Абсолютная погрешность измерения линейки: ЛАБОРАТОРНЫЕ РАБОТЫ ПО ФИЗИКЕ

Абсолютная погрешность измерений. Узнаем как рассчитать абсолютную погрешность измерений?

Физические величины характеризуются понятием «точность погрешности». Есть высказывание, что путем проведения измерений можно прийти к познанию. Так удастся узнать, какова высота дома или длина улицы, как и многие другие.

Введение

Разберемся в значении понятия «измерить величину». Процесс измерения заключается в том, чтобы сравнить её с однородными величинами, которые принимают в качестве единицы.

Для определения объёма используются литры, для вычисления массы применяются граммы. Чтобы было удобнее производить расчеты, ввели систему СИ международной классификации единиц.

За измерение длины вязли метры, массы – килограммы, объёма – кубические литры, времени – секунды, скорости – метры за секунду.

При вычислении физических величин не всегда нужно пользоваться традиционным способом, достаточно применить вычисление при помощи формулы. К примеру, для вычисления таких показателей, как средняя скорость, необходимо поделить пройденное расстояние на время, проведенное в пути. Так производятся вычисления средней скорости.

Применяя единицы измерения, которые в десять, сто, тысячу раз превышают показатели принятых измерительных единиц, их называют кратными.

Наименование каждой приставки соответствует своему числу множителя:

1. Дека.
2. Гекто.
3. Кило.
4. Мега.
5. Гига.
6. Тера.

В физической науке для записи таких множителей используется степень числа 10. К примеру, миллион обозначается как 10⁶.

В простой линейке длина имеет единицу измерения – сантиметр. Она в 100 раз меньше метра. 15-сантиметровая линейка имеет длину 0,15 м.

Линейка является простейшим видом измерительных приборов для того, чтобы измерять показатели длины. Более сложные приборы представлены термометром – чтобы измерять температуру, гигрометром – чтобы определять влажность, амперметром – замерять уровень силы, с которой распространяется электрический ток.

Насколько точны будут показатели проведенных измерений?

Возьмем линейку и простой карандаш. Наша задача заключается в измерении длины этой канцелярской принадлежности.

Для начала потребуется определить, какова цена деления, указанная на шкале измерительного прибора. На двух делениях, которые являются ближайшими штрихами шкалы, написаны цифры, к примеру, «1» и «2».

Необходимо подсчитать, сколько делений заключено в промежутке этих цифр. При правильном подсчете получится «10». Вычтем от того числа, которое является большим, число, которое будет меньшим, и поделим на число, которое составляют деления между цифрами:

(2-1)/10 = 0,1 (см)

Так определяем, что ценой, определяющей деление канцелярской принадлежности, является число 0,1 см или 1 мм. Наглядно показано, как определяется показатель цены для деления с применением любого измерительного прибора.

Измеряя карандаш с длиной, которая немного меньше, чем 10 см, воспользуемся полученными знаниями. При отсутствии на линейке мелкого деления, следовал бы вывод, что предмет имеет длину 10 см. Это приблизительное значение названо измерительной погрешностью. Она указывает на тот уровень неточности, которая может допускаться при проведении измерений.

Определяя параметры длины карандаша с более высоким уровнем точности, большей ценой деления достигается большая измерительная точность, которая обеспечивает меньшую погрешность.

При этом абсолютно точного выполнения измерений не может быть. А показатели не должны превышать размеры цены деления.

Установлено, что размеры измерительной погрешности составляют ½ цены, которая указана на делениях прибора, который применяется для определения размеров.

После выполнения замеров карандаша в 9,7 см определим показатели его погрешности. Это промежуток 9,65 — 9,85 см.

Формулой, измеряющей такую погрешность, является вычисление:

А = а ± D (а)

А — в виде величины для измерительных процессов;

а — значение результата замеров;

D — обозначение абсолютной погрешности.

Если слаживать или вычитать величины с учетом погрешности, это число будет составлять сумму цифр, которые и обозначают погрешность, и имеются у каждой отдельно взятой величины.

При вычитании или складывании величин с погрешностью результат будет равен сумме показателей погрешности, которую составляет каждая отдельная величина.

Знакомство с понятием

Если рассматривать классификацию погрешностей в зависимости от способа её выражения, можно выделить такие разновидности:

• Абсолютную.
• Относительную.
• Приведенную.

Абсолютная погрешность измерений обозначается буквой «Дельта» прописной. Это понятие определяется в виде разности между измеренными и действительными значениями той физической величины, которая измеряется.

Выражением абсолютной погрешность измерений являются единицы той величины, которую необходимо измерить.

При измерении массы она будет выражаться, к примеру, в килограммах. Это не эталон точности измерений.

Как рассчитать погрешность прямых измерений?

Есть способы изображения погрешности измерения и их вычисления. Для этого важно уметь определять физическую величину с необходимой точностью, знать, что такое абсолютная погрешность измерений, что её никто никогда не сможет найти.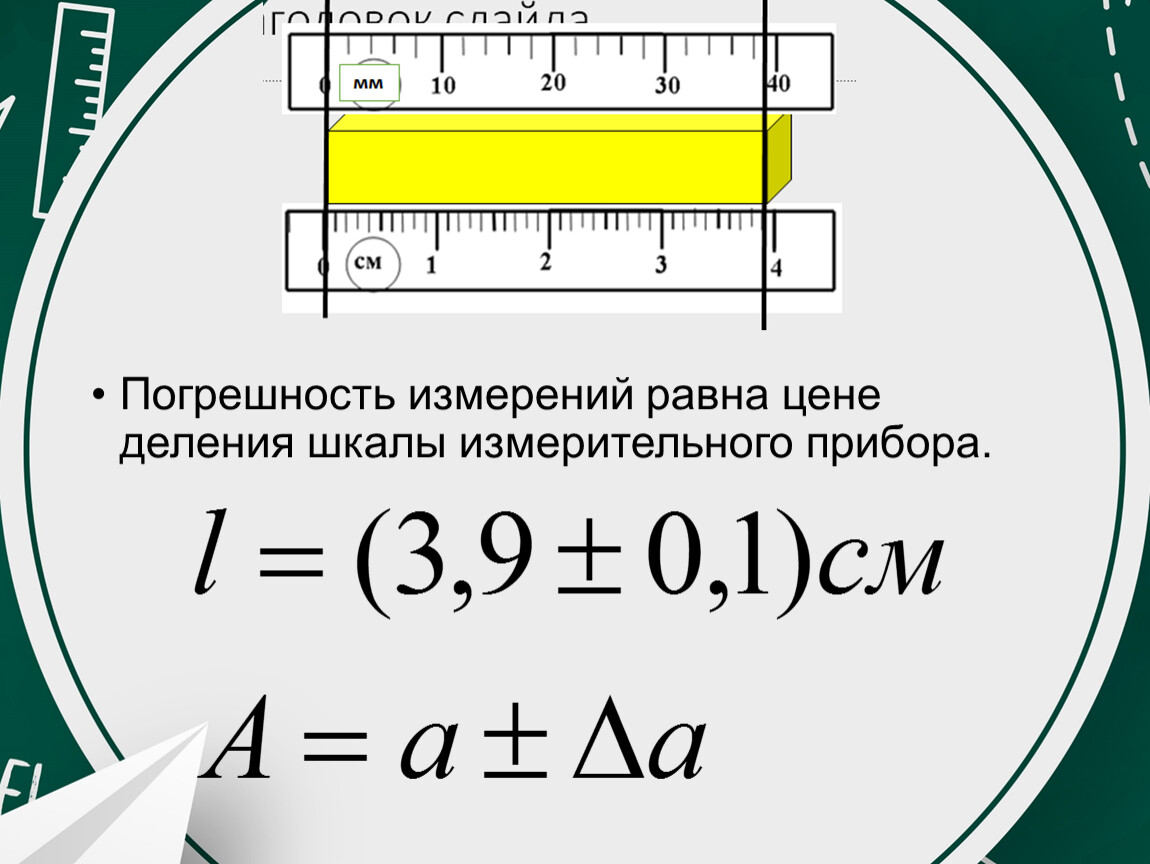 Можно вычислить только её граничное значение.

Даже если условно употребляется этот термин, он указывает именно на граничные данные. Абсолютная и относительная погрешность измерений обозначаются одинаковыми буквами, разница в их написании.

При измерении длины абсолютная погрешность будет измеряться в тех единицах, в которых исчисляться длина. А относительная погрешность вычисляется без размеров, так как она является отношением абсолютной погрешности к результату измерения. Такую величину часто выражают в процентах или в долях.

Абсолютная и относительная погрешность измерений имеют несколько разных способов вычисления в зависимости от того, какой метод измерения физических величин.

Понятие прямого измерения

Абсолютная и относительная погрешность прямых измерений зависят от класса точности прибора и умения определять погрешность взвешивания.

Прежде чем говорить о том, как вычисляется погрешность, необходимо уточнить определения. Прямым называется измерение, при котором происходит непосредственное считывание результата с приборной шкалы.

Когда мы пользуемся термометром, линейкой, вольтметром или амперметром, то всегда проводим именно прямые измерения, так как применяем непосредственно прибор со шкалой.

Есть два фактора, которые влияют на результативность показаний:

• Погрешностью приборов.
• Погрешностью системы отсчета.

Граница абсолютной погрешности при прямых измерениях будет равна сумме погрешности, которую показывает прибор, и погрешности, которая происходит в процессе отсчета.

D = D (пр.) + D (отс.)

Пример с медицинским термометром

Показатели погрешности указаны на самом приборе. На медицинском термометре прописана погрешность 0,1 градусов Цельсия. Погрешность отсчета составляет половину цены деления.

D отс. = С/2

Если цена деления 0,1 градуса, то для медицинского термометра можно произвести вычисления:

D = 0,1^{oС ₊ 0,1o С _/ 2 ₌ 0,15o С}

На тыльной стороне шкалы другого термометра есть ТУ и указано, что для правильности измерений необходимо погружать термометр всей тыльной частью. Точность измерения не указана. Остается только погрешность отсчета.

Если цена деления шкалы этого термометра равна 2^o С, то можно измерять температуру с точностью до 1^o С. Таковы пределы допускаемой абсолютной погрешности измерений и вычисление абсолютной погрешности измерений.

Особую систему вычисления точности используют в электроизмерительных приборах.

Точность электроизмерительных приборов

Чтобы задать точность таких устройств, используется величина, называемая классом точности. Для её обозначения применяют букву «Гамма». Чтобы точно произвести определение абсолютной и относительной погрешности измерений, нужно знать класс точности прибора, который указан на шкале.

Возьмем, к примеру, амперметр. На его шкале указан класс точности, который показывает число 0,5. Он пригоден для измерений на постоянном и переменном токе, относится к устройствам электромагнитной системы.

Это достаточно точный прибор. Если сравнить его со школьным вольтметром, видно, что у него класс точности – 4.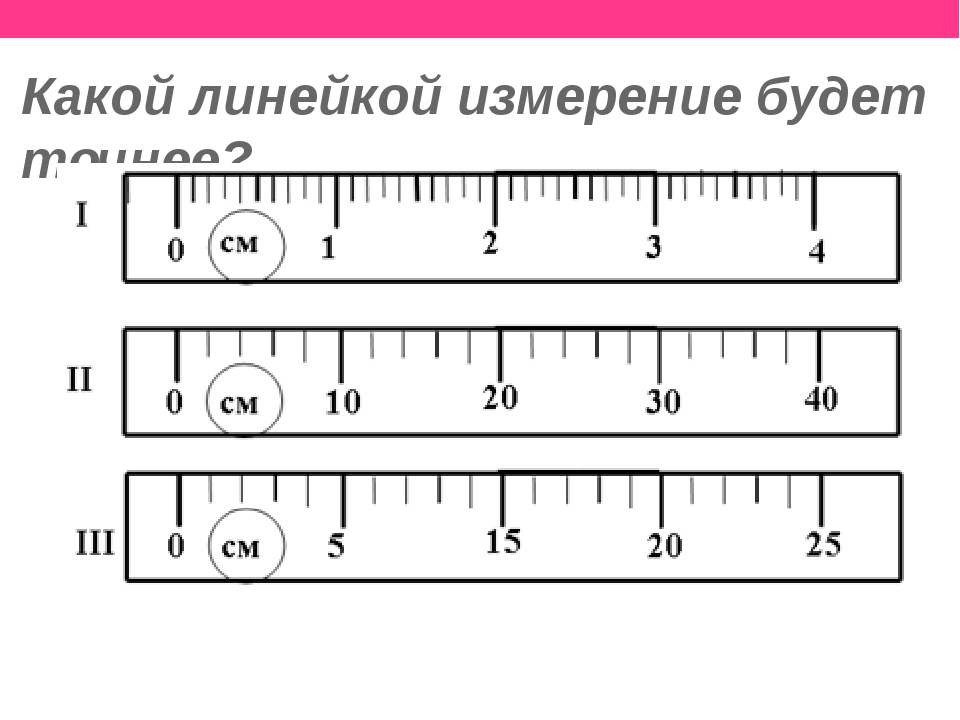 Эту величину обязательно знать для дальнейших вычислений.

Применение знаний

Таким образом, D c = c (max) Х γ /100

Этой формулой и будем пользоваться для конкретных примеров. Воспользуемся вольтметром и найдем погрешность измерения напряжения, которое дает батарейка.

Подключим батарейку непосредственно к вольтметру, предварительно проверив, стоит ли стрелка на нуле. При подключении прибора стрелка отклонилась на 4,2 деления. Это состояние можно охарактеризовать так:

1. Видно, что максимальное значение U для данного предмета равно 6.
2. Класс точности –(γ) = 4.
3. U(о) = 4,2 В.
4. С=0,2 В

Пользуясь этими данными формулы, абсолютная и относительная погрешность измерений вычисляется так:

D U = DU (пр.)+ С/2

D U (пр.) = U (max) Х γ /100

D U (пр.) = 6 В Х 4/100 = 0, 24 В

Это погрешность прибора.

Расчет абсолютной погрешности измерений в этом случае будет выполнен так:

D U = 0,24 В + 0,1 В = 0,34 В

По рассмотренной формуле без труда можно узнать, как рассчитать абсолютную погрешность измерений.

Существует правило округления погрешностей. Оно позволяет найти средний показатель между границей абсолютной погрешности и относительной.

Учимся определять погрешность взвешивания

Это один из примеров прямых измерений. На особом месте стоит взвешивание. Ведь у рычажных весов нет шкалы. Научимся определять погрешность такого процесса. На точность измерения массы влияет точность гирь и совершенство самих весов.

Мы пользуемся рычажными весами с набором гирь, которые необходимо класть именно на правую чашу весов. Для взвешивания возьмем линейку.

Перед началом опыта нужно уравновесить весы. Линейку кладем на левую чашу.

Масса будет равна сумме установленных гирь. Определим погрешность измерения этой величины.

D m = D m (весов) + D m (гирь)

Погрешность измерения массы складывается из двух слагаемых, связанных с весами и гирями. Чтобы узнать каждую из этих величин, на заводах по выпуску весов и гирь продукция снабжается специальными документами, которые позволяют вычислить точность.

Применение таблиц

Воспользуемся стандартной таблицей. Погрешность весов зависит от того, какую массу положили на весы. Чем она больше, тем, соответственно, больше и погрешность.

Даже если положить очень легкое тело, погрешность будет. Этот связано с процессом трения, происходящим в осях.

Вторая таблица относится к набору гирь. На ней указано, что каждая из них имеет свою погрешность массы. 10-граммовая имеет погрешность в 1 мг, как и 20-граммовая. Просчитаем сумму погрешностей каждой из этих гирек, взятой из таблицы.

Удобно писать массу и погрешность массы в двух строчках, которые расположены одна под другой. Чем меньше гири, тем точнее измерение.

Итоги

В ходе рассмотренного материала установлено, что определить абсолютную погрешность невозможно. Можно лишь установить её граничные показатели. Для этого используются формулы, описанные выше в вычислениях. Данный материал предложен для изучения в школе для учеников 8-9 классов. На основе полученных знаний можно решать задачи на определение абсолютной и относительной погрешности.

Статья «Как провести лабораторную работу по физике дистанционно?»

Всероссийский дистанционный конкурс педагогического мастерства на лучшую статью «Теория и практика современной учебно- воспитательной деятельности в образовательном учреждении» автор учитель физики МБОУ «Средняя школа №30» города Дзержинска Нижегородской области Борцовой Елены Владимировны

Как провести лабораторную работу по физике дистанционно?

Дистанционное обучение вошло в нашу школьную жизнь неожиданно, но надолго. Оно стало «одним из участников» современного учебно- воспитательного процесса. И оголило возникшую проблему, решить которую было трудно или невозможно. Такой проблемой оказалось проведение лабораторных работ по физике дистанционно.

Цифровые платформы, готовые к реализации в учебном процессе на момент введения дистанционного обучения, не давали решения данной проблемы. Можно было «зависнуть» в интернете и найти виртуальные лабораторные работы. Однако это было временно затратно , либо не соответствовало возрасту учащихся. Не все из ребят готовы к выполнению виртуальных лабораторных работ. Поэтому другим способом решения вопроса мне виделись лабораторные работы с помощью подручных средств, того оборудования, которое учащиеся могли найти без труда в домашних условиях. О своем опыте организации учебно- воспитательного процесса в «трудное время» карантина я попытаюсь рассказать.

В качестве примера хочу привести описания двух работ курса 7 класса. Программа А.В. Перышкина «требовала» их проведения в карантинное время.

Лабораторная работа №8

«Определение выталкивающей силы,

действующей на погруженное в жидкость тело»

Цель работы— обнаружить на опыте выталкивающее действие жидкости на погруженное в нее тело и определить выталкивающую силу.

Приборы и материалы: кусок резинки (резинка должна быть мягкая, легко растяжимая), два тела разной формы и объема (определите, какое №1, какое №2), стаканы с водой и насыщенным раствором соли в воде), листок бумаги или картона, прикрепленный к резинке. Листок должен быть по длине больше, чем резинка.

Ход работы.

Отметьте на картоне (листочке) и резинке черточки на одном уровне для начала измерений.

Привяжите к резинке первое тело, пометьте на картонке (листочке) новое положение черточки резинки (резинка растянулась, а картонка- нет). Эта черточка на картонке будет соответствовать весу тела №1 в воздухе.

Измерьте расстояние между черточками на картонке (листочке) в см, с точностью до 0,1 см. Запишите результаты в таблицу ( без единиц измерения).

Опустите тело №1 в воду, отметьте новой положение черточки резинки. Измерьте расстояние между первой черточкой (пункт 1) и вновь полученной в см, с точностью до 0,1 см. Это значение будет соответствовать весу тела в воде. Запишите результат в таблицу без единиц измерения.

Опустите тело №1 в насыщенный раствор соли в воде, отметьте новое положение черточки резинки. Измерьте расстояние между первой черточкой (пункт 1) и вновь полученной в см, с точностью 0,1 см. Запишите результат в таблицу без единиц измерения.. Это значение будет соответствовать весу тела №1 в насыщенном растворе соли в воде.

Поменяйте картонку ( листок) и приступайте к опытам со вторым телом.

Проделайте те же измерения, что и в пунктах 1-5, сменив тело 1 на тело 2. Результаты внесите в таблицу.

Определите выталкивающую силу. Запишите вычисления без единиц измерения для каждого опыта ниже таблицы.

На основе полученных результатов сделайте вывод, от каких величин в ваших опытах зависит выталкивающая сила?

 

Таблица для внесения результатов опытов.

Вес тела в воздухе		Жидкость	Вес тела в жидкости		Выталкивающая сила ( из веса тела в жидкости вычесть вес тела в воздухе)
1 тело	2 тело		1 тело	2 тело		1 тело	2 тело
		Вода
		Насыщенный раствор соли в воде

Работа выполняется на листочках. Листок подписать, заполнить таблицу, сделать вычисления и сформулировать вывод. Полностью оформлять работу не надо!

Выполненную работу, карточки (листочки) с отметками сканировать и отослать в сообщении в ЭлЖур.

 

Лабораторная работа №9

«Выяснение условий плавания тела в жидкости»

Цель работы: на опыте выяснить условия, при которых тело плавает и при которых тело тонет.

Приборы и материалы: пузырёк или маленькая баночка, которые могут закрываться, нитки, емкость, в которую можно налить воды и чтобы в ней мог плавать поплавок (пузырёк или баночка), фломастер или то, что будет писать на емкости с водой, сахарный песок , соль или любые крупы, линейка.

Ход работы.

Отметьте фломастером на емкости уровень налитой воды.

Насыпьте в поплавок 0,5 чайной ложки песка (или то, что вы приготовили) так, чтобы он, закрытый и помещенный в воду, плавал в воде, немного в нее погрузившись.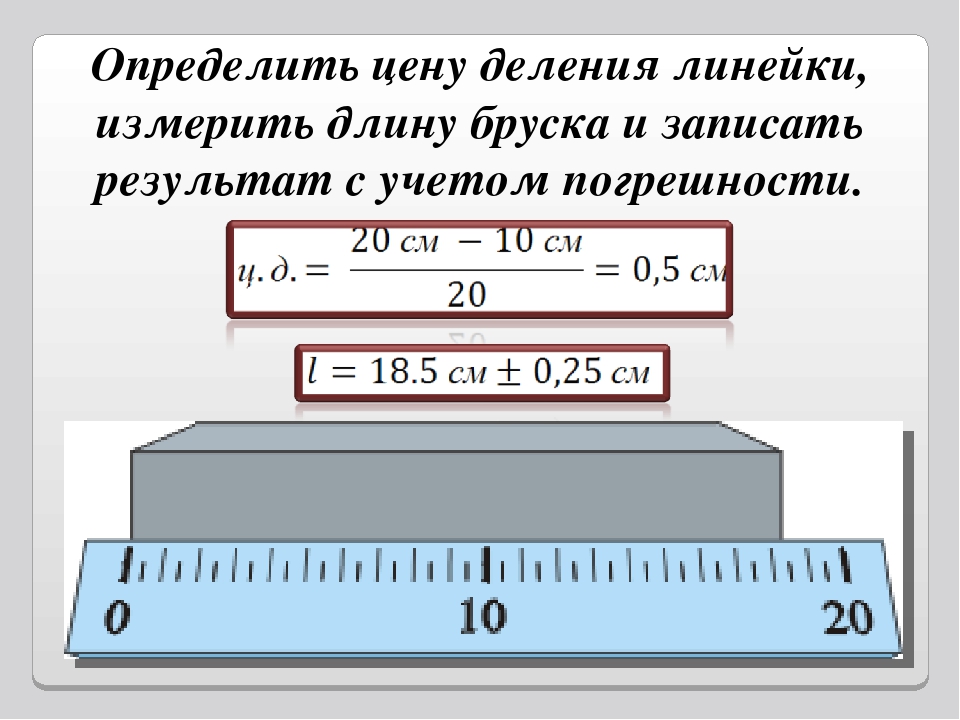 Отметьте новый уровень воды.

Измерьте расстояние между черточками в см. Это будет объем вытесненной воды в условных единицах. Запишите результат в таблицу без единиц измерения.

Вычислите выталкивающую силу, действующую на поплавок по формуле F=ρвgVв. Результат запишите в таблицу без единиц измерения. Все вычисления делаем после таблицы!

Проделайте еще два опыта, насыпая в поплавок сначала 1 чайную ложку песка, потом 1,5 чайной ложки песка, аналогично пунктам 2-4. Результаты запишите в таблицу.

Зафиксируйте поведение поплавка в каждом случае. Результаты внесите в таблицу.

Сделайте вывод об условиях плавания тела.

Таблица.

№ опыта	V воды	Изменение веса поплавка	Выталкивающая сила, F=ρвgVв	Поведение поплавка (плавает или тонет)
1		0,5 чайной ложки
2		1 чайная ложка
3		1,5 чайной ложки

 

Ребята! Полностью оформлять работу не надо.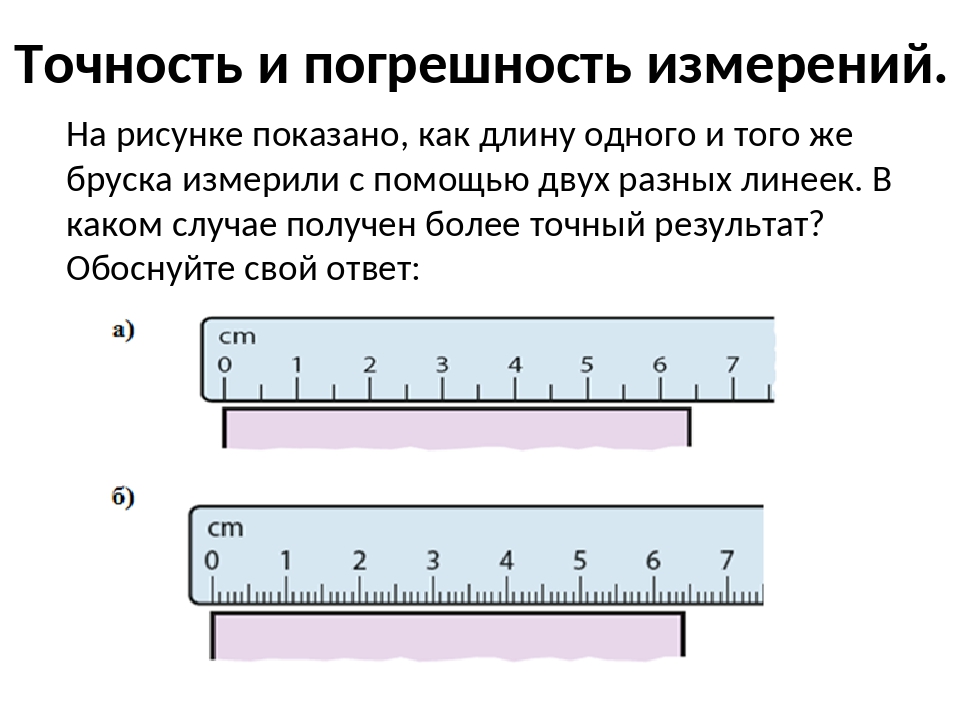 Заполните на листочке таблицу, после нее вычисления выталкивающей силы и вывод. Сделайте скан (фото) своей работы и вышлите его мне в сообщении в ЭлЖур.

Дополнительное задание. При желании можно немного усложнить работу, рассчитав объем вытесняемой воды. Для этого нужно определить не только уровень воды, но и площадь свободной поверхности жидкости . Если емкостью, которую вы используете в работе, будет банка, то определив экспериментально ее диаметр или радиус, по формуле площади круга S=πD2/4 или S=πR2 найдете площадь свободной поверхности воды. Другим способом определения площади круга может стать расчет через длину окружности банки. Если С- длина окружности, то С=πD или С=2πR. Выразив D или R из формулы длины окружности, получим формулы для расчета площади круга S=C2/4π . Умножив S на расстояние между черточками, находим объем вытесненной жидкости.

Дополнительное задание к работе №9 предложили сами дети, поскольку более подготовленным из них это позволяла сделать математическая подготовка.

Такая форма проведения лабораторных работ «на злобу дня» выявила свои плюсы и минусы. В плюсах оказались самостоятельность и заинтересованность ребят, возможность показать, на что они способны без помощи «друга из интернета». Они увидели, каких знаний и навыков им не хватает, над чем еще надо поработать. Кроме того, ребята сами обнаружили, что знания других предметов можно использовать на практике. Например, математика не лежит «мертвым грузом», а работает! И самое важное. Все, что есть вокруг тебя, может быть инструментом для изучения науки!

Минусы тоже были. Не секрет, что современные дети мало читают, неважно пересказывают, и что, самое ужасное, плохо понимают прочитанное. Вот поэтому были ребята, для которых выполнение работ становилось трудным уже на этапе прочтения. Самостоятельность- тоже не самая сильная сторона таких детей.

Возможно, для создания ситуации успеха таким ребятам требовалась дополнительная помощь. Например, этапы выполнения работы снять на видео или сделать фото- фрагменты. Думаю, такого рода шпаргалка была бы им полезна. Может быть в дальнейшем , применяя лабораторные работы из подручных средств, я так и сделаю.

А в качестве примера хочу привести другие лабораторные работы, для выполнения которых можно использовать то, что найдется дома. Это фрагмент работы на одну из городских научно- практических конференций готовила учащаяся 8 класса Тимофеева Светлана. К сожалению, по техническим причинам участие не состоялось. И в описании опытов Светлана как раз и использует фото- помощь.

Лабораторная работа №1

Измерение физических величин с учётом абсолютной погрешности.

 

Цель работы: Приобретение умений оценивать абсолютные погрешности измерений. Научиться пользоваться измерительными приборами и записывать результат измерений и учётом погрешностей.

Приборы и материалы: измерительный цилиндр (мензурка), линейка, термометр, стакан с водой, брусок.

Это школьные приборы и материалы, но если исследовательскую работу необходимо выполнить дома, то следует взять: 2 стакана и водой, линейку, коробку или любую другую вещь прямоугольной формы, шприц, термометр. Эти приборы наверняка имеются дома и с их помощью можно проводить измерения.

Чтобы приступить к лабораторной работе, нужно изучить теорию.

 

Теория.

Для начала рассмотрим размер физической величины, который мы будем измерять с помощью линейки, итак:

Размер физической величины — это количественное содержание характеристики физического объекта или явления.

Это например: 12 см, 1 дюйм.

Линейка — это наш измерительный прибор.

Измерительным прибором называют средство измерения, дающее возможность непосредственно отсчитывать значение измеряемой величины.

 

В этой лабораторной работе мы будем определять абсолютную погрешность.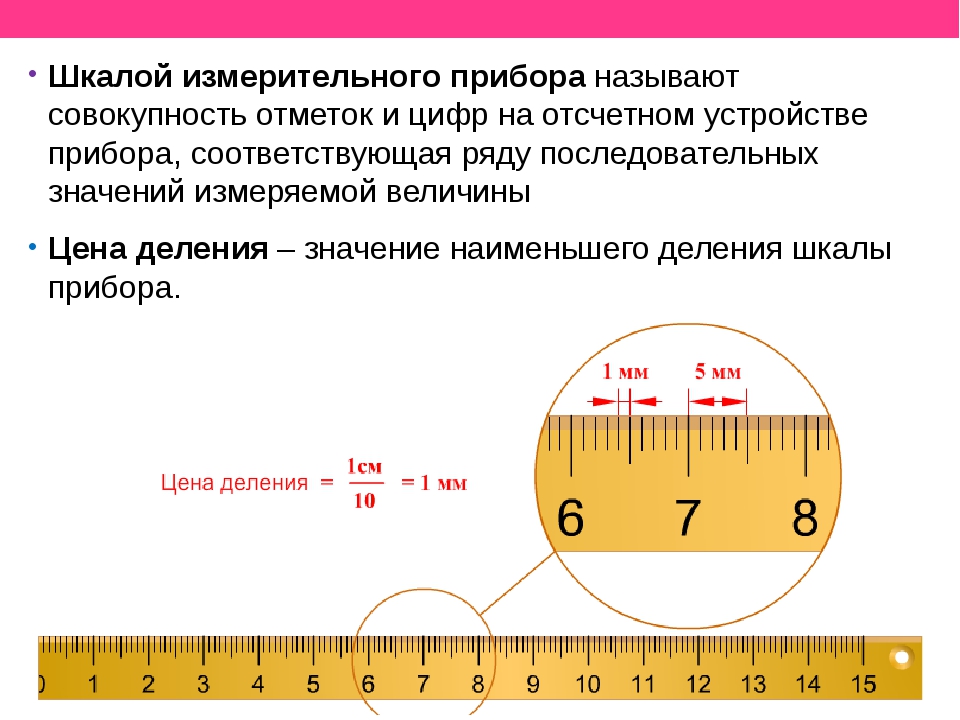

Погрешность — это допускаемая при измерении неточность.

Абсолютная погрешность — это модуль разности результата измерения и истинного значения измеряемой величины.

 

 

Также мы будем вычислять цену деления.

Цена деления — это расстояние между двумя ближайшими штрихами шкалы измерительного прибора.

 

Ход работы.

Определите цену деления шкалы линейки.

Определите абсолютную погрешность измерения линейкой.

Измерьте длину (а), ширину (б) и высоту (h) деревянного бруска.

Запишите значения цены деления, погрешность и результаты измерений в таблицу.

Изготовление мензурки

Определите цену деления шкалы мензурки.

Определите абсолютную погрешность измерения мензуркой.

Налейте в мензурку немного воды из стакана. Измерьте объем воды V1.

Налейте в мензурку еще воды и определите ее объем V2.

Изготовление термометра

Определите цену деления шкалы термометра.

Определите абсолютную погрешность измерения термометром. 13.Измерьте температуру воды в мензурке.

14.Запишите результаты всех измерений в таблицу.

Определение цены деления шкалы линейки

Чтобы определить цену деления, нужно из большей величины, соответствующую отметке шкалы, вычесть меньшую, а потом разделить на количество штрихов, находящихся в промежутке между ними. Я буду использовать в своих измерениях эту линейку. Её цена деления равна:

Определение абсолютной погрешности измерения линейкой.

 

 

Для того, чтобы измерить абсолютную погрешность измерения линейкой, нужен прибор, который бы показывал очень точный результат измерения размера физической величины, например штангенциркуль. Но у меня такого прибора нет, поэтому я воспользуюсь таблицей абсолютных инструментальных погрешностей. Из таблицы видно, что у моей ученической линейки абсолютная погрешность равна+- 1 мм.

Измерение длины, ширины и высоты деревянного бруска.

Деревянный брусок я заменю на маленькую коробочку.

 

Измерение длины

 

 

 

 

 

 

 

 

 

 

 

 

 

Среднее значение длины = (12,5см + 12,6см + 12,5см):3=12,5333см=12,5см Длина равна 12,5см+-1мм с учётом абсолютной погрешности.

Измерение ширины

 

Среднее значение длины = (9см + 8,9см + 8,9см):3=8,93333см=8,9см Ширина равна 8,9см+-1мм с учётом абсолютной погрешности

 

Измерение высоты

 

Высота = 3,5см+-1мм с учётом абсолютной погрешности.

Таблица значений цены деления, погрешности и результат измерений.

 

 

Изготовление мензурки

Для измерения абсолютной погрешности измерения нужно использовать мензурку, но если в домашних условиях её нет, то её можно изготовить с помощью шприца и стакана.

Материалы: стакан, шприц, фломастер, маркер или др.

 

Разрезаем бутылку на 2 части, чтобы было удобней наливать штрихом воду.

 

 

 

берём в шприц воду ( если шприц большой, то можно сразу 10 мл по 2 раза, тогда цена деления будет 20 мл, а если шприц как у меня, то 2 раза по 5 мл или 4 раза до 20 мл).

 

Цена деления моей мензурки будет равна 10 мл.

 

 

 

 

 

Выливаем воду в разрезанную бутылку и помечаем ручкой ( маркёр плохо пишет на бутылке).

 

 

 

 

 

 

 

 

 

 

 

 

 

Повторяем это ещё несколько раз (зависит от размера бутылки и от выбранной цены деления).

 

 

 

 

 

 

 

В итоге деления должны получиться достаточно ровными друг относительно друга

(зависит от формы бутылки) и быть похожи на деления на мензурке.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Я не буду помечать на моей самодельной мензурке деления.

Определение цены деления шкалы мензурки.

Цена деления моей мензурки равна 10 мл. (20-10)/1=10 мл.

Определение абсолютной погрешности измерения мензуркой.

Для определения абсолютной погрешности нужно взять шприц и стакан.

Шприц мы будем использовать как более точный предмет.

Предположим, что абсолютная погрешность этого шприца равна половине его цены деления.

 

Нальём в мензурку воды. Я налила 40 мл.

 

Наливаем воду в шприц и определяем, сколько миллилитров мы нальём за одно деление.

 

В итоге в одном делении оказалось 5 мл+6 мл=11 мл вместо 10 мл.

 

Абсолютная погрешность равна:

 

 

Налейте в мензурку немного воды из стакана. Измерьте объем воды V1.

Налейте в мензурку ещё воды и определите ее объём V2.

 

 

№Опыта Объёмы,V,мл

 

№2

 

С помощью самодельной мензурки мы можем самостоятельно измерять объёмы жидкостей.

Изготовление термометра.

На лабораторных работах в школах не используют ртутные термометры и электронные термометры, которые наверняка есть дома. Следует изготовить водный термометр или термометр с раствором воды и медицинского спирта.

 

Для этого понадобится: бутылка, трубка (медицинская из-под капельницы), вода, медицинский спирт, пластилин, картон.

 

 

Изготовление раствора

Налейте в бутылку наполовину воды.

 

После столько же налейте спирта. Обязательно наливайте до самых краев!

 

Изготовление прибора

Проделываем в крышке маленькую дырочку и продеваем трубку.

 

После плотно заклейте пластилином места вокруг отверстия, чтобы не вытекал раствор. Потом приклейте прямоугольник картона скотчем трубке, чтобы потом на нем отмечать деления.

 

Далее с помощью шприца долейте раствор так, чтобы была заполнена половина трубки.

 

Не нужно заклеивать верхнюю часть трубки, иначе термометр не будет работать!

 

Для того, чтобы измерить цену деления термометра, нужно проделать опыты охлаждения и нагревания прибора для того, чтобы отметить деления. Изначально термометр был при комнатной температуре, равной 20 0С.

Лабораторная работа №2

Измерение массы тела на рычажных весах.

 

Цель работы: определить массу тел с помощью рычажных весов.

Для проведения следующей лабораторной работы нам понадобятся следующие

приборы: самодельные весы, грузы одинаковой массы.

 

Теория

Масса тела — это физическая величина, которая является мерой инертности. Эту величину можно измерить двумя способами:

Сравнивая скорости, приобретённые при взаимодействии.

Для такого измерения массы тела нужно знать приобретённые от взаимодействия скорости тел, и массу одного из тел. Вычисление происходит по формуле

С помощью весов.

При одинаковых массах на весах, тела будут находиться в равновесии.

 

 

Весы могут быть учебные, медицинские, аналитические, аптекарские, электронные и др.

В нашёл лабораторной работе мы будем изготавливать простейшие учебные весы.

 

Ход работы:

Изготовление весов

Придерживаясь правил взвешивания, измерьте массу нескольких твёрдых тел.

Результаты измерений запишите в таблицу.

 

Перед тем, как выполнять лабораторную работу, сделает изучить правила взвешивания: 1.Перед взвешиванием необходимо убедиться, что весы уравновешены. При необходимости для установления равновесия на более лёгкую чашку нужно положить полоски бумаги, картона и т. п.

Взвешиваемое тело кладут на левую чашку весов, а гири — на правую.

Во избежание порчи весов взвешиваемое тело и гири нужно опускать на чашки осторожно, не роняя их даже с небольшой высоты.

Нельзя взвешивать тяжелые тела.

 

Изготовление весов

Для изготовление прибора понадобится: длинная линейка, чашки (из бутылки или кашпо для горшков), нитки.

Склеиваем по сторонам линейки 2 чашки.

 

Ищем центр тяжести наших весов и приклеиваем на отмеченное место веревку.

 

Закрепляем весы так, чтобы они были в равновесии. Для улучшения равновесия внутрь можно положить ватные диски, бумагу и др.

Измерение массы нескольких твёрдых тел.

Так как у меня нет гирек, я буду измерять массу не граммами и миллиграммами, а специальной величиной, которая будет обозначать массу, — монетами, а именно копейками.

взвешивание.

Первым я буду измерять массу брелка, с помощью 10-копеечных монеток.

После уравновешивания весов выяснилось, что масса брелка равна 20 копейкам.

взвешивание.

Во втором взвешивании я уравновесила на весах компьютерную флешку. Для этого я использовала не только 10-копеечную монету, но и монету в 1 копейку.

 

Оказалось, что масса флешки равна 41-ой копейке по массе.

 

Таблица результатов измерений.

 

№ Взвешивания

 

№1

 

№2

Масса груза в специальной величине измерения

— 1 копейка.

 

 

 

Лабораторная работа №3

Градуирование динамометра.

Цель работы: проградуировать пружину, получить шкалу с заданной ценой деления и с её помощью измерить силы.

Теория:

Сила — это векторная физическая величина, являющееся мерой инерции тел. Измеряется в 1Н.

Сила, с которой тела притягиваются тела к Земле, называется сила тяжести. Она также измеряется в Н. Сила тяжести можно вычислить с помощью формулы mg.

Сила упругости — это сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение.

Fупр = kx

x — изменение длины пружины, k — коэффициент пропорциональности или жесткость. Деформация — это любое измерение формы и размера тела. Она бывает упругая и неупругая.

В динамометре сила тяжести груза уравновешивается силой упругости растягиваемой пружины.

Для изготовления самодельного динамометра понадобиться: картон, бумага, скрепка, нитки, резинка.

 

Ход работы:

Изготовление динамометра

Определение цены деления.

Таблица измерений силы тяжести грузов.

 

Изготовление динамометра.

Вырежьте из картона и бумаги основу динамометра

Наклеите прямоугольный кусок бумаги на картон

 

Проделайте в картоне маленькую дырочку и проденьте скрепку. Заклейте её с обеих сторон

Возьмите хорошо растягивающуюся резинку и привяжите её к веревке (можно согнуть резинку вдвое, для увеличения k, а также наклеить стрелочку, там, где привязана веревка)

 

Наденьте на скрепку резинку, отметьте 0 там, где начинается веревка (или там, где показывает стрелочка).

Наверху напишите букву H, что означает, что прибор измеряет в Ньютонах.

 

Прибор готов.

Определение цены деления.

Мой прибор будет иметь цену деления, равную 1 Ньютон. Для того, чтобы измерить 1Н на динамометре, нужен груз весом 102г.

Я возьму мыло равное по массе 100г, этой точности вполне будет достаточно, чтобы получить нужную цену деления.

 

Подвешиваем груз на динамометр и отмечаем штрихом там, где начинается веревка или стрелка. (Измерение №1)

 

Теперь возьмём другой груз, подобрав его так, что при подвешивании на динамометр стрелочка или узел показывали на 1Н. Это будет значит, что сила тяжести второго груза будет равна первому. (Измерение №2)

 

2. 3 Для определения силы в 2Н нужно скрепить 2 груза вместе и подвесить их к динамометру. Отметить штрихом указания стрелочки или узла. (Измерение №3)

 

Теперь у нас есть проградуированный динамометр.

Таблица измерений силы тяжести грузов.

Так как я уже до этого проводили измерения с помощью динамометра, я уже впишу те результаты, которые были при измерении цены деления.

 

Думаю, что такой способ проведения лабораторных работ может быть использован как при дистанционном обучении, так и в обычном, очном, учебно- воспитательном процессе.

 

Оценка погрешностей измерений

Оценка погрешностей измерений

Г.Г.Никифоров (ИОСО РАО), г. Москва

1. Проблема

Несмотря на десятки книг и большое количество диссертационных исследований, значительных успехов в освоении учащимися умения оценивать погрешности измерений не наблюдалось. Причина этого, помимо всего прочего, в объективной сложности материала, а также в отсутствии координации между физикой и математикой. Следует указать и отсутствие соответствующей организации учебной деятельности учеников. По современным представлениям [В.В.Давыдов], ученик должен получать знания как продукт своей работы с изучаемым материалом. По отношению к обсуждаемому вопросу это означает, что представление о погрешностях и методах их оценки должны вытекать из экспериментальной работы самих учащихся.

2. Погрешности средств измерения

Школьные средства измерения имеют вполне нормированные основные погрешности. Включенные в новый «Перечень оборудования», эти средства делятся на стрелочные приборы (амперметры, вольтметры, динамометры и др.), цифровые приборы (мультиметры демонстрационные и лабораторные, счетчик-секундомер и др.), многопредельные меры (линейка, мерная лента, мерный цилиндр), наборы мер (набор грузов по механике и набор гирь, набор резисторов).

Несколько особняком в этой номенклатуре оказываются весы для фронтальных работ и практикума. Весы с точки зрения принципа действия можно отнести к нуль-индикаторам, в которых измерение сводится к прямому сравниванию массы взвешиваемого тела с массой гирь.

Сведения об основных (инструментальных, приборных) погрешностях школьных лабораторных средств измерения приведены в табл. 1 и 2. Погрешности цифрового мультиметра (на примере М3900) приведены ниже. Поясним метрологический смысл приведенных сведений.

особенность погрешностей многопредельных мер (пп. 1–9, табл. 1) состоит в том, что они линейно нарастают вдоль шкалы. Именно поэтому либо указано значение погрешностей номинальных значений (т.е. всей длины), либо значение на 100 мм шкалы. Обратим внимание на то, что погрешности деревянных инструментов меньше, чем пластмассовых. Все инструменты, маркированные знаком «ГОСТ», имеют погрешности меньшие, чем погрешности инструментов, не имеющих этих знаков.

В чем метрологический смысл погрешности меры? Она показывает интервал, внутри которого с вероятностью, близкой к 100% находится неизвестное истинное значение меры. Например, каждый груз из набора грузов имеет номинальное значение массы 100 г, погрешность меры ± 2 г. Следовательно, истинное значение груза находится в интервале (100 – 2) г < m < (100 + 2) г.

Если номинальное значение сопротивления резистора равно 4,0 Ом, а погрешность 0,12 Ом, следовательно, истинное значение сопротивления содержится в интервале   (4,00 – 0,12) Ом Ј  R Ј (4,00 + 0,12) Ом.

Погрешности стрелочных электроизмерительных приборов чаще всего задаются специальной величиной, которая называется классом точности и обозначается символом g. Класс точности g показывает значение допускаемой погрешности в процентах от предела измерения (или суммы пределов для приборов, нуль которых находится внутри шкалы). Например, если класс точности амперметра (табл. 2) равен g = 2,5, то основная погрешность равна  

Если миллиамперметр имеет ноль посередине шкалы, его основная погрешность равна  

В чем смысл основной погрешности стрелочных приборов? Она показывает интервал, внутри которого с вероятностью равной 100% находится истинное значение измеряемой величины, если стрелка прибора совпадает со штрихом шкалы. Например, пусть стрелка амперметра совпадает со штрихом 1,6 А. Следовательно, истинное значение силы тока находится в интервале

(1,60 – 0,05) А Ј I Ј (1,60 + 0,05) А.

Основная погрешность весов складывается из погрешности гирь и чувствительности. Например, если на весах находится взвешиваемое тело и две гири номинальными значениями 100 г и 50 г, то погрешность весов складывается из погрешностей гирь (40 + 30) мг и чувствительности весов, которая определяется из графика, приведенного в п. 5 табл. 2.

Погрешность мультиметра указана двумя числами. Например, для диапазона 700 В записано: «± 1,2% ± 3». Эта запись означает, что погрешность мультиметра в диапазоне от 200 В до 700 В равна сумме единицы младшего разряда считываемого показания U. Пусть считываемое показание равно U = 237 В. Следовательно, погрешность измерения равна

Истинное значение напряжения находится в интервале  (237 – 6) В < U < (237 + 6) В.

3.

 Знакомство учащихся с погрешностью средств измерения

Как показывает многолетний опыт автора, наиболее эффективная организация учебной деятельности школьников по освоению представлений о погрешности средств измерений может быть основана на экспериментах по поверке измерений. Поверка – это процедура сравнения показаний рабочего средства измерения с показаниями образцового. К образцовым средствам измерения относятся такие, основные погрешности которых на порядок (в 10 раз) меньше погрешности рабочего прибора. В процессе поверки учащиеся сами неизбежно обнаружат наличие погрешности средства измерения. В качестве образцовых средств могут быть выбраны весы, набор гирь и стальная линейка. В качестве поверяемых можно взять набор грузов, динамометр и самодельную линейку.

Представление о погрешностях средств измерения может быть сформировано в три этапа уже в самом начале изучения физики, например в 7-м классе.

Первый этап. Поверка самодельной линейки с использованием стальной. В качестве самодельной линейки используется полоска бумаги из тетради в клетку.

Приложив к этой «линейке» стальную, ученики убеждаются в том, что погрешность их «линейки» нарастает и к ее концу достигает примерно 1 мм на длине 10 мм.

Второй этап. Поверка грузов по механике. Образцовое измерительное средство – весы, поверяемое – набор грузов.

Сообщаем учащимся, что в данной работе весы выступают образцовым прибором и его погрешностью можно пренебречь. Поясним учителю. Пусть груз уравновешивается гирями номинальными значениями 100 г и 2 г. Их суммарная погрешность 46 мг. Такова же и чувствительность. Общая погрешность равна 100 мг = 0,1 г. Погрешность же грузов по механике (2 г) в 20 раз больше.

Цель исследования: определить действительные значения масс всех грузов и выяснить, есть ли среди них такие, у которых масса больше 102,00 г или меньше 98,00 г.

Опыт показывает, что работа вызывает у учащихся интерес особенно тогда, когда им поручается изготовить специальные наклейки, на которых указываются масса груза и фамилия «метролога». Или если обнаруживаются грузы, масса которых выходит за пределы (98 г; 102 г). Они должны быть исключены из употребления.

Третий этап. Поверка динамометра. Образцовое средство измерения – набор гирь, поверяемый прибор – динамометр.

К крючку динамометра подвешивается очень легкая коробочка, которую нагружают гирями из набора так, чтобы указатель динамометра совпадал со штрихами 0; 0,1 Н; 0,2 Н; 0,3 Н и т.д. Строят поверочный график. С тыльной стороны динамометра приклеивают фирменный знак «метролога» с его личной подписью, удостоверяющей, что данный динамометр прошел поверку и его погрешность не превосходит 0,05 Н.

Таблица 1. Характеристика мер

№	Меры	Номинальное значение меры	Пределы допускаемой основной погрешности
1	Линейки измерительные металлические, ГОСТ 427-56	150 мм; 300 мм; 500 мм; 1000 мм	± 0,10 мм; ± 0,15 мм; ± 0,20 мм
2	Линейки деревянные с делениями, ГОСТ 12646-67	(200; 250; 300; 400) мм	± 0,1 мм на каждые 100 мм накатанной части
3	Линейка деревянная с делениями	(200; 250; 300; 400) мм	± 0,5 мм
4	Линейки пластмассовые с делениями	(200; 250; 300; 400) мм	± 1,0 мм
5	Угольники деревянные с делениями, ГОСТ 5094-67	(150; 185; 220; 300) мм	± 0,1 мм на каждые 100 мм накатанной части
6	Угольники деревянные с делениями	(150; 185; 220; 300) мм	± 0,5 мм
7	Угольники пластмассовые	(150; 185; 220; 300) мм	± 1,0 мм
8	Метры портновские, ГОСТ 1190-66	1 м 1,5 м	± 1,0 мм ± 3,0 мм
9	Метры портновские	1 м 1,5 м	± 3,0 мм; ± 5,0 мм
10	Термометр лабораторный ртутный	0–100 °С	1 °С
11	Термометры стеклянные жидкостные (не ртутные), ГОСТ 9177-59	Интервал измеряемых температур от –20 до 100 °С	Значение цены деления шкалы, если она равна 1; 2 – 5 град/дел. Две цены деления шкалы, если она равна 0,2; 0,5 град/дел.
12	Набор грузов по механике	100 г	± 2 г
13	Набор гирь 4-го класса	10 мг; 20 мг; 50 мг; 100 мг 200 мг 500 мг 1 г 2 г 5 г 10 г 20 г 50 г 100 г	± 1 мг ± 2 мг ± 3 мг ± 4 мг ± 6 мг ± 8 мг ± 12 мг ± 20 мг ± 30 мг ± 40 мг
14	Набор из трех сопротивлений	1 Ом; 2 Ом; 4 Ом	± 0,03 Ом; ± 0,06 Ом; ± 0,12 Ом

Таблица 2. Характеристики измерительных приборов

№	Измерительный прибор	Диапазон измерения	Класс точн.	Пределы допускаемой основной погрешности
1	Штангенциркули, ГОСТ 166-63	0–125 мм	–	± 0,05 мм при отсчете по нониусу
		0–200 мм	–	0,05 мм или 0,1 мм при отсчете по нониусу 0,1 мм
		0–320 мм	–
2	Микрометры с ценой деления 0,01 мм, ГОСТ 6507-60	0–25 мм	1	± 4 мкм
3	Индикатор часового типа с ценой деления 0,01 мм, ГОСТ 577-68	0–2 мм	1	± 12 мкм
		0–5 мм	1	± 16 мкм
		0–10 мм	1	± 20 мкм
		В пределах 0,1 мм на любом участке шкалы ± 6 мкм, в пределах 1 мм на любом участке шкалы ± 10 мкм
4	Секундомеры механические, ГОСТ 5072-72 (калибр механизма 42 мм)	Емкость шкалы 30–60 мин	2 (3)	Средняя погрешность за 30 мин ± 0,4 с (± 0,7 с) при скачке секундной стрелки 0,1 с; ± 0,6 с (± 1,0 с) при скачке секундной стрелки 0,2 с. Максимальная погрешность за 60 с равна ± 0,2 с при скачке секундной стрелки 0,1 с и ± 0,3 с при скачке секундной стрелки 0,2 с
5	Весы школьные для лабораторных работ	10–200 г	–
6	Весы технические ВЛТ-200	10–200 г	–
7	Динамометр учебный	4 Н	–	0,05 Н
8	Барометр-анероид	720–780 мм рт. ст.	–	В интервале 730–700 мм рт. ст. погрешность равна 3 мм рт. ст. При других показаниях погрешность равна 5 мм рт. ст.
9	Амперметр лабораторный	2 А	2,5	0,05 В
10	Вольтметр лабораторный	6 В	2,5	0,15 В
11	Миллиамперметр	(5–0–5) мА	2,5	0,25 В

 

 

 

 

 

 

Продолжение следует

Приложение. Оценка погрешности измерений ❤️

Погрешности измерений обусловлены неточностью самих приборов и неточностью снятия их показаний, влиянием случайных факторов и т. д. Различают абсолютную и относительную погрешности.

Абсолютной погрешностью называют модуль отклонения измеренного значения физической величины от ее истинного значения. Если ∆A — наибольшее значение абсолютной погрешности, то результат измерения записывают в виде A = Aср ± ∆A. Это означает, что значение физической величины находится между Amin = Aср — ∆A и Amax = Aср + ∆A.

Относительная погрешность

εA = ∆A/A * 100%. Относительная погрешность полнее характеризует точность измерения, чем абсолютная. Например, если длина карандаша и длина комнаты измерены с одной и той же абсолютной погрешностью ∆l = 1 см, то в первом случае измерение не очень точное (относительная погрешность довольно велика), а во втором случае — довольно точное (относительная погрешность мала).

Оценка абсолютной погрешности прямых измерений. При прямом измерении значение величины определяют непосредственно по шкале измерительного прибора (линейки, динамо — метра, часов и т. д.). Если результаты повторных опытов в пределах

точности прибора совпадают, погрешность измерения считают равной цене деления шкалы прибора ∆A = ∆Aш (например, наибольшая абсолютная погрешность измерения длины с помощью линейки с миллиметровыми делениями равна 1 мм). Если же разброс результатов повторных опытов больше ∆Aш, используют усреднение результатов нескольких опытов.

Тогда за измеренное значение принимают Aср = (A1 + A2 + … + AN) / N, где N — число опытов, а погрешность измерения оценивают ∆(Aср) = (|Aср — A1| + |Aср — A2| + … + |Aср — AN|) / N. За абсолютную погрешность измерения ∆A принимают большую из двух величин: ∆(Aср) и ∆Aш.

Оценка абсолютной погрешности косвенных измерений. Косвенным называют измерение, при котором значение измеряемой величины определяют не непосредственно по показаниям приборов, а по формулам, в которые входят значения физических величин, полученные с помощью прямых измерений. Например, для измерения плотности вещества измеряют массу и объем тела и находят плотность по формуле ρ = m/V.

Один из наиболее простых методов оценки погрешности косвенных измерений — это метод границ. Он состоит в том, что с помощью формулы, по которой вычисляют измеряемую величину B, находят два значения: Bmin и Bmax, между которыми находится истинное значение измеренной величины B. Абсолютная погрешность измерения в таком случае ∆B = (Bmax — Bmin)/2, а среднее значение Bср = (Bmax + Bmin)/2.

Округление результатов. Округлять результаты измерений и вычислений следует так, чтобы последняя значащая цифра находилась в том же десятичном разряде, что и абсолютная погрешность измеряемой величины.

Примеры расчета неопределенности измерений — Profilab.by

Примеры расчета неопределенности измерений

Оценивание неопределенности измерений (количественных величин) – одна из важных задач, стоящих перед каждой лабораторией. Требование к оцениванию неопределенности измерений заложено в межгосударственном стандарте ГОСТ ISO/IEC 17025-2019, а также политике ILAC-G17:2002.

Чтобы получить предварительную информацию по теме Неопределенность измерений, посмотрите, пожалуйста, наше обучающее видео:

Международное метрологическое сообщество давно уже разработало и приняло основные принципы концепции неопределенности, закрепив их в серии международных документов JCGM (Joint Committee for Guides in Metrology), а также документах ISO/IEC Guide 98. Разработано много дополнительных руководств по различных подходам оценивания неопределенности измерений в конкретных областях испытаний/измерений (EA, EURACHEM, Nordtest, EUROLAB и т.д.).

---

ОНЛАЙН-КАЛЬКУЛЯТОР

Расчет составляющей неопределенности измерений из-за построения градуировочного графика

ПОДРОБНЕЕ

---

Несмотря на хорошо разработанные и представленные в документах свободного доступа теоретические принципы и подходы оценивания, и даже наличия конкретных примеров, у специалистов лабораторий все еще остаются вопросы по практической реализации этих принципов и подходов для измерений, проводимых в их лаборатории.

Ближайшие семинары:

«Контроль качества измерений в лабораториях: внутрилабораторный контроль и проверки квалификации» — 21-22 февраля (онлайн)

Отсутствие достаточного количества подробных руководящих документов по контролю качества в аналитических измерениях, особенно в части внутрилабораторного контроля, часто сталкивает лаборатории с вопросами практической реализации процедур контроля качества и интерпретации полученных результатов контроля…

ПОДРОБНЕЕ

«Практика проведения электрофизических измерений в электроустановках до 1000 В.

Обеспечение качества результатов измерений, процедуры контроля» — 2-3 марта (очно)

Семинар проводится с целью оказания помощи сотрудникам испытательных лабораторий в изучении ТНПА, устанавливающих требования к объектам испытаний, а также по приобретению навыков выполнения измерений, оформления результатов измерений и расчета неопределенности результатов измерений…

ПОДРОБНЕЕ

«Управление рисками. Методы оценки рисков» — 10 марта (онлайн)

Риски влияют на способность организации достигать своих целей и сроки достижения этих целей. Требования к рассмотрению рисков (идентификации, анализу, оцениванию и обработке) и возможностей, связанных с лабораторной деятельностью, устанавливаются стандартом ГОСТ ISO/IEC 17025-2019…

ПОДРОБНЕЕ

 

С целью наглядного представления основных принципов концепции неопределенности измерений и подхода моделирования предлагаем Вашему вниманию решение нескольких несложных, но часто встречающейся в практике многих испытательных лабораторий, задач:

---

Пример 1.

Оценивание неопределенности измерений массовой доли влаги

---

Пример 2. Оценивание неопределенности измерений сопротивления изоляции

---

Пример 3. Оценивание неопределенности измерений коэффициента поправки титрованного раствора

---

Пример 4. Оценивание неопределенности измерений pH воды

---

Пример 5. Оценивание неопределенности измерений относительного удлинения эластичного герметика

---

Пример 6. Оценивание неопределенности измерений прочности бетона на растяжение при изгибе

---

Пример 7. Оценивание неопределенности измерений твердости по Бриннелю

---

 

---

Пример 1. Оценивание неопределенности измерений массовой доли влаги

---

Исходные данные:

1. Объект измерений – углекислый барий
2. Измеряемая величина – массовая доля влаги
3. Единицы измерений – процент (%)
4. Методика выполнения измерения – ГОСТ 2149-75 «Барий углекислый технический. Технические условия»
5. Метод измерений – метод высушивания пробы до постоянной массы

Этап 1. Составление функции измерений

Функция измерений для измеряемой величины составляется на основании принципа измерений, заложенного в методе измерений, и описанного для реализации в методике выполнения измерений.

Массовую долю влаги бария углекислого Х в процентах вычисляют на основании ГОСТ 2149 (п.3.5) в соответствии с функцией измерений:

где Х_i – массовая доля влаги i-ой пробы углекислого бария, %;

m₁ – масса стаканчика для взвешивания с навеской до высушивания, г;

m₂ – масса стаканчика для взвешивания с навеской после высушивания, г;

m – масса навески углекислого бария, г;

m_cт – масса стаканчика для взвешивания, г;

i – номер параллельной пробы, i = 1, 2;

F – поправочный множитель, учитывающий допускаемое расхождение между параллельными определениями.

Разработка/Валидация МЕТОДИК

Выполним работы по разработке Методик измерений

ПОДРОБНЕЕ ОБ УСЛУГЕ

МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ

В комплекте с автоматизированным расчетом

ПОДРОБНЕЕ ОБ УСЛУГЕ

 

Этап 2. Анализ входных величин

1) Масса стаканчика для взвешивания с навеской до высушивания, m₁

Масса стаканчика для взвешивания с навеской до высушивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:

• для первой пробы m₁₍₁₎ = 41,0055 г,
• для второй пробы m₁₍₂₎ = 41,3842 г.

Неопределенность, связанную с величиной m₁, оцениваем, используя данные производителя на весы. В паспорте на весы лабораторные AV264C для диапазона измерений до 50 г указаны пределы погрешности взвешивания ± 0,001 г. Поскольку значение дано без доверительной вероятности, принимаем прямоугольное распределение значений погрешности взвешивания в этих границах. Стандартная неопределенность массы стаканчика для взвешивания с навеской до высушивания m₁ оценивается по типу В и составляет:

2) Масса стаканчика для взвешивания, m_cт

Масса стаканчика для взвешивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:

• для первой пробы m_ст(1) = 21,0034 г,
• для второй пробы m_ст(2) = 21,3822 г.

Неопределенность массы стаканчика для взвешивания после высушивания обусловлена двумя факторами:

• погрешностью взвешивания стаканчика на весах;
• возможными отклонениями массы стаканчика после высушивания вследствие нечеткого определения в методике выполнения измерений момента, в который масса стаканчика после высушивания будет являться постоянной величиной.

Стандартная неопределенность u₁(m_cт), связанная с погрешностью взвешивания, оценивается на основании данных производителя на весы лабораторные AV264C, определяется аналогично неопределенности величины m₁ и составляет u₁(m_cт) = 0,00058 г.

Стандартную неопределенность u₂(m_cт), обусловленную отклонениями массы стаканчика для взвешивания после высушивания, можно определить на основании информации о том, что разность между двумя последующими взвешиваниями стаканчика для взвешивания после сушки не должна превышать 0,002 г (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает момент, в который масса стаканчика после высушивания будет являться постоянной величиной). Это значение можно рассматривать как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения (предел повторяемости по СТБ ИСО 5725-6). Стандартная неопределенность u₂(m_cт) будет равна стандартному отклонению, рассчитанному на основании указанного интервала по типу В по формуле:

Суммарную стандартную неопределенность величины mcт находим путем суммирования квадратов стандартных неопределенностей перечисленных выше двух вкладов:

3) Масса стаканчика для взвешивания с навеской после высушивания, m₂

Масса стаканчика для взвешивания с навеской после высушивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:

• для первой пробы m₂₍₁₎ = 40,9850 г,
• для второй пробы m₂₍₂₎ = 41,3638 г.

Неопределенность массы стаканчика для взвешивания с навеской после высушивания обусловлена двумя факторами:

• погрешностью взвешивания пробы на весах;
• возможными отклонениями массы пробы после высушивания вследствие нечеткого определения в методе испытаний момента, в который масса пробы после высушивания будет являться постоянной величиной.

Стандартная неопределенность u₁(m₂), связанная с погрешностью взвешивания, оценивается на основании данных производителя на весы лабораторные AV264C, определяется аналогично неопределенности величины m₂ и составляет u₁(m₂) = 0,00058 г.

Стандартную неопределенность u₂(m₂), обусловленную отклонениями массы стаканчика для взвешивания с навеской после высушивания, можно определить на основании информации о том, что разность между двумя последующими взвешиваниями стаканчика для взвешивания с навеской пробы бария углекислого после сушки не должна превышать 0,002 г (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает момент, в который масса пробы после высушивания будет являться постоянной величиной). Это значение можно рассматривать как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения (предел повторяемости по СТБ ИСО 5725-6). Стандартная неопределенность u₂(m₂) будет равна стандартному отклонению, рассчитанному на основании указанного интервала по типу В по формуле:

Суммарную стандартную неопределенность величины m₂ находим путем суммирования квадратов стандартных неопределенностей перечисленных выше двух вкладов:

4) Поправочный множитель, учитывающий допускаемое расхождение между параллельными определениями, F

Значение оценки величины принимается равным единице: F = 1.

Стандартная неопределенность поправочного множителя рассчитывается на основании информации о допускаемом расхождении между параллельными определениями влажности, приведенными в ГОСТ 2149-75 (п.3.5.2). Приведенное допускаемое относительное расхождение составляет r = 20 % и рассматривается как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения. Стандартная неопределенность поправочного множителя будет равна стандартному отклонению, рассчитанному на основании указанного интервала, с учетом того, что за результат измерения принимают среднее арифметические определений двух параллельных проб, по типу В по формуле:

Этап 3. Анализ корреляций

Все входные величины рассматриваются как некоррелированные, поскольку получены независимо друг от друга в различных экспериментах.

ОБУЧЕНИЕ ПРОЦЕДУРЕ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ (химия и аналитика) 

Семинар: «Неопределенность измерения величин: основные принципы и подходы к оцениванию»

ПОДРОБНЕЕ О СЕМИНАРЕ

ОБУЧЕНИЕ ПРОЦЕДУРЕ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ (прямые методы измерений)

Семинар: «Неопределенность измерения величин: основные принципы и подходы к оцениванию»

ПОДРОБНЕЕ О СЕМИНАРЕ

Этап 4. Измеренное значение величины

Массовая доля влаги i-ой пробы углекислого бария рассчитывается по формуле (2):

Расхождение между результатами измерений двух параллельных проб не превышает допускаемого значения, установленного в ГОСТ 2149-75 (п. 3.5.2):

Массовая доля влаги бария углекислого Х в процентах вычисляется в соответствии с функцией измерений (1):

Измеренное значение (оценку измеряемой величины) округляют до четырех знаков после запятой (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает требования к округлению результата измерения).

Этап 5. Суммарная стандартная неопределенность

Стандартную неопределенность измеряемой величины Х получаем по закону распространения неопределенностей путем суммирования квадратов произведений стандартных неопределенностей всех влияющих величин, входящих в функции измерений (1) и (2), на соответствующие коэффициенты чувствительности:

где коэффициенты чувствительности рассчитываются как частные производные функции измерений по входным величинам:

Примечание – Для вычисления коэффициентов чувствительности можно использовать либо минимальные значения масс, полученные при измерении массовой доли влаги i-ой пробы бария углекислого, либо результаты измерений масс, полученные на определенной пробе бария углекислого. В данном примере коэффициенты чувствительности рассчитываются на основании результатов измерений масс для первой пробы.

Суммарная стандартная неопределенность составит

Этап 6. Бюджет неопределенности

В таблице представлен бюджет неопределенности для измеряемой величины.

Вклад в неопределенность от j-ой входной величины рассчитывается как произведение стандартной неопределенности этой величины на соответствующий коэффициент чувствительности.

Этап 7. Расширенная неопределенность

Расширенную неопределенность U получаем умножением суммарной стандартной неопределенности на коэффициент охвата k, который выбирается равным 2 при уровне доверия приблизительно 95 % в предположении нормального распределения вероятностей измеряемой величины:

Этап 8. Представление результата измерения

Результат измерения массовой доли влаги углекислого бария представляют в виде:

«Массовая доля влаги бария углекислого составила (0,1022 ± 0,0150) %, где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 95 %».

Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.

Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.

УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…

---

 

---

Пример 2. Оценивание неопределенности измерений сопротивления изоляции

---

Исходные данные:

1. Объект измерений – кабель силовой АВБбШв
2. Измеряемая величина – сопротивления изоляции
3. Единицы измерений – МОм
4. Измерение сопротивления изоляции выполняется методом непосредственной оценки с помощью мегаомметра Е6-24

Измерения проведены в диапазоне измерений мегаомметра Е6-24 от 100 до 999 МОм при температуре окружающего воздуха 22 °С и относительной влажности воздуха 65 %.

Этап 1. Составление функции измерений

Сопротивление изоляции определяется в соответствии со следующей функцией измерений

где R – сопротивление изоляции, МОм;

R_ind – среднее арифметическое повторных измерений сопротивления изоляции, МОм;

F_Δ – поправка, учитывающая допускаемую основную погрешность измерения сопротивления мегаомметра Е6-24, МОм;

F_с – поправка, учитывающая единицу младшего разряда, выдаваемых мегаомметром Е6-24 показаний сопротивления, МОм.

Примечание – В функции измерений не учитываются поправки F_Δt и F_Δφ на дополнительные погрешности измерения сопротивления мегаомметра Е6-24, вызванные отклонением соответственно температуры и влажности окружающей среды от нормальных условий в рабочем диапазоне. Поправки будут вводиться только в случае, если измеренные значения температуры и/или относительной влажности окружающей среды находятся в рабочем диапазоне, но выходят за диапазон нормальных условий эксплуатации мегаомметра Е6-24 (значения нормальных и рабочих условий эксплуатации указаны в руководстве по эксплуатации мегаомметра Е6-24).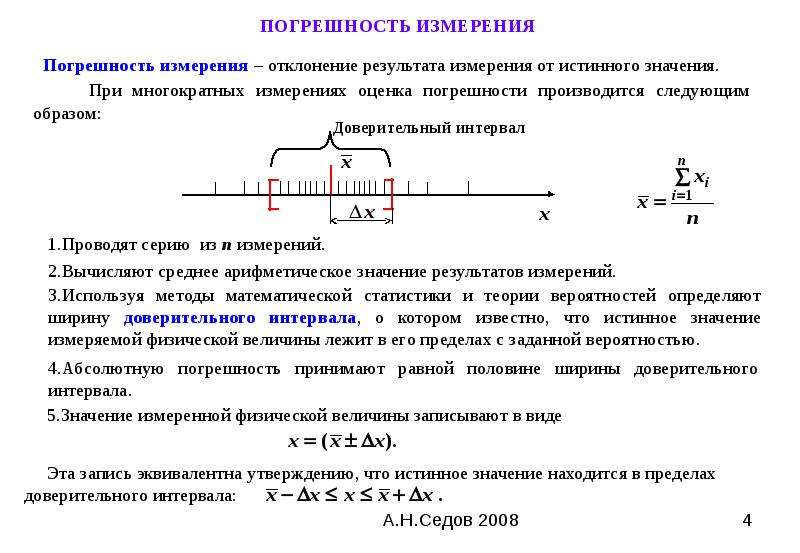

Этап 2. Анализ входных величин

1) Среднее арифметическое повторных измерений сопротивления изоляции R_ind, МОм.

При проведении измерений сопротивления изоляции кабеля силового АВБбШв получены следующие результаты повторных измерений: R₁ = 124 МОм; R₂ = 131 МОм; R₃ = 137 МОм.

Значение оценки величины R_ind определяется по формуле

где R_i – результат i-го повторного измерения сопротивления изоляции, определяемый как показание, снимаемое с дисплея мегаомметра Е6-24, МОм;

n – количество повторных измерений, n = 3.

Стандартная неопределенность измерений величины R_ind, МОм, рассчитывается в предположении нормального распределения вероятностей по формуле

2) Поправка, учитывающая допускаемую основную погрешность измерения сопротивления мегаомметра Е6-24, F_Δ

Значение оценки величины F_Δ принимается равным 0,0 МОм.

Стандартная неопределенность u(F_Δ), МОм, оценивается на основании информации о пределах допускаемой основной абсолютной погрешности измерения сопротивления мегаомметра Е6-24 ± Δ, МОм. В предположении прямоугольного распределения вероятностей значений погрешности в границах ± Δ определяется по формуле

Примечание — согласно [1] пределы допускаемой основной погрешности измерения сопротивления приведены в виде ± (% + е.м.р.) т. е. для получения пределов абсолютной погрешности измерения Δ нужно воспользоваться формулой

где δ» – допускаемая относительная погрешность измерения сопротивления, которая принимается равной первому числу, стоящему в [1] в записи пределов допускаемой основной погрешности измерения сопротивления, %;

100 – коэффициент перехода от долей к процентам, %;

m – второе число стоящее в [1] в записи пределов допускаемой основной погрешности измерения сопротивления, определяющее количество единиц младшего разряда;

с – единица младшего разряда выдаваемого мегаомметром Е6-24 показания сопротивления, МОм.

3) Поправка, учитывающая единицу младшего разряда выдаваемых мегаомметром Е6-24 показаний сопротивления, Fс

Значение оценки величины F_c принимается равным 0,0 МОм.

Стандартная неопределенность u(F_c), МОм, определяется на основании информации о единице младшего разряда выдаваемого мегаомметром Е6-24 показания сопротивления c = 1 МОм (для диапазона измерений мегаомметра Е6-24 от 100 до 999 МОм). В предположении прямоугольного распределения вероятностей значений величины c в границах ± c/2 определяется по формуле

Этап 3. Анализ корреляций

Все величины, входящие в функцию измерений (1), рассматриваются как некоррелированные.

Этап 4. Оценка измеряемой величины

Значение оценки величины R, МОм, «сопротивление изоляции» рассчитывается по формуле (1)

Значение сопротивления изоляции (МОм) округляют до одного знака после запятой.

Этап 5. Суммарная стандартная неопределенность

Суммарная стандартная неопределенность измерений сопротивления изоляции силового кабеля u(R), МОм, определяется по формуле

Процентные вклады неопределенностей влияющих величин в суммарную стандартную неопределенность u(R) определяются по формулам

Этап 6. Бюджет неопределенности

Бюджет неопределенности измерений сопротивления изоляции силового кабеля представлен в таблице 1.

Таблица 1 – Бюджет неопределенности измерений сопротивления изоляции силового кабеля

Этап 7. Расширенная неопределенность

Расширенная неопределенность измерений сопротивления изоляции силового кабеля U(R), МОм, определяется для вероятности 95 % в предположении распределения Стьюдента по формуле

где коэффициент охвата k = 2,26, выбирается в зависимости от числа эффективных степеней свободы v_eff, которое рассчитывается по формуле

Этап 8.

Результат измерения

Сопротивление изоляции силового кабеля АВБбШв составило

(130,7 ± 12,5) МОм (k = 2,26, v_eff = 9,14, Р = 95 %).

Библиография

[1] РЛПА 411218.001 РЭ Руководство по эксплуатации. Мегаомметры Е6-24, E6-24/1 и E6-24/2.

Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.

Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.

УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…

---

 

---

Пример 3. Оценивание неопределенности измерений коэффициента поправки титрованного раствора

---

Исходные данные:

1. Объект измерений – раствор серной кислоты концентрации моль/дм3
2. Измеряемая величина – коэффициента поправки 0,1 моль/дм3 раствора серной кислоты
3. Единицы измерений – безразмерная величина
4. Методика измерений – ГОСТ 25794. 1 83 «Реактивы. Методы приготовления титрованных растворов для кислотно-основного титрования»
5. Метод измерений – титриметрический по безводному углекислому натрию

Этап 1. Составление функции измерений

Значение оценки коэффициента поправки 0,1 моль/дм3 раствора серной кислоты Ki, при единичном определении рассчитывается по формуле:

где m – масса навески безводного углекислого натрия, г;

P – чистота реактива безводного углекислого натрия, P = 1;

M – молярная масса эквивалента безводного углекислого натрия, г/моль;

с – заданная молярная концентрация серной кислоты в 0,1 моль/дм³ растворе серной кислоты, с = 0,1 моль/дм³, рассматривается как постоянная и не учитывается при расчете неопределенности измерений коэффициента K;

V – объем 0,1 моль/дм³ раствора серной кислоты, израсходованный на титрование, см³.

1000 – коэффициент перехода единицы измерения объема см³ в дм³.

Значение оценки коэффициента K вычисляется как среднее арифметическое трех повторных определений коэффициента поправки раствора серной кислоты по формуле:

где F – поправочный коэффициент, учитывающий расхождение между результатами повторных определений коэффициента поправки раствора серной кислоты, F = 1.

Расхождение между результатами трех повторных определений коэффициента поправки раствора серной кислоты не должно превышать значения 0,001, установленного ГОСТ 25794.1 (п. 1.11).

Этап 2. Анализ входных величин

2.1 Масса навески безводного углекислого натрия, m

Значение массы навески безводного углекислого натрия, m, г, определяется как разность показаний весов при взвешивании стаканчика с навеской установочного вещества и пустого стаканчика. При выполнении измерения были получены следующие значения выходной величины для трех повторных определений коэффициента поправки: m₁ = 0,1648 г; m₂ = 0,1643 г; m₃ = 0,1649 г.

Стандартная неопределенность измерений массы навески установочного вещества, u(m), г, оценивается на основании информации о пределах допускаемой погрешности используемых весов ВСЛ-200/0,1А ± Δm = ± 0,001 г в диапазоне измерений от 0,01 до 50 г, и дискретности отсчета весов d = 0,0001 г, установленных в технической документации на весы. В предположении прямоугольного распределения вероятностей значений погрешности и дискретности в границах ± Δm и ± d/2 соответственно и учитывая двойное взвешивание (пустого стаканчика и стаканчика с навеской установочного вещества) стандартная неопределенность u(m) рассчитывается по формуле:

2.2 Чистота реактива безводного углекислого натрия, P

Значение оценки величины P принимается равным 1.

Стандартная неопределенность измерений степени чистоты реактива углекислого натрия u(P) оценивается на основании информации о том, что согласно ГОСТ 83-79 «Реактивы. Натрий углекислый. Технические условия» массовая доля углекислого натрия в реактиве безводного углекислого натрия составляет не менее 99,8 %. Неопределенность измерений u(P) рассчитывается исходя из отклонения значения чистоты реактива от 1 в предположении прямоугольного распределения величины Р в границах ± (1 – 0,998) по формуле:

2.3 Молярная масса эквивалента безводного углекислого натрия, M

Значение оценки величины M, г/моль, определяется как произведение фактора эквивалентности безводного углекислого натрия f_э = 1/2 на молярную массу установочного вещества M₀, г/моль, по формуле:

где молярная масса безводного углекислого натрия (Na2CO3) рассчитывается на основании значений атомных масс натрия, углерода и кислорода A, взятых из таблиц атомных масс IUPAC (//www. sbcs.qmul.ac.uk/iupac/AtWt/), и количества атомов этих элементов в молекуле безводного углекислого натрия n (A_Na ≈ 22,98976928, A_с = 12,011, A₀ = 15,999, n_Na= 2, n_с = 1, n₀ = 3):

Стандартная неопределенность измерений молярной массы эквивалента безводного углекислого натрия, u(M), г/моль, определяется на основании возможных разбросов значений атомных масс углерода и кислорода ΔА = A_max – A_min и неопределенности последней цифры атомной массы натрия ΔA, а также количества атомов этих элементов в молекуле безводного углекислого натрия n. Данные по разбросам значений атомных масс углерода и кислорода и неопределенности последней цифры атомной массы натрия выбираются из таблиц атомных масс IUPAC (//www.sbcs.qmul.ac.uk/iupac/AtWt/). Стандартная неопределенность значений атомных масс химических элементов рассчитывается в предположении прямоугольного распределения вероятностей атомных масс элементов в границах ± ΔА/2 (для углерода и кислорода) и в границах ± ΔA (для натрия). Неопределенность для вклада атомов одного элемента рассчитывается умножением стандартной неопределенности атомной массы элемента на количество атомов элемента. Стандартная неопределенность измерений молярной массы эквивалента безводного углекислого натрия, u(M), г/моль, определяется по формуле:

2.4 Объем раствора серной кислоты, израсходованный на титрование, V

Значение оценки величины V, см³, определяется по шкале бюретки номинальной вместимостью 25 см3 2-го класса точности по ГОСТ 29251-91 «Посуда лабораторная стеклянная. Бюретки. Часть 1. Общие требования». При выполнении измерения были получены следующие значения выходной величины для трех повторных определений коэффициента поправки: V₁= 31,1 см³; V₂= 31,0  см³; V₃= 31,1 см³.

Стандартная неопределенность измерений объема 0,1 моль/дм³ раствора серной кислоты, израсходованного на титрование, u(V), см³, состоит из следующих основных вкладов:

• стандартная неопределенность, обусловленная погрешностью измерения объема сливаемой жидкости используемой бюретки, u(V_Δ), см³;
• стандартная неопределенность, обусловленная ценой наименьшего деления шкалы используемой бюретки, u(V_c), см³;
• стандартная неопределенность, обусловленная отличием температуры, при которой проводятся измерения, от температуры, при которой нормируется погрешность измерения объема сливаемой жидкости бюретки, u(V_t), см3.

Стандартная неопределенность u(V_Δ), см3, рассчитывается на основании информации о пределах погрешности измерения сливаемой жидкости бюреткой ± ΔV = 0,1 см³, установленных ГОСТ 29251 в предположении треугольного распределения погрешности в установленных пределах по формуле:

Стандартная неопределенность u(V_c), см3, рассчитывается на основании информации о цене наименьшего деления шкалы используемой бюретки см3, в предположении прямоугольного распределения вероятностей цены деления в пределах ± dV/2 по формуле:

Стандартная неопределенность u(V_t), см3, рассчитывается в предположении прямоугольного распределения исходя из возможных пределов изменения объема жидкости при условии колебания температуры в лаборатории при измерении в пределах (20 ± 5) °С (Δt = 5 °С) и коэффициента объемного расширения жидкости kV, ºС^-1, равного 0,00021 ºС^-1 для воды (основное вещество в растворе) по формуле:

Примечание – Для оценивания стандартной неопределенности u(V_t) используется измеренное значение объема раствора серной кислоты, пошедшего на титрование, полученное для первой навески безводного углекислого натрия.

Суммарная стандартная неопределенность измерений объема 0,1 моль/дм³ раствора серной кислоты, израсходованного на титрование, u(V), см³ вычисляется путем суммирования стандартных неопределенностей перечисленных выше вкладов по формуле:

2.5 Поправочный коэффициент, учитывающий расхождение между результатами повторных определений коэффициента поправки раствора серной кислоты, F

Значение оценки величины F принимается равным 1.

Стандартная неопределенность измерений поправочного коэффициента, учитывающего расхождение между результатами повторных определений коэффициента поправки раствора серной кислоты, u(F), определяется на основании установленного ГОСТ 25794.1 (п. 1.11) допускаемого расхождения между результатами повторных определений коэффициента поправки r = 0,001, которое рассматривается как предел повторяемости согласно СТБ ИСО 5725-6-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике». С учетом того, что за результат измерения принимается среднее арифметическое трех определений, стандартная неопределенность u(F) определяется по формуле:

Этап 3. Анализ корреляций

Все входные величины рассматриваются как некоррелированные, поскольку получены независимо друг от друга в различных экспериментах.

Этап 4. Оценка измеряемой величины

Значения коэффициента поправки раствора серной кислоты при i-ом определении согласно формуле (1) составляют:

Максимальное расхождение между результатами трех определений не превышает допускаемого значения, установленного ГОСТ 25794.1:
Значение коэффициента поправки раствора серной кислоты определяется по формуле (2) на основании результатов параллельных определений, которые рассчитываются по формуле (1):

Коэффициент поправки вычисляют с точностью до четвертого десятичного знака. Полученное значение коэффициента поправки раствора серной кислоты удовлетворяет требованию ГОСТ 25794. 1 (п. 1.11) о том, что значение коэффициента поправки должно соответствовать диапазону .

Этап 5. Суммарная стандартная неопределенность

Суммарная стандартная неопределенность измерений коэффициента поправки K определяется по закону распространения неопределенностей путем суммирования относительных стандартных неопределенностей всех влияющих величин, входящих в функции измерений (1) и (2), по формуле:

Примечание — Для оценивания суммарной стандартной неопределенности u(K) используются значения оценок влияющих величин (измеренные значения), полученные для первой навески безводного углекислого натрия.

Значения относительных стандартных неопределенностей влияющих величин рассчитываются как отношение стандартной неопределенности влияющей величины к значению оценки влияющей величины.

Значения процентных вкладов неопределенностей влияющих величин в суммарную стандартную неопределенность рассчитываются как умноженное на 100 % отношение квадрата относительной стандартной неопределенности влияющей величины к квадрату относительной суммарной стандартной неопределенности.

Этап 6. Бюджет неопределенности

В таблице представлен бюджет неопределенности измерений коэффициента поправки серной кислоты.

Этап 7. Расширенная неопределенность

Расширенная неопределенность измерений коэффициента поправки серной кислоты, U(K), получается умножением суммарной стандартной неопределенности, u(K), на коэффициент охвата k, который выбирается равным 2 при уровне доверия приблизительно 95 % в предположении нормального распределения вероятностей измеряемой величины:

Этап 8. Результат измерения

Коэффициент поправки раствора серной кислоты концентрации c(H₂SO₄) = 0,1 моль/дм³ составляет (1,0001 ± 0,0108), где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 95 %.

Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.

Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.

УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…

---

 

---

Пример 4. Оценивание неопределенности измерений pH воды

---

Измерительная задача

Метод основан на измерении разности потенциалов гальванического элемента с использованием соответствующего рН-метра. Измерения проводят рН-метром/иономером ИТАН. Перед измерением пробы воды про-водится двухточечная калибровка по буферным растворам. Температура пробы питьевой воды и температура буферных растворов измеряется термодатчиком, встроенным в рН-метр. рН-метр автоматически учитывает разность температур буферных растворов и пробы питьевой воды в выдаваемых показаниях.

Этап 1. Составление функции измерений

Измеряемой величиной является рН пробы питьевой воды, ед. рН, которая определяется согласно функции измерений:

где рНизм – показания рН-метра, ед. рН;
δкал – поправка на погрешность калибровки рН-метра, ед. рН;
δсх – поправка на повторяемость измерений, ед. рН.
Измеренное значение величины округляют до одного десятичного знака.

Результаты измерений

Температура пробы питьевой воды, измеренная термодатчиком рН-метра, составила 10 °С. При измерении пробы питьевой воды с цифрового дисплея рН-метра было снято показание рН равное 6,52 ед. рН.

Этап 2. Анализ входных величин

2.1 Показания рН-метра (рНизм)

Показание рН-метра составило рНизм = 6,52 ед. рН.
Стандартная неопределенность величины рНизм рассчитывается на основании информации о пределах основной допускаемой абсолютной погрешности рН-метра в предположении прямоугольного распределения вероятностей. В паспорте на рН-метр/иономер ИТАН указаны пределы основной допускаемой абсолютной погрешности измерения рН (измерительным преобразователем в комплекте с электродной системой в растворах с температурой от 10 °С до 60 °С) ± Δ = ± 0,050 ед. рН. Стандартная неопределенность величины рНизм рассчитывается по формуле:

Примечание – Неопределенностью измерений, обусловленной разрешающей способностью цифрового дисплея рН-метра пренебрегаем, поскольку данная составляющая неопределенности значительно ниже составляющей, обусловленной основной допускаемой абсолютной погрешностью рН-метра.

2.2 Поправка на погрешность калибровки рН-метра (δкал)

Поправка на погрешность калибровки рН-метра оценивается значением «нуль»
δкал = 0 ед. рН.
Стандартная неопределенность измерений величины δкал рассчитывается на основании информации о допускаемом отклонении значений рН, при проверке калибровки, от значений рН буферных растворов в контрольных точках ± Δк = ± 0,03 ед. рН. Стандартная неопределенность величины δкал рассчитывается в предположении прямо-угольного распределения вероятностей в указанных границах по формуле:

Примечание – Неопределенностью измерений рН буферных растворов пренебрегаем, т.к. значения расширенных неопределенностей измерений рН буферных растворов не превышают 1/3 от допускаемого отклонения Δк.

2.3 Поправка на повторяемость измерений (δсх)

Поправка на повторяемость измерений рН оценивается значением «нуль» δсх = 0 ед. рН.
Стандартная неопределенность измерений величины δсх рассчитывается на основании информации о стандартном отклонении повторяемости в предположении нормального распределения вероятностей. Для питьевой воды в диапазоне рН от 6,35 до 6,46 ед. рН при межлабораторном исследовании метода измерений рН было установлено значение стандартного отклонения повторяемости σr = 0,011 ед. рН. В лаборатории при внедрении метода измерений установленное значение показателя повторяемости было подтверждено и распространено на диапазон измерений, содержащий измеренное значение рН в исследуемой пробе питьевой воды. Стандартная неопределенность величины δсх рассчитывается по формуле:

Этап 3. Анализ корреляций

Все входные величины рассматриваются как некоррелированные.

Этап 4. Измеренное значение величины

рН пробы питьевой воды будет оцениваться в соответствии с выражением (1) и составит:

Этап 5. Суммарная стандартная неопределенность

Суммарная стандартная неопределенность измерений величины рН рассчитывается по формуле:

Коэффициенты чувствительности для всех влияющих величин, входящих в функцию измерений (1), будут равны 1.

Этап 6. Бюджет неопределенности

В таблице представлен бюджет неопределенности для измеряемой величины и произведены соответствующие расчеты для нахождения ее стандартной неопределенности.

Таблица – Бюджет неопределенности для рН пробы питьевой воды

Этап 7. Расширенная неопределенность

Расширенная неопределенность U получается умножением суммарной стандартной неопределенности на коэффициент охвата k, который выбирается равным 2 при уровне доверия 95 % в предположении нормального распределения вероятностей измеряемой величины:

Этап 8.

Представление результата измерения

Результат измерения записывается в виде:
«рН пробы воды составила (6,5 ± 0,1) ед. рН, k = 2, P = 95 %».

Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.

Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.

УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…

 

---

Пример 5. Оценивание неопределенности измерений относительного удлинения эластичного герметика

---

Измерительная задача

Относительное удлинение герметика полиуретанового определяется по ГОСТ 21751-76 «Герметики. Метод определения условной прочности относительного удлинения при разрыве и относительной остаточной деформации после разрыва» с применением разрывной машины РМ-30-1 методом растяжения образцов с постоянной скоростью при заданной температуре до разрыва с последующим измерением геометрических параметров образца. Длина рабочего участка образца до и после приложения нагрузки измеряется линейкой металлической по ГОСТ 427-75 с пределом измерений 300 мм и ценой деления 1 мм.
Образцы герметика для испытаний типа 1 вырезают длиной (115 ± 1) мм специальным ножом согласно ГОСТ 21751 (пп. 1.3, 2.1-2.4). Общее количество испытываемых образцов – 5. Испытания проводят при температуре окружающего воздуха (20 ± 3) ºС и относительной влажности (65 ± 5) %.

Этап 1. Составление функции измерений

Относительное удлинение каждого испытываемого образца, εрi, в процентах рассчитывается на основании функции измерений:

где lpi – длина рабочего участка образца в момент разрыва, мм;
l0 – первоначальная длина рабочего участка образца, мм.
Относительное удлинение герметика полиуретанового  рассчитывается как среднее арифметическое относительных удлинений, εрi, полученных для каждого из испытываемых образцов:

где  – среднее арифметическое измерений относительного удлинения пяти образцах, %;
t – количество испытанных образцов герметика;
Fr – поправка на рассеяние результатов измерений относительных удлинений, полученных на всех испытанных образцах, %.
Результат измерения округляется до целых чисел.

Результаты измерений

При определении относительного удлинение герметика полиуретанового было испытано 5 образцов. Результаты испытаний представлены в таблице 1.

Таблица 1 – Результаты испытаний образов герметика полиуретанового на относительное удлинение

Этап 2. Анализ входных величин

2.1 Среднее арифметическое измерений относительного удлинения пяти образцах ()

Значение оценки рассчитывается по формуле

Возможное рассеяние результатов измерений относительного удлинения на пяти единичных образцах герметика учитывается через влияющую величину F.

2.2 Первоначальная длина рабочего участка образца (l0i)

Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Значение оценки: получают путем снятия показаний со шкалы линейки при прямых измерениях длины рабочего участка образца до проведения испытаний, мм; значения для каждого образца представлены в таблице 1
Стандартная неопределенность: u(l0i) = 0,294 мм
Неопределенность, связанная с величиной l0i, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 300 мм ±Δl = ±0,10 мм и цене деления линейки d = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:

2.3 Длина рабочего участка образца в момент разрыва (lpi)

Вид распределения: трапецеидальное
Значение оценки: получают путем снятия показаний со шкалы линейки при прямых измерениях длины рабочего участка образца после проведения испытаний, мм; значения для каждого образца представлены в таблице 1
Стандартная неопределенность: u(lpi) = 0,294 мм
Неопределенность, связанная с величиной lpi, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 300 мм ±Δl = ±0,10 мм и цене деления линейки d = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:

2.4 Поправка на рассеяние результатов измерений относительных удлинений, полученных на всех испытанных образцах (Fr )

Тип оценивания неопределенности: А
Вид распределения: нормальное
Значение оценки: Fr = 0,0 %
Стандартная неопределенность: u(Fr) = 22,80 %
Стандартная неопределенность поправки рассчитывается как стандартное отклонение среднего арифметического измерений относительного удлинения пяти образцах по типу А в предположении нормального распределения и составляет:

Этап 3. Анализ корреляций

Все входные величины рассматриваются как некоррелированные.

Этап 4. Измеренное значение величины

Оценка измеряемой величины – относительное удлинение герметика, εр, в процентах, рассчитывается по формуле (1) используя полученные в Этапе 2 значения оценок входных величин:

Этап 5.

Суммарная стандартная неопределенность

Стандартную неопределенность измеряемой величины εр, %, рассчитываем по закону распространения неопределенностей путем суммирования квадратов произведений стандартных неопределенностей влияющих величин, входящих в функции измерений (1) и (2), на соответствующие коэффициенты чувствительности:

Коэффициенты чувствительности рассчитываются как частные производные функции измерений (1) по входным величинам:

Примечание – Для расчета коэффициентов чувствительности используются значения параметров, полученные при испытаниях первого образца герметика.

Вклад в неопределенность от j-ой входной величины рассчитывается как произведение стандартной неопределенности этой величины на соответствующий коэффициент чувствительности. Процентный вклад рассчитывается как отношение квадрата вклада входной величины к квадрату суммарной стандартной неопределенности (выражается в процентах):

Этап 6.

Бюджет неопределенности

Бюджет неопределенности для относительного удлинения герметика представлен в таблице 3.

Таблица 3 – Бюджет неопределенности для относительного удлинения

Этап 7. Расширенная неопределенность

Расширенную неопределенность U получаем умножением суммарной стандартной неопределенности на коэффициент охвата k. Поскольку в бюджете неопределенности доминирует составляющая, распределенная по нормальному закону распределения и рассчитанная на малом объеме экспериментальных данных (менее 10), то значение коэффициента охвата выбирается в предположении распределения Стьюдента для измеряемой величины как квантиль распределения Стьюдента при вероятности 95 % и числе эффективных степеней свободы, которые рассчитываются по формуле Уэлча-Саттертуэта

Значение коэффициента охвата принимается равным k = 2,57. Расширенная неопределенность будет рассчитываться по формуле:

Этап 8. Представление результата измерения

Результат измерения представляют в виде:
«Относительное удлинение герметика полиуретанового  составило (580 ±63) %, где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2,78, основанный на предполагаемом распределении Стьюдента и числе эффективных степеней свободы νeff = 5, и определяет интервал, соответствующий вероятности охвата 95 %».

Библиография
ГОСТ 21751-76 Герметики. Метод определения условной прочности относительного удлинения при разрыве и относительной остаточной деформации после разрыва
ГОСТ 427-75 Линейки измерительные металлические. Технические условия

Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.

Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.

УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…

 

---

Пример 6. Оценивание неопределенности измерений прочности бетона на растяжение при изгибе

---

Измерительная задача
Прочность на растяжение при изгибе бетона класса прочности на растяжение при изгибе Вtb3,6 определяется по ГОСТ 10180-2012 «Бетоны. Методы определения прочности по контрольным образцам» путем разрушающих кратковременных статических испытаний специально изготовленных контрольных образцов бетона. В качестве контрольных образцов используются изготовленные согласно ГОСТ 10180 (п. 4) образцы бетона в форме призмы квадратного сечения 100×100×400 мм. Количество контрольных образцов в серии – три.
Испытания контрольных образцов на прочность на растяжение при изгибе проводят на универсальной испытательной машине C093-03A. Линейные размеры образцов измеряют линейкой металлической по ГОСТ 427-75 с пределом измерений 500 мм и ценой деления 1 мм.

Этап 1. Составление функции измерений

Прочность бетона на растяжение при изгибе для i-го образца в серии Rtb,i, МПа, вычисляется в соответствии со следующей функцией измерений:

где δ – масштабный коэффициент для приведения прочности бетона к прочности бетона в образцах базовых размера и формы;
Fi – разрушающая нагрузка для i-го контрольного образца, Н;
ai – ширина поперечного сечения призмы для i-го контрольного образца, мм;
bi – высота поперечного сечения призмы для i-го контрольного образца, мм;
l – расстояние между опорами, мм.
Прочность бетона на растяжение при изгибе Rtb, МПа, вычисляется в соответствии со следующей функцией измерений:

где Fr – поправочный коэффициент, учитывающий расхождение между результатами измерений прочности n образцов, Fr = 1;
n – количество образцов в серии, n = 3.
Измеренное значение прочности бетона на растяжение при изгибе округляется с точностью до 0,01 МПа.

Результаты измерений
При проведении испытаний трех контрольных образцов бетона на растяжение при изгибе были получены значения параметров, представленные в таблице 1.

Таблица 1 – Результаты испытаний контрольных образцов бетона на прочность на растяжение при изгибе

Этап 2. Анализ входных величин

2.1 Масштабный коэффициент для приведения прочности бетона к прочности бетона в образцах базовых размера и формы (δ)

Значение оценки выбирается согласно ГОСТ 10180 (таблица 1) и составляет δ = 0,92.
Величина рассматривается как постоянная.

2.2 Разрушающая нагрузка для i-го контрольного образца (Fi)

Значение оценки величины Fi для каждого контрольного образца определяется по шкале отсчетного устройства испытательной машины и представлено в таблице 1
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(F) = 164,04 Н
Неопределенность, связанная с величиной F, оценивается на основании информации о пределах допускаемой относительной погрешности показания силы ± δF = ± 1 % и цене деления шкалы стрелочного индикатора d = 500 Н. Поскольку значения приведены без вероятности, принимаем прямоугольное распределение значений погрешности показаний силы и ошибки оператора при снятии показаний со шкалы индикатора в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:

Примечание – Для расчета стандартной неопределенности разрушающей нагрузки используется значение параметра, полученное при испытаниях первого контрольного образца.

2.3 Ширина поперечного сечения призмы для i-го контрольного образца (ai)

Значение оценки величины аi для каждого контрольного образца определяется по шкале линейки металлической и представлено в таблице 1
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(а) = 0,301 мм
Неопределенность, связанная с величиной а, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 500 мм ±Δl = ±0,15 мм и цене деления линейки dl = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:

2.4 Высота поперечного сечения призмы для i-го контрольного образца (bi)

Значение оценки величины bi для каждого контрольного образца определяется по шкале линейки металлической и представлено в таблице 1
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(b) = 0,301 мм
Неопределенность, связанная с величиной b, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 500 мм ±Δl = ±0,15 мм и цене деления линейки dl = 1 мм.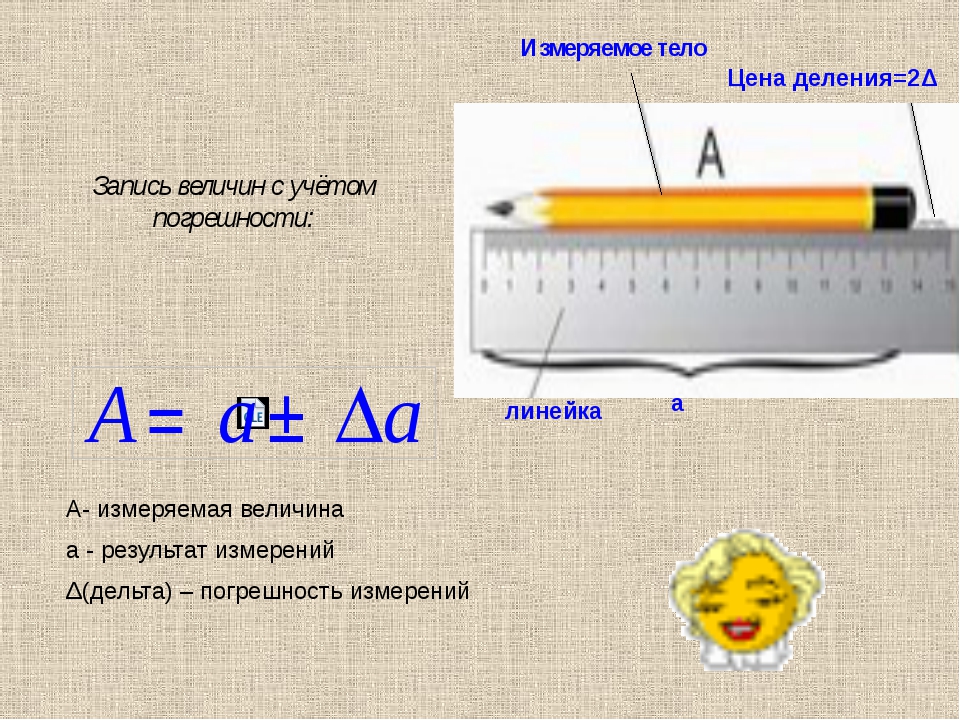 Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:

2.5 Расстояние между опорами (l)

Значение оценки величины l = 300 мм и определяется по шкале линейки металлической
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(l) = 0,301 мм
Неопределенность, связанная с величиной l, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 500 мм ±Δl = ±0,15 мм и цене деления линейки dl = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:

2.6 Поправочный коэффициент, учитывающий расхождение между результатами измерений прочности n образцов (Fr)

Значение оценки: Fr = 1
Тип оценивания неопределенности: B
Вид распределения: нормальное
Стандартная неопределенность: u(Fr) = 0,06
Стандартная неопределенность поправки рассчитывается на основании среднего внутрисерийного коэффициента вариации прочности бетона, установленного в лаборатории согласно ГОСТ 10180 (Приложение А) и равного 6 %. Стандартная неопределенность оценивается по типу В в предположении нормального распределения и составляет:

Примечание – Для использования в расчетах установленного в лаборатории среднего внутрисерийного коэффициента вариации следует проверить соответствие реального разброса результатов измерений прочности бетона на растяжение при изгибе, полученного на испытанных контрольных образцах, установленному среднему внутрисерийному коэффициенту вариации используя положения СТБ ИСО 5725-6 и следующее неравенство:

где f(n) – коэффициент критического размаха, выбирается в зависимости от количества контрольных образцов в серии n по СТБ ИСО 5725-6 (таблица 1).
Для нашего примера f(n=3) = 3,3 и неравенство (8) выполняется:

Этап 3. Анализ корреляций

При измерении величин а и b, близких по измеренным значением, присутствуют корреляционные эффекты, связанные с применением одного средства измерений (линейки металлической) в одной точке диапазона измерений (узком диапазоне измерений) и вызванные погрешностью применяемого средства измерений. Однако, учитывая, что вклад этой составляющей в стандартные неопределенности величин а и b незначителен (в процентном выражении составляет 8,3 %), существующей корреляцией пренебрегаем и не учитываем при расчете суммарной стандартной неопределенности измеряемой величины: прочности бетона на растяжение при изгибе.
Все остальные входные величины рассматриваются как некоррелированные.

Этап 4. Измеренное значение величины

Оценка измеряемой величины – прочности бетона на растяжение при изгибе, Rtb, МПа, рассчитывается по формуле (2) используя полученные в таблице 1 значения оценок входных величин:

Этап 5.

Суммарная стандартная неопределенность

Стандартную неопределенность измеряемой величины Rtb, МПа, рассчитываем по закону распространения неопределенностей путем суммирования квадратов относительных стандартных неопределенностей влияющих величин, входящих в функции измерений (1) и (2):

и составляет для нашего примера

Примечание – Для расчета относительных стандартных неопределенностей входных величин используются значения величин, полученные для первого контрольного образца.
Значения процентных вкладов неопределенностей влияющих величин в суммарную стандартную неопределенность рассчитываются как умноженное на 100 % квадрат отношения относительной стандартной неопределенности влияющей величины к относительной суммарной стандартной неопределенности:

Этап 6. Бюджет неопределенности

Бюджет неопределенности для прочности бетона на растяжение при изгибе представлен в таблице 3.

Таблица 3 – Бюджет неопределенности для прочности бетона на растяжение при изгибе

Этап 7.

Расширенная неопределенность

Расширенную неопределенность U получаем умножением суммарной стандартной неопределенности на коэффициент охвата k = 2 в предположении нормального распределения при уровне доверия приблизительно 95 %:

Этап 8. Представление результата измерения

Результат измерения представляют в виде:
«Прочность бетона на растяжение при изгибе бетона класса прочности на растяжение при изгибе Вtb3,6 составила (3,65  0,45) МПа, где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 95 %».

Библиография
ГОСТ 10180-2012 Бетоны. Методы определения прочности по контрольным образцам
ГОСТ 427-75 Линейки измерительные металлические. Технические условия
СТБ ИСО 5725-6-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике

Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.

Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.

УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…

 

---

Пример 7. Оценивание неопределенности измерений твердости по Бриннелю

---

Измерительная задача
Измерение твердости трубопровода из Стали 10Г2СД по шкале Бриннеля выполняется твердомером ТКМ-459

Условия проведения измерений:

• температура окружающего воздуха +15 ºС;
• относительная влажность 60 %;
• толщина контролируемого участка детали 10 мм;
• шероховатость поверхности, на которой производится измерение Rа 1,2.

Этап 1. Составление функции измерений

Измеряемой величиной является твердость контролируемого участка объекта контроля по шкале Бринелля, Н, которая определяется как:

где Низм – показания твердомера, НВ;
δт – поправка на погрешность твердомера, НВ;
δр – поправка на разрешающую способность дисплея твердомера, НВ.

Результаты измерений
На контролируемом участке были получены следующие единичные результаты наблюдения твердости по шкале Бринелля:
h2 = 180 НВ
h3 = 184 НВ
h4 = 175 НВ
h5 = 172 НВ
H5 = 183 НВ

Этап 2. Анализ входных величин

2.1 Показания твердомера (Низм)

Показания твердомера оцениваются как среднее арифметическое из 5 единичных результатов наблюдений твердости контролируемого участка объекта контроля по формуле:

Стандартная неопределенность величины Низм рассчитывается как среднее квадратическое отклонение среднего арифметического из 5 единичных результатов наблюдений по формуле:

Примечание – Данная составляющая может не учитываться, если отклонение максимального единичного показания твердости от минимального не превышает предела основной допускаемой погрешности твердомера.

2.2 Поправка на погрешность твердомера (δт)

Поправка на погрешность твердомера оценивается значением «нуль». В паспорте на твердомер установлены пределы абсолютной погрешности ± Δ = ± 15 НВ при измерении по шкале Бринелля (НВ). Стандартная неопределенность поправки определяется по типу В на основании установленных пределов абсолютной погрешности твердомера в предположении прямоугольного закона распределения: 2.3 Поправка на разрешающую способность дисплея твердомера (δр)

Поправка на разрешающую способность дисплея твердомера оценивается значением «нуль». Стандартная неопределенность поправки определяется через величину единицы наименьшего разряда дисплея (а = 1 НВ).
Стандартная неопределенность поправки на разрешающую способность дисплея твердо-мера оценивается по типу В в предположении прямоугольного распределения из выражения:

Этап 3. Анализ корреляций

Все входные величины рассматриваются как некоррелированные.

Этап 4. Измеренное значение величины

Твердость контролируемого участка трубопровода будет оцениваться в соответствии с выражением (1) и составит:

Этап 5. Суммарная стандартная неопределенность

Суммарная стандартная неопределенность, приписываемая результату измерения Н, рас-считывается по формуле:

Коэффициенты чувствительности для всех влияющих величин, входящих в функцию измерений (1), будут равны 1.

Этап 6. Бюджет неопределенности

В таблице представлен бюджет неопределенности для измеряемой величины и произведены соответствующие расчеты для нахождения ее стандартной неопределенности.

Таблица – Бюджет неопределенности для твердости по шкале Бриннеля Н

Этап 7. Расширенная неопределенность

Суммарное распределение измеряемой величины предполагаем прямоугольным (по-скольку доминирует составляющая неопределенности от величины δт, процентный вклад составляет более 90 %). Коэффициент охвата для уровня доверия 95 % принимается равным k = 1,65. Расширенную неопределенность рассчитываем по формуле:

Этап 8. Представление результата измерения

Результат измерения записывается в виде:
«Твердость по Бринеллю контролируемого участка трубопровода из Стали 10Г2СД со-ставила (180 ± 15) НВ, k = 1,65, P = 95 %».

Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.

Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.

УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…

 

Урок 5: Выражение ошибки в измерениях

Каждый раз, когда проводится эксперимент, следует ожидать определенной степени неопределенности. В основном есть три причины, по которым у вас может быть ошибка в измерении.

1. физические ошибки в измерительном приборе
   Пример 1: Ваш термометр упал и в нем есть небольшие пузырьки воздуха.

2. неправильное или небрежное использование измерительного прибора
   Пример 2: Когда вы использовали свой термометр, вы измеряли значения в градусах Фаренгейта, а не в градусах Цельсия.

3. условия окружающей среды (температура, давление и т.д.)
   Пример 3: Измеряя длину деревянного бруска на улице зимой с помощью металлической линейки, вы забываете, что металл сжимается на морозе, делая линейку короче.

Какой бы ни была шкала (единицы) измерительного прибора, погрешность, которую вы должны записать, составляет половину наименьшего деления.

• Часто это указывается как « возможная ошибка » в измерении.

Пример 4: Если вы измерили длину карандаша с помощью обычной линейки (они обычно имеют деление 1 мм) и обнаружили, что длина карандаша составляет 102 мм, вам следует записать…

102 ± 0. 5 мм

«плюс-минус» (±) означает «плюс-минус» столько же, сколько возможная ошибка. Длина карандаша могла быть как 101,5 мм, так и 102,5 мм.

Иногда для измерения может быть допустимое значение (проверено в лабораториях с очень высокими стандартами).

• Некоторые из этих номеров указаны на обратной стороне паспорта. Обычно они даются с тремя знаками раскопок.
• Часто бывает полезно сравнить ваши измерения с принятым значением, чтобы оценить, насколько вы точны.

Существует три распространенных способа расчета ошибки: абсолютная ошибка, разница в процентах и ​​ошибка в процентах.

Абсолютная ошибка — это когда вы вычитаете принятое значение из измеренного значения…

Абсолютная ошибка = измеренное значение — принятое значение

• Положительный ответ означает, что вы превысили допустимое значение.
• Отрицательный ответ означает, что вы находитесь ниже принятого значения

Погрешность в процентах — это наиболее распространенный способ измерения погрешности и часто самый простой для понимания.

Процентная ошибка = Абсолютная ошибка / Допустимое значение

Итак, если вы измерили карандаш длиной 102 мм, а независимая лаборатория с высокотехнологичным оборудованием измерила его как 104 мм, процентная ошибка составит…

Процентная ошибка = (102 мм — 104 мм) / (104 мм) = -0,02

Это означает, что вы получили ошибку -2%. Знак минус просто означает, что вы были ниже принятого значения .

В школьных лабораторных работах не удивляйтесь, если вы получите ошибки в 25%.Важная часть, можете ли вы объяснить свои ошибки!

Разница в процентах полезна, если у вас есть два измерения, которые вы сделали, и вы хотите увидеть, насколько они отличаются в процентах. Это удобно, когда , а не имеют допустимое значение для сравнения.

Процентная разница = (разница в измерениях) / (среднее значение измерений)

Не путайте это с процентной ошибкой. Здесь у нас есть два измерения, которые вы сделали, но нет «принятого значения».» Например, вы дважды измерили длину стола и получили числа 1,15 м и 1,13 м.

Разница в процентах = (1,15-1,13) / [(1,15+1,13)/2] = 0,0175

Процентная разница 1,75%.

Видео с вопросами: Определение формулы абсолютной погрешности измерения

Стенограмма видео

Какая из следующих формул является правильной для значения абсолютной погрешности измерения Δ𝑥, учитывая принятое значение 𝑥 ноль и измеренное значение 𝑥? (a) Δ𝑥 равно 𝑥, деленному на 𝑥 ноль.(b) Δ𝑥 равно 𝑥 нулю, деленному на 𝑥. (c) Δ𝑥 равно 𝑥 минус 𝑥 ноль. (d) Δ𝑥 равно 𝑥 ноль минус 𝑥. (e) Δ𝑥 равно абсолютному значению 𝑥 ноль минус 𝑥.

В этом вопросе нам предлагается определить правильную формулу для величины, в данном случае абсолютной погрешности измерения. Как и во всех подобных вопросах, мы могли бы сразу же найти правильный ответ, просто вспомнив правильную формулу. Здесь этим ответом является выбор (e). И мы знаем, что (е) верно, потому что мы вспомнили определение абсолютной ошибки как абсолютной величины разницы между принятым значением и измеренным значением.Сейчас иногда необходимо и почти всегда весьма полезно запоминать соответствующие физические формулы. Однако запомнить все возможные формулы неэффективно и невозможно. Вместо этого мы хотим иметь возможность определить, что вариант (e) является правильным ответом, учитывая то, что мы знаем об абсолютной ошибке и ошибке измерения в целом.

Это также полезно, потому что даже если мы запомнили формулу, иногда мы забываем ее, когда нам нужно ее использовать. Итак, начнем с того, что вспомним, что абсолютная ошибка — это общая величина, на которую измеренное значение отличается от принятого значения.Глядя на наши варианты ответов, мы можем сразу исключить варианты (а) и (б). Поскольку количества 𝑥, деленные на 𝑥 ноль, и 𝑥 ноль, деленные на 𝑥, не дают величины, на которую различаются вещи. Они скорее сравнивают относительные размеры двух величин. С другой стороны, варианты от (c) до (e) представляют собой некоторую разницу между измеренным значением и принятым значением. А абсолютная ошибка определяется как общая сумма, на которую различаются эти две величины.

Теперь нам нужно определить правильный порядок разности или выбрать абсолютное значение, где порядок не имеет значения.Наша первая подсказка заключается в том, что абсолютная ошибка определяется как общая сумма, на которую различаются два значения, а не насколько больше одно конкретное значение, чем другое конкретное значение. Таким образом, нас не интересует, насколько измеренное значение больше принятого значения, и нас не интересует, насколько принятое значение больше измеренного значения. Скорее нас интересует величина, которая не зависит от того, больше ли измеренное или принятое значение, и это абсолютное значение разницы между ними.

В качестве примера рассмотрим измерение длины этого карандаша с помощью линейки длиной 10 сантиметров с делениями по одному сантиметру. С точностью до градации длина этого карандаша составляет семь сантиметров. Однако, поскольку градации отстоят друг от друга на один сантиметр, погрешность измерения этой линейкой составляет максимум полсантиметра, поэтому мы можем записать длину карандаша, измеренную этой линейкой, как семь сантиметров плюс-минус полсантиметра, потому что мы в лучшем случае завышаем или занижаем наши измерения на полсантиметра.

Половина сантиметра — абсолютная погрешность измерения. И это потому, что он ссылается на ошибку между измеренной градацией и истинной длиной карандаша. Это не зависит от фактического числа, которое мы измерили на линейке.

Важно понимать, что мы выразили это значение как плюс или минус некоторое положительное число. Плюс или минус, по сути, означает, что мы допускаем возможность либо переоценки, либо недооценки истинного значения.Теперь мы можем понять, почему мы всегда используем положительное число для абсолютной ошибки. То есть мы выражаем его через абсолютную величину.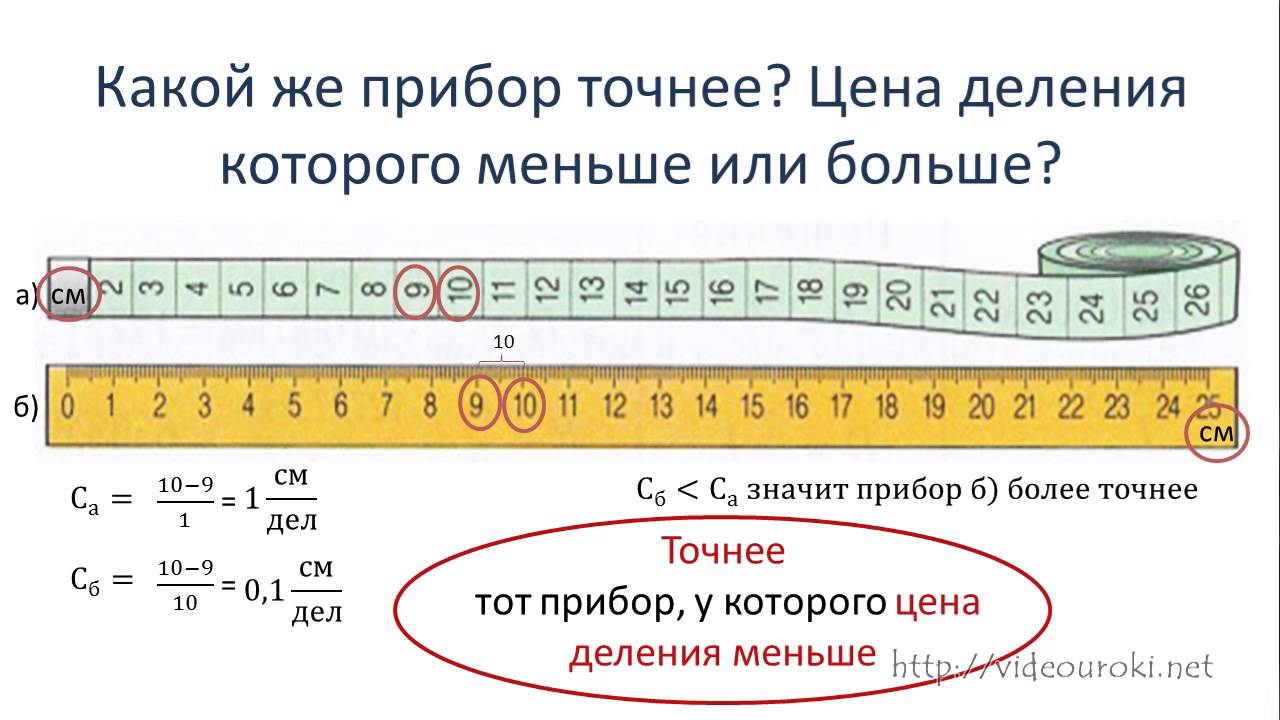 Знак разницы, будь то положительный или отрицательный, говорит нам только о том, является ли измеренное значение завышенным или заниженным значением принятого значения. Однако независимо от того, является ли измеренное значение завышенным или заниженным, положительное число, то есть абсолютное значение этой разницы, по-прежнему говорит нам точно, насколько различаются два значения, что является определенной нами абсолютной ошибкой.

Абсолютная и относительная ошибка: определение и формула — видео и стенограмма урока

Говорят, что инструменты измерения точны до определенной степени. Предположим, что измерительная лента, которую Дэн использовал для измерения своей новой половицы, имеет точность до 1 дюйма. Это означает, что существует 1-дюймовый диапазон или «окно» вокруг измерения, в котором действительно может быть расположено истинное значение. Из измеренного значения это полдюйма с каждой стороны. Дэн измерил длину новой половицы в 36 дюймов, но реальная длина могла быть где-то между 35. 5 дюймов и 36,5 дюймов в длину. В этом случае половица была фактически на более длинном конце. Мы говорим, что измерение составляет 36 ± 0,5 дюйма.

Диаграмма, изображающая возможный диапазон истинной длины половой доски

Абсолютная ошибка

Существует два типа ошибок, на которые влияет точность измерительных инструментов. Абсолютная ошибка определяется как абсолютное значение (или величина) разницы между измеренным значением и истинным значением.Таким образом, пусть:

• e a = абсолютная ошибка
• x м = измеренное значение
• x t = истинное значение

Формула для вычисления абсолютной ошибки:

e a = | x м — x т |

Есть только одна загвоздка — обычно мы не знаем истинное значение. В этом случае нам просто нужно подумать о точности измерительного инструмента. В качестве примера возьмем мерную ленту Дэна. Точность составляет 1 дюйм, что означает, что истинное значение любого измерения может быть на полдюйма меньше или на полдюйма больше фактического измерения. Максимально возможная разница между измерением и его истинным значением составляет полдюйма. Следовательно, абсолютная ошибка составляет 0,5 дюйма.

Диаграмма, изображающая абсолютную погрешность измерительной ленты

Относительная погрешность

Существует еще один тип погрешности, на который влияет точность измерительных инструментов.Относительная ошибка определяется как абсолютная ошибка относительно размера измерения. Все, что вам нужно сделать, это разделить абсолютную погрешность на измеренное значение. В дополнение к переменным, пусть:

Тогда формула для вычисления относительной ошибки:

В ситуации Дэна абсолютная ошибка составляет 0,5 дюйма, и он измерил половицу длиной 36 дюймов, поэтому относительная ошибка:

e r = 0,5 дюйма/36 дюймов = 0,014 (округлено до ближайшей тысячной)

Относительная погрешность не имеет единиц измерения, поскольку они сокращаются во время вычисления. Относительная ошибка является пропорцией, поэтому мы также можем выразить ее в процентах, умножив относительную ошибку на 100%, например:

e r = 0,014 * 100% = 1,4%

Мы можем сказать, что абсолютная погрешность составляет 1,4% от измеренного значения.

Сравнение относительных ошибок

Относительная ошибка зависит как от абсолютной ошибки, так и от измеренного значения. Давайте посмотрим, что произойдет, если вы измерите два объекта разных размеров одним и тем же измерительным инструментом.Скажем, Дэн использовал ту же рулетку, чтобы измерить ширину половицы в 6 дюймов. Абсолютная погрешность по-прежнему составляет 0,5 дюйма. Какова относительная ошибка? Это:

e r = 0,5 дюйма/6 дюймов = 0,083 (округлено до ближайшей тысячной)

Это также может быть выражено в процентах следующим образом: 100% = 8,3%

Диаграмма, изображающая относительные погрешности измерений ширины и длины половицы

Относительная ошибка тем больше, чем меньше измеряемый размер. Это имеет смысл, потому что абсолютная погрешность в полдюйма имеет большое значение, когда вы измеряете что-то длиной всего 6 дюймов по сравнению с длиной 36 дюймов.

Что происходит с относительной погрешностью при выполнении одного и того же измерения с использованием двух разных измерительных инструментов? Давайте сравним измерительную ленту Дэна с точностью до 1 дюйма с линейкой с точностью до 0,5 дюйма (это означает, что абсолютная погрешность составляет 0,25 дюйма). Мы будем использовать ширину половицы в качестве примера. И измерительная лента, и линейка говорят, что длина половицы составляет 6 дюймов.Рассчитаем относительные погрешности:

• Рулетка : e r = 0,5 дюйма/6 дюймов = 0,083 * 100% = 8,3%
• Линейка : e r = 0,25 дюйма/6 дюймов = 0,042 * 100% = 4,2%

Относительная погрешность при использовании линейки меньше относительной погрешности при использовании рулетки, поскольку абсолютная погрешность линейки меньше абсолютной погрешности рулетки.

Итоги урока

Давайте повторим. Абсолютная погрешность определяется как абсолютное значение разницы между измеренным значением и истинным значением измерения и обычно указывается как максимально возможная погрешность с учетом степени точности измерительного инструмента. Абсолютная ошибка имеет те же единицы измерения, что и измерение. Относительная ошибка определяется как абсолютная ошибка относительно размера измерения, и она зависит как от абсолютной ошибки, так и от измеренного значения. Относительная ошибка велика, когда измеренное значение мало, или когда велика абсолютная ошибка.Относительная ошибка не имеет единиц.

Ошибка измерения (ошибка наблюдения) — Статистические инструкции

Смещение > Ошибка измерения

Что такое ошибка измерения?

Ошибка измерения (также называемая ошибкой наблюдения) — это разница между измеренной величиной и ее истинным значением. Он включает случайную ошибку (естественные ошибки, которые следует ожидать при любом эксперименте) и систематическую ошибку (вызванную неправильно откалиброванным прибором, который влияет на все измерений).

Допустим, вы измеряете вес 100 спортсменов-марафонцев. Весы, которые вы используете, отклоняются на один фунт: это систематическая ошибка , которая приведет к тому, что расчеты массы тела всех спортсменов будут отклонены на фунт. С другой стороны, предположим, что ваши весы были точными. Некоторые спортсмены могут быть более обезвожены, чем другие. У некоторых может быть более влажная (и, следовательно, более тяжелая) одежда или 2 унции. моноблок в кармане. Это случайных ошибок и их следует ожидать.На самом деле все собранные выборки будут иметь случайные ошибки — они, по большей части, неизбежны.

Ошибки измерения могут быстро увеличиваться при использовании в формулах. Например, если вы используете небольшую ошибку в измерении скорости для расчета кинетической энергии, ваши ошибки могут легко увеличиться в четыре раза. Чтобы учесть это, вы должны использовать формулу для распространения ошибки всякий раз, когда вы используете неопределенные меры в эксперименте для вычисления чего-то еще.

Различные измерения ошибки

Различные меры погрешности включают:

1. Абсолютная погрешность: величина ошибки в вашем измерении.Например, если вы наступаете на весы, и они показывают 150 фунтов, но вы знаете, что ваш истинный вес составляет 145 фунтов, то абсолютная погрешность весов составляет 150 фунтов – 145 фунтов = 5 фунтов.
2. Максимально возможная ошибка: определяется как половина единицы измерения. Например, если вы используете линейку, измеряющую в целых ярдах (т. е. без дробей), то наибольшая возможная погрешность составит половину ярда.
3. Ошибка прибора: ошибка , вызванная неточным прибором (например, неисправность весов или неправильно составленная анкета).
4. Допустимая погрешность: сумма выше и ниже вашего измерения. Например, вы можете сказать, что средний ребенок весит 8 фунтов с погрешностью 2 фунта (± 2 фунта).
5. Ошибка местоположения измерения : вызвано размещением прибора в недопустимом для него месте, например, термометром, оставленным под прямыми солнечными лучами.
6. Ошибка оператора : человеческий фактор, вызывающий ошибку, например неправильное чтение весов.
7. Процентная ошибка : еще один способ выражения погрешности измерения.Определяется как:
   
8. Относительная ошибка: отношение абсолютной ошибки к принятому измерению. В формуле это:
   

Способы уменьшения погрешности измерения

• Дважды проверьте точность всех измерений. Например, дважды введите все входные данные на двух листах и ​​сравните их.
• Дважды проверьте правильность ваших формул.
• Убедитесь, что наблюдатели и лица, проводящие измерения, хорошо обучены.
• Проведите измерение с помощью самого точного прибора.
• Проведите измерения в контролируемых условиях.
• Проведите пилотную проверку ваших измерительных приборов. Например, соберите фокус-группу и спросите, насколько простыми или сложными были вопросы для понимания.
• Используйте несколько мер для одной и той же конструкции. Например, если вы проводите тестирование на депрессию, используйте два разных опросника.

Статистические процедуры для оценки погрешности измерения

Следующие методы оценивают «абсолютную достоверность»:

• Стандартная ошибка измерения (SEM) : оценивает, как повторные измерения, проведенные на одном и том же приборе, оцениваются относительно истинной оценки.
• Коэффициент вариации (CV) : мера изменчивости распределения повторных оценок или измерений. Меньшие значения указывают на меньшую вариацию и, следовательно, значения ближе к истинному показателю.
• Пределы согласия (LOA) : дает оценку интервала, в котором доля различий лежит между измерениями.

Каталожные номера

Бейер, Стандартные математические таблицы WH CRC, 31-е изд. Бока-Ратон, Флорида: CRC Press, стр.536 и 571, 2002 г.
Додж, Ю. (2008 г.). Краткая энциклопедия статистики. Спрингер.
Фогт, В.П. (2005). Словарь статистики и методологии: нетехническое руководство по социальным наукам. МУДРЕЦ.
Уилан, К. (2014). Голая статистика. WW Norton & Company

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

B. Точность в сравнении с прецизионностью и ошибка в сравнении с неопределенностью :: Физика

Когда мы обсуждаем измерения или результаты измерительных приборов, возникает несколько различных понятий, которые часто путают друг с другом. В этом разделе описываются четыре важные идеи и устанавливаются различия между ними.Первое различие между Точностью и Прецизионностью.

Точность

Точность означает соответствие между измерением и истинным или правильным значением. Если часы бьют двенадцать, когда солнце находится точно над головой, говорят, что часы точны. Измерение часов (двенадцать) и явление, которое они должны измерять (Солнце в зените), согласуются. Точность не может осмысленно обсуждаться, если истинное значение не известно или не известно. (Примечание: истинное значение измерения никогда не может быть известно.)

Точность относится к совпадению измерения и истинного значения и не говорит вам о качестве прибора. Инструмент может быть высокого качества и все же не соответствовать истинной стоимости. В приведенном выше примере предполагалось, что цель часов состоит в том, чтобы измерять положение солнца, когда оно кажется движущимся по небу. Однако в нашей системе часовых поясов солнце находится прямо над головой в двенадцать часов, только если вы находитесь в центре часового пояса. Если вы находитесь на восточном краю часового пояса, солнце находится прямо над головой примерно в 11:30, а на западном краю солнце находится прямо над головой примерно в 12:30.Таким образом, с обеих сторон показания двенадцати часов не согласуются с явлением, когда солнце находится в местном зените, и мы можем пожаловаться на то, что часы не точны. Здесь на точность показаний часов влияет наша система часовых поясов, а не дефект часов.

Однако в случае часовых поясов часы измеряют нечто более абстрактное, чем положение солнца. Мы определяем часы в центре часового пояса как правильные, если они совпадают с солнцем, затем мы определяем все остальные часы в этом часовом поясе как правильные, если они совпадают с центральными часами.Таким образом, часы на восточной окраине часового пояса, которые показывают 11:30, когда солнце находится над головой, все равно будут точными, поскольку они согласуются с центральными часами. Часы, показывающие 12:00, не будут точны в это время. Идея, к которой нужно привыкнуть, заключается в том, что точность относится только к совпадению между измеренным значением и ожидаемым значением, и что это может что-то сказать или не сказать о качестве измерительного прибора. Часы с остановкой точны по крайней мере один раз в день.

Точность

Точность относится к воспроизводимости измерения.Это не требует от нас знания правильного или истинного значения. Если каждый день в течение нескольких лет часы показывают ровно 10:17, когда солнце находится в зените, эти часы очень точны. Поскольку в году более тридцати миллионов секунд, точность этого прибора превышает одну миллионную часть! Это действительно очень хорошие часы! Здесь вы должны принять к сведению, что нам не нужно учитывать сложности краев часовых поясов, чтобы решить, что это хорошие часы. Истинное значение полудня не важно, потому что нас заботит только то, что часы дают повторяемый результат.

Ошибка

Ошибка относится к расхождению между измерением и истинным или принятым значением. Вы можете быть удивлены, обнаружив, что ошибка не так важна при обсуждении экспериментальных результатов. Это утверждение, безусловно, нуждается в пояснении.

Как и в случае с точностью, вы должны знать истинное или правильное значение, чтобы обсуждать свою ошибку. Но подумайте, что такое наука. Основная цель — открывать для себя что-то новое. Если они новые, то мы не знаем какое истинное значение раньше времени.Таким образом, невозможно обсуждать нашу ошибку. Вы можете предположить, что в эксперименте есть дефектный компонент или неверное предположение, что приведет к ошибке. Конечно, ученого это беспокоит. Как правило, было много дискуссий с другими учеными и обзора методов, чтобы попытаться избежать именно этой возможности. Однако, если произойдет ошибка, мы просто не узнаем об этом. Истинное значение еще не установлено, и другого ориентира нет. Хороший ученый предполагает, что в эксперименте нет ошибки .Это единственный доступный выбор. Более поздние исследования, попытки других ученых повторить результат, надеюсь, выявят какие-либо проблемы, но в первый раз такого руководства нет.

Студенты на уроках естествознания находятся в искусственной ситуации. Их эксперименты обязательно являются повторениями предыдущей работы, поэтому результаты известны.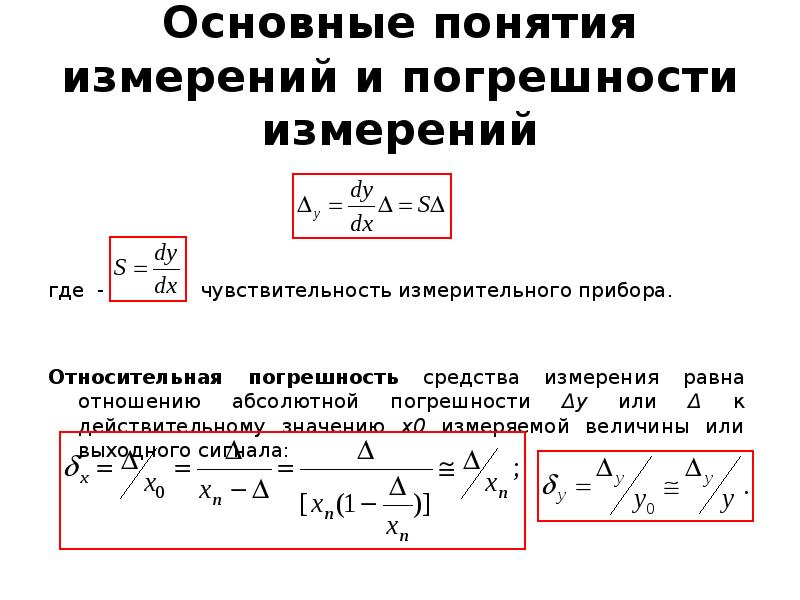 Из-за этого студенты получают плохой урок о науке. Студенты часто очень хорошо осознают ошибку до такой степени, что предполагают, что она происходит в каждом эксперименте.Это отвлекает от проекта стать ученым. Если вы хотите получить наибольшую пользу от своего лабораторного опыта, вам нужно будет разумно притвориться. После того, как эксперимент был проведен, пока вы записываете результат в свой лабораторный отчет, предполагайте, что ошибка не имеет значения. Ваша команда сделала все возможное в лаборатории, и вы должны учитывать результаты на этой основе. Не пишите «человеческий фактор» в отчете лаборатории. Во-первых, это смущает, и по нашему опыту преподавателей редко бывает источником экспериментальных проблем .(Более половины проблем, приводящих к плохим лабораторным результатам, связаны с ошибками анализа в отчете! Сначала посмотрите здесь.)

Неопределенность

Неопределенность измеренного значения представляет собой интервал вокруг этого значения, при котором любое повторение измерения будет давать новый результат, лежащий в пределах этого интервала. Этот интервал неопределенности назначается экспериментатором в соответствии с установленными принципами оценки неопределенности. Одна из целей этого документа — помочь вам научиться назначать интервалы неопределенности и работать с ними.

Неопределенность, а не ошибка, является важным термином для работающего ученого. Каким-то чудесным образом неопределенность позволяет ученому делать совершенно определенные утверждения. Вот пример, чтобы увидеть, как это работает.

Допустим, ваш одноклассник измерил ширину стандартного листа тетради и назвал результат 8,53 ± 0,08 дюйма. Утверждая, что неопределенность составляет 0,08 дюйма, ваш одноклассник с уверенностью заявляет, что каждые разумных измерений этого листа бумаги другими экспериментаторами дадут значение не менее 8.45 дюймов и не более 8,61 дюйма.

Предположим, вы измерили длину своего стола с помощью линейки или рулетки, и результат составил один метр и двадцать сантиметров (L = 1,20 м). Теперь истинная длина здесь неизвестна, отчасти потому, что вы не имеете полных знаний об изготовлении измерительного прибора, и потому, что вы не можете увидеть под микроскопом, чтобы убедиться, что край стола точно соответствует отметкам на приборе. Таким образом, вы не можете обсуждать ошибку в этом случае. Тем не менее, вы бы не сказали с абсолютной уверенностью, что L = 1.20 м.

Однако довольно легко представить себе, что вы можете быть уверены, что размер стола не более чем на десять сантиметров (~ пять дюймов) отличается от ваших измерений. Возможно, у вас есть опыт работы с рулеткой. И, основываясь на этом опыте, вы уверены, что ваша рулетка не может растянуться на пять дюймов по сравнению с ее надлежащей длиной. Если у вас нет этой уверенности, возможно, десять дюймов или фут придадут вам уверенности. После измерения вы можете сказать: «Этот стол не длиннее 1.35 м и не менее 0,95 м». Вы могли бы сделать это заявление с полной уверенностью. Ученый напишет L = 1,20 ± 0,15 м. Формат: « значение плюс или минус неопределенность ».

Обратите внимание, что всегда можно построить совершенно определенное предложение. В худшем случае можно сказать, что стол не короче нуля метров и не длиннее четырех метров (потому что он не помещается в комнате). Это измерение может быть почти бесполезным, но оно совершенно точно! Устанавливая доверительный интервал для измерения, ученый делает утверждения, с которыми должен согласиться любой разумный ученый.Навык заключается в том, чтобы сделать доверительные интервалы (неопределенность) как можно меньше.

Это твоя задача в лаборатории. Каждое измерение, которое вы делаете, должно рассматриваться вместе с доверительным интервалом. Затем вы должны присвоить эту неопределенность измерению во время записи данных.

Неопределенность: Представив пример, вот определение неопределенности.

Неопределенность в заявленном измерении – это доверительный интервал вокруг измеренного значения, при котором измеренное значение точно не выходит за пределы этого установленного интервала.
Неопределенности также могут быть указаны вместе с вероятностью. В этом случае измеренное значение имеет установленную вероятность находиться в пределах доверительного интервала. Особенно распространенным примером является одно стандартное отклонение (SD) для среднего значения случайной выборки.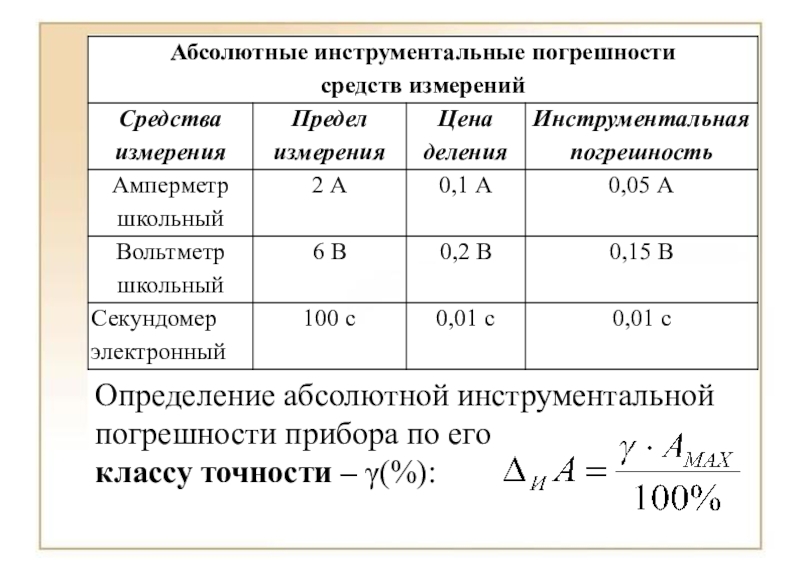 Формат «значение ± 1 стандартное отклонение» означает, что если вы повторите измерение, 68% времени ваше новое измерение будет попадать в этот интервал.

 

Последнее обновление 26 ноября 2014 г.

Неопределенности в измерениях — Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

1. Введение
2. Систематическое или систематическое.Случайная ошибка

Все измерения имеют некоторую степень неопределенности независимо от прецизионности и аккуратности. Это вызвано двумя факторами: ограничениями измерительного прибора (систематическая ошибка) и мастерством экспериментатора, проводящего измерения (случайная ошибка).

Введение

Градуированная бюретка на рис. 1 содержит определенное количество измеряемой воды (с желтым красителем). Количество воды где-то между 19 мл и 20 мл в соответствии с отмеченными линиями.Проверяя, где находится дно мениска, ориентируясь на десять меньших линий, количество воды находится между 19,8 мл и 20 мл. Следующим шагом является оценка неопределенности между 19,8 мл и 20 мл. Делая приблизительное предположение, уровень меньше 20 мл, но больше 19,8 мл. Затем мы сообщаем, что измеренное количество составляет примерно 19,9 мл. Сам градуированный цилиндр может быть деформирован таким образом, что деления шкалы будут содержать неточности, дающие показания, немного отличающиеся от фактического объема присутствующей жидкости.

Рисунок 1 : Вид мениска в бюретке с окрашенной водой. «20,00 мл» — правильное измерение глубины. Щелкните здесь, чтобы получить более полное описание использования бюретки, включая правильное чтение. Рисунок использован с разрешения Википедии.

Систематическая и случайная ошибка

На приведенной ниже диаграмме показано различие между систематическими и случайными ошибками.

Рис. 2: Систематические и случайные ошибки.Рисунок использован с разрешения Дэвида ДиБиасе (Penn State U).

Систематические ошибки: Когда мы используем инструменты, предназначенные для измерения, мы предполагаем, что они правильные и точные, однако измерительные инструменты не всегда правильные. На самом деле, у них есть ошибки, которые возникают естественным образом, называемые систематическими ошибками . Систематические ошибки имеют тенденцию быть постоянными по величине и/или направлению. Если величина и направление ошибки известны, точность можно повысить с помощью аддитивных или пропорциональных поправок. Аддитивная коррекция включает добавление или вычитание постоянного поправочного коэффициента к каждому измерению; пропорциональная коррекция включает умножение измерения(ий) на константу.

Случайная ошибка s: Случайная ошибка, иногда называемая человеческим фактором, определяется навыками или способностью экспериментатора проводить эксперимент и считывать результаты научных измерений. Эти ошибки являются случайными, поскольку полученные результаты могут быть слишком высокими или низкими. Часто случайная ошибка определяет точность эксперимента или ограничивает точность.Например, если бы нам нужно было рассчитать время оборота постоянно вращающегося поворотного круга, случайной ошибкой было бы время реакции. Время нашей реакции будет варьироваться из-за задержки начала (недооценка фактического результата) или задержки остановки (переоценка фактического результата). В отличие от систематических ошибок случайные ошибки различаются по величине и направлению. Однако можно рассчитать среднее значение набора измеренных положений, и это среднее, вероятно, будет более точным, чем большинство измерений.

5. Поскольку Том должен полагаться на прибор для определения абсорбции, а он обеспечивает постоянно разные измерения, это пример систематической ошибки.
6. Большая часть отклонений во времени Клэр, вероятно, может быть связана со случайной ошибкой, такой как усталость после нескольких кругов, непостоянство в технике плавания, небольшое отклонение от времени при запуске и остановке секундомера или бесчисленное множество других мелких факторов, которые влияют на время круга. В гораздо меньшей степени сам секундомер может иметь ошибки в отсчете времени, приводящие к систематической ошибке.
7. Процентная ошибка исследователя составляет около 0,62%.
8. Это известно как ошибка множителя или коэффициента масштабирования.
9. Это называется смещением или ошибкой установки нуля.
10. Процентная ошибка Сьюзан составляет -7,62%. Эта процентная ошибка является отрицательной, поскольку измеренное значение падает на ниже принятого значения на . В задаче 7 процентная ошибка была положительной, потому что она была на выше принятого значения на .
11. Сначала нужно взвесить сам стакан.После получения веса вы добавляете графит в химический стакан и взвешиваете его. Получив этот вес, вы вычитаете вес графита плюс вес стакана минус вес стакана.

Разница между абсолютной ошибкой и относительной ошибкой

9 октября 2015 г. Опубликовано Admin

Ключевая разница — абсолютная ошибка и относительная ошибка
 

Абсолютная ошибка и относительная ошибка — это два способа указания ошибок в экспериментальных измерениях, хотя существует разница между абсолютной ошибкой и относительной ошибкой, основанная на их расчете.Большинство измерений в научных экспериментах содержат ошибки, вызванные инструментальными ошибками и человеческими ошибками. В некоторых случаях для конкретного измерительного прибора существует предопределенное постоянное значение абсолютной погрешности (Наименьшее показание. Например: – линейка = +/- 1 мм.) Это разница между истинным значением и экспериментальным стоимость. Однако относительная ошибка варьируется в зависимости от экспериментального значения и абсолютной ошибки. Его определяют, взяв отношение абсолютной ошибки к экспериментальному значению.Таким образом, ключевое различие между абсолютной ошибкой и относительной ошибкой составляет абсолютная ошибка величина разницы между точным значением и приближением , тогда как относительная ошибка рассчитывается путем деления абсолютной ошибки на величину точного значения.

Что такое абсолютная ошибка?

Абсолютная ошибка указывает на неопределенность измерения. Другими словами, он измеряет, в какой степени истинное значение может отличаться от своего экспериментального значения.Абсолютная погрешность выражается в тех же единицах, что и измерение.

Пример: Допустим, мы хотим измерить длину карандаша с помощью линейки с миллиметровыми отметками. Мы можем измерить его длину с точностью до миллиметра. Если вы получаете значение 125 мм, оно выражается как 125 +/- 1 мм. Абсолютная погрешность составляет +/- 1 мм.

Что такое относительная ошибка?

Относительная ошибка зависит от двух переменных; абсолютная ошибка и экспериментальное значение измерения.Следовательно, эти два параметра должны быть известны, чтобы рассчитать относительную погрешность. Относительная ошибка рассчитывается как отношение абсолютной ошибки к экспериментальному значению. Выражается в процентах или дробях; так что у него нет единиц.

Относительная ошибка интегрирования методом Монте-Карло для вычисления числа пи

В чем разница между абсолютной ошибкой и относительной ошибкой?

Определение абсолютной ошибки и относительной ошибки

Абсолютная ошибка:

Абсолютная ошибка – это значение Δx (значение + или –), где x – переменная; это физическая ошибка в измерении.Она также известна как фактическая ошибка измерения.

Другими словами, это разница между истинным значением и экспериментальным значением.

Абсолютная ошибка = фактическое значение – измеренное значение

Относительная ошибка:

Относительная ошибка – это отношение абсолютной ошибки (Δx) к измеренному значению (x). Она выражается либо в процентах (процентная ошибка), либо в долях (дробная неопределенность).

 

Единицы и расчет абсолютной ошибки и относительной ошибки

Единицы

Абсолютная ошибка:

Имеет те же единицы измерения, что и измеренное значение. Например, если вы измеряете длину книги в сантиметрах (см), абсолютная ошибка также имеет те же единицы измерения.

Относительная ошибка:

Относительная ошибка может быть выражена в виде дроби или процента. Однако оба не имеют единицы в значении.

Ошибка расчета

Пример 1: Фактическая длина земли составляет 500 футов.Измерительный прибор показывает длину 508 футов.

Абсолютная ошибка:

Абсолютная ошибка = [Фактическое значение – измеренное значение] = [508-500] футов = 8 футов

Относительная ошибка:

В процентах:

 

 

Дробью:

 

 

Пример 2:

Студент хотел измерить высоту стены в комнате.Он измерил значение с помощью метровой линейки (с миллиметровыми значениями), оно составило 3,215 м.

Абсолютная ошибка:

Абсолютная погрешность = +/- 1 мм = +/- 0,001 м (Наименьшее значение, которое можно считать с помощью линейки)

Относительная ошибка:

Относительная погрешность = Абсолютная погрешность÷  Экспериментальное значение  = 0,001 м÷ 3,215 м  * 100  = 0,0003%

 

Изображение предоставлено:

«Абсолютная ошибка» DEMcAdams — собственная работа.(CC BY-SA 4.0) через Wikimedia Commons

«Относительная ошибка интегрирования Монте-Карло для вычисления числа пи» Хорхекарлейтао — python и xmgrace. (CC BY-SA 3.0) через Википедию

.