Аксиомы геометрии / Параллельные прямые / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Параллельные прямые
- Аксиомы геометрии
Аксиома — исходное положение о свойствах геометрических фигур, которое принимается без доказательства и на основе которого далее доказываются теоремы и вообще строится вся геометрия. Все аксиомы являются наглядно очевидными и не вызывают сомнений.
Геометрия, в которой сначала формулируются исходные положения — аксиомы, а затем на их основе путем логических рассуждений доказываются другие утверждения, называется евклидовой геометрией
К аксиомам относятся следующие утверждения:
Аксиомы о взаимном расположении точек и прямой
- Каждой прямой принадлежит по крайней мере две точки.
- Имеются по крайней мере три точки, не лежащие на одной прямой.
- Через любые две точки проходит прямая, и притом только одна.
- Из трех точек прямой одна и только одна лежит между двумя другими.
- Каждая точка О прямой разделяет ее на две части (два луча) так, что любые две точки одного и того же луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О.
- Каждая прямая разделяет плоскость на две части (две полуплоскости) так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой , а любые две точки разных полуплоскостей лежат по разные стороны от прямой .
Аксиомы о наложении и равенстве фигур
- Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки.
- На любом луче от его начала можно отложить отрезок, равный данному и притом только один.
- От любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один.
- Любой угол hk можно совместить наложением с равным ему углом
- Любая фигура равна самой себе.
- Если фигура Ф равна фигуре Ф1, то фигура Ф1 равна фигуре Ф.
- Если фигура Ф1 равна фигуре Ф2, а фигура Ф2 равна фигуре Ф3, то фигура Ф1 равна фигуре Ф3.
Аксиомы об измерении отрезков
- При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.
- При выбранной единице измерения отрезков для любого положительного числа существует отрезок, длина которого выражается этим числом.
Аксиома параллельности
- Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Параллельные прямые
Признаки параллельности двух прямых
Практические способы построения параллельных прямых
Аксиома параллельных прямых
Теорема о накрест лежащих углах
Теорема о соответственных углах
Теорема об односторонних углах
Теорема об углах с соответственно параллельными сторонами
Теорема об углах с соответственно перпендикулярными сторонами
Параллельные прямые
Правило встречается в следующих упражнениях:
7 класс
Задание 7, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© 2019 — budu5.com, Буду отличником!
budu5.com
Аксиомы планиметрии — Геометрия — 7 класс
Просмотр содержимого документа
«Аксиомы планиметрии»
ТЕМА 1. АКСИОМЫ ПЛАНИМЕТРИИ
I. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки плоскости можно провести прямую, и только одну.
II. Из трёх точек, лежащих на прямой, одна и только одна лежит между двумя другими.
III. Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
IV. Любая прямая разбивает плоскость на две полуплоскости.
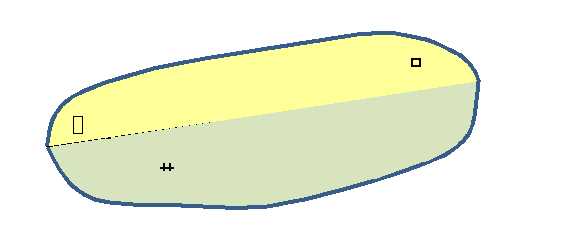
V. Каждый угол имеет определённую градусную меру, большую нуля. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между сторонами этого угла. Градусная мера развёрнутого угла равна 180°.

VI. На любой полупрямой, от её начальной точки можно отложить отрезок заданной длины, и только один.
VII. От любой полупрямой от её начальной точки в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
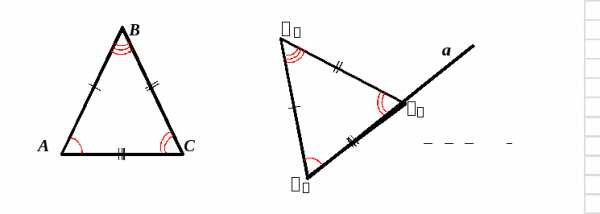
VIII. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.
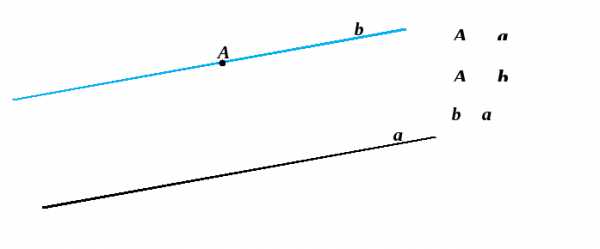
IX. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
§ 1. Прямая и отрезок.
Пересекаются ли отрезки AB и CD?
Пересекаются ли прямые AB и CD?
Отметьте точку М так, чтобы она лежала на прямой CD, но не лежала ни на отрезке AB, ни на отрезке CD.
Отметьте точку N, которая лежит на прямой CD между точками A и B. Как вы назовёте такую точку?
Пересекает ли прямая KL отрезок EF?
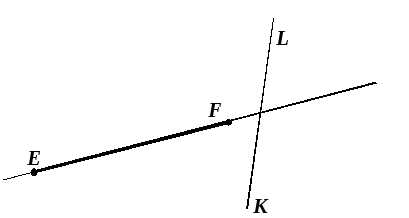
Пересекает ли прямая KL прямую EF?
Отметьте точку А, которая лежит на прямой EF, но не лежит на прямой KL.
Существуют ли точки, которые одновременно лежат на отрезке EF и прямой LK?
Сколько существует различных отрезков с концами в точках A, B, C и D?
Пересекаются ли прямые AB и CD?
Какая из точек, A или D, лежит между точками B и C?
Отметьте точку М, которая лежит на прямой AD, но не лежит на отрезке BC.
Проведите прямую, проходящую через точку Е, которая пересекает прямые AB и BC, но не пересекает отрезок AD.
Сколько существует различных отрезков с концами в точках E, F, M и N?
Пересекаются ли прямые EN и FM?
Какая из точек, A или N, лежит между точками E и F?
Отметьте точку B, которая лежит на отрезке MN, но не лежит на прямой EF.
Проведите прямую, проходящую через точку A, которая пересекает прямые EF и MN, но не пересекает отрезок FM.
Начертите две пересекающиеся прямые и расположите на них два отрезка, не имеющие общих точек.
Сколько точек надо взять между точками A и B, чтобы вместе с отрезком AB получилось шесть различных отрезков?
Даны отрезок AB, точка E, не лежащая на прямой AB, и точка C, лежащая на прямой AB. Каково взаимное расположение прямой EC и отрезка AB?
Можно ли провести прямую, не проходящую через точку A, так, чтобы она пересекала одновременно прямые AB, AC и AD.
Начертите две пересекающиеся прямые и расположите на них два непересекающиеся отрезка так, чтобы точка пересечения прямых принадлежала одному из них.
Проведите прямую, которая пересекает некоторые из указанных на рис. 1 отрезков, так, чтобы вместе с данными отрезками образовалось шесть отрезков.
Дана прямая EF, A∉EF, B∉EF. Может ли прямая AB не пересекать отрезок
Может ли прямая, не проходящая через точку O, одновременно пересекать прямые OA, OB, OC и OD (рис. 2)?
Сколько различных прямых можно провести через 4 точки? Сделайте чертежи.
По рисунку определите число отрезков с концами в обозначенных точках.
Сколько точек пересечения могут иметь четыре попарно пересекающиеся прямые? Для каждого случая сделайте рисунок.
По рисунку определите число отрезков с концами в обозначенных точках.
§ 2. Луч и угол.
а) Сколько лучей с началом в точке О изображено на рисунке?
б) Сколько углов изображено на этом рисунке?
в) Постройте луч ОМ так, чтобы угол АОМ был развёрнутым.
Начертите угол. Отметьте точку М, которая лежит на стороне угла, точку N, лежащую во внутренней области угла, и точку Е, принадлежащую его внешней области.
а) Сколько лучей с началом в точке О изображено на рисунке?
б) Сколько углов изображено на этом рисунке?
в) Постройте луч ОА так, чтобы угол АОN был развёрнутым.
Начертите угол. Изобразите отрезок: а) все точки которого лежат во внутренней области угла; б) все точки которого лежат во внешней области угла; в) часть точек которого лежит во внутренней области угла.
а) Сколько неразвёрнутых и сколько развёрнутых углов изображено на рис. 1?
б) Проведите лучи с началом в точке В, один из которых пересекал бы луч АС, а другой не пересекал бы его.
Даны угол MEF и точка А, лежащая в его внутренней области (рис. 2). Проведите луч с началом в точке Е так, чтобы образовались два угла, такие, что точка А не принадлежала бы их внутренним областям.
а) Сколько неразвёрнутых и сколько развёрнутых углов изображено на рис. 1?
б) Начертите луч CD, проведите два луча с началом в точке A, один из которых пересекал бы луч CD, а другой не пересекал бы его.
Даны угол EKL и точка M, не лежащая в его внутренней области (рис. 2). Проведите из точки К луч так, чтобы образовалось ещё два угла, такие, что точка М не лежала бы в их внутренней области.

Сколько неразвёрнутых и сколько развёрнутых углов изображено на рис. 1?
С началом в точке Е (рис. 2) проведите лучи, один из которых пересекает луч СА, а другой не пересекает луч ВС. Рассмотрите возможные варианты.
Дан неразвёрнутый угол АВС. Проведите лучи с началом в точке В, чтобы образовались при этом шесть углов, из которых один был бы развёрнутым.
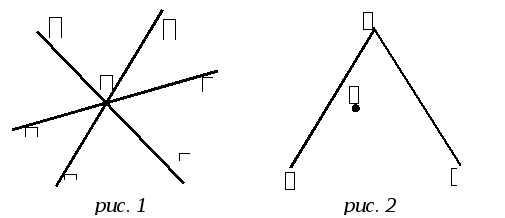
Сколько неразвёрнутых и сколько развёрнутых углов изображено на рис. 1?
С началом в точке Е (рис. 2) проведите лучи, один из которых пересекает луч ВС, а другой не пересекает луч АС. Рассмотрите возможные варианты.
Через заданную точку проведите столько прямых, чтобы при их пересечении образовалось шесть углов.
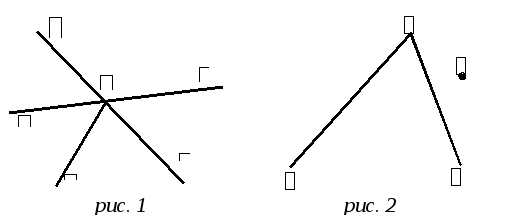
Углы AOB, BOC, COD, DOE и EOA имеют общую вершину О. Прямая а, не проходящая через точку О, пересекает не менее двух лучей, которые являются сторонами этих углов. Рассмотрите все возможные случаи. Сделайте чертежи.
Углы MAF, FAK, KAP, PAQ и QAM имеют общую вершину О. Прямая а, не проходящая через точку О, пересекает не менее трёх лучей, которые являются сторонами этих углов. Рассмотрите все возможные случаи. Сделайте чертежи.
§ 3. Сравнение отрезков и углов.
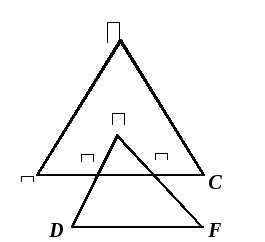
На рис. 1 CB = BE, DE AC. Сравните отрезки AB и DB.
На рис. 2 ∠AOB = ∠DOC. Есть ли ещё на рисунке равные углы?
На рис. 1 EO = NO, OK OL. Сравните отрезки EK и NL.
На рис. 2 ∠MOL = ∠KON. Есть ли ещё на рисунке равные углы?
На прямой а от точки А в одном направлении отложены два отрезка АВ и АС (АС АВ). От точки С на этой прямой отложите такой отрезок СЕ, чтобы АС = ВЕ. Что вы можете сказать о длине отрезка СЕ?
∠AOC = ∠BOD, OM – биссектриса ∠АОВ. Докажите, что OM – биссектриса ∠COD.
На прямой m от точки А отложены два отрезка так, что АС АВ и точка А лежит между точками В и С. От точки С отложен отрезок СМ так, что ВМ = АС. Сравните отрезки МС и АВ.
На рисунке ∠AOC = ∠BOС и ∠AOЕ = ∠BOF. Является ли луч ОС биссектрисой угла EOF?
Если на прямой даны точки A, B, C, D (точка С лежит между А и В) так, что AB = CD, то является ли середина отрезка AD также серединой отрезка ВС? Обоснуйте ответ.
На рисунке ОВ – луч, принадлежащий внутренней области угла АОС. Как нужно провести луч ОЕ, чтобы ∠AOC = ∠BOЕ? Покажите на рисунках возможные варианты.
АВ и АС – отрезки одной прямой (А лежит между точками В и С), точка М – середина отрезка АВ, N – середина АС. Верно ли, что BC = 2MN? Ответ обоснуйте.
На рисунке ОС – луч, принадлежащий внутренней области угла АОВ. Как нужно провести луч OD, чтобы ∠AOD = ∠COB? Покажите на рисунке возможные варианты.
На прямой а от точки А отложены два отрезка АВ и АС, причём ABAC1,99AB. Сравните отрезки ВС и АВ. Ответ обоснуйте.
На рисунке ∠AOC = ∠BOD, OM и ON – биссектрисы углов АОВ и COD. Сравните углы MON и AOC.
На прямой m от точки А отложены два отрезка АВ и АС, причём 0,51ABACAB. Сравните отрезки ВС и АС. Ответ обоснуйте.
На рисунке OM и ON – биссектрисы углов AOB и COD, ∠MON = ∠AOC. Сравните углы АОС и BOD.
§ 4. Измерение отрезков и углов.
На прямой m лежат точки M, N и K, причём MN = 85 мм, NK =1,15 дм. Какой может быть длина отрезка MK в сантиметрах?
∠AOВ = 90°. Проведите луч ОС так, чтобы угол АОС равнялся 45° (рассмотрите два случая).
Чему равен угол СОВ?
Каким углом: острым, тупым или развёрнутым является угол СОВ?
Является ли луч ОС биссектрисой угла АОВ?
Точки А, В и С лежат на прямой а, причём АВ = 5,7 м, ВС = 730 см. Какой может быть длина отрезка АС в дециметрах?
∠AOВ = 120°. Проведите луч ОС так, чтобы угол АОС равнялся 60° (рассмотрите два случая).
Чему равен угол СОВ?
Каким углом: острым, тупым или развёрнутым является угол СОВ?
Является ли луч ОС биссектрисой угла АОВ?
На отрезке MN, равном 8 дм, лежат точки А и В по разные стороны от середины С отрезка MN, СА = 7 см, СВ = 0,24 м. Найдите длины отрезков AN и BN в дециметрах.
∠AOВ = 80°. Луч ОС делит этот угол на два угла так, что ∠AOС = 4∠СОВ.
Найдите эти углы.
Найдите угол DOB, если луч OD проведён так, что ОА – биссектриса угла DOB. Каким углом: острым или тупым является этот угол?
Точка M – середина отрезка EF, длина которого равна 1,2 м. От точки М, по разные стороны от неё, отложены два отрезка MP = 1,6 дм и MQ = 40 см. Найдите длины отрезков EP и QF в сантиметрах.
∠AOВ = 100°. Луч ОЕ делит этот угол на два угла так, что ∠ВОЕ = 3∠АОЕ.
Найдите эти углы.
Найдите угол AOF, если луч OF проведён так, что ОE – биссектриса угла FOB. Каким углом: острым или тупым является этот угол?
На отрезке АВ, равном 192 дм, дана точка С, такая, что АС:СВ = 1:3. На отрезке АС отложен отрезок CD, равный ВС. Найдите расстояние между серединами отрезков AD и CB.
Угол АОВ расположен во внутренней области угла COD. ОЕ и OF – биссектрисы углов СОА и BOD соответственно. Объясните, почему угол EOF прямой, если ∠COD + ∠AOВ = 180°.
На прямой отложены два равных отрезка АС и СВ. На отрезке СВ дана точка D, такая, что 5СD = 4DB. Найдите длину отрезка, концами которого являются середины отрезков АС и DB, если CD = 12 м.
Угол АОВ принадлежит внутренней области угла COD; ∠COD = 140°, а ∠АОВ = 100°. Найдите угол, образованный биссектрисами углов AOC и BOD, если луч ОВ принадлежит внутренней области угла AOD.
Длина отрезка АВ равна 14 см. Найдите на прямой АВ все такие точки D, для которых DA = 3DB.
Прямой угол разделён лучом, исходящим из его вершины, на два угла, такие, что половина одного угла трети другого. Найдите эти углы.
Длина отрезка АВ равна 12 см. Найдите на прямой АВ все такие точки М, для которых МА = 2МВ.
Прямой угол двумя лучами, исходящими из его вершины, разделён на три угла, один из которых равен разности двух других углов. Найдите величину большего из этих углов.
8
multiurok.ru
Аксиомы геометрии и следствия из них
Построение геометрии как науки состоит из выбора основных геометрических понятий, формулирование основных свойств для этих геометрических понятий с помощью утверждений, которые считаются истинными без доказательства и построение других понятий. Такое построение называют аксиоматическим.
Можно рассматривать геометрию на плоскости и в пространстве. Геометрия на плоскости называется планиметрией, в пространстве – стереометрией.
Неопределяемыми или основными понятиями в планиметрии являются точка, прямая, а в стереометрии – точка, прямая и плоскость.
Основные аксиомы геометрии
Аксиомы геометрии можно разбить на пять групп.
1. Аксиомы принадлежности
1.1 Какова бы ни была прямая, существуют точки, принадлежащие ей и не принадлежащие ей.
1.2 Через любые две точки можно провести прямую и притом только одну.
1.3 Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости и точки, не принадлежащие ей.
2. Аксиомы расположения
2.1 Из трех точек на прямой одна и только одна лежит между двумя другими.
2.2 Прямая разбивает плоскость на две полуплоскости.
2.3 Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну.
2.4 Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
3. Аксиомы измерения
3.1 Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
3.2 Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен . Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
4. Аксиомы откладывания.
4.1 На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины и притом только один.
4.2 От любой полупрямой в заданную полуплоскость можно отложить угол, с заданной градусной мерой, меньшей и притом только один.
4.3 Каков бы ни был треугольник, существует треугольник, равный ему, в заданном расположении относительно данной полупрямой.
5. Аксиома параллельности.
5.1 Через точку, не лежащую на данной прямой можно провести не более одной прямой, параллельной данной.
Примеры решения задач
ru.solverbook.com
Презентация к уроку по геометрии (7 класс) по теме: Аксиомы планиметрии Геометрия 7 класс
Презентация по геометрииучителя математикиМКОУ СОШ №1пгт. ПаланаКамчатский крайУчебник геометрии 7 – 9.Авторы: Л.С. Атанасян и другие.Геометрия Евклида
Первым систематическим изложением геометрии, дошедшим до нашего времени, являются “Начала” – сочинения александрийского математика Евклида.
В “Началах” был развит аксиоматический подход к построению геометрии, который состоит в том, что сначала формулируются основные положения (аксиомы), а затем на их основе посредством рассуждений доказываются другие утверждения (теоремы). Изложение геометрии Евклидом долгое время служило недосягаемым образцом точности, безукоризненности и строгости. Только в начале 20 века математики смогли улучшить логические основания геометрии.
«Начала»
Аксиомы планиметрии
Аксиомами называются те основные положения геометрии, которые принимаются в качестве исходных. Или :Аксиомами называются утверждения, которые принимаются без доказательства.
Основные понятия (фигуры) на плоскости: точка и прямая
Используя основные понятия и аксиомы даются определения новых понятий, формулируются и доказываются теоремы о свойствах геометрических фигур.
Аксиомы взаимного расположения точек и прямых:
1.Каждой прямой принадлежит по крайней мере две точки.2. Имеются по крайней мере три точки, не лежащие на одной прямой. 3. Через любые две точки проходит прямая, и притом только одна.
Аксиомы расположения точек на прямой:
4. Из трёх точек прямой одна и только одна лежит между двумя другими.5. Каждая точка О прямой разделяет её на две части(два луча) так, что любые две точки одного и того же луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О.
Аксиома расположения точек на плоскости:
6. Каждая прямая а разделяет плоскость на две части (две полуплоскости) так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а.
Аксиомы наложения или равенства фигур.
Наложение – это отображение плоскости на себя.Если существует наложение, при котором фигура Ф отображается на фигуру Ф1, то говорят, что фигуру Ф можно совместить наложением с фигурой Ф1, или фигура Ф равна фигуре Ф1.
Аксиомы наложения или равенства фигур:
7. Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки. 8. На любом луче от его начала можно отложить отрезок, равный данному и притом только один. 9. От любого луча в данную полуплоскость можно отложить угол, равный данному неразвёрнутому углу, и притом только один.
Аксиомы наложения или равенства фигур:
10. Любой угол hk можно совместить наложением с равным ему углом h2k1 двумя способами: 1)так, что луч h совместится с лучом h2, а луч k – с лучом k1; 2) так, что луч k совместится с лучом k1, а луч h – с лучом h2 . 11. Любая фигура равна сама себе.
Аксиомы наложения или равенства фигур:
12. Если фигура Ф равна фигуре Ф1, то фигура Ф1 равна фигуре Ф.13. Если фигура Ф1 равна фигуре Ф2, а фигура Ф2 равна фигуре Ф3, то фигура Ф1 равна фигуре Ф3.
Аксиомы измерения отрезков:
14. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.
Аксиома существования отрезка данной длины:
15. При выбранной единице измерения отрезков для любого положительного числа существует отрезок, длина которого выражается этим числом.
Аксиома параллельных прямых:
16. Через точку, не лежащую на данной прямой, проходит только одна прямая параллельная данной.
Постулаты Евклида
1. Из каждой точки ко всякой другой точке можно провести прямую;2. Каждую ограниченную прямую можно продолжить неопределённо;3. Из любого центра можно описать окружность любого радиуса;4. Все прямые углы равны;5. И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньше двух прямых, то продолженные эти прямые неограниченно встретятся с той стороны, где углы меньше двух прямых
О чем говорится в V постулате Евклида?
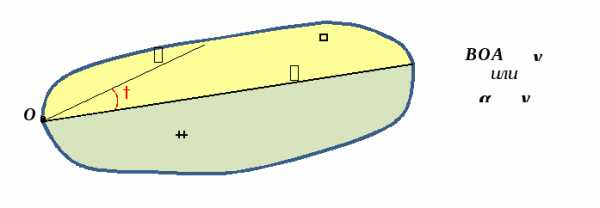
Если две прямые а и в образуют при пересечении с третьей прямой внутренние односторонние углы, сумма величин которых меньше двух прямых углов (т.е. меньше 180°; рис. 1), то эти две прямые обязательно пересекаются, причем именно с той стороны от третьей прямой, по которую расположены углы α и β (составляющие вместе менее 180°).
Аксиомы планиметрии
1.Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.2.Из трех точек на прямой одна и только одна лежит между двумя другими.3.Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.4.Прямая,принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.5.Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180.Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом,проходящим между его сторонами.
Аксиомы планиметрии
6.На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.7.От полупрямой на содержащей ее плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180,и только один.8.Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.9.На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
nsportal.ru
2. Свойства параллельных прямых. Аксиома параллельных прямых
Признаки, которые мы рассматривали в первой части теории, и свойства, которые будем рассматривать в этой части, доказываем разными способами.
Признак — это некоторый факт, благодаря которому мы устанавливаем справедливость интересующего нас суждения о некотором объекте.
Если при пересечении двух прямых третьей секущей накрест лежащие углы равны, то эти две прямые параллельны.
Свойство — если мы уверены в справедливости суждения, мы формулируем свойство объекта.
Если две прямые параллельны, то при пересечении их с третьей секущей накрест лежащие углы равны.
Аксиома, в свою очередь — такая истина, которую не надо доказывать. В каждой науке есть свои аксиомы, на справедливости которых строят все дальнейшие суждения и их доказательства.
Аксиома параллельных прямых.
В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой.
Иногда эту аксиому называют как одно из свойств параллельных прямых, но на справедливости этой аксиомы строятся многие доказательства в геометрии.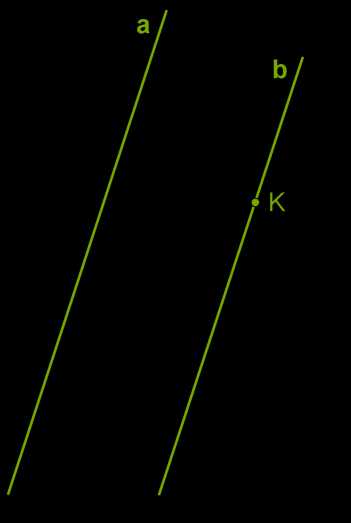
Другие свойства параллельных прямых.
1. Если одна из пары параллельных прямых параллельна третьей прямой, то и другая прямая параллельна третьей прямой.
2. Если некая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую.
Эти свойства в отличие от аксиомы нужно доказать.
Докажем 1. Свойство.
Даны две параллельные прямые \(a\) и \(b\). Верно ли, что если прямая \(c\) параллельна прямой \(a\), то она параллельна и прямой \(b\)?

Используем противоположное суждение.
Допустим, что возможна ситуация, когда прямая \(c\) параллельна одной из параллельных прямых — прямой \(a\) — пересекает другую прямую \(b\) в некоторой точке \(K\).
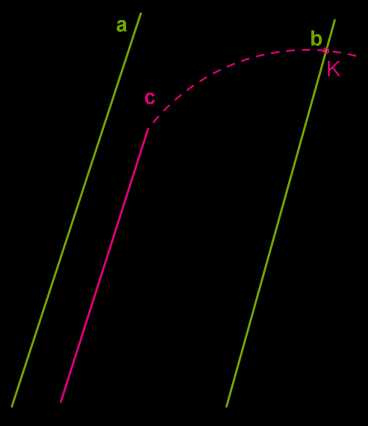
Получается противоречие с аксиомой параллельных прямых. Мы имеем ситуацию, когда через точку проходят две пересекающиеся прямые, которые параллельны одной и той же прямой \(a\). Такого не может быть, значит, прямые \(b\) и \(c\) пересекаться не могут.
Мы доказали, что верно: если одна из пары параллельных прямых параллельна третьей прямой, то и другая прямая параллельна третьей прямой.
Попробуй доказать самостоятельно 2. Свойство.
Если некая прямая \(c\) пересекает одну из двух параллельных прямых \(a\), то она пересекает и вторую параллельную прямую \(b\).
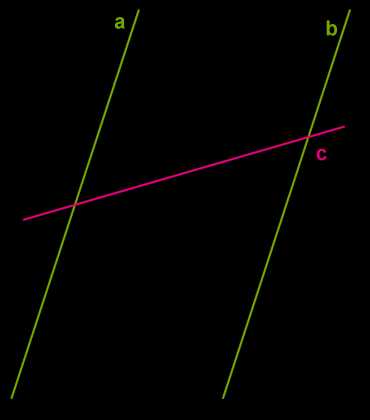
Таким же методом от противоположного суждения попробуй представить, что возможна ситуация, когда прямая пересекает одну из параллельных прямых, но не пересекает другую.
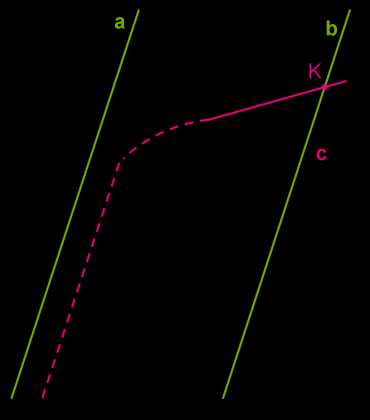
Свойства углов, которые образуются при пересечении двух параллельных прямых с третьей секущей, мы уже назвали в первой части теории.
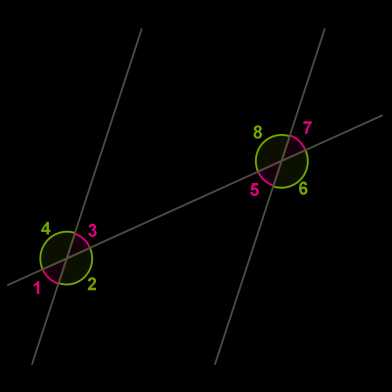
При пересечении двух параллельных прямых третьей секущей:
— накрест лежащие углы равны,
— соответственные углы равны,
— сумма односторонних углов равна \(180°\).
www.yaklass.ru
Презентация по геометрии на тему «Аксиомы геометрии» (7 класс)
Данная презентация необходима для урока об аксиомах геометрии. На уроке рассказывается о том, что есть не только Евклидова геометрия, но и другие, точки зрения на геометрию. Они которые не противоречат друг другу, а просто смотрят на одни и теже вещи под разным углом.
Урок можнот начать со сравнения построения предмета геометрии с домом. Аксиомы Евклида это фундамент на котором строится дом Геометрия теоремы это его стены, Геометрия на плоскости это один этаж, геометрия в пространстве это другой этаж. Следствия, Замечания-окна и двери и т. д.
Для геометрии евклидовой фундамент один, для геометрии лобачевского другой фундамент. Евклид начал с плоскости прямоугольной, а Лобачевский решил раз уж у нас электроны-круглые, атомы-круглые, планета-круглая, значит и основа-плоскость круглая. И начал строить геометрию. А переход от одного к другому существует. Так сказать мост.
Существуют и другие не менее известные подходы к геометрии. Например, эллиптическая геометрия и гиперболическая геометрия, или конформная. Рисунки слайдов 6,7,8. Существуют и другие.
Причем не надо вдаваться в подробности каждой, достаточно просто взлянуть как изображаются и называются( так сказать совсем обзорно).
Все эти подходы можно назвать неевклидовы, т. е. отдичаются от евклидовой.
После такого абстактного подхода можно переходить к более детальной разборке. Рассказать историю, так как без знания истории мы ничто.
«По дошедшим до нас египетским папирусам и древневавилонским текстам видно, что уже за 2 тысячи лет до нашей эры люди умели определять площади треугольников, прямоугольников, трапеций, приближенно вычислять площадь круга, — пишет И. Г. Башмакова. — Они знали также формулы для определения объемов куба, цилиндра, конуса, пирамиды и усеченной пирамиды. Сведения по геометрии вскоре стали необходимы не только при измерении земли. Развитие архитектуры, а несколько позднее и астрономии предъявило геометрии новые требования. И в Египте и в Вавилоне сооружались колоссальные храмы, строительство которых могло производиться только на основе предварительных расчетов. …И все же, несмотря на то что человечество накопило такие обширные знания геометрических фактов, геометрия как наука еще не существовала.
Геометрия стала наукой только после того, как в ней начали систематически применять логические доказательства, начали выводить геометрические предложения не только путем непосредственных измерений, но и путем умозаключений, путем вывода одного положения из другого, и устанавливать их в общем виде. Обычно этот переворот в геометрии связывают с именем ученого и философа VI века до нашей эры Пифагора Самосского».
Однако все новые проблемы и созданные в связи с ними теории привели к тому, что совершенствовались сами способы математических доказательств, возрастала потребность создания стройной логической системы в геометрии.
О жизни Евклида (около 365 г. до нашей эры — 300 г. до нашей эры) почти ничего не известно. До нас дошли только отдельные легенды о нем. Первый комментатор «Начал» Прокл (V век нашей эры) не мог указать, где и когда родился и умер Евклид. По Проклу, «этот ученый муж» жил в эпоху царствования Птолемея I. Некоторые биографические данные сохранились на страницах арабской рукописи XII века: «Евклид, сын Наукрата, известный под именем «Геометра», ученый старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира».
Одна из легенд рассказывает, что царь Птолемей решил изучить геометрию. Но оказалось, что сделать это не так-то просто. Тогда он призвал Евклида и попросил указать ему легкий путь к математике. «К геометрии нет царской дороги», — ответил ему ученый. Так в виде легенды дошло до нас это ставшее крылатым выражение.
Царь Птолемей I, чтобы возвеличить свое государство, привлекал в страну ученых и поэтов, создав для них храм муз — Мусейон. Здесь были залы для занятий, ботанический и зоологический сады, астрономический кабинет, астрономическая башня, комнаты для уединенной работы и главное — великолепная библиотека. В числе приглашенных ученых оказался и Евклид, который основал в Александрии — столице Египта — математическую школу и написал для ее учеников свой фундаментальный труд.
Далее переходим к записи и основных аксиом и следствий.
www.metod-kopilka.ru
аксиомы-определения-теоремы-1 четверть 7кл
1 четверть геометрия 7 класс
ПРЯМЫЕ И ОТРЕЗКИ
Основные геометрические фигуры: точка, прямая, плоскость, пространство.
Аксиома 1. Через любые две точки можно провести прямую, и только одну.
Аксиома 2. Через три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.
Аксиома 3. Прямая, проходящая через две точки плоскости, лежит в этой плоскости.
Определение 1. Любое множество точек называется геометрической фигурой. Часть любой геометрической фигуры также является геометрической фигурой.
Аксиома 4. Для любых двух точек А и В пространства однозначно определено некоторое неотрицательное число АВ, называемое расстоянием между ними и обладающее следующими свойствами:
1) АВ = ВА;
2) АВ = 0 тогда и только тогда, когда точки А и В совпадают;
3) АС = АВ + ВС, причём равенство достигается в том и только в том случае, когда точка В лежит на отрезке АС.
Определение 2. Точка X лежит между точками А и В, если эти точки различны и АХ + ХВ = АВ.
Для любых трёх точек, не лежащих на одной прямой, расстояние АС меньше суммы расстояний АВ и ВС.
Определение 3. Отрезки равны, если равны их длины.
УГЛЫ
Определение 4. Углом называется фигура, состоящая из двух различных лучей с общим началом и ограниченной ими части плоскости.
Определение 5. Развёрнутым углом называется угол, сторонами которого являются дополнительные лучи одной прямой. Два луча с общим началом, дополняющие друг друга до прямой, называются дополнительными.
Определение 6. Фигура называется выпуклой, если любые две её точки можно соединить отрезком, принадлежащим этой фигуре.
Определение 7. Угол, равный 90°, называется прямым углом. Угол, меньший 90°, называется острым углом. Угол, больший 90°, называется тупым углом.
Определение 8. Углы равны, если равны их величины.
Определение 9. Углы называются равными, если их можно совместить наложением друг на друга.
Определение 10. Биссектрисой угла называется луч, который исходит из вершины угла и делит угол пополам.
Определение 11. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами.
Теорема 1. Сумма смежных углов равна 180°.
Следствие 1. Если два угла равны, то смежные с ними углы тоже равны.
Следствие 2. Угол, смежный с прямым углом, есть прямой угол.
Следствие 3. Угол, смежный с острым углом, — тупой; угол, смежный с тупым углом, — острый.
Трёхгранный угол — фигура, состоящая из трёх углов и части пространства, ограниченной этими плоскими углами. Лучи называются рёбрами трёхгранного угла, а углы, ограничивающие трёхгранный угол, — его гранями. Эти углы-грани образуют поверхность трёхгранного угла.
В трёхгранном угле каждый плоский угол меньше суммы двух других плоских углов.
Многогранные углы бывают выпуклыми и невыпуклыми.
Определение 12. Многогранный угол называется выпуклым, если он лежит по одну сторону от каждой плоскости, содержащей его грань.
studfiles.net
