примеры, значение, числовое равенство, правила
Запись, которая состоит из чисел, знаков и скобок, а также имеет смысл, называется числовым выражением.
Например, следующие записи:
- (100-32)/17,
- 2*4+7,
- 13,
- 4*0.7 -3/5,
- 1/3 +5/7
будут являться числовыми выражениями. Следует понимать, что одно число тоже будет являться числовым выражением. В нашем примере, это число 13.
А, например, следующие записи
не будут являться числовыми выражениями, так как они лишены смысла и являются просто набором чисел и знаков.
Значение числового выражения
Так как в качестве знаков в числовых выражениях входят знаки арифметических действий, то мы можем посчитать значение числового выражения. Для этого необходимо выполнить указанные действия.
Например,
(100-32)/17 = 4, то есть для выражения (100-32)/17 значением этого числового выражения будет являться число 4.
2*4+7=15, число 15 будет являться значением числового выражения 2*4+7.
Часто для краткости записи не пишут полностью значение числового выражения, а пишут просто «значение выражения», опуская при этом слово «числового».
Числовое равенство
Если два числовых выражения записаны через знак равно, то эти выражения образуют числовое равенство. Например, выражение 2*4+7=15 является числовым равенством.
Как уже отмечалось выше, в числовых выражениях могут использоваться скобки. Как уже известно скобки влияют на порядок действий.
Вообще, все действия разделены на несколько ступеней.
- Действия первой ступени: сложение и вычитание.
- Действия второй ступени: умножение и деление.
- Действия третей ступени – возведение в квадрат и возведение в куб.
Правила при вычислении значений числовых выражений
При вычислении значений числовых выражений следуют руководствоваться следующими правилами.
- 1. Если выражение не имеет скобок, то надо выполнять действия начиная с высших ступеней: третья ступень, вторая ступень и первая ступень.
 Если имеется несколько действий одной ступени, то их выполняют в порядке в котором они записаны, то есть слева на право.
Если имеется несколько действий одной ступени, то их выполняют в порядке в котором они записаны, то есть слева на право. - 2. Если в выражении присутствуют скобки, то сначала выполняются действия в скобках, а лишь затем все стальные действия в обычном порядке. При выполнении действий в скобках, если их там несколько, следует пользоваться порядком описанным в пункте 1.
- 3. Если выражение представляет собой дробь, то сначала вычисляются значении в числителе и знаменателе, а потом числитель делится на знаменатель.
- 4. Если в выражении присутствуют вложенные скобки, то выполнять действия следует с внутренних скобок.
Нужна помощь в учебе?
Предыдущая тема: Наименьшее общее кратное (НОК): определение, как найти, общая схема
Следующая тема:   Выражения с переменными: разбираем пример с фокусом
Урок 14. числовые выражения. порядок действий в числовых выражениях. скобки. сравнение числовых выражений — Математика — 2 класс
Математика, 2 класс
Урок № 14.
Перечень вопросов, рассматриваемых в теме:
— Что такое числовые выражения?
— Как правильно читать и записывать числовые выражения?
— Как выполнять порядок действий, если есть скобки?
— Как сравнить два выражения?
Глоссарий по теме:
Числовое выражение – это запись, состоящая из чисел и знаков действий между ними.
Значение выражения – это результат выполненных действий.
Сравнить числовые выражения – найти значение каждого из выражений и их сравнить.
Скобки — парные знаки ( )
Порядок выполнения действий – это последовательность проводимых вычислений в данном выражении.
Основная и дополнительная литература по теме:
1. Моро М. И., Бантова М. А., Бельтюкова Г. В.и др. Математика. 2 класс. Учебник для общеобразовательных организаций.
2. Волкова А. Д. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2017, с. 22-27
3. Глаголева Ю. И., Волкова А. Д. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, Учлит, 2017, с.16
Теоретический материал для самостоятельного изучения
Маша и Миша решали пример: из числа 12 вычесть сумму чисел 7 и 3. Они записали его по-разному и получили разные ответы. Маша сначала из 12 вычла 7 и получила 5, потом прибавила 3, получила 8.
Маша: 12 – 7 + 3 = 8
Миша обвёл овалом сумму чисел 7 и 3 и сначала посчитал сумму, получил 10. Затем от 12 отнял 10, получил 2.
Миша: 12 — 7 + 3 = 2
Кто из них вычислил верно? Решил верно, Миша.
В математике для обозначения действий, которые должны выполняться первыми используют специальный знак ( ) —

Запишем пример, который решали дети правильно:
12 — (7 + 3) =2
Вычислим. 7 + 3 равно 10, из 12 вычесть 10, получится 2. Запомните: действия, записанные в скобках, выполняются первыми.
Посмотрим на запись.
9 – (6 + 2) = 1
Запись, в которой разные числа (однозначные и двузначные) соединены знаками «+» и «–» в различных сочетаниях, называется числовым выражением и читается так: «из числа 9 вычесть сумму чисел 6 и 2».
Найти значение выражения – это значит, нужно выполнить все указанные действия в выражении. Значение данного выражения 1.
Теперь мы будем называть примеры числовыми выражениями, а ответы значениями числовых выражений.
9 – (6 + 2) = 1
числовое значение
выражение числового
выражения
Прочитаем выражение: 10 + (8 — 3) =
К числу 10 прибавить разность чисел 8 и 3.
Как найти значение выражения? Нужно выполнить необходимые действия. Но с какого действия нужно начинать? С того, которое записано в скобках. Находим разность чисел 8 и 3, будет 5, к 10 прибавить 5, получится 15.
10+(8-3)=15
Давайте сравним значения двух выражений:
11 — 4 и 16 — 7.
Сначала найдем значение каждого из выражений и их сравним.
11 — 4 = 7
16 — 7 = 9
7 < 9, значит, 11-4 < 16-7
Выводы: Итак, оказывается, порядок должен быть и в действиях, он так и называется «Порядок выполнения действий». Если в числовом выражении стоят скобки, это означает, что действие, которое в них записано, должно быть выполнено первым, а все остальные действия выполняют по порядку.
Тренировочные задания.
1.Выберите правильный ответ. Как правильно прочитать данное числовое выражение: 13 – (7 + 3)?
Вариант ответов:
1. К 13 прибавить сумму чисел 7 и 3
2. Из 13 вычесть 7 плюс 3
3. Из 13 вычесть сумму чисел 7 и 3
Из 13 вычесть сумму чисел 7 и 3
4. Разность чисел 13 и 7 плюс 3
Правильный ответ:
3. Из 13 вычесть сумму чисел 7 и 3
2. Соотнесите числовые выражения с их значениями
3+ (16-6) 15
10-4+9 16
13-(6+4) 13
9+ (13-6) 3
Правильный ответ:
3+ (16 – 6) 13
10 – 4 + 9 15
13 – (6 + 4) 3
9 + (13 – 6) 16
Числовые выражения. Выражения с переменными. Примеры упрощения выражений
Числовое выражение – это совокупность одного или нескольких чисел и функций, соединенных знаками арифметических операций и скобками. Примеры числовых выражений:Значением числового выражения является число.
Операции в числовом выражении выполняются в следующей последовательности:
1. Действия в скобках.
2. Вычисление функций. 3 — 11) = 3 • 4 + (8 — 11) = 3 • 4 + (-3)
3 — 11) = 3 • 4 + (8 — 11) = 3 • 4 + (-3)
2. Умножим 3 на 4:
3 • 4 + (-3) = 12 + (-3)
3. Выполним последовательно операции слева направо:
12 + (-3) = 9.
Выражение с переменными – это совокупность одного или нескольких чисел, переменных и функций, соединенных знаками арифметических операций и скобками. Значения выражений с переменными зависят от значений, входящих в него переменных. Последовательность выполнения операций здесь та же, что и для числовых выражений. Выражения с переменными иногда бывает полезно упрощать, выполняя различные действия – вынесение за скобки, раскрытие скобок, группировки, сокращение дробей, приведение подобных и т.д. Так же для упрощения выражений часто используют различные формулы, например, формулы сокращенного умножения, свойства различных функций и т. д.
Пример: Упростить выражение 3 • (x – 4 • y + 11) + 12 • y – 30
1. Раскроем скобки:
3 • (x – 4 • y + 11) + 12 • y – 30 = 3 • x – 12 • y + 33 + 12 • y – 30;
2. Приведем подобные:
Приведем подобные:
3 • x — 12 • y + 33 + 12 • y – 30 = 3 • x + 3;
3. Теперь можно оставить выражение в таком виде, а можно вынести 3 за скобки:
3 • x + 3 = 3 • (x + 1).
Числовые и буквенные выражения. Формула
Числовые и буквенные выражения. ФормулаСложение, вычитание, умножение, деление — арифметические действия (или арифметические операции). Этим арифметическим действиям соответствуют знаки арифметических действий:
+ (читаем «плюс«) — знак операции сложения,
— (читаем «минус«) — знак операции вычитания,
∙ (читаем «умножить«) — знак операции умножения,
: (читаем «разделить«) — знак операции деления.
Запись, состоящая из чисел, связанных между собой знаками арифметических действий, называется числовым выражением. В числовом выражении могут присутствовать также скобки Например, запись 1290 : 2 – (3 + 20 ∙ 15) является числовым выражением.
В числовом выражении могут присутствовать также скобки Например, запись 1290 : 2 – (3 + 20 ∙ 15) является числовым выражением.
Результат выполнения действий над числами в числовом выражении называется значением числового выражения. Выполнение этих действий называется вычислением значения числового выражения. Перед записью значения числового выражения ставят знак равенства «=». В таблице 1 приведены примеры числовых выражений и их значений.
Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий называется буквенным выражением. В этой записи могут присутствовать скобки. Например, запись a + b – 3 ∙ c является буквенным выражением. Вместо букв в буквенное выражение можно подставлять различные числа. При этом значение букв может изменяться, поэтому буквы в буквенном выражении называют еще переменными.
Подставив в буквенное выражение числа вместо букв и вычислив значение получившегося числового выражения, находят значение буквенного выражения при данных значениях букв (при данных значениях переменных). В таблице 2 приведены примеры буквенных выражений.
Буквенное выражение может не иметь значения, если при подстановке значений букв получается числовое выражение, значение которого для натуральных чисел не может быть найдено. Такое числовое выражение называется некорректным для натуральных чисел. Говорят также, что значение такого выражения «не определено» для натуральных чисел, а само выражение «не имеет смысла». Например, буквенное выражение a – b не имеет значения при a = 10 и b = 17. Действительно, для натуральных чисел, уменьшаемое не может быть меньше вычитаемого. Например, имея всего 10 яблок (a = 10), нельзя отдать из них 17 (b = 17)!
В таблице 2 (колонка 2) приведён пример буквенного выражения. По аналогии заполните таблицу полностью.
По аналогии заполните таблицу полностью.
Для натуральных чисел выражение 10 -17 некорректно (не имеет смысла), т.е. разность 10 -17 не может быть выражена натуральным числом. Другой пример: на ноль делить нельзя, поэтому для любого натурального числа b, частное
Математические законы, свойства, некоторые правила и соотношения часто записывают в буквенном виде (т.е. в виде буквенного выражения). В этих случаях буквенное выражение называют формулой. Например, если стороны семиугольника равны a, b, c, d, e, f, g, то формула (буквенное выражение) для вычисления его периметра p имеет вид:
p = a + b + c + d + e + f + g
При a = 1, b = 2, c = 4, d = 5, e = 5, f = 7, g = 9, периметр семиугольника p = a + b + c + d + e + f + g = 1 + 2 + 4 + 5 +5 + 7 + 9 = 33.
При a = 12, b = 5, c = 20, d = 35, e = 4, f = 40, g = 18, периметр другого семиугольника p = a + b + c + d + e + f + g = 12 + 5 + 20 + 35 + 4 + 40 + 18 = 134.
Блок 1. Словарь
Составьте словарь новых терминов и определений из параграфа. Для этого в пустые клетки впишите слова из списка терминов, приведенного ниже. В таблице (в конце блока) укажите номера терминов в соответствии с номерами рамок. Рекомендуется перед заполнением клеток словаря еще раз внимательно просмотреть параграф.
- Операции: сложение, вычитание, умножение, деление.
2.Знаки «+» (плюс), «-» (минус), «∙» (умножить, «:» (разделить).
3.Запись, состоящая из чисел, которые связанны между собой знаками арифметических действий и в которой могут присутствовать также скобки.
4.Результат выполнения действий над числами в числовом выражении.
5. Знак, стоящий перед значением числового выражения.
Знак, стоящий перед значением числового выражения.
6. Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий (могут присутствовать также скобки).
7. Общее название букв в буквенном выражении.
8. Значение числового выражения, которое получается при подстановке переменных.в буквенное выражение.
9.Числовое выражение, значение которого для натуральных чисел не может быть найдено.
10. Числовое выражение, значение которого для натуральных чисел может быть найдено.
11. Математические законы, свойства, некоторые правила и соотношения, записанные в буквенном виде.
12. Алфавит, малые буквы которого используются для записи буквенных выражений.
Блок 2. Установите соответствие
Установите соответствие между заданием в левой колонке и решением в правой. Ответ запишите в виде: 1а, 2г, 3б…
Ответ запишите в виде: 1а, 2г, 3б…
Блок 3. Фасетный тест. Числовые и буквенные выражения
Фасетные тесты заменяют сборники задач по математике, но выгодно отличаются от них тем, что их можно решать на компьютере, проверять решения и сразу узнавать результат работы. В этом тесте содержится 70 задач. Но решать задачи можно по выбору, для этого есть оценочная таблица, где указаны простые задачи и посложнее. Ниже приведён тест.
- Дан треугольник со сторонами c, d, m, выраженными в см
- Дан четырехугольник со сторонами b, c, d, m, выраженными в м
- Скорость автомобиля в км/ч равна b, время движения в часах равно d
- Расстояние, которое преодолел турист за m часов, составляет с км
- Расстояние, которое преодолел турист, двигаясь со скоростью m км/ч, составляет b км
- Сумма двух чисел больше второго числа на 15
- Разность меньше уменьшаемого на 7
- Пассажирский лайнер имеет две палубы с одинаковым количеством пассажирских мест.
 В каждом из рядов палубы m мест, рядов на палубе на n больше, чем мест в ряду
В каждом из рядов палубы m мест, рядов на палубе на n больше, чем мест в ряду - Пете m лет Маше n лет, а Кате на k лет меньше, чем Пете и Маше вместе
- m = 8, n = 10, k = 5
- m = 6, n = 8, k = 15
- t = 121, x = 1458
ТО:
- Значение данного выражения
- Буквенное выражение для периметра имеет вид
- Периметр, выраженный в сантиметрах
- Формула пути s, пройденного автомобилем
- Формула скорости v, движения туриста
- Формула времени t, движения туриста
- Путь, пройденный автомобилем в километрах
- Скорость туриста в километрах в час
- Время движения туриста в часах
- Первое число равно…
- Вычитаемое равно….
- Выражение для наибольшего количества пассажиров, которое может перевезти лайнер за k рейсов
- Наибольшее количество пассажиров, которое может перевезти лайнер за k рейсов
- Буквенное выражение для возраста Кати
- Возраст Кати
- Координата точки В, если координата точки С равна t
- Координата точки D, если координата точки С равна t
- Координата точки А, если координата точки С равна t
- Длина отрезка BD на числовом луче
- Длина отрезка CА на числовом луче
- Длина отрезка DА на числовом луче
Ответы (равно, имеет вид, не определено):
а)1; б) s=b ∙d; в) 9; г) 40; д) b + c + d + m; е) 7; ж) выражение не имеет смысла (некорректно) для натуральных чисел; з) 2 ∙ m (m + n) ∙ k; и) (m + n) – k; к) 6; л) 15; м) 3760; н) t – 3; о) фигура не может быть треугольником; п) 22; р) t – 3 ∙ 7; с) 0; т) 32; у) 59600; ф) 6019; х) 2880; ц) 10378; ч)1440; ш) на ноль делить нельзя; щ) 13; ы) 1800; э) 496; ю) 2; я) 12; аа) 14; бб) 5; вв) 35; дд) 79200; ее) 1900; жж) 118; зз) 18; ии) 12800; кк) 98; лл) 1458; мм) v = c : m; нн) 100; оо) 19900; пп) t = b : m; рр) 2520; сс) c + d + m; тт) x; уу) 1579; фф) t + 2; хх) 10206; цц) 135; чч) t + 2 ∙ 7; шш) 7 ∙ x; щщ) x – 2; ыы) 7 ∙ x – 2 ∙ 7; ээ) t + x ∙ 7; юю) 10192; яя) t + x; ааа) 123; ббб) 1456; ввв) 10327.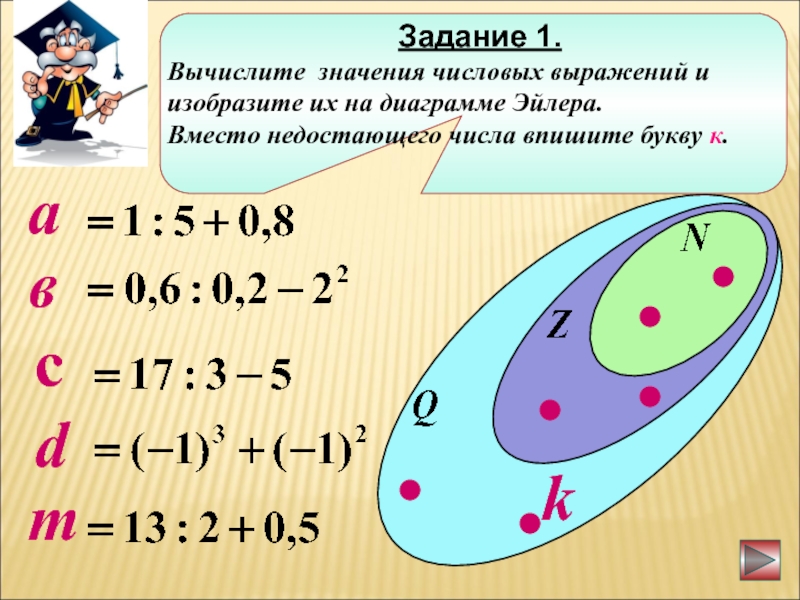
ПОКАЗАТЕЛИ ТЕСТА. Число задач 70, время выполнения 2 – 3 часа, сумма баллов: 1 ∙ 22 + 2 ∙ 24 + 3 ∙ 24 = 142. Для фасетного теста можно использовать следующую шкалу оценок.
Блок 4. Давайте поиграем
Блок 5. Обучающая игра «Уроки кота Леопольда»
Для учителя приводим ответы к блокам параграфа 6
Ответы к игре «Уроки Леопольда»
Западня 1 : 1/2, 1/3, 2/3, 7/8. Западня 2. 12, 2, 13 5. Западня 3. 6
Западня 4. 15. Западня 5. 396
Блок 1. Словарь
Блок 2. Установите соответствие.
Вариант 1: 1и, 2з, 3е, 4б, 5м, 6л, 7а, 8ж, 9в, 10д, 11г, 12к, 13т, 14н, 15ф, 16о, 17у, 18с, 19р, 20п
Вариант 2: 1д, 2е, 3к, 4а, 5г, 6з, 7и, 8б, 9ж, 10в
Блок 3. Фасетный тест. Числовые и буквенные выражения (ответы под заданиями)
Фасетный тест. Числовые и буквенные выражения (ответы под заданиями)
Ответы к игре «Сокровища»
Деревянный – 10250. Оловянный – 21640. Медный – 50400. Серебряный – 191000. Золотой – 289800.
Числовые выражения
Числовые выражения.
Числовое выражение – это любая запись из чисел, знаков арифметических действий и скобок. Числовое выражение может состоять и просто из одного числа. Напомним, что основными арифметическими действиями являются «сложение», «вычитание», «умножение» и «деление». Этим действиям соответствуют знаки «+», «-», «∙», «:».
Конечно же, чтобы у нас получилось числовое выражение, запись из чисел и арифметических знаков должна быть осмысленной. Так, например, такую запись 5 : + ∙ нельзя назвать числовым выражением, так как это случайный набор символов, не имеющий смысла. Напротив, 5 + 8 ∙ 9 — уже настоящее числовое выражение.
Значение числового выражения.
Сразу скажем, что если мы выполним действия указанные в числовом выражении, то в результате мы получим число. Это число называется значением числового выражения.
Это число называется значением числового выражения.
Попробуем вычислить, что у нас получится в результате выполнения действий нашего примера. Согласно порядку выполнения арифметических действий, сначала выполним операцию умножения. Умножим 8 на 9. Получим 72. Теперь сложим 72 и 5. Получим 77.
Итак, 77 – значение числового выражения 5 + 8 ∙ 9.
Числовое равенство.
Можно это записать таким образом: 5 + 8 ∙ 9 = 77. Здесь мы впервые использовали знак «=» («Равно»). Такая запись, при которой два числовых выражения разделены знаком «=», называется числовым равенством. При этом, если значения левой и правой части равенства совпадают, то равенство называют верным. 5 + 8 ∙ 9 = 77 – верное равенство.
Если же мы напишем 5 + 8 ∙ 9 = 100, то это уже будет неверное равенство, так как значения левой и правой части данного равенства уже не совпадают.
Следует отметить, что в числовом выражении мы также можем использовать скобки. Скобки влияют на порядок выполнения действий. Так, например, видоизменим наш пример, добавив скобки: (5 + 8) ∙ 9. Теперь сначала нужно сложить 5 и 8. Получим 13. А затем умножить 13 на 9. Получим 117. Таким образом, (5 + 8) ∙ 9 = 117.
Скобки влияют на порядок выполнения действий. Так, например, видоизменим наш пример, добавив скобки: (5 + 8) ∙ 9. Теперь сначала нужно сложить 5 и 8. Получим 13. А затем умножить 13 на 9. Получим 117. Таким образом, (5 + 8) ∙ 9 = 117.
117 – значение числового выражения (5 + 8 ) ∙ 9.
Как прочитать числовое выражение?
Чтобы правильно прочитать выражение, нужно определить какое именно действие выполняется последним для вычисления значения данного числового выражения. Так, если последнее действие вычитание, то выражение называют «разностью». Соответственно, если последнее действие сумма — «суммой», деление – «частным», умножение – «произведением», возведение в степень – «степенью».
Например, числовое выражение (1+5)(10-3) читается так: «произведение суммы чисел 1 и 5 на разность чисел 10 и 3».
Примеры числовых выражений.
Приведем пример более сложного числового выражения:
\[\left( \frac{1}{4}+3,75 \right):\frac{1,25+3,47+4,75-1,47}{4\centerdot 0,5}\]
В данном числовом выражении используются простые числа, обыкновенные и десятичные дроби.
 Также используются знаки сложения, вычитания, умножения и деления. Черта дроби также заменяет знак деления. При кажущейся сложности, найти значение данного числового выражения довольно просто. Главное уметь выполнять операции с дробями, а также внимательно и аккуратно делать вычисления, соблюдая порядок выполнения действий.
Также используются знаки сложения, вычитания, умножения и деления. Черта дроби также заменяет знак деления. При кажущейся сложности, найти значение данного числового выражения довольно просто. Главное уметь выполнять операции с дробями, а также внимательно и аккуратно делать вычисления, соблюдая порядок выполнения действий.В скобках у нас выражение $\frac{1}{4}+3,75$. Преобразуем десятичную дробь 3,75 в обыкновенную.
$3,75=3\frac{75}{100}=3\frac{3}{4}$
Итак, $\frac{1}{4}+3,75=\frac{1}{4}+3\frac{3}{4}=4$
Далее, в числителе дроби \[\frac{1,25+3,47+4,75-1,47}{4\centerdot 0,5}\] у нас выражение 1,25+3,47+4,75-1,47. Для упрощения данного выражения применим переместительный закон сложения, который гласит: «От перемены мест слагаемых сумма не изменяется». То есть, 1,25+3,47+4,75-1,47=1,25+4,75+3,47-1,47=6+2=8.
В знаменателе дроби выражение $4\centerdot 0,5=4\centerdot \frac{1}{2}=4:2=2$
Получаем $\left( \frac{1}{4}+3,75 \right):\frac{1,25+3,47+4,75-1,47}{4\centerdot 0,5}=4:\frac{8}{2}=4:4=1$
Когда числовые выражения не имеют смысла?
Рассмотрим еще один пример. В знаменателе дроби $\frac{5+5}{3\centerdot 3-9}$ значением выражения $3\centerdot 3-9$ является 0. А, как мы знаем, деление на нуль невозможно. Следовательно, у дроби $\frac{5+5}{3\centerdot 3-9}$ нет значения. Про числовые выражения, у которых нет значения, говорят, что они «не имеют смысла».
В знаменателе дроби $\frac{5+5}{3\centerdot 3-9}$ значением выражения $3\centerdot 3-9$ является 0. А, как мы знаем, деление на нуль невозможно. Следовательно, у дроби $\frac{5+5}{3\centerdot 3-9}$ нет значения. Про числовые выражения, у которых нет значения, говорят, что они «не имеют смысла».
Если мы в числовом выражении помимо чисел будем использовать буквы, то у нас получится уже алгебраическое выражение.
Дата публикации:
Теги: числовые выражения :: 7 класс
Смотрите также учебники, книги и учебные материалы:
Следующие учебники и книги:
Предыдущие статьи:
- Уроки математики, Пособие для учителей, 2 класс, Дорофеев Г.В., Миракова Т.Н., 2009
- Математика, 6 класс, Методические рекомендации, Суворова С.Б., Кузнецова Л.В., Минаева С.С., Рослова Л.О., 2013
- Математика, 6 класс, Методические рекомендации, Потапов М.К., Шевкин А.
 В., 2013
В., 2013 - Математика, 5 класс, Методические рекомендации, Суворова С.Б., Кузнецова Л.В., Минаева С.С., Рослова Л.О., 2013
Числовые выражения — формулы, примеры и алгоритм решения в 7 классе
Основой математики являются числовые выражения. В 7 классе они изучаются подробнее, поскольку к ним применяются специальные методики, позволяющие выполнять операции упрощения. Последние используются для оптимизации вычислений при решении задач по различным дисциплинам с физико-математическим уклоном. Однако специалисты рекомендуют изучить теорию, которая поможет избежать множества ошибок при расчетах величин.
Общие сведения
Многие начинающие математики часто путают два понятия: числовые и алгебраические выражения. Между ними существует разница, которая заключается в определениях. Числовое выражение — вид математического тождества, состоящего только из чисел, скобок и знаков арифметических операций. Например, тождество «5+8/3−4*2» является числовым выражением. Оно означает последовательность математических знаков, объединенных в одну логическую цепочку.
Оно означает последовательность математических знаков, объединенных в одну логическую цепочку.
Алгебраическим называется совокупность переменных и числовых выражений, имеющих логическое завершение. Объяснение смысла логики выражения имеет такой вид: совокупность чисел и переменных, связанных между собой арифметическими операциями умножения, деления, сложения и вычитания. Например, выражение «5t-2/3» — алгебраическое, поскольку в нем присутствует переменная «t».
Математическим выражением не является набор символов, не имеющий логического завершения. Например, 234±4678++* — обыкновенный ряд, который можно составить из цифр и знаков арифметических операций. Последние имеют следующие обозначения:
Произведение — вид арифметической операции, позволяющей умножить одну величину на другую. Она состоит из трех основных элементов. К ним относятся: I множитель, II множитель и произведение (результат). Математики утверждают, что для сокращения сложения применяется умножение, то есть 3+3+3+3+3+3=3*6=18. Если рассчитать оба выражения, то они будут равными между собой.
Математики утверждают, что для сокращения сложения применяется умножение, то есть 3+3+3+3+3+3=3*6=18. Если рассчитать оба выражения, то они будут равными между собой.
Деление — арифметическая операция, используемая для поиска сомножителей искомого числа. Она состоит из следующих обязательных компонентов: делимого, делителя и частного. Первый элемент — составное значение, второй — один из множителей первого, а частное — результат операции деления.
Сложение — простейшая арифметическая операция, составление которой осуществляется минимум из трех элементов и позволяющая увеличивать искомую величину на определенное значение. Компоненты имеют следующие названия: два слагаемых и результат, который называется суммой.
Вычитание — операция, необходимая для уменьшения искомого числа на заданную величину. Она состоит из трех компонентов: уменьшаемого, вычитаемого и разности. Первое — числовое значение, от которого отнимается вычитаемое.
Однако у каждой операции есть определенный приоритет.
Приоритет операций
При вычислении математических выражений существует определенный приоритет арифметических операций. Сначала выполняются умножение и деление. Они обладают максимальной величиной приоритета. Иногда для оптимизации вычислений можно выполнять действие над числами или переменными в любой последовательности, то есть пример «2*26/13» можно решить двумя способами:
В первом случае операция займет больше ресурсов: сначала требуется 2 умножить на 26, высчитать результат, а затем его поделить на 13. Это не слишком удобно. Однако для оптимизации вычислений рекомендуется применять второй способ, поскольку особого труда не составляет 26 разделить на 13, а затем результат перемножить с двойкой.
Сложение и вычитание имеют также одинаковый уровень приоритета. Можно сначала для удобства выполнить сложение, а затем вычитание или наоборот. Специалисты рекомендуют руководствоваться важным принципом: вычисления должны быть максимально упрощены. Чтобы задать приоритет какому-либо математическому действию, необходимо взять часть выражения в скобки (сгруппировать). В результате этого первой будет выполняться операция, находящаяся в скобках.
Можно сначала для удобства выполнить сложение, а затем вычитание или наоборот. Специалисты рекомендуют руководствоваться важным принципом: вычисления должны быть максимально упрощены. Чтобы задать приоритет какому-либо математическому действию, необходимо взять часть выражения в скобки (сгруппировать). В результате этого первой будет выполняться операция, находящаяся в скобках.
Для примера нужно найти значение выражения: 2*2−2 (3−2)*7/14−25/5. Решать его правильно по такой методике с учетом приоритета:
Если не учитывать приоритет выполнения операций, то найти значение числового выражения можно по такой схеме:
Если сравнить два результата, то они не совпадают. На основании этого можно сделать вывод, что приоритет имеет значение при выполнении вычислений и нарушать его нельзя, поскольку исчезнет логика выражения. Однако не только скобки позволяют установить очередность операций. Существуют некоторые исключения.
Частные случаи или исключения
В алгебре, как и во всех дисциплинах с физико-математическим уклоном, учитывается скорость вычислений. Это существенно влияет на время выполнения какого-либо задания. В некоторых случаях выражение можно упростить, используя формулы сокращенного умножения и выполняя математические преобразования с элементами тождества. Для этих целей рекомендуется пользоваться соответствующими правилами:
Следует отметить, что в первом случае обязательно требуется проверить равенство знаменателя нулевому значению. Для этого следует указать величину переменной, которая не должна превращать знаменатель в 0.
Методика вычисления
Математики разработали специальную методику нахождения значения выражения. Она сводится к разбиению числового выражения на части. Этот подход впервые использовал Пифагор. Суть его состоит в следующем:
Для демонстрации алгоритма необходимо решить пример: 9*7−21 (74/(43+31))/7−64-(27−3*9). Практическая реализация методики имеет следующий вид:
Следует отметить, что этот алгоритм позволяет реализовать принцип «дробления» задания на несколько компонентов. Разбивать тождество можно в произвольном порядке.
Таким образом, для расчета значения числового выражения нужно воспользоваться специальным алгоритмом, который позволит существенно оптимизировать вычисления.
ПредыдущаяАлгебраАлгебра как наука — история появления, классификация раздела и понятия
Числовые и буквенные выражения. Порядок действий. 🐲 СПАДИЛО.РУ
Что такое числовое выражение?Числовое выражение – это выражение, состоящее из чисел и знаков действий, а также скобок.
Пример №1. В каждом из этих выражений содержатся числа, между которыми есть знаки действий, а также бывают скобки. Это и есть числовые выражения.
- 256 : 2 + 315×5
- (181 – 19)×6 – 121:11
- 13,5 + 16 – 11
- 122 — 14×8,5
Если выполнить по порядку все действия, которые есть в числовом выражении, то получится определенное число, которое называют значением числового выражения. Порядок действий в числовых выражениях определяется правилами.
Важно!Действия сложение и вычитание принято называть действиями первой ступени, а умножение и деление – действиями второй ступени. Возведение в степень – это действие третьей ступени.
Порядок действий в выражении, не содержащем скобки
Порядок действий без скобок- При наличии действий одной ступени их выполняют по порядку слева направо.
- При наличии действий разных ступеней — выполнение начинается с высшей ступени (то есть с третьей).
Пример №2.
890 – 567 + 2340 – 124
в данном выражении действия одной ступени (сложение и вычитание), поэтому выполняем их по порядку слева направо:
- 890 – 567 = 323
- 323 + 2340=2663
- 2663 – 124=2539
1260:20×3,7:10
в этом выражении также действия одной ступени (умножение и деление), поэтому выполняем их по порядку слева направо:
- 1260:20=63
- 63 3,7=233,1
- 233,1:10=23,31
560:2 + 162 – 3×76,2
здесь присутствуют действия всех ступеней. Поэтому начинаем выполнять их с наивысшей ступени – возведения в степень. Затем слева направо выполняем деление и умножение, а затем слева направо – сложение и вычитание:
- 162=256
- 560:2=280
- 3 76,2=228,6
- 280+256=536
- 536 – 228,6=307,4
Порядок действий в выражении, содержащем скобки
Порядок действий со скобкамиЕсли числовое выражение содержит скобки, то выполняют сначала действия в скобках, следуя правилу, а затем – действия за скобками.
Пример №5.
(3245 + 67,92:2)×3 + (126×2 – 321:3) – 125
здесь числовое выражение содержит скобки, поэтому действия выполняем в скобках слева (деление, затем сложение), затем в скобках справа (умножение, деление, вычитание):
- 67,92:2=33,96
- 3245+33,96=3278,96
- 126×2=252
- 321:3=107
- 252-107=145
Теперь выполняем действия за скобками слева направо (умножение, сложение, вычитание):
- 3278,96×3=9836,88
- 9836,88+145=9981,88
- 9981,88 – 125=9856,88
Буквенные выражения. Числовое значение буквенного выражения.
Какие выражения называют буквенными?Выражения, содержащие не только числа и знаки действий, но и буквы, называют буквенными. Буквы также можно называть «переменная». Обращаем внимание на то, что знак «умножить» между числом и буквой не пишется.
Пример №6. Примеры буквенных выражений:
- 5х + 6у
- 18 + a + b
- 12с – 11
- m + n
- (x + n) – 11m
Числовое значение буквенного выражения – это значение числового выражения, полученного при подстановке конкретных значений переменной в данное выражение.
Пример №7. Найдем значение выражения с + х при с=23, х=0,17. Для этого подставим вместо с и х их данные числовые значения и получим числовое выражение 23 + 0,17. Теперь вычислим результат и получим 23,17. Таким образом, числовое значение буквенного выражения с + х равно 23,17.
Пример №8. Найдем значение выражения 11х +(с — d) при х=10, c=178, d=121. Для этого подставляем вместо каждой переменной соответствующие числовые значения и получим числовое выражение 11×10 + (178 – 121). Выполнив действия, получим ответ 167. Это и есть числовое значение буквенного выражения.
Заметим, что и числовые и буквенные выражения можно называть еще как алгебраические выражения.
Что такое числовое выражение? — Определение, факты и пример
Что такое числовое выражение?
Термин «числовое выражение» состоит из двух слов, числового значения числа и выражения, означающего фразу. Таким образом, это фраза, состоящая из чисел.
Числовое выражение в математике может быть комбинацией чисел, целых чисел, объединенных с использованием математических операторов, таких как сложение, вычитание, умножение или деление.
Примеры числовых выражений
Мы можем сформировать числовое выражение, комбинируя числа с различными математическими операторами.Число операторов, которые может содержать числовое выражение, не ограничено. Некоторые числовые выражения используют только один оператор между двумя числами, а некоторые могут содержать больше.
Некоторые примеры числовых выражений приведены ниже:
10 + 5
250–75
60 × 5 + 10
72 ÷ 8 × 5 — 4 + 1
82 + 4 — 10
Запись числового выражения
Любая математическая словесная задача решается сначала преобразованием в числовое выражение.Ниже приведены некоторые примеры.
У Кэндис 10 плиток шоколада. Она дает 3 сестре, 1 подруге и съедает 2 из них. Позже она навещает свою бабушку, и она (бабушка) предлагает Кэндис еще 12 плиток шоколада. Сколько плиток шоколада у Кэндис сейчас?
Давайте посмотрим на числа, участвующие в указанной выше проблеме. Кэндис начинает с 10 батончиков, раздает 4 (3 + 1), съедает 2 и снова получает еще 12 от бабушки. Итак, числовое выражение
10–3–1–2 + 12
= 7–1–2 + 12
= 6–2 + 12
= 4 + 12
= 16
Это дает нам 16.
Интересные факты
|
Например:
Алгебраические выражения — объяснения и примеры
Алгебра — интересный и увлекательный раздел математики, в котором числа, фигуры и буквы используются для выражения задач.Независимо от того, изучаете ли вы алгебру в школе или сдаете какой-то тест, вы заметите, что почти все математические задачи представлены словами.
Следовательно, необходимость переводить письменные текстовые задачи в алгебраические выражения возникает тогда, когда нам нужно их решить.
Большинство алгебраических задач со словами состоят из рассказов или случаев из реальной жизни. Другие — простые фразы, такие как описание математической задачи. Из этой статьи вы узнаете, как написать алгебраических выражений из простых текстовых задач, а затем перейти к слегка сложным текстовым задачам.
Что такое алгебраическое выражение?
Многие люди попеременно используют алгебраические выражения и алгебраические уравнения, не подозревая, что это совершенно разные термины.
Алгебраика — это математическая фраза, в которой две стороны фразы соединены знаком равенства (=). Например, 3x + 5 = 20 — это алгебраическое уравнение, где 20 представляет собой правую часть (RHS), а 3x +5 представляет собой левую часть (LHS) уравнения.
С другой стороны, алгебраическое выражение — это математическая фраза, в которой переменные и константы объединяются с помощью операционных символов (+, -, × & ÷).В алгебраическом символе отсутствует знак равенства (=). Например, 10x + 63 и 5x — 3 являются примерами алгебраических выражений.
Давайте рассмотрим терминологию, используемую в алгебраическом выражении:
- Переменная — это буква, значение которой нам неизвестно. Например, x — это наша переменная в выражении: 10x + 63.
- Коэффициент — это числовое значение, используемое вместе с переменной. Например, 10 — это переменная в выражении 10x + 63.
- Константа — это терм, который имеет определенное значение.В этом случае 63 — это константа в алгебраическом выражении, 10x + 63.
Существует несколько типов алгебраических выражений, но основной тип включает:
- Мономиальное алгебраическое выражение
Этот тип выражения имеет только один член, например, 2x, 5x 2 , 3xy и т. д.
Алгебраическое выражение, содержащее два, в отличие от членов, например, 5y + 8, y + 5, 6y 3 + 4 и т. д.
Это алгебраическое выражение с более чем одним членом и ненулевыми показателями переменных.Пример полиномиального выражения: ab + bc + ca и т. Д.
Другие типы алгебраических выражений:
Числовое выражение состоит только из чисел и операторов. В числовое выражение не добавляется никакая переменная. Примеры числовых выражений: 2 + 4, 5-1, 400 + 600 и т. Д.
Это выражение содержит переменные вместе с числами, например, 6x + y, 7xy + 6 и т. Д.
Как решить алгебраическое выражение?
Цель решения алгебраического выражения в уравнении — найти неизвестную переменную.Когда два выражения приравниваются, они образуют уравнение, и поэтому становится легче найти неизвестные члены.
Чтобы решить уравнение, поместите переменные с одной стороны, а константы — с другой. Вы можете изолировать переменные, применяя арифметические операции, такие как сложение, вычитание, умножение, деление, квадратный корень, кубический корень и т. Д.
Алгебраические выражения всегда взаимозаменяемы. Это означает, что вы можете переписать уравнение, поменяв местами LHS и RHS.
Пример 1
Вычислите значение x в следующем уравнении
5x + 10 = 50
Решение
Заданное уравнение как 5x + 10 = 50
- Изолируйте переменные и константы;
- Вы можете сохранить переменную на левой стороне, а константы на правой.
5x = 50-10
5x = 40
Разделите обе части на коэффициент переменной;
x = 40/5 = 8
Следовательно, значение x равно 8.
Пример 2
Найдите значение y, когда 5y + 45 = 100
Решение
Изолировать переменные от констант;
5y = 100-45
5y = 55
Разделим обе части на коэффициент;
y = 55/5
y = 11
Пример 3
Определите значение переменной в следующем уравнении:
2x + 40 = 30
Решение
Разделите переменные из константы;
2x = 30-40
2x = -10
Разделите обе стороны на 2;
x = -5
Пример 4
Найдите t, когда 6t + 5 = 3
Решение
Отделите константы от переменной,
6t = 5 — 3
6t = -2
Разделим обе части на коэффициент,
t = -2/6
Упростим дробь,
t = -1/3
Практические вопросы
1.Если x = 4 и y = 2, найдите следующие выражения:
a. 2г + 4
б. 10х + 40л;
г. 15лет — 5x
д. 5x + 7
e. 11y + 6
ф. 6x — 2
г. 8лет — 5
ч. 60 — 5x — 2y
2. Сэм кормит свою рыбу одинаковым количеством корма (пусть равным x ) трижды в день. Сколько еды он накормит рыбу в неделю?
3. Нина испекла по 3 кекса для сестры и по 2 кекса для каждой подруги (пусть равняется x ).Сколько всего кексов она испекла?
4. У Джонса на ферме 12 коров. Большинство коров дают 30 литров молока в сутки (пусть равно х ). Сколько коров не дают 30 литров молока в день?
Предыдущий урок | Главная страница | Следующий урокЧисловые выражения
Числовые выраженияЧисловые выражения
Числовые данные представлены как последовательность цифр (0–9) с необязательная десятичная точка. Ведущий плюс (+) или минус (-) знак может быть использован, но запятые не допускаются.Любые данные, содержащие любые символы, отличные от чисел, и одна десятичная точка будут интерпретироваться в виде строки. Вот некоторые примеры числовых значений:
-34
42368,99
+3.1416
Числовые данные могут содержать до 19 цифр, включая максимум 9 десятичных знаков. позиции. См. Заявление о ТОЧНОСТИ в обзоре операторов и функций mvBASIC для получения информации о том, как установить максимальное количество цифр после дробной части.
Арифметические операторы
Арифметические операции варьируются от простейших вычислений (например, СТОИМОСТЬ = COST + 5) в сложные выражения, объединяющие тригонометрические и логарифмические функции. В общем, когда несколько арифметических операций используются в одном выражении, они следуют общепринятым математическим принципам в приоритет. Арифметические операторы, доступные для mvBASIC, в порядке старшинства, перечислены ниже:
Оператор | Эксплуатация | Пример выражения |
+ | Одинарный плюс | + СТОИМОСТЬ |
– | Унарный минус | –СТОИМОСТЬ |
* | Умножение | СТОИМОСТЬ * РАСХОДЫ |
/ | Отдел | СТОИМОСТЬ / РАСХОДЫ |
+ | Дополнение | СТОИМОСТЬ + РАСХОДЫ |
– | Вычитание | СТОИМОСТЬ — РАСХОДЫ |
В случаях, когда операторы эквивалентны по приоритету (например, * и /) используются, порядок оценки следует слева направо.
Круглые скобки в выражениях
Порядок оценки можно изменить, используя круглые скобки. Операции в выражениях, заключенных в круглые скобки, выполняются раньше остальных.
Пример
В приведенном выше примере выражение оценивается как 112 + 6 + 2 или 120. Вкл. с другой стороны, следующее арифметическое выражение оценивается как 14 * 20/4 или 70:
В арифметических выражениях круглые скобки должны быть правильно расставлены по порядку. для получения желаемого результата.
Строки символов в арифметических выражениях
Если строковая символьная переменная, которая оценивается как число, используется в арифметическое выражение, символьная строка рассматривается как числовая Переменная. То есть числовая символьная строка преобразуется в ее эквивалент. внутреннее число, а затем вычисляется численно в арифметическом выражении.
Предыдущий пример оценивается как 77. Если переменная строки символов который не вычисляется до числа, используется в арифметическом выражении, отображается предупреждающее сообщение, и строка считается нулем.
Следующий пример выражения оценивается как 55:
Отображается сообщение, предупреждающее о том, что данные не являются числовыми, напоминая следующие:
[B16] СТРОКА 16 НЕЧИСЛОВЫЕ ДАННЫЕ, КОТОРЫЕ ЦИФРОВЫЕ ОБЯЗАТЕЛЬНЫЙ; НОЛЬ ИСПОЛЬЗУЕТСЯ! |
Внутренние математические функции
Внутренняя функция — это встроенная функция mvBASIC для использования с числовыми операнды. Ниже приводится список доступных математических функций. в mvBASIC:
Функция | Описание |
АБС | Вычисляет абсолютное значение данного арифметического выражения. |
COS | Возвращает косинус. значение угла, указанное в выражении. |
EXP | Возвращает экспоненту. значение, которое повысит базовое число e (2,7183) до значения выражения. |
ИНТ | Усекает десятичная часть данного арифметического выражения и возвращает целочисленное значение. |
LN | Создает натуральный логарифм (логарифм с основанием е) данного выражения. |
PWR | Повышает значение выражения в степень, обозначенную вторым выражением. |
REM | Делит выражение другим и возвращает только оставшееся значение. |
RND | Создает случайный число в диапазоне от 0 и значение выражения минус 1. |
SIN | Возвращает синус значение угла, указанное в выражении. |
SQRT | Вычисляет квадратный корень из любого положительного числового выражения. |
ТАН | Возвращает тангенс. значение угла, указанное в выражении. |
См. Описание и функции Ссылка для получения полной информации о синтаксисе и поведении этих функции.
См. Также
Строительные выражения
Простое присвоение
Использование операторов и функций
Строковые выражения
Логические данные (логические значения)
Запись и интерпретация числовых выражений Видео от NUMBEROCK
Узнайте все о написании и интерпретации числовых выражений в этом футуристическом музыкальном видео о планете, вращающейся вокруг Альфы Центури.После просмотра числовых выражений видео затем вводит ключевые слова, которые могут помочь нам интерпретировать выражения, задачи со словами и многое другое!
Числовые выражения Текст: Verse 1
Операции и шаги
числового выражения находятся в его словах, которые подробно описывают процесс.
Посмотрите на символы группировки, чтобы определить
, какие вычисления должны быть выполнены перед другими.
Давайте посмотрим, что я имею в виду, на нескольких примерах —
— на нескольких примерах числовых выражений.
Но сначала соло на Бонго… поехали!
Что такое «четырехкратное частное двадцати и десяти»?
Прежде чем умножить, нам нужно найти частное;
заключаем в скобки «двадцать, разделенные на десять» —
получаем «четыре умножить на два» — «восемь» отвечает на вопрос.
Припев
Чтобы писать и интерпретировать числовые выражения,
мы внимательно их читаем и задаем следующие вопросы:
Какие операции описаны в этой задаче?
И в каком порядке мы их будем решать?
Стих 2
Что такое «девяносто, разделенное на разницу в четырнадцать и пять»?
«Четырнадцать минус пять» попадает в скобки — их разница в «девять».
Следующий шаг обозначен знаком деления.
Разделите «девяносто на девять» и «десять», чтобы получить частное.
Давайте посмотрим на пример — еще раз —
с лучшими рифмами, которые вы когда-либо когда-либо находили.
Но сначала соло на Бонго… поехали!
Что такое «в десять раз больше суммы сорока пятидесяти трех»?
Сначала заключите «сорок плюс пятьдесят три» в круглые скобки;
слова говорят нам сначала сложить и получить «девяносто три» —
затем «умножить на десять», чтобы закончить стих.
Мост
Когда математический класс находится в сеансе
и мы читаем числовое выражение,
словных подсказок могут помочь нам выбрать операции,
, чтобы мы могли делать правильные вычисления.
Плюс, все, вместе, всего, всего и сумма…
это все ключевые слова для сложения.
Сколько еще, минус, осталось, меньше, разница…
— все ключевые слова для вычитания.
На, умножение, умножение, произведение на…
— все это ключевые слова для умножения.
Сколько раз, разделить, перейти, частное…
— все это ключевые слова для деления.
Эта песня ориентирована на стандарты обучения Common Core для 5-х классов. Ознакомьтесь с соответствующими стандартами здесь.
Если вы заинтересованы в том, чтобы получить идеи о том, как спланировать надежный и согласованный со стандартами урок по написанию и интерпретации выражений, мы рекомендуем ознакомиться с рекомендациями Instructure для общих основных стандартов 5.OA.2 Эта страница помогает разбить стандартный язык и выставить оценку -соответствующий уровень строгости для каждой концепции и предлагает различные предложения по занятиям (семенам урока), которые помогают учащимся достичь своих учебных целей.
Чтобы продолжить просмотр библиотеки материалов по математике Numberock, щелкните здесь. Чтобы получить доступ к растущей библиотеке премиум-контента Numberock, щелкните здесь.
частей выражения
Алгебраические выражения — это комбинации переменные , числа и хотя бы одну арифметическую операцию.
Например, 2 Икс + 4 y — 9 является алгебраическим выражением.
Срок: Каждое выражение состоит из терминов. Термин может быть числом со знаком, переменной или константой, умноженной на переменную или переменные.
Фактор: То, что умножается на другое. Фактор может быть числом, переменной, термином или более длинным выражением. Например, выражение 7 Икс ( y + 3 ) имеет три фактора: 7 , Икс , а также ( y + 3 ) .
Коэффициент: Числовой коэффициент выражения умножения, содержащего переменную. Рассмотрим выражение на рисунке выше, 2 Икс + 4 y — 9 . В первом семестре 2 Икс , коэффициент равен 2 : во втором семестре, 4 y , коэффициент равен 4 .
Постоянный: Число, которое не может изменить свое значение.В выражении 2 Икс + 4 y — 9 , термин 9 является константой.
Как условия: Термины, содержащие одинаковые переменные, такие как 2 м , 6 м или же 3 Икс y а также 7 Икс y . Если в выражении есть несколько постоянных членов, они также похожи на термины.
|
|
|
|
|
|
|
|
|
|
Пример:
Определите термины, такие как термины, коэффициенты и константы в выражении.
9 м — 5 п + 2 + м — 7
Во-первых, мы можем переписать вычитания как добавления.
9 м — 5 п + 2 + м — 7 знак равно 9 м + ( — 5 п ) + 2 + м + ( — 7 )
Итак термины находятся 9 м , ( — 5 п ) , м , 2 , а также ( — 7 ) .
Как условия — это термины, содержащие одинаковые переменные.
9 м а также 9 м пара как условия . Постоянные условия 2 а также — 7 также похожи на термины.
Коэффициенты — числовые части термина, содержащего переменную.
Итак, вот коэффициенты находятся 9 , ( — 5 ) , а также 1 . ( 1 коэффициент при члене м .)
В постоянный термины — это термины без переменных, в данном случае 2 а также — 7 .
Алгебраические выражения должны быть написаны и интерпретированы осторожно.Алгебраическое выражение 5 ( Икс + 9 ) является нет эквивалентно алгебраическому выражению, 5 Икс + 9 .
Посмотрите разницу между двумя выражениями в таблице ниже.
| Словесные фразы | Алгебраическое выражение |
| В пять раз больше числа и девяти | 5 ( Икс + 9 ) |
| Девять больше, чем в пять раз больше | 5 Икс + 9 |
При написании выражений для неизвестных величин мы часто используем стандартные формулы.Например, алгебраическое выражение «расстояние, если скорость 50 миль в час, а время Т часов «это D знак равно 50 Т (по формуле D знак равно р Т ).
Выражение вроде Икс п называется властью. Здесь Икс это база, а п — показатель степени. Показатель степени — это количество раз, когда основание используется в качестве фактора.Словосочетание для этого выражения: » Икс к п th мощность.»
Вот несколько примеров использования экспонент.
| Словесные фразы | Алгебраическое выражение |
| Семь раз м в четвертой степени | 7 м 4 |
| Сумма Икс в квадрате и 12 времена y | Икс 2 + 12 y |
| Икс раз в кубе y в шестой степени | Икс 3 ⋅ y 6 |
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.ПРОДУКТЫ}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$ select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}} Примерыи связанный синтаксис для числовых выражений
В этом разделе перечислены общие примеры и связанный синтаксис, на который вы можете ссылаться в своем конкретном сценарии.
Синтаксис для получения количества любой линии продуктов, выбранной для предложения:
Apttus_Config2__LineItem__c. $ CartLines ['Apttus_Config2__ProductId__r.Name', 'Product A'] [0] .Apttus_Config2__Quantity__c КОД
Вставить поле > Позиция > CartLines > Выберите поле и укажите фильтр и индекс.
Синтаксис для получения количества опций родственника в одном родительском пакете:
Apttus_Config2__LineItem__c.$ ParentBundle. $ Options ['Apttus_Config2__OptionId__r.Name', 'Solar Panel 80-100 Watt'] [0] .Apttus_Config2__Quantity__c КОД
Вставить поле > Позиция > ParentBundle > Параметры > Выберите поле и укажите фильтр и индекс.
Получение поля продукта пакета
Apttus_Config2__LineItem__c.Apttus_Config2__ProductId__r.Numr_Numb__cКОД
Вставить поле > Отдельная позиция > Продукт > Выберите поле
Получение поля продукта Option при создании выражения для продукта пакета.
Apttus_Config2__LineItem__c. $ Options [поле, значение] [индекс] .Apttus_Config2__OptionId__r.Numr_Numb__cКОД
Вставить поле > Позиция > ParentBundle > Параметры > Выберите поле и укажите фильтр и индекс.
При настройке Bundle-In-Bundle, если вы хотите обновить атрибут дополнительного продукта, минимальное и максимальное количество на основе значения поля из его продукта пакета, который является опцией другого пакета.
Apttus_Config2__LineItem__c. $ ParentBundle.Apttus_Config2__OptionId__r.Numr_Numb__cКОД
В настройке Bundle-In-Bundle, если вы хотите обновить атрибут дополнительного продукта, минимальное и максимальное количество на основе значения поля из верхнего продукта комплекта.
Apttus_Config2__LineItem__c. $ MainBundle.Apttus_Config2__ProductId__r.Numr_Numb__cКОД
Синтаксис для получения значения атрибута продукта как части выражения:
Apttus_Config2__ProductAttributeValue__c.Total_Daily_WattHours__c КОД
Вставить поле > Атрибуты продукта > Выберите поле
Синтаксис, чтобы определить значение атрибута с использованием другого атрибута того же продукта или опции
Apttus_Config2__ProductAttributeValue__c.Длина__c * 0,25 КОД
Синтаксис для получения значения атрибута продукта родительского пакета как части выражения:
Apttus_Config2__LineItem__c. $ ParentBundle.Apttus_Config2__AttributeValueId__r.Battery_Capacity_Needed__c КОД
Вставить поле > Позиция > ParentBundle > AttributeValue > Выберите поле
Синтаксис для определения свертки в заголовке
Укажите объект, который нужно обновить, и поле объекта, которое нужно обновить.В поле выражения значений укажите поля, из которых вы хотите получить значения.
BLANKVALUE ($. AttributeValueId__r.Total_daily_WattHours_required__c, 0) * 3 КОД
Укажите область действия как «Продукт» и введите имя продукта в поле «Продукт». Убедитесь, что вы определяете родительское поле как LineItemId_c в области «Критерии объединения».
Укажите область действия как Продукт, а в области «Соответствие выражению» введите ParentBundleNumber__c == $ condition.PrimaryLineNumber__c
Укажите область как Группа продуктов и введите имя группы продуктов в поле Группа продуктов. Убедитесь, что вы определяете родительское поле как LineItemId_c в области «Критерии объединения».
Синтаксис для определения сводных данных для конкретных номеров предложений или номеров счетов:
Укажите область действия как заголовок и в области «Соответствие выражения» введите
BLANKVALUE (ConfigurationId__r.Proposald__r.Apttus_Proposal__Account__r.Name == 'Имя учетной записи', 0) КОД
Синтаксис для определения наборов опций для определенных пакетов или нескольких пакетов
Укажите область действия как Продукт, укажите имя продукта в поле Продукт и в области Выражение соответствия введите
ParentBundleNumber__c == $ condition.PrimaryLineNumber__c КОД
Убедитесь, что вы определили родительское поле как LineItemId_c в области «Критерии объединения».
Синтаксис для определения свертки на основе суммы значений атрибутов
Укажите область как Продукт, укажите имя продукта в поле Продукт и в области Критерии выражения укажите выражение значения как
BLANKVALUE ($. AttributeValueId__r.PerfAttr1__c, 0) + BLANKVALUE ($. AttributeValueId__r.PerfAttr2__c, 0) + BLANKVALUE ($. AttributeValueId__r.PerfAttr3__c, 014) 909
КОД
Убедитесь, что вы определили родительское поле как LineItemId_c в области «Критерии объединения».
Синтаксис для определения числовой сводной сводной записи в числовом выражении
Для того, чтобы свернуть конкретный атрибут продукта (который является числовым) на основе опций агрегирования количества продукта, выполните следующее.
В свернутом количестве параметров
В разделе «Условие совпадения» укажите Apttus_Config2__LineItem__c.Apttus_Config2__ParentBundleNumber__c! = NULL ()
Выберите SUM в качестве операции объединения.
В разделе «Агрегатное выражение» укажите Apttus_Config2__LineItem__c.Apttus_Config2__Quantity__c
Затем используйте сводную сводку в выражении следующим образом:
Apttus_Config2__LineItem__c. $ Rollups ['fieldName', значение] .Apttus_Config2__TotalQuantity__c КОД
Синтаксис для установки значения атрибута продукта из значения атрибута другого продукта в корзине:
ПУСТО ЗНАЧЕНИЕ (ЗНАЧЕНИЕ (Apttus_Config2__LineItem__c. $ CartLines ['Apttus_Config2__ProductId__r.Семья »,« Ноутбук »]. Apttus_Config2__AttributeValueId__r.Size__c), 17) BLANKVALUE (VALUE (Apttus_Config2__LineItem__c. $ CartLines ['Apttus_Config2__ProductId__r.Name', 'Toshiba Satellite S875-S737617,3 дюйма']. Apttus_Config2__AttributeValueId__r.Size) BLANKVALUE (VALUE (Apttus_Config2__LineItem__c. $ CartLines ['Apttus_Config2__ProductId__r.ProductCode', 'LP104']. Apttus_Config2__AttributeValueId__r.Size__c), 14)КОД
Синтаксис для установки значения атрибута элемента опции со значением атрибута другого элемента опции внутри того же набора.
Apttus_Config2__LineItem__c. $ ParentBundle. $ Options ['Apttus_Config2__OptionId__r.Name', 'Option 1.1']. Apttus_Config2__AttributeValueId__r.Length__c КОД
Синтаксис для установки значения параметра по умолчанию / минимального / максимального количества на основе значения атрибута родительского пакета:
BLANKVALUE (VALUE (Apttus_Config2__LineItem__c. $ ParentBundle.Apttus_Config2__AttributeValueId__r.Data_Transfer_Limit_Month_in_TB__c), 0)
ПУСТОЕ ЗНАЧЕНИЕ (Apttus_Config2__LineItem__c.$ ParentBundle.Apttus_Config2__AttributeValueId__r.Number_of_Users__c + 5, 0) КОД
Синтаксис для условной установки значения атрибута или минимального / максимального / количества по умолчанию элемента опции, в зависимости от значения атрибута из родительского пакета.
IF (Apttus_Config2__LineItem__c. $ ParentBundle.Apttus_Config2__AttributeValueId__r.Edition__c == 'Enterprise', BLANKVALUE (Apttus_Config2__LineItem__c. $ ParentBundle.Apttus_Config2__AttributeValueId__r.Number_of_Users__c + 5, 0),
BLANKVALUE (Apttus_Config2__LineItem__c. $ ParentBundle.Apttus_Config2__AttributeValueId__r.Number_of_Users__c + 10, 0)) КОД
Синтаксис для установки количества опции с использованием количества другой опции в том же наборе.
BLANKVALUE (Apttus_Config2__LineItem__c. $ ParentBundle. $ Options ['Apttus_Config2__OptionId__r.Name', 'Option 1.1']. Apttus_Config2__Quantity__c * 2, 0) КОД
Синтаксис для установки значения атрибута или минимальных / максимальных / значений по умолчанию с использованием числового сведения:
ПУСТО ЗНАЧЕНИЕ (Apttus_Config2__LineItem__c.
