Равноускоренное движение: формулы, примеры
Равноускоренное движение
Равноускоренное движение — это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение — частный случай равноускоренного движения с ускорением, равным нулю.
Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.
В любой точке траектории на тело действует ускорение свободного падения g→, которое не меняется по величине и всегда направлено в одну сторону.
Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.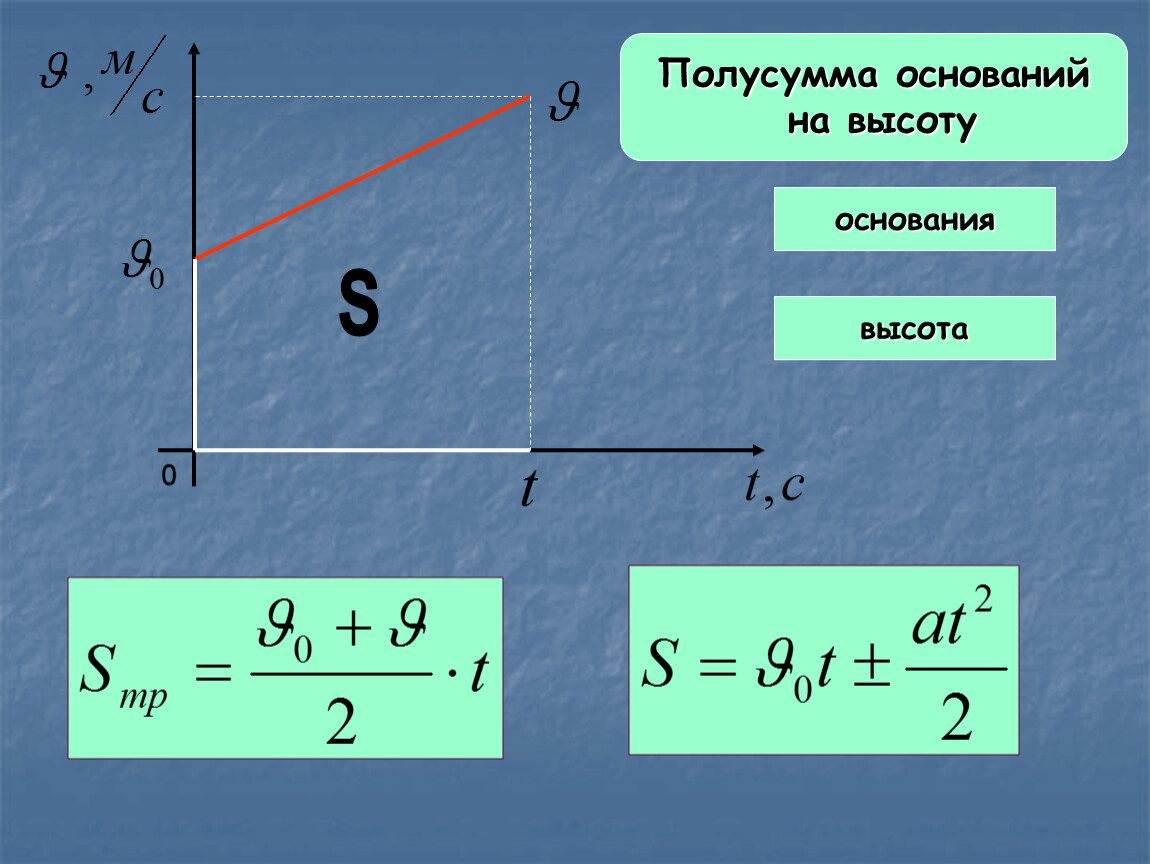
Формулы для равноускоренного движения
Формула для скорости при равноускоренном движении:
v=v0+at.
Здесь v0 — начальная скорость тела, a=const — ускорение.
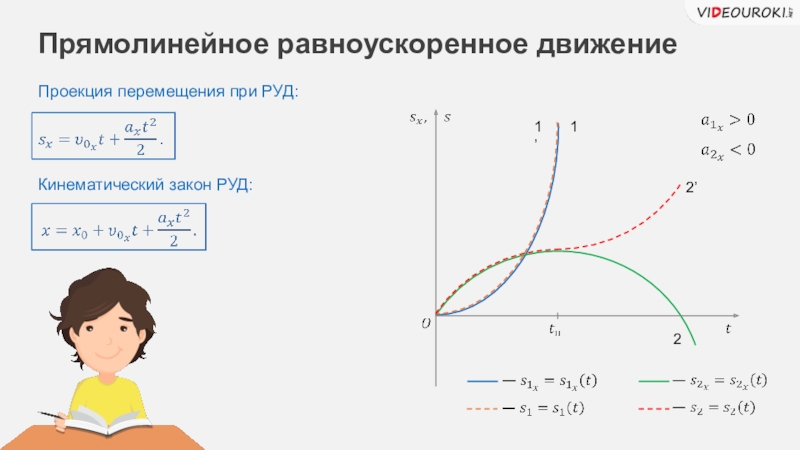
Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии.
Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.
a=v-v0t=BCAC
Чем больше угол β, тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.
Для первого графика: v0=-2 мс; a=0,5 мс2.
Для второго графика: v0=3 мс; a=-13 мс2.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеПо данному графику можно также вычислить перемещение тела за время t. Как это сделать?
Выделим на графике малый отрезок времени ∆t. Будем считать, что он настолько мал, что движение за время ∆t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆t.
Разобьем все время t на бесконечно малые промежутки ∆t. Перемещение s за время t равно площади трапеции ODEF.
s=OD+EF2OF=v0+v2t=2v0+(v-v0)2t.
Мы знаем, что v-v0=at, поэтому окончательная формула для перемещения тела примет вид:
s=v0t+at22
Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.
Закон равноускоренного движения
Закон равноускоренного движенияЕще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения — нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.
Исключая из записанных выше уравнений t и решая их, получаем:
s=v2-v022a.
По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:
v=v02+2as.
При v0=0 s=v22a и v=2as
Важно!Величины v, v0, a, y0, s, входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.
Равноускоренное движение — материалы для подготовки к ЕГЭ по Физике
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное падение.
Равноускоренное движение — это движение с постоянным вектором ускорения . Таким образом, при равноускоренном движении остаются неизменными направление и абсолютная величина ускорения.
Зависимость скорости от времени.
При изучении равномерного прямолинейного движения вопрос зависимости скорости от времени не возникал: скорость была постоянна в процессе движения. Однако при равноускоренном движении скорость меняется с течением времени, и эту зависимость нам предстоит выяснить.
Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:
. (1)
В нашем случае имеем . Что надо продифференцировать, чтобы получить постоянный вектор ? Разумеется, функцию . Но не только: к ней можно добавить ещё произвольный постоянный вектор (ведь производная постоянного вектора равна нулю). Таким образом,
. (2)
Каков смысл константы ? В начальный момент времени скорость равна своему начальному значению: . Поэтому, полагая в формуле (2), получим:
.
Итак, константа — это начальная скорость тела. Теперь соотношение (2) принимает свой окончательный вид:
. (3)
В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей и прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:
Часто хватает двух осей и прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:
, (4)
. (5)
Формула для третьей компоненты скорости, если она необходима, выглядит аналогично.)
Закон движения.
Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела:
Подставляем сюда выражение для скорости, даваемое формулой (3):
(6)
Сейчас нам предстоит проинтегрировать равенство (6). Это несложно. Чтобы получить , надо продифференцировать функцию . Чтобы получить , нужно продифференцировать . Не забудем добавить и произвольную константу :
.
Ясно, что — это начальное значение радиус-вектора в момент времени . В результате получаем искомый закон равноускоренного движения:
. (7)
Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:
. (8)
(8)
. (9)
. (10)
Формулы (8) — (10) дают зависимость координат тела от времени и поэтому служат решением основной задачи механики для равноускоренного движения.
Снова вернёмся к закону движения (7). Заметим, что — перемещение тела. Тогда
получаем зависимость перемещения от времени:
.
Прямолинейное равноускоренное движение.
Если равноускоренное движение является прямолинейным, то удобно выбрать координатную ось вдоль прямой, по которой движется тело. Пусть, например, это будет ось . Тогда для решения задач нам достаточно будет трёх формул:
,
,
где — проекция перемещения на ось .
Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:
и подставим в формулу для перемещения:
.
После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:
.
Эта формула не содержит времени и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.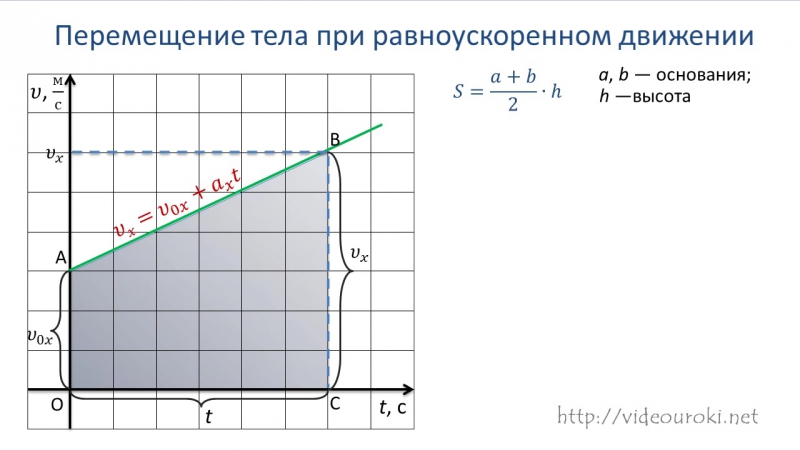
Свободное падение.
Важным частным случаем равноускоренного движения является свободное падение. Так называется движение тела вблизи поверхности Земли без учёта сопротивления воздуха.
Свободное падение тела, независимо от его массы, происходит с постоянным ускорением свободного падения , направленным вертикально вниз. Почти во всех задачах при расчётах полагают м/с.
Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.
Задача. Найти скорость приземления дождевой капли, если высота тучи км.
Решение. Направим ось вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой
.
Имеем: — искомая скорость приземления, . Получаем: , откуда . Вычисляем: м/с. Это 720 км/ч, порядка скорости пули.
На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!
Задача. Тело брошено вертикально вверх со скоростью м/с. Найти его скорость через c.
Тело брошено вертикально вверх со скоростью м/с. Найти его скорость через c.
Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу
.
Здесь , так что . Вычисляем: м/с. Значит, скорость будет равна 20 м/с. Знак проекции указывает на то, что тело будет лететь вниз.
Задача. С балкона, находящегося на высоте м, бросили вертикально вверх камень со скоростью м/с. Через какое время камень упадёт на землю?
Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу
.
Имеем: так что , или . Решая квадратное уравнение, получим c.
Горизонтальный бросок.
Равноускоренное движение не обязательно является прямолинейным. Рассмотрим движение тела, брошенного горизонтально.
Предположим, что тело брошено горизонтально со скоростью с высоты . Найдём время и дальность полёта, а также выясним, по какой траектории происходит движение.
Выберем систему координат так, как показано на рис. 1.
| Рис. 1. Горизонтальный бросок |
Используем формулы:
В нашем случае . Получаем:
. (11)
Время полёта найдём из условия, что в момент падения координата тела обращается в нуль:
.
Дальность полёта — это значение координаты в момент времени :
.
Уравнение траектории получим, исключая время из уравнений (11). Выражаем из первого уравнения и подставляем во второе:
.
Получили зависимость от , которая является уравнением параболы. Следовательно, тело летит по параболе.
Бросок под углом к горизонту.
Рассмотрим несколько более сложный случай равноускоренного движения: полёт тела, брошенного под углом к горизонту.
Предположим, что тело брошено с поверхности Земли со скоростью , направленной под углом к горизонту. Найдём время и дальность полёта, а также выясним, по какой траектории двигается тело.
Найдём время и дальность полёта, а также выясним, по какой траектории двигается тело.
Выберем систему координат так, как показано на рис. 2.
| Рис. 2. Бросок под углом к горизонту |
Начинаем с уравнений:
,
.
В нашем случае . Получаем:
.
Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:
,
,
.
(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость от снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:
.
Равноускоренное движение, вектор ускорения, направление, перемещение. Формулы, определение, законы
Тестирование онлайн
Равноускоренное движение
В этой теме мы рассмотрим очень особенный вид неравномерного движения. Исходя из противопоставления равномерному движению, неравномерное движение — это движение с неодинаковой скоростью, по любой траектории. В чем особенность равноускоренного движения? Это неравномерное движение, но которое «равно ускоряется». Ускорение у нас ассоциируется с увеличением скорости. Вспомним про слово «равно», получим равное увеличение скорости. А как понимать «равное увеличение скорости», как оценить скорость равно увеличивается или нет? Для этого нам потребуется засечь время, оценить скорость через один и тот же интервал времени. Например, машина начинает двигаться, за первые две секунды она развивает скорость до 10 м/с, за следующие две секунды 20 м/с, еще через две секунды она уже двигается со скоростью 30 м/с. Каждые две секунды скорость увеличивается и каждый раз на 10 м/с. Это и есть равноускоренное движение.
Исходя из противопоставления равномерному движению, неравномерное движение — это движение с неодинаковой скоростью, по любой траектории. В чем особенность равноускоренного движения? Это неравномерное движение, но которое «равно ускоряется». Ускорение у нас ассоциируется с увеличением скорости. Вспомним про слово «равно», получим равное увеличение скорости. А как понимать «равное увеличение скорости», как оценить скорость равно увеличивается или нет? Для этого нам потребуется засечь время, оценить скорость через один и тот же интервал времени. Например, машина начинает двигаться, за первые две секунды она развивает скорость до 10 м/с, за следующие две секунды 20 м/с, еще через две секунды она уже двигается со скоростью 30 м/с. Каждые две секунды скорость увеличивается и каждый раз на 10 м/с. Это и есть равноускоренное движение.
Физическая величина, характеризующая то, на сколько каждый раз увеличивается скорость называется ускорением.
Можно ли движение велосипедиста считать равноускоренным, если после остановки в первую минуту его скорость 7км/ч, во вторую — 9км/ч, в третью 12км/ч? Нельзя! Велосипедист ускоряется, но не одинаково, сначала ускорился на 7км/ч (7-0), потом на 2 км/ч (9-7), затем на 3 км/ч (12-9).
Обычно движение с возрастающей по модулю скоростью называют ускоренным движением. Движение же с убывающей скоростью — замедленным движением. Но физики любое движение с изменяющейся скоростью называют ускоренным движением. Трогается ли автомобиль с места (скорость растет!), или тормозит (скорость уменьшается!), в любом случае он движется с ускорением.
Равноускоренное движение — это такое движение тела, при котором его скорость за любые равные промежутки времени изменяется (может увеличиваться или уменьшаться) одинаково
Ускорение тела
Ускорение характеризует быстроту изменения скорости. Это число, на которое изменяется скорость за каждую секунду. Если ускорение тела по модулю велико, это значит, что тело быстро набирает скорость (когда оно разгоняется) или быстро теряет ее (при торможении). Ускорение — это физическая векторная величина, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Определим ускорение в следующей задаче. В начальный момент времени скорость теплохода была 3 м/с, в конце первой секунды скорость теплохода стала 5 м/с, в конце второй — 7м/с, в конце третьей 9 м/с и т.д. Очевидно, . Но как мы определили? Мы рассматриваем разницу скоростей за одну секунду. В первую секунду 5-3=2, во вторую секунду 7-5=2, в третью 9-7=2. А как быть, если скорости даны не за каждую секунду? Такая задача: начальная скорость теплохода 3 м/с, в конце второй секунды — 7 м/с, в конце четвертой 11 м/с.В этом случае необходимо 11-7= 4, затем 4/2=2. Разницу скоростей мы делим на промежуток времени.
Эту формулу чаще всего при решении задач применяют в видоизмененном виде:
Формула записана не в векторном виде, поэтому знак «+» пишем, когда тело ускоряется, знак «-» — когда замедляется.
Направление вектора ускорения
Направление вектора ускорения изображено на рисунках
На этом рисунке машина движется в положительном направлении вдоль оси Ox, вектор скорости всегда совпадает с направлением движения (направлен вправо).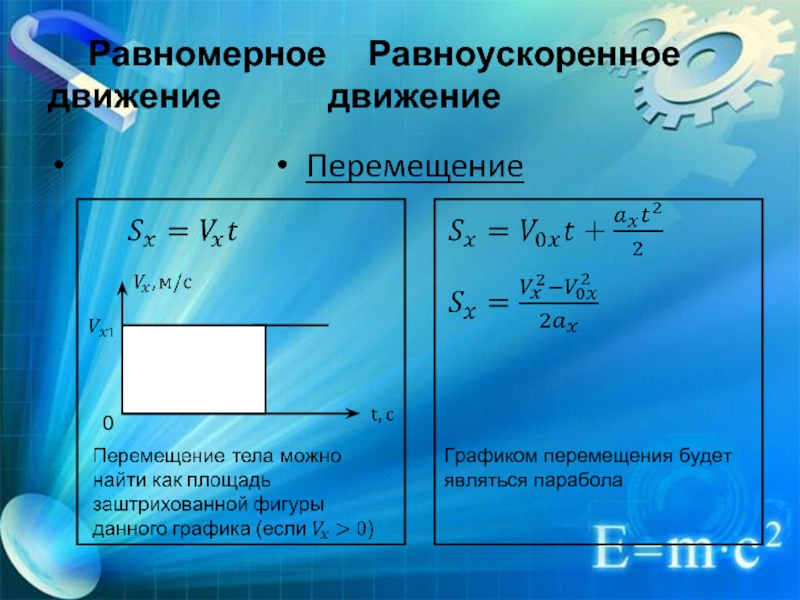 Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.
Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.
При разгоне направление ускорения совпадает с направлением скорости. Ускорение положительное.
На этом рисунке машина движется в положительном направлении по оси Ox, вектор скорости совпадает с направлением движения (направлен вправо), ускорение НЕ совпадает с направлением скорости, это означает, что машина тормозит. Ускорение отрицательное.
При торможении направление ускорения противоположно направлению скорости. Ускорение отрицательное.
Разберемся, почему при торможении ускорение отрицательное. Например, теплоход за первую секунду сбросил скорость с 9м/с до 7м/с, за вторую секунду до 5м/с, за третью до 3м/с. Скорость изменяется на «-2м/с». 3-5=-2; 5-7=-2; 7-9=-2м/с. Вот откуда появляется отрицательное значение ускорения.
При решении задач, если тело замедляется, ускорение в формулы подставляется со знаком «минус»!!!
Перемещение при равноускоренном движении
Дополнительная формула, которую называют безвременной
Формула в координатах
Связь со средней скоростью
При равноускоренном движении среднюю скорость можно рассчитывать как среднеарифметическое начальной и конечной скорости
Из этого правила следует формула, которую очень удобно использовать при решении многих задач
Соотношение путей
Если тело движется равноускоренно, начальная скорость нулевая, то пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел.
Главное запомнить
1) Что такое равноускоренное движение;
2) Что характеризует ускорение;
3) Ускорение — вектор. Если тело разгоняется ускорение положительное, если замедляется — ускорение отрицательное;
3) Направление вектора ускорения;
4) Формулы, единицы измерения в СИ
Упражнения
Два поезда идут навстречу друг другу: один — ускоренно на север, другой — замедленно на юг. Как направлены ускорения поездов?
Одинаково на север. Потому что у первого поезда ускорение совпадает по направлению с движением, а у второго — противоположное движению (он замедляется).
Поезд движется равноускоренно с ускорением a (a>0). Известно, что к концу четвертой секунды скорость поезда равна 6м/с. Что можно сказать о величине пути, пройденном за четвертую секунду? Будет ли этот путь больше, меньше или равен 6м?
Так как поезд движется с ускорением, то скорость его все время возрастает (a>0). Если к концу четвертой секунды скорость равна 6м/с, то в начале четвертой секунды она была меньше 6м/с. Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6м.
Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6м.
Какие из приведенных зависимостей описывают равноускоренное движение?
Уравнение скорости движущегося тела . Каково соответствующее уравнение пути?
*Автомобиль прошел за первую секунду 1м, за вторую секунду 2м, за третью секунду 3м, за четвертую секунду 4м и т.д. Можно ли считать такое движение равноускоренным?
В равноускоренном движении пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Следовательно, описанное движение не равноускоренное.
Формулы равномерного и равноускоренного движения
Равномерное движение
Формула скорости движения при равномерном движении:
v=const
a=0
v — скорость, м/с
s — перемещение, м
t — время, с
Формула перемещения при равномерном движении:
Координата вычисляются через кинематическое уравнение равномерного прямолинейного движения по формуле:
График — Равномерного прямолинейного движения
Равноускоренное движение
Формула скорости при равноускоренном движении:
a=const
v0 — начальная скорость, м/с
a — ускорение, м/с2
Формула для нахождения перемещения при равноускоренном движении:
или
Уравнение равноускоренного движения в проекции на оси координат:
Формула для определения ускорения при равноускоренном прямолинейном движении:
v0 — начальная скорость, м/с
v — мгновенная скорость, м/с
Формула для определения средней скорости движения:
График — Равноускоренное движение при a>0
Равнозамедленное движение
Формула скорости при равнозамедленном движении:
Формула перемещения при равнозамедленном движении:
График — Равнозамедленное движение при a<0
Свободное падение
Постоянная величина скорости свободного падения тела равна g=9,8 м/с2
Формула для вычисления скорости при свободном падении тела:
Формула для вычисления перемещения при свободном падении тела:
Формула координаты при свободном падении тела:
Формула высоты с которой тело свободно падает:
Формула для определения скорости тела в конце свободного падения:
Время свободного падения тела равно:
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.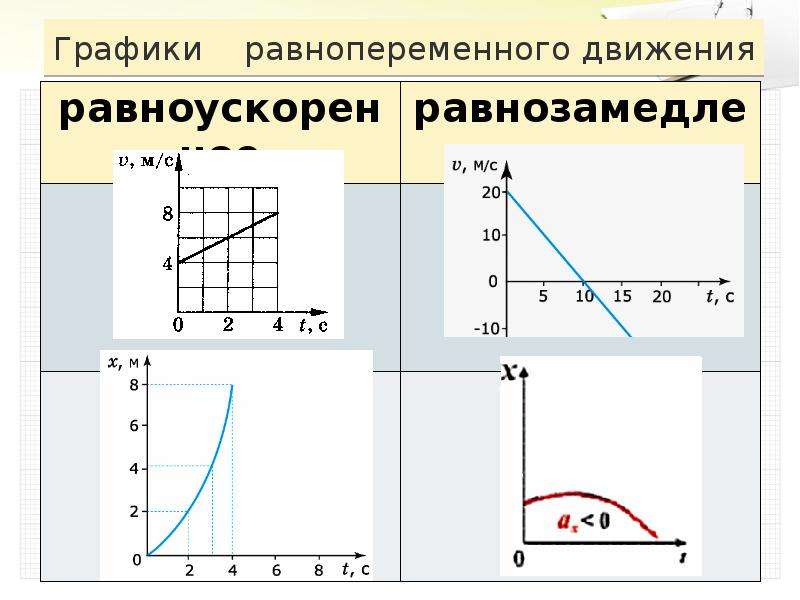 8 / 5. Количество оценок: 6
8 / 5. Количество оценок: 6
Оценок пока нет. Поставьте оценку первым.
Урок 3. равноускоренное движение материальной точки — Физика — 10 класс
Физика, 10 класс
Урок 3.Равноускоренное движение материальной точки
Перечень вопросов, рассматриваемых на уроке:
1) изучение равноускоренного движения;
2) изучение понятий мгновенной скорости, ускорения и скорости равноускоренного движения;
3) вывод формул скорости и пути равноускоренного движения;
4) построения графиков координат и пути равноускоренного движения.
Глоссарий по теме
Неравномерное движение – если тело за одинаковые промежутки времени проходит разные расстояния — то такое движение называется неравномерным.
Скорость – это векторная величина равная отношению пути, пройденного телом за некоторый период времени, к величине этого периода времени.
Средняя скорость при неравномерном движении – отношение вектора перемещения тела к промежутку времени, за который это перемещение произошло.
Мгновенная скорость – это векторная физическая величина, численно равная пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени:
Ускорение – это физическая величина, численно равная изменению скорости за единицу времени. Равноускоренное движение – скорость тела за равные промежутки времени изменяется одинаково, то есть движется с постоянным ускорением.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 31-54
1.Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 40 – 41
Открытые электронные ресурсы:
2. http://kvant.mccme.ru/1983/10/p33.htm
Основное содержание урока.
Неравномерное движение тел может быть не только прямолинейным, но и криволинейным.
Полное описание неравномерного движения тела, возможно при знании его положения и скорости в каждый момент времени. Скорость точки в данный момент времени называется мгновенной скоростью ()
Скорость точки в данный момент времени называется мгновенной скоростью ()
Любая точка в движении при определённой скорости перемещается из начального положения в конечное. Эту скорость называют средней скоростью перемещения точки.
Определяется по формуле:
Кроме мгновенной и средней скоростей перемещения для описания движения чаще пользуются средней путевой скоростью.
Эта средняя скорость определяется отношением пути к промежутку времени, за которое этот путь пройден:
Скорости тел при движении меняются по модулю, по направлению или же одновременно как по модулю, так и по направлению.
Изменения скорости теле могут происходить как быстро, так и медленно.
Ускорением тела называется предел отношения изменения скорости к промежутку
Времени ∆t, в течении которого это изменение призошло, при стремлении ∆t к нулю.
Ускорение обозначается буквой .
Определяется по формуле:
Единица ускорения – м/с2
Выясним зависимости точки от времени при её движении с постоянным ускорением. Для этого воспользуемся формулой:
Для этого воспользуемся формулой:
Пусть о – скорость точки в начальный момент времени to, а – в некоторый момент времени t, тогда:
∆t = to,
и формула для ускорения примет вид:
Если начальный момент времени принять равным нулю, то получим:
Отсюда получим формулу для определения скорости точки в любой момент времени при её движении с постоянным ускорением:
Вектору уравнению соответствуют в случае движения на плоскости два скалярных уравнения для проекций скорости на координатные оси X и Y:
𝑣х = 𝑣ох + 𝒂х t;
𝑣у = 𝑣оу = 𝒂уt.
Мы научились, таким образом, находить скорость материальной точки при движении с постоянным ускорением.
Теперь получим уравнения, которые позволяют рассчитывать для этого движения положение точки в любой момент времени.
Допустим, движение с постоянным ускорением совершается в одной плоскости, пусть это будет плоскость XOY. Если вектор начальной скорости и вектор ускорения не лежат на одной прямой, то точка будет двигаться по кривой линии. Следовательно, в этом случае с течением времени будут изменяться обе ее координаты х и у. Обозначим через хо и уо координаты в начальный момент времени tо = 0, а через х и у координаты времени.
Если вектор начальной скорости и вектор ускорения не лежат на одной прямой, то точка будет двигаться по кривой линии. Следовательно, в этом случае с течением времени будут изменяться обе ее координаты х и у. Обозначим через хо и уо координаты в начальный момент времени tо = 0, а через х и у координаты времени.
Тогда за время ∆t = t – to = t изменения координат будут равны
∆х = х – хо и ∆у = у – уо
Отсюда:
х = хо + ∆х,
у = уо + ∆у
График зависимости v(t)
По формуле для площади трапеции имеем:
Учитывая, что 𝑣ₓ = 𝑣ₒₓ + 𝒂ₓt, получаем формулу:
В обычных условиях задачи даются значения (модули) скоростей и ускорений:
При движении точки в плоскости ХОY двум уравнениям соответствует одно векторное уравнение:
Разбор тренировочных заданий
1. Куда движутся тела и как изменяются их скорости, векторы начальных скоростей и ускорений которых показаны на рисунке 1?
Куда движутся тела и как изменяются их скорости, векторы начальных скоростей и ускорений которых показаны на рисунке 1?
Направление движения определяем по направлению скорости, изменение скорости – по направлению ускорения и скорости.
Решение:
Тело 1 движется вправо; направления ускорения и скорости совпадают, следовательно, скорость его увеличивается.
Тело 2 движется вправо; ускорение направлено в противоположную сторону скорости, следовательно, скорость его уменьшается.
Тело 3 движется влево; направления ускорения и скорости совпадают, следовательно, скорость его увеличивается.
Тело 4 движется влево; ускорение направлено в противоположную сторону скорости, следовательно, скорость его уменьшается.
2. Электропоезд тормозит с ускорением 0,40 м/с2. Определите, за какое время он остановится, если тормозной путь равен 50 м.
Решение:
При прямолинейном движении путь электропоезда равен перемещению s = ∆r.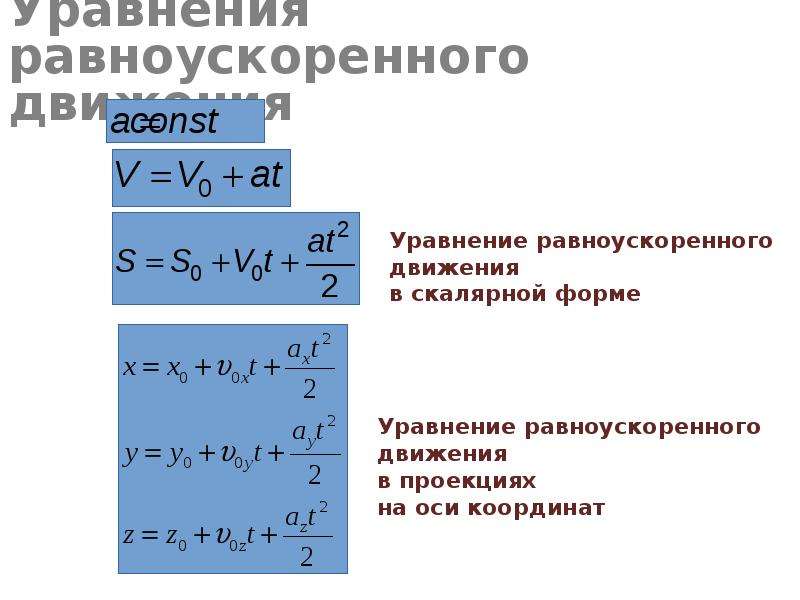
Тогда:
Ответ: t ≈ 16 c.
Механическое движение — определение, формулы, примеры
Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Путь — вектор, проведенный из начальной точки пути в конечную [м].
Чтобы сразу практиковаться, приходите в современную школу для подростков Skysmart. Ученики занимаются на интерактивной платформе по индивидуальной программе, отслеживает прогресс в личном кабинете и чувствуют себя увереннее на школьных контрольных.
Ученики занимаются на интерактивной платформе по индивидуальной программе, отслеживает прогресс в личном кабинете и чувствуют себя увереннее на школьных контрольных.
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю. |
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость → → → |
Средняя путевая скорость V ср.путевая = S/t V ср.путевая — средняя путевая скорость [м/с] |
В чем разница между перемещением и путем?
Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уравнение движения
Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения x(t) = x0 + vxt x(t) — искомая координата [м] |
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
Уравнение движения при движении против оси x(t) = x0 — vxt x(t) — искомая координата [м] |
Графики
Изменение любой величины можно описать графически. Вместо того, чтобы писать множество значений, можно просто начертить график — это проще.
В видео ниже разбираемся, как строить графики кинематических величин и зачем они нужны.
Прямолинейное равноускоренное движение
Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».
Итак, прямолинейное движение — это движение с ускорением по прямой линии.2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с2.
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
Примеров механического движения в жизни — масса. Узнайте больше у преподавателей онлайн-школы Skysmart. Каждый урок по физике — это новый эксперимент: интерактивный, живой и очень увлекательный.
Приходите на бесплатный вводный урок и начните заниматься физикой в удовольствие уже завтра!
К зачету физика 10-1
10 класс
Материалы к зачету по теме «
Основные законы механики «1. Механическое движение.
Явление механического движения тел (материальных точек)состоит в том, что положение тела относительно других тел, т. е. его координаты, с течением времени изменяется.Чтобы найти координаты тела в любой момент времени, нужно знать начальные координаты и вектор перемещения тела. Изменение координаты тела равно проекции вектора перемещения на соответствующую ось координат.
Прямолинейное равномерное движение — это самый простой вид движения.При таком движении нужно определять лишь одну координату потому, что координатную ось можно направить вдоль направления движения тела. Координату х тела (материальной точки) в любой момент времени t можно вычислить по формуле:
,
где — начальная координата тела, а — проекция вектора его скорости на ось х. При вычислениях по этой формуле знаки входящих в нее величин определяются условием задачи.
Механическое движение относительно. Это значит, что перемещение и скорость тела относительно различных систем координат, движущихся друг относительно друга, различны.
Покой также относителен. Если относительно какой-то системы координат тело покоится, то существуют и такие системы отсчета, относительно которых оно движется.
2. Основная задача механики
состоит в нахождении положения тела в любой момент времени. Решение этой задачи идет по своеобразной «цепочке»:
чтобы найти координату точки, нужно знать ее перемещение, а чтобы вычислить перемещение, нужно знать скорость движения.
По такой цепочке: скорость → перемещение → координата решают задачи механики для прямолинейного равномерного движения.
Если движение ускоренное, то нужно знать ускорение, так что при таком движении задачи решают по «цепочке» ускорение → скорость → перемещение → координата. И для равномерного, и для ускоренного движения должны быть известны начальные условия — начальные координаты и начальная скорость.
При прямолинейном ускоренном движении мгновенная скорость тела (материальной точки) непрерывно изменяется от одного момента времени к другому. Поэтому для вычисления скорости в любой момент времени и в любой точке нужно знать быстроту ее изменения, т.е. ускорение:
.
Проекцию скорости тела на выбранную координатную ось в любой момент времени t вычисляют по формуле:
.
Координату тела находят по формуле:
.
Проекцию перемещения находят по формуле:
.
Из приведенных формул получаются формулы для скорости, координат и перемещений при равномерном прямолинейном движении, если принять, что а x = 0.
Значение проекции перемещения при равноускоренном движении можно определить также по формуле:
.
| Так как | , то для координаты тела х имеем: |
При вычислениях по приведенным формулам знаки проекций векторов , а также знак начальной координаты х, определяются условием задачи и направлением оси координат.
3. При криволинейном движении непрерывно изменяется направление вектора скорости, и в каждой точке траектории он направлен по касательной к траектории в данной точке. Поэтому даже равномерное движение по криволинейной траектории, при котором значение модуля скорости постоянно, есть ускоренное движение. Движение тела (материальной точки) по окружности описывают не только с помощью линейных величин — перемещения и скорости, но и с помощью угловых величин — угла поворота радиуса φ, проведенного из центра окружности к телу, и угловой скорости ω.
Связь между линейной и угловой скоростью выражается формулой:
,
где r — радиус окружности.
При равномерном движении по окружности вектор ускорения в любой точке окружности перпендикулярен вектору скорости и направлен к центру окружности. Модуль вектора центростремительного ускорения выражается равенством:
.
Относительно вращающегося стержня (оси) не закрепленное на нем тело (точка) движется вдоль стержня по направлению от оси вращения.
Пример решения задачи:
1. Ширина реки 200 м. Лодка, держа курс перпендикулярно течению реки, достигла противоположного берега за 140 с. Скорость течения воды в реке 0,8 м/с. Определите скорость и перемещение лодки относительно берега.
Ответ: Скорость лодки относительно берега 1,6 м/с, перемещение 112 м.
Решите задачи самостоятельно:
1. Через реку переправляется лодка, выдерживая курс перпендикулярно течению. Скорость лодки
4 м/с, скорость течения реки 3 м/с. Какова ширина реки, если лодку снесло на 60 м?
2. 9 км/ч = … м/с; 10 м/с = … км/ч; 8 км/с = … км/ч, 54 км/ч = …м/с.
3. Автомобиль движется: а) с постоянной скоростью; б) с постоянным ускорением;
в) с положительным ускорением; г) с отрицательным ускорением.
Назовите вид каждого движения и изобразите соответствующие графики скорости.
Попробуйте решить задачи из раздела «Кинематика»
вернуться на страницу «Физика» | вверх |
Уравнения движения с постоянным ускорением
Равномерно ускоренное прямолинейное движение (u.a.r.m.) , также известное как движение с постоянным ускорением , представляет собой прямолинейное движение с постоянным ускорением, отличным от нуля. В этом разделе мы собираемся изучить:
Концепция движения с постоянным ускорением
Движение с постоянным ускорением довольно часто встречается в вашей повседневной жизни. Хорошими примерами этого являются объект, которому разрешено падать и который не встречает на своем пути никаких препятствий (свободное падение), или лыжник, который спускается по склону непосредственно перед тем, как прибыть в зону прыжка.Движение с постоянным ускорением или равноускоренное прямолинейное движение (u.a.r.m) имеет следующие свойства :
Тело движется с постоянным ускорением движение или равноускоренное прямолинейное движение (u.a.r.m) , когда его траектория является прямой и его ускорение постоянно и отличается от 0 . Это означает, что скорость увеличивается или уменьшается равномерно .
Равномерно ускоренное прямолинейное движение
В нашем примере автомобиль описывает u.a.r.m, поскольку он движется по прямой с постоянным ускорением, равным 2 м / с 2 . [Обратите внимание, что каждую секунду скорость и расстояние, пройденное телом, увеличиваются в зависимости от значения ускорения за предыдущую секунду.]
Обратите внимание, что хотя в разговорной речи мы проводим различие между ускоряющимся и тормозящим телом, с точки зрения физики, оба являются равноускоренными прямолинейными движениями .Разница в том, что у одного ускорение положительное, а у другого — отрицательное.
Уравнения движения с постоянным ускорением
уравнений движения с постоянным ускорением или равноускоренного прямолинейного движения (u.a.r.m.) :
Где:
- x , x 0 : Положение тела в данный момент времени ( x ) и в начальный момент времени ( x 0 ).Его единица измерения в Международной системе (СИ) — метр (м) .
- v , v 0 : Скорость тела в данный момент времени ( v ) и в начальный момент времени ( v 0 ). Его единица измерения в Международной системе — метр в секунду (м / с) .
- a : Разгон кузова. Остается постоянным при значении, отличном от 0. Его единица измерения в международной системе — метр в секунду (м / с 2 )
- t : Время изучается.Его единица измерения в Международной системе — вторая ( с )
Хотя первые являются основными уравнениями u.a.r.m. и единственные, необходимые для решения упражнений, иногда полезно знать следующее выражение:
v2 = v02 + 2 · a · ∆x
Приведенная выше формула позволяет связать скорость и пройденное расстояние, если ускорение известно и может быть выведено из предыдущих, как вы можете видеть ниже.
v = v0 + a · tx = x0 + v0 · t + 12 · a · t2⇒t = v-v0a∆x = v0 · t + 12 · a · t2⇒∆x = v0v-v0a + 12 · a · v-v0a2;
2 · a · ∆x = v2-v02
Вывод уравнений движения с постоянным ускорением
Для вывода уравнений движения с постоянным ускорением или равноускоренного прямолинейного движения (u.a.r.m) , необходимо учитывать, что:
- Нормальное или центростремительное ускорение равно нулю: an = 0
- Среднее ускорение, мгновенное ускорение и тангенциальное ускорение имеют одинаковое значение: a = aa = at = cst
С этими ограничениями получаем:
aa = aaa = ΔvΔt = v-v0t-t0 = ⏟t0 = 0x-x0t → v-v0 = a⋅t → v = v0 + a⋅t
Это первое уравнение связывает скорость тела с его ускорением в любой момент времени и представляет собой прямую линию ( v ), наклон которой совпадает с величиной ускорения, а ее координата y в начале координат является начальной скоростью. ( против 0 ).Нам нужно получить уравнение, которое позволит нам получить позицию. Есть разные методы, чтобы вывести это. Мы будем использовать теорему о средней скорости или правило равномерного ускорения Мертона :
«Тело с равномерно ускоренным движением в любой момент времени преодолевает такое же расстояние, которое могло бы пройти тело, движущееся с постоянной скоростью, равной средней скорости первого тела».
Это означает, что
∆x = va⋅t
Значение средней скорости при постоянном ускорении четко видно на следующем рисунке:
ва = v + v02
Если мы разработаем уравнения, которые мы видели до сих пор, мы получим уравнение положения в равномерно ускоренном прямолинейном движении (u.а.р.м.) :
∆x = x-x0 = va⋅t = ⏞1v + v02t = ⏞2v0 + at + v02t = 2v0 + at2t = 22v0t + at22⇒x = x0 + v0t + 12at2
Куда мы обращались:
ва = v + v02
v = v0 + a⋅t
Наконец, обратите внимание, что в предыдущих уравнениях движение учитывалось по оси x . Если мы перемещаемся по оси по оси Y , например, при свободном падении или вертикальном старте, просто замените положение x на y , в результате получится следующее уравнение:
Пример
Велосипедист начинает утреннюю поездку и через 10 секунд его скорость равна 7.2 км / ч. В этот момент он видит приближающуюся собаку и тормозит на 6 секунд, пока велосипед не остановится. Вычислить:
а) Ускорение до тех пор, пока он не начнет замедляться.
б) Тормозное ускорение велосипеда.
c) Общее пройденное расстояние.
Верен ли такой вывод координат для равноускоренного движения в теории относительности?
Верен ли такой вывод координат для равноускоренного движения в теории относительности? — Обмен физическими стекамиСеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Physics Stack Exchange — это сайт вопросов и ответов для активных исследователей, ученых и студентов-физиков.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 87 раз
$ \ begingroup $Я пытался вывести координаты равномерно ускоренного движения (в теории относительности).2} $$ Если я интегрирую это, я не получу ничего близкого к решению проблемы. Не ошибаюсь ли я в этом выводе? есть ли способ исправить это, чтобы он давал правильное решение?
Создан 25 мар.
ПамПам46722 серебряных знака1010 бронзовых знаков
$ \ endgroup $ 5 Physics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Equations of Motion — The Physics Hypertextbook
Обсуждение
постоянное ускорение
Для точности этот раздел должен называться «Одномерные уравнения движения при постоянном ускорении».Учитывая, что такое название было бы стилистическим кошмаром, позвольте мне начать этот раздел со следующей оговорки. Эти уравнения движения действительны только тогда, когда ускорение постоянное и движение ограничено прямой линией.
Учитывая, что мы живем в трехмерной вселенной, в которой единственной константой является изменение, у вас может возникнуть соблазн сразу отказаться от этого раздела. Было бы правильно сказать, что ни один объект никогда не двигался по прямой с постоянным ускорением в любом месте Вселенной в любое время — ни сегодня, ни вчера, ни завтра, ни пять миллиардов лет назад, ни тридцать миллиардов лет в будущем. , никогда.Об этом я могу сказать с абсолютной метафизической уверенностью.
Так что же тогда хорошего в этом разделе? Что ж, во многих случаях полезно предположить, что объект действительно двигался или будет двигаться по прямому пути с почти постоянным ускорением; то есть любое отклонение от идеального движения можно по существу игнорировать. Движение по криволинейной траектории можно считать фактически одномерным, если имеется только одна степени свободы для задействованных объектов.Дорога может извиваться и поворачиваться и исследовать всевозможные направления, но автомобили, движущиеся по ней, имеют только одну степень свободы — свободу двигаться в одном или противоположном направлении. (Вы не можете двигаться по дороге по диагонали и надеетесь остаться на ней надолго.) В этом отношении это мало чем отличается от движения, ограниченного прямой линией. Аппроксимация реальных ситуаций моделями, основанными на идеальных ситуациях, не считается обманом. Так поступают в физике. Это настолько полезный метод, что мы будем использовать его снова и снова.
Наша цель в этом разделе — вывести новые уравнения, которые можно использовать для описания движения объекта в терминах его трех кинематических переменных: скорости ( v ), положения ( с ) и времени ( т ). Есть три способа объединить их в пары: скорость-время, положение-время и скорость-положение. В этом порядке их также часто называют первым, вторым и третьим уравнениями движения, но нет веских причин для изучения этих имен.
Поскольку мы имеем дело с движением по прямой линии, направление будет обозначено знаком — положительные величины указывают в одну сторону, а отрицательные величины указывают в противоположную сторону.Определение того, какое направление является положительным, а какое отрицательным, совершенно произвольно. Законы физики изотропны ; то есть они не зависят от ориентации системы координат. Однако некоторые проблемы легче понять и решить, если одно направление предпочтительнее другого. Пока вы последовательны в решении проблемы, это не имеет значения.
скорость-время
Связь между скоростью и временем проста при равномерно ускоренном прямолинейном движении.Чем дольше ускорение, тем больше изменение скорости. Изменение скорости прямо пропорционально времени, когда ускорение постоянно. Если скорость увеличивается на определенную величину за определенное время, она должна увеличиваться вдвое на эту величину в два раза быстрее. Если объект уже стартовал с определенной скоростью, то его новая скорость будет равна старой скорости плюс это изменение. Вы должны быть в состоянии увидеть уравнение уже мысленным взором.
Это самое простое из трех уравнений, которое можно вывести с помощью алгебры.Начнем с определения ускорения.
Расширить ∆ v до v — v 0 и сжать ∆ t до t .
Затем найдите v как функцию от t .
v = v 0 + at [1]
Это первое уравнение движения . Он записывается как полином — постоянный член ( v 0 ), за которым следует член первого порядка ( на ).Поскольку наивысший порядок равен 1, правильнее называть его линейной функцией .
Символ v 0 [vee naught] называется начальной скоростью , или скоростью t = 0. Его часто называют «первой скоростью», но это довольно наивный способ Опишите это. Лучшее определение было бы сказать, что начальная скорость — это скорость, которую имеет движущийся объект, когда он впервые становится важным в проблеме. Скажем, метеор был замечен глубоко в космосе, и проблема заключалась в том, чтобы определить его траекторию, тогда начальная скорость, вероятно, будет той скоростью, которую он имел при первом наблюдении.Но если проблема заключалась в том, что тот же самый метеор сгорает при входе в атмосферу, то начальная скорость, вероятно, равна скорости, которую он имел при входе в атмосферу Земли. Ответ на вопрос «Какая начальная скорость?» «Это зависит от обстоятельств». Это оказывается ответом на множество вопросов.
Обозначение v — это скорость через некоторое время t после начальной скорости. Ее часто называют конечной скоростью , но это не делает ее «последней скоростью» объекта. Возьмем случай с метеором.Какая скорость обозначена символом v ? Если вы внимательно слушали, значит, вы должны были ожидать ответа. По-разному. Это может быть скорость метеора, когда он проходит мимо Луны, входит в атмосферу Земли или ударяется о поверхность Земли. Это также может быть скорость метеорита, находящегося на дне кратера. (В этом случае v = 0 м / с.) Является ли какое-либо из этих значений конечной скоростью? Кто знает. Кто-то мог извлечь метеорит из дыры в земле и уехать вместе с ним.Это актуально? Наверное, нет, но это зависит от обстоятельств. Для такого рода вещей нет правил. Вы должны проанализировать текст задачи на предмет физических величин, а затем присвоить значение математическим символам.
Последняя часть этого уравнения на — это изменение скорости по сравнению с начальным значением. Вспомните, что a — это скорость изменения скорости, а t — это время после некоторого начального события . Ставка раз время меняется. Учитывая, что объект ускоряется со скоростью 10 м / с 2 , через 5 с он будет двигаться на 50 м / с быстрее.Если бы он стартовал со скоростью 15 м / с, то его скорость через 5 с была бы…
15 м / с + 50 м / с = 65 м / с
позиция-время
Смещение движущегося объекта прямо пропорционально скорости и времени. Двигайся быстрее. Иди дальше. Двигайтесь дольше (как и дольше). Иди дальше. Ускорение усугубляет эту простую ситуацию, поскольку скорость теперь также прямо пропорциональна времени. Попробуйте сказать это словами, и это прозвучит нелепо. «Смещение прямо пропорционально времени и прямо пропорционально скорости, которая прямо пропорциональна времени.»Время удваивается, поэтому смещение пропорционально квадрату времени. Автомобиль, ускоряющийся в течение двух секунд, преодолеет в четыре раза расстояние, превышающее скорость автомобиля, ускоряющегося всего за одну секунду (2 2 = 4). Автомобиль, ускоряющийся в течение трех секунды покрыли бы расстояние в девять раз большее (3 2 = 9).
Если бы это было так просто. Этот пример работает, только когда начальная скорость равна нулю. Смещение пропорционально квадрату времени, когда ускорение постоянное, а начальная скорость равна нулю.Истинное общее утверждение должно учитывать любую начальную скорость и то, как она менялась. Это приводит к ужасно запутанному утверждению соразмерности. Смещение прямо пропорционально времени и пропорционально квадрату времени, когда ускорение постоянно. Функция, которая является одновременно линейной и квадратной, называется квадратичной , что позволяет нам значительно сжать предыдущее утверждение. Смещение является квадратичной функцией времени при постоянном ускорении
Формулировки пропорциональности полезны, но не столь общие, как уравнения.Мы до сих пор не знаем, каковы константы пропорциональности для этой проблемы. Один из способов понять их — использовать алгебру.
Начнем с определения средней скорости.
Расширить ∆ с до с — с 0 и сжать ∆ t до t .
Найдите позицию.
с = с 0 + vt [a]
Чтобы продолжить, нам нужно прибегнуть к небольшому трюку, известному как теорема о средней скорости или правило Мертона .Я предпочитаю второй вариант, поскольку правило может применяться к любой величине, которая изменяется с одинаковой скоростью, а не только к скорости. Правило Мертона было впервые опубликовано в 1335 году в Мертон-колледже, Оксфорд, английским философом, математиком, логиком и калькулятором Уильямом Хейтсбери (1313–1372). Когда скорость изменения величины постоянна, ее среднее значение находится на полпути между ее конечным и начальным значениями.
v = ½ ( v + v 0 ) [4]
Подставьте первое уравнение движения [1] в это уравнение [4] и упростите его, исключив v .
| v = ½ [( v 0 + при ) + v 0 ] v = ½ (2 v 0 + при |
Теперь замените [b] на [a], чтобы исключить v [vee bar].
с = с 0 + ( v 0 + ½ при ) т
И, наконец, найдите s как функцию от t .
с = с 0 + v 0 t + ½ при 2 [2]
Это второе уравнение движения . Он записывается как полином — постоянный член ( s 0 ), за которым следует член первого порядка ( v 0 t ), за которым следует член второго порядка (½ at 2 ). ). Поскольку наивысший порядок равен 2, правильнее называть его квадратичным .
Символ s 0 [ess naught] часто рассматривается как начальная позиция . Символ s — это позиция на t позже. Если хотите, вы можете назвать ее конечной позицией . Изменение положения (∆ s ) называется смещением или расстоянием (в зависимости от обстоятельств), и некоторые люди предпочитают писать второе уравнение движения таким образом.
∆ с = v 0 t + ½ при 2 [2]
скорость-позиция
Первые два уравнения движения описывают одну кинематическую переменную как функцию времени.По сути…
- Скорость прямо пропорциональна времени при постоянном ускорении ( v ∝ t ).
- Смещение пропорционально квадрату времени при постоянном ускорении (∆ с ∝ t 2 ).
Объединение этих двух утверждений дает начало третьему, не зависящему от времени. При замене должно быть очевидно, что…
- Смещение пропорционально квадрату скорости при постоянном ускорении (∆ s ∝ v 2 ).
Это утверждение особенно важно для безопасности вождения. Когда вы вдвое увеличиваете скорость автомобиля, требуется в четыре раза больше расстояния, чтобы его остановить. Увеличьте скорость втрое, и вам понадобится в девять раз больше расстояния. Это хорошее практическое правило, которое следует запомнить.
Концептуальное введение сделано. Пришло время вывести формальное уравнение.
метод 1
Объедините первые два уравнения таким образом, чтобы исключить время как переменную. Самый простой способ сделать это — начать с первого уравнения движения…
v = v 0 + at [1]
решить на время…
и подставляем во второе уравнение движения…
с = с 0 + v 0 t + ½ при 2 [2]
нравится…
| с = | с 0 + с 0 | ⎛ ⎜ ⎝ | в — в 0 | ⎞ ⎟ ⎠ | + ½ a | ⎛ ⎜ ⎝ | в — в 0 | ⎞ 2 ⎟ ⎠ |
| с — с 0 = | vv 0 — v 0 2 | + | v 2 -2 vv 0 + v 0 2 |
| 2 a |
| 2 a ( с — с 0 ) = 2 ( vv 0 — v 0 2 ) + ( v 2 — 2 vv 0 + v 0 2 ) | |
| 2 a ( s — s 0 ) = v 2 — v 0 2 | |
Возведите объект в квадрат скорости, и все готово.
v 2 = v 0 2 + 2 a ( s — s 0 ) [3]
Это третье уравнение движения . Еще раз, символ s 0 [ess naught] — это начальная позиция , , а s, — это позиция через некоторое время t . Если вы предпочитаете, вы можете написать уравнение, используя ∆ s — изменение положения на , смещение на или на расстояние в зависимости от ситуации.
v 2 = v 0 2 + 2 a ∆ s [3]
метод 2
Более сложный способ вывести это уравнение — начать со второго уравнения движения в этой форме…
∆ с = v 0 t + ½ при 2 [2]
и решите ее на время. Это непростая работа, поскольку уравнение квадратично. Переставьте термины так…
½ при 2 + v 0 t — ∆ s = 0
и сравните его с общей формой квадратичной.
топор 2 + bx + c = 0
Решение этого дается известным уравнением…
| x = | — b ± √ ( b 2 — 4 ac ) |
| 2 |
Замените символы в общем уравнении эквивалентными символами из нашего преобразованного второго уравнения движения…
| т = | — v 0 ± √ [ v 0 2 — 4 (½ a ) (∆ s )] |
| 2 (½ a ) |
почисти немного…
| т = | — v 0 ± √ ( v 0 2 -2 a ∆ s ) |
, а затем подставьте его обратно в первое уравнение движения.
v = v 0 + at [1]
| v = v 0 + a | ⎛ ⎜ ⎝ | — v 0 ± √ ( v 0 2 -2 a ∆ s ) | ⎞ ⎟ ⎠ |
Материал отменяется, и мы получаем это…
v = ± √ ( v 0 2 + 2 a ∆ s )
Выровняйте обе стороны, и все готово.
v 2 = v 0 2 + 2 a ∆ s [3]
Это было не так уж и плохо, не так ли?
исчисления выводов
Исчисление — это сложная математическая тема, но она значительно упрощает вывод двух из трех уравнений движения. По определению, ускорение — это первая производная скорости по времени. Возьмите операцию в этом определении и отмените ее. Вместо того, чтобы дифференцировать скорость, чтобы найти ускорение, интегрируйте ускорение, чтобы найти скорость.Это дает нам уравнение скорость-время. Если мы предположим, что ускорение постоянное, мы получим так называемое первое уравнение движения [1].
| = | |||
| дв | = | a dt | |
| = | |||
| v — v 0 | = | при | |
| v | = | v 0 + at [1] | |
Опять же, по определению, скорость — это первая производная положения по времени.Выполните эту операцию в обратном порядке. Вместо того, чтобы различать положение для определения скорости, интегрируйте скорость, чтобы найти положение. Это дает нам уравнение положения-времени для постоянного ускорения, также известное как второе уравнение движения [2].
| v | = | |||||||||
| DS | = | v dt | ||||||||
| DS | = | ( v 0 + at ) dt | ||||||||
| = |
| |||||||||
| с — с 0 | = | v 0 t + ½ at 2 | ||||||||
| с | = | s 0 + v 0 t + ½ at 2 [2] | ||||||||
В отличие от первого и второго уравнений движения, нет очевидного способа вывести третье уравнение движения (то, которое связывает скорость с положением) с помощью расчетов.Мы не можем просто перепроектировать это по определению. Нам нужно разыграть довольно изощренный трюк.
Первое уравнение движения связывает скорость со временем. По сути, мы вывели его из этой производной…
Второе уравнение движения связывает положение со временем. Это произошло от этой производной…
Третье уравнение движения связывает скорость с положением. По логике, это должно происходить от производной, которая выглядит так…
Но что это значит? Ну, ничего по определению, но, как и все количества, оно равно самому себе.Он также равен самому себе, умноженному на 1. Мы будем использовать специальную версию 1 ( dt dt ) и специальную версию алгебры (алгебра с бесконечно малыми). Посмотрите, что происходит, когда мы это делаем. Мы получаем одну производную, равную ускорению ( dv dt ), и другую производную, равную обратной скорости ( dt ds ).
| дв | = | дв | 1 | |
| DS | DS | |||
| дв | = | дв | дт | |
| DS | DS | дт | ||
| дв | = | дв | дт | |
| DS | дт | DS | ||
| дв | = | a | 1 | |
| DS | v |
Следующий шаг, разделение переменных.Соберите вместе похожие вещи и интегрируйте их. Вот что мы получаем при постоянном ускорении…
| = | ||||
| в дв | = | a DS | ||
| = | ||||
| ½ ( v 2 — v 0 2 ) | = | a ( с — с 0 ) | ||
| v 2 | = | v 0 2 + 2 a ( s — s 0 ) [3] | ||
Безусловно, умное решение, и оно было не так уж сложно, чем первые два варианта.Однако на самом деле это сработало только потому, что ускорение было постоянным — постоянным во времени и постоянным в пространстве. Если бы ускорение каким-либо образом менялось, этот метод был бы неудобно трудным. Мы вернемся к алгебре, чтобы спасти наше здравомыслие. Не то чтобы в этом что-то не так. Алгебра работает, а здравомыслие стоит сэкономить.
| v = | v 0 + at | [1] |
| + | ||
| с = | s 0 + v 0 t + ½ при 2 | [2] |
| = | ||
| v 2 = | v 0 2 + 2 a ( s — s 0 ) | [3] |
Принцип эквивалентности, равномерно ускоренные системы отсчета и однородное гравитационное поле
% PDF-1.7 % 1 0 obj > / Metadata 2 0 R / Outlines 6 0 R / Pages 3 0 R / StructTreeRoot 7 0 R / Type / Catalog / Viewer Preferences >>> эндобдж 5 0 obj > эндобдж 2 0 obj > поток application / pdf
3.4 Движение с постоянным ускорением — Университетская физика, том 1
Цели обучения
К концу этого раздела вы сможете:
- Определите, какие уравнения движения следует использовать для решения неизвестных.
- Используйте соответствующие уравнения движения для решения задачи преследования двух тел.
Вы можете догадаться, что чем больше ускорение, скажем, у автомобиля, удаляющегося от знака «Стоп», тем больше смещение автомобиля за данный момент времени.Но мы не разработали конкретное уравнение, которое связывает ускорение и смещение. В этом разделе мы рассмотрим некоторые удобные уравнения кинематических отношений, начиная с определений смещения, скорости и ускорения. Сначала мы исследуем движение одного объекта, называемого движением одного тела. Затем мы исследуем движение двух объектов, называемое задачами преследования двух тел.
Обозначение
Во-первых, сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением.Поскольку прошедшее время равно Δt = tf − t0Δt = tf − t0, взятие t0 = 0t0 = 0 означает, что Δt = tfΔt = tf, последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть x0x0 — это начальная позиция , а v0v0 — начальная скорость . Мы не ставим нижние индексы на окончательные значения. То есть t — это конечный момент времени , x — конечная позиция , а v — конечная скорость . Это дает более простое выражение для затраченного времени: Δt = tΔt = t.Это также упрощает выражение для смещения x , которое теперь равно Δx = x − x0Δx = x − x0. Кроме того, это упрощает выражение для изменения скорости, которое теперь равно Δv = v − v0Δv = v − v0. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,
Δt = tΔx = x − x0Δv = v − v0, Δt = tΔx = x − x0Δv = v − v0,, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает конечное значение в любом рассматриваемом движении.
Теперь мы делаем важное предположение, что ускорение постоянно .Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, то есть
a– = a = постоянная. a– = a = постоянная.Таким образом, мы можем использовать символ a для ускорения в любое время. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не ухудшает точность нашего лечения. Во-первых, ускорение равно постоянным в большом количестве ситуаций.Более того, во многих других ситуациях мы можем точно описать движение, приняв постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, во время которого ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.
Смещение и положение от скорости
Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:
Подставляя упрощенные обозначения для ΔxΔx и ΔtΔt, получаем
v– = x − x0t.v– = x − x0t.Решение для x дает нам
x = x0 + v – t, x = x0 + v – t,3,10
, где средняя скорость
v– = v0 + v2.v– = v0 + v2.3,11
Уравнение v– = v0 + v2v– = v0 + v2 отражает тот факт, что при постоянном ускорении v – v– представляет собой просто среднее значение начальной и конечной скоростей. Рисунок 3.18 графически иллюстрирует эту концепцию. В части (а) рисунка ускорение является постоянным, а скорость увеличивается с постоянной скоростью. Средняя скорость в течение 1-часового интервала от 40 км / ч до 80 км / ч составляет 60 км / ч:
v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.В части (b) ускорение не является постоянным. В течение 1-часового интервала скорость ближе к 80 км / ч, чем к 40 км / ч. Таким образом, средняя скорость больше, чем в части (а).
Рис. 3.18 (a) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости v0andvv0andv. Средняя скорость равна 12 (v0 + v) = 60 км / ч 22 (v0 + v) = 60 км / ч. (б) График зависимости скорости от времени с изменением ускорения со временем. Средняя скорость не равна 12 (v0 + v) 12 (v0 + v), но превышает 60 км / ч.Решение окончательной скорости по ускорению и времени
Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:
Подстановка упрощенных обозначений для ΔvΔv и ΔtΔt дает
а = v − v0t (константа). a = v − v0t (константа).Решение для v дает
v = v0 + at (constanta). v = v0 + at (constanta).3,12
Пример 3,7
Расчет конечной скорости
Самолет приземляется с начальной скоростью 70.0 м / с, а затем ускоряется против движения со скоростью 1,50 м / с 2 за 40,0 с. Какова его конечная скорость?Стратегия
Сначала мы идентифицируем известные: v0 = 70 м / с, a = -1,50 м / с2, t = 40sv0 = 70 м / с, a = -1,50 м / с2, t = 40 с.Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость vfvf.
Наконец, мы определяем, какое уравнение использовать. Для этого мы выясняем, какое кинематическое уравнение дает неизвестное в терминах известных. Мы рассчитываем окончательную скорость, используя уравнение 3.12, v = v0 + atv = v0 + at.
Решение
Подставьте известные значения и решите: v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с.Рисунок 3.19 представляет собой эскиз, показывающий векторы ускорения и скорости.
Рис. 3.19. Самолет приземляется с начальной скоростью 70,0 м / с и замедляется до конечной скорости 10,0 м / с, прежде чем направиться к терминалу. Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.
Значение
Конечная скорость намного меньше начальной скорости, требуемой при замедлении, но все же положительная (см. Рисунок). С реактивными двигателями обратная тяга может поддерживаться достаточно долго, чтобы остановить самолет и начать движение назад, на что указывает отрицательная конечная скорость, но в данном случае это не так.Помимо полезности при решении задач, уравнение v = v0 + atv = v0 + at дает нам представление о взаимосвязях между скоростью, ускорением и временем.Мы видим, например, что
- Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
- Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v 0 ), как и ожидалось (другими словами, скорость постоянна)
- Если a отрицательное, то конечная скорость меньше начальной скорости
Все эти наблюдения соответствуют нашей интуиции. Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.
Решение для конечного положения с постоянным ускорением
Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволяет нам вычислить окончательное положение объекта, испытывающего постоянное ускорение. Начнем с
Добавление v0v0 к каждой стороне этого уравнения и деление на 2 дает
v0 + v2 = v0 + 12at. v0 + v2 = v0 + 12at.Так как v0 + v2 = v – v0 + v2 = v– для постоянного ускорения, имеем
v– = v0 + 12at.v– = v0 + 12at.Теперь мы подставляем это выражение для v – v– в уравнение для смещения, x = x0 + v – tx = x0 + v – t, что дает
х = х0 + v0t + 12at2 (константа).х = х0 + v0t + 12at2 (константа).3,13
Пример 3.8
Расчет смещения ускоряющегося объекта
Драгстеры могут развивать среднее ускорение 26,0 м / с 2 . Предположим, драгстер ускоряется из состояния покоя с этой скоростью в течение 5,56 с. Рис. 3.20. Как далеко он пролетит за это время?Рис. 3.20. Пилот Top Fuel в армии США Тони «Сержант» Шумахер начинает гонку с контролируемого выгорания. (Источник: подполковник Уильям Термонд. Фото любезно предоставлено США.Армия.)
Стратегия
Сначала нарисуем набросок Рис. 3.21. Нас просят найти смещение, которое составляет x , если мы примем x0x0 равным нулю. (Думайте о x0x0 как о стартовой линии гонки. Она может быть где угодно, но мы называем ее нулевой и измеряем все остальные позиции относительно нее.) Мы можем использовать уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 когда мы идентифицируем v0v0, aa и t из постановки задачи.Рис. 3.21. Эскиз разгоняющегося драгстера.
Решение
Во-первых, нам нужно определить известные.Запуск из состояния покоя означает, что v0 = 0v0 = 0, a задается как 26,0 м / с 2 и t задается как 5,56 с.Во-вторых, мы подставляем известные значения в уравнение, чтобы найти неизвестное:
x = x0 + v0t + 12at2.x = x0 + v0t + 12at2.Поскольку начальное положение и скорость равны нулю, это уравнение упрощается до
Подстановка идентифицированных значений на и t дает
x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м. x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м.Значение
Если мы переведем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартному расстоянию для дрэг-рейсинга. Итак, наш ответ разумный. Это впечатляющий водоизмещение всего за 5,56 с, но первоклассные драгстеры могут преодолеть четверть мили даже за меньшее время. Если бы драгстеру была присвоена начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении использовать те же ускорение и время, пройденное расстояние будет намного больше.Что еще мы можем узнать, исследуя уравнение x = x0 + v0t + 12at2? X = x0 + v0t + 12at2? Мы видим следующие отношения:
- Смещение зависит от квадрата истекшего времени, когда ускорение не равно нулю. В примере 3.8 драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени.
- Если ускорение равно нулю, то начальная скорость равна средней скорости (v0 = v -) (v0 = v–), и x = x0 + v0t + 12at2becomesx = x0 + v0t.x = x0 + v0t + 12at2becomesx = x0 + v0t.
Расчет конечной скорости по расстоянию и ускорению
Четвертое полезное уравнение может быть получено путем другой алгебраической манипуляции с предыдущими уравнениями. Если мы решим v = v0 + atv = v0 + at для t , мы получим
Подставляя это и v– = v0 + v2v– = v0 + v2 в x = x0 + v – tx = x0 + v – t, получаем
v2 = v02 + 2a (x − x0) (constanta). v2 = v02 + 2a (x − x0) (constanta).3,14
Пример 3.9
Расчет конечной скорости
Рассчитайте конечную скорость драгстера в Примере 3.8 без использования информации о времени.Стратегия
Уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) идеально подходит для этой задачи, поскольку оно связывает скорости, ускорение и смещение и не требует информации о времени.Решение
Сначала мы идентифицируем известные значения. Мы знаем, что v 0 = 0, поскольку драгстер запускается из состояния покоя. Мы также знаем, что x — x 0 = 402 м (это был ответ в примере 3.8). Среднее ускорение было равно , = 26.0 м / с 2 .Во-вторых, мы подставляем известные в уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) и решаем относительно v :
v2 = 0 + 2 (26,0 м / с2) (402 м). v2 = 0 + 2 (26,0 м / с2) (402 м).Таким образом,
v2 = 2,09 × 104 м2 / с2 v = 2,09 × 104 м2 / с2 = 145 м / с. v2 = 2,09 × 104 м2 / с2v = 2,09 × 104 м2 / с2 = 145 м / с.Значение
Скорость 145 м / с составляет около 522 км / ч или около 324 миль / ч, но даже эта головокружительная скорость не достигает рекорда для четверти мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение.Изучение уравнения v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) может дать дополнительное понимание общих соотношений между физическими величинами:
- Конечная скорость зависит от величины ускорения и расстояния, на котором оно действует.
- При фиксированном ускорении автомобиль, который едет вдвое быстрее, не просто останавливается на удвоенном расстоянии. Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)
Объединение уравнений
В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций.Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для облегчения поиска необходимых уравнений. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных, и нам нужно два уравнения из набора для решения для неизвестных. Для решения данной ситуации нам нужно столько уравнений, сколько неизвестных.
Сводка кинематических уравнений (константа
a ) х = х0 + v0t + 12at2x = x0 + v0t + 12at2 v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0)Прежде чем мы перейдем к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях.Переставляя уравнение 3.12, получаем
Из этого мы видим, что в течение конечного времени, если разница между начальной и конечной скоростями мала, ускорение невелико, приближаясь к нулю в пределе, когда начальная и конечная скорости равны. Напротив, в пределе t → 0t → 0 при конечной разности начальной и конечной скоростей ускорение становится бесконечным.
Аналогичным образом, преобразовав уравнение 3.14, мы можем выразить ускорение в терминах скоростей и смещения:
а = v2-v022 (х-х0).а = v2-v022 (х-х0).Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе смещение приближается к нулю. Ускорение приближается к нулю в пределе, разница в начальной и конечной скоростях приближается к нулю для конечного смещения.
Пример 3.10
Как далеко уезжает машина?
На сухом бетоне автомобиль может ускоряться противоположно движению со скоростью 7,00 м / с 2 , тогда как на мокром бетоне он может ускоряться противоположно движению со скоростью всего 5 м / с.00 м / с 2 . Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите смещение от точки, где водитель видит, что светофор становится красным, принимая во внимание время его реакции 0,500 с, чтобы нажать ногой на тормоз.Стратегия
Для начала нам нужно нарисовать набросок Рис. 3.22. Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.Рис. 3.22. Пример эскиза для визуализации ускорения, противоположного движению и тормозному пути автомобиля.
Решение
- Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v 0 = 30,0 м / с, v = 0 и a = −7,00 м / с 2 ( a отрицательно, потому что оно находится в направлении, противоположном скорости) . Возьмем x 0 равным нулю. Ищем смещение ΔxΔx, или x — x 0 .
Во-вторых, мы определяем уравнение, которое поможет нам решить проблему. Лучшее уравнение для использования — v2 = v02 + 2a (x − x0). v2 = v02 + 2a (x − x0). Это уравнение лучше всего, потому что оно включает только одно неизвестное, x . Мы знаем значения всех других переменных в этом уравнении. (Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которое мы не знаем. Мы могли бы их использовать, но это потребовало бы дополнительных вычислений.)
В-третьих, мы изменим уравнение, чтобы найти x : x − x0 = v2 − v022ax − x0 = v2 − v022a и подставляем известные значения: х − 0 = 02− (30.0 м / с) 22 (-7,00 м / с2). X-0 = 02- (30,0 м / с) 22 (-7,00 м / с2). Таким образом, x = 64,3 м на сухом бетоне. x = 64,3 м на сухом бетоне. - Эта часть может быть решена точно так же, как (а). Единственное отличие состоит в том, что ускорение составляет −5,00 м / с 2 . Результат xwet = 90,0 м по мокрому бетону. xwet = 90,0 м по мокрому бетону.
- Когда водитель реагирует, тормозной путь такой же, как в (a) и (b) для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно вычислить, как далеко проехал автомобиль за время реакции, а затем добавить это время ко времени остановки.Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.
Для этого мы снова определяем известные и то, что мы хотим решить. Мы знаем, что v– = 30,0 м / sv– = 30,0 м / с, treaction = 0,500streaction = 0,500s и areaction = 0areaction = 0. Примем x0-реакцию x0-реакцию равной нулю. Ищем xreactionxreaction.
Во-вторых, как и раньше, мы определяем лучшее уравнение для использования. В этом случае x = x0 + v – tx = x0 + v – t работает хорошо, потому что единственное неизвестное значение — x , что мы и хотим найти.
В-третьих, мы подставляем известные для решения уравнения: x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. Это означает, что автомобиль проезжает 15,0 м, в то время как водитель реагирует, в результате чего общее смещение в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем если бы он реагировал мгновенно.
Наконец, мы добавляем смещение во время реакции к смещению при торможении (рис. 3.23), xbraking + xreaction = xtotal, xbraking + xreaction = xtotal, и найдите (a) равным 64,3 м + 15,0 м = 79.3 м в сухом виде и (b) должно составлять 90,0 м + 15,0 м = 105 м во влажном состоянии.
Рис. 3.23. Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны значения тормозного пути для сухого и мокрого покрытия, рассчитанные в этом примере для автомобиля, изначально движущегося со скоростью 30,0 м / с. Также показано общее расстояние, пройденное от точки, когда водитель впервые видит, что свет загорается красным, при условии, что время реакции составляет 0,500 с.
Значение
Смещения, обнаруженные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля.Остановка автомобиля на мокром асфальте должна длиться дольше, чем на сухом. Интересно, что время реакции значительно увеличивает смещения, но более важен общий подход к решению проблем. Мы идентифицируем известные и определяемые величины, а затем находим соответствующее уравнение. Если существует более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных необходимо решить. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но представленные здесь решения являются самыми короткими.Пример 3.11
Время расчета
Предположим, автомобиль въезжает в движение по автостраде на съезде длиной 200 м. Если его начальная скорость равна 10,0 м / с, а он ускоряется со скоростью 2,00 м / с 2 , сколько времени потребуется автомобилю, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)Стратегия
Сначала мы рисуем набросок Рис. 3.24. Нам предлагается решить за время т . Как и раньше, мы идентифицируем известные величины, чтобы выбрать удобную физическую связь (то есть уравнение с одной неизвестной, t .)Рис. 3.24. Эскиз автомобиля, ускоряющегося на съезде с автострады.
Решение
Опять же, мы идентифицируем то, что нам известно, и то, что мы хотим решить. Мы знаем, что x0 = 0, x0 = 0,v0 = 10 м / с, a = 2,00 м / с2v0 = 10 м / с, a = 2,00 м / с2 и x = 200 м.
Нам нужно решить для т . Уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 работает лучше всего, потому что единственной неизвестной в уравнении является переменная t , которую нам нужно решить. Из этого понимания мы видим, что когда мы вводим известные значения в уравнение, мы получаем квадратное уравнение.
Нам нужно изменить уравнение, чтобы найти t , затем подставив известные значения в уравнение:
200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2. 200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2.Затем мы упрощаем уравнение. Единицы измерения отменяются, потому что они есть в каждом члене. Мы можем получить единицы секунд для отмены, взяв t = t с, где t — величина времени, а s — единица измерения. Остается
.Затем мы используем формулу корней квадратного уравнения, чтобы найти t ,
t2 + 10t − 200 = 0t = −b ± b2−4ac2a, t2 + 10t − 200 = 0t = −b ± b2−4ac2a,, что дает два решения: t = 10.0 и t = -20,0. Отрицательное значение времени неразумно, так как это будет означать, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,
Значение
Всякий раз, когда уравнение содержит неизвестный квадрат, есть два решения. В некоторых проблемах имеют смысл оба решения; в других разумно только одно решение. Ответ 10,0 с кажется разумным для типичной автострады на съезде.Проверьте свое понимание 3.5
Ракета ускоряется со скоростью 20 м / с. 2 во время пуска.Сколько времени нужно, чтобы ракета достигла скорости 400 м / с?
Пример 3.12
Ускорение космического корабля
Космический корабль покинул орбиту Земли и направляется к Луне. Разгоняется со скоростью 20 м / с 2 за 2 мин и преодолевает расстояние в 1000 км. Каковы начальная и конечная скорости космического корабля?Стратегия
Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не дает ответа.Мы должны использовать одно кинематическое уравнение для решения одной из скоростей и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость. Таким образом, мы решаем два кинематических уравнения одновременно.Решение
Сначала мы решаем для v0v0, используя x = x0 + v0t + 12at2: x = x0 + v0t + 12at2: x − x0 = v0t + 12at2x − x0 = v0t + 12at21.0 × 106m = v0 (120.0s) +12 (20,0 м / с2) (120,0 с) 21,0 × 106 м = v0 (120,0 с) +12 (20,0 м / с2) (120,0 с) 2v0 = 7133,3 м / с. V0 = 7133,3 м / с.Затем мы подставляем v0v0 в v = v0 + atv = v0 + at, чтобы найти окончательную скорость:
v = v0 + at = 7133.3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с. V = v0 + at = 7133,3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с.Значение
Есть шесть переменных смещения, времени, скорости и ускорения, которые описывают движение в одном измерении. Начальные условия данной задачи могут быть множеством комбинаций этих переменных. Из-за такого разнообразия решения могут быть не такими простыми, как простая подстановка в одно из уравнений. Этот пример показывает, что решения кинематики могут потребовать решения двух одновременных кинематических уравнений.Освоив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также увидели общий подход к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений. Следующий уровень сложности в наших задачах кинематики связан с движением двух взаимосвязанных тел, называемых задачами преследования двух тел .
Задачи преследования двух тел
До этого момента мы рассматривали примеры движения с участием одного тела.Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задаче преследования двух тел движения объектов связаны, то есть искомое неизвестное зависит от движения обоих объектов. Чтобы решить эти проблемы, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на Рисунке 3.25.
Рис. 3.25. Сценарий преследования с двумя телами, в котором автомобиль 2 имеет постоянную скорость, а автомобиль 1 идет сзади с постоянным ускорением.Автомобиль 1 догонит автомобиль 2 позже.
Время и расстояние, необходимое для того, чтобы автомобиль 1 догнал автомобиль 2, зависит от начального расстояния, на которое автомобиль 1 находится от автомобиля 2, а также от скорости обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.
Рассмотрим следующий пример.
Пример 3.13
Гепард ловит газель
Гепард прячется за кустом. Гепард замечает пробегающую мимо газель со скоростью 10 м / с.В тот момент, когда газель проходит мимо гепарда, гепард из состояния покоя ускоряется со скоростью 4 м / с 2 , чтобы поймать газель. а) Сколько времени требуется гепарду, чтобы поймать газель? б) Что такое смещение газели и гепарда?Стратегия
Мы используем систему уравнений для постоянного ускорения, чтобы решить эту проблему. Поскольку есть два движущихся объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но то, что связывает уравнения, — это общий параметр, который имеет одинаковое значение для каждого животного.Если мы внимательно посмотрим на проблему, становится ясно, что общим параметром для каждого животного является их положение x в более позднее время t . Поскольку оба они начинаются с x0 = 0x0 = 0, их смещения будут такими же в более позднее время t , когда гепард догонит газель. Если мы выберем уравнение движения, которое решает смещение для каждого животного, мы можем затем установить уравнения, равные друг другу, и решить для неизвестного, то есть времени.Решение
- Уравнение для газели: Газель имеет постоянную скорость, которая является ее средней скоростью, поскольку она не ускоряется.Поэтому мы используем уравнение 3.10 с x0 = 0x0 = 0: x = x0 + v – t = v – t. x = x0 + v – t = v – t. Уравнение для гепарда: гепард ускоряется из состояния покоя, поэтому мы используем уравнение 3.13 с x0 = 0x0 = 0 и v0 = 0v0 = 0: x = x0 + v0t + 12at2 = 12at2.x = x0 + v0t + 12at2 = 12at2. Теперь у нас есть уравнение движения для каждого животного с общим параметром, который можно исключить, чтобы найти решение. В этом случае мы решаем для t : x = v – t = 12at2t = 2v – a.x = v – t = 12at2t = 2v – a. Газель имеет постоянную скорость 10 м / с, что составляет ее среднюю скорость.Ускорение гепарда составляет 4 м / с 2 . Оценив t , время, за которое гепард достигнет газели, имеем t = 2v – a = 2 (10 м / с) 4m / s2 = 5s.t = 2v – a = 2 (10 м / с) 4m / s2 = 5s.
- Чтобы получить смещение, мы используем уравнение движения гепарда или газели, поскольку оба они должны дать одинаковый ответ.
Смещение гепарда: x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. Водоизмещение газели: x = v – t = 10 м / с (5) = 50 м. x = v – t = 10 м / с (5) = 50 м.Мы видим, что оба смещения равны, как и ожидалось.
Значение
Важно анализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания отдельного движения. Также важно иметь хорошую визуальную перспективу задачи преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.Проверьте свое понимание 3.6
Велосипед имеет постоянную скорость 10 м / с. Человек начинает с отдыха и начинает бежать, чтобы догнать велосипед через 30 секунд, когда велосипед находится в том же положении, что и человек.Какое ускорение у человека?
Равномерно ускоренное движение в общей теории относительности: полнота нерастяжимых траекторий
Бим, Дж. К., Эрлих, П. Э., Исли, К. Л .: Глобальная лоренцианская геометрия. Марсель Деккер, Чистая и прикладная математика 202 , (1996)
Кандела А.М., Ромеро А., Санчес М .: Полнота траекторий релятивистских частиц в стационарных магнитных полях. Int. J. Geom. Методы Мод. Phys., 10 , 1360007 (1–8), (2013)
Кандела А.М., Ромеро А., Санчес М .: Полнота траекторий частиц, связанных с общим силовым полем. Arch. Рацион. Мех. Анальный. 208 , 255–274 (2013)
Артикул МАТЕМАТИКА MathSciNet Google Scholar
Чен Б.Ю .: Геометрия подмногообразий и ее приложения. Токийский научный университет, Токио (1981)
MATH Google Scholar
Кобаяси С., Номидзу К .: Основы дифференциальной геометрии, т. II. Уайли, Нью-Йорк (1969)
MATH Google Scholar
Фридман, Ю., Скар, Т .: Создание ковариантного уравнения релятивистской динамики: явные решения для движения под действием постоянной силы. Phys. Scr. 86 , 065008 (7pp) (2012)
Фридман Ю., Скарр, Т.: Преобразования пространства-времени из равномерно ускоренной системы отсчета, Phys.Scr. 87 , 055004 (8 стр.) (2013)
Икава, Т .: О кривых и подмногообразиях в неопределенно-римановом многообразии. Цукуба. J. Math. 9 , 353–371 (1985)
MATH MathSciNet Google Scholar
Мардер, Л .: О равномерном ускорении в специальной и общей теории относительности. Математика. Proc. Camb. Фил. Soc. 53 , 194–198 (1957)
Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА MathSciNet Google Scholar
Машхун, Б., Мюнч, У .: Измерение длины в ускоренных системах. Аня. Phys. 11 , 532–547 (2002)
Артикул МАТЕМАТИКА Google Scholar
Макмиллан Э.М.: «Парадокс часов» и космические путешествия. Наука 126 , 381–384 (1957)
Статья ОБЪЯВЛЕНИЯ Google Scholar
Миснер, К.В., Торн, К.С., Уиллер, Дж. А .: Гравитация.W.H. Фриман и Ко, Лондон (1973)
Google Scholar
Номидзу К., Яно К .: Об окружностях и сферах в римановой геометрии. Математика. Аня. 210 , 163–170 (1974)
Артикул МАТЕМАТИКА MathSciNet Google Scholar
О’Нил, Б .: Полуриманова геометрия. Academic Press, Massachusetts (1983)
MATH Google Scholar
Ponge, R., Reckziegel, H .: Скрученные произведения в псевдоримановой геометрии. Geom. Dedicata 48 , 15–25 (1993)
Артикул МАТЕМАТИКА MathSciNet Google Scholar
Риндлер У. Гиперболическое движение в искривленном пространстве-времени. Phys. Ред. 119 , 2082–2089 (1960)
Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА MathSciNet Google Scholar
Риндлер, В .: Парадокс сокращения длины. Являюсь. J. Phys. 24 , 365–366 (1961)
Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar
Ромеро, А., Санчес, М .: Полнота компактных лоренцевых многообразий, допускающих времяподобное конформное векторное поле Киллинга. Proc. Являюсь. Математика. Soc. 123 , 2831–2833 (1995)
Артикул МАТЕМАТИКА Google Scholar
Сакс, Р.К., Ву, Х .: Общая теория относительности для математиков. Град. Тексты по математике, т. 48. Springer, New York (1977)
MATH. Google Scholar
Санчес, М .: О геометрии обобщенного пространства-времени Робертсона – Уокера: геодезические. Gen. Relativ. Gravit. 30 , 914–932 (1998)
Google Scholar
Равномерно ускоренное движение в одном измерении
Описание движения за заданный промежуток времени.
u = скорость частицы в начале интервала.
v = скорость частицы в конце интервала.
a = постоянное ускорение частицы.
с = смещение частицы в заданном интервале времени
x i = координата частицы вдоль линии движения в начале интервала.
x f = координата частицы вдоль линии движения в конце интервала.
= временной интервал.
Рисунок описывает положение, скорость и координату частицы, движущейся вдоль оси x в два разных момента времени и. (A) По определению:
a ср. = v-u / t₂ — t₁
Если ускорение частицы постоянно, то
a ср. = a inst = a
Отсюда a = v — u / t, где t = t₂ — t₁
(B) Смещение частицы
s = x f — x i =
Если частица движется с постоянным ускорением, средняя скорость определяется как
с = (v + u) / 2 x t
с = (u + at) + u / 2 x t
As v = u + at из уравнения
с = ut + ½ at²
(C) Из уравнения a = (v — u) / t, t = (V — u) / a
Если мы поместим это значение t в уравнение s == [(V + u) / 2] t, мы получим
s = (v + u) / 2 x (v — u) / a, v² = u² + 2 как
Кинематические уравнения: Следующие производные уравнения известны как кинематические уравнения.
(i) v = u + при
(ii) s = ut + ½ at²
(iii) v² = u² + 2as.
Примечание:
(a) Любое из приведенных выше уравнений может использоваться непосредственно для решения проблем тогда и только тогда, когда ускорение частицы является постоянным.
(b) Вы должны учитывать знак соответствующих количеств.
Пример: Частица движется по прямой с постоянным ускорением. В точке A на линии его скорость равна 4 м / с, а в точке B — 6 м / с.Если расстояние между этими двумя точками равно 2 м, найдите
.(а) Ускорение частицы
(b) Время, необходимое частице, чтобы перейти к точке B от точки A.
(c) Если в момент времени t = 0, частица находится в точке A, найдите расстояние, на которое она переместилась за 5 th секунд.
Решение:
(a) В данной ситуации начальная скорость u = 4 м / с и конечная скорость v = 6 м / с смещение s = 2 м
∵ v² = u² + 2as
=> a = v² — u² / 2s
=> (36 м² / с² — 16 м² / с²) / 2×2 м = 5 м / с²
(b) u = 4 м / с, v = 6 м / с и a = 5 м / с².
