Как найти Объем Параллелепипеда?
Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения объема (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, вина в бочке, земли в клумбе.
Два свойства объёма
|
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Объем прямоугольного параллелепипеда
Давайте вспомним, какие виды параллелепипедов бывают.
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань которой называется параллелограмм.
Призма — это многогранник, в основаниях которого лежат равные многоугольники, а его боковые грани — это параллелограммы.
Какие бывают призмы:
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.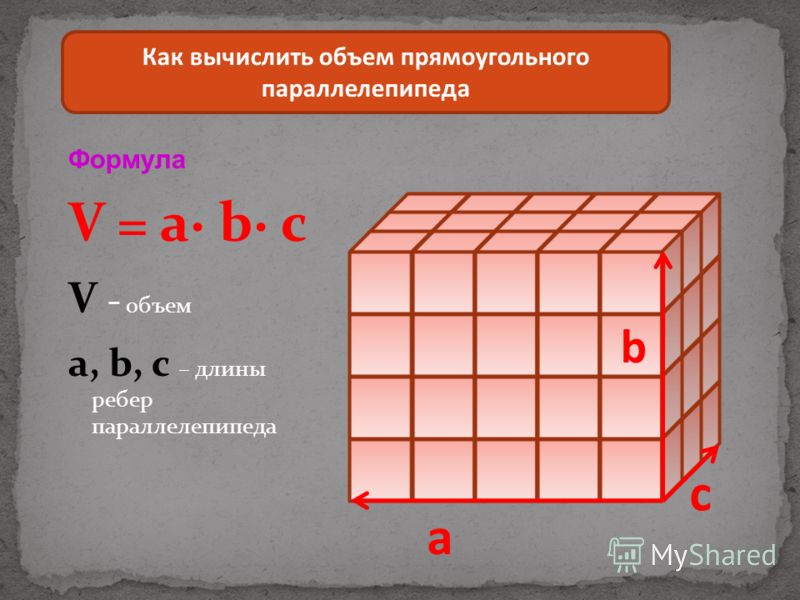
Прямоугольным параллелепипедом называют параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: V = a * b * h |
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
a | длина параллелепипеда |
b | ширина параллелепипеда |
h | высота параллелепипеда |
P (осн) | периметр основания |
S (осн) | площадь основания |
S (бок) | площадь боковой поверхности |
S (п.п.) | площадь полной поверхности |
V | объем |
Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.
a = 9 см
b = 6 см
h = 3 см
V = a * b * h
V = 9 * 6 * 3 = 162 см3.
Ответ: объем прямоугольного параллелепипеда равен 162 см3.
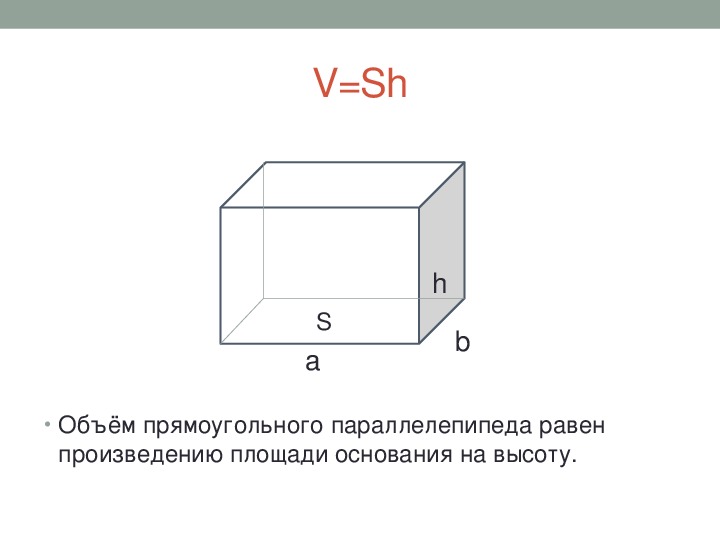
Следствие 1 Объем параллелепипеда равен произведению площади основания на высоту. V = S осн * h |
Из этого следствия выведем формулу нахождения площади основания параллелепипеда.
S осн = V : h
Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 82 см3, а высота 8 см.
V = 82 см3
h = 8 см
V = S осн * h
S осн = V : h
S осн = 82 см3: 8 см = 10,25 см2.
Ответ: площадь основания параллелепипеда равна 10,25 см2.
Следствие 2 Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту. V = S осн * h |
Пример 3. Основанием прямой призмы служит прямоугольный треугольник с катетами 6 и 8 см. Боковое ребро равно 5. Найдем объем призмы.
V = S * h = 12* a * b * h
a = 6
b = 8
h = 5
V = 1/2 * 6 * 8 * 5 = 120 см3.
Ответ: объём прямой призмы, основанием которой является прямоугольный треугольник, равен 120 см3.
С каждым годом геометрия становится все более объемной. Формулы множатся, а задачки усложняются. В детской онлайн-школе Skysmart ваш ребенок сможет заполнить пробелы, разобрать сложные темы и научиться доказывать любые теоремы.
Записывайтесь на бесплатный вводный урок и знакомьтесь с устройством учебной платформы лично.
Вычисление площади
Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.
Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.
Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания.
- S п.п. = 2 (ab + ac + bc)
Пример 4. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.
S п.п. = 2 (ab + ac + bc)
S п.п. = 2(6 * 4 + 6 * 3 + 4 * 3) = 2 * (24 + 18 + 12) = 2 * 54 = 108 см2.
Ответ: площадь поверхности параллелепипеда — 108 см2.
Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно. В интернете есть много онлайн-калькуляторов, которые помогут вам быстро вычислить объем:
В интернете есть много онлайн-калькуляторов, которые помогут вам быстро вычислить объем:
Задачи на самопроверку
Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.
Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.
Как решаем:
a = 18 см
b = 10 см
h = 7 см
Формула нахождения объема параллелепипеда:
V = a * b * h
Подставляем наши числа:
V = 18 * 10 * 7 = 1260 см3.
Ответ: объём параллелепипеда = 1260 см3.
Задачка 2. Найдите площадь основания параллелепипеда, если его объём = 120 см3, а высота — 15 см.
Как решаем:
V = 120 см3
h = 15 см
V = S осн * h
S осн = V : h
S осн = 120 см3: 15 см = 8 см2.
Ответ: площадь основания параллелепипеда = 8 см2.
Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания = 30 сантиметров, ширина = 12 см, а высота = 5 см.
Как решаем:
S п.п. = 2 (ab + ac + bc)
S п.п. = 2(30 * 12 + 30 *5 + 12 * 5) = 2 * (360 + 150 + 60) = 2 * 570 = 1140 см2.
Ответ: площадь полной поверхности параллелепипеда = 1140 см2.
Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.
V параллелепипеда | V = a * b * h |
| V = S осн * h |
S боковой поверхности | S б.п. = 2(ac + bc) |
S полной поверхности | S п.п. = 2 (ab + ac + bc) |
Диагональ параллелепипеда | d2 = a2+ b2 + c2 |
На уроках математики в современной школе Skysmart нет скучных учебников, надоевших задачек и неинтересных тетрадей.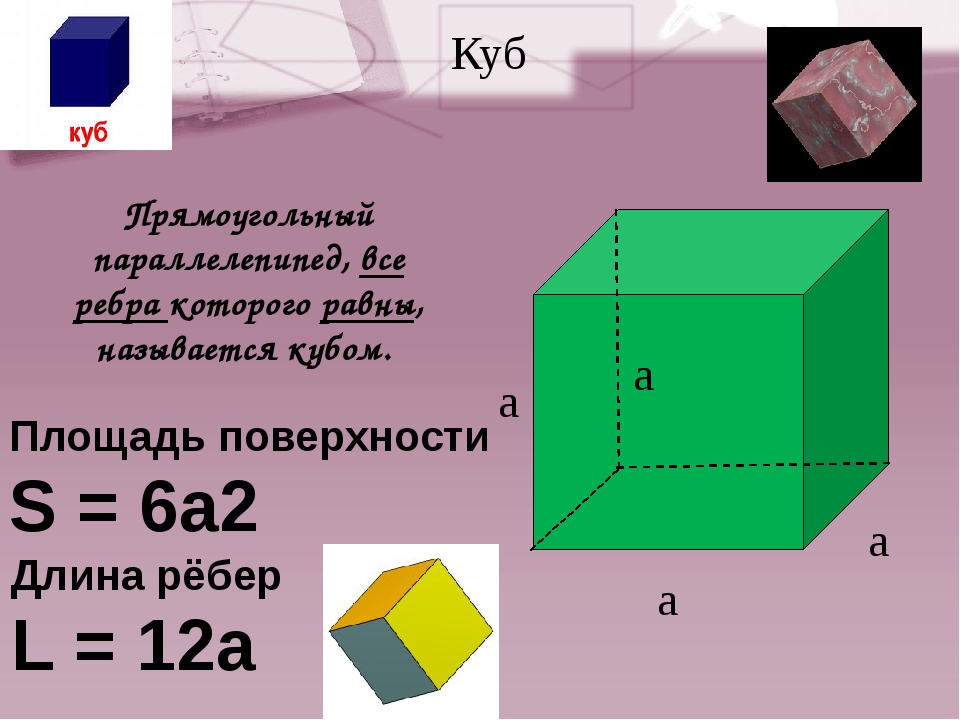 Ученики занимаются по интерактивному учебнику, чертят на настоящей онлайн-доске и решают занимательные примеры.
Ученики занимаются по интерактивному учебнику, чертят на настоящей онлайн-доске и решают занимательные примеры.
Математика может быть по-настоящему увлекательной. Записывайтесь на бесплатный вводный урок, чтобы проверить, так ли это на самом деле.
Формулы объема геометрических фигур.
Объем геометрической фигуры
— количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a3
где V — объем куба,
a — длина грани куба.
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
V = So h
где V — объем призмы,
So — площадь основания призмы,
h — высота призмы.
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
V = So · h
где V — объем параллелепипеда,
So — площадь основания,
h — длина высоты.
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
V = a · b · h
где V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
где V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды.
Объем правильного тетраэдра
Формула объема правильного тетраэдра:
где V — объем правильного тетраэдра,
a — длина ребра правильного тетраэдра. 2 \cdot h$
2 \cdot h$
$S = 2\cdot\pi\cdot r \cdot h$
Площадь полной поверхности:$S = 2\cdot\pi\cdot r(h + r)$
Тест: объём и площадь поверхности
Как найти объём параллелепипеда
1. Заполните, пожалуйста размеры рёбер параллелепипеда 2. Для вычисления необходимо знать ширину, высоту и длину 3. Онлайн калькулятор параллелепипеда вычислит объём, моментально решит задачу и напишет решение которое вам останется только переписать!
Формула используемая в нашем калькуляторе найдёт объём прямоугольного параллелепипеда. А если ваш параллелепипед имеет косые грани, вместо длины соответствующего косого ребра — необходимо ввести значение высоты этой части фигуры.
Формула объёма прямоугольного параллелепипеда
L * H * N = V
Чтобы его найти, необходимо знать размеры рёбер: высоту, ширину и длину. По формуле, размеры граней параллелепипеда необходимо перемножить в произвольном порядке.
Объём можно представить в литрах или куб.см., кубических миллиметрах.
Формула площади поверхности параллелепипеда
S1*2 + S2*2 + S3*2 = S
По формуле площади параллелепипеда необходимо найти площади всех сторон параллелепипеда, а затем их сложить. Противоположные стороны, грани, и рёбра параллелепипеда равны между собой, по этому при вычислении площадей можно применять умножение на два.
Основание параллелепипеда
В некоторых случаях бывает известна площадь основания параллелепипеда, тогда для того, что бы найти объём достаточно площадь основания умножить на высоту. ! ВАЖНО ! — это верно, только для прямоугольного параллелепипеда.
Как найти объём параллелепипеда?
Проще всего найти объём введя три известных значения в графы онлайн калькулятора объёма! Затем — нажми на кнопу — получишь результат )!
Калькулятор вычислит объём параллелепипеда abcda1b1c1d1 и распишет решение подробно и с комментариями. Вам останется только переписать строчное решение параллелепипеда себе в тетрадь. Подробное текстовое решение с разъяснениями позволит найти понимание методики решения таких задач и при необходимости снять вопросы, дав развёрнутый и грамотный ответ.
Вам останется только переписать строчное решение параллелепипеда себе в тетрадь. Подробное текстовое решение с разъяснениями позволит найти понимание методики решения таких задач и при необходимости снять вопросы, дав развёрнутый и грамотный ответ.
Расчёты объёма и площадь параллелограмма — это элементарная основа для многих технических и бытовых расчётов! Например для расчёта ремонта в комнате, вычисления данных для отопления помещений или их кондиционирования.
Параллелограмм это объёмная геометрическая фигура, имеющая шесть сторон, каждая из сторон при этом параллелограмм. Стороны параллелограмма обычно называются гранями. Если все грани параллелепипеда имеют форму прямоугольника — то это уже прямоугольный параллелограмм! Обозначается эта фигура буквами abcda1b1c1d1.
Как правильно с помощью формул найти объем прямоугольного параллелепипеда?
Прямоугольный параллелепипед, с точки зрения математики, является объемной фигурой с шестью гранями. Увидеть его можно, если посмотреть на прямоугольный бассейн, кирпич или спичечный коробок.
Эта фигура очень часто встречается в повседневной жизни, однако, нередко возникает необходимость узнать ее объем, что для многих представляет некоторые трудности. Например, какого объема необходим бак для воды на дачном участке, или каким размером делать бассейн.
Во многих других ситуациях возникает проблема, как найти объем параллелепипеда правильно.
Между тем вычислить это значение очень просто. Достаточно лишь знать ширину, длину и высоту предмета или объекта. И также необходимо знать формулу, с помощью которой и находят объем данной геометрической фигуры.
Основные особенности и формула для расчета
Для того чтобы найти объем параллелепипеда необходимо:
- определить длину, высоту и ширину объекта;
- и после этого перемножить данные значения друг на друга;
- получившиеся данные и будут объемом.

Это все предельно просто и не таит никаких подводных камней. Главное — это знать требуемые значения, без которых выполнить расчет будет невозможно.
При этом важно знать, что определить параметр можно в сантиметрах, кубометрах, дециметрах и некоторых других размерностях в зависимости от требований. Если говорить о Международной системе единиц (СИ), параметр рассчитывают в сантиметрах. Это оптимальный вариант. Но при желании всегда можно перевести значение в требуемые размерности.
Формула расчета в двух вариантах
Итак, для расчета по формуле нужно знать длину, ширину и высоту измеряемого предмета. Эти данные следует обозначить соответственно как А, B и C, а объем обычно представляют буквой V. Формула для определения объема прямоугольного параллелепипеда при этом будет выглядеть следующим образом: V = A x B x C.
Если определятся объем бассейна, то необходимо его длину, ширину и глубину перемножить. Для более простого восприятия давайте разберем правила расчета объема параллелепипеда на примере. Допустим, что его длина составляет 10 метров, ширина достигает 3 метров, а глубина — 1,5. В этом случае объем этого объекта определяется следующим образом: 10x3x1,5=45 кубометров, или 45 кубических метров.
Можно выделить и другую формулу, которая имеет некоторое отличие. Она представляет собой произведение площади основания на высоту. Формула выглядит следующим образом: V = S x h. Здесь h — высота параллелепипеда. S — площадь основания, которая представлена произведением двух сторон основания. Обычно их обозначают, как a и b: S = a x b.
При расчете можно пользоваться любой из двух приведенных формул. Обе являются верными и позволяют получить точные данные. Последний вариант удобен, когда уже известна площадь основания. Если же она неизвестна, проще перемножать сразу три линейных размера, исключая необходимость в лишней процедуре.
О чем еще следует знать для правильности расчета?
Для вычисления объема параллелепипеда необходимо понять, что это за фигура. Она представляет собой призму, основание которой — параллелограмм. Параллелепипед имеет 6 граней, каждый из которых является параллелограммом. При этом выделяют несколько видов фигур. Принцип расчета не имеет конкретных отличий, но сами фигуры внешне отличаются. Итак, можно выделить такие виды:
Она представляет собой призму, основание которой — параллелограмм. Параллелепипед имеет 6 граней, каждый из которых является параллелограммом. При этом выделяют несколько видов фигур. Принцип расчета не имеет конкретных отличий, но сами фигуры внешне отличаются. Итак, можно выделить такие виды:
- Прямоугольный параллелепипед. Эта фигура представляет собой параллелепипед, который имеет все грани в виде прямоугольников.
- Прямым параллелепипедом является фигура, у которой 4 боковые грани — прямоугольники.
- Куб — это еще один вид параллелепипеда. Он представляет собой прямоугольный параллелепипед, все стороны которого равны между собой. Другими словами, все шесть граней такой фигуры, как куб — это равные квадраты.
И также важно помнить о том, что в процессе выполнения расчета у каждой составляющей формулы должна быть одна и та же размерность. Если опустить это простое правило, получить верный результат не удастся. Если вы выполняете расчеты просто на уроках математики, проблемой могут стать только неудовлетворительные оценки. А при проектировании и наличии ошибок в расчетах проблемы могут быть более серьезными.
Не стоит думать, что основные математические формулы по определению объемов геометрических фигур встречаются исключительно на уроках математики. В большинстве случаев они пригодятся и в последующей жизни. В частности, во время ремонтных или строительных работ, при проектировании и декорированию интерьера, а также в ряде других случаев. Именно тогда без правильной формулы обойтись не удастся.
Можно подвести итог: объем параллелепипеда равен произведению трех линейных размеров — длины, ширины, высоты. Параметр напрямую зависит от трех единиц измерения при любом вращении и повороте. Результат будет неизменным.
Видео
Видео поможет вам научиться находить объем прямоугольного параллелепипеда.
Объем прямоугольного параллелепипеда: онлайн калькулятор, формулы, примеры решений
Параллелепипед — это призматическая фигура, все грани которой являются параллелограммами. Если в роли граней выступают обычные прямоугольники, то параллелепипед является прямоугольным и именно форму данной фигуры имеют такие реальные объекты как панельные дома, аквариумы, книги, принтеры или кирпичи.
Если в роли граней выступают обычные прямоугольники, то параллелепипед является прямоугольным и именно форму данной фигуры имеют такие реальные объекты как панельные дома, аквариумы, книги, принтеры или кирпичи.
Геометрия параллелепипеда
Прямоугольный параллелепипед ограничен шестью гранями, при этом противоположные грани фигуры равны и параллельны друг другу. Данная геометрическая фигура представляет собой частный случай прямой четырехугольной призмы. Параллелепипед имеет 12 ребер и 8 вершин. В каждой из вершин сходятся по три ребра фигуры, которые являются длиной, шириной и высотой параллелепипеда или его измерениями. Если длина, ширина и высота фигуры равны, то параллелепипед превращается в куб.
Параллелепипеды в реальной жизни
Большое количество существующих в реальности объектов имеют форму параллелепипеда. Широкое распространение такая форма получила благодаря легкости производства, удобству хранения и транспортировки, идеальной сочетаемости одинаковых параллелепипедов, устойчивости и постоянству размеров. Параллелепипедную форму имеют такие объекты, как кирпичи, коробки, смартфоны, блоки питания, дома, комнаты и многое другое.
Объем параллелепипеда
Важным свойством любого геометрического тела является его вместимость, то есть объем фигуры. Объем — это характеристика объекта, которая показывает, сколько единичных кубов он способен вместить. В общем случае объем любой призматической фигуры рассчитывается по формуле:
V = So × h,
где So – площадь основания фигуры, а h – ее высота.
Данная формула легко иллюстрируется следующим примером. Представьте, что у вас есть один лист бумаги А4. Это обычный прямоугольник, который характеризуется строго определенной площадью. Грубо говоря, лист — это плоскость. Теперь представьте стандартную пачку бумаги из 500 листов формата А4. Это уже объемная фигура, имеющая форму параллелепипеда. Узнать ее объем легко, достаточно перемножить площадь листа, лежащего в основании, на их количество, то есть, на высоту призмы.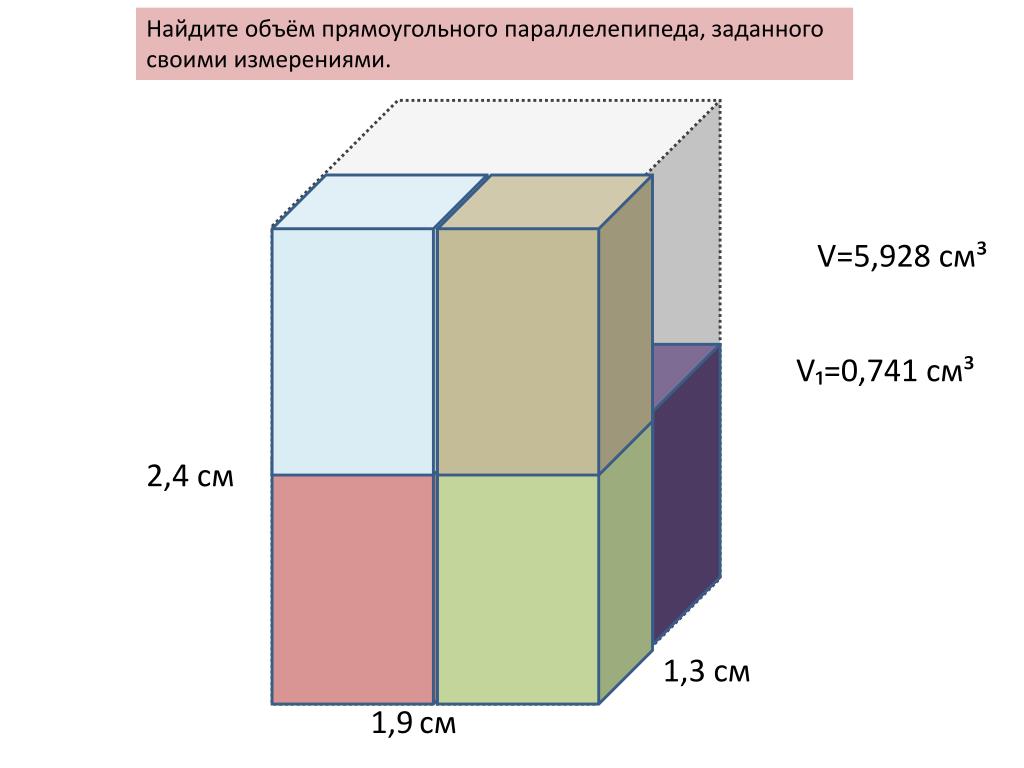
Параллелепипед — это частный случай призмы, в основании которой лежит прямоугольник. Площадь прямоугольника представляет собой простое произведение его сторон, следовательно, для параллелепипеда:
So = a × b
Для определения объема достаточно умножить So на высоту фигуры. Таким образом, объем прямоугольного параллелепипеда считается по простой формуле, представляющей перемножение трех сторон тела:
V = a × b × h,
где a – длина, b – ширина, h – высота геометрической фигуры.
Для определения объема прямоугольного параллелепипеда вам достаточно замерить три этих параметра и просто перемножить их. Если вы не хотите постоянно держать в голове формулы определения объемов и площадей геометрических фигур, то воспользуйтесь нашим каталогом онлайн-калькуляторов: каждый инструмент подскажет вам, какие параметры вы должны замерить и мгновенно вычислит результат. Рассмотрим пару примеров, когда вам может понадобиться определить объем параллелепипеда.
Примеры из жизни
Аквариум
К примеру, вы купили старый аквариум в форме параллелепипеда, но вам никто не сказал, какой объем имеет данная конструкция. Объем аквариума — важный параметр, по которому определяется мощность системы обогрева для морских обитателей. Вычислить данную характеристику несложно — достаточно замерить длину, ширину и высоту аквариума и ввести эти данные в форму калькулятора. Допустим, длина аквариума составляет 1 м, ширина — 50 см, а высота — 70 см. Для правильного расчета важно выразить все стороны в одних единицах измерения, допустим, в метрах.
V = 1 × 0,5 × 0,7 = 0,35
Таким образом, объем аквариума составит 0,35 кубических метров или 350 литров. Зная объем, вы без проблем подберете мощность для системы обогрева.
Строительство
Допустим, вы заливаете плитный фундамент для своей дачи и вам необходимо узнать, сколько бетона понадобится для заливки основания. Плитный фундамент — это цельная монолитная плита, которая располагается под всей площадью здания. Для того чтобы узнать требуемый объем бетона, необходимо вычислить объем плиты. Плита, к счастью, имеет форму прямоугольного параллелепипеда, поэтому вы без проблем можете подсчитать нужное количество бетона. Допустим, ваша дача — это стандартный домик 6 на 6 метров. Вы уже знаете два из трех необходимых параметров. Согласно требованиям, толщина плитного фундамента должна быть не менее 10 см, и вы можете сами выбрать подходящий размер. К примеру, вы решили залить плиту толщиной 20 см. Для правильного расчета задайте все параметры в одних единицах измерения, то есть метрах, и получите результат:
Для того чтобы узнать требуемый объем бетона, необходимо вычислить объем плиты. Плита, к счастью, имеет форму прямоугольного параллелепипеда, поэтому вы без проблем можете подсчитать нужное количество бетона. Допустим, ваша дача — это стандартный домик 6 на 6 метров. Вы уже знаете два из трех необходимых параметров. Согласно требованиям, толщина плитного фундамента должна быть не менее 10 см, и вы можете сами выбрать подходящий размер. К примеру, вы решили залить плиту толщиной 20 см. Для правильного расчета задайте все параметры в одних единицах измерения, то есть метрах, и получите результат:
V = 6 × 6 × 0,2 = 7,2
Следовательно, для заливки фундамента вам понадобится 7,2 кубических метров бетона.
Заключение
Определение объема параллелепипедных фигур может пригодиться вам во многих случаях: от бытовых проблем до производственных вопросов, от школьных заданий до проектных задач. Наш онлайн-калькулятор поможет вам решить задания любой сложности.
| Прямой параллелепипед – это параллелепипед с ребром, перпендикулярным плоскости основания. | ||
| Геометрические фигуры. Прямой параллелепипед. | ||
| Призма — многогранник, 2 грани это конгруэнтные (равные) многоугольники, которые лежат в параллельных плоскостях, а оставшиеся грани — параллелограммы, имеющие общие стороны с этими многоугольниками. | ||
| Геометрические фигуры. Призма. Объем призмы. | ||
| Наклонный параллелепипед — это параллелепипед , у которого боковые грани расположены, относительно оснований, под не прямым углом . | ||
| Геометрические фигуры. Наклонный параллелепипед. Объем наклонного параллелепипеда. | ||
Формула кваркового объема для параллелепипеда |
Начиная с повсеместного тройная идентификация продукта |
для векторов в R 3 , у нас сразу есть удобная формула для перекрестного произведения двух крестов товары |
Теперь предположим, что мы определяем три новые векторы в терминах A , B , C следующим образом |
Хорошо известно, что тройное произведение A ‘∙ ( B ‘ x C ‘) — это просто квадрат тройного произведения A ∙ ( B х С ).Чтобы понять почему это правда, обратите внимание, что, используя (2) «затравленное» тройное произведение может можно выразить как |
Так как количество ( A x B ) ∙ C равен объему параллелепипеда с векторами A , B , C образуя смежные кромки, ясно, что ( A x B ) ∙ A = 0, потому что два из
три края идентичны. |
Но это не очень изящно. Из конечно, в частном случае, когда A , B , C взаимно ортогональных следует, что попарно перпендикулярные векторы A , B , C также ортогональны, поэтому два тройных произведения — это просто объемы двух прямоугольных тел, одно со сторонами A , B , C а другой со сторонами A ‘= BC , B ‘ = AC , C ‘ = AB , из чего очевидно, что второй объем является квадратом первый.Это основано на формуле объема V = | A || B || C | для прямоугольных тел, и такая же степень очевидности может быть достигнута в общем случае, если бы у нас была подходящая формула для объема общего параллелепипеда. |
Тройное произведение A ∙ ( B x C ) соответствует объему общего параллелепипеда с прилегающими ребрами A , B , C , и этот объем можно выразить формулой |
где S — произведение
синусы парных углов θ AB , θ BC ,
θ CA между векторами A , B , C ,
а S ‘- произведение синусов углов θ AB , θ BC ,
θ CA между двойными векторами A , B , C . |
Величины грунтованного векторов |
, значит, у нас |
Интересно, как 2/3 и 1/3 показателя на S и S ‘, кажется, имитируют комбинаторное поведение свойства кварков.Также интересно, что S 1/3 — это просто геометрическое среднее трех попарных синусов, поэтому, если мы представим прямоугольный сплошной с длиной кромки, равной трем синусам, количество S 1/3 будет краем куба с таким же объемом. |
Возврат в главное меню MathPages |
Формулы объема и поверхности
Объем выражает количество чего-то (например, воды), которое нам нужно заполнить в форме.Космические фигуры имеют только объем. Плоские фигуры (треугольники, квадраты) не имеют объема.
Стандартное обозначение для тома — V.
Прямоугольный параллелепипед
Прямоугольный параллелепипед имеет 6 прямоугольных граней.
Если стороны прямоугольника внизу — это и
b, а высота параллелепипеда равна c
(третье ребро прямоугольного параллелепипеда).
Формула объема:
$ V = а \ cdot b \ cdot c $
Площадь поверхности = $ 2 (a \ cdot b + a \ cdot c + b \ cdot c) $
Куб
Куб — это прямоугольный параллелепипед, грани и ребра которого равны. 2 $
2 $
Цилиндр
Круглый цилиндр — это фигура, имеющая два одинаковых и параллельных круглых основания.3 $, то объем параллелепипеда, образованного между этими тремя векторами, можно вычислить по следующей формуле: $ \ mathrm {Volume} = \ mathrm {abs} (\ vec {u} \ cdot (\ vec {v} \ times \ vec {w})) = \ mathrm {abs} \ begin {vmatrix} u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \\ w_1 & w_2 & w_3 \ end {vmatrix} $.
- Доказательство: Напомним, что формула параллелепипеда определяется формулой $ V = (\ mathrm {Area \: of \: base}) (\ mathrm {height}) $. Площадь основания параллелепипеда будет площадью параллелограмма, определяемой векторами $ \ vec {u} $ и $ \ vec {v} $, которые мы уже вычислили как $ A = \ | \ vec {u} \ times \ vec {v} \ | $.Теперь нам нужно рассчитать высоту параллелепипеда.
- Сначала давайте посмотрим на следующее изображение:
- Заметим, что высота параллелепипеда — это просто норма проекции векторного произведения $ \ vec {u} \ times \ vec {v} $ на $ \ vec {w} $, то есть $ h = \ | \ mathrm {proj} _ {\ vec {u} \ times \ vec {v}} \ vec {w} \ | $. S
\ begin {align} h = \ | \ mathrm {proj} _ {\ vec {u} \ times \ vec {v}} \ vec {w} \ | = \ frac {\ mid \ vec {w} \ cdot (\ vec {u} \ times \ vec {v}) \ mid} {\ | \ vec {u} \ times \ vec {v} \ |} \ end {align}
- Подставляя это обратно в нашу формулу для объема параллелепипеда, получаем:
\ begin {align} V = \ | \ vec {u} \ times \ vec {v} \ | \ frac {\ mid \ vec {w} \ cdot (\ vec {u} \ times \ vec {v}) \ mid} {\ | \ vec {u} \ times \ vec {v} \ |} \\ V = \ mid \ vec {w} \ cdot (\ vec {u} \ times \ vec {v}) \ mid \ end {align}
- Заметим, что эта формула дает абсолютное значение скалярного тройного произведения между векторами $ \ vec {u}, \ vec {v}, \ vec {w} $, то есть:
\ begin {align} V = \ mathrm {abs} \ begin {vmatrix} w_1 & w_2 & w_3 \\ v_1 & v_2 & v_3 \\ u_1 & u_2 & u_3 \ end {vmatrix} \ end {align}
- Конечно, перестановка строк в этом определителе не влияет на определитель, когда мы вычисляем абсолютное значение результата, и поэтому наше доказательство завершено.
 3 $ — это ноль. Поскольку каждый вектор в $ \ {\ vec {u}, \ vec {v}, \ vec {w} \} $ уже должен лежать в той же плоскости, что и другой вектор из набора, то, поскольку объем равен нулю, должны существовать вектор в этом наборе, лежащий в той же плоскости, что и два других. Без ограничения общности предположим, что $ \ vec {u} $ лежит на одной плоскости с $ \ vec {v} $ и $ \ vec {w} $. Тогда $ \ vec {v} $ также должен лежать в той же плоскости, что и $ \ vec {u} $ и $ \ vec {w} $, и то же самое касается $ \ vec {w} $. Следовательно, все три вектора лежат в одной плоскости.3 $ и $ \ vec {u} = (1, 0, 1) $, $ \ vec {v} = (1, 1, 0) $ и $ \ vec {w} = (w_1, 0, 1). $, найдите значение $ w_1 $, при котором все три вектора лежат в одной плоскости.
3 $ — это ноль. Поскольку каждый вектор в $ \ {\ vec {u}, \ vec {v}, \ vec {w} \} $ уже должен лежать в той же плоскости, что и другой вектор из набора, то, поскольку объем равен нулю, должны существовать вектор в этом наборе, лежащий в той же плоскости, что и два других. Без ограничения общности предположим, что $ \ vec {u} $ лежит на одной плоскости с $ \ vec {v} $ и $ \ vec {w} $. Тогда $ \ vec {v} $ также должен лежать в той же плоскости, что и $ \ vec {u} $ и $ \ vec {w} $, и то же самое касается $ \ vec {w} $. Следовательно, все три вектора лежат в одной плоскости.3 $ и $ \ vec {u} = (1, 0, 1) $, $ \ vec {v} = (1, 1, 0) $ и $ \ vec {w} = (w_1, 0, 1). $, найдите значение $ w_1 $, при котором все три вектора лежат в одной плоскости. Как мы только что узнали, три вектора лежат на одной плоскости, если их тройное скалярное произведение равно нулю, и поэтому мы должны оценить следующий определитель как равный нулю:
(4)\ begin {align} \ begin {vmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ w_1 & 0 & 1 \ end {vmatrix} = 0 \ end {align}
Давайте оценим этот определитель по третьей строке, чтобы получить $ w_1 \ begin {vmatrix} 0 & 1 \\ 1 & 0 \ end {vmatrix} + \ begin {vmatrix} 1 & 0 \\ 1 & 1 \ end {vmatrix} = 0 $, что в упрощенном виде составляет $ -w_1 + 1 = 0 $.Следовательно, если $ w_1 = 1 $, то все три вектора лежат в одной плоскости.
404 не найдено
404 не найденоЗапрошенный URL /~jmckerna/teaching/14-15/autumn/20f/l_17.pdf не найден на этом сервере.
Наиболее частые причины этой ошибки:- Вы неправильно ввели URL-адрес, к которому вы пытаетесь получить доступ. Тщательно проверьте орфографию, пунктуацию и чувствительность к регистру URL-адреса и повторите попытку.
- Файл или каталог, к которому вы пытаетесь получить доступ, больше не существует или был перемещен в другое место.

Информацию о веб-сайтах класса см. В списке веб-сайтов класса по адресу http://www.math.ucsd.edu/resources/course-websites/.Для других веб-страниц, пожалуйста, начните с веб-сайта верхнего уровня математического факультета UCSD по адресу http://www.math.ucsd.edu/.
Чтобы связаться с администраторами веб-сервера, отправьте электронное письмо по адресу [email protected].Чтобы мы могли должным образом устранить проблему, включите:
- Точный URL-адрес, который вы пытаетесь получить, указан в вашем веб-браузере:
REQUEST_URI = http: // www.math.ucsd.edu/~jmckerna/teaching/14-15/autumn/20f/l_17.pdf - Предыдущая ссылающаяся веб-страница или ссылка, которая привела вас на этот URL:
HTTP_REFERER = (нет) - Полное имя используемого вами веб-браузера, включая номер его версии:
HTTP_USER_AGENT = Mozilla / 5.0 (X11; Linux x86_64; rv: 33.0) Gecko / 20100101 Firefox / 33.0 - Любые сообщения об ошибках или подробное описание возникшей проблемы.
- Название вашей операционной системы, включая номер ее версии.
- Текущий IP-адрес или имя хоста вашего компьютера:
REMOTE_ADDR (REMOTE_HOST) = 81.222.188.26 ((нет)) - Точная дата и время, когда вы столкнулись с проблемой:
DATE_LOCAL = среда, 7 апреля 2021 года 01:05:29 PDT
Расчет объема прямоугольника
Описание:
Онлайн-калькулятор позволяет рассчитать объем прямоугольника по его длине, ширине и высоте.
volume_rectangle онлайнОписание:
Калькулятор может рассчитать в режиме онлайн объем прямоугольного параллелепипеда , другими словами, вычислить объем прямоугольного кубоида . Объем прямоугольного параллелепипеда определяется формулой `(L * l * h)`, где L — длина, ширина с одной стороны и h по высоте.
 Калькулятор объема поддерживает как числовые, так и буквальные выражения.
Калькулятор объема поддерживает как числовые, так и буквальные выражения.Калькулятор объема может рассчитать объем прямоугольного параллелепипеда по переменным числовые, возвращаются точные и приблизительные результаты.
Таким образом, вычисляя объем прямоугольного кубоида длиной 3, шириной 2, а высота равна 4, вычисляется по следующей формуле volume_rectangle (`3; 2; 4`).
Калькулятор объема может выполнять символьные или буквальные вычисления.Чтобы вычислить, например, объем прямоугольного параллелепипеда длиной x, шириной x + 1 и высотой `x / 2`, введите следующую формулу volume_rectangle (`x; 1 + x; x / 2`), после вычисления возвращается результат.
Онлайн-калькулятор позволяет рассчитать объем прямоугольника по его длине, ширине и высоте.Синтаксис:
прямоугольник_объема (длина; ширина; высота)Примеры:
volume_rectangle (`3; 2; 4`), возвращает 24 Рассчитать онлайн с volume_rectangle (объем прямоугольного параллелепипеда)Расчет формулы объема и площади в Excel
Программа Excel — лучший калькулятор.Мы привыкли использовать для расчетов традиционные бухгалтерские калькуляторы, хотя все их возможности поддерживаются программой Excel. Более того, у него есть неоспоримые преимущества.
В некоторых формулах можно выполнить только один математический расчет для расчета калькуляции. В таких случаях, если данные изменяются, вам нужно все изменить. Но если все данные распределены по ячейкам и формула будет относиться только к единицам, то при любых изменениях менять не нужно.
Взаимодействие с другими людьми Одна формула может использоваться много раз. Чтобы понять, как это работает, лучше привести несколько практических примеров.
Одна формула может использоваться много раз. Чтобы понять, как это работает, лучше привести несколько практических примеров.Как рассчитать объем и площадь в Excel
В ячейку A1 записываем формулу для расчета объема параллелепипеда: a = 6 см; б = 8 см; c = 12 см.
В ячейку А2 записываем формулу расчета площади круга: r = 25 см.
В ячейке A3 формула содержит функцию без аргументов PI (), которая сама по себе содержит общее количество PI (а не 3.). Если писать все в одну строчку, то надо соблюдать правила арифметической последовательности. Для этого нужно использовать круглые скобки.
Взаимодействие с другими людьмиФормула для расчета объема сферы в Excel
Например, нам нужно регулярно рассчитывать объемы сфер разного радиуса.
Формула для вычисления объема шара выглядит так:
Предыдущие примеры плохо подходят для решения этой проблемы, так как они не используют значения переменных в формулах, а только константы.3 (A2 — ссылка на ячейку).
- В ячейку A2 мы введем разные радиусы, и после каждого ввода в ячейку B2 мы получим результат вычисления объема сфер, соответствующего его радиусу.
Примечание. Если вы используете несколько вычислений в Excel или формулы, которые содержат ссылки на ячейки в качестве значений переменных, вам всегда нужно подписывать каждую ячейку входящими данными и формулами. Это позволит избежать ошибок и легко прочитать значения или результаты расчета формул.
Формула площади и объема для геометрических фигур
пи (π) = 3.1415926535 …
Формула периметра | |||
| Квадрат | 4 × сторона | ||
| Прямоугольник | 2 × (длина + ширина) | ||
| Параллелограмм | 2 × (сторона1 + сторона102) | 2 × 9 (сторона1 + сторона102) | сторона1 + сторона2 + сторона3 |
| Правильный n-полигон | n × сторона | ||
| Трапеция | высота × (основание1 + основание2) / 2 | ||
| основание × трапеция | высота1 + [ csc (theta1) + csc (theta2)] | ||
| Окружность | 2 × pi × радиус | ||
| Эллипс | 4 × radius1 × E (k, pi / 2) E (k, pi / 2) — полный эллиптический интеграл второго рода k = (1 / radius1) × sqrt (radius1 2 — radius2 2 ) | ||
Формула площади | |||
| Квадрат | сторона 2 | ||
| Прямоугольник | длина × ширина | ||
| Параллелограмм | основание × высота | ||
| Треугольник | основание × высота / 2 | 2110||
| основание × высота / 2 | 2110|||
| Трапеция | высота × (base1 + base2) / 2 | ||
| Окружность | pi × радиус 2 | ||
| Эллипс | пи × радиус1 × радиус2 | ||
| Куб (поверхность) | 6 × сторона 2 | ||
| Сфера (поверхность) | 4 × пи × радиус 2 | ||
| Цилиндр ( | вс сторона стороны) | периметр окружности × высота | |
| 2 × pi × радиус × высота | |||
| Цилиндр (вся поверхность) | Площади верхней и нижней окружностей + Площадь стороны | ||
| 2 (пи × радиус 2 ) + 2 × пи × радиус × высота | |||
| Конус (поверхность) | пи × радиус × сторона | ||
| Тор (поверхность) | пи 2 × (радиус2 2 — радиус1 2 ) | ||
Формула объема | |||
| Куб | сторона 3 | ||
| Прямоугольная призма | сторона1 × сторона2 × сторона3 | Сфера||
| Эллипсоид | (4/3) × пи × радиус1 × радиус2 × радиус3 | ||
| Цилиндр | пи × радиус 2 × высота | Конус | (1/3) × pi × радиус 2 × высота |
| Пирамида | (1/3) × (площадь основания) × высота | ||
| Тор | (1/4) × pi 2 × (r1 + r2) × (r1 — r2) 2 | ||
Источник: Spiegel, Murray R.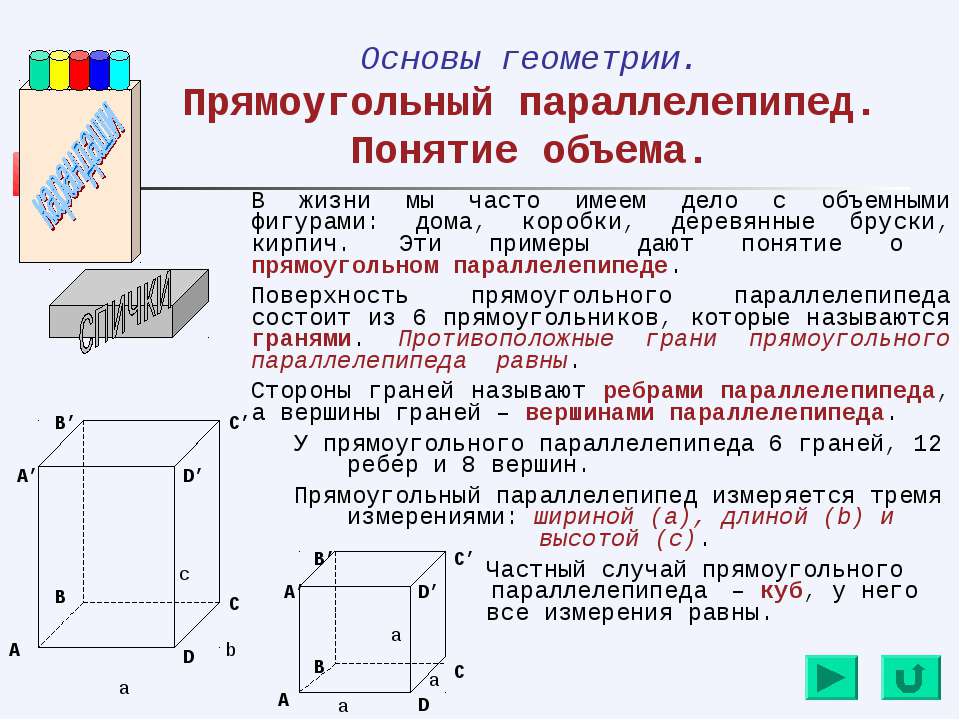

 У прямоугольного параллелепипеда каждая из граней является прямоугольником.
У прямоугольного параллелепипеда каждая из граней является прямоугольником.
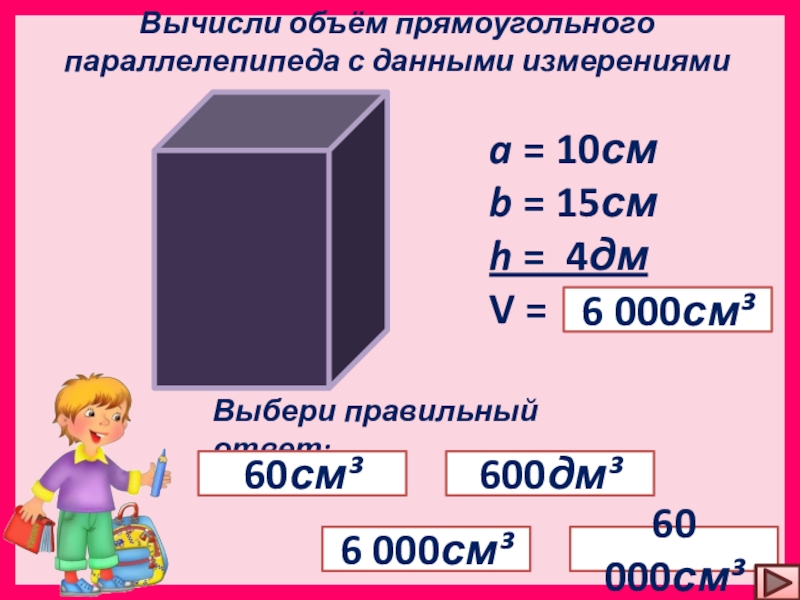 Для чего же может потребоваться формула нахождения объема фигуры? Подобную форму имеют книги, упаковочные коробки и еще множество вещей из повседневной жизни. Комнаты в жилых и офисных домах, как правило, являются прямоугольными параллелепипедами. Для установки вентиляции, кондиционеров и определение количества обогревательных элементов в комнате необходимо рассчитать объем помещения.
Для чего же может потребоваться формула нахождения объема фигуры? Подобную форму имеют книги, упаковочные коробки и еще множество вещей из повседневной жизни. Комнаты в жилых и офисных домах, как правило, являются прямоугольными параллелепипедами. Для установки вентиляции, кондиционеров и определение количества обогревательных элементов в комнате необходимо рассчитать объем помещения.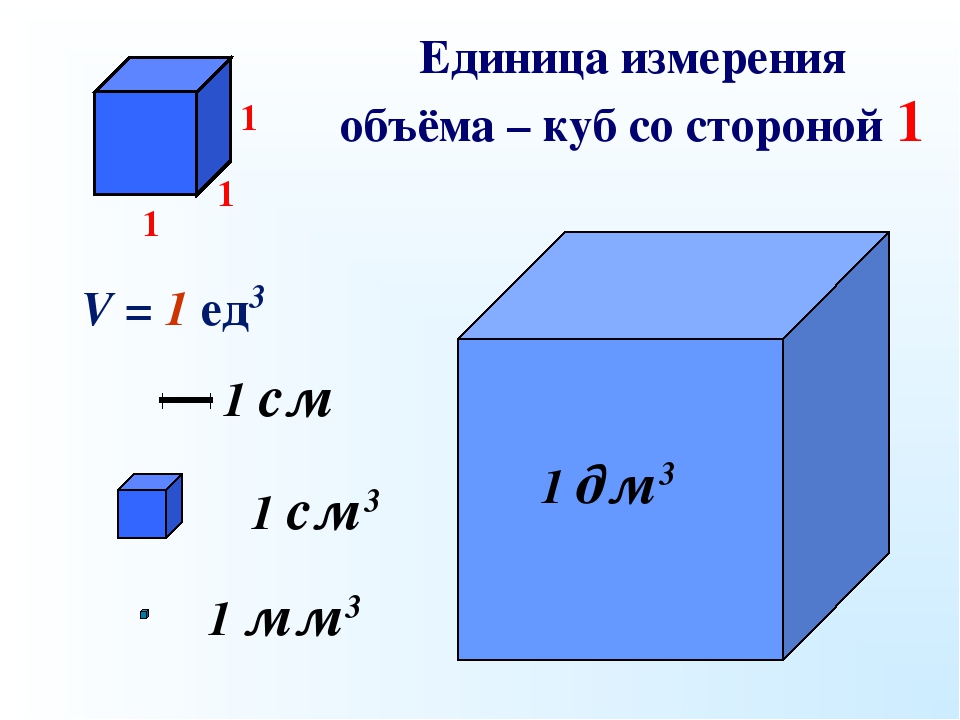 Призма. Объем призмы.
Призма. Объем призмы.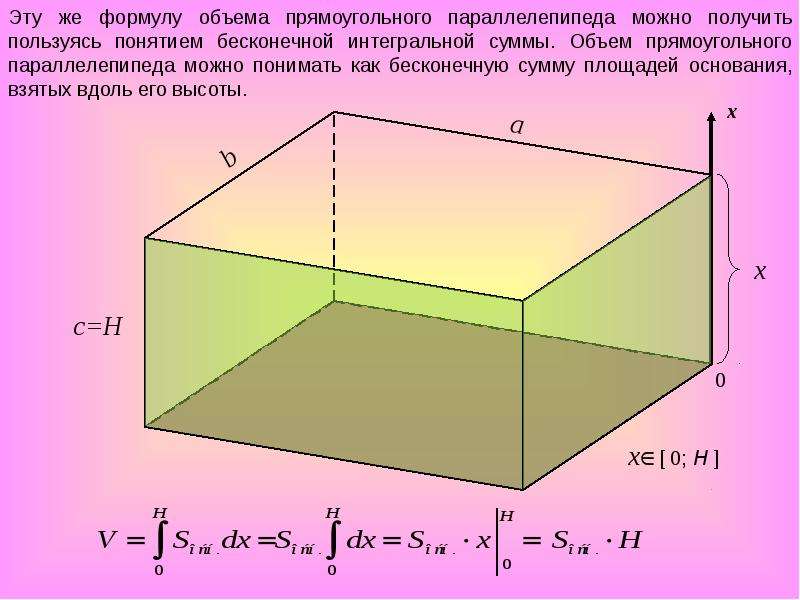 Как найти высоту прямоугольного параллелепипеда? Очень просто – в нем высота всегда совпадает с одной из граней. Поэтому, чтобы ее найти, не требуется специальных формул. Здесь понадобятся формулы для нахождения длины граней. Например, формула объема параллелепипеда:
Как найти высоту прямоугольного параллелепипеда? Очень просто – в нем высота всегда совпадает с одной из граней. Поэтому, чтобы ее найти, не требуется специальных формул. Здесь понадобятся формулы для нахождения длины граней. Например, формула объема параллелепипеда: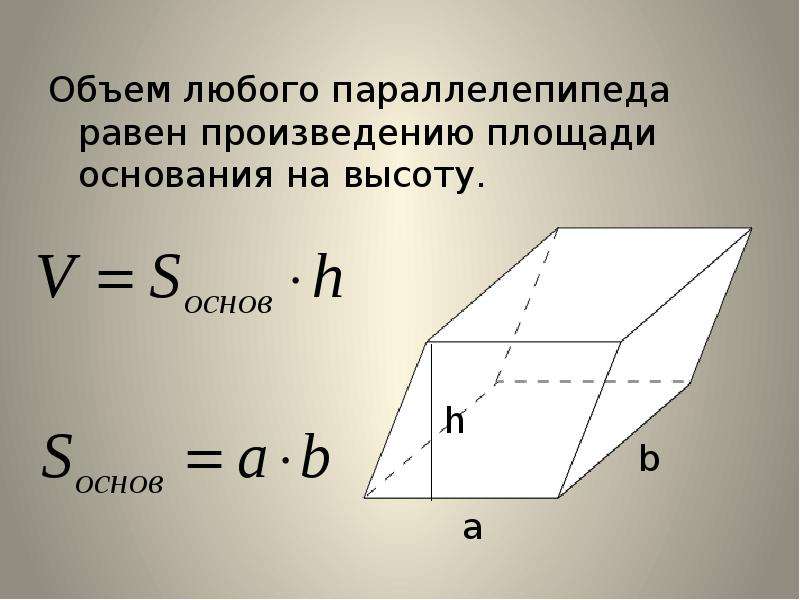
 html
html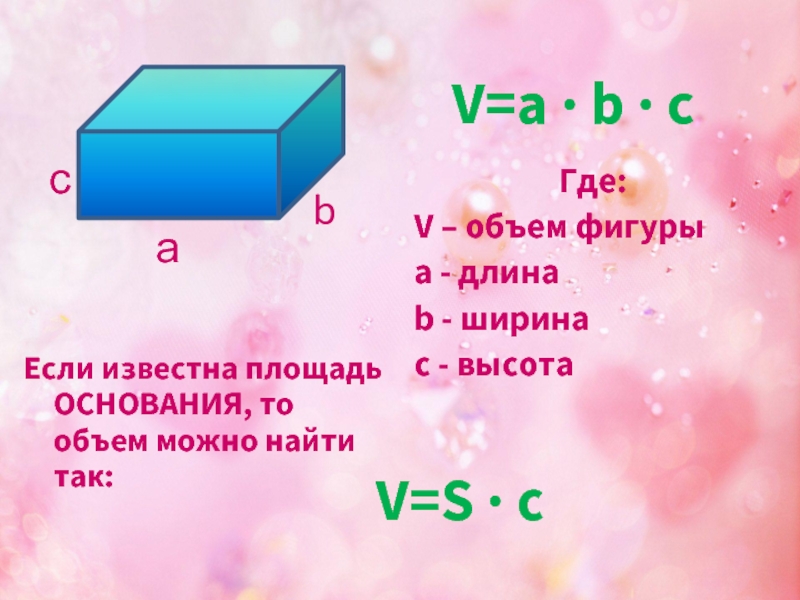 Таким образом, крайний правый член в предыдущем
выражение выпадает, и результирующая величина просто ( B x C ) ∙ A [( A x B ) ∙ C ],
которое ввиду ассоциативности скалярного умножения над точкой
product, то же самое, что [( B x C ) ∙ A ] [( A x B ) ∙ C ]. Оба фактора равны объему
параллелепипед с ребрами A , B , C , поэтому произведение равно
[ A ∙ ( B x С )] 2 .
Таким образом, крайний правый член в предыдущем
выражение выпадает, и результирующая величина просто ( B x C ) ∙ A [( A x B ) ∙ C ],
которое ввиду ассоциативности скалярного умножения над точкой
product, то же самое, что [( B x C ) ∙ A ] [( A x B ) ∙ C ]. Оба фактора равны объему
параллелепипед с ребрами A , B , C , поэтому произведение равно
[ A ∙ ( B x С )] 2 . (Эту формулу можно проверить, подставив векторные выражения для S
и S ‘.) Аналогично, объем двойного параллелепипеда равен
(Эту формулу можно проверить, подставив векторные выражения для S
и S ‘.) Аналогично, объем двойного параллелепипеда равен