Формула электрического заряда, q
Определение и формула электрического заряда
Фундаментальным свойством электрического заряда является существование двух видов зарядов: положительных и отрицательных. Заряды, имеющие один знак, отталкиваются. Взаимодействие зарядов разного знака определяют как притяжение. Телу можно сообщить заряд любого знака. В макроскопическом теле заряды разных знаков могут взаимно компенсировать друг друга.
Электрический заряд является релятивистски инвариантной величиной. Это значит, что величина заряда не зависит от системы отсчета, не важно, движется заряд (заряженное тело) или покоится.
Электрический заряд тела находят как суммарный заряд его частей.
Разделения электрических зарядов разных знаков можно добиться путем электризации посредством непосредственного контакта тел (например, трением) или без контакта, например посредством электрической индукции. При зарядке тела, мы создаем на нем избыток электронов или недостаток в сравнении с их нормальным количеством, при котором тело не имеет заряда. При этом электроны берутся у другого тела или удаляются из заряжаемого тела, но не уничтожаются или создаются. Важно запомнить, что процесс зарядки и разрядки тел является процедурой перераспределения электронов, при этом общее их число не изменяется.
При соединении заряженного проводника с незаряженным, заряд перераспределяется между обоими телами. Допустим, что одно тело несет отрицательный заряд, его соединяют с незаряженным телом. Электроны заряженного тела под воздействием сил взаимного отталкивания переходят на незаряженное тело. При этом заряд первого тела уменьшается, заряд второго увеличивается, до тех пор, пока не наступит равновесие.
Элементарный заряд
Немецкий физик и физиолог Г. Гельмгольц обратил внимание на то, что заряды, которые переносят ионы при явлении электролиза, являются целыми, кратными некоторой величине, равной Кл. Каждый одновалентный ион переносит такой заряд. Любой двухвалентный ион несет заряд, равный Кл, и так далее. Гельмгольц сделал вывод о том, что заряд Кл является минимальным количеством электричества, которое существует в природе. Данный заряд получил название элементарного заряда.
Закон сохранения заряда
Закон сохранения заряда является фундаментальным законом природы. Он был установлен на основании обобщения экспериментальных данных. Подтвержден в 1843 г. английским физиком М. Фарадеем.
Формулировка закона: В любой замкнутой системе алгебраическая сумма зарядов – это неизменная величина, и не важно, какие процессы происходят в этой системе:
где N – количество зарядов.
Закон Кулона
На вопрос: С какими силами взаимодействуют неподвижные точечные заряды? Отвечает закон Кулона, который можно записать в виде формулы как:
где – сила, с которой заряд действует на заряд ; – радиус вектор, который проведен от второго заряда к первому; – электрическая постоянная; – диэлектрическая проницаемость вещества в котором находятся заряды. В соответствии с третьим законом Ньютона первый заряд действует на второй с силой равной по модулю и противоположной по направлению силе Обратите внимание, что заряды в формуле (2) точечные.
Примеры решения задач по теме «Электрический заряд»
ru.solverbook.com
Основные законы и формулы
58
ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК
Закон Кулона:
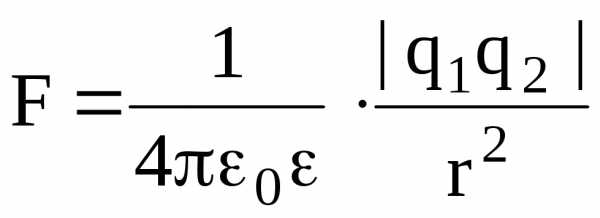 ,
,
где F – сила взаимодействия двух точечных зарядов q1 и q2; r – расстояние между зарядами; — диэлектрическая проницаемость среды; 0 — электрическая постоянная
.
Закон сохранения заряда:
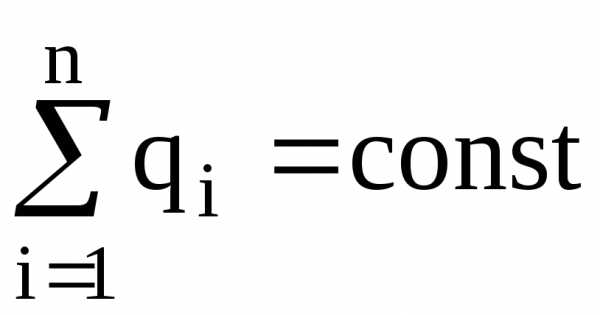
где 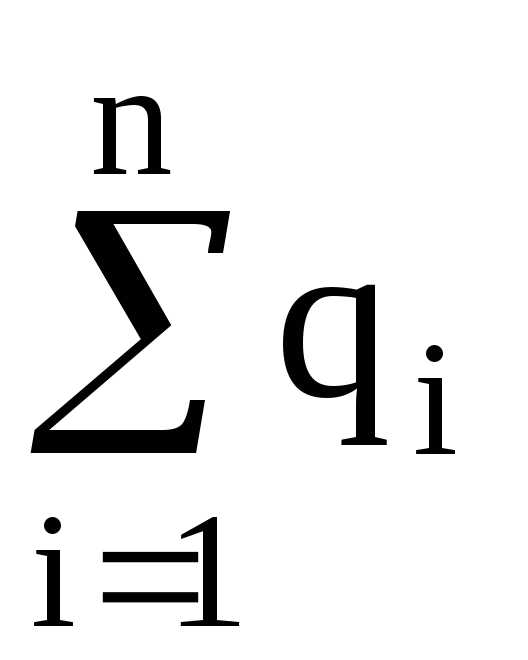 – алгебраическая сумма зарядов, входящих
в изолированную систему;n
– число зарядов.
– алгебраическая сумма зарядов, входящих
в изолированную систему;n
– число зарядов.
Напряженность и потенциал электростатического поля:
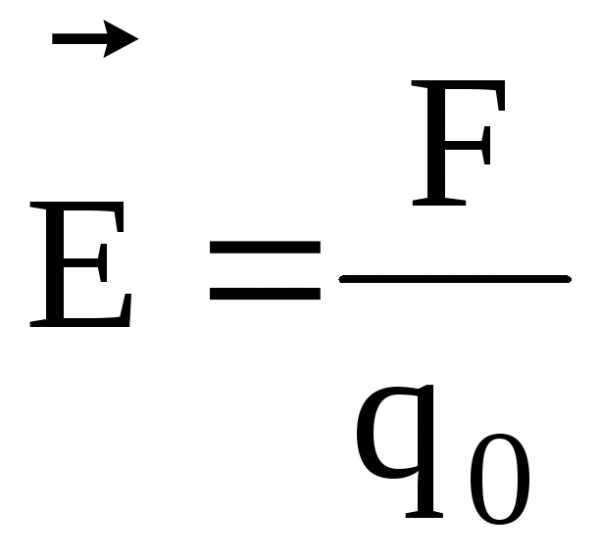 ;
; 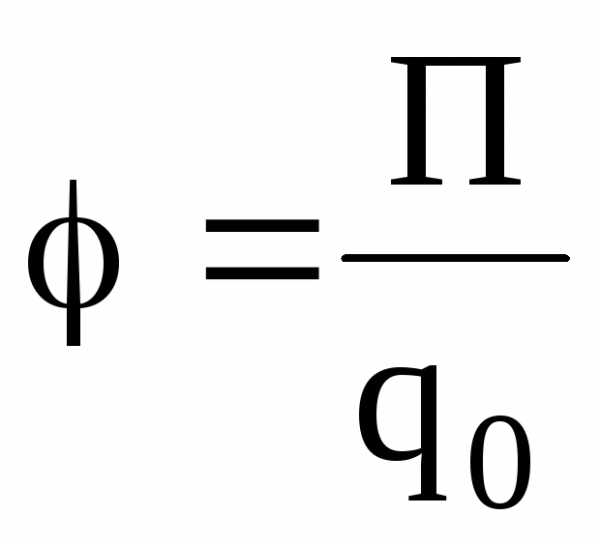 ,
или
,
или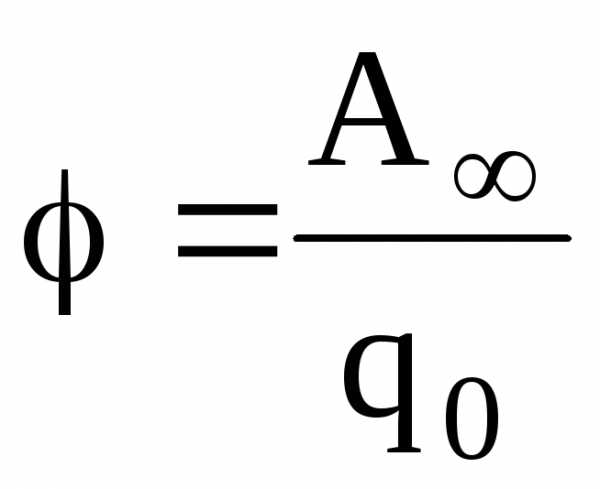 ,
,
где  – сила, действующая на точечный
положительный зарядq0,
помещенный в данную точку поля; П –
потенциальная энергия заряда; А∞ — работа,
затраченная на перемещение заряда q0 из данной точки поля в бесконечность.
– сила, действующая на точечный
положительный зарядq0,
помещенный в данную точку поля; П –
потенциальная энергия заряда; А∞ — работа,
затраченная на перемещение заряда q0 из данной точки поля в бесконечность.
Поток
вектора напряженности  электрического поля:
электрического поля:
а) через произвольную поверхность S, помещенную в неоднородное поле:
,
или 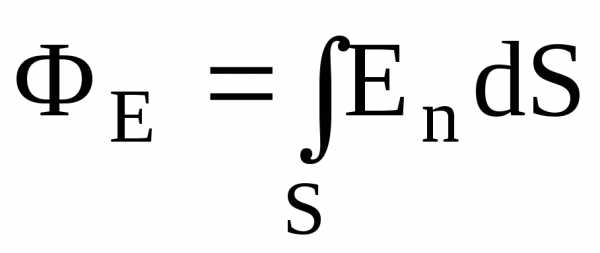
где
– угол между вектором напряженности  и нормалью
и нормалью к элементу поверхности;dS
– площадь элемента поверхности; En – проекция вектора напряженности на
нормаль;
к элементу поверхности;dS
– площадь элемента поверхности; En – проекция вектора напряженности на
нормаль;
б) через плоскую поверхность, помещенную в однородное электрическое поле:
.
Поток
вектора напряженности  через замкнутую поверхность –
через замкнутую поверхность –
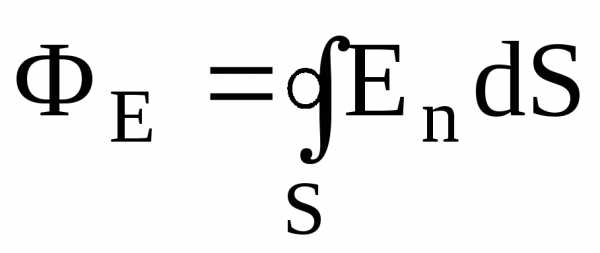
(интегрирование ведется по всей поверхности).
Теорема Остроградского-Гаусса. Поток вектора напряженностичерез любую замкнутую поверхность, охватывающую зарядыq1,q2, …,qn, –
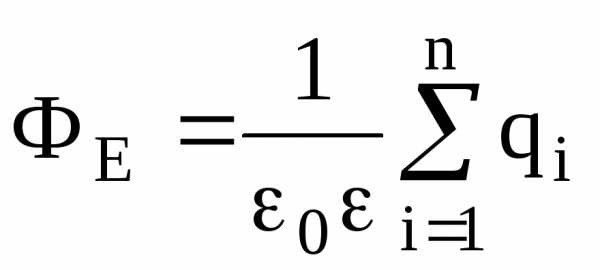 ,
,
где 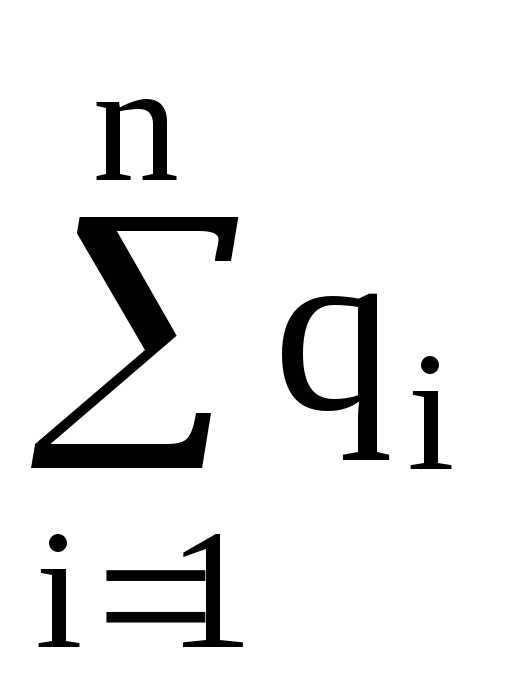 – алгебраическая
сумма зарядов, заключенных внутри
замкнутой поверхности; n
– число зарядов.
– алгебраическая
сумма зарядов, заключенных внутри
замкнутой поверхности; n
– число зарядов.
Напряженность электростатического поля, создаваемого точечным зарядом q на расстоянии r от заряда, –
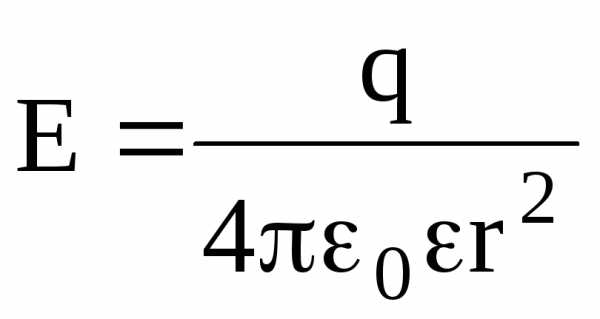 .
.
Напряженность электрического поля, создаваемого сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы такова:
внутри сферы (r R) Е=0;
на
поверхности сферы (r=R) 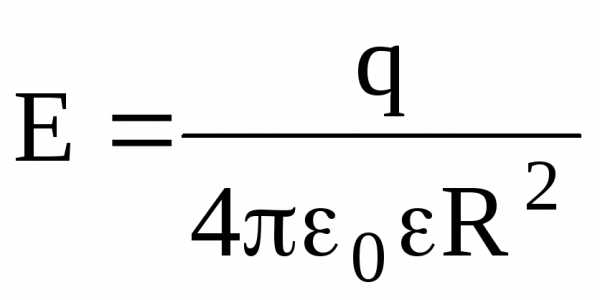 ;
;
вне
сферы (r
R) 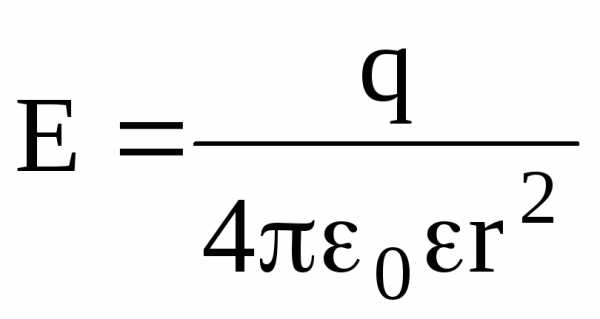 .
.
Принцип суперпозиции (наложения)
электростатических полей, согласно
которому напряженность  результирующего поля, созданного двумя
(и более) точечными зарядами, равна
векторной (геометрической) сумме
напряженностей складываемых полей,
выражается формулой
результирующего поля, созданного двумя
(и более) точечными зарядами, равна
векторной (геометрической) сумме
напряженностей складываемых полей,
выражается формулой
.
 иабсолютное значение вектора напряженности
составляет
иабсолютное значение вектора напряженности
составляет,
где
— угол между векторами  и
и .
.
Напряженность поля, создаваемого бесконечно длинной и равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси, –
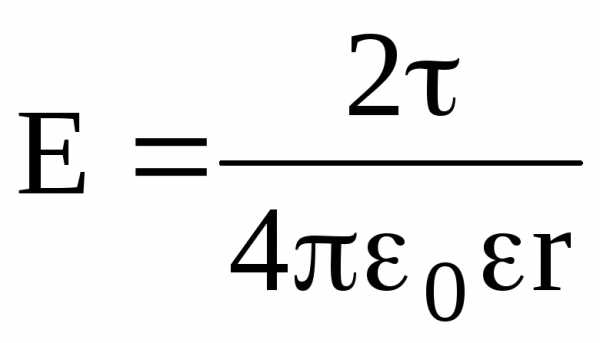 ,
,
где — линейная плотность заряда.
Линейная плотность заряда есть величина, равная его отношению к длине нити (цилиндра):
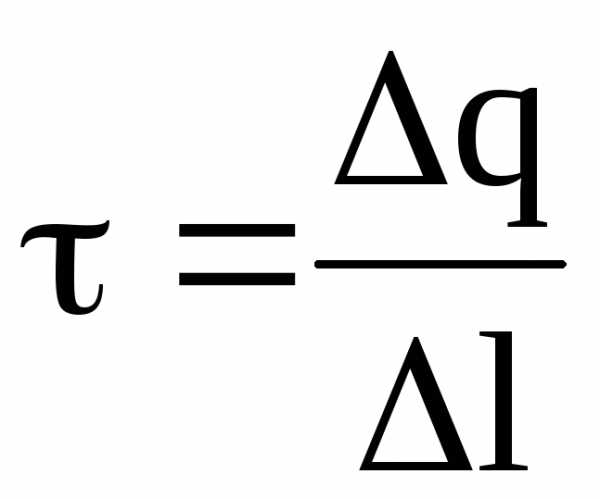 .
.
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, –
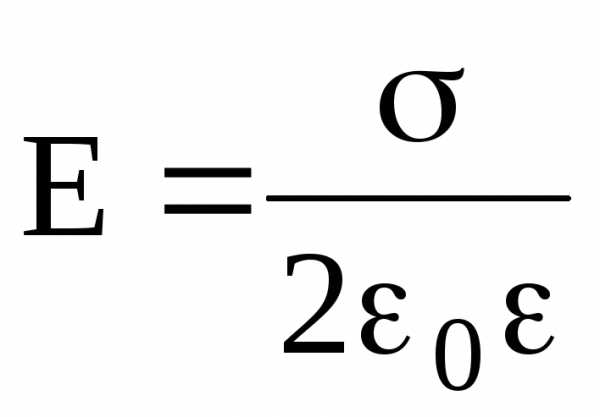
где — поверхностная плотность заряда.
Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к ее площади:
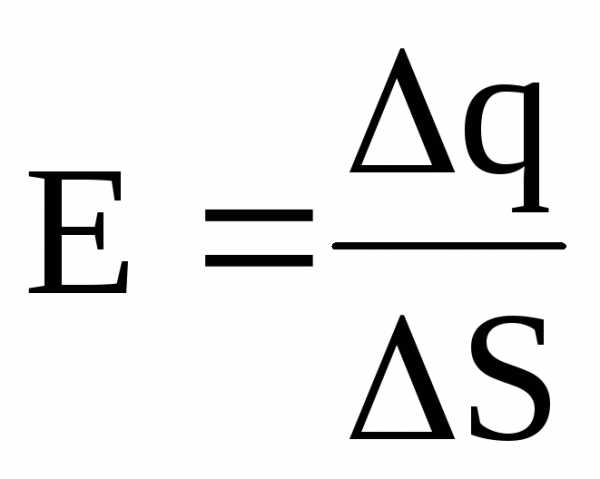 .
.
Напряженность поля, создаваемого двумя бесконечными и параллельными плоскостями, заряженными равномерно и разноименно, с одинаковой по абсолютному значению поверхностной плотностью заряда (поле плоского конденсатора) –
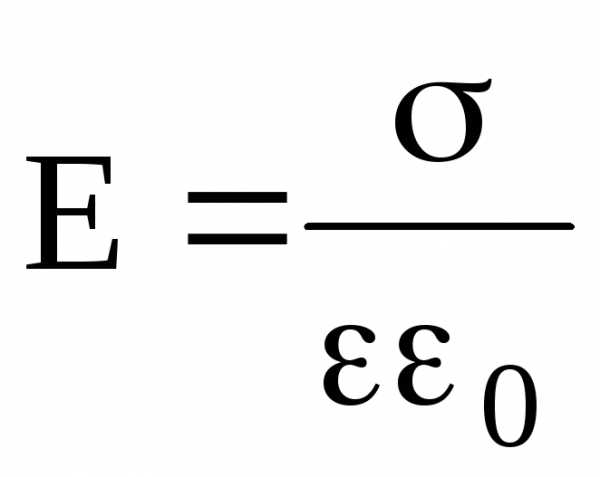 .
.
Приведенная формула справедлива при вычислении напряженности поля между пластинами плоского конденсатора (в его средней части) только в том случае, если расстояние между пластинами намного меньше линейных размеров пластин конденсатора.
Электрическое
смещение  связано с напряженностью
связано с напряженностью
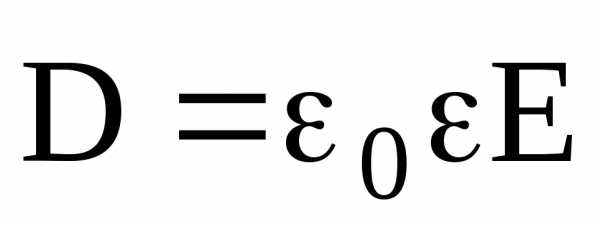 ,
,
которое справедливо только для изотропных диэлектриков.
Потенциал электрического поля есть величина, равная отношению потенциальной энергии и точечного положительного заряда, помещенного в данную точку поля:
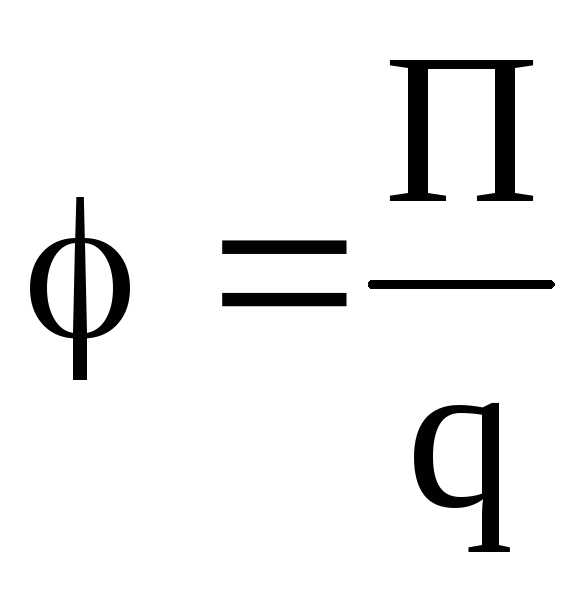 .
.
Иначе говоря, потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к величине этого заряда:
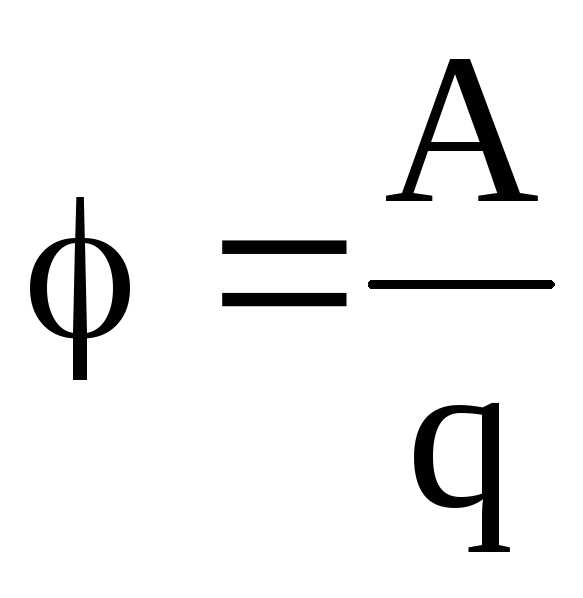 .
.
Потенциал электрического поля в бесконечности условно принят равным нулю.
Потенциал электрического поля, создаваемый точечным зарядом q на
расстоянии r от заряда, – 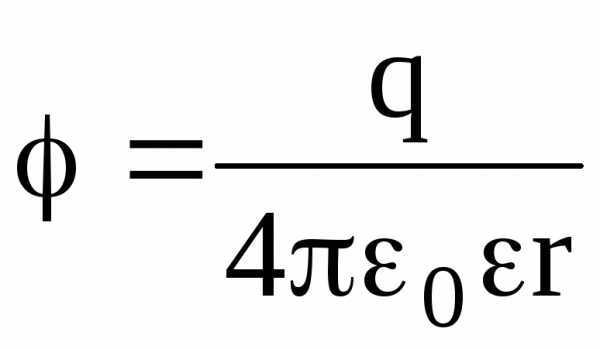 .
.
Потенциал электрического поля, создаваемый металлической сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы таков:
внутри
сферы (r
R) 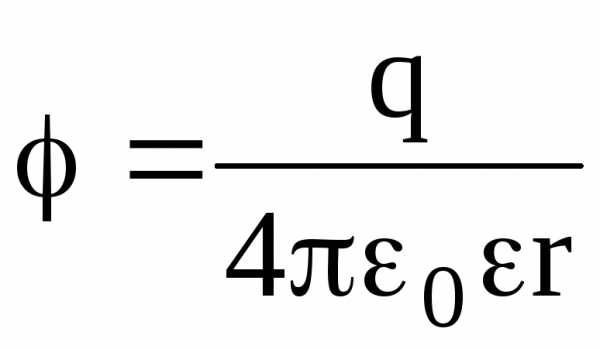 ;
;
на
поверхности сферы (r
= R) 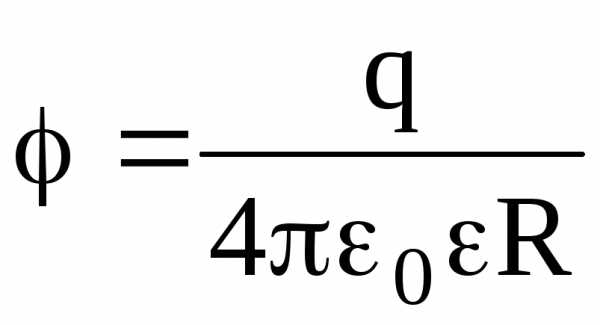 ;
;
вне
сферы (r
R) 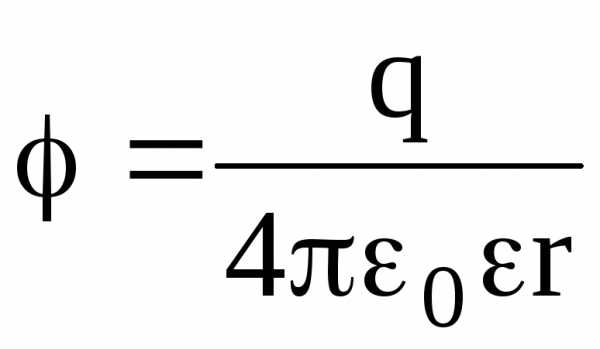 .
.
Во всех формулах, приведенных для потенциала заряженной сферы, есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.
Потенциал электрического поля, образуемого системой n точечных зарядов в данной точке в соответствии с принципом суперпозиции электрических полей, равен алгебраической сумме потенциалов , создаваемых отдельными точечными зарядами:
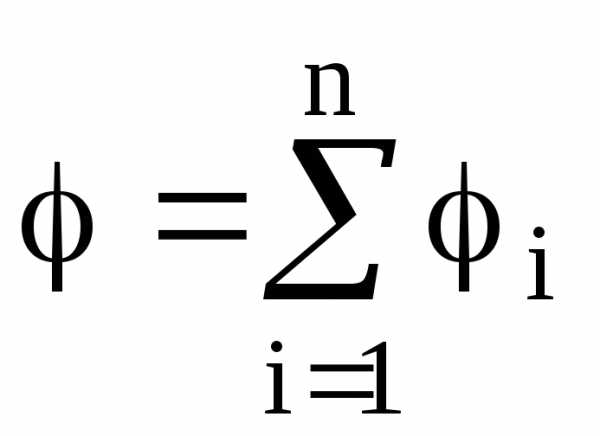 .
.
Энергия W взаимодействия системы точечных зарядов определяется работой, которую эта система может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой
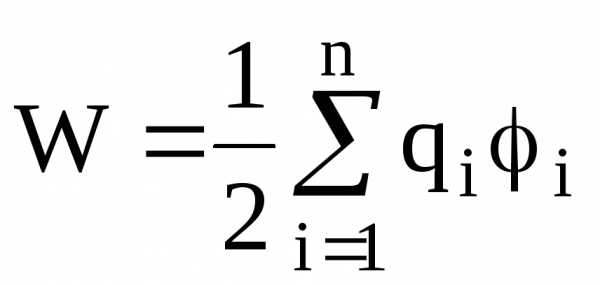 ,
,
где  — потенциал поля, создаваемый всеми
(n-1)
зарядами (за исключением i-го)
в точке, где находится заряд
— потенциал поля, создаваемый всеми
(n-1)
зарядами (за исключением i-го)
в точке, где находится заряд 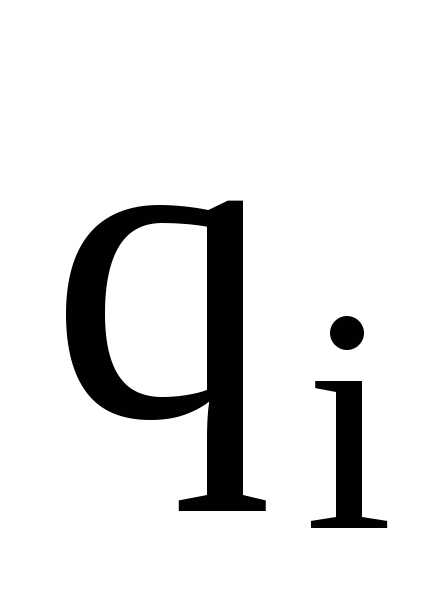 .
.
Потенциал связан с напряженностью электрического поля соотношением
.
В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой
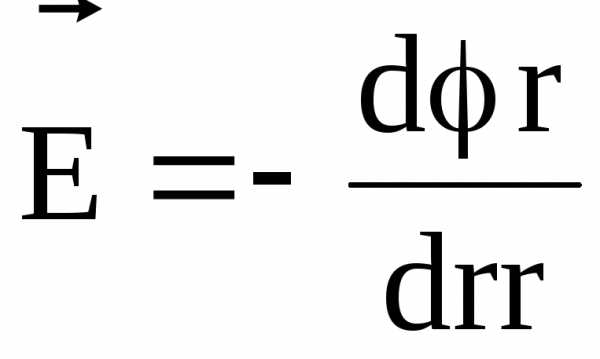 ,
,
или в скалярной форме
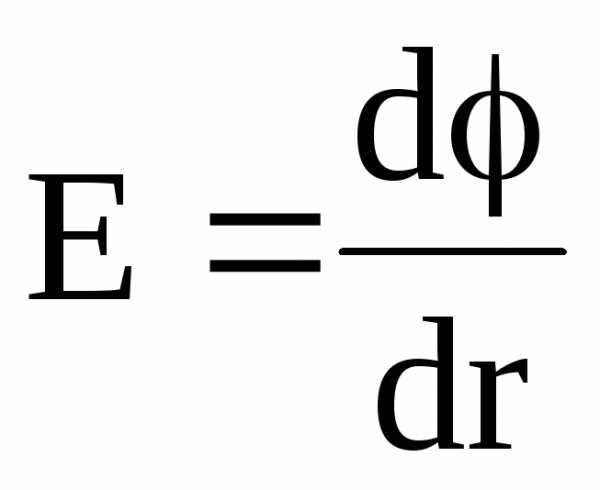 .
.
В случае однородного поля, т.е. поля, напряженность которого в каждой его точке одинакова как по абсолютному значению, так и по направлению, –
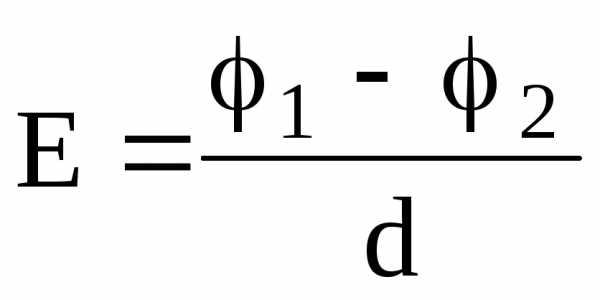 ,
,
где 1 и 2 – потенциалы точек двух эквипотенциальных поверхностей; d — расстояние между этими поверхностями вдоль электрической силовой линии.
Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал 1, в другую, имеющую потенциал 2, равна
,
или 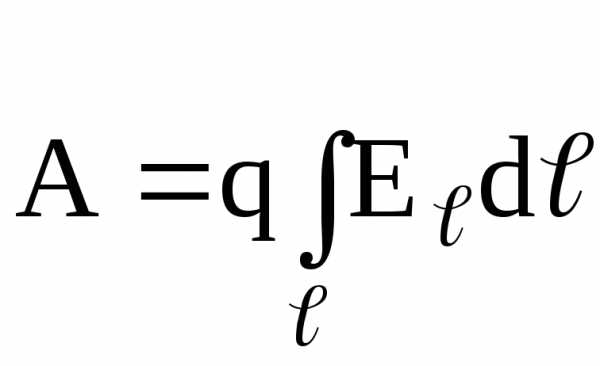 ,
,
где
E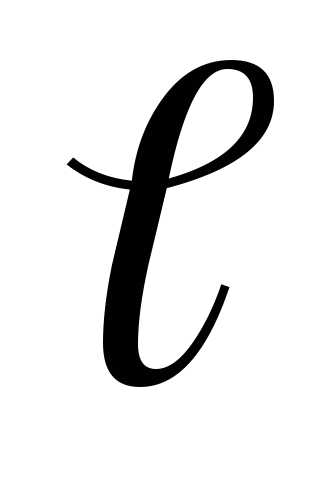 – проекция вектора
– проекция вектора  на направление перемещения;
на направление перемещения;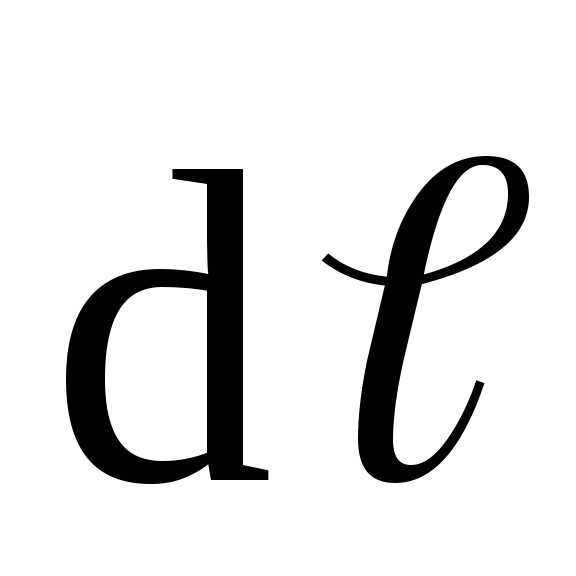 — перемещение.
— перемещение.
В случае однородного поля последняя формула принимает вид
,
где 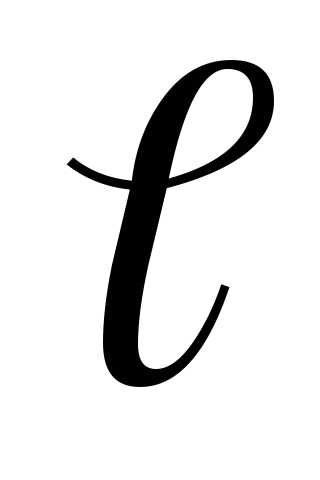 – перемещение;
— угол между направлениями вектора
– перемещение;
— угол между направлениями вектора  и перемеще-ния
и перемеще-ния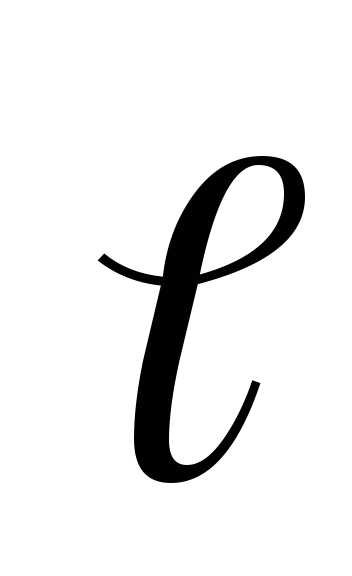 .
.
Диполь есть система двух точечных (равных по абсолютному значению и противоположных по знаку) зарядов, находящихся на некотором расстоянии друг от друга.
Электрический
момент 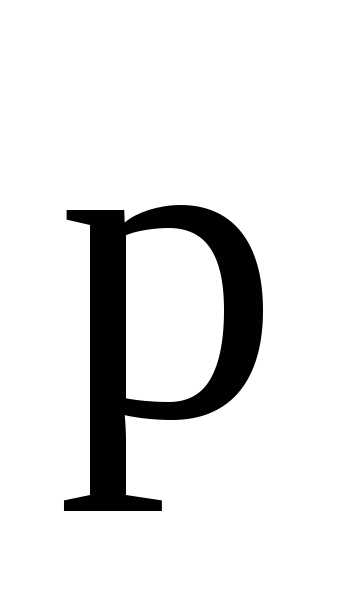 диполя есть вектор, направленный от
отрицательного заряда к положительному,
равный произведению заряда
диполя есть вектор, направленный от
отрицательного заряда к положительному,
равный произведению заряда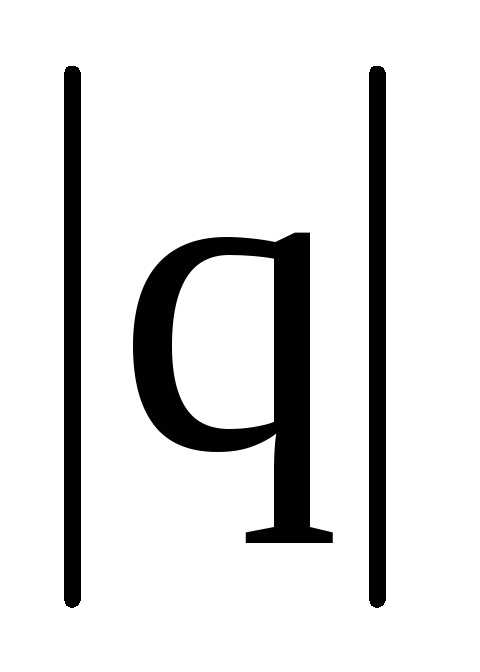 на вектор
на вектор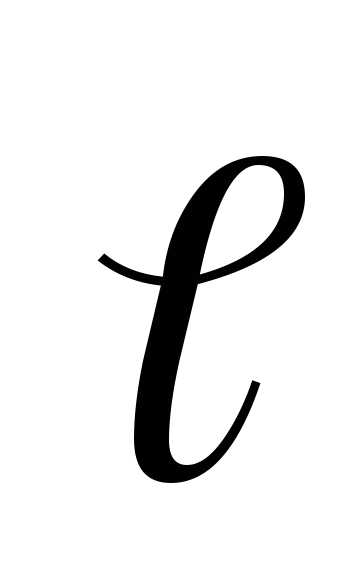 ,
проведенный от отрицательного заряда
к положительному, и называемый плечом
диполя, т.е.
,
проведенный от отрицательного заряда
к положительному, и называемый плечом
диполя, т.е.
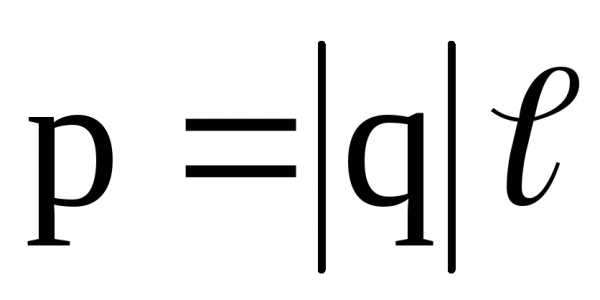 .
.
Диполь
называется точечным, если его плечо 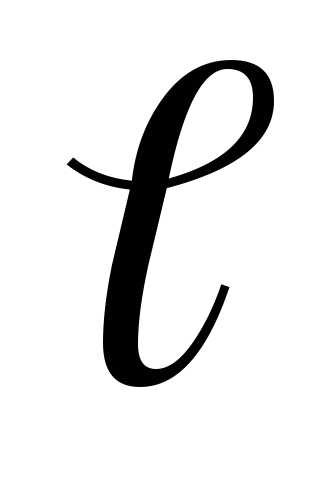 намного меньше расстоянияr
от центра диполя до точки, в которой нас
интересует действие диполя (
намного меньше расстоянияr
от центра диполя до точки, в которой нас
интересует действие диполя (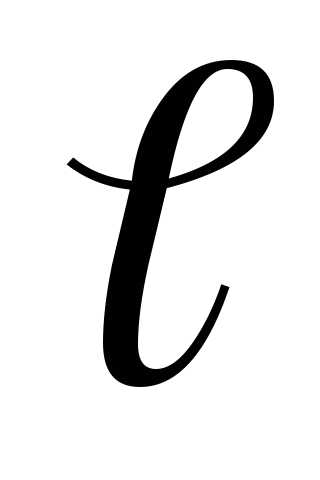
r),
см. рис. 1.
r),
см. рис. 1.
Рис. 1
Напряженность поля точечного диполя:
,
где
р – электрический момент диполя; r
– абсолютное значение радиус-вектора,
проведенного от центра диполя к точке,
напряженность поля в которой нас
интересует;
— угол между радиус-вектором  и плечом
и плечом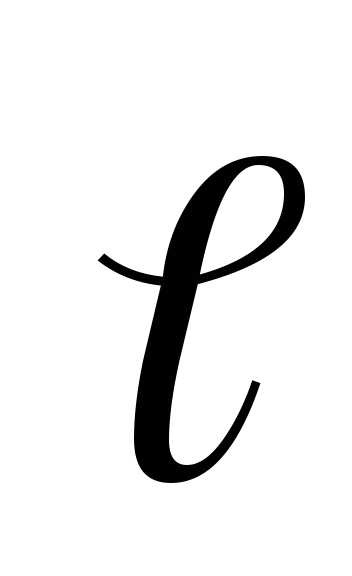 диполя.
диполя.
Напряженность поля точечного диполя в точке, лежащей на оси диполя
(=0), находится по формуле
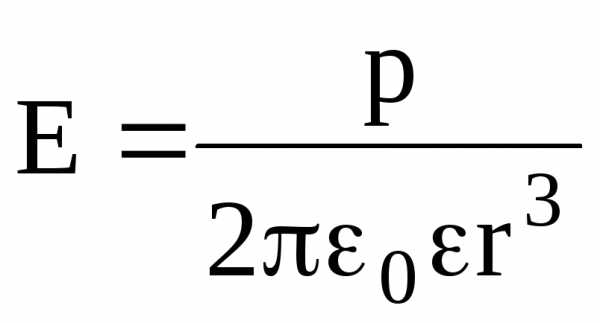 ;
;
в
точке, лежащей на перпендикуляре к плечу
диполя, восстановленном из его середины 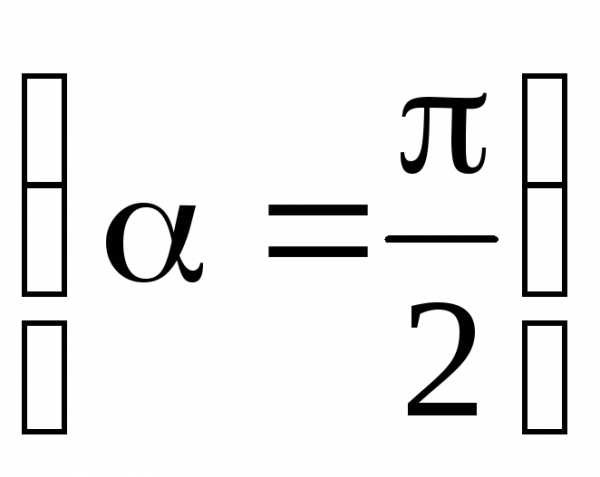 ,
– по формуле
,
– по формуле
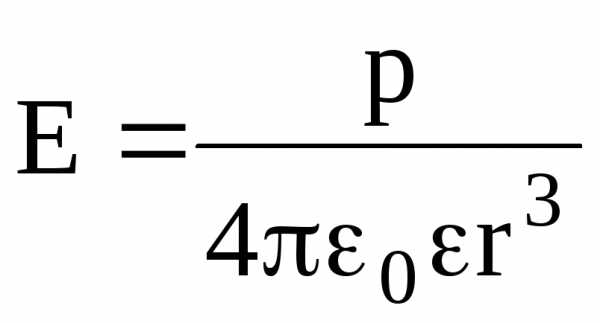 .
.
Потенциал поля точечного диполя в точке, лежащей на оси диполя (=0), составляет
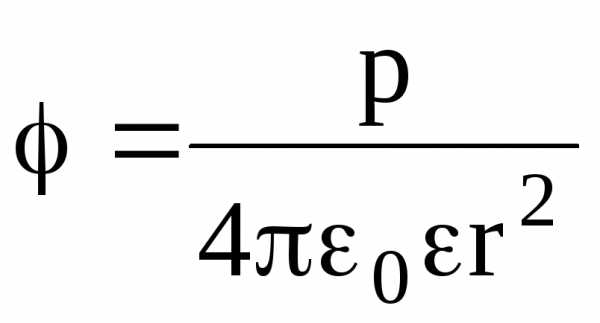 ,
,
а
в точке, лежащей на перпендикуляре к
плечу диполя, восстановленном из его
середины 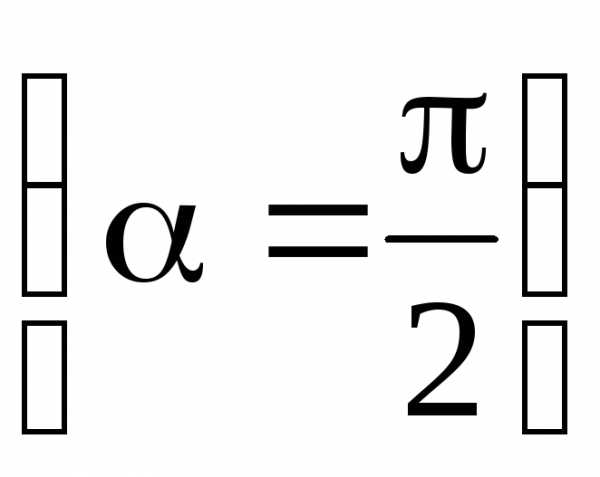 ,
–
,
–
=0.
Напряженность и потенциал неточечного диполя определяются так же как и для системы зарядов.
Механический момент, действующий на диполь с электрическим моментом р, помещенный в однородное электрическое поле с напряженностью Е, –
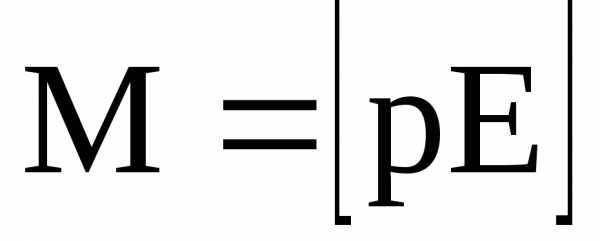 ,
или
,
,
или
,
где
— угол между направлениями векторов 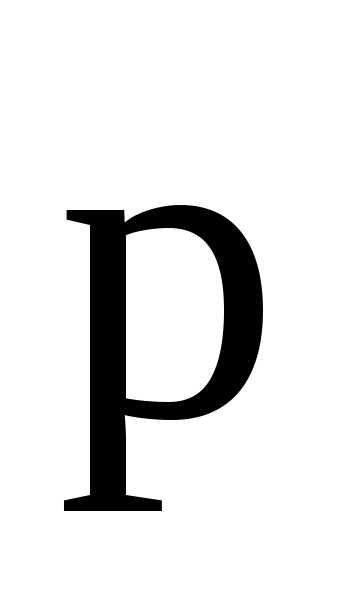 и
и .
.
Электроемкость уединенного проводника или конденсатора –
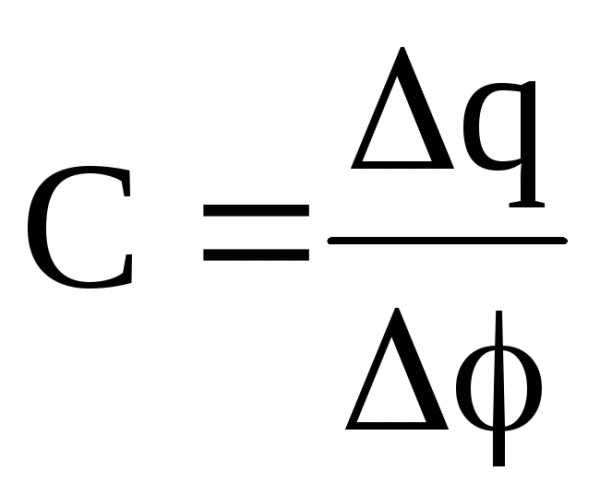 ,
,
где
q
– заряд, сообщенный проводнику;  —
изменение потенциала,
вызванное этим зарядом.
—
изменение потенциала,
вызванное этим зарядом.
Электроемкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью , –
.
Если сфера полая и заполнена диэлектриком, то ее электроемкость при этом не изменяется.
Электроемкость плоского конденсатора:
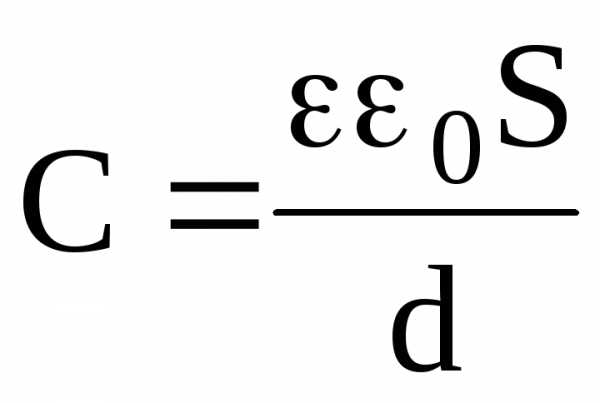 ,
,
где S – площадь каждой пластины конденсатора; d – расстояние между пластинами; — диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.
Электроемкость плоского конденсатора, заполненного n слоями диэлектрика толщиной di и диэлектрической проницаемостью i каждый (слоистый конденсатор), составляет
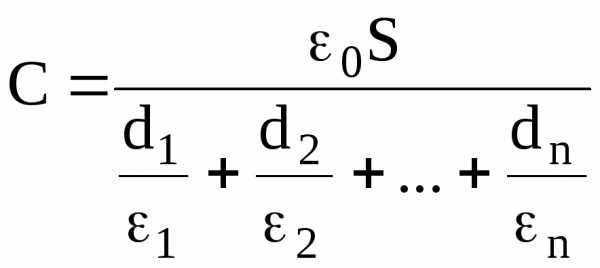 .
.
Электроемкость сферического конденсатора (две концентрические сферы радиусом R1 и R2 , пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ) находится так:
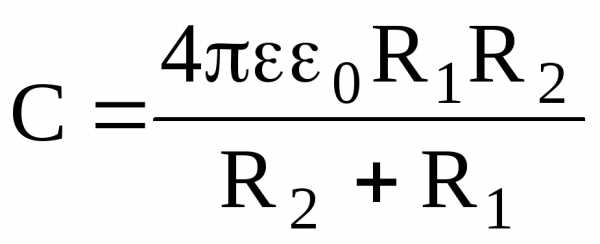 .
.
Электроемкость последовательно соединенных конденсаторов составляет:
в общем случае –
,
где n – число конденсаторов;
в случае двух конденсаторов –
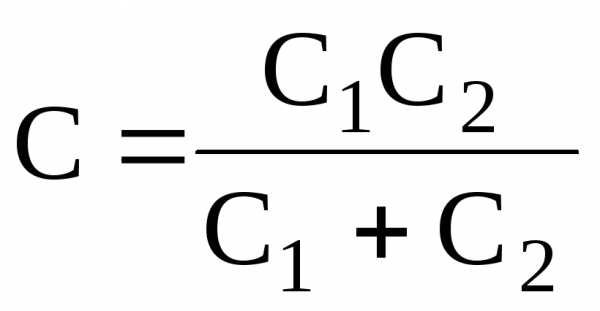 ;
;
в случае n одинаковых конденсаторов с электроемкостью С1 каждый –
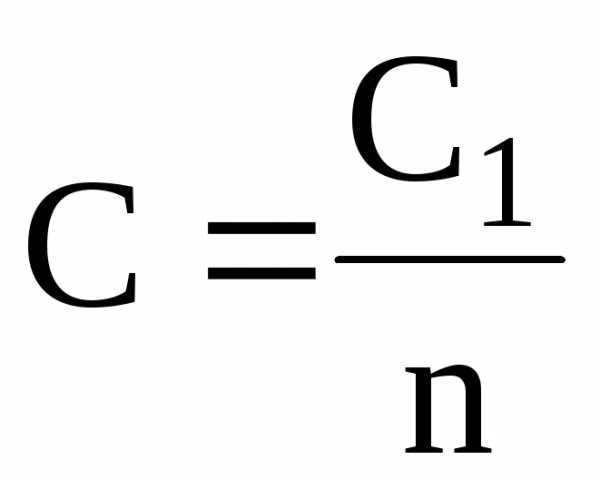 .
.
Электроемкость параллельно соединенных конденсаторов определяется следующим образом:
в общем случае –
С=С1+С2+…+Сn;
в случае двух конденсаторов –
С= С1+С2;
в случае n одинаковых конденсаторов с электроемкостью С1 каждый –
С=nС1.
Энергия заряженного проводника выражается через заряд q, потенциал и электроемкость С проводника следующим образом:
.
Энергия заряженного конденсатора –
,
где q – заряд конденсатора; С – электроемкость конденсатора; U – разность потенциалов на его пластинах.
studfiles.net
Электрическое поле (к задачнику Рымкевича для 10-11 классов). Формула заряда q
Формула электрического заряда, q
Определение и формула электрического заряда
Фундаментальным свойством электрического заряда является существование двух видов зарядов: положительных и отрицательных. Заряды, имеющие один знак, отталкиваются. Взаимодействие зарядов разного знака определяют как притяжение. Телу можно сообщить заряд любого знака. В макроскопическом теле заряды разных знаков могут взаимно компенсировать друг друга.
Электрический заряд является релятивистски инвариантной величиной. Это значит, что величина заряда не зависит от системы отсчета, не важно, движется заряд (заряженное тело) или покоится.
Электрический заряд тела находят как суммарный заряд его частей.
Разделения электрических зарядов разных знаков можно добиться путем электризации посредством непосредственного контакта тел (например, трением) или без контакта, например посредством электрической индукции. При зарядке тела, мы создаем на нем избыток электронов или недостаток в сравнении с их нормальным количеством, при котором тело не имеет заряда. При этом электроны берутся у другого тела или удаляются из заряжаемого тела, но не уничтожаются или создаются. Важно запомнить, что процесс зарядки и разрядки тел является процедурой перераспределения электронов, при этом общее их число не изменяется.
При соединении заряженного проводника с незаряженным, заряд перераспределяется между обоими телами. Допустим, что одно тело несет отрицательный заряд, его соединяют с незаряженным телом. Электроны заряженного тела под воздействием сил взаимного отталкивания переходят на незаряженное тело. При этом заряд первого тела уменьшается, заряд второго увеличивается, до тех пор, пока не наступит равновесие.
Элементарный заряд
Немецкий физик и физиолог Г. Гельмгольц обратил внимание на то, что заряды, которые переносят ионы при явлении электролиза, являются целыми, кратными некоторой величине, равной Кл. Каждый одновалентный ион переносит такой заряд. Любой двухвалентный ион несет заряд, равный Кл, и так далее. Гельмгольц сделал вывод о том, что заряд Кл является минимальным количеством электричества, которое существует в природе. Данный заряд получил название элементарного заряда.
Закон сохранения заряда
Закон сохранения заряда является фундаментальным законом природы. Он был установлен на основании обобщения экспериментальных данных. Подтвержден в 1843 г. английским физиком М. Фарадеем.
Формулировка закона: В любой замкнутой системе алгебраическая сумма зарядов – это неизменная величина, и не важно, какие процессы происходят в этой системе:
где N – количество зарядов.
Закон Кулона
На вопрос: С какими силами взаимодействуют неподвижные точечные заряды? Отвечает закон Кулона, который можно записать в виде формулы как:
где – сила, с которой заряд действует на заряд ; – радиус вектор, который проведен от второго заряда к первому; – электрическая постоянная; – диэлектрическая проницаемость вещества в котором находятся заряды. В соответствии с третьим законом Ньютона первый заряд действует на второй с силой равной по модулю и противоположной по направлению силе Обратите внимание, что заряды в формуле (2) точечные.
Примеры решения задач по теме «Электрический заряд»
ru.solverbook.com
Формула заряда конденсатора, q
По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.
Формула заряда конденсатора
Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:
где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.
Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Заряд на пластинах плоского конденсатора равен:
где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.
Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Заряд на обкладках сферического конденсатора найдем как:
где – радиусы обкладок конденсатора.
Заряд конденсатора связан с энергией поля (W) внутри него:
Из формулы (6) следует, что заряд можно выразить как:
Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.
При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.
Примеры решения задач по теме «Заряд конденсатора»
ru.solverbook.com
Основные законы и формулы
58
ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК
Закон Кулона:
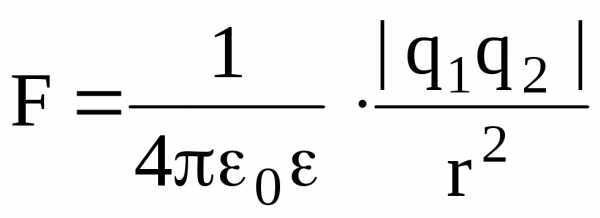 ,
,
где F – сила взаимодействия двух точечных зарядов q1 и q2; r – расстояние между зарядами; — диэлектрическая проницаемость среды; 0 — электрическая постоянная
.
Закон сохранения заряда:
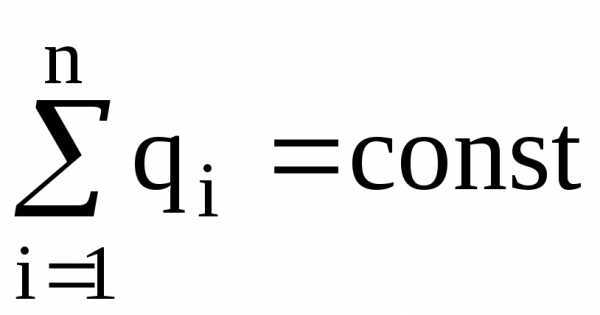 ,
,
где 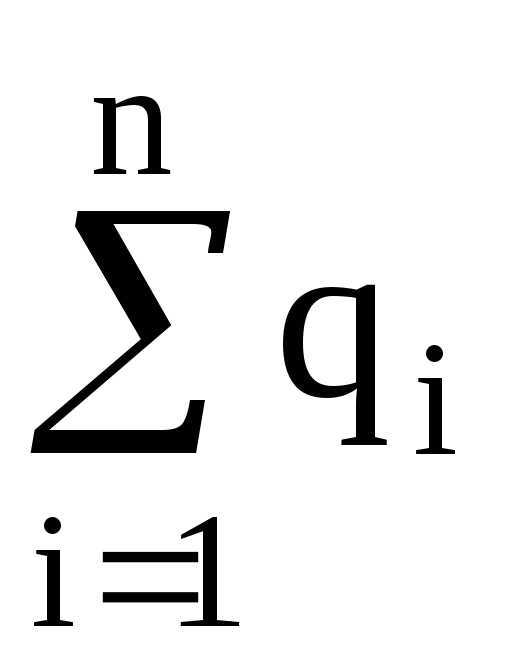 – алгебраическая сумма зарядов, входящих в изолированную систему;n – число зарядов.
– алгебраическая сумма зарядов, входящих в изолированную систему;n – число зарядов.
Напряженность и потенциал электростатического поля:
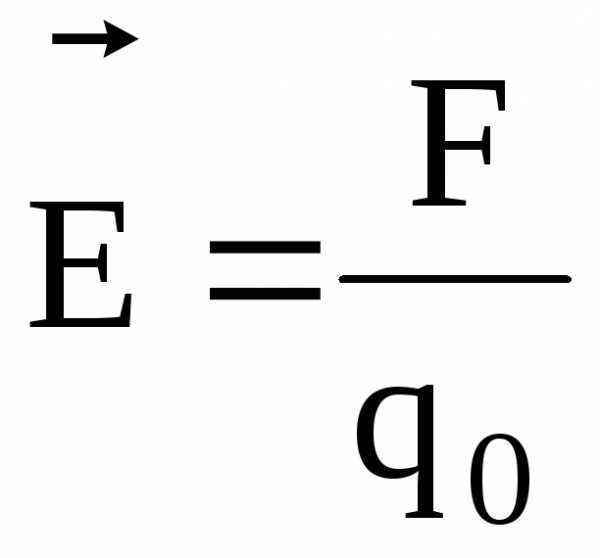 ;
; 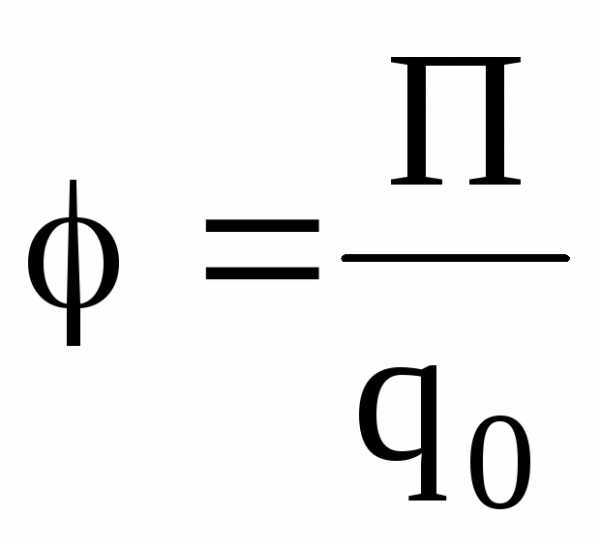 , или
, или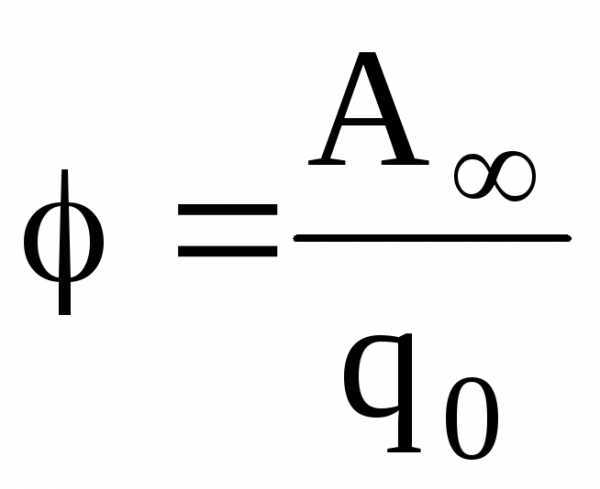 ,
,
где  – сила, действующая на точечный положительный зарядq0, помещенный в данную точку поля; П – потенциальная энергия заряда; А∞ — работа, затраченная на перемещение заряда q0 из данной точки поля в бесконечность.
– сила, действующая на точечный положительный зарядq0, помещенный в данную точку поля; П – потенциальная энергия заряда; А∞ — работа, затраченная на перемещение заряда q0 из данной точки поля в бесконечность.
Поток вектора напряженности  электрического поля:
электрического поля:
а) через произвольную поверхность S, помещенную в неоднородное поле:
, или 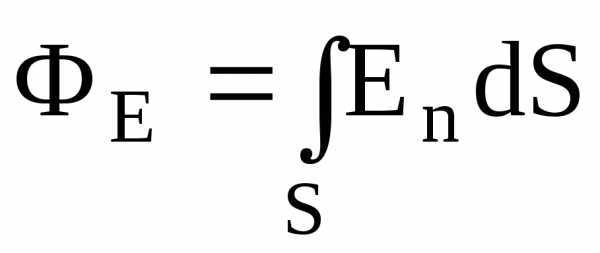 ,
,
где – угол между вектором напряженности  и нормалью
и нормалью к элементу поверхности;dS – площадь элемента поверхности; En – проекция вектора напряженности на нормаль;
к элементу поверхности;dS – площадь элемента поверхности; En – проекция вектора напряженности на нормаль;
б) через плоскую поверхность, помещенную в однородное электрическое поле:
.
Поток вектора напряженности  через замкнутую поверхность –
через замкнутую поверхность –
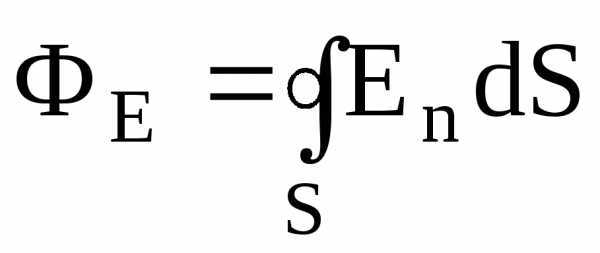
(интегрирование ведется по всей поверхности).
Теорема Остроградского-Гаусса. Поток вектора напряженностичерез любую замкнутую поверхность, охватывающую зарядыq1,q2, …,qn, –
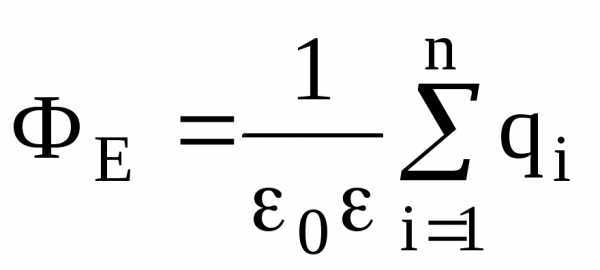 ,
,
где 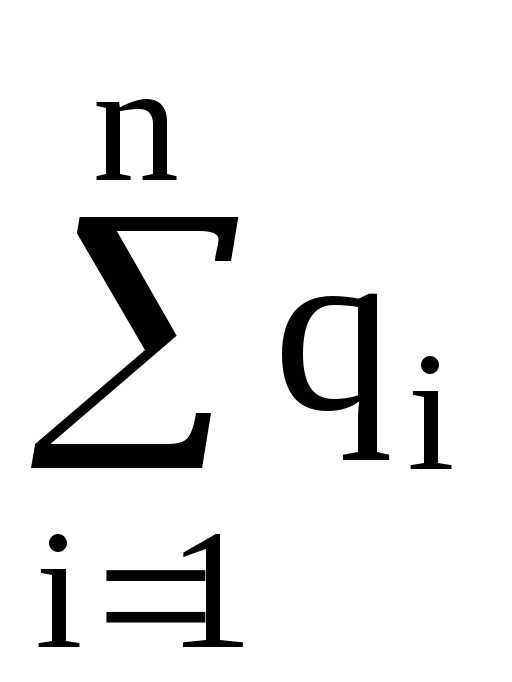 – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; n – число зарядов.
– алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; n – число зарядов.
Напряженность электростатического поля, создаваемого точечным зарядом q на расстоянии r от заряда, –
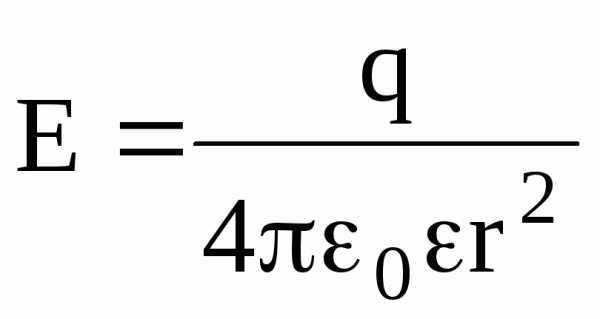 .
.
Напряженность электрического поля, создаваемого сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы такова:
внутри сферы (r R) Е=0;
на поверхности сферы (r=R) 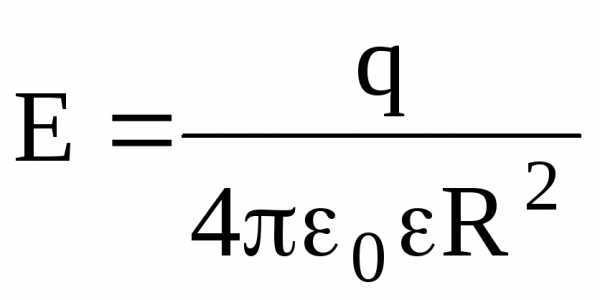 ;
;
вне сферы (r R) 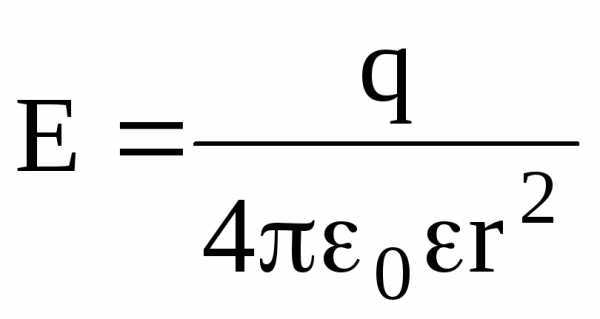 .
.
Принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность  результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей, выражается формулой
результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей, выражается формулой
.
В случае двух электрических полей с напряженностями 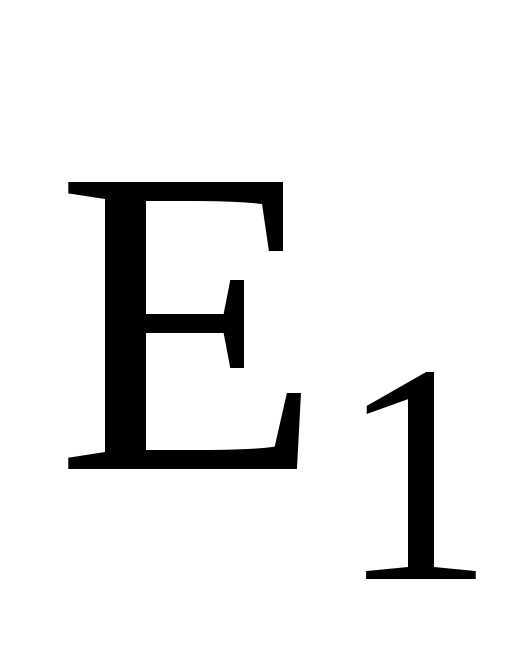 иабсолютное значение вектора напряженности составляет
иабсолютное значение вектора напряженности составляет
,
где — угол между векторами 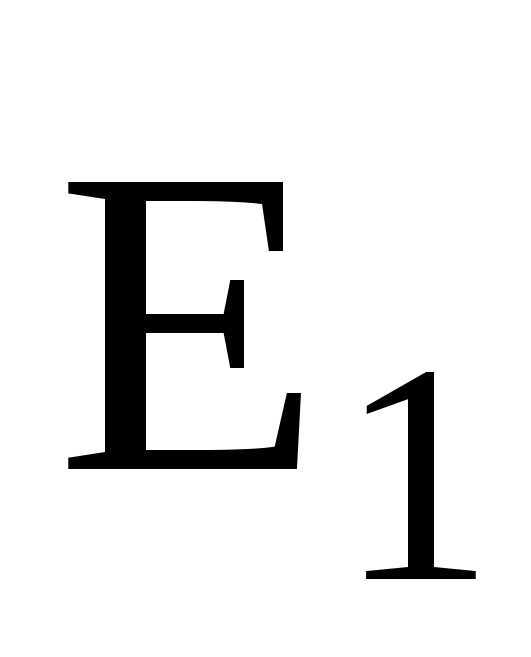 и
и .
.
Напряженность поля, создаваемого бесконечно длинной и равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси, –
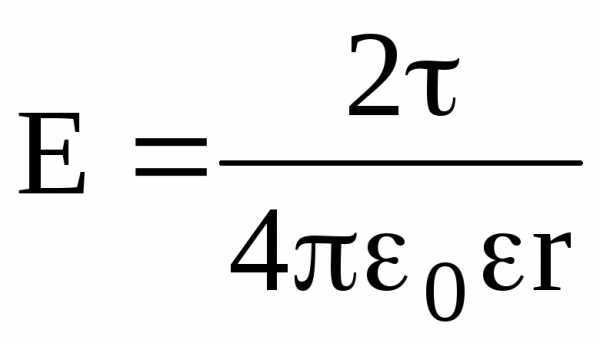 ,
,
где — линейная плотность заряда.
Линейная плотность заряда есть величина, равная его отношению к длине нити (цилиндра):
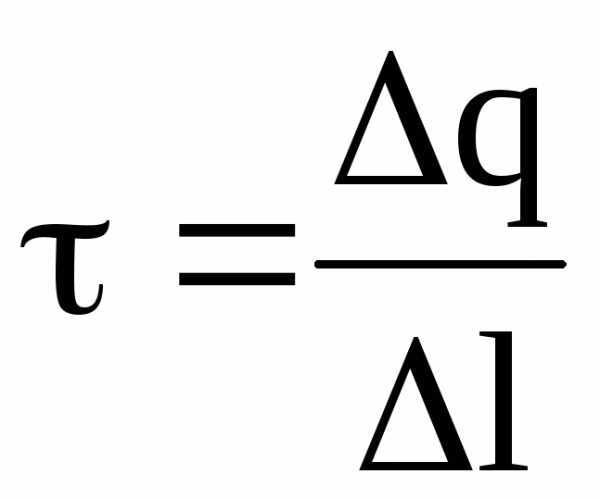 .
.
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, –
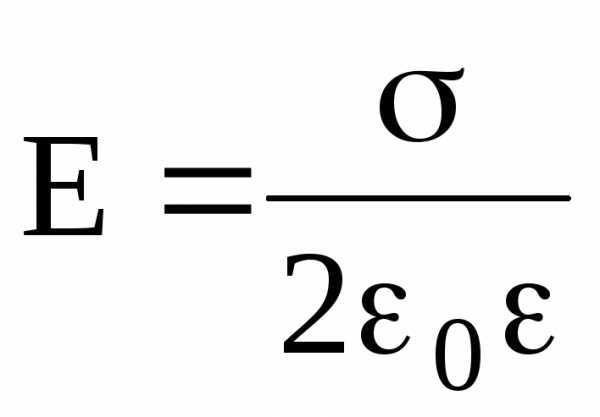 ,
,
где — поверхностная плотность заряда.
Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к ее площади:
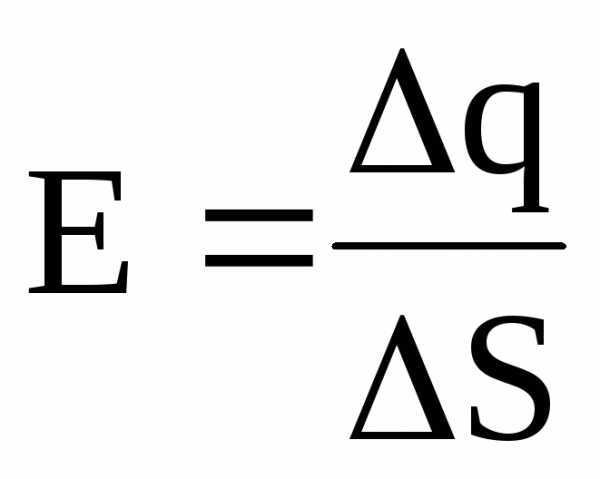 .
.
Напряженность поля, создаваемого двумя бесконечными и параллельными плоскостями, заряженными равномерно и разноименно, с одинаковой по абсолютному значению поверхностной плотностью заряда (поле плоского конденсатора) –
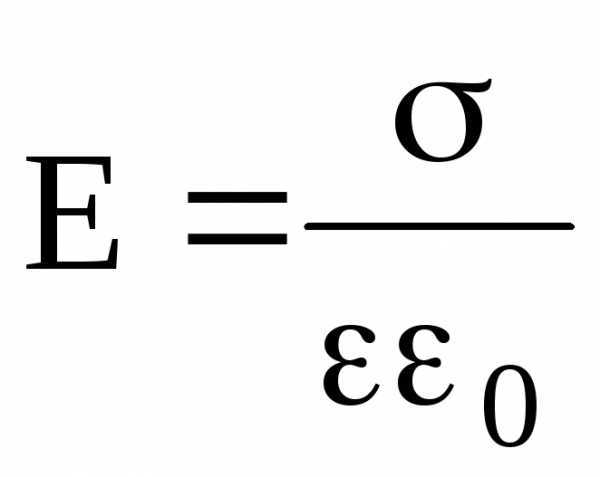 .
.
Приведенная формула справедлива при вычислении напряженности поля между пластинами плоского конденсатора (в его средней части) только в том случае, если расстояние между пластинами намного меньше линейных размеров пластин конденсатора.
Электрическое смещение  связано с напряженностью
связано с напряженностью электрического поля соотношением
электрического поля соотношением
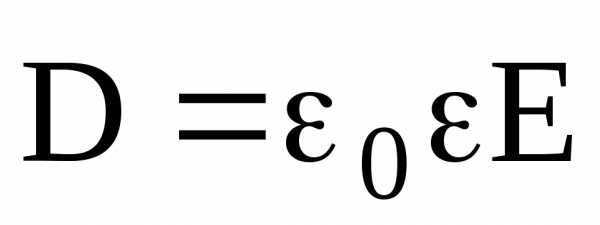 ,
,
которое справедливо только для изотропных диэлектриков.
Потенциал электрического поля есть величина, равная отношению потенциальной энергии и точечного положительного заряда, помещенного в данную точку поля:
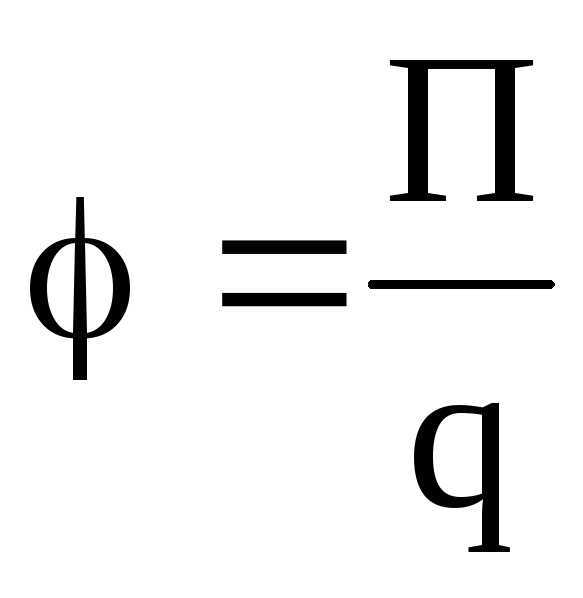 .
.
Иначе говоря, потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к величине этого заряда:
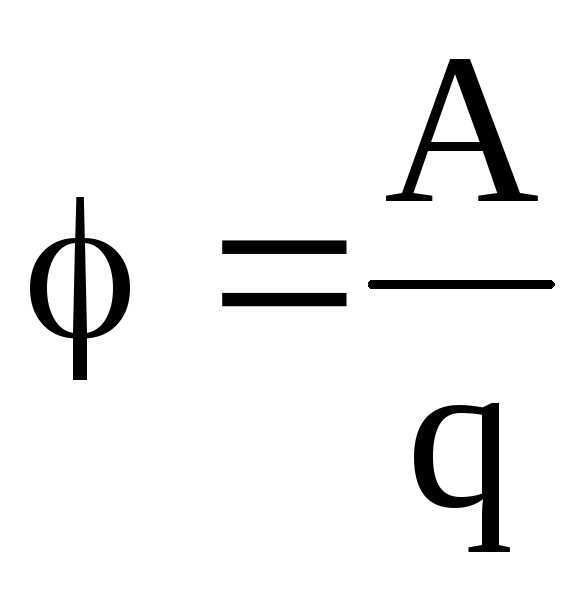 .
.
Потенциал электрического поля в бесконечности условно принят равным нулю.
Потенциал электрического поля, создаваемый точечным зарядом q на
расстоянии r от заряда, –
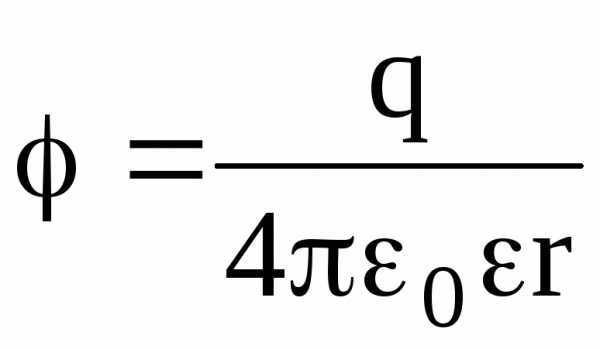 .
.
Потенциал электрического поля, создаваемый металлической сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы таков:
внутри сферы (r R) 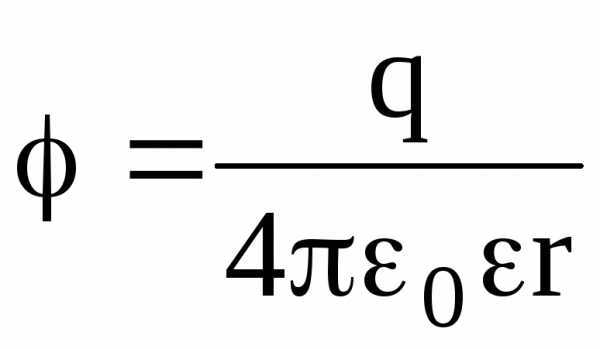 ;
;
на поверхности сферы (r = R) 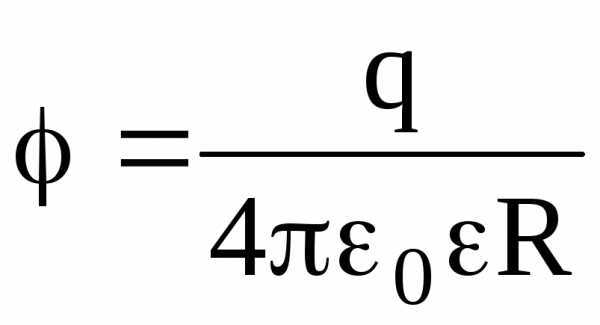 ;
;
вне сферы (r R) 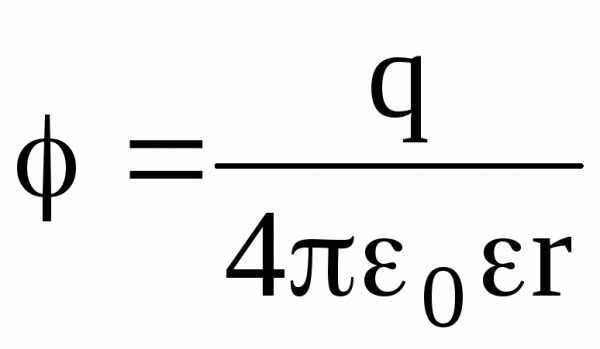 .
.
Во всех формулах, приведенных для потенциала заряженной сферы, есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.
Потенциал электрического поля, образуемого системой n точечных зарядов в данной точке в соответствии с принципом суперпозиции электрических полей, равен алгебраической сумме потенциалов , создаваемых отдельными точечными зарядами:
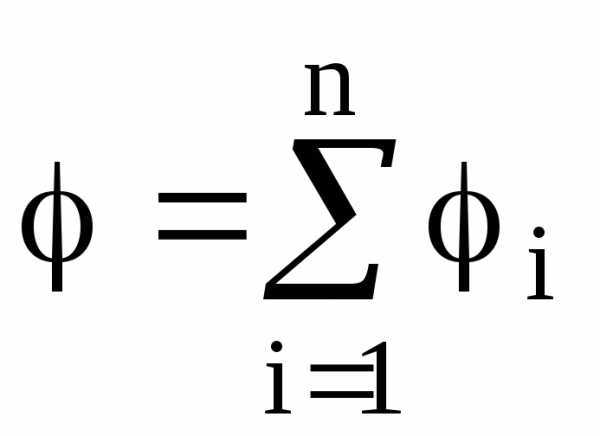 .
.
Энергия W взаимодействия системы точечных зарядов определяется работой, которую эта система может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой
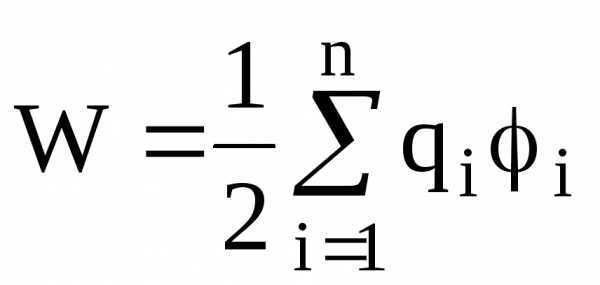 ,
,
где  — потенциал поля, создаваемый всеми (n-1) зарядами (за исключением i-го) в точке, где находится заряд
— потенциал поля, создаваемый всеми (n-1) зарядами (за исключением i-го) в точке, где находится заряд 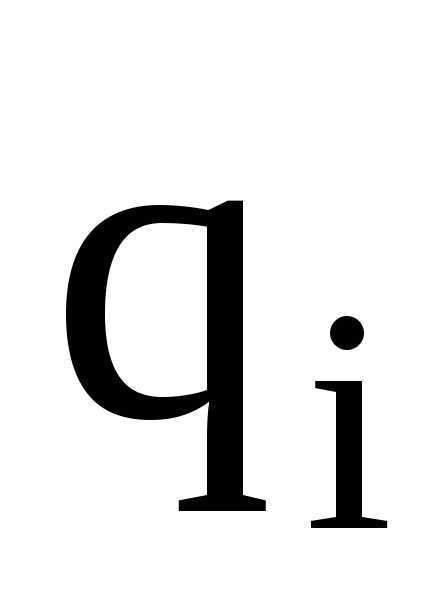 .
.
Потенциал связан с напряженностью электрического поля соотношением
.
В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой
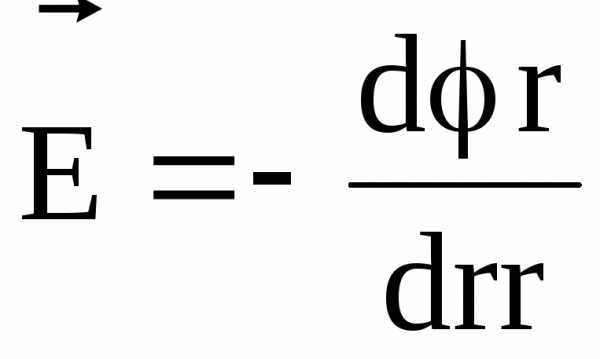 ,
,
или в скалярной форме
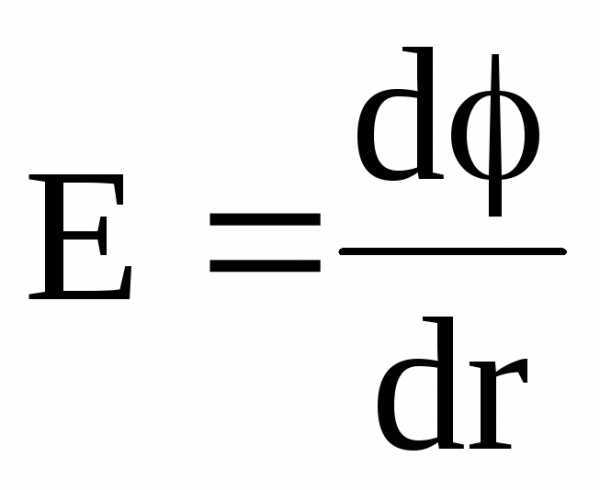 .
.
В случае однородного поля, т.е. поля, напряженность которого в каждой его точке одинакова как по абсолютному значению, так и по направлению, –
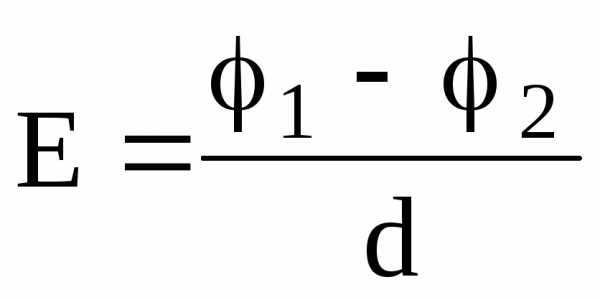 ,
,
где 1 и 2 – потенциалы точек двух эквипотенциальных поверхностей; d — расстояние между этими поверхностями вдоль электрической силовой линии.
Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал 1, в другую, имеющую потенциал 2, равна
, или 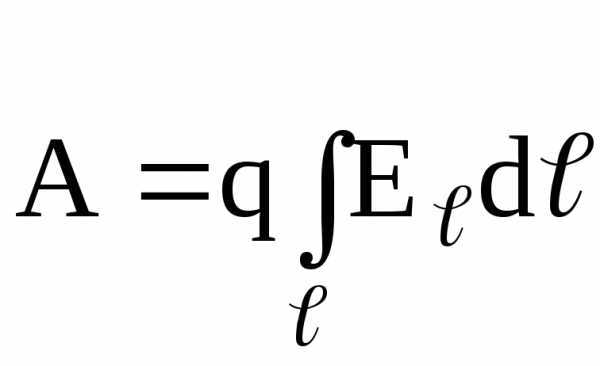 ,
,
где E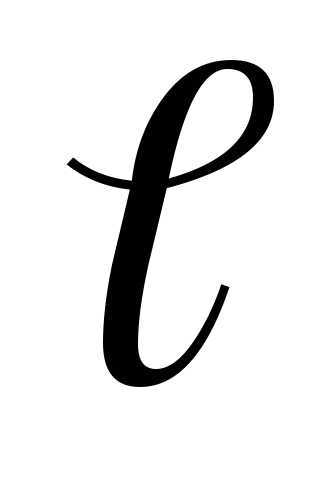 – проекция вектора
– проекция вектора  на направление перемещения;
на направление перемещения;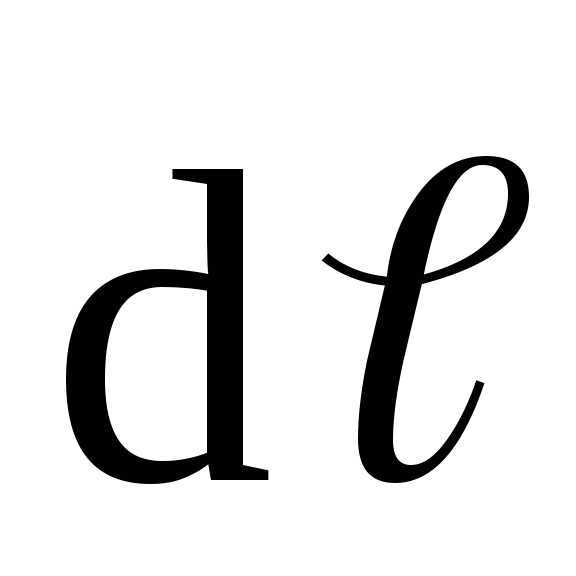 — перемещение.
— перемещение.
В случае однородного поля последняя формула принимает вид
,
где 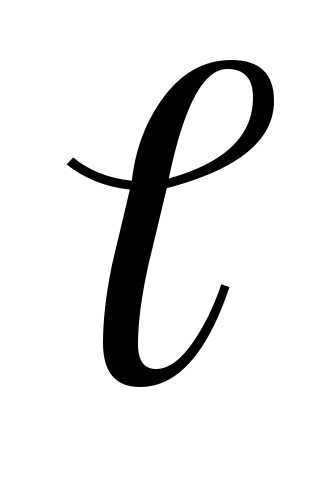 – перемещение; — угол между направлениями вектора
– перемещение; — угол между направлениями вектора  и перемеще-ния
и перемеще-ния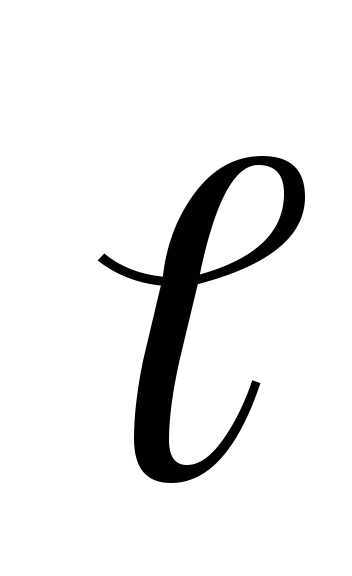 .
.
Диполь есть система двух точечных (равных по абсолютному значению и противоположных по знаку) зарядов, находящихся на некотором расстоянии друг от друга.
Электрический момент 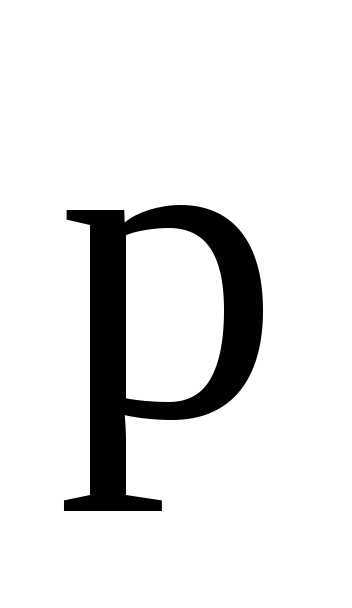 диполя есть вектор, направленный от отрицательного заряда к положительному, равный произведению заряда
диполя есть вектор, направленный от отрицательного заряда к положительному, равный произведению заряда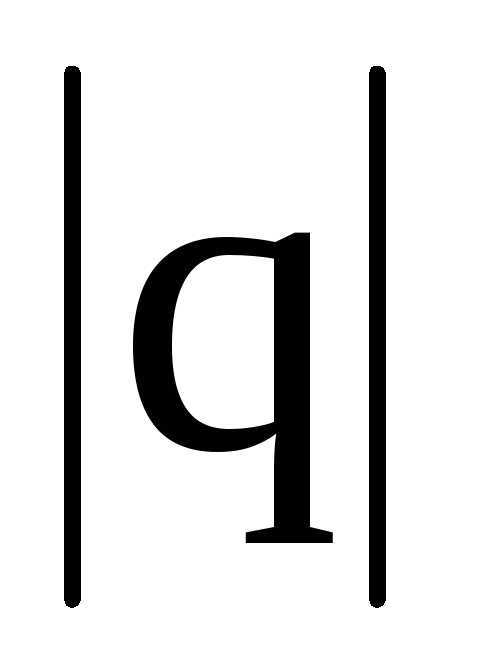 на вектор
на вектор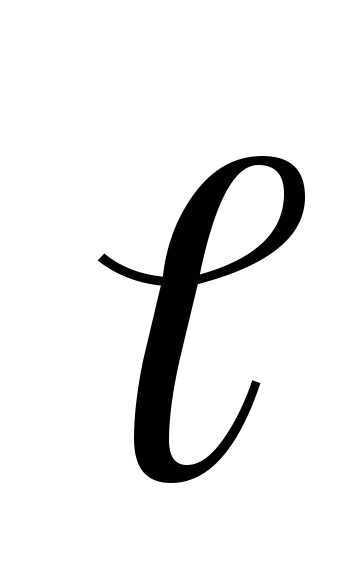 , проведенный от отрицательного заряда к положительному, и называемый плечом диполя, т.е.
, проведенный от отрицательного заряда к положительному, и называемый плечом диполя, т.е.
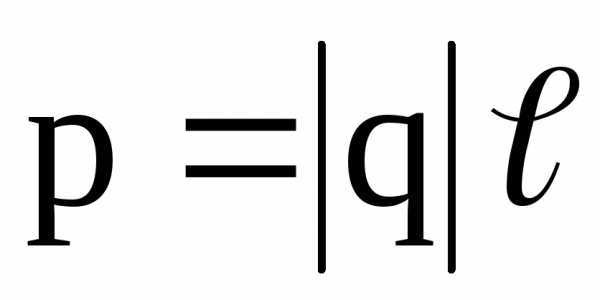 .
.
Диполь называется точечным, если его плечо 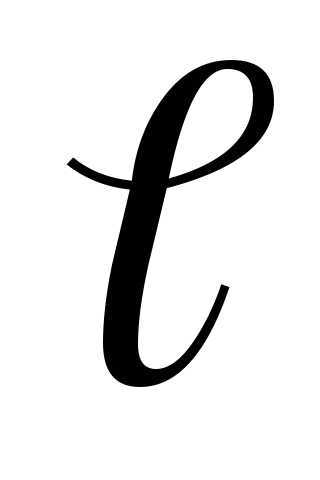 намного меньше расстоянияr от центра диполя до точки, в которой нас интересует действие диполя (
намного меньше расстоянияr от центра диполя до точки, в которой нас интересует действие диполя (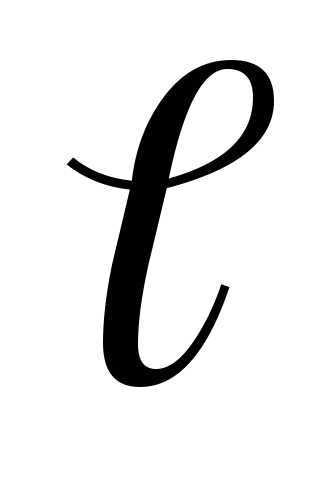 r), см. рис. 1.
r), см. рис. 1.
Рис. 1
Напряженность поля точечного диполя:
,
где р – электрический момент диполя; r – абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; — угол между радиус-вектором  и плечом
и плечом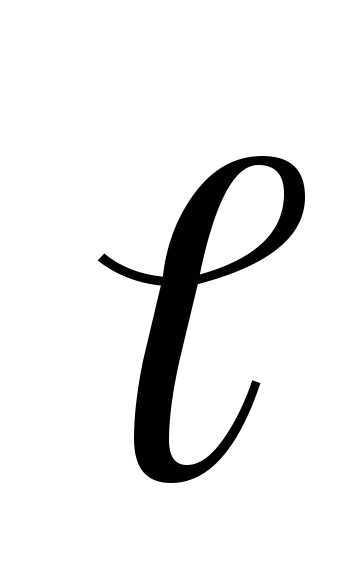 диполя.
диполя.
Напряженность поля точечного диполя в точке, лежащей на оси диполя
(=0), находится по формуле
 ;
;
в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины 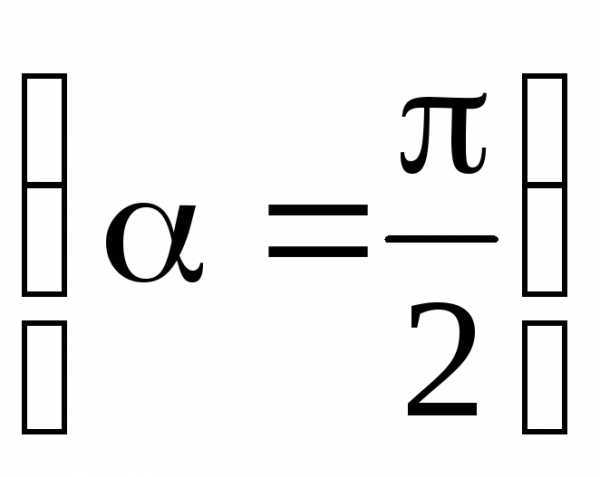 , – по формуле
, – по формуле
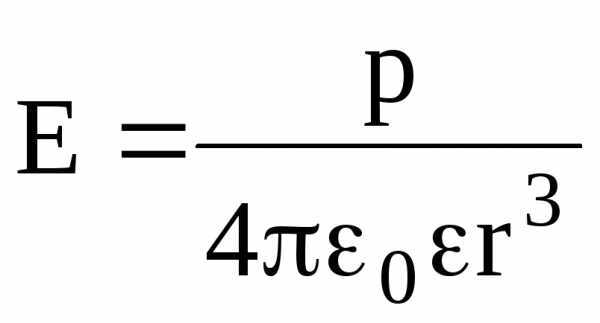 .
.
Потенциал поля точечного диполя в точке, лежащей на оси диполя (=0), составляет
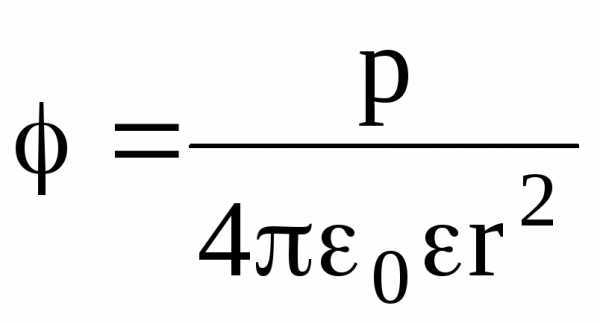 ,
,
а в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины 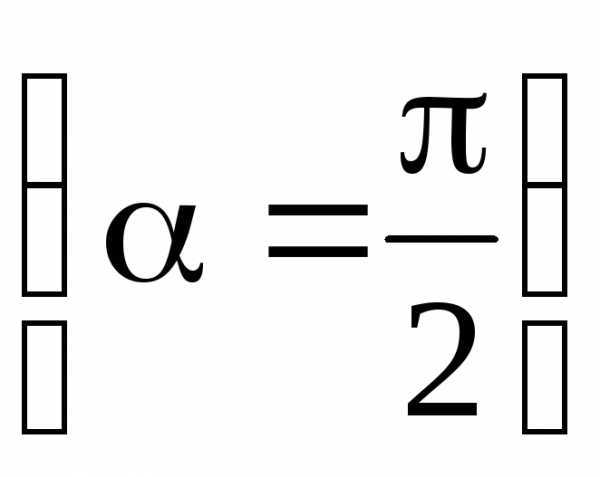 , –
, –
=0.
Напряженность и потенциал неточечного диполя определяются так же как и для системы зарядов.
Механический момент, действующий на диполь с электрическим моментом р, помещенный в однородное электрическое поле с напряженностью Е, –
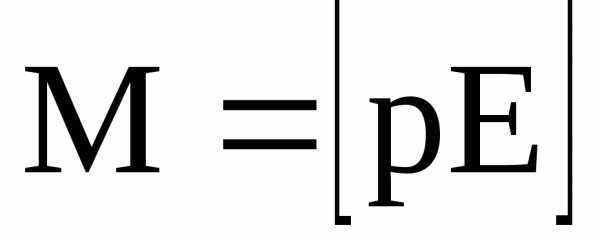 , или ,
, или ,
где — угол между направлениями векторов 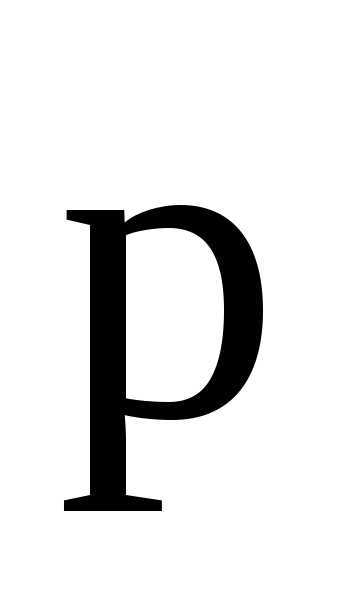 и
и .
.
Электроемкость уединенного проводника или конденсатора –
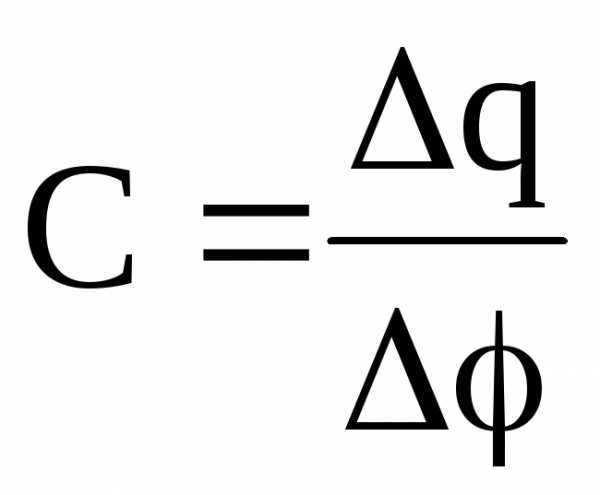 ,
,
где q – заряд, сообщенный проводнику;  — изменение потенциала, вызванное этим зарядом.
— изменение потенциала, вызванное этим зарядом.
Электроемкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью , –
.
Если сфера полая и заполнена диэлектриком, то ее электроемкость при этом не изменяется.
Электроемкость плоского конденсатора:
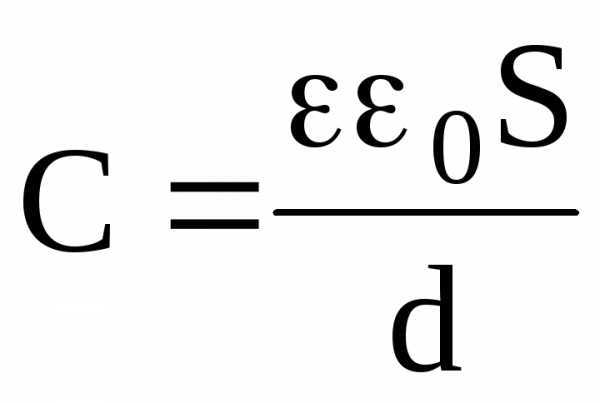 ,
,
где S – площадь каждой пластины конденсатора; d – расстояние между пластинами; — диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.
Электроемкость плоского конденсатора, заполненного n слоями диэлектрика толщиной di и диэлектрической проницаемостью i каждый (слоистый конденсатор), составляет
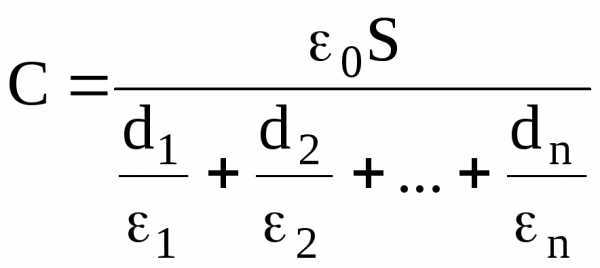 .
.
Электроемкость сферического конденсатора (две концентрические сферы радиусом R1 и R2 , пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ) находится так:
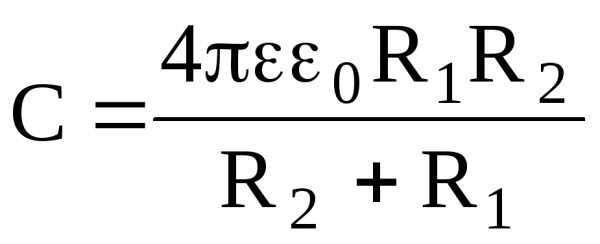 .
.
Электроемкость последовательно соединенных конденсаторов составляет:
в общем случае –
,
где n – число конденсаторов;
в случае двух конденсаторов –
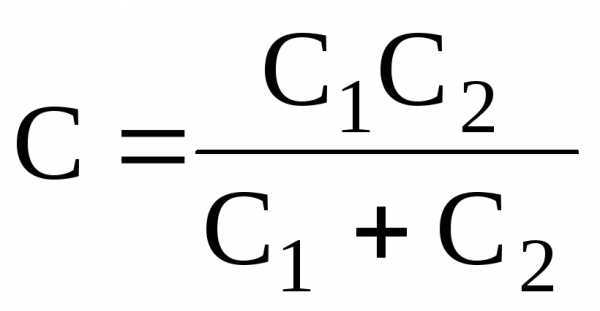 ;
;
в случае n одинаковых конденсаторов с электроемкостью С1 каждый –
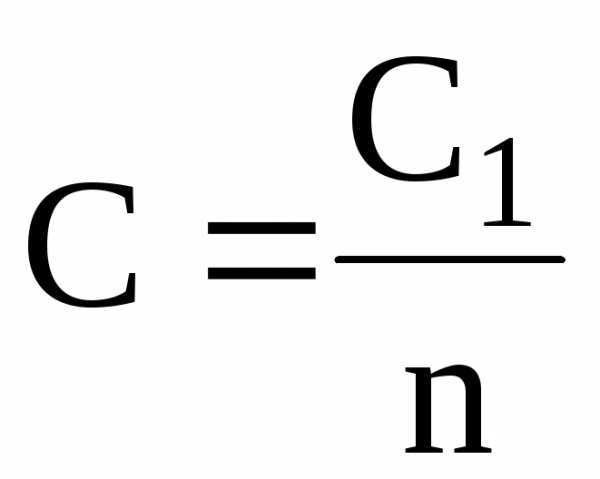 .
.
Электроемкость параллельно соединенных конденсаторов определяется следующим образом:
в общем случае –
С=С1+С2+…+Сn;
в случае двух конденсаторов –
С= С1+С2;
в случае n одинаковых конденсаторов с электроемкостью С1 каждый –
С=nС1.
Энергия заряженного проводника выражается через заряд q, потенциал и электроемкость С проводника следующим образом:
.
Энергия заряженного конденсатора –
,
где q – заряд конденсатора; С – электроемкость конденсатора; U – разность потенциалов на его пластинах.
studfiles.net
Формула напряжённости электрического поля
Здесь – напряжённость электрического поля, – сила, действующая на заряд, – величина заряда.
Единица измерения напряжённости электрического поля – В/м (вольт на метр) или Н/Кл (ньютон на кулон).
Напряжённость – векторная величина, характеризующая интенсивность воздействия электрического поля на заряжённую частицу в конкретной точке. Напряжённость поля в различных точках вообще говоря различна, то есть электрическое поле – это векторное поле, направление векторов которого зависит от того, как было создано это поле. По указанной формуле можно рассчитать не только силу воздействия электрического поля на точечный заряд, но и силу воздействия этого поля на заряжённое тело, если распределение заряда в нём известно.
Примеры решения задач по теме «Напряжённость электрического поля»
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
| Напряженность поля точечного заряда. | |
Обозначим: q — заряд, создающий поле, q0 — заряд, помещенный в поле (внешний заряд). Закон Кулона: . Напряженность поля: . Тогда напряженность поля точечного заряда: | |
Теорема Гаусса. Потоком вектора напряженности наз. величина Ф, равная произведению модуля вектора напряженности на площадь контура S, ограничивающую некоторую площадь, и на косинус угла между вектором напряженности и нормалью (перпендикуляром) к площадке. |
|
Если считать, что напряженность пропорциональна числу силовых линий, приходящихся на единицу площади поверхности (т.е. густоте), то поток напряженности пропорционален полному числу силовых линий, пересекающих данный контур. | |
Поток линий напряженности электростатического поля через произвольную замкнутую поверхность прямо пропорционален величине заряда, находящегося в области пространства, ограниченного данной поверхностью. | |
Применения теоремы Гаусса. |
|
1. Напряженность поля заряженной проводящей сферы радиуса R. Сфера заряжена по поверхности. А) Внутри сферы заряда нет . Е=0 | |
Б) Снаружи сферы. | |
На поверхности сферы: | |
2. Напряженность поля шара заряженного по объему. |
|
Введем понятие объемной плотности заряда: Объемная плотность заряда показывает, какой заряд содержится в единице объема заряженного по всему объему тела. Объем шара произвольного радиуса . Обозначим q — заряд шара, q0 — заряд, находящийся внутри объема произвольного радиуса. | |
Тогда заряд сферы радиуса r , будет: Следовательно: . – напряженность поля внутри шара, равномерно заряженного по объему. Снаружи — см. 1. | |
3. Напряженность поля бесконечной заряженной плоскости. |
|
Введем понятие поверхностной плотности заряда: . Тогда . Коэффициент 2 появляется, т.к. плоскость окружена двумя поверхностями площадью S. Поле бесконечной заряженной плоскости не зависит от расстояния от плоскости! Можно пользоваться, когда расстояние много меньше размеров плоскости. 4. Напряженность поля плоского воздушного конденсатора. Из рисунка видим, что снаружи конденсатора поля пластин взаимно скомпенсированы, и общее поле равно нулю. Внутри конденсатора поля складываются. Используя вывод п.3 получаем: . Формула справедлива при условии, что расстояние между пластинами много меньше размеров самих пластин и вдали от краев пластин. | |
www.eduspb.com
Электрическое поле (к задачнику Рымкевича для 10-11 классов)
Электрическое поле к задачнику по физике за 10-11 классы «Физика. 10-11 класс. Пособие для общеобразовательных учебных заведений» Рымкевич А.П.
Электрическое поле и электрический заряд — первичные понятия, которые не определяются аналогично понятиям точки и прямой в геометрии. Неподвижный заряд создает вокруг себя электрическое поле. Если замкнутая система обладала зарядом q, то при любых изменениях в ней заряд q сохраняется. Это фундаментальное утверждение носит название закона сохранения заряда.
Точечным зарядом называется заряд исчезающе малых размеров. Из эксперимента известно, что два точечных заряда q1 и q2 на расстоянии r взаимодействуют с силой F, значение которой определяется законом Кулона:
где
— коэффициент пропорциональности. Когда заряды одноименные, то они отталкиваются, когда разноименные — притягиваются.
Силовой характеристикой электрического поля является вектор напряженности E;. Рассмотрим некоторый заряд q, внесенный в электрическое поле E;. Тогда на него будет действовать сила F;, которая определяется формулой: F; = qE;. Это формула может служить определением вектора напряженности электрического поля. Для графического представления электростатического поля пользуются понятием линий напряженности. Эти линии начинаются на положительных зарядах и заканчиваются на отрицательных. Касательная в каждой точке линии напряженности направлена также, как и вектор E; . Если имеется N зарядов, каждый из которых создает свое поле E1;, E2;,…, EN; , то полная напряженность в любой точке пространства E; определяется как векторная сумма этих напряженностей (принцип суперпозиции):
Для точечного заряда q значение напряженности E в точке, удаленной от него на расстоянии r, выражается формулой:
Проводником называется тело, содержащее свободные заряды. Если мы сообщим проводнику некоторый заряд q, то он распределится по поверхности, а внутри проводника поле будет равно нулю. Поверхностной плотностью о называется отношение заряда к площади поверхности проводника
Поле заряженного проводящего шара снаружи от него совпадает с полем точечного заряда, а внутри него равно нулю. Поле бесконечной заряженной проводящей плоскости с поверхностной плотностью заряда о определяется формулой:
где ε0 = 8,854⋅10-12 Ф/м — электрическая постоянная.
Диэлектриком называется тело, в котором отсутствуют свободные заряды. При помещении диэлектрика в электрическое поле происходит его поляризация, при этом поле E в диэлектрике уменьшается в ε раз:
где E0 — напряженность поля вне диэлектрика, ε — диэлектрическая проницаемость. При перемещении заряда q в электрическом поле E; на
расстояние
совершается работа A:
Изменение потенциальной энергии ΔWP равно:
Потенциал φ — энергетическая характеристика электрического поля, он определяется формулой:
Эквипотенциальные поверхности — это такие поверхности, в каждой точке которых потенциал постоянен. Потенциал поля φ в некоторой точке пространства, созданный N зарядами, равен алгебраической сумме потенциалов φ1, φ2,…, φN созданных отдельными зарядами (принцип суперпозиции): φ = φ1 + φ2 + … +
φN- Потенциал поля точечного заряда q на расстоянии r от него определяется формулой:
Напряжением U между точками A и B называется разность потенциалов:
где φ1 — потенциал в точке A, φ2 — потенциал в точке B. Напряжение U связано с напряженностью E электрического поля следующей формулой:
Конденсатором называется устройство, способное накапливать заряд. Емкость конденсатора C определяется как отношение заряда q на его обкладках к приложенному напряжению U:
Емкость не зависит от заряда и напряжения на нем, а определяется его геометрическими свойствами (формой и размером) и родом среды. Для плоского конденсатора емкость равна:
где ε — диэлектрическая проницаемость среды между обкладками, S — площадь обкладок, d — расстояние между обкладками. Энергия заряженного конденсатора W определяется формулой:
Плотность энергии ω электрического поля E выражается формулой:
5terka.com
Электрический заряд определение и формула. Основные законы и формулы
Закон Кулона:
где F – сила взаимодействия двух точечных зарядов q 1 и q 2 ; r – расстояние между зарядами; — диэлектрическая проницаемость среды; 0 — электрическая постоянная
.
Закон сохранения заряда:
,
где – алгебраическая сумма зарядов, входящих в изолированную систему;n – число зарядов.
Напряженность и потенциал электростатического поля:
;
, или
,
где – сила, действующая на точечный положительный зарядq 0 , помещенный в данную точку поля; П – потенциальная энергия заряда; А ∞ — работа, затраченная на перемещение заряда q 0 из данной точки поля в бесконечность.
Поток вектора напряженности электрического поля:
а) через произвольную поверхность S, помещенную в неоднородное поле:
, или
,
где – угол между вектором напряженности и нормальюк элементу поверхности;dS – площадь элемента поверхности; E n – проекция вектора напряженности на нормаль;
б) через плоскую поверхность, помещенную в однородное электрическое поле:
.
Поток вектора напряженности через замкнутую поверхность –
(интегрирование ведется по всей поверхности).
Теорема Остроградского-Гаусса. Поток вектора напряженностичерез любую замкнутую поверхность, охватывающую зарядыq1,q2, …,qn, –
,
где – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; n – число зарядов.
Напряженность электростатического поля, создаваемого точечным зарядом q на расстоянии r от заряда, –
.
Напряженность электрического поля, создаваемого сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы такова:
внутри сферы (r R) Е=0;
на поверхности сферы (r=R)
;
вне сферы (r R)
.
Принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей, выражается формулой
В случае двух электрических полей с напряженностями иабсолютное значение вектора напряженности составляет
где — угол между векторами и.
Напряженность поля, создаваемого бесконечно длинной и равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси, –
,
где — линейная плотность заряда.
Линейная плотность заряда есть величина, равная его отношению к длине нити (цилиндра):
ruscos.ru
les66.ru
Глава 17. Взаимодействие электрических зарядов. Закон Кулона, принцип суперпозиции
Взаимодействие электрических зарядов описывается законом Кулона, который утверждает, что сила взаимодействия двух покоящихся точечных зарядов в вакууме равна
(17.1) |
где и — модули зарядов, — расстояние между ними. Коэффициент пропорциональности в формуле (17.1) зависит от системы единиц. В международной системе единиц СИ этот коэффициент принято записывать в виде
(17.2) |
где величина называется электрической постоянной, размерность величины сводится к отношению размерности длины к размерности электрической емкости (Фарада). Электрические заряды бывают двух типов, которые условно принято называть положительным и отрицательным. Как показывает опыт, заряды притягиваются, если они разноименные и отталкиваются, если одноименные.
В любом макроскопическом теле содержится огромное количество электрических зарядов, поскольку они входят в состав всех атомов: электроны заряжены отрицательно, протоны, входящие в состав атомных ядер — положительно. Однако большинство тел, с которыми мы имеем дело, не заряжены, поскольку количество электронов и протонов, входящих в состав атомов, одинаково, а их заряды по абсолютной величине в точности совпадают. Тем не менее, тела можно зарядить, если создать в них избыток или недостаток электронов по сравнению с протонами. Для этого нужно передать электроны, входящие в состав какого-нибудь тела, другому телу. Тогда у первого возникнет недостаток электронов и соответственно положительный заряд, у второго — отрицательный. Такого рода процессы происходят, в частности, при трении тел друг о друга.
Если заряды находятся в некоторой среде, которая занимает все пространство, то сила их взаимодействия ослабляется по сравнению с силой их взаимодействия в вакууме, причем это ослабление не зависит от величин зарядов и расстояния между ними, а зависит только от свойств среды. Характеристика среды, которая показывает, во сколько раз ослабляется сила взаимодействия зарядов в этой среде по сравнению с силой их взаимодействия в вакууме, называется диэлектрической проницаемостью этой среды и, как правило, обозначается буквой . Формула Кулона в среде с диэлектрической проницаемостью принимает вид
(17.3) |
Если имеется не два, а большее количество точечных зарядов для нахождения сил, действующих в этой системе, используется закон, который называется принципомсуперпозиции1. Принцип суперпозиции утверждает, что для нахождения силы, действующей на один из зарядов (например, на заряд ) в системе из трех точечных зарядов , и надо сделать следующее. Сначала надо мысленно убрать заряд и по закону Кулона найти силу, действующую на заряд со стороны оставшегося заряда . Затем следует убрать заряд и найти силу, действующую на заряд со стороны заряда . Векторная сумма полученных сил и даст искомую силу.
Принцип суперпозиции дает рецепт поиска силы взаимодействия неточечных заряженных тел. Следует мысленно разбить каждое тело на части, которые можно считать точечными, по закону Кулона найти силу их взаимодействия с точечными частями, на которое разбивается второе тело, просуммировать полученные вектора. Ясно, что такая процедура математически очень сложна, хотя бы потому, что необходимо сложить бесконечное количество векторов. В математическом анализе разработаны методы такого суммирования, однако в школьный курс физики они не входят. Поэтому, если такая задача и встретится, то суммирование в ней должно легко выполняться на основе тех или иных соображений симметрии. Например, из описанной процедуры суммирования следует, что сила, действующая на точечный заряд, помещенный в центр равномерно заряженной сферы, равна нулю.
Кроме того, школьник должен знать (без вывода) формулы для силы, действующей на точечный заряд со стороны равномерно заряженной сферы и бесконечной плоскости. Если имеется сфера радиуса , равномерно заряженная зарядом , и точечный заряд , расположенный на расстоянии от центра сферы, то величина силы взаимодействия равна
(17.4) |
если точечный заряд находится снаружи сферы, и
(17.5) |
если заряд находится внутри (причем не обязательно в центре). Из формул (17.4), (17.5) следует, что сфера снаружи создает такое же электрическое поле как весь ее заряд, помещенный в центре, а внутри — нулевое.
Если имеется очень большая плоскость с площадью , равномерно заряженная зарядом , и точечный заряд , то сила их взаимодействия равна
(17.6) |
где величина имеет смысл поверхностной плотности заряда плоскости. Как следует из формулы (17.6) сила взаимодействия точечного заряда и плоскости не зависит от расстояния между ними. Обратим внимание читателя на то, что формула (17.6) является приближенной и «работает» тем точнее, чем дальше точечный заряд находится от ее краев. Поэтому при использовании формулы (17.6) часто говорят, что она справедлива в рамках пренебрежения «краевыми эффектами», т.е. когда плоскость считается бесконечной.
Рассмотрим теперь решение данных в первой части книги задач.
Согласно закону Кулона (17.1) величина силы взаимодействия двух зарядов из задачи 17.1.1 выражается формулой
Заряды отталкиваются (ответ 2).
Поскольку капелька воды из задачи 17.1.2 имеет заряд ( – заряд протона), то она имеет в избытке электронов по сравнению с протонами. Значит при потере трех электронов их избыток уменьшится, и заряд капельки станет равен (ответ 2).
Согласно закону Кулона (17.1) величина силы взаимодействия двух зарядов при увеличении в раз расстояния между ними уменьшится в раз (задача 17.1.3 — ответ 4).
Если заряды двух точечных тел увеличить в раз при неизменном расстоянии между ними, то сила их взаимодействия, как это следует из закона Кулона (17.1), увеличится в раз (задача 17.1.4 — ответ 3).
При увеличении одного заряда в 2 раза, а второго в 4, числитель закона Кулона (17.1) увеличивается в 8 раз, а при увеличении расстояния между зарядами в 8 раз — знаменатель увеличивается в 64 раза. Поэтому сила взаимодействия зарядов из задачи 17.1.5 уменьшится в 8 раз (ответ 4).
При заполнении пространства диэлектрической средой с диэлектрической проницаемостью = 10, сила взаимодействия зарядов согласно закону Кулона в среде (17.3) уменьшится в 10 раз (задача 17.1.6 — ответ 2).
Сила кулоновского взаимодействия (17.1) действует как на первый, так и на второй заряд, а поскольку их массы одинаковы, то ускорения зарядов, как это следует из второго закона Ньютона, в любой момент времени одинаковы (задача 17.1.7 — ответ 3).
Похожая задача, но массы шариков разные. Поэтому при одинаковой силе ускорение шарика с меньшей массой в 2 раза больше ускорения шарика с меньшей массой , причем этот результат не зависит от величин зарядов шариков (задача 17.1.8 — ответ 2).
Поскольку электрон заряжен отрицательно, он будет отталкиваться от шара (задача 17.1.9). Но поскольку начальная скорость электрона направлена к шару, он будет двигаться в этом направлении, но его скорость будет уменьшаться. В какой-то момент он на мгновение остановится, а потом будет двигаться от шара с увеличивающейся скоростью (ответ 4).
В системе двух заряженных шариков, связанных нитью (задача 17.1.10), действуют только внутренние силы. Поэтому система будет покоиться и для нахождения силы натяжения нити можно использовать условия равновесия шариков. Поскольку на каждый из них действуют только кулоновская сила и сила натяжения нити, то из условия равновесия заключаем, что эти силы равны по величине.
Отсюда
где (ответ 1).
Система трех шариков в задаче 17.2.1 покоится, поэтому силы натяжения должны компенсировать силы кулоновского отталкивания крайних зарядов. Последние найдем по закону Кулона и принципу суперпозиции. Каждый крайний заряд отталкивается от центрального заряда и другого крайнего. Для суммы этих сил получаем
Этой величине и будет равна сила натяжения нитей (ответ 4). Отметим, что рассмотрение условия равновесия центрального заряда не помогло бы найти силу натяжения, а привело бы к заключению, что силы натяжения нитей одинаковы (впрочем, это заключение и так очевидно благодаря симметрии задачи).
Для нахождения силы, действующей на заряд — в задаче 17.2.2, используем принцип суперпозиции. На заряд — действуют силы притяжения к левому и правому зарядам (см. рисунок). Поскольку расстояния от заряда — до зарядов одинаковы, модули этих сил равны друг другу и они направлены под одинаковыми углами к прямой, соединяющей заряд — с серединой отрезка — . Поэтому сила, действующая на заряд — направлена вертикально вниз (вектор результирующей силы выделен жирным на рисунке; ответ 4).
Задача 17.2.3 похожа на предыдущую, но изменен знак одного из зарядов. Поэтому сила, действующая на заряд — со стороны правого заряда, не изменившись по величине, изменится по направлению (см. рисунок). Поэтому вектор результирующей силы будет направлен влево (вектор результирующей силы выделен жирным на рисунке; ответ 1). |
|
На каждый заряд в задаче 17.2.4 действуют силы отталкивания со стороны двух других зарядов (см. рисунок), причем значения этих сил одинаковы (из-за равенства величин всех зарядов и расстояний между ними) и равны |
Из-за равенства значений сил-слагаемых параллелограмм сложения сил представляет собой ромб, и, следовательно, вектор результирующей силы направлен вдоль биссектрисы треугольника из зарядов (выделен жирным на рисунке). Поэтому угол, отмеченный на рисунке дугой равен 30°, а значение результирующей силы равно
(ответ 3).
Из формулы (17.6) заключаем, что правильный ответ в задаче 17.2.5 — 4. В задаче 17.2.6 нужно использовать формулу для силы взаимодействия точечного заряда и сферы (формулы (17.4), (17.5)). Имеем = 0 (ответ 3).
В задаче 17.2.7 необходимо применить принцип суперпозиции к двум сферам. Принцип суперпозиции утверждает, что взаимодействие каждой пары зарядов не зависит от наличия других зарядов. Поэтому каждая сфера действует на точечный заряд независимо от другой сферы, и для нахождения результирующей силы нужно сложить силы со стороны первой и второй сфер. Поскольку точечный заряд расположен внутри внешней сферы, она не действует на него (см. формулу (17.5)), внутренняя действует с силой
где . Поэтому и результирующая сила равна этому выражению (ответ 2)
В задаче 17.2.8 также следует использовать принцип суперпозиции. Если заряд поместить в точку , то силы, действующие на него со стороны зарядов и , направлены влево. Поэтому по принципу суперпозиции имеем для равнодействующей силы
где — расстояния от зарядов до исследуемых точек. Если поместить положительный заряд в точку , то силы будут направлены противоположно, и на основании принципа суперпозиции находим результирующую силу
В точке на заряд будут действовать силы, направленные направо, и потому
Из этих формул следует, что наибольшей сила будет в точке — ответ 1.
Пусть, для определенности, заряды шариков и в задаче 17.2.9 положительны. Так как шарики одинаковы, заряды после их соединения распределяться между ними равномерно и для сравнения сил, нужно сравнить друг с другом величины
(1) |
которые представляют собой произведения зарядов шариков до и после их соединения. После извлечения квадратного корня сравнение (1) сводится к сравнению среднего геометрического и среднего арифметического двух чисел. А поскольку среднее арифметическое любых двух чисел больше их среднего геометрического, то сила взаимодействия шариков возрастет независимо от величин их зарядов (ответ 1).
Задача 17.2.10 очень похожа на предыдущую, а ответ — другой. Непосредственной поверкой легко убедиться, что сила может как увеличиться, так и уменьшиться в зависимости от величин зарядов. Например, если заряды равны по величине, то после соединения шариков их заряды станут равны нулю, поэтому нулевой будет и сила их взаимодействия, которая, следовательно, уменьшится. Если один из первоначальных зарядов равен нулю, то после соприкосновения шариков заряд одного из них распределится между шариками поровну, и сила их взаимодействия увеличится. Таким образом, правильный ответ в этой задаче — 3.
online.mephi.ru
Формула определения заряда. Основные законы и формулы
Закон Кулона:
где F – сила взаимодействия двух точечных зарядов q 1 и q 2 ; r – расстояние между зарядами; — диэлектрическая проницаемость среды; 0 — электрическая постоянная
.
Закон сохранения заряда:
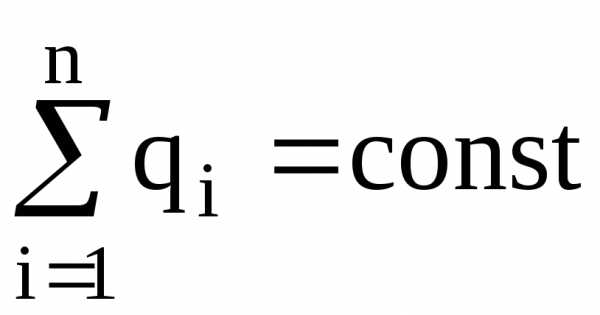 ,
,
где 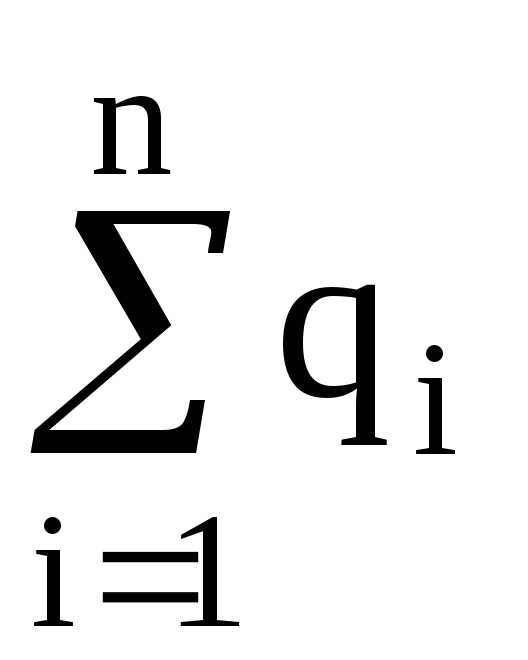 – алгебраическая сумма зарядов, входящих
в изолированную систему;n
– число зарядов.
– алгебраическая сумма зарядов, входящих
в изолированную систему;n
– число зарядов.
Напряженность и потенциал электростатического поля:
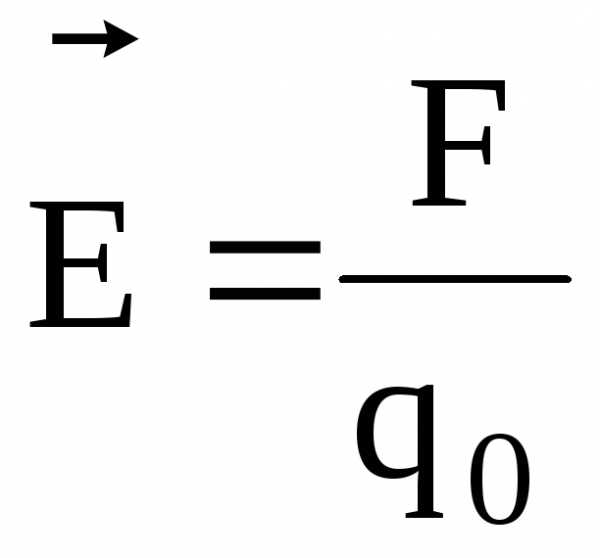 ;
;
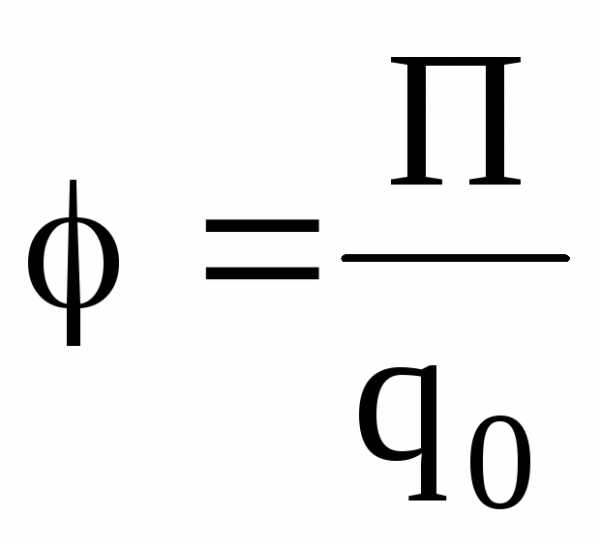 ,
или
,
или
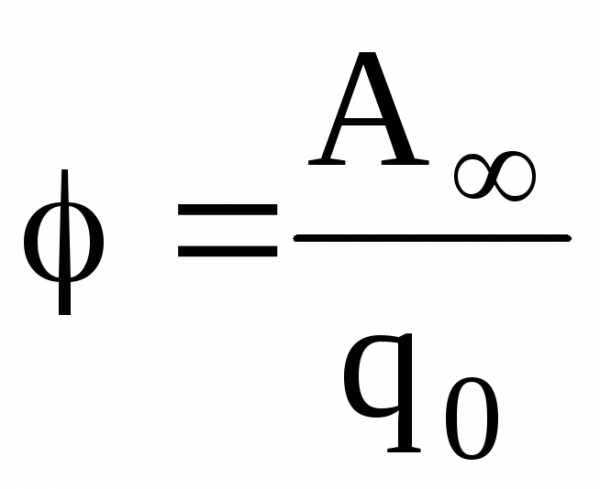 ,
,
где  – сила, действующая на точечный
положительный зарядq 0 ,
помещенный в данную точку поля; П –
потенциальная энергия заряда; А ∞
— работа,
затраченная на перемещение заряда q 0
из данной точки поля в бесконечность.
– сила, действующая на точечный
положительный зарядq 0 ,
помещенный в данную точку поля; П –
потенциальная энергия заряда; А ∞
— работа,
затраченная на перемещение заряда q 0
из данной точки поля в бесконечность.
Поток
вектора напряженности  электрического поля:
электрического поля:
а) через произвольную поверхность S, помещенную в неоднородное поле:
,
или
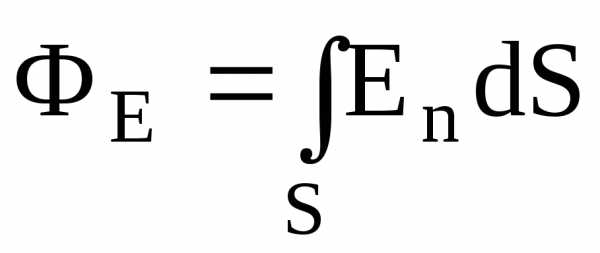 ,
,
где
– угол между вектором напряженности  и нормалью
и нормалью к элементу поверхности;dS
– площадь элемента поверхности; E n
– проекция вектора напряженности на
нормаль;
к элементу поверхности;dS
– площадь элемента поверхности; E n
– проекция вектора напряженности на
нормаль;
б) через плоскую поверхность, помещенную в однородное электрическое поле:
.
Поток
вектора напряженности  через замкнутую поверхность –
через замкнутую поверхность –
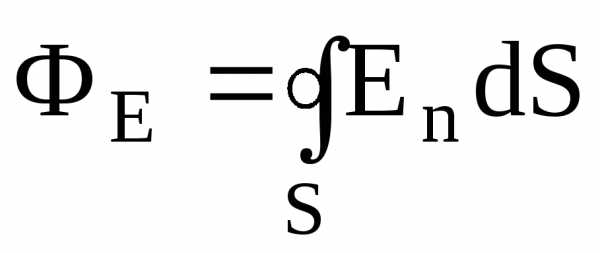
(интегрирование ведется по всей поверхности).
Теорема Остроградского-Гаусса. Поток вектора напряженностичерез любую замкнутую поверхность, охватывающую зарядыq1,q2, …,qn, –
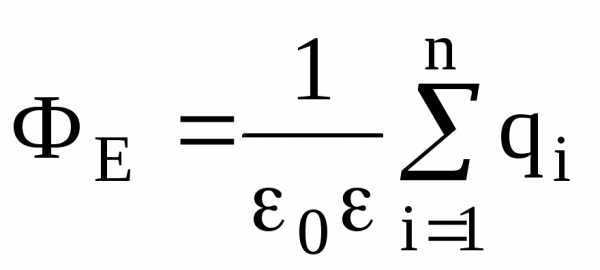 ,
,
где 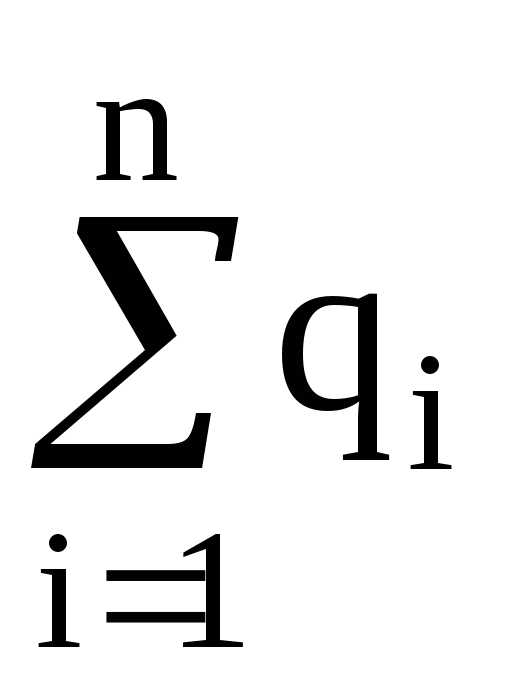 – алгебраическая
сумма зарядов, заключенных внутри
замкнутой поверхности; n
– число зарядов.
– алгебраическая
сумма зарядов, заключенных внутри
замкнутой поверхности; n
– число зарядов.
Напряженность электростатического поля, создаваемого точечным зарядом q на расстоянии r от заряда, –
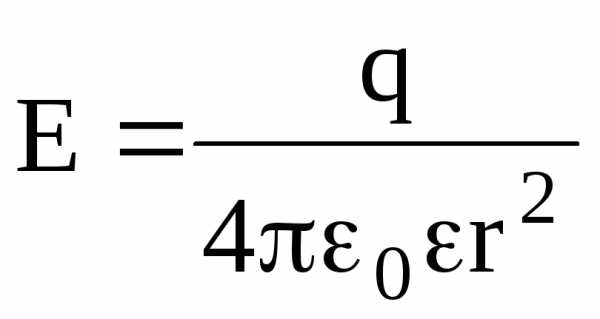 .
.
Напряженность электрического поля, создаваемого сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы такова:
внутри сферы (r R) Е=0;
на поверхности сферы (r=R)
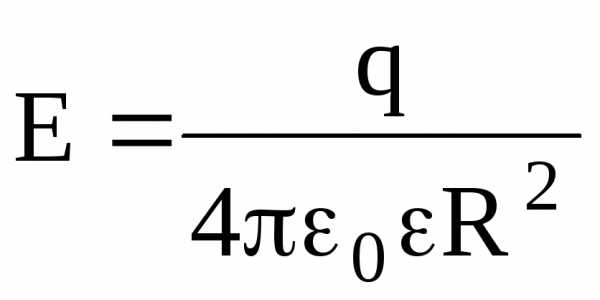 ;
;
вне сферы (r R)
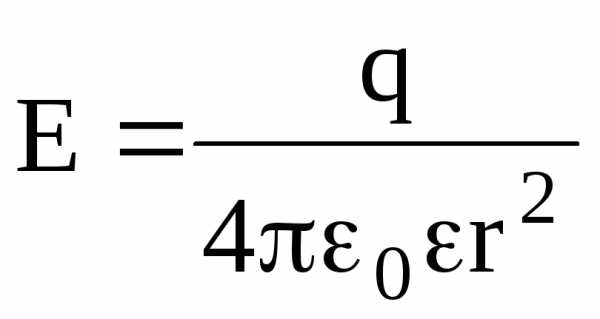 .
.
Принцип суперпозиции (наложения)
электростатических полей, согласно
которому напряженность  результирующего поля, созданного двумя
(и более) точечными зарядами, равна
векторной (геометрической) сумме
напряженностей складываемых полей,
выражается формулой
результирующего поля, созданного двумя
(и более) точечными зарядами, равна
векторной (геометрической) сумме
напряженностей складываемых полей,
выражается формулой
В
случае двух электрических полей с
напряженностями 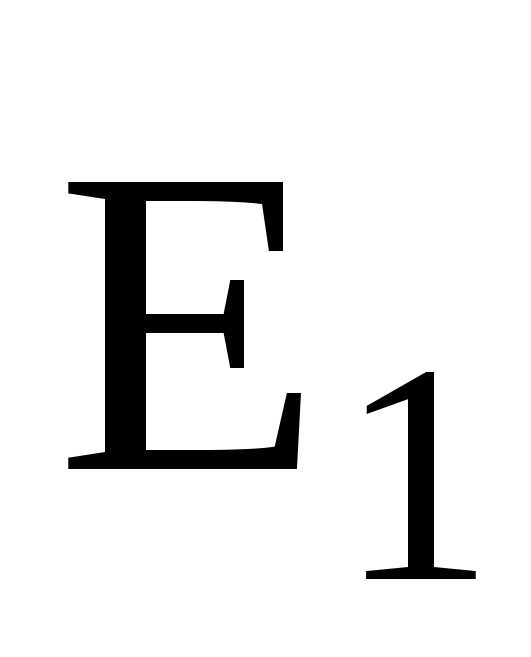 иабсолютное значение вектора напряженности
составляет
иабсолютное значение вектора напряженности
составляет
где
— угол между векторами 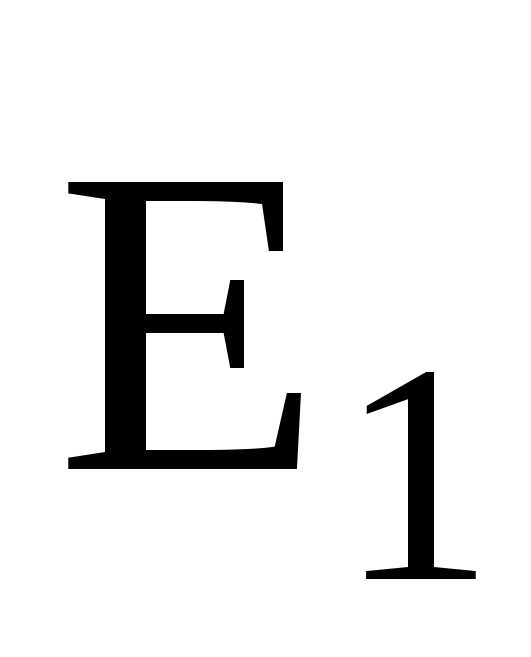 и.
и.
Напряженность поля, создаваемого бесконечно длинной и равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси, –
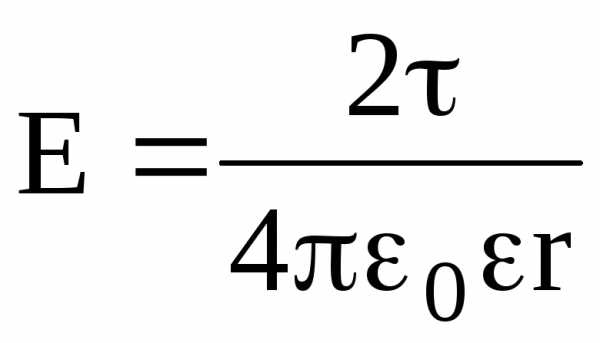 ,
,
где — линейная плотность заряда.
Линейная плотность заряда есть величина, равная его отношению к длине нити (цилиндра):
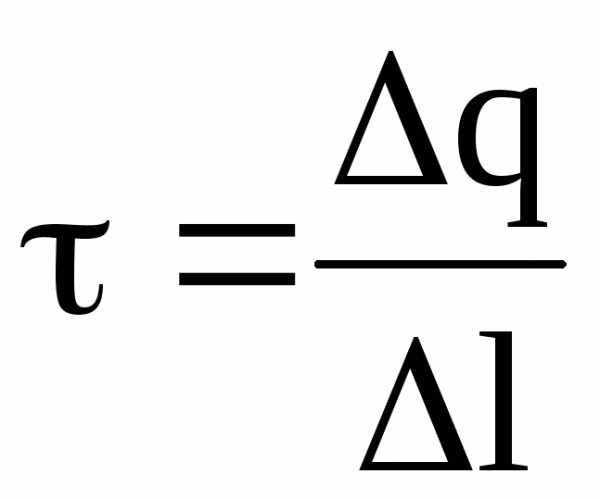 .
.
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, –
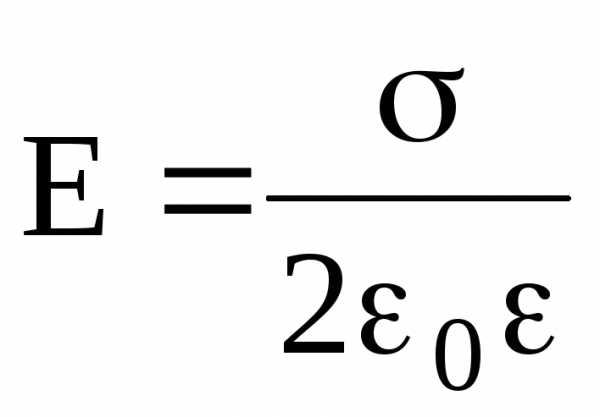 ,
,
где — поверхностная плотность заряда.
Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к ее площади:
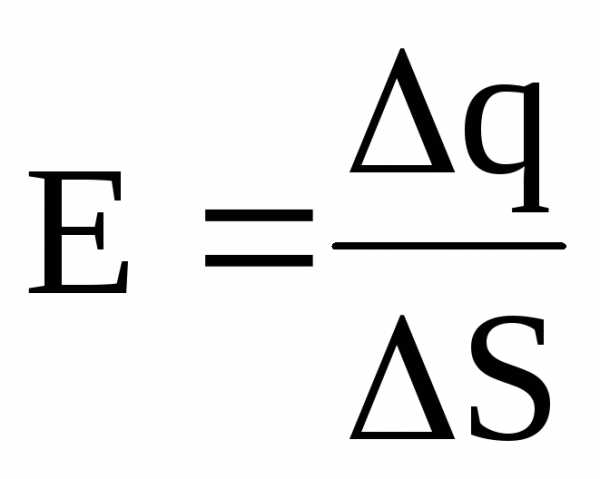 .
.
Напряженность поля, создаваемого двумя бесконечными и параллельными плоскостями, заряженными равномерно и разноименно, с одинаковой по абсолютному значению поверхностной плотностью заряда (поле плоского конденсатора) –
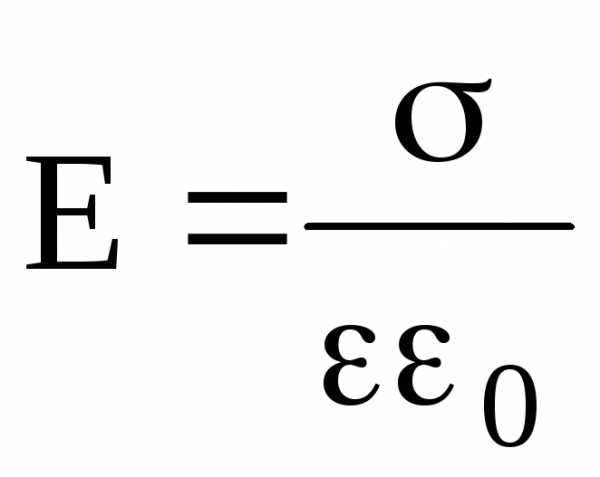 .
.
Приведенная формула справедлива при вычислении напряженности поля между пластинами плоского конденсатора (в его средней части) только в том случае, если расстояние между пластинами намного меньше линейных размеров пластин конденсатора.
Электрическое
смещение  связано с напряженностью
связано с напряженностью электрического поля соотношением
электрического поля соотношением
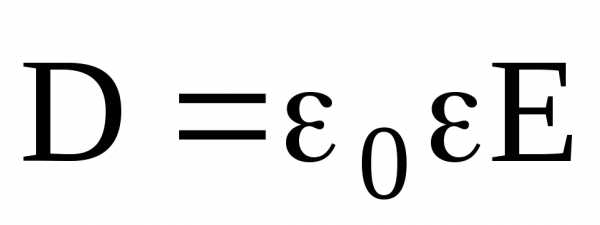 ,
,
которое справедливо только для изотропных диэлектриков.
Потенциал электрического поля есть величина, равная отношению потенциальной энергии и точечного положительного заряда, помещенного в данную точку поля:
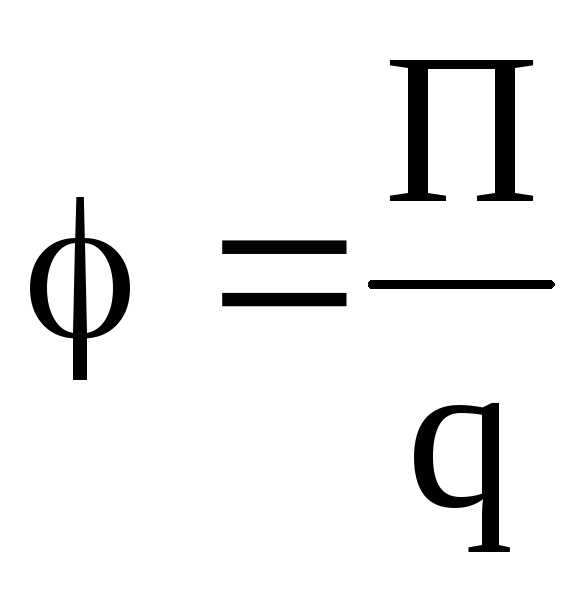 .
.
Иначе говоря, потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к величине этого заряда:
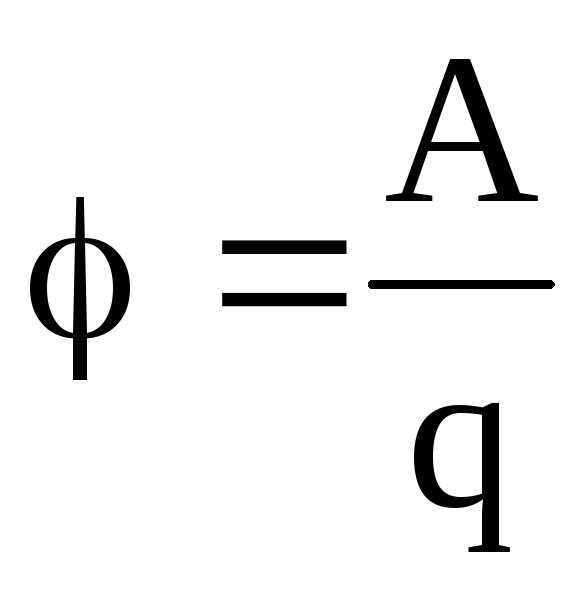 .
.
Потенциал электрического поля в бесконечности условно принят равным нулю.
Потенциал электрического поля, создаваемый точечным зарядом q на
расстоянии r от заряда, –
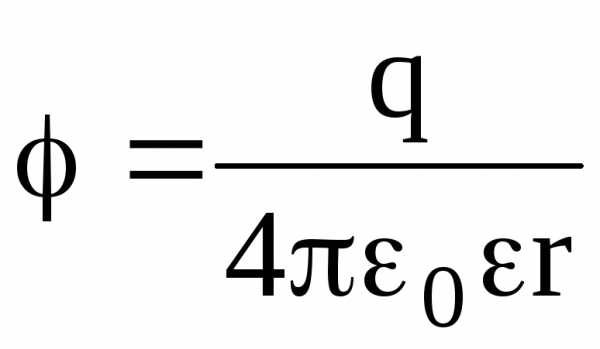 .
.
Потенциал электрического поля, создаваемый металлической сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы таков:
внутри сферы (r R)
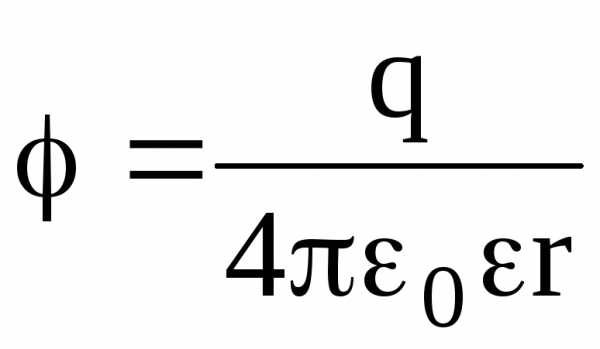 ;
;
на поверхности сферы (r = R)
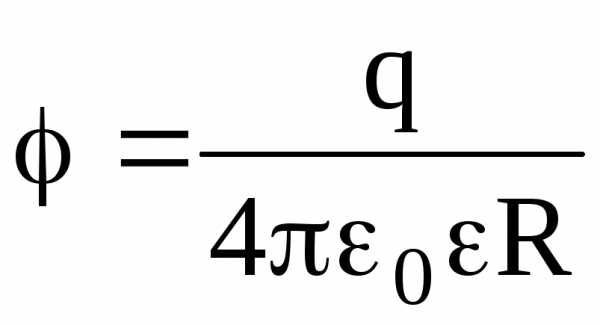 ;
;
вне сферы (r R)
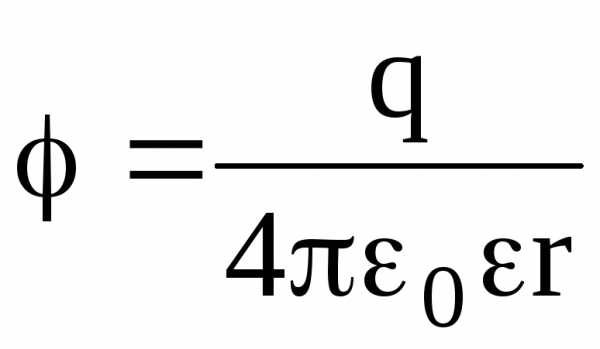 .
.
Во всех формулах, приведенных для потенциала заряженной сферы, есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.
Потенциал электрического поля, образуемого системой n точечных зарядов в данной точке в соответствии с принципом суперпозиции электрических полей, равен алгебраической сумме потенциалов
, создаваемых отдельными точечными зарядами
:
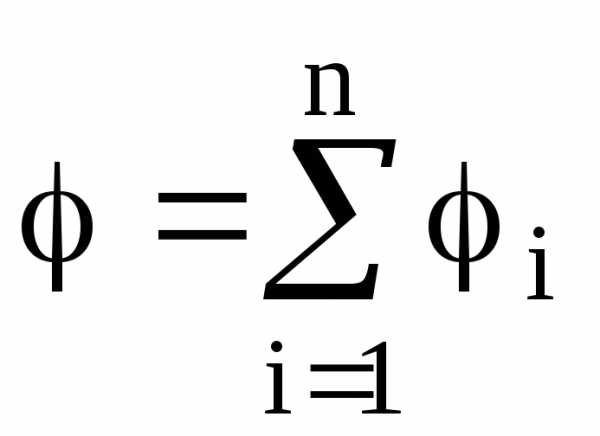 .
.
Энергия W взаимодействия системы точечных зарядов
определяется работой, которую эта система может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой
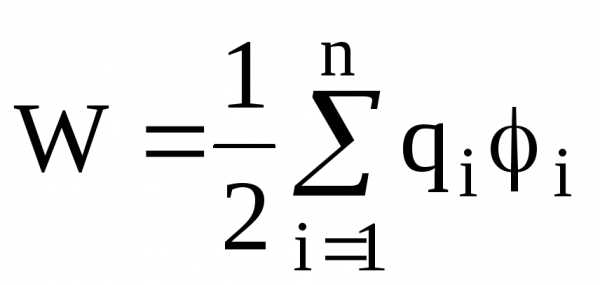 ,
,
где  — потенциал поля, создаваемый всеми
(n-1)
зарядами (за исключением i-го)
в точке, где находится заряд
— потенциал поля, создаваемый всеми
(n-1)
зарядами (за исключением i-го)
в точке, где находится заряд 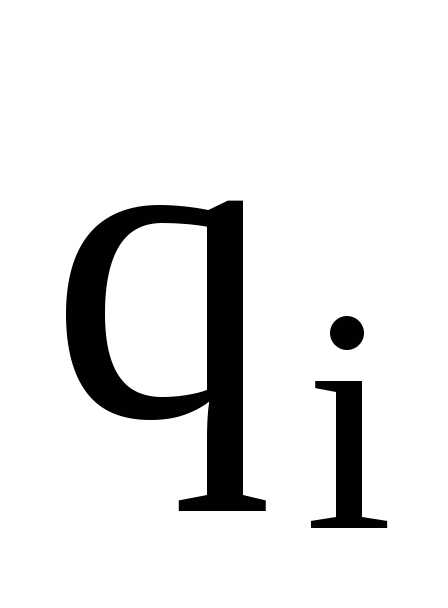 .
.
Потенциал связан с напряженностью электрического поля соотношением
.
В случае электрического поля, обладающего сферической симметрией, эта
electrician-top.ru
| Напряженность поля точечного заряда. | |
Обозначим: q — заряд, создающий поле, q0 — заряд, помещенный в поле (внешний заряд). Закон Кулона: . Напряженность поля: . Тогда напряженность поля точечного заряда: | |
Теорема Гаусса. Потоком вектора напряженности наз. величина Ф, равная произведению модуля вектора напряженности на площадь контура S, ограничивающую некоторую площадь, и на косинус угла между вектором напряженности и нормалью (перпендикуляром) к площадке. |
|
Если считать, что напряженность пропорциональна числу силовых линий, приходящихся на единицу площади поверхности (т.е. густоте), то поток напряженности пропорционален полному числу силовых линий, пересекающих данный контур. | |
Поток линий напряженности электростатического поля через произвольную замкнутую поверхность прямо пропорционален величине заряда, находящегося в области пространства, ограниченного данной поверхностью. | |
Применения теоремы Гаусса. |
|
1. Напряженность поля заряженной проводящей сферы радиуса R. Сфера заряжена по поверхности. А) Внутри сферы заряда нет . Е=0 | |
Б) Снаружи сферы. | |
На поверхности сферы: | |
2. Напряженность поля шара заряженного по объему. |
|
Введем понятие объемной плотности заряда: Объемная плотность заряда показывает, какой заряд содержится в единице объема заряженного по всему объему тела. Объем шара произвольного радиуса . Обозначим q — заряд шара, q0 — заряд, находящийся внутри объема произвольного радиуса. | |
Тогда заряд сферы радиуса r , будет: Следовательно: . – напряженность поля внутри шара, равномерно заряженного по объему. Снаружи — см. 1. | |
3. Напряженность поля бесконечной заряженной плоскости. |
|
Введем понятие поверхностной плотности заряда: . Тогда . Коэффициент 2 появляется, т.к. плоскость окружена двумя поверхностями площадью S. Поле бесконечной заряженной плоскости не зависит от расстояния от плоскости! Можно пользоваться, когда расстояние много меньше размеров плоскости. 4. Напряженность поля плоского воздушного конденсатора. Из рисунка видим, что снаружи конденсатора поля пластин взаимно скомпенсированы, и общее поле равно нулю. Внутри конденсатора поля складываются. Используя вывод п.3 получаем: . Формула справедлива при условии, что расстояние между пластинами много меньше размеров самих пластин и вдали от краев пластин. | |
www.eduspb.com
Формула заряда конденсатора, q
По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.
Формула заряда конденсатора
Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:
где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.
Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Заряд на пластинах плоского конденсатора равен:
где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.
Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Заряд на обкладках сферического конденсатора найдем как:
где – радиусы обкладок конденсатора.
Заряд конденсатора связан с энергией поля (W) внутри него:
Из формулы (6) следует, что заряд можно выразить как:
Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.
При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.
Примеры решения задач по теме «Заряд конденсатора»
ru.solverbook.com
