Формулы заряд: нахождения величины заряда и количество заряда

Содержание

нахождения величины заряда и количество заряда

Электрический заряд – это основа работы любого электронного прибора и та величина, без которой невозможно посчитать ни один важный показатель в электродинамике и электростатике. Подробная расшифровка термина, описание формулы нахождения электрического заряда и образец решения типовой задачи приведены в данной статье.

Что такое электрический заряд q

Электрический заряд, обозначаемый в международной системе единиц буквами q и Q, считается скалярной физической величиной, которая определяет свойство частицы или тела выступать в качестве источника электромагнитного поля и вступать в прямое взаимодействие с ним. В физике существует несколько видов электромагнитных заряженных частиц, и они называются положительными или отрицательными. Обе единицы измеряются в Кулонах, а найти их можно путём вычисления произведения одного Ампера с одной секундой.

Понятие из учебного пособия

Формула нахождения заряда

Определить искомую величину можно из физико-математической формулы силы тока.

-19 Кулон.

Обратите внимание! Формула заряда является следствием прямой зависимости напряженности электромагнитного поля от потенциала его частицы, что является основным правилом нахождения емкости заряженного конденсатора и величины энергии, накопленной в нём. Кроме того, вычислить количество заряда можно через силу Лоренца.

Основные формулы

Как вычислять с помощью законов

Поскольку q и Q являются скалярными единицами, вычислить их с помощью законов можно через точные формулы, выведенные известными учеными-физиками. К примеру, в соответствии с законом Кулона, можно найти величину и силовое направление взаимодействия заряженных частиц между несколькими неподвижными телами.

Закон сохранения

Все элементарные частицы подразделяются на нейтральные или заряженные. Они вступают во взаимодействие друг с другом внутри электромагнитного поля. Частицы, которые имеют одноименный электрон, отталкиваются, а разноименный – притягиваются. В первом случае наблюдается избыток электронов, а во втором – их недостаток.

Оба типа частиц заряжаются посредством электризации. На практике, при возникновении данного явления, заряженные частицы равны по модулю, несмотря на противоположность знаков. Когда разные частицы притягиваются, то между ними происходит электризация и сохранение электрона. При этом, сумма всех изолированных системных частиц не изменяется, то есть, q + q + q…= const.

Закон сохранения

Закон Кулона

Выше было сказано, что электрические заряженные микрочастицы бывают как положительными, так и отрицательными, а их наличие подтверждается силовым взаимодействием, которое с помощью экспериментов на весах описал в 1785 году О. Кулон, создав свой физико-математический закон.

Закон Кулона представляет собой физическую закономерность, которая описывает взаимодействие наэлектризованных частиц между не электризованными, в зависимости от промежутка между ними. В соответствии с этой формулировкой, чем больше электронов имеет частица, тем ближе она расположена к другой элементарной единице заряда, и, соответственно, сила возрастает.

Обратите внимание! При увеличении расстояния между частицами, сал их взаимодействия неизменно убывает. В математической формуле это выглядит так: F1 = F2 = K*(q1*q2/r2), где q1 и q2 считаются модулями заряженных микрочастиц, k является коэффициентом пропорциональности, который зависит от системного выбора единицы, а r — расстоянием.

Закон Кулона

Образец решения задач по теме «Электрический заряд»

Ниже приведены образцы решения простых задач по электростатике, в частности, на закон Кулона.

Задача 1. Несколько одинаковых заряженных шаров имеют показатели q1 = 6 микрокулон и q2 = -18 микрокулон. Они располагаются друг от друга на 36 сантиметров (0,36 метров). Насколько будет меняться сила их взаимодействия при соприкосновении друг с другом и разведении в сторону?

Чтобы решить эту задачу, нужно воспользоваться эл заряд формулой F=K*(q1*q2/r2), подставив вместо букв известные величины. В результате, выйдет число 7,5.

Задача 2. Маленькие одинаковые шары находятся на промежутке в 0,15 метра и притягиваются с силой 1 микроньютон. -7 или 10 микрокулон.

Формула для решения

В целом, электрический заряд представляет собой физическую скалярную величину, которая определяет способность тел являться источником электромагнитного поля и участвовать во взаимодействии с ним. Отыскать величину, которая обозначается буквами q и Q, для решения задач или для выполнения другой работы, можно через закон сохранения, Кулона и представленные выше основные физические формулы.

Формула электрического заряда, q

Определение и формула электрического заряда

Фундаментальным свойством электрического заряда является существование двух видов зарядов: положительных и отрицательных. Заряды, имеющие один знак, отталкиваются. Взаимодействие зарядов разного знака определяют как притяжение. Телу можно сообщить заряд любого знака. В макроскопическом теле заряды разных знаков могут взаимно компенсировать друг друга.

Электрический заряд является релятивистски инвариантной величиной. Это значит, что величина заряда не зависит от системы отсчета, не важно, движется заряд (заряженное тело) или покоится.

Электрический заряд тела находят как суммарный заряд его частей.

Разделения электрических зарядов разных знаков можно добиться путем электризации посредством непосредственного контакта тел (например, трением) или без контакта, например посредством электрической индукции. При зарядке тела, мы создаем на нем избыток электронов или недостаток в сравнении с их нормальным количеством, при котором тело не имеет заряда. При этом электроны берутся у другого тела или удаляются из заряжаемого тела, но не уничтожаются или создаются. Важно запомнить, что процесс зарядки и разрядки тел является процедурой перераспределения электронов, при этом общее их число не изменяется.

При соединении заряженного проводника с незаряженным, заряд перераспределяется между обоими телами. Допустим, что одно тело несет отрицательный заряд, его соединяют с незаряженным телом. Электроны заряженного тела под воздействием сил взаимного отталкивания переходят на незаряженное тело. При этом заряд первого тела уменьшается, заряд второго увеличивается, до тех пор, пока не наступит равновесие.

Элементарный заряд

Немецкий физик и физиолог Г. Гельмгольц обратил внимание на то, что заряды, которые переносят ионы при явлении электролиза, являются целыми, кратными некоторой величине, равной Кл. Каждый одновалентный ион переносит такой заряд. Любой двухвалентный ион несет заряд, равный Кл, и так далее. Гельмгольц сделал вывод о том, что заряд Кл является минимальным количеством электричества, которое существует в природе. Данный заряд получил название элементарного заряда.

Закон сохранения заряда

Закон сохранения заряда является фундаментальным законом природы. Он был установлен на основании обобщения экспериментальных данных. Подтвержден в 1843 г. английским физиком М. Фарадеем.

Формулировка закона: В любой замкнутой системе алгебраическая сумма зарядов – это неизменная величина, и не важно, какие процессы происходят в этой системе:

где N – количество зарядов.

Закон Кулона

На вопрос: С какими силами взаимодействуют неподвижные точечные заряды? Отвечает закон Кулона, который можно записать в виде формулы как:

где – сила, с которой заряд действует на заряд ; – радиус вектор, который проведен от второго заряда к первому; – электрическая постоянная; – диэлектрическая проницаемость вещества в котором находятся заряды. В соответствии с третьим законом Ньютона первый заряд действует на второй с силой равной по модулю и противоположной по направлению силе Обратите внимание, что заряды в формуле (2) точечные.

Примеры решения задач по теме «Электрический заряд»

Глава 17. Взаимодействие электрических зарядов. Закон Кулона, принцип суперпозиции

Взаимодействие электрических зарядов описывается законом Кулона, который утверждает, что сила взаимодействия двух покоящихся точечных зарядов в вакууме равна

(17.

где и — модули зарядов, — расстояние между ними. Коэффициент пропорциональности в формуле (17.1) зависит от системы единиц. В международной системе единиц СИ этот коэффициент принято записывать в виде

(17.2)

где величина называется электрической постоянной, размерность величины сводится к отношению размерности длины к размерности электрической емкости (Фарада). Электрические заряды бывают двух типов, которые условно принято называть положительным и отрицательным. Как показывает опыт, заряды притягиваются, если они разноименные и отталкиваются, если одноименные.

В любом макроскопическом теле содержится огромное количество электрических зарядов, поскольку они входят в состав всех атомов: электроны заряжены отрицательно, протоны, входящие в состав атомных ядер — положительно. Однако большинство тел, с которыми мы имеем дело, не заряжены, поскольку количество электронов и протонов, входящих в состав атомов, одинаково, а их заряды по абсолютной величине в точности совпадают.

Тем не менее, тела можно зарядить, если создать в них избыток или недостаток электронов по сравнению с протонами. Для этого нужно передать электроны, входящие в состав какого-нибудь тела, другому телу. Тогда у первого возникнет недостаток электронов и соответственно положительный заряд, у второго — отрицательный. Такого рода процессы происходят, в частности, при трении тел друг о друга.

Если заряды находятся в некоторой среде, которая занимает все пространство, то сила их взаимодействия ослабляется по сравнению с силой их взаимодействия в вакууме, причем это ослабление не зависит от величин зарядов и расстояния между ними, а зависит только от свойств среды. Характеристика среды, которая показывает, во сколько раз ослабляется сила взаимодействия зарядов в этой среде по сравнению с силой их взаимодействия в вакууме, называется диэлектрической проницаемостью этой среды и, как правило, обозначается буквой . Формула Кулона в среде с диэлектрической проницаемостью принимает вид

(17. 3)

Если имеется не два, а большее количество точечных зарядов для нахождения сил, действующих в этой системе, используется закон, который называется принципомсуперпозиции¹. Принцип суперпозиции утверждает, что для нахождения силы, действующей на один из зарядов (например, на заряд ) в системе из трех точечных зарядов , и надо сделать следующее. Сначала надо мысленно убрать заряд и по закону Кулона найти силу, действующую на заряд со стороны оставшегося заряда . Затем следует убрать заряд и найти силу, действующую на заряд со стороны заряда . Векторная сумма полученных сил и даст искомую силу.

Принцип суперпозиции дает рецепт поиска силы взаимодействия неточечных заряженных тел. Следует мысленно разбить каждое тело на части, которые можно считать точечными, по закону Кулона найти силу их взаимодействия с точечными частями, на которое разбивается второе тело, просуммировать полученные вектора. Ясно, что такая процедура математически очень сложна, хотя бы потому, что необходимо сложить бесконечное количество векторов. В математическом анализе разработаны методы такого суммирования, однако в школьный курс физики они не входят. Поэтому, если такая задача и встретится, то суммирование в ней должно легко выполняться на основе тех или иных соображений симметрии. Например, из описанной процедуры суммирования следует, что сила, действующая на точечный заряд, помещенный в центр равномерно заряженной сферы, равна нулю.

Кроме того, школьник должен знать (без вывода) формулы для силы, действующей на точечный заряд со стороны равномерно заряженной сферы и бесконечной плоскости. Если имеется сфера радиуса , равномерно заряженная зарядом , и точечный заряд , расположенный на расстоянии от центра сферы, то величина силы взаимодействия равна

(17.4)

если точечный заряд находится снаружи сферы, и

(17.5)

если заряд находится внутри (причем не обязательно в центре). Из формул (17.4), (17.5) следует, что сфера снаружи создает такое же электрическое поле как весь ее заряд, помещенный в центре, а внутри — нулевое.

Если имеется очень большая плоскость с площадью , равномерно заряженная зарядом , и точечный заряд , то сила их взаимодействия равна

(17.6)

где величина имеет смысл поверхностной плотности заряда плоскости. Как следует из формулы (17.6) сила взаимодействия точечного заряда и плоскости не зависит от расстояния между ними. Обратим внимание читателя на то, что формула (17.6) является приближенной и «работает» тем точнее, чем дальше точечный заряд находится от ее краев. Поэтому при использовании формулы (17.6) часто говорят, что она справедлива в рамках пренебрежения «краевыми эффектами», т.е. когда плоскость считается бесконечной.

Рассмотрим теперь решение данных в первой части книги задач.

Согласно закону Кулона (17. 1) величина силы взаимодействия двух зарядов из задачи 17.1.1 выражается формулой

Заряды отталкиваются (ответ 2).

Поскольку капелька воды из задачи 17.1.2 имеет заряд ( – заряд протона), то она имеет в избытке электронов по сравнению с протонами. Значит при потере трех электронов их избыток уменьшится, и заряд капельки станет равен (ответ 2).

Согласно закону Кулона (17.1) величина силы взаимодействия двух зарядов при увеличении в раз расстояния между ними уменьшится в раз (задача 17.1.3 — ответ 4).

Если заряды двух точечных тел увеличить в раз при неизменном расстоянии между ними, то сила их взаимодействия, как это следует из закона Кулона (17.1), увеличится в раз (задача 17.1.4 — ответ 3).

При увеличении одного заряда в 2 раза, а второго в 4, числитель закона Кулона (17. 1) увеличивается в 8 раз, а при увеличении расстояния между зарядами в 8 раз — знаменатель увеличивается в 64 раза. Поэтому сила взаимодействия зарядов из задачи 17.1.5 уменьшится в 8 раз (ответ 4).

При заполнении пространства диэлектрической средой с диэлектрической проницаемостью = 10, сила взаимодействия зарядов согласно закону Кулона в среде (17.3) уменьшится в 10 раз (задача 17.1.6 — ответ 2).

Сила кулоновского взаимодействия (17.1) действует как на первый, так и на второй заряд, а поскольку их массы одинаковы, то ускорения зарядов, как это следует из второго закона Ньютона, в любой момент времени одинаковы (задача 17.1.7 — ответ 3).

Похожая задача, но массы шариков разные. Поэтому при одинаковой силе ускорение шарика с меньшей массой в 2 раза больше ускорения шарика с меньшей массой , причем этот результат не зависит от величин зарядов шариков (задача 17.1.8 — ответ 2).

Поскольку электрон заряжен отрицательно, он будет отталкиваться от шара (задача 17. 1.9). Но поскольку начальная скорость электрона направлена к шару, он будет двигаться в этом направлении, но его скорость будет уменьшаться. В какой-то момент он на мгновение остановится, а потом будет двигаться от шара с увеличивающейся скоростью (ответ 4).

В системе двух заряженных шариков, связанных нитью (задача 17.1.10), действуют только внутренние силы. Поэтому система будет покоиться и для нахождения силы натяжения нити можно использовать условия равновесия шариков. Поскольку на каждый из них действуют только кулоновская сила и сила натяжения нити, то из условия равновесия заключаем, что эти силы равны по величине.

Отсюда

где (ответ 1).

Система трех шариков в задаче 17.2.1 покоится, поэтому силы натяжения должны компенсировать силы кулоновского отталкивания крайних зарядов. Последние найдем по закону Кулона и принципу суперпозиции. Каждый крайний заряд отталкивается от центрального заряда и другого крайнего. Для суммы этих сил получаем

Этой величине и будет равна сила натяжения нитей (ответ 4). Отметим, что рассмотрение условия равновесия центрального заряда не помогло бы найти силу натяжения, а привело бы к заключению, что силы натяжения нитей одинаковы (впрочем, это заключение и так очевидно благодаря симметрии задачи).

Для нахождения силы, действующей на заряд — в задаче 17.2.2, используем принцип суперпозиции. На заряд — действуют силы притяжения к левому и правому зарядам (см. рисунок). Поскольку расстояния от заряда — до зарядов одинаковы, модули этих сил равны друг другу и они направлены под одинаковыми углами к прямой, соединяющей заряд — с серединой отрезка — . Поэтому сила, действующая на заряд — направлена вертикально вниз (вектор результирующей силы выделен жирным на рисунке; ответ 4).

Задача 17.2.3 похожа на предыдущую, но изменен знак одного из зарядов. Поэтому сила, действующая на заряд — со стороны правого заряда, не изменившись по величине, изменится по направлению (см. рисунок). Поэтому вектор результирующей силы будет направлен влево (вектор результирующей силы выделен жирным на рисунке; ответ 1).

На каждый заряд в задаче 17.2.4 действуют силы отталкивания со стороны двух других зарядов (см. рисунок), причем значения этих сил одинаковы (из-за равенства величин всех зарядов и расстояний между ними) и равны

Из-за равенства значений сил-слагаемых параллелограмм сложения сил представляет собой ромб, и, следовательно, вектор результирующей силы направлен вдоль биссектрисы треугольника из зарядов (выделен жирным на рисунке). Поэтому угол, отмеченный на рисунке дугой равен 30°, а значение результирующей силы равно

(ответ 3).

Из формулы (17.6) заключаем, что правильный ответ в задаче 17.2.5 — 4. В задаче 17.2.6 нужно использовать формулу для силы взаимодействия точечного заряда и сферы (формулы (17.4), (17.5)). Имеем = 0 (ответ 3).

В задаче 17.2.7 необходимо применить принцип суперпозиции к двум сферам. Принцип суперпозиции утверждает, что взаимодействие каждой пары зарядов не зависит от наличия других зарядов. Поэтому каждая сфера действует на точечный заряд независимо от другой сферы, и для нахождения результирующей силы нужно сложить силы со стороны первой и второй сфер. Поскольку точечный заряд расположен внутри внешней сферы, она не действует на него (см. формулу (17.5)), внутренняя действует с силой

где .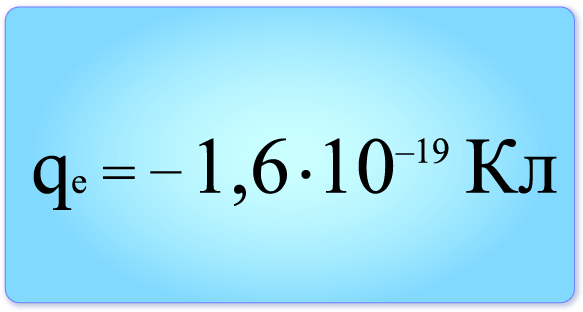 Поэтому и результирующая сила равна этому выражению (ответ 2)

В задаче 17.2.8 также следует использовать принцип суперпозиции. Если заряд поместить в точку , то силы, действующие на него со стороны зарядов и , направлены влево. Поэтому по принципу суперпозиции имеем для равнодействующей силы

где — расстояния от зарядов до исследуемых точек. Если поместить положительный заряд в точку , то силы будут направлены противоположно, и на основании принципа суперпозиции находим результирующую силу

В точке на заряд будут действовать силы, направленные направо, и потому

Из этих формул следует, что наибольшей сила будет в точке — ответ 1.

Пусть, для определенности, заряды шариков и в задаче 17. 2.9 положительны. Так как шарики одинаковы, заряды после их соединения распределяться между ними равномерно и для сравнения сил, нужно сравнить друг с другом величины

(1)

которые представляют собой произведения зарядов шариков до и после их соединения. После извлечения квадратного корня сравнение (1) сводится к сравнению среднего геометрического и среднего арифметического двух чисел. А поскольку среднее арифметическое любых двух чисел больше их среднего геометрического, то сила взаимодействия шариков возрастет независимо от величин их зарядов (ответ 1).

Задача 17.2.10 очень похожа на предыдущую, а ответ — другой. Непосредственной поверкой легко убедиться, что сила может как увеличиться, так и уменьшиться в зависимости от величин зарядов. Например, если заряды равны по величине, то после соединения шариков их заряды станут равны нулю, поэтому нулевой будет и сила их взаимодействия, которая, следовательно, уменьшится. Если один из первоначальных зарядов равен нулю, то после соприкосновения шариков заряд одного из них распределится между шариками поровну, и сила их взаимодействия увеличится. Таким образом, правильный ответ в этой задаче — 3.

Глава 18. Напряженность и потенциал электрического поля.Силовые линии электрического поля

Для характеристики создаваемого зарядами электрического поля вводятся две величины — напряженность электрического поля и его потенциал. Напряженность характеризует силу, действующую со стороны поля на внесенный в него пробный заряд. Если в какой-то точке поля на заряд действует сила , то напряженность электрического поля в этой точке равна

(18.1)

где — заряд, который мы взяли, чтобы «попробовать» поле в данной точке. Такой заряд называется «пробным». Пробный заряд не должен искажать распределение зарядов, создающих поле, и потому должен быть достаточно мал.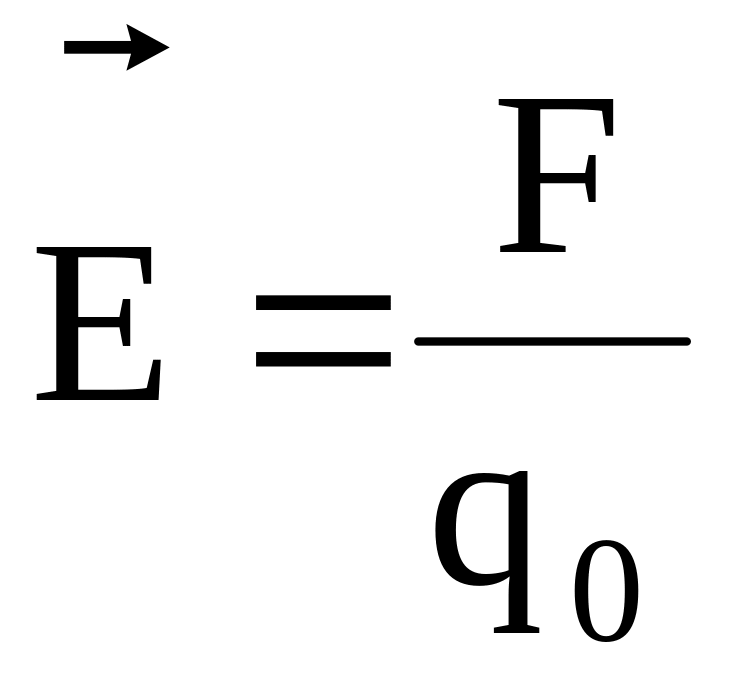 В формулу (18.1) пробный заряд входит со своим знаком (не модуль), поэтому, как следует из (18.1), вектор напряженности поля в некоторой точке направлен так же, как и вектор силы, действующей в этой точке на положительный пробный заряд.

Найдем напряженность электрического поля, создаваемого точечным зарядом . Для этого возьмем произвольный пробный заряд и поместим его в точку, находящуюся на расстоянии от заряда . Сила, действующую на пробный заряд со стороны заряда , определяется законом Кулона (17.1), (17.2). Поэтому согласно (18.1) имеем

(18.2)

где . Направлен вектор напряженности от заряда , если , и к нему, если .

Пусть поле создается несколькими зарядами … В этом случае его напряженность равна векторной сумме напряженностей тех полей, которые создаются каждым зарядом в отдельности. Действительно, из принципа суперпозиции следует, что на пробный заряд в этом случае действует сила . .., где … — силы, действующие на пробный заряд со стороны каждого заряда … Поэтому из (18.1) получаем

(18.3)

где … — напряженности тех полей, которые создавались бы каждым зарядом в отдельности в отсутствие других зарядов. Утверждение (18.3) называется принципом суперпозиции для полей. Формула (18.2) и принцип суперпозиции позволяют вычислить поле, создаваемое любым заряженным телом — с помощью мысленного разбиения его на точечные части и суммирования напряженностей, создаваемых всеми таким частями. Однако из-за математической сложности такой процедуры, она не входит в программу школьного курса физики. Школьник должен знать без вывода результат ее применения к заряженным сферам и плоскостям. Из формул (17.4), (17.5) получаем для напряженности поля сферы радиуса , равномерно заряженной зарядом , в точке на расстоянии от центра сферы:

(18. 4)

где , а из формулы (17.6) для напряженности поля равномерно заряженной плоскости

(18.5)

где — заряд плоскости, — площадь, — поверхностная плотность зарядов плоскости.

Электрическое поле можно изобразить графически (на современном русском языке — визуализировать) с помощью силовых линий. Силовые линии — это такие воображаемые линии, касательные к которым в каждой точке совпадают по направлению с вектором напряженности в этой точке. Вообще говоря, силовые линии проходят через каждую точку поля (кроме тех точек, где ), но поскольку так их нарисовать нельзя, условились проводить их с определенной густотой в зависимости от величины поля: чем гуще расположены силовые линии, тем больше величина напряженности поля.

Второй характеристикой электрического поля является его потенциал. Основная идея введения этой величины заключается в следующем.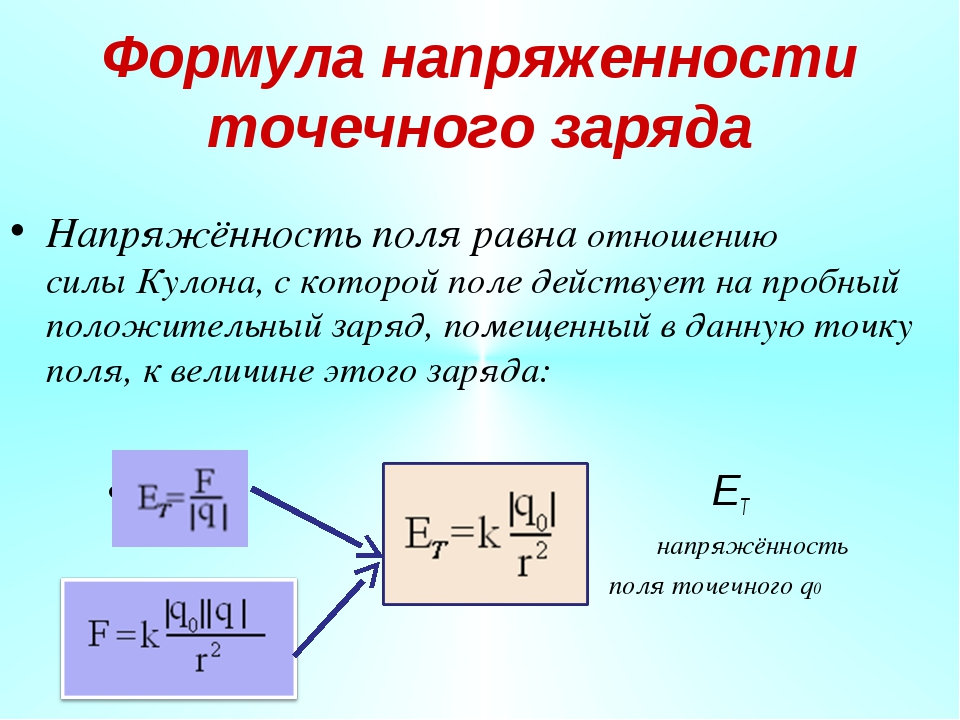 Если электрический заряд перемещается в электрическом поле (созданном другими зарядами), то со стороны поля на него действуют силы, и, следовательно, поле совершает работу. Потенциал поля — это такая функция точки поля , что работа , совершаемая полем над точечным пробным зарядом при его перемещении из точки с радиусом-вектором в точку с радиусом-вектором , равна

(18.6)

(именно в такой последовательности). Из формулы (18.6) следует, что работа, которую совершает поле при перемещении заряда, не зависит от формы траектории, а определяется только начальной и конечной ее точками. В частности, при перемещении тела по замкнутой траектории поле совершает нулевую работу.

Поскольку в формулу (18.6), входит разность потенциалов двух точек поля, потенциал определен с точностью до постоянной. Эту постоянную всегда можно выбрать так, что потенциал любой заданной точки поля можно сделать равным нулю. Как правило, в качестве такой точки выбирают бесконечно удаленную от зарядов точку поля, считая ее потенциал равным нулю. Из формулы (18.6) следует, что потенциал любой точки поля равен отношению работы, которую совершает электрическое поле при перемещении пробного заряда из этой точки в ту точку, потенциал которой выбран равным нулю, к пробному заряду.

Можно доказать, что если поле создается точечным зарядом , то потенциал на расстоянии от заряда при условии, что потенциал бесконечно удаленной точки принят за нуль, равен

(18.7)

Важно отметить, что в формулу (18.7) входит заряд со знаком (не модуль!), т.е. потенциал поля, создаваемого положительным зарядом, — положительный, отрицательным — отрицательный.

Для потенциалов справедлив принцип суперпозиции: если поле создается несколькими точечными зарядами, то потенциал любой его точке равен алгебраической сумме потенциалов (18. 7), создаваемых в этой точке каждым точечным зарядом. Это правило позволяет найти потенциал поля, создаваемого протяженным заряженным телом: нужно мысленно разделить тело на малые («точечные») части, по формуле (18.7) найти потенциал поля, создаваемого каждой такой частью, а затем сложить полученные результаты.

Для решения задач ЕГЭ нужно знать (без вывода) формулу потенциала поля равномерно заряженной сферы. Пусть имеется сфера радиуса , равномерно заряженная зарядом . Тогда потенциал точки поля, расположенной на расстоянии центра сферы, равен

(18.8)

(точка нулевого потенциала выбрана на бесконечности).

Часто в задачах ЕГЭ по физике используется связь напряженности однородного электрического поля и разности потенциалов двух точек поля, лежащих на одной силовой линии. Для нахождения этой связи возьмем положительный пробный заряд , перенесем его из первой точки во вторую вдоль силовой линии и найдем работу, которую совершает при этом электрическое поле.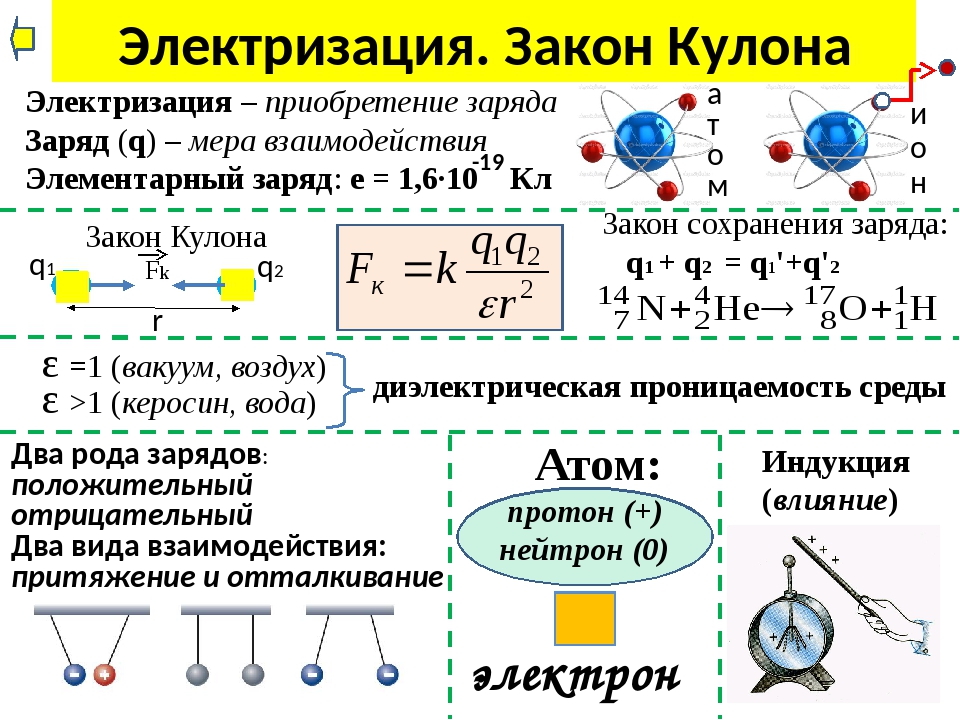 Поскольку поле действует на заряд с постоянной силой , угол между перемещением и этой силой равен нулю (заряд движется вдоль силовой линии), поэтому работа сил поля равна , где — расстояние между исследуемыми точками. С другой стороны, по определению потенциала работа поля равна . Приравнивая эти работы, находим

(18.9)

Подчеркнем, что формула (18.9) справедлива только для однородного поля, а точки 1 и 2 должны лежать на одной силовой линии.

Рассмотрим теперь задачи.

Величина напряженности электрического поля, создаваемого точечным зарядом (задача 18.1.1), определяется формулой (18.2)

где (ответ 1).

Размерность напряженности электрического поля (задача 18.1.2) можно найти из связи напряженности поля и потенциала (см. формулу (18. 9)). А поскольку размерность потенциала в международной системе единиц СИ – вольт, из формулы (18.9) имеем:

где квадратные скобки обозначают размерность (ответ 3).

Для определения напряженности поля используют пробный заряд (см. формулу (18.1)). Однако напряженность (18.1) ни от знака, ни от величины пробного заряда не зависят (задача 18.1.3). Это связано с тем, что сила в (18.1) линейно зависит от пробного заряда , и он сокращается в (18.1). Если взять пробный заряд отрицательным, то направление вектора числителе (18.1) изменится по сравнению со случаем положительного пробного заряда, но отношение будет направлено противоположно вектору , т.е. направление вектора не изменится (ответ 4).

Для нахождения поля, созданного двумя точечными зарядами (задача 18.1.4), используем принцип суперпозиции. Напряженности полей, создаваемых в точке каждым зарядом в отдельности, показаны тонкими векторами и отмечены как и . Поскольку модули этих векторов равны, вектор их суммы направлен вертикально вниз (ответ 4).

По определению силовые линии — это такие воображаемые линии, касательные к которым в каждой точке совпадают по направлению с вектором напряженности в этой точке (задача 18.1.5 — ответ 4).

Поскольку силовые линии поля в задаче 18.1.6 направлены направо, то направо направлен и вектор напряженности в каждой точке. Поэтому направо будет направлен и вектор силы, действующий со стороны этого поля на положительные точечный заряд (ответ 2).

Поскольку все траектории движения заряда I, II и III в задаче 18.1.7 начинаются и заканчиваются в тех же точках, то работа поля над зарядом при его движении по всем трем траекториям одинакова (ответ 4).

Разность потенциалов двух точек однородного электрического поля (задача 18.1.8) найдем по формуле (18.9):

(ответ 1).

Поскольку вектор напряженности электрического поля в любой точке направлен от заряда, то силовые линии поля расходятся радиально, являясь везде прямыми (см.рисунок). Таким образом, правильный ответ в задаче 18.1.9 — 1.

По определению потенциала имеем для работы поля в задаче 18.1.10

(ответ 3).

Силовые линии электрического поля строятся так, что их густота пропорциональна величине поля: чем гуще силовые линии, тем больше величина напряженности. Поэтому в задаче 18.2.1 (ответ 2).

Рисунок в задаче 18.2.2 — тот же самый, что и в предыдущей задаче, однако логика получения ответа совсем другая. Чтобы сравнить потенциалы в точках 1 и 2 перенесем из первой точке во вторую положительный пробный заряд и найдем работу поля. Так как , и если работа положительна, то , если отрицательна — наоборот. Очевидно, работа поля при перемещении положительного заряда из точки 1 в точку 2 положительна. Действительно, стрелки на силовых линиях направлены вправо, следовательно, и сила, действующая на положительный заряд, направлена вправо, туда же направлен и вектор перемещения заряда, поэтому косинус угла между силой и перемещением положителен на всех элементарных участках траектории, поэтому положительна работа. Таким образом (ответ 1), причем этот результат является следствием направления стрелок на силовых линиях, а не переменной густоты силовых линий.

В задаче 18.2.3 используем формулу для потенциала поля точечного заряда. Поскольку потенциал поля обратно пропорционален расстоянию до заряда, создающего поле (см. формулу (18.7)),

(ответ 2). Другими словами, на втрое большем расстоянии от точечного заряда потенциал его поля втрое меньше.

Очевидно, искомая в задаче 18.2.4 точка, находится между зарядами. В этой точке величины напряженностей полей и , создаваемых каждым зарядом, должны быть равны (см. рисунок). Используя формулу (18.2), получаем

где . Отсюда находим (ответ 3).

Используя принцип суперпозиции для потенциалов и формулу для потенциала поля точечного заряда (18.7), получим для искомой точки (задача 18.2.5)

где . Отсюда находим (ответ 2).

Поскольку все заряды в задаче 18.2.6 одинаковы, то напряженность поля, созданного в центре квадрата каждой парой зарядов, лежащих на одной диагонали, равна нулю. Поэтому равна нулю и напряженность электрического поля, созданного всеми четырьмя зарядами (ответ 2).

В задачах 18.2.7 и 18.2.8 используем принцип суперпозиции. Векторы напряженности полей, создаваемых верхней и нижней пластинами и соответственно показаны на рисунках (левый рисунок относится к задаче 18.2.7, правый — к 18.2.8). Из этих рисунков следует, что в области II для задачи 18. 2.7 и в областях I и III для задачи 18.2.8 векторы и направлены противоположно. А поскольку величина напряженности поля плоскости не зависит от расстояния до нее (формула (18.5)), а заряды плоскостей одинаковы по величине, напряженность суммарного поля в этих областях равна нулю.

Таким образом, правильный ответ в задаче 18.2.7 — 2, в задаче 18.2.8 — 3. Отметим, что полученный результат является приближенным и справедлив в пределе бесконечно больших пластин. Для конечных пластин поле в указанных областях будет малым, но отличным от нуля, причем величина поля будет наибольшей около краев пластин.

По принципу суперпозиции для потенциалов имеем (задача 18.2.9) . Если убрать либо первый, либо второй заряды, то потенциал в исследуемой точке станет равным соответственно или . Отсюда находим (ответ 2).

Согласно формуле (18.8) потенциал поля в любой точке внутри сферы равен потенциалу на ее поверхности

где . Поэтому правильный ответ в задаче 18.2.10 — 4.

Работа и мощность тока — урок. Физика, 8 класс.

При прохождении тока в цепи электрическое поле совершает работу по перемещению заряда. В этом случае работу электрического поля называют работой электрического тока.

При прохождении заряда \(q\) по участку цепи электрическое поле будет совершать работу: \(A=q\cdot U\), где \(U\) — напряжение электрического поля, \(A\) — работа, совершаемая силами электрического поля по перемещению заряда \(q\) из одной точки в другую.

Для выражения любой из этих величин можно использовать приведённый ниже рисунок.

Рис. \(1\). Зависимость между работой, напряжением и зарядом

Количество заряда, прошедшее по участку цепи, пропорционально силе тока и времени прохождения заряда: q=I⋅t.

Работа электрического тока на участке цепи пропорциональна напряжению на её концах и количеству заряда, проходящего по этому участку: A=U⋅q.

Работа электрического тока на участке цепи пропорциональна силе тока, времени прохождения заряда и напряжению на концах участка цепи: A=U⋅I⋅t.

Чтобы выразить любую из величин из данной формулы, можно воспользоваться рисунком.

Рис. \(2\). Зависимость между работой, силой тока и временем прохождения заряда

Единицы измерения величин:

работа электрического тока \([A]=1\) Дж;

напряжение на участке цепи \([U]=1\) В;

сила тока, проходящего по участку \([I]=1\) А;

время прохождения заряда (тока) \([t]=1\) с.

Для измерения работы электрического тока нужны вольтметр, амперметр и часы. Например, для определения работы, которую совершает электрический ток, проходя по спирали лампы накаливания, необходимо собрать цепь, изображённую на рисунке. Вольтметром измеряется напряжение на лампе, амперметром — сила тока в ней. А при помощи часов (секундомера) засекается время горения лампы.

Рис. \(3\). Схема и часы для измерения

Например:

I = 1,2 АU = 5 Вt = 1,5 мин = 90 сА = U⋅I⋅t = 5⋅1,2⋅90 = 540 Дж

Обрати внимание!

Работа чаще всего выражается в килоджоулях или мегаджоулях.

\(1\) кДж = 1000 Дж или \(1\) Дж = \(0,001\) кДж;
\(1\) МДж = 1000000 Дж или \(1\) Дж = \(0,000001\) МДж.

Для потребителей электрической энергии существуют приборы, позволяющие в пределах ошибки измерения получать числовые данные о ее расходе в единицу времени.

Рис. \(4\). Электросчетчик

Механическая мощность численно равна работе, совершённой телом в единицу времени: N = Аt. Чтобы найти мощность электрического тока, надо поступить точно также, т.е. работу тока, A=U⋅I⋅t, разделить на время.

Мощность электрического тока обозначают буквой \(Р\):

P=At=U⋅I⋅tt=U⋅I. Таким образом:

Мощность электрического тока равна произведению напряжения на силу тока: P=U⋅I.

Из этой формулы можно определить и другие физические величины.
Для удобства можно использовать приведённый ниже рисунок.

Рис. \(5\). Зависимость между мощностью, напряжением и силой тока

За единицу мощности принят ватт: \(1\) Вт = \(1\) Дж/с.

Из формулы P=U⋅I следует, что

\(1\) ватт = \(1\) вольт ∙ \(1\) ампер, или \(1\) Вт = \(1\) В ∙ А.

Обрати внимание!

Используют также единицы мощности, кратные ватту: гектоватт (гВт), киловатт (кВт), мегаватт (МВт).
\(1\) гВт = \(100\) Вт или \(1\) Вт = \(0,01\) гВт;
\(1\) кВт = \(1000\) Вт или \(1\) Вт = \(0,001\) кВт;
\(1\) МВт = \(1 000 000\) Вт или \(1\) Вт = \(0,000001\) МВт.

Пример:

Измерим силу тока в цепи с помощью амперметра, а напряжение на участке — с помощью вольтметра.

Рис. \(6\). Схема

Так как мощность тока прямо пропорциональна напряжению и силе тока, протекающего через лампочку, то перемножим их значения:

I=1,2АU=5ВP =U⋅I=5⋅1,2=6Вт.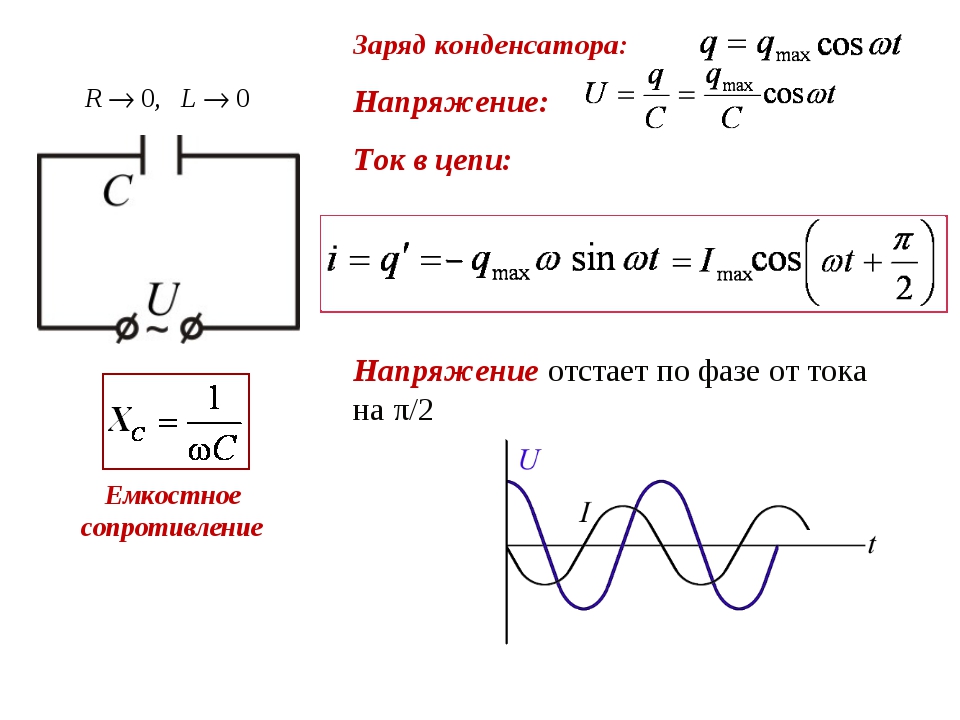

Ваттметры измеряют мощность электрического тока, протекающего через прибор. По своему назначению и техническим характеристикам ваттметры разнообразны.

В зависимости от сферы применения у них различаются пределы измерения.

Аналоговый ваттметр	Аналоговый ваттметр	Аналоговый ваттметр	Цифровой ваттметр

Рис. \(7\). Приборы для измерения

Подключим к цепи по очереди две лампочки накаливания, сначала одну, затем другую и измерим силу тока в каждой из них. Она будет разной.

Рис. \(8\). Лампы различной мощности в цепи

Сила тока в лампочке мощностью \(25\) ватт будет составлять \(0,1\) А. Лампочка мощностью \(100\) ватт потребляет ток в четыре раза больше — \(0,4\) А. Напряжение в этом эксперименте неизменно и равно \(220\) В. Легко можно заметить, что лампочка в \(100\) ватт светится гораздо ярче, чем \(25\)-ваттовая лампочка. Это происходит оттого, что её мощность больше. Лампочка, мощность которой в \(4\) раза больше, потребляет в \(4\) раза больше тока. Значит:

Обрати внимание!

Мощность прямо пропорциональна силе тока.

Что произойдёт, если одну и ту же лампочку подсоединить к источникам различного напряжения? В данном случае используется напряжение \(110\) В и \(220\) В.

Рис. \(8\). Лампа, подключенная к источнику тока с различным напряжением

Можно заметить, что при большем напряжении лампочка светится ярче, значит, в этом случае её мощность будет больше. Следовательно:

Обрати внимание!

Мощность зависит от напряжения.

Рассчитаем мощность лампочки в каждом случае:

I=0,2АU=110ВP=U⋅I=110⋅0,2=22Вт

I=0,4АU=220ВP=U⋅I=220⋅0,4=88Вт.

Можно сделать вывод о том, что при увеличении напряжения в \(2\) раза мощность увеличивается в \(4\) раза.
Не следует путать эту мощность с номинальной мощностью лампы (мощность, на которую рассчитана лампа). Номинальная мощность лампы (а соответственно, ток через нить накала и её расчётное сопротивление) указывается только для номинального напряжения лампы (указано на баллоне, цоколе или упаковке).

Рис. \(9\). Маркировка

В таблице дана мощность, потребляемая различными приборами и устройствами:

Таблица \(1\). Мощность различных приборов

Название	Рисунок	Мощность
Калькулятор		\(0,001\) Вт
Лампы дневного света		\(15 — 80\) Вт
Лампы накаливания		\(25 — 5000\) Вт
Компьютер		\(200 — 450\) Вт
Электрический чайник		\(650 — 3100\) Вт
Пылесос		\(1500 — 3000\) Вт
Стиральная машина		\(2000 — 4000\) Вт
Трамвай		\(150 000 — 240000\) Вт

Источники:

Рис. 1. Зависимость между работой, напряжением и зарядом. © ЯКласс.
Рис. 3. Схема и часы для измерения. © ЯКласс.
Рис. 5. Зависимость между мощностью, напряжением и силой тока. © ЯКласс.
Рис. 6. Схема. © ЯКласс.
Таблица 1. Мощность различных приборов. Компьютер. Указание авторства не требуется, 2021-08-14, Pixabay License, https://pixabay.com/ru/photos/яблоко-стул-компьютер-1834328/.

Закон сохранения заряда в физике

Закон сохранения заряда:

Закон сохранения заряда. Изменится ли общий заряд тела, когда тело электризуется? Чтобы ответить на этот вопрос, проведем следующий опыт (рис. 7.1а).

Возьмем электрометр, на его стержень установим металлический диск. Накрыв диск кусочком плотной ткани, потрем его другим диском, который имеет изолированную ручку. При этом стрелка электрометра будет наклоняться. Это показывает, что на ткани и диске появились электрические заряды.

Продолжим опыт. Диск, которым натерли ткань, соединяем со стрелкой второго электрометра (рис. 7.1б). В этом случае стрелка второго электрометра тоже повернется. Угол наклона стрелки равняется углу наклона стрелки первого электрометра. Это показывает, что оба диска зарядились одинаково. Если соединить стержни каждого из двух электрометров металлическим проводником, мы увидим, что стрелки обоих электрометров приходят в нулевое положение. Это явление показывает, что электрометры имели равные по количеству, но разные по знаку заряды. Поэтому сумма этих зарядов равна нулю.

Все опыты по электризации показали, что невозможно зарядить только одно тело. Чтобы зарядить тело, обязательно требуется второе тело. Какой отрицательный заряд получает одно из тел в процессе зарядки, такой же положительный заряд получит второе тело. В результате общее количество зарядов тела остается без изменения.

Алгебраическая сумма зарядов всех тел, входящих в любую закрытую систему, остается постоянной, т.е.:

Этот вывод называется законом сохранения электрических зарядов.
Закон сохранения зарядов открыт в 1750 году американским ученым и политическим деятелем Бенджамином Франклином.

Согласно теории Фарадея и Максвелла, вокруг наэлектризованных тел создается электрическое поле. Взаимодействие происходит как раз посредством этого электрического поля. Это поле невозможно потрогать руками или увидеть глазами. Его можно только почувствовать. Изучение воздействия электрического поля на заряженные частицы показало, что воздействие поля вблизи заряженного тела сильнее, а с удалением от него воздействие становится слабее. Чтобы показать, насколько сильно поле, созданное электрическим зарядом, введена величина, которая называется напряженностью электрического поля. Напряженность электрического поля определяется формулой:

Здесь – напряженность поля в определенной его точке; – количество заряда, помещенного в эту точку поля; – сила, действующая на помещенный заряд со стороны электрического поля.
Электрическое поле характеризуется с помощью силовых линий или линий напряженности (рис. 7.2 и 7.3). Напряженность электрического поля является векторной величиной и направлена по направлению силовых линий.

Единица напряженности или .
Подсчитаем напряженность поля точечного заряда на расстоянии :

Здесь – расстояние от точечного заряда до точки, где определяется напряженность поля; .
Электрическое поле в основном создают системы зарядов. Например, если в определенную точку поля, созданного системами зарядов и ввести пробный заряд, то на него со стороны каждого заряда будут действовать силы и (рис. 7.4). Среднее значение сил, воздействующих на пробный заряд, равно:

В этом случае напряженность поля в точке равняется:

На основании выражения (7.5) делаем следующий вывод:
Напряженность электростатического поля, создаваемого в данной точке системой зарядов, равна векторной сумме напряженностей полей, создаваемых в этой точке каждым зарядом в отдельности.

Это уравнение называется принципом суперпозиции электрического поля.

Смысл слова «суперпозиция» означает «суммирование или «сложения».
Вычислим по принципу суперпозиции напряженность поля, создаваемого в определенной точке двумя точечными зарядами, расположенными на расстоянии r друг от друга (рис. 7.4). Напряженность поля каждого заряда в рассматриваемой точке определяется выражением и .

Итоговая напряженность поля заряда в данной
точке по принципу суперпозиции вычисляется на основании следующей формулы:

Здесь и соответственно напряженности полей точечных зарядов в рассматриваемой точке, – угол между векторами напряженности поля.

Образец решения задачи:

Два противоположно заряженных точечных заряда величиной по 4 нКл каждый расположены на расстоянии 10 см друг от друга. Чему равна напряженность поля в точке, расположенной на расстоянии 8 см от первого заряда, 6 см от второго заряда?
Дано:

Найти:

Формула и решение:

Ответ:

Потенциал, работа электростатического поля.

Потенциальная энергия, разность потенциалов, принцип суперпозиции. Тесты, формулы

Тестирование онлайн

Работа электростатического поля

Рассмотрим ситуацию: заряд q₀ попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q₀ со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.

Потенциал

Система «заряд — электростатическое поле» или «заряд — заряд» обладает потенциальной энергией, подобно тому, как система «гравитационное поле — тело» обладает потенциальной энергией.

Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля.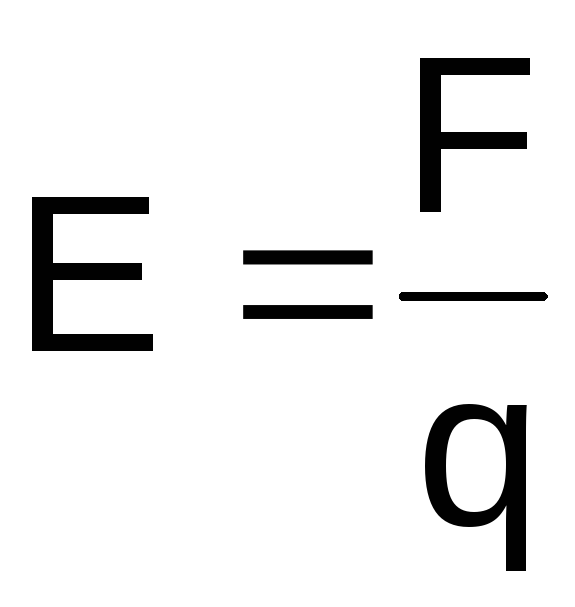 В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал — это характеристика электростатического поля.

Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.

Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.

В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело — наоборот.

Потенциальная энергия поля — это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.

Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.

Разность потенциалов

Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов

Эту формулу можно представить в ином виде

Эквипотенциальная поверхность (линия) — поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.

Напряжение

Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.

Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.

От величины напряжения зависит ток в цепи и энергия заряженной частицы.

Принцип суперпозиции

Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности

При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.

На рисунке изображены линии напряженности. В какой точке поля потенциал больше?

Верный ответ — точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.

Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком «минус». Чем дальше от отрицательного заряда, тем потенциал поля больше.

Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак «+», работа имеет знак «-«.

Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.

Напряжение в клетках сетчатки глаза при попадания в них света около 0,01 В.
Напряжение в телефонных сетях может достигать 60 В.
Электрический угорь способен создавать напряжение до 650 В.

Из определения потенциала следует, что потенциальная энергия электростатического взаимодействия двух зарядов q₁ и q₂, находящихся на расстоянии r друг от друга, численно равна работе, которая совершается при перемещении точечного заряда q₂ из бесконечности в данную точку поля, созданного зарядом q₁

Аналогично Тогда энергия взаимодействия двух точечных зарядов

Энергия взаимодействия n зарядов

Как рассчитать официальное обвинение

Эй! Добро пожаловать в Master Organic Chemistry, на тот случай, если вы посетитель впервые.

В этом сообщении в блоге я объясню, как рассчитать формальный заряд для молекул. Тем не менее, вы можете найти мои видео, содержащие 10 решенных примеров формальных задач заряда, быть еще более полезными. Просто думал, что вы должны знать!

Нужно выяснить, является ли атом отрицательным, положительным или нейтральным? Вот формула для определения «формального заряда» атома:

Формальный заряд = [количество валентных электронов] – [электроны в неподеленных парах + 1/2 числа связывающих электронов]

В этой формуле явно указано отношение между числом связывающих электронов и их отношением к тому, сколько формально «принадлежит» атому.

Например, применив это к BH ₄ (верхний левый угол на изображении ниже), мы получим:

Число валентных электронов для бора равно 3 .
Количество несвязанных электронов равно ноль .
Общее количество связывающих электронов вокруг бора равно 8 (полный октет). Половина этого числа равна 4 .

Таким образом, формальный платеж = 3 – (0 + 4) = 3 – 4 = –1

Однако существует более простой способ сделать это.

Поскольку химическая связь имеет два электрона, «число связывающих электронов, деленное на 2», по определению равно числу связей, окружающих атом, . Таким образом, мы можем вместо этого использовать эту сокращенную формулу :

Формальный заряд = [количество валентных электронов на атоме] – [несвязанные электроны + количество связей].

Повторное применение к BH ₄ (верхний левый угол).

Число валентных электронов для бора равно 3 .
Количество несвязанных электронов равно ноль .
Количество связей вокруг бора 4 .

Таким образом, формальный заряд = 3 – (0 + 4) = 3 – 4 = –1

Формальный заряд B в BH ₄ отрицателен 1.

Применим его к _{CH :}

7 :

7 3 (один справа от BH ₄ )
Число валентных электронов для углерода 4
Число несвязанных электронов два (у него неподеленная пара) количество связей вокруг углерода 3 .
Таким образом, формальный заряд = 4 – (2 +3) = 4 – 5 = –1
Формальный заряд C в :CH ₃ отрицательный 1.
Тот же формальный заряд, что и у BH ₄ !
Давайте сделаем последний пример. Давайте сделаем CH ₃ ⁺ (без неподеленных пар на углероде). Это оранжевый в нижнем ряду.
Количество валентных электронов для углерода равно 4
Количество несвязанных электронов равно нулю
Количество связей вокруг углерода равно 3 .
Таким образом, формальный заряд = 4 – (0 +3) = 4 – 3 = +1
Вы можете применить эту формулу к любому атому, который вы хотите назвать.
Вот схема некоторых простых молекул ряда B C N O . Я надеюсь, что бериллий и фтор не слишком обиделись, что я их пропустил, но они не так интересны для целей этой таблицы.
Обратите внимание на интересную схему геометрии (выделено цветом): BH ₄ (–), CH ₄ и NH ₄ (+) имеют ту же геометрию, что и CH ₃ (–), NH ₃ и OH ₃ (+).Карбкатион CH ₃ (+) имеет ту же электронную конфигурацию (и геометрию), что и нейтральный боран BH ₃ . Знакомая изогнутая структура воды H ₂ O характерна для аниона амида NH ₂ (–). Эта общая геометрия является одним из интересных следствий теории отталкивания пар электронов валентной оболочки (VSEPR — произносится как « vesper », точно так же, как «Favre» произносится как « Farve» ). и тройные связи:
Вот вопрос.Алканы, алкены и алкины нейтральны, так как существует четыре связи и нет несвязанных электронов: 4 – [4+0] = 0. Для каких других значений [связи + несвязанные электроны] вы также получите значение, равное нулю, и как могут выглядеть эти структуры? (Некоторые из этих сооружений вы встретите позже).
Последний вопрос. Как вы думаете, почему это называется «официальное обвинение»?
Подумайте о том, каким будет официальное обвинение BF ₄. Отрицательный заряд бора.Какой здесь самый электроотрицательный элемент? Фторид, разумеется, с электроотрицательностью 4,0, с бором, равным 2,0. Как вы думаете, где находится этот отрицательный заряд на самом деле ?
Ну, это не на боре. На самом деле он распространяется через более электроотрицательные ионы фтора, которые становятся более богатыми электронами. Таким образом, хотя «формальный» адрес отрицательного заряда находится на боре, электронная плотность фактически распределена по фторидам. Другими словами, в данном случае формальное обвинение не имеет ничего общего с действительностью.
Еще одно напоминание — 10 видео с примерами решения формальных задач о заряде, прямо здесь (см. самый верх страницы)
Учебник по физике: напряженность электрического поля
В предыдущем разделе урока 4 было введено понятие электрического поля. Было заявлено, что концепция электрического поля возникла в попытке объяснить силы действия на расстоянии. Все заряженные объекты создают электрическое поле, распространяющееся наружу в окружающее их пространство.Заряд изменяет это пространство, вызывая воздействие этого поля на любой другой заряженный объект, который входит в это пространство. Сила электрического поля зависит от того, насколько заряжен объект, создающий поле, и от расстояния до заряженного объекта. В этом разделе Урока 4 мы будем исследовать электрическое поле с численной точки зрения — напряженность электрического поля .

Коэффициент силы на заряд

Напряженность электрического поля является векторной величиной; она имеет как величину, так и направление.Величина напряженности электрического поля определяется способом ее измерения. Предположим, что электрический заряд можно обозначить символом Q . Этот электрический заряд создает электрическое поле; поскольку Q является источником электрического поля, мы будем называть его исходным зарядом . Напряженность электрического поля исходного заряда можно измерить любым другим зарядом, помещенным где-нибудь в его окружении. Заряд, используемый для измерения напряженности электрического поля, называется тестовым зарядом , поскольку он используется для проверки напряженности поля.Испытательный заряд имеет количество заряда, обозначенное символом q . Помещенный в электрическое поле, пробный заряд будет испытывать электрическую силу — либо притягивающую, либо отталкивающую. Как обычно, эта сила будет обозначаться символом F . Величина электрического поля просто определяется как сила, приходящаяся на заряд пробного заряда.

Если напряженность электрического поля обозначить символом E , то уравнение можно переписать в символьной форме как

Стандартные метрические единицы напряженности электрического поля вытекают из его определения. Поскольку электрическое поле определяется как сила, приходящаяся на один заряд, его единицами измерения будут единицы силы, деленные на единицы заряда. В этом случае стандартными метрическими единицами являются Ньютон/Кулон или N/C.

В приведенном выше обсуждении вы заметите, что упоминаются два заряда — исходный заряд и тестовый заряд. Два заряда всегда были бы необходимы, чтобы столкнуться с силой. В электрическом мире для притяжения или отталкивания нужны двое.Уравнение для напряженности электрического поля ( E ) имеет одну из двух перечисленных в нем величин заряда. Поскольку задействованы два заряда, учащийся должен быть предельно осторожным, чтобы использовать правильное количество заряда при вычислении напряженности электрического поля. Символ q в уравнении представляет собой количество заряда испытательного заряда (не исходного заряда). Напомним, что напряженность электрического поля определяется с точки зрения того, как она измеряется или проверяется; таким образом, пробный заряд входит в уравнение.Электрическое поле — это сила, приходящаяся на количество заряда на пробный заряд .

Напряженность электрического поля не зависит от количества заряда на испытательном заряде. Если вы немного подумаете об этом утверждении, оно может вас обеспокоить. (Конечно, если вы вообще не думаете — никогда — вас ничего не беспокоит. Неведение — это блаженство.) В конце концов, количество заряда пробного заряда ( q ) находится в уравнении для электрического поля. Так как же может напряженность электрического поля не зависеть от q , если q входит в уравнение? Хороший вопрос.Но если вы подумаете об этом еще немного, вы сможете ответить на свой собственный вопрос. (Невежество может быть блаженством. Но, немного подумав еще, вы можете достичь прозрения, состояния, намного лучшего, чем блаженство. ) Увеличение количества заряда на пробном заряде, скажем, в 2 раза, увеличит знаменатель уравнения. в 2 раза. Но согласно закону Кулона, чем больше заряд, тем больше электрическая сила ( F ). В самом деле, двукратное увеличение q будет сопровождаться двукратным увеличением F .Таким образом, при увеличении знаменателя в уравнении в два (или в три, или в четыре раза) числитель увеличивается во столько же раз. Эти два изменения компенсируют друг друга, так что можно с уверенностью сказать, что напряженность электрического поля не зависит от количества заряда пробного заряда. Таким образом, независимо от того, какой тестовый заряд используется, напряженность электрического поля в любом заданном месте вокруг исходного заряда Q будет измерена одинаковой.

Другая формула напряженности электрического поля

Вышеприведенное обсуждение относилось к определению напряженности электрического поля с точки зрения того, как она измеряется. Теперь мы исследуем новое уравнение, определяющее напряженность электрического поля через переменные, влияющие на напряженность электрического поля. Для этого нам придется вернуться к уравнению закона Кулона. Закон Кулона гласит, что электрическая сила между двумя зарядами прямо пропорциональна произведению их зарядов и обратно пропорциональна квадрату расстояния между их центрами. Применительно к нашим двум зарядам — заряду источника ( х ) и испытательному заряду ( q ) — формула для электрической силы может быть записана как

Если выражение для электрической силы, данное законом Кулона, заменить силой в приведенном выше уравнении E = F/q, можно получить новое уравнение, как показано ниже.

Обратите внимание, что приведенный выше вывод показывает, что пробный заряд q был исключен как из числителя, так и из знаменателя уравнения. Новая формула для напряженности электрического поля (показана внутри рамки) выражает напряженность поля через две переменные, влияющие на нее. Напряженность электрического поля зависит от количества заряда источника заряда ( Q ) и расстояния ( d ) от источника заряда.

Закон обратных квадратов

Как и все формулы в физике, формулы для напряженности электрического поля можно использовать для алгебраического решения задач по физике.И, как и все формулы, эти формулы напряженности электрического поля также можно использовать для того, чтобы направлять наши размышления о том, как изменение одной переменной может (или не может) повлиять на другую переменную. Одной из особенностей этой формулы напряженности электрического поля является то, что она иллюстрирует обратную квадратичную зависимость между напряженностью электрического поля и расстоянием. Напряженность электрического поля, создаваемого зарядом источника Q , обратно пропорциональна квадрату расстояния от источника. Это известно как закон обратных квадратов . 2).

Используйте этот принцип обратной квадратичной зависимости между напряженностью электрического поля и расстоянием, чтобы ответить на первые три вопроса в разделе «Проверьте свое понимание» ниже.

Возвращение к аналогии с вонючим полем

В предыдущем разделе Урока 4 была представлена несколько грубая, но поучительная аналогия — аналогия с вонючим полем. Аналогия сравнивает концепцию электрического поля, окружающего заряд источника, с вонючим полем, которое окружает вонючий подгузник младенца.Как каждый вонючий подгузник создает вонючее поле, так и каждый электрический заряд создает электрическое поле. И если вы хотите узнать силу вонючего поля, вы просто используете вонючий детектор — нос, который (насколько я знаю) всегда отталкивающе реагирует на вонючий источник. Точно так же, если вы хотите узнать силу электрического поля, вы просто используете детектор заряда — тестовый заряд, который будет реагировать притягивающим или отталкивающим образом на исходный заряд. И, конечно же, сила поля пропорциональна воздействию на детектор.Более чувствительный детектор (лучший нос или более заряженный тестовый заряд) почувствует эффект сильнее. Тем не менее напряженность поля определяется как эффект (или сила) на чувствительность детектора; поэтому напряженность поля вонючего подгузника или электрического заряда не зависит от чувствительности детектора.

Если вы измерите вонючее поле подгузника, имеет смысл только то, что оно не будет зависеть от того, насколько вы вонючие. Человек, измеряющий силу вонючего поля подгузника, может создать свое собственное поле, сила которого зависит от того, насколько он вонючий.Но поле этого человека не следует путать с вонючим полем подгузника. Вонючее поле подгузника зависит от того, насколько вонючий подгузник. Точно так же сила электрического поля заряда источника зависит от того, насколько заряжен заряд источника. Кроме того, как и в случае с вонючим полем, наше уравнение электрического поля показывает, что по мере того, как вы приближаетесь к источнику поля, эффект становится все больше и больше, а напряженность электрического поля увеличивается.

Аналогия с вонючим полем оказывается полезной для передачи как концепции электрического поля, так и математики электрического поля.Концептуально он иллюстрирует, как источник поля может воздействовать на окружающее пространство и оказывать влияние на чувствительные детекторы в этом пространстве. И математически это показывает, как сила поля зависит от источника и расстояния от источника и не зависит от каких-либо характеристик, связанных с детектором.

Направление вектора электрического поля

Как упоминалось ранее, напряженность электрического поля является векторной величиной.В отличие от скалярной величины, векторная величина не может быть полностью описана, если с ней не связано направление. Величина вектора электрического поля рассчитывается как сила, приходящаяся на заряд на любом заданном пробном заряде, находящемся в пределах электрического поля. Сила на пробном заряде могла быть направлена либо в сторону исходного заряда, либо прямо от него. Точное направление силы зависит от того, имеют ли пробный заряд и исходный заряд один и тот же тип заряда (в котором происходит отталкивание) или противоположный тип заряда (в котором возникает притяжение).Чтобы решить дилемму, направлен ли вектор электрического поля к источнику заряда или от него, было принято соглашение. Всемирное соглашение, используемое учеными, состоит в том, чтобы определять направление вектора электрического поля как направление, в котором положительный пробный заряд толкается или притягивается в присутствии электрического поля. Используя соглашение о положительном испытательном заряде, каждый может согласиться с направлением E .

Учитывая это условное обозначение положительного пробного заряда, можно сделать несколько общих выводов о направлении вектора электрического поля.Положительный исходный заряд создаст электрическое поле, оказывающее отталкивающее действие на положительный пробный заряд. Таким образом, вектор электрического поля всегда будет направлен в сторону от положительно заряженных объектов. С другой стороны, положительный пробный заряд будет притягиваться к отрицательному исходному заряду. Поэтому векторы электрического поля всегда направлены в сторону отрицательно заряженных объектов. Вы можете проверить свое понимание направления электрического поля, ответив на вопросы 6 и 7 ниже.

Мы хотели бы предложить… Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения «Положи заряд в цель» и/или нашего интерактивного «Пейзажа электростатики». Оба интерактива можно найти в разделе Physics Interactives на нашем веб-сайте. Оба интерактива обеспечивают привлекательную среду для изучения электрических полей и действий на расстоянии.

Проверьте свое понимание

Используйте свое понимание, чтобы ответить на следующие вопросы. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.

1. Заряд Q действует как точечный заряд, создавая электрическое поле. Его прочность, измеренная на расстоянии 30 см, составляет 40 Н/Кл. Какова величина напряженности электрического поля, которую вы ожидаете измерить на расстоянии …

а. на расстоянии 60 см?
б. на расстоянии 15 см?
в. на расстоянии 90 см?
д. на расстоянии 3 см?
в. на расстоянии 45 см?

2. Заряд Q действует как точечный заряд для создания электрического поля. Его прочность, измеренная на расстоянии 30 см, составляет 40 Н/Кл.Какой будет напряженность электрического поля…

а. 30 см от источника с зарядом 2Q?
б. 30 см от источника с зарядом 3Q?
в. 60 см от источника с зарядом 2Q?
д. 15 см от источника с зарядом 2Q?
эл. 150 см от источника с зарядом 0,5Q?

3. Используйте свое понимание напряженности электрического поля, чтобы заполнить следующую таблицу.

4. Найдите в приведенной выше таблице не менее двух строк, иллюстрирующих, что напряженность вектора электрического поля равна …

а. напрямую связано с количеством заряда на исходном заряде ( Q ).
б. обратно пропорциональна квадрату разделительного расстояния ( d ).
в. независимо от количества заряда на пробном заряде ( q ).

5. Следующая единица, безусловно, не является стандартной единицей для выражения величины напряженности электрического поля.

кг • м/с ²/С

Тем не менее, это может быть приемлемой единицей для E . Используйте модульный анализ, чтобы определить, является ли приведенный выше набор единиц приемлемой единицей измерения напряженности электрического поля.

6.Замечено, что воздушный шар А заряжен отрицательно. Воздушный шар B оказывает отталкивающее воздействие на воздушный шар A. Будет ли вектор электрического поля, создаваемого воздушным шаром B, направлен к B или от B? ___________ Объясните свои рассуждения.

7. Отрицательный заряд источника ( Q ) показан на диаграмме ниже. Этот исходный заряд может создавать электрическое поле. Различные места в поле помечены.Для каждого местоположения нарисуйте вектор электрического поля в соответствующем направлении с соответствующей относительной величиной. То есть нарисуйте длину вектора E длинной там, где величина велика, и короткой там, где величина мала.

Формула плотности заряда

| Решенные примеры вопросов

Поток заряда очень важен для определения электрического поля.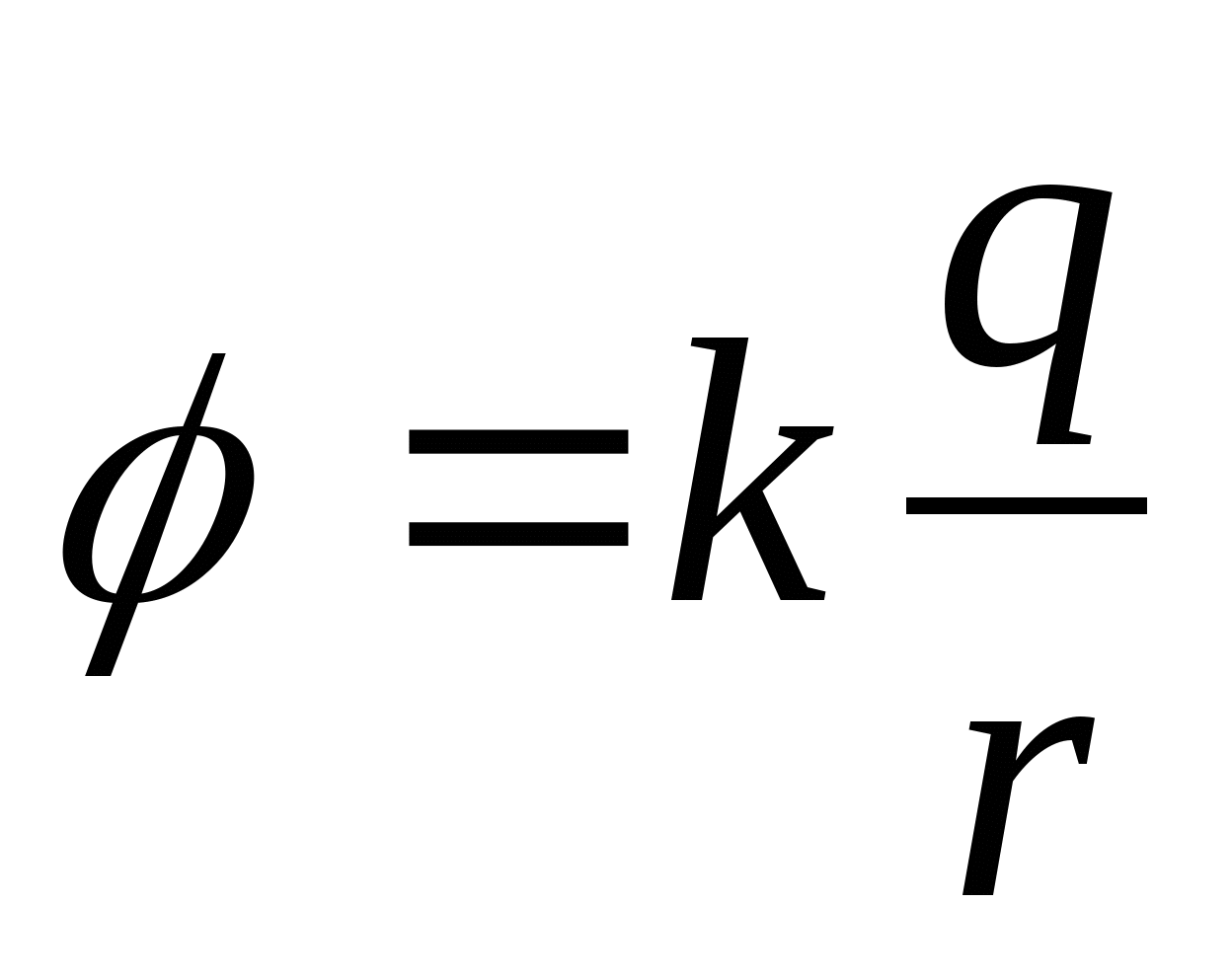 У них есть набор электрических зарядов. и, таким образом, плотность заряда очень важно рассчитать для многих целей. Плотность заряда рассчитывается на основе площади поверхности и объема электрического объекта. Формула плотности заряда — очень интересная и важная тема.

Плотность заряда является мерой накопления электрического заряда в данном конкретном поле. Ниже приведены некоторые из измерений, в которых измеряется плотность заряда:

Линейная плотность заряда: \[\lambda = \frac{q}{l} \] , где q — заряд, а l — длина который он распространяется.Единицей СИ будет Кулон м-1.
Поверхностная плотность заряда: \[ \sigma = \frac{q}{A}\], где q — заряд, а A — площадь поверхности. Единицей СИ является кулон м-2.
Объемная плотность заряда: \[ \rho = \frac{q}{V}\], где q — заряд, а V — объем распределения. {2} \]
Плотность заряда; \[\сигма = 2.{-2} \]
Плата прилагается; q= \[\sigma\] A =2,5 \[\times\] 10 ⁻² \[\times\]15 \[\times\]10 ⁻⁴
= 37,5 \[\times\] 10 ⁻⁶
C = 37,5 мкКл
Вычисление формального заряда: определение и формула — видео и стенограмма урока
Пошаговый метод
Теперь, когда мы знаем формулу для определения формального заряда, давайте применим ее на практике и шаг за шагом рассмотрим, как определить формальный заряд для каждого атома в молекуле.Формула формального платежа:
Давайте начнем с чего-то простого, например с углекислого газа. Углекислый газ имеет один атом углерода и два атома кислорода. Его структура Льюиса выглядит так:
Шаг 1: Рассчитайте формальный заряд C
Углерод (C) находится в группе 14, что означает, что он имеет 4 валентных электрона. Вокруг углерода нет точек, значит, у него нет несвязывающих электронов.Вокруг углерода 4 линии, и одна линия соответствует двум связывающим электронам. Таким образом, углерод имеет 8 связывающих электронов.
VE равно 4
NE равно 0
BE равно 8
Теперь подставим значения, и мы получим:
формальный заряд = 4 — 0 — 8/2 = 0
Формальный заряд углерода равен 0
Шаг 2: Рассчитайте формальный заряд кислорода слева
Кислород (O) находится в группе 16, значит, у него 6 валентных электронов.Вокруг кислорода 4 точки, значит, у него 4 несвязывающих электрона. К кислороду присоединены 2 линии, и одна линия соответствует двум связывающим электронам. Таким образом, кислород имеет 4 связывающих электрона.
VE равно 6
NE равно 4
BE равно 4
Теперь подставим значения и получим:
формальный заряд = 6 — 4 — 4/2 = 0
Формальный заряд кислорода ) равно 0.
Шаг 3: Рассчитайте формальный заряд кислорода справа
Кислород (O) находится в группе 16, что означает, что он имеет 6 валентных электронов.Вокруг кислорода 4 точки, значит, у него 4 несвязывающих электрона. К кислороду присоединены 2 линии, и одна линия соответствует двум связывающим электронам. Таким образом, кислород имеет 4 связывающих электрона.
VE равно 6
NE равно 4
BE равно 4
Теперь подставим значения и получим:
6 — 4 — 4/2 = 0
Формальный заряд кислорода (справа) равняется 0.
Шаг 4: Проверьте общий заряд
Теперь добавим все формальные заряды атомов в молекуле углекислого газа.Тот факт, что двуокись углерода не имеет надстрочного индекса, относящегося к заряду, означает, что общий заряд должен быть равен нулю. Давайте перепроверим.
Все формальные сборы равны нулю. Если мы сложим их все, сумма будет равна нулю. Мы знаем, что углекислый газ является нейтральной молекулой, а это означает, что его общий заряд равен нулю. Мы только что подтвердили это, подсчитав вместе все формальные расходы и получив сумму, равную нулю.Значения совпадают, значит, мы сделали это правильно.
Пример
Рассмотрим другой пример. Рассмотрим отрицательно заряженный нитрат-ион. Знак минус в верхней правой части структуры Льюиса означает, что ее общий заряд равен -1. Найдем формальные заряды азота и трех атомов кислорода. Мы пометим каждый кислород цифрой красного цвета.
Теперь мы можем вычислить формальные заряды для всех атомов в молекуле нитрата:
Азот:
Азот (N) находится в группе 15, поэтому у него 5 валентных электронов (VE).Вокруг него четыре линии, значит, у него 8 связывающих электронов (BE), а вокруг него нет точек, значит, нет несвязывающих электронов (NE).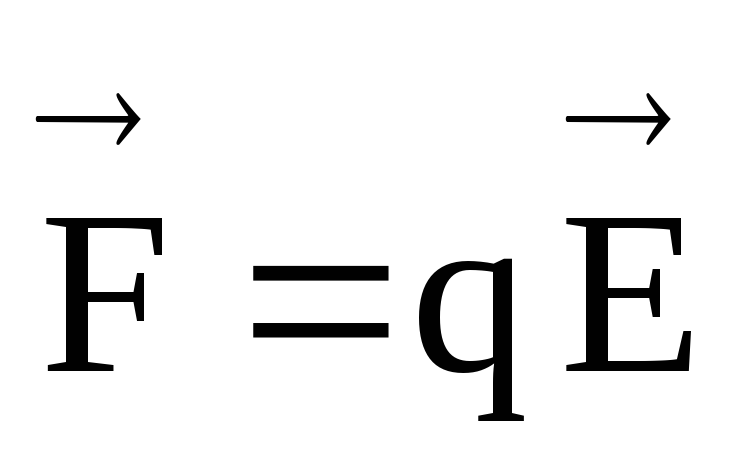
Кислород 1:
Кислород (O) находится в группе 16, поэтому у него 6 валентных электронов (VE). К нему присоединены 2 линии, значит, у него 4 связывающих электрона (BE), а вокруг него 4 точки, значит, 4 несвязывающих электрона (NE).
Кислород 2:
Кислород (O) находится в группе 16, поэтому у него 6 валентных электронов (VE).К нему присоединена 1 линия, значит, у него 2 связывающих электрона (BE), а вокруг него 6 точек, значит, 6 несвязывающих электронов (NE).
Кислород 3:
Кислород (O) находится в группе 16, поэтому у него 6 валентных электронов (VE). К нему присоединена 1 линия, значит, у него 2 связывающих электрона (BE), а вокруг него 6 точек, значит, 6 несвязывающих электронов (NE).
Общий заряд:
Теперь добавим все формальные расходы:
0 + (+1) + (-1) + (-1) = -1
Общий заряд равен -1. Это согласуется с правильным общим зарядом нитрат-иона. Это дает нам хороший намек, верны ли наши расчеты.
Итоги урока
Давайте повторим. Формальный заряд вычисляет индивидуальный заряд атома в молекуле. Это указывает на то, имеет ли атом положительный, отрицательный или нейтральный заряд. Формальный заряд определяется валентными электронами (VE), несвязывающими электронами (NE) и связывающими электронами (BE) по следующей формуле:
Вычислив формальный заряд каждого атома в молекуле, мы можем определить общий заряд молекулы.
Ключевые термины
Формальный заряд — заряд атома в молекуле
Структура Льюиса — рисунок молекулы, на котором показаны все связывающие и несвязывающие электроны
Связывающие электроны – электроны, которые являются общими для атомов в молекуле
Несвязывающие электроны – электроны, которые не являются общими для атомов в молекуле
Валентные электроны самых внешних оболочек атом
Результаты обучения
На этом уроке вы научились:
- Определять связывающие, несвязывающие и валентные электроны атома
- Рассчитайте формальный заряд атомов в молекуле
- Определить общий заряд молекулы и определить, является ли он положительным, отрицательным или нейтральным
Формула закона Кулона
Объекты с электрическим зарядом притягиваются и отталкиваются друг от друга под действием сил. Заряды одного знака отталкиваются, а заряды противоположного знака притягиваются. Величину электростатической силы между зарядами можно найти с помощью закона Кулона. Электростатическая сила зависит от величины зарядов, расстояния между ними и постоянной Кулона, которая равна . Постоянная Кулона также может быть записана через диэлектрическую проницаемость свободного пространства . В таком виде постоянная Кулона равна . Значения электрических зарядов измеряются в кулонах, Кл. Заряды часто записываются как кратные наименьшему возможному заряду, .Единицей электростатической силы является ньютон (Н).
F = электростатическая сила между двумя точечными зарядами ()
k = постоянная Кулона ()
q ₁ = заряд первой точки (C)
q ₂ = заряд второго точечного заряда (C)
r = расстояние между зарядами (м)
Формула закона Кулона Вопросы:
1) Два маленьких заряженных шара находятся на расстоянии 0,300 м друг от друга. Первый имеет заряд -3.00 мкКл (микрокулоны), а второй имеет заряд -12,0 мкКл. Эти заряженные сферы притягиваются или отталкиваются? Какова величина электростатической силы, действующей на каждый шар?
Ответ: Шары имеют заряды одного знака, поэтому сила между ними отталкивающая. Направление силы, действующей на каждую сферу, направлено в сторону от другой. Чтобы найти величину силы, необходимо перевести заряд частиц в кулоны. Приставка «µ», означающая «микро», указывает на то, что число масштабируется на 10 ^-6 , и поэтому 1 мкКл = 10 ^-6 Кл.Заряд первой сферы:
q ₁ = -3,00 мкКл
Заряд второй сферы:
Величину электростатической силы, действующей на каждую сферу, можно найти с помощью закона Кулона:
Величина силы, действующей на каждую сферу, равна 3. 595 Н (Ньютонов).
2) Электрон и протон находятся на расстоянии 1000 нм (нанометр) друг от друга. Заряд электрона равен , а заряд протона равен . Эти заряды притягиваются или отталкиваются? Какова величина электростатической силы, действующей на эти заряженные частицы?
Ответ: Электрон и протон имеют заряды противоположных знаков, поэтому сила притяжения между ними есть. Направление силы, действующей на каждую частицу, совпадает с направлением другой. Чтобы найти величину силы, расстояние между частицами нужно сначала перевести в метры.Приставка «n», означающая «нано», указывает на то, что число увеличено до 10 ^-9 , поэтому 1 нм = 10 ^-9 м. Расстояние между заряженными частицами:
r = 1000 нм
Величина электростатической силы между частицами может быть найдена с помощью закона Кулона:
Величина силы между электроном и протоном равна 2. 307 х 10 ^-10 Н (Ньютоны).
Расчет + ярлык для студентов, изучающих органическую химию
Формальное обвинение — это надоедливая концепция, появившаяся в начале органической химии и почему-то кажется, что она никогда не исчезнет.
Почему я называю это надоедливым?
Потому что уравнение в вашем учебнике длинное, запутанное и излишне раздражающее.
Как вы можете позволить себе столько времени при работе над многоэтапным синтезом?
Нельзя!
Вам не нужно.
Тем не менее, понимание природы формального заряда является важным компонентом, когда речь идет о освоении реакций и механизмов органической химии. Формальный заряд помогает вам понять закономерности реакции, показывая, почему конкретный атом атакует и почему его «жертва» принимает атаку.
Так что же такое официальное обвинение?
Формальный заряд — это фактический заряд отдельного атома в более крупной молекуле или многоатомном ионе.
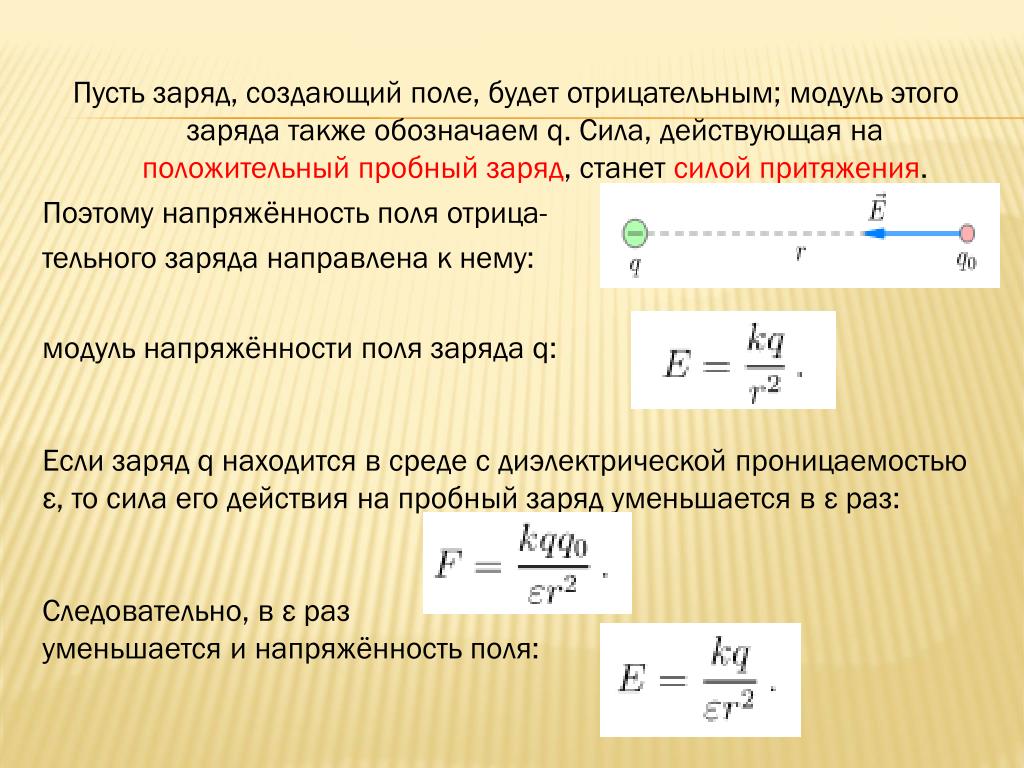
Сумма формальных зарядов любой молекулы или иона дает суммарный общий заряд.
Эта концепция достаточно проста для небольших ионов. Очевидно, что хлорид имеет отрицательный заряд. Даже отрицательный заряд гидроксида кислорода понять несложно.
Но что, если у вас есть гораздо большая группа связанных атомов с общим суммарным зарядом? Например, отрицательный нитрат или тройной отрицательный фосфат.
Откуда берется заряд?
Какой именно атом отвечает за общий заряд?
Может ли быть более одного атома?
А что, если вы изучаете незаряженную молекулу — могут ли отдельные атомы нести заряд, несмотря на общую нейтральность?
Ответы: да, да, да и еще раз да.
Вспомните общую химию, когда вы изучали образование ионов. Ион — это просто атом или молекула, которые приобрели или потеряли электроны, чтобы получить суммарный заряд.
Если в атоме всего на один отрицательный электрон больше, чем протонов, он будет иметь суммарный отрицательный заряд.
Если атом теряет отрицательные электроны и, следовательно, имеет хотя бы один дополнительный ПОЛОЖИТЕЛЬНЫЙ протон в своем ядре, он будет нести в целом положительный заряд.
Теперь, когда вы знаете, ЧТО мы изучаем, давайте посмотрим, КАК! — Вот тут я могу тебе помочь.
Как рассчитать официальное обвинение
Когда я впервые изучал официальное обвинение, я был потерян. Формула в моем учебнике была длинной, утомительной и жестокой. Долгая, надоедливая поездка в рабочее время моего профессора позволила мне понять это, но это все равно было чрезвычайно УТОМИТЕЛЬНЫМ!
Давайте начнем с правильной формулы, а затем выучим ярлык.
Формальное уравнение оплаты
Формальный заряд = [# валентных электронов на нейтральном атоме] – [(# неподеленных электронных пар) + (½ # связывающих электронов)]
- Валентные электроны = соответствует номеру группы периодической таблицы (для репрезентативных элементов).
- Одиночные пары = одинокие электроны, сидящие на атоме. Каждый электрон считается за один, поэтому пара считается за два.
- ½ # связывающие электроны = Поскольку связь образуется путем обмена 2 электронами между 2 атомами, каждый атом в связи может получить кредит только за один из 2 электронов. Двойная связь, содержащая четыре электрона, позволяет каждому атому претендовать на 2. Тройная связь из 6 электронов позволяет каждому атому претендовать на три.
Вы запутались?
Вы боитесь повторять это каждый раз, когда заканчиваете реакцию?
Я с тобой.
Да, уравнение работает, но оно слишком утомительно и раздражает! Слишком много шагов и расчетов.
Вот еще вариант, МОЙ вариант — проще, быстрее, а результат тот же!
Ярлык для формального расчета стоимости
Вот моя версия этого уравнения.
Готов?
Официальное обвинение = Должен – Есть

Определенно быстрее, верно?
Этот ярлык гарантированно сэкономит драгоценные секунды на вашем экзамене, ЕСЛИ И ТОЛЬКО ЕСЛИ вы понимаете, как его применять.
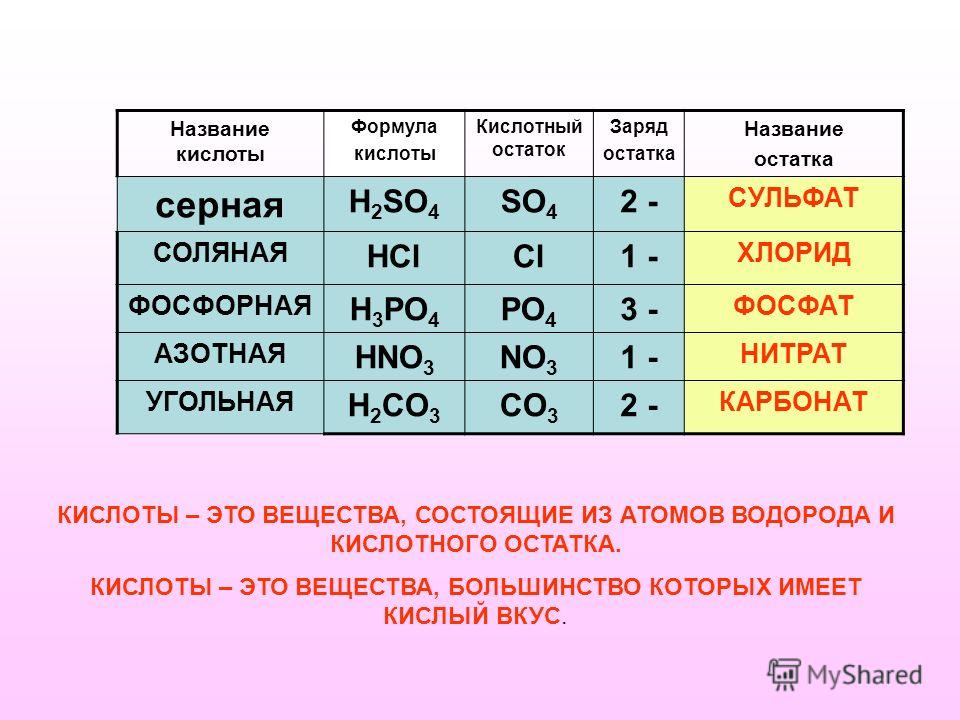
Но когда вы это поймете, вы сможете решить формальный заряд в уме менее чем за 8 секунд на атом.
Убедитесь, что вы понимаете этот ярлык
Should = число валентных электронов, которое ДОЛЖЕН иметь нейтральный атом.
Имеет = количество электронов, которые непосредственно присоединены к атому, касаясь рассматриваемого атома.
Неподеленные пары представляют собой 2 электрона, сидящих на атоме, так что Has = 2
Каждая связь имеет значение только для одного электрона, так как второй электрон в связи касается другого атома.
Хотите, чтобы этот ярлык ожил? Смотрите мое официальное видео об оплате ниже

Когда вы впервые изучаете формальный заряд, это помогает вычертить структуру Льюиса для каждой рассматриваемой молекулы. Когда вы освоитесь с этой темой, вы сможете выбирать связи на чертежах скелетных линий связи.
А пока давайте остановимся на основах (или лучше — давайте будем проще) и рассмотрим несколько примеров, используя контрольный список, представленный в видеоролике Lewis Structures ниже.Это обязательный контрольный список — так что, если вы еще не смотрели, просмотрите это видео:

Когда вы работаете со структурами Льюиса, полезно иметь под рукой периодическую таблицу. Поскольку мы работаем над тем, чтобы сэкономить ваше время, наиболее эффективными результатами будут запоминание следующих 10 атомов. Когда вы будете запоминать их порядок и расположение, обратите особое внимание на следующие тренды:
- Номера групп, указанные сверху
- Электроотрицательность увеличивается вверх и вправо
- Размер увеличивается вниз и влево
Начнем с более простого примера. Мы уже обсуждали гидроксид, поэтому давайте посмотрим на структуру ОН-Льюиса.
Следуя контрольному списку в видеоролике Lewis Structures, мы имеем кислород, связанный с водородом, с 3 неподеленными парами вокруг кислорода.
Применим ярлык:
Водород должен иметь 1 валентный электрон.
Водород имеет один присоединенный электрон.
Нейтральный кислород должен иметь 6 валентных электронов
Кислород имеет 7 присоединенных электронов, как показано красным
Должен – Имеет = 6 – 7 = -1
Гидроксид имеет отрицательный формальный заряд на атоме кислорода.
Что насчет нитратов?
Давайте проанализируем структуру NO3-Льюиса и формальный заряд
Следуя контрольному списку, мы рисуем наши атомы, связи и электроны.
Из-за резонанса мы бы показали три структуры для нитрата. Однако мы просто посмотрим на один ради нашего эксперимента.
Теперь официальное обвинение
Должно – Есть = 5 – 4 = +1
Нейтральный азот должен иметь 5 валентных электронов, но на нашем рисунке показано только 4 присоединенных.
Далее мы рассмотрим двойной связанный кислород.
Должно – есть = 6 – 6 = 0
Кислород с двойной связью счастлив, стабилен и имеет общий нейтральный заряд.
Наконец, у нас есть 2 одиночных связанных атома кислорода с 3 неподеленными парами каждый. Поскольку они идентичны, мы должны вычислить только один, чтобы получить ответ для обоих.
Должен – Имеет = 6 – 7 = -1
Кислород должен иметь 6 валентных электронов, каждый из оставшихся атомов кислорода имеет 7 присоединенных электронов для общего отрицательного заряда.
Давайте попробуем еще один простой, но хитрый пример. Оксид углерода.
Простой, потому что в нем всего 2 атома.
Сложно, потому что окись углерода нейтральна, но пусть вас это не смущает. Многие гемоглобины были обмануты углекислым газом, что сделало его таким смертельным ядом.
Есть 2 типа молекул с нулевым зарядом
1. молекулы без формального заряда
2. молекулы с формальным зарядом, которые компенсируют чистый нулевой формальный заряд.
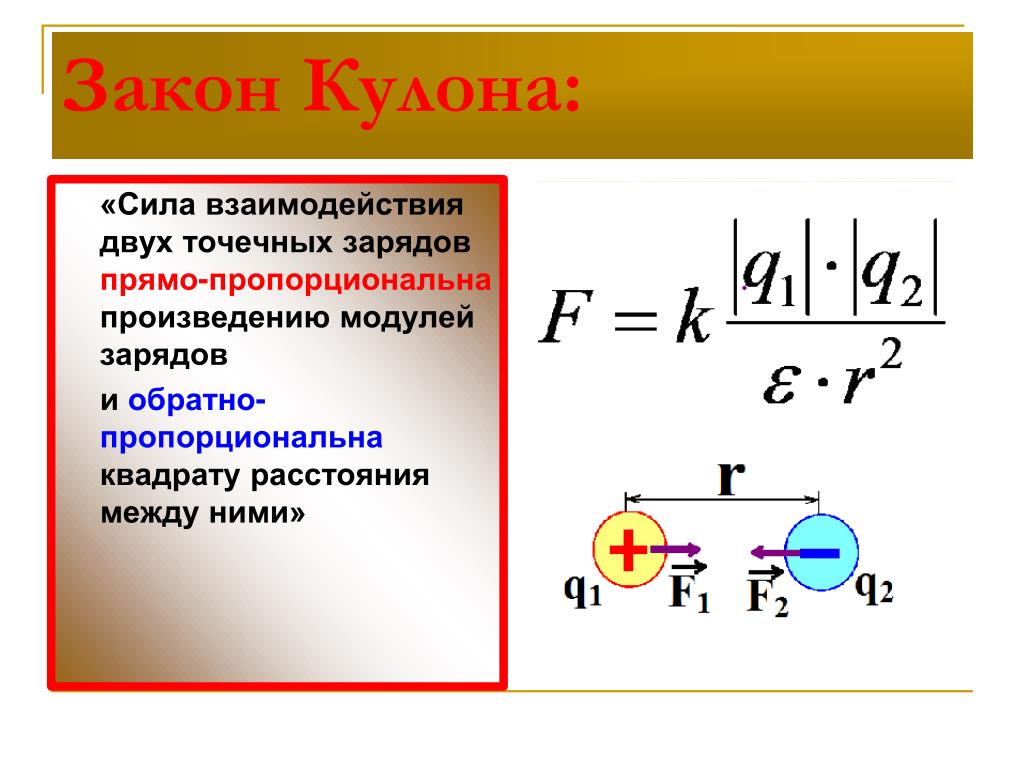
CO Структура Льюиса и формальный заряд
Начните с контрольного списка Льюиса
Теперь займемся отдельными атомами.
Углерод должен иметь 4, прилагается 5, формальный заряд = -1
Кислород должен иметь 6, прилагается 5, формальный заряд = +1
Что вы думаете? Вы по-прежнему находите официальное обвинение таким же утомительным и пугающим, как когда вы впервые узнали об этом? Будем надеяться, что сокращение «должно было» придало вам уверенности, что вы просто смотрите на молекулу и получаете мгновенные формальные заряды.
Или вам нужно больше практики со структурами Льюиса, формой, гибридизацией и многим другим? Смотрите ниже!

Буду рад прочитать ваши отзывы в комментариях ниже!
Готовы проверить свои навыки резонанса? Попробуйте мою БЕСПЛАТНУЮ викторину по практике резонанса.
Видео с вопросами
: определение формулы, связывающей заряд, ток и время
Стенограмма видео
Что из следующего является Правильная формула количества заряда, протекающего через точку цепи в данное время? 𝑄 представляет собой сумму заряда, 𝐼 представляет ток, а 𝑡 представляет время.
В этом примере мы ищем правильную формулу из четырех вариантов, которые нам даны, A, B, C и D, что представляет собой количество заряда 𝑄, протекающего через точку в цепи по данное время. Другими словами, мы хотим знать как математически связаны заряд 𝑄, ток 𝐼 и время 𝑡.
Нам будет полезно вспомнить общее определение того, что такое ток.Текущий является мерой количества потока материала, проходящего через точку за некоторое время. Что касается электрического тока, этот текущий материал является зарядом. Обозначим это буквой 𝑄. И мы можем представить некоторое количество время с помощью буквы 𝑡.
Поскольку ток связан с количество заряда, проходящего через точку в единицу времени, мы можем разделить 𝑄 на 𝑡, и что даст нам ток, который мы обозначаем 𝐼.Теперь у нас есть математическое уравнение для тока. Посмотрим, найдем ли мы это уравнение где-нибудь среди наших вариантов ответа.
Рассматривая сначала вариант ответа А, мы видим, что это утверждает, что ток равен заряду, умноженному на время. Но наше уравнение показывает, что ток равен заряду, деленному на время. Это означает, что вариант А не является правильная формула. Все остальные варианты после у этого есть 𝑄, изолированный сам по себе с одной стороны уравнения.Чтобы увидеть, как наше уравнение сравнивает, давайте алгебраически переставим его так, чтобы 𝑄 была на одной стороне сама по себе.