Обозначение корня: √ — Квадратный корень: U+221A radic

знак корня — это… Что такое знак корня?

Знак корня — √ Знак корня (знак радикала) в математике  условное обозначение для корней, по умолчанию квадратных. В общем случае (для корней n й степени) показатель степени ставится над «птичкой»: знак используется для кубических корней,   для… …   Википедия

знак корня — радикал — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы радикал EN radical sign …   Справочник технического переводчика

Знак радикала — √ Знак корня (знак радикала) в математике условное обозначение для корней, по умолчанию квадратных. В общем случае (для корней n й степени) показатель степени ставится над «птичкой»: знак используется для кубических корней, для корней 4 й степени …   Википедия

Знак процента — % Знак процента Пунктуация апостроф (’ …   Википедия

Знак деления

— ÷ Знак деления Пунктуация апостроф (’ ) …   Википедия

% (знак) — % %  знак, чаще всего обозначающий проценты. Происхождение обозначения …   Википедия

Знак умножения — × • Знак умножения (×)  математический знак операции умножения. Знак умножения изображают как крестик (×), точку …   Википедия

Знак плюс-минус — У этого термина существуют и другие значения, см. Плюс минус (значения). ± ∓ Знак плюс минус (±)  математический символ, который ставится перед некоторым выражением и означает, что значение этого выражения может быть как положительным, так и …   Википедия

Знак градуса — У этого термина существуют и другие значения, см. Градус. ° Знак градуса Пунктуация апостроф …   Википедия

Знак равенства — …   Википедия

Знак тильда — Тильда (исп. tilde, от лат. titulus  надпись)  название нескольких типографских знаков в виде волнистой черты. Содержание 1 Диакритический знак 1.1 Надстрочный …   Википедия

подкоренное число и показатель корня

Корень  n-ой  степени из числа  a  — это число,  n-ая  степень которого равна  a.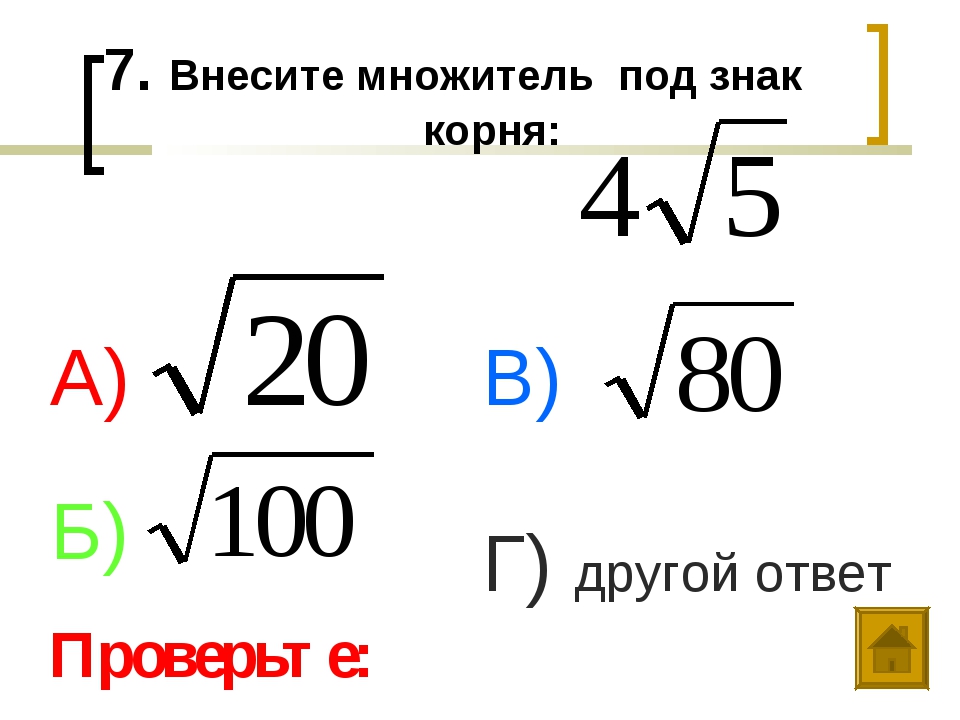   Например, корнем второй степени из  36  будет число  6,  так как:

6² = 36.

Для записи корня используется знак  √    (знак корня  или  радикал). Под чертой знака записывается подкоренное число, а над знаком, в левом верхнем углу, показатель корня:

²√36.

Подкоренное число — это степень, показатель корня — это показатель степени, корень — основание степени. Если

,

то

.

Эта запись читается так: корень  n-ой  степени из числа  a  равен  x.

Извлечение корня — это действие, обратное возведению в степень, с помощью которого по данной степени и по данному показателю степени находят основание степени.

Примеры:

³√125 = 5,   так как   5³ = 125;

²√81 = 9,   так как   9² = 81;

⁵√32 = 2,   так как   2⁵ = 32.

Квадратный корень

Квадратным корнем из числа  a  называется число, квадрат которого равен  a.

Например, квадратными корнями из числа  16  являются числа  4  и  -4:

²√16 = 4   или   ²√16 = -4.

Рассмотрим уравнение

x² = a

при различных значениях   a:

1. a < 0:

   В данном случае уравнение не будет иметь решений, так как квадрат любого числа всегда является положительным числом или нулём. Следовательно,  x²  не может быть равен отрицательному числу.

2. a = 0:

   В этом случае уравнение имеет единственное решение:

   x = 0.

3. a > 0:

   В этом случае уравнение имеет два корня: положительный и отрицательный, модули которых равны. Так как вторая степень отрицательного числа является числом положительным:

   x = ±√a .

Из рассмотренного примера можно сделать вывод, что для того чтобы из числа можно было извлечь квадратный корень, необходимо, чтобы оно было числом положительным или нулём

.

Арифметический квадратный корень

Арифметический квадратный корень из положительного числа  a  — это положительное число  x,  квадрат которого равен  a:

²√a = x,   следовательно   x² = a.

При обозначении квадратного корня показатель корня опускается, то есть квадратный корень обозначается знаком корня без показателя. Например:

√a  — квадратный корень из  a.

Обратите внимание, что при чтении выражения слово арифметический опускается.

Действие, с помощью которого вычисляется квадратный корень, называется извлечением квадратного корня.

Извлечение квадратного корня — действие обратное возведению в квадрат (или возведению числа во вторую степень).

При возведении в квадрат известно число, требуется найти его квадрат. При извлечении квадратного корня известен квадрат числа, требуется по нему найти само число.

Поэтому для проверки полученного результата можно найденный корень возвести во вторую степень, если степень будет равна подкоренному числу, значит корень был найден правильно.

Рассмотрим извлечение арифметического квадратного корня и его проверку на примере. Найдём  √36,  для этого надо найти число, при возведении которого во вторую степень получится  36.  Таким числом является  6,  так как

6² = 36.

Значит,  √36 = 6.  Корень  -6  мы не рассматриваем, потому что арифметический корень является положительным числом.

Урок 16. арифметический корень натуральной степени — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок №16 Название темы: Арифметический корень натуральной степени.

Перечень тем, рассматриваемых на уроке:

• преобразование и вычисление арифметических корней,
• свойства арифметического корня натуральной степени,
• корень нечетной степени из отрицательного числа,
• какими свойствами обладает арифметический корень натуральной степени.

Глоссарий

1. Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.
2. Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.
3. Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.
4. Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.
5. Арифметическим корнем натуральной степени, где n ≥ 2, из неотрицательного числа
   a называется неотрицательное число, n-я степень которого равна a.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл.– М.: Просвещение, 2014.

1. Сканави М. И., Зайцев В. В., Рыжков В. В. «Элементарная математика». – Книга по требованию, 2012.
2. Семенова А.Л., Ященко И.В. ЕГЭ 3000 задач с ответами, математика под редакцией Москва, 2017.
3. Ященко И. В. ЕГЭ 3300 задач с ответами, математика профильный уровень под редакцией Москва, 2017.

Объяснение темы «Арифметический корень натуральной степени»

Решим задачу.

Площадь квадрата S=16 м².

Обозначим сторону квадрата а, м.

Тогда, а

² = 16.

Решим данное уравнение:

a=4 и а= –4.

Проверим решение:

4² = 16;

(–4)² = 16.

Ответ: длина стороны квадрата равна 4 м.

Определение:

Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.

Определение:

Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.

Обозначение: .

Определение:

Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.

Обозначение: .

Например:

.

.

.

На основании определений квадратного и кубического корней, можно сформулировать определения корня n-ой степени и арифметического корня n-ой степени.

Определение:

Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.

Определение:

Арифметическим корнем натуральной степени, где n≥2, из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.

Обозначение: – корень n-й степени, где

n–степень арифметического корня;

а– подкоренное выражение.

Давайте рассмотрим такой пример: .

Мы знаем, что (–4)³ = –64, следовательно, .

Еще один пример: .

Мы знаем, что (–3)⁵ = –243, следовательно, .

На основании этих примеров, можно сделать вывод:

, при условии, что n –нечетное число.

Свойства арифметического корня натуральной степени:

Если а ≥ 0, b ≥ 0 и n, m – натуральные числа, причем n ≥ 2, m ≥ 2, то справедливо следующее:

1. .

Примеры:

.

.

1. .

Примеры:

.

.

1. .

Пример:

.

1. .

Пример:

.

1. Для любогоа справедливо равенство:

Пример:

Найдите значение выражения , при 3 <x< 6.

Степени заданных арифметических корней 4 и 2, четные числа, следовательно, мы можем применить свойство №5:

=|x – 3| = х – 3, т. к. х>3;

=|x – 6|=6 – x, т.к. х<6.

Получаем: х – 3 + 6 – х= 3.

Примеры заданий.

Первый пример.

Задача:

Выберите верные утверждения:

Разбор задания.

Применим определение арифметического корня: Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a. Следовательно, верными могут быть только неотрицательные выражения.

Ответ: ; ;

Второй пример.

Задача:

Выделите самое маленькое число:

Разбор задания:

Корень из отрицательного числа будет отрицательным числом, следовательно, наименьшее число –

Ответ: 4.

Знак корня

Знак корня (знак радикала) (√) в математике — условное обозначение {displaystyle {sqrt {quad }}} для корней, по умолчанию квадратных. В общем случае (для корней n-й степени) показатель степени ставится над «птичкой»: знак 3 {displaystyle {sqrt[{3,}]{quad }}} используется для кубических корней, 4 {displaystyle {sqrt[{4,}]{quad }}} — для корней 4-й степени и т. п.; для квадратного корня также можно использовать «полное» обозначение 2 {displaystyle {sqrt[{2,}]{quad }}} .

Корни чётной степени из вещественных чисел неоднозначны — например, у числа 9 существуют два квадратных корня, + 3 {displaystyle +3} и − 3.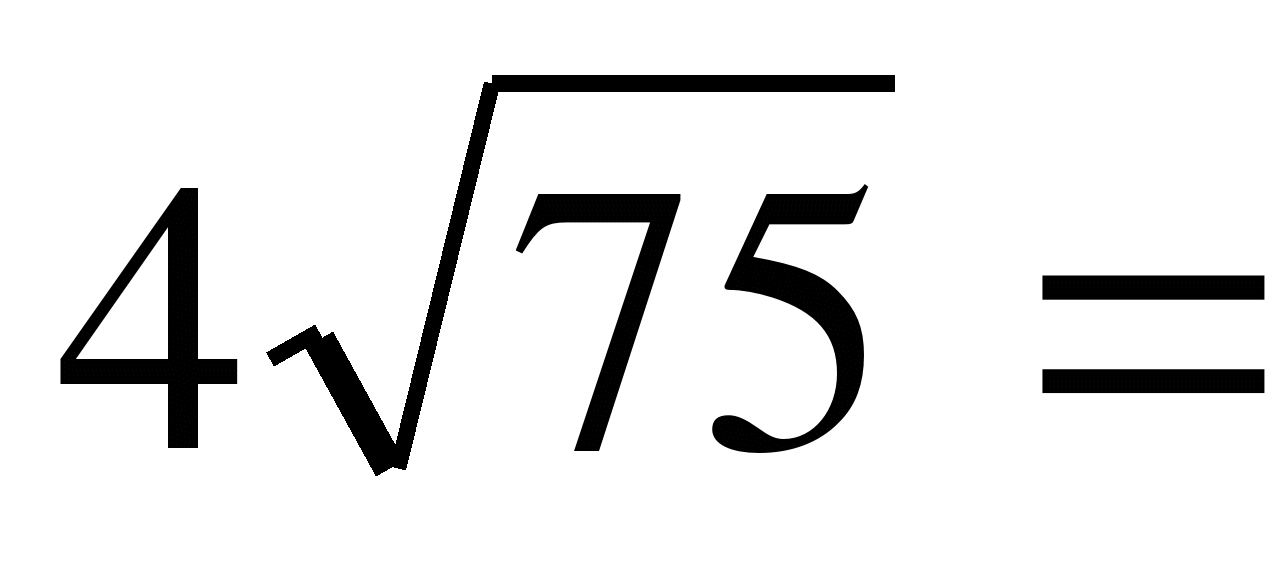 {displaystyle -3.} Во избежание недоразумений принято соглашение, что под знаком корня чётной степени из вещественного числа может находиться только неотрицательное число (см. Арифметический корень). Для корней в комплексной области знак радикала обычно либо не используется, либо обозначает не функцию корня, а множество всех корней; в последнем случае, во избежание ошибок, знак радикала не должен использоваться в арифметических операциях (см. Комплексные корни).

История

Знак корня происходит из строчной латинской буквы r (начальной в лат. radix — корень), сросшейся с надстрочной чертой: ранее надчёркивание выражения использовалось вместо нынешнего заключения его в скобки. Так что a + b {displaystyle {sqrt {a+b}}} есть всего лишь видоизменённый способ записи выражения   r a + b ¯ {displaystyle r{overline {a+b}}} .

Впервые такое обозначение использовал немецкий математик Кристоф Рудольф в 1525 году. Им также были изобретены символы и для корней третьей и четвёртой степеней соответственно, однако они не закрепились в науке.

Типографика

• американский вариант

• немецкий вариант

• русский вариант

• вариант TeX

В некоторых типографских традициях (например, в германской) принято верхнюю черту знака корня снабжать справа небольшой обращённой вниз засечкой. В Американской типографике (в частности, системе TEΧ) этой детали нет.

Длина и высота знака корня должны быть такими, чтобы полностью покрывать подкоренное выражение. При соседстве в одной строке нескольких подкоренных выражений разной (но близкой) высоты часто бывает принято все знаки корня подстраивать под самое высокое из них.

Знак корня используют только для выражений, помещающихся в пределах строки, а для более длинных вместо a b c d e … n {displaystyle {sqrt[{n,}]{abcdedots }}} применяют эквивалентную запись ( a b c d e … ) 1 / n {displaystyle (abcdedots )^{1/n}} . Впрочем, в некоторых руководствах по набору и вёрстке упоминается разрыв подкоренного выражения на несколько строк; при этом знак корня ставится над первой, а над продолжением подкоренного выражения ставится черта; в месте разрыва строк и знак корня, и черта над продолжением снабжаются стрелками, обращёнными наружу.

Арифметический квадратный корень. Вынесение, внесение множителя под знак корня

Математика->Модуль числа. Корень числа->квадратный корень->

Тестирование онлайн

• Квадратный корень. Вычисления

• Квадратный корень. Вычисления (часть 2)

• Квадратный корень. Алгебраические выражения и преобразования

• Квадратный корень. Алгебраические выражения и преобразования (часть 2)

• Квадратный корень. Алгебраические выражения и преобразования (часть 3)

• Тождество

• Вынесение множителя из-под знака квадратного корня

• Внесение множителя под знак квадратного корня

• Значение переменной в выражении с квадратным корнем

• Вынесение и внесение множителя (средний уровень)

• Алгебраические преобразования с квадратным корнем (выше среднего)

• Алгебраические преобразования, вычисление. Повторение (выше среднего)

Арифметический квадратный корень

Обозначение знака квадратного арифметического корня , подразумеваем , но «2» не пишется.

Неотрицательный квадратный корень из числа a называется арифметическим квадратным корнем из числа a. Например,

Выражения не имеют смысла!

Тождество

При любом значении a имеет место равенство

Согласно определению модуля получим

Вынесение и внесения множителя под знак корня

При любом значении a и при любом положительном значении b верно равенство

Обратное равенство имеет вид

Среднее арифметическое и среднее геометрическое чисел

Средним арифметическим двух чисел a и b называется выражение

Средним геометрическим двух неотрицательных чисел a и b называется выражение

Среднее арифметическое неотрицательных чисел a и b не меньше их среднего геометрического.

Если среднее арифметическое двух неотрицательных чисел равно их среднему геометрическому, то эти числа равны.

О знаке квадратного корня. Историческая справка репетитора по математике

Ззнак квадратного корня знаком всем. Его используют школьники и студенты, преподаватели и репетиторы по математике, доктора наук и академики. Однако не все знают, что современная форма и появилась не сразу. Эволюция знака радикала длилась почти пять веков, начиная с в далекого XIII в., когда итальянские и некоторые европейские математики впервые называли квадратный корень латинским словом Radix (корень) или сокращенно R.

В XV в. Н.Шюке писал вместо . Современный знак корня произошел от обозначения, применяемого немецкими математиками XV-XVI вв., называвшие алгебру — наукой «Косс», а математиков -алгебраистов «коссистами». (Математики XII-XV вв. писали все свои труды исключительно на латинском языке. Они называли неизвестное — res (вещь). Итальянские математики перевели слово res как cosa. Последний термин заимствовали немцы, от которых и появилось коссисты и косс.)

В XV в. некоторые немецкие коссисты для обозначения квадратного корня пользовались точкой перед выражением или числом. В скорописи эти точки заменялись черточками, а позже они перешли в символ
Один такой знак означал обычный квадратный корень. Если нужно было обозначить корень четвертой степени, то применялся сдвоенный знак знак Для обозначения кубического корня использовали утроенный знак

Комментарий репетитора по математике: остается только гадать, как именно обозначался корень восьмой степени. Если брать аналогию с четвертой степенью, то этот знак должен был отождествлять трехкратное извлечение квадратного корня, то есть для этого нужно было поставить три квадратика. Однако, это обозначение занято кубическим корнем.

Скорее всего, в последствии от таких обозначений как раз и образовался знак V, близкий по записи к знакомому школьникам современному знаку, но без верхней черты. Впервые этот знак был замечен в немецкой алгебре «Красивый и быстрый счет при помощи искусных правил алгебры»:

Автором этого труда был преподаватель математики из Вены, уроженец Чехии Криштоф Рудольф. Книга пользовалась большим успехом и постоянно переиздавалась на протяжении всего XVI в. и после аж до 1615г. Знаком корня, предложенного Криштофом пользовались А.Жирар, С.Стевин (он писал показатель корня справа от знака радикала в кружке: V (2) или V (3).

В 1626г. нидерландский математик А.Жирар видоизменил знак корня Рудольфа и ввел совсем близкое к современному обозначение Такая форма записи начала вытеснять прежний знак R. Однако некоторое время знак корня писали разрывая верхнюю черту, а именно так: .

И только в 1637 году Рене Декарт соединил горизонтальную черту с галочкой, применив новое обозначение в своей книге «геометрия».

Но и здесь не было точной копии современной формы. Запись Декарта несколько отличалась от той, к который мы с вами привыкли одной деталью. У него было записано: , где буква С, поставленная сразу после радикала, указывала на запись кубического корня. В современном виде это выражение выглядело бы так: .

Самое близкое к современному написанию радикала применял Ньютон в своей «Универсальной арифметике» (1685 г.) Впервые запись корня, полностью совпадающая с сегодняшней, встречается в книге французского математика Ролля «Руководство алгебры», вышедшей в 1690 г. Только через некоторое время после ее написания математики планеты принята, наконец, единую и окончательная форма записи квадратного корня:

Колпаков А.Н. Профессиональный репетитор по математике.

Метки: Алгебра

Свойства арифметического квадратного корня

1 октября 2020

0.

{2n+1}} \right) \\ \end{align}\]

Мы будем использовать эти свойства на всю катушку в третьей части урока. А пока начнём с более простых вещей.

1. Корни из точных степеней

При работе с корнями многие ученики допускают одну и ту же ошибку. Они пытаются подменить чёткие правила алгебры интуитивными размышлениями. И на первый взгляд всё выглядит хорошо. Взгляните на примеры:

Во всех трёх случаях мы видим, что под корнем стоят точные квадраты. Их можно переписать так:

Может показаться, что для упрощения выражения достаточно убрать степень и знак корня. На практике это не так:

Из третьей строки видно, что просто убрать степень и корень с отрицательного основания нельзя, ведь корень не может быть отрицательным! Вторая строка объясняет нам, что именно происходит: квадрат делает число под корнем положительным, а дальше мы извлекаем этот самый корень и вновь получаем положительное число. В итоге строки 1 и 2 ведут к извлечению корня из одного и того же числа — 64.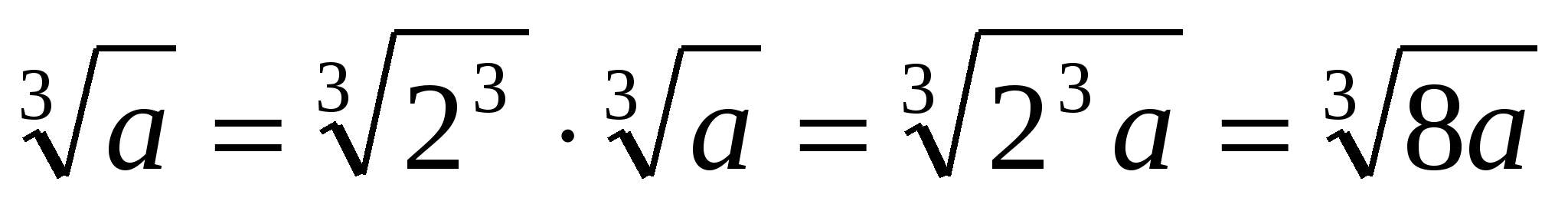

Вывод?

1.1. Корень из точного квадрата

А вывод такой: корень из квадрата не меняет положительные числа, а отрицательные меняет на противоположные. Это в точности совпадает с определением модуля:

Для удобства дальнейших размышлений предлагаю взять на вооружение вот такое определение модуля:

Это определение чрезвычайно полезно для решения сложных задач с параметрами. Об этом как-нибудь в следующий раз. А пока давайте потренируемся:

Опыт моих учеников: поначалу довольно непривычно выписывать эти множители (1, 0 и −1), но затем человек привыкает и пишет всё на автомате. А затем и вовсе перестаёт писать — всё происходит в его голове, но навык добавления множителей остаётся (и очень пригодится, когда мы считаем коэффициенты многочленов).

Потренируйтесь самостоятельно:

Задание. Найдите значение выражения:

[Показать ответы]

Отдельное внимания заслуживают двойные корни, вложенные друг в друга:

Для них замена корня модулем тоже работает, но возникает вопрос: как корректно раскрыть модуль? Придётся сравнивать корни:

Откуда такое смелое утверждение во второй строке? Существует два способа доказать неравенство в красных скобках:

• 1. Использовать свойства корней;
• 2.Составить цепочку неравенств.

Я приведу оба:

Сравнение корней — отдельная серьёзная тема. Ей посвящён целый урок. Поэтому давайте просто решим второе задание:

Задание. Вычислите значение выражения:

[показать ответ]

1.2. Корень из чётной степени

Идём дальше. Вновь запишем нашу волшебную формулу:

Капитан очевидность как бы намекает: эта формула верна не только для квадратов, но и для всех чётных степеней:

Другими словами, корень из любой чётной степени понижает эту степень ровно в два раза, но взамен навешивает на неё модуль! Рассмотрим примеры:

Обратите внимание на последнюю строку: изначально под корнем стоит довольно громоздкое число. Вычислять его напролом — возводить в квадрат, а затем извлекать корень — безумие. Но формула понижения степени редуцирует задачу до устной — отличная экономия времени на экзамене.:)

Попробуйте сами:

Задание 2. Найдите значение выражения:

[Показать ответы]

Вывод: если видите корень из степени, то смело понижайте степень вдвое, убирайте корень, но взамен ставьте модуль. Всегда. Обязательно. Ок? Переходим ко второй части урока.

2. Корни из произведения и частного

Перед тем как давать какие-либо новый формулы, напомню важный факт. Корень из суммы не равен сумме корней:

Иначе мы бы получили вот такие бредовые выкладки:

Вроде бы, капитаноочевидно, но многие даже в старших классах допускают такие ошибки.

А теперь разберём ещё два свойства корней.

2.1. Умножение и деление корней

Корни можно умножать и делить. Правила просты:

Примеры:

Попробуйте сами:

Задание 3. Найдите значение выражения:

[показать ответы]

Как видите, с помощью формул мы разбиваем сложный корень на несколько простых.

Мы знаем, то все формулы работают как слева-направо, так и справа-налево, поэтому корни можно «склеивать». При этом новый корень может легко вычисляться, хотя исходные части — не вычисляются вообще. Например:

Попробуйте повторить этот трюк:

Задание 4. Найдите значение выражения:

[показать ответы]

2.

2. Проблемы с областью определения

Но есть одна тонкость. Взгляните, например, на формулу произведения корней:

Напомню: знак радикала обозначает арифметический квадратный корень, который извлекается только из неотрицательных чисел и сам является числом неотрицательным.

С левой стороны от знака равенства стоит один корень, а справа — целых два. Поэтому области определения левой и правой части этого равенства различны:

В чём конкретно состоит различие?

В первой строке мы видим произведение, поэтому неравенство (1) верно всякий раз, когда знаки множителей совпадают. В частности, оба множителя могут быть отрицательными, но их произведение всё равно будет положительным.

Вторая строка — система из двух неравенств, и здесь отрицательные числа нас уже не устроят. Вывод:

Красным я выделил ситуацию, которая допустима для корня из произведения, но становится недопустимой для произведения корней.

Поскольку любое равенство определено лишь тогда, когда определена и левая, и правая его части, дополним исходные правила специальными требованиями:

И вот в таком виде их уже можно использовать — везде и всегда!

Может показаться, что эти ограничения несущественны. Или искусственны. Чуть выше мы никак их не учитывали и всё прекрасно посчитали. Поэтому вопрос: когда ограничения области определения становятся существенным?

Ответ: когда под корнями стоят не конкретные числа, а переменные. К примеру, пусть даны числа:

Очевидно, что произведение двух отрицательных чисел будет положительным. И хотя корень из произведения будет определён, извлекать корни из отдельных множителей нельзя:

Значит, нужно сделать так, чтобы множители под корнем стали положительными. И тут нам на помощь приходит старое доброе число −1:

Добавление минусов к каждому из двух множителей нисколько не повлияло на произведение, но привело к возникновению двух новых множителей, каждый из которых уже точно положителен:

Помните об этом преобразовании, когда сталкиваетесь с произведением отрицательных выражений под знаком корня. Источником такой отрицательности могут быть условия задачи, либо следствия из области определения (такое часто встречается в логарифмических уравнениях и неравенствах, которые изучаются в 10—11 классах).

Ну а мы немного потренируемся и пойдём к третьей части урока — работе с переменными.

Задание 5. Найдите значение выражения:

[показать ответы]

Переходим к самому весёлому.:)

3. Работа с переменными

Если не считать определения, то мы знаем о корнях две вещи. Во-первых, корни понижают степени, но добавляют модули:

Во-вторых, корни можно умножать и делить. Но не всегда:

До сих пор мы тренировались лишь на конкретных числах. И многие могут удивляться: зачем все эти рассуждения про модули и ограничения?

Сейчас мы заменим числа буквами — и задача резко усложнится. Или не усложнится — если вы внимательно изучите то, что написано дальше.:)

3.1. Раскрытие модуля через свойства степеней

Начнём с простого. Мы уже знаем, как избавляться от точной степени:

Попробуем применить эту формулу к двум различным выражениям:

В первой строке мы без труда раскрыли модуль, поскольку знаем, что число под модулем отрицательно. Затем посчитали — получили ответ.

Но как раскрыть модуль во второй строке? Ведь правила раскрытия будут меняться в зависимости от того, какое значение принимает переменная. И если никаких дополнительных ограничений на переменную нет, то модуль так и останется нераскрытым. Взгляните:

Замените выражение тождественно равным, не содержащим знака корня:

Из приведённых примеров видно:

• В строках (2) и (4) мы можем раскрыть модуль, ничего не зная о переменной;
• В строках (1) и (3) раскрыть модуль не удалось.

Почему? Чётные степени в строках (2) и (4) при любом значении переменной будут положительным числом или нулём. Поэтому модуль однозначно раскрывается со знаком «плюс».

Нечётная степень в строках (1) и (3) таким свойством не обладает: она может оказаться как положительным числом, так и отрицательным. Поэтому модуль раскрыть нельзя.

Попробуйте сами:

Задание. Замените выражение тождественно равным, не содержащим знака корня:

[показать ответ]

Чётные степени всегда неотрицательны, нечётные степени могут принимать любой знак:

Тем не менее, модуль нечётной степени тоже можно раскрыть. Если в задаче есть дополнительные условия.

3.2. Учёт дополнительных ограничений

Зачастую в самом условии задачи содержатся ограничения на переменную, которые помогают однозначно раскрыть модуль. Пример:

Упростите выражение:

Работаем по тем правилам, которые изучали выше:

Обратите внимание: в строке (2) чётные степени под корнем дают три неотрицательных числа, поэтому корень можно разбить на три изолированных множителя — область определения при этом не поменяется; затем в строке (3) мы видим чётную степень под модулем и раскрываем его.

Ещё раз запишем результат и дополним его исходными условиями:

В первом случае выражение под модулем положительно или ноль, поэтому модуль однозначно раскрывается со знаком «плюс». Во втором — отрицательно или ноль, поэтому модуль раскрывается со знаком «минус»:

Возможно, у вас возникает вопрос: почему мы пишем множитель 1 или −1, но не рассматриваем отдельно множитель 0? В этом фишка модуля:

Таким образом, в нуле модуль можно раскрывать любым удобным способом.

Попробуйте самостоятельно:

Задание. Упростите выражение:

[показать ответ]

Это были весьма примитивные выражения, сводящиеся к раскрытию модуля. На них мы отработали важный новый навык. Теперь воспользуемся этим навыком для решения более интересных задач.

3.3. Упрощение выражений

Последний и самый интересный раздел этого урока.

Откуда берутся дополнительные ограничения на переменные? Существует ровно два источника таких ограничений:

• 1.Условие задачи. Например, если переменная — это длина отрезка на чертеже, то можно без ущерба для здоровья полагать, что она неотрицательна (а если всё-таки отрицательна, то у вас неправильный чертёж).
• 2.Неявные следствия из исходного выражения / уравнения / неравенства. Тут всё намного интереснее: анализ следствий из исходного условия — увлекательный процесс, доступный лишь хорошо подготовленным ученикам.

Начнём с первого пункта — ограничений, явно указанных в условии задачи. Примеры:

Упростите выражение:

С первым выражением всё просто:

Со вторым уже интереснее. Заметим, что в первом числителе стоит формула сокращённого умножения, а дробь под корнем гарантированно имеет неотрицательный числитель и знаменатель:

Вспомним исходные ограничения:

И раскроем модули:

Как видите, нам удалось избавиться не только от модулей, но и от дробей.:)

Обратите внимание

Материал, представленный дальше, относится скорее к следующему уроку — «Внесение и вынесение множителей из-под знака корня». Его изучение прямо сейчас не является обязательным, но может оказаться весьма полезным для сильных учеников.

Наконец, разберёмся с неявными ограничениями. Ещё раз запишем самую первую формулу:

Пусть известно, что подмодульное выражение неотрицательно. Тогда модуль можно убрать:

С отрицательными величинами тоже можно провернуть такой трюк:

Но любое равенство работает как слева-направо, так и справа-налево. Следовательно, если нам известен знак переменной, мы можем внести её под знак корня:

Это замечание позволит упрощать выражения, которые неподготовленному ученику покажутся неприступными.

Остаётся лишь один вопрос: где взять знак переменной? Ответ: ограничения на переменную часто скрыты в области определения. Например:

Упростите выражения:

Решение:

В первой строке мы видим корень, поэтому выпишем область определения. Это даст нам ограничения на переменную и поможет внести её под знак корня:

То же самое со вторым выражением:

В итоге мы получили выражение, тождественно равное нулю. Однако помните: это равенство сохраняется только для отрицательных значений переменной! Для положительных значений исходное выражение вообще не определено.

Операция, которую мы только что провернули, как раз и называется внесением переменной под знак радикала.

В заключение хотел бы рассмотреть типичную ситуацию для сложных алгебраических задач, когда под корнем стоят, на первый взгляд, противоположные числа.

Упростите выражение:

Заметим, что самый первый корень накладывает жёсткие ограничения на переменную:

Под остальными корнями стоят неотрицательные выражения, поэтому дальше всё просто:

Наличие неявного ограничения позволило нам раскрыть модуль даже у нечётной степени. Обратите внимание на этот переход:

Как мы помним из краткой вводной, минусы можно выносить (и вносить) из основания нечётной степени. Это можно сделать как после раскрытия модуля, так и в самом начале — прямо под корнем:

Красным я отметил одинаковые выражения, стоящие под корнем и в основании степени. Именно такая форма записи (а не игра с минусами) является предпочтительной, например, в логарифмических уравнениях и неравенствах.

Но это тема совсем другого урока. А на сегодня хватит.:)

Смотрите также:

1. Умножение корней n-й степени
2. Корень степени N
3. Тест к уроку «Площади многоугольников на координатной сетке» (средний)
4. Задача B3 — работа с графиками
5. Пробный ЕГЭ 2012 от 7 декабря. Вариант 8 (без производной)
6. Как решать биквадратное уравнение

Решено: STP: корневой порт по сравнению с назначенным портом

Кевин

Взгляните на прилагаемую схему.

sw1 — корневой мост.

Корневой порт (RP) — это порт, который ведет к корневому мосту, поэтому корневой мост не имеет корневых портов. Все порты корневого моста пересылаются, и все они являются назначенными портами (DP).

Как вы можете видеть, в вышеупомянутой сети есть петля, поэтому одна из ссылок должна быть заблокирована (BLK).

Когда коммутаторы загружаются, они обмениваются BPDU, и первое, что они делают, это выбирают корневой мост. В этом случае выбирается SW1.

Далее каждый коммутатор должен найти путь к корневому мосту с наименьшими затратами. Я не включил затраты на каждую ссылку в этой диаграмме, но из приведенного выше

SW3 считает, что направление подключения к SW1 является наименьшей стоимостью, поэтому его порт на этом канале становится RP.

SW2 считает свое направление подключения к SW1 наименее затратным, поэтому его порт на этом канале становится RP.

После того, как коммутаторы согласовали корневой мост и свои RP, им теперь нужно найти назначенные им порты. Назначенные порты — это порты, отвечающие за пересылку трафика в сегмент сети. Подумайте об этом так:

RP ведут к корневому мосту

DP ведут от корневого моста

, потому что корневой мост не имеет блокирующих портов, все его порты являются DP.

Таким образом, единственный другой сегмент, не учтенный в приведенной выше диаграмме, — это SW2 -> SW3.Один из портов, соединяющих этот сегмент, должен пересылать трафик в этот сегмент, иначе этот сегмент никогда не получит никакого трафика. Но они не могут оба продвигаться вперед, так как тогда будет цикл, т.е. пакет, отправленный из SW1, перейдет в SW3 -> SW2 и обратно в SW1 и т. д.

Итак, SW2 и SW3 сравнивают затраты на этот сегмент в BPDU, отправленных между собой, и один из них имеет лучшую стоимость, в данном случае SW3. Он помещает свой порт в переадресацию, и он становится DP. Чтобы разорвать петлю, SW2 теперь должен перевести свой порт в режим блокировки.

Надеюсь, это помогло. Все вышеперечисленное сделано по затратам, но я не включил их, чтобы не путать основные концепции.

Йон

Посмотреть решение в исходном сообщении

Cisco CCNA — Протокол связующего дерева (корневой мост, корневые / назначенные / заблокированные порты) — CertificationKits.com

Мы будем использовать рисунок 1 для объяснения этих трех проблем.

Предположим, что на рисунке выше ПК-1 отправляет кадр на ПК-2.Этот кадр получен на Порте 1 как коммутатора A, так и коммутатора B. Поскольку оба коммутатора не знают адрес назначения, они просто рассылают кадр через все порты, кроме того, на котором он был получен, в данном случае — Порт 2. Копия фрейм получен на Порте 2 обоих Коммутаторов, поскольку каждый Коммутатор отправляет фрейм на Порт 2, а другой получает тот же самый фрейм от другого коммутатора. Процесс повторяется снова, и лавинная рассылка происходит в указанном выше сегменте. Это продолжается и продолжается, и создается широковещательный шторм, который потребляет все ресурсы сети.

В процессе, описанном выше, ПК-2 может получить несколько копий одного и того же кадра от коммутатора A и коммутатора B. Это может вызвать проблемы, поскольку многие протоколы не могут обрабатывать повторяющиеся кадры.

Другой проблемой, которая может быть вызвана петлями, является нестабильность таблицы MAC-адресов. Когда ПК-1 отправляет кадр на ПК-2 и получает его через порт 1 обоих коммутаторов, которые затем устанавливают MAC-адрес ПК-1 в таблице MAC-адресов и связывают его с портом 1. Оба коммутатора затем лавинно отправляют кадр из порта 2 .Коммутатор A получает кадр, который был передан коммутатором B, и обновляет его таблицу MAC-адресов, связывая MAC-адрес ПК-1 с портом 2. Тот же процесс происходит и на коммутаторе B, и таблица MAC-адресов обоих коммутаторов повреждена и, как следствие, трафик переключается не на те интерфейсы.

Протокол связующего дерева был разработан, чтобы избежать петель путем поиска избыточных каналов в сети и их отключения. Чтобы предотвратить создание мостовых петель, необходимо определить и заблокировать избыточные пути.Связующее дерево не только блокирует избыточные пути, но и повторно открывает их в случае сбоя канала.

Как следует из названия, STP вычисляет дерево, охватывающее все коммутаторы в сети. Все коммутаторы взаимодействуют друг с другом с помощью блоков данных протокола моста (BPDU). Контрольная точка согласовывается всеми коммутаторами в сети, и на основе этой контрольной точки идентифицируются и блокируются все избыточные ссылки, и только один путь может пересылать трафик. Если ссылка, которая ранее перенаправлялась, не работает, STP автоматически включает одну из избыточных заблокированных ссылок в качестве нового активного пути.

Обработка связующего дерева

Для получения топологии без петель STP использует три шага, указанные ниже.

• Выбор одного корневого моста
• Выберите один корневой порт на некорневых мостах
• Выберите один назначенный порт на каждом сегменте

Мы будем использовать рисунок 2 в наших объяснениях этих трех шагов

Выбор корневого моста

Корневой мост — это эталонная точка для всех коммутаторов в топологии связующего дерева.На всех подключенных коммутаторах происходит процесс выбора, и мост с наименьшим идентификатором моста выбирается в качестве корневого моста. Идентификатор моста — это 8-байтовое значение, состоящее из 2-байтового приоритета моста и 6-байтового идентификатора системы, который записан в MAC-адрес коммутатора.
Первоначально все коммутаторы начали рекламировать себя как корневую невесту в BPDU, но как только они получат вышестоящий BPDU, имеющий более низкий идентификатор моста, они прекращают передачу сообщений и начинают пересылку вышестоящих BPDU.
На приведенном выше рисунке все коммутаторы начинались с объявления себя корневым мостом.Когда коммутатор B получает BPDU от коммутатора A, он сравнивает свой идентификатор моста с идентификатором коммутатора A. Поскольку приоритеты одинаковы, MAC-адрес используется в качестве прерывателя связи, и, таким образом, коммутатор A выигрывает из-за более низкого MAC-адреса. Коммутатор B прекращает отправку своего BPDU и пересылает BPDU от A. Этот процесс повторяется также на коммутаторе C, и он прекращает генерацию BPDU и вместо этого пересылает BPDU от A. Теперь выбирается единственная эталонная точка для сети, которая является коммутатором A, все остальные коммутаторы теперь пересылают пакеты BPDU STP, полученные от корневого моста.

Прежде чем мы перейдем к следующему шагу, мы должны знать, что каждый порт в топологии связующего дерева окажется в одной из трех ролей портов.

• Корневой порт
• Назначенный порт
• Неназначенный / блокирующий порт

Выберите один корневой порт на некорневых мостах

После выбора корневого моста все некорневые мосты выбирают корневой порт. Это порт с наименьшей совокупной стоимостью пути к корневому мосту. Корневой порт — это восходящий порт, который всегда указывает на текущий корневой мост.

Таблица 1 перечисляет стоимость портов по умолчанию в соответствии с IEEE 802.1D

.

Пропускная способность канала	STP Стоимость
4 Мбит / с	250
10 Мбит / с	100
100 Мбит / с	19
1 Гбит / с	4
10 Гбит / с	2

На рисунке 2, как упомянуто выше, коммутатор A будет корневым мостом и будет отправлять BPDU через свои интерфейсы каждые 2 секунды со стоимостью корневого пути, равной 0, поскольку все его порты подключены к себе.После получения BPDU коммутаторы B и C добавят стоимость пути для порта Gi0 / 0, которая равна 4. Оба коммутатора затем пересылают BPDU со стоимостью корневого пути 4 из интерфейса Gi0 / 1. Затем они получат BPDU от другого коммутатора на Gi0 / 1 и добавят стоимость пути, равную 4.
Таким образом, оба коммутатора будут иметь стоимость корневого пути 4 на Gi0 / 0 и стоимость корневого пути 8 на Gi0 / 1 и как результат Gi0 / 0 будет корневым портом как на коммутаторе A, так и на коммутаторе B
Выберите один назначенный порт в каждом сегменте

Последний шаг — выбрать один назначенный порт в каждом сегменте.Порт, который объявляет самую низкую стоимость корневого пути в сегменте, выбирается как назначенный порт. Давайте рассмотрим сегмент между коммутатором B и коммутатором C. Оба коммутатора объявляют 4 как стоимость корневого пути, теперь есть связь. Каждый раз при выборе корневых портов или назначенных портов, если два или более порта сообщают об одинаковой стоимости корневого пути, возникает следующий механизм разрешения конфликтов

• Самый низкий идентификатор моста отправителя
• Самый низкий приоритет порта отправителя
• Самый низкий номер порта отправителя

Таким образом, порт Gi0 / 1 коммутатора B будет выбран в качестве назначенного порта для сегмента между коммутатором B и коммутатором C, поскольку коммутатор B объявил сегменту самый низкий идентификатор моста.

Все порты корневого моста являются назначенными портами, и любой порт, не являющийся корневым портом или назначенным портом, становится блокирующим портом и блокируется для предотвращения образования петель.

На рис. 3 (а) показана окончательная конвергентная топология без петель. Порт Gi0 / 1 коммутатора C переводится в состояние блокировки, петля эффективно удаляется, и мы получаем топологию, аналогичную топологии на рисунке 3 (b).

Обратите внимание, что если есть топологические изменения, STP повторно сойдется.В случае сбоя связи между коммутатором A и коммутатором B заблокированный порт коммутатора C будет переведен в состояние пересылки.

Когда когда-либо порт включен и запускается процесс STP, или всякий раз, когда STP повторно сходится к стабильной топологии, порт должен переходить в другое состояние порта STP. Существует пять состояний порта STP, которые указаны ниже

.

• Отключено
• Блокировка
• Прослушивание
• Обучение
• Экспедирование

Все порты при административном отключении попадают в категорию неактивного состояния.Когда порт включен, он запускается в состоянии блокировки, чтобы предотвратить любые петли, и, таким образом, пересылка трафика не происходит, и порт не узнает какие-либо MAC-адреса. Заблокированный порт будет обрабатывать только BPDU, полученные от соседних коммутаторов.

Порт, который можно выбрать как корневой порт или назначенный порт, перейдет в состояние прослушивания. В этом состоянии порту также будет разрешено отправлять пакеты BPDU, чтобы он мог активно участвовать в связующем дереве.

После периода времени, называемого задержкой пересылки (15 секунд по умолчанию), порт может перейти в состояние обучения, в котором он может изучать MAC-адреса и отправлять / получать BPDU, но по-прежнему не может пересылать или получать трафик.

После еще одной задержки пересылки порт переходит в состояние пересылки, и теперь он может отправлять и получать трафик и является полностью функциональным портом.

Знак квадратного корня (сделайте символ корня на клавиатуре)

Квадратный корень √ — это математический текстовый символ (о его значении мы поговорим позже), который люди переписывали с тех времен, когда была разработана кодировка ASCII. И вы можете набрать его прямо с клавиатуры. Я покажу вам, как это сделать, используя разные методы в зависимости от вашей операционной системы и вкусов.

Математика	≠	≤	≥	∫
	Σ	√	π	½

Математика корня

Квадратный корень из некоторого числа «А» — это число «Х», такое, что «Х», умноженное само на себя, будет «А». Каждое положительное число «A» имеет два квадратных корня: положительный и отрицательный ± √a. Хотя главный квадратный корень положительного числа является только одним из двух квадратных корней, обозначение «квадратный корень» часто используется для обозначения главного квадратного корня.Для положительного «A» главный квадратный корень можно также записать в экспоненциальной нотации как A ^1/2 .

Но корней больше, чем просто квадратные! Мы можем сказать, что N-й корень числа «X» — это число «R», которое при возведении в степень «N» равно «X» и обозначается как Rⁿ = X. Также в случае, если эти корни имеют парную мощность (2, 4, 6 …), у них будет 2 решения, положительное и отрицательное. И те, у кого есть непарная сила (1, 3, 5…) имел бы только одно положительное решение.

Я дам вам несколько примеров использования для наглядности.

Квадратный корень из 9 равен ± 3 (обозначается как ± √9 = 3), потому что (± 3) ² = 9 (3 · 3 = 9)
Пятый корень из 34 равен 2,024397 … (обозначается как ⁵√34 = 2,024397 …), потому что 2,024397 ⁵ = 34

Как ввести квадратный корень

Выберите свою систему, чтобы узнать.

Окна

Состояния переключения

Настройте раскладку клавиатуры в Windows так, чтобы вы могли вводить все дополнительные символы так же легко, как и любой другой текст.На настройку уходит около 5-10 минут, но вы будете печатать как начальник. Вы можете назначить математический квадратный корень √ и любые другие текстовые символы на клавиатуре, используя эту технику.

Карта персонажей

CharMap позволяет вам просматривать и использовать все символы и символы, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере. Вы можете ввести символ квадратного корня, используя его.

Mac

Emoji на iOS (iPhone, iPad и iPod touch)

Простой и красивый способ узнать, как добавить виртуальную клавиатуру для символов Emoji, отображаемых в виде небольших изображений.Сама клавиатура предустановлена ​​на вашем устройстве iOS, поэтому вам не нужно ничего скачивать или покупать.

Средство просмотра клавиатуры

Палитра символов

Палитра символов позволяет вам просматривать и использовать все символы и символы, включая знак квадратного корня, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере.

Linux

С клавиатуры

Карта символов

Карта символов позволяет вам просматривать и использовать все символы и символы, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере.Он также может помочь вам найти коды Unicode для ввода символов с клавиатуры.

HTML код

Ниже приведен список объектов HTML и JavaScript для символа квадратного корня. В Javascript вы должны написать как = «этот \ u2669 символ», если вы хотите включить специальный символ в строку.

Обозначение высокого качества для курса естественной биологии

Энтузиазм и опыт в области новаторской науки заработали знак высокого качества для онлайн-курса, преподаваемого профессором Университета Флориды.

Лоренцо Росси, доцент кафедры биологии корней растений Института продовольственных и сельскохозяйственных наук (UF / IFAS) Индийского речного исследовательского и образовательного центра (IRREC) в Форт-Пирсе, является ученым-исследователем, чей курс «Экология корней и ризосферы» был признан Центром передового опыта UF в области преподавания.

«Биология корней растений превратилась в захватывающую область сельскохозяйственных исследований только в течение последних 20 лет», — сказал Рональд Д. Кейв, директор IRREC. «Мы ожидаем, что биология корней растений будет способствовать развитию производства продовольственных культур во многих отношениях, и д-р.Опыт и энтузиазм Росси находятся в центре исследований Флориды по этой теме. Его работа феноменально повлияет на многих студентов и производственную практику ».

Корневая архитектура — это пространственная конфигурация растения, его корневая система и множество микросистем, окружающих корни растений. Каждое растение имеет уникальную корневую систему в зависимости от вида и состава почвы, в которой оно растет. Другие аспекты архитектуры корня растений связаны с питательными веществами, микроорганизмами и живыми насекомыми или нематодами рядом с корнями растений.

Новаторы с университетским центром передового опыта в области преподавания помогают профессорам с помощью электронных обучающих платформ для повышения качества обучения с помощью новых технологий дистанционного обучения. Кроме того, центр оценивает проведение онлайн-курсов и стремится к совершенству. Текущие онлайн-предложения прошли экспертную оценку на предмет инноваций, качества содержания курсов и доставки, сказал Кейв.

Когда коллеги Росси оценивали курс коренной науки, они отметили, что его студенты постоянно отмечали энтузиазм Росси по поводу этой темы.Материал курса новый и важный — новаторские научные знания, применимые к широкому кругу наук о растениях и почвах.

Были признаны технические аспекты курса. Например, «технология зеленого экрана» помогает студентам видеть доктора Росси, когда он читает лекции с «закадровым голосом» в слайд-модулях каждой лекции курса. Для наглядности лекции в правом нижнем углу каждого слайда появляется небольшое изображение лица Росси, читающего лекцию.Анимация иллюстрирует более сложные научные теории, и Росси активно присутствует во время дискуссий и встреч со студентами. Он выделяет текст или изображения и отвечает на вопросы студентов.

«Технология зеленого экрана дает нам инструменты для увеличения присутствия преподавателей в онлайн-обучении», — сказал Росси. «Студенты чувствуют себя более связанными с профессором, и они чувствуют себя частью класса». Несколько студентов, оценивавших курс Росси, отметили ценность этого курса для их академической работы.

Содержание курса охватывает биологию корней растений — актуальную тему сельскохозяйственных исследований, которая, как ожидается, произведет революцию в производстве продуктов питания.

«Идея о том, что корневую систему растений можно улучшить, нова, — сказал Росси. «Сельское хозяйство зародилось 2000 лет назад, и только в течение последних 20 лет ученые осознали, что структура корня растений влияет на урожай. Раньше их беспокоили только деревья и растения над землей ».

Росси сказал, что корневеды теперь знают, что оптимальная пространственная конфигурация корневой системы может помочь поглощать питательные вещества и воду, что полезно для плодовых деревьев.Росси также отмечает, что улучшенная корневая система позволит выращивать фрукты в развивающихся странах, где почвы не подходят для выращивания сельскохозяйственных культур.

«С улучшением архитектуры корневой системы мы можем это изменить», — сказал Росси.

«Экология корней и ризосферы — растущая и очень важная тема», — написал недавний бывший студент в анонимной оценке курса. «Я поражен, увидев, сколько технологий доступно для изучения корней, а сколько еще предстоит изучить».

Отмеченный наградами курс «Экология корней и ризосферы» предлагается на осенний семестр 2020 года в онлайн-формате для зарегистрированных студентов UF.В настоящее время идет регистрация; курс начнется 31 августа. Абитуриенты могут получить доступ к программе курса по этой ссылке. Чтобы зарегистрироваться на курс, посетите следующую страницу веб-сайта Колледжа сельскохозяйственных и медико-биологических наук UF / IFAS. Конкретные вопросы о курсе можно направлять доктору Росси по электронной почте: [email protected]

.

Foundation Level 2018 — Международная квалификационная комиссия по тестированию программного обеспечения ISTQB®

Аудитория

Программа базового уровня составляет основу схемы сертифицированных тестировщиков Международного совета по тестированию программного обеспечения (ISTQB®).

ISTQB® Foundation Level актуален для всех практик доставки программного обеспечения, включая Waterfall, Agile, DevOps и Continuous Delivery.

Квалификация базового уровня 2018 подходит для всех, кому необходимо продемонстрировать практические знания фундаментальных концепций тестирования программного обеспечения, включая людей, выполняющих такие роли, как тестировщики, аналитики тестирования, инженеры по тестированию, консультанты по тестированию, менеджеры тестирования, тестеры приемлемости пользователей и разработчики программного обеспечения.

Он также подходит для людей, которым необходимо базовое понимание тестирования программного обеспечения, включая руководителей проектов, менеджеров по качеству, менеджеров по разработке программного обеспечения, бизнес-аналитиков, ИТ-директоров и консультантов по управлению.

Новая программа 2018 признана предпосылкой для других сертификатов ISTQB®, где требуется уровень Foundation (примечание: все предыдущие выпуски уровня Foundation, включая программу 2011 года и «унаследованные» сертификаты уровня Foundation, останутся в силе).

Обучение

для уровня базового уровня сертифицированного тестировщика 2018 доступно у аккредитованных поставщиков обучения (классное, виртуальное и электронное обучение). Мы настоятельно рекомендуем посещать аккредитованный тренинг, поскольку членский совет ISTQB® оценит материалы на предмет соответствия и согласованности с программой.Информацию об аккредитованных поставщиках услуг обучения можно найти здесь или связаться с вашим местным советом членов ISTQB® или поставщиком экзаменов

.

Самостоятельное обучение с использованием учебной программы и рекомендованных материалов для чтения также является вариантом при подготовке к экзамену базового уровня. Ваш местный совет членов ISTQB® или поставщик экзаменов сможет предоставить информацию об экзаменах, например: доступные языки, где найти экзаменационный центр и т. д.

Посмотрите вводное видео уровня Foundation.

В начало

Содержание

В начало

Результаты деятельности

Бизнес-результаты, ожидаемые от кандидата, получившего сертификат Foundation Level 2018, следующие:

• Способствуйте эффективному общению, используя общий словарь для тестирования программного обеспечения.
• Понимать фундаментальные концепции тестирования программного обеспечения.
• Продемонстрировать понимание того, как различные методы разработки и тестирования, а также различные ограничения на тестирование могут применяться при оптимизации тестирования в различных контекстах.
• Эффективно вносить вклад в обзоры.
• Используйте установленные методы для разработки тестов на всех уровнях тестирования.
• Интерпретировать и выполнить тесты на основе заданных тестовых спецификаций. Отчет о результатах тестирования.
• Понимать принципы управления тестированием ресурсов, стратегий, планирования, контроля проектов и управления рисками
• Напишите и сообщите четкие и понятные отчеты о дефектах
• Понимание факторов проекта, определяющих приоритеты тестирования и подход к тестированию
• Понять ценность, которую тестирование программного обеспечения приносит заинтересованным сторонам
• Оцените, насколько действия по тестированию и рабочие продукты согласуются с целями, мерами и задачами проекта
• Помощь в выборе и внедрении инструмента для тестирования

В начало

Цели обучения

Цели обучения указаны для каждого раздела учебной программы и классифицируются следующим образом:

• K1: запомнить, распознать, вспомнить
• K2: понимать, объяснять, приводить причины, сравнивать, классифицировать, категоризировать, приводить примеры, резюмировать
• K3: применить, использовать
• K4: анализировать

В программе Foundation на 2018 год 62 цели обучения:

Цели базового обучения на 2018 год следующие:

Глава 1 Основы тестирования

1.1 Что такое тестирование?
ЛО-1.1.1	Определите типичные цели тестирования (K1)
ЛО-1.1.2	Отличие тестирования от отладки (K2)

1.2 Почему необходимо тестирование?
ЛО-1.2.1	Приведите примеры того, почему необходимо тестирование (K2)
ЛО-1.2,2	Опишите взаимосвязь между тестированием и обеспечением качества и приведите примеры того, как тестирование способствует повышению качества (K2)
ЛО-1.2.3	Различать ошибку, дефект и отказ (K2)
ЛО-1.2.4	Различать первопричину дефекта и его последствия (K2)

1.3 Семь принципов тестирования (K2)
ЛО-1.3,1	Объясните семь принципов тестирования (K2)

1,4 Процесс тестирования
ЛО-1.4.1	Объясните влияние контекста на процесс тестирования (K2)
ЛО-1.4.2	Опишите действия по тестированию и соответствующие задачи в рамках процесса тестирования (K2)
ЛО-1.4.3	Различение рабочих продуктов, поддерживающих процесс тестирования (K2)
ЛО-1.4,4	Объясните значение поддержания прослеживаемости между тестовой базой и тестовыми рабочими продуктами (K2)

1.5 Психология тестирования (K2)
ЛО-1.5.1	Определите психологические факторы, влияющие на успех тестирования (K1)
ЛО-1.5.2	Объясните разницу между мышлением, необходимым для тестовых заданий, и мышлением, необходимым для действий в области развития (K2)

Глава 2 Тестирование на протяжении жизненного цикла разработки программного обеспечения

2.1. Модели жизненного цикла разработки программного обеспечения
ЛО-2.1.1	Объясните взаимосвязь между действиями по разработке программного обеспечения и действиями по тестированию в жизненном цикле разработки программного обеспечения (K2)
ЛО-2.1.2	Определите причины, по которым модели жизненного цикла разработки программного обеспечения должны быть адаптированы к контексту проекта и характеристик продукта (K1)
ЛО-2.1.3	Вспомните характеристики хорошего тестирования, применимые к любой модели жизненного цикла (K1)

2.2 уровня тестирования (K2)
ЛО-2.2.1	Сравните различные уровни тестирования с точки зрения целей, основы тестирования, объектов тестирования, типичных дефектов и отказов, подходов и обязанностей (K2)

2.3 Типы испытаний (K2)
ЛО-2.3.1	Сравнение функционального, нефункционального тестирования и тестирования методом белого ящика (K2)
ЛО-2.3,2	Признать, что функциональные и структурные тесты проводятся на любом уровне тестирования (K1)
ЛО-2.3.3	Признать, что функциональные, нефункциональные тесты и тесты белого ящика проводятся на любом уровне тестирования (K1)
ЛО-2.3.4	Сравните цели подтверждающего тестирования и регрессионного тестирования (K2)

2.4 Техническое тестирование (K2)
ЛО-2.4,1	Обобщение триггеров для технического обслуживания (K2)
ЛО-2.4.2	Опишите роль анализа воздействия в тестировании технического обслуживания (K2)
ЛО-2.4.3	Опишите роль анализа воздействия в тестировании технического обслуживания (K2)

Глава 3 Статические испытания

3.1 Основы статического тестирования
ЛО-3.1,1	Распознавать типы рабочих продуктов программного обеспечения, которые можно исследовать с помощью различных методов статического тестирования (K1)
ЛО-3.1.2	Используйте примеры для описания значения статических испытаний (K2)
ЛО-3.1.3	Объясните разницу между статическими и динамическими методами, учитывая цели, типы дефектов, которые необходимо идентифицировать, и роль этих методов в жизненном цикле программного обеспечения (K2)

3.2 Процесс проверки
ЛО-3.2.1	Обобщите действия процесса обзора рабочего продукта (K2)
ЛО-3.2.2	Признать различные роли и обязанности в формальной проверке (K1)
ЛО-3.2.3	Объясните различия между разными типами обзора: неформальный обзор, пошаговое руководство, технический обзор и проверка (K2)
ЛО-3.2,4	Применение метода обзора к рабочему продукту для поиска дефектов (K3)
ЛО-3.2.5	Объясните факторы, способствующие успешной проверке (K2)

Глава 4 Методы тестирования

4.1 Категории методов испытаний
ЛО-4.1.1	Объясните характеристики, общие черты и различия между методами тестирования черного ящика, методами тестирования белого ящика и методами тестирования, основанными на опыте (K2)

4.2 Методики тестирования черного ящика
ЛО-4.2.1	Применить разделение эквивалентности для получения тестовых примеров из заданных требований (K3)
ЛО-4.2.2	Применение анализа граничных значений для получения тестовых примеров из заданных требований (K3)
ЛО-4.2.3	Применить тестирование таблицы решений для получения тестовых примеров из заданных требований (K3)
ЛО-4.2,4	Применить тестирование перехода между состояниями для получения тестовых примеров из заданных требований (K3)
ЛО-4.2.5	Объясните, как получить тестовые примеры из варианта использования (K2)

4.3 Методики тестирования белого ящика
ЛО-4.3.1	Объяснение заявления (K2)
ЛО-4.3.2	Объясните покрытие решения (K2)
ЛО-4.3,3	Объясните значение заявления и покрытия решений (K2)

4.4 Методы тестирования, основанные на опыте
ЛО-4.4.1	Объясните угадывание ошибок (K2)
ЛО-4.4.2	Объяснение исследовательского тестирования (K2)
ЛО-4.4.3	Объяснение тестирования на основе контрольного списка (K2)

Глава 5 Управление тестированием

5.1 Испытательная организация
ЛО-5.1.1	Объясните преимущества и недостатки независимого тестирования (K2)
ЛО-5.1.2	Определить задачи тест-менеджера и тестировщика (K1)

5.2 Планирование и оценка тестирования
ЛО-5.2.1	Обобщите цель и содержание плана тестирования (K2)
ЛО-5.2,2	Различия между различными подходами к тестированию (K2)
ЛО-5.2.3	Приведите примеры потенциальных критериев входа и выхода (K2)
ЛО-5.2.4	Применить знания о приоритезации, а также технических и логических зависимостях, чтобы запланировать выполнение теста для заданного набора тестовых примеров (K3)
ЛО-5.2.5	Определите факторы, которые влияют на усилия, связанные с тестированием (K1)
ЛО-5.2,6	Объясните разницу между двумя методами оценки: методом на основе показателей и методом на основе экспертов (K2)

5.3 Контроль и контроль испытаний
ЛО-5.3.1	Показатели отзыва, использованные для тестирования (K1)
ЛО-5.3.2	Обобщите цели, содержание и аудитории для отчетов об испытаниях (K2)

5.4 Управление конфигурацией
ЛО-5.4.1	Обобщите, как управление конфигурацией поддерживает тестирование (K2)

5.5 Риски и тестирование
ЛО-5.5.1	Определите уровень риска, используя вероятность и влияние (K1)
ЛО-5.5.2	Различать риски проекта и продукта (K2)
ЛО-5.5,3	Опишите на примерах, как анализ риска продукта может повлиять на тщательность и объем тестирования (K2)

5.6 Управление дефектами
ЛО-5.6.1	Напишите отчет о дефектах, описывающий дефекты, обнаруженные во время тестирования (K3)

Глава 6. Поддержка инструментов для тестирования

6.1 Рекомендации по тестированию
ЛО-6.1.1	Классифицируйте инструменты тестирования в соответствии с их назначением и поддерживаемыми ими тестовыми действиями (K2)
ЛО-6.1.2	Определение преимуществ и рисков автоматизации тестирования (K1)
ЛО-6.1.3	Помните об особенностях выполнения тестов и инструментов управления тестами (K1)

6.2 Планирование и оценка тестирования (K3)
ЛО-6.2.1	Определите основные принципы выбора инструмента (K1)
ЛО-6.2.2	Напомнить цели использования пилотных проектов для внедрения инструментов (K1)
ЛО-6.2.3	Определите факторы успеха для оценки, внедрения, развертывания и постоянной поддержки инструментов тестирования в организации (K1)

В начало

Программа обучения

Программа базового уровня является основой для международной квалификации по тестированию программного обеспечения на базовом уровне.

Международная квалификационная комиссия по тестированию программного обеспечения ^® (ISTQB ^®) предоставляет национальным экзаменационным органам возможность аккредитовать поставщиков услуг обучения и составить экзаменационные вопросы на их местном языке.

Провайдеры обучения будут производить учебные материалы и определять соответствующие методы обучения для аккредитации, а программа обучения поможет кандидатам в подготовке к экзамену.

Сертифицированный тестировщик Базовый уровень тестирования программного обеспечения

Квалификация базового уровня предназначена для всех, кто занимается тестированием программного обеспечения.Сюда входят люди с такими ролями, как тестировщики, аналитики тестирования, инженеры по тестированию, консультанты по тестированию, менеджеры по тестированию, тестеры приемлемости пользователей и разработчики программного обеспечения.

Эта квалификация базового уровня также подходит для всех, кто хочет получить базовые знания о тестировании программного обеспечения, например для менеджеров проектов, менеджеров по качеству, менеджеров по разработке программного обеспечения, бизнес-аналитиков, ИТ-директоров и консультантов по менеджменту. Обладатели сертификата Foundation смогут перейти на более высокий уровень квалификации по тестированию программного обеспечения.

Программа базового уровня 2018 доступна в разделе «Материалы для скачивания».

В начало

Структура экзамена

Экзамен базового уровня состоит из 40 вопросов с несколькими вариантами ответов, при этом проходная оценка 65% должна быть завершена в течение 60 минут. Участники, которые сдают экзамен не на своем разговорном языке, получат дополнительно 25% времени, в общей сложности 75 минут.

Модуль	Количество вопросов	Продолжительность экзамена (минуты)	Продолжительность экзамена + 25% (минуты)
Базовый уровень	40	60	75

Аккредитованные учебные заведения

Экзамены можно сдавать как часть курса, проводимого Аккредитованным провайдером обучения, или сдавать самостоятельно в экзаменационном центре или на государственном экзамене.

Типичная продолжительность обучения базового уровня, предлагаемого аккредитованным провайдером обучения, составляет 3 дня. Завершение аккредитованного учебного курса не является обязательным условием для сдачи экзамена.

Пожалуйста, посетите веб-сайты советов членов ISTQB ^® и ISTQB ^® аккредитованных поставщиков обучения, чтобы узнать о наличии экзаменов и тренингов.

В начало

материалы для загрузки

Syllabus Документы:

Экзаменационных документов:

Общие файлы:

В начало

терминология — Почему такое название «квадратный корень»?

Этот вопрос недавно появился на сайте StackExchange по английскому языку и использованию (здесь).Я воспроизведу здесь ответ, который дал там.

Короче говоря, корень — это перевод латинского слова radix , которое само по себе является неправильным переводом арабского слова jadhr. Это слово имеет несколько значений в арабском языке, одно из которых действительно , корень . Но арабоязычные математики ¹ , которые представили его, использовали его в другом значении: «основание», «основание», «низшая часть».

^{1 Я говорю «говорящие по-арабски», потому что некоторые из них были неарабами и писали на арабском языке, лингва-франка своего времени и места.Например, Мухаммад ибн Муса аль-Хваризми, который традиционно считается основателем алгебры, был персом. В частности, слово алгебра происходит от арабского слова al-jabr , «балансировка», которое фигурирует в названии его самого известного труда.}

Обсуждение

Согласно Британской энциклопедии,

В IX веке арабские писатели обычно называли один из равных множителей числа jadhr («корень»), а их средневековые европейские переводчики использовали латинское слово radix (от которого происходит радикальное прилагательное).

Но почему авторы математических трактатов на арабском языке использовали слово jadhr ?

Причина связана с различием между «конкретными» и «абстрактными» числами (см., Например, здесь), которое, по-видимому, было очень важно для математиков того времени:

конкретное число: число, относящееся к определенному объекту или объектам, как в три собаки, десять человек
абстрактное число: число, которое не обозначает количество какого-либо конкретного вида вещей

Словарь Коллинза, здесь и здесь

(В настоящее время эти вопросы обычно относят к науке и технике под названием размерный анализ.)

Похоже, что существовала традиция мышления, восходящая к древнему Египту, что для вычисления, например, площадь прямоугольника, нельзя просто перемножить два абстрактных числа, обозначающих длины сторон прямоугольника. Скорее, одно из этих чисел нужно сначала умножить на «основу» площади (я не уверен, есть ли какое-либо концептуальное различие между этим типом «основы» и современной концепцией единицы измерения). Именно эту «основу» математики, говорящие на арабском языке, назвали jadhr , арабское слово, означающее «основа», «основание», «низшая часть».Однако джадхр также означает «корень», и многие переводчики арабских слов на другие языки (включая латинский и китайский) ошибочно полагали, что джадхр используется в текстах с таким значением. Вот соответствующий отрывок из источника, который я процитирую более подробно ниже:

Таким образом, египтянин вычислил квадрат, сначала умножив одну сторону (9 ккет ) на единицу квадрата. Это был квадратный базис ( джадхр ), который нужно было умножить на другую сторону, представляя чистое число.Тот же самый процесс также описан аль-Ховаризми, который говорит: «И в каждом квадратном рисунке одна из его сторон, умноженная на квадратную единицу, — это его джадхр … а мы делаем другую сторону, а именно, hj , три и это номер его джадхр ».

С. Гандз, О происхождении термина «корень». Вторая статья ,
The American Mathematical Monthly, vol.35, стр. 74, 1928.

Расширенное обсуждение

Следующее взято из статьи О происхождении термина «корень» С. Гандца (The American Mathematical Monthly vol. 33, 261–265, 1926):

Термин «корень» имеет арабское происхождение. «Латинские произведения переведены с арабские имеют основание для общего термина, в то время как те, унаследованные от У римской цивилизации latus ». ² Radix («корень») — это арабский jadhr, , а latus (греч. πλευρά, Pleura, означает «ребро» или «сторона») — сторона геометрического квадрата. .

^{2 См. Smith, History of Mathematics, vol. II, стр. 150.}

Это, конечно, довольно странно, что в этой связь. Это предполагает, что если основное число является корнем, квадрат может быть куст, и так далее в своего рода математическом саду.

Китайцы действительно используют слово кун для обозначения корня, травы и кустарника, и индусы также используют слово мула для обозначения корня растения, но это было очень вероятно, из-за арабского влияния, которое так часто наблюдается в Китае и которое возможно, распространился в Индию через Китай.Однако факт, что таким образом пока что у нас нет удовлетворительного объяснения того, почему этот ботанический термин должен нашли место в теории чисел. …

Следовательно, стоящая перед нами проблема, как уже ясно сформулировал профессор Смит, состоит в том, чтобы выяснить, были ли средневековые латинские авторы правы в своем переводе арабского слова jadhr на radix («корень»). …

Таким образом, писатель начал исследовать истинное значение слова слово jadhr , не зависящее от лексиконов или латинских версий тринадцатого века, но ищущих значение, как оно проявляется в рукописях самих старых арабских математиков.

Мухаммад ибн Муса аль-Хваризми (ок. 825 г.) — старейший арабский математик с большой известностью, и именно его ‘Ильм аль-джабр ва’ль мнукабала дал Европе как имя, так и основополагающие принципы алгебры. . Его глава Баб аль Мисаха («О геометрии») начинается следующим образом: «Знайте, что значение выражения« один в одном »- это« площадь »; и его значение составляет один локоть (в длину) на один локоть ( и всякая крыша с равными сторонами и углами, каждая сторона которой имеет один локоть, является единицей (квадратом).Но если у него два локтя с каждой стороны и равные стороны и углы, то вся крыша в четыре раза больше крыши, имеющей один локоть на один локоть. … И в каждой квадратной крыше с равными сторонами одна из ее сторон (умноженная) на квадратную единицу — это ее джадхр ; или если то же самое умножить на два (квадратные единицы), то это будет как два из его джазов , будь эта крыша маленькая или большая ». …

Джадхр означает не только «корень», но также «основание», «фундамент», «низшая часть».Мухаммед ибн Муса … начинает свою главу о площадях с введения нового понятия квадратной единицы. Затем он говорит, что для того, чтобы получить площадь любой фигуры, мы должны сначала умножить одну сторону на квадратную единицу; тогда это основа, которую нужно умножить на другую сторону. Мы умножаем не одну сторону на одну сторону, а одну джадхр , представляющую квадратную основу, на одну сторону, представляющую число. Такое же определение и идея можно найти и в других местах его алгебры. …

Термин [ джадхр ] означает не «корень», а «квадратный базис», умножением которого мы получаем квадратную площадь.Это было причиной того, что джадхр использовалось более поздними авторами, такими как Омар Хайям, в качестве основного числа квадратного числа. Последний больше ничего не знал об исходном значении джадхр , и он использовал это слово в широком смысле для обозначения дил ‘ (греч. πλευρά ), что означает« ребро »или« сторона ». Но он, как и аль-Ховаризми, все же знал, что это конкретное число в отличие от абстрактного числа.

Ко времени Беха Эддина (ок. 1600 г.) первоначальное значение было полностью забыто.В своем Kholdsat al-Hisdb («Суть арифметики») он говорит: «То, что умножается на себя, называется джадхр в арифметике, дил ‘ (« сторона ») в геометрии и шай’ ( «Вещь», «причина») в алгебре ». Он определенно понимал под джадхр абстрактный «корень». В этой неверно истолкованной форме термин jadhr вошел в средневековую латынь как radix .

и О происхождении термина «корень». Вторая статья того же автора (The American Mathematical Monthly, vol.35, 67–75, 1928), находим дальнейшее объяснение:

Теперь интересно обнаружить, что этот довольно странный процесс возведения площади в квадрат сохранился в Математическом папирусе Райнда как самый старый метод вычисления площади, использовавшийся египтянами еще в 1650 году до нашей эры. Таким образом, вполне возможно, что при формулировании этого геометрического определения джадхр ал-Ховаризми были подсказаны не только математические соображения, но и старые исторические воспоминания о египетской геометрии.

Египетской единицей длины при измерении земли была хет в 100 локтей. Самой распространенной единицей площади был сетат или квадрат Khet , который содержал 10 000 квадратных локтей. Для практических целей при измерении земли они использовали единицу, называемую локтем земли или локтем — полосой. Это была узкая полоска земли в сто локтей в длину и в один локоть в ширину. Меньшие части setat были выражены в таких локтях. Чтобы получить площадь прямоугольника, в хетах иногда умножали его длину в локтях на ширину.Это дало им правильный ответ в локтях. Тем не менее, в задаче 48 мы более четко видим, что при умножении 8 кхет на 8 кхет и 9 кхет на 9 кхет «фактически написанное произведение выглядит как умножение 9 ‘ сет в на чистое число 9 ».

Таким образом, египтянин вычислил квадрат, сначала умножив одну сторону (9 ккет ) на единицу квадрата. Это был квадратный базис ( джадхр ), который нужно было умножить на другую сторону, представляя чистое число.Тот же процесс описан аль-Ховаризми, который говорит: «И в каждой квадратной фигуре одна из его сторон, умноженная на квадратную единицу, является его джадхром … и мы делаем другую сторону, а именно, hj , три, и это номер его джадхра ».

Этот архаический способ вычисления квадрата находит свое оправдание не только в «своеобразной египетской системе умножения», но и в самой природе примитивных вычислений. Древние египтяне не вычисляли площади и не измеряли свои поля в соответствии с абстрактными правилами.Первоначально они определили площадь экспериментальным практическим способом, взяв небольшую квадратную меру и попробовав, сколько раз она содержалась в измеряемом поле, «как мы сегодня измеряем ткань по ярдам». Для этой цели простая мера длины, Khet или шнур, не могла быть использована. Поэтому они должны были создать квадратную единицу, полосу в локтях, равную кхет в длину и один локоть в ширину. Это был первый джадхр на квадратной основе, использовавшийся в практической жизни.

Эта полоска в локтевую полоску также, по всей вероятности, могла быть основной идеей египетской концепции квадратного корня. Идея квадратного корня существовала в Египте, и технический термин для ее обозначения был Knbt , буквально «угол» или «угол». У Пита есть объяснение этому, что длина каждой из двух сторон квадрата, содержащего любой его угол, была его квадратным корнем. Однако не чистая, одномерная сторона содержит «угол», а только jadhr , сторона, умноженная на квадратную единицу, содержит «угол».«Угол» или «угол» — это простое слово для обозначения маленькой квадратной единицы. Аполлоний (ок. 225 г. до н. Э.) Определяет угол как сжатие поверхности в одной точке под ломаной линией. Поскольку слово «угол», «краеугольный камень» обычно подразумевает также значение «нижняя часть», «основание, основание», мы можем видеть в египетском Knbt источник и происхождение греческого pythmenes (основания), арабского асс и джадхр, ивритские иккар и аш и индуистские мула .

Таким образом, мы можем проследить происхождение нашего термина «корень» из алгебраической термин, обозначающий конкретное число с основанием, первой степенью ( x ) и геометрический термин, обозначающий основную квадратную единицу ( x · 1 ² ). Все три концепции содержатся в арабском джадхр и сохранены в определениях аль-Ховаризми.

Политика и процедуры дозорных событий

Совместная комиссия приняла официальную Политику дозорных событий в 1996 году, чтобы помочь больницам, которые испытывают серьезные неблагоприятные события, повысить безопасность и извлечь уроки из этих дозорных событий.Тщательное расследование и анализ событий, связанных с безопасностью пациентов (событий, не связанных в первую очередь с естественным течением болезни или основным состоянием пациента), а также оценка корректирующих действий необходимы для снижения риска и предотвращения причинения вреда пациенту. Политика Sentinel Event объясняет, как Объединенная комиссия сотрудничает с организациями здравоохранения, которые пережили серьезное событие, связанное с безопасностью пациентов, для защиты пациента, улучшения систем и предотвращения дальнейшего вреда.

Дозорное событие — это Событие безопасности пациента, которое достигает пациента и приводит к любому из следующих событий:

Событие также может считаться дозорным событием, даже если его результатом не была смерть, необратимый вред, серьезный временный вред и вмешательство, необходимое для поддержания жизни.См. Список ниже.

Такие события называются «дозорными», потому что они сигнализируют о необходимости немедленного расследования и реагирования. Каждой аккредитованной организации настоятельно рекомендуется, но не обязательно, сообщать Совместной комиссии о дозорных событиях. Организации получают выгоду от самоотчетности следующим образом:

• Совместная комиссия может предоставить поддержку и экспертизу во время рассмотрения дозорного события.

• Возможность сотрудничать со специалистом по безопасности пациентов в отделе по борьбе с событиями Совместной комиссии Управления качества и безопасности пациентов.

• Отчетность повышает уровень прозрачности в организации и способствует культуре безопасности.

• Reporting сообщает общественности о том, что организация здравоохранения делает все возможное, чтобы предотвратить подобные события, связанные с безопасностью пациентов, в будущем.

Кроме того, сообщение о событии позволяет добавить «извлеченные уроки» из этого события в базу данных о дозорных событиях Объединенной комиссии, тем самым способствуя общему знанию о дозорных событиях и снижению риска таких событий.