Содержание

Как найти время, скорость и расстояние

Расстояние

Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.

Расстояние — это длина от одного пункта до другого.

  • Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.

Расстояние обозначается латинской буквой s.

Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).

Формула пути

Чтобы найти расстояние, нужно умножить скорость на время движения:

s = v × t

Скорость

Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.

Скорость определяет путь, который преодолеет объект за единицу времени.

Скорость обозначается латинской буквой v.

Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.

Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.

Формула скорости

Чтобы найти скорость, нужно разделить путь на время:

v = s : t

Показатели скорости чаще всего выражаются в м/сек или км/час.

Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.

Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.

Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.

Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.

Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.

Время

Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.

Время — это продолжительность каких-то действий, событий.

  • Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.

Время движения обозначается латинской буквой t.

Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.

Формула времени

Чтобы найти время, нужно разделить расстояние на скорость:

t = s : v

Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Как рассуждаем:

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:

v = 50 м/мин

t = 15 мин

s = v × t = 50 × 15 = 750 (м)

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?

Как рассуждаем:

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

100 : 25 = 4

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

100 : 50 = 2

Значит, скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

4 (м/с) > 2 (м/с)

Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.

Ответ: первый школьник добежал быстрее.

Если известны скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?

Как рассуждаем:

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:

s = 500 м

v = 100 м/мин

t = s : v = 500 : 100 = 5 (мин)

Ответ: от школы до стадиона мы дойдем за 5 минут.

Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

Урок 35. задачи на движение — Математика — 5 класс

Математика

5 класс

Урок № 35

Задачи на движение

Перечень вопросов, рассматриваемых в теме:

  1. Понятия скорости, времени, расстояния.
  2. Формулы нахождения скорости, времени, расстояния.
  3. Понятия скорости сближения, скорости удаления.

Глоссарий по теме

Расстояние – это длина от одного пункта до другого.

Большие расстояния, в основном, измеряются в метрах и километрах.

Расстояние обозначается латинской буквой S.

Чтобы найти расстояние, надо скорость умножить на время движения:

S = v ∙ t

Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.

Скорость обозначается латинской буквой v.

Чтобы найти скорость, нужно расстояние разделить на время движения:

v = S : t

Время – это продолжительность каких-то действий, событий.

Время движения обозначается маленькой латинской буквой t.

Чтобы найти время, нужно расстояние разделить на скорость движения:

t = S : v

Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Чтобы найти скорость сближения, нужно сложить скорости объектов.

Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Чтобы найти скорость удаления, нужно сложить скорости объектов.

Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.

Основная литература

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010

Дополнительная литература

1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014

2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.

3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010

Теоретический материал для самостоятельного изучения

Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.

Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.

Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.

Рассмотрим задачу:

Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?

Решение:

Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.

Давайте найдём скорость первого школьника.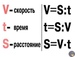 Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:

200 м : 50 с = 4

Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч). 

У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:

200 м : 50 с = 4 (м/с)

Скорость движения первого школьника составляет 4 метра в секунду.

Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:

200 м : 100 c = 2 (м/с)

Скорость движения первого школьника – 4 (м/с).

Скорость движения второго школьника – 2 (м/с).

4 (м/с) > 2 (м/с)

Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.

Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.

Рассмотрим задачу:

От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?

Решение:

Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:

1200 : 600 = 2 (мин)

Ответ: мы доедем до спортивной секции за 2 минуты.

Скорость, время и расстояние связаны между собой.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:

S = v ∙ t

Рассмотрим задачу:

Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?

Решение:

Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:

v = 60 (м/мин)

t = 15 (минут)

S = v ∙ t = 60 ∙ 15 = 900 (метров)

Ответ: мы прошли 900 метров.

Если известно время и расстояние, то можно найти скорость:

v = S : t

Рассмотрим задачу:

Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?

Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?

Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:

S = 800 метров

t = 8 минут

v = S : t = 800 : 8 = 100 (м/мин)

Ответ: скорость школьника была 100 м/мин.

Если известна скорость и расстояние, то можно найти время:

t = S : v

Рассмотрим задачу:

От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?

Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?

Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:

S = 600 метров

v = 120 (м/мин)

t = S : v = 600 : 120 = 5 (минут).

Ответ: мы дойдём до спортивной секции за 5 минут.

Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:

Теперь рассмотрим типы задач на движение.

Задачи на сближение.

Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.

Чтобы найти скорость сближения, нужно сложить скорости объектов.

Задача.

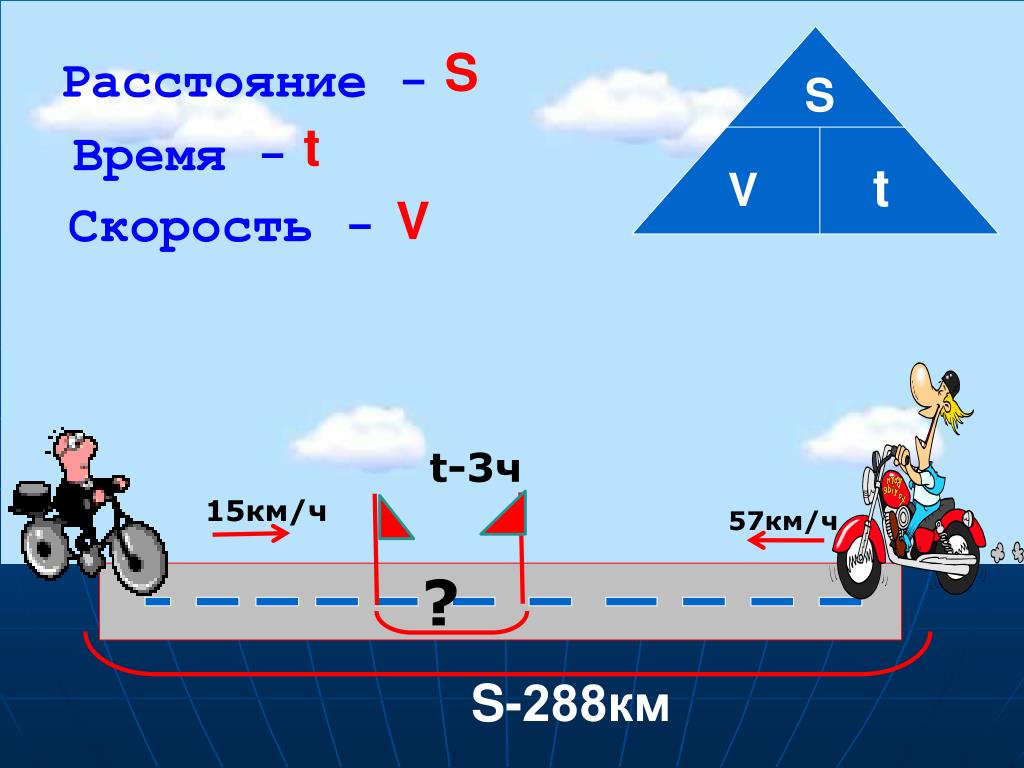
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.

Решение:

  1. Найдём скорость сближения велосипедистов:

13 км/ч + 15 км/ч = 28 км/ч

  1. Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:

28 ∙ 3 = 84 км

Ответ: расстояние между населёнными пунктами 84 км.

Задачи на скорость удаления.

Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.

Чтобы найти скорость удаления, нужно сложить скорости объектов.

Рассмотрим задачу:

С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?

Решение:

  1. Определим скорость удаления. Для этого сложим их скорости:

60 + 130 = 190 км/ч.

Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.

  1. Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:

190 ∙ 2 = 380 км.

Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.

Задачи на движение объектов в одном направлении.

В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.

Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.

Рассмотрим задачу:

Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?

Решение:

  1. Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:

130 км/ч − 90 км/ч = 40 км/ч

  1. Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:

40 ∙ 3 = 120 км

Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.

Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.

Задача.

Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?

Решение:

  1. Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:

90 ∙ 3 = 270 метров

  1. Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 255 метров:

85 ∙ 3 = 255 метров

  1. Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):

900 + 255 = 1155 м

1155 – 270 = 885 м

Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):

900 – 270 = 630 м

630 + 255 = 885 м

Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.

  1. Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?

В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:

90 ∙ 1 = 90 м

85 ∙ 1 = 85 м

900 + 85 – 90 = 985 – 90 = 895 м

Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров.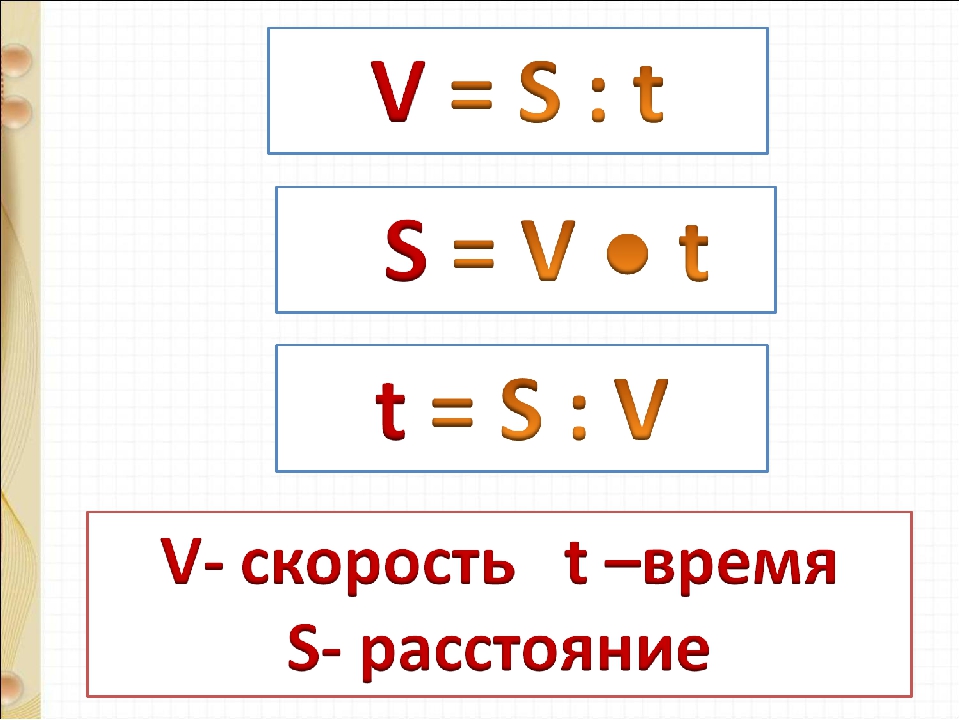 Это был наш ответ на первый вопрос задачи:

90 ∙ 3 = 270 м

85 ∙ 3 = 255 м

900 + 255 – 270 = 1155 – 270 = 885 м

Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.

А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:

900 : 5 = 180 минут.

Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.

Разбор решения заданий тренировочного модуля

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Заполните таблицу:

S

v

t

1.

135 км

9 км/ч

____ ч

2.

____ м

12 м/с

4 с

3.

132 м

____ м/мин

11 мин

Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:

  1. Надо найти время: t = S : v

135 : 9 = 15 часов.

  1. Надо найти расстояние: S = v ∙ t

12 ∙ 4 = 48 м.

  1. Надо найти скорость: v = S : t

132 : 11 = 12 м/мин.

Верный ответ:

S

v

t

1.

135 км

9 км/ч

15 часов

2.

48 м

12 м/с

4 с

3.

132 м

12 м/мин

11 мин

№2. Тип задания: единичный / множественный выбор

Выберите верный ответ к задаче:

Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?

Варианты ответов:

  1. 70
  2. 30
  3. 270
  4. 240

Эта задача относится к типу задач на сближение, т.е. нам надо:

  1. сложить скорости мотоциклиста и автомобилиста:

60 + 30 = 90 км/ч – скорость сближения;

  1. узнать, сколько километров они пройдут за 3 часа вместе. Для этого:

90 ∙ 3 = 270 км;

  1. из общего расстояния нам осталось вычесть пройденное:

300 – 270 = 30 км

Верный ответ: 2. 30 км.

Урок математики по теме «Скорость. Время. Расстояние». 4-й класс

Цели:

  • закрепить знания нахождения скорости, времени, расстояния;
  • ввести формулы;
  • учиться решать задачи с этими величинами по формулам и без них;
  • развивать мышление и память;
  • прививать любовь к математике.

Ход урока

1. Организация учащихся.

2. Сообщение темы.

— Сегодня на уроке мы закрепим знания нахождения скорости, времени, расстояния. Будем учиться решать задачи с помощью формул.

— А работать мы будем в форме соревнований трех команд:

  • 1 ряд — автомобилисты
  • 2 ряд — летчики
  • 3 ряд — мотоциклисты

— Баллы будем выставлять на доске

3. Соотнести записи с картинкой.

— Как вы думаете, что написано на доске? (Скорости)

— Соотнесите их с нужной картинкой.

(12 км/ч, 60 км/ч, 5 км/ч, 70 км/ч, 120 км/ч, 800 км/ч, 8 км/с, 50 км/ч,250 км/ч.

Автобус, самолет, ракета, пешеход, поезд, велосипедист , автомобиль, пароход, мотоциклист) Каждая команда выставляет по 3 ученика.

— Как вы понимаете км/сек, км/ч, м/мин.

Решение задач.

а) В тетрадь записываете ответ с наименованием.

Таблица на интерактивной доске.

Скорость
V		 Время
t		 Расстояние
S
5 м/с 15 сек. ? м.

Муха летела со скоростью 5 м/сек. 15 сек. Какое расстояние она пролетела?

— Что известно?

— Повторите вопрос задачи.

— Как найти расстояние?

— Кто может записать буквами это правило?

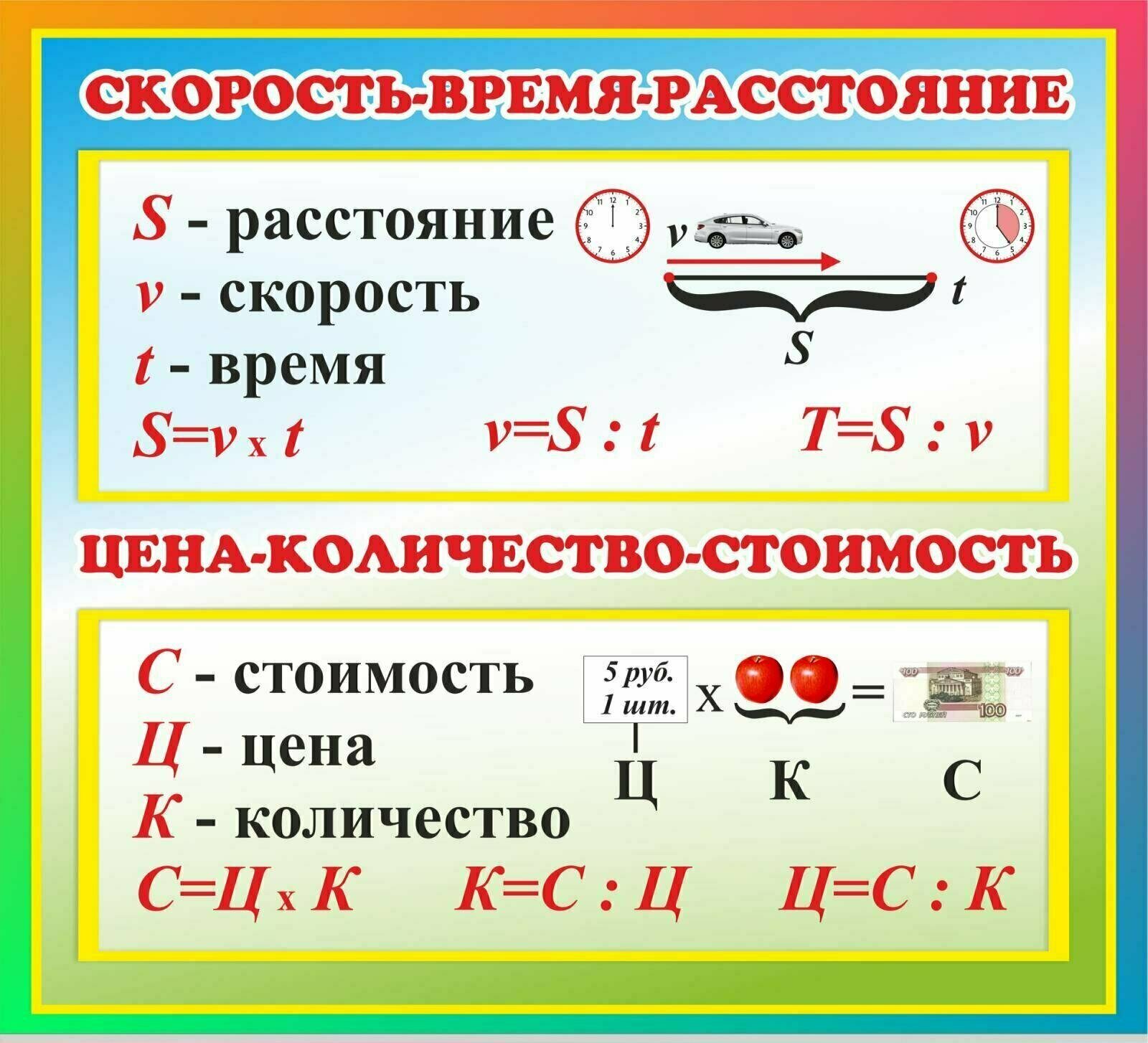
— Запишите эту формулу в тетрадь s=v * t.

Скорость
V		 Время
t		 Расстояние
S
? м/с 3 сек. 78 м.

За 3 сек. Сокол пролетел 78 метров. Какова скорость сокола?

— Что известно?

— Повторите вопрос задачи.

— Как найти скорость?

— Кто может записать буквами это правило?

— Запишите эту формулу в тетрадь v=s:t.

Скорость
V		 Время
t		 Расстояние
S
10 м./сек ? сек. 100 м.

Грач пролетел 100 метров со скоростью 10 м/сек. Сколько времени он был в пути?

— Что известно?

— Повторите вопрос задачи.

— Как найти время?

— Кто может записать буквами это правило?

— Запишите эту формулу в тетрадь t=s:v.

Баллы. Молодцы!

б) Составление задач.

  • 1 ряд — нахождение V
  • 2 ряд — нахождение t
  • 3 ряд — нахождение S

Баллы. Отлично.

в) Заполнить таблицу.

Скорость
V		 Время
t		 Расстояние
S
90 км/ч 6 ч. ? км.
? км/ч 30 ч. 1500 км
70 м/мин. ? мин. 840 м

Решение записываете в тетрадь с наименованием, рядом записываете формулу.

Самостоятельная работа.

Проверка.

90 * 6 = 540 (км)

s=v*t

1500:30=50 (км/ч) v=s:t

840:70=12 (ч) t=s:v

Замечательно!

4. Работа с учебником.

Коллективное решение задачи стр. 60 №4

Две бабы-яги поспорили, что быстроходнее ступа или помело? Одну и ту же дистанцию в 228 км баба-яга в ступе пролетела за 4 ч, а баба яга на помеле за 3 ч. Что больше, скорость ступы или помела?

а) составление таблицы.

  Скорость
V		 Время
t		 Расстояние
S
ступа      
помело      

б) решение у доски и в тетрадях.

1) 288:4=72 (км/ч) — скорость ступы

2) 288:3=96 (км/ч) — скорость помела

3) 96-72=24 (км/ч) — больше скорость помела, чем скорость ступы.

Ответ запишите самостоятельно.

Баллы.

5. Физминутка.

6. Задача повышенной сложности.

Это очень интересно (на доске написана задача)

— Кто видел счетчик в автомобиле, который ведет отчет километров, которые проехал автомобиль?

— Как он называется (спидометр).

Счетчик автомобиля показал 12921 км. Через 2 час на счетчике опять появилось число, которое читалось одинаково в обоих направлениях. С какой скоростью ехал автомобиль?

Решение.

1) 13031 — 12921=110 (км) — проехал за 2 ч.

2) 110 :2 = 55 (км/ч) — скорость автомобиля.

Ответ.

7. Итоги урока.

— Как найти расстояние, скорость, время (формула).

— Баллы. Итог.

Молодцы! Всем огромное спасибо!

Дополнительная задача.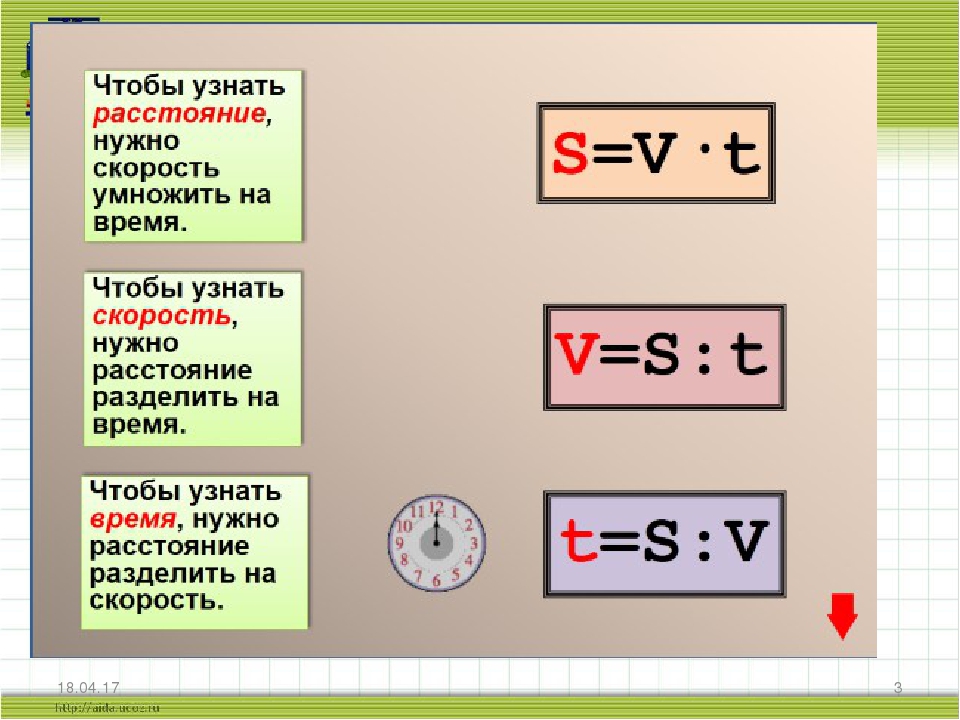

Туристы ехали в первый день 5 ч. На лодке со скоростью 12 км/ч. Во второй день они были в пути столько же времени, увеличив скорость на 3 км/ч. Сколько километров проехали туристы на лодке во второй день?

Самостоятельно заполнить таблицу и решить задачу.

Математика 4 класс Богданович. Решебник. ГДЗ. Скорость, время, расстояние.

Сложение и вычитание многозначных чисел.

Категория: —>> Математика 4 класс Богданович  
Задание:  —>>     381 — 400  401 — 418 



наверх

Задание 381.

Рассмотри решение задачи и прочитай объяснение.
Задача. За 2ч автобус проехал 120 км, проезжая за каждый час одинаковое расстояние. Сколько километров автобус проезжал за 1 ч?
Решение: 120 : 2 = 60 (км). Ответ: за 1 ч автобус проезжал 60 км.
Объяснение. Если за каждый час автобус проезжает 60 км, то говорят, что он движется со скоростью 60. км в час.
Это записывают так: 60 км/ч.
Чтобы найти скорость, надо расстояние поделить на время.

Задание 382.

По данным таблицы вычисли скорость движения велосипедиста, пассажирского самолёта, ласточки.


Решение:
  • Скорость велосипедиста: 28 км : 2 ч = 14 км/ч.
  • Скорость ласточки: 180 км : 2 ч = 90 км/ч.
  • Скорость самолета: 1500 км : 3 ч = 500 км/ч.



Задание 383.

Велосипедист был в пути 6 ч, а мотоциклист 2 ч. Велосипедист проехал 72 км, а мотоциклист 100 км. На сколько скорость мотоциклиста больше скорости велосипедиста?

План решения
  • 1) Какова скорость велосипедиста?
  • 2) Какова скорость мотоциклиста?
  • 3) На сколько скорость мотоциклиста больше скорости велосипедиста?

Решение:
  • 1) 72 : 6 = 12 (км/ч) скорость велосипедиста;
  • 2) 100 : 2 = 50 (км) скорость мотоциклиста;
  • 3) 50 — 12 = 38 (км/ч).
  • Ответ: скорость мотоциклиста на 38 км/ч больше, чем скорость велосипедиста.

Задание 384.

Расстояние 400 м мальчик пробежал туда и обратно за 4 мин. С какой скоростью бежал мальчик?


Решение:
  • 1) 400 : 4 = 100 (м/мин).
  • Ответ: скорость мальчика 100 м/мин.

Задание 385.

Расстояние между условными пунктами K и M на орбите искусственного спутника Земли составляет 320 км. Четвёртую часть этого расстояния спутник пролетел за 10 с. С какой скоростью он летел?


Решение:
  • 1) 320 : 4 = 80 (км) четвертая часть расстояния;
  • 2) 80 : 10 = 8 (км/с).
  • Ответ: скорсть спутника 8 км/с.

Задание 386.


Решение:
1)
8000 + 7000 = 1500090000 + 7000 = 970001500 − 300 = 12001210 − 300 = 910
600 + 7000 = 760023000 + 7000 = 300002000 − 300 = 17005200 − 300 = 4900
60 + 7000 = 706045000 + 7000 = 52000900 − 300 = 60011000 − 300 = 10700
    2)
  • 20 грн 08 к − 59 к = 2008 к − 59 к = 949 к = 9 грн 49 к .
  • 12 грн 70 к − 8 грн 07 к = 4 грн 63 к .

3) 3 грн 60 к : 3 = 360 : 3 = 120 к = 1грн 20 к .

Задание 387.

Расстояние между двумя пристанями 320 км. Половину этого расстояния моторная лодка прошла за 4 ч. С какой скоростью шла лодка?


Решение:
  • 1) 320 : 2 = 160 (км) половина расстояния;
  • 2) 160 : 4 = 40 (км/ч).
  • Отвтет: скорость лодки 40 км/ч.

Задание 388.

Расстояние 20 км всадник проехал туда и обратно за 4 ч. С какой скоростью ехал всадник?


Решение:
  • 1) 20 + 20 = 40 (км) расстояние туда и обратно;
  • 2) 40 : 4 = 10 (км/ч).
  • Ответ: скорость всадника 10 км/ч.

Задание 389.

Прочитай задачу и рассмотри её решение.

  • Задача. Лыжник был в пути 3 ч, двигаясь со скоростью 12 км/ч. Какое расстояние прошёл лыжник?
  • Решение: 12 — 3 = 36 (км).
  • Ответ: за 3 ч лыжник прошёл 36 км.
Чтобы найти расстояние, надо скорость умножить на время

Задание 390.

Пассажирский катер шёл 4 ч, а буксирный 7 ч. Какой из них прошёл большее расстояние и на сколько километров, если скорость пассажирского катера 24 км/ч, а буксирного 14 км/ч?


Решение:
  • 1) 24 * 4 = 96 (км) прошел пассажирский катер;
  • 2) 14 * 7 = 98 (км) прошел буксирный катер;
  • 3) 98 — 96 = 2 (км).
  • Ответ: буксирный катер прошел на 2 км больше.

Задание 391.

По данным таблицы найди расстояния.


Решение:
  • Пешеход: 5км/ч * 4ч = 20 км .
  • Такси: 70 км/ч * 2 ч = 140 км .
  • Электропоезд: 120 км/ч * 3 ч = 360 км .

Задание 392.

В течение дня туристы шли пешком 2 ч, на автобусе ехали 3 ч. Пешком они двигались со скоростью 4 км/ч, на автобусе ехали со скоростью 45 км/ч. Какой путь преодолели туристы за день?


Решение:
  • 1) 2 * 4 = 8 (км) преодолели туристы пешком;
  • 2) 3 * 45 = 135 (км) преодолели турсты на автобусе;
  • 3) 8 + 135 = 143 (км).
  • Ответ: за день туристы преодолели 143 км.

Задание 393.


Решение:
  • 54408 + 351875 + 973 = 406283 + 973 = 407256
  • 10 ц 3 кг − 4 ц 12 кг = 5 ц 91 кг
  • 48350 − 9405 + 598 = 38945 + 598 = 39543
  • 8365 − (2120 + 1080) = 8365 − 3200 = 5165

Задание 394.

На птичьем дворе было 16 цыплят, а утят — в 4 раза больше.

    По условию задачи можно поставить такие вопросы:
  • 1) Сколько утят было на птичьем дворе?
  • 2) Сколько было цыплят и утят вместе?
  • 3) На сколько больше было утят, чем цыплят? Выполни устно вычисления и запиши ответы.

Решение:
  • 1) 16 * 4 = 64 Утят — 64;
  • 2) 16 + 64 = 80 — цыплят и утят.
  • 3) 64 — 16 = 48 — Утят на 48 больше, чем цыплят.

Задание 395.

В течение двух дней велосипедист был в дороге 12 ч и за это время проехал 180 км. Сколько километров проедет мотоциклист за 20 ч, если его скорость на 36 км/ч больше скорости велосипедиста?


Решение:
  • 1) 180 : 12 = 15 (км/ч) скорость велосипедиста;
  • 2) 15 + 36 = 51 (км/ч) скрость мотоциклиста;
  • 3) 51 * 20 = 1020 (км).
  • Ответ: мотоциклист проедет 1020 км.

Задание 396.


Решение:
  • 1) 10 ц 08 кг − 4 ц 12 кг = 5 ц 96 кг
  • 2) 12 км 750 м + 4 км 75 м = 16 км 825 м
  • 3) 47650 − 875 − 6588 = 46775 − 6588 = 40187
  • 4) 3358 − (12 + 778) = 3358 − 790 = 2568

Задание 397.

Автомобиль ехал 2 ч со скоростью 66 км/ч. После этого ему осталось проехать расстояние в 3 раза большее, чем он уже проехал. Какое расстояние должен был проехать автомобиль?


Решение:
  • 1) 2 * 66 = 132 (км) проехал автомобиль;
  • 2) 132 * 3 = 396 (км) осталось проехать автомобилю;
  • 3) 396 + 132 = 528 (км).
  • Ответ: автомобиль должен был проехать 528 км.

Задание 398.

Прочитай задачу и рассмотри ее решение.

  • Задача. Пассажир проехал на автобусе 180 км. Скорость автобуса 60 км/ч. Сколько времени ехал пассажир на автобусе?
  • Решение: 180 : 60 = 3 (ч).
  • Ответ: пассажир ехал на автобусе 3 ч.

Чтобы найти время, надо расстояние поделить на скорость.

Задание399.

По данным таблицы найди время движения.


Решение:
  • Лыжник: 26 км : 13 км/ч = 2 ч.
  • Поезд: 240 км : 60 км/ч = 4 ч.
  • Легковой автомобиль: 240 км : 80 км/ч = 3 ч.

Задание 400.

По асфальтированной дороге автомобиль проехал расстояние 210 км со скоростью 70 км/ч, а по грунтовой — 90 км со скоростью 45 км/ч. За какое время автомобиль проехал всё расстояние?


Решение:
  • 1) 210 : 70 = 3 (ч) ехал автомобиль по асфальтированной дорогое4;
  • 2) 90 : 45 = 2 (ч) ехал автомобиль по грунтовой дороге;
  • 3) 3 + 2 = 5 (ч).
  • Ответ: автомобиль проехал все расстояние за 5 ч.



Задание:  —>>     381 — 400  401 — 418 

Скорость, время, расстояние / Задачи / Справочник по математике для начальной школы

  1. Главная
  2. Справочники
  3. Справочник по математике для начальной школы
  4. Задачи
  5. Скорость, время, расстояние

Скорость движения – это расстояние, пройденное за единицу времени.

Единицей времени является 1 секунда, 1 минута или 1 час.

Чтобы определить скорость движения, нужно использовать величины — расстояние и время.

Чтобы найти скорость, нужно расстояние разделить на время.

В качестве единиц измерения скорости мы будем пользоваться единицами длины и единицами времени. Обычно используют такие единицы скорости, как метр в секунду, метр в минуту, километр в час и другие, а записывают так: м/с, м/мин, км/ч. Обратите внимание, что предлог “в” в математике заменили чёрточкой “ / ”.

Например, скорость страуса — 7 км/ч.

Скорость черепахи — 5 м/с.

Прибор для измерения скорости: спидометр.

Чем меньше времени затрачено на дорогу, тем больше скорость движения.

Чем меньше скорость движения, тем больше времени требуется на дорогу.

Чтобы найти время, нужно расстояние разделить на скорость.

Чтобы найти расстояние, нужно скорость умножить на время.

При решении задач на движение стоит помнить, что при движении навстречу друг другу скорости складываются, а при движении друг за другом – вычитается.

Складывая две скорости при движении навстречу, мы получаем скорость, с которой пешеходы приближаются друг к другу. Её мы будем называть скоростью сближения.

Складывая две скорость при движении в противоположных направлениях, мы получаем скорость, с которой объекты удаляются друг от друга. Её мы будем называть скоростью удаления.

Место встречи всегда ближе к пункту, из которого вышел пешеход, у которого скорость меньше.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Образцы оформления задачи

Обратные задачи

Цена. Количество. Стоимость

Задачи

Правило встречается в следующих упражнениях:

4 класс

Страница 54. Проверочные работа. Вариант 1., Моро, Волкова, Проверочные работы

Страница 59. Вариант 2. Проверочная работа 2, Моро, Волкова, Проверочные работы

Страница 10, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 11, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 21, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 26, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 29, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 38, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 102, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 30, Моро, Волкова, Рабочая тетрадь, часть 2

5 класс

Задание 135, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 428, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 808, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1526, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1709, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1784, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 459, Мерзляк, Полонский, Якир, Учебник

Номер 473, Мерзляк, Полонский, Якир, Учебник

Номер 2, Мерзляк, Полонский, Якир, Учебник

Номер 937, Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 207, Мерзляк, Полонский, Якир, Учебник

Номер 491, Мерзляк, Полонский, Якир, Учебник

Номер 492, Мерзляк, Полонский, Якир, Учебник

Номер 2, Мерзляк, Полонский, Якир, Учебник

Номер 1339, Мерзляк, Полонский, Якир, Учебник

Задание 481, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 676, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 782, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1232, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1350, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 15, Мерзляк, Полонский, Якир, Учебник

Номер 16, Мерзляк, Полонский, Якир, Учебник

Номер 107, Мерзляк, Полонский, Якир, Учебник

Номер 108, Мерзляк, Полонский, Якир, Учебник

Номер 111, Мерзляк, Полонский, Якир, Учебник

Номер 122, Мерзляк, Полонский, Якир, Учебник

Номер 146, Мерзляк, Полонский, Якир, Учебник

Номер 255, Мерзляк, Полонский, Якир, Учебник

Номер 389, Мерзляк, Полонский, Якир, Учебник

Номер 525, Мерзляк, Полонский, Якир, Учебник

© budu5. com, 2022

Пользовательское соглашение

Copyright

Движение вдогонку | Математика

Рассмотрим задачи на движение вдогонку, в которых объекты движутся в одном направлении, но выезжают из разных пунктов, находящихся на некотором расстоянии друг от друга.

При движении вдогонку объекты могут как сближаться, так и удаляться.

Если скорость объекта, который идет впереди, меньше скорости идущего вслед за ним объекта, то второй догоняет первого и они сближаются.

Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:

   

   

Если скорость идущего впереди объекта больше скорости объекта, который движется следом, то второй не сможет  догнать первого и они удаляются друг от друга.

Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:

   

   

Скорость, время и расстояние связаны между собой формулой пути:

   

Задача 1.

Расстояние между двумя пунктами 20 км. Из этих пунктов в одном направлении одновременно выехали автомобиль и мотоциклист, причем автомобиль двигался впереди. Через 5 часов расстояние между ними стало 170 км. Найти скорость мотоциклиста, если скорость автомобиля 70 км/ч.

Решение:

v, км/ч

t, ч

s, км

Автомобиль

70

5

?

Мотоциклист

?

5

?

1) 170-20=150 (км) на столько увеличилось расстояние между автомобилем и мотоциклистом за 5 часов

2) 150:5=30 (км/ч) скорость удаления автомобиля от мотоциклиста

3) 70-30=40 (км/ч) скорость мотоциклиста.

Ответ: 40 км/ч.


Задача 2.

Расстояние между двумя станциями 40 км. Из этих станций одновременно в одном направлении вышли скорый и товарный поезда, причем товарный поезд едет впереди. Через сколько часов скорый поезд догонит товарный, если его скорость равна 80 км/ч, а скорость товарного поезда — 60 км/ч?

Решение:

v, км/ч

t, ч

s, км

Пассажирский

80

?

? на 40 км больше

Товарный

60

?

?

1) 80-60=20 (км/ч) скорость сближения поездов

2) 40:20=2 (ч) через такое время скорый поезд догонит товарный.

Ответ: через 2 ч.

Задача 3.

Расстояние между пунктами равно 50 км. Из этих пунктов одновременно в одном направлении выезжают велосипедист и мотоциклист, причем велосипедист едет впереди. Скорость велосипедиста равна 13 км/ч, скорость мотоциклиста — 38 км/ч. На каком расстоянии от пункта своего выезда мотоциклист догонит велосипедиста?

Решение:

v, км/ч

t, ч

s, км

Мотоциклист

38

?

? на 50 км больше

Велосипедист

13

?

?

1) 38-13=25 (км/ч) скорость сближения мотоциклиста и велосипедиста

2) 50:25=2 (ч) через столько часов после своего выезда мотоциклист догонит велосипедиста

3) 38∙2=76 (км) на таком расстоянии от пункта своего выезда мотоциклист догонит велосипедиста.

Ответ: 76 км.

Текстовые задачи. Задачи на движение с решениями

Задачи на движение с решениями

перейти к содержанию курса текстовых задач

  1. Первый турист проехал 2 ч на велосипеде со скоростью 16 км/ч. Отдохнув 2 ч, он отравился дальше с прежней скоростью. Спустя 4 ч после старта велосипедиста ему вдогонку выехал второй турист на мотоцикле со скоростью 56 км/ч. На каком расстоянии от места старта мотоциклист догонит велосипедиста? Решение
  2. Из пункта A в пункт B отправились три машины друг за другом с интервалом в 1 ч. Скорость первой машины равна 50 км/ч, а второй — 60 км/ч. Найти скорость третьей машины, если известно, что она догнала первые две машины одновременно. Решение
  3. Поезд был задержан в пути на 12 мин, а затем на расстоянии 60 км наверстал потерянное время, увеличив скорость на 15 км/ч. Найти первоначальную скорость поезда. Решение
  4. Расстояние между станциями A и B равно 103 км. Из A в B вышел поезд и, пройдя некоторое расстояние, был задержан, а потому оставшийся до B путь проходил со скоростью, на 4 км/ч большей, чем прежняя.  Найти первоначальную скорость поезда, если известно, что оставшийся до B путь был на 23 км длиннее пути, пройденного до задержки, и что на прохождение пути после задержки было затрачено на 15 мин больше, чем на прохождение пути до нее. Решение
  5. Скорость автомобиля по ровному участку на 5 км/ч меньше, чем скорость под гору, и на 15 км/ч больше, чем скорость в гору. Дорога из A в B идет в гору и равна 100 км. Определить скорость автомобиля по ровному участку, если расстояние от A до B и обратно он проехал за 1 ч 50 мин. Решение
  6. Автобус проходит расстояние между пунктами A и B по расписанию за 5 ч. Однажды, выйдя из A, автобус был задержан на 10 мин в 56 км от A и, чтобы прибыть в B по расписанию, он должен был оставшуюся большую часть пути двигаться со скоростью, превышающей первоначальную на 2 км/ч. Найти скорость движения автобуса по расписанию и расстояние между пунктами A и B, если известно, что это расстояние превышает 100 км. Решение
  7. Поезд проходит мимо платформы за 32 с. За сколько секунд поезд проедет мимо неподвижного наблюдателя, если длина поезда равна длине платформы? Решение
  8. Два поезда отправляются навстречу друг другу с постоянными скоростями, один из А в В, другой из В в А. Они могут встретиться на середине пути, если поезд из А отправится на 1,5 ч раньше. Если бы оба поезда вышли одновременно, то через 6 ч расстояние между ними составило бы десятую часть первоначального. Сколько часов каждый поезд тратит на прохождение пути между А и В? Решение
  9. От пристани А одновременно отправились вниз по течению катер и плот. Катер спустился вниз на 96 км, потом повернул обратно и вернулся в А через 14 ч. Найти скорость катера в стоячей воде и скорость течения, если известно, что катер встретил плот на обратном пути расстоянии 24 км от А. Решение
  10. Пункт В находится по реке ниже пункта А. В одно и то же время из пункта А отплыли плот и первая моторная лодка, а из пункта В — вторая моторная лодка. Через некоторое время лодки встретились в пункте С, а плот за это время проплыл третью часть пути от А до С. Если бы первая лодка без остановки доплыла до пункта В, то плот за это время прибыл бы в пункт С. Если бы из пункта А в пункт В отплыла вторая лодка, а из пункта В в пункт А — первая лодка, то они встретились бы в 40 км от пункта А. Какова скорость обеих лодок в стоячей воде, а также расстояние между пунктами А и В, если скорость течения реки равна 3 км/ч? Решение
  11. Два тела, двигаясь по окружности в одном направлении, встречаются через каждые 112 мин, а двигаясь в противоположных направлениях — через каждые 16 мин. Во втором случае расстояние между телами уменьшилось с 40 м до 26 м за 12 с. Сколько метров в минуту проходит каждое тело и какова длина окружности? Решение
  12. Две точки, двигаясь по окружности в одном направлении, встречаются каждые 12 мин, причем первая обходит окружность на 10 с быстрее, чем вторая. Какую часть окружности проходит за 1 с каждая точка? Решение
  13. Два тела движутся навстречу друг другу из двух точек, расстояние между которыми 390 м. Первое тело прошло в первую секунду 6 м, а в каждую последующую секунду проходило на 6 м больше, чем в предыдущую. Второе тело двигалось равномерно со скоростью 12 м/c и начало движение спустя 5 с после первого. Через сколько секунд после того, как начало двигаться первое тело, они встретятся? Решение

Задачи для самостоятельного решения

  1. Дорога от A до D длиной в 23 км идет сначала в гору, затем — по ровному участку, а потом — под гору. Пешеход, двигаясь из A в D, прошел весь путь за 5 ч 48 мин, а обратно, из D в A, — за 6 ч 12 мин. Скорость его движения в гору равна 3 км/ч, по ровному участку — 4 км/ч, а под гору — 5 км/ч. Определить длину дороги по ровному участку. Ответ:  8 км
  2. В 5 ч утра со станции A вышел почтовый поезд по направлению к станции B, отстоящей от A на 1080 км. В 8 ч утра со станции B по направлению к A вышел пассажирский поезд, который проходил в час на 15 км больше, чем почтовый. Когда встретились поезда, если их встреча произошла в середине пути AB? Ответ: в 5 ч дня
  3. Из пункта A впунктB отправились три велосипедиста. Первый из них ехал со скоростью 12 км/ч. Второй отправился на 0,5 ч позже первого и ехал со скоростью 10 км/ч. Какова скорость третьего велосипедиста, который отправился на 0,5 ч позже второго, если известно, что он догнал первого через 3 ч после того как догнал второго? Ответ: 15 км/ч
  4. Два поезда — товарный длиной в 490 м и пассажирский длиной в 210 м — двигались навстречу друг другу по двум параллельным путям. Машинист пассажирского поезда заметил товарный поезд, когда он находился от него на расстоянии 700 м; через 28 с после этого поезда встретились. Определить скорость каждого поезда, если известно, что товарный поезд проходит мимо светофора на 35 с медленнее пассажирского. Ответ:  36 км/ч; 54 км/ч
  5. Турист A и турист B должны были выйти одновременно навстречу друг другу из поселка M ипоселкаN соответственно. Однако турист A задержался и вышел позже на 6 ч. При встрече выяснилось, что A прошел на 12 км меньше, чем B. Отдохнув, туристы одновременно покинули место встречи и продолжили путь с прежней скоростью. В результате A пришел в поселок N через 8 ч, а B пришел в поселок M через 9 ч после встречи. Определить расстояние MN и скорости туристов. Ответ:  84 км; 6 км/ч; 4 км/ч.
  6. Пешеход, велосипедист и мотоциклист движутся по шоссе в одну сторону с постоянными скоростями. В тот момент, когда пешеход и велосипедист находились в одной точке, мотоциклист был на расстоянии 6 км позади них, а тот момент, когда мотоциклист догнал велосипедиста, пешеход отстал от них на 3 км. На сколько километров велосипедист обогнал пешехода в тот момент, когда пешехода настиг мотоциклист? Ответ: 2 км
  7. Два туриста вышли одновременно из пункта A в пункт B.Первый турист проходил каждый километр на 5 мин быстрее второго. Пройдя 20% расстояния от A до B, первый турист повернул обратно, пришел в A, пробыл там 10 мин, снова пошел в B и оказался там одновремен-
    но со вторым туристом. Определить расстояние от A до B, если второй турист прошел его за 2,5 ч. Ответ: 10 км
  8. Рыбак проплыл на лодке от пристани против течения 5 км и возвратился обратно на пристань. Скорость течения реки равна 2,4 км/ч. Если бы рыбак греб с той же силой в неподвижной воде озера на лодке с парусом, увеличивающим скорость на 3 км/ч, то он за то же время проплыл бы 14 км. Найти скорость лодки в неподвижной воде. Ответ:  9,6 км/ч
  9. Моторная лодка проплыла по озеру, а потом спустилась вниз по реке, вытекающей из озера. Расстояние, пройденное лодкой по озеру, на 15% меньше расстояния, пройденного по реке. Время движения лодки по озеру на 2% больше, чем по реке. На сколько процентов скорость движения лодки вниз по реке больше скорости движения по озеру? Ответ: на 20%
  10. Турист проплыл в лодке по реке из города A в город B и обратно, затратив на это 10 ч. Расстояние между городами равно 20 км. Найти скорость течения реки, зная, что турист проплывал 2 км против течения реки за такое же время, как 3 км по течению. Ответ: 5/6 км/ч
  11. По окружности длиной 60 м равномерно в одном направлении движутся две точки. Одна из них совершает полный оборот на 5 с быстрее другой. При этом совпадение точек происходит каждый раз через 1 мин. Определить скорости точек. Ответ:  4 м/с; 3 м/с.
  12. Из точек A и B одновременно начали двигаться два тела навстречу друг другу. Первое в первую минуту прошло 1 м, а в каждую последующую проходило на 0,5 м больше, чем в предыдущую. Второе тело проходило каждую минуту по 6 м. Через сколько минут оба тела встретились, если расстояние между A и B равно 117 м? Ответ: через 12 мин.
  13. Два приятеля в одной лодке прокатились по реке вдоль берега и вернулись по одной и той же речной трассе через 5 ч с момента отплытия. Протяженность всего рейса составила 10 км. По их подсчетам получилось, что на каждые 2 км против течения в среднем потребовалось столько же времени, сколько на каждые 3 км по течению. Найти скорость течения реки, а также время проезда туда и время проезда обратно. Ответ:  5/12 км/ч; 2 ч и 3 ч.

 

Метки движение, текстовые задачи. Смотреть запись.

Калькулятор скорости, расстояния, времени

Использование калькулятора

Рассчитайте скорость, расстояние или время по формуле d = st, расстояние равно скорости, умноженной на время. Калькулятор скорости, расстояния, времени может найти неизвестное sdt значение с двумя известными значениями.

Время можно ввести или вычислить в секундах (с), минутах (мин), часах (ч) или часах, минутах и ​​секундах (чч:мм:сс).Видеть ярлыки для форматов времени ниже.

Чтобы найти расстояние, используйте формулу для расстояния d = st, или расстояние равно скорости, умноженной на время.

расстояние = скорость x время

Скорость и скорость похожи, так как они оба представляют некоторое расстояние в единицу времени, например мили в час или километры в час. Если скорость r то же, что и скорость с , r = s = d/t.Вы можете использовать эквивалентную формулу d = rt, что означает, что расстояние равно скорости, умноженной на время.

расстояние = скорость x время

Чтобы найти скорость или скорость, используйте формулу скорости: s = d/t, что означает, что скорость равна расстоянию, деленному на время.

скорость = расстояние/время

Чтобы найти время, используйте формулу для времени: t = d/s, что означает, что время равно расстоянию, деленному на скорость.

время = расстояние/скорость

Форматы ввода времени чч:мм:сс

Вы можете использовать тире (-), точку (.) или двоеточие (:) в качестве разделителей и всегда должны использовать 2 разделителя. Например, 15-06-22, 15.06.22 и 15:06:22 интерпретируются как 15 часов 6 минут 22 секунды или 15:06:22.

Допустимые пределы входа:

  • часов от 0 до 999
  • минут от 0 до 59
  • секунд от 0 до 59

Ярлыки формата времени

Х..

5. .

5 часов : 0 минут : 0 секунд

05:00:00

Х.Ю.

5.22.

5 часов : 22 минуты : 0 секунд

05:22:00

XYZ

5.22.10
5.01.15
5.3.6

5 часов : 22 минуты : 10 секунд
5 часов : 1 минута : 15 секунд
5 часов : 3 минуты : 6 секунд

05:22:10
05:01:15
05:03:06

. Ю.

.22.

22 минуты

00:22:00

.YZ

.22.15

22 минуты : 15 секунд

00:22:15

..Z

..5

5 секунд

00:00:05

Х..З

5..05

5 часов : 0 минут : 5 секунд

05:00:05

Связанные калькуляторы

Для физических расчетов со скоростью, перемещением и скоростью используйте наш Калькулятор смещения для расчета смещения с , средняя скорость против или время t .

Math Fact Benchmarks: почему скорость письма имеет значение

Математические упражнения используются, чтобы помочь учащимся усвоить основные математические факты с однозначными числами. Цель состоит в том, чтобы помочь учащимся ответить на основные математические факты из памяти и развить автоматизм. Единственный способ узнать, вспоминает ли учащийся ответ, а не выясняет его, — использовать математические упражнения в качестве эталона. Но ученики не могут научиться вспоминать целую страницу математических фактов, тренируя их.Упражнения, вероятно, вызовут беспокойство и разочарование у студентов. Вот несколько распространенных ошибок, которых следует избегать при обучении студентов основным фактам, касающимся однозначных чисел.

Общие проблемы с математикой Контрольные показатели 

Школы обычно устанавливают контрольные показатели, чтобы оценить, достигли ли учащиеся своих образовательных целей. Когда дело доходит до запоминания математических фактов, школы устанавливают контрольные точки, чтобы отличить знание ответов путем быстрого припоминания от медленного процесса выяснения фактов. У этих тестов есть две основные проблемы.

Учились по одному.

Первая проблема заключается в том, что математические факты изучаются индивидуально, и учащиеся решают одну задачу за раз. Контрольный показатель должен заключаться в том, чтобы решить проблему менее чем за секунду. Если бы они могли, то было бы ясно, какие математические факты студент запомнил, а какие нет. В школах чаще проводят тесты по всем фактам операции, и эти тесты не могут сказать школам, какие факты запоминаются. Более содержательным отчетом было бы то, какие факты в операции студент может ответить мгновенно.

 

Время написать ответ.

Вторая основная проблема заключается в том, что как бы хорошо ученики ни знали факты, они не могут писать ответы на факты быстрее, чем пишут. Учащиеся начальной школы различаются по скорости и могут писать ответы от 10 до 50 ответов в минуту. Если учащийся может ответить на 40 задач в минуту, он достиг мастерства в математических фактах. Но если они не могут писать ответы так быстро, они не могут соответствовать требованиям своей школы. Чтобы установить разумный стандарт, учителя должны знать, насколько быстро учащиеся могут писать, и тест на скорость письма поможет определить это.

Свободное владение математическими фактами Common Core не должно вызывать беспокойства

Общая основная идея гласит, что учащиеся должны быстро запоминать математические факты, чтобы успешно продвигаться по математике. Почему-то почти все дети запомнили 2+2=4 и могут ответить на эту задачу по памяти.Это не напряжно, не сложно и не вызовет математической фобии. Итак, мы знаем, что научиться решать математическую задачу мгновенно по памяти выполнимо, и это можно сделать без стресса. Сложность в том, что есть много фактов, которые нужно изучить, но, если брать их понемногу, все они могут быть изучены одинаково легко.

Однако для этого требуются систематические усилия, ежедневная практика и тщательный контроль. Учителям нужна какая-то программа по сбору фактов, чтобы помочь ученикам запоминать большое количество фактов.До разработки принципов проектирования, лежащих в основе Rocket Math, я думал, что это почти невыполнимая задача. Но за последние 20 лет я видел, как Rocket Math успешно использовался для обучения студентов математическим фактам. Имея достаточно времени, терпения и поддержки, учащиеся могут научиться вспоминать математические факты по памяти, а с помощью Rocket Math они могут делать это, развлекаясь.

Тест скорости письма по Rocket Math

 Тест скорости письма для Rocket Math

Вот простой и удобный в использовании тест скорости письма, который поможет выяснить, насколько быстро учащийся может ответить, когда у него есть все факты в операция запоминается.Тест представляет собой смесь однозначных и двузначных чисел, поэтому он работает со сложением и умножением.

Просто дайте тест своим ученикам и попросите их в течение одной минуты написать числа, которые они видят в каждой клетке. Вы сможете узнать, сколько ящиков они могут заполнить за одну минуту. Это число является верхним пределом задач по математике, на которые вы можете ожидать, что они смогут ответить, если они отвечают на припоминание, а не на их вычисление.

Скорость записи определяется количеством заполненных ящиков.  

Когда учащийся закончит тест, у вас будет количество ящиков, которые он может заполнить за минуту. Вы можете ожидать, что учащийся сможет закончить не менее 80% этого числа, если он сможет мгновенно вспомнить факты. Если студент может ответить на 90%, ему не нужна работа с фактами. Если они составляют от 80 до 90% от этого числа, они хороши, но больше фактов поможет им. Что-нибудь ниже 80%, и они должны остановиться, чтобы выяснить некоторые факты и нуждаются в дополнительной работе.

Если вам не интересно снова и снова заниматься математикой, вот таблица целей для предварительных тестов, в которой цифры рассчитаны для вас. Вы можете распечатать его по этой ссылке.

Контрольные показатели должны основываться на скорости записи.  

Контрольные показатели, не учитывающие скорость, с которой дети могут писать, оставляют у многих детей невыполнимые ожидания. Просьба детей сделать что-то, на что они физически не способны, вызовет много ненужных страданий.

 

 

Контрольные показатели по математике для детского сада

Учеников следует учить правильно и эффективно писать числительные в детском саду. Способы рисования цифр, которые дети изобретают самостоятельно, могут быть медленными, громоздкими и неэффективными, что впоследствии приводит к снижению скорости письма. Rocket Math Writing for Numerals — это систематический метод, который поможет учащимся научиться составлять свои числительные. Контрольные показатели для дошкольников должны быть сосредоточены на скорости написания числительных, что требует большого количества практики и обучения.

Детский сад цифры письма беглости ориентиры (цифры)

              • 1
                • 40 цифр / минута

    Тесты по математике для первоклассников

    Первоклассники должны свободно писать числительные. Не каждый детский сад делает это, поэтому учителя должны тестировать и давать какую-то программу для письма с цифрами ученикам, которые не соответствуют этим стандартам письма.

    Первый сорт цифры письма беглости ориентиры (цифры)

              • 40 цифр в минуту
            • 9002
              • цифр в минуту                       
            •   Конец года     

          Скорость письма учащегося — это количество клеток, которые он может заполнить за одну минуту.

          Первый сорт Математические факты Белнокольные ориентиры (Проблемы)

                  • Дополнение 20% скорости письма
                • 9009
                    • Дополнение 40% скорости письма
                • 1 конец года
                  • дополнение 80% скорости записи
                  • вычитание 20% скорости записи

              математические ориентиры второго класса

              Во втором классе мы хотим, чтобы учащиеся освоили вычитание так же, как и сложение.

                    • 1 начало года
                      • дополнение 80% скорости записи
                  • 1
                  • 1
                    • Дополнение 80% скорости записи
                    • Вычитание 40% скорости записи
                • 7 Конец года
                      • Вычитание 80% скорости письма

                  Математические ориентиры третьего класса

                  в третьем Важно, чтобы учащиеся освоили вычитание и начали работать над умножением.

                        • Добавление 80% скорости письма
                    • 1 середине года
                      • Дополнение 80% скорости письма
                      • Вычитание 80% скорости письма

                      • Дополнение 80% скорости записи
                      • Вычитание 80% скорости записи
                      • Умножение 80% скорости письма

                  Контрольные показатели математики для четвертого класса

                  В четвертом классе учащимся важно освоить умножение и начать деление.

                            • Добавление 80% скорости записи
                            • Вычитание 80% скорости письма
                            • Умновидение 80% скорости записи
                          • 1 в середине года
                              • дополнение 80% скорости письма
                              • Умновидение 80% скорости записи
                              • Division 40% скорости записи
                              • Дополнение 80% скорости записи
                                • % скорости записи
                              • умножение 80% скорости записи
                              • Division 80% скорости записи

                          и выше) тесты математических фактов

                          В пятом классе это важно t для того, чтобы учащиеся освоили свои основные математические факты, а также сложение, вычитание, умножение и деление.

                                • Добавление 80% скорости записи
                                • Умновидение 80% скорости записи
                                • Division 80% скорости записи

                                  • Дополнение 80% скорости письма
                                  • Вычитание 80% скорости написания
                                  • Умножение 80% скорости записи
                                  • Отдел 80% Скорость записи
                            • конец года
                              • дополнение 80% скорости письма
                                • % скорости письма
                              • Умножение 80% скорости записи
                              • Division 80% скорость                     
                            • 900 51

                            Все 1-минутные предварительные тесты, тесты на скорость письма и лист целей можно найти на этой странице https://rocketmath. com/предварительные тесты/.

                            Rocket Math — это забавный путь для студентов, чтобы узнать

                            Rocket Math имеет системный подход к обучению студентам, как свободно владеть основными математическими фактами и при этом получать удовольствие от изучения математики. Математика может показаться сложной для изучения, и если ее не преподавать должным образом, используя хорошую математическую программу, у учащихся может развиться математическая фобия.Учителя используют Rocket Math уже более 20 лет и считают его бесценным инструментом, помогающим их ученикам изучать математику.

                             

                            Почему беглость математики должна быть больше направлена ​​на понимание, а не на скорость

                            Взгляните на приведенное ниже уравнение. Ответ правильный, так в чем же проблема?

                            В математике мы часто приравниваем успех к скорости. Студент, который приходит к ответу, быстро получает золотую звезду. Но слишком часто ученик, который является самым быстрым, демонстрирует поверхностное понимание или способность запоминать, а не осмысливать математику.

                             

                            Возьмем, к примеру, описанную выше проблему. Студент, который работал над этим, четко запомнил ряд шагов или алгоритм достижения успеха, но вы можете видеть, что отсутствует понимание концепции, лежащей в основе алгоритма. Если бы учащийся понял, как числа связаны друг с другом, ему не понадобился бы стандартный алгоритм «пойти по соседству, чтобы одолжить» или перегруппироваться. Нам нужно выйти за рамки запоминания алгоритмов и перейти к более глубокому пониманию математических концепций, чтобы учащиеся понимали, как числа связаны друг с другом.

                             

                            В математике мы часто приравниваем успех к скорости. Студент, который приходит к ответу, быстро получает золотую звезду. Но слишком часто ученик, который является самым быстрым, демонстрирует поверхностное понимание или способность запоминать, а не осмысливать математику.

                            Мы говорим о знании математики, но что это значит? Учащийся, свободно владеющий математикой, — это ученик, демонстрирующий точность, работоспособность, и   гибкость . Это учащийся, который может опираться на предыдущие знания, а затем вырабатывать стратегию, чтобы увидеть несколько путей решения одной проблемы. Конечно, этому ученику может потребоваться больше времени, чтобы найти ответ, но в итоге его понимание намного глубже. Нам нужно проявлять такое же терпение к нашим студентам-математикам, как и к нашим читателям. Если учащийся быстро читает текст, мы просим его замедлить темп, подумать о словах, которые он читает, и обдумать сообщение автора. Так почему же тогда мы повышаем скорость с помощью математики, а не лелеем такое же понимание числовых отношений?

                             

                            Подумайте обо всех приложениях и компьютерных играх для iPad, которые призваны помочь учащимся улучшить свои математические навыки. Большинство из них имеют встроенный таймер и просят ученика выполнить заданный набор за определенное время, чтобы добиться успеха. Почему важно, как быстро вы сможете решить проблему? В начальных классах, когда учащиеся развивают свой математический склад ума и только начинают рассматривать себя как математиков, важно дать им пространство и время для разработки своих стратегий, сосредоточиться на своем мышлении и поразмышлять о том, как числа относятся друг к другу.Замедление на этом этапе, погружение в хитросплетения чисел и обсуждение своих стратегий друг с другом неизбежно позволят им развить глубокое чувство понимания. Это, в свою очередь, позволит им ускориться и стать более автоматическими, поскольку они продолжают свою математическую траекторию.

                             

                             

                            Мы должны предоставить нашим учащимся-математикам такую ​​же возможность исследовать, задавать вопросы, общаться, устанавливать связи с предыдущими знаниями и размышлять, что мы делаем по другим нашим предметам. Математика сама по себе является языком, и для ее понимания требуется время. Учащиеся должны быть осведомлены о том, что они могут опираться на предыдущие знания, чтобы устанавливать новые связи и, следовательно, лучше понимать концепции более высокого уровня. Учащиеся станут более эффективными, точными и гибкими, когда у них будет время подумать о своем мышлении и пообщаться друг с другом о различных стратегиях и о том, какие из них использовать в определенных ситуациях, тем самым развивая и углубляя свое понимание.

                             

                            Предоставление учащимся времени для совместной работы и общения друг с другом даст результаты, подобные приведенным ниже.Студенты, которые могут решить эту задачу пятью, шестью или 10 различными способами, гораздо глубже понимают концепцию вычитания!

                            Эти ученики создают набор инструментов, который они могут использовать в будущих ситуациях. Они закладывают основу для алгебры, исчисления и многого другого, тратя время на изучение математики, высказывая свое мнение и размышляя над наиболее эффективной и действенной стратегией. Это учащиеся, которые выйдут за рамки запоминания и смогут применить свое понимание к новым и различным ситуациям.Это математики, которых мы хотим воспитать.

                            Полный курс ускоренной ведической математики

                            У вас или у вашего ребенка проблемы с математикой? Хотите повеселиться с математикой? Если да, то этот курс для вас!

                            Все, что вы хотели знать о высокоскоростной ведической математике и многом другом.

                            Этот курс содержит более 15 часов материала о самой быстрой в мире системе счета в уме и более тысячи решенных примеров и упражнений. Это займет вас более чем по 60 темам, улучшит ваши математические навыки и даст вам конкурентное преимущество.

                            Автором этого курса является Гаурав Текривал, президент Форума ведической математики в Индии. Курс содержит подробно представленные примеры и прекрасно объясненные методы. Методы были объяснены более чем 3-мя различными способами с помощью демонстраций на белой доске, компьютерных презентаций и анимации.

                            Курс ведической математики пользуется спросом в академических кругах и был создан благодаря многолетнему опыту автора в обучении этому предмету более 4 миллионов студентов по всему миру.

                            Сможете ли вы умножить 998 x 997 за пять секунд?

                            Изучите высокоскоростную ведическую математику, которая позволит вам считать намного быстрее по сравнению с обычной системой. Вы сможете выполнять, казалось бы, сложные вычисления, такие как 998 x 997, за доли секунды, что значительно повлияет на вашу уверенность и самооценку. Ваши навыки расчета улучшатся, вы сможете работать лучше, и вы будете полны уверенности, которая поразит людей.

                            Объем области, которую охватывает ведическая математика, намного больше, чем у других систем.С помощью Ведической математики вы можете выполнять вычисления по арифметике, алгебре и даже тригонометрии, а также упростить и ускорить вычисления. Вы можете видеть результаты, и люди по всему миру любят нас за то, что мы приносим пользу им и их детям.

                            Чем вам может помочь высокоскоростная ведическая математика

                            · Более чем в 1500% раз быстрее, чем обычная математика: это делает ее самой быстрой в мире.
                            · Полностью устраняет страх перед математикой. Итак, если у вашего ребенка фобия математики, высокоскоростная ведическая математика — это веселый способ заниматься математикой и вызывает интерес у вашего ребенка.
                            · Значительно улучшенная успеваемость в школе и мгновенные результаты. Просто посмотрите первое упражнение и поверьте в это сами. Просмотрите примеры, приведенные в учебниках, вы будете поражены.
                            · Обостряет ум, повышает сообразительность и интеллект.
                            · Увеличивает вашу скорость и точность. Станьте Ментальным Калькулятором сами.
                            · Улучшает память и повышает уверенность в себе.
                            · Вызывает у вас интерес к числам.
                            · Развивает левое и правое полушария мозга, используя интуицию и инновации.Было замечено, что гении используют правое полушарие мозга для достижения исключительных результатов.
                            · Простота освоения и применения. Вам просто нужно знание таблиц, чтобы узнать это.
                            · От 11 лет и старше. Этот курс был разработан, чтобы обратиться к большому слою общества — студентам, учителям, родителям, специалистам, абитуриентам вступительных экзаменов, бизнесменам и людям, которые проявляют большой интерес к математике и хотели бы изучить что-то исключительное, что занимает Мир штурмом.

                            Вы узнаете, как ускорить вычисления, которые являются камнем преткновения в математике. Эти концепции помогут вам в подготовке к университетским экзаменам, а также к вступительным экзаменам, с которыми вы столкнетесь в своей жизни.

                            Вы узнаете, как ускорить умножение, деление, сложение, вычитание, как находить квадраты менее чем за 5 секунд, кубы, находить кубические корни за 3 секунды, находить квадратные корни, оттачивать свои навыки алгебраических уравнений и делать это мысленно, изучите правила делимости для каждого числа в системе счисления, ускорьте понятия геометрии, узнайте правила делимости для каждого числа в системе счисления, календари и многое другое. Эта система изменит ваше представление о математике, и вы сможете получать от нее больше удовольствия, чем когда-либо.

                            Этот курс поможет вам реализовать свой скрытый потенциал, развить математические способности и значительно повысить успеваемость. Большинство студентов по всему миру после прохождения курса говорят нам, почему этим методам не учат в школе? На что мы отвечаем, что мы должны реалистично относиться к нашей образовательной политике в любой стране и понимать, что нынешняя система не изменится радикально, чтобы принять совершенно новый способ преподавания математики.

                            Я считаю, что для того, чтобы древняя система ведической математики стала общепринятой, учителям необходимо постепенно интегрировать ее в свою учебную программу и демонстрировать ее положительные результаты, например, учащиеся лучше справляются с тестами благодаря упрощенной и понятной системе. — осваивать и применять методы. Практикумы, семинары и математические выставки по этому предмету стимулируют мозг ребенка и пробуждают в нем интерес к математике, а затем его можно научить более сложным высшим понятиям, поскольку он находится в рецептивном режиме.

                            Темы

                            За 15 часов курса вы научитесь ускорять:-
                            · Высокоскоростное умножение
                            · Быстрое деление
                            · Ускоренное сложение
                            · Мгновенное вычитание
                            · Цифровые корни
                            · Алгебра: линейная, одновременная, Квадратные и прочие уравнения
                            · Квадраты
                            · Кубы
                            · Квадратные корни
                            · Кубические корни
                            · Математическая медитация — выполнение математических расчетов без ручки и бумаги!
                            · Делимость
                            · Календари
                            · Теорема Пифагора

                            Эти и другие темы изучаются более чем за 15 часов с помощью демонстраций на белой доске, компьютерных презентаций и документальных фильмов.Каждая тема рассматривается подробно, и несколько примеров различных уровней сложности решаются шаг за шагом. Зритель может осветить каждую тему в своем собственном темпе и может повторить тему, если ему нужно дополнительное понимание.

                            Курс изобилует многочисленными примерами и практическими упражнениями. Каждый пример подробно объясняется для лучшего понимания, и есть много иллюстраций по каждой теме, чтобы обеспечить понимание предмета.

                            Премиальное время в классе, бесплатная поддержка по телефону.

                            Помимо этого курса, для обеспечения высокого уровня интерактивности мы предлагаем более 3 часов нашей интерактивной поддержки в виртуальном классе, где ваши сомнения и вопросы будут рассмотрены для лучшего понимания и ясности. Наш виртуальный класс оснащен аудио-видео, PowerPoint и WhiteBoard, так что можно давать различные объяснения. Мы будем рады ответить на ваши вопросы по мере того, как вы будете углубляться в тему и помогать вам. Мы также будем рады предложить вам поддержку по электронной почте, телефону и в чате.

                            Отзывы

                            » Курс представляет собой обширный материал по ведической математике. Было проделано много тяжелой работы, чтобы оживить эту работу, которая становится очевидной, когда вы ее видите, и это должно быть оценено по достоинству. Содержание и редактирование было сделано профессионально, и у меня был потрясающий опыт просмотра. Моим детям очень понравились методы умножения, особенно квадраты методом дуплекса. Теперь они могут делать это за то время, которое требуется для того, чтобы упавшая булавка достигла земли. Потрясающе, я говорю.»

                            Лайам Кэффри
                            Ирландия

                            «Древние индийские секреты, которые должен знать учитель математики»

                            Неру Лалл
                            Великобритания

                            «Отличная работа Гаурав. Ваш Форум оказывает услугу обществу, передавая эти навыки новому поколению. Им нужно это, чтобы избавиться от математической фобии, распространенной в классах, и я думаю, что ваш набор КУРС подходит сюда прекрасно. Предлагаемые объяснения и повторение методов помогают детям понять метод.»

                            Martyn Rosser
                            Southern Pines, NC
                            United States

                            » Я учитель математики в Хьюстоне и вот уже два месяца как я изучил эти методы в Индии с помощью набора Complete High Speed ​​Vedic Math COURSE. Я начал обучать этим методам своих учеников, которых я тренирую, и их глаза сияют от волнения, когда я обучаю их этим методам. Они хотят узнать больше, и эти подростки, которые предпочли бы играть в компьютерные игры, просят меня увеличить время их занятий, чтобы изучить эти новые методы. Я за 9 лет своего служения ни разу не сталкивался с этим, и удивительно, что система высокоскоростной ведической математики способна на это!» получить оценку А на следующем экзамене по математике. Возможно. Методы ведической математики профессора Текривала не от мира сего. Это похоже на магию Гарри Поттера, работающую с математикой».

                            Рональд Кэй
                            Понтипул, Торфэн
                            Великобритания

                            «Метод деления, которому вы научили и объяснили, самый быстрый.Ты прав. Теперь я могу бросить вызов своим друзьям, чтобы они ответили правильно с точностью до 5 знаков после запятой быстрее, чем я. Я победил их по всем пунктам».

                            Фрэнсис Райан
                            Перт, Западная Австралия
                            Австралия

                            «У моего ребенка Вивиан была фобия математики. Когда я нашла ваш сайт и узнала о преимуществах набора КУРС, я подумала, что он может помочь Вивиан. Поначалу было очень трудно заставить его высидеть набор COURSE. Но вдруг, когда зашла речь о базовом методе… что-то привлекло его внимание, и он просидел целых 3 часа. Он просидел до позднего вечера и что-то строчил в своей записной книжке, которая, когда я увидел, была заполнена вычислениями, которые он решил с помощью вашего ведического математического метода. Сейчас Вивиан очень хочет пройти курс и считает, что эти методы являются дружественными и помогут ему. Спасибо, мистер Текривал, за то, что указали путь моему ребенку».

                            Уильям Перри
                            Колумбус, Огайо
                            США

                            «Я обучаю своего ребенка дома. Этот индийский метод привлек меня, когда я выполняла некоторые уроки, представленные на веб-сайте.Я думал, что это поможет моему сыну решить его проблемы с математикой. Я получил набор КУРСОВ ведической математики и показал некоторые методы. Я скептически относился к тому, что это ошеломит моего ребенка, поэтому я подумал о том, чтобы сначала пройти его самостоятельно, и, к моему удивлению, эти КУРСЫ прекрасно разъясняют математические концепции без какой-либо истерии по поводу скорости. Идея состоит в том, чтобы вычислить сумму, используя базовую простую систему, а затем, если это произойдет быстро, вы получите бонус. Теперь ко мне присоединился Томас, и мы вместе решаем задачи.Иногда он учит меня новой концепции. Спасибо.»

                            Terrence Brannon
                            Taylorsville, CA
                            United States

                            «Это просто волшебно, и это познакомило меня с Страной чудес чисел»

                            Margaret Rittenhouse
                            Leonia, NJ
                            United States

                            » Спасибо за ваше разрешение на позвольте нам провести 2-часовой показ Ведической математической системы из вашего КУРСА для нашей школы. Это было успешно, и дети были замечены, делая заметки. Мы делаем это впервые, и я думаю, что в ближайшем будущем у нас будет больше таких сессий.Мы дали нашим студентам задания и проектную работу по высокоскоростной ведической математике, которая поможет им понять концепции». ://www.vedicmathsindia.org

                            Speed ​​Mathematics |guruparents

                            Разве не удивительно, какие сокровища можно найти в местной библиотеке? На прошлой неделе я случайно наткнулся на книгу Билла Хэндли по обучению умножению под названием «Быстрая математика: секретные навыки для быстрого вычисления
                            ».

                            Книга обещала раскрыть секрет молниеносных вычислений в уме, чем и зацепила меня. В течение пяти минут я просмотрел книгу, чтобы понять различные техники, а через пятнадцать минут я вернулся домой, читая введение.

                            Это было большим открытием для меня. Как и большинство людей, я был воспитан на запоминании своей таблицы умножения путем повторения, за которым следовали еще большие повторения. Сложение и вычитание были медленными методическими процессами.Вычисление квадратных корней и деление в длину были просто пыткой. В книге Хэндли он описывает простые, быстрые и высокоэффективные математические методы.

                            Как это работает?

                            Методы, изложенные в книге, используют справочные числа для быстрого расчета правильных ответов.

                            Возьмем пример, такой как 7 x 8.
                            С помощью традиционных методов умножения у ребенка есть три варианта решения этого вопроса:

                            • добавить семь восьмерок (т.е. 8 + 8 + 8 + 8 + 8 + 8 + 8)
                            • запомнили свои таблицы умножения на 7 или 8
                            • использовал комбинацию этих методов (т. е. 5 x 8 = 40 плюс еще две восьмерки, чтобы получить 56).

                            Все эти методы подвержены ошибкам для маленького ребенка.

                            Умножение скорости может упростить расчет за счет использования справочного числа. В приведенном ниже примере в качестве ссылочного номера используется 10.

                            В следующем примере в качестве ссылочного номера используется 100.

                            В чем преимущество воспитания?

                            Обучение детей методам быстрой математики, вероятно, даст вашим детям множество преимуществ:

                            • Более высокие оценки – у них будет преимущество перед одноклассниками, поскольку они будут использовать более совершенную технику умножения
                            • Повышение уверенности – способность выполнять упражнения и тесты быстрее, чем их сверстники
                            • Удовольствие от математики – получать удовольствие от способности умно и легко решать сложные задачи на умножение
                            • Потенциал прорыва . Если у вашего ребенка возникли проблемы с традиционными методами умножения, то попытка альтернативного метода может привести к успеху

                            Недостатки:

                            • Ресурсы – чтобы научить ваших детей ускоренной математике, вам нужно будет купить соответствующие учебные пособия и потратить время или иным образом заплатить репетитору для обучения вашего ребенка.
                            • Путаница – вы будете обучать одной технике дома, а другой – в школе

                            Другие идеи

                            Существует ряд различных систем скоростной математики, которые имеют уникальные преимущества и недостатки. Вы также можете изучить ведическую математическую систему или систему Трахтенберга.

                            Алгебра: Задачи на скорость и расстояние

                            Задачи на скорость и расстояние

                            Вы когда-нибудь слышали о словесной задаче, подобной этой? «Поезд А движется на север со средней скоростью 95 миль в час, покидая свою станцию ​​в тот самый момент, когда другой поезд, поезд Б, отправляется с другой станции, направляясь на юг со средней скоростью 110 миль в час. Если эти поезда случайно поставят на один и тот же путь и отправятся на расстоянии ровно 1300 миль друг от друга, сколько времени пройдет, прежде чем они столкнутся?»

                            Если эта проблема кажется вам знакомой, это, вероятно, потому, что вы смотрите много телевизора (как и я). Всякий раз, когда телепередачи говорят Что касается математики, то обычно это происходит в контексте того, как главный герой пытается, но с треском проваливается, решить классическую «задачу о невозможном поезде». столько математики.

                            Предостережения Келли

                            Убедитесь, что единицы измерения совпадают в задаче о перемещении. Например, если в задаче сказано, что вы проехали 70 миль за 90 208 часов 90 209 за 15 90 208 минут 90 209 , то 90 208 r 90 209 = 70 и 90 208 t 90 209 = 0,25. Так как скорость дана в милях за час , время также должно быть в часах, а 15 минут равны 0,25 часа. Я получил это десятичное число, разделив 15 минут на количество минут в часе: 15 60 = 1 4 = 0. 25.

                            На самом деле это не так уж и сложно. Это, как и любая задача о расстоянии и скорости перемещения, требует только одной простой формулы:

                            Пройденное расстояние ( D ) равно вашей скорости ( r ), умноженной на время ( t ), которое вы прошли скорость. Что делает большинство задач на расстояние и скорость сложными, так это то, что у вас обычно есть две вещи, путешествующие одновременно, поэтому вам нужно использовать формулу дважды в одно и то же время. В этой задаче вы будете использовать его один раз для поезда А и один раз для поезда Б.

                            Чтобы не упускать из виду, вам следует использовать небольшие описательные индексы. Например, используйте формулу D 9089 A = R R T T T A A A для тренировки расстояние, скорость и значения времени и времени и используйте формулу D B = R 9 T T T T B для поезда B.

                            Критическая точка

                            Маленький A в формуле D A = R A t A не влияют на значения D, r и t .Это всего лишь маленькие метки, гарантирующие, что вы подставите в эту формулу только те значения, которые соответствуют поезду А.

                            Пример 4 : Поезд А движется на север со средней скоростью 95 миль в час, покидая свою станцию ​​в тот самый момент, когда другой поезд, Поезд В, отправляется с другой станции, направляясь на юг со средней скоростью 110 миль в час. час. Если эти поезда случайно поставят на один и тот же путь и отправятся на расстоянии ровно 1300 миль друг от друга, сколько времени пройдет, пока они не столкнутся?

                            Решение : Два поезда означает два дистера расстояния: D A = R = R T T D и D B = г Б т Б . Ваша первая цель — подставить любые значения, которые вы можете определить из задачи. Поскольку поезд А движется со скоростью 95 миль в час, r A = 95; аналогично, r B = 110.

                            Обратите внимание, что в задаче также говорится, что поезда отправляются в одно и то же время. Это означает, что их время в пути точно совпадает. Поэтому вместо того, чтобы обозначать их время в пути как t A и t B (что предполагает, что они разные), я буду писать их как t (что предполагает, что они равны). .На данный момент ваши формулы выглядят следующим образом:

                            Предостережения Келли

                            Даже если вы добавили расстояния в этой задаче, вы не всегда будете это делать, это зависит от формулировки задачи. Например, в задаче 3 вы не будете вычислять сумму.

                            Вот хитрый шаг. Поезда движутся навстречу друг другу по пути длиной 1300 миль. Следовательно, они должны столкнуться, когда оба поезда вместе пройдут в общей сложности 1300 миль. Конечно, поезд Б проедет больше из этих 1300 миль, чем поезд А, поскольку он движется быстрее, но это не имеет значения.Вам даже не нужно придумывать, как далеко проедет каждый поезд. Важно только то, что когда D A + D B = 1300, это шторы. К счастью, вы знаете, что такое D A и D B (95 t и 110 t соответственно)

                            У вас есть проблемы

                            Проблема 3: Дэйв ехал на велосипеде от дома до 7-11 со средней скоростью 17 миль в час, и поездка заняла 1.25 часов. Однако, подъезжая к магазину, он наехал на стекло, в результате чего обе шины спустились. Из-за этой неудачи ему пришлось толкать свой велосипед домой со средней скоростью 3 мили в час. Сколько времени заняла дорога домой?

                            • D A + D B B = 1300
                            • 95 T + 110 T = 1300
                            • 205

                              T = 1300

                            • T 6. 341 час

                            Итак, поезда столкнутся примерно через 6.341 час.

                            Выдержки из The Complete Idiot’s Guide to Algebra 2004 У. Майкла Келли. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.

                            Вы можете приобрести эту книгу на Amazon.com и в Barnes & Noble.

                            Преподавание математики — скорость не нужна

                            «Что нужно знать учителям об обучении математике? Стратегия важнее скорости, а математические размышления важнее механического запоминания.— Стэнфордский профессор доктор Джо Боулер

                            Ознакомьтесь с советами Джо из ее новой статьи «Рабочая память блоков скорости и давления времени» (ниже).

                            «Я всегда был глубоко не уверен в своих интеллектуальных способностях; Я думал, что я неразумен. И это правда, что я был и остаюсь довольно медлительным. Мне нужно время, чтобы схватить вещи, потому что я всегда должен понимать их полностью. К концу одиннадцатого класса я втайне считал себя глупым. Я беспокоился об этом в течение длительного времени.

                            Я все такой же медлительный. . . . В конце одиннадцатого класса я измерил ситуацию и пришел к выводу, что быстрота не имеет точного отношения к интеллекту. Важно глубоко понимать вещи и их отношения друг к другу. Вот где кроется интеллект. Факт быстрого или медленного на самом деле не имеет значения».
                            –     Лоран Шварц, полевой медалист, один из величайших математиков всех времен

                            «Когда я спрашиваю их, что привело к их отвращению к математике, многие говорят о тестах на время во втором или третьем классе как о главном поворотном моменте, когда они решили, что математика не для них.
                            – Доктор Джо Боулер, Стэнфорд

                            Чего нельзя делать:    Тестирование на время в младших классах, чрезмерный упор на механическую математику

                            Что делать:  Обучайте стратегии вместо того, чтобы заучивать наизусть, привлекайте внимание к интересным математическим моделям, знакомьтесь с визуальной математикой

                            Вот еще один визуальный математический ресурс, на который стоит обратить внимание. Это бесплатное приложение Number Line от Центра обучения математике. Он доступен для iPad, Windows и Интернета! Ознакомьтесь также с некоторыми другими приложениями Math Center!

                            Вопрос о тестах на время и стратегии обучения особенно актуален для учащихся с дислексией, у многих из которых медленная обработка (особенно в начальных классах), проблемы с механической памятью и трудности с поиском по времени.

                            Большое спасибо доктору Джо Боалер из

                            В приведенном ниже видео вы можете ознакомиться с веб-семинаром доктора Боулера о дислексическом преимуществе. Она говорила о мышлении и математическом беспокойстве. Нас поразило то, что они обнаружили, что у детей в возрасте 5 лет может развиться математическая тревожность.

                             

                            Загрузка.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *