Контрольная работа по алгебре 8 класс. Повторение
Контрольная работа 8 класс. Повторение тем: «Степени»,
«Формулы сокращенного умножение», «Линейные уравнение и системы уравнения»
1 вариант
Представьте в виде многочлена Преобразуйте трёхчлен в квадрат двучлена Выполните умножение многочленов a) b) Упростите выражение a) b) | Графически решите систему уравнений При решении используйте метод подстановки При решении используйте метод сложения |
Контрольная работа 8 класс. Повторение тем: «Степени»,
«Формулы сокращенного умножение», «Линейные уравнение и системы уравнения»
2 вариант
Представьте в виде многочлена a) b) Преобразуйте трёхчлен в квадрат двучлена a) b) Выполните умножение многочленов a) b) Упростите выражение a) b) | Графически решите систему уравнений При решении используйте метод подстановки При решении используйте метод сложения |
Контрольная работа 8 класс. Повторение тем: «Степени»,
Повторение тем: «Степени»,
«Формулы сокращенного умножение», «Линейные уравнение и системы уравнения»
3 вариант
Представьте в виде многочлена a) b) Преобразуйте трёхчлен в квадрат двучлена a) b) Выполните умножение многочленов a) b) Упростите выражение a) b) | Графически решите систему уравнений При решении используйте метод подстановки При решении используйте метод сложения |
Контрольная работа 8 класс. Повторение тем: «Степени»,
«Формулы сокращенного умножение», «Линейные уравнение и системы уравнения»
4 вариант
Представьте в виде многочлена a) b) Преобразуйте трёхчлен в квадрат двучлена a) b) Выполните умножение многочленов a) b) Упростите выражение a) b) | Графически решите систему уравнений При решении используйте метод подстановки При решении используйте метод сложения |
Адрес публикации: https://www. prodlenka.org/metodicheskie-razrabotki/153246-kontrolnaja-rabota-po-algebre-8-klass-povtore
prodlenka.org/metodicheskie-razrabotki/153246-kontrolnaja-rabota-po-algebre-8-klass-povtore
Самостоятельная работа .Итоговая повторения курса алгебры . 8 класс
Вариант1.
1.Найдите значение выражения
2.Найдите значение выражения .
3.Найдите значение выражения
4.Найдите значение выражения
5.Решите уравнение .
6.Решите неравенство
7.Найдите корни уравнения .
8.Решить неравенство
9.Установите соответствие между графиками функций и формулами, которые их задают.
1)
2)
3)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
А
Б
В
Вариант№2
1. Найдите значение выражения
Найдите значение выражения
2.Найдите значение выражения
3.Найдите значение выражения .
4.Найдите значение выражения
5.Решите уравнение
6.Решите неравенство
7.Найдите корни уравнения
8.Решить неравенство Решите неравенство
9.Установите соответствие между графиками функций и формулами, которые их задают.
1)
2)
3)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
А
Б
В
Вариант№3
1.Найдите значение выражения
2.Найдите значение выражения
3.Найдите значение выражения
4.Найдите значение выражения
5.Решите уравнение
6.
7.Найдите корни уравнения
8.Решить неравенство
9.Установите соответствие между графиками функций и формулами, которые их задают.
1)
2)
3)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
А
Б
В
ГДЗ самостоятельные работы по алгебре 8 класс Александрова Мнемозина
Заблаговременная подготовка к проверочной — отличная идея для получения высокой оценки за работу с минимумом усилий для достижения этой цели. Чтобы все складывалось максимально удачно, рекомендуется воспользоваться специализированным справочником-помощником. В числе наиболее грамотных и эффективных при решении этих задач называют гдз по алгебре за 8 класс самостоятельные работы Александрова — при условии правильной работы с ними.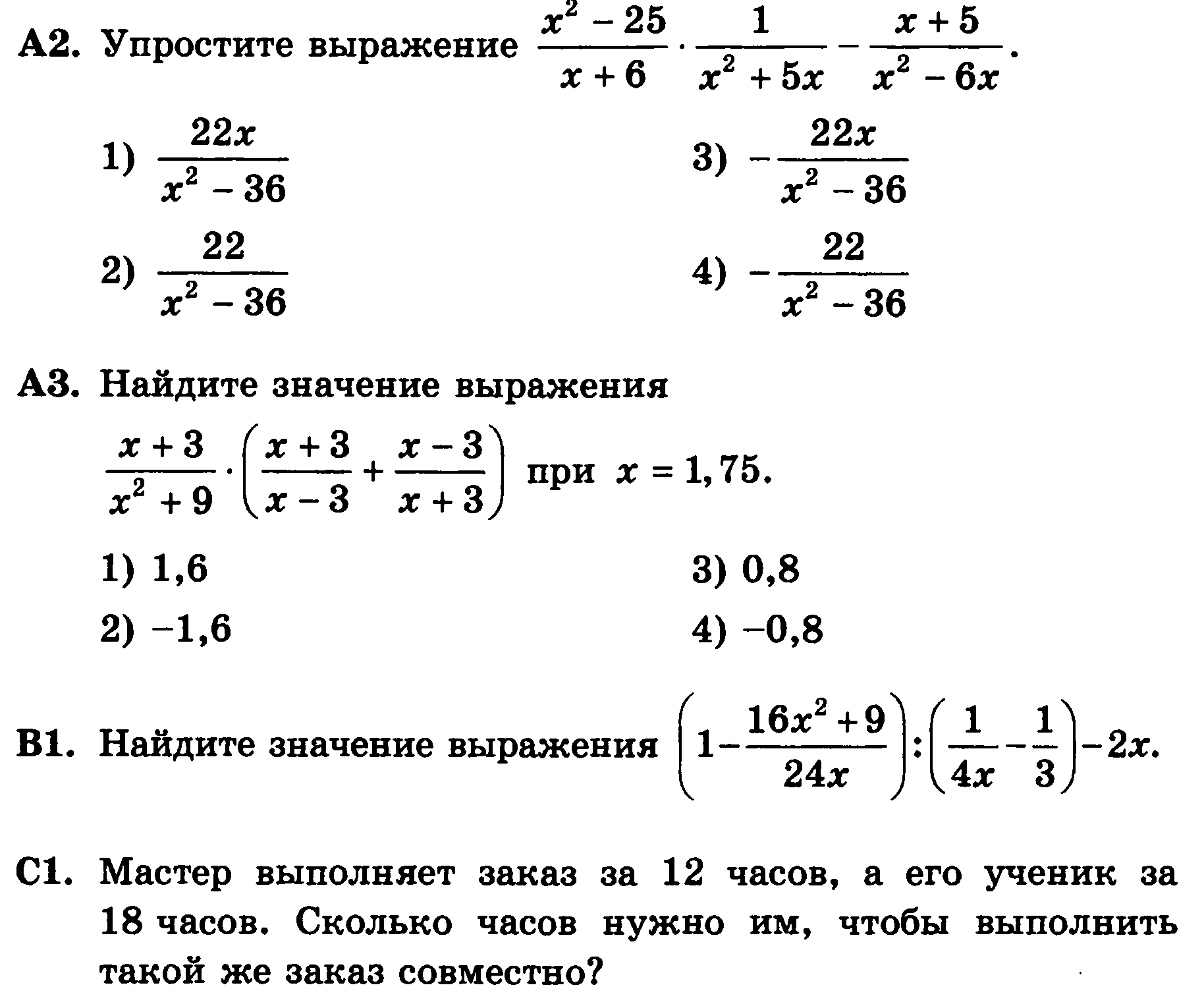
Кто и для чего использует онлайн помощники в учебном процессе?
Среди тех, кто системно и регулярно применяет подробные решения по алгебре 8 класс для самостоятельных работ Александрова — такие группы пользователей:
- восьмиклассники, по тем или иным причинам часто пропускающие занятия (дети, которые часто болеют, профессиональные спортсмены, выезжающие на сборы и соревнования, творческие личности, участвующие во всевозможных конкурсах и пр.). Для них сборник станет источником для получения нужных знаний, позволяющих им правильно написать проверочную;
- подростки, переведенные на дистанционную форму образования, избравшие домашний/семейный формат обучения.
 В этом случае материалы позволят дополнить объяснение учителя и получить на проверке хорошую отметку;
В этом случае материалы позволят дополнить объяснение учителя и получить на проверке хорошую отметку; - педагоги-предметники, которым надо оперативно проверить большое количество сданных школьниками работ. Ресурс поможет им сэкономить время на решение срочных дел (плановых, отчетных и т. д.), не рискуя качеством результата;
- родители восьмиклассников, справедливо полагающие, что приведенные ответы позволят им проверить степень готовности своего ребенка к предстоящим в школе проверочным. При этом — не вникать глубоко в суть программы, в темы и разделы школьного алгебраического курса.
Очевидные преимущества применения ответов к самостоятельным работам по алгебре за 8 класс (автор Александрова)
Правда, некоторые родители и учителя до сих пор не оценили всех преимуществ еуроки ГДЗ, считая, что подростки просто бездумно списывают с них готовые решения. Но это совсем не так. Польза у ресурса огромна:
- он доступен в любое время и всем;
- при возникновении сложностей с решением всегда можно найти здесь подсказку, проработать задание еще до того, как за его выполнение будут ставить оценку в классе;
- вся информация представлена в соответствии с действующими образовательными Стандартами, включая требования к оформлению;
- это экономически выгодное решение, позволяющее сократить расходы на репетиторов или даже полностью отказаться от них.

Применяя сборник готовых решений, школьники учатся работать со справочной литературой в условиях ограниченного времени на выполнение задачи. Этот ценный навык пригодится им и сейчас, и впоследствии.
ГДЗ Алгебра 8 класс Александрова
Алгебра 8 класс
Самостоятельные работы (Углубленный уровень)
Александрова
Мнемозина
Очень многое зависит от программы, по которой учатся подростки. Если используется обычная, то, как правило, разобраться с ней бывает намного проще. А вот если директор решает принять в своем учебном заведении усложненный курс, то тут школьникам навряд ли поможет штудирование материала, если они что-то упустили. Соответственно от направленности проводятся и проверочные работы, которые тоже имеют несколько категорий сложности. Решебник к учебнику «Алгебра. Самостоятельные работы 8 класс (углубленный уровень)» Александрова поможет справиться даже с самыми трудными заданиями.
Как построен сборник.
В издание вошло шестьдесят шесть самостоятельных работ, включая и нулевую, которая помогает вспомнить материал предыдущего класса. Каждая имеет по четыре варианта, в них имеется различное количество заданий. ГДЗ по алгебре 8 класс Александрова содержит развернутые и детальные решения по всем номерам.
Каждая имеет по четыре варианта, в них имеется различное количество заданий. ГДЗ по алгебре 8 класс Александрова содержит развернутые и детальные решения по всем номерам.
В чем именно он поможет.
Вполне понятно, что школьники должны справляться с трудностями, которые встают по пути к знаниям. Но одно дело, когда те сами виноваты в том, что чего-то недопоняли и совсем другое, когда это вина преподавателя. Если бы учителя хоть половину того времени, что тратят на заполнение различных бумажек, расходовали на разъяснение материала, то и проблем у ребят было бы значительно меньше. Особенно дефицит информации ощущается во время проверочных работ, когда нет возможности обратиться к дополнительным источникам за помощью. Именно поэтому требуется хорошая подготовка к подобным мероприятиям. Оказать ее может решебник к учебнику «Алгебра. Самостоятельные работы 8 класс (углубленный уровень)» Александрова, в котором подробно расписана вся программа этого курса и имеются полновесные решения по каждому пункту.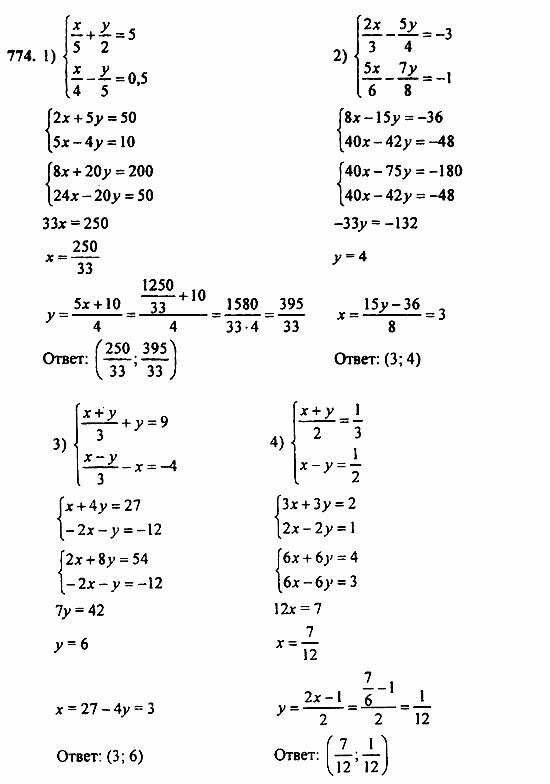 «Мнемозина», 2018 г.
«Мнемозина», 2018 г.
Самостоятельная работа 0 Повторение курса алгебры 7-го класса
Самостоятельная работа 1
Варианты:
Самостоятельная работа 2
Варианты:
Самостоятельная работа 3
Варианты:
Самостоятельная работа 4
Варианты:
Самостоятельная работа 5
Варианты:
Самостоятельная работа 6
Варианты:
Самостоятельная работа 7
Варианты:
Самостоятельная работа 8
Варианты:
Самостоятельная работа 9
Варианты:
Самостоятельная работа 10
Варианты:
Самостоятельная работа 11
Варианты:
Самостоятельная работа 12
Варианты:
Самостоятельная работа 13
Варианты:
Самостоятельная работа 14
Варианты:
Самостоятельная работа 15
Варианты:
Самостоятельная работа 16
Варианты:
Самостоятельная работа 17
Варианты:
Самостоятельная работа 18
Варианты:
Самостоятельная работа 19
Варианты:
Самостоятельная работа 20
Самостоятельная работа 21
Варианты:
Самостоятельная работа 22
Варианты:
Самостоятельная работа 23
Варианты:
Самостоятельная работа 24
Варианты:
Самостоятельная работа 25
Варианты:
Самостоятельная работа 26
Варианты:
Самостоятельная работа 27
Варианты:
Самостоятельная работа 28
Варианты:
Самостоятельная работа 29
Варианты:
Самостоятельная работа 30
Варианты:
Самостоятельная работа 31
Варианты:
Самостоятельная работа 32
Варианты:
Самостоятельная работа 33
Варианты:
Самостоятельная работа 34
Варианты:
Самостоятельная работа 35
Варианты:
Самостоятельная работа 36
Варианты:
Самостоятельная работа 37
Варианты:
Самостоятельная работа 38
Варианты:
Самостоятельная работа 39
Варианты:
Самостоятельная работа 40
Самостоятельная работа 41
Варианты:
Самостоятельная работа 42
Варианты:
Самостоятельная работа 43
Варианты:
Самостоятельная работа 44
Варианты:
Самостоятельная работа 45
Варианты:
Самостоятельная работа 46
Варианты:
Самостоятельная работа 47
Варианты:
Самостоятельная работа 48
Варианты:
Самостоятельная работа 49
Варианты:
Самостоятельная работа 50
Варианты:
Самостоятельная работа 51
Варианты:
Самостоятельная работа 52
Варианты:
Самостоятельная работа 53
Варианты:
Самостоятельная работа 54
Варианты:
Самостоятельная работа 55
Варианты:
Самостоятельная работа 56
Варианты:
Самостоятельная работа 57
Варианты:
Самостоятельная работа 58
Варианты:
Самостоятельная работа 59
Варианты:
Самостоятельная работа 60
Самостоятельная работа 61
Варианты:
Самостоятельная работа 62
Варианты:
Самостоятельная работа 63
Варианты:
Самостоятельная работа 64
Варианты:
Самостоятельная работа 65
Варианты:
Алгебра 8 класс.
 Тесты и ТренажерыТесты и тренажеры по алгебре
Тесты и ТренажерыТесты и тренажеры по алгебреКонтрольные работы с ответами:
УМК МЕРЗЛЯК: Дидактические материалы: Контрольные работы (7 КР)
УМК МЕРЗЛЯК (угл.): КиСР — Контрольные работы 8 кл (10 КР).
УМК МАКАРЫЧЕВ: Жохов Дидактические материалы — Контрольные (10 КР)
УМК МАКАРЫЧЕВ: Жохов Дидактические материалы — Самостоятельные (57 СР)
УМК МАКАРЫЧЕВ: Глазков. Контрольно измерительные работы (10 КР)
УМК МАКАРЫЧЕВ: Дудницын. Тематические тесты для 8 класса
УМК МАКАРЫЧЕВ: Рурукин. Поурочные разработки: Контрольные (10 КР)
УМК МАКАРЫЧЕВ (угл.): Карачинский. Самостоятельные и контрольные работы 8 кл
УМК МОРДКОВИЧ: Попов М.А. Дидактические материалы: Контрольные (7 КР)
УМК МОРДКОВИЧ: Александрова. Контрольные работы в 8 классе
УМК МОРДКОВИЧ: Домашние контрольные работы из уч. «Алгебра 8 класс. Часть 2-я»
«Алгебра 8 класс. Часть 2-я»
УМК НИКОЛЬСКИЙ: Потапов. Дидактические материалы — Контрольные (7 КР)
УМК ДОРОФЕЕВ: Кузнецова и др. Контрольные работы для 8 класса (итоговая)
УМК АЛИМОВ: Жохов и др. Дидактические материалы — Контрольные (9 КР)
К любому УМК (базовому) — Ершова. Самост. и контр. работы по алгебре и геометрии (итоговая)
Электронные версии учебников и конспекты
Конспекты по математике (5-6 классы) и алгебре (7-9 классы)
Онлайн учебник: Алгебра 8 кл. Макарычев, Миндюк, Суворова (Просвещение 2019)
Онлайн учебник: Алгебра 8 класс. Мордкович, Семенов (Просвещение, 2018)
Онлайн учебник: Алгебра 8 (углубленное изучение). Мерзляк, Поляков (2019)
Рекомендуемые материалы для очного контроля знаний
по предмету «Алгебра 8 класс»:
Контрольно-измерительные материалы по алгебре в 8 классе / В. В.Черноруцкий — М.: ВАКО, 2018
В.Черноруцкий — М.: ВАКО, 2018
Алгебра. Тематические тесты. 8 класс. Кузнецова Л.В., Минаева С.С., Рослова Л.О. и др. (2014, 142с.)
Алгебра 8 класс. Контрольные работы. Кузнецова Л.В., Минаева С.С., Рослова Л.О., Суворова С.Б. (2016, 80с.)
Алгебра. 7-9 классы. Контрольные работы. Кузнецова Л.В., Минаева С.С., Рослова Л.О. (2011, 110с.)
Алгебра. Дидактические материалы. 8 класс. Евстафьева Л.П., Карп А.П. (2017, 144с.)
Алгебра. 8 класс. Дидактические материалы. Ткачева М.В., Федорова Н.Е., Шабунин М.И. (2013, 96с.)
Алгебра. 8 класс. Тематические тесты. Ткачева М.В. (2014, 80с.)
Алгебра 8 класс. Дидактические материалы. Жохов В.И., Макарычев Ю.Н., Миндюк Н.Г. (2012, 160с.)
Алгебра. 8 класс. Контрольные измерительные материалы. Глазков Ю.А., Гаиашвили М.Я. (2014, 96с.)
Алгебра. 8 класс. Тестовые материалы для оценки качества обучения. Гусева И.Л., Пушкин С.А. и др. (2013, 96с.)
Алгебра. Тематические тесты. 8 класс. Дудницын Ю. П., Кронгауз В.Л. (2012, 128с.)
П., Кронгауз В.Л. (2012, 128с.)
Алгебра. 8 класс. Дидактические материалы к учебнику Макарычева Ю.Н. — Звавич Л.И., Дьяконова Н.В. (2014, 240с.)
Самостоятельные и контрольные работы по алгебре. 8 класс. К учебнику Макарычева Ю.Н. и др. Глазков Ю.А., Гаиашвили М.Я. (2012, 144с.)
Тесты по алгебре. 8 класс: к учебнику Макарычева Ю.Н. и др. — Глазков Ю.А., Гаиашвили М.Я. (2013, 112с.)
Алгебра. 8 класс. Дидактические материалы к учебнику Макарычева. Углубленное изучение. (2013, 173с.)
Алгебра. Дидактические материалы. 8 класс. Пос. для школ с углубл. изучен. математики. Макарычев Ю.Н., Миндюк Н.Г. (2010, 157с.)
Тесты по алгебре. 8 класс. К учебнику Мордковича А.Г. Ключникова Е.М., Комиссарова И.В. (2011, 96с.)
Алгебра. 7-9 классы. Контрольные работы. Мордкович А.Г. (2011, 127с.)
Алгебра 8 класс. Контрольные работы. Александрова Л.А. (2014, 40с.)
Алгебра. 7-9 классы. Контрольные работы. Мордкович А.Г. (2011, 127с.)
Алгебра. 8 класс. Тематические тесты. Чулков П.В., Струков Т.С. (2012, 95с.)
8 класс. Тематические тесты. Чулков П.В., Струков Т.С. (2012, 95с.)
Тесты по алгебре. 8 класс. К учебнику Никольского С.М. и др. — Журавлев С.Г., Ермаков В.В. и др. (2013, 144с.)
Алгебра. 7-8 классы. Тренажер. Тематические тесты и итоговые работы. Под ред. Лысенко Ф.Ф., Кулабухова С.Ю. (2013, 96с.)
Алгебра. 8 класс. Сборник тестов и контрольных заданий. Дюмина Т.Ю. (2010, 83с.)
Вы смотрели «Тесты по алгебре в 8 классе. Контрольные работы по алгебре 8 класс с ответами». Вернуться
Решебник к сборнику самостоятельных работ по алгебре для 8 класса Александровой ОНЛАЙН
Решения самостоятельных работ по алгебре из сборника для 8 класса Александровой Л. А. Рукопись. — 2014.
Настоящее пособие содержит решения самостоятельных работ из сборника «Александрова Л. А. Алгебра. Самостоятельные работы для 8 класса общеобразовательных учреждений / K. А. Александрова ; под ред. А. Г. Мордковича. — 3-е изд., перераб. — М. : Мнемозина, 2007. — 112 с.»
— М. : Мнемозина, 2007. — 112 с.»
Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы по математике.
Внимание! Рукопись не проверялась, возможны ошибки!
Содержание
Тема 1
АЛГЕБРАИЧЕСКИЕ ДРОБИ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД АЛГЕБРАИЧЕСКИМИ ДРОБЯМИ
1. Основные понятия С-1
2. Основное свойство алгебраической дроби С-2
3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями С-3
4. Сложение и вычитание алгебраических дробей с разными знаменателями С-4, 5
5. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень С-6, 7
6. Преобразование рациональных выражений С-8
7. Первые представления о рациональных уравнениях С-9
8. Степень с отрицательным целым показателем С-10
Тема 2
ФУНКЦИЯ у = Vx. СВОЙСТВА КВАДРАТНОГО КОРНЯ
9. Множество рациональных чисел С-11
10. Понятие квадратного корня из неотрицательного числа С-12
11. Иррациональные числа С-13
Иррациональные числа С-13
12. Множество действительных чисел С-14
13. Функция у = k/х , ее свойства и график С-15
14. Свойства квадратных корней С-16
15. Преобразование выражений, содержащих операцию извлечения квадратного корня С-17—20
16. Модуль действительного числа С-21, 22
Тема 3
КВАДРАТИЧНАЯ ФУНКЦИЯ. ФУНКЦИЯ у = k/x
17. Функция у = kx², ее свойства и график С-23, 24
18. Функция у = k/x, ее свойства и график С-25, 26
19. Как построить график функции у = f(х + l) если известен график функции у = f(x) С-27
20. Как построить график функции у = f(x) + m, если известен график функции у = f(x) С-28
21. Как построить график функции у = f(x + l) + m, если известен график функции у = f(x) С-29
22. Функция у = ах² + bx + с, ее свойства и график С-30, 31
23. Графическое решение квадратных уравнений С-32
Тема 4 КВАДРАТНЫЕ УРАВНЕНИЯ
24. Основные понятия С-33
25. Формулы корней квадратного уравнения С-34
26. Рациональные уравнения С-35
27. Рациональные уравнения как математические модели реальных ситуаций С-36
Рациональные уравнения как математические модели реальных ситуаций С-36
28. Еще одна формула корней квадратного уравнения С-37
29. Теорема Виета С-38, 39
30. Иррациональные уравнения С-40
Тема 5 НЕРАВЕНСТВА
31. Свойства числовых неравенств С-41
32. Исследование функций на монотонность С-42
33. Решение линейных неравенств С-43
34. Решение квадратных неравенств С-44, 45
35. Приближенные значения действительных чисел С-46
36. Стандартный вид числа С-47
Итоговое повторение
ВНИМАНИЕ! Все права на публикацию рукописей принадлежат сайту gdz.math-helper.ru. Копирование и распространение материалов запрещено!
САМОСТОЯТЕЛЬНЫЕ И КОНТРОЛЬНЫЕ РАБОТЫ ПО АЛГЕБРЕ
СБОРНИК ЗАДАЧ ПО АЛГЕБРЕ
А Н РУРУКИН, Н Н ГУСЕВА, Е А ШУВАЕВА СБОРНИК ЗАДАЧ ПО АЛГЕБРЕ 8 класс МОСКВА «ВАКО» 016 УДК 75 ББК 14 Р87 6+ Издание допущено к использованию в образовательном процессе на основании приказа Министерства
ПодробнееПОУРОЧНОЕ ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
ПОУРОЧНОЕ ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ (4 ч в неделю I полугодие, 3 ч в неделю II полугодие, всего 119 ч) ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ 7-ГО КЛАССА 4 2. 09-7.09 1 Разложение на множители 1 2.09 2 Формулы сокращенного
09-7.09 1 Разложение на множители 1 2.09 2 Формулы сокращенного
ГЕОМЕТРИЯ. Издание четвертое. 10 класс
ГЕОМЕТРИЯ Издание четвертое 10 класс МОСКВА «ВАКО» 2017 УДК 372.851 ББК 74.262.21 К65 6+ Издание допущено к использованию в образовательном процессе на основании приказа Министерства образования и науки
ПодробнееРАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ 8 КЛАСС
РАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ 8 КЛАСС Пояснительная записка Рабочая программа составлена на основе: — Федерального компонента государственного образовательного стандарта основного общего образования по
ПодробнееПояснительная записка
Пояснительная записка Рабочая программа составлена на основе: — Федерального компонента государственного образовательного стандарта основного общего образования по математике — Примерные программы по математике.
ИНФОРМАТИКА 8 класс МОСКВА «ВАКО» 2017
ИНФОРМАТИКА 8 класс МОСКВА «ВАКО» 2017 УДК 372.862 ББК 74.262.8 К65 6+ Издание допущено к использованию в образовательном процессе на основании приказа Министерства образования и науки РФ от 09.06.2016
ПодробнееСБОРНИК ЗАДАЧ ПО АЛГЕБРЕ
А. Н. РУРУКИН, Н. Н. ГУСЕВА, Е. А. ШУВАЕВА СБОРНИК ЗАДАЧ ПО АЛГЕБРЕ 9 класс МОСКВА «ВАКО» 06 УДК 7.5 ББК.4 Р87 6+ Издание допущено к использованию в образовательном процессе на основании приказа Министерства
ПодробнееПояснительная записка.
Пояснительная записка. Данная рабочая программа ориентирована на учащихся 8 класса и реализуется на основе следующих документов:. Государственный стандарт начального общего, основного общего и среднего
ПодробнееРАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ.
 8 класс
8 классМУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА 40 г. ЛИПЕЦКА РАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ для учащихся с ограниченными возможностями здоровья по слуху 8 класс
ПодробнееПояснительная записка
Пояснительная записка Настоящая программа по алгебре для основной общеобразовательной школы 8 класса составлена на основе федерального компонента государственного стандарта основного общего образования
ПодробнееАЛГЕБРА. Издание четвертое. 9 класс
АЛГЕБРА Издание четвертое 9 класс МОСКВА «ВАКО» 2017 УДК 372.851 ББК 74.262.21 К65 6+ Издание допущено к использованию в образовательном процессе на основании приказа Министерства образования и науки РФ
ПодробнееОТКРЫТЫЕ УРОКИ АЛГЕБРЫ
Н. Л. БАРСУКОВА ОТКРЫТЫЕ УРОКИ АЛГЕБРЫ 7 8 классы МОСКВА «ВАКО» 2010 УДК 372.851 ББК 74.262.21 Б26 Книга подготовлена совместно с ООО «Парус». Б26 Барсукова Н.Л. Открытые уроки алгебры: 7 8 классы. М.:
Л. БАРСУКОВА ОТКРЫТЫЕ УРОКИ АЛГЕБРЫ 7 8 классы МОСКВА «ВАКО» 2010 УДК 372.851 ББК 74.262.21 Б26 Книга подготовлена совместно с ООО «Парус». Б26 Барсукова Н.Л. Открытые уроки алгебры: 7 8 классы. М.:
Тематическое планирование
Тематическое планирование Тема урока Колво часов Тип урока Характеристика деятельности учащихся или виды учебной деятельности Виды контроля, измерители Требования к уровню подготовки обучающихся Домашнее
ПодробнееАЛГЕБРА ТЕМАТИЧЕСКИЕ ТЕСТЫ. 8 класс
АЛГЕБРА ТЕМАТИЧЕСКИЕ ТЕСТЫ класс МОСКВА «ВАКО» 01 УДК 7.51 ББК 7..1 А5 + Издание допущено к использованию в образовательном процессе на основании приказа Министерства образования и науки РФ от 1.1.009
ПодробнееОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
УДК 788:5 ББК 5я7 Г7 Рекомендовано для учащихся 8 классов, соответствует действующей программе по математике для общеобразовательных учебных заведений, утвержденной МИНИСТЕРСТВОМ ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ПодробнееАЛГЕБРА.
 Издание третье. 7 класс
Издание третье. 7 классАЛГЕБРА Издание третье 7 класс МОСКВА «ВАКО» 2017 УДК 372.851 ББК 74.262.21 К65 6+ Издание допущено к использованию в образовательном процессе на основании приказа Министерства образования и науки РФ от
ПодробнееМАТЕМАТИКА. Издание восьмое. 2 класс
МАТЕМАТИКА Издание восьмое 2 класс МОСКВА «ВАКО» 2017 УДК 372.851 ББК 74.262.21 К65 Издание допущено к использованию в образовательном процессе на основании приказа Министерства образования и науки РФ
ПодробнееАннотация к рабочей программе
Аннотация к рабочей программе 8 класс, алгебра ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа по алгебре для основной общеобразовательной школы 8 класса составлена на основе: Федерального компонента государственного
ПодробнееРАБОЧАЯ ПРОГРАММА Артамошиной Н.
 А.
А.РАБОЧАЯ ПРОГРАММА Артамошиной Н.А. по алгебре для 8-х классов 2017-2018 учебный год Москва 2017 Раздел 1. Пояснительная записка Рабочая программа по алгебре для 8 класса составлена на основе федерального
ПодробнееISBN К 22.14я721 ISBN
ДК 373:512 К 22.14721 49 49 аа, аьяа Маа.. 7 9 /.М.. М : Э, 2018. 128. (. ). ISBN 978-5-04-093533-8, 7 9-. П ё -. П,. П 7 9-,, -. ДК 373:512 К 22.14я721 ISBN 978-5-04-093533-8 аа.м., 2018 О. ООО «Иаь «Э»,
ПодробнееРабочая программа. по алгебре
Муниципальное бюджетное общеобразовательное учреждение Гимназия 4 г. Химки УТВЕРЖДАЮ: Директор МБОУ Гимназия 4 /Н.Н. Козельская / Приказ от 2015 г. Рабочая программа по алгебре (базовый уровень) 8 класс
ПодробнееРАБОЧАЯ ПРОГРАММА. Алгебра 8 класс
РАБОЧАЯ ПРОГРАММА Алгебра 8 класс Используемые учебные пособия: Ю. Н. Макарычев, Н.Г. Миндюк, К.И.Нешков, С.Б.Суворова Алгебра 8 класс Учебник для обшеобразовательных учреждений М.: Просвещение ОАО «Московские
Н. Макарычев, Н.Г. Миндюк, К.И.Нешков, С.Б.Суворова Алгебра 8 класс Учебник для обшеобразовательных учреждений М.: Просвещение ОАО «Московские
Пояснительная записка
Пояснительная записка Данная рабочая программа учебного курса по алгебре для 8 класса разработана на основе программы основного общего образования по математике с учетом требований федерального компонента
ПодробнееПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа составлена к учебнику «Алгебра 8» авторов Ю.Н.Макарычева, Н.Г.Миндюк, К.И.Нешкова, С.Б.Суворовой. Цель изучения курса алгебры в 8 классе развить интерес к решению
ПодробнееСБОРНИК ЗАДАЧ ПО АЛГЕБРЕ
А. Н. РУРУКИН, Н. Н. ГУСЕВА, Е. А. ШУВАЕВА СБОРНИК ЗАДАЧ ПО АЛГЕБРЕ 7 класс МОСКВА «ВАКО» 06 УДК 7. 5 ББК.4 Р87 6 Издание допущено к использованию в образовательном процессе на основании приказа Министерства
5 ББК.4 Р87 6 Издание допущено к использованию в образовательном процессе на основании приказа Министерства
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа учебного предмета «Алгебра» составлена в соответствии с требованиями федерального компонента государственного стандарта общего образования и примерной программы
ПодробнееПояснительная записка
Пояснительная записка Цель: Познакомить учащихся со способами решения систем линейных уравнений с двумя переменными. Выработать умение выполнять тождественные преобразования рациональных выражений. Систематизировать
ПодробнееРабочая программа. по алгебре 8«Б»класс
Рабочая программа по алгебре 8«Б»класс Петухова Ольга Алексеевна учитель математики высшей квалификационной категории Учебник Алгебра 8 класс под редакцией С. А.Теляковского М.: Просвещение, 2015 г. Руза
А.Теляковского М.: Просвещение, 2015 г. Руза
ИНФОРМАТИКА. 11 класс
ИНФОРМАТИКА 11 класс МОСКВА «ВАКО» 2018 УДК 372.862 ББК 74.262.8 К65 6+ Издание допущено к использованию в образовательном процессе на основании приказа Министерства образования и науки РФ от 09.06.2016
ПодробнееРабота по алгебре для 8 класса.
Работа по алгебре для 8 класса. 1.Вид работы: итоговая работа по алгебре в 8 классе Цель работы: оценка уровня достижения учащимися 8 класса планируемых результатов обучения алгебре 2.Перечень проверяемых
Подробнее12 необычных действий с уравнениями в один шаг
Мы ожидаем, что в 8-м классе ученики уже знают, как решать одношаговые уравнения. Многие из них делают это, но есть и другие, которые борются с ними. Я работаю со студентами, которые имеют право на математическую лабораторию, вторая доза математики в течение дня. Большинство моих учеников пропустили базовые понятия, когда они должны были выучить их в предыдущем классе. Итак, практика решения одношаговых уравнений работает как обзор для большинства студентов, но для других это кажется новой темой.
Я работаю со студентами, которые имеют право на математическую лабораторию, вторая доза математики в течение дня. Большинство моих учеников пропустили базовые понятия, когда они должны были выучить их в предыдущем классе. Итак, практика решения одношаговых уравнений работает как обзор для большинства студентов, но для других это кажется новой темой.
Сегодня я поделюсь с вами 12 заданиями и идеями, которые помогут вашим ученикам понять и попрактиковаться в решении одношаговых уравнений.
За прошедшие годы я усвоил одну вещь: смотреть на навыки преподавания по-разному, в зависимости от того, что нужно ученикам. Для решения одношаговых уравнений это действительно должно быть автоматическим. Студентам не нужно много думать, решая их. Это должно стать естественным. Таким образом, практика решения одношаговых уравнений выглядит иначе, чем более сложные концептуальные темы.Ключом к тому, чтобы ученики свободно владели этими навыками, является повторение, повторение, повторение. Я упоминал повторение?
Я упоминал повторение?
В упражнениях, которые я собрал в этом списке, большое внимание уделяется практике беглости речи. Некоторые занятия проводятся с партнерами или небольшими группами. Другие отлично подходят для самостоятельной практики на математических станциях, выполнения домашних заданий и т. Д. В целом, если ваши ученики регулярно отрабатывают эти виды деятельности, они очень свободно овладевают этим навыком.
Лабиринты с одношаговыми уравнениями
Понг с одношаговыми уравнениями
Игра в крестики-нолики
Доски для совместной работы
Активность ловушки Кути для одношаговых уравнений
Колеса Equation
Снежный бой
Line Puzzle Activity
Соответствующие карты
Kahoot для решения одношаговых уравнений
Викторина на Quizizz
Опасность
Давайте углубимся в деятельность
Давайте рассмотрим каждое из занятий и то, что они могут предложить вашему классу. По мере того, как вы узнаете больше об упражнениях, вы будете видеть задания для всего класса, небольшой группы и самостоятельной практики. Кроме того, эти упражнения работают для звонков, практических занятий, а некоторые из них могут работать и для домашних заданий.
По мере того, как вы узнаете больше об упражнениях, вы будете видеть задания для всего класса, небольшой группы и самостоятельной практики. Кроме того, эти упражнения работают для звонков, практических занятий, а некоторые из них могут работать и для домашних заданий.
Если вы раньше не использовали математические лабиринты в классе, я предлагаю вам попробовать их. Я не всегда был верующим, но однажды я использовал их в отчаянии и никогда не оглядывался назад. Лабиринты отлично подходят для того, чтобы побудить студентов решать проблемы и практиковаться, не осознавая, сколько проблем они на самом деле решают.Каждый день в начале урока мы проходим один из этих лабиринтов. Вы можете положить их в конверт или карман для сухого стирания, если у вас несколько занятий в течение дня.
Я использую лабиринты как с продвинутыми учениками, так и на лабораторных занятиях по математике. Этот конкретный набор лабиринтов включает 4 лабиринта, и их сложность увеличивается от одного лабиринта к другому. Первый — это сложение и вычитание, второй — целые числа, третий — умножение и деление, а последний — смесь одношаговых уравнений со всеми операциями.Это упражнение — отличный способ постоянно практиковаться в этом навыке.
Первый — это сложение и вычитание, второй — целые числа, третий — умножение и деление, а последний — смесь одношаговых уравнений со всеми операциями.Это упражнение — отличный способ постоянно практиковаться в этом навыке.
Если вы хотите еще больше увлекательных математических лабиринтов, мы отправляем БЕСПЛАТНЫЙ лабиринт по математическим концепциям средней школы исключительно членам клуба «Лабиринт месяца». Если вы хотите присоединиться и получить БЕСПЛАТНЫЕ математические лабиринты, которых нет нигде, , и , зарегистрируйтесь здесь:
Запишитесь в клуб «Лабиринт месяца».
Дети любят возвращаться к вещам очень давней давности (и я знаю некоторых учителей, которым они тоже нравятся!).Забавно, как они думали, что 10 лет назад это были древние времена. Что ж, эта игра с уравнениями от XP Math восходит к временам Pong и добавляет в процесс решения одношаговых уравнений. Есть несколько способов настроить эту игру: по уровню математических задач и по уровню владения компьютером. Я бы посоветовал дать ученикам калькулятор, потому что некоторые из используемых ими чисел не являются обычными.
Я бы посоветовал дать ученикам калькулятор, потому что некоторые из используемых ими чисел не являются обычными.
Кроме того, вы можете сыграть в эту игру вместе со студентами, чтобы они соревновались с вами.Им это понравится, и они будут очень соревноваться.
Крестики-нолики — это интересный способ попрактиковаться в одношаговых уравнениях во многих различных формах. Эту игру можно использовать как совместную работу, игру, занятие в небольшой группе, для быстрого завершения или для всего класса. Моим ученикам нравится играть в крестики-нолики, и они забывают, что учатся решать одношаговые уравнения. Эта игра в крестики-нолики для одношаговых уравнений включает 8 игр, сложность которых возрастает от сложения и вычитания до целых чисел и умножения и деления.Это отличный способ повторить решение одношаговых уравнений.
Когда учащиеся играют вдвоем, каждый из них берет по символу x или o. Они ходят вперед и назад, решая уравнения, и, если они делают это правильно, помещают свой символ в квадрат. Мои дети действительно увлекаются этой игрой, и мне нравится слышать, как они рассказывают о проблемах, которые они решают.
Мои дети действительно увлекаются этой игрой, и мне нравится слышать, как они рассказывают о проблемах, которые они решают.
Дети учатся решать одноэтапные уравнения в совместной работе с классной доской, используя какую-либо доску и решая задачи на своем разделе / доске.Вы можете заставить их всех работать над одной и той же проблемой, а затем они сверится друг с другом, чтобы убедиться, что у них одинаковые ответы. Другой вариант — каждый работает над другой проблемой, но ответы на все проблемы одинаковы. Вы можете установить это в центрах и попросить учеников сменять друг друга.
Ссылка на эту идею ведет на сообщение в блоге с множеством идей для решения уравнений. В середине страницы она описывает то, что она называет «уравнениями салфеток», которые можно сделать с помощью рукавов для сухого стирания или больших студенческих досок.Вы можете скачать несколько бесплатных салфеток, но они представляют собой двухступенчатые уравнения. Если вам нужен набор задач для этого упражнения, вы можете щелкнуть эту ссылку, чтобы просмотреть список проблем, который вы могли бы использовать.
Несколько лет назад я попробовал ловушку для кути со своими учениками, и им это понравилось. Я не очень часто играю в эту игру со студентами, так что когда мы это делаем, это новость. Этот одношаговый уловитель кути включает в себя два разных уловителя кути. Один из них — ночь, а другой — день. У вас есть ученики, сражающиеся друг с другом с помощью ловцов для кути.Если вы хотите, чтобы они просто выполнили задачи, они тоже могут это сделать. Убедитесь, что вы показываете им пример, прежде чем заставлять их играть.
Эта загрузка включает в себя 2 ловушки для кути с 8 одношаговыми уравнениями для каждой ловушки для кути, протокол учащегося, ключи ответов и наглядное руководство по складыванию ловушки для кути. Сами задачи не очень сложные, и лучше всего работает, когда учащиеся только изучают эти концепции.
Я хочу попробовать это упражнение Equations Wheels от Miss Calculate в моем классе математической лаборатории в качестве быстрого завершающего упражнения. Его можно использовать со многими другими темами, а не только с одношаговыми уравнениями. Вам понадобятся одношаговые уравнения и много прищепок. Вы пишете уравнения на колесе, а ответы на его обратной стороне. Также ответы будут написаны на обеих сторонах прищепок. Глядя на изображения в ее посте, я понял, как это работает. Вы также можете скачать пустое колесо из связанного сообщения в блоге.
Его можно использовать со многими другими темами, а не только с одношаговыми уравнениями. Вам понадобятся одношаговые уравнения и много прищепок. Вы пишете уравнения на колесе, а ответы на его обратной стороне. Также ответы будут написаны на обеих сторонах прищепок. Глядя на изображения в ее посте, я понял, как это работает. Вы также можете скачать пустое колесо из связанного сообщения в блоге.
Снежный бой
Снежный бой в классе украсит день каждого, независимо от времени года.Для создания снежного кома каждый должен написать на листе бумаги одношаговое уравнение. Затем вы скомкаете бумагу в «снежный ком». Когда вы говорите «иди», все начинают кидать снежки, пока вы не скажете «Стоп». На этом этапе все разворачивают бумагу и решают задачу о снежном коме. Вы снова бросаете снежки, и все проверяют, правильный ли ответ.
Этот метод также работает с рефлексией или заданием вопросов. Это происходит из-за разлома мозга.Одна из лучших частей заключается в том, что никакой подготовки не требуется.
Это упражнение-головоломка — это бесплатная игра, которую вы можете загрузить на TeachersPayTeachers. Аспект головоломки делает занятия с одношаговыми уравнениями увлекательными. Я никогда раньше не видел подобной головоломки. Убедитесь, что у ваших учеников есть линейка, когда они это сделают, чтобы ученики могли быть точными в своих ответах. Вы заметите, что некоторые ответы являются отрицательными целыми числами, поэтому ваши ученики должны быть знакомы с целыми числами для этого упражнения.Это отлично подходит в качестве практического занятия для учеников 7-8 классов.
Вы можете поймать бесплатный набор совпадающих карточек для практики решения одношаговых уравнений из блога Math in the Middle. В своем блоге она рассказывает о различных занятиях, которые вы можете попробовать с ними. Она предоставляет набор карточек, состоящий из 8 групп по четыре штуки. Эти карты можно использовать несколькими способами. Во-первых, вы можете дать каждому карточку по пути в комнату. Затем они должны посмотреть, смогут ли они найти трех других людей, у которых есть то же решение, что и у них.
Затем они должны посмотреть, смогут ли они найти трех других людей, у которых есть то же решение, что и у них.
Кроме того, вы можете попросить учащихся работать в парах и попытаться найти 8 наборов совпадающих карточек. Кроме того, это действительно может быть использовано в качестве быстрого финишера.
Kahoot имеет несколько различных применений. Моя любимая часть в этом — возможность использовать эту игру для формирующего оценивания. В конце игры вы можете загрузить довольно подробный технический паспорт на свой Google Диск.
Эта игра Kahoot состоит из 20 вопросов. 18 вопросов выглядят как простые выражения одношаговых уравнений.Последние два вопроса повышают уровень и представляют собой проблемы со словами. Эта игра отлично подходит как для предварительной оценки, так и для практики.
Quizizz похожа на Kahoot, за исключением того, что учащиеся могут идти в своем собственном темпе (я предпочитаю использовать опцию домашнего задания). Вы получите много отчетов об успеваемости учащихся от Quizizz. В этой игре-викторине есть множество одношаговых уравнений, которые я бы использовал в классе. Эта конкретная игра-викторина сочетает в себе как традиционные вопросы, так и пару словесных задач.Мне нравится использовать Quizizz как разминку, циклический обзор для студентов. Можно пару недель заниматься одной и той же темой. Это дает студентам возможность улучшить свои навыки.
В этой игре-викторине есть множество одношаговых уравнений, которые я бы использовал в классе. Эта конкретная игра-викторина сочетает в себе как традиционные вопросы, так и пару словесных задач.Мне нравится использовать Quizizz как разминку, циклический обзор для студентов. Можно пару недель заниматься одной и той же темой. Это дает студентам возможность улучшить свои навыки.
Jeopardy имеет много особенностей, которые я ищу в игре-обзоре. Весь класс может играть одновременно, и вам не нужно проходить всю игру, чтобы она была эффективной. В моем классе, когда мы играем в Jeopardy, все отвечают на все вопросы. Я не играю в командном стиле. Кажется, что в командном стиле большинство детей не занимается.Я прошу студентов отслеживать свои собственные баллы и следить за тем, какие студенты получают их, а какие нет.
В этой конкретной игре Jeopardy вы найдете уравнения для решения следующих категорий: сложение, вычитание, умножение, деление и десятичные дроби. Всего 25 вопросов. Студентам придется работать с отрицательными числами, так что это лучше подходит для студентов с такими навыками.
Студентам придется работать с отрицательными числами, так что это лучше подходит для студентов с такими навыками.
Попробуй одно ..
Этот сборник одноэтапных упражнений с уравнениями поможет вам внести немного остроты в повседневную практику ваших учеников.Вам не нужно пытаться объединить все действия. Я бы начал с одного и посмотрел, как оно пойдет. Используйте один для циклического повторения для всего класса или для звонаря, когда они входят в класс. Помните, что практика одношаговых вопросов заложит основу для многих других концепций, которым мы учим в средней школе. Эти занятия помогут вам дать им много-много возможностей для практики.
Большое спасибо за чтение. До скорого!
СвязанныеКто повторяет алгебру I и как начальные результаты связаны с улучшением результатов при повторении курса?
Описание
Это исследование Западной Западной образовательной лаборатории (REL West) изучает распространенность студентов, повторяющих Алгебру I, которые, скорее всего, повторят курс, и уровень улучшения для студентов, которые повторяют курс.
REL West провели исследование, основанное на данных за шесть лет, полученных в когорте из 3 400 учеников седьмого класса в школьном округе Калифорнии.
Ключевые выводы
- Сорок четыре процента студентов повторили Алгебру I
- В целом успеваемость учащихся улучшилась в среднем примерно на половину буквенной оценки и чуть менее чем на одну треть уровня успеваемости по Калифорнийскому стандартному тесту (CST), когда ученики повторяли Алгебру I
- Когда данные были дезагрегированы на основе начальной успеваемости в классе, более успешные ученики испытали разницу в уровнях успеваемости
- Повторяющиеся студенты, которые первоначально получили средние оценки по курсу не менее «C» по алгебре. Я получил более высокие баллы CST, но в среднем более низкие оценки по курсу, когда они повторяли курс
- У студентов, которые изначально набрали уровень владения алгеброй I CST, оценки по курсу повысились, но в среднем они снизились при повторном прохождении курса
В целом, эти результаты показывают, что учащиеся с более низкой успеваемостью, вероятно, улучшат свои оценки и оценки CST, когда они повторяют Алгебру I. Более успешные студенты, вероятно, испытают улучшение по одним показателям успеваемости и снижение по другим показателям, когда они повторяют курс.
Более успешные студенты, вероятно, испытают улучшение по одним показателям успеваемости и снижение по другим показателям, когда они повторяют курс.
Эти результаты могут помочь преподавателям изучить варианты курсов, доступные студентам с разным уровнем успеваемости, а также процессы, с помощью которых студенты попадают на курсы математики.
Сведения о ресурсе
Информация о продукте
Авторские права: 2014Формат: PDF
Страницы: 31
Издатель: U.S. Департамент образования, Институт педагогических наук
Оставайтесь на связи
Подпишитесь на E-Bulletin и получайте регулярные обновления об исследованиях, бесплатных ресурсах, решениях и объявлениях о вакансиях от WestEd.
Подписаться
Ваша загрузка начнется после того, как вы подпишетесь или выберете нет, спасибо.
Онлайн-курс алгебры для средней школы | 8 класс по математике
Этот список является репрезентативным для материалов, предоставленных или используемых в этом курсе. Имейте в виду, что фактически используемые материалы могут отличаться в зависимости от школы, в которую вы записаны, и от того, проходите ли вы курс как независимое обучение.
Чтобы получить полный список материалов, которые будут использоваться в этом курсе вашим зачисленным студентом, посетите MyInfo . Все списки могут быть изменены в любое время.
Scope & Sequence: Scope & Sequence документы описывают, что охвачено в курсе (объем), а также порядок , в каких темах охватываются (последовательность). В этих документах перечислены учебные цели и навыки, которые необходимо освоить.K12 Объем и последовательность документов для каждого курса включают:
В этих документах перечислены учебные цели и навыки, которые необходимо освоить.K12 Объем и последовательность документов для каждого курса включают:
Обзор курса
Студенты развивают беглость алгебры, приобретая навыки, необходимые для решения уравнений и выполнения операций с числами, переменными, уравнениями и неравенствами. Они также изучают основные понятия абстракции и обобщения, которые делает возможной алгебра. Студенты учатся использовать числовые свойства для упрощения выражений или обоснования утверждений; описывать множества с обозначением множеств и находить объединение и пересечение множеств; упрощать и оценивать выражения, включающие переменные, дроби, показатели степени и радикалы; работать с целыми числами, рациональными числами и иррациональными числами; создавать графики и решать уравнения, неравенства и системы уравнений.Они учатся определять, является ли отношение функцией, и как описывать его область и диапазон; использовать факторинг, формулы и другие методы для решения квадратных и других полиномиальных уравнений; формулировать и оценивать достоверные математические аргументы, используя различные типы рассуждений; и преобразовать текстовые задачи в математические уравнения, а затем использовать уравнения для решения исходных задач. Ожидается, что студенты, изучающие алгебру, овладеют навыками и концепциями, представленными в курсе предварительной алгебры K12 (или его эквиваленте).
Ожидается, что студенты, изучающие алгебру, овладеют навыками и концепциями, представленными в курсе предварительной алгебры K12 (или его эквиваленте).
Краткое содержание курса
SEMESTER ONE
Раздел 1: Основы алгебры
Английское слово algebra и испанское слово algebrista происходят от арабского слова al-jabr , что означает «восстановление». В средневековье цирюльник часто называл себя альгебристом. Альгебрист также был костоправом, который восстанавливал или фиксировал кости. Сегодня математики используют алгебру для решения задач.Алгебра может находить решения и «исправлять» определенные проблемы, с которыми вы сталкиваетесь.
- Введение в семестр
- Выражения
- Переменные
- Перевод слов в переменные выражения
- Уравнения
- Перевод слов в уравнения
- Запасные наборы
- Решение проблем
Блок 2: Свойства действительных чисел
Есть много разных типов чисел. Отрицательные числа, положительные числа, целые числа, дроби и десятичные дроби — это лишь некоторые из многих групп чисел.Что общего у этих разновидностей чисел? Все они подчиняются правилам арифметики. Их можно складывать, вычитать, умножать и делить.
Отрицательные числа, положительные числа, целые числа, дроби и десятичные дроби — это лишь некоторые из многих групп чисел.Что общего у этих разновидностей чисел? Все они подчиняются правилам арифметики. Их можно складывать, вычитать, умножать и делить.
- Номер строки
- Наборы
- Сравнение выражений
- Количество объектов недвижимости
- Измерение, точность и оценка
- Распределительная собственность
- Алгебраическое доказательство
- Противоположности и абсолютная ценность
Раздел 3: Операции с действительными числами
Есть много разных типов чисел.Отрицательные числа, положительные числа, целые числа, дроби и десятичные дроби — это лишь некоторые из многих групп чисел. Что общего у этих разновидностей чисел? Все они подчиняются правилам арифметики. Их можно складывать, вычитать, умножать и делить.
- Дополнение
- Вычитание
- Умножение
- Взаимные и деление
- Приложения: проблемы с числами
Раздел 4: Решение уравнений
Греческого математика Диофанта часто называют «отцом алгебры». В его книге «Арифметика » описаны решения 130 проблем. Он не открыл все эти решения сам, но он собрал множество решений, которые были найдены греками, египтянами и вавилонянами до него. Некоторым людям давным-давно явно нравилось заниматься алгеброй. Это также помогло им — и может помочь вам — решить множество реальных проблем.
В его книге «Арифметика » описаны решения 130 проблем. Он не открыл все эти решения сам, но он собрал множество решений, которые были найдены греками, египтянами и вавилонянами до него. Некоторым людям давным-давно явно нравилось заниматься алгеброй. Это также помогло им — и может помочь вам — решить множество реальных проблем.
- Уравнения сложения и вычитания
- Уравнения умножения и деления
- Узоры
- Множественные преобразования
- Переменные с обеих сторон уравнения
- Преобразование формул
- Оценка решений
- Проблемы затрат
Раздел 5: Устранение неравенств
Каждый математик знает, что 5 меньше 7, но когда y Что общего у масштабного рисунка, велосипедной шестерни и распродажи в местном магазине? Все они представляют проблемы, которые можно решить с помощью уравнений с дробями. Вы, наверное, слышали фразу: «Вот где я провожу черту!» В алгебре это выражение можно понимать буквально.Линейные функции и их графики играют важную роль в нескончаемом стремлении к моделированию реального мира. Когда встречаются два человека, они часто обмениваются рукопожатием или здороваются. Солнечная батарея — это небольшая машина, которая поглощает солнечную энергию и вырабатывает электричество.Математическая функция — это машина, которая принимает число на входе и производит другое число на выходе. Рациональные числа очень уравновешенные? Сложно ли рассуждать с иррациональными числами? Не совсем, но у рациональных и иррациональных чисел есть что-то общее и то, что их отличает. Подобно тому, как поезд строится из железнодорожных вагонов, полином строится путем объединения терминов и их связывания знаками плюс или минус. Многочлен — это выражение, в котором есть переменные, представляющие числа. Число может быть разложено на множители, так что вы должны иметь возможность разложить на множители многочлен, не так ли? Иногда можно, а иногда нет.Поиск способов записать многочлен как произведение множителей может быть весьма полезным. Решение уравнений может помочь вам найти ответы на многие проблемы повседневной жизни. У дроби всегда есть число в числителе и знаменателе.Однако на самом деле эти числа могут быть выражениями, представляющими числа, а это значит, что вы можете делать с дробями всевозможные интересные вещи. Дроби с переменными выражениями в числителе и знаменателе могут помочь вам решить многие проблемы. Профессионалы используют логические рассуждения по-разному. Два дополнительных раздела обеспечивают дополнительную курсовую работу.«Измерение и геометрия» предоставляет некоторые из основных предметов для начинающих студентов-геометров, а «Счет, вероятность и статистика» обеспечивает прочную основу для дальнейших исследований в области статистики и вероятности. Тесселяция — это способ повторения формы снова и снова, чтобы покрыть плоскую поверхность. Художник Мауриц Корнелис (М.К.) Эшер был очарован мозаикой. Он использовал мозаику и геометрические идеи, такие как точки, сегменты, углы и конгруэнтность, чтобы создать множество красивых и интересных произведений искусства. Сколько кукурузы может получить фермер с акра земли? Какие страны экспортируют больше всего кукурузы? Как цена на кукурузу изменилась с течением времени и как она изменится в будущем? Данные повсюду вокруг нас.Имея хорошее представление о вероятности и статистике, люди могут принимать более обоснованные решения. Всего уроков: Цель этой страницы — познакомить вас с инструментами, используемыми при распределении по математике с восьмого по девятый класс, и предоставить вам диапазоны, которые мы используем в качестве руководства. ОПИСАНИЕ УРОВНЯ CCHS В CCHS есть четыре уровня математики, разработанные для соответствия различным стилям обучения учащихся. В значительной степени учебный план и порядок преподавания тем согласованы на каждом из четырех уровней конкретной предметной области.Основные различия между уровнями заключаются в способе представления нового контента, темпах прохождения курса и количестве повторений ранее изученных тем. Ниже приведены более подробные описания каждого уровня. Honors Geometry: Этот уровень разработан для учащихся, продемонстрировавших высочайший уровень владения нестандартными, абстрактными и сложными математическими концепциями. У студентов хорошо развитые, независимые и продуктивные навыки работы. Enriched Geometry: Это расширенный уровень, разработанный для учащихся, продемонстрировавших высокий уровень владения абстрактными и сложными математическими понятиями. Учащиеся выработали привычки продуктивной работы, могут продемонстрировать владение ранее изученными темами и продолжить обучение с ограниченным повторным обучением и повторением.Студенты изучают новые темы в быстром темпе с некоторым повторением. На практике студенты могут применять и синтезировать концепции для решения некоторых новых задач (в том числе в тестовых ситуациях). Интегрированная математика A: Этот уровень включает в себя последовательность из трех курсов, каждый из которых включает стандарты алгебры, геометрии, статистики и тригонометрии. Integrated Math B: Этот уровень включает в себя последовательность из трех курсов, каждый из которых включает стандарты алгебры, геометрии, статистики и тригонометрии.Интегрированный подход, используемый на этом уровне, позволит учащимся решать проблемы, используя различные стратегии. Студенты будут использовать ранее изученный материал и развивать новые навыки в темпе, который дает значительное время для концептуального понимания. Примечание: стрелки указывают типичных пути в математической последовательности, а не исключают других перемещений между уровнями. Процесс зачисления в высшую школу по математике Для студентов, изучающих независимую и управляемую алгебру 8-го класса, следующие критерии будут использоваться для зачисления в классы математики CCHS. Геометрия с отличием 95 + Расширенная геометрия 80-94 Интегрированная математика A 60 — 79 Интегрированная математика B — 59 Для тех студентов, изучающих алгебру, которые в настоящее время изучают направленную математику в 8 классе, следующие критерии будут использоваться для зачисления в классы математики CCHS Интегрированная математика A 80 + Интегрированная математика B 0 — 79 Перечисленные оценки включают средние оценки за единицу (не средние значения по домашнему заданию / успеваемости). Черил начала урок с чтения Спагетти и Фрикадельки для всех! вслух классу. По сюжету мистер и миссис Комфорт приглашают 32 члена семьи и друзей на встречу и устанавливают восемь квадратных столов, чтобы разместить по четыре человека за каждым, по одному в стороне.По мере того, как гости приходят, у всех есть свои идеи о том, как переставить столы, чтобы группы разного размера могли сидеть вместе. Миссис Комфорт протестует, зная, что позже возникнут проблемы с сиденьем, но ее протесты игнорируются. Вечеринка превращается в веселую смесь переставленных столов, стульев, тарелок, стаканов и еды. Однако, в конце концов, все сработает, когда миссис Комфорт оказалась права. Когда Черил закончила читать рассказ, она спросила класс: «Что это была за миссис Билл?Беспокоитесь о комфорте? » Николь сначала ответила: «Здесь не будет достаточно места, потому что, когда вы складываете столы вместе, вы теряете стулья», — сказала она. «Что ты имеешь в виду?» — спросила Черил. «Это как если вы сложите два стола вместе, вы потеряете места там, где они соприкасаются. Это трудно объяснить.» Николь нарисовала в воздухе два стола, указывая на стороны, где они встретились. Черил нарисовала на доске два квадрата, нарисовав стрелку там, где стороны касались друг друга. «Вы имеете в виду потерять стулья здесь?» она спросила.Николь кивнула. (См. Рисунок 1). Выслушав идеи других студентов о проблеме миссис Комфорт, Черил сказала: «Давайте использовать цветные плитки, чтобы изучить различные способы расстановки всего четырех столов. Начнем всего с четырех столов ». Черил дала классным указаниям по расстановке квадратных «столов». «Когда плитки соприкасаются, — сказала она, — они должны касаться всей стороны. Прикосновение к частям сторон или только к углам недопустимо ». Она продемонстрировала на диапроекторе.(См. Рисунок 2.) Шерил также разместила плитки таким образом, чтобы не следовать ее правилу, и попросила учеников объяснить, почему. Затем она выполнила инструкции. «В своей группе поделитесь плитками, которые я положил на ваш стол, и найдите разные способы расставить четыре плитки. Обязательно следуй моему правилу ». Черил разложила около 70 плиток для каждой группы из четырех учеников. Пока ученики работали, Черил ходила по классу, наблюдая за учениками и отвечая на вопросы по мере необходимости.Когда у всех была возможность поработать над проблемой, она прервала студентов и попросила их внимания. «Что вы сделали?» — спросила Черил. «Кто бы хотел описать расположение, чтобы я мог построить его из плитки наверху?» «Вы можете провести прямую линию», — сообщил Брэндон. «Как это?» — спросила Черил, складывая четыре плитки в прямоугольник 1 на 4. Брэндон кивнул. «Сделайте квадрат со всеми четырьмя из них», — сказала Рахиль. Черил построила квадрат из четырех плиток. «Я сделала тройку и одну», — сказала Николь. «Что ты имеешь в виду?» — спросила Черил. «Один маленький столик, как у Натана, — объяснила Николь, — а затем столик 1 на 3». «Вы можете сделать четыре отдельных стола», — сказал Натан. «Ты мог бы поставить Т», — сказал Зак. «Положите три в ряд и один под средним». «Я тоже сделал это, но мой перевернут», — сказал Эрик. Шерил построила аранжировку Эрика под руководством Зака и указала классу, что когда вы можете перевернуть, повернуть или сдвинуть фигуру, чтобы она точно соответствовала другой фигуре, фигуры совпадают.«Мы будем считать конгруэнтные формы одинаковыми», — пояснила она. Когда расположение студентов заполнило накладные расходы, Черил спросила: «Что, если бы мы использовали только отдельные прямоугольные столы, сделанные из четырех плиток? Какие формы мы должны удалить? » «Я предложил четыре отдельные таблицы, — сказал Натан. Рифка добавила: «И та, которая похожа на букву Т». «Вы также должны снять мою», — сказала Николь. «Это не один прямоугольник». Когда Малкия предложила убрать квадрат, разговор разгорелся.Некоторые ученики помнили, что квадрат — это прямоугольник, а другие — нет. Черил пояснила: «Квадрат — это особый вид прямоугольника, потому что все его стороны имеют одинаковую длину. Но, как и прямоугольник, квадрат по-прежнему имеет четыре угла в 90 градусов, а противоположные стороны параллельны ». Шерил хотела убедиться, что ученики умеют маркировать построенные ими прямоугольники. Она нарисовала на доске прямоугольник размером 1 на 4. «Я могу записать это двумя способами», — сказала она и записала под прямоугольником: Затем Черил нарисовала квадрат 2 на 2 и пометила его. Черил указала на квадратный стол 2 на 2 и спросила: «Если один человек сидит сбоку от небольшого квадратного стола, и никто не сидит по углам или в щелях между столами, сколько людей может сидеть здесь? ” «Легко, восемь», — ответила Николь. «Просто сосчитайте по два человека с каждой стороны, умноженные на четыре стороны». «Когда вы подсчитываете количество людей, которые могут сесть за стол, вы фактически находите его периметр», — объяснила Шерил. «Это потому, что каждый человек сидит по одну сторону от меньшего квадрата и занимает одну единицу длины.Таким образом, периметр прямоугольника 2 на 2 составляет 8 единиц ». «Периметр стола размером 1 на 4 равен 10», — заметил Эрик. Черил попросила остальных проверить заявление Эрика, а также изобразить периметр нескольких других прямоугольников. Затем она представила другую проблему. — Давайте вспомним вечеринку мистера и миссис Комфорт, — начала Черил. «Предположим, миссис Комфорт решила, что все 32 человека должны сесть за один большой массивный прямоугольный стол, и она хотела выяснить, сколько маленьких квадратных столов можно арендовать.Посмотрите, сможете ли вы найти все возможные прямоугольные столы разных размеров и форм, на которых могут разместиться 32 человека ». «Должен ли каждый стол вмещаться ровно 32?» JT хотел знать. «Да», — ответила Черил. «Сколько плиток мы используем?» — спросила Малкия. «Это будет зависеть от столов, которые вы построите», — ответила Черил. «Можем ли мы работать с партнером?» — спросила Николь. «Да, — ответила Черил, — но веди свой личный учет». Больше вопросов не было.Черил дала последнее указание. «Используйте плитки, но нарисуйте свои решения на листе бумаги. Обязательно запишите размеры каждого стола и количество людей, за которыми он может разместиться ». Остаток урока Черил наблюдала за учениками за работой и при необходимости оказывала помощь. Она наблюдала, как Кэтлин составляла прямоугольник 16 на 2. «Хм, — громко сказала Кэтлин, работая, — давайте посмотрим, 32 человека. Это должно сработать, потому что 16 умножить на 2 равно 32.Кэтлин сосредоточенно нахмурилась, считая стороны квадратов. Затем она с удивлением посмотрела на Шерил. «Я не понимаю», — сказала она. «Еще 36. Ага». Кэтлин пожала плечами, перемешала 16 плиток обратно в стопку в центре стола и начала строить еще один прямоугольник. «Что ты делаешь?» — спросила ее Шерил. «Что ж, я, должно быть, напортачила, потому что первая, которую я сделал, не сработала, поэтому я попробую что-нибудь еще», — ответила Кэтлин. «Что ты собираешься попробовать?» — спросила Черил. «Не знаю. Я просто собираюсь повозиться и посмотреть, что будет », — сказала она. Черил наблюдала, как Кэтлин начала складывать плитки в длинный ряд шириной в один квадрат. Она продолжала считать стороны одну за другой каждый раз, когда добавляла новую плитку. Наконец она улыбнулась. «Это работает! Этот вмещает 32 человека. Это 1 на 15. А теперь записать это ». Кэтлин начала рисовать прямоугольник на бумаге. Алекс сидел напротив Кэтлин. «О», — ответила Кэтлин и начала строить прямоугольник шириной четыре квадрата. Натан подошел к Шерил. «Я не рисую на бумаге прямоугольники, как все, — сказал он. «Вместо этого я решил использовать Xs. Но Люк сказал мне, что это неправильно. Разве я не могу нарисовать крестики, если захочу? » Натан показал Шерил свою газету. Черил попросила Натана объяснить, что он сделал. Удовлетворенная тем, что он понимает, что делает, Шерил сказала: «То, что вы сделали, имеет для меня смысл.” Натан вернулся к Люку. «Я сказал вам, что она скажет, что все в порядке», — сказал он. Черил продолжила движение по классной комнате. К концу периода она увидела, что все студенты нашли некоторые прямоугольники, а некоторые нашли их все. Она попросила детей убрать плитку и собрала их бумаги. Шерил планировала продолжить урок на следующий день. На следующее утро Черил дала классу возможность подумать над расширением. Примерно через 10 минут Черил прервала учеников, чтобы начать обсуждение в классе. «Какие варианты есть у Comforts, чтобы посадить всех 32 человека за один стол?» — спросила Черил. Руки студентов вскинулись. «У них будет группа, точнее, восемь», — сказала Рэйчел. Большинство студентов кивнули или пробормотали свое согласие. «Может ли кто-нибудь описать размеры таблиц, которые будут работать?» — спросила Черил. «Я запишу их на доске». Эрик сообщил: «Один раз-15, 2-раз-14, 3-раз-13, 4-раз-12, 5-раз-11, 6-раз-10, 7-раз-9 и 8-раз-8. .После того, как Шерил записала размеры, она вернулась и зарисовала каждый соответствующий прямоугольник. «О, я вижу закономерность!» — сказала Анферни. «Могу я показать это?» Черил кивнула, и Анферни подошла к доске. «А другая сторона идет вниз», — добавила Анн Мария. «О да, я этого не видела», — сказала Анферни. «Ага, 15, 14, 13 и так далее». Он снова сел. «Разве список не должен продолжаться?» — спросила Черил.»Разве не следует прямоугольник 9 на 7?» (См. Рисунок 6.) «Он у тебя уже есть», — сказала Малкия. «Да, 9 на 7 и 7 на 9 — это одно и то же», — добавила Николь. «Все числа после 8-умножить на 8 — это повторения, — сказала Кирстен, — так что вы не можете их сосчитать». «Давайте подумаем, сколько квадратных столов придется арендовать мистеру и миссис Комфорт для каждого большого прямоугольника», — сказала Шерил. «Сколько им придется арендовать за стол размером 15 на 1?» «Пятнадцать.Легко, — ответили несколько студентов. «А как насчет 2 на 14?» Черил продолжила. «Сколько столов придется арендовать Комфортс для такой договоренности?» «Двадцать восемь», — звали многие дети. «А как насчет расположения 3х13?» — спросила Черил. Класс быстро понял, чем занимается Шерил. «Вы просто размножаетесь», — сказала Рифка. «Просто сделай это для всех — 28, 39, 48, 55, 60, 63 и 64». «Что вы заметили в форме столов?» Затем спросила Черил. Малкия сказала: «Размер 8 на 8 — квадрат, а все остальные — прямоугольники». «Но ведь размер 8 на 8 тоже прямоугольник, помнишь?» Эрин напомнила Малкию. «Смотрите, — сказал Брэндон. «Если они устроят длинный тонкий прямоугольник для 32 человек, то они смогут сделать это всего с 15 столами. Так дешевле всего. «И они также сэкономили место, поскольку 1-умноженный на 15 занимает меньше всего места», — добавил Шарнет. «Но вам понадобится длинная комната, — добавила Николь, — как для королевского банкета.” Затем Шерил прервала беседу и дала письменное задание оценить мышление каждого ученика. Она написала на доске три вопроса, чтобы дети могли ответить: Учащиеся работали над заданием для остальной части класса. Альфи Кон Все еще доминирующая модель старой школы начинается с предположения, что детям в первую очередь необходимо усвоить «математические факты»: способность говорить «42», как только они слышат стимул «6 x 7», и знакомство с пошаговой инструкцией. -шаговые процедуры (иногда называемые алгоритмами) для всех видов проблем — перенос чисел при вычитании, вычитание при делении, приведение дробей к наименьшему общему знаменателю и т. д. Когда объект определен таким образом, нет большой загадки относительно того, какая техника будет использоваться. «Когда процесс обучения арифметике задуман как простое приобретение отдельных, независимых фактов, процесс обучения превращается в административное упражнение» [1]. Если учащиеся не могут дать правильный ответ, это «рассматривается только как доказательство необходимости дальнейшего обучения» [2]. Как мы видели, именно это, как мы видели, объясняется именно этим: чем больше не работает, тем очевиднее вам это нужно.И, как и в случае с традиционными способами обучения детей чтению, большинство классов математики основано на модели передачи: ученикам просто фактов и процедур учитель и учебник. Один урок математики, или учитель, отличается от следующего только относительно тривиальными вопросами: количеством задач, которые нужно решить за классной доской по сравнению с на своем месте по сравнению с дома, ясностью объяснений учителя или сложностью расчеты в каждой задаче.Решения, которые действительно имеют значение, уже приняты: рассматривать математику как набор истин «где-то там», которые нужно прививать ученикам посредством повторяющихся упражнений. Эти элементы присутствуют даже в классах, которые, по общему мнению, являются высококачественными, с уважаемыми учителями, внимательными учениками и хорошими результатами на стандартных тестах. [4] «Бездумная мимикрическая математика», как ее называет Национальный исследовательский совет [5], стала нормой в наших школах. Более 70 лет назад преподаватель математики по имени Уильям Браунелл заметил, что «интеллект не играет никакой роли» в этом стиле обучения. Даже сейчас большинство студентов по-прежнему обучаются математике «как рутинному навыку», — говорит Лорен Резник. «Они не развивают способности более высокого порядка для организации и интерпретации информации» [6]. Таким образом, студенты могут запомнить тот факт, что 0.4 = 4/10, или успешно следовать рецепту решения для x , но традиционный подход оставляет их в неведении относительно важности того, что они делают. Не чувствуя общей картины, они склонны подставлять числа механически, следуя методике, которой они научились. Их нельзя назвать «успешными в количественном мышлении», потому что для этого, как объяснил Браунелл, «нужен фонд значений, а не мириады« автоматических ответов ». В результате стандартного подхода к обучению математике учащиеся часто не могут использовать методы, которым их учили, и применить их к задачам, даже немного отличающимся от тех, к которым они привыкли. Например, семилетняя девочка может отлично складывать числа, когда они расположены на странице вертикально, но затем поднимает руки, когда та же задача написана горизонтально. Или она может обладать «богатой неформальной базой знаний, полученной в результате работы с количествами в повседневных ситуациях» [8], которая позволяет ей выяснить, сколько печенек у нее было бы, если бы она начала с 16, а затем получила еще девять — но при этом учитывайте это понимание совершенно отдельно от того, как вы должны учиться в школе (где она вполне может получить неправильный ответ).[9] Преподаватели математики постоянно находят примеры того, как дети могут выполнять вычисления, даже не зная, что они делают. Дети задали задачу начал кропотливо складывать, а затем делить, упуская из виду тот факт, что им не нужно было беспокоиться — факт, который был бы очевиден, если бы они действительно понимали, что такое умножение и деление. Еще один поразительный пример — это то, как 13-летние дети справились с проблемой, которая появилась в Национальной оценке успеваемости в образовании (NAEP). Вопрос был такой: «В армейском автобусе 36 солдат. Если к месту тренировок едут 1128 солдат, сколько потребуется автобусов? » Если разделить первое число на второе, получится 31 с остатком 12, что означает, что для перевозки всех солдат потребуется 32 автобуса. Этот вид роботизированных вычислений отражает не умственную неполноценность учащихся, а торжество модели обучения математике с возвратом к основам и навыками. И это мнение не только одного человека. Аналитики данных NAEP для Службы образовательного тестирования отметили, что учащиеся могут «декламировать правила», но часто не имеют «представления о том, разумны ли их ответы».«Нелепые ответы», которые часто получаются в результате, могут быть связаны с «общим чрезмерным акцентом в современных учебных программах на навыки, связанные с вычислениями, или с тенденцией преподавать навыки и знания до интеграции приложений и решения проблем в обучение» [13]. В некоторых случаях ученикам может быть полезно попрактиковаться в каком-либо навыке — после они пришли к полному пониманию основной идеи. Но когда тренировка начинается слишком рано или занимает слишком много времени в классе, она приносит мало пользы уже успевающим ученикам [14] и абсолютно ничего не делает для тех, кто этого не делает, за исключением того, что заставляет их чувствовать себя еще более некомпетентными. Стоит заниматься математикой Все это заметили люди, которые зарабатывают на жизнь размышлениями о том, как следует преподавать математику.В нескольких документах по реформированию этой области, в том числе, в первую очередь, в стандартах, распространенных в 1989 г. Национальным советом учителей математики (NCTM), говорится, что занятия по математике должны вращаться вокруг осмысления (как и в случае с нетрадиционными подходами к чтению и письму) и способствовать мышлению, а не запоминанию правил. Студентов следует поощрять писать и говорить о своих идеях, понимать основные концепции и уметь выразить их словами. абстрагирование, применение, убеждение, классификация, вывод, организация, представление, изобретение, обобщение, специализация, сравнение, объяснение, формирование паттернов, проверка, доказательство, предположение, анализ, подсчет, измерение, синтез и упорядочивание [потому что] это виды деятельности, которая, как считается, характеризует работу математиков.[16] Учащиеся в классах, где математическое мышление поощряется с самого раннего возраста, учатся оценивать и предсказывать. («Как вы думаете, сколько карандашей во всей школе? Есть ли способ узнать наверняка, не считая?») Они приобретают базовые навыки в процессе решения значимых проблем — часто со своими сверстниками. Они могут использовать калькуляторы, как это часто делают взрослые, чтобы они могли решать более сложные и увлекательные задачи, чем это было бы возможно, если бы им пришлось направить свою энергию на вычисления.В отличие от класса, основная деятельность которого заключается в том, чтобы слушать учителя и заполнять рабочие листы, такая учебная среда отличается тем, что учащиеся «сидят в группах, обсуждают идеи, проводят эксперименты, составляют диаграммы, используют конкретные объекты для проверки своих предположений, следуя слепому принципу». Некоторые особенности таких классных комнат уже должны показаться вам знакомыми.Во-первых, сотрудничество — важная часть обучения. Иногда дети решают задачи в парах с последующим обсуждением в классе. Учителя прилагают особые усилия для создания заботливого сообщества, чтобы несогласие с ответами друг друга не превратилось в соревнование и не побудило некоторых детей высказаться. Во-вторых, студенты более активны, больше сосредоточены на классе, чем в традиционной модели; их выбор имеет значение, и их голоса слышны.И, как и в случае с «Целым языком», в котором используются преимущества естественного употребления слов и идей, учителя математики всегда ищут реальные проблемы и действия, которые могут предложить «детям возможности участвовать в числовых рассуждениях». [18] Новости статьи из утренней газеты поднимают вопросы о вероятности; приготовление пищи обеспечивает подлинные проблемы фракций; можно использовать даже учет посещаемости («Какая часть нашего класса отсутствует?»). Некоторым из нас все это сразу покажется привлекательным, возможно, потому, что мы видим в этом освежающий контраст с бессмысленной скукой , которую нам, , пришлось вынести на уроках математики в прошлом.Но другие отвергнут это видение по той же причине: это не то, к чему они привыкли. Даже родители, готовые к убеждению в ценности целостного языка, могут скептически относиться к концептуальным подходам к математике. Идея чтения для понимания достаточно ясна (в конце концов, мало кто из взрослых тратит свое время на выделение тематических предложений или обводку гласных), но многие ли из нас имеют какой-либо опыт обучения математике, в котором подчеркивается понимание? [19] Мы думаем о математике как о предмет, на который вы набираете правильные или неправильные ответы, и мы можем опасаться, что что-либо, кроме обычных методов упражнений и навыков, оставит наших детей неспособными давать правильные ответы, когда для них придет время пройти стандартизированный тест .В самом деле, от людей многое требуется поддержать или даже разрешить перейти от чего-то, что они знают, к чему-то совершенно незнакомому. Тем не менее, именно об этом просят нас большинство экспертов в данной области — и не без оснований. Как и в случае с любым из вопросов, обсуждаемых в этой книге, существует три основных способа убедить скептиков. Во-первых, есть теория: объяснение целей и причин, по которым нужно делать что-то по-другому. Это то, что я пытался сделать в этом и предыдущем разделе.Во-вторых, это исследование, которое будет рассмотрено в Приложении А [перепечатано ниже]. Наконец, есть примеры, идеально почерпнутые из непосредственного наблюдения за необычными классными комнатами — или, что еще лучше, описания, которые дают представление о том, как эти идеи выглядят на практике, и как они сравниваются с обычной платой за проезд. Представьте, что учитель говорит своим ученикам, что такое «коэффициент», ожидая, что они запомнят определение. А теперь представьте учителя, у которого первоклассники выясняют, сколько пластиковых звеньев, размещенных на одной стороне весов, эквивалентно одной металлической шайбе на другой стороне. Представьте себе класс, в котором третьеклассники открывают свои учебники математики для надуманных «задач со словами» на странице 39. («Поезд отправляется из Вашингтона, округ Колумбия, движется на запад со скоростью 65 миль в час…»). Теперь представьте себе класс, где учеников просят сравнить вес двух кусков жевательной резинки (с сахаром и без него) до и после того, как каждый кусок был пережеван — прогнозирование, запись результатов, объяснение различий, все время сложение, вычитание, умножение, деление, а также использование десятичных дробей и процентов, учимся оценивать и экстраполировать.В каком классе они с большей вероятностью будут рассматривать математику как актуальную, привлекательную и что-то, в чем они могут добиться успеха? Рассмотрим то же самое, полное задач на дроби для учащихся старших классов начальной школы: «1/2 + 1/3 = ___» и так далее. Наконец, рассмотрите — то есть запомните — обычную математическую программу средней или старшей школы.А теперь представьте класс, в котором ученики на протяжении года занимаются изучением различных концепций и вместе пишут учебник для учеников, которые займут свое место в той же аудитории в следующем году. Что более строго? Что вы хотите для своего ребенка? [20] Изобретательские факты Это довольно резкий контраст между математикой, определяемой в основном в терминах навыков, и математикой, определяемой в основном в терминах понимания. Но если нас убеждает конструктивистский подход к обучению, даже последнего недостаточно.Когда традиционалисты настаивают на том, что детям очень важно «знать свои математические факты», мы можем ответить не только оспаривая эти приоритеты, но и спросив, что имеется в виду под , знаю . В начале 1998 года в статье, опубликованной в газете New York Times , упоминалось о важности того, чтобы учащиеся разрабатывали и проводили свои собственные эксперименты по математике.«Только подумайте, — саркастически ответила женщина в письме редактору, — таким образом студенты могут заново изобрести теорему Пифагора». Она заключила: может быть, таким образом мы сможем «побороться за последнее место в следующем году» в международных сравнениях. [21] Неважно, что плохие результаты американских студентов в последних тестах, вероятно, были результатом того самого учебного плана, который предпочитал этот автор письма. (Ее можно простить за незнание этой детали, поскольку она не упоминалась практически во всех обсуждениях этих результатов в популярной прессе.Более интересным является ее убеждение в том, что было бы, очевидно, нелепо, если бы студенты заново изобрели математические законы. По совпадению, тот же самый пример был предложен Пиаже несколькими десятилетиями ранее, чтобы аргументировать в пользу такого рода обучения. «Незнание теоремы Пифагора гарантирует свободное проявление силы личного рассуждения», — писал он. «Он заключается в том, чтобы заново открыть для себя его существование и его использование. Цель интеллектуального образования не в том, чтобы уметь повторять или сохранять готовые истины »; скорее, человек получает образование, «научившись самому постигать истину.[22] Когда детям не вручают линейки, а на самом деле просят их изобрести, когда они конструируют для себя идею соотношений, когда они воссоздают удивительно последовательную связь между тремя сторонами прямоугольного треугольника (и обнаруживают ее отношение к реальные проблемы дизайна), то они действительно учатся. Обдумывая возможности, учащиеся придумывают собственные способы поиска решений. Им приходится изобретать свои собственные процедуры. На практике это означает столь же прямолинейно, сколь и нелогично: учителей обычно воздерживаются от показа своим классам, как решать задачи . Этот подход был подробно описан Констанс Ками, ведущей ученицей Пиаже, в серии из трех книг о том, как дети в первом, втором и третьем классе соответственно могут «заново изобрести арифметику». В конечном итоге, конечно, имеет значение, придумают ли студенты правильный ответ, но если они будут думать, что это все, что имеет значение, они вряд ли поймут, что происходит. Таким образом, говорит Камии, «если ребенок говорит, что 8 + 5 = 12, лучшей реакцией было бы воздержаться от исправления его и. У учителя в таком классе очень сложная работа.Ему приходится много прикусывать язык, а также воздерживаться от того, чтобы дети слишком рано записывали свои ответы на бумаге, поскольку это может помешать по-настоящему обдумать проблемы. Он должен знать, когда бросить вызов студентам: если все они придумают один и тот же метод и правильный ответ, он, вероятно, будет склонен спросить: «Это единственный способ сделать это?» (Качество обучения математике в любом классе можно почти измерить как функцию того, как часто задают этот вопрос. Я считаю, что весь этот подход имеет смысл по четырем причинам.Во-первых, это отражает суровую реальность того, что знания о числах и их соотношении нельзя научить (то есть дать) детям. Его нужно построить. Как комментирует Камии, Педагоги находятся в иллюзии, что они преподают арифметику, когда все, что они на самом деле преподают, — это самые поверхностные аспекты, такие как конкретные суммы (4 + 4 = 8, 4 + 5 = 9…) и общепринятые значения письменных знаков (например, 4 и +). . . . Если ребенок не может построить отношения, тогда все объяснения в мире не позволят ему понять утверждения учителя.. . . Ребенок должен изменить неправильные идеи. Учитель не может их устранить. [25] Даже если учитель ничего не делает, кроме как требует запоминания фактов и практики с процедурами, ученики обычно придумывают и используют свои собственные стратегии в любом случае — по сути, конструируют свой собственный смысл — иногда, притворяясь, что они решают проблемы так, как им сказали. Во-вторых, явное предложение детям составить свои собственные процедуры дает учителю гораздо лучшее представление о том, что они понимают и в чем им нужна помощь.Открытое приглашение к решению нового типа проблемы позволяет учителю увидеть, как они думают, могут ли они интегрировать более ранние концепции и где именно они застряли, — в отличие от того, чтобы судить только о том, получили ли они правильный ответ. Вспомните, что с конструктивистской точки зрения один из наиболее важных аспектов работы учителя — знать как можно больше о мышлении каждого ученика. Третий аргумент в пользу этого подхода — то, что он действительно работает. Я представлю научное исследование позже, а пока давайте послушаем второклассную учительницу, которая объявила, что раздала 22 леденца на палочке из пакета 40.Она хотела знать, сколько осталось. Я наблюдал за детьми, которые пытались мысленно решить проблему. Они были очень тихими. Некоторые из них пристально смотрели в космос, как будто решали задачу на невидимой доске. После того, как прошло несколько минут размышлений, большинство детей подняли руку, чтобы сообщить мне, что у них есть ответ, которым они могут поделиться с группой.Предложенные ими ответы были 29, 22, 18, 28 и 12. Я написал каждый ответ на доске без комментариев, а затем спросил: «Есть ли здесь какие-то ответы, которые вас беспокоят?» Дети сразу же начали обдумывать предложенные ответы. . . . Эллисон тихо сказала: «Я не думаю, что ответ может быть 29, но я не знаю почему». Многие дети согласно кивнули головами. Стив, с другой стороны, не был столь осторожен. Он одновременно поднял руку, встал и начал говорить.«Потому что 29 — это слишком много», — настаивал он. Если взять 20 из 40, получится 20. Значит, 29 — это слишком много ». Бен едва дождался, когда Стив остановится и переведет дух. Он указал на доску и авторитетно заявил: «40 минус 20 равно 4 минус 2 равняется 2. Стив прокомментировал: «Я не согласен; 20 take away 2 не может быть больше 20, потому что вы забираете вещи.’ После дополнительного обсуждения дети разбились на группы и использовали блоки (пример того, что педагоги называют «манипуляторами»), чтобы придать конкретную форму обсуждаемым ими идеям. В течение следующих нескольких недель они боролись с другими проблемами. В конечном итоге, сообщает учитель, «они заново изобрели перегруппировку». Они не только самостоятельно выяснили, как решать такие проблемы, но и поняли идею этого метода [27]. Пока вы не увидите, как это работает, может быть очень трудно принять идею о том, чтобы доверять детям решать незнакомые задачи — более того, даже идею о том, что математика является «творческим» делом, связанным с «изобретениями».Иногда предполагается, что, если взрослый не вмешивается немедленно, чтобы сказать «правильно» или «нет, не совсем», детям дают понять, что все ответы одинаково приемлемы. Наряду с обвинением в релятивизме конструктивистов иногда обвиняют в том, что они верят в то, что дети просто автоматически усваивают математику без необходимости что-либо делать учителю. Но мы можем сказать больше, чем то, что этот подход эффективен. Окончательное оправдание такого обучения математике состоит в том, что традиционный метод передачи может нанести серьезный вред. Учитель (или родитель), для которого правильный ответ означает все, — это тот, кто, естественно, захочет рассказать ребенку, как наиболее эффективно получить этот правильный ответ. Это создает бессмысленность. Такая ученица, вооруженная алгоритмами, приобретает привычку смотреть на взрослого или на книгу, вместо того, чтобы думать об этом через себя.Она чувствует себя менее автономной, более зависимой. Застряв в середине проблемы, она не пытается понять, что имеет смысл делать ; она пытается вспомнить, что ей нужно сделать , чтобы сделать дальше. [29] Короче говоря, это наследие традиционного образования. * Когда я читал литературу по нетрадиционному математическому образованию и наблюдал за таким обучением в действии, меня осенило, что здесь работает интересный парадокс. С одной стороны, важно подождать, пока дети научатся понимать концепцию, прежде чем вводить ее в заблуждение.Это предостережение следует из всех выводов Пиаже о качественных изменениях в детском мышлении. Вы можете попросить малышей запомнить слова «пятнадцать в квадрате — двести двадцать пять». В самом деле, у меня есть друзья, которые развлекают себя и своих гостей, заставляя своих детей повторять невероятно не по годам развитые фразы. Но с таким же успехом эти дети могут учить бессмысленные слоги. Родители часто удивляются тому, как рано их дети умеют считать (в том смысле, что они могут говорить «один, два, три, четыре…»), но вскоре понимают, что не понимают относительных величин, обозначаемых каждым числом.В этом случае очевидны ограничения в развитии. Но это не так просто увидеть — хотя и так же верно — в случае, если шестилетний ребенок выполняет сложение в две колонки. Он может следовать инструкциям, но почти наверняка не может понять значение разряда — то есть, как столбец десятков соотносится со столбцом единиц. Такой традиционалист, как Э.Д. Хирш, по образованию профессор английского языка в колледже, кстати, не испытывает угрызений совести, утверждая, что «сообщаемые трудности, с которыми сталкиваются американские дети в возрасте до десяти лет в понимании значения места, очень вероятно из-за отсутствия у них последовательного обучения и практики. арифметика.[30] Но правда в том, что вы можете заставить детей тренироваться, пока коровы не вернутся домой, и они все еще не поймут, что значит говорить о «десятках», пока они не будут готовы. [31] Таким образом, нет смысла заставлять их делать наизусть то, что для них не имеет смысла. Все, что они делают, — это учат их рассматривать математику как нечто, что люди, , от не должны понимать. Парадокс заключается в том, что, хотя конструктивисты внимательно относятся к тому, что дети не могут сделать, они также необычайно щедро уважают то, что дети могут делать — спонтанно и в очень раннем возрасте.«Обучение детей начинается задолго до того, как они пойдут в школу», — отметил известный российский психолог Лев Выготский. У них «своя собственная дошкольная арифметика, которую могут игнорировать только близорукие психологи». [32] На самом деле близорукость не обязательно, чтобы это пропустить: все, что вам нужно сделать, — это заставить детей запоминать факты и следовать рецептам. Учителя, которые тратят свое время на то, чтобы рассказывать, а не спрашивать, инструктировать, а не приглашать, могут годами стоять перед детьми, не имея представления о том, на что они способны.Учитель начальной школы-ветеран отражает: Я никогда не считал детей достаточно умными, чтобы изобретать решения. Учителю требовалось много дополнительных усилий, чтобы выслушать то, что они пытались сказать, и много самоконтроля, чтобы подавить побуждение воспользоваться быстрым и легким способом навязывания моих взрослых взглядов и методов. Но было так много всего, чему никогда не нужно было учить, потому что дети придумывали всевозможные вещи, которые даже не приходили мне в голову. Теперь, когда я занимаюсь математикой, я вижу на лицах детей волнение, энтузиазм и сосредоточенность.Я слышу голоса, исходящие от детей, которые уверены в себе, редко застенчивы и молчат, только когда думают. Я задаюсь вопросом, как учителя могут продолжать работу в зависимости от рабочих тетрадей и заданий. Но я также вспоминаю, насколько скептически и неуверенно я был поначалу, не показывая детям, как решить проблему «правильным» способом [33]. Сказать, что обучение с конструктивистской точки зрения характеризуется парадоксом — не давать маленьким детям больше, чем они могут справиться, но дать им возможность показать вам, на что они способны, — значит сказать об этом положительно.Обратной стороной является то, что «старой школе» удается облажаться по обоим пунктам, одновременно не понимая ограничений развития детей («Тренируйте их, пока они не достигнут») и не цените их умы («Используйте технику, которую я вам показал». ). Эта двойная ошибка — это то, что, возможно, имела в виду Лилиан Кац, когда говорила о педагогах, которые «переоценивают детей в учебе и недооценивают их интеллектуально» [34]. Нетрадиционные учителя стараются избегать обеих ловушек. [из Приложения A] Твердые доказательства: результаты математики «Достаточно ли хорошо» учащихся в США по математике — это, конечно, вопрос для суждения. Но насколько бы мы не были удовлетворены их квалификацией, есть все основания полагать, что традиционная модель обучения несет большую часть ответственности. В середине и конце 1990-х годов было проведено всеобъемлющее международное сравнение преподавания математики и естествознания, известное под аббревиатурой TIMSS, которое затем было опубликовано по частям.Часть исследования включала серию обычных тестов, которые давались учащимся всего мира, эквивалентным четвертым, восьмым и двенадцатым классам. Учащиеся из США неплохо учились в четвертом классе, довольно плохо — в восьмом и ужасно — в двенадцатом, хотя были подняты вопросы относительно данных, лежащих в основе этих выводов. TIMSS не ограничивался стандартизованными результатами испытаний; он также включал анализ учебных материалов и аудиторных практик. В одном из сегментов исследования Джеймс Стиглер и его коллеги сняли на видео более 200 учителей математики восьмого класса, чтобы пересмотреть их методы, а также распространили анкеты, чтобы понять цели учителей.Трое из пяти учителей в США заявили, что их больше всего интересует «развитие навыков». Только один из четырех японских учителей ответил так: подавляющее большинство заявило, что они хотят, чтобы их ученики понимали определенную математическую концепцию. Эта цель побудила этих учителей включить дедуктивное мышление в свое обучение, которое сыграло свою роль в 62 процентах уроков японского и 0 процентах уроков в США. Японские учителя также изучали тонкости конкретных математических понятий со своими учениками, а не просто называли эти понятия американским стилем.В японских классах меньше математических задач рассматривалось более глубоко, и учащиеся активно участвовали в предложении различных способов решения этих задач. Кроме того, что интересно, домашние задания назначались редко. [35] Общий вывод, к которому пришли исследователи TIMSS — который почему-то не попал в заголовки или даже в новости, когда были опубликованы результаты тестирования — заключался в том, что традиционных форм обучения и упор на основы , в значительной степени способствовали низкому положению американских студентов старшего возраста .Еще до того, как была опубликована последняя фаза исследования (глядя на последний год средней школы и обнаруживая худшие результаты для студентов из США), авторы TIMSS писали: «Обучение в этой стране все еще кажется — по сравнению с обучением в некоторых других странах. — в большей степени ориентированы на студентов как на пассивных поглощателей знаний, а не как на активных участников, которые конструируют, трансформируют и интегрируют знания ». Далее они предсказали, что «широко распространенный выбор сосредоточиться на« основах »в американских школах, вероятно, приведет к« соответствующим различиям в успеваемости учащихся, и эти различия должны быть кумулятивными, с U.Студенты S. все больше отстают по мере продвижения по классам »- что и произошло. Эти результаты нельзя объяснить с точки зрения «естественных различий» между учащимися, то есть врожденных способностей, или даже с точки зрения того, сколько усилий прикладывают учащиеся, из-за «различий в учебных программах. . . влияет на сколько студентов могут достичь даже трудясь «. Изучая данные со всего мира, исследователи обнаружили, что студенты, которым посчастливилось жить в странах, которые избегали подхода к обучению «назад к основам», «справлялись сравнительно лучше» на тестах на понимание.[36] Напомним, что эти выводы в точности повторяют выводы Национальной оценки успеваемости в образовании (NAEP), основной оценки успеваемости учащихся в США с точки зрения обучения математике. Они также подтверждаются исследованием преподавания математики в старших классах начальной школы, которое показало, что «сильный упор на развитие навыков и небольшое внимание к концепциям и приложениям могут помочь объяснить относительно низкое положение Соединенных Штатов среди других стран по проблеме математики. -разрешающая способность студентов.»[37] Другой вид поддержки пришел в 1998 году, когда исследователь сравнил использование компьютеров студентами с их оценками по математике NAEP. Общий вывод, что достаточно удивительно, заключался в том, что чем больше времени ученики проводили за компьютерами в школе, тем хуже они сдавали экзамен. Но при ближайшем рассмотрении оказалось, что нетрадиционное использование компьютеров, например, для моделирования и обучающих игр, было полезным. Отрицательный эффект успеваемости был ограничен теми учащимися, которые использовали компьютеры в основном для отработки основных навыков.[38] Очевидно, даже использования новых технологий недостаточно для смягчения разрушительного воздействия старой педагогики. Достаточно недавних данных о традиционных подходах к обучению математике. Что мы можем сказать об усилиях по внедрению более концептуальных и конструктивистских альтернатив? Исследования, проводимые по таким программам, были сосредоточены в начальных классах, и они указывают на результат, который можно резюмировать в шести словах: лучше рассуждать без ущерба для вычислительных навыков — интересный отголосок того, что мы только что видели в нетрадиционных подход к обучению чтению (а именно, лучшее понимание прочитанного без ущерба для навыков декодирования). В одном исследовании сорок учителей первого класса в Висконсине прошли специальную подготовку по тому, как сделать решение задач организационным центром обучения арифметике. Когда тесты на успеваемость, сданные их учениками, позже сравнивались с тестами детей, обучающихся по традиции, результаты показали скромное, хотя и стабильное преимущество для первой группы. «Сосредоточение внимания на решении проблем не обязательно приводит к снижению производительности вычислительных навыков», — пишут авторы [39]. Несколько лет спустя некоторые исследователи из Делавэра попытались сделать нечто подобное с небольшой группой учителей второго класса.Дети в нетрадиционных классах решали намного меньше задач в течение года, но, по-видимому, с большей осознанностью и пониманием, потому что в конечном итоге они лучше справлялись с тестами, особенно когда им приходилось решать задачи, которых они раньше не видели [40]. Третье исследование подтвердило, что более концептуальный подход к обучению математике как на начальном, так и на среднем уровне не повлек за собой жертв в стандартизированных результатах тестов, даже при переходе от традиционного обучения.[41] Четвертый проект в Мэриленде показал, что такое обучение математике повысило успеваемость учащихся с низким доходом, в основном из числа меньшинств, хотя потребовалось несколько лет, чтобы эти преимущества достигли статистической значимости. [42] Еще одна группа исследователей из Университета Пердью в Индиане разработала очень специфическую схему для обучения второклассников задачам местного школьного округа по математике. Детям были предложены задачи, над которыми они могли работать в парах, после чего весь класс собрался вместе, чтобы обсудить то, что они придумали.Не было ни оценок, ни похвалы за правильные ответы, ни учебников или рабочих листов, ни требований для решения определенного количества задач, ни демонстрации учителем «правильного» способа их решения. Учителя старались поощрять продуктивное сотрудничество и создавать благоприятную среду, в которой дети могли бы безопасно оспаривать идеи друг друга. [43] После того, как пилотный класс был создан и проанализирован, исследователи были готовы сравнить эффекты своей модели с эффектами традиционных классов в трех школах.Практически не было разницы в том, насколько хорошо дети выполняли базовые вычисления, но те, кто учился в альтернативных классах, демонстрировали значительно более высокий уровень математических рассуждений. [44] Затем все студенты провели следующий год в обычных классах и снова прошли тестирование. Те, чей второй класс был нетрадиционным, были на человек, но на человек лучше справлялись с концептуально сложными задачами [45]. Тем временем исследователи расширили свой проект на большее количество классов для второклассников, а также на некоторые классы для третьих классов, что позволило им оценить эффект от проведения двух лет подряд в месте, где «закономерности, отношения и значения не имеют себе равных. образованный студентами », и где математический класс преобразован в« сообщество, в котором происходит взаимный обмен и всестороннее взаимодействие.«Дополнительный год в таких условиях действительно имел значение. Было протестировано множество различных видов математической компетентности, и хотя не все измерения показали статистически значимый эффект, ни один из них не показал лучших результатов у студентов с традиционными инструкциями, чем у тех, кто два года занимался альтернативной математикой. Последние студенты были гораздо более искусными в понимании задач, представленных в форматах, отличных от учебников, и они также лучше справлялись с базовыми вычислениями — даже после того, как они провели год в обычном классе.Те, кто проучился конструктивистской математикой всего один год, с большей вероятностью будут отброшены обратно на уровень обучающихся — не только по своим достижениям, но и по своим установкам: они пришли к выводу, что математика — это «решение задач». используя один метод »вместо того, чтобы полагать, как это было раньше, что речь идет о« попытке понять и выяснить для себя »[46]. В меньшем и более неформальном масштабе теоретик-конструктивист Констанс Камии проверила несколько элементарных классов, в которых дети решали все задачи самостоятельно, без каких-либо алгоритмов.В соответствии с другими исследованиями, она обнаружила, что два конструктивистских второклассника показали такие же результаты, как и два обычных класса, по стандартизированному тесту достижений, но показали лучшие результаты по критериям мышления. [47] Последующее сравнение третьеклассников также показало, что «Группа конструктивистов использовала различные процедуры, получала более правильные ответы и делала более разумные ошибки, когда получали неправильные ответы. Группа сравнения в целом имела только один способ решения каждой проблемы — традиционный алгоритм — и, как правило, получала неправильные ответы, которые свидетельствовали о плохом понимании чисел.»[48] И последний момент, который не так уж случаен: учительница, работающая с Камии, отметила, что после того, как она приняла нетрадиционный подход к обучению, ее классы «проявили любовь к математике, которую я не видел в течение моего первого десятилетия преподавания» [ 49]. Хотя нет достоверных данных, подтверждающих это впечатление (как в случае с Whole Language), оно определенно совпадает с тем, что исследователи Purdue наблюдали в своих экспериментальных классах. Они сообщили, что посетители «неизменно отмечали увлечение математикой, которое проявляли дети, когда они решали задания.Дети часто подпрыгивали, обнимали друг друга и бросались рассказывать учителю, когда они решают особенно сложную задачу ». Более того, они в необычной степени упорствовали в решении сложных проблем и радовались успехам друг друга [50]. Конечно, это, вероятно, связано с отсутствием наклеек, оценок, похвалы и других подкреплений, которые, как правило, мешают детям получать удовольствие от самого обучения. Но задачи должны быть достаточно увлекательными и открытыми, чтобы успех был потенциально восхитительным — что-то гораздо менее вероятно, когда дети просто пройдут через утвержденные шаги, чтобы получить правильные ответы на рабочем листе. ПРИМЕЧАНИЯ [Полные цитаты см. В справочном разделе документа «Школы, которых заслуживают наши дети». ] Стандарты математической практики описывают различные виды знаний, которые преподаватели математики на всех уровнях должны стремиться развивать у своих учеников.Эти практики опираются на важные «процессы и навыки», имеющие давнюю важность в математическом образовании. Первыми из них являются стандарты процесса NCTM для решения проблем, обоснования и доказательства, коммуникации, представления и связей. Вторые — это направления математической подготовки, указанные в отчете Национального исследовательского совета Adding It Up : адаптивное мышление, стратегическая компетентность, концептуальное понимание (понимание математических концепций, операций и отношений), беглость процедур (умение гибко выполнять процедуры, точно, эффективно и уместно) и продуктивному расположению (привычная склонность считать математику разумной, полезной и стоящей, в сочетании с верой в усердие и собственную эффективность). Студенты со знанием математики начинают с объяснения себе значения проблемы и поиска точек входа для ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто предпринимают попытки решения. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной проблемы, чтобы получить представление о ее решении.Они отслеживают и оценивают свой прогресс и при необходимости меняют курс. Старшие ученики могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или изменять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую информацию. Математически опытные студенты могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и отношений, графических данных и искать закономерности или тенденции. Младшие ученики могут полагаться на использование конкретных предметов или изображений, чтобы помочь осмыслить и решить проблему.Математически опытные ученики проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понимать подходы других к решению сложных проблем и определять соответствия между разными подходами. Учащиеся со знанием математики понимают величины и их отношения в проблемных ситуациях. Они привносят две взаимодополняющие способности для решения проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагироваться от данной ситуации и представлять ее символически и манипулировать репрезентативными символами, как если бы они жили своей собственной жизнью, не обязательно обращая внимание на своих референтов. — и возможность контекстуализировать , при необходимости останавливаться во время процесса манипуляции, чтобы исследовать референты для задействованных символов.Количественные рассуждения влекут за собой привычку создавать связное представление о рассматриваемой проблеме; с учетом задействованных единиц; внимание к значению количеств, а не только к тому, как их вычислить; знание и гибкое использование различных свойств операций и объектов. Студенты со знанием математики понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов.Они делают предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они могут анализировать ситуации, разбивая их на случаи, распознавать и использовать контрпримеры. Они оправдывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, приводя правдоподобные аргументы, учитывающие контекст, из которого данные возникли. Математически опытные учащиеся также могут сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и — если в аргументе есть изъян — объяснять, что это такое.Учащиеся начальной школы могут строить аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не принимаются формально до более поздних оценок. Позже студенты учатся определять области, к которым применим аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы. Студенты со знанием математики могут применять полученные знания для решения задач, возникающих в повседневной жизни, в обществе и на рабочем месте. В младших классах это может быть так же просто, как написать дополнительное уравнение для описания ситуации. В средних классах учащийся может применять пропорциональное рассуждение для планирования школьного мероприятия или анализа проблемы в сообществе. В старшей школе ученик может использовать геометрию для решения проектной задачи или использовать функцию, чтобы описать, как одна интересующая величина зависит от другой.Математически опытные студенты, которые могут применять то, что они знают, комфортно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что они могут потребовать пересмотра позже. Они могут определять важные величины в практической ситуации и отображать свои отношения с помощью таких инструментов, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически проанализировать эти отношения, чтобы сделать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не служит своей цели. Студенты со знанием математики рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Опытные студенты в достаточной мере знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как понимание, которое необходимо получить, так и их ограничения.Например, старшеклассники со знанием математики анализируют графики функций и решений, сгенерированные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценки и другие математические знания. Создавая математические модели, они знают, что технологии могут позволить им визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Учащиеся с математическими знаниями в различных классах могут определять соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач.Они могут использовать технологические инструменты для изучения и углубления понимания концепций. Учащиеся со знанием математики стараются общаться с другими именно так. Они пытаются использовать четкие определения в обсуждениях с другими и в своих собственных рассуждениях. Они заявляют значение выбранных символов, в том числе используют знак равенства последовательно и надлежащим образом. Они осторожны при указании единиц измерения и маркировке осей, чтобы уточнить соответствие количеству в проблеме.Они производят точные и эффективные вычисления, выражают числовые ответы со степенью точности, соответствующей контексту проблемы. В начальных классах ученики дают друг другу тщательно сформулированные объяснения. К моменту поступления в среднюю школу они научились проверять утверждения и четко использовать определения. Студенты, разбирающиеся в математике, внимательно приглядываются, чтобы различить образец или структуру. Например, молодые студенты могут заметить, что три и семь больше равны семи и еще трем, или они могут отсортировать набор фигур в зависимости от того, сколько сторон у них.Позже учащиеся увидят, что 7 × 8 равно хорошо запоминающимся 7 × 5 + 7 × 3, при подготовке к изучению свойства распределения. В выражении x 2 + 9 x + 14 старшие школьники могут видеть 14 как 2 × 7 и 9 как 2 + 7. Они осознают значение существующей линии в геометрической фигуре и могут использовать стратегия рисования вспомогательной линии для решения задач. Они также могут сделать шаг назад для обзора и изменения перспективы. Они могут видеть сложные вещи, такие как некоторые алгебраические выражения, как отдельные объекты или как составленные из нескольких объектов.Например, они могут видеть 5-3 ( x — y ) 2 как 5 минус положительное число, умноженное на квадрат, и использовать это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y . Студенты, разбирающиеся в математике, замечают, если вычисления повторяются, и ищут как общие методы, так и ярлыки. Ученики старших классов могут заметить при делении 25 на 11, что они повторяют одни и те же вычисления снова и снова, и придут к выводу, что у них есть повторяющаяся десятичная дробь.Обращая внимание на вычисление наклона, поскольку они неоднократно проверяют, находятся ли точки на прямой, проходящей через (1, 2) с наклоном 3, ученики средней школы могут абстрагироваться от уравнения ( y — 2) / ( x — 1) = 3. Обращая внимание на закономерность в том, как условия отменяются при раскрытии ( x — 1) ( x + 1), ( x — 1) ( x 2 + x + 1), и ( x — 1) ( x 3 + x 2 + x + 1) может привести их к общей формуле для суммы геометрического ряда.Работая над решением задачи, ученики с математическими навыками следят за процессом, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов. Стандарты математической практики описывают способы, с помощью которых развивающиеся студенты, практикующие математическую дисциплину, должны все больше вовлекаться в предмет по мере того, как они растут в математической зрелости и опыте на протяжении младших, средних и старших классов школы.Разработчики учебных программ, оценок и повышения квалификации должны уделять внимание необходимости увязать математические практики с математическим содержанием в обучении по математике. Стандарты математического содержания представляют собой сбалансированное сочетание процедуры и понимания. Ожидания, начинающиеся со слова «понять», часто являются особенно хорошей возможностью связать практики с содержанием. Студенты, которым не хватает понимания темы, могут слишком сильно полагаться на процедуры.Без гибкой основы для работы они с меньшей вероятностью будут рассматривать аналогичные проблемы, связно представлять проблемы, обосновывать выводы, применять математику к практическим ситуациям, осознанно использовать технологии для работы с математикой, точно объяснять математику другим ученикам, сделайте шаг назад, чтобы получить обзор, или отклонитесь от известной процедуры, чтобы найти ярлык. Короче говоря, непонимание фактически мешает студенту заниматься математической практикой. Блок 6: Применение дробей
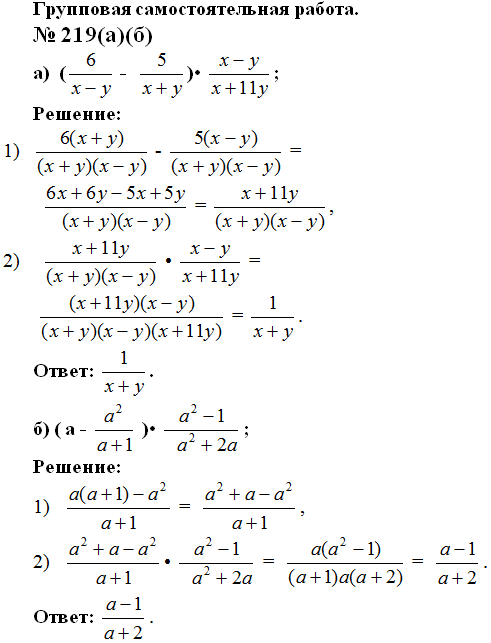
Раздел 7: Линейные уравнения и неравенства
Раздел 8: Системы уравнений
 Как только они начнут разговаривать друг с другом, они смогут узнать, что у них общего. Что происходит, когда встречаются две линии? Они что-нибудь говорят? Наверное, нет, но всякий раз, когда встречаются две линии, вы знаете, что у них есть по крайней мере одна общая точка. Определение точки, в которой они встречаются, может помочь вам решить проблемы в реальном мире.
Как только они начнут разговаривать друг с другом, они смогут узнать, что у них общего. Что происходит, когда встречаются две линии? Они что-нибудь говорят? Наверное, нет, но всякий раз, когда встречаются две линии, вы знаете, что у них есть по крайней мере одна общая точка. Определение точки, в которой они встречаются, может помочь вам решить проблемы в реальном мире. Раздел 9: Обзор семестра и тест
СЕМЕСТР ВТОРОЙ
Раздел 1: Взаимосвязи и функции
 Есть много видов функций. У некоторых есть графики, которые выглядят как линии, в то время как у других есть графики, которые изгибаются как парабола. Функции также могут принимать другие формы. Не у каждой функции есть график, похожий на линию или параболу. Не у каждой функции есть уравнение. Важно помнить, что если вы поместите какой-либо действительный ввод в функцию, вы получите единственный результат.
Есть много видов функций. У некоторых есть графики, которые выглядят как линии, в то время как у других есть графики, которые изгибаются как парабола. Функции также могут принимать другие формы. Не у каждой функции есть график, похожий на линию или параболу. Не у каждой функции есть уравнение. Важно помнить, что если вы поместите какой-либо действительный ввод в функцию, вы получите единственный результат. Раздел 2: Рационалы, иррациональные элементы и радикалы
Раздел 3: Работа с многочленами
 Вы можете выполнять основные операции с многочленами так же, как вы складываете, вычитаете, умножаете и делите числа.
Вы можете выполнять основные операции с многочленами так же, как вы складываете, вычитаете, умножаете и делите числа. Раздел 4: Факторинговые многочлены
Раздел 5: Квадратичные уравнения
 Линейные уравнения обычно имеют одно решение, но как насчет квадратных? Как их решить и как выглядят решения?
Линейные уравнения обычно имеют одно решение, но как насчет квадратных? Как их решить и как выглядят решения? Раздел 6: Рациональные выражения
Раздел 7: Логика и рассуждение
 Подобно тому, как юристы используют логические рассуждения для формулирования убедительных аргументов, математики используют логические рассуждения для формулирования и доказательства теорем. Освоив использование индуктивного и дедуктивного рассуждений, вы сможете приводить и понимать аргументы во многих областях.
Подобно тому, как юристы используют логические рассуждения для формулирования убедительных аргументов, математики используют логические рассуждения для формулирования и доказательства теорем. Освоив использование индуктивного и дедуктивного рассуждений, вы сможете приводить и понимать аргументы во многих областях. Раздел 8: Обзор семестра и тест
ДОПОЛНИТЕЛЬНЫЕ УСТАНОВКИ
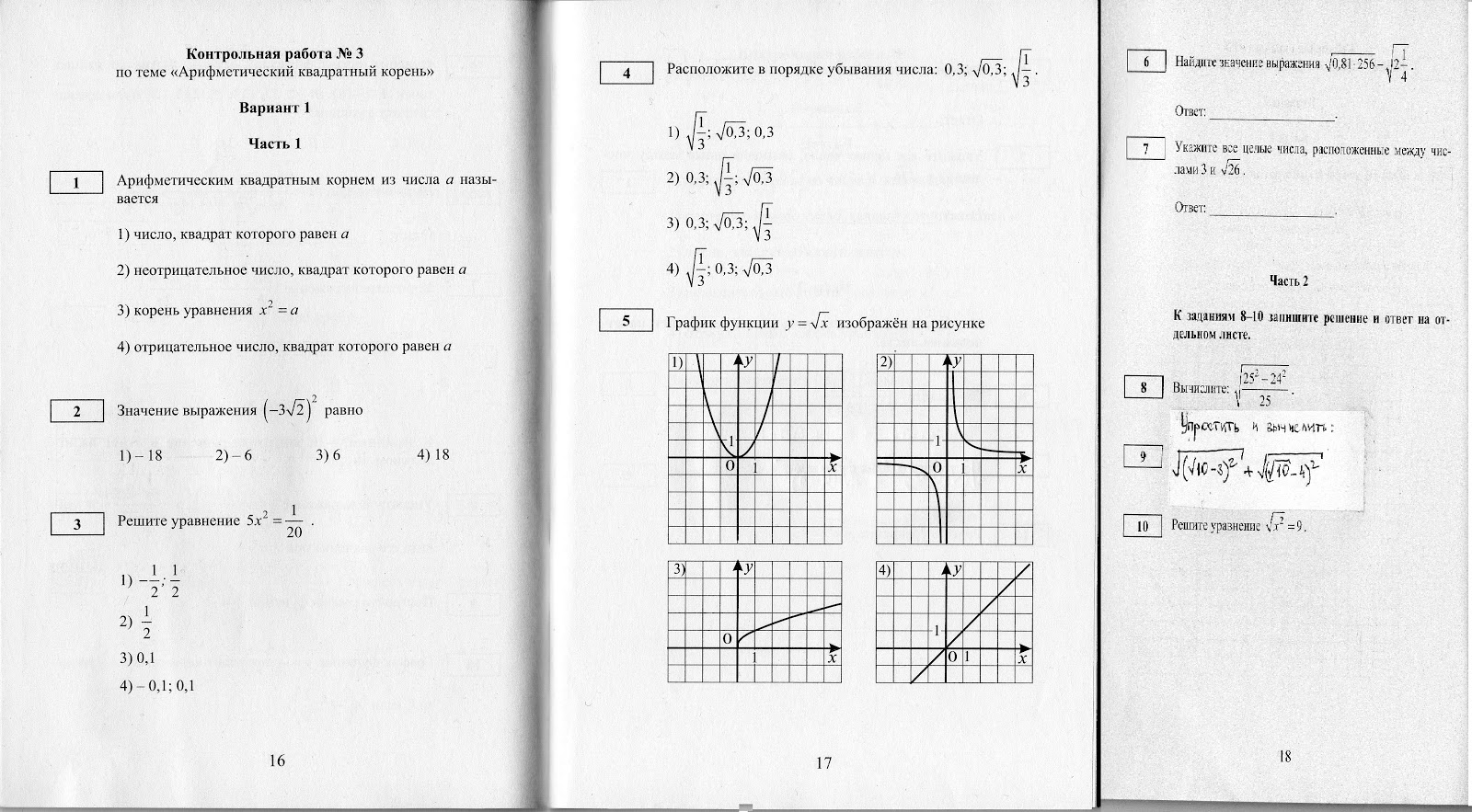
A – 1: Измерения и геометрия
A – 2: Подсчет, вероятность и статистика
наверх Количество уроков и расписание
Критерии зачисления по математике 8-9 классы
 Распределение по математике — это не то, что происходит в конце года. Скорее, это непрерывный процесс с определенными этапами в течение года. Математический факультет также считает важным включить общее описание каждого курса CCHS.
Распределение по математике — это не то, что происходит в конце года. Скорее, это непрерывный процесс с определенными этапами в течение года. Математический факультет также считает важным включить общее описание каждого курса CCHS. Студенты последовательно демонстрируют владение ранее изученными темами и сохраняют знания без повторного обучения.Студенты изучают новые темы в ускоренном темпе с минимальным повторением и могут легко применять и синтезировать концепции для решения новых задач (в том числе в тестовых ситуациях).
Студенты последовательно демонстрируют владение ранее изученными темами и сохраняют знания без повторного обучения.Студенты изучают новые темы в ускоренном темпе с минимальным повторением и могут легко применять и синтезировать концепции для решения новых задач (в том числе в тестовых ситуациях). Теория, лежащая в основе этого подхода, заключается в том, что в реальном мире проблемы не требуют особого подхода. Используя «интегрированный» подход, студенты могут решить, какие навыки использовать для решения конкретной проблемы, независимо от области содержания.Студенты овладевают некоторыми ранее изученными темами и продолжают обучение с повторным обучением и повторением. Студенты узнают, как использовать комбинацию навыков из алгебры, геометрии, статистики и тригонометрии в зависимости от их анализа и подхода к решению проблем. Этот уровень преподается в умеренном темпе с достаточным количеством повторений.
Теория, лежащая в основе этого подхода, заключается в том, что в реальном мире проблемы не требуют особого подхода. Используя «интегрированный» подход, студенты могут решить, какие навыки использовать для решения конкретной проблемы, независимо от области содержания.Студенты овладевают некоторыми ранее изученными темами и продолжают обучение с повторным обучением и повторением. Студенты узнают, как использовать комбинацию навыков из алгебры, геометрии, статистики и тригонометрии в зависимости от их анализа и подхода к решению проблем. Этот уровень преподается в умеренном темпе с достаточным количеством повторений. Студенты узнают, как использовать комбинацию навыков из алгебры, геометрии, статистики и тригонометрии в зависимости от их анализа и подхода к решению проблем.
Студенты узнают, как использовать комбинацию навыков из алгебры, геометрии, статистики и тригонометрии в зависимости от их анализа и подхода к решению проблем. В июне CMS предоставит CCHS текущие оценки учащихся, которые CCHS сверит с диапазонами оценок за февраль на предмет возможных изменений уровня учащихся.
В июне CMS предоставит CCHS текущие оценки учащихся, которые CCHS сверит с диапазонами оценок за февраль на предмет возможных изменений уровня учащихся. уроков в классе | Математические решения

 (См. Рисунок 3.)
(См. Рисунок 3.)



Наблюдая за детьми
 «Я насчитал 36 мест. Но в этом нет смысла, потому что 16 умножить на 2 равно 32. Может, я неправильно посчитал ». Она снова сосчитала стороны.
«Я насчитал 36 мест. Но в этом нет смысла, потому что 16 умножить на 2 равно 32. Может, я неправильно посчитал ». Она снова сосчитала стороны. «Я тоже нашел это», — сказал он. «Теперь я пробую что-то вдвое».
«Я тоже нашел это», — сказал он. «Теперь я пробую что-то вдвое». На следующий день
 «Какой самый дешевый способ разместить 32 человека за одним большим прямоугольным столом? А какой самый дорогой способ? Чтобы ответить, некоторым из вас нужно будет найти больше расстановок столов.”
«Какой самый дешевый способ разместить 32 человека за одним большим прямоугольным столом? А какой самый дорогой способ? Чтобы ответить, некоторым из вас нужно будет найти больше расстановок столов.” Она сказала, указывая: «Сверху вниз идет 1, затем 2, затем 3, затем 4, затем 5 и так далее, вплоть до 8».
Она сказала, указывая: «Сверху вниз идет 1, затем 2, затем 3, затем 4, затем 5 и так далее, вплоть до 8».

Что работает лучше, чем традиционные инструкции по математике
Из главы 9: «Как правильно сделать 3 Р»
в
Школы, которых заслуживают наши дети (Бостон: Houghton Mifflin, 1999) Почему основы просто не складываются
 Вы решаете одну задачу за другой, пока не решите ее. Это может заставить вас бояться всего предмета (и по возможности избегать его), но именно так это и нужно делать. Более того, математика на уроке алгебры в старшей школе почти такая же, как и на дополнительном уроке в первом классе.Учитель начинает с демонстрации правильного способа решения задачи, затем дает бесчисленное количество примеров одной и той же задачи (за исключением разных номеров), идея состоит в том, чтобы ученики имитировали метод, который им показали, а учитель при необходимости корректирует их усилия.
Вы решаете одну задачу за другой, пока не решите ее. Это может заставить вас бояться всего предмета (и по возможности избегать его), но именно так это и нужно делать. Более того, математика на уроке алгебры в старшей школе почти такая же, как и на дополнительном уроке в первом классе.Учитель начинает с демонстрации правильного способа решения задачи, затем дает бесчисленное количество примеров одной и той же задачи (за исключением разных номеров), идея состоит в том, чтобы ученики имитировали метод, который им показали, а учитель при необходимости корректирует их усилия. На самом деле, учебники по математике часто рассматриваются как учениками, так и учителями как источник истины — «загадочный, но авторитетный документ», так что задача каждого состоит в том, чтобы выяснить, «что, , хочет, чтобы вы сделали» [3].
На самом деле, учебники по математике часто рассматриваются как учениками, так и учителями как источник истины — «загадочный, но авторитетный документ», так что задача каждого состоит в том, чтобы выяснить, «что, , хочет, чтобы вы сделали» [3]. Одно из последствий этого проявляется каждый раз, когда взрослый небрежно описывает себя ненавидящим математику и неспособным к ней.Поколения бывших студентов списали со счетов этот предмет, а также свою собственную компетенцию, по крайней мере частично, в результате обучения старой школе.
Одно из последствий этого проявляется каждый раз, когда взрослый небрежно описывает себя ненавидящим математику и неспособным к ней.Поколения бывших студентов списали со счетов этот предмет, а также свою собственную компетенцию, по крайней мере частично, в результате обучения старой школе. . . . Дрель не развивает смыслов.Повторение не ведет к пониманию »[7].
. . . Дрель не развивает смыслов.Повторение не ведет к пониманию »[7]. [10] Один исследователь задал задачи типа 7 + 52 + 186 учащимся второго, третьего и четвертого классов и обнаружил, что те, кого учили обычным способом — с установленной процедурой переноса чисел с разряда единиц на разряды десятков, а затем от десятков до сотен — не просто делали ошибки: они допускали ошибки настолько диковинные, что предполагали полную неспособность уловить задействованные количества.Эти студенты ответили: 29, 30, 989 и 9308. [11] (Как мы увидим позже, ученики того же возраста, которых учили нетрадиционно — без учебников, рабочих листов или какой-либо презентации учителя о «правильном способе» сложения, — справились гораздо лучше.)
[10] Один исследователь задал задачи типа 7 + 52 + 186 учащимся второго, третьего и четвертого классов и обнаружил, что те, кого учили обычным способом — с установленной процедурой переноса чисел с разряда единиц на разряды десятков, а затем от десятков до сотен — не просто делали ошибки: они допускали ошибки настолько диковинные, что предполагали полную неспособность уловить задействованные количества.Эти студенты ответили: 29, 30, 989 и 9308. [11] (Как мы увидим позже, ученики того же возраста, которых учили нетрадиционно — без учебников, рабочих листов или какой-либо презентации учителя о «правильном способе» сложения, — справились гораздо лучше.)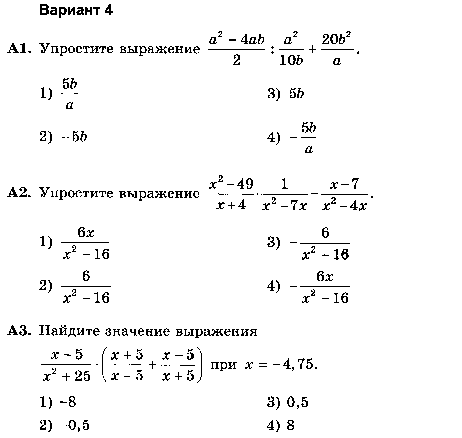 Большинство студентов правильно ответили на вопросы, но менее одного из четырех правильно ответили на вопрос. Наиболее частым ответом был «31 остаток 12». [12]
Большинство студентов правильно ответили на вопросы, но менее одного из четырех правильно ответили на вопрос. Наиболее частым ответом был «31 остаток 12». [12] В самом деле, — самое важное, что — избегать этого сценария для студентов, которым сложно понять, что происходит: чем больше им дают алгоритмов и точно говорят, что делать, тем дальше они отстают в понимании. . [15] К настоящему времени мы не должны удивляться, обнаружив, что школы США поступают наоборот, подвергая этих учеников, в частности, бесконечному режиму тренировок.
В самом деле, — самое важное, что — избегать этого сценария для студентов, которым сложно понять, что происходит: чем больше им дают алгоритмов и точно говорят, что делать, тем дальше они отстают в понимании. . [15] К настоящему времени мы не должны удивляться, обнаружив, что школы США поступают наоборот, подвергая этих учеников, в частности, бесконечному режиму тренировок. Они должны потратить свое время
Они должны потратить свое время переулков, и время от времени испытывая удовлетворение от открытия чего-то, чего они не знали раньше »[17].
переулков, и время от времени испытывая удовлетворение от открытия чего-то, чего они не знали раньше »[17].

 Затем, обнаружив, что нужно снова добавить такое же количество звеньев, чтобы уравновесить дополнительную шайбу, дети начинают понимать концепцию соотношения для себя. Как вы думаете, какой подход приведет к более глубокому пониманию?
Затем, обнаружив, что нужно снова добавить такое же количество звеньев, чтобы уравновесить дополнительную шайбу, дети начинают понимать концепцию соотношения для себя. Как вы думаете, какой подход приведет к более глубокому пониманию? Теперь представьте, что вместо этого их просят объяснить, используя слова и числа: «Почему не равно 1/2 + 1/3 1/5?» Как вы думаете, какой вопрос поможет учителю лучше понять, как думает каждый ученик?
Теперь представьте, что вместо этого их просят объяснить, используя слова и числа: «Почему не равно 1/2 + 1/3 1/5?» Как вы думаете, какой вопрос поможет учителю лучше понять, как думает каждый ученик?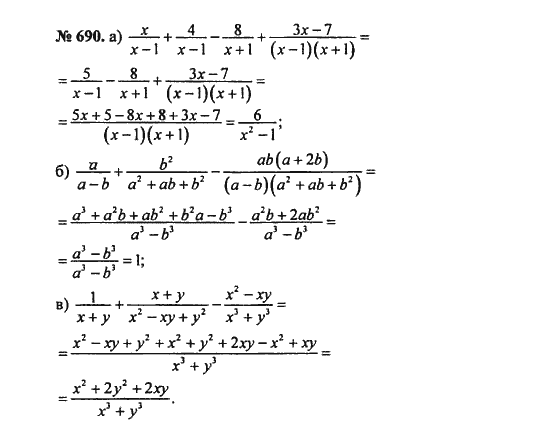 Ключевой вопрос заключается в том, поглощается ли понимание пассивно или активно. В последнем случае математика фактически превращается в творческую деятельность.
Ключевой вопрос заключается в том, поглощается ли понимание пассивно или активно. В последнем случае математика фактически превращается в творческую деятельность.
 Вместо демонстрации «правильной» процедуры сложения двузначных чисел, например, учителя второго класса могут поставить проблему и затем позволить учащимся (индивидуально или парами) найти способы ее решения, побуждая их попробовать различные методы, дайте им достаточно времени, прежде чем снова созвать их для обсуждения, чтобы они могли объяснить, что они сделали, оспорить ответы друг друга (в дружеской и поддерживающей манере), задать вопросы, пересмотреть свои собственные подходы и выяснить, что работает и почему.
Вместо демонстрации «правильной» процедуры сложения двузначных чисел, например, учителя второго класса могут поставить проблему и затем позволить учащимся (индивидуально или парами) найти способы ее решения, побуждая их попробовать различные методы, дайте им достаточно времени, прежде чем снова созвать их для обсуждения, чтобы они могли объяснить, что они сделали, оспорить ответы друг друга (в дружеской и поддерживающей манере), задать вопросы, пересмотреть свои собственные подходы и выяснить, что работает и почему. . . спросите ребенка: «Как вы получили 12?» Дети часто поправляются, пытаясь объяснить свои рассуждения кому-то другому ». [23] Поскольку этот« кто-то другой »может быть ровесником, детям часто имеет смысл объяснять их рассуждения друг другу. Более того, как исправление неправильных ответов не особенно полезно, так и похвала за правильные ответы не приносит особой пользы. Опять же, важен сам процесс — или, точнее, понимание процесса ребенком, что может быть выявлено с помощью вопроса «Как вы получили 13 баллов?» [24]
. . спросите ребенка: «Как вы получили 12?» Дети часто поправляются, пытаясь объяснить свои рассуждения кому-то другому ». [23] Поскольку этот« кто-то другой »может быть ровесником, детям часто имеет смысл объяснять их рассуждения друг другу. Более того, как исправление неправильных ответов не особенно полезно, так и похвала за правильные ответы не приносит особой пользы. Опять же, важен сам процесс — или, точнее, понимание процесса ребенком, что может быть выявлено с помощью вопроса «Как вы получили 13 баллов?» [24] )
) для этого. [26]
для этого. [26] Остальные сидели, кивая головами, словно в ритме чисел. Некоторые манипулировали пальцами, а один ребенок закусил губу и выглядел весьма озадаченным.
Остальные сидели, кивая головами, словно в ритме чисел. Некоторые манипулировали пальцами, а один ребенок закусил губу и выглядел весьма озадаченным.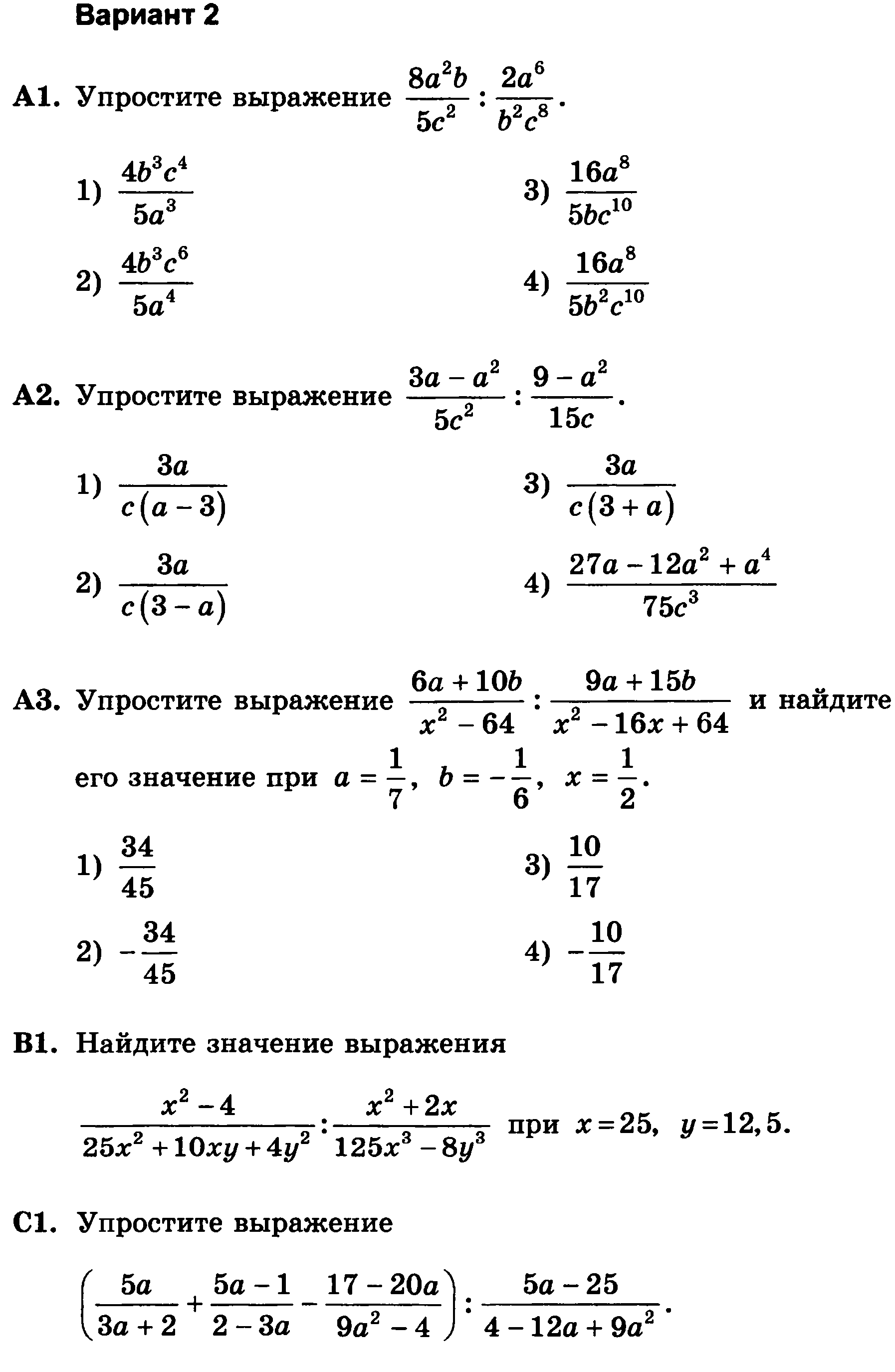 Итак, 40 минус 20 — это 20. Уберите еще 2». Это 28 ». . . Я надеялся, что кто-то из детей заметит ошибку и привлечет внимание Бена. Я не был разочарован.
Итак, 40 минус 20 — это 20. Уберите еще 2». Это 28 ». . . Я надеялся, что кто-то из детей заметит ошибку и привлечет внимание Бена. Я не был разочарован. На самом деле, однако, не только неверно утверждать, что конструктивистский математический класс основан на этой релятивистской предпосылке, но и верно прямо противоположное. Именно тот факт, что у «40 минус 22» есть только один правильный ответ, заставляет этот подход работать. «Дети в конечном итоге дойдут до истины, если они будут думать и спорить достаточно долго, потому что в [математике] нет абсолютно ничего произвольного», — говорит Камии.[28] Даже те ошибки, которые дети делают на пути к пониманию, отражают определенные предсказуемые закономерности, мало чем отличающиеся от их ранних орфографических ошибок. (Например, маленькие дети, пытающиеся вычислить, сколько чисел отделяют 3 от 8, часто начинают считать с 3, а не с 4, тем самым получая ответ, который отличается на единицу.)
На самом деле, однако, не только неверно утверждать, что конструктивистский математический класс основан на этой релятивистской предпосылке, но и верно прямо противоположное. Именно тот факт, что у «40 минус 22» есть только один правильный ответ, заставляет этот подход работать. «Дети в конечном итоге дойдут до истины, если они будут думать и спорить достаточно долго, потому что в [математике] нет абсолютно ничего произвольного», — говорит Камии.[28] Даже те ошибки, которые дети делают на пути к пониманию, отражают определенные предсказуемые закономерности, мало чем отличающиеся от их ранних орфографических ошибок. (Например, маленькие дети, пытающиеся вычислить, сколько чисел отделяют 3 от 8, часто начинают считать с 3, а не с 4, тем самым получая ответ, который отличается на единицу.)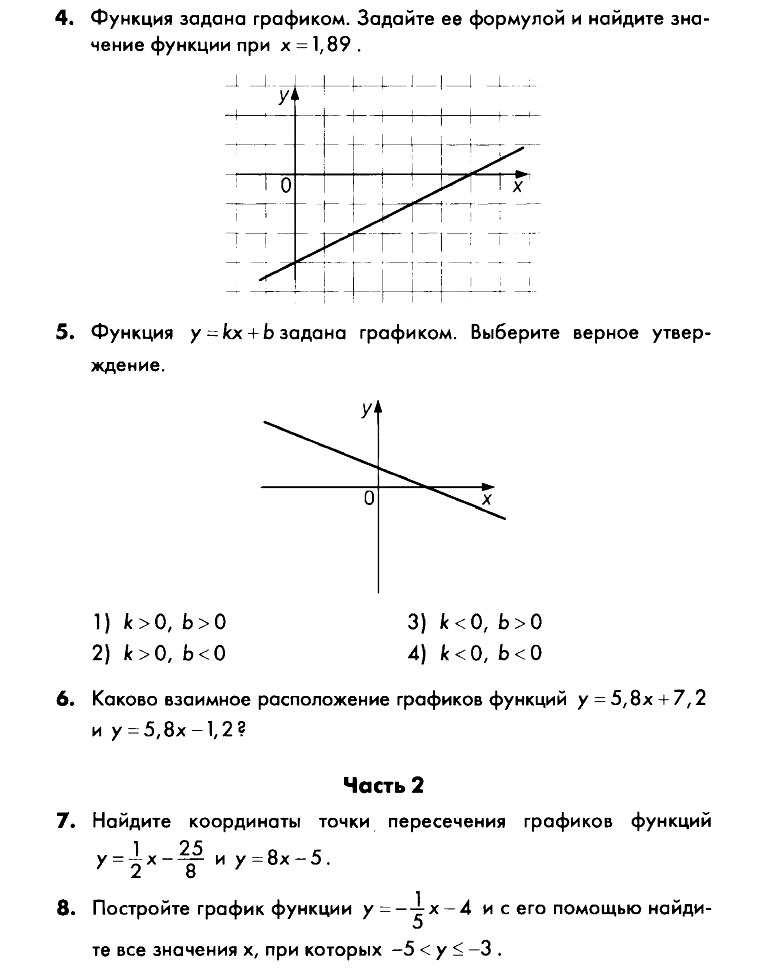 Это, конечно, всего лишь еще одна версия ошибочного приравнивания прогрессивного образования к своего рода невмешательству романтизма: расслабьтесь, и дети будут учиться. Поскольку в сознании многих традиционалистов «обучение» приравнивается к прямому наставлению, отсутствие этого конкретного метода означает, что учитель вообще ничего не делает. К настоящему моменту мы понимаем, что учитель жизненно активен, органично вовлечен. Она настраивает вещи так, чтобы ученики могли поиграть с возможностями, обдумать проблемы, поговорить и исправить.Это бесконечно труднее, чем выполнить образец задачи и раздать рабочие листы.
Это, конечно, всего лишь еще одна версия ошибочного приравнивания прогрессивного образования к своего рода невмешательству романтизма: расслабьтесь, и дети будут учиться. Поскольку в сознании многих традиционалистов «обучение» приравнивается к прямому наставлению, отсутствие этого конкретного метода означает, что учитель вообще ничего не делает. К настоящему моменту мы понимаем, что учитель жизненно активен, органично вовлечен. Она настраивает вещи так, чтобы ученики могли поиграть с возможностями, обдумать проблемы, поговорить и исправить.Это бесконечно труднее, чем выполнить образец задачи и раздать рабочие листы. Стандарты математической практики | Инициатива Common Core State Standards
Стандарты в этой области:
CCSS.Math.Practice.MP1 осмысливать проблемы и настойчивость в их решении.
CCSS.Math.Practice.MP2 Размышляйте абстрактно и количественно.
CCSS.Math.Practice.MP3 Создавайте жизнеспособные аргументы и критикуйте рассуждения других.
CCSS. Математика. Практика.Модель MP4 с математикой.
CCSS.Math.Practice.MP5 Стратегически используйте соответствующие инструменты.
CCSS.Math.Practice.MP6 Внимание к точности.
CCSS.Math.Practice.MP7 Ищите и используйте структуру.
CCSS.Math.Practice.MP8 Ищите и выражайте закономерность в повторяющихся рассуждениях.
Соединение стандартов математической практики со стандартами математического содержания
