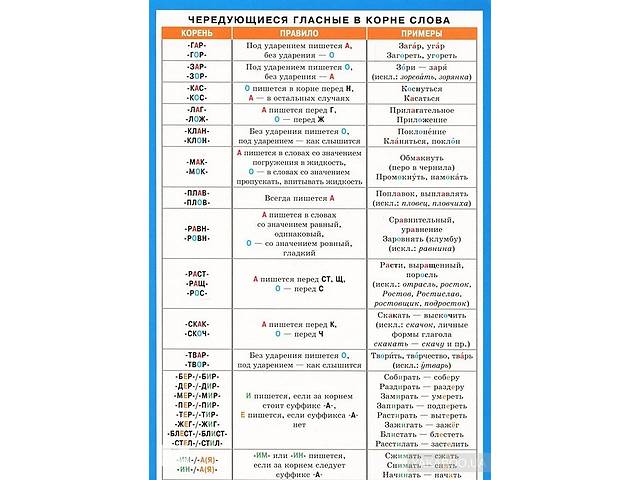
| -ГАР- -ГОР- | Под ударением пишется А, без ударения — О | Уга́рный, зага́р загоре́лый, погоре́лец Исключение: вы́гарки, и́згарь, при́гарь |
| -КЛАН- -КЛОН- | Без ударения пишется буква О, под ударением то, что слышится | кла́няться склоне́ние, укло́н, наклони́ться |
| -ТВАР- -ТВОР- | Без ударения пишется буква О, под ударением в соответствии с произношением | тварь, сотвори́ть, затво́р, притво́р Исключение: у́тварь |
| -ЗАР- -ЗОР- | Без ударения пишется А, под ударением то, что слышится | зарни́ца, за́рево зо́ри, зо́ренька Исключение: зорева́ть |
| -ПЛАВ- -ПЛОВ- | Всегда пишется буква А, кроме двух слов | сплавля́ть, поплаво́к, плаву́честь плове́ц, пловчи́ха |
| -КАС- -КОС- | Буква А пишется, если за корнем следует -а-, О – в остальных случаях | касание, касательная коснись, прикосновение |
| -МАК- -МОК- | Буква А пишется в корне со значением «погружать в жидкость», буква О — «пропускать, впитывать жидкость» | макать вымокнуть, намокнуть |
| -РАВН- -РОВН- | А пишется в корне, имеющем значение «одинаковый, равный, сходный», О — при значении «ровный, прямой, гладкий» | равноправие, сравнять (счет) подровнять Исключение: равнина, уровень, поравняться, поровну |
| -РАСТ- -РАЩ- -РОС- | Буква А пишется перед ст, щ, О — перед остальными буквами | отрасти, наращенный, поросль Исключение: отрасль, росток, ростовщик, Ростов, Ростислав |
| -СКАК- -СКОЧ- | Буква А пишется перед к, О — перед ч | скакалка, выскочка Исключение: скачок, личные формы глагола скакать – скачу и пр.  |
| -ЛАГ- -ЛОЖ- | Буква А пишется перед г, О — перед ж | полагать, облагать отложить, обложение |
| -БЕР-/-БИР- -ДЕР-/-ДИР- -МЕР-/-МИР- -ПЕР-/-ПИР- -ТЕР-/-ТИР- -ЖЕГ-/-ЖИГ- -БЛЕСТ-/-БЛИСТ- -СТЕЛ-/-СТИЛ- -ЧЕТ-/-ЧИТ- | Буква И пишется, если за корнем следует -а-, Е — в остальных случаях | набирать — наберу отдирать — отдерешь отмирать — отмереть отпирать — отпереть стирать — стереть прижигать — прижёг блистать — блестящий застилать — застелить вычитать — вычеты |
| -ИМ-/-А(Я) -ИН-/-А(Я)- | Сочетание -ИМ- или -ИН- пишется, если за корнем следует -а- | пережимать — пережать занимать — занять начинать — начать |
Таблица «Корни с чередующимися гласными» | Учебно-методический материал по русскому языку на тему:
Корни с чередующимися гласными А/О
1. Зависимость от ударения
Зависимость от ударения
Корни | Правило | Примеры | Исключения |
Гар-/гор- | Независимо от того, какой гласный пишется под ударением (а или о), в безударном положении пишется о. | Зага́р – загорелый, угореть, погорелец. | Пригарь, изгарь, выгарки. |
Клан-/клон- | Кла́няться, покло́н – поклониться, склонять, наклонение, склонение. | ||
Твар-/твор- | Тва́рь, тво́рчество – творить, сотворить, претворить, притвориться. | Утварь. | |
Зар-/зор- | Независимо от того, какой гласный пишется под ударением (а или о), в безударном положении пишется а. | За́рево, зо́рька – заря, зарница, озарять. | Зоревать, зорянка. |
Плав-/плов- | Независимо от того, какой гласный пишется под ударением (а, о, илиы), в безударном положении пишется а. | Пла́вать, плы́ть – плавучесть, поплавок, жук-плавунец. | Пловец, пловчиха; |
2. Зависимость от конечных согласных корня
Корни | Правило | Примеры | Исключения |
Раст- | Перед ст и щ пишется а, перед с пишется о. | Расти, растение, выращивать, наращение – выросший, заросли, поросль. | а) Ростов, Ростислав, росток, ростовщик, выросток (и производные от них, например:ростовщический). |
Скак-/скоч- | Независимо от того, какой гласный пишется под ударением (а или о), в безударном положении перед кпишется а, перед ч пишется о. | Скакать, проскакать, на скаку – выскочка, заскочить, выскочить. | Скачу, скачок, скачи, вскачь. |
Лаг-/лож- | Перед г пишется а, перед ж пишется о. | Слагаемое, полагать, разлагать – сложить, положить, разложить. | Полог. |
3. Зависимость от наличия суффикса -а-
Корни | Правило | Примеры |
Кас-/кос- | Если за корнем следует суффикс -а-, то в корне пишется а, если суффикса нет, то в корне пишется о. | Касаться, касательная – коснуться, прикоснуться. |
4. Зависимость от значения
Корни | Правило | Примеры | Исключения |
Мак-/мок- | Корень мак- (мач-) пишется в словах, имеющих значение «погружать в жидкость». | Обмакнуть перо в чернила («погрузить»), макать хлеб в сметану («погружать») –промокнуть пятно («пропустить жидкость»), промокательная бумага(«пропускающая жидкость»), смочить («сделать мокрым»). | |
Равн-/ровн- | Корень равн- пишется в словах, имеющих значение «одинаковый, наравне, равный». | Поравняться («оказаться на одной линии, в одинаковом положении»), уравнение(«математическое равенство») – подровнять кусты («сделать ровными»),разровнять песок («сделать ровным, гладким»). | Равнина, поровну, уровень, ровесник. |
Корни с чередующимися гласными И/Е
Корни | Правило | Примеры |
Бир-/бер- | Если за корнем следует суффикс -а-, то в корне пишется и, если суффикса нет, то в корне пишется е. . | Забирать – заберу. |
Жиг-/жег- | Выжигать – выжегший. | |
Стил-/стел- | Застилать – постелить. | |
Блист-/блест- | Блистать – блестеть. | |
Мир-/мер- | Умирать – умереть. | |
Тир-/тер- | Стирать – стереть. | |
Дир-/дер- | Раздирать – раздерёт. | |
Пир-/пер- | Запирать – запереть. | |
Чит-/чет- | Вычитать – вычеты. Исключения: сочетание, сочетать, чета. |
Обратите внимание!
1) Чередование и/е в корнях мир-/мер- характерно только для слов со значениями «мёртвый», «умирать», «замереть, стать неподвижным» и т.п.
Вымирать – вымереть, замирать – замереть.
В словах с корнем мир- со значением «отсутствие войны, вражды» всегда пишется и.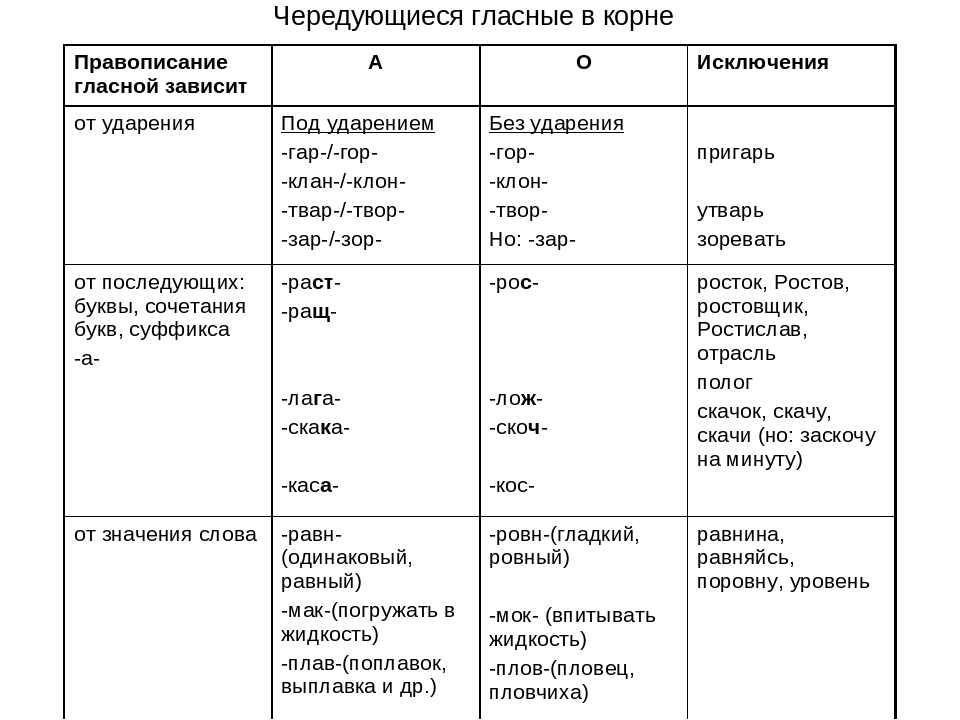
Мир, мирный, усмирять.
В словах с корнем мер- со значением «мерить, измерять» всегда пишется е.
Мерить, измерять, примерять платье, мерило.
2) Чередование и/е в корнях пир-/пер- характерно только для слов со значениями «закрыть», «открыть», «двигать», «выдаться вперёд, выдавиться» и т.п.
Запирать – запереть, отпирать – отпереть, выпирать – выпереть.
В словах с корнем пир- со значением «обильное угощение, пиршество» всегда пишется и.
Пир, пировать.
Чередование A(Я)/им(ин)
Корни | Правило | Примеры |
Корни с чередованиема(я)/им(ин) | Если за корнем следует суффикс -а-, то в корне пишетсяим(ин), если суффикса нет, то в корне пишется а/я. | Пожимать – пожать, нажимать – нажать, разминать – размять, понимать – понять, начинать – начать, поминать – память. |
Корень | Правило | Примеры, исключения. |
Лож/лаг | Пишется –а- при наличии суффикса –а- в основе, иначе – о- | Прилагать, изложение Искл.: полог |
Кос/кас | Пишется –а- при наличии суффикса –а- в основе, иначе — -о- | Касаться, коснуться |
Рос/раст/ращ | Пишется –а- перед ст, щ; -о- перед –с- | Расти, росли, выращен Искл.: отрасль, росток, Ростов, Ростислав, ростовщик |
Скак/скоч | Пишется –а- перед –к— о- перед ч- | Скакать, выскочить Искл.: скачок, скачу. |
Гор/гар | Пишется –а- под ударением. Иначе –о- | Загар, загорелый |
Зор/зар | Пишется –а-без ударения, под ударением – то, что слышится. | Озарить, зори. Зарево Искл.: зоревать, птица зорянка |
Клан/клон | Пишется – о – без ударением, под ударением – то что слышится. | Поклон, кланяться, поклониться |
Твор/твар | Пишется — о – без ударением, под ударением – то, что слышится. | Тварь, творчество, творить. Искл.: утварь. |
Плов/плав | Пишется всегда –а-, кроме слов пловец, пловчиха. плывун. | Плавать, поплавок |
Мок/мак | Пишется –а-, если слово имеет значение «погружать в жидкость», -о-, если слово имеет значение «пропускать, впитывать жидкость». | Макать в сметану, Промокнуть под дождем |
Ровн/равн | Пишется –а-, если слово имеет значение «равный, одинаковый», -о-, если слово имеет значение «прямой, гладкий, ровный». | Сравнить с образцом, уровень воды. Искл.: равнина, равнение |
Бир/бер Блист/блест Дир/дер Жиг/жечь Мир/мер Стил/стел Тир/тер Чит/чет | Пишется –и- при наличии суффикса –а-. иначе — -е- | Собирать, соберу; Блистать, блестеть; Раздирать, раздеру; Сжигать, сжечь; Умирать, умереть; Расстилать, расстелить; Стирать, стереть; Вычитать, четность |
Им/а(я) Ин/а)я) | Пишется –им-, -ин- при наличии суффикса –а- | Обнимать, обнять; Начинать, начать. |
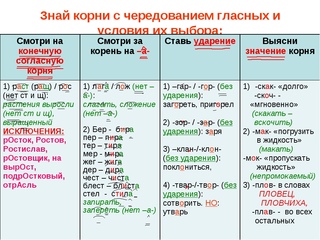
Условия выбора гласной. | Корень. | Примеры |
1.Выбор зависит от конечной согласной корня. | -раст— ращ— рос— | раСТи, выраЩенный, зароСли Исключение: росток, Ростов, Ростислав, ростовщик, отрасль |
— скак – скоч— | скакать, выскочить Исключение: скачок, скачу | |
2. | -бер – бир—А -дер – дир—А -мер – мир—А -пер – пир—А -тер – тир—А -блест – блист- А -жег – жиг -А -стел – стил-А -чет – чит—А | выберешь – выбираешь выдернуть – выдираешь замер – замирать запер – запиратьвытер – вытирать блестящий – блистательный выжег – выжигать постелить – застилать вычет – вычитать Искл. |
-кос – кас-А -лож- лаг-А | Коснулся-касАлся Изложить- излагАть | |
-а(я) – им-А -а(я) – ин -А | нанять=нанимать снять — снимать, начать – начинать | |
3. От ударения. | — гор – гар- без ударения О | угар — угореть |
-твор — твар- -клон — клан без ударения О | творец, сотворить склони′ть, покло′н, кла′няться | |
-зор – зар- без ударения А | зорька – з аря НО! зоревать, зорянка (птица) | |
Плав- плов без ударения пишется А | плавательный, поплавок Исключения: пловец, пловчиха, плывуны | |
4. | -мак – мок- мак- (погружать в жидкость) мок-(пропускать жидкость) | обмакнуть перо непромокаемый плащ |
равн – ровн- ра -ровн- (прямой, гладкий) | Уравнение, заровнять Исключения: уровень, ровесник, равнина, равняйсь, равнение направо. |
|
Корни, в которых написание гласной зависит от суффикса, следующего за корнем |
Корни, в которых написание гласной зависит от ударения |
Корни, в которых написание гласной зависит от буквы (букв), стоящей (стоящих) за гласной
|
Корни, в которых написание гласной зависит от смысла |
-бер-/-бир- -дер-/-дир- -мер-/-мир- -пер-/-пир- -тер-/-тир- -блест-/-блист- -жег-/-жиг- -стел-/-стил- -чет-/-чит- Пишется И, если за корнем следует суффикс -а- ∆замирать – замереть, блистать — блестеть Исключения: сочетать, сочетание
-лаг-/-лож- Пишется А, если за корнем следует суффикс -а- ∆касаться – коснуться, предлагать – предложить |
—гар-/-гор- -клан-/-клон- -твар-/-твор- Под ударением – А, без ударения – О. ∆загар – загорать поклон – кланяться творить – тварь Исключения: пригарь, выгарки, утварь
-зар-/-зор- Под ударением – в соответствии с произношением, без ударения – А. ∆зори – зарево – заря Исключение: зоревать
-плав-/-плов- Без ударения О пишется только в словах: пловец, пловчиха |
-раст- (-ращ-)/-рос- Пишется А перед ст, щ, в остальных случаях – О ∆расти, сращение – росла Исключения: росток, рост, ростовщик, подростковый, Ростов, Ростислав, отрасль
-скак-/-скоч- Пишется А перед К, пишется О перед Ч ∆скакать – вскочить Исключения: скачок, скачу |
-мак-/-мок- мак = «погружать в жидкость», «макать» мок = «пропускать жидкость», «мокнуть» ∆макать (хлеб в молоко) – вымокнуть (под дождем)
-равн-/-ровн- равн = «равный, одинаковый, наравне» ровн = «ровный, гладкий, прямой»∆выровнять (поверхность) – сравнивать |
Таблица по русскому языку по теме: «Корни с чередованиями»
Запомни! Корни с чередованием нельзя проверять ударением!
Условиявыбора
гласного
Чередующиеся
корни
Условия
выбора
гласного
Что пишут?
Примеры
Правила
Исключения
От наличия или отсутствия суффикса -А-
ЛАГ — ЛОЖ
Есть –А-
Нет –А-
-ЛАГ-
-ЛОЖ-
Полагать.
Положить.
В корне -ЛАГ– напишем А,
Получается –АГА.
Перед Ж напишем О –
Это знаем мы давно!
Полог
КАС — КОС
Есть –А-
Нет –А-
-КАС-
-КОС-
Касаться.
Коснуться.
Есть за корнем суффикс -А-?
-КАС- напишем мы всегда!
-КОС- напишем мы тогда,
Когда нет за корнем -А-!
БЕР – БИР
ПЕР – ПИР
ДЕР – ДИР
ТЕР – ТИР
СТЕЛ – СТИЛ
МЕР – МИР
БЛЕСТ – БЛИСТ
ЖЕГ – ЖИГ
ЧЕТ – ЧИТ
Есть –А-
Нет –А-
В корне –И-
В корне –Е-
Убирать, запирать,
удирать, вытирать,
застилать, умирать,
блистать, выжигать,
вычитать.
Уберу, запереть,
удеру, вытереть,
стелить, умереть,
блестеть, выжег,
вычесть.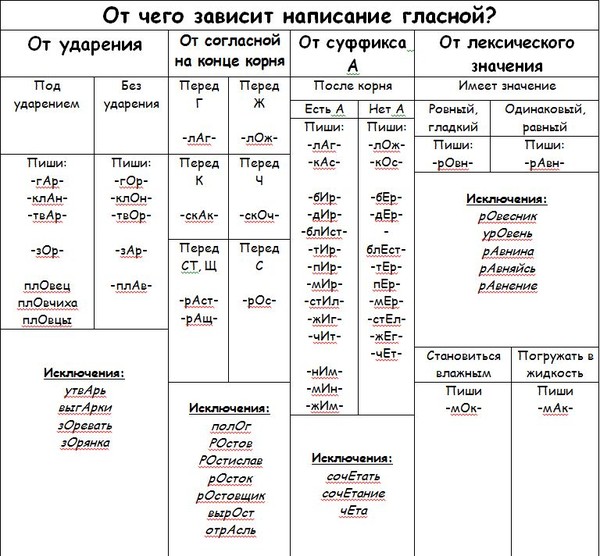
Если есть за корнем –А-,
В корне будет И всегда,
Вот пример, запоминай:
Ноги вытер? – Вытирай!
А(я) – им(ин)
(НЯ — НИМ)
Есть –А-
Нет –А-
В корне –
-им(ин)-
– А(я) –
Сжимать, приминать,
начинать, сочинять.
Сжать, примять, начать.
Сочетание,
сочетать.
От последующих
согласных
РАСТ(РАЩ) –
РОС
Перед СТ,Щ
Перед С
-РАСТ(РАЩ)-
-РОС-
Возраст, наращение.
Росла.
О напишем в корне РОС:
Вырос, перерос, подрос.
Перед СТ и Щ всегда
Мы напишем букву А.
Росток, росточек,
Ростислав, Ростов,
ростовец, ростовщик,
отрасль, отраслевой.
СКАК – СКОЧ
Перед К
Перед Ч
А
О
Скакать, поскакать.
Вскочить, подскочить.
Скачок, скачу,
скачи
(повелит. накл.)
Условия
выбора
гласного
Чередующиеся
корни
Условия
выбора
гласного
Что пишут?
Примеры
Правила
Исключения
От ударения
ГОР – ГАР
КЛОН – КЛАН
ТВОР – ТВАР
Без ударения
Под
ударением
О
Что слышим
Наклонение, творение,
загореть.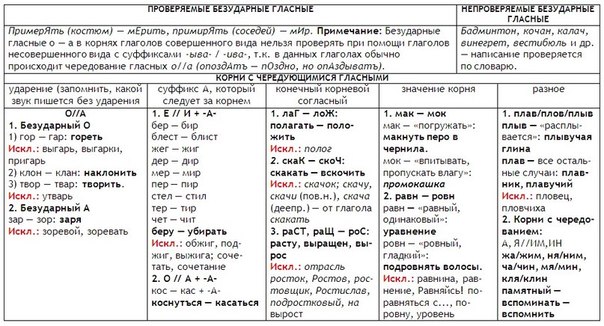
Угар, наклон, кланяться,
затвор.
КЛОН – запомните: поклон,
ТВОР – подсказка вам:
затвор,
КЛОН? ТВОР? ГОР? —
себя спрошу.
Сомневаюсь? О пишу!
Утварь,
выгарки
ЗАР – ЗОР
ПЛАВ – ПЛОВ
Без ударения
Под
ударением
А
Что слышим
Заря, зарница, озаренный.
Плавник, плавучий.
Зори, зарево.
Запомни:
ГОР КЛОН ТВОР – О
ЗАР ПЛАВ – А
Зоревать,
зорянка.
Пловец,
пловчиха,
плывун.
От значения слова
МАК – МОК
«Погружение
в жидкость»
«Пропускать
жидкость,
становиться
влажным»
-МАК-
-МОК-
Макать (хлеб в молоко).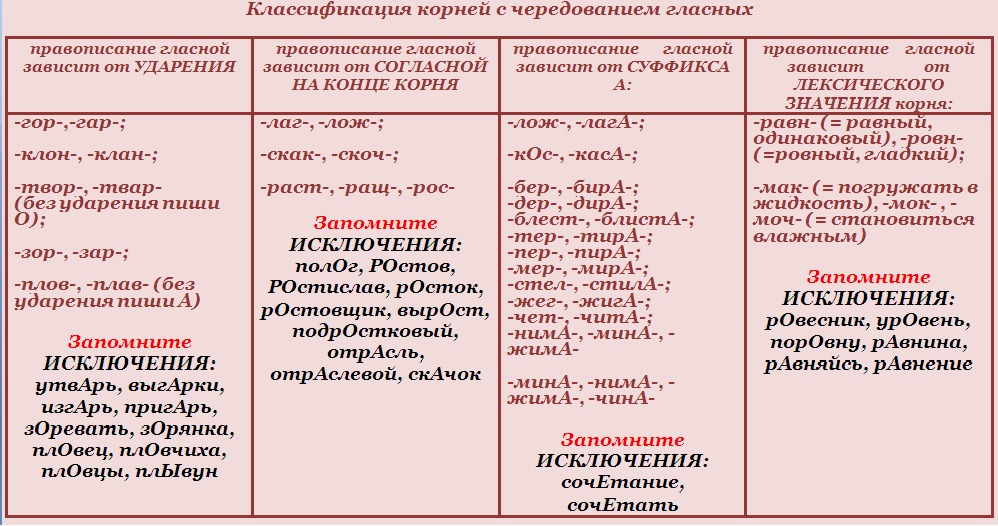
Обмакнуть
(перо в чернильницу).
Сапоги промокают.
РАВН – РОВН
Слово =
«равный,
одинаковый»
Слово =
«ровный,
гладкий,
прямой»
-РАВН-
-РОВН-
Равномерный, уравнять.
Ровнять (дорожки),
заровнять (яму),
подровнять (клумбы).
Равнение,
равняться,
равняйтесь,
поравняйтесь,
равнина.
Чередующиеся гласные в корнях
Условиявыбора
гласного
Чередующиеся
корни
Условия
выбора
гласного
Что пишут?
Примеры
Правила
Исключения
ЗАВИСИТ ОТ НАЛИЧИЯ СУФФИКСА — А —
ЛАГ – ЛОЖ
Эти корни никогда не употребляются
без приставки!
Есть –А-
Нет –А-
-ЛАГ-
-ЛОЖ-
Полагать.
Положить.
В корне –ЛАГ– напишем А,
Получается –АГА.
Перед Ж напишем О –
Это знаем мы давно!
Полог
КАС — КОС
Есть –А-
Нет –А-
-КАС-
-КОС-
Касаться.
Коснуться.
Есть за корнем суффикс -А-?
-КАС- напишем мы всегда!
-КОС- напишем мы тогда,
Когда нет за корнем -А-!
БЕР – БИР
ПЕР – ПИР
ДЕР – ДИР
ТЕР – ТИР
СТЕЛ – СТИЛ
МЕР – МИР
БЛЕСТ – БЛИСТ
ЖЕГ – ЖИГ
ЧЕТ – ЧИТ
Есть –А-
Нет –А-
В корне –И-
В корне –Е-
Убирать, запирать,
удирать, вытирать,
застилать, умирать,
блистать, выжигать,
вычитать.
Уберу, запереть,
удеру, вытереть,
стелить, умереть,
блестеть, выжег,
вычесть.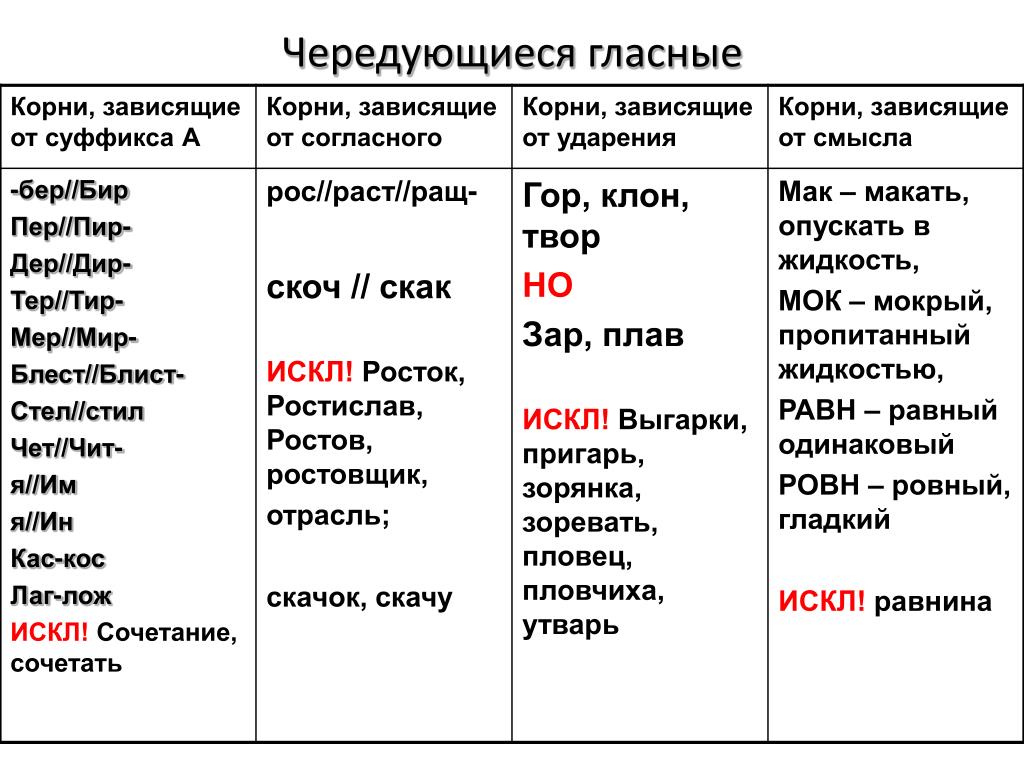
Если есть за корнем –А-,
В корне будет И всегда,
Вот пример, запоминай:
Ноги вытер? – Вытирай!
А(я) – им(ин)
Есть –А-
Нет –А-
В корне –
-им(ин)-
– А(я) –
Сжимать, приминать,
начинать, сочинять.
Сжать, примять, начать.
Сочетание,
сочетать.
ЗАВИСИТ ОТ
СОГЛАСНЫХ
В КОРНЕ
РАСТ(РАЩ) –
РОС
Перед СТ,Щ
Перед С
-РАСТ(РАЩ)-
-РОС-
Возраст, наращение.
Росла.
О напишем в корне РОС:
Вырос, перерос, подрос.
Перед СТ и Щ всегда
Мы напишем букву А.
Росток,
росточек,
Ростислав,
Ростов,
ростовец,
ростовщик,
отрасль,
отраслевой.
СКАК – СКОЧ
Перед К
Перед Ч
А
О
Скакать, подскакать.
Вскочить, подскочить.
Скачок,
скачу,
скачи
(повелит. накл.)
ЗАВИСИТ ОТ УДАРЕНИЯ
КЛАН – КЛОН
ТВАР – ТВОР
ГАР – ГОР
Без ударения
Под
ударением
О
Что слышим
Наклонение, творение,
загореть.
Угар, наклон, кланяться,
затвор.
КЛОН – проверьте так:
поклон,
ТВОР – подсказка вам:
«затвор»,
КЛОН? ТВОР? ГОР?
Себя спрошу. Сомневаюсь? О пишу!
Утварь,
выгарки,
изгарь, пригарь
ЗАР – ЗОР
ПЛАВ – ПЛОВ
Без ударения
Под
ударением
А
Что слышим
Заря, зарница, озаренный.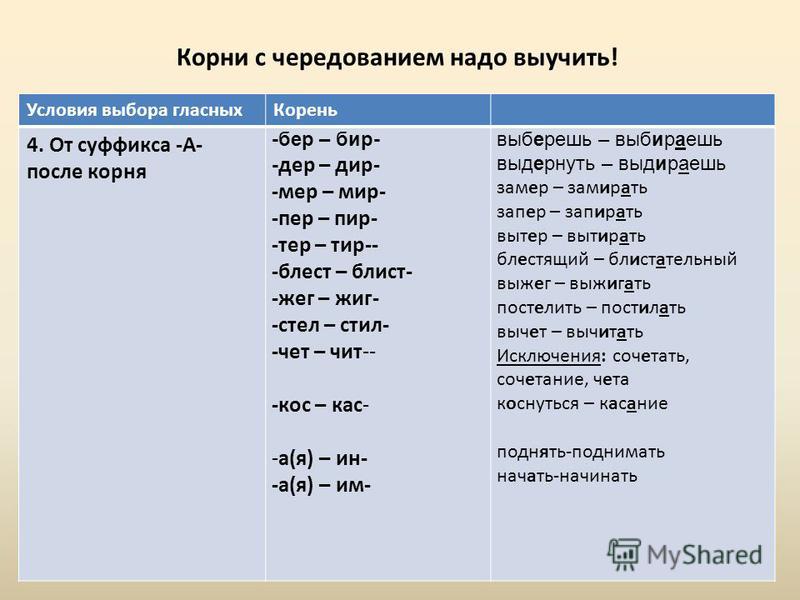
Плавник, плавучий.
Зори, зарево.
Запомни:
КЛОН ТВОР ГОР – О
ЗАР ПЛАВ – А
Зоревать,
зоревой,
зорянка.
Пловец,
пловчиха,
плывун,
плывучий
ЗАВИСИТ ОТ ЗНАЧЕНИЯ СЛОВА
МАК – МОК
«Погружение
в жидкость»
«Пропускать
жидкость,
становиться
влажным»
-МАК-
-МОК-
Макать (хлеб в молоко).
Обмакнуть
(перо в чернильницу).
Сапоги промокают.
РАВН – РОВН
Слово =
«равный,
одинаковый»
Слово =
«ровный,
гладкий,
прямой»
-РАВН-
-РОВН-
Равномерный, уравнять.
Ровнять (дорожки),
заровнять (яму),
подровнять (клумбы).
Равнение,
равняться,
равняйтесь,
поравняйтесь,
равнина.
Запомни! Корни с чередованием нельзя проверять ударением!
Правописание корней | ЕГЭ по русскому языку
Корень — это основная смысловая часть слова.
Корни можно разделить на три группы:
1) корни с безударными проверяемыми гласными
2) корни с безударными непроверяемыми гласными
3) корни с чередованием
Рассмотрим каждую из них.
Корни с безударными проверяемыми гласными
Выбор гласной буквы в безударном положении в корне определяется способом проверки. Проверять необходимо формами того же слова или однокоренными словами, в которых проверяемый гласный находится под ударением.
Например: звезда — звёздный, скреплять — скрепка, смотреть — смотрит
Есть несколько особенностей, на которые следует обратить внимание при такой проверке:
1. Есть слова старославянского по происхождения с сочетаниями ра/ла, которые в русском языке имеют сочетания оро/оло.
Есть слова старославянского по происхождения с сочетаниями ра/ла, которые в русском языке имеют сочетания оро/оло.
Например: врата-ворота, глава-голова, бразды-борозда.
2. Нельзя проверять безударную гласную о в корнях глаголов совершенного вида формами несовершенного вида.
Например: затопить-топка (а не затапливать), опоздать — поздно (а не опаздывать), проглотить — глотка (а не проглатывать).
3. При выборе написания о или а в безударных глагольных корнях не следует использовать для проверки глаголы несовершенного вида с суффиксом -ыва-/-ива-.
Например: бросать — бросить (а не набрасывать), топтать — топчет (а не вытаптывать) и т.п.
Корни с безударными непроверяемыми гласными
В русском языке есть множество слов, в которых нельзя проверить безударную гласную. Это, так назваемые, словарные слова. Их написание следует проверять по орфографическому словарю.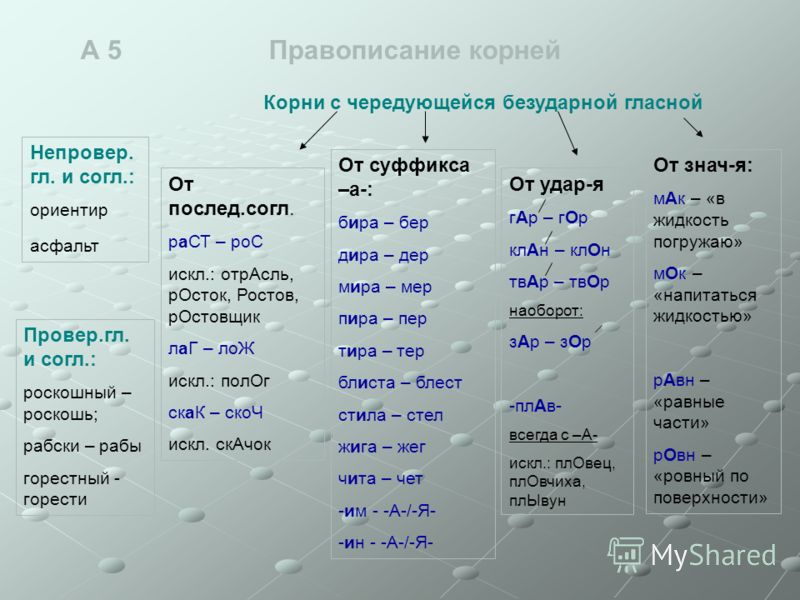
Например: винегрет, дирижабль, макулатура и т. п.
Корни с чередованием
1. Корни с чередующимися е//и завсисит от наличия/отсутствия суффикса -а-.
Если после корня есть суффикс -а-, то в корне пишем -и-, если суффикса -а- нет, то выбираем -е-.
Исключения: сочетать, сочетание
2. Корни с чередующимися о//а
Правописание корней -гар-//-гор-, -зар-//-зор-, -клан-//-клон-, -твар-//-твор- зависит от ударения.
-Гор-, -клон-, -твор-, -плав-, -зар- — так пишутся эти корни без ударения.
| и перед суффиксом -а- | е в остальных случаях | ||
| -бир(а)- | собирать | -бер- | соберет |
| -дир(а)- | обдирать | -дер- | обдерет |
| -мир(а)- | замирать | -мер- | замереть |
| -тир(а)- | обтирать | -тер- | обтереть |
| -пир(а)- | запирать | -пер- | запереть |
| -жиг(а)- | выжигать | -жег- | выжег |
| -стил(а)- | расстилать | -стел- | расстелить |
| -блист(а)- | блистать | -блест- | блестеть-чит(а)- |
| -чит(а)- | вычитать | -чет- | вычет |
Правописание корней -мок- //-моч-//-мак-, -равн-//-ровн- зависит от значения.
| Без ударения | Под ударением | |
| -гар-//-гор- | загорел, горелый | загар |
| -зар-//-зор- | заря, озарение | зорька |
| -клан-//-клон- | наклонять, склонение | кланяться |
| -твар-//-твор- | творить,творение | тварь |
Правописание корней -кос-//-кас- завсисит от наличия/отсутствия суффикса -а-.
| -мок-(-моч-) | в значении «пропускать жидкость» | непромокаемый вымокнуть |
| -мак- | в значении «погружать в жидкость» | макать |
| -равн- | в значении «равный, наравне, одинаковый» | приравнять, уравнение |
| -ровн- | в значении «прямой, гладкий, ровный» | выровнять |
| -кас- | касаться, прикасаться |
| -кос- | прикоснуться, прикосновение |
Правописание корней -лаг-//-лож-, -раст-//-ращ-//-рос-, -скак-//-скоч- зависит от последующей согласной корня.

| -лаг- | полагать, прилагательное |
| -лож- | положить, предложить, изложить |
| -раст- | возраст, растить |
| -ращ- | выращивать, приращение |
| -рос- | заросли, вырос |
| -скак- | выскакивать, скакать |
| -скоч- | выскочить, перескочить |
5.5 Чередующиеся серии — Calculus Volume 2
Цели обучения
- 5.5.1 Используйте тест чередующихся серий для проверки сходимости чередующихся серий.
- 5.5.2 Оценить сумму переменного ряда.
- 5.5.3 Объясните значение абсолютной и условной конвергенции.
До сих пор в этой главе мы в основном обсуждали ряды с положительными терминами. В этом разделе мы вводим чередующиеся серии — те серии, члены которых чередуются по знаку. В следующей главе мы покажем, что эти ряды часто возникают при изучении степенных рядов. После определения чередующихся серий мы вводим тест чередующихся серий, чтобы определить, сходится ли такой ряд.
В следующей главе мы покажем, что эти ряды часто возникают при изучении степенных рядов. После определения чередующихся серий мы вводим тест чередующихся серий, чтобы определить, сходится ли такой ряд.
Испытание чередующейся серии
Ряд, члены которого чередуют положительные и отрицательные значения, является чередующимся рядом. Например, серия
∑n = 1∞ (−12) n = −12 + 14−18 + 116− ⋯ ∑n = 1∞ (−12) n = −12 + 14−18 + 116− ⋯5,11
и
∑n = 1∞ (−1) n + 1n = 1−12 + 13−14 + ⋯ ∑n = 1∞ (−1) n + 1n = 1−12 + 13−14 + ⋯5.12
— это чередующиеся серии.
Определение
Любая серия, члены которой чередуются между положительными и отрицательными значениями, называется чередующейся серией. Переменный ряд можно записать в виде
∑n = 1∞ (−1) n + 1bn = b1 − b2 + b3 − b4 + ⋯ ∑n = 1∞ (−1) n + 1bn = b1 − b2 + b3 − b4 + ⋯5,13
или
∑n = 1∞ (−1) nbn = −b1 + b2 − b3 + b4− ⋯ ∑n = 1∞ (−1) nbn = −b1 + b2 − b3 + b4− ⋯5,14
Где bn≥0bn≥0 для всех натуральных чисел n .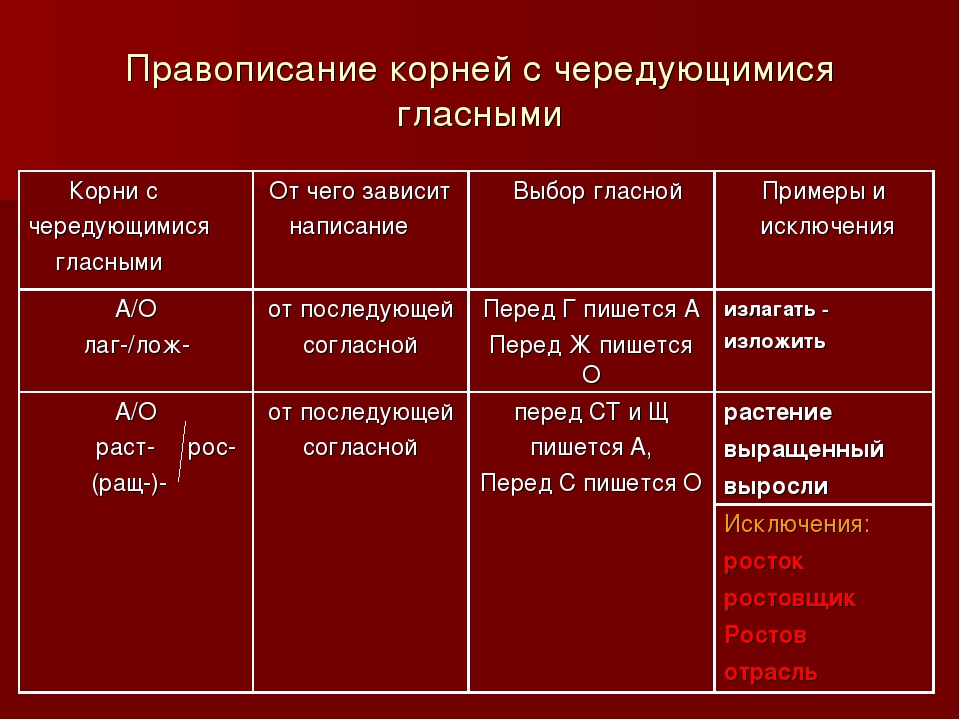
(1), показанная в уравнении 5.11, представляет собой геометрический ряд. Поскольку | r | = | −1/2 | <1, | r | = | −1/2 | <1, ряд сходится. Ряд (2), показанный в уравнении 5.12, называется серией переменных гармоник. Мы покажем, что в то время как гармонический ряд расходится, знакопеременный гармонический ряд сходится.
Чтобы доказать это, рассмотрим последовательность частичных сумм {Sk} {Sk} (рис. 5.17).
Проба
Рассмотрим нечетные члены S2k + 1S2k + 1 для k≥0.k≥0. Поскольку 1 / (2k + 1) <1 / 2k, 1 / (2k + 1) <1 / 2k,
S2k + 1 = S2k − 1−12k + 12k + 1 Следовательно, {S2k + 1} {S2k + 1} ограничено снизу. Поскольку {S2k + 1} {S2k + 1} — убывающая ограниченная снизу последовательность, по теореме о монотонной сходимости {S2k + 1} {S2k + 1} сходится. Точно так же четные члены {S2k} {S2k} образуют возрастающую последовательность, ограниченную сверху, поскольку
Точно так же четные члены {S2k} {S2k} образуют возрастающую последовательность, ограниченную сверху, поскольку
и
S2k = 1 + (- 12 + 13) + ⋯ + (- 12k − 2 + 12k − 1) −12k <1.S2k = 1 + (- 12 + 13) + ⋯ + (- 12k − 2 + 12k − 1) −12k <1.Следовательно, по теореме о монотонной сходимости последовательность {S2k} {S2k} также сходится. С
г. S2k + 1 = S2k + 12k + 1, S2k + 1 = S2k + 12k + 1,мы знаем, что
limk → ∞S2k + 1 = limk → ∞S2k + limk → ∞12k + 1.limk → ∞S2k + 1 = limk → ∞S2k + limk → ∞12k + 1. Полагая S = limk → ∞S2k + 1S = limk → ∞S2k + 1 и используя тот факт, что 1 / (2k + 1) → 0,1 / (2k + 1) → 0, заключаем, что limk → ∞S2k = S.limk → ∞S2k = S. Поскольку нечетные и четные члены в последовательности частичных сумм сходятся к одному и тому же пределу S, S, можно показать, что последовательность частичных сумм сходится к S, S, и, следовательно, чередующийся гармонический ряд сходится к S. С.
С.
Также можно показать, что S = ln2, S = ln2, и мы можем написать
∑n = 1∞ (−1) n + 1n = 1−12 + 13−14 + ⋯ = ln (2). N = 1∞ (−1) n + 1n = 1−12 + 13−14 + ⋯ = ln (2). Рис. 5.17. Для переменного гармонического ряда нечетные члены S2k + 1S2k + 1 в последовательности частичных сумм убывают и ограничены снизу. Четные члены S2kS2k возрастают и ограничены сверху.□
В более общем смысле, любой чередующийся ряд вида (3) (уравнение 5.13) или (4) (уравнение 5.14) сходится, пока b1≥b2≥b3≥ ⋯ b1≥b2≥b3≥ ⋯ и bn → 0bn → 0 (рисунок 5.18). Доказательство аналогично доказательству для знакопеременного гармонического ряда.
Рисунок 5.18 Для знакопеременного ряда b1 − b2 + b3− ⋯ b1 − b2 + b3− ⋯, в котором b1> b2> b3> ⋯, b1> b2> b3> ⋯, нечетные члены S2k + 1S2k + 1 в последовательности частичные суммы убывают и ограничены снизу. Четные члены S2kS2k возрастают и ограничены сверху.Теорема 5.13
Испытание чередующейся серии
Чередование серий формы
∑n = 1∞ (−1) n + 1bnor∑n = 1∞ (−1) nbn∑n = 1∞ (−1) n + 1bnor∑n = 1∞ (−1) nbnсходится, если
- 0≤bn + 1≤bn0≤bn + 1≤bn для всех n≥1n≥1 и
- limn → ∞bn = 0.
 limn → ∞bn = 0.
limn → ∞bn = 0.
Это известно как испытание чередующейся серии.
Заметим, что эта теорема верна в более общем смысле, пока существует некоторое целое число NN такое, что 0≤bn + 1≤bn0≤bn + 1≤bn для всех n≥N.n≥N.
Пример 5.19
Конвергенция переменных серий
Для каждого из следующих чередующихся рядов определите, сходится он или расходится.
- ∑n = 1∞ (−1) n + 1 / n2∑n = 1∞ (−1) n + 1 / n2
- ∑n = 1∞ (−1) n + 1n / (n + 1) ∑n = 1∞ (−1) n + 1n / (n + 1)
Решение
- С
1 (n + 1) 2 <1n2and1n2 → 0,1 (n + 1) 2 <1n2and1n2 → 0,
ряд сходится. - Поскольку n / (n + 1) ↛0n / (n + 1) ↛0 при n → ∞, n → ∞, мы не можем применить тест чередующейся серии. Вместо этого мы используем n -й критерий дивергенции. С
limn → ∞ (−1) n + 1nn + 1 ≠ 0, limn → ∞ (−1) n + 1nn + 1 ≠ 0,
серия расходится.
КПП 5.18
Определите, сходится или расходится ряд ∑n = 1∞ (−1) n + 1n / 2n∑n = 1∞ (−1) n + 1n / 2n.
Остаток чередующейся серии
Трудно явно вычислить сумму большинства чередующихся рядов, поэтому обычно сумма приближается с использованием частичной суммы.При этом нас интересует количество ошибок в нашем приближении. Рассмотрим чередующуюся серию
∑n = 1∞ (−1) n + 1bn∑n = 1∞ (−1) n + 1bn, удовлетворяющий гипотезам теста чередующихся серий. Обозначим через SS сумму этого ряда, а {Sk} {Sk} — соответствующую последовательность частичных сумм. Из рисунка 5.18 видно, что для любого целого числа N≥1, N≥1 остаток RNRN удовлетворяет
| RN | = | S-SN | ≤ | SN + 1-SN | = bn + 1. | RN | = | S-SN | ≤ | SN + 1-SN | = bn + 1.Теорема 5.14
Остатки в чередующемся ряду
Рассмотрим чередующийся ряд вида
∑n = 1∞ (−1) n + 1bnor∑n = 1∞ (−1) nbn∑n = 1∞ (−1) n + 1bnor∑n = 1∞ (−1) nbn, который удовлетворяет гипотезам теста чередующихся серий.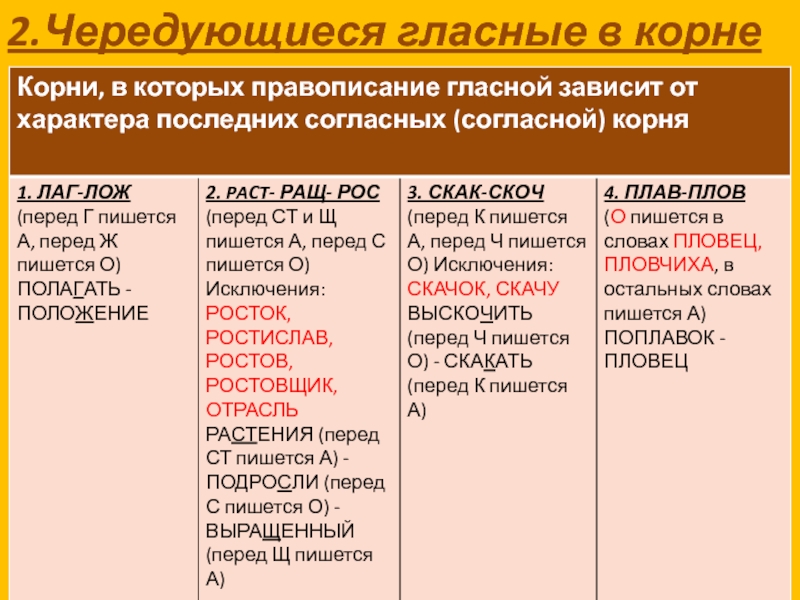 Пусть SS обозначает сумму ряда, а SNSN обозначает N-ю частичную сумму. Для любого целого числа N≥1, N≥1 остаток RN = S − SNRN = S − SN удовлетворяет условию
Пусть SS обозначает сумму ряда, а SNSN обозначает N-ю частичную сумму. Для любого целого числа N≥1, N≥1 остаток RN = S − SNRN = S − SN удовлетворяет условию
Другими словами, если выполняются условия теста чередующихся серий, то ошибка аппроксимации бесконечного ряда N-йN-й частичной суммой SNSN по величине не превосходит размер следующего члена bN + 1.bN + 1.
Пример 5.20
Оценка остатка чередующейся серии
Рассмотрим чередующуюся серию
∑n = 1∞ (−1) n + 1n2.∑n = 1∞ (−1) n + 1n2.Используйте оценку остатка, чтобы определить границу ошибки R10R10, если мы аппроксимируем сумму ряда частичной суммой S10.S10.
Решение
Из приведенной выше теоремы
| R10 | ≤b11 = 1112≈0,008265. | R10 | ≤b11 = 1112≈0,008265.
КПП 5.19
Найдите оценку для R20R20, аппроксимируя ∑n = 1∞ (−1) n + 1 / n∑n = 1∞ (−1) n + 1 / n с помощью S20.S20.
Абсолютная и условная сходимость
Рассмотрим ряд ∑n = 1∞an∑n = 1∞an и связанный с ним ряд ∑n = 1∞ | an |. ∑n = 1∞ | an |. Здесь мы обсуждаем возможности взаимосвязи между сходимостью этих двух рядов. Например, рассмотрим переменный гармонический ряд ∑n = 1∞ (−1) n + 1 / n.n = 1∞ (−1) n + 1 / n. Ряд, члены которого являются модулями этих членов, является гармоническим рядом, поскольку ∑n = 1∞ | (−1) n + 1 / n | = ∑n = 1∞1 / n.∑n = 1∞ | ( −1) n + 1 / n | = ∑n = 1∞1 / n. Поскольку чередующийся гармонический ряд сходится, но гармонический ряд расходится, мы говорим, что чередующийся гармонический ряд демонстрирует условную сходимость.
∑n = 1∞ | an |. Здесь мы обсуждаем возможности взаимосвязи между сходимостью этих двух рядов. Например, рассмотрим переменный гармонический ряд ∑n = 1∞ (−1) n + 1 / n.n = 1∞ (−1) n + 1 / n. Ряд, члены которого являются модулями этих членов, является гармоническим рядом, поскольку ∑n = 1∞ | (−1) n + 1 / n | = ∑n = 1∞1 / n.∑n = 1∞ | ( −1) n + 1 / n | = ∑n = 1∞1 / n. Поскольку чередующийся гармонический ряд сходится, но гармонический ряд расходится, мы говорим, что чередующийся гармонический ряд демонстрирует условную сходимость.
Для сравнения рассмотрим ряд ∑n = 1∞ (−1) n + 1 / n2.∑n = 1∞ (−1) n + 1 / n2. Ряд, члены которого являются модулями членов этого ряда, есть ряд ∑n = 1∞1 / n2.∑n = 1∞1 / n2. Поскольку оба этих ряда сходятся, мы говорим, что ряд ∑n = 1∞ (−1) n + 1 / n2∑n = 1∞ (−1) n + 1 / n2 демонстрирует абсолютную сходимость.
Определение
Ряд ∑n = 1∞an∑n = 1∞an демонстрирует абсолютную сходимость, если ∑n = 1∞ | an | ∑n = 1∞ | an | сходится. Ряд ∑n = 1∞an∑n = 1∞an демонстрирует условную сходимость, если ∑n = 1∞an∑n = 1∞an сходится, но ∑n = 1∞ | an | ∑n = 1∞ | an | расходится.
Ряд ∑n = 1∞an∑n = 1∞an демонстрирует условную сходимость, если ∑n = 1∞an∑n = 1∞an сходится, но ∑n = 1∞ | an | ∑n = 1∞ | an | расходится.
Как показывает чередующийся гармонический ряд, ряд ∑n = 1∞an∑n = 1∞an может сходиться, но ∑n = 1∞ | an | ∑n = 1∞ | an | могут расходиться.Однако в следующей теореме мы покажем, что если ∑n = 1∞ | an | ∑n = 1∞ | an | сходится, то n = 1∞an∑n = 1∞an сходится.
Теорема 5.15
Абсолютная сходимость влечет сходимость
Если ∑n = 1∞ | an | ∑n = 1∞ | an | сходится, то ∑n = 1∞an∑n = 1∞an сходится.
Проба
Предположим, что ∑n = 1∞ | an | ∑n = 1∞ | an | сходится. Мы покажем это, используя тот факт, что an = | an | an = | an | или an = — | an | an = — | an | и поэтому | an | + an = 2 | an || an | + an = 2 | an | или | an | + an = 0. | an | + an = 0. Следовательно, 0≤ | an | + an≤2 | an |.0≤ | an | + an≤2 | an |. Следовательно, при проверке сравнения, поскольку 2∑n = 1∞ | an | 2∑n = 1∞ | an | сходится, серия
∑n = 1∞ (| an | + an) ∑n = 1∞ (| an | + an) сходится. Используя алгебраические свойства сходящихся рядов, заключаем, что
Используя алгебраические свойства сходящихся рядов, заключаем, что
сходится.
□
Пример 5.21
Абсолютная и условная сходимость
Для каждого из следующих рядов определите, сходится ли ряд абсолютно, сходится условно или расходится.
- ∑n = 1∞ (−1) n + 1 / (3n + 1) ∑n = 1∞ (−1) n + 1 / (3n + 1)
- ∑n = 1∞cos (n) / n2∑n = 1∞cos (n) / n2
Решение
- Мы видим, что
∑n = 1∞ | (−1) n + 13n + 1 | = ∑n = 1∞13n + 1∑n = 1∞ | (−1) n + 13n + 1 | = ∑n = 1∞13n + 1
расходится при использовании теста сравнения пределов с гармоническим рядом. Фактически
limn → ∞1 / (3n + 1) 1 / n = 13. limn → ∞1 / (3n + 1) 1 / n = 13.
Следовательно, ряд не сходится абсолютно. Однако с
13 (n + 1) +1 <13n + 1 и 13n + 1 → 0,13 (n + 1) +1 <13n + 1 и 13n + 1 → 0,
ряд сходится. Можно заключить, что ∑n = 1∞ (−1) n + 1 / (3n + 1) ∑n = 1∞ (−1) n + 1 / (3n + 1) условно сходится.
Можно заключить, что ∑n = 1∞ (−1) n + 1 / (3n + 1) ∑n = 1∞ (−1) n + 1 / (3n + 1) условно сходится. - Отметив, что | cosn | ≤1, | cosn | ≤1, чтобы определить, сходится ли ряд абсолютно, сравните
∑n = 1∞ | cosnn2 | ∑n = 1∞ | cosnn2 |
с рядом ∑n = 1∞1 / n2.n = 1∞1 / n2. Поскольку ∑n = 1∞1 / n2∑n = 1∞1 / n2 сходится, по результатам сравнения ∑n = 1∞ | cosn / n2 | ∑n = 1∞ | cosn / n2 | сходится, поэтому ∑n = 1∞cosn / n2∑n = 1∞cosn / n2 сходится абсолютно.
КПП 5.20
Определите, сходится ли ряд ∑n = 1∞ (−1) n + 1n / (2n3 + 1) ∑n = 1∞ (−1) n + 1n / (2n3 + 1) абсолютно, сходится ли условно или расходится.
Чтобы увидеть разницу между абсолютной и условной сходимостью, посмотрите, что происходит, когда мы, , переставляем члены чередующегося гармонического ряда ∑n = 1∞ (−1) n + 1 / n. (n = 1∞ (−1 ) п + 1 / п. Мы показываем, что мы можем переставить члены так, чтобы новый ряд расходился. Конечно, если мы переставим члены конечной суммы, сумма не изменится. Однако, когда мы работаем с бесконечной суммой, могут происходить интересные вещи.
Однако, когда мы работаем с бесконечной суммой, могут происходить интересные вещи.
Начните с добавления достаточного количества положительных членов, чтобы получить сумму, превышающую некоторое действительное число M> 0.М> 0. Например, пусть M = 10, M = 10, и найдите такое целое число kk, что
1 + 13 + 15 + ⋯ + 12k − 1> 10,1 + 13 + 15 + ⋯ + 12k − 1> 10.(Мы можем это сделать, потому что ряд ∑n = 1∞1 / (2n − 1) ∑n = 1∞1 / (2n − 1) расходится до бесконечности.) Затем вычтем 1 / 2,1 / 2. Затем добавляйте больше положительных членов, пока сумма не достигнет 100. То есть найдите другое целое число j> kj> k такое, что
1 + 13 + ⋯ + 12k − 1−12 + 12k + 1 + ⋯ + 12j + 1> 100,1 + 13 + ⋯ + 12k − 1−12 + 12k + 1 + ⋯ + 12j + 1> 100. Затем вычтите 1 / 4,1 / 4. Продолжая таким образом, мы нашли способ переупорядочить слагаемые в чередующемся гармоническом ряду так, чтобы последовательность частичных сумм для переставленного ряда была неограниченной и, следовательно, расходилась.
Члены в чередующемся гармоническом ряду также можно переставить так, чтобы новый ряд сходился к другому значению. В примере 5.22 мы показываем, как переставить члены, чтобы создать новый ряд, сходящийся к 3ln (2) /2.3ln (2) / 2. Отметим, что чередующиеся гармонические ряды можно переставить, чтобы создать ряд, сходящийся к любому действительному числу r; r; однако доказательство этого факта выходит за рамки этого текста.
В общем, любой ряд ∑n = 1∞an∑n = 1∞an, который условно сходится, можно переупорядочить так, чтобы новый ряд расходился или сходился к другому действительному числу.Сходящийся ряд абсолютно не обладает этим свойством. Для любого абсолютно сходящегося ряда ∑n = 1∞an∑n = 1∞an значение ∑n = 1∞an∑n = 1∞an одинаково при любой перестановке слагаемых. Этот результат известен как теорема Римана о перестановке, что выходит за рамки этой книги.
Пример 5.22
Перестановка серии
Используйте тот факт, что
1−12 + 13−14 + 15− ⋯ = ln21−12 + 13−14 + 15− ⋯ = ln2, чтобы переставить члены в чередующемся гармоническом ряду так, чтобы сумма преобразованного ряда была 3ln (2) / 2. 3лн (2) / 2.
3лн (2) / 2.
Решение
Let
∑n = 1∞an = 1−12 + 13−14 + 15−16 + 17−18 + ⋯ .∑n = 1∞an = 1−12 + 13−14 + 15−16 + 17−18 + ⋯.Поскольку ∑n = 1∞an = ln (2), ∑n = 1∞an = ln (2), в силу алгебраических свойств сходящихся рядов,
∑n = 1∞12an = 12−14 + 16−18 + ⋯ = 12∑n = 1∞an = ln22.∑n = 1∞12an = 12−14 + 16−18 + ⋯ = 12∑n = 1∞ an = ln22.Теперь введем ряд ∑n = 1∞bn∑n = 1∞bn такой, что для всех n≥1, n≥1, b2n − 1 = 0b2n − 1 = 0 и b2n = an / 2.b2n = an / 2 . Тогда
∑n = 1∞bn = 0 + 12 + 0−14 + 0 + 16 + 0−18 + ⋯ = ln22.∑n = 1∞bn = 0 + 12 + 0−14 + 0 + 16 + 0−18 + ⋯ = ln22.Тогда, используя алгебраические предельные свойства сходящихся рядов, поскольку ∑n = 1∞an∑n = 1∞an и ∑n = 1∞bn∑n = 1∞bn сходятся, ряд ∑n = 1∞ (an + bn ) ∑n = 1∞ (an + bn) сходится и
∑n = 1∞ (an + bn) = ∑n = 1∞an + ∑n = 1∞bn = ln2 + ln22 = 3ln22.∑n = 1∞ (an + bn) = ∑n = 1∞an + ∑n = 1∞bn = ln2 + ln22 = 3ln22.Теперь, сложив соответствующие члены, anan и bn, bn, мы видим, что
∑n = 1∞ (an + bn) = (1 + 0) + (- 12 + 12) + (13 + 0) + (- 14−14) + (15 + 0) + (- 16 + 16) + (17 + 0) + (18−18) + ⋯ = 1 + 13−12 + 15 + 17−14 + ⋯ . ∑n = 1∞ (an + bn) = (1 + 0) + (- 12 + 12 ) + (13 + 0) + (- 14−14) + (15 + 0) + (- 16 + 16) + (17 + 0) + (18−18) + ⋯ = 1 + 13−12 + 15 + 17−14 + ⋯.
∑n = 1∞ (an + bn) = (1 + 0) + (- 12 + 12 ) + (13 + 0) + (- 14−14) + (15 + 0) + (- 16 + 16) + (17 + 0) + (18−18) + ⋯ = 1 + 13−12 + 15 + 17−14 + ⋯.Мы замечаем, что ряд справа от знака равенства представляет собой перестановку переменного гармонического ряда. Поскольку ∑n = 1∞ (an + bn) = 3ln (2) / 2, ∑n = 1∞ (an + bn) = 3ln (2) / 2, заключаем, что
1 + 13−12 + 15 + 17−14 + ⋯ = 3ln (2) 2,1 + 13−12 + 15 + 17−14 + ⋯ = 3ln (2) 2.Таким образом, мы нашли перестановку переменного гармонического ряда, обладающую желаемым свойством.
Раздел 5.5 Упражнения
Укажите, сходится ли каждый из следующих рядов абсолютно, условно или нет вообще.
250.∑n = 1∞ (−1) n + 1nn + 3∑n = 1∞ (−1) n + 1nn + 3
251.∑n = 1∞ (−1) n + 1n + 1n + 3∑n = 1∞ (−1) n + 1n + 1n + 3
252.∑n = 1∞ (−1) n + 11n + 3∑n = 1∞ (−1) n + 11n + 3
253.∑n = 1∞ (−1) n + 1n + 3n∑n = 1∞ (−1) n + 1n + 3n
254.∑n знак равно 1∞ (−1) N + 11n! ∑n = 1∞ (−1) N + 11n!
255.
∑n знак равно 1∞ (−1) n + 13nn! ∑n = 1∞ (−1) n + 13nn!
256.∑n = 1∞ (−1) n + 1 (n − 1n) n∑n = 1∞ (−1) n + 1 (n − 1n) n
257.∑n = 1∞ (−1) n + 1 (n + 1n) n∑n = 1∞ (−1) n + 1 (n + 1n) n
258.∑n = 1∞ (−1) n + 1sin2n∑n = 1∞ (−1) n + 1sin2n
259.∑n = 1∞ (−1) n + 1cos2n∑n = 1∞ (−1) n + 1cos2n
260.∑n = 1∞ (−1) n + 1sin2 (1 / n) ∑n = 1∞ (−1) n + 1sin2 (1 / n)
261.∑n = 1∞ (−1) n + 1cos2 (1 / n) ∑n = 1∞ (−1) n + 1cos2 (1 / n)
262.∑n = 1∞ (−1) n + 1ln (1 / n) ∑n = 1∞ (−1) n + 1ln (1 / n)
263.∑n = 1∞ (−1) n + 1ln (1 + 1n) ∑n = 1∞ (−1) n + 1ln (1 + 1n)
264.∑n = 1∞ (−1) n + 1n21 + n4∑n = 1∞ (−1) n + 1n21 + n4
265.∑n = 1∞ (−1) n + 1ne1 + nπ∑n = 1∞ (−1) n + 1ne1 + nπ
266.∑n = 1∞ (−1) n + 121 / n∑n = 1∞ (−1) n + 121 / n
267.∑n = 1∞ (−1) n + 1n1 / n∑n = 1∞ (−1) n + 1n1 / n
268. ∑n = 1∞ (−1) n (1 − n1 / n) ∑n = 1∞ (−1) n (1 − n1 / n) ( Подсказка: n1 / n≈1 + ln (n) / nn1 / n≈1 + ln (n) / n для больших n. ) n.)
) n.)
∑n = 1∞ (−1) n + 1n (1 − cos (1n)) ∑n = 1∞ (−1) n + 1n (1 − cos (1n)) ( Подсказка: cos (1 / n) ≈1−1 / n2cos (1 / n) ≈1−1 / n2 для больших n.) n.)
270.∑n = 1∞ (−1) n + 1 (n + 1 − n) ∑n = 1∞ (−1) n + 1 (n + 1 − n) ( Подсказка: Рационализируйте числитель.)
271.∑n = 1∞ (−1) n + 1 (1n − 1n + 1) ∑n = 1∞ (−1) n + 1 (1n − 1n + 1) ( Подсказка: Найдите общий знаменатель, затем рационализируйте числитель .)
272.∑n = 1∞ (−1) n + 1 (ln (n + 1) −lnn) ∑n = 1∞ (−1) n + 1 (ln (n + 1) −lnn)
273.∑n = 1∞ (−1) n + 1n (tan − 1 (n + 1) −tan − 1n) ∑n = 1∞ (−1) n + 1n (tan − 1 (n + 1) −tan −1n) ( Подсказка: Используйте теорему о среднем значении.)
274.∑n = 1∞ (−1) n + 1 ((n + 1) 2 − n2) ∑n = 1∞ (−1) n + 1 ((n + 1) 2 − n2)
275.∑n = 1∞ (−1) n + 1 (1n − 1n + 1) ∑n = 1∞ (−1) n + 1 (1n − 1n + 1)
276.
∑n = 1∞cos (nπ) n∑n = 1∞cos (nπ) n
277.∑n = 1∞cos (nπ) n1 / n∑n = 1∞cos (nπ) n1 / n
278.∑n = 1∞1nsin (nπ2) ∑n = 1∞1nsin (nπ2)
279.∑n = 1∞sin (nπ / 2) sin (1 / n) ∑n = 1∞sin (nπ / 2) sin (1 / n)
В каждой из следующих задач используйте оценку | RN | ≤bN + 1 | RN | ≤bN + 1, чтобы найти значение NN, которое гарантирует, что сумма первых NN членов переменного ряда ∑n = 1∞ (−1) n + 1bn∑n = 1∞ (−1) n + 1bn отличается от бесконечной суммы не более чем на данную ошибку. Рассчитайте частичную сумму SNSN для этого N.N.
280.[T] bn = 1 / n, bn = 1 / n, погрешность <10-5 <10-5
281.[T] bn = 1 / ln (n), bn = 1 / ln (n), n≥2, n≥2, ошибка <10−1 <10−1
282.[T] bn = 1 / n, bn = 1 / n, погрешность <10-3 <10-3
283.[T] bn = 1 / 2n, bn = 1 / 2n, ошибка <10-6 <10-6
284.
[T] bn = ln (1 + 1n), bn = ln (1 + 1n), ошибка <10−3 <10−3
285.[T] bn = 1 / n2, bn = 1 / n2, ошибка <10-6 <10-6
Для следующих упражнений укажите, является ли каждое из следующих утверждений истинным или ложным. Если утверждение неверно, приведите пример, в котором оно неверно.
286.Если bn≥0bn≥0 убывает и limn → ∞bn = 0, limn → ∞bn = 0, то ∑n = 1∞ (b2n − 1 − b2n) ∑n = 1∞ (b2n − 1 − b2n) сходится абсолютно.
287.Если bn≥0bn≥0 убывает, то ∑n = 1∞ (b2n − 1 − b2n) ∑n = 1∞ (b2n − 1 − b2n) сходится абсолютно.
288.Если bn≥0bn≥0 и limn → ∞bn = 0limn → ∞bn = 0, то ∑n = 1∞ (12 (b3n − 2 + b3n − 1) −b3n) ∑n = 1∞ (12 (b3n − 2 + b3n − 1) −b3n) сходится.
289.Если bn≥0bn≥0 убывает и ∑n = 1∞ (b3n − 2 + b3n − 1 − b3n) ∑n = 1∞ (b3n − 2 + b3n − 1 − b3n) сходится, то ∑n = 1∞b3n −2∑n = 1∞b3n − 2 сходится.
290. Если bn≥0bn≥0 убывает и ∑n = 1∞ (−1) n − 1bn∑n = 1∞ (−1) n − 1bn сходится условно, но не абсолютно, то bnbn не стремится к нулю.
Пусть an + = anan + = an, если an≥0an≥0, и an — = — anan — = — an, если an <0.an <0. (Также an + = 0ifan <0an + = 0ifan <0 и an− = 0ifan≥0.) An− = 0ifan≥0.) Если ∑n = 1∞an∑n = 1∞an сходится условно, но не абсолютно, то ни ∑n = 1∞an + ∑n = 1∞an + и ∑n = 1∞an − ∑n = 1∞an− сходятся.
292.Предположим, что anan — это последовательность положительных действительных чисел и что ∑n = 1∞an∑n = 1∞an сходится.
Предположим, что bnbn — произвольная последовательность единиц и минус единиц. Обязательно ли сходится ∑n = 1∞anbn∑n = 1∞anbn?
293.Предположим, что anan — это последовательность, такая что ∑n = 1∞anbn∑n = 1∞anbn сходится для любой возможной последовательности bnbn нулей и единиц. Сходится ли ∑n = 1∞an∑n = 1∞ абсолютно?
Следующая серия не удовлетворяет гипотезе испытания чередующейся серии, как указано.
В каждом случае укажите, какая гипотеза не выполняется. Укажите, сходится ли серия абсолютно.
294.∑n = 1∞ (−1) n + 1sin2nn∑n = 1∞ (−1) n + 1sin2nn
295.
∑n = 1∞ (−1) n + 1cos2nn∑n = 1∞ (−1) n + 1cos2nn
296.1 + 12-13-14 + 15 + 16-17-18 + 1 + 12-13-14 + 15 + 16-17-18 + ⋯
297.1 + 12-13 + 14 + 15-16 + 17 + 18-19 + ⋯ 1 + 12-13 + 14 + 15-16 + 17 + 18-19 + ⋯
298.Покажите, что чередующийся ряд 1−12 + 12−14 + 13−16 + 14−18 + ⋯ 1−12 + 12−14 + 13−16 + 14−18 + ⋯ делает
не сходятся. Какая гипотеза теста чередующихся серий не выполняется?
299.Предположим, что an∑an абсолютно сходится.Покажите, что ряд, состоящий из положительных членов anan, также сходится.
300.Покажите, что знакопеременный ряд 23−35 + 47−59 + ⋯ 23−35 + 47−59 + ⋯ не сходится. Какая гипотеза теста чередующихся серий не выполняется?
301. Формула cosθ = 1 − θ22! + Θ44! −θ66! + ⋯ cosθ = 1 − θ22! + Θ44! −θ66! + ⋯ будет выведена в следующей главе. Используйте остаток | RN | ≤bN + 1 | RN | ≤bN + 1, чтобы найти границу ошибки оценки cosθcosθ с помощью пятой частичной суммы 1 − θ2 / 2! + Θ4 / 4! −θ6 / 6! + Θ8 / 8! 1 − θ2 / 2! + Θ4 / 4! −θ6 / 6! + Θ8 / 8! для θ = 1, θ = 1, θ = π / 6, θ = π / 6 и θ = π. θ = π.
θ = π.
Формула sinθ = θ − θ33! + Θ55! −θ77! + ⋯ sinθ = θ − θ33! + Θ55! −θ77! + ⋯ будет выведена в следующей главе. Используйте остаток | RN | ≤bN + 1 | RN | ≤bN + 1, чтобы найти оценку ошибки в оценке sinθsinθ с помощью пятой частичной суммы θ − θ3 / 3! + Θ5 / 5! −θ7 / 7! + Θ9 / 9! Θ − θ3 / 3! + Θ5 / 5! −θ7 / 7! + Θ9 / 9! для θ = 1, θ = 1, θ = π / 6, θ = π / 6 и θ = π.θ = π.
303.Сколько членов в cosθ = 1 − θ22! + Θ44! −θ66! + ⋯ cosθ = 1 − θ22! + Θ44! −θ66! + ⋯ необходимо для аппроксимации cos1cos1 с точностью не более 0,00001? 0,00001?
304.Сколько членов в sinθ = θ − θ33! + Θ55! −θ77! + ⋯ sinθ = θ − θ33! + Θ55! −θ77! + ⋯ необходимо для аппроксимации sin1sin1 с точностью не более 0,00001? 0,00001?
305. Иногда знакопеременный ряд ∑n = 1∞ (−1) n − 1bn∑n = 1∞ (−1) n − 1bn сходится к некоторой доле абсолютно сходящегося ряда ∑n = 1∞bn∑n = 1∞ млрд. руб. более быстрыми темпами. Учитывая, что ∑n = 1∞1n2 = π26, ∑n = 1∞1n2 = π26, находим 12 = 1−122 + 132−142 + ⋯ . 12 = 1−122 + 132−142 + ⋯. Какой из рядов 6∑n = 1∞1n26∑n = 1∞1n2 и S∑n = 1∞ (−1) n − 1n2S∑n = 1∞ (−1) n − 1n2 дает лучшую оценку π2π2 с использованием 10001000 терминов?
12 = 1−122 + 132−142 + ⋯. Какой из рядов 6∑n = 1∞1n26∑n = 1∞1n2 и S∑n = 1∞ (−1) n − 1n2S∑n = 1∞ (−1) n − 1n2 дает лучшую оценку π2π2 с использованием 10001000 терминов?
Следующие чередующиеся ряды сходятся к заданным кратным π.π. Найдите значение NN, предсказанное оценкой остатка, такое, что N-я N-я частичная сумма ряда точно аппроксимирует левую часть с точностью до заданной ошибки. Найдите минимальный NN, для которого выполняется граница ошибки, и дайте желаемое приблизительное значение в каждом случае. До 1515 знаков после запятой, π = 3,1415
[T] π4 = ∑n = 0∞ (−1) n2n + 1, π4 = ∑n = 0∞ (−1) n2n + 1, ошибка <0,0001 <0,0001
307.[T] π12 = ∑k = 0∞ (−3) −k2k + 1, π12 = ∑k = 0∞ (−3) −k2k + 1, ошибка <0.0001 <0,0001
308. [T] Ряд ∑n = 0∞sin (x + πn) x + πn∑n = 0∞sin (x + πn) x + πn играет важную роль в обработке сигналов. Докажите, что ∑n = 0∞sin (x + πn) x + πn∑n = 0∞sin (x + πn) x + πn сходится всякий раз, когда 0
Докажите, что ∑n = 0∞sin (x + πn) x + πn∑n = 0∞sin (x + πn) x + πn сходится всякий раз, когда 0
[T] Если ∑n = 1N (−1) n − 11n → ln2, ∑n = 1N (−1) n − 11n → ln2, то что равно 1 + 13 + 15−12−14−16 + 17 + 19 + 111−18−110−112 + ⋯? 1 + 13 + 15−12−14−16 + 17 + 19 + 111−18−110−112 + ⋯?
310.[T] Постройте ряд ∑n = 1100cos (2πnx) n∑n = 1100cos (2πnx) n для 0≤x <1.0≤x <1. Объясните, почему ∑n = 1100cos (2πnx) n∑n = 1100cos (2πnx) n расходится при x = 0,1.x = 0,1. Как ведет себя серия для других x? X?
311.[T] Постройте ряд ∑n = 1100sin (2πnx) n∑n = 1100sin (2πnx) n для 0≤x <10≤x <1 и прокомментируйте его поведение
312. [T] Постройте ряд ∑n = 1100cos (2πnx) n2∑n = 1100cos (2πnx) n2 для 0≤x <10≤x <1 и опишите его график.
[T] Переменный гармонический ряд сходится из-за сокращения его членов.Его сумма известна, поскольку отмену можно описать явно. Случайный гармонический ряд имеет вид ∑n = 1∞Snn, ∑n = 1∞Snn, где snsn — это случайно сгенерированная последовательность ± единиц ± 1, в которой значения ± 1 ± 1 имеют равную вероятность появления. Используйте генератор случайных чисел для получения 10001000 случайных ± 1 с ± 1 с и нанесите на график частичные суммы SN = ∑n = 1NsnnSN = ∑n = 1Nsnn вашей случайной гармонической последовательности для N = 1N = от 1 до 1000,1000. Сравните с графиком первых 1000–1000 частичных сумм гармонического ряда.
314. [T] Оценки ∑n = 1∞1n2∑n = 1∞1n2 можно ускорить , записав его частичные суммы как ∑n = 1N1n2 = ∑n = 1N1n (n + 1) + ∑n = 1N1n2 (n + 1) ∑n = 1N1n2 = ∑n = 1N1n (n + 1) + ∑n = 1N1n2 (n + 1) и вспоминая, что ∑n = 1N1n (n + 1) = 1−1N + 1∑n = 1N1n (n + 1) = 1−1N + 1 сходится к единице при N → ∞. N → ∞. Сравните оценку π2 / 6π2 / 6 с использованием суммы ∑n = 110001n2∑n = 110001n2 с оценкой с использованием 1 + ∑n = 110001n2 (n + 1) .1 + ∑n = 110001n2 (n + 1).
N → ∞. Сравните оценку π2 / 6π2 / 6 с использованием суммы ∑n = 110001n2∑n = 110001n2 с оценкой с использованием 1 + ∑n = 110001n2 (n + 1) .1 + ∑n = 110001n2 (n + 1).
[T] Преобразование Эйлера переписывает S = ∑n = 0∞ (−1) nbnS = ∑n = 0∞ (−1) nbn как S = ∑n = 0∞ (−1) n2 − n −1∑m = 0n (нм) bn − m.S = ∑n = 0∞ (−1) n2 − n − 1∑m = 0n (нм) bn − m. Для знакопеременного гармонического ряда он принимает вид ln (2) = ∑n = 1∞ (−1) n − 1n = ∑n = 1∞1n2n.ln (2) = ∑n = 1∞ (−1) n −1n = ∑n = 1∞1n2n. Вычислите частичные суммы ∑n = 1∞1n2n∑n = 1∞1n2n, пока они не приблизятся к ln (2) ln (2) с точностью до 0,0001,0,0001. Сколько нужно терминов? Сравните этот ответ с количеством членов переменного гармонического ряда, необходимых для оценки ln (2) .ln (2).
316. [T] В тексте было сказано, что условно сходящийся ряд может быть преобразован так, чтобы сходиться к любому числу. Вот немного более простой, но похожий факт. Если an≥0an≥0 таково, что an → 0an → 0 при n → ∞n → ∞, но ∑n = 1∞an∑n = 1∞an расходится, то для любого числа AA существует последовательность snsn из ± 1 ± 1 такие, что ∑n = 1∞ansn → A.∑n = 1∞ansn → A. Покажем это для A> 0A> 0 следующим образом.
Вот немного более простой, но похожий факт. Если an≥0an≥0 таково, что an → 0an → 0 при n → ∞n → ∞, но ∑n = 1∞an∑n = 1∞an расходится, то для любого числа AA существует последовательность snsn из ± 1 ± 1 такие, что ∑n = 1∞ansn → A.∑n = 1∞ansn → A. Покажем это для A> 0A> 0 следующим образом.
- Рекурсивно определить snsn как sn = 1sn = 1, если Sn − 1 = ∑k = 1n − 1aksk
- Объясните, почему в конечном итоге Sn≥A, Sn≥A и для любого мм больше этого n, n, A − am≤Sm≤A + am.A − am≤Sm≤A + am.
- Объясните, почему из этого следует, что Sn → ASn → A при n → ∞.п → ∞.
— Исчисление, том 2
Цели обучения
- Используйте тест чередующихся серий для проверки сходимости чередующихся серий.
- Оценить сумму переменного ряда.
- Объясните значение абсолютной и условной конвергенции.
До сих пор в этой главе мы в основном обсуждали ряды с положительными терминами. В этом разделе мы вводим чередующиеся серии — те серии, члены которых чередуются по знаку.В следующей главе мы покажем, что эти ряды часто возникают при изучении степенных рядов. После определения чередующихся серий мы вводим тест чередующихся серий, чтобы определить, сходится ли такой ряд.
В этом разделе мы вводим чередующиеся серии — те серии, члены которых чередуются по знаку.В следующей главе мы покажем, что эти ряды часто возникают при изучении степенных рядов. После определения чередующихся серий мы вводим тест чередующихся серий, чтобы определить, сходится ли такой ряд.
Испытание чередующейся серии
Ряд, члены которого чередуют положительные и отрицательные значения, является чередующимся рядом. Например, серия
и
— это чередующиеся серии.
Определение
Любая серия, члены которой чередуются между положительными и отрицательными значениями, называется чередующейся серией.Переменный ряд можно записать в виде
или
Где для всех натуральных чисел n .
Серия (1), показанная на (Рисунок), представляет собой геометрическую серию. Поскольку ряд сходится. Ряд (2), изображенный на (рис.), Называется переменным гармоническим рядом. Мы покажем, что в то время как гармонический ряд расходится, знакопеременный гармонический ряд сходится.
Чтобы доказать это, мы рассмотрим последовательность частичных сумм ((рисунок)).
Проба
Рассмотрим странные термины для С
Следовательно, это убывающая последовательность.Также
Следовательно, ограничено снизу. Поскольку — ограниченная снизу убывающая последовательность, по теореме о монотонной сходимости сходится. Точно так же четные члены образуют возрастающую последовательность, ограниченную сверху, потому что
и
Следовательно, по теореме о монотонной сходимости последовательность также сходится. С
г.мы знаем, что
Допуская и используя тот факт, что мы заключаем, что Поскольку нечетные члены и четные члены в последовательности частичных сумм сходятся к одному и тому же пределу, можно показать, что последовательность частичных сумм сходится к, и, следовательно, чередующийся гармонический ряд сходится к
Также можно показать, что и мы можем написать
Для переменного гармонического ряда нечетные члены в последовательности частичных сумм убывают и ограничены снизу. Четные члены возрастают и ограничены сверху.
Четные члены возрастают и ограничены сверху.□
В более общем смысле, любой чередующийся ряд формы (3) ((Рисунок)) или (4) ((Рисунок)) сходится до тех пор, пока и ((Рисунок)). Доказательство аналогично доказательству для знакопеременного гармонического ряда.
Испытание чередующейся серии
Переменный ряд формы
сходится, если
- для всех и
Это известно как испытание чередующейся серии.
Заметим, что эта теорема верна в более общем смысле, пока существует такое целое число, что для всех
Определите, сходится ли ряд или расходится.
Подсказка
Уменьшается? Что такое
Абсолютная и условная сходимость
Рассмотрим ряд и связанный ряд Здесь мы обсуждаем возможности взаимосвязи между сходимостью этих двух рядов. Например, рассмотрим чередующийся гармонический ряд. Ряд, члены которого являются абсолютными значениями этих членов, является гармоническим рядом, поскольку поскольку чередующийся гармонический ряд сходится, но гармонический ряд расходится, мы говорим, что чередующийся гармонический ряд демонстрирует условную сходимость.
Для сравнения рассмотрим ряд. Ряд, члены которого являются абсолютными значениями членов этого ряда, и есть ряд. Поскольку оба ряда сходятся, мы говорим, что ряд демонстрирует абсолютную сходимость.
Как показывает чередующийся гармонический ряд, ряд может сходиться, но может расходиться. Однако в следующей теореме мы показываем, что если сходится, то сходится.
Абсолютная конвергенция подразумевает конвергенцию
Если сходится, значит сходится.
Проба
Предположим, что сходится. Мы показываем это, используя тот факт, что или, следовательно, или Следовательно, следовательно, с помощью сравнительного теста, поскольку сходится, ряд
сходится. Используя алгебраические свойства сходящихся рядов, заключаем, что
сходится.
□
Абсолютная и условная сходимость
Для каждого из следующих рядов определите, сходится ли ряд абсолютно, сходится условно или расходится.
Определите, сходится ли ряд абсолютно, сходится условно или расходится.
Серия абсолютно сходится.
Подсказка
Сначала проверьте абсолютную сходимость.
Чтобы увидеть разницу между абсолютной и условной сходимостью, посмотрите, что происходит, когда мы переставляем члены чередующегося гармонического ряда. Мы показываем, что мы можем переставить члены так, чтобы новый ряд расходился.Конечно, если мы переставим члены конечной суммы, сумма не изменится. Однако, когда мы работаем с бесконечной суммой, могут происходить интересные вещи.
Начните с добавления достаточного количества положительных членов, чтобы получить сумму, превышающую некоторое действительное число. Например, позвольте и найти такое целое число, что
(Мы можем это сделать, потому что ряд расходится до бесконечности.) Затем вычтите Затем добавьте больше положительных членов, пока сумма не достигнет 100. То есть найдите другое целое число, такое, что
Затем вычесть Продолжая таким образом, мы нашли способ переупорядочить члены в чередующемся гармоническом ряду так, чтобы последовательность частичных сумм для переставленного ряда была неограниченной и, следовательно, расходилась.
Члены в чередующемся гармоническом ряду также можно переставить так, чтобы новый ряд сходился к другому значению. На (Рисунок) мы показываем, как переставить термины, чтобы создать новый ряд, который сходится к. Мы указываем, что чередующийся гармонический ряд может быть перегруппирован для создания ряда, сходящегося к любому действительному числу, однако доказательство этого факта невозможно объем этого текста.
В общем, любой ряд, который условно сходится, можно переупорядочить так, чтобы новый ряд расходился или сходился к другому действительному числу.Сходящийся ряд абсолютно не обладает этим свойством. Для любого ряда, который абсолютно сходится, значение одинаково при любой перестановке членов. Этот результат известен как теорема Римана о перестановке, что выходит за рамки этой книги.
Перестановка серии
Используйте тот факт, что
, чтобы переставить члены в чередующемся гармоническом ряду так, чтобы сумма преобразованного ряда была
Ключевые уравнения
- Переменная серия
Укажите, сходится ли каждый из следующих рядов абсолютно, условно или нет.
Не сходится при тестировании расхождения. Сроки не стремятся к нулю.
Условно сходится при проверке чередующихся серий, так как убывает. Совершенно не сходится по сравнению с р -серия
Абсолютно сходится по сравнению с лимитом к примеру.
Расхождения по результатам теста расхождения с
г.Не сходится.Сроки не стремятся к нулю.
Расхождения по тесту дивергенции.
Сходится при испытании чередующихся серий.
Условно сходится при испытании чередующихся серий. Абсолютно не сходится по предельному сравнению с р -серия,
Diverges; сроки не стремятся к нулю.
Сходится при испытании чередующихся серий. Абсолютно не сходится по предельному сравнению с гармоническими рядами.
Абсолютно не сходится по предельному сравнению с гармоническими рядами.
( Подсказка: Рационализируйте числитель.)
( Подсказка: Найдите общий знаменатель, затем рационализируйте числитель.)
Абсолютно сходится по сравнению с серией p после применения подсказки.
( Подсказка: Используйте теорему о среднем значении.)
Сходится при проверке чередующихся серий, так как при больших значениях уменьшается до нуля. Абсолютно не сходится при сравнении предельных значений с гармоническими рядами после применения подсказки.
сходится абсолютно, т.к. являются членами телескопической серии.
Термины не стремятся к нулю. Серия расходится по тесту дивергенции.
Сходится при испытании чередующихся серий. Абсолютно не сходится по предельному сравнению с гармоническими рядами.
Абсолютно не сходится по предельному сравнению с гармоническими рядами.
В каждой из следующих задач используйте оценку, чтобы найти значение, которое гарантирует, что сумма первых членов чередующегося ряда отличается от бесконечной суммы не более чем на заданную ошибку.Рассчитайте частичную сумму для этого
[T] ошибка
[T] ошибка
[T] ошибка
[T] ошибка
[T] ошибка
Для следующих упражнений укажите, является ли каждое из следующих утверждений истинным или ложным. Если утверждение неверно, приведите пример, в котором оно неверно.
Если убывает, а затем сходится абсолютно.
Если убывает и сходится условно, но не абсолютно, то не стремится к нулю.
Верно. Если одно сходится, то и другое должно сходиться, что подразумевает абсолютное схождение.
Предположим, что это сходящаяся последовательность положительных действительных чисел.
Предположим, что это произвольная последовательность единиц и минус единиц. Обязательно сходится?
Предположим, что это такая последовательность, которая сходится для всех возможных последовательностей нулей и единиц.Сходится абсолютно?
Следующая серия не удовлетворяет гипотезе испытания чередующейся серии, как указано.
В каждом случае укажите, какая гипотеза не выполняется. Укажите, сходится ли серия абсолютно.
Не уменьшается. Не сходится абсолютно.
Не чередуется. Может быть выражено как что расходится по сравнению с
Показать, что чередующийся ряд соответствует
не сходятся.Какая гипотеза теста чередующихся серий не выполняется?
Предположим, что абсолютно сходится. Покажите, что ряд, состоящий из положительных членов, также сходится.
Показать, что чередующиеся ряды не сходятся. Какая гипотеза теста чередующихся серий не выполняется?
Сколько членов необходимо для приблизительного вычисления с погрешностью не более
Сколько членов необходимо для приблизительного вычисления с погрешностью не более
Следующие чередующиеся ряды сходятся к заданным кратным значениям Найти значение, предсказанное оценкой остатка, так что частичная сумма ряда точно аппроксимирует левую часть с точностью до заданной ошибки.Найдите минимум, для которого сохраняется граница ошибки, и дайте желаемое приблизительное значение в каждом случае. С точностью до десятичных знаков,
[T] ошибка
[T] Серия играет важную роль в обработке сигналов. Показать, что сходится всякий раз, когда ( Подсказка: Используйте формулу для синуса суммы углов.)
[T] Если что такое
Частичная сумма такая же, как и для переменного гармонического ряда.
[T] Постройте ряд для и опишите его график.
Вот типичный результат. Верхняя кривая состоит из частичных сумм гармонического ряда. Нижняя кривая отображает частичные суммы случайного гармонического ряда.
Квадрат, куб, квадратный корень и кубический корень
Калькулятор квадрата, куба, квадратного корня и кубического корня
Квадрат, куб, квадратный корень и кубический корень для чисел с диапазоном 0-100
| Число x | Квадрат x 2 | Куб x 3 | Квадратный корень x 1/2 | Кубический корень x 1/3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 908 1.000 | 1.000 | |||||||
| 2 | 4 | 8 | 1.414 | 1.260 | ||||||
| 3 | 9 | 27 | 1,732 | 2. 000 000 | 1,587 | |||||
| 5 | 25 | 125 | 2,236 | 1,710 | ||||||
| 6 | 36 | 216 | 2.449 | 1,817 | ||||||
| 7 | 49 | 343 | 2,646 | 1,913 | ||||||
| 8 | 64 | 512 | 2,828 | 8 | 3.000 | 2.080 | ||||
| 10 | 100 | 1000 | 3.162 | 2.154 | ||||||
| 11 | 121 | 1331 | 3.317 | 2,224 | ||||||
| 12 | 144 | 1728 | 3,464 | 2,289 | ||||||
| 13 | 169 | 2197 | 3,608 9036 | 2197 | 3,608 903 | 3,742 | 2,410 | |||
| 15 | 225 | 3375 | 3,873 | 2,466 | ||||||
| 16 | 256 | 4096 | 4.000 | 2,520 | ||||||
| 17 | 289 | 4913 | 4,123 | 2,571 | ||||||
| 18 | 324 | 5832 | 4,243 198368 | 9036 | 4,243 2,621 | 4,359 | 2,668 | |||
| 20 | 400 | 8000 | 4,472 | 2,714 | ||||||
| 21 | 441 | 9261 | 4. 583 583 | 2,759 | ||||||
| 22 | 484 | 10648 | 4,690 | 2,802 | ||||||
| 23 | 529 | 12167 | 835529 | 12167 | 8358359 | 12167 | 8358 903 | 8358 | 4,899 | 2,884 |
| 25 | 625 | 15625 | 5.000 | 2,924 | ||||||
| 26 | 676 | 17576 | 099 | 2,962 | ||||||
| 27 | 729 | 19683 | 5,196 | 3,000 | ||||||
| 28 | 784 | 21952 | 8 3,0 | 5,385 | 3,072 | |||||
| 30 | 900 | 27000 | 5,477 | 3,107 | ||||||
| 31 | 961 | 29791 | 5.568 | 3,141 | ||||||
| 32 | 1024 | 32768 | 5,657 | 3,175 | ||||||
| 33 | 1089 | 35937 | 8358358 9036 903 | 5,831 | 3,240 | |||||
| 35 | 1225 | 42875 | 5,916 | 3,271 | ||||||
| 36 | 1296 | 46656 | 000 | 3,302 | ||||||
| 37 | 1369 | 50653 | 6,083 | 3,332 | ||||||
| 38 | 1444 | 54872 | 8 6,13562 9036 | 54872 | 8 6,13562 9036 9036 | 6,245 | 3,391 | |||
| 40 | 1600 | 64000 | 6,325 | 3,420 | ||||||
| 41 | 1681 | 68921 | 6. 403 403 | 3,448 | ||||||
| 42 | 1764 | 74088 | 6,481 | 3,476 | ||||||
| 43 | 1849 | 79507 | 8 6,5578 9036 903 | 6,633 | 3,530 | |||||
| 45 | 2025 | 6,708 | 3,557 | |||||||
| 46 | 2116 | 97336 6.782 | 3,583 | |||||||
| 47 | 2209 | 103823 | 6,856 | 3,609 | ||||||
| 48 | 2304 | 110592 | 8 9036 117 9036 903 | 7.000 | 3.659 | |||||
| 50 | 2500 | 125000 | 7.071 | 3.684 | ||||||
| 51 | 2601 | 132651 | 141 | 3,708 | ||||||
| 52 | 2704 | 140608 | 7,211 | 3,733 | ||||||
| 53 | 2809 | 148877 | 2809 | 148877 | 2809 | 148877 | 8358 9036 | 8 9036 906 | 7,348 | 3,780 |
| 55 | 3025 | 166375 | 7,416 | 3,803 | ||||||
| 56 | 3136 | 175616 | 483 | 3,826 | ||||||
| 57 | 3249 | 185193 | 7,550 | 3,849 | ||||||
| 58 | 3364 | 195112 | 8 | 8 903 8358 903 | 7,681 | 3,893 | ||||
| 60 | 3600 | 216000 | 7,746 | 3,915 | ||||||
| 61 | 3721 | 226981 7 | 810 3. 936 936 | |||||||
| 62 | 3844 | 238328 | 7.874 | 3.958 | ||||||
| 63 | 3969 | 250047 | 8 9036 | 8 9036 909 | 8.000 | 4.000 | ||||
| 65 | 4225 | 274625 | 8.062 | 4.021 | ||||||
| 66 | 4356 | 287496 8.124 | 4,041 | |||||||
| 67 | 4489 | 300763 | 8,185 | 4,062 | ||||||
| 68 | 4624 | 314432 | 8 8,2358 | 314432 | 8 8,246 | 8,307 | 4,102 | |||
| 70 | 4900 | 343000 | 8,367 | 4,121 | ||||||
| 71 | 5041 | 357911 | 426 | 4,141 | ||||||
| 72 | 5184 | 373248 | 8,485 | 4,160 | ||||||
| 73 | 5329 | 389017 | 8358 9036 | 8 9036 | 8 903 836 908 | 8,602 | 4,198 | |||
| 75 | 5625 | 421875 | 8,660 | 4,217 | ||||||
| 76 | 5776 | 4389735 8. 718 718 | 4,236 | |||||||
| 77 | 5929 | 456533 | 8,775 | 4,254 | ||||||
| 78 | 6084 | 474552 | 8358 9036 9036 | 8,8328 903 | 8,888 | 4,291 | ||||
| 80 | 6400 | 512000 | 8,944 | 4,309 | ||||||
| 81 | 6561 | 531441 9.000 | 4,327 | |||||||
| 82 | 6724 | 551368 | 9,055 | 4,344 | ||||||
| 83 | 6889 | 571787 | 8358358 9036 9062 | 9,110 9036 | 9,165 | 4,380 | ||||
| 85 | 7225 | 614125 | 9,220 | 4,397 | ||||||
| 86 | 7396 | 63603556 | 2739,434 | 4,465 | ||||||
| 90 | 8100 | 729000 | 9,487 | 4,481 | ||||||
| 91 | 8281 | 753571 93571 | 5394,498 | |||||||
| 92 | 8464 | 778688 | 9,592 | 4,514 | ||||||
| 93 | 8649 | 804357 | 8 9036 | 8 | 9,695 | 4,547 | ||||
| 95 | 9025 | 857375 | 9,747 | 4,563 | ||||||
| 96 | 9216 | 884736 9,836 | 798 | 4,579 | ||||||
| 97 | 9409 | 3 | 9,849 | 4,595 | ||||||
| 98 | 9604 | 941192 | 8 | 9. 950 950 | 4.626 | |||||
| 100 | 10000 | 1000000 | 10.000 | 4,642 |
Загрузите и распечатайте квадрат, куб, квадратный корень
и кубический корень
. 3D-модельИспользуйте расширение Engineering ToolBox Sketchup — для добавления кубических линий в модели Sketchup.
Упражнения: чередующиеся серии — Ximera
Упражнения, относящиеся к чередующимся рядам и абсолютной или условной сходимости.
Для бесконечного ряда функция is не положительный, а isis нет уменьшение когда. Кроме того, это не стремятся к нулю как. Тест чередующейся серии не применять и подразумевает конвергенциюпредполагает расхождения ничего не говорит о ряд . Для бесконечного ряда функция is не положительный, а isis нет уменьшение когда.Кроме того, это не стремятся к нулю как. Тест чередующейся серии не применять и подразумевает конвергенциюпредполагает расхождения ничего не говорит о ряд . Для бесконечного ряда функция is не
положительный, а isis нет
уменьшение когда. Кроме того, это не
стремятся к нулю как. Тест чередующейся серии не
применять и подразумевает конвергенциюпредполагает расхождения ничего не говорит о
ряд
. Для бесконечного ряда функция is не
положительный, а isis нет
уменьшение когда.Кроме того, это не
стремятся к нулю как. Тест чередующейся серии не
применять и подразумевает конвергенциюпредполагает расхождения ничего не говорит о
ряд
. Для бесконечного ряда функция is не
положительный, а isis нет
уменьшение когда. Кроме того, это не
стремятся к нулю как. Тест чередующейся серии не
применять и подразумевает конвергенциюпредполагает расхождения ничего не говорит о
ряд
.Сначала определите, чередуются ли серии. Применяется ли к серии испытание чередующейся серии?
Для бесконечного ряда функция is не
положительный, а isis нет
уменьшение когда. Кроме того, это не
стремятся к нулю как. Тест чередующейся серии не
применять и подразумевает конвергенциюпредполагает расхождения ничего не говорит о
ряд
. Для бесконечного ряда функция is не
положительный, а isis нет
уменьшение когда.Кроме того, это не
стремятся к нулю как. Тест чередующейся серии не
применять и подразумевает конвергенциюпредполагает расхождения ничего не говорит о
ряд
. Для бесконечного ряда функция is не
положительный, а isis нет
уменьшение когда. Кроме того, это не
стремятся к нулю как. Тест чередующейся серии не
применять и подразумевает конвергенциюпредполагает расхождения ничего не говорит о
ряд
.Сначала определите, чередуются ли серии. Применяется ли к серии испытание чередующейся серии?Да Нет, это не так чередование Нет, слагаемые не уменьшаются Нет, слагаемые не уходят в ноль
Если да, то при каком минимальном значении вы можете быть уверены, что оно отличается от сумма ряда не более чем на? Если таковых нет, напишите N / A. Если
применяется тест чередующейся серии, нам потребуется величина (т. е. абсолютная
значение) первого члена , не включенного в частичную сумму , не более
.Найдите отрезок длины, содержащий сумму бесконечного ряда Частичное
суммы переменного ряда также чередуются выше и ниже суммы ряда
сам.
Если
применяется тест чередующейся серии, нам потребуется величина (т. е. абсолютная
значение) первого члена , не включенного в частичную сумму , не более
.Найдите отрезок длины, содержащий сумму бесконечного ряда Частичное
суммы переменного ряда также чередуются выше и ниже суммы ряда
сам.Примеры вопросов викторины
Для каждого ряда ниже определите, сходится ли он абсолютно (A), сходится ли условно (C), либо расходится (D). Покажите, как вы использовали тесты сходимости для приду к вашему ответу.
I: C, II: D, III: D I: C, II: A, III: C I: A, II: C, III: A I: D, II: C, III: D I: C, II: D, III: C I: C, II: A, III: A
I: сходится условно.Значение альтернатив. Члены уменьшаются до нуля, поэтому ряд сходится по критерию знакопеременности. Сериал не совсем сходится, потому что -серия с расходится.II: сходится абсолютно. Ряд абсолютно сходится при прямом сравнении с -серия с.
III: сходится условно. Ряд сходится по критерию знакопеременного ряда.
потому что уменьшается до as и чередуется по значению между и.Однако для всех
большой, поэтому при прямом сравнении с гармоническим рядом этот ряд не совсем
сходящийся. Поэтому сходимость условна.
Ряд сходится по критерию знакопеременного ряда.
потому что уменьшается до as и чередуется по значению между и.Однако для всех
большой, поэтому при прямом сравнении с гармоническим рядом этот ряд не совсем
сходящийся. Поэтому сходимость условна.
Для каждого ряда ниже определите, сходится ли он абсолютно (A), сходится ли условно (C), либо расходится (D). Покажите, как вы использовали тесты сходимости для приду к вашему ответу.
I: D, II: D, III: D I: D, II: A, III: C I: C, II: C, III: A I: A, II: C, III: D I: D, II: D, III: C I: D, II: A, III: A
Я: расходится.Ряд расходится потому, что это означает, что члены не стремятся к нулю. Тест дивергенции -го члена подразумевает дивергенцию.II: расходится. Сериал расходится потому (потому что). По предельному сравнению по теореме, это означает, что серия имеет то же поведение, что и-серия с, что означает он расходится.
III: сходится условно. Ряд сходится, потому что это сумма
два сходящихся ряда: один с членами (который является сходящимся рядом
чередующийся тест серии, потому что уменьшается до нуля) и второй с членами (которые
является сходящейся-серией). Однако ряд не совсем сходится,
потому что для, который является суммой расходящихся -серий с и абсолютно
сходящиеся чередующиеся -серии с. Таким образом, ряд условно сходится.
Однако ряд не совсем сходится,
потому что для, который является суммой расходящихся -серий с и абсолютно
сходящиеся чередующиеся -серии с. Таким образом, ряд условно сходится.
Какой из следующих интервалов содержит значение бесконечного ряда
Функция положительна и уменьшается до нуля, поэтому с помощью теста чередующихся серий мы знайте, что частичные суммы чередуются выше и ниже фактического значения суммы. В в частности, если мы называем значение суммы, то и так далее.Последние два неравенства вместе подразумевают, что принадлежит интервалу.
Образцы вопросов к экзамену
Определите, сходятся ли следующие ряды абсолютно (A), сходятся ли условно (C), или расходятся (D). Для полного доверия не забудьте объяснить свои доводы и укажите, какие тесты использовались.
оба A один A, другой C один A, другой D оба C один C, другой D оба D
Альтернативное капельное орошение с частичной корневой зоной улучшает эффективность использования воды и азота сладко-восковой кукурузы с азотным фертигацией

Ран, М. Ю. Текущая ситуация и меры противодействия эксплуатации и использованию региональных водных ресурсов в Китае. J. Sichuan Normal Univ. (Естественные науки) 24 , 416–419 (2015).
Google Scholar
Кан, С. З. На пути к водной и продовольственной безопасности в Китае. Подбородок. J. Eco – Agric. 22 , 880–885 (2014).
Google Scholar
Кан, С. З., Чжан, Дж. Х., Лян, З. С., Ху, X. Т. и Цай, Х. Дж. Управляемое альтернативное орошение — новый подход к регулированию экономии воды на сельскохозяйственных угодьях. Agric. Res. Засушливые районы. 15 , 1–6 (1997).
Google Scholar
Кан, С. З. и Чжан, Дж. Х. Контролируемое альтернативное частичное орошение корневых зон: его физиологические последствия и влияние на эффективность использования воды. J. Exp. Бот. 55 , 2437–2446 (2004).
J. Exp. Бот. 55 , 2437–2446 (2004).
CAS Статья PubMed Google Scholar
Зорица, Дж., Радмила, С., Биляна, В. и Прабхака, М. Частичная сушка корневой зоны увеличивает содержание WUE, азота и антиоксидантов в полевом картофеле. евро. J. Agron. 33 , 124–131 (2010).
Артикул Google Scholar
Сонг, Л. и др. . Влияние альтернативного полива с частичной корневой зоной на рост, урожайность и эффективность использования воды персика. Подбородок. J. Appl. Эко. 19 , 1631–1636 (2008).
Google Scholar
Ду, Т. С., Кан, С. З., Чжан, Дж. Х. и Ли, Ф. С. Реакция водопользования и урожайности хлопка на альтернативное частичное капельное орошение корневой зоны в засушливых районах северо-западного Китая. Ирриг. Sci. 26 , 147–159 (2008).
Ирриг. Sci. 26 , 147–159 (2008).
Артикул Google Scholar
Ли, Ф. С., Лян, Дж. Х., Кан, С. З. и Чжан, Дж. Х. Преимущества альтернативного частичного орошения корневой зоны на рост, эффективность использования воды и азота, измененную удобрением и водным статусом почвы для кукурузы. Почва растений. 295 , 279–291 (2007).
CAS Статья Google Scholar
Хуанг, G.Q. Исследование характеристик развития и устойчивости индустрии химических удобрений в Китае. Пекин: докторская диссертация в Китайском сельскохозяйственном университете. 1–2 (2014).
Йокинен, К., Сяркка, К., Няккиля, Дж. И Тахвонен, Р. Раздельное корневое фертигация увеличивает урожай огурцов как в открытых, так и в полузакрытых теплицах. Sci. Хорти. 130 , 808–814 (2011).
Артикул Google Scholar
Сингандхупе, Р. Б., Рао, Г. Г. С. Н., Патил, Н. Г. и Брахмананд, П. С. Исследования фертигации и планирование полива в системе капельного орошения посевов томатов ( Lycopersicon esculentum L.). евро. J. Agron. 19 , 327–340 (2003).
Артикул Google Scholar
Bhat, R., Sujatha, S. & Balasimha, D. Влияние капельного фертигации на урожайность ареканута ( Areca catechu L.). Agric. Управление водными ресурсами. 90 , 101–111 (2007).
Артикул Google Scholar
Choi, ST, Kang, SM, Park, DS, Hong, KP & Rho, CW Комбинированное влияние соотношения листьев / плодов и уровней фертигации N и K на рост и распределение питательных веществ в выращиваемых в горшках деревьях хурмы . Sci. Хорти. 128 , 364–368 (2011).
Sci. Хорти. 128 , 364–368 (2011).
CAS Статья Google Scholar
Бай, М. Дж., Сюй, Д., Чжан, С. Х. и Ли, Ю. Характеристики пространственно-временного распределения воды и азота и оценка эффективности для бассейнового орошения с использованием обычных удобрений и методов фертигации. Agric. Управление водными ресурсами. 126 , 75–84 (2013).
Артикул Google Scholar
Кастелланос, М. Т. и др. . Азотное фертигация: комплексное агрономическое и экологическое исследование. Agric. Управление водными ресурсами. 120 , 46–55 (2012).
Артикул Google Scholar
Махаджан Дж. И Сингх К. Г. Реакция тепличных томатов на орошение и фертигацию. Agric. Управление водным хозяйством. 84 , 202–206 (2006).
84 , 202–206 (2006).
Артикул Google Scholar
Антонио, Дж. С. Н., Сержио, З. и Даниэла, К. Л. Разработка и оценка автоматизированной системы контроля фертигации при выращивании томатов без почвы. Comput. Электрон. Agric. 103 , 17–25 (2014).
Артикул Google Scholar
Лян, Х. Л., Ли, Ф. С. и Нонг, М.L. Влияние чередующегося частичного орошения корневой зоны на урожайность и водопользование сладко-восковой кукурузы при фертигации. Agric. Управление водными ресурсами. 116 , 242–247 (2013).
Артикул Google Scholar
Раджпут, Т. Б. С. и Патель, Н. Движение воды и нитратов в луке капельного орошения при фертигации и орошении. Agric. Управление водными ресурсами. 79 , 293–311 (2006).
79 , 293–311 (2006).
Артикул Google Scholar
Чжан, Х. X., Чи, Д. К., Ван, К., Цзюнь, Ф. и Фанг, X. Урожайность и качество огурца реакция на орошение и азотные удобрения при подпочвенном капельном орошении в солнечной теплице. Agric. Sci. Подбородок. 10 , 921–930 (2011).
CAS Статья Google Scholar
Ван, Ю. Ф., Цай, Х. Ю., Чжан, X. Х., Гао, Х. и Сун, X. Влияние альтернативного орошения с разделением корней на физиологические характеристики и урожайность табака дымовой сушки. Agric. Res. Засушливые районы. 24 , 93–98 (2006).
CAS Google Scholar
Нонг, М. Л., Ли, Ф. С. и Лю, С. Влияние частичного орошения корневой зоны и уровней N, K на накопление сухой массы, использование воды и питательных веществ кукурузы. Plant Nutri. Fert. Sci. 16 , 1539–1545 (2010).
Plant Nutri. Fert. Sci. 16 , 1539–1545 (2010).
CAS Google Scholar
Вэй, З. Х. и др. . Дискриминация изотопов углерода показывает более высокую эффективность использования воды при попеременном частичном орошении корневой зоны выращиваемых в поле томатов. Agric. Управление водными ресурсами. 165 , 33–43 (2016).
Артикул Google Scholar
Е., Ю. С. и др. . Чередование увлажняющего и высушивающего полива и азотных удобрений с контролируемым высвобождением для позднего риса: влияние на накопление сухого вещества, урожай, использование воды и азота. Field Crops Res. 144 , 212–224 (2013).
Артикул Google Scholar
Лю, Л. Дж. и др. . Комбинация управления азотом на конкретном участке и попеременного орошения с помощью увлажнения и сушки увеличивает урожай зерна, а также эффективность использования азота и воды в супер-рисе. Field Crops Res. 154 , 226–235 (2013).
. Комбинация управления азотом на конкретном участке и попеременного орошения с помощью увлажнения и сушки увеличивает урожай зерна, а также эффективность использования азота и воды в супер-рисе. Field Crops Res. 154 , 226–235 (2013).
Артикул Google Scholar
Du, W. B. Влияние капельного фертигации на помидоры в солнечной теплице. J. Shanxi Agric. Sci. 37 , 58–60 (2009).
CAS Google Scholar
Кабельо, М. Дж., Кастелланос, М.Т., Ромохаро, Ф., Мартинес-Мадрид, К. и Рибаса., Ф. Урожайность и качество дыни, выращенной при разном поливе и нормах азота. Agric. Управление водными ресурсами. 96 , 866–874 (2009).
Артикул Google Scholar
Hebbar, S. S., Ramachandrappa, B. K., Nanjappa, H. V. & Prabhakar, M. Исследования капельного фертигации NPK в полевых помидорах ( Lycopersicon esculentum Mill.). евро. J. Agron. 21 , 117–127 (2004).
S., Ramachandrappa, B. K., Nanjappa, H. V. & Prabhakar, M. Исследования капельного фертигации NPK в полевых помидорах ( Lycopersicon esculentum Mill.). евро. J. Agron. 21 , 117–127 (2004).
Артикул Google Scholar
Ауйла, М. С., Тинд, Х. С. и Буттар, Г. С. Урожайность фруктов и эффективность использования воды баклажанами ( Solanum melongema L.) под влиянием различных количеств азота и воды, вносимых при капельном и бороздковом орошении. Sci. Хорти. 112 , 142–148 (2007).
CAS Статья Google Scholar
Zheng, Y. M., Ding, Y. F. & Wang, Q. S. Благоприятное влияние азота перед пересадкой на распределение и эффективность использования азота в почве ризосферы риса. Sci. Agric. Грех. 40 , 314–321 (2007).
CAS Google Scholar
Цяо, Дж., Ян, Л.З., Янь, Т. М., Сюэ, Ф. и Чжао, Д. Снижение производства риса с использованием азотных удобрений в течение двух лет подряд в районе озера Тайху. Agric. Экосист. Environ. 146 , 103–112 (2012).
CAS Статья Google Scholar
Hartmann, T. E. et al. . Урожайность и эффективность использования азота в системе возделывания кукурузы и пшеницы в зависимости от различных стратегий управления удобрениями на фермерском поле Северо-Китайской равнины. Field Crops Res. 174 , 30–39 (2015).
Артикул Google Scholar
Peng, S. et al. . Стратегии преодоления низкой агрономической эффективности использования азота в орошаемых рисовых системах в Китае. Field Crops Res. 96 , 37–47 (2006).
Field Crops Res. 96 , 37–47 (2006).
ADS Статья Google Scholar
Кассман, К. Г. и др. . Возможности повышения эффективности использования азота за счет улучшенного управления ресурсами в орошаемых рисовых системах. Field Crops Res. 56 , 7–39 (1998).
Артикул Google Scholar
Rathore, V. S., Nathawat, N. S., Meel, B. & Bhardwaj, S. Культуры и нормы внесения азота влияют на урожайность и эффективность использования азота пшеницей в жарких засушливых регионах. Proc. Natl. Акад. Sci. Индия, разд. B Biol. Sci . (2016).
Ли, Ф. С., Канг, С. З., Чжан, Дж. Х. и Коэн, С. Влияние атмосферного CO 2 обогащения, состояния воды и внесенного азота на эффективность использования воды и азота пшеницей. Почва растений. 254 , 279–289 (2003).
254 , 279–289 (2003).
CAS Статья Google Scholar
Лопес – Беллидо, Р.Дж. И Лопес – Беллидо, Л. Эффективность азота в пшенице в средиземноморских условиях: влияние обработки почвы, севооборота и азотных удобрений. Field Crops Res. 71 , 31–46 (2001).
Артикул Google Scholar
Li, Y. Z., Wang, F. X. & Huang, Y. F. Эффективность использования почвенной воды и питательных веществ: сравнение нескольких определений. Подбородок. J. Почвоведение. 4 , 150–155 (2000).
Google Scholar
Кан, С. З., Ши, У. Дж., Цао, Х. Х. и Чжан, Дж. Попеременный полив в вертикальном профиле почвы повышает эффективность водопользования кукурузы ( Zea mays L.). Field Crops Res. 77 , 31–41 (2002).
Артикул Google Scholar
Чжан, Дж. Дж., Ли, Дж. С., Чжао, Б. К. и Ли, Ю.Моделирование динамики воды и азота в зависимости от стратегии капельного фертигации. J. Integre. Agric. 14 , 2434–2445 (2015).
CAS Статья Google Scholar
Helrich, K. Официальные методы анализа Ассоциации официальных химиков-аналитиков . Арлингтон: Ассоциация официальных химиков-аналитиков Inc. (1990).
11.{n-1} \ over n} = {1 \ over1} + {- 1 \ over2} + {1 \ over3} + {- 1 \ over4} + \ cdots = {1 \ over1} — {1 \ over2} + {1 \ over3} — {1 \ over4} + \ cdots. \]
В этой серии размеры термов уменьшаются, то есть \ (| a_n | \) образует убывающую последовательность, но этого не требуется в чередующейся серии. Однако, как и в случае с положительными термальными рядами, когда члены действительно имеют уменьшающийся размер, их легче анализировать, что гораздо проще, чем положительные термальные ряды.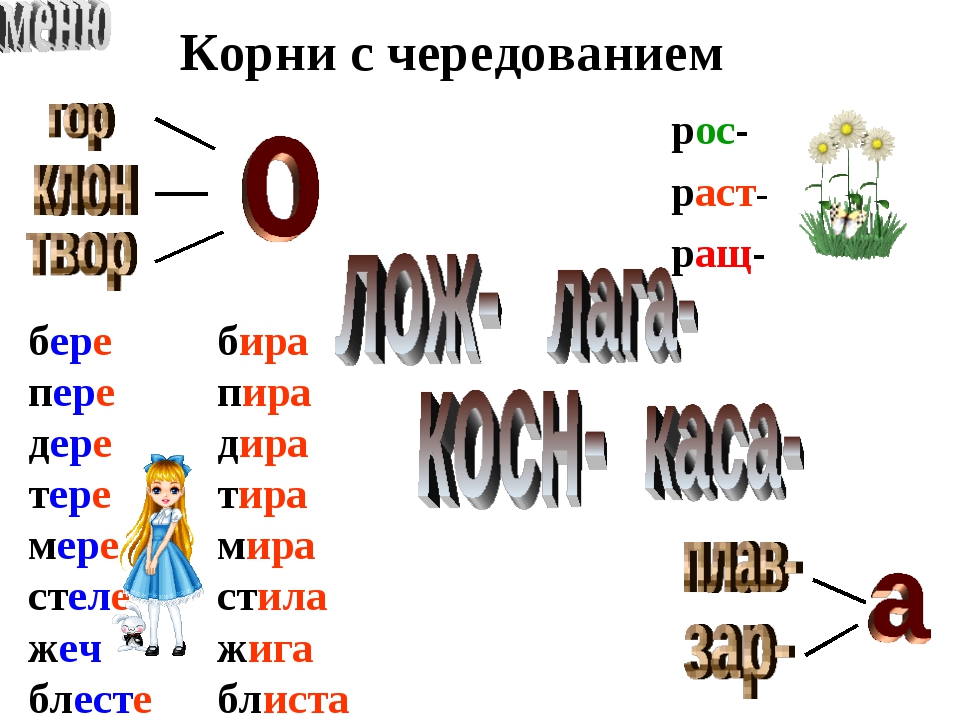 Рассмотрим наглядно, что происходит в чередующемся гармоническом ряду, показанном на рисунке 11.4.1. Поскольку размеры членов \ (a_n \) уменьшаются, частичные суммы \ (s_1 \), \ (s_3 \), \ (s_5 \) и так далее образуют убывающую последовательность, ограниченную снизу величиной \ ( s_2 \), поэтому эта последовательность должна сходиться. Точно так же частичные суммы \ (s_2 \), \ (s_4 \), \ (s_6 \) и т. Д. Образуют возрастающую последовательность, ограниченную сверху значением \ (s_1 \), поэтому эта последовательность также сходится. Поскольку все частичные суммы с четными номерами меньше, чем все суммы с нечетными номерами, и поскольку «скачки» (то есть члены \ (a_i \)) становятся все меньше и меньше, две последовательности должны сходиться к одному и тому же значению. , что означает, что вся последовательность частичных сумм \ (s_1, s_2, s_3, \ ldots \) также сходится.{n-1} a_n \) сходится.
Рассмотрим наглядно, что происходит в чередующемся гармоническом ряду, показанном на рисунке 11.4.1. Поскольку размеры членов \ (a_n \) уменьшаются, частичные суммы \ (s_1 \), \ (s_3 \), \ (s_5 \) и так далее образуют убывающую последовательность, ограниченную снизу величиной \ ( s_2 \), поэтому эта последовательность должна сходиться. Точно так же частичные суммы \ (s_2 \), \ (s_4 \), \ (s_6 \) и т. Д. Образуют возрастающую последовательность, ограниченную сверху значением \ (s_1 \), поэтому эта последовательность также сходится. Поскольку все частичные суммы с четными номерами меньше, чем все суммы с нечетными номерами, и поскольку «скачки» (то есть члены \ (a_i \)) становятся все меньше и меньше, две последовательности должны сходиться к одному и тому же значению. , что означает, что вся последовательность частичных сумм \ (s_1, s_2, s_3, \ ldots \) также сходится.{n-1} a_n \) сходится.
Проба
Нечетные пронумерованные частичные суммы, \ (s_1 \), \ (s_3 \), \ (s_5 \), и так далее, образуют невозрастающую последовательность, потому что \ (s_ {2k + 3} = s_ {2k + 1} -a_ {2k + 2} + a_ {2k + 3} \ le s_ {2k + 1} \), поскольку \ (a_ {2k + 2} \ ge a_ {2k + 3} \).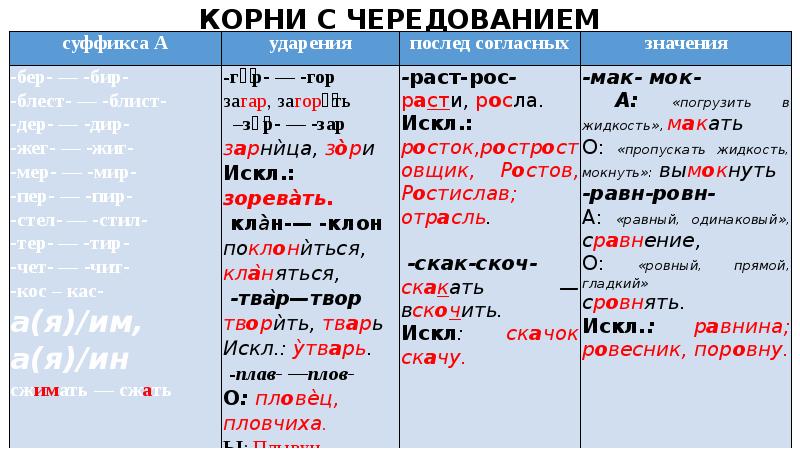 {n-1} a_n.{п-1} а_н. \) В зависимости от того, является ли \ (N \) нечетным или четным, второе будет больше или меньше первого.
{n-1} a_n.{п-1} а_н. \) В зависимости от того, является ли \ (N \) нечетным или четным, второе будет больше или меньше первого.
Пример 11.4.2
Приближают чередующиеся гармонические ряды к одному десятичному знаку.
Раствор
Нам нужно примерно перейти к точке, в которой следующий член, который нужно добавить или вычесть, будет \ (1/10 \). Сложив первые девять и первые десять членов, мы получим примерно \ (0,746 \) и \ (0,646 \). Они находятся на расстоянии \ (1/10 \) друг от друга, но неясно, как будет округлено правильное значение.п а_н \) и др.
Авторы и авторство
Хотя следующий процесс якобы предназначен для нахождения наименьших верхних и наибольших нижних интегральных границ для действительных корней полиномиальных уравнений, у него есть приятное побочное преимущество — пары последовательных целых чисел, между которыми находится действительный корень. также обнаруживаются при нахождении этих границ. По этой причине в следующих примерах я буду указывать как на границы, так и на пары целых чисел, которые «улавливают» действительные корни. также обнаруживаются при нахождении этих границ. По этой причине в следующих примерах я буду указывать как на границы, так и на пары целых чисел, которые «улавливают» действительные корни.
Общая информация: Как вы, возможно, уже догадались, поиск корней (или решений) уравнения обычно не является тривиальным процессом. В настоящий момент нас интересует поиск корней (или решений) полиномиального уравнения. Теперь многочлены являются одним из самых основных алгебраических выражений, поскольку нет экспонент, логарифмов, дробей с переменными в знаменателе или переменных под радикалами. (полином — это алгебраическое выражение, в котором показатели переменных являются целыми числами, а в знаменателе нет переменных) Однако найти решения полиномиальных уравнений непросто. Решениями полиномиальных уравнений могут быть действительные или мнимые числа. Прямо сейчас мы займемся только реальными решениями. Напомним, что если действительное число r является решением полиномиального уравнения P (x) = 0, то P (r) = 0. Обратите внимание, что мы говорим, что график касается оси x в точке x = r. Это означает, что он может либо проходить через ось, либо нет, но график будет соприкасаться с осью x. Никакие старые границы не годятся : Иногда бывает полезно найти границы действительных корней многочлена. Это означает, что мы ищем число, которое больше всех корней (верхняя граница) и число, которое меньше всех корней (нижняя граница) . На самом деле это довольно просто для многочленов, с которыми мы столкнемся в этом классе, потому что я могу просто выбрать действительно большое число, скажем 1000000, и вычислить, что ни один корень не будет больше 1 миллиона. Точно так же я могу предположить, что ни один корень не будет меньше -1000000, и, вероятно, буду прав. Но знание того, что график коснется оси x где-то в интервале (-1000000, 1000000), на самом деле не дает много полезной информации о местоположении корней.
Наименьшая верхняя граница и наилучшая нижняя граница Что действительно помогло бы, так это если бы мы могли определить МАЛЕНЬКИЙ верхнюю границу и НАИЛУЧШУЮ нижнюю границу , чтобы корни были ограничены наименьшим возможным интервалом. Если корни оказываются иррациональными, тогда не существует наименьшей верхней границы, потому что сам корень является непрерывным, неповторяющимся десятичным числом, поэтому мы не можем найти число, которое будет находиться рядом с ним на числовой строке.Итак, мы идем на компромисс и ищем верхнюю границу LEAST INTEGER (LUB) и нижнюю границу GREATEST INTEGER (GLB) , которые мы можем найти. (Напомним, что целые числа: {…..- 3, -2, -1, 0, 1, 2, 3, ….}) Чтобы помочь нам определить границы действительных корней, мы воспользуемся теоремой из вашего текста:
Мы используем эту теорему очень систематически, чтобы найти первое положительное целое число, удовлетворяющее условию оценки сверху.То есть мы пробуем 1, затем 2, затем 3 (и так далее), пока не найдем первое действующее положительное целое число. Чтобы найти нижнюю границу, мы делаем то же самое. Попробуйте -1, затем -2, затем -3 (и так далее), пока мы не найдем первое отрицательное целое число, удовлетворяющее условию нижней границы.
Вот пример: Определите верхнюю границу наименьшего интеграла и нижнюю границу наибольшего интеграла для действительных корней многочлена x 4 — 3 x 2 + x — 12 = 0 Как было сказано ранее, мы будем использовать синтетическое деление, чтобы сначала попробовать 1, затем 2 и так далее, пока не найдем FIRST POSITIVE INTEGER , который проходит проверку верхней границы.Для консолидации синтетического деления будут показаны только третьи строки каждого этапа синтетического деления Поскольку последняя строка не содержит отрицательных чисел, мы можем объявить, что 3 — это верхняя граница наименьшего целого, которую мы можем найти с помощью этой теоремы. Теперь поищем наибольшую нижнюю границу. В этом случае мы ищем FIRST NEGATIVE INTEGER , который проходит проверку верхней границы. Мы будем пробовать, -1, -2 и так далее, пока последняя строка синтетического деления не поменяется знаками.Опять же, чтобы закрепить синтетическое разделение, будут показаны только третьи строки каждого этапа синтетического разделения Поскольку в последней строке чередуются положительные и отрицательные значения, мы можем объявить, что — 3 — это наибольшая нижняя граница интеграла, которую мы можем найти с помощью этой теоремы . ПРИМЕЧАНИЕ. Не всегда верхняя и нижняя границы будут аддитивно инвертировать друг друга.
РАСПОЛОЖЕНИЕ НАСТОЯЩИХ КОРНЕЙ МЕЖДУ ПОСЛЕДУЮЩИМИ Целыми числами Мы можем почерпнуть еще одну полезную информацию из этих двух таблиц.Для этого мы обратимся к теореме о расположении.
Из таблиц видим следующее: P (0) = — 12 P (2) и P (3) имеют противоположные знаки, поэтому согласно теореме о местонахождении, уравнение P (x) = 0 имеет по крайней мере один НАСТОЯЩИЙ корень между 2 и 3.Также существует настоящий корень между -3 и — 2. Примечание: Обычно мы заинтересованы в нахождении действительных корней между последовательными целыми числами по двум причинам.
И последнее замечание: Почему мы не находим границ мнимым корням, а также реальным корням? Это потому, что у мнимых чисел нет свойства порядка, которое применяется к набору действительных чисел. Это означает, что концепция <и> не имеет значения для мнимых чисел.Было бы неплохо, если бы мы могли сказать, что все корни <НАИМЕНЕЕ ВЕРХНЕЙ ОГРАНИЧЕНИЯ (LUB), но это утверждение не имеет значения для мнимых корней. Итак, лучшее, что мы можем сказать, это то, что все НАСТОЯЩИЕ корни - это © 1999 Jo Steig |



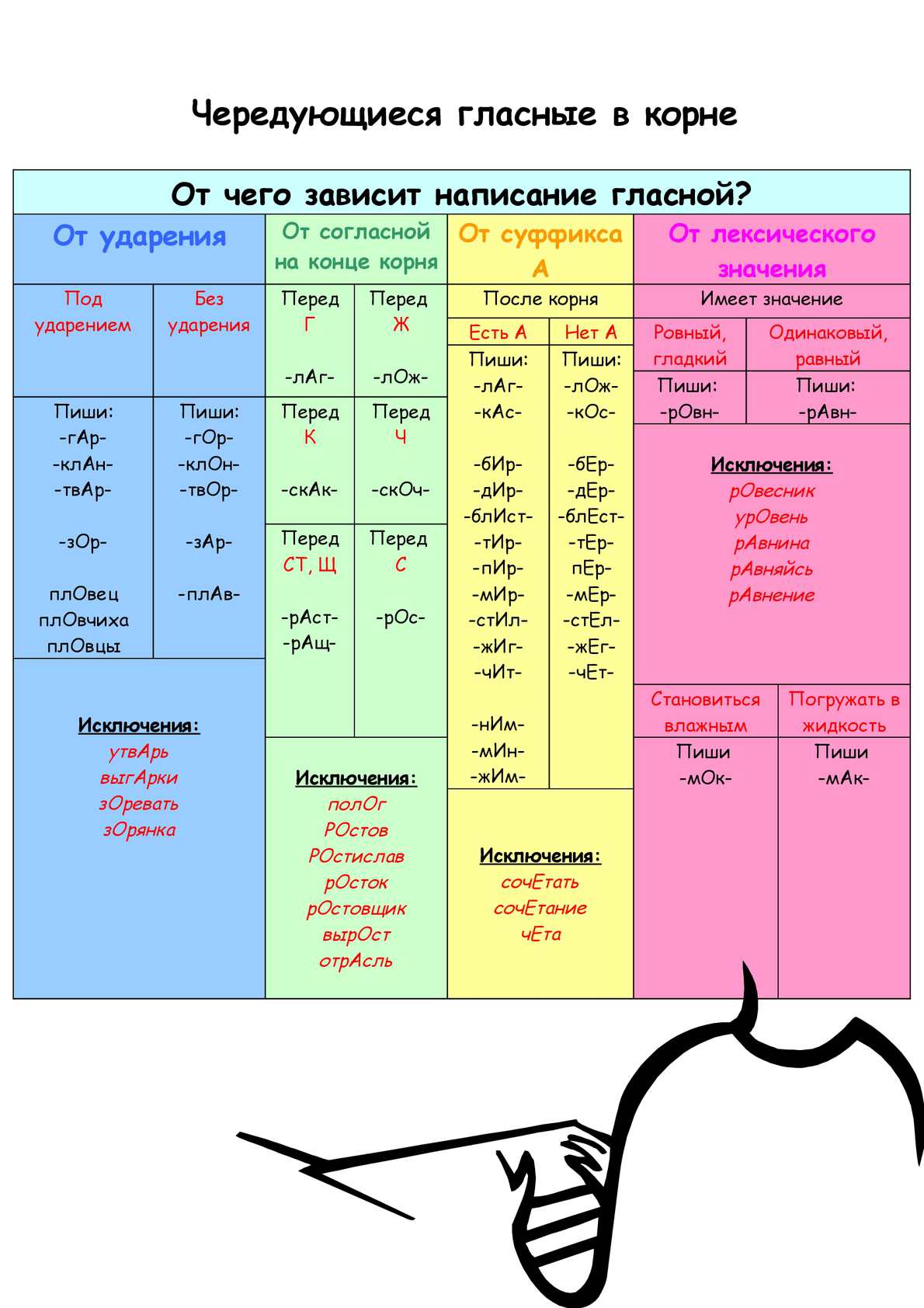




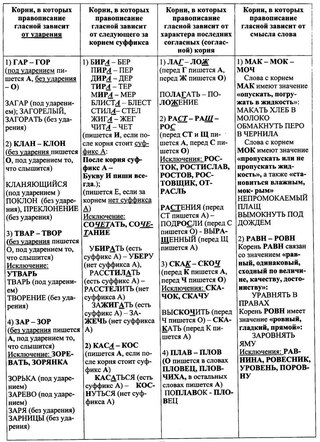

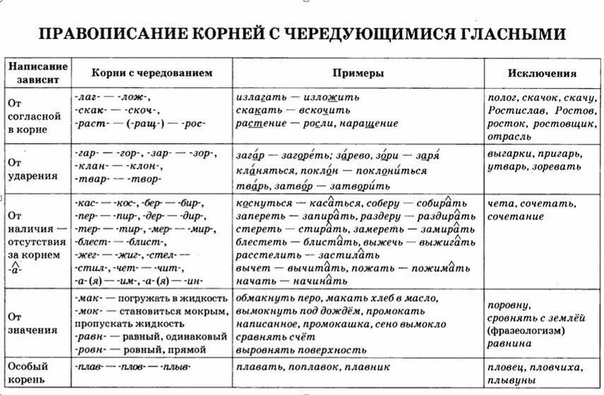 :сочетать,
сочетание,
чета
:сочетать,
сочетание,
чета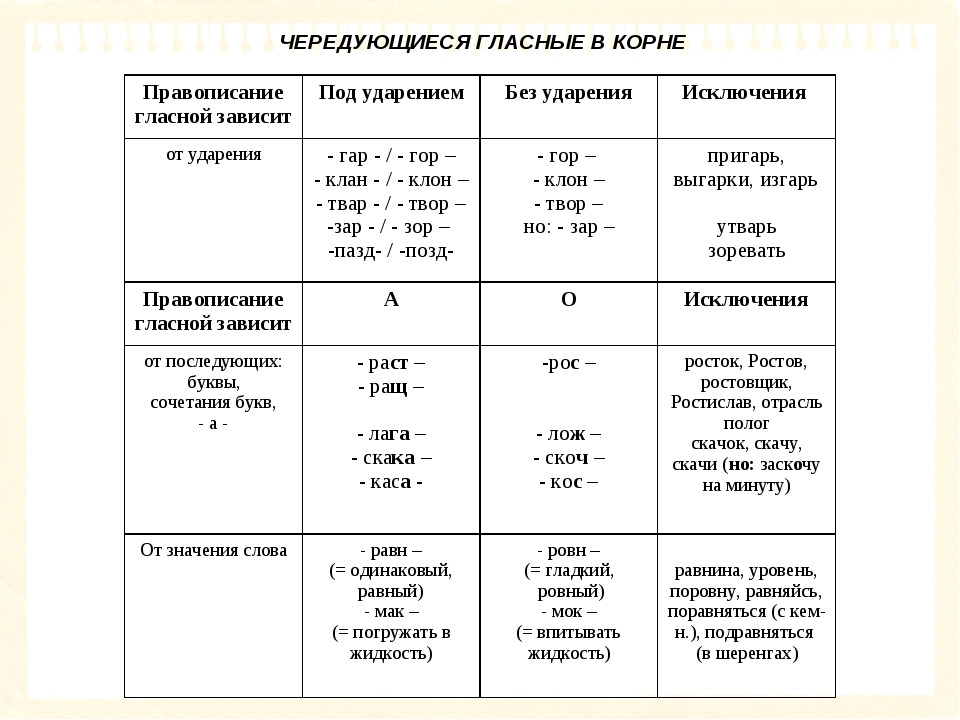 От
лексического значения.
От
лексического значения.
.jpg) 2 + x — 2 будет касаться оси x, где x = 1.
2 + x — 2 будет касаться оси x, где x = 1.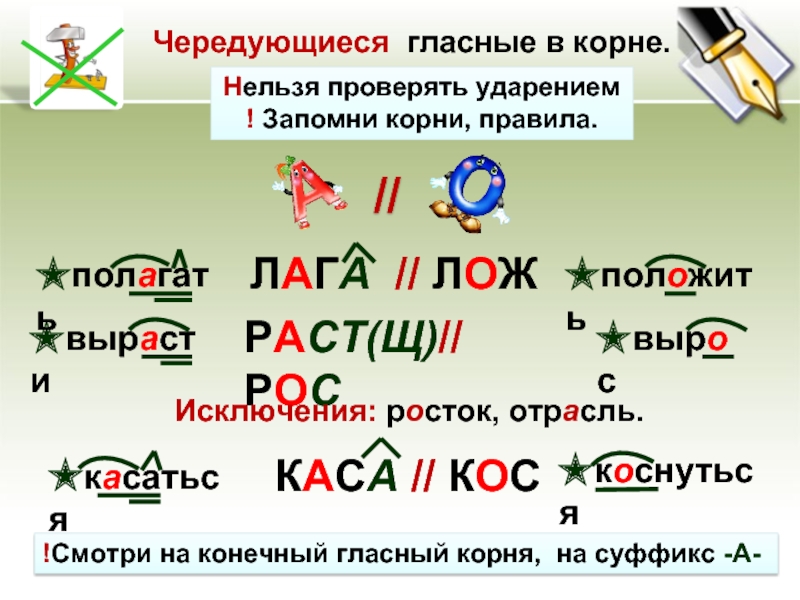 Хотелось бы, чтобы расположение корней было более конкретным.
Хотелось бы, чтобы расположение корней было более конкретным.