Выражения по математике 4 класс на порядок действий со скобками: Урок 2. числовые выражения. порядок выполнения действий. сложение нескольких слагаемых - Математика

Содержание

Урок 2. числовые выражения. порядок выполнения действий. сложение нескольких слагаемых — Математика — 4 класс

Математика, 4 класс

Урок №2. Числовые выражения. Порядок выполнения действий.

Сложение нескольких слагаемых

Перечень вопросов, рассматриваемых в теме:

— что такое «числовые выражения»?

— что значит «Найти значение выражения»?

— как устанавливается порядок действий в выражениях со скобками и без?

Глоссарий по теме:

Сложение чисел – математическая операция по объединению частей в одно целое. На письме обычно обозначается с помощью знака «плюс»

Вычитание чисел – математическая операция по вычитанию из целого части. На письме обычно обозначается с помощью знака «минус».

Умножение чисел – математическая операция, в результате которой находят сумму одинаковых слагаемых.

Деление чисел – математическая операция обратная умножению.

Числовое выражение – числа, соединенные знаками арифметических действий для выполнения вычисления.

Значение выражения –число, которое получается после выполнения всех действий.

Скобки в выражениях – знаки «( )», которые позволяют разграничить и определить порядок действий.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 4 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 7-9

2. Математика: 4 класс: учебник в 2 ч. Ч.1/ В. Н. Рудницкая, Т. В. Юдачева. – М. Вентана-Граф, 2016. – с. 13-15

3. Математика: 4 класс/ Т. Е. Демидова, С. А. Козлова, А. П. Тонких О. – М.; БАЛАСС, 2008. – с. 11-12

Теоретический материал для самостоятельного изучения

Существуют следующие правила порядка действий в числовых выражениях.

Правило 1. Если числовое выражение содержит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку.

Правило 2.Если числовое выражение содержит не только сложение и вычитание, но и умножение и деление, то сначала выполняются по порядку (слева направо) действия умножение и деление, а потом – сложение и вычитание (слева направо).

Правило 3.Если числовое выражение содержит одну пару или несколько пар скобок, то сначала находят значение выражения в скобках, а затем выполняют действия по правилам 1 и 2.

Задания тренировочного модуля:

1. Найдите правильное значение выражения:

15 ∙ 10 + (30 — 20) ∙ 5

Правильный ответ:

200

2. Заполните таблицу:

слагаемое	170		90	80
слагаемое	230	40			37
сумма		330	160	80	37

Правильный ответ:

слагаемое	170	290	90	80	74
слагаемое	230	40	70	0	37
сумма	400	330	160	80	37

3. Расставьте порядок действий:

80 — (42 : 7 ∙ 15 — 29)

Правильный вариант:

ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ Урок математики 4 класс

ВЫ НАС УЗНАЛИ? l К нам на урок l пришли l математические l действия

Действие «сложение» считает, что день надо начинать с утренней гимнастики, а урок математики – с гимнастики ума. l Вычислите устно 25 * 3 : 15 + 29 : 17 ——? 2 15 * 4 + 16 : 19 -4 ——? 0 16 * 3 — 12 : 12 * 23 ——? 69

А действие «вычитание» предлагает вам найти значение выражения 1 4 2 5 3 l 245 : 7 – 35 : 5 + 11 *10 = 138 1 2 3 4 5 l 245 : 7 – 35 : 5 + 11 *10 = 110

ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ. • СЛОЖЕНИЕ И ВЫЧИТАНИЕ чисел называют действиями первой ступени. • УМНОЖЕНИЕ И ДЕЛЕНИЕ чисел называют действиями второй ступени Порядок выполнения действий при нахождении значений выражений определяется правилами. Расскажем эти правила для Буратино.

Порядок выполнения действий при нахождении значений выражений определяется следующими правилами: l Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку слева направо. l Если выражение содержит действия первой и второй ступени и в нем нет скобок, то сначала выполняют действия второй ступени, потом – действия первой ступени. l Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2)

Каждое выражение задает программу своего вычисления. Она состоит из команд. (814 + 36 * 27) : (101 – 2052 : 38) = 38 1. Перемножить числа 36 и 27 (972) 2. Сложить 814 с результатом (1786) команды 1. (54) 3. Разделить 2052 на 38 4. Вычесть из 101 результат (47) команды 3 5. Разделить результат команды (38) 2 на результат команды 4.

Действие «умножения» предлагает вам гимнастику для глаз. А действие «деление» — гимнастику для вас «истинно – ложно» : Если предположение верное, то вы сидите. Если предположение ложное, вы встаете и один из вас объясняет, почему оно ложное.

Во всем нужна сноровка, закалка, тренировка. l № 202 (с. 105) l № 203

Семь раз отмерь – один отрежь Выполни тест 1. В выражении 200 + (20 – 10 : 2) * 8 последним выполняется действие: А) умножение; Б) деление В)вычитание; Г) сложение 2. Составьте выражение для решения задачи: У Белоснежки и 7 гномов было 25 конфет. Белоснежка съела 4 конфеты, а остальные конфеты гномы разделили между собой поровну. Сколько конфет стало у каждого гнома? А) (25– 4): 7; Б) (25 – 7): 4; В) 25 – 4: 7; Г) 25 : 7 – 4 3. Не производя вычислений определить , в каком из примеров указанный порядок действий приводит к неверному результату:

Проверь тест Номер задания 1 2 3 Правильный ответ А В Г

ДОМАШНЕЕ ЗАДАНИЕ с.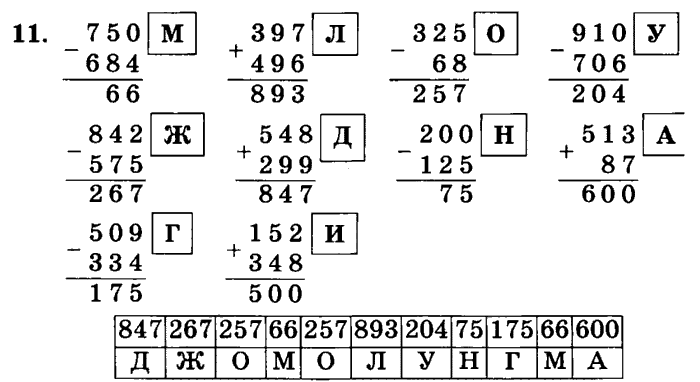 106, № 205 l. Что на уроке у вас хорошо получалось? l. Над чем еще надо работать?

СПАСИБО ЗА УРОК

Как решать примеры со скобками порядок действий. Порядок выполнения действий, правила, примеры

Правила порядка выполнения действий в сложных выражениях изучаются во 2 классе, но практически некоторые из них дети используют еще в 1 классе.

Сначала рассматривается правило о порядке выполнения действий в выражениях без скобок, когда над числами производят либо только сложение и вычитание, либо только умножение и деление. Необходимость введения выражений, содержащих два и более арифметических действий одной ступени, возникает при знакомстве учеников с вычислительными приемами сложения и вычитания в пределах 10, а именно:

Аналогично: 6 — 1 — 1, 6 — 2 — 1, 6 — 2 — 2.

Так как для нахождения значений этих выражений школьники обращаются к предметным действиям, которые выполняются в определенном порядке, то они легко усваивают тот факт, что арифметические действия (сложение и вычитание), которые имеют место в выражениях, выполняются последовательно слева направо.

С числовыми выражениями, содержащими действия сложения и вычитания, а также скобки, учащиеся впервые встречаются в теме «Сложение и вычитание в пределах 10». Когда дети встречаются с такими выражениями в 1 классе, например: 7 — 2 + 4, 9 — 3 — 1 , 4 +3 — 2; во 2 классе, например: 70 — 36 +10, 80 — 10 — 15, 32+18 — 17; 4*10:5, 60:10*3, 36:9*3, учитель показывает, как читают и записывают такие выражения и как находят их значение (например, 4*10:5 читают: 4 умножить на 10 и полученный результат разделить на 5). К моменту изучения во 2 классе темы «Порядок действий» учащиеся умеют находить значения выражений этого вида. Цель работы на данном этапе — опираясь практические умения учащихся, обратить их внимание на порядок выполнения действий в таких выражениях и сформулировать соответствующее правило. Учащиеся самостоятельно решают подобранные учителем примеры и объясняют, в каком порядке выполняли; действия в каждом примере. Затем формулируют сами или читают по учебнику вывод: если в выражении без скобок указаны только действия сложения и вычитания (или только действия умножения и деления), то их выполняют в том порядке, в каком они записаны (т.

е. слева направо).

Несмотря на то, что в выражениях вида а+в+с, а+(в+с) и (а+в)+с наличие скобок не влияет на порядок выполнения действий в силу сочетательного закона сложения, на этом этапе учащихся целесообразнее сориентировать на то, что сначала выполняется действие в скобках. Это связано с тем, что для выражений вида а — (в+с) и а — (в — с) такое обобщение неприемлемо и учащимся на начальном этапе довольно трудно будет сориентироваться в назначении скобок для различных числовых выражений. Использование скобок в числовых выражениях, содержащих действия сложения и вычитания, в дальнейшем получает свое развитие, которое связано с изучением таких правил, как прибавление суммы к числу, числа к сумме, вычитание суммы из числа и числа из суммы. Но при первом знакомстве со скобками важно нацелить учащихся на то, что сначала выполняется действие в скобках.

Учитель обращает внимание детей на то, как важно соблюдать это правило при вычислениях, иначе можно получить неверное равенство. Например, учащиеся объясняют, каким образом, получены значения выражений: 70 — 36 +10=24, 60:10 — 3 =2, почему они неверны, какие значения в действительности имеют эти выражения. Аналогично изучают порядок действий в выражениях со скобками вида: 65 — (26 — 14), 50:(30 — 20), 90:(2 * 5). С такими выражениями учащиеся также знакомы и умеют их читать, записывать и вычислять их значение. Объяснив порядок выполнения действий в нескольких таких выражениях, дети формулируют вывод: в выражениях со скобками первым выполняется действие над числами, записанными в скобках. Рассматривая эти выражения нетрудно показать, что действия в них выполняются не в том порядке, в каком записаны; чтобы показать другой порядок их выполнения, и использованы скобки.

Следующим вводится правило порядка выполнения действий в выражениях без скобок, когда в них содержатся действия первой и второй ступени. Поскольку правила порядка действий приняты по договоренности, учитель сообщает их детям или же учащиеся знакомятся с ними по учебнику. Чтобы учащиеся усвоили введенные правила, наряду с тренировочными упражнениями включают решение примеров с пояснением порядка выполнения их действий. Эффективны также упражнения в объяснении ошибок на порядок выполнения действий. Например, из заданных пар примеров предлагается выписать только те, где вычисления выполнены по правилам порядка действий:

После объяснения ошибок можно дать задание: используя скобки, изменить порядок действий так, чтобы выражение имело заданное значение. Например, чтобы первое из приведенных выражений имело значение, равное 10, надо записать его так: (20+30):5=10.

Особенно полезны упражнения на вычисление значения выражения, когда ученику приходится применять все изученные правила. Например, на доске или в тетрадях записывается выражение 36:6+3*2. Учащиеся вычисляют его значение. Затем по заданию учителя дети изменяют с помощью скобок порядок действий в выражении:

36:6+3-2
36:(6+3-2)
36:(6+3)-2
(36:6+3)-2

Интересным, но более трудным является обратное упражнение: расставить скобки так, чтобы выражение имело заданное значение:

72-24:6+2=66
72-24:6+2=6
72-24:6+2=10
72-24:6+2=69

Также интересными являются упражнения следующего вида:

1. Расставьте скобки так, чтобы равенства были верными:
25-17:4=2 3*6-4=6
24:8-2=4
2. Поставьте вместо звездочек знаки «+» или «-» так, чтобы получились верные равенства:
38*3*7=34
38*3*7=28
38*3*7=42
38*3*7=48
3. Поставьте вместо звездочек знаки арифметических действий так, чтобы равенства были верными:
12*6*2=4
12*6*2=70
12*6*2=24
12*6*2=9
12*6*2=0

Выполняя такие упражнения, учащиеся убеждаются в том, что значение выражения может измениться, если изменяется порядок действий.

Для усвоения правил порядка действий необходимо в 3 и 4 классах включать все более усложняющиеся выражения, при вычислении значений которых ученик применял бы каждый раз не одно, а два или три правила порядка выполнения действий, например:

90*8- (240+170)+190,
469148-148*9+(30 100 — 26909).

При этом числа следует подбирать так, чтобы они допускали выполнение действий в любом порядке, что создает условия для сознательного применения изученных правил.

При расчётах примеров нужно соблюдать определённый порядок действий. С помощью правил ниже, мы разберёмся в каком порядке выполняются действия и для чего нужны скобки.

Если в выражении скобок нет, то:

сначала выполняем слева направо все действия умножения и деления;

а потом слева направо все действия сложения и вычитания.

Рассмотрим порядок действий в следующем примере.

Напоминаем вам, что порядок действий в математике расставляется слева направо (от начала к концу примера).

При вычислении значения выражения можно вести запись двумя способами.

Первый способ

Каждое действие записывается отдельно со своим номером под примером.
После выполнения последнего действия ответ обязательно записывается в исходный пример.

При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.

Второй способ

Второй способ называется запись «цепочкой». Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.

Если выражение содержит скобки, то сначала выполняют действия в скобках.

Внутри самих скобок действует правило порядка действий как в выражениях без скобок.

Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.

Порядок действий и возведение в степень

Если в примере содержится числовое или буквенное выражение в скобках, которое надо возвести в степень, то:

Сначала выполняем все действия внутри скобок
Затем возводим в степень все скобки и числа, стоящие в степени, слева направо (от начала к концу примера).
Выполняем оставшиеся действия в обычном порядке

Порядок выполнения действий, правила, примеры.

Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .

В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.

Навигация по странице.

Сначала умножение и деление, затем сложение и вычитание

В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :

действия выполняются по порядку слева направо,
причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.

Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.

Выполните действия 7−3+6 .

Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .

Кратко решение можно записать так: 7−3+6=4+6=10 .

Укажите порядок выполнения действий в выражении 6:2·8:3 .

Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.

сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.

Вычислите значение выражения 17−5·6:3−2+4:2 .

Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .

На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .

Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.

Действия первой и второй ступени

В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.

Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .

В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).

Порядок выполнения арифметических действий в выражениях со скобками

Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Выполните указанные действия 5+(7−2·3)·(6−4):2 .

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .

Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Выполните действия в выражении 4+(3+1+4·(2+3)) .

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .

Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями

Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.

Рассмотрим решения примеров.

Выполните действия в выражении (3+1)·2+6 2:3−7 .

В этом выражении содержится степень 6 2 , ее значение нужно вычислить до выполнения остальных действий. Итак, выполняем возведение в степень: 6 2 =36 . Подставляем это значение в исходное выражение, оно примет вид (3+1)·2+36:3−7 .

Дальше все понятно: выполняем действия в скобках, после чего остается выражение без скобок, в котором по порядку слева направо сначала выполняем умножение и деление, а затем – сложение и вычитание. Имеем (3+1)·2+36:3−7=4·2+36:3−7= 8+12−7=13 .

Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.

cleverstudents.ru

Онлайн игры,тренажеры,презентации,уроки,энциклопедии,статьи

Примеры со скобками, урок с тренажерами.

Мы рассмотрим в этой статье три варианта примеров:

1. Примеры со скобками (действия сложения и вычитания)

2. Примеры со скобками (сложение, вычитание, умножение, деление)

3. Примеры, в которых много действий

1 Примеры со скобками (действия сложения и вычитания)

Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:

Мы видим, что порядок действий в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.

Если в примере нет скобок , мы выполняем все действия по порядку, слева направо.
Если в примере есть скобки , то сначала мы выполняем действия в скобках, и лишь потом все остальные действия, начиная слева направо.

*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.

Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем все действия по порядку, слева направо:

В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.

А теперь — тренажеры!

1) Примеры со скобками в пределах до 20.

2) Примеры со скобками в пределах до 100. Онлайн тренажер.

3) Примеры со скобками. Тренажер №2

4) Вставь пропущенное число — примеры со скобками. Тренажер

2 Примеры со скобками (сложение, вычитание, умножение, деление)

Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.

Сначала рассмотрим примеры без скобок:

Если в примере нет скобок , сначала выполняем действия умножения и деления по порядку, слева направо. Затем — действия сложения и вычитания по порядку, слева направо.
Если в примере есть скобки , то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.

Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:

Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:

3 Примеры, в которых много действий

Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).

Эти знаки и будут делить наш пример на блоки:

Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.

А теперь закрепляем решение примеров на порядок действий на тренажерах!

1.

2. Тренажер по математике 2 — 3 класс «Расставь порядок действий (буквенные выражения).»

3. Порядок действий (расставляем порядок и решаем примеры)

Порядок действий в математике 4 класс

Начальная школа подходит к концу, скоро ребёнок шагнёт в углубленный мир математики. Но уже в этот период школьник сталкивается с трудностями науки. Выполняя простое задание, ребёнок путается, теряется, что в результате приводит к отрицательной отметке за выполненную работу. Чтобы избежать подобных неприятностей, нужно при решении примеров, уметь ориентироваться в порядке, по которому нужно решать пример. Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.

Перед выполнением задания попросите своё чадо пронумеровать действия, которые он собирается выполнить. Если возникли затруднения – помогите.

Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:

Если в задании необходимо выполнить ряд действий, нужно сначала выполнить деление или умножение, затем сложение. Все действия выполняются по ходу письма. В противном случае, результат решения будет не верным.

Если в примере требуется выполнить сложение и вычитание, выполняем по порядку, слева направо.

27-5+15=37 (при решении примера руководствуемся правилом. Сначала выполняем вычитание, затем – сложение).

Научите ребёнка всегда планировать и нумеровать выполняемые действия.

Ответы на каждое решённое действие записываются над примером. Так ребёнку гораздо легче будет ориентироваться в действиях.

Рассмотрим ещё один вариант, где необходимо распределить действия по порядку:

Как видим, при решении соблюдено правило, сначала ищем произведение, после — разность.

Это простые примеры, при решении которых, необходима внимательность. Многие дети впадают в ступор при виде задания, в котором присутствует не только умножение и деление, но и скобки. У школьника, не знающего порядок выполнения действий, возникают вопросы, которые мешают выполнить задание.

Как говорилось в правиле, сначала найдём произведение или частное, а потом всё остальное. Но тут же есть скобки! Как поступить в этом случае?

Решение примеров со скобками

Разберём конкретный пример:

При выполнении данного задания, сначала найдём значение выражения, заключённого в скобки.
Начать следует с умножения, далее – сложение.
После того, как выражение в скобках решено, приступаем к действиям вне их.
По правилам порядка действий, следующим шагом будет умножение.
Завершающим этапом станет вычитание.

Как видим на наглядном примере, все действия пронумерованы. Для закрепления темы предложите ребёнку решить самостоятельно несколько примеров:

Порядок, по которому следует вычислять значение выражения уже расставлен. Ребёнку останется только выполнить непосредственно решение.

Усложним задачу. Пусть ребёнок найдёт значение выражений самостоятельно.

7*3-5*4+(20-19) 14+2*3-(13-9)
17+2*5+(28-2) 5*3+15-(2-1*2)
24-3*2-(56-4*3) 14+12-3*(21-7)

Приучите ребёнка решать все задания в черновом варианте. В таком случае, у школьника будет возможность исправить не верное решение или помарки. В рабочей тетради исправления не допустимы. Выполняя самостоятельно задания, дети видят свои ошибки.

Родители, в свою очередь, должны обратить внимание на ошибки, помочь ребёнку разобраться и исправить их. Не стоит нагружать мозг школьника большими объёмами заданий. Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.

Делайте перерыв. Ребёнок должен отвлекаться и отдыхать от занятий. Главное помнить, что не все обладают математическим складом ума. Может из вашего ребёнка вырастет знаменитый философ.

detskoerazvitie. info

Урок по математике 2 класс Порядок действий в выражениях со скобками.

Успейте воспользоваться скидками до 50% на курсы «Инфоурок»

Цель: 1.

3. Закрепить знание таблицы умножения и деления на 2 – 6, понятия делителя и

4. Учить работать в парах с целью развития коммуникативных качеств.

Оборудование * : + — (), геометрический материал.

Раз, два – выше голова.

Три, четыре – руки шире.

Пять, шесть – всем присесть.

Семь, восемь – лень отбросим.

Но сначала придется узнать его название. Для этого нужно выполнить несколько заданий:

6 + 6 + 6 … 6 * 4 6 * 4 + 6… 6 * 5 – 6 14 дм 5 см… 4 дм 5 см

Пока мы вспоминали о порядке действий в выражениях, с замком происходили чудеса. Мы были только что у ворот, а теперь попали в коридор. Смотрите, дверь. А на ней замок. Откроем?

1. Из числа 20 вычесть частное чисел 8 и 2.

2. Разность чисел 20 и 8 разделить на 2.

— Чем отличаются результаты?

— Кто сможет назвать тему нашего урока?

(на массажных ковриках)

По дорожке, по дорожке

Скачем мы на правой ножке,

Скачем мы на левой ножке.

По тропинке побежим,

Наше предположение было полностью правильно7

Где выполняются действия сначала, если в выражении есть скобки?

Смотрите перед нами «живые примеры». Давайте «оживим» их.

* : + — ().

m – c * (a + d) + x

k: b + (a – c) * t

6. Работа в парах.

Для их решения вам понадобиться геометрический материал.

Учащиеся выполняют задания в парах. После выполнения проверка работы пар у доски.

Что нового вы узнали?

8. Домашнее задание.

Тема: Порядок действий в выражениях со скобками.

Цель: 1. Вывести правило порядка действий в выражениях со скобками, содержащих все

4 арифметических действия,

2. Формировать способность к практическому применению правила,

4.Учить работать в парах с целью развития коммуникативных качеств.

Оборудование : учебник, тетради, карточки со знаками действий * : + — (), геометрический материал.

1 .Физминутка.

Девять, десять – тихо сесть.

2. Актуализация опорных знаний.

Сегодня мы с вами отправляемся в очередное путешествие по стране Знаний городу математика. Нам предстоит посетить один дворец. Что-то я забыла его название. Но не будем расстраиваться, вы сами сможете мне подсказать его название. Пока я переживала, мы подошли к воротам дворца. Войдем?

1. Сравните выражения:

2. Расшифруй слово.

3. Постановка проблемы. Открытие нового.

Так как же называется дворец?

А когда в математике мы говорим о порядке?

Что вы уже знаете о порядке выполнения действий в выражениях?

— Интересно, нам предлагают записать и решить выражения (учитель читает выражения, учащиеся записывают их и решают).

20 – 8: 2

(20 – 8) : 2

Молодцы. А что интересного в этих выражениях?

Посмотрите на выражения и их результаты.

— Что общего в записи выражений?

— Как вы думаете, почему получились разные результаты, ведь числа были одинаковые?

Кто рискнет сформулировать правило выполнения действий в выражениях со скобками?

Правильность этого ответа мы сможем проверить в другой комнате. Отправляемся туда.

4. Физминутка.

И по этой же дорожке

До горы мы добежим.

Стоп. Немножко отдохнем

И опять пешком пойдем.

5. Первичное закрепление изученного.

Вот мы и пришли.

Нам нужно решить еще два выражения, чтобы проверить правильность нашего предположения.

6 * (33 – 25) 54: (6 + 3) 25 – 5 * (9 – 5) : 2

Для проверки правильности предположения откроем учебники на стр. 33 и прочитаем правило.

Как нужно выполнять действия после решения в скобках?

На доске написаны буквенные выражения и лежат карточки со знаками действий * : + — (). Дети выходят к доске по одному, берут карточку с тем действием, которое нужно сделать сначала, потом выходит второй ученик и берет карточку со вторым действием и т. д.

а + (а –в)

а * (в +с) : d – t

m – c * ( a + d ) + x

k : b + ( a – c ) * t

(a – b) : t + d

6. Работа в парах. Автономная некоммерческая организация Бюро судебных экспертиз Судебная экспертиза. Несудебная экспертиза Рецензия на экспертизу. Оценка Автономная некоммерческая организация «Бюро судебных экспертиз» в Москве – центр […]

Особенности бухгалтерского учета субсидий Государство стремится поддержать малое и среднее предпринимательство. Такая поддержка наиболее часто выражается в форме предоставления субсидий – безвозмездных выплат из […]
Жалоба на педиатра Жалоба на педиатра — официальный документ, устанавливающий требования пациента и описывающий суть возникновения таких требований. Согласно статье 4 Федерального закона «О порядке рассмотрения […]
Ходатайство об уменьшении размера исковых требований Один из видов уточнения иска — ходатайство об уменьшении размера исковых требований. Когда истец неправильно определил цену иска. Или ответчик частично исполнил […]
Черный рынок доллара в Киеве Валютный аукцион по покупке доллара в Киеве Внимание: администрация не несёт ответственности за содержание объявлений на валютном аукционе. Правила публикации объявлений на валютном […]

Мы рассмотрим в этой статье три варианта примеров:

1. Примеры со скобками (действия сложения и вычитания)
2. Примеры со скобками (сложение, вычитание, умножение, деление)
3. Примеры, в которых много действий

1 Примеры со скобками (действия сложения и вычитания)

Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:

А теперь — тренажеры!

1) Примеры со скобками в пределах до 20. Онлайн тренажер.

2) Примеры со скобками в пределах до 100. Онлайн тренажер.

3) Примеры со скобками. Тренажер №2

4) Вставь пропущенное число — примеры со скобками.

Тренажер

2 Примеры со скобками (сложение, вычитание, умножение, деление)

Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.

Сначала рассмотрим примеры без скобок:

3 Примеры, в которых много действий

Эти знаки и будут делить наш пример на блоки:

А теперь закрепляем решение примеров на порядок действий на тренажерах!

Если у вас не открываются игры или тренажёры, читайте .

Видеоурок «Порядок выполнения действий» подробно поясняет важную тему математики — последовательность выполнения арифметических операций при решении выражения. В ходе видеоурока рассматривается, какой приоритет имеют различные математические операции, как это применяется в вычислении выражений, приводятся примеры для усвоения материала, обобщаются полученные знания в решении заданий, где имеются все рассмотренные операции. С помощью видеоурока учитель имеет возможность быстрее достичь целей урока, повысить его эффективность. Видео может применяться в качестве наглядного материала, сопровождающего объяснение учителя, а также в качестве самостоятельной части урока.

В наглядном материале используются приемы, которые помогают лучше достичь понимания темы, а также запомнить важные правила. С помощью цвета и разного написания выделяются особенности и свойства операций, отмечаются особенности решения примеров. Анимационные эффекты помогают подавать последовательно учебный материал, а также обратить внимание учеников на важные моменты. Видео озвучено, поэтому дополняется комментариями учителя, помогающими ученику понять и запомнить тему.

Видеоурок начинается с представления темы. Затем отмечается, что умножение, вычитание являются операциями первой ступени, операции умножения и деления названы операциями второй ступени. Данным определением нужно будет оперировать дальше, выведено на экран и выделено цветным крупным шрифтом. Затем представляются правила, составляющие порядок выполнения операций. Выводится первое правило порядка, которое указывает, что при отсутствии скобок в выражении, наличию действий одной ступени, данные действия необходимо производить по порядку. Во втором правиле порядка утверждается, что при наличии действий обеих ступеней и отсутствии скобок, производятся первыми операции второй ступени, потом производятся операции первой ступени. Третье правило устанавливает порядок выполнения операций, для выражений, включающих скобки. Отмечается, что в этом случае сначала производятся операции в скобках. Формулировки правил выделены цветным шрифтом и рекомендованы к запоминанию.

Далее предлагается усвоить порядок выполнения операций, рассматривая примеры. Описывается решение выражения с содержанием только операций сложения, вычитания. Отмечаются основные особенности, которые влияют на порядок вычислений — отсутствуют скобки, присутствуют операции первой ступени. Ниже расписано по действиям, как выполняются вычисления, сначала вычитание, затем два раза сложение, а затем вычитание.

Во втором примере 780:39·212:156·13 требуется вычислить выражение, выполняя действия согласно порядку. Отмечается, что в данном выражении содержатся исключительно операции второй ступени, без скобок. В данном примере все действия производятся строго слева направо. Ниже поочередно расписываются действия, постепенно подходя к ответу. В результате вычисления получается число 520.

В третьем примере рассматривается решение примера, в котором есть операции обеих ступеней. Отмечается, что в данном выражении отсутствуют скобки, но есть действия обеих ступеней. Согласно порядку выполнения операций, производятся операции второй ступени, после этого — операции первой ступени. Ниже — по действиям расписывается решение, в котором выполняются сначала три операции — умножение, деление, еще одно деление. Затем с найденными значениями произведения и частных производятся операции первой ступени. В ходе решения фигурными скобками объединены действия каждой ступени для наглядности.

В следующем примере содержатся скобки. Поэтому демонстрируется, что первые вычисления производятся над выражениями в скобках. После них производятся операции второй ступени, следом — первой.

Далее представлено замечание о том, в каких случаях можно не записывать скобки при решении выражений. Замечено, что это возможно только в случае, когда устранение скобок не изменить порядок выполнения операций. Примером служит выражение со скобками (53-12)+14, которое содержит только операции первой ступени. Переписав 53-12+14 с устранением скобок, можно отметить, что порядок поиска значения не изменится — сначала выполняется вычитание 53-12=41, а затем сложение 41+14=55. Ниже отмечается, что менять порядок операций при нахождении решения выражения можно, используя свойства операций.

В конце видеоурока изученный материал обобщается в выводе, что каждое выражение, требующее решения, задает определенную программу для вычисления, состоящую из команд. Пример такой программы представляется при описании решения сложного примера, представляющего собой частное (814+36·27) и (101-2052:38). Заданная программа содержит пункты: 1) найти произведение 36 с 27, 2) добавить к 814 найденную сумму, 3) поделить на 38 число 2052, 4) отнять из числа 101 результат деления 3 пункта, 5) поделить результат выполнения пункта 2 на результат пункта 4.

В конце видеоурока представлен перечень вопросов, на которые предлагается ответить ученикам. В их числе умение отличить действия первой и второй ступеней, вопросы о порядке выполнения действий в выражениях с действиями одной ступени и разных ступеней, о порядке выполнения действий при наличии скобок в выражении.

Видеоурок «Порядок выполнения действий» рекомендуется применять на традиционном школьном уроке для повышения эффективности урока. Также наглядный материал будет полезен для проведения дистанционного обучения. Если ученику необходимо дополнительное занятие для освоения темы или он изучает ее самостоятельно, видео может быть рекомендовано для самостоятельного изучения.

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

Yandex.RTB R-A-339285-1

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

Все действия выполняются слева направо.
В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Пример 1

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 6: 2 · 8: 3 ?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Пример 3

Условие: подсчитайте, сколько будет 17 − 5 · 6: 3 − 2 + 4: 2 .

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:

17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6: 3 − 2 + 4: 2 = 7 .

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

Определение 2

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Определение 3

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Пример 4

Условие: вычислите, сколько будет 5 + (7 − 2 · 3) · (6 − 4) : 2 .

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7:

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + (7 − 2 · 3) · (6 − 4) : 2 = 5 + 1 · 2: 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + (7 − 2 · 3) · (6 − 4) : 2 = 6 .

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Пример 5

Условие: вычислите, сколько будет 4 + (3 + 1 + 4 · (2 + 3)) .

Решение

У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · (2 + 3) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .

Ответ: 4 + (3 + 1 + 4 · (2 + 3)) = 28 .

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет (4 + (4 + (4 − 6: 2)) − 1) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Пример 6

Условие: найдите, сколько будет (3 + 1) · 2 + 6 2: 3 − 7 .

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид (3 + 1) · 2 + 36: 3 − 7 .

(3 + 1) · 2 + 36: 3 − 7 = 4 · 2 + 36: 3 − 7 = 8 + 12 − 7 = 13

Ответ: (3 + 1) · 2 + 6 2: 3 − 7 = 13 .

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Страница 27 — ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 1

Вернуться к содержанию учебника

Числа, которые больше 1000. Нумерация

Вопрос

117. Сравни числа.

94875 и 94895

5999 и 6000

19400 и 19399

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

118. Объясни, как меняется значение цифры 5 в записи чисел 5, 50, 500, 5000, 50000, 500000.

Подсказка

Повтори состав многозначных чисел.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

119. Ученики записали число девять тысяч сорок так: 940, 900040, 9040. Найди правильную запись.

Подсказка

Повтори состав многозначного числа.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

120. У трёх тракторов такие заводские номера: 250000, 249999, 250001. Какой из них сошёл с конвейера первым? вторым? третьим?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

121. С помощью скобок измени порядок выполнения действий и найди значения выражений.

740 — 240 + 60	66 — 6 • 9 + 1	500 : 100 • 5
840 — 40 : 8	120 — 20 + 4 • 5	300 : 10 : 10

Подсказка

Повтори порядок действий, действия со скобками, умножение и деление круглых чисел, а также:

♦ Если число разделить на 1, то получится число, которое делили.

♦ Если число, не равное 0, разделить на себя, то частное будет равно 1.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

122. Рабочий за восьмичасовой рабочий день вытачивает 80 деталей, а его ученик работает 6 ч в день и вытачивает 42 такие детали. На сколько больше деталей вытачивает за 1 ч рабочий, чем его ученик?

Измени вопрос задачи, чтобы она решалась так:

80 : 8 + 42 : 6

Подсказка

Повтори единицу времени — час.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

123.

705 — 296 • 2	(365 + 175) : 5	(904 — 268) : 4
(705 — 296) • 2	265 + 175 : 5	904 — 268 : 4

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

124. 1) Что обозначает цифра 1 в записи чисел 1, 10, 100, 1000?

2) Во сколько раз 1 десяток больше, чем 1 единица? 1 сотня больше, чем 1 единица?

Подсказка

Повтори состав многозначного числа.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Сравни числа: 376689 и 37690; 47308 и 46309.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Ребус:

Подсказка

Повтори алгоритм письменного деления.

Ответ

Поделись с друзьями в социальных сетях:

Вернуться к содержанию учебника

Пользовательское соглашение

Порядок действий

В уроке выражения мы узнали, что они бывают числовые и буквенные. Мы рассмотрели несколько числовых и буквенных выражений. Это были самые простейшие выражения.

Настало время сдвинуться с мёртвой точки и рассмотреть более сложные выражения. В данном уроке мы познакомимся с порядком выполнения действий.

Выражения могут состоять из нескольких чисел. Таковыми к примеру являются следующие выражения:

10 − 1 + 2 + 3
(3 + 5) + 2 × 3
5 × 2 + (5 − 3) : 2 + 1

Такие выражения нельзя вычислить сразу, то есть поставить знак равенства и записать значение выражения. Да и выглядят они не так просто, как 2 + 2 или 9 − 3.

Для подобных выражений принято соблюдать так называемый порядок действий. Суть в том, что выражение вычисляется кусочками по определённому порядку.

Когда нам требуется решить подобные примеры, мы сразу должны мысленно прочитать следующее правило:

Сначала вычислить то, что находится в скобках!

Посмотрим на выражение 10 − 1 + 2 + 3. Видим, что в нём нет никаких скобок. Тогда переходим к следующему правилу, которое выглядит так:

Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!

Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Видим, что в нём нет никакого умножения или деления. Тогда переходим к следующему правилу:

Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию!

Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Встречаем вычитание 10 − 1. Сразу выполняем эту операцию: 10 − 1 = 9. Полученную девятку запишем в главном выражении вместо 10 − 1

Затем снова читаем те, правила, которые мы прочитали выше. Читать их нужно в следующем порядке:

1. Сначала вычислить то, что находится в скобках!

2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же применяем эту операцию!

3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же применяем эту операцию!

Сейчас у нас имеется выражение 9 + 2 + 3 Читаем его слева направо и встречаем сложение 9 + 2. Выполняем эту операцию: 9 + 2 = 11. Запишем число 11 в главном выражении вместо 9 + 2:

Осталось простейшее выражение 11 + 3, которое вычисляется легко:

11 + 3 = 14

Таким образом, значение выражения 10 − 1 + 2 + 3 равно 14

10 − 1 + 2 + 3 = 14

Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:

И далее можно выполнить действия по отдельности, что очень удобно:

1) 10 − 1 = 9

2) 9 + 2 = 11

3) 11 + 3 = 14

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий. Например, решение для выражения 10 − 1 + 2 + 3 можно записать следующим образом:

Но если человек не научился быстро считать в уме, то не рекомендуется использовать такой способ.

Пример 2. Найти значение выражения (3 + 5) + 2 × 3

Применим правила порядка действий. Прочитаем правила в порядке их приоритета.

Сначала вычислить то, что находится в скобках!

Посмотрим на выражение (3 + 5) + 2 × 3. Видим, что в нём есть выражение в скобках (3 + 5). Вычислим то, что в этих скобках: 3 + 5 = 8. Запишем полученную восьмёрку в главном выражении вместо выражения в скобках:

8 + 2 × 3

Снова читаем первое правило:

Сначала вычислить то, что находится в скобках!

Видим, что в выражении 8 + 2 × 3 нет никаких скобок. Тогда читаем следующее правило:

Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!

Посмотрим на наше выражение 8 + 2 × 3. Видим, что в нём есть умножение 2 × 3. Выполним эту операцию: 2 × 3 = 6. Запишем полученную шестёрку в главном выражении вместо 2 × 3

8 + 6

Осталось простейшее выражение 8 + 6, которое вычисляется легко:

8 + 6 = 14

Таким образом, значение выражения (3 + 5) + 2 × 3 равно 14

(3 + 5) + 2 × 3 = 14

Также, этот пример можно решить, расставив порядок действий над самим выражением. Действие в скобках будет первым действием, умножение — вторым действием, а сумма — третьим:

И далее можно выполнить действия по отдельности, что очень удобно:

1) 3 + 5 = 8

2) 2 × 3 = 6

3) 8 + 6 = 14

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Но опять же, используя такой способ, нужно быть очень внимательным.

Пример 3. Найти значение выражения 5 × 2 + (5 − 3) : 2 + 1

Расставим порядок действий над выражением. Действие в скобках будет первым действием, умножение — вторым действием, деление — третьим действием, четвёртое и пятое действие являются суммами и они будут выполнены в порядке их следования:

1) 5 − 3 = 2

2) 5 × 2 = 10

3) 2 : 2 = 1

4) 10 + 1 = 11

5) 11 + 1 = 12

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Четвёртое и пятое действие заключалось в том, чтобы вычислить оставшееся простейшее выражение 10 + 1 + 1. Мы не стали тратить время на выполнение каждого из этих действий, а поставили знак равенства и записали ответ 12.

Пример 4. Найти значение выражения (3250 − 2905) : 5

Расставим порядок действий над выражением. Действие в скобках будет первым действием, а деление — вторым

1) 3250 − 2905 = 345

2) 345 : 5 = 69

В скобках могут выполняться два и более действия. Бывает даже так, что в скобках встречаются другие скобки. В таких случаях нужно применять те же правила, которые мы изучили ранее.

Пример 5. Найти значение выражения (6 411 × 8 − 40799) × 6

Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется умножение и вычитание. Согласно порядку действий, умножение выполняется раньше вычитания.

В данном случае сначала нужно 6 411 умножить на 8, и из полученного результата вычесть 40 799. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат будет умножен на 6.

В результате будем иметь следующий порядок:

1) 6 411 × 8 = 51 288

2) 51 288 − 40 799 = 10 489

3) 10 489 × 6 = 62 934

Пример 6. Найти значение выражения: 1 657 974 : 822 × 106 − (50 377 + 20 338)

Расставим порядок действий над выражением. Действие в скобках будет первым действием, деление будет вторым действием, умножение — третьим, вычитание — четвёртым.

1) 50 377 + 20 338 = 70 715

2) 1 657 974 : 822 = 2 017

3) 2 017 × 106 = 213 802

4) 213 802−70 715 = 143 087

Пример 7. Найти значение выражения: 14 026 − (96 : 4 + 3680)

Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется деление и сложение. Согласно порядку действий деление выполняется раньше сложения.

В данном случае сначала нужно 96 разделить на 4, и полученный результат сложить с 3 680. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат нужно вычесть из 14 026. В результате будем иметь следующий порядок:

1) 96 : 4 = 24

2) 24 + 3 680 = 3 704

3) 14026 − 3 704 = 10 322

Задания для самостоятельного решения

Задание 1. Найдите значение выражения:

5 + 2 − 2 − 1

Решение

Задание 2. Найдите значение выражения:

14 + (6 + 2 × 3) − 6

Решение

Задание 3. Найдите значение выражения:

486 : 9 − 288 : 9

Решение

Задание 4. Найдите значение выражения:

756 : 3 : 4 × 28

Решение

Задание 5. Найдите значение выражения:

807 : 3 − (500 − 58 × 4)

Решение

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Порядок выполнения математических действий | интернет проект BeginnerSchool.

Сегодня мы поговорим о порядке выполнения математических действий. Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.

Читаем выражение слева направо и выбираем порядок действий по приоритету. Сначала выполняем действия в скобках. Затем умножение и/или деление. Далее складываем и вычитаем.

Если скобки имеют несколько вложений, то есть если внутри скобок есть ещё скобки, то сначала выполняем действия во внутренних скобках. Для простоты понимания, выражение в скобках можно воспринимать как самостоятельное выражение, то есть как отдельный пример, который надо решить. Внутри скобок действия выполняются согласно тому же порядку: Действия в скобках, затем умножение/деление, затем сложение/вычитание.

Умножение и деление не имеет между собой приоритета и выполняются слева направо, также как и сложение с вычитанием.

Рассмотрим пример:

38 – (10 + 6) = 22;

Итак, вспомним о том, что сначала вычисляются выражения в скобках

1) в скобках: 10 + 6 = 16;

2) вычитание: 38 – 16 = 22.

Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.

10 ÷ 2 × 4 = 20;

Порядок выполнения действий:

1) слева направо, сначала деление: 10 ÷ 2 = 5;

2) умножение: 5 × 4 = 20;

10 + 4 – 3 = 11, т.е.:

1) 10 + 4 = 14;

2) 14 – 3 = 11.

Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.

18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7

Порядок выполнения действий:

1) 18 ÷ 2 = 9;

2) 2 × 3 = 6;

3) 12 ÷ 3 = 4;

4) 9 – 6 = 3; т. е. слева направо – результат первого действия минус результат второго;

5) 3 + 4 = 7; т.е. результат четвертого действия плюс результат третьего;

Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.

30 + 6 × (13 – 9) = 54, т.е.:

1) выражение в скобках: 13 – 9 = 4;

2) умножение: 6 × 4 = 24;

3) сложение: 30 + 24 = 54;

Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:

1) действия, заключенные в скобках;

2) умножение и деление;

3) сложение и вычитание.

Если вы хотите получать анонсы наших статей подпишитесь на рассылку “Новости сайта“.

Понравилась статья — поделитесь с друзьями:

Оставляйте пожалуйста комментарии в форме ниже

Урок 2.

Выражение и его значение. Порядок выполнения действий

№ 11

Условие:

Решение:

Советы:

Правило, определяющее порядок выполнения действий в выражениях без скобок:
1) действия выполняются по порядку слева направо,
2) причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

№ 12

Условие:

Решение:

Советы:

Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо. Например, в числовом выражении 3 арифметических действия: сложение, вычитание и вычитание. Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо

№ 13

Условие:

Решение:

Советы:

Сначала найди сколько р. в 8 монетах.

№ 14

Условие:

Решение:

Советы:

Сначала найди сколько в одном вагоне.

№ 15

Условие:

Решение:

Советы:

Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.  Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое. Чтобы найти неизвестное уменьшаемое, нужно к разность прибавить вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого.

№ 16

Условие:

Решение:

Советы:

если к числу прибавить ноль, получится это же число.

если к нулю прибавить число, получится это же число.

если из числа вычесть ноль, получится это же число.

если из числа вычесть само себя, получится ноль.

№ 17

Условие:

Решение:

Советы:

Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое. Чтобы найти неизвестное уменьшаемое, нужно к разность прибавить вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого.

№ 18

Условие:

Решение:

Советы:

Соотнеси пример с условием задачи.

№ 19

Условие:

Решение:

Советы:

Напишите условие задачи.

№ 20

Условие:

Решение:

Советы:

Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое. Чтобы найти неизвестное уменьшаемое, нужно к разность прибавить вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого.

№ 21

Условие:

Решение:

Советы:

Вспомните порядок действий.

№ 22

Условие:

Решение:

Советы:

Пробуйте различные варианты.

№*

Условие:

Решение:

Советы:

Не забывайте про порядок действий.

Порядок действий: PEMDAS

Purplemath

Если вас просят упростить что-то вроде «4 + 2 × 3», естественно возникает вопрос: «Как мне это сделать? Потому что есть два варианта!» Я мог бы добавить первым:

4 + 2 × 3 = (4 + 2) × 3 = 6 × 3 = 18

. ..или я мог сначала умножить:

4 + 2 × 3 = 4 + (2 × 3) = 4 + 6 = 10

Какой ответ правильный?

MathHelp.com

Кажется, ответ зависит от того, как вы смотрите на проблему.Но у нас не может быть такой гибкости в математике; математика не будет работать, если вы не можете быть уверены в ответе или если можно вычислить одно и то же выражение, чтобы вы могли прийти к двум или более различным ответам.

Чтобы устранить эту путаницу, у нас есть некоторые правила приоритета, установленные, по крайней мере, еще в 1500-х годах, которые называются «порядком операций». «Операциями» являются сложение, вычитание, умножение, деление, возведение в степень и группирование; «порядок» этих операций указывает, какие операции имеют приоритет (выполняются) перед другими операциями.

Распространенным методом запоминания порядка действий является сокращение (или, точнее, «акроним») «PEMDAS», которое превращается в мнемоническую фразу «Пожалуйста, извините, моя дорогая тетя Салли». Эта фраза означает «круглые скобки, экспоненты, умножение и деление, сложение и вычитание» и помогает запомнить их порядок. В этом списке указаны ранги операций: скобки опережают показатели, которые превосходят умножение и деление (но умножение и деление находятся в одном ранге), а умножение и деление превосходят сложение и вычитание (которые вместе находятся в нижнем ранге).Другими словами, приоритет:

Круглые скобки (внутри них упростить)
Экспоненты
Умножение и деление (слева направо)
Сложение и вычитание (слева направо)

Когда у вас есть несколько операций одного ранга, вы просто действуете слева направо. Например, 15 ÷ 3 × 4 не 15 ÷ (3 × 4) = 15 ÷ 12, а скорее (15 ÷ 3) × 4 = 5 × 4, потому что, идя слева направо, вы попадаете в разделение подпишитесь первым.

Если вы не уверены в этом, проверьте это на своем калькуляторе, который был запрограммирован с иерархией порядка операций. Например, набрав указанное выше выражение в графическом калькуляторе, вы получите:

Используя приведенную выше иерархию, мы видим, что в вопросе «4 + 2 × 3» в начале этой статьи ответ 2 был правильным, потому что мы должны выполнить умножение, прежде чем выполнять сложение.

(Примечание: носители британского английского часто вместо этого используют аббревиатуру «BODMAS», а не «PEMDAS». BODMAS означает «скобки, порядки, деление и умножение, а также сложение и вычитание». и «порядки» совпадают с показателями, два акронима означают одно и то же. Кроме того, вы можете видеть, что буквы «M» и «D» перевернуты в британо-английской версии; это подтверждает, что умножение и деление того же «звания» или «уровня». Канадцы, говорящие по-английски, разделяют разницу, используя BEDMAS.)

Порядок операций был определен во избежание недопонимания, но PEMDAS может создать свою собственную путаницу; некоторые студенты иногда склонны применять иерархию, как будто все операции в задаче находятся на одном «уровне» (просто идут слева направо), но часто эти операции не «равны». Во многих случаях это помогает решать проблемы изнутри, а не слева направо, потому что часто некоторые части проблемы находятся «глубже», чем другие.Лучший способ объяснить это — привести несколько примеров:

Мне нужно упростить термин с показателем, прежде чем пытаться добавить 4:

Я должен упростить в круглых скобках, прежде чем я смогу прописать экспоненту. Только тогда я смогу добавить 4.

4 + (2 + 1) ² = 4 + (3) ² = 4 + 9 = 13

Упростить 4 + [–1 (–2 — 1)]
².

Я не должен пытаться делать эти вложенные круглые скобки слева направо; этот метод слишком подвержен ошибкам. Вместо этого я постараюсь работать изнутри. Сначала я упрощу внутри фигурных скобок, затем упрощу внутри квадратных скобок и только потом займусь квадратом. После этого я наконец могу добавить 4:

4 + [–1 (–2 — 1)] ²

= 4 + [–1 (–3)] ²

= 4 + [3] ²

= 4 + 9

= 13

Нет особого смысла в использовании квадратных скобок («[» и «]» выше) вместо скобок.Скобки и фигурные скобки (символы «{» и «}») используются, когда есть вложенные круглые скобки, как помощь для отслеживания того, какие круглые скобки к которым идут. Различные символы группировки используются только для удобства. Это похоже на то, что происходит в электронной таблице Excel, когда вы вводите формулу, используя круглые скобки: каждый набор скобок имеет цветовую кодировку, поэтому вы можете определить пары:

Упростить 4 (
^–2/₃ + ⁴/₃).

Сначала я упрощу внутри скобок:

Итак, мой упрощенный ответ

⁸/₃

На следующей странице есть больше примеров отработанных примеров ….

URL: https: // www.purplemath.com/modules/orderops.htm

Порядок операций — определение, правила, примеры, проблемы

Порядок операций — это набор правил, которым необходимо следовать в определенной последовательности при решении выражения. В математике под словом «операции» мы подразумеваем процесс вычисления любого математического выражения, включающий арифметические операции, такие как деление, умножение, сложение и вычитание.Давайте узнаем подробно о порядке выполнения правил и о том, насколько хорошо мы можем запоминать правила, используя короткие приемы.

Каков порядок действий?

Порядок операций — это математическое правило, которое гласит, что сначала мы оцениваем скобки / скобки, на втором месте — экспоненты / порядок, на третьем — деление или умножение (слева направо, в зависимости от того, что наступит раньше), а затем сложение или вычитание. (слева направо, в зависимости от того, что наступит раньше).В математике при вычислении выражения может потребоваться выполнить несколько операций, и упрощение в конце дает разные результаты. Однако на любое выражение у нас может быть только один правильный ответ. Чтобы определить правильный ответ, мы упрощаем любое данное математическое выражение, используя определенный набор правил. Эти правила вращаются вокруг всех основных операторов, используемых в математике. Такие операторы, как сложение (+), вычитание (-), деление (÷) и умножение (×). Посмотрите на данное изображение, чтобы получить представление о том, как именно выглядит порядок операций.

Определение порядка операций

Как мы обсуждали выше Порядок операций можно определить как набор основных правил приоритета, которые мы используем при решении любого математического выражения, включающего несколько операций. Когда между двумя операторами появляется подвыражение, первым должен применяться оператор, который идет первым в соответствии со списком, приведенным ниже. Порядок действий, правила изложены здесь:

Кронштейны (), {}, []
Экспоненты
Деление (÷) и умножение (×)
Сложение (+) и вычитание (-)

Вышеупомянутый набор правил всегда меняется в зависимости от соответствующих заданных математических выражений.

Порядок операций

Выполняя какие-либо операции с соответствующими числами, присутствующими в выражении, мы будем следовать данным основным правилам в конкретной последовательности.

Порядок действий Правило 1: Обратите внимание на выражение. Первое правило — решать числа, заключенные в круглые или квадратные скобки. Решаем операции группировки изнутри наружу. Обратите внимание на образец скобок, присутствующий в выражении, существует определенный порядок решения скобок, т.е.е., [{()}]. Сначала решите круглые скобки () → фигурные скобки {} → квадратные скобки []. В скобках следует соблюдать порядок действий.
Порядок операций Правило 2: После решения чисел в круглых скобках найдите любой член, представленный в форме экспонент, и решите его.
Порядок операций Правило 3: Теперь у нас остались четыре основных оператора. Ищите числа с помощью операции умножения или деления, решайте их слева направо.
Порядок операций Правило 4: Наконец, найдите члены со сложением или вычитанием и решите их слева направо.

У этих правил есть конкретное сокращенное название. Мы называем их PEMDAS или BODMAS. Давайте теперь узнаем, что такое PEMDAS или BODMAS.

Порядок операций — PEMDAS против BODMAS

PEMDAS или BODMAS — это два разных акронима, которые используются для изучения правил. Эти два имени указывают порядок, в котором должны выполняться операции в выражении.Вот подробный термин для каждой буквы, используемой в упомянутых акронимах. Сначала мы обсудим PEMDAS.

Порядок работы PEMDAS

P означает круглые скобки (), {}, []
E обозначает экспоненты (a ²) (например, здесь a — это число с показателем степени 2 )
M означает умножение (×)
D обозначает Подразделение (÷)
A означает дополнение (+)
S означает вычитание (-)

Порядок работы BODMAS

B — скобки (), {}, []
O обозначает заказ
D обозначает Подразделение (÷)
M означает умножение (×)
A означает дополнение (+)
S означает вычитание (-)

С помощью приведенных выше обозначений мы можем легко решить математические выражения и получить правильный ответ.

Как использовать порядок операций?

Давайте рассмотрим различные примеры, упомянутые ниже, чтобы понять точность правил, используемых в порядке операций.

1) Для решения скобок в порядке операций :

Выражение: 4 × (5 + 2)
Решение: 4 × ( 7 ) = 28 (Правильно (✔). Это правильный способ решить скобки)
Давайте посмотрим на другой подход к тому же выражению.
4 × ( 5 + 2) = 20 + 2 = 22 (Неверно (✘). Это неправильный способ решения скобок)

2) Для решения показателей в порядке операций

Выражение: 4 × (5 ²)
Решение: 4 × ( 25 ) = 100 (Правильно (✔). Это правильный способ решения показателей)
Давайте посмотрим на другой подход к тому же выражению.
4 × ( 5 ²) = 20 ² = 400 ((Неверно (✘). Это неправильный способ решения экспонент)

3) Для умножения или деления и сложения или вычитания

Выражение: 3 + 5 × 2
Решение: 3 + 5 × 2 = 3 + 10 = 13 (Правильно (✔). Это правильный способ.)
Давайте посмотрим на другой подход к тому же выражению.
3 + 5 × 2 = 8 × 2 = 16 (Неверно (✘). Это неправильный способ.)

Выражение: 3-6 ÷ 2
Решение: 3- 6 ÷ 2 = 3- 3 = 0 (Правильно (✔).Это правильный путь.)
Давайте посмотрим на другой подход к тому же выражению.
3 — 6 ÷ 2 = (-3) ÷ 2 = -3/2 (Неверно (✘). Это неправильный способ.)

Всегда помните, следуя правилам порядка операций, делайте умножение или деление перед сложением или вычитанием

Способы запомнить порядок действий

Мы только что прочитали о двух разных словах PEMDAS и BODMAS. Это лучший способ запомнить порядок действий. PEMDAS можно запомнить по фразе «Прошу прощения, моя дорогая тетя Салли». В порядке операций это означает «круглые скобки, экспоненты, умножение и деление, а также сложение и вычитание». Здесь умножение и деление, сложение и вычитание вместе. Точно так же мы можем запомнить порядок операций со словом BODMAS (скобки, порядки, деление, умножение, сложение и вычитание).

Самый простой способ узнать порядок работы — выполнить следующие шаги:

Начните с упрощения терминов в квадратных скобках
Решите экспоненциальные члены.
Выполните деление или умножение.
Выполните сложение или вычитание.

Примечание: Выполняя порядок операций с любым заданным выражением, мы должны соблюдать шаблон операторов.

Реальные приложения порядка операций

Многие действия в нашей жизни требуют определенного порядка действий для их правильного выполнения. Возьмем повседневную проблему. Предположим, вы пошли купить пять пицц пепперони по 20 долларов каждая и хотите поровну разделить общую стоимость между 5 людьми.Чтобы узнать, сколько должен заплатить каждый человек, воспользуемся порядком действий здесь.

Общее количество человек = 5
Общее количество пицц = 5
Стоимость одной пиццы = 20
$ Обозначим выражение в формате PEMDAS:
Выражение: (20 + 20 + 20 + 20 + 20) ÷ 5 или (5 × 20) ÷ 5
Решение: в соответствии с PEMDAS или BODMAS сначала решим скобки.
(100) ÷ 5 = 20
Согласно порядку операций, каждому человеку нужно заплатить 20 долларов.

Подобно вышеупомянутой проблеме, у нас есть много повседневных реальных случаев, когда мы используем порядок операций для решения наших проблем.

☛Сопутствующие статьи о порядке работы

Ознакомьтесь с интересными статьями ниже и узнайте подробнее о теме Порядок операций и его приложениях.

Часто задаваемые вопросы о порядке работы

Каков порядок операций в математике?

Порядок операций в математике — это набор правил, касающихся 4 основных операторов.В соответствии с порядком операций существует определенная последовательность, которой мы должны следовать для каждого оператора при решении данного математического выражения.

Как решить порядок операций?

Чтобы определить порядок операций, сначала обратите внимание на выражение и обратите внимание, какому образцу оно следует в точности. Теперь начните использовать PEMDAS или BODMAS для решения данного выражения. В соответствии с правилами порядка операций сначала ищите круглые скобки, затем показатели, затем переходите к умножению или делению и сложению или вычитанию слева направо.

Как выполнить порядок операций с целыми числами?

Мы знаем, что целые числа — это положительные и отрицательные числа. Мы можем легко выполнить порядок операций с целыми числами, выполнив следующие шаги:

Найдите целые числа в круглых или квадратных скобках и решите их.
После решения целых чисел в круглых скобках найдите любой целочисленный член в форме экспонент и решите его.
Теперь у нас остались четыре основных оператора, которые нужно выполнить с целыми числами.Найдите целые числа с помощью операции умножения или деления и решите их слева направо.
Наконец, найдите целые числа с помощью сложения или вычитания и решите их.
В случае с целыми числами нам нужно убедиться, что мы правильно умножаем знаки. Такие, что (-) × (-) = + и (+) × (-) = —

Как запомнить порядок операций?

Чтобы запомнить порядок действий, мы используем два известных акронима, т.е.е. ПЕМДАС и БОДМАС. Мы используем любой из двух в соответствии с правилами порядка операций. PEMDAS или BODMAS помогают запомнить процесс решения любого порядка операций для любого числа n выражений.

Как выполнить порядок операций с экспонентами?

Согласно PEMDAS, буква E обозначает показатель степени, который является вторым шагом в порядке операций. Давайте посмотрим на приведенный пример, чтобы наглядно понять, как делать порядок операций с показателями.
Выражение: 7 × (2 ²)
Решение: 7 × ( 4 ) = 28 (Правильно (✔). Это правильный способ решения показателей)
Давайте посмотрим на другой подход к тому же выражению.
7 × ( 2 ²) = 14 ² = 196 ((Неверно (✘). Это неправильный способ выполнения порядка операций с показателями)

Каков правильный порядок действий?

Правильный порядок действий можно легко выразить с помощью слов PEMDAS или BODMAS.Эти два слова можно описать как PEMDAS (круглые скобки, экспоненты, умножение или деление и сложение или вычитание). Аналогично для BODMAS (скобки, порядки, деление, умножение, сложение и вычитание)

Каков порядок операций без скобок?

Следуя правилам порядка операций, если убрать круглые скобки, то останется EMDAS. EMDAS означает (Показатели, Умножение или Деление, Сложение или Вычитание). Если в выражении нет экспоненциального члена, тогда нам нужно сначала выполнить умножение или деление, а затем продолжить сложение или вычитание.Ситуация может варьироваться в зависимости от операторов, присутствующих в данном выражении

Когда мы используем порядок операций?

Многие экземпляры в нашей жизни проходят через какой-то порядок операций, чтобы выполнить это хорошо. Каждый день мы сталкиваемся с таким сценарием. Например, идя на продуктовый рынок и покупая вещи, мы быстро выполняем в голове порядок действий. Это помогает нам сократить время обработки заказа на счетчике выставления счетов.

Какая операция выполняется первой в порядке операций?

В приведенных выше разделах мы читаем о двух акронимах BODMAS и PEMDAS.Согласно обоим аббревиатурам, в порядке операций мы сначала упрощаем скобки или скобки.

Для чего нужен калькулятор порядка работы?

Калькулятор порядка операций — это онлайн-инструмент и самый быстрый метод, с помощью которого мы можем вычислить любое числовое выражение, учитывая правила порядка операций. Чтобы использовать калькулятор порядка работы, нам нужно ввести числовое выражение в правильном формате. Попробуйте калькулятор порядка операций Cuemath и быстро решите выражения за секунды.

☛Также проверьте:

Для большей практики попробуйте эти:

Каковы четыре порядка действий?

Четыре основных порядка операций:

Круглые скобки.
Экспоненциальный член.
Умножение или деление.
В конце сложение или вычитание.

Четыре порядка операций можно легко вызвать в любой момент времени, выучив аббревиатуры PEMD AS или B ODMAS .

Круглые, фигурные и квадратные скобки в математике — стенограмма видео и урока

Порядок операций

Самая основная и распространенная причина использования скобок, скобок и фигурных скобок — контролировать порядок операций. Порядок операций — это метод определения того, какую часть математического выражения выполнить в первую очередь. Возможно, вы слышали такие аббревиатуры, как BEDMAS, PEDMAS или даже PEMDAS. Существует множество версий, но все они имеют одну и ту же цель: сообщить вам, в каком порядке выполнять математические операции.Например, PEMDAS, самая популярная версия в США, означает p arentheses, e xponents, m ultiplication, d ivision, a ddition и s ubtraction. Сначала вы заполняете круглые скобки, затем показатели, затем умножение и так далее. Это важно, потому что, если вы оцениваете выражение в неправильном порядке, вполне возможно, что вы получите неправильный ответ.

Первое в списке — скобки.По правде говоря, первое, что стоит в списке, — это любая комбинация скобок, скобок и фигурных скобок. Когда используются для порядка операций, скобки используются первыми и являются наиболее распространенными. Например, в приведенном ниже выражении вы сначала должны вычислить 5 минус 2, даже если умножение обычно идет первым, если бы не было круглых скобок:

8 * (5-2)

Иногда вам нужно несколько слоев скобок. Вот тогда и можно использовать скобки и скобки. Внутренний слой состоит из скобок, следующий слой состоит из квадратных скобок, а внешний слой состоит из скобок.Это позволяет вам иметь такое сложное выражение:

{4 — [8 * (5-2)] + 3} * 6

В этом случае вы должны сначала вычислить 5 минус 2 (скобки), а затем умножить на 8 (скобки), затем завершите деталь внутри фигурных скобок и, наконец, умножьте на 6.

Массивы и наборы

Есть еще пара ситуаций, в которых вы можете использовать скобки и фигурные скобки.

Скобки используются для записи чего-то, что называется массивом. Массив — это набор чисел, который соответствует определенному шаблону и содержит числа в строках и столбцах.Чаще всего они используются в сложной математике, например, при использовании матриц для анализа векторов в физике. Их также можно использовать в молодом возрасте при обучении умножению впервые: семь, умноженные на четыре, — это всего лишь быстрый способ сосчитать до семи четыре раза подряд. Итак, если вы считаете винные бутылки в коробке, которая имеет семь бутылок в поперечнике и четыре бутылки в глубину, вы можете просто 7 умножить на 4.

Скобки, с другой стороны, можно использовать в наборах и последовательностях. Набор — это набор объектов, которые каким-то образом связаны между собой.Последовательность номеров — это когда набор имеет определенный шаблон, например {1, 2, 3, 4} или {2, 4, 6, 8}. В обычном наборе порядок чисел не имеет значения. В определенной последовательности это так.

Вот и все. Так мы используем круглые, квадратные и фигурные скобки в математике.

Резюме урока

Круглые, квадратные и фигурные скобки — это способы отделения частей математического выражения друг от друга, и все они выглядят очень похоже. Круглые скобки — гладкие и изогнутые (), квадратные скобки, — квадратные [], и фигурные скобки, — фигурные {}.

В математике они в основном используются для определения порядка операций. Сначала вычисляются самые внутренние круглые скобки, за ними следуют скобки, которые образуют следующий слой наружу, а затем скобки, которые образуют третий слой наружу. В круглых, квадратных и фигурных скобках и за их пределами вы следуете обычному порядку операций, изложенному в PEMDAS или других акронимах. Скобки также используются для представления массивов, а фигурные скобки используются в наборах и последовательностях.

Порядок операций — BODMAS

Операции

«Операции» означают такие вещи, как сложение, вычитание, умножение, деление, возведение в квадрат и т. Д.Если это не число, это, вероятно, операция.

Но, когда вы видите что-то вроде …

7 + (6 × 5 ² + 3)

… какую часть нужно рассчитать в первую очередь?

Начать слева и пойти направо?
Или идти справа налево?

Предупреждение: вычисляйте их в неправильном порядке, и вы можете получить неправильный ответ!

Итак, давным-давно люди согласились следовать правилам при расчетах, а это:

Порядок действий

Сначала делайте что-то в скобках

		4 × (5 + 3)	=	4 × 8	=	32
		4 × (5 + 3)	=	20 + 3	=	23	(неверно)

Показатели (степени, корни) перед умножением, делением, сложением или вычитанием

		5 × 2 ²	=	5 × 4	=	20
		5 × 2 ²	=	10 ²	=	100	(неверно)

Умножьте или разделите перед сложением или вычитанием

		2 + 5 × 3	=	2 + 15	=	17
		2 + 5 × 3	=	7 × 3	=	21	(неверно)

В противном случае просто идите слева направо

		30 ÷ 5 × 3	=	6 × 3	=	18
		30 ÷ 5 × 3	=	30 ÷ 15	=	2	(неверно)

Как я все это запомню.

..? БОДМЫ!

Б	B ракетки первые
О	O rders (т. Е. Степени, квадратные корни и т. Д.)
DM	D ivision и M ultiplication (слева направо)
КАК	A ddition и S ubtraction (слева направо)

Разделение и Умножение ранжируются одинаково (и идут слева направо).

Сложить и вычесть ранг одинаково (и идти слева направо)

Так сделай так:

После того, как вы сделали «B» и «O», просто идите слева направо, выполняя любую «D» или «M», как вы их найдете.

Затем идите слева направо, выполняя любую букву «A» или «S», если найдете их.

Примечание: единственное странное название — «Заказы». «Экспоненты» используется в Канаде, поэтому вы можете предпочесть «БЕДМЫ».Также есть «Индексы», что делает его «БИДМАС». В США вместо скобок пишут «круглые скобки», поэтому это «PEMDAS»

Примеры

Пример: как вы работаете

3 + 6 × 2 ?

M ultiplication до A ddition:

Сначала 6 × 2 = 12 , затем 3 + 12 = 15

Пример: как вычислить

(3 + 6) × 2 ?

B первая ракетка:

Сначала (3 + 6) = 9 , затем 9 × 2 = 18

Пример: как вы работаете

12/6 × 3/2 ?

M ultiplication и D ivision ранжируются одинаково, поэтому просто идите слева направо:

Сначала 12/6 = 2 , затем 2 × 3 = 6 , затем 6/2 = 3

Практический пример:

Пример: Сэм бросил мяч прямо вверх со скоростью 20 метров в секунду, как далеко он улетел за 2 секунды?

Сэм использует эту особую формулу, которая включает гравитацию:

высота = скорость × время — (1/2) × 9. 8 × время ²

Сэм устанавливает скорость 20 метров в секунду и время 2 секунды:

высота = 20 × 2 — (1/2) × 9,8 × 2 ²

Теперь о расчетах!

Начать с: 20 × 2 — (1/2) × 9,8 × 2 ²

Кронштейны сначала: 20 × 2 — 0,5 × 9,8 × 2 ²

Then Orders (2 ² = 4): 20 × 2 — 0,5 × 9,8 × 4

Затем умножается: 40-19.6

Вычесть и СДЕЛАНО! 20,4

Мяч достигает 20,4 метра за 2 секунды

Показатели экспоненты …

А как насчет этого примера?

4 ^{3 ²}

Показатели — особые: идут сверху вниз (сначала экспонента сверху). Итак, вычисляем так:

Начать с:		4 ^{3 ²}
3 ² = 3 × 3:		4 ⁹
4 ⁹ = 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4:		262144

Итак 4 ^{3 ²} = 4 ^{(3 ²)}, а не (4 ³) ^²

И, наконец, как насчет примера с самого начала?

Начать с: 7 + (6 × 5 ² + 3)

Кронштейны сначала, а затем «Заказы» : 7 + (6 × 25 + 3)

Затем Умножить : 7 + (150 + 3)

Затем Добавьте : 7 + (153)

Кронштейны в комплекте: 7 + 153

Последняя операция — это Добавить : 160

295, 1565, 1571, 296, 1567, 380, 1569, 3852, 3853, 382

Сначала умножить или сложить? Обучение правилам порядка операций

Что первично в порядке операций?

Со временем математики согласовали набор правил, названный порядком операций , чтобы определить, какую операцию выполнить в первую очередь. Когда выражение включает только четыре основных операции, вот правила:

Умножайте и делите слева направо.
Сложить и вычесть слева направо.

При упрощении выражения, такого как \ (12 \ div 4 + 5 \ times 3-6 \), сначала вычислите \ (12 \ div 4 \), поскольку порядок операций требует сначала оценки любого умножения и деления (в зависимости от того, что произойдет первый) слева направо перед вычислением сложения или вычитания. В данном случае это означает сначала вычисление \ (12 \ div 4 \), а затем \ (5 \ times 3 \).После того, как все умножение и деление будут завершены, продолжайте, добавляя или вычитая (в зависимости от того, что наступит раньше) слева направо. Шаги показаны ниже.

\ (12 \ div 4 + 5 \ times 3-6 \)
\ (3 + 5 \ times 3-6 \)	Потому что \ (12 \ div 4 = 3 \)
\ (3 + 15-6 \)	Потому что \ (5 \ times 3 = 15 \)
\ (18-6 \)	Потому что \ (3 + 15 = 18 \)
\ (12 \)	Потому что \ (18-6 = 12 \)

Рассмотрим в качестве примера другое выражение:

\ (6 + 4 \ times 7-3 \)
\ (6 + 28-3 \)	Потому что \ (4 \ times 7 = 28 \), что выполняется первым, потому что умножение и деление оцениваются в первую очередь.
\ (34-3 \)	Потому что \ (6 + 28 = 34 \)
\ (31 \)	Потому что \ (34-3 = 31 \)

Иногда мы можем захотеть убедиться, что сначала выполняется сложение или вычитание. Группировка символов , таких как круглых скобок \ (() \), скобок \ ([] \) или фигурных скобок \ (\ {\} \), позволяет нам определить порядок, в котором выполняются определенные операции. выполненный.

Порядок операций требует, чтобы операции внутри символов группировки выполнялись перед операциями вне их.Например, предположим, что выражение 6 + 4 заключено в круглые скобки:

\ ((6 + 4) \ times 7-3 \)
\ (10 \ times 7-3 \)	Потому что \ (6 + 4 = 10 \), что и сделано во-первых, потому что он заключен в круглые скобки.
\ (70 — 3 \)	Потому что \ (10 \ times 7 = 70 \), и скобок больше нет.
\ (67 \)	Потому что \ (70-3 = 67 \)

Обратите внимание, что выражение имеет совершенно другое значение! Что, если вместо этого мы заключим \ (7 — 3 \) в круглые скобки?

\ (6 + 4 \ times (7-3) \)
\ (6 + 4 \ times 4 \)	На этот раз \ (7-3 \) находится в скобках, так что мы делаем это в первую очередь.
\ (6 + 16 \)	Поскольку \ (4 \ times 4 = 16 \) и когда скобок не осталось, мы продолжаем умножение перед сложением.
\ (22 \)	Потому что \ (6 + 16 = 22 \)

Этот набор скобок дает еще один ответ. Итак, когда используются круглые скобки, правила для порядка операций следующие:

Выполнять операции в скобках или группировать символы.
Умножайте и делите слева направо.
Сложить и вычесть слева направо.

PEMDAS — Незабываемое сокращение | Студенческая жизнь

Пейдж Фабер, партнер ACDC

Помните, в седьмом классе вы обсуждали порядок операций в классе математики, и учитель сказал вам запоминающееся сокращение «PEMDAS» (скобки, показатели, умножение, деление, сложение, вычитание), чтобы помочь вам запомнить? Запоминающиеся сокращения — не единственный способ запоминать концепции. Вот несколько способов помочь вам в изучении курсовой работы.

Сделайте карточки или викторины

Запись информации поможет вам запомнить ее, так что сделайте несколько карточек! Карточки — это простой и быстрый способ проверить свои знания по теме. Цифровым эквивалентом карточек будет Quizlet. Кроме того, в Quizlet есть не только карточки, но и тесты и игры для запоминания. Вы можете создать учетную запись Quizlet на этом веб-сайте.

Сделайте сокращения или фразы

Если вы изобретательны в словах, попробуйте сделать аббревиатуру из первых букв ваших важных понятий, например, PEMDAS в математике (круглые скобки, экспоненты, умножение, деление, сложение, вычитание).Если аббревиатура вам не подходит, попробуйте составить фразу, например, четыре P маркетинга (продукт, цена, размещение, продвижение).

Попробуй

Ничто так не укоренилось в головах людей, как запоминающийся джингл или песня. Чтобы вам было легче запоминать, поставьте тему изучения на мелодию вашей любимой песни. Возможно, вам будет сложно запомнить пародию на всю песню (если вы не Майли Стюарт из Hannah Montana ), поэтому постарайтесь просто спеть припев песни.Эта тактика запоминания удобна тем, что ее можно практиковать из любого места в любое время.

Создание движений

Кинестетические ученики в мире могли бы лучше запоминать курсовую работу, если бы они сочетали часть информации с физическим движением. Эта тактика задействует разум и тело, что позволяет использовать два разных способа запоминания. Примерами движений могут быть простой жест рукой или движение руки.

Если вы попросите партнера или группу по изучению запоминания вместе с этими приемами, вы также сможете усвоить материал.

Вопросы? Свяжитесь с нами по телефону 402.554.3672 или посетите наш веб-сайт.

Математическое уравнение, которое попыталось поставить в тупик Интернет

Подробнее о математике в The Times от Стивена Строгаца

Чтобы помочь учащимся в США запомнить этот порядок операций, учителя вставляют в них аббревиатуру PEMDAS: скобки, показатели, умножение, деление, сложение, вычитание. Другие учителя используют эквивалентную аббревиатуру BODMAS: скобки, порядки, деление и умножение, а также сложение и вычитание.Третьи советуют своим ученикам запомнить маленькую частушку: «Прошу прощения, моя дорогая тетя Салли».

[ Эта математическая задача — не первый раз, когда Интернет разделился. Помните Янни и Лорел? Как насчет цвет этого платья ? ]

А теперь поймите, что следование за тетей Салли — это чисто условный вопрос. В этом смысле PEMDAS произвольна. Более того, по моему опыту математика, выражения вроде 8 ÷ 2 × 4 выглядят абсурдно надуманными.Ни один профессиональный математик никогда не написал бы что-то столь явно неоднозначное. Мы бы вставили круглые скобки, чтобы обозначить наше значение и указать, следует ли сначала выполнить деление или умножение.

В последний раз, когда это появилось в Твиттере, я отреагировал возмущенно: казалось смешным, что мы тратим так много времени в школьной программе на такую софизму. Но теперь, будучи просветленным некоторыми из моих компьютерных друзей в Твиттере, я пришел к пониманию того, что условности важны и от них могут зависеть жизни.Мы знаем это всякий раз, когда выезжаем на шоссе. Если все остальные едут по правой стороне дороги (как в США), вам будет разумно последовать их примеру. То же самое, если все остальные едут слева, как в Соединенном Королевстве. Неважно, какая конвенция будет принята, если все ее соблюдают.

Точно так же важно, чтобы каждый, кто пишет программное обеспечение для компьютеров, электронных таблиц и калькуляторов, знал правила порядка операций и следовал им. Для остальных из нас сложности PEMDAS менее важны, чем более крупный урок о том, что условности имеют свое место.Это двойная желтая линия по центру дороги — бесконечный знак равенства — и общее соглашение о понимании друг друга, совместной работе и избежании лобовых столкновений. В конечном счете, 8 ÷ 2 (2 + 2) — это не столько утверждение, сколько кирпичная кладка; это все равно что написать фразу «ест побеги и листья» и прийти к выводу, что язык капризен.

Урок 2. числовые выражения. порядок выполнения действий. сложение нескольких слагаемых — Математика — 4 класс

ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ Урок математики 4 класс

Как решать примеры со скобками порядок действий. Порядок выполнения действий, правила, примеры

Первый способ

Второй способ

Порядок действий и возведение в степень

Порядок выполнения действий, правила, примеры.

Сначала умножение и деление, затем сложение и вычитание

Действия первой и второй ступени

Порядок выполнения арифметических действий в выражениях со скобками

Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями

Онлайн игры,тренажеры,презентации,уроки,энциклопедии,статьи

Post navigation

Примеры со скобками, урок с тренажерами.

1) Примеры со скобками в пределах до 20.

2) Примеры со скобками в пределах до 100. Онлайн тренажер.

3) Примеры со скобками. Тренажер №2

4) Вставь пропущенное число — примеры со скобками. Тренажер

1.

2. Тренажер по математике 2 — 3 класс «Расставь порядок действий (буквенные выражения).»

Порядок действий в математике 4 класс

Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:

Решение примеров со скобками

Урок по математике 2 класс Порядок действий в выражениях со скобками.

1) Примеры со скобками в пределах до 20. Онлайн тренажер.

2) Примеры со скобками в пределах до 100. Онлайн тренажер.

3) Примеры со скобками. Тренажер №2

4) Вставь пропущенное число — примеры со скобками.

Что такое действия первой и второй ступени

Порядок вычислений в выражениях со скобками

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Страница 27 — ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 1

Вопрос

Ответ

Вопрос

Подсказка

Ответ

Вопрос

Подсказка

Ответ

Вопрос

Ответ

Вопрос

Подсказка

Ответ

Вопрос

Подсказка

Ответ

Вопрос

Ответ

Вопрос

Подсказка

Ответ

Вопрос

Ответ

Вопрос

Подсказка

Ответ

Порядок действий

Задания для самостоятельного решения

Навигация по записям

Порядок выполнения математических действий | интернет проект BeginnerSchool.

Урок 2.

Порядок действий: PEMDAS

Purplemath

MathHelp.com

Упростить 4 + [–1 (–2 — 1)]

Упростить 4 (

Порядок операций — определение, правила, примеры, проблемы

Каков порядок действий?

Определение порядка операций

Порядок операций

Порядок операций — PEMDAS против BODMAS

Порядок работы PEMDAS

Порядок работы BODMAS

Как использовать порядок операций?

Способы запомнить порядок действий

Реальные приложения порядка операций

Часто задаваемые вопросы о порядке работы

Каков порядок операций в математике?