Задачи на проценты математика: Как решать задачи с процентами? Примеры Решений Задач

Проценты. Задачи на проценты: нахождение процента от величины и величины по её проценту. Математика, 5 класс: уроки, тесты, задания.

1.	Проценты как несократимая дробь Сложность: среднее	2
2.	Проценты как десятичная дробь Сложность: лёгкое	1
3.	Проценты в виде десятичной дроби (сотни) Сложность: лёгкое	1
4.	Проценты в виде десятичной дроби (десятичная дробь) Сложность: лёгкое	1
5.	Десятичные дроби в виде процентов (тысячные) Сложность: лёгкое	1
6.	Десятичные дроби в виде процентов (сотые) Сложность: лёгкое	2
7.	Десятичная дробь как проценты Сложность: среднее	2
8.	Обыкновенная дробь в виде процентов Сложность: среднее	1
9.	Нахождение процентов от данного числа Сложность: среднее	2
10.	Нахождение числа по его процентам (десятичная дробь) Сложность: среднее	2
11.	Проценты и прямоугольник Сложность: среднее	2
12.	Проценты от величины, тысячи Сложность: среднее	2
13.	Сравнение процентов и дроби (переход к процентам) Сложность: среднее	2
14.	Покупка для засолки Сложность: среднее	2
15.	Себестоимость детали Сложность: среднее	2
16.	Количество страниц в книге Сложность: среднее	2
17.	Количество девочек в школе Сложность: среднее	2
18.	Мука из пшеницы Сложность: сложное	4
19.	Части прямого угла Сложность: сложное	3
20.	Участок прямоугольной формы Сложность: сложное	6

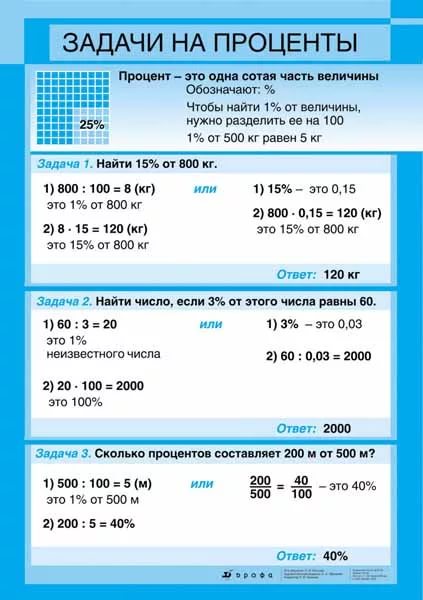
Решение задач на проценты.

Решение задач по теме проценты.

Решение задач на проценты

Задача 1. Найди какой процент числа \(80\) от \(160\)?

 

Решение:

 

\(\frac{80}{160}* 100=50\%\)

Ответ: \(50\%\).

Процент: увеличение и  уменьшение

Когда число увеличивается до другого числа, то сумма увеличения вычисляется по формуле:

 

 \(Увеличение = новое \quadчисло-старое \quadчисло \)

 

Когда число уменьшается до другого числа, то  сумма уменьшения задается как:

 

  \(Уменьшение = старое \quadчисло-новое \quadчисло \)

 

Процент увеличения или уменьшения числа всегда выражается на основании старого числа.

 

 

 \( Увеличение = 100\frac{ новое \quadчисло-старое \quadЧисло} {старое \quad число}\)

\( Уменьшение = 100\frac{ старое \quadчисло-новое \quadЧисло} {старое \quad число}\)

 

Задача 2.  У вас есть \(80 \) почтовых марок, и вы начинаете собирать больше в течение этого месяца до тех  пока общее количество марок не достигнет 120. Процент увеличения количества марок, которые у вас есть в настоящее время:

Решение:

 

\(\frac{120-80}{80}×100=50\%\)

Ответ: \(50\%\).

Задача 3. У тебя  120 марок. Некоторые из них ты отдал другу в обмен на игру Lego , так что осталось 100 марок. Чему в этом случае равно процентное уменьшение. 

Решение:

 

\(\frac{120-100}{120}*100\)\(=\frac{20}{120}*100=16,67\%\)

Ответ: \(16,67\%\).

Задача 4. Сергей начал  бизнес в сфере торговли. В первый месяц он купил продукты за \(650$\) и продал их за \(800$\), а во второй месяц он купил за \(800$\) и продал за \(1200$\). Сколько  получил  прибыли Сергей.

 

Решение:

Мы не можем сразу сказать  увеличивается ли прибыль Сергея или нет, так как количество его расходов и прибыли отличаются каждый месяц. Для того, чтобы решить эту задачу, мы нужно отнести все значения к фиксированному базовому значению, которое составляет \(100\).   Выразим процент  прибыли относительно  расходов Сергея за первый месяц:

\( \frac{800\: -\: 650} { 650} *100 = 23,08\%\)

 

Это означает, что, если бы Сергей потратил \(100$\), он бы получил прибыль \(23,08\%\) за первый месяц.

 

Теперь расчитаем прибыль за второй месяц:

 

\(\frac{1200 — 800} {800} *100 = 50\%\)

 

Итак, на второй месяц, если бы Сергей потратил \(100$\), он получил бы прибыль в \(50$\). Теперь ясно, что прибыль Сергея растет.

 

---

Задача 5. Райан любит собирать крышки от coca-cola. Он собрал 32  крышки от fanta, 25 крышек от sprite и 47 крышек от  cola. Каков процент от общего количества крышек?

 

Решение:

1. \(32 + 25 + 47 = 104\) — общее количество 
2. \(\frac{32}{104} * 100 = 30,8\%\) —  крышки от fanta
3. \(\frac{25}{104} *100 = 24\%\)  — крышки от sprite
4. \(\frac{47}{104} *100 = 45.2\%\) — крышки от  cola

Задача 6. У тебя была математическая викторина на уроке. В викторине было \(5\) вопросов; три из них по \(3\) бала, а два  по \(4\) бала . Вам удалось правильно решить \(2\) вопроса по \(3\) бала и один вопрос с 4 баллами. Каков процент оценок, которые вы получили в этой викторине?

 

Решение:

1. \(3*3 + 2х4 = 17-\)общая оценки
2. \(2*3 + 4 = 10-\)количество баллов за правильные ответы
3. \(3*3 + 2*4 = 17-\) максимальное количество баллов
4. \(\frac{10}{17} *100 = 58,8\%-\)процент полученных баллов

 

 

 

 

Сложные задачи на проценты | Шевкин.Ru

25.04.2017

Задачи этого раздела являются необязательными для всех учащихся, среди них есть действительно сложные задачи, но есть и такие, в которых всем учащимся разобраться полезно. Это задачи на так называемые сложные проценты — проценты начисляемые на процентные деньги. Первая задача этого раздела была дана на олимпиаде Малого мехмата МГУ для семиклассников в 1991 году. Шутливое отражение в ней политических страстей того времени не должно отвлечь учащихся от важного вопроса: что получится, если число сначала увеличить, а потом уменьшить на 50 % (на одно и то же число процентов). Полученный здесь опыт поможет решить и другие олимпиадные задачи.

344.* В начале года винтики, шпунтики и гаечки продавались по одинаковой цене 1 р. за 1 кг. 30 февраля Верховный Совет СССР принял закон о повышении цен на винтики на 50 % и снижению цен на шпунтики на 50 %. 31 февраля Верховный Совет РСФСР принял закон о снижении цен на винтики на 50 % и повышению цен на шпунтики на 50 %. Какой товар будет самым дорогим и какой самым дешевым в марте?

Ошибочное решение задачи 345 нетрудно предвидеть: учащиеся сложат проценты от разных величин.

345. * 1) Число увеличили на 10 %, потом еще на 10 %. На сколько процентов увеличили число за два раза?

2) Число увеличили на 10 %, результат уменьшили на 10 %. Какое получилось число — большее или меньшее первоначального? На сколько процентов?

346.* Вася прочитал в газете, что за последние 3 месяца цены на продукты питания росли в среднем на 10 % за каждый месяц. На сколько процентов выросли цены за 3 месяца?

347.* Женя за весну похудел на 20 %, потом поправился за лето на 30 %, за осень опять похудел на 20 % и за зиму прибавил в весе 10 %. Остался ли за этот год его вес прежним?

Если Женя весил x кг, то после уменьшения веса на 20 % он стал весить 0,8x кг, а после увеличения веса на 30 % – 0,8x·1,3 кг и т. д., в итоге Женя весил 0,8x·1,3·0,8·1,1 или 0,9152x кг, что меньше x кг. Значит, Женя похудел.

348.* Две противоположные стороны прямоугольника увеличили на 10 %. На сколько процентов увеличилась его площадь? Зависит ли результат от того, какую пару сторон увеличили на 10 %?

349.* Все стороны прямоугольника увеличили на 10 %. На сколько процентов увеличилась его площадь?

350.* Каждую сторону квадрата увеличили на 20 %. На сколько процентов увеличилась его площадь?

351.* Две противоположные стороны прямоугольника увеличили на 20 %, две другие — уменьшили на 20 %. Как изменилась площадь прямоугольника?

352.* Две противоположные стороны прямоугольника увеличили на 20 %, две другие — уменьшили на 10 %. На сколько процентов увеличилась площадь прямоугольника?

353.* Длину прямоугольника уменьшили на 20 %. На сколько процентов надо увеличить ширину прямоугольника, чтобы его площадь не изменилась?

354.* Магазин продал на прошлой неделе некоторый товар. На этой неделе запланировано продать того же товара на 10 % меньше, но по цене на 10 % больше. Большую или меньшую сумму выручит магазин от продажи товара на этой неделе и на сколько процентов?

355.* На некотором участке пути машинист уменьшил скорость поезда на 25 %. На сколько процентов увеличится время движения на этом участке?

356.* Арбуз массой 20 кг содержал 99 % воды. Когда он немного усох, содержание воды в нем уменьшилось до 98 %. Какова теперь масса арбуза?

На первый взгляд кажется, что масса арбуза мало изменилась, но это на первый взгляд! Масса «сухого вещества» арбуза составляла 100 – 99 = 1 (%). Это 20·0,01 = 0,2 кг. После усушки его масса составляла уже 100 – 98 = 2 (%). То есть те же самые 0,2 кг составляют 2 % от новой массы арбуза. Найдем эту новую массу: 0,2:0,02 = 10 (кг).

Интересная переформулировка этой известной задачи встретилась недавно на олимпиаде.

357.* Некий леспромхоз решил вырубить сосновый лес, но экологи запротестовали. Тогда директор леспромхоза всех успокоил, сказав: «В нашем лесу 99% сосны. После рубки сосна будет составлять 98% всех деревьев». Какую часть леса может вырубить леспромхоз?

Если бы экологи хорошо знали проценты, то они смогли бы возразить предприимчивому директору леспромхоза, планирующему вырубить как минимум половину леса – это при условии, что вырубать будут только сосны. Если же топор коснется и других деревьев, то от соснового леса можно оставить меньше половины. Ведь удовлетворить условию задачи можно, оставив в лесу 50 деревьев: 49 сосен и 1 березу.

358.* а) Яблоки, содержащие 70 % воды, потеряли при сушке 60 % своей массы. Сколько процентов воды содержат сушеные яблоки?

б) Груши, содержащие 65 % воды, потеряли при сушке 50 % своей массы. Сколько процентов воды содержат сушеные груши?

Объясняя решение задачи 358 (а), воспользуемся следующей иллюстрацией.

Вода составляла 70 % массы яблок, 60 из них испарилось, а 10 осталось. Теперь 10 частей воды приходится на 30 частей «сухого вещества» яблок или на 40 частей массы сушеных яблок. Масса воды составляет 10:40 = 0,25, или 25 % массы сушеных яблок?

359.* а) Сколько граммов воды нужно добавить к 600 г раствора, содержащего 15 % соли, чтобы получить 10%-й раствор соли?

б) Сколько граммов воды нужно добавить к 120 г раствора, содержащего 30 % сахара, чтобы получить раствор, содержащий 20 % сахара?

360.* На коробке вермишели написано: «Масса нетто 500 г при влажности 13 %». Какова масса вермишели, если она хранится при влажности 25 %?

361.* Для получения томат-пасты протертую массу томатов выпаривают в специальных машинах. Сколько томат-пасты, содержащей 30 % воды, получится из 28 т протертой массы томатов, содержащей 95 % воды?

362.* Из 40 т руды выплавили 20 т металла, содержащего 6 % примесей. Сколько процентов примесей в руде?

363.* Свежие фрукты содержат 72 % воды, а сухие — 20 %. Сколько сухих фруктов получится из
40 кг свежих?

364.* До сушки влажность зерна составляла 23 %, а после сушки составила 12 %. Сколько процентов массы теряет зерно при сушке?

365.* В драмкружке число мальчиков составляет 80 % от числа девочек. Сколько процентов составляет число девочек от числа мальчиков в этом кружке?

I способ. Число мальчиков составляют 80 % от числа девочек (100 %). Определим, сколько процентовсоставляют 100 % от 80 % :

¹⁰⁰/₈₀ = ^100×100/₈₀ % = 125 %.

II способ. Число мальчиков (m) составляют 80 % от числа девочек (d), значит, m = 0,8d. Отсюда d = 1,25m, то есть число девочек составляет 125 % от числа мальчиков.

III способ. На 10 девочек приходится 8 мальчиков, число девочек составляет ¹⁰/₈  или 125 %  от числа мальчиков.

366. С 1 октября 1993 г. за хранение денег на срочном депозите в течение года Сбербанк выплачивал доход из расчета 150% от вложенной суммы; в течение полугода — 130% годовых, в течение трех месяцев — 120 % годовых. Каким образом за год на условиях Сбербанка можно было получитьнаибольший доход на 100 000 р.? Каков этот наибольший доход?

На первый взгляд самое выгодное вложение денег на год — под 150 % годовых (через год сумма обратится в 100·2,5 = 250 тыс. р.). Но это только на первый взгляд! Давайте для сравнения положим деньги на полгода, а через полгода получим их обратно с доходом 130:2 =
= 65 (%) от вложенной суммы. Затем все полученные деньги положим еще на полгода. Таким образом через год мы получим:

100·1,65·1,65 = 272,25 (тыс. р.).

Это несколько больше полученной ранее суммы. Попросите учащихся провести расчеты для третьего случая. Пусть они убедятся, что знание процентов может быть полезным при выборе более выгодного способа вложения денег.

367.* Компания X выплачивает доход по своим акциям ежегодно из расчета 140 % годовых. Компания Y выплачивает доход по акциям 1 раз в полгода из того же расчета. В акции какой компании выгоднее вложить деньги на 1 год?

368.* Производительность труда повысили на 25 %. На сколько процентов уменьшится время выполнения задания.

369.* Если при повышении производительности труда рабочего на 10 % повысить его зарплату на 6,7 %, то это позволит снизить расход на оплату труда в расчете на единицу продукции на 3 %. Проверьте это.

370.* Рабочий повысил производительность труда на 15 %, а его зарплата увеличилась на 10,4 %. На сколько процентов уменьшился расход на оплату труда в расчете на единицу продукции?

371.* Купили конфеты и печенье. За 1 кг конфет заплатили на 50 % больше, чем за 1 кг печенья, но их купили на 50 % меньше, чем печенья. За что заплатили больше?

372. * Кусок сплава весом 700 г, содержащий 80 % олова, сплавили с куском олова весом 300 г. Определите процентное содержание олова в полученном сплаве.

373.* Имеется 500 г 40 %-го раствора кислоты. Сколько воды требуется добавить, чтобы получить 25 %-й раствор кислоты?

374.* В первый день рабочий перевыполнил дневное задание на 2 %, во второй день он перевыполнил дневное задание на 4 %. На сколько процентов рабочий перевыполнил задание двух дней?

375.* В автоинспекции города N подсчитали, что число легковых автомобилей увеличивалось в последние годы на 15 % ежегодно. Во сколько раз увеличится число легковых автомобилей за пять лет, если эта тенденция сохранится?

376.* Деньги, вложенные в акции известной фирмы, приносят ежегодно 20 % дохода. За сколько летвложенная сумма удвоится?

377. * В спортивной секции девочки составляют 60 % числа мальчиков. Сколько процентов числа всех участников секции составляют девочки?

Если число мальчиков принять за 100 %, то число девочек от него составляет 60 %, а число всех участников секции 160 % от числа мальчиков. 60 % от 160 % составляет ^60×100/₁₆₀ = 37,5 (%). Но понять это решение из-за нагромождения процентов нелегко. Если же число мальчиков обозначитьбуквой x, то те же самые действия легче объяснить и понять. Итак, число девочек равно 0,6x, а число всех участников секции x + 0,6x = 1,6x. Определим, сколько процентов от 1,6х составляет число 0,6х:

^0,6x×100/_1,6x = 37,5 (%).

378. В некотором царстве, в некотором государстве пятиклас­сники стали изучать математику не 6, а 5 уроков в неделю. Кроме того, урок у них стал длиться не 45, а 40 минут. Сколько процентов учебного времени потеряли пятиклассники? Ответ округлите до десятых.

Эту задачу могли бы решить учителя математики всего несколько лет назад, чтобы объяснить себе катастрофическую нехватку времени, которая стала ощущаться в связи с указанными в условии задачи нововведениями.

Учебное время теперь составляет ⁵/₆×⁴⁰/₄₅ = ²⁰/₂₇ от прежнего. Потеря составила 1 – ²⁰/₂₇ = 
=  ⁷/₂₇ = 0,2592…, или примерно 25,9 %.

379.* а) Торговец продал книгу со скидкой 5 % от назначенной цены и получил 14 % прибыли. Сколько процентов прибыли планировал получить торговец при продаже книги?

б) Торговец продал товар, имевший небольшой дефект, уступив покупателю 30 % от назначенной цены. При этом он имел 16 % убытка. Какой процент прибыли планировал получить торговец при продаже товара?

Рассмотрим решение первой задачи. Пусть торговец планировал продать книгу за a р., тогда он продал ее за (1 – 0,05)a = 0,95a р. Эта сумма составила 100 + 14 = 114 (%) цены, по которой торговец сам купил книгу и которая составляла ^0,95а/_1,14 = ⁵/₆ а р. Подсчитаем доход, который планировал получить торговец (в процентах): 

a: ⁵/₆ a ·100 = 120 (%).

Торговец планировал получить 120 – 100 = 20 % дохода.

Алгебра: проблемы с процентами

Проблемы с процентами

Есть три веские причины положить свои сбережения на банковский счет, а не прятать их в шкафу или матрасе:

1. В банке безопаснее, и если ваши деньги украдут , обычно существуют федеральные законы, которые страхуют ваши инвестиции.
2. Банк предоставляет вам уникальную возможность писать ручками, прикованными к столу. Несмотря на то, что ваши деньги позволяют банкам самим загребать деньги, по какой-то причине они очень непреклонны, чтобы вы случайно не взяли их ручки, каждая из которых стоит всего гроши.
3. Вы зарабатываете проценты на свои деньги вообще без каких-либо усилий.

Talk the Talk

Сумма денег, которую вы изначально вкладываете в процентную ставку, называется основной суммой .

Интерес — это здорово. Это бесплатные деньги, которые вы зарабатываете, просто храня деньги в надежном месте. В алгебре вас могут попросить решить задачи, в которых вы вычисляете проценты, полученные от некоторых первоначальных инвестиций (которые называются основной суммой ) за некоторый промежуток времени.В частности, вас могут попросить решить два основных типа проблем с процентами: простые проценты и сложные проценты.

Простые проценты

Если ваши деньги растут в соответствии с простыми процентами, вы в основном зарабатываете небольшой процент от своих первоначальных инвестиций каждый год в виде процентов. Например, если основная сумма счета составляет 100 долларов США, а ваша годовая процентная ставка составляет 6,75%, в конце каждого года вы заработаете дополнительно 6,75 доллара США (поскольку 6,75 доллара США равны 6.75% от 100 долларов).

Вот и плохая новость: даже если ваш счет будет немного расти с каждым годом, вы не будете зарабатывать больше процентов! При простых проблемах с процентами вы получаете проценты только на первоначальные инвестиции, независимо от того, как долго у вас был активный банковский счет или сколько процентов были начислены на эти деньги.

Формула для расчета простых процентов:

, где p — ваша основная сумма, r — годовая процентная ставка, выраженная в десятичной дроби, а i — это проценты, которые вы заработали после того, как деньги были инвестированы в т. гг.

Пример 1 : Вы были очень экономным и экономным ребенком. Вместо того, чтобы тратить деньги, которые зубная фея дала вам на молочные зубы, вы в подростковом возрасте вложили эти деньги единовременно в размере 32 долларов США на банковский счет с фиксированной годовой процентной ставкой 7,75%. Каков остаток на счете ровно 30 лет спустя?

Критическая точка

Чтобы преобразовать процент в десятичную дробь, отбросьте знак процента и умножьте его на 0,01. Например, десятичный эквивалент 6.75% равно (6,75) (0,01) = 0,0675. (И наоборот, чтобы преобразовать десятичную дробь в процент, умножьте ее на 100 и приклейте знак процента в конце. Следовательно, процентный эквивалент 0,45 равен (0,45) (100) = 45%.)

Решение : Чтобы рассчитать баланс счета, просто добавьте проценты, которые вы заработали, к основной сумме. Конечно, вам все еще нужно понять, что это за интерес. Используйте формулу i = prt , где p = 32, r = 0,0775 (десятичный эквивалент 7,75%) и t = 30.

• i = prt
• i = (32) (. 0775) (30)
• i = 74,4

Вы заработали 74,40 доллара США в виде процентов за этот 30-летний период, поэтому, если вы добавите при первоначальных инвестициях ваш общий баланс составляет:

• остаток = основная сумма + полученные проценты
• = 32 доллара + 74,40 доллара
• = 106,40 доллара

Сложные проценты

Большинство банков не используют простые проценты; чем больше денег вы вкладываете, тем больше денег они потенциально могут заработать, поэтому они хотят побудить вас внести как можно больше на свой счет.Один из способов сделать это — использовать сложных процентов , в которых вы зарабатываете деньги на основе вашей первоначальной основной суммы и процентов, которые вы накопили к этому моменту.

Talk the Talk

Если на ваш банковский счет начисляются сложных процентов , то вы получаете проценты на основе всего вашего баланса, а не только начальных инвестиций.

Допустим, вы вносите 100 долларов на счет, на который ежегодно начисляются проценты по ставке 6,0%. В конце первого года у вас будет баланс в размере 106 долларов, как и с простыми процентами.Однако в конце второго года вы заработаете 6,0% процентов от нового баланса в размере 106 долларов, а не только от первоначального баланса в 100 долларов.

Еще лучше то, что большинство банков не увеличивают проценты раз в год. Суммируются ли они еженедельно (52 раза в год), ежемесячно (12 раз в год) или ежеквартально (4 раза в год), может иметь большое значение для вашей чистой прибыли.

Формула расчета сложных процентов немного сложнее простых процентов; это выглядит так:

Critical Point

Чем больше будет начисляться процент на вашем счете, тем больше денег вы заработаете.Наилучшим возможным сценарием было бы непрерывное начисление процентов, которое составляет бесконечное количество раз. Подобные вещи возможны; фактически, вы научитесь делать это в предварительном исчислении.

Предостережения Келли

Обратите внимание, что формула сложных процентов дает вам общий остаток , тогда как формула простых процентов дает вам проценты , только вам нужно было добавить основную сумму к процентам в Примере 1, чтобы рассчитать простой процент. остаток средств.

В этой формуле p — это основная инвестиция, r — это еще раз годовая процентная ставка в десятичной форме, n — количество раз, когда проценты начисляются за один год, а b — это остаток. на вашем счете по прошествии ровно t лет.

Пример 2 : Сколько больше денег вы заработали бы, если бы вложили 3000 долларов на сберегательный счет, годовая процентная ставка которого 6,25% начислялась ежемесячно, а не ежеквартально, если вы планировали оставить деньги в покое на 18 месяцев? (Чтобы наши ответы были единообразными, округлите все десятичные дроби до семи десятичных знаков при вычислении. )

Решение : вам нужно будет рассчитать два отдельных баланса: один с n = 12 для ежемесячного начисления сложных процентов и один с n = 4 для квартальных процентов. Остальные переменные будут соответствовать обеим задачам: p = 3000, r = 0,0625 и t = 1,5. Будь осторожен! Переменная t должна измерять годы, а не месяцы; поскольку 18 месяцев — это ровно полтора года, t = 1,5, а не 18.

Предостережения Келли

Как в простых, так и в сложных задачах с процентами t должны измеряться годами.Следовательно, если ваши инвестиции приносят проценты в течение 24 месяцев, t = 2, а не 24, поскольку 24 месяца равны двум годам.

Рассчитайте остаток, если начисляете ежемесячно.

• = 3000 (1 + .0052083) ¹⁸
• = 3000 (1.0980173)
• = 3294,0519

Поскольку банки не присуждают доли пенни, ваш окончательный ответ должен содержать только 2 десятичных знака: 3294,05 доллара . Теперь рассчитайте баланс, если проценты начисляются только ежеквартально.

• 3000 (1 + 0,015625) ⁶
• 3000 (1.0974893)
• = 3292,4679

На этот раз ваш баланс составляет 3292,47 доллара США. Вычтите два остатка, чтобы найти общую разницу: 3294,05 доллара — 3292,47 доллара = 1,58 доллара. Конечно, 1,58 доллара — это не большая разница, но чем больше сумма основного долга и чем дольше вы оставляете деньги, тем больше эта разница будет расти.

У вас проблемы

Задача 1. Рассчитайте остаток на счете, если его основная сумма в 5000 долларов приносит:

(a) Простые проценты по годовой процентной ставке 8.25% на 20 лет.

(b) Начисление процентов еженедельно ( n = 52) по годовой процентной ставке 8,25% в течение 20 лет.

При необходимости округлите десятичные дроби до 7 знаков при расчетах.

Выдержки из Полное руководство для идиотов по алгебре 2004 У. Майкла Келли. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.

Вы можете приобрести эту книгу на Amazon.com и Barnes & Noble.

Какое уравнение использовать? — Математика для нашего мира

Какую формулу использовать?

Теперь, когда мы изучили основные используемые виды финансовых расчетов, не всегда может быть очевидно, какой из них использовать, когда вам нужно решить проблему. Вот несколько советов по выбору уравнения, основанного на формулировке задачи.

Кредиты

Самый простой тип проблем — это ссуды. Проблемы ссуды почти всегда включают такие слова, как ссуды , амортизировать (причудливое слово для ссуд), финансы (т.е. автомобиль), или ипотека (жилищный заем). Ищите такие слова, как ежемесячный или годовой платеж.

Формула ссуды предполагает, что вы производите платежи по ссуде по регулярному графику (каждый месяц, год, квартал и т. Д.) И платите проценты по ссуде.

Формула ссуды

• P ₀ — это остаток на счете в начале (основная сумма или сумма ссуды).
• d — ваш платеж по кредиту (ежемесячный платеж, годовой платеж и т. Д.)
• r — годовая процентная ставка в десятичной форме.
• k — количество периодов начисления сложных процентов в году.
• N — срок кредита в годах.

Счета с процентным доходом

Счета, на которые начисляются проценты, делятся на две основные категории. Первый — это когда вы один раз кладете деньги на счет и позволяете им оставаться, а второй — когда вы делаете регулярные платежи или снимаете деньги со счета, как на пенсионном счете.

Проценты

• Если вы позволяете деньгам оставаться на счете, а только проценты меняют баланс, то перед вами задача сложных процентов .Ищите такие слова, как составные или APY. Сложные проценты предполагают, что вы кладете деньги на счет один раз и позволяете им оставаться там, зарабатывая проценты.

СЛОЖНЫЙ ПРОЦЕНТ

• P _N — остаток на счете после N лет.
• P ₀ — начальный баланс счета (также называемый начальным депозитом или основной суммой)
• r — годовая процентная ставка в десятичной форме
• k — количество периодов начисления сложных процентов в году
  • Если начисление сложных процентов производится ежегодно (один раз в год), k = 1.
  • Если начисление сложных процентов производится ежеквартально, тыс. = 4.
  • Если начисление процентов производится ежемесячно, тыс. = 12.
  • Если начисление сложных процентов производится ежедневно, k = 365.

• Исключение составляют облигации и другие инвестиции, проценты по которым не реинвестируются; в этих случаях вы смотрите на простые проценты .

ПРОСТОЙ ПРОЦЕНТ НА ​​ВРЕМЯ

(1)

Единицы измерения (годы, месяцы и т. Д.).) для времени должно соответствовать периоду времени для процентной ставки.

Аннуитеты

• Если вы вкладываете деньги на счет на регулярной основе (ежемесячно / ежегодно / ежеквартально), то вы сталкиваетесь с проблемой базовой аннуитета . Базовые аннуитеты — это когда вы экономите деньги. Обычно в случае проблемы с аннуитетом ваша учетная запись начинает пустовать, и в будущем на ней будут деньги. Аннуитеты предполагают, что вы кладете деньги на счет на регулярной основе (каждый месяц, год, квартал и т. Д.)) и пусть сидит, зарабатывая проценты.

ФОРМУЛА ГОДА

• P _N — остаток на счете после N лет.
• d — обычный депозит (сумма, которую вы вносите каждый год, каждый месяц и т. Д.)
• r — годовая процентная ставка в десятичной форме.
• k — количество периодов начисления сложных процентов в году.

Если частота начисления сложных процентов явно не указана, предположим, что в год такое же количество соединений, как и вкладов, сделанных за год.

• Если вы регулярно снимаете деньги со счета , то вы сталкиваетесь с проблемой выплаты аннуитета . Аннуитеты на выплату используются для таких вещей, как пенсионный доход, когда вы начинаете с денег на своем счете, регулярно вытаскиваете деньги, а в будущем ваш счет оказывается пустым. Аннуитеты на выплату предполагают, что вы снимаете деньги со счета регулярно (каждый месяц, год, квартал и т. Д.), А остальным позволяете сидеть и получать проценты.

ФОРМУЛА ГОДОВОЙ ВЫПЛАТЫ

• P ₀ — это остаток на счете в начале (начальная сумма или основная сумма).
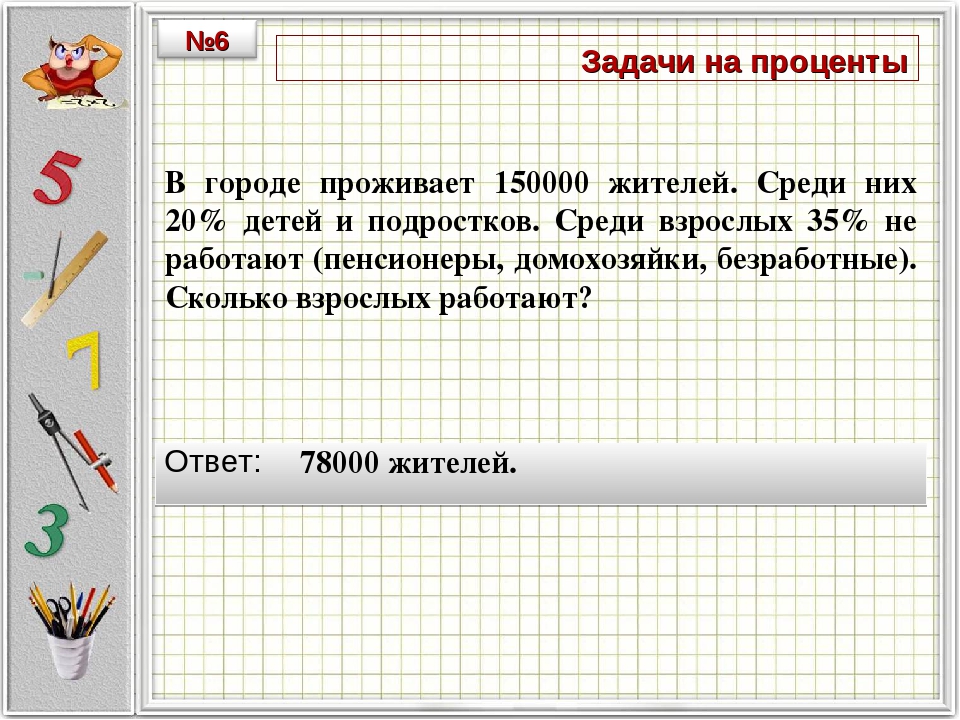
• d — это обычное снятие средств (сумма, которую вы снимаете каждый год, каждый месяц и т. Д.)
• r — годовая процентная ставка (в десятичной форме. Пример: 5% = 0,05)
• k — количество периодов начисления сложных процентов в году.
• N — количество лет, в течение которых мы планируем снимать средства

Помните, что самая важная часть ответа на любой вопрос, будь то денежный или какой-либо другой, — это сначала правильно определить, что на самом деле задается вопросом, а затем определить, какой подход лучше всего позволит вам решить проблему.

Попробуй

Для каждого из следующих сценариев определите, является ли это проблемой сложных процентов, проблемой сберегательного аннуитета, проблемой аннуитета выплат или проблемой ссуд. Затем решите каждую проблему.

1. Марси получила наследство в размере 20 000 долларов и вложила его под 6%. Она собирается использовать его для учебы в колледже, снимая деньги на обучение и расходы каждый квартал. Сколько она может вынимать ежеквартально, если ей осталось 3 года обучения в школе?
2. Пол хочет купить новую машину.Вместо того, чтобы брать ссуду, он решает откладывать 200 долларов в месяц на счете, зарабатывающем 3% годовых, начисляемых ежемесячно. Сколько он накопит через 3 года?
3. Кейша управляет инвестициями в некоммерческой компании. Они хотят вложить немного денег в счет, приносящий 5% годовых, с целью иметь 30 000 долларов на счете через 6 лет. Сколько Кейше следует положить на счет?
4. Miao собирается профинансировать новое офисное оборудование под 2% в течение 4 лет.Если она может позволить себе ежемесячные платежи в размере 100 долларов, сколько нового оборудования она сможет купить?
5. Сколько вам нужно ежемесячно откладывать на счете с доходностью 4%, чтобы накопить 5000 долларов за два года?

Решения:

1. Это проблема с выплатой аннуитета. Она может получать 1833,60 доллара за квартал.
2. Это проблема сберегательного аннуитета. Он накопит 7 524,11 долл. США
3. Это проблема сложных процентов. Ей нужно будет внести 22 386 долларов.46. ​​
4. Это проблема с кредитами. Она может купить новое оборудование
на 4 609,33 доллара.
5. Это проблема сберегательного аннуитета. Вам нужно будет экономить 200,46 долларов в месяц

В следующем видео мы представляем больше примеров того, как использовать язык в вопросе, чтобы определить, какой тип уравнения использовать для решения финансовой проблемы.

В следующем видео-примере мы показываем, как решить финансовую проблему, которая состоит из двух этапов: первый этап — проблема сбережений, а второй этап — проблема вывода средств.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Атрибуции

Эта глава содержит материал, взятый из Math in Society (в OpenTextBookStore) Дэвида Липпмана и используется по лицензии CC Attribution-Share Alike 3.0 United States (CC BY-SA 3.0 US).

Эта глава содержит материал, взятый из книги Math for the Liberal Arts (по Lumen Learning) компании Lumen Learning и используется по лицензии CC BY: Attribution .

Простые и сложные проценты — математика для нашего мира

Результаты обучения

• Расчет единовременных простых процентов и простых процентов с течением времени
• Определить APY с учетом процентного сценария
• Расчет сложных процентов

Надо работать с деньгами каждый день. В то время как баланс вашей чековой книжки или подсчет ваших ежемесячных расходов на эспрессо требует только арифметики, когда мы начинаем экономить, планируем выход на пенсию или нуждаемся в ссуде, нам нужно больше математики.

Простые проценты

Обсуждение процентов начинается с основной суммы или суммы, с которой начинается ваш счет. Это могут быть стартовые инвестиции или стартовая сумма кредита. Проценты в самой простой форме рассчитываются как процент от основной суммы долга. Например, если вы взяли у друга 100 долларов и согласились выплатить их с 5% -ной процентной ставкой, тогда сумма процентов, которую вы заплатите, будет всего лишь 5% от 100: 100 долларов (0,05) = 5 долларов. Общая сумма, которую вы должны выплатить, составит 105 долларов, включая первоначальную основную сумму плюс проценты.

Простые разовые проценты

(1)

Примеры

Друг просит одолжить 300 долларов и соглашается выплатить его в течение 30 дней под 3% годовых. Сколько процентов вы заработаете?

Решение:

(3) = 300 долларов США	основной
r = 0,03	3% ставка
I = 300 долларов (0.03) = 9 долларов.	Вы получите проценты в размере 9 долларов.

В следующем видео подробно рассматривается этот пример.

Одноразовые простые проценты обычно используются только для чрезвычайно краткосрочных ссуд. По долгосрочным займам проценты обычно выплачиваются ежедневно, ежемесячно, ежеквартально или ежегодно. В этом случае проценты будут начисляться регулярно.

Например, облигации — это, по сути, ссуды, предоставленные эмитенту облигаций (компании или правительству) вами, держателем облигации. В обмен на ссуду эмитент соглашается выплачивать проценты, часто ежегодно. Облигации имеют дату погашения, когда эмитент выплачивает первоначальную стоимость облигации.

Упражнения

Предположим, ваш город строит новый парк и выпускает облигации, чтобы собрать деньги на его строительство. Вы получаете облигацию на сумму 1000 долларов, по которой выплачивается 5% годовых со сроком погашения 5 лет. Сколько процентов вы заработаете?
[раскрыть-ответ q = «14596 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 14596 ″] Каждый год вы будете зарабатывать 5% годовых: 1000 долларов (0.05) = 50 долларов США в виде процентов. Таким образом, в течение пяти лет вы заработаете в общей сложности 250 долларов в виде процентов. Когда срок погашения облигации истечет, вы получите обратно 1000 долларов, которые вы изначально заплатили, в результате чего у вас останется 1250 долларов. [/ Hidden-answer]

Дальнейшее объяснение решения этого примера можно увидеть здесь.

Мы можем обобщить эту представляющую простой интерес идею с течением времени.

Простой процент с течением времени

(4)

Единицы измерения (годы, месяцы и т. Д.).) для времени должно соответствовать периоду времени для процентной ставки.

APR — Годовая процентная ставка

Процентные ставки обычно задаются как годовая процентная ставка (APR) — общая процентная ставка, которая будет выплачиваться в течение года. Если проценты выплачиваются меньшими временными интервалами, годовая процентная ставка будет разделена.

Например, ежемесячная выплата 6% годовых будет разделена на двенадцать платежей по 0,5%.

Ежеквартальная ставка 4%, выплачиваемая ежеквартально, будет разделена на четыре выплаты по 1%.

Пример

Казначейские облигации (казначейские ноты) — это облигации, выпущенные федеральным правительством для покрытия его расходов. Предположим, вы получаете казначейские облигации на сумму 1000 долларов США с годовой ставкой 4%, выплачиваемой раз в полгода, со сроком погашения через 4 года. Сколько процентов вы заработаете?

Решение:

Поскольку проценты выплачиваются раз в полгода (два раза в год), процентная ставка 4% будет разделена на две выплаты по 2%.

(6) = 1000 долларов США	основной
r = 0.02	Ставка 2% за полгода
т = 8	4 года = 8 полугодий
I = 1000 (0,02) (8) = 160 долларов.	Вы заработаете 160 долларов в течение четырех лет.

Это видео объясняет решение.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Попробуй

Кредитная компания взимает 30 долларов за ссуду на один месяц в размере 500 долларов.Найдите годовую процентную ставку, которую они взимают.

Решение:

I = 30 долларов процентов
= 500 долларов основной суммы
r = неизвестно
t = 1 месяц

Используя, получаем. Решая, получаем r = 0,06, или 6%. Поскольку время было ежемесячным, это ежемесячные проценты. Годовая ставка будет в 12 раз больше: 72% годовых.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Сложные проценты

С простыми процентами мы предположили, что получили проценты, когда получили их.На стандартном банковском счете любые проценты, которые мы зарабатываем, автоматически добавляются к нашему балансу, и мы будем получать проценты с этих процентов в будущие годы. Это реинвестирование процентов называется , составляющим .

Предположим, что мы помещаем 1000 долларов на банковский счет с ежемесячной ставкой 3% годовых. Как наши деньги будут расти?

3% годовых — это годовая процентная ставка (APR) — общая сумма процентов, подлежащих выплате в течение года. Поскольку проценты выплачиваются ежемесячно, каждый месяц мы будем зарабатывать 3% ÷ 12 = 0.25% в месяц.

В первый месяц

• P ₀ = 1000 долларов США
• r = 0,0025 (0,25%)
• I = 1000 долларов США (0,0025) = 2,50 доллара США
• A = 1000 USD + 2,50 USD = 1002,50 USD

В первый месяц мы заработаем 2,50 доллара на процентах, в результате чего баланс нашего счета увеличится до 1002,50 доллара.

Во второй месяц

• P ₀ = 1002,50 долларов США
• I = 1002 доллара.50 (0,0025) = 2,51 USD (округлено)
• A = 1002,50 USD + 2,51 USD = 1005,01 USD

Обратите внимание, что во второй месяц мы заработали больше процентов, чем в первый месяц. Это потому, что мы заработали проценты не только на первоначальную 1000 долларов, которые мы вложили, но мы также получили проценты на 2,50 доллара процентов, которые мы заработали в первый месяц. Это ключевое преимущество, которое дает нам , составляющая процентов.

Если подсчитать еще несколько месяцев, получим:

Месяц	Начальное сальдо	Полученные проценты	Конечное сальдо
1	1000.00	2,50	1002,50
2	1002,50	2,51	1005.01
3	1005.01	2,51	1007,52
4	1007,52	2,52	1010,04
5	1010,04	2,53	1012,57
6	1012,57	2,53	1015. 10
7	1015,10	2,54	1017,64
8	1017,64	2,54	1020,18
9	1020,18	2,55	1022,73
10	1022,73	2,56	1025.29
11	1025.29	2,56	1027,85
12	1027.85	2,57	1030,42

Мы хотим упростить процесс расчета сложных процентов, потому что создание таблицы, подобной приведенной выше, занимает много времени. К счастью, математика хороша в том, что дает вам короткие пути. Чтобы найти уравнение, представляющее это, если P _m представляет сумму денег через m месяцев, то мы могли бы написать рекурсивное уравнение:

P ₀ = 1000 долларов США

P _м = (1 + 0. 0025) П _м-1

Вы, вероятно, узнаете в этом рекурсивную форму экспоненциального роста. Если нет, мы проделаем шаги, чтобы построить явное уравнение для роста в следующем примере.

Пример

Постройте явное уравнение для роста 1000 долларов, депонированных на банковском счете с ежемесячной ставкой 3% годовых.

Решение:

• P ₀ = 1000 долларов США
• П ₁ = 1.0025 P ₀ = 1,0025 (1000)
• P ₂ = 1,0025 P ₁ = 1,0025 (1,0025 (1000)) = 1,0025 2 (1000)
• P ₃ = 1,0025 P ₂ = 1,0025 (1,00252 (1000)) = 1,00253 (1000)
• P ₄ = 1,0025 P ₃ = 1,0025 (1,00253 (1000)) = 1,00254 (1000)

Наблюдая закономерность, можно сделать вывод

Обратите внимание, что 1000 долларов в уравнении были P ₀ , начальная сумма.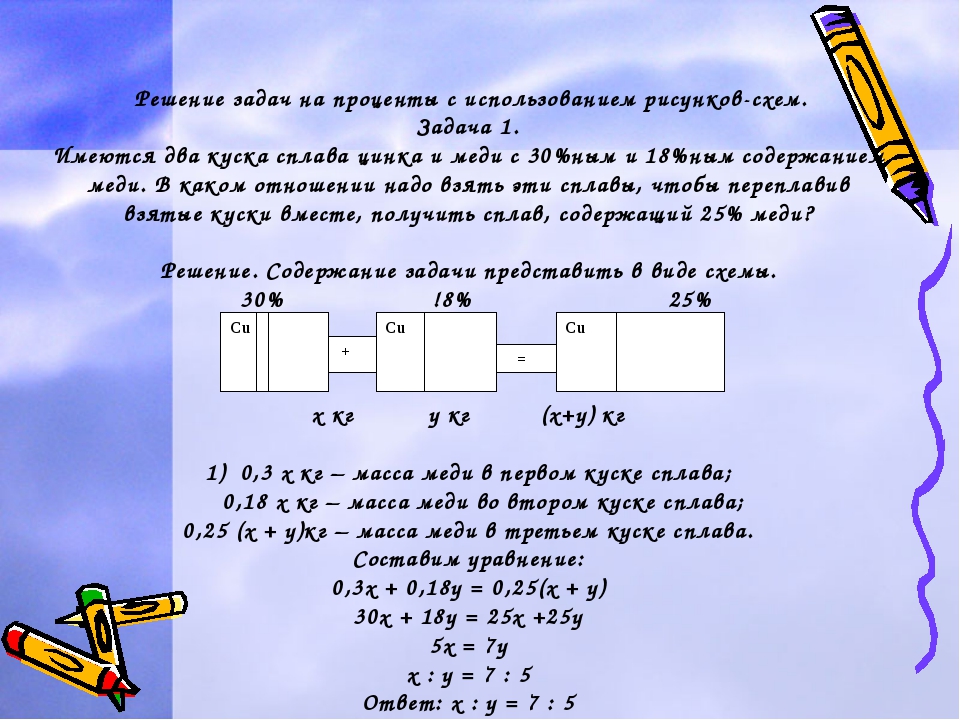 Мы нашли 1,0025, прибавив единицу к скорости роста, разделенной на 12, так как мы увеличивали 12 раз в год.

Обобщая наш результат, мы можем написать

В этой формуле:

• м — количество периодов начисления сложных процентов (в нашем примере месяцев)
• r — годовая процентная ставка
• k — количество соединений в год.

Просмотрите это видео, чтобы ознакомиться с концепцией сложных процентов.

Хотя эта формула работает нормально, чаще используется формула, которая включает количество лет, а не количество периодов начисления сложных процентов. Если N — количество лет, то m = N k . Это изменение дает нам стандартную формулу для сложных процентов.

Сложные проценты

• P _N — остаток на счете после N лет.
• P ₀ — начальный баланс счета (также называемый начальным депозитом или основной суммой)
• r — годовая процентная ставка в десятичной форме
• k — количество периодов начисления сложных процентов в году
  • Если начисление сложных процентов производится ежегодно (один раз в год), k = 1.
  • Если начисление сложных процентов производится ежеквартально, тыс. = 4.
  • Если начисление процентов производится ежемесячно, тыс. = 12.
  • Если начисление сложных процентов производится ежедневно, k = 365.

Самая важная вещь, которую следует помнить при использовании этой формулы, заключается в том, что она предполагает, что мы помещаем деньги на счет один раз и позволяем им оставаться там, зарабатывая проценты.

В следующем примере мы покажем, как использовать формулу сложных процентов, чтобы найти остаток на депозитном сертификате через 20 лет.

Пример

Депозитный сертификат (CD) — это сберегательный инструмент, который предлагают многие банки. Обычно он дает более высокую процентную ставку, но вы не можете получить доступ к своим инвестициям в течение определенного периода времени. Предположим, вы вкладываете 3000 долларов на компакт-диск с ежемесячной выплатой 6% годовых. Сколько у вас будет на счету через 20 лет?

Решение:

В этом примере

P 0 = 3000 долл. США	начальный депозит
r = 0.06	6% годовая ставка
к = 12	12 месяцев в 1 год
N = 20	, поскольку мы ищем, сколько у нас будет через 20 лет

Итак (округлите ответ до ближайшей копейки)

Видео-пошаговое руководство по этому примеру проблемы доступно ниже.

Давайте сравним сумму денег, полученную от начисления сложных процентов, с суммой, которую вы заработали бы от простых процентов

Годы	Простой процент (15 долларов в месяц)	6% начисленных ежемесячно = 0.5% каждый месяц.
5	$ 3900	$ 4046,55
10	$ 4800	$ 5458,19
15	$ 5700	$ 7362,28
20	$ 6600	$ 9930.61
25	$ 7500	$ 13394.91
30	$ 8400	$ 180 67,73
35	$ 9300	24370 долларов.65

Как видите, в течение длительного периода времени начисление сложных процентов сильно влияет на баланс счета. Вы можете понять разницу между линейным и экспоненциальным ростом.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Пример

Вы знаете, что вам понадобится 40 000 долларов на образование вашего ребенка через 18 лет. Если ваша учетная запись зарабатывает 4% в квартал, сколько вам нужно будет внести сейчас, чтобы достичь своей цели?

Решение:

В этом примере мы ищем P ₀ .

r = 0,04	4%
к = 4	4 квартала за 1 год
N = 18	Поскольку мы знаем баланс за 18 лет
P 18 = 40 000 долларов США	Сумма у нас за 18 лет

В этом случае нам нужно будет составить уравнение и решить для P ₀ .

(7)

Итак, вам нужно будет внести 19 539,84 доллара сейчас, чтобы получить 40 000 долларов через 18 лет.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Округление

Если вы не вводите всю свою формулу в Desmos и выбираете делать это по частям, важно быть очень осторожным с округлением при вычислении значений с показателями. В общем, вы хотите использовать как можно больше десятичных знаков во время вычислений. Убедитесь, что в строке должно быть не менее 3 значащих цифр (цифры после любых ведущих нулей).Округление от 0,00012345 до 0,000123 обычно дает «достаточно близкий» ответ, но всегда лучше оставить больше цифр.

Пример

Чтобы понять, почему так важно не завышать округление, если вы решите не вводить свою формулу сразу в Desmos, предположим, что вы инвестируете 1000 долларов под 5% -ную ставку ежемесячно в течение 30 лет.

P 0 = 1000 долларов США	начальный депозит
r = 0.05	5%
к = 12	12 месяцев в 1 год
N = 30	, поскольку мы ищем сумму через 30 лет

Если мы сначала вычислим r / k , мы найдем 0,05 / 12 = 0,00416666666667

Вот результат округления до разных значений:

r / k округляется до:	Возвращает P30 к:	Ошибка
0. 004	$ 4208.59	$ 259,15
0,0042	$ 4521,45	$ 53,71
0,00417	$ 4473,09	$ 5,35
0,004167	$ 4468,28	0,54 долл. США
0,0041667	$ 4467,80	0,06 $
без округления	$ 4467,74

Если вы работаете в банке, вы, конечно, вообще не станете округлять.Для наших целей ответ, который мы получили путем округления до 0,00417, трех значащих цифр, достаточно близок — 5 долларов от 4500 долларов не так уж и плохо. Конечно, сохранение четвертого десятичного разряда не повредило бы.

Просмотрите следующее для демонстрации этого примера.

Использование калькулятора Desmos

Во многих случаях вы можете полностью избежать округления, введя значения в калькулятор.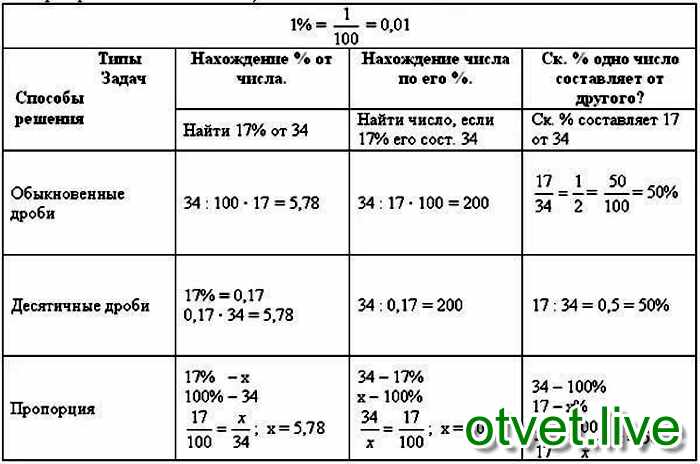 Например, в приведенном выше примере нам нужно было вычислить

Мы можем быстро вычислить это на калькуляторе Desmos, введя формулу сразу:

Чтобы ввести это в калькулятор, введите следующее:

1000 * (1 +.05/12) a ^b (12 * 30)

Примечание: a ^b находится в первой строке, втором столбце главного меню выше. Теперь вы можете округлить окончательный ответ до ближайшего цента.

Атрибуции

Эта глава содержит материал, взятый из Math in Society (в OpenTextBookStore) Дэвида Липпмана и используется по лицензии CC Attribution-Share Alike 3.0 United States (CC BY-SA 3.0 US).

Эта глава содержит материал, взятый из книги Math for the Liberal Arts (по Lumen Learning) компании Lumen Learning и используется по лицензии CC BY: Attribution .

Проблемы слова «Инвестиции»

«Инвестиционный» Проблемы Word (стр. 1 из 2) Инвестиционные проблемы обычно включают простые годовые проценты (в отличие от сложных интерес), используя формула процента I = Prt , где I стоит для процентов на первоначальные инвестиции P обозначает сумму первоначальных инвестиций (называемую «основной суммой»), r — процентная ставка (выраженная в десятичной форме), а t — время. На годовой процент , время t должно быть в годах. Если они дадут вам время, скажем, девять месяцев, вы должны сначала преобразуйте это в 9 / 12 = 3 / 4 = 0,75 года. В противном случае вы получите неправильный ответ. Единицы времени должны соответствовать единицам процентной ставки. Если вы получили ссуду в дружелюбном районе ростовщик, где процентная ставка ежемесячная, а не годовая, тогда ваше время нужно измерять месяцами. Инвестиционные проблемы со словом обычно не очень реалистичны; в «реальной жизни», интерес почти всегда каким-то образом усугубляется, и инвестиции обычно не все за целые годы. Но вы получите более «практичный» прочее позже; это просто разминка, чтобы подготовить вас к дальнейшим действиям. Во всех случаях этих проблем, вы захотите подставить всю известную информацию в « I = Prt «уравнение, а затем решите все, что осталось. Вы вкладываете 1000 долларов в инвестицию с доходностью 6% годовых; вы оставили деньги на два года. Сколько процентов вы получите в конце этих двух лет? В этом случае P = 1000 долларов, r = 0,06 (потому что мне нужно преобразовать процент в десятичную форму), а время составляет t = 2. Подставляя, Я получаю: I = (1000) (0. 06) (2) = 120 Я получу 120 долларов в виде процентов. Другой пример: Вы инвестировали $ 500 и через три года получили $ 650 . Какая была процентная ставка? Для этого упражнения я Сначала нужно найти сумму процентов.Поскольку проценты добавляются к принципалу, а поскольку P = 500 долларов, то I = 650 — 500 = 150 долларов. Время t = 3. Подставляя все эти значения в формулу простого процента, я получаю: Конечно, мне нужно не забудьте преобразовать это десятичное число в проценты. Самое сложное приходит, когда упражнения требуют многократных вложений.Но в этих что делает их довольно простыми в обращении. Авторские права © Элизабет Стапель 1999-2011 Все права защищены У вас есть 50 000 долларов для инвестирования, и два фонда, в которые вы хотите инвестировать. Фонд You-Risk-It (Фонд Y) приносит 14% годовых. Экстра-скучный фонд (Fund X) приносит 6% годовых. Из-за финансовой помощи колледжа вы не думаете вы можете позволить себе заработать более 4500 долларов в виде процентного дохода в этом году.Сколько вы должны вложить в каждый фонд? « Проблема здесь из-за того, что я разделяю эти 50 000 долларов в основном на две меньшие суммы. Вот как с этим справиться: х I п. r т Фонд ? ? 0.06 1 Фонд Y ? ? 0,14 1 всего 4,500 50 000 — — Как мне заполнить эти вопросительные знаки? Начну с основного P . Допустим, я поставил « x » долларов в Фонд X и « y » долларов в Фонд Y. Тогда x + y = 50 000. Это мало помогает, так как я знаю только, как решать уравнения в одна переменная. Но затем я замечаю, что могу решить x + y = 50 000, чтобы получить y = 50 000 долларов — x . ЭТА МЕТОДИКА ЯВЛЯЕТСЯ ВАЖНЫЙ! г. сумма в Фонде Y (общая) меньше (что мы уже учли в Фонде X), или 50 000 — х .Вам понадобится эта техника, конструкция «сколько осталось», в будущем, поэтому убедитесь, что вы понимаете это сейчас. х I п. r т Фонд ? x 0.06 1 Фонд Y ? 50 000 — х 0,14 1 всего 4,500 50 000 — — Теперь я покажу вам, почему Я поставил стол вот так. Организуя столбцы в соответствии с формулу процента, теперь я могу умножить (справа налево) и заполните графу «проценты». х I п. r т Фонд 0. 06 x x 0,06 1 Фонд Y 0,14 (50 000 — х ) 50 000 — х 0,14 1 всего 4,500 50 000 — — Так как проценты от Фонд X и проценты от Фонда Y в сумме составят 4500 долларов, я могу добавить вниз по столбцу «проценты» и установите эту сумму равной общая сумма процентов: 0. 06 x + 0,14 (50 000 — x ) = 4500 0,06 x + 7000 — 0,14 x = 4500 7 000 — 0,08 x = 4500 –0,08 x = –2 500 x = 31 250 Тогда y = 50 000 — 31 250 = 18 750. Я должен вложить 31 250 долларов в Фонд X и 18 750 долларов в Фонд Y. Обратите внимание, что ответ сделал не включать «аккуратные» значения, такие как «10 000 долларов» или «35 000 долларов».Вы должны понимать, что это означает, что вы не всегда можете ожидать уметь использовать «угадывай и проверяй», чтобы найти ответы. Вы действительно действительно нужно знать, как делать эти упражнения. Вверх | 1 | 2 | Возвращаться к указателю Вперед >> Цитируйте эту статью как: Стапель, Елизавета. «Проблемы со словом« инвестиции »». Purplemath . Доступна с https://www.purplemath.com/modules/investmt.htm . Дата обращения [Дата] [Месяц] 2016 г.

Проблемы со словом про интересов

Проблемы со словом про интерес Проблемы со словом «интерес»

Сначала несколько определений:

Основная сумма деньги, вложенные на счет

Проценты деньги, выплачиваемые за инвестирование главный

Простые проценты проценты, рассчитываемые с использованием формула Проценты = (Основная сумма) × (Ставка) × (Время).Эта формула часто обозначается сокращением I = PRT. Если время равно через год формула становится I = PR.

В наиболее интересных задачах мы постараемся найти сумма денег (основная сумма), вложенная на каждый из двух банковских счетов. Помогать найдем эти вещи, нам сообщат общую сумму вложенных денег и общая сумма процентов, выплаченных по двум счетам.

Давайте рассмотрим пример типичной проблемы со словом «интерес».

Сэм вкладывает 6000 долларов на два банковских счета. Один из на счетах выплачивается 8% годовых, а на другом счете — 10%. в год. Если общий процент, полученный от инвестиций, составляет 560 долларов после в год, сколько денег было вложено в каждый счет?

1. Что мы должны найти в этой проблеме? Последний Часть проблемы дает нам ответ на этот вопрос.Мы пытаемся чтобы узнать сумму денег, которая была вложена в каждый счет.

Давайте определим переменную. Мы не знаем сколько денег был вложен в любую учетную запись, поэтому примите решение использовать x, чтобы представляют собой сумму денег, вложенную в первый счет (тот, который зарабатывает 8% в год). Как мы называем сумму денег, вложенных в второй аккаунт? Мы могли бы дать ему другое имя переменной, например y, но в этой главе мы собирались ограничить наши проблемы одной переменной.

Итак, представьте: Сэм несет стек в 6000 долларов в первый банк и говорит: «Я хотел бы положить x долларов на счет, который платит 8% годовых «. Затем кассир снимает x долларов с свои 6000 долларов, а Сэм кладет оставшиеся деньги в другой банк. Помнить что для вас значили слова «забрать», когда вы были в начальной школе студент-математик? Вычесть, верно ?? Так что «забери x долларов из 6000 долларов» можно быть записано символически как 6,000-x.Вот сколько денег вложено в второй банк.

При проблемах с процентами часто бывает полезно использовать диаграмму систематизировать информацию в задаче. Хорошо промаркируйте верхнюю часть график с двумя объектами, которые искали (деньги, вложенные под 8% и деньги, вложенные под 10%), и хорошо пометьте сторону графика две части информации, которую предоставляет проблема (основной и заработанные проценты). Поскольку проблема дает нам информацию о общая сумма основного долга и общий процент, а также столбец для итогов.

	деньги под 8%	деньги под 10%	всего
основной
процентов

На данный момент известно следующее:

долларов вложено под 8%

6000 x долларов было вложено под 10%

общая сумма инвестиций составила 6000 долларов США.

общая сумма полученных процентов составила 560 долларов США

Давайте поместим эту информацию в нашу диаграмму:

	деньги под 8%	деньги под 10%	всего
основной	Икс	6000 — х	6000
процентов			560

Чтобы заполнить поля процентов, помните, что через один год время I = PR. Итак, в каждом поле процентов мы умножаем сумму основного долга. вкладывается в этот счет по процентной ставке, полученной на эти деньги. Сейчас наша диаграмма выглядит так:

	деньги под 8%	деньги под 10%	всего
основной	Икс	6000 — х	6000
процентов	.08x	0,10 (6000 х)	560

Наше уравнение берется из последней строки на графике. С проценты, полученные на первом счете, плюс проценты, заработанные на второй счет должен равняться общей сумме процентов, мы можем написать:

0,08x + 0,10 (6000 x) = 560

Чтобы решить уравнение, сначала умножьте обе части уравнения на 100, чтобы убрать десятичные дроби. Помните, умножение на 100 сместит одну десятичную точку в каждом члене вправо на два разряда.

100 [0,08x + 0,10 (6000 x)] = 100 [560]

8x + 10 (6000 x) = 56000

8x + 60,000 10x = 56,000

-2x + 60 000 = 56 000

-2x = -4,000

х = 2,000

Поскольку x представляет собой сумму денег, вложенных в По первому счету можно сказать, что 2000 долларов было вложено под 8%.

Нам нужно решить проблему. Нас спросили, сколько деньги были вложены в каждый счет, и, поскольку мы еще не знаем, сколько деньги были вложены под 10%, у нас есть только половина нашего ответа. В соответствии с на нашем графике сумма денег, вложенных во второй счет, равна до 6000- x, поэтому

6000 x = 6000 2000 = 4000

$ 4000 вложено под 10%

Прежде чем мы оставим эту проблему, давайте проверим наш ответ с помощью слова проблемы:

слов	проверка
$ 6000 вложено во все	2 000 + 4 000 = 6 000
560 долл. США было получено в виде процентов	Процентная ставка 8%: .08 (2,000) = 160 Процентный доход по ставке 10%: 0,10 (4,000) = 400Общий процент заработанных процентов: 160 + 400 = 560

Наши ответы проверяют. Были сделаны!

Простой процент | Математика для гуманитарных наук

Результаты обучения

• Расчет единовременных простых процентов и простых процентов с течением времени
• Определить APY с учетом процентного сценария
• Расчет сложных процентов

Основная сумма и проценты

Обсуждение процентов начинается с основной суммы или суммы, с которой начинается ваш счет.Это могут быть стартовые инвестиции или стартовая сумма кредита. Проценты в самой простой форме рассчитываются как процент от основной суммы долга. Например, если вы взяли у друга 100 долларов и согласились выплатить их с 5% -ной процентной ставкой, тогда сумма процентов, которую вы заплатите, будет всего лишь 5% от 100: 100 долларов (0,05) = 5 долларов. Общая сумма, которую вы должны выплатить, составит 105 долларов, включая первоначальную основную сумму плюс проценты.

Простые разовые проценты

[латекс] \ begin {align} & I = {{P} _ {0}} r \\ & A = {{P} _ {0}} + I = {{P} _ {0}} + {{P } _ {0}} r = {{P} _ {0}} (1 + r) \\\ end {align} [/ latex]

• I — проценты
• A — конечная сумма: основная сумма плюс проценты
• [латекс] \ begin {align} {{P} _ {0}} \\\ end {align} [/ latex] — основная сумма (начальная сумма)
• r — процентная ставка (в десятичной форме.Пример: 5% = 0,05)

Примеры

Друг просит одолжить 300 долларов и соглашается выплатить его в течение 30 дней под 3% годовых. Сколько процентов вы заработаете?

Показать решение

[латекс] \ begin {align} {{P} _ {0}} \\\ end {align} [/ latex] = 300 долларов США	основной
r = 0,03	3% ставка
I = 300 долларов (0,03) = 9 долларов.	Вы получите проценты в размере 9 долларов.

В следующем видео подробно рассматривается этот пример.

Одноразовые простые проценты обычно используются только для чрезвычайно краткосрочных ссуд. По долгосрочным займам проценты обычно выплачиваются ежедневно, ежемесячно, ежеквартально или ежегодно. В этом случае проценты будут начисляться регулярно.

Например, облигации — это, по сути, ссуды, предоставленные эмитенту облигаций (компании или правительству) вами, держателем облигации. В обмен на ссуду эмитент соглашается выплачивать проценты, часто ежегодно. Облигации имеют дату погашения, когда эмитент выплачивает первоначальную стоимость облигации.

Упражнения

Предположим, ваш город строит новый парк и выпускает облигации, чтобы собрать деньги на его строительство. Вы получаете облигацию на сумму 1000 долларов, по которой выплачивается 5% годовых со сроком погашения 5 лет. Сколько процентов вы заработаете?

Показать решение

Каждый год вы будете зарабатывать 5% процентов: 1000 долларов (0,05) = 50 долларов процентов. Таким образом, в течение пяти лет вы заработаете в общей сложности 250 долларов в виде процентов. Когда срок погашения облигации наступит, вы получите обратно 1000 долларов, которые вы изначально заплатили, в результате чего у вас останется 1250 долларов.

Дальнейшее объяснение решения этого примера можно увидеть здесь.

Мы можем обобщить эту представляющую простой интерес идею с течением времени.

Простой процент с течением времени

[латекс] \ begin {align} & I = {{P} _ {0}} rt \\ & A = {{P} _ {0}} + I = {{P} _ {0}} + {{P } _ {0}} rt = {{P} _ {0}} (1 + rt) \\\ end {align} [/ latex]

• I — проценты
• A — конечная сумма: основная сумма плюс проценты
• [латекс] \ begin {align} {{P} _ {0}} \\\ end {align} [/ latex] — основная сумма (начальная сумма)
• r — процентная ставка в десятичной форме
• т время

Единицы измерения (годы, месяцы и т. Д.)) для времени должно соответствовать периоду времени для процентной ставки.

APR — Годовая процентная ставка

Процентные ставки обычно задаются как годовая процентная ставка (APR) — общая процентная ставка, которая будет выплачиваться в течение года. Если проценты выплачиваются меньшими временными интервалами, годовая процентная ставка будет разделена.

Например, ежемесячная выплата 6% годовых будет разделена на двенадцать платежей по 0,5%.
[латекс] 6 \ div {12} = 0,5 [/ латекс]

Ежеквартальная ставка 4%, выплачиваемая ежеквартально, будет разделена на четыре выплаты по 1%.
[латекс] 4 \ div {4} = 1 [/ латекс]

Пример

Казначейские облигации (казначейские ноты) — это облигации, выпущенные федеральным правительством для покрытия его расходов. Предположим, вы получаете казначейские облигации на сумму 1000 долларов США с годовой ставкой 4%, выплачиваемой раз в полгода, со сроком погашения через 4 года. Сколько процентов вы заработаете?

Показать решение

Поскольку проценты выплачиваются раз в полгода (два раза в год), процентная ставка 4% будет разделена на две выплаты по 2%.

[латекс] \ begin {align} {{P} _ {0}} \\\ end {align} [/ latex] = 1000 долларов США	основной
r = 0.02	Ставка 2% за полгода
т = 8	4 года = 8 полугодий
I = 1000 (0,02) (8) = 160 долларов.	Вы заработаете 160 долларов в течение четырех лет.

Это видео объясняет решение.

Попробуй

Кредитная компания взимает 30 долларов за ссуду на один месяц в размере 500 долларов. Найдите годовую процентную ставку, которую они взимают.

Показать решение

I = 30 долларов процентов
[латекс] P_0 [/ latex] = 500 долларов основной суммы
r = неизвестно
t = 1 месяц

Используя [latex] I = P_0rt [/ latex], получаем [latex] 30 = 500 · r · 1 [/ latex]. Решая, получаем r = 0,06, или 6%. Поскольку время было ежемесячным, это ежемесячные проценты. Годовая ставка будет в 12 раз больше: 72% годовых.

Мы вас заинтересовали?

июнь 2000

Введение

«Ни заемщиком, ни кредитором быть не может.«

Сегодня никто не прислушивается к совету Полония его сыну-ученику Лаэрту. Все постоянно занимают и ссужают.

• Дети кладут карманные деньги на банковский счет, чтобы накопить на велосипеде.
• Студенты берут ссуды для финансирования учебы.
• Кредитные карты широко используются для краткосрочного заимствования.
• Молодые пары покупают дома по ипотеке от 20 до 30 лет и откладывают на пенсию.

Понимание кредитов и займов означает понимание сложных процентов.Для карьеры в мире финансов это понимание должно быть широким и основательным.

В этой статье мы не будем пытаться всесторонне охватить все сложные детали предмета, но постараемся показать, что сложные проценты

• — важный компонент математических навыков,
• включает в себя интересную математику,
• время от времени дает удивительные, даже парадоксальные результаты.

Кусочек истории

Рисунок 1: Настоящее предназначение зиккурата?

Применение математики в торговле и финансах старо, как сама математика.История показывает, что как только цивилизация развивает письменность, в том числе запись чисел, новые технологии используются в финансовых транзакциях, и соответствующие математические идеи быстро развиваются.

Более 4000 лет назад шумерские купцы Вавилона и Ниневии записывали счета, квитанции и долговые расписки клинописью на глиняных табличках. Они составили таблицы умножения и таблицы обратных величин, квадратов, кубов и экспонент и использовали их для расчета сложных процентов и выплат по ипотеке.Глиняная табличка, хранящаяся сейчас в Лувре, решает проблему того, как долго она продлится. возьмите денежную сумму в два раза по ставке 20%.

индуистских математиков 500–1000 гг. Нашей эры умели суммировать арифметические и геометрические ряды и могли решать задачи, связанные с расчетом скидок и процентов.

Есть запись о кредитном соглашении в Лондоне от 1183 года. Взимаемые проценты составляли 2 пенса. в фунтах стерлингов в неделю, составляя 43% годовых. Еще более высокая ставка была установлена ​​в 1235 году лондонскими купцами, которые ссужали деньги монастырю, требуя «каждые два месяца одну марку за каждые десять марок в качестве компенсации за убытки» — годовая процентная ставка 60%.

Рисунок 2: Таблица умножения на девять в вавилонской клинописи

В Италии 15 века коммерческая деятельность резко возросла. Была введена двойная бухгалтерия и изданы учебники по арифметике: на латыни для классиков в церковных школах и на просторечии для подготовки студентов к коммерческой карьере.

Логарифмы

(изобретенные Джоном Нэпиром в 1614 году) произвели революцию в финансовой математике. Только в ХХ веке на смену им пришли механические, а позже и электронные калькуляторы.

Время — деньги

Рисунок 3: Время — деньги?

Когда вы занимаете деньги у кредитора, такого как банк, вы платите кредитору процентов — плату за использование денег. Проценты начисляются как процент от принципа (сумма ссуды) за согласованный период, обычно год.

Если принцип и процентная ставка равны, то проценты равны. В конце года необходимо погасить ссуду плюс проценты: в общей сложности.

Если вы не производите погашение, ваш долг является текущим, который должен быть погашен в конце второго года с процентами: в общей сложности.

Через три года вы будете должны, а через несколько лет вы будете должны

Это основная формула для расчета сложных процентов.

Та же формула применяется, когда вы кладете деньги на сберегательный счет. Теперь вы ссужаете деньги банку, который выплачивает вам проценты по вашему вкладу.Если вы внесете сумму под процентную ставку, через несколько лет ваши вложения окупятся.

Таким образом, стоимость денег зависит от времени. Если обозначает приведенную стоимость денежной суммы и обозначает ее будущую стоимость в годах при процентной ставке, то

Эти простые формулы являются ключом к пониманию сложных схем инвестирования и погашения долга.

Частое начисление сложных процентов

Основная формула сложных процентов предполагает, что проценты выплачиваются один раз в год.Иногда проценты выплачиваются чаще. По инвестициям с фиксированным депозитом проценты могут выплачиваться ежеквартально, а ссуды на покупку автомобиля и ипотека выплачиваются ежемесячно.

Если 1000 фунтов стерлингов инвестируются под 8% в течение года, они будут стоить в конце года

Эффективная ставка начисления сложных процентов 8%	ежеквартально	8,243%
	ежемесячно	8.300%
	еженедельно	8,322%
	ежедневно	8,327%

По мере увеличения частоты начисления сложных процентов эффективная ставка увеличивается, но постепенно все медленнее.

Как правило, если проценты начисляются раз в год по процентной ставке, через несколько лет инвестиции вырастут до

Что происходит как?

Непрерывное компаундирование

Основной математической проблемой здесь является поведение последовательности

как.

Каждый учебник по математическому анализу показывает, что эта последовательность возрастает, но не неограниченно (это несложно доказать для всех). Фактически, последовательность сходится к пределу, значение которого (до 7 знаков после запятой) составляет 2,7182818. Это число обозначается. Он играет очень важную роль в исчислении.

Тогда можно доказать, что, as,

, которая представляет собой стоимость инвестиции через несколько лет по процентной ставке, непрерывно начисляемой.

Альтернативный метод вывода формулы для непрерывно начисленных процентов состоит в создании и решении дифференциального уравнения .

Позвольте быть стоимостью инвестиции в данный момент, которая приносит процент по ставке. Первоначальные вложения (когда) есть. Затем за короткий промежуток времени от до заработанные проценты равны, и, следовательно,

Позволяет получить дифференциальное уравнение

Это разделимое дифференциальное уравнение, которое решается следующим образом:

, которая представляет собой формулу непрерывного начисления процентов, полученную нами ранее.

Финансы и физика

Дифференциальное уравнение описывает экспоненциальный рост или спад. Подобные уравнения возникают в физике, особенно при радиоактивном распаде. Это не случайность, поскольку в финансовой математике есть ряд проблем, в которых лежащая в основе математика также моделирует физический процесс. Броуновское движение описывает молекулярное движение в жидкости, а также случайные движения фондового рынка. Знаменитое уравнение Блэка-Шоулза, используемое при ценообразовании опционов и деривативов, имеет близкие аналогии в уравнениях, описывающих диффузионные процессы в физике.

Сколько дней в году?

При расчете процентов за часть года, скажем, 137 дней, было бы естественно использовать дробь (или високосный год). Некоторые финансовые учреждения, однако, используют «процентный год» из 360 дней. Это может иметь большое значение. Процентная ставка на миллион фунтов стерлингов под 8% годовых в течение тысячи лет составляет 30444,44 фунта стерлингов; в год составляет 30027,40 фунтов стерлингов: на 417,04 фунтов стерлингов меньше.

360-дневный процентный год используется в нескольких европейских странах и США.В Великобритании и Японии процентный год составляет 365 дней, даже в високосный год. Некоторые выпуски облигаций евро-фунт стерлингов допускают, что високосный год составляет 366 дней.

Для ежедневного начисления сложных процентов, однако, очень мало разницы, принимается ли год за 360, 365 или 366 дней. Например, при 8%

На миллион фунтов в течение одного года разница составляет не более 16 пенсов.

Удвойте свои деньги

Сколько времени потребуется, чтобы ваши деньги удвоились, если они вложены на сберегательный счет под 5%? И сколько времени потребуется, чтобы удвоить 7%? Простое эмпирическое правило гласит, что при% деньги со временем удвоятся.Таким образом, при 5% депозит удваивается через 14 лет, а при 7% он удваивается через 10 лет. Это «Правило 70».

Как выводится правило? Если сумма инвестируется под процентную ставку, проблема состоит в том, чтобы определить, что

Простая алгебра дает

Используемая функция журнала может относиться к любому основанию, но оказывается, что лучше использовать журналы для определения базы (натуральные логарифмы, обозначаемые).Тогда

Причина выбора натурального логарифма заключается в том, что функция представлена ​​в виде серии Маклорена

Поскольку мала, условиями расширения Маклорена можно пренебречь, так что. Так

Замена 0.6931 по более красивому округленному числу 0,7000 дает

когда%. В таблице ниже сравнивается время удвоения, заданное правилом 70, с правильным временем удвоения.

	Правило 70:	Правильный ответ:
1%	70	69.66
2%	35	35,00
5%	14	14,21
7%	10	10,24
10%	7	7.27

Правило 70 было бы более точным как «Правило 69.3». Но 70 — это более управляемое число. Фактически, 72 имеет больше делителей, чем 70, и «Правило 72» работает почти так же хорошо, как Правило 70.

Правило 70 было выведено с учетом годового сложения. Что происходит при непрерывном начислении процентов? Теперь необходимо решить уравнение

без использования разложения Маклорена.

Регулярные инвестиции окупаются

В начале каждого года сумма вкладывается на сберегательный счет, на который выплачиваются проценты по определенной ставке.Сколько будет на счету по истечении лет?

Когда Алисе и Бобу было по 19 лет, они устроились на новую работу.Алиса начала сберегательную программу, инвестируя 1000 фунтов стерлингов в начале каждого года под 10% годовых. По прошествии 7 лет ее счет показывает в общей сложности 10435,89 фунтов стерлингов (см. Расчет выше).

Боб, который до сих пор не откладывал ни копейки, впечатлен размером яйца Алисы и решает начать инвестировать таким же образом. Алиса решает больше не вкладывать средства на свой счет, просто позволяя ему расти со скоростью 10% в год. Боб полон решимости наращивать свои вложения до тех пор, пока они не станут больше, чем у Алисы.Сколько времени потребуется, чтобы вложения Боба превзошли вложения Алисы?

Удивительный ответ: на это уйдет 32 года!

Если вам трудно в это поверить, проверьте приведенные ниже расчеты.

Через 31 год инвестиции Алисы будут стоить

Будущая стоимость первого платежа
Будущая стоимость второго платежа
Будущая стоимость ого платежа

Инвестиции Боба составят

и Алиса все еще опережает Боба.

Через 32 года инвестиции Алисы будут стоить

Инвестиции Боба составят

и Боб наконец догнал Алису.

Погашение кредитов

Когда вы покупаете дом или машину, вы берете взаймы покупную цену в банке и соглашаетесь возвращать деньги регулярными равными частями в течение определенного времени.Если сумма ссуды равна, процентная ставка и количество выплат, то какова сумма выплаты?

Ключевым моментом является взглянуть на проблему с точки зрения банка: их кредит должен быть сбалансирован текущей стоимостью выплат.

Текущая стоимость первого погашения составляет
текущая стоимость второго погашения
и в целом
текущая стоимость n-го платежа составляет

Таким образом, общая приведенная стоимость всех выплат составляет

, который представляет собой геометрическую серию членов с первым членом и обычным соотношением.Сумма ряда равна

. При равенстве получаем

.

Например, ссуда в размере 100 000 фунтов стерлингов подлежит погашению в течение 25 лет равными ежемесячными платежами. Если годовая процентная ставка составляет 7%, какова ежемесячная выплата?

Вот и (так как выплаты ежемесячные). Итак,

Выплаты состоят из двух компонентов: процентов на непогашенный остаток и суммы погашения капитала.В таблице ниже представлена ​​разбивка первых трех выплат.

	Проценты	Капитал	выдающиеся
		Погашение	Капитал
1	583.33	123,45	99876,55
2	582,61	124,17	99752,38
3	581,89	124,89	99627,49

Первоначально ежемесячная выплата в основном представляет собой проценты, всего 17 процентов.46% от погашения капитала. По мере осуществления выплат процентная составляющая падает, а выплата капитала увеличивается.

Какая часть капитала была возвращена через 20 лет? Ответ можно найти, продолжив приведенную выше таблицу на 240 строк, что является легким упражнением с электронной таблицей. Более элегантное решение состоит в том, чтобы понять, что после 240 платежей непогашенный капитал в точности равен приведенной стоимости оставшихся 60 платежей:

Таким образом, более трети капитала все еще остается непогашенным, даже после того, как было произведено 80% выплат. .

Предположим, что для чисто числовой аккуратности решено округлить ежемесячный платеж с 706,78 фунтов стерлингов до 710 фунтов стерлингов. Как это влияет на количество выплат?

Из формулы, относящейся и

получаем

и оттуда, положив, и получаем

Таким образом, при очень небольшом «округлении» получается существенная экономия более чем на 3 погашения.Вместо 300 платежей на сумму 706,78 фунтов стерлингов на общую сумму 212034 фунтов стерлингов производится 296,35 платежей на сумму 710 фунтов стерлингов на общую сумму 210408,50 фунтов стерлингов. Разница составляет 1625,50 фунтов стерлингов!

Округление выплат до 720 фунтов стерлингов в месяц позволяет сэкономить еще 10 выплат в конце. Проверяйте цифры сами!

Обман сложных процентов

Как мы уже неоднократно видели, сложные проценты могут преподносить сюрпризы. Нечестные рекламодатели могут обернуть неожиданный способ работы сложных процентов. Вот пример.

Заем в размере 2000 фунтов стерлингов предлагается под «всего 5%» с погашением в течение года ежемесячными платежами. Загвоздка в неправильном, но правдоподобном способе расчета взносов.

«При 5% годовых процентная ставка на 2000 фунтов стерлингов составляет 100 фунтов стерлингов, что в сумме составляет 2100 фунтов стерлингов. Таким образом, ежемесячные выплаты равны».

Более пристальный взгляд показывает, что истинная процентная ставка составляет немногим более 9%. Чтобы найти истинную процентную ставку, воспользуемся формулой

с.Месячная ставка неизвестна. Складывание и умножение дает

, что упрощается до

(Очевидное решение, которое явно соответствует, не является решением исходной задачи. Но затем мы вспоминаем, что мы умножили на, и именно так появилось это решение.) Итак, мы должны найти решение

кроме. Метод проб и ошибок с помощью калькулятора показывает, что это решение, соответствующее процентной ставке 0,75872% в месяц или немногим более 9,1% годовых.

Проблема Саймона Стевина

Рисунок 4: Статуя Саймона Стевина в Брюгге

Математик Саймон Стевин из Брюгге (1548-1620) известен тем, что ввел десятичные дроби в арифметику.В учебнике коммерческой арифметики, изданном в 1585 году, он поставил и решил следующую задачу:

Долг в 1500 фунтов стерлингов в год, подлежащий погашению в течение следующих 22 лет, погашается единовременным платежом в размере 15 300 фунтов стерлингов. Какова была процентная ставка?

Его метод решения состоял в том, чтобы обратиться к таблицам процентов, чтобы найти процентную ставку, которая лучше всего соответствовала цифрам, которая оказалась 8%. Это был единственный эффективный метод решения таких проблем до появления калькуляторов и компьютеров.

С математической точки зрения проблема Стевина аналогична задаче из предыдущего раздела, поэтому мы закончим это введение в сложный процент словами из многих учебников математики: «детали лучше оставить читателю».