Контрольные работы по геометрии 11 класс
Геометрия 11 класс
Контрольная работа № 1 по теме:
«Координаты точки и координаты вектора»
Вариант 1
Найдите координаты вектора
 , если А (5;-1; 3), В (2;-2; 4).
, если А (5;-1; 3), В (2;-2; 4).Даны векторы
 (3; 1;-2) и
(3; 1;-2) и  (1; 4;-3). Найдите
(1; 4;-3). Найдите 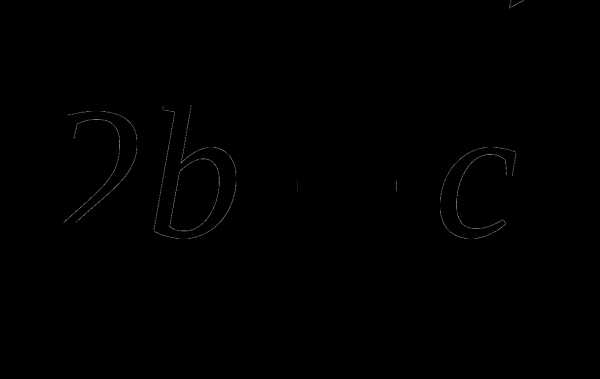 .
.Изобразите систему координат Охуz и постройте точку А (1;-2;-4). Найдите расстояния от этой точки до координатных плоскостей.
Вариант 2
Найдите координаты вектора

Даны вектора
 (5;-1; 2) и
(5;-1; 2) и  (3; 2;-4). Найдите
(3; 2;-4). Найдите 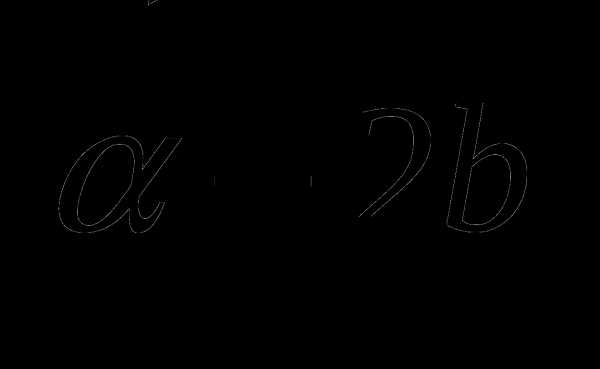 .
.Изобразите систему координат Охуz и постройте точку В (-2;-3; 4). Найдите расстояния от этой точки до координатных плоскостей.
Геометрия 11 класс
Контрольная работа № 1 по теме:
«Координаты точки и координаты вектора»
Вариант 1
Найдите координаты вектора
 , если А (5;-1; 3), В (2;-2; 4).
, если А (5;-1; 3), В (2;-2; 4).Даны векторы
(3; 1;-2) и
 (1; 4;-3). Найдите
(1; 4;-3). Найдите 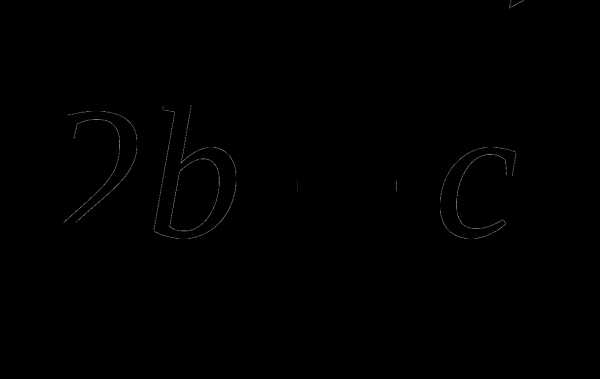 .
.Изобразите систему координат Охуz и постройте точку А (1;-2;-4). Найдите расстояния от этой точки до координатных плоскостей.
Вариант 2
Найдите координаты вектора
 , если С (6; 3;-2), D (2; 4;-5).
, если С (6; 3;-2), D (2; 4;-5).Даны вектора
 (5;-1; 2) и
(5;-1; 2) и  (3; 2;-4). Найдите
(3; 2;-4). Найдите 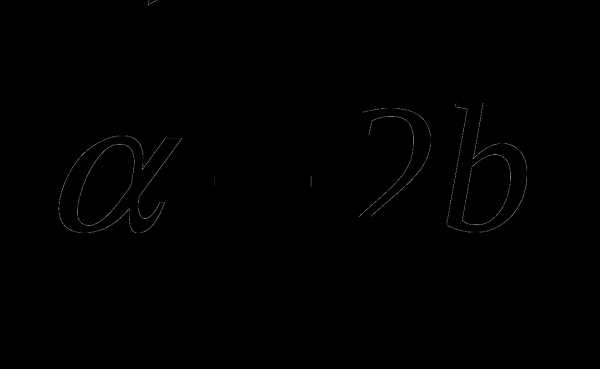 .
.Изобразите систему координат Охуz и постройте точку В (-2;-3; 4). Найдите расстояния от этой точки до координатных плоскостей.
Геометрия 11 класс
Контрольная работа № 2 по теме:
«Метод координат в пространстве»
Вариант 1
Вычислите скалярное произведение векторов
 , если
, еслиДан куб АВСДА1В1С1Д1. Найдите угол между прямыми АД1 и ВМ, где М – середина ребра ДД1.
При движении прямая b отображается на прямую b1, а плоскость — на плоскость 1 и b׀׀1. Докажите, что b1׀׀1.
Вариант 2
Вычислите скалярное произведение векторов
, если
Дан куб АВСДА1В1С1Д1. Найдите угол между прямыми АС и ДС1.
При движении прямая а отображается на прямую а1, а плоскость — на плоскость 1 и а
 . Докажите, что а1
. Докажите, что а1 1.
1.
Геометрия 11 класс
Контрольная работа № 2 по теме:
«Метод координат в пространстве»
Вариант 1
Вычислите скалярное произведение векторов
 , если
, еслиДан куб АВСДА1В1С1Д1. Найдите угол между прямыми АД
При движении прямая b отображается на прямую b1, а плоскость — на плоскость 1 и b׀׀1. Докажите, что b1׀׀1.
Вариант 2
Вычислите скалярное произведение векторов
 , если
, еслиДан куб АВСДА1В1С1Д1. Найдите угол между прямыми АС и ДС1.
При движении прямая а отображается на прямую а1, а плоскость — на плоскость 1 и а
 . Докажите, что а1
. Докажите, что а1 1.
1.
Контрольная работа №2 по теме: «Метод координат».
Вариант 1
С(-3,2,-4). Найдите сумму расстояний от точки С до оси Ох и точки С до плоскости Оуz.
Известны координаты вершин треугольника С(-2;3;1), Д(2;-4;3), Е(-2;-3;1). ДК – медиана треугольника. Найдите ДК.
При параллельном переносе точка А (-3;4;6) переходит в точку А1 (2;-4;5). Найдите сумму координат точки В1, в которую при этом параллельном переносе переходит точка В(-2;-4;1).
Найдите площадь треугольника АВС, если А (3;0;0), В(0;-4;0), С(0;0;1).
Вариант 2
А(3,-2,-4). Найдите сумму расстояний от точки А до оси Оу и точки А до плоскости Оxz.
При параллельном переносе точка М (-3;2;-5) переходит в точку М1 (1;-3;-2). Найдите сумму координат точки К1, в которую при этом параллельном переносе переходит точка К(1;-2;-5).
Найдите площадь треугольника АВС, если А (3;0;0), В(0;-4;0), С(0;0;1).
Контрольная работа №2 по теме: «Метод координат».
Вариант 1
С(-3,2,-4). Найдите сумму расстояний от точки С до оси Ох и точки С до плоскости Оуz.
Известны координаты вершин треугольника С(-2;3;1), Д(2;-4;3), Е(-2;-3;1). ДК – медиана треугольника. Найдите ДК.
При параллельном переносе точка А (-3;4;6) переходит в точку А1 (2;-4;5). Найдите сумму координат точки В 1, в которую при этом параллельном переносе переходит точка В(-2;-4;1).
Найдите площадь треугольника АВС, если А (3;0;0), В(0;-4;0), С(0;0;1).
Вариант 2
А(3,-2,-4). Найдите сумму расстояний от точки А до оси Оу и точки А до плоскости Оxz.
Известны координаты вершин треугольника А(2;-1;-3), В(-3;5;2), С(-2;3;-5). ВМ – медиана треугольника. Найдите ВМ.
При параллельном переносе точка М (-3;2;-5) переходит в точку М1 (1;-3;-2). Найдите сумму координат точки К1, в которую при этом параллельном переносе переходит точка К(1;-2;-5).
Найдите площадь треугольника АВС, если А (3;0;0), В(0;-4;0), С(0;0;1).
Геометрия 11 класс
Контрольная работа № 3 по теме:
Вариант 1
Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16 см2. Найдите площадь поверхности цилиндра.
Высота конуса равна 6 см, угол при вершине осевого сечения равен 120. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30;
б)площадь боковой поверхности конуса.Диаметр шара равен 2т. Через конец диаметра проведена плоскость под углом 45 к нему. Найдите длину линии пересечения сферы с этой плоскостью.
Вариант 2
Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь поверхности цилиндра.
Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30. Найдите:
б) площадь боковой поверхности конуса.
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60;Диаметр шара равен 4т. Через конец диаметра проведена плоскость под углом 30 к нему. Найдите площадь сечения шара этой плоскостью.
Геометрия 11 класс
Контрольная работа № 3 по теме:
«Цилиндр, конус и шар»
Вариант 1
Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16 см2. Найдите площадь поверхности цилиндра.
Высота конуса равна 6 см, угол при вершине осевого сечения равен 120. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30;
б)площадь боковой поверхности конуса.Диаметр шара равен 2т. Через конец диаметра проведена плоскость под углом 45 к нему. Найдите длину линии пересечения сферы с этой плоскостью.
Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь поверхности цилиндра.
Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60;
б) площадь боковой поверхности конуса.Диаметр шара равен 4т. Через конец диаметра проведена плоскость под углом 30 к нему. Найдите площадь сечения шара этой плоскостью.
Геометрия 11 класс
Контрольная работа № 4 по теме:
«Объемы тел»
Вариант 1
Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен 60. Найдите объем пирамиды.
В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45. Найдите объем цилиндра.
Вариант 2
Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол в 60. Найдите объем пирамиды.
В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол в 45. Найдите объем конуса.
Геометрия 11 класс
Контрольная работа № 4 по теме:
«Объемы тел»
Вариант 1
Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен 60. Найдите объем пирамиды.
В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45. Найдите объем цилиндра.
Вариант 2
Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол в 60. Найдите объем пирамиды.
В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол в 45. Найдите объем конуса.
Геометрия 11 класс
Контрольная работа № 5 по теме:
«Объем шара и площадь сферы»
Вариант 1
Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60. Найдите отношение объемов конуса и шара.
Объем цилиндра равен 96 см3, площадь его осевого сечения 48 см2. Найдите площадь сферы, описанной около цилиндра.
Вариант 2
В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов цилиндра и шара.
Геометрия 11 класс
Контрольная работа № 5 по теме:
«Объем шара и площадь сферы»
Вариант 1
Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60. Найдите отношение объемов конуса и шара.
Объем цилиндра равен 96 см3, площадь его осевого сечения 48 см2. Найдите площадь сферы, описанной около цилиндра.
Вариант 2
В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов цилиндра и шара.
Геометрия 11 класс
Итоговая контрольная работа
Вариант 1
1. В правильной четырехугольной пирамиде МАВСD сторона основания равна 6, а боковое ребро -5. Найдите:
площадь боковой поверхности пирамиды;
объем пирамиды;
угол наклона боковой грани к плоскости основания;
скалярное произведение векторов ;
площадь описанной около пирамиды сферы;
угол между ВD и плоскостью DMC.
Вариант 2
1. В правильной треугольной пирамиде МАВС сторона основания равна 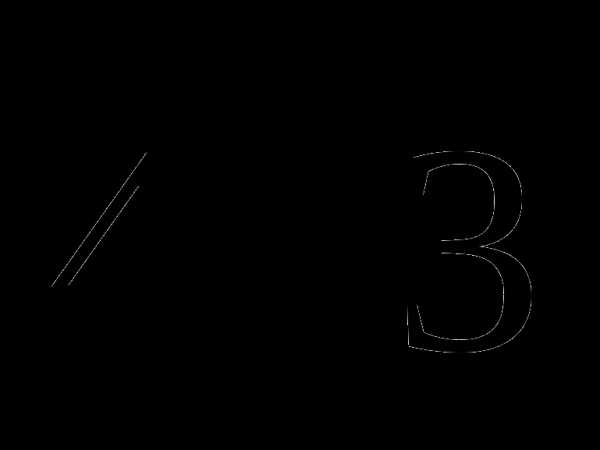 , а боковое ребро -5. Найдите:
, а боковое ребро -5. Найдите:
площадь боковой поверхности пирамиды;
объем пирамиды;
угол наклона боковой грани к плоскости основания;
скалярное произведение векторов
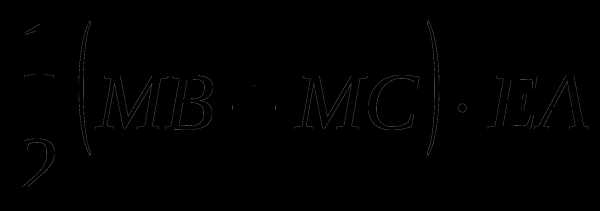 , где Е – середина ВС;
, где Е – середина ВС;объем вписанного в пирамиду шара;
угол между стороной основания и плоскостью боковой грани.
Геометрия 11 класс
Итоговая контрольная работа
Вариант 1
1. В правильной четырехугольной пирамиде МАВСD сторона основания равна 6, а боковое ребро -5. Найдите:
площадь боковой поверхности пирамиды;
объем пирамиды;
угол наклона боковой грани к плоскости основания;
скалярное произведение векторов ;
площадь описанной около пирамиды сферы;
угол между ВD и плоскостью DMC.
Вариант 2
1. В правильной треугольной пирамиде МАВС сторона основания равна 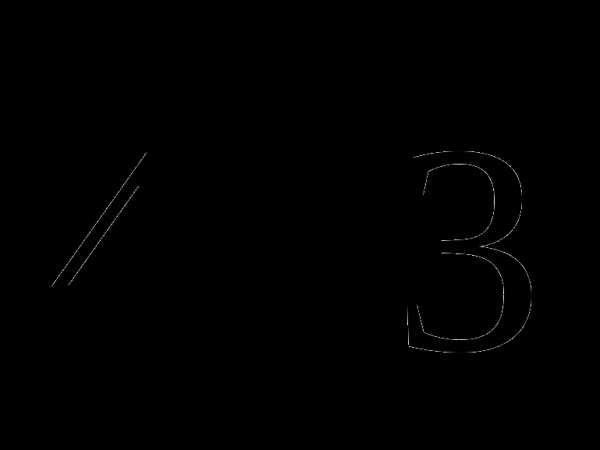 , а боковое ребро -5. Найдите:
, а боковое ребро -5. Найдите:
площадь боковой поверхности пирамиды;
объем пирамиды;
угол наклона боковой грани к плоскости основания;
скалярное произведение векторов
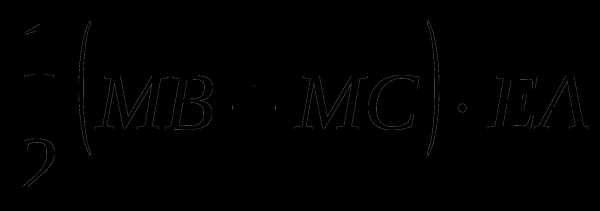 , где Е – середина ВС;
, где Е – середина ВС;объем вписанного в пирамиду шара;
угол между стороной основания и плоскостью боковой грани.
doc4web.ru
КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(–4; 6; –3), В(7; –3; 5), С(–5; –4; 0), D(3; 0; –5). Изобразить их на координатной плоскости. Найти: 1) координаты 2) расстояние между точками B и А 3) координаты середины Р отрезка СВ 4) 5) угол между векторами 6) | КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(4; –6; 3), В(–5; 2; –5), С(0; –3; –4), D(–6; –3; 0). Изобразить их на координатной плоскости. Найти: 1) координаты 2) расстояние между точками А и D 3) координаты середины Х отрезка СВ 4) 5) угол между векторами 6) |
КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(–3; -5; –6), В(5; –2; -4), С(0; 4; 3), D(–6; –3; 0). Изобразить их на координатной плоскости. Найти: 1) координаты 2) расстояние между точками B и D 3) координаты середины М отрезка АВ 4) 5) угол между векторами и 6) | КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(3; –5; 6), В(–3; -1; 4), С(–4; 0; -3), D(0; –3; –5). Изобразить их на координатной плоскости. Найти: 1) координаты 2) расстояние между точками С и D 3) координаты середины К отрезка АС 4) 5) угол между векторами и 6) |
КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(4; 6; –3), В(7; 3; 5), С(–5; –4; 0), Найти: 1) координаты 2) расстояние между точками B и А 3) координаты середины Р отрезка СВ 4) 5) угол между векторами 6) | КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(4; 6; 3), В(–5; -2; –5), С(0; –3; –4),D(–6; –3; 0). Изобразить их на координатной плоскости. Найти: 1) координаты 2) расстояние между точками А и D 3) координаты середины Х отрезка СВ 4) 5) угол между векторами 6) |
КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(–3; 5; 6), В(5; –4; 4), С(0; 6; 3), Найти: 1) координаты 2) расстояние между точками B и D 3) координаты середины М отрезка АВ 4) 5) угол между векторами и 6) | КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(4; –5; 6), В(–3; 2; –4), С(–4; 0; 3), D(0; –3; –5). Изобразить их на координатной плоскости. Найти: 1) координаты 2) расстояние между точками С и D 3) координаты середины К отрезка АС 4) 5) угол между векторами и 6) |
КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(–4; 6; 3), В(7; –3; 6) С(–5; –4; 0), D(3; 0; –5). Изобразить их на координатной плоскости. Найти: 1) координаты 2) расстояние между точками B и А 3) координаты середины Р отрезка СВ 4) 5) угол между векторами 6) | КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(6; –6; 3), В(–5; 2; –5), С(0; –3; –6), D(–6; –3; 0). Изобразить их на координатной плоскости. Найти: 1) координаты 2) расстояние между точками А и D 3) координаты середины Х отрезка СВ 4) 5) угол между векторами 6) |
КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(3; 6; –6), В(7; –2; 4), С(0;- 4; 3), Найти: 1) координаты 2) расстояние между точками B и D 3) координаты середины М отрезка АВ 4) 5) угол между векторами и 6) | КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(3; –5; -6), В(3; 1; –4), С(–4; 0; -3), D(0; –3; –5). Изобразить их на координатной плоскости. Найти: 1) координаты 2) расстояние между точками С и D 3) координаты середины К отрезка АС 4) 5) угол между векторами и 6) |
КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(–4; 6; –3), В(8; –3; 5),С(–5; –4; 0), \ D(4; 0; –5). Изобразить их на координатной плоскости. Найти: 1) координаты 2) расстояние между точками B и А 3) координаты середины Р отрезка СВ 4) 5) угол между векторами 6) | КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(-4; –6; 3), В(–5; 2; –6),С(0; –3; –4),\ D(–5; –3; 0). Изобразить их на координатной плоскости. Найти: 1) координаты 2) расстояние между точками А и D 3) координаты середины Х отрезка СВ 4) 5) угол между векторами 6) |
КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(–3; 6; –6), В(5; –2; 4), С(0; 6; 3), Найти: 1) координаты 2) расстояние между точками B и D 3) координаты середины М отрезка АВ 4) 5) угол между векторами и 6) | КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ по теме «КООРДИНАТЫ, ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ» I. Даны точки А(3; –5; 6), В(–2; 1; –4),С(–4; 0; 3), D(0; –4; –5). Изобразить их на координатной плоскости. Найти: 1) координаты 2) расстояние между точками С и D 3) координаты середины К отрезка АС 4) 5) угол между векторами и 6) |
multiurok.ru
Контрольные работы по геометрии 11 класс
Контрольные работы
по геометрии
в 11 классе
по учебнику атанасян л.с.
Контрольная работа № 1
Тема: Векторы
(на 20 мин)
Вариант 1
1. Найдите координаты вектора  , если А (5; –1; 3), В (2; –2; 4).
, если А (5; –1; 3), В (2; –2; 4).
2. Даны векторы  (3; 1; –2) и
(3; 1; –2) и  (1; 4; –3). Найдите
(1; 4; –3). Найдите 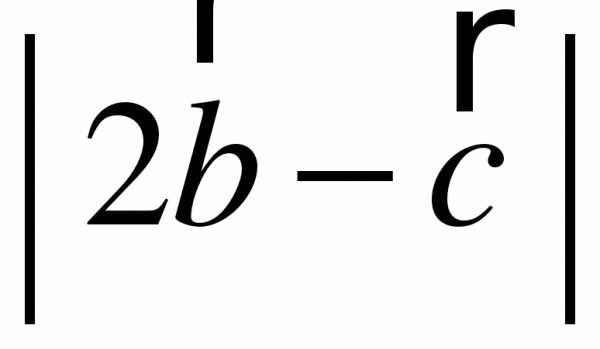 .
.
3. Изобразите систему координат Oxyz и постройте точку А (1; –2; –4). Найдите расстояния от этой точки до координатных плоскостей.
Контрольная работа № 1
Тема: Векторы
(на 20 мин)
Вариант 2
1. Найдите координаты вектора  , если С (6; 3; – 2), D (2; 4; – 5).
, если С (6; 3; – 2), D (2; 4; – 5).
2. Даны вектора  (5; – 1; 2) и
(5; – 1; 2) и 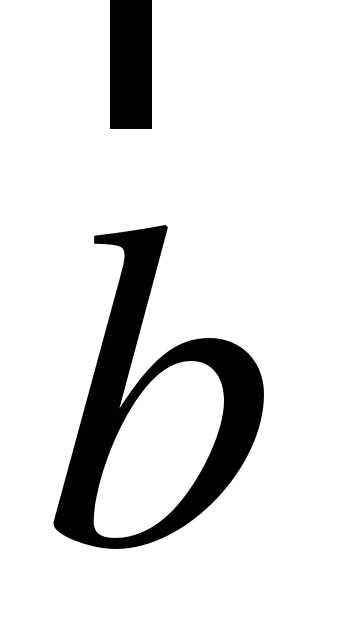 (3; 2; – 4). Найдите
(3; 2; – 4). Найдите 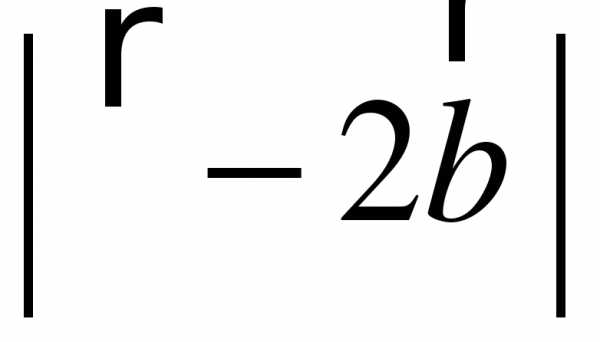 .
.
3. Изобразите систему координат Oxyz и постройте точку В (– 2; – 3; 4). Найдите расстояние от этой точки до координатных плоскостей.
Контрольная работа № 2
Тема: Скалярное произведение векторов. Движения.
Вариант 1
1. Вычислите скалярное произведение векторов  и
и  , если , ,
, если , , 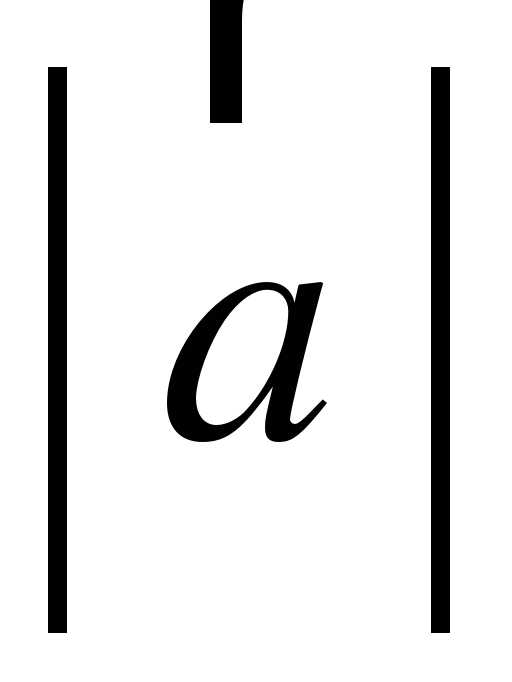 = 2,
= 2, 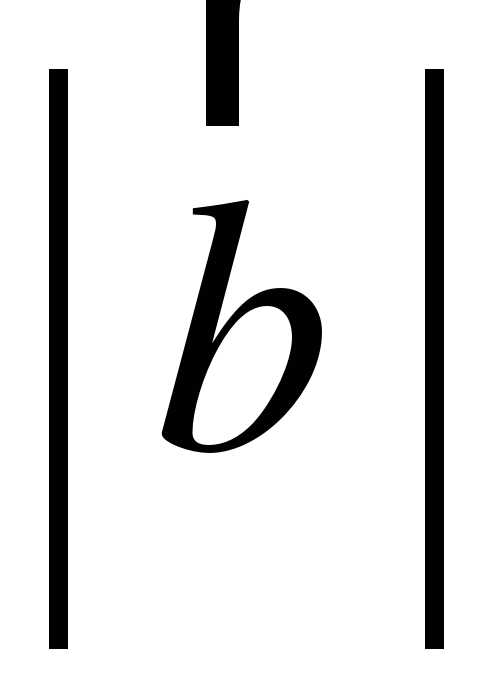 = 3,
= 3, 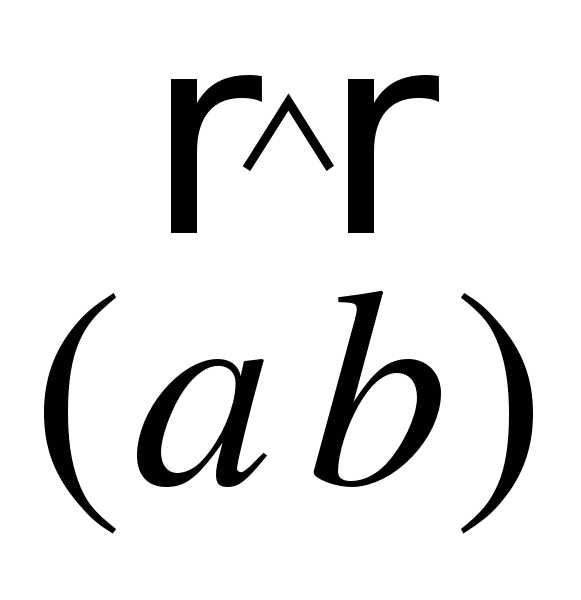 = 60°,
= 60°, 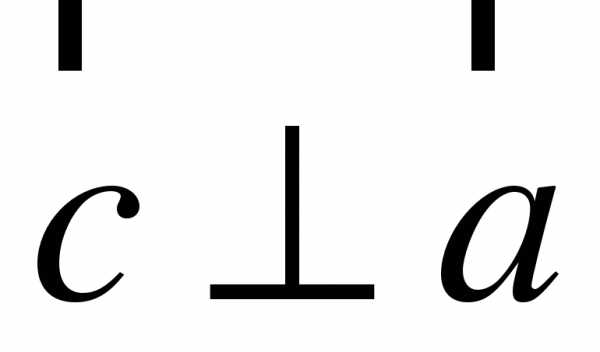 ,
, 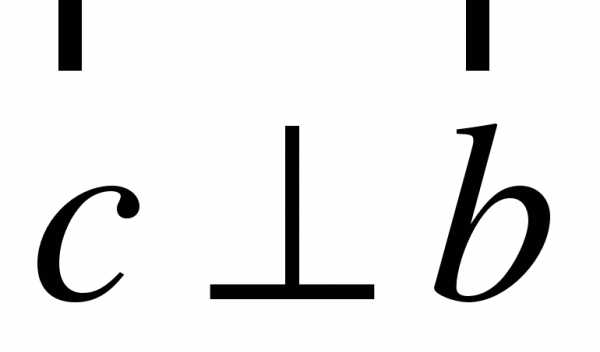 .
.
2. Дан куб ABCDA1B1C1D1. Найдите угол между прямыми AD1 и BM, где M – середина ребра DD1.
3. При движении прямая отображается на прямую b1, а плоскость β – на плоскость β1 и b || β1.
Контрольная работа № 2
Тема: Скалярное произведение векторов. Движения.
Вариант 2
1. Вычислите скалярное произведение векторов 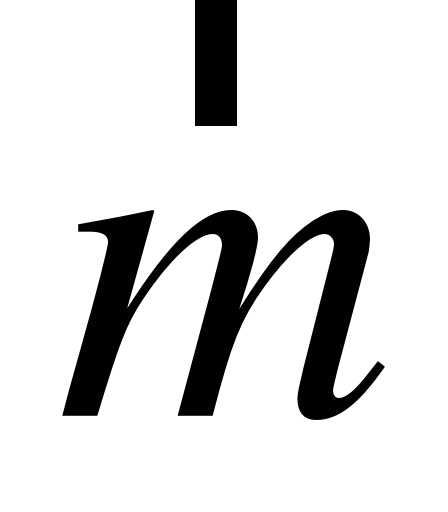 и
и 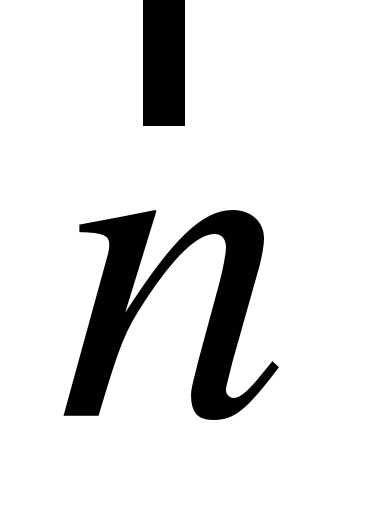 , если , ,
, если , ,  = 3,
= 3, 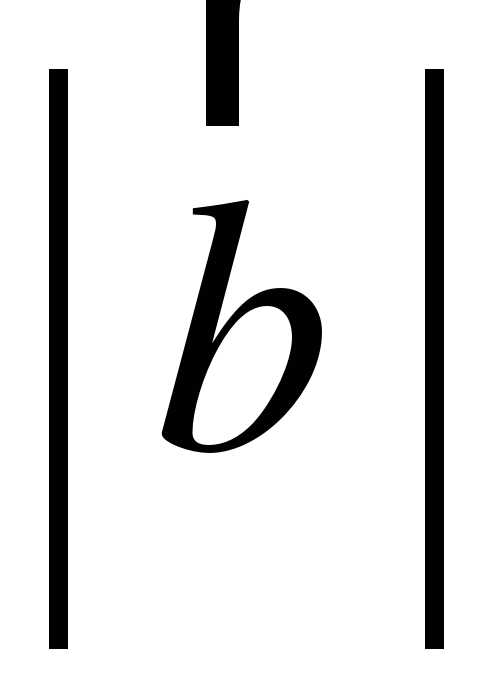 = 2,
= 2, 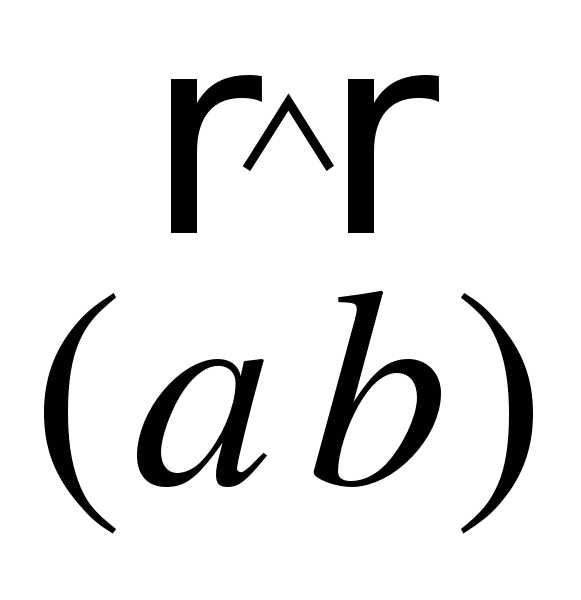 = 60°,
= 60°, 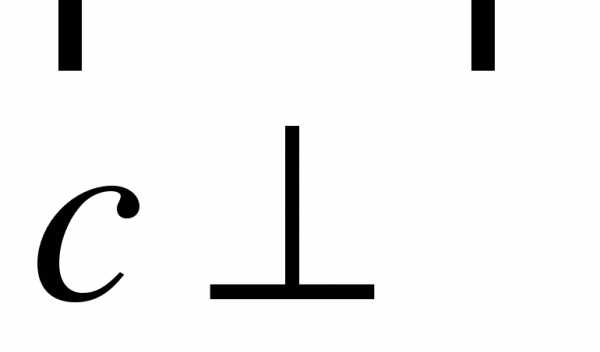 ,
, 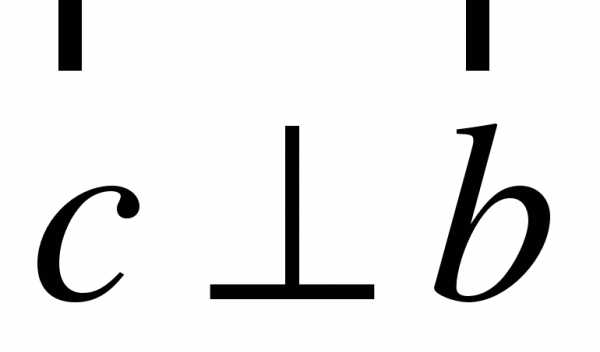 .
.
2. Дан куб ABCDA1B1C1D1. Найдите угол между прямыми AC и DC1.
3. При движении прямая a отображается на прямую a1, плоскость α – на плоскость α1, и . Докажите, что .
Контрольная работа № 3
Тема: Цилиндр, конус, шар.
Вариант 1
1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16π см2. Найдите площадь поверхности цилиндра.
2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 120°. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30°;
б) площадь боковой поверхности конуса.
3. Диаметр шара равен 2m. Через конец диаметра проведена плоскость под углом 45° к нему. Найдите длину линии пересечения сферы с этой плоскостью.
Контрольная работа № 3
Тема: Цилиндр, конус, шар.
Вариант 2
1. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь поверхности цилиндра.
2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30°. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60°;
б) площадь боковой поверхности конуса.
3. Диаметр шара равен 4m. Через конец диаметра проведена плоскость под углом 30° к нему. Найдите площадь сечения шара этой плоскостью.
Контрольная работа № 4
Тема: Объемы тел.
Вариант 1
1. Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен 60°. Найдите объем пирамиды.
2. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2a, а прилежащий угол равен 30°. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45°. Найдите объем цилиндра.
Контрольная работа № 4
Тема: Объемы тел.
Вариант 2
1. Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол в 60°. Найдите объем пирамиды.
2. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2a, а прилежащий угол равен 30°. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол в 45°. Найдите объем конуса.
Контрольная работа № 5
Тема: Объем шара и площадь сферы.
Вариант 1
1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60°. Найдите отношение объемов конуса и шара.
2. Объем цилиндра равен 96π см3, площадь его осевого сечения 48 см2. Найдите площадь сферы, описанной около цилиндра.
Контрольная работа № 5
Тема: Объем шара и площадь сферы.
Вариант 2
1. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов цилиндра и шара.
videouroki.net
Тексты контрольных работ по геометрии для 11 класса (учебник Л.С. Атанасяна)
Контрольные работы
по геометрии
в 11 классе
по учебнику атанасянА л.с.
Контрольная работа № 1
Тема: Векторы
(на 20 мин)
Вариант 1
1. Найдите координаты вектора , если А (5; –1; 3), В (2; –2; 4).
2. Даны векторы (3; 1; –2) и (1; 4; –3). Найдите .
3. Изобразите систему координат Oxyz и постройте точку А (1; –2; –4). Найдите расстояния от этой точки до координатных плоскостей.
Контрольная работа № 1
Тема: Векторы
(на 20 мин)
Вариант 2
1. Найдите координаты вектора , если С (6; 3; – 2), D (2; 4; – 5).
2. Даны вектора (5; – 1; 2) и (3; 2; – 4). Найдите .
3. Изобразите систему координат Oxyz и постройте точку В (– 2; – 3; 4). Найдите расстояние от этой точки до координатных плоскостей.
Контрольная работа № 2
Тема: Скалярное произведение векторов. Движения.
Вариант 1
1. Вычислите скалярное произведение векторов и , если , , = 2, = 3, = 60°, , .
2. Дан куб ABCDA1B1C1D1. Найдите угол между прямыми AD1 и BM, где M – середина ребра DD1.
3. При движении прямая отображается на прямую b1, а плоскость β – на плоскость β1 и b || β1.
Контрольная работа № 2
Тема: Скалярное произведение векторов. Движения.
Вариант 2
1. Вычислите скалярное произведение векторов и , если , , = 3, = 2, = 60°, , .
2. Дан куб ABCDA1B1C1D1. Найдите угол между прямыми AC и DC1.
3. При движении прямая a отображается на прямую a1, плоскость α – на плоскость α1, и . Докажите, что .
Контрольная работа № 3
Тема: Цилиндр, конус, шар.
Вариант 1
1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16π см2. Найдите площадь поверхности цилиндра.
2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 120°. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30°;
б) площадь боковой поверхности конуса.
3. Диаметр шара равен 2m. Через конец диаметра проведена плоскость под углом 45° к нему. Найдите длину линии пересечения сферы с этой плоскостью.
Контрольная работа № 3
Тема: Цилиндр, конус, шар.
Вариант 2
1. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь поверхности цилиндра.
2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30°. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60°;
б) площадь боковой поверхности конуса.
3. Диаметр шара равен 4m. Через конец диаметра проведена плоскость под углом 30° к нему. Найдите площадь сечения шара этой плоскостью.
Контрольная работа № 4
Тема: Объемы тел.
Вариант 1
1. Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен 60°. Найдите объем пирамиды.
2. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2a, а прилежащий угол равен 30°. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45°. Найдите объем цилиндра.
Контрольная работа № 4
Тема: Объемы тел.
Вариант 2
1. Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол в 60°. Найдите объем пирамиды.
2. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2a, а прилежащий угол равен 30°. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол в 45°. Найдите объем конуса.
Контрольная работа № 5
Тема: Объем шара и площадь сферы.
Вариант 1
1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60°. Найдите отношение объемов конуса и шара.
2. Объем цилиндра равен 96π см3, площадь его осевого сечения 48 см2. Найдите площадь сферы, описанной около цилиндра.
Контрольная работа № 5
Тема: Объем шара и площадь сферы.
Вариант 2
1. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов цилиндра и шара.
infourok.ru
Контрольные работы по геометрии по теме «Векторы в пространстве» 11 класс
11 класс Контрольная работа по теме « Векторы в пространстве» вариант 1
Какому из указанных векторов равен вектор
 (1; 2;3)?
(1; 2;3)?
А)  (2; 3; 1) Б)
(2; 3; 1) Б)  (3;1;2) В)
(3;1;2) В) 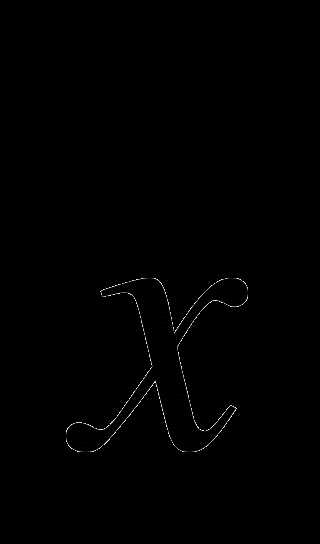 (1;2;3) Г)
(1;2;3) Г) 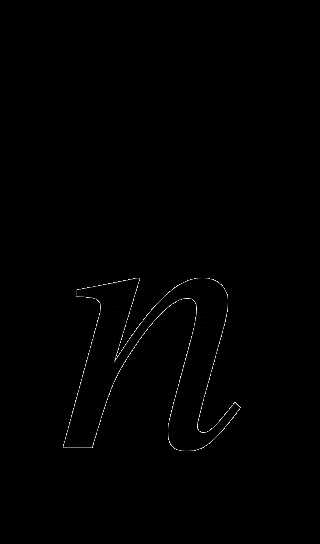 (1;3;2)
(1;3;2)
Найдите скалярное произведение векторов
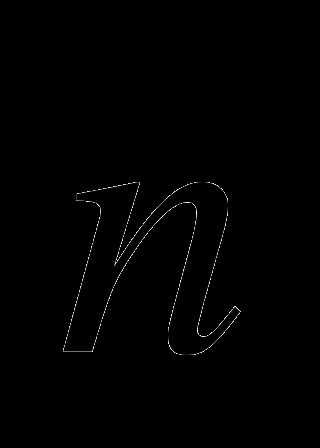 (-1; 3; -2) и
(-1; 3; -2) и  (0; -1; 5)
(0; -1; 5)
А) -14; Б) -13; В) 0; Г) 7; Д) 4.
3. При каких значениях n векторы  (1;-1; n) и
(1;-1; n) и  (n; 1; n) коллинеарны?
(n; 1; n) коллинеарны?
А) ни при каких; Б) при n=-1; В) при n=1; Г) при n= 1.
1.
Часть 2
Вычислите длину вектора
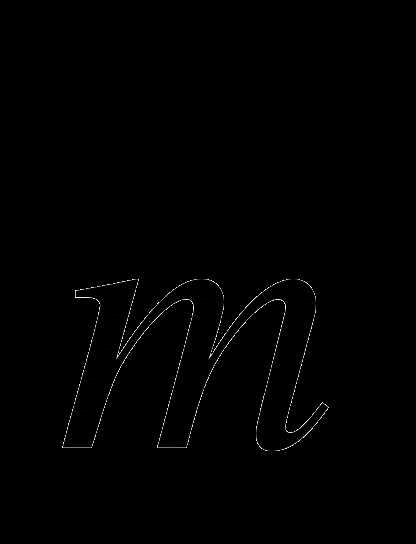 = 2
= 2 + 3
+ 3 , если
, если  (1;1;-1),
(1;1;-1),  (2; 0; 0).
(2; 0; 0).При каком значении р векторы
 (3; р; -1) и
(3; р; -1) и  (р; -2; 5) взаимно перпендикулярны?
(р; -2; 5) взаимно перпендикулярны?Разложите вектор
 (5; -17; 11) по векторам
(5; -17; 11) по векторам 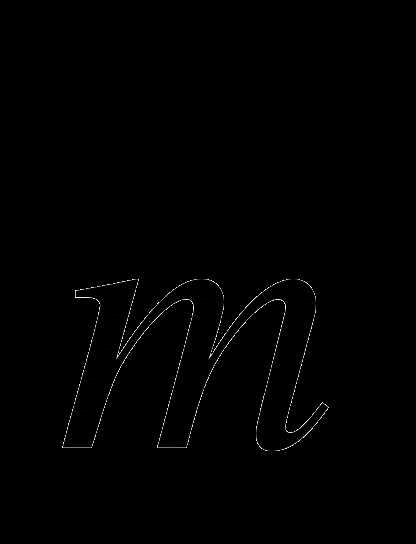 (3; -2; 0),
(3; -2; 0), 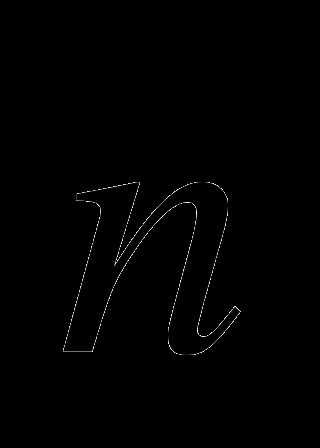 (-2; 4; 1) и
(-2; 4; 1) и  (-1; -3; 4)
(-1; -3; 4)
Часть 3
Найдите градусную меру угла φ между векторами
 = 3
= 3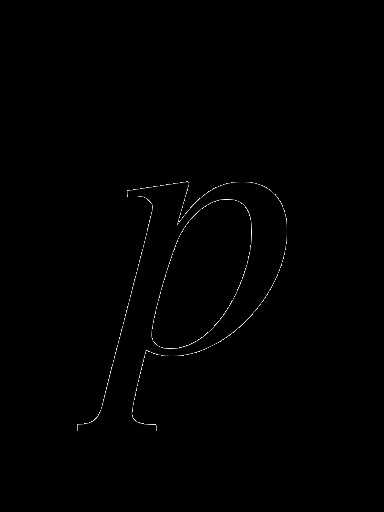 +
+ и
и 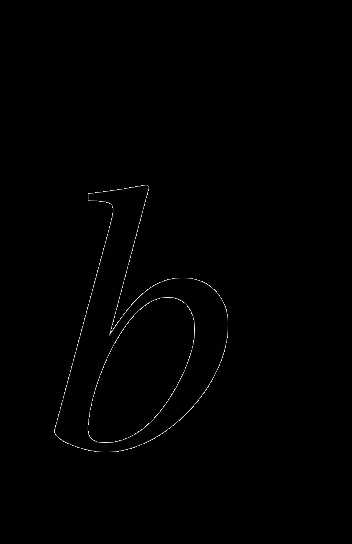 =
= 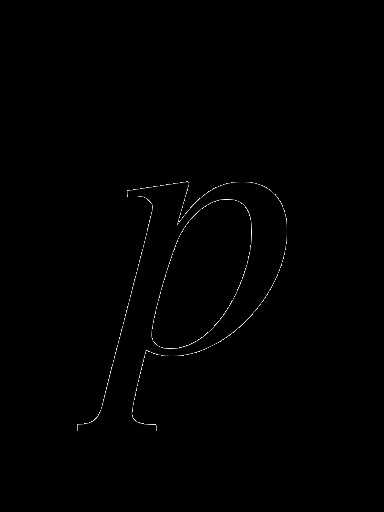 + 2
+ 2 , где
, где 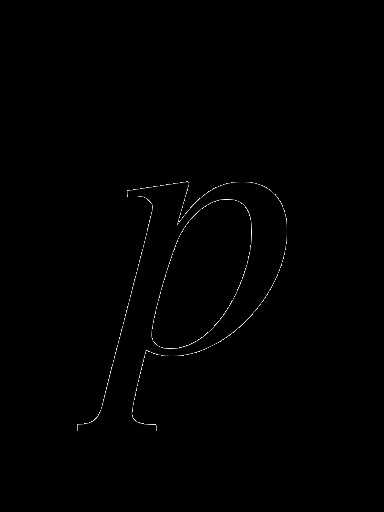 и
и  — единичные и взаимно перпендикулярные векторы.
— единичные и взаимно перпендикулярные векторы.
11 класс Контрольная работа по теме « Векторы в пространстве» вариант 2
1. Какому из указанных векторов равен вектор  (3; 1;2)?
(3; 1;2)?
А)  (2; 3; 1) Б)
(2; 3; 1) Б)  (3;1;2) В)
(3;1;2) В)  (1;2;3) Г)
(1;2;3) Г) 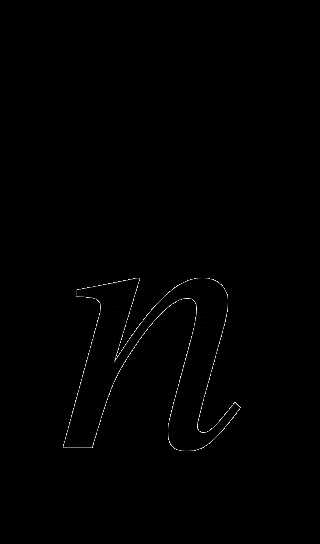 (1;3;2)
(1;3;2)
2. Найдите координаты вектора 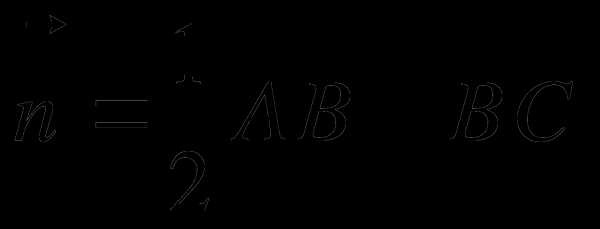 , если А(-3;-2; -1), В(-1; 2; 3), С(0; -1; -2)
, если А(-3;-2; -1), В(-1; 2; 3), С(0; -1; -2)
А) 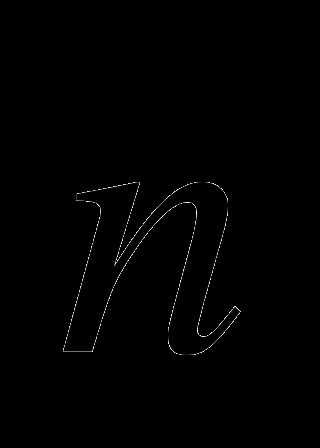 (0; -5; -7) Б)
(0; -5; -7) Б) 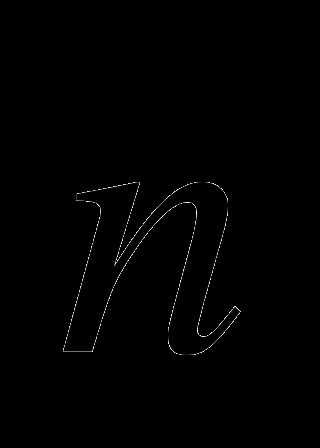 (-2; 1; 3) В)
(-2; 1; 3) В) 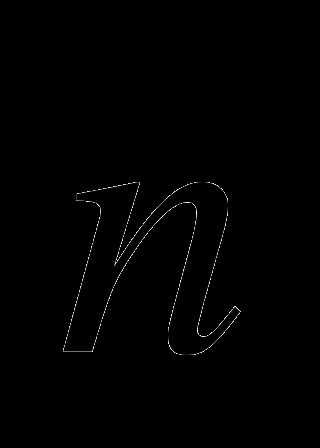 (-3; 1; 2)
(-3; 1; 2)
Г) 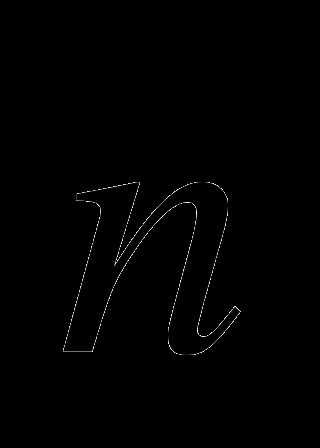 (2; -1; -3) Д)
(2; -1; -3) Д) 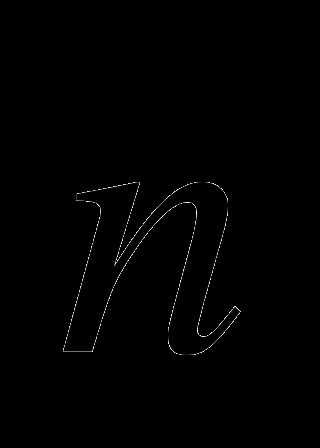 (0; 5; 7)
(0; 5; 7)
3. При каких значениях n векторы  (2; 1; n) и
(2; 1; n) и  (n; 1; n) перпендикулярны?
(n; 1; n) перпендикулярны?
А) ни при каких; Б) при n=-1; В) при n=1; Г) при n= 1.
1.
Часть 2
При каких значениях n и m векторы
 (-1; 4; -2) и
(-1; 4; -2) и  (-3; m; n) коллинеарны?
(-3; m; n) коллинеарны?Дан треугольник АВС: А(0;1;-1), В(1;-1;2) и С(3;1;0). Найти косинус угла А треугольника АВС
Разложите вектор
 (1; 4; 3) по векторам
(1; 4; 3) по векторам 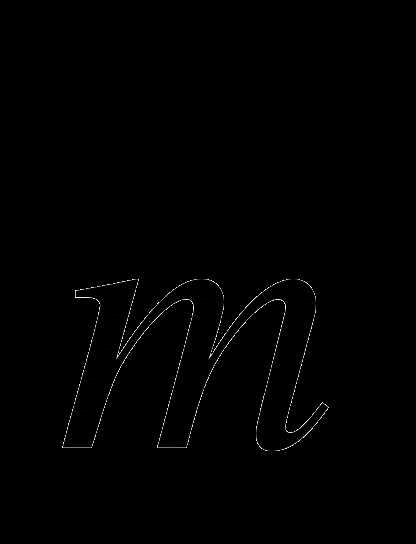 (1; -1; 0),
(1; -1; 0), 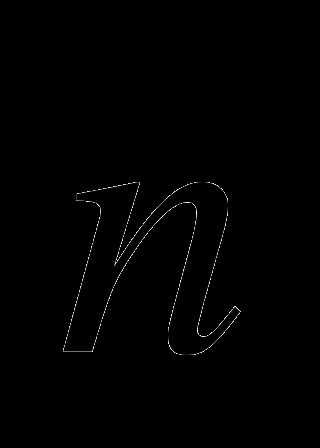 (0; 1; 1) и
(0; 1; 1) и
 (1; 0; -1)
(1; 0; -1)
Часть 3
Вычислите длину вектора
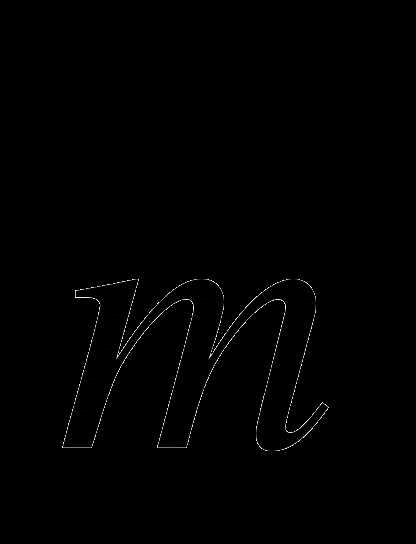 =
=  — 2
— 2 , если
, если  = 2,
= 2,  =1, а угол между векторами
=1, а угол между векторами  и
и  равен 600 .
равен 600 .
11 класс. Векторы в пространстве вариант 3
1. Вычислите координаты вектора 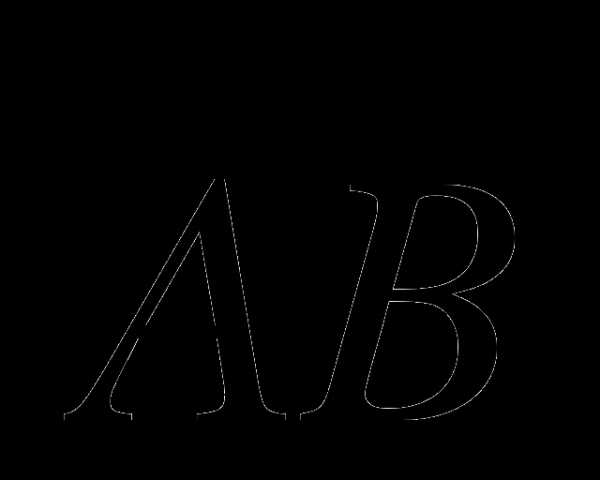 , если А(2;3;1), В(1;0;2)
, если А(2;3;1), В(1;0;2)
А)  (1;3;-1) Б)
(1;3;-1) Б)  (
( ;
; ;
; ) В)
) В)  (-1;-3;1) Г) другой ответ
(-1;-3;1) Г) другой ответ
2. Найдите скалярное произведение векторов  (4; -3; 1) и
(4; -3; 1) и  (-2; 1; -1)
(-2; 1; -1)
А) -24; Б) -12; В) 0; Г) -1; Д) -10.
3. Вычислите длину вектора  = — 2
= — 2 , если
, если  (-1;2;-2)
(-1;2;-2)
А) 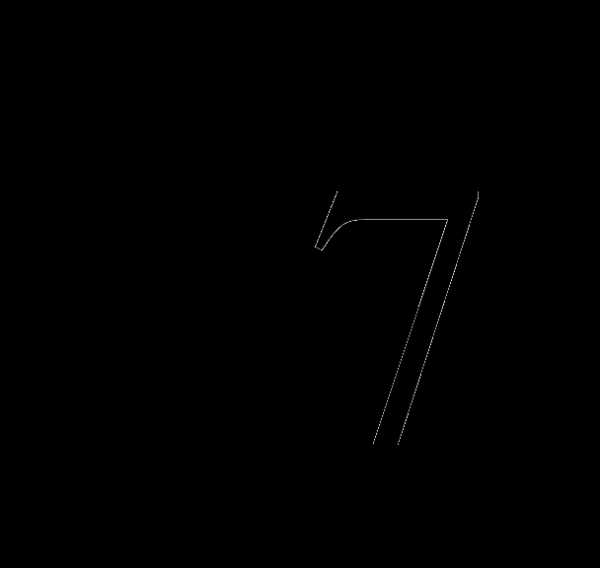 Б) 3 В) 1 Г) 6 Д) другой ответ
Б) 3 В) 1 Г) 6 Д) другой ответ
Часть 2
4.При каких значениях n и m векторы  (-2;8; -4) и
(-2;8; -4) и  (-6; m; n) коллинеарны?
(-6; m; n) коллинеарны?
5. Разложите вектор  (11; -4; 11) по векторам
(11; -4; 11) по векторам 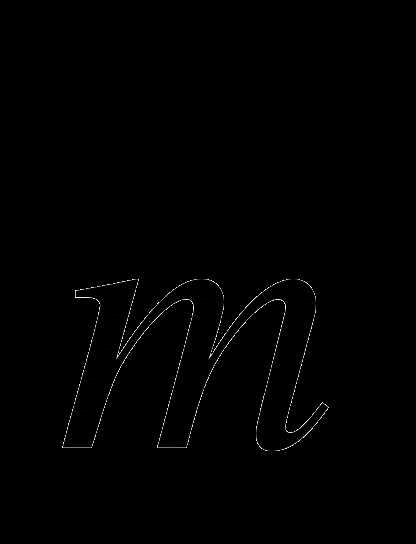 (1; 2; 3),
(1; 2; 3), 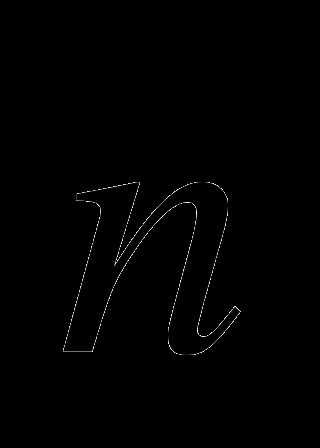 (2; -1; 1) и
(2; -1; 1) и  (3; -5; 2)
(3; -5; 2)
6. Дан треугольник АВС: А(2; 1; 7), В(-1; 1; 3) и С(-8; 1; 2). Найти внутренний угол при вершине В.
Часть 3
7.Угол между векторами  и
и  равен 60
равен 60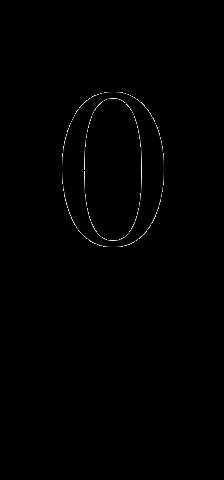 ;
;

 ,
, 

 , причем длины векторов
, причем длины векторов  ,
,  и
и  равны 1. Найдите скалярное произве-дение (
равны 1. Найдите скалярное произве-дение ( -2
-2 )
) 2
2 +
+ ).
).
11 класс. Векторы в пространстве вариант 4
Вычислите координаты вектора
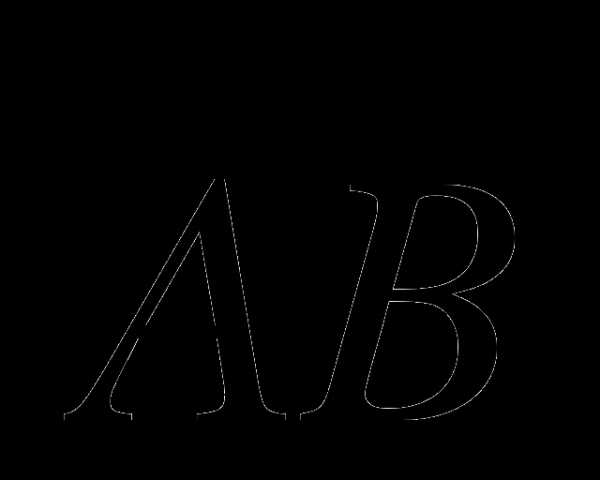 , если А(-2;4;1), В(1;0;-2)
, если А(-2;4;1), В(1;0;-2)
А) 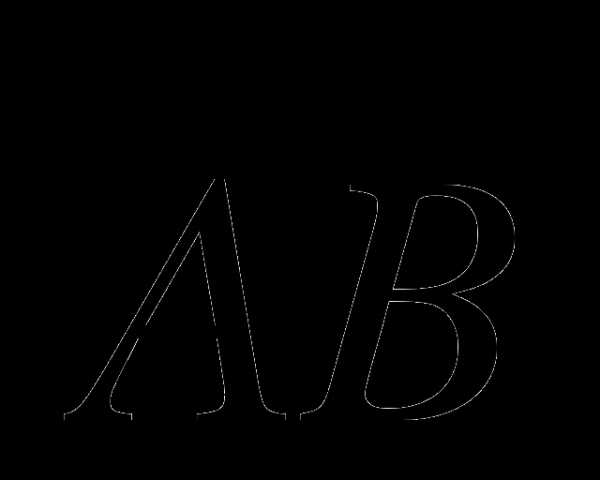 (3;-4;-3) Б)
(3;-4;-3) Б) 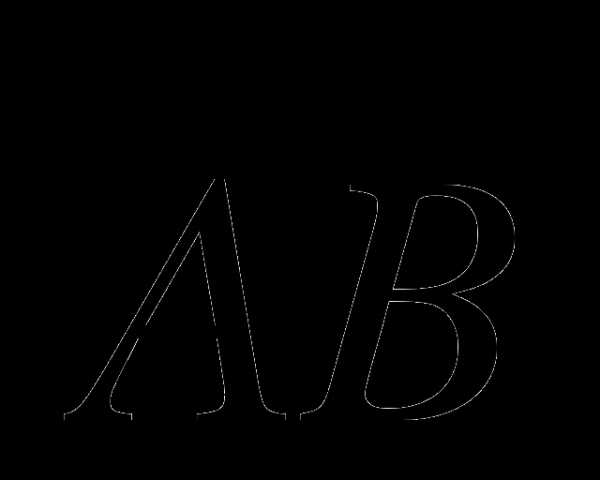 (-
(- ; 2; —
; 2; — ) В)
) В) 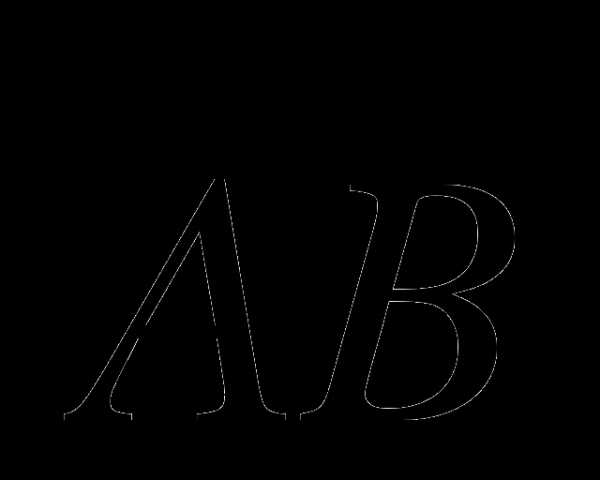 (-1;4;-1) Г) другой ответ
(-1;4;-1) Г) другой ответ
2. Какому из указанных векторов равен вектор  (4; 2;3)?
(4; 2;3)?
А)  (2; 3; 4) Б)
(2; 3; 4) Б)  (3;4;2) В)
(3;4;2) В)  (4;2;3) Г)
(4;2;3) Г) 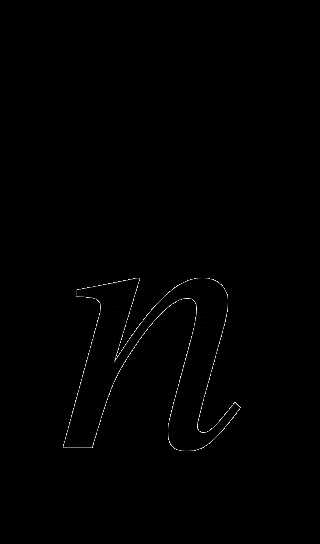 (4;3;2))
(4;3;2))
3. Являются ли векторы 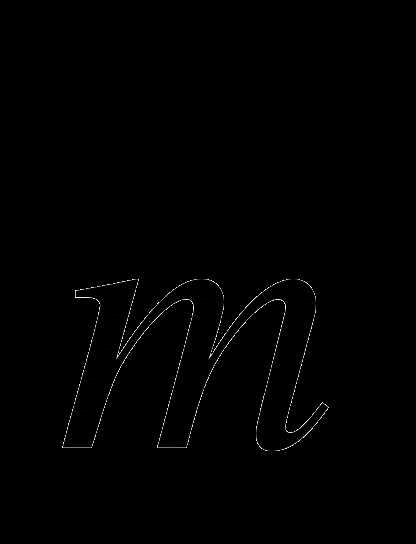 (8;-4;3) и
(8;-4;3) и  (-4;2;-
(-4;2;- ) коллинеарными?
) коллинеарными?
А) да Б) нет В) невозможно определить
Часть 2
Вычислите длину вектора
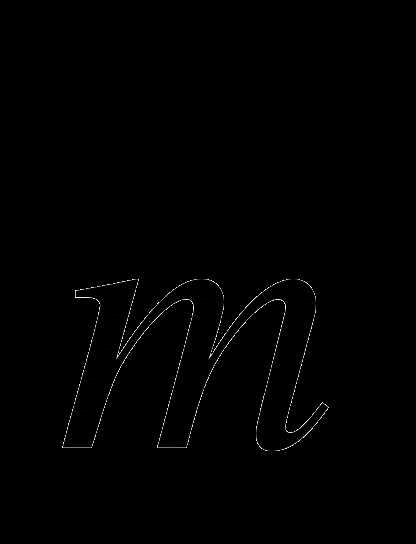 = 2
= 2 + 3
+ 3 , если
, если (3;1;0),
(3;1;0),  (0;1;-1).
(0;1;-1).Дан треугольник АВС: А(-1; -2; 4), В(-4; -2; 0) и С(3; -2; 1). Найти внутренний угол при вершине В.
Разложите вектор
 (4; 0; -7) по векторам
(4; 0; -7) по векторам 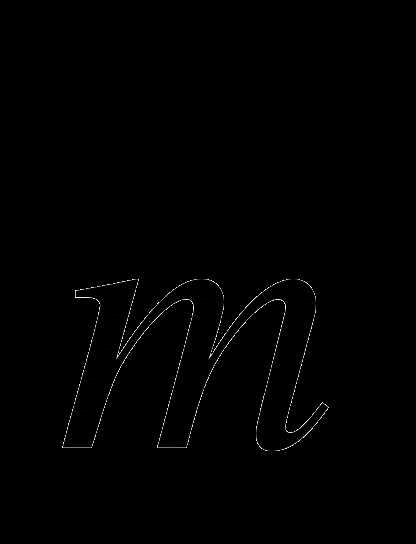 (1; 2; -3),
(1; 2; -3),  (0; 3; 1) и
(0; 3; 1) и  (2; 5; 2)
(2; 5; 2)
Часть 3
Векторы
 ,
,  и
и  — единичные;
— единичные;  и
и  образуют угол 600, а вектор
образуют угол 600, а вектор  перпендикулярен им. Найдите длину вектора
перпендикулярен им. Найдите длину вектора  +
+  +
+ .
.
infourok.ru
Контрольная работа № 1. Метод координат в пространстве в пространстве | |
1 вариант.
А( -2; 0; 1 ), В( -1; 2; 3 ), С( 8; -4; 9 ). Найдите координаты вектора , если ВМ – медиана ∆АВС. | 2 вариант.
А(6; 3; -2), В(2; 4; -5).
А ( -1; 2; 3 ), В ( 1; 0; 4 ), С ( 3; -2; 1 ). Найдите координаты вектора , если АМ – медиана ∆АВС. |
26.12 Контрольная работа № 2. Цилиндр. Конус и шар | |
1 вариант 1. Радиус основания цилиндра равен 5 см, а высота цилиндра равна 6 см. Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 см от нее. 2. Радиус шара равен 17 см. Найдите площадь сечения шара, удаленного от его центра на 15 см. 3. Радиус основания конуса равен 3 м, а высота 4 м. Найдите образующую и площадь осевого сечения. | 2 вариант 1. Высота цилиндра 8 дм, радиус основания 5 дм. Цилиндр пересечен плоскостью параллельно оси так, что в сечении получился квадрат. Найдите расстояние от этого сечения до оси цилиндра. 2. Радиус сферы равен 15 см. Найдите длину окружности сечения, удаленного от центра сферы на 12 см. 3. Образующая конуса l наклонена к плоскости основания под углом в 300. Найдите высоту конуса и площадь осевого сечения. |
01.03 Контрольная работа № 3 Объемы тел. Объем призмы, цилиндра, конуса | |
1 вариант 1. Образующая конуса равна 60 см, высота 30 см. Найдите объём конуса. 2. Основание прямой призмы – прямоугольный треугольник с катетом 6 см и острым углом 450. Объем призмы равен 108 см3. Найдите площадь полной поверхности призмы. 3. Осевым сечением цилиндра является квадрат, диагональ которого равна см. Найдите объем цилиндра. | 2 вариант 1. Образующая конуса, равная 12 см, наклонена к плоскости основания под углом 300. Найдите объём конуса. 2. Основанием прямой призмы является ромб со стороной 12 см и углом 600. Меньшее из диагональных сечений призмы является квадратом. Найдите объем призмы. 3. Осевым сечением цилиндра является квадрат, диагональ которого равна см. Найдите объем цилиндра. |
26.04 Контрольная работа № . Итоговая контрольная работа | |
1 вариант 1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол, равный 600. Найдите отношение объёмов конуса и шара. 2. Объём цилиндра равен 96π см3, площадь его осевого сечения 48см2. Найдите площадь сферы, описанной около цилиндра. 3. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2р, а прилежащий угол равен . Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол . Найдите объём конуса. | 2 вариант 1. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объёмов шара и цилиндра. 2. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса. 3. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2р, а прилежащий угол равен . Диагональ большей боковой грани призмы составляет с плоскостью её основания угол . Найдите объём цилиндра. |
multiurok.ru
Контрольная работа по геометрии для 11 класса Тема: «Векторы»
Контрольная работа
по геометрии для 11 класса
Тема: «Векторы»
Цели: проверить знания по данной теме, знать как упростить выражение по правилу треугольника, уметь находить координаты вектора, уметь находить длины отрезков по заданным координатам.
Просмотр содержимого документа
«Контрольная работа по геометрии для 11 класса Тема: «Векторы»»
Контрольная работа
по геометрии для 11 класса
Тема: «Векторы»
Цели: проверить знания по данной теме, знать как упростить выражение по правилу треугольника, уметь находить координаты вектора, уметь находить длины отрезков по заданным координатам.
Ход урока
Организационный момент. ( Сообщение темы и целей урока )
Контрольная работа.
Вариант 1.
1. Упростите выражение:

2. Даны векторы 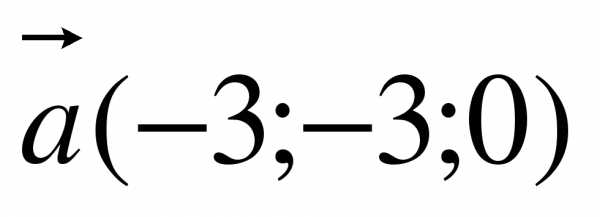 ,
, 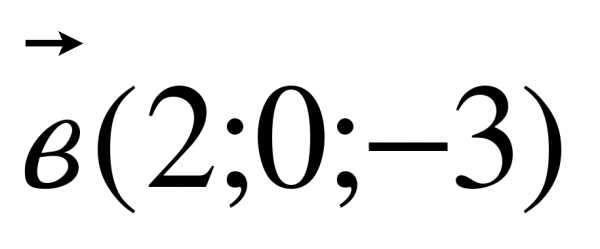 ,
, 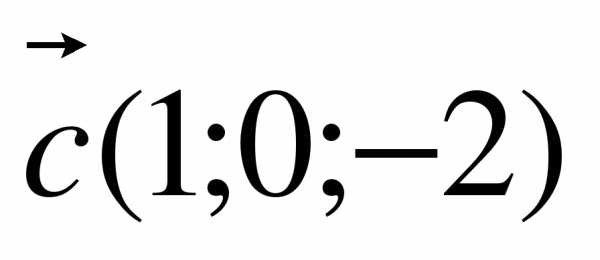
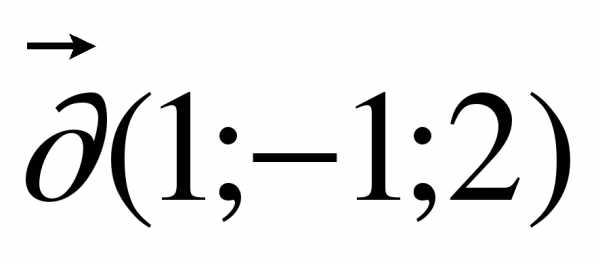 .
.
Найдите координаты векторов .
3. Даны точки А(9;3;-5), В(2;10;-5), С(2;3;2), Д(3;7;-4), Е(5;-3;2), F(1;3;-10)? K(-4;3;0).
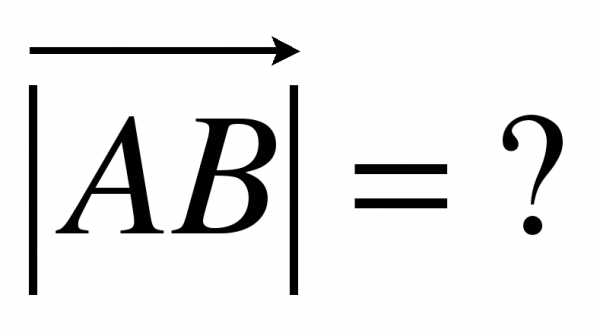
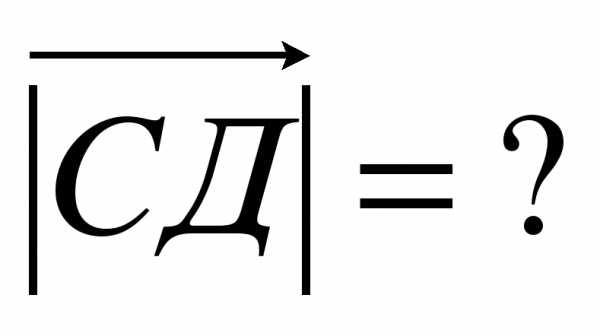
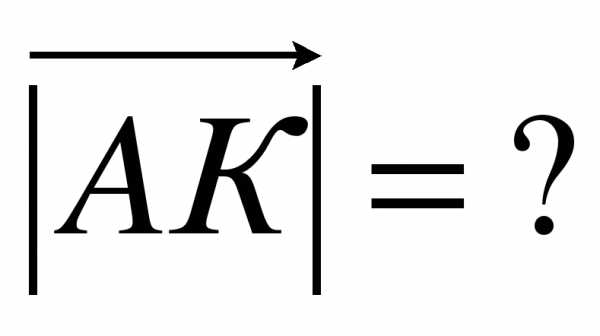
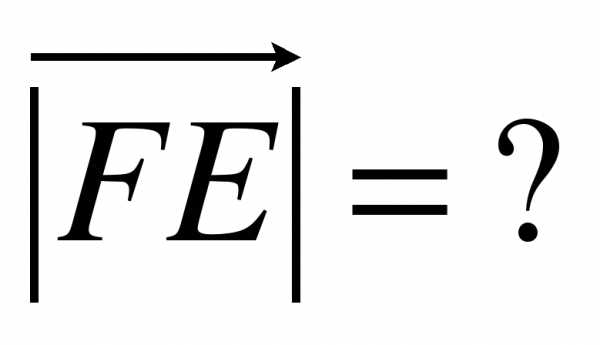
Вариант 2.
1. Упростите выражение:

2. Даны векторы 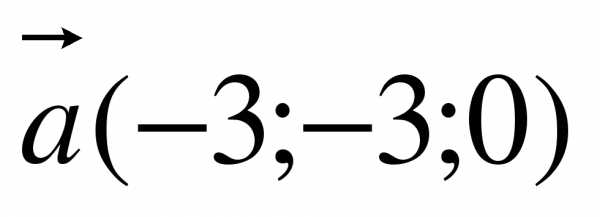 ,
, 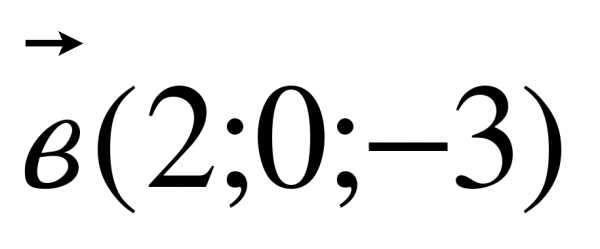 ,
, 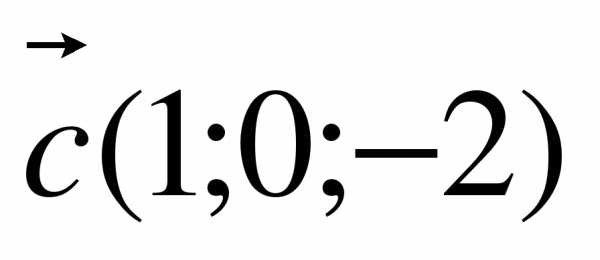
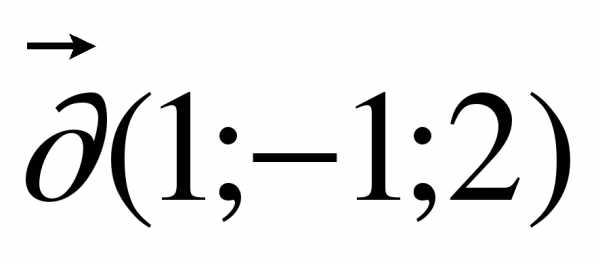 .
.
Найдите координаты векторов .
3. Даны точки А(9;3;-5), В(2;10;-5), С(2;3;2), Д(3;7;-4), Е(5;-3;2), F(1;3;-10)? K(-4;3;0).
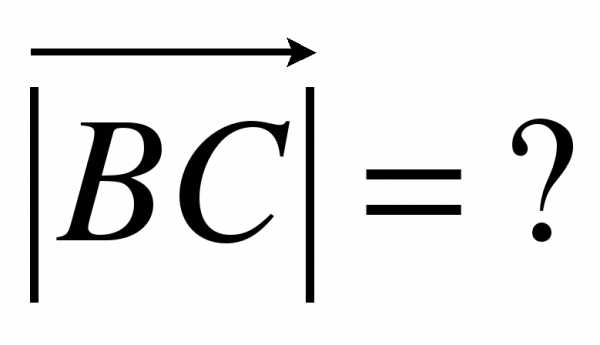
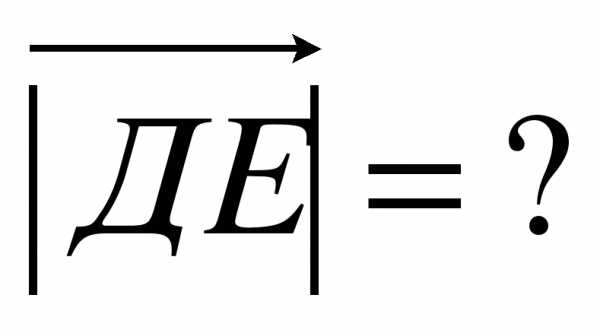
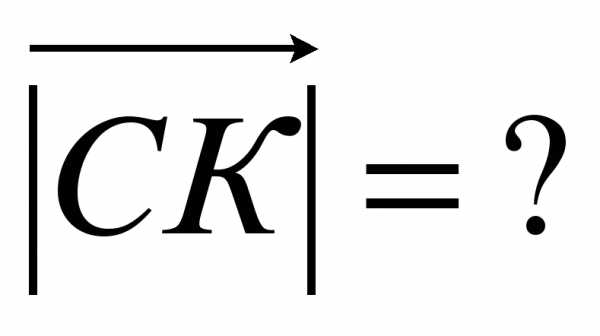
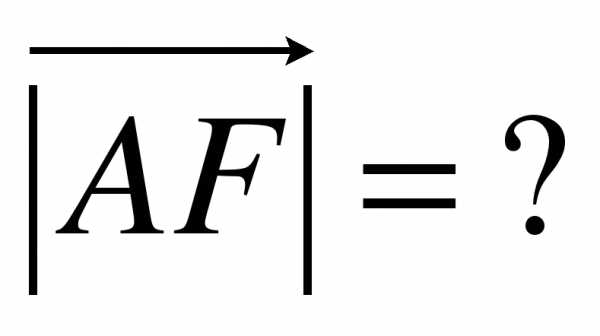
III. Итоги урока.
Учащиеся сдают тетради для контрольных работ.
Спасибо за урок.
multiurok.ru
