Математика 7 класс уравнения – Тест: Уравнения — Математика 7 класс

Линейные уравнения 7 класс | Алгебра

Линейные уравнения, решение которых начинается в курсе алгебры (7 класс) — это уравнения вида

   

где a и b — числа, x — переменная.

Уравнения, сводящиеся к виду ax=b при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей на число, отличное от нуля (то есть при помощи равносильных преобразований), также часто называют линейными (правильнее называть их уравнениями, сводящимися к линейным).

Рассмотрим примеры уравнений, сводящихся к линейным, которые встречаются в начале курса алгебры 7 класса.

   

Раскрываем скобки. Если перед скобками стоит множитель, умножаем этот множитель на каждое слагаемое в скобках. Если перед скобками стоит знак «+», знаки  не меняем. Если перед скобками стоит знак «-«, знаки меняем на противоположные:

   

Неизвестные слагаемые переносим в одну сторону, известные — в другую. При переносе знаки слагаемых меняем на противоположные:

   

   

Обе части уравнения делим на число, стоящее перед иксом:

   

   

Ответ: -9.

   

Раскрываем скобки:

   

Неизвестные слагаемые перенесём в левую часть, известные — в правую. Знак каждого слагаемого при переносе из одной части уравнения в другую меняем на противоположный:

   

(Обратите внимание: хотя сумма слагаемых  с переменной равна нулю, результат записываем не как 0, а как 0x).

Какое бы число мы не подставили в это уравнение вместо x, получим верное равенство.

Ответ: x — любое число.

   

Раскрываем скобки:

   

Можно сначала привести подобные слагаемые, чтобы упростить уравнение:

   

а уже потом перенести: неизвестные — в одну сторону, известные — в другую:

   

   

Это уравнение не имеет корней.

Ответ: нет корней.

   

Раскрываем скобки:

   

Приводим подобные слагаемые:

   

Переносим неизвестные слагаемые в одну сторону, известные — в другую, изменив при этом их знаки:

   

   

Обе части уравнения делим на число, стоящее перед иксом:

   

Ответ:

   

В следующий раз рассмотрим сводящиеся к линейным уравнениям уравнения с дробями.

www.algebraclass.ru

Решение уравнений по алгебре в 7 классе

ИТОГОВОЕ ПОВТОРЕНИЕ ПО АЛГЕБРЕ В 7 КЛАССЕ

Тема: Решение уравнений

Подобранные уравнения могут быть использованы как при изучении темы, так и при повторении или при подведении итогов. Уравнения отличаются своей тематикой и сложностью. Таким образом их применение возможно при дифференцированном подходе к каждому ученику. Есть уравнения, которые можно использовать в классах с углубленным изучением математики.

№

А

В

С

Д

Е

F

5х – 2 = 8

7 (2х -3) – х = 3х — 11

— (3 — х) : 12 = 3

|х – 4 |= 2

3а – 2(b – x) + 2 = b

-5,6(x — 3) + 2,1x = -3,5x + 10

2(x — 4) = 15

-4x + 34 = -2(x — 5)

(x — 4) : 5 = (2x — 3) : 3

|2x — 1| = 3

3a + bx = 12 – 3a

7(x – 4) + 3 = 3(2x — 7) + x — 8

3 – 4x = -5

2,5(x — 4) + 2 = 0,5x

(-6x + 1) : 4 = 2x : 3

|x + 4| = 9

4b – ax + 12 = 0

-12x + 4(x — 3) = -8x — 12

12 – 3x = 7

-5x + 12(x — 1) = 2

(8 — x) : 4 = (x — 3) : 3

|2x — 3| = 5

4(a – 2x) + b = 6

10(x — 3) + 1 = 5(2x + 3)

35(x + 1) = -14

-12(2 — x) = -6x + 2

(x + 3) : 4 = (2x — 1) : 3

|3x + 1| = 4

a(b – 3x) + 2 = 23

12(x + 2) – 2,1 = 2(6x + 12) — 3x

14 – (x – 2) = 23

-(x – 3) + 2(3 — x) = 5

-2(x + 1) : 3 = (3x — 1) : 2

|2x — 5| = 3

b – ax + 12 = ax

2,1x + 0,3(7 – x ) = 2,1

32x + (2 – 3x) = 5

-4x + 21 + (3 — x) = 12

x : 4 = 2x : 3

|x — 3| = 12

3b – a(x — 3) = 2

-2(x + 21) – 3(x — 14) = -5x

34(x — 2) = 2

-2(x — 3) + (4 — x) = 12

(13 — x) : 12 = 3(x — 2) : 5

|2x — 13| = 1

a(3x — b) = 12

-2(x + 21) – 3(x — 4) = -5(x +6)

3x – 12 + x = 4

23x – 2(3x — 4) = 12

(3x — 1) : 2 = 2(x + 2) : 3

|3x — 13| = 2

3xa – 2b = 3a — 4

2,1(x – 0,3) + 0,7x = 2,8x

11(x — 3) = 33

23(x + 2) – (2x — 1) = 1

-x : 4 = (3 – 2x) : 5

|5x + 1| = 4

-b(x — 3) = a

2,4(x – 0,01) = 24x : 10

3x + 12 + x = -4

-(3 — x) + 2(x — 3) = 3

(x – 3,4) : 3 = (2x — 3) :2

|x + 12| = 1

(x — a) :b = 12

-11(x — 2) + (2x — 3) = -9x + 19

2(x — 3) + 4 = 1

2(3x — 2) – (3 — x) = 5

(3 — x) : 3 = (2x — 1) : 2

|2x — 7| = 3

xb + a(x — 2) = 0

-11(x — 2) + (2x — 3) = -9(x + 2)

-3x + 2 = 17

-2(x — 3) + 3(2 — x) =1

2(x — 1) :3 = 3(2x + 1) : 2

|3x — 1| = 3

b + 2(ax — 4) = 2

-1,7(x +2) – 0,3x = 2(2 — x)

12 – (x — 2) = 3

-(2x — 1) – 2(5 – 3x) = 0

-(x — 2) : 5 = 2x : 3

|5x — 1| = 2

ax – 4bx + 12 = 9

-11(x — 2) + 2(3 – 2x) + 15x = 0

3x + 12 = 3

5(x — 2) + 2(3 — x) = 12

(4x — 3) : 3 = 2x : 5

|x + 1| = 1

bx – 2ax + 5 = 2bx

2(x — 23) + 3(15 — x) = -(x + 1)

43(x — 2) = 12

12(x — 2) + (-4 + x) = 0

-(0,6 + x) : 25 = x : 3

|x – 2| = 3

a(x — b) = 12

2(x — 23) + 3(15 — x) = -x + 1

4x – 21 = 4

-(2 — x) + 3(2x — 3) = 2

3 : x = 2 : (3 — x)

|21x + 2| = 23

a : (3x — b) = 21

2,1(2 — x) + 1,4(1,5x – 3) = 0

3 : (2x — 1) = 3

2(3 — x) – 21(x — 1) = 0

(2 – 3x) : 2 = (3 – 2x) : 3

|x + 3| = 12

b – 2ax + 4 = 0

2,1(2 – x) + 1,4(1,5x — 3) = 2

2 : (3 – 2x) = 1

-2(x — 12) – 3(x + 1) = 1

-(-3x -1) : 2 = x : 2

|3x — 2| = 4

(2ax — 3) : b = 1

21(2x — 1) = 14(3x — 4)

3(5x + 2) = 12

-7(2 — x) + 2(x — 3) = 0

(x — 2) : 5 = x : 3

|x — 6| = 3

bx – 4a = 8

21(x — 3) + 20 = 7(3x — 2)

21x – 3 = 12

7(2x — 1) + (4 — x) = 2x

(21x + 1) : 3 = 2x

|21x — 1| = 20

b : (ax – 5) + 1 = 0

7(2x — 3) + 1 = 2(7x — 10)

21(x — 3) = 12

2(7x + 1) – (x — 4) = 0

21 : x = 7 : (x — 3)

|21x + 1| = 20

2(bx – 4a) + 8x = 0

2(8x — 1) – 8(2x — 3) = 13

21(3 – x) = 12

3x – 2(2 — x) = 7(x — 2)

12 : (1 — x) = 4 : (3x — 1)

|x + 11| = 1

2b – 2(a + 3x) = 2b

8(2x — 1) – 2(8x – 3) = 2

21 : (x — 3) = 7

-2(x — 2) + 3(2x – 1) = 0

(3 + x) : 2 = (3x — 1) : 3

|7x — 1| = 6

3(ax — 1) = 2b

8(2x — 1) – 2(8x — 3) = -2

7(3x + 1) = -14

-12(2x — 1) – (x – 1) = x

(-12x + 1) : 2 = 3x

|7x + 3| = 4

2(x – 3a) = 4b

11(2x — 3) = 5(4x — 6) + 2x

3x + 12 – 2x = 11

-2(x — 2) – (3x + 1) = 3

3x : 2 = (3 + x) : 4

|x — 23| = 22

3(a + x) = 2b

9(2x — 1) + 2 = 2(9x — 3) — 1

5x – 2 = 13

-3(4 — x) + (2 – x) = 3x

(3x + 2) : 4 = (x + 3) : 3

|2x — 5| = 5

3bx + 2a = 4a

9(2x — 1) + 2 = 2(9x — 3)

5(x — 2) = 15

-(2x — 1) + 2(2 — x) = x

(x + 2) : 3 = x : 2

|2x + 5| = 5

ax – 4b = 2

3(x + 2) = 2(1,5x + 4)

www.metod-kopilka.ru

Памятка по теме «Решение уравнений» для 7 класса

Памятка для учащихся 7 класса

по теме: «Решение уравнений»

Алгоритм решения:

1. Умножьте обе части уравнения на общий знаменатель дробей (НОК).

2. Запишите дополнительные множители к каждой дроби, которые получаются после сокращения. Не забудьте умножить на общий знаменатель и целую часть уравнения!

3. Умножьте

числители на дополнительный множитель.

4. Раскройте скобки, если необходимо.

5. Перенесите неизвестные члены уравнения в левую часть, а известные — в правую.

6. Приведите подобные слагаемые в левой части уравнения и найдите значение правой части.

Получилось линейное уравнение вида ax=b, где x=b:a.

Примеры решения уравнений с дробной частью.

1) Или:

Решение:

— пропорция

Решение:

1 / 3/

|•6

x — 7 = 3(x+1)

x – 7 = 3x + 3

x — 3x = 3+7

-2x = 10

x = 10: (–2)

x = –5

Основное свойство пропорции: произведение крайних членов пропорции

равно произведению ее средних членов.

(x – 7)·2 = 6·(x+1)

2 x – 14 = 6x + 6

2 x –6 x = 6 + 14

-4x = 20

x = 20: (-4)

x = –5

Решение:

8/ 7/ 56/

= 5 |·56

8(5y + 8) – 7(3y — 1) = 56·5

40y + 64 – 21y +7 = 280

19y = 280 – 64 – 7

19y = 209

y = 209 : 19

y = 11

Решение:

3/ 5/ 15/

— 7 |·15

3(х — 5) = 5(2х + 1) — 15·7

3х – 15 = 10х +5 – 105

3х – 10х = -100 + 15

-7х = -85

х = -85: (-7)

х = 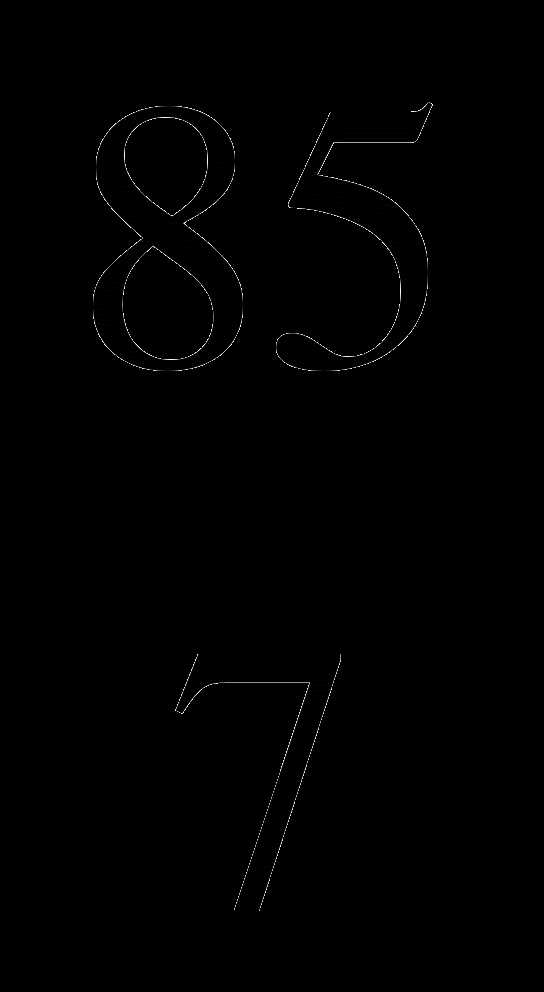= 12

Решение:

3/ 2/ 42/

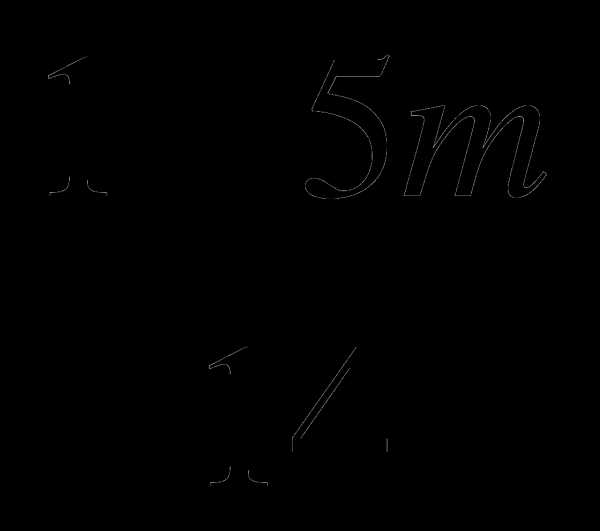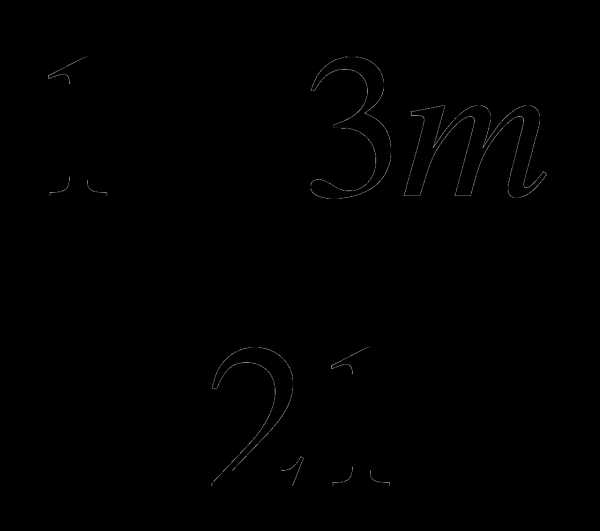– + = 0 |·42

–3(1 – 5m) + 2(1 +3m) = 0

–3 + 15m + 2 + 6m = 0

21m = 0 + 3 – 2

21m = 1

m = 1 : 21

m =

Решение:

6/ 2/ 3/ 6/

2x — = + 6 |·6

6·2x – 2(16 – x) = 3(x +3) +6·6

12x – 32 + 2x = 3x + 9 + 36

14x – 3x = 45 + 32

11x = 77

x= 77 : 11

x = 7

Ответ: 1) —5; 2) 11; 3) 12; 4) ; 5) 7.

infourok.ru

Решение линейных уравнений — Математика

Решение линейных уравнений, 7 класс

Разноуровневые карточки для проверки знаний учащихся по теме: «Линейные уравнения» содержат 5 уравнений разного уровня сложности. Их можно применять не только на уроках в данной теме, но и при повторении материала.

Вариант I (Уровень А)

Вариант II (Уровень В)

Вариант III (Уровень С)

Вариант I (Уровень А)

Вариант II (Уровень В)

Вариант III (Уровень С)

Вариант I (Уровень А)

Вариант II (Уровень В)

Вариант III (Уровень С)

 

 

 

Просмотр содержимого документа
«Решение линейных уравнений»

multiurok.ru

Практика. Линейные уравнения и их системы. Видеоурок. Алгебра 7 Класс

Пример . Решить уравнение: .

Решение

Вспомним, что деление, по определению, операция, обратная умножению (деление на какое-либо число – это то же самое, что и умножение на обратное к этому числу):

Разделим обе части уравнения на  или умножим на :

Упростим выражение в левой части уравнения:

Упростим выражение в правой части уравнения:

Таким образом, решением уравнения будет:

Ответ: .

 

Пример . Решить уравнение: .

Решение

Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .

Упростим уравнение – выполним действия в обеих частях уравнения: .

Разделим обе части уравнения на :

Решением уравнения является .

Ответ: .

 

Пример . Решить уравнение: .

Решение

Раскроем скобки в правой и левой частях уравнения. Для выражения в левой части уравнения используем распределительный закон: .

Тогда . Вспомним, что если перед скобками стоит знак минус, то при раскрытии скобок все знаки всех слагаемых внутри скобок меняются на противоположный: .

Перепишем уравнение после применения преобразований: .

Как и в предыдущем примере, перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .

Выполнив действия в обеих частях уравнения, получим тождество: .

Таким образом, данное равенство верно всегда, при любых значениях переменной.

Ответ:  – любое число.

 

Пример . Решить уравнение: .

Решение

Раскроем скобки в правой и левой частях уравнения, используя распределительный закон .

Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .

Получаем .

Данное равенство неверно всегда, т.е. оно не выполняется ни при каких значениях переменной.

Ответ: нет решений.

 

Пример . Решить уравнение: .

Решение

Избавимся от знаменателей дробей – умножим обе части уравнения на общий знаменатель всех дробей, т.е. число :

Получим: .

Выполним сокращения и избавимся от знаменателей: .

Раскроем скобки:

Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .

Выполнив действия в обеих частях уравнения, получим следующее уравнение: .

Найдем :

Ответ: .

В общем виде системы линейных уравнений выглядят следующим образом:  где  – переменные, – произвольные числа.

Есть несколько методов решения систем уравнений.

1. Метод подстановки.
2. Метод сложения.
3. Графический метод.

Пример . Решить систему: .

Решение (несколько способов)

1. Метод подстановки – необходимо в уравнении выразить одну переменную через другую и подставить во второе уравнение.

Из первого уравнения выразим , для этого перенесем  из левой части уравнения в правую: .

Затем умножим обе части первого уравнения на : .

Теперь подставим во второе уравнение полученное выражение: .

Теперь во втором уравнении только одна переменная , решим его (мы уже умеем это делать – получилось обычное линейное уравнение с одной переменной).

Раскроем скобки во втором уравнении: .

Во втором уравнении перенесем все слагаемые с переменной в левую часть, а без переменной – в правую: .

Выполним действия в обеих частях второго уравнения: .

Найдем : .

Подставим в первое уравнение найденное значение переменной:

Решением системы будет: .

Ответ: .

 

2. Метод сложения – нужно преобразовать уравнения так, чтобы при одной переменной в разных уравнениях были противоположные коэффициенты, после этого нужно сложить правые и левые части уравнений.

Избавимся от переменной . Умножим первое уравнение на : .

Теперь система имеет вид: .

Сложим уравнения системы: .

Получим следующее уравнение: . Выполним действия: .

Найдем :

Подставим найденное значение в любое из уравнений исходной системы, например, в первое: .

Выразим : . Решением системы будет: .

Ответ: .

 

3. Графический метод

 

Сначала перепишем каждое из уравнений так, чтобы они задавали линейную функцию в привычном для нас виде , т.е. выразим  через :

Графиком линейной функции является прямая. Построим обе прямые по двум точкам. Вместо  возьмем произвольные значения и подставим их в соответствующие уравнения прямых:

Отметим точки на координатной плоскости и проведем через них прямые (Рис. 1).

Рис. 1. Иллюстрация к примеру 6

Видно, что точкой пересечения прямых является точка с координатами . Поскольку точка лежит на каждой из прямых, а прямая – это множество решений уравнения, то точка пересечения прямых является решением каждого из уравнений, т.е. является решением системы. Координаты точки пересечения и будут решением системы.

Дополнительно нужно подставить координаты точки в исходную систему, чтобы убедиться в правильности: .

Ответ: .

 

Пример . Решить систему: .

Решение

Сначала упростим уравнения системы – избавимся от знаменателей дробей. Для этого умножим каждое уравнение на общий знаменатель дробей, которые в него входят (чтобы найти это число, нужно рассмотреть наименьшее общее кратное чисел, которые стоят в знаменателе):

Получим:

Выполним сокращения и избавимся от знаменателей:

Раскроем скобки:

Приведем подобные слагаемые:

Умножим второе уравнение на :

Сложим уравнения системы:

Получим уравнение:

Выполним действия:

Найдем :

Подставим в первое уравнение найденное значение переменной:

Решением системы будет: .

Ответ: .

Задача

Провод длиной  метров разрезали на  части (Рис. 2), причем первая часть в  раза длиннее третьей, а вторая – на  метров длиннее третьей. Найти длину каждой части провода.

Рис. 2. Иллюстрация к задаче 1

Решение

1. Провод длиной  метров разрезали на  части:

Первая часть в  раза длиннее третьей:

Вторая часть на  метров длиннее третьей:

Теперь все выражено через часть , поэтому все замены можно переписать так:

2. Обозначим длину части  за :

Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую:

Выполним действия:

Найдем

interneturok.ru

РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ — Алгебра 7 класс — Учебно-методическое пособие — Старова Е. А. — 2015 год

Урок № 54. РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ

Цели:

• учебная: сформировать умение решать линейные уравнения;

• развивающая: развивать творческие способности, смекалку учащихся; способствовать совершенствованию вычислительных навыков;

• воспитательная: воспитывать настойчивость в достижении цели, дисциплинированность, внимательность;

Тип урока: усвоение новых знаний, умений, навыков.

Оборудование и наглядность:

Ход урока

И. ОРГАНИЗАЦИОННЫЙ ЭТАП

______________________________________________________

______________________________________________________

______________________________________________________

II. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ

1. Проверка задания, заданного по учебнику

______________________________________________________

______________________________________________________

2. Выполнение тестовых заданий

Обведите кружочком букву, которая, по вашему мнению, соответствует правильному ответу

Вариант 1

1) Какое из приведенных уравнений является линейным?

А) 2х² = 4; Б) 3х = 4; В) x(x — 2) = 0; Г) 5/x = 1.

2) Какое из приведенных уравнений равносильно уравнению 2х = 8?

3) Какое из приведенных уравнений не имеет ни одного решения?

4) Какое уравнение получим, если в уравнении 3х — 5 = 4х + 6 члены со сменными перенести из правой части в левую, а без переменных — наоборот?

А) 7х = 1; Б) х = 11; В) -х = 11; Г) х = 1.

5) Какое уравнение получим, если обе части уравнения разделить на одно и то же число?

Вариант 2

1) Какое из приведенных уравнений является линейным?

А) 2х² = 8; Б) 5х = 9; В) 3/x = 1; Г) х(4 — х) = 0.

2) Какое из приведенных уравнений равносильно уравнению 3х = 9?

3) Какое из приведенных уравнений имеет множество решений?

4) Какое уравнение получим, если в уравнении 5х — 9 = 6х + 7 члены со сменными перенести из правой части в левую, а без переменных — наоборот?

А) 11х = 16; Б) x = 2; В) x = -2; Г) -х = 16.

5) Какое уравнение получим, если обе части уравнения разделить на одно и то же число?

Ответы

Вариант 1	1 — Б, 2 — Г, 3 — А, 4 — В, 5 — Б
Вариант 2	1 — Б, 2 — Б, 3 — Б, 4 — Г, 5 — В

III. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

1. Схема решения линейных уравнений с одной переменной .

2. Примеры уравнений, сводящихся к линейным, и схема их решения:

______________________________________________________

______________________________________________________

IV. УСВОЕНИЕ НОВЫХ ЗНАНИЙ И УМЕНИЙ

1. Работа по учебнику

______________________________________________________

______________________________________________________

2. Дополнительные задания

Найдите корни уравнений с точностью до 0,01:

V. ИТОГИ УРОКА

1.

______________________________________________________

______________________________________________________

2. Самостоятельная работа с последующей взаимопроверкой

Вариант 1	Вариант 2
1) Решите уравнение:
2) При каком значении х
значение выражения 5х +11 равно значению выражения 7х + 31?	значение выражения 3х + 5 равно значению выражения 5х + 13?
3) Составьте уравнение, которое имеет тот же корень, что и уравнение
2х — 3 = 5х + 6	3х — 4 = 6х + 5
Укажите этот корень

VI. ДОМАШНЕЕ ЗАДАНИЕ

1. Задание по учебнику:

______________________________________________________

______________________________________________________

2. Дополнительное задание. Решите уравнение ах + b = 0, где a — корень уравнения 3(х — 4) + 5 = х — 6, b — корень уравнения 4(2х + 15) = 7(20 — х) + 20.

Ответ. -200.

schooled.ru

Решение уравнений 7 класс — математика, уроки

Ф. И. О. автора: Пеньковская Вера Константиновна

место работы: МБОУ Самарская СОШ

должность: учитель математики

предмет: Алгебра

класс: 7

тема урока: Решение уравнений

базовый учебник: «Алгебра, 7» Макарычев Ю.Н., Миндюк Н.Г. и др.

Цель: Формирование навыка решения уравнения с одним неизвестным. решать уравнения с различным количеством корней.

задачи урока:

1. Повторение понятия, связанные с уравнением, закрепление знания и умения по данной теме; формирование умения свободно решать уравнения.

2. Развитие внимания, логическое мышление, долговременной памяти, математической речи.

3. Воспитание чувства взаимопомощи, самоконтроля, математической культуры.

Тип урока: урок обобщения и систематизации

Формы работы учащихся: фронтальная, индивидуальная.

Необходимое техническое оборудование: мультимедийные средства (проектор), таблица “Алгоритм решения линейного уравнения», карточки для запоминания “Исследование количества корней линейного уравнения ax=b.”, карточки для самостоятельной работы, коробочки – копилки; жетоны (выдаются за правильное решение).

План урока:

1. Организационный момент

2. Домашнее задание

3. Актуализация знаний и умений

4. Физминутка

5. Составление таблицы

6. Закрепление знаний и умений

7. Самостоятельная работа

8. Итог

ХОД УРОКА

1. Организационный момент

Если только улыбнуться, то настанут чудеса. От улыбок проясняться и глаза, и небеса. Ну – ка, взрослые и дети, улыбнитесь поскорей! Чтобы стало на уроке и светлее и теплей!

Спасибо за ваши улыбки! И теперь с хорошим настроением начнем урок!

В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. Вот сегодня мы и поговорим о неизвестном.

1. Как называется равенство, содержащее неизвестную? (Уравнение)

Зачем нам нужно решать уравнения? В чем нам эти знания пригодятся? (Для нахождения неизвестного. При решении задач и упражнений)

1. Как вы думаете, какой же будет тема сегодняшнего урока? (Решение уравнений)

Запишите сегодняшнее число и тему урока в тетрадь.

1. Домашнее задание

1. Придумать 4 уравнения: по одному для каждого вида.

2. Записать их на карточку (для обмена карточками), заготовить решения.

3. № 291 – решить

1. Актуализация знаний

Что значит решить уравнение? (Найти все его корни или доказать, что корней нет.)

У меня есть такая волшебная коробочка. Она не пустая. И сейчас мы узнаем, что же там находится. (внутри лежат коробочки — копилки для жетонов, на которых написаны уравнения)

1. 12/х = 3

2. 14х = 56

3. 2х – 2х = 4

4. 3х – 4 = 3х – 4

5. 1/2х – 1/3

6. -0,3х = 5 – 5

Является ли уравнение линейным, почему?

Приводится ли уравнение к линейному, как?

1. Физминутка

1. Заполнить таблицу:

а	b	Вид уравнения	Примеры (могут быть такими)	Количество корней
a 0	b0	ax = b	14x =56	Один корень
a 0	b = 0	ax = 0	14x=0	0
a = 0	b0	0x =b	3x-3x=9	Нет корней
a = 0	b = 0	0x = 0	3x-8=3x-8	бесконечно много корней

У каждого ученика заготовка таблицы “Исследование количества корней линейного уравнения ax=b”

Для проверки выполняется заполнение таблицы на доске.

1. Закрепление знаний и умений

1. Сколько решений имеют следующие уравнения? (Устное решение)

1. 6х = 0;

2. 3х – 1 = 3х;

3. 1 – 7х = -1;

4. 2(х + 3) – 2х = 6.

2. Решение уравнений. Решение уравнений(с комментированием) у доски. Записи сохранить до конца урока, так как учащиеся при решении уравнений самостоятельной работы будут опираться на выполненные решения.

а) 3х + 7 = (9 + х) + 2х /нет корней/

б) 5х – 1 = 4(х + 2) – (9 – х) / бесконечно много корней /

в) 1,5(х + 4) = -9,9 – 3(х – 5,3) /х=0/

г) /х=1,7/

Сколько корней может иметь линейное уравнение? (Уравнение может иметь один корень, не иметь корней и бесконечно много корней)

Что нужно сделать, чтобы ответить на этот вопрос?

1. Раскрыть скобки.

2. Перенести слагаемые, меняя знак коэффициента

3. Привести подобные слагаемые.

4. Разделить уравнение на коэффициент

1. Самостоятельная работа

(взаимопроверка)

1 вариант

1) 5х – 2 = 8

2) 7(2х – 3) – х = 13х – 11

3) 2/3х = -9

4) -12х + 4(х-3) =-8х -12

2 вариант

1) 7х = 9

2) 48 – 3х = 0

3) 15(x + 2) – 15х = 30

4) 12(х + 2) – 2,1 = 2(6х + 12)

3 вариант

1) 5х = -50

2) 12х – 1 = 35

3)

4) -12х + 4(х – 3) = -8х – 12

5) 21(х – 3) + 7х = 28х

4 вариант

1) -15х = 6

2) — х + 4 = 47

3)

4) 3(х + 2) = 2( 1,5 х + 4)

5) 9(2х – 1) + 2 = 2(9х – 3) -1

1. Итог урока

Теперь посчитаем, кто же больше всего скопил жетонов.

Что мы сегодня научились делать?

Что было интересно?

Выставление отметок.

Сейчас давайте улыбнемся еще раз. И пусть все, уйдет и останется только хорошее. Я желаю вам хорошего дня. Спасибо за урок!

ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА

№	Этап урока	Деятельность учителя	Деятельность ученика
1	Организационный момент	Если только улыбнуться, то настанут чудеса. От улыбок проясняться и глаза, и небеса. Ну – ка, взрослые и дети, улыбнитесь поскорей! Чтобы стало на уроке и светлее и теплей! Спасибо за ваши улыбки! И теперь с хорошим настроением начнем урок! В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. Вот сегодня мы и поговорим о неизвестном. Как называется равенство, содержащее неизвестную? Зачем нам нужно решать уравнения? В чем нам эти знания пригодятся? Как вы думаете, какой же будет тема сегодняшнего урока? Запишите сегодняшнее число и тему урока в тетрадь.	Учащиеся улыбаются друг другу Уравнение. Для нахождения неизвестного. При решении задач Решение уравнений Записывают число и тему урока в тетради
2	Домашнее задание	1. Придумать 4 уравнения: по одному для каждого вида. 2. Записать их на карточку (для обмена карточками), заготовить решения. 3. № 291 – решить	Запись домашнего задания
3	Актуализация знаний, умений	Что значит решить уравнение? (Найти все его корни или доказать, что корней нет.) Является ли уравнение линейным, почему? Приводится ли уравнение к линейному, как? 12/х = 3 14х = 56 2х – 2х = 4 3х – 4 = 3х – 4 1/2х – 1/3 -0,3х = 5 – 5	Найти все его корни или доказать, что корней нет. 12/х = 3 = х = 4 14х = 56 = х = 4 2х-2х=4 = 0х=4 = корней нет 3х-4=3х-4 = 0х=0 – бесконечно много корней Нет -0,3х = 5-5 = х=0
4	Физминутка
5	Составление таблицы	Заполнить таблицу: У каждого ученика заготовка таблицы “Исследование количества корней линейного уравнения ax=b.” а b Вид уравнения Примеры (могут быть такими) Количество корней a 0 b0 ax = b 14x =56 Один корень a 0 b = 0 ax = 0 14x=0 0 a = 0 b0 0x =b 3x-3x=9 Нет корней a = 0 b = 0 0x = 0 3x-8=3x-8 R Для проверки выполняется заполнение таблицы на доске.	Заполняют таблицу: a b Вид уравнения Примеры Количество корней a 0 b0 ax = b Один корень a 0 b = 0 ax = 0 0 a = 0 b0 0x =b Нет корней a = 0 b = 0 0x = 0 R Дети карандашом заполняют таблицу. При заполнении таблицы ученики анализируют уже полученную информацию, делают аргументированные выводы, оформляют результаты обсуждения в таблице.
6	Закрепление знаний и умений	1. Сколько решений имеют следующие уравнения? (Устное решение) 6х = 0; 3х – 1 = 3х; 1 – 7х = -1; 2(х + 3) – 2х = 6. 2. Решение уравнений. Решение уравнений(с комментированием) у доски. Записи сохранить до конца урока, так как учащиеся при решении уравнений самостоятельной работы будут опираться на выполненные решения. а) 3х + 7 = (9 + х) + 2х /нет корней/ б) 5х – 1 = 4(х + 2) – (9 – х) / бесконечно много корней / в) 1,5(х + 4) = -9,9 – 3(х – 5,3) /х=0/ г) /х=1,7/ Сколько корней может иметь линейное уравнение? Что нужно сделать, чтобы ответить на этот вопрос?	Учащиеся решают уравнения и проговаривают, к какому виду относится данное уравнение. х = 0; нет решения; х = 2/7; бесконечно много корней а) 3х + 7 = (9 + х) + 2х /нет корней/ б) 5х – 1 = 4(х + 2) – (9 – х) 5х – 1 = 4х + 8 – 9 + х 5х – 4х – х = 8 – 9 + 1 0х = 0 / бесконечно много корней / в) 1,5(х + 4) = -9,9 – 3(х – 5,3) 1,5х + 6 = — 9,9 – 3х + 15,9 1,5х + 3х = — 9,9 – 6 + 15,9 4,5х = 0 х = 0 / один корень / г) 6х = 10,2 х = 1,7 Уравнение может иметь один корень, не иметь корней и бесконечно много корней Раскрыть скобки. Перенести слагаемые, меняя знак коэффициента Привести подобные слагаемые. Разделить уравнение на коэффициент
7	Самостоятельная работа	1 вариант 1) 5х – 2 = 8 2) 7(2х – 3) – х = 13х – 11 3) 2/3х = -9 4) -12х + 4(х-3) =-8х -12 2 вариант 1) 7х = 9 2) 48 – 3х = 0 3) 15(x + 2) – 15х = 30 4) 12(х + 2) – 2,1 = 2(6х + 12) 3 вариант 1) 5х = -50 2) 12х – 1 = 35 3) 4) -12х + 4(х – 3) = -8х – 12 5) 21(х – 3) + 7х = 28х 4 вариант 1) -15х = 6 2) — х + 4 = 47 3) 4) 3(х + 2) = 2( 1,5 х + 4) 5) 9(2х – 1) + 2 = 2(9х – 3) -1	1 вариант 1) х = 2 2) 0х = 10 = решений нет 3) х = -13,5 4) бесконечно много корней 2 вариант 1) х = 2) х = 16 3) бесконечно много решений 4) 0х = 2,1 = решений нет 3 вариант 1) х = -10 2) х = 3 3) х =15 и х = -15 4) бесконечно много решений 5) 0х = 63 = решений нет 4 вариант 1) х = 2) х = -43 3) х = 9 и х = -9 4) 0х = 2 = решений нет 5) бесконечно много решений
8	Итог урока	Теперь посчитаем кто же больше всего скопил жетонов. Что мы сегодня научились делать? Что было интересно? Выставление отметок. Сейчас давайте улыбнемся еще раз. И пусть все, уйдет и останется только хорошее. Я желаю вам хорошего дня. Спасибо за урок!	Учащиеся открывают коробочки и считают жетоны. Отвечают на вопросы

kopilkaurokov.ru