Расчет погрешности измерений
Измерения называются прямыми, если значения величин определяются приборами непосредственно (например, измерение длины линейкой, определение времени секундомером и т. д.). Измерения называютсякосвенными, если значение измеряемой величины определяется посредством прямых измерений других величин, которые связаны с измеряемой определенной зависимостью.
Случайные погрешности при прямых измерениях
Абсолютная и относительная погрешность. Пусть проведеноNизмерений одной и той же величиныxв отсутствии систематической погрешности. Отдельные результаты измерений имеют вид:x1,x2, …,xN. В качестве наилучшего выбирается среднее значение измеренной величины:
. (1)
Абсолютной погрешностью
.
Среднее значение абсолютной погрешности Nединичных измерений:
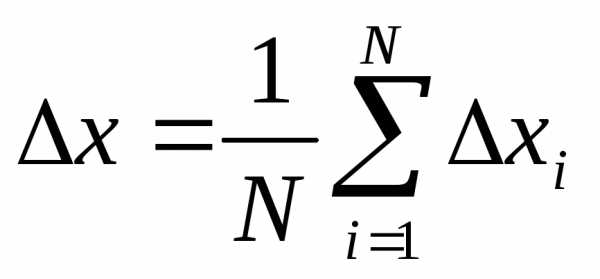 (2)
(2)
называется средней абсолютной погрешностью.
Относительной погрешностью называется отношение средней абсолютной погрешности к среднему значению измеряемой величины:
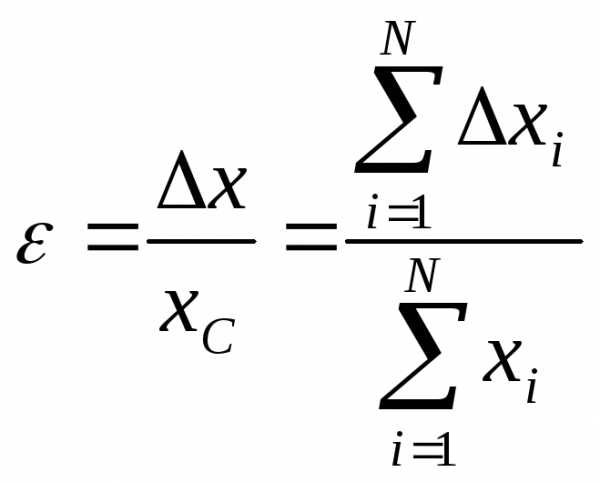 .
(3)
.
(3)
Приборные погрешности при прямых измерениях
Если нет особых указаний, погрешность прибора равна половине его цены деления (линейка, мензурка).
Погрешность приборов, снабженных нониусом, равна цене деления нониуса (микрометр – 0,01 мм, штангенциркуль – 0,1 мм).
Погрешность табличных величин равна половине единицы последнего разряда (пять единиц следующего порядка за последней значащей цифрой).
Погрешность электроизмерительных приборов вычисляется согласно классу точности С, указанному на шкале прибора:
Например: 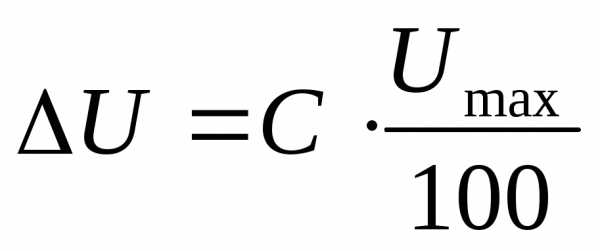 и
и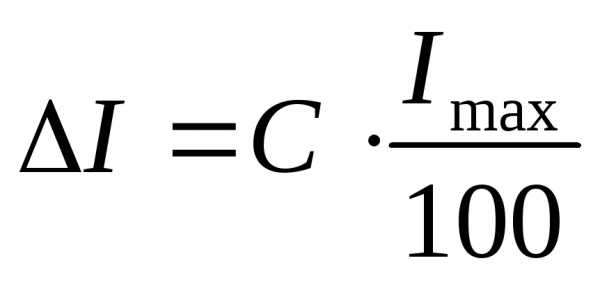 ,
,
где Umax и Imax – предел измерения прибора.
Погрешность приборов с цифровой индикацией равна единице последнего разряда индикации.
После оценки случайной и приборной погрешностей в расчет принимается та, значение которой больше.
Вычисление погрешностей при косвенных измерениях
Большинство измерений являются косвенными. В этом случае искомая величина Х является функцией нескольких переменных
Среднее арифметическое результата косвенных измерений будет равно:
X = f(a,b,c…).
Одним из способов
вычисления погрешности является способ
дифференцирования натурального логарифма
функции Х = f(a,b,c…).
Если, например, искомая величина Х
определяется соотношением Х = 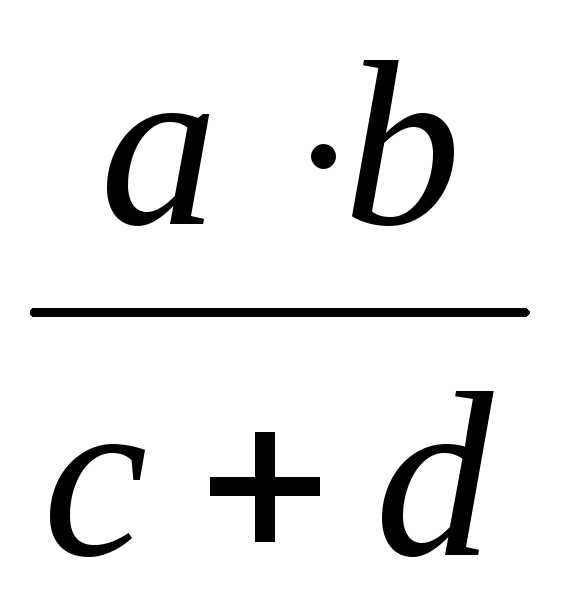 ,
то после логарифмирования получаем:lnX
= lna + lnb + ln(c+d).
,
то после логарифмирования получаем:lnX
= lna + lnb + ln(c+d).
Дифференциал этого выражения имеет вид:
.
Применительно к вычислению приближенных значений его можно записать для относительной погрешности в виде:
= . (4)
Абсолютная погрешность при этом рассчитывается по формуле:
Х = Х(5)
Таким образом, расчет погрешностей и вычисление результата при косвенных измерениях производят в следующем порядке:
1) Проводят измерения всех величин, входящих в исходную формулу для вычисления конечного результата.
2) Вычисляют средние арифметические значения каждой измеряемой величины и их абсолютные погрешности.
3) Подставляют в исходную формулу средние значения всех измеренных величин и вычисляют среднее значение искомой величины:
X = f(a,b,c…).
4) Логарифмируют исходную формулу Х = f(a,b,c…) и записывают выражение для относительной погрешности в виде формулы (4).
5)
Рассчитывают относительную погрешность
= 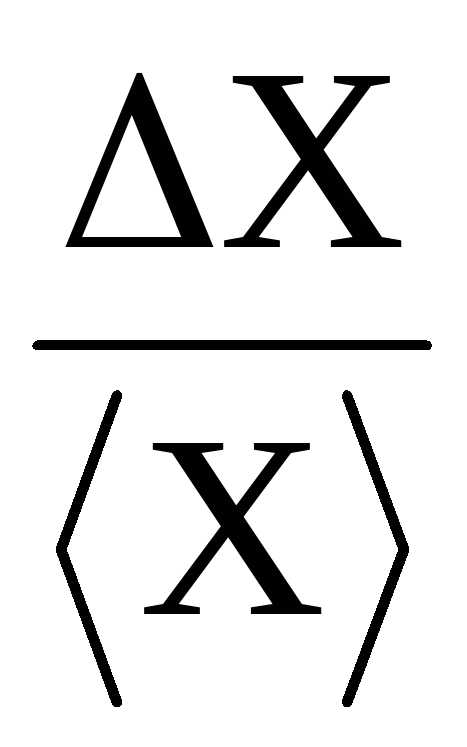 .
.
6) Рассчитывают абсолютную погрешность результата по формуле (5).
7) Окончательный результат записывают в виде:
Х = ХсрХ
= …%
Абсолютные и относительные погрешности простейших функций приведены в таблице:
Функция | Абсолютная погрешность | Относительная погрешность |
| a+b | a+b |
|
a-b | a+b |
|
ab | ab+ba |
|
|
|
|
|
|
|
sin a |
|
|
cos a |
|
|
studfiles.net
Лабораторная работа №1 по физике 9 класс (ответы)
Лабораторная работа №1 по физике 9 класс (ответы) — Определение абсолютной и относительной погрешностей прямых измерений
3. Вычислите и занесите в таблицу среднее значение промежутка времени <t>.
< t > = (1.79 + 1.62 + 1.62 + 1.69 + 1.62) : 5 = 1.668 ≈ 1.7
4. Вычислите абсолютную случайную погрешность при каждом измерении и среднее значение Δtслуч при пяти измерениях.
Δt = |1.79 — 1.68| = 0.11
Δt = |1.62 — 1.68| = 0.06
Δt = |1.62 — 1.68| = 0.06
Δt = |1.69 — 1.68| = 0.01
Δt = |1.62 — 1.62| = 0.06
< Δt > = (0.11 + 0.06 + 0.06 + 0.01 + 0.06) : 5 = 0.06
5. Определите максимальное значение случайной погрешности.
Δt = 3 · 0.06 = 0.18
Δt = 0.05 с + 0,05 с = 0,1 с
7. Вычислите значение абсолютной погрешности Δt прямого измерения промежутка времени.
Δt = 0,18 + 0,1 = 0,28
8. Вычислите значение относительной погрешности ε прямого промежутка времени t.
ε = 0,28/1,7 · 100% = 16%
9. Запишите окончательный результат измерений в интервальной форме.
t = (1,7 ± 0,28) с; ε = 16%
| № | t | Δtслуч | Δt = k | Δtсист | Δt | εt |
| 1 | 1,79 | 0,11 | 0,18 | 0,1 | 0,28 | 16 |
| 2 | 1,62 | 0,06 | ||||
| 3 | 1,62 | 0,06 | ||||
| 4 | 1,69 | 0,01 | ||||
| 5 | 1,62 | 0,06 | ||||
| Ср. | 1,7 | 0,06 |
Ответьте на контрольные вопросы
1. Почему нельзя абсолютно точно измерить прибором физическую величину?
Потому что несовершенство измерений приборов не позволяют это сделать, а также из-за округления чисел при подсчётах.
2. Будет ли одинаковой относительная погрешность измерения промежутка времени, если нить с шариков отклонить на угол 45°? Почему?
Нет. Из-за большего градуса шарику понадобится больше времени для движения. Чем меньше времени тратит шарик, тем меньше погрешность.
3. Если при трёх и более повторных измерениях данным прибором получены одинаковые значения физической величины, то чему равны абсолютные случайная и систематическая погрешности? Относительная погрешность?
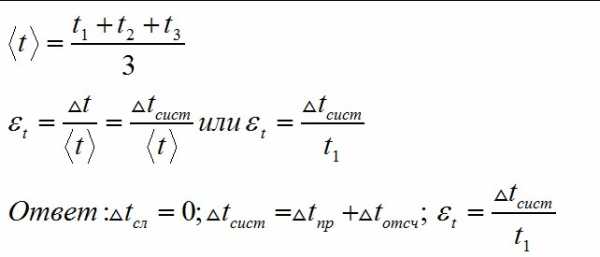
Выводы: научился определять абсолютную и относительную погрешность прямых измерений, представлять измерения в интервальной форме.
belmathematics.by
Погрешность измерений | КИПиА Портал
Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.
Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.
По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные
Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.
(1.2), где X — результат измерения; Х0 — истинное значение этой величины.
Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением
(1.3), где Хд — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.
Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:
(1.4)
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные.
Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.
Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.
Систематические и прогрессирующие погрешности средств измерений вызываются:
- первые — погрешностью градуировки шкалы или ее небольшим сдвигом;
- вторые — старением элементов средства измерения.
Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.
Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.
По происхождению различают инструментальные и методические погрешности средств измерений.
Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.
Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.
Погрешности средств измерений.
Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:
(1.5), где Xн – номинальное значение меры; Хд – действительное значение меры
Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:
(1.6), где Xп – показания прибора; Хд – действительное значение измеряемой величины.
Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному
(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).
(1.7)
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).
(1.8)
Предел допускаемой погрешности средств измерений – наибольшая без учета знака погрешность средства измерений, при которой оно может быть признано и допущено к применению. Данное определение применяют к основной и дополнительной погрешности, а также к вариации показаний. Поскольку свойства средств измерений зависят от внешних условий, их погрешности также зависят от этих условий, поэтому погрешности средств измерений принято делить на основные и дополнительные.
Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.
Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.
Погрешности средств измерений подразделяются также на статические и динамические.
Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.
Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.
Факторы влияющие на погрешность измерений.
Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений
Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.
Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.
Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.
Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.
Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.
Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.
Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.
Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.
Шумы — любой сигнал не несущий полезной информации.
kipia-portal.ru
Определение абсолютной и относительной погрешностей прямых измерений
3. Вычислите и занесите в таблицу среднее значение промежутка времени <t>.
< t > = (1.79 + 1.62 + 1.62 + 1.69 + 1.62) : 5 = 1.668 ≈ 1.7
4. Вычислите абсолютную случайную погрешность при каждом измерении и среднее значение Δtслуч при пяти измерениях.
Δt = |1.79 — 1.68| = 0.11
Δt = |1.62 — 1.68| = 0.06
Δt = |1.62 — 1.68| = 0.06
Δt = |1.69 — 1.68| = 0.01
Δt = |1.62 — 1.62| = 0.06
< Δt > = (0.11 + 0.06 + 0.06 + 0.01 + 0.06) : 5 = 0.06
5. Определите максимальное значение случайной погрешности.
Δt = 3 · 0.06 = 0.18
6. Определите и занесите в таблицу значение абсолютной систематической погрешности.
Δt = 0.05 с + 0,05 с = 0,1 с
7. Вычислите значение абсолютной погрешности Δt прямого измерения промежутка времени.
Δt = 0,18 + 0,1 = 0,28
8. Вычислите значение относительной погрешности ε прямого промежутка времени t.
ε = 0,28/1,7 · 100% = 16%
9. Запишите окончательный результат измерений в интервальной форме.
t = (1,7 ± 0,28) с; ε = 16%
| № | t | Δtслуч | Δt = k | Δtсист | Δt | εt |
| 1 | 1,79 | 0,11 | 0,18 | 0,1 | 0,28 | 16 |
| 2 | 1,62 | 0,06 | ||||
| 3 | 1,62 | 0,06 | ||||
| 4 | 1,69 | 0,01 | ||||
| 5 | 1,62 | 0,06 | ||||
| Ср. | 1,7 | 0,06 |
Ответьте на контрольные вопросы
1. Почему нельзя абсолютно точно измерить прибором физическую величину?
Потому что несовершенство измерений приборов не позволяют это сделать, а также из-за округления чисел при подсчётах.
2. Будет ли одинаковой относительная погрешность измерения промежутка времени, если нить с шариков отклонить на угол 45°? Почему?
Нет. Из-за большего градуса шарику понадобится больше времени для движения. Чем меньше времени тратит шарик, тем меньше погрешность.
3. Если при трёх и более повторных измерениях данным прибором получены одинаковые значения физической величины, то чему равны абсолютные случайная и систематическая погрешности? Относительная погрешность?
Выводы: научился определять абсолютную и относительную погрешность прямых измерений, представлять измерения в интервальной форме.
101.3dn.ru
Относительная погрешность — это… Что такое Относительная погрешность?
Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.
Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).
В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».
Определение погрешности
В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.
- Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:
- Средняя квадратическая погрешность:
- Средняя квадратическая погрешность среднего арифметического:
Классификация погрешностей
По форме представления
- Абсолютная погрешность — ΔX является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины Xmeas. При этом равенство:
ΔX = | Xtrue − Xmeas | ,
где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.
.
Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
- Приведенная погрешность — относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле
,
где Xn — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:
— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
Приведенная погрешность — безразмерная величина (может измеряться в процентах).
По причине возникновения
- Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
- Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
- Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.
В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.
Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.
Обобщенной характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведенных основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10n, где n = 1; 0; -1; -2 и т.д.
По характеру проявления
- Случайная погрешность — погрешность, меняющаяся (по величине и по знаку) от измерения к измерению. Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т.п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления), с особенностями самой измеряемой величины (например при измерении количества элементарных частиц, проходящих в минуту через счётчик Гейгера).
- Систематическая погрешность — погрешность, изменяющаяся во времени по определенному закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т.п.), неучтёнными экспериментатором.
- Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.
- Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора, если произошло замыкание в электрической цепи).
По способу измерения
- Погрешность прямых измерений
- Погрешность косвенных измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:
Если F = F(x1,x2…xn), где xi — непосредственно измеряемые независимые величины, имеющие погрешность Δxi, тогда:
См. также
Литература
- Назаров Н. Г. Метрология. Основные понятия и математические модели. М.: Высшая школа, 2002. 348 с.
- Лабораторные занятия по физике. Учебное пособие/Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др.; под ред. Гольдина Л. Л. — М.: Наука. Главная редакция физико-математичекой литературы, 1983. — 704 с.
Wikimedia Foundation. 2010.
dic.academic.ru
Иногда относительная погрешность выражается в процентах:
I I. Погрешность при косвенных измерениях.
В большинстве случаев в лабораторном практикуме нельзя определить искомую физическую величину непосредственно по приборам. В этом случае прибегают к косвенным измерениям. Косвенными измерениями являются измерения, полученные на основе прямых измерений и подсчитанные по математическим формулам.
Например,
объем цилиндра определяется по формуле 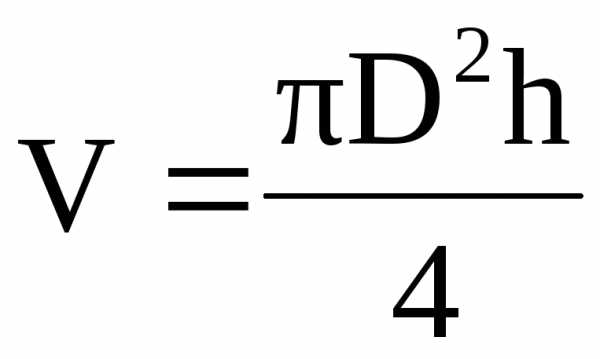 , где с помощью прямых измерений
определяется диаметр цилиндра D
и его высота h,
объем же получается в результате
косвенных измерений.
, где с помощью прямых измерений
определяется диаметр цилиндра D
и его высота h,
объем же получается в результате
косвенных измерений.
В таких случаях погрешность косвенного измерения зависит не только от погрешностей прямых измерений, но и от вида той математической формулы, по которой находится физическая величина.
Для нахождения погрешностей косвенных измерений удобно воспользоваться правилами дифференциального исчисления, считая искомую величину функцией, а величины, непосредственно измеряемые приборами, ее аргументами. Пусть вид функциональной зависимости определяется формулой , где А результат косвенного измерения, результаты прямых измерений. По определению относительная погрешность равна
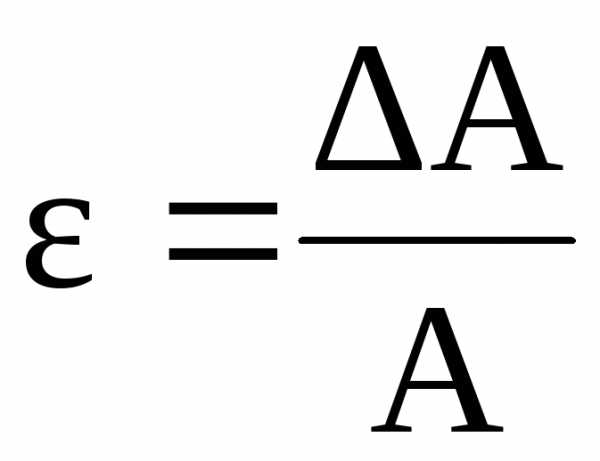 (5)
(5)
С
другой стороны 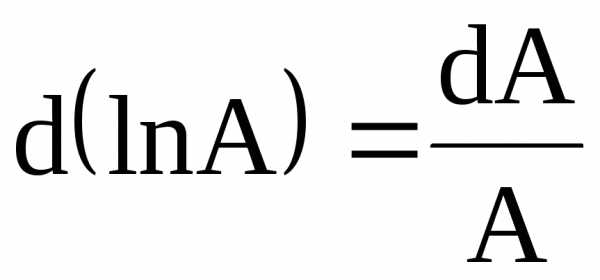 .
Так как погрешность
.
Так как погрешность всегда много меньше измеряемой величиныА, ошибки можно считать малыми величинами.
Это дает возможность замены знака
дифференциала d
на знак абсолютной ошибки
всегда много меньше измеряемой величиныА, ошибки можно считать малыми величинами.
Это дает возможность замены знака
дифференциала d
на знак абсолютной ошибки  .
То есть, можно записать:
.
То есть, можно записать: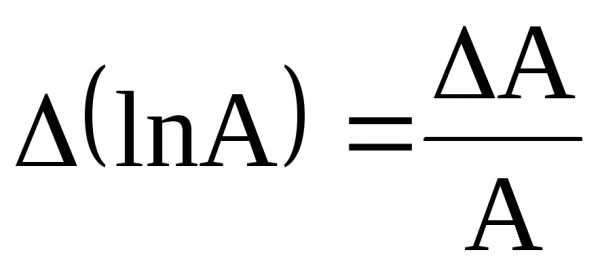 .
.
5
Из сопоставления приведенных формул следует, что относительную погрешность косвенного измерения можно найти путем:
логарифмирования исходного выражения ;
последующего дифференцирования ;
заменой знака дифференциала d на знак абсолютной погрешности
 ;
;заменой всех знаков минус на знаки плюс перед знаками абсолютных погрешностей
 .
.
Пример.
Для определения плотности цилиндрического тела применяется формула:
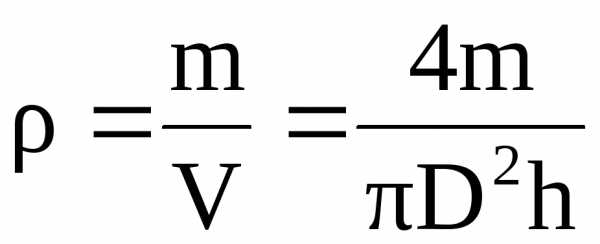 ,
,
где
m
масса тела, D
диаметр, h
высота. Величины m,
D,
h
определяются в результате прямых измерений.
Плотность  определяется из косвенных
измерений. Для нахождения относительной
погрешности, выполняем следующие
действия:
определяется из косвенных
измерений. Для нахождения относительной
погрешности, выполняем следующие
действия:
находим натуральный логарифм исходного выражения

,
выполняем дифференцирование : ,
заменяем знак d на знак
 :,
:,
перед всеми знаками
 ставим
знаки плюс.
ставим
знаки плюс.
Далее можно найти абсолютную погрешность: ,
где 
абсолютная погрешность косвенного
измерения,
абсолютная погрешность косвенного
измерения, 
среднее значение
искомой величины, ε – относительная
погрешность.
среднее значение
искомой величины, ε – относительная
погрешность.
Примечание.
Иногда в зависимости от расчетной формулы удобнее вначале найти абсолютную погрешность непосредственно, не связывая ее с относительной погрешностью. Для этого используют следующее правило для нахождения абсолютной ошибки при косвенном измерении:
6
1) дифференцируют исходное выражение;
2)
заменяют знак дифференциала d на знак
погрешности  ;
;
3)
перед всеми знаками  ставят
знаки плюс.
ставят
знаки плюс.
Пример.
1)
2) ,
3) .
III. Запись результата косвенного измерения.
При записи результата косвенного измерения необходимо соблюдать следующие правила:
1.
Величину абсолютной погрешности  необходимо округлить до двух значащих
цифр, если первая из них единица, и до
одной во всех остальных случаях (значащими
цифрами называются все цифры, кроме
нулей, стоящие впереди числа слева).
Нули в середине числа и в конце являются
значащими. Например, в числе 0.0305 три
значащие цифры, в числе 5100
четыре значащие цифры.
необходимо округлить до двух значащих
цифр, если первая из них единица, и до
одной во всех остальных случаях (значащими
цифрами называются все цифры, кроме
нулей, стоящие впереди числа слева).
Нули в середине числа и в конце являются
значащими. Например, в числе 0.0305 три
значащие цифры, в числе 5100
четыре значащие цифры.
Пример. Если при определении объема цилиндра V абсолютная ошибка оказалась равной , ее следует округлить до двух значащих цифр:. Если, ее следует округлить до одной значащей цифры.
Среднее значение измеряемой величины
 следует записать таким образом, чтобы
результат заканчивался в том же разряде,
что и абсолютная погрешность.
следует записать таким образом, чтобы
результат заканчивался в том же разряде,
что и абсолютная погрешность.
Пример. Если объем цилиндра при расчете по
формуле 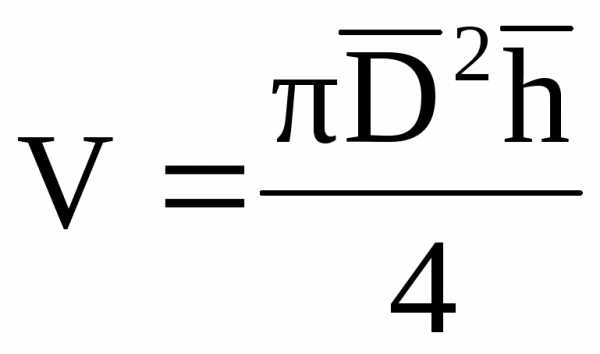 получается равным
,
а абсолютная ошибка после округления
равна, то объем следует записать также только
до десятых
получается равным
,
а абсолютная ошибка после округления
равна, то объем следует записать также только
до десятых
Окончательный результат записывается в виде: .
Такая запись показывает, в каких пределах содержится истинное значение измеряемой величины.
В случае нашего примера для объема цилиндра окончательный результат записывается следующим образом: .
Такая запись указывает, что истинный результат лежит в пределах:
.
7
ПРИМЕР ОБРАБОТКИ РЕЗУЛЬТАТОВ КОСВЕННЫХ ИЗМЕРЕНИЙ.
При определении ускорения свободного падения g с помощью математического маятника используется расчетная формула:
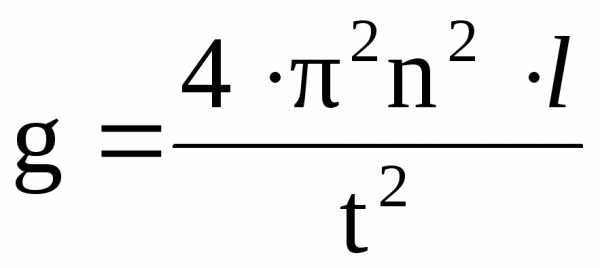 ,
,
где l длина математического маятника, измеряемая миллиметровой линейкой, n — число колебаний маятника, t — время десяти колебаний маятника, определяемое секундомером. После прямых измерений времени и длины получаем следующие данные:
t = 14.72с, 14.74с, 14.75с, 14.73с, 14.76; n = 10;
l= 54.2 см ±0.05 см = (54.2 ±0.05)10-2 м
1) Результаты измерений заносим в таблицу
Результаты измерений и расчетов. Таблица.
№ | | | l, м | Δl, м |
1 2345 | 14.72 14.74 14.77 14.76 14.71 | 0.02 0 0.03 0.02 0.03 | 54.210-2 | 0.0510-2 |
| 0,02 | |||
| | |||
g
=(9.84 ±0.05) м/с2, | ||||
2) Определяем погрешности при прямых измерениях:
t = (14.74±0.02) c.
8
б) Так как измерения длины производились один раз, в качестве абсолютной погрешности берем погрешность инструмента (линейки), т.е. половину деления ее шкалы
3) Определяем относительную погрешность при косвенном измерении g:
а)
берем натуральный логарифм от выражения: 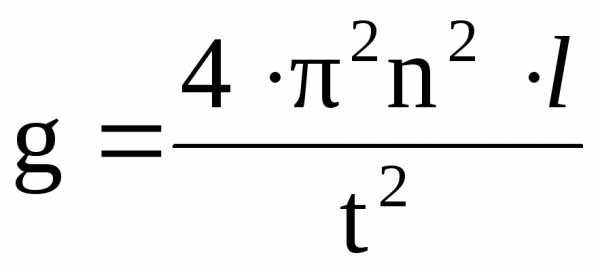
б) выполняем дифференцирование
в)
знак d
заменяем на знак 
,
г)
знак минус перед знаком  заменяем на знак плюс
заменяем на знак плюс
.
Число Если ограничиться значением, то
относительная
погрешность 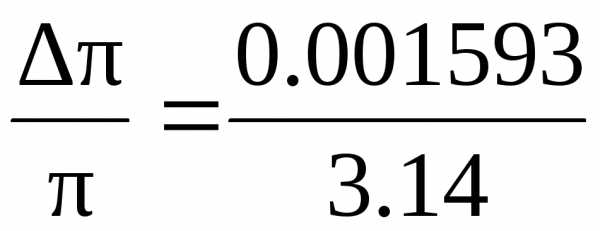 и
и
.
Запись окончательного результата. Находим среднее значение ускорения свободного падения
.
Найдем
абсолютную погрешность:
.
Округляем полученный результат до одной
значащей цифры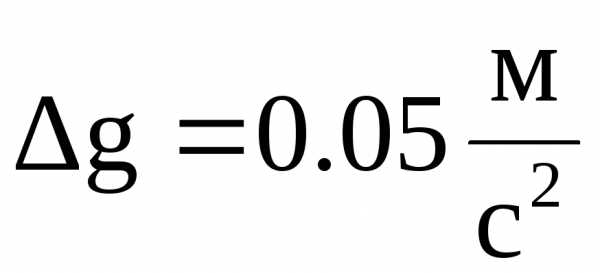 .Записываем
окончательный результат:
.Записываем
окончательный результат:
.
studfiles.net
Относительная погрешность — это… Что такое Относительная погрешность?
Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.
Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).
В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».
Определение погрешности
В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.
- Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:
- Средняя квадратическая погрешность:
- Средняя квадратическая погрешность среднего арифметического:
Классификация погрешностей
По форме представления
- Абсолютная погрешность — ΔX является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины Xmeas. При этом равенство:
ΔX = | Xtrue − Xmeas | ,
где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.
.
Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
- Приведенная погрешность — относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле
,
где Xn — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:
— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
Приведенная погрешность — безразмерная величина (может измеряться в процентах).
По причине возникновения
- Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
- Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
- Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.
В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.
Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.
Обобщенной характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведенных основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10n, где n = 1; 0; -1; -2 и т.д.
По характеру проявления
- Случайная погрешность — погрешность, меняющаяся (по величине и по знаку) от измерения к измерению. Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т.п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления), с особенностями самой измеряемой величины (например при измерении количества элементарных частиц, проходящих в минуту через счётчик Гейгера).
- Систематическая погрешность — погрешность, изменяющаяся во времени по определенному закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т.п.), неучтёнными экспериментатором.
- Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.
- Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора, если произошло замыкание в электрической цепи).
По способу измерения
- Погрешность прямых измерений
- Погрешность косвенных измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:
Если F = F(x1,x2…xn), где xi — непосредственно измеряемые независимые величины, имеющие погрешность Δxi, тогда:
См. также
Литература
- Назаров Н. Г. Метрология. Основные понятия и математические модели. М.: Высшая школа, 2002. 348 с.
- Лабораторные занятия по физике. Учебное пособие/Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др.; под ред. Гольдина Л. Л. — М.: Наука. Главная редакция физико-математичекой литературы, 1983. — 704 с.
Wikimedia Foundation. 2010.
dik.academic.ru


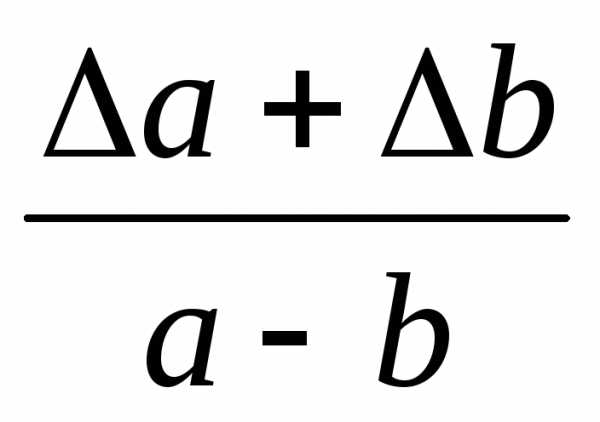
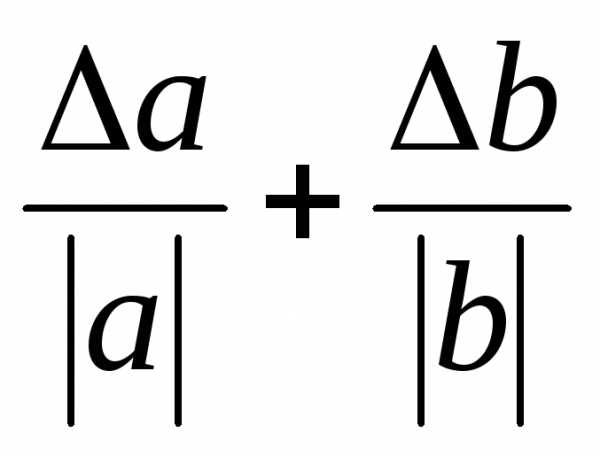

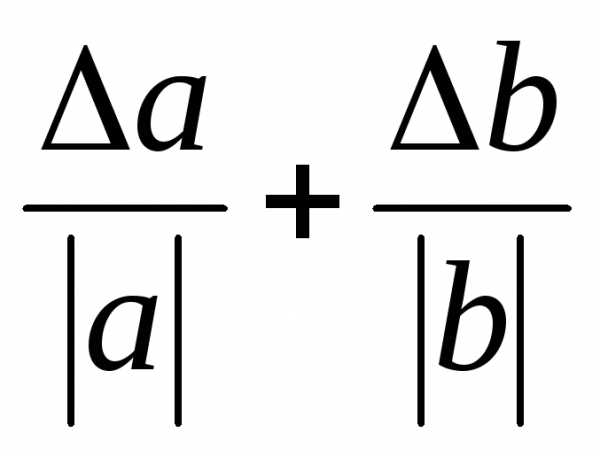


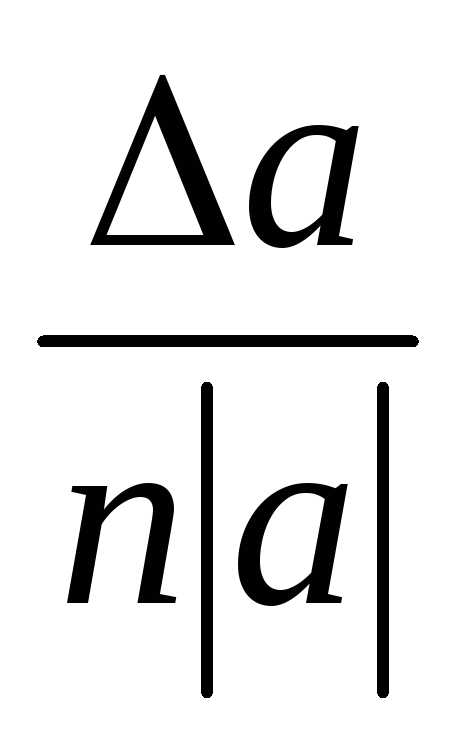

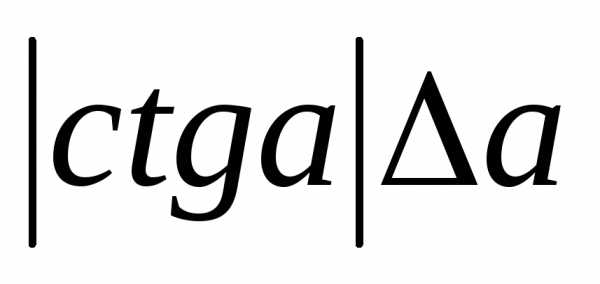

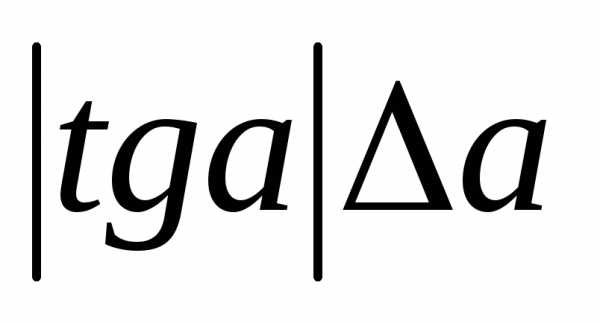
 ,
с
,
с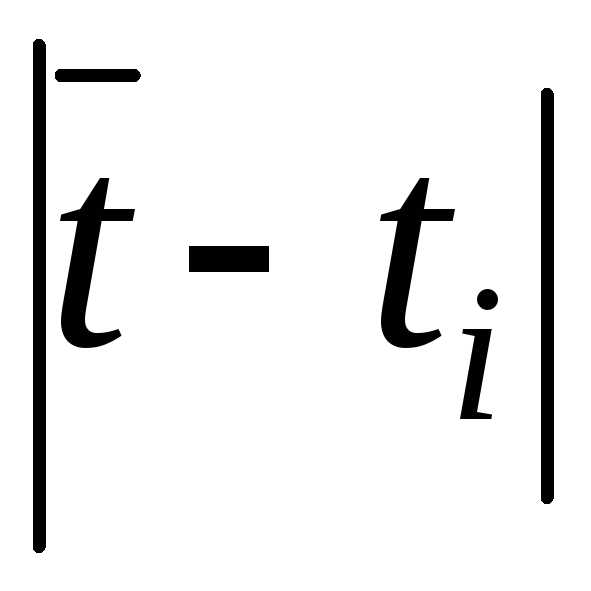 ,
с
,
с =14.74
=14.74 =(14.74±0.02)
с
=(14.74±0.02)
с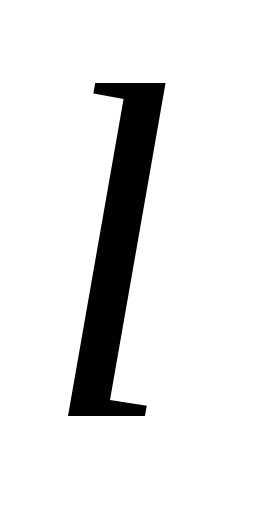 =
(54,20 + 0,05)10-2 м
=
(54,20 + 0,05)10-2 м = 0.005
= 0.005