1. Абсолютная и относительная погрешности числа(определения, предельные погрешности, примеры)
Абсолютная и относительная погрешность числа.
В качестве характеристик точности приближенных величин любого происхождения вводятся понятия абсолютной и относительной погрешности этих величин.
Обозначим через а приближение к точному числу А.
Определени. Величина называется погрешностью приближенного числаа.
Определение. Абсолютной погрешностью 
приближенного
числа а
называется
величина 
.
Практически точное число А обычно неизвестно, но мы всегда можем указать границы, в которых изменяется абсолютная погрешность.
Определение. Предельной абсолютной погрешностью 
,
которую можно найти при данном способе
получения числаа. На практике в
качестве 
выбирают одну
из верхних границ для 
,
достаточно близкую к наименьшей.
Поскольку 
,
то.
Иногда пишут:.
Абсолютная погрешность — это разница между результатом измерения
и истинным (действительным) значением измеряемой величины.
Абсолютная погрешность и предельная абсолютная погрешность не достаточны для характеристики точности измерения или вычисления. Качественно более существенна величина относительной погрешности.
Определение. Относительной погрешностью 
Определение. Предельной относительной погрешностью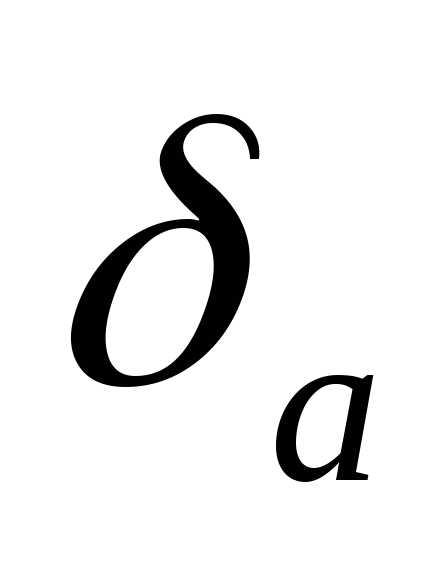 
приближенного
числа а назовем
величину
Так как .
Таким образом, относительная погрешность определяет фактически величину абсолютной погрешности, приходящейся на единицу измеряемого или вычисляемого приближенного числа а.
Пример. Округляя точные числа А до трех значащих цифр, определить
абсолютную Dи относительную δ погрешности полученных приближенных
чисел.
Дано:
А=-13,327
Найти:
∆-абсолютная погрешность
δ –относительная погрешность
Решение:
=|А-а|
А=а±.
a=-13.3
=|-13.327-(-13.3)|=0.027
,a
0
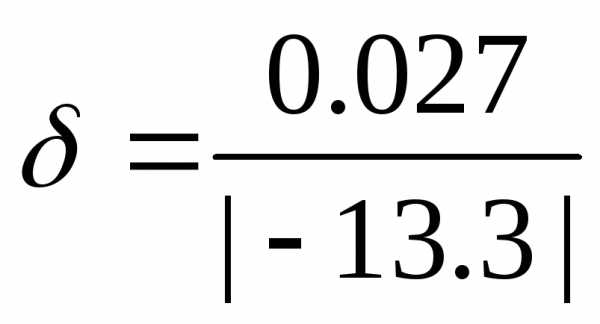*100%=0.203%
Ответ: =0,027; δ=0.203%
2.Десятичная запись приближенного числа. Значащая цифра. Верные знаки числа(определение верных и значащих цифр, примеры; теория о связи относительной погрешности и числа верных знаков).
Верные знаки числа.
Определение. Значащей цифрой приближенного числа а называется всякая цифра, отличная от нуля, и нуль, если он расположен между значащими цифрами или является представителем сохраненного десятичного разряда.
Например, в числе 0,00507 = имеем 3 значащие цифры, а в числе 0,005070=значащие цифры, т.е. нуль справа, сохраняя десятичный разряд, является значащим.
Условимся впредь нули справа записывать, если только они являются значащими. Тогда, иначе говоря,
значащими являются все цифры числа а, кроме нулей слева.
В десятичной системе счисления всякое число а может быть представлено в виде конечной или бесконечной суммы (десятичной дроби):
где
, 
— первая значащая
цифра, m —
целое число, называемое старшим десятичным
разрядом числа а.
Например, 518,3 =, m=2.
Пользуясь записью , введем понятие о верных десятичных знаках (в значащих цифрах) приближенно-
го числа.
Определение. Говорят, что в приближенном числе а
формы n —
первых значащих цифр 
,
где i= m, m-1,…, m-n+1 являются верными, если абсолютная погрешность этого числа не превышает половины единицы разряда, выражаемого n-й значащей цифрой:
В противном случае
последняя цифра 
называется
сомнительной.
При записи приближенного числа без указания его погрешности требуют, чтобы все записанные цифры
были верными. Это требование соблюдено во всех математических таблицах.
Термин “n верных знаков” характеризует лишь степень точности приближенного числа и его не следует понимать так, что n первых значащих цифр приближенного числа а совпадает с соответствующими цифрами точного числа А. Например, у чисел А=10, а=9,997 все значащие цифры различны, но число а имеет 3 верных значащих цифры. Действительно, здесь m=0 и n=3 (находим подбором).
На практике
отыскание n из при
известных 
и
m требует
решения нелинейного неравенства, что
составляет непростую задачу. Правильный
выбор n возможен
из тривиального линейного равенства
по следующей методике.
Величину 
записываем в
виде
,
где 0,05<d≤0,5,
что всегда возможно. Тогда в неравенство для
коэффициентов выполняется (d≤1/2), основания степеней справа и слева одинаковы , поэтому можем приравнять показатели степеней: s=m-n+1, поэтому n=m-s+1.
ТЕОРЕМА 1 .
Если положительное приближенное число
а имеет
n верных
десятичных знаков, то для относительной
погрешности 
этого числа
справедлива оценка:
где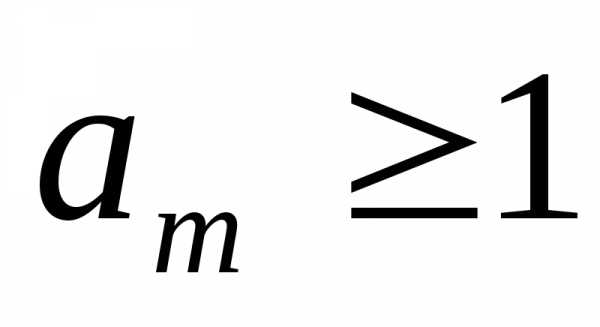 
— первая значащая
цифра числа а.
Доказательство.
Пусть число а
определено
формулой со знаком +
перед скобкой.
По условию а
имеет n
верных знаков,
следовательно 
Тогда
Следствие. В качестве предельной относительной погрешности числа а можно принять
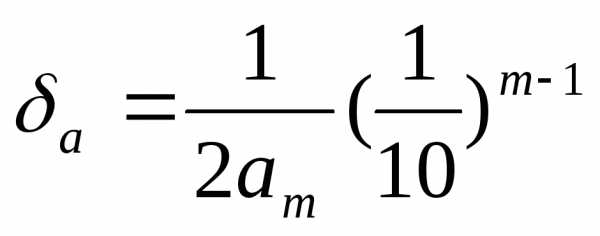
studfiles.net
Относительная и абсолютная погрешность: понятие и примеры
Как уже говорилось ранее, когда мы сравниваем точность измерения некоторой приближенной величины, мы используем абсолютную погрешность.
Понятие абсолютной погрешности
Абсолютная погрешность приближенного значения — это модуль разности точного значения и приближенного значения.
Абсолютную погрешность можно применять для сравнения точности приближений одинаковых величин, а если мы собираемся сравнивать точности приближения различных величин, тогда одной абсолютной погрешности недостаточно.
Например: Длина листа бумаги формата А4 равна (29.7 ± 0.1) см. А расстояние от Санкт-Петербурга до Москвы равно (650± 1) км. Абсолютная погрешность в первом случае не превосходит одного миллиметра, а во втором – одного километра. Вопрос, сравнить точность этих измерений.
Если вы думаете, что длина листа измерена точнее потому, что величина абсолютной погрешности не превышает 1 мм. То вы ошибаетесь. Напрямую сравнить эти величины нельзя. Проведем некоторые рассуждения.
При измерении длины листа абсолютная погрешность не превышает 0.1 см на 29.7 см, то есть в процентном соотношении это составляет 0.1/29.7 *100% = 0.33% измеряемой величины.
Когда мы измеряем расстояние от Санкт-Петербурга до Москвы абсолютная погрешность не превышает 1 км на 650 км, что в процентном соотношении составляет 1/650 *100% = 0.15% измеряемой величины. Видим, что расстояние между городами измерено точнее, чем длинна листа формата А4.
Понятие относительной погрешности
Здесь для оценки качества приближения вводится новое понятие относительная погрешность. Относительная погрешность – это частное от деления абсолютной погрешности на модуль приближенного значений измеряемой величины. Обычно, относительную погрешность выражают в процентах. В нашем примере мы получили две относительных погрешности равные 0.33% и 0.15%.
Как вы уже догадались, относительная погрешность величина всегда положительная. Это следует из того, что абсолютная погрешность всегда положительная величина, и мы делим её на модуль, а модуль тоже всегда положителен.
Нужна помощь в учебе?
Предыдущая тема: Абсолютная погрешность: понятие, как вычислить + примеры
Следующая тема:   Многочлен: понятие и его стандартный вид, степень многочлена
Все неприличные комментарии будут удаляться.
www.nado5.ru
какая разница между относительной и абсолютной погрешностью? спасибо, если можно на примерах
Абсолютной погрешностью или, короче, погрешностью приближенного числа называется разность между этим числом и его точным значением (из большего числа вычитается меньшее) *.Пример 1. На предприятии 1284 рабочих и служащих. При округлении этого числа до 1300 абсолютная погрешность составляет 1300 — 1284=16. При округлении до 1280 абсолютная погрешность составляет 1284 — 1280 = 4.
Относительной погрешностью приближенного числа называется отношение (11, 48) абсолютной погрешности приближенного числа к самому этому числу.
Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная погрешность составляет 200 — 197 = 3. Относительная погрешность равна 3/197 или, округленно, 3/197 = 1,5 %.
В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности. Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.
Пример 3. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая — 50 г. Взвешивание дало 3600 г. Это число – приближенное. Точный вес арбуза неизвестен. Но абсолютная погрешность не превышает 50 г.
Относительная погрешность не превосходит 50/3600 ≈ 1,4%.
Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей) , называется предельной абсолютной погрешностью. Число, заведомо превышающее относительную погрешность (или в худшем случае равное ей) , называется предельной относительной погрешностью.
В примере 3 за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность – 1,4 %.
Величина предельной погрешности не является вполне определенной. Так, в примере 3 можно принять за предельную абсолютную погрешность 100 г, 150 г и вообще всякое число, большее чем 50 г. На практике берется по возможности меньшее значение предельной погрешности. В тех случаях, когда известна точная величина погрешности, эта величина служит одновременно предельной погрешностью. Для каждого приближенного числа должна быть из¬вестна его предельная погрешность (абсолютная или oотносительная) . Когда она прямо не указана, подразумевается что предельная абсолютная погрешность составляет половину единицы последнего выписанного разряда. Так, если приведено приближенное число 4,78 без указания предельной погрешности, то подразумевается, что предельная абсолютная погрешность составляет 0,005. Вследствие этого соглашения всегда можно обойтись без указания предельной погрешности числа.
Предельная абсолютная погрешность обозначается греческой буквой Δ («дельта») ; предельная относительная погрешность — греческой буквой δ («дельта малая») . Если приближенное число обозначить буквой а, то
δ = Δ/a.
Пример 4. Длина карандаша измерена линейкой с миллиметровыми делениями. Измерение показало 17,9 см. Какова предельная относительная погрешность этого измерения?
Здесь а = 17,9 см; можно принять Δ = 0,1 см, так как с точностью до 1 мм измерить карандаш нетрудно, a значительно уменьшить, предельную погрешность ни удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но у самого карандаша ребра могут разниться на бoльшую величину) . Относительная погрешность равна 0,1/17,9. Округляя, находим δ = 0,1/18 ≈ 0,6%.
Пример 5. Цилиндрический поршень имеет около 35 мм в диаметре. С какой точностью нужно его измерить микрометром, чтобы предельная относительная погрешность составляла 0,05%?
Решение. По условию, предельная абсолютная погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная абсолютная погрешность равна 36*(0,05/100) = 0,0175 (мм) или, усиливая, 0,02 (мм) . Можно воспользоваться формулой δ = Δ/a. Подставляя в неё а = 35, δ = 0,0005, имеем 0,0005 = Δ/35. Значит, Δ = 35 • 0,0005 = 0,0175 (мм) .
otvet.mail.ru
Абсолютная и относительная погрешность | Бесплатные курсовые, рефераты и дипломные работы
Абсолютной погрешностью приближенного числа называется модуль разности между этим числом и его точным значением. . Отсюда следует, что заключено в пределах или .
Пример 1. На предприятии 1284 рабочих и служащих. При округлении этого числа до 1300 абсолютная погрешность составляет |1300 — 1284|=16. При округлении до 1280 абсолютная погрешность составляет |1280 — 1284| = 4.
Относительной погрешностью приближенного числа называется отношение абсолютной погрешности …
приближенного числа к модулю значения числа .
Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная погрешность составляет |200 — 197| = 3. Относительная погрешность равна 3/|197| или 1,5 %.
В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности. Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.
Пример 3. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая — 50 г. Взвешивание дало 3600 г. Это число – приближенное. Точный вес арбуза неизвестен. Но абсолютная погрешность не превышает 50 г. Относительная погрешность не превосходит 50/3600 ≈1,4%.
В примере 3 за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность – 1,4 %.
Абсолютная погрешность обозначается греческой буквой Δ («дельта») или Da; относительная погрешность — греческой буквой δ («дельта малая»). Если приближенное число обозначить буквой А, то δ = Δ/|А|.
Значащей цифрой приближенного числа А называется всякая цифра в его десятичном представлении, отличная от нуля, и нуль, если он содержится между значащими цифрами или является представителем сохраненного десятичного разряда
Пример. А= 0,002080. Здесь только первые три нуля не являются значащими.
n первых значащих цифр приближенного числа А являются верными, если абсолютная погрешность этого числа не превышает половины разряда, выражаемого n – й значащей цифрой, считая слева направо. Цифры, не являющиеся верными, называются сомнительными.
Пример. Если в числе a= 0,03450 все цифры верные, то .
| Правила приближенных вычислений | ||
| понятие | определение | пример или примечание |
| Приближенные вычисления | Вычисления, производимые над числами, которые известны нам с определённой точностью, например, полученными в эксперименте. | Выполняя вычисления, всегда необходимо помнить о той точности, которую нужно или которую можно получить. Недопустимо вести вычисления с большой точностью, если данные задачи не допускают или не требуют этого. И наоборот. |
| Погрешности | Разница между точным числом а и его приближенным значением А называется погрешностью данного приближенного числа. Если известно, что | а — А | < D, то величина D называется абсолютной погрешностью приближенной величины А. Отношение D /|А| = δ называется относительной погрешностью; последнюю часто выражают в процентах. | 3,14 является приближенным значением числа а, погрешность его равна 0,00159…, абсолютную погрешность можно считать равной 0,0016, а относительную погрешность δ равной 0.0016/3.14 = 0,00051 = 0,051%. |
| Значащие цифры | все цифры числа, начиная с 1-й слева, отличной от нуля, до последней, за правильность которой можно ручаться. | Приближенные числа следует записывать, сохраняя только верные знаки. Если, например, абсолютная погрешность числа 52438 равна 100, то это число должно быть записано, например, в виде 524 .102 или 0,524 .105. Оценить погрешность приближенного числа можно, указав, сколько верных значащих цифр оно содержит. Если число А = 47,542 получено в результате действий над приближенными числами и известно, что δ = 0,1%, то a имеет 3 верных знака, т.е. А = 47,5 |
| Округление | Если приближенное число содержит лишние (или неверные) знаки, то его следует округлить. | При округлении сохраняются только верные знаки; лишние знаки отбрасываются, причем если первая отбрасываемая цифра больше или равна 5, то последняя сохраняемая цифра увеличивается на единицу. |
| Действия над приближенными числами | Результат действий над приближёнными числами представляет собой также приближённое число. Число значащих цифр результата можно вычислить при помощи следующих правил: 1. При сложении и вычитании приближённых чисел в результате следует сохранять столько десятичных знаков, сколько их в приближённом данном с наименьшим числом десятичных знаков. 2. При умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет приближённое данное с наименьшим числом значащих цифр. |
Результат действий с приближенными числами есть тоже приближенное число. При этом неточными могут оказаться и те цифры, которые получены действиями над точными цифрами данных чисел.
Пример 5. Перемножаются приближенные числа 60,2 и 80,1. Известно, что все выписанные цифры верны, так что истинные величины могут отличаться от приближенных лишь сотыми, тысячными и т. д. долями. В произведении получаем 4822,02. Здесь могут быть неверными не только цифры сотых и десятых, но и цифры единиц. Пусть, например, сомножители получены округлением точных чисел 60,25 и 80,14. Тогда точное произведение будет 4828,435, так что цифра единиц в приближенном произведении (2) отличается от точной цифры (8) на 6 единиц.
Теория приближенных вычислений позволяет:
1) зная степень точности данных, оценить степень точности результатов еще до выполнения действий;
2) брать данные с надлежащей степенью точности, достаточной, чтобы обеспечить требуемую точность результата, но не слишком большой, чтобы избавить вычислителя от бесполезных расчетов;
3) рационализировать сам процесс вычисления, освободив его от тех выкладок, которые не окажут влияния на точные цифры результата.
refac.ru
Абсолютная и относительная погрешности — Мегаобучалка
На практике обычно числа, над которыми производятся вычисления, являются приближенными значениями тех или иных величин. Для краткости речи приближенное значение величины называют приближенным числом. Истинное значение величины называют точным числом. Приближенное число имеет практическую ценность лишь тогда, когда мы можем определить, с какой степенью точности оно дано, т.е. оценить его погрешность. Напомним основные понятия из общего курса математики.
Обозначим: x — точное число (истинное значение величины), а -приближенное число (приближенное значение величины).
Определение 1. Погрешностью ( или истинной погрешностью) приближенного числа называется разность между числом x и его приближенным значением а. Погрешность приближенного числа а будем обозначать . Итак,
| . | (2.1) |
Погрешность может быть числом положительным, отрицательным или равным нулю.
Определение 2. Абсолютной погрешностью приближенного числа а называется модуль разности между числом х и его приближенным значением а.
Абсолютную погрешность приближенного числа а будем обозначать , т.е.
| . | (2.2) |
Точное число x чаще всего бывает неизвестно, поэтому найти истинную и абсолютную погрешности не представляет возможным. С другой стороны, бывает необходимо оценить абсолютную погрешность, т.е. указать число, которого не может превысить абсолютная погрешность. Например, измеряя длину предмета данным инструментом, мы должны быть уверены в том, что погрешность полученного числового значения не превысит некоторого числа, например 0,1 мм. Другими словами, мы должны знать границу абсолютной погрешности. Эту границу будем называть предельной абсолютной погрешностью.
Определение 3. Предельной абсолютной погрешностью приближенного числа а называется положительное число такое, что , т.е.
| . | (2.3) |
Из формулы (2.3) получаем:
| (2.4) |
Значит, есть приближенное значение числа х по недостатку, — по избытку. Применяют также такую запись:
| . | (2.5) |
Ясно, что предельная абсолютная погрешность определяется неоднозначно: если некоторое число есть предельная абсолютная погрешность, то любое большее число тоже есть предельная абсолютная погрешность. На практике стараются выбирать возможно меньшее и простое по записи (с 1-2 значащими цифрами) число , удовлетворяющее неравенству (2.3).
Пример. Определить истинную, абсолютную и предельную абсолютную погрешности числа а = 0,17, взятого в качестве приближенного значения числа .
Истинная погрешность:
Абсолютная погрешность:
За предельную абсолютную погрешность можно принять число и любое большее число. В десятичной записи будем иметь: Заменяя это число большим и возможно более простым по записи, примем:
Замечание. Если а есть приближенное значение числа х, причем предельная абсолютная погрешность равна h, то говорят, что а есть приближенное значение числа х с точностью до h.
Знания абсолютной погрешности недостаточно для характеристики качества измерения или вычисления. Пусть, например, получены такие результаты при измерении длины. Расстояние между двумя городами S1=500 1 км и расстояние между двумя зданиями в городе S2=10 1 км. Хотя абсолютные погрешности обоих результатов одинаковы, однако существенное значение имеет то, что в первом случае абсолютная погрешность в 1 км приходится на 500 км, во втором — на 10 км. Качество измерения в первом случае лучше, чем во втором. Качество результата измерения или вычисления характеризуется относительной погрешностью.
Определение 4. Относительной погрешностью приближенного значения а числа х называется отношение абсолютной погрешности числа а к абсолютному значению числа х:
| . | (2.6) |
Так, как точное число обычно бывает неизвестно, его заменяют приближенным числом:
| . | (2.7) |
Определение 5. Предельной относительной погрешностью приближенного числа а называется положительное число такое, что .
Так как , то из формулы (2.7) следует, что можно вычислить по формуле
| . | (2.8) |
Для краткости речи в тех случаях, когда это не вызывает недоразумений, вместо “предельная относительная погрешность” говорят просто “относительная погрешность”.
Предельную относительную погрешность часто выражают в процентах.
Пример 1. . Полагая , можем принять = . Производя деление и округляя (обязательно в сторону увеличения), получим =0,0008=0,08%.
Пример 2. При взвешивании тела получен результат: p=23,4 0,2 г. Имеем =0,2. . Производя деление и округляя, получим =0,9%.
Формула (2.8) определяет зависимость между абсолютной и относительной погрешностями. Из формулы (2.8) следует:
| . | (2.9) |
Пользуясь формулами (2.8) и (2.9), мы можем, если известно число а, по данной абсолютной погрешности находить относительную погрешность и наоборот.
Заметим, что формулы (2.8) и (2.9) часто приходится применять и тогда, когда мы еще не знаем приближенного числа а с требуемой точностью, а знаем грубое приближенное значение а. Например, требуется измерить длину предмета с относительной погрешностью не выше 0,1%. Спрашивается: возможно ли измерить длину с нужной точностью при помощи штангенциркуля, позволяющего измерить длину с абсолютной погрешностью до 0,1 мм? Пусть мы еще не измеряли предмет точным инструментом, но знаем, что грубое приближенное значение длины — около 12 см. По формуле (1.9) находим абсолютную погрешность:
мм
Отсюда видно, что при помощи штангенциркуля возможно выполнить измерение с требуемой точностью.
В процессе вычислительной работы часто приходится переходить от абсолютной погрешности к относительной, и наоборот, что делается с помощью формул (1.8) и (1.9).
megaobuchalka.ru
12. Погрешность, классификация погрешностей.
Результат измерений физической величины всегда отличается от истинного значения на некоторую величину, которая называется погрешностью
КЛАССИФИКАЦИЯ:
1. По способу выражения: абсолютные, приведенные и относительные
2. По источнику возникновения: методические и инструментальные.
3. По условиям и причинам возникновения: основные и дополнительные
4. По характеру изменения: систематические и случайные.
5. По зависимости от входной измеряемой величины: аддитивные и мультипликативные
6. По зависимости от инерционности: статические и динамические.
13. Абсолютная, относительная и приведенная погрешности.
Абсолютная погрешность — это разность между измеренным и действительным значениями измеряемой величины:
(1)
где Аизм, А — измеряемое и действительное значения; ΔА — абсолютная погрешность.
Абсолютную погрешность выражают в единицах измеряемой величины. Абсолютную погрешность, взятую с обратным знаком, называют поправкой.
Относительная погрешность р равна отношению абсолютной погрешности ΔА к действительному значению измеряемой величины и выражается в процентах:
(2)
Приведенная погрешность измерительного прибора — это отношение абсолютной погрешности к номинальному значению. Номинальное значение для прибора с односторонней шкалой равно верхнему пределу измерения, для прибора с двусторонней шкалой (с нулем посередине) — арифметической сумме верхних пределов измерения:
пр. ном.
14. Методическая, инструментальная, систематическая и случайная погрешности.
Погрешность метода обусловлена несовершенством применяемого метода измерения, неточностью формул и математических зависимостей, описывающий данный метод измерения, а также влиянием средства измерения на объект свойства которого изменяются.
Инструментальная погрешность (погрешность инструмента) обусловлена особенностью конструкции измерительного устройства, неточностью градуировки, шкалы, а также неправильностью установки измерительного устройства.
Инструментальная погрешность, как правило, указывается в паспорте на средство измерения и может быть оценена в числовом выражении.
Систематическая погрешность — постоянная или закономерно изменяющаяся погрешность при повторных измерениях одной и той же величины в одинаковых условиях измерения. Например, погрешность, возникающая при измерении сопротивления ампервольтметром, обусловленная разрядом батареи питания.
Случайная погрешность — погрешность измерения, характер изменения которой при повторных измерениях одной и той же величины в одинаковых условиях случайный. Например, погрешность отсчета при нескольких повторных измерениях.
Причиной случайной погрешности является одновременной действие многих случайных факторов, каждый из которых в отдельности мало влияет.
Случайная погрешность может быть оценена и частично снижена путём правильной обработки методами математической статистики, а также методами вероятности.
15. Основная и дополнительная, статическая и динамическая погрешности.
Основная погрешность — погрешность, возникающая в нормальных условиях применения средства измерения (температура, влажность, напряжение питания и др.), которые нормируются и указываются в стандартах или технических условиях.
Дополнительная погрешность обуславливается отклонением одной или нескольких влияющих величин от нормального значения. Например, изменение температуры окружающей среды, изменение влажности, колебания напряжения питающей сети. Значение дополнительной погрешности нормируется и указывается в технической документации на средства измерения.
Статическая погрешность — погрешность при измерении постоянной по времени величины. Например, погрешность измерения неизменного за время измерения напряжения постоянного тока.
Динамическая погрешность — погрешность измерения изменяющейся во времени величины. Например, погрешность измерения коммутируемого напряжения постоянного тока, обусловленная переходными процессами при коммутации, а также ограниченным быстродействием измерительного прибора.
studfiles.net
Абсолютная и относительная погрешность
Элементы теории погрешностей
Точные и приближенные числа
Точность числа, как правило, не вызывает сомнений, когда речь идет о целых значениях данных(2 карандаша, 100 деревьев). Однако, в большинстве случаев, когда точное значение числа указать невозможно (например, при измерении предмета линейкой, снятии результатов с прибора и т.п.), мы имеем дело с приближенными данными.
Приближенным значением называется число, незначительно отличающееся от точного значения и заменяющее его в вычислениях. Степень отличия приближенного значения числа от его точного значения характеризуется погрешностью.
Различают следующие основные источники погрешностей:
1. Погрешности постановки задачи, возникающие в результате приближенного описания реального явления в терминах математики.
2. Погрешности метода, связанные с трудностью или невозможностью решения поставленной задачи и заменой ее подобной, такой, чтобы можно было применить известный и доступный метод решения и получить результат, близкий к искомому.
3. Неустранимые погрешности, связанные с приближенными значениями исходных данных и обусловленные выполнением вычислений над приближенными числами.
4. Погрешности округления, связанные с округлением значений исходных данных, промежуточных и конечных результатов, получаемых с применением вычислительных средств.
Абсолютная и относительная погрешность
Учет погрешностей является важным аспектом применения численных методов, поскольку погрешность конечного результата решения всей задачи является продуктом взаимодействия всех видов погрешностей. Поэтому одной из основных задач теории погрешностей является оценка точности результата на основании точности исходных данных.
Если – точное число и – его приближенное значение, то погрешностью (ошибкой) приближенного значения является степень близости его значения к его точному значению .
Простейшей количественной мерой погрешности является абсолютная погрешность, которая определяется как
(1.1.2-1)
Как видно из формулы 1.1.2-1, абсолютная погрешность имеет те же единицы измерения, что и величина . Поэтому по величине абсолютной погрешности далеко не всегда можно сделать правильное заключение о качестве приближения. Например, если , а речь идет о детали станка, то измерения являются очень грубыми, а если о размере судна, то – очень точными. В связи с этим введено понятие относительной погрешности, в котором значение абсолютной погрешности отнесено к модулю приближенного значения ().
(1.1.2-2)
Использование относительных погрешностей удобно, в частности, тем, что они не зависят от масштабов величин и единиц измерений данных. Относительная погрешность измеряется в долях или процентах. Так, например, если
,а , то , а если и ,
то тогда .
Чтобы численно оценить погрешность функции, требуется знать основные правила подсчета погрешности действий:
· при сложении и вычитании чиселабсолютные погрешности чисел складываются
· при умножении и делении чисел друг на друга складываются их относительные погрешности
· при возведении в степень приближенного числа его относительная погрешность умножается на показатель степени
Пример 1.1.2-1. Дана функция: . Найти абсолютную и относительную погрешности величины (погрешность результата выполнения арифметических операций), если значения известны, а 1 – точное число и его погрешность равна нулю.
Определив, таким образом, значение относительной погрешности, можно найти значение абсолютной погрешности, как ,где величина вычисляется по формуле при приближенных значениях
Поскольку точное значение величины обычно неизвестно, то вычисление и по приведенным выше формулам невозможно. Поэтому на практике проводят оценку предельных погрешностей вида:
(1.1.2-3)
где и – известные величины, которые являются верхними границами абсолютной и относительной погрешностей, иначе их называют – предельная абсолютная и предельная относительная погрешности. Таким образом, точное значение лежит в пределах:
или
Если величина известна, то , а если известна величина , то
Предельная абсолютная погрешность функции вида , дифференцируемойв заданной области, при известных значениях аргументов , а также при известных предельных абсолютных погрешностях аргументов , вычисляется по формуле:
(1.1.2-4)
а, соответственно, предельная относительная погрешность функции
(1.1.2-5)
В частном случае для функции от одной переменной (при m=1):
Пример1.1.2-2.Оценить абсолютную и относительную погрешности приближенного числа .
Число – трансцендентное число, представляется бесконечной непериодической дробью .
Приближенное значение числа .
Граница абсолютной погрешности , относительная погрешность числа
Похожие статьи:
poznayka.org