Задачи на проценты математика – задачи на проценты | математика-повторение

Как решать задачи на проценты?

Понятие процент встречается в нашей жизни слишком часто, поэтому очень важно знать, как решать задачи на проценты. В принципе, это дело не сложное, главное, понять принцип работы с процентами.

Что такое процент

Мы оперируем с понятием 100 процентов, и соответственно, один процент это сотая доля определенного числа. И все счисления ведутся уже исходя из этого соотношения.

Например, 1% от 50 это 0,5, 15 от 700 это 7.

Как решать

1. Зная, что один процент это одна сотая от представленного числа, можно найти любое количество требуемых процентов. Для того чтобы было нагляднее, попробуем найти 6 процентов от числа 800. Делается это просто.
   • Сначала находим один процент. Для этого 800 делим на 100. Получается 8.
   • Теперь этот самый один процент, то есть 8, умножаем на нужное нам количество процентов, то есть на 6. Получается 48.
   • Закрепим результат повторением.

   15% от 150. Решение: 150/100*15=22.

   28% от 1582. Решение: 1582/100*28=442.

2. Бывают другие задачки, когда вам даются величины, а вам нужно найти проценты. Например, вам известно, что в магазине 5 алых роз из 75 белых, и вам нужно узнать, каков процент алых. Если мы не знаем этот процент, значит, обозначим его как х.

   Для этого есть формула: 75 – 100%

   5 — х%

   В этой формуле цифры умножаются крест на крест, то есть х=5*100/75. Получается, что х=6% Значит процент алых роз составляет 6%.

3. Существует еще один тип задач на проценты, когда вам надо найти на сколько процентов одно число больше или меньше другого. Как решать задачи с процентами в этом случае?

   В классе учится 30 человек, из них 16 мальчиков. Вопрос, на сколько процентов мальчиков больше, чем девочек. Для начала необходимо сосчитать, какой процент составляют учащиеся мальчики, затем нужно узнать, сколько процентов девочек. А уж в конце найти разницу.

   Итак, приступим. Составляем пропорцию 30 уч. – 100%

   16 уч. –х %

   Теперь считаем. Х=16*100/30, х=53,4 % от всех учащихся в классе составляют мальчики.

   Теперь найдем процент дево

elhow.ru

Задачи на проценты | Математика

Удобнее всего решать задачи на проценты в 6 классе с помощью пропорций.  Для составления пропорции нет необходимости выяснять вид задачи на проценты.  Нахождение числа по его процентам, процентов от числа и процентного отношения чисел  в этом случае  проходит по одинаковой схеме, что существенно упрощает решение.

Задачи на проценты относятся к задачам на прямую пропорциональную зависимость, но при составления условия стрелки обычно не рисуют. Условие оформляется максимально просто: в первом столбце — единицы измерения, во втором — проценты.

Рассмотрим примеры задач на проценты,  решаемые с помощью пропорции.

1)  Сколько килограммов соли содержится в 40 кг 3-процентного раствора?

Решение:

Пусть х кг соли содержится в растворе.  Составляем пропорцию: 

(Здесь пропорцию составили по строкам. Можно также составлять ее по столбцам, например, в направлении от большой величины —  к меньшей: 40:х=100:3).

Значит, в растворе содержится 1,2 кг соли.

Ответ: 1,2 кг.

2) В саду растет 64 вишневых дерева, что составляет 16% всех деревьев. Сколько всего деревьев в саду?

Решение:

Пусть х деревьев всего в саду.  Составляем пропорцию:

Значит, всего в саду 400 деревьев.

Ответ: 400 деревьев.

3) В книге 130 страниц. Саша прочитал 104 страницы. Сколько процентов книги прочитал Саша?

Решение:

Пусть х% книги составляют прочитанные страницы. Составим и решим пропорцию:

130 и 100 сокращаем на 10, затем 13 и 104 сокращаем на 13:

Значит, Саша прочитал 80% книги.

Ответ: 80%.

В некоторых случаях задачи на проценты можно легко решать устно. Как это делается, я расскажу позже.

www.for6cl.uznateshe.ru

математика-повторение-задачи на проценты | математика-повторение

Записи с меткой «математика-повторение-задачи на проценты»

Задача 1. Первое число составляет 80% от второго. А сколько процентов второе число составляет от первого?

Решение. Обозначим второе число через х. Тогда первое число по равно 0,8х. Найдем, сколько второе число составляет от первого. Для этого разделим второе число на первое, и результат умножим на 100%.

Ответ: второе число составляет 125% от первого.

Задача 2. На сколько процентов увеличится площадь квадрата, если его сторону увеличить на 30%?

Решение. Если сторона квадрата равна а, то площадь квадрата S=а². После увеличения стороны на 30% ее длина составит 130% от а. Это 1,3а. Новая площадь S₁=(1,3a)²=1,69a². Разница составила 0,69а². Обращаем десятичную дробь 0,69 в проценты и получаем 69%. Ответ: Если сторону квадрата увеличить на 30%, то площадь квадрата увеличится на 69%.

Задача 3. Яблоки, содержащие 70% воды, потеряли при сушке 60% своей массы. Сколько процентов воды содержат сушеные яблоки?

Решение. Пусть было х яблок по массе. В них содержится 70% воды, значит, 30% сухого концентрата. 30% от х – это 0,3х. После сушки яблок это количество 0,3х сухого вещества так и остается. Известно, что при сушке яблоки потеряли 60% своей массы. Следовательно, осталось 40% от х, Это 0,4х. То, что осталось, примем за 100%. В этой массе 0,3х сухого вещества. Узнаем, сколько это процентов.

В сушеных яблоках 75% сухого вещества, значит, воды в сушеных яблоках 100%-75%=25%. Ответ: в сушеных яблоках 25% воды.

Задача 4. Свежие грибы содержат 90% влаги, сушеные – 12%. Сколько сушеных грибов получится из 13,2 кг свежих?

Решение. Пусть из 13,2 кг свежих грибов получится х кг сушеных грибов. Тогда сухого вещества в х кг будет содержаться 100%-12%=88%. Получается 0,88х кг. В 13,2 кг свежих грибов сухого вещества содержится 100%-90%=10%. В килограммах получается 0,1∙13,2=1,32 кг. Имеем равенство: 0,88х=1,32, отсюда х=1,32 : 0,88;

х=1,5 кг. Ответ: из 13,2 кг свежих грибов получается 1,5 кг сушеных грибов.

Задача 5. Сколько литров воды нужно разбавить с 300 г соли для получения раствора с концентрацией 15%?

Решение. Пусть нужно х граммов воды разбавить с 300 г соли для получения раствора с концентрацией 15%. Выразим количество соли в х г воды 15%-го раствора. Это 15% от х. Получаем 0,15х г. По условию соли 300 г. Получаем равенство:

0,15х=300, отсюда х=300:0,15=30000:15=2000 г = 2 л воды.

Ответ: нужно разбавить 2 л воды.

Задача 6. В раствор сахарной воды массой 200 г с концентрацией 30% налили 100 г чистой воды. Сколько процентов составляет концентрация сахара в последнем растворе?

Решение. В 200 г сахарной воды с концентрацией 30% содержится 0,3∙200=60 г сахара. После того, как в раствор налили 100 г чистой воды, масса раствора стала равной 300 г, а сахара в нем по-прежнему 60 г. Найдем процентное отношение массы сахара к массе раствора.

Ответ: концентрация сахара в последнем растворе составляет 20%.

Задача 7. В раствор соленой воды массой 600 г с концентрацией 15% добавили раствор соленой воды массой 240 г с концентрацией 50%. Сколько процентов соли в полученной смеси?

Решение. В 600 г соленой воды с концентрацией 15% содержится 15% от 600 г соли. Это 0,15∙600=90 г соли. В 240 г соленой воды с концентрацией 50% содержится 50% от 240 г соли. Это 0,5∙240=120 г соли. Масса полученной смеси равна 600+240=840 г. Соли в этой массе 90+120=210 г. Найдем процент соли в полученной смеси.

Ответ: в полученной смеси содержится 25% соли.

Задача 8. Цену товара сначала снизили на 20%, затем новую цену снизили еще на 25%. На сколько процентов снизили первоначальную цену товара?

Решение. Обозначив первоначальную стоимость товара через х, выразим окончательную стоимость товара и найдем, сколько процентов последняя цена товара будет составлять от первоначальной. После первого снижения на 20%  товар стал стоить 80% от первоначальной цены. Это 80% от х или 0,8х Эту цену снизили еще на 25%, стоимость стала составлять 75% от последней цены, равной 0,8х. Тогда последняя цена составит 75% от 0,8х или 0,75∙0,8х=0,6х. Находим, сколько процентов 0,6х (последняя цена товара) составляет от х (первоначальной цены товара).

Получается, что новая цена составляет 60% от первоначальной цены. Это означает, что цена товара после двух снижений уменьшилась на 40%. Ответ: цену товара снизили на 40%.

Задача 9. Число увеличили на 25%. На сколько процентов нужно уменьшить полученное число, чтобы вновь получилось заданное?

Решение. Пусть заданное число было равно х. После увеличения оно составит 1,25х (это 125% от х). Выясним, сколько процентов от  числа 1,25х нужно взять, чтобы опять получить х. Получается, что:

Так как х составляет от 1,25х только 80%, то это означает, что, для того, чтобы получить заданное число, нужно полученное число уменьшить на 100%-80%=20%.   Ответ: на 20%.

Если вы хотите научиться решать задачи на проценты, то полезной будет эта книга: перейдите по ссылке.

Математика. 5 класс.             Тест 8. Вариант 2.

1. В школьной библиотеке 3400 книг, из них 2890 учебников. Сколько процентов всех книг составляют учебники?

А) 70%; B) 75%; C) 90%; D) 80%; E) 85%.

2. Автотуристы в первый день проехали 36% всего пути, во второй день 39% всего пути, а в третий день — оставшиеся 200 км. Каков весь путь?

А) 700 км; В) 600 км; С) 800 км; D) 1000 км; Е) 900 км.

3. …, на которые точка разбивает прямую, называются дополнительными лучами.

А) отрезки; В) прямые; С) фигуры; D) лучи; Е) стороны.

4. Найти градусные меры / ABC и / MNK.

А) / ABC=135°, / MNK=45°;

B) /  ABC=120°, /  MNK=45°;

C) / ABC=105°, /  MNK=135°;

D) /  ABC=45°, / MNK=135°;

E) /  ABC=60°, / MNK=135°.

5. Угол АОВ равен 87°. Внутри этого угла проведен луч ОС. Найдите градусную меру угла АОС, если / ВОС=61°.

А) 36°; В) 31°; С) 26°; D) 16°; E) 158°.

6. Решить задачу, составив уравнение. Угол МОК равен 120°. Внутри этого угла проведен луч OD. Угол MOD больше угла DOK на 50°. Сколько градусов содержит угол DOK?

A) 35°; B) 85°; C) 45°; D) 60°; E) 70°.

7. … угол равен половине развернутого угла.

А) тупой; В) острый; С) любой; D) полный; Е) прямой.

8. Сколько градусов содержит угол, если он составляет 3/5 развернутого угла?

А) 45°; В) 72°; С) 135°; D) 120°; Е) 108°.

9. Сколько градусов составляет угол, если он равен 7/15 прямого угла?

А) 54°; В) 36°; С) 60°; D) 42°; Е) 66°.

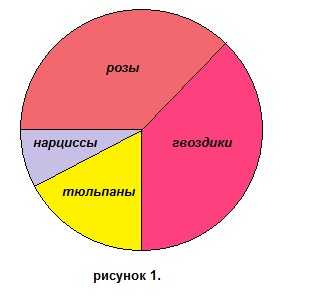10. Определить по круговой диаграмме, изображенной на рисунке 1, процентное содержание гвоздик в цветнике. Результат округлить до целых.

А) 38 %;

В) 44%;

С) 17%;

D) 8 %;

Е) 25 %.

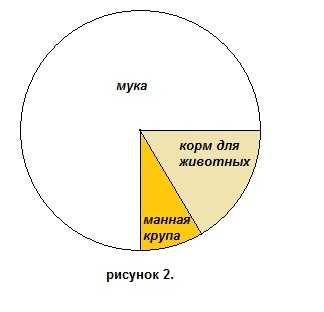11. Используя круговую диаграмму, приведенную на рисунке 2, найти процентное количество корма для животных, получающегося в результате помола пшеницы. Округлить до целых.

А) 4 %;

В) 17 %;

С) 25 %;

D) 80 %;

Е) 60 %.

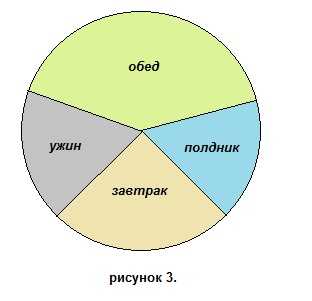12. Используя круговую диаграмму, приведенную на рисунке 3, найти в процентах норму пищи, рекомендуемую к употреблению за завтраком. Округлить до целых.

А) 17 %;

В) 10 %;

С) 45 %;

D) 35 %;

Е) 25 %.

Ответы к тестам Вы найдете на странице «Ответы«.

Нужно учиться решать задачи на проценты, так как тема «Проценты» уже никогда не закончится! Приобретайте лучшее наглядное пособие «Как решать задачи на проценты». В электронной книге не только правила и текстовые объяснения, но и обучающие видео (круговым диаграммам в книге также нашлось место!) Посмотреть подробнее можно здесь! 

www.mathematics-repetition.com

Задачи на тему Проценты | Математика

1562 Запишите в процентах десятичные дроби: 0,87; 0,07; 1,45; 0,035; 2,672; 0,907
РЕШЕНИЕ

1563 Запишите обыкновенные дроби 1/2, 1/4, 3/4, 2/5, 17/50 в виде десятичных, а потом в виде процентов
РЕШЕНИЕ

1564 Заполните таблицу
РЕШЕНИЕ

1565 В школьной библиотеке 7000 книг. Маша прочитала одну сотую всех этих книг. Сколько библиотечных книг прочитала Маша? Сережа прочитал 1% всех книг школьной библиотеки. Сравните число библиотечных книг, прочитанных Машей и Сережей.
РЕШЕНИЕ

1566 В палатку завезли 850 кг огурцов. Первый покупатель взял для соления 1% всех огурцов, а второй 3% всех огурцов. Сколько килограммов огурцов купил каждый из них?
РЕШЕНИЕ

1567 На поле, площадь которого 620 га, работали хлопкоуборочные машины. За сутки они убрали 15% всего поля. Сколько гектаров хлопка убрали за сутки?
РЕШЕНИЕ

1568 Бригаде поручили отремонтировать участок дороги длиной 760 м. Сколько метров дороги бригада отремонтирует, когда выполнит: 30% задания; 50% задания; 10% задания?
РЕШЕНИЕ

1569 Предприятие изготовило за квартал 500 насосов, из которых 60% имели высшую категорию качества. Сколько насосов высшей категории качества изготовило предприятие?
РЕШЕНИЕ

1570 В плодовом саду собирали яблоки. За день было собрано 4840 кг. 25% собранных яблок отправили в магазин, а остальные на склад. Сколько килограммов яблок отправили на склад?
РЕШЕНИЕ

1571 Себестоимость изготовления одной детали равна 650 р. Внедрение новой технологии позволило снизить себестоимость детали на 2%. Какова стала себестоимость такой детали?
РЕШЕНИЕ

1572 Поле на рисунке 158 разбито на 100 долей. Закрашенная на рисунке часть засеяна горохом. Найдите площадь всего поля, если горохом засеяно 24,8 га.
РЕШЕНИЕ

1573 Сколько человек было в кино, если 1% всех зрителей составляет 7 человек?
РЕШЕНИЕ

1574 Мотоциклист за день проехал некоторое расстояние. 1% пути он ехал по проселочной дороге, что составило 3,2 км. Какое расстояние проехал мотоциклист за день?
РЕШЕНИЕ

1575 Двор разбит на 100 равных частей. Часть площади двора, закрашенная на рисунке 159, отведена под стоянку машин. Найдите площадь двора, если стоянка занимает 146,4 м2.
РЕШЕНИЕ

1576 Ученик прочитал 138 страниц, что составляет 23% числа всех страниц в книге. Сколько страниц в книге?
РЕШЕНИЕ

1577 Масса медвежонка составляет 15% массы белого медведя. Найдите массу белого медведя, если масса медвежонка 120 кг.
РЕШЕНИЕ

1578 Сливочное мороженое содержит 14% сахара. На приготовление мороженого израсходовали 35 кг сахара. Сколько сделали порций мороженого, если в каждой порции 100 г?
РЕШЕНИЕ

1579 Применяя интенсивную технологию, бригада изготовила сверх плана 250 деталей, перевыполнив тем самым план на 5%. Сколько деталей изготовила бригада?
РЕШЕНИЕ

1580 В школе 700 учащихся. Среди них 357 мальчиков. Сколько процентов учащихся этой школы составляют мальчики?
РЕШЕНИЕ

1581 Фрекен Бок испекла 80 пирожков, и Карлсон тут же съел 10 пирожков. Сколько процентов всех пирожков съел Карлсон?
РЕШЕНИЕ

1582 В механическом цехе установлено 350 станков, из которых 35 находятся в ремонте. Сколько процентов станков находятся в действующем состоянии?
РЕШЕНИЕ

1583 При плане 35 деталей в день рабочий сделал 42 детали. На сколько процентов он выполнил норму? На сколько процентов он перевыполнил норму?
РЕШЕНИЕ

1584 Сколько процентов соли содержит раствор, приготовленный из 35 г соли и 165 г воды?
РЕШЕНИЕ

1585 В 4 А классе 40 учеников. С задачей справились 32 ученика. В 4 Б классе 35 учеников, а с задачей справились 28 учеников. Какой класс лучше справился с задачей?
РЕШЕНИЕ

1586 Найдите 0,3 числа: а) 150; б) 600; в) 100; г) 5
РЕШЕНИЕ

1587 Вычислите устно
РЕШЕНИЕ

1588 Представьте в виде десятичной дроби числа
РЕШЕНИЕ

1589 Восстановите цепочки вычислений и попробуйте объяснить, почему они приводят к одному ответу
РЕШЕНИЕ

1590 Собственная скорость катера 18 км/ч. Отметьте ее на координатном луче. Вычислите и отметьте на этом луче скорости катера против течения и по течению, если скорость течения 1,5 км/ч. Используя чертеж, подумайте: а) как найти собственную скорость катера, если известны его скорости по течению и против течения; б) как найти скорость катера против течения, если известны скорость течения и скорость катера по течению; в) на сколько скорость катера по течению больше его скорости против течения.
РЕШЕНИЕ

1591 Попробуйте представить правило нахождения среднего арифметического нескольких чисел и средней скорости в виде последовательности команд по схемам:
РЕШЕНИЕ

1592 Найдите значение выражения. Проверьте ответ с помощью микрокалькулятора.
РЕШЕНИЕ

1593 Автобус шел 3 ч по шоссе, 1,5 ч по грунтовой дороге и 0,5 ч по проселочной дороге. Известно, что скорость автобуса по грунтовой дороге была в 2 раза больше скорости по проселочной дороге, а скорость по шоссе в 3,5 раза больше скорости по проселочной дороге. Найдите скорость движения автобуса по проселочной дороге, если средняя скорость автобуса на всем пути 33,6 км/ч.
РЕШЕНИЕ

1594 Марина сварила варенье, истратив 5/8 имевшегося у нее сахара. Сколько сахара осталось у Марины, если на варенье она израсходовала 0,8 кг сахара?
РЕШЕНИЕ

1595 В куске было 112,2 м материи. В первый раз отрезали 3/17 кyска а во второй раз 7/17 куска. Сколько метров материи было отрезано за оба раза?
РЕШЕНИЕ

1596 Выполните действия
РЕШЕНИЕ

1597 Решите задачу: 1) Первое число в 2,4 раза больше третьего, а второе число на 0,6 больше третьего числа. Найдите эти три числа, если их среднее арифметическое равно 2,4. 2) Второе число на 0,8 больше первого, а третье число в 3,2 раза больше первого. Найдите эти три числа, если их среднее арифметическое равно 4,6.
РЕШЕНИЕ

1598 Запишите в виде процентов десятичные дроби 6,51; 2,3; 0,095
РЕШЕНИЕ

1599 Запишите в виде десятичной дроби 42%; 8%; 7,25%; 568%
РЕШЕНИЕ

1600 Слесарь и его ученик изготовили 1200 деталей. Ученик сделал 30% всех деталей. Сколько деталей сделал ученик?
РЕШЕНИЕ

1601 На водопой пригнали 220 лошадей и жеребят. Жеребята составляли 15% всего табуна. Сколько жеребят было в табуне?
РЕШЕНИЕ

1602 Геологи проделали путь длиной 2450 км. 10% пути они пролетели на самолете, 60% пути проплыли в лодках, а остальную часть прошли пешком. Сколько километров геологи прошли пешком?
РЕШЕНИЕ

1603 Из молока получается 10% творога. Сколько творога получится из 32,8 кг молока? Из 58,7 кг молока?
РЕШЕНИЕ

1604 Площадь одной комнаты 12 м2, и она составляет 25% площади всей квартиры. Найдите площадь всей квартиры.
РЕШЕНИЕ

1605 Автотурист проехал в первый день 120 км, что составляет 15% всего намеченного пути. Какой длины намеченный путь?
РЕШЕНИЕ

1606 Засеяли 24% поля. Осталось засеять 45,6 га этого поля. Найдите площадь всего поля.
РЕШЕНИЕ

1607 Из пшеницы получается 80% муки. Сколько смололи пшеницы, если получили 2,4 т муки? Сколько муки получится из 2,5 т пшеницы?
РЕШЕНИЕ

1608 Масса сушеных яблок составляет 16% массы свежих яблок. Сколько надо взять свежих яблок, чтобы получить 4 т сушеных? Сколько сушеных яблок получится из 4,5 т свежих яблок?
РЕШЕНИЕ

1609 Из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелые арбузы?
РЕШЕНИЕ

1610 В классе 17 мальчиков, а девочек на 6 больше. Сколько процентов класса составляют девочки и сколько процентов класса составляют мальчики?
РЕШЕНИЕ

1611 В санатории отдыхали мужчины и женщины. Мужчины составляли 40% всех отдыхающих. Какой процент всех отдыхающих составляли женщины?
РЕШЕНИЕ

1612 Выполните действия
РЕШЕНИЕ

famiredo.ru

Задачи на проценты | Математика

Задачи на проценты

Автор: Купцова Ирина Николаевна

Организация: ГОУ «Перевальская гимназия №1»

Населенный пункт: г. Перевальск

Урок сопровождается презентацией “ Задачи на проценты”, разработанной автором ( приложение 1)

Тема. Задачи на проценты ( слайд 1)

Цель: рассмотреть решение задач на проценты составлением пропорции

( слайд 3)

Задачи урока:

Образовательная: повторить понятие процента, сформировать умение решать задачи на проценты составлением пропорции.

Развивающая: создать условия для развития навыков самостоятельной работы, самоконтроля и самооценки, развития интеллектуальных качеств: внимания, воображения, памяти, умения анализировать, обобщать, выделять главное.

Воспитательная: воспитывать самостоятельность мышления, уважение к мнению других, умение работать в паре, формировать культуру устной и письменной речи, умение слушать и слышать.

УУД ( универсальные учебные действия)

Регулятивные УУД:

— самостоятельно формулировать цель урока после предварительного обсуждения;

— составлять план решения задачи совместно с учителем;

— определять степень успешности выполнения своей работы, исходя из имеющихся критериев оценки знаний.

Познавательные УУД:

— ориентироваться в своей системе знаний (предполагать, какая информация нужна для решения учебной задачи).

Коммуникативные УУД:

-оформлять свою мысль в устной и письменной речи;

-умение работать в коллективе.

Личностные УУД:

развивать готовность и способность учащихся к саморазвитию

Тип урока: урок усвоения новых знаний

Формы обучения: индивидуальная, фронтальная, коллективная, групповая

Дидактические средства

1.карточки для самооценки;

2.мультимедийная установка;

3.презентация.

Методы обучения

1.словесные;

2.наглядные;

3.практические;

4.проблемно-поисковые;

5.продуктивные;

6.объяснительно-иллюстративные.

Форма:

урок – восхождение

Метод:

создание ситуации успеха

Технологии:

коллективно – индивидуальной мыследеятельности

Приемы:

мозговой штурм, лови ошибку, самоконтроль, беседа – диалог, наблюдательное чтение, кто быстрее, неоконченное предложение, работа в парах, один ум – хорошо, а много лучше

Структура урока

1.Организационный момент (психологический настрой на работу на уроке)

2.Актуализация опорных знаний – устная работа, с помощью которой ведется повторение основных фактов, ведущих идей и основных теорий на основе систематизации знаний

3.Мотивационная беседа с последующей постановкой цели учащимися

4.Изложение нового материала

5.Релаксация

6.Первичное осмысление и закрепление нового материала

7.Подведение итогов урока, оценивание знаний учащихся

8. Домашнее задание

9.Рефлексия

Ход урока

1.Организационный момент

Вступительное слово учителя (психологический настрой на работу на уроке)

( слайд 2)

Учитель. Здравствуйте, ребята. Садитесь.

Создадим хорошее, дружелюбное настроение

— Я улыбнусь вам, а вы улыбнитесь друг другу и подумайте, как хорошо, что мы сегодня все вместе.

— Мы спокойны, добры, приветливы, ласковы. Мы все здоровы.

— Я желаю вам хорошего настроения и бережного отношения друг к другу. Я уверена, что у нас всё получится.

Девиз урока: «Дорогу осилит идущий, а математику – мыслящий”.

Пифагор( слайд 4)

2.Актуализация опорных знаний

(прием «Мозговой штурм»)

Учитель. Как называлась тема, которую мы изучали на прошлом уроке?

Ученики отвечают. (Понятие о проценте)

Учитель. Повторим материал, который изучили.

Прием «Лови ошибку»( слайд 5)

а)5 % = 5100,

б)120 % = 12100( 1210 ),

в)3100 = 3 %;

г)15 = 20%;

д)12 = 25% ( 50%)

Учитель. Давайте вспомним основные задачи на проценты.

Учитель выслушивает ответы учеников, направляет, консультирует.

а) как найти процент от числа?( слайд 6)

Найдите: 24% от 300

Ученики.

1.Запишем 24% в виде дроби.

2.Умножим полученное число на 300

Решение:

24% = 0,24

300 ×0,24 =72

Ответ. 72

Найти ( слайд 7)

а)1% от 300 (3)

б)5 % от 40 (2)

в)7% от 20 (14)

Учитель.

б) как найти по проценту целую величину?( слайд 8)

Ученики.

1.Запишем проценты в виде дроби

Разделим данное число на полученное число

Найдите: число, 9 % которого равны 18

Решение: 9% = 0,09

18 : 0,09 =200

Ответ. 200

Учитель. Как найти процентное соотношение одного числа от другого?

( слайд 9)

Сколько процентов составляет 120 от 480?

Ученики.

1.Разделим120 на 480

2.Полученный результат умножим на 100

Решение: 120 : 480 ×100% = 25%.

Ответ. 25%

Сколько процентов составляет:( слайд 10)

а) число 17 от числа 100 (17%)

б) число 10 от числа 5 (200%)

Учитель.Очень хорошо, перейдем к проверке домашнего задания

а) проверка домашнего задания

Учитель отвечает на вопросы, которые возможно возникли во время выполнения домашнего задания.

Проверка письменного домашнего задания (№ 107, 118а, 120 б)

Решения предоставлены на доске

№ 107 ( прием «Самоконтроль») ( слайд 11)

Решение

1.400: 100 = 4 (г) сплава приходится на 1 %

2.4×62 = 248 (г) олова в сплаве

3.4 ×38=152 (г) или 400 – 248 = 152 (г) свинца в сплаве

Ответ. 248 г, 152 г

№ 118а( слайд 12)

1.50 : 100 = 0,5( семян приходится на 1 %)

2.47 :0,5=94 (%)

Ответ. 94 %

№ 120 б

1.12 + 18 = 30 дней составляет месяц

2.30 : 100 = 0,3 ( приходится на 1 %)

3.18:0,3= 60 % составили пасмурные дни

Ответ. 60 %

Учитель подводит итог работы учащихся: обобщает, одобряет

3.Мотивация учебной деятельности учащихся, постановка темы, цели урока

Прием «Беседа – диалог»

Учитель.

Ребята! Как вы думаете, что самое ценное на Земле? ( выслушиваются ответы учащихся)

Учитель.

Вот какой ответ дал известный ученый Ал – Бируни: «Знание – самое ценное превосходное из владений. Все стремятся к нему, само же оно не приходит»( слайд 13)

Учитель. Вдумайтесь в эти слова.

Учитель. На прошлом уроке мы познакомились с понятием о проценте. Как вы думаете, чему мы должны посвятить сегодняшний урок?

Ученики. Решать задачи на проценты

Учитель. Правильно, ребята. Тема нашего урока «Задачи на проценты».

Учитель. А как вы думаете, пригодится ли эта тема вам? Встречаются ли проценты в жизни?

Предполагаемые ответы учащихся.

В нашей жизни человек очень часто сталкивается с понятием процента: и в магазине, и в банке, и в аптеке, и в газете, и в журналах и по телефону

( слайд 14)

Учитель.

Итак, мы осознаем, как часто встречается понятие процента, как необходимо знать и понимать что это. И цель нашего сегодняшнего урока: рассмотреть способы решения задач на проценты.

Учитель.

Сядьте ровно,

Всё ль в порядке?

Открывайте – ка тетрадки

И, какой сегодня день,

Все запишем…

Нам не лень!( слайд 15,16)

Дети записывают дату.

Какие орфограммы присутствуют в словах, записанных на доске. Какими правилами будете пользоваться, чтобы написать правильно

« Одиннадцатое сентября. Классная работа»?

Выслушиваются ответы учащихся.

Учитель одобряет, дополняет

4. Изложение нового материала

Прием « Наблюдательное чтение» — работа с учебником

Учитель. Откройте учебник на странице 19, повторите решение задачи 1.

Ученики работают с учебником.

Учитель. Какая зависимость рассмотрена в задаче 1?

Ученики отвечают ( прямая пропорциональность)

Учитель. Какова схема решения задач на проценты?

Предполагаемые ответы учащихся.

Читаем задачу, проводим анализ содержания, пишем краткую запись в тетрадях, а затем- анализ решения по вопросам:

-Что нужно узнать в задаче?

-Как можно ответить на вопрос задачи?

Учитель обобщает, одобряет ответы учащихся

Учитель. Задачи на проценты можно решать как задачи на прямую пропорциональность. Рассматриваются основные задачи на проценты, решаются с участием учащихся, ведутся записи в тетрадях.

Прием «Один ум – хорошо, а много – лучше»

Пример 1. Найдем 9 % от числа 45 ( слайд 17)

Решение. Пусть х – искомое число, тогда

45 — 100%

х — 9 %

45х = 1009 , х = 45* 9100 , х = 4,05

Ответ. 4,05

Пример 2.Найдем число, 17 % которого равны 51.( слайд 18)

Решение. Пусть х – искомое число, тогда

х – 100%

51 – 17%

х51 = 10017, х = 51*10017, х = 300

Ответ. 300

Пример 3. Сколько процентов составляет число 6 от числа 30?( слайд 19)

Решение.

Пусть 6 от 30 составляет х процентов, тогда

30 – 100 %

6 – х %

306 = 100х, х =6*10030, х = 20

Ответ. 20 %

Задача.( слайд 20)

Из 140 кг свежих вишен получают 21 кг сушеных. Сколько выйдет сушеных вишен из 160 кг свежих?

Решение

140 кг свежих вишен – 21 кг сушки

160 кг свежих вишен — х кг сушки

140160 = 21х , х =160*21140 = 24 ( кг) сушеных вишен

Ответ. 24 кг

Учитель подводит итог работы: обобщает, одобряет.

5.Релаксация ( звучит музыка)(Приложение 2) ( слайды 21 — 25)

Учитель.

Сядьте удобнее, послушайте музыку, постарайтесь расслабиться.

Учитель. Продолжим работу. Переходим к закреплению изученного материала

6.Первичное осмысление и закрепление нового материала

Учитель.

«Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их»

Д.Пойа( сайд 26)

Решение упражнений

Учитель.

Читаем задачу, проводим анализ содержания, пишем краткую запись в тетрадях, а затем — анализ решения по вопросам:

-Что нужно узнать в задаче?

-Как можно ответить на вопрос задачи?

Задача 122 а( коллективное решение – фронтальная работа) ( слайд 27)

1 способ

Решение

2500 кг лука – 100 %

х кг лука – 30 %

250х = 10030 , х = 250*30100 = 750 ( кг) продали

2500 – 750 = 1750 ( кг) осталось продать

2 способ( слайд 28)

Решение

100 % — 30 % = 70% ( осталось продать)

2500 кг лука – 100 %

Х кг лука — 70 %

2500х = 10070, х =2500*70100 = 1750 ( кг) – осталось продать

— Мы ответили на вопрос задачи? (да)

Ответ. 1750 кг

Задача 123– самостоятельно ( прием «Кто быстрее!») ( слайд 29)

Данную задачу ребята решают самостоятельно, учитель контролирует процесс решения, работает со слабыми учащимися, учащийся, который выполнил работу раньше всех, комментирует решение

Решение

1способ

100 кг свежих груш – 100 %

х кгсушеных груш — 20 %

100х = 10020, х =100*20100 = 20 ( кг) сушеных груш из 100 кг свежих

2 способ( слайд 30)

20% = 15, значит 100* 15 = 20 ( кг)

— Мы ответили на вопрос задачи? (да)

Ответ. 20 кг

Учитель предлагает работу в парах. Объясняет задание

Задача 124 – самостоятельная работа в парах по рядам, один из учащихся от ряда озвучивает решение( слайд 31)

Учитель выслушивает предложения учеников, направляет,одобряет

100 % — 70 % = 30% получается изюма

100 кг винограда – 100 %

х кг изюма — 30%

100х = 10030, х =100*30100 = 30 (кг) изюма из 100 кг

250 кг винограда – 100 %

х кг изюма — 30%

250х = 10030, х = 250*30100 = 75 ( кг) изюма из 250 кг

80 кг винограда — 100 %

х кг изюма — 30%

80х = 10030, х = 80*30100 = 24 ( кг) изюма из 80 кг

— Мы ответили на вопрос задачи? (да)

Ответ. 30 кг, 75 кг, 24 кг

Задача 125( 3 человека выполняют у доски, комментируют решение)

( слайд 32)

Учитель и учащиеся помогают

300 г припоя – 100 %

х г олова — 40%

300х = 10040 , х = 300*40100 = 120 ( г) олова в припое

300 г припоя — 100 %

х г сурьмы — 2%

300х = 1002, х = 300*2100 = 6 ( г) сурьмы в припое

300 – 120 – 6 = 174 (г) свинца в припое

или

100% — 40% — 2 % = 58% свинца в припое

300 г припоя — 100 %

х г свинца — 58%

300х = 10058 , х = 300*58100 = 174 (г) свинца в припое

— Мы ответили на вопрос задачи? (да)

Ответ. 120 г, 6 г, 174 г

7.Подведение итогов урока, оценивание знаний учащихся

Учитель.

Наш урок незаметно подошёл к концу. Вы трудились усердно и дружно. Молодцы!

Прием «Неоконченное предложение»( слайд 33)

Учитель.

Итак, ребята, сегодня мы с вами …

Предполагаемые ответы учащихся:

— рассмотрели способы решения задач на проценты

— научились решать задачи на проценты.

Учитель обобщает, одобряет ответы учащихся

Учащиеся анализируют свою работу, заполняя листы самооценки

( приложение 3), сдают эти листы.

Учитель выставляет оценки за работу на уроке самым активным учащимся, комментирует отметки.

8.Домашнее заданиеп.1.7 ( с.28) прочитать, решить письменно № 122б, № 129 устно и придумать и оформить задачу на проценты из жизненных ситуаций ( слайд 34)

Информирование учащихся о домашнем задании

Учащиеся записывают домашнее задание.

9.Рефлексия

Учитель читает притчу( слайд 35)

Притча.

Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал вопрос каждому. У первого спросил: «А что ты делал целый день?». И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнил свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»

Учитель.- Ребята! Давайте мы попробуем с вами оценить каждый свою работу за урок.

— Кто работал как первый человек?

— Кто работал добросовестно?

— Кто принимал участие в строительстве храма своих знаний?

Пусть каждый сам оценит свою работу на уроке.(Сигнальные карточки)

Кто работал как первый человек? Поднимает синюю карточку.

Кто работал как второй человек? Поднимает зелёную карточку.

Кто работал как третий человек? Поднимает красную карточку.

Я желаю вам всегда работать с радостью и удовольствием.

Надеюсь, что урок прошел с пользой для вас.

Поаплодируйте себе! Спасибо за урок!( слайд 36)

Список использованных источников

1.Примерные программы по математике (базовый уровень, углубленный, профильный уровень), утвержденные приказом МОН ЛНР от 27.12.2016 г. №483.

2.Математика. Сборник рабочих программ 5-6 классы: пособие для учителей общеобразовательных организаций / [Сост. Т.А. Бурмистрова]. – 3-е изд. – М.: Просвещение, 2014. (Базовый уровень).

3.Математика 6: учебник для общеобразовательных организаций / С.М. Никольский и др. – 6 – е изд. М.: Просвещение, 2016. – 256 с.

4.Дидактические материалы для 5 – 6 классов / М.К.Потапов и др. — 13- е изд.- М.:2017. – 128 с.

Интернет – источники:

http://mp3parade.ru/music-files/МУЗЫКА%20ДЛЯ%20РЕЛАКСАЦИИ

Приложения:

1. kuptsova-in_ed7346dc-911c-.. 38,5 МБ
2. razrabotka-uroka.docx.. 37,8 КБ

Опубликовано: 19.10.2017

www.1urok.ru

Математика 5-6 классы. 17. Проценты. Решение задач на проценты

• Главная
• Видеотека
  • Естествознание
    • Физика
    • Математика
    • Химия
    • Биология
    • Экология
  • Обществознание
    • Обществознание — как наука
    • Иностранные языки
    • История
    • Психология и педагогика
    • Русский язык и литература
    • Культурология
    • Экономика
    • Менеджмент
    • Логистика
    • Статистика
    • Философия
    • Бухгалтерский учет
  • Технические науки
    • Черчение
    • Материаловедение
    • Сварка
    • Электротехника
    • АСУТП и КИПИА
    • Технологии
    • Теоретическая механика и сопромат
    • САПР
    • Метрология, стандартизация и сертификация
    • Геодезия и маркшейдерия
  • Программирование и сеть
    • Информатика
    • Языки программирования
    • Алгоритмы и структуры данных
    • СУБД
    • Web разработки и технологии
    • Архитектура ЭВМ и основы ОС
    • Системное администрирование
    • Создание программ и приложений
    • Создание сайтов
    • Тестирование ПО
    • Теория информации и кодирования
    • Функциональное и логическое программирование
  • Программы
    • Редакторы и компиляторы
    • Офисные программы
    • Работа с аудио видео
    • Работа с компьютерной графикой и анимацией
    • Автоматизация бизнеса
  • Прочие
    • Музыка
    • Природное земледелие
    • Рисование и живопись
• Библиотека
  • Естествознание
    • Физика
    • Математика
    • Химия
    • Биология
    • Экология
    • Астрономия
  • Обществознание
    • Иностранные языки
  • Технические науки
    • Теоретическая механика и сопромат
    • Сварка
    • Железная дорога
  • Паспорта и техническая документация
    • Металлообра-батывающие станки
    • Деревообра-батывающие станки
    • Сварочное оборудование
• Правила
• Контакты

• Вы здесь:  
• Главная
• Видеотека

forkettle.ru