Урок 16. окружность. задачи на построение — Геометрия — 7 класс
Геометрия
7 класс
Урок № 16
Окружность. Задачи на построение
Перечень рассматриваемых вопросов:
- Геометрическое место точек, примеры ГМТ.
- Изображение на рисунке окружности и ее элементов.
- Решение задач на построение.
- Выполнение построений прямого угла, отрезка, угла равного данному, биссектрисы угла, перпендикулярных прямых, середины отрезка с помощью циркуля и линейки.
Тезаурус:
Радиус окружности – отрезок соединяющий центр окружности с какой-либо точкой окружности.
Окружность – это геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Хорда – отрезок, соединяющий две точки окружности.
Диаметр – хорда, проходящая через центр окружности.
Основная литература:
- Атанасян Л.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М.А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М.А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Ранее мы узнали некоторые геометрические фигуры, например, угол, отрезок, треугольник, научились их строить и измерять.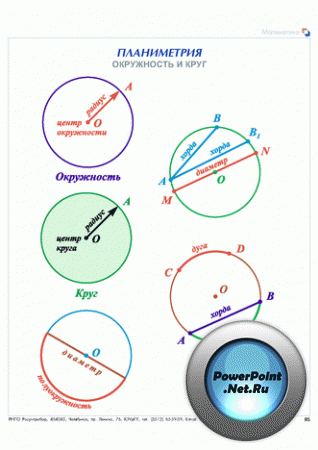
Сегодня мы введём определение ещё одной фигуры – окружности, рассмотрим её элементы и выполним построения геометрических фигур с помощью циркуля и линейки.
Для начала дадим определение геометрической фигуры, называемой окружностью.
Окружность – это геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Но можно использовать и другое определение окружности.
Окружность ‑ это геометрическое место точек, удалённых на одно и то же расстояние от точки, называемой центром окружности. Это расстояние называют радиусом окружности. В нашем случае точки О.
При этом стоит пояснить, что геометрическое место точек – это фигура речи, употребляемая в математике для определения геометрической фигуры, как множества всех точек, обладающих некоторым свойством.
Вспомним элементы окружности.
Радиус окружности – отрезок соединяющий центр окружности с какой-либо точкой окружности.
По определению окружности все её радиусы имеют одну и ту же длину.
OM = OA
Отрезок, соединяющий две точки окружности, называется хордой.
AC, BD – хорды
Хорда, проходящая через центр окружности, называется диаметром.
AB – диаметр,
OB – радиус,
AB = 2OB,
O – середина диаметра.
Любые две точки окружности делят её на две части. Каждая из этих частей называется дугой окружности.
AMB, ALB – дуги окружности.
Построим окружность радиусом 3 см. Для этого поставим точку О. Возьмём циркуль и выставим с помощью линейки расстояние между ножками циркуля, равное 3 см. Поставим иголочку циркуля в точку О и построим окружность, вращая ножку циркуля с грифелем вокруг этой точки. Грифель описывает замкнутую кривую линию, которую называют окружностью.
Часть плоскости, которая лежит внутри окружности, вместе с самой окружностью, называют кругом, т. е. окружность ‑ граница круга.
Итак, мы можем с помощью циркуля строить окружность, но с его помощью можно построить и угол равный данному.
Для построения воспользуемся ещё и линейкой.
Дано: A, OM – луч.
Построить: EOМ = A.
Построение.
1. Окр. (A; r), r – произвольный радиус.
2. Окр. (A; r) ∩ AB = B.
3. Окр. (A; r) ∩ AС = С.
4. Окр. (O; r) ∩ OM = D.
5. Окр. (D; BС) ∩ Окр. (O; r) = E
6. OЕ, ЕОD = BAC (из равенства ∆ОЕD и ∆ABC). EOM – искомый.
Теперь выполним построение биссектрисы угла.
Дано: CAB.
Построить: AE – биссектриса
Построение.
- Окр. (A; r), r – произвольный радиус.
- Окр. (A; r) ∩ AB = B.
- Окр. (A; r) ∩ AC = C.
- Окр. (C; CB) ∩ Окр. (B; CB) = E.
- AE – искомая биссектриса BAC, т. к. ABE =CBE (из равенства ∆ACE и ∆ABE).
Рассмотрим ещё одно построение с помощью циркуля и линейки. Построим середину отрезка АВ.
Для этого построим две окружности с центрами на концах отрезка , т. е. в точках А и В.
Окружности пересекутся в точках Р и Q. Проведём прямую через точки Р и Q. Прямая РQ пересечёт прямую АВ в точке О, которая и будет являться искомой серединой отрезка АВ. Докажем это. Для этого рассмотрим ∆APQ и ∆BPQ. Они равны по трём сторонам, следовательно, ∠1 = ∠2, поэтому РО– биссектриса равнобедренного ∆АВР, а соответственно РО ещё и медиана. Следовательно, точка О – середина отрезка АВ.
Разбор заданий тренировочного модуля.
№ 1. АВ и СК – диаметры окружности, с центром в точке О. По какому признаку равенства треугольников равны треугольники АОС и ОКВ?
Решение:
Так как О – центр окружности, то точка О делит диаметры пополам, следовательно отрезки АО, ОВ, ОС, ОК равны. ∠СОА = ∠КОВ (как вертикальные). Поэтому треугольники АОС и ОКВ равны по первому признаку равенства треугольников (по двум сторонам и углу между ними).
Ответ: 1 признак равенства треугольников.
№ 2. На рисунке O – центр окружности, АВ – диаметр окружности.
Отрезки АD и ВС, перпендикулярны к отрезку АВ. АВ = 8 см, ОС = 5 см, СВ = 3 см. Чему равен периметр ∆AOD?
Решение:
Периметр треугольника AOD равен сумме сторон АО, AD, DO. Найдём эти стороны.
По условию O – центр окружности, то она делит диаметр пополам, следовательно отрезок АО равен отрезку ОВ, т. е. АО = АВ:2 = 8 см :2 = 4 см.
По условию отрезки АD и ВС, перпендикулярны к отрезку АВ, следовательно ∠СВО = ∠ОАD = 90°, ∠АОD = ∠СОВ (как вертикальные). Поэтому ∆АОD = ∆СОВ (по 2 признаку равенства треугольников). Следовательно, AD = СВ = 3 см, DO = ОС = 5 см.
Р∆AOD = АО + AD + DO = 4 см + 3 см + 5 см = 12 см.
Ответ: Р∆AOD = 12 см.
Окружность. Задачи на построение — урок. Геометрия, 7 класс.
Окружность — геометрическая фигура, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от данной точки.
Эту точку называют центром окружности, а заданное расстояние — радиусом окружности.
Радиус — это отрезок, соединяющий центр окружности с любой точкой окружности. Из определения следует, что можно провести бесконечное количество радиусов, и они все имеют одинаковую длину.
Отрезок, который соединяет две точки на окружности, называют хордой.
Если хорда проходит через центр окружности, то её называют диаметром окружности.
Диаметр — самая длинная хорда.
В окружности также можно провести бесконечное количество диаметров.
Если соединить две точки окружности не отрезком, а кривой, проходящей по самой окружности, то часть окружности между двумя точками называют дугой.
Если на окружности отметить две точки, то получаются две дуги. Поэтому для названия дуги используют три латинские буквы, которые могут быть как маленькие, так и большие.
На рисунке выше можем назвать: дуга \(BDH\), дуга \(ACG\) и другие.
На рисунке ниже нарисованы: дуга \(AxB\) и дуга \(AyB\).
Часть плоскости, ограниченная окружностью, называется кругом.
Задачи на построение
В задачах, где необходимо выполнить конструкции, используются циркуль и линейка.
Очень важно запомнить, что в этих задачах линейка используется не как инструмент для измерения, а исключительно только для того, чтобы провести прямую, луч или отрезок через две данные точки, то есть, чтобы провести прямую линию. Циркуль используется для построения окружности или дуги окружности.
Рассмотрим пять основных построений, в которых используем упомянутые действия — построение прямой линии и окружности:
1. на данном луче от его начала отложить отрезок, равный данному.
2. Построение угла, равного данному.
3. Построение биссектрисы угла.
4. Построение перпендикулярных прямых.
5. Построение середины отрезка.
1. На данном луче от его начала отложить отрезок, равный данному.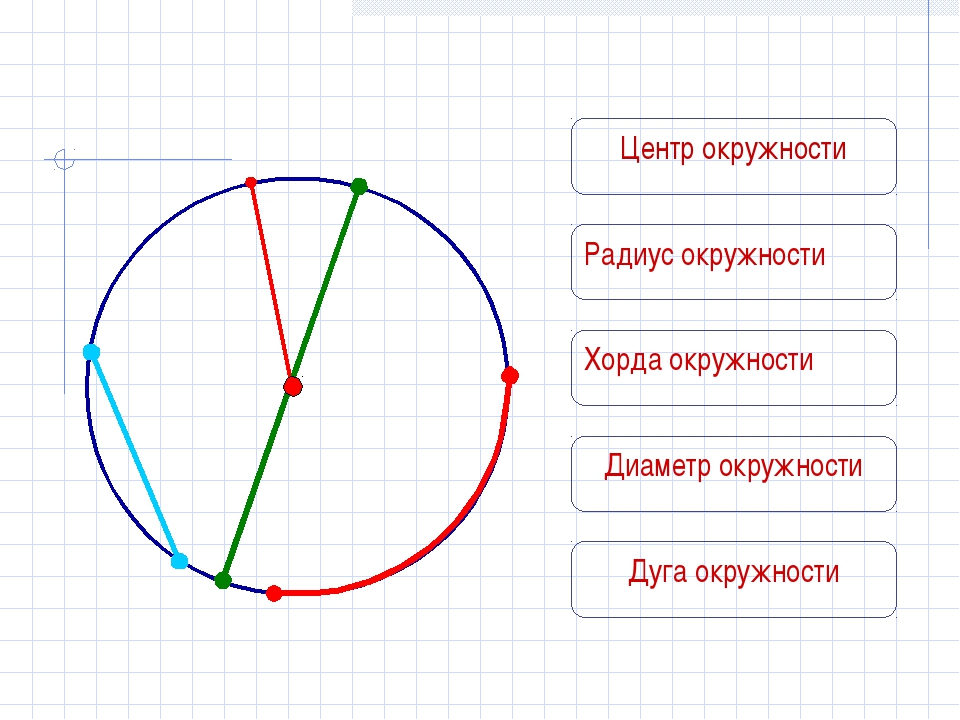
См. видео.
Ясно, что таким образом мы получили отрезок, равный данному. Соответственно определению окружности, она состоит из точек, расположенных на заданном расстоянии (радиусе) от некоей точки (центра окружности).
Если центром служит начальная точка луча \(C\), радиусом — данный отрезок \(AB\), то точка пересечения окружности и луча \(D\) и есть искомая конечная точка отрезка \(CD\), равного данному отрезку \(AB\).
2. Построение угла, равного данному.
См. видео.
Докажем, что построенный угол \(ECD\) и есть тот искомый угол, равный данному углу \(AOB\).
Если мы построили окружность с центром \(C\) — начальной точкой луча и таким же радиусом, как у окружности с центром \(O\), то \(CD\) \(=\) \(OB\).
Если далее мы построили окружность с центром \(D\) и радиусом, равным отрезку \(BA\), и получили точку пересечения обеих окружностей \(E\), то \(BA\) \(=\) \(DE\).
Провели луч \(CE\). Очевидно, \(OA\) \(=\) \(CE\).
Значит, треугольники \(AOB\) и \(ECD\) равны по третьему признаку равенства треугольников, у них равны и углы, в том числе угол \(ECD\) равен углу \(AOB\).
3. Построение биссектрисы угла.
См. видео.
Чтобы доказать, что \(OC\) действительно делит угол \(AOB\) пополам, достаточно рассмотреть треугольники \(AOC\) и \(BOC\).
\(OA = OB\) как радиусы одной окружности, а \(AC = BC\), так как мы при построении выбрали одинаковые радиусы для обеих окружностей.
Сторона \(OC\) — общая.
Эти треугольники равны по третьему признаку.
Следовательно, их соответствующие углы равны.
Значит, \(AOC\) и \(BOC\) — две равные части одного угла, это означает, что луч \(OC\) делит угол пополам.
4. Построение перпендикулярных прямых.
См. видео.
Почему \(DE\) является перпендикулярной к \(BC\)?
\(AB = AC\) — так эти точки были отложены при построении.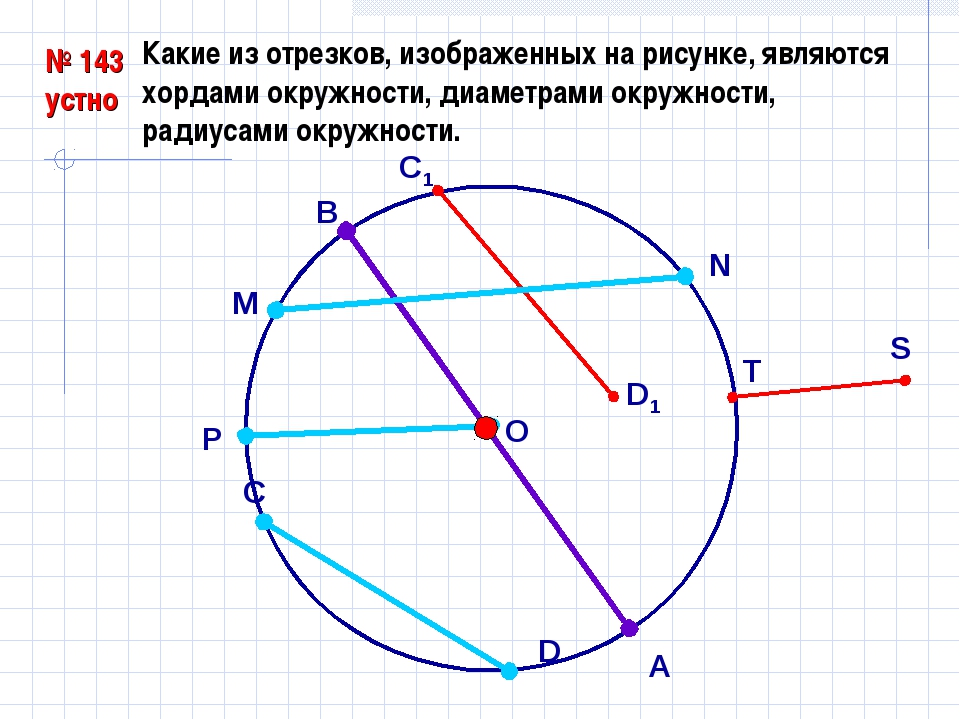
\(BD = CD\), так как мы обе окружности построили с одинаковыми радиусами.
Значит, \(DA\) или \(EA\) — медианы, проведённые к основанию равнобедренных треугольников \(BDC\) или \(BEC\).
Медиана в равнобедренном треугольнике является также высотой, то есть перпендикулярна к основанию.
5. Построение середины отрезка.
См. видео.
Эта конструкция такая же, как в случае построения перпендикулярных прямых, и уже доказано, что \(DC\) или \(EC\) делит \(AB\) пополам, то есть \(C\) — серединная точка отрезка \(AB\).
Тест по геометрии «Окружность» 7 класс
Вариант 1
Продолжите предложения:
Треугольник называется вписанным, если окружность…
а) касается его сторон; б) проходит через его вершины;
в) пересекает его стороны; г) проходит через одну из вершин.
Радиусом окружности называется отрезок, соединяющий …
а) две точки окружности; б) любые две точки;
в) центр и любую точку окружности; г) нет правильного ответа.
Касательная и радиус окружности в точке касания образуют угол равный…
а) 90; б) 180; в) 360; г) нет правильного ответа.
Касание окружностей называется внутренним, если центры этих окружностей лежат… общей касательной.
а) по одну сторону от; б) на самой;
в) по разные стороны от; г) нет правильного ответа.
Через точку А окружности с центром С проведена касательная АВ. Найдите АВС, если АСВ=63.
а) 27; б) 63; в) 90; г) 180; д) нет правильного ответа.
Точка М – середина хорды ВС, О – центр окружности. Найдите углы ВОМ, если BОС=146.
а) 17, 17 и 146; б) 17, 73 и 90;
в) 34, 56 и 90; г) нет правильного ответа.
Точка М – середина хорды ВС, О – центр окружности. Найдите углы ВОМ, если BСО=70.
а) 35, 55 и 90; б) 55, 55 и 70;
в) 20, 70 и 90; г) нет правильного ответа.
В окружности с центром О проведена хорда КМ. Найдите углы ОKМ, если ОМК=46.
а) 23, 67 и 90; б) 46, 46 и 88;
в) 44, 46 и 90; г) нет правильного ответа.
В окружности с центром О проведена хорда КМ. Найдите углы ОKМ, если МОК=84.
а) 48, 48 и 84; б) 42, 48 и 90;
в) 12, 84 и 84; г) нет правильного ответа.
Точка О – центр окружности, АВ и КМ – равные хорды. Тогда АВО=КМО по… признаку.
а) первому; б) второму; в) третьему; г) нет правильного ответа.
Вариант 2
Продолжите предложения:
Треугольник называется описанным, если окружность…
а) касается его сторон; б) проходит через его вершины;
в) пересекает его стороны; г) проходит через одну из вершин.
Хордой называется отрезок, соединяющий…
а) две точки окружности; б) любые две точки;
в) центр и любую точку окружности; г) нет правильного ответа.
Касательная и диаметр окружности в точке касания образуют угол равный…
а) 90; б) 180; в) 360; г) нет правильного ответа.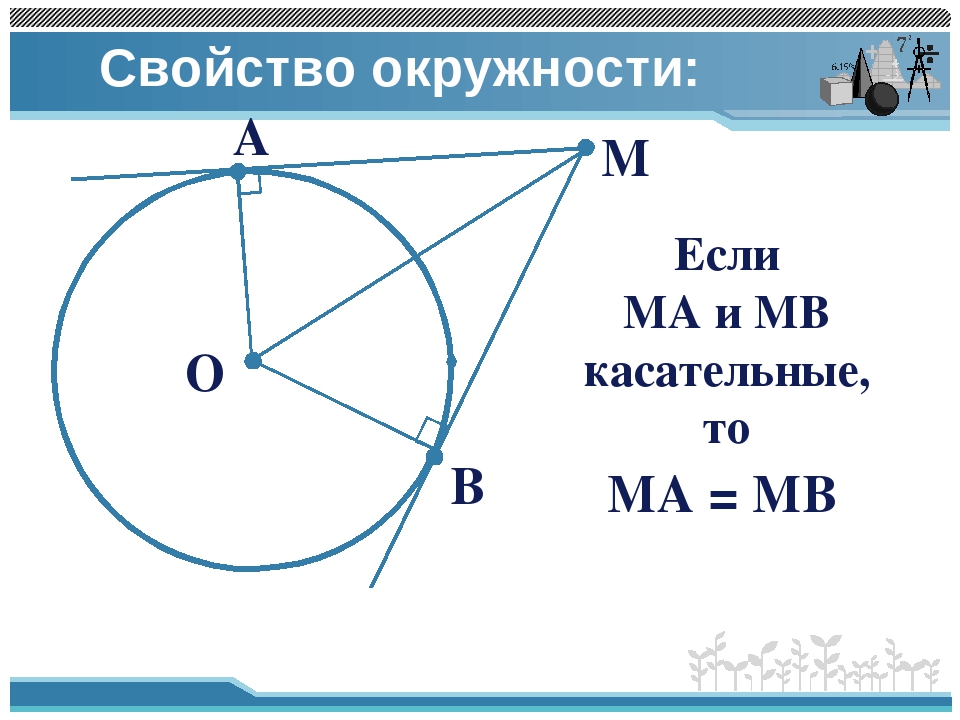
Касание окружностей называется внешним, если центры этих окружностей лежат… общей касательной.
а) по одну сторону от; б) на самой;
в) по разные стороны от; г) нет правильного ответа.
Через точку А окружности с центром С проведена касательная АВ. Найдите АСВ, если АВС=59.
а) 31; б) 59; в) 90; г) 180; д) нет правильного ответа.
Точка М – середина хорды ВС, О – центр окружности. Найдите углы СОМ, если BОС=136.
а) 44, 44 и 92; б) 22, 22 и 136;
в) 22, 68 и 90; г) нет правильного ответа.
Точка М – середина хорды ВС, О – центр окружности. Найдите углы СОМ, если СBО=80.
а) 50, 50 и 80; б) 10, 80 и 90;
в) 40, 50 и 90; г) нет правильного ответа.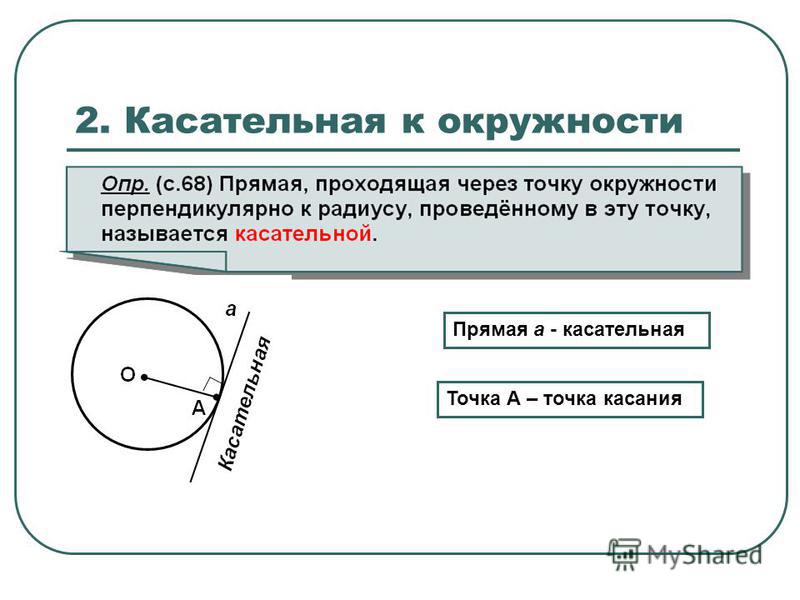
В окружности с центром О проведена хорда КМ. Найдите углы ОKМ, если ОКМ=56.
а) 34, 56 и 90; б) 28, 62 и 90;
в) 56, 56 и 68; г) нет правильного ответа.
В окружности с центром О проведена хорда КМ. Найдите углы ОKМ, если КОМ=68.
а) 34, 56 и 90; б) 56, 56 и 68;
в) 44, 68 и 68; г) нет правильного ответа.
Точка О – центр окружности, АВ и ВС – хорды. Если АОВ=ВОС, АВО=ВСО по… признаку.
а) первому; б) второму; в) третьему; г) нет правильного ответа.
Вариант 3
Продолжите предложения:
Окружность называется вписанной в треугольник, если она…
а) пересекает его стороны; б) проходит через его вершины;
в) касается его сторон; г) проходит через одну из вершин.
Касательной называется прямая, проходящая через точку окружности…
а) параллельно радиусу; б) перпендикулярно радиусу;
в) параллельно хорде; г) перпендикулярно хорде.
Касательная и диаметр окружности в точке касания образуют угол равный…
а) 360; б) 180; в) 90; г) нет правильного ответа.
Касание окружностей называется внутренним, если центры этих окружностей лежат… общей касательной.
а) по разные сторону от; б) на самой;
в) по одну стороны от; г) нет правильного ответа.
Через точку В окружности с центром С проведена касательная АВ. Найдите ВАС, если ВСА=42.
а) 42; б) 48; в) 90; г) 180; д) нет правильного ответа.
Точка М – середина хорды ВС, О – центр окружности. Найдите углы СОМ, если BОС=126.
а) 27, 63 и 90; б) 27, 27 и 126;
в) 54, 63 и 63; г) нет правильного ответа.
Точка М – середина хорды ВС, О – центр окружности. Найдите углы СОМ, если СBО=60.
а)60, 60 и 60; б) 30, 60 и 90;
в) 30, 30 и 120; г) нет правильного ответа.
В окружности с центром О проведена хорда КМ. Найдите углы ОKМ, если ОКМ=62.
а) 56, 62 и 62; б) 31, 59 и 90;
в) 59, 59 и 62; г) нет правильного ответа.
В окружности с центром О проведена хорда КМ. Найдите углы ОKМ, если КОМ=76.
а) 38, 52 и 90; б) 38, 38 и 104;
в) 52, 52 и 76; г) нет правильного ответа.
Точка О – центр окружности, АВ и ВС – равные хорды. Тогда АВО=ВСО по… признаку.
а) первому; б) второму; в) третьему; г) нет правильного ответа.
Вариант 4
Продолжите предложения:
Окружность называется описанной около треугольника, если она…
а) пересекает его стороны; б) проходит через его вершины;
в) касается его сторон; г) проходит через одну из вершин.
Диаметром окружности называется…
а) половина радиуса; б) отрезок, соединяющий точки окружности;
в) хорда, проходящая через центр; г) нет правильного ответа.
Касательная и радиус окружности в точке касания образуют угол равный…
а) 360; б) 180; в) 90; г) нет правильного ответа.
Касание окружностей называется внешним, если центры этих окружностей лежат… общей касательной.
а) по разные сторону от; б) на самой;
в) по одну стороны от; г) нет правильного ответа.
Через точку В окружности с центром С проведена касательная АВ. Найдите ВСА, если ВАС=36.
а) 36; б) 54; в) 90; г) 180; д) нет правильного ответа.
Точка М – середина хорды ВС, О – центр окружности. Найдите углы ВОМ, если BОС=116.
а) 32, 32 и 116; б) 58, 58 и 64;
в) 32, 58 и 90; г) нет правильного ответа.
Точка М – середина хорды ВС, О – центр окружности. Найдите углы ВОМ, если BСО=50.
а) 25, 75 и 90; б) 40, 50 и 90;
в) 50, 65 и 65; г) нет правильного ответа.
В окружности с центром О проведена хорда КМ. Найдите углы ОKМ, если ОМК=74.
а) 16, 74 и 90; б) 32, 74 и 74;
в) 37, 37 и 106; г) нет правильного ответа.
В окружности с центром О проведена хорда КМ. Найдите углы ОKМ, если МОК=58.
а) 32, 58 и 90; б) 58, 61 и 61;
в) 29, 61 и 90; г) нет правильного ответа.
Точка О – центр окружности, АВ и КМ – хорды. Если АОВ=КОМ, АВО=КМО по… признаку.
а) первому; б) второму; в) третьему; г) нет правильного ответа.
ОКРУЖНОСТЬ И КРУГ — ОКРУЖНОСТЬ И КРУГ. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ — Учебник Геометрия 7 класс Бевз Г.П. — Возрождение 2015 год
Круг — первая самая простая и самая совершенная фигура.
Прокл
РАЗДЕЛ 4 ОКРУЖНОСТЬ И КРУГ.
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯВ этом разделе вы расширите и углубите свои знания о круге и круг, приобретенные в предыдущих классах, узнаете о взаимное расположение на плоскости прямой и окружности, двух окружностей; о свойствах касательной к окружности, касательных окружностей; окружности вписанные и описанные вокруг треугольника А еще поймете, что такое геометрическое место точек, научитесь выполнять основные геометрические построения и решать более сложные задачи на построение циркулем и линейкой.
§ 17. ОКРУЖНОСТЬ И КРУГ
Круг — это фигура, состоящая из всех точек плоскости, равноудаленных от данной точки. Эту точку называют центром окружности.
Отрезок, соединяющий любую точку окружности с его центром, называют радиусом. Отрезок, соединяющий две произвольные точки окружности, называют хордой круга.
Хорду, проходящую через центр окружности, называют диаметром (рис. 209). Каждый Диаметр окружности состоит из двух радиусов, поэтому его длина вдвое больше длины радиуса.
Если хорда не проходит через центр окружности, ее длин а меньшая от длины диаметра. (Почему?)
Круг на бумаге изображают с помощью циркуля.
Считают, что из данного центра на плоскости можно описать только одну окружность данного радиуса (рис. 210).
Прямая и окружность могут иметь две общие точки (рис. 211, а), одну общую точку (мат. 211,6) или не иметь ни одной (рис. 211, в).
Прямую, имеющую с окружностью две общие точки, называют секущей.
Прямую, имеющую с окружностью только одну общую точку, называется касательной к окружности. Их общую точку называют точкой касания. (Речь идет о фигуры на одной плоскости.) Точка касания лежит на круге, поэтому касательная удалена от центра круга на расстояние, равное длине радиуса. Поскольку все остальные точки касательной лежат вне круга, расстояния от них до центра окружности больше длины радиуса. Из этого следует, такое утверждение.
Рис. 209
Рис.
210
Касательная к окружности перпендикулярна к ного радиуса, проведенного в точку касания.
Рис.211
Чтобы через данную на окружности точку К провести касательную к этой окружности, надо провести радиус ОК, а потом — прямую KM, перпендикулярную этому радиусу (рис. 212).
Если два круга имеют две стальные точки, то говорят, что данные окружности пересекаются в этих точках. Точки пересечения двух кот лежат по разные стороны от прямой, которая проходит через центры этих окружностей. На рисунке 213 изображены круги с центрами О и O, пересекаются в точках А и В.
Если две окружности имеют только одну общую точку, говорят, что они соприкасаются в этой точке. Касание двух окружностей может быть внешним (рис. 214) или внутренним (рис. 215). В обоих случаях точка касания и центры окружностей лежат на одной прямой.
Два круга одной плоскости, имеющих общий центр, называются концентрическими кругами (рис. 216).
Обычно круги чертят, пользуясь циркулем.
Окружность делит плоскость на две части (области). Объединение круга с его внутренней областью называют кругом. Граница круга — окружность. Центром, радиусам, диаметром, хордой круга называют соответственно центр, радиус, диаметр, хорду окружности, которая является границей данного круга (рис. 217).
Рис. 212
Рис. 213
Рис. 214
Рис. 215
Рис. 216
Рис. 217
Форму круга имеет обруч, форму круга — дно ведра, видимый диск Солнца и тому подобное. Колесо на рельсе — материальная модель круга, что примыкает к прямой. На схематическом изображении подшипника (рис. 218) есть несколько соприкасающихся кругов.
Как вам известно из предыдущих классов, длину С окружности и площадь S круга выражается через радиус r следующим формулам:
С = 2 пг, S = пг2.
Строгие доказательства этих формул будут рассматриваться в старших классах.
Рис. 218
Для любознательных
Слово круг — древнеукраинское. Оно масс один корень со словами колода, колоть, колотить, сколоть. Околотами называли праукраинцев, которые жили на землях современной Украины за скифов и еще раньше. А еще слово коло в русском языке служит предлогом, как и вокруг, вокруг. Если к забитому в землю колу (кола) привязывали животное, то она ходила вокруг, вокруг.
Раньше круг также называли кругом, например, пели: «Ой сойди, сойди, ясень месяцу, как мельничный круг». Хоть и полнолуние, и камень в мельнице имеют форму круга, а не круга. Нередко круг называли также колесом; кое-кто считает, что первые колеса научились делать мастеровые люди в наших краях.
В геометрии круг играет важную роль. Существует даже отдельная часть геометрии — геометрия кругов, в которой исследуются важные и интересные свойства геометрических фигур, связанных с кругом.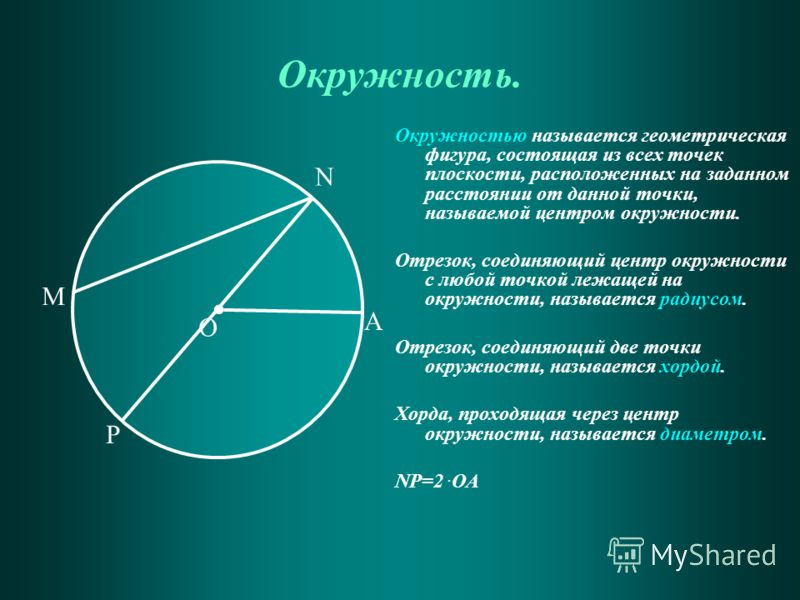
Вопросы и задания для самоконтроля
1. Что такое круг; центр окружности; радиус; диаметр; хорда?
2. Что такое круг? Чем отличается круг от окружности?
3. Сколько общих точек могут иметь: а) прямая и окружность; б) два круга?
4. Сформулируйте определение касательной к окружности. Какое свойство имеет касательная к окружности?
5. Какие круги называют касательными? Что такое точка соприкосновения?
6. Как могут соприкасаться два круга?
7. Какие окружности называют концентрическими?
Выполним вместе
1. Докажите, что точки касания окружности к сторонам угла равноудалены от его вершины.
— Пусть круг с центром О касается сторон угла А в точках В и С (рис. 219). Докажем, что АВ = АС.
Радиусы OD и ОС, проведенные в точки касания, перпендикулярны к соответствующим касательным и уровне. Поэтому прямоугольные треугольники АВО и АСО равны по гипотенузой и катетом.
Следовательно, АВ = АС.
2. Докажите, что диаметр окружности, проведенный через середину хорды, отличной от диаметра, перпендикулярен к хорде.
Пусть АВ — хорда окружности, не проходящая через центр О окружности, а КР — диаметр круга, КОТОРЫЙ проходит через середину М хорды АВ (рис. 220). Треугольник ОАВ равнобедренный, так как ОА = ОВ. А медиана ОМ равнобедренного треугольника, проведенная к его основанию, является также высотой треугольника. Поэтому ОМ ⏊ АВ, а следовательно, и КР ⏊ АВ.
3. Найдите площадь кольца, ограниченного двумя концентрическими окружностями радиусов r и r1 (рис. 221) .
Площадь S кольца равна разности площадей кругов радиусов r и r1:
S = пг2 — пг2 = п (r2 – r21).
Рис. 219
Рис. 220
ЗАДАЧИ И УПРАЖНЕНИЯ
Выполните устно
497. Сколько разных окружностей можно провести через: а) одну точку; б) две точки; в) три точки?
498. Сколько общих точек могут иметь: а) окружность и прямая; б) два круга;
в) круг и треугольник; г) круг и плоскость?
499. Дано окружность с центром О. Сколько общих точек имеет окружность с: а) прямой ОА; б) лучом ОМ?
500. Сколько различных касательных к данной окружности можно провести через данную точку, лежащую: а) на окружности; б) вне окружности; в) внутри круга?
501. Сколько пар соприкасающихся кругов на рисунке 218? А сколько пар концентрических кругов?
Рис. 221
А
502. Начертите круг. Проведите его радиус, диаметр, хорду.
503. Докажите, что диаметр — наибольшая из хорд данного круга.
504. Даны окружность и отрезок, меньшинств от диаметра. Проведите хорду, длина которой равна длине данного отрезка.
505. Найдите расстояние между центрами окружностей радиусов 5 м и 7 м, которые касаются:
а) внешним способом; б) внутренним способом.
506. Имеют ли общие точки две окружности, радиусы которых равны 3 см и 4 см, если расстояние между их центрами равно 5 см?
507. АВ и CD — равные хорды окружности с центром О. Докажите, что ∆АВО = ∆CDO.
508. Окружности с центрами О и О1 пересекаются в точках А и В. Докажите, что:
1) ∆ОАО1 = ∆ОВО1; 2) ∆ОАВ и О1АВ — равнобедренные.
509. Окружности с центрами О и О1 пересекаются в точках А и В, причем каждое из них проходит через центр другой. Найдите ∠AOB и ∠OAO1.
Бы
510. Каждое из трех окружностей проходит через центры двух других. Докажите, что их центры — вершины равностороннего треугольника.
511. Докажите, что равные хорды окружности равноудалены от центра.
512. Как построить касательную к данной окружности:
а) параллельную данной прямой;
б) перпендикулярную к данной прямой?
513. Садовник описывает круг для клумбы с помощью колышков и веревки (рис. 222).
Почему описанная таким способом фигура — круг? Получится круг, если веревка намотуватиметься на колышек?
Рис. 222
514. Найдите радиусы двух соприкасающихся окружностей, если они относятся как 1 : 3, а расстояние между центрами окружностей равно 16 см. Рассмотрите два случая.
515. Из точки А к окружности с центром О проведены касательные АВ и АС. Докажите, что АО — биссектриса угла ВАС.
516. Из точки А к окружности с центром О проведены две касательные, угол между которыми равен 60°. Найдите радиус окружности, если ОА = 10 см.
517. Из точки А к окружности проведены две касательные. Найдите угол между ними, если расстояние от точки А до точки касания равно радиусу круга.
518. Круг касается сторон угла А в точках В и С так, что АВ = ВС. Найдите меру угла А.
519. Три равные окружности с центрами O1, О2, О3 попарно касаются друг друга в точках К, Р и Т. Докажите, что:
1 )В1В2 = В2В3 = В2В1; 2) КР = РТ = ТК.
520. Из центра круга провели три луча, которые разбили данное окружность на три дуги, длина каждой из которых равна 3 см. Найдите углы между этими лучами и радиус круга.
521. Докажите, что площадь кольца, ограниченного двумя концентрическими окружностями радиусов r и r1 равна среднему арифметическому длин этих окружностей, умноженному на разницу радиусов, то есть S = lm (рис. 223).
Рис. 223
Практическое задание
522. Подготовьте презентацию на тему: а) «Круг вокруг нас»; б) «Круг вокруг нас».
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
523. Отрезок длиной а поделен на 3 равные части. Какую часть составляет расстояние между серединами первой и третьей частей?
524. Найдите длину биссектрисы треугольника с периметром 40 см, если она разбивает его на два треугольника с периметрами 20 см и 30 см.
525. Найдите площадь квадрата ABCD, если АС = 10 см.
Окружность и круг. Решение задач. 7 класс
ТеорияЗадания на проверку теоретических знаний
1
2
3
4
5
6
7
8
9
17
18
ГМТ. Окружность и круг
10
11
12
13
14
15
16
Свойства окружности. Касательная к окружности
19
20
21
22
23
Описанная и вписанная окружности треугольника
24
25
26
27
28
29
30
Геометрическим местом точек
(ГМТ)
называют множество всех точек,
обладающих определённым
свойством.
А
СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР
отрезка является геометрическим
местом точек, равноудалённых
от концов этого отрезка
А
БИССЕКТРИСА угла является
геометрическим местом точек,
принадлежащих углу и равноудалённых
от его сторон
О
ОКРУЖНОСТЬЮ называют
геометрическое место точек,
равноудалённых от заданной точки
О
КРУГОМ называют
геометрическое место точек, расстояние
от которых до заданной точки не больше
данного положительного числа
О
Отрезок, соединяющий две точки
окружности, называют
ХОРДОЙ окружности
О
Хорду, проходящую через
центр окружности,
называют ДИАМЕТРОМ
О
Диаметр окружности, перпендикулярный
хорде, делит эту хорду пополам.
. . . .
Диаметр окружности, делящий пополам
хорду, отличную от диаметра,
перпендикулярен этой хорде.
О
Прямую, имеющую с окружностью
только одну общую точку называют
КАСАТЕЛЬНОЙ к окружности
О
Касательная к окружности
перпендикулярна радиусу,
проведённому в точку касания
О
Если прямая, проходящая через точку
окружности, перпендикулярна радиусу,
проведённому в эту точку то эта прямая
является касательной к данной окр-ти
О
r
Если расстояние от центра окружности
до некоторой прямой равно радиусу
окружности, то эта прямая является
касательной к данной окружности
О
r
Если расстояние от центра окружности
до некоторой прямой равно радиусу
окружности, то эта прямая является
касательной к данной окружности
О
А
Отрезки касательных
к окружности,
проведённых из одной точки, равны
п составляют равные углы с прямой,
проходящей через эту точку и центр окр-ти
Необходимо
выбрать правильный ответ.
1
2
3
4
5
6
7
1.
Даны три точки, не лежащие на
одной прямой. Сколько точек
содержит геометрическое место
точек, равноудалённых от данных?
с
В
Бесконечно
много
Подумай!
С
Не Две
верно!
Одну
ВЕРНО
Ни одной
Подумай!
А
К
КС KВ КА
Подсказка
2.
Даны три точки, лежащие на
одной прямой. Сколько точек
содержит геометрическое место
точек, равноудалённых от данных?
Одну
Подумай!
Не Две
верно!
с
А
В
Бесконечно
много
Подумай!
С
Ни
одной
ВЕРНО
Подсказка
3.
Сколько точек содержит
геометрическое место точек,
принадлежащих углу и
равноудалённых от его сторон и вершины?
с
В
Одну
ВЕРНО
Не Две
верно!
Бесконечно
много
Подумай!
Ни одной
Подумай!
К
О
А
КО KА КВ
4.
Точка К принадлежит окружности
с центром в точке О радиуса R.
Какое из следующих утверждений
неверно?
ОК ≤ R
Подумай!
К
ОК ≥ R
Подумай!
ОК
МОЛОДЕЦ
ОК > R
Подумай!
с
O
5.
Прямая имеет две общие точки с
окружностью с центром О радиуса R.
Какую фигуру образуют все точки Х
данной прямой, такие, что ОХ ≥ R?
Отрезок
Подумай!
А
Два
луча
ВЕРНО
Луч
Подумай!
Прямую
Не
верно!
с
С
О
6.
На окружности отметили точку В,
Х – произвольная точка прямой а.
Какое из следующих утверждений
неверно?
ОX > OB
МОЛОДЕЦ
ОX ≥ OA
Подумай!
с
В
O
ОX ≥ OB
Подумай!
ОA = OB
Подумай!
A
a
7.
Какое утверждение верно?
Если две хорды перпендикулярны,
Подумай!
то одна из них является диаметром
Если две хорды точкой пересечения
Не
верно!
делятся пополам, то они перпендикулярны
Если касательная, проведённая через конец
ВЕРНО
хорды, перпендикулярна ей, то это — диаметр
Если одна из хорд делит другую пополам, то
Подумай!
эта хорда — диаметр
| Слайд №2 | |
| Задание: Найдите в оглавлении учебника геометрии название § 4 Главы 2 § 4 Задачи на построение п. 21 Окружность п. 22 Построения циркулем и линейкой п. 23 Примеры задач на построение Предположите, о каких понятиях пойдет речь сегодня на уроке??? | |
| Слайд №3 | |
| Задание: прочитайте п. 21, проставьте на полях учебника карандашом следующие знаки: Знак Значение знака V Отмечается уже известная информация + Отмечается новое знание, новая информация — Отмечается то, о чем думал иначе ? Отмечается то, что осталось непонятным | |
| Слайд №4 | |
| Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. | |
| Слайд №5 | |
| (O,r) или (O,R) Любой отрезок, соединяющий какую-нибудь точку окружности с ее центром, называется радиусом окружности Отрезок соединяющий две точки окружности, называется ее хордой Хорда, проходящая через центр окружности, называется диаметром | |
| Слайд №6 | |
| Часть плоскости, ограниченная окружностью, называется кругом | |
| Слайд №7 | |
| Способы построения окружности | |
| Слайд №8 | |
| Хорды окружности: Диаметры окружности: Радиусы окружности: | |
| Слайд №9 | |
| Разгадайте кроссворд, прочитайте слово по вертикали п е р п е н д и к у л я р н ы е т е о р е м а т р и с е к ц и я ц е н т р ц и р к у л ь х о р д а о п р е д е л е н и е о к р у ж н о с т ь р а д и у с д и а м е т р | |
| Слайд №10 | |
| В геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов: циркуля и линейки без масштабных делений. Линейка позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки; с помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | |
| Слайд №11 | |
| Домашнее задание Выучить определения п. 21 наизусть, №144, 145, 146 Принести циркуль | |
Тесты Окружность (7 класс) по теме геометрии
Сложность: знаток.Последний раз тест пройден 1 час назад.
Вопрос 1 из 10
В прямоугольном треугольнике катеты 5 см и 12 см. Найти радиус описанной окружности
- Правильный ответ
- Неправильный ответ
- Вы и еще 74% ответили правильно
- 74% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветитьВопрос 2 из 10
Гипотенуза прямоугольного треугольника равна 12 см. Радиус описанной окружности :
- Правильный ответ
- Неправильный ответ
- Вы и еще 81% ответили правильно
- 81% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 3 из 10
Из точки А к окружности с центром О проведена касательная АВ (В — точка касания). Угол АВО:
- Правильный ответ
- Неправильный ответ
- Вы и еще 66% ответили правильно
- 66% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 4 из 10
Центр окружности, описанной около прямоугольного треугольника, лежит на середине:
- Правильный ответ
- Неправильный ответ
- Вы и еще 67% ответили правильно
- 67% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 5 из 10
Окружности радиусов 3 см и 7 см касаются внешним образом. Расстояние между их центрами равно:
- Правильный ответ
- Неправильный ответ
- Вы и еще 62% ответили правильно
- 62% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 6 из 10
Ширина кольца, образованного двумя концентрическими окружностями с диаметрами 10 см и 16 см, равна:
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 62% участников
- 38% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 7 из 10
Из точки А к окружности проведены касательные АВ и АС (В и С — точки касания). Какое утверждение верно?
- Правильный ответ
- Неправильный ответ
- Вы и еще 67% ответили правильно
- 67% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 8 из 10
Стороны треугольника равны 6 см, 8 см и 10 см. Радиус вписанной окружности:
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 59% участников
- 41% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 9 из 10
Центр окружности, описанной около треугольника, лежит в точке пересечения:
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 53% участников
- 47% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 10 из 10
Окружность поделена точками А, В, С в отношении 5:7:8. Найти наименьший угол в треугольнике АВС
- Правильный ответ
- Неправильный ответ
- Вы и еще 52% ответили правильно
- 52% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
ТОП-3 тестакоторые проходят вместе с этимРейтинг теста
Средняя оценка: 3.5. Всего получено оценок: 152.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Окружность круга — Common Core: 7-й класс по математике
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Go Math Grade 7 Answer Key Key 9 Окружность, площадь и объем — Go Math Answer Key
Практическое руководство — Стр. № 268
Найдите длину окружности каждого круга.
Вопрос 1.
________ в
Ответ: 56,57 из
Пояснение:
Окружность круга = 2πr = 2 x 22/7 x 9 = 56,57 дюйма
Вопрос 2.
________ см
Ответ: 44 см
Пояснение:
Окружность круга = 2πr = 2 x 22/7 x 7 = 44 см
Найдите длину окружности каждого круга. Используйте 3.14 или \ (\ frac {22} {7} \) для π. При необходимости округлите до ближайшей сотой.
Вопрос 3.
______ м
Вопрос 4.
______ ярд
Ответ: 30,15 ярдов
Пояснение:
Окружность круга = 2πr = 2 x 3,14 x 4,8 = 30,144 ярда
Вопрос 5.
______ в
Ответ: 7,5 из
Пояснение:
Окружность круга = 2πr = 2 x 3,14 x 7,5 = 47,1 дюйма
Вопрос 6.
Круглый бассейн имеет окружность 66 футов. Карлос хочет купить веревку, чтобы протянуть ее по всему диаметру бассейна.Веревка стоит 0,45 доллара за фут, а Карлосу нужно на 4 фута больше диаметра бассейна. Сколько Карлос заплатит за веревку?
$ ______
Ответ: 6.525 $
Пояснение:
Окружность бассейна = 66 футов
πd = 66
22/7 xd = 66
d = 66 x 7/22 = 10,5
Диаметр бассейна = 10,5 футов
Карлосу нужно на 4 фута больше, чем диаметр бассейна.
Общая необходимая веревка = 10,5 + 4 = 14,5 футов
Стоимость веревки на фут = 0,45 доллара США
Общая стоимость веревки = 14.5 x 0,45 доллара = 6,525 доллара
Следовательно, общая стоимость веревки = 6,525 доллара
Найдите каждое недостающее измерение с точностью до сотых. Используйте 3,14 для π.
Вопрос 7.
r =
d =
C = π ярд
r = ________ ярд
d = ________ ярд
Ответ:
r = 0,5 ярда
d = 1 ярд
Пояснение:
Окружность = π ярд
2πr = π ярд
r = 1/2 ярда = 0,5 ярда
d = 2r = 2 [1/2] = 1 ярд
Вопрос 8.
r ≈
d ≈
C = 78.8 футов
r ≈ ________ футов
d ≈ ________ футов
Ответ:
r = 495,31 фута
d = 990,62 фута
Пояснение:
Окружность = 78,8 футов
2πr = 78,8 футов
r = 2 x 22/7 x 78,8 = 495,31 футов
d = 2 x 495,31 = 990,62 футов
Вопрос 9.
r ≈
d ≈ 3,4 дюйма
C =
r ≈ ________ в
C = ________ в
Ответ:
r = 1,7 дюйма
c = 10,68 дюйма
Пояснение:
Диаметр = 3,4 дюйма
Окружность = πd = 22/7 x 3.4 дюйма = 10,68 дюйма
r = d / 2 = 1,7 дюйма
Регистрация основных вопросов
Вопрос 10.
Нора знает, что диаметр круга составляет 13 метров. Как бы вы сказали ей найти окружность?
Тип ниже:
____________
Ответ: Окружность = 16,82 метра
Пояснение:
Дано,
Диаметр = 13 метров
Окружность = πd = 22/7 x 13 = 16,82 метра
Независимая практика — Стр. № 269
Для 11–13 найдите длину окружности каждого круга.Используйте 3.14 или \ (\ frac {22} {7} \) для π. При необходимости округлите до ближайшей сотой.
Вопрос 11.
_______ футов
Ответ:
Cicumference = 18,526 футов = 19 футов (приблизительно)
Пояснение:
Дано:
Диаметр = 5,9 футов
Cicumference = πd = 3,14 x 5,9 = 18,526 футов = 19 футов (приблизительно)
Вопрос 12.
_______ см
Ответ:
Cicumference = 176 см
Пояснение:
Дано:
Радиус = 56 см
Cicumference = πd = 22/7 x 56 = 176 см
Вопрос 13.
_______ в
Ответ:
Cicumference = 110 из
Пояснение:
Дано:
Диаметр = 35 дюймов
Cicumference = πd = 22/7 x 35 = 110 дюймов
Вопрос 14.
Для каких задач в упражнениях 11–13 вы использовали \ (\ frac {22} {7} \) для π? Объяснить свой выбор.
Введите ниже:
_____________
Ответ:
11-й вопрос как 3.14, а 12 и 13 вопросы как π
Пояснение:
Мы можем принять 3,14 в качестве π для 11-го вопроса, потому что диаметр дан в десятичных точках.
И в вопросах 12 и 13 нам нужно взять π, потому что радиус и диаметр даны в виде целых чисел.
Вопрос 15.
Круглый фонтан имеет радиус 9,4 фута. Найдите его диаметр и длину окружности с точностью до десятых.
d = _________ футов
C = _________ футов
Ответ:
d = 19 футов
C = 59 футов
Пояснение:
Дано:
Радиус = 9,4 фута
Диаметр = 2r = 2 x 9,4 = 18,8 фута = 19 футов (приблизительно)
Окружность = πd = 22/7 x 18.8 = 59,08 = 59 футов (приблизительно)
Вопрос 16.
Найдите радиус и окружность компакт-диска диаметром 4,75 дюйма.
r = _________ в
C = _________ в
Ответ:
r = 2,4 дюйма
C = 15 дюймов
Пояснение:
Дано:
Диаметр = 4,75 дюйма
Радиус = r / 2 = 4,75 / 2 = 2,37 дюйма = 2,4 дюйма (приблизительно)
Окружность = πd = 22/7 x 4,75 = 14,92 дюйма = 15 дюймов (приблизительно)
Вопрос 17.
Дартс имеет диаметр 18 дюймов. Каковы его радиус и окружность?
r = _________ в
C = _________ в
Ответ:
r = 9 в
C = 56.6 из
Пояснение:
Дано:
Диаметр = 18 дюймов
Радиус = r / 2 = 18/2 = 9 дюймов
Окружность = πd = 22/7 x 18 = 56,57 дюйма = 56,6 дюйма (приблизительно)
Вопрос 18.
Multistep
Круглый сад Рэнди имеет радиус 1,5 фута. Он хочет оградить сад бордюром, который стоит 0,75 доллара за фут. Примерно сколько будет стоить окантовка? Объяснять.
$ _______
Ответ:
Пояснение:
Дано:
Радиус сада = 1,5 фута
Окружность сада = 2πr = 2 x 22/7 x 1.5 = 9,42 фута
Стоимость огораживания сада за фут = 0,75 доллара США
Общая стоимость окантовки = 9,42 x 0,75 доллара США = 7,06 доллара США = 7 долларов США (приблизительно)
Вопрос 19.
Представляют проблемы реального мира
Показанное колесо обозрения совершает 12 оборотов за поездку. Как далеко можно проехать за одну поездку?
_______ футов
Ответ: Общее расстояние, пройденное за одну поездку, составляет 4752 фута
Пояснение:
Дано:
Диаметр колеса обозрения = 63 фута
Окружность колеса обозрения = 2πr = 2 x 22/7 x 63 = 396 футов
Общее количество оборотов = 12
Общее пройденное расстояние = 12 x 396 = 4,752 футов
Вопрос 20.
Диаметр велосипедного колеса 2 фута. Примерно сколько оборотов делает колесо, чтобы проехать 2 километра? Объяснять. Подсказка: 1 км ≈ 3,280 футов
_______ оборотов
Ответ:
1044 оборотов
Пояснение:
Дано:
Диаметр велосипедного колеса = 2 фута
Общее пройденное расстояние = 2 километра
Мы знаем, что
1 км ≈ 3280 футов
2 км = 2 x 3280 = 6560 футов
Окружность велосипеда = Расстояние проехал за один оборот = πd = 22/7 x 2 = 6.28 футов = 6,3 фута
Общее количество оборотов = Общее пройденное расстояние / расстояние, пройденное за один оборот
= 6560 / 6,28 = 1044 оборотов
Вопрос 21.
Multistep
На карте общественного парка показан круглый пруд. Вдоль пруда диаметром 0,25 мили проложен мост. Вы переходите мост, а ваш друг обходит половину пруда, чтобы встретить вас на другой стороне моста. Насколько дальше ваш друг идет?
_______ миля
Ответ:
Пояснение:
Дано,
Диаметр водоема = 0.25 миль
Длина моста = Диаметр пруда = 0,25 миль
Затем расстояние, пройденное человеком = 0,25 миль
Расстояние, пройденное другом = На полпути вокруг пруда, чтобы встретить вас на другой стороне моста = πd / 2
= 22/7 x 0,25 / 2 = 0,39 = 0,4 мили
Друг прошел большее расстояние по сравнению с человеком
Чем больше расстояние, пройденное другом = 0,39 — 0,25 = 0,14 мили
Стр. № 270
Вопрос 22.
Архитектура
Ротонда Капитолия соединяет Дом и Сенат стороны U.С. Капитолий. Заполнить таблицу. Округлите свои ответы до ближайшего фута
Тип ниже:
_____________
Ответ:
Радиус = 48 футов
Диаметр = 96 футов
Пояснение:
Учитывая
Высота = 180 футов
Окружность = 301,5 футов
πd = 301,5
22/7 x d = 301,5
d = 95,93 = 96 футов
r = d / 2 = 96/2 = 48 футов
H.O.T.
Фокус на мышлении высшего порядка
Вопрос 23.
Multistep
Хранитель музея создает сад полукруглых скульптур диаметром 30 футов.Вокруг сада будет забор. Ограждение стоит 9,25 доллара за погонный фут. Примерно сколько вообще будет стоить ограждение?
$ _______
Ответ:
Общая стоимость ограждения = 712 $
Пояснение:
Дано,
Диаметр = 30 футов
Окружность сада в форме круга = 2πr
Окружность полукруга = πr = πd / 2 = 22/7 x 30/2 = 47,14 фута
Стоимость ограждения за каждую ногу = 9,25 $
Общая стоимость ограждения полукруглого сада = 47.14 x 9,25 доллара США + 30 x 9,25 доллара США = 712 долларов США (приблизительно)
Вопрос 24.
Критическое мышление
Сэм развешивает веревочные светильники по краю круглого патио диаметром 18 футов. Фары бывают длиной 54 дюйма. Сколько нитей света ему нужно, чтобы окружить край патио?
_______ прядей
Ответ: 12 с половиной прядей светлых = 13 прядей (примерно)
Пояснение:
Дано,
Диаметр круглого внутреннего дворика = 18 футов = 216 дюймов
Окружность круглого внутреннего дворика = πd = 22/7 x 216 = 678.85 дюймов
Светильники будут иметь длину (в одной нитке) = 54 дюйма
Общее количество нитей света, необходимое для круглого внутреннего дворика
= Окружность круглого внутреннего дворика / Светильники будут иметь длину (в одной нитке) = 678,85 / 54 = 12,57 = 12 с половиной прядей светлых
Вопрос 25.
Представляют проблемы реального мира
Круговой путь шириной 2 фута имеет внутренний диаметр 150 футов. Насколько дальше он от внешнего края пути, чем от внутреннего края?
_______ футов
Ответ: около 12.6 футов
Пояснение:
Дано,
Ширина круговой траектории = 2 фута
Внутренний диаметр круговой траектории = 150 футов
Внешний диаметр круговой траектории = 150 + 2 (2) = 154 фута
Внутренняя окружность = πd = 150 π
Наружная окружность = πd = 154π
Расстояние между внешним и внутренним краем = 154 π — 150 π = 4 π = 12,6 фута
Вопрос 26.
Рассуждения критики
Шестерня на велосипеде имеет форму круга. Одна шестерня имеет диаметр 4 дюйма, а меньшая — 2 дюйма.Джастин говорит, что окружность большой шестерни на 2 дюйма больше, чем окружность меньшей шестерни. Вы согласны? Поясните свой ответ.
_______
Ответ:
Заявление Джастина неверно.
Пояснение:
Окружность большей шестерни = πd = 4π
Окружность меньшей шестерни = πd = 2π
Так как 2 x 2π = 4π, окружность большей шестерни в два раза больше окружности меньшей шестерни.
Так как = 4π — 2π = 2π = 6.28
Следовательно, большая окружность не на 2 дюйма больше, чем меньшая окружность
Вопрос 27.
Настойчиво решайте проблемы
Рассмотрим два круглых бассейна. Бассейн A имеет радиус 12 футов, а бассейн B — 7,5 метров. У какого бассейна больше окружность? Насколько больше? Обоснуйте свои ответы.
_______
Ответ:
Бассейн Б около 0,9 метра
Пояснение:
Дано,
Бассейн A имеет диаметр = 24 фута,
Бассейн B имеет диаметр = 7.5 м
Мы знаем, что
1 фут = 0,3 метра
24 фута = 7,2 метра
Бассейн B имеет больший диаметр, поэтому он имеет большую окружность.
Окружность бассейна A = 7,2π
Окружность бассейна B = 7,5π
Разница между окружностями = 7,5π — 7,2π = 0,9 метра.
Практическое руководство — Страница № 274
Найдите площадь каждого круга. При необходимости округлите до ближайшей десятой. Используйте 3,14 для π.
Вопрос 1.
_______ м 2
Ответ: 153.9 м 2
Пояснение:
Дано:
Диаметр = 14 м
Радиус = 14/2 = 7 м
Площадь круга = πr 2
= 3,14 x 7 x 7 = 153,86 = 153,9 м 2
Вопрос 2.
_______ мм 2
Ответ: 452,2 мм 2
Пояснение:
Дано:
Радиус = 12 мм
Площадь круга = πr 2
= 3,14 x 12 x 12 = 3,14 (144) = 452,2 мм 2
Вопрос 3.
_______ ярд 2
Ответ: 314 ярдов 2
Пояснение:
Дано:
Диаметр = 20 ярдов
Радиус = 20/2 = 10 ярдов
Площадь круга = πr 2
= 3,14 x 10 x 10 = 3,14 (100) = 314 ярдов 2
Решить. Используйте 3,14 для π.
Вопрос 4.
Циферблат имеет радиус 8 дюймов. Какова площадь циферблата? Округлите ответ до ближайшей сотой.
_______ в 2
Ответ: 200.96 из 2
Пояснение:
Дано:
Радиус = 8 дюймов
Площадь циферблата = πr 2
= 3,14 x 8 x 8 = 3,14 (64) = 200,96 дюйма 2
Вопрос 5.
DVD имеет диаметр 12 сантиметров. Какова площадь DVD? Округлите ответ до ближайшей сотой.
_______ см 2
Ответ: 113,04 см 2
Пояснение:
Дано:
Диаметр = 12 см
Радиус = 12/2 = 6 см
Площадь DVD = πr 2
= 3.14 x 6 x 6 = 3,14 (36) = 113,04 см 2
Вопрос 6.
Компания производит стальные крышки диаметром 13 дюймов. Какова площадь каждой крышки? Округлите ответ до ближайшей сотой.
_______ в 2
Ответ: 132,67 в 2
Пояснение:
Дано:
Диаметр = 13 дюймов
Радиус = 13/2 = 6,5 дюйма
Площадь каждой крышки = πr 2
= 3,14 x 6,5 x 6,5 = 3,14 (42,25) = 132,67 дюйма 2
Найдите площадь каждого круга.Дайте свои ответы в терминах π.
Вопрос 7.
C = 4π
A =
Тип ниже:
______________
Ответ: 4π
Пояснение:
Дано:
Центр окружности = 4π
2πr = 4π
Радиус = 4/2 = 2 единицы
Площадь круга = πr 2
= π x 2 x 2 = π (4) = 4π квадратных единиц
Вопрос 8.
C = 12π
A =
Тип ниже:
______________
Ответ: 36π
Пояснение:
Дано:
Центр окружности = 12π
2πr = 12π
Радиус = 6 единиц
Площадь круга = πr 2
= π x 6 x 6 = π (36) = 36π квадратных единиц
Вопрос 9.
C = \ (\ frac {π} {2} \)
A =
Введите ниже:
______________
Ответ: π / 16
Пояснение:
Дано:
Центр окружности = \ (\ frac {π} {2} \)
2πr = \ (\ frac {π} {2} \)
Радиус = 1/4 единицы
Площадь круга = πr 2
= π x 1/4 x 1/4 = π (1/16) = π / 16 квадратных единиц
Вопрос 10.
Круглая ручка имеет площадь 64π квадратных ярда. Какова окружность пера? Дайте свой ответ в виде π
Введите ниже:
______________
Ответ: 16π
Пояснение:
Дано:
Площадь круглого пера = 64π квадратных ярда
πr 2 = 64π
r = 8 ярдов
Окружность круга = 2πr = 2 x 8 x π = 16π ярдов
Регистрация основных вопросов
Вопрос 11.
Какова формула площади A круга через радиус r?
Тип ниже:
______________
Ответ: πr 2
Пояснение:
Площадь круга = πr 2
Независимая практика — Стр. № 275
Вопрос 12.
Самая популярная пицца в Pavone’s Pizza — это 10-дюймовая персональная пицца с одной начинкой. Какова площадь пиццы диаметром 10 дюймов? Округлите ответ до ближайшей сотой.
_______ в 2
Ответ: 78,5 дюйма 2
Пояснение:
Дано:
Диаметр = 10 дюймов
Радиус = 10/2 = 5 дюймов
Площадь пиццы = πr 2
= 3,14 x 5 x 5 = 3,14 (25) = 78,5 дюймов 2
Вопрос 13.
Колпак имеет радиус 16 сантиметров. Какова площадь колпака? Округлите ответ до ближайшей сотой.
_______ см 2
Ответ: 803,84 см 2
Пояснение:
Дано:
Радиус = 16 см
Площадь круга = πr 2
= 3.14 x 16 x 16 = 3,14 (256) = 803,84 см 2
Вопрос 14.
Витраж имеет форму полукруга. Нижний край окна составляет 36 дюймов в длину. Какова площадь витража? Округлите ответ до ближайшей сотой.
_______ в 2
Ответ: 508,68 из 2
Пояснение:
Площадь полукруга = 1/2 πr 2 = 1/2 (3,14) (18) (18) = 1/2 (3,14) (324) = 1,57 (324) = 508,68 дюйм 2
Вопрос 15.
Анализ взаимосвязей
Точка (3,0) лежит на окружности с центром в начале координат. Какова площадь круга с точностью до сотых?
_______ шт. 2
Ответ: 28,26 шт. 2
Пояснение:
Радиус = 3
Площадь круга = πr 2 = π (3) 2 = 3,14 (9) = 28,26 единиц 2
Вопрос 16.
Multistep
Радиостанция передает сигнал на территорию с радиусом 50 миль.Станция может ретранслировать сигнал и транслировать на территорию в радиусе 75 миль. Насколько больше зона вещания при ретрансляции сигнала? Округлите ответ до ближайшей квадратной мили.
_______ миля 2
Ответ: 9813 mi 2
Пояснение:
Дано:
Радиус радиостанции, передающей сигнал (r) = 50 миль
Наибольший радиус, на который может быть ретранслирована передача (R) = 75 миль
Наибольшая площадь региона вещания, когда сигнал передается = πR 2 -πr 2 = π (75) (75) — π (50) (50)
= 5625π — 2500π
= 3125π
= 3125 (3.14) = 9813 миль 2 (приблизительно)
Вопрос 17.
Multistep
Стороны квадратного поля равны 12 метрам. Спринклер в центре поля опрыскивает круглую область с диаметром, соответствующим стороне поля. Какая часть поля не обрабатывается дождевальной машиной? Округлите ответ до ближайшей сотой.
_______ м. 2
Ответ: 30,96 м 2
Пояснение:
Дано:
Сторона квадрата = 12 метров
Диаметр круглой площади поля в центре = Сторона квадрата = 12 метров
Радиус поля = 12/2 = 6 метров
Площадь поля, которое не достигает ороситель = Площадь квадрата — Площадь круглой площади
= (сторона) 2 -πr 2 = (12) (12) — π (6) (6)
= 144 — 36 (3.14)
= 144 — 113,04
= 30,96 м 2
Вопрос 18.
Обоснование рассуждений
Небольшой блинчик с серебряным долларом, который подают в ресторане, имеет окружность 2π дюйма. Обычный блин имеет окружность 4π дюйма. Площадь обычного блина вдвое больше, чем у блина с серебряным долларом? Объяснять.
_______
Ответ: Нет, площадь обычного блина в 4 раза больше площади блина с серебряным долларом
. Пояснение:
Блин с серебряным долларом:
Окружность блина с серебряным долларом = 2π дюйма
2πr = 2π
r = 1 дюйм
Площадь блина с серебряным долларом = πr 2 = π (1) (1) = π дюймов 2
Обычный блин:
Окружность обычного блина = 4π дюйма
2πr = 4π
r = 2 дюйма
Площадь блина с серебряным долларом = πr 2 = π (2) (2) = 4π дюйм 2
Таким образом, площадь обычного блина в 4 раза больше площади блина с серебряным долларом
Вопрос 19.
Анализ взаимосвязей
Пекарня предлагает небольшой круглый торт диаметром 8 дюймов. Он также предлагает большой круглый торт диаметром 24 дюйма. В три раза больше верхней части большого торта, чем у маленького торта? Если нет, то насколько больше его площадь? Объяснять.
_______
Ответ: Нет, площадь большого торта в 9 раз больше площади маленького торта
Пояснение:
Маленький торт:
Диаметр маленького торта = 8 дюймов
Радиус маленького торта = 8/2 = 4 дюйма
Площадь маленького торта = πr 2 = π (4) (4) = 16 π дюйм 2
Большой торт:
Диаметр большого торта = 24 дюйма
Радиус большого торта = 24/2 = 12 дюймов
Площадь большого торта = πr 2 = π (12) (12) = 144 π в 2
Так как 144 π / 16 π = 9
Следовательно,
большого торта в 9 раз больше площади маленького торта.{2}} {4π} \), чтобы найти площадь круга по окружности. Опишите еще один способ найти площадь круга по окружности.
Тип ниже:
____________
Ответ: Площадь = C 2 / 4π
Пояснение:
Окружность круга = 2πr
C = 2πr
Разделите обе стороны на 2π
, тогда r = C / 2π
Площадь круга = πr 2
Замените C / 2π на r:
Площадь = π (с / 2π) 2 = С 2 / 4π
Вопрос 21.
Выводы розыгрыша
Марк хочет заказать пиццу. Какая сделка лучше? Объяснять.
_____
Ответ: Пицца 18 дюймов — лучшее предложение
Пояснение:
Дано:
Диаметр пиццы = 12 дюймов
Радиус пиццы = 12/2 = 6 дюймов
Площадь круга = πr 2
= (3,14) (6) (6) = 113 (приблизительно) в 2
Общая стоимость пиццы = 10 долларов США
Стоимость пиццы за дюйм = 10 долларов США / 113 = 0,09 доллара США за квадратный дюйм
Диаметр пиццы = 18 дюймов
Радиус пиццы = 18/2 = 9 дюймов
Площадь круга = πr 2
= (3.14) (9) (9) = 254 (приблизительно) в 2
Общая стоимость пиццы = 20 долларов США
Стоимость пиццы за дюйм = 20 долларов США / 254 = 0,08 доллара США за дюйм
Вопрос 22.
Multistep
Медведь был замечен возле кемпинга. На поиски медведя в регион были отправлены поисковики.
а. Предположим, медведь может ходить в любом направлении со скоростью 2 мили в час. Предположим, медведя в последний раз видели 4 часа назад. Насколько большую площадь должны покрыть искатели? Используйте 3,14 для π. Округлите ответ до ближайшей квадратной мили.
_____ миля 2
Ответ: 201mi 2
Пояснение:
Медведь может пройти расстояние = 2 x 4 = 8 миль
Так как он проходит 2 мили в час в течение 4 часов
Радиус медведя = 8 миль
Площадь круга = πr 2
= (3,14) (8) (8) = 201 (приблизительно) миль 2
Вопрос 22.
б. Что, если? Какую дополнительную площадь пришлось бы охватить поисковикам, если бы медведя последний раз видели 5 часов назад?
_____ миля 2
Ответ: 113mi 2
Пояснение:
Если медведь 5 часов, то
Медведь может пройти расстояние = 2 x 5 = 10 миль
Так как он проходит 2 мили в час в течение 5 часов
Радиус медведя = 10 миль
Площадь круг = πr 2
= (3.14) (10) (10) = 314 (приблизительно) миль 2
Дополнительная площадь, охваченная поисками = 314 — 201 = 113 миль 2
H.O.T.
Фокус на мышлении высшего порядка
Вопрос 23.
Анализировать взаимосвязи
Две окружности имеют одинаковый радиус. Совпадает ли объединенная площадь двух кругов с площадью круга с удвоенным радиусом? Объяснять.
_____
Ответ: Нет
Пояснение:
Если радиус двух окружностей одинаковый.
тогда, Пусть радиусы кругов равны 1.
Площадь каждого круга = π квадратных единиц
Объединенная площадь 2 кругов = π + π = 2π квадратных единиц
Если радиус увеличен вдвое.
тогда, Пусть радиусы кругов равны 2
Площадь каждого круга = 4π квадратных единиц
Объединенная площадь 2 кругов = 4π + 4π = 8π квадратных единиц
Следовательно, области в обоих случаях не совпадают.
Вопрос 24.
Ищите узор
Как изменится площадь круга, если радиус умножить на коэффициент n, где n — целое число?
Тип ниже:
____________
Ответ: Тогда новая площадь в n 2 раз больше площади исходного круга.
Пояснение:
Если радиус умножить на коэффициент «n»
, тогда новый радиус = rn
Площадь круга (с радиусом rn) = π (rn) 2 = n 2 (πr 2 ).
Следовательно, новая площадь в n 2 раз больше площади исходного круга.
Вопрос 25.
Представляют проблемы реального мира
Прицел на цель имеет диаметр 3 дюйма. Вся цель имеет диаметр 15 дюймов. Какая часть цели является мишенью? Объяснять.
Тип ниже:
____________
Ответ: 1/25 от целевого
Пояснение:
Глаз быка:
Диаметр бычьего глаза = 3 дюйма
Радиус бычьего глаза = 3/2 = 1,5 дюйма
Площадь бычьего глаза = π (r) 2 = π (1,5) 2 = 2,25π
Цель:
Диаметр цели = 15 дюймов
Радиус цели = 15/2 = 7,5 дюймов
Площадь цели = π (r) 2 = π (7,5) 2 = 56,25π
Доля «Бычьего глаза» во всей мишени = 2.25π / 56,25π = 1/25
Следовательно, 1/25 всей цели — это «Бычий глаз».
Практическое руководство — Страница № 280
Вопрос 1.
Установщик плитки рисует неправильную форму на сетке. Каждый квадрат в сетке соответствует 1 квадратному сантиметру. Какова площадь неправильной формы?
_____ см 2
Ответ: Площадь неправильной формы = 34 см 2
Пояснение:
ШАГ1 Сначала разделите неправильные формы на многоугольники.
STEP2 Неправильная форма может быть разделена на треугольник, прямоугольник, параллелограмм
STEP3 Площади многоугольников
Площадь треугольника = 1/2 (основание x высота) = 1/2 (4 x 2) = 4 см 2
Площадь прямоугольника = длина x ширина = 5 x 3 = 15 см 2
Площадь параллелограмма = основание x высота = 5 x 3 = 15 см 2
Площадь неправильной формы = (15 + 15 + 5 ) см 2 = 34 см 2
Вопрос 2.
Покажите два разных способа разделить составную фигуру.Найдите область в обоих направлениях. Покажи свою работу ниже.
_____ см 2
Ответ: Площадь фигуры в обе стороны = 288 см 2
Пояснение:
Первый способ разделить составную фигуру — это разделить ее на прямоугольник 8 на 9 и прямоугольник 12 на 18.
Площадь первого прямоугольника = длина x ширина = 9 x 8 = 72 см 2
Площадь второго прямоугольника = длина x ширина = 18 x 12 = 216 см 2
Общая площадь фигуры = 72 + 216 = 288 см 2
Вопрос 3.
Сал облицовывает свой подъезд плиткой. План этажа нарисован на единичной сетке. Каждая единица длины соответствует 1 футу. Плитка стоит 2,25 доллара за квадратный фут. Сколько Сал заплатит за то, чтобы выложить плитку в подъезде?
$ _____
Ответ: Сал заплатит 97,875 долларов
Пояснение:
Разделите эту фигуру на трапецию и параллелограмм.
Площадь трапеции = 1/2 (a + b) h = 1/2 (7 + 4) 5 = 1/2 (11) 5 = 27,5 футов 2
Площадь параллелограмма = основание x высота = 4 x 4 = 16 футов 2
Общая площадь фигуры = 27.5 + 16 = 43,5 фута 2
Стоимость каждого квадратного фута = 2,25 доллара США
Сумма, уплаченная Sal = 43,5 x 2,25 = 97,875 доллара США
Регистрация основных вопросов
Вопрос 4.
Каков первый шаг в поиске площади составной фигуры?
Тип ниже:
______________
Ответ:
Первый шаг в поиске площади составной фигуры — разделить ее на более мелкие базовые формы.
Пояснение:
Первый шаг в определении площади составной фигуры — разделить ее на более мелкие базовые формы, такие как треугольники, квадраты, прямоугольники, параллелограммы, круги и трапеции.
Затем вычислите площадь каждой фигуры и сложите их, чтобы найти площадь фигуры.
Независимая практика — стр. № 281
Вопрос 5.
Баннер состоит из квадрата и полукруга. У квадрата длина сторон 26 дюймов. Одна сторона квадрата также равна диаметру полукруга. Какая общая площадь баннера? Используйте 3,14 для π.
_____ в 2
Ответ: 941,33 из 2
Пояснение:
Площадь квадрата = сторона x сторона = 26 x 26 = 676 дюймов 2
Площадь полукруга = 1/2 πr 2 = 1/2 (3.14) (13) (13) = 1/2 (3,14) (169) = 265,33 дюйма 2
Площадь фигуры = 676 + 265,33 = 941,33 дюйма 2
Вопрос 6.
Multistep
Эрин хочет застелить пол в своем туалете. Показан план этажа туалета.
а. Сколько ковра нужно Эрин?
_____ фут 2
Ответ: 61 фут 2
Пояснение:
Площадь прямоугольника = длина x ширина = 4 x 10 = 40 футов
Площадь треугольника = 1/2 x основание x высота = 1/2 x 6 x 7 = 21 фут
Общая площадь фигуры = 40 + 21 = 61 фут 2
Вопрос 6.
г. Ковер, который выбрала Эрин, стоит 2,50 доллара за квадратный фут. Во сколько ей будет стоить ковровое покрытие на полу?
$ _____
Ответ: 152,50 $
Пояснение:
Стоимость квадратного фута ковра = 2,50 доллара США
Общая стоимость ковра на полу = 61 x 2,50 доллара США = 152,50 доллара США
Вопрос 7.
Множественные представления
Шестиугольник ABCDEF имеет вершины A (-2, 4), B (0, 4), C (2, 1), D (5, 1), E (5, -2) и F (-2, -2). Нарисуйте фигуру на координатной плоскости. Какова площадь шестиугольника?
_____ ед. 2
Ответ: Площадь рисунка 30 квадратных единиц
Пояснение:
Разделите фигуру на трапецию и прямоугольник.
Площадь трапеции = 1/2 (a + b) h = 1/2 (2 + 4) x 3 = 1/2 (6) 3 = 9 квадратных единиц
Площадь прямоугольника = длина x ширина = 7 x 3 = 21 квадрат
Общая площадь фигуры = 9 + 21 = 30 квадратных единиц
Вопрос 8.
Поле имеет форму, как показано на рисунке. Какая площадь поля? Используйте 3,14 для π.
_____ м. 2
Ответ: 146,24 м 2
Пояснение:
Разделите фигуру на квадрат, треугольник и четверть круга.
Площадь квадрата = сторона x сторона = 8 x 8 = 64 м 2
Площадь четверти круга = 1/4 (πr 2 ) = 1/4 (3,14 x 8 2 )
= 1/4 (200,96) = 50,24 м 2
Площадь треугольника = 1/2 x основание x высота = 1/2 x 8 x 8 = 32 м 2
Общая площадь фигуры = 64 + 32 +50,24 = 146,24 м 2
Вопрос 9.
Закладка имеет форму прямоугольника с полукругом на обоих концах. Прямоугольник 12 см в длину и 4 см в ширину.Диаметр каждого полукруга равен ширине прямоугольника. Какая область закладки? Используйте 3,14 для π.
_____ см 2
Ответ: 60,56 см 2
Пояснение:
Закладка разделена на прямоугольник, полукруг.
Площадь прямоугольника = длина x ширина = 12 x 4 = 48 см 2
Диаметр полукруга = ширина прямоугольника = 4 см
Радиус полукруга = 4/2 = 2 см
Площадь полукруга = πr 2 = 3.14 x 2 x 2 = 12,56 см 2
Общая площадь закладки = 12,56 + 48 = 60,56 см 2
Вопрос 10.
Multistep
Алекс делает 12 подвесок для школьной ярмарки. Узор, который он использует для изготовления вымпелов, показан на рисунке. Ткань для вымпелов стоит 1,25 доллара за квадратный фут. Сколько будет стоить Алекс, чтобы сделать 12 вымпелов?
$ _____
Ответ: 52,50 $
Пояснение:
Каждый кулон состоит из прямоугольника и треугольника.
Площадь прямоугольника = длина x ширина = 3 x 1 = 3 фута 2
Площадь треугольника = 1/2 x основание x высота = 1/2 x 1 x 1 = 0,5 фута 2
Общая площадь подвески = 3 + 0,5 = 3,5 фута 2
Количество подвесок = 12
Площадь подвесок = 12 x 3,5 = 42 фута 2
Стоимость каждого квадратного фута подвески = 1,25 доллара США
Общая стоимость для всех 12 кулонов = 12 x 1,25 доллара США = 52,50 доллара США
Вопрос 11.
Рассуждения
Составная фигура образуется путем объединения квадрата и треугольника.Его общая площадь составляет 32,5 футов 2 . Площадь треугольника составляет 7,5 футов 2 . Какова длина каждой стороны квадрата? Объяснять.
_____ футов
Ответ: 5 футов
Пояснение:
Дано:
Площадь составной фигуры = 32,5 футов 2
Площадь треугольника = 7,5 футов 2
Площадь квадрата = 32,5 — 7,5 = 25
сторона x сторона = 25
сторона 2 = 25
сторона = корень 25 = 5 футов
H.O.T. — Страница №282
Фокус на мышлении высшего порядка
Вопрос 12.
Представляют проблемы реального мира
Кристина изобразила форму своего сада на миллиметровой бумаге. По ее оценкам, с каждой квадратной единицы она получит около 15 морковок. Она планирует использовать весь сад для выращивания моркови. Сколько моркови она может вырастить? Объяснять.
______ морковь
Ответ: 300 морковок
Пояснение:
Эта фигура разделена на два треугольника и квадрат.
Площадь рисунка = 2 (1/2 x 2 x 2) + 4 (4) = 4 + 16 = 20 квадратных единиц
Количество моркови на квадратную единицу = 300
Общее количество моркови = 20 x 15 = 300
Вопрос 13.
Анализ взаимосвязей
Показанная фигура состоит из треугольника и квадрата. Периметр фигуры 56 дюймов. Какая площадь у фигуры? Объяснять.
_____ в 2
Ответ: 192 из 2
Пояснение:
Дано:
Периметр фигуры = 56 дюймов
Фигура разделена на квадрат и треугольник.
10 + 10 + 3s = 56
3s = 36
s = 12
Площадь треугольника = 1/2 x 12 x 8 = 48 дюймов 2
Площадь квадрата = 12 x 12 = 144 дюйма 2
Общая площадь фигуры = 144 + 48 = 192 дюйма 2
Вопрос 14.
Критическое мышление
Справа показан образец шарфа. Какая площадь у шарфа? Используйте 3,14 для π.
_____ в 2
Ответ: 243 из 2
Пояснение:
Площадь прямоугольника на данном рисунке = 28 x 15 = 420 дюймов 2
Площадь двух полукругов = 2 (1/2 πr 2 ) = 3.14 x 7,5 x 7,5 = 176,625 дюйма 2
Площадь заштрихованной области = 420 — 176,625 = 243 дюйма 2 (приблизительно)
Вопрос 15.
Настойчиво решайте проблемы
Показанный дизайн палладиевого окна имеет полукруглую форму вверху. Дно образовано квадратами одинакового размера. Тень для окна будет выступать на 4 дюйма за периметр окна, показанный пунктирной линией вокруг окна. Каждый квадрат в окне имеет площадь 100 из 2 .
а. Какая площадь окна? Используйте 3,14 для π.
_____ в 2
Ответ: а) 2228 в 2
Пояснение:
Площадь квадрата = 100 дюймов 2
Сторона x сторона = 100
Сторона = 10 дюймов
Так как сторона каждого квадрата равна 10 дюймам и имеется 4 квадрата.
Длина стороны большего квадрата (ов) = 40 дюймов
Площадь большего квадрата = сторона x сторона = 40 x 40 = 1600 дюймов 2
Так как сторона каждого квадрата равна 10 дюймам и имеется 2 квадрата.
Радиус полукруга = 20 дюймов
Площадь полукруга = 1/2 (πr 2 ) = 1/2 (3,14 x 20 2 ) = 628 дюймов 2
Площадь окно = 1600 + 628 = 2228 в 2
Вопрос 15.
б. Какая площадь тени? Округлите ответ до ближайшего целого числа.
_____ в 2
Ответ: б) 3016 в 2
Пояснение:
Шторка выходит за пределы форм на 4 дюйма, поэтому длина нижнего прямоугольника составляет 40 + 4 + 4 = 48 дюймов.
Длина проходит ниже исходного квадрата.
Высота теперь = 40 + 4 = 44 дюйма
Радиус полукруга = 20 + 4 = 24 дюйма
Новая площадь фигуры = 48 (44) + 1/2 (3,14 x 24 2 ) = 2112 + 904,32 = 3016,32 = 3016 дюйм 2
Практическое руководство — Страница № 286
Найдите площадь поверхности каждой твердой фигуры.
Вопрос 1.
Общая площадь: _____ футов 2
Ответ: 150 футов 2
Пояснение:
Основание представляет собой треугольник с длинами сторон 8 футов, 5 футов, 5 футов, поэтому периметр основания = P = 8 + 5 + 5 = 18 футов
Высота призмы = 7 футов
Основание представляет собой треугольник.
Площадь треугольника = 1/2 (8) (3) = 12 футов 2
Формула площади поверхности для призмы: S = Ph + 2b
P = Периметр = 18 h = высота = 7 b = основание = площадь треугольника = 12
Площадь поверхности призмы = 18 (7) + 2 (12) = 126 + 24 = 150 футов 2
Вопрос 2.
Общая площадь: _____ м 2
Ответ: 503 м 2
Пояснение:
Дано:
Размеры кубоида:
Длина = 11 м
Ширина = 9 м
Высота = 7 м
Площадь поверхности кубоида = 2 (фунт + bh + hl) = 2 (11 x 9 + 9 x 7 + 7 x 11) = 478м 2
Размеры куба:
Длина стороны = 2.5 м
Площадь поверхности куба = 6a 2 = 6 x 2,5 x 2,5 = 37,5 м 2
Площадь поверхности прямоугольной призмы = 2,5 x 2,5 = 6,25
Площадь поверхности фигуры = перекрытие площадь — площадь основания куба
= 37,5 + 478-2 (6,25) = 503 м 2
Регистрация основных вопросов
Вопрос 3.
Как определить площадь поверхности композитного твердого тела, состоящего из призм?
Введите ниже:
_____________
Ответ: Площадь поверхности призм, сложите их, а затем дважды вычтите перекрывающиеся области.
Пояснение:
Площадь поверхности составного твердого тела состоит из призм путем нахождения площадей поверхности призм, их сложения, а затем увеличения и последующего вычитания перекрывающихся областей.
Независимая практика — стр. № 287
Вопрос 4.
Карла упаковывает подарок в показанную коробку. Сколько ей нужно оберточной бумаги, не считая нахлеста?
_____ в 2
Ответ: 164 из 2
Пояснение:
Площадь поверхности прямоугольника без верха = 2h (l + b) + lb = 2 x 4 (13) + 10 x 3 = 164 дюйма 2
Длина оберточной бумаги = Площадь поверхности прямоугольника без верха = 164 дюйма 2
Вопрос 5.
Дмитрий хочет покрыть верх и стороны показанной коробки стеклянной плиткой квадратной формы 5 мм. Сколько плиток ему нужно?
_____ плитки
Ответ: 3720 плиток
Пояснение:
Площадь поверхности куба без учета дна = 2h (l + b) + lb = 2 x 9 (35) + 20 x 15 = 930 см 2
5 мм = 0,5 см
Площадь плитки = Площадь квадрата = a 2 = 0,5 см x 0,5 см = 0,25 см 2
Общее количество плиток = 930 / 0,25 = 3720 плиток
Вопрос 6.
Шера строит кабинет. Делает деревянные распорки для углов шкафа. Найдите площадь поверхности каждой скобки.
_____ в 2
Ответ: 45 из 2
Пояснение:
Периметр фигуры = P = 3 (3) + 2 (1) = 11 дюймов
Основание = B = 3 (2) = 6 дюймов
Высота = h = 3
Площадь поверхности фигуры = Ph + 2B = 11 x 3 +2 (6) = 33 + 12 = 45 дюймов 2
Вопрос 7.
В показанной конуре есть пол, но нет окон.Найдите общую площадь конуры, включая дверь.
_____ фут 2
Ответ: 66 футов 2
Пояснение:
Периметр основания пятиугольника (P) = 2 (2,5) + 2 (2) + 3 = 5 + 4 + 3 = 12
Площадь основания пятиугольника путем сложения площади треугольника и площади основания прямоугольник (B) = 1/2 (3) (2) + 2 (3) = 9
Высота (h) = 2 + 2 = 4
Площадь поверхности фигуры = Ph + 2B = 12 (4) + 2 (9) = 48 + 18 = 66 футов 2
Эдди построил показанный пандус, чтобы обучать своего щенка трюкам.Используйте цифру для 8–9.
Вопрос 8.
Анализировать взаимосвязи
Опишите два способа определения площади поверхности пандуса.
Тип ниже:
____________
Ответ: Один из способов — использовать формулу S = Ph + 2B. Другой способ — найти площадь каждой грани призмы и сложить их, чтобы получить общую площадь поверхности.
Пояснение:
Самый первый способ использования формулы S = Ph + 2B, где трапеции являются основанием. Второй способ — найти площадь каждой грани призмы, а затем сложить их, чтобы получить общую площадь поверхности.
Вопрос 9.
Какова площадь пандуса?
_____ в 2
Ответ: 3264 из 2
Пояснение:
P = Периметр фигуры = 16 (3) + 2 (20) + 16 = 104
B = Основание фигуры = 1/2 (12) (16 + 3 (16)) = 6 (16 + 48) = 6 (64) = 384
h = Высота фигуры = 2
Площадь поверхности фигуры = Ph + 2B = 104 (2) + 2 (384) = 2496 + 768 = 3264 дюйма 2
Марко и Элейн строят стенд, подобный показанному, чтобы показать трофеи.Используйте цифру 10–11.
Вопрос 10.
Какова площадь стенда?
_____ фут 2
Ответ: 58 футов 2
Пояснение:
Верх:
Периметр = P = 4 (1) = 4
Основание = B = 1 (1) = 1
Высота = h = 3
Площадь верхней поверхности = Ph + 2B = 4 (3) + 2 ( 1) = 14 футов 2
Низ:
Периметр = P = 2 (7) + 2 (1) = 14 + 2 = 16
Основание = B = 7 (1) = 7
Высота = h = 2
Верх площадь поверхности = Ph + 2B = 16 (2) + 2 (7) = 46 футов 2
Площадь перекрытия = 1 (1) = 1
Площадь поверхности фигуры = площадь поверхности верха + площадь поверхности дна — площадь перекрытия = 14 + 46-2 = 60-2 = 58 футов 2
Вопрос 11.
Critique Reasoning
Марко и Элейн хотят покрасить весь стенд в серебристый цвет. Банка с краской покрывает 25 квадратных футов и стоит 6,79 доллара. Они отложили 15 долларов на краску. Этого достаточно? Объяснять.
_____
Ответ: Нет
Пояснение:
Так как площадь поверхности составляет 58 футов 2 , им потребуется 3 банки с краской. Так как каждая банка рисует 25 футов 2 , и мы не можем купить часть банок.
3 банки тогда будут стоить 6,79 x 3 = 20,37, так что этого недостаточно.
Стр.288
Вопрос 12.
Генри хочет закрыть показанную коробку бумагой без нахлеста. Сколько квадратных сантиметров будет покрыто бумагой?
_____ см 2
Ответ: 2316 см 2
Пояснение:
Дано:
Длина = 24 см Ширина = 27 см Высота = 10 см
P = Периметр = 2 (24) + 2 (27) = 48 + 54 = 102
B = Основание = 24 (27) = 648
h = Высота = 10
Площадь фигуры = Ph + 2B = 102 (10) + 2 (648) = 1020 + 1296 = 2316 см 2
Вопрос 13.
Что если?
Предположим, что длина и ширина коробки в упражнении 12 удвоены. Удваивается ли площадь поверхности S? Объяснять.
_____
Ответ: Нет
Пояснение:
Дано:
Длина = 24 см x 2 = 48 см Ширина = 27 см x 2 = 54 см Высота = 10 см
P = 2 (48) + 2 (54) = 96 + 108 = 204
B = 48 (54 ) = 2592
Новая площадь поверхности = Ph + 2B = 204 (10) + 2 (2592) = 2040 + 5184 = 7224 см 2
Двойная площадь поверхности = 2 (2316) = 4632 см 2
Итак, площадь новой поверхности не вдвое больше первоначальной.
H.O.T.
Фокус на мышлении высшего порядка
Вопрос 14.
Настойчиво решайте проблемы
Эния строит шкаф для хранения в форме прямоугольной призмы. Прямоугольная призма имеет квадратное основание с длиной сторон 2,5 фута и высотой 3,5 фута. Сравните количество краски, которое она использовала бы, чтобы закрасить всю призму, кроме нижней, с количеством краски, которое она использовала бы, чтобы нарисовать всю призму.
Тип ниже:
______________
Ответ: Разница только в площади нижней поверхности.Это было бы на 6,25 фута на 2 меньше.
Пояснение:
Разница в количестве краски — это только площадь нижней поверхности. Площадь нижней поверхности (2,5) 2 = 6,25.
Следовательно, она бы нарисовала на 6,25 фута 2 меньше, если бы она закрасила всю поверхность, кроме нижней, по сравнению с закрашиванием всей призмы.
Вопрос 15.
Интерпретация ответа
Показанная коробка овсянки имеет форму цилиндра. С помощью сетки найдите площадь поверхности S коробки с овсянкой с точностью до десятых.Затем найдите количество квадратных футов картона, необходимое для 1500 коробок овсянки. Округлите ответ до ближайшего целого числа
_____ ft 2
Ответ: 138,28 дюйма 2 , 1440 футов 2
Пояснение:
Дано:
Размеры цилиндра:
Радиус: 2 дюйма
Высота: 9 дюймов
Общая площадь поверхности цилиндра = 2πr (r + h) = 2 x 22/7 x 2 (2 + 9) = 138,28 дюйма 2
Общее количество квадратных дюймов, необходимых для 1500 коробок овсянки = 1500 x 138.28 = 207 300 дюймов 2
1 фут = 12 дюймов
(1 фут) 2 = (12 дюймов) 2
1 фут 2 = 144 дюйма 2
Общее количество квадратных футов, необходимое для 1500 коробок овсянки (с точностью до ближайшего целого числа)
= 207300/144 = 1440 футов 2
Вопрос 16.
Анализировать взаимосвязи
Призма состоит из сантиметровых кубов. Как найти площадь поверхности призмы на рисунке 1 без использования сетки или формулы? Как изменяется площадь поверхности на рисунках 2, 3 и 4? Объяснять.
Тип ниже:
______________
Ответ: Площадь первых трех фигур одинакова. Площадь поверхности на рисунке 4 больше, чем площадь поверхности на рисунке 1-3.
Пояснение:
Площадь первых трех фигур одинакова. 3 новые грани на рис. 2 имеют те же области, что и 3 видимые грани, которые были удалены при удалении верхнего углового куба. Тогда площадь поверхности будет такой же, как на рисунке 1. Точно так же площади новых видимых граней на рисунке 3 равны площадям видимых граней, удаленных после удаления угловых кубов, поэтому площади поверхности такие же, как на рисунке 3. фигура 1.Площадь поверхности на рисунке 4 больше, чем площадь поверхности на рисунках 1-3. При удалении куба были удалены 2 видимые грани (одна сверху и одна спереди), но добавлены 4 видимые грани, так что площадь поверхности увеличилась. .
Практическое руководство — Решение проблем с объемом — Стр. № 292
Вопрос 1.
Найдите объем треугольной призмы.
_____ фут 3
Ответ: 84 фута 3
Пояснение:
Площадь основания призмы = 1/2 x 8 x 3 = 12 футов 2
Высота призмы = 7 футов
Объем призмы = (12 x 7) футов 3
Вопрос 2.
Найдите объем трапециевидной призмы.
_____ м. 3
Ответ: 330 м 3
Пояснение:
Площадь основания призмы = 1/2 x (15 + 5) x 3 = 30 м 2
Высота призмы = 11 м
Объем призмы = (30 x 11) м 3 = 330 м 3
Вопрос 3.
Найдите объем составной фигуры.
_____ фут 2
Ответ: Составная фигура: 360 футов 3
Пояснение:
Объем треугольной призмы:
Площадь основания призмы = 1/2 x 4 x 6 = 12 футов 2
Высота = 6 футов
Объем треугольной призмы = 12 x 6 = 72 фут 3
Объем прямоугольной призмы:
Площадь основания призмы = 4 x 6 = 24 фута 2
Высота = 12 футов
Объем треугольной призмы = 12 x 24 = 288 футов 3
Объем составной фигуры = (288 + 72) футов 3 = 360 футов 3
Найдите объем каждой фигуры.
Вопрос 4.
На рисунке показан сарай, который мистер Фаулер строит для своей фермы.
_____ фут 3
Ответ: 40 000 футов 3
Пояснение:
Треугольная призма:
B = Площадь основания = 1/2 x 10 (40) = 200 см 2
Высота = 50 см
Объем треугольной призмы = Bh = 200 x 50 = 10 000 см 3
Прямоугольная призма:
B = Площадь основания = 40 x 15 = 600 см 2
Высота = 50 см
Объем треугольной призмы = Bh = 600 x 50 = 30 000 см 3
Общий объем призмы = 10 000 + 30 000 = 40 000 см 3
Вопрос 5.
На рисунке показан контейнер в форме трапециевидной призмы, который Пит наполнил песком.
_____ см 3
Ответ: 385 см 3
Пояснение:
B = Площадь основания = 1/2 x 5 (10 + 12) = 55 см 2
Высота = 7 см
Объем контейнера = Bh = 55 x 55 = 385 см 3
Регистрация основных вопросов
Вопрос 6.
Как определить объем составного твердого тела, образованного двумя или более призмами?
Тип ниже:
______________
Ответ: Нахождение объема каждой фигуры, складывая их, чтобы получить объем составного твердого тела.
Пояснение:
Чтобы найти объем составной фигуры, которую можно разделить на 2 или более призм, найдите объем каждой призмы и сложите их, чтобы получить объем составного твердого тела.
Независимая практика — Стр. № 293
Вопрос 7.
Ловушка для насекомых имеет форму треугольной призмы. Площадь основания 3,5 дюйма 2 , а высота призмы 5 дюймов. Каков объем этой ловушки?
_____ в 3
Ответ: 17.5 из 3
Пояснение:
Объем ловушки = Площадь основания x высота = 3,5 x 5 = 17,5 дюйма 3
Вопрос 8.
Арлетта построила картонную рампу для игрушечных машинок своих младших братьев. Определите форму пандуса. Затем найдите его объем.
Форма: _________
Площадь: _________ в 3
Ответ: 525 из 3
Пояснение:
Площадь основания = 1/2 x 6 x 25 = 75 дюймов 2
Высота = 7 дюймов
Объем фигуры = 75 x 7 = 525 дюймов 3
Вопрос 9.
Алекс сделал эскиз самодельных футбольных ворот, которые планирует построить. Цель будет иметь форму треугольной призмы. Ноги прямоугольных треугольников по сторонам его ворот имеют размер 4 фута и 8 футов, а отверстие вдоль передней части — 24 фута. Сколько места содержится в этой цели?
_____ фут 3
Ответ: 384 футов 3
Пояснение:
Площадь основания = 1/2 x 4 x 8 = 16 футов 2
Высота = 24 фута
Объем фигуры = 16 x 24 = 384 футов 3
Вопрос 10.
Подарочная коробка имеет форму трапециевидной призмы с длиной основания 7 дюймов и 5 дюймов и высотой 4 дюйма. Высота подарочной коробки — 8 дюймов. Какой объем подарочной коробки?
_____ в 3
Ответ: 192 из 3
Пояснение:
Площадь основания = 1/2 x 4 x (7 + 5) = 24 дюйма 2
Высота = 8 дюймов
Объем фигуры = 24 x 8 = 192 Площадь основания = 1/2 x 6 x 25 = 75 дюймов 2
Высота = 7 дюймов
Объем фигуры = 75 x 7 = 525 дюймов 3
Вопрос 11.
Объясните ошибку
Студент написал следующее утверждение: «Треугольная призма имеет высоту 15 дюймов и площадь основания 20 квадратных дюймов. Объем призмы составляет 300 квадратных дюймов ». Определите и исправьте ошибку.
Тип ниже:
____________
Ответ: Погрешность — единица измерения.
Пояснение:
Объем призмы:
площадь основания x высота = 20 x 15 = 300 дюймов 3
Найдите объем каждой фигуры. При необходимости округлите до ближайшей сотой.
Вопрос 12.
_____ в 3
Ответ: 97,2 дюйма 3
Пояснение:
Объем шестиугольной призмы = 23,4 x 3 = 70,2 дюйма 3
Площадь основания прямоугольной призмы = 3 x 3 = 9 дюймов 2
Объем прямоугольной призмы = Bh = 9 x 3 = 27 дюймов 3
Общий объем фигуры = 70,2 + 27 = 97,2 дюйма 3
Вопрос 13.
_____ м 3
Ответ: 316.41 метр 3
Пояснение:
Объем прямоугольной призмы слева = Bh = [7,5 x 3,75] (3,75) = 105,47 м 3
Объем прямоугольной призмы справа = Bh = [7,5 x 3,75] (7,5 ) = 210,94 м 3
Общий объем составной фигуры = 105,47 + 210,94 = 316,41 м 3
Вопрос 14.
Multi-Step
У Джози 260 кубических сантиметров свечного воска. Она хочет сделать свечу с шестиугольной призмой с площадью основания 21 квадратный сантиметр и высотой 8 сантиметров.Еще она хочет сделать треугольную свечу-призму высотой 14 сантиметров. Может ли площадь основания свечи треугольной призмы составлять 7 квадратных сантиметров? Объяснять.
_____
Ответ: Нет
Пояснение:
Объем шестиугольной призмы = 21 x 8 = 168
Общий объем парафина 260 равен сумме объемов каждой призмы.
B — площадь основания треугольной призмы.
168 + 14B = 260 см 3
14B = 260 — 168
B = 6,6 см 3
Стр.294
Вопрос 15.
Кинотеатр предлагает попкорн в двух разных емкостях по одинаковой цене. Один контейнер представляет собой трапециевидную призму с площадью основания 36 квадратных дюймов и высотой 5 дюймов. Другой контейнер представляет собой треугольную призму с площадью основания 32 квадратных дюйма и высотой 6 дюймов. Какой контейнер лучше? Объяснять.
Тип ниже:
___________
Ответ: Треугольная призма — лучшее предложение, так как она имеет больший объем
Пояснение:
Площадь основания трапециевидной призмы = 36 дюймов 2
Объем трапециевидной призмы = Bh = 36 x 5 = 175 дюймов 3
Площадь основания треугольной призмы = 32 дюйма 2
Объем прямоугольной призмы = Bh = 32 x 6 = 192 дюйма 3
Треугольная призма — лучшее решение, так как она имеет больший объем.
H.O.T.
Фокус на мышлении высшего порядка
Вопрос 16.
Критическое мышление
Показанный детский бассейн представляет собой трапециевидную призму с общим объемом 286 кубических футов. Какое недостающее измерение?
______ фут.
Ответ: 3,5 фута
Пояснение:
Площадь трапециевидной призмы = B = 1/2 x 13 (2 + x)
Объем фигуры = 286 кубических футов
V = Bh
286 = 1/2 x 13 (2 + x) (8 )
5,5 = (2 + x)
x = 3.5 футов
Вопрос 17.
Упорство в решении проблем
Линетт имеет металлический дверной упор с указанными размерами. Каждый кубический сантиметр металла в дверном упоре имеет массу около 8,6 грамма. Найдите объем металла в дверном упоре. Затем найдите массу дверного упора.
______ грамм
Ответ: 75 кубических сантиметров, 645 граммов
Пояснение:
V = Bh
B = Площадь основания треугольника = 10 см, высота = 6 см = 1/2 x 10 x 6 = 30 квадратных сантиметров
V = 30 x 2.5 = 75 кубических сантиметров
1 кубический сантиметр = 8,6 грамма по массе
V = 75 кубических сантиметров x 8,6 = 645 граммов
Вопрос 18.
Анализ взаимосвязей
Как утроение всех размеров треугольной призмы повлияет на ее объем? Объясните свои рассуждения.
Тип ниже:
____________
Ответ: Объем в 27 раз превышает исходный объем.
Пояснение:
Площадь основания = B = 1/2 (3b) (3h) = 9/2 (bh)
H — высота призмы
Объем будет = 9/2 (bh) x ( 3H) = 27 [1/2 (bhH)]
Следовательно, объем в 27 раз превышает исходный объем.
Вопрос 19.
Настойчиво решайте проблемы
Каждая из двух трапециевидных призм имеет объем 120 кубических сантиметров. У призм нет общих размеров. Укажите возможные размеры для каждой призмы.
Тип ниже:
____________
Ответ: Возможная комбинация размеров: высота 8 см, основание 2 см и 3 см.
Пояснение:
Числа, которые умножаются, чтобы получить 120: 20 и 6, поэтому пусть первая призма имеет площадь основания 20 квадратных сантиметров и высоту 6 см.
Если площадь основания равна 20, высота трапеции и длина оснований могут быть 8,2 и 3 соответственно.
Другие числа, которые умножаются, чтобы получить 120: 4 и 30, поэтому пусть вторая призма имеет площадь основания 30 квадратных сантиметров и высоту 4 см.
Если площадь основания 30, высота трапеции и длина оснований могут быть 10,1 и 5 соответственно.
9.1, 9.2 Окружность и площадь кругов — Стр. № 295
Найдите длину и площадь каждого круга.Используйте 3,14 для π. При необходимости округлите до ближайшей сотой.
Вопрос 1.
C = _________ м
A = _________ м 2
Ответ:
C = 43,96 м
A = 153,86 м 2
Пояснение:
C = 2 πr = 2 π (7) = 14 (3,14) = 43,96 м
A = πr 2 = 3,14 (7) 2 = 153,86 м 2
Вопрос 2.
C = _________ футов
A = _________ футов 2
Ответ:
C = 37.68 футов
A = 113,04 футов 2
Пояснение:
Диаметр = 12 футов
Радиус = d / 2 = 12/2 = 6 футов
C = 2 πr = 2 π (6) = 6 (3,14) = 37,68 футов
A = πr 2 = 3,14 ( 6) 2 = 113,04 футов 2
9.3 Площадь составных фигур
Найдите площадь каждой фигуры. Используйте 3,14 для π.
Вопрос 3.
______ м 2
Ответ: 180,48 м 2
Пояснение:
Площадь треугольника = 1/2 x 16 x 10 = 80 м 2
Площадь полукруга = 1/2 πr 2 = 1/2 (3.14) (8) 2 = 100,48 м 2
Общая площадь фигуры = 80 + 100,48 = 180,48 м 2
Вопрос 4.
______ см 2
Ответ: 200 см 2
Пояснение:
Площадь параллелограмма = 4,5 (20) = 90 см 2
Площадь прямоугольника = 20 (5,5) = 110 см 2
Общая площадь фигуры = 90 + 110 = 200 см 2
9.4, 9.5 Решение задач площади и объема поверхности
Найдите площадь и объем каждой фигуры.
Вопрос 5.
S = _________ см 2
V = _________ см 3
Ответ:
S = 132 см 2
V = 60 см 3
Пояснение:
Периметр = 3 + 4 + 5 = 12 см
Площадь основания = Площадь треугольника = 1/2 x 3 x 4 = 6
S = Ph + 2B = 12 (10) + 2 (6) = 120 +12 = 132 см 2
V = Bh = 6 x 10 = 60 см 3
Вопрос 6.
S = _________ ярдов 2
V = _________ ярдов 3
Ответ:
S = 54.5 ярдов 2
V = 27,5 ярдов 3
Пояснение:
Периметр = 2 (2,5) + 2 (2) + 4 = 13 см
Площадь основания = Площадь треугольника + Площадь прямоугольника = 1/2 x 1,5 x 4 + 4 (2) = 11
S = Ph + 2B = 13 (2,5) + 2 (11) = 32,5 +22 = 54,5 ярда 2
V = Bh = 11 x 2,5 = 27,5 ярда 3
Основной вопрос
Вопрос 7.
Как можно использовать геометрические фигуры для решения реальных задач?
Тип ниже:
______________
Ответ: Мы можем решить реальные проблемы, определив площадь поверхности и объем.
Пример: Мы можем найти количество жидкости в резервуаре, вычислив его объем.
Пояснение:
Реальные проблемы с определением площади поверхности и объема.
Пример 1: Мы можем найти количество жидкости в резервуаре, вычислив его объем.
Пример 2: Мы можем найти площадь дома и количество краски, необходимое для покраски дома.
Стр. № 296
Вопрос 1.
Какова длина окружности?
а. 34,54 м
г.69.08 м
г. 379,94 м
г. 1519,76 м
Ответ: б. 69,08 м
Пояснение:
Окружность = 2 πr = 2 π (11) = 22 (3,14) = 69,08 м
Вопрос 2.
Какова площадь круга?
Опции:
а. 23,55 м 2
б. 47,1 м 2
г. 176,625 м 2
г. 706,5 м 2
Ответ: c. 176,625 м 2
Пояснение:
Диаметр = 15 м
Радиус = 7,5 м
Площадь круга = πr 2 = 3.14 (7,5) 2 = 176,625 м 2
Вопрос 3.
Какова площадь фигуры?
Опции:
а. 28,26 м 2
г. 36 м 2
г. 64,26 м 2
г. 92,52 м 2
Ответ: c. 64,26 м 2
Пояснение:
Площадь квадрата = 6 x 6 = 36 м 2
Радиус = 6 м
Площадь четверти круга = 1/4 πr 2 = 1/4 x 3,14 (6) 2 = 28.26 м 2
Общая площадь фигуры = 36 + 28,26 = 64,26 м 2
Вопрос 4.
Годовое членство в клубе здоровья стоит 480 долларов. Это включает плату в размере 150 долларов США для новых членов, которая выплачивается при присоединении. Какое уравнение представляет ежемесячную стоимость x в долларах для нового участника?
Опции:
а. 12x + 150 = 480
б. \ (\ frac {x} {12} \) + 150 = 480
с. 12x + 480 = 150
г. \ (\ frac {x} {12} \) + 480 = 150
Ответ: а. 12x + 150 = 480
Пояснение:
Если x — ежемесячная плата, то 12x — это общая ежемесячная плата.
Плата за присоединение = 150 долларов
Общая стоимость = 480 долларов
тогда
12x + 150 = 480
Вопрос 5.
Какой объем призмы?
Опции:
а. 192 футов 3
б. 48 футов 3
c. 69 футов 3
г. 96 футов 3
Ответ: d. 96 футов 3
Пояснение:
B = Площадь основания треугольника = 1/2 x 8 x 2 = 8 футов 2
Высота = 12 футов
Объем треугольной формы = Bh = 8 (12) = 96 футов 3
Вопрос 6.
В школьном снек-баре продается смесь мюсли и изюма. Смесь включает 2 фунта гранолы на каждые 3 фунта изюма. Сколько фунтов гранолы нужно для смеси, включающей 24 фунта изюма?
Опции:
а. 16 фунтов
б. 36 фунтов
c. 48 фунтов
г. 120 фунтов
e. 120 фунтов
Ответ: а. 16 фунтов
Пояснение:
2/3 равно x / 24, то 3 умноженное на 8 равно 24, а если 2 умноженное на 8 равно 16.
Вопрос 7.
Найдите процентное изменение с 20 до 25 долларов.
Опции:
а. Снижение на 25%
б. 25% рост
c. Снижение на 20%
d. 20% увеличение
Ответ: б. 25% увеличение
Объяснение:
25-20 = 5 разделить на 20 = 1/4
Когда мы найдем процент, мы получим 25.
Таким образом, мы можем сказать, что есть увеличение на 25%
Вопрос 8.
Каждый размер меньшей призмы составляет половину соответствующего размера большей призмы.
а. Какая площадь поверхности фигуры?
_____ в 2
Ответ: 856 из 2
Пояснение:
Высота верхней призмы = 10/2 = 5
Длина верхней призмы = 16/2 = 8
Ширина верхней призмы = 8/2 = 4
Периметр = 2l + 2w = 2 (8) + 2 (4) = 16 + 8 = 24 дюйма
B = lw = 8 (4) = 32 дюйма
Площадь поверхности верхней призмы = Ph + 2B = 24 (5) + 2 (32) = 184 дюйма 2
Высота призмы = 10
Длина призмы = 16
Ширина призмы = 8
Периметр = 2l + 2w = 2 (16) + 2 (8) = 32 + 16 = 48 дюймов
B = lw = 16 (8) = 128 дюймов
Площадь поверхности нижней призмы = Ph + 2B = 48 (10) + 2 (128) = 736 дюймов 2
Площадь перекрывающейся области = 32 дюйма 2
Общая площадь поверхности призмы
= Площадь поверхности верхней призмы + Площадь поверхности нижней призмы — 2 [Площадь перекрывающейся области]
= 184 + 736 — 2 (32) = 856 дюймов 2
Вопрос 8.
г. Какой объем фигуры?
_____ в 3
Ответ: 1440 из 3
Пояснение:
Объем верхней призмы = Bh = 32 (5) = 160 дюймов 3
Объем нижней призмы = Bh = 128 (10) = 1280 дюймов 3
Общий объем фигуры = 160 + 1280 = 1440 дюймов 3
УПРАЖНЕНИЯ — Стр. № 298
Вопрос 1.
На масштабном чертеже парка масштаб 1 см: 10 м. Найдите площадь настоящего парка.
_____ м. 2
Ответ: 450 м 2
Пояснение:
Умножьте размеры чертежа в масштабе на 10, так как 1 см = 10 м
3 см на 1,5 см = 30 м на 15 м
Площадь = 30 (15) = 450 м 2
Вопрос 2.
Найдите значение y и меру ∠YPS.
y = __________ °
mYPS = __________ °
Ответ: y = 8
mYPS = 40 °
Пояснение:
140 + 5y = 180 [сумма углов на прямой = 180 °]
5y = 40
y = 8
mYPS = mRPZ = 5y [вертикально противоположные углы]
mYPS = 5 (8) = 40 °
Вопрос 3.
Канье хочет сделать треугольную клумбу из бревен указанной ниже длины, чтобы сформировать границу. Может ли Канье образовать треугольник из бревен, не разрезая ни одного из них? Объяснять.
_____
Ответ: Нет
Пояснение:
Сторона треугольника должна быть больше, чем разность двух других сторон, и меньше, чем сумма двух других сторон.
Сумма первых двух сторон = 3 + 4 = 7 <8
Следовательно, он не может образовать треугольник, пока не разрежет бревна.
Вопрос 4.
В магазине Адриана строит пирамиду с квадратным основанием 4 дюйма и высотой 6 дюймов. Затем она разрезает пирамиду вертикально пополам, как показано. Какова площадь каждой поверхности среза?
_____ в 2
Ответ: 12 из 2
Пояснение:
Основание = 4 дюйма
Высота = 6 дюймов
Площадь треугольника = 1/2 x 6 x 4 = 12 дюймов 2
Стр. № 300
Найдите длину и площадь каждого круга.Округлить до ближайшей сотой.
Вопрос 1.
C = __________ в
A = __________ в 2
Ответ:
C = 69,08 дюйма
A = 379,94 дюйма 2
Пояснение:
Диаметр = 22 дюйма
Радиус = d / 2 = 22/2 = 11 дюймов
C = 2 πr = 2 π (11) = 22 (3,14) = 69,08 дюйма
A = πr 2 = 3,14 ( 11) 2 = 379,94 дюйма 2
Вопрос 2.
C = __________ м
A = __________ м 2
Ответ:
C = 28.26 м
A = 63,59 м 2
Пояснение:
Радиус = 4,5 м
C = 2 πr = 2 π (4,5) = 9 (3,14) = 28,26 м
A = πr 2 = 3,14 (4,5) 2 = 63,59 м 2
Найдите площадь каждой составной фигуры. При необходимости округлите до ближайшей сотой.
Вопрос 3.
______ в 2
Ответ: 99 из 2
Пояснение:
Площадь квадрата = 9 x 9 = 81 дюйм 2
Основание треугольника = 13 — 9 = 4 дюйма
Площадь треугольника = 1/2 x 4 x 9 = 18 дюймов 2
Общая площадь фигуры = 81 + 18 = 99 2
Вопрос 4.
______ см 2
Ответ: 420,48 см 2
Пояснение:
Площадь прямоугольника = 16 x 20 = 320 см 2
Диаметр = 16 см
Радиус = 16/2 = 8 см
Площадь полукруга = 1/2 πr 2 = 1/2 x 3,14 (8) 2 = 100,48 см 2
Общая площадь фигуры = 320 + 100,48 = 420,48 см 2
Найдите объем каждой фигуры.
Вопрос 5.
______ в 3
Ответ: 420 из 3
Пояснение:
B = 7 (5) = 35 дюймов 2
V = Bh = 35 x 12 = 420 дюймов 3
Вопрос 6.
Объем треугольной призмы составляет 264 кубических фута. Площадь основания призмы 48 квадратных футов. Найдите высоту призмы.
______ в
Ответ: 5,5 футов
Пояснение:
V = Bh
264 = 48 часов
h = 264/48 = 5,5 футов
Стр. № 301
Стеклянное пресс-папье имеет сложную форму: квадратную пирамиду, точно помещающуюся на вершине 8-сантиметрового куба. Пирамида имеет высоту 3 см. Каждое треугольное лицо имеет высоту 5 сантиметров.
Вопрос 7.
Какой объем пресс-папье?
______ см 3
Ответ: 576 см 3
Пояснение:
Пирамида:
B = 8 x 8 = 64 см 2
V = 1/3 Bh = 1/3 x 64 x 3 = 64 см 3
Призма:
B = 8 x 8 = 64 см 2
V = Bh = 64 x 8 = 512 см 3
Общий объем фигуры = 64 + 512 = 576 см 3
Вопрос 8.
Какова общая площадь поверхности пресс-папье?
______ см 2
Ответ: 400 см 2
Пояснение:
Пирамида:
P = 4 (8) = 32 см
S = 1/2 Pl + B = 80 + 64 = 144 см 2
Призма:
P = 4 (8) = 32 см
S = Ph + 2B = 32 (8) + 2 (64) = 384 см 2
Общая площадь поверхности призмы
= Площадь призмы + Площадь пирамиды — 2 [Площадь перекрывающейся области]
= 144 + 384 — 2 (64) = 400
Блок 4 Задачи производительности
Вопрос 9.
Инженер по дизайну продукта
Миранда — инженер по дизайну продукта, работающая в компании по производству спортивных товаров. Она оформляет палатку в виде треугольной призмы. Размеры палатки указаны на схеме.
а. Сколько квадратных футов материала нужно Миранде, чтобы сделать палатку (включая пол)? Показать свою работу.
______ футов 2
Ответ: 261 3/4 фута 2
Пояснение:
P = 2 x 7 1/2 + 8 = 22 1/2
B = 4/2 (8) (6) = 24
S = Ph + 2B = 22 1/2 x 9 1/2 + 2 (24) = 213 3/4 + 48 = 261 3/4 фута 2
Вопрос 9.
г. Какой объем палатки? Показать свою работу.
______ футов 3
Ответ: 228 футов 3
Пояснение:
V = Bh = 24 x 9 1/2 = 228 футов 3
Вопрос 9.
c. Предположим, Миранда хочет увеличить объем палатки на 10%. Характеристики высоты (6 футов) и ширины (8 футов) должны оставаться неизменными. Как Миранда может удовлетворить это новое требование? Объясните
Тип ниже:
____________
Ответ: Увеличьте высоту до 10.45 футов
Пояснение:
Новый объем = 1,10 x 228 = 250,8
250,8 = 24 часа
h = 10,45 футов
Раздел 4 Рабочие задачи (продолжение) — Стр. № 302
Вопрос 10.
Ли делает стенд для демонстрации скульптуры, созданной в художественном классе. Стенд будет иметь ширину 45 сантиметров, длину 25 сантиметров и высоту 1,2 метра.
а. Какой объем стенда? Напишите свой ответ в кубических сантиметрах.
______ см 3
Ответ: 135000 см 3
Пояснение:
B = 45 x 25 = 1125 см 2
V = Bh = 1125 x 120 = 135000 см 3
Вопрос 10.
г. Ли нужно засыпать подставку песком, чтобы она была тяжелой и устойчивой. Каждый кусок дерева имеет толщину 1 сантиметр. Доски собираются вместе, как показано на рисунке, который не в масштабе. Сколько кубических сантиметров песка ей нужно, чтобы засыпать подставку? Объясните, как вы нашли свой ответ.
______ см 3
Ответ: 116,702 см 3
Пояснение:
Ширина = 45-2 (1) = 43 фута
Длина = 25-2 (1) = 23 фута
Высота = 120-2 (1) = 118 футов
B = 43 x 23 = 989 футов 2
V = Bh = 989 x 118 = 116,702 футов 3
Выбранный ответ — стр.303
Вопрос 1.
Школьный флаг имеет форму прямоугольника с удаленным треугольником, как показано.
Какова мера угла x?
Опции:
а. 50 °
б. 80 °
с. 90 °
г. 100 °
Ответ: d. 100 °
Пояснение:
x = 50 + 50 = 100 ° [Сумма двух углов, образованных двумя линиями]
Вопрос 2.
На карте с масштабом 2 см = 1 км расстояние от дома Бо до пляжа составляет 4,6 сантиметра. Какое реальное расстояние?
Опции:
а.2.3 км
б. 4.6 km
c. 6.5 км
д. 9.2 км
Ответ: а. 2.3 км
Пояснение:
2/1 = 4,6 / x
x = 4,6 / 2 = 2,3 км
Вопрос 3.
Лаласа и Ясмин проектируют треугольный баннер, который нужно повесить в школьном спортзале. Сначала они рисуют дизайн на бумаге. Треугольник имеет основание 5 дюймов и высоту 7 дюймов. Если 1 дюйм на чертеже эквивалентен 1,5 футам на фактическом баннере, какова будет площадь фактического баннера?
Опции:
а.17,5 футов 2
б. 52,5 футов 2
c. 39,375 футов 2
г. 78.75 футов 2
Ответ: c. 39,375 футов 2
Пояснение:
1 дюйм = 1,5 фута
Основание треугольника = 5 дюймов = 1,5 (5) футов = 7,5 футов
Высота = 7 дюймов = 7 (1,5) футов = 10,5 футов
Площадь треугольника = 1/2 x 7,5 x 10,5 = 39,375 футов 2
Вопрос 4.
У Сони четыре соломинки разной длины: 2 см, 8 см, 14 см и 16 см. Сколько треугольников она может сделать из соломинки?
Опции:
а.нет треугольника
b. один треугольник
c. два треугольника
г. более двух треугольников
Ответ: б. один треугольник
Пояснение:
Третья сторона треугольника должна быть меньше суммы двух других сторон, чтобы получился треугольник.
2 + 8 = 10 <14
2 + 8 = 10 <16
8 + 14 = 22> 14
8 + 14 = 22> 16
2 + 14 = 16 = 16
2 + 16 = 18> 16
Следовательно, можно образовать только один треугольник со сторонами 8, 14, 16.
Вопрос 5.
Пицца с одной начинкой стоит 15 долларов.00. Каждая дополнительная доливка стоит 1,25 доллара США. Пусть x будет количеством дополнительных покрытий. У вас есть 20 долларов, которые можно потратить. Какое уравнение вы можете решить, чтобы найти количество дополнительных начинок, которые можно добавить в пиццу?
Опции:
а. 15x + 1,25 = 20
б. 1.25x + 15 = 20
с. 15x — 1,25 = 20
г. 1,25x — 15 = 20
Ответ: б. 1,25x + 15 = 20
Пояснение:
Если x — количество дополнительных начинок, то 1,25 x — это стоимость дополнительных начинок.
Это дает общую стоимость 1.25x + 15
, тогда
1,25x + 15 = 20
Вопрос 6.
Банк предлагает ссуду на улучшение жилья с простой процентной ставкой 12% годовых. J.T. занимает $ 14 000 сроком на 3 года. Сколько он вообще вернет?
Опции:
а. $ 15680
б. $ 17360
в. $ 19040
г. $ 20720
Ответ: c. $ 19040
Пояснение:
Простые проценты = 14 000 x 0,12 x 2 = 5 040 долларов США
Сумма = 14 000 долларов США + 5 040 долларов США = 19040 долларов США
Вопрос 7.
Каков объем треугольной призмы длиной 75 сантиметров с основанием площадью 30 квадратных сантиметров?
Опции:
а.2,5 см 3
б. 750 см 3
c. 1125 см 3
г. 2250 см 3
Ответ: d. 2250 см 3
Пояснение:
V = Bh = 30 (75) = 2250 см 3
Вопрос 8.
Рассмотрим показанный правый круговой конус.
Если вертикальная плоскость пересекает конус, образуя два идентичных полуконуса, какова форма их поперечного сечения?
Опции:
а. прямоугольник
б. площадь
г.треугольник
г. круг
Ответ: c. треугольник
Пояснение:
Если разрезать вершину для создания двух одинаковых полуконусов, получится поперечное сечение, представляющее собой треугольник.
Стр. № 304
Вопрос 9.
Радиус круга указан в метрах. Какова длина окружности? Используйте 3,14 для π.
а. 25,12 м
г. 50,24 м
г. 200.96 м
г. 803,84 м
Ответ: б. 50,24 м
Пояснение:
Окружность = 2 πr = 2 π (8) = 16 (3.14) = 50,24 м
Вопрос 10.
Размеры фигуры указаны в миллиметрах. Какова площадь двумерной фигуры?
Опции:
а. 39 мм 2
б. 169 мм 2
c. 208 мм 2
d. 247 мм 2
Ответ: c. 208 мм 2
Пояснение:
Площадь квадрата = 13 x 13 = 169 мм 2
Площадь треугольника = 1/2 x 13 x 6 = 39 мм 2
Общая площадь фигуры = 169 + 39 = 208 мм 2
Вопрос 11.
Лесничий хочет определить радиус ствола дерева. Ее окружность составляет 8,6 футов. Каков радиус ствола с точностью до десятых долей фута?
Опции:
а. 1,4 фута
б. 2,7 футов
c. 4,3 фута
г. 17,2 футов
Ответ: а. 1,4 фута
Пояснение:
Окружность = 2 πr = 8,6 фута
r = 8,6 / 2 π = 1,4 фута
Вопрос 12.
Какая величина угла в градусах является дополнительной к углу 74 °?
Опции:
а.16 °
б. 74 °
с. 90 °
г. 106 °
Ответ: d. 106 °
Пояснение:
Сумма дополнительных углов = 180 °
x + 74 ° = 180 °
x = 106 °
Вопрос 13.
Каков объем в кубических сантиметрах прямоугольной призмы, имеющей длину 6,2 см, ширину 3,5 см и высоту 10 см?
Опции:
а. 19,7 см 3
б. 108,5 см 3
c. 217 см 3
г. 237,4 см 3
Ответ: c.217 см 3
Пояснение:
V = Bh
B = 6,2 x 3,5 = 21,7 см 2
h = 10 см
V = 21,7 x 10 = 217 см 3
Вопрос 14.
Внутренний дворик имеет форму круга с указанным диаметром.
Какова площадь дворика? Используйте 3,14 для π.
Опции:
а. 9 м 2
б. 28,26 м 2
г. 254,34 м 2
г. 1017,36 м 2
Ответ: c. 254,34 м 2
Пояснение:
Диаметр = 18 м
Радиус = 18/2 = 9 м
Площадь патио = πr 2 = 3.14 (9) 2 = 254,34 м 2
Вопрос 15.
Петра наполняет маленькую картонную коробку песком. Размеры коробки 3 дюйма на 4 дюйма на 2 дюйма.
а. Какой объем коробки?
______ в 3
Ответ: 24 из 3
Пояснение:
V = Bh
B = 3 x 4 = 12 дюймов 2
V = 12 x 2 = 24 дюймов 3
Вопрос 15.
б. Петра решает наклеить коробку на оберточную бумагу.Сколько оберточной бумаги ей нужно, чтобы покрыть все шесть сторон коробки?
______ в 2
Ответ: 76 из 2
Пояснение:
P = 2 (3) + 2 (4) = 6 + 8 = 14 дюймов
S = Ph + 2B = 14 x 2 + 2 x 24 = 76 дюймов 2
Вопрос 15.
c. У Петры есть вторая, более крупная коробка размером 6 на 8 на 4 дюйма. Во сколько раз больше объем второй коробки? Площадь поверхности?
Объем в _________ раз больше.
Площадь поверхности в _________ раз больше
Ответ: Площадь около 2.В 7 раз больше
Пояснение:
B = 6 x 8 = 48 дюймов 2
V = Bh = 48 x 4 = 192 дюймов 3
192/24 = 8
P = 2 (6) + 2 (8) = 12 + 16 = 28
S = Ph + 2B = 28 (4) + 2 (48) = 112 + 96 = 208 дюймов 2
208/76 = 2,7
Понимание окружности и площади круга План урока 7 класс
Обсуждение / Введение
Это третий урок из серии, посвященной кругам. Он следует Элементам Кругового плана урока для 7-го класса и Пониманию Плана урока Пи для 7-го класса.По завершении всех трех уроков учащиеся должны иметь твердое представление о том, что образует круг, что представляет собой число «пи» и как найти площадь и длину окружности круга. Этот урок требует, чтобы учащиеся чувствовали себя комфортно с пи, и позволяли дифференцировать и писать.
Объектив
- Учащиеся поймут, что пи — это отношение.
- Студенты смогут найти площадь и длину окружности.
- Учащиеся поймут связь между площадью квадрата и площадью круга.
Принадлежности
- Рабочий лист «Эффект пульсации»
- Калькуляторы
- Ножницы (1 пара на группу из 4 человек)
- Клей-карандаш (1 на группу из 4 шт.)
- 3 листа квадратной бумаги разного цвета (хорошо подходит бумага для оригами) на группу из 4 учеников
- Рабочий лист «Площадь круга»
- Складные фигурки учеников по кругу из последних двух занятий (начаты в «Элементы плана урока по кругу седьмого класса»)
Методология / процедура
Понимание окружности
- На этом этапе учащиеся должны понять следующие моменты.Если этот урок проводится в другой день, я рекомендую ознакомиться с этими ключевыми моментами, прежде чем начинать дневные уроки. Вся информация должна быть найдена на раскладушках учеников.
- Окружность — это расстояние по окружности.
- Диаметр — это расстояние по окружности, проходящей через центр.
- Радиус — это расстояние от любой точки окружности до центра.
- Диаметр в два раза больше радиуса.
- Пи — это соотношение.
- Пи можно округлить до 3.14.
- Разделите учащихся в группы по 4 человека и раздайте лист «Эффект ряби». Обратите внимание, что первые 2 страницы очень ориентированы. Для цифр могут потребоваться калькуляторы, но это все еще в строю. Последние две страницы могут быть использованы либо в качестве дополнительного материала, либо в качестве дополнительного домашнего задания / задания по вовлечению семьи.
- Добавьте информацию об окружности в складной круг.
- Домашнее задание / обзор для этого занятия может представлять собой рабочий лист по окружности.
Понимание площади круга
- Попросите учащихся остаться со своей четверкой из предыдущего задания.
- Раздайте каждой группе 3 одинаковых квадратных листа бумаги разных цветов, ножницы и клей-карандаш.
- Попросите 1 ученика из группы сложить один лист пополам, а затем еще раз пополам («снежинка»). С этого момента попросите ученика вырезать форму четверти круга. Будьте осторожны, чтобы они не отрезали сторону «открытого клапана».Это должен быть самый большой круг, чтобы дуга проходила в оба угла. Порекомендуйте, чтобы они были действительно широкими, иначе круг будет искажен. Вам понадобятся дополнительные листы под рукой. Приклейте этот круг поверх квадрата со складками по горизонтали и вертикали. (В комплект входит лист с изображениями вырезов квадрата / круга / ромба.)
- Попросите другого ученика сложить третий лист пополам, а затем еще раз пополам («складка снежинки»). Отсюда пусть ученик прорежет от одного угла до диагонального угла.Будьте осторожны, чтобы они не отрезали сторону «открытого клапана». Это должно сформировать ромб / ромб / квадрат. Приклейте этот ромбик поверх круга со складками по горизонтали и вертикали.
- Проведите в классе короткое обсуждение форм и напомните об их свойствах.
- Попросите другого ученика разрезать большую фигуру на четыре равные части. Каждый студент получит по одной части.
- В ходе обсуждения в классе задайте следующие вопросы:
- Какая у нас форма внизу?
- Если квадрат представляет наше целое, какая часть целого — треугольник? Откуда вы знаете?
- Площадь четверти круга больше или меньше площади треугольника? Откуда вы знаете?
- Так как площадь четверти круга больше площади треугольника, она больше или меньше ½ площади квадрата?
- Площадь четверти круга больше или меньше площади квадрата? Откуда вы знаете?
- Поскольку площадь четверти круга меньше площади квадрата, она больше или меньше 1 площади квадрата?
- Можем ли мы выразить это в форме сложного неравенства? Четверть круга больше _________ квадрата, но меньше __________ квадрата.
- Раздайте рабочий лист «Площадь круга»: попросите учащихся поработать в группе над первой половиной. Проведите в классе обсуждение обратной стороны.
- В качестве подведения итогов дня попросите учащихся добавить информацию о площади круга в свои Складные Круги.
- Домашнее задание / обзор для этого занятия может быть рабочим листом в области круга.
Скачать урок и распечатки
Общие основные стандарты
CCSS.MATH.CONTENT.7.G.B.4
- Знать формулы площади и длины окружности и использовать их для решения задач; дают неформальный вывод отношения между окружностью и площадью круга.
Обращается ко всем 8 стандартам математической практики
Интернет-ресурсы / дополнительные исследования
10 заданий по поиску площади и окружности круга
Площадь и окружность круга часто дают нашим ученикам первое представление о геометрии в течение года.Кроме того, похоже, что студенты впервые видят формулы при изучении этой темы. Обычно они не приходят к нам, понимая, как подставлять значения в формулы. Это означает, что мы должны научить их пользоваться формулами, а также находить площадь и длину окружности. Хотя это может показаться сложным, но самое замечательное в кругах и геометрии то, что они довольно легко поддаются применению. У нас определенно есть возможность дать ученикам возможность увидеть площадь и окружность на практике.Этот пост полон увлекательных, увлекательных занятий и заданий по окружности для учеников средней математики.
Иногда я слышу, как учителя говорят о том, следует ли им сначала учить площадь или окружность. Лично я считаю, что вы должны учить их вместе, и этот ученик действительно должен понимать различия. Слишком часто наши ученики делают что-то изолированно, а позже они не знают, что делать, потому что мы идем в другом порядке, или им приходится применять свои знания, не зная, что проблема — это «проблема области» или « проблема окружности ».Следующий список заданий предоставит вашим ученикам множество возможностей попрактиковаться в работе и решении задач, связанных с нахождением площади и окружности кругов.
Список мероприятий по площади и окружности:
Лабиринт
Бинго по площади и окружности
Лаборатория открытий
Практическое занятие по вырезанию круга
Мнемонический урок и упражнение
Рабочий лист площади и рабочий лист
Бумажная тарелка Activity
Онлайн-игра на запоминание окружности
Инструмент Online Circle
Опасность
Погрузимся в
Читая этот список, вы заметите, что некоторые задания подходят для звонарей, а другие — это игры для проверки всего класса.Вы найдете широкий спектр видов деятельности и возможных применений в вашем классе. Получайте удовольствие от изучения этих увлекательных занятий.
Студенты любят лабиринты, потому что для них нет больших ставок. Это дает им возможность практиковаться в непринужденной обстановке. Мы каждый день используем лабиринты в моей комнате в качестве звонка, и мне нравится тон, который они задают для класса.
Этот набор из 3 лабиринтов — один из моих любимых. Мне нравится тот факт, что в формуле кругов есть число «пи», а пироги — это круги.Это дает мне возможность использовать пироги в своей деятельности, а дети любят говорить о пирогах. Итак, я могу использовать свой клипарт с пирогом в этих лабиринтах. В одном из лабиринтов ученики находят площадь области, в следующем — окружность, а в последнем — и площадь, и окружность. Некоторые ответы даны в терминах числа пи, а другие ответы используют 3,14 в качестве приближения для числа пи.
Хотите еще больше БЕСПЛАТНЫХ лабиринтов, доставленных прямо на ваш почтовый ящик каждый месяц? Присоединяйтесь к клубу Math Idea Galaxy Maze of the Month Club, и каждый месяц вы будете получать эксклюзивные математические лабиринты, подобные приведенному выше, по электронной почте.
Да! Подпишите меня в клуб «Лабиринт месяца».
Если вы еще не в клубе, надеюсь увидеть вас там!
Одно из моих любимых занятий — вдохновлять коллег пробовать что-то новое. Я работаю в школе, где мои 12 лет преподавания меньше, чем у всех других учителей математического факультета. Мы ветеран ядро. У всех нас есть традиционная черта, и мы все пытались вырваться из нее, чтобы заинтересовать наших студентов. Одна из моих коллег, в частности, говорила мне, что ненавидит лото.Затем, буквально на днях, когда я вошел в ее класс, она играла со своим классом в бинго. Она даже разыграла небольшие призы. Было потрясающе видеть, как усердно трудятся за призы даже неохотные восьмиклассники.
Эта игра в бинго по площади и окружности кругов полна задач со словами. Студенты должны найти площадь и окружность с разными измерениями, а иногда и в единицах числа пи. Некоторые вопросы немного проще, когда нужно просто найти диаметр или радиус.Каждый вопрос основан на картинке: например, парень держит 10 коробок пиццы, собака ловит фрисби или девушка считает монеты. Мне нравится использовать эту игру для обзора всего класса в конце раздела. Попробуйте эту игру, и ваши ученики будут учиться весело и увлекательно.
Эта лаборатория по обнаружению областей и окружностей — одна из моих любимых. Лаборатории Discovery — отличный способ познакомить студентов с темой и позволить им найти закономерности и сделать выводы. Это помогает им усвоить знания и прочнее закрепить их в своем сознании.Что я понял с лабораториями открытий, так это то, что они должны быть очень сфокусированными, и студенты не должны пытаться изучить слишком много вещей одновременно. В этой лабораторной работе основное внимание уделяется выявлению различий между площадью и окружностью. Учащиеся будут работать над созданием концептуальной основы того, как окружность является одномерной, а площадь — двумерной.
Для этого задания ученики раскрашивают область, а затем используют викистики или пряжу, чтобы измерить окружность. Они аппроксимируют площадь квадратами на бумаге.Мы пока не используем формулы. Подсчитывая квадратные дюймовые квадраты, ученики действительно понимают, почему площадь измеряется в квадратных дюймах. Это дает им возможность действительно увидеть, что происходит, когда мы говорим о площади и окружности. Тогда у вас всегда есть опыт, к которому они могут вернуться, когда у них на лице появляется такое выражение: «Какая из них — площадь, а какая — окружность?» Вы можете узнать больше в этом пошаговом руководстве о том, как это упражнение знакомит учащихся с процессом открытия, в этом посте.
Я нашел это упражнение с вырезанным кружком в Правилах математики средней школы, но в нем не было кружков, которые можно было бы использовать. Итак, я создал свой собственный набор кругов, который вы можете скачать здесь. Студенты могут измерять круги линейкой и вычислять различные части круга. Он отлично подходит для математической станции или для практики с партнером.
Вы можете попросить учащихся вырезать круги, что займет у них больше времени, чем следовало бы, или они могут просто измерить их на бумаге.Кроме того, вы можете попросить их пометить круги с различными размерами или они могут использовать графический органайзер (включен в загрузку кругов) для анализа различных форм.
Мнемоника работает, потому что наш мозг любит структуру. Я не использую их много, но когда я найду тот, который помогает детям запомнить что-то вроде формул для площади и окружности круга, я воспользуюсь им. Несмотря на то, что я очень долго находил площадь и окружность круга, я все еще путаю две формулы, и мне приходится останавливаться и думать о них.
Многие студенты находятся в одной лодке. Не говоря уже о том, насколько важны такие вещи, как мнемонические устройства, для студентов, которым нужна дополнительная поддержка. Студенты, которые борются с управляющими функциями и организацией информации в своем мозгу, действительно процветают, когда у них есть способ запоминать. Вот где приходит на помощь замечательная мнемоническая стратегия от Джанин Халди из Owlcation. Я взяла эту идею и создала вкладыш для интерактивных записных книжек моих учеников.
Студенты помнят следующее высказывание:
Вишневый пирог восхитителен!
Яблочные пироги тоже!
Если они могут это запомнить, тогда они смогут придерживаться двух формул.Для этого мы используем графический органайзер (скачать здесь БЕСПЛАТНО) в нашей интерактивной записной книжке. Каждый день какое-то время мы тренируемся писать формулы на доске, произнося это утверждение, пока все не получат его. Иногда большое значение имеют мелочи.
Это упражнение с бумажной тарелкой из книги «Читающие друзья» привнесет в ваш класс немного искусства и визуальных упражнений. Студенты иногда с трудом запоминают части круга. Создание собственного красочного круга поможет им запомнить.В этом упражнении показано, как использовать бумажные тарелки для обзора словаря и формул, которые мы используем, когда говорим о площади и окружности круга.
Кроме того, вы можете попросить учащихся поделиться своими тарелками с другими людьми и поговорить с ними по математике. В конце занятия они могут повесить свои творения на стену и совершить прогулку по галерее, чтобы посмотреть на тарелки других людей. В сообщении в блоге, где мне пришла эта идея, это упражнение использовалось для Дня Пи, и они украшали тарелки как пирог. Я думаю, что его можно использовать во время Дня Пи или в любое время года, когда ваш прибор находится на площади и окружности кругов.
Если вам нужен предварительный набор, вы можете использовать эту онлайн-игру на запоминание окружности. Студенты могут играть сами или с партнером. Они должны найти окружность 6 разных кругов, а затем сыграть в игру на сопоставление памяти. Это мило и добавляет немного удовольствия их тренировкам.
Мне нравится этот онлайн-инструмент круга от Illuminations. У него три функции, и вам не нужно ничего готовить. В нем есть вводный экран, экран расследования и, наконец, есть некоторые практические проблемы.Вы можете открыть его на своем компьютере и показать студентам, что вы хотите, чтобы они делали на экране в передней части комнаты. Затем студенты могут работать самостоятельно или вместе с партнерами над исследованием и решением некоторых практических задач.
Когда они закончат упражнение, я прошу их написать отражение своего опыта использования этого инструмента. Это прекрасная возможность узнать, что учащиеся понимают в нахождении площади и окружности кругов.Кроме того, вы также можете увидеть некоторые заблуждения.
Мои дети любят делать обзоры, используя игры для всего класса. Jeopardy — одна из игр, в которую мы периодически играем. Эта игра Jeopardy дает студентам возможность попрактиковаться в нахождении радиуса, диаметра, площади и окружности. Я не играю в Jeopardy в командах. Когда я играю, все ученики пишут свои ответы на доске или SmartPal. Я считаю, что если каждый должен записывать ответы, он будет более ответственным. Это задание отлично подходит для дня, когда вы представляете тему, или за день до теста.
Попробуйте одно
В этом посте мы представили множество идей. Эти упражнения можно использовать для практики или повторения, и ваши ученики будут практиковаться в поиске площади и окружности круга. Моя задача — попробовать что-то одно. Просмотрите список и попробуйте что-нибудь новенькое. Я считаю, что когда я пробую что-то новое, это вовлекает меня в процесс обучения. Студенты оценят это, потому что они устают делать одно и то же снова и снова.Итак, удачи в вашем обучении или рассмотрении этой темы. Просто помните, великие учителя всегда совершенствуют свое мастерство. Я надеюсь, что вы нашли здесь несколько упражнений или инструментов, которые помогут вам вывести свои единицы измерения площади и окружности на новый уровень. Спасибо за прочтение! До скорого.
СвязанныеЗнать формулы площади и окружности круга и использовать их для решения задач; дают неформальный вывод отношения между окружностью и площадью круга.
MAFS.7.G.2.4 — Знать формулы площади и окружности круга и использовать их для решения задач; дают неформальный вывод отношения между окружностью и площадью круга.Веб-сайт несовместим с используемой вами версией браузера. Не все функции могут быть доступны. Пожалуйста, обновите ваш браузер до последней версии.
Знать формулы площади и окружности круга и использовать им решать проблемы; дать неформальный вывод отношений между окружностью и площадью круга.
Общая информация
Предметная область: Математика
Класс: 7
Домен-Поддомен: Геометрия
Кластер: Уровень 2: Базовое применение навыков и концепций
Дата принятия или изменения: 14.02
Дата последней оценки: 14.02
Статус: Утверждено Государственным советом
Оценено: Да
Образцы тестовых заданий (4)
- Тестовый элемент №: Образец задания 1
- Вопрос:
Показан круг с его размерами в сантиметрах (см).
Какова площадь круга в квадратных сантиметрах?
- Сложность: НЕТ
- Тип: EE: Редактор уравнений
- Тестовый элемент №: Образец задания 2
- Вопрос: Круг с размерами в дюймах (дюймах.), Показано.
Какова площадь половины круга в квадратных дюймах?
- Сложность: НЕТ
- Тип: EE: Редактор уравнений
- Тестовый элемент №: Образец задания 4
- Вопрос:
Длина окружности 53.38 сантиметров.
Какова площадь в квадратных сантиметрах? Используйте 3,14 для
- Сложность: НЕТ
- Тип: EE: Редактор уравнений
Связанные точки доступа
Альтернативная версия этого теста для учащихся со значительными когнитивными нарушениями.
Связанные ресурсы
Проверенные ресурсы преподаватели могут использовать для обучения концепциям и навыкам, связанным с этим тестом.
Уроки STEM — Образцовая деятельность по выявлению
Прототипы жевательной резинки Bubble Burst Corporation:Студенты будут вычислять скорость и длину окружности, сравнивать и упорядочивать десятичные дроби, конвертировать метрические единицы и округлять десятичные дроби.Корпорация Bubble Burst разработала несколько прототипов жевательной резинки и попросила студентов помочь в выборе прототипов жевательной резинки для массового производства, используя как количественные, так и качественные данные для ранжирования прототипов Bubble Burst Corporation.
Устройство плиточного пола:Этот MEA требует от студентов сформулировать основанное на сравнении решение проблемы, связанной с поиском наилучшего плана укладки плиточного пола с учетом различных аспектов.Студентам предоставляется контекст проблемы, письмо-запрос от клиента с просьбой дать рекомендацию и данные, относящиеся к ситуации. Учащиеся используют данные для создания надежного модельного решения для представления клиенту.
Формирующие оценки MFAS
Разбитые круги:Учащимся предлагается заполнить и объяснить неформальный вывод взаимосвязи между окружностью и площадью круга.
Формула площади круга:Учащимся предлагается написать формулу площади круга, объяснить, что представляет каждый символ, и обозначить радиус на диаграмме.
Формула окружности:Учащимся предлагается написать формулу длины окружности, объяснить, что представляет каждый символ, и обозначить переменные на диаграмме.
Оригинальные уроки по математике для учащихся — 6–8 классы
Пицца Пи: Площадь:В этом интерактивном руководстве узнайте, как вычислить площадь кругов в единицах числа «Пи» и с помощью аппроксимации числа «Пи».Вы также столкнетесь с ситуациями с неправильной площадью, которые потребуют использования формулы площади круга.
Пицца Пи: Окружность:Исследуйте происхождение числа Пи как отношения окружности к диаметру круга. В этом интерактивном руководстве вы будете работать с формулой окружности, чтобы определить длину окружности, и работать в обратном направлении, чтобы определить диаметр и радиус окружности.
Плавание кругами:В этом интерактивном руководстве научитесь решать задачи, связанные с окружностью и площадью бассейнов в форме круга.
Ресурсы для учащихся
Ресурсы, прошедшие проверку, учащиеся могут использовать для изучения концепций и навыков, используемых в этом тесте.
Оригинальные учебные пособия для студентов
Пицца Пи: Окружность:Исследуйте происхождение числа Пи как отношения окружности к диаметру круга. В этом интерактивном руководстве вы будете работать с формулой окружности, чтобы определить длину окружности, и работать в обратном направлении, чтобы определить диаметр и радиус окружности.
Тип: Оригинальное учебное пособие для учащихся
Пицца Пи: Площадь:В этом интерактивном руководстве узнайте, как вычислить площадь кругов в единицах числа «Пи» и с помощью аппроксимации числа «Пи». Вы также столкнетесь с ситуациями с неправильной площадью, которые потребуют использования формулы площади круга.
Тип: Оригинальное учебное пособие для учащихся
Плавание кругами:В этом интерактивном руководстве научитесь решать задачи, связанные с окружностью и площадью бассейнов в форме круга.
Тип: Оригинальное учебное пособие для учащихся
Перспективы видео: эксперт
Задача по решению проблем
Восемь кругов:Учащимся предлагается найти площадь затененной области, используя диаграмму и предоставленную информацию.Цель этого задания — улучшить понимание учащимися местности.
Тип: Задача по решению проблем
Учебники
Окружность круга:В этом видео показано, как найти длину окружности, расстояние по окружности, учитывая площадь.
Тип: Учебное пособие
Площадь круга:В этом видео вы увидите, как мы находим площадь круга при заданном диаметре.
Тип: Учебное пособие
Виртуальный манипулятор
Инструмент Круг:Этот апплет позволяет студентам исследовать отношения между площадью и длиной окружности круга, его радиусом и диаметром.На сайте три раздела: Введение, Исследование и Проблемы.
- Во вводном разделе учащиеся могут изменять размер круга и видеть, как это влияет на радиус, диаметр и длину окружности. Учащиеся также могут воспроизвести видеоклип, чтобы наглядно увидеть, как связаны эти измерения.
- Раздел «Исследование» позволяет учащимся собирать точки данных, перетаскивая радиус круга на разную длину, и записывать в таблицу данные для радиуса, диаметра, окружности и площади.Нажатие кнопки x / y позволяет учащимся изучить взаимосвязь между любыми двумя показателями. При нажатии на кнопку графика студенты переходят к графику данных. Они могут нанести любой из четырех показателей на ось x против любого из четырех показателей на оси y.
- Раздел «Задачи» содержит вопросы, которые ученики должны решить, и записать свои ответы в правильном блоке.
(Подсветка NCTM)
Тип: виртуальный манипулятор
Ресурсы для родителей
Проверенные ресурсы, которые могут использовать воспитатели, чтобы помочь учащимся изучить концепции и навыки, используемые в этом тесте.
Перспективы видео: эксперт
Задача по решению проблем
Восемь кругов:Учащимся предлагается найти площадь затененной области, используя диаграмму и предоставленную информацию.Цель этого задания — улучшить понимание учащимися местности.
Тип: Задача по решению проблем
Видео / Аудио / Анимация
История Пи:Это видео динамически показывает, как работает Pi и как он используется.
Тип: видео / аудио / анимация
Виртуальный манипулятор
Круг:Этот интерактивный урок знакомит студентов с кругом, его атрибутами и формулами для определения его окружности и площади.Затем учащиеся выполняют несколько вычислений, чтобы попрактиковаться в определении площади и длины окружности кругов с учетом диаметра.
Тип: виртуальный манипулятор
Загрузка….
| Вы здесь: Главная → Рабочие листы → Круг Этот генератор создает рабочие листы для вычисления радиуса, диаметра, длины окружности или площади круга, если задан один из них (задан радиус, диаметр, окружность или площадь). Они могут быть выполнены в форматах PDF или html. Вариантов множество: вы можете выбрать метрические или обычные единицы измерения или и то, и другое, вы можете включать или не включать простые изображения круга в задачи или случайным образом позволить некоторым задачам иметь изображение круга, а некоторым нет. Вы также можете выбрать 3,14 или 3,1416 в качестве значения Пи в расчетах, а затем выбрать точность округления для ответов. Измените различные параметры, чтобы увидеть, каков их эффект. После того, как вы создали рабочий лист, вы можете просто обновить страницу из окна браузера (или нажать F5), чтобы получить другой рабочий лист с другими проблемами, но с теми же параметрами. Все рабочие листы имеют ключ ответа. Вы можете распечатать рабочий лист прямо из браузера или сохранить его на диск с помощью команды «Сохранить как» в браузере. Если проблемы на листе не умещаются на странице или на нем недостаточно рабочего места, выберите меньший шрифт, меньше полей для ячеек или меньшее количество столбцов с проблемами. Примеры рабочих листов (окружность, диаметр, радиус, площадь круга)Круглые Рабочие Листы
Вот простой способ подготовить студентов к формальной геометрии. Ключ к геометрии Рабочие тетради знакомят учащихся с широким спектром геометрических открытий, поскольку они делают пошаговые построения. Используя только карандаш, циркуль и линейку, учащиеся начинают с рисования линий, деления углов пополам и воспроизведения сегментов. Позже они создают сложные конструкции, включающие более дюжины шагов, и им предлагается сформулировать свои собственные обобщения. Когда они закончат, учащиеся познакомятся со 134 геометрическими терминами и будут готовы к формальным доказательствам. => Узнать больше |
Как рассчитать окружность и площадь круга
Ключевые термины
o Круг
o Эквидистант
o Радиус
o Диаметр
o Окружность
o Pi ( π )
Цели
o Определите некоторые основные части круга, такие как радиус и диаметр
o Вычислить длину окружности
o Вычислить площадь круга
В этой статье мы рассмотрим геометрическую фигуру, которая не состоит из отрезков прямых, а вместо этого изогнута: круг.Мы применим то, что мы знаем об алгебре, к изучению окружностей и тем самым определим некоторые свойства этих фигур.
Знакомство с кругами
Представьте себе точку P , имеющую определенное местоположение; Затем представьте все возможные точки, которые находятся на некотором фиксированном расстоянии r от точки P. . Некоторые из этих точек проиллюстрированы ниже. Если бы мы нарисовали все (бесконечное количество) точек, которые находятся на расстоянии r от P, , мы получили бы круг, который показан ниже сплошной линией.
Таким образом, круг — это просто набор всех точек , находящихся на одинаковом расстоянии (то есть на одинаковом расстоянии) от центральной точки ( P в приведенном выше примере). Расстояние r от центра круга до самого круга называется радиусом ; Диаметр в два раза больше (2 r ) называется диаметром . Радиус и диаметр показаны ниже.
Окружность круга
Как и в случае с треугольниками и прямоугольниками, мы можем попытаться вывести формулы для площади и «периметра» круга.В отличие от треугольников, прямоугольников и других подобных фигур, расстояние по внешней стороне круга называется окружностью , а не периметром — однако концепция, по сути, та же. Однако вычислить длину окружности не так просто, как вычислить периметр прямоугольника или треугольника. Учитывая, что объект в реальной жизни имеет форму круга, один из подходов может заключаться в том, чтобы ровно один раз обернуть нить вокруг объекта, а затем выпрямить нить и измерить ее длину.Такой процесс проиллюстрирован ниже.
Очевидно, что по мере увеличения диаметра (или радиуса) круга круг становится больше, и, следовательно, длина окружности также увеличивается. Нас заставляют думать, что, следовательно, существует некоторая взаимосвязь между окружностью и диаметром. Оказывается, если мы измеряем длину окружности и диаметр любого круга, мы всегда обнаруживаем, что длина окружности чуть более чем в три раза больше диаметра.Два примера окружностей ниже иллюстрируют эту точку, где D — диаметр, а C — длина окружности каждого круга.
Опять же, в каждом случае длина окружности чуть больше трех диаметров круга. Если мы разделим длину окружности любого круга на его диаметр, мы получим постоянное число. Эта константа, которую мы обозначаем греческим символом π ( pi ), приблизительно равна 3.141593. Точное значение π неизвестно, и есть подозрение, что пи — иррациональное число (неповторяющееся десятичное число, которое, следовательно, не может быть выражено в виде дроби с целым числителем и целым знаменателем). Давайте запишем упомянутую выше взаимосвязь: частное окружности ( C ), деленное на диаметр ( D ), является постоянным числом π.
Мы можем получить выражение для окружности через диаметр, умножив обе части выражения выше на D, , таким образом выделив C.
Поскольку диаметр в два раза больше радиуса (другими словами, D = 2 r ), мы можем заменить 2 r на D в приведенном выше выражении.
Таким образом, мы можем вычислить длину окружности, если мы знаем радиус круга (или, следовательно, его диаметр).Для большинства вычислений, требующих десятичного ответа, часто достаточно оценки π как 3,14. Например, если круг имеет радиус 3 метра, тогда его окружность C будет следующей.
Ответ выше точный (хотя он написан в терминах символа π ). Если нам нужен приблизительный числовой ответ, мы можем оценить π как 3.14. Затем,
Символ ≈ просто означает «примерно равно».
Практическая задача : Окружность имеет радиус 15 дюймов. Какая у него окружность?
Решение : Начнем с рисования диаграммы ситуации. Этот подход может быть очень полезным, особенно в ситуациях, связанных с кругами, где радиус и диаметр легко спутать.
Поскольку нам дан радиус, мы должны либо вычислить длину окружности ( C ), используя выражение в терминах радиуса, либо мы должны преобразовать радиус в диаметр (удвоенный радиус) и использовать выражение в терминах диаметр. Для простоты воспользуемся первым подходом.
Это точный результат. Если нам нужен приблизительный десятичный результат, мы можем использовать π ≈ 3.14.
Площадь круга
Так же, как вычисление длины окружности сложнее, чем у треугольника или прямоугольника, так вычисляется и площадь. Давайте попробуем оценить площадь круга, нарисовав круг внутри квадрата, как показано ниже. Область круга заштрихована.
Нарисуем в окружности вертикальный и горизонтальный диаметры; мы обозначим эти диаметры как имеющие длину D. Обратите внимание на то, что по сравнению с квадратом, квадрат также должен иметь стороны длиной D .
Мы знаем, что квадрат (который представляет собой прямоугольник, длина и ширина которого равны) со сторонами длиной D имеет следующую площадь A квадрат (обратите внимание, что мы добавляем нижний индекс, чтобы идентифицировать эту область как площадь квадрат — аналогичный индекс добавим в случае площади круга):
Поскольку круг диаметром D , очевидно, имеет меньшую площадь, чем квадрат со сторонами длиной D, , мы знаем, что площадь круга должна быть меньше D 2 .Осмотрев, мы можем предположить, что площадь A круга круга составляет примерно три четверти площади квадрата. Таким образом,
Как оказалось, это предположение близко к реальному результату. Посредством некоторой более сложной математики, которая выходит за рамки учебника, можно показать, что площадь круга в точности следующая:
Обратите внимание, что снова появляется число π .Давайте теперь сравним этот точный результат с нашим предположением сверху. Мы просто немного изменим выражение, имея в виду, что радиус ( r ) равен половине диаметра ( D ), другими словами, D = 2 r.
Так как D = 2 r, , то
Подставим это значение для r в выражение для площади круга; мы должны сделать замену дважды.Затем мы можем несколько упростить выражение.
Так как π приблизительно равно 3,14, то
Таким образом, наше предположение было очень близко к фактической площади!
Практическая задача : Диаметр круга 6 сантиметров.Какая у него площадь?
Решение : Обратите внимание на то, что указан диаметр , а не радиус. Таким образом, если мы хотим использовать выражение для площади в терминах радиуса, мы должны преобразовать диаметр в радиус (просто разделив диаметр пополам).
Теперь мы можем рассчитать площадь по следующей формуле.
Опять же, 9 квадратных сантиметров точный. Но,
Это приблизительный результат, но его будет достаточно во многих контекстах.
Практическая задача : Окружность окружности составляет 8 π футов.Какая у него площадь?
Решение : Мы узнали, что длина окружности тесно связана с радиусом (и диаметром).