| 1. |
Перемена знаков числителя и знаменателя дроби
Сложность: лёгкое |
1 |
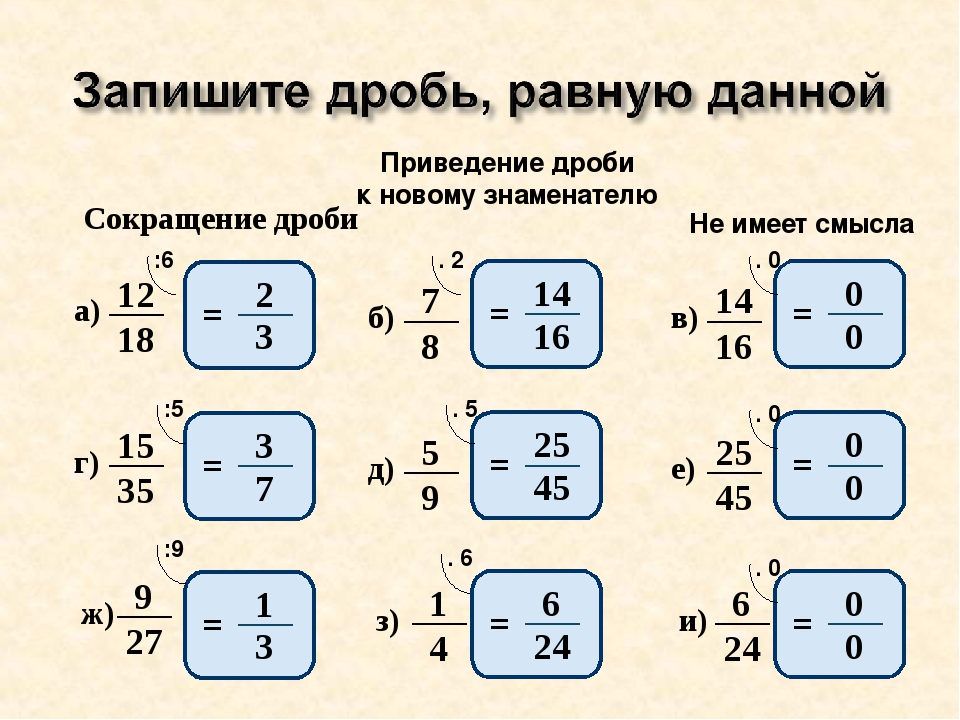
| 2. |
Сокращение алгебраической дроби, вынесение общего множителя за скобки
|
2 |
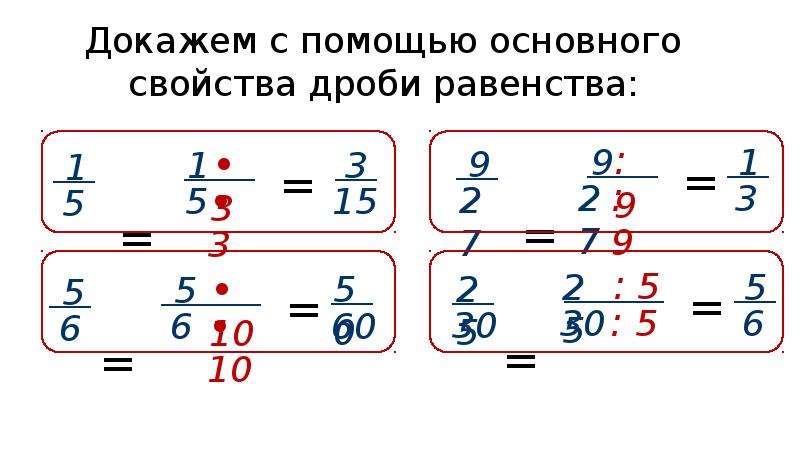
3.
|
Расширение алгебраической дроби (неизвестный числитель)
Сложность: лёгкое |
1,5 |
| 4. |
Расширение дроби
Сложность: среднее |
2 |
5. |
Общий знаменатель (противоположные знаменатели)
Сложность: среднее |
4 |
| 6. |
Дроби с одинаковыми знаменателями
Сложность: среднее |
3 |
7.
|
Дроби с общим знаменателем (две дроби)
Сложность: среднее |
4 |
| 8. |
Дроби с общим знаменателем (разность квадратов)
Сложность: среднее |
6 |
9.
|
Дроби с общим знаменателем (три дроби, разность квадратов)
Сложность: среднее |
4 |
| 10. |
Сокращение алгебраической дроби, разложение на множители способом группировки
Сложность: среднее |
3 |
11.
|
Дроби с одинаковыми знаменателями (общий множитель, способ группировки)
Сложность: сложное |
7 |
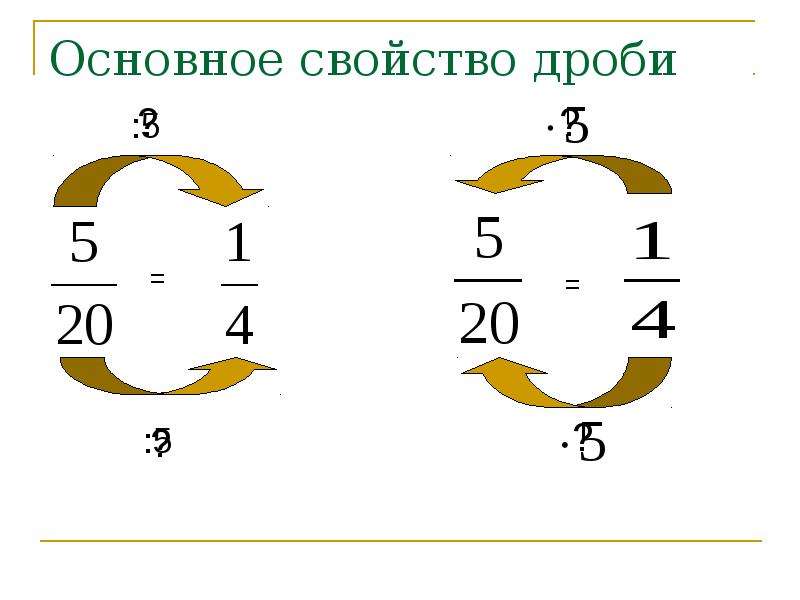
Тест «Основное свойство дроби» 5 класс
Тест «Основное свойство дроби» 5 класс * Обязательно
Фамилия Имя, класс *
1.Какие из представленных дробей правильные? 4/3; 99/101; 5/6; 8/7; 3/3; *
б)99\101
в)5\6
г)8\7
д)3\3
2.Какая из следующих дробей является неправильной? *
а)77/80
б)99/59
в)100/101
г)39/50
3.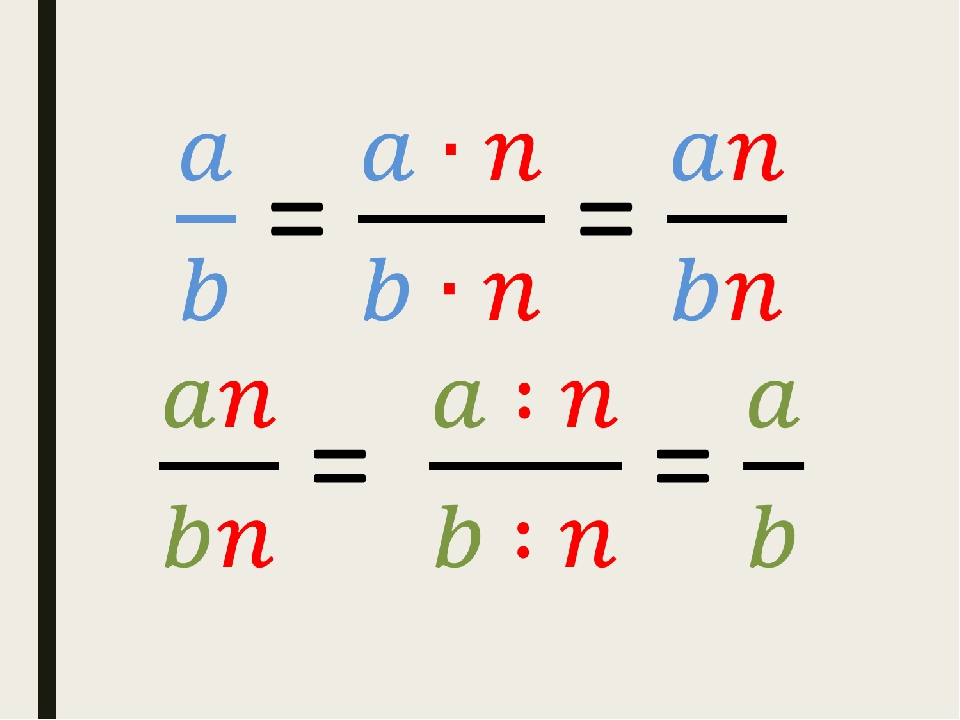 В саду растут яблони и груши. Груши составляют 3\7 всех деревьев. Какую часть всех деревьев составляют яблони? *
В саду растут яблони и груши. Груши составляют 3\7 всех деревьев. Какую часть всех деревьев составляют яблони? *
а)3/7
б)4/7
в)5/7
г)7/7
4.В коробке 5 зеленых карандашей и 6 красных. Какую часть всех карандашей составляют красные? *
а)6/5
б)5/6
в)6/11
г)5/11
5.На полке 40 книг, 5\8 из них учебники. Сколько учебников на полке?
Ответ:______________________________________________________________
6.Чему равна длина отрезка, если 1\10 его длины составляет 9 см *
Ответ:______________________________________________________________
7.Представьте дробь 3/5 в виде дроби со знаменателем 15 и выберите правильный ответ:6/15; 8/15; 9/15; 12/15; 15/15; *
а)1/15
б)8/15
в)9/15
г)12/15
д)15/15
8.Какие из представленных дробей равны дроби 8/12 ? 4/6; 6/8; 2/3; 5/6; 16/24; *
а)4/6
б)6/8
в)2/3
г)5/6
д)16/24
9. Какое число нужно написать в числителе, чтобы равенство стало верным? 21/49=?/7 *
Какое число нужно написать в числителе, чтобы равенство стало верным? 21/49=?/7 *
Ответ:___________________________________________________________
10.На плане одного из районов города клетками изображены кварталы, каждый из которых имеет форму квадрата со стороной 150 м. Ширина всех улиц в этом районе — 25 м. Найдите длину пути от точки А до точки В, изображенных на плане. *
Ответ:______________________________________________________________________
Сравнительный анализ тональности комментариев в YouTube (осторожно, ненормативная лексика)
Привет! Чем еще заняться на каникулах любителю Data Scienсe как не анализом тональности комментариев под новогодними обращениями?! На эту мысль меня натолкнули алгоритмы YouTube, выдавшие к просмотру первого января 2022 года два видео, с очень разными по эмоциональной окраске комментариями.
Тогда я подумал, что пошаговый разбор решения задачи классификации этих комментариев по их тональности мог бы стать довольно наглядным примером для знакомства с базовыми техниками обработки естественного языка, а о том, насколько это получилось предлагаю судить вам.
Итак, в процессе классификации наших комментов мы поучимся :
Писать парсер комментариев YouTube
Предобрабатывать тексты для их последующего анализа
Получать частотность слов в наборах текстов
Создавать красивые графики «облака тэгов»
Находить размеченные наборы текстов и оценивать их пригодность для задачи
Получать векторные представления текстов bag of words и TF-IDF
Классифицировать комментарии с помощью логистической регрессии
Оценивать качество классификации с помощью графиков ROC-кривых и матрицы ошибок
Визуализировать наиболее важные для классификации слова
Применять полученный классификатор для анализа тональности комментариев
A для работы нам понадобится только: компьютер, доступ в интернет, настроенная среда Jupyter Notebook и пару вечеров свободного времени.
Все материалы и код используемые в этой статье я выложил в github, a для тех, кому удобнее смотреть чем читать, записал видео-туториал c разбором кода на своем канале:
Парсинг комментариев
Для парсинга комментариев воспользуемся python библиотекой Selenium которая с помощью модуля WebDriver позволяет автоматизировать действия в браузере предоставляя для их реализации API. Для того чтобы парсить комментарии с видео в YouTube c помощью API WebDriver необходимо дополнительно скачать драйвер для того браузера в котором вы хотели бы производить действия, в нашем случае это ChromeDriver, кратко разберем код парсера, который я подсмотрел тут
Для того чтобы парсить комментарии с видео в YouTube c помощью API WebDriver необходимо дополнительно скачать драйвер для того браузера в котором вы хотели бы производить действия, в нашем случае это ChromeDriver, кратко разберем код парсера, который я подсмотрел тут
# Импортируем webdriver
from selenium import webdriver
# Импортируем визуализатор счетчика итераций
from tqdm import tqdm
# Создаем список для результатов парсинга
scrapped = []
# Инициализируем наш экземпляр webdriver
with webdriver.Chrome(executable_path =\
# указываем путь к .exe файлу драйвера Google Chrome
'/path_chrome_driver/chromedriver.exe'
) as driver:
# Указываем время ожидания в секундах и URL видео
wait = webdriver.support.ui.WebDriverWait(driver,1)
driver.get("https://www.youtube.com/watch?v=wCycCRk_Eak")
# Задаем количество прокруток для загрузки комментариев
# для сбора более чем 3300 комментариев мне было достаточно
# 200 итераций
for item in tqdm(range(200)):
wait.
until(webdriver.support.expected_conditions\
.visibility_of_element_located(
(By.TAG_NAME, "body")))\
.send_keys(webdriver.common.keys.Keys.END)
# Указываем время ожидания в секундах после каждой прокрутки
time.sleep(2)
# Получаем комментарии по тэгу "#content"
for comment in wait.until(webdriver.support.expected_conditions\
.presence_of_all_elements_located(
(By.CSS_SELECTOR, "#content"))):
# Добавляем тексты комментариев в список
scrapped.append(comment.text) Если вы все сделаете правильно, то после запуска кода у вас откроется окошко с браузером и начнет смотреть видео прокручивая и собирая комментарии.
Предобработка текстов комментариев и визуализация частотности слов
Любые исходные данные это руда которую нужно обрабатывать и после того как мы получили комментарии их также необходимо очистить чтобы с ними можно было работать дальше. А-яЁё]+’, ‘ ‘, text).lower()
return ‘ ‘.join(clear_text.split()) # напишем функцию удаляющую стоп-слова
def clean_stop_words(text : str,
stopwords : list):
«»»
Функция получает:
* text — строчку текста
* stopwords — список стоп слов для исключения
из текста Возвращает строчку текста с исключенными стоп словами «»»
text = [word for word in text.split() if word not in stopwords]
return » «.join(text)
А-яЁё]+’, ‘ ‘, text).lower()
return ‘ ‘.join(clear_text.split()) # напишем функцию удаляющую стоп-слова
def clean_stop_words(text : str,
stopwords : list):
«»»
Функция получает:
* text — строчку текста
* stopwords — список стоп слов для исключения
из текста Возвращает строчку текста с исключенными стоп словами «»»
text = [word for word in text.split() if word not in stopwords]
return » «.join(text)
Выведем пару примеров обработки текстов:
# Протестируем работу функции очистки текста
for _ in range(3):
text = comments_shulman_df.sample(n = 1)['comment'].values[0][:70]
print(text)
print('=======================================')
print(clean_stop_words((clear_text(text)), stopwords))
print()
>>>
Спасибо️
=======================================
спасибо
С Новым годом! Именно такие слова и такое пожелание я хотела услышать!
=======================================
новым годом именно такие слова такое пожелание хотела услышать
Спасибо, Екатерина Михайловна! Прекрасные слова. =======================================
спасибо екатерина михайловна прекрасные слова
=======================================
спасибо екатерина михайловна прекрасные словаЛемматизация текстов
Лемматизация — приведение всех слов текста к их леммам — изначальным формам:
для существительных — именительный падеж, единственное число;
для прилагательных — именительный падеж, единственное число, мужской род;
для глаголов, причастий, деепричастий — глагол в инфинитиве (неопределённой форме) несовершенного вида.
Лемматизация позволяет еще больше универсализировать наши тексты, привести их так сказать к общему знаменателю, но тут есть и обратная сторона — лишая наши предложения падежей и времен мы теряем достаточно много информации которая может содержать эмоциональную окраску.
При решении конкретно этой задачи лемматизация оказала хоть и не значительное но негативное влияние на качество классификации, поэтому в примерах далее мы будем использовать не лемматизированые тексты.
Но возможно в других задачах лемматизация может оказаться полезной, поэтому давайте напишем функцию для лемматизации, использующую библиотеку от Яндекса pymystem3. У этой библиотеки есть некоторые сложности с параллелизацией запросов, поэтому для ускорения обработки больших массивов приходится несколько исхитрятся и объединять сразу большое количество текстов в батч вставляя перед этим символ разделения затем получая результат лемматизации извлекать его обратно получая исходные тексты. Кстати это решение я подсмотрел тут же, на Хабре.
У этой библиотеки есть некоторые сложности с параллелизацией запросов, поэтому для ускорения обработки больших массивов приходится несколько исхитрятся и объединять сразу большое количество текстов в батч вставляя перед этим символ разделения затем получая результат лемматизации извлекать его обратно получая исходные тексты. Кстати это решение я подсмотрел тут же, на Хабре.
import numpy as np
import pandas as pd
from pymystem3 import Mystem
from tqdm import tqdm
def lemmatize(df : (pd.Series, pd.DataFrame),
text_column : (None, str),
n_samples : int,
break_str = 'br',
) -> pd.Series:
"""
Принимает:
df -- таблицу или столбец pandas содержащий тексты,
text_column -- название столбца указываем если передаем таблицу,
n_samples -- количество текстов для объединения,
break_str -- символ разделения, нужен для ускорения,
количество текстов записанное в n_samples объединяется
в одит большой текст с предварительной вставкой символа
записанного в break_str между фрагментами
затем большой текст лемматизируется, после чего разбивается на
фрагменты по символу break_str
Возвращает:
Столбец pd. Series с лемматизированными текстами
в которых все слова приведены к изначальной форме:
* для существительных — именительный падеж, единственное число;
* для прилагательных — именительный падеж, единственное число,
мужской род;
* для глаголов, причастий, деепричастий — глагол в инфинитиве
(неопределённой форме) несовершенного вида.
"""
result = []
m = Mystem()
if df.shape[0] % n_samples == 0 :
n_iterations = df.shape[0] // n_samples
else:
n_iterations = (df.shape[0] // n_samples) + 1
for i in tqdm(range(n_iterations)) :
start = i * n_samples
stop = start + n_samples
sample = break_str.join(df[text_column][start : stop].values)
lemmas = m.lemmatize(sample)
lemm_sample = ''.join(lemmas).split(break_str)
result += lemm_sample
return pd.Series(result, index = df.
Series с лемматизированными текстами
в которых все слова приведены к изначальной форме:
* для существительных — именительный падеж, единственное число;
* для прилагательных — именительный падеж, единственное число,
мужской род;
* для глаголов, причастий, деепричастий — глагол в инфинитиве
(неопределённой форме) несовершенного вида.
"""
result = []
m = Mystem()
if df.shape[0] % n_samples == 0 :
n_iterations = df.shape[0] // n_samples
else:
n_iterations = (df.shape[0] // n_samples) + 1
for i in tqdm(range(n_iterations)) :
start = i * n_samples
stop = start + n_samples
sample = break_str.join(df[text_column][start : stop].values)
lemmas = m.lemmatize(sample)
lemm_sample = ''.join(lemmas).split(break_str)
result += lemm_sample
return pd.Series(result, index = df. index)
index)Выведем несколько результатов работы функции:
поздравление здорового человека
======================================================================
поздравление здоровый человек
здоровья вашей семье спасибо екатерина михайловна новым годом
======================================================================
здоровье ваш семья спасибо екатерина михайловна новый год
новым годом екатерина михайловна благодаря эта настойчивость
======================================================================
новый год екатерина михайловна благодаря этот настойчивостьВизуализация частотности слов. Облако тэгов «Word cloud»
Визуализация данных — это большая часть Data Science и важна не только в качестве презентации результатов, но и в как важный инструмент при анализе данных. Глядя на гистограммы, боксплоты или тепловые карты корреляций можно очень быстро получить представление о том с какими выборками мы имеем дело и какие зависимости могут быть в наших данных, да и просто это как правило очень красиво.
Посмотрим на визуализацию 100 наиболее частотных слов, уникальных для каждого набора наших обработанных наборов комментариев.
Разберем подробнее как получить такой график. Для начала нам нужно пройтись по каждому набору текстов и посчитать частоту встречаемости каждого уникального слова.
Несложно написать соответсвующую функцию, но мы воспользуемся уже готовым классом CountVectorizer из библиотеки scikit-learn:
import numpy as np
import pandas as pd
from sklearn.feature_extraction.text import CountVectorizer
# Для каждого коруса текстов инциализируем свой экземпляр класса
shulman_counter = CountVectorizer(ngram_range=(1, 1))
putin_counter = CountVectorizer(ngram_range=(1, 1))
# Получаем словарь уникальных слов (fit)
# и сразу же считаем частотность для каждого текста (transform)
shulman_count = shulman_counter.fit_transform(comments_shulman_df['text_clear'])
putin_count = putin_counter.fit_transform(comments_putin_df['text_clear'])
shulman_frequence = pd. DataFrame(
# получаем словарь из CountVectorizer
# c помощью .get_feature_names_out()
{'word' : shulman_counter.get_feature_names_out(),
# получаем частотность слов
# находя сумму компонент векторов
'frequency' : np.array(shulman_count.sum(axis = 0))[0]
}).sort_values(by = 'frequency', ascending = False)
putin_frequence = pd.DataFrame(
{'word' : putin_counter.get_feature_names_out(),
'frequency' : np.array(putin_count.sum(axis = 0))[0]
}).sort_values(by = 'frequency', ascending = False)
# Убираем с помощью запроса пересекающиеся слова
# Оставляем 100 наиболее частотных
putin_frequence_filtered = putin_frequence\
.query('word not in @shulman_frequence.word')[:100]
shulman_frequence_filtered = shulman_frequence\
.query('word not in @putin_frequence.word')[:100]
DataFrame(
# получаем словарь из CountVectorizer
# c помощью .get_feature_names_out()
{'word' : shulman_counter.get_feature_names_out(),
# получаем частотность слов
# находя сумму компонент векторов
'frequency' : np.array(shulman_count.sum(axis = 0))[0]
}).sort_values(by = 'frequency', ascending = False)
putin_frequence = pd.DataFrame(
{'word' : putin_counter.get_feature_names_out(),
'frequency' : np.array(putin_count.sum(axis = 0))[0]
}).sort_values(by = 'frequency', ascending = False)
# Убираем с помощью запроса пересекающиеся слова
# Оставляем 100 наиболее частотных
putin_frequence_filtered = putin_frequence\
.query('word not in @shulman_frequence.word')[:100]
shulman_frequence_filtered = shulman_frequence\
.query('word not in @putin_frequence.word')[:100]Затем мы обращаемся к функции WordCloud и передаем ей словарь с частотой слов, по которым она генерирует красивые картинки, которые мы в свою очередь выводим на экран с помощью библиотеки matplotlib. pyplot
pyplot
from wordcloud import WordCloud
import matplotlib.pyplot as plt
# Генерируем красивые картинки со словами
# на которых размер шрифта соответствует частотности
wordcloud_shulman = WordCloud(background_color="black",
colormap = 'Blues',
max_words=200,
mask=None,
width=1600,
height=1600)\
.generate_from_frequencies(
dict(putin_frequence_filtered.values))
wordcloud_putin = WordCloud(background_color="black",
colormap = 'Oranges',
max_words=200,
mask=None,
width=1600,
height=1600)\
.generate_from_frequencies(
dict(shulman_frequence_filtered.values))
# Выводим картинки сгенерированные вордклаудом
# С помощью matplotlib. pyplot
fig, ax = plt.subplots(1, 2, figsize = (20, 12))
ax[0].imshow(wordcloud_shulman, interpolation='bilinear')
ax[1].imshow(wordcloud_putin, interpolation='bilinear')
ax[0].set_title('title_1',
fontsize = 20
)
ax[1].set_title('title_2',
fontsize = 20
)
ax[0].axis("off")
ax[1].axis("off")
plt.show()
pyplot
fig, ax = plt.subplots(1, 2, figsize = (20, 12))
ax[0].imshow(wordcloud_shulman, interpolation='bilinear')
ax[1].imshow(wordcloud_putin, interpolation='bilinear')
ax[0].set_title('title_1',
fontsize = 20
)
ax[1].set_title('title_2',
fontsize = 20
)
ax[0].axis("off")
ax[1].axis("off")
plt.show()Классификация комментариев по эмоциональной окраске
Хорошо, мы предобработали и немного поиграли с нашими текстами, теперь можем перейти к решению задачи sentiment analysis. В нашем случае сведем решение этой задачи к задаче бинарной классификации, то есть присвоению каждому комментарию числовой метки в интервале от 0 до 1, где 0 будет соответствовать негативному комментарию, а 1 позитивному. Верхнеуровнево наметим план решения задачи:
Поиск похожего набора текстов с размеченными интонациями
Проведение обработки текстов размеченного датасета
Получение векторных представлений текстов
Обучение классификатора на полученных векторах
Оценка качества полученного классификатора
Классификация комментариев с помощью обученной модели
Оценка адекватности полученной классификации
Поиск подходящего датасета для обучения
Это очень важный этап от которого зависит качество всех последующих результатов. При поиске датасета для задачи анализа тональности текстов важно учесть что лексикон — набор специфических слов и устойчивых выражений может сильно зависеть от конкретной площадки.
При поиске датасета для задачи анализа тональности текстов важно учесть что лексикон — набор специфических слов и устойчивых выражений может сильно зависеть от конкретной площадки.
Например для оценки комментариев нам точно не подойдет корпус текстов новостей, поскольку это довольно сильно отличающиеся тексты, в новостях как правило вы не найдете нецензурных слов, там будет гораздо меньше слов с ошибками и интернет слэнга.
Перебрав в течении часа не слишком большой набор доступных датасетов с русскоязычными текстами я в итоге остановился на наборе состоящем из 114,911 положительных, 111,923 отрицательных постов Twitter сделанных на русском языке за период с конца ноября 2013 года до конца февраля 2014 года, которые были автоматически размечены на два класса positive и negative (ссылка на источник https://study.mokoron.com/). Вот так выглядит набор данных после аналогичной предобработки и объединения всех комментариев в одну таблицу:
Всего в корпусе позитивных комментариев употребляется 100 143 слова, а в корпусе позитивных — 119 363. Посмотрим на 100 наиболее частотных слов специфичных для каждого класса комментариев:
Посмотрим на 100 наиболее частотных слов специфичных для каждого класса комментариев:
Получение векторных представлений мешок слов и TF-IDF
Чтобы производить обучение классификатора нам для начала необходимо будет преобразовать каждый текст в набор чисел. От способа, которым тексты переводятся в численные вектора очень сильно зависит качество классификации. Один такой способ мы уже рассмотрели — это просто посчитать количество упоминаний в каждом тексте каждого уникального слова. Такие вектора называются мешками слов (bag of words) потому что не учитывают порядок слов.
Еще один способ, не учитывающий порядок слов но более чувствительный к специфичным, редким словам — это вектора TF-IDF. В случае TF-IDF мы также получаем вектор длины равной количеству уникальных слов, но сама оценка строится немного по другому — каждый компонент такого вектора состоит из двух сомножителей:
TF — term frequency — частота встречаемости слова в тексте
IDF — inverse document frequency — логарифм от обратной частоты встречаемости документов с указанным словом.
 Например если обычная частота встречаемости документа с указанным словом — это количество документов со словом деленное на количество всех документов, то обратная частота по аналогии с обратной функцией — переворачивает эту дробь и мы получаем количество всех документов разделить на количество документов с нужным словом.
Например если обычная частота встречаемости документа с указанным словом — это количество документов со словом деленное на количество всех документов, то обратная частота по аналогии с обратной функцией — переворачивает эту дробь и мы получаем количество всех документов разделить на количество документов с нужным словом.
TF-IDF может быть полезен для снижения веса часто встречаемых слов и повышения веса редких слов, которые могут быть важны для классификации текста.
В более сложные способы получения векторного представления с помощью глубоких нейронных сетей мы пока лезть не будем, но надеюсь, что руки дойдут написать статью и про них тоже (подписывайтесь на меня если интересна эта тема).
Классификация с помощью логистической регрессии
Для нашей задачи мы воспользуемся логистической регрессией, давайте кратко рассмотрим как она работает. По сути это линейная регрессия к результату которой в конце применяется логистическая функция.
То есть для каждого компонента вектора (читай для каждого слова из словаря), который мы подаем на вход, логистическая регрессия подбирает некоторое число — вес, таким образом, чтобы после умножения каждого компонента вектора на свой вес и последующего суммирования всех произведений мы бы для каждого текста получали число в интервале от 0 до 1, которое бы говорило нам о том насколько данный текст близок к классу 0 — негативных комментариев или классу 1 — позитивных комментариев.
Первая часть с подбором весов умножением на компоненты векторов и сложением — это линейная регрессия, мы как-бы регрессируем из большого набора чисел в одно число. Логистическая же функция в самом конце масштабирует любое полученное число на интервал от нуля до единицы. И если можно было бы показать только одну-единственную формулу в этой статье, то я бы без раздумий выбрал логистическую функцию, взгляните на эту красавицу:
Где e — число Эйлера равное примерно 2.71828, а основные свойства этой формулы зависят от показателя его степени, то есть с увеличением x, мы будем получать увеличение отрицательной степени у числа e, а значит экспоненциальное стремление знаменателя дроби к единице. С другой стороны, при больших отрицательных значениях аргумента мы будем получать экспоненциальный рост знаменателя к бесконечности и следовательно стремление всей дроби к нулю. График функции при x от -6 до +6 выглядит так:
Симметричная, гладкая, монотонная — прелесть а не функция 🙂Логистическая регрессия очень удобна для нашей задачи, поскольку позволяет нам не только интерпретировать ответ классификатора, как вероятность принадлежности текста к классу, но также и получать веса признаков, то есть слов из нашего словаря.
Давайте напишем код расчёта векторного представления для комментариев, не забыв предварительно разделить выборку на обучающую и тестовую в пропорции 4 к 1. Ведь если мы начнем считать статистики слов используя полный корпус текстов то не сможем потом проверить, как себя будет вести классификатор встретившись с незнакомыми текстами.
import numpy as np
import pandas as pd
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
# предварительно разделим выборку на тестовую и обучающую
train, test = train_test_split(
labeled_tweets,
test_size = 0.2,
stratify = labeled_tweets['label'],
random_state = 12348,
)
# инцициализируем векторайзер и укажем размер n-грамм
counter_idf = TfidfVectorizer(ngram_range=(1,1))
# Получаем словарь и idf только из тренировочного набора данных
count_train = counter_idf. fit_transform(train['text'])
# Применяем обученный векторайзер к тестовому набору данных
count_test = counter_idf.transform(test['text'])
# Инициализируем модель с параметрами по умолчанию
model_lr = LogisticRegression(random_state = 12345,
max_iter = 10000,
n_jobs = -1)
# Подбираем веса для слов с помощь fit на тренировочном наборе данных
model_lr.fit(count_train, train['label'])
# Получаем прогноз модели на тестовом наборе данных
predict_count_proba = model_lr.predict_proba(count_test)
fit_transform(train['text'])
# Применяем обученный векторайзер к тестовому набору данных
count_test = counter_idf.transform(test['text'])
# Инициализируем модель с параметрами по умолчанию
model_lr = LogisticRegression(random_state = 12345,
max_iter = 10000,
n_jobs = -1)
# Подбираем веса для слов с помощь fit на тренировочном наборе данных
model_lr.fit(count_train, train['label'])
# Получаем прогноз модели на тестовом наборе данных
predict_count_proba = model_lr.predict_proba(count_test)Давайте сразу выведем веса наших слов, возьмем 100 слов с наибольшими отрицательными весами и 100 слов с наибольшими положительными весами и нарисуем из них облака тэгов:
# Объединим в таблицу словарь из нашего векторайзера
# и веса для слов из обученной модели
weights = pd.DataFrame({'words': counter_idf.get_feature_names_out(),
'weights': model_lr.coef_.flatten()})
# Создаем копию отсортированную по возрастанию
weights_min = weights. sort_values(by= 'weights')
# И еще одну отсортированную по убыванию
weights_max = weights.sort_values(by= 'weights', ascending = False)
sort_values(by= 'weights')
# И еще одну отсортированную по убыванию
weights_max = weights.sort_values(by= 'weights', ascending = False)Код построения графиков используем тот же:
Оценка качества классификации. Матрица ошибок
Веса слов выглядят довольно правдоподобно, теперь давайте численно оценим качество полученного классификатора. Есть довольно много метрик классификации, в числе которых accuracy, precision, recall, F1, но в большинстве случаев вам достаточно понимать как устроена матрица ошибок (confusion matrix), поскольку все перечисленные метрики вычисляются из неё.
Посмотрим на матрицу ошибок нашего классификатора:
from sklearn.metrics import confusion_matrix
matrix = confusion_matrix(test['label'],
# В качестве порогового значения вероятности
# ниже которого объекты будут принадлежать
# к классу негативных выберем 0.5
(predict_lr_base_proba_1[:, 0] < 0.5).astype('int'),
normalize='true',
)
matrix
>>>
array([[0. 70199178, 0.29800822],
[0.2416975 , 0.7583025 ]])
70199178, 0.29800822],
[0.2416975 , 0.7583025 ]])Вкратце о том, с чем едят матрицу ошибок. Так как мы разделяли объекты на два класса в нашей матрице будет 2 строки и 2 столбца. Главное что нужно запомнить — строчки это истинные классы объектов, столбцы — это то, как наша модель назначила этим объектам классы.
По главной диагонали (от верхнего левого числа к нижнему правому) в матрице ошибок отображаются доли верно классифицированных объектов каждого класса. В каждой строчке по соседству с долей верно классифицированных комментариев находится доля объектов данного класса, которую классификатор ошибочно записал в другой класс. Нарисуем красивый график матрицы ошибок:
Например если у нас было 1000 негативных комментариев и 1000 положительных комментариев то поскольку мы видим что в первой строчке стоят числа 0.702, 0.298, это значит из нашей тысячи негативных комментариев 702 были распознаны верно, но при этом 298 были ошибочно классифицированы как позитивные, а во второй строчке мы видим по соседству числа 0. 242 , 0.758, значит что из 1000 позитивных комментариев мы ошибочно признали негативными 242.
242 , 0.758, значит что из 1000 позитивных комментариев мы ошибочно признали негативными 242.
Построение графиков ROC-кривых
Но мы же помним, что логистическая регрессия выдает в качестве ответа число в интервале от 0 до 1 и мы можем сами определять ту границу после которой мы считаем прогноз негативным. По умолчанию если мы выведем прогноз модели с помощью метода predict() эта граница устанавливается равной 0.5, но мы можем вывести сырой прогноз с помощью predict_proba() как мы и сделали и теперь например мы можем сказать — окей пусть все тексты для которых ответ меньше 0.7 — считаются положительными. Это может позволить увеличить охват верно классифицированных положительных текстов, но если классификатор обучился не достаточно хорошо, то это также увеличит и количество негативных текстов которые будут ошибочно классифицированы как положительные, то есть возрастет количество ложных срабатываний. И на переборе различных значений граничных значений основана еще одна очень наглядная техника оценки классификатора — построение графика ROC кривой (Receiver Operating Characteristic).
Вот, например как выглядят ROC кривые для наших классификаторов, обученных на разных векторных представлениях: bag of words, TF-IDF и на TF-IDF на лемматизированных текстах:
Давайте заодно разберем как понимать график ROC-кривой. Если наш классификатор обучился очень хорошо его ответы будут очень близки единице для большинства положительных негативных текстов и очень близки к нулю для большинства позитивных текстов. Например прогнозы для 90% отрицательных текстов будут находится в интервале ответов от 0 до 0.3, и 90% положительных текстов в интервале от 0.7 до 1.
Тогда сдвиг границы в интервале от 0.3 до 0.7 не будет особо менять долю ложно классифицированных объектов, а доля верно классифицированных объектов будет близка к единице. На графике мы будем видеть резкий подъем к высоким значениям по оси Y при низких значения по оси X.
И чем более не уверенный классификатор мы получим, тем при увеличении порогового значения, будет более равномерно увеличиваться и доля ложно классифицированных объектов.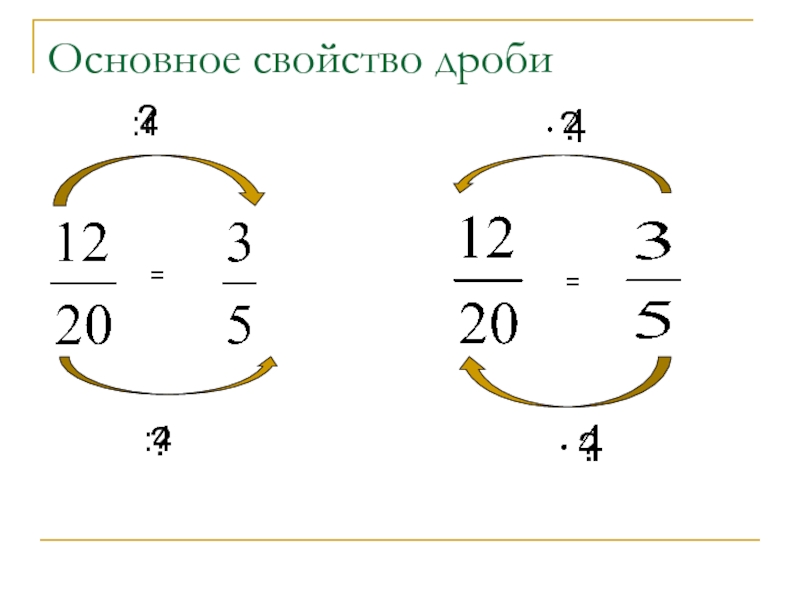 У самого плохого классификатора, который в качестве прогноза будет выдавать случайное число, при сдвиге границы будет происходить симметричный рост ложно классифицированных объектов. На графике мы будем видеть линию которая близка к диагонали, как на графике выше у пунктирной линии «Coin» по аналогии с прогнозом при подбрасывании монетки.
У самого плохого классификатора, который в качестве прогноза будет выдавать случайное число, при сдвиге границы будет происходить симметричный рост ложно классифицированных объектов. На графике мы будем видеть линию которая близка к диагонали, как на графике выше у пунктирной линии «Coin» по аналогии с прогнозом при подбрасывании монетки.
Чтобы не разглядывать форму кривой можно просто замерять площадь под ней, рандомный классификатор всегда будет иметь площадь около 0.5, отличных классификаторов эта площадь будет 0.9 и выше, у нашего лучшего варианта — чуть не дотягивает до 0.81.
Как видим из графика выше у нашей классификации качество довольно среднее. И это так же можно видеть на гистограмме распределения текстов каждого из классов по прогнозу классификатора:
Подбор оптимального порогового значения
Пересечение классов у нашего классификатора, как мы видим на графике выше довольно большое и как не выбирай границу по оси x, мы всгеда будем захватывать довольно много объектов другого класса. Но мы можем несколько про оптимизировать границу, максимизируя общее количество верно классифицированных объектов. Или если этого требует бизнес-задача, несколько сместить акцент на один из классов поступившись охватом другого класса.
Но мы можем несколько про оптимизировать границу, максимизируя общее количество верно классифицированных объектов. Или если этого требует бизнес-задача, несколько сместить акцент на один из классов поступившись охватом другого класса.
Например мы можем поставить задачу верно классифицировать не менее 75% негативных комментариев. Тогда пройдемся по всем значениям от 0.01 до 0.99 и запишем в таблицу долю верно классифицированных положительны и отрицательных объектов а также общую сумму соответствующие каждому пороговому значению, а затем выведем только те значения порогов в которых доля классифицированных негативных текстов не меньше 0,75 и отсортируем по убыванию общей суммы true positive rate + true negative rate, также сравним полученное пороговое значение с оптимальным, то есть дающим наибольшее значение true positive + true negative
В целом мы видим, что наша задача выполняется ценой не слишком большой потери в качестве, порядка десятых долей процента.
Классификация не размеченных комментариев
Теперь когда наша модель обучена и оценено её качество, давайте посмотрим как она справляется с боевой задачей классификации собранных комментариев.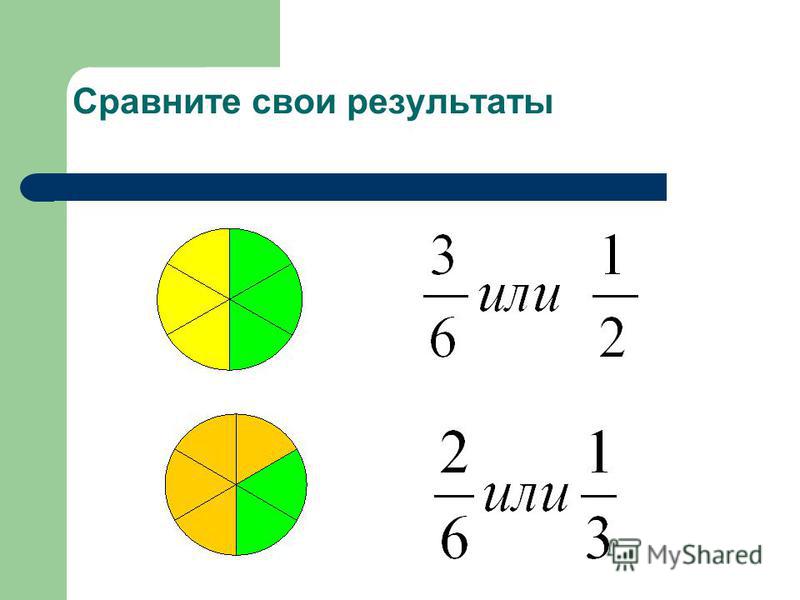 Сначала самостоятельно оценим, на сколько адекватно работает модель, будем выводить по 5 случайных комментов, переводить их в вектора с помощью обученного векторайзера и подавать числа в обученную модель, получая вероятность негатива:
Сначала самостоятельно оценим, на сколько адекватно работает модель, будем выводить по 5 случайных комментов, переводить их в вектора с помощью обученного векторайзера и подавать числа в обученную модель, получая вероятность негатива:
# Выведем 5 случайных комментариев c оценкой негатива первого видео
for _ in range(5):
source = comments_putin_df.sample(n=1)
text_clear = source['text_clear'].values[0]
text = source['comment'].values[0]
print(text[:100])
tf_idf_text = count_idf_1.transform([text_clear])
toxic_proba = model_lr_base_1.predict_proba(tf_idf_text)
print('Вероятность негатива: ', toxic_proba[:, 0])
print()Результат будет выглядеть так:
И для второго видео:
Мы видим, что работа классификатора далека от идеала, но в среднем, похоже что основные интонации он улавливает. Получим вероятность негатива для всех комментариев из первого и второго видео и отобразим распределение комментариев каждого видео по полученным оценкам в виде сглаженных гистограмм или т.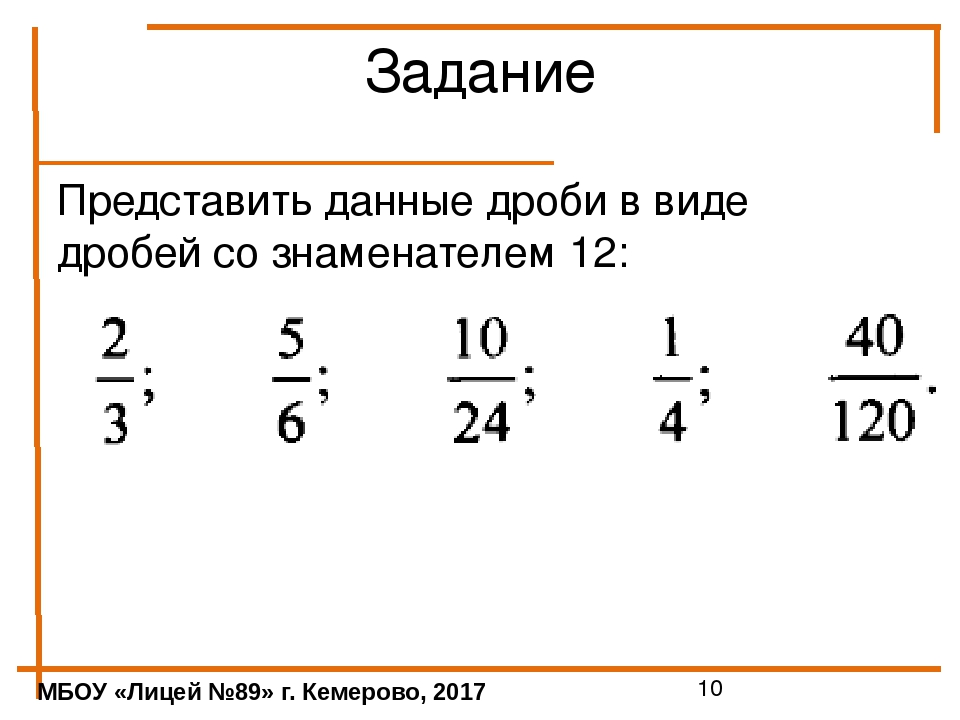 н. скрипичных диограмм (violin plots)
н. скрипичных диограмм (violin plots)
# Получим вектора tf-idf
putin_tf_idf = counter_tf_idf.transform(comments_putin_df['text_clear'])
shulman_tf_idf = counter_tf_idf.transform(comments_shulman_df['text_clear'])
# Получим прогноз негативности комментария
putin_negative_proba = model_lr.predict_proba(putin_tf_idf)
shulman_negative_proba = model_lr.predict_proba(shulman_tf_idf)
# Добавим прогнозы в таблицу
comments_putin_df['negative_proba'] = putin_negative_proba[:, 0]
comments_shulman_df['negative_proba'] = shulman_negative_proba[:, 0]
# Посчитаем доли негативных комментариев при подобранном пороговом значении
putin_share_neg = (comments_putin_df['negative_proba'] > 0.45).sum()\
/ comments_putin_df.shape[0]
shulman_share_neg = (comments_shulman_df['negative_proba'] > 0.45).sum()\
/ comments_shulman_df.shape[0]
# Отобразим полученные данные в виде графиков скрипичных диаграмм
fig = make_subplots(1,1,
subplot_titles=\
['Распределение комментариев по оценке негативности']
)
fig. add_trace(go.Violin(
x = comments_shulman_df['negative_proba'],
meanline_visible = True,
name = 'Shulman (N = %i)' % comments_shulman_df.shape[0],
side = 'positive',
spanmode = 'hard'
))
fig.add_trace(go.Violin(
x = comments_putin_df['negative_proba'],
meanline_visible = True,
name = 'Putin (N = %i)' % comments_putin_df.shape[0],
side = 'positive',
spanmode = 'hard'
))
fig.add_annotation(x=0.8, y=1.5,
text = "%0.2f — доля негативных комментариев (при p > 0.45)"\
% putin_share_neg,
showarrow=False,
yshift=10)
fig.add_annotation(x=0.8, y=0.5,
text = "%0.2f — доля негативных комментариев (при p > 0.45)"\
% shulman_share_neg,
showarrow=False,
yshift=10)
fig.update_traces(orientation='h',
width = 1.5,
points = False
)
fig.update_layout(height = 500,
xaxis_zeroline=False,
template = 'plotly_dark',
font_color = 'rgba(212, 210, 210, 1)',
legend=dict(
y=0.
add_trace(go.Violin(
x = comments_shulman_df['negative_proba'],
meanline_visible = True,
name = 'Shulman (N = %i)' % comments_shulman_df.shape[0],
side = 'positive',
spanmode = 'hard'
))
fig.add_trace(go.Violin(
x = comments_putin_df['negative_proba'],
meanline_visible = True,
name = 'Putin (N = %i)' % comments_putin_df.shape[0],
side = 'positive',
spanmode = 'hard'
))
fig.add_annotation(x=0.8, y=1.5,
text = "%0.2f — доля негативных комментариев (при p > 0.45)"\
% putin_share_neg,
showarrow=False,
yshift=10)
fig.add_annotation(x=0.8, y=0.5,
text = "%0.2f — доля негативных комментариев (при p > 0.45)"\
% shulman_share_neg,
showarrow=False,
yshift=10)
fig.update_traces(orientation='h',
width = 1.5,
points = False
)
fig.update_layout(height = 500,
xaxis_zeroline=False,
template = 'plotly_dark',
font_color = 'rgba(212, 210, 210, 1)',
legend=dict(
y=0. 9,
x=-0.1,
yanchor='top',
),
)
fig.update_yaxes(visible = False)
fig.show()
9,
x=-0.1,
yanchor='top',
),
)
fig.update_yaxes(visible = False)
fig.show()Результат:
На графике выше мы можем видеть сравнение распределений комментариев под двумя видео. Пунктирной линией выделено медианное значение, то есть такое значение правее и левее которого находится одинаковое количество текстов. Для комментариев под видео с участием Владимира Путина полученное медианное значение оценки негативности составило 0.45, а для видео с Екатериной Шульман — 0.34, можно сказать что общая оцененная вероятность негатива в комментариях под первым видео значительно выше чем под вторым, что в целом соответствует общему изначальному ожиданию которое сформировалось после прочтения нескольких сотен случайно выбранных комментариев.
Наметим стратегию улучшения классификатора.
Парсим много много-много комментариев порядка сотен тысяч.
С помощью обученного классификатора оцениваем негативность и позитивность не размеченных комментариев, и забираем из выборки только те комментарии, в которых классификатор очень уверен, например, с оценками больше 0.
 8 или меньше 0.2
8 или меньше 0.2Добавляем наиболее уверенно классифицрованные тексты в корпус размеченных текстов, снова получаем по ним вектора tf-idf и обучаем модель
Убираем наиболее уверенно классифицированные тексты из не размеченной выборки
Возвращаемся на шаг № 2
Итоги
Чему мы научились и узнали:
Парсить тексты комментариев из YouTube и собирать из них базы данных
Предобрабатывать тексты и получать их векторные представления tf-idf и bag of words
Классифицировать тексты с помощью логистической регрессии и оценивать качество классификации с помощью confusion matrix и ROC-curve
Строить красивые графики облаков слов и скрипичных диаграмм
Надеюсь, что этот data-sci-pop туториал был вам полезен и вы узнали что-то новое для себя, буду рад если подпишитесь на меня тут или на мой канал на YouTube, там планирую и дальше делать разборы решений задач из различных областей DataSciense и стараться, чтобы это было не скучно. Всем желаю максимизации счастья и минимизации страданий!
Всем желаю максимизации счастья и минимизации страданий!
Common Core математические стандарты восьмого класса
8.NS Система счисления
8.NS.A Знайте, что есть числа не рациональные, и аппроксимируйте их рациональными числами.
8.NS.A.1 Знайте, что нерациональные числа называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число.
8.NS.A.2 Используйте рациональные приближения иррациональных чисел, чтобы сравнить размер иррациональных чисел, расположить их приблизительно на диаграмме числовых линий и оценить значение выражений (например, pi²).
Возможность контрольно-пропускного пункта
8.
 EE Выражения и уравнения
EE Выражения и уравнения8.EE.A Работа с радикалами и целыми показателями.
8.EE.A.1 Знать и применять свойства целочисленных показателей степени для создания эквивалентных числовых выражений.
8.EE.A.2 Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x² = p и x³ = p, где p — положительное рациональное число. Вычислите квадратные корни из маленьких совершенных квадратов и кубические корни из маленьких совершенных кубов. Знайте, что квадратный корень из 2 иррационален.
8.EE.A.3 Используйте числа, выраженные в виде одной цифры, умноженной на целую степень числа 10, для оценки очень больших или очень малых величин и для выражения того, во сколько раз одно больше другого.
8.EE.A.4 Выполнение операций с числами, выраженными в экспоненциальном представлении, включая задачи, в которых используются как десятичные, так и экспоненциальные представления.
 Используйте экспоненциальное представление и выбирайте единицы соответствующего размера для измерения очень больших или очень малых величин (например,г., используйте миллиметры в год для расширения морского дна). Интерпретировать научную нотацию, созданную технологией.
Используйте экспоненциальное представление и выбирайте единицы соответствующего размера для измерения очень больших или очень малых величин (например,г., используйте миллиметры в год для расширения морского дна). Интерпретировать научную нотацию, созданную технологией.Возможность контрольно-пропускного пункта
8.EE.B Понимать связи между пропорциональными отношениями, линиями и линейными уравнениями.
8.EE.B.5 Графики пропорциональных отношений, интерпретация удельной скорости как наклона графика.Сравните два разных пропорциональных отношения, представленных по-разному.
8.EE.B.6 Используйте подобные треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для прямой, проходящей через начало координат, и уравнение y = mx + b для прямой, пересекающей вертикальную ось в точке b.

Возможность контрольно-пропускного пункта
8.EE.C Анализируйте и решайте линейные уравнения и пары одновременных линейных уравнений.
8.EE.C.7 Решение линейных уравнений с одной переменной.
8.EE.C.7a Приведите примеры линейных уравнений с одной переменной с одним решением, бесконечным числом решений или отсутствием решений. Покажите, какая из этих возможностей имеет место, последовательно преобразовывая данное уравнение в более простые формы, пока не получится эквивалентное уравнение вида x = a, a = a или a = b (где a и b — разные числа).
8.EE.C.7b Решите линейные уравнения с коэффициентами рациональных чисел, включая уравнения, решения которых требуют расширения выражений с использованием свойства дистрибутивности и сбора подобных членов.

8.EE.C.8 Анализ и решение пар одновременных линейных уравнений.
8.EE.C.8a Поймите, что решения системы двух линейных уравнений с двумя переменными соответствуют точкам пересечения их графиков, потому что точки пересечения удовлетворяют обоим уравнениям одновременно.
8.EE.C.8b Алгебраически решать системы двух линейных уравнений с двумя переменными и оценивать решения, изображая уравнения в виде графиков. Решите простые случаи путем проверки.
8.EE.C.8c Решайте реальные и математические задачи, приводящие к двум линейным уравнениям с двумя переменными.
Возможность контрольно-пропускного пункта
8.F-функции
8.
 F.A Определение, оценка и сравнение функций.
F.A Определение, оценка и сравнение функций.8.F.A.1 Поймите, что функция — это правило, которое назначает каждому входу ровно один выход. График функции представляет собой набор упорядоченных пар, состоящих из входа и соответствующего выхода.
8.F.A.2 Сравните свойства двух функций, каждая из которых представлена по-разному (алгебраически, графически, численно в таблицах или словесными описаниями).
8.F.A.3 Интерпретировать уравнение y = mx + b как определяющее линейную функцию, график которой представляет собой прямую линию; приведите примеры функций, которые не являются линейными.
Возможность контрольно-пропускного пункта
8.F.B Используйте функции для моделирования отношений между величинами.
8.
 F.B.4 Построить функцию для моделирования линейной зависимости между двумя величинами.Определить скорость изменения и начальное значение функции по описанию зависимости или по двум значениям (x, y), в том числе прочитать их из таблицы или из графика. Интерпретируйте скорость изменения и начальное значение линейной функции с точки зрения ситуации, которую она моделирует, и с точки зрения ее графика или таблицы значений.
F.B.4 Построить функцию для моделирования линейной зависимости между двумя величинами.Определить скорость изменения и начальное значение функции по описанию зависимости или по двум значениям (x, y), в том числе прочитать их из таблицы или из графика. Интерпретируйте скорость изменения и начальное значение линейной функции с точки зрения ситуации, которую она моделирует, и с точки зрения ее графика или таблицы значений.8.F.B.5 Качественно описать функциональную связь между двумя величинами, анализируя график (например, где функция возрастает или убывает, линейна или нелинейна).Нарисуйте график, демонстрирующий качественные характеристики функции, описанной словесно.
Возможность контрольно-пропускного пункта
8.G Геометрия
8.G.A Понимание конгруэнтности и сходства с использованием физических моделей, прозрачных пленок или программного обеспечения для геометрии.
8.G.A.1 Экспериментально проверить свойства вращения, отражения и перемещения:
8.G.A.1a Линии превращаются в прямые, а отрезки прямых в отрезки прямой одинаковой длины.
8.G.A.1b Углы принимают за углы одной меры.
8.G.A.1c Параллельные прямые превращаются в параллельные прямые.
8.G.A.2 Понять, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность.
8.G.A.3 Описать эффект расширения, перемещения, поворота и отражения двухмерных фигур с использованием координат.
8.
 G.A.4 Понять, что двумерная фигура подобна другой, если вторая может быть получена из первой посредством последовательности поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.
G.A.4 Понять, что двумерная фигура подобна другой, если вторая может быть получена из первой посредством последовательности поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.8.G.A.5 Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образованных при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников.
Возможность контрольно-пропускного пункта
8.G.B Понимать и применять теорему Пифагора.
8.G.B.6 Объясните доказательство теоремы Пифагора и ее обращение.
8.RUS.7 Применение теоремы Пифагора для определения неизвестных длин сторон в прямоугольных треугольниках в реальных и математических задачах в двух и трех измерениях.
8.RUS.8 Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.
Возможность контрольно-пропускного пункта
8.G.C. Решайте реальные и математические задачи, связанные с объемом цилиндров, конусов и сфер.
8.G.C.9 Знать формулы объемов конусов, цилиндров и сфер и использовать их для решения реальных и математических задач.
Возможность контрольно-пропускного пункта
8.SP Статистика и вероятность
8.SP.A Исследуйте закономерности ассоциации в двумерных данных.
8.SP.A.1 Построение и интерпретация диаграмм рассеяния для двумерных данных измерений для изучения закономерностей связи между двумя величинами.
 Опишите шаблоны, такие как кластеризация, выбросы, положительная или отрицательная связь, линейная связь и нелинейная связь.
Опишите шаблоны, такие как кластеризация, выбросы, положительная или отрицательная связь, линейная связь и нелинейная связь.8.SP.A.2 Знайте, что прямые линии широко используются для моделирования отношений между двумя количественными переменными.Для точечных диаграмм, которые предполагают линейную связь, неформально аппроксимируют прямую линию и неформально оценивают соответствие модели, оценивая близость точек данных к линии.
8.SP.A.3 Использование уравнения линейной модели для решения задач в контексте данных двумерных измерений, интерпретация наклона и точки пересечения.
8.SP.A.4 Поймите, что закономерности ассоциации также можно увидеть в двумерных категориальных данных, отображая частоты и относительные частоты в двусторонней таблице.Постройте и интерпретируйте двустороннюю таблицу, обобщающую данные по двум категориальным переменным, собранным у одних и тех же субъектов.
 Используйте относительные частоты, рассчитанные для строк или столбцов, чтобы описать возможную связь между двумя переменными.
Используйте относительные частоты, рассчитанные для строк или столбцов, чтобы описать возможную связь между двумя переменными.Возможность контрольно-пропускного пункта
Общие базовые стандарты штата © Copyright 2010. Центр передового опыта Национальной ассоциации губернаторов и Совет руководителей школ штата.Все права защищены.
Common Core 8 класс Математика
Common Core 8 класс МатематикаВключите сценарии (или JavaScript) в веб-браузере и затем перезагрузите эту страницу.
Главы
В этих интерактивных уроках используется динамическая графика и управляемое исследование для укрепления и объединения
символическое и визуальное мышление. Они дают учащемуся практическую визуальную экспозицию всех общих
Основные темы по математике для 8 класса, подкрепленные адаптивными упражнениями и случайно сгенерированными тестами. Все упражнения и тесты проверяются и оцениваются автоматически. Наведите указатель мыши на ссылку ниже
чтобы увидеть пример из этого урока, или нажмите на тестовую ссылку, чтобы увидеть краткий
конспект группы уроков. Перечислены соответствующие стандарты
после упражнений каждого урока. Мы также предоставляем
глоссарий курса.
Все упражнения и тесты проверяются и оцениваются автоматически. Наведите указатель мыши на ссылку ниже
чтобы увидеть пример из этого урока, или нажмите на тестовую ссылку, чтобы увидеть краткий
конспект группы уроков. Перечислены соответствующие стандарты
после упражнений каждого урока. Мы также предоставляем
глоссарий курса.
Учащиеся должны иметь в наличии черновую бумагу, доступ к (программному или аппаратному) числовому калькуляторы, за исключением главы «Обзор арифметики», и других учеников или учителя, чтобы спросить за помощью, когда они застряли. Всем учащимся рекомендуется как давать, так и получать математические объяснения со своими сверстниками. Пожалуйста присылайте нам свои комментарии, вопросы и предложения.
Арифметический обзор
- Арифметика на сетке: счетная единица квадраты. Сумма, разность, произведение, частное.
- Двузначное сложение: двузначные числа
показано как $a(10)+b$ на сетке. Дополнение с перегруппировкой, переноской.

Упражнения: сложение - Вычитание двух цифр и
Умножение: вычитание с заимствованием, умножение с перегруппировкой.
Упражнения: вычитание, умножение, разделение - Отрицательные числа: зеленые квадраты
имеют значение $+1$, розовые квадраты имеют значение $-1$. Суммы и разности. Текстовые задачи
с участием долга.
Упражнения: добавление, вычитание - Умножение и
Деление с отрицательными числами: произведения и частные с отрицательными числами на
сетка, введенная через аналогию и сопоставление с образцом.
Упражнения: умножение, разделение - Сложение дробей и
Вычитание: Визуализация дробей с использованием секторов пирога.Сведение к самым низким условиям.
Нахождение общих знаменателей.
Упражнения: добавление, вычитание - Умножение дробей и
Деление: использование расширенной сетки для визуализации дробей.
Упражнения: умножение, разделение - Арифметический тест
Переменные, выражения и простые уравнения
- Переменные и выражения:
Выражения как количества.
 Простые линейные выражения. Ползунки для переменных.
Простые линейные выражения. Ползунки для переменных.
Упражнения: оценка - Word Проблемы: стоимость $n$ предметов.Многовариантные выражения.
Упражнения: выражения - Более сложный
Выражения: Примеры с отрицательными числами, делением, дробями.
Упражнения: оценка, разделение - Уравнения в виде предложений:
Решение уравнений методом проб и ошибок или путем перемещения ползунка. Обратные задачи как слово
проблемы.
Упражнения: решение - Группировка в дополнение и
Задачи на вычитание: скобки, ассоциативный закон сложения, порядок действий.
для сложения и вычитания.Упрощение выражений с использованием ассоциативности
дополнение к перегруппировке, в том числе для вычитания.
Упражнения: оценка, упрощение - Решение $x+b=c$: добавление константы к обоим
стороны.
Упражнения: решение - Группировка при умножении
Задачи: Порядок действий, включая умножение. Умножая три числа,
Ассоциативный закон умножения и его использование для упрощения выражений.

Упражнения: оценка 1, оценка 2, умножение, разделение - Решение $ax+b=c$: добавление $-b$, а затем
умножение на $$1/a$$ или деление на $a$.
Упражнения: решение 1, решение 2 - Применение линейных
Уравнения: сбалансированная шкала, составление бюджета, преобразование температуры.
Упражнения: решение - Переменные, выражения и простые Уравнения Тест 1
- Распределительный закон и объединение
Подобные термины: расширение $a(x+c)$, $a(bx+c)$, $-(bx+c)$. Упрощение $ax+bx$ до
$[а+б]х$.
Упражнения: упрощение 1, упрощение 2, объединение подобных терминов - Управление линейным
Выражения: сложение, вычитание, масштабирование, упрощение.Коммутативность сложения
и умножение. Законы ноль и один.
Упражнения: упрощение 1, упрощение 2 - Решение $ax+b=cx+d$: Добавление $-cx-b$ к обоим
стороны.
Упражнения: решение 8.EE.7 - Упрощение и решение
Уравнения: расширение и упрощение каждой части уравнения. Нахождение количества
решения уравнения.
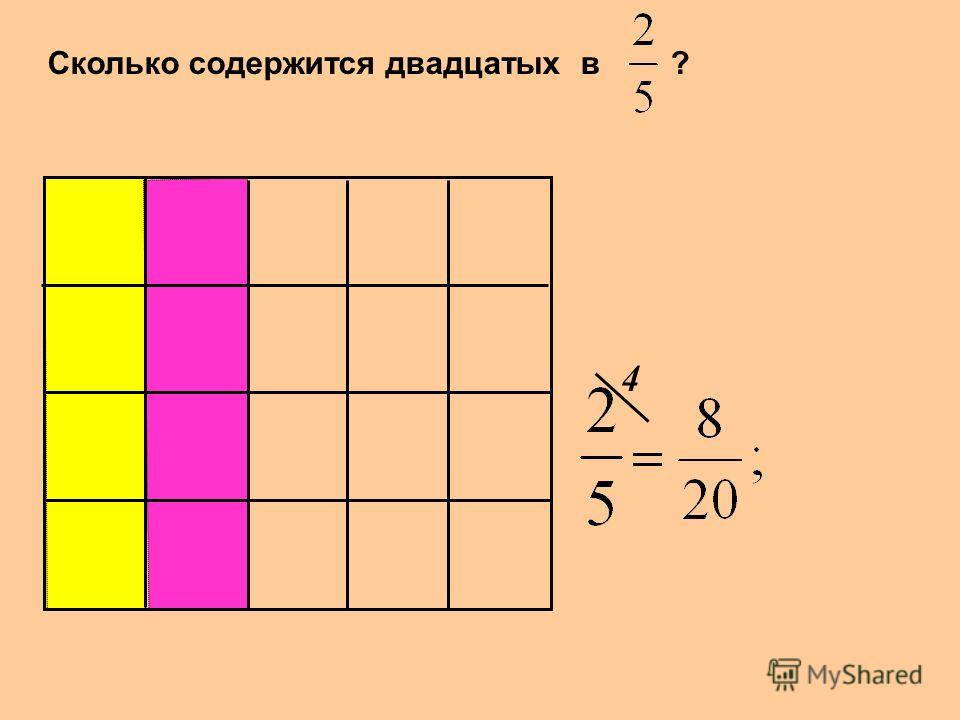
Упражнения: упрощение и решение, количество решений 8.EE.7 - Переменные, выражения и простые Уравнения Тест 2
Конгруэнтность, подобие и координаты
- Жесткие движения: перемещения, вращения и размышления.Они сохраняют длины, углы, линии и параллелизм. 8.G.1
- Конгруэнтность: определение конгруэнтности с использованием жестких
движения. SAS-критерий конгруэнтности треугольников.
Упражнения: конгруэнтные фигуры 8.G.2 - Правила соответствия: ASA и SSS
критерии равенства треугольников. AAA не подразумевает конгруэнтность, равно как и SSSS для
четырехугольники.
Упражнения: конгруэнтные треугольники 8.G.2 - Связанные углы: острый, тупой и правый
углы.Дополнительные и вертикальные углы. Переводы, параллельные линии и
трансверсали.
Упражнения: связанные углы 8.G.5 - Углы в треугольниках: углы в
треугольник в сумме дает 180°. Сумма внешних углов треугольника равна 360˚.
Упражнения: углы в треугольниках 8. G.5
G.5 - Расширения: Определение расширения.
Расширение переводит линию в ту же или параллельную линию, сохраняет угловые размеры и
измеряет длину одним общим множителем.
Упражнения: расширения 8.Г.4 - Сходство: определение сходства с использованием жестких
движений и дилатаций. Подобные треугольники имеют одинаковые углы и пропорциональные
сторон, и наоборот, любой из этих критериев для двух треугольников подразумевает сходство.
Упражнения: правило АА, пропорциональный сторона правило 1, пропорциональный сторона правило 2 8.Г.4, 8.Г.5 - Применение
Подобие и связанные углы: длина пандуса. Расчет высоты
флагшток от теней. Окружность земли.
Упражнения: решение подобных треугольники - Точки и координаты:
Соединение упорядоченной пары $(x, y)$ с координатной плоскостью. Квадранты.
Упражнения: квадранты, координаты - Преобразования и
Координаты: координаты точек после перемещений, отражений, вращений и
расширения.
Упражнения: координаты после перевод, координаты после отражение, координаты после вращение, координаты после расширение 8. G.3
G.3 - Конгруэнтность, сходство и Тест координат
Линейные графики
- Исследование $y=x+b$:
Нахождение $y$-отрезка $(0,b)$ прямой.
Упражнения: $y$-перехваты - Исследование $y=mx$: Линии с наклоном $m$,
положительное или отрицательное.
Упражнения: наклоны 8.EE.5, 8.F.2 - Исследование $y=mx+b$: наклон
и $y$-перехват.
Упражнения: $y$-перехваты 1, склоны 1, $y$-перехваты 2, склоны 2, уравнения - Решение уравнений графически:
Построение графика каждой стороны и нахождение пересечения, e.г. для $ax+b=cx+d$.
Упражнения: решение 8.ЕЕ.7б, 8.ЕЕ.8а - Склоны,
Скорость изменения и подобные треугольники: вычисление наклона линии по любым двум
точки на нем. Вывод уравнения $y=mx$ или $y=mx+b$ из наклона линии и
$y$-перехват.
Упражнения: вычисление склоны 8.EE.6, 8.F.4 - Поиск уравнений для линий:
Точечно-наклонная форма.
Упражнения: точечно-наклонная форма - Параллельный и
Перпендикулярные линии: наклоны $m$ и $$-1/m$$.

Упражнения: параллельные линии, перпендикулярные линии 8.ЕЕ.8с - Линейные функции: линейные и нелинейные
функции. Высота мяча.
Упражнения: определение функций, свойства функций 8.F.1, 8.F.3, 8.F.5 - Тест линейных графиков
Описательная статистика
- Ассоциации между Категории: Двусторонние таблицы частот. Возможные ассоциации между двумя способами деления населения. 8.СП.4
- Нахождение формул для приблизительно линейных Данные: введение в диаграммы рассеяния и линейные модели.8.СП.1, 8.СП.2
- Точечные диаграммы: кластеризация, выбросы, положительная или отрицательная ассоциация, линейная ассоциация и нелинейная ассоциация. Интерпретация наклона и $y$-перехвата линейной модели. 8.СП.1, 8.СП.3
Системы линейных уравнений
- Уравнения для линий в стандарте
Форма: $Ax + By = C$. Преобразование в форму пересечения наклона. Вычисление уклонов,
$x$- и $y$-перехваты.
Упражнения: преобразование в форма пересечения наклона, $y$-перехваты, $x$-перехватов - Решающие системы линейных
Уравнения в виде графиков: решения представляют собой пересечения графиков.

Упражнения: проверка, решение 8.ЕЕ.8а - Решающие системы линейных
Уравнения на вычитание: решение для разности, равной 0.
Упражнения: решение 8.EE.8b - Применение систем линейных Уравнения: Стоимость, выручка, прибыль. Рождаемость и смертность. 8.EE.8c, 8.SP.3
- Системы линейных уравнений Контрольная работа
Экспоненты, корни и действительные числа
- Целочисленные показатели: основные свойства
экспоненты.Значения экспоненциальных выражений с нулевыми или отрицательными показателями.
Упражнения: вычисление, упрощение 8.EE.1 - Научное обозначение: Преобразование
между десятичной и экспоненциальной записью. Арифметика с научным обозначением. Массы
планетные системы, количество клеток в организме человека.
Упражнения: конверсия, добавление и вычитание, умножение и деление 1, умножение и деление 2 8.ЕЕ.3, 8.ЕЕ.4 - Квадратные и кубические корни: геометрические
интерпретация второй и третьей степеней.
 2$ для прямоугольного треугольника, а также его обратное.треугольник 1-1-√2 как
особый случай.
2$ для прямоугольного треугольника, а также его обратное.треугольник 1-1-√2 как
особый случай.
Упражнения: Теорема Пифагора, разговаривать 8.G.6 - Расстояния с использованием
Теорема Пифагора: расстояние от $(x_1, y_1)$ до $(x_2, y_2)$.
Длина диагоналей сторон и диагоналей пространства в прямоугольном блоке.
Упражнения: диагональные длины, расстояния с использованием координаты 8.Г.7, 8.Г.8 - Твердая геометрия:
Объем призм, цилиндров, пирамид, конусов и сфер.
Упражнения: призмы и пирамиды, цилиндры, конусы, сферы 8.G.9 - Теорема Пифагора, Расстояние, и объемный тест
Модуль 2: Дроби, десятичные числа, отношения и проценты — курсы по математике
Дроби, десятичные числа и проценты связаны между собой и могут использоваться для выражения одного и того же числа или пропорции по-разному.
Понимание 1
Соотношение десятичных дробей, дробей и процентов
Учебная деятельность в предыдущих двух модулях была сосредоточена на числах, представленных в виде дробей, десятичных дробей и отношений. Этот модуль фокусируется на процентах, еще одном способе представления рациональных чисел.
Этот модуль фокусируется на процентах, еще одном способе представления рациональных чисел.
Любое рациональное число, будь то дробь или целое число, может быть записано в виде дроби, десятичной дроби или процента.
Термин «проценты» — это просто другое название сотых, поэтому проценты — это рациональные числа со знаменателем 100. Например, 25% (двадцать пять процентов) — это то же самое, что (двадцать пять сотых). 25% или также можно записать в десятичной системе счисления как 0,25 (ноль целых две десятых пять).
К концу этого модуля вы сможете заполнить таблицу, подобную этой.
Номер | Фракция | Десятичный | Процент |
|---|---|---|---|
пять | 5. | 500% | |
две и одна восьмая | 2,125 | 212,5% | |
три четверти | 0.75 | 75% |
Учебное задание 1
Соотношение десятичных дробей, дробей и процентов
Перейдите по ссылке ниже и выполните действия, предложенные ниже.
Математика — это весело, виртуальный манипулятор
Упражнения для демонстрации взаимосвязи между дробями, десятичными знаками и процентами, а также для закрепления и расширения вашего понимания того, что проценты являются еще одним способом представления дробей:
1. Поместите курсор на пиццу в положение «3 часа» или 90 градусов. В этом месте показана одна целая пицца, сетка 100 полностью заштрихована (100 процентов или 100%), а число один указано в строке от нуля до единицы.
Поместите курсор на пиццу в положение «3 часа» или 90 градусов. В этом месте показана одна целая пицца, сетка 100 полностью заштрихована (100 процентов или 100%), а число один указано в строке от нуля до единицы.
(одно целое) = 100% (сто из ста равных частей) = 1
2. Вращая курсор против часовой стрелки вокруг пиццы, заштриховывая сетку или перемещаясь по числовой строке, вы можете выбрать часть пиццы.
Закрасьте один из 100 квадратов сетки. Это одна из 100 равных частей, следовательно, 1% (процент) сетки. Обратите внимание, что появляется одна сотая часть пиццы, а указатель находится на очень небольшом расстоянии от нуля на числовой прямой.
Представьте себе числовую прямую от нуля до 1, разделенную на сто равных частей. Одна из этих частей равна одной сотой, или 0,01. Эта часть также составляет одну десятую десятой или одну десятую от 0,1.
(одна сотая) = 1% = 0. 01 (ноль целых ноль один)
01 (ноль целых ноль один)
3. Выделите верхнюю строку сетки, то есть десять из ста квадратов. Вы выделили одну десятую часть квадрата и заметите, что появилась одна из десяти равных частей пиццы. Стрелка показывает одну десятую или 0,1 (ноль целых один) на числовой прямой. Это также можно записать как 0,10, показывая, что одна десятая точно такая же, как десять сотых. и 10/100 — эквивалентные дроби (добавить ссылку — FDRP LO1).
(одна десятая) = 10% = 0.1 (ноль целых один)
4. Переместите курсор, чтобы отобразить:
. (одна половина) = 50% = 0,5 (ноль целых пять десятых) или 0,50
(одна четверть) = 25% = 0,25 (ноль целых две целых пять десятых)
(семь сотых) = 7% = 0,07 (ноль целых семь десятых)
(три четверти) = 75% = 0,75 (ноль целых семь десятых)
(семь сотых) = 7% = 0,07 (ноль целых семь десятых)
(девять десятых) = 90% = 0,9 (ноль целых девять десятых) или 0,90
( девяносто девять сотых) = 99% = 0,99 (ноль целых девять сотых)
Понимание 2
Представление десятичных долей до тысячных
Тысячную сетку можно использовать для представления одного целого (1) и для демонстрации десятичных долей до тысячных.
Вся сетка представляет собой одно (1) или одно целое.
Сетка может быть разделена на 10 равных частей или десятых частей. Одна из этих десяти равных частей, или одна десятая сетки (), заштрихована красным цветом.
Одна десятая, красная часть, может быть разделена на десять равных частей (желтая часть показывает это). Желтая часть — это одна сотая (), так как 100 из них составляют целое.
Сотая (желтая часть) также может быть разделена на десять равных частей (синяя часть показывает это).Синяя часть представляет одну тысячную () целого, так как 1000 этих тысяч составляют целое.
Можно сделать следующие заявления:
Одна десятая + одна сотая + одна тысячная
() или (0,1 + 0,01 + 0,001) или () или ()
Учебное задание 2
Сетка тысячи: визуальная модель десятичных дробей
В следующем видео аналогичным образом используется сетка тысячных, чтобы продемонстрировать запись десятичных дробей:
Во втором примере в видео показана заштрихованная область, равная 500 одной тысячной от целой 1000 (составляющей одну тысячную).Написано как 0.500.
Легко видеть, что эта заштрихованная область составляет половину всей сетки.
Эту заштрихованную область также можно разбить на 50 сотых. Дробь 50 сотых () эквивалентна 500 тысячным ().
Кроме того, заштрихованную область на видео можно разбить на пять десятых. Дробь пять десятых () эквивалентна дроби 50 сотых () и 500 тысячных ().
Все эти дроби имеют одинаковое значение половины (), и поэтому они являются эквивалентными дробями.
Десятичная запись
0,5 = 0,50 = 0,500
Десятичная запись не требует нулей после пятерки. В отличие от целых чисел, ноль в конце (справа) не меняет значение десятичной дроби. Однако нули иногда могут помочь при сложении и вычитании десятичных знаков.
Однако нули иногда могут помочь при сложении и вычитании десятичных знаков.
Учебное задание 3
Дроби больше единицы
Нажмите на следующую ссылку из Ресурсов иллюминации для преподавания математики:
Дробные модели
Следуйте этим инструкциям:
- Выберите вкладку «Широкий диапазон» в верхней части экрана.Это устанавливает диапазон числителя в нижней части экрана от 0 до 100, а диапазон знаменателя от 1 до 25. Следовательно, дроби будут неправильными или больше 1, потому что числитель будет больше знаменателя.
- Выберите вариант модели «площадь», расположенный справа под столом. Используйте вкладки «плюс» и «минус» по обе стороны от настроек числителя и знаменателя, чтобы выбрать числитель, равный 5, и знаменатель, равный 3. Вы увидите пять третей, представленных на модели площади на экране.Выше вы увидите, как это число выражается в виде дроби (или неправильной дроби), смешанного числа (), десятичного числа (1,6667) и процента (166,67%).
 Обратите внимание, что десятичные дроби и проценты округлены в большую сторону; иначе они продолжались бы вечно.
Обратите внимание, что десятичные дроби и проценты округлены в большую сторону; иначе они продолжались бы вечно.
Посмотрите на разные модели (длина, площадь, область, набор). - Попробуйте другие числа больше единицы, взглянув на различные визуальные представления. Обратите внимание, как они выражаются в неправильных дробях, смешанных числах, десятичных дробях и процентах.
Понимание 3
Соотношение десятичных дробей, дробей и процентов с помощью числовой строки
Числовая строка ниже размечена с шагом в одну сотую от нуля до 0,36. Обратите внимание, где в числовой строке расположены следующие десятичные числа, содержащие одинаковые цифры, но в разных местах:
0,257 | 0.05 | 0,023 | 0,307 | 0,175 | 0,12 |
|---|
Десятичное число 0,023 содержит ноль в десятых долях, поэтому оно меньше одной десятой (0,023). 1). В нем десятичное число 0,023 состоит из двух сотых. У него также есть 3 тысячных, так что это только за отметку в 2 сотые (три десятых за отметку).
1). В нем десятичное число 0,023 состоит из двух сотых. У него также есть 3 тысячных, так что это только за отметку в 2 сотые (три десятых за отметку).
Десятичное число 0,05 содержит ноль в десятых долях, поэтому оно меньше одной десятой (0,1). больше 0,023, так как в нем больше сотых.
Десятичное число 0,12 имеет 1 десятую и 2 сотые, то есть две сотые после знака одной десятой (0,1).
Десятичное число 0,175 также находится между 0,1 и 0,2, но оно ближе к 0,2, поскольку состоит из семи десятых.Он находится на полпути между отметками семи и восьми десятых, потому что у него также есть 5 тысячных.
Десятичное число 0,257 находится между 0,2 и 0,3. У него пять сотых, так что это где-то посередине между 0,2 и 0,3. У него также есть 7 тысячных, так что это чуть больше половины пути между 0,2 и 0,3.
Десятичное число 0,302 всего на 2 тысячных больше, чем 0,3, поэтому оно лишь немного превышает отметку 0,3.
На этот раз три различных представления рациональных чисел: дроби, десятичные дроби и проценты были помещены в пустую числовую строку.
15% | 0,28 |
| 70% | 0,115 | 1 |
|
| 0.3 |
|---|
15% | 0,28 | 70% | 0,115 | 1 | 0. | |||
|
|
|
| * |
| * |
|
|
* и являются близкими приближениями.Десятичное число 0,115 на самом деле составляет 5 тысячных и чуть больше, потому что это 0,3333333.
Примеры того, как проценты используются в реальной жизни
Пример 1
В универмаге проходит распродажа товаров для дома с 25% выбранных товаров. Сервиз перед распродажей стоил 130 долларов.
Сколько это будет стоить вам сейчас? Решение: Мы признаем, что 25% равны. Затем мы можем работать из 130 долларов, что составляет 32,50 доллара.
(мы знаем это, потому что половина от 130 — это 65, а половина от 65 — это 32.5. Это то же самое, что 130 разделить на 4).
Таким образом, вы можете приобрести столовый сервиз за 130 долларов – 32,5 доллара = 97,50 долларов США.
Пример 2
Недвижимость, которая в прошлом году была выставлена на продажу за 450 000 долларов, снизилась в цене на 10%. Сколько вы сэкономите, купив его сейчас? Решение: Мы понимаем, что 10% — это то же самое, что и . Сейчас 450 000 долларов — это 45 000 долларов. Таким образом, вы сэкономите 45 000 долларов, купив недвижимость сейчас.
(Обратите внимание, что скидка 10% на небольшой предмет, например, на футболку за 20 долларов, составляет всего несколько долларов, в данном случае 2 доллара.Принимая во внимание, что 10% скидка на недвижимость за 450 000 долларов — это очень стоящая сумма в 45 000 долларов. Таким образом, значение того, что может означать для нас скидка 10%, зависит от того, с чего мы начали).
Таким образом, значение того, что может означать для нас скидка 10%, зависит от того, с чего мы начали).
Распространенные заблуждения относительно десятичных дробей и дробей
Десятичные дроби останавливаются на сотых — NO
Примеры десятичных знаков после сотых:
Миллиметр (мм) составляет одну тысячную метра
1 мм = 0,001 м
2,44 микрограмма равно 0,00244 миллиграмма.
Распространенные заблуждения относительно упорядочивания дробей
1. Чем больше знаменатель, тем больше дробь
Это справедливо для единичных дробей (дроби с числителем, равным единице). Существует обратная зависимость между количеством частей и размером каждой части: чем больше количество частей (знаменатель), тем меньше размер каждой части (числитель). Если контекст задачи не указывает на то, что две дроби относятся к разным целым, мы предполагаем, что обе относятся к одному и тому же целому. Имея это в виду, имеет смысл, что чем больше частей, на которые делится целое, тем меньше они будут.
Имея это в виду, имеет смысл, что чем больше частей, на которые делится целое, тем меньше они будут.
Пример: Сравните одну восьмую с одной пятой
Если мы имеем в виду одно и то же целое, например часть торта (смоделированную ниже), мы можем видеть, что чем больше частей, на которые оно разделено, тем меньше будет каждая часть.
В визуальном представлении мы можем ясно видеть, что это больше, чем.
Пять человек делят торт, каждый
Восемь человек делят торт одинакового размера.
Когда мы сравниваем только одну из каждой части, например одну восьмую с одной пятой (), чем больше знаменатель, тем меньше будет каждая часть.
Числитель равен единице ()
Когда одна или обе дроби не являются единичными дробями:
На этот раз мы сравним одну пятую() и три восьмых(). Мы знаем, что восьмые меньше пятых, но мы должны отметить, что на этот раз восьмых не одна, а три.
На диаграмме ниже мы видим, что это большая часть.
Человек А съел пятую часть () торта.
Человек Б съел три восьмых () торта.
Если мы не можем надежно сравнить дроби с разными знаменателями визуально, как на диаграмме выше, нам нужно заменить одну или обе дроби на равнозначные дроби для общего знаменателя.
Легко признать, что четыре пятых () больше, чем две пятых (), потому что каждая из частей (пятых) имеет одинаковый размер.Четыре больше двух, поэтому должно быть больше .
Как насчет сравнения четырех пятых () и семи десятых (), у которых разные знаменатели?
Как видно на стенке дроби, каждая пятая часть равна двум десятым. Это показано в модели ниже:
Замена четырех пятых () на эквивалентную дробь восьми десятых () значительно упрощает понимание того, что четыре пятых () больше, чем семь десятых ().
Практическое задание 1
1) Заполните таблицу так, чтобы числа в каждой строке, представленные дробями, десятичными знаками и процентами, были эквивалентны:
Фракция | Десятичный | Процент |
|---|---|---|
1.1 | 110% | |
0,04 | ||
25% | ||
350% | ||
0. |
2) Упорядочить следующие номера от меньшего к большему:
0,125
1,5
1,45
0,25
0,81
0,09
1.1065
3) Напишите не менее четырех эквивалентных дробей для каждой из следующих дробей:
Нажмите здесь , чтобы проверить свои ответы
Практическое задание 2
1) Отношение десятичных дробей, дробей и процентов с помощью числовой строки
Нажмите на ссылку ниже и завершите задание, поместив все дроби, десятичные запятые и проценты в числовые строки из ICTgames.
Эквивалентность дробей, десятичных знаков и процентов
2) Поместите следующие дроби, десятичные запятые и проценты в одну числовую строку:
10%
0,375
50%
1,3
128%
0,002
3) Просматривайте дневную газету и выделяйте каждый раз, когда процент упоминается или используется .Этим видом деятельности могут заниматься и учащиеся.
Нажмите здесь , чтобы проверить свои ответы
Проверьте свое понимание взаимосвязи между дробями, десятичными числами и процентами
Цель этого раздела состояла в том, чтобы продемонстрировать следующее понимание;
- Число может быть представлено дробью или десятичной дробью.

- Процент — это доля от ста, очень часто используемая в повседневной жизни.Проценты также можно понимать как сотые доли
Теперь это имеет для вас смысл?
Перейдите на следующую вкладку
Понимать дробь a/b с a > 1 как сумму дробей 1/b. Понимать сложение и вычитание дробей как соединение и разделение частей, относящихся к одному и тому же целому. Разлагайте дробь на сумму дробей с одним и тем же знаменателем более чем одним способом, записывая каждое разложение уравнением. Обоснуйте разложения, т.е.г., используя модель визуальной дроби. Примеры: 3/8 = 1/8 + 1/8 + 1/8; 3/8 = 1/8 + 2/8; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8. Сложите и вычтите смешанные числа с одинаковыми знаменателями, например, заменив каждое смешанное число эквивалентной дробью и/или используя свойства операций и взаимосвязь между сложением и вычитанием. Решайте текстовые задачи, включающие сложение и вычитание дробей, относящихся к одному и тому же целому и имеющих одинаковые знаменатели, например, с помощью визуальных моделей дробей и уравнений для представления задачи.
 MAFS.4.NF.2.3 — понимать дробь a/b с a > 1 как сумму дробей 1/b. Понимать сложение и вычитание дробей как соединение и разделение частей, относящихся к одному и тому же целому. Разлагайте дробь на сумму дробей с одним и тем же знаменателем более чем одним способом, записывая каждое разложение уравнением. Обоснуйте разложения, например, с помощью визуальной дробной модели. Примеры: 3/8 = 1/8 + 1/8 + 1/8; 3/8 = 1/8 + 2/8; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8.Складывать и вычитать смешанные числа с одинаковыми знаменателями, например, заменяя каждое смешанное число эквивалентной дробью и/или используя свойства операций и связь между сложением и вычитанием. целыми и имеющими одинаковые знаменатели, например, с помощью моделей визуальных дробей и уравнений для представления проблемы.
MAFS.4.NF.2.3 — понимать дробь a/b с a > 1 как сумму дробей 1/b. Понимать сложение и вычитание дробей как соединение и разделение частей, относящихся к одному и тому же целому. Разлагайте дробь на сумму дробей с одним и тем же знаменателем более чем одним способом, записывая каждое разложение уравнением. Обоснуйте разложения, например, с помощью визуальной дробной модели. Примеры: 3/8 = 1/8 + 1/8 + 1/8; 3/8 = 1/8 + 2/8; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8.Складывать и вычитать смешанные числа с одинаковыми знаменателями, например, заменяя каждое смешанное число эквивалентной дробью и/или используя свойства операций и связь между сложением и вычитанием. целыми и имеющими одинаковые знаменатели, например, с помощью моделей визуальных дробей и уравнений для представления проблемы.Веб-сайт несовместим с используемой версией браузера.Не все функции могут быть доступны. Пожалуйста, обновите ваш браузер до последней версии.
Под дробью a/b, где a > 1, понимается сумма дробей 1/b.
- Понимать сложение и вычитание дробей как соединение и разделение частей, относящихся к одному и тому же целому.
- Разложите дробь на сумму дробей с одинаковым знаменателем более чем одним способом, записывая каждое разложение уравнением. Обоснуйте разложения, например, с помощью визуальной дробной модели. Примеры: 3/8 = 1/8 + 1/8 + 1/8 ; 3/8 = 1/8 + 2/8; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8.
- Сложение и вычитание смешанных чисел с одинаковыми знаменателями, например.г., заменяя каждое смешанное число эквивалентной дробью и/или используя свойства операций и взаимосвязь между сложением и вычитанием.
- Решайте текстовые задачи на сложение и вычитание дробей, относящихся к одному и тому же целому и имеющих одинаковые знаменатели, например, используя визуальные модели дробей и уравнения для представления задачи.
Разъяснения
Примеры возможностей для углубленного изучения Этот стандарт представляет собой важный шаг в многоуровневой прогрессии сложения и вычитания дробей. Учащиеся расширяют свое прежнее понимание сложения и вычитания, чтобы складывать и вычитать дроби с одинаковыми знаменателями, думая о сложении или
вычитая так много единичных дробей.
Учащиеся расширяют свое прежнее понимание сложения и вычитания, чтобы складывать и вычитать дроби с одинаковыми знаменателями, думая о сложении или
вычитая так много единичных дробей.
Общая информация
Предметная область: Математика
Класс: 4
Домен-поддомен: Число и операции — дроби
Кластер: Уровень 2: Базовое применение навыков и понятий
Дата принятия или пересмотра: 14 февраля
Дата последней оценки: 14/02
Статус: Утвержден Государственным советом
Оценено: Да
Образцы тестовых заданий (5)
- Тестовый образец #: Образец образца 3
- Вопрос:
Сью выпила стакан муки.
 Она использовала чашку.
Она использовала чашку.Сколько муки в чашках осталось у Сью?
- Сложность: Н/Д
- Тип: EE: Редактор формул
Связанные точки доступа
Альтернативная версия этого теста для учащихся с серьезными когнитивными нарушениями.
MAFS.4.NF.2.AP.3a: Используя представление, разложите дробь на несколько копий единичной дроби (например, 3/4 = 1/4 + 1/4+ 1/4).MAFS.4. NF. 2.AP.3b: Складывать и вычитать дроби с одинаковыми знаменателями (2, 3, 4 или 8), используя представления. MAFS.4.NF.2.AP.3c: Решать текстовые задачи на сложение и вычитание дробей с одинаковыми знаменатели (2, 3, 4 или 8).
2.AP.3b: Складывать и вычитать дроби с одинаковыми знаменателями (2, 3, 4 или 8), используя представления. MAFS.4.NF.2.AP.3c: Решать текстовые задачи на сложение и вычитание дробей с одинаковыми знаменатели (2, 3, 4 или 8).Связанные ресурсы
Проверенные ресурсы, которые преподаватели могут использовать для обучения концепциям и навыкам в этом эталонном тесте.
Формирующие оценки MFAS
Анна Мари и пицца: Учащихся просят решить текстовую задачу на сложение дробей с одинаковыми знаменателями. Затем учащиеся анализируют текстовую задачу, включающую сложение разнородных величин.
Затем учащиеся анализируют текстовую задачу, включающую сложение разнородных величин.
Учащихся просят решить текстовую задачу на вычитание дробей с одинаковыми знаменателями. Затем учащиеся анализируют текстовую задачу на вычитание разнородных величин.
Оригинальные учебники для учащихся по математике — классы K-5
Ресурсы для учащихся
Проверенные ресурсы, которые учащиеся могут использовать для изучения концепций и навыков в этом эталонном тесте.
Оригинальный учебник для студентов
Дилемма оставшегося десерта:Узнайте, как разложить дробь на сумму дробей с общими знаменателями с помощью этого интерактивного руководства.
Тип: оригинальное учебное пособие для учащихся
Образовательная игра
Фракция Викторина: Проверьте свои навыки фракции, отвечая на вопросы на этом сайте. В этом тесте вам предлагается упростить дроби, преобразовать дроби в десятичные числа и проценты, а также ответить на вопросы по алгебре, связанные с дробями. Вы даже можете выбрать уровень сложности, типы вопросов и ограничение по времени.
В этом тесте вам предлагается упростить дроби, преобразовать дроби в десятичные числа и проценты, а также ответить на вопросы по алгебре, связанные с дробями. Вы даже можете выбрать уровень сложности, типы вопросов и ограничение по времени.
Тип: обучающая игра
Задачи решения проблем
Делаем 22 семнадцатых разными способами: Это простое задание на сложение дробей с одинаковыми знаменателями.Основная цель состоит в том, чтобы подчеркнуть, что есть много способов разложить дробь как сумму дробей.
Тип: Задача решения проблем
Сравнение двух разных пицц:Основное внимание в этом задании уделяется пониманию того, что дроби в явном контексте являются дробями определенного целого.В этой задаче есть три разных целого: средняя пицца, большая пицца и две пиццы вместе взятые. Это задание лучше всего подходит для обучения. Студенты могут практиковаться в объяснении своих рассуждений друг другу в парах или в рамках группового обсуждения.
Тип: Задача решения проблем
Запись смешанного числа в виде эквивалентной дроби: Цель этого задания — помочь учащимся понять и сформулировать причины действий обычного алгоритма преобразования смешанного числа в эквивалентную дробь. Второй шаг показывает, что алгоритм — это просто способ найти общий знаменатель между двумя дробями. Эта концепция является важным предшественником сложения смешанных чисел и дробей с одинаковыми знаменателями, и поэтому на втором этапе следует сделать акцент. Это задание подходит как для обучения, так и для формирующего оценивания.
Второй шаг показывает, что алгоритм — это просто способ найти общий знаменатель между двумя дробями. Эта концепция является важным предшественником сложения смешанных чисел и дробей с одинаковыми знаменателями, и поэтому на втором этапе следует сделать акцент. Это задание подходит как для обучения, так и для формирующего оценивания.
Тип: Задача решения проблем
Персики: Это задание предоставляет контекст, в котором учащиеся могут вычитать дроби с общим знаменателем; его можно использовать как для оценки, так и для учебных целей.Для этой конкретной задачи учителя должны предусмотреть два типа подходов к решению: один, когда учащиеся вычитают целые числа и дроби по отдельности, и другой, когда учащиеся преобразуют смешанные числа в неправильные дроби, а затем приступают к вычитанию.
Тип: Задача решения проблем
Пластиковые строительные блоки:Цель этого задания – предложить учащимся складывать смешанные числа с одинаковыми знаменателями.Это задание иллюстрирует различные подходы к решению, которые учащиеся могут применить к такой задаче. Следует предусмотреть два общих подхода: один, когда учащиеся точно подсчитывают, сколько ведер блоков у мальчиков есть для определения ответа, и второй, когда учащиеся сравнивают полученные числа с эталонными числами.
Тип: Задача решения проблем
Учебники
Сравнение дробей: Этот учебник для студенческой аудитории поможет учащимся лучше понять, что дроби — это способ показать часть целого. Однако некоторые дроби больше других. Таким образом, этот учебник поможет освежить понимание сравнения дробей. Студенты смогут перемещаться по обучающей части учебника в своем собственном темпе и проверять свое понимание после каждого шага урока с помощью раздела «Попробуйте это». Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется.
Однако некоторые дроби больше других. Таким образом, этот учебник поможет освежить понимание сравнения дробей. Студенты смогут перемещаться по обучающей части учебника в своем собственном темпе и проверять свое понимание после каждого шага урока с помощью раздела «Попробуйте это». Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется.
Тип: Учебник
Виртуальный манипулятор
Дробная игра: Этот виртуальный манипулятор позволяет отдельным учащимся работать с дробными отношениями. (Есть также ссылка на версию для двух игроков.)
(Есть также ссылка на версию для двух игроков.)
Тип: виртуальный манипулятор
Ресурсы для родителей
Проверенные ресурсы, которые опекуны могут использовать, чтобы помочь учащимся освоить концепции и навыки в этом эталонном тесте.
Задачи решения проблем
Делаем 22 семнадцатых разными способами: Это простое задание на сложение дробей с одинаковыми знаменателями. Основная цель состоит в том, чтобы подчеркнуть, что есть много способов разложить дробь как сумму дробей.
Основная цель состоит в том, чтобы подчеркнуть, что есть много способов разложить дробь как сумму дробей.
Тип: Задача решения проблем
Сравнение двух разных пицц:Основное внимание в этом задании уделяется пониманию того, что дроби в явном контексте являются дробями определенного целого.В этой задаче есть три разных целого: средняя пицца, большая пицца и две пиццы вместе взятые. Это задание лучше всего подходит для обучения. Студенты могут практиковаться в объяснении своих рассуждений друг другу в парах или в рамках группового обсуждения.
Тип: Задача решения проблем
Запись смешанного числа в виде эквивалентной дроби: Цель этого задания — помочь учащимся понять и сформулировать причины действий обычного алгоритма преобразования смешанного числа в эквивалентную дробь.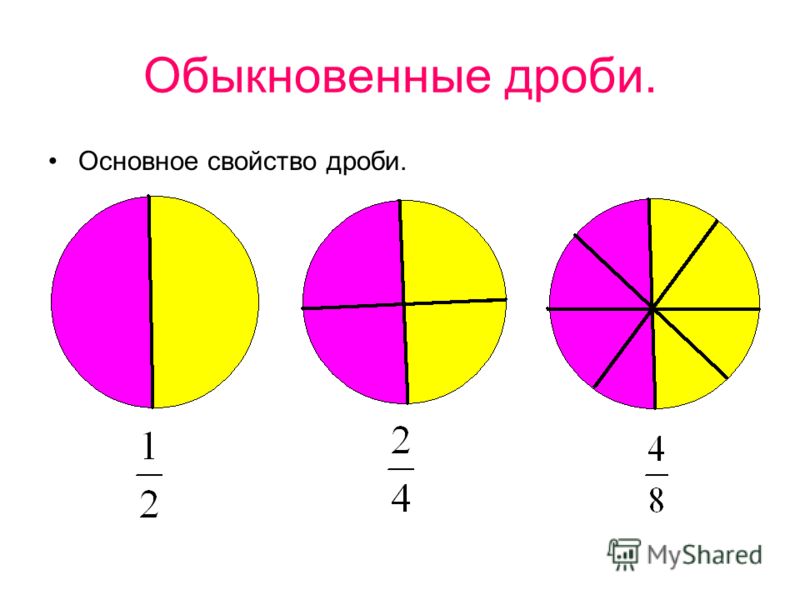 Второй шаг показывает, что алгоритм — это просто способ найти общий знаменатель между двумя дробями. Эта концепция является важным предшественником сложения смешанных чисел и дробей с одинаковыми знаменателями, и поэтому на втором этапе следует сделать акцент. Это задание подходит как для обучения, так и для формирующего оценивания.
Второй шаг показывает, что алгоритм — это просто способ найти общий знаменатель между двумя дробями. Эта концепция является важным предшественником сложения смешанных чисел и дробей с одинаковыми знаменателями, и поэтому на втором этапе следует сделать акцент. Это задание подходит как для обучения, так и для формирующего оценивания.
Тип: Задача решения проблем
Персики: Это задание предоставляет контекст, в котором учащиеся могут вычитать дроби с общим знаменателем; его можно использовать как для оценки, так и для учебных целей.Для этой конкретной задачи учителя должны предусмотреть два типа подходов к решению: один, когда учащиеся вычитают целые числа и дроби по отдельности, и другой, когда учащиеся преобразуют смешанные числа в неправильные дроби, а затем приступают к вычитанию.
Тип: Задача решения проблем
Пластиковые строительные блоки:Цель этого задания – предложить учащимся складывать смешанные числа с одинаковыми знаменателями.Это задание иллюстрирует различные подходы к решению, которые учащиеся могут применить к такой задаче. Следует предусмотреть два общих подхода: один, когда учащиеся точно подсчитывают, сколько ведер блоков у мальчиков есть для определения ответа, и второй, когда учащиеся сравнивают полученные числа с эталонными числами.
Тип: Задача решения проблем
Руководство
Сравнение дробей: Этот учебник для студенческой аудитории поможет учащимся лучше понять, что дроби — это способ показать часть целого. Однако некоторые дроби больше других. Таким образом, этот учебник поможет освежить понимание сравнения дробей. Студенты смогут перемещаться по обучающей части учебника в своем собственном темпе и проверять свое понимание после каждого шага урока с помощью раздела «Попробуйте это». Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется.
Однако некоторые дроби больше других. Таким образом, этот учебник поможет освежить понимание сравнения дробей. Студенты смогут перемещаться по обучающей части учебника в своем собственном темпе и проверять свое понимание после каждого шага урока с помощью раздела «Попробуйте это». Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется.
Тип: Учебник
Загрузка….
Рабочие листы по математике — бесплатные печатные рабочие листы для 1–10 классов
Рабочие листы по математике предназначены для разных классов и тем. Эти рабочие листы усиливают пошаговый механизм обучения, который помогает учащимся стратегически подходить к проблеме, признавать свои ошибки и развивать математические навыки. Рабочие листы по математике состоят из наглядных материалов, которые помогают учащимся визуализировать различные концепции и смотреть на вещи с более широкой точки зрения, что может значительно улучшить обучение.Это также помогает учащимся в активном обучении, поскольку создает увлекательный опыт обучения с помощью различных вопросов, а не пассивного потребления видео- и аудиоконтента. Рабочие листы по математике дают учащимся огромную гибкость во времени и позволяют им решать задачи в своем собственном темпе.
Эти рабочие листы усиливают пошаговый механизм обучения, который помогает учащимся стратегически подходить к проблеме, признавать свои ошибки и развивать математические навыки. Рабочие листы по математике состоят из наглядных материалов, которые помогают учащимся визуализировать различные концепции и смотреть на вещи с более широкой точки зрения, что может значительно улучшить обучение.Это также помогает учащимся в активном обучении, поскольку создает увлекательный опыт обучения с помощью различных вопросов, а не пассивного потребления видео- и аудиоконтента. Рабочие листы по математике дают учащимся огромную гибкость во времени и позволяют им решать задачи в своем собственном темпе.
Ссылки на список рабочих листов по математике, доступных по различным темам, расположены в алфавитном порядке для вашего удобства. Итак, выберите тему и начните свое обучение!
Рабочие листы по математике доступны для учащихся всех классов с 1 по 10 класс.Нажмите на свою оценку ниже, чтобы получить доступ к рабочим листам тем из этой оценки.
Лучший способ изучить любую тему — решить практические задачи. Вы можете найти несколько хорошо организованных рабочих листов по всем математическим темам ниже.
Рабочие листы по математике состоят из множества вопросов, таких как вопросы с множественным выбором (MCQ), «Заполните пропуски», вопросы в формате эссе, вопросы на соответствие, вопросы с перетаскиванием и многие другие. Эти рабочие листы по математике для 1-8 классов содержат визуальные симуляции, которые помогают учащимся увидеть вещи в действии и получить более глубокое понимание тем.
Рабочие листы по математике могут предложить различные преимущества и помочь в эффективном обучении. Это может помочь студентам повысить их логическое мышление. Это также помогает в развитии навыков рассуждения. Эти навыки важны и могут дать учащимся преимущество на всю жизнь. Эти рабочие листы могут в значительной степени улучшить обучение студентов, тем самым давая им прочную математическую основу. Решение задач по математике по разным темам также может повысить уверенность учащегося и помочь ему получить хорошие оценки в школе и на конкурсных экзаменах.
Рабочие листы по математике играют очень важную роль в четком изучении понятий. Это помогает учителю назначать детям вопросы по всем темам в виде рабочих листов. Регулярное выполнение этих математических заданий помогает учащимся улучшить свою скорость и точность за счет четкого понимания концепций. Организация заполненных рабочих листов поможет родителям отслеживать прогресс ребенка.
Каждый лист по математике тщательно подобран таким образом, чтобы он не только дополнял школьные знания, но и побуждал ребенка к совершенствованию.Рабочие листы по математике будут доступны для всего спектра понятий, которые ребенок будет изучать в своем конкретном классе. С программой Cuemath ваш ребенок получит лучшие в своем классе рабочие листы, которые были профессионально разработаны нашей высококвалифицированной командой по учебным программам. Наши рабочие листы по математике существуют для достижения двух целей:
Часто задаваемые вопросы по математическим таблицам
Что такое математические рабочие листы?
Рабочие листы по математике — это документы, доступные в Интернете или в автономном режиме, которые состоят из списка практических вопросов по определенной теме. Они направлены на то, чтобы дополнить обучение ребенка в школе и помочь ему улучшить свои математические навыки. Вопросы представлены в структурированном виде, чтобы помочь учащимся разработать кристально четкие концепции.
Они направлены на то, чтобы дополнить обучение ребенка в школе и помочь ему улучшить свои математические навыки. Вопросы представлены в структурированном виде, чтобы помочь учащимся разработать кристально четкие концепции.
Нужно ли использовать математические рабочие листы?
Рабочие листы по математике — отличный способ найти множество практических сумм. Поскольку дети сталкиваются с несколькими типами задач, они получают представление о том, какие вопросы будут сформулированы на экзамене. Таким образом, рекомендуется включить математические рабочие листы в вашу обычную учебную программу.
Могут ли рабочие листы по математике помочь в понимании концепций?
После того, как ребенок знакомится с темой, единственный способ проверить его понимание — это решать практические вопросы. Рабочие листы по математике помогают детям прививать кристально четкие концепции, проверяя знания ребенка и помогая им улучшить свои навыки в областях, которые могут быть проблематичными. Следовательно, они оказываются хорошим ресурсом, который дети могут использовать для привития надежной математической основы.
Следовательно, они оказываются хорошим ресурсом, который дети могут использовать для привития надежной математической основы.
Как математические рабочие листы могут помочь улучшить навыки решения задач?
Рабочие листы по математике помогают детям анализировать задачи, разбивать их на части, а затем решать.По мере того, как дети привыкают к интерпретации того, почему и как стоит вопрос, они могут улучшить свои способности решать проблемы. В дополнение к этому они также изучают множество передаваемых навыков, таких как критическое мышление, логика, рассуждение и аналитические способности.
Как лучше всего задавать вопросы по математике?
Хорошо структурированный рабочий лист по математике содержит разделы с постепенным повышением уровня сложности. Следовательно, всегда решайте математический лист в заданном порядке организации, чтобы получить максимальную пользу, и старайтесь не пропускать ни одного вопроса.
Полезны ли рабочие листы по математике для конкурсных экзаменов?
Цель рабочих листов по математике состоит в том, чтобы предоставить детям практические задачи, позволяющие им быстро освоить тему. Таким образом, эти рабочие листы созданы таким образом, чтобы независимо от экзамена, будь то школьный или конкурсный, ребенок развивал необходимые знания и навыки, чтобы успешно сдать его.
Как можно использовать математические рабочие листы для повышения уровня концентрации?
Некоторые онлайн-рабочие листы по математике являются интерактивными с соответствующими изображениями.Кроме того, они оснащены забавной графикой, которая повышает уровень вовлеченности и мотивации для решения большего количества задач. Если дети весело проводят время, решая вопросы с рабочим листом, их концентрация автоматически улучшается.
Общие базовые стандарты для 8-го класса
Ниже приведены общие базовые стандарты для 8-го класса со ссылками на поддерживающие их ресурсы. Мы также поощряем множество упражнений и работу с книгами.
8 класс | Система счисления
Знай, что есть нерациональные числа, и аппроксимируй их рациональными числами.
8.NS.A.1Знайте, что числа, не являющиеся рациональными, называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число.
Преобразование дробей в десятичные Природа Золотое сечение и числа Фибоначчи8.NS.A.2Используйте рациональные аппроксимации иррациональных чисел, чтобы сравнить размер иррациональных чисел, расположить их приблизительно на диаграмме с числовыми линиями и оценить значение выражений (например,2). Например, усекая десятичное разложение квадратного корня из 2, покажите, что квадратный корень из 2 находится между 1 и 2, а затем между 1,4 и 1,5, и объясните, как продолжить, чтобы получить более точные приближения.
Упражнение: Найдите приблизительное значение для Pi, класс 8 | Выражения и уравнения
Работа с радикалами и целыми показателями.3) = 1/27.9, и определить, что население мира более чем в 20 раз больше.
Обозначение индекса — степени 108.EE.A.4 Выполнение операций с числами, выраженными в экспоненциальном представлении, включая задачи, в которых используются как десятичные, так и экспоненциальные представления. Используйте научные обозначения и выбирайте единицы соответствующего размера для измерения очень больших или очень малых величин (например, используйте миллиметры в год для распространения по морскому дну). Интерпретировать научную нотацию, созданную технологией.
Обозначение индекса — степени 10Понимать связи между пропорциональными отношениями, линиями и линейными уравнениями.
8.EE.B.5 Нарисуйте пропорциональные отношения, интерпретируя удельную скорость как наклон графика. Сравните два разных пропорциональных отношения, представленных по-разному. Например, сравните график «расстояние-время» с уравнением «расстояние-время», чтобы определить, какой из двух движущихся объектов имеет большую скорость.
8.EE.B.6Используйте подобные треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для прямой, проходящей через начало координат, и уравнение y = mx + b для прямой, пересекающей вертикальную ось в точке b.
Анализ и решение линейных уравнений и пар одновременных линейных уравнений.
8.EE.C.7 Решите линейные уравнения с одной переменной.
а. Приведите примеры линейных уравнений от одной переменной с одним решением, бесконечным числом решений или отсутствием решений. Покажите, какая из этих возможностей имеет место, последовательно преобразовывая данное уравнение в более простые формы, пока не получится эквивалентное уравнение вида x = a, a = a или a = b (где a и b — разные числа).
б. Решите линейные уравнения с коэффициентами рациональных чисел, включая уравнения, решения которых требуют расширения выражений с использованием дистрибутивного свойства и сбора подобных членов.
8.EE.C.8 Анализировать и решать пары одновременных линейных уравнений.
а. Поймите, что решения системы двух линейных уравнений с двумя переменными соответствуют точкам пересечения их графиков, потому что точки пересечения удовлетворяют обоим уравнениям одновременно.
б. Решите системы двух линейных уравнений с двумя переменными алгебраически и оцените решения, построив уравнения в виде графика. Решите простые случаи путем проверки. Например, 3x + 2y = 5 и 3x + 2y = 6 не имеют решения, потому что 3x + 2y не может быть одновременно 5 и 6.
c. Решайте реальные и математические задачи, приводящие к двум линейным уравнениям с двумя переменными. Например, зная координаты двух пар точек, определите, пересекает ли прямая, проходящая через первую пару точек, прямую, проходящую через вторую пару.
класс 8 | Функции
Определение, оценка и сравнение функций.
8.F.A.1 Поймите, что функция — это правило, которое назначает каждому входу ровно один выход. График функции представляет собой набор упорядоченных пар, состоящих из входа и соответствующего выхода. (Обозначение функции не требуется в 8 классе.)
Диапазон доменов и кодовый домен Инъективный Сюръективный и Биективный8.F.A.2 Сравните свойства двух функций, каждая из которых представлена по-разному (алгебраически, графически, численно в таблицах или словесными описаниями).2, дающая площадь квадрата как функцию длины его стороны, нелинейна, потому что ее график содержит точки (1,1), (2,4) и (3,9), которые не лежат на прямой.
График функций и калькуляторИспользуйте функции для моделирования отношений между величинами.
8.F.B.4 Создайте функцию для моделирования линейной зависимости между двумя величинами. Определить скорость изменения и начальное значение функции по описанию зависимости или по двум значениям (x, y), в том числе прочитать их из таблицы или из графика.Интерпретируйте скорость изменения и начальное значение линейной функции с точки зрения ситуации, которую она моделирует, и с точки зрения ее графика или таблицы значений.
8.F.B.5 Качественно описать функциональную связь между двумя величинами, анализируя график (например, где функция возрастает или убывает, линейна или нелинейна). Нарисуйте график, демонстрирующий качественные характеристики функции, описанной словесно.
График функций и калькулятор Возрастающие и убывающие функции8 класс | Геометрия
Понимание конгруэнтности и сходства с помощью физических моделей, прозрачных пленок или программного обеспечения для геометрии.
8.G.A.1 Экспериментально проверить свойства вращения, отражения и переноса:
а. Линии превращаются в прямые, а отрезки прямых в отрезки прямой одинаковой длины.
б. Углы принимаются равными углам.
с. Параллельные прямые переводятся в параллельные прямые.
8.G.A.2Понять, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность.
8.G.A.3Описать эффект расширения, перемещения, поворота и отражения двухмерных фигур с использованием координат.
Симметрия — отражение и вращение8.G.A.4Понять, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.
Загадка жонглера Сэма Лойда Симметрия — отражение и вращение8.G.A.5Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образованных при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников. Например, расположите три копии одного и того же треугольника так, чтобы казалось, что три угла образуют линию, и приведите аргумент в терминах секущей, почему это так.
Поймите и примените теорему Пифагора.
8.RUS6 Объясните доказательство теоремы Пифагора и ее обращение.
8.RUS.7 Применение теоремы Пифагора для определения неизвестных длин сторон в прямоугольных треугольниках в реальных и математических задачах в двух и трех измерениях.
8.RUS.8 Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.
Расстояние между 2 точками Упражнение: Прогулка по пустынеРешите реальные и математические задачи на объем цилиндров, конусов и сфер.
8.G.C.9Знать формулы объемов конусов, цилиндров и сфер и использовать их для решения реальных и математических задач.
Площадь круга Треугольник Квадрат Прямоугольник Параллелограмм Трапеция Эллипс и секторКласс 8 | Статистика и вероятность
Исследование закономерностей связи в двумерных данных.
8.SP.A.1 Построение и интерпретация диаграмм рассеяния для данных двумерных измерений для изучения закономерностей связи между двумя величинами. Опишите шаблоны, такие как кластеризация, выбросы, положительная или отрицательная связь, линейная связь и нелинейная связь.
8.SP.A.2Знайте, что прямые линии широко используются для моделирования отношений между двумя количественными переменными. Для точечных диаграмм, которые предполагают линейную связь, неформально аппроксимируют прямую линию и неформально оценивают соответствие модели, оценивая близость точек данных к линии.
8.SP.A.3Используйте уравнение линейной модели для решения задач в контексте данных двумерных измерений, интерпретируя наклон и точку пересечения. Например, в линейной модели биологического эксперимента интерпретируйте наклон равным 1.5 см/час, что означает, что дополнительный час солнечного света каждый день связан с дополнительными 1,5 см высоты взрослого растения.
8.SP.A.4 Поймите, что закономерности ассоциации также можно увидеть в двумерных категориальных данных, отображая частоты и относительные частоты в двусторонней таблице. Постройте и интерпретируйте двустороннюю таблицу, обобщающую данные по двум категориальным переменным, собранным у одних и тех же субъектов. Используйте относительные частоты, рассчитанные для строк или столбцов, чтобы описать возможную связь между двумя переменными.Например, соберите данные от учеников вашего класса о том, соблюдается ли у них комендантский час по вечерам в школе и есть ли у них работа по дому. Есть ли доказательства того, что те, у кого комендантский час, также, как правило, занимаются домашними делами?
Сводные таблицы и графики
дробей — Рациональные числа — Документация Python 3.10.1
Исходный код: Lib/fractions.py
Модуль дробей обеспечивает поддержку арифметики рациональных чисел.
Экземпляр Fraction может быть создан из пары целых чисел, из другое рациональное число или из строки.
- класс
дроби.Дробь( числитель=0 , знаменатель=1 ) - класс
дроби.Фракция( other_fraction ) - класс
дроби.Дробь( с плавающей запятой ) - класс
дроби.Дробь( десятичная ) - класс
дроби.Дробь( строка ) Первая версия требует, чтобы числитель и знаменатель были экземплярами из
.чисел. Rationalи возвращает новый экземплярFractionсо значениемчислитель/знаменатель. Если знаменатель равен0, то вызывает ошибкуZeroDivisionError.Вторая версия требует, чтобы other_fraction является экземпляромnumbers.Rationalи возвращаетДробный экземплярс одинаковым значением. Следующие две версии принимают либос плавающей запятой, либоdecimal.Decimal, и вернитеДробный экземплярс точно таким же значением. Отметим, что из-за обычные проблемы с двоичными числами с плавающей запятой (см. Арифметика с плавающей запятой: проблемы и ограничения), аргумент дляДробь (1.1)не совсем равно 11/10, так чтоFraction(1.1)возвращает вместоFraction(11, 10), как и можно было ожидать. (Но см. документацию по методуlimit_denominator()ниже.) Последняя версия конструктора ожидает строку или экземпляр Unicode. Обычная форма для этого экземпляра:[знак] числитель ['/' знаменатель]
, где необязательный знак
числительизнаменатель(если есть) представляют собой строки десятичные цифры.Кроме того, любая строка, представляющая конечный значение и принимается конструкторомfloatтакже принимается конструкторомFraction. В любой форме входная строка также может иметь начальные и/или конечные пробелы. Вот несколько примеров:>>> из импорта дробей Дробь >>> Дробь(16, -10) Дробь (-8, 5) >>> Дробь(123) Дробь(123, 1) >>> Дробь() Фракция (0, 1) >>> Дробь('3/7') Фракция (3, 7) >>> Дробь('-3/7') Дробь (-3, 7) >>> Дробь('1.414213 \т\п') Дробь(1414213, 1000000) >>> Дробь('-.125') Дробь (-1, 8) >>> Дробь('7e-6') Дробь(7, 1000000) >>> Дробь (2,25) Дробь(9, 4) >>> Дробь(1.1) Дробь(2476979795053773, 2251799813685248) >>> из десятичного импорта Decimal >>> Дробь (десятичная ('1.1')) Дробь(11, 10)Класс
Fractionнаследуется от абстрактного базового классачисел. Rationalи реализует все методы и операции из этого класса.Дробьэкземпляров можно хэшировать, и следует рассматривать как неизменяемый. Кроме того,Дробьимеет следующие свойства и методы:Изменено в версии 3.9: функция
math.gcd()теперь используется для нормализации числителя . и знаменатель .math.gcd()всегда возвращает типint. Раньше тип GCD зависел от числителя и знаменателя .-
числитель Числитель младшей дроби.
-
знаменатель Знаменатель младшей дроби.
-
as_integer_ratio() Возвращает кортеж из двух целых чисел, отношение которых равно к дроби и с положительным знаменателем.
-
from_float( этаж ) Этот метод класса
создает дробь, представляющую точную значение fl , которое должно быть числомс плавающей запятой.Остерегайтесь этогоFraction.from_float(0.3)не совпадает со значениемFraction(3, 10).Примечание
Начиная с Python 3.2, вы также можете создать
Экземпляр фракциинепосредственно из числа с плавающей запятой
-
from_decimal( дек ) Этот метод класса
создает дробь, представляющую точную значение dec , которое должно быть десятичным числом.Десятичный экземпляр.
-
предельный_знаменатель( максимальный_знаменатель=1000000 ) Находит и возвращает ближайшую
дробьксобственной личности, которая имеет знаменатель не больше max_denominator. Этот метод удобен для нахождения рациональные приближения к заданному числу с плавающей запятой:>>> из импорта дробей Дробь >>> Дробь('3.1415926535897932').limit_denominator(1000) Дробь(355, 113)или для восстановления рационального числа, представленного в виде числа с плавающей запятой:
>>> из математического импорта pi, cos >>> Дробь(cos(pi/3)) Дробь(4503599627370497,
- 99254740992) >>> Дробь (cos (pi/3)).предел_знаменатель() Фракция (1, 2) >>> Дробь(1.1).limit_denominator() Дробь(11, 10)
-
__этаж__() Возвращает наибольшее значение
int<= self. Этот метод может также можно получить через функциюmath.floor():>>> с этажа импорта математики >>> пол(Дробь(355, 113)) 3
-
__ceil__() Возвращает наименьшее
int>= self.Этот метод может также можно получить через функциюmath.ceil().
-
__круглый__() -
__round__( ndigits ) Первая версия возвращает ближайший
intкself, округление половины до четного. Вторая версия округляетдодо ближайшее кратноеFraction(1, 10**ndigits)(логически, еслиndigitsотрицательно), снова округляя половину до четного.Этот Доступ к методу также можно получить с помощью функцииround().
-
См. также
- Модуль
чисел Абстрактные базовые классы, составляющие числовую башню.

 0
0 3
3 125
125