Алгебра сокращение дробей 8 класс – Сокращение алгебраических дробей — урок. Алгебра, 8 класс.

Основное свойство алгебраической дроби. Видеоурок. Алгебра 8 Класс

На данном уроке будет рассмотрено основное свойство алгебраической дроби. Умение правильно и без ошибок применять это свойство является одним из важнейших базовых умений во всем курсе школьной математики и будет встречаться не только на протяжении изучения данной темы, но и практически во всех изучаемых в дальнейшем разделах математики. Ранее уже было изучено сокращение обыкновенных дробей, а на данном уроке будет рассмотрено сокращение рациональных дробей. Несмотря на довольно большое внешнее отличие, существующее между рациональными и обыкновенными дробями, у них очень много общего, а именно – и обыкновенным, и рациональным дробям присущи одинаковое основное свойство и общие правила выполнения арифметических действий. В рамках урока мы столкнемся с понятиями: сокращение дроби, умножение и деление числителя и знаменателя на одно и то же выражение – и рассмотрим примеры.

Вспомним основное свойство обыкновенной дроби: значение дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число. Напомним, что деление числителя и знаменателя дроби на одно и то же отличное от нуля число называется

сокращением.

Например: , при этом значение дробей не изменяется. Однако зачастую при применении данного свойства многие допускают стандартные ошибки:

1)  — в приведенном примере допущена ошибка деления только одного слагаемого из числителя на 2, а не всего числителя. Правильная последовательность действий выглядит таким образом:  или .

2)  — здесь мы видим похожую ошибку, однако, кроме этого еще в результате деления  получен 0, а не 1, что является еще более частой и грубой ошибкой.

Теперь необходимо перейти к рассмотрению алгебраической дроби. Вспомним это понятие из предыдущего урока.

Определение. Рациональная (алгебраическая) дробь – дробное выражение вида , где  – многочлены.  – числитель,   – знаменатель.

Алгебраические дроби являются, в некотором смысле, обобщением обыкновенных дробей и над ними можно проводить те же операции, что и над обыкновенными дробями.

Основное свойство алгебраической дроби – и числитель, и знаменатель дроби можно умножать и делить на один и тот же многочлен (одночлен) или число, отличное от нуля. Это будет тождественное преобразование алгебраической дроби. Вспомним, что как и ранее, деление числителя и знаменателя дроби на одно и то же отличное от нуля выражение называется сокращением.

Основное свойство алгебраической дроби позволяет сокращать дроби и приводить их к наименьшему общему знаменателю.

Для сокращения обыкновенных дробей мы прибегали к основной теореме арифметики, разлагали и числитель, и знаменатель на простые множители.

Определение.Простое число – натуральное число, которое делится только на единицу и само себя. Все остальные натуральные числа называются составными. 1 не является ни простым, ни составным числом.

Пример 1. а), где множители, на которые разложены числители и знаменатели указанных дробей, являются простыми числами.

Ответ.; .

Следовательно, для сокращения дробей необходимо предварительно разложить на  множители числитель и знаменатель дроби, а затем разделить их на общие множители. Т.е. следует владеть методами разложения многочленов на множители.

Пример 2. Сократить дробь а), б) , в)  .

Решение. а) . Необходимо заметить, что в числителе находится полный квадрат, а в знаменателе разность квадратов. После сокращения необходимо указать, что , во избежание деления на ноль.

б) . В знаменателе выносится общий числовой множитель, что полезно делать практически в любом случае, когда это возможно. Аналогично с предыдущим примером указываем, что .

в) . В знаменателе выносим за скобки минус (или, формально, ). Не забываем, что при сокращении .

Ответ. ;; .

Теперь приведём пример на приведение к общему знаменателю, делается это аналогично с обыкновенными дробями.

Пример 3. Привести к общему знаменателю дроби  и .

Решение. Для нахождения наименьшего общего знаменателя необходимо найти наименьшее общее кратное (НОК) двух знаменателей, т.е. НОК(3;5). Иными словами, найти наименьшее число, которое делится на 3 и на 5 одновременно. Очевидно, что это число 15, записать это можно таким образом: НОК(3;5)=15 – это и будет общий знаменатель указанных дробей.

Чтобы преобразовать знаменатель 3 в 15, его необходимо умножить на 5, а для преобразования 5 в 15, его необходимо умножить на 3. По основному свойству алгебраической дроби следует умножить на те же числа и соответствующие числители указанных дробей.

 и .

Ответ.; .

Пример 4.

Привести к общему знаменателю дроби  и .

Решение. Проведем аналогичные предыдущему примеру действия. Наименьшее общее кратное знаменателей НОК(12;18)=36. Приведем к этому знаменателю обе дроби:

 и .

Ответ.; .

Теперь рассмотрим примеры, демонстрирующие применение техники сокращения дробей для их упрощения в более сложных случаях.

Пример 5. Вычислить значение дроби: а) , б) , в) .

а) . При сокращении пользуемся правилом деления степеней .

б) .

в) .

После того, как мы повторили использование основного свойства обыкновенной дроби, можно перейти к рассмотрению алгебраических дробей.

Пример 6. Упростить дробь  и вычислить при заданных значениях переменных: а) ; , б) ;

Решение. При подходе к решению возможен следующий вариант – сразу же подставить значения переменных и начать расчет дроби, но в таком случае решение сильно усложняется и необходимое на его решение время увеличивается, не говоря уже об опасности ошибиться в сложных вычислениях. Поэтому удобно сначала упростить выражение в буквенном виде, а затем уже подставить значения переменных.

а) . При сокращении на множитель  необходимо проверить, не обращается ли он в ноль в указанных значениях переменных. При подстановке получаем  , что дает возможность сокращения на данный множитель.

б) . В знаменателе выносим минус, как мы это уже делали в примере 2. При сокращении на  снова проверяем не делим ли мы на ноль: .

Ответ.; .

Пример 7. Привести к общему знаменателю дроби а)  и

interneturok.ru

План-конспект урока по алгебре (8 класс) на тему: Алгебра 8 класс . Сокращение дробей.

У р о к
СОКРАЩЕНИЕ ДРОБЕЙ

Цели: формировать умение применять основное свойство дроби при сокращении дробей.

Ход урока

I. Организационный момент.

II. Устная работа.

– Сократите дробь:

а) ;                б) ;                в) ;                г) ;

д) ;                е) ;                ж) ;                з) .

III. Объяснение нового материала.

Для успешной работы учащихся на уроке им необходимо не только использовать основное свойство дроби, но и применять ряд других знаний и умений, полученных и сформированных ранее.

Учащиеся должны помнить формулы сокращенного умножения и основные приёмы разложения многочлена на множители. Поэтому начать необходимо с актуализации знаний и умений.

З а д а н и я   и   в о п р о с ы  учащимся:

1. Какие существуют способы разложения многочлена на множители?

2. В чём состоит каждый из этих способов?

3. Разложите на множители многочлен:

а) х2у – 2х;                        д) х2 + 6х + 9;

б) 3a2b – 9ab2;                        е) а2 – 10а + 25;

в) т2 – 4п;                        ж) ax + bx + ay + by.

г) а3 – а;                                з) ab – b + 3a – 3.

После проведения этой работы следует разобрать пример 3 из учебника и сделать  в ы в о д: чтобы сократить рациональную дробь, нужно сначала разложить на множители её числитель и знаменатель.

IV. Формирование умений и навыков.

1. № 29, № 30 (а, в, д), № 32 (а, в).

2. № 31, № 34.

3. № 35 (а, в).

Р е ш е н и е

а) .

в) .

Д о п о л н и т е л ь н о  можно выполнить № 36 (а).

Р е ш е н и е

Областью определения этой функции является множество всех чисел, кроме х = –5. Сократим дробь, задающую функцию:

.

Графиком функции  является прямая, а графиком функции  – та же прямая, но с «выколотой» точкой (–5; –5).

V. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– В чём состоит основное свойство дроби?

– Когда применяется основное свойство дроби?

– Что нужно сделать, чтобы сократить рациональную дробь?

– Какие существуют способы разложения многочлена на множители?

Домашнее задание: № 30 (б, г, е), № 32 (б, г), № 33, № 35 (б, г).

Д о п о л н и т е л ь н о: № 36 (б).

nsportal.ru

Презентация урока для интерактивной доски по алгебре (8 класс) по теме: 8 класс Алгебра Основное свойство дроби. Сокращение дробей. Урок 1 и 2

Слайд 1

МсСВУ ФГКОУ Московское суворовское военное училище 07.10.2013 Основное свойство дроби Урок 1-2 Преподаватель математики Каримова С.Р.

Слайд 2

Формулы сокращенного умножения: квадрат суммы двух выражений; квадрат разности двух выражений; разность квадратов двух выражений; сумма кубов двух выражений; разность кубов двух выражений; куб суммы двух выражений; куб разности двух выражений. Устно

Слайд 3

1. Что значит сократить дробь? – Сократим дробь . Для этого разделим числитель и знаменатель на их общий множитель. – Сократите дроби :

Слайд 4

2. Как привести дробь к новому знаменателю? – Приведём дробь к знаменателю 28. Для этого умножим числитель и знаменатель дроби на 4: – Приведите дроби к знаменателю 60 .

Слайд 5

3. Каким свойством мы воспользовались при сокращении дробей и приведении дробей к новому знаменателю? Сформулируйте основное свойство дроби .

Слайд 6

д в а т и п а з а д а н и й, при выполнении которых применяется основное свойство дроби : – приведение дробей к новому знаменателю; – сокращение дробей. ОСНОВНОЕ СВОЙСТВО ДРОБИ Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Слайд 7

2) (сократить дробь). Примеры

Слайд 8

Упражнения 1. Умножьте числитель и знаменатель дроби на указанное число. а) на 5; б ) на 2; в ) на 6.

Слайд 9

2. Разделите числитель и знаменатель дроби на указанное число: а) на 2 ; б ) на 3 ; в ) на 5. Упражнения

Слайд 10

3. Заполните пустые места так, чтобы равенство было верным : ; 2) ; 3) ; 4) ; 5 ) ; 6 ) . Упражнения

Слайд 11

4. № 23, № 25(а, в, д), № 26, № 28 (а, б). 5. № 47. Упражнения

Слайд 12

Р е ш е н и е № 23

Слайд 13

Р е ш е н и е № 25(а, в, д ) № 26 а) б) в) г)

Слайд 14

№ 28 (а, б). Р е ш е н и е № 47.

Слайд 15

Сокращение дробей

Слайд 16

а ) ; б) ; в ) ; г) ; д ) ; е) ; ж) ; з ) . Устно – Сократите дробь:

Слайд 17

Вынесение общего множителя за скобки: 2) Способ группировки: = 3) Применение формул сокращенного умножения: =( = = Способы разложения многочлена на множители:

Слайд 18

Разложите на множители многочлен: а) х 2 у – 2 х ; д ) х 2 + 6 х + 9; б) 3 a 2 b – 9 ab 2 ; е ) а 2 – 10 а + 25; в) т 2 – 4 п ; ж ) ax + bx + ay + by . г) а 3 – а ; з ) ab – b + 3 a – 3. З а д а н и я и в о п р о с ы :

Слайд 19

в ы в о д: чтобы сократить рациональную дробь, нужно сначала разложить на множители её числитель и знаменатель.

Слайд 20

Упражнения 1. № 29, № 30 (а, в, д), № 32 (а, в). 2. № 31 (а, б ) , № 34. 3. № 35 (а, в ). 4 . № 36 (а )*.

Слайд 21

Решение № 29

Слайд 22

Решение № 30 (а, в, д )

Слайд 23

Решение № 32 (а, в )

Слайд 24

Решение № 31 (а, б)

Слайд 25

Решение № 34

Слайд 26

Решение № 35 (а, в ) а ) в)

Слайд 27

Решение № 36 (а)*. Областью определения этой функции является множество всех чисел, кроме х = –5. Сократим дробь, задающую функцию: Графиком функции является прямая, а графиком функции –та же прямая, но с «выколотой» точкой (– 5 ;– 5).

Слайд 28

Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных. Если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному.

Слайд 29

Самостоятельная работа Вариант 1 1. В чём состоит основное свойство дроби? 2. Что нужно сделать, чтобы сократить рациональную дробь? 3. Формулы: квадрат разности двух выражений; сумма кубов двух выражений. Сократить дробь: 4 . 5. Вариант 2 1. Когда применяется основное свойство дроби? 2. Что нужно сделать, чтобы сократить рациональную дробь? 3. Формулы: разность квадратов двух выражений ; куб суммы двух выражений. Сократить дробь: 4. 5 .

Слайд 30

– В чём состоит основное свойство рациональной дроби? – Что такое тождество? – Когда применяется основное свойство дроби? В о п р о с ы:

Слайд 31

Задание на самоподготовку: № 24, № 25 (б, г, е ) № 30 (б, г, е), № 32 (б, г), № 33 .

Слайд 32

Алгебpа . 8 класс. Учебник. ФГОС. Ю.Н. Макарычев, Н.Г. Миндюк , К.И. Нешков , С.Б. Суворова. Под ред. С.А.Теляковского . 2013г . Алгебра, 8 класс, Поурочные планы, Дюмина Т.Ю., Махонина А.А., 2012: CD; http://www.arms-expo.ru/049049052052124049051054055.html http://s4.goodfon.ru/wallpaper/previews-middle/219776.jp Литература и Интернет–ресурсы :

nsportal.ru

Основное свойство алгебраической дроби. Алгебра, 8 класс: уроки, тесты, задания.

1.	Перемена знаков числителя и знаменателя дроби Сложность: лёгкое	1
2.	Сокращение алгебраической дроби, вынесение общего множителя за скобки Сложность: лёгкое	2
3.	Расширение алгебраической дроби (неизвестный числитель) Сложность: лёгкое	1,5
4.	Расширение дроби Сложность: среднее	2
5.	Общий знаменатель (противоположные знаменатели) Сложность: среднее	4
6.	Дроби с одинаковыми знаменателями Сложность: среднее	3
7.	Дроби с общим знаменателем (две дроби) Сложность: среднее	4
8.	Дроби с общим знаменателем (разность квадратов) Сложность: среднее	6
9.	Дроби с общим знаменателем (три дроби, разность квадратов) Сложность: среднее	4
10.	Сокращение алгебраической дроби, разложение на множители способом группировки Сложность: среднее	3
11.	Дроби с одинаковыми знаменателями (общий множитель, способ группировки) Сложность: сложное	7

www.yaklass.ru

Технологическая карта к уроку по алгебре 8 класс «Сокращение дробей»

ООО Учебный центр «ПРОФЕССИОНАЛ»

План-конспект урока

по математике

в 8 классе муниципального бюджетного общеобразовательного учреждения

«Средняя школа № 2 им. Е. В. Камышева»

на тему «Сокращение дробей»

Разработал:Филова Елена Викторовна

ФИО

слушатель курсов профессиональной переподготовки «Математика: теория и методика преподавания в образовательной организации»

Проверил: ________________________

ФИО руководителя практики

Г.Гагарин , 2016

Урок по алгебре 8 класса. По УМК Ю.Н. Макарычев и др. Дата 13.09

Дата проведения

Тип урока

Виды деятельности (элементы содержания, контроль)

Планируемые результаты

предметные

Метапредметные УУД: коммуникативные, регулятивные, познавательные; личностные

6

Сокращение дробей

13.09

Урок общеметодической направленности

Формирование у учащихся навыков деятельностях способностей и способностей к структурированию и систематизации изучаемого предметного содержания: работа с опорным конспектами, опрос по теоретическому материалу, проектирование способов выполнения, комментирование выставленных оценок

Познакомится с принципами тождественных преобразований дробей. Научится тождественно сокращать рациональные дроби; формулировать основное свойство рациональных дробей и применять его для преобразований

К: вступать в диалог, участвовать в коллективном обсуждении проблем

Р: вносить коррективы и дополнения в составленные планы

П: выбирать смысловые единицы текста и устанавливать отношения между ними

Л: формирование навыков самодиагностики и самокоррекции деятельности, способности к волевому усилию в преодолении препятствий

Технологии: здоровьесбережения, проблемного обучения, развития исследовательских навыков, дифференцированного подхода в обучении, поэтапного формирования умственных действий

Решаемые проблемы: основное свойство рациональной дроби. Тождества. Тождественные преобразования дробей. Сокращение рациональных дробей

Основная дидактическая цель урока: формировать умение применять основное свойство дроби при сокращении дробей.

Развивать: логическое и критическое мышление

Воспитывать: аккуратность, уважения мнения товарищей, трудолюбие

Оборудование: доска, мел

Учитель приветствует учащихся, проверяет их готовность к уроку.

 Учащиеся готовы к началу работы

 Л: самоопределение.

Р: целеполагание.

II. Устная работа.

– Сократите дробь:

а) ; б) ; в) ; г) ;

д) ; е) ; ж) ; з)

Решают, выполняют работу

 Умение быстрого счета, и анализировать, сопоставлять

П: самостоятельное выделение проблемы, решение проблемы, построение логической цепи рассуждение.

Р: контроль и коррекция

III. Объяснение нового материала

З а д а н и я и в о п р о с ы учащимся:

1. Какие существуют способы разложения многочлена на множители?

2. В чём состоит каждый из этих способов?

3. Разложите на множители многочлен:

а) х²у – 2х; д) х² + 6х + 9;

б) 3a²b – 9ab²; е) а² – 10а + 25;

в) т² – 4п; ж) ax + bx + ay + by.

г) а³ – а; з) ab – b + 3a – 3.

После проведения этой работы следует разобрать пример 3 (с.9) из учебника и сделать в ы в о д: чтобы сократить рациональную дробь, нужно сначала разложить на множители её числитель и знаменатель.

Для успешной работы учащихся на уроке им необходимо не только использовать основное свойство дроби, но и применять ряд других знаний и умений, полученных и сформированных ранее.

Учащиеся должны помнить формулы сокращенного умножения и основные приёмы разложения многочлена на множители. Поэтому начать необходимо с актуализации знаний и умений.

IV. Формирование умений и навыков

1. № 30 (а, в, д), № 32 (в).

2.№ 34(в,г).

3. № 35 (а, в).

Р е ш е н и е

а) .

в) .

Д о п о л н и т е л ь н о можно выполнить № 36 (а).

Р е ш е н и е

Областью определения этой функции является множество всех чисел, кроме х = –5. Сократим дробь, задающую функцию:

.

Графиком функции является прямая, а графиком функции – та же прямая, но с «выколотой» точкой (–5; –5).

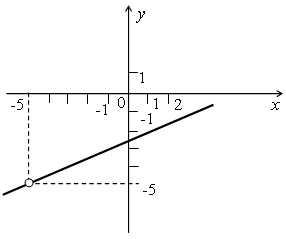
Слушают, анализируют, решают

Решать примеры и задачи , вспоминать правила

 К: инициативное сотрудничество.

П: самостоятельное выделение проблемы, решение проблемы, построение логической цепи рассуждение, доказательства

Р: контроль, коррекция

V. Домашнее задание

§2. №32 (б), 35 (б,г), 40 (а,в,д), 50(а,в, д)

Записывают домашнее задание

VI. Итоги урока

VII. Рефлексия

– В чём состоит основное свойство дроби?

– Когда применяется основное свойство дроби?

– Что нужно сделать, чтобы сократить рациональную дробь?

– Какие существуют способы разложения многочлена на множители?

— оцените себя на сколько Вы поняли тему урока.

 

Отвечают на вопросы

Каждый оценивает свою работу.

 К: умение с достаточной полнотой и точностью выражать свои мысли

П: рефлексия

infourok.ru

Основное свойство дроби. Сокращение дробей

Вы уже знакомы с основным свойством дроби. Давайте вспомним его:

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, отличное от нуля, то значение дроби не изменится.

Иначе говоря, при любых a, b и c верны равенства

Хотелось бы сразу уточнить, что деление числителя и знаменателя на одно и то же число называется сокращением дроби.

Равенство,  справедливо и не только при натуральных, но и при любых значениях переменных a, b и c при которых знаменатель не равен нулю.

Рациональные дроби  тоже можно преобразовывать таким же образом.

Рациональная дробь – это дробь, числитель и знаменатель которой многочлены.

Основное свойство рациональной дроби сводится к тому, что:

Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Если числитель и знаменатель рациональной дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Например

 

Это равенство верно при всех допустимых значениях переменной. Такие равенства называют тождествами.

Определение:

Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Два выражения, принимающие равные значения при всех допустимых значениях переменных, называются тождественно равными.

Замену одного такого выражения другим называют тождественным преобразованием выражения.

Равенство

Основное свойство рациональной дроби позволяет сокращать дроби и приводить дробь к новому знаменателю.

Чтобы сократить рациональную дробь, нужно предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общие множители.

Задание

Сократить дробь.

Решение:

Задание

Привести дробь к указанному знаменателю.

Решение:

Итоги:

Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Если числитель и знаменатель рациональной дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Основное свойство рациональной дроби позволяет сокращать дроби и приводить дробь к новому знаменателю.

videouroki.net

План-конспект урока по алгебре (8 класс) по теме: Сценарий урока «Рациональные дроби. Сокращение дробей»

Сценарий урока

На тему: «Рациональные дроби. Сокращение дробей»

Ход занятия

1. Организационный момент

Взаимное приветствие учителя и учащихся, проверка готовности учеников к занятию, организация внимания, формулирование правил работы на уроке:

Учитель: Здравствуйте ребята! Напомним правила работы на уроке:

1 правило: не выкрикивать, не перебивать и слушать друг друга;

2 правило: выполнив задание, подними руку и дождись когда тебя спросят;

3 правило: быть активными и помогать друг другу.

2. Постановка цели и задач урока

(Слайд1)

Учитель: Как сказал французский писатель и литературный критик Анатоль Франс:  «Учиться можно весело… Чтобы переваривать знания, надо поглощать их с аппетитом»

 (Слайд 2)

С этим девизом мы и начнем урок! Выполним устно задание и соберем «Математический пазл».

(Слайд 3)

Для этого нам необходимо устно найти значение выражения и открыть соответствующую часть картинки.

Учащиеся  устно выполняют вычисления, сообщают свои ответы учителю. Результатом выполнения этого задания станет красочная подсказка на интерактивной доске, с помощью которой учащиеся формулируют тему, цель и задачи урока.

Учитель: Как вы думаете, что это? А какая цель урока?

Учитель:  Математику  не зря называют  «царицей наук», ей больше, чем какой — либо другой науке, свойственны красота, изящность и точность. Одно из замечательных качеств всех математиков – любознательность. Постараемся доказать это на уроке. Вы уже знакомы с рациональными дробями и умеете с ними работать. Знания не только надо иметь, но и надо уметь их показать, что вы и сделаете, а я вам в этом помогу.

3. Оперирование знаниями и способами деятельности в стандартных и нестандартных ситуациях

1. Работа с интерактивными моделями

Для начала вспомним, какую дробь называют рациональной? Приведите пример. Что означает, сократить дробь? Что необходимо сделать, чтобы сократить дробь? А какие способы разложения на множители вы знаете?

Применим на практике все правила, которые вы только что озвучили. Для этого обратимся к планшетам. В электронном учебнике перейдем в каталог, в содержании выберем первый параграф и перейдем в интерактивные модели «Сократи дробь и расшифруй слово».

Кто готов продемонстрировать свои результаты? Какое слово было зашифровано? Все познакомились со значением этого слова? Молодцы!

2. Работа в парах

Ребята, а что мы свами делаем каждый день, перед тем как начать урок? Правильно, мы здороваемся друг с другом. А вы знаете, что здороваться, как и «Здравия желаю» , повелось с древних времен и считалось жестом уважения при приветствии. Выражение произошло от слова «здравствовать» — быть здоровым, благополучно существовать. Речевое приветствие «Здравствуйте» является повелительной формой глагола, которая сформировалась к концу 17 века из описательных оборотов, типа «повелеваю тебе здравствовати» , «здравия тебе желаю» и т. д. «Здравствуйте же многие лета» – находили же в рукописи 1057 года, это самое древнее дошедшее до нас пожелание нашего предка.  

Наиболее распространенное приветствие в русском языке – «здравствуйте», в английском … , в немецком …

Работая в парах, выполните умножение на карточках. Используя найденные ответы и данные таблицы, узнайте, как это приветствие звучит на других языках.

Оставшийся ответ соответствует арабскому языку.

3. Индивидуальная работа (тестовые задания)

Сегодня на уроке вы повторили понятие рациональной дроби, закрепили навыки разложения на множители и сокращения дробей. А теперь пришло время оценить ваши знания. И помогут нам в это наши планшеты. Я попрошу вас перейти в раздел контроль, выбрать тест «Сокращение дробей» и приступить к его выполнению. По завершению работы заполните карточку «Результаты теста», которая лежит у каждого на столе.

4. Формулирование и разъяснение домашнего задания

Математика – удивительная наука. Изучать математику можно весело! Вот и домашнее задание я подготовила необычным и интересным. На ваших столах лежит материал с тремя заданиями. Ваша задача выполнить одно задание по выбору, пользуясь инструкцией, раздобыть интересную информацию и познакомить нас с ней на следующем уроке.

5. Рефлексия

А в завершении урока, я попрошу вас заполнить рефлексионную карту следующим образом: напротив каждого понятия поставьте знак «+», если вам данное понятие сегодня было хорошо известно, «!» — данное понятие необходимо повторить, «-» — мне не известно это понятие, я буду его изучать.

Мне было очень приятно с вами работать, вы молодцы! Спасибо за урок!

nsportal.ru