Что такое площадь по математике: Площадь (математика, 5 класс) – что такое, правило обозначения и понятие

Урок 22. площадь прямоугольника — Математика — 3 класс

Математика, 3 класс

Урок №22. Площадь прямоугольника

Перечень вопросов, рассматриваемых в теме:

1. Как вычислить площадь прямоугольника?
2. В каких единицах измеряется площадь?
3. Какими способами можно сравнить геометрические фигуры?

Глоссарий по теме:

Площадь – внутренняя часть любой плоской геометрической фигуры.

Квадрат – это прямоугольник, у которого все стороны равны.

Прямоугольник – это четырёхугольник, у которого все углы прямые.

Квадратный сантиметр – квадрат со стороной 1 сантиметр.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.

2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с.

38-43.

3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.

Теоретический материал для самостоятельного изучения

Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат.  Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки.

И названия всем геометрическим фигурам дали тоже древнегреческие учёные.

Найдём площадь геометрической фигуры.

Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.

Найдём площадь прямоугольника со сторонами 6 см и 3 см.

Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см²

Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.

S = a ∙ b

S – площадь

a – длина

b – ширина

Задания тренировочного модуля:

1. Заполните пропуски в таблице.

Правильный ответ:

2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.

12 см; 32 см; 24 см²; 32 см²; 24; 12 см².

Правильный ответ:^32см2.

Математика – 5 класс. Площадь геометрической фигуры

Дата публикации: 08 апреля 2017.

Определение и понятие площади фигуры

Чтобы лучше понять, что такое площадь фигуры, рассмотрим рисунок.
Эта произвольная фигура разбита на 12 маленьких квадратика. Сторона каждого квадратика равна 1 см. А площадь каждого квадратика равна 1 квадратному сантиметру, что записывается так: 1 см².

Тогда площадь фигуры равна 12 квадратным сантиметрам. В математике площадь обозначается латинской буквой S.
Значит, площадь нашей фигуры равна: S _фигуры= 12 см².

Площадь фигуры равна площади всех маленьких квадратиков, из которых она состоит!

Ребята, запомните!
Площадь измеряется квадратными единицами длины. Единицы измерения площади:
1. Квадратный километр – км² (когда площади очень большие, например, страна или море).
2. Квадратный метр – м² (вполне подходит для того, чтобы измерять площадь участка или квартиры).
3. Квадратный сантиметр – см² (обычно используется на уроках математики, когда рисуют фигуры в тетради).
4. Квадратный миллиметр – мм².

Площадь треугольника

Рассмотрим два вида треугольников: прямоугольный и произвольный.

Чтобы найти площадь прямоугольного треугольника необходимо знать длину основания и высоту. В прямоугольном треугольнике высоту заменяет одна из сторон. Поэтому в формулу площади треугольника вместо высоты подставляем одну из сторон. В нашем примере стороны равны 7 см и 4 см. Формула для расчета площади треугольника записывается так:

S _{прямоугольного треугольника АВС} = ВС * СА : 2

Подставим в формулу наши данные и получим:
S _{прямоугольного треугольника АВС} = 7 см * 4 см : 2 = 14 см²

Теперь рассмотрим произвольный треугольник.
Для такого треугольника необходимо провести высоту к основанию.
В нашем примере высота равна 6 см, а основание равно 8 см. Как и в предыдущем примере, рассчитываем площадь по формуле:
S _{произвольного треугольника АВС} = ВС * h : 2.

Подставим в формулу наши данные и получим:
S _{произвольного треугольника АВС} = 8 см * 6 см : 2 = 24 см².

Площадь прямоугольника и квадрата

Возьмем прямоугольник АВСD со сторонами 5 см и 8 см. Формула расчета площади прямоугольника записывается так:
S_{прямоугольника АВСD}

= АВ * ВС.

Подставим в формулу наши данные и получим:
S прямоугольника АВСD = 8 см * 5 см = 40 см².

Теперь рассчитаем площадь квадрата. В отличии от прямоугольника и треугольника, для нахождения площади квадрата необходимо знать только одну сторону. В нашем примере сторона квадрата ABCD равна 9 см. S_{квадрата АВСD} = АВ * ВС = АВ ².

Подставим в формулу наши данные и получим:
S_{квадрата АВСD} = 9 см * 9 см = 81 см².

Что такое площадь в математике? Единицы площади

Есть проблемы с элементарной геометрией? Эта статья поможет вам решить одну из них. Здесь вы узнаете о том, что такое площадь в математике, об единицах ее измерения и других важных аспектах этой темы. Разбор некоторых конкретных примеров даст вам возможность глубже изучить вопрос.

Что такое площадь в математике?

Площадь — это мера того, сколько пространства есть на плоской поверхности. Например, есть два одинаковых куска бумаги, чья суммарная площадь, очевидно, больше чем у каждого из них по отдельности.

Площади фигур в математики вычисляются разными путями, зависимо от их формы. Например, в случае с прямоугольником необходимо найти произведение его высоты и ширины. Посмотрим на рисунок.

Имеем ответ: 2 × 4 = 8 см2. Задача решена.

Проверить его можно вручную подсчитав количество больших квадратиков внутри прямоугольника. Подобной задачи достаточно для того чтобы объяснить, что такое площадь в математике. Но в этой теме есть еще и другие важные нюансы.

Единица измерения площади в математике

Измеряется площадь в квадратных единицах. То есть ее можно определить как некоторое количество четырехугольников, чьи стороны равны 1. При этом если поменять местами значения длины и высоты, конечный результат не изменится.

Примечание! Все величины должны быть в одинаковых единицах измерения.

Допустим, что данные заданы в сантиметрах. Как тогда правильно обозначить это на бумаге?

Вместо того чтобы писать «восемь квадратных сантиметров», можно использовать запись вида «8 см2». Достаточно просто возвести сокращенную форму меры во вторую степень.

Перевод величин

У студента или ученика может возникнуть потребность перевести значение из одних единиц измерения в другие. Существует только один верный способ это сделать. Правда, для этого необходимо вспомнить, как правильно переводить одни единицы измерения в другие.

Допустим имеем 9000 м2. Нужно найти, сколько это гектаров. Известно что 1 га = 10 000 м2. Разделим исходную площадь на десять тысяч. В результате получим 0,9 га. Это и будет искомым значением. Главное иметь информацию об отношении двух величин между собой.

А теперь проверим.

Другие фигуры

К сожалению, для нахождения площади не всегда достаточно перемножить два числа. Ситуации бывают разные. Рабочая формула для каждой из них будет видоизменяться из раза в раз. Ниже приведены наиболее часто встречаемые вариации фигур.

Пример

Теперь вы знаете, что такое площадь в математике. Основной теоретический материал усвоен, и можно переходить к практике. Для закрепления решим конкретную задачу.

Условие. Имеется квадрат со стороной 3 сантиметра и круг с радиусом такой же длины. Найдите, чья площадь больше и на сколько.

Решение. Для начала произведем вычисления для каждой из фигур по отдельности:

Sквад = 3 × 3 = 9. Итак, площадь квадрата равна 9 см2.

А вот площадь круга вычисляется уже по другой формуле. Для ее нахождения необходимо вспомнить значение ∏:

Sкруг = ∏ × 3 × 3 ≈ 28,26 см2.

По результатам видим, что площадь круга в несколько раз больше. Осталось лишь посчитать на сколько. Для этого найдем разницу двух чисел.

Sкруг — Sквад = 28,26 — 9 = 19,26 см2.

Ответ найден.

Обычно, решая такие задачи, человек должен сводить все к готовым формулам. Затем уже искать неизвестные, выражать величины одну через другую и использовать смекалку.

Конспект урока математики для 1 класса на тему: «Площадь»

Конспект урока по предмету «математика»

Класс: 1

Тема: «Площадь. Решение задач с использованием краеведческого материала»

Цель: знакомство с понятием «площадь»; формирование представлений об измерении площади одинаковыми геометрическими фигурами (квадратами, прямоугольниками и др. ).

Задачи:

Образовательные: научить вычислять периметр многоугольника и закрепить умение складывать и вычитать числа в пределах 20 без перехода через десяток

Способствовать развитию: пространственных представлений учащихся, отработка изученных приёмов вычислений во втором десятке.

Воспитывать: аккуратность, точность.

Тип урок: открытие новых знаний.

УМК: «Планета знаний», учебники «Математика» М.И. Башмакова, М.Г. Нефёдова, рабочие тетради.

Ход урока.

1. Организационный момент.

Приветствие учащихся. Подведение к теме урока.

2. Устный счет.

— Обратите внимание на задание. Выполнив его, мы назовем тему сегодняшнего урока. Итак, вычислив устно данные выражения, расположим ответы в порядке убывания.

Щ 9-1=

П 11+7=

Д 10-5=

А 6+1=

Л 10+5=

Ь 4-2=

О 20-10=

— Правильно, тема урока «Площадь». На предыдущих уроках вы уже познакомились с понятиями линия, ломанная линия, длина ломанной, периметр.

Что же такое «площадь»?

3. Объяснение нового материала.

— Ребята, посмотрите № 1 в учебнике (на интерактивную доску). Читаем задание: Что общего у этих фигур? А чем они отличаются?

Похожи эти фигуры тем, что каждая из них построена из 5 клеточек.

А отличаются эти фигуры тем, что у них разная форма.

— Ребята, все эти фигуры занимают одинаковое место на странице учебника, ведь так? Тогда говорят, что у них одинаковая площадь.

— Переходим к следующему заданию, № 2. Оно есть на странице учебника, и выведено на доску. Читаем задание: «В цветочном городе все улицы и площади носят названия цветов».

— Итак, давайте вместе с вами назовем эти улицы и площади. (Улицы: Ромашек, Лилий, Маков, Тюльпанов, Нарциссов. Площади: Георгинов, Роз, Ирисов).

В городе 5 улиц и 3 площади.

— Чтобы узнать, какая улица в цветочном городе самая длинная, нужно подсчитать количество клеток каждой улицы. Длина улиц на рисунке определяется подсчетом числа отрезков (сторон клеток).

Улица Ромашек – 5;

Улица Лилий – 8;

Улица Маков – 10;

Улица Тюльпанов – 12;

Улица Нарциссов – 9.

Самая длинная улица – улица Тюльпанов.

А самая короткая?

— Какая площадь самая большая? Как это определить? Правильно, нужно сосчитать количество клеток на каждой площади.

Площадь Георгинов – 8 клеток;

Площадь Роз – 9 клеток;

Площадь Ирисов – 7 клеток.

Самая большая площадь – площадь Роз.

А самая маленькая?

№ 3.

Прочитайте предложение.

В городе была красивейшая площадь с фонтанами.

О какой площади идет в речь?

Поля с капустой занимают большую площадь, чем поля со свеклой.

О какой площади идет речь?

Ребята, последнее предложение можно исправить и сказать так: « Капуста занимает больше места, чем свекла».

4. Физкультминутка.

Встанем, надо отдохнуть,

Наши пальчики встряхнуть.

Поднимайтесь, ручки, вверх,

Шевелитесь, пальчики, –

Так шевелят ушками

Серенькие зайчики.

Крадемся тихо на носочках,

Как лисы бродят по лесочку.

Волк озирается кругом,

И мы головки повернем.

Теперь садимся тише, тише –

Притихнем, словно в норках мыши.

5. Закрепление нового материала.

№ 4.

На четырех участках посадили овощи. Какая площадь у свеклы? (4). А какая площадь у репы? (4). Что занимает большую площадь: репа или свекла?

Какая площадь у капусты? А какая площадь у моркови? Что занимает большую площадь: капуста или морковь? Можно ли сравнить площади полей под капустой и репой? Почему? Потому, что у них разные клеточки.

№ 5. Вычислительный тренинг.

№ 6. Прочитаем задание.

А) Начерти в тетради квадрат со стороной 4 клетки.

Б) Начерти прямоугольник со сторонами 3 и 5 клеток.

В) Какая фигура занимает большую площадь?

Г) Сравни периметры этих фигур.

— Ребята, как определить площадь начерченных фигур (квадрата и прямоугольника)? Площадь начерченных фигур определяется количеством клеток, занимаемых этими фигурами. Квадрат – 16 клеток. Прямоугольник – 15 клеток.

— А теперь сравним периметры этих фигур.

Площадь – это место, которое занимает фигура, периметр – длина границы фигуры.

Периметр определяется числом отрезков – сторон клеток, ограничивающий квадрат и прямоугольник. Периметр квадрата – 16, периметр прямоугольника – 16.

— Ребята, делаем вывод, что у разных фигур с разной площадью периметры могут быть одинаковы.

№ 7.

— Какую единицу измерения площади удобно выбрать для каждой фигуры?

— Какова площадь первой фигуры? Второй? Третьей? Четвертой?

— Верно ли, что площади фигур одинаковы? Почему?

Сравнить площади этих фигур нельзя, так как они измерялись разными мерками.

— Можно ли измерить площадь какой-нибудь фигуры кругами? Почему?

Можно, но ответ получится неточный, так как круги неплотно прилегают друг к другу и не покрывают всей площади, которую занимает фигура.

— Наш урок подходит к концу. Вы все хорошо работали на протяжении всего урока.

— Какие знания помогали нам в работе?

Сегодня на уроке я узнал …

Сегодня на уроке я научился …

Сегодня на уроке мне понравилось…

Периметр, площадь и объем

Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.

Периметр геометрической фигуры

Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.

Вычислим периметр следующей фигуры:

Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.

У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:

Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:

P = 9 см + 4 см + 9 см + 4 см = 26 см.

Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»

P = 2 × (9 + 4) = 18 + 8 = 26 см.

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»

Чтобы вычислить периметр, сложим все стороны:

P = 5 см + 5 см + 5 см + 5 см = 20 см

Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза

P = 5 см × 4 = 20 см

---

Площадь геометрической фигуры

Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.

Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.

Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.

Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.

Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:

Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.

Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:

Допустим, потребовалось измерить площадь следующей комнаты:

Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:

Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:

Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.

---

Площадь прямоугольника

В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.

Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.

Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.

Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:

Теперь измерим ширину. Пусть она составила 3 метра:

Умножим длину (4 м) на ширину (3 м).

4 × 3 = 12

Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:

Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:

---

Площадь квадрата

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см

Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.

Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см

3 × 3 = 9

В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:

Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 3².

Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.

---

Обозначения

Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу

S = a²

где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.

Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см². Это обозначение заменяет словосочетание «квадратный сантиметр».

Например, вычислим площадь квадрат со стороной 2 см.

Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:

Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м². Это обозначение заменяет словосочетание «квадратный метр».

Вычислим площадь квадрата со стороной 3 метра

Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:

Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:

S = a × b

Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см², м², км². Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.

Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см

Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:

В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).

---

Перевод единиц измерения площади

Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.

1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.

Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см

Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100

S = 100² = 10 000 см²

Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.

1 м²  = 10 000 см²

Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.

Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.

А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.

Например, переведём 100 000 см² в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см² это один квадратный метр, то сколько раз 100 000 см² будут содержать по 10 000 см²»

100 000 см² : 10 000 см² = 10 м²

Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км² в квадратные метры.

Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000

S = 1000² = 1 000 000 м²

Получается, что на один квадратный километр приходится один миллион квадратных метров:

1 км²  = 1 000 000 м²

Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.

Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.

Итак, вернёмся к нашей задаче. Требовалось перевести 2 км² в квадратные метры. Умножим 2 км² на 1 000 000

2 км² × 1 000 000 = 2 000 000 м²

А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.

Например, переведём 3 500 000 м² в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м² это один квадратный километр, то сколько раз 3 500 000 м² будут содержать по 1 000 000 м²»

3 500 000 м² : 1 000 000 м² = 3,5 км²

---

Пример 2. Выразить 7 м² в квадратных сантиметрах.

Умножим 7 м² на 10 000

7 м² = 7 м² × 10 000 = 70 000 см²

---

Пример 3. Выразить 5 м² 13 см² в квадратных сантиметрах.

5 м² 13 см² = 5 м² × 10 000 + 13 см² = 50 013 см²

---

Пример 4. Выразить 550 000 см² в квадратных метрах.

Узнаем сколько раз 550 000 см² содержит по 10 000 см². Для этого разделим 550 000 см² на 10 000 см²

550 000 см² : 10 000 см² = 55 м²

---

Пример 5. Выразить 7 км² в квадратных метрах.

Умножим 7 км² на 1 000 000

7 км² × 1 000 000 = 7 000 000 м²

---

Пример 6. Выразить 8 500 000 м² в квадратных километрах.

Узнаем сколько раз 8 500 000 м² содержит по 1 000 000 м². Для этого разделим 8 500 000 м² на 1 000 000 м²

8 500 000 м² × 1 000 000 м² = 8,5 км²

---

Единицы измерения площади земельных участков

Площади небольших земельных участков удобно измерять в квадратных метрах.

Площади более крупных земельных участков измеряются в арах и гектарах.

Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м²). В виду частого распространения такой площади (100 м²) она стала использоваться, как отдельная единица измерения.

Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м² каждый, то есть:

3 а = 100 м² × 3 = 300 м²

В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м². Примеры:

1 сотка = 100 м²

2 сотки = 200 м²

10 соток = 1000 м²

Гектар (сокращенно: га) — это площадь, равная 10 000 м². Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м² каждый, то есть:

20 га = 10 000 м² × 20 = 200 000 м²

---

Прямоугольный параллелепипед и куб

Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:

Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.

Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:

Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:

---

Объём геометрической фигуры

Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.

Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.

Измерить объём какой-нибудь фигуры означает выяснить сколько  кубических единиц вмещается в данную фигуру.

Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:

Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:

Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см³). Тогда объём V рассмотренного нами параллелепипеда равен 12 см³

V = 12 см³

Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .

Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

V = abc

где, a — длина, b — ширина, c — высота

Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см³. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат

Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.

Например, вычислим объём куба, длина которого 3 см.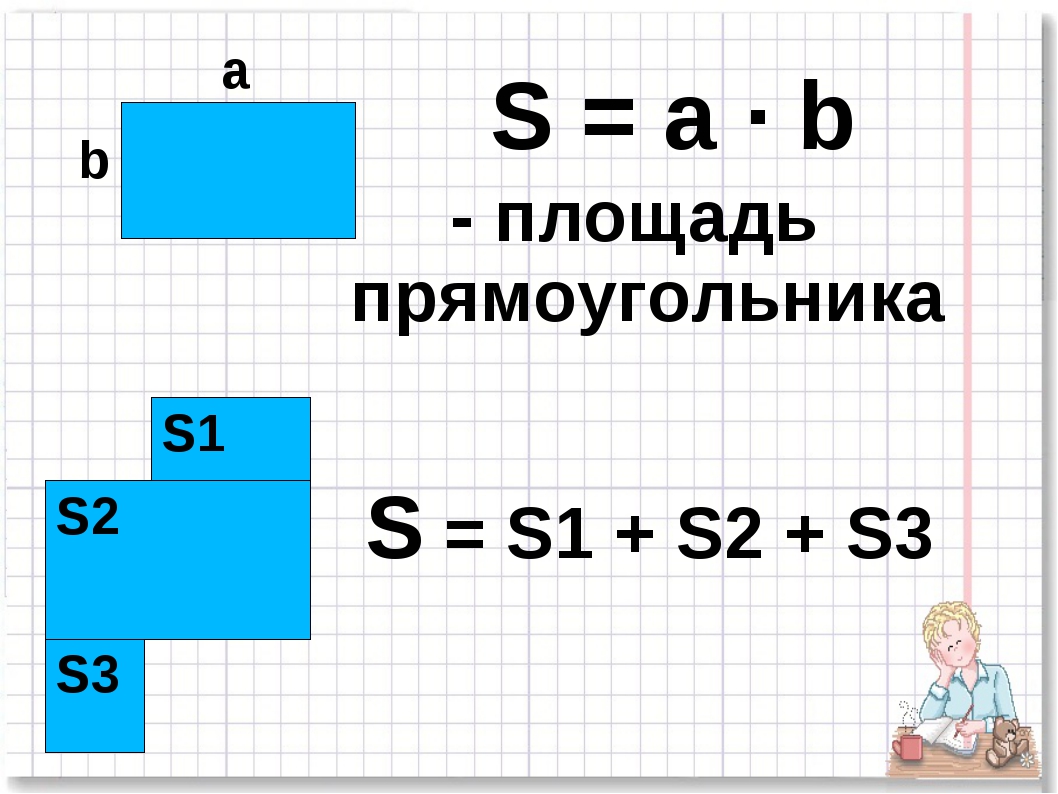 У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:

Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:

V = 3 × 3 × 3 = 27 см³

Действительно, в исходный куб вмещается 27 кубиков длиной 1 см

При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 3³.

V = 3³ = 27 см³

Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.

Таким образом, объём куба вычисляется по следующему правилу:

V = a³

Где a — длина куба.

---

Кубический дециметр. Кубический метр

Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м³). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм³).

Другое название одного кубического дециметра – один литр.

1 дм³ = 1 литр

---

Перевод единиц измерения объёма

Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 кубический метр в кубических сантиметрах.

Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.

Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см

Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:

V = 100³ = 1 000 000 см³

Получается, что на один кубический метр приходится один миллион кубических сантиметров:

1 м³  = 1 000 000 см³

Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.

Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.

А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.

Например, переведём 300 000 000 см³ в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см³ это один кубический метр, то сколько раз 300 000 000 см³ будут содержать по 1 000 000 см³»

300 000 000 см³ : 1 000 000 см³ = 300 м³

---

Пример 2. Выразить 3 м³ в кубических сантиметрах.

Умножим 3 м³ на 1 000 000

3 м³ × 1 000 000 = 3 000 000 см³

---

Пример 3. Выразить 60 000 000 см³ в кубических метрах.

Узнаем сколько раз 60 000 000 см³ содержит по 1 000 000 см³. Для этого разделим 60 000 000 см³ на 1 000 000 см³

60 000 000 см³ : 1 000 000 см³ = 60 м³

---

Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.

1 литр = 1 дм³

Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм³. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.

Пример 1. Перевести 5 литров в кубические дециметры.

Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1

5 л × 1 = 5 дм³

---

Пример 2. Перевести 6000 литров в кубические метры.

Шесть тысяч литров это шесть тысяч кубических дециметров:

6000 л × 1 = 6000 дм³

Теперь переведём эти 6000 дм³ в кубические метры.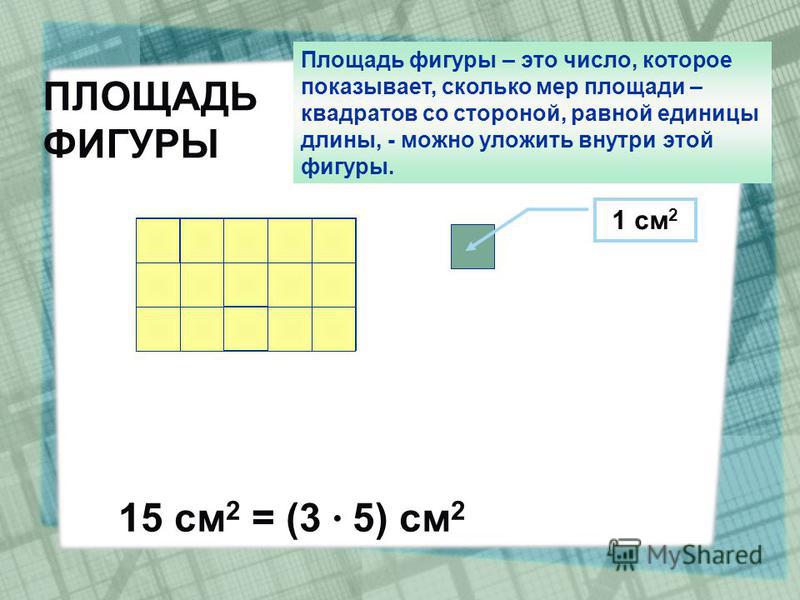

Длина, ширина и высота одного кубического метра равны 10 дм

Если вычислить объём этого куба в дециметрах, то получим 1000 дм³

V = 10³= 1000 дм³

Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм³ содержит по 1 000 дм³

6 000 дм³ : 1 000 дм³ = 6 м³

Значит, 6000 л = 6 м³.

---

Таблица квадратов

В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.

Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.

Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.

Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.

Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576

24² = 576

---

Таблица кубов

Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.

Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.

35³ = 42875

---

Задания для самостоятельного решения

Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.

Решение

P = 2(a + b)

a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см

Ответ: периметр прямоугольника равен 16 см.

Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.

Решение

S = ab
a = 6, b = 2
S = 6 × 2 = 12 см²

Ответ: площадь равна 12 см².

Задача 3. Площадь прямоугольника составляет 12 см². Длина составляет 6 см. Найдите ширину прямоугольника.

Решение

S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2

Ответ: ширина прямоугольника составляет 2 см.

Задача 4. Вычислите площадь квадрата со стороной 8 см

Решение

S = a²
a = 8
S = 8² = 64 см²
Ответ: площадь квадрата со стороной 8 см равна 64 см²

Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.

Решение

V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см³.

Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см³

Задача 6. Объем прямоугольного параллелепипеда составляет 200 см³. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см

Решение

V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4

Ответ: высота прямоугольного параллелепипеда равна 4 см.

Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га

Решение

Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.

Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.

Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза

4 × 3 = 12 га

Ответ: пшеницей засеяно 12 га.

Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м³ его весит 740 кг.

Решение

a — длина
b — ширина
c — высота

a = 42 м
b = м
c = 42 × 0,1 = 4,2 м

Определим объем зернохранилища:

V = abc = 42 × 30 × 4,2 = 5292 м³

Определите сколько тонн зерна вмещает зернохранилище:

5292 × 740 = 3916080 кг

Переведём килограммы в тонны:

Ответ: зернохранилище вмещает 3916,08 тонн зерна.

Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.

Решение

Определим сколько литров в минуту вливается через вторую трубу:

25 л/мин × 0,75 = 18,75 л/мин

Определим сколько литров в минуту вливается в бассейн через обе трубы:

25 л/мин + 18,75 л/мин = 43,75 л/мин

Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин

43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л

1 л = 1 дм³

35 525 л = 35 525 дм³

Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:

35 525 дм³ : 1000 дм³ = 35,525 м³

Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:

V = 35,525
a = 5.8
b = 3.5
c = x

35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м

с = 1,75

Ответ: высота (глубина) бассейна составляет 1,75 м.

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Площадь многоугольника. Площадь квадрата и прямоугольника 8 класс онлайн-подготовка на Ростелеком Лицей

Площадь многоугольника. Площадь квадрата и прямоугольника.

Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.

За единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков.

Например, единица измерения отрезков 1 мм, а единица измерения площади 1 мм² – квадратный миллиметр.

1 см – единица измерения отрезков, а единица измерения площади 1 см² – квадратный сантиметр.

1 м – единица измерения отрезков, а 1 м² – единица площади – квадратный метр.

При выбранной единице измерения площадей площадь каждого многоугольника выражается положительным числом. Это число показывает, сколько раз единица измерения и ее части укладываются в данном многоугольнике.

Если форма многоугольника сложная, то данный процесс усложняется, и на практике неудобен. Поэтому обычно измеряют некоторые отрезки, связанные с многоугольником, и затем вычисляют площадь многоугольника по специальным формулам.

Вывод этих формул основан на свойствах площадей.

1. Равные многоугольники имеют равные площади.

2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

    

    

   Площадь первой фигуры равна сумме площадей двух маленьких фигур, из которых состоит эта фигура.

   Площадь второй фигуры равна сумме площадей трех маленьких фигур, из которых состоит эта фигура.

   Эти два свойства называют основными свойствами площадей.

3. Площадь квадрата равна квадрату его стороны.

    

    

4. Площадь прямоугольника равна произведению длины на ширину.

    

    

    

   S = ab

    

В геометрии, когда нужно сравнить площади фигур, используют следующие понятия: равновеликие многоугольники и равносоставленные.

Равновеликие многоугольники – это многоугольники, которые имеют равные площади.

Равносоставленные многоугольники – это многоугольники, которые составлены из многоугольников, имеющих равные площади. На следующем рисунке изображены два равносоставленных многоугольника.

 

 

Любые два равносоставленных многоугольника – равновеликие.

Верно и обратное утверждение: если два многоугольника равновеликие, то они равносоставленные.

Интересная математика. Учимся измерять площадь

0.00 avg. rating (0% score) — 0 votes

Конечно же, тему «площадь» будут проходить в школе, как и многие другие темы. Но почему-то многое в школе или непонятно, или неинтересно, или и то, и другое.

Я знакомила своих детей с разными математическими темами задолго до школы. Но, конечно же, не на школьном уровне — а просто для формирования понятий.

Например, тема «Площадь» доступна примерно с 5 лет. Как только ребёнок может сосчитать кубики или квадратики, то он уже готов.

С чего начинать?

Можно начать с игр с кубиками.

Сложите из кубиков одинакового размера (из строительного набора, или из игры «Сложи узор», или игры «Уникуб») любую фигуру. Для начала попроще и поменьше. Предложите ребенку пальцем сосчитать все кубики, которые составляют фигуру. Скажите, что общее их количество называется площадью фигуры.

Сколько места занимает фигура в некоторых единицах измерения, так в числовом виде выражается ее площадь. А единица измерения здесь – квадратик – грань кубика.
Впрочем, показать проще, чем объяснить, даже если объяснять простыми словами. Поэтому сложите несколько фигур разной формы и площади и вместе с ребенком сосчитайте их площадь.

Предложите ребенку самостоятельно сосчитать площади других фигур, выстроенных из кубиков. Это не должны быть только квадраты и прямоугольники — фигуры могут быть очень разными!
Потом пусть ребёнок построит фигуры для вас, а вы считайте площадь.

Измеряем площадь плитками

Если у вас дома есть место, где пол выложен плиткой одинаковой формы (без вставок бордюров), предложите ребёнку измерить площадь комнаты (ванной комнаты, например) в плитках. То есть, сосчитать, сколько плиток занимает площадь пола. Если кроме целых плиток есть половинки или кусочки плиток, попробуйте складывать их (примерно, приблизительно!) в целые в уме и в итоге получить площадь с точностью до «столько-то плиток и еще такой-то кусочек» (половинка или меньше половинки, например).

Засаживаем полянку

Можно использовать конструктор «Лего», тогда площадь будем считать «пупырышками». И можно использовать детали из 2 пупырышков, четырех, восьми. Можно брать «однушки» — с одним пупырышком, или длинные детали, где пупырышки в один ряд.

Предложите ребёнку засадить разными «цветами» поляку для игровых человечков или других персонажей.
Полянка может быть любой формы. Но лучше начать с квадратной или прямоугольной. Посчитайте площадь.
Обратите внимание ребенка на то, что можно сосчитать не только площадь целиком, но и сколько рядов деталей или пупырышков и сколько их в каждом ряду. После этого говорите что-то вроде: «шесть рядов по три — получилось восемнадцать». Не надо требовать запоминания, достаточно, чтобы ребёнок слышал.

Площадь фигур на математическом планшете

Одно из моих любимых математических пособий — планшет с гвоздиками. На нём мы изучали очень много математических тем, в том числе — высчитывали площадь фигур.
Начинали с квадратов, прямоугольников. Потом я подбрасывала идею попробовать найти площадь треугольника. Немного помучившись, дети доходили до решения своим умом. И это было на уровне открытия! Не зная никаких правил, теорем, формул, дети догадываются, как на пальцах высчитать площадь треугольника, а потом и любой сложный многоугольник им по плечу!

Кроме вычисления площади уже готовых фигур, на планшете можно предложить детям рисовать резиночками фигуры заданной площади, но разной формы. И тут уж простор для творчества! Только не надо никуда спешить!

Квадратный сантиметр

Ваши дети уже знают, что такое сантиметр? А теперь узнают, что такое квадратный сантиметр.
Скажите ребёнку, что квадратик, у которого все стороны равны 1 см и называется квадратный сантиметр.
Нарежьте из миллимитровой бумаги 20 квадратных сантиметров и попробуйте заполнять им, например, поверхность спичечного коробка, ластика, небольшой коробочки.
Нарисуйте на лист обычной бумаги в клетку несколько фигур разной формы, разделенных на квадратные сантиметры. Предложите ребёнку сосчитать, сколько квадратных сантиметров составляет площадь каждой из фигур.

Квадратный метр

Изобразите на полу квадратный метр. Например, малярным скорчем или просто выложите метровыми лентами. Можно вырезать квадратный метр из куска широких обоев. Можно еще разбить его на квадратные дециметры. А один из них — на квадратные сантиметры или вообще — один из них заклеить кусочком миллиметровки, чтобы показать и квадратные сантиметры и квадратные миллиметры.

Попробуйте, сколько людей может встать на один квадратный метр. Сколько игрушек туда войдет? Сколько коробок от обуви (например, если у вас есть такие коробки) надо выложить, чтобы его заполнить и так далее.
Попробуйте измерять площадь комнаты в квадратных метрах (если у вас есть вырезанный из бумаги квадратный метр), сделайте вывод, что это неудобно. Но пока не говорите, как лучше сосчитать площадь.

Что дальше?

Вообще, в дошкольном возрасте этого достаточно. Хорошо, если в дальнейших играх вы так или иначе будете обращать внимание ребёнка на площадь фигуры. Рано или поздно это станет столь же естественным, как счёт.

Кстати, тема «Площадь» детям даётся даже проще, чем периметр. Потому что площадь можно увидеть наглядно, пощупать, ощутить, а периметр «пощупать» сложнее.

О периметре мы поговорим как-нибудь в другой раз.

Акция! До 1-го декабря скидка на набор презентаций по математике, записи прямых эфиров и на спецкурсы «Матемашка»!

>>Узнать подробнее

Не забудьте подписаться на обновления блога:

Подобные записи

0. 00 avg. rating (0% score) — 0 votes

Что такое площадь? — Определение, факты и пример

Что такое площадь? В геометрии площадь можно определить как пространство, занимаемое плоской формой или поверхностью объекта. Площадь фигуры — это количество единичных квадратов, покрывающих поверхность замкнутой фигуры. Площадь измеряется в квадратных единицах, таких как квадратные сантиметры, квадратные футы, квадратные дюймы и т. Д.

Площадь приведенных ниже квадратов со стороной 1 сантиметр каждый будет измеряться в квадратных сантиметрах (см²).

Здесь площадь фигур ниже будет измеряться в квадратных метрах (м²) и квадратных дюймах (дюйм²).

Слово «площадь» происходит от латинского «площадь», что означает свободный участок ровной поверхности. Происхождение далее привело к неправильному получению площади как «определенного количества пространства, заключенного в пределах набора границ».

Мы часто находим площадь пола комнаты, чтобы определить размер покупаемого ковра. Покрытие пола плиткой, покрытие стен краской или обоями или строительство бассейна — другие примеры, где площадь вычисляется.

Обычные простые формы и многоугольники имеют свои собственные формулы для вычисления площади. Вот как вычисляется площадь обычных двухмерных или двумерных фигур:

Двумерные геометрические формы:

Название формы:	Изображение формы:	Формула площади:
Круг		Площадь = πr², где r — радиус.
Треугольник		Площадь = бх, где b — база, А h — высота.
Квадрат		Площадь = l × l, где l — длина каждой стороны.
Прямоугольник		Площадь = l × w, где l длина и w — ширина.
Параллелограмм		Площадь = b × h, где b — база, h — высота по перпендикуляру.
Трапеция		Площадь = (а + б) з, где a и b — длины параллельных сторон, h — высота по перпендикуляру.

В реальной жизни не каждую плоскую фигуру можно однозначно классифицировать как прямоугольник, квадрат или треугольник. Чтобы найти площадь составной фигуры, которая состоит из более чем одной формы, нам нужно найти сумму площадей обеих или всех фигур, образующих составную фигуру.

Площадь внешней поверхности твердой или трехмерной формы называется площадью поверхности. Например, прямоугольная призма имеет 6 прямоугольных оснований и боковые грани.Итак, общая площадь поверхности — это сумма площадей всех 6 прямоугольников.

Интересные факты Среди всех фигур с одинаковым периметром круг имеет наибольшую площадь.

Давайте споем!

Для посадки овощей в приусадебном участке,

Найдите площадь поля — все внутри.

Умножьте его длину на ширину,

И вот формула площади, которую вы применили!

Давайте сделаем это!

Вместо того, чтобы раздавать детям рабочие листы по математике, вовлекайте их в проекты по благоустройству дома.Сообщите им о комнате, которую вы собираетесь покрасить. Попросите их подсчитать общую площадь стен, чтобы узнать, сколько требуется краски.

Обсудите, как все стены в комнате могут отличаться друг от друга, и, таким образом, проведение общих измерений с последующим вычитанием площади двери, окон или книжных полок поможет оценить необходимое количество краски.

Вы также можете попросить рассмотреть возможность определения общей площади подарка, который они упаковывают, чтобы найти необходимое количество оберточной бумаги.

Связанный математический словарь

Что такое площадь?

Площадь — это размер поверхности!

Пример:

У всех этих фигур одинаковая площадь 9:

.

Это помогает представить , сколько краски покроет форму.

Площадь простых форм

Для определенных форм существуют специальные формулы:

Пример: Какова площадь этого прямоугольника?

Формула:

Площадь = ш × в
ш = ширина
в = высота

Ширина равна 5, а высота равна 3, поэтому мы знаем, что w = 5 и h = 3 :

Площадь = 5 × 3 = 15

Узнайте больше в Area of ​​Plane Shapes.

Площадь по счету квадратов

Мы также можем нанести фигуру на сетку и посчитать количество квадратов:

Прямоугольник имеет площадь 15

Пример: когда каждый квадрат равен 1 метр со стороны, тогда площадь составляет 15 м ² (15 квадратных метров)

Квадратный метр vs Квадратный метр

Базовая единица площади в метрической системе — квадратных метров. — квадрат, каждая сторона которого имеет 1 метр:

1 квадратный метр

Будьте осторожны, говоря «квадратные метры», а не «квадратные метры»:

Есть также «квадратный мм», «квадратный см» и т. Д., Подробнее см. Метрическая площадь.

Приблизительная площадь по подсчету квадратов

Иногда квадраты не совсем соответствуют форме, но мы можем получить «приблизительный» ответ.

В одну сторону:

• больше чем половина квадрата считается как 1
• меньше чем половина квадрата считается как 0

Как это:

Этот пятиугольник имеет площадь примерно 17

Или мы можем сосчитать один квадрат, когда кажется, что

областей в сумме дают .

Пример: Здесь область, обозначенная « 4 », кажется равной примерно 1 целому квадрату (также для « 8 »):

Этот круг имеет площадь примерно 14

Но лучше всего использовать формулу (когда это возможно):

Пример: круг имеет радиус 2,1 метра:

Формула:

Площадь = π × r ²

Где:

Радиус 2. 1м , итого:

Площадь = 3,1416 … × (2,1 м) ²

= 3,1416 … × (2,1 м × 2,1 м)

= 13,854 … м ²

Таким образом, круг имеет площадь 13,85 квадратных метров (с точностью до 2 знаков после запятой)

Область сложных форм

Иногда мы можем разбить фигуру на две или более простые формы:

Пример: Какова площадь этой формы?

Разобьем область на две части:

Часть А представляет собой квадрат:

Площадь A = ² = 20м × 20м = 400м ²

Часть B представляет собой треугольник.При взгляде сбоку он имеет основание 20 м и высоту 14 м.

Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м ²

Итак, общая площадь:

Площадь = Площадь A + Площадь B

Площадь = 400 м ² + 140 м ²

Площадь = 540м ²

Площадь путем сложения треугольников

Мы также можем разбить фигуру на треугольники:

Затем измерьте основание ( b ) и высоту ( h ) каждого треугольника:

Затем рассчитайте каждую площадь (используя Area = ½b × h) и сложите их все.

Площадь по координатам

Когда мы знаем координаты каждой угловой точки, мы можем использовать метод «Площадь неправильных многоугольников».

Есть область многоугольника с помощью инструмента рисования, который тоже может помочь.

Что такое площадь в математике? — Определение и формула — Видео и стенограмма урока

Формулы площади

Чтобы найти площадь прямоугольника, используйте следующую формулу:

Площадь = длина * ширина

Площадь квадрата определяется по следующей формуле:

Площадь = s2, где s = сторона

Формула площади треугольника:

Площадь = (1/2) b * h, где b = основание, а h = высота

Чтобы найти площадь круга, используйте эту формулу :

Площадь = pi * r2, где r = радиус

Площадь параллелограмма определяется по следующей формуле:

Площадь = b * h, где b = основание, а h = высота по вертикали

формула для площади трапеции:

Площадь = (1/2) * (a + b) * h, где a = основание 1, b = основание 2 и h = высота по вертикали

Площадь эллипса находится так:

Area = pi * a * b, где a = радиус большой оси и b = радиус малой оси

90 002 Единицы площади

Для определения площади формы всегда требуется умножение двух длин. В квадрате это сторона, умноженная на бок. В круге это радиус в квадрате. Для эллипса это радиус большой оси, умноженный на радиус малой оси. Благодаря этому единицы измерения площади всегда будут квадратными (футы в квадрате, дюймы в квадрате и т. Д.). Все, что умножено на себя, возводится в квадрат, будь то число или нет.

Пример поиска области

Давайте попрактикуемся в поиске области с помощью нескольких примеров задач.

Какова площадь квадрата со стороной 5 дюймов?

Помните, формула для определения площади квадрата: A = s 2.Стороны этого квадрата равны 5 дюймам. Подставьте это в формулу, чтобы получить A = 52 = 25 дюйм2.

Какова площадь этого параллелограмма?

Параллелограмм например проблема

Помните, формула: A = b * h . Итак, для этого примера площадь будет A = 3 * 12 = 36 мм2.

Поиск области необычных форм

Если вас попросят найти область необычной формы, это можно сделать, разбив фигуру на более общие формы, найдя площадь этих фигур, а затем сложив области вместе.Давайте посмотрим на несколько примеров:

Найдите площадь этой формы:

Форма, например, проблема

Первым шагом к решению этой проблемы является разделение формы на формы, площадь которых мы можем легко найти. Эту форму можно разделить на треугольник и квадрат.

Чтобы найти площадь, разделите необычные формы на общие.

Вы можете использовать предоставленную информацию для определения длины, необходимой для расчета площади.Поскольку вы знаете, что высота от точки треугольника до нижней части квадрата составляет 10 см, а высота квадрата 8 см, высота треугольника должна составлять 2 см. Основание треугольника равно стороне квадрата, равной 8 см. Вы можете использовать эти числа для определения площади. A квадрата = с 2 = 82 = 64 см2. A треугольника = (1/2) * b * h = (1/2) * 8 * 2 = 8 см2. Затем вы просто складываете области вместе, чтобы получить общую площадь фигуры. A = 64 + 8 = 72 см2.

Найдите область фигуры, заштрихованную красным, учитывая, что размеры прямоугольника 11 дюймов на 7 дюймов

Найдите область красной части.

Этот пример немного отличается, поскольку вам нужна только площадь небольшой части фигуры. Эту фигуру можно разбить только на прямоугольник и круг, на этот раз площадь круга нужно вычесть из площади прямоугольника, чтобы получить оставшуюся площадь. прямоугольника = l * w = 11 * 7 = 77 дюймов2. A круга = пи * r 2 = пи * (3,52) = 38,47 дюйм2.

Радиус круга определяется по диаметру круга, который равен ширине прямоугольника, потому что ширина круга равна ширине прямоугольника. Радиус составляет половину диаметра (1,2 * 7 = 3,5). A = 77 — 38,47 = 38,53 дюйма2.

Резюме урока

Площадь двумерной фигуры — это расчет пространства, занимаемого фигурой.Такие фигуры, как квадраты, треугольники, круги и другие, имеют определенные формулы, которые можно использовать для определения их площади. Площадь других фигур можно определить, разбив фигуру на части, площадь которых легко определить.

Результаты обучения

По мере того, как вы смотрите видеоурок, ваши расширяющиеся знания могут подготовить вас к:

• Назовите определение области и узнайте ее приложения
• Экспресс-единицы площади
• Определите и примените формулы для поиска области общих форм
• Найдите области необычных форм

Что такое площадь? Определение, Формула площади форм

Площадь — это пространство, занимаемое двухмерной фигурой. Другими словами, это величина, которая измеряет количество единичных квадратов, покрывающих поверхность замкнутой фигуры. Стандартная единица площади — квадратные единицы, которые обычно представлены как квадратные дюймы, квадратные футы и т. Д. Давайте узнаем, как рассчитать площадь различных геометрических фигур с помощью примеров и практических вопросов.

Что означает площадь?

Слово «площадь» означает свободную поверхность. Площадь фигуры рассчитывается по ее длине и ширине.Длина является одномерной и измеряется в таких единицах, как футы (футы), ярды (ярды), дюймы (дюймы) и т. Д. Однако площадь фигуры является двумерной величиной. Следовательно, он измеряется в квадратных единицах, таких как квадратные дюймы или (в ² ), квадратные футы или (футы ² ), квадратные ярды или (ярды ² ) и т. Д. Большинство объектов или форм имеют края и углы. Длина и ширина этих краев учитываются при расчете площади конкретной формы.

Как рассчитать площадь?

Давайте посмотрим, как вычислить площадь фигуры с помощью сетки.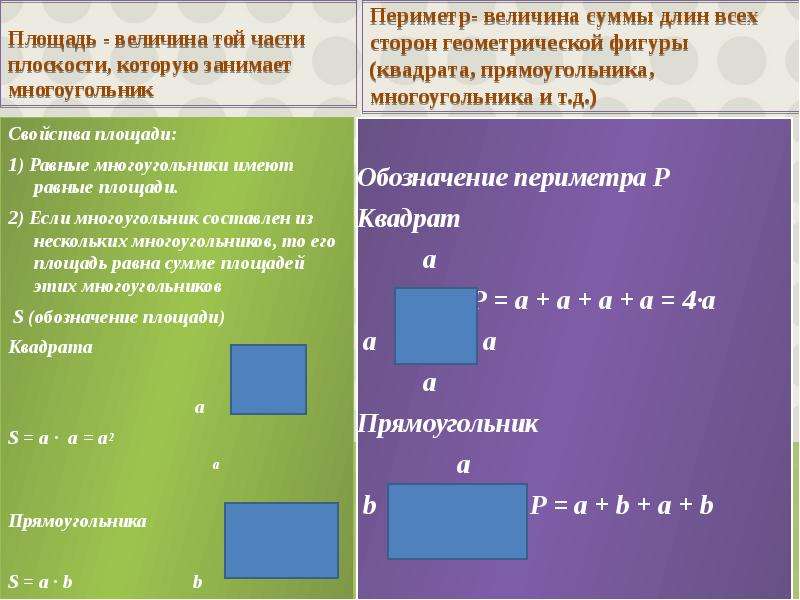 Площадь любой формы — это количество единичных квадратов, которые могут в нее поместиться. Сетка состоит из множества квадратов со сторонами 1 единица на 1 единицу. Площадь каждого из этих квадратов составляет 1 квадратную единицу. Следовательно, каждый квадрат известен как единичный квадрат. Посмотрите на рисунок, показанный ниже. Найдем площадь нарисованной фигуры в сетке.

Площадь этой фигуры равна количеству заштрихованных единичных квадратов.

Таким образом, площадь фигуры = 9 квадратных единиц. Теперь давайте посмотрим на другой пример.Когда фигура не занимает полный единичный квадрат, мы можем приблизительно определить и найти ее значение. Если он занимает около 1/2 единицы квадрата, мы можем объединить две такие половинки, чтобы получить площадь в 1 квадратную единицу. Обратите внимание на рисунок, приведенный ниже.

Здесь площадь, занимаемая фигурой, равна 4 полным квадратам и 8 полуквадратам. Вместе это составляет 8 квадратных единиц.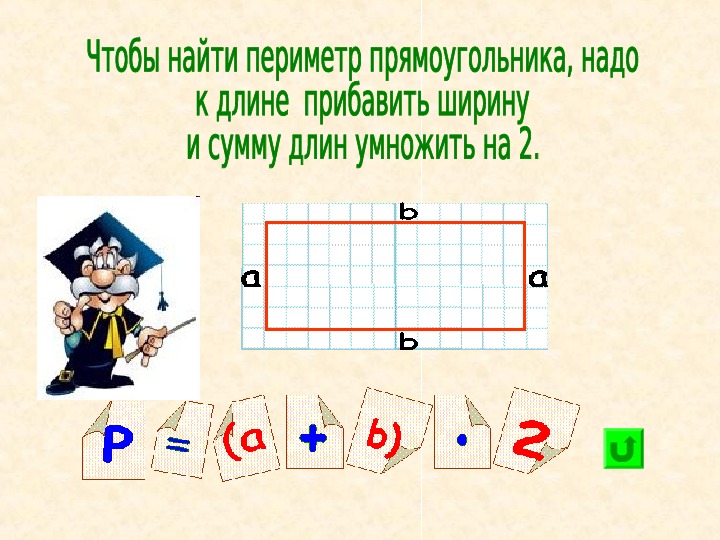 Если заштрихованная область меньше 1/2, мы можем опустить эти части. Для правильных форм у нас есть определенные формулы для расчета их площади.Обратите внимание, что это только приблизительное значение.

Площадь прямоугольника

Площадь прямоугольника — это занимаемое им пространство. Рассмотрим желтый прямоугольник в сетке. Он занял 6 единиц.

В приведенном выше примере длина прямоугольника составляет 3 единицы, а ширина — 2 единицы. Площадь прямоугольника получается путем умножения его длины и ширины, что аналогично подсчету единичных квадратов. Таким образом, формула для площади прямоугольника : Площадь прямоугольника = длина × ширина. В данном случае это будет 2 × 3 = 6 квадратных единиц.

Площадь квадрата

Площадь квадрата — это занимаемая площадь. Посмотрите на цветной квадрат, показанный в сетке ниже. Он занимает 25 квадратов.

Из рисунка видно, что длина каждой стороны цветного квадрата равна 5 единицам. Следовательно, площадь квадрата — это произведение его сторон, которое можно представить формулой: Площадь квадрата = сторона × сторона. Итак, площадь этого квадрата = 5 × 5 = 25 квадратных единиц.

Площадь круга

Круг имеет изогнутую форму. Площадь круга — это количество пространства, заключенного в пределах круга. Узнайте больше о π и радиусе, прежде чем мы перейдем к формуле для площади круга.

Площадь круга вычисляется по формуле: π r ² , где π — математическая константа, значение которой приблизительно равно 3,14 или 22/7, а r — радиус круга.

Площадь геометрических фигур — Формула

Каждая форма имеет разные размеры и формулы.В следующей таблице представлен список формул для площади различных форм.

Форма	Площадь фигур — Формула
Квадрат	Площадь квадрата = x 2 квадратных единиц
Прямоугольник	Площадь прямоугольника = длина × ширина = квадратные единицы l × w
Круг	Площадь круга = π r 2 квадратных единиц
Треугольник	Площадь треугольника = \ (\ dfrac {1} {2} \ times b \ times h \) единиц квадрата
Параллелограмм	Площадь параллелограмма = основание × высота = b × h квадратных единиц
Равнобедренная трапеция	Площадь равнобедренной трапеции = \ (\ dfrac {1} {2} (a + b) h \) квадратных единиц
Ромб	Площадь ромба = \ (\ dfrac {1} {2} \ times (d1) \ times (d2) \) квадратных единиц
Воздушный змей	Площадь воздушного змея = \ (\ dfrac {1} {2} \ times (d1) \ times (d2) \) квадратных единиц

☛ Связанные темы в области

Ознакомьтесь со следующими темами, относящимися к областям различной формы, и узнайте больше о формулах площади.

Советы и хитрости

• Мы часто заучиваем формулы для вычисления площади фигур. Более простой способ — использовать линии сетки, чтобы понять, как была получена формула.
• Мы часто путаемся между площадью и периметром фигуры. Полное понимание может быть достигнуто, отслеживая поверхность любой формы и наблюдая, что область — это, по сути, пространство или область, покрытая формой.

Часто задаваемые вопросы по Area

Что такое площадь?

Площадь формы — это двумерная величина, которая измеряется в квадратных единицах, таких как квадратные дюймы или (в ² ), квадратные футы или (футы ² ), квадратные ярды или (ярды ² ) и т. Д. .

Как найти область неправильной формы?

Площадь неправильной формы можно найти, разделив форму на единичные квадраты. Когда фигура не занимает весь единичный квадрат, мы можем приблизительно определить и найти ее значение.

Как доказать площадь круга?

Если круг складывается в треугольник, радиус становится высотой треугольника, а периметр становится его основанием, равным 2 × π × r. Мы знаем, что площадь треугольника определяется путем умножения его основания и высоты, а затем деления на 2, что составляет: ½ × 2 × π × r × r.Следовательно, площадь круга равна π r ² .

Что такое периметр и площадь треугольника?

Общая длина границы замкнутой формы называется ее периметром. Другими словами, периметр — это сумма сторон двухмерной фигуры. Периметр треугольника равен сумме трех сторон треугольника, а площадь треугольника равна

.

Каковы формулы площади и периметра квадрата и прямоугольника?

Формулы для вычисления площади и периметра квадрата и прямоугольника следующие.Площадь квадрата = сторона × сторона. Периметр квадрата = 4 × стороны. Площадь прямоугольника = длина × ширина. Периметр прямоугольника = 2 × (длина + ширина)

Почему площадь выражается в квадратных единицах?

Площадь фигуры — это количество единичных квадратов, необходимых для ее полного покрытия. Поэтому он измеряется и выражается в квадратных единицах.

Что такое площадь в математике? | Определение и формула

Определение площади в математике

В геометрии площадь — это пространство, которое плоская форма — такие фигуры, как многоугольник, круг или эллипс — занимает на плоскости.

Площадь сбивает с толку многих людей, потому что площадь измеряется в квадратных единицах независимо от формы. Где количество квадратных единиц в круге? Как только вы узнаете, как квадратные единицы соотносятся с площадью, вы сможете найти площадь практически любой двухмерной формы.

Содержание

1. Определение площади в математике
2. Как найти площадь формы
3. Формула площади

Как найти площадь формы

Плоские формы имеют два измерения:

1. Ширина
2. Длина

Квадрат, например, имеет ширину, равную его длине, потому что все стороны одинаковы.Эллипс тоже имеет ширину и длину.

Мы можем легко увидеть, как квадрат можно разделить на маленькие квадратные единицы, как на координатной плоскости. Вы не можете легко понять, как эллипс может состоять из маленьких квадратов, но это возможно.

Поскольку он имеет ширину и длину, он покрывает пространство, и это пространство, даже с изогнутыми сторонами эллипса, можно разделить на квадратные единицы:

Подсчитать квадратные единицы в квадрате легко: один, два, три и т. Д..

Но как можно сосчитать все квадратные единицы эллипса? Как вы определяете, какая часть квадрата находится под верхней кривой? А как насчет кривых на левом и правом концах?

К счастью, у математики есть быстрый способ сложить все квадратные единицы, не считая их на самом деле.

Квадратные единицы — это единицы измерения площади, потому что плоские фигуры или плоские формы всегда можно разделить на квадраты известных размеров, например:

• мм2
• см2
• фут2
• ярда2
• ярда2
• км2
• mi2

Если вы находите площадь четырехугольника, такого как трапеция и ромб, или любую другую замкнутую фигуру, площадь всегда будет квадратной.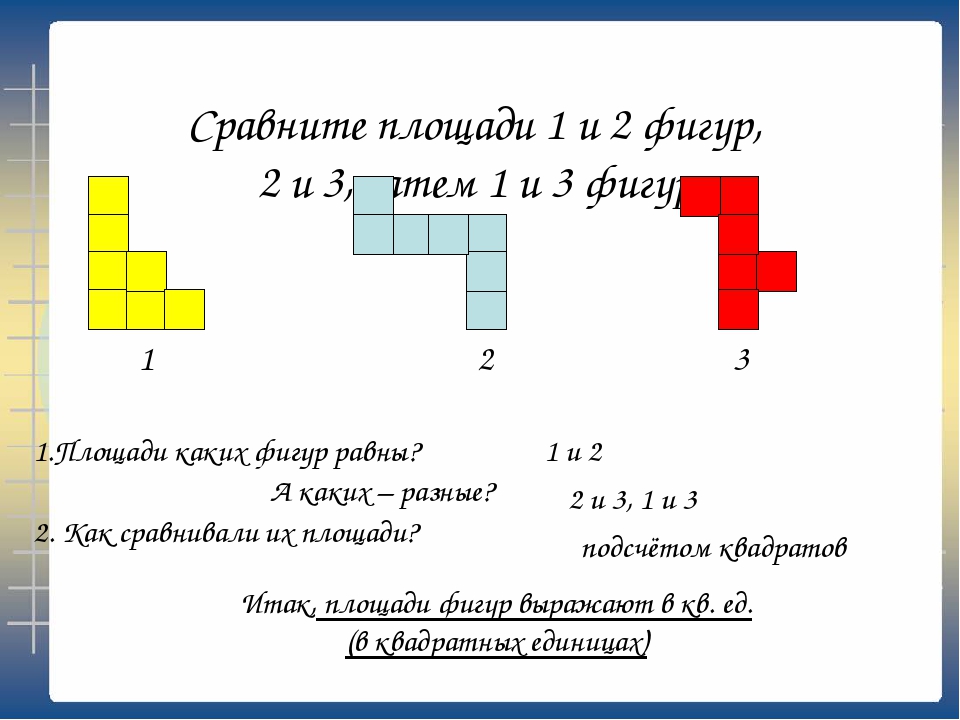

Формула площади

Используемая формула площади зависит от формы, для которой вы пытаетесь найти площадь.

Площадь квадратов и прямоугольников

Чтобы найти площадь простых форм, таких как квадрат или площадь прямоугольника, вам нужны только его ширина, w, и длина, l (или основание, b). Площадь: длина умноженная на ширину:

.

Площадь всегда квадратная. Вы всегда будете выражать площадь в квадратных единицах, производных от линейных единиц.

Вот прямоугольник шириной 90 метров и длиной 120 метров (самый большой размер футбольного поля ФИФА).Какова его площадь этого прямоугольника?

A = длина × ширина

A = 120 м × 90 м

A = 10 800 м2

Поскольку футбольное поле измеряется в погонных метрах, его площадь составляет квадратные метры. Площадь прямоугольника составляет 10 800 квадратных метров.

Площадь формулы квадрата на самом деле даже проще, чем записать длину × ширину, потому что все стороны равны:

Вот квадрат со сторонами 15 дюймов в длину, такого же размера, как основания на бейсбольном поле MLB. Расчетная площадь этого квадрата выглядит так:

А = s2

А = 152

A = 225 дюйм2

Площадь других форм

Все остальные многоугольники нелегко разделить на квадратные единицы. Взгляните на параллелограмм :

Две стороны пересекают множество квадратных единиц. Конечно, параллелограмм — это просто перевернутый прямоугольник.

Итак, математически, если бы мы могли отрезать один конец и прикрепить его к другому, мы получили бы площадь в квадратных единицах.Мы можем сделать именно это, поскольку площадь параллелограмма с основанием b и шириной или высотой h определяется по следующей формуле:

Это та же формула, что и для квадрата или прямоугольника!

Если разделить параллелограмм по диагонали, что получится? Два треугольника. Это означает, что площадь любого треугольника равна половине площади параллелограмма с такой же длиной основания и высотой. Помните, что параллелограмм использует ту же формулу, что и прямоугольник.

Площадь треугольника равна половине основания b, умноженной на высоту h:

Вот прямоугольный треугольник, парус 45-футовой парусной лодки Morgan с базой 20 14 футов и высотой 44 12 футов.Какая у него площадь?

Для удобства умножения дроби можно поменять на десятичные:

А = 12bh

A = 12 (20,25 футов × 44,5 футов)

A = 12 (901,125 фут2)

A = 450,5625 фут2

Площадь треугольного паруса составляет примерно 450,6 квадратных футов.

Как насчет домашней пластины бейсбольного поля MLB? Мы можем рассчитать площадь пятиугольника на домашней плите , рассматривая его как две формы:

1. Прямоугольник 17 дюймов × 8.5 дюймов
2. Равнобедренный прямоугольный треугольник с ногами 12 дюймов

Сначала воспользуемся формулой, чтобы найти площадь прямоугольника:

A = длина × ширина

A = 17 дюймов × 8,5 дюймов

A = 144,5 дюйма2

Теперь мы вычислим площадь оставшегося треугольника, используя формулу площади треугольника:

А = 12bh

A = 12 (12 дюймов × 12 дюймов)

A = 12 (144 дюйм2)

A = 72 дюйм2

Сложите эти две площади, чтобы найти общую площадь в квадратных дюймах:

144. 5 дюймов2 + 72 дюймов2 = 216,5 дюймов2

Найдите площадь круга

Некоторые двумерные формы даже не являются многоугольниками, как наш эллипс или круг. Площадь окружности с радиусом r определяется по следующей формуле:

Если у вас есть круг с радиусом 4 сантиметра, вы можете легко вычислить площадь круга по приведенной выше формуле:

А = πr2

А = π (4) 2

А = π (16)

А = 3,14 × 16

А ≈ 50,24

Площадь круга примерно 50.24 квадратных сантиметра.

Найдите площадь эллипса

Площадь эллипса определяется с использованием двух его осей, большой оси (длина от центра), обычно обозначаемой как a, и малой оси (ширины от центра), обычно обозначаемой как b, по следующей формуле:

Если вы имеете дело с правильным многоугольником или неправильной плоской фигурой, вы можете найти область!

Следующий урок:

Площадь поверхности прямоугольной призмы

Периметр, площадь и объем

1. В периметр из многоугольник (или любая другая замкнутая кривая, например окружность) — это расстояние вокруг внешней стороны.

2. В площадь из простая замкнутая плоская кривая — это количество внутреннего пространства.

3. В объем из твердый 3 D shape — это количество перемещаемого им пространства.

Некоторые формулы для общих 2 -мерные плоские фигуры и 3 -мерные тела приведены ниже.Ответов один, два, или три измерения; периметр измеряется в линейные единицы , площадь измеряется в квадратные единицы , и объем измеряется в кубические единицы .

Таблица 1 . Формулы периметра
Форма	Формула	Переменные
Квадратный	п знак равно 4 s	s длина стороны квадрата.
Прямоугольник	п знак равно 2 L + 2 W	L и W — длины сторон прямоугольника (длина и ширина).
Треугольник	а + б + c	а , б , и c — длины сторон.
	п знак равно а + б + а 2 + б 2	а и б длины двух катетов треугольника
Круг		р это радиус и d это диаметр.

Таблица 2. Формулы площади
Форма	Формула	Переменные
Квадратный		s длина стороны квадрата.
Прямоугольник		L и W — длины сторон прямоугольника (длина и ширина).
Треугольник	А знак равно 1 2 б час	б и час основание и высота
Треугольник	А знак равно s ( s — а ) ( s — б ) ( s — c ) где s знак равно а + б + c 2	а , б , и c длины сторон и s полупериметр
Параллелограмм		б длина основания и час это высота.
Трапеция	А знак равно б 1 + б 2 2 час	б 1 и б 2 — длины параллельных сторон и час расстояние (высота) между параллелями.
Круг	А знак равно π р 2	р это радиус.

Таблица 3. Формулы объема
Форма	Формула	Переменные
Куб		s длина стороны.
Правая прямоугольная призма		L это длина, W это ширина и ЧАС это высота.
Призма или цилиндр		А площадь основания, час это высота.
Пирамида или конус		А площадь основания, час это высота.
Сфера		р это радиус.

Что такое площадь? | TheSchoolRun

Мы объясняем, что означает термин «площадь» и как детей учат вычислять площадь фигуры.

или зарегистрируйтесь, чтобы добавить к сэкономленным ресурсам

Что такое площадь?

Площадь — это термин, используемый для определения объема пространства, занимаемого двухмерной формой или поверхностью. We измеряет площадь в квадратных единицах : см² или м².

Площадь рассчитывается как умножения длины фигуры на ее ширину . В этом случае мы могли бы определить площадь этого прямоугольника, даже если бы он не был на бумаге прямоугольной формы, просто вычислив 5 см x 5 см = 25 см² (фигура не масштабируется).

Изучение области в начальной школе

Дети знакомятся с областью в 4 классе , где им будет предложено найти площадь различной формы, просто посчитав квадраты размером 1 см², которые они занимают на бумаге:

Ожидается, что в году 5 детей будут использовать формулу (длина х ширина), чтобы вычислить площадь прямоугольника.Им часто будут рисовать прямоугольники, не масштабированные, поэтому эту формулу необходимо запомнить. Также им нужно оценить площадь неправильной формы.

В классе 6 детям нужно будет выяснить, как найти область неправильной формы , например, следующую. Часто, чтобы усложнить задачу, будут указаны не все размеры каждой стороны.

Хороший способ найти площадь такой формы — разделить ее на более мелкие и затем проработать площадь каждой из них.Затем можно сложить области меньших фигур, чтобы найти ответ.

Дети 6-го класса также учатся вычислять площадь параллелограммов (основание x высота) и треугольников (основание x высота ÷ 2).

Иногда детей просят разгадывать сформулированные головоломки или исследовать территорию, на которой нет графического изображения, например:

Прямоугольник имеет периметр 36 см. Какой может быть площадь этой формы?

На этот вопрос есть несколько возможных ответов.Один из способов найти возможный ответ — нарисовать прямоугольник, а затем определить, какими могут быть стороны, если периметр равен 36 см.

Это, вероятно, потребует большого количества проб и ошибок. Наконец-то ребенок может прийти к меркам: 10см и 8см. Чтобы найти площадь, им нужно запомнить формулу для площади (длина x ширина), поэтому умножив 10 x 8, получится 80 см².