Физика что такое погрешность: Измерение физических величин. Точность и погрешность измерений. 7 класс

Измерение физических величин. Точность и погрешность измерений. 7 класс

Измерение физических величин. Точность и погрешность измерений. 7 класс

Подробности

Просмотров: 358

При изучений физических явлений проводят различные измерения.
Физики измеряют физические величины.

Например:

При изучении падение тела, надо измерить высоту, с которой падает тело, массу тела, его скорость и время падения.
Чтобы узнать, например, зависит ли объем воды или другой жидкости от ее температуры и как зависит, нужно, нагревая воду, измерять и объем, и температуру.
Объем и температура, время и длина, площадь, скорость, масса, сила — это физические величины.

1. Что значит измерить?

Измерить какую-либо физическую величину — это значит сравнить ее с однородной величиной, принятой за единицу этой величины.

Например:

Измерить длину стола — значит сравнить ее с другой длиной, которая принята за единицу длины, например с метром.

В результате измерения величины получаем ее числовое значение, выраженное в принятых единицах.

2. Какие бывают единицы имерения?

Для каждой физической величины приняты свои единицы измерения.

Очень удобно пользоваться одинаковыми единицами физических величин во всех странах мира.
Поэтому с 1963 г. применяется Международная система единиц — СИ (система интернациональная).

Основные единицы в системе СИ:

единица длины — 1 метр (1м),
единица времени — 1 секунда (1с),
единица массы — 1 килограмм (1 кг).

Кроме того, используются кратные единицы (кратные основной единице), которые в 10, 100, 1000 и т. д. раз больше.

Эти единицы получили наименования с приставками, взятыми из греческого языка.
«Дека» — 10, «гекто» — 100, «кило» — 1000 и др.

Используются и дольные единицы, которые в 10, 100, 1000 и т. д. раз меньше принятых единиц величин.
В них применяют приставки, также взятые из латинского языка. «Деци» — 0,1, «санти» — 0,01, «милли» — 0,001 и др.

Некоторые приставки к названиям единиц:

г — гекто (100 или 10²)
к — кило (1000 или 10³)
М — мега (1 000 000 или 10⁶)

д — деци (0,1 или 10^-1)
с — санти (0,01 или 10^-2)
м — милли (0,001 или 10^-3)

Например:

Длина столовой ложки 20 см.
Ее длина в метрах (м):
20 см = 0,20 м или 2 • 10^-1 м.

3. Что такое измерителный прибор?

Для измерения физических величин нужны измерителные приборы.

Есть измерителные приборы для простых измерений. Например, измерительная линейка, рулетка, мензурка, применяемая для измерения объема жидкости.
Есть сложные измерительные приборы: секундомеры, термометры и другие.
По мере развития физики и техники приборы усложнялись и появились, например, приборы, при помощи которых изучают строение вещества.

У измерительных приборов есть измерительная шкала, на которой штрихами нанесены деления и написаны значения величин.

Между двумя большими штрихами могут быть дополнительно нанесены несколько делений, не обозначенных числами.

Значение измеряемой величины между ближайшими штрихами называется ценой деления прибора.

Например, у обычной школьной линейки расстояние между двумя ближайшими штрихами составляет 1 мм, это цена деления линейки.

4. Как определить цену деления измерительной шкалы прибора?

Прежде чем использовать измерительный прибор, надо определить цену деления этого прибора.
Надо установить, какому значению величины соответствует каждое самое малое деление.

Для того чтобы определить цену деления, необходимо:
— найти два ближайших штриха шкалы, возле которых написаны значения величины;
— вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

5. Примеры определения цены деления

а) Определение цены деления секундомера.
Используем любые два штриха, около которых нанесены значения измеряемой величины (времени), например штрихи с обозначениями 5 и 10 с.

Расстояние между этими штрихами разделено на 10 делений. Значит, цена каждого деления равна:

Секундомер показывает 22 с.

б) Определение цены деления термометра.
Возьмем, например, ближайшие друг к другу штрихи с обозначениями 10 °С и 20 °С. Расстояния между ними разделены на 10 делений. Следовательно,
цена каждого деления будет равна: 20 °С — 10 °С = 10 °С, далее 10 °С : 10 = 1 °С.
Термометр показывает 24 °С.

6. Что такое точность и погрешность измерений?

Любое измерение может быть выполнено с большей или меньшей точностью.
В физике допускаемую при измерении неточность называют погрешностью измерения.
Погрешность измерения не может быть больше цены деления измерительного прибора.

Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора.
Чем меньше цена деления, тем больше точность измерения.
При измерении принято считать, что: погрешность измерений равна половине цены деления шкалы измерительного прибора.

При записи величин, с учетом погрешности, пользуются формулой:

где А — измеряемая величина,
а — результат измерений,
дельта а — погрешность измерений (треуголник — греч. буква «дельта»).

Например:

Если длина книги 20 см, а цена деления линейки 1 мм, то погрешность измерения будет равна 0,5 мм, или 0,05 см.
Следовательно, длину книги можно записать так:
L = (20 ±0,05) см,
где L — длина книги.
Истинное значение длины книги находится в интервале от 19,95 см до 20,05 см.

Главное:

Измерить какую-либо величину — это значит сравнить ее с однородной величиной, принятой за единицу этой величины.
Основные единицы системы СИ: метр, килограмм, секунда.
Для того чтобы определить цену деления, необходимо:
— найти два ближайших штриха шкалы, возле которых написаны значения величины;
— вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

Следующая страница — смотреть

Назад в «Оглавление» — смотреть

Физические величины. Точность и погрешность измерений

Физические величины. Точность и погрешность измерений

Измерять – значит, познавать

Данная тема посвящена физическим величина и их измерениям. В физике часто приходится измерять те или иные величины. Измерить можно высоту дома или длину улицы.

Можно измерить объём воды в колбе или массу воды в стакане.

Но что означают эти измерения? Измерить какую-либо величину – значит сравнить её с однородной величиной, принятой за единицу. Из приведённых выше примеров, можно заметить, что, например, единицей объёма является литр, а единицей массы является грамм. Для удобства была введена международная система единиц, которая называется СИ.

В этой системе длина измеряется в метрах, масса в килограммах, объём — в кубических метрах, время – в секундах и так далее. В процессе изучения физики будут вводиться новые величины и соответствующие им единицы измерения. Иногда физические величины можно не измерять, а вычислять по формуле. Например, для того, чтобы вычислить среднюю скорость нужно пройденное расстояние разделить на время. То есть, данная формула помогает вычислить такую физическую величину, как

средняя скорость.

Известно что, иногда применяются единицы измерения, которые в десятки, сотни, тысячи и так далее раз больше принятых единиц измерения. Такие единицы измерения называются кратными.

Каждая приставка соответствует тому или иному множителю. Например, «Дека» означает в 10 раз больше, «гекто» — в сто раз больше, «кило» - в тысячу раз больше, «мега» — в миллион раз больше и так далее. Необходимо отметить, что в физике принято записывать такие множители в виде степени числа 10. Например, вместо миллиона записывается 10⁶. Также, могут быть использованы единицы, которые в десятки, сотни, тысячи и так далее раз меньше принятых единиц измерения.

Такие единицы измерения называются дольными.

Каждая приставка соответствует тому или иному множителю. Например, «Деци» означает в 10 раз меньше, «санти» — в сто раз меньше, «милли» — в тысячу раз меньше, «микро» — в миллион раз меньше и так далее. Эти приставки также записываются в виде степени числа 10. Например, вместо записи числа 0,000001 записывается 10^–6.

У каждого ученика имеется линейка, длина которой измеряется в сантиметрах, то есть в единицах, которые в сто раз меньше метра. Поэтому, если длина линейки составляет 15 сантиметров, мы можем сказать, что её длина 0,15 метра.

Линейка – это прибор для измерения длины

. Конечно, линейка относится к самым простым измерительным приборам. Существуют значительно более сложные приборы: например, термометр, который применяется для измерения температуры, гигрометр, который используется для измерения влажности или амперметр, который используется для измерения силы электрического тока.

Важно знать, как пользоваться измерительными приборами и насколько могут быть точны те или иные измерения. У каждого ученика есть линейка и карандаш. Можно попытаться измерить длину карандаша. В первую очередь нужно определить, какова цена деления измерительного прибора. Для этого необходимо найти два ближайших штриха шкалы, возле которых указаны значения величины (например, 1 см и 2 см). Далее нужно сосчитать число делений, заключенных между цифрами 1 и 2. При подсчёте получается, что количество этих делений равно 10. Таким образом, между отметками 1 см и 2 см заключено десять делений. Вычитаем из большего числа меньшее и делим на количество делений между ними. В результате вычислений получаем, что цена деления линейки составляет 0,1 см или 1 мм. Данный пример объясняет, как определить цену деления любого измерительного прибора.

Как видно из рисунка, длина карандаша чуть меньше десяти сантиметров. Если бы на этой линейке не было миллиметровых делений, то можно было сказать, что длина карандаша равна десяти сантиметрам. Но это было бы не совсем точное измерение. Такую неточность называют погрешностью измерения. В представленном случае, на линейке есть миллиметровые деления, поэтому можно измерить длину карандаша с более высокой точностью – 9,8 см. Это говорит о том, что чем меньше цена деления, тем больше точность измерения. Ну а большая точность измерения означает меньшую погрешность. Однако абсолютно точных измерений не существует. Если дать один и тот же карандаш каждому ученику из класса и попросить измерить длину карандаша, не у всех получится одинаковый результат. Тем не менее, погрешность измерения не может быть больше цены деления. Например, если видно, что длина карандаша не точно 9,8 см, а чуточку больше, то понятно, что длина карандаша находится в промежутке от 9,8 см до 9,9 см.

Погрешность измерений принято считать равной половине цены деления измерительного прибора. То есть, в рассмотренном случае, погрешность измерений составляет 0,5 мм. Поэтому, после того, как измерили карандаш и записали, что его длина равна 9,8 см, следует записать погрешность.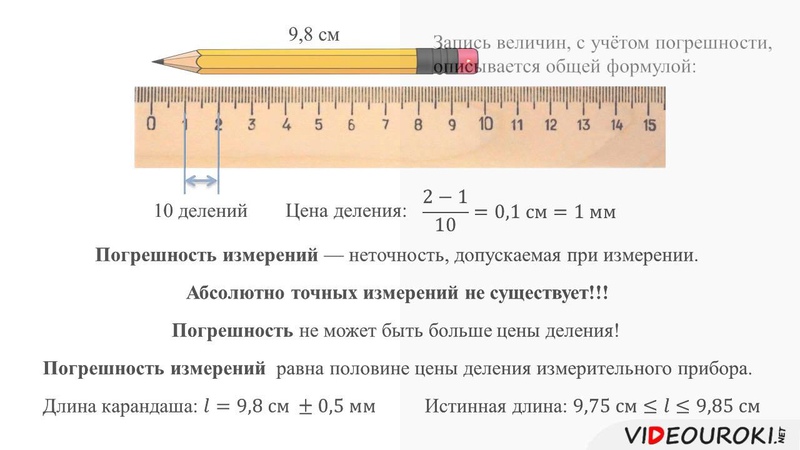

Знак «±» означает, что указанная длина может быть на полмиллиметра больше или на полмиллиметра меньше. Таким образом, истинное значение длины карандаша находится в промежутке от 9,75 см до 9,85 см.

В общем случае запись измеряемых величин с учетом погрешности имеет следующий вид:

где А – измеряемая величина;

а – результат измерения;

Da – погрешность измерений.

Необходимо отметить, что при сложении или вычитании величин с погрешностью, погрешность результата равна сумме погрешностей каждой величины. В этом легко убедиться на примере. На рисунке показаны два отрезка AB и CD, длины которых измерены с определенной погрешностью.

Рассчитаем сумму длин этих отрезков. Из рисунка видно, что отрезок AB равен 1 м ± 1 см. Истинная длина этого отрезка находится в промежутке 99 см ≤ АВ ≤ 101 см. Отрезок CD равен 12 см ± 0,5 см. Истинная длина этого отрезка находится в промежутке от 11,5 см ≤ CD ≤ 12,5 см. Поэтому, сумма длин этих отрезков будет иметь еще большую погрешность. Прежде чем производить вычисления, необходимо перевести обе длины в одинаковые единицы измерения.

Таким образом, получаем, что сумма длин отрезков AB и CD равна

Важно отметить, что этот же промежуток мы бы получили, если бы сложили наименьшие и наибольшие длины отрезков AB и CD. Следовательно, при сложении или вычитании величин, измеренных с погрешностями, погрешность результата равна сумме погрешностей каждой из величин.

Упражнения.

Упражнение 1. Заполните таблицу, указав, что из перечисленных слов является физическим телом, единицей измерения, физической величиной или физическим явлением: ветер, Луна, килограмм, дерево, длина, скорость, испарение.

Решение:

Упражнение 2. Родители измерили рост братьев Димы и Васи с помощью рулетки, цена деления которой 1 см. Подсчитайте, насколько см Дима выше, чем Вася.

Решение:

Упражнение 3. Найдите суммарную массу животных с погрешностью.

Решение:

Основные выводы:

– Для описания физических тел или физических явлений вводится физическая величина, которую можно измерить с помощью измерительных приборов или вычислить по формуле.

– Измерение величины – это сравнение её с однородной величиной, принятой за единицу.

– Кратные приставки – это приставки означающие увеличение в десятки, сотни, тысячи и так далее раз.

– Дольные приставки – это приставки, означающие уменьшение в десятки, сотни, тысячи и так далее раз.

– Погрешность измерений – неточность допускаемая при измерении. За погрешность измерений данного прибора принимают половину цены деления этого прибора.

– При сложении или вычитании величин с погрешностями, погрешность результата вычислений равна сумме погрешностей каждой величины.

ГДЗ конспекты по физике 7 класс Задание: Физические величины Точность и погрешность измерений Измерение физических величин

Изображения обложек учебников приведены на страницах данного сайта исключительно в качестве иллюстративного материала (ст. 1274 п. 1 части четвертой Гражданского кодекса Российской Федерации)

Вид УМК: конспекты

Серия: Краткое содержание параграфов учебника для устного ответа

На данной странице представлено детальное решение задания Физические величины. Точность и погрешность измерений. Измерение физических величин по физике для учеников 7 классa автор(ы)

Физические величины. Точность и погрешность измерений. Измерение физических величин

Физическая величина – это количественная характеристика предметов, которую можно измерить.

Измерить физическую величину – сравнить её с величиной, принятой за единицу.

В 1963 г. была принята международная система единиц.

1) 1,08 км = 1080 м;

2) 0,02 км = 20 м;

3) 24,015 км = 24015 м.

Цена деления – расстояние между двумя ближайшими штрихами на шкале измерительного прибора.

Для того, чтобы определить цену деления, необходимо:

1) найти два ближайших штриха шкалы, возле которых написаны значения величины;

2) вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

Измерение физических явлений, единицы:

0,1 мм = 0,01 см

0,1 мм = 0,001 м

0,1 мм = 100 мкм

0,1 мм = 100000 нм

1 мкм = 0,0000001 м

1 м = 1000000 мкм

1 нм = 0,000000001 м

Рис. 1. ГДЗ конспекты по физике 7 класс Задание: Физические величины Точность и погрешность измерений Измерение физических величин

Add

Новыe решебники

© 2021Copyright.  Все права защищены. Правообладатель SIA Ksenokss.
Адрес: 1069, Курземес проспект 106/45, Рига, Латвия.
Тел.: +371 29-851-888 E-mail: [email protected]

Точность измерений и погрешности в физике

Содержание:

При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с  точностью до сантиметра, размеры дома, стадиона – с точностью до метра.

Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.

При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.

Пример:

Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).

Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением 
шкалы линейки совпадает второй край стола  (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)

Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.  

Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.

Относительная погрешность измерения ε (ЭПСИЛОН)

Иногда важно знать, какую часть составляет наша погрешность от значения 
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: .  То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой  (эпсилон): 

     (5.1)

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения –  плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.

Стандартная запись результата измерений и выводы

Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 0,5) мм — Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.

На точность измерения влияет много факторов, в частности:

1. При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
2. Не вполне ровно установили рулетку.
3. Наша рулетка является копией эталона и может несколько отличаться от оригинала.

Все это необходимо учитывать при проведении измерений.

Итоги:

• Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
• Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.  
• Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:   и указывает на качество измерения. Ее можно выразить в процентах.

Измерительные приборы

Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.

Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.

Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.

Как определяют единицы длины и времени

В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.

Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).

Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.

Можно ли расстояние измерять годами

Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!

Что надо знать об измерительных приборах

Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?

Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.

Как определить цену деления шкалы? Для этого необходимо:

1. выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
2. подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
3. вычесть из большего значения меньшее (4 см — 3 см = 1 см) и результат разделить на число делений.

Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.

• Для линейки 1: 
• Для линейки 2: 
• Для линейки 3: 

Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2: 

А какими линейкой и мензуркой можно измерить точнее?

Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.

Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше  Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы ), мензуркой 2 — с точностью до 1 мл (сравните с ценой деления ). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.

Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.

Главные выводы:

1. Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
2. Цена деления шкалы равна значению наименьшего деления шкалы.
3. Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.

Для любознательных:

В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г.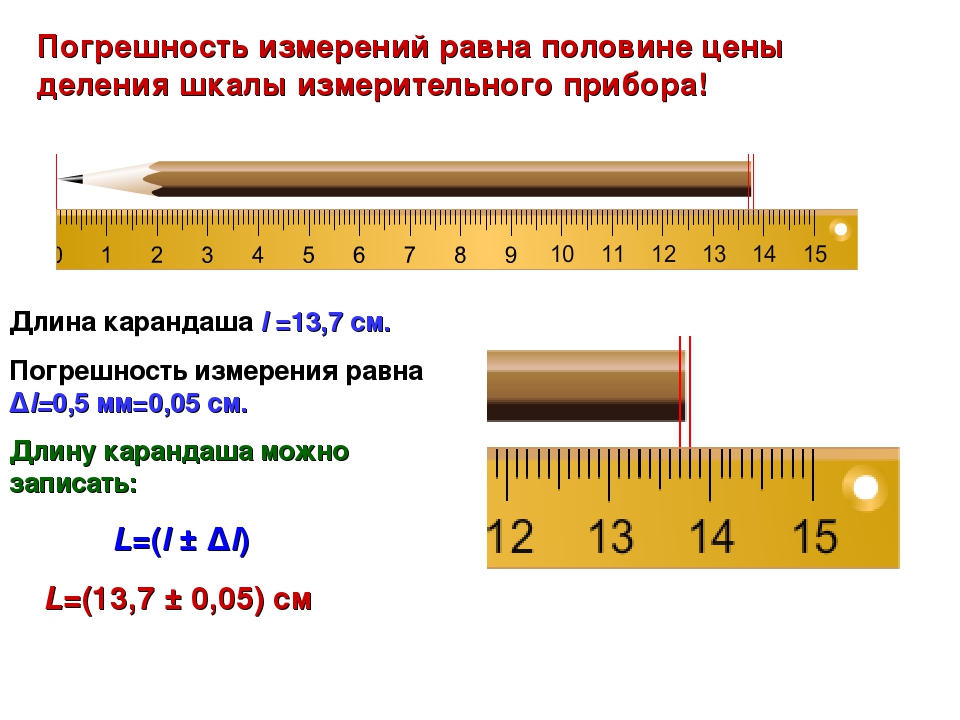 одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.

Пример решения задачи

Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:

1) Цена деления нижней шкалы:

Цена деления средней шкалы: 

Цена деления верхней шкалы:

2) Определенный но нижней шкале с точностью до 10° определенный по средней шкале с точностью до 5° определенный по верхней шкале с точностью до 1°

Оценка погрешностей измерений ❤️ | Физика

Погрешности измерений обусловлены неточностью самих приборов и неточностью снятия их показаний, влиянием случайных факторов и т. д. различают абсолютную и относительную погрешности.

Абсолютной погрешностью называют модуль отклонения измеренного значения физической величины от ее истинного значения. Если ∆A — наибольшее значение абсолютной погрешности, то результат измерения записывают в виде A = Aср ± ∆A. Это означает, что значение физической величины находится между Amin = Aср — ∆A и Amax = Aср + ∆A.

Относительная погрешность εA = ∆A/A

* 100% . Относительная погрешность полнее характеризует точность измерения, чем абсолютная. Например, если длина карандаша и длина комнаты измерены с одной и той же абсолютной погрешностью ∆l = 1 см, то в первом случае измерение не очень точное (относительная погрешность довольно велика), а во втором случае — довольно точное (относительная погрешность мала).

Оценка абсолютной погрешности прямых измерений. При прямом измерении значение величины определяют непосредственно по шкале измерительного прибора (линейки, динамо — метра, часов и т. д.). Если результаты повторных опытов в пределах точности прибора

совпадают, погрешность измерения считают равной цене деления шкалы прибора ∆A = ∆Am (например, наибольшая абсолютная погрешность измерения длины с помощью линейки с миллиметровыми делениями равна 1 мм). Если же разброс результатов повторных опытов больше ∆Am, используют усреднение результатов нескольких опытов.

Тогда за измеренное значение принимают Aср = (A1 + A2 + … + AN) / N, где N — число опытов, а погрешность измерения оценивают по формуле ∆(Aср) = (|Aср — A1| + |Aср — A2| + … + |Aср — AN|) / N. За абсолютную погрешность измерения ∆A принимают большую из двух величин: ∆(Aср) и ∆Am.

Оценка абсолютной погрешности косвенных измерений. Косвенным называют измерение, при котором значение измеряемой величины определяют не непосредственно по показаниям приборов, а по формулам, в которые входят значения физических величин, полученные с помощью прямых измерений. Например, для измерения плотности вещества измеряют массу и объем тела н находят плотность по формуле ρ = m/V.

Один из наиболее простых методов оценки погрешности косвенных измерений — это метод границ. Он состоит в том, что с помощью формулы, по которой вычисляют измеряемую величину B, находят два значения: Bmin и Bmax, между которыми находится истинное значение измеренной величины B.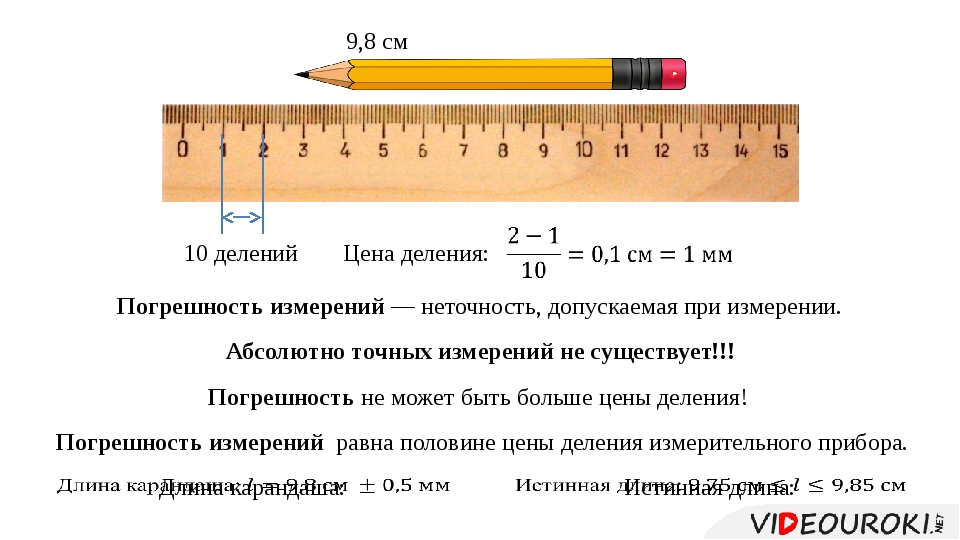 Абсолютная погрешность измерения в таком случае ∆B = (Bmax — Bmin) / 2, а среднее значение Bср = (Bmax + Bmin) / 2.

Округление результатов. Округлять результаты измерений и вычислений следует так, чтобы последняя значащая цифра находилась в том же десятичном разряде, что и абсолютная погрешность измеряемой величины.

P>Интернет-ресурсы для дополнительного изучения физики:

«Физические величины, измерение физических величин. Точность и погрешность измерений»

«Физические величины, измерение  физических величин. Точность и погрешность измерений»

Цели урока: познакомиться с понятием «физическая величина»; на­учиться измерять физические величины при помощи простейших из­мерительных средств.

Оборудование: линейка, мензурка, секундомер, термометр, другие из­мерительные приборы.

Ход урока

I. Повторение

В самом начале урока следует повторить материал прошлого урока. Для этого можно ответить на вопросы:

1.           Существует ли разница между физическими понятиями «материя» и «вещество»?
2.           Как вы понимаете слова «тело», «вещество»? Приведите примеры физических тел и веществ.
3.           Что означают слова: «Это тело материально»?
4.           Приведите примеры физических явлений. Какие группы явлений изучает физика?
5.           Приведите примеры физических явлений и укажите их причины.
6.           Приведите примеры физических явлений, которые не получили научного объяснения. Как вы думаете, сумеем ли мы когда-либо объяснить причины этих явлений?
7.           Может ли существовать в природе какое-либо явление, не имею­щее причины?
8.           Какую роль играет в физике опыт? Приведите примеры из области механических (тепловых, электрических и др. ) явлений.
9.           Каковы источники наших знаний о явлениях природы?

 

10.       Что необходимо предпринять для того, чтобы получить научные знания об окружающем нас мире?
11.       Сумеете ли вы возразить вашему собеседнику, если он скажет: «В изучении живых организмов знания по физике нам совсем не помогают»?

12. Зачем нужно изучать науку о природе?
Подведите итоги проверки домашнего задания.

П. Изучение нового материала

С давних пор люди сталкивались с необходимостью определять рас­стояния, длины предметов, время, площади, объемы и т. д.

Значение измерений возрастало по мере развития общества и, в час­тности, по мере развития науки. А чтобы измерять, необходимо было придумать единицы различных физических величин. Вспомните, как написано в учебнике: «Измерять какую-нибудь величину — это значит сравнить ее с однородной величиной, принятой за единицу».

Знаете ли вы, какие существовали и существуют сейчас единицы дли­ны, каково их происхождение?

Самыми древними единицами были субъективные единицы. Так, на­пример, моряки измеряли путь трубками, т. е. расстоянием, которое проходит судно за время, пока моряк выкурит трубку. В Испании похо­жей единицей была сигара, в Японии — лошадиный башмак, т. е. путь, ко­торый проходила лошадь, пока не износится привязанная к ее копытам соломенная подошва, заменявшая подкову. В Египте распространенной единицей длины был стадий — путь, проходимый мужчиной за время между первым лучом Солнца и появлением на небе всего солнечного диска, т. е. примерно за две минуты.

У многих народов для определения расстояния использовалась еди­ница длины стрела — дальность полета стрелы. Наши выражения: «не подпускать на ружейный выстрел», позднее «на пушечный выстрел»

— напоминают о подобных единицах длины.

Древние римляне расстояния измеряли шагами или двойными шагами (шаг левой ногой, шаг правой). Тысяча двойных шагов составляла милю (лат. «милле» — тысяча).

Длину веревки или ткани неудобно измерять шагами или стадиями. Для этого оказались пригодными встречающиеся у многих народов еди­ницы с названиями частей человеческого тела. Локоть — расстояние от конца пальцев до локтевого сустава. На Руси долгое время в качестве единицы длины использовали аршин (примерно 71 см). Эта мера возник­ла при торговле с восточными странами (перс, «арш» — локоть). Мно­гочисленные выражения: «Словно аршин проглотил», «Мерить на свой аршин» и другие — свидетельствуют о ее широком распространении.

Для измерения меньших длин применяли пядь — расстояние между концами расставленных большого и указательного пальцев. Пядь или, как ее еще называли, четверть (« 18 см) составляла] аршина.

В странах Западной Европы издавна применяли в качестве единиц длины дюйм (2,54 см) — длина сустава большого пальца (от голл. «дюйм»

— большой палец) и фут (30 см) — средняя длина ступни человека (от англ. «фут» — ступня).

С развитием торговых связей между народами в каждой стране наряду с ранее применявшимися мерами стали употреблять меры чужих стран. Таким образом, росло число единиц для измерения одной и той же ве­личины.

Громадное число различных мер, неудобные для расчетов соотноше­ния между единицами создали много затруднений. Ошибок, обманов и злоупотреблений. Всевозможные расчеты в промышленности и торгов­ле были очень сложны и требовали много времени, труда и внимания.

Назрела необходимость уточнить основные единицы и упорядочить всю систему мер. И первым шагом к этому явилось создание постоян­ных образцов (эталонов) мер длины в виде металлических линеек или стержней и массы в виде металлических гирь — эталонов.

В I960 г. XI Генеральная конференция по мерам и весам, в которой принимали участие крупные ученые многих стран, в том числе и СССР, приняла резолюцию об установлении Международной системы единиц — СИ (читается «эс — с» от первых букв слов «система интернациональ­ная»).

В качестве основных единиц были выбраны следующие: метр — единица длины, килограмм — единица массы, секунда — единица времени, кельвин — единица температуры, ампер —единица силы тока, кандела — единица силы света, моль — единица количества вещества.

Интересно знать

В древние времена самой точной мерой длины считалась толщина волоса верблюда или мула (около О, 1 мм), причем только в том случае, если волос был выдернут из хвоста.

Англичане столкнулись с большими трудностями при переходе в 1977 г. на Международную метрическую систему мер. Они настолько привыкли к старым английским мерам, что долго не могли без ошибок применять но­вые единицы. Так, например, 20-летний лондонский полицейский опреде­лил, что его рост около 7м, а одна 23-летняя женщина ответила, что ее рост… 55см.

Чтобы было удобнее измерять физические величины, кроме основных еди­ниц используют кратные единицы, которые в 10, 100, 1000 и т.д. больше основных и дольные, которые в 10, 100, 1000меньше основной единицы. Для их обозначения используют специальные приставки (см. таблицу).

 

 

 

Наименование приставки	Обозначение приставки	Множитель	Наименование множителя
нано	н	109=0,00000000!	одна миллиардная
микро	мк	io-b=o,oooooi	одна миллионная
МИЛЛИ	м	10-3=0,001	одна тысячная
санти	с	io-2o,oi	одна сотая
деци	д	10-‘=0,1	одна десятая
дека	да	10’=10	десять
гекто	г	102=100	сто
кило	к	103=1000	тысяча
мега	М	106=1 ООО ООО	миллион
гига	Г	109= 1 ООО ОООООО	миллиард

Упражнение 1.

«Семь пядей во лбу» — говорят об умном человеке; «косая сажень в плечах» — о могучем, сильном человеке. Не известны ли вам другие по­говорки — что-нибудь о золотнике, фунте, футе?

Упражнение 2.

Пофантазируем! Пусть эталон, например брусок, длина которого при­нята за 1 м, по какой-то причине стал чуть-чуть короче, причем никто об этом не знает, в том числе и хранители эталона. Попробуйте нарисовать кошмарную картину, которая возникнет на Земле через некоторое время.

Упражнение 3.

Запишите с помощью сокращающих приставок следующие значения величин: 0,0000052 м; 2 560 000 000 м.

Запишите в обычном виде следующие значения величин: 2,37 Мм; 7,5 мкс.

Для измерения физических величин применяют измерительные прибо­ры. Самыми простыми измерительными приборами являются рулетка, мензурка (измерительный цилиндр). Более сложными являются термо­метр, секундомер.

Любой измерительный прибор имеет шкалу. На шкалу нанесены мет­ки, каждая из которых соответствует определенному численному зна­чению измеряемой величины. Рядом с крупными метками нанесены соответствующие цифры. Между крупными метками нанесены мелкие, но без цифр. По шкале экспериментатор может определить две важные характеристики прибора: предел измерения и цену деления.

Пределы измерения определяются цифрами у первого и последнего деления. Цена деления (Ц)—это численное значение измеряемой ве­личины, которое соответствует одному (самому маленькому) делению шкалы.

Например, при помощи линейки, у которой между делениями \сми 2см нанесено 10 равных делений, мы можем измерить длину с точнос­тью до 1мм.

Перед проведением измерений всегда определяют цену деления прибора.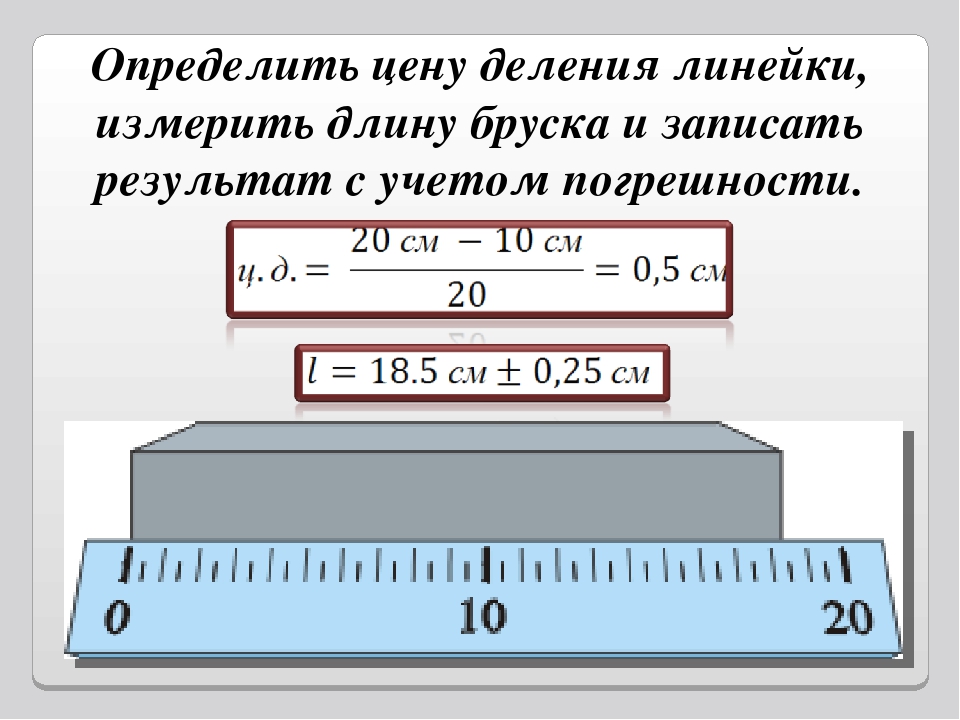

Для определения цены деления прибора необходимо взять два бли­жайших деления с числовым обозначением, из большего вычесть мень­шее и разделить на число делений между ними.

 

III. Работа у доски

Зная цену деления, мы всегда с данной точностью можем измерить физическую величину.

Можно предложить определить цену деления измерительных прибо­ров (секундомер, линейка, термометр), которые есть в кабинете физи­ки.

 

Физики уменьшили погрешность атомных часов

Сотрудники Института лазерной физики СО РАН вместе с учеными из США и Франции предложили новый метод, позволяющий уменьшить полевой сдвиг в атомных часах. Для этого исследователи искусственно создали антисдвиг. Статья исследователей опубликована в журнале Physical Review Applied.

«Атомные часы на сегодняшний день самые точные приборы для измерения времени. Если бы такте часы запустили в момент образования Вселенной, то к сегодняшнему дню они отклонились бы на доли секунды», — рассказал порталу «Наука в Сибири» один из авторов проекта, главный научный сотрудник ИЛФ СО РАН доктор физико-математических наук Валерий Юдин.

Такие приборы сегодня используют на космических станциях, для навигации в системах ГЛОНАСС и GPS и в некоторых других областях. Поэтому важна их точность и стабильность. При работе атомных часов, несмотря на их огромную точность, могут возникать отклонения, которые влияют на результаты измерений. Например, сегодня системы спуниковой навигации позволяют рассчитать координаты с точностью до нескольких метров. Усовершенствование технологии атомных часов позволит сократить это значение до нескольких сантиметров.

На данный момент атомные часы обладают нестабильностью от 10^-16 до 10^-18. Во многих случаях такая нестабильность возникает из-за полевого сдвига. Такой сдвиг обусловлен действием электромагнитного поля, которое генерирует локальный осциллятор в самих часах. Помимо своей основной работы по созданию нужных частот в приборе, этот элемент формирует электромагнитные импульсы, которые смещают частоту колебаний в атомах. Поэтому чтобы увеличить стабильность и точность атомных часов ученые стараются создать методы уменьшения этого сдвига.

Часто в атомных часах физики используют лазер для создания необходимой частоты колебаний. Такой лазер может влиять на поведение полевого сдвига. Российские исследователи нашли способ уменьшить полевой сдвиг в атомных часах с помощью антисдвига. Эти воздействия одинаковые по силе, но разные по знаку, поэтому компенсируют друг друга, тем самым снижая нестабильность прибора.

В своей работе ученые использовали принцип двух петель обратной связи. Петля представляет собой кольцевую систему причинно-связанных элементов, которые влияют друг на друга. На первой петле стабилизируется частота лазера, а на второй компенсируются «естественный» и искусственный сдвиги. Чтобы создать антисдвиг, ученые запрограммировали лазер таким образом, чтобы он «выстрелил» по атомным часам с дополнительным отрицательным частотным сдвигом.

Новый метод оказался довольно простым и легко корректируемым. Теперь физики планируют исследовать применение нового метода и понять, как его лучше реализовать на практике.

Ошибки и их виды: постоянные, случайные, систематические и др.

Наука > Физика > Единицы и измерения > Ошибки и их виды

В этой статье мы изучим ошибки, их виды и терминологию ошибок.

Ошибка определяется как разница между фактическим или истинным значением и измеренным ценность.

Ошибку не следует путать с ошибкой, ошибки можно избежать, а ошибки нельзя избежать, но их можно уменьшить (минимизировать).

Типы ошибок:

1) Постоянная ошибка, 2) Постоянные или систематические ошибки 3) Случайные или случайные ошибки 4) Грубые ошибки

Постоянные ошибки:

Когда результаты серии наблюдений имеют одинаковую ошибку, говорят, что ошибка является постоянной ошибкой. Систематическая ошибка из-за неисправного оборудования вызывает постоянную ошибку.

Систематическая ошибка:

Ошибка вызвано несовершенной техникой измерения, дефектным или несовершенным оборудованием или какие-то личные причины называют систематической ошибкой.

Причины систематической ошибки:

• Дефект в аппарате : Например, для метровая шкала имеет фактическую длину 99 см, но используется как 100 см.
• Неисправный прибор: а) Ноль весов не совпадает со стрелкой. б) Микрометрический винтовой калибр может иметь погрешность, если нулевая отметка на круглой шкале не совпадает с нулевой отметкой на основной шкале при закрытых губках.
• Личные ошибки:  Особые привычки человека во время измерения могут вызвать ошибки.Большинство таких ошибок в том же направлении. Если для расчета не используется надлежащая формула, это приведет к введению ошибки.

Случайные ошибки:

Ошибка в измерение, вызванное факторами, которые варьируются от одного измерения к другому, называется случайной ошибкой.

Причины случайных ошибок:

• Нестабильные условия: например изменение температуры или окружающей среды может привести к ошибке в измерении.В тепловых или электрических экспериментах возможны такие ошибки.
• Незначительные помехи: Небольшие помехи, такие как вибрации, могут внести погрешность в измерения.
• Ошибка оценки: Возможны отклонения в оценке измерения.
• Неспособность определить качество: Если качество объекта, измерения которого должны быть выполнены, существует вероятность внесения ошибки.

Ошибки могут можно свести к минимуму, взяв несколько показаний, а затем найдя среднее значение сняты показания.

Терминология ошибок: 

Наиболее вероятное значение:

Когда берется достаточно большое количество показаний, то среднее значение этих показаний называется наиболее вероятным значением.

Абсолютная ошибка:

величина разницы между наиболее вероятным значением (средним) и единичное измерение называется абсолютной погрешностью измерения.

Окончательная абсолютная ошибка:

Среднее арифметическое всех абсолютных ошибок называется окончательной абсолютной ошибкой

Финал абсолютная ошибка = сумма всех абсолютных ошибок / общее количество абсолютных ошибок

Относительная ошибка:

Отношение абсолютной погрешности измерения величины к наиболее вероятному значению называется относительной погрешностью

Родственник Ошибка = окончательная абсолютная ошибка / наиболее вероятное значение

Относительная ошибка в процентах:

Если относительную ошибку умножить на 100, полученное значение называется процентной относительной ошибкой.

Процент относительная ошибка = относительная ошибка × 100

Расчет относительной ошибки в процентах: 

Пример – 01:

Длину металлической пластины измеряли с помощью штангенциркуля с наименьшим шагом 0,01 см. Полученные показания составили 3,11 см, 3,13 см, 3,14 см, 3,14 см. Найдите среднюю длину, среднюю абсолютную ошибку, относительную ошибку и процентную ошибку измерения длины.

Решение:

Показания 3.11 см, 3,13 см, 3,14 см и 3,14 см

Средняя длина = (3,11 см + 3,13 см + 3,14 см + 3,14 см) / 4 = 12,53 см/4 = 3,13 см

Средняя абсолютная ошибка = [|3,11 -3,13| + |3,13 -3,13| +|3,14 -3,13| +|3,14 -3,13|] / 4

Средняя абсолютная ошибка = [0,02 + 0,00 + 0,01 + 0,01] / 4 = 0,04 / 4 = 0,01 см

Относительная ошибка = Окончательная абсолютная ошибка / Среднее значение = 0,01 / 3,13 = 0,00319

Относительная ошибка в процентах = Относительная ошибка × 100 = 0,00319 × 100 = 0,319 %

Пример – 02:

Масса тела измеряется с помощью физических весов, и полученные показания равны 5.04 г, 5,06 г, 4,97 г, 5,00 г и 4,93 г. Найдите процент ошибки в измерении.

Решение:

Показания: 5,04 г, 5,06 г, 4,97 г, 5,00 г и 4,93 г

Средняя длина = (5,04 г + 5,06 г + 4,97 г + 5,00 г + 4,93 г) / 5 = 25 г/5 = 5,00 г

Средняя абсолютная ошибка = [|5,04 – 5,00| + |5,06 -5,00| +|4,97 -5,00| +|5. 00 -5.00| + |4,93 – 5,00|] / 5

Средняя абсолютная ошибка = [0,04 + 0,06 + 0,03 + 0,00 + 0,07] / 5 = 0,2 / 5 = 0.04 г

Относительная ошибка = Окончательная абсолютная ошибка / Среднее значение = 0,04 / 5 = 0,008

Относительная ошибка в процентах = Относительная ошибка × 100 = 0,008 × 100 = 0,8 %

Пример – 03:

Предмет был взвешен на физических весах и после получены показания: 5,04 г, 5,06 г, 4,97 г, 5 г и 4,93 г. Найдите а) среднее значение b) абсолютная ошибка и c) процентная ошибка

Решение:

Показания 5,04 г, 5.06 г, 4,97 г, 5 г и 4,93 г

Средний вес = (5,04 г + 5,06 г + 4,97 г + 5 г + 4,93 г) / 5 = 25 г/5 = 5 г

Средняя абсолютная ошибка = [|5,04 – 5| + |5.06 – 5| +|4,97 – 5| +|5 – 5| + |4,93 – 5|] / 5

Средняя абсолютная ошибка = [0,04 + 0,06 + 0,03 + 0 + 0,07] / 5 = 0,2/5= 0,04 г

Относительная ошибка = Окончательная абсолютная ошибка / Среднее значение = 0,04 / 5 = 0,008

Относительная ошибка в процентах = Относительная ошибка × 100 = 0,008 × 100 = 0,8 %

Ответ: а) среднее значение = 5 г, б) абсолютная ошибка = 0.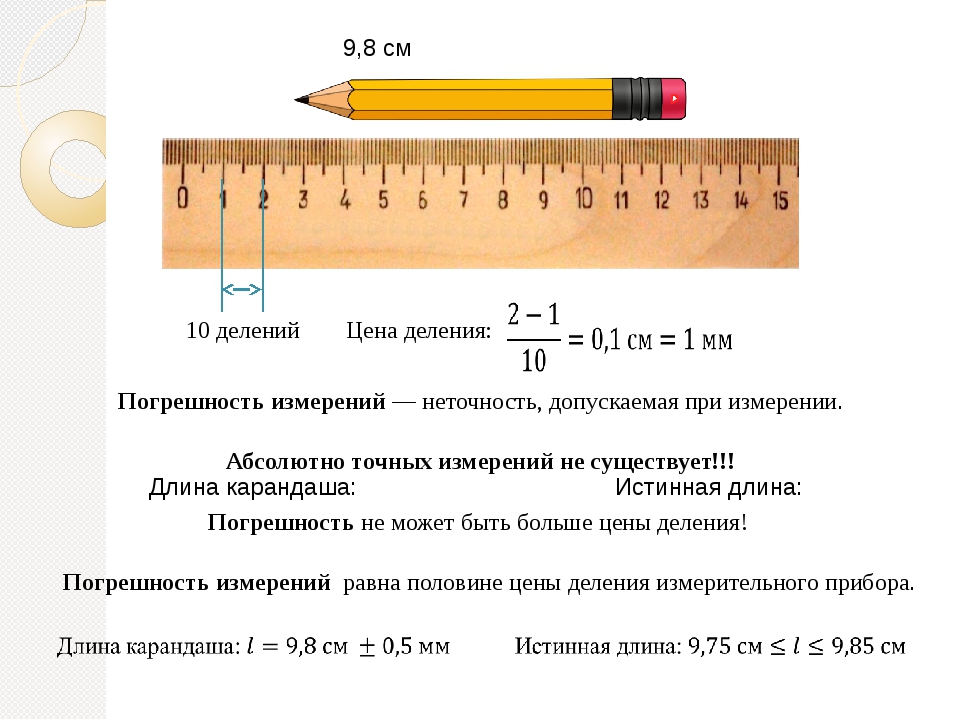 04 г, в) процентная ошибка = 0,8 %

Пример – 04:

Значения радиуса стеклянной палочки, измеренные тремя студентами составляют 0,301 см, 0,323 см и 0,325 см. Найдите средний радиус.

Решение:

Показания: 0,301 см, 0,323 см и 0,325 см.

Средний вес = (0,301 см + 0,323 см + 0,325 см) / 3 = 0,949 см/3 = 0,316 см

Средняя абсолютная ошибка = [|0,301 – 0,316| + |0,323 – 0,316| +|0,325 – 0,316| ] /3

Средняя абсолютная ошибка = [0.015 + 0,007 + 0,009] / 3 = 0,031/ 3= 0,010 см

Относительная ошибка = Окончательная абсолютная ошибка / Среднее значение = 0,010 / 0,316 = 0,0316

Относительная ошибка в процентах = Относительная ошибка × 100 = 0,0316 × 100 = 3,16 %

Ответ:  процент ошибка = 3,16 %

Пример – 05:

Измерение диаметра проволоки 0,74 мм. Если наименьший отсчет прибора составляет 0,01 см, рассчитайте процентную погрешность измерения.

Решение:

Измерение диаметра проволоки = 0.74 мм

Наименьшее количество инструментов = 0,01 см = 0,1 мм

Отсюда возможная погрешность измерения = 0,1 мм

Процентная ошибка = (Возможная ошибка / Измерение) × 100

∴  Процентная ошибка = (0,1/0,74) × 100 = 13,51 %

Ответ: Процентная ошибка = 13,51 %

Предыдущая тема: Значимые цифры и порядок величин

Следующая тема: Распространение ошибок

Наука > Физика > Единицы и измерения > Ошибки и их типы

Научная практика: научная ошибка

 

Когда одно измерение сравнивается с другим одиночным измерением того же объекта, значения обычно не идентичны.Различия между отдельными измерениями обусловлены ошибкой. Ошибки — это различия между наблюдаемыми значениями и тем, что истинно в природе. Ошибка приводит к неточным или вводящим в заблуждение результатам и может искажать природу.

 

Научно принятые значения — это наилучшие на данный момент приближения или описания природы учеными. По мере совершенствования информации и технологий и уточнения, повторения и переосмысления исследований понимание природы учеными становится все ближе к описанию того, что на самом деле существует в природе.Однако природа постоянно меняется. То, что было наилучшей качественной интерпретацией природы в один момент времени, может отличаться от лучшего научного описания в другой момент времени.

 

Ошибки не всегда возникают из-за ошибок. Ошибки бывают двух видов: случайные и систематические. Случайная ошибка возникает случайно. При измерении всегда есть некоторая изменчивость. Случайная ошибка может быть вызвана небольшими колебаниями в приборе, окружающей среде или способе считывания измерения, которые не вызывают каждый раз одну и ту же ошибку.Чтобы устранить случайную ошибку, ученые использовали репликацию. Репликация — многократное повторение измерения и получение среднего значения.

 

Систематическая ошибка дает измерения, которые постоянно отличаются от истинных значений в природе, часто из-за ограничений инструментов или процедуры. Систематическая ошибка является одной из форм предвзятости. Многие люди могут думать о недобросовестном поведении исследователя, например, о записи и сообщении только определенных результатов, когда они думают о предвзятости.Однако важно помнить, что предвзятость может быть вызвана и другими факторами. Погрешность часто вызывается приборами, которые постоянно смещают измеренное значение от истинного значения, например, весы, которые всегда показывают на 5 грамм больше реального значения.

 

Ошибка не может быть полностью устранена, но ее можно уменьшить, зная общие источники ошибок и используя продуманные и осторожные методы. Общие источники ошибок включают инструментальные, экологические, процедурные и человеческие.Все эти ошибки могут быть как случайными, так и систематическими в зависимости от того, как они влияют на результаты.

 

• Инструментальная ошибка возникает, когда используемые инструменты неточны, например, весы не работают (SF рис. 1.4). pH-метр, который показывает 0,5 или калькулятор, который неправильно округляет, может быть источником ошибки прибора.
• Ошибка среды возникает, когда какой-либо фактор среды, например необычное событие, приводит к ошибке.Например, если вы пытаетесь измерить массу яблока на весах, а в вашем классе дует ветер, ветер может привести к неправильному показанию весов.
• Процедурная ошибка возникает, когда для ответа на один и тот же вопрос используются разные процедуры, которые дают немного разные ответы. Если два человека округляют, и один округляет в меньшую сторону, а другой в большую, то это процедурная ошибка.
• Человеческая ошибка связана с небрежностью или ограниченностью человеческих возможностей.Два типа человеческих ошибок — это ошибка транскрипции и ошибка оценки.
  
  • Ошибка транскрипции возникает, когда данные записываются или записываются неправильно. Примерами этого являются случаи, когда номер телефона копируется неправильно или когда номер пропускается при вводе данных в компьютерную программу из таблицы данных.
  • Ошибка оценки может возникнуть при считывании измерений на некоторых приборах. Например, читая линейку, вы можете прочесть, что длина карандаша равна 11.4 сантиметра (см), а ваш друг может прочесть как 11,3 см.
     

Ученые тщательно планируют эксперименты или проводят измерения, чтобы уменьшить количество ошибок, которые могут возникнуть.

 

Проведение эксперимента, часть 1: понимание ошибки

В каждом физическом эксперименте есть ошибка. Позвольте мне показать вам, как понять, принять и сообщить о своей неуверенности.

В предыдущих сообщениях мы сосредоточились на теоретической стороне изучения физики, рассматривая различные методы, которые позволят вам решать проблемы, будь то SAT 2 по физике, GRE по физике или курс физики в средней школе или колледже. уверенно и легко.В следующих двух постах давайте больше сосредоточимся на экспериментальной стороне изучения физики.

Всякий раз, когда вы проводите эксперимент и записываете результаты, измеряете ли вы время колебания маятника на своем первом уроке физики в старшей школе или отправляете пятую статью в журнал Nature, вам необходимо учитывать ошибки в ваших измерениях. Ни одно измерение не является совершенным; каждое измерение, которое вы делаете, будет иметь некоторую конечную неопределенность, связанную с ним, и вы должны убедиться, что ваш окончательный результат точно отражает неизбежное несовершенство вашего измерения.

Наш эксперимент: измерение гравитации

Например, представьте, что нас попросили найти g ускорение свободного падения при падении мяча с заданной высоты. Какие два измерения нам нужно сделать? Нам нужно измерить время t , за которое мяч упадет на землю, и высоту t , с которой мы его уронили. Затем мы можем найти г , используя формулу

.

 

Это очень простой эксперимент — все, что для этого нужно, — это мяч и секундомер — и ошибки, которые мы рассматриваем, специфичны для данного измерения, но он иллюстрирует несколько концепций, применимых к любому эксперименту, который вы, возможно, захотите провести.

Время измерения: точность против точности

Во-первых, давайте посмотрим на наши измерения t и спросим себя, насколько они точны и точны (а это два разных вопроса). точность измерения отражает то, насколько точным является измеренное вами число. В нашем примере это соответствует количеству цифр на дисплее нашего секундомера. Скажем, мы считываем все цифры секундомера, что дает нам 0,62 с. Тогда точность этого единственного измерения равна 0.01 с.

Насколько точны эти измерения? То есть насколько мы уверены, что 0,62 с — это реальное время, которое потребовалось мячу для удара об пол? Точность измерения отражает насколько хорошо измеренное вами значение соответствует фактической величине, которую вы пытаетесь измерить.  Среднее время реакции человека составляет около 200 мс, поэтому не имеет смысла утверждать, что мы можем провести измерение на глаз с точностью до 10 мс, что является нашей точностью. Мы просто недостаточно быстры с нашими пальцами на спусковом крючке.

Какую неопределенность мы заявляем?

Теперь, когда мы понимаем точность нашего измерения времени (0,01 с) и имеем некоторое представление об ошибках, которые присутствуют в нашем эксперименте (время нашей человеческой реакции), какую неопределенность в наших измерениях мы можем ответственно заявить? Это та часть, которая требует некоторого суждения, и мы должны помнить, что цель указания ошибки в нашем измерении состоит в том, чтобы показать, насколько мы уверены в своем ответе. Таким образом, мы должны руководствоваться мыслью, что лучше признать, когда вы не уверены в результате, чем заявлять о результате с уверенностью, но ошибаться.

Но что мы записываем? Во-первых, давайте заметим, что время нашей человеческой реакции (200 мс) намного больше, чем точность секундомера (10 мс), поэтому мы можем игнорировать неопределенность из-за точности нашего измерения и сосредоточиться на точности. То есть ограничивающим фактором в эксперименте является наш спусковой палец, а не секундомер.

Итак, на что мы можем претендовать? Давайте начнем с самой простой и консервативной оценки, а затем спросим себя, можем ли мы сделать какие-либо предположения.Среднее время реакции на нажатие кнопки секундомера составляет 200 мс, поэтому предположим, что при каждом нажатии мы можем опоздать от 0 до 400 мс. Тогда как время начала, так и время окончания имеют погрешность ±0,2 с. Поскольку мы добавляем абсолютные неопределенности сумм, которые добавляются или вычитаются , время спада t , определяемое как

 

имеет неопределенность.

 

Таким образом, измеренное время, которое мы можем указать, равно 0.6 ± 0,4 с.

Обратите внимание, что мы считываем с секундомера 0,62 с, но опускаем второй знак fig с 0,62 и заявляем только 0,6 ± 0,4 с. Я скажу об этом больше, когда мы будем обсуждать, как мы представляем наш окончательный результат, но если наша неопределенность намного больше, чем наша точность, то нет смысла давать такое точное число. Представьте, что вы пытаетесь описать человека, которого только что встретили; имеет ли смысл утверждать, что она была ростом 5 футов 4,175 дюйма, плюс-минус 2 дюйма?

Можем ли мы сделать лучше?

Однако это огромная неопределенность! Мы говорим, что время падения мяча может быть всего 0.2 с или целых 1,0 с, разница в 5 раз! Можем ли мы ответственно претендовать на меньшую неопределенность? Здесь нам следует более тщательно подумать о том, что на самом деле происходит во время эксперимента. Мы могли бы заметить, что среднее время реакции человека составляет около 200 мс, но статистика более подробная.

Если мы предположим, что реагируем исключительно на вид мяча, начинающего падать или ударяющегося о землю, то можно предположить, что время нашей реакции соответствует статистическому распределению для населения в целом.Тогда мы можем обоснованно утверждать, что с высокой вероятностью мы опоздали на 150–350 мс при нажатии обеих кнопок. И время начала, и время остановки запаздывают в среднем на 0,25 с, что компенсируется с погрешностью 0,1 с. При таком предположении мы можем указать измеренное время 0,6 ± 0,2 с, что является гораздо более точным результатом.

По возможности не предполагайте – измеряйте!

Если все эти предположения и оправдания вызывают у вас дискомфорт, возможно, так и должно быть.Когда вы даете результат, любое заявление, которое вы делаете, имеет силу только в той мере, в какой обоснованы ваши действия и предположения, которые вы делаете. Что, если наше предположение о том, что мы просто реагируем на удар мяча о землю, было неверным? Что, если мы проследим путь падающего мяча и попытаемся предугадать, когда он ударит?

Мы также могли пропустить другие источники ошибок. Что, если есть вещи, которые наши рассуждения упустили? Как скоро после того, как наш партнер отпускает мяч, мы можем сказать, что он действительно падает? Если бы мы были теми, кто сказал «иди», наш партнер уронил мяч через 200 мс после того, как мы начали отсчет времени, а не наоборот? Зачастую очень сложно предсказать все источники ошибок, которые могут исказить наши измерения, причем некоторые из них весьма незаметны.

Когда это возможно, мы должны попытаться измерить нашу неопределенность, а не строить догадки, предположения и обоснования. В следующем посте давайте рассмотрим, как мы можем измерить эту неопределенность и прийти к более точному и точному результату.

систематических и случайных ошибок в физике

Введение в систематические и случайные ошибки

В Части 2 Руководства по практическим навыкам физики мы рассмотрели надежность, точность и достоверность, а также то, как на них влияют различные типы ошибок.В этой части Руководства по практическим навыкам физики мы более подробно рассмотрим экспериментальные ошибки (систематические и случайные).

В этой статье мы обсуждаем:

 

Экспериментальные ошибки

Что такое экспериментальные ошибки?

Существует два типа экспериментальной ошибки:

1. Случайная ошибка
2. Систематическая ошибка

Систематические ошибки влияют на точность, тогда как случайные ошибки влияют на надежность экспериментальных результатов.

 

Получите преимущество перед следующим практическим тестом по физике

Получите глубокие знания и понимание всего модуля до того, как его начнут преподавать в школе. Узнайте больше о нашем семестровом курсе по физике.

 

Систематические и случайные ошибки

Что такое систематические ошибки?

Систематические ошибки будут постоянно смещать измерения от их истинного значения на одну и ту же величину или долю и в одном и том же направлении. Они не влияют на надежность (поскольку они всегда одинаковы), но влияют на точность.Обычно они возникают из-за проблемного или неправильно используемого оборудования, т.е. плохая калибровка.

Что такое случайные ошибки?

Случайные ошибки будут сдвигать каждое измерение от его истинного значения на случайную величину и в случайном направлении. Они повлияют на надежность (поскольку они случайны), но могут не повлиять на общую точность результата.

Каковы источники систематических или случайных ошибок?

Ниже перечислены различные типы ошибок и их происхождение. Каждая из них может быть описана как случайная или систематическая ошибка.

Ошибка	Описание	Систематическая или случайная ошибка
Ошибка весов	Если часть оборудования неправильно откалибрована (например, деревянная линейка села), все измерения будут смещены на одну и ту же долю.	Систематическая ошибка
Ошибка нуля	Если часть оборудования имеет смещение (например, массовый баланс показывает ненулевое значение, когда на нем ничего нет), все измерения будут смещены на одинаковую величину.	Систематическая ошибка
Ошибка параллакса	Если вы выполняете измерение, сравнивая индикатор со шкалой (например, считывая показания вольтметра или используя ртутный термометр), угол, под которым вы смотрите на него, будет влиять на показания.	Систематическая ошибка, если вы всегда смотрите на циферблат под одним и тем же углом. Случайная ошибка, если вы каждый раз смотрите на циферблат под случайным углом.
Ошибки, возникающие из-за окружающей среды	В идеале управляющие переменные остаются постоянными, но некоторые из них могут быть вне вашего контроля, например.г. атмосферное давление, температура, влажность, вибрации.	Изменения контрольных переменных могут привести как к систематическим, так и к случайным ошибкам. Одно последовательное изменение даст систематическую ошибку. Случайные изменения дадут случайные ошибки.
Время реакции	Если измерение зависит от времени вашей реакции, то вы можете отреагировать слишком рано или слишком поздно на разное количество времени.	Случайная ошибка.
Ошибки измерения из-за недостаточной точности	Если вы измеряете что-то, что находится между двумя отметками на шкале (например,г. вы используете линейку, чтобы измерить что-то длиной 10,25 мм), вы не можете измерить точное значение, и вам нужно будет округлить его в большую или меньшую сторону (это выглядит как 10 мм или 10,5 мм?).	Случайная ошибка.

 

Как насчет «человеческой ошибки»?

«Человеческая ошибка» не является источником экспериментальной ошибки. Вы должны классифицировать конкретные ошибки как случайные или систематические и указать источник ошибки.

Человеческая ошибка не может считаться ошибкой эксперимента.

 

Ошибки в процентах

Ошибки в процентах выражают неопределенность или несоответствие значения в процентах от значения.

Неопределенность описывает диапазон значений, которые может принимать результат или измерение, и связана с надежностью или точностью. Если значение указано как x ± 5%, то значение может быть больше или меньше на 5%.

Расхождение связано с разницей между окончательным результатом эксперимента и принятым значением и, следовательно, относится к точности.

 

Как уменьшить систематические ошибки

Систематическая ошибка возникает из-за оборудования , поэтому самый прямой способ ее устранения состоит в использовании калиброванного оборудования и устранении любых ошибок нуля или параллакса .

Даже если это повлияет на ваши измерения, при анализе данных можно устранить некоторые систематические ошибки. При анализе мы обычно рисуем график, который дает прямую линию, мы рисуем линию наилучшего соответствия и измеряем ее градиент. Измеряя градиент, мы рассматриваем только изменения, а не абсолютные значения.Нулевые ошибки приведут к смещению линии вверх и вниз (т. е. к пересечению графика по оси Y), но не повлияют на градиент. Следовательно, мы устраняем нулевые ошибки, что повышает точность.

 

Как уменьшить количество случайных ошибок

Так как случайные ошибки носят случайный характер и могут сдвигать значения как в большую, так и в меньшую сторону, их можно устранить путем повторения и усреднения . Истинная случайная ошибка усреднится до нуля, если будет проведено и усреднено достаточное количество измерений (через линию наилучшего соответствия).Вот почему повторение измерений может повысить надежность конечного результата эксперимента.

В анализе рисование графика и линии наилучшего соответствия служит для уменьшения случайной ошибки в окончательном экспериментальном результате. Во-первых, выбросы могут быть устранены. Во-вторых, линия наилучшего соответствия рисуется так, чтобы вместить как можно больше данных, разрезая набор точек данных. Таким образом, данные усредняются, при этом наибольший вес присваивается наиболее близким значениям.Это снижает влияние случайной ошибки и повышает надежность.

 

 

 

© Matrix Education и www.matrix.edu.au, 2022. Несанкционированное использование и/или копирование этого материала без письменного разрешения автора и/или владельца этого сайта строго запрещено. Выдержки и ссылки могут быть использованы при условии полной и четкой ссылки на Matrix Education и www.matrix.edu.au с соответствующим и конкретным указанием на исходный контент.

Ручной хронометраж в физических экспериментах: Ошибка и неопределенность: Американский журнал физики: Том 87, № 2

Ручные цифровые устройства хронометража, такие как секундомеры, повсеместно используются в образовательном секторе для экспериментальной работы, где автоматизированный электронный хронометраж недоступен или нецелесообразен. Недостаток ручного измерения времени заключается в том, что экспериментатор вносит дополнительную систематическую ошибку и случайную неопределенность в измерение, которое до сих пор можно было только приблизить и которое маскирует полезную информацию о неопределенности из-за изменений в физических условиях эксперимента.Модель времени реакции хронометриста, использующего секундомер, на одиночный ожидаемый визуальный стимул типа, встречающегося в физических экспериментах, получена из набора 4304 времен реакции хронометристов на соревнованиях по плаванию. Установлено, что время реакции хорошо смоделировано нормальным распределением N ( ε , σ ² ) = N (0,11, 0,07 ² ) в единицах секунд, где ε и σ ² — систематическая ошибка и дисперсия для одного измерения времени.Согласованность между хронометристами показана очень хорошо. Таким образом, время реакции для запуска и остановки эксперимента с секундомером можно смоделировать с помощью N (0, 0,10 ² ), предполагая, что среднее время реакции одинаково в обоих случаях. Это вносит существенный вклад в погрешность большинства измерений, синхронизируемых вручную. Эту временную неопределенность можно вычесть из изменений, наблюдаемых при повторных измерениях в реальном эксперименте, чтобы выявить неопределенность, связанную исключительно с колебаниями физических условий эксперимента.

БЛАГОДАРНОСТИ

Авторы очень благодарны официальным лицам клуба плавания Hart, Флит, Хэмпшир, Великобритания, которые предоставили доступ к данным о заплывах.

Типы, определение, примеры, систематическая ошибка, случайные ошибки

Ошибки в измерениях — обычное явление для любого метода. Результат каждого измерения, выполненного с помощью любого измерительного прибора, содержит некоторую неопределенность. Эта неопределенность называется ошибкой. В любой физической или математической системе всегда есть калиброванная шкала для измерения физической величины.При измерении числовое значение считывается с этой предопределенной шкалы.

Например: когда мы измеряем длину объекта, мы используем сантиметровую шкалу с заранее заданными отметками. Эта шкала имеет наименьшее деление 0,1 см, как показано ниже на диаграмме.

Это наименьшее деление шкалы также известно как наименьшее число , поэтому наименьшее число или наименьшее деление, которое мы можем измерить с помощью сантиметровой шкалы, составляет 1 мм.

Чтобы получить подробную информацию о кинетической теории газов, кандидаты могут посетить статью по ссылке.

Точность и прецизионность

Точность: Точность измерения является мерой того, насколько близко измеренное значение к истинному значению величины.

Точность: Точность означает близость двух или более измерений друг к другу. Точность говорит нам, с каким разрешением или пределом измеряется величина.

Теперь, чтобы проиллюстрировать разницу между точностью и точностью, давайте представим, что мы проводим эксперимент, в котором мы измеряем длину объекта 4 раза подряд.Затем тот же эксперимент повторяют еще три студента.

Студент

Измеренные значения 1	70	Измеренное значение 3	Измеренное значение 4
Студент 1	12. 36 см	12,37 см	12,36 см	12,36 см
Студент 2	12.36 см	12.32 см	12.38 см	12.38 см	12.17 см	12.17 см
	12,3 см	12.2 см	12.2 см	12,4 см	12.1 см

От вышеуказанного эксперимента, мы можем обратите внимание, что длина, измеренная студентом 3, не была ни точной, ни точной, в то время как показания, сделанные студентом 2, были точными, но менее точными по сравнению с студентом 1.

Таким образом, точность и прецизионность инструмента играют жизненно важную роль в любом измерительном устройстве.

Подробнее о расстоянии и смещении см. в статье по ссылке.

Существует общая путаница между Точность и Точность . Давайте проясним путаницу простым способом. На изображении ниже вы можете наблюдать изменение точности и точности и его значение.

Хорошей аналогией для понимания точности и аккуратности является представление баскетболиста, бросающего мяч в корзину. Если игрок стреляет точно, его цель всегда будет приводить мяч близко к корзине или в нее.Если игрок стреляет точно, его цель всегда будет направлять мяч в одно и то же место, которое может быть или не быть близко к корзине. Хороший игрок будет точен и точен, каждый раз бросая мяч одинаково и каждый раз попадая в корзину.

Точность прибора: Разрешение/наименьшее значение прибора.

Ознакомьтесь со статьей о равномерном круговом движении здесь.

Типы ошибок

В физике ошибки в основном представляют собой отклонение фактического значения от расчетного, и они классифицируются следующим образом:

• Систематическая ошибка : это ошибки из-за системы.Систематическая ошибка далее классифицируется как
  • Инструментальная погрешность: , возникающая из-за ошибок из-за несовершенной конструкции или калибровки измерительного прибора. Например:
    1. Ошибка нуля в штангенциркуле возникает, когда нулевые отметки нониусной шкалы могут не совпадать с нулевыми отметками основной шкалы,
    2. Обычная метровая шкала может быть стерта с одного конца.
  • Ошибка в методике измерения : Для определения температуры тела человека термометр, помещенный под мышку, всегда будет показывать температуру ниже фактического значения температуры тела.
  • Личные ошибки: возникающие из-за предвзятости человека, неправильной настройки прибора или небрежности человека при записи наблюдений
• Случайные ошибки: случайны по знаку и размеру. Они могут возникать из-за случайных и непредсказуемых колебаний экспериментальных условий. Например: если человек берет несколько показаний для одного и того же эксперимента, возможно, что каждое снятое показание будет уникальным и отличным от других.
• Наименьшая ошибка счета: Наименьшее значение, которое может быть измерено измерительным прибором, называется его наименьшим счетом . Например, штангенциркуль имеет наименьшее значение 0,01 см; сферометр может иметь наименьший счет 0,001 см. Используя инструменты более высокой точности, совершенствуя экспериментальную технику и т. д., мы можем уменьшить наименьшую ошибку счета.

Получите подробную информацию о вихревых токах и токах смещения.

Абсолютная ошибка

Величина разницы между отдельным измерением и истинным значением величины называется абсолютной ошибкой измерения.Это обозначается |∆a |

Предположим, что в нескольких измерениях получены значения a1, a2, a3…., an.

\(a_{mean}={(a_1+a_2+a_3+…+a_n)\over n}\)

Тогда отклонения отдельных значений измерений от истинного значения равны

∆a1 = a1 – \ (a_{среднее}\)

∆a2 = a2 – \(a_{среднее}\)

….

….

\(∆a_n\) = \(a_n\) – \(a_{mean}\)

Вычисленное выше ∆a может быть положительным в некоторых случаях и отрицательным в некоторых других случаях.Но абсолютная ошибка |∆a| всегда будет положительным.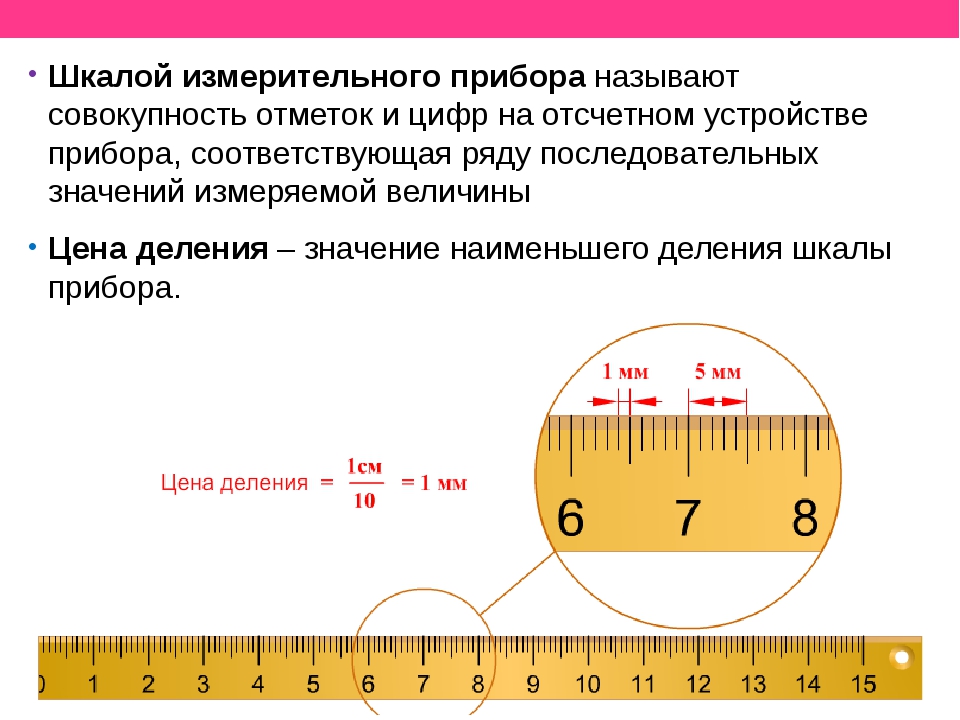

Среднее арифметическое всех абсолютных погрешностей принимается за окончательную или среднюю абсолютную погрешность значения физической величины а. Он представлен как \(∆a_{mean}\)

Подробную информацию о проверке мощности в цепи переменного тока см. здесь.

Относительная погрешность или погрешность в процентах (δa)

Относительная погрешность представляет собой отношение средней абсолютной погрешности \(∆a_{mean}\) к среднему значению \(∆a_{mean}\) измеряемой величины .

\(\text{Относительная ошибка}={\Delta{a_{mean}}\over{a_{mean}}}\\\)

\(\text{Процентная ошибка}(\delta a)={ \Delta{a_{mean}}\over{a_{mean}}}\times 100 \%\)

Прочтите об атоме и ядрах здесь.

Применение ошибок в арифметических операциях

Ошибка из-за суммы/разности

Предположим, что мы вычисляем задачу, в которой есть две величины A и B, и ожидается, что их измеренные значения будут примерно A ± ΔA и B ± ΔB соответственно, где ΔA и ΔB — абсолютная погрешность A и B соответственно.

Теперь мы хотим найти ожидаемое значение (т. е. Z + ΔZ) при суммировании этих физических величин. Здесь ΔZ — чистая абсолютная ошибка.

Таким образом, идеальное уравнение, когда мы добавляем две физические величины, может быть выражено как

Z= A+B

Аналогично, математическое ожидание суммы с ошибкой может быть задано как

(Z ± ΔZ) = (A ± ΔA) + (B ± ΔB)

∴ Z ± ΔZ = A + B ± ΔA ± ΔB

Но поскольку Z = A+B, уравнение может быть записано как

i.т. е., ⇒ Δ Z = ΔA + ΔB

И аналогично для отличия можно выразить как

(Z + ΔZ) = (A ± ΔA) – (B ± ΔB)

∴ Z ± ΔZ = A – B ± ΔA ± ΔB

Но поскольку Z = A+B, уравнение может быть представлено как

± Δ Z = ± ΔA ± ΔB

Кроме того, подробно ознакомьтесь с Типами термодинамических процессов , чтобы улучшить свою подготовку.

В. Какой будет общая длина провода, если соединить два провода длиной 10 ± 1 см и 12 ± 2 см соответственно?

А. Учитывая, что

Длина первого провода, L1 = 10 ± 1 см

Длина второго провода, L1 = 12 ± 2 см

Тогда общая длина провода, L = L1 + L2

∴ L ± ΔL = 10 ± 1 + 12 ± 2 = 22 ± 3 см

Подробнее о колебаниях см. в статье по ссылке.

Ошибка из-за продукта или подразделения

Предположим, мы рассчитываем задачу, в которой есть две величины A и B, и ожидается, что их измеренные значения будут около A ± ΔA и B ± ΔB соответственно, где ΔA и ΔB — абсолютная ошибка А и Б соответственно.

Теперь мы хотим найти ожидаемое значение (т. е. Z + ΔZ) при перемножении этих физических величин. Здесь ΔZ — чистая абсолютная ошибка.

В этом случае идеальное уравнение может быть выражено как

Z = AB

Таким образом, математическое ожидание суммы с ошибкой может быть задано как

(Z ± ΔZ) = (A ± ΔA) × (B ± ΔB)

Z ± ΔZ = AB ±A(ΔB) ± B(ΔA) ± ΔAΔB

Теперь, разделив обе стороны с Z, получим

\({Z\over Z}\pm{\Delta Z \over Z}={AB\over AB}\pm{A(\Delta B)\over AB}\pm{B(\Delta A)\over AB}\pm{(\Delta A)(\Delta B) \over AB}\\\)

\(\следовательно 1\pm{\Delta Z\over Z}=1\pm{A(\Delta B)\over AB}\pm{B(\Delta A)\ над AB}\pm{(\Delta A)(\Delta B)\над AB}\)

(здесь мы взяли Z = AB в правой части уравнения)

При этом, поскольку ΔA и ΔB действительно малы по сравнению с A и B, поэтому их произведением можно пренебречь. Итак, окончательное уравнение выглядит так:

Это выражение то же самое и для деления.

\({\Delta Z\over Z}={(\Delta B)\over B}+{(\Delta A)\over A}\)

Правило умножения или деления :

Когда две величины умножаются или делятся, относительная ошибка результата равна сумме относительных ошибок множителей.

Вы также можете проверить подробности о законах термодинамики.

Ошибка в случае степени

Как мы уже обсуждали, как вычисляются ошибки при умножении физических величин, таким образом, взятие квадрата, куба или любой степени физической величины есть не что иное, как многократное умножение одной и той же величины.r}}\)

Ознакомьтесь со статьей «Применение термодинамики» здесь.

Правило для степени :

Относительная погрешность физической величины, возведенной в степень k, равна относительной погрешности отдельной величины, умноженной на k.

Надеюсь, эта статья помогла вам понять основы ошибок в измерениях. Если вам нужна более интерактивная подготовка, попробуйте приложение Testbook. Здесь вы можете потренироваться на бесплатных пробных тестах

Часто задаваемые вопросы об ошибках измерений

Q.1 Что подразумевается под ошибками измерения?

Ответ 1 Результат каждого измерения любым измерительным прибором содержит некоторую неопределенность. Эта неопределенность называется ошибкой.

Q.2 Что подразумевается под точностью?

Ответ 2 Точность означает близость двух или более измерений друг к другу. Точность говорит нам, с каким разрешением или пределом измеряется величина.

В.3 Что подразумевается под точностью?

Ответ.3 Точность измерения – это мера того, насколько близко измеренное значение к истинному значению величины.

В.4 Что подразумевается под абсолютной ошибкой?

Ответ 4 Величина разницы между индивидуальным измерением и истинным значением величины называется абсолютной погрешностью измерения.

В.5 Что подразумевается под относительной ошибкой?

Ответ 5 Относительная погрешность представляет собой отношение средней абсолютной погрешности ∆amean к среднему значению amean измеряемой величины.

Создайте бесплатную учетную запись, чтобы продолжить чтение

• Получайте мгновенные оповещения о вакансиях бесплатно!

• Получите ежедневные капсулы GK и текущих событий и PDF-файлы

• Получите более 100 бесплатных пробных тестов и викторин

Подпишитесь бесплатно У вас уже есть аккаунт? Войти

Следующий пост

Написание анализа ошибки

Заключение вашего лабораторного отчета должно быть основано на анализе ошибки в эксперименте.Анализ ошибок является одним из наиболее точных критериев, доступных преподавателю, с помощью которого можно оценить научную проницательность студента. Для того, чтобы этот анализ был выполнен правильно, необходимы комментарии о факторах, влияющих на то, в какой степени экспериментальные результаты согласуются с теоретическим значением (какие факторы влияют на процентную ошибку), об ограничениях и ограничениях используемых инструментов (какие факторы влияют на неопределенность). ), и правомерность предположений.

Физики обычно используют фразу «источники ошибок» (или «источники неопределенности»), чтобы описать, как пределы измерения распространяются в расчете (см. Распространение неопределенностей), чтобы повлиять на неопределенность в конечном результате.Этот тип «анализа ошибок» дает представление о точности результата. Рекомендации по анализу ошибок содержат вопросы, которые могут помочь вам описать, какое из нескольких измерений может наиболее эффективно улучшить точность результата, чтобы вы могли получить представление о точности результата. Точность позволяет оценить достоверность (истинность) лежащих в основе отношений, а точность позволяет оценить точность. Иными словами, небольшая разница в процентов обычно используется для обозначения небольшой ошибки в процентов.Иными словами, неточные измерения всегда кажутся точными.

Подраздел A.2.1 Технически ошибки не являются ошибками

¶

В вашем отчете не следует указывать «человеческую ошибку», потому что большинство студентов неправильно понимают этот термин как означающий «места, в которых я мог совершить ошибку», а не как «ограничивающий фактор при правильном использовании оборудования». В разделе «Нахождение точности измерения» обсуждаются неопределенности измерения, как они определены выше.

В приведенном выше примере с яблоком тот факт, что у одного человека \(0.33 \pm 0,04\) яблока , а не , отражают «ошибку» в разрезании, а скорее отражают ограниченность резчика в точности. Важно использовать неопределенность, чтобы выразить, насколько хорошо можно повторно разрезать яблоко на три части. Абсолютная неопределенность \(0,04\) обычно интерпретируется как указание на то, что большинство случаев (примерно \(68\%\text{,}\) как объяснено в разделе Неопределенность множественных, повторяющихся измерений) разрезания яблока таким образом приведет к тому, что между \(0.29\) до \(0,37\) яблока для любого заданного кусочка.

При описании причины ошибки (отличие от теоретического значения) или неопределенности (насколько вы доверяете числу), вы обычно можете классифицировать этот источник ошибки как случайную ошибку (причина, которая может слишком сильно исказить результат). или слишком мало) или как систематическая ошибка (причина, которая имеет тенденцию искажать результат в одном конкретном направлении).

Случайная ошибка

Окружающие обстоятельства, как правило, не поддающиеся контролю, которые иногда делают результат измерения слишком высоким, а иногда делают его слишком низким непредсказуемым образом.Случайные ошибки могут иметь статистическое происхождение, т. е. они обусловлены случайностью. Например, если на стол брошено сто пенни, в среднем мы ожидаем, что пятьдесят выпадут орлом. Но мы не должны удивляться, если пятьдесят три или сорок семь действительно выпадут один на один. Это отклонение носит статистический характер, потому что то, как приземляется пенни, зависит от случая. Случайные ошибки иногда можно уменьшить либо за счет сбора большего количества данных и усреднения показаний, либо за счет использования приборов с большей точностью.

Систематическая ошибка

Систематическая ошибка может быть приписана фактору, который имеет тенденцию отклонять результат в определенном направлении от теоретического значения.