Конспект урока определение координаты движущегося тела 9 класс – Презентация по физике, 9 класс. Путь. Перемещение. Определение координаты движущегося тела

Содержание

Определение координаты движущегося тела. Видеоурок. Физика 9 Класс

Представьте: вы изо всей силы бросили мяч. Как определить, где он будет находиться через две секунды? Можно подождать две секунды и просто посмотреть, где он. Но, даже не глядя, вы приблизительно можете предсказать, где будет мяч: бросок был сильнее обычного, направлен под большим углом к горизонту, значит, полетит высоко, но недалеко… Используя законы физики, можно будет точно определить положение нашего мяча.

Определить положение движущегося тела в любой момент времени – это и есть основная задача кинематики.

Начнем с того, что у нас есть тело: как определить его положение, как объяснить кому-то, где оно находится? Об автомобиле мы скажем: он на дороге за 150 метров перед светофором или на 100 метров за перекрестком (см. рис. 1).

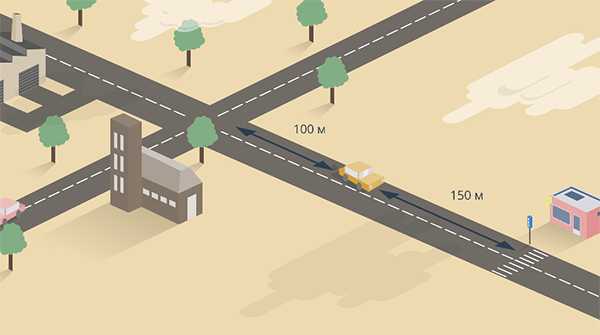
Рис. 1. Определение местоположения машины

Или на трассе за 30 км к югу от Москвы. О телефоне на столе скажем: он сантиметров на 30 правее клавиатуры или рядом с дальним углом стола (см. рис. 2).

Рис. 2. Положение телефона на столе

Заметьте: мы не сможем определить положение автомобиля, не упомянув другие объекты, не привязавшись к ним: светофор, город, клавиатуру. Мы определяем положение, или координаты, всегда относительно чего-то.

Координаты – это набор данных, по которому определяется положение того или иного объекта, его адрес.

Примеры упорядоченных и неупорядоченных имен

Координата тела – это его адрес, по которому мы его можем найти. Он упорядоченный. Например, зная ряд и место, мы точно определяем, где находится наше место в зале кинотеатра (см. рис. 3).

Рис. 3. Зал кинотеатра

Буквой и цифрой, например e2, точно задается положение фигуры на шахматной доске (см. рис. 4).

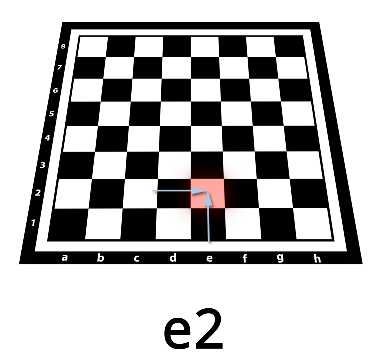
Рис. 4. Положение фигуры на доске

Зная адрес дома, например улица Солнечная 14, мы будем искать его на этой улице, на четной стороне, между домами 12 и 16 (см. рис. 5).

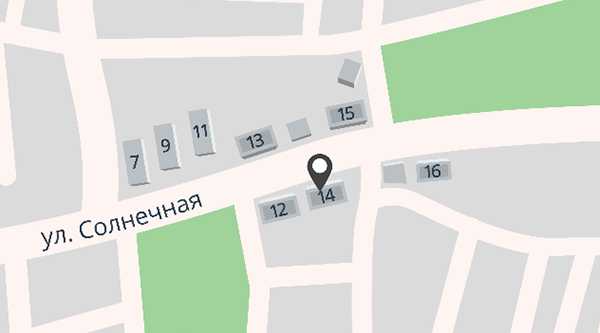
Рис. 5. Поиск дома

Названия улиц не упорядочены, мы не будем искать Солнечную улицу по алфавиту между улицами Розовой и Тургенева. Также не упорядочены номера телефонов, номерные знаки автомобилей (см. рис. 6).

Рис. 6. Неупорядоченные имена

Эти номера, идущие подряд, – это лишь совпадение, не означающее соседства.

Мы можем задать положение тела в разных системах координат, как нам удобно. Для того же автомобиля, можно задать точные географические координаты (широту и долготу) (см. рис. 7).

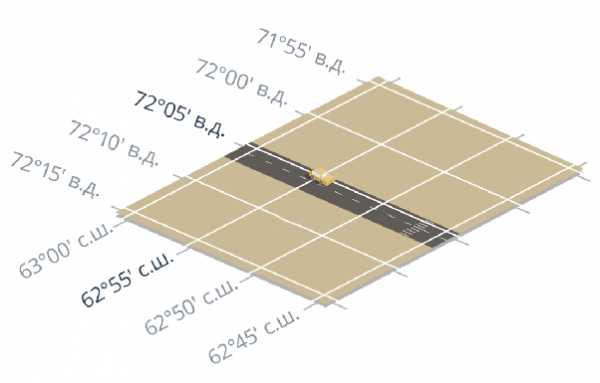
Рис. 7. Долгота и широта местности

Можно выбрать любую точку в городе и считать, сколько километров нужно проехать на юг и сколько на восток, чтобы найти автомо

interneturok.ru

Определение координаты движущегося тела

На прошлом уроке мы с вами говорили о пути и перемещении тела. Давайте вспомним, что путь — это скалярная величина, равная длине траектории, которую описывает тело за некоторый промежуток времени.

А перемещением называется направленный отрезок прямой, соединяющий начальное и конечное положения тела.

Так как перемещение — это векторная величина, то есть имеет модуль и направление, то складывать и вычитать перемещения необходимо по правилам сложения и вычитания векторов. Однако при решении большинства задач, используется понятие не вектора, а проекции вектора на ось координат.

— А что такое проекция вектора и каковы её свойства?

На это вопрос мы с вами и попытаемся сегодня ответить. Начнём с простого — с понятия проекция точки на ось. Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.

На представленном рисунке точка А₁ — это проекция точки А на ось Ox, а точка B₁ — проекция точки B на ось Oy.

Теперь разберёмся с проекцией вектора на ось. Согласно определению, проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора на эту ось, взятая со знаком «плюс» или «минус».

Знак «плюс» берут, если угол между вектором и осью острый, а «минус» — если угол тупой.

Обозначать проекцию вектора будем той же буквой, что и вектор, но с индексом внизу (например, a_x — это проекция вектора a на ось Ox).

— А если вектор перпендикулярен оси?

Тогда проекция этого вектора равна нулю.

Проекцию вектора можно выразить через его модуль и угол между вектором и осью. Итак, пусть у нас есть вектор a направленный под некоторым острым углом к координатной оси Ox. Укажем проекцию этого вектора на ось.

У нас с вами получился прямоугольный треугольник, гипотенуза которого равна длине вектора a, а катет AB₁ — это проекция вектора a на ось Ox.

Тогда, на основании определения косинуса острого угла, мы можем записать, что п

роекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью:

Это правило справедливо при любых значениях угла φ. Например, для углов, больше 90^о, косинус угла φ отрицательный. Тогда по формуле получается, что проекция вектора на ось также отрицательна, как и должно быть по определению проекции.

— А можно ли найти модуль и направление вектора по его проекциям на координатные оси?

Чтобы ответить на этот вопрос рассмотрим вектор, лежащий в плоскости xOy. Вектор, лежащий в заданной плоскости, определяется двумя проекциями на оси координат.

Обратим внимание на важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.

Но вернёмся к нашему прошлому уроку. На нём мы с вами говорили о том, что положение тела, которое совершило некоторое перемещение, можно найти графически. Для этого достаточно отложить вектор перемещения от начального положения этого тела. Однако в большинстве случаев необходимо уметь вычислять положение тела, то есть уметь определять его координаты. Давайте на примере решения задачи посмотрим, как можно определить координату движущегося тела, зная координату его начального положения и вектор перемещения.

Итак, два поезда идут по параллельным путям в противоположных направлениях и встречаются в шестидесяти километрах к востоку от железнодорожного вокзала. Продолжив движение через некоторое время t первый поезд удалился от места встречи на 50 километров в восточном направлении, а второй — на 80 километров в западном. Определите координаты каждого поезда относительно вокзала и расстояние между ними через промежуток времени t.

videouroki.net

«Конспект урока по физике «Определение координаты движущегося тела» 9 класс»

Тема урока: «Определение координаты движущегося тела»

Цель урока: Ввести понятия векторная и скалярная величина, координата, проекция вектора, модуль вектора. Сформулировать правила определения знака проекции.
Тип уроки: Комбинированный урок.
Проверка знаний:
1. Что называется механическим движением?
2. Что входит в понятие «система отсчета»?
3. Почему невозможно описать движение без выбора системы отсчета?
4. Какие точки катящегося вагона движутся и какие находятся в покое относительно дороги?
5. Что такое материальная точка?
6. Какое движение называется поступательным?
7. Что такое траектория?
8. Что такое пройденный путь?
9. Что такое перемещение?
10. ответить на вопросы к §2.
11. ответить на вопросы упр. 2 № 1,2.
Траектории движения двух материальных точек пересекаются. Означает ли это, что тела сталкиваются? Приведите пример, подтверждающий ваш ответ.

Тело, брошенное вертикально вверх, поднялось на высоту 20 м и упало в ту же точку. Чему равен путь, пройденный телом за то время, пока оно двигалось вверх? За время, пока оно двигалось вниз? За все время движения?
При каком условии путь равен модулю перемещения тела? Может ли модуль перемещения быть больше пройденного пути? Приведите примеры таких движений.
Автомобиль проехал 100 км. а) Какие точки колеса совершили максимальное перемещение? Минимальное? б) Какие точки колеса прошли максимальный путь? Минимальный?
Два тела, двигаясь прямолинейно, совершили одинаковые перемещения. Обязательно ли одинаковы пройденные ими пути? Ответ поясните примером.

План изложения нового материала:
Определение координаты движущегося тела.
Векторные и скалярные величины.
Проекция вектора.
Правило определения знака проекции.
Уравнение, с помощью которого можно определить координату тела.

Модуль вектора.

1. Изложение нового материала.
Определение координаты движущегося тела. При решении задач обычно составляют уравнения, связывающие физические величины, а затем решают эти уравнения. Если величины векторные, приходится «следить» не только за модулем каждой такой величины, но и за ее направлением. Решение задач значительно упрощается благодаря тому, что одну векторную величину можно задать с помощью нескольких скалярных величин следующим образом.
Любую векторную величину можно представить в виде суммы трех векторных величин, направленных вдоль осей координат. Эти векторные величины называют ее составляющими. Каждую составляющую векторной величины можно охарактеризовать просто числом: модуль этого числа равен модулю составляющей, а знак числа определяется направлением составляющей. Если она направлена в положительном направлении оси координат, это чис

schoolfiles.net

Конспект урока по физике «Определение координаты движущегося тела» 9 класс

Тема урока: «Определение координаты движущегося тела»

Цель урока: Ввести понятия векторная и скалярная величина, координата, проекция вектора, модуль вектора. Сформулировать правила определения знака проекции.

Тип уроки: Комбинированный урок.

Проверка знаний:

1. Что называется механическим движением?

2.Что входит в понятие «система отсчета»?

3.Почему невозможно описать движение без выбора системы отсчета?

4.Какие точки катящегося вагона движутся и какие находятся в покое относительно дороги?

5. Что такое материальная точка?

6. Какое движение называется поступательным?

7. Что такое траектория?

8. Что такое пройденный путь?

9. Что такое перемещение?

10. ответить на вопросы к §2.

11. ответить на вопросы упр. 2 № 1,2.

Траектории движения двух материальных точек пересекаются. Означает ли это, что тела сталкиваются? Приведите пример, подтверждающий ваш ответ.
Тело, брошенное вертикально вверх, поднялось на высоту 20 м и упало в ту же точку. Чему равен путь, пройденный телом за то время, пока оно двигалось вверх? За время, пока оно двигалось вниз? За все время движения?
При каком условии путь равен модулю перемещения тела? Может ли модуль перемещения быть больше пройденного пути? Приведите примеры таких движений.
Автомобиль проехал 100 км. а) Какие точки колеса совершили максимальное перемещение? Минимальное? б) Какие точки колеса прошли максимальный путь? Минимальный?
Два тела, двигаясь прямолинейно, совершили одинаковые перемещения. Обязательно ли одинаковы пройденные ими пути? Ответ поясните примером.

План изложения нового материала:

Определение координаты движущегося тела.
Векторные и скалярные величины.
Проекция вектора.
Правило определения знака проекции.
Уравнение, с помощью которого можно определить координату тела.
Модуль вектора.

1. Изложение нового материала.

Определение координаты движущегося тела. При решении задач обычно составляют уравнения, связывающие физические величины, а затем решают эти уравнения. Если величины векторные, приходится «следить» не только за модулем каждой такой величины, но и за ее направлением. Решение задач значительно упрощается благодаря тому, что одну векторную величину можно задать с помощью нескольких скалярных величин следующим образом.

Любую векторную величину можно представить в виде суммы трех векторных величин, направленных вдоль осей координат. Эти векторные величины называют ее составляющими. Каждую составляющую векторной величины можно охарактеризовать просто числом: модуль этого числа равен модулю составляющей, а знак числа определяется направлением составляющей. Если она направлена в положительном направлении оси координат, — это число положительное, а если в отрицательном, — отрицательное. Это число называется проекцией данной векторной величины на соответствующую координатную ось.

Проекции векторной величины а на оси координат х, у, z обозначаются а_х, а_у и а_г. Они измеряются в тех же единицах, что и модуль этой величины. Например, проекция перемещения измеряется в метрах, а проекция скорости — в метрах в секунду.

Свяжем проекции перемещения тела с его координатами. Для наглядности ограничимся движением на плоскости.

Пусть тело из точки с координатами х_0, у₀ переместилось в точку с координатами х, у. Тогда перемещение s — это вектор, проведенный из точки с координатами х_0,, у₀ в точку с координатами х, у. Следовательно,

s_x = х — х₀, s_y=y-y_0. • Таким образом,

x = x₀ + s_x, y = y_Q+s_y.

Обращаем внимание: в этих формулах стоит знак «плюс», независимо от того, в каком направлении двигалось тело — в положительном направлении оси или в отрицательном.

2. Отработка знаний и умений.

Решение задачи упр.3 №1

Задание на дом: §3 упр.3 №2.

best-4info.ru

9 класс | Социальная сеть работников образования

Слайд 2

Физика Законы взаимодействия и движения тел. Механические колебания и волны. Звук ЭМ-поле. Строение атома и атомного ядра.

Слайд 3

Тема 1 «Законы взаимодействия и движения тел» Урок 1. Материальная точка. Система отсчета. Перемещение Юлия Ринатовна Залялиева , учитель физики и математики МБОУ СОШ №8 . 2.09.2015 г

Слайд 4

Движение – это неотъемлемое свойство материи Движение

Слайд 5

Механическое движение – изменение положения тела в пространстве относительно других тел с течением времени. Механическое движение

Слайд 6

Пройденный путь; Скорость; Траектория; Перемещение ; Координаты тела. Характеристики движения:

Слайд 7

Траектория – это линия, вдоль которой движется тело Пройденный путь – это длина траектории Перемещение – вектор, соединяющий начальное положение тело с его последующим положением s (м ) s (м )

Слайд 8

Скорость – это величина, характеризующая быстроту движения Скорость υ (м / с)

Слайд 9

Координата тела — положение тела в пространстве в любой момент времени Координата тела

Слайд 10

с ловесный табличный г рафический а налитический (формулы) Способы описания движения

Слайд 11

Словесное описание Выехав из пункта А, поезд 2 часа ехал со скоростью 100 км/ч, затем час стоял, и в пункт Б прибыл через 3 часа, все это время двигаясь с постоянной скоростью 50 км/ч.

Слайд 12

Табличное описание Графическое описание

Слайд 13

Аналитическое описание

Слайд 14

Способы описания движения

Слайд 15

Материальная точка — тело, размерами которого можно пренебречь в условиях данной задачи Материальная точка

Слайд 16

Условия , при которых тело можно считать МТ: если его размеры малы по сравнению с расстоянием , которое оно проходит. если оно движется поступательно ( все точки движутся одинаково).

Слайд 17

Например За материальную точку очень часто рассматривают Землю, если исследуют её движение вокруг Солнца.

Слайд 18

Можно ли считать материальными точками тела, описанные в следующих ситуациях ? 1.Рассчитывают путь Земли по орбите вокруг Солнца. 3.Для определения объема шарика его опускают в мензурку. 4.Для измерения массы лимона его кладут на весы. 5. Ваши примеры

Слайд 19

Чтобы определить положение тела (материальной точки) в пространстве надо : задать тело отсчета ; выбрать систему координат; иметь прибор для отсчёта времени (часы)

Слайд 20

Что такое тело отсчета? Тело отсчёта — это тело, относительно которого определяется положение других (движущихся) тел .

Слайд 21

Система координат

Слайд 22

Система отсчета:

Слайд 23

Повторим Что такое механическое движение? Что такое материальная точка? В каких случаях тело можно считать материальной точкой? Какое движение называется поступательным? Что такое система отсчета?

Слайд 24

§ 1-2, вопросы после параграфа Упр. 1 (2,4), Упр.2 (1) Знать все определения (!) Домашнее задание:

Слайд 25

+ 1 балл № Вид движения Определение Примеры 1 Поступательное 2 Прямолинейное 3 Вращательное 4 Криволинейное 5 Равномерное 6 Неравномерное

Слайд 26

Тема урока. ОПРЕДЕЛЕНИЕ КООРДИНАТЫ ДВИЖУЩЕГОСЯ ТЕЛА Урок 2

Слайд 27

Скалярные и векторные величины траектория путь перемещение

Слайд 28

Слайд 29

Определение пройденного пути и перемещения

Слайд 30

0 X X 0 X

Слайд 31

Задача1. Автомобиль переместился из точки с координатой Х 0 =200 м в точку с координатой Х=-200 м. Определите проекцию перемещения автомобиля. Дано: Х 0 =200 м Х=-200 м S х -? Решение Вычисления S х =-200 м-200 м= -400 м Ответ: S х =-400 м

Слайд 32

Определите по графику пройденный путь и модуль перемещения материальной точки. S =АВ+ВС+С D=8 м+4 м+8 м=20 м |S| =А D=4 м

Слайд 33

Сборник задач по физике А.П. Рымкевич №и 9 №11 № 17

nsportal.ru

Конспект урока по физики на тему: Определение координат движущегося тела 9 класс

Физика 9 класс
Урок 2. Траектория, путь и перемещение. Определение координаты движущегося тела.
Цели урока: введение понятий “перемещение”, “путь”, “траектория”.
Задачи урока:
образовательная: научить определять координаты движущегося тела.
развивающая: развивать логическое мышление, правильную физическую речь, использовать соответствующую терминологию.воспитательная: достигать высокой активности класса, внимания, сосредоточенности учащихся.
Ход урока.
1. Организационный момент (1 мин).
Здравствуйте, ребята. Сегодня мы с вами продолжим изучать тему “Законы взаимодействия и движения тел” и на уроке познакомимся с тремя новыми понятиями из этой темы.
2. Актуализация знаний. Проверка домашнего задания (10 мин).
А пока проверим выполнение вами домашнего задания к данному уроку.
У доски работает 3 человека устно по вопросам к § 1 и упражнение 1.
Четверо учеников работают по карточкам с индивидуальными заданиями, которые выполняются во время устного ответа. (Приложение 1)
3. Изучение нового теоретического материала (15 мин).
Тема урока «Траектория, путь и перемещение. Определение координаты движущегося тела».
Слайд 1
С изменениями координат тела связана величина, вводимая для описания движения, – перемещение.
2971800298450Перемещением тела (материальной точки) называется вектор, проведенный из начального положения тела в его конечное положение.
Перемещение принято обозначать буквой . В СИ перемещение измеряется в метрах (м).
Перемещение – величина векторная, т.е. кроме числового значения имеет еще и направление. Векторную величину изображают в виде отрезка, который начинается в некоторой точке и заканчивается острием, указывающим направление. Такой отрезок-стрелка называется вектором.
Слайд 2
В процессе движения материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом движущаяся точка “описывает” в пространстве какую-то линию. Иногда эта линия видна, – например, высоко летящий самолет может оставлять за собой след в небе. Более знакомый пример – след куска мела на доске.
Воображаемая линия в пространстве, по которой движется тело называется траекторией движения тела.
Траектория движения тела – это непрерывная линия, которую описывает движущееся тело (рассматриваемое как материальная точка) по отношению к выбранной системе отсчета.
Длина траектории – это путь. Путь увеличивается, если тело движется. И остается неизменным, если тело покоится. Таким образом, путь не может уменьшаться с течением времени.
Слайд 3
Движение, при котором все точки тела движутся по одинаковым траекториям, называется поступательным.
В зависимости от траектории движения могут быть прямолинейными (падение тел в опыте Галилея) и криволинейными (движение брошенного под углом к горизонту мяча).
Траектория одного и того же движения различна в разных системах отсчета.
Например, для пассажира равномерно двигающегося поезда падающий в вагоне мячик двигается вертикально вниз, а для человека, стоящего на перроне, тот же мячик двигается по параболической траектории.
Слайд 4
Чем же отличается путь от перемещения? Эти два понятия часто смешивают, хотя на самом деле они очень сильно отличаются друг от друга. Рассмотрим эти отличия:
Путь – скаляр, а перемещение вектор.
Путь зависит от траектории, а перемещение нет.
Перемещение м

univerfiles.com

Урок 03. Определение координаты движущегося тела (Федосова О.А.).

Название предмета - физика
Класс - 9
УМК (название учебника, автор, год издания) - Физика. 9 кл.: учебник/ А.В. Перышкин, Е.М. Гутник. - М.: Дрофа, 2014.
Уровень обучения (базовый, углубленный, профильный) - базовый
Тема урока -Определение координаты движущегося тела.
Общее количество часов, отведенное на изучение темы - 1
Место урока в системе уроков по теме - 3/3
Цель урока - нахождение координаты тела по его начальной координате и проекции вектора перемещения.
Задачи урока -
ввести понятия векторная и скалярная величина, координата, проекция вектора, модуль вектора; сформулировать правила определения знака проекции; научить определять проекцию вектора перемещения на выбранную ось, определять модуль перемещения; находить координаты тела по его начальной координате и проекции вектора перемещения; научить строить проекцию вектора перемещения на выбранную ось;
формировать у обучающихся логическое мышление; развивать познавательный интерес к предмету; развивать умение оперировать ранее полученными знаниями; развивать умение планировать свою деятельность;
воспитывать умение самостоятельно мыслить, ответственности за выполняемую работу, аккуратности при выполнении работы.
Планируемые результаты -
Знать:
Определение: вектор, проекция вектора, модуль вектора, координата тела.
Уметь:
находить проекцию вектора перемещения на выбранную ось;
определять модуль перемещения;
использовать знания из области математики (нахождение координаты тела)
строить проекцию вектор перемещения.
Техническое обеспечение урока -компьютер, мультимедийный проектор
Дополнительное методическое и дидактическое обеспечение урока (возможны ссылки на интернет-ресурсы) – презентация к уроку, тест 01 «Механическое движение. СО. Траектория, путь и перемещение» Автор: © 2014, ООО "КОМПЭДУ", http://compedu.ru
Содержание урока
1. Организационный этап
1. Взаимное приветствие учителя и обучающихся; проверка отсутствующих по журналу.
2. Актуализация субъектного опыта обучающихся

Для повторения материала прошлого урока учащимся предлагаются следующие вопросы:
1. Что называется механическим движением?
2. Что входит в понятие «система отсчета»?
3. Почему невозможно описать движение без выбора системы отсчета?
4. Какие точки катящегося вагона движутся и какие находятся в покое относительно дороги?
5. Что такое материальная точка?
6. Какое движение называется поступательным?
7. Что такое траектория?
8. Что такое пройденный путь?
9. Что такое перемещение?
10. Ответить на вопросы к §2.
11. Ответить на вопросы упр. 2 № 1,2.
Индивидуальная работа с тестом 01.Механическое движение. СО. Траектория, путь и перемещение.
3. Изучение новых знаний и способов деятельности (работа со слайдами презентации)
Определение координаты движущегося тела. При решении задач обычно составляют уравнения, связывающие физические величины, а затем решают эти уравнения. Если величины векторные, приходится «следить» не только за модулем каждой такой величины, но и за ее направлением. Решение задач значительно упрощается благодаря тому, что одну векторную величину можно задать с помощью нескольких скалярных величин следующим образом.
Любую векторную величину можно представить в виде суммы трех векторных величин, направленных вдоль осей координат. Эти векторные величины называют ее составляющими. Каждую составляющую векторной величины можно охарактеризовать просто числом: модуль этого числа равен модулю составляющей, а знак числа определяется направлением составляющей. Если она направлена в положительном направлении оси координат, — это число положительное, а если в отрицательном, — отрицательное. Это число называется проекцией данной векторной величины на соответствующую координатную ось.
Проекции векторной величины а на оси координат х, у, z обозначаются ах, ау и аz. Они измеряются в тех же единицах, что и модуль этой величины. Например, проекция перемещения измеряется в метрах, а проекция скорости — в метрах в секунду.
Свяжем проекции перемещения тела с его координатами. Для наглядности ограничимся движением на плоскости.
Проекция вектора на координатную ось

Пусть тело из точки с координатами х0, у0 переместилось в точку с координатами х, у. Тогда перемещение s — это вектор, проведенный из точки с координатами х0,, у0 в точку с координатами х, у. Следовательно,
sx = х - х0, sy=y-y0. • Таким образом,
x = x0 + sx, y = yо+sy.
Обращаем внимание: в этих формулах стоит знак «плюс», независимо от того, в каком направлении двигалось тело — в положительном направлении оси или в отрицательном.

4.Первичная проверка понимания изученного
Рассмотрим задачу на стр.13.

5.Закрепление изученного
Запишем условие задачи и решим ее

Решим задачу

6. Обобщение и систематизация

7.Домашнее задание: §3 упр.3 №2

56bit.ru