Содержание

Разработка урока математики в 6 классе по теме «Пропорция»


Приложение 1
DOC / 50 Кб

/data/files/d1604482565.doc (Приложение 1)


Приложение 2
DOC / 48.5 Кб

/data/files/w1604482598.doc (Приложение 2)


Приложение 3
DOC / 39.5 Кб

/data/files/m1604482624.doc (Приложение 3)


Приложение 4
DOC / 23.5 Кб

/data/files/s1604482646.doc (Приложение 4)


Презентация к уроку
PPT / 628.5 Кб

/data/files/t1604482688.ppt (Презентация к уроку)Разработка урока математики в 6 классе по теме «Пропорция»

Илатовская Ирина Анатольевна – учитель математики МБОУ «Бестужевская СОШ» Устьянского района Архангельской области

УМК: Математика 6 класс: учебник для общеобразовательной школы/ Виленкин Н. Я. М.: «Мнемозина», 2014г.

Тип урока: урок обобщения и закрепления знаний.

Цели урока:

Образовательная: обобщение и систематизация знаний обучающихся по данной теме; совершенствование умений обучающихся решать пропорций.

Развивающая: расширение кругозора обучающихся; формирование правильной математической речи; развитие умений обобщать, анализировать, делать выводы.

Воспитательная: активизация познавательной активности обучающихся; воспитание интереса к предмету; воспитание чувства прекрасного.

Формы организации учебной деятельности: Фронтальная работа, индивидуальная работа, работа в малых группах

Оборудование: проектор, экран, компьютер, карточки с заданиями.

Ход урока

1. Мотивация к учебной деятельности (2 мин)

Учитель: Здравствуйте, ребята! Я рада видеть вас на своем уроке. Урок мы начнем с ребуса. (Слайд 1)

Ответ: Пропорция

Итак, вы все догадались, что урок посвящен теме «Пропорция». Сформулируем цель урока.

2. Формулирование темы урока, постановка цели (3 мин)

Учащиеся: Цель: Закрепление понятия «Пропорция», основного свойства пропорции.

У вас на столах лежат оценочные листы, с которыми мы будем работать на уроке. Рассмотрите их и составьте план урока. (Приложение 1)

Учащиеся: План урока:

1. Повторить, что такое отношение и пропорция, члены пропорции.

2. Повторить основное свойство пропорции.

3. Применить знания для решения пропорций.

Учитель: Итак, мы отправляемся с вами в Путешествие по стране «Пропорция» (Слайд 2).

Хвала пропорции: (Слайд 3)

Чтобы здания построить, чтобы возводить мосты,

Надо правило усвоить. Здесь пропорции важны.

Блюдо будет идеально, если все пропорционально.

И фигура – просто класс, говорю вам без прикрас.

Ведь расчёт во всём нам нужен, будь с пропорцией ты дружен

Первая остановка. «Отношения и пропорция». Математический диктант (Слайд 4).

3. Актуализация знаний (7 мин)

(Слайд 5)

Поменяйтесь тетрадями и проверьте друг друга (Слайд 6).

Поставьте в оценочный лист количество баллов 0-7

4. Обобщение и систематизация знаний (13 мин)

Учитель: Поезд приходит на вторую станцию «Основное свойство пропорции». Давайте вспомним это свойство (Слайд 7).

Учащиеся: Произведение крайних членов верной пропорции равно произведению средних членов (Слайд 8).

Фронтальная работа: на доске написаны пропорции. Проверить верные они или неверные по основному свойству пропорции и по определению. Двое работают у доски, остальные на местах.

Учитель: я каждому предлагаю вытянуть карточку с пропорцией и проверить верна ли она, если она верная, прикрепить свою карточку к слову «Верная». Если пропорция неверная – прикрепить к слову «Неверная» (Слова «Верная» и «Неверная» висят на магнитной доске Приложение 4). Раздать карточки с пропорциями (Приложение 2).

Учащиеся: решают, выходят к доске и прикрепляют на магниты свои карточки, делаем проверку (Слайд 9)

Оцените себя баллами 0-5, запишите в оценочный лист.

5. Применение знаний и умений в новой ситуации (15 мин)

Учитель: И вот, мы прибываем на третью станцию «Вычислительная» (Слайд 10).

Сейчас вы будете работать в группах. Ваша задача найти неизвестный член пропорции и отгадать слово (Приложение 3).

Учащиеся: работают в малых группах по 3-4 ученика или парах. Ученики делятся на группы или пары сильный-сильный, слабый – слабый, слабых учеников можно в группы по 3 -4 человека.

Учитель: Оцените друг друга в группах поставьте в оценочный лист баллы 0-5. Мы приезжаем на последнюю станцию «Историческая» (Слайд 12, 13). Учитель зачитывает историческую справку

(Слайд 14) Ничто не нравится, кроме красоты,

в красоте – ничто, кроме форм,

в формах – ничто, кроме пропорций,

в пропорциях – ничто, кроме числа.

Аврелий Августин философ, влиятельнейший проповедник, Отец христианской церкви

6. Рефлексия учебной деятельности на уроке. Итог урока. Домашнее задание. (5 мин)

Учитель: Подведем итоги урока. Поставьте в оценочный лист отметку за урок, в зависимости от количества заработанных баллов. Запишем домашнее задание:

Рабочая тетрадь стр 115-116 :

№10 – любые четыре пропорции

№11 – любые две пропорции

№12.

Вернуться к цели и задачам урока, посмотреть, что успели, что нет.

Спасибо за урок.

Литература:

Виленкин Н. Я. Математика 6 класс: учебник для общеобразовательной школы. М.: «Мнемозина», 2014г.

Глейзер Г. И. История математики в школе М.: Просвещение, 1981г.

Ерина Т. М. Рабочая тетрадь Математика 6 класс Москва Экзамен 2013 год

Чесноков А. С., Нешков К. И. Дидактические материалы по математике 6 класс. Москва Классик Стиль 2013 год

Википедия. Свободная энциклопедия. Пропорция. https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE%D0%BF%D0%BE%D1%80%D1%86%D0%B8%D1%8F_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)

Яндекс картинки. https://yandex.ru/images/search?text=%D1%86%D0%B8%D1%86%D0%B5%D1%80%D0%BE%D0%BD

Конспект урока по математике «Пропорции» 6 класс

Урок ознакомления с новым материалом по математике в 6 классе. По учебнику Виленкина Н. Я. и др.

Тема урока: Пропорции

Цели: ввести понятие пропорции, ее членов; ознакомить с двумя способами проверки верной пропорции, развивать грамотную математическую речь; воспитывать умение внимательно выслушивать мнение других.

Оборудование: компьютер, проектор, карточки, рисунок треугольника.

Ход урока

  1. Организационный момент

  1. Актуализация опорных знаний учащихся

  1. Проверка домашнего задания

  2. Устный счет

  1. Найдите: 50% от 500, 205 от 300, 25% от 200,250% от 800.

  2. Найдите значений выражений: ; ; ; ; ; ; .

  3. Сколько треугольников на чертеже.

3. Сообщение темы урока

— Решите примеры и соответствующие буквы расставьте по возрастанию.

— Прочитайте слово. Правильно: пропорция. Сегодня мы познакомимся с пропорциями, узнаем, что они могут быть верными и неверными. Научимся составлять верные пропорции.

4. Изучение нового материала

А) Подготовительная работа.

— Придумайте отношение, равное 5.

Записать на доске все ответы и составить из них равенства:

200:100=8:4

45:9=50:10

=40:8

-Можно ли частное записать в виде дроби?

.

Определение. Равенство двух отношений называют пропорцией.

Б) Работа над новой темой.

Запишем пропорцию в буквенном виде: или a:b=c:d , где a

-Читают: отношение a к b равно отношению c к d.

-Или « a так относится к b , как с относится к d »

-Прочитайте по — разному пропорции, и запишите в тетрадях.

-Числа а и d называют крайними членами пропорции, а числа b и c средними членами пропорции.

— Назовите крайние и средние члены пропорций.

Рассмотрим первую пропорцию:

— Найдем произведение ее крайних и произведение ее средних членов.

— Сравните эти произведения.

— Что интересного заметили?

— Какой вывод можно сделать? (

Произведение крайних членов равно произведению средних членов. )

— В верной пропорции произведение крайних членов равно произведению средних членов.

— Сформулируйте обратное утверждение. (Если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна)

— Это свойство называется основным свойством пропорции.

— Запишите это свойство в буквенном виде:

Запись в тетради.

Крайние члены

средние члены

a и d – крайние члены

b и c – средние члены

a ≠ 0; c ≠ 0; b ≠ 0; c ≠ 0; d ≠ 0.

  1. Релаксация

Упражнение для глаз. Расслабьтесь. Закройте глаза. Представьте, что кончик носа – это ручка, которой можно писать. Теперь напишите свое имя, нарисуйте солнышко, облака, домик с дымом из трубы. Подумайте о чем — нибудь приятном. Откройте глаза.

  1. Закрепление изученного материала

№ 760 стр. 125

Решение:

А) 5 : 3 = 2 : 1,2; = ; =1 ; = = =1 ;

Б) 0,9 : = 45: 16 ; 0,9 : = = 2,7; 45 : 16 = = = 2,7

В) : 0,1 = 14 : 4,9 ; : 0, 1 = = = 2 ;

14: 4,9 = 14 * = =2

— Какой вывод можно сделать? (Отношения равны, значит пропорции составлены верно)

— Если отношения равны, то пропорция составлена верно.

— Если отношения не равны, то пропорция составлена неверно.

  1. Работа над задачей

№ 774 стр. 127 (На обратной стороне доски и в тетрадях.)

— Решить задачу двумя способами.

— Разобрать только с теми учащими, которые не понимают, как решить. Они решают только одним способом.

— Зная, что вместо 280 ц винограда фактически собрали 350 ц, что можно узнать? (Сколько винограда собрали сверх нормы.)

— Зная, сколько ц собрали сверх нормы и зная сколько собрали по плану, что можно узнать? (На сколько процентов бригада выполнила задание.)

Решение:

1 способ

  1. 350 – 280 = 70 (ц) – собрали сверх нормы

  2. 70 : 280 = = = 0, 25 = 25% — перевыполнила бригада.

2 способ

  1. = = 1,25 =125 % — выполнила бригада.

  2. 125 – 100 = 25 %

(Ответ: 25%)

8. Подведение итогов урока

— Что такое пропорция?

— Как называются числа k и r пропорции ?

— Как называют числа m и n в пропорции ?

— Какая пропорция называется верной?

— Верно ли обратное утверждение?

9.

Домашнее задание
№776, 778, 772 стр. 127.

Выставление оценок за урок.

4

п

о

ц

о

п

и

р

я

р

Конспект урока математики в 6 классе по теме: «Пропорции» | План-конспект урока по алгебре (6 класс) на тему:

Урок математики по теме: «Пропорции»

Класс: 6

Предмет: математика

Дидактическая цель урока: ввести определение пропорции;

организовать деятельность учащихся по выведению основного свойства пропорции;

 создать условия для формирования у учащихся умения применять основное свойство пропорции для нахождения неизвестного члена пропорции.

Тип урока: изучение нового материала.

Планируемые результаты:

Предметные: учащиеся учатся записывать пропорции, проверять полученные пропорции, определяя отношения чисел;

учатся записывать основное свойство пропорции и применять его для нахождения неизвестного члена пропорции.

Метапредметные: понимать и принимать учебную задачу, поставленную учителем на разных этапах обучения;

Осуществлять анализ своих действий и делать выводы;

Участие в диалоге, отражение в письменной форме своих решений;

Личностные: ответственное отношение к учению;

ясно, точно грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи на выполнение действий с отношениями чисел;

коммуникативная компетентность в общении и сотрудничестве со сверстниками в образовательной учебно–исследовательской и других видах деятельности;

уважительное отношение к другому мнению при ведении диалога.

Образовательная цель: создать условия для приобретения знаний по теме «Пропорция»;

 способствовать осознанию правила нахождения неизвестного члена пропорции через применения основного свойства пропорции.

Развивающая цель: способствовать формированию умений анализировать и систематизировать информацию.

Воспитательная цель: продолжать развитие теоретического мышления, математической речи, коммуникативных умений делового общения.

Методы обучения: исследовательский; частично-поисковый.

Средства обучения: математика 6 класс: учебник для общеобразовательных учреждений Н.Я. Виленкин; наглядный материал.

Формы организации познавательной деятельности: фронтальная, парная, групповая.

Оборудование: компьютер, проектор, интерактивная доска.

Структура урока:

  1. Организационный момент.
  2. Формулирование темы урока.
  1. Изучение нового материала.
  2. Применение знаний.
  3. Практическая работа.
  4. Физминутка.

7.   Самостоятельная работа.

     8.   Подведение итогов.

     9.  Домашнее задание.

Конспект урока


1. Организационный момент:

– Эпиграфом к нашему уроку станут следующие слова Льва Толстого:

«Человек подобен дроби: в знаменателе – то, что он о себе думает, в числителе – то, что он есть на самом деле. Чем больше знаменатель, тем меньше дробь».

Перед вами на столе лежат детали белого и зеленого цветов.

Пододвиньте к себе детали белого цвета и попробуйте собрать из них фигурку человечка.

Вам нравится эта фигурка? (нет) Почему? (она не пропорциональная.)

Теперь пододвиньте детали зеленого цвета и соберите из них фигурку. Что про нее можете сказать? (Она пропорциональная).

Само слово «пропорция» (от латинского proportio) означает «соразмерность», определенное соотношение частей между собой. Значит, в первом случае  не учтена пропорциональность размеров объектов и фигурка теряет привлекательность, красоту.
Учение о пропорциях особенно успешно развивалось в IV в до н. э. в Древней Греции, славившейся произведениями искусства, архитектуры, развитыми ремеслами. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке. Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета .Вот примеры.

2.Формулировка темы урока.

Давайте сформулируем тему урока.

Пропорции

1)Открываем тетради   записываем дату и тему урока.

Клоун решил найти отношение массы мышки к массе слона. Мышка весит – 30 г, слон – 5т. “Составляем отношение: 30/5, — сказал клоун. – Мышка в 6 раз тяжелее слона!”

 Публика смеялась: все видели, что клоун, что сделал ошибку. Какую?

 (Использовал разные единицы массы)

 Составьте правильное отношение и найдите, какую часть массы слона составляет масса мышки.

1т=1000кг         1кг=1000г             5т. =5000 000 г        =   

30: 5000 000 = 6:1000 000

Вывод. Что за выражение получилось? Что мы о нем можем сказать?

К этим вопросам мы вернёмся в конце урока.

3.Изучение нового материала.

1) Найдём числовые значения двух отношений:

30:3 и 10 :5?

6:3=2 и 10:5=2

Следовательно, можем записать равенство 6:3=10:5

Такое равенство называется пропорцией.

Значит, равенство двух отношений называется пропорцией.

2)  a: b=c :d

=

a,d -крайние члены пропорции

b,c-  средние члены пропорции

6:3=10:5

=    30:5000 000 =6 :1000 000

4.Применение знаний.

1)Какие из равенств являются пропорциями?

а) 2,5 : 0,5 = 45 : 9;
б) 2,5 : 0,5 = 3 + 2;
в) 0,5 * 12 = 24 : 4.

2)Назовите пропущенные числа.

а) 105 :  __ = 70 : 2    б) 15 : 3 =  __ : __

3) Прочитайте пропорцию:

а) 18 : 6 = 24 : 8
б) 30 : 5 = 42 : 7
в)36 : 9 = 50 : 10.

4) Назовите крайние и средние члены пропорции.

5) Верно ли составлены пропорции? Проверьте.

— Как проверить верно, ли составлена пропорция? (Вычисляют числовое значение каждого отношения, составляющего пропорцию. Если эти отношения равны, то пропорция составлена, верно; если не равны, то пропорция составлена неверно.)

— Оказывается можно проверить и по-другому. Можно проверить пропорцию с помощью основного свойства пропорции.

5.Практическая работа

1). Заполните таблицу. Игра-соревнование.  (Проверка заполнение на интерактивной доске).

Работа в группах.

Пропорция

a : b = c : d

18 : 6 = 24 : 8

0,5 : 0,3 = 5 : 3

1/50 : 0,04 = 1 : 2

Крайние члены

 

 

 

 

Средние члены

 

 

 

 

Произведение
крайних членов

 

 

 

 

Произведение

средних членов

 

 

 

 

— Что вы заметили? (Произведение крайних членов верной пропорции равно произведению средних членов пропорции. )

— Это свойство называют основным свойством пропорции. Для пропорции a : b = c : d оно записывается a * d = b * c.

Верно и обратное утверждение: “Если a * d = b * c, то a : b = c : d.”

-Чтобы убедиться в том, что пропорция составлена, верно, достаточно проверить, равны ли произведения крайних и средних членов. Если эти произведения равны, то пропорция составлена, верно.

2)Запись на доске учителем.

Примеры: 1) Пропорция 0,9 : 3,6 = 0,4 : 1,6 составлена верно, так как 0,9 x 1,6 = 1,44 и 0,4 x 3,6 = 1,44.

2) Пропорция 5,4 : 1,8 = 4 : 3 составлена неверно, так как 5,4 x 3 = 16,2; а 1,8 x 4 = 7,2.

3)Работа с учебником.

 (Учащиеся работают у доски с объяснением, начиная с первой парты, по очереди)

Выполнить № 760, № 762. 

4)Работа в парах:

Составить, если можно, пропорции из четырёх данных чисел:

а) 100; 80; 4; 5.
б) 5; 10; 9; 4,5.
в) 45; 15; 8; 75.

6.Физминутка. (Видео физминутка)

7. Самостоятельная работа.

В – 1      Тест по теме «Пропорция»

Выберите один верный ответ: 

1. Отношением двух чисел называют:
а) произведение этих чисел;

с) частное этих чисел.

2. В пропорции a:b=c:d  числа b и с называют

      ч) средними членами пропорции;

      п) крайними членами пропорции.

3. Верна ли пропорция 2,4:6=1,6:4

а) да

б) нет

4. Найдите произведение средних членов пропорции

 2,4 : 20 = 0,24 : 2.

т) 4,8    с)5,4   м)48

5. Из данных пропорций выберите верную:

а) 36: 2 = 64 : 3 ; б)15 : 8 = 13 : 6; ь) 17 : 2 = 34 : 4;

г) 22 : 5 = 81 : 4.

6. Найдите произведение крайних членов пропорции:

4,8:8= 1,2:2

т) 0,3   р)4      я)9,6

В – 2     Тест по теме «Пропорция»

Выберите один верный ответ: 

1. Отношение показывает:
в) во сколько раз первое число больше второго или какую часть первое составляет от второго;
т) на сколько первое число больше второго или какую часть второе составляет от первого.

2. В пропорции a:b=c:d  числа a и d называют

          д)средними членами пропорции;

          е) крайними членами пропорции.

3. Верна ли пропорция 2,5:5=1,5:2

а) да

з) нет

4 . Найдите произведение средних членов пропорции

 2,1 : 7 = 1,5 : 0,5.

н) 10,5  с)5,4   м)48

5. Из данных пропорций выберите верную:

а) 36: 2 = 64 : 3 ; б)15 : 8 = 13 : 6; ь) 17 : 2 = 34 : 4;

г) 22 : 5 = 81 : 4.

6. Найдите произведение крайних членов пропорции:

4,8:8= 1,2:2

т) 0,3   р)4      я)9,6

8. Итог урока.

1) Однажды учёные нашли в Индии древнюю рукопись. Их заинтересовала запись:

 

Впоследствии выяснилось, что индусы так записывали пропорцию.

Проверьте, верна ли эта пропорция?

2) Сформулируйте основное свойство пропорции.

=    30:5000 000 =6 :1000 000 ( Запись на доске.)

Что за выражение? Что можете о нем сказать? Каким правилам оно подчиняется?

– Что называется пропорцией?
– Основное свойство пропорции.
– Сколько верных пропорций можно составить из заданной?

— Оцените свою деятельность на лестнице знаний. 

9. Информация о домашнем задании и инструктаж по его выполнению.

п.21, № 776.Составить три пропорции из любой верной пропорции.

Сценарий открытого урока «Пропорции» (6 класс, Виленкин)

Образовательные: познакомить с понятием “пропорция”, научить использовать свойства пропорции для решения различных уравнений;

Развивающие: формировать умение пересказывать, выделять главное, задавать вопросы, оценивать;

Воспитательные: развивать умение работать в коллективе.

2. Актуализация знаний.

а) Давайте вспомним тот материал, который мы изучали на прошлом уроке.

— Что называется “отношением”? (Частное двух чисел называется “отношением”).

— Что показывает “отношение”? (Отношение показывает, во сколько раз первое число больше второго или какую часть первое число составляет от второго).

б) Учитель просит взять в руки листы с заданиями.

в) Устный счет.

Задачи, приводящие к равенству двух отношений, возникли примерно в VI веке до н.э. в эпоху Пифагора. Как же греки называли равенство двух отношений?

Для того чтобы ответить на этот вопрос, выполните вычисления и зачеркните в таблице буквы, соответствующие найденному ответу. Из оставшихся букв получится искомое слово (слайд 2 презентации).

Вычислить:

1. ;

2. ;

3. ;

4. ;

5. 

6. ;

7. ;

8. .

В результате должно получиться слово АНАЛОГИЯ.

Словом АНАЛОГИЯ греки называли равенство двух отношений.

3. Объяснение нового материала.

Равенство двух отношений в более поздние времена стали называть пропорцией

Это тема нашего урока «Пропорция», сегодня мы узнаем, что называется пропорцией и какими свойствами она обладает.

Латинское слово “пропорция”, для обозначения равенства двух отношений стали использовать, начиная с I века нашей эры.

Итак, равенство двух отношений называют пропорцией.

С помощью букв пропорцию можно записать так:

a : b = c : d

Эти записи читают следующим образом:

  • “Отношение a к b равно отношению с к d”;

  • “a так относится к b, как с относится к d”.

Числа a и d называют крайними членами пропорции, а числа b и с – средними.

Рисунок на слайде учащиеся переносят в тетрадь.

б) Прочитайте пропорцию и назовите крайние и средние члены ее члены.

28:7=16:4

32:8=24:6

.

в) Давайте выясним, каким свойством обладает пропорция №2.

Крайние члены

Средние члены

Произведение крайних членов

Произведение средних членов

Что мы обнаружили? Сделайте вывод.

Учащиеся с помощью учителя делают вывод: в верной пропорции произведение крайних членов равно произведению средних.

Верно и обратное утверждение: если произведение крайних членов равно произведению средних, то пропорция верна.

Это основное свойство пропорции.

г) Прочитайте пропорции и проверьте, верные ли они, используя основное свойство пропорции:

2:9=4:8

5:15=4:12

 (три ученика работают на доске по очереди, остальные в тетрадях).

д) Поменяйте местами средние члены пропорции (слайд 7 презентации).

Вы получите новую пропорцию. Проверьте, верная ли пропорция получилась?

20:16=5:4

(ученик работает на доске, остальные в тетрадях).

е) Теперь поменяйте местами крайние члены пропорции (слайд 8 презентации). Также проверьте, получили ли вы верную пропорцию. Какой вывод можно сделать?

20:16=5:4

(ученик работает на доске, остальные в тетрадях).

Учащиеся с помощью учителя делают вывод (слайд 9 презентации): если в верной пропорции поменять местами средние члены или крайние члены, то получившиеся новые пропорции тоже верны.

№ 762 (а-г) (если успеем)

5. Итог урока. №3

Для того, чтобы проверить достигли ли мы поставленной цели и все ли вы уяснили, я предлагаю решить кроссворд, и вы узнаете, что означает слово «пропорция». Для этого впишите по горизонтали ответы на вопросы. Прочтите слово в выделенном столбце.

  1. Частное двух чисел.

  2. Равенство двух отношений.

  3. В пропорции а : b = с : d члены a и d
    называются …

  4. В пропорции а : b = с : d члены b и с
    называются …

  5. Пропорция 5 : 2 = 10 : 4 является …

  6. В верной пропорции произведение
    крайних членов равно произведению
    средних членов. Это правило называют…
    свойство пропорции.

Ответ: СОРАЗМЕРНЫЙ

ВЫВОД:

1. Что называется пропорцией?

2. Как проверить, верна ли пропорция или нет?

3. Основное свойство пропорции?

4. Какие члены пропорции можно менять местами, чтобы также получить верную пропорцию?

Выполните № 4 на рабочих листах

Домашнее задание

Математика 6 Виленкин Контрольная 5 + ОТВЕТЫ

Контрольная работа по математике 6 класс Виленкин с ответами «Отношения. Пропорции.
Масштаб» (4 варианта). Цитаты из пособия «Дидактические материалы по математике 6 класс к учебнику Н.Я. Виленкина и др. «Математика 6 класс» ФГОС (к новому учебнику) / М.А. Попов — М.: Издательство «Экзамен», 2017» использованы в учебных целях. Математика 6 Виленкин Контрольная 5. Проверочные работы ориентированы на школьный учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд «Математика 6 класс». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.

Математика 6 класс (Виленкин)


Контрольная работа № 5

Отношения. Пропорции. Прямая и обратная пропорциональные зависимости.
Масштаб. Длина окружности и площадь круга

КР-05. Вариант 3 (транскрипт)

1. Найдите длину окружности радиуса 6 см. Число п округлите до сотых.
2. Решите уравнение: х/2,2 = 5/7.
3. Найдите площадь круга с диаметром 4 см. Число π округлите до десятых.
4. Во сколько раз увеличится t из формулы S = vt, если S увеличить в 3 раза, a v уменьшить в 2 раза?
5. Отрезку на карте длиной в 5 см соответствует расстояние на местности в 100 км. Какой масштаб у карты?
6. Выпишите все решения неравенства 1135 < х < 1215, кратные 43.

КР-05. Вариант 4 (транскрипт)

1. Найдите длину окружности радиуса 8 см. Число к округлите до сотых.
2. Решите уравнение: 3/x = 7/18.
3. Найдите площадь круга с диаметром 10 см. Число π округлите до десятых.
4. Во сколько раз уменьшится S из формулы S = vt, если v увеличить в 5 раз, a t уменьшить в 10 раз?
5. Отрезку на карте длиной в 3 см соответствует расстояние на местности 300 км. Какой масштаб у карты?

6. Выпишите все решения неравенства 577< х < 700, кратные 47.

 

ОТВЕТЫ на контрольную работу

ВАРИАНТ 1.       1. 18,84 см.      2. 7/9.      3. 151,9 см2.      4. в 1,5 раза.      5. 1 : 1 000 000.      6. 1147, 1184, 1221.

ВАРИАНТ 2.        1. 31,4 см.    2. 3,36.    3. 49,6 см2.    4. в 6 раз.    5. 1 : 500 000.    6. 1025, 1066.

ВАРИАНТ 3.       1. 37,68 см.    2. 11/7 = 14/7.    3.12,4см2.    4. в 6 раз.     5. 1 : 2 000 000.     6. 1161, 1204.

ВАРИАНТ 4.       1. 50,24 см.

    2. 54/7 = 75/7.    3. 77,5 см2.    4. в 2 раза.    5. 1 : 10 000 000.    6. 611, 658.

 

Вы смотрели: Контрольная работа по математике 6 класс Виленкин «Отношения. Пропорции.
Масштаб» с ответами (4 варианта). Цитаты из пособия «Дидактические материалы по математике 6 класс к учебнику Н.Я. Виленкина и др. «Математика 6 класс» (к новому учебнику) / М.А. Попов — М.: Издательство «Экзамен», 2017» использованы в учебных целях. Математика 6 Виленкин Контрольная 5. Проверочные работы ориентированы на школьный учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд «Математика 6 класс».

Вернуться к Списку контрольных работ по математике в 6 классе по УМК Виленкин и др.

 

Пропорции тест (6 класс) по математике онлайн

Сложность: новичок.Последний раз тест пройден 1 час назад.

Материал подготовлен совместно с учителем высшей категории

Опыт работы учителем математики — более 33 лет.

  1. Вопрос 1 из 10

    Верно ли утверждение 3 : 3,6 = 5 : 6?

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 86% ответили правильно
    • 86% ответили правильно на этот вопрос

    В вопросе ошибка?

    Следующий вопросОтветить

  2. Вопрос 2 из 10

    Найдите произведение средних членов пропорции 3 : 5 = 15 : 25

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 84% ответили правильно
    • 84% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  3. Вопрос 3 из 10

    Решите уравнение 6,4 : 0,16 = 4 : у

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 67% ответили правильно
    • 67% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  4. Вопрос 4 из 10

    Какая из данных пропорций неверна?

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 76% ответили правильно
    • 76% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  5. Вопрос 5 из 10

    Решите пропорцию 42 : (4 * х) = 21 : 4

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 83% ответили правильно
    • 83% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  6. Вопрос 6 из 10

    Найдите произведение крайних членов пропорции 2 : 7 = 12 : 42

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 79% ответили правильно
    • 79% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  7. Вопрос 7 из 10

    Решите уравнение 0,75 : 1,5 = 5 : х

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 62% ответили правильно
    • 62% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  8. Вопрос 8 из 10

    Верно ли утверждение 4 : 0,2 = 280 : 13?

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 73% ответили правильно
    • 73% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  9. Вопрос 9 из 10

    Деревянный брусок объемом 4 куб. см весит 36 г. Сколько грамм весит брусок объемом 5 куб. см?

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 81% ответили правильно
    • 81% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  10. Вопрос 10 из 10

    Запишите пропорцию: 5 так относится к 7 как 25 к 35:

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 74% ответили правильно
    • 74% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

Доска почёта

Чтобы попасть сюда — пройдите тест.

    

  • Ярослав Степанов

    10/10

  • Максим Струков

    9/10

  • Артём Переладов

    9/10

  • Стёпа Лаврентьев

    4/10

  • Саша Кнутович

    9/10

  • Валера Рощин

    10/10

  • Елена-Алексеевна Чернолых

    8/10

  • Vlad Mnatsakanov

    9/10

  • София Никитан

    10/10

  • Егор Высоцкий

    10/10

ТОП-2 тестакоторые проходят вместе с этим

Тест «Пропорции» (6 класс) рассчитан на учеников средних классов, которые хотят оценить или закрепить свои знания по теме. Вопросы проверяю теорию, а также умение решать пропорции. Задания теста проверяют все необходимые аспекты раздела, поэтому являются прекрасным помощников для экспресс-подготовки к контрольной работе. Задания удобно просматривать в онлайн режиме с любого доступного устройства.

Тест по математике «Пропорции» – это один из самых эффективных методов самооценивания и самоподготовки к занятиям.

Рейтинг теста

Средняя оценка: 3.8. Всего получено оценок: 1146.

А какую оценку получите вы? Чтобы узнать — пройдите тест.

Контрольная работа «Отношения. Пропорции. Прямая и обратная пропорциональная зависимость» 6 класс

Контрольная работа

Отношения. Пропорции. Прямая и обратная пропорциональная зависимость.

6 класс. Виленкин Н.Я.

Вариант 1

1. Найдите отношение 1,2 км к 10 м.

2. Проверьте, верна ли пропорция или нет:

А)7:2,1=2:0,6 В)



3.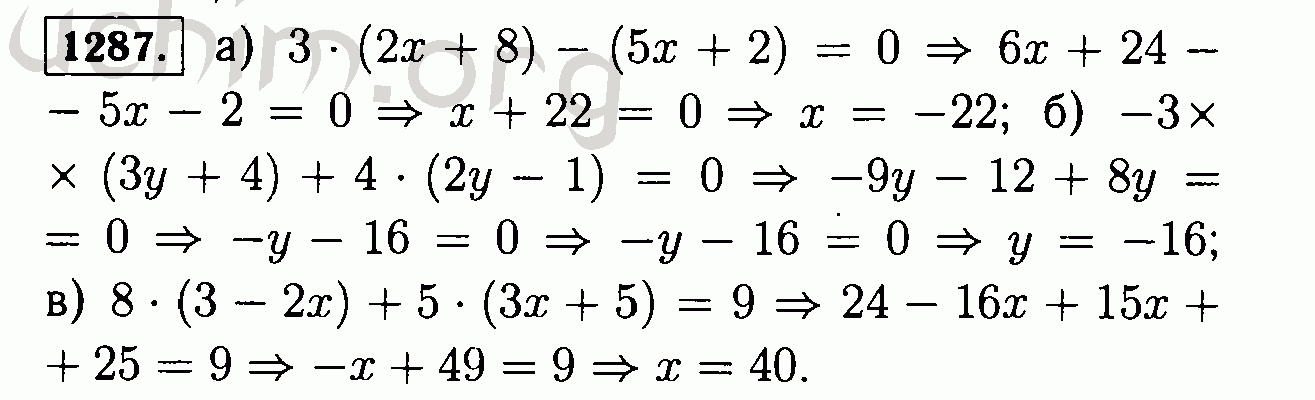 Найдите неизвестный член пропорции:



 

;



 





4. За 2 ч пешеход прошел

всего пути . За какое время он пройдет

всего пути?

5. Средняя скорость самолета 500 км/ч, а машины 80км/ч.

Сколько времени потребуется машине, чтобы проехать путь, на который самолет

потратит 4 часа?

Вариант 2

1. Найдите отношение 573 мм к 10 см.

2. Проверьте, верна ли пропорция или нет:

А)

 

  



=







3. Найдите неизвестный член пропорции:





 





 







4. За 3 ч вагон разгружают на

его объема. За какое время вагон разгрузят на



?

5. Дорога до дачи на автомашине занимает 2ч. при скорости 75 км/ч. Сколько

потребуется времени, чтобы добраться до дачи на велосипеде со скоростью 15

км/ч.

Вариант 3

1. Найдите отношение 2,8 км к 100 м.

2. Проверьте, верна ли пропорция или нет:

А)2,1:3,15=2:3 В)





3. Найдите неизвестный член пропорции:



 

;



 





4. За 3 ч пешеход прошел

всего пути . За какое время он пройдет

всего пути?

5. Средняя скорость скорого поезда 110 км/ч, а скорость сапсана 200км/ч.

Сколько времени потребуется скорому поезду, чтобы проехать путь, на который

сапсан преодолевает за 3 часа?

Вариант 4

1. Найдите отношение 64,3 дм к 10 см.

2. Проверьте, верна ли пропорция или нет:

А)

 

  



=







3. Найдите неизвестный член пропорции:





 





 







4. За 4 ч вагон загружают на

его объема. За какое время вагон загрузят на





?

5. Дорога до дачи на автомашине занимает 2ч. при скорости 85 км/ч. Сколько

потребуется времени, чтобы добраться до дачи на автобусе со скоростью 55 км/ч.

Deoma — Продукты — Алгебра

Электронный учебник «Интерактивная математика» для 6 класса предназначен для использования возможности компьютера в обучении математике в 6 классе. Ты можешь выбрать конфигурация электронного учебника, соответствующая печатной учебник, который прилагает учитель. Адаптация электронного учебника предусмотрены печатные книги авторов: Виленкина, Зубарева и Мордковича, Шарыгин.Электронное приложение включает интерактивные разработки для обучение основам математики, в частности, таким темам как: целые числа и отрицательные целые числа, делимость, пропорции, десятичные дроби, основы выражений упрощение, координатная линия, координатная плоскость, понятие математической модель; используются математические игры.

Последняя версия продукта от 12 августа 2015 г .:

Скачать «Интерактивная математика» 6 класс v1.4.3.21 для Windows

Снимки экрана программы перечислены ниже.

Вы можете увеличивать рисунки ↓

Версия 1.4.3.21 от 12 августа 2015 (последняя)

Показать предыдущие версии

Версия 1.4.3.20 от 11 августа 2015 г.

Версия 1.4.3.19 от 11 августа 2015 г.

Версия 1. 4.3.18 от 17 ноября 2012 г.

Версия 1.4.3.17 от 9 октября 2011 г.

Версия 1.4.3.16 от 28 июня 2011 г.

Версия 1.4.3.15 от 6 мая 2011

Версия 1.4.3.14 от 18 апреля 2011

Версия 1.4.3.12 от 23 января 2011

Версия 1.4.3.11 от 4 января 2011

Версия 1.4.3.10 от 4 ноября 2010 г.

Версия 1.4.3.9 от 4 ноября 2010 г.

Версия 1.4.3.8 от 5 сентября 2010 г.

Версия 1.4.3.7 от 5 сентября 2010

Версия 1.4.3.6 от 24 августа 2010

Версия 1.4.3.5 от 16 августа 2010

Версия 1.4.3.4 от 13 июня 2010

Версия 1.4.3.3 от 10 мая 2010 г.

Версия 1.4.3.2 от 10 мая 2010 г.

Версия 1.4.3.0 от 23 марта 2010 г.

Версия 1.4.2.0 от 17 марта 2010

Версия 1.4.1.0 от 1 марта 2010 г.

Версия 1.4.0.0 от 20 февраля 2010 г.

Версия 1.3.15.0 от 10 февраля 2010 г.

Версия 1.3.14 от 4 февраля 2010 г.

Версия 1.3.13 от 10 января 2010 г.

Версия 1.3.12 от 5 января 2010 г.

Версия 1.3.11 от 25 декабря 2009 г.

Версия 1.3.10 от 24 декабря 2009 г.

Версия 1.3.9 от 15 декабря 2009 г.

Версия 1.3.8 от 14 декабря 2009 г.

Версия 1.3,6 от 11 октября 2009 г.

Версия 1.3.5 от 9 октября 2009 г.

Версия 1.3.4 от 2 октября 2009 г.

Версия 1.3.3 от 27 сентября 2009 г.

Версия 1.3.2 от 20 сентября 2009 г.

Версия 1. 3.1 от 13 сентября 2009 г.

Версия 1.3.0 от 25 августа 2009 г.

Версия 1.0,2 из 12 апреля 2009 г.

Версия 1.0.1 из 16 марта 2009 г.

Скрыть предыдущие версии

Алгебры Клиффорда и их приложения в математической физике

Об этой книге

Введение

Уильям Кингдон Клиффорд опубликовал статью с определением его «геометрических алгебр» в 1878 году, за год до своей смерти.Алгебра Клиффорда является обобщением n-мерного пространства кватернионов, которое Гамильтон использовал для представления скаляров и векторов в реальном трехмерном пространстве: это также развитие алгебры Грассмана, включающее в фундаментальные отношения скалярные произведения, определенные в терминах метрики космос. Странно, что векторные методы Гиббса Хевисайда стали доминировать в научной и технической литературе, в то время как кватернионы и алгебры Клиффорда, истинные ассоциативные алгебры пространств со скалярными произведениями, почти столетие рассматривались просто как интересные математические курьезы. В этот период Паули, Дирак и Майорана использовали алгебры, носящие их имена, для описания свойств элементарных частиц, в частности их спина. Кажется вероятным, что ни один из этих выдающихся физиков-математиков не осознавал, что они использовали алгебры Клиффорда. Некоторые исследователи, такие как Фютер, осознали всю мощь этой алгебраической схемы, но этот предмет стал цениться более широко только после публикации книги Шевалле «Алгебраическая теория спиноров» в 1954 году и лекций Марселя Рисса в Мэриленде в 1954 году. 1959 г.Некоторые из авторов этого тома, Жорж Дешам, Эрик Фольке Болиндер, Альберт Крумейролле и Дэвид Хестенес, работали в этой области примерно в то время и, в свою очередь, убедили других в важности предмета.

Ключевые слова

алгебра исчисление дифференциальное уравнение калибровочная теория математическая физика минимум

Редакторы и сотрудники

    w3.org/1999/xhtml»>
  • Дж.С. Р. Чизхолм
  • А. К. Коммон
  1. 1. Математический институт Кентского университета Кентербери, КентUK

Библиографическая информация

  • Заголовок книги Алгебры Клиффорда и их приложения в математической физике
  • Редакторы Дж.S.R. Чисхолм
    А.К. Обычный
  • Название серии Серия НАТО ASI
  • DOI https://doi. org/10.1007/978-94-009-4728-3
  • Информация об авторских правах Springer Science + Business Media B.V.1986 г.
  • Имя издателя Спрингер, Дордрехт
  • электронные книги Архив книг Springer
  • ISBN в твердом переплете 978-90-277-2308-6
  • ISBN в мягкой обложке 978-94-010-8602-8
  • электронная книга ISBN 978-94-009-4728-3
  • Серия ISSN 1389-2185
  • Номер издания 1
  • Количество страниц XX, 592
  • Количество иллюстраций 0 ч / б иллюстраций, 0 иллюстраций в цвете
  • Темы Анализ
    Алгебра
  • Купить эту книгу на сайте издателя
Обзор

: [Без названия] на JSTOR

Информация о журнале

Ежемесячный журнал публикует статьи, а также заметки и другие материалы о математике и профессии. Его читатели охватывают широкий спектр математических интересов и включают профессиональных математиков, а также студентов-математиков на всех университетских уровнях. Авторам предлагается присылать статьи и заметки, которые знакомят с интересными математическими идеями широкую аудиторию читателей Monthly. Читатели The Monthly ожидают высокого уровня изложения; они ожидают, что статьи будут информировать, стимулировать, бросать вызов, просвещать и даже развлекать. Ежемесячные статьи предназначены для чтения, просмотра и обсуждения, а не для архивирования.Статьи могут быть изложением старых или новых результатов, историческими или биографическими эссе, размышлениями или окончательными трактовками, обширными разработками или исследованиями одного приложения. Новизна и общность гораздо менее важны, чем ясность изложения и широкая привлекательность. Приветствуются соответствующие рисунки, схемы и фотографии. Примечания короткие, четкие и, возможно, неформальные. Часто они представляют собой жемчужины, обеспечивающие новое доказательство старой теоремы, новое изложение знакомой темы или живое обсуждение одного вопроса.

Информация об издателе

Основываясь на двухвековом опыте, Taylor & Francis за последние два десятилетия быстро выросла и стала ведущим международным академическим издателем. Группа издает более 800 журналов и более 1800 новых книг каждый год, охватывая широкий спектр предметных областей и включая отпечатки журналов Routledge, Carfax, Spon Press, Psychology Press, Martin Dunitz, Taylor & Francis. Taylor & Francis полностью привержены публикации и распространению научной информации высочайшего качества, и сегодня это остается основной целью.

Примечание: Эта статья представляет собой обзор другой работы, такой как книга, фильм, музыкальная композиция и т. Д. Оригинальная работа не включена в покупку этого обзора.

Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей (Технический отчет)

Холм Д. Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей .США: Н. П., 1976. Интернет. DOI: 10,2172 / 7348957.

Холм Д. Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей . Соединенные Штаты. https://doi.org/10.2172/7348957

Holm, D D. Thu. «Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей».Соединенные Штаты. https://doi.org/10.2172/7348957. https://www.osti.gov/servlets/purl/7348957.

@article {osti_7348957,
title = {Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей},
author = {Holm, D D},
abstractNote = {Физика жидкостей основана на определенных принципах кинематической инвариантности, которые относятся к системам координат, размерам и системе отсчета Галилея. Другие, термодинамические, принципы симметрии вводятся в описании материала. В настоящей работе взаимодействие между этими двумя видами принципов инвариантности используется для решения классов одномерных нестационарных изэнтропических движений жидкости, уравнение состояния которой относится к типу Ми-Грюнайзена. Также на уровне приближения Бюргерса изучается изменение профиля и затухание слабых ударных волн в диссипативной среде с точки зрения лежащей в основе структуры симметрии.Математический метод подхода основан на теории бесконечно малых групп Ли. Движения жидкости охарактеризованы в соответствии с неэквивалентными подгруппами группы полной инвариантности описания течения и представлены точные групповые приводимые решения.},
doi = {10.2172 / 7348957},
url = {https://www.osti.gov/biblio/7348957}, journal = {},
number =,
объем =,
place = {United States},
год = {1976},
месяц = ​​{7}
}

Квантовая гравитация — обзор

Петли

Основными причинами интереса к петлевой квантовой гравитации являются: ее физические допущения — это только КМ и ОТО, а именно хорошо проверенные теории; тот факт, что теория не зависит от фона; и что это хорошо разработанная попытка включить общие релятивистские представления о пространстве и времени в КТП.Теория не претендует на то, чтобы быть окончательной «Теорией всего». Он конечен в ультрафиолете, не требуя высокоэнергетических модификаций ОТО, суперсимметрии, дополнительных измерений или другой ненаблюдаемой физики.

Петлевая квантовая гравитация была представлена ​​в 1988 году. Теория является результатом слияния двух направлений исследований, которые, как оказалось, решают трудности друг друга [Rovelli and Smolin, 1988; Ровелли, Смолин, 1990].

Первой из них была теория Уиллера-деВитта. Как и в подходе Уиллера-деВитта, петлевая квантовая гравитация представляет собой прямое квантование ОТО с его обычными связями материи и не основывается ни на каких конкретных физических предположениях, кроме ОТО и КМ.Следуя основным правилам КМ, квантовые состояния петлевой квантовой гравитации получаются из представления алгебры полевых переменных ОТО; их физическая интерпретация получается путем диагонализации самосопряженных операторов, представляющих физические величины. Отличие от старой теории Уиллера-ДеВитта состоит в выборе алгебры петлевых переменных в качестве основных переменных для квантования. Благодаря этому плохо определенная теория Уиллера-ДеВитта становится четко определенным формализмом, в котором могут быть вычислены конечные физические величины.

Вторым входом была идея о том, что калибровочные теории естественным образом описываются в терминах петлевых возбуждений. Эта идея восходит к самому началу теории поля, интуиции Фарадея. Фарадей понимал электрические и магнитные явления в терминах линий, «линий Фарадея», заполняющих пространство. При наличии зарядов линии Фарадея могут начинаться и заканчиваться на зарядах; при отсутствии зарядов они замыкаются, образуя «петли». Максвелл перевел интуицию Фарадея в математическую физику, представив электрическое и магнитное поля, которые являются векторными полями, повсюду касательными к линиям Фарадея, тем самым открыв путь к современной физике, которая полностью основана на понятии поля.Идею о том, что калибровочные теории поля лучше понимать в терминах петель, отстаивали многие ученые, включая Полякова, Мандельштама, Вильсона и других. Квантовое возбуждение одиночной линии Фарадея называется «петлевым состоянием».

Формулировка QFT в терминах состояний петель жизнеспособна и хорошо понимается в контексте приближения решетки; но он сталкивается с трудностями при определении на континуальном пространственно-временном фоне. Однако эти трудности исчезают в независимом от фона контексте.Причина в том, что при наличии фона состояния петли локализованы в фоновом пространстве-времени: для каждой позиции петли в пространстве существует свое состояние. В случае с гравитацией, напротив, отсутствует фоновое пространство-время. Сами петлевые состояния являются квантовыми возбуждениями пространства. Следовательно, состояния петель не погружены в пространство: они сами «плетут» физическое пространство, точно так же, как ансамбль нитей может плести ткань футболки.

Точнее, состояния цикла QG имеют точки самопересечения, называемые «узлами».Узел представляет собой элементарное квантовое возбуждение пространства или отдельный атом пространства. Два узла, непосредственно соединенные петлей, представляют собой соседние атомы пространства. Узлы и связи, соединяющие узлы, образуют граф и несут квантовые числа. Эти квантовые числа определяют квантованный объем атомов пространства и квантованную площадь элементарных поверхностей, разделяющих соседние узлы. Граф с этими квантовыми числами называется «спин-сетью», потому что квантовые числа на связях оказываются полуцелыми числами или спинами.

Состояние спиновой сети не имеет позиции. Важны только комбинаторные отношения, определяющие граф, а не его форма или положение в пространстве. Фактически, состояние спиновой сети — это не в пространстве : это — это пространство. Следовательно, несмотря на свои консервативные базовые предположения (КМ и ОТО), петлевая квантовая гравитация приводит к радикально новой картине пространства.

Возможные значения, которые может принимать объем физической области или площадь физической поверхности, определяются спектрами соответствующих операторов в соответствии со стандартными правилами QM.Они оказываются дискретными, давая гранулярную структуру пространства планковского масштаба. Эти спектры были вычислены и представляют собой количественные физические предсказания петлевой квантовой гравитации: прогнозируется, что точное измерение любой площади или объема в масштабе Планка даст в результате только значения в этих спектрах. Например, (основная последовательность) спектр области определяется выражением [Rovelli and Smolin, 1995]

(9) A = 8πγℏG∑iji (ji + 1),

, где j i представляет собой набор полуцелых чисел n (соответствующий квантовым числам звеньев состояния спиновой сети, пересекающих поверхность, площадь которой измеряется).γ — параметр Иммирци, упомянутый в разделе 2.1.

Динамика определяется уравнением Уиллера-деВитта на пространстве состояний спиновой сети. Его ультрафиолетовая конечность — следствие зернистой структуры пространства. Построены различные конечные и четко определенные версии этого уравнения. В настоящее время еще не ясно, какой из них является физически правильным, если таковой имеется.

Приложения теории включают вывод энтропии черной дыры Бекенштейна, упомянутый в разделе 2.1, приложения к описанию классических сингулярностей, таких как особенности в центре блоковых дыр, и приложения к космологии. Теория, похоже, способна контролировать сингулярности черных дыр и начальную сингулярность Большого взрыва. Косвенные эмпирические доказательства, подтверждающие предсказания теории, активно исследуются в астрофизической и космологической областях.

Основные трудности петлевой квантовой гравитации заключаются в восстановлении феноменологии низких энергий. Квантовые состояния, соответствующие вакууму Минковского и его возбуждению, еще не построены, а амплитуды рассеяния частиц не вычислены.Этот недостаток ослабляет силу утверждения о конечности и отвечает одному из ключевых требований квантовой теории гравитации: полное восстановление физики низких энергий. Динамика все еще плохо изучена: уравнение Уиллера-деВитта существует более чем в одной версии.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *