Найдите площадь боковой поверхности прямоугольного параллелепипеда: Площадь поверхности прямоугольного параллелепипеда – формула (5 класс, математика)

Площадь поверхности и объём призмы — урок. Геометрия, 11 класс.

Площадь боковой поверхности прямой призмы Sбок.=Pосн.⋅H,

где \(H\) — высота призмы.

 

Площадь полной поверхности призмы — сумма площадей всех граней призмы.

Она состоит из площади боковой поверхности и площади оснований

Sполн.=Sбок.+2⋅Sосн.

 

Все грани куба — квадраты, поэтому рациональнее использовать формулу

Sполн. пов. куба=6⋅a2.

  

Объём прямой призмы находится по формуле:

V=Sосн.⋅H.

 

Для прямоугольного параллелепипеда можно использовать формулу \(V = abc\) , где \(a\), \(b\), \(c\) — измерения прямоугольного параллелепипеда (длина, ширина, высота).

 

Для куба используется формула V=a3, где \(a\) — ребро куба.

 

Основанием призмы может быть любой \(n\)-угольник, поэтому важно знать формулы вычисления их площадей.

 

Важные формулы нахождения площади \(n\)-угольников

  

Квадрат	a2
Прямоугольник	a⋅b
Ромб	a⋅b⋅sinα	a⋅h	d1⋅d22
Параллелограмм	a⋅b⋅sinα	a⋅h
Равносторонний треугольник	a234
Прямоугольный треугольник	a⋅b2	a⋅h3
Произвольный треугольник	a⋅b⋅sinα2	a⋅h3	p⋅p−ap−bp−c
Трапеция	a+b2⋅h

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

 

 

  

  

  

Формула нахождения площади правильного шестиугольника

 

Рис. \(1\). Правильный шестиугольник

Правильный шестиугольник состоит из \(6\) правильных треугольников.   Sправ. ш.=6⋅a234, где \(a\) — сторона шестиугольника

Источники:

Рис. 1. Правильный шестиугольник, © ЯКласс. 

Подготовка к ЕГЭ. Геометрические задачи.

ЗАДАНИЕ 16 Вариант 1

1.Стороны основания правильной четырёхугольной пирамиды равны 14, боковые рёбра равны 25. Найдите площадь поверхности этой пирамиды.

 

2. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 8 и 9. Диагональ параллелепипеда равна 17. Найдите объём параллелепипеда.

3. Два ребра прямоугольного параллелепипеда равны 7 и 4, а объём параллелепипеда равен 140. Найдите площадь поверхности этого параллелепипеда.

4. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4 и 8. Диагональ параллелепипеда равна 12. Найдите объём параллелепипеда.

6. Стороны основания правильной четырёхугольной пирамиды равны 30, боковые рёбра равны 25. Найдите площадь поверхности этой пирамиды. 
7. Стороны основания правильной шестиугольной пирамиды равны 14, боковые рёбра равны 25. Найдите площадь боковой поверхности этой пирамиды.

8. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 7 и 5. Объём параллелепипеда равен 210. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

 

ЗАДАНИЕ 16 Вариант 2

1.

Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17.

2. Стороны основания правильной шестиугольной пирамиды равна 14, боковые ребра 25. Найдите площадь боковой поверхности этой пирамиды.

3. Вычислите площадь полной поверхности прямоугольного параллелепипеда, диагональ которого равна 25 см, а диагонали боковых граней равны 15 см и 4√34 см.

4. Высота основания правильной треугольной пирамиды равно 9 а высота боковой грани пирамиды проведенная к ребру основания равна корень из 73. Найдите боковое ребро пирамиды

5. Стороны основания правильной шестиугольной пирамиды равны 24, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.

6. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что ВВ1 = 16, А1В1 = 2, A1D1 = 8. Найдите длину диагонали AC1

7.  В правильной треугольной пирамиде SABC медианы основания АВС пересекаются в точке О. Площадь треугольника АВС равна 2; объём пирамиды равен 4. Найдите длину отрезка OS.

8. Стороны основания правильной четырехугольной пирамиды равны 14, боковые ребра равны 25. Найдите площадь поверхности этой пирамиды.
9.. В правильной треугольной пирамиде SABC точка K – середина ребра BC, S – вершина. Известно, что AB = 6, а длина отрезка SK = 7. Найдите площадь боковой поверхности пирамиды.

 

 

 

ЗАДАНИЕ 16

Вариант 3

1. В прямоугольном параллелепипеде АВСDA1B1C1D1 AB=5, AD=√3, CC1=2√2. Найдите длину диагонали параллелепипеда АС1.

2. Конус вписан в шар. Объём шара равен 14. Найдите объём конуса, если известно, что радиус основания конуса равен радиусу шара.

3. В основании пирамиды SABC лежит правильный треугольник АВС со стороной 2, а боковое ребро SA перпендикулярно основанию и равно 5√3. Найдите объём пирамиды SABC.

 

 

 

 

4. Сторона основания правильной треугольной призмы АВСА1В1С1 равна 5, а высота этой призмы равна √3. Найдите объем призмы АВСА1В1С1.

 

 

 

 

 

5. Даны два шара с радиусами 6 и 3. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего?

 

 

 

 

 

6. Даны два шара с радиусами 6 и 1. Во сколько раз объём большего шара больше объёма меньшего?

 

7. Даны два конуса. Радиус основания и образующая первого конуса равны, соответственно, 6 и 8, а второго — 4 и 8. Во сколько раз площадь боковой поверхности первого конуса больше площади боковой поверхности второго?

 

 

8. Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17.

 

 

 

 

9. Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.

 

 

 

10. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13.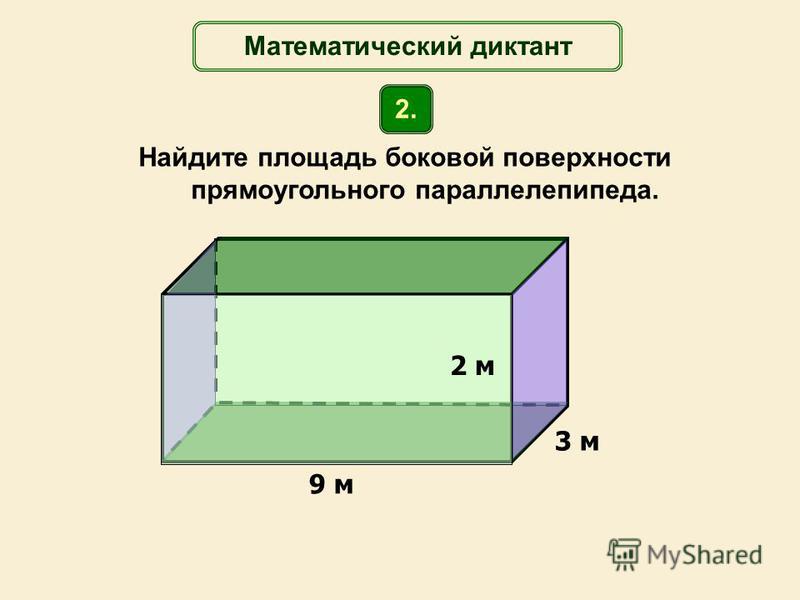 Найдите площадь боковой поверхности пирамиды.

 

 

 

 

 

11. Площадь основания конуса равна 16π, высота — 12. Найдите площадь осевого сечения конуса.

12. В кубе ABCDA1B1C1D1 точки Е, F, Е1 и F1 являются серединами рёбер ВС, DC, В1С1 и D1C1 соответственно. Объём треугольной призмы, отсекаемой от куба плоскостью EFF1, равен 29. Найдите объём куба.

13. В основании прямой призмы лежит правильный треугольник со стороной, равной 6. Высота ее равна √3/24. Найти объем призмы.

14. В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 4, а гипотенуза равна 4·√2. Найдите объём призмы, если её высота равна 3.

 

 

 

 

15. В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра АB, AD и диагональ AB1равны соответственно 6, 2 и √45. Найдите объём параллелепипеда ABCDA1B1C1D1.

 

Найдите объем параллелепипеда ABCDA 1 B 1 C

Описание презентации Найдите объем параллелепипеда ABCDA 1 B 1 C по слайдам

Найдите объем параллелепипеда ABCDA 1 B 1 C 1 D 1 , если объем треугольной пирамиды ABDA 1 равен 3. №№ 11 Ответ: 1 8. h. SVABCDдапар h. SVABDABDA 3 1 1 ABCDABDSS 2 1 1 способ дапар. ABCDABDAVh. SV 6 1 2 1 3 1 1 183666 1 ABDAABDдапар. Vh. SV С 1 В 1 А С ВDА

Найдите объем параллелепипеда ABCDA 1 B 1 C 1 D 1 , если объем треугольной пирамиды ABDA 1 равен 3. №№ 11 Ответ: 1 8. С 1 В 1 А С ВDА 1 D 1 2 способ

Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.

№№ 22 Ответ: 1, 5. С 1 В 1 А С ВDА 1 D 1 M NQ P 5, 112 8 1 8 1 32 призмы ABCDпризмы V ааа. V h. SV

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). №№ 33 Решение. Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 4, 3, 2 и двух площадей прямоугольников со сторонами 2, 1 (выделены цветом): Ответ: 48. 3 24 2 2 S пов. = 2(4· 3 + 4· 2 + 3· 2 – 2· 1) =

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). №№ 44 Решение. Площадь поверхности данного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 4, 5, 4: Ответ: 112. 5 1 4 24 1 S пов. = 2(4· 5 + 4· 4 + 4· 5) =

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). №№ 55 Решение: Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 6, 5, 1 и двух прямоугольников со сторонами 1 и 2, уменьшенной на площадь двух прямоугольников со сторонами 2 и 2: Ответ: 78.

S пов. = 2(6· 5 + 6· 1 + 5· 1 + 1· 2 – 2· 2) =

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). №№ 66 Решение: Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с длиной ребер 2, 3, 2 минус площади двух прямоугольников с длинами сторон 2 и 5 – 2 = 3 уменьшенной на удвоенную площадь прямоугольника со сторонами 2, 3: Ответ: 50. S пов. = 2(5· 2 + 5· 3 + 2· 3 – 2· 3) =

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). №№ 77 Решение: Площадь поверхности заданного многогранника равна сумме площадей большого и маленького параллелепипедов с ребрами 1, 4, 7 и 2, 1, 2, уменьшенной на 4 площади прямоугольника со сторонами 2, 2 — передней грани маленького параллелепипеда, излишне учтенной при расчете площадей поверхности параллелепипедов: Ответ: 78. S пов. = 2(7· 4 + 7· 1 + 4· 1 + 1· 2 + 2· 2 – 2· 2· 2) =

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). №№ 88 Решение: Площадь поверхности заданного многогранника равна сумме площадей большого и маленького параллелепипедов с ребрами 6, 6, 2 и 4, 4, 3, уменьшенной на 2 площади квадрата со сторонами 4, 4 — общей для обоих параллелепипедов, излишне учтенной при расчете площадей поверхности параллелепипедов: 5 4 4 6 63 S пов. = 2(6· 6 + 6· 2 + 4· 4 + 4· 3 – 4· 4) = 168 Ответ: 168.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 3. Площадь поверхности этого параллелепипеда равна 262. Найдите третье ребро, выходящее из той же вершины. №№ 99 Решение: Площадь поверхности параллелепипеда равна S пов. = 2 S осн. + S бок. S осн. = ab = 3 · 1 = 3 S бок. = Р осн. · h = 2·(3 + 1) · h = 8 h Имеем, 262 = 2 · 3 + 8 h , откуда найдем третье ребро 8 h = 262 – 6 8 h = 256 h = 32 Ответ: 32.

Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 4, а высота − 7. №№ 1010 Решение: Площадь боковой поверхности правильной призмы равна S бок. = Р осн. · h S бок. = 6 · 4 · 7 = 16 8 Ответ: 168.

Площадь поверхности куба равна 1682. Найдите его диагональ. №№ 1111 Решение: Площадь поверхности куба равна S куба = 6 а 2 d 2 = 3 a 2 – ква драт диагонали куба d 2 = S куба /2 = 168 2/2 = 84 1 d = √ 841 = 29 Ответ: 29.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 20 и 60. Площадь поверхности параллелепипеда равна 4800. Найдите его диагональ. №№ 1212 Решение: Площадь поверхности параллелепипеда равна S пов. = 2 S осн. + S бок. S осн. = ab = 60 · 20 = 1200 S бок. = Р осн. · h = 2·( 60 + 20 ) · h = 160 h Имеем, 4800 = 2 · 1200 + 160 h , откуда найдем третье ребро 160 h = 4800 – 2400 160 h = 2400 h = 15 d 2 = a 2 + b 2 + c 2 d 2 = 60 2 + 20 2 + 15 2 = 4225 d = 65 – диагональ параллелепипеда Ответ: 65.

Если каждое ребро куба увеличить на 5, то его площадь поверхности увеличится на 390. Найдите ребро куба. №№ 1313 Решение: Площадь поверхности куба равна S 1 куба = 6 а 2 Если ребро увеличить на 5, то S 2 куба = 6(а + 5) 2 , что на 390 больше. Откуда имеем, 6(а + 5) 2 − 6 а 2 = 390 Поделив на 6, получим: (а + 5) 2 − а 2 = 65 (а + 5 − а)(а + 5 + а) = 65 5(2 а + 5) = 65 2 а + 5 = 13 а = 4 Ответ: 4.

Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10. №№ 1414 Решение: Площадь поверхности параллелепипеда равна S пов. = 2 S осн. + S бок. S осн. = ½ d 1 · d 2 = ½ · 6 · 8 = 24 S бок. = Р осн. · h = 4 · 5 · 10 = 200. Где сторону основания нашли по теореме Пифагора, т. к. диагонали ромба перпендикулярны. S пов. = 2 · 24 + 200 = 248. Ответ: 248.

Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 18, а площадь поверхности равна 1368. №№ 1515 Решение: Площадь поверхности параллелепипеда равна S пов.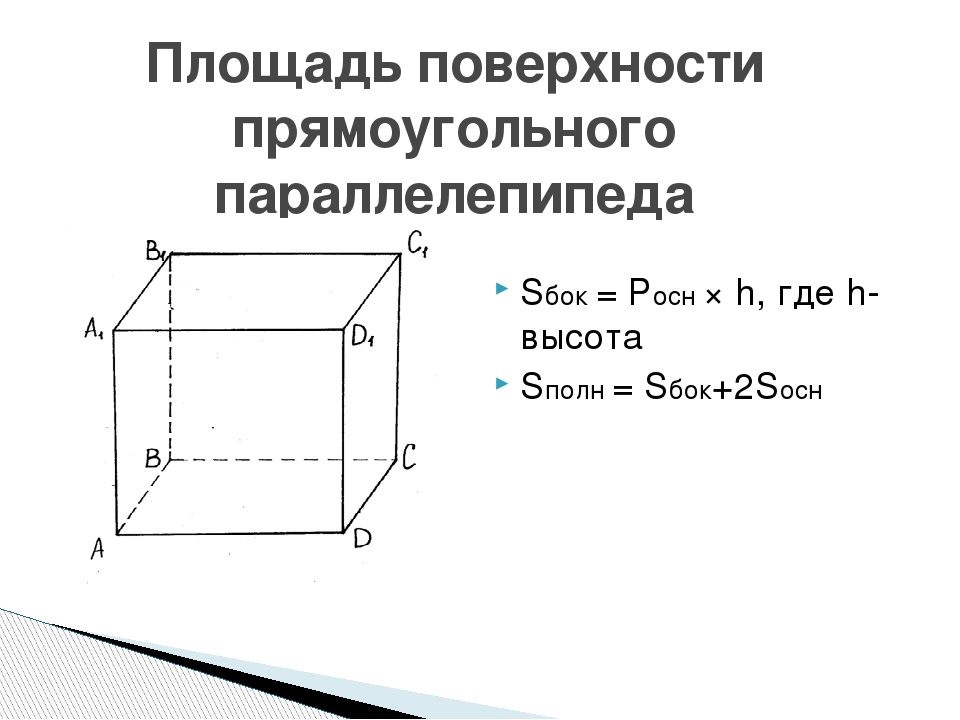 = 2 S осн. + S бок. S осн. = а 2 = 1 8 2 = 3 24 S бок. = Р осн. · h = 4 · 18 · h = 72 h. 1368 = 2 · 3 24 + 72 h Откуда , 72 h = 1368 – 648 h = 10. Ответ: 10.

Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 98 , проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы. №№ 11 66 Решение: Площадь боковых граней отсеченной призмы вдвое меньше соответствующих площадей боковых граней исходной призмы. Поэтому площадь боковой поверхности отсеченной призмы вдвое меньше площади боковой поверхности исходной. S бок. = 98/2 = 49. Ответ: 49.

Стороны основания правильной четырехугольной пирамиды равны 48, боковые ребра равны 25. Найдите площадь поверхности этой пирамиды. №№ 1515 Решение: Площадь поверхности пирамиды равна S пов. = S осн. + S бок. S осн. = а 2 = 14 2 = 196 S бок. = ½ Р осн. · l = ½ · 4 · 14 · l = 28 · l.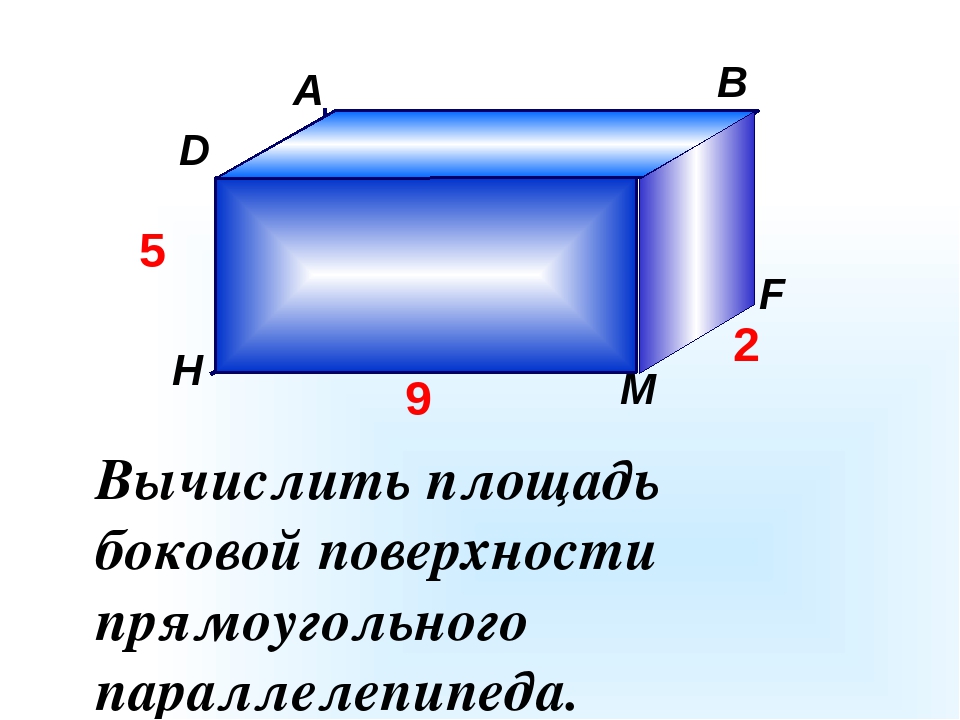 l – апофема (высота боковой грани SK ), которую найдем из п/у ∆ SKC по теореме Пифагора l 2 = SK 2 = SC 2 – CK 2 = 25 2 – (½ · 14 ) 2 l 2 = 576 ⟹ l = 24 S пов. = 196 + 28 · 24 = 868. Ответ: 868. 1414 25 С ВD А S K

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0, 6 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба. №№ 11 66 Решение: Площадь поверхности получившегося многогранника равна сумме площадей боковых граней куба со стороной 1 и призмы со сторонами 1 ; 0, 6; 0, 6 и 2 площади основания куба с вырезанными основаниями призмы: Ответ: 7, 68. 11 1 0, 6 S = 4 · 1 + 4(0, 6 · 1) + + 2( 1 · 1 – 0, 6 · 0, 6) = 7,

Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 12, 16 и 9. Найдите ребро равновеликого ему куба. №№ 1717 Решение: Равновеликие тела имеют равные объемы V пар-да = а bc = 9 · 12 · 1 6 = 1728 V куба = а 3 = 1728 a = 12.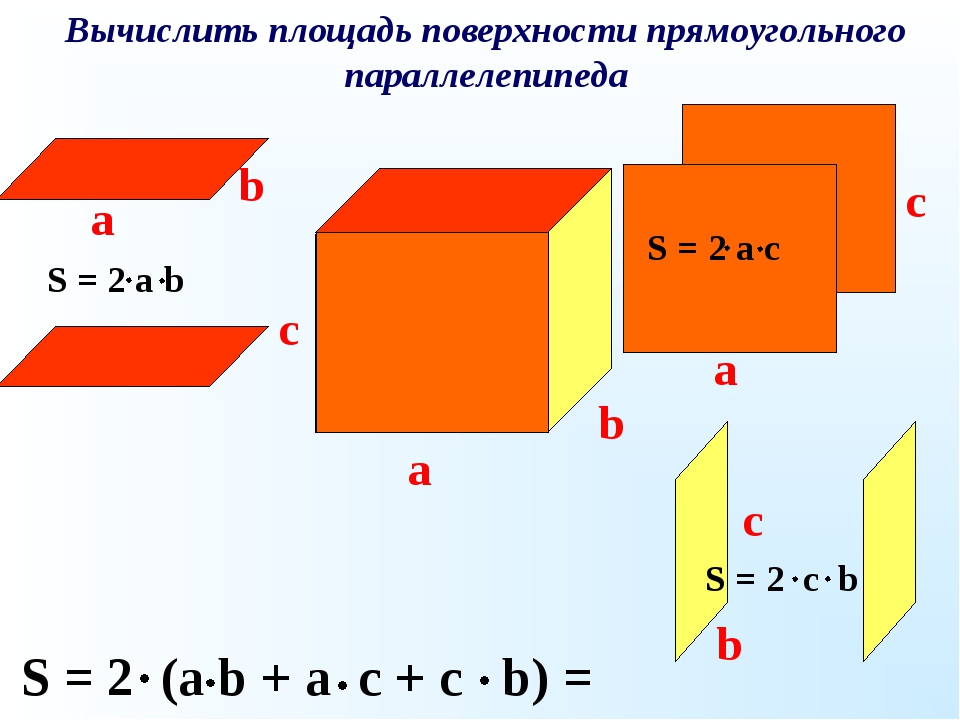 Ответ: 12.

Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в 12 раз? №№ 1818 Решение: Площадь поверхности куба равна S 1 куба = 6 а 2 Если ребро увеличить в 12 раз, то S 2 куба = 6(12 · а) 2 = 6 · 144 · а 2. Откуда имеем, S 2 куба / S 1 куба = (6 · 144 · а 2 )/(6 · а 2 ) S 2 куба / S 1 куба = 144. Ответ: 144.

В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 13 и отстоит от других боковых ребер на 12 и 5. Найдите площадь боковой поверхности этой призмы. №№ 1919 Решение: Площадь боковой поверхности призмы равна S бок. = Р ⊥ · l, где l – длина бокового ребра, а Р ⊥ – площадь перпендикулярного сечения призмы ( п/у ∆ со сторонами 15, 36 и 39 ) S бок. = (5 + 12 + 13)· 13 = 390. Ответ: 390.

Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 10 и 24. Площадь ее поверхности равна 1680.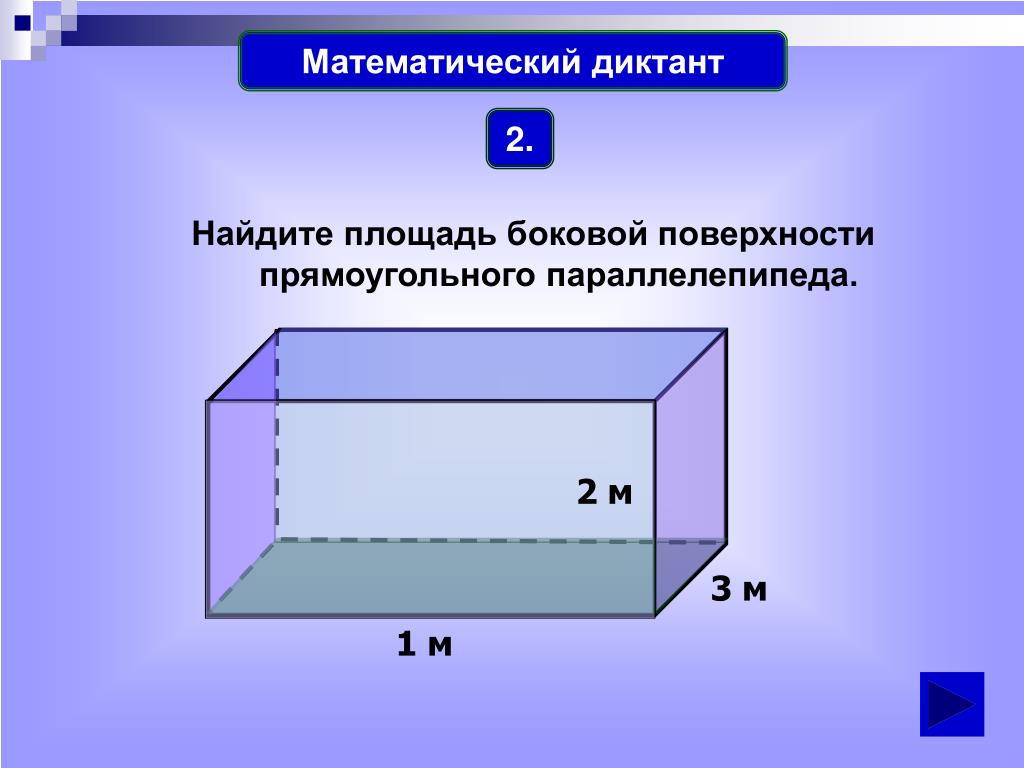 Найдите высоту призмы. №№ 2020 Ответ: 24. 24 10 Решение: Площадь поверхности призмы равна S пов. = 2 S осн. + S бок. S осн. = ½ ab = ½ · 10 · 24 = 120 S бок. = Р осн. · h = ( 2 4 + 10 + 26 ) · h = 60 h Гипотенузу п/у ∆ находим по теореме Пифагора, она рана 26. Имеем, 1680 = 2 · 120 + 60 h , откуда найдем высоту призмы 60 h = 1680 – 240 60 h = 1440 h = 24.

Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов. №№ 2121 Ответ: 30. Решение: Площадь поверхности креста равна площади поверхности 6 -ти кубов, у которых отсутствует одна из шести граней. Имеем, S пов. = 6 S куба – 6 а 2 = 6 · а 2 – 6 а 2 S пов. = 36 – 6 = 30.

Ребра тетраэдра равны 12. Найдите площадь сечения, проходящего через середины четырех его ребер. №№ 2222 12 12 Решение: Данное сечение – квадрат, т. к. каждая сторона является средней линией соответствующей грани, которая, в 2 раза меньше параллельной ей стороны и равна поэтому ½ · 12 = 6. Стороны сечения перпендикулярны, т. к. они параллельны соответственно двум скрещивающимся перпендикулярным ребрам тетраэдра. Тогда площадь сечения равна S сеч. = а 2 = 6 2 = 36. Ответ: 36.

Площадь поверхности тетраэдра равна 3. Найдите площадь поверхности многогранника, вершинами которого являются середины ребер данного тетраэдра. №№ 2323 Решение. Искомая поверхность состоит из 8 равносторонних треугольников со стороной, площадь которого в 4 раза меньше площади одной грани тетраэдра. Поверхность исходного тетраэдра состоит из 16 -ти таких треугольников, поэтому искомая площадь равна половине площади поверхности тетраэдра и равна 1, 5. Ответ: 1, 5.

Используемые материалы • http: //mathege. ru/or/ege/Main − Материалы открытого банка заданий по математике 2013 года

ГДЗ 5 класс. Математика. Никольский, Потапов. Учебник. Упражнение 506

Ответы к упражнению 506

содержание

Другие решебники 5 класс:

Рёбра прямоугольного параллелепипеда равны 3 см, 4 см и 5 см.
а) Найдите площадь его основания и площадь боковой поверхности, то есть сумму площадей боковых граней.
Вариант 1:

1) 5 * 4 = 20 (см²) − площадь основания
2) 3 * 4 = 12 (см²) − площадь первой грани
3) 3 * 5 = 15 (см²) − площадь второй грани
4) (12 + 15) * 2 = 17 * 2 = 54 (см²) − площадь боковой поверхности
Ответ: 20 см² − площадь основания, 54 см² − площадь боковой поверхности.

Вариант 2:

1) 4 * 3 = 12 (см²) − площадь основания
2) 5 * 4 = 20 (см²) − площадь первой грани
3) 5 * 3 = 15 (см²) − площадь второй грани
4) (20 + 15) * 2 = 35 * 2 = 70 (см²) − площадь боковой поверхности
Ответ: 12 см² − площадь основания, 70 см² − площадь боковой поверхности.

Вариант 3:

1) 3 * 5 = 15 (см²) − площадь основания
2) 4 * 3 = 12 (см²) − площадь первой грани
3) 4 * 5 = 20 (см²) − площадь второй грани
4) (12 + 20) * 2 = 32 * 2 = 64 (см²) − площадь боковой поверхности
Ответ: 15 см²− площадь основания, 64 см²− площадь боковой поверхности.

б) Найдите площадь полной поверхности прямоугольного параллелепипеда.
1) 5 * 4 = 20 (см²) – площадь первой грани
2) 5 * 3 = 15 (см²) – площадь второй грани
3) 3 * 4 = 12 (см²) – площадь третьей грани
4) (20 + 15 + 12) * 2 = 47 * 2 = 94 (см²) – площадь полной поверхности.
Ответ: площадь полной поверхности равна 94 см².

Объясните, почему в задании «а» могут получиться три разных ответа.
Могут получиться 3 разных ответа, т.к. прямоугольный параллелепипед состоит из трех пар граней, и за основание можно взять одну из каждой пары.

Поделись с друзьями в социальных сетях:

Математика для блондинок: Прямоугольный параллелепипед

Вновь поступил вопрос про прямоугольный параллелепипед. И вопрос этот не простой, смотрите сами:

Рёбра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите площадь его поверхности. Подскажите, как это переварить?

Вопрос, конечно, не простой — что такое прямоугольный параллелепипед, как и с чем его едят? В частности, как найти рецепт приготовления площади поверхности этого то ли фрукта, то ли овоща? Так, для начала давайте посмотрим, что это вообще такое — прямоугольный параллелепипед? Вот картинка прямоугольного параллелепипеда.

Как видите, прямоугольный параллелепипед — это, собственно, обыкновенный кирпич. Кстати, если бы Ньютону на голову упала не сфера в виде яблока, а прямоугольный параллелепипед в виде кирпича, то в школе мы вряд ли бы учили его законы. Прямоугольная комната — это тоже прямоугольный параллелепипед, который позволяет вам совершить обзорную экскурсию по его достопримечательностям прямо изнутри. Если вы хотите произвести внешний осмотр достопримечательностей сего математического чуда, тогда возьмите в руки коробку из-под обуви и можете вертеть её, сколько душе угодно.

И так, прямоугольный параллелепипед на картинке дает нам возможность увидеть вершины, ребра и диагонали. Вершины мы можем потрогать пальцем, ребра мы можем измерять, диагональ можем высчитать. Нам сейчас диагональ не нужна. Закон движения учеников в классе знаете? Если леди-учитель покидает класс, класс движется быстрее. Закон решения задач очень похож: чем меньше всякой ерунды нам нужно искать, тем проще задача.

Первая проблема, с которой мы сталкиваемся в задаче, это проблема сленга. Задача сформулирована на бытовом сленге, а все формулы и определения в математике формулируются на математическом сленге. Поэтому нам самим предстоит выполнить перевод. Приступаем к поэтапному переводу, по фразам.

«Рёбра прямоугольного параллелепипеда, выходящие из одной вершины …» — собственно, здесь говорится о тех ребрах, которые позволяют нам определить размеры прямоугольного параллелепипеда и на основании этих размеров выполнить все необходимые вычисления. На картинке это ребра a, b и c. Кто бы сомневался, что именно эти три ребра нам дадут по условию, но только не я. Ни один математик вам этого не скажет (не потому, что они этого не знают, а из боязни нарваться на очень неудобные вопросы), но если в условии задачи дать две длины параллельных ребер и одного перпендикулярного им, то нашу задачу в принципе решить будет невозможно. В прямоугольном параллелепипеде из любой вершины всегда выходит три взаимно перпендикулярных ребра. Вот по этому в нашей задаче прямо говорится об этом. Если верить Священным Писаниям разных религий, то именно из одного такого ребра сотворены все прямоугольные параллелепипеды, задачи о которых решает вся прекрасная половина человечества.

Следующая фраза «… равны 1, 2, 3» обозначает, что нам не нужно искать этот злополучный прямоугольный параллелепипед и свою линейку, чтобы измерить длины его граней, как это показано на рисунке. Тот, кто эту задачу придумал, уже сам всё измерил (или выдумал эти размеры, что в данном случае принципиального значения не имеет). Кто есть кто в этом списке чисел? Где длина, ширина, высота нашего параллелепипеда? Нам это без разницы. Как бы мы этот прямоугольный параллелепипед не крутили, площадь его поверхности всегда будет оставаться неизменной. Предыдущие поколения математиков этот факт не единожды проверили. Когда мы доберемся до решения, мы сами в этом убедимся.

Теперь вопрос, в чём же конкретно измеряется наш прямоугольный параллелепипед и площадь его поверхности? В каких единицах измерения? Ответ довольно прост — в любых единицах измерения длины. Англичане и американцы любят дюймы, футы, мили. Мы предпочитаем сантиметры, метры, километры. В чем измеряют длину инопланетяне? Мы вообще не знаем. Да нам эти единицы измерения и не важны. В чем бы мы не измеряли длину граней, циферки возле длин и площади будут одинаковыми. Циферки остаются, единицы измерения меняются. Вот два способа получения результата в математике.

разные числа + одинаковые единицы измерения = разный результат

одинаковые числа + разные единицы измерения = разный результат

Приблизительно, как в этом счетчике. Крутим одно колесико — меняются числа. Крутим другое колесико — меняются единицы измерения. Так устроена настоящая математика, маленький кусочек которой мы сейчас рассматриваем.

Это уже не детская математика, придуманная специально для того, чтобы мучить нас задачками. Это взрослая математика, одинаковая для всех.

В нашей задаче мы измеряем всё в абстрактных единицах измерения длины. Соответственно, полученная нами площадь будет измеряться в этих же единицах измерения, возведенных в квадрат.

Теперь нам осталось только достать из глубокого кармана шпаргалку с формулами для прямоугольного параллелепипеда и посмотреть, чего полезного для нас там имеется.

Что вообще есть в этой шпаргалке? Формула диагонали прямоугольного параллелепипеда, формула объема. Есть несколько формул для площади поверхности: полная, основания, боковая. Вот одна из этих формул нам как раз нужна. Разберемся в площадях на примере коробки для обуви. Площадь основания — это площадь донышка или крышки коробки. Площадь боковой поверхности — это боковые стеночки коробки без донышка и крышки. Полная площадь — это боковые стеночки вместе с донышком и крышкой.

Теперь смотрим в условие задачи и определяем, «чё тебе надобно, старче?». А надобно ему (ей, им) «площадь поверхности». Если уточнений типа «боковой» или «основания» нет, значит искать нужно полную площадь поверхности прямоугольного параллелепипеда. Длины трех граней у нас есть, формула тоже, можно произвести расчет. Заморачиваться с основаниями и боками нам нет смысла.

Как видим, полная площадь поверхности нашего прямоугольного параллелепипеда получилась равной 22 единицы в квадрате. Какие именно единицы? А какие вам не жалко или какие вы больше всего любите.

По просьбе учащихся добавляю картинку про сумму длин ребер прямоугольного параллелепипеда.

Сумма ребер прямоугольного параллелепипеда

Сумму длин всех ребер параллелепипеда я обозначил через букву «P», поскольку она очень похожа на периметр прямоугольника. Кстати, в формуле длин всех ребер я этого не записал, но если мы возьмем три фигурообразующие грани прямоугольного параллелепипеда, которыми являются прямоугольники, то сумма длин всех ребер параллелепипеда будет равна сумме периметров этих прямоугольников.

Спонсор страницы: был, да сплыл.

Боковая область: определение, формула и примеры — видео и стенограмма урока

Боковая поверхность правого кругового цилиндра

Найдем боковую поверхность правого кругового цилиндра.

В этом примере нам дан цилиндр высотой 6 см и диаметром 10 см. Помните, что в правом круговом цилиндре основания — это круги. Чтобы найти площадь боковой поверхности, мы находим периметр, который в данном случае является окружностью (расстояние по окружности), а затем умножаем его на высоту цилиндра.

Длина окружности находится по следующей формуле:

C обозначает окружность, d обозначает диаметр, а символ пи округляется до 3,14. Итак, мы находим окружность основания 3,14 * 10 = 31,4, а затем умножаем ее на высоту 6.

Причина, по которой мы используем окружность при определении площади боковой поверхности, заключается в том, что когда мы открываем круговой цилиндр и складываем стороны из квартиры мы получаем прямоугольник.Представьте бумажное полотенце. Рулон бумажных полотенец представляет собой цилиндр, но когда вы снимаете бумажное полотенце с рулона, вы получаете прямоугольник. Длина — это окружность, а ширина — это высота рулона.

Чтобы найти площадь сторон этого цилиндра, нам нужно умножить длину окружности на высоту. Итак, у нас есть формула для площади боковой поверхности правого кругового цилиндра:

Площадь боковой поверхности правого кругового цилиндра = окружность * высота

Площадь боковой поверхности прямоугольной призмы

Давайте попробуем другой пример, на этот раз с прямоугольной призмой.

Как видите, указаны длина, ширина и высота. Итак, боковые поверхности — это все поверхности по бокам. Нам нужно найти площадь каждой из четырех сторон … но есть более быстрый способ — вы его видите? Если бы мы нашли периметр основания, а затем умножили его на высоту, мы получили бы площадь боковой поверхности.

У нас есть две длины и две ширины. Как и в предыдущем примере, основная формула для площади боковой поверхности:

Как и круглый цилиндр, если мы положим прямоугольную призму плоско, она будет выглядеть так:

Итак, сложите длину и ширину и умножьте на высоту, чтобы найти площадь боковой поверхности.Более кратко это можно записать так:

Площадь боковой поверхности правого кругового цилиндра и правой прямоугольной призмы в основном одинакова; найти периметр основания и умножить на высоту фигуры.

Площадь боковой поверхности пирамиды

Далее мы собираемся найти площадь боковой поверхности пирамиды.

Пирамида — это фигура с многоугольным основанием и несколькими сторонами, называемыми гранями, которые все соединяются в одной точке, называемой вершиной.Чтобы найти площадь боковой поверхности, найдем половину периметра основания и умножим ее на наклонную высоту боковых треугольников. Каждый треугольник имеет наклонную высоту. Наклонная высота — это высота каждого треугольника, а не высота пирамиды. Почему, спросите вы, мы находим половину периметра? Это потому, что каждая из сторон пирамиды представляет собой треугольник, а формула для площади треугольника равна половине основания, умноженному на высоту.

Чтобы найти площадь боковой поверхности пирамиды, вы можете найти площадь каждого треугольника: A = 1/2 bh или A = 1/2 lw , а затем умножить на количество треугольников. , который будет зависеть от количества сторон основания; или можно взять половину периметра и умножить на наклонную высоту.

Давайте попробуем оба варианта на этой пирамиде:

Определение площади боковой поверхности путем нахождения площади каждого треугольника и последующего умножения на количество треугольников: l обозначает наклонную высоту:

Определение площади боковой поверхности по формуле: LSA = 1/2 периметра, умноженного на наклонную высоту:

Определение площади боковой поверхности конуса такое же, как у пирамиды, за исключением того, что наше основание представляет собой круг, поэтому мы используем половину длины окружности, умноженную на наклонную высоту.Итак, допустим, у нас есть конус с наклонной высотой 12.

Резюме урока

Площадь боковой поверхности — это площадь поверхности сторон любой трехмерной фигуры. Каждая фигура может иметь различное основание, но площадь боковой поверхности определяется одинаково. Найдите периметр основания, а затем умножьте его на высоту любой трехмерной призмы.

При нахождении площади боковой поверхности пирамиды или конуса формула:

Калькулятор прямоугольной призмы (кубоид)

Прямоугольная призма

l = длина
w = ширина
h = высота
d = диагональ
S _tot = общая площадь поверхности
S _lat = площадь боковой поверхности
S _верх = площадь верхней поверхности
S _bot = площадь нижней поверхности
V = объем

Использование калькулятора

Введите любые 3 переменные для прямоугольной призмы в этот онлайн-калькулятор, чтобы вычислить другие 3 неизвестные переменные. Куб — это частный случай, когда l = w = h для прямоугольной призмы.

Единицы: Обратите внимание, что единицы показаны для удобства, но не влияют на вычисления. Единицы измерения указывают на порядок результатов, например футы, футы ² или футы ³ . Например, если вы начинаете с мм и знаете h, l и w в мм, в результате ваших вычислений d в мм, S в мм ² и V в мм ³ .

Формулы для прямоугольной призмы:

• Объем прямоугольной призмы :
• Площадь поверхности прямоугольной призмы :
• Пространственная диагональ прямоугольной призмы : (аналогично расстояние между 2 точками)

Куб — это особый случай, когда l = w = h. Таким образом, вы можете найти объем куба или площадь поверхности куба, установив эти значения равными друг другу.

Расчеты для прямоугольной призмы:

1. Зная длину, ширину и высоту, найдите объем, площадь поверхности и диагональ прямоугольной призмы

• h, l и w известны; найти V, S и d
• V = lwh
• S = 2 (lw + lh + wh)
• d = √ (l ² + w ² + h ² )

2.Зная площадь поверхности, длину и ширину, найдите высоту, объем и диагональ прямоугольной призмы

.

• S, l и w известны; найти h, V и d
• ч = (S — 2lw) / (2l + 2w)
• V = lwh
• d = √ (l ² + w ² + h ² )

3. Зная объем, длину и ширину, найдите высоту, площадь поверхности и диагональ прямоугольной призмы

• V, l и w известны; найти h, S и d
• ч = об / л
• S = 2 (lw + lh + wh)
• d = √ (l ² + w ² + h ² )

4. Зная диагональ, длину и ширину, найдите высоту, объем и площадь поверхности прямоугольной призмы

.

• d, l и w известны; найти h, V и S
• h = √ (d ² — l ² — w ² )
• V = lwh
• S = 2 (lw + lh + wh)

Для получения дополнительной информации о кубоидах см .: Weisstein, Eric W. Cuboid. От MathWorld — Интернет-ресурс Wolfram, Кубоид.

Площадь поверхности кубоида

Общая площадь поверхности (TSA) кубоида — это сумма площадей его 6 граней, которая определяется по формуле:

TSA = 2 (lw + wh + hl)

Помните, что площадь поверхности — это общая площадь всех граней трехмерной формы.
Площадь боковой поверхности кубоида определяется как:
LSA = 2 (lh + wh) = 2 h (l + w)

Пример 1: Найдите общую площадь поверхности кубоида размером 8 см по формуле 6 см на 5 см.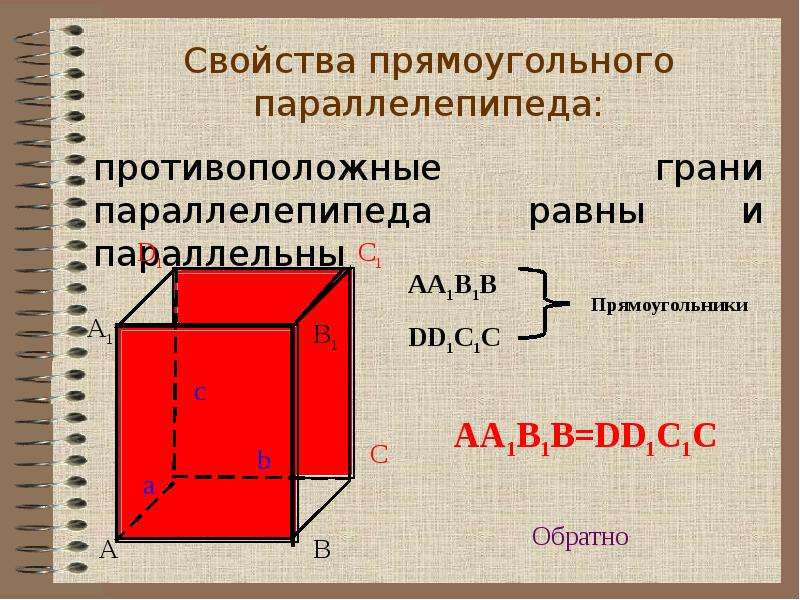
TSA = 2 (lw + wh + hl)
TSA = 2 (8 * 6 + 6 * 5 + 5 * 8)
TSA = 2 (48 + 30 + 40)
TSA = 236
Итак, общая площадь этого кубоида составляет 236 см ² .

Пример 2: Найдите площадь поверхности кубоида размером 4,8 см, 3,4 см и 7,2 см.
Решение:
Площадь лица 1: 4,8 × 7,2 = 34,56 см²
Площадь лица 2: 3,4 × 7,2 = 24,48 см²
Площадь лица 3: 4.8 × 3,4 = 16,32 см²

Сумма площади этих трех граней дает 75,36 см², поскольку каждая грань дублируется на противоположной стороне, общая площадь поверхности кубоида будет:
TSA = 2 (75,36) = 150,72 см²

Пример 3: Длина, ширина и высота прямоугольного прямоугольника составляют 10 см, 8 см и 7 см соответственно. Найдите площадь боковой поверхности кубоида.
Решение:
Площадь боковой поверхности кубоида определяется как:
LSA = 2h (l + w)
где,
l = длина = 10 см
w = ширина = 8 см
h = высота = 7 см

Вставьте эти значения в формулу, которую мы получим:

Пример 4: Длина, ширина и высота кубовида составляют 16 см, 14 см и 10 см соответственно. Найдите общую площадь поверхности кубоида.
Решение:
Общая площадь поверхности кубоида определяется как:
TSA = 2 (l * b + b * h + h * l)

Подставляя значения в уравнение, мы получим
TSA = 2 (16 * 4 + 14 * 10 + 10 * 16)
TSA = 2 (224 + 140 + 160)
TSA = 2 * 524
TSA = 1048 см ²

Пример 5: Учитывая ящик для хлопьев длиной 20 см, высотой 30 см и шириной 8 см.Найдите площадь поверхности коробки.
Решение:
Чтобы найти поверхность коробки, нам нужно найти площадь каждой прямоугольной грани и сложить их все.
Площадь лицевой стороны: 20 х 30 = 600 см2.
Площадь верхней грани: 20 x 8 = 160 см2.
Площадь боковой грани: 8 x 30 = 240 см2.

Теперь сложите эти значения вместе, и мы получим: 600 + 160 + 240 = 1000 см2.

Таким образом, общая площадь поверхности составляет 1000 x 2 = 2000 см2.

Пример 6: Найдите площадь поверхности кубоида со сторонами 3 см на 6 см на 10 см.
Решение:
Площадь поверхности кубоида определяется как:
TSA = 2 (16 * 4 + 14 * 10 + 10 * 16)
TSA = 2 (3 x 6 + 6 x 10 + 3 x 10)
TSA = 2 (18 + 60 + 30)
TSA = 216 см ²

Решение задач геометрии — прямоугольник или параллелепипед

Решатель задач с геометрией

Кубоид или параллелепипед

Параллелепипед и пирамида вместе

Куб и параллелепипед вместе

Параллелепипед и сфера вместе

Параллелепипед и призма вместе

Параллелепипед и конус вместе

Параллелепипед и цилиндр вместе

Они указывают на то, что некоторые проблемы могут быть решены автоматически, числовые значения не имеют значения в различных примерах.

Track 1

Прямоугольный параллелепипед имеет прямоугольное основание размерами 30 см и 50 см, высота 100 см. Рассчитайте объем твердого тела и боковую поверхность.

Track 2

Сколько уходит в бетонную стену длиной 500 см, высотой 300 см и шириной 20 см?

Дорожка 3

Контейнер имеет внутреннюю площадь 14200 см, площадь внутреннего основания 1500 см, размер другого составляет 3/5.Рассчитывает высоту сосуда и его возможности, зная, что он имеет форму прямоугольного параллелепипеда.

Дорожка 4

Размеры основания прямоугольного параллелепипеда составляют 3/4 другого, а диагональ основания длиной 30 см соответствует высоте параллелепипеда. Вычислите площадь общей площади коробки.

Дорожка 5

Вычислите общую площадь прямоугольного параллелепипеда, зная, что сумма трех его измерений составляет 17 см, а два из них составляют соответственно 1/2 и 1/5 высоты. .

Дорожка 6

В прямоугольном параллелепипеде сумма измерений трех измерений составляет 60 см; зная, что размеры основания составляют 3/4 другого, а высота составляет 5/3 второстепенного размера, вычисляет площадь общей площади и объем твердого тела.

Дорожка 7

Край куба совпадает с диагональю прямоугольного параллелепипеда с размерами 24 см, 32 см и 30 см. Вычислите площадь общей площади куба.

Дорожка 8

Край куба длиной 30 см. Определяет размер основания прямоугольного параллелепипеда высотой 30 см, зная, что размер основания является двойным размером другого и что боковая поверхность параллелепипеда эквивалентна боковой поверхности куба.

Направляющая 9

Прямоугольный параллелепипед имеет размеры соответственно 10 см, 20 см, 30 см. Рассчитайте боковую площадь, общую площадь и объем.

Колея 10

Длина и ширина прямоугольного параллелепипеда составляют 20 м и 30 м.Зная, что общая площадь 6200 м, рассчитываем высоту ящика и измеряем объем.

Дорожка 11

Вычислите объем и диагональ прямоугольного параллелепипеда размером 14 см, 48 см и 120 см.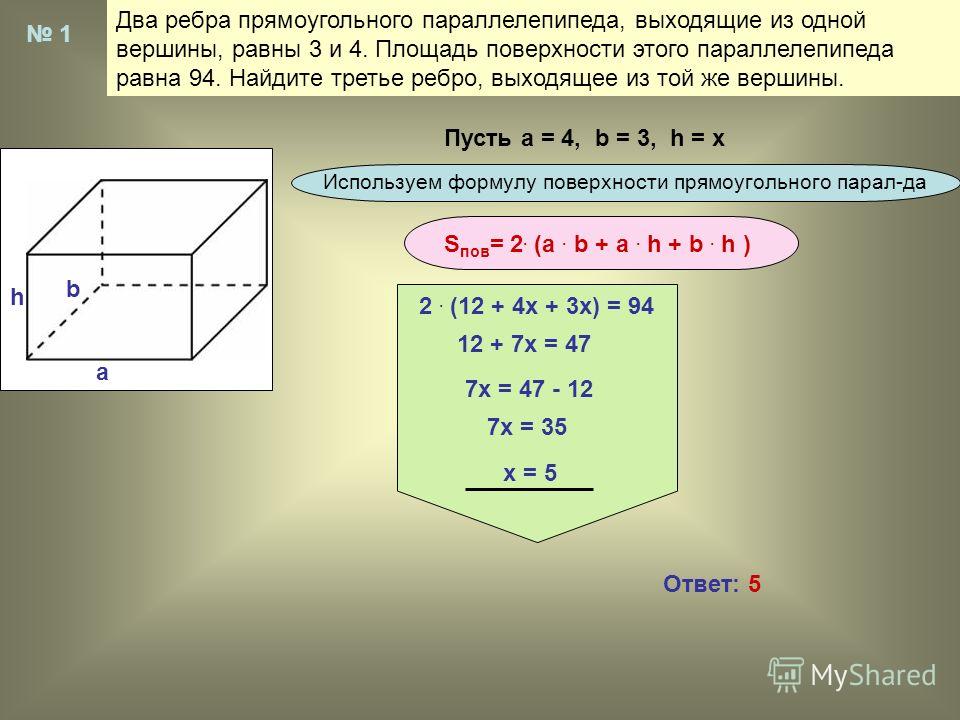

Дорожка 12

На одном листе вырезана коробка длиной 20 см, шириной 25 см и высотой 30 см. Если бы бумага имела площадь 1 м, сколько квадратных метров бумаги было бы свободным?

Дорожка 13

Параллелепипед образован тремя сложенными кубиками, равными друг другу.Зная, что край каждого куба размером 10 см, вычисляет площадь общей поверхности и объем твердого тела.

Дорожка 14

Общая площадь поверхности куба равна площади боковой поверхности прямоугольного параллелепипеда с размерами основания соответственно 30 см в длину и 10 см. Вычислите объем куба, зная, что базовый периметр коробки составляет 8/3 высоты.

Дорожка 15

Общая площадь куба равна одной стороне прямоугольного параллелепипеда высотой 30 см.Вычислите объем куба, зная, что размеры параллелепипеда втрое больше другого, а их сумма равна 40 см.

Дорожка 16

Высота прямоугольного параллелепипеда размером 100 см и его объем составляет 1 50000 см. Вычислите боковую площадь и общую площадь, зная, что размеры основания составляют 3/5 другого.

Колея 17

Площадь боковой поверхности прямоугольного параллелепипеда 160 дм; зная, что размер основания и высота твердого тела соответственно 5 и 10 дм дм, вычисляет вес параллелепипеда.(Ps = 8 кг / дм)

Дорожка 18

Площадь боковой поверхности прямоугольного параллелепипеда 11200 см, размер основания 50 см, высота 7/5. Определяет площадь общей поверхности и объем параллелепипеда.

Дорожка 19

Общая площадь параллелепипеда составляет 14200 см, а площадь основания 1500 см. В прямоугольнике основания одна сторона составляет 3/5 другой. Определяет длину коробки по трем измерениям и объем.

Колея 20

Прямоугольный параллелепипед имеет площадь боковой поверхности 13000 см и периметр основания 260 см. Зная, что размеры основания равны 8/5 другого, вычисляет:
а) площадь общей поверхности параллелепипеда;
б) высота правильной четырехугольной призмы, эквивалентной данному параллелепипеду и имеющей длину края основания 50 см.

Путь 21

Кран может поднимать груз не более 2 тонн.Г-н Питер зарядил 40 бетонных блоков (1,2 пс), длиной 50 см, шириной 20 см и высотой 25 см. В порядке?

Трасса 22

Бассейн имеет форму прямоугольного параллелепипеда. Его ширина составляет 3,5 м, а длина 10,5 м. Луиджи потребляет 44,1 м воды, чтобы заполнить его. Какая высота воды в этом бассейне?

Программа для решения задач может давать совершенно неправильные ответы.

Площадь поверхности и объем пирамид, призм, цилиндров и конусов (Геометрия, Площадь) — Mathplanet

Площадь поверхности — это область, которая описывает материал, который будет использоваться для покрытия геометрического тела.Когда мы определяем площади поверхности геометрического твердого тела, мы берем сумму площадей для каждой геометрической формы внутри твердого тела.

Объем — это мера того, сколько может вместить фигура, и измеряется в кубических единицах. Объем говорит нам кое-что о вместимости фигуры.

Призма — это сплошная фигура, имеющая две параллельные конгруэнтные стороны, называемые основаниями, которые соединены боковыми гранями, являющимися параллелограммами. Есть как прямоугольные, так и треугольные призмы.

Чтобы найти площадь поверхности призмы (или любого другого геометрического тела), мы открываем твердое тело, как картонную коробку, и расплющиваем его, чтобы найти все включенные геометрические формы.

Чтобы найти объем призмы (неважно, прямоугольная она или треугольная), мы умножаем площадь основания, называемую площадью основания B, на высоту h.

$$ V = B \ cdot h $$

Цилиндр — это труба, состоящая из двух параллельных конгруэнтных окружностей и прямоугольника, основание которого является окружностью окружности.{2} \ cdot h $$

Пирамида состоит из трех или четырех треугольных боковых поверхностей и трех- или четырехсторонней поверхности соответственно в основании. Когда мы вычисляем площадь поверхности пирамиды ниже, мы берем сумму площадей четырех треугольников и основного квадрата. Высота треугольника внутри пирамиды называется наклонной высотой.

Объем пирамиды составляет одну треть объема призмы.

$$ V = \ frac {1} {3} \ cdot B \ cdot h $$

Основание конуса — круг, и это легко увидеть.{3} $$

---

Видеоурок

Найдите площадь поверхности цилиндра радиуса 4 и высоты 8

---

Найти объем конуса высотой 5 и радиусом 3

Видео с вопросом: Определение площади диагонального прямоугольника внутри прямоугольного параллелепипеда с учетом его размеров

Стенограмма видео

𝐴𝐵𝐶𝐷 простое 𝐵 простое 𝐶 простое простое число — это прямоугольный параллелепипед, три измерения которого: 𝐴𝐵 равны 69 сантиметрам, 𝐵𝐶 равны 55 сантиметрам, а 𝐴𝐴 простое число равно 92 сантиметрам. Определите площадь прямоугольника 𝐶𝐵𝐴 простой простой.

Начнем с заполнения данных измерений. — 69 сантиметров, 𝐵𝐶 — 55 сантиметров, а 𝐴𝐴 — 92 сантиметра. Нам сказали, что трехмерная фигура на этом рисунке — параллелепипед. И обычно мы можем увидеть такой рисунок. Тем не мение. Простое число простое число 𝐶 простое число 𝐷 простое число описывается как прямоугольный параллелепипед, который является особым типом параллелепипеда, в котором все шесть граней являются прямоугольниками. В качестве альтернативы мы можем представить эту форму как кубовидную или прямоугольную призму.Это означает, что у нас будут прямые углы здесь, здесь и здесь.

Итак, давайте посмотрим, что нас просят вычислить. Это площадь прямоугольника 𝐶𝐵𝐴 простое 𝐷 простое число. Это будет плоскость, которая прорезает твердое тело. Напомним, что для определения площади прямоугольника мы умножаем длину на ширину. Мы знаем, что одним из размеров этого прямоугольника будет 55 сантиметров, но нам нужно вычислить эту длину «простого». Нам не дается никакой информации о длине этого отрезка прямой простого, но давайте рассмотрим его как часть этого прямоугольного треугольника.

Мы знаем, что треугольник 𝐴 простое число будет прямоугольным, потому что он является частью этого прямоугольного параллелепипеда. Поскольку нам даны две длины в этом прямоугольном треугольнике, и мы хотим найти длину этой третьей стороны, мы можем применить теорему Пифагора. Эта теорема говорит нам, что квадрат гипотенузы равен сумме квадратов на двух других сторонах. И это часто записывается как в квадрате равно в квадрате плюс в квадрате, где 𝑐 — гипотенуза, а 𝑎 и 𝑏 — две другие стороны.

Итак, допустим, мы определяем длину отрезка 𝐴 prime 𝐵 буквой. Затем мы можем заполнить данные значения. Гипотенуза будет. Это самая длинная сторона, и она всегда противоположна прямому углу. А квадраты двух других сторон можно записывать в любом порядке, так что в квадрате равно 92 в квадрате плюс 69 в квадрате. Используя метод без использования калькулятора, мы можем вычислить эти квадраты как 8464 плюс 4761, что дает нам 13225. Затем нам нужно извлечь квадратный корень из обеих частей этого уравнения, чтобы найти значение 𝑥.

Итак, 𝑥 равно квадратному корню из 13225. Единицами измерения будут сантиметры, поскольку 𝑥 — длина. Обычно в этот момент, когда мы работаем с теоремой Пифагора в трех измерениях или тригонометрией в трех измерениях, и у нас есть значение, которое мы еще не закончили использовать в наших вычислениях, мы бы сказали, чтобы сохранить это значение в форме квадратного корня. . Однако 13225 на самом деле является точным квадратом, а это означает, что, когда мы находим квадратный корень, мы получаем целое число.

Этот квадратный корень из 13225 фактически равен 115.Итак, 𝑥 составляет 115 сантиметров. Итак, теперь у нас есть длина и ширина прямоугольника 𝐶𝐵𝐴 простое 𝐷 простое число. Следовательно, мы можем найти площадь, умножив длину и ширину. Итак, мы вычислим 115, умноженное на 55. Это дает нам площадь прямоугольника 𝐶𝐵𝐴 простое простое число 6325 квадратных сантиметров.

Твердые тела — объемы и поверхности

Куб

Объем

V = a ³ (1)

где

V = объем (м ^{3 )}

a = сторона (м, футы)

Площадь поверхности

A ₀ = 6 a ² (1b)

где

A ₀ = площадь поверхности (м ² , фут ² )

Диагональ

d = a 3 ^1/2 (1c)

где

d = внутренняя диагональ (м, фут)

Диагональ кубической грани

d _s = a 2 ^1/2 (1d)

Кубоид — квадратная призма

90 005

Объем

V = abc (2)

где

V = объем твердого тела (м ³ , футы ³ )

a = длина прямоугольной призмы (м , футы)

b = ширина прямоугольной призмы (м, футы)

c = высота прямоугольной призмы (м, футы)

Диагональ

d = ( _² + b ^₂ + c ^₂ ) ^1/2 (2b)

Площадь поверхности

A ₀ = 2 (ab + ac + bc) (2c)

где

A ₀ = площадь поверхности твердого тела (м ² , футы ² )

Параллелепипед 9028 1

Объем

V = A ₁ h (3a)

где

A ₁ = боковая площадь (м ² , фут ² )

Компоненты Sketchup из Engineering ToolBox

• Геометрические фигуры — цилиндры, прямоугольники, конусы, плоскости, сферы, линии, кривые и многое другое. .

— бесплатный плагин Engineering ToolBox для использования с удивительным приложением для рисования / моделирования 3D Sketchup.

Цилиндр

Объем

V = π r ² h = ( π / 4) d ² h (4a)

35

35

35

35

35

d = диаметр цилиндра (м, фут)

r = радиус цилиндра (м, фут)

h = высота цилиндра (м, фут)

Поверхность

A = 2 π rh + 2 π r ² (4b)

Полый цилиндр

Объем

V = π / 4 h (D ² — d ² ) (5)
(5)

Пирамида

Объем

V = 1/3 ч A ₁ (6)

где

A _{1 90 234 = площадь основания (м ² , фут ² )}

h = перпендикулярная высота пирамиды (м, фут)

Поверхность

A = ∑ сумма площадей треугольников, образующих стороны + A _b (6b)

где

площади поверхностей треугольных граней будут иметь разные формулы для оснований разной формы

Frustum of Pyramid

Volume

/ 3 (A ₁ + A ₂ + (A ₁ A ₂ ) ^1/2 ) (7)

Конус

Объем

V = 1/3 π r ² h (8a)

где

r = радиус основания конуса (м, футы)

h = высота конуса (м, футов)

Поверхность

A = π rl + π r ² (8b)

где

l = (r ² + h ² ) = длина стороны конуса (м, футы)

Сторона

м = (h ² + r ² ) ^1/2 (8c)

A ₂ / A ₁ = x ² / h ² (8d)

Уголок конуса

Объем

V = π / 12 h (D ² + D d + d ² ) (9a)

m = (((D — d) / 2) ² + h ² ) ^1/2 (9c)

Сфера

Объем

V = 4/3 π r ³

= 1/6 π d ³ (10a)

где

r = радиус сферы (м, фут)

Поверхность

A = 4 π r ²

= π d ² (10b)

35 м :

Поверхность:

Сферы с дробным диаметром — площадь поверхности и объем

Зона сферы

V = π / 6 h (3a ² + 3b ² + h) ( 11a)

A _m = 2 π rh (11b)

A ₀ = π (2 rh + a ² + b ² ) (11c)

Сегмент сферы

V = π / 6 h (3/4 с ² + h ² )

= π h ² (r — h / 3) (12a)

A _м = 2 π rh

= π / 4 (s ² + 4 h ² ) (12b)

Сектор сферы

V = 2/3 π r ² h (13a)

A ₀ 32 = /2 r (4 ч + с) (13b)

Сфера с цилиндрическим растачиванием

V = π / 6 h ³ (14a)

A 90 233 0 = 4 π ((R + r) ³ (R — r)) ^1/2

= 2 π h (R + r) (14b)

h = 2 (R ² — r ² ) ^1/2 (14c)

Сфера с коническим растачиванием

V = 2/3 π R ² h (15a)

A ₀ = 2 π R (h + (R ² — h ² /4) ^1/2 ) (15b)

h = 2 (R ² — r ² ) ^1/2 (15c)

Тор

V = π ² /4 D d ² (16a)

А ₀ = π ² D d (16b)

Нарезанный цилиндр

V = π / 4 d ² h

= π r ^{2 (1 (h h ₂ ) / 2)} (17a)

A _m = π dh

= 2 π r ((h ₁ 902 + h 902) / 2) (17b)

где

A _м = площадь боковых стенок

A ₀ = π r (h + h + h + h + r + (r ² + (h ₁ — h ₂ ) ² /4) ^1/2 ) (17c)

где

A ₀ знак равно площадь поверхности

Ungula

V = 2/3 r ² h (18a)

A _m = 2 rh (18b)

= A _м + π / 2 r ² + π / 2 r (r ² + h ² ) ^1/2 (18c)

Ствол

V ≈ π / 12 ч (2 D ² + d ² ) (19a)

.