Лабораторная работа измерение коэффициента жесткости пружины. Лабораторная работа«Измерение жесткости пружины» методическая разработка по физике на тему
МОУ «Гимназия №6» Физический практикум 10 класс
Лабораторная работа №3
Измерение жесткости пружины
Цель работы : найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести , уравновешивающей силу упругости
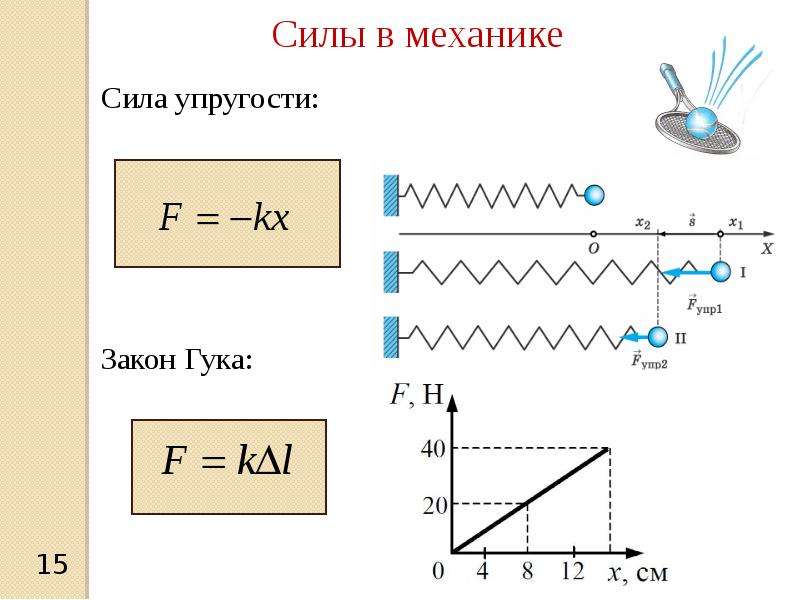
на основе закона Гука:
. В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т.е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости
от модуля удлинения х . При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
.
Результат измерения обычно записывается в виде выражения
, где
— наибольшая абсолютная погрешность измерения. Известно, что относительная погрешность () равна отношению абсолютной погрешности
к значению величины k :
, откуда
.
В данной работе
. Поэтому
, где
;
;
.
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Лабораторная работа «Измерение жесткости пружины» Учитель физики ГБОУ СОШ №145 Калининского района Санкт- Петербурга Карабашьян М.
проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины. Цель работы Оборудование: набор «Механика» из комплекта L-micro- штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузов известной массы (по 50 г), линейка с миллиметровыми делениями.
Подготовительные вопросы Что такое сила упругости? Как вычислить силу упругости, возникающую в пружине при подвешивании к ней груза массой m кг? Что такое удлинение тела? Как измерить удлинение пружины при подвешивании к ней груза? В чем заключается закон Гука?
Правила техники безопасности Будьте осторожны при работе с растянутой пружиной. Не роняйте и не бросайте грузы.
Описание работы: Согласно закону Гука, модуль F силы упругости и модуль х удлинения пружины связаны соотношением F = kx . Измерив F и х, можно найти коэффициент жесткости k по формуле
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения \ х\ . При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F yпp =k\x\ . Это связано с погрешностями измерений. В этом случае график надо проводить так, чтобы примерно одинаковое число точек, оказалось, по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика) определите по нему соответствующие этой точке значения силы упругости и удлинения, и вычислите жесткость k . Она и будет искомым средним значением жесткости пружины k ср.
Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения \ х\ . При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F yпp =k\x\ . Это связано с погрешностями измерений. В этом случае график надо проводить так, чтобы примерно одинаковое число точек, оказалось, по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика) определите по нему соответствующие этой точке значения силы упругости и удлинения, и вычислите жесткость k . Она и будет искомым средним значением жесткости пружины k ср.
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком). 2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями. 3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины. 4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины. 5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение \ х\ пружины. По результатам измерений заполните таблицу ХОД РАБОТЫ:
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями. 3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины. 4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины. 5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение \ х\ пружины. По результатам измерений заполните таблицу ХОД РАБОТЫ:
№ опыта m, кг mg, H х, м 1 0,1 2 0,2 3 0,3 4 0,4
6. Начертите оси координат х и F, выберите удобный масштаб и нанесите полученные экспериментальные точки. 7. Оцените (качественно) справедливость закона Гука для данной пружины: находятся ли экспериментальные точки вблизи одной прямой, проходящей через начало координат. 8. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k ср. 9. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k cp 10.
Контрольные вопросы: Как называется зависимость между силой упругости и удлинением пружины? Пружина динамометра под действием силы 4Н удлинилась на 5 мм. Определите вес груза, под действием которого эта пружина удлиняется на 16 мм.
Лабораторные работы по физике 9 класс Генденштейн Орлов Ход работы
1 — Закрепите конец пружины в штативе. Измерьте высоту на которой находится нижний конец пружины над столом.
2 — Подвесьте к пружине груз массой 100 грамм. Измерьте высоту, на которой находится теперь нижний конец пружины над столом. Вычислите удлинение пружины.
3 — Повторите измерения, подвешивая к пружине два, три и четыре грузы массой по 100 грамм.
4 — Запишите результаты в таблицу.
5 — Начертите систему координат для построения графика зависимости силы упругости от удлинения пружины.
7 — Определите, как зависит сила упругости от удлинения пружины.
Чем больше удлинение пружины, тем больше сила упругости, то есть чем длиннее растягивается пружина, тем больше сила упругости.
8 — По построенной прямой найдите жесткость пружины.
k = Fупр /|x|k = 4/0.1 = 40 H/m
9 — Определите, зависит ли жесткость пружины от ее длины, и если зависит, то как она изменяется при уменьшении длины пружины.
Жесткость пружины не зависит от удлинения длины пружины. У каждой пружины есть k(жесткость пружины) и она постоянна, не зависит от Fупр и от ΔxПо
физике
за 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год),
задача №2
к главе «ЛАБОРАТОРНЫЕ РАБОТЫ ».
Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести
уравновешивающей силу упругости на основе закона Гука:
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях.
Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k ср.
Результат измерения обычно записывается в виде выражения k = = k cp ±Δk, где Δk — наибольшая абсолютная погрешность измерения. Из курса алгебры (VII класс) известно, что относительная погрешность (ε k) равна отношению абсолютной погрешности Δk к значению величины k:
откуда Δk — ε k k. Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются.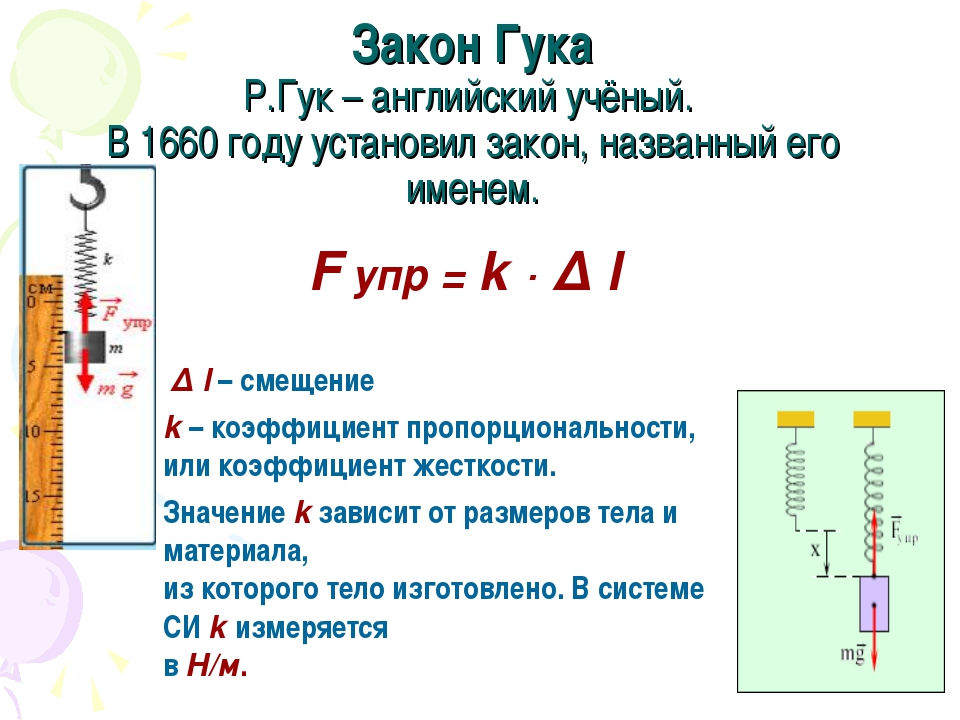 В данной работе
В данной работе
Средства измерения: 1) набор грузов, масса каждого равна m 0 = 0,100 кг, а погрешность Δm 0 = 0,002 кг; 2) линейка с миллиметровыми делениями.
Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.
Порядок выполнения работы
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:
6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k cp .
7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k ср (из опыта с одним грузом). В формуле (1)
так как погрешность при измерении удлинения Δx=1 мм, то
8. Найдите
и запишите ответ в виде:
1 Принять g≈10 м/с 2 .
Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
Закон Гука
Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
где F — приложенная к пружине сила, а х — изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m 0 = (0,1±0,002) кг.
Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.
Порядок выполнения работы описан в учебнике и комментариев не требует.
масса, кг | удлинение |х|, | |||
Лабораторная работа № 2 «Измерение жесткости пружины»
Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести
уравновешивающей силу упругости на основе закона Гука:
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости Fупр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины kср.
В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины kср.
Результат измерения обычно записывается в виде выражения k = = kcp±Δk, где Δk — наибольшая абсолютная погрешность измерения. Из курса алгебры (VII класс) известно, что относительная погрешность (εk) равна отношению абсолютной погрешности Δk к значению величины k:
откуда Δk — εkk. Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе
Поэтому
Средства измерения: 1) набор грузов, масса каждого равна m0 = 0,100 кг, а погрешность Δm0 = 0,002 кг; 2) линейка с миллиметровыми делениями.
Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.
Порядок выполнения работы
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:
|
Номер опыта |
m, кг |
mg1, Н |
|х|, м |
6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины kcp.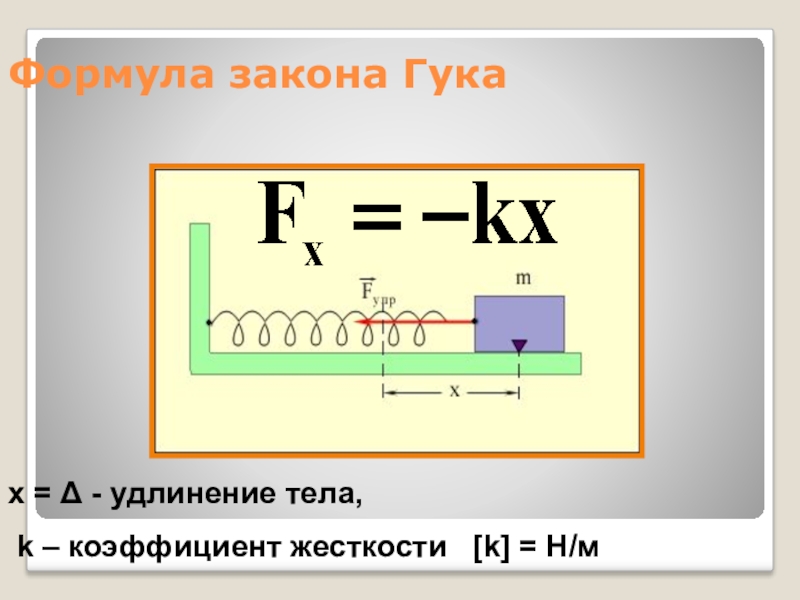
7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение kср (из опыта с одним грузом). В формуле (1)
так как погрешность при измерении удлинения Δx=1 мм, то
8. Найдите
и запишите ответ в виде:
1 Принять g≈10 м/с2.
Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
Закон Гука
Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
где F — приложенная к пружине сила, а х — изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m0 = (0,1±0,002) кг.
Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.
Порядок выполнения работы описан в учебнике и комментариев не требует.
|
№ опыта |
масса, кг |
удлинение |х|, |
К, Н/м | |
|
м | ||||
|
1 |
0,1 |
1 |
0,036 |
27,78 |
|
2 |
0,2 |
2 |
0,074 |
27,03 |
|
3 |
0,3 |
3 |
0,112 |
26,79 |
|
4 |
0,4 |
4 |
0,155 |
25,81 |
* Ускорение свободного падения примем равным 10 м/с2.
Вычисления:
Вычисление погрешности измерения:
εх максимально когда х — наименьшее, т.е., в нашем случае, для опыта с одним грузом
Можно записать результат измерений как:
или округляя:
т.к. в нашем случае отклонения вычисленных R1; R2; R3; R4 от Rср велики из-за разности условий опытов принимаем
оцените качественно справедливость закона Гука для данной пружины: находятся ли
На рисунке изображены: линза, предмет, ход луча 1 через линзу и фокусное расстояние.а) с помощью условного обозначения покажите вид линзы изображённой … на рисунке и постройте изображение даваемое этой линзой,.б) вычислите оптическую силу линзы. с) вычислите расстояние от линзы до изображения применяя формулу тонкой линзы. d) вычислите линейное увеличенное изображения предмета 50 БАЛЛОВ
На рисунке изображены: линза, предмет, ход луча 1 через линзу и фокусное расстояние. а) с помощью условного обозначения покажите вид линзы изображённой
… на рисунке и постройте изображение даваемое этой линзой,.б) вычислите оптическую силу линзы. с) вычислите расстояние от линзы до изображения применяя формулу тонкой линзы. d) вычислите линейное увеличенное изображения предмета
а) с помощью условного обозначения покажите вид линзы изображённой
… на рисунке и постройте изображение даваемое этой линзой,.б) вычислите оптическую силу линзы. с) вычислите расстояние от линзы до изображения применяя формулу тонкой линзы. d) вычислите линейное увеличенное изображения предмета
Помогите пожалуйста!!!
Задание 5 Длина рычага 4 м действуют силы равные 10 Н и 30 Н. Чтобы получить состояние равновесия мы должны расположить точку опоры на расстоянии А) 3 … 00 см от 30Н В) 100 см от 30 Н Б) 3 м от 10 Н Г) 1 м от 10 Н 10 points!!!
Перед рассеивающей линзой с фокусным расстоянием 0,3 м на расстоянии 15 см от нее поставлен предмет. На каком расстоянии от линзы получается его изобр … ажение?Дано: SI:Решение:
8. Рисунок 1 = 2 м h = 1 м F = 200H P = 300H. 8.1) Что такое простой механизм? 8.2) Полезная работа 8.3) Полная трость, выполняемая рабочим 8.4) Опред … елить КПД механизмаДАМ 20 БАЛЛОВ
Потяг рухається зі швидкістю 30 м/с. Скільки часу триватиме подорож якщо відстань між двома містами дорівнює 765 км
Скільки часу триватиме подорож якщо відстань між двома містами дорівнює 765 км
Решите пожалуйста!!!
Помогите плиз с физикой 7 класс. Фейкответы баню.
КРОССВОРД «ПовтоРИМ ПРОЙДЕННОЕПо горизонтали:1. Воздушный шар, предназначенный дляполетов в стратосферу. 2. Газовая оболочка,окружающая Землю. 3. Отно … шение силы дав-ления к площади. 4. Прибор для измерениядавления, большего или меньшего атмосфер-ного. 5. Единица давления. 6. Инструмент длявзятия проб различных жидкостей. 7. Баро-метрический высотомер, используемый в авиа-ции.По вертикали:1. Масса воды, вытесняемой плавающим суд-ном. 2. Судно, приводимое в движение с по-мощью двигателя внутреннего сгорания.Глубина, на которую плавающее судноПогружается в воду. 4. Летательныйаппарат,применяемый в воздухоплавании. 5. ПриборДля измерения атмосферного давления.
Лабораторная работа«Измерение жесткости пружины» | Методическая разработка по физике на тему:
Слайд 1
Лабораторная работа «Измерение жесткости пружины» Учитель физики ГБОУ СОШ №145 Калининского района Санкт- Петербурга Карабашьян М. В.
В.Слайд 2
проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины. Цель работы Оборудование : набор «Механика» из комплекта L-micro- штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузов известной массы (по 50 г), линейка с миллиметровыми делениями.
Слайд 3
Подготовительные вопросы Что такое сила упругости? Как вычислить силу упругости, возникающую в пружине при подвешивании к ней груза массой m кг? Что такое удлинение тела? Как измерить удлинение пружины при подвешивании к ней груза? В чем заключается закон Гука?
Слайд 4
Правила техники безопасности Будьте осторожны при работе с растянутой пружиной. Не роняйте и не бросайте грузы.
Слайд 5
Описание работы: Согласно закону Гука, модуль F силы упругости и модуль х удлинения пружины связаны соотношением F = kx . Измерив F и х , можно найти коэффициент жесткости k по формуле
Слайд 6
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения \ х\ . При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F yпp =k\x\ . Это связано с погрешностями измерений. В этом случае график надо проводить так, чтобы примерно одинаковое число точек, оказалось, по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика) определите по нему соответствующие этой точке значения силы упругости и удлинения, и вычислите жесткость k . Она и будет искомым средним значением жесткости пружины k ср .
е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения \ х\ . При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F yпp =k\x\ . Это связано с погрешностями измерений. В этом случае график надо проводить так, чтобы примерно одинаковое число точек, оказалось, по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика) определите по нему соответствующие этой точке значения силы упругости и удлинения, и вычислите жесткость k . Она и будет искомым средним значением жесткости пружины k ср .
Слайд 7
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком). 2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями. 3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины. 4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины. 5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение \ х\ пружины. По результатам измерений заполните таблицу ХОД РАБОТЫ:
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями. 3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины. 4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины. 5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение \ х\ пружины. По результатам измерений заполните таблицу ХОД РАБОТЫ:
Слайд 8
№ опыта m, кг mg, H х , м 1 0,1 2 0,2 3 0,3 4 0,4
Слайд 9
6. Начертите оси координат х и F, выберите удобный масштаб и нанесите полученные экспериментальные точки. 7. Оцените (качественно) справедливость закона Гука для данной пружины: находятся ли экспериментальные точки вблизи одной прямой, проходящей через начало координат. 8. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k ср . 9. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k cp 10. Запишите сделанный вами вывод.
Запишите сделанный вами вывод.
Слайд 10
Контрольные вопросы: Как называется зависимость между силой упругости и удлинением пружины? Пружина динамометра под действием силы 4Н удлинилась на 5 мм. Определите вес груза, под действием которого эта пружина удлиняется на 16 мм.
1.1-01. Закон Гука. — Лабораторная экспериментальная площадка для школьников
В данной работе Вы изучите упругое растяжение нескольких пружин под действием силы тяжести. Проведёте серию экспериментов для нахождения коэффициента жёсткости этих пружин. В ходе эксперимента увидите влияние массы пружины на растяжение и как его можно учесть при проведении эксперимента. Дополнительным заданием будет определение коэффициента жёсткости системы пружин при параллельном и последовательном соединении.
Теоретический минимум: закон Гука, сила, сила упругости, сила тяжести, ускорение свободного падения, масса, коэффициент жёсткости, деформация, упругая деформация, неупругая деформация.
Лабораторная работа рекомендуется для учащихся 8, 9 классов.
Краткое методическое описание.
Цель работы:Познакомиться с законом Гука на примере деформации пружин. Определить жёсткость двух или более пружин, проверить линейную зависимость силы упругости от удлинения пружины. Научиться проводить измерения и обрабатывать экспериментальные данные.
Порядок выполнения лабораторной работы:Задание. Измерение жёсткости пружин №1 и №2.
- Закрепить пружину №1 на стержне с крючком и отметить на шкале с помощью курсора нижний край пружины.
- Подобрать начальную массу груза, и измерить его массу вместе с держателем для груза.
- Подвесить держатель с грузом на нижний край пружины.
- Отметить вторым курсором положение нижнего края пружины после её растяжения под действием силы тяжести.
- Определить растяжение пружины и внести измеренные величины в таблицу.

Таблица 1. Экспериментальные данные. № m, г Fт, Н x0, мм x’, мм l, 10-3м … … … … … … - Добавить груз на держатель и повторить пункты 3-5. Провести измерения для 5 разных масс.
- Построить график зависимости силы от удлинения пружины.
- По графику определить жёсткость пружины.
- Оценить погрешность измерений и полученной величины.
- Закрепить пружину №2 и повторить пункты 1-9 для второй пружины.
Дополнительное задание. Параллельное и последовательное соединение пружин.
- Закрепить параллельно пружины №1 и №2 и повторить задание «Измерение жёсткости пружин №1 и №2» для параллельного соединения пружин.

- Закрепить последовательно пружины №1 и №2 и повторить задание «Измерение жёсткости пружин №1 и №2» для последовательно соединения пружин.
- Провести расчёт жёсткости систем при последовательном и параллельном соединении пружин и сравнить результаты с экспериментальными данными.
Метки: 8 класс, 9 класс
Лабораторная работа «Экспериментальная проверка закона Гука» Цели работы: проверить справедливость закона Гука для пружины и измерить жесткость этой пружины. Оборудование: штатив с муфтой и зажимом, пружина, набор грузов известной массы (по 100 г), линейка с миллиметровыми делениями. Описание работы Согласно закону Гука модуль F силы упругости и модуль x удлинения пружины связаны соотношением F=kx. Ход работы
| Лабораторная работа «Экспериментальная проверка закона Гука» Цели работы: проверить справедливость закона Гука для пружины и измерить жесткость этой пружины. Оборудование: штатив с муфтой и зажимом, пружина, набор грузов известной массы (по 100 г), линейка с миллиметровыми делениями. Описание работы Согласно закону Гука модуль F силы упругости и модуль x удлинения пружины связаны соотношением F=kx. Измерив F и x, можно найти жесткость k по формуле k=F/x (1). Ход работы
|
Лабораторная работа № 2 «Измерение жесткости пружины» — Динамика — МЕХАНИКА — ВСЕ УРОКИ ФИЗИКИ 10 класс — конспекты уроков — План урока — Конспект урока — Планы уроков — разработки уроков по физике
1-й семестр
МЕХАНИКА
2. Динамика
Динамика
Урок 13/33
Тема. Лабораторная работа № 2 «Измерение жесткости пружины»
Цель урока: проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины
Тип урока: контроля и оценивания знаний
Оборудование: штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузиков известной массы (по 100 г), линейка с миллиметровыми делениями
ХОД РАБОТЫ
1. Закрепите динамометр в штативе на достаточно большой высоте.
2. Подвешивая разное количество грузиков (от одного до четырех), вычислите для каждого случая соответствующее значение F = mg, а также измерьте соответствующее удлинение пружины х.
3. Результаты измерений и вычислений запишите в таблицу:
№ опыта |
m, кг |
mg, Н |
х, м |
1 |
0,1 |
|
|
2 |
0,2 |
|
|
3 |
0,3 |
|
|
4 |
0,4 |
|
|
4. Начертите оси координат х и F, выберите удобный масштаб и нанесите полученные во время эксперимента точки.
Начертите оси координат х и F, выберите удобный масштаб и нанесите полученные во время эксперимента точки.
5. Оцените (качественно) справедливость закона Гука для данной пружины: приближаются экспериментальные точки одной прямой, проходящей через начало координат.
6. Вычислите коэффициент жесткости по формуле k = F/x, используя результаты опыта № 4 (это обеспечивает наибольшую точность).
7. Для вычисления погрешности следует использовать опыт, который мы получили во время поведення опыта № 4, потому что ему соответствует наименьшая относительная погрешность измерений. Вычислите пределы Fmin и Fmax, в которых находится истинное значение F, считая, что Fmin = F — ΔF, F = F + ΔF. Примите ΔF = 4Δm · g, где Δm — погрешность во время изготовления грузиков (для оценки можно считать, что Δm = 0,005 кг):
где Δх = 0,5 мм.
8. Пользуясь методом оценки погрешности косвенных измерений, вычислите:
9. Вычислите среднее значение kcep и абсолютную погрешность измерения Δk по формулам:
Вычислите среднее значение kcep и абсолютную погрешность измерения Δk по формулам:
10. Вычислите относительную погрешность измерений:
11. Заполните таблицу:
Fmin, H |
Fmax, H |
xmin, м |
xmax, м |
kmin, Н/м |
kmax, Н/м |
kсэр, Н/м |
Δk, Н/м |
εk |
|
|
|
|
|
|
|
|
|
12.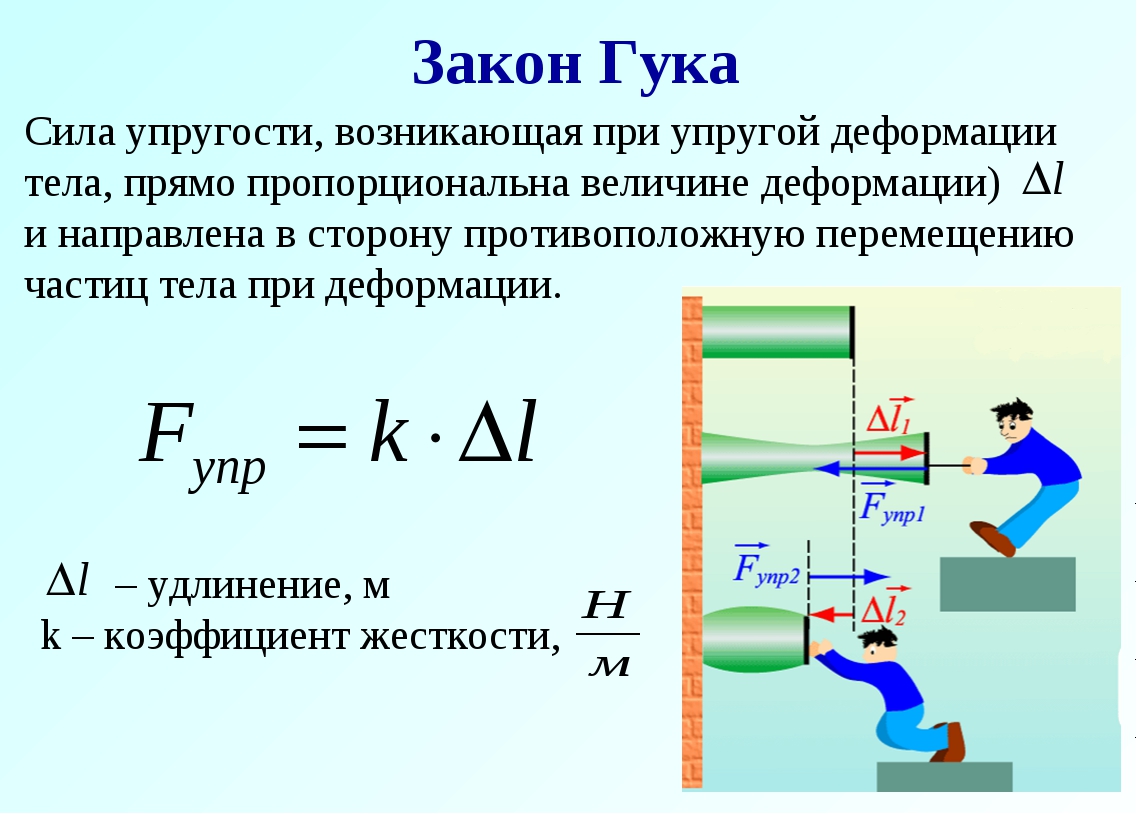 Запишите в тетради для лабораторных работ результат в виде k = kcep ± Δk, подставив в эту формулу числовые значения найденных величин.
Запишите в тетради для лабораторных работ результат в виде k = kcep ± Δk, подставив в эту формулу числовые значения найденных величин.
13. Запишите в тетради для лабораторных вывод: что вы измеряли и какой получили результат.
Напряжение и деформация) — X-Douglas College Physics 1107 Fall 2019 Custom Textbook
Сводка
- Закон штата Гука.
- Объясните закон Гука, используя графическое представление между деформацией и приложенной силой.
- Обсудить деформации, такие как изменение длины
- Определите изменение длины с учетом массы, длины и радиуса.
Силы могут повлиять на форму объекта. Если бульдозер втолкнет машину в стену, машина не двинется с места, но заметно изменит форму.Изменение формы из-за приложения силы — это деформация . Известно, что даже очень небольшие силы вызывают некоторую деформацию. При малых деформациях наблюдаются две важные характеристики. Во-первых, объект возвращается к своей исходной форме, когда сила снимается, то есть деформация является упругой для небольших деформаций. Во-вторых, размер деформации пропорционален силе, то есть для малых деформаций соблюдается закон Гука . В форме уравнения закон Гука определяется как
Во-первых, объект возвращается к своей исходной форме, когда сила снимается, то есть деформация является упругой для небольших деформаций. Во-вторых, размер деформации пропорционален силе, то есть для малых деформаций соблюдается закон Гука . В форме уравнения закон Гука определяется как
[латекс] \ boldsymbol {F = k \ Delta {L},} [/ латекс]
, где Δ L — величина деформации (например, изменение длины), создаваемая силой F , а k — константа пропорциональности, которая зависит от формы и состава объект и направление силы.Обратите внимание, что эта сила является функцией деформации Δ L — она не постоянна, как кинетическая сила трения. Иногда мы используем Δ x вместо Δ L. Деформация может происходить по любой оси. Переставляем это на
[латекс] \ boldsymbol {\ Delta {L} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {F} {k}} [/ latex]
дает понять, что деформация пропорциональна приложенной силе.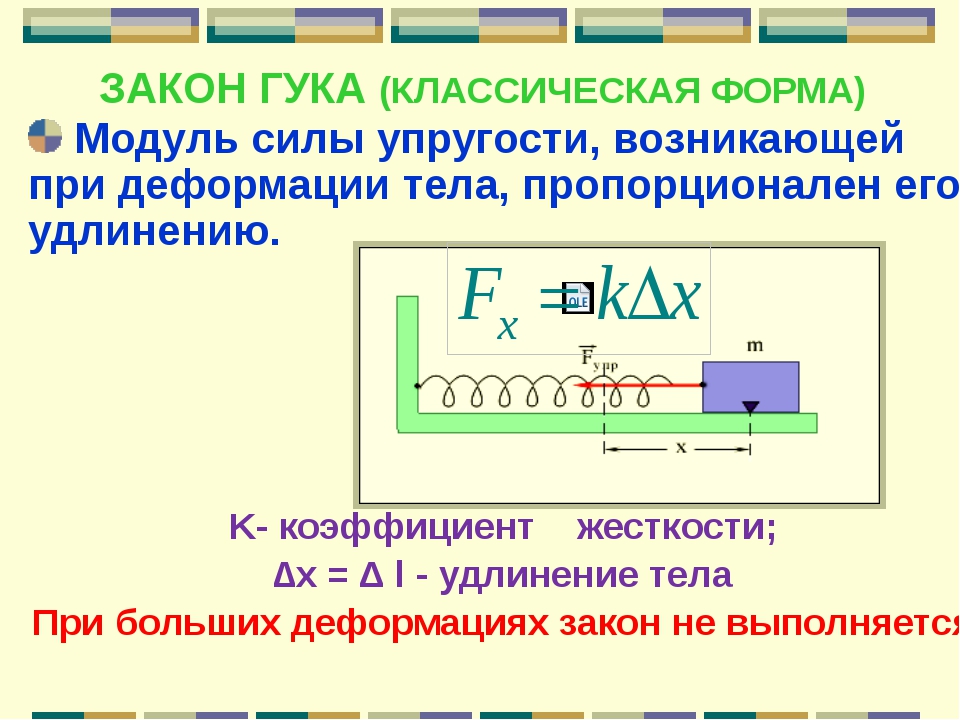 На рисунке 1 показано соотношение по закону Гука между удлинением Δ L пружины или человеческой кости. Для металлов или пружин область прямой линии, к которой относится закон Гука, намного больше. Кости хрупкие, эластичная область небольшая, а перелом резкий. В конце концов, достаточно большое напряжение материала приведет к его разрушению или разрушению. Предел прочности на разрыв — это разрушающее напряжение, которое вызывает остаточную деформацию или разрушение материала.
На рисунке 1 показано соотношение по закону Гука между удлинением Δ L пружины или человеческой кости. Для металлов или пружин область прямой линии, к которой относится закон Гука, намного больше. Кости хрупкие, эластичная область небольшая, а перелом резкий. В конце концов, достаточно большое напряжение материала приведет к его разрушению или разрушению. Предел прочности на разрыв — это разрушающее напряжение, которое вызывает остаточную деформацию или разрушение материала.
ЗАКОН КРЮКА
[латекс] \ boldsymbol {F = k \ Delta {L},} [/ латекс]
, где Δ L — величина деформации (например, изменение длины), создаваемая силой F , а k — константа пропорциональности, которая зависит от формы и состава объект и направление силы.
[латекс] \ boldsymbol {\ Delta {L} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {F} {k}} [/ latex]
Рисунок 1. График зависимости деформации Δ L от приложенной силы F . Прямой отрезок — это линейная область, в которой соблюдается закон Гука. Уклон прямого участка 1 / k . Для больших сил график изогнут, но деформация остается упругой — Δ L вернется к нулю, если сила будет устранена. Еще большие силы деформируют объект до тех пор, пока он не сломается. Форма кривой возле трещины зависит от нескольких факторов, в том числе от того, как прикладывается сила F .Обратите внимание, что на этом графике наклон увеличивается непосредственно перед трещиной, указывая на то, что небольшое увеличение F дает большое увеличение L рядом с трещиной.
График зависимости деформации Δ L от приложенной силы F . Прямой отрезок — это линейная область, в которой соблюдается закон Гука. Уклон прямого участка 1 / k . Для больших сил график изогнут, но деформация остается упругой — Δ L вернется к нулю, если сила будет устранена. Еще большие силы деформируют объект до тех пор, пока он не сломается. Форма кривой возле трещины зависит от нескольких факторов, в том числе от того, как прикладывается сила F .Обратите внимание, что на этом графике наклон увеличивается непосредственно перед трещиной, указывая на то, что небольшое увеличение F дает большое увеличение L рядом с трещиной. Константа пропорциональности k зависит от ряда факторов для материала. Например, гитарная струна из нейлона растягивается при затягивании, и удлинение Δ L пропорционально приложенной силе (по крайней мере, для небольших деформаций). Более толстые нейлоновые и стальные струны меньше растягиваются при одной и той же приложенной силе, что означает, что они имеют большее значение k (см. Рисунок 2). Наконец, все три струны возвращаются к своей нормальной длине, когда сила снимается, при условии, что деформация мала. Большинство материалов будут вести себя таким образом, если деформация будет меньше примерно 0,1% или примерно 1 часть на 10 3 .
Более толстые нейлоновые и стальные струны меньше растягиваются при одной и той же приложенной силе, что означает, что они имеют большее значение k (см. Рисунок 2). Наконец, все три струны возвращаются к своей нормальной длине, когда сила снимается, при условии, что деформация мала. Большинство материалов будут вести себя таким образом, если деформация будет меньше примерно 0,1% или примерно 1 часть на 10 3 .
НЕМНОГО РАСТЯНИСЬ
Как бы вы измерили константу пропорциональности k резиновой ленты? Если резинка растянулась на 3 см, когда к ней была прикреплена 100-граммовая масса, то насколько она растянулась бы, если бы две одинаковые резинки были прикреплены к одной и той же массе — даже если их соединить параллельно или, наоборот, если связать вместе последовательно?
Концептуальные вопросы
1: Чем лук и стрела похожи на пружину?
Задачи и упражнения
- Груз подвешен на вертикальной пружине так, что он оказывает направленное вниз усилие величиной 5.
 02 ньютона на пружине. Пружина растягивается на 0,0456 метра, когда к ней прикреплен груз. Что такое постоянная пружины в ньютон / м? Подсказка: Подвешенный означает висеть в воздухе, не двигаясь. Какова суммарная сила, действующая на неподвижную массу?
02 ньютона на пружине. Пружина растягивается на 0,0456 метра, когда к ней прикреплен груз. Что такое постоянная пружины в ньютон / м? Подсказка: Подвешенный означает висеть в воздухе, не двигаясь. Какова суммарная сила, действующая на неподвижную массу? - Амортизаторы моей машины имеют жесткость пружины 97 722 ньютон / метр. Когда некий человек садится в машину, он прикладывает к машине нисходящую силу в 987 ньютонов. Как далеко «вниз» переместится машина после того, как они сядут в нее? (Посмотрите фильм «Работа по-итальянски» и узнайте, как они использовали этот тип физики, чтобы выяснить, какой грузовик на самом деле перевозил золото.)
- Пружинные весы имеют жесткость пружины 34,5 Н / м и растягиваются на 3,21 см, когда к ним присоединяется неизвестная масса. Какая сила в ньютонах приложена к пружине неизвестной массой?
- Если приложенная сила в 12 ньютонов растягивает определенную пружину на 4,0 сантиметра, сколько растяжения произойдет для приложенной силы в 18 ньютонов?
Решения
Задачи и упражнения
1) 110 Н / м
2) 0.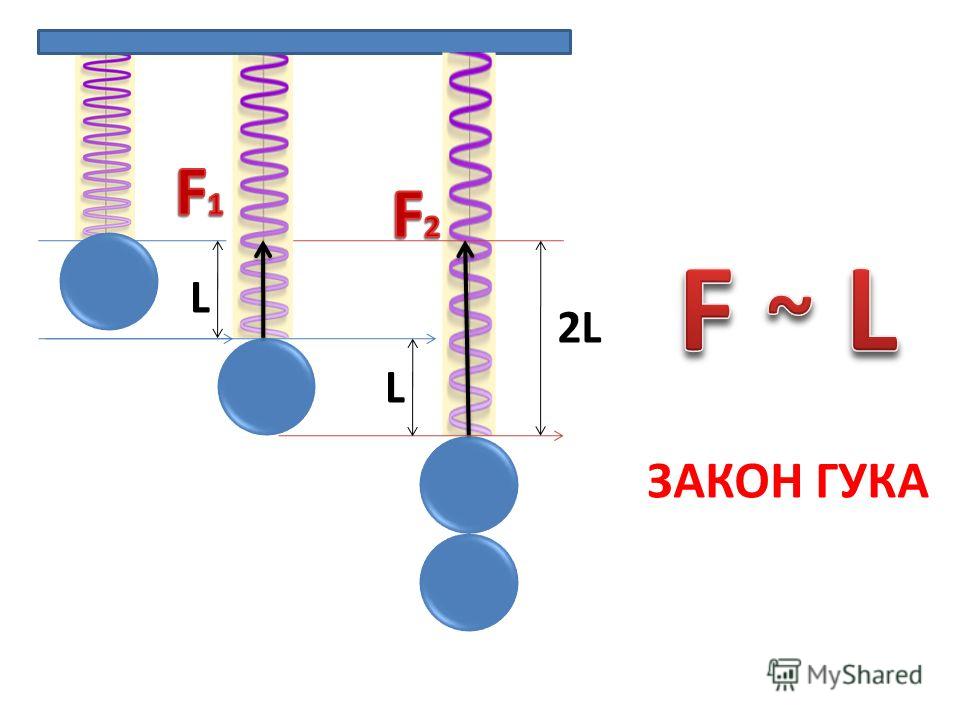 0101 м = 1,01 см
0101 м = 1,01 см
3) 1,11 ньютона
4) 6,0 см По соотношению и соотношению 12 Н / 4,0 см = 18 Н /? так ? = 18 х 4/12 =
Теперь рассмотрим тип деформации, вызывающий изменение длины (растяжение и сжатие). Существуют также боковые силы, вызывающие сдвиг (напряжение) и изменения объема, но мы не будем подробно останавливаться на них в этом курсе.
Изменение длины Δ L происходит, когда к проволоке или стержню прилагается сила, параллельная ее длине L 0 , либо растягивая (натяжение), либо сжимая.(См. Рисунок 3.)
Рис. 3. (a) Натяжение. Стержень растягивается на длину Δ L , когда сила прилагается параллельно его длине. (б) Сжатие. Тот же стержень сжимается силами той же величины в противоположном направлении. Для очень малых деформаций и однородных материалов Δ L примерно одинаково для одинаковой величины растяжения или сжатия. При больших деформациях площадь поперечного сечения изменяется при сжатии или растяжении стержня.
При больших деформациях площадь поперечного сечения изменяется при сжатии или растяжении стержня.Эксперименты показали, что изменение длины ( Δ L ) зависит только от нескольких переменных. Как уже отмечалось, Δ L пропорционально силе F и зависит от вещества, из которого сделан объект. Кроме того, изменение длины пропорционально исходной длине L 0 и обратно пропорционально площади поперечного сечения проволоки или стержня. Например, длинная гитарная струна растягивается больше, чем короткая, а толстая струна растягивается меньше, чем тонкая.Мы можем объединить все эти факторы в одно уравнение для Δ L :
[латекс] \ boldsymbol {\ Delta {L} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {Y} \ frac {\ vec {\ textbf {F}}} {A} } [/ latex] [латекс] \ boldsymbol {L_0}, [/ latex]
, где Δ L — изменение длины, F приложенная сила, Y — коэффициент, называемый модулем упругости или модулем Юнга, который зависит от вещества, A — это площадь поперечного сечения, а L 0 — исходная длина.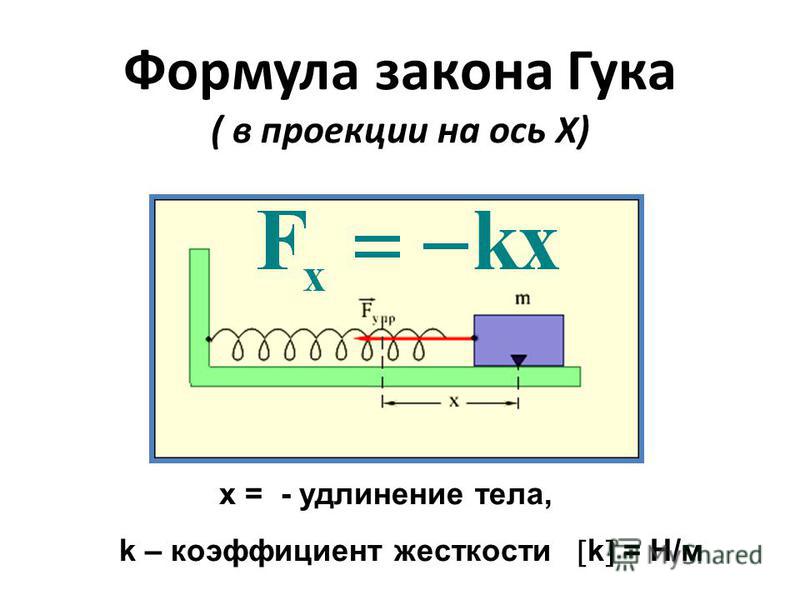 2)} [/ латекс]
2)} [/ латекс]
 7
7Модули Юнга не указаны для жидкостей и газов в таблице 3, потому что они не могут быть растянуты или сжаты только в одном направлении.Обратите внимание, что существует предположение, что объект не ускоряется, поэтому на самом деле существуют две приложенные силы величиной F , действующие в противоположных направлениях. Например, струны на Рисунке 3 тянут вниз силой величиной w и удерживаются за потолок, который также оказывает силу величиной w .
Пример 1: Растяжение длинного кабеля
Подвесные тросы используются для перевозки гондол на горнолыжных курортах.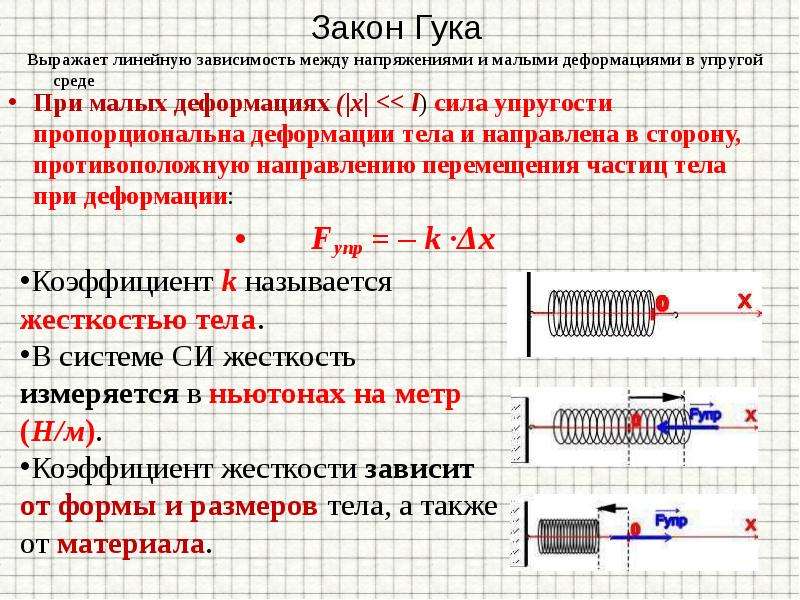 (См. Рис. 4). Рассмотрим подвесной трос, длина которого без опоры составляет 3 км. Рассчитайте степень растяжения стального троса. Предположим, что кабель имеет диаметр 5,6 см и максимальное выдерживаемое натяжение составляет 3,0 × 10 6 N .
(См. Рис. 4). Рассмотрим подвесной трос, длина которого без опоры составляет 3 км. Рассчитайте степень растяжения стального троса. Предположим, что кабель имеет диаметр 5,6 см и максимальное выдерживаемое натяжение составляет 3,0 × 10 6 N .
Стратегия
Сила равна максимальному натяжению, или F = 3.2}) (3020 \ textbf {m})} [/ latex]
[латекс] \ boldsymbol {= 18 \ textbf {m}}. [/ Латекс]
Обсуждение
Это довольно большая длина, но она составляет всего 0,6% от длины без опоры. В этих условиях влияние температуры на длину может быть важным.
Кости в целом не ломаются от растяжения или сжатия. Скорее они обычно ломаются из-за бокового удара или изгиба, что приводит к срезанию или разрыву кости. Поведение костей при растяжении и сжатии важно, потому что оно определяет нагрузку, которую кости могут нести. Кости классифицируются как несущие конструкции, такие как колонны в зданиях и деревья. Несущие конструкции обладают особенностями; колонны в здании имеют стальные арматурные стержни, а деревья и кости — волокнистые. Кости в разных частях тела выполняют разные структурные функции и подвержены разным нагрузкам. Таким образом, кость в верхней части бедренной кости расположена в виде тонких листов, разделенных костным мозгом, в то время как в других местах кости могут быть цилиндрическими и заполненными костным мозгом или просто твердыми.Люди с избыточным весом имеют тенденцию к повреждению костей из-за длительного сжатия костных суставов и сухожилий.
Кости классифицируются как несущие конструкции, такие как колонны в зданиях и деревья. Несущие конструкции обладают особенностями; колонны в здании имеют стальные арматурные стержни, а деревья и кости — волокнистые. Кости в разных частях тела выполняют разные структурные функции и подвержены разным нагрузкам. Таким образом, кость в верхней части бедренной кости расположена в виде тонких листов, разделенных костным мозгом, в то время как в других местах кости могут быть цилиндрическими и заполненными костным мозгом или просто твердыми.Люди с избыточным весом имеют тенденцию к повреждению костей из-за длительного сжатия костных суставов и сухожилий.
Другой биологический пример закона Гука встречается в сухожилиях. Функционально сухожилие (ткань, соединяющая мышцу с костью) должно сначала легко растягиваться при приложении силы, но обеспечивать гораздо большую восстанавливающую силу для большего напряжения. На рисунке 5 показана зависимость напряжения от деформации человеческого сухожилия.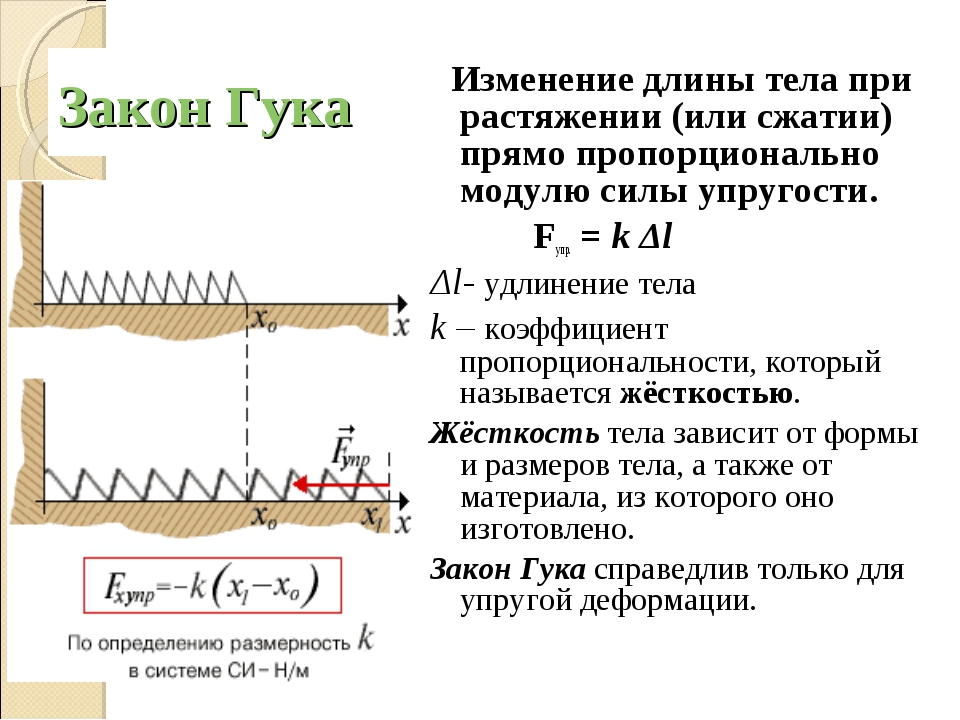 Некоторые сухожилия имеют высокое содержание коллагена, поэтому деформация или изменение длины относительно невелико; другие, например, опорные сухожилия (например, в ноге) могут изменять длину до 10%.Обратите внимание, что эта кривая напряжения-деформации является нелинейной, поскольку наклон линии изменяется в разных областях. В первой части растяжения, называемой областью пальца, волокна сухожилия начинают выравниваться в направлении напряжения — это называется разжим . В линейной области фибриллы будут растянуты, а в области разрушения отдельные волокна начнут разрываться. Простую модель этой взаимосвязи можно проиллюстрировать параллельными пружинами: разные пружины активируются при разной длине растяжения.Примеры этого приведены в задачах в конце этой главы. Связки (ткань, соединяющая кость с костью) ведут себя аналогичным образом.
Некоторые сухожилия имеют высокое содержание коллагена, поэтому деформация или изменение длины относительно невелико; другие, например, опорные сухожилия (например, в ноге) могут изменять длину до 10%.Обратите внимание, что эта кривая напряжения-деформации является нелинейной, поскольку наклон линии изменяется в разных областях. В первой части растяжения, называемой областью пальца, волокна сухожилия начинают выравниваться в направлении напряжения — это называется разжим . В линейной области фибриллы будут растянуты, а в области разрушения отдельные волокна начнут разрываться. Простую модель этой взаимосвязи можно проиллюстрировать параллельными пружинами: разные пружины активируются при разной длине растяжения.Примеры этого приведены в задачах в конце этой главы. Связки (ткань, соединяющая кость с костью) ведут себя аналогичным образом.

В отличие от костей и сухожилий, которые должны быть прочными и эластичными, артерии и легкие должны быть легко растяжимыми. Эластичные свойства артерий важны для кровотока. Когда кровь выкачивается из сердца, давление в артериях увеличивается, и стенки артерий растягиваются.Когда аортальный клапан закрывается, давление в артериях падает, и артериальные стенки расслабляются, чтобы поддерживать кровоток. Когда вы чувствуете свой пульс, вы чувствуете именно это — эластичное поведение артерий, когда кровь хлынет через каждый насос сердца. Если бы артерии были жесткими, вы бы не почувствовали пульс. Сердце также является органом с особыми эластичными свойствами. Легкие расширяются за счет мышечного усилия, когда мы вдыхаем, но расслабляемся свободно и эластично, когда мы выдыхаем. Наша кожа особенно эластична, особенно для молодых.Молодой человек может подняться от 100 кг до 60 кг без видимого провисания кожи. С возрастом снижается эластичность всех органов. Постепенное физиологическое старение за счет снижения эластичности начинается в начале 20-х годов. 2}) (\ frac {607.{-5} \ textbf {m}}. [/ Latex]
2}) (\ frac {607.{-5} \ textbf {m}}. [/ Latex]
Обсуждение
Это небольшое изменение длины кажется разумным, поскольку мы знаем, что кости жесткие. Фактически, даже довольно большие силы, возникающие при напряженных физических нагрузках, не сжимают и не сгибают кости в больших количествах. Хотя кость жесткая по сравнению с жиром или мышцами, некоторые из веществ, перечисленных в таблице 3, имеют более высокие значения модуля Юнга Y . Другими словами, они более жесткие.
Уравнение изменения длины традиционно переставляют и записывают в следующем виде:
[латекс] \ boldsymbol {\ frac {F} {A}} [/ latex] [латекс] \ boldsymbol {= Y} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta {L}} {L_0 }}. [/ latex]
Отношение силы к площади, [латекс] \ boldsymbol {\ frac {F} {A}}, [/ latex] определяется как напряжение (измерено в Н / м 2 ), а соотношение изменения длины к длине, [латекс] \ boldsymbol {\ frac {\ Delta {L}} {L_0}}, [/ latex] определяется как деформация (безразмерная величина).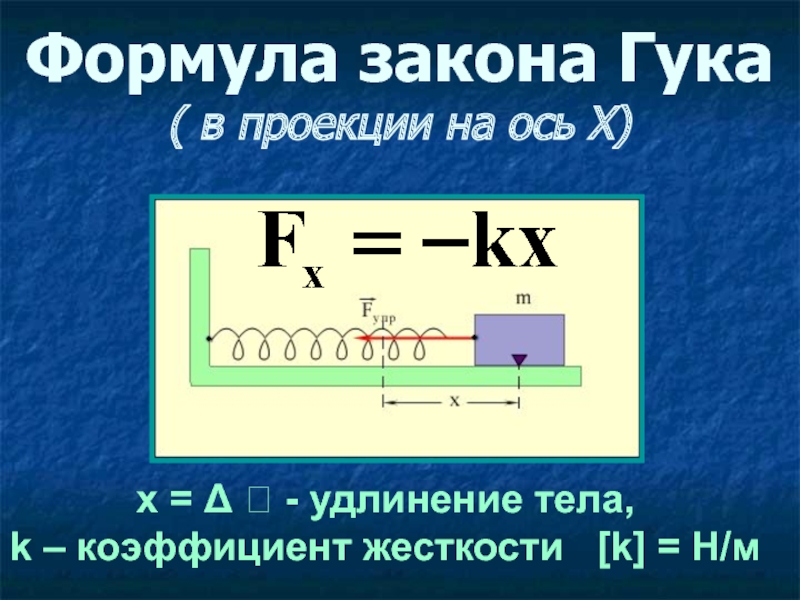 Другими словами,
Другими словами,
[латекс] \ boldsymbol {\ textbf {stress} = Y \ times \ textbf {stretch}}. [/ Latex]
В этой форме уравнение аналогично закону Гука с напряжением, аналогичным силе, и деформацией, аналогичной деформации. Если снова переписать это уравнение к виду
[латекс] \ boldsymbol {F = YA} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta {L}} {L_0}}, [/ латекс]
мы видим, что он совпадает с законом Гука с константой пропорциональности
[латекс] \ boldsymbol {k \: =} [/ latex] [латекс] \ boldsymbol {\ frac {YA} {L_0}}.[/ латекс]
Эта общая идея о том, что сила и вызываемая ею деформация пропорциональны небольшим деформациям, применима к изменениям длины, боковому изгибу и изменениям объема.
СТРЕСС
Отношение силы к площади, [латекс] \ boldsymbol {\ frac {F} {A}}, [/ latex] определяется как напряжение, измеренное в Н / м 2 .
ШТАМ
Отношение изменения длины к длине, [латекс] \ boldsymbol {\ frac {\ Delta {L}} {L_0}}, [/ latex], определяется как деформация (безразмерная величина). Другими словами,
Другими словами,
[латекс] \ boldsymbol {\ textbf {stress} = Y \ times \ textbf {stretch}}. [/ Latex]
- Закон Гука дан
[латекс] \ boldsymbol {F = k \ Delta {L}}, [/ latex] или [латекс] \ boldsymbol {F = k \ Delta {x}}, [/ latex]
, где Δ L — величина деформации (изменение длины), F — приложенная сила, а k — константа пропорциональности, которая зависит от формы и состава объекта. и направление силы.Соотношение между деформацией и приложенной силой также можно записать как
[латекс] \ boldsymbol {\ Delta {L} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {Y} \ frac {F} {A}} [/ латекс] [латекс] \ boldsymbol {L_0}, [/ латекс]
, где Y — это модуль Юнга , который зависит от вещества, A — площадь поперечного сечения, а L 0 — исходная длина.
- Отношение силы к площади, [латекс] \ boldsymbol {\ frac {F} {A}}, [/ latex] определяется как напряжение , измеренное в Н / м 2 .

- Отношение изменения длины к длине, [латекс] \ boldsymbol {\ frac {\ Delta {L}} {L_0}}, [/ latex] определяется как деформация (безразмерная величина). Другими словами,
[латекс] \ boldsymbol {\ textbf {stress} = Y \ times \ textbf {stretch}}. [/ Latex]
Концептуальные вопросы
1: Эластичные свойства артерий важны для кровотока. Объясните важность этого с точки зрения характеристик кровотока (пульсирующего или непрерывного).
2: Что вы чувствуете, когда прощупываете пульс? Измерьте частоту пульса в течение 10 с и 1 мин. Есть ли разница в 6 раз?
3: Изучите различные типы обуви, включая спортивную обувь и стринги. С точки зрения физики, почему нижние поверхности устроены именно так? Какие различия будут иметь для этих поверхностей сухие и влажные условия?
4: Ожидаете ли вы, что ваш рост будет различаться в зависимости от времени суток? Почему или почему нет?
5: Почему белка может прыгнуть с ветки дерева на землю и убежать целой, а человек может сломать кость при таком падении?
Задачи и упражнения
1: Во время циркового номера один артист качается вверх ногами, висит на трапеции, держа другого, также перевернутого, за ноги.Если восходящая сила, действующая на более низкую спортсменку, в три раза превышает ее вес, насколько растягиваются кости (бедра) в ее верхних конечностях? Вы можете предположить, что каждый из них эквивалентен одинаковому стержню длиной 35,0 см и радиусом 1,80 см. Ее масса 60,0 кг.
2: Во время схватки борец 150 кг ненадолго встает на одну руку во время маневра, призванного сбить с толку его и без того умирающего противника. Насколько укорачивается длина кости плеча? Кость может быть представлена однородным стержнем 38.0 см в длину и 2,10 см в радиусе.
3: (a) «Грифель» в карандашах — это графитовая композиция с модулем Юнга примерно 1 × 10 9 Н / м 2 . Вычислите изменение длины грифеля автоматического карандаша, если постучите им прямо по карандашу с усилием 4,0 Н. Грифель имеет диаметр 0,50 мм и длину 60 мм. б) разумен ли ответ? То есть согласуется ли это с тем, что вы наблюдали при использовании карандашей?
4: Антенны телевещания — самые высокие искусственные сооружения на Земле.В 1987 году физик весом 72,0 кг разместил себя и 400 кг оборудования на вершине одной антенны высотой 610 м для проведения гравитационных экспериментов. Насколько была сжата антенна, если считать ее эквивалентом стального цилиндра радиусом 0,150 м?
5: (a) Насколько альпинист весом 65,0 кг натягивает нейлоновую веревку диаметром 0,800 см, когда она висит на 35,0 м ниже выступа скалы? б) Соответствует ли ответ тому, что вы наблюдали для нейлоновых веревок? Имел бы смысл, если бы веревка была на самом деле тросиком?
7: По мере бурения нефтяной скважины каждая новая секция бурильной трубы выдерживает собственный вес, а также вес трубы и бурового долота под ней.Рассчитайте растяжение новой стальной трубы длиной 6,00 м, которая поддерживает 3,00 км трубы, имеющей массу 20,0 кг / м, и буровое долото 100 кг. Труба эквивалентна по жесткости сплошному цилиндру диаметром 5 см.
8: Рассчитайте усилие, которое настройщик рояля применяет для растяжения стальной рояльной проволоки на 8,00 мм, если изначально проволока имеет диаметр 0,850 мм и длину 1,35 м.
12: Чтобы рассмотреть влияние проводов, подвешенных на столбах, мы возьмем данные из главы 4.7 Пример 2, в котором были рассчитаны натяжения проводов, поддерживающих светофор. Левая проволока образовывала угол 30,0 ° ниже горизонтали с верхней частью своего столба и выдерживала натяжение 108 Н. Полый алюминиевый столб высотой 12,0 м эквивалентен по жесткости сплошному цилиндру диаметром 4,50 см. а) Насколько он наклонен в сторону? б) Насколько он сжат?
15: Эта проблема возвращается к канатоходцу, изученному в главе 4.5, пример 2, который создал натяжение 3.94 × 10 3 Н в тросе, имеющем угол 5,0 ° ниже горизонтали с каждой опорной стойкой. Подсчитайте, насколько это натяжение растягивает стальную проволоку, если изначально она была 15 м в длину и 0,50 см в диаметре.
Сноски
- Приблизительные и средние значения. Модули Юнга Y для растяжения и сжатия иногда различаются, но здесь они усреднены. Кость имеет существенно разные модули Юнга для растяжения и сжатия.
Глоссарий
- деформация
- изменение формы из-за приложения силы
- Закон Гука
- пропорциональная зависимость между силой F на материале и деформацией Δ L , которую она вызывает, F = k Δ L
- предел прочности
- разрушающее напряжение, которое вызовет остаточную деформацию или часть материала
- напряжение
- отношение силы к площади
- штамм
- отношение изменения длины к исходной длине
- деформация сдвига
- деформация перпендикулярно исходной длине объекта
Решения
Задачи и упражнения
1: [латекс] \ boldsymbol {1.2}. [/ Latex] Это примерно 36 атм, больше, чем может выдержать обычная банка.
15: $$ \ boldsymbol {1.4 \ textbf {cm}} $$
Лаборатория закона Гука
Аннотация
Сегодня вы исследуете взаимосвязь между силой, приложенной к пружине, и расстоянием, на которое она растягивается — это соотношение называется законом Гука. На этой неделе в классе вы подробно обсудите пружины. На следующей неделе в лаборатории вы определите, подчиняется ли резинка закону Гука.
ДЕНЬ ПЕРВЫЙ
Предварительные упражнения
Опишите метод измерения силы, прилагаемой пружиной, когда пружина растягивается. Для этого метода вы можете использовать любое общедоступное оборудование.
Цели
После завершения сегодняшнего эксперимента вы сможете:
- Опишите словами из своего опыта, как сила, прикладываемая пружиной, соотносится с ее растяжением
- Свяжите свой эксперимент с будущим обсуждением в классе закона Гука
- Обсудить относительные достоинства нескольких методов измерения силы
Материалы / процедура:
Вы должны построить график, который поясняет взаимосвязь между силой, прилагаемой пружиной, F , и расстоянием, на которое пружина растягивается, x .
Вы можете использовать любое оборудование, имеющееся в лаборатории.
Безопасность и утилизация
Если исходить из здравого смысла лабораторных протоколов (т.е. не стрелять друг другу в глаза резиновыми лентами!), Единственная проблема безопасности возникает, когда пружины или резиновые ленты растягиваются почти до предела своей конструкции. В этом случае пригодятся защитные очки.
Лабораторные советы:
Сила F , приложенная к пружине, может быть измерена различными способами с использованием различных материалов.Будь креативным. Вы можете использовать свой ответ на предварительное упражнение; вы можете запросить предложения у других групп.
Для каждой приложенной силы измерьте расстояние x , на котором пружина растянута на от ее исходного , нерастянутого положения. Линейка или измерительная линейка будут наиболее эффективным инструментом для измерения этого расстояния.
Данные / наблюдения
Хотя вам не следует ломать пружину, убедитесь, что вы проверили широкий диапазон перемещений.
Для некоторых пружин график может быть нелинейным при малых перемещениях. Иногда это происходит потому, что катушки слипаются. Если это произойдет, допустимо приложить ровно столько силы, чтобы разложить катушки, а затем переопределить положение равновесия до точки, где катушки едва разделяются.
Это будет вам на пользу экспериментам других групп. Обратите внимание, какие другие возможные методы измерения силы вы видите. Также обратите внимание на сходства и различия между вашей пружиной и пружинами других групп.
Анализ
Вероятно, вы обнаружите линейную зависимость между силой и смещением. Определите и укажите наклон вашего графика (конечно, с соответствующими единицами измерения!).
Наклон графика F по сравнению с x называется жесткостью пружины и обозначается переменной k .
Прежде чем отвечать на вопросы для обсуждения, поделитесь данными как минимум с двумя другими группами. В записной книжке запишите постоянные пружины, определенные этими двумя другими группами.Будьте осторожны с единицами измерения — для корректного сравнения все константы пружины должны быть помещены в одни и те же единицы. Также будет полезно написать краткое описание пружин других групп, обращая внимание на то, чем их пружины отличаются от ваших.
Вопросов к ответу:
- Опишите словами, что жесткость пружины говорит вам о пружине. Включите в свое обсуждение конкретную ссылку на пружины других групп (и их пружинные константы).
- В подвеске автомобиля (или поезда) колесо в сборе соединено с пассажирским салоном с помощью нескольких пружин.Возможно, вы даже видели эти источники раньше. Прокомментируйте, как жесткость пружины автоматической пружины сравнивается с жесткостью пружины, которую вы измерили сегодня.
ДЕНЬ ВТОРОЙ
Предварительные упражнения
Опишите метод, с помощью которого можно определить, подчиняется ли резинка закону Гука. Вы можете использовать любое доступное лабораторное оборудование.
Цели
После сегодняшнего эксперимента вы сможете:
- Примените свое понимание закона Гука к неканоническим ситуациям
- Интерпретировать график, который не представляет собой простую математическую функцию
- Объясните пределы действия закона Гука
Материалы / процедура:
Вы должны определить, подчиняется ли подаренная вам резинка закону Гука.Вы можете использовать любое имеющееся в лаборатории оборудование.
Лабораторные советы:
Обязательно проверьте широкий диапазон перемещений.
Данные / наблюдения
Запишите любые данные и графики, которые вы считаете необходимыми, чтобы определить, подчиняется ли резинка закону Гука.
Как минимум, вы должны иметь возможность:
Обоснование отсутствия пружинной постоянной со ссылкой на лабораторию на прошлой неделе
или
Обоснуйте подчинение резиновой ленты закону Гука на основе графика
Обратите внимание, что ответ, скорее всего, будет более сложным, чем просто «да» или «нет».»
Анализ
Вы напишете очень краткий отчет об эксперименте на этой неделе. Ваш аккаунт будет состоять из двух абзацев:
Параграф 1: Эксперимент
Опишите, что вы измерили и как вы это измерили. Это должно занять не более трех-четырех предложений. Было бы полезно включить диаграмму, но диаграмма не заменяет словесное описание.
Параграф 2: Анализ
Укажите, подчиняется ли резинка закону Гука, и обоснуйте свой ответ ссылкой на свои данные.Помните, что ответ, скорее всего, будет более сложным, чем просто «да» или «нет».
Эта учетная запись должна быть очень короткой — она не может занимать больше, чем рукописную страницу. Итак, включите только существенной информации, которая поспособствовала вашему заключению. Удалите вспомогательные материалы, такие как списки оборудования или не относящуюся к делу информацию о процессе записи данных.
Грег Джейкобс преподает физику B и C в школе Вудберри Форест в центральной Вирджинии. Он выпускник Хаверфордского колледжа и имеет степень магистра инженерных наук Северо-Западного университета.Когда он не преподает, Грег транслирует по Интернету бейсбольные матчи университета Вудберри Форест; он репортер STATS, Inc., освещающий бейсбол, баскетбол и футбол; и он является читателем и консультантом программы AP Physics Совета колледжей. Грег живет в кампусе Вудберри со своей женой Шари и сыном Майло Себу.
% PDF-1.5 % 4 0 obj > эндобдж xref 4 187 0000000016 00000 н. 0000004525 00000 н. 0000004633 00000 н. 0000005621 00000 н. 0000005655 00000 н. 0000006096 00000 н. 0000010258 00000 п. 0000014181 00000 п. 0000018069 00000 п. 0000018429 00000 п. 0000018578 00000 п. 0000018733 00000 п. 0000023037 00000 п. 0000025250 00000 п. 0000025527 00000 п. 0000027682 00000 п. 0000027810 00000 н. 0000027966 00000 н. 0000028122 00000 п. 0000028282 00000 п. 0000028438 00000 п. 0000028566 00000 п. 0000028878 00000 п. 0000029153 00000 п. 0000029525 00000 п. 0000030002 00000 п. 0000030386 00000 п. 0000030887 00000 п. 0000031423 00000 п. 0000031551 00000 п. 0000031863 00000 п. 0000032126 00000 п. 0000032309 00000 п. 0000032482 00000 н. 0000032741 00000 п. 0000032904 00000 п. 0000033032 00000 п. 0000033160 00000 п. 0000033288 00000 п. 0000035464 00000 п. 0000039586 00000 п. 0000042234 00000 п. 0000042347 00000 п. 0000042377 00000 п. 0000042449 00000 п. 0000043962 00000 п. 0000044289 00000 п. 0000044352 00000 п. 0000044466 00000 п. 0000044496 00000 п. 0000044568 00000 п. 0000055158 00000 п. 0000055482 00000 п. 0000055545 00000 п. 0000055659 00000 п. 0000055774 00000 п. 0000055887 00000 п. 0000055998 00000 п. 0000056067 00000 п. 0000056146 00000 п. 0000057213 00000 п. 0000057455 00000 п. 0000057612 00000 п. 0000057637 00000 п. 0000057933 00000 п. 0000058002 00000 п. 0000058081 00000 п. 0000059217 00000 п. 0000059459 00000 п. 0000059620 00000 п. 0000059645 00000 п. 0000059948 00000 н. 0000060017 00000 п. 0000060096 00000 п. 0000061199 00000 п. 0000061441 00000 п. 0000061598 00000 п. 0000061623 00000 п. 0000061920 00000 п. 0000061945 00000 п. 0000062242 00000 п. 0000062267 00000 п. 0000062564 00000 н. 0000062589 00000 п. 0000062886 00000 п. 0000064686 00000 п. 0000065027 00000 п. 0000065400 00000 п. 0000065484 00000 п. 0000065869 00000 п. 0000066122 00000 п. 0000067096 00000 п. 0000067377 00000 п. 0000068427 00000 н. 0000068695 00000 п. 0000068784 00000 п. 0000069121 00000 п. 0000069370 00000 п. 0000073746 00000 п. 0000074141 00000 п. 0000074605 00000 п. 0000074697 00000 п. 0000078513 00000 п. 0000078980 00000 п. 0000079504 00000 п. 0000081251 00000 п. 0000081573 00000 п. 0000081945 00000 п. 0000082029 00000 н. 0000085636 00000 п. 0000086072 00000 п. 0000086533 00000 п. 0000087722 00000 п. 0000088033 00000 п. 0000088379 00000 п. 0000106190 00000 п. 0000106439 00000 н. 0000106808 00000 п. 0000119526 00000 н. 0000119782 00000 н. 0000120100 00000 н. 0000121156 00000 н. 0000121387 00000 н. 0000122603 00000 н. 0000122834 00000 н. 0000123976 00000 н. 0000124015 00000 н. 0000124409 00000 н. 0000124448 00000 н. 0000125171 00000 н. 0000125210 00000 н. 0000125933 00000 н. 0000125972 00000 н. 0000126695 00000 н. 0000126734 00000 н. 0000127121 00000 н. 0000127218 00000 н. 0000127362 00000 н. 0000129154 00000 н. 0000129476 00000 н. 0000129839 00000 н. 0000130224 00000 н. 0000130297 00000 н. 0000130659 00000 н. 0000131298 00000 н. 0000131329 00000 н. 0000131402 00000 н. 0000132784 00000 н. 0000133112 00000 н. 0000133178 00000 п. 0000133294 00000 н. 0000134058 00000 н. 0000134097 00000 н. 0000138301 00000 н. 0000138340 00000 н. 0000138413 00000 н. 0000138444 00000 н. 0000138517 00000 н. 0000140392 00000 н. 0000140712 00000 н. 0000140778 00000 н. 0000140894 00000 н. 0000140967 00000 н. 0000141092 00000 н. 0000141385 00000 н. 0000141815 00000 н. 0000141888 00000 н. 0000142185 00000 н. 0000145267 00000 н. 0000145340 00000 н. 0000145639 00000 п. 0000145712 00000 н. 0000146011 00000 н. 0000146084 00000 н. 0000154607 00000 н. 0000161762 00000 н. 0000162142 00000 н. 0000162555 00000 н. 0000162944 00000 н. 0000163391 00000 н. 0000163464 00000 н. 0000163902 00000 н. 0000164324 00000 н. 0000164809 00000 н. 0000165307 00000 н. 0000166246 00000 н. 0000004036 00000 н. трейлер ] / Назад 169116 >> startxref 0 %% EOF 190 0 объект > поток htK [QKLbԐb> (@ * «P EbB- ⢎ «» «KpxA2tO ({@
Dynamics — эксперимент по закону Гука
Dynamics — эксперимент по закону ГукаНазначение:
- Для исследования закона Гука (связь между силой и растяжка для пружины)
- Для исследования законов Ньютона и действия пружины. шкала.
Обсуждение:
Всем известно, что когда вы прикладываете силу к пружине или резинка, она тянется. Ученый спросит: «Как сила что вы применяете в связи с количеством растяжки? »Этот вопрос был ответил Роберт Гук, современник Ньютона, и ответ стал называться законом Гука.
Закон Гука, хотите верьте, хотите нет, но очень важный и широко используемый закон в физике и технике.Его приложения идут далеко помимо пружин и резинок.
Вы можете исследовать закон Гука, измерив, сколько известных сил растянуть пружину. Удобный способ применения точно известной силы позволить вес известной массы быть силой, используемой для растяжения весна. Сила может быть рассчитана из W = mg. Протяженность пружину можно измерить, отметив положение конца пружина до и во время приложения силы.
Оснащение:
пружина | резинка | подставка для колец | |
Зажимы кольцевые | хомут | пружинная шкала | линейка или метр |
набор известных масс |
Указания по безопасности:
- Не допускайте попадания ног в зону какие массы упадут, если пружина или резинка порвутся!
- Обязательно прижмите кольцевую подставку к лабораторному столу или утяжелите ее. с несколькими книгами, чтобы масса не стягивала с Таблица.
- Вам нужно подвесить достаточно массы до конца пружины, чтобы получить
измеримое растяжение, но слишком большое усилие навсегда
Повреждение пружины . (Инженер сказал бы, что
превысил «предел упругости » ). «Ты сломаешь это, ты
купил. «
Процедура:
- Соберите устройство, как показано на схеме справа. Быть обязательно закрепите кольцевую подставку на лабораторном столе или утяжелите ее несколько книг.
- Создайте таблицу данных. Вам нужно будет записать массу, которая вы висите на пружине и положение конца пружины до и после добавления массы. Исходя из этого, вы рассчитаете сила, приложенная к пружине, и результирующее растяжение весна. Вы должны разрешить как минимум 8-10 попыток. (Пример данных таблица приведена ниже.)
- Для каждого испытания запишите массу, начальное положение пружина (перед навешиванием груза) и конечное положение пружина (пока она растягивается).
- Повторите процесс для резинки.
Результатов:
- Рассчитайте силу, прилагаемую к пружине / резиновой ленте в каждом испытание (W = мг) Используйте g = 9,8 м / с 2 .
- Рассчитайте растяжение пружины / резинки в каждом испытании. (разница в начальной и конечной позиции).
- Нарисуйте графики зависимости усилия от растяжения для пружины и резинка.Вы можете разместить оба графика на одном листе. миллиметровой бумаги, в зависимости от данных.
Выводы:
Закон Гука гласит, что растяжение пружины прямо пропорционально приложенной силе. (Инженеры говорят: «Стресс — это пропорционально деформации «. В символах F = kx, где F — сила, x — растяжение, а k — постоянная пропорциональности. Если Гука Закон верен, тогда график зависимости силы от растяжения будет прямая линия.
Подтверждают ли ваши результаты закон Гука или противоречат ему? Пожалуйста
разрабатывать.
Вопросы:
Осмотрите пружинную шкалу. Это простое устройство для измерения силы измеряя величину, на которую сила растягивает пружину.
- Повесьте объект (в состоянии покоя) на пружинных весах. Нарисуйте набор
диаграммы, показывающие все действующие силы:
- на объекте
- по пружинной шкале
- Какова чистая сила:
- объект?
- пружинная шкала?
- Силы, действующие на объект, равны и противоположны? Находятся они пара сил третьего закона Ньютона?
- Равны ли силы, действующие на пружинную шкалу, и противоположный? Являются ли они парой сил третьего закона Ньютона?
- Для каждой силы на диаграммах (вопрос 1) укажите ее «Партнер» третьего закона Ньютона.Обязательно укажите (а) что сила толкает или тянет, и (б) ее направление.
адаптировано из Робинсона, Лаборатория концептуальной физики Руководство , Addison-Wesley, Experiment 15, Tug-of-War
последнее обновление 6 ноября 2002 г., автор: JL Stanbrough
Напряжение, деформация и закон Гука — Урок
(0 оценок) Спасибо за оценку!Быстрый просмотр
Уровень оценки: 11 (10-12)
Требуемое время: 1 час 15 минут
Зависимость урока:
Тематические области: Физические науки, физика
Резюме
Студенты знакомятся с законом Гука, а также с отношениями стресс-напряжение.Сначала они изучают основные уравнения, затем работают над несколькими примерами задач, сначала индивидуально, а затем в классе. В ходе занятия, состоящего из двух частей, учащиеся: 1) изучают закон Гука путем экспериментального определения неизвестной жесткости пружины, а затем 2) применяют полученные знания для создания графика деформации, изображающего опухоль, с помощью Microsoft Excel®. После занятий урок завершается тестом на стресс-напряжение, чтобы оценить понимание понятий каждым учащимся.Инженерное соединение
Более 300 лет назад Роберт Гук определил пропорциональность, которая до сих пор остается фундаментальной концепцией для физиков и инженеров.Хотя его «закон» был установлен только для пружин, с тех пор он был применен ко всем материалам с известной площадью поверхности. Взаимосвязь, которую сегодня чаще всего используют, — это прямая пропорциональность между напряжением и напряжением. Вместе инженеры-строители, инженеры-механики и специалисты по материалам тщательно выбирают конструкционные материалы, которые способны безопасно выдерживать повседневные нагрузки, оставаясь при этом в упругой области кривой зависимости напряжения от деформации, в противном случае возникает необратимая деформация. Архитекторы, которые когда-то выбирали камень из-за его эстетической привлекательности, теперь выбирают сталь из-за ее долговечности.Для биомедицинских инженеров титан часто является материалом выбора из-за его биосовместимости и, что более важно, его способности выдерживать растягивающее и сжимающее напряжение веса тела. В предоставленном наборе задач учащиеся изучают приложения закона Гука и отношения напряжения и деформации. В частности, в задаче 7 студенты применяют эти отношения к тканям тела, как это сделали бы биомедицинские инженеры.
Цели обучения
После этого урока учащиеся должны уметь:
- Объясните концепции напряжения и деформации и взаимосвязь между ними.
- Объясните закон Гука и примените его для анализа пружин.
- Используйте Microsoft Excel®, чтобы построить простой график деформации.
- Соотнесите напряжение и деформацию с инженерной задачей устройства.
Образовательные стандарты
Каждый урок или задание TeachEngineering соотносится с одним или несколькими научными дисциплинами K-12, образовательные стандарты в области технологий, инженерии или математики (STEM).
Все 100000+ стандартов K-12 STEM, охватываемых TeachEngineering , собираются, обслуживаются и упаковываются сетью стандартов достижений (ASN) , проект D2L (www.achievementstandards.org).
В ASN стандарты иерархически структурированы: сначала по источникам; например , по штатам; внутри источника по типу; например , естественные науки или математика; внутри типа по подтипу, затем по классу, и т. д. .
Общие основные государственные стандарты — математика- Докажите, что для данной системы двух уравнений с двумя переменными замена одного уравнения суммой этого уравнения и кратным другим дает систему с такими же решениями.(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Используйте единицы как способ понять проблемы и направить решение многоэтапных проблем; последовательно выбирать и интерпретировать единицы в формулах; выбрать и интерпретировать масштаб и начало координат на графиках и дисплеях данных.(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Обобщение, представление и интерпретация данных по одному счету или измеряемой переменной
(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Обобщение, представление и интерпретация данных по двум категориальным и количественным переменным.
(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Телемедицина отражает конвергенцию технологических достижений в ряде областей, включая медицину, телекоммуникации, виртуальное присутствие, компьютерную инженерию, информатику, искусственный интеллект, робототехнику, материаловедение и психологию восприятия.(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Определите критерии и ограничения и определите, как они повлияют на процесс проектирования.(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Используйте компьютеры и калькуляторы для доступа, извлечения, организации, обработки, обслуживания, интерпретации и оценки данных и информации в целях общения.(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Используйте единицы как способ понять проблемы и направить решение многоэтапных проблем; последовательно выбирать и интерпретировать единицы в формулах; выбрать и интерпретировать масштаб и начало координат на графиках и дисплеях данных.(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Обобщение, представление и интерпретация данных по одному счету или измеряемой переменной
(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Обобщение, представление и интерпретация данных по двум категориальным и количественным переменным.
(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Докажите, что для данной системы двух уравнений с двумя переменными замена одного уравнения суммой этого уравнения и кратным другим дает систему с такими же решениями.(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
Какое альтернативное выравнивание вы предлагаете для этого контента?
Рабочие листы и приложения
Посетите [www.teachengineering.org/lessons/view/van_cancer_lesson2], чтобы распечатать или загрузить.Больше подобной программы
Механика упругого твердого телаУчащиеся вычисляют напряжение, деформацию и модуль упругости, а также узнают о типовой инженерной диаграмме напряжения-деформации (графике) упругого материала.
Эластичность и модуль Юнга для анализа тканейВ рамках процесса инженерного проектирования для создания тестируемых моделей сердечных клапанов учащиеся узнают о силах, действующих в человеческом теле, чтобы открывать и закрывать аортальные клапаны.Они узнают о силах кровотока, эластичности, напряжениях, деформациях, структуре клапана и свойствах тканей, а также о модуле Юнга, включая …
Применение закона Гука для обнаружения ракаСтуденты изучают закон Гука, работая в небольших группах на своих лабораторных скамьях.Они собирают данные о смещении пружин с неизвестной константой пружины k путем добавления различных масс известного веса.
Напряженная и деформированнаяСтуденты знакомятся с концепциями стресса и напряжения с примерами, которые иллюстрируют характеристики и важность этих сил в нашей повседневной жизни.Они исследуют факторы, влияющие на стресс, почему инженеры должны знать о нем, и способы, которыми инженеры описывают силу материи …
Предварительные знания
Базовые знания алгебры и способность решать простые алгебраические выражения. Кроме того, понимание проблемы обнаружения рака, представленной на предыдущем уроке.
Введение / Мотивация
В сегодняшнем уроке мы начнем узнавать о законе Гука, а затем узнаем, как применить эту пропорциональность к тканям тела. Мы точно узнаем, что описывают термины «напряжение» и «деформация», а также взаимосвязь между ними. После изучения материала урока я раздам раздаточный материал с примерами задач. Сначала проработайте их в меру своих возможностей независимо; затем мы рассмотрим проблемы всем классом.
После знакомства с использованием новых уравнений мы исследуем закон Гука в соответствующей деятельности (Применение закона Гука к обнаружению рака) путем экспериментального определения неизвестной константы пропорциональности. После изучения закона Гука во второй части упражнения мы начнем применять полученные знания для разработки средств визуализации тканей тела, и вскоре мы сможем обнаруживать злокачественные опухоли!
Вы также попрактикуетесь в графическом отображении подготовленных данных для изображения раковой ткани.После того, как мы усвоим этот материал, у нас будет тест на стресс, деформацию и закон Гука. Пожалуйста, делайте подробные записи и обязательно задавайте любые вопросы о примерах проблем, над которыми мы будем работать.
Возвращаясь к унаследованному циклу, который мы обсуждали в предыдущем уроке, сегодняшний урок представляет собой фазу исследования и пересмотра. Вернитесь к своим первоначальным заметкам с мыслями и запишите любую новую информацию, которая применима к решению проблемы. Ваша цель сегодня — пересмотреть, пересмотреть и расширить свои текущие знания! Теперь давайте узнаем, как обнаружить рак.
Предпосылки и концепции урока для учителей
Устаревшая информация цикла
Этот урок относится к этапу «Исследование и пересмотр » традиционного цикла. Студенты начинают изучать основные концепции, необходимые для построения графика деформации для изображения раковой ткани. После этого урока попросите учащихся пересмотреть свои первоначальные мысли, а по завершении соответствующего задания учащиеся должны обладать навыками, необходимыми для Go Public с решением.Но до того, как станет общедоступным , попросите учащихся пройти тест на стресс, напряжение и закон Гука в рамках фазы Test Your Mettle традиционного цикла. Викторина служит формирующей оценкой, в то время как этап Go Public следующего урока представляет собой итоговую оценку.
Информация о лекции
В конце 1600-х годов Роберт Гук заявил, что «сила любого упругого тела находится в той же пропорции, что и расширение». Хотя закон Гука остался в силе и сегодня, его формулировка была исправлена, заменив власть силой.Этот закон объясняется прямой пропорциональностью между сжатием или расширением пружины и возникающей восстанавливающей силой. Соотношение задается следующим образом: F = -k * Δx , где Δx — это расстояние, на которое была растянута пружина, F — возвращающая сила, прикладываемая пружиной, а k — жесткость пружины, которая характеризует упругие свойства материал пружины. Этот закон действует в пределах упругости линейной пружины, когда она действует по поверхности без трения.
Продолжая исследование пружин Гука, становится очевидным, что большинство материалов действуют как пружины с силой, прямо пропорциональной смещению. Но по сравнению с пружинами другие материалы обладают площадью, которую необходимо учитывать. Заменяя силу мерой напряжения и смещения мерой деформации, можно получить следующее выражение: σ = E * ε . Теперь мы исследуем меры стресса и деформации.
Напряжение — это мера средней силы на единицу площади, определяемая по формуле σ = F / A , где среднее напряжение σ равно силе F , действующей по площади, A .Единица измерения напряжения в системе СИ — паскали (Па), что равно 1 Ньютону на квадратный метр. Пси — это альтернативная единица измерения в фунтах на квадратный дюйм. Единицы напряжения равны единицам давления, которые также являются мерой силы на единицу площади.
Напряжение нельзя измерить напрямую, поэтому его можно вычислить из меры деформации и константы, известной как модуль упругости Юнга. Соотношение задается следующим образом: σ = E * ε , где σ представляет напряжение, ε представляет деформацию, а E представляет модуль упругости Юнга.Используя этот способ определения напряжения, деформация является геометрической мерой деформации, а модуль Юнга — мерой, используемой для характеристики жесткости упругого материала. Деформация не имеет единицы измерения, но модуль Юнга имеет значение Па.
Деформация характеризуется отношением полной деформации или изменения длины к исходной длине. Это соотношение задается соотношением ε = Δ л / л 0 , где деформация, ε , представляет собой изменение в l , деленное на начальную длину, l 0 .
Следующие ниже задачи могут быть решены независимо и рассмотрены в классе, побуждая учащихся ближе познакомиться с приведенными выше уравнениями. Раздайте каждому ученику по экземпляру набора задач по закону стресса, напряжения и Гука.
Вы должны ПОКАЗАТЬ ВСЕ РАБОТЫ. Полезные константы, представленные в таблице ниже. (Предположим, что заданные константы имеют три значащих цифры (SF). Также обратите внимание, что отношения, которые мы только что обсудили, приведены ниже.
Материал
- Модуль Янга: 200×10 9 E (Па)
- чугун
- Модуль Юнга: 100×10 9 E (Па)
- бетон
- Модуль Юнга: 20.0×10 9 E (Па)
F = m * a σ = F / A ε = Δl / l 0 σ = E * ε F = -k * Δx
- Шар 3340 Н поддерживается вертикально стальным тросом диаметром 1,90 см. Предполагая, что длина кабеля составляет 10,3 м, определите напряжение и деформацию в кабеле.
- Рассмотрим железный стержень с площадью поперечного сечения 3,81 см2, к которому приложено усилие 66 700 Н. Найдите напряжение в стержне.
- Бетонный столб с 50.Диаметр 8 см выдерживает сжимающую нагрузку 8910 Ньютонов. Определите нагрузку на столб.
- Бетонный столб в предыдущей задаче имеет начальную высоту 0,55 м. Насколько короче стойка после приложения нагрузки (в мм)?
- Строительный кран с кабелем диаметром 1,90 см имеет максимальное рабочее напряжение 138 МПа. Найдите максимальную нагрузку, которую может выдержать кран.
- Рассмотрим закон Гука как простую пропорциональность, где F прямо пропорционально Δx.Следовательно, мы знаем, что сила, растягивающая пружину, прямо пропорциональна расстоянию, на которое она растягивается. Если 223 Н растягивает пружину на 12,7 см, какое растяжение мы можем ожидать от 534 Н?
- На фиг.1 показан столбец жировой ткани, определяющий деформацию в каждой из трех областей. Рисунок 1. Столбик жировой ткани.
Сопутствующие мероприятия
- Применение закона Гука к обнаружению рака — группы студентов изучают закон Гука, собирая данные о смещении пружин с неизвестной константой пружины, добавляя различные массы известного веса.Ответив на ряд вопросов по применению, они применяют свое новое понимание для исследования ткани с известной площадью поверхности. Затем примените соответствующие соотношения, чтобы изобразить раковую опухоль среди нормальной ткани, создав график Microsoft Excel®.
Словарь / Определения
Радиолог: медицинский специалист, изучающий фотографии тканей, органов, костей для использования при лечении заболеваний.
деформация: деформация тела или конструкции в результате приложенной силы. Вытягивайтесь за правильную точку или предел.
стресс: физическое давление, притяжение или другая сила, оказываемая на систему другим человеком. Нагрузка, сила или система сил, вызывающая деформацию. Отношение силы к площади.
Оценка
Оценка после ознакомления:
Набор задач : Попросите учащихся выполнить в классе набор задач по закону стресса, напряжения и Гука, чтобы оценить их понимание.Последний вопрос из набора задач и прикладные вопросы из связанного упражнения служат для оценки понимания учащимися задачи. Используйте эти вопросы как средство проверки того, применяют ли учащиеся полученные знания для решения инженерной задачи.
Оценка после урока:
Викторина : Проведите тест на стресс, напряжение и закон Гука в качестве формирующей оценки после урока, служащей частью фазы «Проверьте свой характер» традиционного цикла.
Рекомендации
Dictionary.com. ООО «Издательская группа« Лексико ». По состоянию на 28 декабря 2008 г. (Источник словарных определений с некоторой адаптацией) http://www.dictionary.com
Авторские права
© 2013 Регенты Университета Колорадо; оригинал © 2007 Университет ВандербильтаАвторы
Люк Даймонд; Меган МерфиПрограмма поддержки
VU Bioengineering RET Program, Школа инженерии, Университет ВандербильтаБлагодарности
Содержание этой учебной программы по цифровой библиотеке было разработано в рамках грантов №№ RET Национального научного фонда.0338092 и 0742871. Тем не менее, это содержание не обязательно отражает политику NSF, и вы не должны рассчитывать на одобрение со стороны федерального правительства.
Последнее изменение: 30 апреля 2021 г.
Закон Гука и жесткость пружин
Мы анализируем линейные и обратные отношения, содержащиеся в законе Гука.
Закон Гука — это фундаментальное соотношение, объясняющее, как вес на пружине растягивается этой пружиной.Здесь есть фундаментальная прямая пропорциональность с константой пропорциональности, называемой жесткостью пружины \ (\ normalsize {k} \). Однако, когда мы спрашиваем о соотношении между \ (\ normalsize {k} \) и длиной пружины, мы обнаруживаем обратную пропорциональность! Закон Гука объясняет колебания пружины и связь с круговыми функциями. На этом этапе вы узнаете- о математической форме закона Гука
- о том, как жесткость пружины изменяется в зависимости от длины пружины
- , как колебания пружины являются моделью для гармонического движения.
Закон Гука: восстанавливающая сила пропорциональна смещению
В физике движение колеблющейся пружины является важным колебанием, которое дает знакомые косинусные и синусоидальные круговые функции в виде амплитуд в зависимости от времени. Истоки этого движения лежат в особенно простой линейной зависимости, которую имеют пружины до определенной точки, когда вы их смещаете.© «Пружины закона Крюка» Svjo / Wikimedia Commons CC BY SA На диаграмме мы видим, что удвоение силы удваивает смещение.Это еще одна формулировка закона Гука. Это было обнаружено британским физиком Робертом Гуком в 1660 году и обозначено как \ [\ Large {F = kx} \], где \ (\ normalsize {F} \) — сила, необходимая для создания смещения \ (\ normalsize { x} \) в положении пружины. (Иногда этот закон появляется с отрицательным знаком и значение силы меняется на противоположное.) Это действительный закон только для относительно небольших значений \ (\ normalsize {x} \), но в этом диапазоне, если вы хотите удвоить смещение , вам нужно удвоить усилие на пружине.В этом случае коэффициент пропорциональности \ (\ normalsize {k} \) зависит от жесткости пружины.
Пример
Предположим, что у нас есть пружина, длина которой естественным образом равна \ (\ normalsize 6 \) см, когда она свободно висит. Если мы поместим на пружину небольшой груз размером \ (\ normalsize 30 \) г, мы заметим, что она растягивается на \ (\ normalsize 2 \) мм. Исходя из этого, мы можем использовать линейную зависимость, чтобы предсказать, какие расширения мы получим с другими массами. Если мы удвоим массу до \ (\ normalsize 60 \) gm, мы ожидаем, что струна растянется вдвое дальше, до \ (\ normalsize 4 \) мм.Если, с другой стороны, мы заменим массу на \ (\ normalsize 10 \) gm, то мы ожидаем, что расширение также уменьшится на треть от того, что было, а именно до \ (\ normalsize 2/3 \) мм.Q1 (E): если масса \ (\ normalsize 10 \) кг на тяжелой промышленной пружине размером \ (\ normalsize 100 \) см создает удлинение на \ (\ normalsize 3 \) мм, то как большое расширение было бы вызвано \ (\ normalsize 15 \) кг? Какую массу нам придется приложить к исходной пружине, чтобы получить удлинение на \ (\ normalsize 5 \) мм?
Как жесткость пружины зависит от длины?
Но разве мы не обсуждаем обратные отношения? Как мы обсуждали на первой неделе, закон Гука является примером прямой пропорциональности.Но за этим законом стоит другой закон, который является прекрасным примером обратной пропорциональности.
Предположим, у нас есть заданная пружина с заданной жесткостью пружины \ (\ normalsize {k} \). Что произойдет, если мы разрежем эту пружину на две части одинакового размера? Одна из этих более коротких пружин будет иметь новую жесткость пружины, которая будет \ (\ normalsize {2k} \). В более общем смысле, жесткость пружины составляет , обратно пропорциональна длине пружины, предполагая, что мы говорим о пружине из определенного материала и толщины.
Итак, предположим, что мы разрезаем пружину в приведенном выше примере ровно на две части, создавая две более короткие пружины, каждая длиной \ (\ normalsize 3 \) см. Одна из меньших пружин будет иметь жесткость пружины , вдвое превышающую исходную . Это потому, что жесткость пружины и длина пружины обратно пропорциональны. Это означает, что исходная масса \ (\ normalsize 30 \) gm даст только растяжение на \ (\ normalsize 1 \) мм на более короткой пружине. Чем больше жесткость пружины, тем меньше растяжение, создаваемое данной силой.
Надеюсь, это имеет интуитивный смысл — это не должно быть сюрпризом. Если представить исходную пружину как две более короткие пружины, соединенные вместе, то масса \ (\ normalsize 30 \) растягивает обе меньшие пружины на \ (\ normalsize 1 \) мм, давая общее растяжение \ (\ normalsize 2 \) мм.
Для тех, кто физически склонен, с соответствующими единицами измерения в этом случае сила составляет \ (\ normalsize {F = 0.3} \) ньютонов, а исходное смещение составляет \ (\ normalsize {x = 0.002} \) м. Итак, поскольку \ (\ normalsize {F = kx} \), в этих единицах \ (\ normalsize k = \ frac {0.2 \).
Q2 (M): если заданная сила \ (\ normalsize {F} \) на пружине создает смещение на \ (\ normalsize {8} \) см, мы разрезаем эту пружину на три равных частей, какое усилие нужно приложить к одной из частей, чтобы создать смещение на \ (\ normalsize {4} \) см?
Колебание пружины и гармоническое движение
Особенно простая связь между возвращающей силой и смещением в законе Гука имеет прекрасные последствия для движения колеблющейся пружины.Если вы опустите вес на пружину и отпустите ее, она будет колебаться вокруг своего среднего положения в так называемом гармоническом движении .
Довольно удивительно, но это в точности идентично другому фундаментальному движению: \ (\ normalsize {y} \) — координата частицы, которая движется по единичной окружности равномерно с постоянной скоростью. Если вы посмотрите на эти два примера, надеюсь, вы увидите сходство в движениях.
Причина этого кажущегося совпадения связана с дифференциальными уравнениями, но сводится к относительно простому соотношению закона Гука.
Ответы
A1. Поскольку по закону Гука расширение прямо пропорционально силе, которая для подвешенного груза прямо пропорциональна массе, мы утверждаем, что если масса \ (\ normalsize 10 \) кг создает расширение \ (\ normalsize 3 \) мм, то масса в \ (\ normalsize 15 \) кг вызовет расширение на \ (\ normalsize 4.5 \) мм. Чтобы получить расширение \ (\ normalsize 5 \) мм, нам потребуется масса m, где
\ [\ Large \ frac {10} {m} = \ frac {3} {5}.\]Решая, получаем \ (\ normalsize m = 50/3 = 16,7 \) кг.
A2. Если жесткость пружины изначально равна \ (\ normalsize {k} \), то по закону Гука приложенная сила равна \ (\ normalsize {F = 8k} \). Теперь для одной из меньших частей, мы знаем, что жесткость пружины утроилась, до \ (\ normalsize k_1 = 3k \). Если новая требуемая сила равна \ (\ normalsize {F_1} \), то \ (\ normalsize {F_1 = 4k_1 = 4 (3k)} \). Отсюда следует, что
\ [\ Large {\ frac {F} {F_1} = \ frac {8k} {12k} = \ frac {2} {3}} \]и так \ (\ normalsize {F_1} \) должно быть \ (\ normalsize {\ frac {3} {2}} = 1.В 5 \) раз больше, чем \ (\ normalsize {F} \).
16.1 Закон Гука: снова о стрессе и напряжении — College Physics
Рис. 16.2 При смещении из своего вертикального положения равновесия эта пластиковая линейка колеблется взад и вперед из-за возвращающей силы, противодействующей смещению. Когда линейка находится слева, справа есть сила, и наоборот.
Первый закон Ньютона подразумевает, что объект, колеблющийся вперед и назад, испытывает силы.Без силы объект будет двигаться по прямой с постоянной скоростью, а не колебаться. Рассмотрим, например, отщипывание пластиковой линейки слева, как показано на рисунке 16.2. Деформация линейки создает силу в противоположном направлении, известную как восстанавливающая сила. После высвобождения возвращающая сила заставляет линейку возвращаться к своему устойчивому положению равновесия, где результирующая сила, действующая на нее, равна нулю. Однако к тому времени, когда линейка попадает туда, она набирает обороты и продолжает двигаться вправо, создавая противоположную деформацию.Затем он перемещается влево, обратно через равновесие, и процесс повторяется до тех пор, пока диссипативные силы не заглушат движение. Эти силы удаляют механическую энергию из системы, постепенно уменьшая движение, пока линейка не остановится.
Простейшие колебания возникают, когда возвращающая сила прямо пропорциональна смещению. Когда напряжение и деформация были охвачены третьим законом движения Ньютона, эта связь между силой и смещением была названа законом Гука:
F = −kx.F = −kx. размер 12 {F = — ital «kx»} {}16,1
Здесь FF размер 12 {F} {} — возвращающая сила, xx размер 12 {x} {} — смещение от равновесия или деформация, а размер kk 12 {k} {} — постоянная величина, связанная со сложностью деформирования системы. Знак минус указывает на то, что возвращающая сила направлена в направлении, противоположном смещению.
Рис. 16.3 (a) Пластиковая линейка высвобождена, и возвращающая сила возвращает линейку в положение равновесия.(b) Чистая сила равна нулю в положении равновесия, но линейка имеет импульс и продолжает двигаться вправо. (c) Возвратная сила в противоположном направлении. Он останавливает линейку и снова возвращает ее к равновесию. (г) Теперь у правителя есть импульс влево. (e) При отсутствии демпфирования (вызванного силами трения) линейка достигает своего исходного положения. Оттуда движение повторится.
Силовая постоянная kk размер 12 {k} {} связана с жесткостью (или жесткостью) системы — чем больше силовая постоянная, тем больше восстанавливающая сила и тем жестче система.Единицы измерения kk размером 12 {k} {} — это ньютоны на метр (Н / м). Например, размер kk 12 {k} {} напрямую связан с модулем Юнга, когда мы растягиваем струну. На рис. 16.4 показан график зависимости абсолютного значения восстанавливающей силы от смещения для системы, которая может быть описана законом Гука — в данном случае простой пружины. Наклон графика равен силовой постоянной kk размером 12 {k} {} в ньютонах на метр. Обычное физическое лабораторное упражнение — измерить восстанавливающие силы, создаваемые пружинами, определить, соответствуют ли они закону Гука, и вычислить их силовые константы, если они это сделают.
Рис. 16.4 (a) Отображается график абсолютного значения возвращающей силы в зависимости от смещения. Тот факт, что график представляет собой прямую линию, означает, что система подчиняется закону Гука. Наклон графика — это силовая постоянная kk размером 12 {k} {}. (b) Данные на графике были получены путем измерения смещения пружины из состояния равновесия при поддержании различных грузов. Возвратная сила равна поддерживаемому весу, если масса неподвижна.Пример 16.1
Насколько жестки автомобильные пружины?
Рис. 16.5 Масса автомобиля увеличивается из-за въезда пассажира. Это влияет на смещение автомобиля в системе подвески. (кредит: exfordy на Flickr)
Какова силовая константа для системы подвески автомобиля, которая опускается на 1,20 см, когда в него садится человек весом 80,0 кг?
Стратегия
Считайте, что автомобиль находится в положении равновесия x = 0x = 0 размер 12 {x = 0} {} до того, как человек сядет в него.Затем автомобиль устанавливается на 1,20 см, что означает, что он перемещается в положение x = -1,20 × 10–2 м x = -1,20 × 10–2 м, размер 12 {x = — 1 «». «20» умножить на «10» rSup {размер 8 {- 2}} м} {}. В этот момент пружины обеспечивают восстанавливающую силу FF размером 12 {F} {}, равную весу человека w = mg = 80,0 кг 9,80 м / с2 = 784Nw = mg = 80,0 кг 9,80 м / с2 = 784N размер 12 {w = ital «mg» = left («80» «.» 0` «kg» right) left (9 «.» «80» `» m / s «rSup {size 8 {2}} right) =» 784 » `N} {}. Мы принимаем эту силу как FF, размер 12 {F} {} по закону Гука.Зная FF размер 12 {F} {} и xx размер 12 {x} {} , мы можем затем решить силовую постоянную kk размер 12 {k} {} .
Решение
- Решите закон Гука, F = −kxF = −kx size 12 {F = — ital «kx»} {}, для размера kk 12 {k} {} : k = −Fx.k = −Fx. размер 12 {k = — {{F} больше {x}}} {}
16,2
Подставляем известные значения и решаем kk размер 12 {k} {}:
k = −784 N − 1,20 × 10−2 м = 6,53 × 104 Н / м. k = −784 N − 1,20 × 10−2 м = 6.53 × 104 Н / м. Выравнивание {stack { размер 12 {k = — {{«784» «N»} больше {- 1 «.» «20» умножить на «10» rSup {размер 8 {- 2}} «м»}}} {} # « = 6 дюймов. » «53» умножить на «10» rSup {размер 8 {4}} «Н / м» {} }} {}16,3
Обсуждение
Обратите внимание, что FF размера 12 {F} {} и xx размера 12 {x} {} имеют противоположные знаки, потому что они направлены в противоположные стороны — восстанавливающая сила вверх, а смещение вниз. Также обратите внимание, что автомобиль будет раскачиваться вверх и вниз, когда человек садится в него, если бы не демпфирование (из-за сил трения), обеспечиваемое амортизаторами.Подскакивающие машины — верный признак плохих амортизаторов.
Энергия в законе деформации Гука
Чтобы вызвать деформацию, необходимо проделать работу. То есть сила должна передаваться на расстоянии, независимо от того, дергаете ли вы гитарную струну или сжимаете автомобильную пружину. Если единственным результатом является деформация, и никакая работа не переходит в тепловую, звуковую или кинетическую энергию, тогда вся работа изначально сохраняется в деформированном объекте в виде некоторой формы потенциальной энергии. Потенциальная энергия, запасенная в пружине, равна PEel = 12kx2PEel = 12kx2 размер 12 {«PE» rSub {size 8 {«el»}} = {{1} over {2}} ital «kx» rSup {size 8 {2} }} {}.Здесь мы обобщаем идею упругой потенциальной энергии для деформации любой системы, которая может быть описана законом Гука. Следовательно,
PEel = 12kx2, PEel = 12kx2, размер 12 {«PE» размер 8 {«el»} = {{1} больше {2}} ital «kx» rSup {size 8 {2}}} {}16.4
где PEelPEel размером 12 {«PE» rSub {size 8 {«el»}}} {} — это упругая потенциальная энергия, запасенная в любой деформированной системе, которая подчиняется закону Гука и имеет смещение xx размером 12 {x} { } от равновесия и силовая постоянная kk величиной 12 {k} {}.
Можно найти работу, проделанную при деформации системы, чтобы найти запасенную энергию. Эта работа выполняется за счет приложенной силы FappFapp размером 12 {F rSub {size 8 {«app»}}} {}. Приложенная сила прямо противоположна возвращающей силе (действие-противодействие), поэтому Fapp = kxFapp = kx размер 12 {F rSub {size 8 {ital «app»}} = ital «kx»} {}. На рисунке 16.6 показан график зависимости приложенной силы от деформации xx размером 12 {x} {} для системы, которую можно описать законом Гука. Работа, выполняемая с системой, представляет собой силу, умноженную на расстояние, которое равно площади под кривой или (1/2) kx2 (1/2) kx2 размер 12 {\ (1/2 \) ital «kx» rSup {size 8 { 2}}} {} (метод A на рисунке).Другой способ определить работу — заметить, что сила увеличивается линейно от 0 до kxkx размера 12 {ital «kx»} {} , так что средняя сила составляет (1/2) kx (1/2) kx size 12 {\ (1/2 \) ital «kx»} {}, пройденное расстояние составляет xx размер 12 {x} {}, поэтому W = Fappd = [(1/2) kx] (x) = (1 / 2) kx2W = Fappd = [(1/2) kx] (x) = (1/2) kx2 размер 12 {W = F rSub {размер 8 {ital «app»}} «.» d = \ [\ (1/2 \) ital «kx» \] \ (x \) = \ (1/2 \) ital «kx» rSup {size 8 {2}}} {} (Метод B в фигура).
Рисунок 16.6 Отображается график зависимости приложенной силы от расстояния для деформации системы, которая может быть описана законом Гука. Работа, проделанная над системой, равна площади под графиком или площади треугольника, которая равна половине его основания, умноженному на его высоту, или W = (1/2) kx2W = (1/2) kx2 размер 12 {W = \ (1/2 \) ital «kx» rSup {size 8 {2}}} {}.Пример 16.2
Расчет накопленной энергии: Пружина пистолета с транквилизатором
Мы можем использовать пружинный механизм игрушечного пистолета, чтобы задать два простых вопроса и ответить на них: а) сколько энергии хранится в пружине пистолета с транквилизатором, имеющего постоянную силы 50.0 Н / м и сжимается 0,150 м? б) Если пренебречь трением и массой пружины, с какой скоростью будет выброшен снаряд массой 2,00 г из пушки?
Рисунок 16.7 (a) На этом изображении пистолета пружина не сжимается перед взведением. (b) Пружина сжата на расстояние xx размер 12 {x} {}, и снаряд находится на месте. (c) При отпускании пружина преобразует упругую потенциальную энергию PEelPEel размером 12 {«PE» rSub {size 8 {«el»}}} {} в кинетическую энергию.Стратегия для
(a): Энергия, запасенная в пружине, может быть найдена непосредственно из уравнения упругой потенциальной энергии, поскольку даны размер kk 12 {k} {} и размер xx 12 {x} {}.
Решение для
Ввод заданных значений для размера kk 12 {k} {} и размера xx 12 {x} {} дает
PEel = 12kx2 = 1250,0 N / m 0,150 m2 = 0,563Nm = 0,563JPEel = 12kx2 = 1250,0 N / m0.150 m2 = 0.563Nm = 0.563Jalignl {stack { размер 12 {«PE» размер 8 {«el»} = {{1} больше {2}} ital «kx» rSup {size 8 {2}} = {{1} больше {2}} влево («50» «.» 0 «Н / м» справа) влево (0 «.» «150» «м» справа) rSup {size 8 {2}} = 0 «.». «563» N cdot M} {} # = 0 «.» «563» J {} }} {}16,5
Стратегия для b
Поскольку трение отсутствует, потенциальная энергия полностью преобразуется в кинетическую энергию.Выражение для кинетической энергии может быть решено для скорости снаряда.
Решение для b
- Укажите известные количества:
KE
ж
знак равно
PE
эль
или1 / 2mv2 = (1/2) kx2 = PEel = 0,563 Дж
KE
ж
знак равно
PE
эль
или же
KE_f = PE_el
1 / 2mv2 = (1/2) kx2 = PEel = 0,563J размер 12 {1/2 ital «mv» rSup {size 8 {2}} = \ (1/2 \) ital «kx» rSup {size 8 { 2}} = ital «PE» rSub {size 8 {e1}} = 0 «.» «563» J} {}
16.6
- Решите для размера vv 12 {v} {}:
v = 2PEelm1 / 2 = 20,563 Дж0,002 кг1 / 2 = 23,7Дж / кг1 / 2v = 2PEelm1 / 2 = 20,563 Дж0,002 кг1 / 2 = 23,7Дж / кг1 / 2 размер 12 {v = левый [{{2 » PE «размер 8 {» el «}} над {m}} справа] rSup {размер 8 {1/2}} = слева [{{2 слева (0». «» 563 «» J «справа)} над { 0 «.» «002» «кг»}} справа] rSup {size 8 {1/2}} = «23» «.» 7 дюймов слева («Дж / кг» справа) rSup {размер 8 {{{1} больше {2}}}}} {}
16,7
- Перевести единицы: 23,7 м / s 23.7 м / s 23,7 м / с
Обсуждение
(a) и (b): Эта скорость снаряда впечатляет для пистолета с транквилизатором (более 80 км / ч). Цифры в этой задаче кажутся разумными. Сила, необходимая для сжатия пружины, достаточно мала, чтобы ею мог управлять взрослый, а энергия, передаваемая дротику, достаточно мала, чтобы ограничить ущерб, который он может нанести. Тем не менее, скорость дротика достаточно велика, чтобы он мог пройти приемлемое расстояние.
Проверьте свое понимание
Представьте, что вы держите конец линейки одной рукой и деформируете его другой.Когда вы отпускаете, вы можете видеть колебания линейки. Каким образом вы могли бы изменить этот простой эксперимент, чтобы повысить жесткость системы?
Решение
Вы можете держать линейку посередине так, чтобы колеблющаяся часть линейки была вдвое короче, чем в исходном эксперименте.

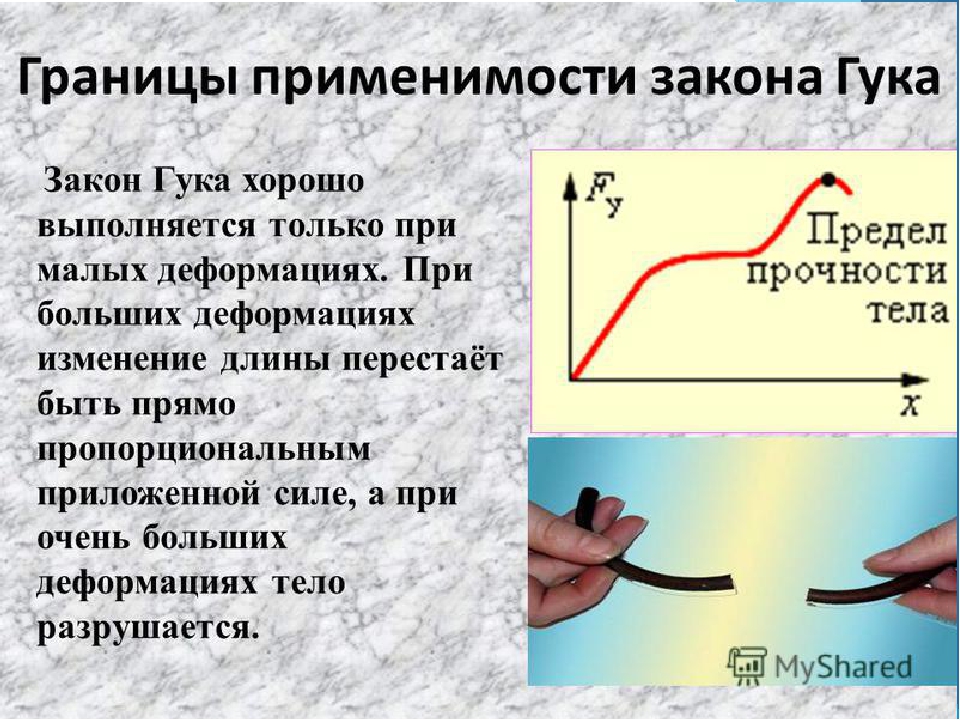 Измерив F и x, можно найти жесткость k по формуле k=F/x (1).
Измерив F и x, можно найти жесткость k по формуле k=F/x (1).
