Погрешность произведения, степени и частного величин с примерами
Погрешность произведения
Пусть в результате измерений получено:
$$ x = x_0 \pm \Delta x, \quad y = y_0 \pm \Delta y, \quad x, y \gt 0 $$
Найдём границы для произведения этих величин: z = xy
$$ {\left\{ \begin{array}{c} x_0- \Delta x \le x \le x_0+ \Delta x \\ y_0- \Delta y \le y \le y_0+ \Delta y \end{array} \right.} \Rightarrow (x_0- \Delta x)(y_0-\Delta y) \le xy \le (x_0+ \Delta x)(y_0+ \Delta y) \Rightarrow $$
$$ \Rightarrow x_0 y_0-( \Delta xy_0+x_0 \Delta y- \Delta x \Delta y) \le xy \le x_0 y_0-( \Delta xy_0+x_0 \Delta y+ \Delta x \Delta y) $$
(О правилах умножения двух неравенств, см. §36 данного справочника).
Абсолютные погрешности $\Delta x ≪ x_0, \Delta y≪y_0$ заметно меньше $x_0$ и $ y_0$, поэтому будем считать, что произведение $\Delta x \Delta y \approx 0$, и им можно пренебречь. Получаем:
$$ x_0 y_0-( \Delta xy_0+x_0 \Delta y) \le xy \le x_0 y_0-( \Delta xy_0+x_0 \Delta y) $$
$$ z = z_0 \pm \Delta z: z_0 = x_0 y_0, \quad \Delta z = \Delta xy_0+x_0 \Delta y $$
$$ δ_z = \frac{\Delta z}{z_0} = \frac{\Delta xy_0+x_0 \Delta y}{x_0 y_0} = \frac{\Delta x}{x_0} + \frac{\Delta y}{y_0} = δ_x+δ_y $$
$$ δ_{xy} = δ_x+δ_y $$
При умножении приближенных величин их относительные погрешности складываются. n} = n δ_x $$
n} = n δ_x $$
При возведении приближенной величины в натуральную степень n, её относительная погрешность увеличивается в n раз.
Погрешность частного
Пусть в результате измерений получено:
$$x = x_0 \pm \Delta x, \quad y = y_0 \pm \Delta y, \quad x,y \gt 0 $$
Найдём границы для частного этих величин: $z = \frac{x}{y}$
$$ {\left\{ \begin{array}{c} x_0- \Delta x \le x \le x_0 + \Delta x \\ y_0- \Delta y \le y \le y_0+ \Delta y \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c}x_0- \Delta x \le x \le x_0+ \Delta x \\ \frac{1}{y_0-\Delta y} \ge \frac{1}{y} \ge \frac{1}{y_0+ \Delta y} \end{array} \right.} \Rightarrow $$
$$ \Rightarrow {\left\{ \begin{array}{c} x_0- \Delta x \le x \le x_0+ \Delta x \\ \frac{1}{y_0+ \Delta y} \le \frac{1}{y} \le \frac{1}{y_0- \Delta y} \end{array} \right.} \Rightarrow \frac{x_0- \Delta x}{y_0+ \Delta y} \le \frac{x}{y} \le \frac{x_0+ \Delta x}{y_0- \Delta y} \Rightarrow $$
$$ \Rightarrow \frac{ (x_0- \Delta x)(y_0- \Delta y)}{(y_0+ \Delta y)(y_0- \Delta y)} \le \frac{x}{y} \le \frac{(x_0+ \Delta x)(y_0+ \Delta y)}{(y_0- \Delta y)(y_0+ \Delta y)} \Rightarrow $$
$$ \Rightarrow \frac{x_0 y_0-( \Delta xy_0+x_0 \Delta y- \Delta x \Delta y)}{y_0^2- \Delta y^2} \le \frac{x}{y} \le \frac{x_0 y_0+( \Delta xy_0+x_0 \Delta y+ \Delta x \Delta y)}{y_0^2- \Delta y^2} $$
О правилах умножения двух неравенств и обращения положительных сторон, см. 2}\right) \cdot \frac{y_0}{x_0} = \frac{\Delta x}{x_0} + \frac{\Delta y}{y_0} = δ_x+δ_y $$
2}\right) \cdot \frac{y_0}{x_0} = \frac{\Delta x}{x_0} + \frac{\Delta y}{y_0} = δ_x+δ_y $$
$$ δ_{\frac{x}{y}} = δ_x+δ_y $$
При делении приближенных величин их относительные погрешности складываются.
Внимание!
Как при умножении, так и при делении приближённых величин, их относительные погрешности складываются.
Точность произведения или частного всегда меньше точности исходных величин.
Примеры
Пример 1. Точное значение выражения:
$$5,31 \cdot 4,16+2,19 \cdot 1,51 = 22,0896+3,3069 = 25,3965 $$
Считая все величины, входящие в выражение, приближёнными с абсолютной погрешностью $\Delta$ x = 0,01, выясните, нужно ли округлять ответ.
Во сколько раз абсолютная погрешность результата больше абсолютной погрешности исходных данных? Во сколько раз относительная погрешность результата больше относительной погрешности сомножителя 5,31?
Обозначим a = 5,31, b = 4,16, c = 2,19, d = 1,51.
Относительные погрешности (округление с избытком):
$$δ_a = \frac{0,01}{5,31} \cdot 100 \text{%} = 0,19 \text{%}, \quad δ_b = \frac{0,01}{4,16} \cdot 100 \text{%} = 0,25 \text{%} $$
$$δ_c = \frac{0,01}{2,19} \cdot 100 \text{%} = 0,46 \text{%}, \quad δ_d = \frac{0,01}{1,51} \cdot 100 \text{%} = 0,67 \text{%} $$
Относительные погрешности произведений:
$$ δ_{ab} = δ_a+δ_b = 0,19 \text{%} + 0,25 \text{%} = 0,44 \text{%} $$
$$ δ_{cd} = δ_c+δ_d = 0,46 \text{%} +0,67 \text{%} = 1,13 \text{%} \approx ↑ 1,2 \text{%} $$
Абсолютные погрешности произведений:
$$ \Delta_{ab} = δ_{ab} \cdot ab = 0,0044 \cdot 22,0896 \approx 0,09719 \approx ↑ 0,098 $$
$$ \Delta_{cd} = δ_{cd} \cdot cd = 0,012 \cdot 3,3069 \approx 0,03968 \approx 0,040 $$
Оставляем в промежуточных оценках 2 значащие цифры для последующего округления. Абсолютная погрешность выражения:
Абсолютная погрешность выражения:
$$ \Delta_{ab+cd} = \Delta_{ab} + \Delta_{cd} = 0,098+0,040 = 0,138 \approx ↑ 0,2 $$
Таким образом, ответ нужно округлить до десятых:
$$ 5,31 \cdot 4,16+2,19 \cdot 1,51 \approx 25,4 ± 0,2 $$
Отношение абсолютной погрешности результата к погрешности исходных данных:
$ \frac{0,2}{0,01} = 20$ — абсолютная погрешность увеличилась в 20 раз.
Относительная погрешность результата: $δ = \frac{0,2}{25,4} \cdot 100 \text{%} \approx 0,79 \text{%} $
По отношению к $δ_a: \frac{δ}{δ_a} = \frac{0,79}{0,19} \approx 4,2$ — относительная погрешность результата в 4,2 раза больше.
Пример 2. а) Границы приближенных величин $5 \le x \le 6,6 \le y \le 7$. Оцените сумму, разность, произведение и частное этих величин.
б) Считая x и y точными величинами, принимающими значения на заданных отрезках, найдите границы суммы, разности и произведения этих величин.
а) По условию:
$$ {\left\{ \begin{array}{c} x_0-\Delta x = 5 \\ x_0+\Delta x = 6 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} 2x_0 = 5+6 = 11 \\ 2 \Delta x = 6-5 = 1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x_0 = 5,5 \\ \Delta x = 0,5 \end{array} \right.} \Rightarrow δ_x = \frac{0,5}{5,5} \cdot 100 \text{%} \approx 9,1 \text{%} $$
} \Rightarrow {\left\{ \begin{array}{c} 2x_0 = 5+6 = 11 \\ 2 \Delta x = 6-5 = 1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x_0 = 5,5 \\ \Delta x = 0,5 \end{array} \right.} \Rightarrow δ_x = \frac{0,5}{5,5} \cdot 100 \text{%} \approx 9,1 \text{%} $$
$$ {\left\{ \begin{array}{c} y_0- \Delta y = 6 \\ y_0+ \Delta y = 7 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 2y_0 = 6+7 = 13 \\ 2 \Delta y = 7-6 = 1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} y_0 = 6,5 \\ \Delta y = 0,5 \end{array} \right.} \Rightarrow δ_y = \frac{0,5}{6,5} \cdot 100 \text{%} \approx 7,7 \text{%} $$
Абсолютная погрешность суммы: $\Delta_{x+y} = \Delta_x+\Delta_y = 0,5+0,5 = 1$
$$ x+y = (5,5+6,5) \pm 1 = 12 \pm 1 $$
Границы суммы: $ 11 \le x+y \le 13$
Абсолютная погрешность разности: $\Delta _{x-y} = \Delta _x + \Delta _y = 0,5+0,5 = 1$
$$ x-y = (5,5-6,5) \pm 1 = -1 \pm 1 $$
Границы разности: $-2 \le x-y \le 0$
Относительная погрешность произведения:
$$δ_{xy} = δ_x+δ_y = 9,1 \text{%} +7,7 \text{%} = 16,8 \text{%} \approx 17 \text{%}$$
Абсолютная погрешность произведения:
$$ \Delta_{xy} = δ_{xy} \cdot x_0 y_0 = 0,17 \cdot 5,5 \cdot 6,5 = 6,0775 \approx ↑ 7 $$
$$ xy = (5,5 \cdot 6,5) \pm 7 \approx 36 \pm 7 $$
Границы произведения: $29 \le xy \le 43$
Относительная погрешность частного:
$$ δ_{x/y} = δ_x+δ_y = 9,1 \text{%} +7,7 \text{%} = 16,8 \text{%} \approx 17 \text{%} $$
Абсолютная погрешность частного:
$$ \Delta_{\frac{x}{y}} = δ_{\frac{x}{y}} \cdot \frac{x_0}{y_0} = 0,17 \cdot \frac{5,5}{6,5} \approx 0,14 \approx ↑ 0,2 $$
$$ \frac{x}{y} = \left( \frac{5,5}{6,5} \right) \pm 0,2 \approx 0,8 \pm 0,2 $$
Границы частного: $0,6 \le \frac{x}{y} \le 1,0$
б) Для точных величин получаем следующие границы:
Границы суммы:
$$ {\left\{ \begin{array}{c} 5 \le x \le 6 \\ 6 \le y \le 7 \end{array} \right. } \Rightarrow 5+6 \le x+y \le 6+7 \Rightarrow 11 \le x+y \le 13 $$
} \Rightarrow 5+6 \le x+y \le 6+7 \Rightarrow 11 \le x+y \le 13 $$
Границы разности:
$$ {\left\{ \begin{array}{c} 5 \le x \le 6 \\ 6 \le y \le 7 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5 \le x \le 6 \\ -7 \le -y \le -6 \end{array} \right.} \Rightarrow 5-7 \le x-y \le 6-6 \Rightarrow -2 \le x-y \le 0 $$
Границы произведения:
$$ {\left\{ \begin{array}{c} 5 \le x \le 6 \\ 6 \le y \le 7 \end{array} \right.} \Rightarrow 5 \cdot 6 \le xy \le 6 \cdot 7 \Rightarrow 30 \le xy \le 42 $$
Границы частного:
$$ {\left\{ \begin{array}{c} 5 \le x \le 6 \\ 6 \le y \le 7 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5 \le x \le 6 \\ \frac{1}{7} \le \frac{1}{y} \le \frac{1}{6} \end{array} \right.} \Rightarrow \frac{5}{7} \le \frac{x}{y} \le 1 $$
Пример 3. В эксперименте по определению плотности вещества получен объём V = 9, 7 $\pm$ 0,05 мл и масса m = 107 $\pm$ 2 г. Найдите плотность.
Это свинец или железо?
Плотность:
$$ ρ = \frac{m}{V}, ρ_0 = \frac{m_0}{V_0} = \frac{107 \cdot 10^{-3} кг}{9,7 \cdot 10^{-6} м^3} \approx 11031 \frac{кг}{м^3} $$
Относительные погрешности (округление с избытком):
$$ δ_V = \frac{0,05}{9,7} \cdot 100 \text{%} \approx 5,2 \text{%}, δ_m = \frac{2}{107} \cdot 100 \text{%} \approx 1,9 \text{%} $$
$$ δ_ρ = δ_V+δ_m = 5,2 \text{%} +1,9 \text{%} = 7,1 \text{%} $$
Абсолютная погрешность для плотности (округление с избытком):
$$ Δ_ρ = δ_ρ \cdot ρ_0 = 0,071 \cdot 11031 \approx 800 \frac{кг}{м^3} $$
$$ ρ = 11000 \pm 800 \frac{кг}{м^3} $$
Это – свинец (табличное значение $ρ_{таб} = 11340 \frac{кг}{м^3}$ ).
Численные методы решения прикладных задач
16
сумме предельных абсолютных погрешностей уменьшаемого и
вычитаемого.
Предельная относительная погрешность разности
A
x
x
u
2
1
δ
,
(1.7)
где
А
– точное значение абсолютной величины разности чисел
x
1
и
x
2
.
Замечание о потере точности при вычитании близких чисел
. Если
приближенные числа
x
1
и
x
2
достаточно близки друг к другу и имеют
малые абсолютные погрешности, то число
A
мало. Из формулы (1.7)
вытекает, что предельная относительная погрешность в этом случае
может быть весьма большой, в то время как относительные погрешности
уменьшаемого и вычитаемого остаются малыми, т. е. здесь происходит
е. здесь происходит
потеря точности.
1.8. Погрешность произведения
Теорема.
Относительная погрешность произведения нескольких
приближенных чисел, отличных от нуля, не превышает суммы
относительных погрешностей этих чисел.
Доказательство.
Пусть
n
x xx u
…
21
.
Предполагая для простоты, что приближенные числа
n
x x
x
,. ..,
..,
,
2
1
положительны, будем иметь
n
x
x x
u
ln …
ln
ln ln
2
1
.
Отсюда, используя приближенную формулу
x
x
x d
x
ln
ln
, находим
n
n
x
x
x
x
x
x
u
u
. ..
..
2
2
1
1
.
Оценивая последнее выражение по абсолютной величине, получим
n
n
x
x
x
x
x
x
u
u
. ..
..
2
2
1
1
.
Если
i
A
)
,…,
2,1
(
n
i
точные значения сомножителей
x
i
и
i
x
, как это
бывает обычно, малы по сравнению с
x
i
, то приближенно можно
положить
i
i
i
i
i
A
x
x
x
и
δ
u
u, где
i
δ
относительные погрешности
сомножителей
i
x
n
i
,. .., 2,1
.., 2,1
и
δ
относительная погрешность
произведения.
Следовательно,
n
δ …
δ
δ δ
2
1
.
(1.8)
Какова погрешность измерения — Измерения
Спасибо за помощь.Но понятно мне пока не всё.
Вы пишете, что «отнисительная погрешность произведения или частного двух величин равна корню из суммы квадратов относительных погрешностей этих величин». (мы рассматриваем случай без корреляции) А я читала , что:
«Относительная погрешность произведения приближенных чисел равна сумме относительных погрешностей множителей.»
Смотрите страницы:
http://solidbase.karelia.ru/edu/meth_calc/files/02.shtm
http://schools.techno.ru/sch2567/metod/pogr.htm
Может я что-то не так поняла?
Объясните, кто прав?
Увы, в случае с http://solidbase.karelia.ru/edu/meth_calc/files/02.shtm вы не так поняли, там речь идет о погрешности вычислений за счет округления чисел, что же касается http://schools.techno.ru/sch2567/metod/pogr.htm , то это вообще какой-то несолидный ресурс, лабораторная для школьников, написанная каким-то учителем, далеким от метрологии. Могу предложить следующие ссылки:
http://users.kpi.kharkov. ua/fmp/biblio/BOOK1/1-10.html
ua/fmp/biblio/BOOK1/1-10.html
http://www.nntu.sci-nnov.ru/RUS/fakyl/VECH…trology/6_3.htm
http://window.edu.ru/window_catalog/redir?…file=errors.pdf
Попытаюсь на пальцах объяснить в чем разница между погрешностью округления и погрешностью измерения.
Допустим некоторые числовые значения округляются до ближайшего целого, при этом, увидев округленное число, например, 10, мы вправе предположить, что исходное число с равной вероятностью могло находиться в интервале 9,5 — 10,5, то есть график распределения вероятностей представляет собой прямоугольную функцию, с четкими границами. Если же мы в результате измерения с допустимой погрешностью 0,5% получили значение 10, то это вовсе не означает, что истинное значение измеряемой величины с абсолютно одинаковой вероятностью распределяется в интервале 9,5 — 10,5, и даже то, что оно вообще находится в этом интервале (хотя вероятность выхода за интервал допуска пренебрежительно мала). График распределения вероятности истинности того или иного значения представляет собой (за исключением особых случаев) экспоненциальный колокол, так, что, вероятность того, что истинное значение в рассматриваемом случае будет, допустим 10,1 выше, чем, например, 10. 4. В связи с таким неравномерным распределением вероятностей формулы для определения пределов допустимой погрешности при косвенных измерениях выводятся с использованием частных производных. Я как-то давно еще, несмотря на нелюбовь к математике, потратил целый вечер, и вывел формулы для множества разных функций от двух переменных, потом, конечно потерял листочек с записями, а больше мне такой подвиг совершать не хотелось (математику страшно не люблю!), но на самом деле, практически, при косвенных измерениях, как правило встречаются в основном произведение/частное и сумма/разность величин. При произведении/делении предел допустимой результирующей относительной погрешности равен геометрической (квадратичной) сумме пределов относительных погрешностей измеренных величин, в случае суммы/разности формула для относительного выражения погрешности получается слишком громоздкой, поэтому лучше использовать абсолютные выражения, тоже получается геометрическая сумма.
4. В связи с таким неравномерным распределением вероятностей формулы для определения пределов допустимой погрешности при косвенных измерениях выводятся с использованием частных производных. Я как-то давно еще, несмотря на нелюбовь к математике, потратил целый вечер, и вывел формулы для множества разных функций от двух переменных, потом, конечно потерял листочек с записями, а больше мне такой подвиг совершать не хотелось (математику страшно не люблю!), но на самом деле, практически, при косвенных измерениях, как правило встречаются в основном произведение/частное и сумма/разность величин. При произведении/делении предел допустимой результирующей относительной погрешности равен геометрической (квадратичной) сумме пределов относительных погрешностей измеренных величин, в случае суммы/разности формула для относительного выражения погрешности получается слишком громоздкой, поэтому лучше использовать абсолютные выражения, тоже получается геометрическая сумма.
Когда окончательный результат измерения представляет собой функцию только одной измеренной величины, то все гораздо проще, формула для пересчета предела допустимой относительной погрешности определяется с помощью обычной производной. Например, результирующая величина равна квадрату измеренной, то предел результирующей погрешности в два раза больше исходной, когда корню — то наоборот.
Например, результирующая величина равна квадрату измеренной, то предел результирующей погрешности в два раза больше исходной, когда корню — то наоборот.
Урок 16. Абсолютная и относительная погрешность
Значит,
∆ = 35 × 0,0005 = 0,0175 мм.
Действия над приближёнными числами.
Сложение и вычитание приближённых чисел.
Абсолютная погрешность суммы двух величин равна сумме абсолютных погрешностей отдельных слагаемых.
ПРИМЕР:
Складываются приближённые числа
265 и 32.
РЕШЕНИЕ:
Пусть предельная погрешность первого есть 5, а второго 1. Тогда предельная погрешность суммы равна
5 + 1 = 6.
Так, если истинное значение первого есть 270, а второго 33, то приближённая сумма
265 + 32 = 297
на 6 меньше истинной
270
+ 33 = 303.
ПРИМЕР:
Найти сумму приближённых чисел:
0,0909 + 0,0833 + 0,0769 + 0,0714 + 0,0667
+ 0,0625 + 0,0588 + 0,0556 + 0,0526.
РЕШЕНИЕ:
Сложение даёт следующий результат – 0,6187.
Предельная погрешность каждого слагаемого
0,00005.
Предельная погрешность суммы:
0,00005 ∙ 9 = 0,00045.
Значит, в последнем (четвёртом) знаке суммы возможна ошибка до 5 единиц. Поэтому округляем сумму до третьего знака, то есть до тысячных. Получаем 0,619, здесь все знаки верные.
При значительном
числе слагаемых обычно происходит взаимная компенсация погрешностей, поэтому
истинная погрешность суммы лишь в исключительных случаях совпадает с предельной
погрешностью или близка к ней. Насколько редки эти случаи, видно из предыдущего
примера, где 9 слагаемых. Истинная величина каждого из них может
отличаться в пятом знаке от взятого приближённого значения на 1, 2, 3, 4 или даже на 5 единиц в ту и в другую сторону.
Например, первое слагаемое может быть больше своего истинного значения на 4 единицы пятого знака, второе – на две, третье – меньше истинного на одну единицу и так далее.
Расчёт показывает, что число всех возможных случаев распределения погрешностей составляет около одного миллиарда. Между тем лишь в двух случаях погрешность суммы может достигнуть предельной погрешности 0,00045, это произойдёт:
– когда истинная величина каждого слагаемого больше приближённой величины на 0,00005;
– когда истинная величина каждого слагаемого меньше приближённой величины на 0,00005.
Значит, случаи, когда погрешность суммы совпадает с предельной, составляют только 0,0000002% всех возможных случаев.
Дальнейший расчёт
показывает, что случаи, когда погрешность суммы девяти слагаемых может
превысить три единицы последнего знака, тоже очень редки. Они составляют
лишь 0,07%
из числа всех
возможных. Две единицы последнего знака погрешность может превысить 2% всех возможных случаев, а одну единицу –
примерно в 25%.
В остальных 75% случаев погрешность девяти слагаемых не
превышает одной единицы последнего знака.
Две единицы последнего знака погрешность может превысить 2% всех возможных случаев, а одну единицу –
примерно в 25%.
В остальных 75% случаев погрешность девяти слагаемых не
превышает одной единицы последнего знака.
ПРИМЕР:
Найти сумму точных чисел:
0,0909 + 0,0833 + 0,0769 + 0,0714 + 0,0667
+ 0,0625 + 0,0588 + 0,0556 + 0,0526.
РЕШЕНИЕ:
Сложение даёт следующий результат – 0,6187.
Округлим их до тысячных и сложим:
0,091 + 0,083 + 0,077 + 0,071 + 0,067
+ 0,062 + 0,059 + 0,056 + 0,053 = 0,619.
Предельная погрешность суммы:
0,0005 ∙ 9 = 0,0045.
Приближённая сумма отличается от истинной на 0,0003, то есть на треть единицы последнего знака приближённых чисел. Все три знака приближённой суммы верны, хотя теоретически последняя цифра могла быть грубо неверной.
Произведём в наших слагаемых округление до сотых. Теперь предельная погрешность суммы будет:
0,005
∙ 9 = 0,045.
Между тем получим:
0,09 + 0,08 + 0,08 + 0,07 + 0,07
+ 0,06 + 0,06 + 0,06 + 0,05 = 0,62.
Истинная погрешность составляет только 0,0013.
Предельная абсолютная погрешность разности двух величин равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого.
ПРИМЕР:
Пусть предельная погрешность приближённого уменьшаемого 85 равна 2, а предельная погрешность вычитаемого 32 равна 3. Предельная погрешность разности
85 – 32 = 53
есть
2 + 3 = 5.
В самом деле, истинное значение уменьшаемого и вычитаемого могут равняться
85 + 2 = 87 и
32 – 3 = 29.
Тогда истинная разность есть
87 – 29 = 58.
Она на 5 отличается от приближённой разности 53.
Относительная погрешность суммы и разности.
Предельную относительную погрешность суммы и разности легко найти, вычислив сначала предельную абсолютную погрешность.
Предельная относительная погрешность суммы (но не разности!) лежит между наименьшей и наибольшей из относительных погрешностей слагаемых. Если все слагаемые имеют одну и ту же (или примерно одну и ту же) предельную относительную погрешность, то и сумма имеет ту же (или примерно ту же) предельную относительную погрешность. Другими словами, в этом случае точность суммы (в процентном выражении) не уступает точности слагаемых. При значительном же числе слагаемых сумма, как правило, гораздо точнее слагаемых.
ПРИМЕР:
Найти предельную абсолютную и предельную относительную погрешность суммы чисел:
24,4 + 25,2 + 24,7.
РЕШЕНИЕ:
В каждом слагаемом суммы
24,4 + 25,2 + 24,7 = 74,3
предельная относительная погрешность примерно одна и та же, а именно:
0,05
: 25 = 0,2%.
Такова же она и для суммы.
Здесь предельная абсолютная погрешность равна 0,15, а относительная
0,15 : 74,3 ≈ 0,15 : 75 = 0,2%.
В противоположность сумме разность приближённых чисел может быть менее точной, чем уменьшаемое и вычитаемое. <<Потеря точности>> особенно велика в том случае, когда уменьшаемое и вычитаемое мало отличаются друг от друга.
Относительные погрешности при сложении и вычитании складывать нельзя.
Умножение и деление приближённых чисел.
При делении и умножении чисел требуется сложить относительные погрешности.
ПРИМЕР:
Пусть перемножаются приближённые числа 50 и 20, и пусть предельная относительная погрешность первого сомножителя есть 0,4%, а второго 0,5%.
Тогда предельная относительная погрешность произведения
50 × 20 = 1000
приближённо равна 0,9%. В самом деле предельная абсолютная погрешность первого сомножителя есть
В самом деле предельная абсолютная погрешность первого сомножителя есть
50 × 0,004 = 0,2,
а второго
20 × 0,005 = 0,1.
Поэтому истинная величина произведения не больше чем
(50 + 0,2)(20 + 0,1) = 1009,02,
и не меньше, чем
(50 – 0,2)(20 – 0,1) = 991,022.
Если истинная величина произведения есть 1009,2, то погрешность произведения равна
1009,2 – 1000 = 9,02,
а если 991,02, то погрешность произведения равна
1000 – 991,02 = 8,98.
Рассмотренные два случая – самые неблагоприятные. Значит, предельная абсолютная погрешность произведения есть 9,02. Предельная относительная погрешность равна
9,02 : 1000 = 0,902%,
то есть приближённо 0,9%.Погрешность частная — Энциклопедия по машиностроению XXL
Относительная погрешность частного [c.221]Погрешность субъективная Погрешность суммарная Погрешность теоретическая Погрешность частная Подвид измерений Подвижность средства измерений Подтверждение типа Подтверждение типа средств измерений Показание
[c. 104]
104]
При умножении приближенного числа на точное число N абсолютная погрешность произведения возрастает в N раз, относительная погрешность произведения равна относительной погрешности приближенного числа. Погрешность частного приближенных величин также проще вычислять через относительные ошибки. [c.61]
Наибольшая относительная погрешность частного приближенных величин равняется сумме абсолютных значений относительных погрешностей делимого и делителя. Наибольшая абсолютная погрешность частного вычисляется по относительным ошибкам [c.61]
При делении приближенного числа на точное число N абсолютная погрешность частного уменьшается в N раз, относительная погрешность частного равна относительной погрешности делимого. [c.61]
При существенной случайной составляющей погрешности частные динамические характеристики контролируют посредством обработки серии п наблюдений. Число наблюдений п не должно быть более 10. [c.252]
[c.252]
Улучшение характеристик противоточной системы с помощью принципа механического торможения изучалось автором совместно с сотрудниками не только при каскадно расположенных вставках, рассмотренных выше. Представляется, что наиболее эффективным осуществлением этого принципа является применение винтовых сетчатых вставок (одно- или многозаходных). Экспериментальное изучение таких вставок проводилось методами меченых частиц, р-просвечивания и отсечек [Л. 21, 84]. В первом случае экспериментальная установка состояла из стенда торможенной газовзвеси и электронного блока для регистрации заряженных частиц. Стенд торможенной газовзвеси включал в себя прозрачную цилиндрическую камеру из органического стекла высотой 0,8 и диаметром 0,34 м, в которую вставлялись сменные винтовые сетчатые вставки. Источником излучения являлась частица алюмосиликата di = = 4,35 мм, меченная Со активностью 0,5 мг-экв. Для проверки методики вначале были проведены опыты по определению времени свободного падения одиночной меченой частицы, которое сопоставлялось с теоретически рассчитанной величиной. Время находилось по (2-45) при у = 0, Vo.a=VT,a=0. Многократное определение времени, в течение которого меченая частица проходила контрольный участок камеры, совпадало с расчетным с погрешностью 4%, что лежит в пределах точности эксперимента и служит частной проверкой
[c.95]
Время находилось по (2-45) при у = 0, Vo.a=VT,a=0. Многократное определение времени, в течение которого меченая частица проходила контрольный участок камеры, совпадало с расчетным с погрешностью 4%, что лежит в пределах точности эксперимента и служит частной проверкой
[c.95]
Оболочками в теории упругости называют тела, ограниченные двумя криволинейными поверхностями, расстояние между которыми h (толщина) мало по сравнению с другими размерами тела. Поверхность, которая делит толщину оболочки пополам, называют срединной. В частном случае плоской срединной поверхности оболочка превращается в пластину. Поэтому, так же как арки называют кривыми стержнями, оболочки иногда называют кривыми пластинами. Этот термин удачен для незамкнутых оболочек, применяемых для перекрытия больших площадей без промежуточных опор, но неудачен для замкнутых оболочек, таких, как сферическая и цилиндрическая (резервуары и т. п.). Можно использовать оба термина. Для краткости будем использовать только термин оболочка . Под тонкими оболочками понимаются такие, у которых отнощение толщины h к наименьшему радиусу кривизны R срединной поверхности мало по сравнению с единицей. Допуская обычную для технических расчетов погрешность в 5%, будем считать тонкими оболочками такие, у которых max (/г/i ) [c.214]
Под тонкими оболочками понимаются такие, у которых отнощение толщины h к наименьшему радиусу кривизны R срединной поверхности мало по сравнению с единицей. Допуская обычную для технических расчетов погрешность в 5%, будем считать тонкими оболочками такие, у которых max (/г/i ) [c.214]
Пунктиром показаны графики, полученные для частного случая, когда i=0. Результаты позволяют оценить погрешность, которая получается, если при афл 2 не учитывать осевую аэродинамическую силу I qi I. [c.260]
Равенство (11.32) является приближенным и им следует пользоваться с известной осторожностью, поскольку иногда оно может привести к большим погрешностям. Однако в одном частном случае, когда материал тела не обладает свойством старения, а функция е t) при неограниченном увеличении времени стремится к константе Ёсо, можно показать, что соотношение (11.32) дает точное решение при t оо
[c. 369]
369]
Примеры аппроксимаций. Заменяя в дифференциальном уравнении частные производные теми или иными разностными отношениями, мы аппроксимируем его на некотором шаблоне. Это наиболее простой способ аппроксимации. Для описания точности аппроксимации отдельных производных естественно использовать введенное выше понятие погрешности аппроксимации по отношению к классу функций. Аппроксимация производных уже рассматривалась в 1.3. Там же были приведены главные члены погрешности аппроксимации. Односторонние двухточечные аппроксимации первой производной (1.22) имеют первый порядок точности, а симметричные (центральные) [c.77]
Однако следует отметить здесь те цели, которые имеются в виду при отыскании решений. Приближенные методы отыскания напряжений и деформаций в упругих телах, основанные на частных гипотезах простейшего характера, принято относить к тому, что называется сопротивлением материалов. Примером может служить приближенная теория растяжения и изгиба стержней, изложенная в гл. 2, 3 и 5. Теория упругости позволяет получить точное решение задачи изгиба для определенных случаев и сравнить его с приближенным таким образом, находится строгая оценка погрешности элементарной теории.
[c.266]
2, 3 и 5. Теория упругости позволяет получить точное решение задачи изгиба для определенных случаев и сравнить его с приближенным таким образом, находится строгая оценка погрешности элементарной теории.
[c.266]
Главное достоинство теории Мора заключается в принципе подхода к рассматриваемому вопросу. К сожалению, на это далеко не всегда обращают внимание, и часто теорию Мора ставят в один ряд с общеизвестными гипотезами, а то обстоятельство, что в частных случаях расчетная формула Мора совпадает с расчетной формулой гипотезы касательных напряжении, усиливает впечатление о равноценности этих подходов. Между тем феноменологический подход Мора, т.е. подход, основанный на логическом описании явления, является наиболее естественным и правильным. При обнаружении погрешностей или несоответствий этот подход сохраняет за нами возможность внести в теорию дополнительные уточнения. Так, если в дальнейшем удастся провести испытания образцов в области положительных [c. 359]
359]
Таким образом, максимальная относительная погрешность произведения или частного равна сумме относительных погрешностей исходных величин. [c.128]
Пусть результат измерения рассчитывается как произведение или частное прямых измерений, относительная систематическая погрешность которых одинакова и равна В этом случае максимальная погрешность находится по формуле (4.24), в которой принимается 0= =7 [c.167]
Пусть, например, измеряется удельный. объем газа при =400°С и р=300-10 Па, причем эти параметры измеряются с абсолютной погрешностью Дг=0,03°С и Ар = = 0,15-10 Па. Следовательно, при проведении опыта температура может быть не 400 °С, а, например (в худшем случае), 400,03°С, давление соответственно 299,85-10 Па. Экспериментатор же, получив значение удельного объема, приписывает его параметрам =400 °С и р=300-10 Па, хотя на самом деле параметры в опыте другие и в пределах отклонений этих параметров удельный объем изменится. Это изменение будет зависеть от интенсивности изменения ИСКОМОЙ величины под влиянием изменения температуры и давления (т. е. от значений частных производных).
[c.171]
Это изменение будет зависеть от интенсивности изменения ИСКОМОЙ величины под влиянием изменения температуры и давления (т. е. от значений частных производных).
[c.171]
Если ограничение линейной зависимостью Ар от Ад( (/ = = 0,1,. .., п) приводит к недопустимым неточностям расчетов, то можно учитывать члены, пропорциональные второй степени погрешностей [двойная сумма в равенстве (6.2)]. Частные [c.112]
Поверители проводили внезапные ревизии (определяли погрешности средств измерения и устанавливали препоны к применению неисправных весов) в торговых заведениях, лавках, магазинах, складах на фабриках, заводах, мастерских, ремесленных заведениях и тому подобных промышленных предприятиях, в аптеках, почтамтах, на железнодорожных и пароходных складах, банках, интендантских, военных складах и других казенных, общественных, частных учреждениях, приписанных к Уфимской палатке. [c.21]
В неявных абсолютно устойчивых разностных схемах рассмотренного типа допустимый шаг по времени выбирается только из соображений требуемой точности, причем погрешность аппроксимации как явной, так и неявной схемы пропорциональна Ас и (Ах) .
 Однако в частных случаях, когда Ас и Ах выбраны так, что аАс/(Ах) — 1/6, эта погрешность существенно уменьшается и становится пропорциональной (Аг) и (Ах)» .
[c.91]
Однако в частных случаях, когда Ас и Ах выбраны так, что аАс/(Ах) — 1/6, эта погрешность существенно уменьшается и становится пропорциональной (Аг) и (Ах)» .
[c.91]Величина частной погрешности определяется величиной первичной ошибки А[c.110]
Таким образом, погрешность положения можно представить как сумму частных погрешностей, возникающих от неточностей параметров г, I, h [c.111]
Метод преобразованного механизма.. Сущность этого графоаналитического метода, называемого методом преобразованного механизма, заключается в определении частных погрешностей механизма построением планов скоростей для некоторого преобразованного механизма. По этому плану, называемому планом малых [c.111]
Пример определения погрешности положения ведомого звена, возникшей в кривошипно-ползунном механизме из-за зазора в кинематической паре А, показан на рис. 1.72, б, в. Отрезок рлЬ и будет соответствовать частной погрешности А5б в масштабе цд. [c.114]
[c.114]
Отрезок АЗц = 8 — 8 является ошибкой положения ведомого звена. Зависимость между первичной ошибкой АЛ и частной погрешностью механизма А8н найдем из треугольника ВВ В» [c.117]
Для оценки точности одного механизма необходимо определить его первичные ошибки, связанные с изготовлением и эксплуатацией, затем найти максимальное значение ошибки положения (перемещения) механизма. С этой целью приходится определять погрешности в нескольких положениях механизма. По полученным данным строится график величина погрешности — положение ведущего звена механизма , по которому легко найти погрешность механизма в заданном положении. Погрешность механизма целесообразно представлять в виде суммы частных погрешностей, обусловленных отдельными первичными ошибками. Такие графики дают возможность определить не только максимальную погрешность, но и наглядно показывают удельный вес каждой из частных погрешностей. Последнее особенно важно для установления точности изготовления деталей и способов регулировки механизма. [c.118]
[c.118]
Угловая погрешность положения ведомого колеса Аф является суммой частных погрешностей, вызванных первичными ошибками. [c.284]
Общие правила вычисления погрешностей для обоих случаев могут быть легко выведены с помощью дифференциального исчисления. Вначале мы ограничимся простыми частными задачами. [c.60]
Простейший случай, когда интересующая нас величина являлась суммой двух или нескольких независимо измеряемых величин, мы уже разбирали и написали для вычисления случайных погрешностей правило сложения дисперсий (26). Теперь дадим правила вычисления погрешностей для случаев произведения и частного. [c.61]
Величина определяется сравнением экспериментальных данных и аналитических зависимостей, полученных при различных допущениях, и считается независящей от радиальной и продольной координат. Несмотря на определенную погрешность такого подхода (линеаризация решений, идеализация граничных условий, анизотропия турбулентности и т. д), данный метод оказался в некоторых частных случаях наиболее удобным для практических расчетов.
[c.112]
д), данный метод оказался в некоторых частных случаях наиболее удобным для практических расчетов.
[c.112]
Формально это уравнение совпадает с уравнением линейной зависимости, оцениваемой по методу наименьших квадратов 126]. Однако при оценке линейной зависимости задача состоит в том, чтобы сгладить отклонения от линейной зависимости, вызванные погрешностями наблюдений или отклонениями самой зависимости от строгой линейности. В этом случае уравнение (2) описывает прямую по наименьшим квадратам , а параметры уравнения получают путем приравнивания нулю частных производных [c.13]
Если jo = 1 ( — е. ji = )), то при описании движения тела в рамках линеаризованных уравнений движения мы получаем, что отклонение тела от его равновесного положения = О неограниченно возрастает со временем, так как уравнение (41) имеет частное решение вида (36) при и = jo, а = 2). При нелинейной трактовке задачи о движении твердого тела при резонансе ситуация иная. В самом деле, пусть в начальный момент = О, ф = 0. Тогда (с погрешностью, порядок которой не ниже чем е ) и R = при t = 0. Следовательно, в интеграле % = h постоянная h равна нулю и во все время движения
[c.512]
В самом деле, пусть в начальный момент = О, ф = 0. Тогда (с погрешностью, порядок которой не ниже чем е ) и R = при t = 0. Следовательно, в интеграле % = h постоянная h равна нулю и во все время движения
[c.512]
Таким образом, коэффициент вязкости зависит от мгновенного состояния материала и условий его нагружения, которые в частном случае могут быть охарактеризованы величиной пластической деформации и скорости деформации. С учетом зависимости коэффициента вязкости от деформации и скорости деформации различные методы определения коэффициента вязкости приводят к сопоставимым величинам с учетом возможного разброса результатов и погрешности расчетов. Квазистатические испытания с высокими скоростями обеспечивают получение наиболее надежных данных о величине коэффициента вязкости с учетом его зависимости от деформации и скорости деформации. [c.136]
Следует отметить, что решения безмоментной задачи и задачи чистого изгибания — медленно меняющиеся функции. Поэтому при их определении теория пологих оболочек может дать существенную погрешность, если только рассматриваемая область оболочки не мала по сравнению. с радиусом Для быстро изменяющихся решений уравнения (7.72) точность рассматриваемой теории вполне достаточна. Поэтому для сферических оболочек можно рекомендовать расчет на основе безмоментной теории (см. гл. 6), дополняя его решением уравнения (7.72) при = О и частным решением уравнения (7.74).
[c.343]
Поэтому при их определении теория пологих оболочек может дать существенную погрешность, если только рассматриваемая область оболочки не мала по сравнению. с радиусом Для быстро изменяющихся решений уравнения (7.72) точность рассматриваемой теории вполне достаточна. Поэтому для сферических оболочек можно рекомендовать расчет на основе безмоментной теории (см. гл. 6), дополняя его решением уравнения (7.72) при = О и частным решением уравнения (7.74).
[c.343]
Тонкая пластина представляет собой частный случай трехмерного тела, и для нее были введены гипотезы Кирхгофа, согласно которым члены Озбез, Tijfisig, 1. 36623 в фигурных скобках подынтегрального выражения для приращения энергии деформации bU (см. 8.2) могут быть опущены в силу их малости с погрешностью h IU . Поэтому [c.385]
Строгая оценка погрешности опытных данных может быть получена методом, основанным на теории вероятности и теории вычислений, получившими достаточное освещение в литературе. В каждом частном случае определение погрешности результатов опыта составляет довольно сложную задачу, так как погрешности, возникающие в процессе определения опытных данных, представляют сумму погрешностей двух видовгпроведения эксперимента и вычисления.
[c.9]
В каждом частном случае определение погрешности результатов опыта составляет довольно сложную задачу, так как погрешности, возникающие в процессе определения опытных данных, представляют сумму погрешностей двух видовгпроведения эксперимента и вычисления.
[c.9]
Результаты, полученные для графитоэпоксидных композитов, подтверждают перспективность использованного подхода к планированию эксперимента. Тензорно-полиномиальный критерий разрушения, построенный по результатам основных экспериментов, хорошо согласуется с результатами многочисленных контрольных экспериментов на сложное напряженное состояние. Кроме этого, получается количественная оценка погрешностей, к которым приводит применение частных видов критерия разрушения. [c.485]
Но этого еще недостаточно для того, чтобы привести доступные нам эксперименты к той схематической простоте, которая позволила бы выяснить характеристические свойства, присущие понятию о силе. Все тела обладают известным протяжением) мы видели при изучении кинематики, что даже в частном случае движения твердой системы кинематические элементы (скорости, ускорения, траектории) отдельных точек, вообще говоря, отличаются друг от друга. Поскольку мы здесь предполагаем сделать общие индуктивные выводы о характере. сил путем анализа их динамического эффекта, совершенно ясно, что указанное многообразие одновременных кинематических особенностей неизбежно должно маскировать явления и даже отвлекать наше внимание от возможного схематического изображения всего процесса в целом. Чтобы элиминировать. это многообразие усложняющих обстоятельств, целесообразно ограничиться сначала телами настолько малыми (по сравнению с размерами области, в которой происходит движение), чтобы положение тела можно было определить без значительной погрешности геометрической точкой. 13сякое тело, рассматриваемое о этой точки зрения, принято называть материальной точкой. Это название не только не противоречит нашим наглядным представлепяям о конкретных явлениях, но, как было уже указано в кинематике (II, рубр. 1), соответствует уже установившимся взглядам так, например, положение судна на море обыкновенно определяют долготой и широтой места но в действительности эти координаты определяют только одну геометрическую точку на земной поверхности, которую мы отолсествляем с нашим судном в силу его незначительных размеров по сравнению с размерами земли точно так же, чтобы привести пример, еще лучше соответствующий приведенному выше определению, мы изображаем все звезды точками на небесной сфере, хорошо зная, как велики их размеры по сравнению с телами на земле.
Поскольку мы здесь предполагаем сделать общие индуктивные выводы о характере. сил путем анализа их динамического эффекта, совершенно ясно, что указанное многообразие одновременных кинематических особенностей неизбежно должно маскировать явления и даже отвлекать наше внимание от возможного схематического изображения всего процесса в целом. Чтобы элиминировать. это многообразие усложняющих обстоятельств, целесообразно ограничиться сначала телами настолько малыми (по сравнению с размерами области, в которой происходит движение), чтобы положение тела можно было определить без значительной погрешности геометрической точкой. 13сякое тело, рассматриваемое о этой точки зрения, принято называть материальной точкой. Это название не только не противоречит нашим наглядным представлепяям о конкретных явлениях, но, как было уже указано в кинематике (II, рубр. 1), соответствует уже установившимся взглядам так, например, положение судна на море обыкновенно определяют долготой и широтой места но в действительности эти координаты определяют только одну геометрическую точку на земной поверхности, которую мы отолсествляем с нашим судном в силу его незначительных размеров по сравнению с размерами земли точно так же, чтобы привести пример, еще лучше соответствующий приведенному выше определению, мы изображаем все звезды точками на небесной сфере, хорошо зная, как велики их размеры по сравнению с телами на земле. [c.300]
[c.300]
Урок 15. Абсолютная и относительная погрешность
Урок 15. Абсолютная и относительная погрешность
Абсолютная погрешность.
Разность между истинным значением измеряемой величины и её приближённым значением называется абсолютной погрешностью.
Истинное значение измеряемой величины известно бывает лишь в очень редких случаях, а поэтому и действительная величина абсолютной погрешности почти никогда не может быть вычислена. Но при выполнении различных измерений мы обычно представляем себе границы абсолютной погрешности и всегда можем сказать, какого определённого числа она не превосходит. Например, торговые весы могут дать абсолютную погрешность, не превышающую 5 г, а аптекарские – не превышающую одной сотой грамма.
ПРИМЕР:
На предприятии 1284 рабочих и служащих. При округлении этого числа до 1300 абсолютная погрешность составляет
1300
– 1284 = 16.
При округлении до 1280 абсолютная погрешность составляет
1284 – 1280 = 4.
Но абсолютная погрешность не даёт нам представление о качестве измерения, т. е. о том, насколько тщательно это измерение выполнено. Чтобы понять эту мысль, достаточно разобраться в таком примере.
ПРИМЕР:
Допустим, что при измерении коридора длиной в 20 м мы допустили абсолютную погрешность всего только в 1 см. Теперь представим себе, что, измеряя корешок книги, имеющий 18 см длины, мы тоже допустили абсолютную погрешность в 1 см. Тогда понятно, что первое измерение нужно признать превосходным, но зато второе – совершенно неудовлетворительным. Это значит, что на 20 м ошибка в 1 см вполне допустима и неизбежна, но на 18 см такая ошибка является очень грубой.
Отсюда
ясно, что для оценки качества измерения существенна не сама абсолютная
погрешность, а та доля, какую она составляет от измеряемой величины. При измерении
коридора длиной в 20 м погрешность в 1
см составляет
При измерении
коридора длиной в 20 м погрешность в 1
см составляет
долю измеряемой величины, а при измерении корешка книги погрешность в 1 см составляет
долю измеряемой величины. составляет
Если ошибка, возникающая при измерении линейкой или каким либо другим измерительным инструментом, значительно меньше, чем деления шкалы этой линейки, то в качестве абсолютной погрешности измерения обычно берут половину деления. Если деления на линейке нанесены достаточно точно, то ошибка при измерении близка к нулю. Тогда значение измеряемой длины предмета будет значение ближайшей метки линейки. Поэтому, если измерение выполнено аккуратно, то истинная длина предмета может отличаться от измеренной длины не более чем на половину деления шкалы, то есть 0,5 мм.
Абсолютная погрешность суммы двух величин равна сумме абсолютных
погрешностей отдельных слагаемых.
Абсолютная погрешность разности двух величин равна сумме абсолютных погрешностей уменьшаемого и вычитаемого.
Относительная погрешность.
Отношение абсолютной погрешности к приближённому числу называется относительной погрешностью.
Абсолютная погрешность, как мы убедились, не даёт возможности судить о качестве измерения. Относительная же погрешность позволяет судить об этом, Например, сравнивая относительные погрешности, полученные при измерении коридора и корешка книги, т. е. числа
мы видим, что первая дробь меньше второй почти в 110 раз. Это значит, что качество первого измерения значительного выше второго.
Относительные погрешности при сложении и вычитании складывать нельзя.
Относительная погрешность произведения приближённо равна сумме
относительных погрешностей отдельных сомножителей.
ПРИМЕР:
В школе 197 учащихся. Округляем это число до 200. Абсолютная погрешность составляет
200 – 197 = 3.
Относительная погрешность равна 3 : 197 или, округлённо,
3/197 = 1,5%.
В большинстве случаев невозможно узнать точное значение приближённого числа, а значит, и точную величину погрешности. Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.
ПРИМЕР:
Продавец взвешивает арбуз на чашечных весах. В наборе наименьшая гиря – 50 г. Взвешивание показало 3600 г. Это число – приближённое. Точный вес арбуза неизвестен. Но абсолютная погрешность не превышает 50 г. Относительная погрешность не превосходит
50/3600 ≈ 1,4%.
Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью.
Число, заведомо превышающее относительную погрешность (или в худшем случае равное ей), называется предельной относительной погрешностью.
В предыдущем примере за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность 1,4%.
Величина
предельной погрешности не является вполне определённой. Так в предыдущем
примере можно принять за предельную абсолютную погрешность 100 г, 150 г и вообще
всякое число, большее чем 50 г. На практике
берётся по возможности меньшее значение предельной погрешности. В тех случаях,
когда известна точная величина погрешности, эта величина служит одновременно
предельной погрешностью. Для каждого приближённого числа должна быть известна
его предельная погрешность (абсолютная или относительная). Когда она прямо не
указана, подразумевается что предельная абсолютная погрешность составляет
половину единицы последнего выписанного разряда. Так, если приведено
приближённое число 4,78 без указания предельной
погрешности, то подразумевается, что предельная абсолютная погрешность
составляет 0,005. В следствии
этого соглашения всегда можно обойтись без указания предельной погрешности
числа.
Когда она прямо не
указана, подразумевается что предельная абсолютная погрешность составляет
половину единицы последнего выписанного разряда. Так, если приведено
приближённое число 4,78 без указания предельной
погрешности, то подразумевается, что предельная абсолютная погрешность
составляет 0,005. В следствии
этого соглашения всегда можно обойтись без указания предельной погрешности
числа.
Предельная абсолютная погрешность обозначается греческой буквой ∆ (<<дельта>>), предельная относительная погрешность – греческой буквой δ (<<дельта малая>>). Если приближённое число обозначить буквой а, то
ПРИМЕР:
Длина карандаша измерена линейкой с миллиметровым делением. Измерение показало 17,9 см. Какова предельная относительная погрешность этого измерения ?
РЕШЕНИЕ:
Здесь а = 17,9 см. Можно
принять ∆ =
0,1см,
так как с точностью до 1 мм измерить карандаш
нетрудно, а значительно уменьшить предельную погрешность не удастся (при навыке
можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но у самого
карандаша рёбра могут отличаться на большую величину). Относительная погрешность равна
Относительная погрешность равна
Округляя, находим
ПРИМЕР:
Цилиндрический поршень имеет около 35 мм в диаметре. С какой точностью нужно его измерить микрометром, чтобы предельная относительная погрешность составляла 0,05% ?
РЕШЕНИЕ:
По условию, предельная абсолютная погрешность должна
составлять 0,05% от 35 мм. Следовательно, предельная абсолютная погрешность равна
или, усиливая, 0,02 мм. Можно воспользоваться формулой
Подставляя в формулу
а = 35,𝛿 = 0,0005,
имеем
Значит,
∆ = 35 × 0,0005 = 0,0175 мм.
ПРИМЕР:
Для измерения длины болта использованы метровая
линейка с делениями 0,5 см и линейка с
делениями 1 мм. В обоих случаях получен
результат 35 см. Ясно, что в первом случае отклонение найденной
длины 3,5 см от истинной, не должно по модулю
превышать 0,5 см, во втором случае 0,1 см.
Если этот же результат получится при измерении штангенциркулем, то
p(l; 3,5) = |l – 3,5 ≤ 0,01|.
Данный пример показывает зависимость абсолютной погрешности и границ, в которых находится точный результат, от точности измерительных приборов. В одном случае ∆l = 0,5 и, следовательно,
3 ≤ l ≤ 4,
в другом – ∆l = 0,1 и
3,4 ≤ l ≤ 3,6.
Оценка погрешностей арифметических действий.
ПРИМЕР:
Складываются приближённые числа
265 и 32.
Пусть предельная погрешность первого есть 5, а второго 1. Тогда предельная погрешность суммы равна
5 + 1 = 6.
Так, если истинное значение первого есть 270, а второго 33, то приближённая сумма
265 + 32 = 297
на 6 меньше истинной
270 + 33 = 303.
ПРИМЕР:
Пусть предельная погрешность приближённого уменьшаемого 85 равна 2, а предельная погрешность вычитаемого 32 равна 3. Предельная погрешность разности
85 – 32 = 53
есть
3 + 3 = 5.
В самом деле, истинное значение уменьшаемого и вычитаемого могут равняться
85 + 2 = 87 и
32 – 3 = 29.
Тогда истинная разность есть
87 – 29 = 58.
Она на 5 отличается от приближённой разности 53.
ПРИМЕР:
Пусть перемножаются приближённые числа 50 и 20, и пусть предельная относительная погрешность первого сомножителя есть 0,4%, а второго 0,5%.
Тогда предельная относительная погрешность произведения
50 × 20 = 1000
приближённо равна 0,9%. В
самом деле предельная абсолютная погрешность первого сомножителя есть
В
самом деле предельная абсолютная погрешность первого сомножителя есть
50 × 0,004 = 0,2,
а второго
20 × 0,005 = 0,1.
Поэтому истинная величина произведения не больше чем
(50 + 0,2)(20 + 0,1) = 1009,02,
и не меньше, чем
(50 – 0,2)(20 – 0,1) = 991,022.
Если истинная величина произведения есть 1009,2, то погрешность произведения равна
1009,2 – 1000 = 9,02,
а если 991,02, то погрешность произведения равна
1000 – 991,02 = 8,98.
Рассмотренные два случая – самые неблагоприятные. Значит, предельная абсолютная погрешность произведения есть 9,02. Предельная относительная погрешность равна
9,02 : 1000 = 0,902%,
Скачано с www.znanio.ru
Абсолютная и относительная погрешность вычислений.
 Погрешность приближения
Погрешность приближенияРассчитывая значения систематической, случайной и суммарной погрешностей, особенно при использовании электронного калькулятора, получают значение с большим числом знаков. Однако исходные данные для этих расчетов всегда указываются с одной или двумя значащими цифрами. Действительно, класс точности прибора на его шкале указывается не более чем с двумя значащими цифрами, а среднее квадратическое отклонение не имеет смысла записывать с более чем двумя значащими цифрами, так как точность этой оценки при 10 измерениях не выше 30 %. Вследствие этого и в окончательном значении расчетной погрешности должны быть оставлены только первые одна — две значащие цифры. При этом необходимо учитывать следующее. Если полученное число начинается с цифры 1 или 2, то отбрасывание второго знака приводит к очень большой ошибке (до 30– 50 %), это недопустимо. Если же полученное число начинается, например, с цифры 9, то сохранение второго знака, то есть указание погрешности, например, 0,94 вместо 0,9, является дезинформацией, так как исходные данные не обеспечивают такой точности.
В итоге можно сформулировать правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения:
1. Абсолютная погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной, – если первая есть 3 и более.
2. Среднее значение измеренной величины округляется до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности.
3. Относительную погрешность, выраженную в процентах, достаточно записать двумя значащими цифрами.
4. Округление производится лишь в окончательном ответе, а все предварительные вычисления проводятся с одним лишним знаком.
Пример:
На вольтметре класса точности 2,5 с пределом измерений 300 В были произведены несколько повторных измерений одного и того же напряжения. При этом оказалось, что все замеры дали одинаковый результат 267,5 В .
Отсутствие различий между знаками говорит о том, что случайная погрешность пренебрежимо мала, поэтому суммарная погрешность совпадает с систематической (см. рис. 1а).
рис. 1а).
Сначала найдем абсолютную, а затем относительную погрешности. Абсолютная погрешность градуировки прибора равна:
Так как первая значащая цифра абсолютной погрешности больше трех, то это значение должно быть округлено до 8 В . Относительная погрешность:
В значении относительной погрешности должны быть сохранены два значащих разряда: 2,8 %.
Таким образом, в окончательном ответе должно быть сообщено “Измеренное напряжение U=(268+8) В при относительной погрешности d U =2,8 % ”.
учитель математики МОУ «Упшинская ООШ»
Оршанского района Республики Марий Эл
(К учебнику Ю.А.Макарычева Алгебра 8)
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ
Найдем по графику значение у при х = 1,5
у=х 2
у ≈2,3
Найдем значение у при х = 1,5 по формуле
у =1,5 2 = 2,25
Приближенное значение отличается от точного на 2,3 – 2,25 = 0,05
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ
Найдем по графику значение у при х = 1,8
у=х 2
у ≈3,2
Найдем значение у при х = 1,8 по формуле
у =1,8 2 = 3,24
Приближенное значение отличается от точного на 3,24 – 3,2 = 0,04
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ
х
1,5
Точное значение у
(по формуле)
1,8
2,25
Приближенное значение у (по графику)
3,24
2,3
3,2
у=х 2
Определение. Абсолютной погрешностью
Абсолютной погрешностью
у = 2,3 А.П. = |2,25 – 2,3| = |- 0,0 5| = 0,05
у = 3,2 А.П. = |3,24 – 3,2| = | 0,0 4| = 0,04
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ
Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.
Пример 1 пуд равна 16,38. Округлите это значение до целых и найдите абсолютную погрешность приближенного значения.
Решение. 1 6 ,38 ≈ 16
16,38 – точное значение;
16 – приближенное значение.
А.П. = | 16,38 – 16 | = |0 ,38 | = 0, 38
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ
Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.
Пример 2 верста равна 1067 м. Округлите это значение до десятков и найдите абсолютную погрешность приближенного значения.
Решение. 10 6 7 ≈ 1070
1067 – точное значение;
1070 – приближенное значение.
А.П. = | 1067 – 1070 | = |-3| = 3
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ
Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.
Пример 3 . Старинная русская мера длины сажень равна 2,13 м. Округлите это значение до десятых и найдите абсолютную погрешность приближенного значения.
Решение. 2, 1 3 ≈ 2,1
2,13 – точное значение;
2,1 – приближенное значение.
А.П. = | 2,13 – 2,1 | = | 0,03 | = 0,03
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ
Пример 4 . Представьте дробь в виде бесконечной периодической дроби. Округлите результат до сотых и найдите абсолютную погрешность приближенного значения.
Представьте дробь в виде бесконечной периодической дроби. Округлите результат до сотых и найдите абсолютную погрешность приближенного значения.
ТОЧНОСТЬ ПРИБЛИЖЕНИЯ
Всегда ли можно найти абсолютную погрешность?
АВ ≈ 5,3 см
Найдем длину отрезка АВ
Точного значения длины отрезка АВ мы определить не можем, поэтому и абсолютную погрешность приближенного значения найти невозможно.
В подобных случаях в качестве погрешности указывают такое число, больше которого абсолютная погрешность быть не может.
В нашем примере в качестве такого числа можно взять число 0,1.
ПОЧЕМУ? Цена деления линейки равна 0,1 см и поэтому абсолютная погрешность приближенного значения 5,3 не больше 0,1.
ТОЧНОСТЬ ПРИБЛИЖЕНИЯ
Говорят, что число 5,3 есть приближенное значение длины отрезка АВ (в санти-метрах) с точностью до 0,1
АВ ≈ 5,3 см
t ≈ 28 0 с точностью до 1
t ≈ 14 0 с точностью до 2
Определите точность приближенных значений величин, полученных при измерении приборами, изображенными на рисунках 1- 4
ТОЧНОСТЬ ПРИБЛИЖЕНИЯ
Говорят, что число 5,3 есть приближенное значение длины отрезка АВ (в сантиметрах) с точностью до 0,1
АВ ≈ 5,3 см
Если х ≈ а и абсолютная погрешность приближенного значения не превосходит некоторого числа h , то число а называют приближенным значением х с точностью до h
х ≈ а с точностью до h
х = а ± h
ТОЧНОСТЬ ПРИБЛИЖЕНИЯ
АВ ≈ 5,3 см
с точностью до 0,1
t ≈ 28 0 с точностью до 1
с точностью до 2
Определение . Относительной погрешностью (точностью) приближенного значения называется отношение абсолютной погрешности (точности) к модулю приближенного значения
Относительной погрешностью (точностью) приближенного значения называется отношение абсолютной погрешности (точности) к модулю приближенного значения
Для оценки качества измерения можно использовать определения относительной погрешности и относительной точности
l = 100,0 ± 0,1
b = 0,4 ± 0,1
ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ
Определение .
Пример 5 . Старинная русская мера массы пуд равна 16,38. Округлите это значение до целых и найдите относительную погрешность приближенного значения.
Решение. 1 6 ,38 ≈ 16
16,38 – точное значение;
16 – приближенное значение.
А.П. = | 16,38 – 16 | = |0 ,38 | = 0, 38
ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ
Определение . Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения
Пример 6 . Старинная русская мера длины верста равна 1067 м. Округлите это значение до десятков и найдите относительную погрешность приближенного значения.
Старинная русская мера длины верста равна 1067 м. Округлите это значение до десятков и найдите относительную погрешность приближенного значения.
Решение. 10 6 7 ≈ 1070
1067 – точное значение;
1070 – приближенное значение.
А.П. = | 1067 – 1070 | = |-3| = 3
ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ
Пример 7 . Представьте дробь в виде бесконечной периодической дроби. Округлите результат до сотых и найдите относительную погрешность приближенного значения.
Абсолютная и относительная погрешность числа.
В качестве характеристик точности приближенных величин любого происхождения вводятся понятия абсолютной и относительной погрешности этих величин.
Обозначим через а приближение к точному числу А.
Определени . Величина называется погрешностью приближенного числаа.
Определение . Абсолютной погрешностью приближенного
числа а
называется
величина
.
Практически точное число А обычно неизвестно, но мы всегда можем указать границы, в которых изменяется абсолютная погрешность.
Определение . Предельной абсолютной погрешностью приближенного числа а называется наименьшая из верхних границ для величины , которую можно найти при данном способе получения числаа.
На практике в качестве выбирают одну из верхних границ для , достаточно близкую к наименьшей.
Поскольку
,
то
.
Иногда пишут:
.
Абсолютная погрешность — это разница между результатом измерения
и истинным (действительным) значением измеряемой величины.
Абсолютная погрешность и предельная абсолютная погрешность не достаточны для характеристики точности измерения или вычисления. Качественно более существенна величина относительной погрешности.
Определение . Относительной погрешностью приближенного числа а назовем величину:
Определение . Предельной относительной погрешностью приближенного числа а назовем величину
Так как
.
Таким образом, относительная погрешность определяет фактически величину абсолютной погрешности, приходящейся на единицу измеряемого или вычисляемого приближенного числа а.
Пример. Округляя точные числа А до трех значащих цифр, определить
абсолютную Dи относительную δ погрешности полученных приближенных
Дано:
Найти:
∆-абсолютная погрешность
δ –относительная погрешность
Решение:
=|-13.327-(-13.3)|=0.027
,a0
*100%=0.203%
Ответ: =0,027; δ=0.203%
2.Десятичная запись приближенного числа. Значащая цифра. Верные знаки числа(определение верных и значащих цифр, примеры; теория о связи относительной погрешности и числа верных знаков).
Верные знаки числа.
Определение . Значащей цифрой приближенного числа а
называется
всякая цифра, отличная от нуля, и нуль,
если он расположен между значащими
цифрами или является представителем
сохраненного десятичного разряда.
Например, в числе
0,00507 =
имеем
3 значащие цифры, а в числе 0,005070=
значащие цифры,
т.е. нуль справа, сохраняя десятичный
разряд, является значащим.
Условимся впредь нули справа записывать, если только они являются значащими. Тогда, иначе говоря,
значащими являются все цифры числа а, кроме нулей слева.
В десятичной системе счисления всякое число а может быть представлено в виде конечной или бесконечной суммы (десятичной дроби):
где
,
— первая значащая
цифра, m —
целое число, называемое старшим десятичным
разрядом числа а.
Например, 518,3 =, m=2.
Пользуясь записью , введем понятие о верных десятичных знаках (в значащих цифрах) приближенно-
го числа.
Определение . Говорят, что в приближенном числе а формы n — первых значащих цифр ,
где i= m, m-1,…, m-n+1 являются верными, если абсолютная погрешность этого числа не превышает половины единицы разряда, выражаемого n-й значащей цифрой:
В противном случае
последняя цифра
называется
сомнительной.
При записи приближенного числа без указания его погрешности требуют, чтобы все записанные цифры
были верными. Это требование соблюдено во всех математических таблицах.
Термин “n верных знаков” характеризует лишь степень точности приближенного числа и его не следует понимать так, что n первых значащих цифр приближенного числа а совпадает с соответствующими цифрами точного числа А. Например, у чисел А=10, а=9,997 все значащие цифры различны, но число а имеет 3 верных значащих цифры. Действительно, здесь m=0 и n=3 (находим подбором).
Имея дело в вычислениях с бесконечными десятичными дробями, приходится для удобства выполнять приближение этих чисел, т. е. округлять их. Приблизительные числа получаются также при различных измерениях.
Бывает полезно узнать, как сильно приближенное значение числа отличается от его точного значения. Понятно, что чем это различие меньше, тем лучше, тем точнее выполнено измерение или вычисление.
Для определения точности измерений (вычислений) вводят такое понятие как погрешность приближения . По-другому его называют абсолютной погрешностью . Погрешность приближения представляет собой взятую по модулю разность между точным значением числа и его приближенным значением.
По-другому его называют абсолютной погрешностью . Погрешность приближения представляет собой взятую по модулю разность между точным значением числа и его приближенным значением.
Если a — это точное значение числа, а b — его приближенное значение, то погрешность приближения определяется по формуле |a – b|.
Допустим, что в результате измерений было получено число 1,5. Однако в результате вычисления по формуле точное значение этого числа равно 1,552. В таком случае погрешность приближения будет равна |1,552 – 1,5| = 0,052.
В случае с бесконечными дробями погрешность приближения определяется по той же формуле. На месте точного числа записывается сама бесконечная дробь. Например, |π – 3,14| = |3,14159… – 3,14| = 0,00159… . Здесь получается, что погрешность приближения выражена иррациональным числом.
Как известно, приближение может выполняться как по недостатку, так и по избытку. То же число π при приближении по недостатку с точностью до 0,01 равно 3,14, а при приближении по избытку с точностью до 0,01 равно 3,15. Причина, по которой в вычислениях используется его приближение по недостатку, заключается в применении правил округления. Согласно этим правилам, если первая отбрасываемая цифра равна пяти или больше пяти, то выполняется приближение по избытку. Если меньше пяти, то по недостатку. Так как третьей цифрой после запятой у числа π является 1, то поэтому при приближении с точностью до 0,01 оно выполняется по недостатку.
Причина, по которой в вычислениях используется его приближение по недостатку, заключается в применении правил округления. Согласно этим правилам, если первая отбрасываемая цифра равна пяти или больше пяти, то выполняется приближение по избытку. Если меньше пяти, то по недостатку. Так как третьей цифрой после запятой у числа π является 1, то поэтому при приближении с точностью до 0,01 оно выполняется по недостатку.
Действительно, если вычислить погрешности приближения до 0,01 числа π по недостатку и по избытку, то получим:
|3,14159… – 3,14| = 0,00159…
|3,14159… – 3,15| = 0,0084…
Так как 0,00159…
Говоря о погрешности приближения, также как и в случае с самим приближением (по избытку или недостатку), указывают его точность. Так в приводимом выше примере с числом π следует сказать, что оно равно числу 3,14 с точностью до 0,01. Ведь модуль разности между самим числом и его приближенным значением не превышает 0,01 (0,00159… ≤ 0,01).
Точно также π равно 3,15 с точностью до 0,01, так как 0,0084. .. ≤ 0,01. Однако если говорить о большей точности, например до 0,005, то мы можем сказать, что π равно 3,14 с точностью до 0,005 (так как 0,00159… ≤ 0,005). Сказать же это по отношению к приближению 3,15 мы не можем (так как 0,0084… > 0,005).
.. ≤ 0,01. Однако если говорить о большей точности, например до 0,005, то мы можем сказать, что π равно 3,14 с точностью до 0,005 (так как 0,00159… ≤ 0,005). Сказать же это по отношению к приближению 3,15 мы не можем (так как 0,0084… > 0,005).
При выполнении вычислений часто возникает необходимость в округлении чисел, т.е. в замене их числами с меньшим количеством значащих цифр.
Существуют три способа округления чисел:
Округление с недостатком до k -й значащей цифры состоит в отбрасывании всех цифр, начиная с (k+1) -й.
Округление с избытком отличается от округления с недостатком тем, что последняя сохраняемая цифра увеличивается на единицу.
Округление с наименьшей погрешностью отличается от округления с избытком тем, что увеличение на единицу последней сохраняемой цифры производится лишь в том случае, когда первая из отбрасываемых цифр больше 4.
Исключение: если округление с наименьшей погрешностью сводится к отбрасыванию только одной цифры 5, то последняя сохраняемая цифра не изменяется если она четная, и увеличивается на 1, если она нечетная.
Из вышеуказанных правил округления приближенных чисел следует, что погрешность, вызываемая округлением с наименьшей погрешностью, не превышает половины единицы последнего сохраняемого разряда, а при округлении с недостатком или с избытком погрешность может быть и больше половины единицы последнего сохраняемого разряда, но не более целой единицы этого разряда.
Рассмотрим это на следующих примерах.
1. Погрешность суммы. Пусть x а , у — некоторое приближение величины b . Пусть х и у — абсолютные погрешности соответствующих приближений х и у . Найдем границу абсолютной погрешности h a+b суммы х+у , являющейся приближением суммы а+b .
a = x + х,
b = y + y.
Сложим эти два равенства, получим
a + b = x + y + х + y.
Очевидно, что погрешность суммы приближений x и у равна сумме погрешностей слагаемых, т.е.
(x + y) = x + y
Известно, что модуль суммы меньше или равен сумме модулей слагаемых. Поэтому
Поэтому
(x + y) = x + y x + y
Отсюда следует, что абсолютная погрешность суммы приближений не превышает суммы абсолютных погрешностей слагаемых. Следовательно, за границу абсолютной погрешности суммы можно принять сумму границ абсолютных погрешностей слагаемых.
Обозначив границу абсолютной погрешности величины а через h a , а величины b через h b будем иметь
h a+b = h a + h b
2. Погрешность разности. Пусть х и у — погрешности приближений x и у соответственно величин a и b.
a = x + х,
b = y + y.
Вычтем из первого равенства второе, получим
a — b = (x — y) + (x — y)
Очевидно, что погрешность разности приближений равна разности погрешностей уменьшаемого и вычитаемого, т. е.
(x — y) = x — y) ,
(x — y) = x + (-y)
А тогда, рассуждая так же, как в случае сложения, будем иметь
(x — y) = x + (-y) x + y
Отсюда следует, что абсолютная погрешность разности не превышает суммы абсолютных погрешностей уменьшаемого и вычитаемого.
За границу абсолютной погрешности разности можно принять сумму границ абсолютных погрешностей уменьшаемого и вычитаемого. Таким образом.
h a-b = h a + h b (9)
Из формулы (9) следует, что граница абсолютной погрешности разности не может быть меньше границы абсолютной погрешности каждого приближения. Отсюда вытекает правило вычитания приближений, применяемое иногда при вычислениях.
При вычитании чисел, являющихся приближениями некоторых величин, в результате следует оставить столько цифр после запятой, сколько их имеет приближение с наименьшим числом цифр после запятой.
3. Погрешность произведения. Рассмотрим произведение чисел х и у , являющихся приближениями величин a и b . Обозначим через x погрешность приближения х , а через у — погрешность приближения у ,
a = x + х,
b = y + y.
Перемножив эти два равенства, получим
Абсолютная погрешность произведения ху равна
И поэтому
Разделив обе части полученного неравенства на ху , получим
Учитывая, что модуль произведения равен произведению модулей сомножителей, будем иметь
Здесь левая часть неравенства представляет собой относительную погрешность произведения ху , — относительную погрешность приближения х , а — относительную погрешность приближения у . Следовательно, отбрасывая здесь малую величину, получим неравенство
Следовательно, отбрасывая здесь малую величину, получим неравенство
Таким образом, относительная погрешность произведения приближений не превышает суммы относительных погрешностей сомножителей. Отсюда следует, что сумма границ относительных погрешностей сомножителей является границей относительной погрешности произведения, т.е.
E ab = E a + E b (10)
Из формулы (10) следует, что граница относительной погрешности произведения не может быть меньше границы относительной погрешности наименее точного из сомножителей. Поэтому здесь, как и в предыдущих действиях, не имеет смысла сохранять в сомножителях излишнее количество значащих цифр.
Иногда при вычислениях для сокращения объема работы полезно руководствоваться следующим правилом: При умножении приближений с различным числом значащих цифр в результате следует сохранить столько значащих цифр, сколько их имеет приближение с наименьшим числом значащих цифр.
4. Погрешность частного. Если x — приближение величины а, погрешность которого x, а у — приближение величины b с погрешностью y, то
Погрешность частного. Если x — приближение величины а, погрешность которого x, а у — приближение величины b с погрешностью y, то
Вычислим сначала абсолютную погрешность частного:
а затем относительную погрешность:
Принимая во внимание, что y мало по сравнению с y , абсолютную величину дроби можно считать равной единице. Тогда
из последней формулы вытекает, что относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя. Следовательно, можно считать, что граница относительной погрешности частного равна сумме границ относительных погрешностей делимого и делителя, т.е.
5. Погрешность степени и корня. 1) Пусть u = a n , где n — натуральное число, и пусть а х. Тогда, если E a — граница относительной погрешности приближения x величины a , то
и поэтому
Таким образом, граница относительной погрешности степени равна произведению границы относительной погрешности основания на показатель степени, т. е.
е.
E u = n E a (11)
2) Пусть, где n — натуральное число, и пусть ах .
По формуле (11)
и, следовательно,
погрешность вычитаемый вычисление
Таким образом, граница относительной погрешности корня n -й степени в n раз меньше границы относительной погрешности подкоренного числа.
6. Обратная задача приближенных вычислений. В прямой задаче требуется найти приближенное значение функции u=f(х,у,…,n) по данным приближенным значениям аргументов
и границу погрешности h a , которая выражается через погрешности аргументов некоторой функции
h u = (h x , h y , …, h z ) (12)
На практике нередко приходится решать и обратную задачу, в которой требуется узнать, с какой точностью должны быть заданы значения аргументов х, у, …, z , чтобы вычислить соответствующие значения функции u = f(х, у, …, z) с наперед заданной точностью h u .
Таким образом, при решении обратной задачи искомыми являются границы погрешностей аргументов, связанные с заданной границей погрешности функции h u уравнением (12), и решение обратной задачи сводится к составлению и решению уравнения h u = (h x , h y , …, h z ) относительно h x , h y , …, h z . Такое уравнение или имеет бесконечное множество решений, или совсем не имеет решений. Задача считается решенной, если найдено хотя бы одно решение такого уравнения.
Для решения обратной задачи, которая часто бывает неопределенной, приходится вводить добавочные условия об отношениях искомых погрешностей, например считать их равными и тем самым сводить задачу к уравнению с одним неизвестным.
3.1 ВВЕДЕНИЕ
После того, как каждому элементу данных присвоены оценки ошибок, мы должны выяснить
как эти ошибки влияют на ошибку в результате. Ошибка в количестве может быть
рассматривается как вариация или «изменение» значения этой величины. Результаты есть
полученные математическими операциями над данными, и небольшие изменения в любых данных
количество может повлиять на ценность результата.Мы говорим, что «ошибки в данных распространяются
путем вычислений, чтобы получить ошибку в результате.»
Ошибка в количестве может быть
рассматривается как вариация или «изменение» значения этой величины. Результаты есть
полученные математическими операциями над данными, и небольшие изменения в любых данных
количество может повлиять на ценность результата.Мы говорим, что «ошибки в данных распространяются
путем вычислений, чтобы получить ошибку в результате.»
3.2 МАКСИМАЛЬНАЯ ОШИБКА
Сначала мы рассмотрим, как ошибки данных распространяются при вычислениях, чтобы повлиять на пределы ошибок (или максимальная ошибка) результатов. Проще всего сначала рассмотреть детерминированных ошибок , которые имеют явный знак. Это приводит к полезным правилам распространения ошибок. Затем мы изменим и распространить правила на другие меры ошибок, а также на неопределенные ошибки.
В основе лежит математика «конечных разностей», алгебра для работы с
числа, на которые наложены относительно небольшие вариации. Конечные различия, которые мы
интересуют отклонения от «истинных значений», вызванные ошибками эксперимента.
Рассмотрим результат R, вычисленный из суммы двух величин данных A и B. Для этого обсуждение мы будем использовать ΔA и ΔB для представления ошибок в A и B соответственно. Количества данных записываются, чтобы показать ошибки явно:
Мы допускаем возможность того, что ΔA и ΔB могут быть как положительными, так и отрицательными, причем знаки находятся «в» символы «ΔА» и «ΔВ».»
Результат сложения А и В выражается уравнением: R = А + В. При ошибках явно включены, написано:
Таким образом, результат с явно показанной ошибкой ΔR форма R + ΔR, составляет:
Ошибка в R: ΔR = ΔA + ΔB.
Делаем вывод, что ошибка в сумме двух величин есть сумма ошибок в тех количества. Вы можете легко решить случай, когда результат вычисляется из разность двух величин.В этом случае ошибка в результате есть разница в ошибки. Итого:
Правило суммы и разности. При сложении (или вычитании) двух величин
их определенные ошибки складываются (или вычитаются).
Теперь рассмотрим умножение: R = AB. С явно включенными ошибками:
R + ΔR = (A + ΔA)(B + ΔB) = AB + (ΔA)B + A(ΔB) + (ΔA)(ΔB)
или : ΔR = (ΔA)B + А(ΔВ) + (ΔА)(ΔВ)
Это не похоже на простое правило.Однако, когда мы выражаем ошибки в относительная форма , все выглядит лучше. Когда ошибка a мала по сравнению с A, а ΔB мало по сравнению с B, то (ΔA)(ΔB) заведомо мала по сравнению с АБ. Он также мал по сравнению с (ΔA)B и A(ΔB). Поэтому мы можем выбросить член (ΔA)(ΔB), так как нас интересует только в оценках ошибок до одной-двух значащих цифр. Относительная ошибка в R как
ΔR ΔAB + ΔBA ΔA ΔB —— ≈ ————————— = —— + —— , Р АБ А Б
это дает нам очень простое правило:
Правило продукта. При умножении двух величин их относительные детерминированные ошибки доп.
Аналогичная процедура используется для отношения двух величин, R = A/B.
(A + ΔA) B — A (B + ΔB) (ΔA)B — B(ΔA) ΔA ΔB = ————————————————————— ≈ ————————————— ≈ —— — —— А(В + ΔВ) АВ А ВА + ΔА А (А + ΔА) В А (В + ΔВ) —————— — ———————— — — ————————— ΔR B + ΔB B (B + ΔB) B B (B + ΔB) —— = —————————— = ——————————————————————— Р А А — — Б Б
Приближение, сделанное на предпоследнем шаге, заключалось в том, чтобы пренебречь ΔB в знаменателе, что справедливо при относительных ошибках маленькие.Итак, результат:
Частное правило. Когда две величины делятся, относительная детерминация ошибка частного — это относительная детерминированная ошибка числителя минус относительная детерминированная ошибка знаменателя.
Следствием правила произведения является следующее:
Силовое правило. Когда величину Q возводят в степень P, относительная
детерминированная ошибка в результате равна P, умноженной на относительную детерминированную ошибку в Q. Это также справедливо
для отрицательных степеней, т. е. относительная детерминированная ошибка квадратного корня из Q составляет половину
относительная детерминированная ошибка в Q.
Это также справедливо
для отрицательных степеней, т. е. относительная детерминированная ошибка квадратного корня из Q составляет половину
относительная детерминированная ошибка в Q.
3.3 РАСПРОСТРАНЕНИЕ НЕОПРЕДЕЛЕННЫХ ОШИБОК.
Неопределенные ошибки имеют неизвестный знак. Если предположить, что измерения имеют симметричное распределение относительно их среднего значения, то ошибки несмещены по знаку. Кроме того, если неопределенные ошибки в различных измерениях не зависят друг от друга, их знаки имеют тенденцию компенсировать друг друга, когда величины объединяются посредством математических операции.
Когда нас интересуют только пределы ошибки (или максимальной ошибки), мы принять «наихудшую» комбинацию знаков. В операции вычитания А — В наихудшие Случай отклонения ответа возникает, когда ошибки составляют либо +ΔA и -ΔB, либо -ΔA и +ΔB. В любом случае, максимальная ошибка будет (ΔA + ΔB).
В операции деления A/B наихудшее отклонение результата происходит, когда
ошибки в числителе и знаменателе имеют противоположный знак, либо +ΔA и -ΔB, либо -ΔA и +ΔB. В любом случае,
максимальный размер относительной ошибки составит (ΔA/A + ΔB/B).
В любом случае,
максимальный размер относительной ошибки составит (ΔA/A + ΔB/B).
Результаты сложения и умножения такие же, как и раньше. В итоге, максимум неопределенных ошибок распространяются в соответствии со следующими правилами:
Правило сложения и вычитания. Добавлены абсолютные неопределенные ошибки.
Правило произведения и частного. Добавлены относительные неопределенные ошибки.
Следствием правила произведения является следующее:
Силовое правило. Когда количество Q возводится в степень P, относительная ошибка в результате P умножается на относительную ошибку в Q. Это также верно для отрицательных степеней, т.е. относительная ошибка квадратного корня Q составляет половину относительной ошибки Q.
Эти правила применяются только при объединении независимых ошибок, которые
отдельные измерения, ошибки которых имеют размер и знак, независимые друг от друга.
Можно показать (но не здесь), что эти правила достаточно хорошо применимы и к ошибкам выражены в виде средних отклонений. Одним из недостатков является то, что оценки ошибок, сделанные таким образом, еще слишком консервативен. Они не полностью учитывают тенденцию ошибок, связанных с независимые ошибки компенсируют друг друга. Это, однако, небольшая поправка, мало значение в нашей работе в этом курсе.
При необходимости могут быть получены правила распространения ошибок для других математических операций.Например, правила для ошибок в тригонометрических функциях могут быть получены с помощью тригонометрические тождества с использованием приближений: sin θ ≈ θ и cos θ ≈ 1, справедливые, когда θ достаточно мало. Также можно вывести правила для экспонент.
При объединении математических операций правила могут последовательно применяться к
каждой операции. Таким образом, можно алгебраически вывести уравнение, выражающее
ошибка в результате с точки зрения ошибок в данных. Такое уравнение всегда можно привести к
Стандартная форма , в которой каждый источник ошибки появляется только в одном термине. Пусть Δx представляет ошибку в x, Δy
ошибка в y и т. д. Тогда ошибка в любом результате R, рассчитанная по любой комбинации математических
операций со значениями данных x, y, z и т. д. определяется как:
Такое уравнение всегда можно привести к
Стандартная форма , в которой каждый источник ошибки появляется только в одном термине. Пусть Δx представляет ошибку в x, Δy
ошибка в y и т. д. Тогда ошибка в любом результате R, рассчитанная по любой комбинации математических
операций со значениями данных x, y, z и т. д. определяется как:
ΔR = (c x ) Δx + (c y ) Δy + (c z ) Δz … и т. д.,
, которые всегда можно алгебраически преобразовать в:
ΔR Δx Δy Δz —— = {С} —— + {С} —— + {С} —— ... и т.д. R х х y y z z
Коэффициенты {c x } и {C x } и т. д. в каждом члене чрезвычайно важны, потому что они, наряду с размерами ошибок определить, насколько сильно каждая ошибка влияет на результат. Это является относительным размером членов этого уравнения, которое определяет относительную важность источников ошибок .
Если это уравнение ошибки получено из правил определяемой ошибки ,
относительные ошибки могут иметь знаки + или -. Коэффициенты также могут иметь знаки + или -,
поэтому сами термины могут иметь знаки + или -. Поэтому, вероятно, для членов ошибки
компенсировать друг друга, уменьшая ΔR/R.
Коэффициенты также могут иметь знаки + или -,
поэтому сами термины могут иметь знаки + или -. Поэтому, вероятно, для членов ошибки
компенсировать друг друга, уменьшая ΔR/R.
Если это уравнение ошибки получено из правил неопределенной ошибки , ошибка меры Δx, Δy и т. д. по своей сути положительный. Коэффициенты также окажутся положительными, поэтому члены не могут компенсировать друг с другом.
Уравнение неопределенной ошибки может быть получено непосредственно из определенной ошибки уравнения, просто выбрав «наихудший случай», т.е.е., взяв абсолютное значение каждого термина. Это заставляет все термины быть положительными. Этот шаг следует выполнять только после определите уравнение ошибки, Eq. 3-6 или 3-7, был полностью выведен в стандартной форме.
Уравнение ошибки в стандартной форме является одним из самых полезных инструментов для экспериментальных исследований.
проектирование и анализ. Он должен быть выведен (в алгебраической форме) еще до начала эксперимента. начал, как руководство к экспериментальной стратегии. Он может показать, какие источники ошибок преобладают, и
которые незначительны, тем самым экономя время, которое вы могли бы потратить на возню с неважными
соображения.Он может подсказать, как можно свести к минимуму влияние источников ошибок с помощью соответствующих
выбор размеров переменных. Он может сказать вам, насколько хороший измерительный прибор необходим для
добиться желаемой точности результатов.
начал, как руководство к экспериментальной стратегии. Он может показать, какие источники ошибок преобладают, и
которые незначительны, тем самым экономя время, которое вы могли бы потратить на возню с неважными
соображения.Он может подсказать, как можно свести к минимуму влияние источников ошибок с помощью соответствующих
выбор размеров переменных. Он может сказать вам, насколько хороший измерительный прибор необходим для
добиться желаемой точности результатов.
Студент, который пренебрегает выводом и использованием этого уравнения, может провести весь лабораторный период использование инструментов, стратегии или ценностей, недостаточных для требований эксперимента. То студент может понятия не иметь почему результаты были не такими хорошими, как должны были быть был.
Последнее замечание для тех, кто хочет использовать стандартные отклонения как неопределенную ошибку измерения: Поскольку стандартное отклонение получается из среднего значения в квадрате отклонения , уравнение 3-7 необходимо изменить — каждый член уравнения (обе части) должен быть в квадрате:
(r/R) 2 = (C x ) 2 (x/X) 2 + (C y ) 2 (y/Y) 2 + (C ) 2 (г/я) 2
Это правило приводится здесь без доказательства.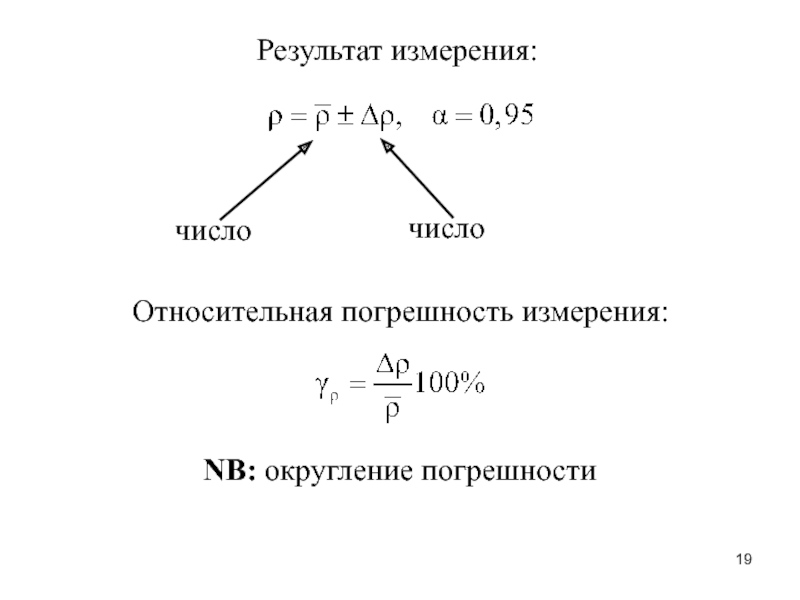 Этот метод объединения членов ошибки называется
«суммирование в квадратурах».
Этот метод объединения членов ошибки называется
«суммирование в квадратурах».
3.4 ПРИМЕР АНАЛИЗА РАСПРОСТРАНЕНИЯ ОШИБКИ
Физические законы, с которыми вы сталкиваетесь в начальных курсах физики, выражаются как уравнений, а это комбинации элементарных операций сложения, вычитание, умножение, деление, возведение в степень и т. д. Лабораторные опыты часто принимают форму проверки физического закона путем измерения каждой величины в законе.Если измерения согласуются в пределах погрешности, то говорят, что закон соблюден. проверено экспериментом.
Например, говорят, что тело падает прямо вниз в отсутствие сил трения. соблюдать закон:
1 2 s = v т + — а т о 2
где s — расстояние падения, vo — начальная скорость, t — время падения, а — время падения.
ускорение.В этом случае a представляет собой ускорение свободного падения g, которое, как известно, имеет
постоянная величина около 980 см/сек2, в зависимости от широты и высоты. Точнее
доступны значения g, сведенные в таблицу для любого места на Земле. Есть общая формула
для g вблизи Земли, называемой формулой Гельмерта, которую можно найти в Справочнике по
Химия и физика.
Точнее
доступны значения g, сведенные в таблицу для любого места на Земле. Есть общая формула
для g вблизи Земли, называемой формулой Гельмерта, которую можно найти в Справочнике по
Химия и физика.
Студент может разработать эксперимент, чтобы проверить эту связь и определить значение g, измеряя время падения тела на измеренное расстояние.
Одно упрощение можно сделать заранее, измеряя s и t из положения и Мгновение тело находилось в состоянии покоя, как только оно было освобождено и начало падать. Тогда v o = 0 и весь первый член в правой части уравнения выпадает, остается:
1 2 с = — г т 2
Студент, конечно, повторит эксперимент несколько раз, чтобы получить среднее значение. время падения.Средние значения s и t будут использоваться для вычисления g с использованием переставленного уравнение:
2 с г = —— 2 т
Экспериментатор использовал данных , состоящих из измерений s и t, для вычисления результат , г. Ошибки в s и t объединяются, чтобы произвести ошибку в
экспериментально определенное значение g.Ошибка в g может быть рассчитана из
сформулированные ранее правила распространения ошибок, если мы знаем ошибки в s и t.
Ошибки в s и t объединяются, чтобы произвести ошибку в
экспериментально определенное значение g.Ошибка в g может быть рассчитана из
сформулированные ранее правила распространения ошибок, если мы знаем ошибки в s и t.
Пусть fs и ft представляют дробные ошибки в t и s. Точно так же fg будет представлять дробная ошибка в g. Число «2» в уравнении не является измеряемой величиной, поэтому он считается безошибочным или точным.
Таким образом, дробная ошибка в числителе уравнения. 11 по правилу продукта:
, так как f 2 = 0.
Дробная ошибка в знаменателе по правилу степени равна 2f t . Используя правило деления, дробная ошибка во всей правой части уравнения. 3-11 — дробная ошибка в числитель минус дробная ошибка в знаменателе.
которую мы указали, также является дробной ошибкой в g.
Абсолютная ошибка в g:
Уравнения, подобные 3-11 и 3-13, называются уравнениями детерминированной ошибки , так как мы
использовали правила детерминированных ошибок. Рекомендуется сначала получить их, даже до того, как вы
решить, являются ли ошибки детерминированными, неопределенными или и теми, и другими.
Рекомендуется сначала получить их, даже до того, как вы
решить, являются ли ошибки детерминированными, неопределенными или и теми, и другими.
Некоторые студенты предпочитают выражать дробные погрешности величины Q в виде ΔQ/Q. Используя этот стиль, наши результаты:
Δg Δs Δt Δs Δt —— = —— - 2 —— , а Δg = g —— - 2g —— г с т с т
В этом эксперименте мы можем распознать возможные источники определенной ошибки: время реакции при использовании секундомера натяжение веревки используется для измерения расстояния падения.Но если ты распознать определенную ошибку, вы должны принять меры для ее устранения, прежде чем предпринимать окончательный набор данных.
Неопределенные ошибки проявляются как разброс в независимых измерениях,
особенно в измерении времени. Экспериментатор должен изучить эти
измерений и выбрать соответствующую оценку величины этого разброса, чтобы
присвойте значение неопределенным ошибкам.
Затем эти оценки используются в уравнении определяемой ошибки в .Тот легко получить. Посмотрите на уравнение детерминированной ошибки и выберите знаки термины для «наихудшего» случая распространения ошибки. В уравнениях 3-13 через 3-16 мы должны изменить знак минус на знак плюс:
е + 2 е = е с т г
Δg = г f = г (f + 2 f ) г с т
Δg Δs Δt Δs Δt —— = —— + 2 —— , а Δg = g —— + 2g —— г с т с т
3.5 ПРИМЕРОВ:
(1) Две величины данных, X и Y, используются для вычисления результата, R = XY. Х = 38,2 ± 0,3 и Y = 12,1 ± 0,2. Какая ошибка в R?
Решение: Сначала рассчитайте R без учета ошибок:
Правило произведения требует измерения дробной ошибки. Дробная ошибка в X составляет 0,3/38,2.
= 0,008 примерно, а дробная ошибка в Y составляет примерно 0,017. Добавление этих
дает дробную ошибку в R: 0.025. Умножение этого результата на R дает 11,56 в качестве абсолютного
ошибка в R, поэтому мы записываем результат как R = 462 ± 12. Обратите внимание, что, как только мы узнаем ошибку, ее размер говорит нам, насколько округлить результат (сохраняя первую неопределенную цифру). Обратите внимание также, что мы округляем саму ошибку до одной или максимум двух цифр. Вот почему мы могли безопасно делать приближения при расчетах ошибок.
Добавление этих
дает дробную ошибку в R: 0.025. Умножение этого результата на R дает 11,56 в качестве абсолютного
ошибка в R, поэтому мы записываем результат как R = 462 ± 12. Обратите внимание, что, как только мы узнаем ошибку, ее размер говорит нам, насколько округлить результат (сохраняя первую неопределенную цифру). Обратите внимание также, что мы округляем саму ошибку до одной или максимум двух цифр. Вот почему мы могли безопасно делать приближения при расчетах ошибок.
Этот результат один и тот же независимо от того, являются ли ошибки определенными или неопределенными, поскольку в уравнении детерминированной ошибки появились отрицательные члены.
(2) Величина Q рассчитывается по закону: Q = (G+H)/Z, и данные:
Вычисление Q требует как сложения, так и деления, и дает Q = 0,340. То
поэтому вычисление ошибки требует как правила сложения, так и правила деления,
применялись в том же порядке, в каком выполнялись операции при вычислении Q.
Во-первых, правило сложения гласит, что абсолютные ошибки в G и H складываются, поэтому ошибка в числитель (G+H) равен 0.5 + 0,5 = 1,0. Поэтому дробная ошибка в числитель 1,0/36 = 0,028. Дробная ошибка в знаменателе 1,0/106 = 0,0094. Дробная детерминированная ошибка в Q составляет 0,028 — 0,0094 = 0,0186, что составляет 1,86%. Абсолютная дробно-детерминированная ошибка равна (0,0186)Q = (0,0186)(0,340) = 0,006324. Приведем результат в стандартной форме: Q = 0,340 ± 0,006.
Если бы мы знали, что ошибки в детерминированы по своей природе, мы бы добавили дробные ошибки числителя и знаменателя, чтобы получить наихудший случай.Дробный тогда неопределенная ошибка в Q составляет 0,028 + 0,0094 = 0,122, или 12,2%. Абсолютная ошибка в Q тогда 0,04148. Приводим результат Q = 0,340 ± 0,04.
3.6 УПРАЖНЕНИЯ:
(3.1) Разработайте неисчислимое доказательство правил произведения.
(3. 2) Разработайте неисчислимое доказательство частных правил. Сделайте это для неопределенного
правило ошибок и правило детерминированных ошибок. Подсказка: возьмем частное от (A + ΔA) и (B — ΔB), чтобы найти дробную ошибку в A/B.Попробуйте все другие комбинации знаков плюс и минус.
2) Разработайте неисчислимое доказательство частных правил. Сделайте это для неопределенного
правило ошибок и правило детерминированных ошибок. Подсказка: возьмем частное от (A + ΔA) и (B — ΔB), чтобы найти дробную ошибку в A/B.Попробуйте все другие комбинации знаков плюс и минус.
(3.3) Математическая операция определения разности двух величин данных часто дают гораздо большую дробную ошибку в результате, чем в данных. Почему это может произойти? Следует ли это из приведенных выше правил? При каких условиях это порождает очень большие ошибки в результатах?
(3.4) Покажите с помощью правил, что максимальная ошибка в среднем нескольких количество равно максимальной ошибке каждой из отдельных величин.Это показывает один из недостатков этих правил для максимальной ошибки; вроде нет плюсов взяв среднее. Но об этом будет сказано позже.
3.7 РАСПРОСТРАНЕНИЕ ОШИБОК В ДРУГИХ МАТЕМАТИЧЕСКИХ ОПЕРАЦИЯХ
Приведены правила сложения, вычитания, умножения и деления. Повышение до
сила была частным случаем умножения. Иногда вы будете сталкиваться с вычислениями с
тригонометрические функции, логарифмы, квадратные корни и другие операции, для которых эти правила не применимы.
достаточный.
Повышение до
сила была частным случаем умножения. Иногда вы будете сталкиваться с вычислениями с
тригонометрические функции, логарифмы, квадратные корни и другие операции, для которых эти правила не применимы.
достаточный.
Метод исчисления, описанный в главе 6, работает для любых математических операция. Но для тех, кто не знаком с исчислением, всегда найдутся не исчисления. стратегии, чтобы выяснить, как распространяются ошибки.
Хитрость заключается в применении общего принципа, подразумеваемого во всех предыдущих обсуждения и специально использованный ранее в этой главе для установления правил добавления и умножение.Этот принцип можно сформулировать:
Максимальная ошибка в результате определяется путем определения того, насколько сильно произошло изменение в результат, когда максимальные ошибки в данных сочетаются наихудшим образом.
Пример : Измеренный угол равен 30° ±0,5°. Что ошибка в синусе этого угла?
Решение: Воспользуйтесь электронным калькулятором.
Синус 30° равен 0,5; синус 30,5° равен 0.508; синус 29,5° равен 0,492. Таким образом, если угол на полградуса больше, синус становится на 0,008 больше, а если он меньше на полградуса, синус становится на 0,008 меньше. ( изменение в обоих случаях оказывается почти одинакового размера.) Таким образом, ошибка в синусе будет написано ±0,008.
Размер ошибки в тригонометрических функциях зависит не только от размера ошибки по углу, но и по величине угла. Ошибка в полградуса при угле 90° выдаст ошибку только 0.00004 в синусе.
3.8 НЕЗАВИСИМЫЕ НЕОПРЕДЕЛИМЫЕ ОШИБКИ
Экспериментальные исследования обычно требуют измерения ряда различных физических величин, каждая из которых может иметь ошибку. Говорят, что ошибки быть независимым , если ошибка в каждом из них никак не связана с другими. Ошибки, встречающиеся в элементарной лаборатории, обычно независимы, но есть важные исключения.
Когда ошибки независимы, математические операции, приводящие к результату, имеют тенденцию
усреднить последствия ошибок. Это снижает вероятность того, что ошибки в результатах будут такими большими, как предсказывает правило максимальной ошибки.
Это снижает вероятность того, что ошибки в результатах будут такими большими, как предсказывает правило максимальной ошибки.
Простая модификация этих правил дает более реалистичные прогнозы размера ошибок. в результатах. Эти модифицированные правила представлены здесь без доказательства. На самом деле они несколько произвольны, но дают реалистичные оценки, которые легко вычислить.
Предыдущие правила изменены заменой «сумма из» на «квадратный корень из суммы квадратуры». Вместо суммирования мы «суммируем в квадратурах».
Эта модификация используется только при работе с неопределенными ошибками, поэтому мы повторяем изменены правила неопределенных ошибок:
Правило суммы и разности: Неопределенная ошибка в сумме или разнице нескольких величин есть квадратный корень из суммы квадратов погрешностей отдельных величин.[Суммировать квадратурные ошибки.]
Правило произведения и частного: дробная неопределенная ошибка в произведении или частном нескольких величин есть квадратный корень из суммы квадратов дробных ошибок отдельных величин.
[Сумма дробных ошибки в квадратуре.]
Возведение числа в степень может показаться простым случаем умножения: A 2 = А × А.Но здесь два числа, умноженные вместе, тождественны, и, следовательно, не является независимым. подвеска . Таким образом, модификация правила здесь неуместна, и исходное правило стенды:
Степенное правило: Задана дробная неопределенная ошибка в величине An в n раз больше дробной ошибки в A.
3.9 УПРАЖНЕНИЯ (3.10) Какова дробная неопределенная ошибка в A -n через дробную ошибку в A?
(3.11) Какова дробная неопределенная ошибка в A A (A в степени A)?
(3.12) Какова дробная неопределенная ошибка в 3А? (Цифра 3 без ошибок).
3.10 ОШИБКА В СРЕДНЕМ
В качестве примера этих правил рассмотрим случай усреднения нескольких величин.
Ранее мы заявляли, что процесс усреднения не уменьшил размер ошибки. Теперь, когда мы признаем, что повторные измерения независимы , мы должны применить
изменены правила раздела 9.
Теперь, когда мы признаем, что повторные измерения независимы , мы должны применить
изменены правила раздела 9.
Предположим, что произведено n измерений величины Q. Дробная ошибка может быть считается примерно одинаковым для всех этих измерений. Назовите это ф. Тогда наши данные таблица:
Q±fQ 1 1 Q±fQ 2 2 .... Q±fQ 3 3Первым шагом в получении среднего значения является добавление Q. Ошибка в сумме определяется модифицированным правилом сумм:
Но каждое из значений Q почти равно их среднему значению, , поэтому ошибка в сумме
это:
Следующим шагом в вычислении среднего является деление суммы на n.Нет ошибки в n (счет — это одно из немногих измерений, которые мы можем делать идеально.) Таким образом, дробная ошибка в частное того же размера, что и дробная ошибка в числителе.
Таким образом, дробная ошибка в среднем равна , уменьшенной на коэффициент 1/√n. За
Например, относительная погрешность среднего значения четырех измерений составляет половину погрешности одного измерения.
измерение. Обратите внимание, что эта дробь сходится к нулю при больших n, предполагая, что нулевая ошибка
было бы получено только при усреднении бесконечного числа измерений! У нас было бы
достигнуто неуловимое «истинное» значение!
За
Например, относительная погрешность среднего значения четырех измерений составляет половину погрешности одного измерения.
измерение. Обратите внимание, что эта дробь сходится к нулю при больших n, предполагая, что нулевая ошибка
было бы получено только при усреднении бесконечного числа измерений! У нас было бы
достигнуто неуловимое «истинное» значение!
3.11 УПРАЖНЕНИЙ
(3.13) Выведите выражение для дробной и абсолютной ошибки среднего значения n измерения величины Q, когда каждое измерение Q имеет различных дробная ошибка. Результат проще всего выразить с помощью обозначения суммирования, обозначающего каждое измерение на Q i и его относительная ошибка на f i .
© 1996, 2004, Дональд Э. Симанек.
(PDF) Оценка наименьшей относительной погрешности продукта
arXiv:1309.0220v1 [stat.ME] 1 сентября 2013 г.
Оценка относительной погрешности наименьшего произведения
Кани ЧЕНЬ, Юаньюань ЛИН, Чжанфэн ВАНГ и Чжилян ЙИНГ
Критерий относительной погрешности наименьшего произведения предлагается для моделей мультипликативной регрессии. Это —
Это —
вариант при масштабном преобразовании исхода и ковариат. Кроме того, целевая функция
гладкая и выпуклая, что дает простую и однозначно определенную оценку параметра регрессии.
Показано, что оценка асимптотически нормальна и справедлива простая оценка дисперсии с включением
.Результаты моделирования подтверждают, что предложенный метод работает хорошо. Приложение
для расчета телесного жира представлено для иллюстрации нового метода.
Ключевые слова: линейная гипотеза; Мультипликативная регрессионная модель; Форма продукта; Относительная ошибка, шкала
инвариантность; Оценка дисперсии.
1 Введение
В регрессионном анализе наименьшие квадраты (LS) и наименьшее абсолютное отклонение (LAD) являются наиболее часто используемыми критериями, основанными на абсолютных ошибках (Stigler, 1981; Portnoy & Koenker, 1997).Однако в некоторых
ситуациях более желательны критерии, основанные на относительных ошибках, которые не зависят от масштаба и менее чувствительны к выбросам (Narula & Wellington, 1977; Makridakis et al. , 1984; Khoshgoftaar et al.,
, 1984; Khoshgoftaar et al.,
). 1992; Ye, 2007; Park & Stefanski, 1998; Chen et al., 2010; Zhang & Wang, 2012). Рассмотрим
в соответствии с моделью мультипликативной регрессии переменные с первым компонентом
, равным 1 (отрезок), β — соответствующий p-вектор параметров регрессии с первым компонентом
, являющимся точкой пересечения, а ii — член ошибки, который является строго положительным.Дополнительное ограничение на ǫ
1 Кани Чен — профессор факультета математики Гонконгского университета науки и технологии, Коулун,
Гонконг, Китай (электронная почта: [email protected]). Юаньюань Линь — доцент кафедры статистики Школы экономики
и Института экономических исследований Ван Яньань Сямэньского университета, Китай (электронная почта: [email protected]).
Ван Чжаньфэн — доцент кафедры статистики и финансов Научно-технического университета
Китай, Хэфэй 230026, Китай (Электронная почта: [email protected]). Чжилян Ин — профессор кафедры статистики Колумбийского университета
, Нью-Йорк, штат Нью-Йорк, 10027 (электронная почта: zying@stat. columbia.edu).
columbia.edu).
1
Новая мера относительной ошибки для векторов на JSTOR
АбстрактныйСтатья определяет новую меру относительной ошибки вектора y как приближение к вектору x при произвольной норме. Показано, что это метрика, тогда как традиционная мера |y — x|/|x| только примерно так.Он обобщает соответствующую меру Ф. В. Дж. Олвера для скаляров, имеет явную формулу для пространств внутренних произведений и предлагается в качестве инструмента для анализа ошибок округления.
Информация о журналеЖурнал SIAM по численному анализу содержит исследовательские статьи. по разработке и анализу численных методов, в том числе их сходимость, стабильность и анализ ошибок, а также связанные результаты в функциональный анализ и теория приближений. Вычислительные эксперименты также включены новые типы числовых приложений.
Информация об издателе «Общество промышленной и прикладной математики является ведущим
международная ассоциация прикладной математики и ее публикации
могли бы стать ядром адекватной коллекции по математике.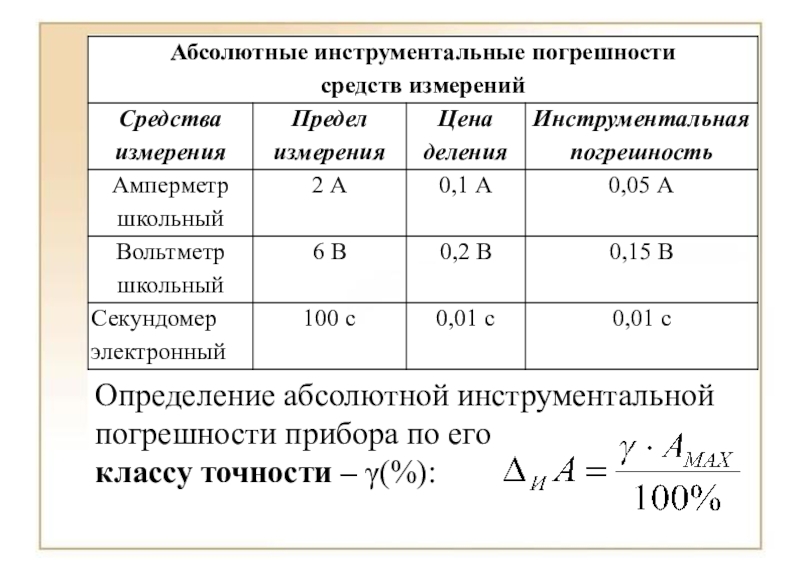 Один из
цели этой организации состоит в том, чтобы сделать поток информации между
университет и промышленность более гладкими. Прекрасно справляется с этой задачей
и многие из ведущих академических учреждений мира являются членами.»
— Журналы для библиотек, восьмое издание, 1995 г., R. R.
Боукер, Нью-Провиденс, Нью-Джерси
Общество промышленной и прикладной математики (SIAM), штаб-квартира
в Филадельфии, была основана в 1951 году для продвижения применения
математики в науку и промышленность, продвигать математические исследования и
предоставить средства для обмена информацией и идеями между
математиков, инженеров и ученых.
SIAM имеет комплексную программу публикаций в области прикладных и вычислительных
математике, включая 11 престижных исследовательских журналов.Для полного
описание наших журналов и недавно анонсированных SIAM Journals Online,
зайдите на http://www.siam.org/.
Один из
цели этой организации состоит в том, чтобы сделать поток информации между
университет и промышленность более гладкими. Прекрасно справляется с этой задачей
и многие из ведущих академических учреждений мира являются членами.»
— Журналы для библиотек, восьмое издание, 1995 г., R. R.
Боукер, Нью-Провиденс, Нью-Джерси
Общество промышленной и прикладной математики (SIAM), штаб-квартира
в Филадельфии, была основана в 1951 году для продвижения применения
математики в науку и промышленность, продвигать математические исследования и
предоставить средства для обмена информацией и идеями между
математиков, инженеров и ученых.
SIAM имеет комплексную программу публикаций в области прикладных и вычислительных
математике, включая 11 престижных исследовательских журналов.Для полного
описание наших журналов и недавно анонсированных SIAM Journals Online,
зайдите на http://www.siam.org/.
Подход к оценке относительной ошибки для мультипликативной модели с одним индексом
Chen KN, Guo SJ, Lin YY, et al. , Оценка наименьшей абсолютной относительной ошибки, Journal of the American Statistical Association, 2010, 105 (491): 1104–1112.
, Оценка наименьшей абсолютной относительной ошибки, Journal of the American Statistical Association, 2010, 105 (491): 1104–1112.
MathSciNet Статья МАТЕМАТИКА Google Scholar
Chen K N, Lin Y Y, Wang Z F, et al., Оценка относительной ошибки наименьшего продукта, Journal of Multivariate Analysis, 2016, 144 : 91–98.
MathSciNet Статья МАТЕМАТИКА Google Scholar
Парк Х.С. и Стефански Л.А. Прогноз относительной ошибки, Statistics & Probability Letters, 1998, 40 (3): 227–236.
MathSciNet Статья МАТЕМАТИКА Google Scholar
Ye J M, Ценовые модели и значимость бухгалтерской информации, Электронный журнал SSRN , http://ssrn.com/abstract=1003067, 2007.
Google Scholar
Zhang Q Z и Wang Q H, Подход к оценке локальной наименьшей абсолютной относительной ошибки для частично линейной мультипликативной модели, Statistica Sinica, 2013, 23 (3): 1091–1116.
MathSciNet МАТЕМАТИКА Google Scholar
Wang Z F, Liu W X и Lin Y Y, Проблема точки изменения в регрессии на основе относительных ошибок, TEST , 2015, 24 (4): 835–856.
MathSciNet Статья МАТЕМАТИКА Google Scholar
Христаче М., Юдицкий А. и Спокойный В., Прямая оценка коэффициента индекса в модели с одним индексом, Статистические анналы, 2001, 29 (3): 595–623.
MathSciNet Статья МАТЕМАТИКА Google Scholar
Рупперт Д., Ванд М. П. и Кэрролл Р. Дж., Полупараметрическая регрессия , Cambridge University Press, Лондон, 2003.
Книга МАТЕМАТИКА Google Scholar
Stute W и Zhu L X, Непараметрические проверки для моделей с одним индексом, The Annals of Statistics, 2005, 33 (3): 1048–1083.
MathSciNet Статья МАТЕМАТИКА Google Scholar
Zhu LX и Xue LG, Доверительные области эмпирического правдоподобия в частично линейной модели с одним индексом, Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2006, 68 (3) : 549–570.
MathSciNet Статья МАТЕМАТИКА Google Scholar
Ван Дж. Л., Сюэ Л. Г., Чжу Л. X и др., Оценка частично линейной модели с одним индексом, The Annals of Statistics, 2010, 38 (1): 246–274.
MathSciNet МАТЕМАТИКА Google Scholar
Chang Z Q, Xue L G и Zhu L X, Об асимптотически более эффективной оценке одноиндексной модели, Journal of Multivariate Analysis, 2010, 101 (8): 1898–1901.
MathSciNet Статья МАТЕМАТИКА Google Scholar
Kong E и Xia Y C, Модель одноиндексной квантильной регрессии и ее оценка, Econometric Theory , 2012, 28 (4): 730–768.
MathSciNet Статья МАТЕМАТИКА Google Scholar
Хердле В.К., Мюллер М., Сперлих С. и др., Непараметрические и полупараметрические модели , Springer Science & Business Media, Берлин, 2012.
МАТЕМАТИКА Google Scholar
Fan J Q and Gijbels I, Локальное полиномиальное моделирование и его приложения: монографии по статистике и прикладной теории вероятностей, CRC Press, London, 1996.
MATH Google Scholar
Carroll R J, Fan J Q, Gijbels I, et al., Обобщенные частично линейные одноиндексные модели, Journal of the American Statistical Association, 1997, 92 (438): 477–489.
MathSciNet Статья МАТЕМАТИКА Google Scholar
Yu Y и Ruppert D, Оценка сплайнов со штрафом для частично линейных моделей с одним индексом, Journal of the American Statistical Association, 2002, 97 (460): 1042–1054.
MathSciNet Статья МАТЕМАТИКА Google Scholar
Li K C, Нарезная обратная регрессия для уменьшения размерности, Journal of the American Statistical Association, 1991, 86 (414): 316–327.
MathSciNet Статья МАТЕМАТИКА Google Scholar
Xia YC, Tong H, Li WK и др., Адаптивная оценка пространства уменьшения размерности, Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2002, 64 ( 3): 363–410.
MathSciNet Статья МАТЕМАТИКА Google Scholar
Li T T, Yang H, Wang J L, et al., Поправка на оценку частично-линейной модели с одним индексом, The Annals of Statistics, 2011, 39 (6): 3441–3443.
MathSciNet Статья МАТЕМАТИКА Google Scholar
Произошла ошибка при настройке пользовательского файла cookie
Произошла ошибка при настройке пользовательского файла cookie Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.

- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к
остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Например, сайт
не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к
остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Robust Relative Error Estimation
Entropy (Basel). 2018 Sep; 20(9): 632.
Kei Hirose
1 Institute of Mathematics for Industry, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka 819-0395, Japan
2 RIKEN Center for Advanced Intelligence Project, 1-4-1 Nihonbashi, Chuo-ku, Tokyo 103-0027, Japan
Hiroki Masuda
3 Faculty of Mathematics, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka 819-0395, Japan
1 Institute of Mathematics for Industry, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka 819-0395, Japan
2 RIKEN Center for Advanced Intelligence Project, 1-4-1 Nihonbashi, Chuo-ku, Tokyo 103-0027, Japan
3 Faculty of Mathematics, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka 819-0395, Japan
Received 2018 Jul 11; Accepted 2018 Aug 20.
Abstract
Оценка относительной ошибки недавно использовалась в регрессионном анализе. Важным недостатком существующих процедур оценки относительной ошибки является то, что они чувствительны к выбросам. Чтобы решить эту проблему, мы используем функцию правдоподобия γ, которая строится на основе γ-перекрестной энтропии с сохранением исходной статистической модели.Оценочное уравнение обладает свойством повторного спуска, желательным свойством надежной статистики для широкого класса распределений шума. Чтобы найти минимизатор отрицательной функции γ-правдоподобия, строится алгоритм мажорной минимизации (ММ). Предлагаемый алгоритм гарантированно уменьшает отрицательную функцию γ-правдоподобия на каждой итерации. Мы также выводим асимптотическую нормальность соответствующей оценки вместе с простой последовательной оценкой асимптотической ковариационной матрицы, так что мы можем легко построить приближенные доверительные множества. Моделирование методом Монте-Карло проводится для исследования эффективности предложенной процедуры. Анализ реальных данных иллюстрирует полезность предложенной нами процедуры.
Моделирование методом Монте-Карло проводится для исследования эффективности предложенной процедуры. Анализ реальных данных иллюстрирует полезность предложенной нами процедуры.
Ключевые слова: γ-дивергенция, оценка относительной ошибки, робастная оценка
1. Введение
В регрессионном анализе многие аналитики используют оценку методом наименьших квадратов (со штрафом), целью которой является минимизация среднеквадратичной ошибки прогноза [1] . С другой стороны, относительная (процентная) ошибка часто более полезна и/или адекватна, чем среднеквадратическая ошибка.Например, в эконометрике сравнение эффективности прогнозов между разными ценами на акции с разными единицами измерения должно производиться по относительной ошибке; среди прочего мы ссылаемся на [2,3]. Кроме того, ошибка прогноза производства фотоэлектрической энергии или потребления электроэнергии оценивается не только среднеквадратичной ошибкой, но и относительной ошибкой (см., например, [4]). Мы ссылаемся на [5] относительно полезности и важности относительной ошибки.
Мы ссылаемся на [5] относительно полезности и важности относительной ошибки.
При оценке относительной ошибки мы минимизируем функцию потерь на основе относительной ошибки.Преимущество использования такой функции потерь состоит в том, что она не зависит от масштаба или единицы измерения. Недавно несколько исследователей предложили различные функции потерь, основанные на относительной ошибке [2,3,6,7,8,9]. Некоторые из этих процедур были распространены на непараметрическую модель [10] и модель случайных эффектов [11]. Оценка относительной ошибки с помощью регуляризации L1, включая наименьшее абсолютное сокращение и оператор (лассо; [12]), а также групповое лассо [13], также была предложена несколькими авторами [14,15,16], чтобы учесть анализ многомерных данных.
На практике переменная отклика y(>0) может оказаться очень большой или близкой к нулю. Например, потребление электроэнергии компанией может быть низким в праздничные дни и высоким в исключительно жаркие дни. Эти отклики часто можно рассматривать как выбросы, к которым чувствительна оценка относительной ошибки, поскольку функция потерь расходится, когда y→∞ или y→0. Следовательно, необходимо рассмотреть оценку относительной ошибки, устойчивую к выбросам. Недавно Чен и соавт. [8] обсудили надежность различных процедур оценки относительной ошибки путем исследования соответствующих распределений и пришли к выводу, что распределение оценки относительной ошибки наименьшего произведения (LPRE), предложенное в [8], имеет более тяжелые хвосты, чем другие, подразумевая, что LPRE может быть более надежнее других в практических приложениях.Однако наши численные эксперименты показывают, что ЖРД не так надежен, как ожидалось, поэтому робастификация ЖРД еще предстоит исследовать как с теоретической, так и с практической точек зрения.
Следовательно, необходимо рассмотреть оценку относительной ошибки, устойчивую к выбросам. Недавно Чен и соавт. [8] обсудили надежность различных процедур оценки относительной ошибки путем исследования соответствующих распределений и пришли к выводу, что распределение оценки относительной ошибки наименьшего произведения (LPRE), предложенное в [8], имеет более тяжелые хвосты, чем другие, подразумевая, что LPRE может быть более надежнее других в практических приложениях.Однако наши численные эксперименты показывают, что ЖРД не так надежен, как ожидалось, поэтому робастификация ЖРД еще предстоит исследовать как с теоретической, так и с практической точек зрения.
Чтобы получить оценку относительной ошибки, устойчивую к выбросам, в этой статье используется функция правдоподобия γ для регрессионного анализа Кавасима и Фудзисава [17], которая построена на основе энтропии γ-перекрестка [18]. Показано, что оценочное уравнение обладает ренисходящим свойством, желательным свойством в литературе по робастной статистике [19]. Чтобы найти минимизатор отрицательной функции γ-правдоподобия, мы строим алгоритм мажорной минимизации (ММ). Показано, что функция потерь нашего алгоритма на каждой итерации выпукла, хотя исходная отрицательная функция γ-правдоподобия невыпукла. Наш алгоритм гарантированно уменьшает целевую функцию на каждой итерации. Кроме того, мы получаем асимптотическую нормальность соответствующей оценки вместе с простой последовательной оценкой асимптотической ковариационной матрицы, что позволяет нам напрямую создавать приблизительные доверительные наборы.Моделирование методом Монте-Карло проводится для исследования эффективности предлагаемой нами процедуры. Анализ данных о потреблении электроэнергии представлен для иллюстрации полезности нашей процедуры. Дополнительный материал включает наш пакет R rree (надежная оценка относительной погрешности), который реализует наш алгоритм, а также пример программы rree .
Чтобы найти минимизатор отрицательной функции γ-правдоподобия, мы строим алгоритм мажорной минимизации (ММ). Показано, что функция потерь нашего алгоритма на каждой итерации выпукла, хотя исходная отрицательная функция γ-правдоподобия невыпукла. Наш алгоритм гарантированно уменьшает целевую функцию на каждой итерации. Кроме того, мы получаем асимптотическую нормальность соответствующей оценки вместе с простой последовательной оценкой асимптотической ковариационной матрицы, что позволяет нам напрямую создавать приблизительные доверительные наборы.Моделирование методом Монте-Карло проводится для исследования эффективности предлагаемой нами процедуры. Анализ данных о потреблении электроэнергии представлен для иллюстрации полезности нашей процедуры. Дополнительный материал включает наш пакет R rree (надежная оценка относительной погрешности), который реализует наш алгоритм, а также пример программы rree .
Напоминание об этом документе организовано следующим образом: Раздел 2 рассматривает несколько процедур оценки относительной ошибки. В разделе 3 мы предлагаем оценку относительной ошибки, которая устойчива к выбросам с помощью функции γ-правдоподобия. В разделе 4 представлены теоретические свойства: свойство рениспускания нашего метода и асимптотическое распределение оценки, доказательство последнего отложено до Приложения А. В разделе 5 строится алгоритм ММ для нахождения минимизатора отрицательного γ-вероятности функция. В разделе 6 исследуется эффективность предложенной нами процедуры с помощью моделирования методом Монте-Карло.В разделе 7 представлен анализ данных о потреблении электроэнергии. Наконец, заключительные замечания даны в разделе 8. …,yn)T — вектор положительных откликов. Рассмотрим модель мультипликативной регрессии
В разделе 3 мы предлагаем оценку относительной ошибки, которая устойчива к выбросам с помощью функции γ-правдоподобия. В разделе 4 представлены теоретические свойства: свойство рениспускания нашего метода и асимптотическое распределение оценки, доказательство последнего отложено до Приложения А. В разделе 5 строится алгоритм ММ для нахождения минимизатора отрицательного γ-вероятности функция. В разделе 6 исследуется эффективность предложенной нами процедуры с помощью моделирования методом Монте-Карло.В разделе 7 представлен анализ данных о потреблении электроэнергии. Наконец, заключительные замечания даны в разделе 8. …,yn)T — вектор положительных откликов. Рассмотрим модель мультипликативной регрессии
yi=exp(xiTβ)εi=exp∑j=1pxijβjεi,(i=1,⋯,n),
(1)
где β=(β1,⋯,βp)T — p -мерный вектор коэффициентов, а εi — положительные случайные величины.Предикторы xi∈Rp могут быть случайными и последовательно зависимыми, в то время как мы часто устанавливаем xi1=1, то есть включаем точку пересечения в показатель степени. Пространство параметров B⊂Rp для β — это ограниченная выпуклая область такая, что β0∈B. Мы неявно предполагаем, что модель задана корректно, так что существует истинный параметр β0=(β1,0,⋯,βp,0)∈B. Мы хотим оценить β0 по выборке {(xi,yi), i=1,⋯,n}.
Пространство параметров B⊂Rp для β — это ограниченная выпуклая область такая, что β0∈B. Мы неявно предполагаем, что модель задана корректно, так что существует истинный параметр β0=(β1,0,⋯,βp,0)∈B. Мы хотим оценить β0 по выборке {(xi,yi), i=1,⋯,n}.
Прежде всего отметим, что условие xi1=1 обеспечивает безмасштабность модели (1) по переменным εi, что существенно отличается от модели линейной регрессии yi=xiTβ+εi.В частности, умножение положительной константы σ на εi приводит к переводу точки пересечения в показатель степени:
yi=exp(xiTβ)σεi=exp(logσ+xiTβ)εi
так что переход от εi к σεi эквивалентен переходу от β1 к β1+logσ. См. замечание 1 о распределении ε1.
Чтобы дать простое выражение функций потерь на основе относительной ошибки, мы пишем
ti=ti(β)=exp(xiTβ),(i=1,⋯,n).
Чен и др. [6,8] указали, что критерий потерь для относительной ошибки может зависеть от |(yi-ti)/yi| и/или |(yi-ti)/ti|.Эти авторы также предложили общие критерии относительной ошибки (GRE), определяемые как
G(β)=∑i=1ngyi-tiyi,yi-titi,
(2)
где g:[0,∞)×[0,∞)→[0,∞). Большинство функций потерь, основанных на относительной ошибке, включены в GRE. Парк и Стефански [2] рассмотрели функцию потерь g(a,b)=a2. Он может сильно зависеть от малого yi, поскольку он включает члены 1/yi2, и тогда оценка может быть численно нестабильной. Непротиворечивость и асимптотическая нормальность не могут быть установлены при общих условиях регулярности [8].Функции потерь, основанные на g(a,b)=max{a,b} [3] и g(a,b)=a+b (оценка наименьшей абсолютной относительной ошибки, [6]), могут иметь желаемые асимптотические свойства [3]. ,6]. Однако минимизация функции потерь может быть сложной задачей, особенно для многомерных данных, когда функция негладкая или невыпуклая.
Большинство функций потерь, основанных на относительной ошибке, включены в GRE. Парк и Стефански [2] рассмотрели функцию потерь g(a,b)=a2. Он может сильно зависеть от малого yi, поскольку он включает члены 1/yi2, и тогда оценка может быть численно нестабильной. Непротиворечивость и асимптотическая нормальность не могут быть установлены при общих условиях регулярности [8].Функции потерь, основанные на g(a,b)=max{a,b} [3] и g(a,b)=a+b (оценка наименьшей абсолютной относительной ошибки, [6]), могут иметь желаемые асимптотические свойства [3]. ,6]. Однако минимизация функции потерь может быть сложной задачей, особенно для многомерных данных, когда функция негладкая или невыпуклая.
На практике были бы полезны следующие два критерия:
Оценка относительной погрешности наименьшего продукта (LPRE) Chen et al. [8] предложили ЖРД, определяемую формулой g(a,b)=ab.LPRE пытается минимизировать произведение |1-ti/yi|×|1-yi/ti|, не обязательно оба слагаемых одновременно.

Оценка относительной погрешности методом наименьших квадратов (LSRE) Chen et al. В [8] рассматривался LSRE, заданный формулой g(a,b)=a2+b2. LSRE стремится минимизировать как |1-ti/yi| и |1-йи/ти| через сумму квадратов (1-ti/yi)2+(1-yi/ti)2.
Функции потерь ЖРД и ЛРД гладкие и выпуклые, а также обладают желаемыми асимптотическими свойствами [8]. Вышеописанные критерии GRE и их свойства обобщены в .В частности, «выпуклость» в случае g(a,b)=a+b имеет место, когда εi>0, εi≠1 и ∑i=1nxixiT положительно определена, поскольку матрица Гессе соответствующей G(β) есть ∑i=1n|εi-εi-1|xixiT как
Таблица 1
Несколько примеров общих критериев относительной ошибки (GRE) и их свойств. «Вероятность» во втором столбце означает существование функции правдоподобия, соответствующей функции потерь. Свойства «Выпуклости» и «Гладкости» в последних двух столбцах соответственно указывают на свойства по отношению к β соответствующей функции потерь.
| г (а, б) | правдоподобие Выпуклость | ||
|---|---|---|---|
| a2 | √ | ||
| а + б | √ | √ | |
| тах {а, Ь} | √ | ||
| абы | √ | √ | √ |
| a2 + b2 | √ | √ | √ |
Хотя не важно, мы предполагаем, что переменные εi в уравнении (1) являюсь я. я бы. с общей функцией плотности ч . Как и в Chen и соавт. [8], мы рассмотрим следующий класс ч , связанного с г :
я бы. с общей функцией плотности ч . Как и в Chen и соавт. [8], мы рассмотрим следующий класс ч , связанного с г :
ч (ε): = С (г) εexp-р (е) I + (е),
(3)
где
ρ (& epsi;) = ρ (& epsi;; г): = g1-1ε, | 1-& epsi; |,
и С (г) представляет собой нормирующий константа (∫h (ε) dε = 1) и I + обозначает индикаторную функцию множества (0, ∞). Кроме того, мы предполагаем, что свойство симметрии г (а, б) = г (Ь, а), а, b≥0, из которого следует, что ε1~ε1-1. Последнее свойство необходимо для функции балла, чтобы быть связана с градиентом функции потерь GRE, следовательно, будучи мартингалом относительно подходящей фильтрации, которая часто влечет за собой эффективность оценки.Действительно, асимметрия g(a,b) (т. е. g(a,b)≠g(b,a)) может привести к существенному смещению в оценке [3]. Весь набор наших условий регулярности будет показан в разделе 4.3. Условия в нем относительно g легко проверяются как для ЖРД, так и для ЖРД.
В этой статье мы неявно предполагаем, что i=1,⋯,n обозначают «временные» индексы. Как обычно, чтобы иметь дело со случаями неслучайных и случайных предикторов унифицированным образом, мы используем структуру частичного правдоподобия.В частности, в выражении совместной плотности (с очевидными обозначениями плотностей)
F (x1, ⋯, xn, y1, ⋯, yn) = f (x1) πi = 2nf (xi | x1`, ⋯, xi-1, y1, ⋯, ⋯, x 1) f (y1 | x1 ) Πi = 2nf (yi | x1, ⋯, xi, y1, ⋯, yi-1),
Мы игнорируем первый продукт {⋯} и только смотрите на второй {⋯}, который определяется как частичная вероятность. Далее мы предполагаем, что I -этап шума εi независим от (x1, ⋯, xi, y1, ⋯, yi-1), так что ввиду уравнения (1) у нас есть
F (Yi | X1, ⋯, Xi, Y1, ⋯, Yi-1) = F (Yi | Xi), i = 1, ⋯, n.
Функция плотности отклика y при заданном xi равна
f(y|xi;β)=exp(-xiTβ)hyexp(-xiTβ)
(4)
Из уравнения (3) мы видим, что оценка максимального правдоподобия (MLE), основанная на распределении ошибок в Уравнение (5) получается путем минимизации уравнения (2).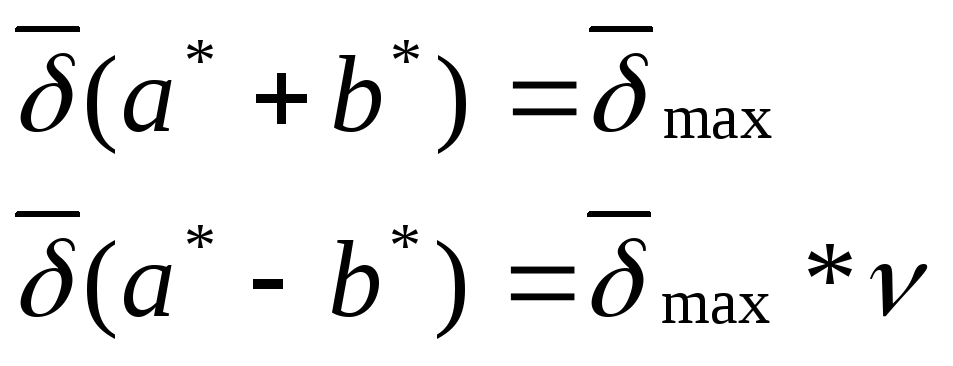 Например, функции плотности ЖРД и ЖРД имеют вид
Например, функции плотности ЖРД и ЖРД имеют вид
LPRE:f(y|xi)=12K0(2)y-1exp-yti-tiy,(y>0),LSRE:f(y|xi)=CLSREy-1exp-1-tiy2-1-yti2, (у>0),
(6)
где Kν(z) обозначает модифицированную функцию Бесселя третьего рода с индексом ν∈R:
Kν(z)=zν2ν+1∫0∞t-ν-1exp-t-z24tdt
а CLSRE — постоянный термин.Постоянные члены рассчитываются численно как K0(2)≈0,1139 и CLSRE≈0,
1. Плотность (6) является частным случаем обобщенного обратного распределения Гаусса (см., например, [20]). Примечание 1.Мы предполагаем, что плотность шума h полностью определена в том смысле, что при заданном g плотность h не содержит неизвестных величин. Однако это никогда не является обязательным. Например, для LPRE, определяемого уравнением (6), мы могли бы естественным образом включить в h еще один параметр σ>0, в результате чего форма h(ε) будет равна
ε↦12K0(σ)ε-1exp-σ2ε+1εI+(ε).
Тогда мы можем проверить, что эквивалентность распределений ε1∼ε1-1 выполняется при любом значении σ. В частности, оценка параметра σ действительно имеет статистический смысл, и, действительно, можно вывести асимптотическую нормальность совместной оценки максимального (частного) правдоподобия (β, σ). В этой статье мы не обращаем внимания на такой возможный дополнительный параметр, а вместо этого рассматриваем его (когда бы он ни существовал) как мешающий параметр, как в дисперсии шума в оценке методом наименьших квадратов модели линейной регрессии.
В частности, оценка параметра σ действительно имеет статистический смысл, и, действительно, можно вывести асимптотическую нормальность совместной оценки максимального (частного) правдоподобия (β, σ). В этой статье мы не обращаем внимания на такой возможный дополнительный параметр, а вместо этого рассматриваем его (когда бы он ни существовал) как мешающий параметр, как в дисперсии шума в оценке методом наименьших квадратов модели линейной регрессии.
3. Надежная оценка с помощью γ-вероятности
На практике часто можно наблюдать выбросы. Например, данные о потреблении электроэнергии могут иметь выбросы в очень жаркие дни. Методы оценки с помощью критериев GRE, включая LPRE и LSRE, неустойчивы к выбросам, поскольку соответствующие функции плотности обычно не имеют тяжелых хвостов. Следовательно, необходим метод оценки относительной ошибки, устойчивый к выбросам. Для этого мы рассматриваем минимизацию отрицательной функции γ-(частного) правдоподобия на основе γ-кросс-энтропии [17].
Определим теперь отрицательную Г- (выборочная) функция правдоподобия по
ℓγ, п (β) = — 1γlog1nΣi = 1nf (уг | Xi; β) γ + 11 + γlog1nΣi = 1n∫0∞f (у | Xi; β) 1 + γdy,
(7 )
где γ> 0 является параметром, который управляет степени надежности; γ → 0 соответствует отрицательной функции логарифмического правдоподобия, и повышается надежность, как гамма возрастает. С другой стороны, слишком большой γ может снизить эффективность устройства оценки [18]. На практике значение гамма может быть выбран с помощью перекрестной проверки на основе гамма-кросс энтропии (см.,г., [18,21]). Мы ссылаемся на Кавасиму и Фудзисаву [22] для более поздних наблюдений по сравнению γ-расхождений между Фудзисавой и Эгучи [18] и Кавасимой и Фудзисава [17].
Существует несколько функций правдоподобия, которые дают надежную оценку. Примеры включают Lq-вероятность [23] и вероятность, основанную на дивергенции степени плотности [24], называемую β-вероятностью. Показано, что γ-вероятность, Lq-вероятность и β-вероятность тесно связаны между собой. Отрицательная функция β-правдоподобия ℓα,n(β) и отрицательная функция Lq-правдоподобия ℓq,n(β) соответственно выражаются как
Отрицательная функция β-правдоподобия ℓα,n(β) и отрицательная функция Lq-правдоподобия ℓq,n(β) соответственно выражаются как
ℓα,n(β)=-1α1n∑i=1nf(yi|xi;β)α+11+α1n∑i=1n∫0∞f(y|xi;β)1+αdy,
(8 )
ℓq,n(β)=-∑i=1nf(yi|xi;β)1-q-11-q.
(9)
Разница между γ-правдоподобием и β-вероятностью заключается лишь в существовании логарифма на ℓγ,n(β). Кроме того, подстановка q=1-α в уравнение (9) дает нам
ℓq,n(β)=-1α∑i=1nf(yi|xi;β)α+const.
Следовательно, минимизация отрицательной функции правдоподобия Lq эквивалентна минимизации отрицательной функции β-правдоподобия без второго члена в правой части уравнения (8). Обратите внимание, что γ-правдоподобие обладает свойством повторного спуска, желательным свойством в литературе по надежной статистике, как показано в разделе 4.2. Более того, известно, что γ-правдоподобие является практически единственной дивергенцией, устойчивой к сильному загрязнению (подробности см. в [18]). С другой стороны, мы не показали, обладают ли Lq-правдоподобие и/или β-правдоподобие свойством повторного спуска или нет.
Интегрирование ∫f(y|xi;β)1+γdy во втором члене правой части уравнения (7) равно
∫0∞f(y|xi;β)1+γdy=1ti1+γ∫0∞hyti1+γdy=:ti-γC(γ,h),
где
C(γ,h):=∫0∞h(v)1+γdv
(10)
является постоянным членом, который предполагается конечным.Тогда уравнение (7) выражается как
ℓγ,n(β)=-1γlog∑i=1nf(yi|xi;β)γ︸=:ℓ1(β)+11+γlog∑i=1nti-γ︸=:ℓ2(β)+C0( γ,h),
(11)
где C0(γ,h) — постоянный член, свободный от β. Мы определяем оценку максимального γ-правдоподобия как любой элемент, такой что
4. Теоретические свойства
4.1. Технические допущения
Пусть →p обозначает сходимость по вероятности.
Предположение A1 (Стабильность из предиктора ) .Существует вероятностная мера π(dx) на пространстве состояний X предикторов и положительных констант δ,δ′>0 такая, что
1n∑i=1n|xi|3expδ′|xi|1+δ=Op(1),
и тот
1n∑i=1nη(xi)→p∫Xη(x)π(dx),n→∞,
, где предел конечен для любого измеримого η, удовлетворяющего
supx∈Rp|η(x)|(1+|x|3)expδ′|x|1+δ<∞.
АО положительный и.и.д. случайные величины ε1,ε2,⋯ имеют общую положительную плотность h вида (3):
h(ε)=C(g)εexp-ρ(ε)I+(ε),
, для которого выполняются следующие условия.
Функция g:[0,∞)×[0,∞)→[0,∞) трижды непрерывно дифференцируема на (0,∞) и удовлетворяет
Существуют константы κ0,κ∞>0 и c>1 такие, что
1cε-κ0∨εκ∞≤ρ(ε)≤cε-κ0∨εκ∞
для каждого ε>0.
Существуют константы C0, C∞≥0 такое, что
SUPε> 0ε-C0∨εC∞-1maxk = 1,2,3∂εkρ (ε) <∞.
Вот и в продолжении, для переменной A , мы обозначаем с помощью частичной дифференциальной дифференциации K , по отношению к A .
Успенцем 1 необходимо для определения стохастических пределов большого образец нескольких ключевых количеств в доказательствах: без них мы не сможем вывести явную асимптотическую нормальность результата. Предположение 2 справедливо для многих случаев, включая ЖРД и ЛРД (т. е. g(a,b)=ab и a2+b2), за исключением g(a,b)=a2 и g(a,b)=b2. Условие гладкости h на (0,∞) не является существенным и может быть ослаблено в свете теории M -оценок ([25], гл. 5). При этих предположениях мы можем вывести следующие утверждения.
Предположение 2 справедливо для многих случаев, включая ЖРД и ЛРД (т. е. g(a,b)=ab и a2+b2), за исключением g(a,b)=a2 и g(a,b)=b2. Условие гладкости h на (0,∞) не является существенным и может быть ослаблено в свете теории M -оценок ([25], гл. 5). При этих предположениях мы можем вывести следующие утверждения.
h трижды непрерывно дифференцируема на (0,∞), и для каждого α>0
∫0∞hα(ε)dε<∞иmaxk=0,1,2,3supε>0∂εkh(ε)α<∞.
Для каждого γ>0 и α>0 (напомним, что задано значение γ>0),
limε↓0h(ε)γuh(ε)α=limε↑∞h(ε)γuh(ε)α=0,
(12)
где
uh(z):=1+z∂zlogh(z)=1+zh′(z)h(z).
Проверки являются прямыми, поэтому опущены.
Наконец, мы накладываем следующее предположение:
Предположение A3 (Идентифицируемость) .Мы имеем β=β0, если
ρe-xTβy=ρe-xTβ0yπ(dx)⊗λ+(dy)-a.е.(х,у),
, где λ+ обозначает меру Лебега на (0,∞).
4.2. Восходящее свойство
Оценочная функция, основанная на отрицательной функции γ-вероятности, определяется выражением
В нашей модели мы рассматриваем не только слишком большие yis, но и слишком маленькие ys как выбросы: говорят, что оценочное уравнение обладает ренисходящим свойством, если
известковый→∞ψ(y|x;β0)=известковый→+0ψ(y|x;β0)=0
для каждого х. Свойство повторного спуска известно как желательное свойство в литературе по робастной статистике [19].Здесь мы показываем, что предложенная процедура обладает свойством ренисхождения.
Уравнение оценки, основанное на отрицательной функции правдоподобия γ, имеет вид
-∑i=1nf(yi|xi;β)γs(yi|xi;β)∑j=1nf(yj|xj;β)γ+∂∂βℓ2(β)=0,
где
s(y|x;β)=∂logf(y|x;β)∂β.
У нас есть выражение
ψ(y|x;β)=f(y|x;β)γs(y|x;β)-∂∂βℓ2(β).
Обратите внимание, что ∂∂βℓ2(β) не содержит y . Для каждого (x,β) прямые вычисления дают оценку
ψ(y|x;β)≤C(x;β)hexp(-xTβ)yγuhexp(-xTβ)y
(13)
для некоторой константы C(x;β), свободной от y . Следовательно, уравнение (12) в сочетании с неравенством (13) приводит к свойству рениспускания.
Следовательно, уравнение (12) в сочетании с неравенством (13) приводит к свойству рениспускания.
4.3. Асимптотическое распределение
Вспомним уравнение (10) для определения C(γ,h) и пусть
C1(γ,h):=∫0∞εh(ε)γh′(ε)dε,C2(γ,h):=∫0∞uh(ε)2h(ε)2γ+1dε,Πk(γ ):=∫x⊗kexp(-γxTβ0)π(dx),k=0,1,2,
где x⊗0:=1∈R, x⊗1:=x∈Rp и x⊗2:=xxT∈Rp⊗Rp; Предположения 1 и 2 гарантируют, что все эти величины конечны при каждом γ>0. Кроме того,
Hγ′(β0):=∫∫f(y|x;β0)γ+1dyπ(dx)=C(γ,h)Π0(γ),Hγ′′(β0):=∫∫f(y |x;β0)γ+1s(y|x;β0)dyπ(dx)=-C(γ,h)+C1(γ,h)Π1(γ),Δγ(β0):=C(γ,h )2C2(γ,h)Π0(γ)2Π2(2γ)+C(γ,h)+C1(γ,h)2C(2γ,h)Π0(2γ)Π1(γ)⊗2-2C(γ, h)C(γ,h)+C1(γ,h)C(2γ,h)+C1(2γ,h)Π0(γ)Π1(2γ)Π1(γ)T,
(14)
Jγ (β0):=C(γ,h)C2(γ/2,h)Π0(γ)Π2(γ)-C(γ,h)+C1(γ,h)2Π1(γ)⊗2.γ)→pΠk(γ),k=0,1,2.
(17)
Доказательство теоремы 1 будет дано в Приложении A. Отметим, что при γ→0 имеем C(γ,h)→1, C1(γ,h)→-1 и C2 (γ,h)→∫0∞uh(ε)2h(ε)dε, откуда, в частности, следует Hγ′→1 и Hγ″→0. Тогда и Δγ, и Jγ стремятся к информационной матрице Фишера
I0:=∫∫s(y|x;β0)⊗2f(y|x,β0)π(dx)dy=∫0∞uh(ε)2h(ε)dε∫x⊗2π(dx)
при γ→0, так что асимптотическое распределение Np(0,Jγ-1ΔγJγ-1) становится Np(0,I0-1), обычным для MLE.
Заметим также, что без подробностей мы могли бы вывести дивергенцию плотности-степени (также известную как β-дивергенция [26]), аналог теоремы 1, аналогично, но с немного меньшими вычислительными затратами; в этом случае мы рассматриваем целевую функцию ℓα,n(β), определяемую уравнением (8), вместо γ-(частного) правдоподобия (7).См. Basu et al. [24] и Jone et al. [21] для деталей расхождения плотности-мощности.
5. Алгоритм
Даже если критерий GRE в уравнении (2) является выпуклой функцией, отрицательная функция γ-вероятности невыпукла. Поэтому сложно найти глобальный минимум. Здесь мы выводим алгоритм MM (мажоризация-минимизация) для получения локального минимума. Алгоритм ММ монотонно уменьшает целевую функцию на каждой итерации. Мы обращаемся к Хантеру и Ланге [27] за кратким описанием алгоритма ММ.
Пусть β(t) значение параметра на t -й итерации. Отрицательная функция γ-вероятности в уравнении (11) состоит из двух невыпуклых функций, ℓ1(β) и ℓ2(β). Функции мажорации ℓj(β), скажем, ℓ˜j(β|β(t)) (j=1,2), построены так, чтобы оптимизация minβℓ˜j(β|β(t)) была намного проще. чем у minβℓj(β). Функции мажорации должны удовлетворять следующим неравенствам:
Функции мажорации ℓj(β), скажем, ℓ˜j(β|β(t)) (j=1,2), построены так, чтобы оптимизация minβℓ˜j(β|β(t)) была намного проще. чем у minβℓj(β). Функции мажорации должны удовлетворять следующим неравенствам:
ℓ˜j(β|β(t))≥ℓj(β),
(18)
ℓ˜j(β(t)|β(t))= ℓj (β (т)).
(19)
Здесь мы строим мажорантные функции ℓ˜j(β|β(t)) для j=1,2.
5.1. Функция мажорации для ℓ1(β)
Пусть
wi(t)=f(yi|xi;β(t))γ∑j=1nf(yj|xj;β(t))γ,
(20)
ri(t)=∑j= 1nf(yj|xj;β(t))γf(yi|xi;β)γf(yi|xi;β(t))γ.
(21)
Очевидно, что ∑i=1nwi(t)=1 и wi(t)ri(t)=f(yi|xi;β)γ. Применяя неравенство Дженсена к y=-logx, получаем неравенство
-log∑i=1nwi(t)ri(t)≤-∑i=1nwi(t)logri(t).
(22)
Подстановка уравнения (20) и уравнения (21) в уравнение (22) дает
ℓ1(β)≤-∑i=1nwi(t)logf(yi|xi;β)+C,
где C=1γ∑iwi(t)logwi(t). Обозначая
ℓ˜1(β|β(t))=-∑i=1nwi(t)logf(yi|xi;β)+C,
(23)
мы видим, что уравнение (23) удовлетворяет уравнению (18) и уравнению (19). Показано, что ℓ˜1(β|β(t)) является выпуклой функцией, если исходная функция потерь относительной ошибки выпукла. В частности, функции мажорации ℓ˜1(β|β(t)) на основе LPRE и LSRE являются выпуклыми.
Показано, что ℓ˜1(β|β(t)) является выпуклой функцией, если исходная функция потерь относительной ошибки выпукла. В частности, функции мажорации ℓ˜1(β|β(t)) на основе LPRE и LSRE являются выпуклыми.
5.2. Функция мажорации для ℓ2(β)
Пусть θi=-γxiTβ. Мы рассматриваем ℓ2(β) как функцию θ=(θ1,⋯,θn)T. Позволять
s(θ):=log∑i=1nti-γ=log∑i=1nexp(θi).
(24)
Взяв производную от s(θ) по θ, получим
∂s(θ)∂θi=πi,∂2s(θ)∂θj∂θi=πiδij-πiπj,
где πi=exp(θi)/{∑k=1nexp(θk)}. Обратите внимание, что ∑i=1nπi=1 для любого θ.
Разложение Тейлора s(θ) при θ=θ(t) выражается как
s(θ)=s(θ(t))+π(t)T(θ-θ(t))+12(θ-θ(t))T∂2s(θ*)∂θ∂θT( θ-θ(t)),
(25)
где π(t)=(π1(t),⋯,πn(t))T и θ* — n -мерный вектор, расположенный между θ и θ(t).Определим матрицу B размера n × n следующим образом:
Из [28] следует, что в матричном смысле
∂2s(θ)∂θ∂θT≤B
(26)
для любого θ. Объединяя уравнение (25) и уравнение (26), мы имеем
s(θ)≤s(θ(t))+π(t)T(θ-θ(t))+12(θ-θ(t))TB(θ-θ(t)).
(27)
Подстановка уравнения (24) в уравнение (27) дает
log∑i=1nexp(-γxiTβ)≤log∑i=1nexp(-γxiTβ(t))-γπ(t)TX(β-β(t))+γ22(β-β(t))TXTBX( β-β(t)),
где X=(x1,⋯,xn)T. Затем мажорантная функция ℓ2(β) строится по формуле
ℓ˜2(β|β(t))=γ22(1+γ)βTXTBXβ-γ1+γβT(XTπ(t)+γXTBXβ(t))+C,
(28)
где C — постоянный член, свободный от β.Заметим, что ℓ˜2(β|β(t)) в уравнении (28) удовлетворяет уравнению (18) и уравнению (). Показано, что ℓ˜2(β|β(t)) — выпуклая функция, поскольку XTBX положительно полуопределена.
5.3. Алгоритм ММ для надежной оценки относительной погрешности
В разделах 5.1 и 5.2 мы построили мажорирующие функции как для ℓ1(β), так и для ℓ2(β). Алгоритм ММ, основанный на этих функциях мажорации, подробно описан в алгоритме 1. Функция мажорации ℓ˜1(β|β(t))+ℓ˜2(β|β(t)) является выпуклой, если исходная функция потерь относительной ошибки равна выпуклый.В частности, функции мажорации LPRE и LSRE являются выпуклыми.
| Алгоритм 1 Алгоритм робастной оценки относительной погрешности. |
|
Вместо алгоритма ММ можно напрямую использовать квазиньютоновский метод, такой как алгоритм Бройдена-Флетчера-Гольдфарба-Шанно (BFGS), для минимизации отрицательной функции γ-правдоподобия. По нашему опыту, алгоритм BFGS быстрее, чем алгоритм MM, но более чувствителен к начальному значению, чем алгоритм MM.Сильные стороны алгоритмов BFGS и MM будут разделены при использовании следующего гибридного алгоритма: .
По нашему опыту, алгоритм BFGS быстрее, чем алгоритм MM, но более чувствителен к начальному значению, чем алгоритм MM.Сильные стороны алгоритмов BFGS и MM будут разделены при использовании следующего гибридного алгоритма: .
Сначала проведем алгоритм ММ с небольшим количеством итераций.
Затем выполняется алгоритм BFGS. Мы используем оценку, полученную алгоритмом ММ, в качестве начального значения алгоритма BFGS.
Стабильность алгоритма ММ исследуется посредством анализа реальных данных в разделе 7.
Примечание 3.Для работы с многомерными данными мы часто используем регуляризацию L1, такую как лассо [12], эластичную сеть [29] и Smoothly Clipped Absolute Deviation (SCAD) [30]. При надежной оценке относительной ошибки функция потерь, основанная на лассо, выражается как 90 814.
ℓγ,n(β)+λ∑j=1p|βj|,
(29)
, где λ>0 — параметр регуляризации. Однако функция потерь в уравнении (29) невыпуклая и недифференцируемая.Вместо прямой минимизации невыпуклой функции потерь в уравнении (29) мы можем использовать алгоритм ММ; следующая выпуклая функция потерь минимизируется на каждой итерации:
Однако функция потерь в уравнении (29) невыпуклая и недифференцируемая.Вместо прямой минимизации невыпуклой функции потерь в уравнении (29) мы можем использовать алгоритм ММ; следующая выпуклая функция потерь минимизируется на каждой итерации:
ℓ˜1(β|β(t))+ℓ˜2(β|β(t))+λ∑j=1p|βj|.
(30)
Минимизация уравнения (30) может быть реализована с помощью метода переменного направления алгоритма множителей [14] или алгоритма координатного спуска с квадратичной аппроксимацией ℓ˜1(β|β(t))+ℓ˜2(β|β (т)) [31].
6.Моделирование методом Монте-Карло
6.1. Настройка
Мы рассматриваем следующие две имитационные модели следующим образом:
Модель1:β0=(1,1,1)T, Модель2:β0=(0,5,⋯,0,5︸6,0,⋯,0)︸45T.
Количество наблюдений установлено равным n=200. Для каждой модели мы генерируем T=10 000 наборов данных предикторов xi (i=1,⋯,n) в соответствии с N(0,(1-ρ)I+ρ11T). Здесь мы рассматриваем случай ρ=0,0 и ρ=0,6. Ответы yi генерируются из распределения смеси
(1-δ)f(y|xi;β0)+δq(y)(i=1,⋯,n),
где f(y|x;β0) — функция плотности, соответствующая LPRE, определяемому уравнением (6), q(y) — функция плотности распределения выбросов, а δ (0≤δ<1) — отношение выбросов . (t) — оценка, полученная из набора данных {(xi(t),yi(t));i=1,⋯,n}, а yinew(t) — наблюдение из yinew(t) |xi(t).Здесь yinew(t)|xi(t) следует распределению f(y|xi(t);β0) и не зависит от yi(t)|xi(t). показывает медиану и планку ошибок {RPE(1), ⋯, RPE( T )} и {MSE(1), ⋯, MSE( T )}. Планки погрешностей очерчены 25-м и 75-м процентилями.
(t) — оценка, полученная из набора данных {(xi(t),yi(t));i=1,⋯,n}, а yinew(t) — наблюдение из yinew(t) |xi(t).Здесь yinew(t)|xi(t) следует распределению f(y|xi(t);β0) и не зависит от yi(t)|xi(t). показывает медиану и планку ошибок {RPE(1), ⋯, RPE( T )} и {MSE(1), ⋯, MSE( T )}. Планки погрешностей очерчены 25-м и 75-м процентилями.
Медиана и планка погрешности относительной ошибки прогнозирования (ООП) в уравнении (31) и среднеквадратичной ошибки (СКО) β в уравнении (32), когда параметры логарифмически нормального распределения (распределение выбросов) равны (μ,σ )=(±5,1). Планки погрешностей очерчены 25-м и 75-м процентилями.
Мы наблюдаем следующие тенденции по результатам в:
По мере увеличения коэффициента выбросов производительность ухудшается во всех случаях. Интересно, что длина полосы ошибок RPE увеличивается по мере увеличения отношения выбросов.
Предлагаемый метод становится устойчивым к выбросам по мере увеличения значения γ.
 Мы наблюдаем, что слишком большое значение γ, такое как γ=10, приводит к крайне низким значениям RPE и MSE, поскольку большинство наблюдений расцениваются как выбросы.Следовательно, не слишком большое γ, такое как γ=0,5, используемое здесь, обычно приводит к лучшей точности оценки, чем MLE.
Мы наблюдаем, что слишком большое значение γ, такое как γ=10, приводит к крайне низким значениям RPE и MSE, поскольку большинство наблюдений расцениваются как выбросы.Следовательно, не слишком большое γ, такое как γ=0,5, используемое здесь, обычно приводит к лучшей точности оценки, чем MLE.Случаи ρ=0,6, когда предикторы коррелированы, хуже, чем случаи ρ=0. В частности, когда γ=0, значение RPE ρ=0,6 становится большим при большом коэффициенте выбросов. Однако увеличение γ привело к равномерному повышению производительности оценки.
Результаты для разных имитационных моделей при одном и том же значении γ обычно различаются, что означает, что соответствующее значение γ может изменяться в соответствии с механизмами генерации данных.
6.3. Исследование асимптотического распределения
Асимптотическое распределение получено в предположении, что истинное распределение y|xi соответствует f(y|xi;β0), то есть δ=0. Однако мы ожидаем, что при достаточно большом γ и умеренном δ асимптотическое распределение может хорошо аппроксимировать истинное распределение, что было подчеркнуто Фудзисава и Эгучи ([18], теорема 5. γ-β0.
γ-β0.
Из уравнения (16) следует, что
Мы ожидаем, что гистограмма zj, полученная в результате моделирования, будет аппроксимировать функцию плотности стандартного нормального распределения при отсутствии (или при наличии нескольких) выбросов. Когда существует значительное количество выбросов, асимптотическое распределение zj может не быть N(0,1), но ожидается, что оно будет близко к N(0,1) для больших γ. показаны гистограммы T = 10 000 выборок z2 вместе с функцией плотности стандартного нормального распределения для μ = 5 в модели 1.
Гистограммы T = 100,00 выборок z2 вместе с функцией плотности стандартного нормального распределения для µ=5 в модели 1.
Когда нет выбросов, распределение z2 близко к стандартному нормальному распределению независимо от выбрано значение γ. Когда отношение выбросов велико, гистограмма z2 далека от функции плотности N(0,1) для малого γ. Однако, когда значение γ велико, гистограмма z2 близка к функции плотности N(0,1), что означает, что асимптотическое распределение в уравнении (16) надлежащим образом аппроксимирует распределение оценок даже при наличии выбросов. Заметим, что результат асимптотического распределения для других zjs показывает ту же тенденцию, что и для z2.
Заметим, что результат асимптотического распределения для других zjs показывает ту же тенденцию, что и для z2.
7. Анализ реальных данных
Мы применяем предложенный метод к данным о потреблении электроэнергии из репозитория машинного обучения UCI (Калифорнийский университет, Ирвин) [32]. Набор данных состоит из 370 наблюдений за потреблением электроэнергии домохозяйствами с января 2011 г. по декабрь 2014 г. Потребление электроэнергии выражено в кВтч с 15-минутными интервалами. Рассматривается задача прогнозирования потребления электроэнергии на следующий день по прошлому потреблению электроэнергии.t становится «ценой дисбаланса», которая обычно выше обычной цены. За подробностями обращайтесь к Сиошанси и Пфаффенбергеру [33].
Для исследования эффективности предлагаемой процедуры мы выбираем одно домохозяйство, которое включает небольшие положительные значения потребления электроэнергии. Данные о потреблении за 25 декабря 2014 г. были удалены, поскольку соответствующие значения данных равны нулю. Мы прогнозируем потребление электроэнергии с января 2012 г. по декабрь 2014 г. (данные 2011 г. используются только для оценки параметра).Данные о фактическом потреблении электроэнергии с января 2012 г. по декабрь 2014 г. показаны на рис.
Мы прогнозируем потребление электроэнергии с января 2012 г. по декабрь 2014 г. (данные 2011 г. используются только для оценки параметра).Данные о фактическом потреблении электроэнергии с января 2012 г. по декабрь 2014 г. показаны на рис.
Потребление электроэнергии с января 2012 г. по декабрь 2014 г. для одного из 370 домохозяйств.
Мы видим, что несколько значений данных близки к нулю от . В частности, с октября по декабрь 2014 г. наблюдается несколько всплесков, достигающих практически нулевых значений. В этом случае точность оценки с обычными критериями GRE низкая, как показано в нашем численном моделировании в предыдущем разделе.
Мы используем модель мультипликативной регрессии в уравнении (1) для прогнозирования потребления электроэнергии. Пусть yt обозначает потребление электроэнергии при t (t=1,⋯,T). Количество наблюдений T=(365×3+366-1)×96=146 160. Здесь 96 — это количество измерений за один день, поскольку спрос на электроэнергию выражается в 15-минутных интервалах. Мы определяем xt как xt=(yt-d,⋯,yt-dq)T, где d=96. В нашей модели потребление электроэнергии на уровне т объясняется потреблением электроэнергии за последние q дней за тот же период.Мы устанавливаем q = 5 для анализа данных и используем последние n = 100 дней наблюдений для оценки модели.
Мы определяем xt как xt=(yt-d,⋯,yt-dq)T, где d=96. В нашей модели потребление электроэнергии на уровне т объясняется потреблением электроэнергии за последние q дней за тот же период.Мы устанавливаем q = 5 для анализа данных и используем последние n = 100 дней наблюдений для оценки модели.
Параметры модели оцениваются робастным ЖРД. Значения γ заданы как регулярные последовательности от 0 до 0,1 с шагом 0,01. Чтобы минимизировать отрицательную функцию γ-правдоподобия, мы применяем предложенный нами алгоритм ММ. Поскольку известно, что структура потребления электроэнергии в будние дни полностью отличается от таковой в выходные дни, мы делаем прогнозы отдельно для будних и выходных дней. Результаты относительной ошибки предсказания изображены на .
Относительная ошибка прогноза для различных значений γ для данных о потреблении электроэнергии домохозяйствами.
Относительная ошибка прогнозирования велика, когда γ=0 (т. е. обычная оценка LPRE). Минимальное значение относительной ошибки предсказания составляет 0,049, а соответствующее значение γ равно γ=0,03. Когда мы устанавливаем слишком большое значение γ, снижается эффективность и может увеличиться относительная ошибка прогноза.
Когда мы устанавливаем слишком большое значение γ, снижается эффективность и может увеличиться относительная ошибка прогноза.
показывает прогнозируемое значение, когда γ=0. Мы видим, что существует несколько чрезвычайно больших значений прогноза (например,г., 8 июля 2013 г. и 6 ноября 2014 г.) из-за параметров модели, на которые сильно влияют почти нулевые значения потребления электроэнергии.
Значение прогноза, основанное на потере относительной ошибки наименьшего произведения (LRE) для данных о потреблении электроэнергии домохозяйствами.
показывает прогнозируемые значения при γ=0,03. Чрезвычайно больших значений прогноза не наблюдается, и значения прогноза аналогичны фактическому спросу на электроэнергию в . Таким образом, предлагаемая нами процедура устойчива к выбросам.
Прогнозное значение, основанное на предложенном методе с γ=0,03 для данных о потреблении электроэнергии домохозяйствами.
Кроме того, мы применяем метод Юла-Уокера, одну из самых популярных процедур оценки в авторегрессионной (AR) модели. Обратите внимание, что метод Юла-Уокера не рассматривает небольшое положительное значение yt как выброс, поэтому нам не нужно проводить надежную модель AR для этого набора данных. Относительная ошибка предсказания Юла-Уокера составляет 0,123, что больше, чем у предложенного нами метода (0,123).049).
Обратите внимание, что метод Юла-Уокера не рассматривает небольшое положительное значение yt как выброс, поэтому нам не нужно проводить надежную модель AR для этого набора данных. Относительная ошибка предсказания Юла-Уокера составляет 0,123, что больше, чем у предложенного нами метода (0,123).049).
Кроме того, для исследования устойчивости алгоритма ММ, описанного в разделе 5, мы также применяем метод BFGS для получения минимизатора функции отрицательного γ-правдоподобия. Функция optim в R используется для реализации метода BFGS. При использовании метода BFGS относительные ошибки предсказания расходятся, когда γ≥0,03. Следовательно, алгоритм MM более стабилен, чем алгоритм BFGS для этого набора данных.
8. Обсуждение
Мы предложили процедуру оценки относительной ошибки, устойчивую к выбросам.Предлагаемая процедура основана на γ-функции правдоподобия, которая строится по γ-кросс-энтропии [18]. Мы показали, что предложенный метод обладает свойством повторного спуска, желательным свойством в литературе по надежной статистике. Получены асимптотическая нормальность соответствующей оценки вместе с простой непротиворечивой оценкой асимптотической ковариационной матрицы, что позволяет построить приближенные доверительные множества. Помимо теоретических результатов, мы построили эффективный алгоритм, в котором мы минимизируем выпуклую функцию потерь на каждой итерации.Предлагаемый алгоритм монотонно уменьшает целевую функцию на каждой итерации.
Получены асимптотическая нормальность соответствующей оценки вместе с простой непротиворечивой оценкой асимптотической ковариационной матрицы, что позволяет построить приближенные доверительные множества. Помимо теоретических результатов, мы построили эффективный алгоритм, в котором мы минимизируем выпуклую функцию потерь на каждой итерации.Предлагаемый алгоритм монотонно уменьшает целевую функцию на каждой итерации.
Результаты нашего моделирования показали, что предложенный метод работает лучше, чем обычные процедуры оценки относительной ошибки с точки зрения точности прогнозирования. Кроме того, асимптотическое распределение оценки дало хорошее приближение с соответствующим значением γ, даже когда существовали выбросы. Предложенный метод был применен к данным о потреблении электроэнергии, которые включали небольшие положительные значения.Хотя обычный ЖРД был чувствителен к небольшим положительным значениям, наш метод смог соответствующим образом устранить отрицательное влияние этих значений.
На практике выбор переменных является одной из наиболее важных тем в регрессионном анализе. Обычный AIC (информационный критерий Акаике, Akaike [34]) не может быть непосредственно применен к предлагаемому нами методу, поскольку AIC направлен на минимизацию расхождения Кульбака-Лейблера, тогда как наш метод направлен на минимизацию γ-расхождения. В качестве темы будущих исследований было бы интересно вывести критерий выбора модели для оценки модели, оцениваемой методом γ-вероятности.
Анализ многомерных данных также является важной темой в статистике. В частности, разреженная оценка, такая как лассо [12], является стандартным инструментом для работы с многомерными данными. Как показано в замечании 3, наш метод можно распространить на L1-регуляризацию. Важным моментом в процедуре регуляризации является выбор параметра регуляризации. Хао и др. [14] предложили использовать критерий типа BIC (Байесовский информационный критерий) Wang et al. [35,36] для обычной оценки LPRE.Также было бы интересно рассмотреть проблему выбора параметра регуляризации в высокоразмерном робастном оценивании относительной ошибки.
В регрессионном анализе мы можем сформулировать два типа функций γ-вероятности: формулировку Фудзисавы и Эгучи [18] и формулировку Кавасимы и Фудзисавы [17]. [22] сообщили, что разница в производительности возникает, когда коэффициент выбросов зависит от объясняющей переменной. В модели мультипликативной регрессии в уравнении (1) ответы yi сильно зависят от исследовательских переменных xi по сравнению с обычной моделью линейной регрессии, поскольку yi является экспоненциальной функцией xij.В результате сравнение двух приведенных выше формулировок функций γ-вероятности было бы важно как с теоретической, так и с практической точек зрения.
Благодарности
Авторы хотели бы поблагодарить анонимных рецензентов за конструктивные и полезные комментарии, которые улучшили качество статьи.
Приложение A. Доказательство теоремы 1
Все асимптотики будут взяты при n→∞. Мы пишем an≲bn, если существует универсальная константа c>0 такая, что an≤cbn для любых достаточно больших n . Для любых случайных функций Xn и X0 на B¯ обозначим Xn(β)⇉pX0(β), если supβ∈B¯|Xn(β)-X0(β)|→p0; ниже мы будем писать просто supβ вместо supβ∈B¯.
Для любых случайных функций Xn и X0 на B¯ обозначим Xn(β)⇉pX0(β), если supβ∈B¯|Xn(β)-X0(β)|→p0; ниже мы будем писать просто supβ вместо supβ∈B¯.
Сначала сформулируем предварительную лемму, которая будет неоднократно использоваться в дальнейшем.
Лемма А1.Пусть η(x;β) и ζ(x,y;β) векторнозначные измеримые функции, удовлетворяющие
supβmaxk∈{0,1}∂βkη(x;β)≤η¯(x),supβmaxk∈{0,1}∂βkζ(x,y;β)≤ζ¯(x,y),
для некоторых η¯ и ζ¯ таких, что
η¯+∫0∞ζ¯(·,y)dy∈⋂q>0Lq(π).
Затем,
1n∑i=1nη(xi;β)⇉p∫Xη(x;β)π(dx),
(A1)
1n∑i=1nζ(xi,yi;β)⇉p∫0∞ ∫Xζ(x,y;β)f(y|x,β0)π(dx)dy.
(A2)
Доказательство.Уравнение (A1) является частным случаем уравнения (A2), поэтому мы показываем только последнее. Обратите внимание, что
supβ1n∑i=1nζ(xi,yi;β)-∫∫ζ(x,y;β)f(y|x,β0)π(dx)dy≤1nsupβ∑i=1n1nζ(xi,yi;β )-∫ζ(xi,y;β)f(y|xi,β0)dy+supβ1n∑i=1n∫ζ(xi,y;β)f(y|xi,β0)dy-∫∫ζ(x ,y;β)f(y|x,β0)π(dx)dy=:1nsupβMn(β)+supβCn(β).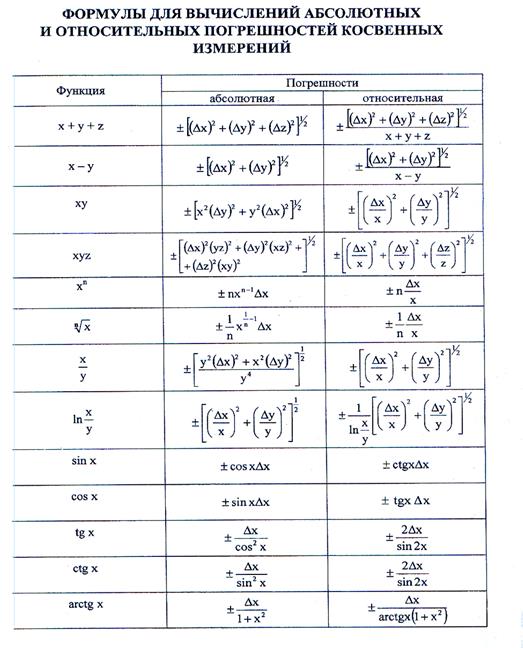
Для первого члена напомним неравенство Соболева ([37], п. 10.2):
EsupβMn(β)q≲supβE|Mn(β)|q+supβE|∂βMn(β)|q
(A7)
для q>p. Слагаемые Mn(β) тривиально образуют массив мартингальных разностей относительно фильтрации Fi:=σ(xj;j≤i), i∈N: поскольку мы предполагаем, что условное распределение yi при заданном {(xi,xi -1,xi-2,⋯),(yi-1,yi-2,⋯)} равно тому, что для данного xi (раздел 2 и раздел 3) каждое слагаемое Mn(β) равно 1nζ(xi,yi;β) -E{ζ(xi,yi;β)|Fi-1}.Отсюда с помощью неравенства Буркхолдера для мартингалов получаем при q>p∨2
supβE|Mn(β)|q≲supβ1n∑i=1nEζ(xi,yi;β)-∫ζ(xi,y;β)f(y|xi,β0)dyq<∞.
Мы можем пойти тем же путем для слагаемых ∂βMn(β), чтобы заключить, что supβE|∂βMn(β)|q<∞. Эти оценки в сочетании с уравнением (A3) затем приводят к выводу, что
Что касается другого члена, мы имеем Cn(β)→p0 для каждого β, а также
supnEsupβ∂βCn(β)<∞.
Последнее влечет тесноту семейства {Cn(β)}n непрерывных случайных функций на компакте B¯, откуда следует, что Cn(β)⇉p0. Доказательство завершено. □
Доказательство завершено. □
Приложение A.1. Непротиворечивость
Пусть fi(β):=f(yi|xi;β) для краткости и
Aγ,n(β):=1n∑i=1nfi(β)γ,A¯γ,n(β):=1n∑i=1n∫f(y|xi;β)γ+1dy=C( γ,h)1n∑i=1nexp(-γxiTβ).
По лемме A1 имеем
Aγ,n(β)⇉pAγ(β):=∫∫f(y|x;β)γf(y|x,β0)π(dx)dy,A¯γ,n(β)⇉pA¯ γ(β):=∫∫f(y|x;β)γ+1π(dx)dy=C(γ,h)∫exp(-γxTβ)π(dx).
Так как infβAγ(β)∧A¯γ(β)>0, то логарифмирование сохраняет равномерность сходимости по вероятности: для функции γ-правдоподобия (7) выполняется равенство
ℓγ,n(β)⇉pℓγ,0(β):=-1γlogAγ(β)+11+γlogA¯γ(β).γ→pβ0. Заметим, что предположение 3 нам не нужно, если ℓγ,n п.н. выпуклая, что, вообще говоря, может не иметь места при γ>0.
Приложение А.2. Асимптотическая нормальность
Прежде всего отметим, что предположение 2 гарантирует, что каждому α>0 соответствует функция F¯α∈L1f(y|x,β0)π(dx)dy такая, что
maxk=0,1,2,3supβ∂βkf(y|x,β)α≤F¯α(x,y).
Эта оценка позволит нам поменять местами порядок ∂β и интегрирования Ди-Лебега, неоднократно используемого ниже без упоминания. n′→pβ0.
n′→pβ0.
(A6)
Сначала докажем уравнение (A5). Прямыми вычислениями и леммой A1 получаем, что
nΨγ,n=A¯γ,nnSγ,nS¯γ,n-nAγ,nA¯γ,nS¯γ,n=∑i=1n1nHγ′fiγsi-∫f(y|xi;β0)γ+1s( y|xi;β0)dy-fiγ-∫f(y|xi;β0)γ+1dyHγ″=:∑i=1nχγ,i.
Последовательность (χγ,i)i≤n является массивом (Fj)-мартингал-разностей. Легко проверить условие Лапунова:
∃α>0,supnsupi≤nEχγ,i2+α<∞.
Следовательно, мартингальная центральная предельная теорема заключает уравнение (A5), если мы покажем следующую сходимость квадратичной характеристики:
1n∑i=1nEχγ,i⊗2|Fi-1→pΔγ.
Из этого следует наблюдение, что
1n∑i=1nEχγ,i⊗2|Fi-1=(Hγ′)21n∑i=1nvarfjγsj|Fi-1+(Hγ′′)⊗21n∑i=1nvarfjγ|Fi-1-2Hγ′1n∑ i=1ncovfjγsj,fjγ|Fi-1Hγ′′=(Hγ′)2∫∫f(y|x;β0)2γ+1s(y|x;β0)⊗2dyπ(dx)-(Hγ″)⊗2+ (Hγ′′)⊗2∫∫f(y|x;β0)2γ+1dyπ(dx)-(Hγ′)2-2Hγ′∫∫f(y|x;β0)2γ+1s(y|x; β0)dyπ(dx)-Hγ′Hγ″(Hγ″)T+op(1)=(Hγ′)2∫∫f(y|x;β0)2γ+1s(y|x;β0)⊗2dyπ( dx)+(Hγ″)⊗2∫∫f(y|x;β0)2γ+1dyπ(dx)-2Hγ′∫∫f(y|x;β0)2γ+1s(y|x;β0)dyπ( dx)(Hγ′′)T+op(1)=Δγ+op(1)
вызвать выражение (4) для последнего равенства.
Далее мы показываем уравнение (A6). При данном условии регулярности мы можем сделать вывод, что
supβ|∂β2Ψγ,n(β)|=Op(1).
Поэтому достаточно проверить, что -∂βΨγ,n(β0)→pJγ(β0)=Jγ. Это следует из прямого вычисления -∂βΨγ,n(β0) в сочетании с применениями леммы A1 (заметим, что A¯γ,n и Aγ,n имеют одинаковый предел по вероятности):
-∂βΨγ,n (β0)=Aγ,n1n∑i=1n∫f(y|xi;β0)γ+1s(y|xi;β0)⊗2dy-S¯γ,nSγ,nT+γSγ,nS¯γ,nT-S ¯γ,nSγ,nT+γAγ,n1n∑i=1n∫f(y|xi;β0)γ+1s(y|xi;β0)⊗2dy-A¯γ,n1n∑i=1nfiγsi⊗2+Aγ, n1n∑i=1n∫f(y|xi;β0)γ+1∂βs(y|xi;β0)dy-A¯γ,n1n∑i=1nfiγ∂βsi=Aγ,n1n∑i=1n∫f( y|xi;β0)γ+1s(y|xi;β0)⊗2dy-S¯γ,nSγ,nT+op(1)=Hγ′∫∫f(y|x;β0)γ+1s(y| x;β0)⊗2dyπ(dx)-(Hγ″)⊗2+op(1)=Jγ+op(1).γ-β0→p0.
Этих наблюдений достаточно, чтобы заключить уравнение (17).
Вклад авторов
К.Х. предложил алгоритм, сделал пакет R бесплатным, провел имитационное исследование и проанализировал реальные данные; Х.М. вывел асимптотику; К.Х. и Х.М. написал бумагу.
Финансирование
Это исследование финансировалось Японским обществом содействия науке KAKENHI 15K15949 и Центром инновационной программы (COI) Японского агентства по науке и технологиям (JST), Япония (K.H.) и номер гранта JST CREST JPMJCR14D7 (H.M.)
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Список литературы
1. Хасти Т., Тибширани Р., Фридман Дж. Элементы статистического обучения. 2-е изд. Спрингер; Нью-Йорк, штат Нью-Йорк, США: 2009 г. (серия Springer по статистике). [Google Академия]2. Парк Х., Стефански Л.А. Предсказание относительной ошибки. Стат. Вероятно. лат. 1998;40:227–236. doi: 10.1016/S0167-7152(98)00088-1. [Перекрестная ссылка] [Академия Google]4.Ван дер Меер Д.В., Виден Дж., Мунхаммар Дж. Обзор вероятностного прогнозирования производства фотоэлектрической энергии и потребления электроэнергии. Продлить. Суст. Энерг. 2018; 81: 1484–1512. doi: 10.1016/j.rser.2017.05.212. [Перекрестная ссылка] [Академия Google] 7. Ли З., Линь Ю., Чжоу Г., Чжоу В. Эмпирическая вероятность регрессии наименьшей абсолютной относительной ошибки. КОНТРОЛЬНАЯ РАБОТА. 2013; 23:86–99. doi: 10.1007/s11749-013-0343-5. [Перекрестная ссылка] [Академия Google]8. Чен К., Линь Ю., Ван З., Ин З. Оценка относительной ошибки наименьшего произведения.J. Многомерный анализ. 2016; 144:91–98. doi: 10.1016/j.jmva.2015.10.017. [Перекрестная ссылка] [Академия Google]9. Дин Х., Ван З., Ву Ю. Оценка на основе относительных ошибок с растущим числом параметров. коммун. Стат. Методы теории. 2017;47:196–209. doi: 10.1080/03610926.2017.1301474. [Перекрестная ссылка] [Академия Google] 10. Демонжо Дж., Хами А., Лаксачи А., Рачди М. Прогноз относительной ошибки в непараметрической функциональной статистике: теория и практика. J. Многомерный анализ. 2016; 146: 261–268. doi: 10.1016/j.жмва.2015.09.019. [Перекрестная ссылка] [Академия Google] 11. Ван З., Чен З., Чен З. H-оценка относительной ошибки для модели мультипликативной регрессии со случайным эффектом. вычисл. Стат. 2018; 33: 623–638. doi: 10.1007/s00180-018-0798-7. [Перекрестная ссылка] [Академия Google] 12. Тибширани Р. Регрессионное сокращение и выбор с помощью лассо. Дж. Р. Стат. соц. Методология серии Б. 1996; 58: 267–288. [Google Академия] 13. Юань М., Лин Ю. Выбор модели и оценка в регрессии со сгруппированными переменными. Дж. Р. Стат. соц. Серия B Стат.Методол. 2006; 68: 49–67. doi: 10.1111/j.1467-9868.2005.00532.x. [Перекрестная ссылка] [Академия Google] 14. Хао М., Лин Ю., Чжао С. Подход к выбору переменных, основанный на относительных ошибках. вычисл. Стат. Анализ данных. 2016;103:250–262. doi: 10.1016/j.csda.2016.05.013. [Перекрестная ссылка] [Академия Google] 15. Лю С., Лин Ю., Ван З. Выбор групповой переменной для регрессии относительной ошибки. Дж. Стат. План. Вывод. 2016;175:40–50. doi: 10.1016/j.jspi.2016.02.006. [Перекрестная ссылка] [Академия Google] 16. Ся С., Лю З., Ян Х. Регулярная оценка для моделей с наименьшими абсолютными относительными ошибками с расходящимся числом ковариат.вычисл. Стат. Анализ данных. 2016;96:104–119. doi: 10.1016/j.csda.2015.10.012. [Перекрестная ссылка] [Академия Google] 17. Кавасима Т., Фудзисава Х. Надежная и разреженная регрессия через γ -дивергенцию. Энтропия. 2017;19:608. doi: 10.3390/e1- 08. [Перекрестная ссылка] [Академия Google] 18. Фудзисава Х., Эгучи С. Надежная оценка параметров с небольшим отклонением от сильного загрязнения. J. Многомерный анализ. 2008;99:2053–2081. doi: 10.1016/j.jmva.2008.02.004. [Перекрестная ссылка] [Академия Google] 19. Маронна Р., Мартин Д., Йохай В.Надежная статистика. Джон Уайли и сыновья; Чичестер, Великобритания: 2006. [Google Scholar]20. Куду А.Э., Лей К. Характеристики законов GIG: обзор. Вероятно. Surv. 2014; 11:161–176. doi: 10.1214/13-PS227. [Перекрестная ссылка] [Академия Google] 21. Джонс М.К., Хьорт Н.Л., Харрис И.Р., Басу А. Сравнение связанных оценок минимального расхождения на основе плотности. Биометрика. 2001; 88: 865–873. doi: 10.1093/биомет/88.3.865. [Перекрестная ссылка] [Академия Google] 22. Кавасима Т., Фудзисава Х. О разнице между двумя типами γ-расхождения для регрессии.[(по состоянию на 20 августа 2018 г.)]; 2018 г. Доступно в Интернете: https://arxiv.org/abs/1805.06144.23. Феррари Д., Ян Ю. Оценка максимального Lq-правдоподобия. Аня. Стат. 2010; 38: 753–783. doi: 10.1214/09-AOS687. [Перекрестная ссылка] [Академия Google] 24. Басу А., Харрис И.Р., Хьорт Н.Л., Джонс М.К. Надежная и эффективная оценка за счет минимизации расходимости мощности по плотности. Биометрика. 1998; 85: 549–559. doi: 10.1093/биомет/85.3.549. [Перекрестная ссылка] [Академия Google] 25. Ван дер Ваарт А.В. асимптотическая статистика; Том. 3, Кембриджская серия по статистической и вероятностной математике.Издательство Кембриджского университета; Кембридж, Великобритания: 1998. [Google Scholar]27. Хантер Д.Р., Ланге К. Учебное пособие по алгоритмам ММ. Являюсь. Стат. 2004; 58:30–37. doi: 10.1198/0003130042836. [Перекрестная ссылка] [Академия Google] 28. Бенинг Д. Алгоритм полиномиальной логистической регрессии. Аня. Инст. Стат. Мат. 1992; 44: 197–200. doi: 10.1007/BF00048682. [Перекрестная ссылка] [Академия Google] 29. Зоу Х., Хасти Т. Регуляризация и выбор переменных с помощью эластичной сети. Дж. Р. Стат. соц. Серия B Стат. Методол. 2005; 67: 301–320. doi: 10.1111/j.1467-9868.2005.00503.х. [Перекрестная ссылка] [Академия Google] 30. Фан Дж., Ли Р. Выбор переменных с помощью невогнутой штрафной вероятности и ее свойств оракула. Варенье. Стат. доц. 2001; 96: 1348–1360. doi: 10.1198/016214501753382273. [Перекрестная ссылка] [Академия Google] 31. Фридман Дж., Хасти Т., Тибширани Р. Пути регуляризации для обобщенных линейных моделей посредством спуска по координатам. Дж. Стат. ПО 2010;33:1. doi: 10.18637/jss.v033.i01. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]33. Сиошанси Ф.П., Пфаффенбергер В.Реформа рынка электроэнергии: международная перспектива. Эльзевир; Оксфорд, Великобритания: 2006. [Google Scholar]34. Акаике Х. Новый взгляд на идентификацию статистической модели. IEEE транс. Автомат. контр. 1974; 19: 716–723. doi: 10.1109/TAC.1974.1100705. [Перекрестная ссылка] [Академия Google] 35. Ван Х., Ли Р., Цай К.Л. Селекторы параметров настройки для метода плавного отсечения абсолютного отклонения. Биометрика. 2007; 94: 553–568. doi: 10.1093/biomet/asm053. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]36. Ван Х., Ли Б., Ленг С. Выбор параметров настройки усадки с расходящимся числом параметров. Дж. Р. Стат. соц. Серия B Стат. Методол. 2009; 71: 671–683. doi: 10.1111/j.1467-9868.2008.00693.x. [Перекрестная ссылка] [Академия Google] 37. Фридман А. Стохастические дифференциальные уравнения и их приложения. Дуврские публикации; Нью-Йорк, штат Нью-Йорк, США: 2006 г. [Google Scholar]
- Статья
- 2 минуты на чтение
Щелкните Пуск , щелкните Все программы , щелкните Microsoft BizTalk Server и щелкните Администрирование BizTalk Server .
В корне консоли разверните Администрирование BizTalk Server , разверните Группа BizTalk и разверните Приложения .
Найдите свое приложение и найдите свой транспорт.
Щелкните правой кнопкой мыши имя транспорта.
Щелкните Свойства .
В списке портов введите выберите правильный порт.
Щелкните Настроить .
Недопустимый адрес (относительный uri требует косой черты («-«)) — BizTalk Server
Пожалуйста, оцените свой опыт
да Нет
Любая дополнительная обратная связь?
Отзыв будет отправлен в Microsoft: при нажатии кнопки отправки ваш отзыв будет использован для улучшения продуктов и услуг Microsoft.Политика конфиденциальности.
Представлять на рассмотрение
Спасибо.
В этой статье
Детали
| Поле | Сведения об ошибке |
|---|---|
| Название продукта | Сервер BizTalk |
| Версия продукта | 3,6 |
| Идентификатор события | 0 |
| Источник событий | 0 |
| Компонент | 0 |
| Символическое имя | 0 |
| Текст сообщения | Неверный адрес; ожидается относительный uri, начинающийся с косой черты («/») |
Пояснение
Вы не указали изолированное расположение получения WCF с корректным относительным адресом.Например, http://localhost/svc не будет работать как относительный адрес. Вы не можете установить для свойства Address изолированного расположения получения WCF абсолютный адрес.
Действие пользователя
Используйте следующую процедуру для настройки адреса.
