Самостоятельные работы по математике за 5 класс к учебнику Виленкина Н.Я. за 1, 2, 3 и 4 четверти
Дата публикации: .
Самостоятельные на темы: «Натуральные числа и их обозначения», «Сложение и вычитание натуральных чисел», «Сравнение натуральных чисел», «Отрезок, прямая, луч», «Умножение натуральных чисел», «Деление натуральных чисел», «Выражения и уравнения», «Квадрат и куб числа», «Окружность и круг», «Обыкновенные дроби», «Сравнение дробей» и др.
Некоторые понятия к учебному материалу.
1. Натуральные числа – используются для счета предметов в повседневной жизни.2. Отрезок. Длина отрезка – расстояние между его крайними точками, концами. Обозначается заглавными латинскими буквами, например AB.
3. Шкала – специальная линейка с делениями (штрихами).
4. Единичный отрезок – отрезок с длиной равной единице.
5. Меньше и больше. Меньше, число, которое при счете называется раньше.
6. Слагаемые числа – числа, которые складываются.
7. Вычитание. Число из которого вычитают – это уменьшаемое. Число, которое вычитается – это вычитаемое. В итоге получаем разность.
Самостоятельная работа №1 (входная работа на повторение)
Вариант I.
1. Определение числа.
а) Определите натуральное число, которое следует за числом 699.б) Определите натуральное число, которое на две единицы меньше числа 1001.
в) Определите натуральное число, которое на единицу больше числа 239 999.
г) Определите натуральное число, которое на единицу меньше числа 394 000.
2. Решите задачу.
В городском сквере посажено 340 деревьев. А в парке посажено 270 деревьев. На сколько деревьев больше в городском сквере, чем в парке?3. Решите примеры.
| а) 492 + 1 220 = | б) 3 495 — 593 = |
| в) 5112 : 6 = | г) 56 * 23 = |
Вариант II.
1. Определение числа.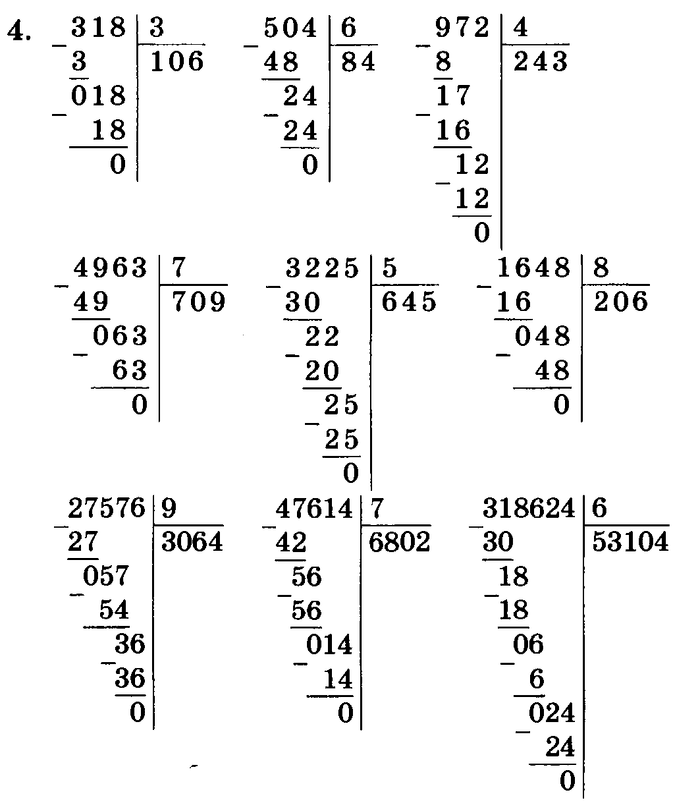
б) Определите натуральное число, которое на единицу меньше числа 2 000.
в) Определите натуральное число, которое на единицу больше числа 722 999.
г) Определите натуральное число, которое на единицу меньше числа 24 000.
2. Решите задачу.
Рыбаки за первую неделю поймали 395 кг рыбы, а за вторую неделю – 239 кг. На сколько кг было поймано меньше за вторую неделю, чем за первую?3. Решите примеры.
| а) 638 + 1 445 = | б) 6 112 — 2 598 = |
| в) 2688 : 3 = | г) 24 * 45 = |
Вариант III.
1. Определение числа.
а) Определите натуральное число, которое следует перед числом 699.б) Определите натуральное число, которое на единицу меньше числа 3 000.
в) Определите натуральное число, которое на единицу больше числа 28 999.
г) Определите натуральное число, которое на единицу меньше числа 12 000.
С первой грядки было собрано 427 помидор, а со второй грядки – 311. На сколько меньше помидор было собрано со второй грядки, чем с первой?3. Решите примеры.
| а) 455 + 3 412= | б) 5 332 — 593 = |
| в) 3648 : 8 = | г) 29 * 41 = |
Самостоятельная работа №2 на тему: «Натуральные числа и их обозначения»
Вариант I.
1. Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
а) число 20;б) число 49.
2. Представьте следующие словосочетания в числовом виде.
а) Шесть миллиардов пятьсот три тысяча семь.б) На единицу больше чем пятьсот девять тысяч девятьсот девяносто девять.
3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
a) 2, 3 и 7.b) 4, 0 и 9.
Вариант II.
1. Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
б) число 38.
2. Представьте следующие словосочетания в числовом виде.
а) Восемь миллиардов триста одна тысяча три.б) На единицу больше чем сто девять тысяч девятьсот девяносто девять.
3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
a) 1, 3 и 9.b) 2, 4 и 0.
Вариант III.
1. Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
а) число 30;б) число 58.
2. Представьте следующие словосочетания в числовом виде.
а) Два миллиарда шестьсот два миллиона триста.б) На единицу больше чем семьсот пять тысяч девятьсот девяносто восемь.
3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
b) 1, 3 и 0.
Самостоятельная работа №3
Вариант I.
1. Переведите из одной единицы измерения в другую.
а) 8 дм 43 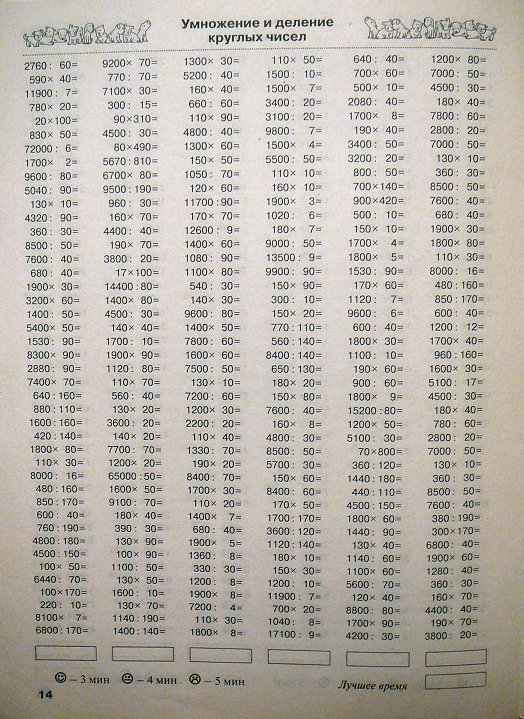см = . .. см | б) 5 км 549 м = … м |
| в) 7 см 18 мм = … мм | г) 249 см =… дм … см |
2. Начертите отрезок AB, равный 17 см 5 мм. Отметьте на нем точки C и D. AC равно 10 см 4 мм, CD равно 4 см 9 мм. Чему равна длина отрезка DB?
3. Решите задачу.
Перед домом построили забор. Забор держится на 18 столбах, расстояние между столбами составляет пять метров. Каково расстояние между шестым и четырнадцатым столбами?4. Начертите четырехугольник ABCD. Отметьте точкой T середину стороны BC. Соедините точки B и D, А и T. Выпишите все многоугольники, которые образовались.
Вариант II.
1. Переведите из одной единицы измерения в другую.
| а) 4 дм 23 см = … см | б) 25 км 50 м = … м |
| в) 16 см 65 мм = … мм | г) 456 см =… дм … см |
2. Начертите отрезок AB, равный 15 см 4 мм, отметьте на нем точки C и D. AC равен 8 см 2 мм, CD равен 3 см 7 мм. Чему равна длина отрезка DB?
3.
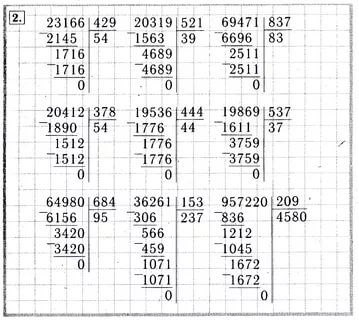Решите задачу.
4. Начертите четырехугольник ABCD. Отметьте середину AB и поставьте точку N. Проведите отрезки DN и АС. Выпишите все многоугольники, которые образовались.
Вариант III.
1. Переведите из одной единицы измерения в другую.
| а) 19 дм 5 см = … см | б) 21 км 678 м = … м |
| в) 43 см 8 мм = … мм | г) 503 см =… дм … см |
2. Начертите отрезок AB, равный 13 см 2 мм, отметьте на нем точки C и D. AC равен 7 см 3 мм. CD равен 3 см 6 мм. Чему равна длина отрезка DB?
3. Решите задачу.
Перед домом построили забор. Забор держится на 16 столбах, расстояние между столбами составляет 3 метра. Каково расстояние между пятым и одиннадцатым столбами?4. Начертите четырехугольник ABCD. Отметьте середину CD и поставьте точку М. Проведите отрезки BM и АС.
Выпишите все многоугольники, которые образовались.
Самостоятельная работа №4 на тему: «Сравнение натуральных чисел»
Вариант I.
1. Сравните числа.
| а) 3 485 660 … 3 458 660 | б) 303 559 … 330 559 |
| в) 2 596 440 … 2 569 440 | г) 45 696 … 44 696 |
2. Представьте в виде двойного неравенства: 18 т 347 кг … 18 т 4 ц 59 кг … 18 568 кг.
Вариант II.
1. Сравните числа.
| а) 34 686 887 … 34 868 887 | б) 3 855 … 3 585 |
| в) 40 955 999 … 40 595 999 | г) 455 776 … 445 776 |
2. Представьте в виде двойного неравенства: 13 км 845 м … 14675 м … 13 км 845 м 3 дм.
Вариант III.
1. Сравните числа.
| а) 678 881 … 687 881 | б) 782 223 … 728 223 |
| в) 2 490 606 … 2 490 660 | г) 13 799 … 13 977 |
2. Представьте в виде двойного неравенства: 15 т 475 кг .
.. 15657 кг … 157 ц 35 кг.
Самостоятельная работа №5 на тему: «Сложение и вычитание натуральных чисел»
Вариант I.
1. Выполните сложение.
| а) 348 588 667 + 239 586 394 = | б) 93 955 483 + 495 868 991 = |
| в) 23 394 596 + 5 697 345 = | г) 3 949 532 + 405 669 = |
2. Выполните вычитание.
| а) 348 588 667 — 283 745 733 = | б) 93 955 483 — 22 394 583 = |
| в) 23 394 596 — 192 485 = | г) 3 949 532 — 4 348 483 = |
3. Решите задачу.
Мастерская закупила 560 гаек. На ремонт первой машины потребовалось 203 гайки, а на ремонт второй машины – еще 293 гайки. Сколько гаек осталось в мастерской?4. Решите задачу.
В концертном зале стояло 454 стула. Для проведения концерта принесли 123 новых стула, а после антракта – еще 13 стульев. Сколько всего стульев стало в концертном зале?Вариант II.
1. Выполните сложение.
| а) 3 484 558 + 9 499 834 = | б) 93 955 483 + 394 585 665 = |
| в) 3 495 863 + 35 384 588 = | г) 5 697 291 + 34 405 669 = |
2. Выполните вычитание.
| а) 4 856 342 — 3 495 384 = | б) 283 495 864 — 232 485 965 = |
| в) 5 965 493 — 3 449 594 = | г) 23 455 303 — 19 485 588 = |
3. Решите задачу.
В рулоне было смотано 327 м ленты. В первый день использовали 103 м, а во второй день – ещё 205 м. Сколько метров осталось в рулоне?4. Решите задачу.
В магазине находилось 4 т 150 кг сахара. В первый день привезли 340 кг сахара, а во второй день – еще 4 ц сахара. Сколько кг сахара стало в магазине?Вариант III.
1. Выполните сложение.
| а) 2 399 388 + 239 586 394 = | б) 435 483 + 495 868 991 = |
| в) 34 567 784 + 13 412 345 = | г) 6 563 544 + 23 876 554 = |
2. Выполните вычитание.
| а) 455 586 661 — 283 745 733 = | б) 40 954 586 — 22 394 583 = |
| в) 495 568 222 — 448 568 338 = | г) 3 949 532 — 2 349 588 = |
3. Решите задачу.
В моток смотано 459 м провода. В первый день истратили 119 м, а на второй день – 239 м провода. Сколько метров провода осталось в мотке?Самостоятельная работа №6
Вариант I.
1. Найдите значение выражения: ( а + 46 ) : ( b — 48 ), если а = 35 и b = 57.
2. Упростите выражения.
а) с + 239 — 93;б) 485 — 483 + d.
3. Составьте уравнение для решения задачи и решите его.
Было задумано некоторое число. К нему прибавили число 194, а потом прибавили ещё число 110 и получили число 322. Какое число было задумано?4. Решите уравнения.
a) (305 — ( ( 45 + х ) — 32 ) + 96 = 223;б) 38 + ( 69 — y ) + 74 = 172.
Вариант II.
1. Найдите значение выражения: ( а — 34 ) * ( b + 9 ), если а = 60 и b = 11.
2. Упростите выражения.
а) 594 — 69 — а;б) 149 + b — 54.
3. Составьте уравнение для решения задачи и решите его.
Было задумано некоторое число. Из этого числа вычли число 424, а затем прибавили число 392. В итоге, получилось число 632. Какое число было задумано?4. Решите уравнения.
a) 209 — ( ( 145 + х ) — 12 ) + 96 = 123;б) 18 + ( 159 — y ) + 34 = 172.
Вариант III.
1. Найдите значение выражения: ( а — 68 ) : b + 2 339, если а = 92 и b = 8.
2. Упростите выражения.
а) с + 239 — 193;б) 485 — d + 384.
3. Составьте уравнение для решения задачи и решите его.
Было задумано некоторое число. Из этого числа вычли число 209, а затем прибавили число 47. В итоге, получилось число 217. Какое число было задумано?4. Решите уравнения.
a) ( 111 — ( 45 + х ) ) + 96 = 123;б) 29 + ( 59 — y ) + 15 = 72.
После завершения второй четверти, учащиеся должны:
1.
уметь умножать натуральные числа и использовать эти знания;
2. уметь производить деление натуральных чисел, в том числе и деление с остатком, и использовать эти навыки при решении задач;
3. знать распределительное свойство умножения, уметь применять это свойство при устных вычислениях и при решении задач;
4. знать, что такое возведение числа в степень. Понимать, что такое корень и куб числа;
5. понимать, что такое формула, и как производить вычисления по формуле.
Самостоятельная работа №7 на тему: «Действия с натуральными числами. Умножение»
Вариант I.
1. Выполните умножение.
| а) 283 * 46 = | б) 29 * 473 = | в) 841 * 93 = | г) 19 * 632 = |
| д) 570 * 340 = | е) 930 * 730 = | ж) 5100 * 360 = | з) 560 * 230 = |
2. Умножьте числа, используя наиболее удобный порядок действий.
а) 25 * 491 * 4 * 200 =б) 4 * 324 * 25 * 300 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 35 * 34 = | 34 * 33 = | 34 * 36 = | 32 * 32 = |
4. Решите задачу.
В двухэтажной школе всего 32 кабинета и в каждом кабинете по 12 парт. В трехэтажной школе 45 кабинетов и в каждом кабинете по 14 парт. Сколько всего парт необходимо городским школам, если в городе 8 двухэтажных и 5 трехэтажных школ?Вариант II.
1. Выполните умножение.
| а) 342 * 57 = | б) 64 * 268 = | в) 342 * 89 = | г) 32 * 864 = |
| д) 920 * 560 = | е) 470 * 990 = | ж) 2300 * 630 = | з) 430 * 540 = |
2. Умножьте числа, используя наиболее удобный порядок действий.
а) 25 * 376 * 4 * 500 =б) 4 * 265 * 25 * 200 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 85 * 84 = | 84 * 83 = | 84 * 86 = | 82 * 82 = |
4. Решите задачу.
В поселке построено 18 домов.
Из них 4 трехэтажных, 6 двухэтажных, остальные одноэтажные дома. В трехэтажных домах – 18 окон, в двухэтажных – 14 окон, в одноэтажных – 8 окон. Сколько окон необходимо для 4 таких же посёлков?Вариант III.
1. Выполните умножение.
| а) 563 * 24 = | б) 32 * 441 = | в) 324 * 87 = | г) 23 * 728 = |
| д) 220 * 680 = | е) 240 * 580 = | ж) 7500 * 290 = | з) 920 * 630 = |
2. Умножьте числа, используя наиболее удобный порядок действий.
а) 25 * 376 * 4 * 300 =б) 4 * 641 * 25 * 100 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 65 * 64 = | 64 * 63 = | 64 * 66 = | 62 * 62 = |
4. Решите задачу.
В один мешок помещается 26 кг картофеля, или 34 кг муки, или 38 кг сахара. Сколько всего весит груз, если в машину погрузили 32 мешка картофеля, 38 мешков муки и 52 мешка сахара?Самостоятельная работа №8 на тему: «Деление натуральных чисел»
Вариант I.
1. Выполните деление.
| а) 475 860 : 5 = | б) 8 412 : 4 = | в) 492 000 000 : 1 000 = |
| г) 270 930 : 3 = | д) 386 240 : 5 = | е) 19 688 : 23 = |
2. Решите уравнения.
| а) X : 85 = 2 210 | б) 36 690 : Y = 10 | в) 792 : X = 4 |
| г) 15 * ( 39 : X ) = 45 | д) Y : 42 = 168 | е) 65 065 : Y = 1 001 |
3. Решите задачу.
Фермеру необходимо вспахать поле размером 318500 м. За сколько дней он вспашет поле, если известно, что за день он может вспахать 45 500 м?4. Остаток равен 18, неполное частное – 35 и делитель – 23. Найдите делимое.
Вариант II.
1. Выполните деление.
| а) 489 560 : 5 = | б) 36 690 : 3 = | в) 657 000 : 1 000 = |
| г) 960 552 : 6 = | д) 522 240 : 2 = | е) 67 065 : 85 = |
2. Решите уравнения.
| а) X : 26 = 456 | б) 4 760 : Y = 85 | в) 792 : X = 8 |
| г) 35 * ( 54 : X ) = 315 | д) Y : 3 = 3015 | е) 524 : Y = 131 |
3.
Решите задачу.
4. Остаток равен 33, неполное частное – 41 и делитель – 25. Найдите делимое.
Вариант III.
1. Выполните деление.
| а) 236 560 : 4 = | б) 36 690 : 6 = | в) 612 345 000 : 1 000 = |
| г) 960 440 : 8 = | д) 678 350 : 2 = | е) 31 464 : 69 = |
2. Решите уравнения.
| а) X : 25 = 14 | б) 1 820 : Y = 28 | в) 1 836 : X = 6 |
| г) 52 * Y = 468 | д) Y : 3 = 7 659 | е) 1048 : Y = 131 |
3. Решите задачу.
Комбайн убирает 30 га пшеницы за 1 час. Сколько дней ему нужно, чтобы убрать площадь равную 1200 га, если в день он будет работать по 10 часов?4. Остаток равен 24, неполное частное – 25 и делитель – 28. Найдите делимое.
Самостоятельная работа №9 на темы: «Выражения, уравнения и решение уравнений», «Квадрат и куб числа»
Вариант I.
1. Решите примеры.
а) 34 + ( 239 — 606 : 6 ) * 4 — 393 : 3 =б) 152 =
в) 73 =
г) ( 14 + 7 )2 — ( 5 + 13 )2 + 287 =
2. Упростите выражение и найдите его значение при с=34: 47с + 34 — 58 + 12с — 58.
3. Решите уравнения.
а) 15 * х = 945б) 3 * y — 45 = 44
4. Решите задачу.
Бабушка и внучка слепили 124 пельмени. Сколько пельменей слепили бабушка и сколько внучка, если бабушка лепила в 3 раза быстрее, чем внучка?Вариант II.
1. Решите примеры.
а) 472 — ( 29 + 124 : 4 ) — 72 : 8 =б) 182 =
в) 63 =
г) ( 5 + 27 )2 — ( 4 + 12 )2 — 64 =
2. Упростите выражение и найдите его значение при с=12: 19с + 57 — 58с + 29с — 38 + 5с.
3. Решите уравнения:
а) 15 * х = 180б) 12 * y + 36 = 96
4. Решите задачу.
Инженер и студент отремонтировали 248 приборов. Инженер ремонтировал приборы в 3 раза быстрее, чем студент. Сколько приборов починил каждый?Вариант III.
1. Решите примеры.
а) 365 + ( 299 — 342 : 2 ) * 5 — 687 : 3 =б) 172 =
в) 83 =
г) ( 4 + 7 )2 — ( 5 + 23 )2 + 787 =
2. Упростите выражение и найдите его значение при с=12: 47 + 56с — 6с + 34 — 12с.
3. Решите уравнения.
а) 32 * х = 1280б) 8 * y + 36 = 356
4. Решите задачу.
Портной и его ученик сшили 213 фартуков. Портной работал в 2 раза быстрее, чем его ученик. Сколько фартуков сшил портной, а сколько ученик?Самостоятельная работа №10 на темы: «Окружность и круг». «Обыкновенные дроби»
Вариант I.
1. Нарисуйте окружность с центром в точке X и радиусом 4 см 6 мм. Нарисуйте отрезок CD так, чтобы он проходил через центр окружности и пересекал ее в точках C и D. Как называются отрезки СX и СD? Определите их длину.
2. Решите задачу.
Оля нашла 26 грибов, из них 18 маслят. Какую часть грибов составляют маслята?3. Решите задачу.
Рыбаки поймали 112 кг рыбы. Из них 10⁄28 – караси.
Сколько карасей поймали рыбаки?4. Решите задачу.
Коля прочитал 85 страниц журнала, что составило 5⁄12 от общего числа страниц. Сколько страниц в журнале?Вариант II.
1. Нарисуйте окружность с центром в точке Y и радиусом 3 см 8 мм. Нарисуйте отрезок EF так, чтобы он проходил через центр окружности и пересекал ее в точках E и F. Как называются отрезки YE и EF? Определите их длину.
2. Решите задачу.
Коля собрал в корзину 31 фрукт, из них 22 фрукта – это груши. Какую часть собранных фруктов составляют груши?3. Решите задачу.
Школьники собрали 104 кг овощей. 13⁄26 от общего числа овощей составляют помидоры. Сколько кг помидор собрали школьники?4. Решите задачу.
Мастер отремонтировал 35 приборов, что составило 5⁄12 от общего количества приборов. Сколько всего приборов надо отремонтировать мастеру?Вариант III.
1. Нарисуйте окружность с центром в точке Z и радиусом 2 см 6 мм.
Нарисуйте отрезок GH так, чтобы он проходил через центр окружности и пересекал ее в точках G и H. Как называются отрезки GZ и GH? Определите их длину.
2. Решите задачу.
У Саши есть 29 карандашей. Из них 19 карандашей – это простые карандаши. Какую часть карандашей составляют цветные карандаши?3. Решите задачу.
Мастер сделал 312 деталей. Из них 3⁄24 часть деталей – деревянные. Сколько деревянных деталей сделал мастер?4. Решите задачу.
Ребята из 5 класса собрали 32 кг ягод. Это составляет 3⁄24 от всего количества собранных ягод. Сколько всего ягод было собрано?Самостоятельная работа №11 на тему: «Сравнение дробей»
Вариант I.
1. Задан луч длиной в 12 единиц. Отметьте на числовом луче:
| а) 2⁄12 части | б) 6⁄12 части | 2⁄3 части | 5⁄4 части |
2. Сравните дроби.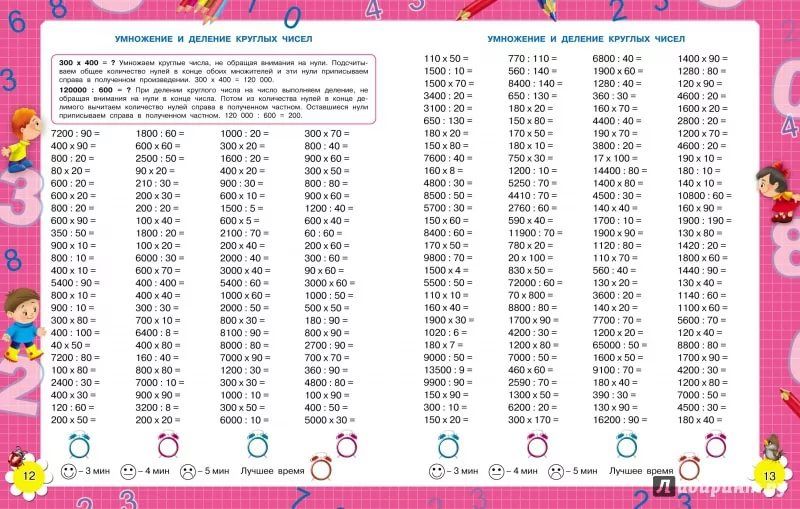
б) 21⁄45 и 15⁄26
3. Найдите три решения неравенства.
а) 21⁄22< x < 22⁄22б) 7⁄11 < z < 8⁄11
4. При каких значениях х:
а) дробь х⁄22 будет правильной?б) дробь 15⁄х будет неправильной?
Вариант II.
1. Задан луч длиной в 15 единиц. Отметьте на числовом луче:
| 4⁄15 части | 3⁄15 части | 3⁄5 части | 2⁄3 части |
2. Сравните дроби.
а) 26⁄34 и 15⁄17б) 22⁄49 и 18⁄21
3. Найдите три решения неравенства.
а) 19⁄20 < x < 20⁄20б) 7⁄9 < z < 8⁄9
4.
При каких значениях y:
б) дробь 23⁄y будет неправильной?
Вариант III.
1. Задан луч длиной в 18 единиц. Отметьте на числовом луче:
| 2⁄18 части | 6⁄18 части | 2⁄3 части | 5⁄6 части |
2. Сравните дроби.
а) 26⁄31 и 18⁄19б) 23⁄41 и 17⁄18
3. Найдите три решения неравенства.
а) 9⁄10< y < 10⁄10б) 5⁄7 < z < 6⁄7
4. При каких значениях z:
а) дробь z⁄29 будет правильной?б) дробь 13⁄z будет неправильной?
Самостоятельная работа №12 на тему: «Сложение и вычитание обыкновенных дробей»
Вариант I.
1. Решите примеры.
а) 26⁄31 + 18⁄31 — 6⁄31;б) 17⁄125 — 5⁄125 + 106⁄125;
в) 19⁄39 + ( 18⁄39 — 6⁄39 ) — 13⁄39;
2. Решите уравнения.
а) x + 6⁄18 = 16⁄18б) 13⁄25 — ( y + 6⁄25 ) = 4⁄25
3. Решите задачу.
Первый спортсмен пробежал 5⁄7 км, а второй спортсмен за тоже время пробежал 6⁄7 км. На сколько метров больше пробежал первый спортсмен?4. Решите задачу.
Из мешка взяли 2⁄9 части муки, а потом – ещё 3⁄9 части. В мешке осталось 14 кг. Сколько кг муки было в мешке?Вариант II.
1. Решите примеры.
а) 15⁄38 + 12⁄38 — 11⁄38;б) 23⁄192 — 8⁄192 + 48⁄192;
в) 19⁄56 + ( 21⁄56 — 12⁄56 ) — 16⁄56;
2.
Решите уравнения.
б) 18⁄23 — ( 7⁄23 + y ) = 5⁄23
3. Решите задачу.
Расстояние от дачи до пруда равно 3⁄5 км, а от дачи до леса равно 4⁄5 км. На сколько метров расстояние от дачи до пруда больше, чем расстояние от дачи до леса?4. Решите задачу.
Из погреба вытащили 3⁄12 части картофеля, а потом – ещё 2⁄12 части. После этого в погребе осталось 56 кг картофеля. Сколько картофеля было в погребе?Вариант III.
1. Решите примеры.
а) 19⁄28 + 12⁄28 — 16⁄28;б) 13⁄176 — 11⁄176 + 49⁄176;
в) 27⁄42 + ( 12⁄42 — 6⁄42 ) — 12⁄42;
2.
Решите уравнения.
б) 28⁄35 — ( y + 16⁄35 ) = 4⁄35
3. Решите задачу.
Расстояние от школы до больницы равно 8⁄9 км, а от школы до бассейна равно 4⁄9 км. На сколько метров расстояние от школы до больницы больше, чем расстояние от школы до бассейна?4. Решите задачу.
Из рулона отрезали 3⁄8 части ткани, а потом – ещё 2⁄8 части. После этого в рулоне осталось 32 метра ткани. Сколько метров ткани было в рулоне?Самостоятельная работа №13 на тему: «Сложение и вычитание смешанных чисел»
Вариант I.
1. Решите примеры.
а) 4 19⁄28 + 6 12⁄28;б) 5 13⁄176 — 2 11⁄176;
в) 12 27⁄43 + 3 12⁄43.
2. Решите уравнения.
б) 7 14⁄16 — y = 3 11⁄16;
в) y + 18 27⁄53 = 24 13⁄53;
3. Решите задачу.
В первый день в мастерской использовали 23 3⁄18 метра проволоки, а во второй день – ещё 18 2⁄18 части. После этого в рулоне осталось 32 метра проволоки. Сколько метров проволоки было в рулоне?Вариант II.
1. Решите примеры.
а) 3 13⁄22 + 3 12⁄22;б) 8 15⁄126 — 4 15⁄126;
в) 13 22⁄49 + 3 14⁄49.
2. Решите уравнения.
а) 2 18⁄43 + х = 3 4⁄43;б) 17 15⁄19 — y = 12 12⁄19;
в) y — 18 38⁄56 = 24 27⁄56.
3. Решите задачу.
В первый день в школе покрасили 17 5⁄23 метра коридора, а во второй день – ещё 23 4⁄23 метра. Сколько метров было покрашено за 2 дня?Вариант III.
1. Решите примеры.
а) 5 19⁄23 + 6 12⁄23;б) 7 13⁄48 — 3 11⁄48;
в) 82 25⁄78 + 34 12⁄78
2. Решите уравнения.
а) 6 17⁄29 + х = 23 4⁄29;б) 8 15⁄128 — y = 6 12⁄128;
в) y — 18 38⁄47 = 5 27⁄47.
3. Решите задачу.
Фермер убрал 13 6⁄13 метра грядки в первый день, а на следующий день – ещё 18 3⁄13 метра. После двух дней работы осталось убрать 6 метров. Какова длина грядки?Самостоятельная работа №14 на темы: «Десятичная запись дробных чисел».
«Сравнение десятичных дробей» Вариант I.
1. Заданные дроби представьте, как десятичные дроби.
а) 5 59⁄10б) 6 1⁄100
в) 17 137⁄1000
2. Сравните числа.
а) 5,596 и 5,629б) 7,34 и 7,339
в) 0,684 и 0,6840
3. Переведите из одной единицы измерения в другую.
а) представьте в тоннах: 92 ц; 887 кг; 14 т 12 кг;б) представьте в квадратных дециметрах: 8 м 2; 57 см 2; 8 м2 77 дм2.
4. Отметьте точки: 0,2; 0,8; 1,1; 2,3; 2,1; 3,7 на числовом отрезке, равном 5 единицам.
Вариант II.
1. Заданные дроби представьте, как десятичные дроби.
а) 18 59⁄1000б) 7⁄10
в) 7 137⁄100
2. Сравните числа.
а) 35,97 и 35,971б) 8,449 и 8,540
в) 0,92 и 0,920
3. Переведите из одной единицы измерения в другую.
а) представьте в тоннах: 3 ц; 239 кг; 23 т 28 кг;б) представьте в квадратных дециметрах: 13 м 2; 2 см 2; 87 м2 32 дм2.
4. Отметьте точки: 0,5; 0,7; 1,1; 2; 2,3; 3,5 на числовом отрезке, равном 6 единицам.
Вариант III.
1. Заданные дроби представьте, как десятичные дроби.
а) 15 43⁄100б) 9 23⁄1000
в) 5⁄10
2. Сравните числа.
а) 29,345 и 29,354б) 171,89 и 171,889
в) 0,93 и 0,930
3. Переведите из одной единицы измерения в другую.
а) представьте в тоннах: 18 ц; 56 кг; 3 т 9 кг;б) представьте в квадратных дециметрах: 4 м 2; 23 см 2; 2 м2 56 дм2.
4. Отметьте точки: 0,4; 0,5; 1,4; 1,9; 2,4; 3,0 на числовом отрезке, равном 4 единицам.
Самостоятельная работа №15 на темы: «Сложение и вычитание десятичных дробей». «Округление чисел»
Вариант I.
1. Решите примеры на сложение десятичных дробей.
а) 29,3 + 4,35 =б) 68,9 + 19,1 =
в) 0,68 + 6,4 =
2. Решите примеры на вычитание десятичных дробей.
а) 35,1 — 13,2 =б) 37 — 27,3 =
в) 13,28 — 5,327 =
3.
Решите задачу:
4. Округлите:
а) целую часть числа 2539,48190 до сотен, до десятков, до единиц;б) дробную часть числа 2539,48190 до тысячных, до сотен, до десятков.
Вариант II.
1. Решите примеры на сложение десятичных дробей.
а) 79,3 + 8,15 =б) 18 + 8,8 =
в) 0,93 + 23,4 =
2. Решите примеры на вычитание десятичных дробей.
а) 48,2 — 4,98 =б) 96 — 48,6 =
в) 37,67 — 13,168 =
3. Решите задачу.
В первом пакете было 15,7 кг песка, во втором – на 350 г больше, чем в первом. В третьем – на 1200 г меньше, чем в первом. Сколько кг песка в трех пакетах?4. Округлите:
а) целую часть числа 3462,9470 до сотен, до десятков, до единиц;б) дробную часть числа 3462,9470 до тысячных, до сотен, до десятков.
Вариант III.
1.
Решите примеры на сложение десятичных дробей.
б) 8 + 47,7 =
в) 0,123 + 23,942 =
2. Решите примеры на вычитание десятичных дробей.
а) 69,2 — 7,88 =б) 91,76 — 18,6 =
в) 8,94 — 5,452 =
3. Решите задачу.
3 дня бабушка пекла блины. В первый день она использовала 1,2 кг муки, во второй день – на 500 г меньше, чем в первый день, а на третий день – на 300 г больше, чем во второй день. Сколько муки она использовала за три дня?4. Округлите:
а) целую часть числа 4392,73910 до сотен, до десятков, до единиц;б) дробную часть числа 4392,73910 до тысячных, до сотен, до десятков.
Самостоятельная работа №16 на тему: «Умножение десятичных дробей на натуральные числа»
Вариант I.
1. Выполните умножение.
| а) 8,3 * 8 = | б) 7,12 * 34 = | в) 0,235 * 93 = | г) 1,93 * 100 = |
2. Найдите значение выражения: х + ( 3,74х — 1,474х ) при х=3; 100; 374; 1000.
3. Решите задачу.
4. Решите задачу.
Машина проехала 360 км за 6 часов. Какое расстояние она преодолеет, передвигаясь с той же скоростью, за 1⁄4 часа, за 2 1⁄3 часа?Вариант II.
1. Выполните умножение.
| а) 7,48 * 12 = | б) 3,57 * 7 = | в) 0,873 * 87 = | г) 1,698 * 1000 = |
2. Найдите значение выражения: 5х + ( 6,59х + 2,483х ) при х=5; 100; 324; 1000.
3. Решите задачу.
Одновременно в противоположных направлениях из города выехали 2 машины. Скорость первой машины составляет 54,7 км/ч, а скорость второй – 76,2 км/ч. Какое расстояние будет между ними через 3 часа?4. Решите задачу.
Велосипедист преодолел 72 км за 3 часа. Какое расстояние он преодолеет, перемещаясь с той же скоростью, за 5⁄6 часа, за 2 1⁄3 часа?Вариант III.
1. Выполните умножение.
| а) 9,4 * 6 = | б) 8,34 * 56 = | в) 0,517 * 62 = | г) 6,787 * 1000 = |
2. Найдите значение выражения: ( 8,45х — 3,594х ) — х при х=8; 100; 843; 1000.
3. Решите задачу.
Одновременно навстречу друг другу из двух городов выехали мотоциклы. Расстояние между городами составляет 234,8 км. Скорость первого мотоциклиста составляет 34,5 км/ч, а скорость второго – 56,2 км/ч. Какое расстояние будет между ними через 2 часа?4. Решите задачу.
Моторная лодка прошла 24 км за 2 часа. Какое расстояние она пройдет, перемещаясь с той же скоростью, за 1⁄4 часа, за 3 1⁄3 часа?Самостоятельная работа №17 на тему: «Деление десятичных дробей на натуральные числа»
Вариант I.
1. Выполните деление.
| а) 2,729 : 6 = | б) 283,85 : 4 = | в) 4 : 13 = | г) 0,095 : 10 = |
2. Решите уравнения.
| а) 5X — 0,4 = 23,6 | б) 48,2 : Y = 10,4 |
3. Решите задачу.
За два дня рабочие отремонтировали 3,6 км дороги. В первый день они отремонтировали 1/4 части дороги. Сколько км дороги они отремонтировали во второй день?4. Решите задачу.
4 класс и 5 класс собирали макулатуру. Пятиклассники собрали в 2 раза больше макулатуры, чем ребята из 4 класса. Вместе они собрали 239,7 кг. Сколько кг собрали ребята из 5 класса и сколько ребята из 4 класса?Вариант II.
1. Выполните деление.
| а) 5,837 : 7 = | б) 291,49 : 5 = | в) 5 : 18 = | г) 0,023 : 10 = |
2. Решите уравнения.
| а) 8X + 2,8 = 18,6 | б) 28,1 : Y = 12,4 |
3. Решите задачу.
За два дня бригада собрала 147,6 кг ягод. В первый день они собрали 4/9 части урожая ягод. Сколько кг ягод они собрали во второй день?4. Решите задачу.
Две бригады собирали картофель.
Первая бригада собрала в 3 раза больше картофеля, чем вторая. Обе бригады вместе собрали 49,6 ц урожая. Сколько центнеров картофеля собрали первая бригада и сколько вторая бригада?Вариант III.
1. Выполните деление.
| а) 4,752 : 9 = | б) 472,49 : 6 = | в) 7 : 19 = | г) 0,044 : 10 = |
2. Решите уравнения.
| а) 5X + 2,5 = 24 | б) 14,2 : Y = 3,4 |
3. Решите задачу.
За 2 дня мотоциклист преодолел 394,1 км. В первый день он проехал 4⁄7 части пути. Сколько км он проехал во второй день?4. Решите задачу.
Мама собрала в 5 раз больше ягод, чем дочка. Вместе они собрали 34,5 кг ягод. Сколько ягод собрала мама и сколько дочка?Самостоятельная работа №18 на тему: «Среднее арифметическое»
Вариант I.
1. Найдите среднее арифметическое четырех чисел: 4,5; 5,6; 4,9; 5,1.
2. Решите задачу.
В течение часа машина двигалась со скоростью 67,5 км/ч, в течение второго часа – со скоростью 51,6 км/ч.
В течение третьего часа её скорость составила 72,3 км/ч. Какова средняя скорость машины? Сколько км она преодолела за 3 часа?3. Решите задачу.
Среднее арифметическое трех чисел составляет 14,5. Первое число – 14,1, а второе число на 0,8 больше третьего числа. Назовите эти числа.4. Решите задачу.
Расстояние между двумя деревнями равно 340 км. Автомобиль преодолел половину пути со скоростью 58 км/ч, а вторую половину – со скоростью 49 км/ч. Какова средняя скорость автомобиля на протяжении всего пути?Вариант II.
1. Найдите среднее арифметическое четырех чисел: 12,3; 12,9; 11,6; 13,1.
2. Решите задачу.
В течение первого часа спортсмен шел со скоростью 11,2 км/ч, в течение второго часа – со скоростью 10,7 км/ч, а в течение третьего часа его скорость составила 9,8 км/ч. Какова средняя скорость спортсмена? Какое расстояние он прошел за 3 часа?3. Решите задачу.
Среднее арифметическое трех чисел составляет 28,5. Первое число – 28,2, а второе на 0,9 больше третьего числа.
Назовите эти числа.4. Решите задачу.
Расстояние между двумя городами составляет 52 км. Первую половину пути велосипедист передвигался со скоростью 18 км/ч, а вторую половину – со скоростью 22 км/час. Какова средняя скорость велосипедиста на всем протяжении пути?Вариант III.
1. Найдите среднее арифметическое четырех чисел: 9,1; 9,9; 11,1; 10,7.
2. Решите задачу.
В течение первого часа лодка двигалась со скоростью 15,5 км/ч, во второй час движения её скорость составила 17,4 км/ч, а в течение третьего часа – 12,7 км/ч. Какая средняя скорость лодки? Сколько км она преодолела за 3 часа?3. Решите задачу.
Среднее арифметическое трех чисел составляет 13,2. Первое число – 13,9, а второе – на 0,7 больше третьего числа. Назовите эти числа.4. Решите задачу.
Расстояние между двумя деревнями составляет 24 км. Первую половину пути пешеход двигался со скоростью 8 км/ч, а вторую половину – со скоростью 9 км/ч. Какова средняя скорость пешехода на всем протяжении пути?Самостоятельная работа №19 на тему: «Проценты, задачи на проценты»
Вариант I.
1. Решите задачу.
В спортивной секции занимается 60 учеников, из них 70% составляют девочки. Сколько мальчиков занимается в спортивной секции?2. Решите задачу.
Ребята четвертых и пятых классов собирали макулатуру. Ребята пятого класса собрали 150 кг макулатуры, что составило 60% общего веса собранной макулатуры. Сколько кг макулатуры собрали ребята?3. Решите задачу.
Из 15 кг яблок получается 12 кг яблочного пюре. Каков процент выхода пюре из яблок?Вариант II.
1. Решите задачу.
В 5 классе числится 30 учеников, 60% из них – мальчики. Сколько девочек учится в 5 классе?2. Решите задачу.
2 бригады собирали помидоры. Первая бригада собрала 320 кг помидор, что составило 40% от общего урожая. Сколько всего помидор собрали обе бригады?3. Решите задачу.
Из 60 семян взошли 55 растений. Найдите процент всхожести семян.Вариант III.
1. Решите задачу.
В школе работает 40 человека. Из них 80% – женщины. Сколько мужчин работает в школе?2.
Решите задачу.
3. Решите задачу.
При перемалывании 40 кг зерна получили 25 кг муки. Найдите процент выхода муки.Урок 14. деление нацело — Математика — 5 класс
Математика
5 класс
Урок № 14
Деление нацело
Перечень вопросов, рассматриваемых в теме:
— деление натуральных чисел;
— свойства деления натуральных чисел.
Тезаурус
Деление – это математическое действие, обратное умножению.
Делимое – это число, которое делят.
Делитель – это число, на которое делят.
Частное – результат деления.
Делить на нуль нельзя.
Любое натуральное число а делится на 1 и само на себя:
а : 1 = а, а : а = 1
Важное свойство частного: делимое и делитель можно одновременно умножить или разделить на одно и то же натуральное число: частное от этого не изменится.
Обязательная литература
- Никольский С. М. Математика: 5 класс. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2017. – 272 с.
- Потапов М. К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.
Дополнительная литература
- Бурмистрова Т. А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
- Потапов М. К. Математика: дидактические материалы. 6 класс. // М. К. Потапов, А. В. Шевкин – М.: Просвещение, 2010.- 118 с.
- Чесноков А. С. Дидактические материалы по математике 5 класс. // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.
Теоретический материал для самостоятельного изучения
Давайте вспомним, что нам уже известно об операции деления. Пусть у нас есть натуральные числа a и b, причём а больше b или равно b (a ≥ b). Говорят, что а делится на b нацело, если существует натуральное число с, при умножении которого на b получается а: a = b ∙ c.
Обычно слово «нацело» в этой фразе опускается. При этом записывают: a : b = с и называют а – делимым, b – делителем, с – частным.
Любое натуральное число а делится на 1 и само на себя:
а : 1 = а, а : а = 1
так как а ∙ 1 = а, 1 ∙ а = а.
Например, 14 делится на 1 и на 14.
14 : 1 = 14, 14 : 14 = 1
При делении ноля на любое натуральное число получается ноль: 0 : а = 0, потому что 0 ∙ а = 0.
Запомните: делить на нуль нельзя!
Любое натуральное число а делить на нуль нельзя, потому что не существует такого числа с, для которого выполнялось бы равенство а : 0 = с (так как с ∙ 0 = 0 ≠ а). Принято считать, что нуль на нуль делить нельзя.
Для деления чисел из двух и более цифр (знаков) применяют деление уголком.
Вспомним, как делить уголком, на примере.
Вычислим 392 : 28 = ?
Для начала запишем делимое и делитель уголком:
Начнём делить 392 на 28 следующим образом.
Во-первых, определим неполное частное. Для этого слева направо сравниваем цифры делимого и делителя.
Рассмотрим цифру 3. Она меньше 28 – значит, нужно взять ещё одну цифру из делимого. 39 больше 28, следовательно, это неполное частное.
Ставим точку в частном (под уголком делителя).
Посчитаем, сколько цифр осталось в делимом, после неполного частного. У нас после 39 стоит только одна цифра – 2. Значит, и в результат добавляем ещё одну точку.
Приступаем к делению: 28 помещается в 39 только один раз, поэтому ставим первой цифрой ответа единицу и вычитаем 28 из 39.
После вычитания в остатке получилось 11, это меньше, чем 28, поэтому к 11 дописываем 2.
112 делится на 28. Получаем 4. Записываем полученный результат второй цифрой в ответе.
В остатке получился нуль – значит, числа разделились нацело. Таким образом, 392 : 28 = 14.
Важное свойство частного: делимое и делитель можно одновременно умножить или разделить на одно и то же натуральное число: частное от этого не изменится.
Вычислим 50 : 25 = ?
Сначала одновременно умножим 50 и 25 на 2. Получим:
100 : 50 = 2.
Теперь разделим 50 и 25 на 5. Получим:
10 : 5 = 2.
В обоих случаях ответ оказался одинаковым. Значит, свойство частного верно.
Если каждое из натуральных чисел a и b делится на натуральное число с, то верно равенство:
(a+ b) : c = a : c + b : c.
Убедимся в правдивости данного свойства на примере.
Вычислим выражение: 124 : 4 + 36 : 4.
Рассмотрим два способа решения.
1 способ. Выполним деление и сложим результаты.
124 : 4 + 36 : 4 = 31 + 9 = 40.
2 способ. Заметим, что у нас есть общий делитель – 4. Вынесем его за скобки. Получим:
(124 + 36) : 4 = 160 : 4 = 40.
В обоих случаях у нас получился один и тот же ответ. Значит, свойство верно.
Разбор решения заданий тренировочного модуля
№ 1. Вычислите 812 : 14 = _____.
Решение: выполним деление уголком.
Ответ: 58.
№ 2. Найдите неизвестный множитель х из равенства: 15 ∙ х = 195.
Выберите верный ответ: х = 3; х = 13; х = 25; х = 15.
Решение: чтобы найти неизвестный множитель, надо произведение поделить на известный множитель, то есть:
15 ∙ х = 195
х = 195 : 15
Выполнив деление уголком, получим:
Ответ: х = 13.
Урок 17. деление с остатком — Математика — 5 класс
Математика
5 класс
Урок № 17
Деление с остатком
Перечень вопросов, рассматриваемых в теме:
— деление с остатком;
— неполное частное;
— остаток.
Тезаурус
Деление с остатком – это деление одного натурального числа на другое, при котором остаток меньше делителя.
Обязательная литература
- Никольский С. М. Математика: 5 класс. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2017. – 272 с.
- Потапов М.
К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.
К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.Дополнительная литература
- Бурмистрова Т. А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
- Потапов М. К. Математика: дидактические материалы. 6 класс. // М. К. Потапов, А. В. Шевкин – М.: Просвещение, 2010.- 118 с.
- Чесноков А. С. Дидактические материалы по математике 5 класс. // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.
Теоретический материал для самостоятельного изучения
Не всегда можно полностью разделить одно число на другое. В примерах на деление может оставаться остаток. Такое деление называется деление с остатком.
Рассмотрим пример. Разделим 16 на 5.
Запишем этот пример в столбик:
Получилось, что 5 помещается в 16 три раза, но остаётся 1 – это остаток.
Читается данное выражение следующим образом: «16 разделить на 5 получится 3, и остаток – 1».
Деление с остатком – это деление одного натурального числа на другое, при котором остаток меньше делителя.
Если при делении натуральных чисел остаток равен нулю, то договорились считать, что делимое делится на делитель без остатка, или делится нацело.
Запишем деление с остатком в общем виде.
Порядок решения выражений на деление с остатком:
1. находим наибольшее число до а, которое делится на b без остатка – это c;
2. вычитаем из делимого найденное число c.
a – c = r
Сравниваем остаток с делителем. Остаток всегда меньше делителя: r < b.
Если получилось, что остаток больше делителя – значит, наибольшее число, которое делится на делитель без остатка, найдено неверно.
При решении более сложных примеров не всегда можно легко найти наибольшее число из пункта 1. Иногда для этого необходимо произвести дополнительные расчёты в столбик.
Рассмотрим ещё один пример.
297 : 25 = ?
Запишем это выражение в столбик:
Получили остаток 22, он меньше, чем 25, значит:
297 : 25 = 11 ост (22)
Как проверить деление с остатком:
- умножить неполное частное на делитель;
- прибавить к полученному результату остаток;
- сравнить полученный результат с делимым.
Проверим ответ предыдущего примера.
297 : 25 = 11 ост (22)
25 · 11 = 275
275 + 22 = 297
Деление с остатком выполнено верно.
Разбор решения заданий модуля
№ 1. Вычислите выражение 312 : 15 = _____ ост (____)
Решение: выполним деление уголком:
Сравним неполное частное с делителем: 12 < 15.
Теперь проверим, верно ли мы нашли неполное частное и остаток:
20 ∙ 15 + 12 = 300 + 12 = 312
Ответ: 312 : 15 = 20 ост (12)
№ 2. Найдите неизвестное делимое в выражении:
х : 17= 18 (остаток 4)
Выберите верный ответ: х = 310; х = 120; х = 250; х = 110.
Решение: чтобы найти неизвестное делимое, надо неполное частное умножить на делитель и прибавить остаток.
х = 18 ∙ 17 + 4
х = 306 + 4
х = 310
Ответ: х = 310.
Свойства умножения и деления. Распределительное и переместительное свойство
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Свойства умножения
Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.
Узнаем, какие бывают свойства умножения и как их применять.
Переместительное свойство умножения
От перестановки мест множителей произведение не меняется. |
То есть, для любых чисел a и b верно равенство: a * b = b * a.
Это свойство можно применять к произведениям, в которых больше двух множителей.
Примеры:
- 6 * 5 = 5 * 6 = 30;
- 4 * 2 * 3 = 3 * 2 * 4 = 24.
Сочетательное свойство умножения
Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением. |
То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).
Пример:
- 3 * 2 * 5 = 3 * (2 * 5) = 3 * 10 = 30
- 3 * 2 * 5 = (3 * 2) * 5 = 6 * 5 = 30.
или
Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.
Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.
Распределительное свойство умножения относительно сложения
Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты. |
То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.
Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.
В обратную сторону распределительное свойство умножения относительно сложения звучит так:
Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить. |
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе. |
То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.
В обратную сторону распределительное свойство умножения относительно вычитания звучит так:
Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе. |
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю. |
То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.
Свойство единицы при умножении
Если умножить любое целое число на единицу, то в результате получится это же число. |
То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.
Свойства деления
Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.
Основные свойства деления целых чисел
|
И еще одно важное свойство деления, которое проходят в 5 классе:
Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится. |
В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.
Применим свойства деления на практике.
Пример 1
Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?
Как решаем:
Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.
Ответ: 2 кг
Пример 2
Вычислить: 500 * (100 : 5).
Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.
Ответ: 500 * (100 : 5) = 10000.
Пример 3
Упростить выражение: 27a – 16a.
Как решаем: 27a – 16a = a * 27 – a * 16 = a * (27 — 16) = a * 11 = 11a.
Ответ: 11a.
Свойства умножения и деления помогают упрощать выражения.
То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.
«Деление с остатком » (5-й класс)
Класс: 5, математика
Тема: Деление с остатком.
Тип урока: Урок изучения нового материала.
Цели
Предметные: сформировать навыки выполнения деления с остатком, разъяснить связь между компонентами действия деления с остатком.
Личностные: развивать интерес к изучению темы и желание применить приобретённые знания и умения.
Метапредметные: формировать умение видеть математическую задачу в контексте проблемной ситуации, в окружающей жизни.
Планируемые результаты: Учащийся получит навык выполнения деления с остатком, получит представление о связи между компонентами действия деления с остатком.
Основные понятия: Остаток, неполное частное, делитель, делимое, правило нахождения делимого, деление нацело.
Ход урока
I.
Организационный момент
II. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
— Решив примеры и заполнив таблицу, вы сумеете узнать тему урока.
На доске:
| |||||||||||||||||||||||||||||||||
|
— Прочитайте тему урока.
— Открыли тетради, записали число, тему урока.
III. Работа по теме урока
Решим устно.
1. Прочитайте выражения:
30 : 5
103 : 10
34 : 5
60 : 7
47 : 6
131 : 11
42 : 6
— На какие две группы их можно разделить? Выпишите и решите те, в которых деление с остатком.
2. Проверим.
Без остатка: | С остатком: | |
30 : 5 |
| 103 : 10 = 10 (ост 3) |
— Расскажите, как выполняли деление с остатком?
— Не всегда одно натуральное число делится на другое число. Но всегда можно выполнить деление с остатком.
— Что, значит, разделить с остатком? Чтобы ответить на этот вопрос, решим задачу.
В гости к бабушке пришли 4 внука. Бабушка решила угостить внуков конфетами. В вазочке было 23 конфеты. Сколько конфет достанется каждому внуку, если бабушка предложит поделить конфеты поровну?
— Давайте рассуждать.
— Сколько конфет у бабушки? (23)
— Сколько внуков пришло в гости к бабушке? (4)
— Что необходимо сделать по условию задачи? (Конфеты нужно разделить поровну, надо разделить 23 на 4; 23 делится на 4 с остатком; в частном получится 5, а в остатке 3.)
— Сколько же конфет достанется каждому внуку? (Каждому внуку достанется по 5 конфет, и в вазочке останется 3 конфеты.)
— Запишем решение.
Решение:
23 : 4=5 (ост 3)
— Как называется число, которое делят? (Делимым.)
— Что такое делитель? (Число, на которое делят.)
— Как называют результат деления с остатком? (Неполное частное.)
— Назовите делимое, делитель, неполное частное и остаток в нашем решении (23 — делимое, 4 — делитель, 5 — неполное частное, 3 – остаток.
)
— Ребята, подумайте и запишите, как найти делимое 23, зная делитель, неполное частное и остаток?
— Проверим.
— Ребята, давайте сформулируем правило, как найти делимое, если известны делитель, неполное частное и остаток.
— Правило.
Делимое равно произведению делителя и неполного частного, сложенному с остатком.
а = вс + d, а — делимое, в — делитель, с — неполное частное, d — остаток.
— Когда выполняется деление с остатком, что мы должны помнить?
— Правильно, остаток всегда меньше делителя.
— А если остаток равен нулю, делимое делится на делитель без остатка, нацело.
IV. Закрепление изученного материала
— Найдите делимое, если:
А) неполное частное равно 7, остаток равен 3, а делитель 6.
Б) неполное частное равно 11, остаток равен 1, а делитель 9.
В) неполное частное равно 20, остаток равен 13, а делитель 15.
V. Работа с учебником
1. Работа над задачей.
2. Оформление решения задачи.
№ 516 (Задачу решает у доски ученик.)
20 х 10 : 18 = 11 (ост 2)
Ответ: 11 деталей по 18 кг можно отлить из 10 болванок, 2 кг чугуна останется.
№ 519 (Рабочая тетрадь, с. 52 №1.)
Первое задание выполняет ученик у доски. Второе и третье — ученики выполняют самостоятельно с самопроверкой.
Устно решаем задачи.
VI. Итог урока
— В вашем классе 17 учеников. Вас построили в шеренги. Получилось несколько шеренг из 5 учеников и одна неполная шеренга. Сколько получилось полных шеренг и сколько человек в неполной шеренге?
— Ваш класс на уроке физкультуры снова построили в шеренги. На этот раз получилось 4 одинаковых полных шеренг и одна неполная? Сколько человек в каждой шеренге? А в неполной?
Отвечаем на вопросы:
— Может ли остаток быть больше делителя? Может ли остаток быть равен делителю?
— Как найти делимое по неполному частному, делителю и остатку?
— Какие могут быть остатки при делении на 5? Приведите примеры.
— Как проверить, верно ли выполнено деление с остатком?
— Оксана задумала число. Если это число увеличить в 7 раз и к произведению прибавить 17, то получится 108. Какое число задумала Оксана?
VII. Домашнее задание
Пункт 13, № 537, 538, рабочая тетрадь, с. 42, №4.
Список литературы
1. Математика : Учеб. для 5 кл. общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 9-е изд., стереотип. – М. : Мнемозина, 2017. – 384 с.: ил.
2. Математика. 5 класс. Рабочая тетрадь №1. натуральные числа / В.Н. Рудницкая. – 7-е изд. – М. : Мнемозина, 2017. – 87 с.: ил.
3. Чесноков А.С., Нешков К.И. Дидактические материалы по математике для 5 класса. – М. : Классикс Стиль, 2017. – 144 с.: ил.
😃 Деление — правила, секретные примеры, упражнения, игры
Деление – одна из четырех основных математических операций (сложение, вычитание, умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни.
Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение. 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть.
число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение. В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1. Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2. На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3.
Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4. Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг. Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг. Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг. Ставим точку под делителем.
5 шаг. После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг. Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг. Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг*. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3)(4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296.
Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления.
Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Презентация на тему «Деление»
Примеры на деление
Легкий уровень
28:4=
16:8=
27:3=
32:8=
64:8=
54:6=
42:6=
49:7=
40:8=
Средний уровень
225:15=
512:8=
144:9=
312:6=
315:7=
625:25=
392:4=
984:8=
Сложный уровень
5712:68=
1035:23=
1121:59=
2352:49=
1610:35=
6300:75=
875:35=
297000:270=
385000:11=
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным.
На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре.
Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание.
Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Играть сейчас
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту.
В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.
После прохождения курса ребенок сможет:
- В 2-5 раз лучше запоминать тексты, лица, цифры, слова
- Научится запоминать на более длительный срок
- Увеличится скорость воспоминания нужной информации
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня.
Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Как улучшить память и развить внимание
Бесплатное практическое занятие от advance.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером.
80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Деление с остатком | Математика
Если одно натуральное число не делится на другое нацело, можно выполнить деление с остатком.
Как и при делении нацело, числа, которые делим, называются делимое и делитель.
Результат деления называется неполным частным.
Число, которое остаётся от делимого в результате деления (это число меньше делителя), называется остаток.
Чтобы выполнить проверку, надо:
- Неполное частное умножить на делитель.
- К полученному произведению прибавить остаток.
- В результате должно получиться делимое.
Рассмотрим конкретные примеры деления с остатком.
Примеры.
Выполнить деление чисел с остатком и сделать проверку:
1) 29 : 8;
2) 613 : 6;
3) 279 : 10;
4) 784 : 23;
5) 4057 : 35;
6) 8591 : 62;
7) 52779 : 2524;
8) 15 : 79.
Решение: 1)
29 : 8 = 3 (остаток 5).
Проверка:
3 · 8 + 5 = 24 + 5 = 29.
2)
513 : 6 = 85 (остаток 3).
513 — делимое, 6 — делитель, 85 — неполное частное, 3 — остаток.
Проверка:
85 · 6 + 3 = 510 + 3 = 513.
3)
279 : 10 = 27 (остаток 9).
279 — делимое, 10 — делитель, 27 — неполное частное, 9 — остаток.
Проверка:
27 · 10 + 9 = 270 + 9 = 279.
4)
784 : 23 = 34 (остаток 2).
784 — делимое, 23 — делитель, 34 — неполное частное, 2 — остаток.
Проверка:
34 · 23 + 2 = 782 + 2 = 784.
5)
4057 : 35 = 115 (остаток 32).
4057 — делимое, 35 — делитель, 115 — неполное частное, 32 — остаток.
Проверка:
115 · 35 + 32 = 4025 + 32 = 4057.
6)
8591 : 62 = 138 (остаток 35).
8591 — делимое, 62 — делитель, 138 — неполное частное, 35 — остаток.
Проверка:
138 · 62 + 35 = 8556 + 35 = 8591.
7)
52779 : 2524 = 20 (остаток 2299).
52779 — делимое, 2524 — делитель, 20 — неполное частное, 35 — 2299.
Проверка:
20 · 2524 + 2299 = 50480 + 2299= 52779.
8) 15 : 79 = 0 (остаток 15).
15 — делимое, 79 — делитель, 0 — неполное частное, 15 — остаток.
( Если делимое меньше делителя, неполное частное всегда равно нулю, а остаток — делимому).
Отдел
Дивизия делится на равные части или группы.
Это результат «честного обмена».
Пример: есть 12 шоколадок, и 3 друга хотят их разделить, как они поделят шоколадки?
12 конфет
12 шоколадок разделить на 3
Ответ: 12 разделить на 3 равно 4. Каждый из них получает по 4.
Символы
÷ /
Мы используем символ ÷ или иногда символ / для обозначения деления:
Давайте использовать оба символа, чтобы привыкнуть к ним.
Другие примеры
Вот еще несколько примеров:
изображения/разделить-simple.js
Противоположное умножению
Деление — это , противоположное умножению . Когда мы знаем факт умножения, мы можем найти факт деления:
Пример: 3 × 5 = 15, поэтому 15/5 = 3.
Также 15/3 = 5.
Почему? Ну, подумайте о числах в строках и столбцах, как на этой иллюстрации:
.| Умножение… | … Подразделение | |
|---|---|---|
| 3 группы по 5 составляют 15… | …значит 15 разделить на 3 будет 5 | |
а также: | ||
| 5 групп по 3 штуки составляют 15… | …так что 15 разделить на 5 будет 3. | |
Итак, имеется четыре связанных факта :
- 3 × 5 = 15
- 5 × 3 = 15
- 15/3 = 5
- 15/5 = 3
Знание таблицы умножения может помочь вам в делении!
Пример: Сколько будет 28 ÷ 7?
Просматривая таблицу умножения, мы обнаруживаем, что 28 равно 4 × 7, поэтому 28 разделить на 7 должно быть 4.
Ответ: 28 ÷ 7 = 4
Имена
Для каждого номера в подразделении есть специальные имена:
делимое ÷ делитель = частное
Пример: через 12 ÷ 3 = 4:
- 12 это делимое
- 3 это делитель
- 4 есть частное
Но иногда это не работает идеально!
Иногда мы не можем точно разделить вещи… может что-то осталось.
Пример: Есть 7 костей, которыми можно поделиться с 2 щенками. Но 7 нельзя разделить точно на 2 группы,
, поэтому каждый щенок получает 3 кости,
, но останется 1 :
Мы называем это Остаток .
Подробнее об этом читайте в Разделе и остатках
Упражнения
Попробуйте эти рабочие листы деления.
1629, 1630, 1631, 1632, 1633, 1634, 3427, 3428, 3429, 3430
Математика 5-го класса — Раздел 2: Умножение и деление целых чисел
Обзор блока
В Разделе 2 учащиеся будут опираться на свою работу по многозначному умножению и делению из 4 класса, а также свое понимание структуры системы счисления с основанием в Разделе 1, чтобы развить беглость с многозначным умножением и расширить многозначный -разрядное деление, чтобы включить двузначные делители.
В 4-м классе учащиеся научились свободно складывать и вычитать многозначные числа (4.NBT.4), что является необходимым навыком для вычисления сумм и разностей в стандартном алгоритме умножения и деления соответственно. Учащиеся также умножали целое число до четырех цифр на однозначное целое число, а также два двузначных числа (4.НБТ.5). К концу 4 класса учащиеся могут вычислять эти продукты с помощью алгоритмов, но «неоднократно рассуждают о связи между математическими рисунками и письменными вычислениями, помогая им увидеть алгоритмы умножения и деления как аббревиатуры или резюме своих рассуждений о количества» (Прогрессии для CCSSM, «Число и операция в десятичной системе счисления, K-5», стр.14). Учащиеся также находят целые числа в частных и остатках с делимыми до четырех цифр и делителями с одной цифрой (4.NBT.6). Подобно умножению, к концу 4 класса учащиеся могут вычислять эти частные, используя алгоритмы наряду с другими стратегиями и представлениями, чтобы алгоритмы были осмысленными, а не заученными.
Модуль 2 5-го класса начинается с написания, оценки и интерпретации простых числовых выражений (5.OA.1, 5.OA.2). Это служит как для просмотра основных фактов умножения и деления, которые поддерживают основной контент позже в модуле, так и для записи вычислений, которые будут становиться все более сложными по мере продвижения модуля.Затем учащиеся закрепляют стандартный алгоритм умножения с вычислительными случаями из 4-го класса, прежде чем расширять его использование на все более и более крупные множители (5.NBT.5). Затем учащиеся следуют аналогичной последовательности с делением, сначала вычисляя частные случаи из 4-го класса, используя различные стратегии, а затем распространяя эти методы на вычисления, включающие двузначные делители. Обратите внимание, однако, что, в отличие от умножения, свободное владение стандартным алгоритмом деления не ожидается до 6 класса (6.НС.2). На протяжении всего модуля учащиеся «учатся использовать [] структуру [десятичных чисел] и свойства операций, чтобы свести вычисление многозначного… произведения или частного к набору однозначных вычислений в различных десятичных единицах.
” (MP.7) (Прогрессии для CCSSM, «Число и операция в базе десяти, K-5», стр. 4). Далее, «повторное рассуждение (MP.8), основанное на единообразии десятичной системы система является частью этого процесса» (Progressions for CCSSM, «Number and Operation in Base Ten, K-5», p.4).
Позже в этом году учащиеся будут опираться на свои знания в области вычислений с целыми числами, чтобы выполнять их с десятичными дробями (5.NBT.7). Они также будут писать, оценивать и интерпретировать выражения с дробями и десятичными знаками в модулях 5 и 6 (5.OA.1, 5.OA.2). Эта работа «в 5 классе предвосхищает их более позднюю работу с переменными выражениями» (6–8.EE) (OA Progression, стр. 32). Кроме того, учащиеся закрепляют беглость алгоритма деления и расширяют беглость всех четырех операций до десятичных дробей (6.EE.2—3). Они также распространяют эти вычисления на еще неизвестные части нашей системы счисления, такие как отрицательные числа (7.NS). Таким образом, к концу этого раздела учащиеся будут просто стесняться бегло выполнять все четыре операции с целыми числами и будут готовы выполнять эти операции с другими типами чисел.
Они также будут готовы думать не только о вычислении числовых выражений, но и об их понимании и интерпретации, намекая на новый мир математики — алгебру.
Темп: 23 учебных дня (20 уроков, 2 гибких дня, 1 день оценки)
Для получения рекомендаций по корректировке темпа на 2021–2022 учебный год см. Рекомендуемые корректировки объема и последовательности для 5-го класса.
Как выполнить длинное деление за 6 шагов [с иллюстрациями]
Вы провели свой класс через большинство больших единиц: сложение, деление, вычитание, умножение. Но вот еще одна хитрость:
Как сделать деление в большую сторону.
Исследование 2012 года, опубликованное в журнале Psychological Science, показало, что понимание пятиклассниками дробей и деления может быть напрямую связано с тем, насколько хорошо они понимают алгебру в старшей школе и успевают ли они на уроках математики более высокого уровня — даже после учета различных социально-экономических факторы.
Никакого давления, верно? Если при мысли об обучении делению на длинные лады у вас холодный пот и липкие ладони, не беспокойтесь — мы сделали всю работу за вас.
1. Повторить
Первый шаг, который вы должны сделать, это шаг назад.
Для ученика 4-го класса деление в большую сторону представляет собой сложную смесь различных операций. Чтобы успешно научиться выполнять деление в большую сторону, им необходимо повторить эти фундаментальные понятия.
Согласно французскому исследованию, «представление и извлечение математических фактов из долговременной памяти» является одним из наиболее важных факторов, определяющих будущие математические успехи учащихся.Согласно тому же исследованию, длинное деление — это «синтез всех арифметических знаний».
Убедитесь, что ваши ученики понимают, что умножение — это результат многократного сложения, а деление — это просто противоположное — многократное вычитание.
Используйте блоки с основанием 10 или деньги, чтобы усилить значение места и чувство числа. Запланируйте занятия, в которых учащимся будет предложено создать «семейство фактов», чтобы убедиться, что учащиеся понимают, как взаимодействуют различные функции.
Используйте игры на умножение и другие математические игры, чтобы заинтересовать учащихся в учебе и развить уверенность в математике, прежде чем продолжить.
2. Начните с простогоДавайте начнем с урока словарного запаса. Уравнение деления на деление состоит из множества частей. Убедитесь, что ваши ученики знают, что они имеют в виду и как их идентифицировать.
Дивиденд — это число в правой части уравнения под чертой. Он представляет собой сумму, которую нужно разделить.
Делитель — это число слева — оно выполняет деление.
Частное — это число сверху.Он представляет собой ответ или количество единиц в каждом разряде после завершения уравнения.
Остаток — это число вверху справа. Он представляет оставшиеся единицы, которые не могут быть равномерно разделены на частное. Во-первых, введите уравнение, которое не имеет остатков, чтобы учащиеся могли привыкнуть к формату и начать понимать новый словарный запас, который они только что изучили:
Спросите учащихся, сколько раз 2 умещается в 4. Это может показаться им сложной концепцией, поэтому используйте идею обмена: если вы хотите разделить 4 предмета между двумя людьми, сколько предметов получит каждый?
Как только они дадут правильный ответ, поставьте 2 над 4.Затем повторите шаг со второй цифрой делимого.
Используйте эти простые уравнения, чтобы усилить позиционное значение. Объясните учащимся, что, когда они спрашивают, сколько раз 2 может превратиться в 4, на самом деле они спрашивают, сколько раз 2 превращается в 40. они удобны с основным форматом. Тогда пришло время двигаться дальше.
Вместо того, чтобы сразу перейти к уравнению с остатками, начните с другого предметного урока .
Разделите учащихся на группы по три, четыре или шесть человек и дайте каждой группе по 50 ватных шариков (или мармеладок, или помпонов, или зефира — любой маленький предмет, доступный в вашем классе).
Попросите учащихся разделить предметы так, чтобы у каждого члена группы было одинаковое количество предметов, а затем наблюдайте и ждите.
В конце концов, они поймут, что не могут разделить его поровну, и всегда будут оставаться какие-то предметы. Вот где вы приходите, чтобы спасти положение и объяснить, как выполнить деление в длинное с остатками .
Сначала покажите учащимся задачу с остатком в единицах:
Теперь начните со столбца десятков и проработайте задачу: 5 входит в 5 ровно один раз, так что там ничего не осталось. Но сколько раз 5 входит в 7, и что вы делаете с остатками?
Показать студенты Новые шаги:
- 0 Divide
- 0 Divide Тема колонны Дивизор Divisor
- Умножьте 1 Диалинт от фактора в правильном месте Колонна
- Вычтите 1 Продукт из колонны
Число, которое они оставили, является остатком.
Обязательно смоделируйте несколько задач всем классом, чтобы учащиеся могли начать понимать этапы и то, как правильно записывать свои ответы.
Это хорошее время на уроке, чтобы научить учащихся проверять свои ответы. Пусть они умножат делитель на частное и прибавят остаток — ответ должен быть таким же, как и делимое, с которого они начали.
4. Остаток в десяткахТеперь пришло время учащимся решить задачи, в которых делитель не помещается точно в столбец десятков или единиц.Шаги более или менее такие же, за исключением одного нового дополнения:
- Разделить делимое в столбце десятков на делитель
- Умножить делитель на частное в столбце десятков
- Вычесть произведение из делителя
- Сократите делимое в столбце единиц и повторите .
Для простоты начните с однозначных делителей и двузначных дивидендов. Помните, что это совершенно новая концепция для учащихся, поэтому найдите время, чтобы смоделировать задачи на доске.
Обсудите, почему эти шаги работают, и помогите им понять, какую важную роль в этом процессе играет значение места.
Вот и все. Либо это?
Дайте учащимся освоиться с формулой и поработать над более мелкими задачами. Когда они обретут уверенность и начнут понимать, как выполнять деление в большую сторону, начните предлагать им задачи с трехзначным делимым, а затем задачи с двузначным делителем.
Напомните учащимся, что шаги остаются одинаковыми, независимо от того, насколько велика задача , и предложите им использовать лист бумаги, чтобы «угадать и проверить» свое умножение по ходу дела. Это хороший момент, чтобы убедиться, что у них нет проблем и что они полностью понимают взаимосвязь деления с разрядным значением и умножением.
Чтобы освежить свои знания, посмотрите это видео от Khan Academy:
6. Как выполнять деление в длинное с десятичными дробями Если вы рассмотрели весь свой контент на первых пяти шагах, поздравляем! Предложите учащимся продолжать практиковаться в делении больших и малых чисел в длину и укреплять взаимосвязь между делением и другими математическими понятиями, которые они изучают.
Но процесс еще не завершен — учащиеся должны понять, как выполнять деление в длинное с десятичными дробями. Для начала вернемся к одному из фундаментальных понятий деления: разрядному значению. Однако на этот раз вы будете двигаться назад, а не вперед.
Предложите учащимся решить задачу, как обычно. Когда они дойдут до шага, на котором они обычно останавливаются с остатком, попросите их поставить десятичную точку в конце частного и делимого и написать несколько нулей после делимого.
Предложите им продолжить обычные шаги деления на один или два знака, опуская нули.
Соедините десятичную дробь с дробью. Попросите их преобразовать частное с десятичной дробью в неправильную дробь. Это должно помочь им понять взаимосвязь между дробями и разрядным значением и может стать хорошей возможностью изучить основы дробей.
Как выполнить деление в длинное число (без деления в длинное число) Поздравляем! Ваш модуль подходит к концу, и вы успешно научили своих учеников выполнять деление в большую сторону.
Но знаете ли вы, что существует несколько способов деления больших чисел? Обучение учащихся другим способам проверки своей работы является важной частью математических стандартов Common Core и может улучшить понимание учащимися того, что на самом деле означает деление в столбцах в данном контексте.
Плоскостные моделиПлоскостные модели — отличный способ для визуалов понять и осмыслить деление, а также улучшить чувство числа.
В этом методе используется сетка, чтобы представить процесс деления в виде задачи площади: например, 148÷4 можно разделить на сетку высотой 4 единицы, площадью 148 квадратных единиц и неизвестным числом единиц ширины.
Учащиеся разбивают сетку на более удобные области: 100 квадратных единиц, 40 квадратных единиц и 8 квадратных единиц. 100÷4 равно 25, 40÷4 равно 10, а 8÷4 равно 2. Эти числа идут вверху модели области и могут быть сложены, чтобы получить ответ.
Частичные частные Подобно модели области, частичные частные побуждают учащихся разбивать вопросы на деление на «более понятные» части.
Это помогает учащимся понять, что деление — это нахождение того, сколько раз одно число может перейти в другое число.
Задайте задачу (в данном случае 450÷23) как уравнение деления на деление. Попросите учащихся умножить делитель на 2 и 5, чтобы использовать его в качестве удобного ориентира.
Спросите, сколько раз 23 входит в число 400, но не ищите точное ближайшее число: сделайте его простым для работы, например, 230 (десять раз). Вычтите 230 из 450 и поставьте 10 справа, чтобы отслеживать результат.
Возьмите разницу и вычтите ее из дивиденда. Ответ должен быть 220.
Спросите, сколько раз 23 входит в число 220.5 x 23 равно 115, так что вычтите это из 220 и запишите 5.
Продолжайте, умножая и вычитая, пока окончательное число не станет слишком маленьким. Когда вы достигли этого шага, вы нашли остаток! Сложите числа в правом столбце, чтобы найти частное.
Частичные частные обладают гибкостью, которой нет в длинном делении. Длинное деление нужно делать точно, но с частичными частными можно просто несколько раз вычесть делитель из делимого и все равно прийти к правильному ответу.
Используйте этот метод, чтобы закрепить позиционное значение и концепцию деления как многократного вычитания.
Упражнения на деление в длинное числоЛучший способ научиться делению в длинное число – практиковаться, практиковаться и еще раз практиковаться.
Вот список из восьми заданий, которые заинтересуют ваш класс делением в длинную и помогут развить прочные математические навыки.
1. ProdigyProdigy — это забавный и увлекательный ресурс для занятий на длинном дивизионе в классе или дома.Учащиеся исследуют мир, полный приключений, где успех зависит от правильных ответов на математические вопросы.
С помощью панели управления учителя вы можете предоставлять контент, ориентированный на урок, в зависимости от оценки, навыков или ученика. Затем учащиеся отвечают на эти вопросы в игре и предоставляют вам обратную связь в режиме реального времени о своем обучении и понимании .
Поощряйте своих учеников практиковать все математические навыки, которые они изучили в классе, включая деление в столбик.Вот как вы можете использовать Prodigy, чтобы:
Студенты играют в увлекательную игровую платформу, где они могут собирать питомцев, выполнять квесты и сражаться с друзьями. И пока они развлекаются, вы помогаете им развивать навыки длинного деления. Это победа для всех!
Зарегистрируйтесь сейчас 2. Деление в натуральную величинуОживите математику с помощью головоломки с делением в натуральную величину. Вырежьте квадраты из цветной бумаги со всеми числами, которые нужны учащимся для решения задачи на деление в длину от начала до конца.Используйте клейкую ленту, чтобы разделить линии на полу, и раздайте учащимся пронумерованные карточки.
Начав с заданного уравнения, попросите учащихся разложить все карточки в правильном порядке, чтобы решить уравнение. Это задание побуждает учащихся замедлиться и подумать о своих шагах, и это особенно полезно для класса, который все еще хочет освоить шаги умножения.
Бинго не просто так является классикой. Каждая из цифр в листе учащегося должна соответствовать вопросу, который вы задали перед классом.Напишите задачу на доске, а затем дайте учащимся черновик и возможность решить ее и посмотреть, есть ли она у них на карточках. Как всегда, побеждает тот, кто первым заполнит весь ряд!
Бросьте вызов своим учащимся, но убедитесь, что вы уделяете этому упражнению достаточно времени — некоторые учащиеся могут испытывать трудности с быстрым решением задач и могут расстраиваться или совершать ошибки, если не смогут справиться с заданием.
4. Книги по математике Повышайте уровень грамотности и обучения математике с помощью забавных книг, посвященных сложным математическим понятиям.Используйте их, чтобы объяснить учащимся деление и остатки в веселой и увлекательной форме и даже охватить более основные понятия, прежде чем они начнут учиться выполнять деление в столбик.
Некоторые книги по математике, которые покрывают отделом:
- Остальная часть одного
9 Elinor J. Pinczes
- Bean Therteen Matthew Mcelligott
- Дверной звонок PAT Hutchins
- Остальная часть одного
5. Получить креатив
В длинном делении много шагов, и их нужно выполнять в правильном порядке, чтобы получить правильный ответ.Учащиеся могут запутаться или расстроиться, если не помнят шагов, что отрицательно сказывается на их уверенности в математике и успеваемости.
Предложите учащимся придумать свой собственный уникальный способ запомнить, как выполнять деление в большую сторону — разделить на , умножить , вычесть и записать — чтобы стимулировать творчество в вашем классе.
Предложите им создать постер, песню, мнемоническое устройство или даже небольшую сценку, которую они могут представить своим одноклассникам.Если они заинтересованы в том, чтобы найти способ запомнить шаги, они, скорее всего, быстро научатся.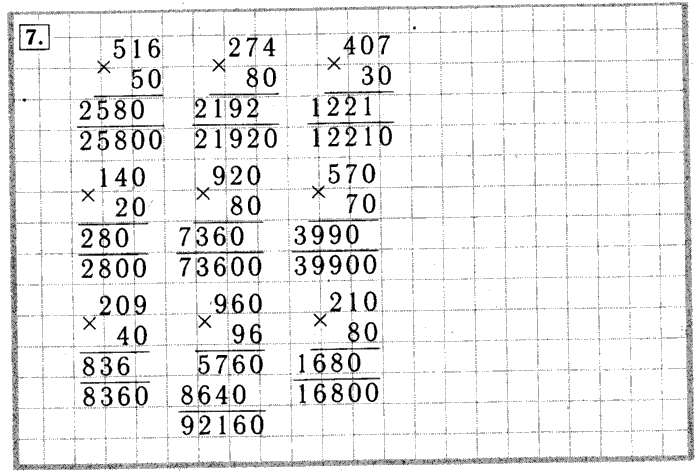
Превратите тренировки на длинные деления в веселую классную игру с эстафетами на длинные деления. Разделите свой класс на команды и сделайте карточки с задачами на деление в длину.
Объедините учеников в группы. Каждая группа получает карточку для начала, и первые учащиеся выполняют первый набор шагов для своей проблемы.
Когда они закончат, второй учащийся ищет ошибки и продолжает решать задачу.Если они решат задачу, они могут позвонить вам, чтобы проверить их работу и обменять правильный ответ на карточку с новой задачей.
Продолжайте, пока каждая группа не ответит на все свои карточки, и посмотрите, какая команда победит!
7. Сундук с сокровищами
Это задание — веселый способ для вашего класса отпраздновать завершение отряда в дивизионе. Возьмите несколько коробок и наполните их небольшим угощением, которое понравится всем в классе. Включите список задач на умножение, которые учащиеся должны решить в группах, чтобы «открыть» коробку.
В качестве дополнительной задачи сделайте это кодом: пусть каждое частное соответствует букве алфавита, чтобы учащиеся должны были правильно расшифровать ключевую фразу, чтобы открыть коробку.
8. Генератор рабочих листовРабочие листы — это проверенный материал на уроках математики. К счастью для вас, существует множество веб-сайтов, которые сделают всю работу за вас и сгенерируют пользовательский рабочий лист, который даст вашим ученикам возможность практиковаться в делении в большую сторону. Вот некоторые из наших фаворитов:
Заключительные мысли по обучению студентов делению в большую сторону Самое важное, что нужно помнить при обучении студентов делению в большую сторону, это не торопиться с материалом.Это большая концепция, которая отличается от всего, что они изучали раньше, и некоторые (если не все) ваши ученики поначалу могут испытывать затруднения. Если вам нужно, вернитесь к более простым уравнениям и некоторым из предыдущих шагов, которые мы описали.
для вас и работайте над ними, пока ваши ученики не почувствуют себя уверенно. Продолжайте поощрять и бросать вызов своим ученикам, и они будут готовы разделять и властвовать в кратчайшие сроки!
Создайте или войдите в свою бесплатную учетную запись учителя в Prodigy – игровой платформе для обучения математике, которую легко использовать как преподавателям, так и учащимся.Он соответствует учебным программам англоязычного мира и используется миллионами учителей и учащихся.Зарегистрируйтесь сейчас
примеров уроков – 5 класс
Пример уроков умножения и деления дробей Единица обучения:
Разделение ванильных вафель: на этом уроке учащиеся будут основываться на своем понимании деления как равных долей, используя пластилин Play-Doh для деления сумм, которые не делятся поровну. Они будут понимать и описывать дроби как деление целых чисел, а также объяснять значение числителя и знаменателя в контексте.
Нажмите на ссылку, чтобы увидеть страницы учеников и инструкции для учителей:
Делимся ванильными вафлями
Умножение дробей на числовой прямой: учащиеся будут использовать числовую прямую для моделирования умножения дробей, рассматривая множитель как представляющий одно расстояние, а другой множитель представляющий часть того расстояния, которое они преодолеют.
Учащиеся будут изучать результаты, чтобы объяснить, когда произведение двух дробей больше, равно или меньше 1. Учащиеся будут смотреть на закономерности с факторами и произведениями, чтобы вывести тот факт, что a/b x c/d = ac/bd.
Нажмите на ссылку, чтобы увидеть страницы учеников и инструкции для учителей:
Умножение дробей на числовом ряду
Деление дробей Часть 1: Учащиеся будут использовать деление в кавычках, чтобы переписать задачи на деление дробей как «Сколько ____ в ___», и использовать это определение с моделью площади для деления целого числа на дробь. Учащиеся сначала поймут это, увидев, сколько меньших блоков шаблона помещается в больший, а затем связав контекст с математикой, стоящей за этим.
Нажмите на ссылку, чтобы увидеть страницы учеников и инструкции для учителей:
Деление дробей I
Как далеко вы можете прыгнуть?: учащиеся должны измерить расстояние (в долях метров), на которое может прыгнуть каждый учащийся, и представить эти данные на линейном графике.
Учащиеся будут отвечать на вопросы, сравнивая расстояния с помощью мультипликативных сравнений, представляя каждый вопрос математическим предложением и решением, применяя четыре операции с дробями.
Нажмите на ссылку, чтобы увидеть страницы учеников и инструкции для учителей:
Как далеко вы можете прыгнуть
Важные математические навыки для пятиклассников
Хотите помочь своему пятикласснику освоить математику? Вот некоторые из навыков, которые ваш пятиклассник будет осваивать в классе.
Сложение, вычитание, умножение и деление
Многозначные целые числа
Быстро и точно умножайте многозначные целые числа. Разделите целые числа (до четырех цифр) на двузначные числа.
Пример:
Решите 4,824 ÷ 12 = ?
Объясните или проиллюстрируйте, как вы решили эту проблему.
Совет: подчеркните реальное использование математики.
По мере того, как математика, которую они изучают, становится все более сложной и менее явно связанной с их повседневным опытом, у некоторых детей начинает развиваться математическая тревожность.
Важно, чтобы ваш ребенок занимался математикой и помогал ему понять практическое применение концепций, которые ваш ребенок изучает в школе. Составление бюджета на школьные принадлежности или ежемесячное пособие — это один из способов попрактиковаться в сложении и вычитании. Попросив их помочь вам с приготовлением пищи или выпечкой, вы покажете им, как работают дроби. Помочь вам рассчитать цены, когда вы покупаете продукты, также является хорошей практикой.
Связанные
Понимание разрядного значения
Расширение понимания разрядного значения: в многозначном числе цифра в одном разряде представляет 1/10 того, что она представляет в разряде слева от нее, и в 10 раз больше как он представляет в месте справа от него.
Сравнение десятичных дробей
Чтение, запись и сравнение десятичных дробей с точностью до тысячных, используя символы > (больше) и < (меньше). Например:
- Прочтите это десятичное число: 23. 002.
- Запишите две и шестьдесят две тысячные в виде десятичного числа.
- Какой знак делает это утверждение верным: 5,389 _?_ 5,420
- Исследователь измеряет количество бактерий, выросших на образцах неохлажденных пищевых продуктов. Ваш ребенок считает 73.343 миллиона бактерий в образце A, 73,431 миллиона бактерий в образце B и 74,399 миллиона бактерий в образце C. Расположите образцы в порядке от наибольшего количества бактерий к наименьшему. Объясните или проиллюстрируйте, как вы упорядочиваете эти образцы.
002.Связанные
Десятичные до сотых
Сложение, вычитание, умножение и деление десятичных долей до сотых.
Совет: потренируйтесь в вычислениях с десятичными дробями.
Свяжите работу с десятичными дробями, которую ваш ребенок выполняет в классе, с реальным миром, побуждая его делать покупки по выгодным ценам.Попросите их разделить стоимость товаров, упакованных оптом, на количество отдельных товаров, чтобы найти стоимость каждого товара.
Итак, сколько вы платите за рулон бумажных полотенец или банку газировки, когда покупаете оптом? Или попросите ребенка подсчитать, сколько вы сэкономите на каждой единице товара, если цены со скидкой предлагают оптовые скидки.
Понимание показателей степени
Понимание того, что такое показатель степени. Например, «2» в 10² указывает, сколько раз нужно умножить число само на себя. 10² может быть прочитано как «10 во второй степени» или «10 в степени 2» или «10 в квадрате» и означает 10 x 10 или 100.10³ (или «10 в третьей степени» или «10 в кубе») означает 10 х 10 х 10, или 1000.
Дроби
Решение текстовых задач
Решение текстовых задач на сложение и вычитание дробей.
Пример:
Пятый класс собирает пазл из 600 деталей. Они начали вчера и собрали 100 частей — только одну шестую (1⁄6) пазла. Сегодня они собрали 400 штук. Какая часть головоломки завершена? Нарисуй картинку И запиши математику, чтобы показать, как ты решил задачу.
Совет: подчеркните реальное использование математики.
По мере того, как математика, которую они изучают, становится все более сложной и менее явно связанной с их повседневным опытом, у некоторых детей начинает развиваться математическая тревожность. Важно, чтобы ваш ребенок занимался математикой и помогал ему понять практическое применение концепций, которые он изучает в школе. Составление бюджета на школьные принадлежности или ежемесячное пособие — это один из способов попрактиковаться в сложении и вычитании.Попросив ее помочь вам с приготовлением пищи или выпечкой, вы покажете ей, как работают дроби. Помочь вам рассчитать цены, когда вы покупаете продукты, также является хорошей практикой.
Нахождение общего знаменателя
Решите текстовые задачи на сложение и вычитание дробей с разными знаменателями (нижними числами) путем преобразования их в дроби с одинаковым знаменателем, называемым общим знаменателем.
Пример:
Рост самой высокой девочки в пятом классе 51 7/8 дюйма.
Рост самого высокого мальчика в пятом классе составляет 49 1/2 дюйма. Какая разница в их росте?
После вечеринки осталось две тарелки лимонада. В одной миске 1⁄3 галлона. Другой содержит 1/2 галлона лимонада. Друг говорит, что вы не должны пытаться объединить их в 1-галлонный контейнер, потому что лимонад выльется сверху. Вы согласны? Почему или почему нет?
Умножение дробей
Решение текстовых задач на умножение дробей на другие дроби и умножение дробей на смешанные числа (целое число и дробь, например 11/4 или 21/2).
Пример:
- В оркестре средней школы 1/3 учащихся-музыкантов играют на струнных инструментах. Из учащихся, играющих на струнных инструментах, 3/4 играют на скрипке. Какая часть оркестра играет на скрипке?
- Утром во время экскурсии в яблоневый сад пятиклассники собрали 4/5 бушеля яблок. После обеда в полдень они собрали в 2,5 раза больше яблок. Все ли яблоки, которые они собрали днем, поместятся в ящик емкостью 2 бушеля? Откуда вы знаете?
Совет: попрактикуйтесь в использовании дробей.
Помогите ребенку познакомиться с дробями, попросив его масштабировать рецепты для вашей семьи. Попросите их начать с уменьшения рецепта вдвое или вдвое. Когда они почувствуют себя комфортно, попросите их преобразовать это на 11/2, что позволит рецепту, который должен накормить семью из четырех человек, работать на семью из шести человек.
Деление единичных дробей
Деление единичных дробей (дроби с 1 в числителе или старшее число) на целые числа. Разделите целые числа на единичные дроби.
Пример:
Если три человека поровну поделят ½ фунта шоколада, сколько шоколада получит каждый? Объясните или проиллюстрируйте, как вы решили эту проблему.
Умножение на дроби
Поймите, что умножение числа на дробь меньше 1 даст ответ меньше числа, например: 12 x ¾ = 9. Умножение числа на дробь больше 1 даст в ответе больше числа – например: 12 х 2 ½ = 30.
Измерения и данные
Преобразование единиц и дробей
Преобразование единиц и дробей единиц в рамках той же системы измерения.
Пример:
Сколько минут составляет 1/5 часа? Объясните или проиллюстрируйте, как вы решили эту проблему.
Многоэтапные задачи преобразования единиц
Решите многоэтапные задачи со словами, используя преобразования стандартных единиц измерения разного размера.
Пример:
У меня 75 см ленты.Мне нужно в семь раз больше ленты, чтобы завершить проект. Сколько еще метров ленты мне нужно?
Объясните или проиллюстрируйте, как вы решили эту проблему.
Использование линейного графика
Решите задачи, используя информацию (в дробных единицах), представленную в линейном графике.
Геометрия
Понимание объема
Понимание объема как измерения пространства внутри трехмерной или объемной фигуры. Используйте формулы 90 178 длина x ширина x высота 90 179 или 90 178 основание x высота 90 179, чтобы измерить объем трехмерного или твердого объекта с прямоугольными сторонами, например куба.
Измеряйте объем для решения реальных проблем.
Пример:
Прямоугольный контейнер для мороженого имеет длину 8 дюймов и высоту 4 дюйма. Каков объем сосуда, выраженный в кубических дюймах?
Советы, которые помогут вашему пятикласснику на уроке математики, см. на нашей странице советов по математике для пятого класса.
Ресурсы Parent Toolkit были разработаны NBC News Learn с помощью профильных экспертов и приведены в соответствие с Common Core State Standards.
Интерпретировать дробь как деление числителя на знаменатель (a/b = a b). Решайте текстовые задачи на деление целых чисел, чтобы получить ответы в виде дробей или смешанных чисел, например, используя визуальные модели дробей или уравнения для представления задачи. Например, интерпретируйте 3/4 как результат деления 3 на 4, отметив, что 3/4, умноженное на 4, равно 3, и что, когда 3 целого делятся поровну между 4 людьми, каждый человек получает долю размером 3/4. Если 9 человек хотят разделить 50-фунтовый мешок риса поровну по весу, сколько фунтов риса должен получить каждый? Между какими двумя целыми числами лежит ваш ответ?
МАФС.
5.NF.2.3 — Интерпретировать дробь как деление числителя на знаменатель (a/b = a b). Решайте текстовые задачи на деление целых чисел, чтобы получить ответы в виде дробей или смешанных чисел, например, используя визуальные модели дробей или уравнения для представления задачи. Например, интерпретируйте 3/4 как результат деления 3 на 4, отметив, что 3/4, умноженное на 4, равно 3, и что, когда 3 целого делятся поровну между 4 людьми, каждый человек получает долю размером 3/4. Если 9 человек хотят разделить 50-фунтовый мешок риса поровну по весу, сколько фунтов риса должен получить каждый? Между какими двумя целыми числами лежит ваш ответ?Веб-сайт несовместим с используемой версией браузера.Не все функции могут быть доступны. Пожалуйста, обновите ваш браузер до последней версии.
Интерпретировать дробь как деление числителя на знаменатель
(а/б = а ÷ б).
Решить текстовые задачи на деление целого
числа, ведущие к ответам в виде дробей или смешанных чисел,
например, с помощью моделей визуальных фракций или уравнений для представления
проблема. Например, интерпретируйте 3/4 как результат деления 3 на 4, учитывая
что 3/4, умноженное на 4, равно 3, и что когда 3 целых числа разделены
поровну среди 4 человек каждый имеет долю размером 3/4. Если 9 человек
хотите разделить 50-фунтовый мешок риса поровну по весу, сколько
фунтов риса должен получить каждый человек? Между какими двумя целыми числами
твой ответ лжет?
Общая информация
Предметная область: Математика
Класс: 5
Домен-поддомен: Число и операции — дроби
Кластер: Уровень 2: Базовое применение навыков и понятий
Дата принятия или пересмотра: 14 февраля
Дата последней оценки: 14/02
Статус: Утвержден Государственным советом
Оценено: Да
Спецификации объекта испытаний
- Пределы оценки:
Частные в пунктах деления не могут быть эквивалентны целому числу. Элементы могут содержать дроби больше 1.
В элементах нельзя использовать термины «упрощение» или «самые низкие термины».
Используйте только целые числа для делителя и делимого дроби.
Для заданных дробей в пунктах знаменатели ограничены 1-20. - Калькулятор:
№
- Контекст:
Допустимый
Элементы могут содержать дроби больше 1.
В элементах нельзя использовать термины «упрощение» или «самые низкие термины».
Используйте только целые числа для делителя и делимого дроби.
Для заданных дробей в пунктах знаменатели ограничены 1-20.Образцы тестовых заданий (3)
- Тестовый образец #: Образец 2
- Вопрос:
У Джо есть доска длиной 6 футов.Ему нужно разрезать доску на 15 частей одинаковой длины.
Сколько футов должна быть длина каждой части доски?
- Сложность: Н/Д
- Тип: EE: Редактор формул
- Тестовый образец #: Образец 3
- Вопрос:
Учитель рисования раздает своим ученикам 35 фунтов глины.
Она дает каждому из своих 16 учеников одинаковое количество глины.Сколько фунтов глины получил каждый ученик?
- Сложность: Н/Д
- Тип: EE: Редактор формул
Она дает каждому из своих 16 учеников одинаковое количество глины.Связанные точки доступа
Альтернативная версия этого теста для учащихся с серьезными когнитивными нарушениями.
MAFS.5.NF.2.AP.3a: разделите дроби единиц на целые числа и целые числа на дроби единиц, используя визуальные модели дробей.
Связанные ресурсы
Проверенные ресурсы, которые преподаватели могут использовать для обучения концепциям и навыкам в этом эталонном тесте.
Уроки STEM — Активность по моделированию
Птицы сейчас: В зоомагазине Birds Now расширяется отдел птиц.
Увеличивая количество и виды птиц, им необходимо покупать больше корма для птиц, а тип корма должен быть таким, чтобы его могли есть разные виды птиц. Учащимся необходимо ранжировать компании, торгующие кормом для птиц, по основным требованиям, изложенным в письме клиента.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для того, чтобы выявить мысли учащихся о концепциях, внедренных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Заповедник дикой природы MEA- Кормление животных: Учащиеся используют математические методы, чтобы рекомендовать к заказу продуктовые наборы для заповедника дикой природы Северной Америки.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для того, чтобы выявить мысли учащихся о концепциях, внедренных в реалистичные ситуации.Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Формирующие оценки MFAS
Пять третей: Учащихся просят интерпретировать неправильную дробь, а затем составить текстовую задачу, соответствующую контексту дроби.
Учащихся просят нарисовать наглядную дробную модель для решения задачи на деление слов.
Делимся пиццей:Учащихся просят нарисовать наглядную дробную модель для решения задачи на деление слов.
Две трети:Учащихся просят интерпретировать дробь и написать задачу, соответствующую контексту дроби.
Оригинальные учебники для учащихся по математике — классы K-5
#InterpretAFractionAsDivision: Научитесь определять дробь как деление числителя на знаменатель, используя модели дробей, в этом интерактивном учебном пособии.
Оригинальные учебные пособия для студентов по информатике
Bee A Coder Часть 1: Объявление переменных: Из этого интерактивного руководства вы узнаете, как определять, объявлять и инициализировать переменные, когда начинаете свой путь к кодеру.Переменные — это структуры, используемые компьютерными программами для хранения информации.
Вы будете использовать свои математические навыки для представления дроби в виде десятичной дроби, которая будет храниться в переменной.
Это первая часть из четырех статей о программировании. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Ресурсы для учащихся
Проверенные ресурсы, которые учащиеся могут использовать для изучения концепций и навыков в этом эталонном тесте.
Оригинальные учебные пособия для студентов
Bee A Coder Часть 1: Объявление переменных: Из этого интерактивного руководства вы узнаете, как определять, объявлять и инициализировать переменные, когда начинаете свой путь к кодеру.
Переменные — это структуры, используемые компьютерными программами для хранения информации. Вы будете использовать свои математические навыки для представления дроби в виде десятичной дроби, которая будет храниться в переменной.
Это первая часть из четырех статей о программировании. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Тип: оригинальное учебное пособие для учащихся
#InterpretAFractionAsDivision:Научитесь определять дробь как деление числителя на знаменатель, используя модели дробей, в этом интерактивном учебном пособии.
Тип: оригинальное учебное пособие для учащихся
Образовательная игра
Фракция Викторина: Проверьте свои навыки фракции, отвечая на вопросы на этом сайте.
В этом тесте вам предлагается упростить дроби, преобразовать дроби в десятичные числа и проценты, а также ответить на вопросы по алгебре, связанные с дробями. Вы даже можете выбрать уровень сложности, типы вопросов и ограничение по времени.
Тип: обучающая игра
Задачи решения проблем
Сколько пирога?: Цель этого задания – помочь учащимся увидеть связь между a÷b и a/b в конкретном конкретном примере.Это задание, вероятно, лучше всего подходит для обучения или формирующего оценивания.
Тип: Задача решения проблем
Ресурсы для родителей
Проверенные ресурсы, которые воспитатели могут использовать, чтобы помочь учащимся освоить концепции и навыки в этом эталонном тесте.
Задачи решения проблем
Сколько пирога?: Цель этого задания – помочь учащимся увидеть связь между a÷b и a/b в конкретном конкретном примере.
Это задание, вероятно, лучше всего подходит для обучения или формирующего оценивания.
Тип: Задача решения проблем
Загрузка….
%PDF-1.4 % 448 0 объект > эндообъект внешняя ссылка 448 82 0000000016 00000 н 0000002775 00000 н 0000002922 00000 н 0000003419 00000 н 0000003751 00000 н 0000004062 00000 н 0000004260 00000 н 0000004374 00000 н 0000004486 00000 н 0000004599 00000 н 0000004708 00000 н 0000005172 00000 н 0000005199 00000 н 0000005635 00000 н 0000005662 00000 н 0000006228 00000 н 0000006624 00000 н 0000006651 00000 н 0000006678 00000 н 0000007142 00000 н 0000007282 00000 н 0000007415 00000 н 0000007550 00000 н 0000007687 00000 н 0000008233 00000 н 0000008771 00000 н 0000009330 00000 н 0000009891 00000 н 0000010435 00000 н 0000010462 00000 н 0000010856 00000 н 0000010994 00000 н 0000011520 00000 н 0000011783 00000 н 0000012286 00000 н 0000012575 00000 н 0000012846 00000 н 0000014112 00000 н 0000025731 00000 н 0000025844 00000 н 0000027008 00000 н 0000027316 00000 н 0000027431 00000 н 0000030282 00000 н 0000030600 00000 н 0000030719 00000 н 0000031960 00000 н 0000032273 00000 н 0000032400 00000 н 0000034380 00000 н 0000034704 00000 н 0000034774 00000 н 0000034854 00000 н 0000038726 00000 н 0000039000 00000 н 0000039288 00000 н 0000039358 00000 н 0000039438 00000 н 0000044340 00000 н 0000044609 00000 н 0000044923 00000 н 0000044993 00000 н 0000045073 00000 н 0000069237 00000 н 0000069502 00000 н 0000069902 00000 н 0000069972 00000 н 0000070052 00000 н 00000
00000 н 0000091070 00000 н 0000091413 00000 н 0000091483 00000 н 0000091563 00000 н 0000091772 00000 н 0000091987 00000 н 0000092208 00000 н 0000092447 00000 н 0000112047 00000 н 0000153155 00000 н 0000214671 00000 н 0000002590 00000 н 0000001936 00000 н трейлер ]/Предыдущая 1142289/XRefStm 2590>> startxref 0 %%EOF 529 0 объект >поток hb«b`TA,`$009|_9GSXDqqE’KfZjM]Mg斬`ᑮM|JIS,*ygt2t, ptYoyD,&pIp8 ɯpDZ)DVmzFbSidv}|¡v!-FgF6K9p13i5µp>Lsw϶D#W7* N4 sirY9yEʨoH:9mE/o_?@3NJ
.