Тест по геометрии на тему «Параллельность прямой и плоскости»
ГБПОУ города Москвы «Спортивно-педагогический колледж»
Департамент спорта и туризма города Москвы
преподаватель математики, информатики и ИКТ: Макеева Е.С.
Тест «Параллельность прямых, прямой и плоскости»
Вариант 1
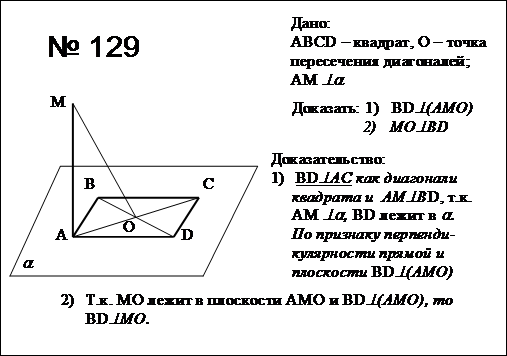
А1. Точки А, В, С, D не лежат в одной плоскости. Точки K, L, M, N- середины отрезков AB, BC, CD, AD соответственно. Укажите прямые, параллельные прямой АС.
1) KL и ML 2)MN и BD 3)KL и MN 4) нет
А2. Точка С лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и С — параллельные прямые, пересекающие эту плоскость в точках . Найдите длину отрезка , если АС:СВ=3:2 и =20 см .
1) 12 см 2)8 см 3)16 см 4) 4 см
А3. Вершина А треугольника АВС лежит в плоскости α, вершины В и С расположены по одну сторону от этой плоскости. Отрезок AD-медиана треугольника АВС. Через точки B, D, C проведены параллельные прямые, пересекающие плоскость α в точках соответственно. Найдите длину D, если = 2 см и =12 см.
1) 7 см 2) 5 см 3) 10 см 4) 8 см
В1. В тетрадке ABCD точки K, L, M, N-середины рёбер АС, ВС, BD, AD, соответственно. Определите вид четырехугольника KLMN и его периметр, если АВ=16 см и CD=18 см.
Ответ:________________________________________________________________________________________________________________________
В2. Точки А и В лежат по одну сторону от плоскости α. Точка С лежит на отрезке АВ и АС:СВ=2:3. Через точки А, В, С проведены параллельные прямые, пересекающие плоскость α соответственно в точках . Найдите , если = α , =b (ba).
Найдите , если = α , =b (ba).
Ответ:________________________________________________________________________________________________________________________
C1. Даны параллелограмм ABCD и не пересекающая его плоскость. Через вершины параллелограмма проведены параллельные прямые, пересекающие данную плоскость в точках ,. Найдите , если = 2 см, =3 см, =8 см.
Ответ:________________________________________________________________________________________________________________________
Тест «Параллельность прямых, прямой и плоскости»
Вариант 2.
А1. Точки А, В, С, D не лежат в одной плоскости. Точки K, L, M, N- середины отрезков AB, BC, CD, AD соответственно. Укажите прямые, параллельные прямой BD.
1) LM и MN 2) KN и LM 3) KN и AC 4) нет
А2. Точка С лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и С — параллельные прямые, пересекающие эту плоскость в точках . Найдите длину отрезка , если АС:СВ=4:3 и =14 см .
Точка С лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и С — параллельные прямые, пересекающие эту плоскость в точках . Найдите длину отрезка , если АС:СВ=4:3 и =14 см .
1) 12 см 2) 7 см 3) 8 см 4) 6 см
А3. Вершина А треугольника АВС лежит в плоскости α, вершины В и С расположены по одну сторону от этой плоскости. Отрезок AD-медиана треугольника АВС. Через точки B, D, C проведены параллельные прямые, пересекающие плоскость α в точках соответственно. Найдите длину D, если = 14см и =8 см.
1) 3 см 2) 11 см 3) 6 см 4) 7 см
В1. В тетрадке ABCD точки K, L, M, N-середины рёбер АС, ВС, BD, AD, соответственно. Определите вид четырехугольника KLMN и его периметр, если АВ=12 см и CD=24 см.
Ответ:________________________________________________________________________________________________________________________
В2. Точки А и В лежат по одну сторону от плоскости α. Точка С лежит на отрезке АВ и АС:СВ=3:4. Через точки А, В, С проведены параллельные прямые, пересекающие плоскость α соответственно в точках . Найдите , если = α, =b (ba).
Точка С лежит на отрезке АВ и АС:СВ=3:4. Через точки А, В, С проведены параллельные прямые, пересекающие плоскость α соответственно в точках . Найдите , если = α, =b (ba).
Ответ:________________________________________________________________________________________________________________________
C1. Даны параллелограмм ABCD и не пересекающая его плоскость. Через вершины параллелограмма проведены параллельные прямые, пересекающие данную плоскость в точках
Ответ:___________________________________________________________________________________________________________________
Ключи к тесту «Параллельность прямых, прямой и плоскости»
№ варианта | А1 | А2 | А3 | В1 | В2 | С1 |
1 | 3 | 1 | 2 | параллелограмм; 34 см | + | 7 см |
2 | 2 | 3 | 1 | параллелограмм; 36 см | + | 12 см |
3
Параллельность прямых и плоскостей в пространстве
Запитання 1
Две прямые в пространстве называются параллельными, если
варіанти відповідей
они не имеют общих точек и лежат в одной плоскости.
они не имеют общих точек.
не имеют общих точек и лежат в разных плоскостях
они не имеют общих точек, и не существует проходящей через них плоскости.
Запитання 2
Какое наибольшее число плоскостей можно провести через различные пары из трех параллельных прямых?
варіанти відповідей
Запитання 3
Через каждую из двух параллельных прямых проведена плоскость. Эти две плоскости пересекаются. Как расположена их линия пересечения относительно данных прямых?
варіанти відповідей
Пересекает их
Скрещивается с ними
Параллельна им
Совпадает с одной из них
Запитання 4
Плоскость a пересекается с прямой a, которая параллельна плоскости b. Как расположены относительно друг друга плоскости a и b?
варіанти відповідей
Определить невозможно
Запитання 5
Параллельной проекцией двух параллельных прямых являются две точки.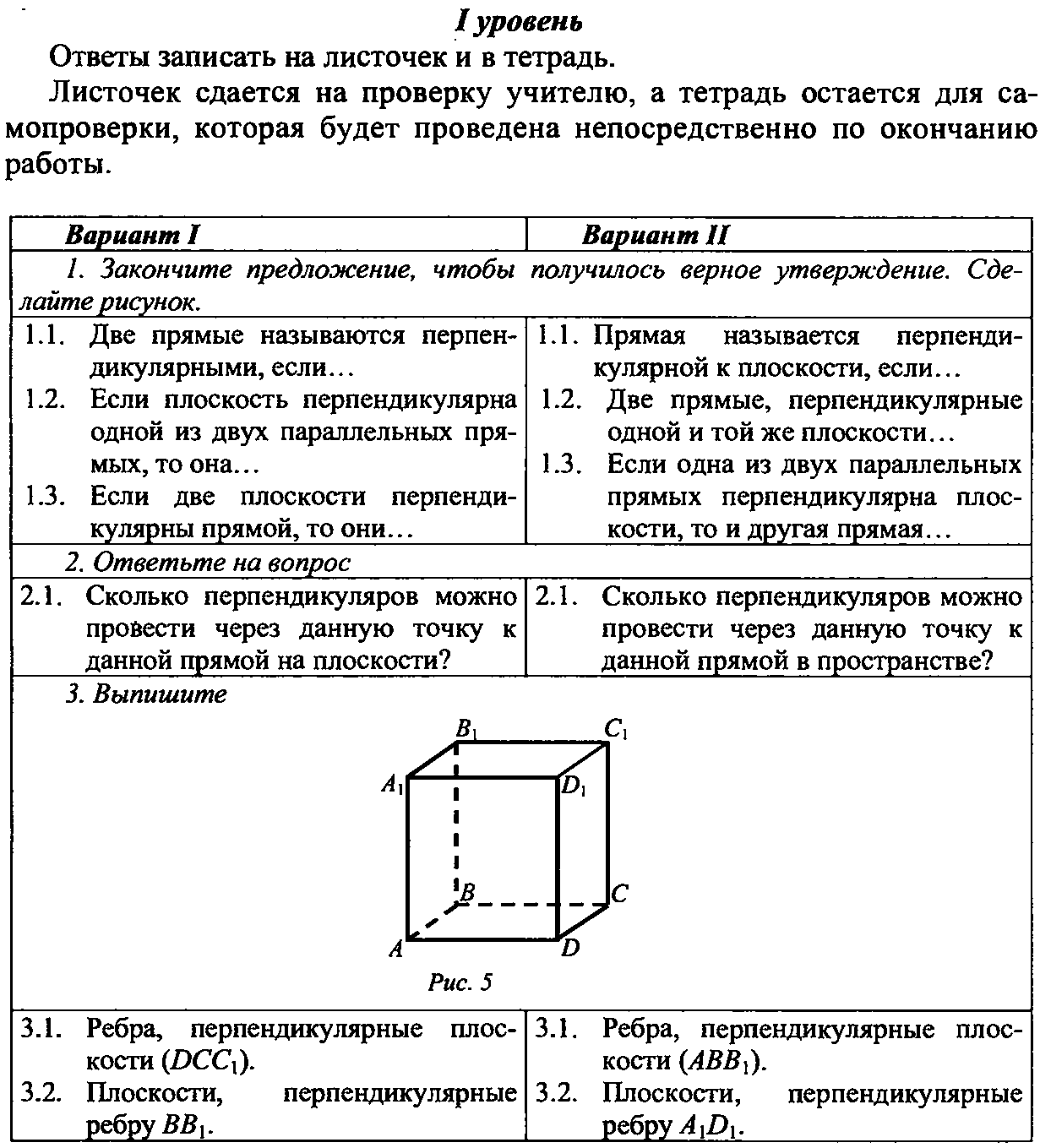 Это значит, что …
Это значит, что …
варіанти відповідей
Плоскость прямых совпадает с плоскостью проектирования
Прямые параллельны плоскости проектирования
Плоскость прямых не параллельна направлению проектирования
Прямые параллельны направлению проектирования
Запитання 6
Дан треугольник АВС и плоскость α. АВ∥α и АС∥α, значит прямая ВС …
варіанти відповідей
параллельна плоскости
пересекает плоскость
перпендикулярна плоскости
лежит в плоскости
Запитання 7
Какое утверждение неверно?
варіанти відповідей
Если каждая из двух пересекающихся прямых одной плоскости параллельна другой плоскости, то эти плоскости параллельны
отрезки прямых, заключённые между параллельными прямыми равны
если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны
если одна из двух параллельных плоскостей параллельна третьей плоскости, то другая плоскость либо тоже параллельна этой плоскости, либо совпадает с ней
Запитання 8
Укажите признак параллельности плоскостей
варіанти відповідей
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны
Если две не совпадающие плоскости перпендикулярны некоторой прямой, то они параллельны
Две прямые параллельные третьей прямой, параллельны
Запитання 9
Примеры параллельных плоскостей:
варіанти відповідей
рельсы и шпалы
лампа дневного света и пол
полки в холодильнике
Запитання 10
Прямая и плоскость в пространстве могут быть
варіанти відповідей
параллельными
скрещивающимися
пересекающимися
Запитання 11
Две прямые пересекаются, если они:
варіанти відповідей
не имеют общих точек
полностью совпадают
имеют две общие точки
имеют одну общую точку
Запитання 12
Даны параллельные прямая a и плоскость α.
варіанти відповідей
бесконечное множество
Створюйте онлайн-тести
для контролю знань і залучення учнів
до активної роботи у класі та вдома
Натисніть «Подобається», щоб слідкувати за оновленнями на Facebook
Тест по теме: «Параллельность плоскостей»
1. МКОУ «Погорельская СОШ» Кощеев М.М.
Вариант 1Вариант 2
Использован шаблон создания тестов в PowerPoint
2. Результат теста
Верно: 14Ошибки: 0
Отметка: 5
Время: 3 мин. 6 сек.
ещё
3. Вариант 1
1. Плоскости параллельны если……а) Прямая одной плоскости параллельна прямой другой плоскости.
б) Две прямые одной плоскости параллельны двум прямым другой
плоскости.
в) Две пересекающиеся прямые одной плоскости параллельны другой
плоскости.
3
4. Вариант 1
2. Дан треугольника АВС и плоскость α, Тогда прямая ВС…
Тогда прямая ВС…а) пересекает плоскость α
б) параллельна плоскости α
в) лежит в плоскости α
4
5. Вариант 1
3. Какое утверждение неверное?а) Отрезки прямых, заключенные между параллельными
плоскостями равны.
б) Если две параллельные плоскости пересечены третьей, то
линии их пересечения параллельны.
в) Если каждая из двух пересекающихся прямых одной плоскости
параллельна другой плоскости, то эти плоскости параллельны.
5
6. Вариант 1
4. Параллелограммы АВСD и АВС₁D₁лежат в разных плоскостях. Тогда
СС₁D₁D не может быть…
а) ромбом
б) прямоугольником
в) трапецией
6
7. Вариант 1
5. (АВСD) ∦ α, еслиа) АВСD- трапеция, АD//ВС, АВ//α, СD//α
б) АВСD – параллелограмм, АВ//α, СD//α
в) АВСD- параллелограмм, АС//α, СD//α
7
8. Вариант 1
6. MN//АВ, MK//АС, АМ=МD. ТогдаD
неверно, что ……
а) NK//ВС
К
М
б) АС=2МК
в) S∆АВС=2S∆MNK
N
С
А
В
8
9.
 Вариант 1 7. α║ẞ, а принадлежит плоскости α,
Вариант 1 7. α║ẞ, а принадлежит плоскости α,b принадлежит плоскости ẞ. Тогда
прямые а и b не могут быть….
а) Параллельными
б) Пересекающимися
в) Скрещивающимися
9
10. Вариант 1
8. Какое утверждение верное?а) Не могут не быть параллельными две плоскости, пересеченные
третьей, если линии пересечения плоскостей параллельны.
б) Не могут быть параллельными плоскости, проходящие через
скрещивающиеся прямые.
в) Если две пересекающиеся плоскости параллельны некоторой
прямой, то линия их пересечения не может быть не параллельна этой
же прямой
10
11. Вариант 1
9. Какое утверждение верное?а) Не могут быть равны два непараллельных отрезка, заключенные
между параллельными плоскостями.
б) Не могут быть скрещивающимися прямые, лежащие в
параллельных плоскостях.
в) Не может прямая, лежащая в одной из параллельных плоскостей,
пересекать другую плоскость.
11
12.
 Вариант 1 10. а║α, а║ẞ, b║α, b║ẞ, α∩ẞ. Тогда
Вариант 1 10. а║α, а║ẞ, b║α, b║ẞ, α∩ẞ. Тогдапрямые а и b ….
а) а║b
б) а и b скрещивающиеся
в) а∩b
12
13. Вариант 1
11. Расстояние между двумяпараллельными плоскостями равно
5см. Тогда расстояние от точки,
лежащей на одной из этих плоскостей,
до второй равно…..
а)
Нельзя
определить
б)
5
в)
Любым в том
числе и 5
13
14. Вариант 1
12. Сторона АС треугольника АВС лежитв плоскости α. Через середину стороны
АВ – точку М – проведена плоскость ẞ,
параллельная плоскости α и
пересекающая ВС в точке К. АС=10см.
Тогда длина отрезка МК равна ….
а)
10
б)
5
в)
15
14
15. Вариант 1
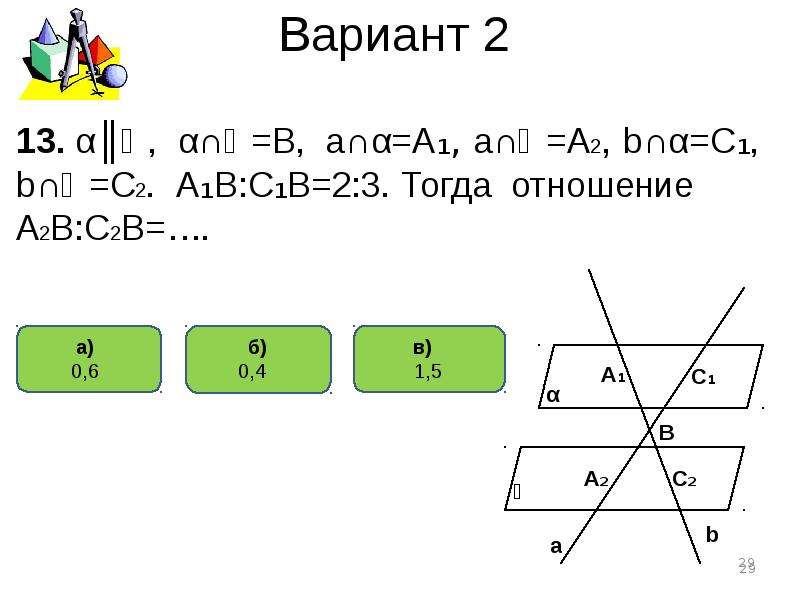
13. α║ẞ, α∩ẞ=В, а∩α=А₁, а∩ẞ=А2, b∩α=C₁,b∩ẞ=C2. А₁В:А₁А2=2:3. Тогда отношение
ВС₁:ВС2=….
В
а)
0,6
б)
2,5
в)
0,4
А₁
α
ẞ
А2
а
С₁
С2
b
15
15
16.
 Вариант 1 14. Три отрезка DD₁, ЕЕ₁, FF₁, не
Вариант 1 14. Три отрезка DD₁, ЕЕ₁, FF₁, нележащие в одной плоскости, имеют
общую середину, тогда плоскости DEF и
D₁E₁F₁ …….
а) пересекаются
б) параллельны
в) нельзя определить
16
17. Вариант 2
1. Чтобы утверждать, что плоскости α иẞ параллельны, достаточно доказать,
что плоскость α проходит через …..
а) Прямую, параллельную плоскости ẞ.
б) Две прямые, параллельные плоскости ẞ.
в) Две пересекающиеся прямые, параллельные плоскости ẞ.
17
18. Вариант 2
2. Диагонали параллелограмма АВСDпараллельны плоскости α. Тогда прямая
АВ…..
а) пересекает плоскость α
б) параллельна плоскости α
в) лежит в плоскости α
18
19. Вариант 2
3. Какое утверждение верное?а) Если через каждую из двух скрещивающихся прямых провести
плоскость, параллельную другой прямой, то эти плоскости будут
параллельны.
б) Если через каждую из двух скрещивающихся прямых провести
плоскость, то эти плоскости будут параллельны
в) Если через каждую из двух параллельных прямых провести
плоскость, то эти плоскости будут параллельны .

19
20. Вариант 2
4. α∩ẞ. Тогда некоторая плоскость ɣ….а) Параллельна плоскостям α и ẞ. .
б) Пересечет только одну из двух плоскостей.
в) Пересечет хотя бы одну из двух плоскостей
20
21. Вариант 2
5. Какое утверждение неверное?а) Если две плоскости пересечены третьей, то линии их
пересечения параллельны.
б) Если прямая параллельная каждой из двух пересекающихся
плоскостей, то она параллельна линии их пересечения.
в) Если прямая параллельна линии пересечения плоскостей и не
лежит в этих плоскостях, то она параллельна этим плоскостям..
21
22. Вариант 2
6. Через вершины ромба АВСDлежащего в одной из двух
параллельных плоскостей, проведены
параллельные прямые, пересекающие
вторую плоскость в точках А₁, В₁, С₁ и
D₁. Тогда А₁В₁С₁D₁ не может быть …
а) прямоугольником
б) квадратом
в) трапецией
22
23. Вариант 2
7. α║ẞ, а принадлежит плоскости α, bпринадлежит плоскости ẞ.
 Тогда
Тогданеверно, что …..
а) а параллельна b
б) а и b скрещивающиеся
в) а пересекает b
23
24. Вариант 2
8. Какое утверждение верное?а) Не могут быть параллельными две плоскости, проходящие
через непараллельные прямые.
б) Если две плоскости пересечены третьей и линии пересечения
плоскостей параллельны, то данные плоскости параллельны.
в) Не могут не быть параллельными две плоскости, если одна из
них проходит через две пересекающиеся прямые, параллельные
другой плоскости.
24
25. Вариант 2
9. Какое утверждение неверное?а) Не могут быть неравными два параллельных отрезка,
заключенные между параллельными плоскостями.
б) Не могут быть равными два непараллельных отрезка,
заключенные между параллельными плоскостями
в) Не могут пересекаться прямые, лежащие в параллельных
плоскостях.
25
26. Вариант 2
10. Прямая р принадлежит α, прямая gпринадлежит α, р∩g, точка А не
принадлежит плоскости α, АВ║α, АС║g,
точка А принадлежит плоскости ẞ, точка
С принадлежит плоскости ẞ.
 Тогда
Тогдаплоскости α и ẞ .….
а) α║ẞ
б) α∩ẞ
в) определить нельзя
26
27. Вариант 2
11. Расстояние от точки, лежащей наодной из параллельных плоскостей, до
второй равно 7см. Тогда расстояние
между плоскостями равно ….
а)
Нельзя
определить
б)
7
в)
Любым в том
числе и 7
27
28. Вариант 2
12. Сторона АВ треугольника АВС лежитв плоскости α. Через середину стороны
АС – точку Р – проведена плоскость ẞ,
параллельная плоскости α и
пересекающая ВС в точке Е. РЕ=7 см.
Тогда длина отрезка АВ равна ….
а)
3,5
б)
14
в)
7
28
29. Вариант 2
13. α║ẞ, α∩ẞ=В, а∩α=А₁, а∩ẞ=А2, b∩α=C₁,b∩ẞ=C2. А₁В:С₁В=2:3. Тогда отношение
А2В:С2В=….
а)
0,6
б)
0,4
в)
1,5
α
А₁
С₁
В
А2
ẞ
а
С2
b
29
29
30. Вариант 2
14. Три отрезка АА₁, ВВ₁, СС₁, нележащие в одной плоскости, имеют
общую середину, тогда плоскости АВС и
А₁В₁С₁ …….

а) пересекаются
б) параллельны
в) нельзя определить
30
Ключи к тесту: Параллельность плоскостей.
1 вариант
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Отв.
в
б
в
а
a
в
а
в
в
а
б
б
в
б
2 вариант
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Отв.
в
б
а
в
а
в
в
в
б
а
б
б
в
б
Литература
Г.И. Ковалева, Н.И. Мазурова Геометрия 10-11 классы. Тесты для текущего и обобщающего
контроля. Изд-во «Учитель», 2009г.
31
Поурочные разработки по геометрии 10 класс
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА
Введение. АКСИОМЫ СТЕРЕОМЕТРИИ И ИХ СЛЕДСТВИЯ
Урок 1. Предмет стереометрии. Аксиомы стереометрии
Урок 2. Некоторые следствия из аксиом
Урок 3. Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий
Урок 4. Решение задач на применение аксиом стереометрии и их следствий
Урок 5. Решение задач на применение аксиом стереометрии и их следствий. Самостоятельная работа
Глава I. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
§ 1. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ, ПРЯМОЙ И ПЛОСКОСТИ
Урок 6. Параллельные прямые в пространстве
Урок 7. Параллельность прямой и плоскости
Урок 8. Решение задач по теме «Параллельность прямой и плоскости»
Урок 9. Решение задач по теме «Параллельность прямой и плоскости»
Урок 10. Решение задач по теме «Параллельность прямой и плоскости»
§ 2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ
Урок 11. Скрещивающиеся прямые
Урок 12. Углы с сонаправленными сторонами. Угол между прямыми
Урок 13. Решение задач по теме «Взаимное расположение прямых в пространстве. Угол между двумя прямыми»
Урок 14. Решение задач по теме «Параллельность прямых и плоскостей»
Урок 15. Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости»
Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости»
§ 3. ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ
Урок 16. Параллельные плоскости
Урок 17. Свойства параллельных плоскостей
§ 4. ТЕТРАЭДР. ПАРАЛЛЕЛЕПИПЕД
Урок 18. Тетраэдр
Урок 19. Параллелепипед
Урок 20. Задачи на построение сечений
Урок 21. Задачи на построение сечений
Урок 22. Закрепление свойств параллелепипеда
Урок 23. Контрольная работа № 1
Урок 24. Зачет № 1
Глава II. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
§ 1. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Урок 25. Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости
Урок 26. Признак перпендикулярности прямой и плоскости
Урок 27. Теорема о прямой, перпендикулярной к плоскости
Урок 28. Решение задач на перпендикулярность прямой и плоскости
Урок 29. Решение задач на перпендикулярность прямой и плоскости
Урок 30. Решение задач на перпендикулярность прямой и плоскости
Решение задач на перпендикулярность прямой и плоскости
§ 2. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Урок 31. Расстояние от точки до плоскости. Теорема о трех перпендикулярах
Урок 32. Угол между прямой и плоскостью
Урок 33. Повторение теории. Решение задач на применение теоремы о трех перпендикулярах (ТПП), на угол между прямой и плоскостью
Урок 34. Решение задач на применение ТТП, на угол между прямой и плоскостью
Урок 35. Повторение (решение задач на теорему о 3-х перпендикулярах)
Урок 36. Угол между прямой и плоскостью (повторение)
§ 3. ДВУГРАННЫЙ УГОЛ. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
Урок 37. Двугранный угол
Урок 38. Признак перпендикулярности двух плоскостей
Урок 39. Прямоугольный параллелепипед
Урок 40. Решение задач на свойства прямоугольного параллелепипеда
Урок 41. Перпендикулярность прямых и плоскостей (повторение)
Урок 42. Решение задач
Урок 43. Контрольная работа по теме «Перпендикулярность прямых и плоскости»
Урок 44. Зачет № 2
Зачет № 2
Глава III. МНОГОГРАННИКИ
§ 1. ПОНЯТИЕ МНОГОГРАННИКА. ПРИЗМА
Урок 45. Понятие многогранника
Урок 46. Призма. Площадь поверхности призмы
Урок 47. Повторение теории, решение задач на вычисление площади поверхности призмы
Урок 48. Решение задач на вычисление площади поверхности призмы
§ 2. ПИРАМИДА
Урок 49. Пирамида
Урок 50. Правильная пирамида
Урок 51. Решение задач по теме «Пирамида»
Урок 52. Решение задач по теме «Пирамида». Самостоятельная работа
Урок 53. Усеченная пирамида. Площади поверхности усеченной пирамиды
§ 3. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Урок 54. Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильных многогранников
Урок 55. Контрольная работе № 3.1 по теме «Многогранники»
Урок 56. Зачет № 3 по теме «Многогранники. Площадь поверхности призмы, пирамиды»
Глава IV. ВЕКТОРЫ В ПРОСТРАНСТВЕ
§ 1. ПОНЯТИЕ ВЕКТОРА В ПРОСТРАНСТВЕ
Урок 57. Понятие векторов. Равенство векторов
Понятие векторов. Равенство векторов
§ 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
Урок 58. Сложение и вычитание векторов. Сумма нескольких векторов
Урок 59. Умножение вектора на число
§ 3. КОМПЛАНАРНЫЕ ВЕКТОРЫ
Урок 60. Компланарные векторы. Правило параллелепипеда
Урок 61. Разложение вектора по трем некомпланарным векторам
Урок 62. Зачет по теме «Векторы в пространстве»
ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ
Урок 63. Итоговое повторение. Аксиомы стереометрии и их следствия
Урок 64. Параллельность прямых и плоскостей
Урок 65. Повторение (теорема о трех перпендикулярах, угол между прямой и плоскостью)
Урок 66. Контрольная работа № 5
Урок 67. Повторение. Векторы в пространстве, их применение к решению задач
Урок 68. Заключительный урок-беседа по курсу геометрии
ПРИЛОЖЕНИЯ
Приложение 1. Контрольные и самостоятельные работы
Урок 5. Самостоятельная работа
Урок 9. Самостоятельная работа обучающего характера
Самостоятельная работа обучающего характера
Урок 10. Проверочная самостоятельная работа
Урок 14. Работа по карточкам
Урок 15. Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости»
Урок 17. Самостоятельная работа
Урок 23. Контрольная работа № 1
Урок 30. Самостоятельная работа
Урок 53. Тест
Урок 55. Контрольная работа № 3.1 по теме «Многогранники»
Урок 63. Теоретический тест с последующей самопроверкой
Урок 66. Контрольная работа № 5
Урок 67. Мини-тест по теории
Приложение 2. Плакаты № 1, 2, 3, 4, рекомендуемые к урокам № 51, 52, 53
Тест с ответами по геометрии для старших классов
1. Раздел геометрии, в котором изучаются свойства фигур в пространстве:
1) стереометрия +
2) планиметрия
3) Евклидова геометрия
4) проективная геометрия
2. Граница шара – это…
1) шар
2) сфера +
3) цилиндр
4) окружность
3. Через любые … точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Через любые … точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
1) 2
2) 3 +
3) 4
4. Если две точки прямой лежат в плоскости, то все точки прямой лежат в … плоскости
1) параллельной
2) прямой
3) диагональной
4) этой +
5. Через … пересекающиеся прямые проходит плоскость, и притом только одна.
1) 2+
2) 3
3) 4
6. Две прямые в пространстве называются …, если они лежат в одной плоскости и не пересекаются.
1) перпендикулярными
2) диагональными
3) параллельными +
4) скрещивающимися
7. Две прямые называются …, если они не лежат в одной плоскости
1) перпендикулярными
2) диагональными
3) параллельными
4) скрещивающимися +
8. Если стороны двух углов соответственно …, то такие углы равны
1) сонаправлены +
2) равны
3) перпендикулярны
4) скрещиваются
9. Поверхность, составленная из двух равных параллелограммов АBCD и А1B1C1D1 и четырех параллелограммов, называется…
1) параллелепипед +
2) октаэдр
3) тетраэдр
4) ромб
10. Прямая называется … к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Прямая называется … к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
1) параллельной
2) соприкасающейся
3) перпендикулярной +
4) сонаправленной
11. Если две прямые перпендикулярны к плоскости, то они …
1) параллельны +
2) перпендикулярны
3) лежат на диагонали
4) лежат на прямой
12. Через … точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
1) одну
2) любую +
3) параллельную
4) диагональную
13. Перпендикуляр, проведенный из данной точки к плоскости, … любой наклонной, проведенной из той же точки к этой плоскости.
1) больше
2) равен
3) меньше +
4) параллелен
14. Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется …
1) расстоянием между параллельными плоскостями +
2) расстоянием между прямой и параллельной ей плоскостью
3) расстоянием между скрещивающимися прямыми
4) расстоянием между сонаправленными плоскостями
15. Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости. В этом случае расстояние от произвольной точки прямой до плоскости называется…
Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости. В этом случае расстояние от произвольной точки прямой до плоскости называется…
1) расстоянием между параллельными плоскостями
2) расстоянием между прямой и параллельной ей плоскостью +
3) расстоянием между скрещивающимися прямыми
4) расстоянием между сонаправленными плоскостями
16. Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется…
1) расстоянием между параллельными плоскостями
2) расстоянием между прямой и параллельной ей плоскостью
3) расстоянием между скрещивающимися прямыми +
4) расстоянием между сонаправленными плоскостями
17. Фигура, образованная прямой и двумя полуплоскостями с общей границей, не принадлежащими одной плоскости
1) двугранный угол +
2) параллельный угол
3) перпендикулярный угол
4) плоскостной угол
18. Полуплоскости, образующие двугранный угол, называются…
1) сторонами
2) гранями +
3) параллелями
4) диагоналями
19. Двугранный угол называется прямым, если он равен…
Двугранный угол называется прямым, если он равен…
1) 45 градусов
2) 90 градусов +
3) 110 градусов
4) 180 градусов
20. Двугранный угол называется острым, если он …
1) меньше 90 градусов +
2) больше 90 градусов
21. Двугранный угол называется тупым, если он …
1) меньше 90 градусов
2) больше 90 градусов +
22. Две пересекающиеся плоскости называются …, если угол между ними равен 90 градусов
1) параллельными
2) сонаправленными
3) соприкасающимися
4) перпендикулярными +
23. Диагонали прямоугольного параллелепипеда …
1) параллельны
2) перпендикулярны
3) равны
4) не равны
24. Сумма плоских углов выпуклого многогранного угла … 360о
1) больше
2) меньше +
3) равна
25. Точка фигуры, не являющаяся граничной, называется…
1) внутренней +
2) ограниченной
3) связной
4) определенной
26. Фигура называется …, если любые две ее точки можно соединить непрерывной линией, целиком принадлежащей данной фигуре.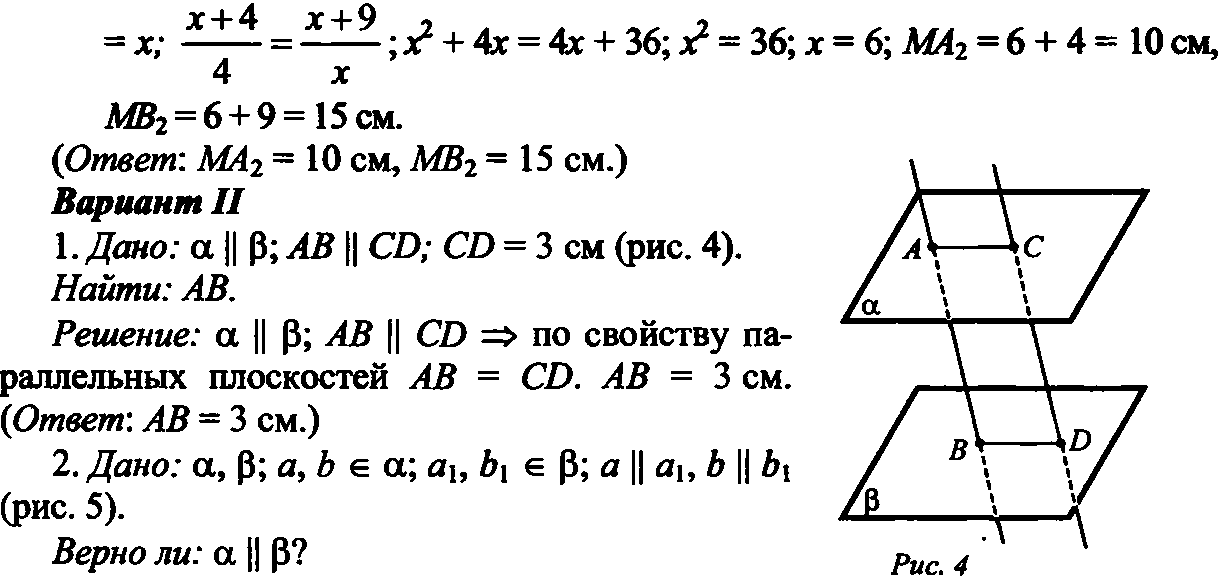
1) внутренней
2) ограниченной
3) связной +
4) определенной
27. Фигура называется …, если ее можно заключить в какую-нибудь сферу.
1) внутренней
2) ограниченной +
3) связной
4) определенной
28. Точка фигуры, не являющаяся граничной, называется … точкой фигуры.
1) внутренней +
2) внешней
3) наружной
4) сквозной
29. Множество всех граничных точек фигуры называется ее …
1) стороной
2) границей
3) диагональю
4) телом
30. В любом выпуклом многограннике сумма числа граней и числа вершин больше числа ребер на …
1) 2+
2) 5
3) 7
4) 9
Урок 8. перпендикулярность прямой и плоскости — Геометрия — 10 класс
Геометрия, 10 класс
Урок № 8 Перпендикулярность прямой и плоскости
Перечень вопросов, рассматриваемых по теме
- Ввести понятие перпендикулярных прямых в пространстве;
- Доказать лемму о перпендикулярности двух параллельных прямых;
- Решать задачи по теме.

Глоссарий по теме
Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90. Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
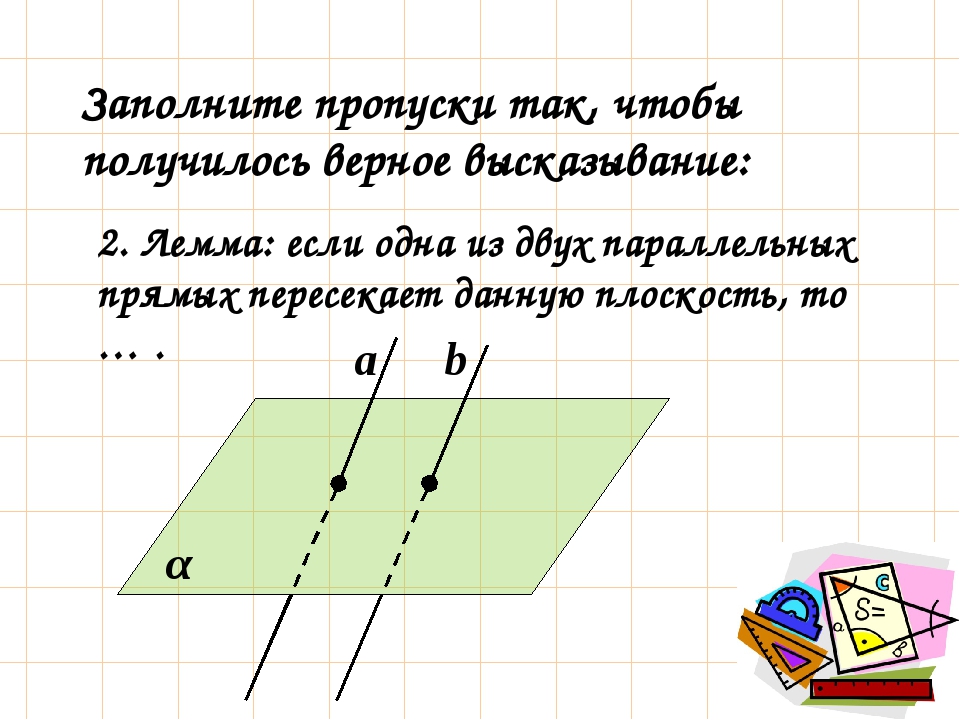
Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости
Теорема о прямой перпендикулярной к плоскости. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.
Основная литература:
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл. Базовый и профильный уровень. М.: Просвещение, 2015. С.1-10.
Геометрия 10-11 кл. Базовый и профильный уровень. М.: Просвещение, 2015. С.1-10.
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 9 класса. Базовый и профильный уровень
Дополнительная литература:
Зив Б.Г. Геометрия. Дидактические материалы. 10-11 класс М.: Просвещение, 2015.
Открытые электронные ресурсы:
Перпендикулярность прямой и плоскости. http://school-collection.edu.ru // Единая коллекция цифровых образовательных ресурсов.
Перпендикулярность прямой и плоскости. https://www.yaklass.ru // Я-класс. Образовательный портал Сколково.
Теоретический материал для самостоятельного изучения
Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой..
Доказательство:
Дано: a ‖ b, a ⊥ c
Доказать: b ⊥ c
Через точку М пространства, не лежащую на данных прямых, проведем прямые МА и МС, параллельные соответственно прямым а и с. Так как а ⊥ с, то ∠АМС=90о.
Так как а ⊥ с, то ∠АМС=90о.
Так как b ‖ a, а а ‖ МА, то b ‖ МА.
Итак, прямые b и с параллельны соответственно прямым МА и МС, угол между ними равен 90о, т.е. b ‖ МА, с ‖ МС, угол между МА и МС равен 90о
Это означает, что угол между прямыми b и с также равен 90о, то есть b ⊥ с.
Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Доказательство:
Дано: a ‖ а1, а ⊥ α
Доказать, что а1 ⊥ α
Проведем какую-нибудь прямую x в плоскости α, т.е. x ∊ α.Так как а ⊥ α, то а ⊥ x.
По лемме о перпендикулярности двух параллельных прямых к третьей а1 ⊥ x.
Таким образом, прямая а1перпендикулярна к любой прямой, лежащей в плоскости α, т.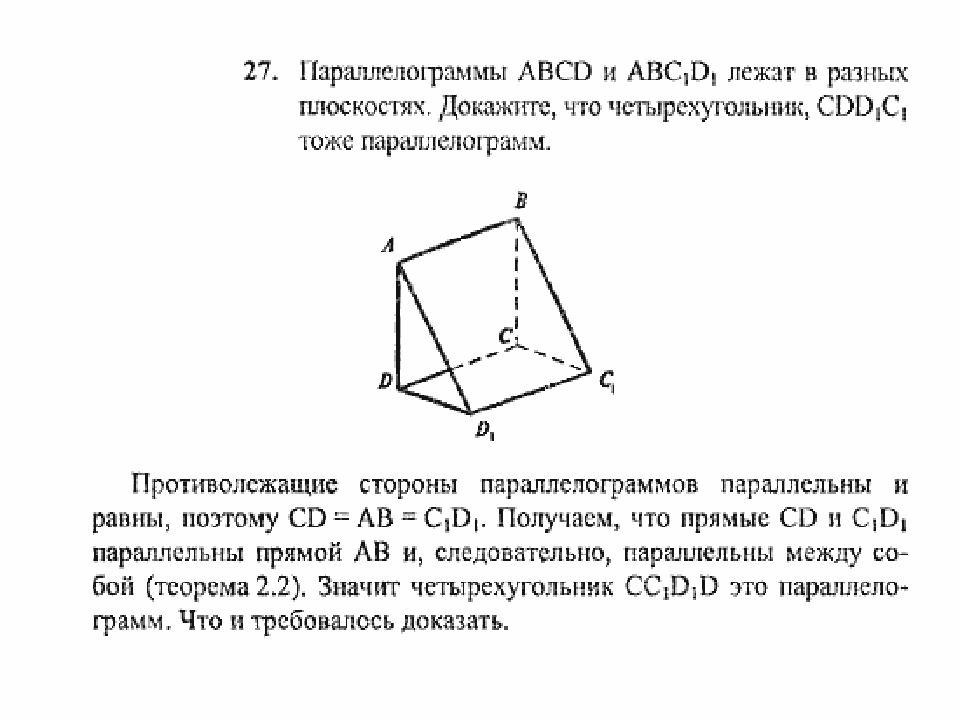 е. а1 ⊥ α
е. а1 ⊥ α
Теорема. Ели две прямые перпендикулярны плоскости, то они параллельны.
Дано: а ⊥ α, b ⊥ α
Доказать, что а ‖ b
Доказательство:
Через какую-нибудь точку М прямой b проведем прямую b1, параллельную прямой а.
М ∊ b, M ∊b1, b1 ‖ a. По предыдущей теореме b1 ⊥ α.
Докажем, что прямая b1 совпадает с прямой b. Тем самым будем доказано, что а ‖ b. Допустим, что прямые b1и b не совпадают. Тогда в плоскости β, содержащей прямые b и b1, через точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости α и β. Но это невозможно, следовательно, а ‖ b, т.е. b ∊ β, b1 ∊ β, α β = c (невозможно)→ а ‖ b
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.
Теорема. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Рис. 2.
Доказательство.
Пусть дана плоскость α и точка М (см. рис. 2). Нужно доказать, что через точку М проходит единственная прямая с, перпендикулярная плоскости α.
Проведем прямую а в плоскости α (см. рис. 3). Согласно доказанному выше утверждению, через точку М можно провести плоскость γ перпендикулярную прямой а. Пусть прямая b – линия пересечения плоскостей α и γ.
Рис. 3.
В плоскости γ через точку М проведем прямую с, перпендикулярную прямой b.
Прямая с перпендикулярна b по построению, прямая с перпендикулярна а (так как прямая а перпендикулярна плоскости γ, а значит, и прямой с, лежащей в плоскости γ).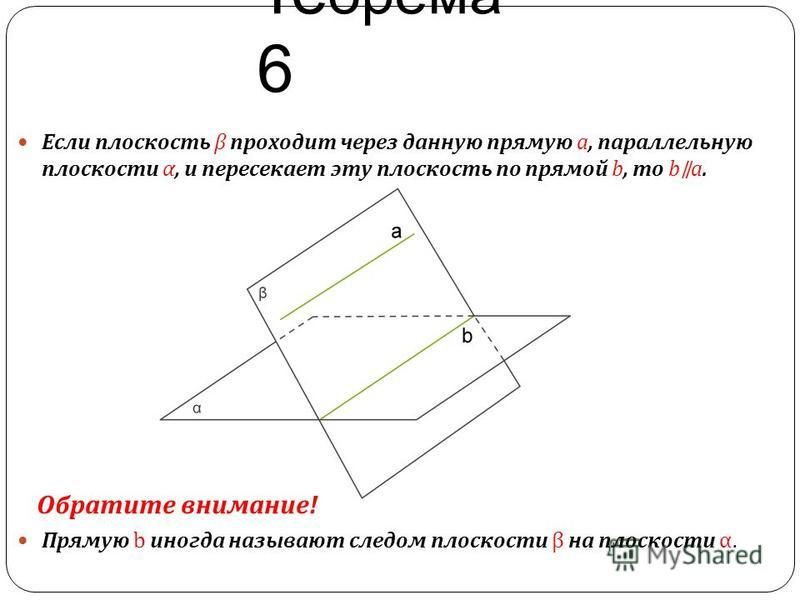 Получаем, что прямая с перпендикулярна двум пересекающимся прямым из плоскости α. Значит, по признаку перпендикулярности прямой и плоскости, прямая с перпендикулярна плоскости α. Докажем, что такая прямая с единственная.
Получаем, что прямая с перпендикулярна двум пересекающимся прямым из плоскости α. Значит, по признаку перпендикулярности прямой и плоскости, прямая с перпендикулярна плоскости α. Докажем, что такая прямая с единственная.
Предположим, что существует прямая с1, проходящая через точку М и перпендикулярная плоскости α. Получаем, что прямые с и с1 перпендикулярны плоскости α. Значит, прямые с и с1 параллельны. Но по построению прямые с и с1пересекаются в точке М. Получили противоречие. Значит, существует единственная прямая, проходящая через точку М и перпендикулярная плоскости α, что и требовалось доказать.
Теоретический материал для углубленного изучения
Теорема о прямой перпендикулярной к плоскости. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.
Рис. 1.
1.
Доказательство (см. рис. 1)
Пусть нам дана прямая а и точка М. Докажем, что существует плоскость γ, которая проходит через точку М и которая перпендикулярна прямой а.
Через прямую а проведем плоскости α и β так, что точка М принадлежит плоскости α. Плоскости α и β пересекаются по прямой а. В плоскости α через точку М проведем перпендикуляр MN (или р) к прямой а, . В плоскости β из точки N восстановим перпендикуляр q к прямой а. Прямые р и q пересекаются, пусть через них проходит плоскость γ. Получаем, что прямая а перпендикулярна двум пересекающимся прямым р и q из плоскости γ. Значит, по признаку перпендикулярности прямой и плоскости, прямая а перпендикулярна плоскости γ.
Примеры и разборы решения заданий тренировочного модуля
Пример 1
Выбор элемента из выпадающего списка
Выпишите ребра, перпендикулярные плоскости (DC).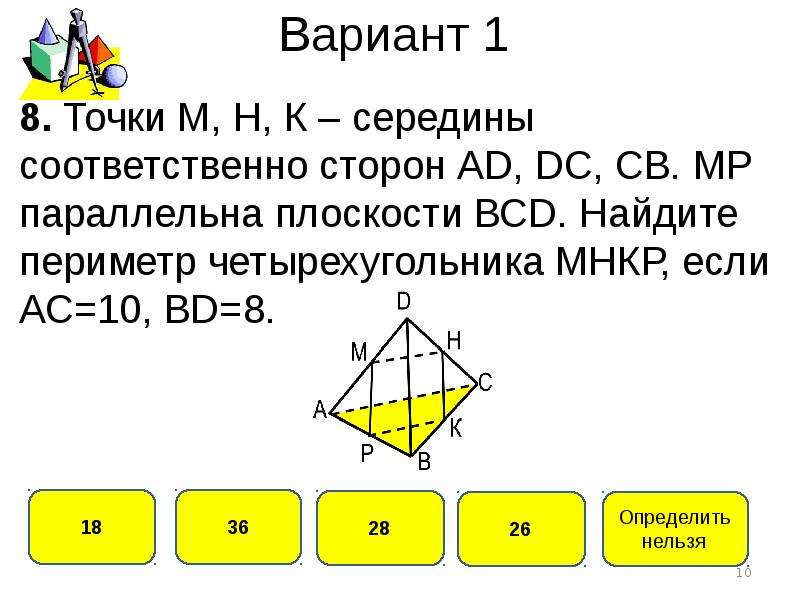
- AD, A1D1, BC, B1C1
- AD, AC, AD1,
- ВС, ВА.
Правильный вариант/варианты (или правильные комбинации вариантов):
Неправильный вариант/варианты (или комбинации):
Все остальные
Подсказка: в кубе все углы по . Плоскость (DC), проходит через грань куба DC.
- Разбор задания: Куб – это геометрическая фигура у которой все углы прямые, следовательно нужно увидеть ребра которые перпендикулярны к плоскости (DC), к грани куба (DDC).Эти ребра — AD, A1D1, BC, B1C1
Пример 2
Ребус – соответствия.
Закончите предложение, чтобы получилось верное утверждение.
Утверждение:
- Две прямые называются перпендикулярными, если …..
- Если плоскости перпендикулярна одной из двух параллельных прямых, то она ……
Варианты ответов:
- параллельны
- один
- она перпендикулярна к любой прямой, лежай в этой плоскости.

- перпендикулярна плоскости.
Правильный вариант/варианты (или правильные комбинации вариантов):
Две прямые называются перпендикулярными, если … | угол между ними равен 90 |
Если плоскость перпендикулярна одной из двух параллельных прямых, то она … | перпендикулярна и другой |
Неправильный вариант/варианты (или комбинации):
Все остальные.
Подсказка:
Лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к третьей прямой.
Теорема: если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Параллельность прямых и плоскостей (10 класс)
Методическая разработка урока геометрии в 10 класса
Параллельность прямых и плоскостей
Нетикова Маргарита Анатольевна,
учитель математики ГБОУ школа №471
Выборгского района Санкт-Петербурга.
Предмет математики настолько серьёзен,
что не надо упускать случая сделать
его немного занимательным.
Б.Паскаль
Тип урока:урок обобщения и систематизации знаний
Форма урока:урок проводится в форме коллоквиума, обеспечивающей повторение и систематизацию учебного материала, контроль знаний учащихся, их коррекцию.
Класс заранее делится на 6 групп по 5 человек.
Урок разбит на 5 блоков:
1. Аксиомы стереометрии
2. Взаимное расположение прямых в пространстве.
3. Взаимное расположение в пространстве прямой и плоскости.
4. Взаимное расположение в пространстве двух плоскостей.
5. Задачи на построение сечений.
Каждый блок, кроме пятого, состоит из учебных элементов (УЭ). УЭ — это последовательные шаги, алгоритм работы учащихся, с которым школьник работает непосредственно:
УЭ — это последовательные шаги, алгоритм работы учащихся, с которым школьник работает непосредственно:
1) актуализация знаний
2) доказательство теорем
3) решение задач.
Ученики выполняют задания, составленные учителем, с той степенью понимания, осмысления и запоминания, которое соответствует индивидуальным возможностям школьника.
Урок дает возможность определить уровень усвоения материала и быстро выявить пробелы в знаниях, создает условия для мотивации, повышения интереса к предмету, способствует развитию и совершенствованию самостоятельной деятельности учащихся; обеспечивает непрерывное образование и устраняет перегрузку домашнего задания.
У учащихся есть возможность:
— работать самостоятельно с дифференцированной программой;
— вернуться к учебному материалу, если в этом есть необходимость;
— получить консультацию и дозированную персональную помощь от учителя или члена группы.
На уроке создается комфортная обстановка:
— индивидуальный темп (для сильных учащихся предлагаются дополнительные задачи),
— «мягкий» контроль (возможность получить помощь товарища).
Учащиеся развивают личностные качества школьника (самостоятельность; умение ставить цели, планировать, организовывать и оценивать свою деятельность). Для самостоятельной оценки деятельности учащимся предлагаются критерии, с помощью которых ученики подсчитывают свои баллы и после 5 блока выставляют себе оценку самостоятельно. Во время самостоятельной работы учитель проверяет объективность выставленных оценок.
Четкая структура урока, дает учителю возможность «видеть» весь класс, работать индивидуально с каждым учеником, оказывать помощь отстающим.
Результат — повышение качества обученности учащихся.
Роль преподавателя на уроке заключается в управлении процессом обучения, консультировании, помощи и поддержке учеников.
Цель урока: обобщить и систематизировать знания и умения учащихся по данной теме, подготовиться к контрольной работе.
Задачи урока
Обучающие: организовать работу учащихся по систематизации знаний основных теоретических вопросов темы;
закрепить и углубить знания и умения учащихсяприменять аксиомы стереометрии, следствия из аксиом, теоремы о параллельности прямых, прямой и плоскости, параллельности плоскостей.
Развивающие:создать условия для развития познавательной активности учащихся, познавательного интереса к предмету;
развивать навыки самостоятельной деятельности учащихся;
развивать навыки самоконтроля;
развивать активность учащихся,
формировать учебно-познавательные действия, коммуникативные, исследовательские навыки учащихся, умение анализировать и устанавливать связь между элементами темы.
Воспитывающие: создать условия успешности ученика на уроке;
воспитывать культуру умственного труда; способность к самоанализу, рефлексии;
развивать умение рецензировать и корректировать ответы товарищей.
воспитывать умение критически относиться к результатам деятельности;
обеспечить гуманистический характер обучения;
Планируемые результаты:
Предметные: знать аксиомы, теоремы по данной теме и уметь их доказывать, применять при решении типовых задач.
Личностные: уметь отстаивать свою точку зрения и работать в группе.
Метапредметные:уметь планировать и оценивать процесс и результат своей деятельности, обрабатывать информацию.
Педагогические технологии: элементы обучения в сотрудничестве (работа в группах) и коллективного взаимообучения.
Оборудование: интерактивная доска, компьютер, раздаточные материалы.
Содержание учебного материала.
1.Аксиомы стереометрии и следствия из них.
2.Признаки параллельности прямых, прямой и плоскости, скрещивающихся прямых; признак и свойства параллельных плоскостей.
3.Задачи на построение сечений тетраэдра и параллелепипеда.
4.Задачи на доказательство параллельности прямых, прямой и плоскости, скрещивающихся прямых.
Структура урока.
1.Организационная часть.
2.Мотивационная часть.
3.Работа по блокам:
«Аксиомы стереометрии»
«Взаимное расположение прямых в пространстве»
«Взаимное расположение в пространстве прямой и плоскости»
« Взаимное расположение в пространстве двух плоскостей»
« Задачи на построение сечений»
4.Подведение итогов урока
5. Домашнее задание.
Домашнее задание.
6.Рефлексия урока.
Технологическая карта урока геометрии в 10 классе по теме:« Параллельность прямых и плоскостей»
|
Этапы урока |
Задачи этапа |
Деятельность учителя |
Деятельность учащихся |
УУД |
|
1.Организационная часть
|
Создание рабочего настроения в начале урока, объяснение правил. |
Здоровается с учениками, проверяет их подготовку к уроку, отмечает отсутствующих, записывает на доске дату, сообщает правила урока |
Готовятся к работе на уроке, приветствуют учителя |
Регулятивные: организация учебной деятельности. |
|
2.Мотивационная часть
|
Создание ситуации успеха. |
Объясняет необходимость и важность данного урока |
Слушают учителя |
Регулятивные:
организация учебной деятельности. |
|
3.Обобщающее повторение (работа по блокам) |
Повторить и систематизировать изученный теоретический материал, рассмотреть основные типы задач по каждому блоку. |
Корректирует и организовывает деятельность учащихся на каждом блоке, собирает бланки с решениями и ответами |
Отвечают на вопросы, доказывают теоремы, выполняют тесты и решают задачи в своих командах. |
Коммуникативные: умение прислушиваться к мнению окружающих. Регулятивные:
оценивание результатов своей деятельности. Познавательные: анализ условий поставленной задачи и поиск её рационального решения. Личностные: оценивание уровня усвоения материала и своих возможностей.
|
|
4.Подведение итогов урока
|
Осознание каждым учащимся: чему, как и зачем он научился сегодня на уроке, и с какими знаниями и умениями он должен прийти на следующий урок. |
Слушает комментарии к уроку у |
|
Регулятивные: умение оценить качество и уровень усвоения |
|
5.
|
Комментарии по домашнему заданию с целью его успешного выполнения. |
Раздаёт каждой команде текст демонстрационного варианта контрольной работы |
Записывают домашнее задание в дневники и задают по нему вопросы. |
|
|
6.Рефлексия урока.
|
Заставить детей задуматься в конце урока о своём настроении, эмоциональном состоянии и результатах взаимодействия с другими участниками образовательного процесса. |
Выходя из кабинета, оцените по пятибалльной шкале своё настроение в конце урока и поставьте оценку на доске. |
Собирают свои вещи, ставят оценки на доске цветными мелками. |
Коммуникативные: умение грамотно и честно выражать свои мысли. Регулятивные: умение оценить достигнутый результат. Личностные: чувство гордости за хорошо проделанную работу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ход урока
1. Организационная часть.
Организационная часть.
Сегодня мы с вами должны подняться ещё на одну ступеньку вверх, «преодолевая» задачи, которые будут рассматриваться на уроке. Мы начинаем повторение темы «Параллельность прямых и плоскостей в пространстве» (слайд 1). Наша задача вспомнить все, что мы знаем по этой теме.
2. Мотивационная часть.
Мы должны закрепить и углубить наши знания по этой теме.
Эти знания пригодятся нам для решения практических задач, для успешной сдачи ЕГЭ.
Вы должны научиться анализировать и устанавливать связь между элементами темы. Развить свою активность, сформировать учебно — познавательные действия, коммуникативные навыки. Хотелось бы создать условия вашей успешности на уроке; чтобы вы проявили способность к самоанализу, рефлексии, умение рецензировать и корректировать ответы товарищей. А каковы пути и средства достижения этих целей?
Домашнее задание к сегодняшнему уроку заключалось в том, чтобы вы повторили пункты 1- 12, просмотрели и еще раз разобрали задачи, которые мы решали в этих пунктах для обобщения и закрепления темы «Параллельность прямых и плоскостей в пространстве».
3.Обобщающее повторение.
Блок 1. Аксиомы стереометрии
Цели блока:
— повторить аксиомы стереометрии и применение их при решении задач ;
-повторить следствия из аксиом;
— закрепить умение применять аксиомы стереометрии и следствия из аксиом при решении задач;.
Актуализация опорных знаний. Проведем теоретическую разминку.
Учащиеся вспоминают учебный материал.
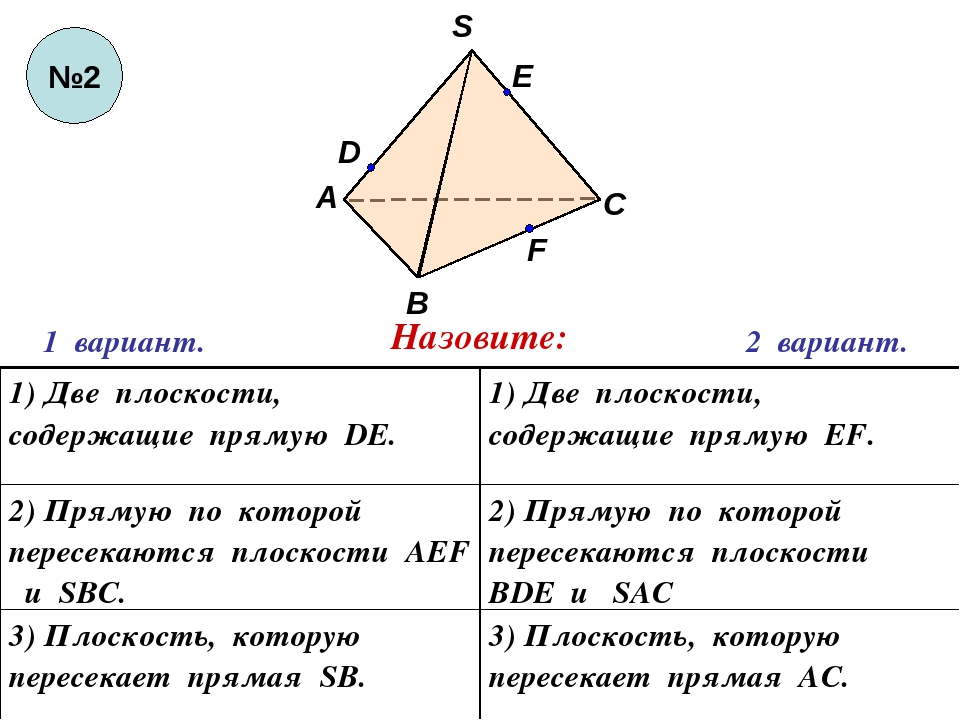
- Посмотрите на чертёж (слайды 2,3).Какие утверждения они иллюстрируют? Сформулируйте их.
В ходе беседы выделяются существенные моменты теории:
а) разъяснение содержания аксиом;
б) чтение учащимися текста аксиом;
в) выполнение чертежа;
Вот и название первого блока нашего урока: Аксиомы стереометрии (слайд 4)
2. Как формулируются следствия из этих аксиом? (слайды 4,5).Кто хочет доказать эти теоремы?
Как формулируются следствия из этих аксиом? (слайды 4,5).Кто хочет доказать эти теоремы?
После обсуждения теоретических вопросовзакрепление полученных знаний.
Задание 1. Как в пространстве можно однозначно задать плоскость?
Учащиеся самостоятельно выполняют задание (проверяем на доске), советуясь в своих командах.
|
Способы задания плоскостей |
Рисунок |
|
I. По трем точкам, не лежащим на одной прямой |
|
|
2. По прямой и не принадлежащей ей точке. |
|
|
3. |
|
|
4. По двум параллельным прямым. |
|
Задание 2. Ответьте на вопросы (слайд 6). Каждая команда отвечает на свой вопрос.
Сколько плоскостей можно провести через выделенные элементы?
1) 2) 3)
4) 5) 6)
Задание 3(слайд 7) Три вершины параллелограмма лежат в некоторой плоскости. Можно ли утверждать, что и его четвертая вершина лежит в этой плоскости?
Команды обсуждают решение и озвучивают ответ.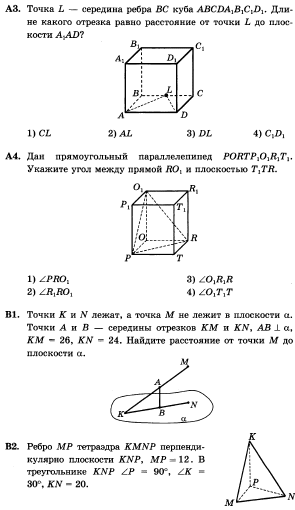
Задание 4: тест по вариантам(для каждого ученика)
|
Тест «Аксиомы стереометрии» Вариант 1 1.Верно ли: любые три точки лежат в одной плоскости. 2.Вставьте пропущенные слова:Единственную плоскость можно задать через три точки, при этом они … на одной прямой.
3.Пересечением двух плоскостей является А) точка Б) прямая В) отрезок
|
Тест «Аксиомы стереометрии» Вариант 2
1.Верно ли: любые четыре точки лежат в одной плоскости. 2.Вставьте пропущенные слова:Если … точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости.
А) две параллельные прямые Б) две скрещивающиеся прямые В) три точки
|
|
Тест «Аксиомы стереометрии» Вариант 3 1.Верно ли: любые четыре точки не лежат в одной плоскости. 2.Вставьте пропущенные слова:Две различные плоскости могут иметь только одну общую …
3.Сколько должно быть общих точек у прямой с плоскостью, чтобы она лежала в этой плоскости? А) одна Б) две В) три |
Тест «Аксиомы стереометрии» Вариант 4
2.Вставьте пропущенные слова:две прямые, параллельные некоторой … , могут пересекаться.
3.Сколько плоскостей задают две пересекающиеся прямые? А) одну плоскость Б) две плоскости В) бесконечно много плоскостей |
|
Тест «Аксиомы стереометрии» Вариант 5
2.Вставьте пропущенные слова:две прямые, параллельные некоторой … , параллельны. 3.Через какие из перечисленных фигуры можно провести единственную плоскость? А) Через три точки Б) Через прямую и не лежащую на ней точку В) Через отрезок |
Тест «Аксиомы стереометрии» Вариант 6
2.Вставьте пропущенные слова: две прямые, параллельные некоторой … , могут пересекаться.
3. Две прямые пересекаются. Что это значит? А) Они имеют две общие точки. Б) Они имеют одну общую точку. В) Они лежат в одной плоскости. |
Блок 2. Взаимное расположение прямых в пространстве.(слайд 8)
Цель блока:
— повторить и обобщить знания по теме «Параллельные прямыев пространстве»;
— систематизировать полученные знания.
Актуализация опорных знаний. Проведем теоретическую разминку.
— Взаимное расположение двух прямых в пространстве (слайд 9)
а ççв аÇв аи в скрещивающиеся
— Какие прямые в пространстве называются параллельными? (Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются)
— Сформулируйте признак параллельности прямых в пространстве. (Две прямые, параллельные третьей прямой, параллельны).
— Какие прямые в пространстве называются скрещивающимися? (Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости и не пересекаются)
-Сформулируйте и докажите признак скрещивающихся прямых.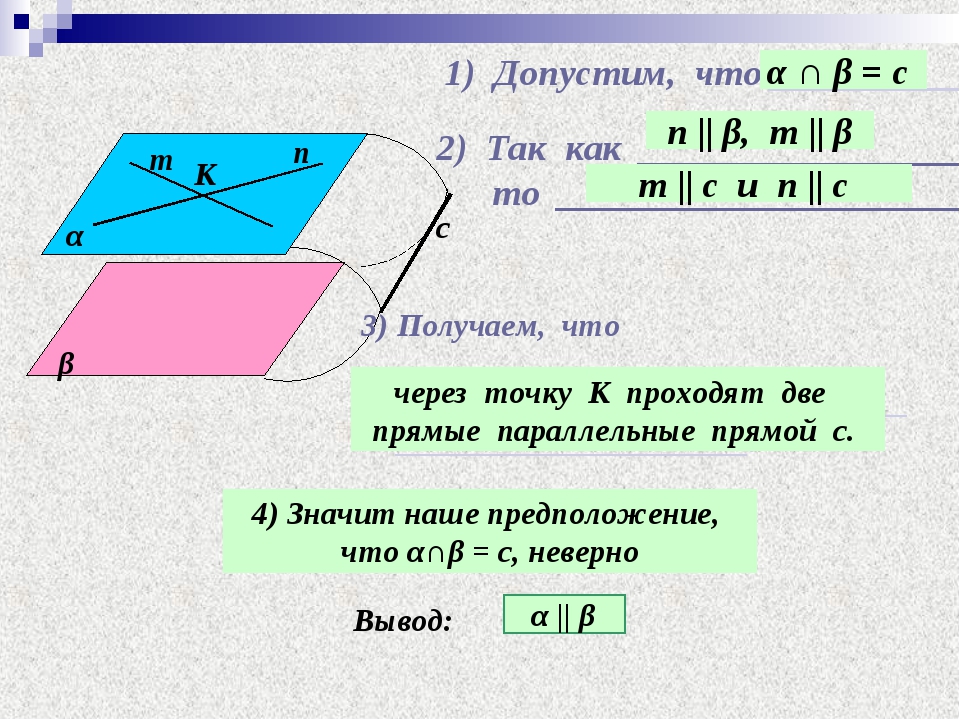
Один ученик доказывает признак параллельности прямых в пространстве (слайд 10), второй ученик доказывает признак скрещивающихся прямых (слайд 10) по чертежу на слайде.
После обсуждения теоретических вопросовзакрепление полученных знаний.
Задание Каждая команда получает карточку с заданием, обсуждает, а затем представляет своё решение (приложение 1)
Блок 3. Взаимное расположение в пространстве прямой и плоскости.(слайд 11)
Цель блока:
— повторить и обобщить знания по теме «Взаимное расположение в пространстве прямой и плоскости»;
— систематизировать полученные знания.
Актуализация опорных знаний. Проведем теоретическую разминку.
— Взаимное расположение в пространстве прямой и плоскости (слайд 12)
а Ìα аççα аÇα
— Какие прямая и плоскость называются параллельными? (Прямая и плоскость называются параллельными, если они не пересекаются)
— Сформулируйте признак параллельности прямой и плоскости в пространстве. (Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.)
Ученик доказывает признак параллельности прямой и плоскости в пространстве по чертежу на слайде (слайд 13).
После обсуждения теоретических вопросовзакрепление полученных знаний.
Задание 1 задача по готовому чертежу (слайд 14)
Задание 2.Тест. Учащиеся получают задание и выполняют его всей командой (приложение 2). Готовое решение сдают учителю.
Блок 4. Взаимное расположение в пространстве двух плоскостей (слайд 15).
Цель блока:
— повторить и обобщить знания по теме «Взаимное расположение в пространстве двух плоскостей»;
— систематизировать полученные знания.
Актуализация опорных знаний. Проведем теоретическую разминку.
— Взаимное расположение в пространстве двух плоскостей (слайд 16)
α Çβ
α иβ — совпадают α ççβ
— Какие плоскости называются параллельными? (Две плоскости называются параллельными, если они не пересекаются)
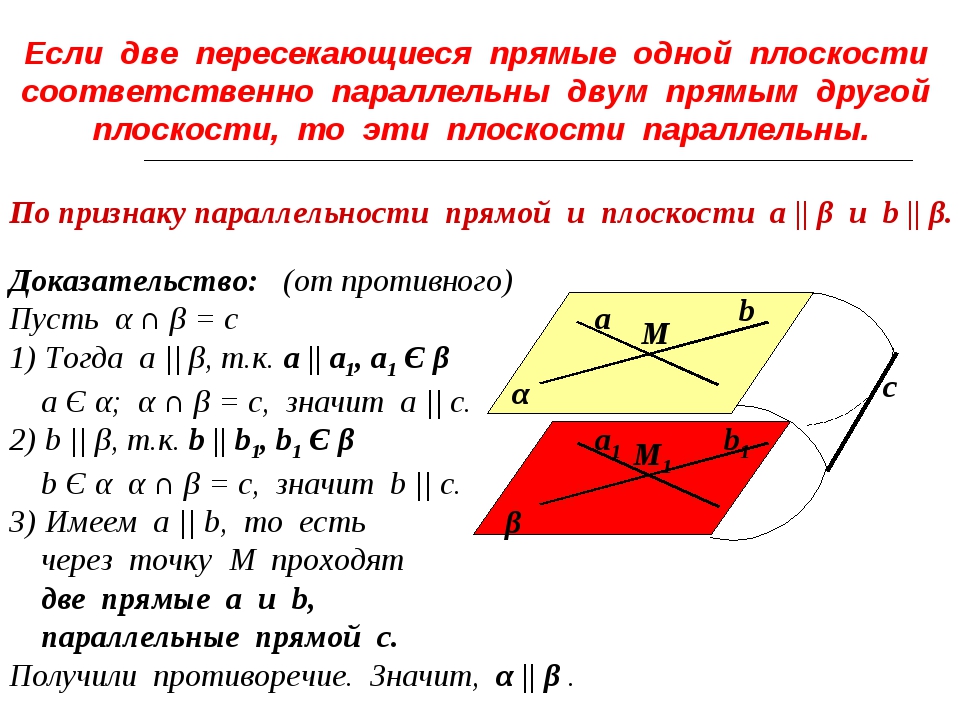
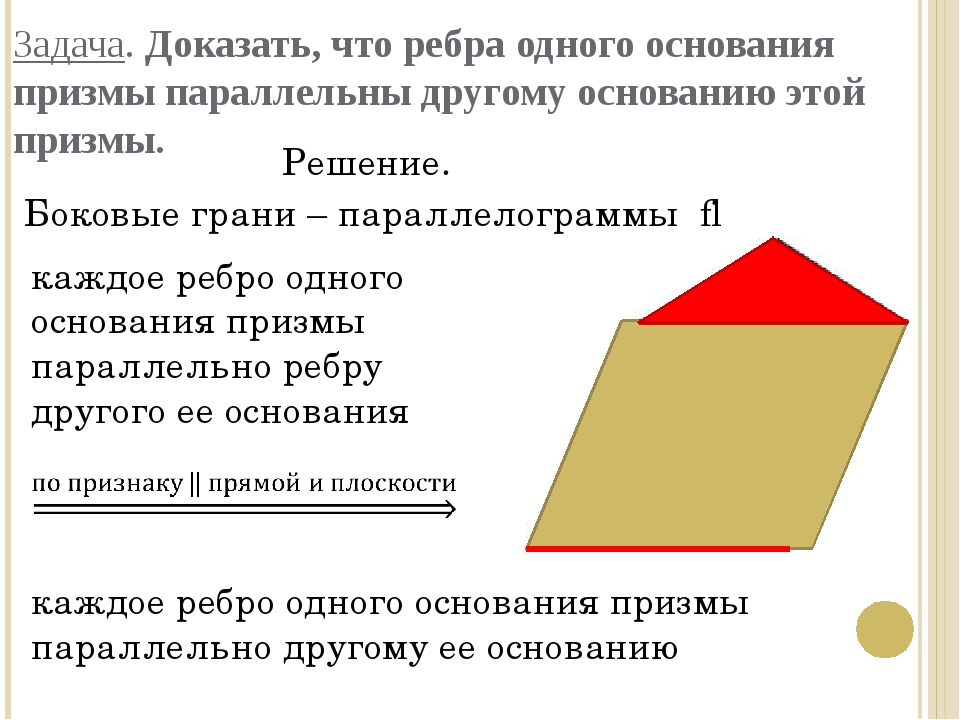
— Сформулируйте и докажите признак параллельности плоскостей в пространстве.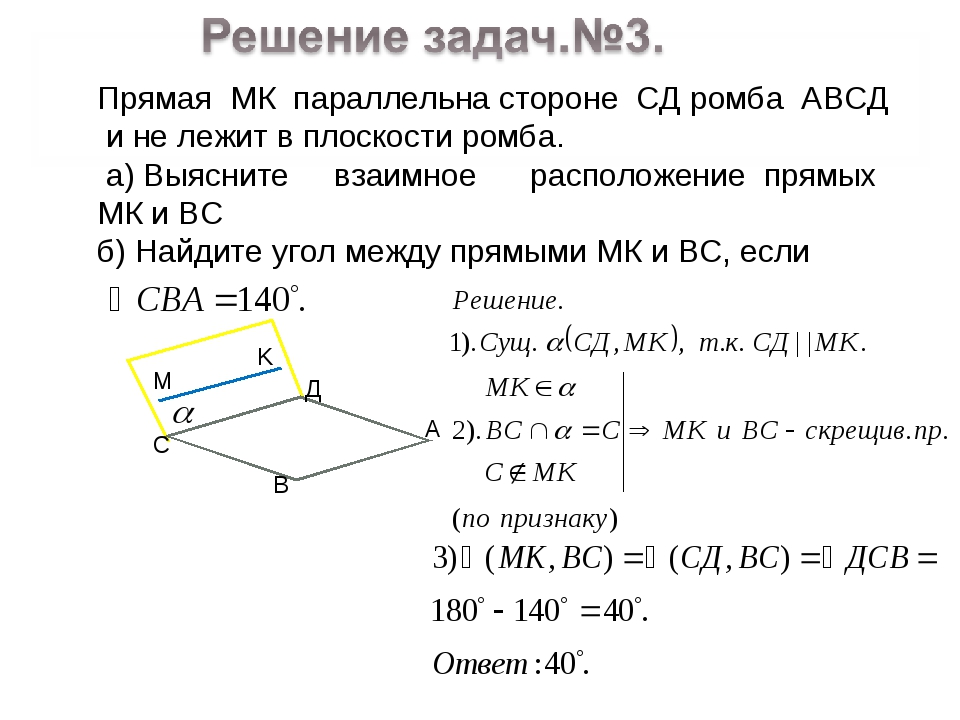 (Если две пересекающиеся прямые одной плоскости параллельны двум прямым другой плоскости, то эти плоскости параллельны) (слайд 17)
(Если две пересекающиеся прямые одной плоскости параллельны двум прямым другой плоскости, то эти плоскости параллельны) (слайд 17)
— Сформулируйте свойство параллельных плоскостей (слайд 18)
После обсуждения теоретических вопросовзакрепление полученных знаний.
Задание 1 Задача по готовому чертежу (слайд 19)
Задание 2 Задача по готовому чертежу каждой команде на карточке (приложение 3)
Блок 5. Построение сечений тетраэдра и параллелепипеда(слайды 20,21).
Каждая команда получает чертежи тетраэдра и параллелепипеда, на них отмечает точки, через которые надо провести сечение, и отдаёт их другой команде. Задание выполняется коллективно, после чего сдаётся учителю.
4. Подведение итогов урока.
Молодцы! Трудились с полной отдачей, ощутили радость своего труда. Оценки за урок вы узнаете после проверки ваших работ.
5. Рефлексия.
У каждого ученика в начале урока лежали на столах смайлики. В конце урока они сдают учителю тот смайлик, который соответствовал их настроению.
|
Мне всё понятно. Вопросов нет. |
Мне ничего не понятно. |
У меня есть вопросы. |
|
|
|
|
Перед вами лежат смайлики. Если у вас на уроке все получалось правильно, если остались от урока положительные эмоции, урок был интересным, то поднимите радостный смайлик. Если вы таскали тяжёлые камни, если всё было не понятно, то поднимите плачущий смайлик, если в течение урокавы добросовестно выполняли свою работу, но у вас возникали проблемы – поднимите читающий смайлик.
Если у вас на уроке все получалось правильно, если остались от урока положительные эмоции, урок был интересным, то поднимите радостный смайлик. Если вы таскали тяжёлые камни, если всё было не понятно, то поднимите плачущий смайлик, если в течение урокавы добросовестно выполняли свою работу, но у вас возникали проблемы – поднимите читающий смайлик.
Оцените свою активность на уроке по шкале от 0-5.
6. Задание на дом.
Демонстрационный вариант контрольной работы
Приложение 1
|
Команда 1
Прямая а не лежит в плоскости параллелограмма ABCD. прямых aи BC,если aIIAB
|
Команда 2
1.Прямая а не лежит в плоскости ABC.Определите взаимное расположение прямых aи AC,если aIIAB
|
Команда 3
1.
|
|
Команда 4
1.Дан тетраэдр ABCD. Определите взаимное расположение прямых ADи BC.
|
Команда 5
1.
|
Команда 6
1.Определите взаимное расположение прямых ANи CM, если NM∩(ABC)
|
Приложение 2
|
Команда 1(4)
1. а) взаимное расположение точно определить нельзя; б) скрещиваются или параллельны; в) параллельны или пересекаются; г) совпадают;
2.Прямые а и b параллельны одной плоскости . Как расположены прямые а и b относительно друг друга? а) параллельны б) пересекаются в) скрещиваются
|
Команда 2(5)
1. а) Две прямые называются параллельными, если они не имеют общих точек; б) две прямые, параллельные третьей прямой, параллельны; в) две прямые, перпендикулярные третьей прямой, параллельны;
2. Прямая а лежит в плоскости. Как расположена относительно плоскости прямая b, если b параллельна а? а) перпендикулярно б) параллельно в) пересекает
|
Команда 3(6)
1.Прямая а, параллельная прямой b, пересекает плоскость α. а) прямые а и с пересекаются; б) прямая с лежит в плоскости α; в) прямые а и с скрещиваются; г) прямая bлежит в плоскости α; д) прямые а и с параллельны.
2. Сколько плоскостей можно провести через две данные точки? а) одну б) две в) много
|
|
Приложение 3
|
||
|
Команда 1
α II β,
a∩b=F. AF:FN=1:3, AB=4. Найти MN.
|
Команда 2
α II β, RK∩NS=M, KM:KR=1:3,NS=9. Найти MS.
|
Команда3
α II β,
a∩b=F. AF:FN=2:5, AB=10. НайтиMN.
|
|
Команда 4
α II β, RK∩NS=M, KN:RS=1:3,MK=2. Найти KR.
|
Команда 5
α II β,
a∩b=F. AB:MN=2:3, AF=10. Найти FN.
|
Команда 6
α II β, RK∩NS=M, MN:NS=1:3,MK=4. НайтиMR.
|
Литература.
1. Селевко Г.К. Современные образовательные технологии: Учебное пособие. — М.: ЮНИТИ-ДАНА, 1998. — 344с.
2. Голощёкина Л.П., Збаровский B.C. Модульная технология обучения: Методические рекомендации. — СПб: ЮНИТИ-ДАНА, 1993.
3. Изучение геометрии 10-11 кл.: книга для учителя / С.М.Саакян, В.Ф. Бутузов. – М.: Просвещение, 2010.
4. Алтынов П.И. Геометрия. 10-11 класс. Тесты. 2001
5. Шарапова В.К. Тематические тесты по геометрии: 10-11 классы, Феникс, 2007
6. Лаппо Л.Д., Морозов А.В. Геометрия. Типовые вопросы и задачи – М.: «Экзамен», 2008.
7. Геометрия 10 класс. Составители Афанасьева Т.Л., Тапилина Л.А. – Волгоград, «Учитель», 2002.
Методическая разработка урока геометрии в 10 классе.
Нетикова Маргарита Анатольевна,
учитель математики ГБОУ школа №471
Выборгского района Санкт- Петербурга.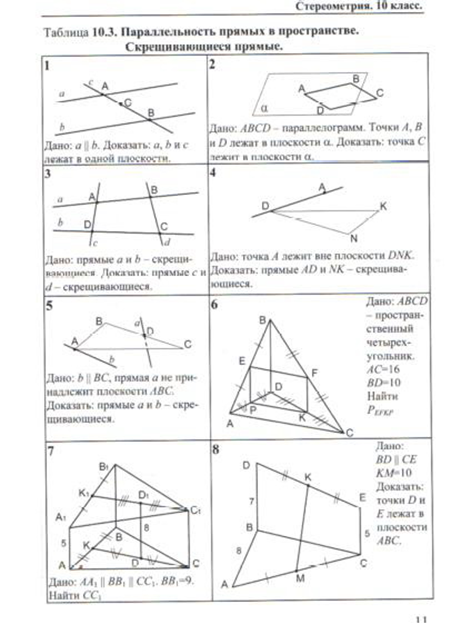
Предмет математики настолько серьёзен, что не надо
упускать случая сделать его немного занимательным.
Б.Паскаль
Тема урока: « Параллельность прямых и плоскостей»
Тип урока:урок обобщения и систематизации знаний
Форма урока:урок проводится в форме коллоквиума, обеспечивающей повторение и систематизацию учебного материала, контроль знаний учащихся, их коррекцию.
Класс заранее делится на 6 групп по 5 человек.
Урок разбит на 5 блоков:
1. Аксиомы стереометрии
2. Взаимное расположение прямых в пространстве.
3. Взаимное расположение в пространстве прямой и плоскости.
4. Взаимное расположение в пространстве двух плоскостей.
5. Задачи на построение сечений.
Каждый блок, кроме пятого, состоит из учебных элементов (УЭ). УЭ — это последовательные шаги, алгоритм работы учащихся, с которым школьник работает непосредственно:
1) актуализация знаний
2) доказательство теорем
3) решение задач.
Ученики выполняют задания, составленные учителем, с той степенью понимания, осмысления и запоминания, которое соответствует индивидуальным возможностям школьника.
Урок дает возможность определить уровень усвоения материала и быстро выявить пробелы в знаниях, создает условия для мотивации, повышения интереса к предмету, способствует развитию и совершенствованию самостоятельной деятельности учащихся; обеспечивает непрерывное образование и устраняет перегрузку домашнего задания.
У учащихся есть возможность:
— работать самостоятельно с дифференцированной программой;
— вернуться к учебному материалу, если в этом есть необходимость;
— получить консультацию и дозированную персональную помощь от учителя или члена группы.
На уроке создается комфортная обстановка:
— индивидуальный темп (для сильных учащихся предлагаются дополнительные задачи),
— «мягкий» контроль (возможность получить помощь товарища).
Учащиеся развивают личностные качества школьника (самостоятельность; умение ставить цели, планировать, организовывать и оценивать свою деятельность). Для самостоятельной оценки деятельности учащимся предлагаются критерии, с помощью которых ученики подсчитывают свои баллы и после 5 блока выставляют себе оценку самостоятельно. Во время самостоятельной работы учитель проверяет объективность выставленных оценок.
Четкая структура урока, дает учителю возможность «видеть» весь класс, работать индивидуально с каждым учеником, оказывать помощь отстающим.
Результат — повышение качества обученности учащихся.
Роль преподавателя на уроке заключается в управлении процессом обучения, консультировании, помощи и поддержке учеников.
Цель урока: обобщить и систематизировать знания и умения учащихся по данной теме, подготовиться к контрольной работе.
Задачи урока
Обучающие: организовать работу учащихся по систематизации знаний основных теоретических вопросов темы;
закрепить и углубить знания и умения учащихсяприменять аксиомы стереометрии, следствия из аксиом, теоремы о параллельности прямых, прямой и плоскости, параллельности плоскостей.
Развивающие:создать условия для развития познавательной активности учащихся, познавательного интереса к предмету;
развивать навыки самостоятельной деятельности учащихся;
развивать навыки самоконтроля;
развивать активность учащихся,
формировать учебно-познавательные действия, коммуникативные, исследовательские навыки учащихся, умение анализировать и устанавливать связь между элементами темы.
Воспитывающие: создать условия успешности ученика на уроке;
воспитывать культуру умственного труда; способность к самоанализу, рефлексии;
развивать умение рецензировать и корректировать ответы товарищей.
воспитывать умение критически относиться к результатам деятельности;
обеспечить гуманистический характер обучения;
Планируемые результаты:
Предметные: знать аксиомы, теоремы по данной теме и уметь их доказывать, применять при решении типовых задач.
Личностные: уметь отстаивать свою точку зрения и работать в группе.
Метапредметные:уметь планировать и оценивать процесс и результат своей деятельности, обрабатывать информацию.
Педагогические технологии: элементы обучения в сотрудничестве (работа в группах) и коллективного взаимообучения.
Оборудование: интерактивная доска, компьютер, раздаточные материалы.
Содержание учебного материала.
1.Аксиомы стереометрии и следствия из них.
2.Признаки параллельности прямых, прямой и плоскости, скрещивающихся прямых; признак и свойства параллельных плоскостей.
3.Задачи на построение сечений тетраэдра и параллелепипеда.
4.Задачи на доказательство параллельности прямых, прямой и плоскости, скрещивающихся прямых.
Структура урока.
1.Организационная часть.
2.Мотивационная часть.
3.Работа по блокам:
«Аксиомы стереометрии»
«Взаимное расположение прямых в пространстве»
«Взаимное расположение в пространстве прямой и плоскости»
« Взаимное расположение в пространстве двух плоскостей»
« Задачи на построение сечений»
4.Подведение итогов урока
5. Домашнее задание.
Домашнее задание.
6.Рефлексия урока.
Технологическая карта урока геометрии в 10 классе по теме:« Параллельность прямых и плоскостей»
|
Этапы урока |
Задачи этапа |
Деятельность учителя |
Деятельность учащихся |
УУД |
|
1.Организационная часть
|
Создание рабочего настроения в начале урока, объяснение правил. |
Здоровается с учениками, проверяет их подготовку к уроку, отмечает отсутствующих, записывает на доске дату, сообщает правила урока |
Готовятся к работе на уроке, приветствуют учителя |
Регулятивные: организация учебной деятельности. |
|
2.Мотивационная часть
|
Создание ситуации успеха. |
Объясняет необходимость и важность данного урока |
Слушают учителя |
Регулятивные:
организация учебной деятельности. |
|
3.Обобщающее повторение (работа по блокам) |
Повторить и систематизировать изученный теоретический материал, рассмотреть основные типы задач по каждому блоку. |
Корректирует и организовывает деятельность учащихся на каждом блоке, собирает бланки с решениями и ответами |
Отвечают на вопросы, доказывают теоремы, выполняют тесты и решают задачи в своих командах. |
Коммуникативные: умение прислушиваться к мнению окружающих. Регулятивные:
оценивание результатов своей деятельности. Познавательные: анализ условий поставленной задачи и поиск её рационального решения. Личностные: оценивание уровня усвоения материала и своих возможностей.
|
|
4.Подведение итогов урока
|
Осознание каждым учащимся: чему, как и зачем он научился сегодня на уроке, и с какими знаниями и умениями он должен прийти на следующий урок. |
Слушает комментарии к уроку у |
|
Регулятивные: умение оценить качество и уровень усвоения |
|
5.
|
Комментарии по домашнему заданию с целью его успешного выполнения. |
Раздаёт каждой команде текст демонстрационного варианта контрольной работы |
Записывают домашнее задание в дневники и задают по нему вопросы. |
|
|
6.Рефлексия урока.
|
Заставить детей задуматься в конце урока о своём настроении, эмоциональном состоянии и результатах взаимодействия с другими участниками образовательного процесса. |
Выходя из кабинета, оцените по пятибалльной шкале своё настроение в конце урока и поставьте оценку на доске. |
Собирают свои вещи, ставят оценки на доске цветными мелками. |
Коммуникативные: умение грамотно и честно выражать свои мысли. Регулятивные: умение оценить достигнутый результат. Личностные: чувство гордости за хорошо проделанную работу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ход урока
1. Организационная часть.
Организационная часть.
Сегодня мы с вами должны подняться ещё на одну ступеньку вверх, «преодолевая» задачи, которые будут рассматриваться на уроке. Мы начинаем повторение темы «Параллельность прямых и плоскостей в пространстве» (слайд 1). Наша задача вспомнить все, что мы знаем по этой теме.
2. Мотивационная часть.
Мы должны закрепить и углубить наши знания по этой теме.
Эти знания пригодятся нам для решения практических задач, для успешной сдачи ЕГЭ.
Вы должны научиться анализировать и устанавливать связь между элементами темы. Развить свою активность, сформировать учебно — познавательные действия, коммуникативные навыки. Хотелось бы создать условия вашей успешности на уроке; чтобы вы проявили способность к самоанализу, рефлексии, умение рецензировать и корректировать ответы товарищей. А каковы пути и средства достижения этих целей?
Домашнее задание к сегодняшнему уроку заключалось в том, чтобы вы повторили пункты 1- 12, просмотрели и еще раз разобрали задачи, которые мы решали в этих пунктах для обобщения и закрепления темы «Параллельность прямых и плоскостей в пространстве».
3.Обобщающее повторение.
Блок 1. Аксиомы стереометрии
Цели блока:
— повторить аксиомы стереометрии и применение их при решении задач ;
-повторить следствия из аксиом;
— закрепить умение применять аксиомы стереометрии и следствия из аксиом при решении задач;.
Актуализация опорных знаний. Проведем теоретическую разминку.
Учащиеся вспоминают учебный материал.
- Посмотрите на чертёж (слайды 2,3).Какие утверждения они иллюстрируют? Сформулируйте их.
В ходе беседы выделяются существенные моменты теории:
а) разъяснение содержания аксиом;
б) чтение учащимися текста аксиом;
в) выполнение чертежа;
Вот и название первого блока нашего урока: Аксиомы стереометрии (слайд 4)
2.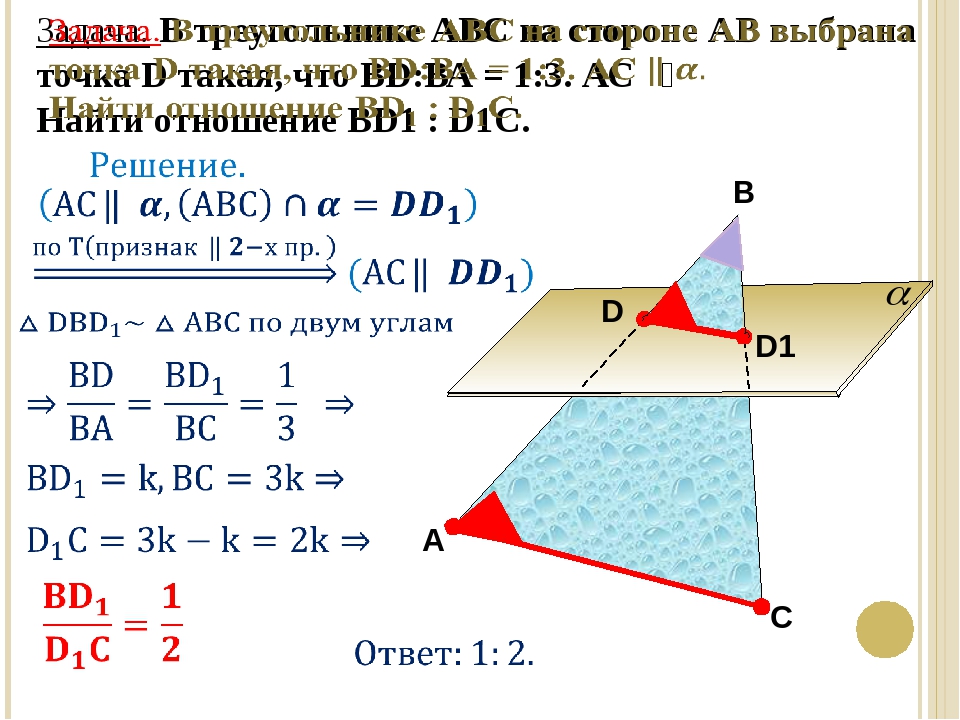 Как формулируются следствия из этих аксиом? (слайды 4,5).Кто хочет доказать эти теоремы?
Как формулируются следствия из этих аксиом? (слайды 4,5).Кто хочет доказать эти теоремы?
После обсуждения теоретических вопросовзакрепление полученных знаний.
Задание 1. Как в пространстве можно однозначно задать плоскость?
Учащиеся самостоятельно выполняют задание (проверяем на доске), советуясь в своих командах.
|
Способы задания плоскостей |
Рисунок |
|
I. По трем точкам, не лежащим на одной прямой |
|
|
2. По прямой и не принадлежащей ей точке. |
|
|
3. |
|
|
4. По двум параллельным прямым. |
|
Задание 2. Ответьте на вопросы (слайд 6). Каждая команда отвечает на свой вопрос.
Сколько плоскостей можно провести через выделенные элементы?
1) 2) 3)
4) 5) 6)
Задание 3(слайд 7) Три вершины параллелограмма лежат в некоторой плоскости. Можно ли утверждать, что и его четвертая вершина лежит в этой плоскости?
Команды обсуждают решение и озвучивают ответ.
Задание 4: тест по вариантам(для каждого ученика)
|
Тест «Аксиомы стереометрии» Вариант 1 1.Верно ли: любые три точки лежат в одной плоскости. 2.Вставьте пропущенные слова:Единственную плоскость можно задать через три точки, при этом они … на одной прямой.
3.Пересечением двух плоскостей является А) точка Б) прямая В) отрезок
|
Тест «Аксиомы стереометрии» Вариант 2
1.Верно ли: любые четыре точки лежат в одной плоскости. 2.Вставьте пропущенные слова:Если … точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости.
А) две параллельные прямые Б) две скрещивающиеся прямые В) три точки
|
|
Тест «Аксиомы стереометрии» Вариант 3 1.Верно ли: любые четыре точки не лежат в одной плоскости. 2.Вставьте пропущенные слова:Две различные плоскости могут иметь только одну общую …
3.Сколько должно быть общих точек у прямой с плоскостью, чтобы она лежала в этой плоскости? А) одна Б) две В) три |
Тест «Аксиомы стереометрии» Вариант 4
2.Вставьте пропущенные слова:две прямые, параллельные некоторой … , могут пересекаться.
3.Сколько плоскостей задают две пересекающиеся прямые? А) одну плоскость Б) две плоскости В) бесконечно много плоскостей |
|
Тест «Аксиомы стереометрии» Вариант 5
2.Вставьте пропущенные слова:две прямые, параллельные некоторой … , параллельны. 3.Через какие из перечисленных фигуры можно провести единственную плоскость? А) Через три точки Б) Через прямую и не лежащую на ней точку В) Через отрезок |
Тест «Аксиомы стереометрии» Вариант 6
2.Вставьте пропущенные слова: две прямые, параллельные некоторой … , могут пересекаться.
3. Две прямые пересекаются. Что это значит? А) Они имеют две общие точки. Б) Они имеют одну общую точку. В) Они лежат в одной плоскости. |
Блок 2. Взаимное расположение прямых в пространстве.(слайд 8)
Цель блока:
— повторить и обобщить знания по теме «Параллельные прямыев пространстве»;
— систематизировать полученные знания.
Актуализация опорных знаний. Проведем теоретическую разминку.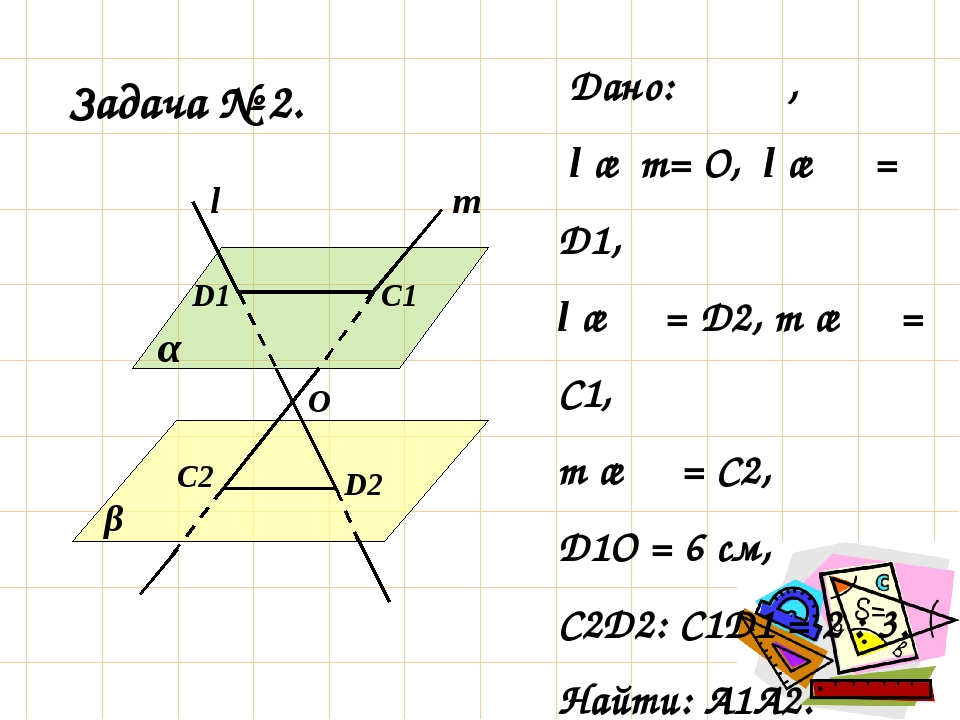
— Взаимное расположение двух прямых в пространстве (слайд 9)
а ççв аÇв аи в скрещивающиеся
— Какие прямые в пространстве называются параллельными? (Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются)
— Сформулируйте признак параллельности прямых в пространстве. (Две прямые, параллельные третьей прямой, параллельны).
— Какие прямые в пространстве называются скрещивающимися? (Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости и не пересекаются)
-Сформулируйте и докажите признак скрещивающихся прямых.
Один ученик доказывает признак параллельности прямых в пространстве (слайд 10), второй ученик доказывает признак скрещивающихся прямых (слайд 10) по чертежу на слайде.
После обсуждения теоретических вопросовзакрепление полученных знаний.
Задание Каждая команда получает карточку с заданием, обсуждает, а затем представляет своё решение (приложение 1)
Блок 3. Взаимное расположение в пространстве прямой и плоскости.(слайд 11)
Цель блока:
— повторить и обобщить знания по теме «Взаимное расположение в пространстве прямой и плоскости»;
— систематизировать полученные знания.
Актуализация опорных знаний. Проведем теоретическую разминку.
— Взаимное расположение в пространстве прямой и плоскости (слайд 12)
а Ìα аççα аÇα
— Какие прямая и плоскость называются параллельными? (Прямая и плоскость называются параллельными, если они не пересекаются)
— Сформулируйте признак параллельности прямой и плоскости в пространстве. (Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.)
Ученик доказывает признак параллельности прямой и плоскости в пространстве по чертежу на слайде (слайд 13).
После обсуждения теоретических вопросовзакрепление полученных знаний.
Задание 1 задача по готовому чертежу (слайд 14)
Задание 2.Тест. Учащиеся получают задание и выполняют его всей командой (приложение 2). Готовое решение сдают учителю.
Блок 4. Взаимное расположение в пространстве двух плоскостей (слайд 15).
Цель блока:
— повторить и обобщить знания по теме «Взаимное расположение в пространстве двух плоскостей»;
— систематизировать полученные знания.
Актуализация опорных знаний. Проведем теоретическую разминку.
— Взаимное расположение в пространстве двух плоскостей (слайд 16)
α Çβ
α иβ — совпадают α ççβ
— Какие плоскости называются параллельными? (Две плоскости называются параллельными, если они не пересекаются)
— Сформулируйте и докажите признак параллельности плоскостей в пространстве. (Если две пересекающиеся прямые одной плоскости параллельны двум прямым другой плоскости, то эти плоскости параллельны) (слайд 17)
(Если две пересекающиеся прямые одной плоскости параллельны двум прямым другой плоскости, то эти плоскости параллельны) (слайд 17)
— Сформулируйте свойство параллельных плоскостей (слайд 18)
После обсуждения теоретических вопросовзакрепление полученных знаний.
Задание 1 Задача по готовому чертежу (слайд 19)
Задание 2 Задача по готовому чертежу каждой команде на карточке (приложение 3)
Блок 5. Построение сечений тетраэдра и параллелепипеда(слайды 20,21).
Каждая команда получает чертежи тетраэдра и параллелепипеда, на них отмечает точки, через которые надо провести сечение, и отдаёт их другой команде. Задание выполняется коллективно, после чего сдаётся учителю.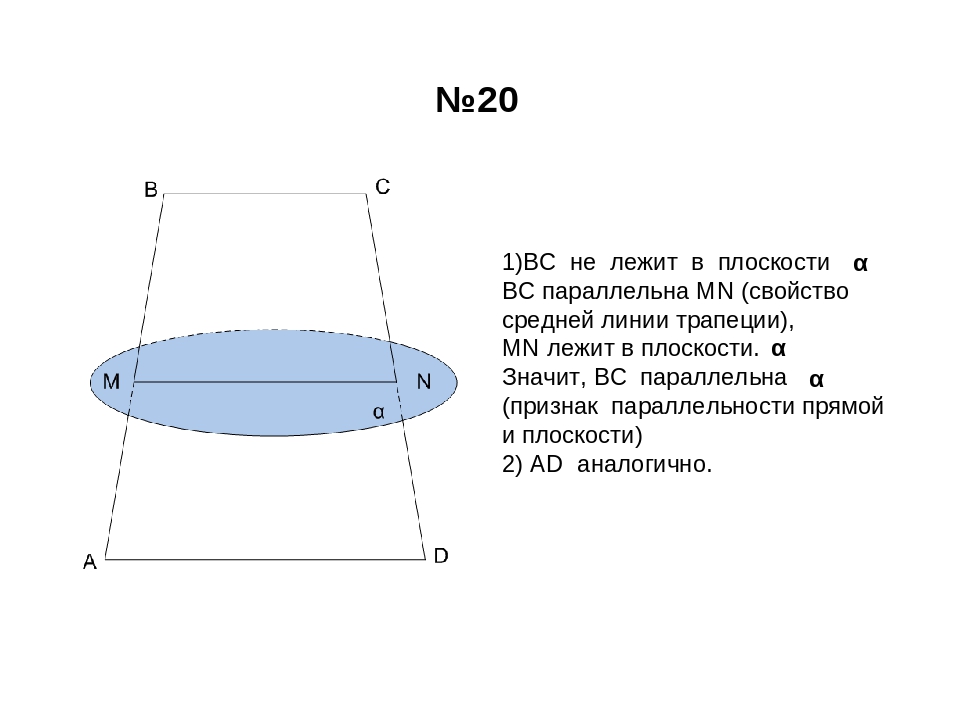
4. Подведение итогов урока.
Молодцы! Трудились с полной отдачей, ощутили радость своего труда. Оценки за урок вы узнаете после проверки ваших работ.
5. Рефлексия.
У каждого ученика в начале урока лежали на столах смайлики. В конце урока они сдают учителю тот смайлик, который соответствовал их настроению.
|
Мне всё понятно. Вопросов нет. |
Мне ничего не понятно. |
У меня есть вопросы. |
|
|
|
|
Перед вами лежат смайлики.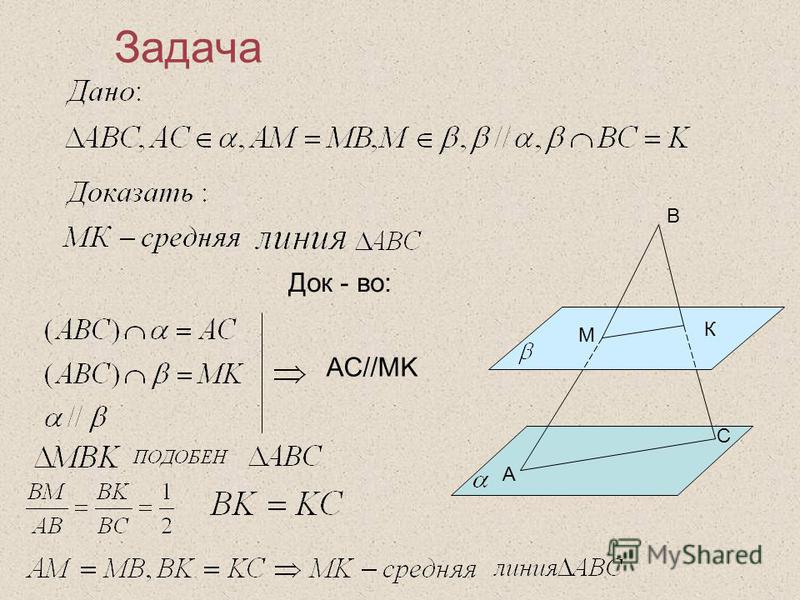 Если у вас на уроке все получалось правильно, если остались от урока положительные эмоции, урок был интересным, то поднимите радостный смайлик. Если вы таскали тяжёлые камни, если всё было не понятно, то поднимите плачущий смайлик, если в течение урокавы добросовестно выполняли свою работу, но у вас возникали проблемы – поднимите читающий смайлик.
Если у вас на уроке все получалось правильно, если остались от урока положительные эмоции, урок был интересным, то поднимите радостный смайлик. Если вы таскали тяжёлые камни, если всё было не понятно, то поднимите плачущий смайлик, если в течение урокавы добросовестно выполняли свою работу, но у вас возникали проблемы – поднимите читающий смайлик.
Оцените свою активность на уроке по шкале от 0-5.
6. Задание на дом.
Демонстрационный вариант контрольной работы
Приложение 1
|
Команда 1
Прямая а не лежит в плоскости параллелограмма ABCD. прямых aи BC,если aIIAB
|
Команда 2
1.Прямая а не лежит в плоскости ABC.Определите взаимное расположение прямых aи AC,если aIIAB
|
Команда 3
1.
|
|
Команда 4
1.Дан тетраэдр ABCD. Определите взаимное расположение прямых ADи BC.
|
Команда 5
1.
|
Команда 6
1.Определите взаимное расположение прямых ANи CM, если NM∩(ABC)
|
Приложение 2
|
Команда 1(4)
1. а) взаимное расположение точно определить нельзя; б) скрещиваются или параллельны; в) параллельны или пересекаются; г) совпадают;
2.Прямые а и b параллельны одной плоскости . Как расположены прямые а и b относительно друг друга? а) параллельны б) пересекаются в) скрещиваются
|
Команда 2(5)
1. а) Две прямые называются параллельными, если они не имеют общих точек; б) две прямые, параллельные третьей прямой, параллельны; в) две прямые, перпендикулярные третьей прямой, параллельны;
2. Прямая а лежит в плоскости. Как расположена относительно плоскости прямая b, если b параллельна а? а) перпендикулярно б) параллельно в) пересекает
|
Команда 3(6)
1.Прямая а, параллельная прямой b, пересекает плоскость α. а) прямые а и с пересекаются; б) прямая с лежит в плоскости α; в) прямые а и с скрещиваются; г) прямая bлежит в плоскости α; д) прямые а и с параллельны.
2. Сколько плоскостей можно провести через две данные точки? а) одну б) две в) много
|
|
Приложение 3
|
||
|
Команда 1
α II β,
a∩b=F. AF:FN=1:3, AB=4. Найти MN.
|
Команда 2
α II β, RK∩NS=M, KM:KR=1:3,NS=9. Найти MS.
|
Команда3
α II β,
a∩b=F. AF:FN=2:5, AB=10. НайтиMN.
|
|
Команда 4
α II β, RK∩NS=M, KN:RS=1:3,MK=2. Найти KR.
|
Команда 5
α II β,
a∩b=F. AB:MN=2:3, AF=10. Найти FN.
|
Команда 6
α II β, RK∩NS=M, MN:NS=1:3,MK=4. НайтиMR.
|
Литература.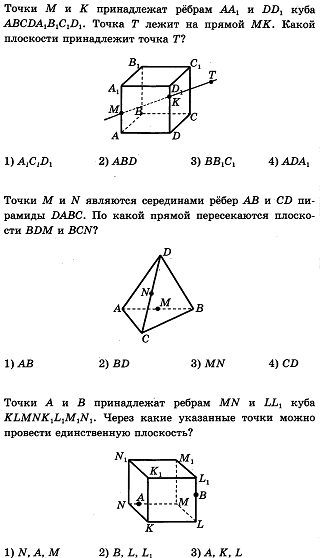
1. Селевко Г.К. Современные образовательные технологии: Учебное пособие. — М.: ЮНИТИ-ДАНА, 1998. — 344с.
2. Голощёкина Л.П., Збаровский B.C. Модульная технология обучения: Методические рекомендации. — СПб: ЮНИТИ-ДАНА, 1993.
3. Изучение геометрии 10-11 кл.: книга для учителя / С.М.Саакян, В.Ф. Бутузов. – М.: Просвещение, 2010.
4. Алтынов П.И. Геометрия. 10-11 класс. Тесты. 2001
5. Шарапова В.К. Тематические тесты по геометрии: 10-11 классы, Феникс, 2007
6. Лаппо Л.Д., Морозов А.В. Геометрия. Типовые вопросы и задачи – М.: «Экзамен», 2008.
7. Геометрия 10 класс. Составители Афанасьева Т.Л., Тапилина Л.А. – Волгоград, «Учитель», 2002.
Что такое параллельные линии? — Определение и концепция — Видео и стенограмма урока
Железнодорожные пути и параллельные линии
Иногда полезно думать о параллельных линиях как о совокупности железнодорожных путей.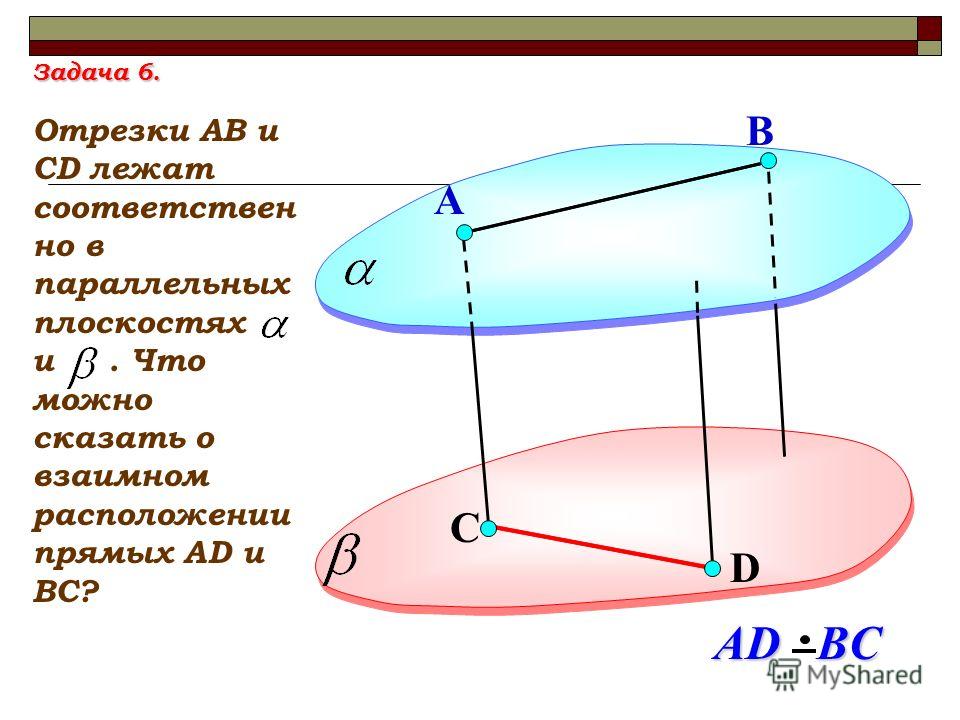 Два рельса рельсового пути созданы для движения колес с каждой стороны поезда. Поскольку колеса поезда всегда находятся на одинаковом расстоянии друг от друга, они не сближаются, даже когда они поворачиваются.
Два рельса рельсового пути созданы для движения колес с каждой стороны поезда. Поскольку колеса поезда всегда находятся на одинаковом расстоянии друг от друга, они не сближаются, даже когда они поворачиваются.
Гусеницы должны быть везде на одинаковом расстоянии друг от друга.Поскольку они созданы людьми, железнодорожные пути не совсем параллельны, но для правильной работы они должны быть очень близко друг к другу.
Еще одно различие между железнодорожными путями и идеально параллельными линиями состоит в том, что они проложены по холмам и долинам. Земля, которую они покрывают, не идеально ровная. С другой стороны, когда математики представляют параллельные линии, они рисуют их на идеально ровной поверхности.
Графические параллельные линии
Когда на графике нанесены две параллельные линии, они всегда должны быть под одним углом, что означает, что они всегда будут иметь одинаковый наклон или крутизну.
Вот график из двух параллельных линий:
Хотя эти две линии не начинаются в одном и том же месте, вы можете видеть, что они одинаково крутые. Они уменьшаются или наклоняются вниз с той же скоростью. Это гарантирует, что они параллельны.
Если вы посмотрите на уравнения этих двух строк, вы можете кое-что заметить: они точно такие же, за исключением чисел в правой части, «6» и «12». Мы можем использовать простую алгебру и переписать два уравнения в форме пересечения угла наклона ( y = mx + b ), формы линии, которая наиболее знакома людям.
Уравнение синей линии будет иметь следующий вид:
y = -3/2 x + 6
В то время как красная линия будет иметь уравнение:
y = -3/2 x + 3
Опять же, вы можете заметить, что эти два уравнения абсолютно одинаковы, за исключением одного: числа справа от x . Это число называется константой , и оно говорит нам, насколько высоко или низко находится линия на графике. Когда линия находится в форме пересечения наклона, это число также сообщает нам пересечение оси y , которое находится именно там, где линия касается оси Y, вертикальной линией, обозначающей ноль на графике.На этом графике две линии абсолютно одинаковы, за исключением того, что одна из них находится над другой.
Это число называется константой , и оно говорит нам, насколько высоко или низко находится линия на графике. Когда линия находится в форме пересечения наклона, это число также сообщает нам пересечение оси y , которое находится именно там, где линия касается оси Y, вертикальной линией, обозначающей ноль на графике.На этом графике две линии абсолютно одинаковы, за исключением того, что одна из них находится над другой.
Когда линии находятся в форме пересечения с уклоном, число, на которое умножается x (это число, которое добавлено к x в вопросе), указывает наклон линии. Вы можете видеть, что обе линии на нашем графике имеют одинаковый наклон, -3/2. Параллельные линии всегда будут иметь одинаковый наклон. Фактически, показать, что наклоны двух прямых равны, — это один из способов доказать, что они параллельны.
Параллельные отрезки линий
В геометрии считается, что линии идут в одно целое навсегда. Отрезки линий с начальной и конечной точками называются не линиями, а отрезками линии . Несмотря на то, что отрезки линии не могут длиться вечно, они все же могут быть параллельны.
Несмотря на то, что отрезки линии не могут длиться вечно, они все же могут быть параллельны.
Однако, в отличие от линий, два отрезка могут никогда не пересекаться и при этом не быть идеально параллельными. Сегменты линии не параллельны , если они расположены ближе друг к другу на одном конце, чем на другом, потому что в конечном итоге они бы встретились, если бы они были продлены дальше.
Если два сегмента прямые, все, что вам нужно сделать, это измерить расстояния между сегментами на обоих концах. Если эти точки находятся на одинаковом расстоянии друг от друга, эти два сегмента, вероятно, параллельны.
Резюме урока
Параллельные линии — это линии, которые всегда находятся на одинаковом расстоянии друг от друга. Поскольку они всегда находятся на одинаковом расстоянии друг от друга, параллельные линии никогда не пересекаются. Вы можете найти параллельные линии во многих местах, включая стороны геометрических фигур, таких как квадраты и прямоугольники, а также железнодорожные пути в вашем районе.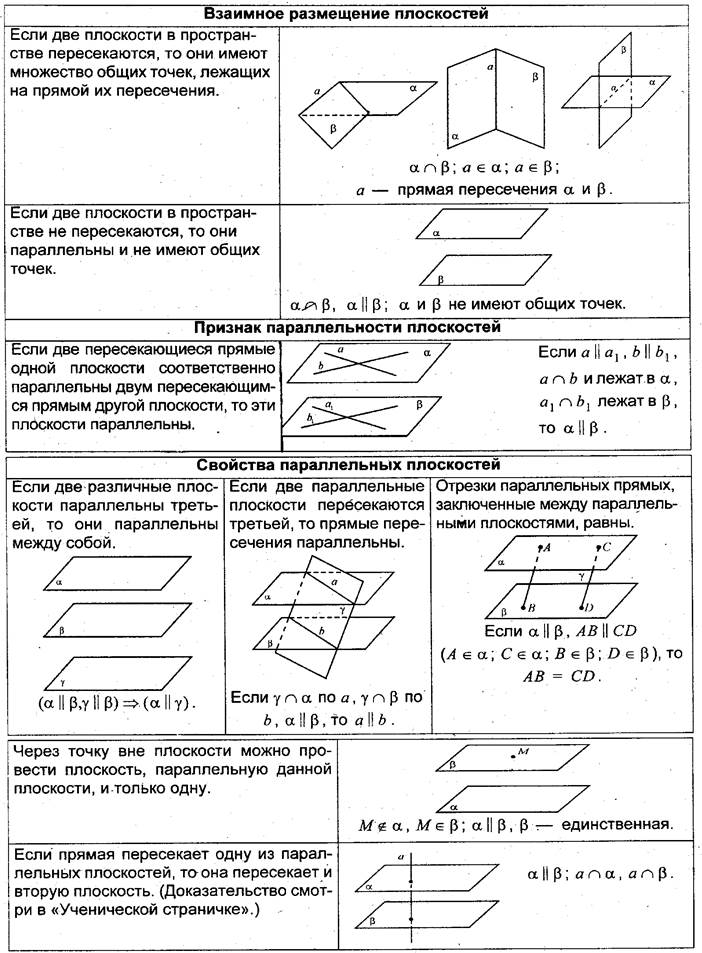
При нанесении на график параллельные линии будут иметь одинаковый наклон . Это легко увидеть, когда уравнения для параллельных линий перечислены в форме пересечения наклона и угла наклона . Если переменная наклона такая же, линии параллельны.
Вот несколько важных вещей, о которых следует помнить:
- Во-первых, каждая линия может иметь несколько параллелей . Линия будет параллельна любой линии с таким же наклоном, поэтому многие линии могут быть параллельны одновременно.
- Во-вторых, сегменты линии могут не быть параллельны, даже если они не пересекаются. Способ узнать наверняка — измерить расстояния на концах. Если они находятся на одинаковом расстоянии друг от друга, то сегменты имеют одинаковый наклон и будут параллельны, если продолжатся дальше.
8.3 Градиент линии | Аналитическая геометрия
Вам дана следующая диаграмма:
Вычислите уравнение прямой \ (AB \).
Чтобы вычислить уравнение прямой, мы сначала вычисляем градиент (\ (m \)) прямой \ (AB \):
\ (\ начало {выровнено} m & = \ frac {y_B — y_A} {x_B — x_A} \\ m & = \ frac {(- \ text {3,5}) — (\ text {2,5})} {(\ text {2}) — (- \ text {1})} \\ м & = — \ текст {2} \\ \ конец {выровнено} \)
Во-вторых, мы вычисляем значение \ (y \) — точки пересечения (\ (c \)) прямой \ (AB \).Мы делаем это подставив либо точку \ (A \), либо \ (B \) в общий вид прямой. Мы будем использовать точку \ (А \).
\ (\ начало {выровнено} у & = мх + с \\ (\ text {2,5}) & = (- \ text {2}) \ times (- \ text {1}) + c \\ c & = \ текст {0,5} \\ \ конец {выровнено} \)
Следовательно, уравнение прямой \ (AB \) выглядит следующим образом:
\ (\ начало {выровнено} у & = — \ текст {2} х + \ текст {0,5} \ конец {выровнено} \)
Вам дана следующая диаграмма:
Вычислите уравнение прямой \ (AB \).
Чтобы вычислить уравнение прямой, мы сначала вычисляем градиент (\ (m \)) прямой \ (AB \):
\ (\ начало {выровнено} m & = \ frac {y_B — y_A} {x_B — x_A} \\ m & = \ frac {(\ text {1,5}) — (- \ text {1})} {(\ text {4}) — (- \ text {1})} \\ м & = \ текст {0,5} \\ \ конец {выровнено} \)
Во-вторых, мы вычисляем значение \ (y \) — точки пересечения (\ (c \)) прямой \ (AB \).Мы делаем это подставив либо точку \ (A \), либо \ (B \) в общий вид прямой. Мы будем использовать точку \ (А \).
\ (\ начало {выровнено} у & = мх + с \\ (- \ text {1}) & = (\ text {0,5}) \ times (- \ text {1}) + c \\ c & = — \ text {0,5} \\ \ конец {выровнено} \)
Следовательно, уравнение прямой \ (AB \) выглядит следующим образом:
\ (\ начало {выровнено} y & = \ text {0,5} x — \ text {0,5} \ конец {выровнено} \)
точки \ (P (-6; 2) \), \ (Q (2; -2) \) и \ (R (-3; r) \) лежат на прямой.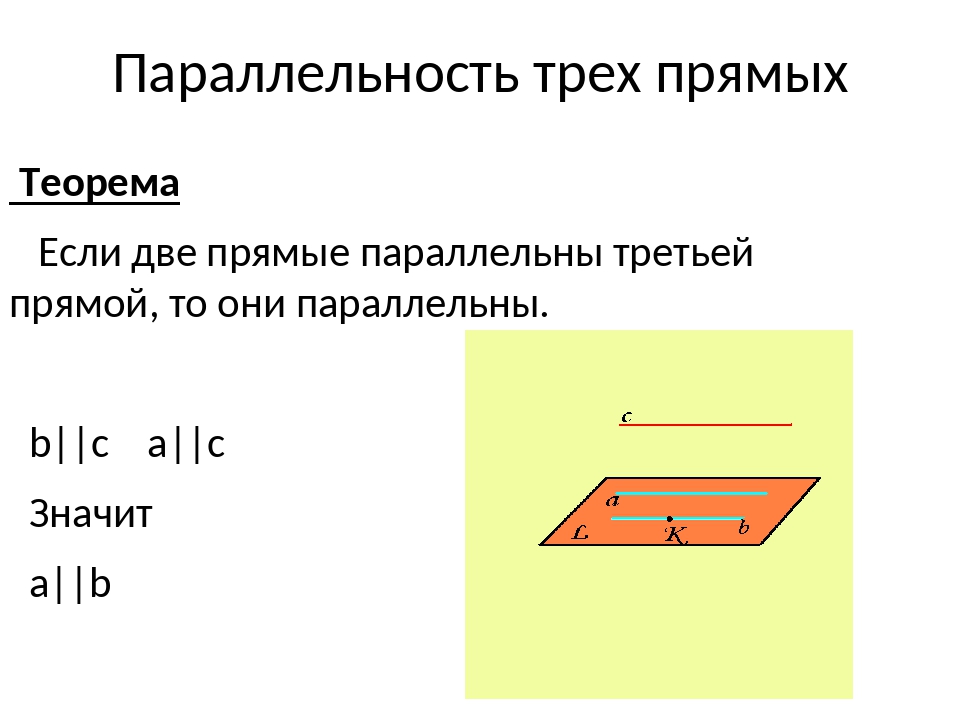 Найдите значение \ (r \).
Найдите значение \ (r \).
Поскольку три точки лежат на прямой, мы можем использовать тот факт, что градиент \ (PQ \) равен к градиенту \ (QR \), чтобы найти \ (r \).
Градиент \ (PQ \) составляет:
\ begin {align *} m_ {PQ} & = \ frac {y_2 — y_1} {x_2 — x_1} \\ & = \ frac {-2 — 2} {2 — (-6)} \\ & = \ frac {-4} {8} \\ & = — \ frac {1} {2} \ end {выровнять *}И градиент \ (QR \) с точки зрения \ (r \) составляет:
\ begin {align *} m_ {QR} & = \ frac {y_2 — y_1} {x_2 — x_1} \\ & = \ frac {r — (-2)} {- 3 — 2} \\ & = \ frac {r + 2} {- 5} \ end {выровнять *}Теперь положим \ (m_ {PR} = m_ {QR} = — \ frac {1} {2} \) и решим для \ (r \):
\ begin {align *} — \ frac {1} {2} & = \ frac {r + 2} {- 5} \\ (-1) \ раз (-5) & = 2 (г + 2) \\ 5 & = 2р + 4 \\ 5 — 4 & = 2р \\ 1 & = 2р \\ г & = \ гидроразрыв {1} {2} \ end {выровнять *} Линия \ (PQ \) с \ (P (-1; -7) \) и \ (Q (q; 0) \) имеет градиент \ (\ text {1} \).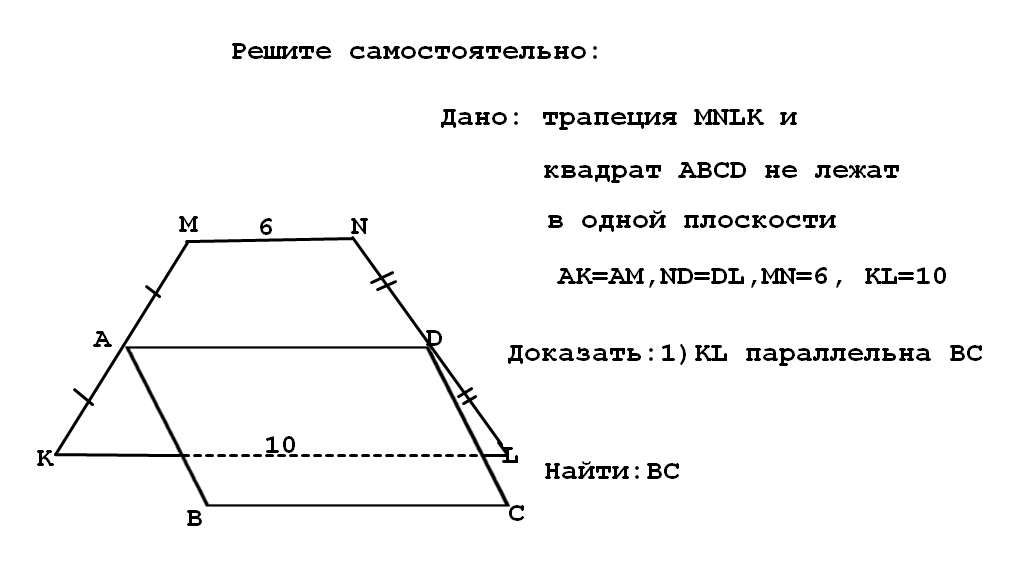 Найдите \ (q \).
Найдите \ (q \).
\ begin {align *} m_ {PQ} & = \ frac {y_2 — y_1} {x_2 — x_1} \\ 1 & = \ frac {0 — (-7)} {q — (-1)} \\ q + 1 & = 7 \\ q & = 6 \ end {выровнять *}
Вам дана следующая диаграмма:
Вам также сообщают, что линия \ (AB \) проходит параллельно следующей линии: \ (y = x — \ text {5} \).Точка \ (A \) находится в \ (\ left (-2; -4 \ right) \).
Найдите уравнение прямой \ (AB \).
Нам говорят, что прямая \ (AB \) параллельна \ (y = x — 5 \), поэтому градиент прямой \ (AB \) равен градиент \ (y = x — 5 \). Градиент \ (y = x — 5 \) равен 1.
Теперь мы можем использовать точку \ (A \) и градиент линии, чтобы найти точку пересечения линии \ (y \):
\ (\ begin {выровнено} у & = мх + с \\ (- \ text {4}) & = (\ text {1}) (- \ text {2}) + c \\ c & = — \ текст {2} \\ \ конец {выровнено} \) Следовательно, уравнение прямой \ (AB \): \ (y = x — 2 \).
Вам дана следующая диаграмма:
Вам также сообщают, что линия \ (AB \) проходит параллельно следующей линии: \ (y = -x + \ text {4,5} \). Точка \ (A \) находится в \ (\ left (-1; \ text {2,5} \ right) \).
Найдите уравнение прямой \ (AB \).
Нам говорят, что линия \ (AB \) параллельна \ (y = -x + \ text {4,5} \), поэтому градиент линии \ (AB \) равен равен градиенту \ (y = -x + \ text {4,5} \).Градиент \ (y = -x + \ text {4,5} \) равен \(-\текст 1}\).
Теперь мы можем использовать точку \ (A \) и градиент линии, чтобы найти точку пересечения линии \ (y \):
\ (\ begin {выровнено} у & = мх + с \\ (\ text {2,5}) & = (- \ text {1}) \ times (- \ text {1}) + c \\ c & = \ текст {1,5} \\ \ конец {выровнено} \) Следовательно, уравнение линии \ (AB \): \ (y = -x + \ text {1,5} \).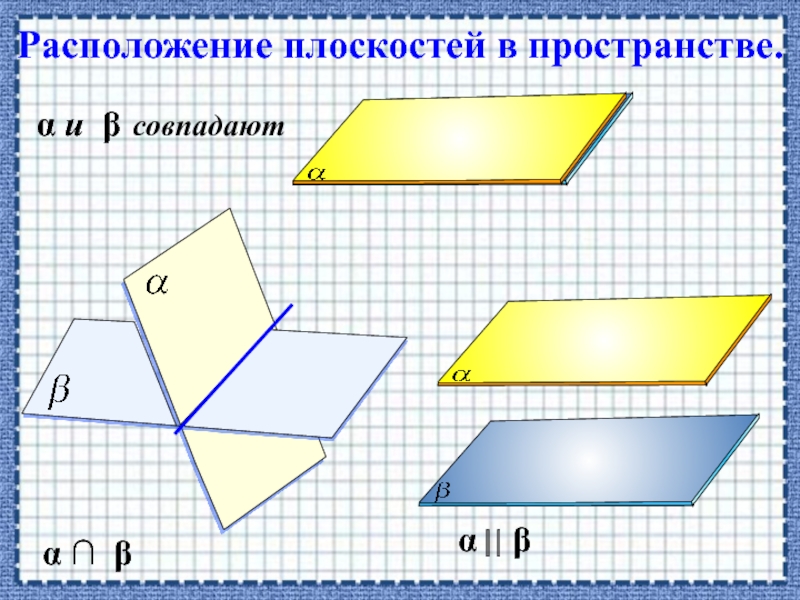
Данная линия \ (AB \), которая проходит параллельно \ (y = \ text {0,5} x — \ text {6} \). Очки \ (A (-1; — \ text {2,5}) \) и \ (B (x; 0) \) также даны.
Вычислить недостающую координату точки \ (B \).
Нам говорят, что линия \ (AB \) параллельна \ (y = \ text {0,5} x — 6 \), поэтому градиент линии \ (AB \) равен равен градиенту \ (y = \ text {0,5} x — 6 \).Градиент \ (y = \ text {0,5} x — 6 \) равен \ (\ text {0,5} \).
Теперь мы можем использовать точку \ (A \) и градиент линии, чтобы найти точку пересечения линии \ (y \):
\ begin {align *} у & = мх + с \\ (- \ text {2,5}) & = (\ text {0,5}) (- \ text {1}) + c \\ c & = — \ текст {2} \\ \ end {выровнять *} Следовательно, уравнение прямой \ (AB \) будет: \ (y = \ text {0,5} x — 2 \).
Теперь мы можем подставить точку \ (B \) в уравнение прямой \ (AB \), чтобы найти \ (x \):
\ begin {align *} у & = \ текст {0,5} х — 2 \\ 0 & = \ text {0,5} x — 2 \\ 4 & = х \ end {выровнять *}Следовательно, координаты точки \ (B \) равны \ ((0; 4) \).
Данная линия \ (AB \), которая проходит параллельно \ (y = — \ text {1,5} x + \ text {4} \). Точки Также указаны \ (A (- \ text {2}; \ text {4}) \) и \ (B (2; y) \).
Вычислите недостающую координату точки \ (B (2; y) \).
Нам говорят, что линия \ (AB \) параллельна \ (y = — \ text {1,5} x + 4 \), поэтому градиент линии \ (AB \) равен
равен градиенту \ (y = — \ text {1,5} x + 4 \).Градиент \ (y = — \ text {1,5} x + 4 \) равен
\ (- \ text {1,5} \).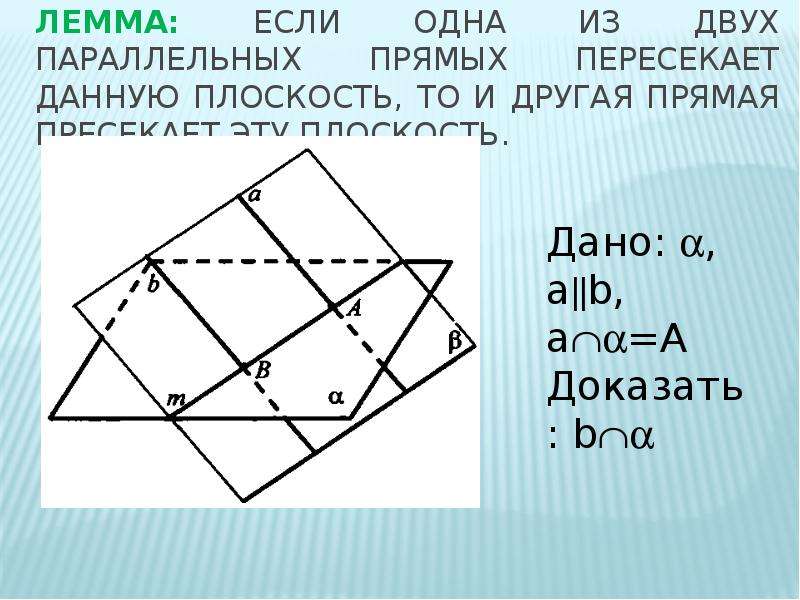
Теперь мы можем использовать точку \ (A \) и градиент линии, чтобы найти точку пересечения линии \ (y \):
\ begin {align *} у & = мх + с \\ (\ text {4}) & = (- \ text {1,5}) (- \ text {2}) + c \\ c & = \ текст {1} \\ \ end {выровнять *}Следовательно, уравнение прямой \ (AB \) будет: \ (y = — \ text {1,5} x + 1 \).
Теперь мы можем подставить точку \ (B \) в уравнение прямой \ (AB \), чтобы найти \ (x \):
\ begin {align *} у & = — \ текст {1,5} х + 1 \\ y & = — \ text {1,5} (2) + 1 \\ y & = -2 \ end {выровнять *}Следовательно, координаты точки \ (B \) равны \ ((2; -2) \).
На графике показана линия \ (AB \). Синяя пунктирная линия перпендикулярна \ (AB \).
Уравнение синей пунктирной линии: \ (y = x + 1 \).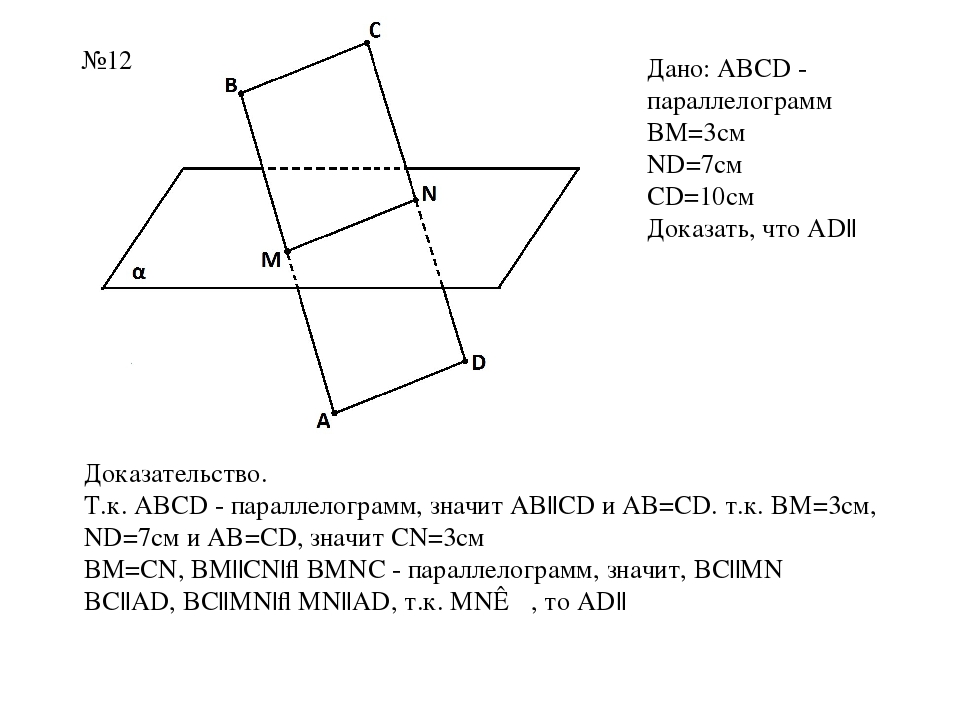 Точка \ (A \) находится в точке \ ((- 2; 4) \).
Точка \ (A \) находится в точке \ ((- 2; 4) \).
Определите уравнение прямой \ (AB \).
Общая форма прямой: \ (y = mx + c \).
Линия \ (AB \) перпендикулярна синей пунктирной линии, поэтому \ (m_ {AB} = \ dfrac {-1} {m _ {\ text {blue линия}}}\).
\ begin {align *} у & = мх + с \\ y & = \ left (\ frac {-1} {m _ {\ text {синяя линия}}} \ right) x + c \\ y & = \ left (\ frac {-1} {\ text {1}} \ right) x + c \\ у & = -x + c \ end {выровнять *}Теперь мы можем подставить координаты точки \ (A \), чтобы найти точку пересечения \ (y \):
\ begin {align *} у & = мх + с \\ (\ text {4}) & = (- \ text {1}) (- \ text {2}) + c \\ c & = \ текст {2} \\ \ end {выровнять *} Следовательно, уравнение прямой \ (AB \): \ (y = -x + 2 \).
На графике показана линия \ (AB \). Синяя пунктирная линия перпендикулярна \ (AB \).
Уравнение синей пунктирной линии: \ (y = — \ text {0,5} x — \ text {0,5} \). Точка \ (A \) находится в \ ((- \ text {1}; — \ text {3,5}) \).
Определите уравнение прямой \ (AB \).
Общая форма прямой: \ (y = mx + c \).
Линия \ (AB \) перпендикулярна синей пунктирной линии, поэтому \ (m_ {AB} = \ dfrac {-1} {m _ {\ text {blue линия}}}\).
\ begin {align *} у & = мх + с \\ y & = \ left (\ frac {-1} {m _ {\ text {синяя линия}}} \ right) x + c \\ y & = \ left (\ frac {-1} {- \ text {0,5}} \ right) x + c \\ у & = 2x + c \ end {выровнять *}Теперь мы можем подставить координаты точки \ (A \), чтобы найти точку пересечения \ (y \):
\ begin {align *} у & = мх + с \\ (- \ text {3,5}) & = (\ text {2}) (- \ text {1}) + c \\ c & = — \ text {1,5} \\ \ end {выровнять *} Следовательно, уравнение прямой \ (AB \) будет: \ (y = 2x — \ text {1,5} \).
Дана прямая \ (AB \), которая проходит перпендикулярно прямой \ (CD \) с уравнением \ (y = -2x + 1 \). Точки \ (A (-5; -1) \) и \ (B (3; a) \) также указаны.
Вычислить недостающую координату точки \ (B \).
Общая форма прямой: \ (y = mx + c \).
Линия \ (AB \) перпендикулярна линии \ (CD \), поэтому \ (m_ {AB} = \ dfrac {-1} {m_ {CD}} \).
\ begin {align *} у & = мх + с \\ y & = \ left (\ frac {-1} {m_ {CD}} \ right) x + c \\ y & = \ left (\ frac {-1} {- \ text {2}} \ right) x + c \\ у & = \ текст {0,5} х + с \ end {выровнять *}Теперь мы можем подставить точку \ (A \) в уравнение, чтобы найти точку пересечения \ (y \):
\ begin {align *} у & = \ текст {0,5} х + с \\ — \ text {1} & = (\ text {0,5}) (- \ text {5}) + c \\ c & = \ текст {1,5} \ end {выровнять *}Затем мы можем подставить в точку \ (B \), чтобы найти недостающую координату:
\ begin {align *} y & = \ text {0,5} x + \ text {1,5} \\ a & = (\ text {0,5}) (\ text {3}) + \ text {1,5} \\ & = \ текст {3} \ end {выровнять *} Следовательно, отсутствует координата \ (B (3; 3) \).
Данная линия \ (AB \), которая проходит перпендикулярно линии \ (CD \) с уравнением \ (y = 2x — \ text {0,75} \). Также указаны точки \ (A (-5; 1) \) и \ (B (a; — \ text {2,5}) \).
Вычислить недостающую координату точки \ (B \).
Общая форма прямой: \ (y = mx + c \).
Линия \ (AB \) перпендикулярна линии \ (CD \), поэтому \ (m_ {AB} = \ dfrac {-1} {m_ {CD}} \).
\ begin {align *} у & = мх + с \\ y & = \ left (\ frac {-1} {m_ {CD}} \ right) x + c \\ y & = \ left (\ frac {-1} {2} \ right) x + c \\ у & = — \ текст {0,5} х + с \ end {выровнять *}Теперь мы можем подставить точку \ (A \) в уравнение, чтобы найти точку пересечения \ (y \):
\ begin {align *} у & = — \ текст {0,5} х + с \\ \ text {1} & = (\ text {0,5}) (- \ text {5}) + c \\ c & = — \ text {1,5} \ end {выровнять *}Затем мы можем подставить в точку \ (B \), чтобы найти недостающую координату:
\ begin {align *} y & = \ text {0,5} x — \ text {1,5} \\ — \ text {2,5} & = \ text {0,5} a — \ text {1,5} \\ а & = — \ текст {2} \ end {выровнять *} Следовательно, отсутствует координата \ (B (-2; — \ text {2,5}) \).
Вам дана следующая диаграмма:
Вам также сообщают, что строка \ (AB \) имеет следующее уравнение: \ (y = — \ text {0,5} x + \ text {1,5} \).
Вычислить недостающую координату точки \ (B \).
Подставляем известное значение точки \ (B \) в уравнение и решаем неизвестное значение:
\ (\ начало {выровнено} y & = (- \ text {0,5}) x + \ text {1,5} \\ a & = (- \ text {0,5}) (\ text {2}) + \ text {1,5} \\ & = \ текст {0,5} \ конец {выровнено} \)
Вам дана следующая диаграмма:
Вам также сообщают, что строка \ (AB \) имеет следующее уравнение: \ (y = \ text {0,5} x — \ text {1} \).
Вычислить недостающую координату точки \ (B \).
Подставляем известное значение точки \ (B \) в уравнение и решаем неизвестное значение:
\ (\ начало {выровнено} y & = (\ text {0,5}) x — \ text {1} \\ a & = (\ text {0,5}) (\ text {1}) — \ text {1} \\ & = — \ текст {0,5} \ конец {выровнено} \)
\ (A \) — это точка \ ((- 3; -5) \), а \ (B \) — это точка \ ((n; -11) \).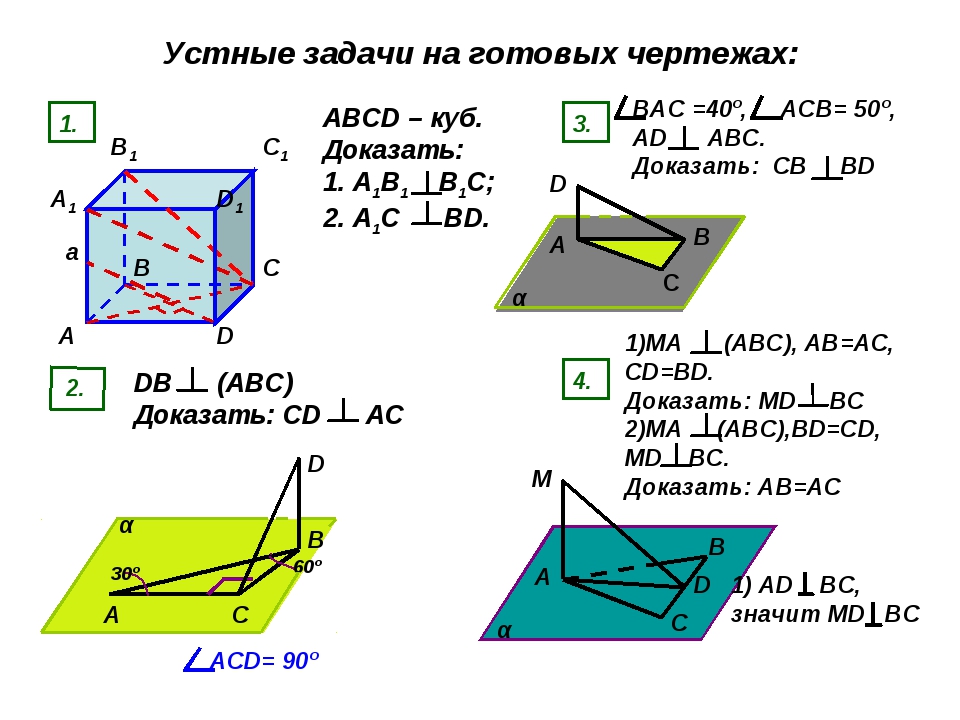 \ (AB \) перпендикулярно прямой
\ (CD \) с уравнением \ (y = \ frac {3} {2} x — 5 \). Найдите значение \ (n \).
\ (AB \) перпендикулярно прямой
\ (CD \) с уравнением \ (y = \ frac {3} {2} x — 5 \). Найдите значение \ (n \).
Линия \ (AB \) перпендикулярна линии \ (CD \), поэтому \ (m_ {AB} = \ dfrac {-1} {m_ {CD}} \).
\ begin {align *} m_ {AB} & = -1 \ div \ frac {3} {2} \\ & = \ frac {-2} {3} \ end {выровнять *}Следовательно:
\ begin {align *} \ frac {-2} {3} & = \ frac {-11 — (-5)} {n — (-3)} \\ \ frac {-2} {3} & = \ frac {-6} {n + 3} \\ \ frac {-2} {3} (n + 3) & = -6 \\ -2 (п + 3) & = -18 \\ п + 3 & = 9 \\ n & = 6 \ end {выровнять *} Даны точки \ (A (4; -3) \), \ (B (-5; 0) \) и \ (C (-3; p) \).Определите значение \ (p \), если \ (A \),
\ (B \) и \ (C \) коллинеарны.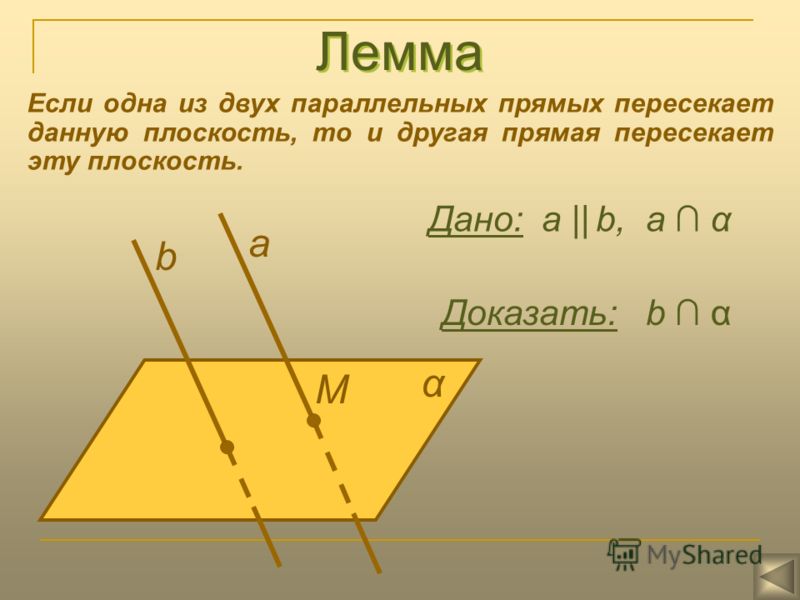
Нам говорят, что \ (A \), \ (B \) и \ (C \) коллинеарны, поэтому \ (m_ {AB} = m_ {BC} \).
\ begin {align *} \ frac {0 + 3} {- 5 — 4} & = \ frac {p} {- 3 + 5} \\ \ frac {3} {- 9} & = \ frac {p} {2} \\ \ поэтому p & = \ frac {6} {- 9} \\ & = \ frac {-2} {3} \ end {выровнять *}Соответствующие углы — пояснения и примеры
Прежде чем перейти к теме соответствующих углов, давайте сначала напомним себе об углах, параллельных и непараллельных прямых и поперечных линиях.
В геометрии угол состоит из трех частей: вершины и двух плеч или сторон. Вершина угла — это место, где встречаются две стороны или линии угла, а ответвления угла — это просто стороны угла.
Параллельные прямые — это две или более прямых на двухмерной плоскости, которые никогда не пересекаются и не пересекаются. С другой стороны, непараллельные прямые — это две или более пересекающихся линий.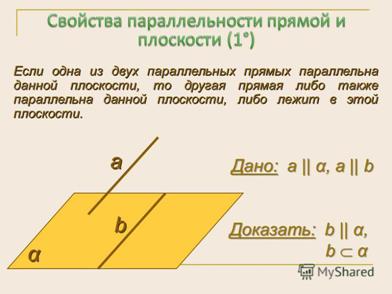 Поперечная линия — это линия, которая пересекает или проходит через две другие линии. Поперечная линия может проходить через две параллельные или непараллельные линии.
Поперечная линия — это линия, которая пересекает или проходит через две другие линии. Поперечная линия может проходить через две параллельные или непараллельные линии.
Что такое соответствующий угол?
Углы, образующиеся, когда поперечная линия пересекает две прямые, известны как соответствующие углы . Соответствующие углы расположены в одном и том же относительном положении, на пересечении поперечной и двух или более прямых линий.
Угловое правило соответствующих углов или соответствующих углов постулирует, что соответствующие углы равны, если трансверсаль пересекает две параллельные линии.
Соответствующие углы равны, если поперечная линия пересекает не менее двух параллельных линий.
На приведенной ниже диаграмме показаны соответствующие углы, образующиеся, когда поперечная линия пересекает две параллельные линии:
Из вышеприведенной диаграммы пара соответствующих углов составляет:
- < a и < e
- < b и < g
- < d и < f
- < c и < h
Доказательство соответствия углов
На приведенном выше параллельном рисунке мы имеем .
Нам нужно это доказать.
У нас есть прямые углы:
Из переходного свойства,
Из теоремы об альтернативном угле,
Используя подстановку, мы имеем,
Следовательно,
Соответствующие углы, образованные непараллельными линиями
Соответствующие углы равны образуется, когда поперечная линия пересекает по крайней мере две непараллельные линии, которые не равны, и на самом деле они не имеют никакого отношения друг к другу.
Иллюстрация:
Соответствующий внутренний угол
Пара соответствующих углов состоит из одного внутреннего и другого внешнего углов.Внутренние углы — это углы, расположенные внутри углов пересечения.
Соответствующий внешний угол
Углы, образующиеся вне пересекающихся параллельных линий. Внешний угол и внутренний угол составляют пару соответствующих углов.
Иллюстрация:
Внутренние углы включают; b, c, e и f, а внешние углы включают; а, г, ж и з.
Следовательно, пары соответствующих углов включают:
Мы можем сделать следующие выводы о соответствующих углах:
- Пара соответствующих углов лежит на одной стороне поперечный.
- Соответствующая пара углов включает один внешний угол и другой внутренний угол.
- Не все соответствующие углы равны. Соответствующие углы равны, если трансверсаль пересекает две параллельные прямые.Если трансверсаль пересекает непараллельные прямые, соответствующие образуемые углы не совпадают и никак не связаны между собой.
- Углы соответствующей формы являются дополнительными углами, если поперечная перпендикулярно пересекает две параллельные прямые.
- Наружные углы на одной стороне поперечной оси являются дополнительными, если линии параллельны. Точно так же внутренние углы являются дополнительными, если две линии параллельны.
Как найти соответствующие углы?
Один из способов решения соответствующих углов — нарисовать букву F на данной диаграмме.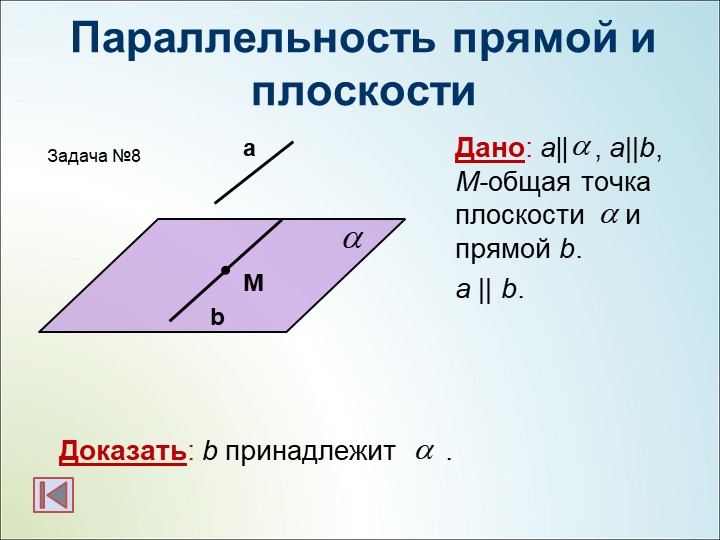 Расположите букву лицом в любом направлении и соответственным образом соотнесите углы.
Расположите букву лицом в любом направлении и соответственным образом соотнесите углы.
Пример 1
При ∠d = 30 ° найдите недостающие углы на диаграмме ниже.
Решение
При условии, что ∠ d = 30 °
∠ d = ∠ b (вертикально противоположные углы)
Следовательно, ∠ b = 30 °
324000 b = ∠ g = 30 ° (соответствующие углы)Теперь ∠ d = ∠ f (Соответствующие углы)
Следовательно, f = 30 °
∠ b + ∠ a = 180 ° (дополнительные углы)
∠ a + 30 ° = 180 °
∠ a = 150 °
∠ a = ∠ e = (соответствующие углы)
Следовательно, ∠e = 150 °
∠ d = ∠ h = 30 ° (соответствующие углы)
Пример 2
Два соответствующих угла фигуры составляют 9x + 10 и 55.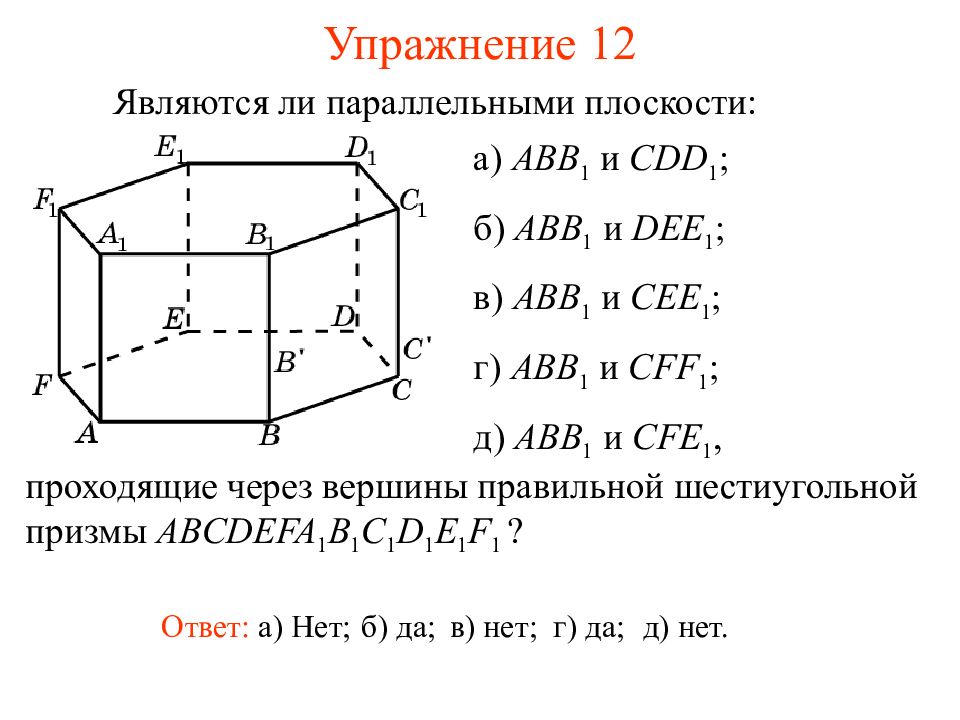 Найдите значение x.
Найдите значение x.
Решение
Два соответствующих угла всегда совпадают.
Следовательно,
9x + 10 = 55
9x = 55-10
9x = 45
x = 5
Пример 3
Два соответствующих угла размера фигуры 7y — 12 и 5y + 6. Найдите величину соответствующего угла.
Решение
Во-первых, нам нужно определить значение y.
Два соответствующих угла всегда совпадают.
Следовательно,
7y — 12 = 5y + 6
7y — 5y = 12 + 6
2y = 18
y = 9
Величина соответствующего угла,
5y + 6 = 5 (9 ) + 6 = 51
Применения соответствующих углов
Существует множество применений соответствующих углов, которые мы игнорируем. Понаблюдайте за ними, если у вас когда-нибудь появится возможность.
- Обычно окна имеют горизонтальные и вертикальные решетки, которые образуют несколько квадратов.Каждая вершина квадрата образует соответствующие углы.

- Мост стоит на столбах. Все столбы соединены таким образом, что соответствующие углы равны.
- Железнодорожные пути спроектированы так, что все соответствующие углы на пути равны.
Использование наклонно-отрезной формы уравнения прямой — элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Распознать связь между графиком и формой углового пересечения в уравнении прямой
- Определите наклон и форму пересечения оси Y уравнения прямой
- Постройте линию, используя ее наклон и точку пересечения
- Выберите наиболее удобный способ построения линии
- Построение графика и интерпретация значений угла наклона и точки пересечения
- Используйте уклоны для обозначения параллельных линий
- Используйте уклоны для обозначения перпендикулярных линий
Перед тем, как начать, пройдите тест на готовность.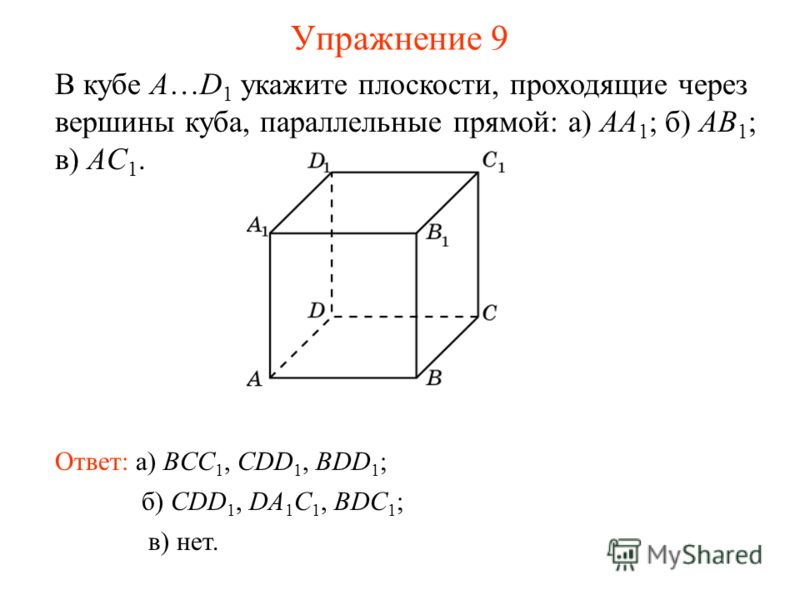
- Добавить:
Если вы пропустили эту проблему, просмотрите (рисунок). - Найдите значение, обратное
. Если вы пропустили эту проблему, просмотрите (рисунок). - Решить.
Если вы пропустили эту проблему, просмотрите (рисунок).
Распознайте связь между графиком и формой наклона-пересечения в уравнении прямой
Мы изобразили линейные уравнения, построив точки, используя точки пересечения, распознавая горизонтальные и вертикальные линии и используя метод точки-наклона.Как только мы увидим, как связаны уравнение в форме угла наклона и пересечения с его графиком, у нас будет еще один метод, который мы можем использовать для построения линий.
В графике линейных уравнений с двумя переменными мы построили линию уравнения, нанеся точки. См. (Рисунок). Давайте найдем наклон этой прямой.
Красные линии показывают, что подъем равен 1, а разбег равен 2. Подставляем в формулу наклона:
Что такое пересечение линии y ? Пересечение y — это место, где линия пересекает ось y , поэтому перехват y находится. Уравнение этой строки:
Уравнение этой строки:
Обратите внимание, в строке есть:
Когда решается линейное уравнение, коэффициент члена представляет собой наклон, а постоянный член представляет собой координату y точки пересечения y . Мы говорим, что уравнение имеет форму «наклон – пересечение».
Форма угла наклона-пересечения прямой
Угловая и угловая форма уравнения прямой с наклоном и точкой пересечения y , составляет,
Иногда форма наклона-пересечения называется формой « y ».”
Используйте график, чтобы найти наклон и пересечение y линии,.
Сравните эти значения с уравнением.
Решение
Чтобы найти наклон линии, нам нужно выбрать две точки на линии. Мы будем использовать точки и.
Наклон такой же, как коэффициент, а координата y интерцепта y такая же, как и постоянный член.
Определите наклон и
y — пересечение с уравнением прямойВ разделе «Понять наклон линии» мы построили линию, используя наклон и точку.Когда нам задают уравнение в форме угла наклона и точки пересечения, мы можем использовать точку пересечения y в качестве точки, а затем отсчитывать оттуда наклон. Попрактикуемся в нахождении значений наклона и отрезка y из уравнения прямой.
Определите наклон и пересечение линии y .
Определите наклон и пересечение линии y .
Если уравнение линии не дано в форме углового пересечения, нашим первым шагом будет решение уравнения для.
Определите наклон и пересечение y линии с помощью уравнения.
Решение
Это уравнение не в форме углового пересечения. Чтобы сравнить его с формой угла наклона и пересечения, мы должны сначала решить уравнение для.
Чтобы сравнить его с формой угла наклона и пересечения, мы должны сначала решить уравнение для.
Определите наклон и пересечение линии y .
Определите наклон и пересечение линии y .
Выберите наиболее удобный метод построения графика линии
Теперь, когда мы увидели несколько методов, которые можно использовать для построения линий графика, как мы узнаем, какой метод использовать для данного уравнения?
Хотя мы могли бы построить точки, использовать форму наклона-пересечения или найти точки пересечения для любого уравнения , если мы найдем наиболее удобный способ построения графика определенного типа уравнения, наша работа будет проще.Как правило, нанесение точек на график — не самый эффективный способ построения линии. Мы видели лучшие методы в разделах 4.3, 4.4 и ранее в этом разделе. Давайте поищем несколько шаблонов, которые помогут определить наиболее удобный метод построения линии.
Вот шесть уравнений, которые мы построили на графиках в этой главе, и метод, который мы использовали для построения графика каждого из них.
Уравнения №1 и №2 имеют только одну переменную. Помните, что в уравнениях такой формы значение одной переменной является постоянным; он не зависит от значения другой переменной.Уравнения этой формы имеют графики, которые представляют собой вертикальные или горизонтальные линии.
В уравнениях № 3 и № 4 оба и находятся на одной стороне уравнения. Эти два уравнения имеют вид. Мы заменили, чтобы найти точку пересечения x и точку пересечения y , а затем нашли третью точку, выбрав другое значение для или.
Уравнения № 5 и № 6 записываются в форме углового пересечения. После определения наклона и пересечения y из уравнения мы использовали их для построения графика линии.
Это приводит к следующей стратегии.
Стратегия выбора наиболее удобного метода построения графика линии
Рассмотрим вид уравнения.
Определите наиболее удобный метод построения графика каждой линии.
ⓐ ⓑ ⓒ ⓓ.
Определите наиболее удобный метод построения графика каждой линии: ⓐ ⓑ ⓒ ⓓ.
ⓐ точки пересечения ⓑ горизонтальная линия ⓒ наклон – точка пересечения ⓓ вертикальная линия
Определите наиболее удобный метод построения графика каждой линии: ⓐ ⓑ ⓒ ⓓ.
ⓐ вертикальная линия ⓑ наклон – точка пересечения ⓒ горизонтальная линия ⓓ точки пересечения
График и интерпретация углов наклона и пересечения
Многие реальные приложения моделируются линейными уравнениями. Здесь мы рассмотрим несколько приложений, чтобы вы могли увидеть, как уравнения, записанные в форме углового пересечения, соотносятся с реальными ситуациями.
Обычно, когда линейное уравнение моделирует реальную ситуацию, для переменных используются разные буквы, а не x и y . Имена переменных напоминают нам о том, какие количества измеряются.
Имена переменных напоминают нам о том, какие количества измеряются.
Уравнение используется для оценки роста женщины в дюймах, h , на основе размера ее обуви, s .
ⓐ Оцените рост ребенка, который носит размер женской обуви 0.
ⓑ Оцените рост женщины, используя размер обуви 8.
ⓒ Интерпретируйте наклон и h — точку пересечения уравнения.
ⓓ Изобразите уравнение.
- ⓐ 50 дюймов
- ⓑ 66 дюймов
- ⓒ Наклон 2 означает, что высота h увеличивается на 2 дюйма, когда размер обуви s увеличивается на 1.Перехват h означает, что когда размер обуви равен 0, высота составляет 50 дюймов.
- ⓓ
Уравнение используется для оценки температуры в градусах Фаренгейта, T , на основе количества щебетаний сверчка, n , за одну минуту.
ⓐ Оценить температуру при отсутствии чириканья.
ⓑ Оцените температуру, когда количество звуковых сигналов за одну минуту равно 100.
ⓒ Интерпретируйте наклон и T — перехват уравнения.
ⓓ Изобразите уравнение.
- ⓐ 40 градусов
- ⓑ 65 градусов
- ⓒ Наклон, означает, что температура по Фаренгейту ( F ) увеличивается на 1 градус, когда количество щебетаний, n , увеличивается на 4. Перехват T означает, что когда количество щебетаний равно 0, температура есть.
- ⓓ
Стоимость ведения бизнеса некоторых типов состоит из двух компонентов: фиксированных затрат , и переменных затрат , .Фиксированная стоимость всегда одинакова, независимо от количества произведенных единиц. Это стоимость аренды, страховки, оборудования, рекламы и других предметов, которые необходимо регулярно оплачивать.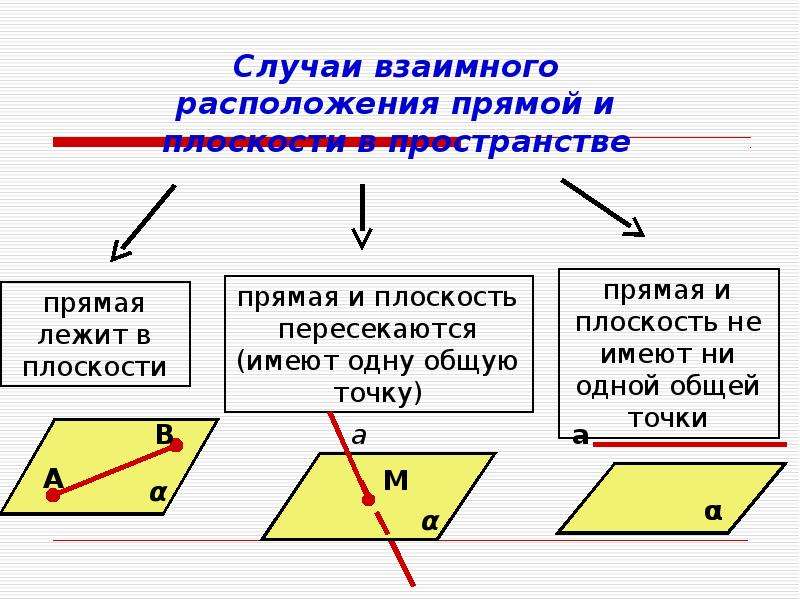 Переменная стоимость зависит от количества произведенных единиц. Это для материалов и рабочей силы, необходимых для производства каждого предмета.
Переменная стоимость зависит от количества произведенных единиц. Это для материалов и рабочей силы, необходимых для производства каждого предмета.
У Стеллы есть домашний бизнес по продаже изысканной пиццы. Уравнение моделирует связь между ее недельной стоимостью C в долларах и количеством пиццы p , которые она продает.
ⓐ Найдите стоимость недели для Стеллы, если она не продает пиццу.
ⓑ Найдите стоимость за неделю, когда она продаст 15 пицц.
ⓒ Интерпретируйте наклон и C -перехват уравнения.
ⓓ Изобразите уравнение.
Сэм водит фургон. Уравнение моделирует связь между его недельной стоимостью, C , в долларах, и количеством миль, м , которые он проезжает.
ⓐ Узнайте стоимость недели для Сэма, когда он проезжает 0 миль.
ⓑ Узнайте стоимость недели, когда он проезжает 250 миль.
ⓒ Интерпретируйте наклон и C -перехват уравнения.
ⓓ Изобразите уравнение.
- ⓐ? 60
- ⓑ? 185
- ⓒ Наклон 0,5 означает, что еженедельная стоимость C увеличивается на 0,50 фунтов стерлингов, когда количество пройденных миль, n, увеличивается на 1. Перехват C означает, что, когда количество пройденных миль 0, еженедельная стоимость? 60
- ⓓ
Лорин занимается каллиграфией.Уравнение моделирует связь между ее недельной стоимостью C в долларах и количеством приглашений на свадьбу n , которые она пишет.
ⓐ Найдите стоимость недели для Лорин, когда она не пишет приглашения.
ⓑ Найдите стоимость за неделю, когда она напишет 75 приглашений.
ⓒ Интерпретируйте наклон и C -перехват уравнения.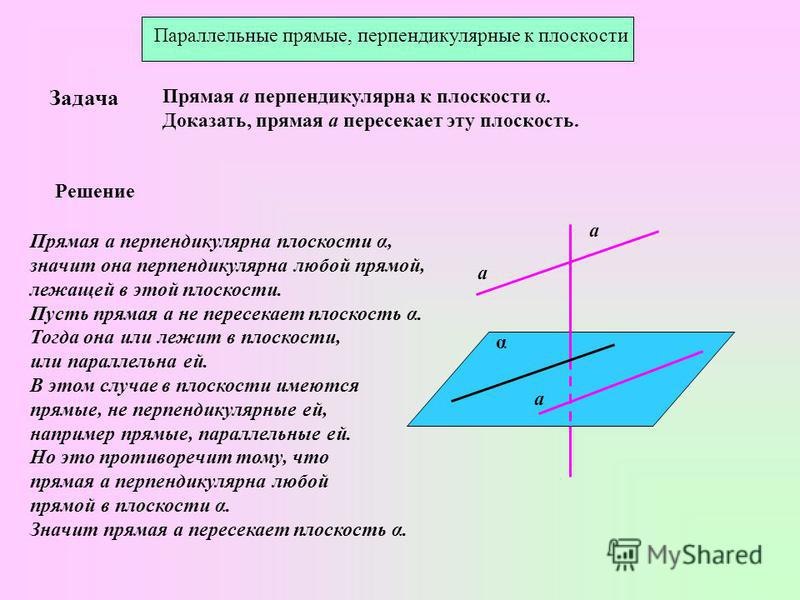
ⓓ Изобразите уравнение.
- ⓐ? 35
- ⓑ? 170
- ⓒ Наклон 1,8 означает, что недельная стоимость C увеличивается на 1 фунт.80, когда количество приглашений, n , увеличивается на 1,80.
Перехват C означает, что при количестве приглашений 0 еженедельная стоимость составляет 35 фунтов стерлингов; - ⓓ
Использование уклонов для определения перпендикулярных линий
Давайте посмотрим на линии, уравнения которых представляют собой и, показанные на (Рисунок).
Эти прямые лежат в одной плоскости и пересекаются под прямым углом. Мы называем эти линии перпендикулярными.
Что вы замечаете в наклонах этих двух линий? При чтении слева направо линия поднимается вверх, поэтому ее наклон положительный.Линия опускается слева направо, поэтому угол наклона отрицательный. Имеет ли для вас смысл, что наклоны двух перпендикулярных линий будут иметь противоположные знаки?
Если мы посмотрим на наклон первой линии, и наклон второй линии, мы увидим, что они являются отрицательными обратными друг другу. Если мы их умножим, их произведение будет
Если мы их умножим, их произведение будет
Это всегда верно для перпендикулярных линий и приводит нас к этому определению.
Перпендикулярные линии
Перпендикулярные линии — это прямые в одной плоскости, образующие прямой угол.
Если — это наклоны двух перпендикулярных прямых, то:
Вертикальные и горизонтальные линии всегда перпендикулярны друг другу.
Мы смогли взглянуть на форму линейного уравнения «наклон – пересечение» и определить, параллельны ли линии. То же самое можно сделать и с перпендикулярными линиями.
Мы находим уравнение в форме углового пересечения и затем смотрим, являются ли наклоны обратными отрицательными. Если произведение уклонов равно, линии перпендикулярны.Перпендикулярные линии могут иметь одинаковые точки пересечения y .
Используйте уклоны, чтобы определить, перпендикулярны ли линии и.
Решение
Наклоны противоположны друг другу, поэтому линии перпендикулярны.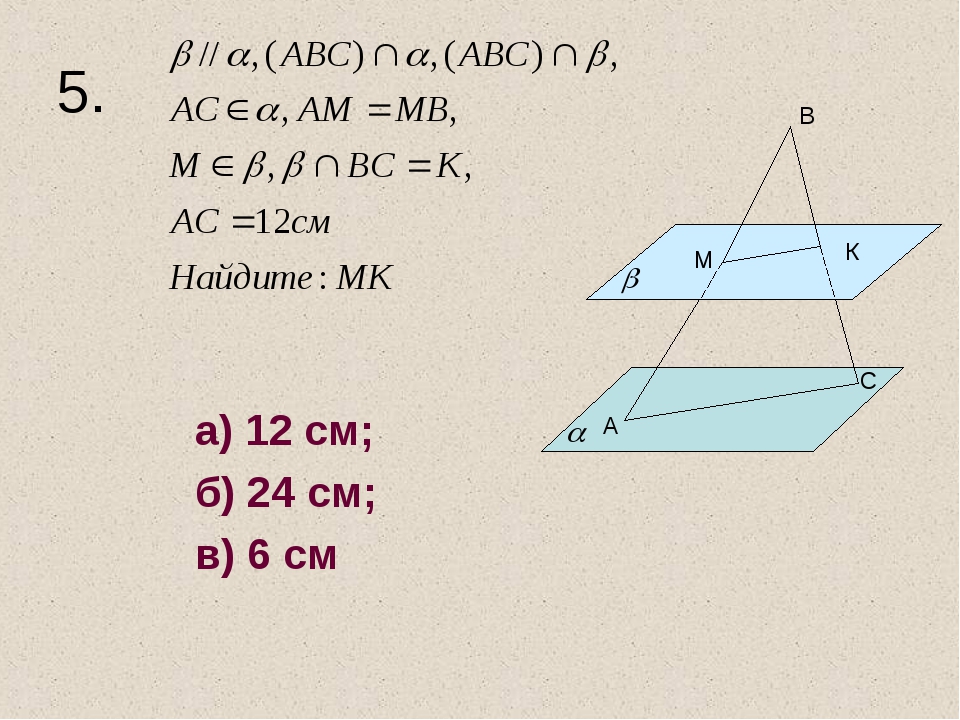 Проверяем умножением уклонов,
Проверяем умножением уклонов,
Используйте уклоны, чтобы определить, перпендикулярны ли линии и.
Используйте уклоны, чтобы определить, перпендикулярны ли линии и.
Используйте уклоны, чтобы определить, перпендикулярны ли линии и.
Решение
Наклоны равны друг другу, но имеют одинаковый знак. Поскольку они не являются отрицательными обратными, линии не перпендикулярны.
Используйте уклоны, чтобы определить, перпендикулярны ли линии и.
Используйте уклоны, чтобы определить, перпендикулярны ли линии и.
Практика ведет к совершенству
Распознайте связь между графиком и формой наклона-пересечения в уравнении прямой
В следующих упражнениях используйте график, чтобы найти наклон и точку пересечения по оси Y каждой линии.Сравните значения с уравнением.
Определить наклон и точку пересечения оси y по уравнению прямой
В следующих упражнениях определите наклон и точку пересечения оси Y каждой линии.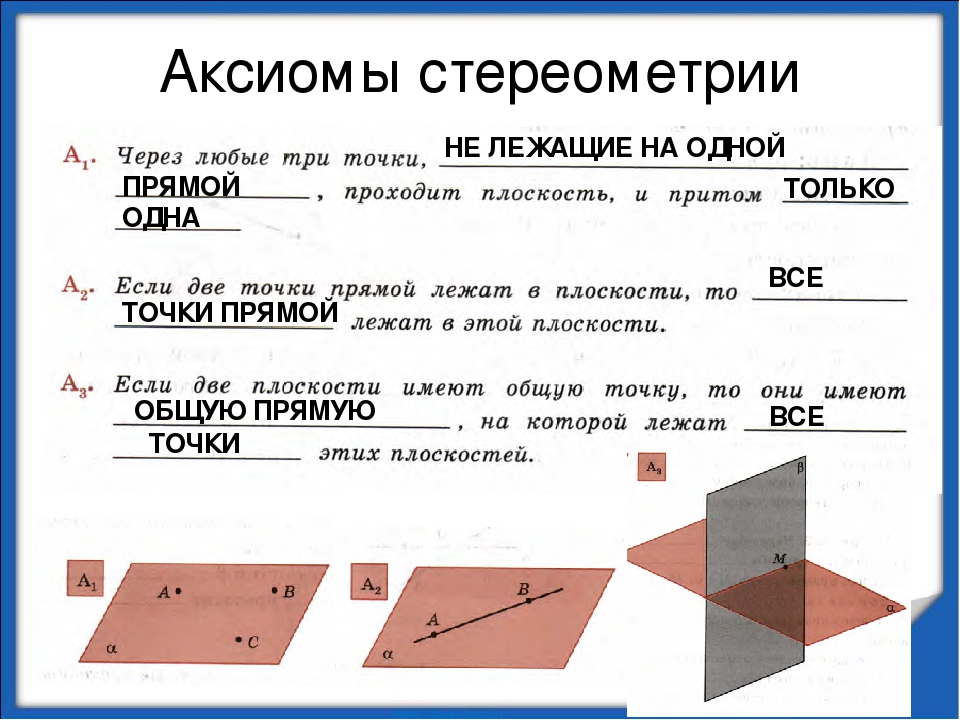
Построение линии с использованием ее наклона и точки пересечения
В следующих упражнениях нарисуйте линию каждого уравнения, используя ее наклон и точку пересечения по оси Y.
Выберите наиболее удобный способ построения графика линии
В следующих упражнениях определите наиболее удобный метод построения графика каждой линии.
График и интерпретация значений наклона и пересечения
Уравнение моделирует связь между суммой ежемесячного платежа Тайета за воду, P , в долларах, и количеством использованных единиц воды, w .
- ⓐ Найдите оплату Тайет за месяц, когда использовано 0 единиц воды.
- ⓑ Найдите оплату Тайет за месяц при использовании 12 единиц воды.
- ⓒ Интерпретируйте наклон и точку пересечения P уравнения.
- ⓓ Изобразите уравнение.
Уравнение моделирует связь между суммой ежемесячного платежа Рэнди по счету за воду, P , в долларах, и количеством использованных единиц воды, w .
- ⓐ Найдите оплату за месяц, когда Рэнди использовал 0 единиц воды.
- ⓑ Найдите оплату за месяц, когда Рэнди использовал 15 единиц воды.
- ⓒ Интерпретируйте наклон и точку пересечения P уравнения.
- ⓓ Изобразите уравнение.
- ⓐ? 28
- ⓑ? 66,10
- ⓒ Наклон 2,54 означает, что платеж Рэнди, P , увеличивается на 2,54 фунта стерлингов, когда количество единиц воды, которые он использовал, w, увеличивается на 1.
 Перехват P означает, что если количество единиц воды воды, которую использовал Рэнди, было 0, оплата составила бы 28 евро.
Перехват P означает, что если количество единиц воды воды, которую использовал Рэнди, было 0, оплата составила бы 28 евро. - ⓓ
Брюс ведет свою машину по работе. Уравнение моделирует соотношение между суммой в долларах , которую ему возмещают, и количеством миль, м , которое он проезжает за один день.
- ⓐ Найдите сумму возмещения Брюсу в день, когда он проезжает 0 миль.
- ⓑ Найдите сумму возмещения Брюсу в день, когда он проезжает 220 миль.
- ⓒ Интерпретируйте наклон и R — точку пересечения уравнения.
- ⓓ Изобразите уравнение.
Жанель планирует арендовать машину на время отпуска. Уравнение моделирует соотношение между стоимостью в долларах, C , в день и количеством миль, м , которое она проезжает за один день.
- ⓐ Узнайте стоимость, если Джанель однажды проехала на машине 0 миль.
- ⓑ Узнайте стоимость в день, когда Джанель проезжает на машине 400 миль.
- ⓒ Интерпретируйте наклон и C –перехват уравнения.
- ⓓ Изобразите уравнение.
- ⓐ? 15
- ⓑ? 143
- ⓒ Наклон 0,32 означает, что стоимость C увеличивается на 0,32 фунта стерлингов, когда количество пройденных миль, м, увеличивается на 1. Перехват C означает, что если Джанель проезжает 0 миль за один день , стоимость будет 15 евро.
- ⓓ
Чери работает в розничной торговле, и ее недельная зарплата включает комиссионные с суммы, которую она продает. Уравнение моделирует связь между ее недельной зарплатой, S , в долларах, и суммой ее продаж, c , в долларах.
- ⓐ Найдите зарплату Чери за неделю, когда ее продажи составляли 0.
- ⓑ Найдите зарплату Чери за неделю, когда ее продажи составляли 3600.
- ⓒ Интерпретировать наклон и S –перехват уравнения.
- ⓓ Изобразите уравнение.
Еженедельная зарплата Патела включает базовую заработную плату плюс комиссионные с его продаж. Уравнение моделирует соотношение между его недельной зарплатой, S , в долларах, и суммой его продаж, c , в долларах.
- ⓐ Найдите зарплату Пателя за неделю, когда его продажи составляли 0.
- ⓑ Найдите зарплату Пателя за неделю, когда его продажи составляли 18 540.
- ⓒ Интерпретируйте наклон и точку пересечения S уравнения.
- ⓓ Изобразите уравнение.
- ⓐ? 750
- ⓑ? 2418,60
- ⓒ Наклон 0,09 означает, что зарплата Пателя, шиллингов , увеличивается на 0,09 фунта стерлингов на каждый фунт увеличения его продаж.
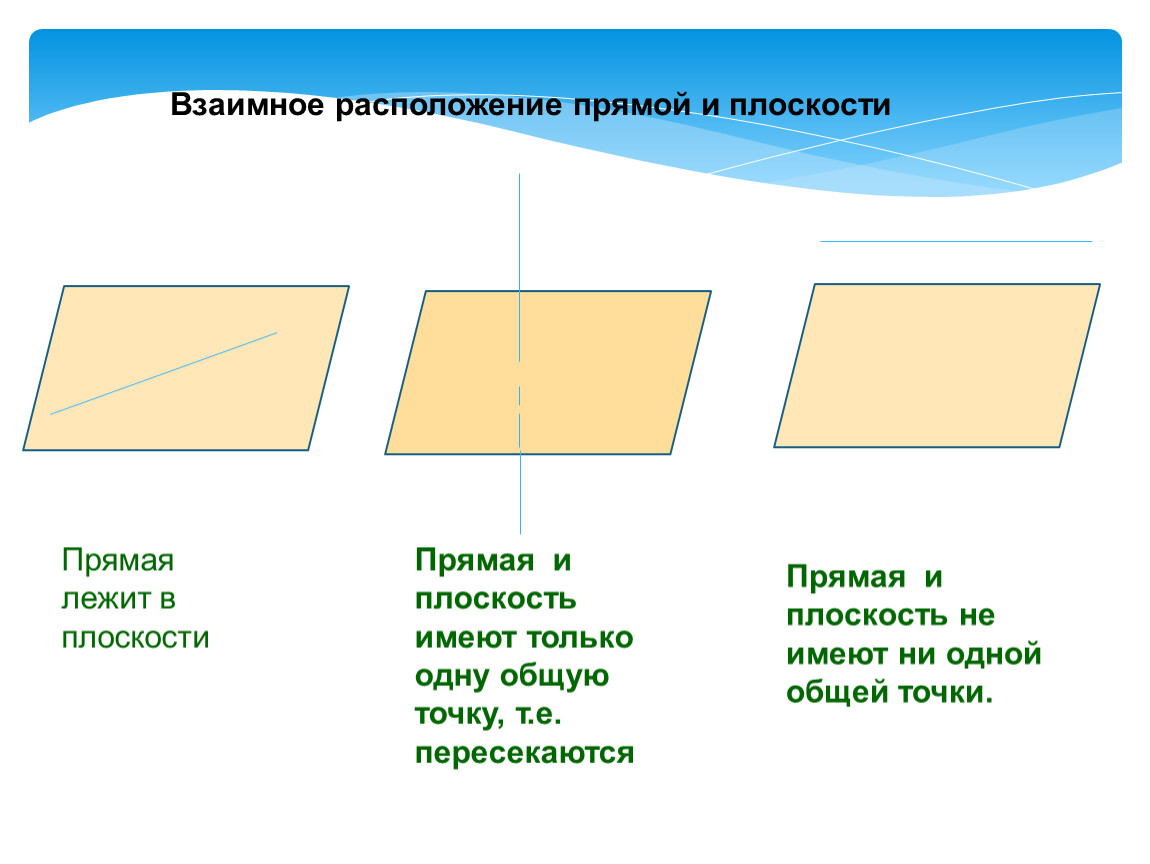 Перехват S означает, что когда его продажи равны 0 евро, его зарплата составляет 750 фунтов стерлингов.
Перехват S означает, что когда его продажи равны 0 евро, его зарплата составляет 750 фунтов стерлингов. - ⓓ
Коста планирует обед-банкет. Уравнение моделирует соотношение между стоимостью банкета C в долларах и количеством гостей г .
- ⓐ Найдите стоимость, если количество гостей 40.
- ⓑ Найдите стоимость, если количество гостей 80.
- ⓒ Интерпретируйте наклон и C -перехват уравнения.
- ⓓ Изобразите уравнение.
Марджи планирует банкетный обед.Уравнение моделирует соотношение между стоимостью банкета C в долларах и количеством гостей г .
- ⓐ Найдите стоимость, если количество гостей 50.
- ⓑ Найдите стоимость, если количество гостей 100.
- ⓒ Интерпретируйте наклон и C –перехват уравнения.

- ⓓ Изобразите уравнение.
- ⓐ? 2850
- ⓑ? 4950
- ⓒ Наклон 42 означает, что стоимость C увеличивается на 42 фунта стерлингов при увеличении количества гостей на 1. C -перехват означает, что, когда количество гостей равно 0, стоимость будет 750 фунтов стерлингов.
- ⓓ
Использование уклонов для определения параллельных линий
В следующих упражнениях используйте наклоны и точки пересечения по оси Y, чтобы определить, параллельны ли линии.
Использование уклонов для определения перпендикулярных линий
В следующих упражнениях используйте наклоны и точки пересечения по оси Y, чтобы определить, перпендикулярны ли линии.
Повседневная математика
Уравнение можно использовать для преобразования температур F по шкале Фаренгейта в температуру ° C по шкале Цельсия.
- ⓐ Объясните, что означает наклон уравнения.
- ⓑ Объясните, что означает перехват C в уравнении.
Уравнение используется для оценки количества щебетаний сверчка, n , за одну минуту на основе температуры в градусах Фаренгейта, T .
- ⓐ Объясните, что означает наклон уравнения.
- ⓑ Объясните, что означает перехват n в уравнении. Это реальная ситуация?
- ⓐ При увеличении на один градус по Фаренгейту количество звуковых сигналов увеличивается на четыре.
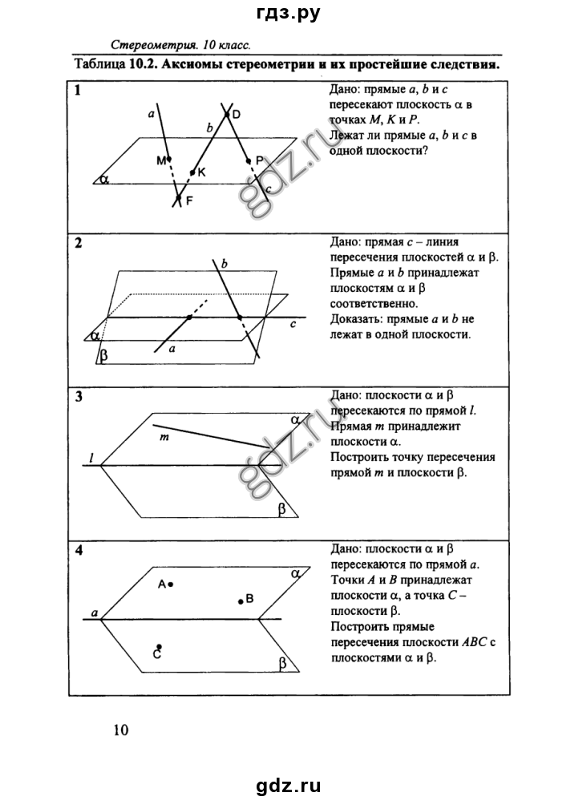
- ⓑ При температуре по Фаренгейту будет слышен щебетание.(Обратите внимание, что это не имеет смысла; эту модель нельзя использовать для всех возможных температур.)
Письменные упражнения
Объясните своими словами, как решить, какой метод использовать для построения линии.
Почему все горизонтальные линии параллельны?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ После просмотра контрольного списка, думаете ли вы, что хорошо подготовились к следующему разделу? Почему или почему нет?
Глоссарий
- параллельные линии
- Непересекающиеся линии в одной плоскости.
- перпендикулярные линии
- Линии в одной плоскости, образующие прямой угол.
- наклонно-отрезная форма уравнения прямой
- Угловая и угловая форма уравнения прямой с наклоном и точкой пересечения y ,.

Что такое прямая линия? (Определение, видео и примеры) // Tutors.com
Что такое прямая линия? (Определение, видео и примеры)
Хорошо, давайте проясним одну вещь … прямую линию.Что может быть проще по геометрии, чем изящная, разреженная, прямая линия? (Честно говоря, точка на проще; совокупность точек составляет прямую линию.) Прямая линия может показаться банальной, но это немного сложнее, и даже можно замаскироваться.
Что вы узнаете:
Проработав этот урок и видео, вы сможете:
- Распознать и построить прямую
- Определить особые виды прямых линий
- Напомним свойства прямых
- Вспомните и назовите фигуры, полученные из прямых линий
- Связать прямые с прямыми углами
Что такое прямая линия?
По определению, прямая линия — это совокупность всех точек между двумя точками и выходящая за их пределы.В большинстве геометрических форм линия — это примитивный объект, который не имеет формальных свойств, кроме длины, своего единственного измерения.
Два свойства прямых в евклидовой геометрии состоят в том, что у них есть только одно измерение, длина, и они простираются в двух направлениях навсегда.
Свойства прямых
- Одномерный
- Может быть горизонтальным, вертикальным или диагональным
- Оба конца тянутся в двух направлениях навсегда
- Делает угол 180 градусов при рисовании угловой дуги от одной точки к другой
Что такое точка?
A точка — простейшая фигура по геометрии.Это место в пространстве без измерения. У него нет ширины, объема, толщины, длины или глубины. Но когда у вас есть две точки, если вы соедините каждую точку между этими двумя точками, у вас будет прямая линия.
Точки на линии коллинеарны (col = «с,» или «вместе» и linear = «строка,» или «строка» ). Для определения линии нужны всего две точки.
Именование и определение прямых линий
Прямые линии называются любыми двумя точками на их длине. Обычно вы называете их слева направо. Вот линия AB:
Обычно вы называете их слева направо. Вот линия AB:
[вставить чертеж линии AB]
Чтобы обозначить линию на письме, вы пишете две точки заглавными буквами и проводите крошечную двуглавую линию над двумя буквами, например:
[вставьте изображение символа]
Как построить прямую
Прямая линия — одно из самых простых геометрических построений. С помощью листа чистой бумаги, карандаша и линейки вы можете легко построить линию:
- Нарисуйте на бумаге две точки на некотором расстоянии друг от друга; это Очки
- Используйте линейку, чтобы соединить две точки линией карандаша, и вытяните линию далеко за обе точки
- Нарисуйте стрелки на концах проведенной линии
Отрезки и лучи линий
Прямые линии считаются бесконечными в двух направлениях по своей длине.Из-за этого вы редко используете чистые линии в повседневной геометрии. Берешь отрывки прямых:
- Сегмент линии — Сегмент линии представляет собой сегмент или конечную часть бесконечной прямой линии
- Луч — Луч — это бесконечный отрезок прямой линии; он имеет единую точку происхождения, но вечно продолжается в одном направлении
Вот отрезок линии CD:
[вставить чертеж линейного сегмента CD]
А вот луч EF:
[вставить чертеж луча EF]
Сегменты линии используются для построения сторон всех многоугольников. Лучи используются для создания углов. Сегменты линий и лучи являются частями или сегментами прямых линий.
Лучи используются для создания углов. Сегменты линий и лучи являются частями или сегментами прямых линий.
А как насчет кривых?
Кривая не является прямой линией, так же как прямая линия не является кривой. Кривая линия содержит точки, которые не являются линейными по отношению к двум заданным точкам. Кривая движется в других направлениях от прямой линии, образованной соединением коллинеарных точек.
Направление прямых
Прямые линии могут быть горизонтальными , то есть перемещаться влево и вправо от точки обзора, навсегда.Прямые линии могут быть вертикальными , то есть подниматься выше и опускаться ниже точки обзора, навсегда. Прямые линии могут быть диагональю , что означает, что они представляют собой любой угол, кроме горизонтального или вертикального.
Прямые линии могут быть одиночными или парами. Пары прямых линий могут проходить параллельно друг к другу, никогда не приближаясь и не отделяясь друг от друга.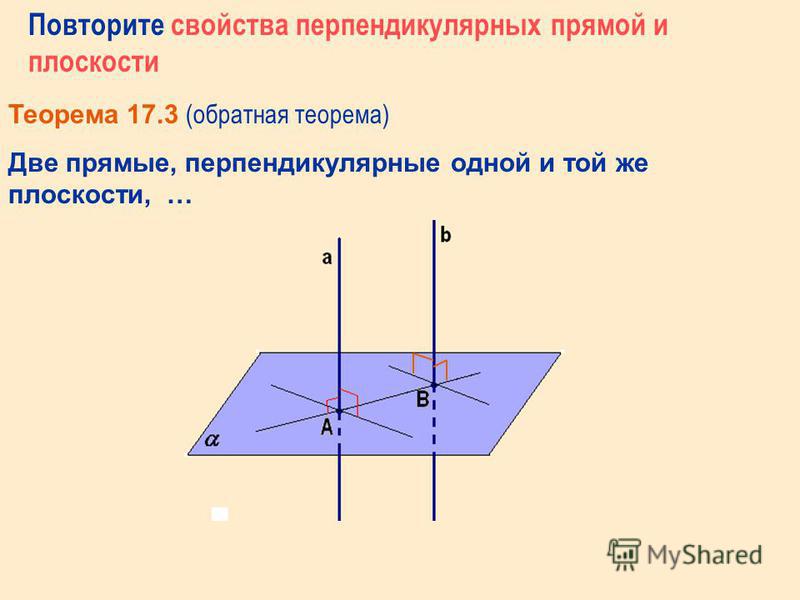 Они обозначены символом ∥.
Они обозначены символом ∥.
Пары прямых также могут пересекаться друг с другом под любым углом.Когда две прямые пересекаются под углом 90 °, это перпендикуляр , обозначенный символом ⊥.
Углы прямые
Прямые линии могут показаться другим рисунком, и наоборот. Прямой угол 180 ° — это прямая линия. Прямой угол состоит из двух лучей с общим концом. Поскольку два луча имеют общую конечную точку, и каждый луч продолжается в одном направлении бесконечно, единственным признаком того, что у вас есть прямой угол (а не прямая линия), могут быть три идентифицированные точки (вместо двух) вдоль фигуры:
[вставить чертеж прямого угла с тремя отмеченными точками слева, в центре и справа]
Краткое содержание урока
Теперь, когда вы изучили урок, вы можете распознать и построить прямую линию, определить особые виды прямых линий (горизонтальные, вертикальные, диагональные, параллельные и перпендикулярные линии), вспомнить свойства прямых линий, а также вспомнить и назовите фигуры, образованные из прямых линий, а именно отрезки и лучи. Вы также можете соотнести прямые линии с прямыми углами, образованными двумя лучами.
Вы также можете соотнести прямые линии с прямыми углами, образованными двумя лучами.
Следующий урок:
Математика, часть II Решения для класса 9 по математике Глава 2
Страница № 17:
Вопрос 1:
На данном рисунке линия RP || линия MS и линия DK являются их поперечными. ∠DHP = 85 °Найдите размеры следующих углов.
(i) ∠RHD (ii) ∠PHG
(iii) ∠HGS (iv) ∠MGKОтвет:
(i) Поскольку RP — прямая линия и на ней стоит луч HD, то
∠RHD + ∠DHP = 180 ∘ (углы в линейной паре)
⇒∠RHD + 85 ∘ = 180 ∘
⇒∠RHD = 180 ∘ -85 ∘ = 95 ∘
(ii) Поскольку прямые RP и DK пересекаются в точке H, тогда
∠PHG = ∠ RHD (вертикально противоположные углы)
⇒∠PHG = 95 ∘
(iii) Так как прямая RP || прямая MS и прямая DK — их трансверсаль, пересекающая их в точках H и G, тогда
∠HGS = ∠DHP (соответствующие углы)
⇒∠HGS = 85 ∘
(iv) Поскольку прямые MS и DK пересекаются в точках G, тогда
∠MGK = ∠HGS (вертикально противоположные углы)
⇒∠MGK = 85 ∘
Страница № 17:
Вопрос 2:
На данном рисунке линия p || линия q и линия l и линия m являются поперечными. Показаны размеры некоторых углов.
Показаны размеры некоторых углов. Следовательно, найдите меры ∠a, ∠b, ∠c, ∠d.
Ответ:
Отметим точки R и S на линии p , T и U на линии q , A и B на линии l и C и D на линии м .
Предположим, что прямые p и q пересекают линию l в точках K и L соответственно и линию m в точках N и M соответственно.
Так как AB — прямая и на ней стоит луч KN, то
∠NKL + ∠NKA = 180 ∘ (Углы в линейной паре)
⇒110 ∘ + a = 180 ∘
⇒ a = 180 ∘ — 110 ∘ = 70 ∘
Так как, строка p || прямая q и линия l — это трансверсаль, пересекающая их в точках K и L, тогда
∠TLB = ∠NKA (Альтернативные внешние углы)
⇒ b = a
⇒ b = 70 ∘
Т.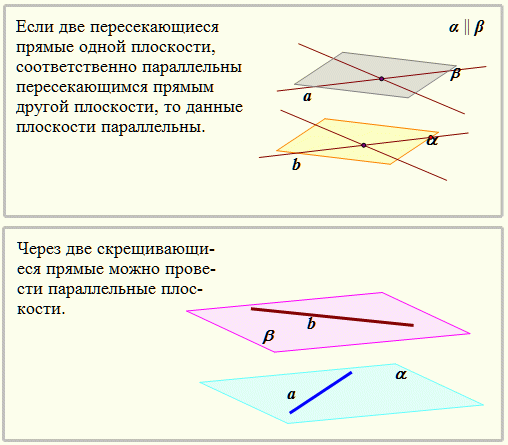 к., строка р || линия q и линия м — это трансверсаль, пересекающая их в точках N и M, тогда
к., строка р || линия q и линия м — это трансверсаль, пересекающая их в точках N и M, тогда
∠CNK = ∠NML (Соответствующие углы)
⇒ c = 115 ∘
Поскольку, CD — прямая линия и луч ML стоит на нем, тогда
∠NML + ∠LMD = 180 ∘ (Углы в линейной паре)
⇒115 ∘ + d = 180 ∘
⇒ d = 180 ∘ –115 ∘ = 65 ∘
Страница № 17:
Вопрос 3:
На данном рисунке линия l || линия м и линия n || линия п .
Найдите ∠a, ∠b, ∠c из заданной меры угла.
Ответ:
Отметим точки R и S на линии n , T и U на линии p , A и B на линии l и C и D на линии m .
Предположим, что прямые n и p пересекают линию l в точках K и L соответственно и линию m в точках M и N соответственно.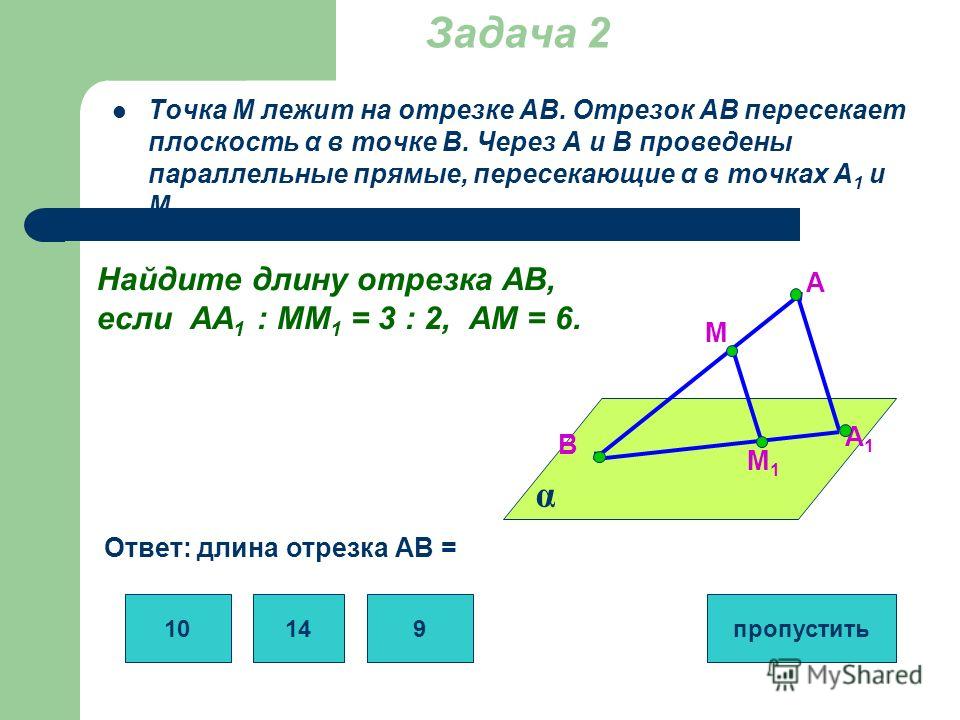
Так как прямая l и линия p пересекаются в точке L, то
∠KLN = ∠BLT (Вертикально противоположные углы)
⇒∠KLN = 45 ∘
Т.к., линия l || линия м и линия p — это трансверсаль, пересекающая их в точках L и N, тогда
∠KLN + ∠MNL = 180 ∘ (Пара внутренних углов на одной стороне трансверсали является дополнительной)
⇒45 ∘ + ∠ a = 180 ∘
⇒∠ a = 180 ∘ — 45 ∘ = 135 ∘
Так как прямая m и линия p пересекаются в точке N, то
∠DNU = ∠MNL (вертикально противоположные углы)
⇒∠ b = ∠ a = 135 ∘
Так как, строка n || линия p и линия м — это трансверсаль, пересекающая их в точках M и N, тогда
∠NMS = ∠DNU (соответствующие углы)
⇒∠ c = ∠ b = 45 ∘
Страница № 17:
Вопрос 4:
На данном рисунке стороны ∠PQR и ∠XYZ параллельны друг другу.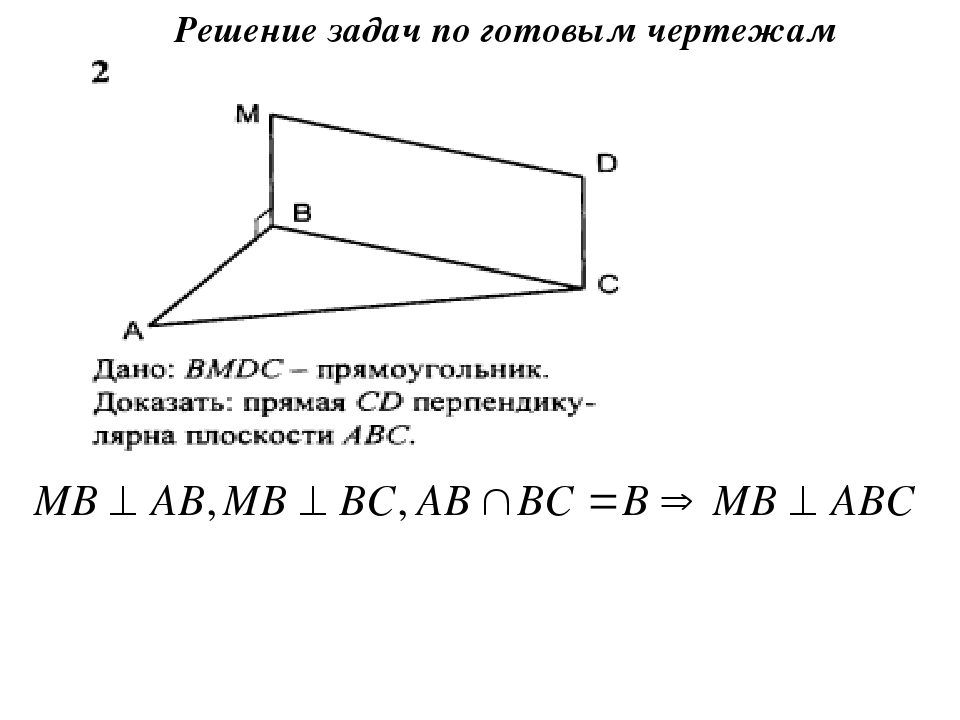
Докажите, что, ∠ PQR ≅∠ XYZ
Ответ:
Имеем, XY || PQ и YZ || QR.
Давайте создадим лучи YZ и YX в обратном направлении к точкам Z ‘и X’ соответственно так, чтобы ZYZ ‘и XYX’ были прямыми линиями.
Аналогичным образом направьте лучи QP и QR к точкам P ‘и R’ соответственно так, чтобы PQP ‘и RQR’ были прямыми линиями.
Предположим, что линия ZYZ ‘пересекает линию PQP’ в точке L, а линия RQR ‘пересекает линию XYX’ в точке K.
Итак, линия XYX ‘|| линия PQP ‘и линия ZYZ’ || линия RQR ‘.
Т.к., строчка ЗЫЗ ‘|| прямая RQR ‘и прямая XYX’ — это трансверсаль, пересекающая их в точках Y и K, тогда
м ∠XYZ = м ∠XKR (Соответствующие углы) …. (1)
Поскольку, прямая XYX ‘|| прямая PQP ‘и линия RQR’ — это трансверсаль, пересекающая их в точках Q и K, тогда
м ∠PQR = м ∠XKR (соответствующие углы) …. (2)
Из (1) и (2) , получаем
м ∠XYZ = м ∠PQR
⇒∠XYZ ≅ ∠PQR
Страница № 18:
Вопрос 5:
На данном рисунке линия AB || Линия CD и линия PQ являются поперечными.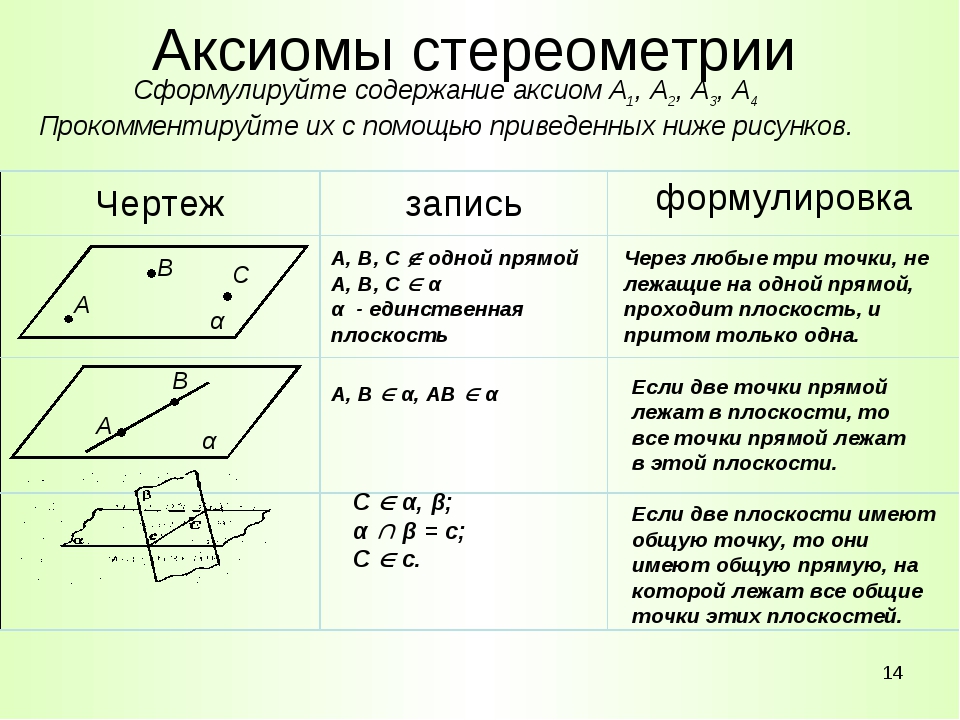 Приведена мера одного из углов. Отсюда найдите меры следующих углов.
Приведена мера одного из углов. Отсюда найдите меры следующих углов.
(i) ∠ART
(ii) ∠CTQ
(iii) ∠DTQ
(iv) ∠PRB
Ответ:
(i) Поскольку AB — прямая линия и на ней стоит луч RT, то
∠ART + ∠BRT = 180 ∘ (Углы в линейной паре)
⇒∠ART + 105 ∘ = 180 ∘
⇒∠ART = 180 ∘ — 105 ∘ = 75 ∘
(ii) Поскольку линия AB || прямая CD и прямая PQ — это трансверсаль, пересекающая их в точках R и T, тогда
∠ART = ∠CTQ (соответствующие углы)
⇒75 ∘ = ∠CTQ
⇒∠CTQ = 75 ∘
(iii) Поскольку линия AB || прямая CD и прямая PQ — это трансверсаль, пересекающая их в точках R и T, тогда
∠BRT = ∠DTQ (соответствующие углы)
⇒105 ∘ = ∠DTQ
⇒∠DTQ = 105 ∘
(iv) Поскольку прямая AB и прямая PQ пересекаются в точке R, тогда
∠PRB = ∠ART (вертикально противоположные углы)
⇒∠PRB = 75 ∘ (∵ ∠ART = 75 ∘ )
Страница № 21:
Вопрос 1:
На данном рисунке y = 108 ° и x = 71 ° Параллельны ли линии m и n ? Оправдывать ?
Ответ:
У нас есть, x = 71 ° и y = 108 °
Теперь, x + y = 71 ∘ + 108 ∘ = 179 461 Итак, 916 , x + y ≠ 180 ∘
Но x и y — это внутренние углы, образованные поперечным углом l двух линий m и n .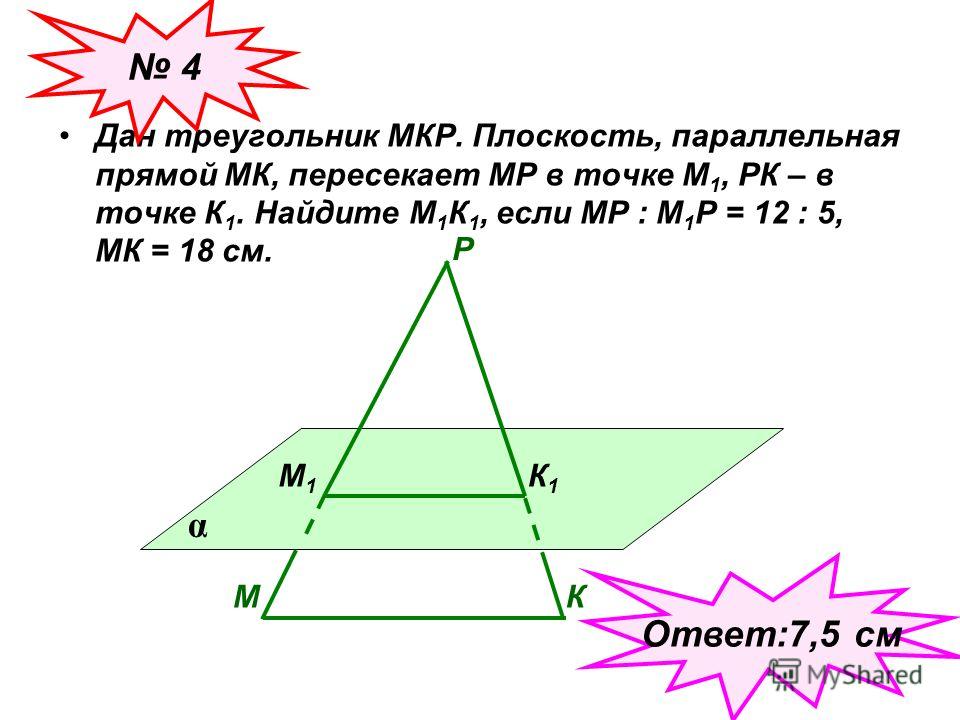
Известно, что если сумма внутренних углов, образованных трансверсалью двух различных прямых, равна 180 ∘ , то эти две прямые параллельны.
∴ линия м не параллельна линии n .
Страница № 21:
Вопрос 2:
Если на данном рисунке ∠a ≅ ∠b, то докажите, что строка l || линия м .
Ответ:
Отметим точки A и B на линии l , C и D на линии m и P и Q на линии n .
Предположим, что линия n пересекает линию l в точке K и линию м в точке L.
Поскольку PQ является прямой линией и на ней стоит луч KA, тогда
m ∠AKP + m ∠AKL = 180 ∘ (Углы в линейной паре)
⇒ м ∠ a + м ∠AKL = 180 ∘
⇒ м ∠ a = 180 ∘ — м AKL .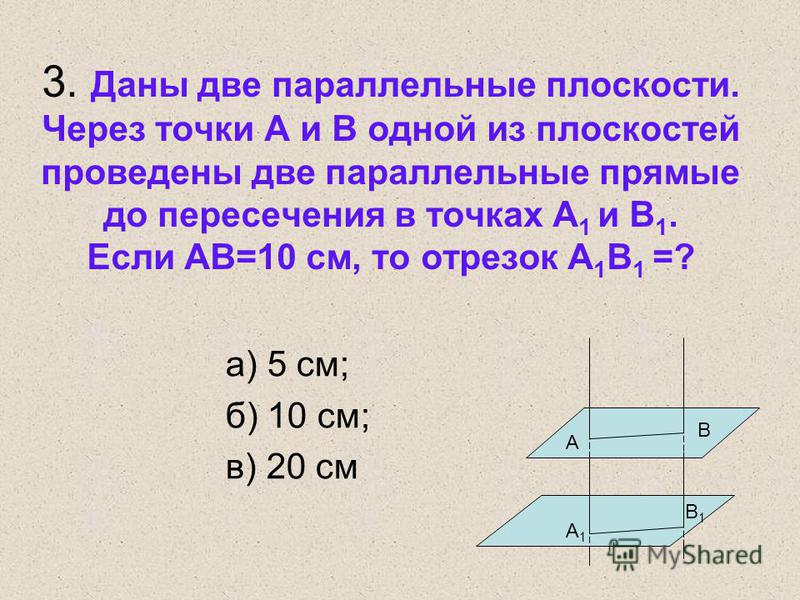 … (1)
… (1)
Поскольку PQ — прямая линия и на ней стоит луч LD, то
м ∠DLQ + м ∠DLA = 180 ∘ (Углы в линейной паре)
⇒ м ∠ b + м ∠DLA = 180 ∘
⇒ м ∠ b = 180 ∘ — м ∠DLA…. (2)
Поскольку, ∠ a ≅ ∠ b , то m ∠ a = m ∠ b .
∴ из (1) и (2), получаем
180 ∘ — м ∠AKL = 180 ∘ — м ∠DLA
⇒ м ∠AKL = м ∠DLA
⇒ ∠AKL ≅ ∠DLA
Известно, что если пара чередующихся внутренних углов, образованных трансверсалью двух прямых, конгруэнтна, то эти две прямые параллельны.
∴ AB || CD или строчка l || линия м .
Страница № 21:
Вопрос 3:
На данном рисунке, если ∠ a ≅∠ b и ∠ x ≅ ∠ y
, тогда докажите, что линия l || линия № .
Ответ:
Мы имеем,
∠ a ≅ ∠ b
⇒ м ∠ a = м ∠ b
Но ∠ a и ∠ b a являются соответствующими углами поперечные к по линии м и по линии л .
∴ линия м || линия l (проверка соответствующих углов)
Также у нас есть,
∠ x ≅ ∠ y
⇒ m ∠ x = м ∠ y
Но ∠ x и ∠ x и ∠ y — это чередующиеся внутренние углы, образованные поперечным углом k линии m и линией n .
∴ линия м || линия n (тест альтернативных углов)
Итак, у нас есть линия m || линия л и линия м || линия п.
Известно, что если две прямые на плоскости параллельны третьей прямой на плоскости, то эти две прямые параллельны друг другу.
∴ строка л || линия н
Страница № 21:
Вопрос 4:
На данном рисунке, если луч BA || луч DE, ∠C = 50 ° и ∠D = 100 ° . Найдите меру ABC.
Ответ:
Проведите линию XY, проходящую через точку C и параллельную AB.
Имеем, АВ || DE и AB || XY.
Известно, что если две прямые на плоскости параллельны третьей прямой на плоскости, то эти две прямые параллельны друг другу.
∴ DE || XY.
С DE || XY и DC — это трансверсаль, пересекающая их в точках D и C, тогда
∠EDC + ∠YCD = 180 ∘ (Пары внутренних углов на одной стороне трансверсали являются дополнительными)
⇒100 ∘ + ∠YCD = 180 ∘
∠YCD = 180 ∘ — 100 ∘ = 80 ∘
Так как сумма всех углов на прямой в точке равна 180 ∘ , тогда
∠XCB + ∠BCD + ∠YCD = 180 ∘
⇒∠XCB + 50 ∘ + 80 ∘ = 180 ∘
⇒∠XCB + 130 ∘ = 180 ∘
⇒∠XCB∘ = 916 —14 130 ∘ = 50 ∘
Поскольку, AB || XY и BC — трансверсаль, пересекающая их в точках B и C, тогда
∠ABC + ∠XCB = 180 ∘ (Пары внутренних углов на одной стороне трансверсали являются дополнительными)
⇒∠ABC + 50 ∘ = 180 ∘
⇒∠ABC = 180 ∘ -50 ∘ = 130 ∘
Страница № 22:
Вопрос 5:
На данном рисунке луч AE || луч BD, луч AF — биссектриса EAB, а луч BC — биссектриса ABD.
Докажите, что линия AF || линия BC.
Ответ:
Поскольку луч AF делит пополам EAB, а луч BC делит пополам ∠ABD, то
∠EAF = ∠FAB = ∠ x = 12∠EAB и ∠CBA = ∠DBC = ∠ y = 12∠ABD
∴ ∠ x = 12∠EAB и ∠ y = 12∠ABD …. (1)
Поскольку, луч AE || луч BD и отрезок AB — это трансверсаль, пересекающая их в точках A и B, тогда
∠EAB = ∠ABD (Альтернативные внутренние углы)
Умножая обе стороны на 12, получаем
12∠EAB = 12∠ABD
Теперь, используя ( 1), мы получаем
∠ x = ∠ y
Но ∠ x и ∠ y — это чередующиеся внутренние углы, образованные поперечными AB луча AF и луча BC.
∴ луч AF || луч BC (Тест альтернативных углов)
Страница № 22:
Вопрос 6:
Трансверсаль EF прямых AB и CD пересекает прямые в точках P и Q соответственно.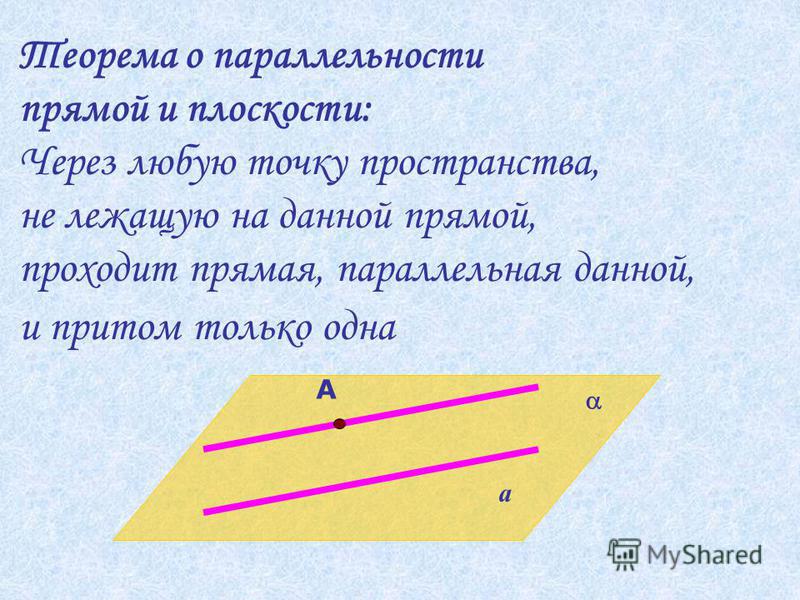 Луч PR и луч QS параллельны и биссектрисы
Луч PR и луч QS параллельны и биссектрисы
∠BPQ и ∠PQC соответственно.
Докажите, что прямая AB || линия CD.
Ответ:
Поскольку луч PR делит пополам ∠BPQ, а луч QS делит пополам ∠PQC, тогда
∠RPQ = ∠RPB = 12∠BPQ и ∠SQP = ∠SQC = 12∠PQC
∴ ∠BPQ = 2∠RPQ и ∠PQC = 2∠ SQP…. (1)
Поскольку PR || QS и PQ — это трансверсаль, пересекающая их в точках P и Q, тогда
∠RPQ = ∠SQP (Альтернативные внутренние углы)
Умножив обе стороны на ‘2’, мы получим
2∠RPQ = 2∠SQP
Теперь, используя ( 1) получаем
∠BPQ = ∠PQC
Но ∠BPQ и ∠PQC — это чередующиеся внутренние углы, образованные поперечным EF прямых AB и CD.
∴ линия AB || линия CD (Тест на альтернативные углы)
Страница № 22:
Вопрос 1:
Выберите правильный вариант и заполните пропуски в следующих утверждениях.
(i) Если трансверсаль пересекает две параллельные прямые, то сумма внутренних углов на одной и той же стороне трансверсали равна …………
(A) 0 ° (B) 90 ° (C) 180 ° (D) 360 °
(ii) Количество углов, образованных трансверсалью двух прямых, равно …………
(А) 2 (В) 4 (В) 8 (Г) 16
(iii) Трансверсаль пересекает две параллельные прямые. Если размер одного из углов равен 40 ∘ , то размер соответствующего ему угла равен………….
(A) 40 ° (B) 140 ° (C) 50 ° (D) 180 °
(iv) In ∆ABC, A = 76 ° , ∠B = 48 ° , ∴ C = …………..
(А) 66 ° (В) 56 ° (С) 124 ° (Г) 28 °
(v) Две параллельные прямые пересекаются трансверсалью. Если размер одного из альтернативных внутренних углов равен 75 ° , то размер другого угла равен .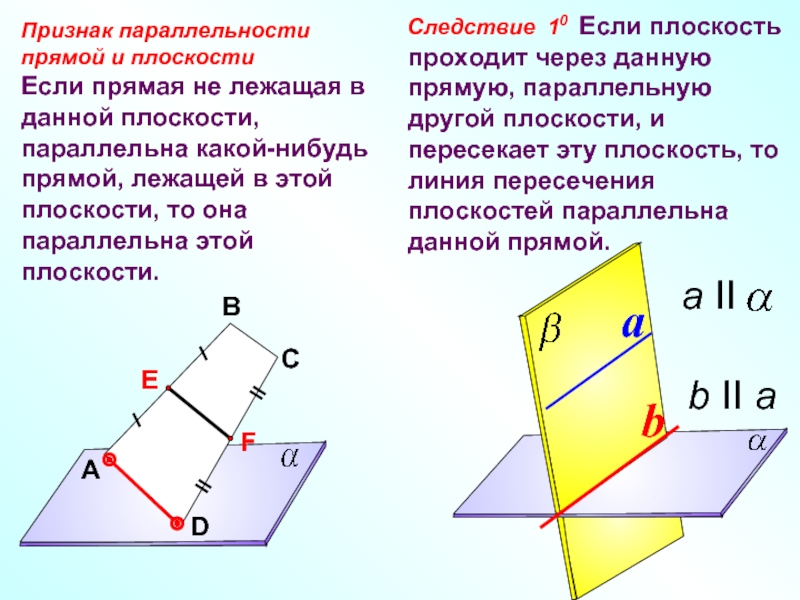 …………
…………
(A) 105 ° (B) 15 ° (C) 75 ° (D) 45 °
Ответ:
(i) Известно, что, когда две параллельные прямые пересекаются трансверсалью, то пары внутренних углов на одной и той же стороне трансверсали являются дополнительными, т. Е. Сумма внутренних углов на одной стороне трансверсали равна 180 ∘ .
Следовательно, правильный ответ — вариант (С).
(ii)
На приведенном выше рисунке линия n является пересечением линии l и линии m . Углы, образованные поперечными n двух прямых l и m , составляют:
a , b , c , d , e , f , g и ч .
∴ количество углов, образованных трансверсией двух прямых, равно 8.
Следовательно, правильный ответ — вариант (C).
(iii)
Предположим, строка RP || прямая MS и прямая DK — это трансверсаль, пересекающая их в точках H и G соответственно.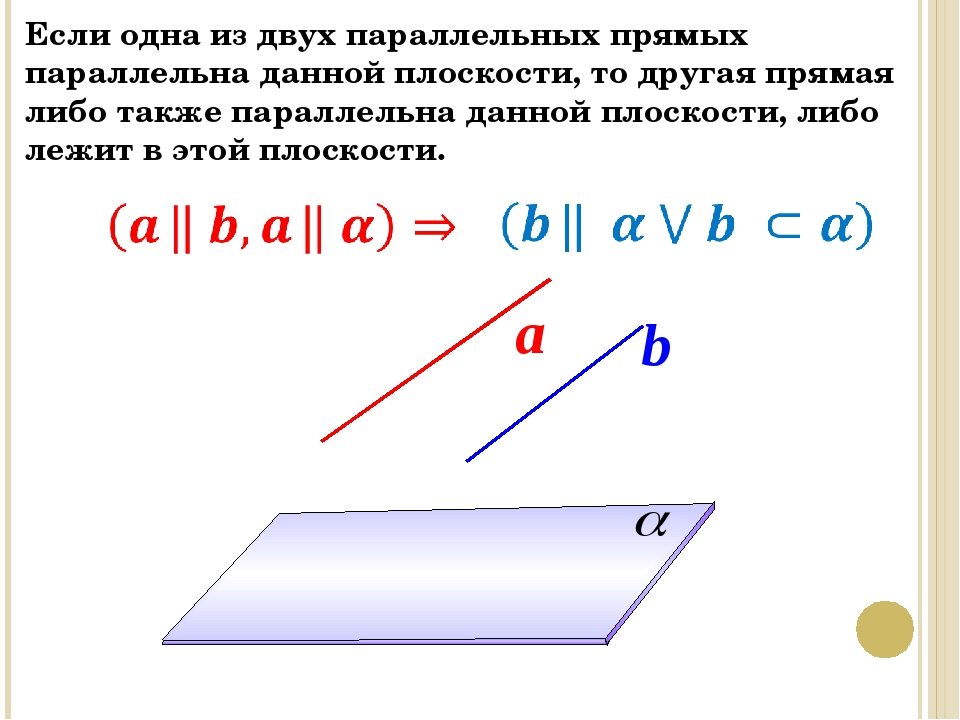
Пусть ∠DHP = 40 ∘
Теперь ∠HGS — это соответствующий угол ∠DHP.
Известно, что соответствующие углы, образованные трансверсалью двух параллельных прямых, равны.
∴ ∠HGS = 40 ∘
Следовательно, правильный ответ — вариант (А).
(iv) In ∆ABC,
∠A + ∠B + ∠C = 180 ∘ (свойство суммы углов треугольника)
⇒76 ∘ + 48 ∘ + ∠C = 180 ∘
⇒124 ∘ + ∠C = 180 ∘
⇒∠C = 180 ∘ –124 ∘ = 56 ∘
Следовательно, правильный ответ — вариант (B).
(v)
Предположим, строка RP || прямая MS и прямая DK — это трансверсаль, пересекающая их в точках H и G соответственно.
Пусть ∠PHG = 75 ∘
Теперь ∠MGH — угол, альтернативный ∠PHG.
Известно, что чередующиеся внутренние углы, образованные трансверсалью двух параллельных прямых, имеют одинаковую меру.
∴ ∠MGH = 75 ∘
Следовательно, правильный ответ — вариант (C).
Страница № 22:
Вопрос 2:
Ray PQ и Ray PR перпендикулярны друг другу.Точки B и A находятся внутри и снаружи ∠QPR соответственно. Луч PB и луч PA перпендикулярны друг другу. Нарисуйте фигуру, показывающую все эти лучи, и напишите —
.
(i) Пара дополнительных углов (ii) Пара дополнительных углов. (iii) Пара конгруэнтных углов.
Ответ:
Так как луч PQ ⊥ луч PR, то м ∠QPR = 90 ∘ и луч PA луч PB, то м ∠APB = 90 ∘ .
(i) Два угла, сумма размеров которых составляет 90 ∘ , называются дополнительными углами.
Здесь м ∠QPR = 90 ∘
⇒ м ∠BPQ + м ∠BPR = 90 ∘
∴ BPQ и ∠BPR — дополнительные углы.
(ii) Два угла, сумма размеров которых составляет 180 ∘ , называются дополнительными углами.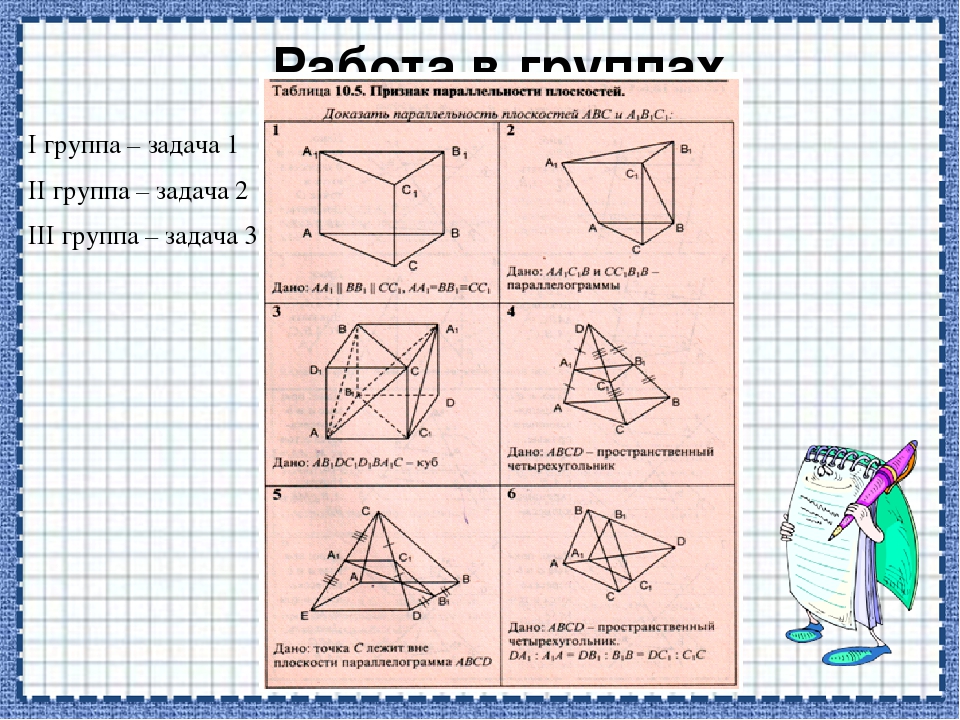
Здесь м ∠APB + м ∠QPR = 90 ∘ + 90 ∘ = 180 ∘
∴ APB и ∠QPR — дополнительные углы.
(iii) Углы с одинаковыми размерами называются конгруэнтными углами.
Здесь м ∠QPR = м ∠APB = 90 ∘
∴ APB и ∠QPR — совпадающие углы.
Страница № 23:
Вопрос 3:
Докажите, что если прямая перпендикулярна одной из двух параллельных прямых, то она также перпендикулярна другой прямой.
Ответ:
Предположим, что m и n — две параллельные прямые, а прямая l — их поперечная.Допустим, линия l ⊥ линия м .
Отметим точки A и B на линии м , C и D на линии n и P и Q на линии l .
Предположим, что линия l пересекает линию m и линию n в точках K и L соответственно.
Так как, строка l ⊥ строка m , то ∠PKB = 90 ∘ .
Поскольку, прямая AB || прямая CD и поперечная PQ пересекают их в точках K и L соответственно, тогда
∠KLD = ∠PKB (соответствующие углы)
⇒∠KLD = 90 ∘
∴ линия l ⊥ линия n .
Страница № 23:
Вопрос 4:
На данном рисунке показаны размеры некоторых углов.
Используя меры, найдите меры ∠x и ∠y и, следовательно, покажите эту прямую l || линия м .
Ответ:
Предположим, что n является трансверсией данных прямых l и m .
Отметим точки A и B на линии l , C и D на линии m и P и Q на линии n .
Предположим, что линия n пересекает линию l и линию m в точках K и L соответственно.
Так как PQ — прямая линия и на ней стоит луч KA, то
∠AKL + ∠AKP = 180 ∘ (углы в линейной паре)
⇒∠ x + 130 ∘ = 180 ∘
⇒∠ x = 180 ∘ — 130 ∘ = 50 ∘
Поскольку CD — прямая линия и луч LK стоит на ней, то
∠KLC + ∠KLD = 180 ∘ (углы в линейной паре)
⇒∠ y + 50 ∘ = 180 ∘
⇒∠ y = 180 ∘ — 50 ∘ = 130 ∘
Теперь, ∠ x + ∠ y = 50 ∘ + 130 ∘ = 180 ∘
Но ∠ x и ∠ y — это внутренние углы, образованные поперечным углом n прямой l и прямой м .
Известно, что если сумма внутренних углов, образованных трансверсалью двух различных прямых, равна 180 ∘ , то эти прямые параллельны.
∴ строка л || линия м .
Страница № 23:
Вопрос 5:
Line AB || строка CD || линия EF и линия QP являются их поперечными. Если y : z = 3: 7, тогда найдите меру ∠ x.
Ответ:
Предположим, что поперечная QP пересекает прямую AB, прямую CD и прямую EF в точках K, L и M соответственно.
Поскольку прямая CD и линия QP пересекаются в точке L, тогда
∠DLM = ∠CLK (вертикально противоположные углы)
⇒∠DLM = ∠ y
Поскольку прямая CD || прямые EF и QP — это трансверсаль, пересекающая их в точках L и M, тогда
∠DLM + ∠FML = 180 ∘ (Пара внутренних углов на одной стороне трансверсали является дополнительной)
⇒∠ y + ∠ z = 180 ∘ …. (1)
Мы имеем, y : z = 3: 7. Пусть y = 3 k и z = 7 k
Теперь, из (1) получаем
3 k + 7 k = 180 ∘
⇒10 k = 180 ∘
⇒ k = 18 ∘
∴ ∠ y = 3 k = 3 × 18 ∘ = 54 ∘ и ∠ z = 7 k = 7 × 18 ∘ = 126 ∘
Поскольку линия AB || прямые CD и QP — это трансверсаль, пересекающая их в точках K и L, тогда
∠AKL + ∠CLK = 180 ∘ (Пара внутренних углов на одной стороне трансверсали является дополнительной)
⇒∠ x + ∠ y = 180 ∘
⇒∠ x + 54 ∘ = 180 ∘
⇒∠ x = 180 ∘ — 54 ∘ = 126 ∘

Страница № 23:
Вопрос 6:
На данном рисунке, если строка q || линия r , линия p является их поперечной, и если a = 80 ° , найдите значения f и g .
Ответ:
Начиная со строки q || прямая r и линия p — их поперечные, тогда
∠ g = ∠ a (Альтернативные внешние углы)
⇒∠ g = 80 ∘
Так как ∠ g и ∠ f образуют линейную пару, тогда
∠ f + ∠ g = 180 ∘ (Углы в линейной паре дополнительные)
⇒∠ f = 180 ∘ — ∠ g
⇒ ∠ f = 180 ∘ — 80 ∘ = 100 ∘
Следовательно, значения f и g равны 100 ∘ и 80 ∘ соответственно.
Страница № 23:
Вопрос 7:
На данном рисунке, если линия AB || линия CF и линия BC || строка ED
, затем докажите, что ∠ABC = ∠FDE.
Ответ:
Отметим точки M и N на прямой BC и точку G на прямой ED.
Начиная с линии AB || прямая PF (или линия CF) и прямая MN их поперечная, тогда
∠PCN = ∠ABC (соответствующие углы)…. (1)
Поскольку строка MN || прямая EG и прямая PF — их поперечная, тогда
∠PCN = ∠CDG (соответствующие углы) …. (2)
Поскольку EG и PF — прямые, пересекающиеся в точке D, то
∠CDG = ∠FDE (вертикально противоположные углы ) …. (3)
∴ из (2) и (3), получаем
∠PCN = ∠FDE …. (4)
∴ из (1) и (4), получаем
∠ABC = ∠FDE
Страница № 23:
Вопрос 8:
На данном рисунке прямая PS представляет собой трансверсию параллельных прямых AB и CD.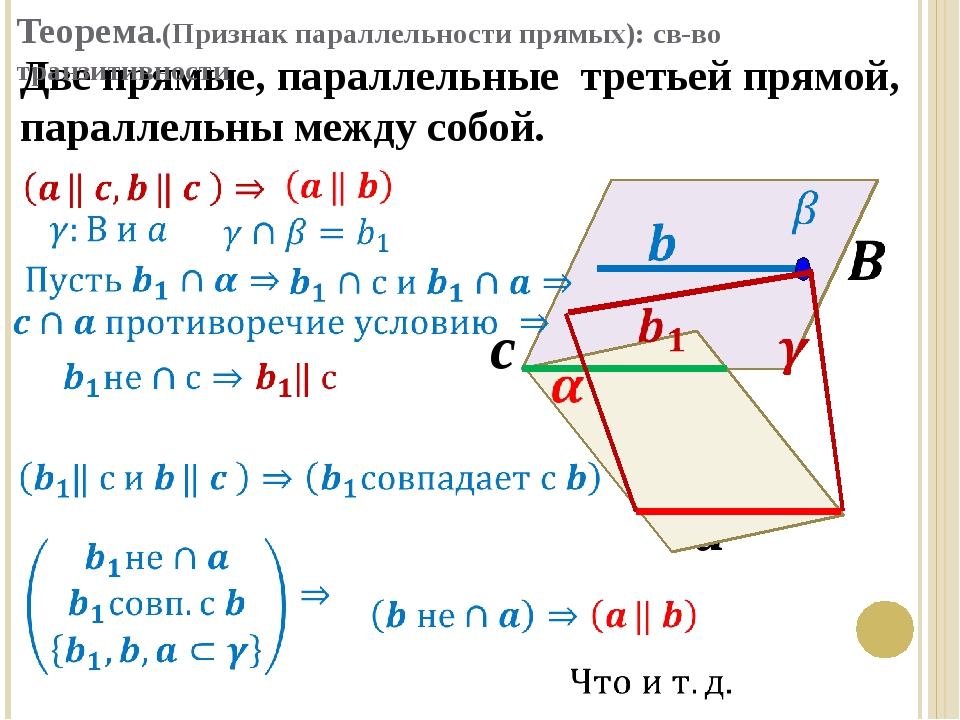 Если луч QX, луч QY, луч RX, луч RY являются биссектрисами угла, тогда докажите, что 123 QXRY — прямоугольник.
Если луч QX, луч QY, луч RX, луч RY являются биссектрисами угла, тогда докажите, что 123 QXRY — прямоугольник.
Ответ:
Дано: AB и CD — две параллельные прямые, которые пересекаются поперечной PS в точках Q и R соответственно. Биссектрисы внутренних углов пересекаются в точках X и Y.
Чтобы доказать: Четырехугольник QXRY является прямоугольником.
Доказательство: Поскольку AB || CD и PS — это поперечное сечение, тогда
∠AQR = ∠DRQ (Альтернативные внутренние углы)
⇒12∠AQR = 12∠DRQ…. (1)
Поскольку QX делит пополам ∠AQR, а RY делит пополам DRQ, то
∠XQR = 12∠AQR и ∠YRQ = 12∠DRQ
∴ из (1), получаем
∠XQR = ∠YRQ
Но ∠XQR и ∠YRQ — альтернативные внутренние углы, образованные поперечным QR с QX и RY соответственно.
∴ QX || RY (Проверка альтернативных углов)
Аналогично, у нас есть RX || QY.
Следовательно, в четырехугольнике QXRY QX || RY и RX || QY.
Известно, что четырехугольник является параллелограммом, если противоположные стороны комплектов параллельны.
∴ QXRY — параллелограмм.
Так как сумма внутренних углов на одной стороне поперечного сечения равна 180 ∘ , то
∠BQR + ∠DRQ = 180 ∘
⇒12∠BQR + 12∠DRQ = 90 ∘ …. (2)
Поскольку QY делит пополам ∠BQR и RY пополам ∠DRQ, то
∠YQR = 12∠BQR и ∠YRQ = 12∠DRQ
∴ из (2), получаем
∠YQR + ∠YRQ = 90 ∘ …. (3)
В ∆QRY мы имеем
∠YQR + ∠YRQ + ∠QYR = 180 ∘ (свойство суммы углов треугольника)
⇒90 ∘ + ∠QYR = 180 ∘ [Используя (3)]
⇒∠QYR = 180 ∘ — 90 ∘ = 90 ∘
Поскольку QXRY — параллелограмм, тогда
∠QXR = ∠QYR (Противоположные углы || gm равны )
⇒∠QXR = 90 ∘ (∵ ∠QYR = 90 ∘ )
Поскольку соседние углы в параллелограмме являются дополнительными, тогда
∠QXR + ∠XRY = 180 ∘
⇒90 ∘ ∘ 916 ∠XRY = 180 ∘ (∵ ∠QXR = 90 ∘ 916 16)
⇒∠XRY = 180 ∘ — 90 ∘ = 90 ∘
Также ∠XQY = ∠XRY = 90 ∘ (Противоположные углы || gm равны)
Таким образом, QXRY представляет собой параллелограмм, в котором все внутренние углы прямые.
Известно, что прямоугольник — это || gm , в котором каждый угол является прямым.
Следовательно, □ QXRY — прямоугольник.
Просмотреть решения NCERT для всех глав класса 9
GRE Multiple-Choice — Выберите один вопрос (для участников тестирования)
Если какое значение x?
- 4
- 7
- 12
Пояснение
Решая уравнение относительно x, вы получаете и поэтому Правильный ответ — вариант A,
Какое из следующих чисел дальше всего от цифры 1 в числовой строке?
- 0
- 5
- 10
Пояснение
Обвод каждого варианта ответа на схеме числовой прямой (рис. 4) показывает, что из данных чисел это наибольшее расстояние от 1.
Рисунок 4
Другой способ ответить на этот вопрос — вспомнить, что расстояние между двумя числами на числовой прямой равно абсолютному значению разницы двух чисел. Например, расстояние между и 1 равно, а расстояние между 10 и 1 равно. Правильный ответ — вариант A,
Например, расстояние между и 1 равно, а расстояние между 10 и 1 равно. Правильный ответ — вариант A,
Рисунок 5
На рисунке выше показан график функции f, определенной для всех чисел x.Для какой из следующих функций g, определенных для всех чисел x, график g пересекает график f?
Пояснение
Вы можете видеть, что все пять вариантов являются линейными функциями, графики которых представляют собой линии с различным наклоном и пересечением по оси Y. График варианта A представляет собой линию с наклоном 1 и точкой пересечения по оси Y, показанной на рисунке 6.
Рисунок 6
Ясно, что эта линия не будет пересекать график f слева от оси y.Справа от оси y график f представляет собой линию с наклоном 2, который больше, чем наклон 1. Следовательно, по мере увеличения значения x значение y увеличивается для f быстрее, чем для g, и, следовательно, графики не пересекаются справа от оси y. Вариант B также исключен. Обратите внимание, что если бы точка пересечения по оси Y любой из линий в вариантах A и B была больше или равна 4, а не меньше 4, они пересекали бы график f.
Вариант B также исключен. Обратите внимание, что если бы точка пересечения по оси Y любой из линий в вариантах A и B была больше или равна 4, а не меньше 4, они пересекали бы график f.
Варианты C и D — это линии с наклоном 2 и пересечением по оси Y меньше 4.Следовательно, они параллельны графику f (справа от оси y) и, следовательно, не будут его пересекать. Любая линия с наклоном больше 2 и точкой пересечения по оси Y меньше 4, например линия в Варианте E, будет пересекать график f (справа от оси Y). Правильный ответ — выбор E,
.Автомобиль проехал 33 мили на галлон, используя бензин по цене 2,95 доллара за галлон. Какова примерная стоимость в долларах бензина, использованного для езды на автомобиле 350 миль?
- $ 10
- $ 20
- $ 30
- $ 40
- $ 50
Пояснение
Просмотр вариантов ответа показывает, что вы можете сделать хотя бы некоторую оценку и при этом ответить уверенно.В машине использовались галлоны бензина, поэтому стоимость составляла доллары. Вы можете оценить продукт, оценив немного ниже, 10, и оценив 2,95 немного выше, 3, чтобы получить приблизительно доллары. Вы также можете использовать калькулятор, чтобы вычислить более точный ответ, а затем округлить ответ до ближайших 10 долларов в соответствии с вариантами ответов. Калькулятор вычисляет десятичную дробь, которая округляется до 30 долларов. Таким образом, правильный ответ — вариант C, 30 долларов.
Вы можете оценить продукт, оценив немного ниже, 10, и оценив 2,95 немного выше, 3, чтобы получить приблизительно доллары. Вы также можете использовать калькулятор, чтобы вычислить более точный ответ, а затем округлить ответ до ближайших 10 долларов в соответствии с вариантами ответов. Калькулятор вычисляет десятичную дробь, которая округляется до 30 долларов. Таким образом, правильный ответ — вариант C, 30 долларов.
В одной банке 60 мармеладов: 22 белых, 18 зеленых, 11 желтых, 5 красных и 4 фиолетовых.Если мармелад должен быть выбран наугад, какова вероятность того, что мармелад не будет ни красным, ни пурпурным?
- 0,09
- 0,15
- 0,54
- 0,85
- 0,91
Пояснение
Поскольку в банке 5 красных и 4 фиолетовых мармелада, 51 мармелад не является ни красным, ни пурпурным, и вероятность выбора одного из них равна. Поскольку все варианты ответов являются десятичными, вы должны преобразовать дробь в ее десятичную дробь.


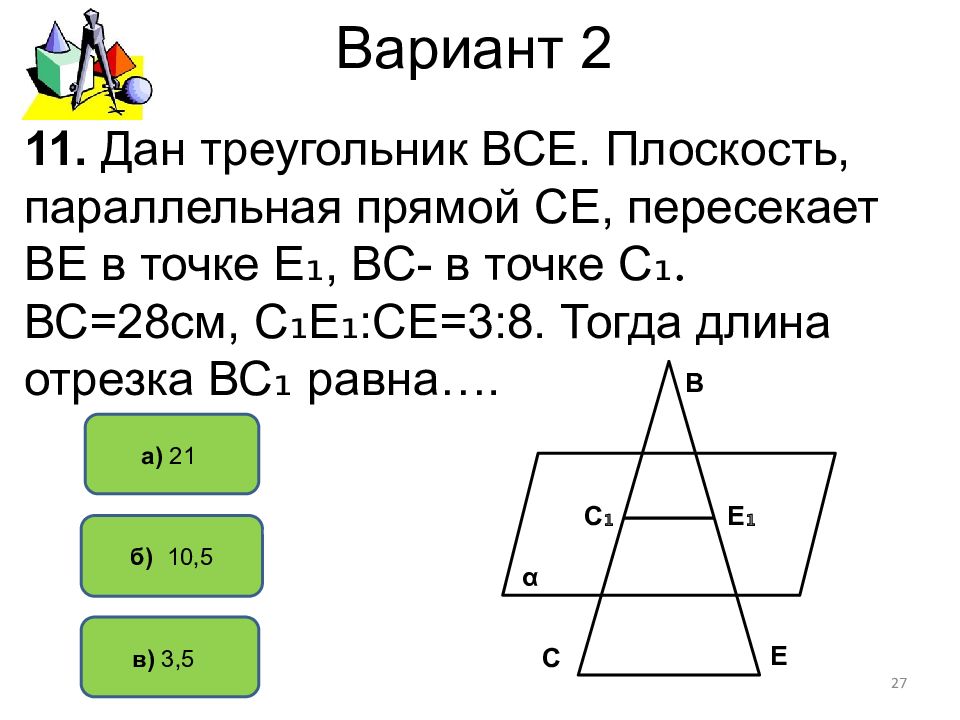

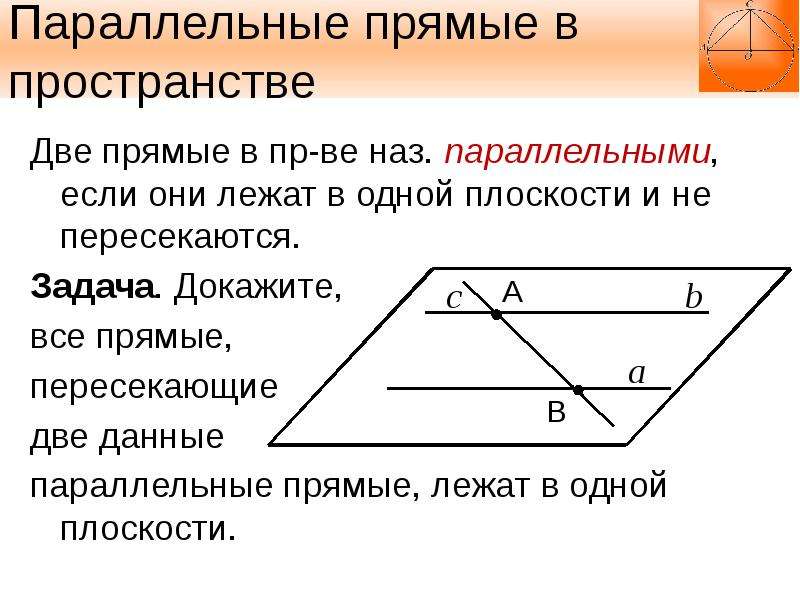 Домашнее задание.
Домашнее задание. Урок закончен, всем спасибо!
Урок закончен, всем спасибо! По двум пересекающимся прямым.
По двум пересекающимся прямым.

 Совпадает ли она с плоскостью квадрата?
Совпадает ли она с плоскостью квадрата?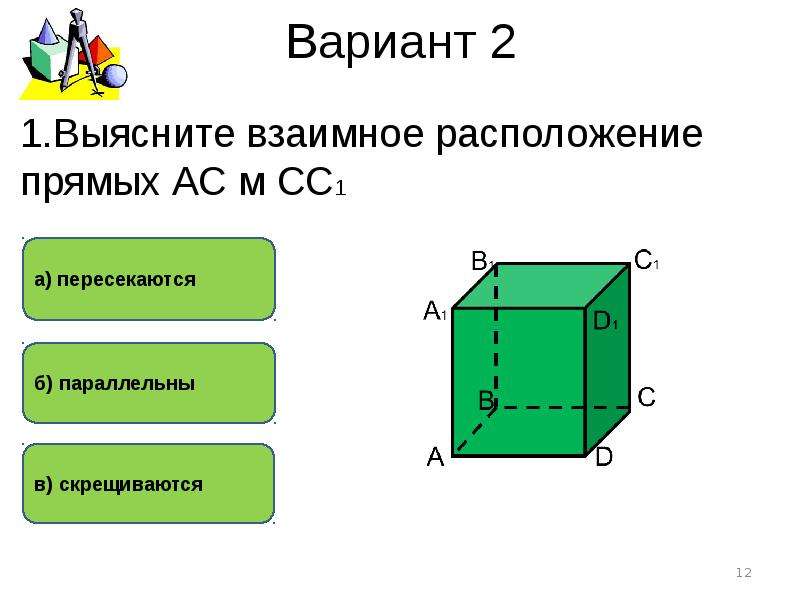 Определите взаимное расположение
Определите взаимное расположение Прямая а не лежит в плоскости трапеции ABCD. Определите взаимное расположение прямых aи BC, если aIIAB.
Прямая а не лежит в плоскости трапеции ABCD. Определите взаимное расположение прямых aи BC, если aIIAB. Определите взаимное расположение прямых MAи DC
Определите взаимное расположение прямых MAи DC Прямые а и bскрещиваются с прямой с. Что можно сказать о прямых а и b?
Прямые а и bскрещиваются с прямой с. Что можно сказать о прямых а и b? Выберите верное утверждение.
Выберите верное утверждение.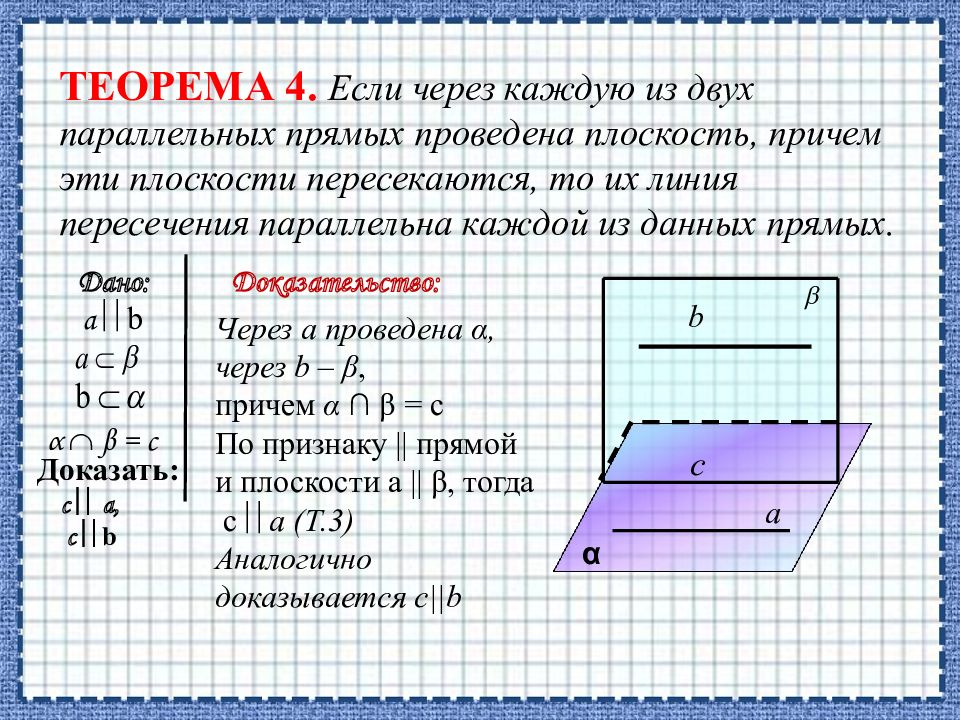 Прямая с параллельна прямой b, тогда:
Прямая с параллельна прямой b, тогда:
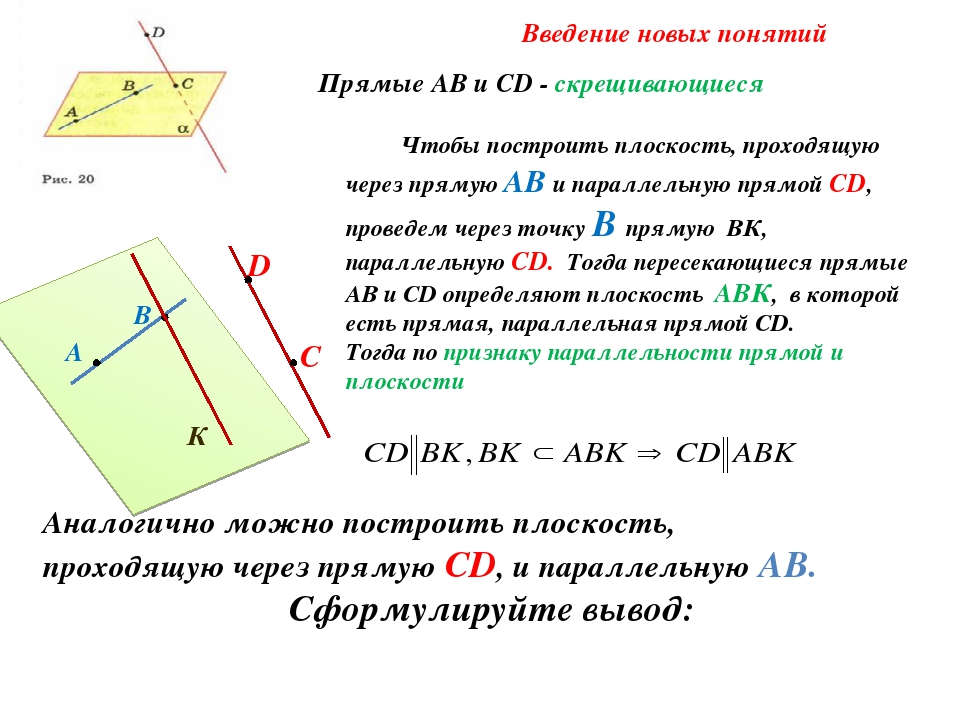
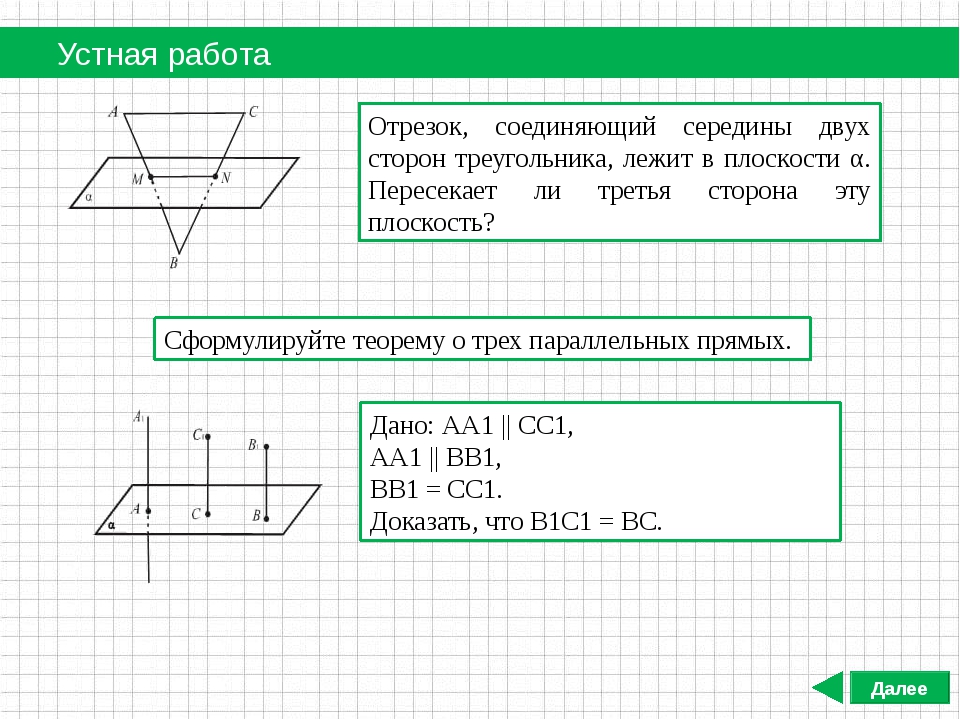
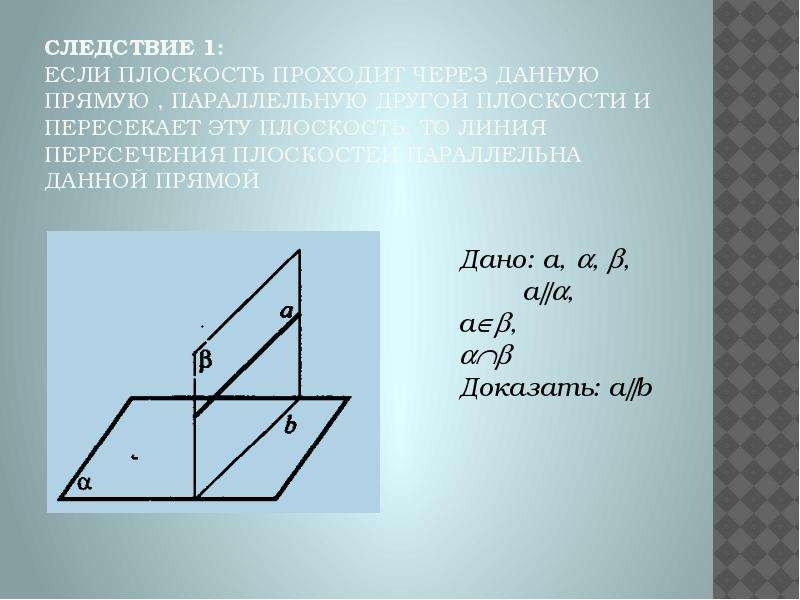

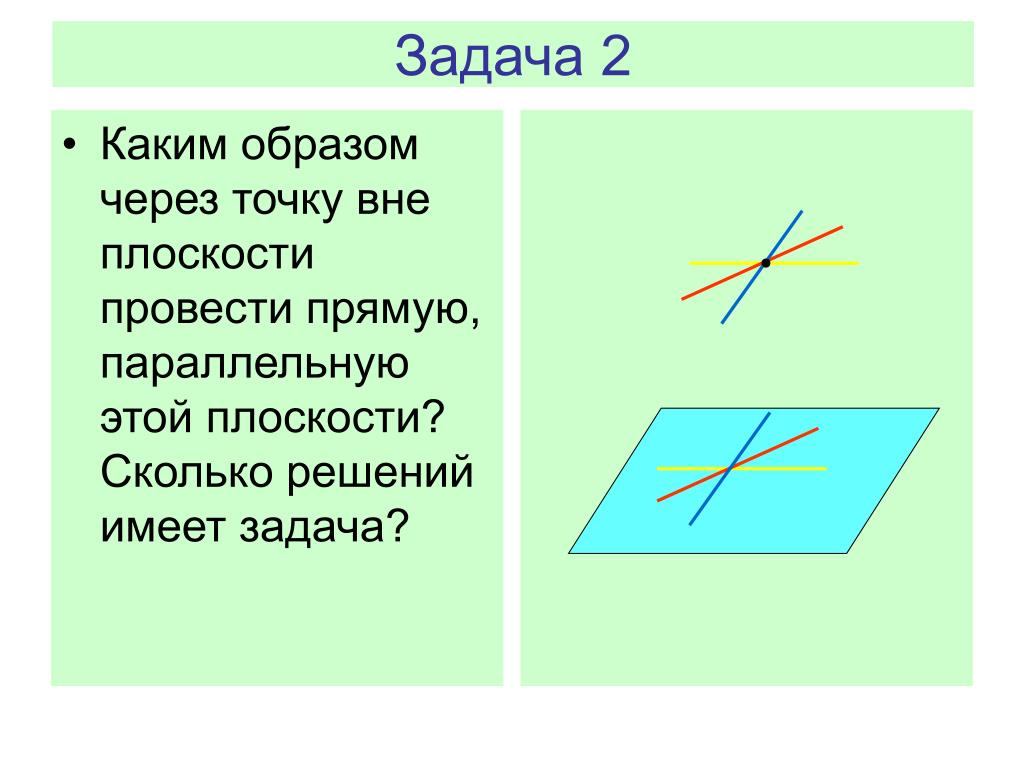
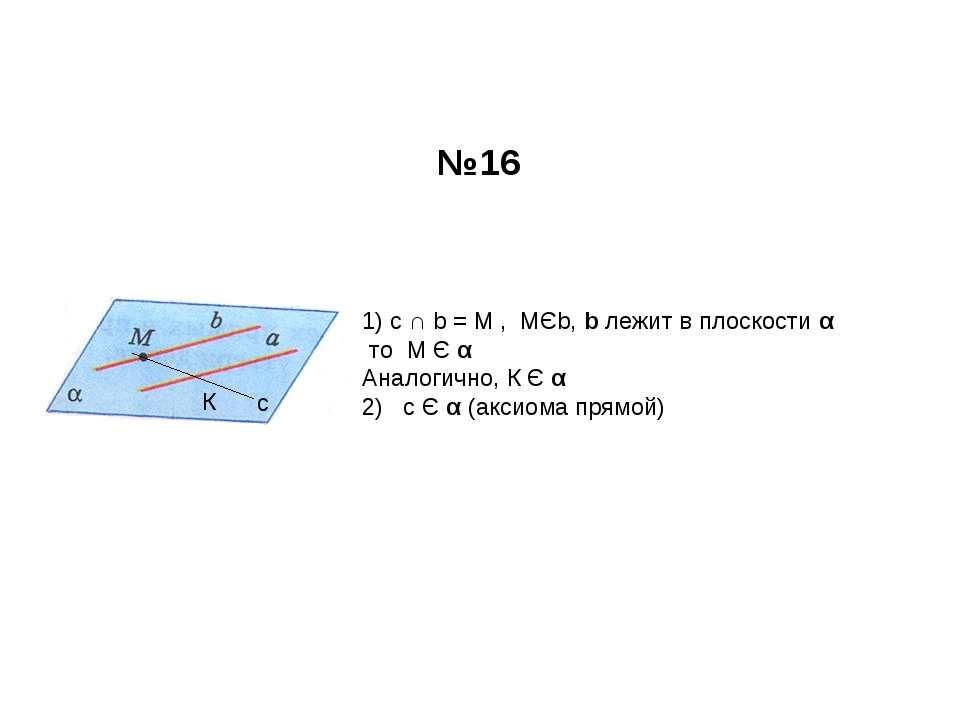 Домашнее задание.
Домашнее задание. Урок закончен, всем спасибо!
Урок закончен, всем спасибо! По двум пересекающимся прямым.
По двум пересекающимся прямым.
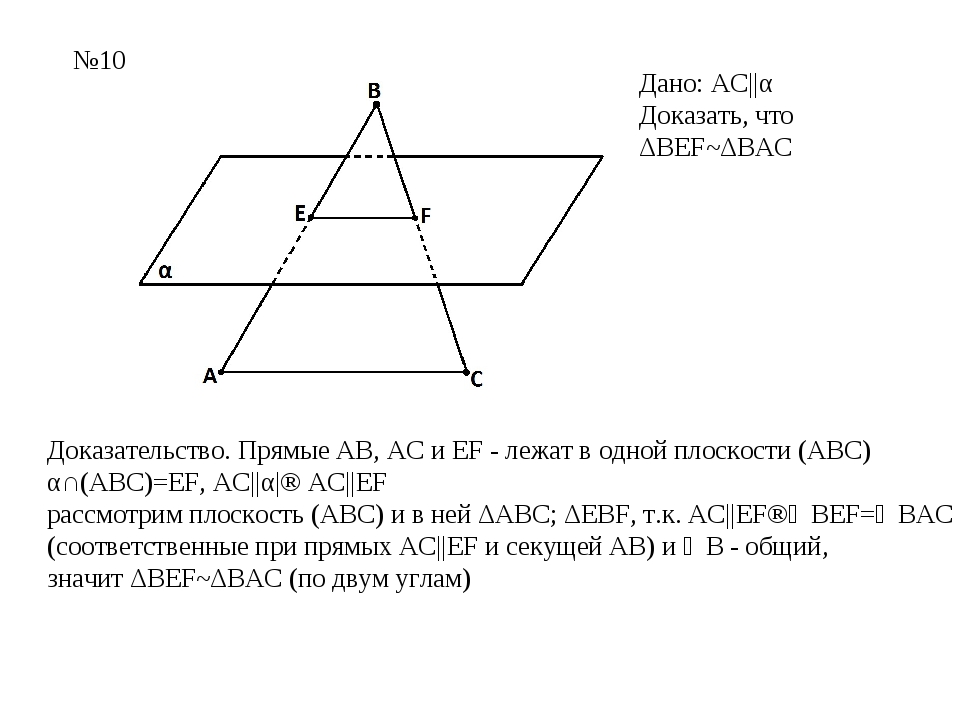
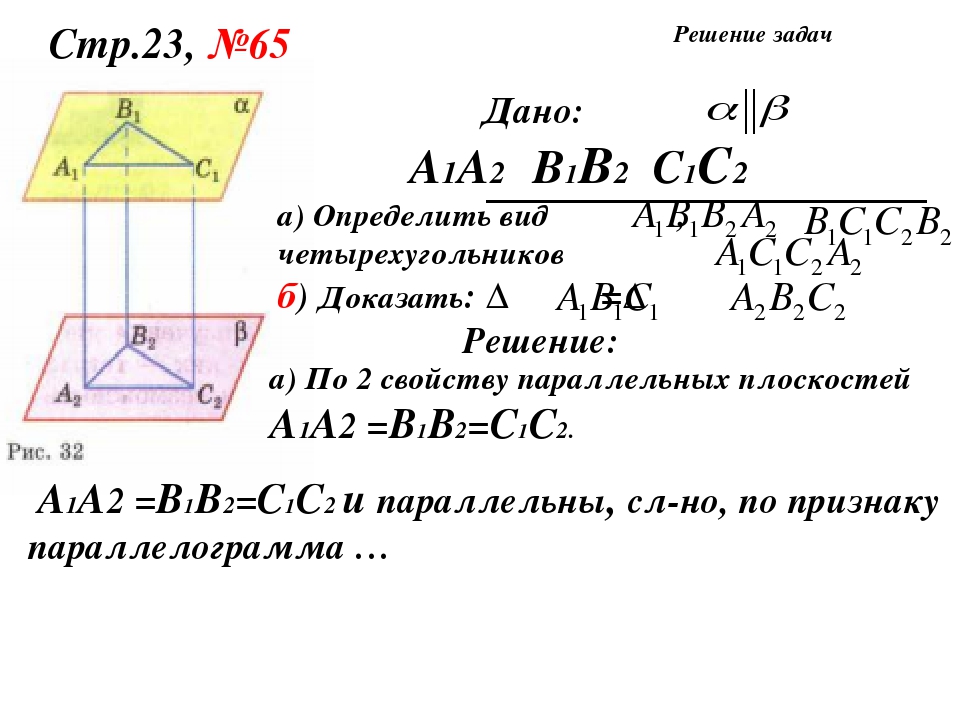 Совпадает ли она с плоскостью квадрата?
Совпадает ли она с плоскостью квадрата? Определите взаимное расположение
Определите взаимное расположение Прямая а не лежит в плоскости трапеции ABCD. Определите взаимное расположение прямых aи BC, если aIIAB.
Прямая а не лежит в плоскости трапеции ABCD. Определите взаимное расположение прямых aи BC, если aIIAB. Определите взаимное расположение прямых MAи DC
Определите взаимное расположение прямых MAи DC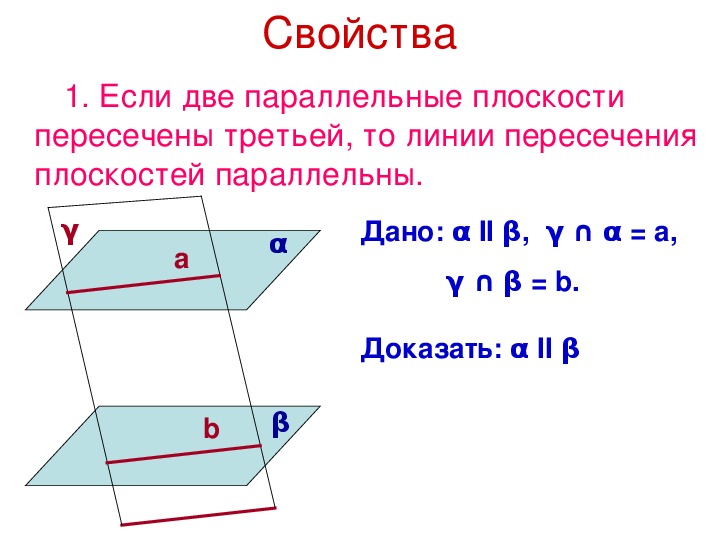 Прямые а и bскрещиваются с прямой с. Что можно сказать о прямых а и b?
Прямые а и bскрещиваются с прямой с. Что можно сказать о прямых а и b?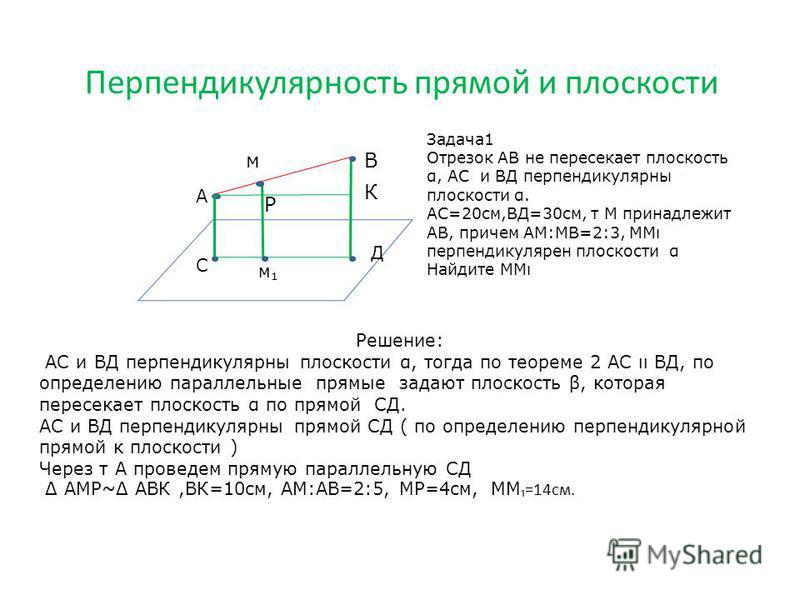 Выберите верное утверждение.
Выберите верное утверждение. Прямая с параллельна прямой b, тогда:
Прямая с параллельна прямой b, тогда: