Тесты тригонометрия: Тесты по теме «Тригонометрия» онлайн

Тест Формулы тригонометрии по алгебре (9 класс)

Сложность: знаток.Последний раз тест пройден 12 часов назад.

Материал подготовлен совместно с учителем высшей категории

Опыт работы учителем математики — более 33 лет.

1. Вопрос 1 из 10

   Упростите выражение: 1 – cos²α

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 86% ответили правильно
   • 86% ответили правильно на этот вопрос

   В вопросе ошибка?

   Следующий вопросОтветить

2. Вопрос 2 из 10

   Найдите значение выражения: (tgα+ctgα)², при α = -π/4

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 66% ответили правильно
   • 66% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

3. Вопрос 3 из 10

   Найдите cos2α , если α = π/2

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 60% ответили правильно
   • 60% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

4. Вопрос 4 из 10

   Вычислите: sin²80+cos²80+1

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 75% ответили правильно
   • 75% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

5. Вопрос 5 из 10

   Упростите выражение: 2sin²x-1+cos²x

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 70% ответили правильно
   • 70% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

6. Вопрос 6 из 10

   Упростите выражения: (1-sin²x)((1+tg²x)

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 71% ответили правильно
   • 71% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

7. Вопрос 7 из 10

   Упростите: tg27°tg63°

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 63% ответили правильно
   • 63% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

8. Вопрос 8 из 10

   Упростите выражение: sin51°cos21°-cos51°sin21°

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 74% ответили правильно
   • 74% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

9. Вопрос 9 из 10

   Упростите выражение: tg²x-sin²x-tg²xsin²x

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 55% ответили правильно
   • 55% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

10. Вопрос 10 из 10

    Вычислите: sin²25+cos²25+5

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 69% ответили правильно
    • 69% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

Доска почёта

Чтобы попасть сюда — пройдите тест.

ТОП-3 тестакоторые проходят вместе с этим

Рейтинг теста

Средняя оценка: 3.8. Всего получено оценок: 387.

А какую оценку получите вы? Чтобы узнать — пройдите тест.

Тригонометрия — Математика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Некоторые рекомендации к выполнению тригонометрических преобразований

К оглавлению…

При выполнении тригонометрических преобразований следуйте следующим советам:

1. Не пытайтесь сразу придумать схему решения примера от начала до конца.
2. Не пытайтесь преобразовывать сразу весь пример. Продвигайтесь вперёд маленькими шагами.
3. Помните, что кроме тригонометрических формул в тригонометрии можно по-прежнему применять все справедливые алгебраические преобразования (вынесение за скобку, сокращение дробей, формулы сокращённого умножения и так далее).
4. Верьте, что всё будет хорошо.

 

Основные тригонометрические формулы

К оглавлению…

Большинство формул в тригонометрии часто применяется как справа налево, так и слева направо, поэтому учить эти формулы нужно так хорошо, чтобы Вы легко смогли применить некоторую формулу в обоих направлениях. Запишем для начала определения тригонометрических функций. Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Формулы двойного угла. Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

 

Дополнительные тригонометрические формулы

К оглавлению. ..

Тригонометрические формулы сложения. Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение. Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Тригонометрические формулы преобразования произведения в сумму. Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени. Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формулы половинного угла.  Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

 

Тригонометрические формулы приведения

К оглавлению…

Функцию косинус называют кофункцией функции синус и наоборот. Аналогично функции тангенс и котангенс являются кофункциями. Формулы приведения можно сформулировать в виде следующего правила:

• Если в формуле приведения угол вычитается (прибавляется) из 90 градусов или 270 градусов, то приводимая функция меняется на кофункцию;
• Если же в формуле приведения угол вычитается (прибавляется) из 180 градусов или 360 градусов, то название приводимой функции сохраняется;
• При этом перед приведенной функцией ставится тот знак, который имеет приводимая (т.е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.

Формулы приведения задаются в виде таблицы:

 

Тригонометрическая окружность

К оглавлению. ..

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

 

Тригонометрические уравнения

К оглавлению…

Для решения некоторого тригонометрического уравнения его нужно свести к одному из простейших тригонометрических уравнений, которые будут рассмотрены ниже. Для этого:

• Можно применять тригонометрические формулы приведенные выше. При этом не нужно пытаться преобразовать сразу весь пример, а нужно двигаться вперед маленькими шагами.
• Нужно не забывать о возможности преобразовать некоторое выражение и с помощью алгебраических методов, т.е. например, вынести что-нибудь за скобку или, наоборот, раскрыть скобки, сократить дробь, применить формулу сокращенного умножения, привести дроби к общему знаменателю и так далее.
• При решении тригонометрических уравнений можно применять метод группировки. При этом нужно помнить, что для того чтобы произведение нескольких множителей было равно нолю, достаточно чтобы любой из них был равен нолю, а остальные существовали.
• Применяя метод замены переменной, как обычно, уравнение после введения замены должно стать проще и не содержать первоначальной переменной. Также нужно не забыть выполнить обратную замену.
• Помните, что однородные уравнения часто встречаются и в тригонометрии.
• Раскрывая модули или решая иррациональные уравнения с тригонометрическими функциями нужно помнить и учитывать все тонкости решения соответствующих уравнений с обычными функциями.
• Помните про ОДЗ (в тригонометрических уравнениях ограничения на ОДЗ в основном сводятся к тому, что делить на ноль нельзя, но не забываем и о других ограничениях, особенно о положительности выражений в рациональных степенях и под корнями четных степеней). Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.

Главное, если не знаете, что делать, делайте хоть что-нибудь, при этом главное правильно использовать тригонометрические формулы. Если то, что Вы при этом получаете становиться все лучше и лучше, значит продолжайте решение, а если становиться хуже, значит вернитесь к началу и попробуйте применить другие формулы, так поступайте пока не наткнетесь на правильный ход решения.

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:

Для остальных тригонометрических функций запись однозначна. Для косинуса:

Для тангенса:

Для котангенса:

Решение тригонометрических уравнений в некоторых частных случаях:

Тесты по тригонометрии

1 вариант

1. Упростить выражение : + cos

A) -1 B) cos C) 1 D) sin E) sin

2. Найти tg, если sin = – , 180

A) 1 B) C) 1 D) E) 2

3. Упростить выражение:

A) cos B) sin C) tg D) sin E) cos

4 Вычислить: sin80 + cos80

A) 0 B) -1 C) 2 D) 1 E) -2

5. Найдите cos2 , если =

A) 0 B) 1 C) 2 D) -1 E)

6. Вычислите: .

7. Вычислите: .

1)

2)

3)

0

4)

1

8. Вычислите: .

9. Найдите значение выражения , если .

1)

0

2)

1

3)

– 1

4)

0,5

10. Найдите значение выражения , если .

1)

1,5

2)

0,5

3)

– 0,5

4)

– 1,5

11. Упростите выражение .

12.Упростите выражение

.

13.Упростите выражение .

14.Упростите выражение .

15.Упростите выражение .

16. Упростите выражение: 

17. Преобразуйте выражение: 

18.Упростите выражение .

19.Упростите выражение .

20.Упростите выражение: 

2 вариант

1.Найдите значение выражения , если .

2. Найдите значение выражения , если .

3. Найдите значение выражения , если .

1)

– 2

2)

– 1

3)

2

4)

1

4. Вычислите: .

5. Вычислите: .

1)

2)

1

3)

− 1

4)

6 Упростить выражение: (sin – cos)+ 2sincos.

A) 1 B) -1 C) cos D) sin E) 2sin

7 Упростить выражение costg и найти его значение при = – 30

A) 0,5 B) C) D) E) 3

8 Найдите сtg, если sin= 0,6,

A) – B) C) D) E)

9 Упростить выражение:

A) — sin B) — cos C) tg D) cos E) sin

10 Найти значение выражения:

A) B) 3 C) D) 2 E)

11. Упростите выражение .

12. Упростите выражение .

13. Упростите выражение .

14. Упростите выражение .

15. Упростите выражение .

16.Упростите выражение .

17. Упростите выражение .

18. Упростите выражение .

19. Упростите выражение sin2xcosx+sinx -cos2xsinx.

20. Упростите выражение .

3 вариант

1 Упростить выражение:

A) B) C) D) 1 E)

2 Упростите выражение:

A) — sin B) 1 C) cos D) — cos E) sin

3 Вычислить : 2sin 30 — sin 60сtg 45tg 30

A) B) C) – () D) E) –

4 Упростите выражение: cos + сtg + sin

A) B) C) 1 D) E)

5 Найдите значение выражения: (tg + сtg )– 2, при = –

A) 0 B) -1 C) 1 D) -2 E) 2

6. Вычислите: .

1)

0

2)

1

3)

4)

7.Вычислите: .

8.Вычислите: .

9. Найдите значение выражения , если .

10. Найдите значение выражения , если .

11. С помощью формул сложения преобразуйте выражение: 

12. С помощью формул сложения преобразуйте выражение: 

13. Представив 105⁰ как сумму 60⁰+ 45⁰, вычислите: 

14. Представив 75⁰ как сумму 30⁰+ 45⁰, вычислите: 

15. Упростите выражение: 

16. Упростите выражение: 

17. Упростите выражение: 

18. Упростите выражение: 

19. Упростите выражение: 

20.  Упростите выражение: 

4 вариант

1. Вычислите: .

1)

0

2)

1

3)

4)

2. Вычислите: .

3. Найдите значение выражения , если .

4. Найдите значение выражения , если .

1)

– 4,5

2)

3,5

3)

4,5

4)

– 3,5

5. Найдите значение выражения , если .

6. Вычислите , если .

7.Вычислите , если .

8.Вычислите , если .

9. Вычислите , если .

10. Вычислите , если .

1)

2)

0

3)

– 4

4)

11. Упростите выражение: 

12. Упростите выражение: 

13. Упростите выражение: 

14. Упростите выражение: 

15. Упростите выражение: 

16. Упростите выражение: 

17. Вычислите: 

18. Вычислите: 

19. Упростите выражение: 

20. Упростите выражение: 

А) 0 В) 1 С) Д)

Ответы

вариант	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	с	а	в	д	д	4	1	1	3	2	1	2	2	3	1	д	с	1	1	а
2	3	4	2	2	1	а	с	а	д	в	3	4	1	4	1	2	2	3	1	2
3	в	е	а	д	е	1	3	3	1	2	а	с	а	с	а	в	д	в	д	в
4	2	4	3	2	4	1	2	2	2	2	а	с	в	а	а	в	д	а	в	а

Тригонометрия.

Задача 9. Единый государственный экзамен, ЕГЭ по математике 2021: уроки, тесты, задания.

1.	Формулы приведения (косинус) Сложность: лёгкое	1
2.	Формулы приведения (тангенс, котангенс) Сложность: лёгкое	1
3.	Вычисление выражения (основное тождество) Сложность: лёгкое	1
4.	Тригонометрические тождества Сложность: среднее	1
5.	Формулы суммы и разности синусов и косинусов Сложность: среднее	1
6.	Упрощение и вычисление выражения Сложность: лёгкое	1
7.	Вычисление выражения (формулы двойного угла) Сложность: лёгкое	1
8.	Использование формул приведения Сложность: лёгкое	1
9.	Формулы двойного угла Сложность: лёгкое	1
10.	Значение косинуса Сложность: лёгкое	1
11.	Вычисление значения тригонометрического выражения Сложность: лёгкое	1
12.	Преобразование буквенного тригонометрического выражения Сложность: лёгкое	1
13.	Преобразование числового тригонометрического выражения Сложность: лёгкое	1

Тест по теме: Тригонометрия (теория)

1. Тест по теме:

Тригонометрия
(теория)
Тест составила Курылева Э. Р.
МОУ « СОШ № 42» г Воркута
Начать
тест

2. Вопрос №1.

Область определения функции y=sin x:
R
1;1
x 0
( 1;1)
Следующий вопрос

3. Вопрос №2.

Функция y=sin x принимает отрицательные
значения в
I и III координатных четвертях
I и II координатных четвертях
III и IV координатных четвертях
II и III координатных четвертях
Следующий вопрос

4.

Вопрос №3. Наименьший положительный период
функции y=cos x
2
2
3
2
Следующий вопрос

5. Вопрос №4.

Нечётные тригонометрические функции:
y sin x, y cos x, y tgx
y sin x, y ctgx, y tgx
y cos x, y sin x, y tgx
y sin x, y cos x, y сtgx
Следующий вопрос

6. Вопрос №5.

Множество значений функции y=sin x:
R
y 0
( 1;1)
1;1
Следующий вопрос

7. Вопрос №6.

Область определения функции y=tgx:
n n
;
2 2
x
2
n, n Z
x n, n Z
0;2 n
Следующий вопрос

8. Вопрос №7.

Основное тригонометрическое тождество:
cos x sin x 1
cos 2 x sin 2 x 1
cos 2 x sin 2 x 1
cos x sin x 1
Следующий вопрос

9. Вопрос №8.

Продолжи формулу cos2x=:
cos x sin x
cos 2 x sin 2 x
cos 2 x sin 2 x
cos x sin x
Следующий вопрос

10. Вопрос №9.

Продолжи формулу cos(x+y)=:
cos x cos y sin x sin y
cos x cos y sin x sin y
cos x sin y sin x cos y
cos x sin y sin x cos y
Следующий вопрос

11.

Вопрос №10. Укажите формулу для понижения степени
синуса:
1 cos 2 x
2
1 cos x
2
sin x
2
cos 2 x 1
2
sin x
2
sin 2 x
sin 2 x
1 cos 2 x
2
Следующий вопрос

12. Вопрос №11.

Продолжи формулу cosx-cosy=:
x y
x y
cos
2
2
x y
x y
2 sin
sin
2
2
x y
x y
2 sin
cos
2
2
x y
x y
2 cos
cos
2
2
2 sin
Следующий вопрос

13. Вопрос №12.

Укажи верную формулу:
1
2
ctg
x 1
2
cos x
1
2
ctg
x 1
sin 2 x
1
2
tg
x 1
2
cos x
1
2
tg
x 1
2
cos x
Следующий вопрос

14. Вопрос №13.

Продолжи формулу tg(x-y)=:
tgx tgy
1 tgx tgy
tgx tgy
1 tgx tgy
tgx tgy
1 tgx tgy
tgx tgy
1 tgx tgy
Следующий вопрос

15. Вопрос №14.

Продолжи формулу sinxcosy+cosxsiny=:
sin( x y )
cos( x y )
sin( x y )
cos( x y )
Следующий вопрос

16. Вопрос №15.

Продолжи формулу tg2α=:
tg 2
1 tg 2
2tg
1 tg 2
tg 2
1 2tg
2tg
1 2tg
Следующий вопрос

17. Вопрос №16.

Продолжи формулу sinα+sinβ=:
2 sin
2 sin
2 cos
2 sin
2
cos
2
2
2
cos
cos
sin
2
2
2
2
Следующий вопрос

18. Вопрос №17.

Продолжи формулу cos²α=:
1 cos 2
2
cos 2 1
2
1 cos 2
4
1 cos 2
2
Следующий вопрос

19. Вопрос №18.

Продолжи формулу sin²α=:
1
ctg 2
1 cos 2
1
1 ctg 2
2 sin cos
Следующий вопрос

20. Вопрос №19.

Продолжи формулу 2sinαcosα=:
sin 2
sin 2
sin
1
sin
2
Следующий вопрос

21. Вопрос №20.

Продолжи формулу sin(α-β)=:
cos cos sin sin
cos sin sin cos
cos cos sin sin
sin cos cos sin
Следующий вопрос

22.

Результаты теста Всего вопросов:
Правильных ответов:
Процент правильных ответов:
Оценка:
Получить результат
Закончить тест

Онлайн-обучение математике с 5 по 11 классы, математический центр в Астане, подготовка НИШ, ЕНТ

Наполни все баки и открывай новую планету

Чтобы не потерять Ваш прогресс — зарегистрируйтесь!

Преимущества регистрации:

Сохранение прогресса обучения

Доступ к итоговым тестам

Получение наград за обучение

Полный доступ ко всему сайту и обучающим урокам

Градусная и радианная меры угла и дуги

Тест — I

---

Выполнено 0 из 5

Тест — II

---

Выполнено 0 из 5

Тест — III

---

Выполнено 0 из 5

Синус, косинус, тангенс и котангенс произвольного угла.

Значения синуса, косинуса, тангенса и котангенса углов

Тест — I

---

Выполнено 0 из 5

Тест — II

---

Выполнено 0 из 5

Тест — III

---

Выполнено 0 из 5

Видео уроки

---

Тригонометрические функции и их свойства

Тест — I

---

Выполнено 0 из 5

Тест — II

---

Выполнено 0 из 5

Тест — III

---

Выполнено 0 из 5

Формулы тригонометрии.

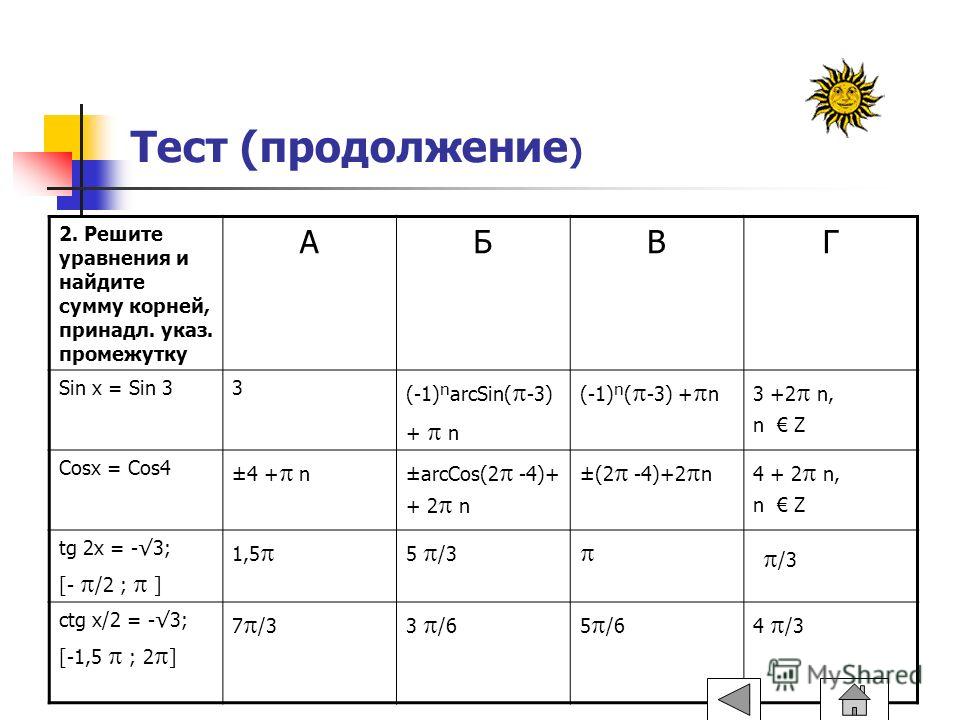Тождественные преобразования тригонометрических выражений

Тест — I

---

Выполнено 0 из 5

Тест — II

---

Выполнено 0 из 5

Тест — III

---

Выполнено 0 из 5

Видео уроки

---

Итоговое тестирование недоступно для Вас. Зарегистрируйте аккаунт или авторизуйтесь, чтобы получить доступ к итоговому тестированию.

Преимущества регистрации:

Сохранение прогресса обучения

Доступ к итоговым тестам

Получение наград за обучение

Полный доступ ко всему сайту и обучающим урокам

тесты по темам из тригонометрии

Тесты по алгебре и началам анализа для 10-11 класса

«Тригонометрические функции»

«Тригонометрические уравнения»

« Преобразование тригонометрических выражений»

2013г.

Данная работа состоит из трех разделов и поможет в организации контроля в тестовой форме на уроках изучения в 10 классе и итоговом повторении при подготовке к ЕГЭ в 11 классе по темам:

1.Тригонометрические функции. (3)

2.Тригонометрические уравнения. (2)

3.Преобразование тригонометрических выражений.(3)

учебник: Мордкович А.Г. «Алгебра10-11». Изд. «Мнемозина», 2010г.

Тесты представлены в двух вариантах.

Ключи к тестам:

Раздел №1

Тест № 1 по теме: « Распознавание графиков тригонометрических функций»

№п/п Вариант	1	2	3	4	5	6	7	8	9	10
1	3	1	4	2	1	2	4	1	2	3
2	4	3	2	3	2	4	4	2	4	2

Тест №2 по теме: « Распознавание графиков тригонометрических функций»

№ п/п Вариант	1	2	3	4	5	6
1	2	2	4	2	4	1
2	3	1	1	1	3	3

Тест №3 по теме: « Область значения тригонометрических функций»

№п/п Вариант	1	2	3	4	5	6	7	8	9	10
1	2	4	1	3	4	4	2	4	2	1
2	3	2	1	4	2	3	1	2	4	1

Раздел №2

Тест №1 по теме: «Простейшие тригонометрические уравнения»

№п/п Вариант	1	2	3	4	5
1	2	2	3	4	3
2	1	4	2	1	3

Тест №2 по теме: «Простейшие тригонометрические уравнения»

№ п/п Вариант	1	2	3	4	5	6	7	8	9	10
1	1	4	2	3	3	2	1	1	2	3
2	1	3	1	2	4	2	3	1	4	1

Раздел №3

Тест №1 по теме: «Формулы сложения»

№ п/п Вариант	1	2	3	4	5	6	7	8	9	10
1	3	4	1	4	1	2	2	3	1	2
2	1	2	2	3	1	1	3	3	1	1

Тест №2 по теме: «Формулы приведения»

№ п/п Вариант	1	2	3	4	5	6	7	8	9	10
1	2	1	4	3	1	3	2	3	4	2
2	2	4	1	3	3	1	2	3	2	3

Тест №3 по теме: «Преобразование тригонометрических выражений»

№ п/п Вариант	1	2	3	4	5	6	7	8	9	10
1	1	2	2	2	2	2	2	4	2	4
2	3	1	1	2	3	1	4	1	1	1

Раздел №1

Тест № 1 по теме: « Распознавание графиков тригонометрических функций»

Вариант №1

1. График какой функции изображен на рисунке?2.График какой функции изображен на рисунке?3.График какой функции изображен на рисунке?4. График какой функции изображен на рисунке?5.График какой функции изображен на рисунке?6.График какой функции изображен на рисунке?7. График какой функции изображен на рисунке?8.График какой функции изображен на рисунке?

9.График какой функции изображен на рисунке?

10.График какой функции изображен на рисунке?

Тест № 1 по теме: « Распознавание графиков тригонометрических функций»

Вариант №2

1.График какой функции изображен на рисунке?

2.График какой функции изображен на рисунке?

3.График какой функции изображен на рисунке?

4.График какой функции изображен на рисунке?5.График какой функции изображен на рисунке?

6.График какой функции изображен на рисунке?

7.График какой функции изображен на рисунке?8. График какой функции изображен на рисунке?9. График какой функции изображен на рисунке?

10. График какой функции изображен на рисунке?

Тест №2 по теме: « Распознавание графиков тригонометрических функций»

Вариант №1

1. На одном из рисунков изображен эскиз графика функции . Укажите номер этого рисунка.

2. На одном из рисунков изображен эскиз графика функции . Укажите номер этого рисунка.

3.На одном из рисунков изображен эскиз графика функции . Укажите номер этого рисунка.

4.На одном из рисунков изображен эскиз графика функции . Укажите номер этого рисунка.

5.На одном из рисунков изображен эскиз графика функции . Укажите номер этого рисунка.

6. График какой функции изображен на рисунке?

Тест №2 по теме: « Распознавание графиков тригонометрических функций»

Вариант №2

1. На одном из рисунков изображен эскиз графика функции . Укажите номер этого рисунка.

2. На одном из рисунков изображен эскиз графика функции . Укажите номер этого рисунка.

3. На одном из рисунков изображен эскиз графика функции . Укажите номер этого рисунка.

4. На одном из рисунков изображен эскиз графика функции . Укажите номер этого рисунка.

5. На одном из рисунков изображен эскиз графика функции . Укажите номер этого рисунка.

6. График какой функции изображен на рисунке?

Тест №3 по теме: « Область значения тригонометрических функций»

Вариант №1

1. Укажите множество значений функции .

2. Укажите множество значений функции.

3. Укажите множество значений функции.

4. Укажите наибольшее значение функции .

5. Какое число не входит в множество значений функции ?

6.Какое число входит в множество значений функции ?

7. Укажите наибольшее значение функции .

8. Укажите наименьшее значение функции .

1)

– 5

2)

– 11

3)

– 2

4)

– 8

9. Укажите наименьшее значение функции .

1)

– 6,5

2)

– 2,5

3)

– 0,5

4)

– 1,5

10. Найдите множество значений функции .

Тест №3 по теме: « Область значения тригонометрических функций»

Вариант №2

1. Укажите множество значений функции .

2. Укажите множество значений функции .

3. Укажите множество значений функции .

4. Укажите множество значений функции .

5. Какое число не входит в множество значений функции ?

6. Какое число входит в множество значений функции ?

1)

15

2)

20

3)

− 5

4)

− 10

7. Укажите наибольшее значение функции .

1)

2)

1

3)

– 0,5

4)

– 1,5

8. Укажите наименьшее значение функции .

9. Укажите наименьшее значение функции .

1)

– 2,5

2)

– 1

3)

– 2

4)

– 3

10. Найдите множество значений функции .

Раздел №2

Тест №1: «Простейшие тригонометрические уравнения»

Вариант №1

1. Решите уравнение .

2. Решите уравнение .

3. Решите уравнение .

4. Решите уравнение .

5. Решите уравнение .

Тест №1: «Простейшие тригонометрические уравнения»

Вариант №2

1. Решите уравнение .

2. Решите уравнение .

3. Решите уравнение .

4. Решите уравнение .

5. Решите уравнение .

Тест №2 по теме: « Простейшие тригонометрические уравнения»

Вариант №1

1. Решите уравнение .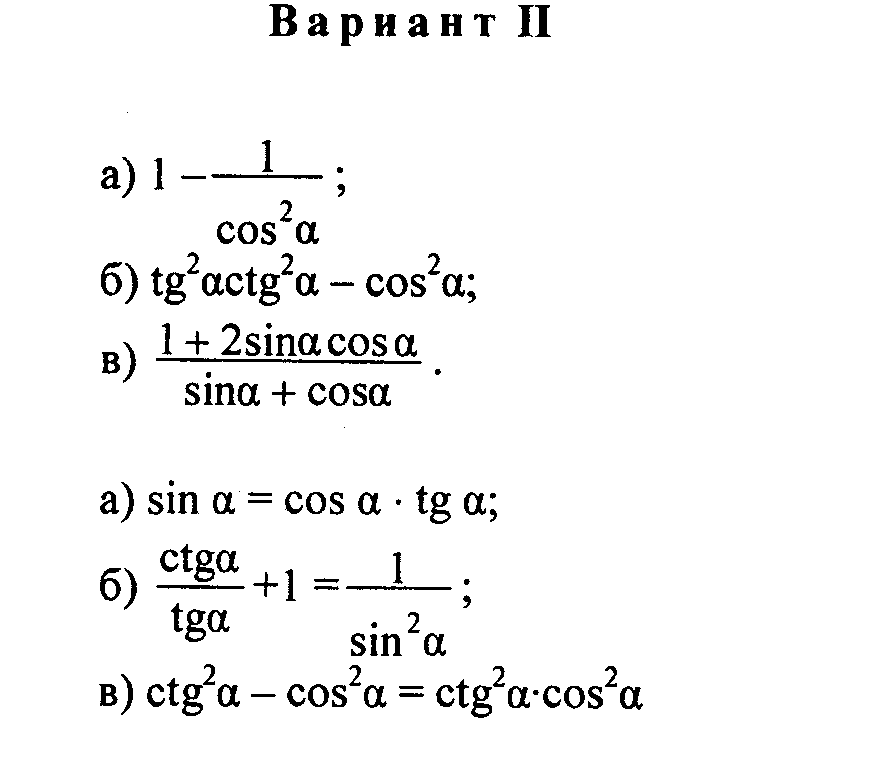

2. Решите уравнение .

3. Решите уравнение .

4. Решите уравнение .

5. Решите уравнение .

6. Решите уравнение .

7. Решите уравнение .

8. Решите уравнение .

9. Решите уравнение .

10. Решите уравнение .

Тест №2 по теме: « Простейшие тригонометрические уравнения»

Вариант №2

1. Решите уравнение .

2. Решите уравнение .

3. Решите уравнение .

4. Решите уравнение .

5. Решите уравнение .

6. Решите уравнение .

7. Решите уравнение .

8. Решите уравнение .

9. Решите уравнение .

10. Решите уравнение .

Раздел №3

Тест №1 по теме: «Формулы сложения»

Вариант №1

1. Упростите выражение .

2. Упростите выражение .

3. Упростите выражение .

4. Упростите выражение .

5. Упростите выражение .

6.Упростите выражение .

7. Упростите выражение .

8. Упростите выражение .

9. Упростите выражение .

10. Упростите выражение .

Тест №1 по теме: «Формулы сложения»

Вариант №2

1.Упростите выражение .

_{2.Упростите выражение}

.

3.Упростите выражение .

4.Упростите выражение .

5.Упростите выражение .

6.Упростите выражение .

7.Упростите выражение .

8.Упростите выражение .

9.Упростите выражение .

10.Упростите выражение .

Тест №2 по теме: « Формулы приведения»

Вариант №1

1. Вычислите: .

2. Вычислите: .

3. Вычислите: .

4. Вычислите: .

5. Вычислите: .

6. Найдите значение выражения , если .

7. Найдите значение выражения , если .

1)

1,5

2)

0,5

3)

– 0,5

4)

– 1,5

8.Найдите значение выражения , если .

9. Найдите значение выражения , если .

10. Найдите значение выражения , если .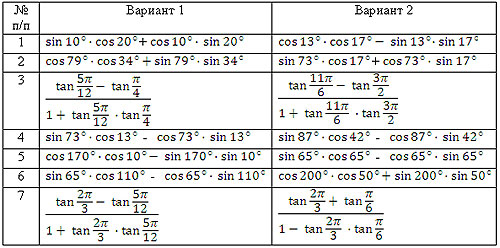

Тест №2 по теме: « Формулы приведения»

Вариант №2

1. Вычислите: .

2. Вычислите: .

3. Вычислите: .

4.Вычислите: .

5. Вычислите: .

6. Найдите значение выражения , если .

7. Найдите значение выражения , если .

8. Найдите значение выражения , если .

9. Найдите значение выражения , если .

1)

– 4,5

2)

3,5

3)

4,5

4)

– 3,5

10. Найдите значение выражения , если .

Тест №3 по теме: «Преобразование тригонометрических выражений»

Вариант №1

1. Вычислите , если .

2.Вычислите , если .

3.Вычислите , если .

4. Вычислите , если .

5. Вычислите , если .

6. Вычислите , если .

7. Вычислите , если .

8. Вычислите , если .

9. Вычислите , если .

10. Вычислите , если .

Тест №3 по теме: «Преобразование тригонометрических выражений»

Вариант №2

1. Вычислите , если

2.Вычислите , если .

3.Вычислите , если .

4. Вычислите , если .

5. Вычислите , если .

6. Вычислите , если .

7. Вычислите , если .

8. Вычислите , если .

9. Вычислите , если .

10. Вычислите , если .

Источники информации:

1.Тексты КДР 2007-2009 г . Автор составитель: Краснодарский краевой институт дополнительного профессионального педагогического образования.

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/199484-testy-po-temam-iz-trigonometrii

Практические тесты по тригонометрии

Пройдите бесплатный диагностический тест Varsity Learning Tools по тригонометрии, чтобы определить, какой академический концепции, которые вы понимаете, и которые требуют вашего постоянного внимания. Каждая проблема тригонометрии связана с основной концепцией, которая проверяется. Результаты диагностического теста тригонометрии показывают, как вы выполняли каждую область теста. Затем вы можете использовать результаты для создания индивидуального учебного плана, основанного на вашей конкретной области потребностей.

Классы тригонометрии в средней школе подробно знакомят учащихся с различными тригонометрическими тождествами, свойствами и функциями. Студенты обычно изучают тригонометрию после завершения предыдущей курсовой работы по алгебре и геометрии, но перед изучением предварительного исчисления и математического анализа. Информация, которую студенты изучают в тригонометрии, помогает им преуспеть в более поздних курсах математики более высокого уровня, а также в таких научных курсах, как физика, где тригонометрические функции используются для моделирования определенных физических явлений.

Как и классы предалгебры, алгебры I и алгебры II, классы тригонометрии сосредоточены на функциях и графах. Тригонометрия, в частности, изучает тригонометрические функции и в процессе учит студентов, как построить график синуса, косинуса, секанса, косеканса, тангенса, котангенса, арксинуса, арккосуса и арктангенса, а также как выполнять фазовые сдвиги и вычислять их периоды и амплитуды. . Также обсуждаются тригонометрические операции, и студенты также узнают о тригонометрических уравнениях, в том числе о том, как понимать, устанавливать и учитывать тригонометрические уравнения, как решать отдельные тригонометрические уравнения, а также системы тригонометрических уравнений, как находить тригонометрические корни и как использовать квадратную формулу для тригонометрических уравнений.

Тригонометрические тождества также обсуждаются в классах тригонометрии; студенты узнают о тождествах суммы и произведения, а также тождества обратных операций, квадратов тригонометрических функций, половинных и удвоенных углов. Студенты также учатся работать с идентичностями с суммами углов, дополнительными и дополнительными идентичностями, пифагорейскими идентичностями, а также основными и определяющими идентичностями.

Другая важная часть тригонометрии — это научиться анализировать особые виды особых треугольников.Студенты учатся определять углы и длины сторон в прямоугольных треугольниках 30-60-90 и 45-45-90, используя закон синусов и закон косинусов, а также узнают, как определять похожие треугольники и определять пропорции, используя пропорциональность.

Тригонометрия также знакомит студентов с единичными кругами и радианами, уделяя особое внимание тому, как преобразовать градусы в радианы и наоборот. Обсуждаются дополнительные, дополнительные и котерминальные углы. Этот акцент на углах в единичном круге также применяется к координатной плоскости, когда исследуются углы в разных квадрантах.

Как теперь может быть очевидно, многие студенты очень опасаются проходить курс тригонометрии и не отставать от него. Такие ресурсы, как бесплатные практические тесты по тригонометрии для университетских репетиторов, могут помочь им направить любую нервозность, которую они испытывают по поводу курса, в процесс активного обзора, который принесет им пользу. Каждый практический тест по тригонометрии включает в себя дюжину вопросов по тригонометрии с несколькими вариантами ответов, и каждый вопрос сопровождается полным пошаговым объяснением, чтобы помочь учащимся, пропустившим его, изучить тестируемые концепции.Вопросы организованы в практических тестах, которые основаны на различных темах, преподаваемых в тригонометрии; вопросы также сгруппированы по концепциям. Итак, если студент хочет сосредоточиться только на ответах на вопросы об использовании закона синусов, вопросы, организованные по концепциям, делают это возможным. Используя бесплатные практические тесты по тригонометрии от Varsity Tutors, студенты могут попрактиковаться в материале, который им кажется трудным, и уменьшить опасения, которые они могут испытывать по поводу тригонометрии.

Наши совершенно бесплатные практические тесты по тригонометрии — идеальный способ улучшить свои навыки.Брать один из наших многочисленных практических тестов по тригонометрии для ответов на часто задаваемые вопросы. Ты получат невероятно подробные результаты оценки в конце вашего практического теста по тригонометрии, чтобы поможет вам определить свои сильные и слабые стороны. Выберите один из наших практических тестов по тригонометрии прямо сейчас и начнем!

Практические тесты по концепции

тригонометрия-угол-приложения

Вопросы : 8

Сложность теста :

тригонометрия-угловая скорость

Вопросы : 8

Сложность теста :

Среднее время нахождения : 2 минуты 15 секунд

длина дуги тригонометрии

Вопросы : 8

Сложность теста :

Среднее время нахождения : 7 минут

тригонометрия-площадь-сектора

Вопросы : 8

Сложность теста :

тригонометрические углы

Вопросы : 4

Сложность теста :

Среднее время нахождения : 16 минут

тригонометрические углы в разных квадрантах

Вопросы : 2

Сложность теста :

Среднее время нахождения : 41 секунда

тригонометрические дополнительные и дополнительные углы

Вопросы : 1

Сложность теста :

Среднее время нахождения : 23 секунды

тригонометрия-терминальные-углы

Вопросы : 1

Сложность теста :

Среднее время нахождения : 33 секунды

тригонометрия-найти-все-углы-в-диапазоне-заданном-конкретном-выходе

Вопросы : 7

Сложность теста :

тригонометрия-комплексные-числа-полярная форма

Вопросы : 11

Сложность теста :

Среднее время нахождения : 6 минут

комплексные числа тригонометрии

Вопросы : 11

Сложность теста :

Среднее время нахождения : 3 минуты

тригонометрия-де-муавр-s-теорема-и-нахождение-корней-комплексных-чисел

Вопросы : 7

Сложность теста :

Среднее время нахождения : 3 минуты

тригонометрия-полярная-форма-комплексных чисел

Вопросы : 8

Сложность теста :

тригонометрия-практические-приложения

Вопросы : 8

Сложность теста :

тригонометрический пеленг

Вопросы : 7

Сложность теста :

тригонометрия, наклонные самолеты и аэронавигация

Вопросы : 7

Сложность теста :

тригонометрические векторы

Вопросы : 8

Сложность теста :

Среднее время нахождения : 5 минут

тригонометрия-сумма-разность-и-произведения-тождества

Вопросы : 8

Сложность теста :

тригонометрия-полное-доказательство-с использованием-сумм-разностей-или-произведений-синусов и косинусов

Вопросы : 10

Сложность теста :

тригонометрическое произведение синусов и косинусов

Вопросы : 8

Сложность теста :

Среднее затраченное время : 21 секунда

тригонометрия-сумма-и-разность-синусов и косинусов

Вопросы : 8

Сложность теста :

Среднее время нахождения : 4 минуты

тригонометрия-треугольники

Вопросы : 5

Сложность теста :

Среднее время нахождения : 9 минут

тригонометрия-площадь-треугольник

Вопросы : 8

Сложность теста :

Среднее время нахождения : 8 минут

тригонометрия-поиск-площадь-треугольника с помощью тригонометрии

Вопросы : 8

Сложность теста :

тригонометрия-закон косинусов и закон синусов

Вопросы : 4

Сложность теста :

Среднее время работы : 9 минут

тригонометрия-неоднозначные-треугольники

Вопросы : 4

Сложность теста :

Среднее время нахождения : 6 минут

тригонометрия-закон косинусов

Вопросы : 2

Сложность теста :

Среднее время нахождения : 12 минут

тригонометрия-закон синусов

Вопросы : 2

Сложность теста :

Среднее время нахождения : 5 минут

тригонометрия-правые треугольники

Вопросы : 7

Сложность теста :

Среднее время нахождения : 1 д 17 часов

тригонометрия-30-60-90-треугольники

Вопросы : 3

Сложность теста :

Среднее время нахождения : 4 минуты

тригонометрия-45-45-90-треугольники

Вопросы : 4

Сложность теста :

Среднее время нахождения : 17 минут

тригонометрия-решение-задач-слов-с-тригонометрией

Вопросы : 4

Сложность теста :

тригонометрия-тригонометрические-приложения

Вопросы : 7

Сложность теста :

Среднее время нахождения : 7 минут

тригонометрия-использование-специальные-треугольники-сделать-выводы

Вопросы : 10

Сложность теста :

тригонометрические-подобные-треугольники

Вопросы : 1

Сложность теста :

Среднее затраченное время : 24 секунды

тригонометрические идентифицирующие-похожие-треугольники

Вопросы : 3

Сложность теста :

Среднее время нахождения : 1 мин 15 сек

тригонометрия-пропорции-в-подобных-треугольниках

Вопросы : 1

Сложность теста :

Среднее время нахождения : 13 секунд

тригонометрия-решающие треугольники

Вопросы : 4

Сложность теста :

Среднее время нахождения : 3 минуты

тригонометрические углы нахождения

Вопросы : 3

Сложность теста :

Среднее время нахождения : 2 минуты 45 секунд

тригонометрические поисковые стороны

Вопросы : 1

Сложность теста :

Среднее время нахождения : 22 секунды

тригонометрия-тригонометрические-уравнения

Вопросы : 5

Сложность теста :

Среднее время нахождения : 5 минут

тригонометрия-решение-тригонометрические-уравнения

Вопросы : 3

Сложность теста :

Среднее время нахождения : 53 минуты

тригонометрия-поиск-тригонометрические-корни

Вопросы : 2

Сложность теста :

Среднее время нахождения : 41 секунда

тригонометрия-квадратичная-формула-с тригонометрией

Вопросы : 2

Сложность теста :

Среднее время нахождения : 6 минут

тригонометрические-системы-тригонометрические-уравнения

Вопросы : 3

Сложность теста :

Среднее затраченное время : 1 минута 58 секунд

тригонометрия-понимание-тригонометрические-уравнения

Вопросы : 2

Сложность теста :

Среднее затраченное время : 2 минуты 0 секунд

тригонометрия-факторизация-тригонометрические-уравнения

Вопросы : 2

Сложность теста :

Среднее время нахождения : 2 минуты 37 секунд

тригонометрия-установка-тригонометрические-уравнения

Вопросы : 6

Сложность теста :

Среднее время нахождения : 2 минуты 45 секунд

тригонометрия-тригонометрические-функции-и-графики

Вопросы : 5

Сложность теста :

Среднее время нахождения : 5 минут

тригонометрия-тригонометрические функции

Вопросы : 3

Сложность теста :

Среднее время нахождения : 2 минуты 56 секунд

тригонометрия определить, какие значения тригонометрических функций не определены

Вопросы : 1

Сложность теста :

тригонометрия-графики-обратных-тригонометрических-функций

Вопросы : 8

Сложность теста :

тригонометрические упрощающие тригонометрические функции

Вопросы : 2

Сложность теста :

Среднее затраченное время : 1 минута 47 секунд

тригонометрия-решить-тригонометрическую функцию-возвести в квадрат обе стороны

Вопросы : 8

Сложность теста :

тригонометрия-тригонометрические функции

Вопросы : 1

Сложность теста :

Среднее время нахождения : 3 минуты

тригонометрия-понимание-знаки-6-тригонометрических функций в каждом квадранте

Вопросы : 1

Сложность теста :

тригонометрия-тригонометрические-графики

Вопросы : 2

Сложность теста :

Среднее время нахождения : 32 секунды

тригонометрия-определение-вертикальные сдвиги

Вопросы : 7

Сложность теста :

тригонометрия, построение графиков, секанс и косеканс

Вопросы : 2

Сложность теста :

Среднее время нахождения : 57 секунд

тригонометрия-график-синус-косинус

Вопросы : 2

Сложность теста :

Среднее затраченное время : 1 минута 13 секунд

тригонометрия-график-касательная-и-котангенс

Вопросы : 3

Сложность теста :

Среднее время нахождения : 2 минуты 46 секунд

тригонометрия-период-амплитуда

Вопросы : 2

Сложность теста :

Среднее время нахождения : 33 секунды

тригонометрия-фазовые сдвиги

Вопросы : 2

Сложность теста :

Среднее время нахождения : 1 мин 28 сек

тригонометрические-тригонометрические-тождества

Вопросы : 4

Сложность теста :

Среднее время нахождения : 2 минуты 27 секунд

тригонометрия-применить-основные-и-определения-тождества

Вопросы : 6

Сложность теста :

Среднее время нахождения : 12 минут

тригонометрические дополнительные и дополнительные тождества

Вопросы : 2

Сложность теста :

Среднее время нахождения : 53 секунды

тригонометрия-полная-основная-тригонометрическая-доказательства

Вопросы : 1

Сложность теста :

тригонометрические тождества удвоенных углов

Вопросы : 2

Сложность теста :

Среднее затраченное время : 1 минута 11 секунд

тригонометрические тождества половинных углов

Вопросы : 2

Сложность теста :

Среднее время нахождения : 2 минуты 54 секунды

тригонометрические тождества обратных операций

Вопросы : 6

Сложность теста :

Среднее время нахождения : 5 минут

тригонометрические тождества квадратов тригонометрических функций

Вопросы : 3

Сложность теста :

Среднее время нахождения : 14 минут

тригонометрические тождества с суммами углов

Вопросы : 4

Сложность теста :

Среднее время нахождения : 6 минут

тригонометрия-пифагорейские тождества

Вопросы : 3

Сложность теста :

Среднее затраченное время : 1 минута 44 секунды

тригонометрические тождества суммы и произведения

Вопросы : 2

Сложность теста :

Среднее время нахождения : 2 минуты 5 секунд

тригонометрия-тригонометрические-операции

Вопросы : 1

Сложность теста :

Среднее затраченное время : 1 минута 4 секунды

тригонометрия-arcsin-arccos-arctan

Вопросы : 1

Сложность теста :

Среднее время нахождения : 2 минуты 8 секунд

тригонометрия-sec-csc-ctan

Вопросы : 3

Сложность теста :

Среднее время нахождения : 2 минуты 4 секунды

тригонометрия-грех-кос-загар

Вопросы : 2

Сложность теста :

Среднее затраченное время : 1 минута 10 секунд

тригонометрия-единица-круг-и-радианы

Вопросы : 2

Сложность теста :

Среднее время нахождения : 45 секунд

тригонометрические углы в единичной окружности

Вопросы : 2

Сложность теста :

Среднее время нахождения : 45 секунд

тригонометрия-радианы-и-преобразования

Вопросы : 2

Сложность теста :

Среднее время нахождения : 38 секунд

тригонометрия-единица-круг

Вопросы : 2

Сложность теста :

Среднее затраченное время : 28 секунд

Все ресурсы по тригонометрии

Основы тригонометрии, Sin, Cos, Tan Test

Выберите лучший ответ. Тригонометрические отношения округлены до тысячных.

1. $ Sin A = \ frac {12} {16} $ для какого из следующих треугольников?

2. $ Tan A = \ frac {13} {12} $ для какого из следующих треугольников?

3. $ Cos B = \ frac {13} {33} $ для какого из следующих треугольников?

4. Какая тригонометрическая функция может быть больше или равна 1.000?
синус
Косинус
Касательная
ничего из вышеперечисленного

5. Самолет поднимается под углом 40 °. Когда он достигает высоты в сто футов, какое расстояние по земле он преодолел? Для решения используйте тригонометрическую диаграмму. Округлите ответ до ближайшей десятой.
64.3 футов
76.6 футов
80,1 футов
119,2 футов

6. 20-футовая балка прислонена к стене. Луч достигает стены на высоте 13,9 фута над землей. Какова мера угла, образованного балкой и землей?
44 °
35 °
55 °
46 °

7. Какой набор углов имеет такое же тригонометрическое соотношение?
Sin 45 и загар 45
Sin 30 и cos 60
Cos 30 и загар 45
Tan 60 и sin 45

8. Какова сумма тригонометрических соотношений Sin 54 и Cos 36?
0,809
1,618
1.000
1,536

9. Какова сумма тригонометрических соотношений Sin 33 и Sin 57?
0,545
1.000
1,090
1,383

10. Какова сумма тригонометрических соотношений Cos 16 и Cos 74?
0.276
0,961
1,237
1,922

11. В ABC вершина C — прямой угол. Какое тригонометрическое соотношение имеет то же тригонометрическое значение, что и Sin A?
Sin B
Косинус A
Косинус B
Tan A

12. In △ ABC, Tan ∠A = 3/4. Гипотенуза треугольника ABC равна
3
4
5
9

13. In ABC, Sin ∠B = 14/17. Гипотенуза треугольника ABC равна
14
17
√485
0,824

14. In △ ABC, Cos ∠C = 22/36. Гипотенуза
22
36
0,611
2√445

Обведите каждый ответ «Верный» или «Неверный».

15. Если Sin∠A = 358, то m∠A = 21 °.
Верно
Ложь

16. Сумма синуса угла и косинуса его дополнения всегда больше 1.000.
Верно
Ложь

17. Тригонометрические отношения sin 45, cos 45 и tan 45 равны.
Верно
Ложь

Практические вопросы по тригонометрии

Если мы наблюдаем прямоугольный треугольник, где a и b — его катеты, а c — его гипотенуза, мы можем использовать тригонометрические функции, чтобы установить связь между углами и сторонами прямоугольного треугольника.

Если прямой угол прямоугольного треугольника ABC находится в точке C, то синус ( sin ) и косинус ( cos ) углов α (в точке A) и β (в точке B) можно найти так:

sinα = кондиционер sinβ = b / c

cosα = b / c cosβ = a / c

Обратите внимание, что sinα и cosβ равны, и то же самое касается sinβ и cosα.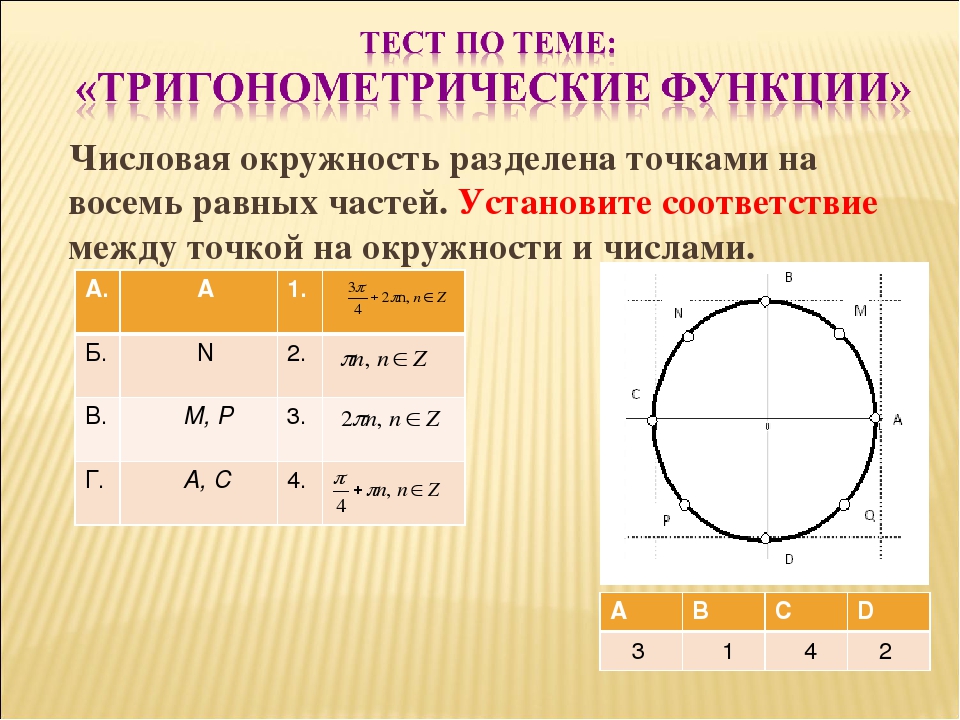 Итак, чтобы найти синус угла, мы делим сторону, противоположную этому углу, и гипотенузу. Чтобы найти косинус угла, мы разделим сторону, образующую этот угол (прилегающую сторону), на гипотенузу.

Есть еще 2 важные тригонометрические функции, тангенс и котангенс:

tgα = sinα / cosα = a / b

ctgα = cosα / sinα = b / a

Для функций синуса и косинуса существует таблица со значениями некоторых углов, которую следует запомнить, так как она очень полезна для решения различных тригонометрических задач.Вот эта таблица:

√

	0	30⁰	45⁰	60⁰	90⁰
sinα	0	1/2	√2 / 2	√3 / 2	1
cosα	1	√3 / 2	√2 / 2	1/2	0

Рассмотрим один пример:

Если a равно 9 см и c равно 18 см, найдите α.

Мы можем использовать синус для этой задачи:

sinα = a / c = 9/18 = 1/2

Из таблицы видно, что если sinα равно 1/2, то угол α равен 30⁰.

В дополнение к градусам мы можем записывать углы с помощью π, где π представляет 180⁰. Например, угол π / 2 означает прямой угол 90⁰.

ACT Тригонометрия: полное руководство

Тригонометрия — это раздел математики, который имеет дело с прямоугольными треугольниками и отношениями между их сторонами и углами.(Слово «триггер» связано со словом «треугольник», чтобы помочь вам запомнить.)

Обычно в тесте ACT есть около 4-6 вопросов, касающихся тригонометрии (официальные инструкции по тестированию ACT говорят, что проблемы тригонометрии составляют 7% теста). На первый взгляд они могут показаться сложными, но большинство из них сводятся к нескольким простым концепциям.

Эта статья будет вашим исчерпывающим руководством по тригонометрии, которое вам нужно знать для ACT. Мы расскажем вам о значении тригонометрии, формулах и понимании, которые вам нужно знать, а также о том, как решать некоторые из самых сложных тригонометрических задач ACT.

Что такое тригонометрия и как ею пользоваться?

Тригонометрия изучает отношения между сторонами и углами прямоугольных треугольников. Соотношения между размерами сторон прямоугольного треугольника и размерами его углов постоянны, независимо от того, насколько большой или маленький треугольник.

Некоторые из множества различных возможных типов прямоугольных треугольников.

Если вы знаете размер одной стороны и один угол, отличный от 90 ° для прямоугольного треугольника, вы сможете определить остальные стороны и углы треугольника.2 = 340 9000 долларов США 3

$ c = √340 $ или $ c = 2√85 $

Но что, если у нас есть только одна длина стороны и мера одного из углов (не девяносто градусов)?

Несмотря на то, что у нас есть длина только одной стороны, мы все равно можем найти другие, используя тригонометрию, потому что у нас есть мера одного из острых углов.

Итак, здесь мы могли бы сказать $ sin 34 ° = 12 / \ hypotenuse \ $

Итак, $ \ hypotenuse \ = 12 / {sin 34 °} $

Не волнуйтесь, если это еще не имеет для вас смысла! Мы разберем каждый шаг по мере продвижения в руководстве.

(Примечание: чтобы найти фактическую величину угла в градусах с использованием двух длин сторон, вам нужно будет выполнить вычисление обратной функции (также называемой функцией «дуги»). Но НЕ БОЙТЕСЬ — ACT никогда не заставит вас Сделайте это! С точки зрения подготовки к математике ACT, поймите, что тест будет предлагать вам вычислить только достаточно далеко, чтобы сказать, например, «$ Cosine‌x = 4/5 $». Вам никогда не придется находить действительную величину угла из х по АКТ.

Мы находим эти меры, понимая отношение определенных сторон треугольника к их соответствующим углам. Это так называемые тригонометрические функции, и есть три, которые вы должны запомнить для ACT: синус, косинус и тангенс. Самый простой способ понять это — использовать мнемоническое устройство SOH, CAH, TOA , о котором мы поговорим чуть позже. > / P>

Тригонометрия широко используется в навигации, а также для расчета высот и расстояний. (На случай, если вам интересно, нужен ли вам триггер в реальной жизни.)

Наиболее распространенные триггерные вопросы ACT

Вопросы по тригонометрии ACT можно разделить на несколько категорий.Мы предоставили несколько реальных математических примеров ACT, чтобы продемонстрировать каждую концепцию.

# 1: Нахождение синуса, косинуса или тангенса (или, реже, косеканса, секанса или котангенса) угла из заданной прямоугольной треугольной диаграммы.

# 2: Нахождение синуса, косинуса или тангенса прямоугольного треугольника из задачи со словами.

Алекс подпирает лестницу к стене. Лестница составляет 23 ° от земли. Если длина лестницы составляет 10 футов, каково выражение для определения расстояния, на котором основание лестницы находится от стены?

А. 10 $ ‌tan‌23 ° $

Б. 10 $ sin‌23 ° $

C. 10 $ cos‌23 ° $

D. $ cos‌ {10/23} $

E. $ sin {10/23}

$

# 3: Нахождение синуса, косинуса или тангенса (или, реже, косеканса, секанса или котангенса) угла от заданного sin, cos или tan и диапазона, в который попадает угол.

Если $ tan‌Θ = 3/4 \ и 180 ° <Θ <270 ° $, что такое $ sinΘ $?

A. $ 4/3 $

Б. $ -4 / 3 $

C. $ -3 / 4 $

Д.$ 3/5 $

-3 Э. $ / 5

# 4: Определение периода или амплитуды графика.

Какова амплитуда графика?

А. 1

Б. 2

К. π

Д. 2π

E. 0

# 5: Закон синусов или закон косинусов.

Для такого вопроса, , они дадут вам формулы закона синусов или закона косинусов , так что вам не нужно беспокоиться об их запоминании.Однако наличие формулы вам не очень поможет, если она вам покажется или звучит как тарабарщина. По мере того, как вы будете изучать это руководство, выполнять практические вопросы по математике ACT, которые мы предоставили, и знакомиться с языком тригонометрии, используемым в этих вопросах, их станет намного легче решать.

Мы рассмотрим, как решить каждую из этих проблем, , но это даст вам представление о том, как будут выглядеть триггерные проблемы ACT в тесте.

SOH, CAH, TOA

Помните эту знаменитую мнемонику? Это спасет вашу жизнь.Давайте пройдемся по каждому.

SOH (синус)

Синус — это функция, в которой значение синуса (также называемого «грехом») угла тета может быть найдено с помощью отношения стороны треугольника, противоположной углу тета, к гипотенузе треугольника.

SOH : S дюйм $ Θ $ = O положительная сторона треугольника / H гипотенуза треугольника

Итак, в этом треугольнике $ sin‌Θ = b / c $, потому что сторона, противоположная углу $ Θ $, равна b , а гипотенуза равна c .

CAH (косинус)

Косинус — это функция, в которой значение косинуса (также называемого «$ cos $») угла тета ($ Θ $) можно найти, используя отношение стороны треугольника, примыкающей к углу $ Θ $ (т. Е. не гипотенуза) над гипотенузой треугольника.

CAH : C os $ Θ $ = A следующая сторона треугольника / H гипотенуза треугольника

Примечание: смежный означает, что сторона треугольника касается угла / помогает создать угол $ Θ $.

В этом же треугольнике $ cos‌Θ = a / c $, потому что сторона, примыкающая к углу $ Θ $, равна a , а гипотенуза равна c .

TOA (касательная)

Касательная — это функция, в которой значение тангенса (также называемого «тангенс») угла тета может быть найдено с помощью отношения стороны треугольника, противоположной углу тета, по соседней стороне треугольника к тета (что не является гипотенуза).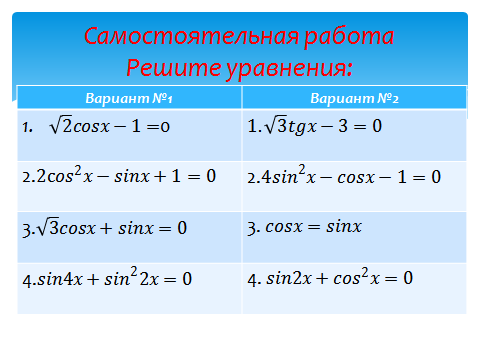

TOA : T и $ Θ $ = O заданная сторона треугольника / A смежная сторона треугольника.

В этом же треугольнике $ tan‌Θ = b / a $, потому что сторона, противоположная углу $ Θ $, равна b , а смежная сторона — a .

Теперь, когда вы знакомы со своими мнемоническими устройствами, вы можете составлять вопросы в несколько этапов. Например, немного более сложный вопрос может выглядеть примерно так:

Вам даны длины двух сторон треугольника, но для решения задачи требуется длина третьей стороны.2 = 21 $

$ x = √21 $

Теперь, когда у вас есть размер третьей стороны, вы можете найти $ tan‌B $.

$ Tan‌B = \ напротив / \ Соседний $

$ TanB = √21 / 2 $

Итак, ответ: F , √21 $ / 2 $

Какие стороны противоположные или смежные?

Гипотенуза треугольника всегда остается неизменной, но противоположные или смежные стороны меняются в зависимости от угла фокусировки.

Например, если вы пытаетесь найти $ sin $ угла $ γ $, вы должны использовать соотношение $ b / c $; если вы пытаетесь найти грех угла $ ξ $, вы должны использовать соотношение $ a / c $.2 = 44 $

$ x = √44 $

Теперь $ sin $ = $ \ Against / \ hypotenuse $, поэтому $ sin‌M = √44 / 12 $.

Итак, ответ — K.

Нет необходимости находить градусную меру (арксинус или обратный синус) угла M на вашем калькуляторе — это все, что вам нужно.

Вам также может быть предоставлено значение угла и длины стороны знаменателя вашего соотношения. В этом случае управляйте уравнением, как алгебраическим уравнением, и умножайте противоположную сторону на знаменатель.

$ sin Θ = \ напротив / \ гипотенуза $

$ гипотенуза $ * sinΘ = $ напротив

Поскольку вас спрашивают о длине лодки до причала, а эта сторона равна против , угол 52 °, вы знаете, что вам понадобится либо sin, либо tan (cos использует смежную и гипотенузу, а не противоположную).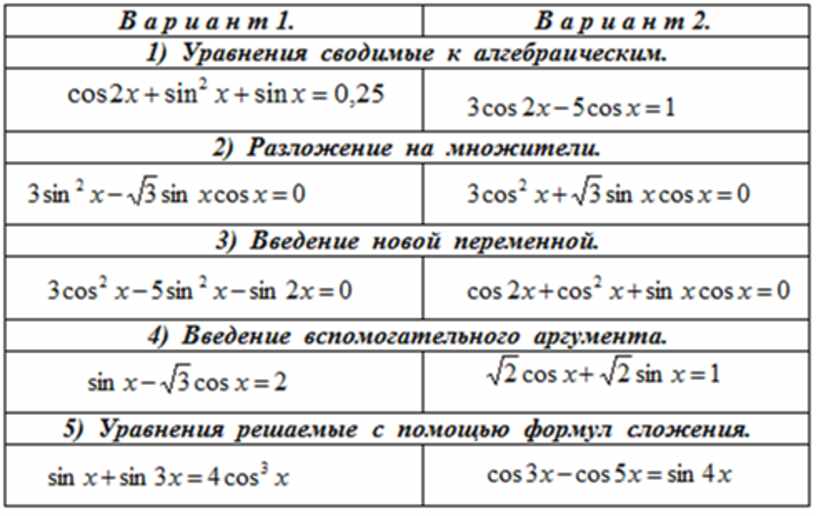

Вам также дается смежной длины , 30 миль, поэтому вы будете использовать tan. (Вы можете сказать, что эта сторона смежная, потому что сторона, противоположная углу 90 °, является гипотенузой, поэтому 30 миль должны быть еще одним катетом треугольника).

$ tan‌Θ = \ напротив / \ рядом $

So $ tan‌52 ° = x / 30 $

30‌ $ тан52 ° = x

долл. США

Итак, ответ — франка, длина лодки до причала 30 тангенциальных 52 °.

И снова проблема со словом из ранее.

Алекс подпирает лестницу к стене. Лестница составляет 23 ° от земли. Если длина лестницы составляет 10 футов, каково выражение для определения расстояния, на котором основание лестницы находится от стены?

А.10 ‌ $ загар‌23 ° $

Б. 10‌ $ sin‌23 ° $

C. 10 $ cos‌23 ° $

D. $ cos‌10 / 23 $

E. $ sin‌10 / 23 $

Во-первых, нарисуйте свою картинку, чтобы легче было представить, о чем вас просят.

Итак, расстояние между лестницей и землей составляет 23 ° $. Также мы работаем с длинами соседней стороны треугольника и гипотенузы. Это означает, что нам понадобится косинус, так как $ cos‌Θ = \ напротив / \ hypoteneuse $

.

Итак, $ cos‌23 ° = \ смежный / 10 $ (Почему 10? Длина лестницы 10 футов)

Это становится 10 $ ‌cos‌23 ° = \ смежный $

Итак, ответ: C , 10 $ ‌cos‌23 ° $

Придется ли мне определять угол?

Короткий ответ: нет, вас не попросят определить точную меру угла с помощью тригонометрии.2)}

долл. США

Когда Sin, Cos и Tan являются положительными или отрицательными?

В зависимости от того, где расположен треугольник в двумерном пространстве, значения sin, cos и tan будут отрицательными или положительными.

В двухмерном пространстве четыре квадранта, разделенных по осям x и y.

• В квадранте I и x, и y положительны.
• В квадранте II x отрицателен, а y положителен
• В квадранте III оба значения x и y отрицательны
• А в квадранте IV x положителен, а y отрицателен

Как и в случае со значениями x и y, sin, cos и tan могут быть положительными или отрицательными в зависимости от квадранта, в котором находится треугольник / угол.

• В квадранте I все положительны
• В квадранте II sin положителен, а cos и tan отрицательны
• В квадранте II tan положительный, а sin и cos отрицательные
• В квадранте IV cos положительна, а sin и tan отрицательны

Хороший способ запомнить это по мнемонической аббревиатуре ASTC — A ll S tudents T ake C hemistry — чтобы увидеть, какая из функций является положительной в зависимости от квадранта.

Итак, A ll положительны в квадранте I, S in положительны в квадранте II, T an положительны в квадранте III, а C ll положительны в квадранте IV

Если $ tan‌Θ = 3/4 $ и $ 180 ° <Θ <270 ° $, что такое $ sinΘ $?

A. $ 4/3 $

Б. $ −4 / 3 $

C. $ -3 / 4 $

D. $ 3/5 $

-3 Э. $ / 5

Чтобы решить эту проблему, сначала определите длины сторон треугольника, используя теорему Пифагора (или используя свои знания о 3-4-5 треугольниках). 2 = 25 9000 долларов США 3

$ c = 5

$

Итак, наша гипотенуза равна 5.

Мы знаем, что $ sin Θ = \ Against / \ hypotenuse $. Итак, $ sin‌Θ = 3/5 $.

Но подождите! Мы еще не закончили. Поскольку они сказали нам, что $ Θ $ лежит между $ 180 ° $ и $ 270 ° $, мы знаем, что значение sin для $ Θ $ отрицательно. Согласно ASTC, только тангенс угла $ Θ $ будет положительным между 180 ° $ и 270 ° $.

Итак, , наш окончательный ответ — евро, $ — 3/5 $

Вторичные триггерные функции

В редких случаях на ACT вас попросят указать одну из вторичных триггерных функций.Это косеканс, секанс и котангенс. Они возникают не более чем по одному вопросу за тест.

Вы могли заметить, что они похожи на основные триггерные функции, которые вы изучили выше. Фактически, эти вторичные функции являются обратными (обратными) sin, cos и касательной.

Чтобы помочь вам запомнить, что есть что, обратите внимание на третью букву каждого слова:

• Co s ecant = обратная величина s ine
• Se c ant = аналог c osine
• Co t Угол = обратный t Угол

Косеканс

Косеканс — величина, обратная синусу.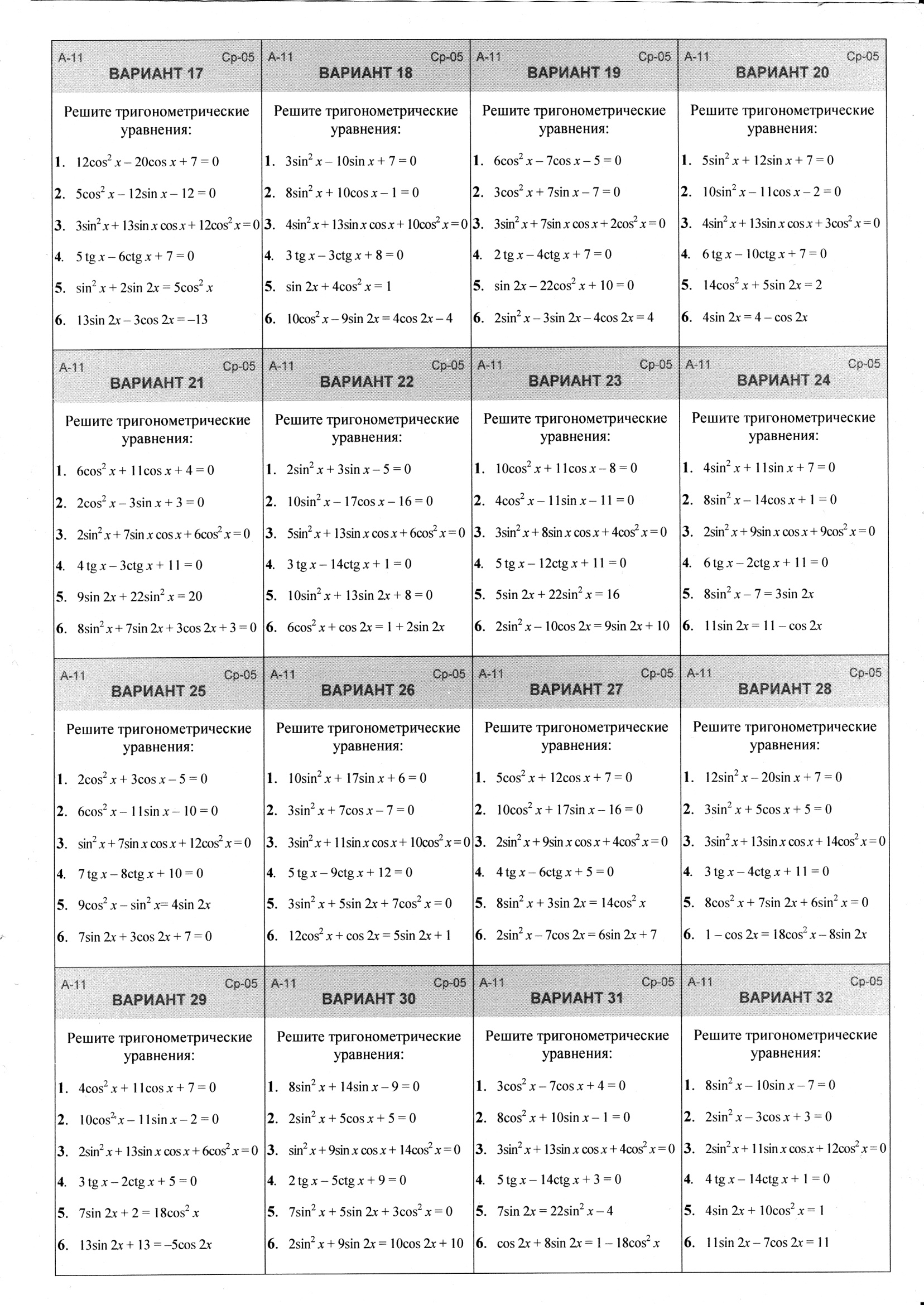 $ Косеканс Θ = \ гипотенуза / \ напротив $

Секант

Секанс — величина, обратная косинусу. $ Секанс Θ = \ гипотенуза / \ смежный $

Котангенс

Котангенс — величина, обратная касательной. $ Котангенс Θ = \ смежный / \ противоположный $

Полезные формулы с Sin, Cos и Tan

Есть две формулы, которые время от времени будут появляться в ACT. Если вы чувствуете, что не можете больше запоминать тригонометрию, не беспокойтесь об их запоминании — они могут ответить максимум на один вопрос за тест .2 {x}) $, что также равно 1.

Итак, мы имеем 1 + 1 = 2

Окончательный ответ: H , 2.

$$ (sin‌Θ) / (cos‌Θ) = tan‌Θ $$

Это уравнение имеет логический смысл, если представить его в виде диаграммы. Допустим, у вас есть треугольник, который выглядит так

$ Sin Θ $ будет 5 $ / 13 $. $ Cos Θ $ будет $ 12/13 $. $ Tan Θ $ составит 5 долларов США / 12%.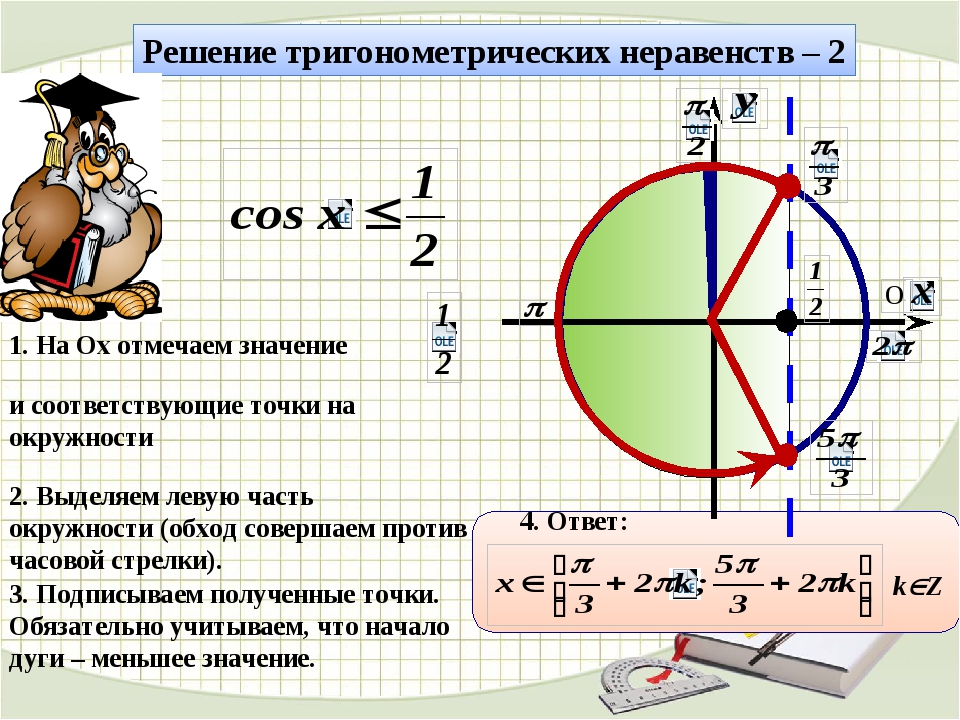

Вы также можете сказать $ tan‌Θ = {sin‌Θ} / {cos‌Θ} = {5/14} / {12/13} = (5/13) (13/12) = 65/156 $ (вы также можете просто отменить обе 13s для упрощения) = 5 $ / 12 $

Графические триггерные функции

ACT не будет запрашивать у вас график триггерной функции, но вам нужно распознать, как каждая функция выглядит в виде графика.

Синус

Синусоидальный график пересекает начало координат в волновой структуре. Он всегда возрастает после $ x = 0 $, после пересечения начала координат.

Это «нечетная» функция, потому что она не симметрична относительно оси y.

Косинус

График косинусов также «волнистый», но не пересекает начало координат. Он спускается после $ x = 0 $.

Это может помочь вам запомнить, что косинус убывает после x = 0, если подумать, что « co — low »

Косинус является «четной» функцией, потому что он симметричен относительно оси y. Это означает, что для всех значений $ x $ $ f (x) = f (-x) $.

Например, на приведенном выше графике $ y = 0,7 $ как при $ x = 1 $, так и при $ x = -1 $

Иногда все, что вам зададут, — это определить, является ли график четным или нечетным, а также является ли график sin или cos. Вам будет легко понять это, если вы запомните основные элементы тригонометрических графиков.

Хотя вы можете понять этот вопрос из предоставленной информации, это займет гораздо меньше времени, если вы узнаете, что график является косинусным и, следовательно, четным.А на ACT время ограничено и ценно.

Касательная

Касательный график выглядит совсем иначе, чем графики sin и cos — вам просто нужно уметь распознавать касательный график, когда вы его видите.

Периоды и амплитуды

ACT иногда просит вас найти период или амплитуду синусоидального или косинусного графика.

Период

Период графика — это расстояние по оси x, с которого график начинает повторяться. Найдите расстояние по оси x, на котором точка возвращается в исходное положение после выполнения полного цикла .

Период синусоидального графика здесь равен 2π. Он должен идти как вверх, так и вниз, прежде чем окончательно вернуться к $ y = 0 $.

Период косинусного графика здесь также равен 2π. Он должен сначала спуститься, а затем снова подняться, чтобы вернуться в исходное положение при $ y = 1 $.

Амплитуда

Амплитуда графика — это его высота от оси x, расстояние между его наивысшим значением $ y $ и $ x = 0 $.

Итак, чтобы использовать тот же график, что и выше:

И синус, и косинус имеют амплитуду 1 (и, опять же, период 2π).

Рад

Радианы — это еще один (более точный) способ измерения расстояния по окружности, а не в градусах. Вместо градусов радианы выражаются через π (и доли π).

Если у вас есть полный круг, это 360 градусов. Это также 2π радиан.

Почему 2π радиан? Что ж, придумайте формулу длины окружности. С = 2πr. Если ваш радиус равен 1, тогда ваша окружность равна 2π, что совпадает с вашей мерой в радианах.

Окружность с радиусом 1 и центром в начале координат называется «единичной окружностью». Радианы удобно рассматривать, размещая их на единичной окружности.

Итак, если у вас есть полукруг, это 180 ° или π радиан.

И так далее. 90 ° — это $ π / 2 $ радиан, 270 ° — $ (3π) / 2 $ радиан.

Чтобы преобразовать градусы в радианы, проще всего использовать преобразование между 180 ° и π .

Преобразовать 45 ° в радианы => $ (45) {π / 180} = π / 4 $ ‌радиан

Преобразовать $ (3π) / 4 $ радиан в градусы => $ {(3π) / 4} (180 / π) $ = 135 °

Шаги к решению триггерного вопроса

Итак, давайте рассмотрим, как разбить триггерный вопрос

# 1: Определите, требует ли проблема тригонометрии. Вы можете сказать, что проблема потребует триггера, когда:

• Проблема упоминает sin, cos или tan в вопросе или в вариантах ответа

• Задача дает вам диаграмму или описывает прямоугольный треугольник, а затем просит вас найти значение, которое нельзя найти, используя только теорему Пифагора.

• Как мы видели в этой задаче ранее — вы можете использовать теорему Пифагора в как задачу тригонометрии, но вы не можете решить тригонометрическую задачу с помощью только , используя теорему Пифагора.

• Проблема показывает «волнистый» график по осям x и y

• Задача запрашивает период или амплитуду графика

# 2: Помните SOH, CAH, TOA.2 {‌Θ} и др.

# 4 :. Вспомните, как выглядят графики синуса, косинуса и тангенса.

И знайте, что:

Период = горизонтальное расстояние

Амплитуда = вертикальное расстояние

# 5: Празднуйте, потому что вы ответили на триггерные вопросы ACT!

Итоги

Хотя проблемы тригонометрии могут показаться устрашающими, почти каждый вопрос о тригонометрии АСТ может быть решен, если вы знаете основные элементы тригонометрии.

Чтобы извлечь максимальную пользу из подготовки к математике ACT, запомните эти три триггерные концепции: SOH, CAH, TOA, как управлять своими уравнениями и как распознавать графики функций. Если вы запомните их, вы обнаружите, что решаете практически все триггерные вопросы, которые ACT может бросить вам.

Что дальше?

Хотите больше математических стратегий и руководств ACT? Прочтите нашу статью по всем математическим темам, протестированным на ACT, чтобы убедиться, что вы их хорошо усвоили. Вы знаете твердотельную геометрию ACT? Не забудьте освежить в памяти все, что вам нужно.

Хотите получить высший балл по математике в ACT? Ознакомьтесь с нашей статьей о том, как набрать 36 баллов по математическому разделу ACT с помощью тестера ACT 36.

Чувствуете себя разбитым? Не знаю, с чего начать? Не ищите дальше наших статей о том, что считается хорошей, плохой или отличной оценкой ACT. Не знаете, в какие дни проводится ACT? Ознакомьтесь с полным списком дат тестирования ACT, чтобы найти подходящие для вашего расписания.

И если вы обнаружите, что у вас не хватает времени на математический раздел, посмотрите нашу статью о том, как перестать не хватать времени на математику ACT.

Хотите улучшить свой результат SAT на 160 баллов?

Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к SAT. Мы гарантируем возврат ваших денег , если вы не улучшите свой SAT на 160 или более баллов.

Наша программа полностью интерактивна, и она адаптирует то, что вы изучаете, к вашим сильным и слабым сторонам. Если вам понравилось это руководство по математической стратегии, вам понравится наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по индивидуальным навыкам, чтобы вы учились наиболее эффективно.Мы также дадим вам пошаговую программу, которой нужно следовать, чтобы вы никогда не запутались, что изучать дальше.

Воспользуйтесь нашей 5-дневной бесплатной пробной версией:

Правила и задачи тригонометрии | Формулы треугольника Sin, Cos, Tan

Правила тригонометрии Страница

На этой странице есть правила тригонометрии, формулы треугольников sin, cos и tan, а также задачи для экзамена.

Тригонометрия включена в экзамен Next Generation по продвинутой алгебре и функциям.

Задачи тригонометрии

Инструкции: Ответьте на вопросы об угле a в правом треугольнике ниже. Длина гипотенузы составляет Y единиц. Две другие стороны имеют длину x и z.

Вы можете обратиться к формулам тригонометрии, особенно к приведенным ниже формулам треугольников sin, cos и tan, прежде чем отвечать на вопросы.

1) загар а =?

2) cos a =?

3) sin ² a =?

4) cos ² a =?

5) sin ² a + cos ² a =?

Ответы на тригонометрические задачи

1) напротив / рядом = Z / X

2) смежный / гипотенуза = X / Y

3) (противоположный / гипотенуза) ² = (Z / Y) ²

4) (рядом / гипотенуза) ² = (X / Y) ²

5) sin ² a + cos ² a всегда равно 1.

Другие задачи тригонометрии

Калькулятор тригонометрии

Правила и формулы тригонометрии:

Запомните следующие правила и формулы тригонометрии для экзамена.

Sin, Cos & Tan — Формулы треугольников

Для экзамена вам нужно будет понять формулы треугольников sin, cos и tan.

Помните, что гипотенуза — это сторона треугольника, противоположная прямому углу.

Соседняя сторона находится рядом с измеряемым углом.

Противоположная сторона находится напротив измеряемого угла.

Итак, наши формулы треугольника sin, cos и tan выглядят следующим образом:

Sin, Cos & Tan — законы треугольника

Вам также будут заданы вопросы о тригонометрических отношениях на экзамене.

Убедитесь, что вы знаете основные правила и формулы тригонометрии.

Это правила тригонометрии, относящиеся к формулам sin, cos и tan для прямоугольных треугольников:

cos ² A + sin ² A = 1

cos ² A = 1 — sin ² A

sin ² A = 1 — cos ² A

тангенс = sin ÷ cos

Правила тригонометрии для радианов

Это правила тригонометрии для радианов.

Радиан можно представить как частичную длину окружности.

θ = s ÷ r [где θ = радианы вытянутого угла; s = длина дуги; и r = радиус]

π × 2 × радиан = 360 °

π × радианы = 180 °

π ÷ 2 × радиан = 90 °

π ÷ 4 × радиан = 45 °

π ÷ 6 × радиан = 30 °

Упражнения «Больше греха, тона и загара» (формула треугольника)

Дополнительная математическая практика

Бесплатный онлайн-тест по продвинутой математике

Получите 400 дополнительных математических задач Accuplacer — PDF

Продвинутые правила математики и тригонометрии, включая формулы треугольников sin, cos и tan, более подробно рассматриваются в нашем бесплатном онлайн-тесте.

гл. 8 Практический тест — алгебра и тригонометрия

Практический тест

Для следующих упражнений нарисуйте график каждой функции для двух полных периодов. Определите амплитуду, период и уравнение средней линии.

5.

f (x) = — cos (x + π3) + 1f (x) = — cos (x + π3) +1

6.

f (x) = 5sin (3 (x − π6)) + 4f (x) = 5sin (3 (x − π6)) + 4

7.

f (x) = 3cos (13x − 5π6) f (x) = 3cos (13x − 5π6).

9.

f (x) = — 2tan (x − 7π6) + 2f (x) = — 2tan (x − 7π6) +2

10.

f (x) = πcos (3x + π) f (x) = πcos (3x + π).

11.

f (x) = 5csc (3x) f (x) = 5csc (3x)

12.

f (x) = πsec (π2x) f (x) = πsec (π2x)

13.

f (x) = 2csc (x + π4) −3f (x) = 2csc (x + π4) −3

Для следующих упражнений определите амплитуду, период и среднюю линию графика, а затем найдите формулу для функции.

14.

Дайте в терминах синусоидальной функции.

15.

Дайте в терминах синусоидальной функции.

16.

Дайте в терминах касательной функции.

Для следующих упражнений найдите амплитуду, период, фазовый сдвиг и среднюю линию.

17.

y = грех (π6x + π) −3y = sin (π6x + π) −3

18.

y = 8sin (7π6x + 7π2) + 6y = 8sin (7π6x + 7π2) +6

19.

Наружную температуру в течение дня можно смоделировать как синусоидальную функцию. Предположим, вы знаете, что температура в полночь составляет 68 ° F, а высокая и низкая температура днем ​​- 80 ° F и 56 ° F соответственно. Предполагая, что tt — это количество часов, прошедших с полуночи, найдите функцию температуры D, D через t.т.

20.

Вода перекачивается в бункер для хранения и опорожняется с периодической скоростью. Глубина воды составляет 3 фута в самом низком месте в 2 часа ночи и 71 футе в самом высоком, что происходит каждые 5 часов. Напишите функцию косинуса, которая моделирует глубину воды как функцию времени, а затем изобразите эту функцию для одного периода.

Для следующих упражнений найдите период и горизонтальный сдвиг каждой функции.

21.

г (x) = 3tan (6x + 42) g (x) = 3tan (6x + 42)

22.

n (x) = 4csc (5π3x − 20π3) n (x) = 4csc (5π3x − 20π3)

23.

Запишите уравнение для графика на рисунке 1 в терминах функции секущей и укажите период и фазовый сдвиг.

Рисунок 1

24.

Если tanx = 3, tanx = 3, найти tan (−x) .tan (−x).

25.

Если secx = 4, secx = 4, найти sec (−x) .sec (−x).

Для следующих упражнений нарисуйте функции в указанном окне и ответьте на вопросы.

26.

График m (x) = sin (2x) + cos (3x) m (x) = sin (2x) + cos (3x) в окне просмотра [−10,10] [- 10,10] на [−3 , 3].[−3,3]. Приблизительно период графика.

27.

График n (x) = 0,02sin (50πx) n (x) = 0,02sin (50πx) в следующих областях в x: x: [0,1] [0,1] и [0,3]. [0 , 3]. Предположим, эта функция моделирует звуковые волны. Почему эти взгляды выглядят так иначе?

28.

График f (x) = sinxxf (x) = sinxx на [−0,5,0,5] [- 0,5,0,5] и объясните любые наблюдения.

Для следующих упражнений пусть f (x) = 35cos (6x) .f (x) = 35cos (6x).

29.

Какое наибольшее возможное значение для f (x)? F (x)?

30.

Какое наименьшее возможное значение для f (x)? F (x)?

31.

Где функция возрастает на интервале [0,2π]? [0,2π]?

Для следующих упражнений найдите и изобразите один период периодической функции с заданными амплитудой, периодом и фазовым сдвигом.

32.

Синусоидальная кривая с амплитудой 3, периодом π3, π3 и фазовым сдвигом (h, k) = (π4,2) (h, k) = (π4,2)

33.

Косинусная кривая с амплитудой 2, периодом π6, π6 и фазовым сдвигом (h, k) = (- π4,3) (h, k) = (- π4,3)

Постройте график функции для следующих упражнений.Опишите график и, если возможно, любое периодическое поведение, амплитуду, асимптоты или неопределенные точки.

34.

f (x) = 5cos (3x) + 4sin (2x) f (x) = 5cos (3x) + 4sin (2x)

Найдите точное значение для следующих упражнений.

38.

cos − 1 (−32) cos − 1 (−32)

39.

cos − 1 (sin (π)) cos − 1 (sin (π))

40.

cos − 1 (tan (7π4)) cos − 1 (tan (7π4))

41.

cos (sin − 1 (1−2x)) cos (sin − 1 (1−2x))

42.

cos − 1 (−0,4) cos − 1 (−0,4)

43.

cos (tan − 1 (x2)) cos (tan − 1 (x2))

Для следующих упражнений предположим, что sint = xx + 1. sin = xx + 1. Оцените следующие выражения.

46.

По рисунку 2 найдите угол θθ с точностью до трех десятичных знаков. Ответ в радианах.

Рисунок 2

Для следующих упражнений определите, истинно ли уравнение или нет.

47.

arcsin (sin (5π6)) = 5π6arcsin (sin (5π6)) = 5π6

48.

arccos (cos (5π6)) = 5π6arccos (cos (5π6)) = 5π6

49.

Уклон дороги 7%. Это означает, что на каждое горизонтальное расстояние в 100 футов по дороге вертикальный подъем составляет 7 футов. Найдите угол между дорогой и горизонтом в радианах.

бесплатных уроков и тестов по математике

Что такое тригонометрия?

Тригонометрия — это раздел математики, изучающий углы и длины сторон треугольников. Тригонометрия, в частности, имеет дело с функциями, которые связывают угол прямоугольного треугольника с длинами его сторон: функция синуса, функция косинуса и функция тангенса.

Оксфордский словарь английского языка определяет тригонометрию как «раздел математики, который имеет дело с измерением сторон и углов треугольников, в частности, с определенными функциями их углов или углов в целом (синус, косинус и тангенс)».

Вот несколько примеров из тригонометрии. Нам может быть интересно найти угол или длину стороны прямоугольного треугольника. Мы могли бы захотеть построить функцию, полученную из отношения длин двух сторон прямоугольного треугольника.Тригонометрия позволяет нам это делать.

Откуда взялась словесная тригонометрия?

Тригонометрия происходит от греческих слов «тригонон» («треугольник») и «метрон» («мера»).

Учебная программа

Уроки сгруппированы в мини-учебные программы, чтобы помочь вам организовать обучение. Краткое описание каждой мини-программы. Нажмите кнопку БОЛЬШЕ , чтобы узнать больше.

Прямой треугольник

Правые треугольники (в американском английском) или прямоугольные треугольники (в английском английском) — это треугольники, содержащие один угол 90 ° (называемый прямым углом).В этой мини-программе вы узнаете о прямоугольных треугольниках и их сторонах.

Теорема Пифагора

Теорема Пифагора касается отношения между длинами трех сторон прямоугольного треугольника. В этой мини-программе вы узнаете о теореме Пифагора и о том, как ее использовать.

Синусоидальная функция

Синусоидальная функция — это тригонометрическая функция. Синус угла в прямоугольном треугольнике равен отношению длины противоположной стороны к длине гипотенузы.В этой мини-программе вы узнаете о функции синуса и о том, как ее можно использовать для определения углов и длин сторон прямоугольного треугольника.

Косинусная функция

Функция косинуса — это тригонометрическая функция. Косинус угла в прямоугольном треугольнике равен отношению длины прилегающей стороны к длине гипотенузы. В этой мини-программе вы узнаете о функции косинуса и о том, как ее можно использовать для определения углов и длин сторон прямоугольного треугольника.

Касательная функция

Касательная функция — это тригонометрическая функция. Тангенс угла в прямоугольном треугольнике равен отношению длины противоположной стороны к длине соседней стороны. В этой мини-программе вы узнаете о функции касательной и о том, как ее можно использовать для определения углов и длин сторон прямоугольного треугольника.

Площадь треугольника по тригонометрии

Хотя тригонометрия в основном касается прямоугольных треугольников, ее можно использовать для любого треугольника.В этой мини-программе вы узнаете, как определить площадь треугольника с помощью тригонометрии.

Помогите нам улучшить математику Монстр

• Вы не согласны с чем-то на этой странице?
• Вы заметили опечатку?

Сообщите нам, используя эту форму .