Содержание

Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой 9 класс онлайн-подготовка на Ростелеком Лицей |

Тема 28.

Уравнение линии на плоскости.

Уравнение окружности.

При изучении алгебры мы строили графики некоторых функций в прямоугольной системе координат, например, график функции у = x. Известно, что графиком этой функции является прямая, проходящая через начало координат O(0; 0). Координаты любой точки M(x; y), лежащей на прямой ОА удовлетворяют уравнению у = x, а координаты любой точки, не лежащей на прямой ОА, этому уравнению не удовлетворяют. Говорят, что уравнение у = x является уравнением прямой ОА.

Введем теперь понятие уравнения произвольной линии.

Пусть на плоскости задана прямоугольная система координат Oxy и дана некоторая линия L.

Уравнение с двумя переменными x и y называется уравнением линии L, если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

При изучении линий методом координат возникают две задачи: 1) по геометрическим свойствам данной линии найти ее уравнение; 2) обратная задача: по заданному уравнению линии исследовать ее геометрические свойства.

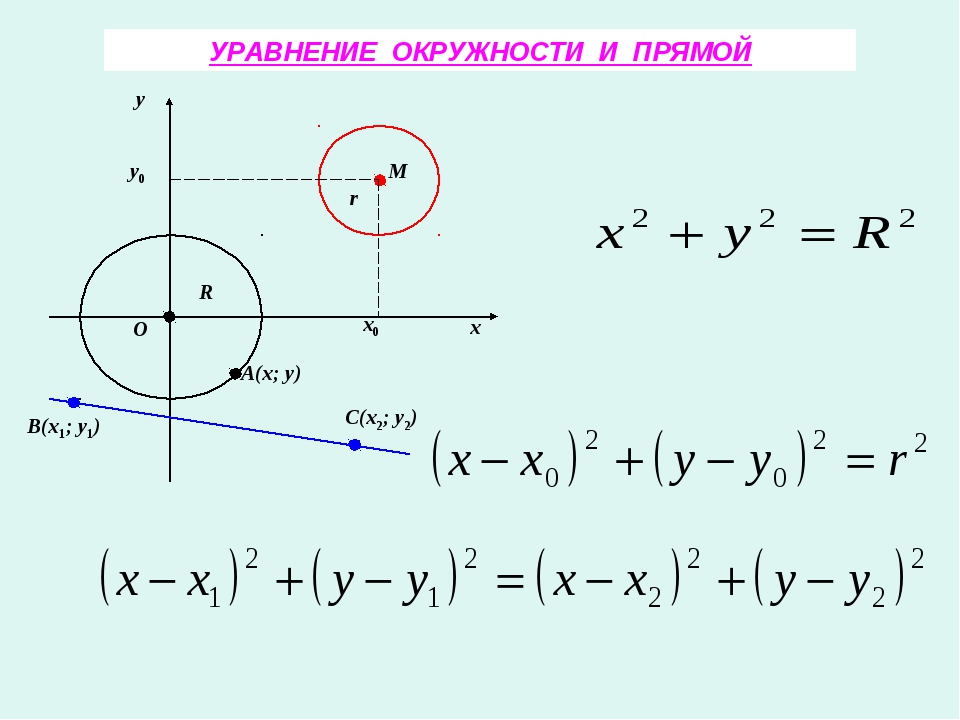
Выведем уравнение окружности радиуса r с центром C в заданной прямоугольной системе координат. Пусть точка C имеет координаты (x0; y0)

Расстояние от произвольной точки M(x; y) до точки C вычисляется по формуле

MC=x-x02+y-y02. Если точка M лежит на данной окружности, то MC = r, или MC2 =

r2, т. е. координаты точки M удовлетворяют уравнению

x-x02+y-y02= r2 (1)

Если же точка M(x; y) не лежит на данной окружности, то MC2 ≠ r2, и, значит координаты точки не удовлетворяют уравнению (1). Следовательно, в прямоугольной системе координат уравнение окружности радиуса r с центром в точке C(x0; y0) имеет вид:

x-x02+y-y02= r2

В частности, уравнение окружности радиуса r с центром в начале координат имеет вид:

x2+y2= r2.

Найти уравнение окружности с центром в точке (-3; 4), проходящей через начало координат.

Центр окружности имеет координаты (-3; 4). Поэтому уравнение этой окружности можно записать в видеx+32+y-42=r2, где

r – пока неизвестный радиус окружности. Найдем его. Для этого воспользуемся тем, что окружность проходит через начало координат, т. е. точка O(0; 0) удовлетворяет этому уравнению: (0 + 3)2 + (0 — 4)2 = r2. Отсюда r2 = 25, и, значит, r = 5. Итак, искомое уравнение окружности имеет вид

x+32+y-42=25

Если раскрыть скобки и привести подобные члены, то получится уравнение x2+y2+6x – 8y=0, которое также является уравнением данной окружности.

Решим еще одну задачу.

Напишем уравнение окружности с диаметром MN, если точка M(-3; 5), а точка N(7; -3).

Для того, чтобы написать уравнение окружности, необходимо найти координаты центра этой окружности. А это середина диаметра. Пусть O(x

; y) – середина диаметра. Итак,

x=-3+72=2y=5-32=1, значит O(2; 1)

Найдем теперь радиус MO, то есть найдем расстояние между точками M и O, получим:

MO=2—32+1-52=41

Подставим все в уравнение окружности:

x-22+y-12=41

Сегодня мы вывели уравнение окружности, а в следующий раз мы выведем уравнение прямой.

Уравнение прямой

Прежде чем приступить к изучению нового материала, давайте повторим формулу для нахождения координат середины отрезка

, , формулу для определения расстояния между двумя точками , вспомним, что называется уравнением линии l, запишем уравнение окружности с радиусом r и центром в точке C (x0;y0). Вспомним уравнение окружности радиуса r и центром в начале координат .

Сегодня на уроке мы выведем уравнение произвольной прямой l.

В координатной плоскости прямая может располагаться либо вертикально (параллельно оси Oy), горизонтально (параллельно оси Ox) либо быть наклонной к обеим осям.

Первым давайте рассмотрим случай, когда прямая параллельна оси Oy.

Возьмем на оси Ox, например, точку с координатой 3 и проведем через эту точку прямую, параллельную оси Oy. Абсцисса любой точки этой прямой равна 3. То есть координаты любой точки этой прямой удовлетворяют уравнению x=3, а координаты любой точки, которая не лежит на данной прямой не удовлетворяют данному уравнению. Значит, уравнение x=3 является уравнением прямой параллельной оси Oy и проходящей через точку с координатами (3;0).

Можно сказать, что произвольная прямая параллельная оси Oy задается уравнением . Уравнение  является уравнением оси .

Задача. Записать уравнения прямых, показанных на рисунке:

Решение.

Для того, чтобы записать уравнение каждой прямой, запишем общее уравнение прямых параллельных оси Oy.

 

 

 

 

Рассмотрим теперь случай когда прямая параллельна оси Ox.

Возьмем на оси Oy, например, точку 5 и проведем через нее прямую параллельную оси Ox. Любая точка этой прямой удовлетворяет уравнению y=5, любая точка, которая не лежит на этой прямой не удовлетворяет этому уравнению, значит, эту прямую задает уравнение y=5.

Можно сказать, что произвольная прямая параллельная оси Ox задается уравнением .Ось Ox задается уравнением .

Задача. Записать уравнения прямых, показанных на рисунке:

Решение.

Запишем общее уравнение прямых параллельных оси Ox.

.

 

 

 

Теперь рассмотрим случай, когда прямая наклонная к обеим осям.

Отметим на координатной плоскости точки с координатами (x1; y1) и (x2; y2) так, чтобы указанная прямая l была серединным перпендикуляром к отрезку AB.

Теперь возьмем произвольную точку M (x;y). Если точка M лежит на прямой  l, то, очевидно, что длины отрезков AM и BM будут равны. Найдем эти отрезки и приравняем их.

Получим уравнение:

Если точка M не лежит на прямой, то, очевидно, что отрезки AM и BM не будут равны и координаты точки M не будут удовлетворять этому уравнению.

Значит, в прямоугольной системе координат уравнение прямой l имеет вид:

.

Раскроем скобки и выполним элементарные преобразования.Введем замену. ;

Получим уравнение .

Так как в самом начале мы говорили, что точки A и B – различные точки, то хотя бы одна из разностей ,  не равна нулю, то есть хотя бы один из коэффициентов a и b не равен нулю. То есть можно сказать, что уравнение прямой в прямоугольной системе координат является уравнением первой степени и имеет вид: .

Задача. Написать уравнение прямой, проходящей через точки  и .

Решение.

Ответ:

Предположим, что в этом уравнении коэффициент .

Тогда получим уравнение .

Число k называется угловым коэффициентом прямой.

Отметим, что две параллельные прямые, не параллельные оси Oy имеют одинаковые угловые коэффициенты и если две прямые имеют одинаковые угловые коэффициенты, то эти прямые параллельны.

Задача. Записать угловой коэффициент прямой, проходящей через точки  и .

Решение.

d

 

 

 

 

 

Ответ:

Задача. Среди предложенных уравнений прямых выберите те, которые задают прямые, параллельные прямой

а)       б)      в)      г) .

Решение. Мы говорили, что две параллельные прямые имеют одинаковые угловые коэффициенты, поэтому искомыми уравнениями будут только уравнения

а)

б)

в)

г)  

Ответ: б)   г) .   

Задача. Укажите пары параллельных прямых

а)  и       б)  и     

в)  и  .   

Решение.

а)

   

б)

   

в)

       

Ответ: б)  и .   

Задача. Даны координаты вершин трапеции

. Написать уравнения прямых, содержащих диагонали .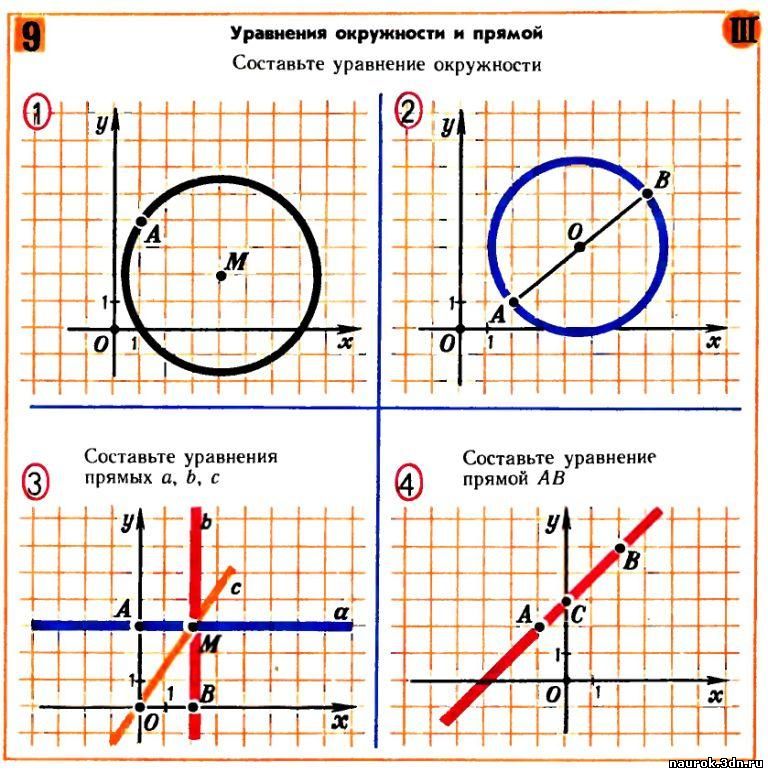

Решение.

Запишем общее уравнение прямой .

Аналогично найдем, что уравнение прямой, которая содержит диагональ BD имеет вид y=1.

Ответ: .

Давайте подведем итоги урока.

Уравнение прямой имеет вид: . Еще один вид уравнения прямой –  – угловой коэффициент прямой.

Уравнение прямой, параллельной оси Ox имеет вид . Уравнение прямой, параллельной оси Oy имеет вид .

Две параллельные прямые, не параллельные оси о игрек имеют одинаковые угловые коэффициенты и если две прямые имеют одинаковые угловые коэффициенты, то эти прямые параллельны.

«Уравнение окружности и прямой»(9 класс)

Самостоятельная работа по геометрии по теме: «Уравнение окружности и прямой».   

Вариант 1.

1.   Начертите окружность заданную уравнение

2.      Напишите уравнение окружности с центром в начале координат, проходящей через точку В(-1;3).

3.      Начертите прямую, заданную уравнением: а)    у=2     б)    х= — 1

4.      Напишите уравнение прямой, проходящей через две данные точки: А(1;-1) и в(-3;2)

 

Самостоятельная работа по геометрии по теме: «Уравнение окружности и прямой».  

Вариант 2.

1.   Начертите окружность заданную уравнение

2.      Напишите уравнение окружности с центром в точке А(0;6), проходящей через точку

В(-3;2).

3.      Начертите прямую, заданную уравнением: а)    у= — 1     б)    х= 2

4.      Напишите уравнение прямой, проходящей через две данные точки: А(2;5) и в(5;2)

Самостоятельная работа по геометрии по теме: «Уравнение окружности и прямой

Вариант 3.

1.   Начертите окружность заданную уравнение

2.      Напишите уравнение окружности с центром в точке А(-3;4), проходящей через начало координат.

3.      Начертите прямую, заданную уравнением: а)    у=3     б)    х= — 1

4.      Напишите уравнение прямой, проходящей через две данные точки: А(0;1) и в(-4;-5)

Самостоятельная работа по геометрии по теме: «Уравнение окружности и прямой

Вариант 4.

1.   Начертите окружность заданную уравнение

2.      Напишите уравнение окружности с центром в точке А(-6;8), проходящей через начало координат.

3.      Начертите прямую, заданную уравнением: а)    у=4     б)    х= — 2

4.      Напишите уравнение прямой, проходящей через две данные точки: А(1;2) и в(3;2)

Самостоятельная работа по геометрии по теме: «Уравнение окружности и прямой».

Вариант 5.

1.   Начертите окружность заданную уравнение

2.       Напишите уравнение окружности с центром в начале координат, проходящей через точку  А(-1;3).

3.      Начертите прямую, заданную уравнением: а)    у= — 3     б)    х= — 2

4.      Напишите уравнение прямой, проходящей через две данные точки: А(1;2) и в(2;3)

 

Уравнение окружности / Метод координат / Справочник по геометрии 7-9 класс

  1. Главная
  2. Справочники
  3. Справочник по геометрии 7-9 класс
  4. Метод координат
  5. Уравнение окружности

Выведем уравнение окружности радиуса с центром в заданной прямоугольной системе координат. Пусть точка имеет координаты :

Расстояние от произвольной точки до точки вычисляется по формуле . Если точка лежит на данной окружности, то = , , т.е. координаты точки удовлетворяют уравнению

      (1)

Если же точка   не лежит на данной окружности, то , и, значит, координаты точки не удовлетворяют уравнению (1).

Частный случай: уравнение окружности радиуса с центром в начале координат:

Задача

Найти уравнение окружности с центром в точке (-3; 4), проходящей через начало координат.

Дано: окр.(), 0 = -3, 0 = 4, окр.()

Найти: уравнение окр.()

Решение:

, следовательно, для данной окружности имеем, что (2).

Найдем : т.к. окр.(), т.е. координаты точки удовлетворяют уравнению (2):

.

Отсюда или .

Итак, искомое уравнение окружности имеет вид .

Раскроем скобки и приведем подобные члены, получим, что: . Полученное уравнение также является уравнением данной окружности.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Разложение вектора по двум неколлинеарным векторам

Координаты вектора

Связь между координатами вектора его начала и конца

Простейшие задачи в координатах

Уравнение линии на плоскости

Уравнение прямой

Взаимное расположение двух окружностей

Метод координат

Правило встречается в следующих упражнениях:

7 класс

Задание 981, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 16, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 24, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1001, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1002, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1010, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1012, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1263, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1265, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

© budu5. com, 2021

Пользовательское соглашение

Copyright

Презентация урока геометрии «Уравнение окружности»

библиотека
материалов

Содержание слайдов

Номер слайда 1

Урок геометрии в 9 классе20.10.2015

Номер слайда 2

«- Что есть больше всего на свете? — Пространство. — Что быстрее всего? — Ум. — Что мудрее всего? — Время. — Что приятнее всего? – Достичь желаемого.»Фалес

Номер слайда 3

Повторение. Даны координаты двух точек А(2;7) и В(-2;7). Найдите: Координаты вектора АВДлину вектора АВРасстояние между точками А и В

Номер слайда 4

Повторение: Определите, принадлежит ли точка К(3;1) графику функции у=4х-11?

Номер слайда 5

Принадлежит ли точка А(2;4) окружности с центром в точке К(3;-2) и радиусом 3?

Номер слайда 6

Уравнение окружности

Номер слайда 7

Номер слайда 8

Вывод формулы: Пусть дана окружность: А(а;b) – центр окружности, С(х ; у) – точка окружности. Найти расстояние между точками А и С.d 2 = АС 2 = (х – а)2 + (у – b)2. Как можно назвать отрезок АС?d = АС = R, следовательно. R 2 = (х – а)2 + (у – b)2

Номер слайда 9

Формула I(х – а)2 + (у – b)2 = R2уравнение окружности, где. А(а;b) − центр, R − радиус,х и у – координаты точки окружности. __________________________

Номер слайда 10

Принадлежит ли точка А(2;4) окружности с центром в точке К(3;-2) и радиусом 3?

Номер слайда 11

Формула II(х – а)2 + (у – b)2 = R 2 . Центр окружности О(0;0), (х – 0)2 + (у – 0)2 = R 2,х2 + у2 = R 2 − уравнение окружности с центром в начале координат. ____________________ .

Номер слайда 12

Для того чтобы составить уравнение окружности, нужно:1) узнать координаты центра;2) узнать длину радиуса;3) подставить координаты центра (а;b) и длину радиуса Rв уравнение окружности(х – а)2 + (у – b)2 = R2. Задачи

Номер слайда 13

1. Определите является данное уравнение уравнением окружности. Найти координаты центра, радиус и диаметр

Номер слайда 14

№ 966(а)РАБОТА ПО УЧЕБНИКУ

Номер слайда 15

Задача: Напишите уравнение окружности с центром в начале координат и диаметром 8. Так как диаметр окружности в два раза больше её радиуса, то r=8÷2=4. Поэтому х²+у²=16.

Номер слайда 16

Постройте в тетради окружности, заданные уравнениями:1) (х – 5)2 + (у + 3)2 = 9;2) (х + 1)2 + (у – 7)2 = 16.

Номер слайда 17

Составьте уравнение окружности с центром А(3;2), проходящей через В(7;5).

Номер слайда 18

r4 RRRR1. Составьте уравнение окружности, изображенной на рисунке: Рисунок 1 R-?

Номер слайда 19

R rr0-1. Составьте уравнение окружности, изображенной на рисунке: Рисунок 2 R-?С (Хо;Уо)-?

Номер слайда 20

1. Составьте уравнение окружности, изображенной на рисунке: Рисунок 3 R-?

Номер слайда 21

№Уравнение окружности. Радиус. Коорд. центра1(х – 5)2 + (у + 3)2 = 36 R= ( ; )2(х – 1)2 + (у + 1)2 = 2 R=( ; )3(х + 1)2 + (у – 7)2 = 49 R=( ; )4х2 + у2 = 81 R=( ; )5(у – 5)2 + (х + 3)2 = 7 R=( ; )6(х + 3)2 + у2 = 14 R=( ; ) Заполните таблицу.

Номер слайда 22

Практическая работа

Номер слайда 23

О чем говорили на уроке?Что хотели получить?Какая цель была поставлена на уроке?Какие задачи позволяет решать сделанное нами «открытие»?

Номер слайда 24

Домашнее задание:§3, п. 91, контрольные вопросы №16,17. Задачи №959(б, г, д),967. Задание ГИА по математике. Окружность, изображенная на рисунке, задается уравнением х2 + у2 = 4. Используя рисунок, установите соответствие между системами уравнений и утверждениями: к каждому элементу первого столбца подберите элемент из второго столбца.

Номер слайда 25

Спасибо за внимание!Успехов в освоении нового!

9 класс Контрольная работа №1 Вариант 1

9 класс Контрольная работа №2(геометрия)

Вариант1(1уровень)

1. Напишите уравнение окружности а)с центром в точке О (2;3) и R=4, б) с центром в начале

координат и R=5.

2.Даны точки А (2;5) и В (4;7). Найдите а) координаты точки С, если С- середина АВ;

б) координаты вектора АВ; в) расстояние между точками А и В.

3.Напишите уравнение прямой, проходящей через точки А (2;5) и В (4;7).

9 класс Контрольная работа №2(геометрия)

Вариант2(1уровень)

1.Напишите уравнение окружности а)с центром в точке О (3;2) и R=9, б) с центром в начале

координат и R=7.

2.Даны точки А (3;8) и В (5;6). Найдите а) координаты точки С, если С- середина АВ;

б) координаты вектора АВ; в) расстояние между точками А и В.

3.Напишите уравнение прямой, проходящей через точки А (3;8) и В (4;7).

9 класс Контрольная работа №2(геометрия)

Вариант1(2уровень)

1. Напишите уравнение окружности : а)с центром в точке О (2;3) и проходящей через точку

А (0;4), б) с центром в начале координат и R=5.

2. Даны точки А (3;8), В (5;6) и С (-6;2) . Найдите: а) длину медианы АМ, б) координаты

вектора АС.

3. Напишите уравнение прямой, проходящей через точки А (-3;8) и В (4;7).

9 класс Контрольная работа №2(геометрия)

Вариант2(2уровень)

1.Напишите уравнение окружности : а)с центром в точке О (2;-3) и проходящей через точку

А (4;0), б) с центром в начале координат и R=9.

2. Даны точки А (3;-8), В (5;7) и С (-6;2) . Найдите: а) длину медианы ВМ, б) координаты

вектора АВ.

3. Напишите уравнение прямой, проходящей через точки А (-3;8) и В (-4;3).

9класс Контрольная работа №3 Вариант 1.

Тема «Решение треугольников»

1. В ΔАВС: ВС=3, В=30˚, С=75˚. Найдите: АС, АВ, А.

2. В ΔАВС: АВ=8, ВС=5, В=60˚.

Найдите: АС, А, С.

3. Найдите соsМ, соsL, cosK в ΔКLМ, если К(1;7), L(-2;4), M(2;0).

4. Найдите скалярное произведение векторов а и b, если |а|=9, |b|=10, a угол между ними равен 125˚.

9класс Контрольная работа №3 Вариант 2.

Тема «Решение треугольников»

1. В ΔАВС: ВС=, В=45˚, А=60˚. Найдите: АС, АВ, С.

2. В ΔАВС: АС=6, ВС=5, С=60˚.

Найдите: АВ, А, В.

3. Найдите соsА, соsВ, cosС в ΔАВС, если А(3;9), В(0;6), С(4;2).

4. Найдите скалярное произведение векторов а и b, если |а|=8, |b|=5, a угол между ними равен 115˚.

9класс Контрольная работа № 4 Вариант 1

Тема: «Длина окружности. Площадь круга»

1. Дуга в 150˚ имеет радиус 3см. Найдите длину этой дуги.

2. Периметр правильного треугольника, вписанного в окружность, равен 45см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность.

3. Найдите площадь круга и длину окружности, если площадь вписанного в неё квадрата равна 49см2.

4. Найдите длину окружности и площадь круга, если радиус равен 5,1см.

9класс Контрольная работа № 4 Вариант 2

Тема: «Длина окружности. Площадь круга»

1. Найдите площадь кругового сектора, если градусная мера его дуги равна 120˚, а радиус круга равен 12см.

2. Периметр правильного шестиуголь-ника, вписанного в окружность, равен 48см. Найдите сторону квадрата, вписанного в ту же окружность.

3. Найдите площадь круга и длину окружности, если периметр вписанного в неё квадрата равна 48см.

4. Найдите длину окружности и площадь круга, если радиус равен 3,6см.

9 класс Контрольная работа Вариант 1

Тема: «Движения»

1)Дана трапеция АВСD с основаниями

АD и ВС. Постройте фигуру, на которую отображается эта трапеция

а)при симметрии относительно прямой, содержащей боковую сторону АВ;

б) при симметрии относительно точки, являющейся серединой боковой стороны СD

в) при повороте вокруг точки А на угол, равныйDАВ, по часовой стрелке;

г) при параллельном переносе на вектор .

2) Постройте ∆А1В1С1, симметрич-ный ∆АВС относительно точки О . Докажите, что ∆АВС= ∆А1В1С1

9 класс Контрольная работа Вариант 2

Тема: «Движения»

1)Дана трапеция АВСD с основаниями АD и ВС. Постройте фигуру, на которую отображается эта трапеция

а) при симметрии относительно прямой, содержащей боковую сторону СD ;

б) при симметрии относительно точки, являющейся серединой боковой стороны АВ

в) при повороте вокруг точки D на угол, равный СDА, по часовой стрелке;

г) при параллельном переносе на вектор DА.

2) Постройте ∆А1В1С1, симметрич-ный ∆АВС относительно точки О. Докажите, что ∆АВС= ∆А1В1С1

9 класс Самостоятельная работа Вариант 1

Тема : «Простейшие задачи в координатах»

1. Найдите координаты середины отрезка АВ, если А(-2;3), В(6;-3)

2. Найдите длину отрезка ЕН, если Е(-3;8), Н(2;-4)

3. Найдите длину вектора {-4; -3}

4. Вершины ∆АВС имеют координаты А(8;-3), В(5;1), С(12;0). Докажите В=С. Найдите S∆АВС

5.Найдите длину вектора,если А(3;-6),В(-4; -7).

9 класс Самостоятельная работа Вариант 2

Тема : «Простейшие задачи в координатах»

1. Найдите координаты середины отрезка ВС, если С(3;-4), В(-6; 3)

2. Найдите длину отрезка КВ, если К(-6;-3), В(2;3)

3. Найдите длину вектора {-6; 8}

4. Вершины четырехугольника АВСD имеют координаты А(-3; -1), В(1; 2), С(5; -3), D(1; -4). Докажите АВСD-ромб. Найдите S∆АВСD

5.Найдите длину вектора,если А(-3;6), В(4; 7).

9 класс Самостоятельная работа Тема: « Уравнение окружности и прямой»

Вариант 1

Вариант 2

1.Напишите уравнение окружности с центром в точке А и радиуса R, если А (4;-5), R=3.

2.Напишите уравнение окружности с центром в начале координат, если она проходит через точку С (-2;3).

3. Напишите уравнение прямой, проходящей через две точки М (-2;-1) и N (3;1).

1.Напишите уравнение окружности с центром в точке А и радиуса R, если А (-7;8), R=9.

2.Напишите уравнение окружности с центром в начале координат, если она проходит через точку С (6;-8).

3. Напишите уравнение прямой, проходящей через две точки М (-1;-2) и N (1;3).

9 класс Самостоятельная работа Тема: «Решение треугольников» Вариант 1.(1ур)

1) Дано: а=5см, В=30˚,С=50˚

Найдите: b, с, А, SАВС

2) Дано: а =6см, с =7см, В= 40˚.

Найдите: b, А.

9 класс Самостоятельная работа

Тема: «Решение треугольников»

Вариант 2.(1ур)

1) Дано: а=6см, В=40˚,С=60˚

Найдите: b, с, А, SАВС.

2) Дано: а =5см, с =8см, В= 30˚.

Найдите: b, С.

9 класс Самостоятельная работа Тема: «Решение треугольников» Вариант 1.(2ур)

1) Дано: АС=0,59см,

В=40˚,С=35˚

Найдите: ВС, АВ, А.

2) Дано: ВС =27см, АВ =16см, В= 140˚.

Найдите: АС, А, С, SАВС.

9 класс Самостоятельная работа

Тема: «Решение треугольников»

Вариант 2.(2ур)

1) Дано: ВС=0,75см,

А=40˚,С=20˚

Найдите: АС, АВ, В.

2) Дано: АС =13см, АВ =42см, А= 100˚.

Найдите: ВС, В, С, SАВС

9класс Самостоятельная работа Вариант1

Тема «Скалярное произведение векторов»

1. Вычислите скалярное произведение векторов а и b, если =2, =3, а угол между ними равен 120˚.

2. Вычислите скалярное произведение векторов а и b, если , .

3. Вычислите косинус угла между векторами а и b, если ,

4. При каком значении х вектора а и b перпендикулярны, если, .

9класс Самостоятельная работа Вариант2

Тема «Скалярное произведение векторов»

1. Вычислите скалярное произведение векторов m и n, если =3, =4, а угол между ними равен 135˚.

2. Вычислите скалярное произведение векторов m и n, если, .

3.Вычислите косинус угла между векторами m и n , если m , n .

4. При каком значении у вектора m и n

перпендикулярны, если m, n/

9 класс Самостоятельная работа Вариант 1

Тема: «Правильные многоугольники»

1) Найдите угол правильного десятиугольника.

2) Найдите сторону правильного ∆ , если радиус описанной около него окружности равен 2см.

3)Найдите радиус окружности, вписанной в квадрат, если радиус описанной около него окружности равен 2м.

4) Найдите площадь правильного ∆ , если расстояние от его центра до вершины равно 2м.

9 класс Самостоятельная работа Вариант 2

Тема: «Правильные многоугольники»

1) Найдите угол правильного девяностоугольника.

2) Найдите сторону квадрата, если расстояние от его центра до вершины равно 2м.

3) Найдите радиус окружности, вписанной в правильный ∆ , если радиус описанной около него окружности равен 2м.

4) Найдите площадь квадрата, если радиус описанной около него окружности равен 2см.

9 класс Самостоятельная работа « Синус, косинус, тангенс угла»

Вариант1

Вариант2

1.Найти: а)tg, если sin= 0,6 , 90˚< <180;

б)sin,если cos=-0,4; в)cos, если sin= .

2.Могут ли одновременно выполняться:

а)sin=0,7, cos=0,3; б) sin=0,8 , cos=0,6?

1.Найти: а)tg, если sin= 0,7 , 90˚< <180; б)sin,если cos=-0,6; в)cos, если sin= .

2. Могут ли одновременно выполняться:

а)sin=0,2, cos=0,8; б) sin= , cos=?

9класс Самостоятельная работа Вариант 1

Тема: «Площадь круга. Длина окружности»

1. Найдите длину окружности и площадь круга, если радиус равен 3,5см. (3)

2. Длина окружности равна 22π см. Найдите площадь соответствующего ей круга. (4)

3. Найдите площадь кругового сектора радиуса 6м, если градусная мера его дуги равна150˚.(3)

4. Длина дуги равна 62,8 м, а её радиус 36м. Найдите градусную меру дуги.(5)

5. Сторона правильного шестиугольника, описанного около окружности равна 4см. Найдите длину этой окружности.(5)

9класс Самостоятельная работа Вариант 2

Тема: «Площадь круга. Длина окружности»

1. Найдите длину окружности и площадь круга, если радиус равен 5,3см. (3)

2. Площадь круга равна 225πсм2. Найдите длину окружности, соответст-вующей этому кругу.(4)

3. Дуга в 110˚ имеет радиус 36см. Найдите длину этой дуги. (3)

4. Площадь кругового сектора равна 3,24см2, его радиус равен 0,18см. Найди-те градусную меру дуги сектора.(5)

5. Сторона правильного треугольника, описанного около окружности равна 4см. Найдите длину этой окружности.(5)

9 класс Самостоятельная работа Вариант 1

Тема: « Отображение плоскости на себя»

9 класс Самостоятельная работа Вариант 2

Тема: « Отображение плоскости на себя»

1. Постройте точку А1, симметрич-ную точке А относительно прямой а

1.Постройте точку А1, симметрич-ную точке А относительно прямой а

2. Постройте отрезок А1В1, симметричный отрезку АВ относительно точки О (центр).

2. Постройте отрезок А1В1, симметричный отрезку АВ относительно точки О (центр).

3. Постройте отрезок А1В1, полученный параллельным переносом отрезка АВ на вектор а.

3. Постройте отрезок А1В1, полученный параллельным переносом отрезка АВ на вектор а.

9 класс Самостоятельная работа Вариант 3

Тема: « Отображение плоскости на себя»

9 класс Самостоятельная работа Вариант 4

Тема: « Отображение плоскости на себя»

1. Постройте квадрат А1В1С1D1, симметричный квадрату АВС D, относительно прямой а.

1.Постройте прямоугольник

А1В1С1D1, симметричный прямоугольнику АВС D, относительно прямой а.

2. Постройте ∆А1В1С1, симметрич-ный ∆АВС относительно точки О (центр).

2. Постройте ∆А1В1С1, симметрич-ный ∆АВС относительно точки О (центр).

3. Постройте трапецию А1В1С1D1, полученную, параллельным переносом трапеции АВСD на вектор ВD

3. Постройте трапецию А1В1С1D1, полученную, параллельным переносом трапеции АВСD на вектор АС

4. Постройте точку А1, получен-ную из точки А поворотом вокруг точки О против часовой стрелки на угол 120˚

4. Постройте точку А1, получен-ную из точки А поворотом вокруг точки О по часовой стрелке на угол 120˚

9 класс Самостоятельная работа Вариант 5

Тема: « Отображение плоскости на себя»

1.Постройте квадрат А1В1С1D1, симметричный квадрату АВС D, относительно прямой а.

9 класс Самостоятельная работа Вариант 2

Тема: « Отображение плоскости на себя»

2. Постройте ∆А1В1С1, симметрич-ный ∆АВС относительно точки О (центр).

1.Постройте точку А1, симметрич-ную точке А относительно прямой а

3. Постройте трапецию А1В1С1D1, полученную, параллельным переносом трапеции АВСD на вектор DВ

2. Постройте отрезок А1В1, симметричный отрезку АВ относительно точки О (центр).

4. Постройте точку А1, получен-ную из точки А поворотом вокруг точки О против часовой стрелки на угол 150˚

3. Постройте отрезок А1В1, полученный параллельным переносом отрезка АВ на вектор а.

Декартовы координаты на плоскости и в пространстве. Координаты точки. Координаты середины отрезка. Расстояние между точками. Уравнение прямой, уравнение плоскости. Уравнение окружности. Уравнение сферы.





 Адрес этой страницы (вложенность) в справочнике dpva. ru:  главная страница  / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа.  / / Декартовы координаты на плоскости и в пространстве. Координаты точки. Координаты середины отрезка. Расстояние между точками. Уравнение прямой, уравнение плоскости. Уравнение окружности. Уравнение сферы.

Поделиться:   

Декартовы координаты на плоскости и в пространстве. Координаты точки. Координаты середины отрезка. Расстояние между точками. Уравнение прямой, уравнение плоскости. Уравнение окружности. Уравнение сферы.
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers

Консультации и техническая
поддержка сайта: Zavarka Team

 Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Уравнение окружности

Круг — это набор всех точек на плоскости на заданном расстоянии (называемый радиус ) из заданной точки (называемой центром).

Отрезок, соединяющий две точки на окружности и проходящий через центр, называется отрезком. диаметр круга.

Предположить, что ( Икс , у ) — координаты точки на изображенной окружности.Центр находится в ( час , k ) , а радиус р .

Использовать Формула расстояния найти уравнение круга.

( Икс 2 — Икс 1 ) 2 + ( у 2 — у 1 ) 2 знак равно d

Заменять ( Икс 1 , у 1 ) знак равно ( час , k ) , ( Икс 2 , у 2 ) знак равно ( Икс , у ) и d знак равно р .

( Икс — час ) 2 + ( у — k ) 2 знак равно р

Выровняйте каждую сторону.

( Икс — час ) 2 + ( у — k ) 2 знак равно р 2

Уравнение окружности с центром ( час , k ) и радиус р единиц ( Икс — час ) 2 + ( у — k ) 2 знак равно р 2 .

7.

{2} + 2x — 8 & = 0 \\ (х — 2) (х + 4) & = 0 \\ \ поэтому x = 2 & \ text {или} x = -4 \\ \ text {If} x = 2 \ quad y & = 2 + 2 = 4 \\ \ text {If} x = -4 \ quad y & = -4 + 2 = -2 \ end {выровнять *}

Это дает баллы \ (P (-4; -2) \) и \ (Q (2; 4) \).2} \\ & = \ sqrt {36 + 36} \\ & = \ sqrt {36 \ cdot 2} \\ & = 6 \ sqrt {2} \ end {выровнять *}

Определите координаты \ (M \), средней точки. хорды \ (PQ \).

\ begin {align *} M (x; y) & = \ left (\ frac {x_ {1} + x_ {2}} {2}; \ frac {y_ {1} + y_ {2}} {2} \ right) \\ & = \ left (\ frac {-4 + 2} {2}; \ frac {-2 + 4} {2} \ right) \\ & = \ left (\ frac {-2} {2}; \ frac {2} {2} \ right) \\ & = \ влево (-1; 1 \ вправо) \ end {выровнять *}

Если \ (O \) — центр круга, покажите, что \ (PQ \ perp OM \).

\ begin {align *} m_ {PQ} & = \ frac {4 — (-2)} {2 — (-4)} \\ & = \ frac {6} {6} \\ & = 1 \\ & \\ m_ {OM} & = \ frac {1 — 0} {- 1 — 0} \\ & = — 1 \\ m_ {PQ} \ times m_ {OM} & = — 1 \\ & \\ \ поэтому PQ & \ perp OM \ end {выровнять *}

Определите уравнения касательных к круг в \ (P \) и \ (Q \).

Касательная в точке \ (P \):

Определите градиент радиуса \ (OP \):

\ begin {align *} m_ {OP} & = \ frac {y_ {2} — y_ {1}} {x_ {2} — x_ {1}} \\ & = \ frac {-2 — 0} {- 4 — 0} \\ & = \ frac {1} {2} \ end {выровнять *}

Пусть градиент касательной в точке \ (P \) равен \ (m_ {P} \).В касательная к окружности перпендикулярна радиусу, поэтому мы можем написать:

\ begin {align *} m_ {OP} \ times m_ {P} & = -1 \\ \ frac {1} {2} \ times m_ {P} & = -1 \\ \ поэтому m_ {P} & = — 2 \ end {выровнять *}

Подставьте \ (m_ {P} = — 2 \) и \ (P (-4; -2) \) в уравнение прямой.

\ begin {align *} y — y_ {1} & = m (x — x_ {1}) \\ y — y_ {1} & = — 2 (x — x_ {1}) \\ \ text {Substitute} P (-4; -2): \ quad y + 2 & = — 2 (x + 4) \\ у & = -2x — 8-2 \\ & = -2x — 10 \ end {выровнять *}

Касательная в точке \ (Q \):

Определите градиент радиуса \ (OQ \):

\ begin {align *} m_ {OQ} & = \ frac {y_ {2} — y_ {1}} {x_ {2} — x_ {1}} \\ & = \ frac {4 — 0} {2 — 0} \\ & = 2 \ end {выровнять *}

Пусть градиент касательной в точке \ (Q \) равен \ (m_ {Q} \). В касательная к окружности перпендикулярна радиусу, поэтому мы можем написать:

\ begin {align *} m_ {OQ} \ times m_ {Q} & = -1 \\ 2 \ times m_ {Q} & = -1 \\ \ поэтому m_ {Q} & = — \ frac {1} {2} \ end {выровнять *}

Замените \ (m_ {Q} = — \ frac {1} {2} \) и \ (Q (2; 4) \) в уравнение прямой.

\ begin {align *} y — y_ {1} & = m (x — x_ {1}) \\ y — y_ {1} & = — \ frac {1} {2} (x — x_ {1}) \\ \ text {Substitute} Q (2; 4): \ quad y — 4 & = — \ frac {1} {2} (x — 2) \\ y & = — \ frac {1} {2} x + 1 + 4 \\ & = — \ frac {1} {2} x + 5 \ end {выровнять *}

Следовательно, уравнения касательных к окружности имеют вид \ (y = -2x — 10 \) и \ (y = — \ frac {1} {2} x + 5 \).

Определите координаты \ (S \) точки, в которой две касательные пересекаются.

Приравняйте два линейных уравнения и решите относительно \ (x \):

\ begin {align *} -2x — 10 & = — \ frac {1} {2} x + 5 \\ -4x — 20 & = — х + 10 \\ -3x & = 30 \\ х & = — 10 \\ \ text {If} x = — 10 \ quad y & = — 2 \ left (- 10 \ right) — 10 \\ & = 10 \ end {выровнять *}

Это дает точку \ (S \ left (- 10; 10 \ right) \). 2} \\ & = \ sqrt {144 + 36} \\ & = \ sqrt {180} \ end {выровнять *}

Определите уравнения двух касательных к круг, оба параллельны прямой \ (y + 2x = 4 \).

Касательная в точке \ (P \), \ (y = -2x — 10 \), параллельна \ (y = — 2х + 4 \). Чтобы найти уравнение второй параллели касательная:

\ begin {align *} у & = -2x + 4 \\ \ поэтому m & = -2 \\ \ поэтому m _ {\ text {radius}} & = \ frac {1} {2} \\ \ text {Ур. {2} & = 16 \\ х & = \ pm 4 \\ \ text {If} x = 4, y & = 2 \\ \ text {Substitute} (4; 2): \ quad y & = -2x + c \\ 2 & = — 2 (4) + с \\ 10 & = с \\ y & = -2x + 10 \ end {выровнять *}

% PDF-1.5 % 1 0 объект > эндобдж 2 0 obj > поток 2013-08-02T10: 03: 13 + 01: 002013-08-02T10: 03: 13 + 01: 002013-08-02T10: 03: 13 + 01: 00ENG Персонал 1-е приложение MID / pdfuuid: bce78d19-e900-4cef-b998 -390e9e44765fuuid: 03d144dc-7cd6-4a5d-8eb3-54c1f9e21311KONICA MINOLTA bizhub C552 конечный поток эндобдж 3 0 obj > эндобдж 5 0 объект > эндобдж 6 0 объект > эндобдж 7 0 объект > эндобдж 23 0 объект >>> / Повернуть 0 / Тип / Страница >> эндобдж 24 0 объект >>> / Повернуть 0 / Тип / Страница >> эндобдж 25 0 объект >>> / Повернуть 0 / Тип / Страница >> эндобдж 26 0 объект >>> / Повернуть 0 / Тип / Страница >> эндобдж 27 0 объект >>> / Повернуть 0 / Тип / Страница >> эндобдж 36 0 объект > поток q 595. 080 0 0 841.680 0 0 см / JI20a Do Q конечный поток эндобдж 37 0 объект > поток

Как построить круг

Графическое изображение окружности

Для построения окружностей требуются две вещи: координаты центральной точки и радиус окружности. Круг — это набор всех точек на одинаковом расстоянии от данной точки, центра круга. Радиус r — это расстояние от этой центральной точки до самого круга.

На графике все эти точки на окружности могут быть определены и нанесены на график с использованием координат (x, y).

Содержание

  1. Построение круга
  2. Круговые уравнения
  3. Использование формы центр-радиус
  4. Как построить круговое уравнение
  5. Как построить круг с помощью стандартной формы

Круговые уравнения

Два выражения показывают, как построить окружность: форма с центральным радиусом и стандартная форма . Где x и y — координаты всех точек круга, h и k представляют значения x и y центральной точки, где r — радиус окружности

Форма центра и радиуса

Форма центрального радиуса выглядит так:

х — h3 + y — k2 = r2

Стандартное уравнение круга

Стандартная или общая форма требует немного больше работы, чем форма с центральным радиусом для получения и построения графика. Уравнение стандартной формы выглядит так:

х2 + у2 + Dx + Ey + F = 0

В общем виде D, E и F задаются значениями, такими как целые числа, которые являются коэффициентами значений x и y.

Использование формы центр-радиус

Если вы не уверены, что подозреваемая формула — это уравнение, необходимое для построения круга, вы можете проверить это. У него должно быть четыре атрибута:

  1. Члены x и y должны быть возведены в квадрат
  2. Все члены в выражении должны быть положительными (что дает возведение значений в скобки в квадрат)
  3. Центральная точка задается как (h, k), координаты x и y
  4. Значение r, радиус, должно быть задано и должно быть положительным числом (что имеет смысл; у вас не может быть отрицательной меры радиуса)

Форма с центральным радиусом дает много информации опытному глазу.Группируя значение h с x x — h3, форма сообщает вам координату x центра круга. То же самое и для значения k; это должна быть координата Y центра вашего круга.

Как только вы определите координаты центра окружности, вы сможете определить радиус окружности, r. В уравнении вы можете видеть не r2, а число, квадратный корень из которого является фактическим радиусом. Если повезет, квадрат значения r будет целым числом, но вы все равно можете найти квадратный корень из десятичных знаков с помощью калькулятора.

Какие формы центрального радиуса?

Попробуйте эти семь уравнений, чтобы увидеть, сможете ли вы распознать форму центрального радиуса. Какие из них являются уравнениями центрального радиуса, а какие — просто уравнениями линии или кривой?

  1. х — 22 + у — 32 = 16
  2. 5x + 3y = 6
  3. х + 12 + у + 12 = 25
  4. у = 6х + 2
  5. х + 42 + у — 62 = 49
  6. х — 52 + у + 92 = 8,1
  7. у = х2 + -6х + 3

Только уравнения 1, 3, 5 и 6 являются формами центрального радиуса. Второе уравнение представляет собой прямую линию; четвертое уравнение представляет собой знакомую форму пересечения наклона; последнее уравнение строит параболу.

Как построить круговое уравнение

Круг можно представить себе как линию графика, которая изгибается как в значениях x, так и в y. Это может показаться очевидным, но рассмотрите следующее уравнение:

у = х2 + 4

Здесь только значение x возведено в квадрат, что означает, что мы получим кривую, но только кривую, идущую вверх и вниз, не замыкаясь на себя.У нас получается параболическая кривая, поэтому она уходит за верхнюю часть нашей сетки, ее два конца никогда не встретятся и больше не будут видны.

Введем второй показатель степени x, и мы получим более живые кривые, но они, опять же, не поворачиваются сами по себе.

Кривые могут изгибаться вверх и вниз по оси Y по мере того, как линия перемещается по оси X, но графическая линия все еще не возвращается сама по себе, как змея, кусающая свой хвост.

Чтобы получить кривую в виде круга, необходимо изменить и , и , и показатель x, и , и , и показатель y. Как только вы возьмете в квадрат значения x и y, вы получите круг, возвращающийся в себя!

Часто форма центрального радиуса не включает никаких ссылок на такие единицы измерения, как мм, м, дюймы, футы или ярды. В этом случае просто используйте одиночные ячейки сетки при подсчете единиц радиуса.

Центр в начале

Когда центральная точка является началом (0, 0) графика, форма центрального радиуса будет в значительной степени упрощенно:

Например, круг с радиусом 7 единиц и центром в точке (0, 0) выглядит как формула и график:

х2 + у2 = 49

Как построить круг с помощью стандартной формы

Если ваше уравнение круга имеет стандартную форму или общую форму , вы должны сначала заполнить квадрат, а затем преобразовать его в форму центрального радиуса.Предположим, у вас есть это уравнение:

х2 + у2 — 8х + 6у — 4 = 0

Перепишите уравнение так, чтобы все ваши x-члены были в первых скобках, а y-члены — во вторых:

x2 — 8x +? 1 + y2 + 6y +? 2 = 4 +? 1 +? 2

Вы изолировали константу справа и добавили значения? 1 и? 2 к обеим сторонам. Значения? 1 и? 2 — каждое число, необходимое в каждой группе для завершения квадрата.

Возьмите коэффициент при x и разделите на 2.Выровняйте это. Это ваше новое значение для? 1:

-82 = -4

-42 = 16

? 1 = 16

Повторите это для значения, которое нужно найти с помощью y-членов:

62 = 3

32 = 9

? 2 = 9

Замените неизвестные значения? 1 и? 2 в уравнении вновь рассчитанными значениями:

x2 — 8x + 16 + y2 + 6y + 9 = 4 + 16 + 9

Упростить:

x2 — 8x + 16 + y2 + 6y + 9 = 29

х — 42 + у + 32 = 29

Теперь у вас есть форма центрального радиуса для графика.Вы можете подставить значения, чтобы найти этот круг с центральной точкой -4, 3 и радиусом 5,385 единиц (квадратный корень из 29):

Предупреждения, на которые следует обратить внимание

На практике помните, что центральная точка, хотя и необходима, на самом деле не является частью круга. Итак, когда вы на самом деле строите свой круг, очень легко отметьте свою центральную точку. Разместите легко подсчитываемые значения по осям x и y, просто подсчитав длину радиуса по горизонтальной и вертикальной линиям.

Если точность не важна, вы можете нарисовать остальную часть круга. Если точность имеет значение, используйте линейку, чтобы сделать дополнительные отметки, или циркуль для рисования, чтобы повернуть весь круг.

Не забывайте и о негативе. Внимательно следите за своими отрицательными значениями, помня, что в конечном итоге все выражения должны быть положительными (потому что ваши значения x и y возведены в квадрат).

Следующий урок:

Завершение площади

Уравнение окружности — Формула, примеры

Уравнение круга предоставляет алгебраический способ описания круга, учитывая центр и длину радиуса круга.Уравнение круга отличается от формул, которые используются для вычисления площади или длины окружности. Это уравнение используется во многих задачах окружностей в координатной геометрии.

Чтобы представить круг на декартовой плоскости, нам потребуется уравнение круга. Круг можно нарисовать на листе бумаги, если мы знаем его центр и длину радиуса. Точно так же на декартовой плоскости мы можем нарисовать круг, если мы знаем координаты центра и его радиус.Круг можно представить во многих формах:

  • Общая форма
  • Стандартная форма
  • Параметрическая форма
  • Полярная форма

В этой статье давайте узнаем об уравнении круга, его различных формах с графиками и решаемых примерах.

Что такое уравнение круга?

Уравнение круга представляет положение круга в декартовой плоскости. Если мы знаем координаты центра круга и длину его радиуса, мы можем написать уравнение круга.2 \).

Различные формы уравнения окружности

Уравнение круга представляет положение круга на декартовой плоскости. На листе бумаги можно нарисовать круг с учетом его центра и длины радиуса. Используя уравнение круга, как только мы найдем координаты центра круга и его радиус, мы сможем нарисовать круг на декартовой плоскости. Есть разные формы для представления уравнения круга,

  • Общая форма
  • Стандартная форма
  • Параметрическая форма
  • Полярная форма

Давайте подробно рассмотрим две общие формы уравнения окружности общего вида и стандартную форму уравнения окружности, а также полярную и параметрическую формы.

Общее уравнение круга

Общая форма уравнения круга: x 2 + y 2 + 2gx + 2fy + c = 0. Эта общая форма используется для нахождения координат центра круга и радиуса, где g, f, c — константы. В отличие от стандартной формы, которую легче понять, общая форма уравнения круга затрудняет поиск каких-либо значимых свойств любого данного круга. Итак, мы будем использовать формулу заполнения квадрата, чтобы быстро преобразовать общую форму в стандартную. 2 \)

Рассмотрим этот пример уравнения окружности (x — 4) 2 + (y — 2) 2 = 36 — это круг с центром в точке (4,2) и радиусом 6.

Параметрическое уравнение окружности

Мы знаем, что общая форма уравнения круга: x 2 + y 2 + 2hx + 2ky + C = 0. Возьмем общую точку на границе круга, скажем (x, y) . Линия, соединяющая эту общую точку и центр круга (-h, -k), составляет угол \ (\ theta \).Параметрическое уравнение окружности можно записать как x 2 + y 2 + 2hx + 2ky + C = 0, где x = -h + rcosθ и y = -k + rsinθ.

Полярное уравнение круга

Полярная форма уравнения круга почти аналогична параметрической форме уравнения круга. Обычно мы пишем полярную форму уравнения окружности для окружности с центром в начале координат. Возьмем точку P (rcosθ, rsinθ) на границе круга, где r — расстояние от точки до начала координат.Мы знаем, что уравнение окружности с центром в начале координат и радиусом p равно x 2 + y 2 = p 2 .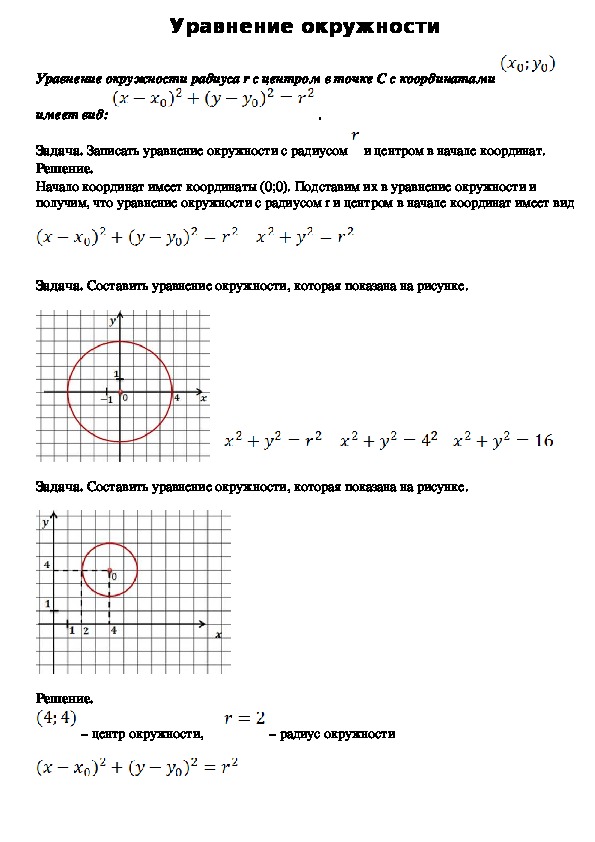

Подставьте значение x = rcosθ и y = rsinθ в уравнение круга.

(rcosθ) 2 + (rsinθ) 2 = p 2
r 2 cos 2 θ + r2sin2θ = p 2
r 2 (cos 2 θ + sin2θ) = p 2
r 2 (1) = p 2
г = р
где p — радиус окружности.

Пример: Найдите уравнение круга в полярной форме при условии, что уравнение круга в стандартной форме имеет следующий вид: x 2 + y 2 = 9.

Решение:

Чтобы найти уравнение круга в полярной форме, замените значения \ (x \) и \ (y \) на:

х = rcosθ
у = rsinθ

х = rcosθ
у = rsinθ
х 2 + y 2 = 9
(rcosθ) 2 + (rsinθ) 2 = 9
r 2 cos 2 θ + r 2 sin 2 θ = 9
r 2 (cos 2 θ + sin 2 θ) = 9
r 2 (1) = 9
г = 3

Уравнение формулы круга

Уравнение круга используется для вычисления уравнения круга. 2 \).

, где \ ((x_1, y_1) \) — центр окружности радиуса r, а (x, y) — произвольная точка на окружности окружности.

Вывод уравнения окружности

Учитывая, что \ ((x_1, y_1) \) — центр окружности радиуса r, а (x, y) — произвольная точка на окружности окружности. Расстояние между этой точкой и центром равно радиусу окружности. Итак, применим формулу расстояния между этими точками.2 \), получаем

\ (x_1 \) = 1, \ (y_1 \) = -2 и r = 3

Итак, центр и радиус равны (1, -2) и 3 соответственно.

Ответ: Центр круга равен (1, -2), а его радиус равен 3.

Построение уравнения окружности

Чтобы показать, как работает уравнение круга, давайте изобразим круг с помощью уравнения (x -3) 2 + (y — 2) 2 = 9. Теперь, прежде чем изобразить это уравнение, нам нужно составить убедившись, что данное уравнение соответствует стандартной форме \ ((x — x_1) ^ 2 + (y — y_1) ^ 2 = r ^ 2 \).

  • Для этого нам нужно только изменить константу 9, чтобы она соответствовала r 2 как (x -3) 2 + (y — 2) 2 = 3 2 .
  • Здесь мы должны отметить, что одна из распространенных ошибок при фиксации — это рассматривать \ (x_ {1} \) как -3 и \ (y_ {1} \) как -2.
  • В уравнении круга, если знак перед \ (x_ {1} \) и \ (y_ {1} \) отрицательный, то \ (x_ {1} \) и \ (y_ {1} \) равны положительные значения и наоборот.
  • Здесь \ (x_ {1} \) = 3, \ (y_ {1} \) = 2 и r = 3

Таким образом, круг, представленный уравнением (x -3) 2 + (y — 2) 2 = 3 2 , имеет центр в (3, 2) и радиус 3.На приведенном ниже изображении показан график, полученный из этого уравнения круга.

Как найти уравнение окружности?

Существует так много разных способов представления уравнения окружности в зависимости от положения окружности на декартовой плоскости. 2} = r \).

  • Шаг 3: Выразите ответ в форме требуемого кругового уравнения.

    • Уравнение окружности с центром в начале координат

    В простейшем случае центр круга находится в начале координат (0, 0), радиус которого равен r. (x, y) — произвольная точка на окружности круга.

    Расстояние между этой точкой и центром равно радиусу окружности. Применим формулу расстояния между этими точками.2 \).

    Если центр находится в начале координат, то \ (x_1 \) = 0 и \ (y_1 \) = 0.

    Ответ: Уравнение окружности, если ее центр находится в начале координат, равно x 2 + y 2 = r 2 .

    Уравнение окружности с центром по оси x

    Рассмотрим случай, когда центр окружности находится на оси x: (a, 0) — центр окружности радиуса r. (x, y) — произвольная точка на окружности круга.

    Расстояние между этой точкой и центром равно радиусу окружности. 2 \)

    Уравнение окружности, касающейся оси x

    Рассмотрим случай, когда окружность круга касается оси x в некоторой точке: (a, r) ​​- центр окружности с радиусом r. Если окружность касается оси x, то координата y центра окружности равна радиусу r.

    (x, y) — произвольная точка на окружности круга. Расстояние между этой точкой и центром равно радиусу окружности.2 \)

    Уравнение окружности, касающейся оси Y

    Рассмотрим случай, когда окружность круга касается оси y в некоторой точке: (r, b) — центр окружности с радиусом r. Если окружность касается оси y, то координата x центра окружности равна радиусу r.

    (x, y) — произвольная точка на окружности круга. Расстояние между этой точкой и центром равно радиусу окружности.2 \)

    Уравнение окружности, касающейся обеих осей

    Рассмотрим случай, когда окружность окружности касается обеих осей в некоторой точке: (r, r) — центр окружности с радиусом r.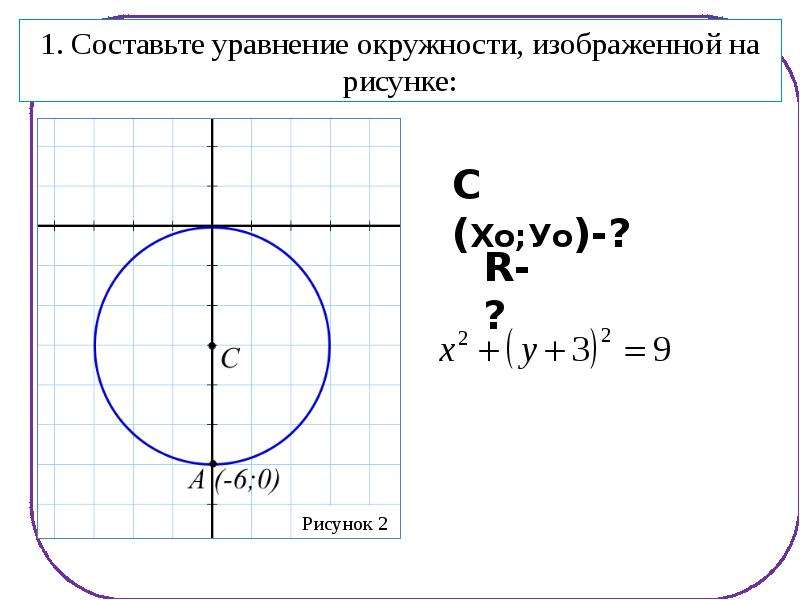 Если круг касается как оси x, так и оси y, то обе координаты центра круга становятся равными радиусу (r, r).

    (x, y) — произвольная точка на окружности круга. Расстояние между этой точкой и центром равно радиусу окружности.2 = 16 \
    г = 4 \)

    Преобразование общей формы в стандартную

    Это стандартное уравнение окружности с радиусом r и центром в точках (a, b): (x — a) 2 + (y — b) 2 = r 2 и рассмотрим общую форму как: x 2 + y 2 + 2gx + 2fy + c = 0. Вот шаги, которые необходимо выполнить, чтобы преобразовать общую форму в стандартную:

    Шаг 1. Объедините одинаковые члены и возьмите константу с другой стороны как x 2 + 2gx + y 2 + 2fy = — c -> (1)

    Шаг 2: Используйте тождество полного квадрата (x + g) 2 = x 2 + 2gx + g 2 , чтобы найти значения выражения x 2 + 2gx и y 2 + 2fy как :

    (x + g) 2 = x 2 + 2gx + g 2 ⇒ x 2 + 2gx = (x + g) 2 — g 2 -> (2)

    (y + f) 2 = y 2 + 2fy + f 2 ⇒ y 2 + 2fy = (y + f) 2 — f 2 -> (3)

    Подставляя (2) и (3) в (1), мы получаем уравнение:

    (x + g) 2 — g 2 + (y + f) 2 — f 2 = — c

    (x + g) 2 + (y + f) 2 = g 2 + f 2 — c

    Сравнивая это уравнение со стандартной формой: (x — a) 2 + (y — b) 2 = r 2 получаем,

    Центр = (-g, -f) и радиус = \ (\ sqrt {g ^ 2 + f ^ 2 — c} \)

    Перед применением формулы необходимо убедиться, что коэффициенты при x 2 и y 2 равны 1. 2 + 2gx + 2fy + c = 0 \), где g, f, c — константы.

    Статьи по теме уравнения окружности

    Посмотрите следующие страницы, связанные с уравнением круга

    Важные примечания по уравнению окружности

    Вот список из нескольких моментов, которые следует помнить при изучении уравнения окружности

    • Общая форма уравнения окружности всегда имеет вначале x 2 + y 2 .
    • Если окружность пересекает обе оси, то есть четыре точки пересечения окружности и осей.2 + axy + C = 0 \), то это не уравнение окружности. В уравнении круга нет члена \ (ху \).
    • В полярной форме уравнение круга всегда представляет в форме \ (r \) и \ (\ theta \).
    • Радиус — это расстояние от центра до любой точки на границе круга. Следовательно, значение радиуса круга всегда положительно.

    Часто задаваемые вопросы по уравнению окружности

    Что такое уравнение окружности в геометрии?

    Уравнение круга представляет геометрическое место точки, расстояние от которой до фиксированной точки является постоянной величиной. 2 \).

    Что такое уравнение окружности, когда центр находится в начале координат?

    В простейшем случае центр круга находится в начале координат (0, 0), радиус которого равен r. (x, y) — произвольная точка на окружности круга. Уравнение окружности с центром в начале координат: x 2 + y 2 = r 2 .

    Что такое общее уравнение круга?

    Общая форма уравнения окружности: x 2 + y 2 + 2gx + 2fy + c = 0.2 + 2hx + 2ky + C = 0 \), где \ (x = -h + rcos \ theta \) и \ (y = -k + rsin \ theta \)

    Что такое C в общем уравнении окружности?

    Общая форма уравнения круга: x 2 + y 2 + 2gx + 2fy + c = 0. Эта общая форма используется для нахождения координат центра круга и радиуса круга. . Здесь c — постоянный член, а уравнение, имеющее значение c, представляет окружность, которая не проходит через начало координат.

    Каковы различные формы уравнений круга?

    Давайте посмотрим на две распространенные формы уравнения:

    • Общая форма x 2 + y 2 + 2gx + 2fy + C = 0
    • Стандартная форма \ ((x — x_1) ^ 2 + (y — y_1) ^ 2 = r ^ 2 \)

    Что такое уравнение окружности, когда центр находится на оси x?

    Рассмотрим случай, когда центр окружности находится на оси x: (a, 0) — центр окружности радиуса r. 2 \)

    Как изобразить уравнение окружности?

    Чтобы изобразить уравнение круга, сначала найдите координаты центра круга и радиус круга с помощью уравнения круга.

    Затем начертите центр на декартовой плоскости и с помощью циркуля измерьте радиус и начертите окружность.

    Как найти общее уравнение круга?

    Если мы знаем координаты центра окружности и радиус, то мы можем найти общее уравнение окружности.2 — 2х — 4у + 1 = 0 \)

    Приведенная выше форма уравнения является общей формой уравнения круга.

    Как написать стандартную форму кругового уравнения с конечными точками?

    Возьмем две конечные точки диаметра: (1, 1) и (3, 3). Сначала вычислите среднюю точку, используя формулу сечения. Координаты центра будут (2, 2). Во-вторых, рассчитайте радиус по формуле расстояния между (1, 1) и (2, 2). Радиус равен \ (\ sqrt {2} \).2 = 2 \).

    Что такое полярное уравнение круга?

    Полярное уравнение круга с центром в качестве начала координат, r = p, где p — радиус круга.

    1,2 Расстояние между двумя точками; Круги

    Учитывая две точки $ (x_1, y_1) $ и $ (x_2, y_2) $, напомним, что их расстояние по горизонтали друг от друга составляет $ \ Delta x = x_2-x_1 $, а их расстояние по вертикали друг от друга составляет $ \ Delta y = y_2-y_1 $. (Фактически, слово «расстояние» обычно означает «положительное расстояние».2 = 16 $. Теперь мы видим, что это круг с радиусом 4 и центром $ (1, -2) $, который легко построить графиком. $ \ квадрат $

    Упражнения 1.2

    Пример 1.2.1 Найдите уравнение окружности радиуса 3 с центром в точке:

    (отвечать)

    Пример 1.2.2 Для каждой пары точек $ A (x_1, y_1) $ и $ B (x_2, y_2) $ найти (i) $ \ Delta x $ и $ \ Delta y $ при переходе от $ A $ к $ B $, (ii) наклон линии, соединяющей $ A $ и $ B $, (iii) уравнение прямой, соединяющей $ A $ и $ B $, в виде $ y = mx + b $, (iv) расстояние от $ A $ до $ B $, и (v) уравнение круг с центром в $ A $, проходящий через $ B $. 2-8лет = 0 $.

    Пример 1.2.6 Найдите стандартное уравнение круга, проходящего через $ (- 2,1) $. и касательная к прямой $ 3x-2y = 6 $ в точке $ (4,3) $. Эскиз. (Подсказка: линия, проходящая через центр круга и точку касания перпендикулярна касательной.) (отвечать)

    Графические круги: определение формулы, центра и радиуса — видео и стенограмма урока

    Формула окружности

    Для определения окружностей мы используем специальное уравнение.2. Круг — это очень простая форма, но имеет сложную формулу. Чтобы узнать, является ли уравнение уравнением круга, нужно запомнить четыре важных момента. Во-первых, члены x и y возводятся в квадрат. Во-вторых, все члены в уравнении положительны. Третья — центральная точка круга ( h , k ). Наконец, r представляет радиус круга.

    h и k — координаты центра, но они не всегда даются по порядку.Легкий способ запомнить — взглянуть на каждую часть уравнения. В первом разделе у нас есть x и h в тех же скобках. Поскольку они вместе, вы можете помнить, что h — это значение x центральной точки. Во втором разделе у нас есть y и k в том же наборе. Поскольку они вместе, мы знаем, что k — это значение y центральной точки. Зная эту формулу, вы можете быстро увидеть координаты центральной точки круга.

    Довольно легко запомнить, что r обозначает радиус. Сложность заключается в том, что вы должны помнить, что r возведено в квадрат в уравнении. Иногда это просто целое число. В этом случае, чтобы найти радиус, вы должны извлечь квадратный корень. Помните, что все три части уравнения должны быть возведены в квадрат, даже если радиус показан в виде целого числа.

    От формулы к графику

    Для любого уравнения важно, чтобы мы знали, как нарисовать его на графике.2, где центр? h = 2 и k = 1. Это координаты центральной точки (2,1). Помните, что если h и k сбивают с толку, число с x является координатой x . Число в скобках с y — это координата центра y .

    Другой важной частью этого графика является радиус. В этом случае радиус r = 5. Чтобы нарисовать этот график, мы начнем с центральной точки и будем использовать радиус, чтобы отмечать точки вверх, вниз, влево и вправо.В этом случае мы начинаем с точки (2,1) и продвигаемся на 5 единиц вверх. Отметьте эту точку. Вернитесь в центр и спуститесь на 5 единиц. Сделайте то же самое, начиная с центра и двигаясь влево и вправо по 5 единиц. Используйте эти 4 точки, показанные ниже, в качестве ориентира при рисовании круга.

    Вы можете использовать эти точки в качестве ориентира при рисовании круга.

    От графика к формуле

    Обнаружив центральную точку, слегка отметьте ее.

    Когда вы видите круг на графике, двумя ключевыми вещами, которые нужно знать, по-прежнему являются центр и радиус. В кружке выше найдем центральную точку. Помните, что центральной точки на самом деле нет на графике, поэтому мы слегка отметим ее и сотрем, когда закончим. Центр круга будет посередине между верхним и нижним краями графика. Это также будет на полпути между левой и правой сторонами. Мы находим центр, вычисляя среднюю точку между каждым набором точек.Средняя точка — это точка, равная половине расстояния между двумя точками . Чтобы найти среднюю точку, мы берем значения x , складываем их и делим на 2. То же самое делаем со значениями y . Это дает нам середину.

    В этом случае мы хотим взять среднюю точку верхней и нижней точки круга. Верхняя точка круга — (-2,4). Нижняя точка находится в (-2, -2). Мы находим среднюю точку, складывая значения x и разделив их на 2. -2 + -2 = -4, -4/2 = -2. Теперь сделайте то же самое для значений y . 4 + -2 = 2, 2/2 = 1. Средняя точка равна (-2,1). Чтобы убедиться, что это идеальный круг, нам нужно найти среднюю точку между левой и правой точками. Нахождение средней точки значений x дает нам -5 + 1 = -4, -4/2 = -2. Средняя точка значений y дает нам 1 + 1 = 2; 2/2 = 1. Средняя точка слева и справа одинакова. Центр круга равен (-2,1), где h = -2 и k = 1.2 = 9. Обратите внимание, что x и y возведены в квадрат, и они положительны. Это уравнение круга.

    Краткое содержание урока

    Хотя x и y оба квадратные, круга нечего бояться. Все, что нам нужно знать, — это центр и радиус. Если мы знаем эти две вещи, мы можем изобразить круг или написать его формулу. Центральная точка дает нам h и k , а радиус дает нам r .Мы можем либо подставить это в уравнение, либо поместить прямо на график. Фигуры помогают нам учиться даже по математике.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *