Виды цифр: Цифры (математика, 5 класс) – виды и классы

Числа: натуральные, целые, рациональные, иррациональные, действительные, комплексные

Тестирование онлайн

• Округление чисел

Натуральные числа

Это числа, которые используются при счете: 1, 2, 3… и т.д.

Ноль не является натуральным.

Натуральные числа принято обозначать символом N.

Целые числа. Положительные и отрицательные числа

Два числа отличающиеся друг от друга только знаком, называются противоположными, например, +1 и -1, +5 и -5. Знак «+» обычно не пишут, но предполагают, что перед числом стоит «+». Такие числа называются положительными. Числа, перед которыми стоит знак «-«, называются отрицательными.

Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.

Рациональные числа

Это конечные дроби и бесконечные периодические дроби . Например,

Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.

Иррациональные числа

Бесконечная непериодическая дробь называется иррациональным числом. Например:

Множество иррациональных чисел обозначается J.

Действительные числа

Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.

Действительные числа обозначаются символом R.

Округление чисел

Рассмотрим число 8,759123… . Округлить до целой части означает записать лишь ту часть числа, которая находится до запятой. Округлить до десятых означает записать целую часть и после запятой одну цифру; округлить до сотых — после запятой две цифры; до тысячных — три цифры и т.д.

Округлить 8,759123… с точностью до целой части.

Округлить 8,759123… с точностью до десятой части.

Округлить 8,759123… с точностью до сотой части.

Округлить 8,759123… с точностью до тысячной части.

Доступные числовые форматы в Excel

В Excel числа, содержащиеся в ячейках, можно преобразовать, например, в денежные единицы, проценты, десятичные числа, даты, номера телефонов или номера социального страхования США.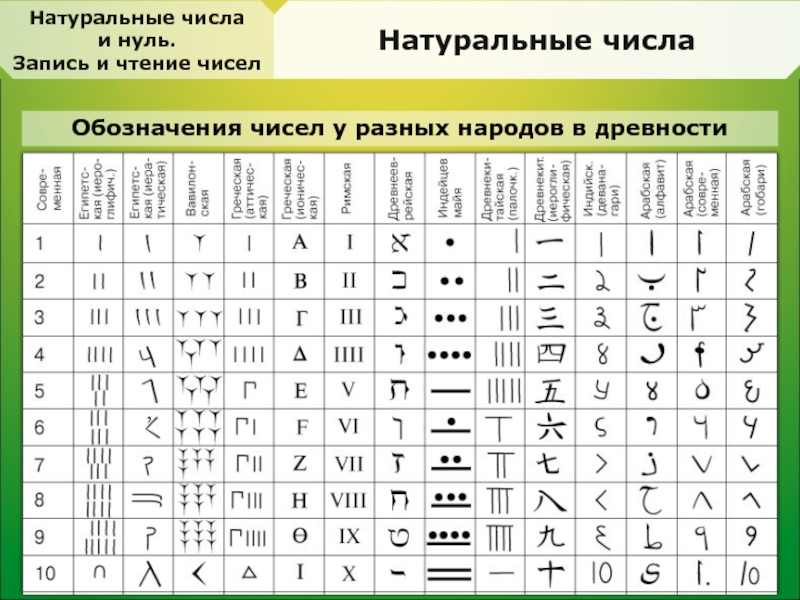

1. Выделите ячейку или диапазон ячеек.

2. На вкладке Главная выберите в раскрывающемся списке формат Числовой.
   
   Можно также выбрать один из следующих вариантов:

   • Нажмите клавиши CTRL+1 и выберите формат Числовой.

   • Щелкните ячейку или диапазон ячеек правой кнопкой мыши, выберите команду Формат ячеек… и формат Числовой.

   • Нажмите кнопку вызова диалогового окна в группе Число  и выберите формат Числовой.

3. Выберите нужный формат.

Числовые форматы

Чтобы просмотреть все доступные числовые форматы, на вкладке Главная в группе Число нажмите кнопку вызова диалогового окна рядом с надписью Число.

Формат	Описание
Общий	При вводе чисел в Excel этот формат используется по умолчанию. В большинстве случаев числа, имеющие формат Общий, отображаются так, как вводятся. Однако если ширины ячейки недостаточно для отображения всего числа, числа в формате Общий округляются. Для чисел, содержащих более 12 знаков, в формате Общий используется научное (экспоненциальное) представление.
Числовой	Используется как основной для вывода чисел. Можно задать количество отображаемых знаков после запятой, применение разделителя групп разрядов и способ отображения отрицательных чисел.
Денежный	Используется для денежных значений и выводит рядом с числом обозначение денежной единицы по умолчанию. Можно задать количество отображаемых знаков после запятой, применение разделителя групп разрядов и способ отображения отрицательных чисел.
Финансовый	Используется для отображения денежных значений с выравниванием обозначений денежных единиц и десятичных разделителей в столбце.
Дата	Отображает числовые представления даты и времени как значения даты в соответствии с заданным типом и языковым стандартом (местоположением). Форматы даты, начинающиеся со звездочки (*), соответствуют формату отображения даты и времени, заданному на панели управления. На форматы без звездочки параметры, заданные на панели управления, не влияют.
Время	Отображает числовые представления даты и времени как значения времени в соответствии с заданным типом и языковым стандартом (местоположением). Форматы времени, начинающиеся со звездочки ( *), соответствуют формату отображения даты и времени, заданному на панели управления. На форматы без звездочки параметры, заданные на панели управления, не влияют.
Процентный	В этом формате значение ячейки умножается на 100, а результат отображается со знаком процента (%). Можно задать количество знаков в дробной части.
Дробный	Отображает число в виде дроби выбранного типа.
Экспоненциальный	Отображает число в экспоненциальном представлении, заменяя часть числа на E+n, где E обозначает экспоненциальное представление, то есть умножение предшествующего числа на 10 в степени n. Например, экспоненциальный формат с двумя знаками в дробной части отображает 12345678901 как 1,23E+10, то есть 1,23, умноженное на 10 в 10-й степени. Можно задать количество знаков в дробной части.
Текстовый	Содержимое ячейки (включая числа) обрабатывается как текст и отображается именно так, как было введено.
Дополнительный	Число отображается в виде почтового индекса, телефонного номера или страхового номера (SSN).
(все форматы)	Позволяет изменять копию существующего кода числового формата. При этом создается пользовательский числовой формат, добавляемый в список кодов числовых форматов. В зависимости от языковой версии Microsoft Excel можно ввести от 200 до 250 пользовательских числовых форматов. Дополнительные сведения см. в статье Создание и удаление пользовательских числовых форматов.

Вы можете применять к числам различные форматы, чтобы изменить способ их отображения. Форматы изменяют только способ отображения чисел и не влияют на значения. Например, если вы хотите, чтобы число отображалось в виде валюты, щелкните ячейку с числом > Денежный.

Форматы влияют только на отображение чисел, но не значения в ячейках, используемые в вычислениях. Фактическое значение можно увидеть в строка формул.

Ниже представлены доступные числовые форматы и описано, как их можно использовать в Excel в Интернете:

Числовой формат	Описание
Общие	Числовой формат по умолчанию. Если ширины ячейки недостаточно, чтобы отобразить число целиком, оно округляется. Например, 25,76 отображается как 26. Кроме того, если число состоит из 12 или более цифр, при использовании формата Общий значение отображается в экспоненциальном виде.
Числовой	Этот формат похож на Общий, но в отличие от него отображает числа с десятичным разделителем, а также отрицательные числа. Ниже представлено несколько примеров отображения чисел в обоих форматах:
Денежный	Отображает рядом с числами денежный символ. Чтобы задать необходимое количество знаков после запятой, нажмите кнопку Увеличить разрядность или Уменьшить разрядность.
Финансовый	Используется для отображения денежных значений с выравниванием символов валюты и десятичных разделителей в столбце.
Краткий формат даты	В этом формате дата отображается в следующем виде:
Длинный формат даты	В этом формате месяц, день и год отображаются в следующем виде:
Системное время	В этом формате числовые представления даты и времени отображаются как значения времени.
Процентный	В этом формате значение ячейки умножается на 100, а результат отображается со знаком процента (%). Чтобы задать необходимое количество знаков после запятой, нажмите кнопку Увеличить разрядность или Уменьшить разрядность.
Дробный	Отображает число в виде дроби. Например, при вводе 0,5 отображается ½.
Экспоненциальный	Отображает числа в экспоненциальной нотации, заменяя часть числа на E+n, где E (степень) умножает предыдущее число на 10 в степени n. Например, экспоненциальный формат с двумя знаками в дробной части отображает 12345678901 как 1,23E+10, то есть 1,23, умноженное на 10 в 10-й степени. Чтобы задать необходимое количество знаков после запятой, нажмите кнопку Увеличить разрядность или Уменьшить разрядность.
Текстовый	Содержимое ячейки (включая числа) обрабатывается как текст и отображается именно так, как было введено. Дополнительные сведения о форматировании чисел в виде текста.

Чем отличаются цифры от чисел?

Первые упоминания о цифрах встречаются ещё около 500 лет до нашей эры, и все давно знают, что такое число и цифра. Но если задать вопрос по-другому, и спросить в чём разница между числом и цифрой, многие не смогут дать правильный ответ. Чтобы понять разницу между этими терминами, стоит более детально разобраться в понятиях «цифра» и «число». Только так можно изучить в чём их отличия.

 

Цифры: виды и особенности

Систему знаков, которую используют для обозначения чисел на письме, называют цифрами. Это различные символы, обозначающие какое-либо число. Знаки «-» и «+» тоже используют для записей, но цифрами они не являются, потому что не обозначают конкретных чисел. Эти знаки используются для записи разных действий с числами.

Цифрами называют цифровой ряд от 0 до 9. Такое название пришло к нам из арабского языка и дословно переводится как пустое место, или ноль. На сегодняшний день существуют различные виды цифр, есть:

• Римские цифры.
• Арабские цифры.
• Шестнадцатеричные цифры.

Это самые распространённые разновидности цифр. Но есть и другие варианты, которые используют разные народы.

Интересно: Раньше, для обозначения чисел, приходилось делать зарубки на скалах и других материалах. Наши предки рисовали палочки и символы в огромном количестве, чтобы вести счёт. С появлением цифр задача упростилась. Теперь, чтобы обозначить большое число, достаточно написать всего несколько символов.

В некоторых языках числа до сих пор записывают буквами, к примеру, в древнегреческом языке. В народе под цифрами понимают различные числа, и используют цифры для записей и расчётов. Цифра не может быть отрицательной, натуральной или дробной, это всего лишь графический символ необходимый для письма.

Европейцы используют арабские цифры, которые впервые упорядочили ещё в 13 веке. До этого счёт вели с помощью римских символов. Теперь такие символы можно встретить только в книгах и на циферблате некоторых часов, а выглядят они как палочки.

Что называют числом?

Качественные характеристики, нумерацию и сравнение, в математике описывают отдельным термином – числом. Записывают числа символами – цифрами.

Ещё в первобытном сообществе появилась необходимость счёта, поэтому люди стали придумывать разные символы, чтобы записывать полученные данные. Число может быть:

• Натуральным – это те числа, которые используют в естественном счёте.
• Целым – это объединение нескольких натуральных чисел.
• Рациональным, которым обозначают дробь.

Есть также комплексные и действительные числа. Последние два варианта часто используются в математическом анализе.

Ранее числа использовали для простых математических расчётов. Сегодня, в связи с бурными темпами развития технологий, роль чисел сложно переоценить.

Основные отличия между цифрой и числом

Подытоживая вышесказанное, можно выделить несколько главных отличий между числами и цифрами:

• В отличие от цифр, числа можно отнимать, прибавлять и выполнять с ними другие математические действия. Цифры никак не поделишь и не отнимешь, это неизменный символ.
• Цифры не могут быть отрицательными, или дробными, а числа могут.
• Чисел может быть множество, они складываются из разных цифр, а цифр всего 10.

Есть различия в этих понятиях и с точки зрения лингвистики, например, для озвучивания статистики и других официальных данных, нужно использовать термин «цифра».

Некоторые придают цифрам магический смысл и считают, что каждое число по-своему влияет на человека, его дальнейшую судьбу. Наука, занимающаяся изучением подобных явлений, называется нумерологией.

Цифры и числа: отличия | НАУМЁНОК

Все знают, что есть цифры и числа. Но если спросить: «Чем отличается цифра от числа?«, то многие дети, а порой и взрослые, затрудняются с ответом. А как объяснить эту разницу ребенку простыми словами?

Чтобы ответить на этот вопрос и понять в чём различие между цифрой и числом надо разобраться с понятиями, что такое цифра и что такое число.

Содержание

1. Что такое цифра?

2. Что такое число?

3. Чем отличается число от цифры?

4. Какие виды чисел изучаются в начальной школе?

5. Как дать характеристику числу?

Что такое цифра?

Цифра — это письменный знак, изображающий число.

Что значит слово цифра? Это слово арабского происхождения и означает ноль или пустое место. Их существует только десять. Они придуманы для обозначения числа. Цифр всего 10.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Что такое число?

Число — это основное математическое понятие.

Его используют для:

• количественной характеристики;
• сравнения;
• обозначения нумерации объектов.

Числа записываются при помощи цифр. Различают несколько видов чисел.

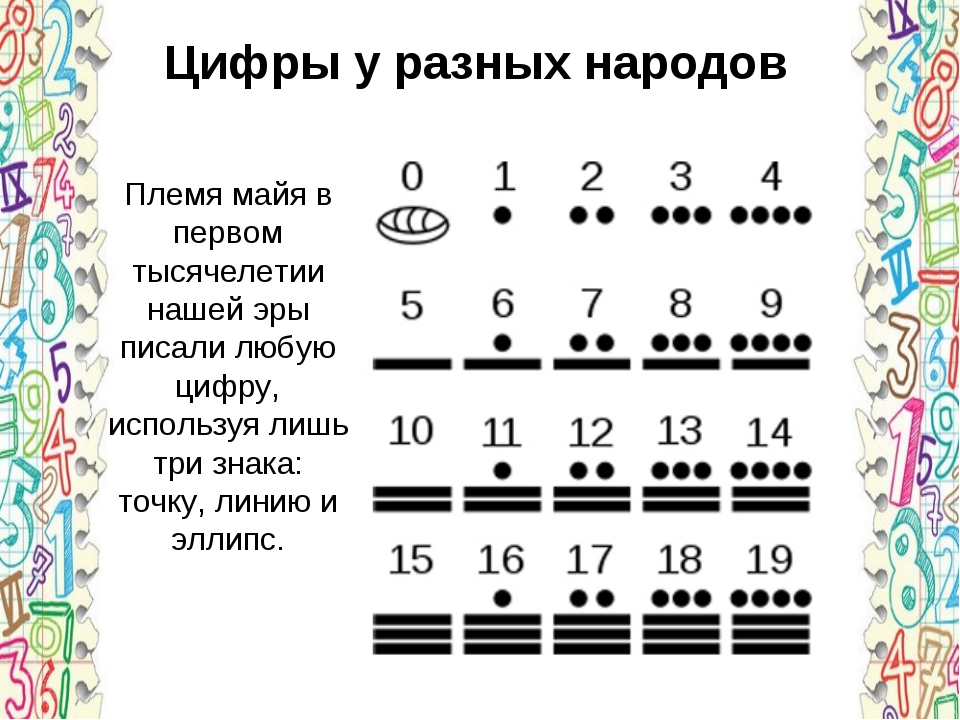
В древнейшие времена цифры обозначали прямолинейными пометками. Палочки до сих пор используются для обозначения римских цифр. Римских цифр 7.

I, V, X, L, C, D, M

Римские числа также, как и арабские, образуются при помощи цифр, только в данном случае римских.

В римских числах желательно разбираться, т.к. они часто используются не только в школьном курсе математики, но и в жизни. Например, на циферблате часов.

Отличия числа от цифры

1. С числами можно проводить различные математические действия. С цифрами такого делать нельзя.
2. Число может быть отрицательным, дробным, в отличие от цифр.
3. Количество арабских цифр всего 10 (римских — 7), а чисел — бесконечное множество, т.к. они состоят из цифр.

Надеюсь, что теперь вам всё понятно, и вы сможете без труда объяснить даже ребёнку, чем отличается число от цифры.

На уроках математики в начальной школе используется очень полезное упражнение. Детей просят дать характеристику числу. Другими словами рассказать о числе все, что знаешь. Не всем детям это задание даётся легко. Чтобы его выполнить пригодятся вышеописанные знания и не только.

Какие виды чисел изучаются в начальной школе?

В начальной школе рассматриваются: натуральные числа, число 0, доли и дроби.  

Натуральные  числа— используются для счёта предметов;

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…

Однозначные числа — состоят из одной цифры;

1, 2, 3, 4, 5, 6, 7, 8, 9

Двузначные числа — состоят из двух цифр;

10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 … 99

Соответственно самое маленькое двузначное число 10, а самое большое — 99.

Аналогично числа можно охарактеризовать как трёхзначные, четырёхзначные и т.д.

Иногда дети затрудняются назвать самое маленькое, например, пятизначное число (10 000) или самое большое семизначное (9 999 999). Просто полезно будет потренироваться это делать.

Чётные — числа, которые делятся пополам без остатка или же заканчиваются  на 0, 2, 4, 6, 8;

2, 4, 6, 8, 10, 12, 14…

Нечетные — числа, которые не делятся на 2 без остатка;

1, 3, 5, 7, 9, 11, 13…

Круглые — числа, которые заканчиваются нулём.

10, 20, 30, 40, 50…

Как дать характеристику числу?

Разберём несколько примеров.

Число 7 — однозначное, нечетное, соседи числа 7 числа 6 и 8.

Также чисел первого десятка можно добавить такое дополнительное задание, как состав числа. Т.е. число 7 можно получить сложением чисел 1 и 6, 2 и 5, 3 и 4.

Число 10 — двузначное, чётное, круглое, соседи числа 9 и 11. Число 10 можно получить сложением чисел 1 и 9, 2 и 8, 3 и 7, 4 и 6, 5 и 5.

Чем крупнее число, тем больше можно о нём рассказать.

Число 999 — наибольшее трёхзначное число, нечётное, соседи 998 и 1000, в числе 9 сотен, 9 десятков и 9 единиц.

Надеюсь, что полученные знания были вам полезны и теперь вы знаете чем отличается цифра от числа, сможете объяснить это ребёнку простыми словами, а также потренироваться давать характеристику числам.

 

С уважением, Ольга Наумова

Заходите в

Книжную лавку  за полезными книгами!

Благодарю, что поделились статьей в социальных сетях!

ОПИСАНИЕ БЛАНКА ПАСПОРТА ГРАЖДАНИНА РОССИЙСКОЙ ФЕДЕРАЦИИ / КонсультантПлюс

Утверждено

Постановлением Правительства

Российской Федерации

от 8 июля 1997 г. N 828

КонсультантПлюс: примечание.

Бланки, изготовленные до 16.07.2021, используются до их израсходования, паспорта, оформленные на таких бланках, действительны впредь до их замены в установленные сроки (Постановление Правительства РФ от 15.07.2021 N 1205).

Список изменяющих документов

(в ред. Постановлений Правительства РФ от 25.09.1999 N 1091,

от 05.01.2001 N 7, от 22.01.2002 N 32, от 02.07.2003 N 392,

от 20.12.2006 N 779, от 27.05.2011 N 424, от 18.02.2014 N 122,

от 29.02.2016 N 154, от 07.07.2016 N 644, от 15.07.2021 N 1205)

1. Бланк паспорта гражданина Российской Федерации (далее именуется — бланк паспорта) изготавливается по единому образцу с указанием всех реквизитов на русском языке.

2. Бланк паспорта имеет размер 88 x 125 мм, состоит из обложки, приклеенных к обложке форзацев и содержит 20 страниц, из них 14 страниц имеют нумерацию в орнаментальном оформлении, продублированную в центре страницы в фоновой сетке.

Бланк паспорта сшит по всей длине корешка двухцветной нитью с пунктирным свечением в ультрафиолетовом излучении.

Бланк паспорта и вкладыш изготавливаются с использованием специальной бумаги, содержащей 3 вида защитных волокон.

Внутренние страницы бланка паспорта и вкладыш имеют видимое на просвет изображение общего водяного знака, содержащего при рассмотрении в проходящем свете объемные начертания букв «РФ».

В бумагу девятнадцатой и двадцатой страниц введена защитная металлизированная нить, меняющая цвет в зависимости от угла зрения, отдельные участки нити видны на поверхности девятнадцатой страницы.

3. Нумерация бланка паспорта состоит из 3 групп цифр. Первые 2 группы, состоящие из 4 цифр, обозначают серию бланка паспорта, третья группа, состоящая из 6 цифр, обозначает номер бланка паспорта.

Нумерация бланка паспорта воспроизведена:

в верхней части второй и третьей страниц, в верхней части левого и правого разворота вкладыша — способом высокой печати;

в нижней части пятой — двадцатой страниц, вкладыша, заднего форзаца и обложки — способом лазерной перфорации. Изображение цифр серии и номера бланка паспорта формируется с помощью прожигаемых лазером в бумаге и переплетном материале видимых на просвет отверстий.

4. Обложка бланка паспорта изготовлена из износостойкого материала темно-красного цвета. В верхней ее части в две строки размещены слова «Российская Федерация», в середине воспроизведен золотистый тисненый Государственный герб Российской Федерации (без щита), а под ним — слово «паспорт».

5. В центре переднего форзаца помещено изображение Московского Кремля, под которым расположены типографский рисунок «розетка».

6. В верхней части первой страницы бланка паспорта воспроизведено цветное изображение Государственного герба Российской Федерации. В середине (под гербом) в орнаментальном оформлении напечатаны в три строки слова «паспорт гражданина Российской Федерации». Под словами расположен типографский рисунок «розетка». Текст и розетка выполнены металлографическим способом печати.

7. Текст реквизитов и строки для внесения записей на второй, третьей, шестнадцатой и семнадцатой страницах бланка паспорта расположены параллельно сгибу бланка. Строки для внесения записей наносятся с интервалом 6,6 мм.

(в ред. Постановлений Правительства РФ от 25.09.1999 N 1091, от 05.01.2001 N 7)

8. В верхней части второй страницы бланка паспорта размещены по центру выполненные офсетным способом печати слова «Российская Федерация», ниже — слова «Паспорт выдан», «Дата выдачи», «Код подразделения», «Личная подпись».

(в ред. Постановлений Правительства РФ от 20.12.2006 N 779, от 15.07.2021 N 1205)

В левом нижнем углу страницы напечатана подстрочная черта для подписи руководителя подразделения, выдавшего паспорт, и отведено место для проставления печати, обозначенное буквами «М.П.».

9. Третья страница бланка паспорта предназначена для размещения сведений о личности владельца паспорта. Страница состоит из 2 частей: верхние три четверти страницы — визуальная зона, в которой слева размещена фотография владельца паспорта размером 35 x 45 мм, а справа — следующие реквизиты, выполненные офсетным способом печати:

«Фамилия»;

«Имя»;

«Отчество»;

«Пол»;

«Дата рождения»;

«Место рождения».

Место для размещения фотографии обозначено уголками. В верхней и нижней частях поля для фотографии располагаются 2 прямоугольные реперные метки черного цвета, которые используются для позиционирования принтера при заполнении бланка. После размещения фотографии реперные метки визуально неразличимы. Нижняя четверть страницы, противоположная сгибу, — зона для внесения машиночитаемых записей.

С целью защиты сведений о личности:

третья страница при высокой температуре ламинируется пленкой с голографическим изображением;

в правом верхнем углу третьей страницы расположен элемент, имеющий форму окружности, с буквами «РФ». В зависимости от угла зрения элемент меняет свой цвет с пурпурного на зеленый.

На четвертой странице записи и отметки не производятся.

Машиночитаемая запись содержит в соответствии с требованиями и стандартами, предъявляемыми к машиночитаемым проездным документам, основную информацию, имеющуюся в этом документе: фамилию, имя, отчество, дату рождения (число, месяц, год) владельца паспорта, пол владельца паспорта, серию и номер паспорта, код подразделения, выдавшего паспорт, дату выдачи паспорта, а также обозначения типа документа, государства, выдавшего паспорт, гражданства владельца паспорта.

Правила и способ формирования машиночитаемой записи устанавливаются Министерством внутренних дел Российской Федерации по согласованию с заинтересованными федеральными органами исполнительной власти.

10. Страницы бланка паспорта с пятой по двенадцатую предназначены для проставления отметок о регистрации гражданина и снятии его с регистрационного учета по месту жительства. В верхней части пятой страницы с ориентацией по центру размещен реквизит «Место жительства».

(в ред. Постановлений Правительства РФ от 25.09.1999 N 1091, от 05.01.2001 N 7)

До 31 декабря 2004 г. на двенадцатую страницу бланка паспорта также вклеиваются фотографии детей — граждан Российской Федерации, не достигших 14-летнего возраста.

11. Тринадцатая страница бланка паспорта предназначена для проставления отметок об отношении гражданина к воинской обязанности. В верхней части тринадцатой страницы с ориентацией по центру размещен реквизит «Воинская обязанность».

12. Четырнадцатая и пятнадцатая страницы бланка паспорта предназначены для производства отметок о регистрации и расторжении брака. В верхней части четырнадцатой страницы с ориентацией по центру размещен реквизит «Семейное положение».

13. Шестнадцатая и семнадцатая страницы бланка паспорта предназначены для внесения сведений о детях владельца паспорта, подписи должностного лица, выдавшего паспорт, и проставления печати территориального органа Министерства внутренних дел Российской Федерации. В верхней части семнадцатой страницы бланка паспорта (параллельно сгибу) с ориентацией по центру размещен реквизит «Дети». На семнадцатой странице с продолжением на шестнадцатую расположена таблица, состоящая из восемнадцати строк и четырех граф (слева направо): «Пол», «Фамилия, имя, отчество», «Дата рождения».

(в ред. Постановлений Правительства РФ от 20.12.2006 N 779, от 07.07.2016 N 644, от 15.07.2021 N 1205)

14. Восемнадцатая и девятнадцатая страницы бланка паспорта предназначены для внесения отметок о группе крови и резус-факторе владельца паспорта, о его идентификационном номере налогоплательщика, о получении основного документа, удостоверяющего личность гражданина Российской Федерации за пределами территории Российской Федерации, а также о ранее выданных основных документах, удостоверяющих личность гражданина Российской Федерации на территории Российской Федерации.

15. Утратил силу. — Постановление Правительства РФ от 18.02.2014 N 122.

16. В верхней части двадцатой страницы бланка паспорта расположен типографский рисунок — орнаментальная бордюрная полоса с ориентацией по центру, под рисунком напечатан заголовок «Информация для владельца паспорта» и далее воспроизведен следующий текст:

«1. Паспорт является основным документом, удостоверяющим личность гражданина Российской Федерации на территории Российской Федерации.

2. Паспорт обязаны иметь все граждане Российской Федерации, достигшие 14-летнего возраста и проживающие на территории Российской Федерации.

3. По достижении гражданином 20-летнего и 45-летнего возраста, в случае изменения сведений о личности, размещенных на третьей странице паспорта, непригодности паспорта для дальнейшего использования, обнаружения неточности или ошибочности произведенных в паспорте записей либо внесения в него сведений, отметок и (или) записей, не предусмотренных Положением о паспорте гражданина Российской Федерации, паспорт подлежит замене.

4. Паспорт, подлежащий замене в связи с достижением гражданином 20-летнего и 45-летнего возраста, является действительным до оформления нового паспорта, но не более чем 90 дней после дня возникновения указанных обстоятельств.

5. Гражданин обязан бережно хранить паспорт. В случае утраты паспорта необходимо незамедлительно обратиться с заявлением в территориальный орган Министерства внутренних дел Российской Федерации.

6. Изъятие у гражданина паспорта, кроме случаев, предусмотренных законодательством Российской Федерации, запрещается.».

17. Гражданин обязан бережно хранить паспорт. Об утрате паспорта гражданин должен незамедлительно заявить в территориальный орган Министерства внутренних дел Российской Федерации.

(в ред. Постановлений Правительства РФ от 20.12.2006 N 779, от 07.07.2016 N 644)

22. Запрещается изъятие у гражданина паспорта, кроме случаев, предусмотренных законодательством Российской Федерации».

17. На пятой, седьмой, девятой, одиннадцатой, тринадцатой, пятнадцатой и девятнадцатой страницах напечатано выполненное стилизованными буквами в орнаментальном оформлении слово «Россия».

(в ред. Постановлений Правительства РФ от 25.09.1999 N 1091, от 05.01.2001 N 7)

В бланке паспорта могут быть применены специально разработанные вшиваемые или вкладываемые элементы, предназначенные для повышения сохранности вносимых записей или для защиты бланка и произведенных в нем записей от подделок.

---

Коды вида операций — «Альфа-Банк»

Как определить какой код вида операции указать при платеже?

Перечень кодов видов валютных операций разделен на группы (условная нумерация группы определяется первыми двумя цифрами кода вида операции) в зависимости от предмета договора, на основании которого осуществляется платеж и /или экономического характера платежа: например, оплата за товары, оплата за услуги, покупка недвижимости, продажа ценных бумаг, выплата заработной платы, оплата штрафа или налога):
01 и 02 группы — конверсионные операции резидентов и нерезидентов в безналичной форме
10 и 11 группы — платежи за товары с вывозом из РФ или ввозом в РФ (экспорт/ импорт товаров)
12 и 13 группы — платежи за товары без ввоза в РФ или вывоза из РФ
20 и 21 группы — платежи за услуги, работы, информацию и результаты интеллектуальной деятельности, исключительные права на них, за аренду (экспорт/ импорт)
22 и 23 группы — платежи по договорам смешанного типа

30 группа — платежи за недвижимое имущество
32 группа — платежи по договорам уступки требования и перевода долга
35 группа — прочие платежи, связанные с внешнеторговой деятельностью
40 и 41 группы — предоставление кредитов и займов
42 и 43 группы — возвраты кредитов и займов и процентов по ним
50 группа — платежи за доли, паи, вклады в имущество
51 и 52 группы — купля -продажа ценных бумаг
55 группа — исполнение обязательств по ценным бумагам
56 группа — платежи по операциям с производными финансовыми инструментами
57 группа — платежи по договорам доверительного управления имуществом
58 группа — платежи по договорам о брокерском обслуживании
59 группа — платежи по договорам об оказании клиринговых услуг
60 группа — переводы нерезидентов (друг другу или сам себе)
61 группа — переводы резидентов (друг другу или сам себе)
70 группа — неторговые операции (налоги, заработная плата, пенсия, благотворительная помощь и т.  п.)
80 группа — операции (резидентов и нерезидентов) по договорам с уполномоченным банком (по аккредитивам, кредитным договорам, оплата банковской комиссии по договору расчетно-кассового обслуживания и т. п.)
90 группа — прочие валютные операции.

Код вида валютной операции зависит также от направления платежа (кто кому платит: резидент нерезиденту или нерезидент резиденту (см. столбец Получатель и Плательщик в таблице ниже)), а также от особенностей расчетов.

Клиент-резидент осуществляет авансовый платеж по импортному договору купли-продажи товара (импорт товара — это ввоз товаров в РФ).

1. Необходимо определить группу кода вида операции, соответствующую виду договора (в нашем случае — это группа 11 «Расчеты между резидентами и нерезидентами при осуществлении внешнеторговой деятельности, связанной с ввозом на территорию Российской Федерации товаров, включая воздушные, морские суда, суда внутреннего плавания и космические объекты».

2. После этого понять кто осуществляет платеж — определить плательщика (в нашем случае — это резидент).

3. Затем необходимо определить особенности (условия) расчетов, предусмотренные договором (оплата по факту или авансом) (в нашем случае — это авансовый платеж- предоплата).

4. Теперь можно определить код валютной операции (в нашем случае получается КВВО 11100).

Полные формулировки кодов видов операций содержатся в Перечне кодов видов операций резидентов и нерезидентов, который является приложением 1 к Инструкции Банка России от 16.08.2017 № 181-И.

Размещения, сочетания и перестановки из трёх элементов

Что изучает комбинаторика

Представьте себе, что вы забыли пароль входа в аккаунт. Помните только, что это было трёхзначное число из цифр 1,2,3 и эти цифры не повторялись. Есть ли у вас шансы с помощью перебора зайти в аккаунт, если даётся всего три попытки? Такие задачи в современной жизни возникают довольно часто, и их решения изучаются в особом разделе математики — комбинаторике.

Комбинаторика – раздел математики, изучающий различные комбинации, которые можно составить из дискретных объектов, входящих в некоторое множество.

«Дискретные объекты» — это какие-то предметы, растения, животные, люди, здания, числа; всё, что можно «отделить» («дискретный» означает «отдельный») . Множество подобных объектов – это какая-то конечная группа, выбранная по какому-нибудь признаку.

Например:

Дискретные объекты – элементы множества

Яблоко, груша, слива, вишня, клубника

Дуб, ель, сосна, береза

Домашние питомцы

Собака, кот, попугай

Виды комбинаций

Составлять из дискретных объектов комбинации можно по-разному, их можно размещать, переставлять, сочетать; а также, брать каждый объект только один раз или помногу.

Комбинации из трёх элементов без повторений

Рассмотрим комбинации из трёх цифр 1,2,3 без повторений.

Перестановки

Нужно переставлять три цифры так, чтобы их порядок был разным:

123, 231, 312, 132, 321, 213

Таких комбинаций 6. 2 = 6$$

Ответ: 6 способов

Пример 4. Сколько всего трёхзначных чисел, в записи которых встречаются только цифры 1 и 2?

Поскольку числа трёхзначные, а цифр только две, цифры буду повторяться. Все возможные двузначные числа из 1 и 2:

Все возможные трёхзначные числа:

Всего – 8 комбинаций.

Ответ: 8 чисел

Пример 5. Сколько всего трехзначных чисел можно записать с помощью цифр 0,1,2 без повторений?

Речь идёт о перестановках без повторений.

012, 120, 201, 021, 210, 102

Из которых нужно исключить 012 и 021, т.к. это – не трёхзначные числа.

120, 201, 210, 102

Получаем 4 комбинации.

Ответ: 4 числа

Пример 6. Сколько всего трехзначных чисел можно записать с помощью цифр 0,1,2 с повторениями?

Все возможные комбинации по 2 из трёх цифр:

Впереди не может быть 0. Получаем возможные трёхзначные числа:

18 комбинаций.

Ответ: 4 числа

Типы чисел — различие и классификация

Можете ли вы представить, какой была бы ваша жизнь, если бы у вас не было возможности представить возраст, вес, дни рождения, время, результаты, банковские счета и номера телефонов? Десять математических цифр (от 0 до 9) используются для определения всех этих величин.

Числа — это цепочки цифр, используемые для представления количества. Величина числа указывает размер количества. Он может быть как большим, так и маленьким. Они существуют в разных формах, например, 3, 999, 0.351, 2/5 и т. Д.

Типы чисел в математике

Так же, как разные члены семьи живут в разных домах, разные числа принадлежат к одной семье, но имеют разные типы. Со временем различные комбинации десяти цифр были классифицированы на множество типов чисел. Эти шаблоны чисел отличаются друг от друга из-за разных представлений и свойств.

Натуральные числа

Натуральные числа или счетные числа — это самые основные типы чисел, которые вы впервые выучили в раннем детстве.Они начинаются с 1 и уходят в бесконечность, то есть 1, 2, 3, 4, 5, 6 и так далее. Их также называют положительными целыми числами. В установленном виде они могут быть записаны как:

{1, 2, 3, 4, 5,…}

Натуральные числа представлены символом N .

Целые числа

Целые числа — это набор натуральных чисел, включая ноль. Это означает, что они начинаются с 0 и увеличиваются до 1, 2, 3 и так далее, т.е.

{0, 1, 2, 3, 4, 5,…}

Целые числа представлены символом W .

Целые числа

Целые числа — это совокупность всех целых чисел и отрицательных чисел натуральных чисел. Они содержат все числа, лежащие между отрицательной бесконечностью и положительной бесконечностью. Они могут быть положительными, нулевыми или отрицательными, но не могут быть записаны в десятичной или дробной форме. Целые числа могут быть записаны в виде набора как

{…, -3, -2, -1, 0, 1, 2, 3,…}

Мы можем сказать, что все целые числа и натуральные числа являются целыми, но не все целые числа — это натуральные или целые числа.

Символ Z представляет целые числа.

Дроби

Дробь представляет собой части целого. Его можно записать в виде a / b , где a и b — целые числа, а b никогда не может быть равным 0. Все дроби являются рациональными числами, но не все рациональные числа являются дробями. .

Далее дроби сокращаются до правильных и неправильных дробей. Неправильные дроби — это дроби, в которых числитель больше знаменателя, в то время как для правильных функций верно обратное, т.е.е., знаменатель больше числителя. Примеры правильных дробей: 3/7 и 99/101, а 7/3 и 101/99 — неправильные дроби. Это означает, что неправильные дроби всегда больше 1.

Все завершающие десятичные дроби и повторяющиеся десятичные дроби могут быть записаны как дроби. Вы можете записать завершающую десятичную дробь 1,25 как 125/100 = 5/4. Повторяющееся десятичное число 0,3333 можно записать как 1/3.

Рациональные числа

Вы можете записывать рациональные числа в форме дробей. Слово «рациональный» происходит от слова «соотношение», поскольку рациональные числа — это отношения двух целых чисел.Например, 0,7 — рациональное число, потому что его можно записать как 7/10. Другими примерами рациональных чисел являются -1/3, 2/5, 99/100, 1,57 и т. Д.

Рассмотрим рациональное число p / q , где p и q — два целых числа. Здесь числитель p может быть любым целым числом (положительным или отрицательным), но знаменатель q никогда не может быть 0, поскольку дробь не определена. Кроме того, если q = 1, то дробь является целым числом.

Символ Q представляет рациональные числа.

Иррациональные числа

Иррациональные числа нельзя записать в дробной форме, т.е.они не могут быть записаны как отношение двух целых чисел. Вот несколько примеров иррациональных чисел: √2, √5, 0,353535…, π и так далее. Вы можете видеть, что цифры в иррациональных числах продолжаются до бесконечности без повторяющегося шаблона.

Символ Q обозначает иррациональные числа.

Вещественные числа

Вещественные числа — это совокупность всех рациональных и иррациональных чисел. Сюда входят все числа, которые можно записать в десятичной форме.Все целые числа являются действительными числами, но не все действительные числа являются целыми числами. Действительные числа включают в себя все целые числа, целые числа, дроби, повторяющиеся десятичные дроби, завершающие десятичные дроби и т. Д.

Символ R представляет действительные числа.

Мнимые числа

Числа, отличные от действительных, являются мнимыми или комплексными числами. Когда мы возводим в квадрат мнимое число, это дает отрицательный результат, что означает, что это квадратный корень из отрицательного числа, например, √-2 и √-5. Когда мы возводим эти числа в квадрат, получаем -2 и -5.Квадратный корень из отрицательной единицы представлен буквой i , т.е.

i = √-1

Пример 1

Что такое квадратный корень из -16? Запишите свой ответ, используя воображаемое число i .

Решение

• Шаг 1. Запишите форму квадратного корня.

√ (-16)

√ (16 × -1)

• Шаг 3. Разделите квадратные корни.

√ (16) × √ (-1)

• Шаг 4: Найдите квадратный корень.

4 × √ (-1)

• Шаг 5: Запишите в форме i.

4 i

Иногда вы получаете мнимое решение уравнений.

Пример 2

Решите уравнение:

x ² + 2 = 0

Решение

• Шаг 1. Возьмите постоянный член с другой стороны уравнения.

x ² = -2

• Шаг 2: извлеките квадратный корень с обеих сторон.

√ x ² = + √-2 или -√-2

x = √ (2) × √ (-1)

x = + √2 i или -√2 i

• Шаг 4. Проверьте ответы, подставив значения в исходное уравнение, и посмотрите, получим ли мы 0.

x ² + 2

(+ √2 i ) ² + 2 = -2 + 2 = 0 (поскольку i = √-1 и квадрат i равен -1)

(-√2 i ) ² + 2 = — 2 + 2 = 0 (поскольку i = √-1 и квадрат i равен -1)

То, что их имя «воображаемое» не означает, что они бесполезны. У них много приложений. Одно из самых больших применений мнимых чисел — их использование в электрических цепях. Вычисления силы тока и напряжения производятся в виде мнимых чисел. Эти числа также используются в сложных вычислительных вычислениях. В некоторых местах мнимое число также обозначается буквой j .

Комплексные числа

Мнимое число комбинируется с действительным числом, чтобы получить комплексное число. Оно представлено как a + bi , где действительная часть и b являются комплексной частью комплексного числа.Действительные числа лежат на числовой прямой, а комплексные числа — на двумерной плоскости.

Подобно мнимым числам, комплексные числа тоже не бесполезны. Они используются во многих приложениях, таких как «Сигналы и системы» и «Преобразование Фурье».

Простые числа и составные числа

Простые и составные числа противоположны друг другу. Простые числа — это целые числа без факторов, кроме них самих и 1, например 2, 3, 5, 7 и т. Д.Число 4 не является простым числом, потому что оно делится на 2. Аналогично, 12 также не является простым числом, потому что оно делится на 2, 3 и 4. Следовательно, 4 и 12 являются примерами составных чисел.

Трансцендентные числа

Числа, которые никогда не могут быть нулем (или корнем) полиномиального уравнения с рациональными коэффициентами, называются трансцендентными числами. Не все иррациональные числа являются трансцендентными числами, но все трансцендентные числа являются иррациональными числами.

Классификация чисел

Семейство чисел, которое мы видели выше, также можно разделить на разные категории. Это похоже на то, что в семье 20 человек, но они живут в двух совместных семейных домах по 10 человек в каждом, что означает, что 10 человек живут в одном доме. Мы можем сказать, что два или более типа чисел могут подпадать под одну категорию.

Дискретные и непрерывные числа

Типы счетных чисел называются дискретными числами, а типы чисел, которые не могут быть подсчитаны, называются непрерывными числами. Все натуральные, целые, целые и рациональные числа дискретны. Это потому, что каждый их набор является счетным. Набор действительных чисел слишком велик и не может быть посчитан, поэтому классифицируется как непрерывные числа. Если мы случайным образом возьмем два ближайших действительных числа, между ними все равно будет существовать бесконечно больше вещественных чисел; следовательно, их нельзя сосчитать.

Наборы номеров

Номера также можно классифицировать в виде наборов. Каждый тип числа является подмножеством другого типа числа.Например, натуральные числа — это подмножество целых чисел. Точно так же целые числа — это подмножество целых чисел. Набор рациональных чисел содержит все числа и дроби. Наборы рациональных чисел и иррациональных чисел образуют действительные числа. Действительные числа относятся к комплексным числам с мнимой частью как 0. Мы можем классифицировать эти числа в иерархической диаграмме, как показано ниже:

Натуральные числа могут быть далее уменьшены до четных, нечетных, простых, простых, составных и точных квадратов. числа.

Предыдущий урок | Главная страница | Следующий урок

Какие бывают типы чисел? — Видео и стенограмма урока

Целые числа

Вернемся ко мне очень быстро, хотя я действительно живу в Купертино, Купертино является частью округа Санта-Клара. Это означает, что, поскольку я житель Купертино, я также житель округа Санта-Клара. Но обратное не обязательно верно, потому что не все, кто живет в округе Санта-Клара, живут в Купертино, поэтому вы должны быть осторожны, путешествуя туда и обратно.

Числа точно такие же. Если мы станем немного менее конкретными, то получим целые числа , . Все натуральные числа являются частью целых чисел, как и все люди, живущие в Купертино, также живут в округе Санта-Клара. Но есть одно целое число, которое не является натуральным числом. Это число 0. Итак, когда мы говорим о целых числах, мы говорим о числах, которые начинаются с 0 и начинают расти на 1, 2, 3 и так далее.

Диаграмма, показывающая разницу между натуральными и целыми числами

Целые числа

Если вернуться назад в моей ситуации, Купертино и округ Санта-Клара являются частями Калифорнии. Опять же, не все жители Калифорнии живут в Санта-Кларе или, точнее, в Купертино. Но если вы живете в Купертино или Санта-Кларе, вы определенно живете в Калифорнии.

Делая шаг вперед с точки зрения чисел, мы получаем так называемые целые числа .Опять же, не все целые числа являются целыми числами и натуральными числами. Но все числа целые и натуральные — целые числа. Целые числа теперь также добавляют к отрицательным числам: -1, -2, -3 и так далее и далее в отрицательном направлении.

Rational Numbers

Сделав еще один шаг назад, я думаю, что большинство людей знают, что Калифорния — это штат, который является частью США, поэтому я также являюсь резидентом Соединенных Штатов. Опять же, каждый, кто является жителем Калифорнии, также является жителем США.С. Но не все, кто живет в США, живут в Калифорнии.

Эта тенденция продолжается с цифрами. Делая еще один шаг назад, мы приходим к так называемому рациональному числу . Новые пополнения в клубе — это фракции. Это означает, что у нас могут быть такие вещи, как -1/2, 1/3, 3/4 или, может быть, 11/7.

Список становится немного сложнее писать, но, опять же, вы можете представить, что здесь много разных типов чисел. По-прежнему верно, что все предыдущие числа, которые мы упомянули, являются рациональными числами, но не все рациональные числа, особенно эти дроби, являются частью чисел в целых числах, целых числах или натуральных числах.

Диаграмма, показывающая различные типы рациональных чисел

Иррациональные числа

Теперь, когда мы взяли место, где я живу, вплоть до того факта, что я живу в Америке, мы, вероятно, не должны упускать из виду людей, которые живут в разных странах. Но они в другой группе. Например, для людей, которые живут в Японии или Франции, вы не живете в Америке, поэтому вы являетесь частью отдельной группы.

У иррационального числа пи нет конца

То же самое происходит с числами. Есть отдельная группа чисел, которая не подходит к остальным. Их называют иррациональными числами . Иррациональные числа — это все числа, которые нельзя описать как дроби.

Таких разных номеров много. Одна из тех, о которых вы, возможно, слышали, называется «пи», то есть 3.14159 … и это все, что я знаю, но это продолжается вечно, и вы не можете представить число Пи в виде дроби, чтобы оно стало точной десятичной дробью. Другой — квадратный корень из 2, что-то вроде 1,4, но опять же, десятичная дробь продолжается вечно, и нет дроби, которая могла бы ее представить.

Эти иррациональные числа представляют собой отдельную группу. Они не являются частью рациональных, натуральных или целых чисел; они не связаны, но разделены.

Реальные числа

Мне не нравится заканчивать рассказ о сепаратизме.Независимо от того, в какой стране вы живете, мы все жители планеты Земля. Цифры такие же. Они счастливы, и им нравится быть вместе. Все они живут под знаменем того, что называется действительными числами . Иррациональное и рациональное соединяются вместе, и вместе они образуют действительные числа.

Резюме урока

Напомним, что наиболее точным набором чисел являются натуральные числа: 1, 2, 3 и так далее, и так далее. Следующий шаг — это целые числа, и вы просто добавляете 0 к группе; все остальное остается прежним.Когда мы переходим к целым числам, мы складываем отрицательные числа: -3, -2, -1, 0, 1, 2, 3. Далее идут рациональные числа, а рациональные числа дают нам дроби.

Иррациональное является отдельным от этого, и это числа, которые не могут быть дробями, например пи и квадратный корень из 2. Действительные числа объединяют рациональное и иррациональное в один большой набор.

Натуральные числа	Также известные как счетные числа, они включают 1,2,3,4,5,6…
Целые числа	Все натуральные числа, включая 0
Целые числа	Все целые числа, включая отрицательные числа
Рациональные числа	Все числа, включая дроби
Иррациональные числа	Числа, которые нельзя выразить дробями, например, пи
Реальные числа	Все номера

Типы чисел в математике с примерами Свойства и определения

Использование чисел в математике может сбивать с толку учащихся.Существует много типов чисел , и некоторые люди могут не знать разницы между ними. Вот список разных типов: натуральные, целые, целые, рациональные, иррациональные. В статье также описывается, как каждый тип используется в математике и как они выглядят, если записать их в виде уравнения или графически на числовой прямой.

В математике существует два типа чисел : целые числа и дроби. Целые числа включают 0–9, а дроби включают все, что имеет десятичную точку, например 3/4 или.75. Существует также другой тип чисел, называемый иррациональным числом, который включает число пи (3,14) и квадратный корень из 2 (0,5).

Типы чисел в математическом списке

• Рациональное число
• Иррациональное число
• Действительное число
• Целое
• Натуральное число
• Дробь
• Комплексное число
• Число
Десятичное число
• Составное число
• Десятичное число
• Квадратное число
• Треугольное число
• Отрицательное число

Рациональное число

Рациональное число — это число, которое может быть выражено как частное или дробное от двух целых чисел, числителя и знаменателя. Рациональные числа являются частью набора действительных чисел, и их десятичные представления продолжаются бесконечно без повторения цифр. Десятичное представление иррационального числа в конечном итоге сформирует шаблон, который повторяется бесконечно.

В математике рациональные числа часто представлены дробями с целыми коэффициентами, а не десятичными, но они также могут быть записаны в любой другой форме, если это облегчает их чтение или понимание.

Например, 1/2 = 0.5 будет представлять точность от половины до одного десятичного знака, а 2/3 = 0,666… будет представлять точность от двух третей до трех десятичных знаков, потому что оба имеют завершающие десятичные знаки.

Попробуйте также: Типы углов

Иррациональное число

Иррациональные числа — забавные вещи. Их нельзя записать дробями, как рациональные числа (a / b). В иррациональных числах есть десятичные дроби, которые продолжаются бесконечно, но не повторяются. Самое известное иррациональное число — Пи, десятичное число которого равно 3. 141592653…

Попробуйте также: Разница между параболой и гиперболой

Действительное число

Действительное число — это число, которое можно вычислить без использования мнимого числа. Они также известны как рациональные числа и представляют собой подмножество всех действительных чисел. Примеры включают 1, 2, 3, 4, 5… и т. Д. Все другие значения, такие как пи (3,14) или π (3,14159…), не считаются действительными числами, потому что они не могут быть выражены на стандартной шкале линейки только целыми числами ( 1-9).

Попробуйте также: Типы треугольников

Целое число

Целое число — это целое число без дробной части. Он может быть положительным, отрицательным или нулевым. Существует много различных типов целых чисел, таких как натуральные числа, рациональные числа и иррациональные числа, и это лишь некоторые из них.

Попробуйте также: 17 разделов математики

Натуральное число

Натуральные числа — это подмножество набора целых чисел. Обычно они используются в счетах, но также имеют много других применений в математике.Например, натуральные числа можно использовать для построения шаблонов, повторяющихся во многих различных масштабах.

Последовательность Фибоначчи — один из таких паттернов; он описывает, как добавление двух последовательных терминов приводит к следующему термину: 1, 1, 2, 3, 5, 8… Эти серии представляют пропорции, встречающиеся в природе и формах искусства, таких как картины или музыкальные композиции.

Свойства натурального числа делают их идеальными для использования в системах моделирования со схожими свойствами, такими как рост населения или химические реакции; они являются важной частью большинства математических областей, включая исчисление и линейную алгебру.

Дробь

Дробь относится к выражению, которое показывает деление, где обе величины являются не целыми числами (целыми числами), а дробями (числами с чертой над ними). Например, 2/3 = 2, разделенные на 3 или 1/4 = 4, разделенные на 4. Это означает, что вы делите одно количество на другое, в результате получается соотношение, такое как 1: 2, и каждый раз, когда вы умножаете два элемента вместе, будет три .

Комплексное число

Комплексное число имеет как мнимую, так и действительную части, которые перемножаются.Действительная часть может быть выражена как x + iy; где x называется действительной составляющей, а y — мнимой составляющей.

Это означает, что если бы вам дали два разных значения для x или y, они составили бы два разных представления одного комплексного числа, потому что одно будет иметь мнимую часть (y), а другое — действительную (x) ».

Число

Числа полезны, потому что они позволяют нам измерять вещи. Например, если у вас есть два яблока и апельсин, но только один пакет чипсов, количество яблок равно 2, а количество апельсинов равно 1.

Десятичное число

Десятичное число используется для отображения чисел с дробями. Математика использует его как способ представления точного числа без использования целой системы счисления. Например, если у меня осталась половина моего файла cookie, я могу представить это, сказав «0,5», что означает, что после десятичной точки стоят две цифры, и они оба являются нулями, потому что у меня будет всего 5 файлов cookie.

Десятичные дроби важны в математике, потому что они позволяют нам выражать очень маленькие или очень большие числа, которые нельзя выразить с помощью натуральных чисел, доступных для счета на руках или пальцах!

Составное число

По мнению математиков, составные числа — это самая большая группа целых чисел.Они образуются путем сложения двух или более простых чисел. Число 10 является составным числом, потому что оно состоит из 2 и 8, которые являются простыми числами. Составные числа обладают множеством интересных свойств, которые отличают их от других групп целых чисел.

Простое число

В математике простое число — это натуральное число, единственными множителями которого являются ровно два различных натуральных числа. Простое число можно записать как 2 ∙ 2, 3 ∙ 3 и 5 ∙ 5 и т. Д. Первые несколько простых чисел — это 2, 3, 4, 5, 7 и 11.

Простые числа важны в математике, потому что они являются строительными блоками всех других целых чисел. Они также очень полезны для решения математических задач, связанных с сложением или умножением с большими целыми числами (числами без десятичной точки).

Например: если вы хотите узнать, что равно 9 + 14, вы должны использовать эту формулу: 9 + 14 = 23, что означает, что 23 — это ответ! И наоборот, если вы хотите узнать, что такое 23-

Квадратное число

Квадратное число — это число, которое имеет нечетное количество цифр и заканчивается цифрой «4» или «9».Слово «квадрат» в математике относится к чему-то, что можно умножить само на себя. Узнать, является ли число квадратом, можно по формуле: (число) 2 = (ответ). Например, 25² = 625.

Треугольное число

Треугольное число — это число, которое можно получить, умножив три последовательных числа вместе. Например, первое треугольное число 1x2x3 = 6. Треугольные числа просты в вычислении и имеют множество приложений в математике. Их также интересно использовать в качестве ответа на математические задачи.

Треугольные числа могут помочь вам решить все виды математических задач. Вы можете не осознавать этого, но на самом деле они используются каждый день, поэтому, если вы знаете, как их использовать, то нет никаких ограничений на то, что вы можете с ними делать!

Отрицательное число

Многие люди думают, что отрицательное число противоположно положительному. Например, если у вас есть два яблока и вы съели одно яблоко, у вас останется одно яблоко. Если кто-то скажет вам, что у него -2 яблока, это будет означать, что у него только 2 яблока (а не 8).

Это означает, что их общее количество яблок было меньше нуля. Отрицательные числа используются в математике, чтобы показать, что осталось после сложения или вычитания других чисел;

например, когда мы вычитаем 3 из 5, мы получаем 2, потому что теперь осталось на две вещи больше, чем раньше (3-5 = 2). Система позиционных значений упрощает понимание этого за счет использования таких цифр, как 1023-35, которые будут иметь разные значения. Типы номеров.

Дискретные и непрерывные числа

Дискретные числа представляют собой точное значение без каких-либо пробелов или пробелов между цифрами, в то время как непрерывные числа имеют бесконечные значения, поэтому нет четкой граничной точки, где заканчивается их величина.99, тогда оно будет считаться непрерывным числом, поскольку вы не можете точно узнать, когда его величина закончится, просто взглянув на него.

Построение чисел

В математике есть разные типы чисел, но построение чисел — сложный процесс, требующий знания системы счисления и принципов. Первый шаг к построению чисел — это понимание того, как считать, начиная с единицы и продолжая, пока не дойдем до «десяти». Сосчитав до десяти, нам нужно понять, сколько раз мы считали по два.

Например: если вы посчитали от 1 до 10 один или два раза, то ваш ответ будет 11 (1 + 2 = 3 × 2). Работая над этой проблемой на бумаге, не забудьте записать, что вы делаете, так как это поможет предотвратить ошибки в будущем.

После того, как ученик определил свой ответ, он должен вычесть шесть из этого числа, потому что между каждым набором из 10 цифр есть шесть шагов (например, разница между 40.

FAQs (Часто задаваемые вопросы)

Q. пять типов чисел?

Ответ: В математике существует пять типов чисел: целые числа, натуральные числа, целые числа, рациональные числа и иррациональные числа.Целые числа состоят из любого числа, кроме дробного или десятичного. Натуральные числа включают в себя все целые числа и ноль. Целые числа могут быть положительными или отрицательными и отражать весь реальный счет, который мы делаем в нашей жизни. Рациональные числа — это дроби, которые содержат целые числа сверху и снизу, в то время как иррациональные числа не могут быть выражены как отношение между двумя целыми числами, такими как пи (3.14).

В. Сколько типов чисел?

Ответ: В математике существует много типов чисел. К ним относятся целые, рациональные, иррациональные и действительные числа.некоторые из них можно найти на графике или линии на координатной плоскости (рациональные числа), которая представляет собой упорядоченную пару (x, y), где x представляет собой расстояние, пройденное на восток от начала координат; y представляет собой расстояние, пройденное на север от исходной точки; оба измеряются в единицах, называемых «метрами» или «пикселями»; координаты представляют собой точки относительно системы осей.

В. Как вы классифицируете числа?

Ответ: Математика — обширный и сложный предмет, имеющий множество разделов. Одно из самых фундаментальных понятий в математике — это классификация, которая относится к тому, как мы идентифицируем и систематизируем различные типы чисел.Например, целые числа — это целые числа без десятичных знаков и дробей; рациональные числа — это числа, которые могут быть выражены в виде отношения, например ½, ⅓, ¼; иррациональные числа — это действительные числа, не повторяющиеся в виде π или √2.

Классификация чисел [Видео и практические вопросы]

Почему мы классифицируем числа? Почему мы даем им имена, например целые, иррациональные или отрицательные числа? По той же причине, по которой мы все классифицируем, мы хотим убедиться, что каждый понимает, какие конкретные числа называются и что они означают.6 \).

Типы чисел

В этом видео Mometrix мы предлагаем обзор чисел и их классификации.

Цифры — наш способ поддерживать порядок. Считаем, сколько денег у нас есть. Измеряем расстояние. Мы используем процентов для обозначения продажи. Числа являются неотъемлемой частью нашего повседневного существования, будь то целые числа, рациональных чисел, или числа первого типа, на которые мы собираемся взглянуть, действительные числа.

Действительные числа

Действительное число — это любое значение непрерывной величины, которое может представлять расстояние на числовой прямой.По сути, это любое число, которое вы можете придумать. Пятьдесят (50) — действительное число. Один миллиард (1 000 000 000) — очень большое действительное число. Действительные числа включают три классификации чисел, о которых мы поговорим чуть позже. Целые числа, рациональные числа и иррациональные числа — все это действительные числа.

Мнимые числа

Мнимые числа не являются действительными числами. Это комплексные числа, которые записываются как действительное число, умноженное на мнимую единицу (\ (i \)). Например, \ (\ sqrt {-1} \) вычисляется как мнимое число «\ (i \)» и \ (\ sqrt {-25} = 5i \).Хотя мнимые числа не являются «действительными числами», они имеют ценность. Электрики используют мнимые числа при работе с токами и напряжением. Мнимые числа также используются в сложных вычислительных вычислениях. Поэтому то, что эти числа называются «воображаемыми», не означает, что они бесполезны.

Целые числа

Целые числа — это числа, которыми мы считаем. 1, 2, 3, 4 и 5 — все целые числа. Таковы -17 и 0. Целые числа не имеют дробей и десятичных знаков.

Все целые числа называются целыми числами .Целые числа могут быть положительными или отрицательными целыми числами.

Рациональные и иррациональные числа

Все целые числа и целые числа являются частью большей группы, называемой рациональными числами . В эту группу также входят дроби и десятичные знаки. Это означает, что \ (\ frac {3} {5} \) и 7.25 — рациональные числа. Рациональные числа также могут быть положительными или отрицательными.

Рациональные числа имеют противоположности, которые называются иррациональными числами . Эти числа нельзя записать в виде простой дроби.Пи (\ (\ pi \)) — самое известное иррациональное число. У нас есть близкое приближение к тому, как вычислить Пи, но это всего лишь близкое приближение. Пи известен тем, что продолжается вечно. Вот почему это иррациональное число. Это непросто записать дробью.

Натуральные и отрицательные числа

Натуральные числа — это те, которые являются положительными целыми числами, хотя есть некоторые споры относительно того, начинаются ли натуральные числа с 0 или 1. Отрицательные числа , ну, именно так.Это числа ниже 0.

Четные и нечетные числа

Есть также несколько других классификаций чисел. Номера делятся на четные и нечетные. Если вы можете разделить число на 2, это число будет четным. Итак, 24, 36 и 74 — все четные числа, потому что если вы разделите их на 2, вы получите 12, 18 и 37. Четные числа всегда заканчиваются на 0, 2, 4, 6 или 8.

Нечетные числа могут Не делим на 2 и оставляем целое число. Любое нечетное число, разделенное на 2, даст дробь.Итак, 17 ÷ 2 = 8,5, а 23 ÷ 2 = 11,5. Все нечетные числа оканчиваются на 1, 3, 5, 7 или 9.

Дроби

Числители и знаменатели образуют дроби, состоящие из двух целых чисел. Число вверху — числитель; число внизу — знаменатель. Числитель , верхнее число, показывает, сколько деталей у нас есть. Знаменатель , нижнее число, показывает, сколько частей составляет одно целое.

Допустим, у вас есть 6 яблок, и 3 из них съедены. Количество оставшихся у вас яблок будет отображаться как \ (\ frac {3} {6} \).

Затем вы разделите 3, верхнее число, на 6, нижнее число, чтобы определить процент оставшихся яблок. В этом случае цифра составляет 50%.

Итак, вот наш взгляд на числа и их классификацию. От целых чисел до иррациональных чисел нам нужно знать, как называть числа, чтобы знать, что они означают.

Надеюсь, этот обзор был вам полезен!

Типы номеров: разница и классификация

Опубликовано в субботу, май.8 января 2021 г., 10:28

Присоединяйтесь к более чем 100 000 подписчиков AFP на Facebook

Приобрести подписку на AFP

Подпишитесь на подкасты AFP в iTunes и Spotify

Новости, пресс-релизы, письма в редакцию: [email protected]

По вопросам рекламы: [email protected]

(© Сашкин– stock.adobe.com)

Числа представляют собой строку цифр, которые используются для обозначения различных количеств и сумм. Каждое число обозначает размер некоторого количества, большого или маленького. Числа могут быть разных типов и форм, например 9, 8/9, 0,599, 56 и т. Д. Эти числа можно разделить на различные подмножества в зависимости от их свойств, таких как натуральные числа, целые числа, действительные числа, рациональные и иррациональные числа. числа.

Типы чисел в математике

Все числа принадлежат одной системе счисления, но имеют разные типы. Существуют различные комбинации десяти цифр (0–9), которые подразделяются на различные типы чисел. Все эти числовые шаблоны отделены друг от друга благодаря своим уникальным представлениям и свойствам.

Натуральные числа

Натуральные числа являются частью исторически использовавшейся системы счисления. Включает в себя все положительные числа, начиная с 1,2,3 и т. Д. Эти числа не имеют нуля; ноль считается частью подмножества целых чисел. Они также известны как положительные целые числа, которые обозначаются символом N. В установленной форме; они могут быть записаны как: {1, 2, 3, 4, 5,…}

Целые числа

Целые числа — это надмножество натуральных чисел. Эти числа включают в себя все положительные числа от 1, 2, 3 до бесконечности. Набор целых чисел также содержит ноль. Все натуральные числа — это целые числа. На числовой строке нанесены целые числа, начинающиеся с 0, 1, 2 и так далее. Примеры целых чисел: 0, 70, 98, 12345 и т. Д. Целые числа обозначаются символом W.

Целые числа

Целые числа — это числа по обе стороны от нуля, что означает, что целые числа включают полный отрицательный набор натуральных чисел и целые числа, у которых есть ноль, и положительный набор натуральных чисел.Совокупность целых чисел обозначается буквой Z в системе счисления. Все целые числа и натуральные числа являются целыми числами, но не все целые числа являются натуральными или целыми числами. Несколько примеров целых чисел: -10, 5, 0, 23, 100 и т. Д. Целые числа могут быть записаны в виде набора как {…, -3, -2, -1, 0, 1, 2, 3,…}

Фракции

Дробь представляет собой части целого. Он записывается в форме a / b, где и a, и b являются целыми числами и никогда не равны 0. Рациональные числа включают в себя все дробные числа.И завершающие, и повторяющиеся десятичные дроби могут быть выражены дробями. Например, мы можем записать завершающую десятичную дробь 0,25 как 25/100 = 5/10 = ½, а повторяющуюся десятичную дробь 0,2222 как ½.

Рациональные числа

Рациональные числа определяются как целые числа и числа, которые можно выразить дробью. То есть рациональное число можно записать как дробь двух целых чисел. Например, 0,5 — рациональное число, потому что его можно записать как 5/10. Другие примеры рациональных чисел: -1/7, 9/5, 77/99, 1.76, пр.

Иррациональные числа

Иррациональные числа включают числа, которые не могут быть представлены в виде дроби; то есть иррациональные числа не могут быть записаны в виде дробей. Например, квадратный корень из 9 и значение числа пи. Все иррациональные числа являются подмножеством вещественных чисел, что означает, что все иррациональные числа являются действительными числами. Для обозначения иррациональных чисел используется символ Q.

.

Реальные числа

Вещественные числа — это числа, представляющие отрицательные числа, положительные числа и ноль.Набор действительных чисел включает набор всех рациональных и иррациональных чисел. Подмножество вещественных чисел включает целые числа, дроби, целые числа, повторяющиеся десятичные дроби, завершающие десятичные дроби и т. Д. Для представления действительных чисел используется символ R.

Мнимые числа

Числа, не являющиеся частью подмножества действительных чисел, называются мнимыми или комплексными числами. Например, √-7 и √-9. Квадрат этих чисел дает -2 и -5. Квадратный корень отрицательных чисел представлен буквой i, i.е., i = √-1.

По рассказу Прашанта Кумара

Связанные

2.1 — Типы чисел

2.1 — Типы чисел

2.1 — Типы чисел

Рассмотрим типы чисел. Посмотрим на натуральные и целые числа, целые числа, рациональные числа, иррациональные числа, действительные числа, мнимые числа и комплексные числа.

---

Натуральные и целые числа

Начнем с натуральных чисел .Это числа 1, 2, 3,… (Символ… означает, что последовательность продолжается бесконечно.) Они используются для подсчета. Если мы включим ноль, то получим целых чисел , 0, 1, 2, 3,….

Натуральные и целые числа обычно считаются точными. (например, у машины 4 колеса, у паука 8 ног). Но иногда они приблизительны (например, в толпе было 1000 человек).

Вот целые числа, указанные в строке номера :

---

Целые числа

Теперь для каждого из чисел 1, 2, 3,… давайте создадим его напротив или отрицательное значение и поместим его напротив сторону числовой прямой, например:

Мы говорим, что 1 и −1 — противоположности, 2 и −2 — противоположности и т. д.и мы также говорим, что −1 — противоположность 1, а 1 — противоположность −1.

Отрицательные числа используются для описания долгов, а не активов, температуры ниже нуля в отличие от температур выше нуля, высоты ниже уровня моря, а не высоты над уровнем моря и т. д.

Набор чисел…, −3, −2, −1, 0, 1, 2, 3,… (целые числа и их противоположности) называется целыми числами .

---

Рациональные числа

Далее идут рациональные числа.Они являются обобщением обычные дроби, так что давайте сначала рассмотрим их. Помните, что обозначение дроби a / b означает, что мы разбиваем что-то на b равных частей, и у нас есть a этих частей. Например, если мы разбиваем пирог на 4 части, и у нас есть 1 кусок, то у нас есть 1/4 части пирога:

Рациональное число определяется как любое число, которое может быть выражено как частное или отношение из два целых числа .Мы используем то же обозначение дробей для выражения рациональных чисел:

Целое число a называется числителем, а целое число b называется знаменателем. Знаменатель не может быть равен нулю.

Обратите внимание, что если a и b являются натуральными числами (1, 2, 3 и т. Д.), То мы получаем обычную дробь. Таким образом, рациональные числа включают обыкновенные дроби.

Обратите внимание, что 3/1 = 3 и −5/1 = −5, поэтому рациональные числа включают все целые числа.

Рациональные числа также можно записывать в десятичной системе счисления вместо дробной. Например:

1/4 = 0,25

Десятичная запись 0,25 означает буквально «25/100», а 25/100 и 1/4 — эквивалентные дроби.

Обратите внимание, что некоторые рациональные числа не имеют точного десятичного эквивалента. Например 1/3 примерно равно 33/100, но не совсем:

1/3 ≈ 0,33

(Символ ≈ означает « приблизительно равно ».) Рациональными числами обычно считаются , точные . По этой причине программа Algebra Coach не преобразует дроби в десятичные, когда работает в точном режиме.

---

Иррациональные числа

Иррациональные числа — это числа, которые нельзя выразить как отношение двух целых чисел. Примерами являются, а также квадратные корни из многих других чисел, и специальные числа, такие как e и π. Получается, что иррациональных чисел столько же как рационально.Иррациональные числа не имеют точных десятичных эквивалентов. Чтобы написать любое иррациональное число в десятичной системе счисления потребуется бесконечное количество десятичных цифр. Таким образом, это только приблизительные значения:

≈ 1,732, e ≈ 2,718 и π ≈ 3,14,

По этой причине программа Algebra Coach не преобразует иррациональные числа в десятичные. когда он работает в точном режиме.

---

Реальные числа

Рациональные числа и иррациональные числа вместе составляют действительных чисел .Реальные числа Говорят, что это плотный . Они включают каждое число, которое находится в числовой строке.

Числовая строка полезна для понимания порядка чисел . Меньшие числа левее и большие числа правее.

Мы используем символ <для обозначения « меньше » и символ> означает « больше ». Вот несколько примеров использования этих символов:

• 5 <8, потому что 5 находится слева от 8.
• −5 <2, потому что −5 находится слева от 2. Фактически любое отрицательное число меньше любого положительного числа.
• 5 <8 и 8> 5 — два способа констатировать один и тот же факт.
• 3,14 <π <3,15 Я называю это «меньше, чем бутерброд». Это означает, что 3.14 <π, а также π <3.15. Другими словами, число π находится где-то между 3,14 и 3,15.

Реальные числа часто получаются в результате измерений, а измерения всегда являются приблизительными.Например, с одним устройством длина объекта может составлять 5,28 (в некоторых единицах). Это не значит, что длина точно 5,28. Это просто означает, что это ближе к 5,28, чем к 5,27 или 5,29. При более точном (и обычно гораздо более дорогом оборудовании) длина может быть измерено как 5,283, что просто означает, что оно ближе к 5,283, чем к 5.282 или 5.284 и так далее. Если выражение содержит приблизительное число, то это все выражение также является приблизительным.

Щелкните здесь, чтобы получить дополнительную информацию о точности и значащих числах.

---

Мнимые числа и комплексные числа

Если действительные числа включают каждое число в числовой строке, то какие еще могут быть числа? Чтобы ответить на этот вопрос, подумайте, как мы до сих пор строили систему счисления:

• Мы начали с целых чисел (например, 3)
• Нам нужны были противоположности для этих чисел, поэтому мы создали целые числа (числа вроде −3)
• Мы хотели разделить эти числа, но нуждались в рациональных числах для описания некоторые результаты (числа вроде 3/4)
• Мы хотели извлечь квадратный корень из этих чисел, но нам потребовались иррациональные числа, чтобы описать некоторые результаты (например,г. )

Теперь мы хотим извлечь квадратный корень из отрицательных чисел, но нам понадобится новый тип числа. описать результат. Определим квадратный корень отрицательного числа быть мнимым числом . Насколько дальше может этот процесс создание новых типов номеров идет? Ответ — еще один шаг. Мы можем добавить действительное число к мнимому. Результат называется комплексным числом . Это конец строки, потому что оказывается, что каждая возможная операция со всевозможным комплексным числом приводит только к другим комплексным числам.Мы говорим, что комплексные числа делают числа полными.

Где на числовой прямой идут мнимые и комплексные числа? Ответ — нет. На этом рисунке показана комплексная плоскость . Он содержит числовую строку (которая теперь называется действительной осью ) и новая ось, называемая мнимая ось , перпендикулярная ей. Реальные числа лежат на действительной оси, мнимые числа лежат на мнимой оси, а комплексные числа обычно лежат вне действительной оси, либо над ним, либо под ним.

Программа Algebra Coach может работать в реальном или сложном режиме. В реальном режиме не будет выполнить любую операцию, которая приводит к не действительному числу (например, извлечение квадратного корня отрицательного числа).

Щелкните здесь, чтобы получить дополнительную информацию о комплексных числах.

---

Если вы нашли эту страницу в веб-поиске, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.Система счисления

: типы чисел

Ниже приведены подробные сведения о различных типах номеров. Для разных ситуаций используются разные типы чисел, поэтому каждый тип чисел имеет свое значение.

Натуральные числа

• Числа, которые используются при счете, называются натуральными числами.
• Набор натуральных чисел обозначается буквой N.

Где N = {1, 2, 3, 4…}

• 1 — наименьшее натуральное число.

Целые числа

• Когда ноль входит в набор натуральных чисел, они называются целыми числами.
• Набор целых чисел обозначается буквой W.

Где W = {0, 1, 2, 3, 4…}

• Все натуральные числа также являются целыми числами.

Факты о целых числах

• Число 0 — первое и наименьшее из всех целых чисел.
• Все натуральные числа вместе с нулем называются целыми числами.
• Здесь нет последнего или наибольшего целого числа, поскольку они бесконечны.
• Все натуральные числа являются целыми числами. Но все числа не являются натуральными. Например, 0 — это целое, а не натуральное число.
• Каждое целое число на 1 больше предыдущего.

Целые числа

• Когда отрицательные числа всех натуральных чисел включены в набор целых чисел, они называются целыми числами.
• Набор целых чисел обозначается буквой Z. Буква Z взята из немецкого слова zahlen, что означает «считать».

Где Z = {… -4, -3, -2, -1, 0, 1, 2, 3, 4…}

• Ноль никогда не может быть положительным или отрицательным целым числом.
• Целые числа можно разделить на два типа:

* Положительные целые числа: Все натуральные числа являются положительными целыми числами.

Пример: I + = {1, 2, 3, 4…}

* Отрицательные целые числа: Все отрицательные числа натуральных чисел являются отрицательными целыми числами.

Пример: I- = {-1, -2, -3, -4…}

Рациональные числа

• Числа, которые могут быть выражены в форме p / q, называются рациональными числами.

Здесь p и q — целые числа, а q не равно 0

• Набор рациональных чисел обозначается буквой Q.

Где Q = {1/2, 1/3, 5/6, 7/2, 5, -2, 0…}

Иррациональные числа

• Числа, которые НЕ МОГУТ быть выражены в форме p / q, называются иррациональными числами.

Здесь также p и q целые числа и q не равно 0

• Набор иррациональных чисел обозначается буквой П.

Где P = {√2, √3, √4, √5…}

Факты об иррациональных числах

• Сумма рациональных и иррациональных чисел также является иррациональным числом

(Пример: 3 + √2, 6 + √4)

• Разница рациональных и иррациональных чисел тоже является иррациональным числом

(Пример: 6-√2, 9-√4)

• Произведение рациональных и иррациональных чисел также является иррациональным числом

(Пример: 2 x √2, 9 x + √4)

---

---

• Действительные числа включают как рациональные, так и иррациональные числа. Другими словами, он включает в себя все натуральные числа, целые числа, а также целые числа.
• Реальные числа обозначаются буквой R.
• Примеры действительных чисел: 2, 0, 5, -7, -10, ½, 1/6, 1,14, 1,789…

Четные числа

• Числа, которые делятся на 2, называются четными числами. Они также кратны 2.
• Набор четных чисел обозначается буквой E, где E = {2, 4, 6, 8, 10…}
• Есть бесконечные четные числа

Нечетные числа

• Числа, которые НЕ делятся на 2, называются нечетными числами.
• Они НЕ кратны 2.
• Множество нечетных чисел обозначается буквой O, где O = {1, 3, 5, 7, 9…}
• Бесконечные нечетные числа

Простые числа

• Числа, которые делятся на 1, и само число называются простыми числами.
• Примеры простых чисел: 2, 3, 5, 7…

Факты о простых числах

• Число 1 не является простым числом.
• Число 2 — единственное четное простое число.
• 25 простых чисел от 1 до 100. Из них 15 от 1 до 50, а остальные 10 от 50 до 100.

Сопоставимые числа

• Два натуральных числа называются взаимными простыми числами, если их наибольший общий множитель (HCF) равен 1.
• Примеры пар взаимных простых чисел: (7, 9), (15, 16) и т. Д.
• Попарно в скобках всегда пишутся попарно.
• Следует отметить, что пара совпадающих простых чисел не обязательно должна быть простыми числами.

Составные числа

• Числа, которые делятся поровну числами, отличными от 1, и сами по себе называются составными числами.
• Например, 9 можно разделить поровну на 3, а также на 1 и 9, поэтому 9 — составное число. Но 7 нельзя разделить поровну, кроме как на 1 и 7, поэтому НЕ является составным числом. Так что это простое число.
• Число 1 нельзя рассматривать как составное число.