Содержание

Тесты по математике. 6 класс. К учебнику Виленкина Н.Я.

В сборнике представлено 32 теста в двух вариантах, примерно одного уровня трудности. Каждый тест относится к определенному параграфу учебника. На выполнение теста выделяется от 15 до 25 минут времени урока. Для учителя даются методические рекомендации по подсчёту баллов и выставлению отметок. В конце приведены ответы ко всем заданиям тестов. Сборник также может быть использован учащимися 6 класса для самостоятельной работы.

СОДЕРЖАНИЕ
Странички для учителя 5
ТЕСТ 1. Делители и кратные 7
Вариант 1 7
Вариант 2 9
ТЕСТ 2. Признаки делимости на 10, на5и на2 11
Вариант 1 11
Вариант 2 13
ТЕСТ 3. Признаки делимости на 9 и на 3 15
Вариант 1 15
Вариант 2 17
ТЕСТ 4 Простые и составные числа 19
Вариант 1 19
Вариант 2 21
ТЕСТ 5. Наибольший общий делитель. Наименьшее общее кратное 23
Вариант 1 23
Вариант 2 25
ТЕСТ 6. Основное свойство дроби. Сокращение дробей 27
Вариант 1 27
Вариант 2 29
ТЕСТ 7.

Приведение дробей к общему знаменателю 31
Вариант 1 31
Вариант 2 33
ТЕСТ 8. Сравнение дробей. Сложение и вычитание 35
Вариант 1 35
Вариант 2 37
ТЕСТ 9. Сложение и вычитание смешанных чисел 39
Вариант 1 39
Вариант 2 41
ТЕСТ 10. Умножение дробей 43
Вариант 1 43
Вариант 2 45
ТЕСТ 11 Нахождение дроби от числа 47
Вариант 1 47
Вариант 2 49
ТЕСТ 12. Применение распределительного свойства умножения 51
Вариант 1 51
Вариант 2 53
ТЕСТ 13. Взаимно обратные числа 55
Вариант 1 55
Вариант 2 57
ТЕСТ 14 Деление дробей 59
Вариант 1 59
Вариант 2 61
ТЕСТ 15 Нахождение числа по его дроби 63
Вариант 1 63
Вариант 2 65
ТЕСТ 16. Отношения 67
Вариант 1 67
Вариант 2 69
ТЕСТ 17. Пропорции 71
Вариант 1 71
Вариант 2 73
ТЕСТ 18. Пропорциональные зависимости 75
Вариант 1 75
Вариант 2 77
ТЕСТ 19. Масштаб 79
Вариант 1 79
Вариант 2 81
ТЕСТ 20. Длина окружности. Площадь круга 83
Вариант 1 83
Вариант 2 85
ТЕСТ 21. Положительные и отрицательные числа 87
Вариант 1 87
Вариант 2 89
ТЕСТ 22. Модуль числа. Сравнение чисел 91
Вариант 1 91
Вариант 2 93
ТЕСТ 23. Сложение 95
Вариант 1 95
Вариант 2 97
ТЕСТ 24. Вычитание 99
Вариант 1 99
Вариант 2 101
ТЕСТ 25. Умножение 103
Вариант 1 103
Вариант 2 105
ТЕСТ 26. Деление 107
Вариант 1 107
Вариант 2 109
ТЕСТ 27. Рациональные числа 111
Вариант 1 111
Вариант 2 113
ТЕСТ 28. Раскрытие скобок 115
Вариант 1 115
Вариант 2 117
ТЕСТ 29. Коэффициент. Подобные слагаемые 119
Вариант 1 119
Вариант 2 121
ТЕСТ 30. Решение уравнений 123
Вариант 1 123
Вариант 2 125
ТЕСТ 31. Координатная плоскость 127
Вариант 1 127
Вариант 2 129
ТЕСТ 32. Итоговый 131
Вариант 1 131
Вариант 2 133
Ответы 135

Тест по математике для 6 класса на делители и кратные (учебник Виленкина)

Перед тем, как договариваться с репетитором по математике о начале реальных занятий Вы можете самостоятельно протестировать Вашего ребенка по основным разделам программы 6 класса (учебник Виленкина). На этой странице размещен тест по теме «делители и кратные». Уровень представленных задач соответствует базовым требованиям к знаниям шестиклассника и предназначен для тематической (долгой) работы репетитора по математике с неглупым (средним) учеником. Решайте и сравнивайте свой уровень! Он-лайн математика для ученика 6 класса. Задачи могут быть использованы для совместного обсуждения их решений и проверяют весь комплекс навыков решения задач на свойства делимости.

Задание 1. Натуральное число b, которое делится без остатка на число

а, называется … 

Выберите ответ:

Задание 2. Укажите название для числа, которое имеет ровно 2 натуральных делителя?

Выберите ответ:

Задание 3. Укажите число, кратное числу 9.

Выберите ответ:

Задание 4. Укажите число, которое делится одновременно на 2, на 3 и на 5.

Выберите ответ:

Задание 5. Какое из чисел является составным? 

Выберите ответ:

Задание 6. Укажите верное разложение числа 840 на простые множители.  

Выберите ответ:

Задание 7. Найдите результат деления числа  на число

Выберите ответ:

Задание 8. Укажите наибольший общий делитель чисел 36 и 60.

Выберите ответ:

Задание 9. Укажите наименьшее общее кратное чисел 108 и 144

Выберите ответ:

Задание 10.  Папа и Денис решили измерить шагами расстояние от дома до речки. Сначала его измерял папа, а затем с той же точки и по той же тропинке пошел Денис. На каком расстоянии от точки старта их следы совпали в первый раз, если шаг папы равен 90см, а шаг Дениса 70 см? 

Выберите ответ:

Задание 11. Мама купила 128 семян гороха и 140 семян фасоли. Она хочет на каждой грядке посадить и горох и фасоль так, чтобы на любых двух грядках росло одинакового количество гороха и одинаковое количество фасоли. Какое наибольшее количество грядок она может сделать?

Выберите ответ:
Я хочу отправить результаты на почту

Меня зовут
и я хочу отправить свои результаты
на e-mail

Варианты ответов выбирались с таким рассчетом, чтобы поймать невнимательного или недостаточно знающего математику ученика на наиболее типичных для данной темы ошибках. Зачастую вместо наибольшего общего делителя дети ищут наименьшее общее кратное, и наоборот. Для определения делимости на 9 регулярно используют последнюю цифру. Если репетитору по математике удастся найти задания, провоцирующие ученика к совершнию этих ошибок и подробно остановиться на каждой из них, это поможет значительно улучшить общую успеваемость. Главное обсуждать ошибки, а не просто их исправлять!

Автор теста, репетитор по математике Колпаков А.Н.
Москва, м. Строгино.

ГДЗ Математика 6 класс Чулков, Шершнёв, Зарапина

Математика 6 класс

Тематические тесты

Чулков, Шершнёв, Зарапина

МГУ- школе

Просвещение

Шестой класс производит на родителей неизгладимое впечатление, так как сложности предыдущих лет начинают казаться просто цветочками.

Иногда приходится бороться с отчаянным нежеланием детей делать уроки и вообще ходить в школу. Любой пропуск уроков грозит снижением оценок по предмету, потому что можно упустить связующую нить между разными материалами. В это время родителям не стоит ослабевать контроль, иначе потом придется бороться с настоящими проблемами. Решебник к учебнику «Математика. Тематические тесты 6 класс» Чулков поможет всегда быть в курсе того, успевает ли ребенок по данной дисциплине или ему требуется настоятельная помощь в изучении.

Фабула данного сборника.

В пособии находится сорок восемь тестов, разделенных по определенным тематическим группам. В принципе каждый из них должен подтвердить, что школьник усвоил определенную тему. Завершает ГДЗ по математике 6 класс Чулков итоговый тест, предусмотренный для двух вариантов.

Для каких целей он подходит.

Разнообразие предметов и обилие уроков часто ведут к своеобразной путанице в голове учащихся.

Естественно требуется время на то, чтобы все уложилось и усвоилось. Но у ребят его попросту нет. Приходится либо повторять что-то, либо заучивать, делать бесконечные проекты, которые по большому счету лишь отвлекаю от учебы, выполнять д/з. И так изо дня в день. Причем многие школьники посещают еще дополнительные секции. Таким образом времени как такового у них на отдых нет совсем, что иногда может негативно сказаться на успеваемости, так как вместо усвоения материала, будет происходить его стирание из памяти. Решебник к учебнику «Математика. Тематические тесты 6 класс» Чулков позволит выявить нуждается ли ребенок в помощи и какие именно разделы ему не даются. «Просвещение», 2018 г.

Название

Решебник №1

Решебник №2

Тест т17 по математике 6 класс виленкин

Тест т17 по математике 6 класс виленкин

Ответы к тестам по математике автора Рудницкая. Тогда вы попали на нужный сайт. Издательство: Академкнига. Математика 6 класс петерсон. Домашние задание по математике для учебника за онлайн гдз для номера 16решебник.

По математике 6 класс Рудницкая к учебнику Виленкина. Ошибка соединения с базой. Математика 6 класс. Рабочая программа математика 6 класс. Рабочая программа по математике 6 класс. На этой странице расположено пособие с гдз на тесты для.

Ранее. Городская олимпиада по математике 6 8 классы. Решебник по математике 6 класс виленкин мобильная версия. Самые свежие решебники по всем школьным предметам в режиме онлайн у нас на сайте. Вашему вниманию предлагаются ответы к тестам.

По математике за 6 класс автора Рудницкая. ФГОС Рудницкая. Умк тесты по математике 6 класс виленкин фгос рудницкая экзамен. Отсутствует подключение к базе данных. Рекомендуем посмотреть. ГДЗ к учебнику 6 класс Виленкин находятся здесь. К учебнику Виленкина Экзамен. Ищите.

Об учебной жизни лицея, условия поступления, задачи вступительных олимпиад. Предлагаю Вашему вниманию тесты по основным темам курса математики изучаемым в 6 классе по учебнику Н. Я. ВИЛЕНКИНА, В. И. ЖОХОВА, А. С. ЧЕСНОКОВА, С. И. ШВАРЦБУРДА приложение к рабочей программе опубликованной.

6 класса, которые применяются при обучении предмету по учебнику Виленкина 6.32 теста в двух вариантах. Авторы: Рудницкая В. Н. Издательство: Экзамен. Гдз по математике 6 класс виленкин. Задачи тезисы по математике. Нужны ответы на тесты.

Вместе с

Тест т17 по математике 6 класс виленкин часто ищут

тесты по математике 6 класс рудницкая.

тесты по математике 6 класс никольский.

итоговые тесты по математике 6 класс виленкин.

тесты по математике 6 класс скачать бесплатно.

тесты по математике 6 класс рудницкая скачать.

итоговый тест по математике 6 класс с ответами.

тесты по математике 6 класс мерзляк.

тесты по математике 6 класс журавлев

Читайте также:

Полный курс математики 4класс узорова гдз

Поппер домашнее задание по обществознанию 10класс

Гиа 9 класс математика 2018 лысенко регать онлайн

История 5 класс рабочая тетрадь ответы часть 1 г и годер

Обществознание 10 класс вопросы и задания к главе ii ответы

ГДЗ к учебникам и тетрадям по Математике за 6 класс.

Готовые ответы бесплатно

Шестая ступень образования – это символический экватор школьной жизни. Он не приносит особого напряжения – в этом году не добавляются новые предметы, да и все знакомые науки не становятся слишком тяжелыми, просто углубляя знание ранее изученного. Но в работе с математикой наступает ответственный момент. В следующем классе предстоит её разделение на две чрезвычайно сложные дисциплины – алгебру и геометрию. И сейчас очень важно проверить, успешно ли освоен весь курс, не появились ли серьёзные пробелы. Уроки математики в школе позволяют не только сформировать навыки счета, но и научиться анализировать материал, а также развить логическое мышление. В шестом классе школьник уже может считать, читать и писать. Это время, когда кругозор ученика расширяется и он становится более самостоятельным в плане учёбы. В шестом классе проходят более сложные темы и задачи, в решении которых помогают онлайн-гдз, которые всегда можно отыскать на нашем сайте. Подросток сможет без труда подготовиться к любой контрольной работе, написанию тестов по любой теме.

Таким образом, минимизируются стрессовые ситуации для детей во время самостоятельных.

Чем же так хорош онлайн-решебник по математике за 6 класс

Данное подспорье было разработано лучшими педагогами страны (именно: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд, С.М. Никольский, М.К. Потапов, Н.Н. Решетников, В. Шевкин, Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова, Е.А. Бунимович, Е. А. Бунимович, Л. В. Кузнецова, С. С. Минаева). Авторы старались создать полезный решебник. По нему могут спокойно заниматься не только отличники и хорошисты, но и те школьники, которым эта дисциплина дается крайне тяжело. Благодаря данной замечательной книге ребята сумеют сэкономить драгоценные часы, и качественно выполнить домашнее задание, не переживая больше о своей успеваемости. Самое сложное в любой науке – точно понять уровень своих знаний, определить в них слабые места, и направить на них все усилия. Сделать это можно только с помощью профессионала. Но учитель не может успеть в течение каждого урока продиагностировать успехи абсолютно всех своих учеников. Тогда приходит на помощь виртуальный репетитор, который проанализирует все. Но самое главное – не просто выявит проблемные темы, а поможет подтянуть знания так, чтобы перейти к следующему учебному году без серьёзных проблем. Издание поможет шестикласснику понять алгоритм выполнения заданий по всем темам программы:

  • противоположные числа;
  • делители и кратные;
  • разложение на простые множители;
  • умножение и деление обыкновенных производных;
  • нахождение дроби от числа;
  • решение задач на координатной плоскости.

Все упражнения даны в двух вариантах, и полностью отражают разделы основного учебника текущего учебного года. Поэтому издание послужит отличным помощником и в седьмом классе, когда начнётся изучение сложнейшего материала, и понадобится повторить пройденный материал.

Лучший помощник – онлайн-сборник по математике для шестых классов

Пособие разработано не в качестве заурядной шпаргалки, из которой копируют готовый ответ. Цель издания – помочь получить твёрдые знания при самостоятельной и добросовестной работе шестиклассника. Справочник имеет массу полезных свойств, помогающих школьнику чувствовать себя увереннее на уроках по технической дисциплине:

  • верные ответы на некоторые номера упражнений содержат уточняющие комментарии, а также полезные подсказки от мастеров своего дела;
  • пятиклассники становятся более независимыми от помощи преподавателя или родителей, развивают в себе дисциплину;
  • составлен под контролем федерального государственного образовательного стандарта второго поколения.

Виленкин 6 кц. Принципы эффективного самостоятельного приготовления

Математика — это особняк среди школьных предметов. Действительно, ее изучению отводится очень много времени. Более того, математика начинается в первом классе и завершается только в конце одиннадцатого. Кроме того, по окончании 9-го и 11-го года обучения именно по математике выдается окончательный аттестат, называемый ОГЭ и ЕГЭ соответственно.

Выхлопные экзамены являются обязательными, т.е. их нельзя избежать ни при каких обстоятельствах.При этом математические способности у разных детей очень разные. Не все это возможно легко. В последнем случае будет полезно воспользоваться вспомогательной литературой, например, онлайн-Виленкинским решебником с содержанием правильных ответов.

Учебно-методический комплекс Н.Я. Виленкин, В. Жокова, А. Чеснокова и С.И. Шварцурбуда распространяется Издательским Домом «Мнемозин» с 2015 по 2019 год. Используется во многих школах Российской Федерации.Соответствующие льготы также довольно легко получить в публичных библиотеках. Многие учителя составляют на своей основе собственные рабочие программы по предмету.

За что школьники любят ГДЗ Виленкина по математике?

В зависимости от врожденных способностей к точным наукам разных людей изучение алгебры требует разного уровня приложенных усилий и вложений. Оснащенный большим количеством полезных прикладных материалов сборник для 6 класса, авторы которого Виленкин, Жохов, чеснок, имеет ряд достоинств:

  • Содержание заданий полностью соответствует ГЭФ;
  • достаточно использовать смартфон, планшет или компьютер с выходом в интернет;
  • вы можете выбрать наиболее понятное решение из нескольких предложенных;
  • поиск нужного упражнения производится с помощью числового индикатора в виде таблицы.

Ответы, данные в ГДЗ по математике, переписать нельзя. Их следует внимательно изучить, найти закономерности и полезные способы решения. Интенсивная работа поможет повысить производительность, легко решить контрольно-проверочные, тесты.

Почему Виленкин и Жоков Решебник за 6 класс могут заменить репетитора?

Если ученик хорошо старается на протяжении всей школьной жизни, то, скорее всего, он получит высокие баллы на выпускном экзамене и сможет поступить в хороший университет.При изучении математики особенно важно не допускать пробелов. В шестом классе необходимо со всей серьезностью подойти к освоению абзацев, решению задач, отработке практических навыков и умений:

  • простые дроби. Числитель и знаменатель;
  • доведение до общей основы. Сложение, вычитание, умножение, деление;
  • линейных уравнений. Правило пропорции;
  • самый большой общий делитель. Наименьшее кратное.

Достаточная практика в решении примеров и упражнений, а также своевременное устранение пробелов избавят школьников от проблем в старшей школе. Поэтому GDZ online может порекомендовать любой шестиклассник, который сталкивается с непонятными темами на уроках или при выполнении домашних заданий. Инструкция с готовыми решениями соответствует требованиям GEF.

Представленное учебное пособие Предназначено для общеобразовательных учреждений с углубленным изучением предмета. Имея под рукой ГДЗ, каждый ученик может увидеть правильное решение и разобраться в своих ошибках.Особенно полезен решебник будет для родителей, которым теперь намного проще проверять домашнее задание своего ребенка.

Учебник дает не только базовые знания, но и позволяет избавиться от всех неточностей в решении задач. Стоит отметить, что в пособии предусмотрена преемственность между курсами начального и старшего классов, помогая безболезненно углубиться в более сложный процесс изучения математики.

ГДЗ по математике 5 Виленкин Содержит ответы на вопросы, позволяет проверить на домашних уроках и поработать над ошибками.Каждый номер сопровождается пояснениями, позволяющими лучше понять материал.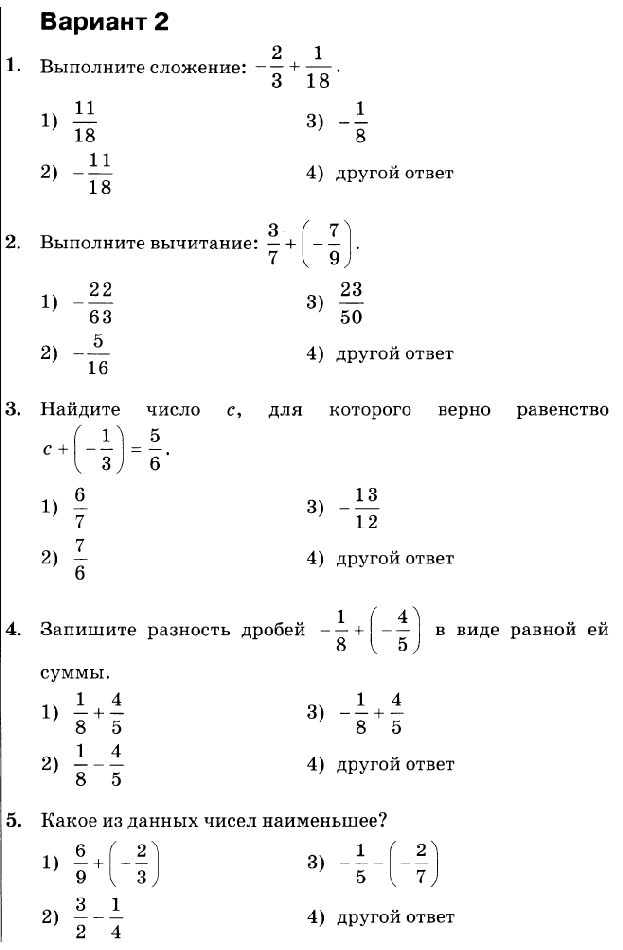 Также номер привязан к определенной задаче, которая выполняется в рабочем блокноте. Каждое математическое действие неразрывно связано, поэтому любое упражнение — это шаг вперед к предметам предмета. Чтобы информация лучше усваивалась, обязательно нужно выполнять домашнее задание.

Новое издание помогает эффективно усвоить материал, а задача становится легкой и непринужденной. Учебник по математике представлен максимально простым и понятным для школьников, поэтому школьники 5 класса, занимающиеся этим учебником, лучше усваивают материал.Виленкин, Жохов, Чесноков, Шварцебрад постарались максимально просто и доходчиво изложить сущность математических действий для базовых средних классов общеобразовательных учреждений.

ГДЗ к рабочей тетради по математике для 5 класса Рудницкая В.Н. Вы можете скачать.

ГДЗ к учебнику по математике для 5 класса Виленкин 1, 2 часть (новый, 2018 г.) можно скачать.

ГДЗ К. Контрольная работа по математике для 5 класса Жохов В. И. Вы можете скачать.

ГДЗ К.Дидактические материалы по математике для 5 класса Попов М.А. Вы можете скачать.

Математический решебник для 5 класса Виленкин представляет собой практическое пособие, представляющее собой сборник готовых домашних заданий, выполненных по классическому учебнику математики, который используется в большинстве общеобразовательных школ РФ. Авторы учебника — авторитетные российские ученые: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбург С.И.

ГДЗ Путина по математике для 5 класса — Виленкин Н.Я.2013-2017 год

ГДЗ по математике для 5 класса Виленкина не является базой для бездумного выбора. Это пошаговый алгоритм выполнения расчетов и онлайн-ответов на задания, позволяющий родителям контролировать успеваемость детей, а школьникам — проверять правильность выполнения примеров и заданий.

Теперь, чтобы пользоваться учебником — совсем не обязательно смотреть на нужную страницу. На нашем сайте вы можете найти желаемое задание, выбрав его номер в таблице выше.

Дополнительные преимущества использования ресурса:

  • Возможность поиска готовых решений Ответы как с ПК, так и с планшета и телефона;
  • Регулярное обновление версий решебников;
  • Наличие нескольких вариантов ответа на одну задачу (из разных решебников).

Наш сайт — серьезный помощник для родителей, которые хотят помочь своим детям в выполнении домашних заданий, но не помнят алгоритмы решения арифметических задач.

Решебник по математике 5 класс: Виленкин, Иоанн, Чесноков, Шварцбург

Номера таблиц соответствуют нумерации заданий в 31-м издании учебника для 5 класса Виленкин Н.Я. Он был опубликован в 2013 году и включает две большие главы:

  • Глава 1 — Натуральные числа;
  • Глава 2 — дробные числа.

В составе обоих разделов рассматриваются понятия, свойства и признаки, основные математические действия. Отдельные параграфы посвящены расчету площадей и объемов.

Благодаря нашему сайту пятиклассники могут самостоятельно разбираться в сложных арифметических примерах и задачах. Родителям больше не нужно пользоваться дорогостоящими репетиторскими услугами: несомненный алгоритм многоэтапного распределения, они смогут самостоятельно помочь своим детям.

В 5 классе в жизни школьника начинается новый образовательный этап. Математика — одно из важнейших звеньев школьного обучения. Ее дети сдают на выпускных экзаменах при поступлении в университет. Поэтому изучение предмета должно проходить на высшем уровне.Чтобы помочь ребенку разобраться во всех тонкостях этой точной науки, стоит использовать онлайн-решебник для 5 класса авторского коллектива: Н.Я. Виленкин, В. Жохов, А. Чесноков, С.И.Шварцборд. В данный сборник вошли все правильные ответы на упражнения из учебника математики ИД «Мнемозина» 2017. Вся информация в нем актуальна на данный момент Time (2019 год). Этот сборник хорошо зарекомендовал себя среди школьных учителей и репетиторов. Они, основанные на уже решенных числах, составляют их уникальную аннотацию для студентов.

Все работы «На отлично» с ГДЗ Виленкин, Жокова, Capsal для пятиклассников

В старшей школе ребенку необходимо запомнить и усвоить большой объем новой информации. На уроке педагог старается максимально подробно разъяснить все правила и законы, привести желаемые примеры и исключения из правил. Студент также должен запомнить всю эту информацию и записать, чтобы затем применить ее на практике. К сожалению, некоторых занятий недостаточно для поддержания высочайшего уровня.Школьник должен делать дома, выполнять все указанные упражнения, усвоить правила. Чтобы все эти манипуляции было проще выполнять, можно воспользоваться онлайн-сборником математики, написанным Виленкиным.

Электронный ресурс

pro Для пользователей:

  • быстрый доступ к информации с любого устройства (компьютера, планшета или телефона). Стоит только включить Интернет;
  • вариативность в решении одной и той же задачи;
  • методических ссылок и пояснений ко многим примерам из учебника;
  • правильные ответы расположены в виде таблицы.В каждой комнате есть отдельная ячейка.

Стоит отметить, что вся информация находится в открытом доступе круглосуточно. Студент может в любой момент открыть нужный вариант и списать «домашнее задание». Хотя бездумное переписывание не приносит никаких полезных результатов. Для повышения производительности стоит для начала самостоятельно разобраться с указанными примерами, а уже проверить их с помощью нужных решений в GDZ.

Рабочая программа по математике с решебником Виленкин

Этот период обучения школьникам достаточно сложен, он требует много эмоциональных и физических сил.Многие родители пытаются успокоить своих детей. Кто-то из взрослых занимается вместе школьником, кто-то нанимает дорогого репетитора. Отличной альтернативой в данной ситуации станет сборник для 5 класса авторов Виленкин, Жохов, Чесноков, Шварцбург. Учебный комплекс рассматривает следующие темы:

  • натуральные числа и шкалы;
  • сложение и вычитание натуральных чисел;
  • умножение I. деление n-x чисел;
  • обыкновенных и десятичных дробей;
  • сложение и вычитание десятичных дробей;
  • умножение и деление десятичных дробей.

Методическое пособие подходит для подготовки к любым поверочным и испытательным работам, тотальным испытаниям и нарезкам.

Если ученик хочет действительно разобраться в сложной вещи, ему придется грамотно насладиться ГДЗ по математике 6 класс Виленкин:

  • Всегда старайтесь сначала решить все домашние задания. Когда не получается, внимательно следите за правильным решением и разбирайтесь на каждом этапе.
  • Выполненные задания и примеры для проверки ответов. Если они не совпали, то сначала попробуйте найти ошибку в их рассуждениях и только потом копаться в доказательствах решебника.
  • Когда совсем нет времени, лучше лучше списать с работы, стараясь запомнить ход решения, а не надеяться на «Авось Учитель не спросит».

Работать нужно только с ГДЗ, которые написаны опытными преподавателями, не содержат опечаток, даже самые сложные понятия подробно и понятно разъясняются. На ГДЗ-Онлайн находится вот такой решебник по математике для 6 класса Виленкин. С ним шестиклассник действительно разберется в дисциплине и повысит успеваемость.

ГДЗ по математике Виленкин 6. Принципы эффективного самообучения

Решебник по математике для 6 класса на Виленкина — это сборник готовых решений и ответов, который составлен на основе учебника математики для шестиклассников, составленного коллективом российских авторов — Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.

Решебник для 6 класса Учебник математики от Виленкина

ГДЗ по математике для 6 класса позволяет учащимся проверить правильность своего домашнего задания.С его помощью им удается самостоятельно разобраться в алгоритме решения сложных задач.

Более того, готовые решения и ответы являются подсказкой для родителей, которые стремятся оказать своим детям посильную помощь в подготовке домашних заданий по математике.

Решебник позволяет снизить учебную нагрузку на шестиклассников, которые не всегда успевают разобраться в решении примера или задачи на уроках.

Интерфейс нашего сайта делает использование учебника максимально удобным для детей и родителей:

  • База ответов доступна с телефона, планшета и компьютера;
  • Таблица чисел позволяет быстро перейти к желаемому ответу;
  • Регулярное обновление решебников исключает вероятность ошибок при подготовке домашних заданий.

Такие опции позволяют сделать процесс выполнения работы по математике максимально эффективным как с точки зрения результата, так и с точки зрения экономии времени.

Учебник математики для 6 класса из Виленкина, Жохова, Чеснокова и Шварцбурга

На нашем сайте представлены готовые решения и ответы на задания учебника для 6 класса от Виленкина Н.Я. В настоящее время большинство школ используют книгу 30-го издания, выпущенную в 2013 году.

В учебном пособии подробно рассматриваются два основных раздела арифметики:

  1. Свойства и операции с натуральными числами;
  2. Знаки, характеристики и математические операции с дробными числами.

В учебнике также приведены сведения о таких арифметических понятиях, как НОК (наименьшее общее кратное) и НОД (наибольший общий делитель), порядок их вычисления, а также особенности составления пропорций.

Книга знакомит шестиклассников с особенностями координат на плоскости, а также с понятием масштаба.Подробно представлены различия между положительными и отрицательными числами, а также правила математических операций с ними.

Математика выделяется среди школьных предметов. Действительно, его изучению уделяется много времени. Причем математика начинается уже в первом классе и заканчивается только в конце одиннадцатого класса. Кроме того, по окончании 9-го и 11-го курсов именно по математике вам необходимо будет сдать итоговые аттестации, называемые ОГЭ и ЕГЭ соответственно.

Выпускные экзамены являются обязательными, т.е. их нельзя избежать ни при каких обстоятельствах. При этом математические способности разных детей очень разные. Не каждому дается предмет без труда. В последнем случае будет полезно использовать вспомогательную литературу, например, онлайн-резолвер Виленкина с содержанием правильных ответов.

Учебно-методический комплекс Н.Я. Виленкина, В. Жохова, А. Чеснокова и С.И.Шварцбурда распространяется издательским домом «Мнемозина» с 2015 по 2019 год.Его используют во многих школах Российской Федерации. Соответствующие руководства также довольно легко получить в публичных библиотеках. Многие учителя на их основе формируют собственные рабочие программы по предмету.

Почему школьники любят ГДЗ Виленкина по математике?

В зависимости от врожденных способностей к точным наукам у разных людей изучение алгебры требует разного уровня усилий и затрат времени. Оснащенный большим количеством полезных прикладных материалов сборник для 6 класса, авторы которого Виленкин, Жохов, Чесноков, имеет ряд преимуществ:

  • Содержание заданий полностью соответствует ФГОС;
  • достаточно использовать смартфон, планшет или компьютер с выходом в Интернет;
  • вы можете выбрать наиболее понятное решение из нескольких предложенных;
  • поиск необходимого упражнения осуществляется с помощью числового указателя в виде таблицы.

Ответы, данные в Maths GDZ, нельзя просто переписать. Их следует внимательно изучить, найти закономерности и полезные решения. Интенсивная работа поможет повысить успеваемость, легко решить контрольно-оценочные работы, тесты.

Почему учитель Виленкина и Жохова в 6 классе может заменить репетитора?

Если ученик усердно старается на протяжении всей школьной жизни, то весьма вероятно, что он получит высокие оценки на выпускном экзамене и сможет поступить в хороший университет.При изучении математики особенно важно избегать пробелов. В шестом классе нужно серьезно отнестись к усвоению абзацев, решению задач, отработке практических навыков:

  • простые дроби. Числитель и знаменатель;
    • Приведение
  • к общей земле. Сложение, вычитание, умножение, деление;
  • линейных уравнений. Правило пропорции;
  • наибольший общий множитель. Как минимум несколько.

Достаточная практика в решении примеров и упражнений, а также своевременное устранение пробелов избавят ученика от проблем в вузе. Поэтому GDZ online можно порекомендовать любому шестикласснику, который сталкивается с непонятными темами в классе или при выполнении домашних заданий. Пособие с готовыми решениями соответствует требованиям ФГОС.

В шестом классе происходит разделение предмета математика на алгебру и геометрию. Это приводит к тому, что студентам необходимо осваивать новые сложные концепции и задачи. Однако не каждый школьник сможет освоить такой материал самостоятельно, и здесь на помощь придет созданное автором решение. Н.Я. Виленкин … Учебник по математике 6 класс станет доступнее, если использовать ГДЗ … Это позволит ученику лучше разбираться в новых для них темах и задачах на решенном примере.

С помощью данного пособия студент может упростить домашнюю подготовку к занятиям. Это также позволяет студентам самостоятельно решать задачи в будущем без каких-либо подсказок. GDZ способствует пониманию языка математики студентами, углубляет их навыки об общих принципах решения математических примеров.

ГДЗ для рабочей тетради по математике для 6 класса Рудницкая В.Н. можно скачать.

ГДЗ для 6 класса учебника математики Виленкин Н.Я. (2018) можно скачать.

ГДЗ для тестов по математике для 6 класса Жохов В.И. можно скачать.

ГДЗ для дидактических материалов по математике для 6 класса Попов М.А. можно скачать

Если ученик хочет действительно разобраться в сложном предмете, ему придется грамотно использовать ГДЗ по математике, 6 класс Виленкин:

  • Всегда сначала пытайтесь решить все домашние числа самостоятельно.Когда не получается, внимательно следите за правильным решением и разбирайтесь с каждым этапом.
  • Проверьте ответы на выполненные задания и примеры. Если они не совпадают, то сначала попробуйте найти ошибку в своих рассуждениях и только потом копайтесь в доказательствах Резервного.
  • Когда совсем некогда хорошо делать уроки, лучше списать работу, стараясь запомнить ход решения, а не надеяться, что учитель может не спросить.

Работать нужно только с теми ГДЗ, которые написаны опытными преподавателями, не содержат опечаток, подробно и понятно объясняют даже самые сложные понятия.На ГДЗ-онлайн есть как раз такое решение по математике для 6 класса Виленкина. С ним шестиклассник действительно разберется в дисциплине и повысит успеваемость.

ГДЗ по математике для 6 класса Виленкин — это онлайн-сборник готовых ответов (из Решебника) на задания одноименного учебника по математике, составленный Н.Я. Виленкин, В. Жохов, А. Чесноков, С.И.Шварцбурд. Он позволяет ученикам проверять правильность домашних заданий и решать сложные задачи, а родителям — оказывать своим детям посильную помощь в подготовке домашних заданий по математике.

Ассистент по изучению математики в 6 классе — решебник Виленкин Н.Я. 2013 год

Курс математики для 6-го класса общеобразовательных школ Российской Федерации включает широкий круг тем, связанных с натуральными и дробными числами. Высокий уровень сложности отдельных задач часто не позволяет ребенку в классе разобраться с алгоритмом решения примера.

Решением этой задачи может быть решатель математики 6-го класса Н.Я. Виленкина, которая представлена ​​на нашем сайте в онлайн-доступе. В чем его преимущества?

  • Благодаря удобному интерфейсу достаточно ввести номер домашнего задания или пример условия (необязательно) в строку поиска — и система предложит список задач с похожими условиями;
  • Для каждого примера дается не только готовый ответ, но и подробный алгоритм его решения.

Такие варианты позволяют ученикам самостоятельно разобраться, как решить ту или иную задачу, а родителям — адекватно проверить домашнее задание учеников.Кроме того, таким образом можно сэкономить много времени.

Что входит в решение по математике в 6 классе: Виленкин, Жохов, Чесноков, Шварцдурд?

Представленное на сайте решение составлено на основе учебника математики для 6 класса под редакцией Н.Я. Виленкин. в 30-м издании (2013 г.). Но это вовсе не означает, что невозможно найти решения для более ранних и более поздних редакций: на самом деле необходимо вбить условия примера в строку поиска — и система найдет искомую проблему.

Учебное пособие Виленкин Н.Я. состоит из двух основных разделов:

  1. Обыкновенные дроби — их понятие, свойства, операции с ними;
  2. Рациональные числа — сущность, роль в выполнении вычислений, математических операций с ними.

В первой части учебника подробно описаны понятие и признаки делимости чисел, механизм вычисления наименьшего общего сокращения (НОК) и наибольшего общего делителя (НОД), а также алгоритм составления и решения пропорций.

Во второй части подробно описаны правила выполнения математических операций с положительными и отрицательными числами, а также порядок решения уравнений с учетом расположения координат на плоскости.

Наш сайт готовых домашних заданий — это не только помощь в решении домашних заданий для 6-х классов и их родителей, но и полноценное практическое пособие, позволяющее самостоятельно постичь азы математики.

Н И Виленкин 6.Принципы эффективного самообучения

Математика стоит особняком среди школьных предметов. Действительно, его изучению уделяется много времени. Причем математика начинается уже в первом классе и заканчивается только в конце одиннадцатого. Кроме того, по окончании 9-го и 11-го курсов именно по математике необходимо будет сдать итоговые аттестации, называемые ОГЭ и ЕГЭ соответственно.

Выпускные экзамены обязательны, т. Е.их нельзя избежать ни при каких обстоятельствах. При этом математические способности разных детей очень разные. Не каждому дается предмет без труда. В последнем случае будет полезно использовать вспомогательную литературу, например, онлайн-резолвер Виленкина с содержанием правильных ответов.

Учебно-методический комплекс Н.Я. Виленкина, В. Жохов, А. Чеснокова и С.И.Шварцбурд распространяется издательством Mnemosyne с 2015 по 2019 год.Его используют во многих школах. Российская Федерация. Соответствующие руководства также довольно легко получить в публичных библиотеках. Многие учителя составляют собственные рабочие программы по этому предмету.

Почему школьники любят ВЛЕНКИН ГДЗ по математике?

В зависимости от врожденных способностей к точным наукам у разных людей изучение алгебры требует разного уровня усилий и затраченного времени. Оснащенный большим количеством полезных прикладных материалов сборник для 6 класса, авторы которого Виленкин, Жохов, Чесноков, имеет ряд преимуществ:

  • Содержание заданий полностью соответствует ГЭФ;
  • просто используйте смартфон, планшет или компьютер с доступом в Интернет;
  • можно выбрать наиболее понятное решение из нескольких предложенных;
  • поиск нужного упражнения осуществляется по указателю в виде таблицы.

Ответы, данные в Госдуме по математике, нельзя просто переписать. Их следует внимательно изучить, чтобы найти закономерности и полезные решения. Интенсивная работа поможет повысить успеваемость, легко управлять контрольными и проверочными рабочими тестами.

Почему ученица Виленкина и Жохова в 6 классе может сменить репетитора?

Если ученик много старается на протяжении всей школьной жизни, то с большой вероятностью он получит высокие баллы на выпускном экзамене и сможет поступить в хороший вуз. При изучении математики особенно важно избегать пробелов. В шестом классе нужно серьезно подойти к освоению абзацев, решению задач и выработке практических навыков:

  • простые дроби. Числитель и знаменатель;
  • снижение к общей основе. Сложение, вычитание, умножение, деление;
  • линейных уравнений. Правило пропорции;
  • наибольший общий множитель. Как минимум несколько.

Достаточная практика в решении примеров и упражнений, а также своевременное заполнение пробелов избавят ученика от проблем в старшей школе.Поэтому GDZ online можно порекомендовать любому шестикласснику, который сталкивается с непонятными темами в классе или в домашней работе. Пособие с готовыми решениями соответствует требованиям GEF.

Если ученик хочет действительно разобраться в сложном предмете, ему придется правильно использовать ГДЗ по математике 6 класс Виленкин:

  • Всегда сначала пытайтесь решить все домашние номера самостоятельно. Когда не получается, внимательно смотрите на правильное решение и разбирайтесь с каждым шагом.
  • Для выполненных задач и примеров проверьте ответы. Если они не совпали, то сначала попробуйте найти ошибку в своих рассуждениях и только потом вникайте в показания поселенца.
  • Когда совсем некогда делать качественные уроки, лучше списать работу, пытаясь запомнить ход решения, а не полагаться на «может учитель не спросит».

Работать нужно только с теми ГДЗ, которые написаны опытными преподавателями, не содержат опечаток, даже самых сложных понятий.На ГДЗ-онлайн есть вот такой решатель математики для 6 класса Виленкин. С ним шестиклассник действительно разберется в дисциплине и повысит успеваемость.

  • Математика в 6 классе включает в себя большой объем знаний. Именно в 6 классе осуществляется переход от простых математических задач к более сложным. Студент уже начинает понимать разницу между алгеброй и геометрией; он должен хорошо разбираться в задачах и формулах.В учебнике есть различные блоки, в которые входят задания и примеры по двум предметам.
  • Решатель математики Виленкина помогает студенту навести порядок. Большой объем материала не всегда хорошо усваивается учениками в школе. Бывает, что студент понимает теорию, но не может понять практику. На конкретных примерах из учебника по расчетам учащиеся сравнивают и перепроверяют свои знания. Благодаря домашнему заданию они имеют возможность досконально разобраться в теме, постепенно обдумывая решение той или иной проблемы.
  • Благодаря GDZ процесс выполнения домашнего задания значительно облегчается, а у ученика развиваются навыки самообучения, теоретический материал находит свое практическое применение, ученик начинает лучше учиться, в нем проявляется тяга к знаниям. Еженедельное выполнение упражнений из учебника поможет школьнику закрепить пройденный материал, подготовиться к контрольной работе и отлично закрыть задание.

    • Принципы эффективного самообучения

  • Шестиклассники продолжают углубленно изучать математику.Классические основы этой дисциплины изучаются в 6 классе. В прошлом году уже с 7-го класса у учеников будет разделение на два самостоятельных предмета — геометрия и алгебра. Чтобы успешно учиться, хорошо подготовиться к текущей и итоговой, диагностической работе, ВПР, шестиклассникам необходимо заранее настроиться на ответственную и систематическую работу. В помощь ученикам качественные учебные материалы, пособия и решатели к ним. Вы можете спланировать свою работу самостоятельно или обратившись за помощью к учителям, репетиторам и родителям.Для того, чтобы самообучение на GDZ было эффективным, вам необходимо:
    — разработать грамотную систему, план работы, исходя из базовых знаний шестиклассника по математике, его интересов, задач и целей. Например, для углубления имеющихся знаний или участия в математических олимпиадах, олимпиадах и т. Д .;
    — придерживаться разработанной схемы, периодически отслеживая достигнутые достижения, выявляя и исправляя недостатки. За динамикой подготовки можно следить после изучения блока: — назначив конкретные даты для мониторинга;
    — Корректировать полученные результаты путем изменения и дополнения программы тренировок.
  • В качестве полезного и интересного базового источника многие учителя, воспитатели и сами шестиклассники называют Н.Я. Учебник Виленкина по математике для 6 класса, в котором сложные темы рассмотрены подробно и полно, для их тщательного и всестороннего изучения есть различные задания. Среди тем, вызывающих наибольшие трудности при изучении математики шестиклассниками, которые подробно рассматриваются в данном пособии, можно выделить:
    — делимость чисел и их знаки;
    — кратность и действия с дробями, имеющими разные знаменатели;
    — пропорции и отношения как математические величины;
    — зависимости прямая и обратная;
    — шкала — раздел, вызывающий наибольшее количество затруднений у шестиклассников;
    — шар, круг, его длина и площадь круга.
  • Для лучшего освоения и закрепления материала желательно дополнить основной учебник практическими занятиями того же автора. Для тех студентов, которые находятся на семейной форме обучения, к учебным материалам можно дополнительно использовать рабочие программы.

Математический решатель для 6 класса по Виленкину — это сборник готовых решений и ответов, основанный на учебнике математики для шестиклассников, составленном коллективом российских авторов — Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.

Решебник для учебника математики, 6 класс от Виленкина

ГДЗ по математике для 6 класса позволяет школьникам проверить правильность домашнего задания. С его помощью им удается понять алгоритм решения. сложные задачи самостоятельно.

Более того, готовые решения и ответы являются подсказкой для родителей, которые стремятся оказать своим детям посильную помощь в подготовке домашних заданий по математике.

Resechnik позволяет снизить нагрузку на шестиклассников, у которых не всегда есть время понять решение примера или проблемы в классе.

Интерфейс нашего сайта делает использование учебника максимально удобным для детей и родителей:

  • База ответов доступна с телефона, планшета и компьютера;
  • Таблица номеров позволяет быстро перейти к желаемому ответу;
  • Регулярное обновление резольверов исключает возможность ошибок при подготовке домашних заданий.

Такие опции позволяют сделать процесс выполнения работы по математике максимально эффективным как с точки зрения результата, так и с точки зрения экономии времени.

Учебник математики для 6 класса от Виленкина, Жохова, Чеснокова и Шварцбурга

На нашем сайте представлены готовые решения и ответы на задания учебника для 6 класса от Н. Виленкина. В настоящее время большинство школ используют книгу 30-го издания, выпущенную в 2013 году.

Учебное пособие IN Подробно рассматриваются два основных раздела арифметики:

  1. Свойства и операции с натуральными числами;
  2. Знаки, характеристики и математические операции с дробными числами.

В учебнике также приведены сведения о таких арифметических понятиях, как НОК (наименьшее общее кратное) и НОД (наибольший общий делитель), приведен порядок их вычисления, а также особенности составления пропорций.

Книга знакомит шестиклассников с особенностями координат на плоскости, а также с понятием масштаба. Подробно описаны различия между положительными и отрицательными числами, а также правила математических действий с ними.

Начало Вселенной | Александр Виленкин

Мы живем после большого взрыва — большого взрыва, произошедшего 13,7 миллиарда лет назад. Во время большого взрыва Вселенная была заполнена огненным шаром, плотной смесью энергичных частиц и излучения. В течение почти столетия физики изучали, как огненный шар расширяется и охлаждается, как частицы объединяются, образуя атомы, и как галактики и звезды постепенно притягиваются друг к другу под действием гравитации. Эта история теперь понятна с мельчайшими количественными подробностями и подтверждена многочисленными данными наблюдений.

Однако остается вопрос, действительно ли Большой взрыв был началом Вселенной. Начало в чем? Чем вызвано? И определяется чем или кем? Эти вопросы побуждали физиков делать все возможное, чтобы избежать космического начала.

В этом эссе я делаю обзор того, где мы сейчас находимся.

Теорема сингулярности Пенроуза

Проблема стоит перед нами с первых дней научной космологии. В 1920-х годах русский математик Александр Фридман дал математическое описание расширяющейся Вселенной, решив уравнения общей теории относительности Альберта Эйнштейна.Фридман для простоты предположил, что распределение материи во Вселенной было совершенно однородным. Его решения имели загадочную особенность: по мере того, как эволюция Вселенной прослеживается в обратном направлении, плотность материи и кривизна пространства-времени неограниченно растут, став бесконечным конечное время назад. Момент бесконечной плотности — космологическая особенность. В этот момент математические выражения, входящие в уравнения общей теории относительности, становятся некорректными, и эволюция не может быть продолжена.Казалось бы, это наводит на мысль, что у Вселенной действительно было начало, но не описываемое законами физики.

Изначально физики надеялись, что сингулярность может быть артефактом упрощающего предположения Фридмана о совершенной однородности, и что она исчезнет при более реалистичных решениях уравнений Эйнштейна. Роджер Пенроуз закрыл эту лазейку в середине 1960-х, показав, что при очень общем предположении сингулярность неизбежна. При условии нулевой конвергенции гравитация всегда заставляет световые лучи сходиться.Это означает, что плотность вещества или энергии, измеренная любым наблюдателем, не может быть отрицательной. Вывод верен для всех известных форм классической материи.

Доказательство Пенроуза основано на концепции неполной геодезической. В общей теории относительности траектории материи представлены прямыми линиями в пространстве-времени или геодезическими. Если пространство-время свободно от сингулярностей, все геодезические должны иметь бесконечную протяженность. Геодезическая, встречающая особенность, не может быть продолжена.Такие геодезические неполны. Пенроуз показал, что пространство-время, удовлетворяющее условию нулевой сходимости (и некоторым дополнительным мягким предположениям), должно содержать неполные геодезические. Кажется, что сингулярность неизбежна.

Аргумент Пенроуза был не совсем убедительным. Хотя классическая материя удовлетворяет условию нулевой сходимости, квантовые флуктуации могут создавать области с отрицательной плотностью энергии. В экстремальных условиях, близких к Большому взрыву, большое значение имеют квантовые флуктуации.Аргумент Пенроуза больше не применим.

Так было до начала 1980-х, когда Алан Гут представил идею космической инфляции.

Вечная инфляция

Инфляция — это период сверхбыстрого ускоренного расширения в ранней истории Вселенной. За доли секунды крошечная субатомная область взрывается до размеров, превышающих размеры всей наблюдаемой в настоящее время Вселенной. Расширение происходит за счет ложного вакуума.

Обычно вакуум считается пустым пространством, но согласно современной физике элементарных частиц пустое пространство — это не ничто.Вакуум — это физический объект, наделенный плотностью энергии и давлением. Он может находиться в разных состояниях или в вакууме. Свойства и типы элементарных частиц различаются от одного вакуума к другому.

Гравитационная сила, вызванная ложным вакуумом, необычна в том смысле, что она отталкивающая. Чем выше энергия вакуума, тем сильнее отталкивание. Такой вакуум нестабилен. Он распадается на низкоэнергетический вакуум, и избыточная энергия производит огненный шар из частиц и излучения.Ложный вакуум был изобретен не для инфляции. Их существование следует из физики элементарных частиц и общей теории относительности.

Теория инфляции предполагает, что в какой-то ранний период своей истории Вселенная занимала высокоэнергетический ложный вакуум. Затем силы отталкивания вызвали сверхбыстрое экспоненциальное расширение Вселенной. Есть характерное время, когда размер Вселенной увеличивается вдвое. В зависимости от модели время удвоения может составлять всего 10 –37 секунд.Примерно за 330 удвоений Вселенная увеличивается в 10 100 раз. Независимо от своего первоначального размера, Вселенная очень быстро становится огромной. Поскольку ложный вакуум нестабилен, он в конечном итоге распадается, образуя огненный шар, знаменующий конец инфляции. Огненный шар продолжает расширяться по инерции и развивается в соответствии со стандартной космологией большого взрыва.

Инфляция объяснила некоторые в остальном загадочные особенности Вселенной, вопросы, которые космология большого взрыва была вынуждена предполагать.Он объяснил расширение Вселенной, ее высокую температуру и наблюдаемую однородность. Инфляционная теория предсказывала, что евклидова геометрия описывает Вселенную в самых больших масштабах. Он также предсказал почти не зависящий от масштаба спектр возмущений малой плотности, вызванных квантовыми флуктуациями во время инфляции. Эти прогнозы подтвердились.

Теория инфляции привела к пересмотру нашего взгляда на Вселенную. Инфляция не заканчивается сразу везде.Области, где ложный вакуум распадается несколько позже, вознаграждаются более сильным инфляционным расширением, поэтому области ложного вакуума имеют тенденцию размножаться быстрее, чем распадаться. В нашем космическом районе инфляция закончилась 13,7 миллиарда лет назад; в отдаленных частях Вселенной это продолжается. Такие регионы, как наш, постоянно формируются. Этот нескончаемый процесс называется вечной инфляцией. Вечная инфляция носит общий характер; и предсказывается большинством моделей.

Распад ложного вакуума зависит от модели.В этом эссе я сосредоточусь на моделях, в которых это происходит через зарождение пузырьков. Вакуумный распад похож на кипение воды. Области с низкой энергией выглядят как микроскопические пузыри и сразу же начинают расти со скоростью, быстро приближающейся к скорости света. Затем пузырьки раздвигаются за счет инфляционного расширения, освобождая место для большего количества пузырьков. Мы живем в одном из этих пузырей, но можем наблюдать лишь небольшую его часть. Независимо от того, как быстро мы путешествуем, мы не можем догнать расширяющуюся границу нашей Вселенной.

Наша вселенная замкнута.

Вечная инфляция открывает интригующую возможность. Если инфляция будет продолжаться и продолжаться в будущем, могла ли она также продолжаться и продолжаться в прошлом? Вселенная без начала избавит от необходимости спрашивать, как она возникла.

Как это часто бывает в физике, непреодолимая сила вот-вот натолкнется на неподвижное препятствие.

Теорема Бордэ-Гута-Виленкина

Препятствие можно найти в теореме Борде-Гута-Виленкина (BGV).Грубо говоря, наша теорема утверждает, что если Вселенная в среднем расширяется, то ее история не может бесконечно продолжаться в прошлом. Точнее, если средняя скорость расширения положительна вдоль данной мировой линии или геодезической, то эта геодезическая должна завершиться через конечный промежуток времени. Разные геодезические, разное время. Важным моментом является то, что прошлая история Вселенной не может быть полной. Схема доказательства приведена в Приложении.

Теорема BGV допускает некоторые периоды сокращения, но в среднем расширение выигрывает.Объем Вселенной со временем увеличивается. Инфляция не может быть вечной и должна иметь какое-то начало.

Теорема BGV широка в своей общности. Он не делает никаких предположений о гравитации или материи. Гравитация может быть притягательной или отталкивающей, световые лучи могут сходиться или расходиться, и даже общая теория относительности может перестать существовать: теорема все равно будет верна.

Ряд физиков построили модели вечной вселенной, в которых теорема BGV больше не актуальна.Джордж Эллис и его сотрудники предположили, что конечная замкнутая Вселенная, в которой пространство замыкается на себя, как поверхность сферы, могла существовать вечно в статическом состоянии, а затем разразиться инфляционным расширением. При усреднении за бесконечное время скорость расширения будет равна нулю, и теорема BGV не будет применяться. Эллис построил классическую модель стабильной замкнутой Вселенной и представил механизм, запускающий начало расширения. Эллис не утверждал, что его модель реалистична; он был задуман как доказательство концепции, показывающей, что вечная вселенная возможна.Не так. Статическая Вселенная нестабильна по отношению к квантовому коллапсу. Она может быть стабильной по законам классической физики, но в квантовой физике статическая Вселенная может внезапно перейти в состояние исчезающего размера и бесконечной плотности. Независимо от того, насколько мала вероятность коллапса, Вселенная не могла существовать бесконечное количество времени до начала инфляции.

Есть еще один способ, по которому Вселенная могла быть вечной в прошлом. Он мог бы проходить через бесконечную последовательность расширений и сокращений.Это понятие было на короткое время популярным в 1930-х годах, но затем от него отказались из-за его явного противоречия второму закону термодинамики. Второй закон требует, чтобы энтропия увеличивалась в каждом цикле космической эволюции. Если бы Вселенная уже завершила бесконечное количество циклов, она достигла бы состояния теплового равновесия и, следовательно, состояния максимальной энтропии. Вся энергия упорядоченного движения превратилась бы в тепло, и повсюду преобладала бы равномерная температура.

Мы не находимся в таком состоянии.

Идея циклической вселенной была недавно возрождена Полом Стейнхардтом и Нилом Туроком. Они предположили, что в каждом цикле расширение больше, чем сжатие, так что объем Вселенной увеличивается. Энтропия вселенной, которую мы сейчас наблюдаем, может быть такой же, как энтропия некоторой подобной области в более раннем цикле; тем не менее, общая энтропия Вселенной увеличилась бы, потому что объем Вселенной теперь больше, чем был раньше. Со временем энтропия и общий объем неограниченно растут, и состояние максимальной энтропии никогда не достигается.Нет максимальной энтропии.

Проблема с этим сценарием состоит в том, что в среднем объем Вселенной все еще растет, и, таким образом, можно применить теорему BGV. Это сразу же приводит к выводу, что циклическая вселенная не может быть вечной в прошлом.

Доказательство Бога

Богословы приветствовали любые свидетельства возникновения вселенной как свидетельства существования Бога. «Что касается первопричины Вселенной, — писал британский астрофизик Эдвард Милн, — читатель может вставить это, но наша картина без Него будет неполной.Некоторые ученые опасались, что космическое начало нельзя описать в научных терминах. «Отрицать бесконечность времени, — утверждал Вальтер Нернст, — значило бы предать сами основы науки».

Ричард Докинз, Лоуренс Краусс и Виктор Стенджер утверждали, что современная наука не оставляет места для существования Бога. Была организована серия дебатов о науке и религии, в которых атеисты вроде Докинза, Дэниела Деннета и Краусса обсуждали теистов, как Уильям Лейн Крейг.Обе стороны апеллировали к теореме BGV, обе стороны обращались ко мне — из всех людей! — для лучшего понимания.

Космологический аргумент в пользу существования Бога состоит из двух частей. Первый простой:

  • все, что начинает существовать, имеет причину;
  • Вселенная начала существовать;
  • Следовательно, у Вселенной есть причина.

Вторая часть утверждает, что причиной должен быть Бог.

Теперь я хотел бы обсудить первую часть аргументации.Современная физика может описать возникновение Вселенной как физический процесс, не требующий причины.

Ничего не может быть создано из ничего, говорит Лукреций, хотя бы потому, что сохранение энергии делает невозможным создание ничего из ничего. Для любой изолированной системы энергия пропорциональна массе и должна быть положительной. Любое начальное состояние до создания системы должно иметь ту же энергию, что и состояние после ее создания.

В этом рассуждении есть лазейка.Энергия гравитационного поля отрицательна; вполне возможно, что эта отрицательная энергия могла бы компенсировать положительную энергию материи, делая полную энергию космоса равной нулю. Фактически, именно это и происходит в замкнутой вселенной, в которой пространство замыкается само на себя, как поверхность сферы. Из законов общей теории относительности следует, что полная энергия такой Вселенной обязательно равна нулю. Другой сохраняющейся величиной является электрический заряд, и снова оказывается, что полный заряд должен исчезнуть в замкнутой Вселенной.

Я проиллюстрирую эти утверждения на примере электрического заряда, используя двумерную аналогию.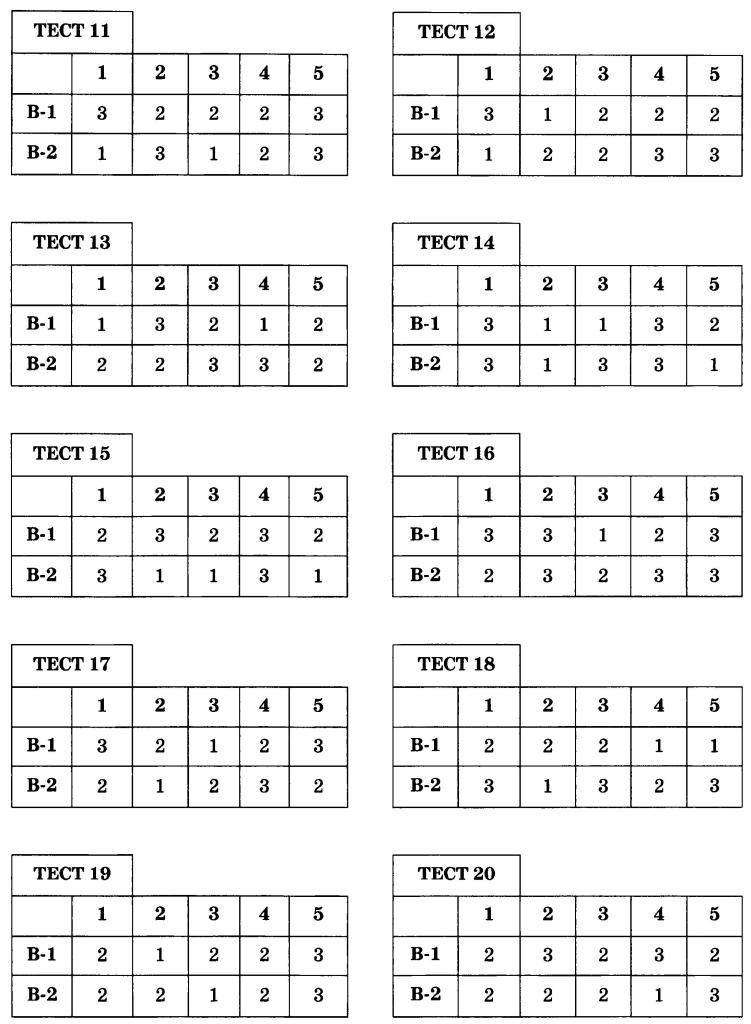 Представьте себе двумерную замкнутую вселенную, которую мы можем представить как поверхность земного шара. Предположим, мы помещаем положительный заряд на северный полюс этой вселенной. Тогда линии электрического поля, исходящие от заряда, охватят сферу и сходятся на южном полюсе. Это означает, что там должен присутствовать отрицательный заряд такой же величины. Таким образом, мы не можем добавить положительный заряд в замкнутую вселенную, не добавив при этом равный отрицательный заряд.Следовательно, полный заряд замкнутой вселенной должен быть равен нулю.

Если все сохраняющиеся числа замкнутой вселенной равны нулю, тогда нет ничего, что могло бы предотвратить спонтанное создание такой вселенной из ничего. А согласно квантовой механике любой процесс, который строго не запрещен законами сохранения, с некоторой вероятностью произойдет.

Новорожденная вселенная может иметь множество различных форм и размеров и может быть заполнена различными видами материи.Как обычно в квантовой теории, мы не можем сказать, какая из этих возможностей действительно реализуется, но мы можем вычислить их вероятности. Это говорит о том, что могло быть множество других вселенных.

Квантовое создание похоже на квантовое туннелирование через энергетические барьеры в квантовой механике. Изящное математическое описание этого процесса можно дать в терминах вращения Вика. Время выражается с помощью мнимых чисел, введенных только для удобства вычислений. Различие между измерениями времени и пространства исчезает.Это описание очень полезно, поскольку оно обеспечивает удобный способ определения вероятностей туннелирования. Наиболее вероятны вселенные с наименьшим начальным размером и наибольшей энергией вакуума. Как только Вселенная сформирована, она сразу же начинает расширяться из-за высокой энергии вакуума.

Это дает начало истории вечной инфляции.

Можно представить, что закрытые вселенные появляются из ничего, как пузыри в бокале шампанского, но эта аналогия не совсем точна.Пузыри выскакивают из жидкости, но в случае вселенных нет места, из которого они могли бы выскочить. Зародившаяся замкнутая вселенная — это все пространство, которое есть, за исключением отдельных пространств других замкнутых вселенных. За ним нет ни места, ни времени.

Что заставляет Вселенную возникать из ничего? Никакой причины не требуется. Если у вас есть радиоактивный атом, он распадется, и квантовая механика дает вероятность распада в заданный интервал времени, скажем, за минуту. Нет причин, по которым атом распался именно в этот момент, а не в другой.Процесс полностью случайный. Для квантового создания Вселенной не нужна причина.

Теория квантового творения — не более чем умозрительная гипотеза. Неясно, как и можно ли это проверить наблюдательными методами. Тем не менее, это первая попытка сформулировать проблему космического происхождения и решить ее количественно.

Тайна без ответа

Ответ на вопрос: «Было ли у вселенной начало?» это: «Вероятно, так оно и было.«У нас нет жизнеспособных моделей вечной вселенной. Теорема BGV дает нам основания полагать, что такие модели просто невозможно построить.

Когда физики или теологи спрашивают меня о теореме BGV, я рад помочь. Но я считаю, что теорема ничего не говорит нам о существовании Бога. Остается глубокая загадка. Законы физики, которые описывают квантовое создание Вселенной, также описывают ее эволюцию. Похоже, это наводит на мысль о том, что у них есть какое-то независимое существование.

Что именно это означает, мы не знаем.

А почему эти законы у нас? Почему не другие законы?

У нас нет возможности начать разгадывать эту загадку.

Приложение: математические детали

В этом приложении я намечаю доказательство теоремы BGV.

Начните с однородной, изотропной и пространственно плоской Вселенной с метрикой:

ds2 = dt2-a2tdx → 2.

Скорость расширения Хаббла равна H = a˙ / a, где точка обозначает производную по времени t.Мы можем представить себе, что Вселенная заполнена сопутствующими частицами, движущимися по времениподобным геодезическим x → = const. Рассмотрим инерционный наблюдатель, мировая линия которого равна xμ (τ), параметризованная собственным временем τ. Для наблюдателя с массой m 4-импульс равен Pμ = m dxμ / dτ, так что dτ = (m / E) dt, где E = P0 = p2 + m2 обозначает энергию, а p — величину 3 -импульс. Из геодезического уравнения движения следует, что p∝1 / a (t), так что pt = a (tf) / a (t) pf, где pf обозначает импульс в некоторый контрольный момент времени tf.

Таким образом:

∫titfHτdτ = ∫a (ti) a (tf) m dam2a2 + pf2a2 (tf) = Fγf-Fγi≤Fγf,

где ti

Обратите внимание:

Fγ = 12lnγ + 1γ-1,

, где γ = 1/1-νrel2 — фактор Лоренца, а νrel = p / E — скорость наблюдателя относительно движущихся частиц.

Для любого несопровождающего наблюдателя γ> 1 и Fγ> 0.

Средняя скорость расширения по мировой линии наблюдателя составляет:

Hav = 1τf-τi∫titfHτdτ.

Предполагая, что

Hav> 0,

и используя первое уравнение, следует, что

τf-τi≤FγfHav.

Это означает, что любая несовместимая направленная в прошлое времениподобная геодезическая, удовлетворяющая условию Hav> 0, должна иметь конечную собственную длину и, следовательно, должна быть неполной в прошлом.

Нет никакой апелляции к однородности и изотропии в произвольном пространстве-времени. Представьте себе, что Вселенная заполнена конгруэнцией сопутствующих геодезических, представляющих пробные частицы, и рассмотрите несопутствующий геодезический наблюдатель, описываемый мировой линией xμ (τ).Пусть uμ и νμ обозначают 4-скорости пробных частиц и наблюдателя.

Тогда коэффициент Лоренца наблюдателя относительно частиц равен

γ = uμνμ.

Чтобы охарактеризовать скорость расширения в общем пространстве-времени, достаточно сосредоточиться на геодезических пробных частицах, которые пересекают мировую линию наблюдателя.

Рассмотрим две такие геодезические, встречающие наблюдателя в моменты времени τ и τ + ∆τ.

Определите параметр

H = lim∆τ → 0∆ur∆r,

где ∆ur — относительная скорость частиц в направлении движения наблюдателя, а ∆r — расстояние между частицами.Обе величины вычисляются в системе покоя одной из частиц.

Для однородной и изотропной Вселенной это определение сводится к параметру Хаббла.

Параметр расширения может быть выражен как полная производная,

H = ddτFγτ.

Интеграл от H вдоль мировой линии наблюдателя по-прежнему определяется разностью F (γ) на ее концах. Выводы об однородных и изотропных вселенных немедленно переносятся на общие вселенные.

Остается нулевой наблюдатель, описанный нулевой геодезической. В этом случае роль собственного времени τ играет аффинный параметр. BGV показал, что при подходящей нормировке τ скорость расширения равна

.

H = ddτFγτ,

с Fγ = 1 / γ, а γ определяется согласно

H = lim∆τ → 0∆ur∆r.

Ясно, что Fγ> 0, и рассуждение продолжается по-прежнему.

Теперь возможна строгая формулировка теоремы BGV. Пусть λ — времениподобная или нулевая геодезическая, максимально продолженная в прошлое, и пусть C — времениподобная геодезическая конгруэнция, определенная вдоль λ.

Если скорость расширения C, усредненная по λ, положительна, то λ должно быть неполным в прошлом.

Александр Виленкин

Биоскетч

Алекс Виленкин — физик, получивший признание за свои работы по космологии ранней Вселенной. Он особенно известен своими исследованиями топологических дефектов, вечной космической инфляции, квантовой космологии, а также теорией киральных магнитных и киральных вихревых эффектов.
Виленкин родился в городе Харькове (бывший Советский Союз) и окончил Харьковский государственный университет в 1971 году по специальности физик. Он иммигрировал в США в 1976 году и получил степень доктора философии. от SUNY Buffalo в следующем году. Проработав год в качестве постдока в Западном резервном университете Кейса, он поступил на факультет Тафтского университета, где в настоящее время является профессором эволюционной науки Л. и Дж. Бернстайнов. Он также является директором Института космологии Тафтса. Виленкин — член Американского физического общества и член Национальной академии наук.

Научные интересы

Исследования Алекса Виленкина сосредоточены в трех основных областях: космические струны, инфляционные модели и квантовая космология. Космические струны могли образоваться как линейные дефекты в ранней Вселенной и в настоящее время вызывать множество наблюдательных эффектов. Виленкин и его сотрудники исследовали формирование, эволюцию и наблюдательные признаки струн, такие как всплески гравитационных волн и частиц высоких энергий.
Космическая инфляция — это период быстрого ускоренного расширения в ранней Вселенной. Он закончился в нашем регионе около 14 миллиардов лет назад, но Виленкин показал, что он, вероятно, продолжится за пределами этого региона и никогда не закончится во всей Вселенной. Он изучил возможные экспериментальные тесты этого сценария вечной инфляции. С помощью А. Борд и А. Гут Виленкин доказал, что, хотя инфляция, вероятно, вечна для будущего, она должна иметь начало в прошлом. Он показал, что расширяющаяся Вселенная может спонтанно возникать в результате квантового процесса, подобного квантовому туннелированию.Виленкин также разработал теорию киральных магнитных и киральных вихревых эффектов, которые имеют множество приложений в космологии и физике конденсированного состояния.

Виленкина уп. Принципы эффективного самообучения

Если ученик хочет действительно разобраться в сложном предмете, ему придется грамотно использовать ГДЗ по математике, 6 класс Виленкин:

  • Всегда сначала пытайтесь решить все домашние числа самостоятельно. Когда не получается, внимательно следите за правильным решением и разбирайтесь с каждым этапом.
  • Проверьте ответы на выполненные задания и примеры. Если они не совпадают, то сначала попробуйте найти ошибку в своих рассуждениях и только потом копайтесь в доказательствах Резервного.
  • Когда совсем некогда хорошо делать уроки, лучше списать работу, стараясь запомнить ход решения, а не надеяться, что учитель может не спросить.

Работать нужно только с теми ГДЗ, которые написаны опытными преподавателями, не содержат опечаток, подробно и понятно объясняют даже самые сложные понятия.На ГДЗ-онлайн есть как раз такое решение по математике для 6 класса Виленкина. С ним шестиклассник действительно разберется в дисциплине и повысит успеваемость.

Математика 6 класс

Виленкин, Чесноков, Шварцбурд

Мнемозина

Никто не говорит, что учиться легко. Но это необходимо не только для образования, но и для развития личности школьников. Ведь именно в школе учатся справляться с препятствиями, идти к цели и развивать множество других полезных навыков.Поэтому, если у ребенка что-то не получается, не нужно торопиться и что-то делать за него. Можно сказать, дать правильное направление, но ученики должны научиться разбираться во всех нюансах самостоятельно. В качестве вспомогательного средства можно использовать книгу ответов к учебнику «Математика 6 класс» Виленкин, Чесноков, , где вся программа изложена наиболее подробно.

Основные моменты в коллекции.

В данном руководстве нумерация ведется по задачам, что позволяет быстро найти то, что вам нужно.Всего в ГДЗ по математике, 6 класс Виленкин насчитывается более полутора тысяч упражнений. Они разделены на тематические главы, чтобы студенты могли повторить любую из них при необходимости.

Решебник поможет тебе в учебе?

Сейчас среди подростков наблюдается довольно пугающая тенденция: большинство из них психически неуравновешенны. Любое затруднение в учебе или какой-то сбой вызывает у них приступы истерии и депрессии.Более того, постоянное давление со стороны учителей и родителей только усугубляет ситуацию. Конечно, это никоим образом не означает, что вам нужно ослабить контроль или позволить детям делать все, что они хотят. Но хотя бы четко объясните ребенку, что препятствия нужно преодолевать, а не пугаться из-за них. А если есть элементарное непонимание предмета или какой-то конкретной темы, всегда можно дополнительно потренироваться, научить и потренироваться. Решебник к учебнику «Математика 6 класс» Виленкин как нельзя лучше подходит для этого.«Мнемозина», 2015

В шестом классе происходит разделение предмета математика на алгебру и геометрию. Это приводит к тому, что студентам необходимо осваивать новые сложные концепции и задачи. Однако не каждый школьник сможет освоить такой материал самостоятельно, и здесь на помощь придет созданное автором решение. Н.Я. Виленкин … Учебник по математике 6 класс станет доступнее, если использовать ГДЗ … Это позволит студенту лучше понять новые для него темы и задачи на решенном примере.

С помощью данного пособия студент может упростить домашнюю подготовку к занятиям. Это также позволяет студентам самостоятельно решать задачи в будущем без каких-либо подсказок. GDZ способствует пониманию языка математики студентами, углубляет их навыки об общих принципах решения математических примеров.

ГДЗ для рабочей тетради по математике для 6 класса Рудницкая В. Можно скачать.

ГДЗ для 6 класса учебника математики Виленкин Н.Я. (2018) можно скачать.

ГДЗ для тестов по математике для 6 класса Жохов В.И. можно скачать.

ГДЗ для дидактических материалов по математике для 6 класса Попов М.А. можно скачать

Решебник по математике для 6 класса на Виленкина — это сборник готовых решений и ответов, который составлен на основе учебника математики для шестиклассников, составленного коллективом российских авторов — Виленкина Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.

Решебник для 6 класса Учебник математики от Виленкина

ГДЗ по математике для 6 класса позволяет учащимся проверить правильность своего домашнего задания. С его помощью им удается самостоятельно разобраться в алгоритме решения сложных задач.

Более того, готовые решения и ответы являются подсказкой для родителей, которые стремятся оказать своим детям посильную помощь в подготовке домашних заданий по математике.

Решебник позволяет снизить учебную нагрузку на шестиклассников, которые не всегда успевают разобраться в решении примера или задачи на уроках.

Интерфейс нашего сайта делает использование учебника максимально удобным для детей и родителей:

  • База ответов доступна с телефона, планшета и компьютера;
  • Таблица чисел позволяет быстро перейти к желаемому ответу;
  • Регулярное обновление решебников исключает вероятность ошибок при подготовке домашних заданий.

Такие опции позволяют сделать процесс выполнения работы по математике максимально эффективным как с точки зрения результата, так и с точки зрения экономии времени.

Учебник математики для 6 класса из Виленкина, Жохова, Чеснокова и Шварцбурга

На нашем сайте представлены готовые решения и ответы на задания учебника для 6 класса от Виленкина Н.Я. В настоящее время большинство школ используют книгу 30-го издания, выпущенную в 2013 году.

В учебном пособии подробно рассматриваются два основных раздела арифметики:

  1. Свойства и операции с натуральными числами;
  2. Знаки, характеристики и математические операции с дробными числами.

В учебнике также приведены сведения о таких арифметических понятиях, как НОК (наименьшее общее кратное) и НОД (наибольший общий делитель), порядок их вычисления, а также особенности составления пропорций.

Книга знакомит шестиклассников с особенностями координат на плоскости, а также с понятием масштаба.Подробно представлены различия между положительными и отрицательными числами, а также правила математических операций с ними.

В шестом классе происходит разделение предмета математика на алгебру и геометрию. Это приводит к тому, что студентам необходимо осваивать новые сложные концепции и задачи. Однако не каждый школьник сможет освоить такой материал самостоятельно, и здесь на помощь придет созданное автором решение. Н.Я. Виленкин … Учебник по математике 6 класс станет доступнее, если использовать ГДЗ … Это позволит ученику лучше разбираться в новых для них темах и задачах на решенном примере.

С помощью данного пособия студент может упростить домашнюю подготовку к занятиям.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *