Задачи на пропорции 6 класс: Задачи на пропорции по математике — примеры с ответами

Задачи на пропорции по математике — примеры с ответами

Понятие пропорции

Чтобы решать задачи на тему пропорции, вспомним главное определение.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин.

Главное свойство пропорции: Произведение крайних членов равно произведению средних. a : b = c : d, где a, b, c, d — члены пропорции, a, d — крайние члены, b, c — средние члены.

Вывод из главного свойства пропорции:

• Крайний член равен произведению средних, которые разделены на другой крайний. То есть для пропорции a/b = c/d:
  
  
• Средний член равен произведению крайних, которые разделены на другой средний. То есть для пропорции a/b = c/d:
  
  

Решить пропорцию — значит найти неизвестный член. Свойство пропорции — главный помощник в решении.

Запомним!

Равенство двух отношений называют пропорцией.

Рассмотрим легкие и сложные задачи, которые можно решить с помощью пропорции. 5, 6, 7, 8 класс — неважно, всем школьникам полезно проанализировать занимательные задачки.

Задачи на пропорции с решением и ответами

Свойства пропорции придумали не просто так! С их помощью можно найти любой из членов пропорции, если он неизвестен. Решим 10 задач на пропорцию.

Задание 1. Найти неизвестный член пропорции: x/2 = 3/1

Как решаем:

В этом примере неизвестен крайний член, поэтому умножим средние члены и разделим полученный результат на известный крайний член:

x = (2 * 3)/1 = 6

Ответ: x = 6.

Задание 2. Найти неизвестный член: 1/3 = 5/y

Как решаем:

y = (3 * 5)/1 = 15

Ответ: y = 15.

Задача 3. Решить пропорцию: 30/x = 5/8

Как решаем:

x = (30 * 8)/5 = 48

Ответ: x = 48.

Задание 4. Решить: 7/5 = y/10

Как решаем:

y = (7 * 10)/5 = 14

Ответ: y = 14.

Задание 5. Известно, что 21x = 14y. Найти отношение x — к y

Как решаем:

• Сначала сократим обе части равенства на общий множитель 7: 21x/7 = 14y/7.

  Получим: 3x = 2y.

• Теперь разделим обе части на 3y, чтобы в левой части убрать множитель 3, а в правой части избавиться от y: 3x/3y = 2y/3y.
• После сокращения отношений получилось: x/y = 2/3.

Ответ: 2 к 3.

На следующем примере мы узнаем как составить пропорцию по задаче💡

Задание 6. Из 300 подписчиков в инстаграм 108 человек — поставили лайк под постом. Какой процент всех подписчиков составляют те, кому понравился пост и они поставили лайк?

Как решаем:

• Примем всех подписчиков за 100% и запишем условие задачи кратко:

  300 — 100%

  108 — ?%

• Составим пропорцию: 300/108 = 100/x.
• Найдем х: (108 * 100) : 300 = 36.

Ответ: 36% всех подписчиков поставили лайк под постом.

Задание 7. Подруга Гарри Поттера при варке оборотного зелья использовала водоросли и пиявки в отношении 5 к 2. Сколько нужно водорослей, если есть только 450 грамм пиявок?

Как решаем:

• Составим пропорцию: 5/2 = x/450.
• Найдем х: (5 * 450) : 2 = 1125.

Ответ: на 450 грамм пиявок нужно взять 1125 гр водорослей.

Задание 8. Известно, что арбуз состоит на 98% из воды. Сколько воды в 5 кг арбуза?

Как решаем:

Вес арбуза (5 кг) составляет 100%. Вода — 98% или х кг.

Составим пропорцию:

5 : 100 = х : 98

х = (5 * 98) : 100

х = 4,9

Ответ: в 5 кг арбуза содержится 4,9 кг воды.

Перейдем к примерам посложнее. Рассмотрим задачу на пропорции из учебника по алгебре за 8 класс.

Задание 9. Папин автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Как рассуждаем:

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Обозначим:

• v1 = 75 км/ч
• v2 = 52 км/ч
• t1 = 13 ч
• t2 = х

Как решаем:

1. Составим пропорцию: v1/v2 = t2/t1.

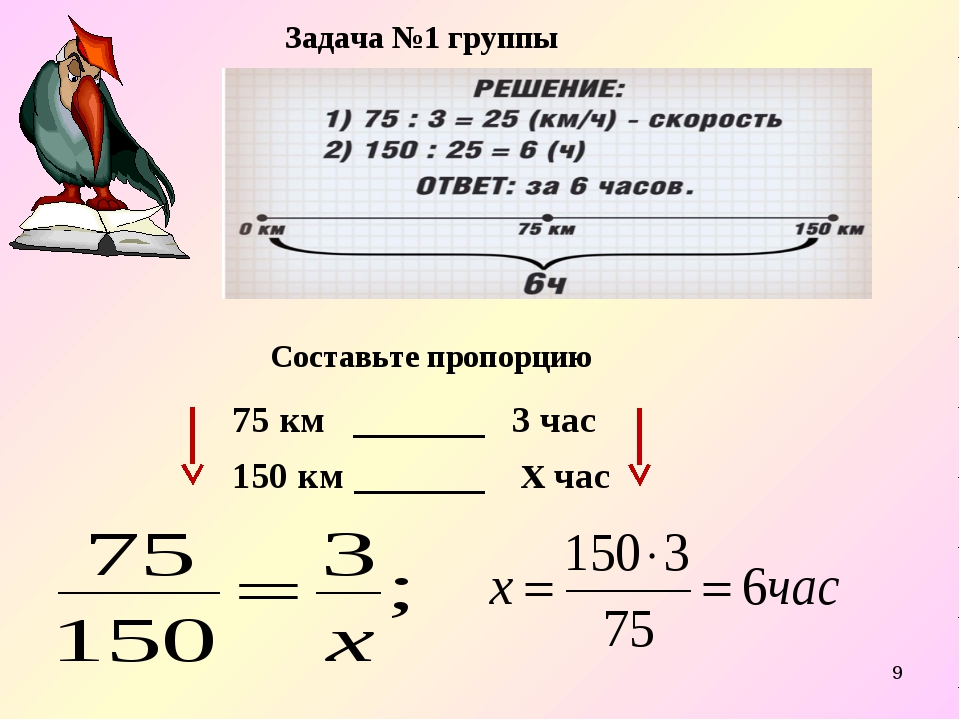
   Соотношения равны, но перевернуты относительно друг друга.



2. Подставим известные значения: 75/52 = t2/13

   t2 = (75 * 13)/52 = 75/4 = 18 3/4 = 18 ч 45 мин

Ответ: 18 часов 45 минут.

Задание 10. 24 человека за 5 дней раскрутили канал в телеграм. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Как рассуждаем:

1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.

3. Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:

Как решаем:

1. Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию:

   30 : 24 = 5 : х



2. Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член:

   х = 24 * 5 : 30

   х = 4



3. Значит, 30 человек раскрутят канал за 4 дня.

Ответ: за 4 дня.

Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.

Урок 5. пропорции — Математика — 6 класс

Математика

6 класс

Урок № 5

Пропорции

Перечень рассматриваемых вопросов:

• Понятие пропорции.
• Основное свойство пропорции.
• Как правильно составить пропорцию.
• Как найти неизвестный член пропорции.

Тезаурус

Равенство двух отношений называют пропорцией.

Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.

Основная литература

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты.
   5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.

Если один член пропорции неизвестен и необходимо его определить, то говорят, что нужно решить пропорцию.

Рассмотрим 3 способа нахождения неизвестного члена пропорции.

1 способ.

2 способ.

Способ 3.

Задача.

Решение:

Ответ:

1) можно;

2) можно;

3) нельзя;

4) нельзя.

Разбор решения заданий тренировочного модуля

№1. Тип задания: сортировка элементов по категориям.

№2. Тип задания: Подстановка элементов в пропуски в тексте.

Найдите неизвестный член пропорции.

Для нахождения неизвестного члена пропорции воспользуемся основным свойством пропорции, из которого следует: чтобы найти неизвестный средний член пропорции, надо произведение крайних членов разделить на известный средний член пропорции.

Ответ: 3.

Задачи по теме «Отношения и пропорции» 6 класс

Математика

6 класс

1. Задачи на отношения.

1. Отрезок АВ разделён точкой С на отрезки АС и ВС в отношении 2:7. Найти длину отрезка АВ, если длина отрезка АС на 5,5 см меньше длины отрезка ВС.

2. С двух участков собрали урожай. Каков урожай на каждом участке, если их отношение равно 11:14, а урожай, собранный со второго участка, на 18 тонн больше, чем с первого?

3. Сплав состоит из меди и цинка. Отношение массы меди к массе цинка равно 7:2. Найдите массу сплава, если масса меди на 4кг больше массы цинка в сплаве.

4. Найти массу сплава цинка и меди, если отношение массы меди к массе цинка в сплаве равно 3:5 и меди на 2,4г меньше, чем цинка.

2. Задачи на прямо пропорциональные величины.

1. Из 90 цветов, посаженных в цветнике, принялись 72. На сколько процентов меньше не принявшихся цветов, чем принявшихся?

2. 0,8 м ткани стоят 560 тенге. На сколько больше заплатят за 3,25 м ткани?

3. 4 м³ зерна ржи весят 2,8 т. На сколько тонн больше весит 6,5 m³ зерна ржи?

4. Поезд за 4,5 часа проехал 360 км. За какое время, двигаясь с тон же скоростью, поезд проедет расстояние, увеличенное на 80 км?

3. Задачи на обратно пропорциональные величины.

1. Все члены бригады работают в одинаковом темпе. Четверо, рабочих успевают выполнить работу за 32ч. Сколько времени понадобится для выполнения этой же работы трем рабочим?

2. Чтобы вывезти товар потребуется 21 автомашина грузоподъёмностью 2,5 т. Сколько потребовалось бы для выполнения этой работы автомашин грузоподъёмностью 3,5 т?

3. 15 рабочих закончили отделку квартир в новом доме за 24 дня. За сколько дней выполнили бы эту работу 18 рабочих?

4. Пешеход затратил на путь 2,5 ч, двигаясь со скоростью 3,6 км/ч. Сколько времени затратит пешеход на тот же путь, если его скорость будет 4,5 км/ч?

4. Задачи на масштаб.

1. Комната имеет прямоугольную форму. Размеры пола этой комнаты на плане 4см и 6см. В действительности меньшая сторона пола 5 м. Найдите площадь комнаты н масштаб плана.

2. 125 м на местности соответствуют 2,5 см на плане. Найти масштаб плана и расстояние между двумя точками на местности, если на плане оно 4,2 см.

3. План земельного участка квадратной формы выполнен в масштабе 1:500. Сторона участка на плане 16см. Вычисли площадь участка.

4. На карте расстояние между годами А и В равно 2,6см. а расстояние между городами В и С – 3,7см, На местности расстояние между- городами В и С равно 296км. Найдите расстояние на местности между годами А и В и масштаб карты.

В гостях у сказки (задачи на пропорции). 6 класс

1. В гостях у сказки (ЗАДАЧИ НА ПРОПОРЦИИ)

6 КЛАСС
(УРОК 3)
Автор: Литвина Марина Николаевна,
учитель математики,
МОУ «СОШ№58 с углубленным
изучением отдельных предметов»
г. Новоуральск, Свердловской области

2. Закончите фразу:

• Прямой пропорциональной
зависимостью называется такая
зависимость величин, при
которой…
• Обратной пропорциональной
зависимостью называется такая
зависимость величин, при
которой…

3. Закончите фразу:

• Если две величины прямо
пропорциональны, то отношение
значений одной величины равно…
• Если две величины обратно
пропорциональны, то отношение
значений одной величины равно…

4.

Выберите в скобках верный ответ: • Скорость движения автомобиля и путь,
пройденный этим автомобилем, (прямо,
обратно) пропорциональны.
• Стоимость покупки и количество купленных
вещей(прямо, обратно) пропорциональны.
• Скорость движения автомобиля и время,
для прохождения определенного расстояния,
(прямо, обратно) пропорциональны.

5. Проверим домашнее задание

№1058
12 тракторов – 88ч
х тракторов – 33ч
Ответ : 32 трактора

6. Проверим домашнее задание

№1059
45м – 2,2м ширины
x м — 1,5м ширины
Ответ : 66м

7. Решите задачу

Ветер по морю гуляет
И кораблик подгоняет;
Он бежит себе в волнах
На раздутых парусах
Мимо острова крутого
Мимо города большого;
Пушки с пристани палят,
Кораблю пристать велят.
С какой скоростью нужно плыть кораблю, чтобы
преодолеть путь от царства царя Салтана до
острова Буяна за 6ч, если при скорости 55км/ч он
проходит это расстояние за 4,5ч?

8.

Решите задачу … Где-то есть
Ель в лесу, под елью белка;
Диво право не безделка –
Белка песенки поет
Да орешки все грызет,
А орешки не простые,
Все скорлупки золотые,
Ядра чистый изумруд…
За 2ч. белка разгрызла 40 орешков. Сколько
орешков она разгрызет за 360 мин., если будет
грызть орешки с той же скоростью?

10. РЕШИТЕ ЗАДАЧУ

Чебурашка и крокодил Гена решили
расчистить площадку для
строительства дома, в котором будут
жить друзья. Для этого 3 экскаватора
работали 330 минут. За сколько минут
эту площадку расчистили бы 10
экскаваторов?

11. РЕШИТЕ ЗАДАЧУ

Однажды Муха-Цокотуха пошла по
полю и нашла денежку, на которой
было написано «12,3 рубля». Муха
пошла на базар и купила ещё 3
самовара к уже имеющемуся.
Сколько самоваров могла бы купить
Муха, если бы нашла денежку, на
которой было бы написано «20,5
рубля»?

12. Решите задачу самостоятельно

Сел Иванушка на Серого Волка верхом и
поскакал – синие леса мимо глаз
пропускает, озера хвостом заметает…
Если бы волк скакал со скоростью
70км/ч, то они бы с Иваном-Царевичем
добрались от царства Берендея до
царства царя Афрона за 4,5ч. С какой
скоростью должен был скакать волк,
чтобы добраться до царства царя
Афрона за 3ч?

13. Проверьте решение

70км/ч – 4,5ч
х км/ч – 3ч
Ответ: Скорость волка должна быть
105км/ч

14. Решите задачу

Хозяйственный кот Матроскин из
Простоквашино завел корову и решил
делать сливочное масло. Масса масла
относится к массе молока как 0,1:2,5.
Сколько молока надо надоить
Матроскину, чтобы получить
100г масла?
Решите задачу
№1064

16. Домашнее задание

Придумать (составить) и решить:
• Задачу на прямую
пропорциональную зависимость;
• Задачу на обратную
пропорциональную зависимость.

Решение задач на пропорции и пропорциональное деление

Решение задач на пропорции и пропорциональное деление

1. Реши задачу методом пропорции:

Бригада из 24 человек за 5 дней отремонтировала квартиру. За сколько дней выполнят эту же работу 15 человек, если будут работать с той же производительностью.

2. Реши задачу методом пропорции:

Чтобы сшить 4 юбки, необходимо 7,2 м ткани. Сколько метров ткани потребуется для 6 юбок?

3. Длины сторон прямоугольника пропорциональны числам 6 и 14. Найди площадь этого прямоугольника, если известно, что его периметр равен 80 см.

4. Реши уравнение:

5. Раздели число:

а) 40 в отношении 3 : 17;

б) 147 в отношении 9 : 2,4 : 18

Решение задач на пропорции и пропорциональное деление

1. Реши задачу методом пропорции:

Бригада из 24 человек за 5 дней отремонтировала квартиру. За сколько дней выполнят эту же работу 15 человек, если будут работать с той же производительностью.

2. Реши задачу методом пропорции:

Чтобы сшить 4 юбки, необходимо 7,2 м ткани. Сколько метров ткани потребуется для 6 юбок?

3. Длины сторон прямоугольника пропорциональны числам 6 и 14. Найди площадь этого прямоугольника, если известно, что его периметр равен 80 см.

4. Реши уравнение:

5. Раздели число:

а) 40 в отношении 3 : 17;

б) 147 в отношении 9 : 2,4 : 18

Тренажёр, 6 класс. Пропорции. Прямая и обратная пропорциональность.

№	Верна ли пропорция?	Решите пропорцию	Решите задачу
1	25 : 5 = 20 : 4	9 : х = 12 : 16	За 6ч. поезд прошел 480км. Какой путь он пройдет за 2ч.?
2	12 : 16 = 18 : 24	х : 4 = 7 : 12	Принтер распечатывает 27 страниц текста за 4,5 минуты. За какое время принтер распечатает 300 страниц?
3	100 : 200 = 4 : 8	28 : 32 = х : 40	На стройке за 2дня забили в землю 25свай. Сколько свай будет забито за 6 дней, если рабочие будут трудиться с той же производительностью?
4	5 : 1,5 = 15 : 4,5	7 : х = 42 : 5	За 2,5часа рабочий обрабатывает 20 деталей. А сколько деталей он обработает за смену(6часов)?
5	1,1 : 22 = 3,3 : 66	0,25 : х = 0,5 : 8,4	Расстояние между двумя городами пассажирский поезд прошел со скоростью 80 км/ч за 3 часа. За сколько часов поезд пройдет то же расстояние со скоростью 60 км/ч?
6	14 : 4,9 =  : 0,1	2,8 : 3,2 = 2,1 : х	Для строительства стадиона 5 бульдозеров расчистили площадку за 210 мин. За какое время 7 бульдозеров расчистили бы эту площадку?
7	2,04: 0,6 = 2,72: 0,8	х :  =  :	В железной руде на 7 частей железа приходится 3 части примесей. Сколько тонн примесей в руде, которая содержит 73,5т железа?
8	0,0112: 0,28 = 0,204: 0,51	: х =  :	Для варки варенья из вишни на 6 кг ягод берут 4 кг сахарного песку. Сколько килограммов сахарного песку надо взять на 12 кг ягод?
9	: 0,3 =  :	:  = х :	Средняя скорость самолета 500 км/ч, а машины 80км/ч. Сколько времени потребуется машине, чтобы проехать путь, на который самолет потратит 4 часа?
10	:  = 21 : 3	х : 2,4 =  :	Двое рабочих могут выполнить задание за 10 дней. Сколько еще рабочих надо пригласить, чтобы все вместе они выполнили ту же работу за 4 дня?
11	420 : 560 =  :	5 :  = х :	За некоторое время велосипедист проехал 5 км со скоростью 10 км/ч. Какое расстояние он проедет за то же время, увеличив свою скорость в полтора раза?

Пропорции математика. Пропорция – это равенство двух отношений. Соотношение.

Пропорция – это равенство, утверждающее, что два отношения равны. Пропорциональный — значит находящийся в определенном отношении к какой-либо величине. Четыре величины \(4, 2, 8 \) и \(4\) находятся в отношении, если \(\frac{4}{2}=\frac{8}{4}\). Произведение крайних членов пропорции равно произведению средних.

​

 

 

Пропорция всегда включает равные коэффициенты. Когда соотношение остается постоянным, это соотношение называется пропорциональным.

Если \(\frac{A}{B} = \frac{C}{D}\), то 

Пропорция состоит из двух равных отношений. Однако если \(\frac{A}{B}\) не равно \(\frac{C}{D}\), то \(A, B, C, D \) не называются пропорцией.

Три величины считаются пропорциональными, если отношение первого ко второму равно соотношению второго и третьего.

\(A, B , C\) находятся в постоянной пропорции, если \(\frac{A}{B} =\frac{C}{D}\) 

Если \(A, B ,C \) находятся в постоянном отношении, то \(B\) называется средней в пропорции.

В косвенной пропорции как одно значение увеличивается, так и другое значение уменьшается.

Задача 1. За  \(5\) дней и \(12\) человек  построили забор. Сколько дней это займет у \(6\) людей?

Решение.

1.  \(12\) человек →  \(5\) дней
2. \(6\) человек → \(x\) дней
3. \(\frac{12}{6} = \frac{x}{5}\)
4. умножаем крест на крест члены пропорции и сокращаем на \(6\):

\(12*5=6x\)

\(60=6x\)

\(x=10\)

Ответ: \(6\) людей будут работать \(10\) дней, чтобы закончить работу.

Задача 2. Найдите значение \(x\), если \(\frac{2}{5}=\frac{x}{15}\)

Решение:

1. \(2*15=5x\)
2. \(30 =5x\)
3. Делим на 5 обе части равенства: \(\frac{30}{5}=x\), откуда находим 

Задача 3. Что должно быть добавлено к каждому из четырех чисел 10, 18, 22, 38, чтобы сделать их пропорцией?

Решение:\(\)

1. \((10+x)(18+x)=(22+x)(38+x)\)
2. \(380+48x+2x=396+40x+2x\)
3. \(8x=16\)
4. \(x=2\)

Задача 4. Найти четвертый член  пропорции \(6,10\) и \(12\)

Решение:

\(\frac{6}{10}=\frac{12}{x}\)

6×х = 120

x = 120/6

x = 20

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Наши преподаватели

Оставить заявку

Репетитор по математике

Кубанский Государственный Университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике для 5-11 классов. Подготовка к ОГЭ, ЕГЭ (базовый и профильный). Люблю математику за то, что она развивает аналитическое и критическое мышление Системно-деятельностный подход Информационно-развивающий и репродуктивный методы Подробное и доступное объяснение, уважительное отношение, индивидуальный подход Умею находить подход к ученикам любого уровня подготовки.

Оставить заявку

Репетитор по математике

БГПУ им. Танка

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-6 классов. Математика сложна, но интересна и увлекательна! При обучении настраиваю на позитивное восприятие всего нового и непонятного и впоследствии мои ученики испытывают радость новых открытий в этом удивительном мире цифр и знаков.

Оставить заявку

Репетитор по математике

Симферопольский государственный университет им. Фрунзе, Таврический национальный университет им Вернадского

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 4-11 классов. Готовлю к ОГЭ и ЕГЭ. С удовольствием окажу помощь школьникам в овладении английским языком, в повышении уровня языковой компетенции. На наших занятиях мы будем использовать упражнения на формирование 4 основных навыков при изучении любого иностранного языка: на формирование навыков чтения, говорения, письма и аудирования, а также будем использовать приемы мнемотехники и скорочтения для достижения большей продуктивности.

Математика 10 класс

• — Индивидуальные занятия
• — В любое удобное для вас время
• — Бесплатное вводное занятие

Похожие статьи

Математика 6 класс

1.     Учащиеся свяжут отношение и скорость с умножением и делением целых чисел и будут использовать понятия отношения и скорости для решения задач.

2.     Учащиеся завершат понимание деления дробей и распространят понятие числа на систему рациональных чисел, которая включает отрицательные числа.

3.     Учащиеся будут писать, интерпретировать и использовать выражения и уравнения.

4.Студенты будут развивать понимание статистического мышления.

Больше заниматься математикой дома

Две важные цели для всех учащихся: 1) научиться ценить математику и 2) стать уверенными в своих способностях заниматься математикой. Родители могут помочь детям развить склонность к математике, воспитывая их естественное любопытство и оказывая им поддержку и поддержку.

Математика повсюду, но многие дети ее не видят.Ищите способы отметить и закрепить математические навыки дома. Например:

·        говорить о том, как вы используете математику на работе или дома

·        вовлекать детей в задачи, которые требуют вычисления, измерения, оценки, построения, следования указаниям, решения проблем и рассуждений

·        ищите занятия, которые требуют от детей использования их математических навыков, таких как построение масштабных моделей, приготовление пищи, планирование поездок и игра в логические игры

Ищите игры и занятия, которые учат и/или укрепляют математику и мышление. Например, ищите игры, которые:

· Требовать и развивать навыки с психическими вычислениями и оценки

· Требовать игроков использовать свои математические навыки

· Влиять на разработку стратегий

· Требовать игроки должны думать о вероятности наступления определенных событий

·        требуется использование навыков пространственной визуализации

·        требуется логическое мышление

Когда вы видите статьи, содержащие данные, которые могут заинтересовать ваших детей (г., спортивная статистика, данные о подростковом курении, факты о стихийных бедствиях), поделитесь ими и расскажите, что означают цифры.

Поделитесь своими стратегиями и методами решения проблем, стратегиями умственных вычислений и стратегиями оценки. Пусть ваши дети научат вас чему-нибудь. Поработайте над одной и той же проблемой, а затем сравните стратегии и ответы.

Предложите своим детям объяснить, что они узнали на уроке математики, или пусть они научат этому вас. Это дает детям возможность прояснить свое мышление, попрактиковаться в новых навыках и попрактиковаться в математическом общении.

Если у ваших детей есть доступ к технологиям, ищите программное обеспечение и приложения, которые укрепляют и обучают математическим понятиям. Помогите своим детям научиться пользоваться математическими утилитами, такими как электронные таблицы и графические программы.

 

Класс 6 Обзор

Соотношение и пропорциональные отношения

·        

·        Словарь

o   Отношение – сравнение двух величин, выраженных как 3/5, 3:5 или 3 к 5.

o   Удельная ставка – ставка с одним из чисел равна 1 или количество 1.

o   Проценты – из 100. o   Прибыль – сумма, на которую доходы превышают расходы.

Система счисления

·        Применить и расширить прежнее понимание умножения и деления для деления дробей на дроби

·        Применить и расширить предыдущее понимание чисел на систему рациональных чисел.

·        Словарь

o   Множитель – одно или несколько целых чисел, которые перемножаются для получения произведения.

o   Множитель – произведение данного целого числа на другое целое число.

o   Простое число — число, имеющее ровно два делителя, единицу и само себя.

o   Составной – число с более чем двумя делителями.

o   Разложение на простые множители – произведение простых чисел, возможно, с некоторыми повторениями, в результате чего получается желаемое число. БЫВШИЙ. 27 = 3 x 3 x 3 или 30 = 2 x 3 x 5

o   Квадратное число – число, являющееся результатом произведения числа на самого себя.

o   Наименьшее общее кратное (НОК) – наименьшее кратное, которое объединяет два или более чисел.

o   Наибольший общий множитель (GCF) – наибольший множитель, общий для двух или более чисел.

o   Экспонента – небольшое выпуклое число, указывающее, сколько раз используется коэффициент.

o   Повторяющаяся десятичная дробь – десятичная дробь с шаблоном фиксированного числа цифр, который повторяется вечно.

o   Конечная десятичная дробь – десятичная дробь, которая заканчивается или завершается.

Выражения и уравнения

·        Применить и расширить прежнее понимание арифметики на алгебраические выражения.

·        Рассуждать и решать уравнения и выражения с одной переменной.

·        Представлять и анализировать количественные отношения между зависимыми и независимыми переменными.

·        Словарь

o   Распределительное свойство – математическое свойство, используемое для перезаписи выражений, включающих сложение и умножение. БЫВШИЙ. 4(5 + x) = 4(5) + 4(x) = 20 + 4x

o   Порядок операций – установленное соглашение о проведении расчетов с одной или несколькими операциями. ( Скобки, Экспоненты, Умножение/деление (движение слева направо), сложение/вычитание (движение слева направо)

o   Эквивалент – равенство по значению

o   Неравенство – Утверждение, которое сравнивает две величины.<, >, < и > используются для выражения неравенства.

o   Выражение – математическая фраза, содержащая числа, переменные и символы операций.

o   Переменная – величина, которая может изменяться, часто обозначается буквой

o   Коэффициент – число, которое умножается на переменную в уравнении или выражении.

Геометрия

·        Решайте реальные и математические задачи, связанные с площадью, площадью поверхности и объемом.

·        Словарь

o   Площадь – мера площади поверхности, ограниченной границей фигуры, количество квадратных единиц в фигуре.

o   Периметр – мера расстояния вокруг двумерной фигуры.

o   Объем – объем пространства, занимаемый трехмерной фигурой, количество единичных кубов, вписывающихся в фигуру.

o   Площадь поверхности – площадь, необходимая для покрытия трехмерной формы.

o   Координаты X и Y – числа в паре координат, используемые для определения точки на координатном графике.

 

Статистика и вероятность

·        Развить понимание статистической изменчивости.

·        Обобщить и описать распределения.

·        Vocabulary

o   Mean – значение, полученное при объединении всех данных и последующем их равномерном распределении (среднее)

o   Median – число, являющееся медианой

o   Mode – число, которое встречается чаще всего в заданном наборе данных.

o   Диапазон – разница между максимальным и минимальным значением в распределении.

o   Линейный график – способ организации данных вдоль числовой строки, где X (или другие символы) над числом показывают, как часто упоминается каждое значение.

o   Таблица частот —

o   Коробчатая диаграмма – отображение, показывающее распределение значений в наборе данных, разделенных на 4 группы одинакового размера, построенные из сводки данных из 5 чисел (минимальное значение, нижний квартиль, медиана, верхний квартиль и максимальное значение)

o   Верхний квартиль — медиана данных слева от медианы.

o   Нижний квартиль – медиана данных справа от медианы.

o   Выброс — значение, которое находится далеко от центра распределения данных и не похоже на другие значения.

 

Скорость, отношение и пропорциональное рассуждение

---

6 класс: Рассуждение о скорости, соотношении и пропорциональности

Рейтинг: 

https:// www.georgiastandards.org/CommonCore/Common%20Core%20Frameworks/CCGPS_Math_6_6thGrade_Unit2SE.pdf

Общие базовые стандарты

Стандарты содержания

6.RP.1 — Понимать концепцию отношения и использовать язык отношений для описания отношения отношения между двумя величинами.

6.RP.2 — Понимать концепцию удельной ставки a/b, связанную с отношением a:b, где b ≠ 0, и использовать формулировку ставок в контексте отношения отношения.

6.RP.3 — Используйте рассуждения об отношении и скорости для решения реальных и математических задач, например, рассуждая о таблицах эквивалентных отношений, ленточных диаграммах, линейных диаграммах с двойным числом или уравнениях.

6.RP.3a — Составьте таблицы эквивалентных отношений, связывающих величины с целыми числами, найдите недостающие значения в таблицах и нанесите пары значений на координатную плоскость. Используйте таблицы для сравнения коэффициентов.

6.RP.3b — Решение проблем с расценками за единицу, в том числе связанных с ценообразованием за единицу и постоянной скоростью.

6.RP.3c — Найти процент от количества как ставку на 100; решать задачи на нахождение целого по заданной части и процентам.

6.RP.3d — Использование рассуждения о соотношении для преобразования единиц измерения; правильно манипулировать и преобразовывать единицы при умножении или делении величин.

Стандарты математической практики

MP. 1  Понимать проблемы и настойчиво решать их.

MP.2  Рассуждайте абстрактно и количественно.

MP.3 Создавать жизнеспособные аргументы и критиковать рассуждения других.

MP.4  Модель с математикой.

Описание блока

Этот модуль «Оценка, отношение и пропорциональные рассуждения с использованием эквивалентных дробей» от Министерства энергетики Джорджии представляет собой набор из 6 заданий, охватывающих основные концепции отношений и пропорций с использованием эквивалентных дробей. Общий блок рассчитан на 3 — 4 недели. В этом блоке учащиеся получат более глубокое понимание пропорциональных рассуждений, понимая, что отношение — это сравнение двух чисел или величин.Студенты будут развивать и использовать мультипликативное мышление и находить проценты, используя тот же процесс для решения ставок и пропорций. Наконец, учащиеся будут решать реальные задачи, связанные с единицами измерения, которые необходимо преобразовать.

Предостережения

Учителя штата Коннектикут

должны знать, что модуль не полностью охватывает область 6. RP.3a, используя таблицы соотношений и ленточные диаграммы для решения задач. В состав блока не входят следующие компоненты:

• дифференциация или поддержка для учащихся, работающих выше/ниже уровня своего класса, изучающих английский язык или учащихся с ограниченными возможностями.
• использование технологий или средств массовой информации.
• явные связи между стандартами математической практики в модуле и содержанием.
• структур для реализации и выполнения исполнительских задач. Инструктивных заметок нет (ключи ответов, рубрики, образцы работ учащихся).

Обоснование выбора

В этом модуле рассматривается одна из основных областей применения этого класса. Стандарты, рассматриваемые в каждой задаче, указаны в начале задачи; есть свидетельство строгости и согласованности в области отношений и пропорциональных рассуждений. Строгие задачи актуальны и заставляют задуматься; они способствуют контекстуальному пониманию стандартов.

12 упражнений для отработки пропорций, которые лопаются

Меня сводит с ума, сколько силы на самом деле несут в себе некоторые навыки, которым мы обучаем. Обучение детей пониманию пропорций и тому, как найти пропущенное значение в пропорциях, — одна из тех концепций, которые продолжают появляться. Понимание пропорций помогает учащимся со многими другими понятиями.Это снова появляется, когда они узнают о склоне. Я чувствую, что ученикам, которые понимают пропорции, гораздо легче понять наклон. Когда я был ребенком, мне нравилось находить закономерности в вещах, и пропорции имеют такую ​​закономерность. Теперь мне нравится помогать учащимся понимать эти закономерности и наблюдать, как загорается лампочка. В этом посте я поделюсь двенадцатью упражнениями, которые определенно помогут студентам получить необходимую им практику с пропорциями.

В прошлом году я работал с группой семиклассников, и мы так много практиковались, что они стали экспертами по пропорциям. Мы практиковались с пропорциями каждый день в течение нескольких недель, пока это не стало для них второй натурой. Они действительно начали смотреть на себя по-другому из-за успеха, который у них был. В посте я поделюсь некоторыми действиями, которые мы выполняли, и объясню, как мы перешли от непонимания к мастерству.

Перечень видов деятельности

Лабиринты

Ловец Кути

Крестики-нолики

Викторина

Битва в лабиринте пропорций

Математические игры

Кахут

Рабочий лист и целевая игра

Раскраска в подарок

Пропорции мотоцикла-внедорожника

Dunk Tank — Соотношения и пропорции

Пакеты с сахаром и безалкогольные напитки. Задача

.

 

Пришло время погрузиться и посмотреть, что может предложить каждое из этих занятий.Некоторые из них отлично подходят для самостоятельной практики, а другие лучше подходят для занятий всем классом. Я использовал их, чтобы изучить и попрактиковаться в пропорциях, а затем еще раз в этом году для повторения. Отрабатывать пропорции можно легко и весело, потому что это навык, а не глубокая сложная концепция. Давайте рассмотрим некоторые идеи и посмотрим, что вы думаете:

Мои ученики учатся и растут на постоянной диете лабиринтов, и когда мы практиковались в решении пропорций, мы часто использовали их. С лабиринтами вы можете натренировать детей, но они думают, что это головоломка.Если однажды у меня не будет лабиринта, мои ученики решат, что что-то не так. Кроме того, это прекрасно работает как способ начать урок. Каждый берет свой лабиринт, входит в класс и приступает к работе.

В этом наборе лабиринтов с тремя пропорциями учащиеся решают найти x с двумя отношениями, разделенными знаком равенства. Я призываю студентов сначала посмотреть, смогут ли они решить ее без калькулятора. Если это не сработает, то они перекрестно размножатся. Чем больше они практикуются, тем более автоматическими они становятся.

Хотите еще больше математических лабиринтов? Присоединяйтесь к клубу «Лабиринт месяца» и ежемесячно получайте бесплатный эксклюзивный математический лабиринт прямо на ваш почтовый ящик. Вы сразу начнете с бесплатного лабиринта целых чисел, а затем получите внутреннюю информацию о ежемесячных лабиринтах и ​​других математических вкусностях.

Да! Я хочу вступить в клуб «Лабиринт месяца»!

Не могу дождаться встречи с вами 🙂

Эта партнерская деятельность по ловле кути идет медленнее, поэтому я использую ее в начале модуля.Студенты могут играть в нее как на дуэли друг против друга, или они могут играть вместе. Для игры у них есть маленькая ловушка для кути, или некоторые люди называют их гадалками. Они складывают его, а затем выбирают символ снаружи и число внутри, как если бы вы использовали их, чтобы предсказать свою судьбу. Многим студентам нравится дополнительное удовольствие, которое это приносит с практикой.

Я считаю, что листы крестики-нолики работают в разных ситуациях. Вы можете предложить учащимся использовать их для игры в крестики-нолики.Кроме того, вы можете использовать их как простой практический рабочий лист.

Играя в крестики-нолики с пропорциями, учащиеся работают с партнером и по очереди отвечают на вопросы. Выигрывает тот, кто первым соберет 5 подряд. Вы можете попросить их сменить партнера и попробовать еще раз. Этот тип игры способствует разговору о математике и выбрасывает математику из их голов, потому что им нужно говорить.

В нашем путешествии по совершенствованию наших безумных навыков решения пропорций мы часто использовали Quizizz. На самом деле мы выполняли одну викторину в день и вели учет нашего прогресса.Студенты отвечали на вопросы и записывали свои баллы в интерактивную тетрадь. Мы стремились к постепенному улучшению, и большинство студентов это видели.

Quizizz — это онлайн-игра, в которой учащиеся получают очки за скорость и точность. Вы можете увидеть, как справился весь класс, на одной странице. У них есть довольно исчерпывающий банк викторин, созданных другими учителями. Вот одна игра Quizizz, в которую мы играли, но вы можете найти и другие. Кроме того, при настройке игры в ней есть функция, позволяющая отключить таймер (лично мне нравится выбирать эту настройку, чтобы ученики сосредоточились на точности, а не на скорости).Затем вы можете легко назначить его из Quizizz в Google Classroom, чтобы учащиеся могли легко найти ссылку.

Если вашим ученикам понравился описанный выше лабиринт, вы можете попробовать пройти битву в лабиринте пропорций. На странице есть два лабиринта. На странице на самом деле три листа бумаги, склеенных вместе. Учащиеся начинают одновременно и хотят добраться до конца быстрее всех. Они могут попросить учителя проверить это в любое время. Если они не спрашивают до конца, а затем у них есть ошибка, они должны пройти весь путь назад.Я люблю деятельность. Похоже на American Ninja Warrior, но в математической версии для средней школы.

Эта игра сочетает в себе старую добрую практику с потрясающей графикой и играми. Студент может выбирать между 8 различными играми. Затем они просто тренируются находить х в пропорции. Вы можете использовать этот онлайн-ресурс снова и снова. Он также имеет рабочий лист для печати внизу страницы и содержит задания по широкому кругу тем. Мне очень нравятся игры Zombie Math и Math Muncher.Мне нравится пробовать игры, чтобы я мог поговорить с детьми о том, во что они играют. Проблемы для этой игры довольно просты.

Иногда вам просто нужна игра для всего класса, и ученики любят Kahoot. Вопросы отображаются на доске, а затем каждый ребенок отвечает на вопрос на своем планшете или компьютере. По ходу игры ученики получают очки и перемещаются вверх и вниз по рейтингу. Одна из моих любимых частей — это функции отчетов в конце. Вы можете получить много формирующих данных из этого отчета.В этой игре Kahoot есть 10 задач, и она идеально подойдет для завершения занятий или повторения в конце года.

   

Веб-сайт Math-Aids создает рабочие листы для практики решения пропорций (не забудьте снять все параметры, кроме выражений мономиальной переменной). Мы редко просто делаем рабочий лист в моем классе. Часто, когда мне нужно, чтобы они потренировались, я добавляю игру, похожую на целевую. По сути, все, что вам нужно, это белая доска и шарик на присоске, чтобы все заработало. Вы можете узнать больше о том, как превратить любой рабочий лист в забавную обзорную игру, сыграв в целевую игру здесь.С помощью этого конкретного рабочего листа вы можете создать рабочий лист. Это означает, что вы можете решить, какие типы проблем вы хотите на нем.

Иногда детям нужна мозговая нагрузка, и я люблю использовать для этого раскраски. Когда я их создаю, я стараюсь не делать раскраску слишком большой, потому что не хочу, чтобы раскрашивание занимало слишком много времени. Я обнаружил, что некоторые ученики не хотят раскрашивать, но я просто требую этого, и это действительно работает, чтобы дать им передышку. Эта раскраска с пропорциями включает в себя 8 решений для x в задачах на пропорции.Это не займет много времени у студентов, но отлично подходит для повторения. Вы можете скачать его БЕСПЛАТНО здесь.

Эта игра с пропорциями грязного байка от Math Playground лучше всего подходит для новичков в этой теме. Кроме того, я использую его со своими студентами математической лаборатории как способ повторения. Вопросы очень простые, но они дают детям интересный способ попрактиковаться. У одной из моих коллег в комнате висит большая клейкая бумага для заметок, и она ведет список высоких результатов. Это дает ей шанс устроить небольшое соревнование между классами.Это будет отлично работать с этой игрой.

Я обнаружил, что этот показатель соотношения и пропорций активности для данк-бака от PBS Learning работает для тех, кто быстро финиширует и долго концентрирует внимание. В серии коротких видеороликов они отвечают на вопросы и зарабатывают баллы. В конце концов, им удается замочить одного из персонажей в баке для данка. Я видел, как некоторым детям это нравится, а другим это будет довольно сложно.

Однажды в летней школе я попробовал это занятие с пакетиками сахара и безалкогольными напитками от Math Equals Love со своими учениками. Им понравилось! И мне понравилось, что они увидели математику в очень актуальном свете. Вы можете адаптировать это для своего класса в зависимости от того, сколько времени вы хотите потратить. Учащиеся смотрят на разные бутылки газировки и сравнивают количество сахара. Они должны выяснить, как сравнить количество сахара, используя пропорции. Кроме того, они увидят, сколько сахара в газировке (что их шокирует). Я бы посоветовал иметь под рукой несколько бутылок газировки и пакеты с сахаром. Тогда учащиеся смогут действительно увидеть, о чем вы говорите.

Попробуйте что-нибудь

Итак, в этом посте есть много идей, которые вы можете попробовать, и иногда это может показаться немного ошеломляющим. Я бы посоветовал вам просто попробовать один из них. Добавьте что-нибудь в свой ящик для инструментов и посмотрите, как отреагируют дети. Помните, что то, что эти занятия доставляют удовольствие, не означает, что дети не тренируются. Если вы сможете больше увлечь студентов, добавив немного новинок, то их математическая практика даст им больше стимула. Получайте удовольствие от преподавания математики!

Большое спасибо за чтение! До скорого.

Родственные

Учебные курсы и коэффициенты {6 класс}

Одним из навыков построения, которым необходимо овладеть в седьмом классе, являются темпы и коэффициенты обучения. В шестом классе ученики изучают основы решения пропорций в седьмом классе. Учащиеся имеют предварительные знания о числах, выражениях и делении, что помогает им научиться решать коэффициенты и отношения.

Я перечислил здесь действия, чтобы просмотреть и попрактиковаться в нормах и соотношениях.Я надеюсь, что они помогут вам начать планирование урока в мире ставок и соотношений. Ключом к тому, чтобы вовлечь учащихся в учебный процесс, является включение интерактивных, наглядных, увлекательных мероприятий, в которых они могли бы активно участвовать.

Эти интерактивные задания в тетради предназначены для того, чтобы помочь учащимся понять концепцию отношения, использовать язык отношений для описания отношений между двумя величинами, понять концепцию удельной нормы, использовать язык норм для описания отношения отношений, а также использовать отношение и скорость рассуждения для решения реальных и математических задач. Включено:

— 4 различных занятия по нормам и соотношениям для привлечения учащихся
— Занятие, организованное учителем в течение 60-90 минут в классе
-Упражнения включают в себя: словарный запас, практику написания таблиц соотношений, чтение словесных задач на соотношения и написание соотношений 3 разными способами, а также нахождение единиц измерения
. -Примеры выполненных интерактивных математических заданий в тетради включены

Эти интерактивные задания для тетрадей предназначены для того, чтобы помочь учащимся понять, как использовать рассуждения об отношении и скорости для решения реальных и математических задач.Учащиеся узнают, как рассуждать о таблицах эквивалентных отношений, использовать линейные диаграммы и уравнения с двойными числами.

Включено:
— 4 различных занятия по нормам и соотношениям для привлечения учащихся
— Занятие, организованное учителем в течение 60-90 минут в классе
-Упражнения включают в себя: словарный запас, практику написания эквивалентных соотношений, поиск расценок за единицу для различных количеств и нахождение цен за единицу продаваемых товаров.
-Примеры выполненных интерактивных математических заданий в тетради включены
.

Это задание на математической станции предназначено для того, чтобы помочь учащимся понять концепцию отношения, использовать язык отношений для описания взаимосвязи между двумя величинами, понять концепцию удельной нормы, использовать язык оценок для описания отношения отношения, а также использовать отношение и скорость рассуждений для решения реальных и математических задач. Включено:
-6 различных станций для привлечения студентов
— Занятие, организованное учителем в течение 60-90 минут в классе
-Станции включают:
1. Словарь
2. Технология (нужны компьютеры в классе и доступ в Интернет к ixl.com)
3. Практика ставок и соотношений
4. Дополнительная практика ставок и коэффициентов
5. Реальные приложения Ratios
6. Словесные задачи Rates & Ratios
-Student Station Guide помогает учащимся записывать свои ответы
— ВСЕ КЛЮЧИ ОТВЕТОВ включены
Эта математическая станция предназначена для того, чтобы помочь учащимся понять, как использовать рассуждения об отношении и скорости для решения реальных и математических задач. Студенты узнают, как рассуждать о таблицах эквивалентных соотношений, использовать линейные диаграммы и уравнения с двойным числом.

Включены:
-6 различных станций для вовлечения учащихся
-Учебная деятельность под руководством учителя в течение 60-90 минут занятий в классе
-Станции включают:
1. Словарь
2. Технология (необходимы компьютеры в классе и доступ в Интернет для ixl .com)
3. Практика ставок и соотношений
4. Дополнительная практика ставок и соотношений
5.Применение коэффициентов в реальных условиях
6. Словесные задачи на коэффициенты и соотношения
-Руководство по студенческой станции помогает учащимся записывать свои ответы
— ВСЕ КЛЮЧИ ОТВЕТОВ включены

Эти математические складки предназначены для того, чтобы учащиеся могли понять концепцию отношения, использовать язык отношений, понять концепцию удельной скорости, использовать рассуждения об отношении и скорости для решения реальных и математических задач, составить таблицы эквивалентных отношений и решать задачи на единицу измерения.

Включает:
— 6 различных складных планшетов NO PREP по математике, чтобы вовлечь учащихся в конспектирование
— Упражнения, проводимые учителем в течение 15-20 минут в классе каждый
— PRINT & GO для обучения, готовые к использованию без PREP
— Инструкции по использованию Математические Складные столы в вашем классе
— Варианты создания строительных лесов с пустыми шаблонами
— Складные столы в комплекте:
Складной: Соотношения и коэффициенты
Складной: Таблицы соотношений
Складной: Пропорции
Складной: Решение пропорций
Складной: Последовательность и выражения
Складной: Пропорции и уравнения
Складной: четыре пустых шаблона

Этот ноябрьский пакет Math NO PREP, который заинтересует ваших шестиклассников! Этот пакет просто весело.Он не только УПАКОВАН основными математическими задачами шестого класса, но и дает учащимся забавные раскраски, головоломки и решения задач. Используйте этот пакет для звонка, работы в классе, дополнительных баллов, быстрых финишеров или домашних заданий!

 Рассматриваемые темы:
— Операции с дробями
— Построение графиков на координатной плоскости
— Операции с десятичными дробями
— Представление соотношений и долей
— Применение соотношений и долей
Я надеюсь, что эти ресурсы помогут вашим учащимся вовлечься в изучение пропорций и соотношений. Активное участие учащихся в учебном процессе гарантирует, что они несут ответственность за собственное обучение. Цель изучения Rates and Ratios состоит в том, чтобы учащиеся приобрели базовые знания, чтобы продолжать расти в седьмом классе.

 

Рабочие листы в формате PDF с ответами на отношения и оценки для 6-го класса

Важные факты о математических упражнениях на отношения и нормы для 6-го класса

Мотивируйте своих детей повеселиться с помощью наших тщательно отобранных заданий на отношения, таких как , запишите соотношение, эквивалентные отношения, таблицы отношений, вычислите соотношение из пропорции, решите пропорцию, определите пропорциональные отношения с помощью графика и т. д. .

В значительной степени, наше основное упражнение на соотношение веселья; — напишите соотношение , имеет большое значение, так как ребенок легко поймет и выучит использование языка соотношения. Это поможет им грамотно описать связь между двумя величинами.

Улучшите математические навыки ребенка с помощью соотношений и пропорциональных рассуждений — решайте математические задачи из реального мира

Понимание соотношений и рассуждений о пропорциях — главный секрет улучшения математических навыков детей в отношении дробей, десятичных знаков, процентов, ставок, единиц и т. д.В результате они получат отличную основу для продвинутой математической алгебры и навыков пропорционального мышления.

Не менее интересно отметить, что навыки отношения и пропорциональные рассуждения очень полезны в некоторых ситуациях реальной жизни, таких как сравнение цен, выпечка (количество сахара на килограмм муки) и т. д.

С помощью наших красиво оформленных моделей соотношений с мультипликативными шаблонами, графиков пропорциональных отношений и представлений таблиц соотношений в наших Рабочих листах пропорций для 6 класса ваш ребенок будет очень вдохновлен умением сравнивать 2 или более величин.

На самом деле, эти модели и представления в виде таблиц являются отличными стратегиями, позволяющими детям узнать эффективную стратегию, которая лучше всего подходит для решения конкретной задачи. Наши вдохновляющие словесные задачи — идеальное руководство для проверки понимания вашим ребенком концепции соотношений и ставок.

Каким образом понятия отношения и доли являются лучшей формой мышления умножения и деления?

Понятия соотношения и нормы являются лучшими формами мышления умножения и деления благодаря следующему;

В первую очередь, глядя на образцы шаблонов в наших листах PDF с ответами на соотношения и оценки для 6-го класса, напишите упражнение на соотношение ,  ваши дети мгновенно поймут идеологию умножения.

Во-вторых, в большинстве упражнений на соотношения и коэффициенты, таких как таблицы соотношений, дети должны использовать свои навыки умножения и деления и исследовать закономерности и структуры.