План урока по теме «Буквенные выражения»
Класс 7. Тема: «Буквенные выражения».
Цели урока:
Личностные: развитие эстетических чувств, доброжелательности и эмоционально – нравственной отзывчивости; развитие мотивов учебной деятельности и формирование личностного смысла учения.
Коммуникативные: уметь находить в тексте информацию, необходимую для решения задачи.
Регулятивные: формировать постановку учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще не известно.
Познавательные: уметь осуществлять сравнения и классификацию по
Оборудование: компоненты УМК «Сферы. Математика 5», проектор, интерактивная доска (ИД).
Этапы урока
Цели и задачи этапа на уровне формирования учебных действий
1.Организационный момент
Создание благоприятных условий для личностного и познавательного развития учащихся.
2.Актуализация знаний учащихся
Развитие математической речи, логического мышления. Развитие умения проводить наблюдение под руководством учителя. Уметь строить рассуждение в форме связи простых суждений об объекте.
3.Изучение нового материала
Организовывать и планировать учебное сотрудничество с учителем и сверстниками.
Корректировать деятельность: вносить изменения в процесс с учетом возникших трудностей и ошибок, намечать способы их устранения. Формировать постановку учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще не известно.
4. Закрепление изученного материала
Уметь осуществлять сравнение и классификацию по заданным критериям. Уметь устанавливать и сравнивать разные точки зрения ,делать выбор. Обмен знаниями между членами группы для эффективных совместных решений; способность брать на себя инициативу в организации совместного действия.
5. Подведение итогов.
Прогнозирование и самоопределение по выполнению домашнего задания. Предметная рефлексия. Формирование регулятивного опыта. Развитие умений формирования вопросов.
6. Домашнее задание.
Саморегуляция, развитие самосознания, ответственного отношения . Формирование заботливого отношения к друзьям.
Ход урока
Этапы
Деятельность учителя
Визуальный ряд
Деятельность учащихся
1
Здравствуйте, ребята.
Нам урок пора начать
Пришло время размышлять
И на трудные вопросы
Вы ответ сумейте дать.
Учащиеся садятся по четыре человека за каждый стол
2
Устные упражнения
Учащиеся считают устно
Учащиеся устно дают характеристику каждой линии
3
Подготовительная работа
Чем выражения записанные на доске отличаются от числовых выражений? Как называются данные выражения?
Как вы думаете чему мы должны сегодня научиться на уроке?
Учитель вводит понятие буквенного выражения
Учащиеся отвечают на наводящие вопросы, формулируют тему урока.
4
Задачник 1.19 – 1.22(а,б)
Учащиеся выполняют номера и записывают их в тетрадь.
5
Перед Вами 2 числа +5 и — 5, как называются эти числа?
Сегодня я оцениваю работу Вашего класса на положительную отметку 5+.
Сегодня я целый урок вас оценивала, о сейчас я попрошу вас оценить меня:
Опустите жетончик в соответствующий кармашек.

Учащиеся дают определение этим числам.
6
Домашнее задание
1.19 – 1.22(в,г)
Записывают домашнее задание в дневник
infourok.ru
Тест по алгебре по теме «Буквенные выражения» (7 класс)
ТЕСТ
по теме «Буквенные выражения»
7 класс
часть А
Выбрать букву, соответствующую верному ответу.
Запишите половину разности чисел a и b
А) 
 Г) ( a : b ): 2
Г) ( a : b ): 22. Из формулы F = ma выразите m через F и a
А) m = Fa Б) m =  В) m =
В) m =  Г) m =F – a
Г) m =F – a
3. Упростите выражение ( х + у ) – 10( 2х – у )
А) 11у – 19х Б) – 9у – 19х В) 11у + 21х Г) 21х – 11у
4. Упростите выражение 4a + ( 3a – ( a + 3 ))
А) 6а — 3 Б) 6а + 3 В) 8а + 3 Г) 2а – 3
5. Найдите значение выражения 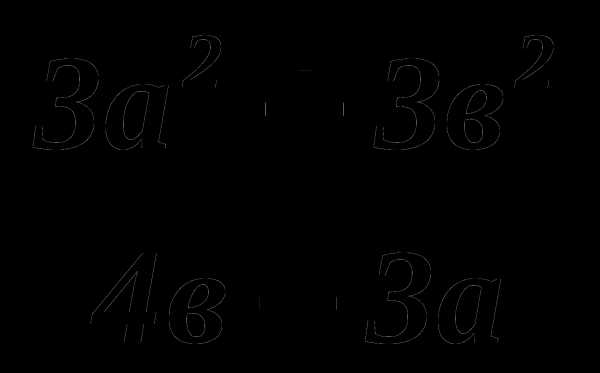 если, а =2; b = -1
если, а =2; b = -1
А) 1,5 Б) — 4,5 В) 4,5 Г) — 1,5
6. Известно, что аn• a = a18 ; bk : b2 = b5 ; (c4 )m = c12
А) n = 18; k = 7; m = 3 Б) n = 17; k = 7; m = 8
В) n = 17; k = 7; m = 3 Г) n = 17; k =10; m = 3
7. Из предложенных пар чисел ( a; b) выделите ту, которая является недопустимой для выражения 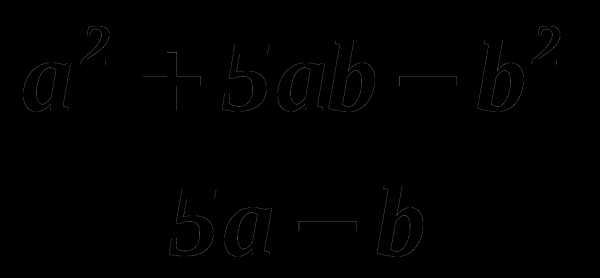
А) a = -1; b = 1 Б) a = 1; b = 1
В) a = 0; b = 5 Г) a = — 2; b = — 10
часть В
Записать ответ.
75% числа а на 10 больше, чем

Переведите на математический язык предложение: «После того, как из первого бидона перелили во второй 15 л молока, во втором бидоне оказалось на 7 л молока меньше, чем в первом. Сколько молока стало во втором бидоне, если первоначально в нём было в три раза меньше, чем в первом ?
Упростите
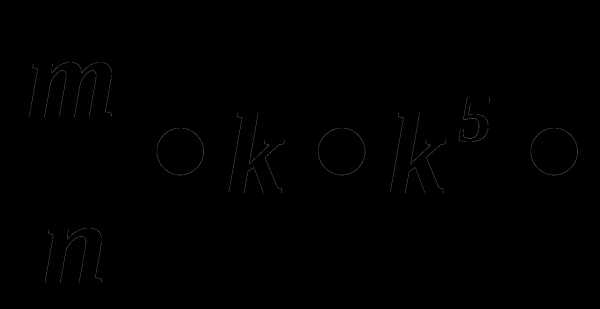
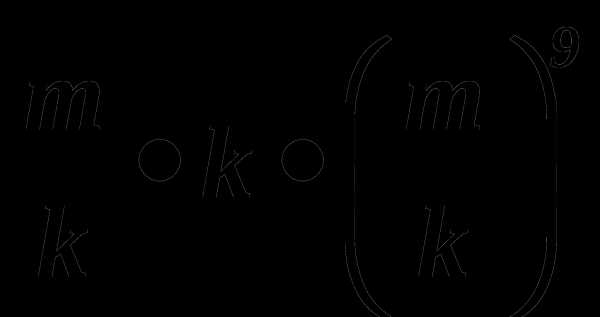
Представьте одночлен в стандартном виде ( — 3 )2ab • 2a2
Выполните действия ( — 3 х у4 )3 • ( — 2 х5 у )2
Представьте в виде квадрата
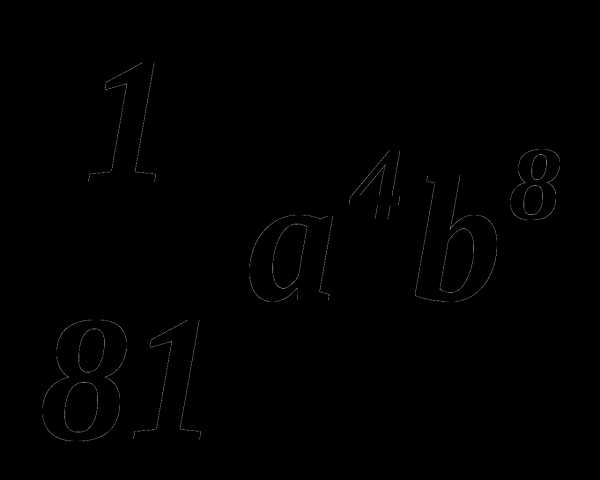
Представьте в виде куба — 0, 001 х6 у9
Найдите площадь квадрата со стороной
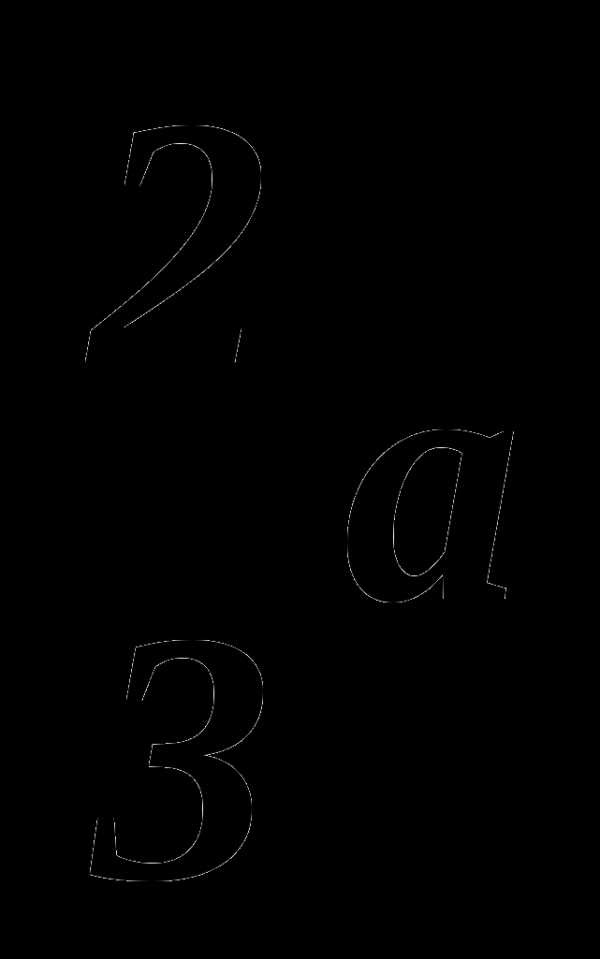
При каких значениях переменных выражение
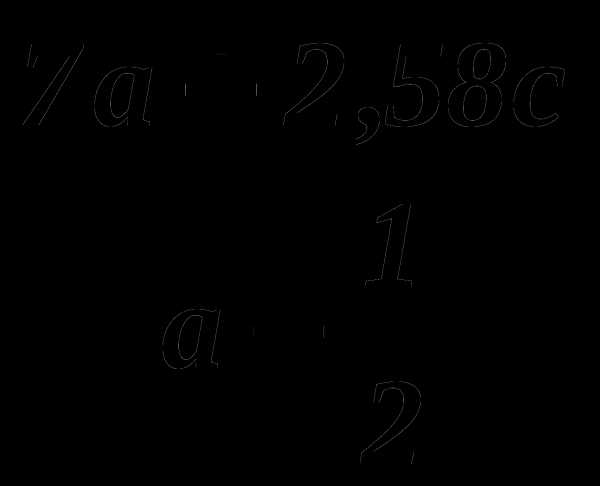 имеет смысл ?
имеет смысл ?Найдите значение одночлена — 200ху3 при х = —
 ; у = — 0,1
; у = — 0,1
Решить.
При каком значении у значение выражения 7у – 2 больше значения выражения
5у – 4 в 2 раза ?
Докажите, что значение выражения не зависит от х:
0,4х – 0,6( х – 4 ) + 2( -1 + 0, 1х ).
Назовите числовой коэффициент одночлена
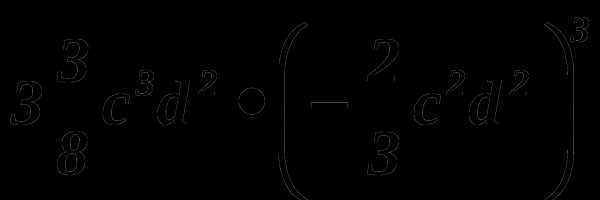
ОТВЕТЫ
к тесту по теме «Буквенные выражения» (7 класс )
часть А часть В часть С
В 2. 3х – 15 = х + 22 или 3х – 22 = х + 15 2. 0,4
А 3.
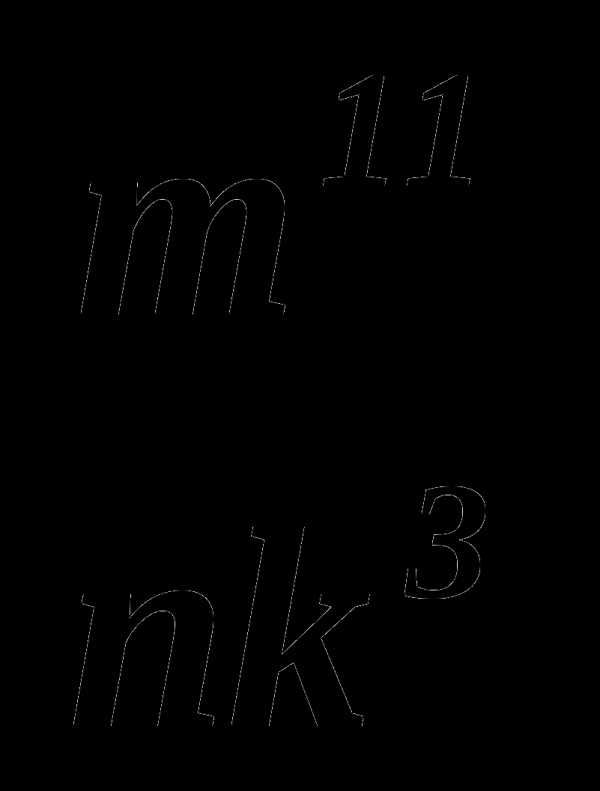 3. — 1
3. — 1А 4. 18 а3 в
Г 5. – 108 х13 у14
В 6.
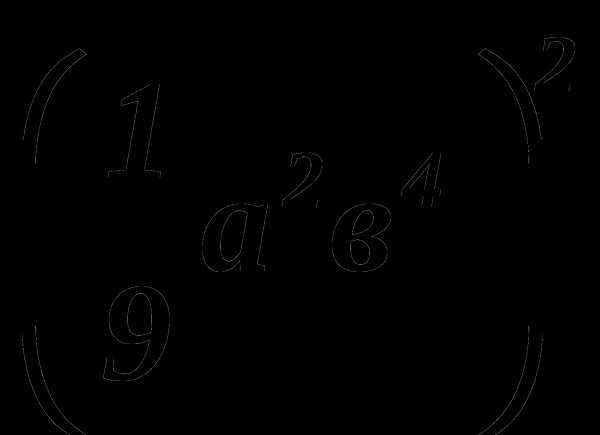
Г 7. ( — 0,1 х2 у3 )3
8.  а2
а2
9. все, кроме а = 
10. – 0,1
infourok.ru
Числовые и буквенные выражения. Формула
Числовые и буквенные выражения.
Формула
Сложение, вычитание, умножение, деление — арифметические действия (или арифметические операции). Этим арифметическим действиям соответствуют знаки арифметических действий:
+ (читаем «плюс«) — знак операции сложения,
— (читаем «минус«) — знак операции вычитания,
∙ (читаем «умножить«) — знак операции умножения,
: (читаем «разделить«) — знак операции деления.
Запись, состоящая из чисел, связанных между собой знаками арифметических действий, называется числовым выражением. В числовом выражении могут присутствовать также скобки Например, запись 1290 : 2 – (3 + 20 ∙ 15) является числовым выражением.
Результат выполнения действий над числами в числовом выражении называется значением числового выражения. Выполнение этих действий называется вычислением значения числового выражения. Перед записью значения числового выражения ставят знак равенства
Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий называется буквенным выражением. В этой записи могут присутствовать скобки. Например, запись a + b – 3 ∙ c является буквенным выражением. Вместо букв в буквенное выражение можно подставлять различные числа. При этом значение букв может изменяться, поэтому буквы в буквенном выражении называют еще переменными.
Подставив в буквенное выражение числа вместо букв и вычислив значение получившегося числового выражения, находят значение буквенного выражения при данных значениях букв (при данных значениях переменных). В таблице 2 приведены примеры буквенных выражений.
Буквенное выражение может не иметь значения, если при подстановке значений букв получается числовое выражение, значение которого для натуральных чисел не может быть найдено. Такое числовое выражение называется некорректным для натуральных чисел. Говорят также, что значение такого выражения «не определено» для натуральных чисел, а само выражение «не имеет смысла». Например, буквенное выражение a – b не имеет значения при a = 10 и b = 17. Действительно, для натуральных чисел, уменьшаемое не может быть меньше вычитаемого. Например, имея всего 10 яблок (a = 10), нельзя отдать из них 17 (b = 17)!
В таблице 2 (колонка 2) приведён пример буквенного выражения. По аналогии заполните таблицу полностью.
Для натуральных чисел выражение 10 -17 некорректно (не имеет смысла), т.е. разность 10 -17 не может быть выражена натуральным числом. Другой пример: на ноль делить нельзя, поэтому для любого натурального числа b, частное b : 0 не определено.
Математические законы, свойства, некоторые правила и соотношения часто записывают в буквенном виде (т.е. в виде буквенного выражения). В этих случаях буквенное выражение называют формулой. Например, если стороны семиугольника равны a, b, c, d, e, f, g, то формула (буквенное выражение) для вычисления его периметра p имеет вид:
p = a + b + c + d + e + f + g
При a = 1, b = 2, c = 4, d = 5, e = 5, f = 7, g = 9, периметр семиугольника p = a + b + c + d + e + f + g = 1 + 2 + 4 + 5 +5 + 7 + 9 = 33.
При a = 12, b = 5, c = 20, d = 35, e = 4, f = 40, g = 18, периметр другого семиугольника p = a + b + c + d + e + f + g = 12 + 5 + 20 + 35 + 4 + 40 + 18 = 134.
Блок 1. Словарь
Составьте словарь новых терминов и определений из параграфа. Для этого в пустые клетки впишите слова из списка терминов, приведенного ниже. В таблице (в конце блока) укажите номера терминов в соответствии с номерами рамок. Рекомендуется перед заполнением клеток словаря еще раз внимательно просмотреть параграф.
- Операции: сложение, вычитание, умножение, деление.
2.Знаки «+» (плюс), «-» (минус), «∙» (умножить, «:» (разделить).
3.Запись, состоящая из чисел, которые связанны между собой знаками арифметических действий и в которой могут присутствовать также скобки.
4.Результат выполнения действий над числами в числовом выражении.
5. Знак, стоящий перед значением числового выражения.
6. Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий (могут присутствовать также скобки).
7. Общее название букв в буквенном выражении.
8. Значение числового выражения, которое получается при подстановке переменных.в буквенное выражение.
9.Числовое выражение, значение которого для натуральных чисел не может быть найдено.
10. Числовое выражение, значение которого для натуральных чисел может быть найдено.
11. Математические законы, свойства, некоторые правила и соотношения, записанные в буквенном виде.
12. Алфавит, малые буквы которого используются для записи буквенных выражений.
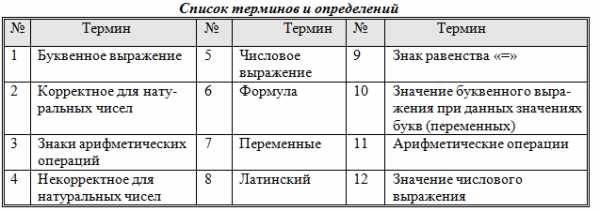
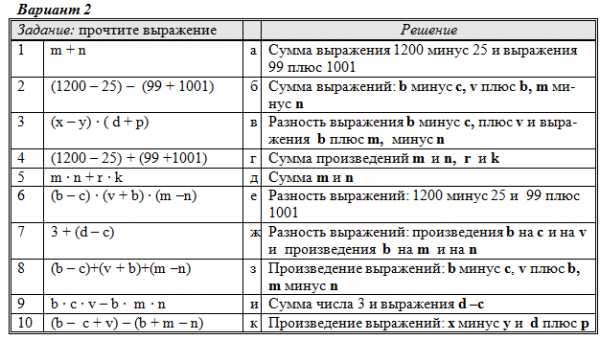
Блок 2. Установите соответствие
Установите соответствие между заданием в левой колонке и решением в правой. Ответ запишите в виде: 1а, 2г, 3б…
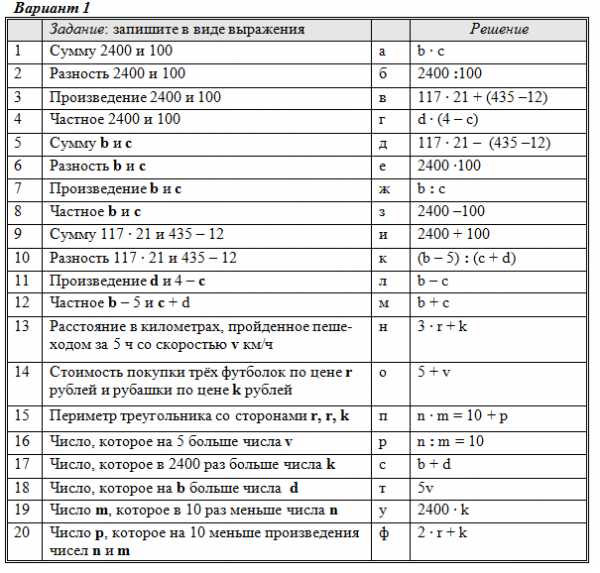
Блок 3. Фасетный тест. Числовые и буквенные выражения
Фасетные тесты заменяют сборники задач по математике, но выгодно отличаются от них тем, что их можно решать на компьютере, проверять решения и сразу узнавать результат работы. В этом тесте содержится 70 задач. Но решать задачи можно по выбору, для этого есть оценочная таблица, где указаны простые задачи и посложнее. Ниже приведён тест.

- Дан треугольник со сторонами c, d, m, выраженными в см
- Дан четырехугольник со сторонами b, c, d, m, выраженными в м
- Скорость автомобиля в км/ч равна b, время движения в часах равно d
- Расстояние, которое преодолел турист за m часов, составляет с км
- Расстояние, которое преодолел турист, двигаясь со скоростью m км/ч, составляет b км
- Сумма двух чисел больше второго числа на 15
- Разность меньше уменьшаемого на 7
- Пассажирский лайнер имеет две палубы с одинаковым количеством пассажирских мест. В каждом из рядов палубы m мест, рядов на палубе на n больше, чем мест в ряду
- Пете m лет Маше n лет, а Кате на k лет меньше, чем Пете и Маше вместе
- m = 8, n = 10, k = 5
- m = 6, n = 8, k = 15
- t = 121, x = 1458
ТО:
- Значение данного выражения
- Буквенное выражение для периметра имеет вид
- Периметр, выраженный в сантиметрах
- Формула пути s, пройденного автомобилем
- Формула скорости v, движения туриста
- Формула времени t, движения туриста
- Путь, пройденный автомобилем в километрах
- Скорость туриста в километрах в час
- Время движения туриста в часах
- Первое число равно…
- Вычитаемое равно….
- Выражение для наибольшего количества пассажиров, которое может перевезти лайнер за k рейсов
- Наибольшее количество пассажиров, которое может перевезти лайнер за k рейсов
- Буквенное выражение для возраста Кати
- Возраст Кати
- Координата точки В, если координата точки С равна t
- Координата точки D, если координата точки С равна t
- Координата точки А, если координата точки С равна t
- Длина отрезка BD на числовом луче
- Длина отрезка CА на числовом луче
- Длина отрезка DА на числовом луче
Ответы (равно, имеет вид, не определено):
а)1; б) s=b ∙d; в) 9; г) 40; д) b + c + d + m; е) 7; ж) выражение не имеет смысла (некорректно) для натуральных чисел; з) 2 ∙ m (m + n) ∙ k; и) (m + n) – k; к) 6; л) 15; м) 3760; н) t – 3; о) фигура не может быть треугольником; п) 22; р) t – 3 ∙ 7; с) 0; т) 32; у) 59600; ф) 6019; х) 2880; ц) 10378; ч)1440; ш) на ноль делить нельзя; щ) 13; ы) 1800; э) 496; ю) 2; я) 12; аа) 14; бб) 5; вв) 35; дд) 79200; ее) 1900; жж) 118; зз) 18; ии) 12800; кк) 98; лл) 1458; мм) v = c : m; нн) 100; оо) 19900; пп) t = b : m; рр) 2520; сс) c + d + m; тт) x; уу) 1579; фф) t + 2; хх) 10206; цц) 135; чч) t + 2 ∙ 7; шш) 7 ∙ x; щщ) x – 2; ыы) 7 ∙ x – 2 ∙ 7; ээ) t + x ∙ 7; юю) 10192; яя) t + x; ааа) 123; ббб) 1456; ввв) 10327.
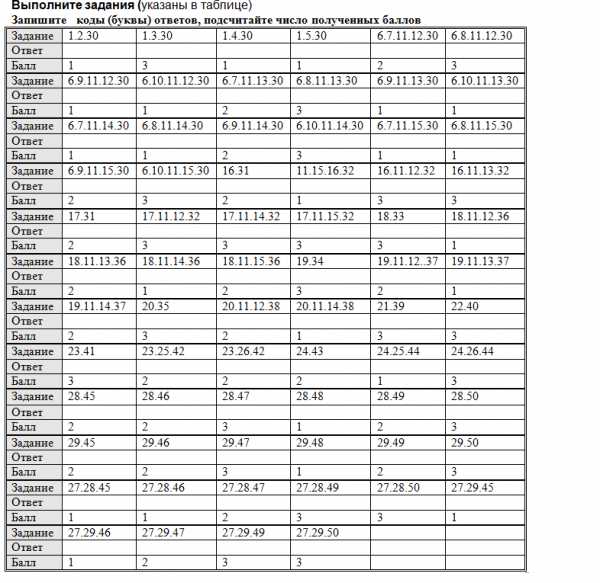
ПОКАЗАТЕЛИ ТЕСТА. Число задач 70, время выполнения 2 – 3 часа, сумма баллов: 1 ∙ 22 + 2 ∙ 24 + 3 ∙ 24 = 142. Для фасетного теста можно использовать следующую шкалу оценок.
Блок 4. Давайте поиграем


Блок 5. Обучающая игра «Уроки кота Леопольда»


Для учителя приводим ответы к блокам параграфа 6
Ответы к игре «Уроки Леопольда»
Западня 1 : 1/2, 1/3, 2/3, 7/8. Западня 2. 12, 2, 13 5. Западня 3. 6
Западня 4. 15. Западня 5. 396
Блок 1. Словарь
Блок 2. Установите соответствие.
Вариант 1: 1и, 2з, 3е, 4б, 5м, 6л, 7а, 8ж, 9в, 10д, 11г, 12к, 13т, 14н, 15ф, 16о, 17у, 18с, 19р, 20п
Вариант 2: 1д, 2е, 3к, 4а, 5г, 6з, 7и, 8б, 9ж, 10в
Блок 3. Фасетный тест. Числовые и буквенные выражения (ответы под заданиями)
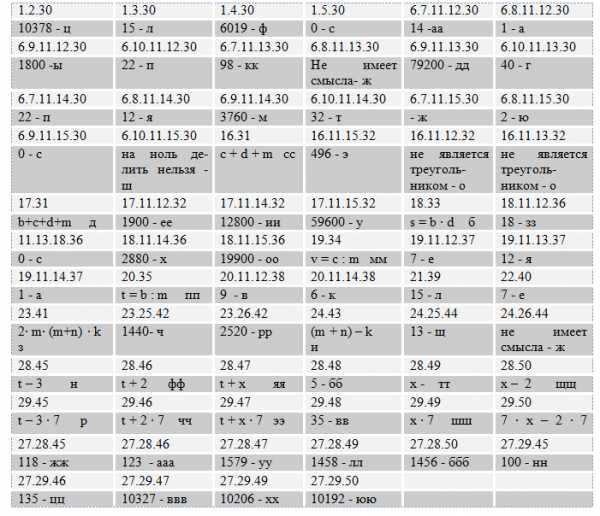
Ответы к игре «Сокровища»
Деревянный – 10250. Оловянный – 21640. Медный – 50400. Серебряный – 191000. Золотой – 289800.
ya-znau.ru
Числовые и буквенные выражения / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Числовое выражение – это запись , состоящая из чисел и знаков действий между ними.
Например, 44 + 32
Значение выражения — это результат выполненных действий.
Например, в записи 44 + 32 = 76, значение выражения — это 76.
Чтение числовых выражений
12 + 9 — сумма
49 — 20 — разность
34 — (8 + 21) — из 34 вычесть сумму чисел 8 и 21
13 + (26 — 8) — к 13 прибавить разность чисел 26 и 8
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Давай сравним значения двух выражений: 14 — 6 и 18 — 9.
Для этого найдем значения каждого из них:
14 — 6 = 8
18 — 9 = 9
8 < 9, значит,
14 — 6 < 18 — 9
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
В этих выражениях буквы могут обозначать различные числа. Число, которым заменяют букву, называют значением.
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
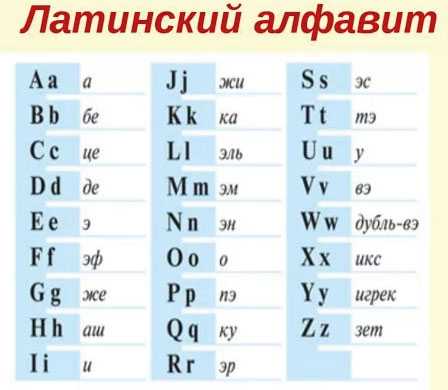
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
Алгоритм — значит, порядок, план выполнения команд.
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Например, 28 – с
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Вычисляем результат:
28 – 4 = 24
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
c = 2, x = 3
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
2 + 3 + 2
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Уравнения
Правило встречается в следующих упражнениях:
2 класс
Страница 42, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 82, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 88, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 45. Вариант 2. № 2, Моро, Волкова, Проверочные работы
Страница 15, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 42, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 48, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 58, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 104, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 33, Моро, Волкова, Рабочая тетрадь, 2 часть
3 класс
Страница 26, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 30, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 36, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 48, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 53, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 65, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 69, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 111, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 23, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 36, Моро, Волкова, Рабочая тетрадь, 1 часть
© 2018 — budu5.com, Буду отличником!
budu5.com
Числовые и буквенные выражения. Значение выражения
Числовые выражения
Числовое выражение – это запись, составленная со смыслом, в которой числа обозначены цифрами (в неё также могут входить знаки арифметических действий и скобки). Числовые выражения так же называются арифметическими выражениями.
7 – числовое выражение
2 + 2 — 1 – числовое выражение
7 — 2 · + : 1 – бессмысленный набор символов
Вычислить значение выражения – это значит выполнить все арифметические действия, указанные в выражении. Действия выполняются в определённом порядке, в зависимости от самих действий и присутствия в выражении скобок. Про порядок выполнения действий можно прочитать тут:
Значение числового выражения – это число, получившееся после выполнения всех вычислений.
Пример 1. Найдите значение числового выражения 4 + 3
Решение:
4 + 3 = 7
Ответ: 7.
Пример 2. Найдите значение числового выражения 4 · 3
Решение:
4 · 3 = 12
Ответ: 12.
Буквенные выражения
Буквенное выражение – это числовое выражение, в котором числа могут быть обозначены и цифрами и буквами. Буквенные выражения так же называются алгебраическими выражениями.
При обозначении чисел буквами обычно используют строчные (маленькие) буквы латинского алфавита:
7 · a – буквенное выражение
a – (b + c) – буквенное выражение
Чаще всего в буквенных выражениях разные числа обозначены разными буквами, но например в выражении:
a = b
подразумевается что a и b являются одним и тем же числом.
Значение буквенного выражения – это число, получившееся после выполнения всех вычислений. Действия в буквенных выражениях выполняются после подстановки вместо букв их численных значений.
Пример. Найдите значение буквенного выражения 2 · a + 3 при a = 7.
Решение:
2 · 7 + 3 = 14 + 3 = 17
Ответ: 17.
В буквенных выражениях знак умножения между числом и буквой, а так же между буквами, не пишут, поэтому считается, что:
7 · a = 7a и x · y = xy
Если в записи выражения одна и та же буква, например a, употребляется несколько раз, то под значением этой буквы во всех случаях мы должны иметь ввиду одно и тоже число.
Пример. Найдите значение буквенного выражения 5x — 2x при x = 4.
Решение:
5 · 4 — 2 · 4 = 20 — 8 = 12
Ответ: 12.
В арифметике буквенные обозначения употребляют, когда необходимо выразить, что некоторое свойство (или правило) принадлежит не каким-нибудь отдельным числам, а является общим для любых чисел. Например:
a + b = b + a
Данное равенство показывает нам, что, как бы мы не переставляли слагаемые, сумма от этого не изменится. Подставив вместо букв любые числа, мы можем в этом убедиться сами:
1 + 2 = 2 + 1
naobumium.info
Урок 27. Буквенные выражения и числовые подстановки | Поурочные планы по алгебре 7 класс
Тема: Буквенные выражения и числовые подстановки.
Цели урока: закрепить и повторить понятия буквенного и числового выражений, переменной; объяснить правила решения и оформления задач с переменными; рассмотреть решение задач – шуток, для развития у детей заинтересованности математикой. В течение урока развивать у учащихся навык решения задач с переменными.
Ход урока:
1. Организационный момент. (2 мин.)
2. Устная работа. (5 мин.)
На карточках или на доске записаны выражения.
Для каждого из выражений ученики должны ответить на следующие вопросы.
• Является ли буквенным данное выражение?
• Сколько действий содержит данное выражение?
• Сколько переменных содержится в данном выражении?
Также на доске рассмотреть задание № 301 из домашнего задания.
3. Актуализация знаний. (14 мин.)
Для закрепления понятия буквенных выражений и вычисления их значений разобрать задания № 307 (а, в), 308, 302. Перед тем, как выполнить последний номер вспомнить определение и привести примеры противоположных чисел и взаимообратных.
4. Новый материал. (9 мин.)
Ввести понятие равенства буквенных выражений. Разобрать задачу № 290. Рассказать о значениях алгебраических выражениях при решении задач. Показать правила решения и оформления таких задач на № 291.
5. Закрепление нового материала. (10 мин.)
Решить задачи № 293, 295, 298, 299 (а), 305.
Также рассмотреть решение задач — шуток:
1) У Коли было a марок, а у Сережи на 8 марок больше. Во время игры Сережа сначала проиграл b марок, а затем выиграл 7. Сколько марок стало у каждого мальчика после игры? У кого из мальчиков стало больше марок и на сколько, если a = 14, b = 13.
2) Катя и Нина на берегу моря собирали ракушки. Но девочки поссорили и разделили ракушки, у Кати осталось x ракушек, а у Нины — y. Пока девочки были в ссоре, Катя нашла еще 7 ракушек, Нина нашла 11 ракушек. Потом девочки помирились и дали клятву, никогда не ссорится, и только после этого объединили богатства — ракушки. Сколько всего стало у девочек ракушек? Найдите значение, если x = 17, y = 15.
6. Итоги урока. (3 мин.)
7. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 3.1.
Решить задания № 299 (б), 292, 307 (б, г), 303.
tak-to-ent.net
