Числовые выражения
Числовые выражения.
Числовое выражение – это любая запись из чисел, знаков арифметических действий и скобок. Числовое выражение может состоять и просто из одного числа. Напомним, что основными арифметическими действиями являются «сложение», «вычитание», «умножение» и «деление». Этим действиям соответствуют знаки «+», «-», «∙», «:».
Конечно же, чтобы у нас получилось числовое выражение, запись из чисел и арифметических знаков должна быть осмысленной. Так, например, такую запись 5 : + ∙ нельзя назвать числовым выражением, так как это случайный набор символов, не имеющий смысла. Напротив, 5 + 8 ∙ 9 — уже настоящее числовое выражение.
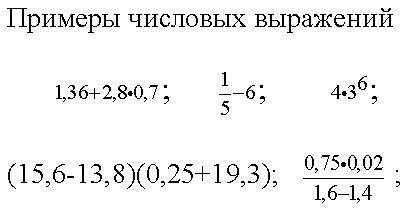
Значение числового выражения.
Сразу скажем, что если мы выполним действия указанные в числовом выражении, то в результате мы получим число. Это число называется значением числового выражения.
Попробуем вычислить, что у нас получится в результате выполнения действий нашего примера. Согласно порядку выполнения арифметических действий, сначала выполним операцию умножения. Умножим 8 на 9. Получим 72. Теперь сложим 72 и 5. Получим 77.
Итак, 77 – значение числового выражения 5 + 8 ∙ 9.
Числовое равенство.
Можно это записать таким образом: 5 + 8 ∙ 9 = 77. Здесь мы впервые использовали знак «=» («Равно»). Такая запись, при которой два числовых выражения разделены знаком «=», называется числовым равенством. При этом, если значения левой и правой части равенства совпадают, то равенство называют верным. 5 + 8 ∙ 9 = 77 – верное равенство.
Если же мы напишем 5 + 8 ∙ 9 = 100, то это уже будет неверное равенство, так как значения левой и правой части данного равенства уже не совпадают.
Следует отметить, что в числовом выражении мы также можем использовать скобки. Скобки влияют на порядок выполнения действий. Так, например, видоизменим наш пример, добавив скобки: (5 + 8) ∙ 9. Теперь сначала нужно сложить 5 и 8. Получим 13. А затем умножить 13 на 9. Получим 117. Таким образом, (5 + 8) ∙ 9 = 117.
Как прочитать числовое выражение?
Чтобы правильно прочитать выражение, нужно определить какое именно действие выполняется последним для вычисления значения данного числового выражения. Так, если последнее действие вычитание, то выражение называют «разностью». Соответственно, если последнее действие сумма — «суммой», деление – «частным», умножение – «произведением», возведение в степень – «степенью».
Например, числовое выражение (1+5)(10-3) читается так: «произведение суммы чисел 1 и 5 на разность чисел 10 и 3».
Примеры числовых выражений.
Приведем пример более сложного числового выражения:
\[\left( \frac{1}{4}+3,75 \right):\frac{1,25+3,47+4,75-1,47}{4\centerdot 0,5}\]
В данном числовом выражении используются простые числа, обыкновенные и десятичные дроби. Также используются знаки сложения, вычитания, умножения и деления. Черта дроби также заменяет знак деления. При кажущейся сложности, найти значение данного числового выражения довольно просто. Главное уметь выполнять операции с дробями, а также внимательно и аккуратно делать вычисления, соблюдая порядок выполнения действий.
В скобках у нас выражение $\frac{1}{4}+3,75$. Преобразуем десятичную дробь 3,75 в обыкновенную.
$3,75=3\frac{75}{100}=3\frac{3}{4}$
Итак, $\frac{1}{4}+3,75=\frac{1}{4}+3\frac{3}{4}=4$
Далее, в числителе дроби \[\frac{1,25+3,47+4,75-1,47}{4\centerdot 0,5}\] у нас выражение 1,25+3,47+4,75-1,47. Для упрощения данного выражения применим переместительный закон сложения, который гласит: «От перемены мест слагаемых сумма не изменяется». То есть, 1,25+3,47+4,75-1,47=1,25+4,75+3,47-1,47=6+2=8.
В знаменателе дроби выражение $4\centerdot 0,5=4\centerdot \frac{1}{2}=4:2=2$
Получаем $\left( \frac{1}{4}+3,75 \right):\frac{1,25+3,47+4,75-1,47}{4\centerdot 0,5}=4:\frac{8}{2}=4:4=1$
Когда числовые выражения не имеют смысла?
Рассмотрим еще один пример. В знаменателе дроби $\frac{5+5}{3\centerdot 3-9}$ значением выражения $3\centerdot 3-9$ является 0. А, как мы знаем, деление на нуль невозможно. Следовательно, у дроби $\frac{5+5}{3\centerdot 3-9}$ нет значения. Про числовые выражения, у которых нет значения, говорят, что они «не имеют смысла».
Если мы в числовом выражении помимо чисел будем использовать буквы, то у нас получится уже алгебраическое выражение.
Дата публикации:
Теги: числовые выражения :: 7 класс
Смотрите также учебники, книги и учебные материалы:
Следующие учебники и книги:
Предыдущие статьи:
- Уроки математики, Пособие для учителей, 2 класс, Дорофеев Г.В., Миракова Т.Н., 2009
- Математика, 6 класс, Методические рекомендации, Суворова С.Б., Кузнецова Л.В., Минаева С.С., Рослова Л.О., 2013
- Математика, 6 класс, Методические рекомендации, Потапов М.К., Шевкин А.В., 2013
- Математика, 5 класс, Методические рекомендации, Суворова С.Б., Кузнецова Л.В., Минаева С.С., Рослова Л.О., 2013
nashol.com
примеры, значение, числовое равенство, правила
Запись, которая состоит из чисел, знаков и скобок, а также имеет смысл, называется числовым выражением.
Например, следующие записи:
- (100-32)/17,
- 2*4+7,
- 13,
- 4*0.7 -3/5,
- 1/3 +5/7
будут являться числовыми выражениями. Следует понимать, что одно число тоже будет являться числовым выражением. В нашем примере, это число 13.
А, например, следующие записи
не будут являться числовыми выражениями, так как они лишены смысла и являются просто набором чисел и знаков.
Значение числового выражения
Так как в качестве знаков в числовых выражениях входят знаки арифметических действий, то мы можем посчитать значение числового выражения. Для этого необходимо выполнить указанные действия.
Например,
(100-32)/17 = 4, то есть для выражения (100-32)/17 значением этого числового выражения будет являться число 4.
2*4+7=15, число 15 будет являться значением числового выражения 2*4+7.
Часто для краткости записи не пишут полностью значение числового выражения, а пишут просто «значение выражения», опуская при этом слово «числового».
Числовое равенство
Если два числовых выражения записаны через знак равно, то эти выражения образуют числовое равенство. Например, выражение 2*4+7=15 является числовым равенством.
Как уже отмечалось выше, в числовых выражениях могут использоваться скобки. Как уже известно скобки влияют на порядок действий.
Вообще, все действия разделены на несколько ступеней.
- Действия первой ступени: сложение и вычитание.
- Действия второй ступени: умножение и деление.
- Действия третей ступени – возведение в квадрат и возведение в куб.
Правила при вычислении значений числовых выражений
При вычислении значений числовых выражений следуют руководствоваться следующими правилами.
- 1. Если выражение не имеет скобок, то надо выполнять действия начиная с высших ступеней: третья ступень, вторая ступень и первая ступень. Если имеется несколько действий одной ступени, то их выполняют в порядке в котором они записаны, то есть слева на право.
- 2. Если в выражении присутствуют скобки, то сначала выполняются действия в скобках, а лишь затем все стальные действия в обычном порядке. При выполнении действий в скобках, если их там несколько, следует пользоваться порядком описанным в пункте 1.
- 3. Если выражение представляет собой дробь, то сначала вычисляются значении в числителе и знаменателе, а потом числитель делится на знаменатель.
- 4. Если в выражении присутствуют вложенные скобки, то выполнять действия следует с внутренних скобок.
Нужна помощь в учебе?
Предыдущая тема: Наименьшее общее кратное (НОК): определение, как найти, общая схема
Следующая тема:   Выражения с переменными: разбираем пример с фокусом
Все неприличные комментарии будут удаляться.
www.nado5.ru
Числовые выражения
Вопросы занятия:
· повторить основные действия, которые можно выполнять над рациональными числами;
· ввести понятия «числовое выражение» и «значение числового выражения»;
· привести примеры нахождения значений числовых выражений;
· решить задачу.
Материал урока
Ранее вы уже изучали различные действия над рациональными числами. Это действие сложение, вычитание, умножение и деление.
Действия сложение, вычитание и умножение можно выполнять для любых чисел, а вот деление – нет.
Определение.
Арифметикой (что с греческого означает «число») называется раздел математики, изучающий числа, их отношения и свойства.
Давайте решим следующую задачу.
На сколько шагов больше сделает ребёнок, чем взрослый, на расстоянии 240 м, если длина шага у ребёнка равна 0,3 м, а у взрослого – 0,8 м?
Решение.
Чтобы найти количество шагов, которые сделал ребёнок, нужно 240 м разделить на длину шага ребёнка – 0,3 м, а чтобы найти количество шагов, которые сделал взрослый, нужно 240 м разделить на длину шага взрослого – нуль 0,8 м.
240 : 0,3 = 800
240 : 0,8 = 300
А тогда, чтобы ответить на вопрос задачи, мы от количества шагов ребёнка отнимем количество шагов взрослого, то есть:
800 – 300 = 500 шагов.
То есть ребёнок сделал на 500 шагов больше взрослого.
Решая задачу, мы получили числовое выражение, выполнив действия которого, нашли значение этого выражения.
Таким образом, сформулируем следующие определения.
Числовым выражением называется запись, составленная из чисел, знаков арифметических действий и скобок, указывающих на порядок выполнения действий.
Значением числового выражения называется число, которое получается при выполнении всех действий числового выражения.
Пример.
Найти значение выражения.
Найдём значение следующего выражения.
Пример.
Давайте найдём значение следующего числового выражения.
Пример.
Пример.
videouroki.net
Числовые выражения. Выражения с переменными. Примеры упрощения выражений
Числовое выражение – это совокупность одного или нескольких чисел и функций, соединенных знаками арифметических операций и скобками.Примеры числовых выражений:
Значением числового выражения является число.
Операции в числовом выражении выполняются в следующей последовательности:
1. Действия в скобках.
2. Вычисление функций.
3. Возведение в степень
4. Умножение и деление.
5. Сложение и вычитание.
6. Однотипные операции выполняются слева на право.
Так значением первого выражения будет само число 12,3
Для того чтобы вычислить значение второго выражения, действия будем выполнять в следующей последовательности:
1. Выполним действия в скобках в следующей последовательности — сначала 2 возведем в третью степень, затем от полученного числа отнимем 11:
3 • 4 + (2^3 — 11) = 3 • 4 + (8 — 11) = 3 • 4 + (-3)
2. Умножим 3 на 4:
3 • 4 + (-3) = 12 + (-3)
3. Выполним последовательно операции слева направо:
12 + (-3) = 9.
Выражение с переменными – это совокупность одного или нескольких чисел, переменных и функций, соединенных знаками арифметических операций и скобками. Значения выражений с переменными зависят от значений, входящих в него переменных. Последовательность выполнения операций здесь та же, что и для числовых выражений. Выражения с переменными иногда бывает полезно упрощать, выполняя различные действия – вынесение за скобки, раскрытие скобок, группировки, сокращение дробей, приведение подобных и т.д. Так же для упрощения выражений часто используют различные формулы, например, формулы сокращенного умножения, свойства различных функций и т. д.
Пример: Упростить выражение 3 • (x – 4 • y + 11) + 12 • y – 30
1. Раскроем скобки:
3 • (x – 4 • y + 11) + 12 • y – 30 = 3 • x – 12 • y + 33 + 12 • y – 30;
2. Приведем подобные:
3 • x — 12 • y + 33 + 12 • y – 30 = 3 • x + 3;
3. Теперь можно оставить выражение в таком виде, а можно вынести 3 за скобки:
3 • x + 3 = 3 • (x + 1).
studyport.ru
Разработка на тему: «Числовые выражения»
7 класс
УРОК № 3. Глава 1. Выражения, тождества, уравнения (22 часа)
Тема. Числовые выражения.
Цель. ввести понятия числового выражения, значения числового выражения; формировать умение находить значение числового выражения, выполняя действия над числами и используя скобки.
Ход урока.
Организационный момент.
Проверка домашнего задания ( фронтально)
Актуализация опорных знаний.
Пример 1. Вычислите. (Устно).
а) 13 – 18,5 = –5,5; б) –19 + 21,3 = 2,3; в) –14 – 71,03 = –85,03;
г) 17 – (–21,3) = 38,3; д) – (–3 – 2,8) = 5,8; е) 3 ∙ 15 – 7 = 38;
ж) (15 – 2) ∙ (–3) = – 39; з) 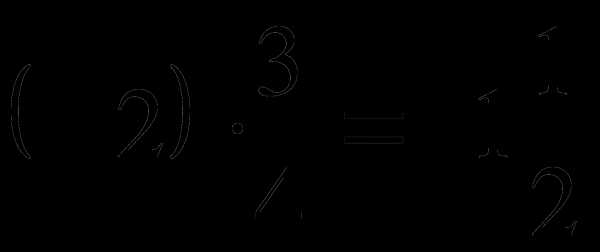 ; к)
; к) 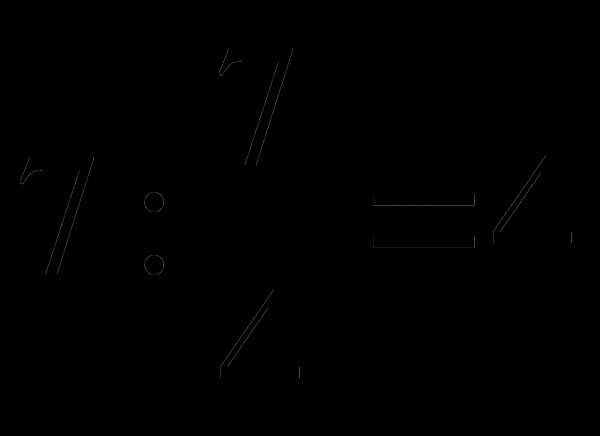 .
.
Объяснение нового материала.
1. При решении многих задач приходится над заданными числами производить арифметические действия: сложение, вычитание, умножение и деление.
Определение. Числовые выражения – выражения, состоящие из чисел и знаков действий.
Но часто, прежде чем доводить до конца каждое из этих действий, удобно заранее указать порядок (план), следуя которому надо производить эти действия. Этот план сводится к тому, что по данным задачи с помощью чисел, знаков действий и скобок составляется числовое выражение.
2. Примеры числовых выражений:
5;  ;
; 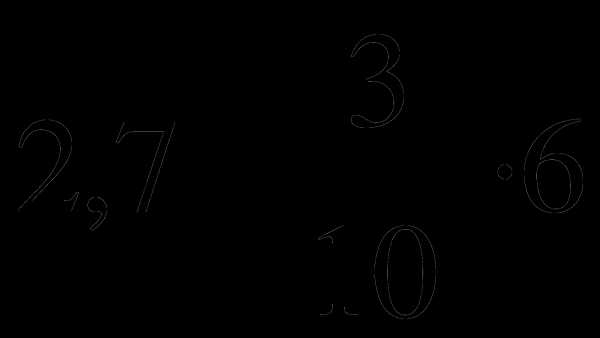 ;
; 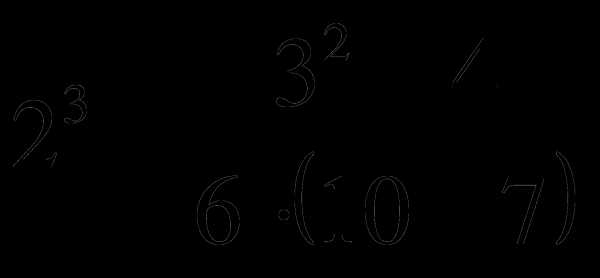 .
.
3. Если в числовом выражении выполнить все указанные в нем действия, то в результате получим действительное число, про которое говорят, что оно равно данному числовому выражению и называется значением выражения.
Определение. Найти значение числового выражения – это значит выполнить все действия в нем.
Пример 2. Найдите значение числового выражения:
.
1) ; 2)  ; 3) .
; 3) .
4.. Всегда возможно произвести сложение, вычитание и умножение любых чисел. А вот делить числа одно на другое возможно, только если делитель не равен нулю: на нуль делить нельзя. Если в данном выражении на некотором его этапе требуется делить на нуль, то это требование неосуществимо. Такое выражение не имеет смысла.
Пример 3. Имеет ли смысл выражение:
; 2)
 .
.
Решение.
Данные выражения не имеют смысла, т.к. при выполнении указанных в нем действий появляется необходимость делить на нуль.
Формирование умений и навыков.
№5 3 столбик (на доске и в тетради)
Ж) 38🙁-0,19)=-200
З) -16:0,2=-80
И) -6,4:(-8)=0,8
№3
3,6:0,08+5,2×2,5=58
(9,885-0,365):1,7+4,410
№13 на доске и в тетради
№14 на доске ив тетради
№17
Подведение итогов урока.
Что называется значением числового выражения?
Для чего в записи числового выражения присутствуют скобки?
Когда числовое выражение имеет смысл? Приведите пример такого выражения.
Когда числовое выражение не имеет смысла? Приведите пример такого выражения.
Что называется значением числового выражения?
Каков порядок выполнения действий при нахождении значения числового выражения?
Домашнее задание. п. 1 (выучить теорию). № 5(1,2 столбик), №6
infourok.ru
Числовые и буквенные выражения. Формулы
Как найти периметр прямоугольника, стороны которого равны 3 см и 5 см (рис. 67)?
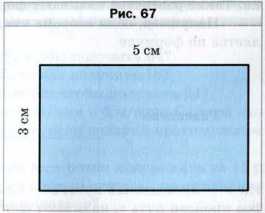
Отвечая на этот вопрос, вы можете сделать такую запись: 2 * 3 + 2 * 5.
Такая запись представляет собой числовое выражение.
Приведем еще несколько примеров числовых выражений: 12 : 4 − 1, (5 + 17) + 11, (19 − 7) * 3. Эти выражения составлены из чисел, знаков арифметических действия и скобок.
Заметим, что не всякая запись, составленная из чисел, знаков арифметических действия и скобок является числовым выражением. Например, запись +) +3 − (2 представляет собой бессмысленный набор символов.
Завершив решение задачи о периметре прямоугольника, получим ответ 16 см. В таких случаях говорят, что число 16 является значением выражения 2 * 3 + 2 * 5.
А чему равен периметр прямоугольника, стороны которого равны 3 см и a см? Ответом будет выражение 2 * 3 + 2 * a.
Запись 2 * 3 + 2 * a представляет собой буквенное выражение.
Приведем еще несколько примеров буквенных выражений: (a + b) + 11, 5 + 3 * x, n : 2 − k * 5. Эти выражения составлены из чисел, букв, знаков арифметических действий и скобок.
Как правило, в буквенных выражениях знак умножения пишут только между числами. В остальных случаях его опускают. Например, вместо 5 * y, m * n, 2 * (a + b) соответственно пишут 5y, mn, 2(a + b).
Пусть стороны прямоугольника равны a см и b см. В этом случае буквенное выражение для нахождения его периметра выглядит так: 2a + 2b.
Подставим в это выражение вместо букв a и b соответственно числа 3 и 5. Получим числовое выражение 2 * 3 + 2 * 5, которое мы уже записывали для нахождения периметра прямоугольника. Если же вместо a и b подставить, например, числа 4 и 9, то получим числовое выражение 2 * 4 + 2 * 9. Вообще, из одного буквенного выражения можно получить бесконечно много числовых выражений.
Обозначим периметр прямоугольника буквой P. Тогда равенство
P = 2a + 2b
можно использовать для нахождения периметра любого прямоугольника. Такие равенства называют формулами.
Например, если сторона квадрата равна a, то его периметр вычисляется по формуле:
P = 4a
Равенство
s = vt
где s − пройденный путь, v − скорость движения, а t − время, за которое пройден путь s, называют формулой пути.
Пример 1. Собранные в саду яблоки фермер разложил в пять ящиков по a кг и в b ящиков по 20 кг. Скоько килограммов яблок собрал фермер? Вычислите значение полученного выражения при a = 18, b = 9.
Решение.
В пяти ящиках содержится 5a кг яблок, а в b ящиках − 20b кг. Всего фермер собрал (5a + 20b) кг яблок.
Если a = 18, b = 9, то получаем: 5 * 18 + 20 * 9 = 90 + 180 = 270 (кг).
Ответ: (5a + 20b) кг, 270 кг.
Пример 2. Найдите, ползуясь формулой пути, скорость, с которой поезд прошел 324 км за 6 ч.
Решение.
Поскольку s = vt, то v = s : t. Тогда можно записать v = 324 : 6 = 54 (км/ч).
Ответ: 54 км/ч.
Пример 3. Буратино купил m булочек по 2 сольдо и торт за 5 сольдо. Составим формулу для вычисления стоимости покупки и найдите эту стоимость, если:
1) m = 4;
2) m = 12.
Решение.
За m булочек Буратино заплатил 2m сольдо.
Обозначив стоимость покупки буквой k, получаем формулу k = 2m + 5.
1) Если m = 4, то k = 2 * 4 + 5 = 13;
2) если m = 12, то k = 2 * 12 + 5 = 29.
Ответ: k = 2m + 5, 13 сольдо, 29 сольдо.
reshalka.com
Числовые выражения, преобразование числовых выражений
Числовые выражения, преобразование числовых выражений (рациональных и иррациональных). Друзья! В этой статье для вас представлено решение числовых рациональных и иррациональных выражений. Это несложные задания на ЕГЭ по математике, достаточно знать свойства степеней и корней. Ещё необходимо уметь работать с дробями (находить их сумму, разность, произведение, частное). Процесс решения такого задания занимает минуты две, не более. Не много теории:
Говоря простым (не математическим) языком рациональные выражения — это целые и дробные выражения. Ниже рассматриваются дробные выражения.
Алгебраическое выражение называется иррациональным, если в выражении, наряду с операциями сложения, вычитания, умножения и деления производится операция возведения в рациональную (не целую) степень.
Обыкновенная дробь – это отношение, вида:
*ОТНОШЕНИЕ это есть действие — ДЕЛЕНИЕ (в данном случае «a» делим на «b»).
Также может быть записано в виде: a/b или a:b (косая черта и знак «:» означает — деление). Примеры обыкновенных дробей:
Как видно, число 4 можно записать в виде дроби 4/1. Есть дроби которые можно сократить, например, 48/8 = 6. Некоторые можно представить как конечные десятичные дроби: ½ = 0,5 ¼ = 0,25.
Если имеем целое число с дробной частью (смешанная дробь) и нам необходимо выполнить действие, то её нужно представить в виде простой дроби. Как?
Имеем число вида:
Чтобы получить дробное равное ему число, целую часть умножаем на знаменатель и прибавляем числитель, результат записываем в числитель, знаменатель остаётся прежний:
Например:
Если нужно вычислить сумму (разность) двух дробей с разными знаменателями, необходимо дроби привести к такому виду, чтобы их знаменатели были равны:
*То есть мы получили общий знаменатель путём умножения числителя и знаменателя первой дроби на знаменатель второй и умножением числителя и знаменателя второй дроби на знаменатель первой. Я намеренно не упоминаю здесь наименьшее общее кратное, так как для некоторых, закончивших школу «давно», возможна перегрузка информацией.
Весь смысл действия в том, чтобы привести дроби к общему знаменателю, так как с разными знаменателями дроби складывать нельзя. Если же дроби имеют общий знаменатель, то результатом суммы дробей будет дробь с тем же знаменателем, а числители складывают.
Если нужно вычислить произведение двух дробей, то результатом будет дробь, числитель которой равен произведению числителей этих дробей, а знаменатель равен произведению знаменателей:
Если одну дробь необходимо разделить на другую, то данное действие сводится к произведению делимого и дроби обратной делителю:
*То есть, говоря простым языком, мы «переворачиваем» ту дробь на которую делим и деление заменяем умножением.
Свойства степени и корня можно посмотреть здесь.
Рассмотрим задания:
77387. Найдите значение выражения
Ответ: 8
77389. Найдите значение выражения
Ответ: 5
77391. Найдите значение выражения
Ответ: 10
77392. Найдите значение выражения
*В данной задаче не нужно вычислять произведения и затем отношение. Глядя на числа видно, что они прекрасно сокращаются. Достаточно произвести несложные преобразования и пример вычисляется устно.
Ответ: 10
86983. Найдите значение выражения
Упрощаем, используя формулу разности квадратов
и вычисляем:
Ответ: 702
61513. Найдите значение выражения
Ответ: 24
62385. Найдите значение выражения
Ответ: 2
62647. Найдите значение выражения
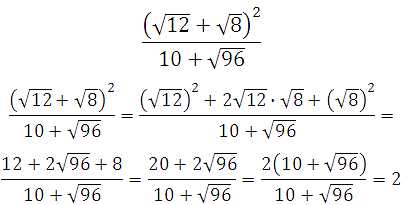
Ответ: 2
68141. Найдите
Определим числитель и знаменатель:
Числитель равен знаменателю. Это означает, что отношение равно единице:
Ответ: 1
26745. Найдите значение выражения
*Если корни имеют разные степени, то преобразования с внесением выражений под один корень выполнять нельзя. Требуется привести все корни к равной степени. Используем свойство:
Ответ: 1
77405. Найдите значение выражения
*На заключительном этапе использовали:
Ответ: 7
Полезным будет посмотреть статью с показательными выражениями.
26900. Найдите значение выражения
Посмотреть решение
77390. Найдите значение выражения
Посмотреть решение
26735. Найдите значение выражения
Посмотреть решение
26736. Найдите значение выражения
Посмотреть решение
26737. Найдите значение выражения
Посмотреть решение
26743. Найдите значение выражения
Посмотреть решение
26744. Найдите значение выражения
Посмотреть решение
26746. Найдите значение выражения
Посмотреть решение
26750. Найдите значение выражения
Посмотреть решение
26752. Найдите значение выражения
Посмотреть решение
На этом всё. Посмотрите, какие чудеса можно нарисовать простым карандашом.
Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
