Что такое биссектриса треугольника в геометрии 7 класс – Треугольники. Геометрия, 7 класс: уроки, тесты, задания.

• Предметы
• Геометрия
• 7 класс

1. Первый признак равенства треугольников

2. Медианы, биссектрисы и высоты треугольника

3. Второй и третий признаки равенства треугольников

4. Задачи на построение

Биссектрисы треугольника / Треугольники / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Треугольники
5. Биссектрисы треугольника

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Треугольник

Равенство треугольников

Первый признак равенства треугольников

Перпендикуляр к прямой

Медианы треугольника

Высоты треугольника

Равнобедренный треугольник

Свойства равнобедренного треугольника

Второй признак равенства треугольников

Третий признак равенства треугольников

Окружность

Построения циркулем и линейкой

Треугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 128, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 131, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 154, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 229, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 235, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 272, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 274, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 275, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

© 2019 — budu5.com, Буду отличником!

Медианы, биссектрисы и высоты треугольника. Видеоурок. Геометрия 7 Класс

Определение: Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

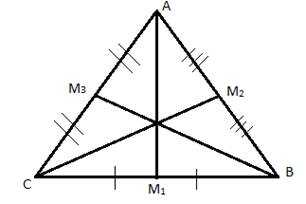
Рис. 1. Медианы треугольника

А, В, С – вершины треугольника.

 – середины сторон треугольника. 

  – медианы треугольника.

У каждого треугольника есть три медианы. В дальнейшем мы докажем, что все медианы треугольника пересекаются в одной точке. И эта точка обладает замечательными свойствами и называется «центром тяжести» треугольника.

Определение: Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника. Стоит заметить, что биссектриса угла – это луч, делящий угол на два равных, а биссектриса треугольника – это отрезок, часть луча, ограниченная стороной треугольника.

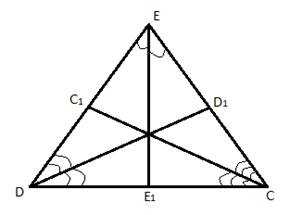
Рис. 2. Биссектрисы треугольника

C, D, E – вершины треугольника.

   – биссектрисы треугольника.

Три биссектрисы любого треугольника пересекаются в одной точке, которая также имеет важное свойство.

Определение: Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

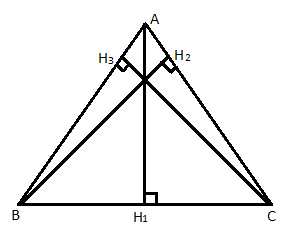
Рис. 3. Высоты остроугольного треугольника

А, В, С – вершины треугольника. 

  – высоты треугольника.

Поскольку у треугольника три вершины, а значит, и три высоты. Далее мы выясним, что все три высоты пересекаются в одной точке. Но в тупоугольном треугольнике высоты расположены следующим образом:

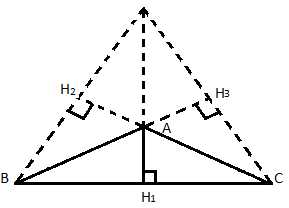
Рис. 4. Высоты тупоугольного треугольника

Перпендикуляр, опущенный с вершины С на прямую ВА, это перпендикуляр , который является высотой треугольника.  – это перпендикуляр, опущенный с вершины В на прямую СА, которая содержит сторону АС.  – это вторая высота треугольника. – третья высота треугольника. Высоты или их продолжения пересекаются в одной точке. Это будет доказано далее.

Пример 1: Медиана AD треугольника АВС продолжена за сторону ВС на отрезок DE, равный AD, и точка Е соединена с точкой С.

1.  Докажите, что ∆АВD = ∆ECD.

2.  Найдите ∠АСЕ, если ∠ACD = , ∠ABD = .

Дано: BD = CD, AD = ED.

Доказать: ∆ABD = ∆ECD.

Доказательство: Выполним пояснительный рисунок:

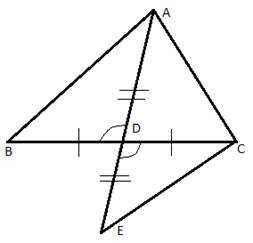
Рис. 5. Чертеж к примеру 1

треугольник ABD = треугольнику ECD по первому признаку равенства треугольников, что и требовалось доказать.

Дано: BD = CD, AD = ED, ∠ACD = , ∠ABD = .

Найти: ∠АСЕ.

Решение: Выполним пояснительный рисунок:

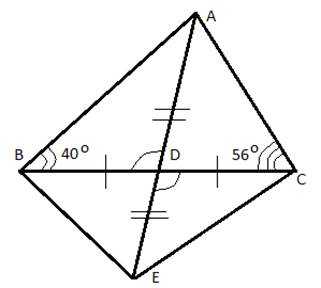
Рис. 6. Чертеж к примеру 1

Воспользуемся результатами предыдущей задачи, что треугольник ABD = треугольнику ECD. Треугольники равны, значит, и равны их соответствующие элементы. ∠ECD =∠ABD = .∠ACE = ∠ECD + ∠ACD = +=.

Ответ: ∠ACE = .

Пример 2: треугольник АВС =  треугольнику .

Доказать: медианы ВМ и  равны.

Доказательство: Выполним пояснительный рисунок:

Рис.7. Чертеж к примеру 2

1 способ:

. 

Отсюда следует, что треугольник АВМ = треугольнику . А из равенства треугольников следует, что ВМ = , что и требовалось доказать.

2 способ: совмещение треугольников АВС и . При этом точка В перейдет в точку , а точка М в точку . Значит, отрезки ВМ и  совместятся. ВМ = .

Ответ: Доказано.

На сегодняшнем уроке мы познакомились с медианами, биссектрисами и высотами треугольника. С этими важными элементами мы будем встречаться неоднократно. На следующем уроке мы рассмотрим равнобедренный треугольник и его свойства.

Список рекомендованной литературы

1. Александров  А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.

2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. – М.: Просвещение.

3. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А.  – М.: Просвещение, 2010.

Рекомендованные ссылки на интернет-ресурсы

1. Обобщающий урок по геометрии в 7-м классе (Источник).

2. Прямая линия, отрезок (Источник).

Рекомендованное домашнее задание

1. №28(а). Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А.  – М.: Просвещение, 2010.

2. На стороне АС треугольника АВС отмечена такая точка К, что периметры треугольников АВК и ВСК отличаются на 5 см. Найдите периметр треугольника АВС, если АВ + АК = 30 см.

3. Какие элементы (части) треугольника совпадут при перегибании его по биссектрисе?

4. *Докажите, что если в треугольнике медиана равна половине стороны, к которой она проведена, то угол, из вершины которого проведена медиана, равен сумме двух других углов. 

interneturok.ru

Биссектриса треугольника | Треугольники

Биссектриса треугольника, в отличие от биссектрисы угла, является отрезком, а не лучом.

Определение

Биссектриса треугольника — это отрезок биссектрисы угла треугольника, проведенной из данной вершины, соединяющий эту вершину с точкой на противолежащей стороне.

Таким образом, биссектриса треугольника является частью биссектрисы угла треугольника (луча), которая находится внутри треугольника.

Все три биссектрисы треугольника пересекаются в одной точке.

Точка пересечения биссектрис треугольника является центром вписанной в треугольник окружности.

Свойство биссектрисы треугольника

Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам:

Более подробно о свойстве биссектрисы мы поговорим позже.

Длина биссектрисы

1) Длина биссектрисы треугольника через длины его сторон.

Если ввести обозначения

длина биссектрисы треугольника АВС, проведенная из вершины А, может быть найдена через длины сторон по формуле

2) Длина биссектрисы треугольника через длины сторон и пропорциональные отрезки.

Если ввести обозначения

формула длины биссектрисы примет вид:

3) Длина биссектрисы треугольника через длины сторон и угол между ними:

Если ввести обозначение ∠CAB=α, формула примет вид:

www.treugolniki.ru

Биссектриса треугольника — что это такое? :: SYL.ru

Геометрия – одна из самых сложных и запутанных наук. В ней то, что кажется на первый взгляд очевидным, очень редко оказывается правильным. Биссектрисы, высоты, медианы, проекции, касательные – огромное количество действительно непростых терминов, запутаться в которых очень легко.

На самом деле при должном желании можно разобраться в теории любой сложности. Когда дело заходит о биссектрисе, медиане и высоте, нужно понимать, что они свойственны не только треугольникам. На первый взгляд это простые линии, но у каждой из них есть свои свойства и функции, знание которых существенно упрощает решение геометрических задач. Итак, что же такое биссектриса треугольника?

Определение

Сам термин «биссектриса» происходит из сочетания латинских слов «два» и «сечь», «резать», что уже косвенно указывает на её свойства. Обычно, когда детей знакомят с этим лучом, им предлагается для запоминания коротенькая фраза: «Биссектриса – это крыса, которая бегает по углам и делит угол пополам». Естественно, такое объяснение не подойдёт для школьников старшего возраста, к тому же у них обычно спрашивают не об угле, а о геометрической фигуре. Так что биссектриса треугольника – это луч, который соединяет вершину треугольника с противоположной стороной, при этом разделяя угол на две равные части. Точка противоположной стороны, в которую приходит биссектриса, для произвольного треугольника выбирается случайным образом.

Базовые функции и свойства

Основных свойств у этого луча немного. Во-первых, из-за того, что биссектриса треугольника делит угол напополам, любая точка, лежащая на ней, будет находиться на равном расстоянии от сторон, образующих вершину. Во-вторых, в каждом треугольнике можно провести три биссектрисы, по числу имеющихся углов (следовательно, в том же четырёхугольнике их будет уже четыре и так далее). Точка, в которой все три луча пересекутся, является центром окружности, вписанной в треугольник.

Свойства усложняются

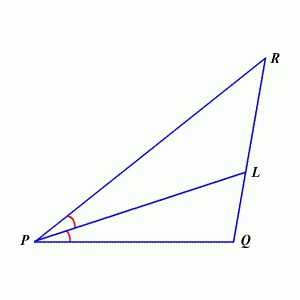
Немного усложним теорию. Ещё одно интересное свойство: биссектриса угла треугольника делит противолежащую сторону на отрезки, отношение которых равно отношению образующих вершину сторон. На первый взгляд это сложно, но на самом деле всё просто: на предложенном рисунке RL:LQ = PR:PK. Кстати, это свойство получило название «Теорема о биссектрисе» и впервые появилось ещё в работах древнегреческого математика Евклида. Вспомнили его в одном из российских учебников только в первой четверти семнадцатого века.

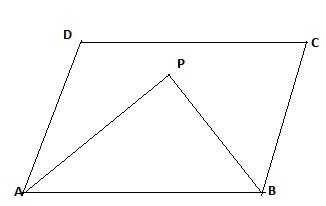
Ещё чуть сложнее. В четырёхугольнике биссектриса отсекает равнобедренный треугольник. На этом рисунке обозначены все равные углы для медианы AF.

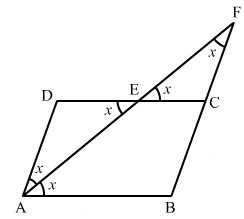
А ещё в четырёхугольниках и трапециях биссектрисы односторонних углов перпендикулярны друг другу. На представленном чертеже угол APB составляет 90 градусов.

В равнобедренном треугольнике

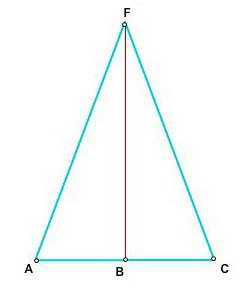
Биссектриса равнобедренного треугольника – гораздо более полезный луч. Она одновременно является не только делителем угла напополам, но и медианой, и высотой.

Медиана – это отрезок, который выходит из какого-то угла и падает на середину противолежащей стороны, разделяя её тем самым на равные части. Высота – это перпендикуляр, опущенный из вершины на противолежащую сторону, именно с её помощью любую задачу можно свести к простой и примитивной теореме Пифагора. В данной ситуации биссектриса треугольника равна корню из разности квадрата гипотенузы и другого катета. Кстати, именно это свойство встречается в геометрических задачах чаще всего.

Для закрепления: в данном треугольнике биссектриса FB является медианой (AB=BC) и высотой (углы FBC и FBA составляют 90 градусов).

В общих чертах

Итак, что же нужно запомнить? Биссектриса треугольника – это луч, который делит его вершину пополам. На пересечении трёх лучей находится центр окружности, вписанной в данный треугольник (единственный минус этого свойства в том, что оно не имеет практической ценности и служит только для грамотного выполнения чертежа). Она же делит противолежащую сторону на отрезки, отношение которых равно отношению сторон, между которыми прошёл этот луч. В четырёхугольнике свойства чуть усложняются, но, признаться, они практически не встречаются в задачах школьного уровня, поэтому обычно не затрагиваются в программе.

Биссектриса равнобедренного треугольника – предел мечтаний любого школьника. Она одновременно является и медианой (то есть делит противолежащую сторону пополам), и высотой (перпендикулярна этой стороне). Решение задач с такой биссектрисой сводится к теореме Пифагора.

Знание базовых функций биссектрисы, а также основных её свойств необходимо для решения геометрических задач как среднего, так и высокого уровня сложности. На самом деле встречается этот луч только в планиметрии, так что нельзя говорить о том, что зазубривание информации о нём позволит справляться со всеми типами заданий.

www.syl.ru

Медианы, биссектрисы и высоты треугольника

Определение:

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Например, возьмём треугольник АВС.

Если точки А₁, В₁ и С₁ - соответственно середины сторон ВС, СА и АВ, то отрезки АА₁, ВВ₁ и СС₁ — медианы этого треугольника. Медианы, проведённые из вершин А, В и С (или их длины) треугольника АВС можно обозначить:

Определение:

Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны.

Например, возьмём некоторый треугольник АВС.

Проведём биссектрису АЕ₁ угла ВАС, ВЕ₂ - угла АВС и СЕ₃ — угла АСВ. Биссектрисы, проведённые из вершин А, В и С (или их длины) треугольника АВС можно обозначить:

Определение:

Высотой треугольника называется перпендикуляр, проведённый из его вершины к прямой, содержащей противоположную сторону.

Изобразим треугольник АВС и отрезки АF1, BF2 и CF3, которые являются высотами нашего треугольника.

Высоты, проведённые из вершин А, В и С (или их длины) треугольника АВС можно обозначить:

Свойства:

1. Медианы треугольника пересекаются в одной точке.

2. Биссектрисы треугольника пересекаются в одной точке.

3. Высоты или прямые, содержащие высоты, пересекаются в одной точке.

Ответим на вопрос: Может ли точка пересечения высот лежать вне треугольника?

Да, когда у него один угол тупой.

А может ли точка пересечения высот лежать в вершине треугольника?

Да, может, когда у треугольника есть прямой угол.

Пример.

Рассмотрим следующую задачу. Отрезок BD - медиана треугольника АВС, отрезок ВЕ — медиана треугольника DBC. Чему равна длина отрезка АС, если отрезок ЕС=4 см.?

Так как ВЕ — медиана треугольника DBC, то отрезок DE=ЕС. Следовательно, сторона DC=2*ЕС, то есть DC=8 см.

BD - медиана треугольника АВС, значит, отрезок AD=DC. Следовательно, сторона АС=2*DC. Так как отрезок DC=8 см., то длина стороны АС=16 см.

Ответ: 16 см.

Пример.

Отрезок AD - медиана треугольника АВС. Точка Е лежит на луче АD так, что AD равняется DЕ. Докажите, что треугольник АDВ равен треугольнику CDE.

Так как AD - медиана треугольника АВС, то СD равняется DB.

Рассмотрим треугольники АDВ и CDE. У них сторона AD равна стороне DЕ по условию задачи; сторона СD равна стороне DB, так как AD - медиана; а углы ADB и CDE равны как вертикальные.

Следовательно, треугольник АDВ равен треугольнику CDE по первому признаку равенства треугольников.

videouroki.net

7 класс. Геометрия. Медианы, биссектрисы и высоты треугольника. — Копия: Медианы, биссектрисы и высоты треугольника.

Комментарии преподавателя

Ме­ди­а­ны, бис­сек­три­сы и вы­со­ты тре­уголь­ни­ка

Опре­де­ле­ние: От­ре­зок, со­еди­ня­ю­щий вер­ши­ну тре­уголь­ни­ка с се­ре­ди­ной про­ти­во­по­лож­ной сто­ро­ны, на­зы­ва­ет­ся ме­ди­а­ной тре­уголь­ни­ка.

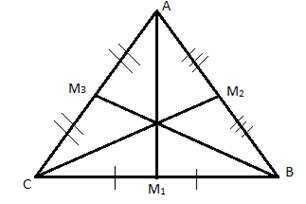
Рис. 1. Ме­ди­а­ны тре­уголь­ни­ка

А, В, С – вер­ши­ны тре­уголь­ни­ка.

 – се­ре­ди­ны сто­рон тре­уголь­ни­ка. 

  – ме­ди­а­ны тре­уголь­ни­ка.

У каж­до­го тре­уголь­ни­ка есть три ме­ди­а­ны. В даль­ней­шем мы до­ка­жем, что все ме­ди­а­ны тре­уголь­ни­ка пе­ре­се­ка­ют­ся в одной точке. И эта точка об­ла­да­ет за­ме­ча­тель­ны­ми свой­ства­ми и на­зы­ва­ет­ся «цен­тром тя­же­сти» тре­уголь­ни­ка.

Опре­де­ле­ние: От­ре­зок бис­сек­три­сы угла тре­уголь­ни­ка, со­еди­ня­ю­щий вер­ши­ну тре­уголь­ни­ка с точ­кой про­ти­во­по­лож­ной сто­ро­ны, на­зы­ва­ет­ся бис­сек­три­сой тре­уголь­ни­ка. Стоит за­ме­тить, что бис­сек­три­са угла – это луч, де­ля­щий угол на два рав­ных, а бис­сек­три­са тре­уголь­ни­ка – это от­ре­зок, часть луча, огра­ни­чен­ная сто­ро­ной тре­уголь­ни­ка.

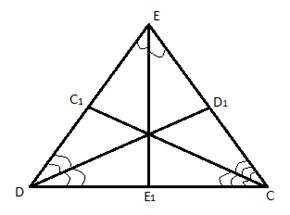
Рис. 2. Бис­сек­три­сы тре­уголь­ни­ка

C, D, E – вер­ши­ны тре­уголь­ни­ка.

   – бис­сек­три­сы тре­уголь­ни­ка.

Три бис­сек­три­сы лю­бо­го тре­уголь­ни­ка пе­ре­се­ка­ют­ся в одной точке, ко­то­рая также имеет важ­ное свой­ство.

Опре­де­ле­ние: Пер­пен­ди­ку­ляр, про­ве­ден­ный из вер­ши­ны тре­уголь­ни­ка к пря­мой, со­дер­жа­щей про­ти­во­по­лож­ную сто­ро­ну, на­зы­ва­ет­ся вы­со­той тре­уголь­ни­ка.

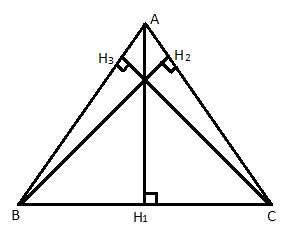
Рис. 3. Вы­со­ты ост­ро­уголь­но­го тре­уголь­ни­ка

А, В, С – вер­ши­ны тре­уголь­ни­ка. 

  – вы­со­ты тре­уголь­ни­ка.

По­сколь­ку у тре­уголь­ни­ка три вер­ши­ны, а зна­чит, и три вы­со­ты. Далее мы вы­яс­ним, что все три вы­со­ты пе­ре­се­ка­ют­ся в одной точке. Но в ту­по­уголь­ном тре­уголь­ни­ке вы­со­ты рас­по­ло­же­ны сле­ду­ю­щим об­ра­зом:

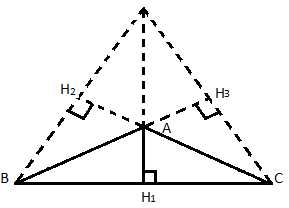
Рис. 4. Вы­со­ты ту­по­уголь­но­го тре­уголь­ни­ка

Пер­пен­ди­ку­ляр, опу­щен­ный с вер­ши­ны С на пря­мую ВА, это пер­пен­ди­ку­ляр , ко­то­рый яв­ля­ет­ся вы­со­той тре­уголь­ни­ка.  – это пер­пен­ди­ку­ляр, опу­щен­ный с вер­ши­ны В на пря­мую СА, ко­то­рая со­дер­жит сто­ро­ну АС.  – это вто­рая вы­со­та тре­уголь­ни­ка. – тре­тья вы­со­та тре­уголь­ни­ка. Вы­со­ты или их про­дол­же­ния пе­ре­се­ка­ют­ся в одной точке. Это будет до­ка­за­но далее.

При­мер 1: Ме­ди­а­на AD тре­уголь­ни­ка АВС про­дол­же­на за сто­ро­ну ВС на от­ре­зок DE, рав­ный AD, и точка Е со­еди­не­на с точ­кой С.

1.  До­ка­жи­те, что ∆АВD = ∆ECD.

2.  Най­ди­те ∠АСЕ, если ∠ACD = , ∠ABD = .

Дано: BD = CD, AD = ED.

До­ка­зать: ∆ABD = ∆ECD.

До­ка­за­тель­ство: Вы­пол­ним по­яс­ни­тель­ный ри­су­нок:

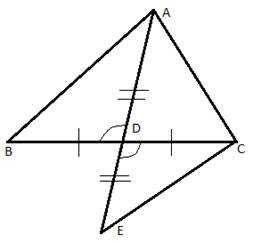
Рис. 5. Чер­теж к при­ме­ру 1

тре­уголь­ник ABD = тре­уголь­ни­ку ECD по пер­во­му при­зна­ку ра­вен­ства тре­уголь­ни­ков, что и тре­бо­ва­лось до­ка­зать.

Дано: BD = CD, AD = ED, ∠ACD = , ∠ABD = .

Найти: ∠АСЕ.

Ре­ше­ние: Вы­пол­ним по­яс­ни­тель­ный ри­су­нок:

Рис. 6. Чер­теж к при­ме­ру 1

Вос­поль­зу­ем­ся ре­зуль­та­та­ми преды­ду­щей за­да­чи, что тре­уголь­ник ABD = тре­уголь­ни­ку ECD. Тре­уголь­ни­ки равны, зна­чит, и равны их со­от­вет­ству­ю­щие эле­мен­ты. ∠ECD =∠ABD = .∠ACE = ∠ECD + ∠ACD = +=.

Ответ: ∠ACE = .

При­мер 2: тре­уголь­ник АВС =  тре­уголь­ни­ку .

До­ка­зать: ме­ди­а­ны ВМ и  равны.

До­ка­за­тель­ство: Вы­пол­ним по­яс­ни­тель­ный ри­су­нок:

Рис.7. Чер­теж к при­ме­ру 2

1 спо­соб:

. 

От­сю­да сле­ду­ет, что тре­уголь­ник АВМ = тре­уголь­ни­ку . А из ра­вен­ства тре­уголь­ни­ков сле­ду­ет, что ВМ = , что и тре­бо­ва­лось до­ка­зать.

2 спо­соб: сов­ме­ще­ние тре­уголь­ни­ков АВС и . При этом точка В пе­рей­дет в точку , а точка М в точку . Зна­чит, от­рез­ки ВМ и  сов­ме­стят­ся. ВМ = .

Ответ: До­ка­за­но.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/7-klass/treugolnikib/mediany-bissektrisy-i-vysoty-treugolnika

http://www.youtube.com/watch?v=Hxp_e6OjgxA

http://school-assistant.ru/?predmet=geometr&theme=mediana_bisektrisa_visota

http://proteacher.ru/2015/01/09/Mediana_bissektrisa_i_vysota_treugolnika_1420794393_62631.ppt

www.kursoteka.ru