Найти сторону прямоугольника через диагональ, периметр или площадь
Четырехугольник, у которого все углы прямые, противоположные стороны равны и параллельны друг другу, называется прямоугольником. Стороной прямоугольника является отрезок, соединяющий две вершины фигуры. Длинная сторона считается длиной, короткая сторона — шириной прямоугольника, прилегающие стороны перпендикулярны, они являются его высотами.
Расчет длины стороны прямоугольника через диагональ и сторону
Отрезок, соединяющий 2 противолежащие вершины прямоугольника, является его диагональю. В прямоугольнике две диагонали одинаковой длины. Каждая из них делит прямоугольник на два прямоугольных треугольника, гипотенузой которых является диагональ, а катетами — стороны прямоугольника. Соответственно, квадрат диагонали можно вычислить через теорему Пифагора: d2 = a2 + b2, а сумма квадратов диагоналей прямоугольника равна сумме квадратов его сторон:
2d2 = 2a2 + 2b
где d — диагональ, а, b — стороны прямоугольника.
Если дана диагональ прямоугольника и одна из его сторон, находим длину другой стороны, как корень из разности: квадрат диагонали минус квадрат известной стороны:
a = √d2 — b2
b = √d2 — a2
где d — диагональ, а, b — стороны прямоугольника.
Расчет стороны прямоугольника через периметр и сорону
Периметр прямоугольника равняется сумме всех его сторон. Если известны длина (а) и ширина (b) прямоугольника, его периметр (Р) будет равен удвоенной сумме сторон, т.к. его противоположные стороны равны:
Р = 2a + 2b = 2 (а + b)
Если известны периметр и одна из сторон прямоугольника, другую находим по формуле:
a = (P — 2b) / 2
b = (P — 2a) / 2
Р — периметр, a — длина, b — ширина прямоугольника
Т.е. сторона прямоугольника равняется половине разности между периметром и удвоенной другой стороной.
Расчет стороны прямоугольника через площадь и сторону
Чтобы рассчитать площадь прямоугольника (S), необходимо его длину а умножить на ширину b:
S = аb
Если известна площадь прямоугольника и одна из его сторон, длину другой находим путем деления площади на длину известной стороны:
a = S / b
b = S / a
где S — площадь прямоугольника, a, b — его стороны.
infofaq.ru
Площадь прямоугольника — формул, пример расчет, калькулятор
Прямоугольник – это параллелограмм, у которого все углы равны 90°, а противоположные стороны попарно параллельны и равны.
У прямоугольника есть несколько неопровержимых свойств, которые применяются в решении множества задач, в формулах площади прямоугольника и его периметра. Вот они:
- Стороны прямоугольника являются его высотами;
- Длины диагоналей равны между собой ;
- Точка пересечения диагоналей делит их пополам;
Длина неизвестной стороны или диагонали прямоугольника вычисляется по формуле площади прямоугольного треугольника или по теореме Пифагора. Площадь прямоугольника можно найти двумя способами – по произведению его сторон или по формуле площади прямоугольника через диагональ. Первая и самая простая формула выглядит так:
Пример расчета площади прямоугольника по этой формуле очень прост. Зная две стороны, к примеру a =3 см, b = 5 см, мы легко высчитаем площадь прямоугольника:
Получаем, что в таком прямоугольнике площадь будет равна 15 кв. см.
Площадь прямоугольника через диагонали
Иногда требуется применить формулу площади прямоугольника через диагонали. Для нее потребуется не только узнать длину диагоналей, но и угол между ними:
Рассмотрим пример расчета площади прямоугольника через диагонали. Пусть дан прямоугольник с диагональю d = 6 см и углом = 30°. Подставляем данные в уже известную формулу:Итак, пример расчета площади прямоугольника через диагональ показал нам, что найти площадь таким образом, если задан угол, довольно просто.
Рассмотрим еще одну интересную задачку, которая поможет нам немного размять мозги.
Итак, у нас есть несколько условий. Для наглядности запишем их, чтобы увидеть все известные и неизвестные параметры:
Стороны фигуры попарно параллельны и равны. Поэтому периметр фигуры равен удвоенной сумме длин сторон:
Из формулы площади прямоугольника, которая равняется произведению двух сторон фигуры, найдем длину стороны b
Подставляем известные данные и находим длину стороны b:
Рассчитываем периметр фигуры:
Вот так, зная несколько легких формул, можно вычислить периметр прямоугольника, зная его площадь.
2mb.ru
Периметр и площадь прямоугольника
Можно ли найти площадь из периметра?
При решении, необходимо принять во внимание, что решить задачу о нахождении площади прямоугольника только из длины его сторон нельзя.
В этом несложно убедиться. Пусть периметр прямоугольника будет равен 20 см. Это будет верно, если его стороны 1 и 9, 2 и 8, 3 и 7 см. Все эти три прямоугольника будут иметь одинаковый периметр, равный двадцати сантиметрам. ( 1 + 9 ) * 2 = 20 точно также как и ( 2 + 8 ) * 2 = 20 см.
Как видно, мы можем подобрать бесконечное количество вариантов
Площадь прямоугольников с заданным периметром 20 см, но с различными сторонами будет различна. Для приведенного примера — 9, 16 и 21 квадратных сантиметров соответственно.
S1 = 1 * 9 = 9 см2
S2 = 2 * 8 = 16 см2
S3= 3 * 7 = 21 см2
Как видим, вариантов площади фигуры при заданном периметре — бесконечное количество.
Таким образом, для того, чтобы вычислить площадь прямоугольника из его периметра, нужно обязательно знать либо соотношение его сторон, либо длину одной из них. Единственной фигурой, которая имеет однозначную зависимость своей площади от периметра, является круг. Только для круга и возможно решение.
В этом уроке:
-
Задача 1. Найти стороны прямоугольника из площади
- Задача 2. Найти стороны прямоугольника из периметра
- Задача 3. Найти площадь прямоугольника из пропорции его сторон
- Задача 4. Изменение длины сторон при сохранении площади прямоугольника
Задача 1. Найти стороны прямоугольника из площади
Периметр прямоугольника равен 32 сантиметрам, а сумма площадей квадратов, построенных на каждой из его сторон — 260 квадратных сантиметров. Найдите стороны прямоугольника.Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=32
Согласно условию задачи, сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, четыре) будет равна
2x2+2y2=260
Решаем полученную систему уравнений. Из первого уравнения выводим, что
x+y=16
x=16-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
2(16-y)2+2y2=260
2(256-32y+y2)+2y2=260
512-64y+4y2-260=0
4y2-64y+252=0
Решаем полученное квадратное уравнение.
D=4096-16×252=64
x1=9
x2=7
Теперь примем во внимание, что исходя из того, что x+y=16 (см. выше) при x=9, то y=7 и наоборот, если x=7, то y=9
Ответ: Стороны прямоугольника равны 7 и 9 сантиметров
Задача 2. Найти стороны прямоугольника из периметра
Периметр прямоугольника 26 см, а сумма площадей квадратов, построенных на двух его смежных сторонах, равна 89 кв. см. Найдите стороны прямоугольника.
Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=26
Сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, два и это квадраты ширины и высоты, поскольку стороны смежные) будет равна
Решаем полученную систему уравнений. Из первого уравнения выводим, что
x+y=13
y=13-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
(13-y)2+y2=89
169-26y+y2+y2-89=0
2y2-26y+80=0
Решаем полученное квадратное уравнение.
D=676-640=36
x1=5
x2=8
Теперь примем во внимание, что исходя из того, что x+y=13 (см. выше) при x=5, то y=8 и наоборот, если x=8, то y=5
Ответ: 5 и 8 см
Задача 3. Найти площадь прямоугольника из пропорции его сторон
Найти площадь прямоугольника если его периметр равен 26 см а стороны пропорциональны как 2 к 3.
Решение.
Обозначим стороны прямоугольника через коэффициент пропорциональности x.
Откуда длина одной стороны будет равна 2x, другой — 3х.
Тогда:
2(2x+3x)=26
2x+3x=13
5x=13
x=13/5
Теперь, исходя из полученных данных, определим площадь прямоугольника:
2x*3x=2*13/5*3*13/5=40,56 см2
Задача 4. Изменение длины сторон при сохранении площади прямоугольника
Длина прямоугольника увеличена на 25%. На сколько процентов надо уменьшить ширину, чтобы его площадь не изменилась?Решение.
Площадь прямоугольника равна
S = ab
В нашем случае один из множителей увеличился на 25%, что означает a2 = 1,25a . Таким образом, новая площадь прямоугольника должна быть равна
S2 = 1,25ab
Таким образом, для того, чтобы вернуть площадь прямоугольника к начальному значению, то
S2 = S / 1.25
поскольку новый размер а изменять нельзя, то
S2 = (1,25a) b / 1.25
1 / 1,25 = 0,8
Таким образом, величину второй стороны нужно уменьшить на ( 1 — 0,8 ) * 100% = 20%
Ответ: ширину нужно уменьшить на 20%.
profmeter.com.ua
Площадь прямоугольника | Треугольники
Как найти площадь прямоугольника? Площадь прямоугольника можно вычислить, если известны длины его сторон либо длина диагонали и угол между диагоналями.
I. Площадь прямоугольника равна произведению его длины на ширину.
Формула площади прямоугольника по сторонам
II. Площадь прямоугольника равна половине произведения квадрата его диагонали на синус угла между диагоналями.
Формула площади прямоугольника по диагонали и углу между диагоналями
В качестве угла между диагоналями может быть взят любой угол — как острый, так и тупой (поскольку синус тупого угла равен синусу смежного с ним острого угла).
Например, площадь прямоугольника
ABCD можно найти как
или
Таким образом, если требуется найти площадь прямоугольника, задача, как правило, сводится к нахождению либо длин его сторон, либо диагонали и угла между диагоналями.
Задача.
Найти площадь прямоугольника, одна сторона которого на 5 см больше другой, а периметр равен 38 см.
Решение:
Формула для нахождения периметра прямоугольника —
Пусть a=x см, тогда b=(x+5) см.
По условию, периметр равен 38 см. Составим уравнение:
Значит, a=7 см, b=7+5=12 см,
Ответ: 84 см².
www.treugolniki.ru
Как вычислить площадь прямоугольника?
Одним из важнейших правил тригонометрии является вычисление площади различных фигур, поэтому многие задумываются над тем, как вычислить площадь прямоугольника.
Стоит отметить, что, зная разнообразные величины: стороны, диагонали, углы и периметр фигуры, — можно вычислить ее площадь.
Площадь по двум сторонам
В задаче необходимо найти площадь прямоугольника, если известны две стороны: одна сторона равна 3 см, а другая — 2 см.
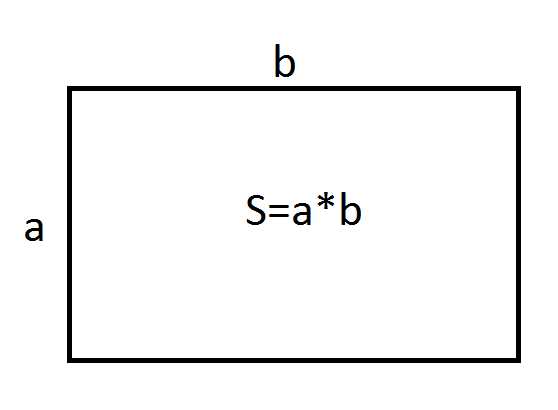
Решение:
Исходя из формулы площади S=a*b, мы получаем, что площадь прямоугольника в данном случае равняется:
Ответ: S = 6 см²
Площадь прямоугольника с известной стороной и диагональю
Чтобы решить задачи с такими условиями, необходимо вспомнить теорему Пифагора.
Например, в задаче необходимо найти площадь прямоугольника ABCD, когда известно, что сторона прямоугольника АВ = 3 см, а прилегающая диагональ АС = 5 см.
Решение:
Для начала необходимо узнать вторую сторону прямоугольника. Для этого следует воспользоваться теоремой Пифагора: а² + b² = c². Исходя из теоремы, мы получаем, что сторону ВС можно вычислить следующим способом:
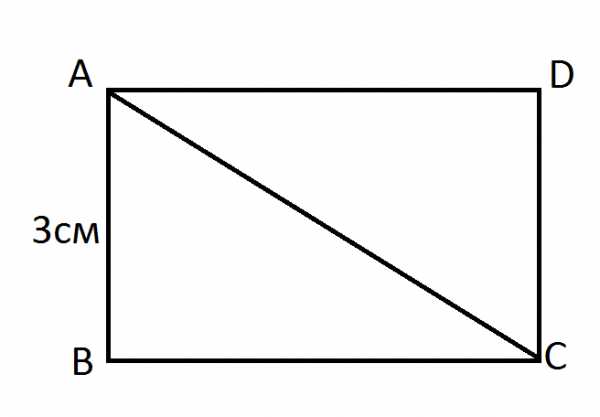ВС2= АС2-АВ2 = (25-9) = 16 см.- ВС=4 см.
ВС2= АС2-АВ2 = (25-9) = 16 см.Таким образом, можно определить и искомое значение:
Ответ: S = 12 см²
О нахождении диагонали прямоугольника можно прочитать в статье Как найти диагональ прямоугольника.
Площадь по диагонали и углу
В задаче необходимо найти площадь прямоугольника, если диагональ равна 10 см, а угол прилегания диагонали к ширине прямоугольника равен 60 градусов.
Решение:
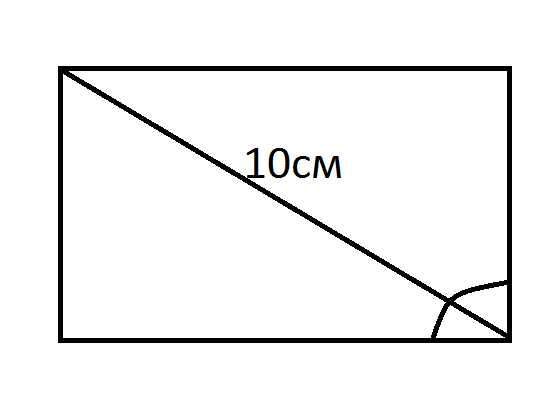Так как угол между одной стороной и диагональю равен 60 градусам, то прямоугольник делится на два треугольника. Используя формулу S=1/2 d2*sin α, определяем:
elhow.ru
Как найти площадь и периметр прямоугольника через диагональ
Математика 6 класс Виленкин. Авторы : Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. Издательство: Мнемозина. В пособии «ГДЗ по математике 6 класс» подробно разобраны упражнения и задачи из учебника по математике для 6 классов общеобразовательных учебных заведений. Книга в.
Площадь прямоугольника
Прямоугольник – это параллелограмм, у которого все углы равны 90°, а противоположные стороны попарно параллельны и равны.
У прямоугольника есть несколько неопровержимых свойств, которые применяются в решении множества задач, в формулах площади прямоугольника и его периметра. Вот они:
- Стороны прямоугольника являются его высотами; Точка пересечения диагоналей делит их пополам;
Длина неизвестной стороны или диагонали прямоугольника вычисляется по формуле площади прямоугольного треугольника или по теореме Пифагора. Площадь прямоугольника можно найти двумя способами – по произведению его сторон или по формуле площади прямоугольника через диагональ. Первая и самая простая формула выглядит так:
Получаем, что в таком прямоугольнике площадь будет равна 15 кв. см.
Площадь прямоугольника через диагонали
Иногда требуется применить формулу площади прямоугольника через диагонали. Для нее потребуется не только узнать длину диагоналей, но и угол между ними:
Итак, пример расчета площади прямоугольника через диагональ показал нам, что найти площадь таким образом, если задан угол, довольно просто.
Рассмотрим еще одну интересную задачку, которая поможет нам немного размять мозги.
Вот так, зная несколько легких формул, можно вычислить периметр прямоугольника, зная его площадь.
Как найти площадь и периметр прямоугольника через диагональ
Как найти площадь и периметр прямоугольника через диагональ
Как найти площадь прямоугольника зная его периметр и диагональ?
- Попроси больше объяснений Следить Отметить нарушение
Dymbay 10.05.2013
Ответы и объяснения
- LFP главный мозг
A² + b² = a² + b² + 2ab — 2ab = (a+b)² — 2ab = d²
Как найти площадь и периметр прямоугольника через диагональ
Площадь прямоугольника
Прямоугольник – это параллелограмм, у которого все углы равны 90°, а противоположные стороны попарно параллельны и равны.
У прямоугольника есть несколько неопровержимых свойств, которые применяются в решении множества задач, в формулах площади прямоугольника и его периметра. Вот они:
- Стороны прямоугольника являются его высотами; Точка пересечения диагоналей делит их пополам;
Длина неизвестной стороны или диагонали прямоугольника вычисляется по формуле площади прямоугольного треугольника или по теореме Пифагора. Площадь прямоугольника можно найти двумя способами – по произведению его сторон или по формуле площади прямоугольника через диагональ. Первая и самая простая формула выглядит так:
Получаем, что в таком прямоугольнике площадь будет равна 15 кв. см.
Площадь прямоугольника через диагонали
Иногда требуется применить формулу площади прямоугольника через диагонали. Для нее потребуется не только узнать длину диагоналей, но и угол между ними:
Итак, пример расчета площади прямоугольника через диагональ показал нам, что найти площадь таким образом, если задан угол, довольно просто.
Рассмотрим еще одну интересную задачку, которая поможет нам немного размять мозги.
Вот так, зная несколько легких формул, можно вычислить периметр прямоугольника, зная его площадь.
poiskvstavropole.ru
Площадь прямоугольника через периметр и диагональ
Пример определения опорных реакций двухопорной балки. Условие задачи. Для заданной двухопорной балки с консольной частью, нагруженной комплексом нагрузок: силой F, моментом m и. Пример решения. Рекомендуем посмотреть наш видеоурок по расчету опорных реакций балки:.
Площадь прямоугольника
Прямоугольник – это параллелограмм, у которого все углы равны 90°, а противоположные стороны попарно параллельны и равны.
У прямоугольника есть несколько неопровержимых свойств, которые применяются в решении множества задач, в формулах площади прямоугольника и его периметра. Вот они:
- Стороны прямоугольника являются его высотами; Точка пересечения диагоналей делит их пополам;
Длина неизвестной стороны или диагонали прямоугольника вычисляется по формуле площади прямоугольного треугольника или по теореме Пифагора. Площадь прямоугольника можно найти двумя способами – по произведению его сторон или по формуле площади прямоугольника через диагональ. Первая и самая простая формула выглядит так:
Получаем, что в таком прямоугольнике площадь будет равна 15 кв. см.
Площадь прямоугольника через диагонали
Иногда требуется применить формулу площади прямоугольника через диагонали. Для нее потребуется не только узнать длину диагоналей, но и угол между ними:
Итак, пример расчета площади прямоугольника через диагональ показал нам, что найти площадь таким образом, если задан угол, довольно просто.
Рассмотрим еще одну интересную задачку, которая поможет нам немного размять мозги.
Вот так, зная несколько легких формул, можно вычислить периметр прямоугольника, зная его площадь.
Площадь прямоугольника через периметр и диагональ
Периметр и площадь прямоугольника
Прямоугольник изучают все школьники и он принадлежит к классу параллелограммов. Наибольший интерес вызывает вычисления площади и периметра прямоугольника.
Напомним что параллелограммы при сторонам имеют как острые так и тупые углы (смотрите рисунок ).
Прямоугольником называют такой параллелограмм у которого все углы прямые. Все это обобщенно, поскольку, если параллелограмм имеет хотя бы один прямой угол то все остальное — также прямые. Большинство предметов которые нас окружают имеют форму прямоугольника: стол, окна, двери, комнаты, участки земли и т. п.
Точки А, В, С и D принято называть вершинами прямоугольника, а отрезки, которые соединяют АВ, ВС, CD и AD — сторонами прямоугольника (ширина и длина). Те из сторон которые имеют общую вершину называются соседними. Остальные не подпадающие этому определению называют противоположными ( Противоположные стороны параллельны между собой).
Отрезок соединяющий наиболее отдаленные вершины называется диагональю прямоугольника.
Свойства прямоугольника
Рассмотрим чем отличается прямоугольник от других фигур.
1. В прямоугольнике противоположные стороны равны.
2. Уровни между собой и имеют 90 градусов все углы прямоугольника.
3. Диагонали прямоугольника равны и в точке пересечения делятся пополам.
4. Диагонали треугольника делят его на два одинаковых треугольника.
Таким образом, если в параллелограмме все углы ровны или один прямой, или одинаковые диагонали то это прямоугольник. Что касается четырехугольников, то среди них прямоугольниками будут только те, у которых все углы равны или хотя бы три прямые. Биссектриса угла прямоугольника отсекает от него равнобедренный треугольник.
Основными геометрическими характеристиками прямоугольника является периметр и площадь.
Периметр прямоугольника — формула
Периметр равен сумме всех сторон, при этом стороны попарно равны между собой. Поэтому формула периметру прямоугольника имеет вид
Пример 1. Стороны прямоугольника равны 5 и 7 см. Найти его периметр.
Решение. Подставляем значения в формулу периметру прямоугольника
Ответ. Периметр равен 24 см.
Формула площади прямоугольника
Площадь прямоугольника равна произведению его ширины на высоту.
Если задано длину диагоналей (d) и угол между ними (alpha) то формула площади прямоугольника равна половине квадрата диагоналей на синус угла между ними.
Не забывайте что площадь измеряется в единицах квадратных, поэтому если размеры заданы в метрах то площадь будет в метрах квадратных, сантиметрах — площадь в сантиметрах квадратных и т. п.
Пример 2. Диагонали прямоугольника пересекаются под углом 30 градусов и ровны 5 см. Какова площадь прямоугольника?
Решение. Подставляем данные в формулу площади прямоугольника через диагонали
Ответ. Площадь равна 6,25 сантиметров квадратных.
Диагонали прямоугольника
В прямоугольнике длину диагонали вычисляют через длины сторон по теореме Пифагора
D=sqrt(a^2+b^2) или
Итак Вы уже знаете как найти площадь прямоугольника, периметр и диагональ.
Стороны прямоугольника
Если известна диагональ и одна сторона то вторую также определяем по теореме Пифагора
или
Описанная и вписанная окружность в прямоугольник
Диаметр или радиус описанной вокруг прямоугольника окружности Вы видимо вычисляли. Однако вряд ли задумывались о вписанной окружности и геометрическом место ее центров.
Диаметр описанной окружности равен диагонали ( d ), соответственно радиус описанной окружности — половине диагонали ( R=d/2 ). Вписанных окружностей в прямоугольник можно построить множество. Радиус вписанной окружности равен половине длины меньшей стороны прямоугольника ( r=b/2 ). Если соединить центры всех возможных вписанных окружностей то получим отрезок MN длина которого равна разности сторон ( MN=a-b ).
Приведенная информация о вписанной и описанной окружности редко пригодится Вам при решении задач но Вы должны знать как в таких случаях вычислять указанные величины.
Задачи на прямоугольник
Стороны прямоугольника
Задача 1. Длина диагонали и стороны прямоугольника составляют 10 и 8 см. Найдите другую сторону.
Решение. По теореме Пифагора вычисляем
Ответ. Сторона равна 6 см.
Задача 2. Длина диагонали прямоугольника равна 5 см. Одна сторона меньше другой на сантиметр. Найдите стороны прямоугольника.
Решение. Обозначим первую сторону через х, тогда по условию вторая – х -1 . Составляем уравнение
Возводим к квадрату и решаем квадратное уравнение
Второе значение не имеет смысла. Для вычисления меньшей стороны выполняем вычитание
Ответ. Стороны прямоугольника равны 3 и 4 см.
Задачи на площадь и периметр прямоугольника
Задача 3. Большая сторона прямоугольника 8 см. Меньшая составляет четверть большой. Какая площадь и периметр прямоугольника?
Решение. Четверть большей означает одна четвертая часть, то есть
Площадь и периметр находим по формулам
Ответ. Периметр 20 см, площадь 16 сантиметров квадратных.
Задача 4. Участок земли имеет площадь 64 квадратных метров. Какой периметр участка если диагонали пересекаются под прямым углом?
Поскольку угол между диагоналями 90 градусов, то это квадрат. Площадь квадрата равна квадрату стороны
Отсюда находим сторону
Периметр находим по формуле
Ответ. Периметр равен 32 метра.
Не забывайте что периметр измеряется в единицах длины, а площадь — в единицах квадратных.
Теперь Вы знаете как найти периметр и площадь прямоугольника. Пользуйтесь формулами на практике и совершенствуйте навыки вычислений указанных величин.
Площадь прямоугольника через периметр и диагональ
Прямоугольник. Формулы и свойства прямоугольника
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют Длиной прямоугольника, а короткую — Шириной прямоугольника.
Стороны прямоугольника одновременно является его высотами.
Основные свойства прямоугольника
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
2 d 2 = 2 a 2 + 2 b 2
∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°
Стороны прямоугольника
Формулы определения длин сторон прямоугольника
Диагональ прямоугольника
Формулы определения длины диагонали прямоугольника
Периметр прямоугольника
Формулы определения длины периметру прямоугольника
P = 2( a + √ d 2 — a 2 ) = 2( b + √ d 2 — b 2 )
P = 2( a + √ 4R 2 — a 2 ) = 2( b + √ 4R 2 — b 2 )
Площадь прямоугольника
Формулы определения площади прямоугольника
S = a √ d 2 — a 2 = b √ d 2 — b 2
S = a √ 4R 2 — a 2 = b √ 4R 2 — b 2
Окружность описанная вокруг прямоугольника
Формулы определения радиуса окружности описанной вокруг прямоугольника
Угол между стороной и диагональю прямоугольника
Формулы определения угла между стороной и диагональю
Угол между диагоналями прямоугольника
Формулы определения угла между диагоналями прямоугольника
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Копирование материалов запрещено.
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
poiskvstavropole.ru