Контрольная работа по теме «Степень с натуральным показателем», 7 класс
Контрольная работа по теме
«Степень с натуральным показателем»,
7 класс
Цель: выявить уровень знаний по данной теме.
Подтемы «Степень и ее свойства», «Одночлены», «Умножение одночленов. Возведение одночлена в степень».
Комментарий для учителя.
В своей работе использую технологию укрупнения дидактических единиц П. Эрдниева, технологию поэтапного формирования умственных действий, развивающие технологии, опережающее обучение, психолого-педагогические рекомендации Я.Груденова. Поэтому
1) в 7 классе ввожу понятие степени с отрицательным показателем, функции у=х2 и у= х3 изучаются после изучения линейной функции;
2) одновременно изучаю прямое и обратное действие, похожие действия ( например, возведение в степень и представление в виде степени,)
3) в систему упражнений постоянно включаю ловушки – задания, провоцирующие ученика на ошибку.

Текст контрольной работы

6. У математиков не сразу сложилось представление о возведении в степень, хотя в самых древних математических текстах Древнего Египта и Междуречья встречаются задачи на вычисление степеней.
Этот древнегреческий математик в своем знаменитом труде описал понятие степени так: «Все числа… состоят из некоторого количества единиц; …среди них находятся: квадраты, получающиеся от умножения некоторого числа самого на себя; это же число называется стороной квадрата, затем кубы, получающиеся от умножения квадратов на их сторону, далее квадрато-квадраты — от умножения квадратов самих на себя, далее квадрато-кубы, получающиеся от умножения квадрата на куб его стороны, далее кубо-кубы — от умножения кубов самих на себя».
Кто он? Фамилия математика состоит из 7 букв. Числа, соответствующие этим буквам согласно алфавиту, удовлетворяют следующим условиям:


6. Кому принадлежат слова: «Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь»? Фамилия автора этих слов состоит из 7 букв. Числа, соответствующие этим буквам согласно алфавиту, удовлетворяют следующим условиям:
Приложение
Алфавит
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
16 17 18 19 20 21 22 23 24 25 26 27 28 29
О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы
30 31 32 33
Ь Э Ю Я
Критерии оценивания:
«2» — 0-11 баллов
«3» — 12-16 баллов
«4» — 17-22 балла
«5» — 23-24 баллов
№ задания | 1 | 2 | 3 | 4 | 5 | 6 |
Количество баллов | 1 | 9 | 2 | 3 | 1 | 8 |
Ответы на задание №6:
вариант 1) — Диофант
вариант 2) — Энгельс
контрольная работа
DOCX / 1013.23 Кб
xn--j1ahfl.xn--p1ai
«Степень с натуральным и целым показателем»
Контрольная работа № 2.
Тема: Степень с натуральным и целым показателем.
I вариант. II вариант.
1. Найдите значение выражения:
; б) ,
если а= -18
1. Найдите значение выражения:
а) ; б) ,
если а = 0,8
2. Выполните действия:
2. Выполните действия:
3. Используя свойство степени, найдите значение выражения:
а) ; б)
3. Используя свойство степени, найдите значение выражения:
а) ; б)
4. Упростите выражение:
4. Упростите выражение:
infourok.ru
Контрольная работа «Степень с целым показателем» 7 класс
Суммативная работа ФИ______________________Класс_______ Дата_________________
РазделСтепень с целым показателем и ее свойства
Цели обучения
7.1.2.3
Знать определение степени с нулевым и целым отрицательным показателем и её свойства;
7.1.2.4
находить числовое значение степени с целым показателем и представлять заданные числа в виде степени;
7.1.2.6
находить допустимые значения переменных в основании степени с нулевым показателем;
7.2.1.1
применять свойства степени с целым показателем при нахождении значений числовых выражений;
Уровень мыслительных
навыков
Знание.
Понимание.
Применение.
Критерий оценивания
Обучающийся:
знает определение степени с нулевым и целым отрицательным показателем и её свойства;
находит числовое значение степени с целым показателем, и представлять заданные числа в виде степени;
находит допустимые значения переменных в основании степени с нулевым показателем;
25 минут
1 задание: Вычислите:
а)= ; б)= в)= ;г)= .
д)=
2 задание: Упростите:
а)= ;
б) = .
3 задание: Найдите допустиму значения переменной х в основании:
а)= ;
б)=.
4 задание : Вычислите:
.
Критерий оценивания
Дескрипторы
Балл
Обучающийся
Знает определение степени с нулевым и целым отрицательным показателем и её свойства.
Умеет представлять число в виде степени с положительным показателем.
4
Находит результат возведения в степень числа.
4Проводить вычислительные расчеты.
6
Записывает ответ.
1
Находит числовое значение степени с целым показателем, и представлять заданные числа в виде степени
Умеет возводить отрицательное число в в степень с четным и нечетным показателем.
1
Умеет представлять выражение в виде степени с положительным показателем.
3
Упрощает выражение, используя свойства степени.
4
Записывает ответ.
1
Находит числовое значение степени с целым показателем, и представлять заданные числа в виде степени
Умеет возводить отрицательное число в в степень с четным и нечетным показателем.
2
3
Упрощает выражение, используя свойства степени.
3
Записывает ответ.
1
Находит допустимые значения переменных в основании степени с нулевым показателем
Умеет возводить любое число, кроме нуля в нулевую степень.
2
Умеет находить значение переменной, при котором выражение обращается в нуль.
2
Записывает ответ.
2
Применяет свойства степени с целым показателем при нахождении значений числовых выражений
Умеет представлять число в виде степени.
4
Умеет представлять число в виде степени с положительным показателем.
2Проводить вычислительные расчеты, используя свойства степени.
6
Записывает ответ.
1
Всего баллов
52
Суммативная работа ФИ______________________Класс_______ Дата_________________
РазделСтепень с целым показателем и ее свойства
Цели обучения
7.1.2.3
Знать определение степени с нулевым и целым отрицательным показателем и её свойства;
7.1.2.4
находить числовое значение степени с целым показателем и представлять заданные числа в виде степени;
7.1.2.6
находить допустимые значения переменных в основании степени с нулевым показателем;
7.2.1.1
применять свойства степени с целым показателем при нахождении значений числовых выражений;
Уровень мыслительных
навыков
Знание.
Понимание.
Применение.
Критерий оценивания
Обучающийся:
знает определение степени с нулевым и целым отрицательным показателем и её свойства;
находит числовое значение степени с целым показателем, и представлять заданные числа в виде степени;
находит допустимые значения переменных в основании степени с нулевым показателем;
Время выполнения
25 минут
1 задание: Вычислите:
а)= ; б)= в)= ;г)= .
д)=
2 задание: Упростите:
а)= ;
б) = .
3 задание: Найдите допустиму значения переменной х в основании:
а)= ;
б)=.
4 задание : Вычислите:
.
Критерий оценивания
Дескрипторы
Балл
Обучающийся
Знает определение степени с нулевым и целым отрицательным показателем и её свойства.
Умеет представлять число в виде степени с положительным показателем.
4
Находит результат возведения в степень числа.
4
Проводить вычислительные расчеты.
6
Записывает ответ.
1
Находит числовое значение степени с целым показателем, и представлять заданные числа в виде степени
Умеет возводить отрицательное число в в степень с четным и нечетным показателем.
1
Умеет представлять выражение в виде степени с положительным показателем.
3
Упрощает выражение, используя свойства степени.
4
Записывает ответ.
1
Находит числовое значение степени с целым показателем, и представлять заданные числа в виде степени
Умеет возводить отрицательное число в в степень с четным и нечетным показателем.
2
Умеет представлять выражение в виде степени с положительным показателем.
3
Упрощает выражение, используя свойства степени.
3
Записывает ответ.
1
Находит допустимые значения переменных в основании степени с нулевым показателем
Умеет возводить любое число, кроме нуля в нулевую степень.
2
Умеет находить значение переменной, при котором выражение обращается в нуль.
2
Записывает ответ.
2
Применяет свойства степени с целым показателем при нахождении значений числовых выражений
Умеет представлять число в виде степени.
4
Умеет представлять число в виде степени с положительным показателем.
2
Проводить вычислительные расчеты, используя свойства степени.
6
Записывает ответ.
1
Всего баллов
52
Суммативная работа ФИ______________________Класс_______ Дата_________________
РазделСтепень с целым показателем и ее свойства
Цели обучения
7.1.2.3
Знать определение степени с нулевым и целым отрицательным показателем и её свойства;
7.1.2.4
находить числовое значение степени с целым показателем и представлять заданные числа в виде степени;
7.1.2.6
находить допустимые значения переменных в основании степени с нулевым показателем;
7.2.1.1
применять свойства степени с целым показателем при нахождении значений числовых выражений;
Уровень мыслительных
навыков
Знание.
Понимание.
Применение.
Критерий оценивания
Обучающийся:
знает определение степени с нулевым и целым отрицательным показателем и её свойства;
находит числовое значение степени с целым показателем, и представлять заданные числа в виде степени;
находит допустимые значения переменных в основании степени с нулевым показателем;
Время выполнения
25 минут
1 задание: Вычислите:
а)= ; б)= в)= ;г)= .
д)=
2 задание: Упростите:
а)= ;
б) = .
3 задание: Найдите допустиму значения переменной х в основании:
а)= ;
б)=.
4 задание : Вычислите:
.
Критерий оценивания
Дескрипторы
Балл
Обучающийся
Знает определение степени с нулевым и целым отрицательным показателем и её свойства.
Умеет представлять число в виде степени с положительным показателем.
4
Находит результат возведения в степень числа.
4
Проводить вычислительные расчеты.
6
Записывает ответ.
1
Находит числовое значение степени с целым показателем, и представлять заданные числа в виде степени
Умеет возводить отрицательное число в в степень с четным и нечетным показателем.
1
Умеет представлять выражение в виде степени с положительным показателем.
3
Упрощает выражение, используя свойства степени.
4
Записывает ответ.
1
Находит числовое значение степени с целым показателем, и представлять заданные числа в виде степени
Умеет возводить отрицательное число в в степень с четным и нечетным показателем.
2
Умеет представлять выражение в виде степени с положительным показателем.
3
Упрощает выражение, используя свойства степени.
3
Записывает ответ.
1
Находит допустимые значения переменных в основании степени с нулевым показателем
Умеет возводить любое число, кроме нуля в нулевую степень.
2
Умеет находить значение переменной, при котором выражение обращается в нуль.
2
Записывает ответ.
2
Применяет свойства степени с целым показателем при нахождении значений числовых выражений
Умеет представлять число в виде степени.
4
Умеет представлять число в виде степени с положительным показателем.
2
Проводить вычислительные расчеты, используя свойства степени.
6
Записывает ответ.
1
Всего баллов
52
infourok.ru
Контрольная работа по алгебре «Степень с натуральным показателем»; 7 класс — К уроку — Математика, алгебра, геометрия
Контрольная работа № 3 7 класс, алгебра
Тема: Степень с натуральным показателем
1 вариант
2 вариант
1.Вычислите:
а) -102∙0,2 б) (-1 )3 в) 17-(-1)7
2.Выполните действия:
а) х4∙х б) у6:у2 в) (-2с6)4
г) д) (m3∙m4)2∙(2m)3
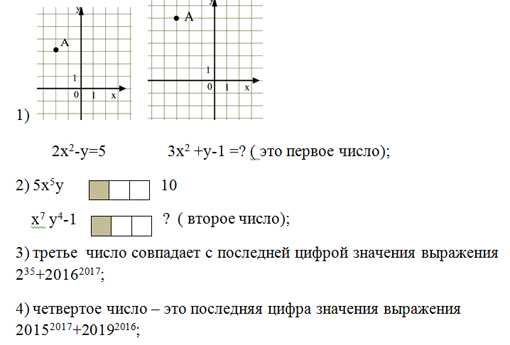
3. Постройте график функции у=х2. Определите по графику значение у, если х=-2.
4. Упростите выражение:
а) 2а5b2∙ba3 б) (-0,1х3)4∙10х
в) ( ab2)3∙ a3b2
5. Используя свойства степени, найдите значение выражения:
а) б)
1.Вычислите:
а) -24∙0,5 б) (-2 )2 в) (-1)9-19
2.Выполните действия:
а) х3∙х7 б) у4:у в) (-3с4)2
г) д) (6х)2∙(х∙х5)4
3. Постройте график функции у=х3. Определите по графику значение у, если х=2.
4. Упростите выражение:
а) 3а2b∙b4 a4 б) (-0,2х2)3∙5х2
в) ( a2 b)2∙ b2а
5. Используя свойства степени, найдите значение выражения:
а) б)
Контрольная работа № 3 7 класс, алгебра
Тема: Степень с натуральным показателем
1 вариант
2 вариант
1.Вычислите:
а) -102∙0,2 б) (-1 )3 в) 17-(-1)7
2.Выполните действия:
а) х4∙х б) у6:у2 в) (-2с6)4
г) д) (m3∙m4)2∙(2m)3
3. Постройте график функции у=х2. Определите по графику значение у, если х=-2.
4. Упростите выражение:
а) 2а5b2∙ba3 б) (-0,1х3)4∙10х
в) ( ab2)3∙ a3b2
5. Используя свойства степени, найдите значение выражения:
а) б)
1.Вычислите:
а) -24∙0,5 б) (-2 )2 в) (-1)9-19
2.Выполните действия:
а) х3∙х7 б) у4:у в) (-3с4)2
г) д) (6х)2∙(х∙х5)4
3. Постройте график функции у=х3. Определите по графику значение у, если х=2.
4. Упростите выражение:
а) 3а2b∙b4 a4 б) (-0,2х2)3∙5х2
в) ( a2 b)2∙ b2а
5. Используя свойства степени, найдите значение выражения:
а) б)
pedsovet.su
Контрольная работа по математике в 7 классе по теме Степень с натуральным показателем
Контрольная работа №2
Степень с натуральным показателем
Вариант 1
А1. Выполните действия: .
А2. Вычислите: .
А3. Упростите выражение: .
______________
В1. Вычислите: 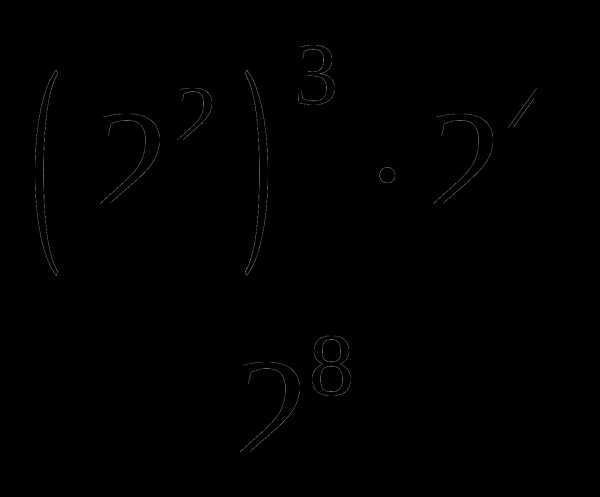 .
.
В2. Решите задачу, выделяя три этапа математического моделирования.
Лодка плыла 2 ч по течению реки, а затем 1 ч против течения. Найдите собственную скорость лодки (т.е. скорость в стоячей воде), если известно, что скорость течения реки равна 3 км/ч, а всего лодкой пройдено расстояние 30 км.
Задания А1-А4 соответствуют уровню обязательной подготовки.
Контрольная работа №2
Степень с натуральным показателем
Вариант 2
А1. Выполните действия: .
А2. Вычислите: .
А3. Упростите выражение: .
______________________
В1. Вычислите: 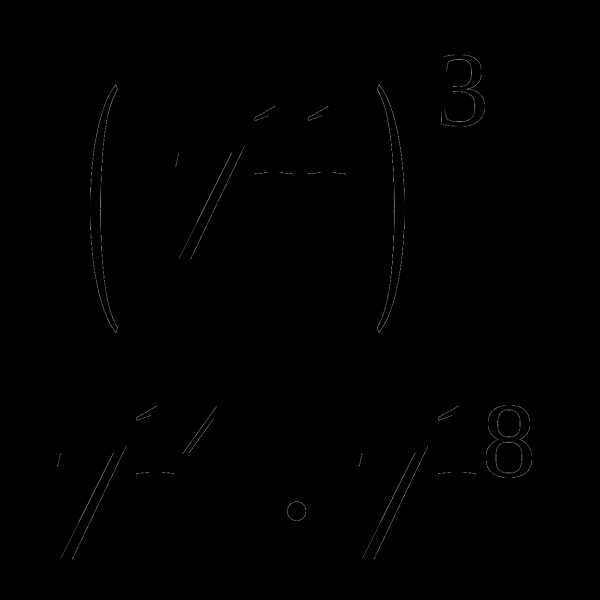 .
.
В2. Решите задачу, выделяя три этапа математического моделирования.
Лодка плыла 4 ч по течению реки, а затем 3 ч против течения. Найдите собственную скорость лодки (т.е. скорость в стоячей воде), если известно, что скорость течения реки равна 3 км/ч, а всего лодкой пройдено расстояние 59 км.
Задания А1-А4 соответствуют уровню обязательной подготовки.
infourok.ru
Контрольная работа № 4 по теме Степень с натуральным показателем — ОДНОЧЛЕНЫ — СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ — Поурочные разработки по алгебре 7 класс — к учебнику Ю.Н. Макарычева
Глава III. СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
§ 8. ОДНОЧЛЕНЫ
Урок 44. Контрольная работа № 4 по теме «Степень с натуральным показателем»
Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.
Ход урока
I. Сообщение темы и цели урока
II. Общая характеристика контрольной работы
Контрольная работа составлена в шести вариантах (варианты 1,2 — самые простые, варианты 3, 4 — средней сложности, варианты 5, 6 — самые сложные). Степень сложности меняется не слишком резко, поэтому можно рекомендовать следующий критерий оценки: при выполнении вариантов 1, 2 оценка «3» ставится за любые три решенные задачи, оценка «4» — за четыре задачи и оценка «5» — за пять задач. Одна задача дает учащимся некоторую свободу выбора. При тех же критериях оценки за решение задач вариантов 3, 4 к набранным баллам добавляются дополнительно 0,5 балла, за решение задач вариантов 5,6 — дополнительно 1 балл (т. е. оценка «5» выставляется уже за четыре задачи). Все задачи в варианте примерно равноценны. Возможно, несколько труднее для учеников задачи 5, 6.
Перед проведением контрольной работы учащихся целесообразно ознакомить с критериями оценки и разной сложностью вариантов. Выбор вариантов может быть осуществлен учителем или предоставлен ученикам (в этом случае предполагается наличие копировальной техники в школе и избыточное количество заданий). При наличии такой техники в классе на стенде (после контрольной) может быть вывешено решение всех задач шести вариантов.
Контрольная работа рассчитана на один урок.
III. Контрольная работа
Вариант 1
1. Дана функция у = х2 + 2. Составьте таблицу значений функции в промежутке -2 ≤ х ≤ 2 с шагом 0,5 и постройте график функции.
2. Выполните действия:
3. Запишите в виде одночлена стандартного вида выражение:
4. Сравните числа 816 и 216 ∙ 415.
5. Решите уравнение:
6. Докажите, что число 1050 — 4 делится на 3.
Вариант 2
1. Дана функция у = 1 — х2. Составьте таблицу значений функции в промежутке -2 ≤ х ≤ 2 с шагом 0,5 и постройте график функции.
2. Выполните действия:
3. Запишите в виде одночлена стандартного вида выражение:
4. Сравните числа 1014 и 215 ∙ 514.
5. Решите уравнение:
6. Докажите, что число 1040 — 7 делится на 3.
Вариант 3
1. Дана функция у = х2 — 2х. Составьте таблицу значений функции в промежутке -1 ≤ х ≤ 3 с шагом 0,5 и постройте график функции.
2. Выполните действия:
3. Запишите в виде одночлена стандартного вида выражение:
4. Сравните числа 230 и 320.
5. Решите уравнение:
6. Докажите, что число 196374 + 391164 — 2 делится на 5.
Вариант 4
1. Дана функция у = х2 + 2х. Составьте таблицу значений функции в промежутке -3 ≤ х ≤ 1 с шагом 0,5 и постройте график функции.
2. Выполните действия:
3. Запишите в виде одночлена стандартного вида выражение:
4. Сравните числа 340 и 430.
5. Решите уравнение:
6. Докажите, что число 171536 + 375164 + 4 делится на 5.
Вариант 5
1. Дана функция у = х2 + 2|х|. Составьте таблицу значений функции в промежутке -3 ≤ х ≤ 3 с шагом 0,5 и постройте график функции.
2. Запишите в виде одночлена стандартного вида выражение:
3. Сравните числа 780 и 4120.
4. Определите последнюю цифру числа (389)162 + (635)236.
5. Решите уравнение
6. Докажите, что число 10316 + 6 не делится на число 1019 — 1.
Вариант 6
1. Дана функция у = 2|х| — х2. Составьте таблицу значений функции в промежутке -3 ≤ х ≤ 3 с шагом 0,5 и постройте график функции.
2. Запишите в виде одночлена стандартного вида выражение:
3. Сравните числа 960 и 490.
4. Определите последнюю цифру числа (289)364 + (536)171.
5. Решите уравнение
6. Докажите, что число 10273 + 7 не делится на число 1019 — 1.
IV. Подведение итогов контрольной работы
1. Распределение работ по вариантам и результаты решения. Данные удобно заносить в таблицу (для каждой пары вариантов).
№ задачи | Итоги | |||
+ | ± | — | Ø | |
1 | 5 | 1 | 1 | 1 |
2 | ||||
… | ||||
6 | ||||
Обозначения:
+ — число решивших задачу правильно или почти правильно;
± — число решивших задачу со значительными погрешностями;
— — число не решивших задачу;
Ø — число не решавших задачу.
Варианты 1, 2 — 8 учащихся.
2. Типичные ошибки при решении задач.
3. Задачи, вызвавшие наибольшие трудности.
V. Разбор задач (ответы и решения)
Вариант 1
6. Доказано.
Вариант 2
6. Доказано.
Вариант 3
6. Доказано.
Вариант 4
6. Доказано.
Вариант 5
1. Для функции у = х2 — 2|х| составим таблицу значений функции в промежутке -3 ≤ х ≤ 3 с шагом 0,5.
x | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
y | 3 | 1,25 | 0 | -0,75 | -1 | -0,75 | 0 | -0,75 | -1 | -0,75 | 0 | 1,25 | 3 |
Отметим точки из таблицы на координатной плоскости и построим график данной функции. Легко проверить, что функция является четной и ее график симметричен относительно оси ординат.
2. Используя правила действий со степенями, запишем одночлен в стандартном виде:
3. Запишем данные числа 780 и 4120 в другом виде: 780 = (72)40 = 4940 и 4120 = (43)40 = 6440. Так как 49 < 64, тo и 4940 < 6440, или 780 < 4120.
(Ответ: 780 < 4120.)
4. Запишем данное число в следующем виде: (389)162 + (635)236 = (3892)81 + (635)236. Число 389 оканчивается цифрой 9. При возведении в квадрат число 3892 оканчивается цифрой 1. Если число оканчивается цифрой 1 или 5, то при возведении такого числа в любую степень оно также будет оканчиваться цифрой 1 или 5. Поэтому данное число оканчивается цифрой 1 + 5 = 6.
(Ответ: 6.)
5. Используя свойства степеней, преобразуем данное уравнение:
Найдем сумму чисел Тогда уравнение имеет вид
Так как равны степени с одинаковым основанием 2, то равны и показатели степеней: 3х + 5 = 50 или 3x = 45, откуда x = 15.
(Ответ: х = 15.)
6. Рассмотрим число 10316 + 6. Число 10316 состоит из одной единицы и 316 нулей. Тогда число 10316 + 6 имеет вид 100…06. Сумма цифр этого числа равна 7, и по признаку делимости оно не делится на 9. Число 1019 состоит из одной единицы и 19 нулей. Поэтому число 1019 — 1 состоит из 19 девяток (т. е. 99…9) и делится на 9. Так как первое число 10316 + 6 не имеет делителя 9, то оно не может без остатка делиться на второе число 1019 — 1.
(Ответ: доказано.)
Вариант 6
1. Для функции 2|х| — х2 составим таблицу значений функции в промежутке -3 ≤ х ≤ 3 с шагом 0,5.
x | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
y | -3 | 1,25 | 0 | 0,75 | 1 | 0,75 | 0 | 0,75 | 1 | 0,75 | 0 | -1,25 | -3 |
Отметим эти точки на координатной плоскости и построим график данной функции. Эта функция является четной, и ее график симметричен относительно оси ординат.
2. Используя правила действий со степенями, запишем одночлен в стандартном виде:
3. Запишем данные числа 960 и 490 в другом виде: 960 = (92)30 = 8130 и 490 = (43)30 = 6430. Так как 81 > 64, то и 8130 > 6430, или 960 > 490.
(Ответ: 960 > 490.)
4. Запишем данное число в следующем виде: (289)364 + (536)171 = (2892)182 + (536)171. Число 289 оканчивается цифрой 9. При возведении в квадрат число 2892 оканчивается цифрой 1. При возведении такого числа в любую степень оно будет также оканчиваться цифрой 1. Число 536 оканчивается цифрой 6. При возведении такого числа в любую степень оно будет также оканчиваться цифрой 6. Поэтому данное число оканчивается цифрой 1 + 6 = 7.
(Ответ: 7.)
5. Используя свойства степеней, преобразуем данное уравнение:
Найдем сумму чисел: Тогда уравнение имеет вид
Так как равны степени чисел с одинаковым основанием 3, то равны и показатели степеней: 4x + 4 = 68 или 4x = 64, откуда х = 16.
(Ответ: х = 16.)
6. Рассмотрим число 10273 + 7. Число 10273 состоит из одной единицы и 273 нулей. Тогда число 10273 + 7 состоит из одной единицы, 273 нулей и цифры 7, т. е. имеет вид 100…07. Сумма цифр этого числа равна 8, и по признаку делимости оно не делится на 9. Число 1019 состоит из одной единицы и 19 нулей. Поэтому число 1019 — 1 состоит из 19 девяток (т. е. 99…9). Очевидно, что такое число делится на 9, так как каждая цифра числа делится на 9. Следовательно, число 10273 + 7 не делится на число 1019 — 1 без остатка, так как не имеет делителя 9.
(Ответ: доказано.)
VI. Подведение итогов урока
compendium.su
В а р и а н т А – 2 К – 4
б)
б) в) 5. Используя свойство степени, найдите значение выражения: | |
Дополнительно: Вычислите: , если . | Дополнительно: Вычислите: , если . |
В а р и а н т В – 1 К – 4
б) в)
б) в)
б) 5. Используя свойства степени, найдите значение выражения: | В а р и а н т В – 2 К – 4
б) в)
б) в)
б) 5. Используя свойства степени, найдите значение выражения: |
Дополнительно: Вычислите: , если | Дополнительно: Вычислите: , если |
www.alllessons.ru

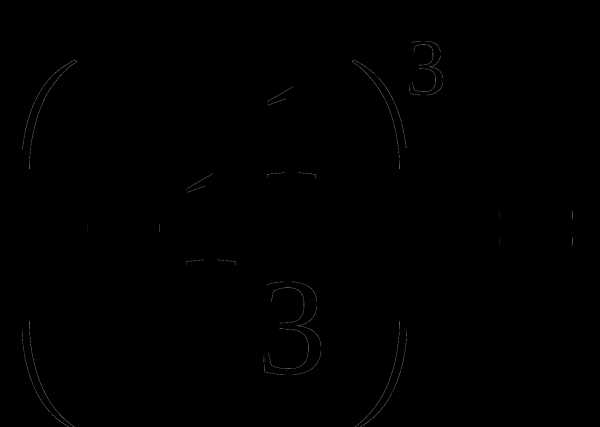 в)
в) 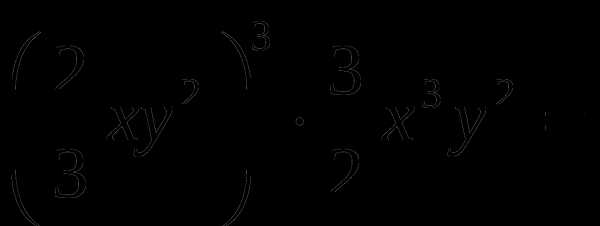
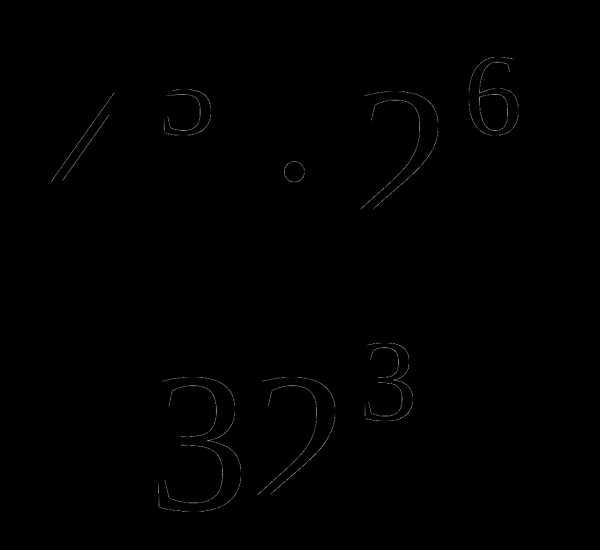
 в)
в) 
 .
.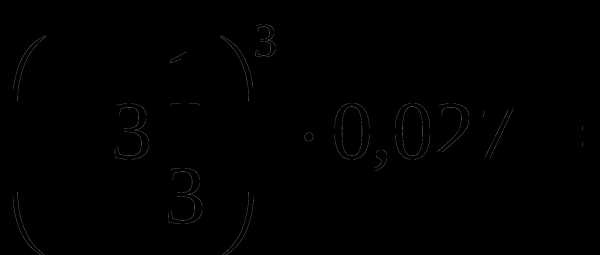
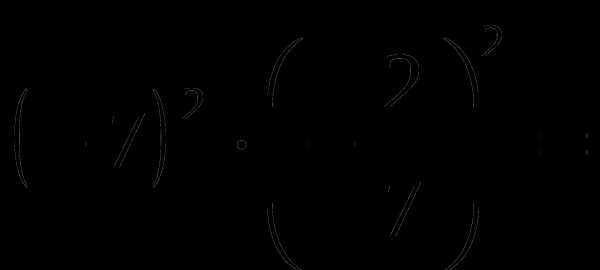
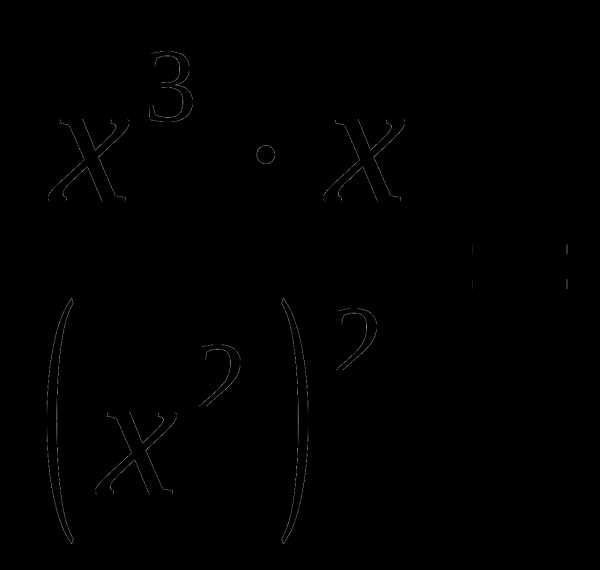
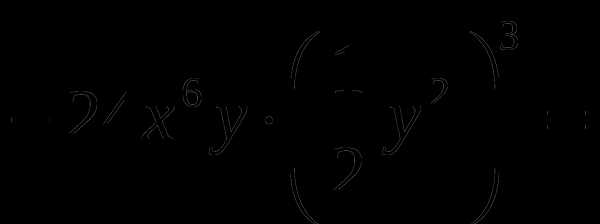 в)
в) 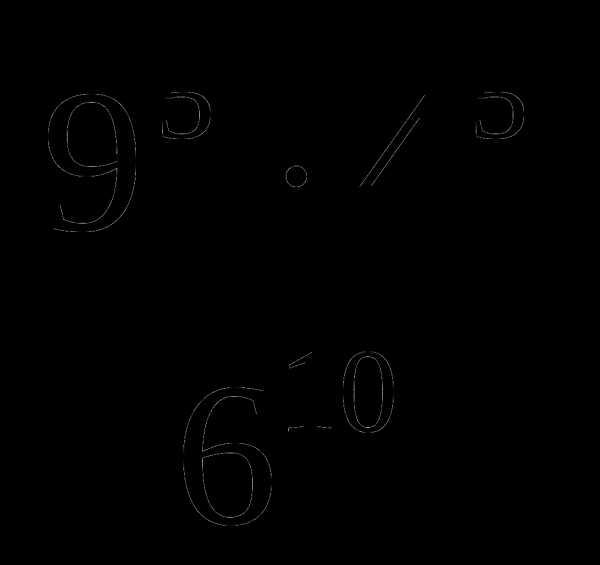 .
.
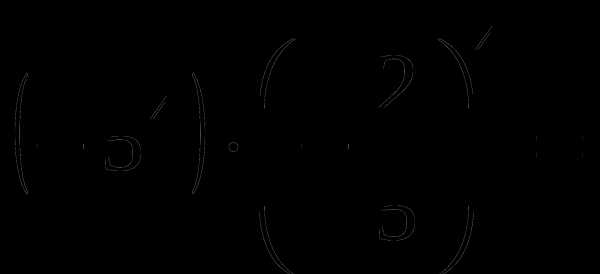
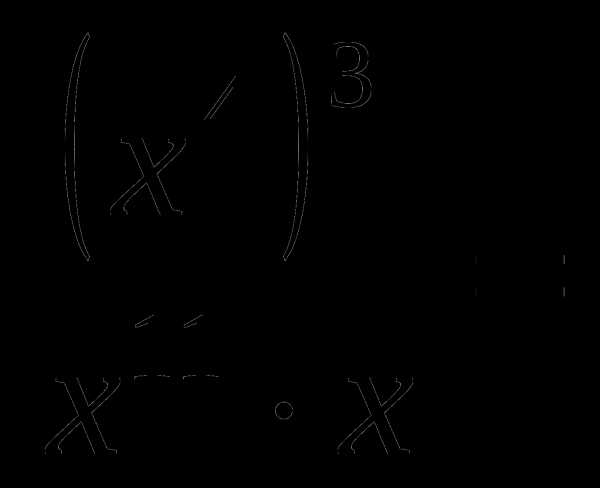
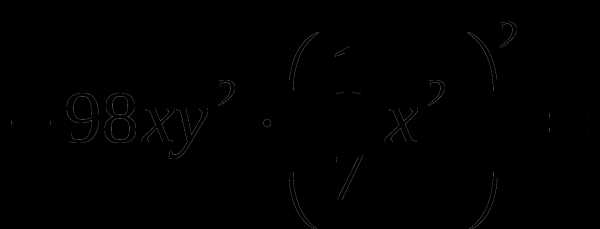 в)
в) 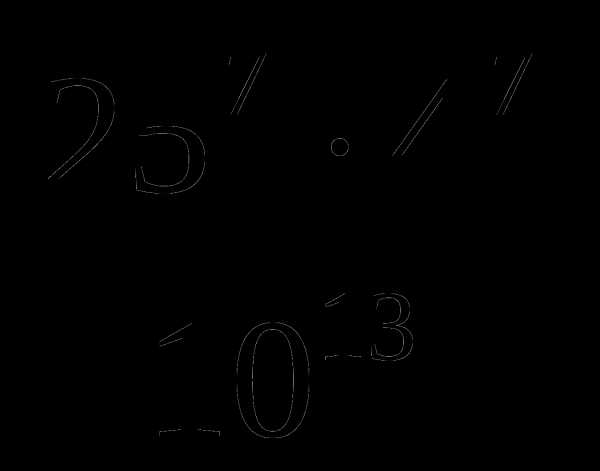 .
.