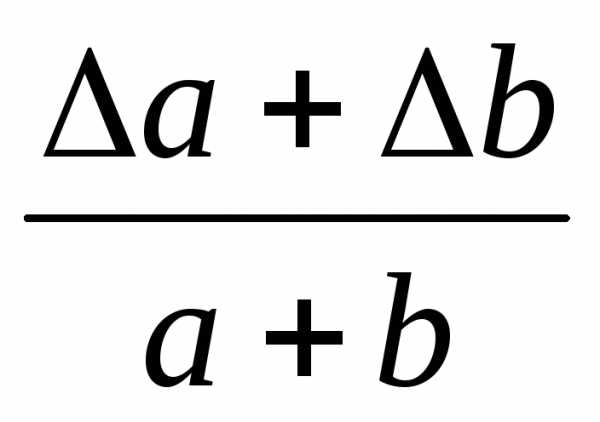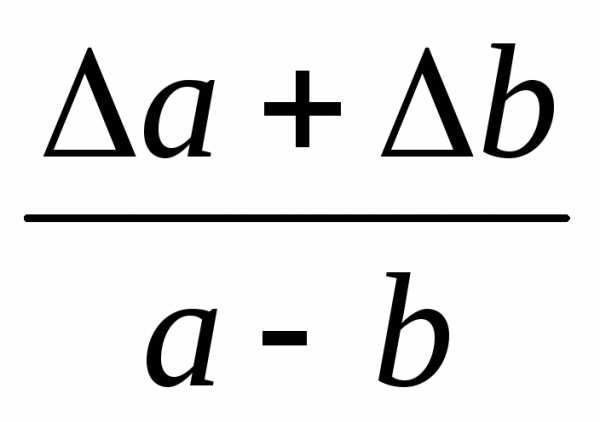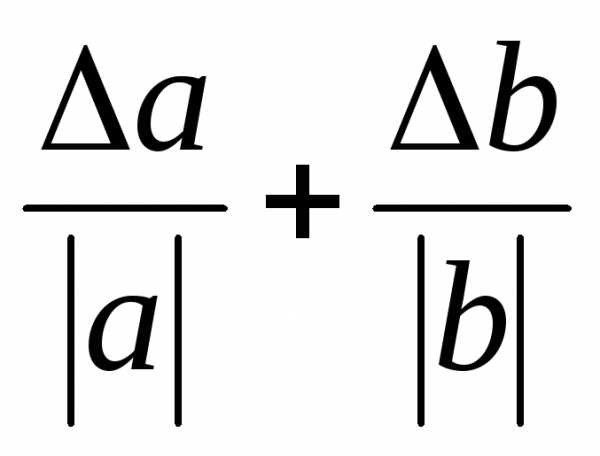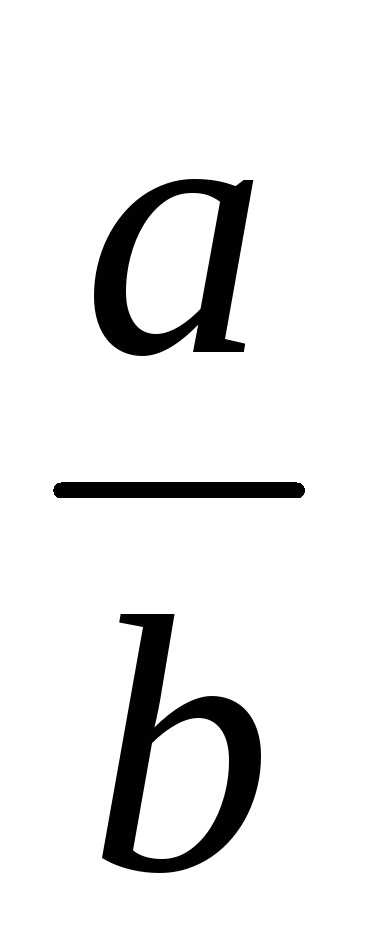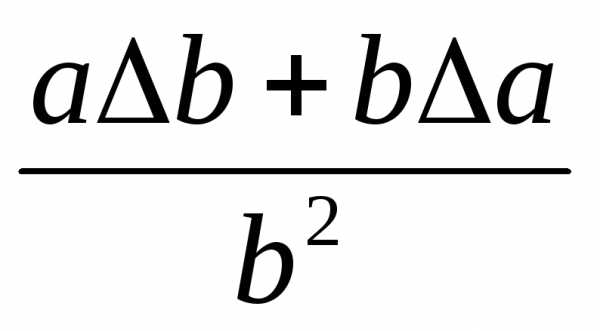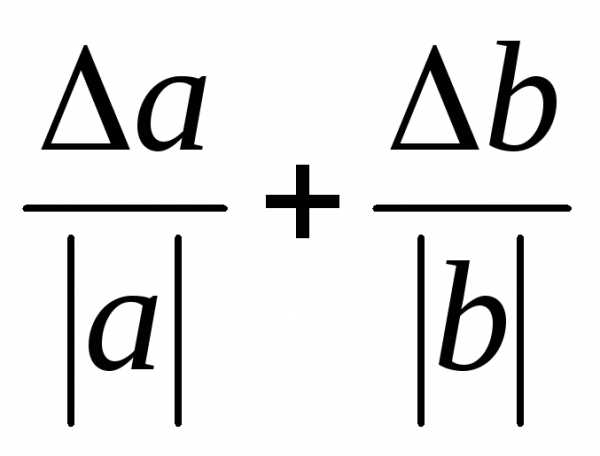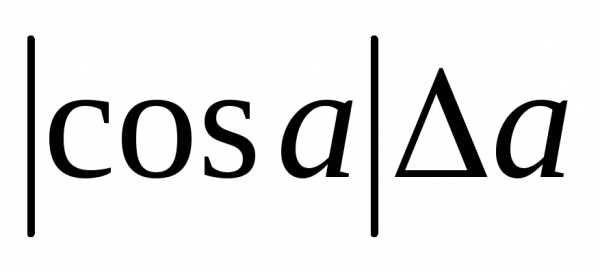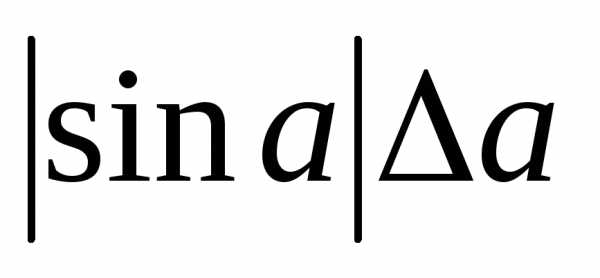Метрология абсолютная погрешность формула – 1.1. Погрешности в метрологии

Содержание

1.1. Погрешности в метрологии

Ни одно измерение не свободно от погрешностей, или, точнее, вероятность измерения без погрешностей приближается к нулю. Род и причины погрешностей весьма разнообразны и на них влияют многие факторы (рис.1.2).

Общая характеристика влияющих факторов может быть систематизирована с различных точек зрения, например, по влиянию перечисленных факторов (рис.1.2).

По результатам измерения погрешности можно разделить на три вида: систематические, случайные и промахи.

Систематические погрешности, в свою очередь, делят на группы по причине их возникновения и характеру проявления. Они могут быть устранены различными способами, например, введением поправок.

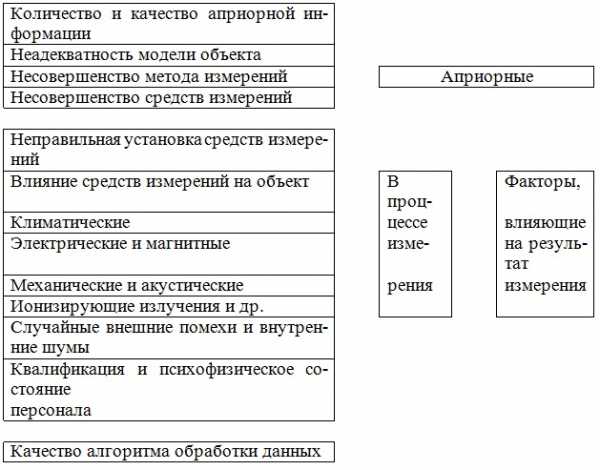
рис. 1.2

Случайные погрешности вызываются сложной совокупностью изменяющихся факторов, обычно неизвестных и трудно поддающихся анализу. Их влияние на результат измерения можно уменьшить, например, путем многократных измерений с дальнейшей статистической обработкой полученных результатов методом теории вероятностей.

К промахам относятся грубые погрешности, которые возникают при внезапных изменениях условия эксперимента. Эти погрешности по своей природе тоже случайны, и после выявления должны быть исключены.

Точность измерений оценивается погрешностями измерений, которые подразделяются по природе возникновения на инструментальную и методическую и по методу вычислений на абсолютную, относительную и приведенную.

Инструментальная погрешность характеризуется классом точности измерительного прибора, который приведен в его паспорте в виде нормируемых основной и дополнительных погрешностей.

Методическая погрешность обусловлена несовершенством методов и средств измерений.

Абсолютная

погрешность есть разность между измеренным G_uи истинным G значениями величины, определяемая по формуле:

Δ=ΔG=G_u-G

Заметим, что величина имеет размерность измеряемой величины.

Относительную погрешность находят из равенства

δ=±ΔG/G_u·100%

Приведенную погрешность рассчитывают по формуле (класс точности измерительного прибора)

δ=±ΔG/G_норм·100%

где G_норм – нормирующее значение измеряемой величины. Ее принимают равной:

а) конечному значению шкалы прибора, если нулевая отметка находится на краю или вне шкалы;

б) сумме конечных значений шкалы без учета знаков, если нулевая отметка расположена внутри шкалы;

в) длине шкалы, если шкала неравномерная.

Класс точности прибора устанавливается при его проверке и является нормируемой погрешностью, вычисляемой по формулам

γ=±ΔG/G_норм·100%, если ΔG

m=const

где ΔG_m – наибольшая возможная абсолютная погрешность прибора;

G_k – конечное значение предела измерения прибора; с и d – коэффициенты, учитывающие конструктивные параметры и свойства измерительного механизма прибора.

Например, для вольтметра с постоянной относительной погрешностью имеет место равенство

δ_m=±c

Относительная и приведенная погрешности связаны следующими зависимостями:

а) для любого значения приведенной погрешности

δ=±γ·G_норм/G_u

б) для наибольшей приведенной погрешности

δ=±γ_m·G_норм/G_u

Из этих соотношений следует, что при измерениях, например вольтметром, в цепи при одном и том же значении напряжения относительная погрешность тем больше, чем меньше измеряемое напряжение. И если этот вольтметр выбран неправильно, то относительная погрешность может быть соизмерима со значением G

н, что является недопустимым. Заметим, что в соответствии с терминологией решаемых задач, например, при измерении напряжения G = U, при измерении тока C = I, буквенные обозначения в формулах для вычисления погрешностей необходимо заменять на соответствующие символы.

Пример 1.1. Вольтметром, имеющим значения γ_m= 1,0 %, U_н = G_норм, G_k = 450 В, измеряют напряжение U_u, равное 10 В. Оценим погрешности измерений.

Решение.

Ответ. Погрешность измерений составляет 45 %. При такой погрешности измеренное напряжение нельзя считать достоверным.

При ограниченных возможностях выбора прибора (вольтметра), методическая погрешность может быть учтена поправкой, вычисленной по формуле

Пример 1.2.

Вычислить абсолютную погрешность вольтметра В7-26 при измерениях напряжения в цепи постоянного тока. Класс точности вольтметра задан максимально приведенной погрешностью γ_m=±2,5 %. Используемый в работе предел шкалы вольтметра U_норм=30 В.

Решение. Абсолютная погрешность вычисляется по известным формулам:

(так как приведенная погрешность, по определению, выражается формулой , то отсюда можно найти и абсолютную погрешность:

Ответ. ΔU = ±0,75 В.

Важными этапами в процессе измерений являются обработка результатов и правила округления. Теория приближенных вычислений позволяет, зная степень точности данных, оценить степень точности результатов еще до выполнения действий: отобрать данные с надлежащей степенью точности, достаточной для обеспечения требуемой точности результата, но не слишком большую, чтобы избавить вычислителя от бесполезных расчетов; рационализировать сам процесс вычисления, освободив его от тех выкладок, которые не окажут влияния на точные цифры результаты.

При обработке результатов применяют правила округления.

Правило 1. Если первая из отбрасываемых цифр больше пяти, то последняя из сохраняемых цифр увеличивается на единицу.

Правило 2. Если первая из отбрасываемых цифр меньше пяти, то увеличение не делается.

Правило 3. Если отбрасываемая цифра равняется пяти, а за ней нет значащих цифр, то округление производится на ближайшее четное число, т.е. последняя сохраняемая цифра остается неизменной, если она четная, и увеличивается, если она не четная.

Если за цифрой пять есть значащие цифры, то округление производится по правилу 2.

Применяя правило 3 к округлению одного числа, мы не увеличиваем точность округления. Но при многочисленных округлениях избыточные числа будут встречаться примерно столь же часто, как недостаточно. Взаимная компенсация погрешности обеспечит наибольшую точность результата.

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью.

Величина предельной погрешности не является вполне определенной. Для каждого приближенного числа должна быть известна его предельная погрешность (абсолютная или относительная).

Когда она прямо не указана, то подразумевается, что предельная абсолютная погрешность составляет половину единицы последнего выписанного разряда. Так, если приведено приближенное число 4,78 без указания предельной погрешности, то подразумевается, что предельная абсолютная погрешность составляет 0,005. Вследствие этого соглашения всегда можно обойтись без указания предельной погрешности числа, округленного по правилам 1-3, т.е., если приближенное число обозначить буквой α, то

, где Δn – предельная абсолютная погрешность; а δ_n – предельная относительная погрешность.

Кроме того, при обработке результатов используются правила нахождения погрешности суммы, разности, произведения и частного.

Правило 1. Предельная абсолютная погрешность суммы равна сумме предельных абсолютных погрешностей отдельных слагаемых, но при значительном числе погрешностей слагаемых обычно происходит взаимная компенсация погрешностей, поэтому истинная погрешность суммы лишь в исключительных случаях совпадает с предельной погрешностью или близка к ней.

Правило 2. Предельная абсолютная погрешность разности равна сумме предельных абсолютных погрешностей уменьшаемого или вычитаемого.

Предельную относительную погрешность легко найти, вычислив предельную абсолютную погрешность.

Правило 3. Предельная относительная погрешность суммы (но не разности) лежит между наименьшей и наибольшей из относительных погрешностей слагаемых.

Если все слагаемые имеют одну и ту же предельную относительную погрешность, то и сумма имеет ту же предельную относительную погрешность. Иными словами, в этом случае точность суммы (в процентном выражении) не уступает точности слагаемых.

В противоположность сумме разность приближенных чисел может быть менее точной, чем уменьшаемое и вычитаемое. Потеря точности особенно велика в том случае, когда уменьшаемое и вычитаемое мало отличаются друг от друга.

Правило 4. Предельная относительная погрешность произведения приближенно равна сумме предельных относительных погрешностей сомножителей: δ=δ₁+δ₂, или, точнее, δ=δ₁+δ₂+δ₁δ₂где δ – относительная погрешность произведения, δ₁δ₂ — относительные погрешности сомножителей.

Примечания:

1. Если перемножаются приближенные числа с одним и тем же количеством значащих цифр, то в произведении следует сохранить столько же значащих цифр. Последняя из сохраняемых цифр будет не вполне надежна.

2. Если некоторые сомножители имеют больше значащих цифр, чем другие, то до умножения следует первые округлить, сохранив в них столько цифр, сколько имеет наименее точный сомножитель или еще одну (в качестве запасной), дальнейшие цифры сохранять бесполезно.

3. Если требуется, чтобы произведение двух чисел имело заранее данное число вполне надежное, то в каждом из сомножителей число точных цифр (полученное измерением или вычислением) должно быть на единицу больше. Если количество сомножителей больше двух и меньше десяти, то в каждом из сомножителей число точных цифр для полной гарантии должно быть на две единицы больше, чем требуемое число точных цифр. Практически же вполне достаточно взять лишь одну лишнюю цифру.

Правило 5. Предельная относительная погрешность частного приближенно равна сумме предельных относительных погрешностей делимого и делителя. Точная величина предельной относительной погрешности всегда превышает приближенную. Процент превышения примерно равен предельно относительной погрешности делителя.

Пример 1.3. Найти предельную абсолютную погрешность частного 2,81 : 0,571.

Решение. Предельная относительная погрешность делимого есть 0,005:2,81=0,2%; делителя – 0,005:0,571=0,1%; частного – 0,2% + 0,1%=0,3%. Предельная абсолютная погрешность частного приближенно составит 2,81:0,571·0,0030=0,015

Значит, в частном 2,81:0,571=4,92 уже третья значащая цифра не надежна.

Ответ. 0,015.

Пример 1.4. Вычислить относительную погрешность показаний вольтметра, включенного по схеме (рис. 1.3), которая получается, если предположить, что вольтметр имеет бесконечно большое сопротивление и не вносит искажений в измеряемую цепь. Классифицировать погрешность измерения для этой задачи.

рис. 1.3

Решение. Обозначим показания реального вольтметра через И, а вольтметра с бесконечно большим сопротивлением через И^∞. Искомая относительная погрешность

Заметим, что

тогда получим

Так как R_И>>R и R > r, то дробь в знаменателе последнего равенства много меньше единицы. Поэтому можно воспользоваться приближенной формулой , справедливой при λ≤1 для любого α. Предположив, что в этой формуле α = -1 и λ= rR (r+R)^-1 R_И^-1, получим δ ≈ rR/(r+R) R_И.

Чем больше сопротивление вольтметра по сравнению с внешним сопротивлением цепи, тем меньше погрешность. Но условие R<<R_И – достаточное, но не необходимое условие малости δ. Погрешность будет мала также и в том случае, когда выполняется условие r≤R_И, т.е. сопротивление вольтметра много больше внутреннего сопротивления источника тока. При этом внешнее сопротивление может быть как угодно велико.

Ответ. Погрешность систематическая методическая.

Пример 1.5. В цепь постоянного тока (рис.1.4) включены приборы: А – амперметр типа М 330 класса точности К_А = 1,5 с пределом измерения I_k = 20 А; А₁ – амперметр типа М 366 класса точности К_А1 = 1,0 с пределом измерения I_к1 = 7,5 А. Найти наибольшую возможную относительную погрешность измерения тока I₂ и возможные пределы его действительного значения, если приборы показали, что I=8,0А. и I₁ = 6,0А. Классифицировать измерение.

рис. 1.4

Решение. Определяем ток I₂ по показаниям прибора (без учета их погрешностей): I₂=I-I₁=8,0-6,0=2,0 А.

Найдем модули абсолютных погрешностей амперметров А и А₁

Для А имеем равенство для амперметра

Найдем сумму модулей абсолютных погрешностей:

Следовательно, наибольшая возможная и той же величины, выраженная в долях этой величины, равна 1 ^. 10³ – для одного прибора; 2·10³ – для другого прибора. Какой из этих приборов будет наиболее точным?

Решение. Точность прибора характеризуется значением, обратным погрешности (чем точнее прибор, тем меньше погрешность), т.е. для первого прибора это составит 1/(1 ^. 10³) = 1000, для второго – 1/(2 ^. 10³) = 500. Заметим, что 1000 > 500. Следовательно, первый прибор точнее второго в два раза.

К аналогичному выводу можно прийти, проверив соответствие погрешностей: 2 ^. 10³ / 1 ^.10³ = 2.

Ответ. Первый прибор в два раза точнее второго.

Пример 1.6. Найти сумму приближенных замеров прибора. Найти количество верных знаков: 0,0909 + 0,0833 + 0,0769 + 0.0714 + 0,0667 + 0.0625 + 0,0588+ 0,0556 + 0,0526.

Решение. Сложив все результаты замеров, получим 0,6187. Предельная наибольшая погрешность суммы 0,00005·9=0,00045. Значит, в последнем четвертом знаке суммы возможна ошибка до 5 единиц. Поэтому округляем сумму до третьего знака, т.е. тысячных, получаем 0,619 – результат, в котором все знаки верные.

Ответ. 0,619. Количество верных знаков – три знака после запятой.

1. Метрология< Предыдущая		Следующая >1.2. Вероятный подход к оценке измерений

xn—-8sbnaarbiedfksmiphlmncm1d9b0i.xn--p1ai

Расчет погрешности измерений

Измерения называются прямыми, если значения величин определяются приборами непосредственно (например, измерение длины линейкой, определение времени секундомером и т. д.). Измерения называютсякосвенными, если значение измеряемой величины определяется посредством прямых измерений других величин, которые связаны с измеряемой определенной зависимостью.

Случайные погрешности при прямых измерениях

Абсолютная и относительная погрешность. Пусть проведеноNизмерений одной и той же величиныxв отсутствии систематической погрешности. Отдельные результаты измерений имеют вид:x₁,x₂, …,x_N. В качестве наилучшего выбирается среднее значение измеренной величины:

. (1)

Абсолютной погрешностьюединичного измерения называется разность вида:

Среднее значение абсолютной погрешности Nединичных измерений:

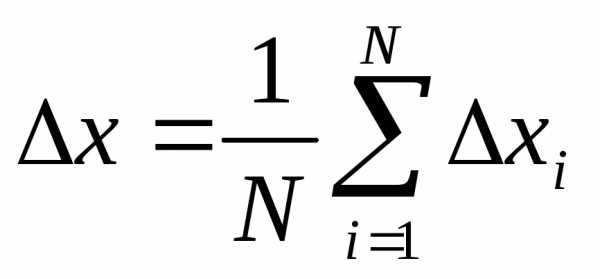(2)

называется средней абсолютной погрешностью.

Относительной погрешностью называется отношение средней абсолютной погрешности к среднему значению измеряемой величины:

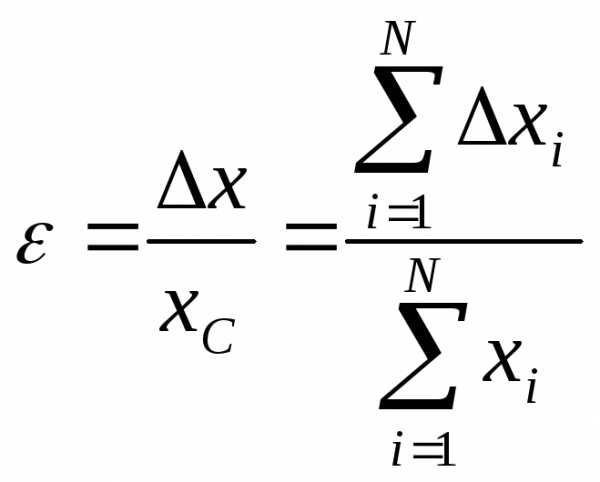. (3)

Приборные погрешности при прямых измерениях

Если нет особых указаний, погрешность прибора равна половине его цены деления (линейка, мензурка).
Погрешность приборов, снабженных нониусом, равна цене деления нониуса (микрометр – 0,01 мм, штангенциркуль – 0,1 мм).
Погрешность табличных величин равна половине единицы последнего разряда (пять единиц следующего порядка за последней значащей цифрой).
Погрешность электроизмерительных приборов вычисляется согласно классу точности С, указанному на шкале прибора:

Например: и,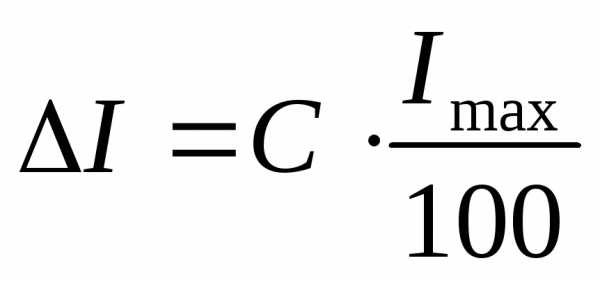

где U_max и I_max – предел измерения прибора.

Погрешность приборов с цифровой индикацией равна единице последнего разряда индикации.

После оценки случайной и приборной погрешностей в расчет принимается та, значение которой больше.

Вычисление погрешностей при косвенных измерениях

Большинство измерений являются косвенными. В этом случае искомая величина Х является функцией нескольких переменных а, b, c…, значения которых можно найти прямыми измерениями: Х = f(a,b,c…).

Среднее арифметическое результата косвенных измерений будет равно:

X = f(a,b,c…).

Одним из способов вычисления погрешности является способ дифференцирования натурального логарифма функции Х = f(a,b,c…). Если, например, искомая величина Х определяется соотношением Х = 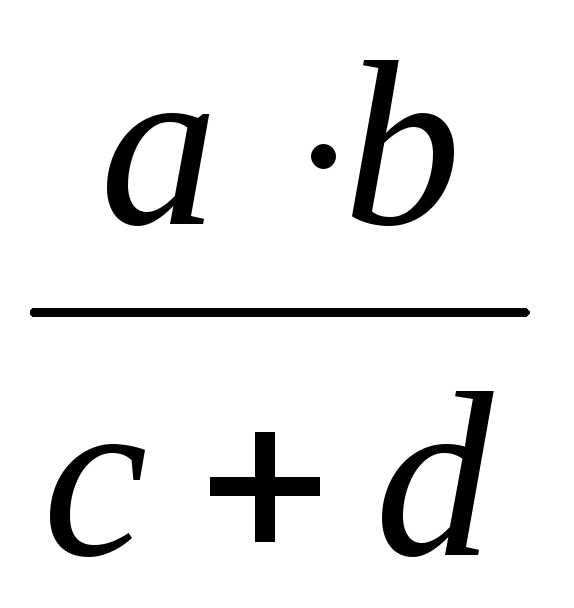, то после логарифмирования получаем:lnX = lna + lnb + ln(c+d).

Дифференциал этого выражения имеет вид:

Применительно к вычислению приближенных значений его можно записать для относительной погрешности в виде:

 = . (4)

Абсолютная погрешность при этом рассчитывается по формуле:

Х = Х(5)

Таким образом, расчет погрешностей и вычисление результата при косвенных измерениях производят в следующем порядке:

1) Проводят измерения всех величин, входящих в исходную формулу для вычисления конечного результата.

2) Вычисляют средние арифметические значения каждой измеряемой величины и их абсолютные погрешности.

3) Подставляют в исходную формулу средние значения всех измеренных величин и вычисляют среднее значение искомой величины:

X = f(a,b,c…).

4) Логарифмируют исходную формулу Х = f(a,b,c…) и записывают выражение для относительной погрешности в виде формулы (4).

5) Рассчитывают относительную погрешность  = .

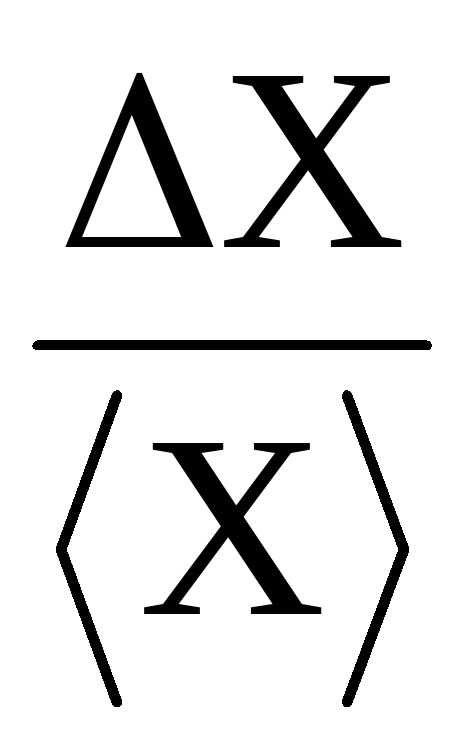6) Рассчитывают абсолютную погрешность результата по формуле (5).

7) Окончательный результат записывают в виде:

Х = Х_срХ

 = …%

Абсолютные и относительные погрешности простейших функций приведены в таблице:

Функция	Абсолютная погрешность	Относительная погрешность
a+b	a+b
a-b	a+b
ab	ab+ba


sin a
cos a

studfiles.net

погрешности измерений

2.2. Погрешности измерений

Ни одно измерение не выполняется идеально точно, всегда по различным причинам существует погрешность, т.е. отклонение результата измерения от истинного значения измеряемой величины. Причиной погрешности может стать несовершенство методики измерения, используемых средств измерений, органов чувств человека-оператора, а также влияние внешних условий.

Все погрешности, не связанные с грубыми ошибками (промахами, возникающими вследствие недосмотра экспериментатора или неисправности аппаратуры), имеют случайную и систематическую составляющие. Случайные погрешности изменяют величину и знак при повторных измерениях одной и той же величины. Значение случайной погрешности измерения невозможно предвидеть и, следовательно, исключить. Для уменьшения их влияния проводят несколько измерений величины и берут среднее арифметическое из полученных значений.

Систематические погрешности остаются постоянными по величине и знаку или закономерно изменяются при повторных измерениях одной и той же величины. Систематические погрешности разделяются на методические (несовершенство метода измерений; в том числе влияние средств измерения на объект, свойство которого измеряется), инструментальные (зависящие от погрешности применяемых средств измерений), внешние (обусловленные влиянием условий проведения измерений) и субъективные (обусловленные индивидуальными особенностями оператора).

Различают абсолютную и относительную погрешность измерения.

Под абсолютной погрешностью измерения понимают разность между полученным в ходе измерения и истинным значением физической величины:

(2.1)

Без сравнения с измеряемой величиной абсолютная погрешность ничего не говорит о качестве измерения. Одна и та же погрешность в 1 мм при измерении длины комнаты не играет роли, при измерении длины тетради уже может быть существенна, а при измерении диаметра проволоки совершенно недопустима.

Поэтому вводят относительную погрешность, показывающую, какую часть абсолютная погрешность составляет от истинного значения измеряемой величины. Относительная погрешность представляет собой отношение абсолютной погрешности к истинному значению измеряемой величины:

(2.2)

Относительная погрешность обычно выражается в процентах.

Результат измерения величины принято записывать в виде:

x_изм± Dх, d=…%.

При записи абсолютной погрешности ее величину округляют до двух значащих цифр, если первая их них является единицей, и до одной значащей цифры во всех остальных случаях. При записи измеренного значения величины последней должна указываться цифра того десятичного разряда, который использован при указании погрешности.

Из формул (2.1) и (2.2) следует, что для нахождения погрешностей измерений необходимо знать истинное значение измеряемой величины. Поэтому этими формулами можно пользоваться только в тех редких случаях, когда проводятся измерения констант, значения которых заранее известны. Цель же измерений, как правило, состоит в том, чтобы найти не известное значение физической величины. Поэтому на практике погрешности измерений не вычисляются, а оцениваются.

В частности, относительную погрешность находят как отношение абсолютной погрешности не к истинному, а к измеренному значению величины:

(2.3)

Способы оценки абсолютной погрешности разные для прямых и косвенных измерений.

Максимальную абсолютную погрешность при прямых измерениях находят как сумму абсолютной инструментальной погрешности и абсолютной погрешности отсчета: Dх=Dх_приб + Dх_отсч(2.4)

Погрешность отсчета является случайной и устраняется при многократных измерениях. Если же проводится одно измерение, она обычно принимается равной половине цены деления шкалы измерительного прибора.

Обратимся теперь к анализу погрешностей средств измерения. В зависимости от условий применения средств измерения различают основную и дополнительную погрешности. Основная погрешность – это погрешность средств измерений, используемых при нормальных условиях; дополнительная погрешность – это погрешность средств измерений, возникающая в результате отклонения значения одной или более влияющих величин от нормального значения.

Способ задания пределов допускаемой основной абсолютной погрешности измерительных средств определяется зависимостью погрешности от значения измеряемой величины. Если абсолютная погрешность измерительного прибора не зависит от измеряемой величины, то погрешность называется аддитивной и ее предел может быть выражен одним числом:

Dх_макс_приб = ± а (2.5)

Зона погрешности в этом случае ограничена двумя прямыми линиями, параллельными оси абсцисс (рис.2.1а). Источники аддитивной погрешности – трение в опорах, неточность отсчета, дрейф, наводки, вибрации и другие факторы. От этой погрешности зависит наименьшее значение величины, которое может быть измерено прибором.

Если погрешность прибора зависит от измеряемой величины, то она называется мультипликативной и предел допускаемой абсолютной погрешности выражается формулой Dх_макс_приб= ± (а + вх), (2.6)

где в – постоянная величина, вх – предельное значение мультипликативной погрешности, а – предельное значение аддитивной погрешности.

Таким образом, мультипликативная погрешность прямо пропорциональна значению измеряемой величины х. Источники мультипликативной погрешности – действие влияющих величин на параметры элементов и узлов средств измерений. Зона погрешности при наличии аддитивной и мультипликативной составляющей показана на рисунке 2.1 б.

Инструментальная погрешность электроизмерительных приборов определяется их классом точности. Класс точности (максимальная приведенная погрешность) – это отношение максимальной абсолютной погрешности прибора к пределу измерения величины (полному значению шкалы). Его, как и относительную погрешность, выражают в процентах. Класс точности показывает, сколько процентов максимальная инструментальная погрешность составляет от всей шкалы прибора:

(2.7)

ГОСТом установлено 8 классов точности измерительных приборов: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Зная класс точности прибора и предельное значение измеряемой величины, можно определить абсолютную и относительную инструментальную погрешность измерения:

(2.8)

(2.9)

Из формулы (2.9) видно, что чем ближе значение измеряемой величины к пределу измерения, тем меньше относительная инструментальная погрешность.

У приборов, аддитивная составляющая погрешности которых преобладает над мультипликативной, класс точности выражается одним числом. К таким приборам относится большинство аналоговых стрелочных приборов. Относительная инструментальная погрешность в этом случае находится просто по формуле (2.9).

Класс точности средств измерения, у которых аддитивная и мультипликативная составляющие основной погрешности соизмеримы, обозначается двумя числами, разделенными косой чертой: c/d. Причем класс точности должен удовлетворять условию c/d>l. К приборам, класс точности которых выражается дробью, относятся цифровые показывающие приборы. Их максимальная относительная погрешность определяется по формуле:

(2.10)

Для сравнения погрешностей измерения цифровых и стрелочных измерительных приборов постройте самостоятельно график зависимости относительной погрешности измерения постоянного напряжения от его величины приборами АВО-63 и Щ4313 на пределе 2В.

Класс точности или максимальная инструментальная погрешность приборов обычно приводится в его паспорте. Для менее точных приборов, если в паспорте ничего не указано, максимальная инструментальная погрешность принимается равной половине цены или цене деления шкалы.

Для прямых измерений сначала оценивается абсолютная погрешность, а затем относительная. При оценке погрешности косвенных измерений величины поступают следующим образом. Сначала находят абсолютные погрешности величин, полученных в ходе прямых измерений. Затем вычисляют относительную погрешность исследуемой величины, пользуясь для этого одной из формул, приведенных в таблице «расчет погрешностей». Формула относительной погрешности зависит от того, по какой формуле находят значение измеряемой величины. И только после этого находят абсолютную погрешность измеряемой величины, выражая ее из формулы (2.3).

ivatv.narod.ru

Абсолютная погрешность измерений. Как рассчитать абсолютную погрешность измерений? Определение абсолютной и относительной погрешности прямых измерений

Физические величины характеризуются понятием «точность погрешности». Есть высказывание, что путем проведения измерений можно прийти к познанию. Так удастся узнать, какова высота дома или длина улицы, как и многие другие.

Введение

Разберемся в значении понятия «измерить величину». Процесс измерения заключается в том, чтобы сравнить её с однородными величинами, которые принимают в качестве единицы.

Для определения объёма используются литры, для вычисления массы применяются граммы. Чтобы было удобнее производить расчеты, ввели систему СИ международной классификации единиц.

За измерение длины вязли метры, массы – килограммы, объёма – кубические литры, времени – секунды, скорости – метры за секунду.

При вычислении физических величин не всегда нужно пользоваться традиционным способом, достаточно применить вычисление при помощи формулы. К примеру, для вычисления таких показателей, как средняя скорость, необходимо поделить пройденное расстояние на время, проведенное в пути. Так производятся вычисления средней скорости.

Применяя единицы измерения, которые в десять, сто, тысячу раз превышают показатели принятых измерительных единиц, их называют кратными.

Наименование каждой приставки соответствует своему числу множителя:

Дека.
Гекто.
Кило.
Мега.
Гига.
Тера.

В физической науке для записи таких множителей используется степень числа 10. К примеру, миллион обозначается как 10⁶.

В простой линейке длина имеет единицу измерения – сантиметр. Она в 100 раз меньше метра. 15-сантиметровая линейка имеет длину 0,15 м.

Линейка является простейшим видом измерительных приборов для того, чтобы измерять показатели длины. Более сложные приборы представлены термометром – чтобы измерять температуру, гигрометром – чтобы определять влажность, амперметром – замерять уровень силы, с которой распространяется электрический ток.

Насколько точны будут показатели проведенных измерений?

Возьмем линейку и простой карандаш. Наша задача заключается в измерении длины этой канцелярской принадлежности.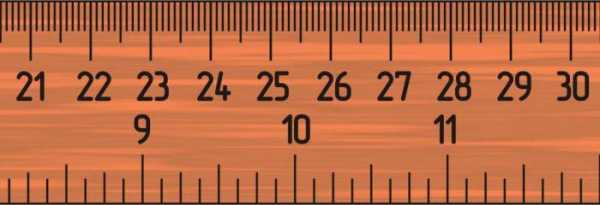

Для начала потребуется определить, какова цена деления, указанная на шкале измерительного прибора. На двух делениях, которые являются ближайшими штрихами шкалы, написаны цифры, к примеру, «1» и «2».

Необходимо подсчитать, сколько делений заключено в промежутке этих цифр. При правильном подсчете получится «10». Вычтем от того числа, которое является большим, число, которое будет меньшим, и поделим на число, которое составляют деления между цифрами:

(2-1)/10 = 0,1 (см)

Так определяем, что ценой, определяющей деление канцелярской принадлежности, является число 0,1 см или 1 мм. Наглядно показано, как определяется показатель цены для деления с применением любого измерительного прибора.

Измеряя карандаш с длиной, которая немного меньше, чем 10 см, воспользуемся полученными знаниями. При отсутствии на линейке мелкого деления, следовал бы вывод, что предмет имеет длину 10 см. Это приблизительное значение названо измерительной погрешностью. Она указывает на тот уровень неточности, которая может допускаться при проведении измерений.

Определяя параметры длины карандаша с более высоким уровнем точности, большей ценой деления достигается большая измерительная точность, которая обеспечивает меньшую погрешность.

При этом абсолютно точного выполнения измерений не может быть. А показатели не должны превышать размеры цены деления.

Установлено, что размеры измерительной погрешности составляют ½ цены, которая указана на делениях прибора, который применяется для определения размеров.

После выполнения замеров карандаша в 9,7 см определим показатели его погрешности. Это промежуток 9,65 — 9,85 см.

Формулой, измеряющей такую погрешность, является вычисление:

А = а ± D (а)

А — в виде величины для измерительных процессов;

а — значение результата замеров;

D — обозначение абсолютной погрешности.

Если слаживать или вычитать величины с учетом погрешности, это число будет составлять сумму цифр, которые и обозначают погрешность, и имеются у каждой отдельно взятой величины.

При вычитании или складывании величин с погрешностью результат будет равен сумме показателей погрешности, которую составляет каждая отдельная величина.

Знакомство с понятием

Если рассматривать классификацию погрешностей в зависимости от способа её выражения, можно выделить такие разновидности:

Абсолютную.
Относительную.
Приведенную.

Абсолютная погрешность измерений обозначается буквой «Дельта» прописной. Это понятие определяется в виде разности между измеренными и действительными значениями той физической величины, которая измеряется.

Выражением абсолютной погрешность измерений являются единицы той величины, которую необходимо измерить.

При измерении массы она будет выражаться, к примеру, в килограммах. Это не эталон точности измерений.

Как рассчитать погрешность прямых измерений?

Есть способы изображения погрешности измерения и их вычисления. Для этого важно уметь определять физическую величину с необходимой точностью, знать, что такое абсолютная погрешность измерений, что её никто никогда не сможет найти. Можно вычислить только её граничное значение.

Даже если условно употребляется этот термин, он указывает именно на граничные данные. Абсолютная и относительная погрешность измерений обозначаются одинаковыми буквами, разница в их написании.

При измерении длины абсолютная погрешность будет измеряться в тех единицах, в которых исчисляться длина. А относительная погрешность вычисляется без размеров, так как она является отношением абсолютной погрешности к результату измерения. Такую величину часто выражают в процентах или в долях.

Абсолютная и относительная погрешность измерений имеют несколько разных способов вычисления в зависимости от того, какой метод измерения физических величин.

Понятие прямого измерения

Абсолютная и относительная погрешность прямых измерений зависят от класса точности прибора и умения определять погрешность взвешивания.

Прежде чем говорить о том, как вычисляется погрешность, необходимо уточнить определения. Прямым называется измерение, при котором происходит непосредственное считывание результата с приборной шкалы.

Когда мы пользуемся термометром, линейкой, вольтметром или амперметром, то всегда проводим именно прямые измерения, так как применяем непосредственно прибор со шкалой.

Есть два фактора, которые влияют на результативность показаний:

Погрешностью приборов.
Погрешностью системы отсчета.

Граница абсолютной погрешности при прямых измерениях будет равна сумме погрешности, которую показывает прибор, и погрешности, которая происходит в процессе отсчета.

D = D (пр.) + D (отс.)

Пример с медицинским термометром

Показатели погрешности указаны на самом приборе. На медицинском термометре прописана погрешность 0,1 градусов Цельсия. Погрешность отсчета составляет половину цены деления.

D отс. = С/2

Если цена деления 0,1 градуса, то для медицинского термометра можно произвести вычисления:

D = 0,1^o^{С ^{₊0,1^o С_/2₌0,15^oС}}

На тыльной стороне шкалы другого термометра есть ТУ и указано, что для правильности измерений необходимо погружать термометр всей тыльной частью. Точность измерения не указана. Остается только погрешность отсчета.

Если цена деления шкалы этого термометра равна 2^oС, то можно измерять температуру с точностью до 1^oС. Таковы пределы допускаемой абсолютной погрешности измерений и вычисление абсолютной погрешности измерений.

Особую систему вычисления точности используют в электроизмерительных приборах.

Точность электроизмерительных приборов

Чтобы задать точность таких устройств, используется величина, называемая классом точности. Для её обозначения применяют букву «Гамма». Чтобы точно произвести определение абсолютной и относительной погрешности измерений, нужно знать класс точности прибора, который указан на шкале.

Возьмем, к примеру, амперметр. На его шкале указан класс точности, который показывает число 0,5. Он пригоден для измерений на постоянном и переменном токе, относится к устройствам электромагнитной системы.

Это достаточно точный прибор. Если сравнить его со школьным вольтметром, видно, что у него класс точности – 4. Эту величину обязательно знать для дальнейших вычислений.

Применение знаний

Таким образом, D c = c (max) Х γ /100

Этой формулой и будем пользоваться для конкретных примеров. Воспользуемся вольтметром и найдем погрешность измерения напряжения, которое дает батарейка.

Подключим батарейку непосредственно к вольтметру, предварительно проверив, стоит ли стрелка на нуле. При подключении прибора стрелка отклонилась на 4,2 деления. Это состояние можно охарактеризовать так:

Видно, что максимальное значение U для данного предмета равно 6.
Класс точности –(γ) = 4.
U(о) = 4,2 В.
С=0,2 В

Пользуясь этими данными формулы, абсолютная и относительная погрешность измерений вычисляется так:

D U = DU (пр.)+ С/2

D U (пр.) = U (max) Х γ /100

D U (пр.) = 6 В Х 4/100 = 0, 24 В

Это погрешность прибора.

Расчет абсолютной погрешности измерений в этом случае будет выполнен так:

D U = 0,24 В + 0,1 В = 0,34 В

По рассмотренной формуле без труда можно узнать, как рассчитать абсолютную погрешность измерений.

Существует правило округления погрешностей. Оно позволяет найти средний показатель между границей абсолютной погрешности и относительной.

Учимся определять погрешность взвешивания

Это один из примеров прямых измерений. На особом месте стоит взвешивание. Ведь у рычажных весов нет шкалы. Научимся определять погрешность такого процесса. На точность измерения массы влияет точность гирь и совершенство самих весов.

Мы пользуемся рычажными весами с набором гирь, которые необходимо класть именно на правую чашу весов. Для взвешивания возьмем линейку.

Перед началом опыта нужно уравновесить весы. Линейку кладем на левую чашу.

Масса будет равна сумме установленных гирь. Определим погрешность измерения этой величины.

D m = D m (весов) + D m (гирь)

Погрешность измерения массы складывается из двух слагаемых, связанных с весами и гирями. Чтобы узнать каждую из этих величин, на заводах по выпуску весов и гирь продукция снабжается специальными документами, которые позволяют вычислить точность.

Применение таблиц

Воспользуемся стандартной таблицей. Погрешность весов зависит от того, какую массу положили на весы. Чем она больше, тем, соответственно, больше и погрешность.

Даже если положить очень легкое тело, погрешность будет. Этот связано с процессом трения, происходящим в осях.

Вторая таблица относится к набору гирь. На ней указано, что каждая из них имеет свою погрешность массы. 10-граммовая имеет погрешность в 1 мг, как и 20-граммовая. Просчитаем сумму погрешностей каждой из этих гирек, взятой из таблицы.

Удобно писать массу и погрешность массы в двух строчках, которые расположены одна под другой. Чем меньше гири, тем точнее измерение.

Итоги

В ходе рассмотренного материала установлено, что определить абсолютную погрешность невозможно. Можно лишь установить её граничные показатели. Для этого используются формулы, описанные выше в вычислениях. Данный материал предложен для изучения в школе для учеников 8-9 классов. На основе полученных знаний можно решать задачи на определение абсолютной и относительной погрешности.

fb.ru

Абсолютные ,относительные и приведенные погрешности измерений

Абсолютная погрешность – это разница между измеренной датчиком величиной Хизм и действительным значением Хд этой величины.

Действительное значение Хд измеряемой величины это найденное экспериментально значение измеряемой величины максимально близкое к ее истинному значению. Говоря простым языком действительное значение Хд это значение, измеренное эталонным прибором, или сгенерированное калибратором или задатчиком высокого класса точности. Абсолютная погрешность выражается в тех же единицах измерения, что и измеряемая величина (например, в м3/ч, мА, МПа и т.п.). Так как измеренная величина может оказаться как больше, так и меньше ее действительного значения, то погрешность измерения может быть как со знаком плюс (показания прибора завышены), так и со знаком минус (прибор занижает).
См.Абсолютная погрешность микрокомпьютерного расходомера скоростемера МКРС
Относительная погрешность – это отношение абсолютной погрешности измерения Δ к действительному значению Хд измеряемой величины.

Относительная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения.
См.Относительная погрешность ультразвукового уровнемера ЭХО-АС-01
Приведенная погрешность – это отношение абсолютной погрешности измерения Δ к нормирующему значению Хn, постоянному во всем диапазоне измерения или его части.

Нормирующее значение Хn зависит от типа шкалы датчика КИП:

Если шкала датчика односторонняя и нижний предел измерения равен нулю (например, шкала датчика от 0 до 150 м3/ч), то Хn принимается равным верхнему пределу измерения (в нашем случае Хn = 150 м3/ч).

Если шкала датчика односторонняя, но нижний предел измерения не равен нулю (например, шкала датчика от 30 до 150 м3/ч), то Хn принимается равным разности верхнего и нижнего пределов измерения (в нашем случае Хn = 150-30 = 120 м3/ч).

Если шкала датчика двухсторонняя (например, от -50 до +150 ˚С), то Хn равно ширине диапазона измерения датчика (в нашем случае Хn = 50+150 = 200 ˚С).

Приведенная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения.

Довольно часто в описании на тот или иной датчик указывается не только диапазон измерения, например, от 0 до 50 мг/м3, но и диапазон показаний, например, от 0 до 100 мг/м3. Приведенная погрешность в этом случае нормируется к концу диапазона измерения, то есть к 50 мг/м3, а в диапазоне показаний от 50 до 100 мг/м3 погрешность измерения датчика не определена вовсе – фактически датчик может показать все что угодно и иметь любую погрешность измерения. Диапазон измерения датчика может быть разбит на несколько измерительных поддиапазонов, для каждого из которых может быть определена своя погрешность как по величине, так и по форме представления. При этом при поверке таких датчиков для каждого поддиапазона могут применяться свои образцовые средства измерения, перечень которых указан в методике поверки на данный прибор.

level-meter.livejournal.com

Погрешность измерения | Наука | FANDOM powered by Wikia

Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.

Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы, но согласно РМГ 29-99^[1] термин ошибка измерения не рекомендуется применять как менее удачный) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2,8±0,1 c. означает, что истинное значение величины T лежит в интервале от 2,7 с. до 2,9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).

В 2004 году на международном уровне был принят новый документ^[2], диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений», однако ГОСТ Р 50.2.038-2004^[3] допускает использовать термин погрешность для документов, использующихся в России.

В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.

Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:

$ \Delta x=\frac{x_{\max}-x_{\min}}{2} $

$ \ S =\left. \sqrt{\sum_{i=1}^{n}\frac{(x_i-\bar{x})^2}{n-1}} \right. $

$ \ S _x= \frac{S} {\sqrt{n}} = \left. \sqrt{\sum_{i=1}^{n}\frac{(x_i-\bar{x})^2}{n(n-1)}} \right. $

По форме представления Править

Абсолютная погрешностъ — $ \Delta X $ является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины $ X_{meas} $. При этом неравенство:

$ \Delta X>|X_{true}-X_{meas}| $ ,

где $ X_{true} $ — истинное значение, а $ X_{meas} $ — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина $ X_{meas} $ распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

$ \delta_x =\frac{ \Delta x}{X} $.

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.

Приведенная погрешность — погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

$ \delta_x =\frac{ \Delta x}{X_n} $,

где $ X_n $ — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

— если шкала прибора односторонняя, то есть нижний предел измерений равен нулю, то $ X_n $ определяется равным верхнему пределу измерений;

— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.

Приведенная погрешность является безразмерной величиной, либо измеряется в процентах).

По причине возникновения Править

Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.

В технике применяют приборы для измерения лишь с определенной заранее заданной точностью — основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.

Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т. п. За нормальную температуру окружающего воздуха принимают 20 °C, за нормальное атмосферное давление 101,325 кПа.

Обобщенной характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведенных основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10ⁿ, где показатель степени n = 1; 0; −1; −2 и т. д.

По характеру проявления Править

Случайная погрешность — погрешность, меняющаяся (по величине и по знаку) от измерения к измерению. Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т. п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления), с особенностями самой измеряемой величины (например при измерении количества элементарных частиц, проходящих в минуту через счётчик Гейгера).

Систематическая погрешность — погрешность, изменяющаяся во времени по определенному закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т. п.), неучтёнными экспериментатором.

Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.

Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора или если произошло замыкание в электрической цепи).

По способу измерения Править

Погрешность прямых измерений
Погрешность косвенных измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:

Если $ F =F(x_1,x_2… x_n) $, где $ x_i $ — непосредственно измеряемые независимые величины, имеющие погрешность $ \Delta x_i $, тогда:

$ \Delta F = \sqrt{\sum_{i=1}^n \left(\Delta x_i \frac{\partial F}{\partial x_i}\right)^2} $

Страница: 0

en: Observational error

de: Messabweichung

↑ РМГ 29-99 Рекомендации по межгосударственной сертификации. Основные термины и определения.
↑ ISO/IEC Guide 2:2004. Standardization and related activities — General vocabulary
↑ ГОСТ Р 50.2.038-2004 Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений

Назаров Н. Г. Метрология. Основные понятия и математические модели. М.: Высшая школа, 2002. 348 с.
Лабораторные занятия по физике. Учебное пособие/Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др.; под ред. Гольдина Л. Л. — М.: Наука. Главная редакция физико-математической литературы, 1983. — 704 с.

Страница 0 — краткая статья
Страница 1 — энциклопедическая статья
Разное — на страницах: 2 , 3 , 4 , 5
Прошу вносить вашу информацию в «Погрешность измерения 1», чтобы сохранить ее

ru.science.wikia.com

1.3 Погрешности как характеристики средств измерений — МЕТРОЛОГИЯ И ЭЛЕКТРОРАДИОИЗМЕРЕНИЯ

1.3.1 Общие сведения

Измерение можно считать законченным, если найден не только результат измерения, но и проведена оценка его погрешности. В метрологии определение «погрешность» является одним из центральных, причем в нем отражены понятия «погрешность результата измерения» и «погрешность средства измерения». Эти два понятия близки друг к другу и обычно их классифицируют по одинаковым признакам.

Погрешностью результата измерения называют отклонение найденного значения от истинного значения измеряемой величины. Так как истинное значение измеряемой величины неизвестно, то при количественной оценке погрешности пользуются действительным значением физической величины. Это значение находится экспериментально и настолько близко к истинному значению, что для поставленной измерительной задачи может быть использовано вместо него.

Погрешность средства измерения представляет собой разность между показаниями средства измерения и истинным (действительным) значением измеряемой физической величины. Она характеризует точность результатов измерений, проводимых используемым средством.

По форме количественного выражения погрешности делят на абсолютные, относительные и приведенные.

Абсолютной погрешностью Δ, выражаемой в единицах измеряемой величины, называют отклонение результата измерения А от истинного значения Х.

Δ = А — Х, (1.7)

Разновидностью абсолютной погрешности является предельная погрешность Δт — погрешность, больше которой в данном измерительном эксперименте не может быть.

Абсолютная погрешность характеризует значение и знак полученной погрешности, но не определяет качество самого измерения. Характеристикой качества измерения является точность измерения, отражающая меру близости результата измерения к истинному значению измеряемой величины. Высокой точности измерений соответствует малая погрешность. Например, измерение силы тока в 10 и 100 А может быть выполнено с идентичной абсолютной погрешностью А = ± 1 А. Однако качество первого измерения хуже второго. Поэтому для сравнения качества измерений, используют относительную погрешность.

Относительной погрешностью δ называют отношение абсолютной погрешности измерения к истинному значению измеряемой величины:

δ = Δ / Х, (1.8)

Мерой точности измерений служит показатель, обратный модулю относительной погрешности: КТ — 1/ | δ |. Относительную погрешность δ часто выражают в процентах:

δ = 100Δ / Х %

Так как обычно Δ << Х то относительная погрешность может быть определена как δ << Δ / А или δ ≈ 100Δ / А %.

Приведенной погрешностью γ, выражающей потенциальную точность измерений, называют отношение абсолютной погрешности Δ к некоторому нормирующему значению XN (например, к конечному значению шкалы):

γ=100 ∆ %,

XN (1.9)

По характеру (закономерности) проявления погрешности делят на три основных класса: систематические, случайные и грубые (промахи).

Систематические погрешности Δс — составляющие погрешности измерений, сохраняющиеся постоянными или закономерно изменяющиеся при многократных измерениях величины в одних и тех же условиях. Такие погрешности выявляют детальным анализом их возможных источников и уменьшают введением соответствующей поправки, применением более точных приборов, калибровкой приборов с помощью рабочих мер и т.п.

Случайные погрешности ∆ — составляющие погрешности измерений, изменяющиеся случайным образом по значению и знаку при повторных измерениях одной и той же физической величины в одних и тех же условиях. Данные погрешности проявляются при повторных измерениях одной и той же физической величины в виде некоторого разброса получаемых результатов. Описание и оценка случайных погрешностей возможны только на основе теории вероятностей и математической статистики.

Грубые погрешности (промахи) — погрешности, существенно превышающие ожидаемые при данных условиях измерения. Они возникают из-за ошибок оператора или неучтенных внешних воздействий. В случае однократного измерения обнаружить промах нельзя. При многократных наблюдениях промахи выявляют и исключают в процессе обработки результатов наблюдений.

Итак, если не учитывать промахи, абсолютная погрешность измерения Δ определяемая выражением (2.1), представляют суммой систематической и случайной составляющих:

∆=∆с +∆, (1.10)

Значит абсолютная погрешность, как и результат измерения — случайная величина.

По причинам возникновения погрешности измерения подразделяют на методические, инструментальные, внешние и субъективные (личные).

Методические погрешности возникают из-за несовершенства метода измерений, некорректности алгоритмов или формул, по которым производят вычисления результатов измерений, из-за влияния выбранного средства измерения на измеряемые параметры сигналов и т.д.

Рисунок 1.3 К примеру 2.1

Пример 2.1 Проанализируем появление методической погрешности при измерении сопротивления методом вольтметра-амперметра (рис. 2.1). Для определения значения сопротивления Rx резистора необходимо измерить ток 1R, протекающий через резистор и падение напряжения на нем UR. В приведенной схеме, реализующей этот метод, падение напряжения на резисторе измеряется вольтметром непосредственно, в то время как амперметр измеряет суммарный ток, одна часть которого протекает через резистор, другая часть через вольтметр. В результате измеренное значение сопротивления будет не RX = UR/IR а R’ = URI(IR + Iy), и появится методическая погрешность ΔR = R’ – RХ,. Методическая погрешность уменьшается и стремится к нулю При токе IV → 0, т.е. при внутреннем сопротивлении вольтметра RV → ∞.

Инструментальные (аппаратурные) погрешности возникают из-за несовершенства средств измерения, т.е. от их погрешностей. Уменьшают инструментальные погрешности применением более точного прибора.

Внешние погрешности связаны с отклонением одной или нескольких влияющих величин от нормальных значений или выходом их за пределы нормальной области.

Субъективные погрешности вызваны ошибками оператора при отсчете показаний (погрешности от небрежности и невнимания оператора).

По характеру поведения измеряемой величины в процессе измерений различают статические и динамические погрешности.

Статические погрешности возникают при измерении установившегося во времени значения измеряемой величины.

Динамические погрешности имеют место при динамических измерениях, когда измеряемая физическая величина изменяется во времени. Причина появления динамических погрешностей состоит в несоответствии скоростных (временных) характеристик прибора и скорости изменения измеряемой величины.

По условиям эксплуатации средства измерений различают основную и дополнительную погрешности.

Основная погрешность средств измерений имеет место при нормальных условиях эксплуатации, оговоренных в регламентирующих документах.

Дополнительная погрешность средств измерений возникает из-за выхода какой-либо из влияющих величин за пределы нормальной области значений.

1.3.2 Классы точности средств измерений

При измерениях в повседневной жизни повышенная точность не всегда нужна. Однако определенная информация о возможной инструментальной составляющей погрешности измерения необходима и поэтому она должна быть каким-либо образом отражена. Такая информация содержится в указании класса точности средства измерения.

Класс точности — обобщенная характеристика средства измерения, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами средств измерений, влияющими на точность, значения которых устанавливают в соответствующих стандартах. Можно отметить такое примечание: «Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполненных с помощью этих средств».

Классы точности присваивают средствам измерений при разработке на основании исследований и испытаний представительной партии таких устройств. Обычно их устанавливают в технических условиях на средство измерения. Пределы допускаемых погрешностей нормируют и выражают в форме абсолютной (∆си = ∆), относительной (δси = δ) или приведенной (γси = γ) погрешностей (далее индекс «си» для упрощения опущен). Форма выражения зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения средства измерения.

Абсолютная погрешность средств измерений ∆СИ = ∆ состоит из аддитивной (суммируемой с измеряемой величиной) и мультипликативной(умножаемой на измеряемую величину) составляющих. Аддитивная составляющая образуется, например, из-за неточности установки на нуль перед измерением и т.д. Мультипликативные погрешности появляются вследствие изменения коэффициента усиления усилителя, коэффициента передачи цепи.

1.3.3 Общие сведения об обработке результатов измерений

Из-за влияния многочисленных и принципиально неустранимых факторов, обусловливающих случайные погрешности, результат каждого измерения Ai будет отличаться от истинного значения X измеряемой величины: Аi — X = Δ Xi. Эту разность называют случайной погрешностью отдельного измерения.

Истинное значение X нам неизвестно. Однако, проведя большое количество измерений исследуемой величины X, можно выявить следующие статистические закономерности:

1) Если проводить серию измерений исследуемой величины и определить среднее значение, то положительные и отрицательные отклонения отдельных результатов измерений от среднего значения имеют приблизительно равную вероятность. Это является причиной того, что имеется равная вероятность (частота) отклонения результатов измерений от истинного значения величины в сторону уменьшения и увеличения, в том случае, когда систематическая погрешность равна нулю.

Среднее арифметическое значение, вычисленное на основании ряда измерений, является наиболее достоверным значением, которое можно приписать измеряемой величине. При вычислении среднего арифметического большого числа измерений погрешности отдельных измерений, имеющие разный знак, взаимно компенсируются.

2) Вероятность (частота) появления больших отклонений от полученного результата значительно меньше вероятности (частоты) появления малых отклонений. Эти статистические закономерности справедливы лишь при многократном повторении измерений.

После обработки результатов измерений, получается не абсолютно достоверный, а наиболее вероятный результат и этим результатом будет среднее арифметическое значение ряда измерений:

A= A0 +A2 +A3 +…+An =∑i=1 Ai

n n , (1.11)

где n — число измерений.

Указанные статистические закономерности большого числа измерений позволяют поставить вопрос о законе, по которому происходит распределение случайных погрешностей. В практике электрорадиоизмерений наиболее распространенным законом распределения погрешностей является гауссовский закон распределения. Аналитически он описывается выражением:

p(∆X) = 1 e−(∆X )2 /2σ2,

σ 2π (1.12)

где р(ΔХ) — плотность вероятности случайной погрешности ΔХ = А-X; σ — параметр, характеризующий степень случайного разброса результатов отдельных измерений относительного истинного значения X.

По своему смыслу плотность вероятности равна отношению вероятности попадания случайной величины внутрь интервала ΔХ к длине этого интервала в предположении, что последняя стремится к нулю.

Величину σ называют средним кнадратическим отклонением случайной погрешности измерения и определяют из соотношения:

σ=

, (1.13)

где Аi- численный результат отдельного измерения, n — число

измерений.

Характер кривых, описываемых (1.13), показан на рис. 1.4, а для трех значений σ. Функция (1.4) графически изображается колоколообразной кривой, симметричной относительно ординат, асимптотически

Рисунок 1.4

приближающейся к оси абсцисс. Максимум этой кривой получается в точке

ΔХ = 0, а величина этого максимума р (ΔХ)max = l/σ 2π. Как видно из рис. 1.4, чем меньше σ, тем уже кривая и, следовательно, тем реже встречаются большие отклонения, т. е. тем точнее выполняются измерения.

Как отмечалось ранее, среднее арифметическое ряда измерений А является лишь наиболее достоверным значением измеряемой величины. Представляет интерес определение погрешности вычисления среднего арифметического значения. Оценивается эта погрешность с помощью величин, аналогичных тем, при посредстве которых производится оценка погрешности отдельного измерения. Если выполнить k серий измерений, в каждом из которых производится п отдельных измерений, и вычислить среднее арифметическое значение для каждой серии, то полученные средние

арифметические значения А 1, А 2, А 3, …, А n будут несколько различаться между собой. Эти средние значения будут отличаться от истинного значения X измеряемой величины на случайные величины и, следовательно, будут распределяться около X по Гауссовскому закону (1.4). Для получения представления о случайном разбросе среднего арифметического относительно точного значения X измеряемой величины нужно вычислить среднее квадратическое отклонение от среднего арифметического. В теории погрешностей доказывается, что это отклонение в n раз меньше средней квадратической погрешности отдельного измерения, т. е.

, (1.14)

σA — средняя квадратическая погрешность среднего

где

арифметического из ряда измерений; σ — средняя квадратическая погрешность отдельного измерения; n — число измерений в серии. Из данного выражения видно, что увеличение числа повторных измерений n приводит к уменьшению

σA результата измерений. средней квадратической погрешности

На практике (особенно при малом значении n) необходимо оценить точность и надежность полученных результатов для среднего значения и среднего квадратического отклонения. Для этой цели пользуются доверительной вероятностью и доверительным интервалом. Под доверительной вероятностью понимают вероятность появления погрешности, не выходящей за некоторые принятые границы. Этот интервал называют доверительным интервалом, а характеризующую его вероятность — доверительной вероятностью.

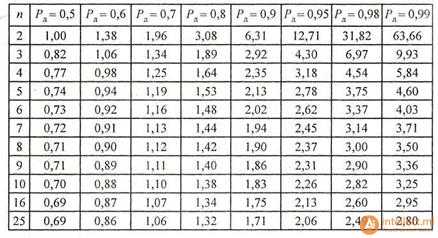
На практике приходится оценивать погрешности по результатам сравнительно небольшого количества измерения. Применение формулы (1.14) в этом случае дает заниженное значение доверительного интервала, т. е. оценка точности измерения оказывается неоправданно завышенной. В этом случае уточнить доверительный интервал можно с помощью коэффициентов Стьюдента tn, которые зависят от задаваемой доверительной вероятности р и числа измерений n.

Для определения доверительного интервала среднюю квадратическую погрешность надо умножить на коэффициент Стьюдента. Окончательный результат можно записать так:

A = A±tnσA , (1.15)

Значения коэффициентов tn, необходимых при расчетах приведены в табл. 1.1.

Общие сведения об обработке результатов измерений

Таблица 1.1 Коэффициенты Стьюдента t (Pд, n)

Контрольные вопросы:

1. Перечислите возможные причины проявления погрешностей.

2. Назовите признаки, по которым классифицируются погрешности.

3. Что называют абсолютной, относительной и приведенной погрешностями?

4. Что такое грубые погрешности (промахи)?

5. Какие характеристики погрешностей вам известны?

6. Сформулируйте свойства систематической, случайной и прогрессирующей составляющих погрешности измерений.

7. Приведите известные вам примеры методических погрешностей.

8. Назовите методы уменьшения систематических погрешностей?

9. Когда погрешность измерения может рассматриваться как случайная величина?

10. Назовите основные законы распределений случайных погрешностей.

11. Как описывается и когда используется распределение Стьюдента?

12. Что называют доверительной вероятностью и доверительным интервалом?

13. Назовите правила округления результатов измерений.

14. Перечислите алгоритмы обработки результатов прямых многократных измерений.

15. Расскажите о критерии «трех сигм».

intellect.ml