Тесты по тригонометрии
Разделы: Математика
Вариант № 1
Часть 1
- Выразить в радианах угол α = 20°
1) π/5 2) π/7 3) π/9 4) π/10
- Выразить в градусах угол α = 4π/45
1) 16º 2) 15º 3) 20º 4) 35º
- Какой четверти числовой окружности принадлежит точка t = 19π/4
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 3cos2α — 6 + 3sin2α
1) 1 2) -5 3) 3 4) -3
- Найти значение выражения 4cos2x + 2 , если sin2x = 0,6
1) 4,56 2) 3,6 3) 4,6 4) 8,4
- Упростить выражение: sin4α — sin6α + cos2α + cos4α — cos6α
1) cos10α + cos2α 2) 2cos2α 3) cosα — cos6α 4) cos2α + sin10α
- Упростить выражение
1) sinα 2) -sinα 3) 2cosα + sinα 4) cosα + sinα
- Найти область значений функции y = sin2x
1) [-1;1] 2) [-2;2] 3) [0;-2] 4) [-2;0]
- Найти tgα, если cosα = -2/3 и
- Решить уравнение sin2x = 1/2
Часть 2
- Найти значение выражения .
- Решить уравнение 2sin22x + 7cos2x = 3
- Решить уравнение 6sin2x + sinx — cosx — cos2x = 2
- Найти значение выражения 169sin2x, если cosx = -5/13, -π < x < 0
- Сколько корней имеет уравнение
- Найти наименьшее целое значение функции .
Вариант № 2
Часть 1
- Выразить в радианах угол α = 240°
1) 4π/5 2) 2π/3 3) 4π/3 4) 3π/2
- Выразить в градусах угол α = 5π/36
1) 40º 2) 35º 3) 25º 4) 50º
- Какой четверти числовой окружности принадлежит точка t = -23π/6
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 9cos2α — 16 + 9sin2α
1) 2 2) -25 3)-15 4) -7
- Найти значение выражения 3 — 2tg2x · cos2x, если sinx = 0,1
1) 2,8 2) 1,02 3) 2,98 4) 3,02
- Упростить выражение: cos3α — cos2α — cosα — sin3α — sin2α
1) cos5α — cosα 2) 0 3) sinα — cosα 4) cos5α + cosα
- Упростить выражение
1) 3cosα 2) cosα 3) 0 4) 2cosα — sinα
- Найти множество значений функции y = sinx — 3
1) [-4;0] 2) [-4;-2] 3) [-3;3] 4) [-3;-2]
- Найти значение выражения
- Решить уравнение
Часть 2
- Найти значение выражения .
- Решить уравнение 2sin2x + 7cosx + 2 = 0
- Решить уравнение 2sin2x -3sinx · cosx + 3cos2x = 2
- Найти значение выражения 5sin2x, если
- Сколько корней имеет уравнение
- Найти наибольшее целое значение функции
Вариант № 3
Часть 1
- Выразить в радианах угол α = 50°
1) 3π/5 2) 6π/7 3) 4π/9 4) 5π/18
- Выразить в градусах угол α = 49π/36
1) 230º 2) 245º 3) 240º 4) 265º
- Какой четверти числовой окружности принадлежит точка t = 37π/4
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: -3cos2α + 8 — 3sin2α
1) 5 2) -5 3)3 4) -3
- Найти значение выражения 3 + 2tg2x · cos2x, если sinx = 0,3
1) 3,18 2) 3,6 3) 4,8 4) 4,82
- Упростить выражение: cos5α · cos7α — cosα + sin5α · sin7α
1) cos12α — cosα 2) sin12α — cosα 3) sin2α — cosα 4) cos2α — cosα
- Упростить выражение
1) sin2α 2) cos2α 3) 3cos2α 4) cos3α
- Найти множество значений функции y = 3sinx — 2
1) [-5;1] 2) [-1;1] 3) (-∞; +∞) 4) [-1;5]
- Найти значение выражения
1) √3 2) √3 + 1 3) 1/2 + 3√3 4) 1
- Решить уравнение 2cos2x — 3sinx = 1/2
Часть 2
- Найти значение выражения
- Решить уравнение 4sin2x + sinx — cosx + cos2x = 2
- Найти значение выражения 26sin2x, если
- Сколько корней имеет уравнение
- Найти наибольшее целое значение функции
Вариант № 4
Часть 1
- Выразить в радианах угол α = 315°
1) 7π/4 2) 4π/7 3) 5π/9 4) 3π/10
- Выразить в градусах угол α = 13π/9
1) 245º 2) 250º 3) 275º 4) 260º
- Какой четверти числовой окружности принадлежит точка t = 27π/4
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 1,5cos2α — 6,5 + 1,5sin2α
1) 1 2) -5 3)3 4) -3
- Найти значение выражения 7sin2x — 3, если cos 2x = 0,7
1) 1 2) -0,9 3) -1,2 4) -1
- Упростить выражение: 2cosα — cosα + sin2α — sinα — sin(α — 6π)
1) cos3α + sinα 2) 2sinα 3) 0 4) cos3α — sinα
- Упростить выражение
1) sin2x 2) -sin2x 3) 4) cos2x
- Найти множество значений функции y = cosx — 3
1) [-1;1] 2) [2;4] 3) [-4;-2] 4) [-3;-2]
- Найти значение выражения
1)1,5 2) 2√3 3) 1 — √3 4) 0,5
- Решить уравнение 2cos 2x — 3sinx = 0
Часть 2
- Найти значение выражения
- Решить уравнение 2cos 2x + 9sinx = 6
- Решить уравнение 4sin2x — 4sinx — cosx + 6cos2x = 3
- Найти значение выражения 7tg2α, если
- Сколько корней имеет уравнение
- Найти наименьшее значение функции
Вариант № 5
Часть 1
- Выразить в радианах угол α = 210°
1) 7π/5 2) 5π/7 3) 7π/6 4) 4π/5
- Выразить в градусах угол α = 19π/9
1) 320º 2) 365º 3) 380º 4) 375º
- Какой четверти числовой окружности принадлежит точка t = 31π/3
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 10cos2α — 7 + 10sin2α
1) 1 2) -5 3)3 4) -3
- Найти значение выражения 6sin2x — 3, если cos2x = 0,3
1) -1,4 2) -0,2 3) 1,2 4) 0,8
- Упростить выражение: sin3α — cos2α + sin2α — cos3α — cos(2π -α)
1) cos3α + sinα 2) 2sinα 3)0 4) cos3α — sinα
- Упростить выражение
1) -6sinx 2) 2sinx 3) 3cosx — sinx 4) -2sinx
- Найти множество значений функции y = sinx + 2
1) [-1;1] 2) [0;2] 3) [1;3] 4) [2;3]
- Найти значение tgα, если
1) -2 2) 2 3) 0,5 4) -0,5
- Решить уравнение 1 + 2cosx — sin2x = 0
Часть 2
- Найти значение выражения
- Решить уравнение 2cos2x = 11sinx + 7
- Решить уравнение sin2x — 2sinx — cosx = cos2x + 1
- Найти значение выражения
- Сколько корней имеет уравнение
- Найти наибольшее целое значение функции
Вариант № 6
Часть 1
- Выразить в радианах угол α = 330°
1) 11π/6 2) 11π/5 3) 10π/9 4) 9π/10
- Выразить в градусах угол α = 2π/5
1) 72º 2) 75º 3) 65º 4) 52º
- Какой четверти числовой окружности принадлежит точка t = -41π/3
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 13cos2α — 15 + 13sin2α
1) 2 2) -2 3) 0 4) 28
- Найти значение выражения 5cos2x — 3, если sin2x = 0,2
1) 1,2 2) 2,1 3) -1 4) 1
- Упростить выражение: sin2,5α — cos1,5α + sin1,5α — cos2,5α + cos(4π — α)
1) sin4α — cosα 2) sinα + cosα 3) sinα — cosα 4) cosα + sin4α
- Упростить выражение
1) sinα 2) cosα 3) cosα + 2sinα 4) 2cosα + sinα
- Найти наибольшее значение функции y = 2cosx — 14
1) -16 2) 2 3) -14 4) -12
- Найти значение выражения
- Решить уравнение
Часть 2
- Найти значение выражения
- Решить уравнение cos2x + 2 sinx = 2
- Решить уравнение 8sin2x + 3sinx — cosx + cos2x = 3
- Найти значение выражения
- Найти сумму корней уравнения принадлежащих промежутку [0; -2π]
- Найти наименьшее целое значение функции
8.07.2010
xn--i1abbnckbmcl9fb.xn--p1ai
тест по тригонометрии с ответами
1. Упростите: (sin4a – sin6a) : (cos5a*sina).
- 1) -2
- 1) 2sina
- 2) -2sina
- 3) -2cosa
2. Упростите: 4 : (ctga – tga).
- 1) tg2a
- 1) ctg2a
- 2) 2tg2a
- 3) sin2a
3. Упростите: cos3a/cosa — sin3a/sina.
- 1) 2
- 1) 2sina
- 2) 2cosa
- 3) -2
4. Упростите: 2 : (tga – ctga).
- 1) cos2а
- 1) ctg2a
- 2) tg2a
- 3) -tg2a
5. В каком ответе знаки cos870°, sin(-490)° и tg670° приведены в порядке их написания?
- 1) -,+,-
- 1) +,-,-
- 2) -,-,+
- 3) -,-,-
| sin2a + 2cosa · cos2a |
| 1 – sina – cos2a + sin3a |
- 1) 2sina
- 1) ctga
- 2) 4tga
- 3) 2tga
7. В каком ответе знаки tg(—850)°, sin670° и cos(-550)° приведены в порядке их написания?
- 1) +,+,-
- 1) +,-,+
- 2) -,-,-
- 3) +,-,-
8. Найдите tgа, если tg(π/4 — а) = 1/3.
9. Упростите:| 1 + sin2a | — cosa |
| sina + cosa |
- 1) cosa
- 1) sina
- 2) -cosa
- 3) -2sina
| 2sina + sin2a |
| 2sina — sin2a |
если cosа = -1/3.
- 1) 1,5
- 1) 0,5
- 2) 3
- 3) 2/3
11. Вычислите: cos30°sin75°- cos60°sin15°.
- 1) 0
- 1) √3/2
- 2) 1/2
- 3) √2/2
12. Найдите tgа, если tg(π/4 + а) = 3.
- 1) 1/3
- 1) -1/2
- 2) -1/3
- 3) 1/2
13. Определите sin2а, если cos2а = 1/2.
- 1) 1/4
- 1) 3/8
- 2) 3/4
- 3) √3/2
- 1) √3/2
- 1) 1
- 2) 1/2
- 3) √2/2
15. Найдите ctgа, если tg(π/4 — а) = -5/3.
- 1) 1/3
- 1) -1/4
- 2) -1/3
- 3) -4
16. В каком ответе знаки sin(-790)°, cos600° и tg475° приведены в порядке их написания?
- 1) -,-,-
- 1) -,-,+
- 2) +,-,-
- 3) -,+,-
17. Найдите ctgа, если tg(π/4 + а) = 5/3.
18. В каком ответе знаки cos590°, sin(-550)° и tg303° приведены в порядке их написания?
- 1) -,+,-
- 1) -,+,+
- 2) -,-,-
- 3) +,+,-
19. В каком ответе знаки sin960°, cos(-440)° и tg480° приведены в порядке их написания?
- 1) +,+,-
- 1) -,-,-
- 2) +,-,-
- 3) -,+,-
20. В каком ответе знаки sin880°, cos(-460)° и tg650° приведены в порядке их написания?
- 1) -,-,-
- 1) +,+,-
- 2) +,-,-
- 3) -,-,+
21. В каком ответе tg(—790)°, cos280° и sin510° знаки приведены в порядке их написания?
- 1) +,-,+
- 1) -,+,+
- 2) -,+,-
- 3) +,-,-
| 1 – cos2a + sin2a |
| 3cos2a |
- 1) 3ctg2a
- 1) 3tg2a
- 2) 1,5ctg2a
- 3) tg2a
23. В каком ответе знаки sin(-910)°, tg220° и cos(-440)° приведены в порядке их написания?
- 1) +,-,+
- 1) -,+,+
- 2) +,+,+
- 3) +,+,-
| 1 + cosa + cos2a + cos3a |
| sin2a + 2sina · cos2a |
- 1) 2sina
- 1) tga
- 2) 2ctga
- 3) ctga
25. В каком ответе знаки cos1030°, sin(-570)° и tg(-490)° приведены в порядке их написания?
- 1) -,+,-
- 1) +,+,-
- 2) +,-,+
- 3) +,+,+
26. В каком ответе знаки tg835°, cos(-430)° и sin220° приведены в порядке их написания?
- 1) +,+,-
- 1) -,+,-
- 2) -,+,+
- 3) +,+,+
27. В каком ответе знаки tg885°, cos(-400)° и sin610° приведены в порядке их написания?
- 1) +,+,-
- 1) -,+,+
- 2) -,+,-
- 3) -,-,-
28. В каком ответе знаки sin751°, tg304° и cos543° приведены в порядке их написания?
- 1) -,-,+
- 1) -,-,-
- 2) +,+,-
- 3) +,-,-
29. В каком ответе знаки sin760°, tg(-460)° и cos470° приведены в порядке их написания?
- 1) +,+,-
- 1) +,-,-
- 2) +,+,+
- 3) -,+,-
30. В каком ответе знаки cos751°, sin304° и tg470° приведены в порядке их написания?
- 1) +,+,-
- 1) +,-,-
- 2) -,-,-
- 3) +,-,+
31. В каком ответе знаки cos580°, sin(-550)° и tg(-440)° приведены в порядке их написания?
- 1) -,+,-
- 1) +,+,-
- 2) +,+,+
- 3) -,-,-
32. Чему равно наибольшее значение: sin2a + 2cos2a?
- 1) 1,2
- 1) 1,4
- 2) 1,6
- 3) 2
- 1) 1/sina
- 1) 1/2cosa
- 2) 1/cosa
- 3) 1/2sina
- 1) tga
- 1) cosa
- 2) -cosa
- 3) 2sina
| 2cos2a – sin2a |
| 2sin2a – sin2a |
37. Упростите: (tgx + ctgx)2 — (tgx — ctgx)2.
- 1) 1/2 sin22a
- 1) sin22a
- 2) cos22a
- 3) 1/2 cos22a
- 1) 1/sin2a
- 1) 1/(2sin2a)
- 2) -1/(2sin2a)
- 3) 1/(2cos2a)
40. Упростите: sin2a + sin2β — sin2a·sin2β + cos2a·cos2β.
41. Упростите выражение:- 1) -sin2a·tg2a
- 1) -sin2a
- 2) cos2a·ctg2a
- 3) -cos2a
42. Упростите выражение: sin2a + cos2a + ctg2a.
- 1) cos2a/2
- 1) 1 / sin2a
- 2) tga/2
- 3) cos2a / 2
| sin(arcsin | √2 | — arccos | √2 | ) |
| 2 | 2 |
- 1) √2/2
- 1) 1
- 2) 0
- 3) √3/2
- 1) 1
- 1) 1,5
- 2) 1,6
- 3) ctg2a
45. Если tga + tgβ = 5/6 и tgatgβ = 1/6 , то чему равно a + β?
- 1) -π/6 + πk, k Є Z
- 1) -π/4 + πk, k Є Z
- 2) π/6 + πk, k Є Z
- 3) π/4 + πk, k Є Z
46. В каких из указанных четвертей должна быть взята α, чтобы выполнялось sinα · cosα > 0 ?
- 1) I или IV
- 1) II или III
- 2) I или II
- 3) I или III
47. Косинус суммы двух углов треугольника равен -1/3. Найдите косинус третьего угла.
- 1) 2/3
- 1) 1/3
- 2) π/3
- 3) -2/3
48. Найдите tgх, если tg(х + у) = 5 и tgу = 1/8.
49. Вычислите:
sin2π/8 + cos23π/8 + sin25π/8 + cos27π/8.
50. В каких из указанных четвертей должна быть взята α, чтобы выполнилось ctgα * cosα > 0 ?
- 1) III или IV
- 1) II или III
- 2) I или II
- 3) I ИЛИ III
geetest.ru
Тест на знание основных тригонометрических формул
Тест по теме: «Тригонометрические формулы»
1. Если осуществить поворот точки Р(1;0) на угол 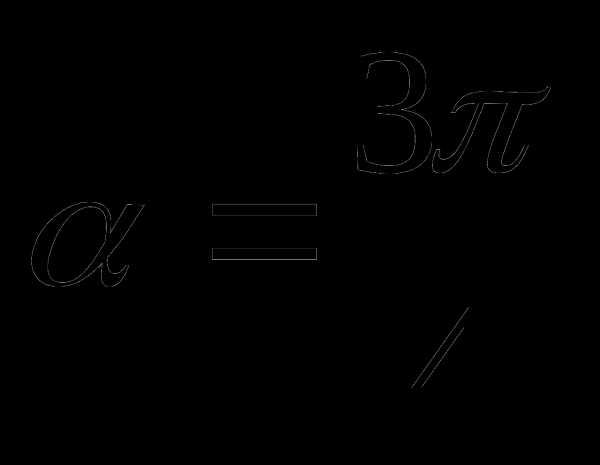 , то точка будет находиться в следующей четверти:
, то точка будет находиться в следующей четверти:
1) I
2) II
3) III
4) IV
2. Значение выражения равно:
1) -7
2) 7
3) 
4) 
3. Решением уравнения является:
1) 
2)
3) 
4)
4. Результатом упрощения выражения 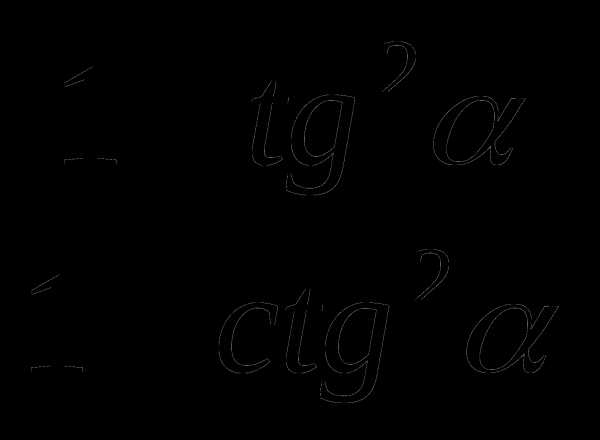 является:
является:
1) 0
2) 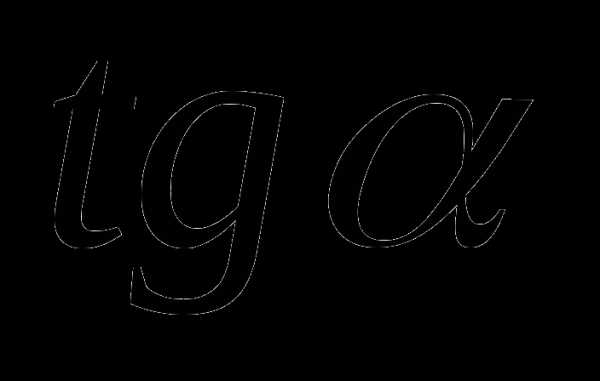
3) 
4) 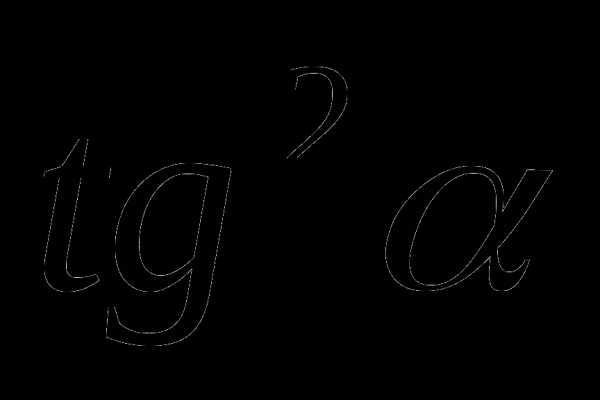
5. Вычислив  , получим значение:
, получим значение:
1) 
2) 
3) 
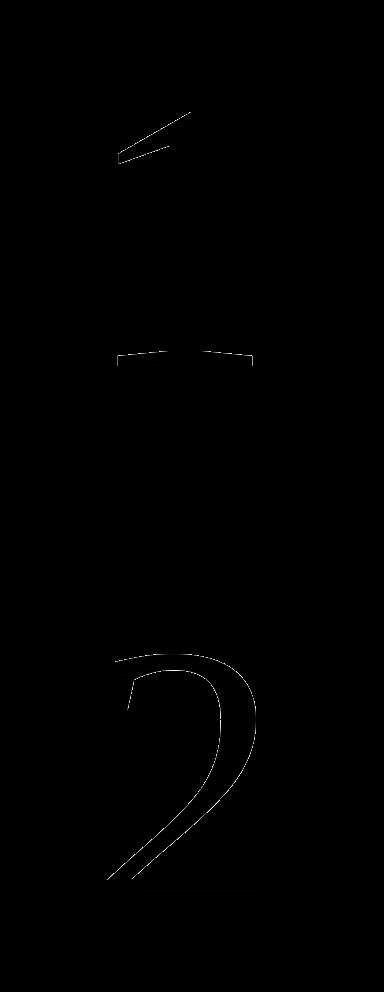
4) 
6. Центральный угол, опирающийся на дугу, длина которого равна радиусу окружности, называется углом в … радиан.
7. Синусом угла  называется … точки, полученной поворотом точки (1;0) вокруг начала координат на угол
называется … точки, полученной поворотом точки (1;0) вокруг начала координат на угол  .
.
8. Градусная мера углов равностороннего треугольника равна … градусам.
9. Отношение синуса угла  к косинусу угла
к косинусу угла  есть … угла
есть … угла  .
.
10. Установить соответствия формул сложения тригонометрических функций:
1) а)
2) б)
3) в)
4) г)
11. Установить соответствие формул суммы и разности тригонометрических функций:
1) а)
2) б)
3) в)
4) г)
12. Установить соответствие между выражениями и результатами:
1) а) 0
2) б) 4
3) в) 
4) г) 
13. Установить соответствие между выражениями и результатами:
1) 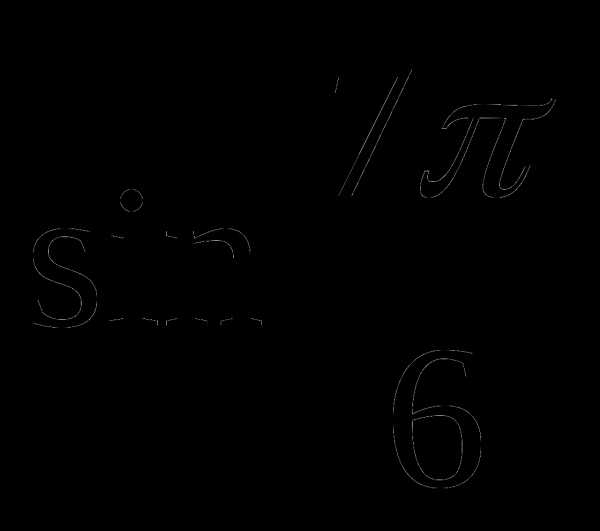 а) 1
а) 1
2)  б)
б) 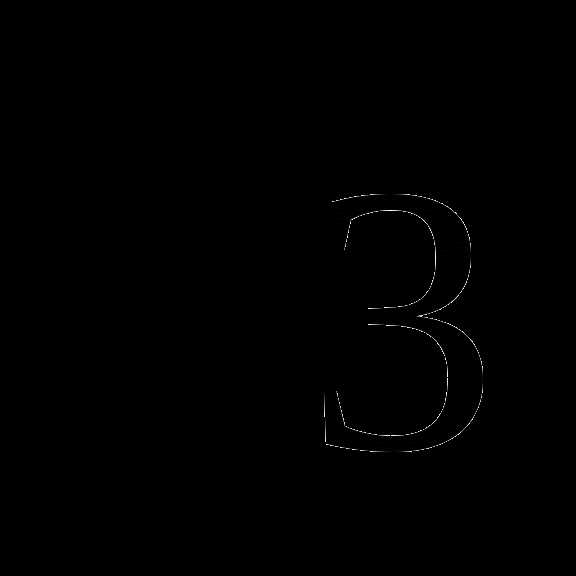
3) 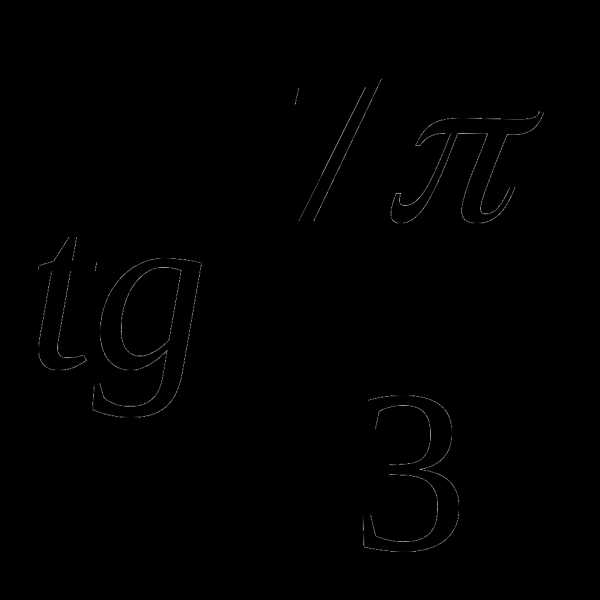 в)
в) 
4)  г)
г) 
14. Расположить в порядке возрастания следующие значения косинуса:
□ 
□ 
□ 
□ 
15. Расположить в порядке убывания следующие значения синуса:
□ 
□ 
□ 
□ 
КЛЮЧ
1. 2)
2. 4)
3. 3)
4. 4)
5. 1)
6. 1
7. ордината
8. 60
9. тангенс
10. 1)-г, 2)-в, 3)-б, 4)-а
11. 1)-в, 2)-г, 3)-а, 4)-б
12. 1)-в, 2)-б, 3)-а, 4)-г
13. 1)-г, 2)-в, 3)-б, 4)-а
14.  ,
,  ,
,  ,
, 
15.  ,
,  ,
,  ,
, 
Инструкция по проведению тестирования
Для учителя, проводящего тестирование:
Учитель, ответственный за проведение теста, после раздачи бланков ответов, но до раздачи заданий знакомит учеников с целью тестирования; с характером учета результатов при оценке их знаний по предмету; с тем, как тест отражает содержание предмета, какие знания и навыки проверяются при его выполнении; демонстрирует правила заполнения бланка ответов. Необходимо также заранее сообщить ученикам, как будет выглядеть процедура завершения теста по истечении срока его выполнения (Процедура сдачи листа с заданиями и бланка ответов). Приблизительно в середине теста следует напомнить о времени, чтобы ученики могли скорректировать скорость выполнения заданий. Это же необходимо сделать и за пять минут до окончания теста.
Перед выполнением ученики получают инструкцию, которая при необходимости повторяется дважды.
Для учеников:
— Общие сведения по тесту. Тест состоит из 15 заданий. Время выполнения – 45 мин. Система оценки: верный ответ на 1 вопрос дает 1 балл (оценка дихотомическая). Для получения отметки «отлично» необходимо выполнить верно не менее 14 заданий, для получения отметки «хорошо» необходимо выполнить верно от 10 до 13 заданий, для получения отметки «удовлетворительно» необходимо выполнить верно от 7 до 9 заданий.
Выполнение теста проходит без использования справочных материалов.
В стандартном бланке ответов черной гелевой ручкой заполняется шапка бланка большими печатными буквами. Верный ответ в заданиях с выбором ответа отмечается крестиком в соответствующей ячейке, при ответах на задания с кратким ответом и на соответствие используются только большие печатные буквы или цифры. При наличии исправлений ответ на данное задание не засчитывается.
— В каждый вариант включены задания четырех видов:
Задания с выбором ответов. Это задания, к которым предложены четыре варианта ответа, из которых три не верных и только один верный. Из четырех предложенных вариантов необходимо выбрать правильный и поставить метку в соответствующей ячейке на бланке ответов. Таких заданий – 5 (33,3%)
Задания с кратким ответом. Задания представляют собой незаконченные утверждения, в которых отсутствует наиболее значимая часть, или вопросы, на которые надо дать правильный ответ. Выполнив задание, необходимо вписать слово или число в соответствующие этому заданию ячейки на бланке ответов. Таких заданий – 4 (26,6%)
Задание на соответствие. Необходимо установить соответствие между элементами стоящими в левом и правом столбце. В бланк ответов вписывать ответы, ставя на первое место букву, на второе – соответствую цифру. Таких заданий – 4 (26,6%)
Задание на упорядочение. Необходимо расположить варианты ответов в требуемом порядке. В бланк ответов записывают числа, порядок которых ученики считают правильным. Таких заданий – 2 (13,3%)
СТРУКТУРА СПЕЦИФИКАЦИИ
Цель создания теста: проверка знаний, умений и навыков по теме: «Тригонометрические формулы».
Исходные документы: Колягин, Ю. М. Алгебра и начала анализа. 10 кл.: учеб. для общеобразоват. учреждений/ Ю. М. Колягин, Ю. В. Сидоров, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин. – 4-е изд. – М.: Мнемозина, 2004. – 364 с.; Федеральный государственный общеобразовательный стандарт среднего (полного) образования.
3. Число заданий в каждом варианте теста – 15
4. Число вариантов теста — 1
5. Тип заданий с указанием количества и процентного содержания заданий каждой формы:
Задания с выбором ответов. Таких заданий – 5 (33,3%)
Задания с кратким ответом. Таких заданий – 4 (26,6%)
Задания на соответствие. Таких заданий – 4 (26,6%)
Задания на упорядочение. Таких заданий – 2 (13,3%)
6. Число ответов к заданиям с выбором ответа — 4
7. Рекомендуемый вес заданий каждой формы при подсчете испытуемых: оценка дихотомическая, за каждое верно выполненное задание, не зависимо от формы, дается один балл.
8. Рекомендуемое время выполнения теста — 45 минут, на каждое задание отводится 3 минуты.
9. Соотношение заданий в тесте по разделам
п/п
Наименование дидактической единицы дисциплины
Количество заданий в теме
Наименование темы
1.
Определение синуса, косинуса, тангенса и котангенса
Тригонометрические формулы
6
2.
Знаки синуса, косинуса, тангенса и котангенса
Тригонометрические формулы
1
3.
Зависимость между синусом, косинусом и тангенсом одного и того же угла
Тригонометрические формулы
6
4.
Формулы сложения
Тригонометрические формулы
1
5.
Формулы суммы и разности
Тригонометрические формулы
1
10.Рекомендации по времени апробации – в конце темы: «Тригонометрические формулы»
12. Общая характеристика охвата требований (программы) в тесте и рекомендации по дополнительным формам проверки. Тест охватывает и теоретическую часть пройденной темы, и практическую часть.
infourok.ru
Тест с ответами по тригонометрии старшие классы
Тема: Тригонометрия
1. tg(x)=
+a)sin(x)/cos(x)
б)cos(x)/sin(x)
в)все вышеперечисленное
2. Что такое синус угла в прямоугольном треугольнике?
+а)отношение противолежащего катета к гипотинузе
б)отношение прилежащего катета к противолежащему
в)отношение прилежащего катета к гипотинузе
3. ctg(x)=
а)sin(x)+cos(x)
б)sin(x)/cos(x)
в)cos(x)/sin(x)
г)1/tg(x)
д)нет правильных ответов
+е) ответ в) и г)
4. cos(0)=
а)100
б)0
+в)1
5. sin(0)=
а)100
+б)0
в)1
6.
а)0
+б)1
в)-1
7.
а) sin(2x)
+б) cos(2x)
в)tg(2x)
8. sin(2x)=
+а)2*sin(x)*cos(x)
б) 2*tg(x)*cos(x)
в) 2*tg(x)*ctg(x)
9. tg(x)*ctg(x)=
а)0
+б)1
в)бесконечность
10. 2*cos(x+y)=
а) 2*(cos(x)*cos(y)+sin(x)*sin(y))
+б)2*(cos(x)*cos(y)-sin(x)*sin(y))
в) 2*(cos(x)*sin(y)-sin(x)*cos(y))
11. sin(x+y)=
а) cos(x)*sin(y)-sin(x)*cos(y)
+б) cos(x)*sin(y)+sin(x)*cos(y)
в) cos(x)*cos(y)+sin(x)*sin(y)
12. cos(-x)=
а)-cos(x)
+б)cos(x)
в)0
13. ctg(-x)=
+а)-ctg(x)
б)ctg(x)
в)tg(x)
14. sin(x+π)=
+а)-sin(x)
б)sin(π)
в)cos(x)
15. cos(x+π/2)=
+а)-sin(x)
б)cos(x)
в)sin(π/2)
16. sin(120)=
+а)cos(30)
б)sin(30)
в)tg(30)
17. cos(150)=
+а)-sin(60)
б)sin(60)
в)cos(60)
18. tg(x)*ctg(y)=
+а)1
б)0
в)100000
19. tg(x)+ctg(y)=
а)1
+б)1/(cos(x)*sin(x))
в)0
20. cos(α) может ли быть больше единицы?
а) не знаю
б)да
+в) нет
21. sin(α) может ли быть больше единицы?
а)не знаю
б)да
+в) нет
22. tg(α) может ли быть больше единицы?
а)нет
б)это не возможно
+в)да
23. sin(x)+sin(y)=
+а)2*sin((x+y)/2)*cos((x-y)/2)
б) 2*cos((x+y)/2)*cos((x-y)/2)
в) 2*sin((x+y)/2)*sin((x-y)/2)
24. tg(x)*tg(x)=
а) (1-sin(2x))/(1+cos(2x))
+б)(1-cos(2x))/(1+cos(2x))
в) 1/(1+cos(2x))
25. В каких четвертях cos(x) принимает положительные значения?
+а) I, IV
б)I, II
в)III, II
26. В каких четвертях sin(x) принимает положительные значения?
+а)I, II
б)I, III
в)II, IV
27. В каких четвертях tg(x), ctg(x) принимает положительные значения?
+а)I, III
б)I, II
в)II, IV
28. tg(x+y)=
а) (cos(x)+tg(y))/(1-tg(x)*tg(y))
+б)(tg(x)+tg(y))/(1-tg(x)*tg(y))
в) (ctg(x)+tg(y))/(1-tg(x)*tg(y))
29. Укажите график ctg(x)
а)
+б)
в)
30. Укажите график sin(x)
+а)
б)
в)
testdoc.ru
Тесты по тригонометрии | Математика
Тест №11 Упрощение тригонометрических выражений1 Упростить выражение : + cos
A) -1
B) cos
C) 1
D) sin
E) sin
2 Найти tg , если sin = – , 180 < < 270
A) 1
B)
C) 1
D)
E) 2
3 Упростить выражение:
A) cos
B) sin
C) tg
D) sin
E) cos
4 Вычислить: sin 80 + cos 80
A) 0
B) -1
C) 2
D) 1
E) -2
5 Найдите cos2 , если =
A) 0
B) 1
C) 2
D) -1
E)
6 Упростить выражение: (sin – cos ) + 2sin cos .
A) 1
B) -1
C) cos
D) sin
E) 2sin
7 Упростить выражение cos tg и найти его значение при = – 30
A) 0,5
B)
C)
D)
E) 3
8 Найдите сtg , если sin = 0,6, < <
A) –
B)
C)
D)
E)
9 Упростить выражение:
A) — sin
B) — cos
C) tg
D) cos
E) sin
10 Найти значение выражения:
A)
B) 3
C)
D) 2
E)
11 Упростить выражение:
A)
B)
C)
D) 1
E)
12 Упростите выражение:
A) — sin
B) 1
C) cos
D) — cos
E) sin
13 Вычислить : 2sin 30 — sin 60 сtg 45 tg 30
A)
B)
C) – ( )
D)
E) –
14 Упростите выражение: cos + сtg + sin
A)
B)
C) 1
D)
E)
15 Найдите значение выражения: (tg + сtg ) – 2, при = –
A) 0
B) -1
C) 1
D) -2
E) 2
16 Упростить выражение:
A) —
B) — sin
C)
D) sin
E) 1
17 Вычислить: 4 cos45 сtg60 tg 60 – 3sin 45
A) 1
B)
C)
D) —
E) —
18 Вычислить: , если tg =
A) —
B) 3
C)
D) — 1
E) 1
19 Упростить выражение: + tg ∙сtg
A) —
B) 1
C)
D) —
E)
20 Упростить выражение:
A) —
B) 1
C)
D)
E) —
21 Вычислить:
A)
B) —
C) 28
D)
E) 15
22 Упростить выражение: tg – sin – tg ∙sin
A) -1
B) 0
C) 1
D) -2
E) сtg
23 Известно, что tg +сtg = m. Найти tg +сtg
A) m – 2
B) m – 2
C) m – 4
D) m + 2
E) m
24 Упростить выражение: sin 2 + cosc2 + сtg 5
A) –
B) sin
C)
D) – 1
E) 1
25 Упростить выражение: (1-cos ) (1+tg )
A) 1
B) — tg
C) -сtg
D) tg
E) tg
Ключи
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C A B D D A C A D B B E A D E C B A E C D B A C E
testent.ru
Тематические тесты по тригонометрии (10 класс)
Тригонометрические функции любого угла
Вариант I
1.Найдите значение выражения .
2.Какое из значений может принимать 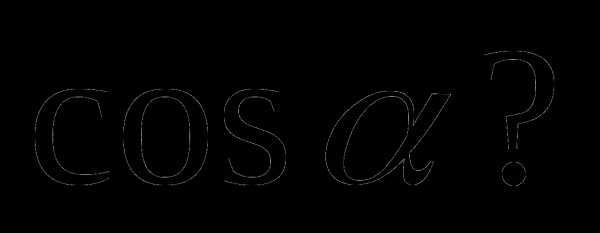
3.Углом, какой четверти является угол
4.Какое из данных чисел положительное?
5.Какое из выражений имеет смысл?
8.Найдите наименьшее значение выражения .
Вариант II
1.Найдите значение выражения .
2.Какое из значений может принимать 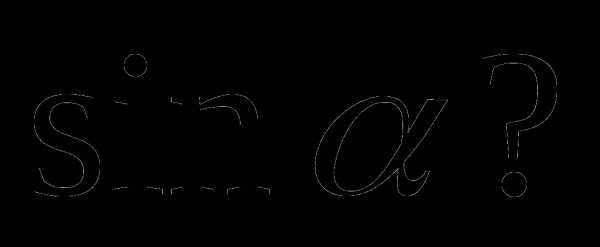
3.Углом, какой четверти является угол
4.Какое из данных чисел отрицательное?
5.Какое из выражений имеет смысл?
4) 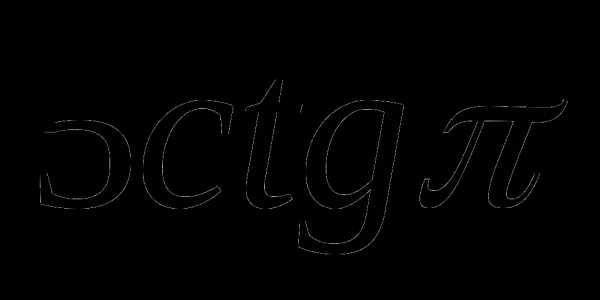
6.Вычислите .
8.Найдите наибольшее значение выражения .
infourok.ru
Формулы приведения, тригонометрические функции углов. Тест
Вопрос 1. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 2. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 3. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 4. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 5. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 6. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 7. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 8. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 9. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 10. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 11. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 12. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 13. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 14. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 15. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 16. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 17. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 18. Замените тригонометрической функцией угла выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 19. Упростите выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 20. Упростите выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 21. Упростите выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 22. Упростите выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 23. Упростите выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 24. Упростите выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 25. Упростите выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 26. Упростите выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 27. Упростите выражение
| A. | 0 |
| B. | |
| C. | 1 |
| D. |
Вопрос 28. Упростите выражение
| A. | |
| B. | 1 |
| C. | |
| D. |
Вопрос 29. Упростите выражение
| A. | |
| B. | |
| C. | |
| D. | 1 |
Вопрос 30. Упростите выражение
| A. | 1 |
| B. | |
| C. | |
| D. |
Вопрос 31. Упростите выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 32. Упростите выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 33. Упростите выражение
| A. | |
| B. | |
| C. | |
| D. | 1 |
Вопрос 34. Упростите выражение
| A. | 0 |
| B. | |
| C. | |
| D. | 1 |
Вопрос 35. Упростите выражение
| A. | |
| B. | |
| C. | 1 |
| D. |
Вопрос 36. Упростите выражение
| A. | |
| B. | 0 |
| C. | 1 |
| D. |
Вопрос 37. Упростите выражение
| A. | |
| B. | |
| C. | 1 |
| D. |
Вопрос 38. Упростите выражение
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 39. Упростите выражение
| A. | |
| B. | 1 |
| C. | |
| D. |
Вопрос 40. Упростите выражение
| A. | |
| B. | |
| C. | |
| D. |
fizmat.by
