Формула куб цилиндра: Расчитать объем цилиндра ✏️ — как найти через формулу. Калькулятор объема цилиндра 🧮

Вычисление объема цилиндра

Цилиндр это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».

Вычисление объема цилиндра

Формула расчёта объема цилиндра

 

Вычисление объема цилиндра производится по следующей формуле:

 

V = π r2h

 

V – объем цилиндра

h – высота цилиндра

r – радиус основания

π – 3.14

Как рассчитать объем цилиндра, все мы проходили в средней школе, и этими знаниями наиболее активно пользуются в своей работе конструкторы различных машин и механизмов, потребительских товаров, а также архитекторы.

Инженерам приходится производить расчет объема цилиндра в тех случаях, когда они занимаются проектированием заданий, снабженных колоннами.

Правда, в последнее время эти архитектурные элементы в их, так сказать, «классическом» варианте (то есть вместе с базой и капителем) встречаются достаточно редко, но их «упрощенные» разновидности, состоящие из одного ствола (который, собственно говоря, и представляет собой цилиндр) используются весьма широко. Нередко с колоннами приходится иметь дело реставраторам различных сооружений, имеющих большую историческую и культурную ценность, правда, в их работе вычисление объема цилиндра – далеко не самая распространенная процедура. Впрочем, если речь идет о полном восстановлении утраченных по тем или иным причинам колонн, то ее также приходится производить.

Расчет объема цилиндра осуществляется тогда, когда ведётся разработка разнообразных емкостей соответствующей формы. В качестве наглядного примера таковых можно привести, скажем, медицинские шприцы, а также колбы термосов. Следует заметить, что в первом случае такой параметр, как объем, имеет очень важное значение, поскольку от него зависит точное количество медикаментов, вводимого пациенту при инъекциях.

В технике цилиндры распространены чрезвычайно широко: достаточно сказать, что их форму имеют практически все валы и их отдельные составные части, используемые, скажем, в двигателях внутреннего сгорания. К тому же, расчет объема цилиндра – одна из важнейших задач, которую приходится решать конструкторами при проектировании современных бензиновых и дизельных силовых агрегатов, ведь от этого параметра зависит множество их характеристик, и в первую очередь такая важнейшая, как мощность. Почти все типы ДВС снабжаются поршнями, которые также имеют цилиндрическую форму.

Чрезвычайно распространенными деталями, которые присутствуют в конструкции многих сложных технических устройств, являются роликовые подшипники. Как нетрудно догадаться по самому их названию, одними из основных их компонентов являются прочные и износостойкие металлические ролики, имеющие цилиндрическую форму. Именно благодаря такой геометрии, эти детали имеют достаточно большую несущую способность и в большинстве случаев способны выдерживать весьма значительные нагрузки, чем их шариковые аналоги. Роликовые подшипники являются высокоточными деталями, и поэтому при их разработке и проектировании правильный расчет объема цилиндра (в данном случае – ролика) играет немаловажную роль.

Формула расчета объема цилиндра: пример решения задачи

Объем является физической величиной, которая присуща телу с ненулевыми размерами вдоль каждого из трех направлений пространства (все реальные объекты). В статье в качестве примера формулы объема рассматривается соответствующее выражение для цилиндра.

Объем тел

Эта физическая величина показывает, какую часть пространства занимает то или иное тело. Например, объем Солнца намного больше этой величины для нашей планеты. Это означает, что принадлежащее Солнцу пространство, в котором находится вещество этой звезды (плазма), превышает земную пространственную область.

Объем изменяется в кубических единицах длины, в СИ это метры в кубе (м³). На практике объемы жидких тел измеряют в литрах. Маленькие объемы могут выражать в кубических сантиметрах, миллилитрах и других единицах.

Для вычисления объема формула будет зависеть от геометрических особенностей рассматриваемого объекта. Например, для куба это тройное произведение длины его ребер. Ниже рассмотрим фигуру цилиндр и ответим на вопрос о том, как найти объем его.

Понятие о цилиндре

Фигура, о которой пойдет речь, является достаточно непростой. Согласно геометрическому определению, она представляет собой поверхность, образованную путем параллельного перемещения прямой (генератрисы) вдоль некоторой кривой (директрисы). Генератриса также называется образующей, а директриса — направляющей.

Если директриса — это окружность, а генератриса перпендикулярна ей, тогда полученный цилиндр называют круглым и прямым. О нем и пойдет дальше речь.

Цилиндр имеет два основания, которые параллельны друг другу и соединены цилиндрической поверхностью. Проходящая через центры двух оснований прямая называется осью круглого цилиндра. Все точки фигуры находятся на одинаковом расстоянии от этой прямой, которое равно радиусу основания.

Круглый прямой цилиндр однозначно определяется двумя параметрами: радиусом основания (R) и расстоянием между основаниями — высота H.

Формула объема цилиндра

Для расчета области пространства, которую занимает цилиндр, достаточно знать его высоту H и радиус основания R. Искомое равенство в этом случае имеет вид:

V = pi*R²*H, здесь pi = 3,1416

Понять эту формулу объема просто: поскольку высота перпендикулярна основаниям, то если ее умножить на площадь одного из них, получается нужная величина V.

Вычисление объема бочки

Для примера решим такую задачу: определим, сколько воды поместится в бочку, имеющую диаметр дна 50 см и высоту 1 метр.

Радиус бочки равен R=D/2=50/2=25 см. Подставляем данные в формулу, получаем:

V = pi*R²*H = 3,1416*25²*100 = 196350 см³

Поскольку 1 л = 1 дм³ = 1000 см³, то получаем:

V = 196350/1000 = 196,35 литра.

То есть в бочку можно налить почти 200 литров воды.

Объём цилиндра. Калькулятор объёма цилиндра онлайн

Цилиндр – это геометрическое тело, которое имеет цилиндрическую поверхность, называемое еще как боковая поверхность цилиндра и имеет две поверхности, которые носят название оснований цилиндра. Круговым цилиндр называют, если у него в основании лежит круг.

Высота цилиндра — это отрезок, соединяющий две любые точки оснований но обязательно расположенный перпендикулярно к ним обоим.

Объем прямого цилиндра

Цилиндр — это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».

Объем цилиндра через радиус основания и высоту цилиндра

Объем цилиндра равен произведению квадрата радиуса основания, высоты цилиндра и числа пи (3. {2} }{4 \cdot H} \]

где:
V — объем цилиндра
π — число пи (3.1415)
D — диаметр основания
H — высота цилиндра

Калькулятор объёма цилиндра

Входные данные

 

Радиус цилиндра r:

 

Высота цилиндра h:

 

Количество знаков после запятой в результате вычислений

1234567

Результат

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox

Формулы объема геометрических фигур.

Объем геометрической фигуры

— количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.

Объем куба

Объем куба равен кубу длины его грани.

Формула объема куба:

V = a³

где V — объем куба,
a — длина грани куба.

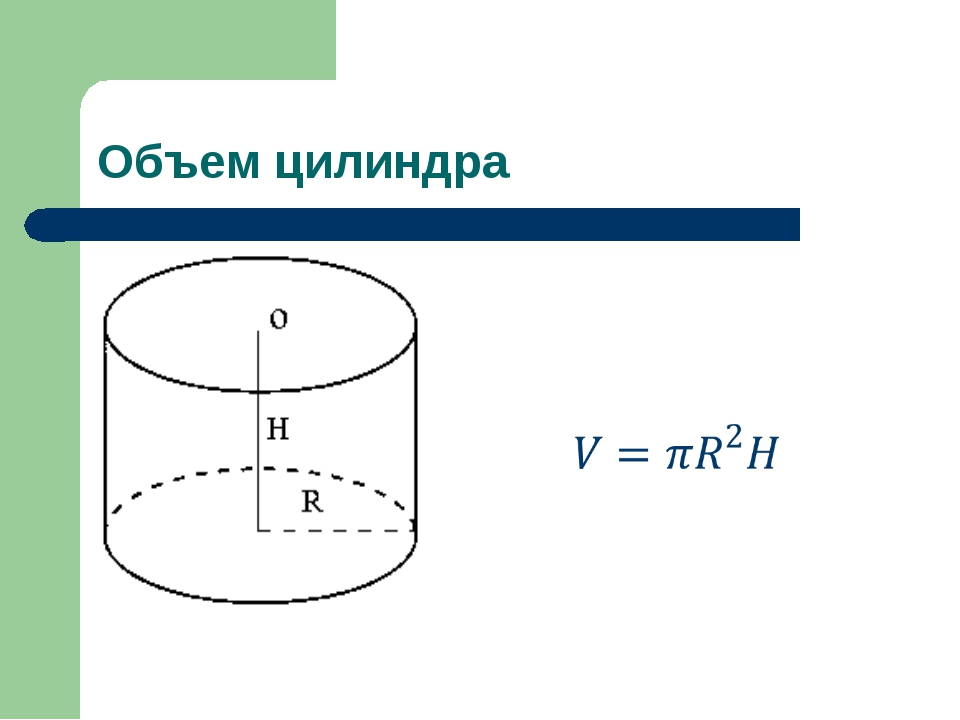
Объем призмы

Объем призмы равен произведению площади основания призмы, на высоту.

Формула объема призмы:

V = S

o h

где V — объем призмы,
S_o — площадь основания призмы,
h — высота призмы.

Объем параллелепипеда

Объем параллелепипеда равен произведению площади основания на высоту.

Формула объема параллелепипеда:

V = S_o · h

где V — объем параллелепипеда,
S_o — площадь основания,
h — длина высоты.

Объем прямоугольного параллелепипеда

Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

Формула объема прямоугольного параллелепипеда:

V = a · b · h

где V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.

Объем пирамиды

Объем пирамиды равен трети от произведения площади ее основания на высоту.

Формула объема пирамиды:

где V — объем пирамиды,
S

o — площадь основания пирамиды,
h — длина высоты пирамиды.

Объем правильного тетраэдра

Формула объема правильного тетраэдра:

где V — объем правильного тетраэдра,
a — длина ребра правильного тетраэдра.

Объем цилиндра

Объем цилиндра равен произведению площади его основания на высоту.

Формулы объема цилиндра: где V — объем цилиндра,
S_o — площадь основания цилиндра,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592.

Объем конуса

Объем конуса равен трети от произведению площади его основания на высоту.

Формулы объема конуса:

где V — объем конуса,
S_o — площадь основания конуса,
R — радиус основания конуса,
h — высота конуса,
π = 3.141592.

Объем шара

Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.

Формула объема шара:

где V — объем шара,
R — радиус шара,
π = 3.141592.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Как правильно рассчитать объем коробки?

Коробка служит тарой для перевозки многих предметов. В бизнесе при доставке товаров используют коробки разных размеров и форм. Тара помогает сохранить внешний вид продуктов при транспортировке. При заказе средств перевозки должны точно знать объем перевозимых товаров. Если тарой служит коробка, то следует определить ее объем. Как правильно рассчитать объем коробки, чтобы вычислить объем груза, узнаем из нижеприведенной статьи.

 

Содержание:

1. Формы коробки
2. Как измерить коробку для вычисления ее объема
3. Какие формулы можно использовать при расчете объема коробки
4. Облегченные расчеты объема коробок онлайн

Формы коробки

Легко сосчитать объем кубической коробки, перемножив величину стороны на три.

На практике применяются разные формы коробок:

• Прямоугольная;
• Кубическая;
• Цилиндрическая;
• Пирамидальная (в виде усеченной пирамиды).

Как измерить коробку для вычисления ее объема

Для определения объема коробки следует снять замеры размеров сторон. Замеры проводить в одной определенной величине: в миллиметрах, сантиметрах, дециметрах. Конечный итог объема переводим в международный стандарт – кубические метры.

Какие формулы можно использовать при расчете объема коробки

Для каждой формы коробки существует определенная форма расчета объема. Несмотря на то, что на сайтах есть калькуляторы расчета объема, нужно знать, по каким формулам рассчитывают объем каждого вида коробки.

Объем прямоугольной коробки

Сначала нам нужно измерить длину коробки. Прикладываем сантиметр или линейку к самой длинной стороне. Полученный результат длины – l записываем. Самая короткая сторона – это ширина. Аналогично проводим замер, записываем результат буквой w.

Далее определяем высоту – h, которую замеряем от высшей точки коробки до низшей.

Объем вычисляем по известной формуле: v = l х w х h, где v – объем коробки. Наглядно это выглядит так: допустим, длина коробки составила 70 см, ширина – 40 см, высота 50 см. Полученный объем будет составлять 140000 кубических сантиметров. Переводим величину в кубические метры, получаем 0,14 м3.

Объем цилиндра

Объем цилиндра высчитывают по формуле: v = π x r² x h, где π – постоянная величина 3,14, r – радиус основания, возведенный в квадрат, h – высота цилиндра.

Радиус измеряем от середины до края круга. Вычисление производим в одной системе.

Объем конуса

Объем конуса высчитывают по формуле v = 1/3 (π x r² x h). Конус – это пирамида с круглым основанием.

Объем пирамиды

Объем пирамиды определяют умножением одной трети площади основания на высоту. В основе пирамиды находится квадрат или прямоугольник, площадь которого рассчитывается умножением длины стороны на ширину.

Облегченные расчеты объема коробок онлайн

Сейчас на многих сайтах есть калькуляторы расчета объема. Результаты произведенных замеров вставляют в формулы и мгновенно получают результат. Это облегчает работу бизнесменам, которым не нужно забивать голову расчетами. Калькулятор подсчитает объем коробок. Полученный результат умножают на количество, и получают объем перевозимого груза.

Остается заказать транспортное средство под требуемый объем товаров. На многих сайтах калькулятор подсчитывает вместе с объемом коробки – объем перевозимого груза и выставляет стоимость перевозки. Деловые люди могут сразу определить насколько выгодна им такая сделка, и выбрать нужный объем перевозимых грузов, чтобы доставка оправдала материальные затраты. Быстрые расчеты помогают принять верное решение в определении способа доставки груза.

Все транспортные компании принимают грузы по объему и весу. Вот почему так важно знать объем коробки, исходя из которого высчитывается объем перевозимой продукции. На практике после нескольких перевозок, бизнесмены уже точно могут определить, сколько потребуется им коробок для транспортировки товара. Сложнее дело обстоит, если приходится иметь дело с разными видами продукции, для которой требуется подбирать соответствующую тару. В это случае выручает те же самые калькуляторы онлайн. При замере коробок лучше сразу замеры записывать в метрах, чтобы облегчить расчеты. Замеры производить внимательно, так как каждая незначительная ошибка может обернуться существенными материальными издержками.

Возможно вам будет также интересна статья: как красиво упаковать подарок.

5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара

Видеоурок: Объем и площадь поверхности многогранников

Лекция: Объём куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара

Для нахождения объема любого тела необходимо произведение трех параметров тела. Именно поэтому, чтобы проверить правильность решения, следует убедиться в том, что в выведенной Вами формуле оказалось в виде множителя три параметра тела.

Куб

Для нахождения объема куба следует перемножить три стороны. Так как в кубе все они равны, следует просто возвести значение стороны в куб: V = a³

Прямоугольный параллелепипед

Так как в данной фигуре все углы прямые, то её объем находится просто, как произведение всех сторон: V = abc

Пирамида и конус

Как уже говорилось ранее, эти две фигуры очень похожи. Различие только в том, что у нее разные основания.

Объем пирамиды и конуса находится, как третья произведения площади основания на высоту: V = S_ocH/3

Для пирамиды данная формула изменяется в зависимости от многоугольника, который будет находится в основании.

У конуса же данная формула стандартна, поскольку в его основании лежит окружность: V = πR²H/3

Цилиндр

Для нахождения объема цилиндра необходимо найти произведение площади основания на высоту. Так как в основании лежит окружность, получается следующая формула: V = πR²H

Не трудно заметить, что формула цилиндра очень похожа на формулу для нахождения объема конуса.

Призма

Как и в нескольких предыдущих случаях, объем призмы находится, как произведение основания на высоту. И не важно, прямая ли эта призма или нет.

Данная формула видоизменяется в зависимости от того, какой многоугольник лежит в основании. Формула очень похожа на формулу нахождения объема пирамиды: V = S_ocH

Шар

Для нахождения объема шара достаточно воспользоваться несложной формулой: V = πR³              

Как рассчитать объем цилиндра в см3: формула расчета / 01.12.2021

Если вам необходимо вычислить объем цилиндра, воспользуйтесь нашим пошаговым путеводителем.

Prostobank.ua рассказывает, как узнать объем цилиндра через высоту и радиус или площадь основания.

Перед расчетом объема цилиндра важно выяснить, что собой представляет цилиндр.

Что такое цилиндр?

Цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Рассмотрим 2 наиболее популярные способы расчета объема цилиндра. В зависимости от ваших данных вы сможете вычислить объем любым из способов.

Формула расчета объема цилиндра через площадь основания и высоту:

V_{цилиндра}=S_{основания}*h, где S_{основания} – площадь основания, h – высота цилиндра

Пример расчета: найти объем цилиндра, если площадь основания равна 20 м², высота цилиндра – 10 см.

Решение: В первую очередь, необходимо, перевести высоту в метры: 10 см=0,1 м.

V_{цилиндра}=S_{основания}*h=20*0,1=2 м³

Если вам необходимо перевести объем в сантиметры кубические или другие единицы измерения объема, воспользуйтесь конвертером.

Формула расчета объема цилиндра через радиус и высоту:

V_{цилиндра}= π*r²*h, где π— число Пи (равно 3,14), r- радиус основания цилиндра, h – высота цилиндра

Пример расчета: найти объем цилиндра, если радиус основания равен 50 см, высота цилиндра – 100 см.

Решение: V_{цилиндра}= π*r²*h= 3,14*50²*100=785000 см³. С помощью конвертера переведем объем цилиндра в кубические метры: 785000 см³=0,785 м³

Объем цилиндров — объяснение и примеры

Объем цилиндра — это мера пространства, занимаемого цилиндром, или мера вместимости цилиндра.

Эта статья покажет вам, как найти объем цилиндра с помощью формулы объема цилиндра.

С точки зрения геометрии цилиндр представляет собой трехмерную форму с двумя равными и параллельными окружностями, соединенными изогнутой поверхностью.

Расстояние между круговыми гранями цилиндра называется высотой цилиндра .Верх и низ цилиндра представляют собой две совпадающие окружности, радиус или диаметр которых обозначены как « r » и « d » соответственно.

Как найти объем цилиндра?

Чтобы вычислить объем цилиндра, вам понадобится радиус или диаметр круглого основания или вершины и высота цилиндра.

Объем цилиндра равен произведению площади круглого основания и высоты цилиндра. Объем цилиндра измеряется в кубических единицах.

Расчет объема цилиндра полезен при проектировании цилиндрических объектов, таких как:

• Цилиндрические резервуары для воды или колодцы
• Кульверты
• Флаконы для духов или химикатов
• Цилиндрические контейнеры и трубы
• Цилиндрические колбы, используемые в химические лаборатории

Формула объема цилиндра

Формула для объема цилиндра имеет следующий вид:

Объем цилиндра = πr ² ч кубических единиц

Где πr ² = площадь круга ;

π = 3. 14;

r = радиус круглого основания и;

h = высота цилиндра.

Для полого цилиндра формула объема имеет следующий вид:

Объем цилиндра = πh (r ₁ ² — r ₂ ² )

Где, r ₁ = внешний радиус и r ₂ = внутренний радиус цилиндра.

Разница внешнего и внутреннего радиуса образует толщину стенки цилиндра, т.е.

Толщина стенки цилиндра = r ₁ — r ₂

Давайте решим несколько примеров задач об объеме цилиндров.

Пример 1

Диаметр и высота цилиндра составляют 28 см и 10 см соответственно. Какой объем цилиндра?

Решение

Дано;

Радиус равен половине диаметра.

Диаметр = 28 см ⇒ радиус = 28/2

= 14 см

Высота = 10 см

По формуле объема цилиндра;

объем = πr ² ч

= 3,14 x 14 x 14 x 10

= 6154. 4 см ³

Итак, объем цилиндра равен 6154,4 см ³

Пример 2

Глубина воды в цилиндрическом резервуаре составляет 8 футов. Предположим, что радиус и высота резервуара составляют 5 футов и 11,5 футов соответственно. Найдите объем воды, необходимый для наполнения бака до краев.

Раствор

Сначала рассчитайте объем цилиндрического резервуара

Объем = 3,14 x 5 x 5 x 11,5

= 902.75 кубических футов

Объем воды в резервуаре = 3,14 x 5 x 5 x 8

= 628 кубических футов.

Объем воды, необходимый для заполнения бака = 902,75 — 628 кубических футов

= 274,75 кубических футов.

Пример 3

Объем цилиндра 440 м ³ , радиус основания 2 м. Рассчитайте высоту резервуара.

Раствор

Объем цилиндра = πr ² ч

440 м ³ = 3.14 x 2 x 2 x h

440 = 12,56h

Разделив 12,56 на обе стороны, мы получим

h = 35

Таким образом, высота резервуара будет 35 метров.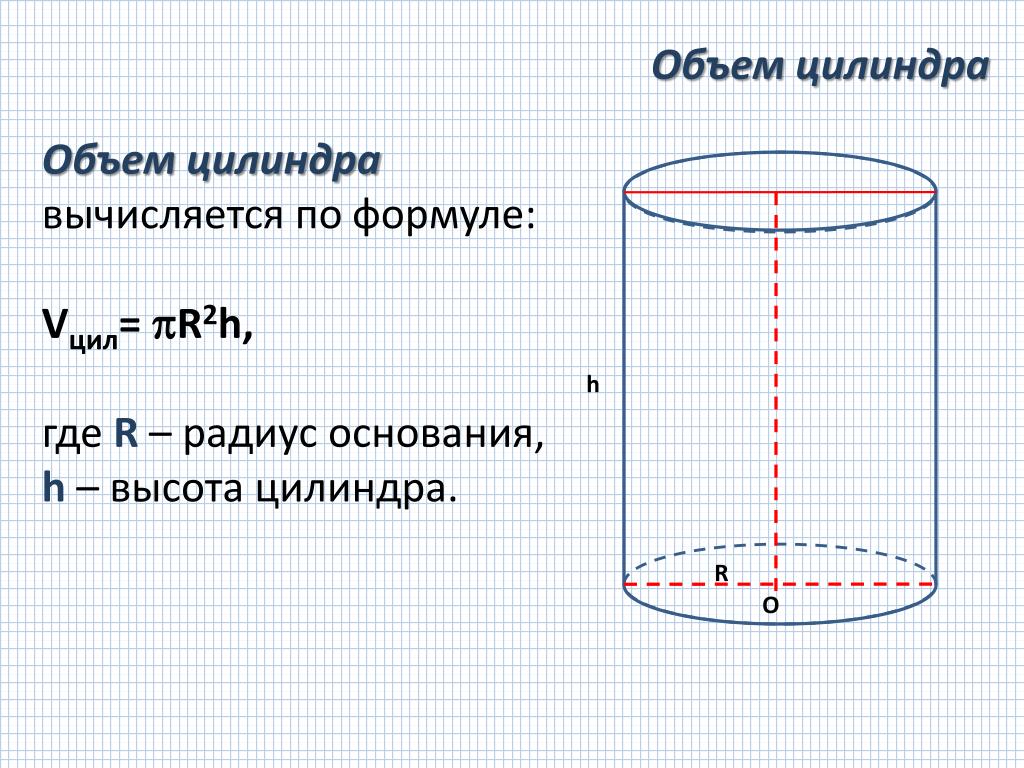

Пример 4

Радиус и высота цилиндрического резервуара для воды составляют 10 см и 14 см соответственно. Найдите объем бака в литрах.

Раствор

Объем цилиндра = πr ² h

= 3,14 x 10 x 10 x 14

= 4396 см ³

Дано, 1 литр = 1000 кубических сантиметров (см ³ )

Следовательно, разделите 4396 на 1000, чтобы получить

Объем = 4.396 литров

Пример 5

Внешний радиус пластиковой трубы составляет 240 мм, а внутренний радиус — 200 мм. Если длина трубы составляет 100 мм, найдите объем материала, из которого изготовлена ​​труба.

Решение

Труба является примером полого цилиндра, поэтому мы имеем

Объем цилиндра = πh (r ₁ ² — r ₂ ² )

= 3,14 x 100 x (240 ² -200 ² )

= 3.14 x 100 x 17600

= 5,5264 x 10 ⁶ мм ³ .

Пример 6

Цилиндрический твердый блок металла должен быть расплавлен с образованием кубов с ребром 20 мм. Предположим, радиус и длина цилиндрического блока равны 100 мм и 490 мм соответственно. Найдите количество кубиков, которые нужно сформировать.

Решение

Рассчитайте объем цилиндрического блока

объем = 3,14 x 100 x 100 x 490

= 1.5386 x 10 ⁷ мм ³

Объем куба = 20 x 20 x 20

= 8000 мм ³

Количество кубиков = объем цилиндрического блока / объем куба

= 1,5386 x 10 ⁷ мм ³ /8000 мм ³

= 1923 куба.

Пример 7

Найдите радиус цилиндра такой же высоты и объема, как у куба со сторонами 4 фута

Решение

Дано:

Высота куба = высота цилиндра = 4 футов и,

объем куба = объем цилиндра

4 x 4 x 4 = 64 кубических фута

Но объем цилиндра = πr ² ч

3. 14 x r ² x 4 = 64 кубических фута

12,56r ² = 64

Разделите обе стороны на 12,56

r ² = 5,1 футов.

r = 1,72

Следовательно, радиус цилиндра будет 1,72 фута.

Пример 8

Сплошная шестиугольная призма имеет длину основания 5 см и высоту 12 см. Найдите высоту цилиндра того же объема, что и призма. Примем радиус цилиндра 5 см.

Раствор

Формула объема призмы имеет вид;

Объем призмы = (h) (n) (s ² ) / [4 tan (180 / n)]

где n = количество сторон

s = базовая длина призмы

h = высота призмы

Объем = (12) (6) (5 ² ) / (4tan 180/6)

= 1800/2.3094

= 779,42 см ³

Объем цилиндра = πr ² h

779,42 = 3,14 x 5 x 5 x h

h = 9,93 см.

Итак, высота цилиндра будет 9,93 см.

Практические вопросы

1. Если объем и радиус цилиндрической коробки для краски составляют 640π кубических см и 8 см соответственно, какова его высота?
2. Рассмотрим цилиндрический резервуар, высота которого в два раза больше его радиуса. Если объем резервуара составляет 4580 единиц, каков радиус резервуара?

Ответы

1. 10 см
2. 9 единиц

Предыдущий урок | Главная страница | Следующий урок

Объем куба, кубоида и цилиндра

Куб, кубоид и цилиндр составляют части трехмерных фигур.Как правило, в трехмерной фигуре вы найдете меры длины, ширины и высоты. Напротив, в случае 2D-фигуры у вас есть только длина и высота. Некоторые из примеров 2D-форм — треугольник, квадрат и круг. А теперь давайте посмотрим, какой же объем в конце концов? Студентам, как правило, сложно работать с трехмерными фигурами. Одна из причин — их склонность запоминать формулы, на самом деле не понимая, что это такое. Итак, было бы хорошо начать с понимания того, что означает объем любой формы?

Причина разницы между объемом куба и цилиндра

Объем любой трехмерной фигуры — это мера площади, заключенной в область фигуры. В буквальном смысле объем обозначает общую емкость или пространство, занимаемое объектом, который имеет все три элемента — длину, высоту и ширину. Различные формулы для каждой трехмерной формы выводятся из структуры образования. Например, структурное различие между кубом и цилиндром вводит необходимость в разных формулах объема для каждой из рассматриваемых форм.

Куб

Куб — первая из трехмерных фигур, которую довольно утомительно отображать. Это фигура, заключенная в шесть одинаковых квадратов.Одна из интересных особенностей куба заключается в том, что в точке пересечения трех ребер образуется одна вершина.

Кубоид

Напоминаем, что любой объект, имеющий форму коробки, является кубоидом. Кубоид по сути представляет собой трехмерную форму, которая характеризуется шестью прямоугольными гранями. Каждая вершина образована под прямым углом.

Цилиндр

Основное различие между кубом и цилиндром, структура — wsie, заключается в наличии третьей меры, то есть высоты. Банка из-под диетического кокса, которую вы держите в руке, читая эту статью, является удачным примером цилиндра.

Цилиндр — это трехмерная форма с двумя параллельными сторонами с круглым или овальным отверстием вверху и внизу. Теперь отверстия могут быть полыми или твердотельными.

Как рассчитать объем куба, кубоида и цилиндра?

Вычислить объем куба, кубоида и цилиндра довольно просто, если вы знаете обходные пути, позволяющие определить размеры фигуры.

Разница между кубом и цилиндром или кубоидом и цилиндром весьма разительна.Кроме того, цилиндры не принадлежат к семейству многогранников трехмерных фигур. Причина исключения указана в FAQ. Давайте посмотрим на объем куба, кубоида и цилиндра по отдельности.

Объем куба

Как упоминалось ранее, куб состоит из шести одинаковых квадратов. Таким образом, каждая сторона куба будет иметь одинаковый размер. Теперь, чтобы рассчитать объем куба, вам просто нужно найти куб с заданным значением стороны.

Например, если размер стороны равен a, тогда объем куба равен i.e V = a3

Объем кубоида

Объем кубоида — это произведение длины, ширины и высоты, которое в просторечии обозначается как «фунт / ч». Для любого кубоида длины L, ширины B и высоты H объем «V» равен LxBxH.

Объем цилиндра

Объем цилиндра включает использование площади круга, умноженной на высоту. Это самый простой способ понять формулы объема цилиндра.

Для любого цилиндра с радиусом R и высотой H объем «V» представлен как V = 𝚷 R2H.

Решенные примеры

Теперь мы рассмотрим некоторые из решенных примеров объема куба Кубоид и цилиндр

1. Найти объем куба со стороной 9 м?

Пусть объем куба равен V. Используя формулу V = a3, мы имеем

V = (9 м) 3 = 729

2. Найдите объем кубоида длиной 12 м, высотой 8 м и ширина 6м?

Используя формулы для объема кубоида, т. е. V = LBH, мы имеем,

V = (12X8X6) m3 = 576m3

3. Найдите объем цилиндра радиусом 14 м и высотой 10 м?

Использование формул для расчета объема цилиндра i.е V = R2H.

Имеем, V = 22/7 x (14 м) 2 X (10 м) = 6,160 м3.

Объем цилиндра с применением теоремы Пифагора для нахождения фактической высоты

1. Найти объем цилиндра с наклонной высотой 10 см и радиусом 3 см?

(Примечание. ** наклонная высота — это гипотенуза, образованная соединением верхнего конца овального отверстия с противоположным нижним концом. Для большей ясности см. Рисунок ниже.)

Как вы можете видеть на наклонной высоте обозначается d.Теперь формула расчета объема цилиндра включает высоту. Но в вопросе у нас нет значения высоты, поэтому мы должны вычислить высоту, используя теорему Пифагора.

h3 (гипотенуза) = L2 (длина) + B2 (квадрат ширины)

Аналогично, здесь мы имеем d2 = h3 + D2 (диаметр)

(10 см) 2 = h3 + (6) 2

Решение В приведенном выше уравнении имеем h = 8 см

Теперь, V = 𝚷 R2H

V = 22/7 x (3) 2 x (8)

Решая приведенное выше уравнение, мы получаем V = 226 (приблизительно).

Факты о кубе, кубоиде и цилиндре

• Квадрат часто называют двумерным заменителем куба.

• Прямоугольный кубоид очень похож на куб, главное отличие состоит в том, что кубоид не имеет трех ребер одинаковой длины.

• В отличие от большинства трехмерных форм, многогранник цилиндр не входит в их число. Причина, по которой цилиндр не является многогранником, заключается в наличии площади поверхности.

Формулы площади поверхности

Формулы площади поверхности

(Математика | Геометрия | Формулы площади поверхности)

( пи = = 3.141592 …)

Поверхность Формулы площади
В общем случае площадь поверхности представляет собой сумму все области всех форм, покрывающие поверхность объекта.

Куб | Прямоугольный Призма | Призма | Сфера | Цилиндр | Единицы

Примечание: «ab» означает «а», умноженное на «б». «а

² » означает «в квадрате», что то же самое, что «а» умножить на «а».

Будьте осторожны !! Количество единиц.Используйте одни и те же единицы для всех измерений. Примеры

Площадь поверхности куба = 6 а 2

(а — длина стороны каждый край куба)

Проще говоря, площадь куба — это площадь шести квадратов, которые накрой это. Площадь одного из них a * a, или ² . Поскольку эти одинаковы, вы можете умножить одно из них на шесть, так что поверхность площадь куба в 6 раз больше квадрата одной из сторон.

Площадь поверхности прямоугольника Призма = 2ab + 2bc + 2ac

(a, b и c — длины трех сторон)

Проще говоря, площадь прямоугольной призмы равна площади шести прямоугольники, которые его покрывают. Но нам не нужно вычислять все шесть, потому что мы знаем, что верх и низ одинаковы, передняя и задняя — это то же самое, и левая и правая стороны такие же.

Площадь верха и низа (длины сторон a и в) = а * с. Поскольку их два, вы получаете 2ac. Передняя и задняя имеют длину стороны b и c. Площадь одного из них b * c, а там их два, поэтому площадь поверхности этих двух равна 2bc.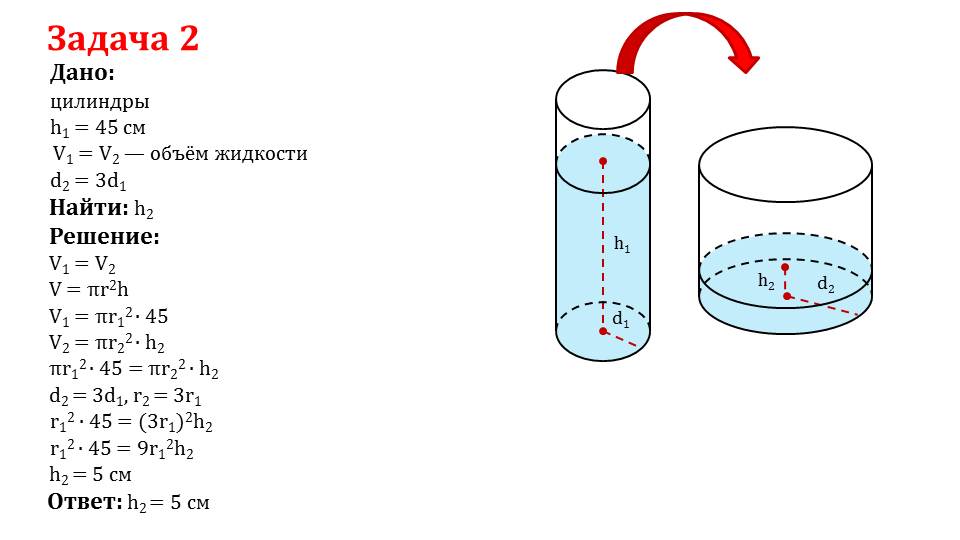 Левая и правая сторона имеет длину сторон a и b, поэтому площадь поверхности одного из их это а * б. Опять же, их два, поэтому их общая площадь поверхности это 2ab.

Площадь любой призмы

(б — форма концов)

Площадь поверхности = Боковая площадь + Площадь двух концов

(Боковая площадь) = (периметр формы b ) * L

Площадь поверхности = (периметр формы b ) * L + 2 * (Площадь формы b )

Площадь поверхности сферы = 4 пи r 2

(r — радиус окружности)

Площадь поверхности цилиндра = 2 pi r 2 + 2 pi r h

(h — высота цилиндра, r — радиус вершины)

Площадь поверхности = Области сверху и снизу + Площадь сбоку

Площадь поверхности = 2 (Площадь верха) + (периметр верха) * высота

Площадь поверхности = 2 ( pi r ² ) + (2 pi r) * h

На словах проще всего представить банку. Площадь поверхности — это площади всех частей, необходимых для закрытия банки. Это верх, низ, и бумажная этикетка, которая оборачивается по центру.

Вы можете найти область вверху (или внизу). Это формула для площади круга ( пи р ² ). Поскольку есть и верх, и дно, умноженное на два.

Сторона похожа на этикетку банки. Если оторвать и положить плоский это будет прямоугольник.Площадь прямоугольника — это произведение с двух сторон. Одна сторона — это высота банки, другая — периметр круга, так как этикетка один раз оборачивается вокруг банки. Так площадь прямоугольника (2 пи r) * h.

Сложите эти две части вместе, и вы получите формулу поверхности. площадь цилиндра.

Площадь поверхности = 2 ( pi r ² ) + (2 pi r) * h

Совет! Не забывайте единицы измерения.

Эти уравнения дадут вам правильные ответы, если вы будете держать единицы прямо. Например — найти площадь поверхности куба со стороной 5 дюймов, уравнение:

Площадь поверхности = 6 * (5 дюймов) ²

= 6 * (25 квадратных дюймов)

= 150 кв. Дюймов

Калькулятор объема

Ниже приводится список калькуляторов объема для нескольких распространенных форм.Заполните соответствующие поля и нажмите кнопку «Рассчитать».

Калькулятор объема сферы

Калькулятор объема конуса

Калькулятор объема куба

Калькулятор объема цилиндра

Калькулятор объема прямоугольного резервуара

Калькулятор объема капсулы

Калькулятор объема сферической крышки

Для расчета укажите любые два значения ниже.

Калькулятор объема конической ствола

Калькулятор объема эллипсоида

Калькулятор объема квадратной пирамиды

Калькулятор объема трубки

Калькулятор площади сопутствующих поверхностей | Калькулятор площади

Объем — это количественная оценка трехмерного пространства, которое занимает вещество.Единица измерения объема в системе СИ — кубический метр, или м ³ . Обычно объем контейнера — это его вместимость и количество жидкости, которое он может вместить, а не количество места, которое фактически вытесняет контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы можно разбить на более простые совокупные формы, и сумма их объемов используется для определения общего объема. Объемы других, еще более сложных фигур можно рассчитать с помощью интегрального исчисления, если существует формула для границы фигуры.Помимо этого, формы, которые нельзя описать известными уравнениями, можно оценить с помощью математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.

Сфера

Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, которые равноудалены от данной точки в ее центре, где расстояние между центром и любой точкой на сфере составляет радиус r . Вероятно, самый известный сферический объект — это идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и расчет их объемов одинаков. Как и в случае с кругом, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема шара приведено ниже:

EX: Клэр хочет заполнить идеально сферический воздушный шар с радиусом 0.15 футов с уксусом для борьбы с ее заклятым врагом Хильдой на воздушных шарах в ближайшие выходные. Необходимый объем уксуса можно рассчитать, используя приведенное ниже уравнение:

объем = 4/3 × π × 0,15 ³ = 0,141 фута ³

Конус

Конус — это трехмерная форма, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован так же, как круг, набором отрезков прямых, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или другое основание).На этой странице рассматривается только случай конечного правого кругового конуса. Конусы, состоящие из полукруглых линий, некруглых оснований и т. Д., Которые простираются бесконечно, не рассматриваются. Уравнение для расчета объема конуса выглядит следующим образом:

, где r — радиус, а h — высота конуса

EX: Би полна решимости выйти из магазина мороженого, потратив свои с трудом заработанные 5 долларов. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, несомненно, больше.Она определяет, что на 15% предпочитает обычные сахарные рожки вафельным рожкам, и ей нужно определить, превышает ли потенциальный объем вафельного рожка на ≥ 15% больше, чем у сахарного рожка. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью следующего уравнения:

объем = 1/3 × π × 1,5 ² × 5 = 11,781 дюйм ³

Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет <15%, и решает купить сахарный рожок. Теперь все, что ей нужно сделать, это использовать свой ангельский детский призыв, чтобы заставить посох выливать мороженое из контейнеров в ее рожок.

Куб

Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых пересекаются в каждой из его вершин, и все они перпендикулярны своим соответствующим смежным граням. Куб является частным случаем многих классификаций геометрических фигур, включая квадратный параллелепипед, равносторонний кубоид и правый ромбоэдр.Ниже приведено уравнение для расчета объема куба:

объем = ³
где a — длина ребра куба

EX: Боб, который родился в Вайоминге (и никогда не покидал штат), недавно посетил свою исконную родину, Небраску. Пораженный великолепием Небраски и окружающей средой, непохожей на какие-либо другие, с которыми он когда-либо сталкивался, Боб знал, что он должен привезти с собой домой часть Небраски. У Боба есть чемодан кубической формы с длиной по краям 2 фута, и он рассчитывает объем почвы, который он может унести с собой домой, следующим образом:

объем = 2 ³ = 8 футов ³

Цилиндр

Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от данной прямой оси.Однако в обычном использовании «цилиндр» относится к правильному круговому цилиндру, где основания цилиндра представляют собой окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . . Уравнение для расчета объема цилиндра показано ниже:

объем = πr ² ч
где r — радиус, а h — высота резервуара

EX: Кэлум хочет построить замок из песка в гостиной своего дома.Поскольку он является твердым сторонником рециркуляции, он извлек три цилиндрических бочки с незаконной свалки и очистил бочки от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который каждая может вместить, используя следующее уравнение:

объем = π × 3 ² × 4 = 113.097 фут ³

Он успешно построил замок из песка в своем доме и в качестве дополнительного бонуса ему удалось сэкономить электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым светом в темноте.

Прямоугольный резервуар

Прямоугольный резервуар — это обобщенная форма куба, стороны которого могут иметь разную длину. Он ограничен шестью гранями, три из которых пересекаются в его вершинах, и все они перпендикулярны своим соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:

объем = длина × ширина × высота

EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к торту.Она планирует отправиться в поход по тропе Калалау на Кауаи, и, несмотря на то, что она в очень хорошей форме, Дарби беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет набить свою идеально прямоугольную упаковку длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она поместит в свою упаковку, рассчитан ниже:

объем = 2 × 3 × 4 = 24 фута ³

Капсула

Капсула — это трехмерная геометрическая форма, состоящая из цилиндра и двух полусферических концов, где полусфера — это полусфера.Отсюда следует, что объем капсулы можно рассчитать, объединив уравнения объема для сферы и правого кругового цилиндра:

объем = πr 2 ч +

πr 3 = πr 2 (

р + з)

где r — радиус, а h — высота цилиндрической части

EX: Имея капсулу радиусом 1,5 фута и высотой 3 фута, определите объем растопленного молочного шоколада, который Джо может унести в капсуле времени, которую он хочет похоронить для будущих поколений на своем пути к самопознанию. Гималаи:

объем = π × 1.5 ² × 3 + 4/3 × π × 1,5 ³ = 35,343 фута ³

Сферический колпачок

Сферический колпачок — это часть сферы, отделенная от остальной сферы плоскостью. Если плоскость проходит через центр сферы, сферический колпачок называется полусферой. Существуют и другие различия, в том числе сферический сегмент, где сфера сегментирована двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу. Уравнение для расчета объема сферической крышки выводится из уравнения для сферического сегмента, где второй радиус равен 0.Относительно сферической крышки, указанной в калькуляторе:

Имея два значения, калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:

Для r и R : h = R ± √R ² — r ²

Для R и h : r = √2Rh — h ²
где r, — радиус основания, R — радиус сферы, а h — высота сферической крышки.

EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, он решает саботировать мяч для гольфа Джеймса.Он отрезает идеальную сферическую крышку от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимый для замены сферической крышки и перекоса веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:

объем = 1/3 × π × 0,3 ² (3 × 1,68 — 0,3) = 0,447 дюйма ³

К несчастью для Джека, за день до игры Джеймс получил новую партию мячей, и все усилия Джека были напрасны.

Коническая усадка

Усеченный конус — это часть твердого тела, которая остается при разрезании конуса двумя параллельными плоскостями. Этот калькулятор рассчитывает объем специально для правильного кругового конуса. Типичные конические усики, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы для питья. Объем усеченного правого конуса рассчитывается по следующей формуле:

объем =

πh (r 2 + rR + R 2 )

где r и R — радиусы оснований, h — высота усеченного конуса

EX: Би успешно приобрела мороженое в сахарном рожке и только что съела его таким образом, чтобы мороженое оставалось упакованным внутри рожка, а поверхность мороженого была ровной и параллельной плоскости отверстия рожка.Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть дна рожка, которая идеально параллельна ранее единственному отверстию. Теперь у Би есть усеченная пирамида правой конической формы, из которой вытекает мороженое, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченной кости 4 дюйма с радиусом 1,5 дюйма и 0,2 дюйма:

объем = 1/3 × π × 4 (0,2 ² + 0,2 × 1,5 + 1,5 ² ) = 10. 849 дюйм ³

Эллипсоид

Эллипсоид является трехмерным аналогом эллипса и представляет собой поверхность, которую можно описать как деформацию сферы посредством масштабирования элементов направления. Центр эллипсоида — это точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки прямых, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным.Уравнение для расчета объема эллипсоида выглядит следующим образом:

, где a , b и c — длины осей

EX: Хабат любит есть только мясо, но его мать настаивает на том, что он ест слишком много, и позволяет ему есть столько мяса, сколько он может уместить в булочке в форме эллипса. Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может уместить в своем сэндвиче. Учитывая, что его булочка имеет длину оси 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат рассчитывает объем мяса, который он может уместить в каждой полой булочке, следующим образом:

объем = 4/3 × π × 1. 5 × 2 × 5 = 62,832 дюйма ³

Квадратная пирамида

Пирамида в геометрии — это трехмерное твердое тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это форма на плоскости, ограниченная конечным числом отрезков прямых линий. Есть много возможных многоугольных оснований пирамиды, но квадратная пирамида — это пирамида, в которой основание представляет собой квадрат. Еще одно отличие пирамид заключается в расположении вершины. У правой пирамиды вершина находится прямо над центром тяжести ее основания.Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды может быть записан как:

Объем обобщенной пирамиды:

, где b — площадь основания, а h — высота

Объем квадратной пирамиды:

, где a — длина края основания

EX: Ван очарован Древним Египтом и особенно любит все, что связано с пирамидами. Будучи старшим из своих братьев и сестер Ту, Дерево и Форе, он может легко загонять и развертывать их по своему желанию. Воспользовавшись этим, Ван решает воссоздать времена Древнего Египта, а его братья и сестры выступают в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать, используя уравнение для квадрата. пирамида:

объем = 1/3 × 5 ² × 12 = 100 футов ³

Трубчатая пирамида

Трубка, часто также называемая трубой, представляет собой полый цилиндр, который часто используется для передачи жидкостей или газа.Для вычисления объема трубы используется та же формула, что и для цилиндра (объем = pr ² h ), за исключением того, что в этом случае используется диаметр, а не радиус, и длина, а не высота. Формула, таким образом, включает в себя измерение диаметров внутреннего и внешнего цилиндров, как показано на рисунке выше, вычисление каждого из их объемов и вычитание объема внутреннего цилиндра из объема внешнего. С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:

где d ₁ — внешний диаметр, d ₂ — внутренний диаметр, а l — длина трубы

EX: Beulah посвящен охране окружающей среды.Ее строительная компания использует только самые экологически чистые материалы. Она также гордится тем, что удовлетворяет потребности клиентов. У одного из ее клиентов есть загородный дом, построенный в лесу за ручьем. Он хочет облегчить доступ к своему дому и просит Беулу построить ему дорогу, следя за тем, чтобы ручей мог течь свободно, чтобы не мешать его любимому месту рыбалки. Она решает, что надоедливые бобровые дамбы будут хорошей точкой для прокладки трубы через ручей. Объем запатентованного бетона с низкой ударопрочностью, необходимый для строительства трубы с внешним диаметром 3 фута и внутренним диаметром 2.5 футов и длина 10 футов можно рассчитать следующим образом:

объем = π ×

× l0 = 21,6 фута 3

Единицы измерения общего объема

9057 9int000473 9055 905 905 Площадь 905 и объем Фигуры

В этом разделе мы вычисляем объем и площадь поверхности трехмерных фигур, таких как куба , кубоида , призмы и цилиндра .

Ед. Изм.	кубических метров	миллилитров
миллилитров (кубических сантиметров)	0,000001	1
кубических дюймов	0,00001639	0,00001639	473
кварта	0,000946	946
литр	0,001	1,000
галлон	0,00376 905	0,00376 905	0,00376
кубический ярд	0,764555	764,555
кубический метр	1	1,000,000
кубический километр	1,000,000,000	кубический километр	1,000,000,000

Куб		Объем = x ³ Площадь = 6 x ²
Кубоид		Объем = xyz Площадь поверхности = 2 xy + 2 xz + 2 yz
Цилиндр		Объем = π r ² h Площадь криволинейной поверхности = 2 π rh Площадь каждого конца = π r ² Общая площадь поверхности = 2 π rh + 2 π r ²
Призма		Призма имеет однородное поперечное сечение Объем = площадь поперечного сечения × длина = А л

Упражнения

Вопрос 5

На схеме показан деревянный брусок, в котором просверлено отверстие.Диаметр отверстия 2 см.
Вычислите объем этого твердого тела, дав правильный ответ с точностью до 2 знаков после запятой.

см³

Объем = блок — отверстие = 4 × 6 × 6 — 1² × π × 6 = 144 — 6 π = 125,15 (до 2 d.p.)

Вопрос 7

На схеме показано сечение трубы длиной 50 см.
Внутренний диаметр трубы составляет 20 см, а внешний — 30 см.

(а)

(б)

Общая площадь поверхности	= 2 × (15² — 10²) × π + 30 π × 50 + 20 π × 50
	= 250 π + 1500 π + 1000 π = 2750 π
	= 8639,379797 см² = 8640 см² (до 3 квадратных футов)

Вопрос 10

Цилиндр имеет диаметр 12 см и площадь криволинейной поверхности 132 π или 415 см² (до 3 значащих цифр).

Вопрос 12

(а)

(б)

Ящик стандартного размера содержит достаточно соли, чтобы заполнить 10 солонек.

(в)

Вопрос 13

(а)

(б)

Каков объем этой призмы?

см³

Площадь поперечного сечения = × основание × высота = × 6 × 8 = 24 см²

Объем призмы = площадь поперечного сечения × длина = 24 × 7 = 168 см³

(в)

Призмы A и B имеют одинаковую площадь поперечного сечения.

Заполните таблицу:

Формула

поперечного сечения — Что такое формула поперечного сечения? Формула

Формула боковой площади используется для определения боковой площади любого твердого объекта. Боковая часть любой фигуры — это только площадь неосновных граней. Формулы боковой поверхности помогают вычислить площадь боковой поверхности различных фигур, включая кубоид, куб, цилиндр, конус и сферу. Давайте посмотрим больше на формулы боковой площади вместе с несколькими решенными примерами.

Что такое формула боковой площади?

Формула боковой площади для разных типов объектов разная. Следовательно, существует множество формул поперечного сечения, которые объясняются ниже. Боковая область не включает базовую область объекта, а также грань, параллельную основанию. Формулы боковой площади для различных объектов приведены в таблице ниже:

Список формул бокового сечения

Измеряем площадь боковой поверхности трехмерных фигур. Ниже приведен подробный табличный список, который поможет вам понять формулу площади боковой поверхности.

Хотите найти сложные математические решения за секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. С Cuemath находите решения простым и легким способом.

Забронируйте бесплатную пробную версию Класс

Примеры по формуле бокового сечения

Давайте взглянем на несколько примеров, чтобы понять концепцию формулы боковой площади

Пример 1: Длина, ширина и высота кубоида составляют 6 единиц, 2 единицы и 16 единиц соответственно.Рассчитайте площадь боковой поверхности кубоида.

Решение:

Найти: Боковая формула кубоида, длина стороны куба
Дано:
Длина куба = 6 шт.
Ширина куба = 2 шт.
Высота куба = 16 шт.
Боковая площадь куба = Боковая площадь кубоида
Используя формулу площади поперечного сечения кубоида,
Боковая площадь кубовида = 2 (длина + ширина) × высота
= 2 (6 + 2) × 16
= 256 единиц

Ответ: Боковая площадь кубоида = 256 единиц

Пример 2: Радиус сферы составляет 4 единицы. Эта сфера разрезана на две равные половины. Вычислите площади боковой поверхности обоих объектов, используя формулу площади боковой поверхности.

Решение:

Найти: Площадь боковой поверхности сферы и полусферы
Дано: Радиус сферы и полусферы = 4 единицы
Используя формулу боковой площади,
Боковая площадь сферы = 4πr ²
= 4 × π × (4) ²
= 201,142 квадратных единицы
Площадь боковой / криволинейной поверхности полусферы = 2πr ²
= 2 × π × (4) ²
= 100.571 кв.

Ответ: Боковая площадь сферы = 201,142 квадратных единицы, а площадь боковой / криволинейной поверхности полусферы = 100,571 квадратных единиц

Пример 3: Найдите боковую площадь куба, используя формулу боковой площади со стороной 7 единиц.

Решение:

Найти: боковая площадь куба
При том, что сторона куба = 7 единиц
Используя формулу боковой площади куба = 4a ²
= 4 * 7 * 7 = 196.

Ответ: Боковая площадь куба составляет 196 квадратных единиц.

Часто задаваемые вопросы по формулам бокового сечения

Какова формула бокового сечения конуса?

Формула боковой площади конуса: LSA = πrl. Где r — радиус конуса, l — наклонная высота конуса, а π (pi) — постоянный член со значением 3,14 или 22/7.

Что такое формула боковой площади сферы?

Площадь боковой поверхности сферы выражается как LSA = 2πrh или 4πr ² (если диаметр сферы = 2r).Где r — радиус сферы, h — высота сферы, а π (pi) — постоянный член со значением 3,14 или 22/7.

Какова формула поперечного сечения цилиндра?

Площадь боковой поверхности цилиндра выражается как LSA = 2πrh. Где r — радиус круглого основания цилиндра, h — высота цилиндра, а π (pi) — постоянный член со значением 3,14 или 22/7.

Что такое формула боковой площади кубоида?

Площадь боковой поверхности кубоида выражается как LSA = 2h (l + b). {2} h, где r — радиус, h — высота. а. Напишите формулу объема куба через s. б. Напишите формулу объема цилиндра через s. c. Напишите формулу в единицах s для объема V металла, оставшегося после снятия цилиндра. d. Разложите формулу на множители из части (c). е. Найдите V в кубических дюймах для s = 15 дюймов. Используйте \ pi = 3,14

Стенограмма видео

Хорошо. Итак, нам дано наличие металлического куба.У него вырезанная из него цилиндрическая форма. Таким образом, размеры куба равны четырем s для каждой стороны. Итак, начните с определения объема куба. Объем любого куба — это длина стороны в третьей степени или четыре s, умноженные на четыре, как для нас. И я использую курсив, чтобы он не выглядел как пятерка. Итак, четыре раза для 16 16 раз для его 64. Итак, это 64 с в степени тройки. Хорошо. Ах, вам дается формула для цилиндра, согласно которой объем цилиндра равен площади круга, умноженному на квадрат радиуса, умноженному на высоту цилиндра. Хорошо, значит, это равно Пи Амар. Радиус s — это квадрат s, умноженный на высоту, которой было дано число 48 дюймов. Так что это равно 48. Извините. 48 раз просили в степени двойки. Хорошо. Затем мы собираемся записать объем металлического куба после того, как цилиндр будет удален. Это означает, что мы возьмем объем куба за вычетом объема цилиндра, который равен 64. Да, в степени трех, минус 48. High s в степени двойки. Таким образом, мы не можем упростить это вообще, потому что они, в отличие от терминов, имеют разные степени s, а также имеют коэффициент.Это число по сравнению с числом, умноженным на пи. Иррациональное число. Хорошо, теперь мы собираемся разложить наш ответ по частям. Видите ли, я собираюсь использовать двойное деление 64 в кубе минус 48. Привет в квадрате, двойное деление. Гм, вещи, которые делают 64 восемь раз восемь и 48 восемь раз секс. Все используют восемь для начала. Я вижу два общих фактора s и один дополнительный в первом. Таким образом, если я вычеркну восемь квадратов в квадрате, у меня останется восемь в первом члене, минус шесть во втором члене.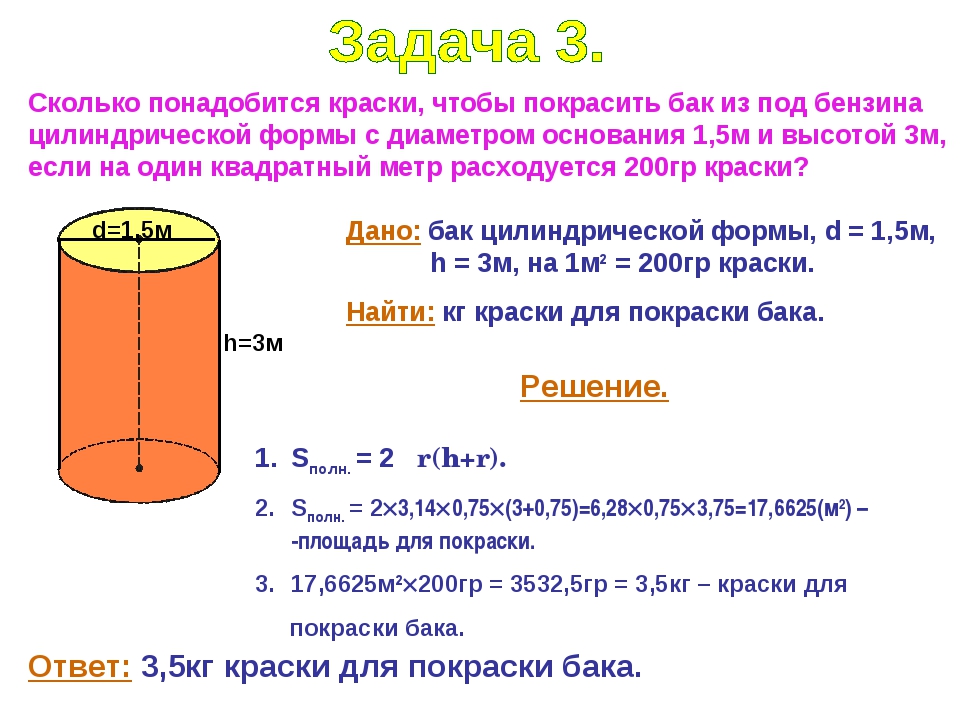 Новые факторы от нас остались.Тогда я буду искать все, что я пропустил. Восемь и шесть имеют общий делитель два s, и круговая диаграмма — не одно и то же. По крайней мере, мы не знаем, если. Итак, это ЦЗ, сколько мы можем вынести. Итак, это четыре секунды минус три пирога. Между ними определенно нет ничего общего, кроме одного. Итак, наш наибольший общий делитель равен восьми умноженным на два раза по 1 16 с в степени, умноженной на двойную величину s минус три пирога. Ладно, наконец, едем. Теох Ми Риз. Все в порядке, мы собираемся найти объем.Если мы знаем, что s равно 15 дюймам, а круговая диаграмма равна, мы будем использовать 3,14, поэтому объем будет равен 16 умноженным на 15 в квадрате, 15 умноженным, 15 умноженным, 4 умноженным на 15 минус 3 умноженным на 3,14. начать здесь. Хм, 15 умножить на 15 будет 225. Однако я найду способ попроще. Это три раза пять в квадрате. Итак, это 25 умножить на девять. 25 умножить на 16 — это то же самое, что 25 умножить на четыре, то есть 100 вещей и больше, то есть 400. Это 400 умножить на девять, то есть 3600. Вы также можете использовать калькулятор, если не хотите делать все эти причудливые рты. или просто умножьте 225 на 16.Я собираюсь использовать калькулятор, чтобы убедиться, что моя увлекательная математика не доставила мне неприятностей. Итак, 225 умноженное на 16 дает 3600. Отлично. Далее в скобках у меня есть 60 минус троекратное приближение пирога. Гм, трижды 14 — это 42 42 сотки, трижды 39 его. Это примерно равно 3600 умноженным на 51 балл. 48. Нет, это не так. 15.48. Так что вычтите 10. Из этого мы получим 50. Но затем еще 48 сотен, прежде чем это дойдет до 10. Итак, это 15,48, и это равно этому.Я воспользуюсь калькулятором. 36 100 умножить на 50,48. Это огромное количество перепроверок. 3600 умножить на 50,48. Хорошо. Ах, объем 181 1007 128 куб. Всего за

.