Формула полной поверхности параллелепипеда: Площадь поверхности прямоугольного параллелепипеда – формула (5 класс, математика)

«Объём и площадь поверхности прямоугольного параллелепипеда»

Формула объема параллелепипеда	Площадь полной поверхности параллелепипеда. а,b,c – ребра параллелепипеда
1) Начертите прямоугольный параллелепипед и найдите его объём, площадь основания, площадь боковых граней, а также площадь полной поверхности, если длина 12см, ширина 7см, высота 16см. 2) Даны два прямоугольных параллелепипеда: ребра одного равны 185, 185 и 37; а ребра другого равны 185,37 и 37. Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда?	5) Сколько кубиков войдет в коробку?
3) Дан прямоугольный параллелепипед, стороны основания которого равны 4 и 5, а боковое ребро равно 3. Найдите наибольшую площадь его грани.	6) Сколько понадобится краски, чтобы покрасить поверхность бруса, длина которого 40 см, ширина 30 см, а высота 20 см, если для покраски 1 дм2 поверхности нужно 2 г краски?
4) Сколько ленты потребуется, чтобы перевязать коробку так, как это изображено на рисунке? На бантик необходимо оставить 2 дм. Ответ дайте в дм.	7) Деревянный куб покрасили со всех сторон, потом распилили его на 27 одинаковых кубиков. Сколько кубиков не окрашено? 8) Длина аквариума 80 см, ширина 45 см, а высота 55 см. Сколько литров воды надо влить в этот аквариум, чтобы уровень воды был ниже верхнего края аквариума на 10 см?
Формула объема параллелепипеда	Площадь полной поверхности параллелепипеда. а,b,c – ребра параллелепипеда
1) Начертите прямоугольный параллелепипед и найдите его объём, площадь основания, площадь боковых граней, а также площадь полной поверхности, если длина 12см, ширина 7см, высота 16см. 2) Даны два прямоугольных параллелепипеда: ребра одного равны 185, 185 и 37; а ребра другого равны 185,37 и 37. Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда?	5) Сколько кубиков войдет в коробку?
3) Дан прямоугольный параллелепипед, стороны основания которого равны 4 и 5, а боковое ребро равно 3. Найдите наибольшую площадь его грани.	6) Сколько понадобится краски, чтобы покрасить поверхность бруса, длина которого 40 см, ширина 30 см, а высота 20 см, если для покраски 1 дм2 поверхности нужно 2 г краски?
4) Сколько ленты потребуется, чтобы перевязать коробку так, как это изображено на рисунке? На бантик необходимо оставить 2 дм. Ответ дайте в дм.	7) Деревянный куб покрасили со всех сторон, потом распилили его на 27 одинаковых кубиков. Сколько кубиков не окрашено? 8) Длина аквариума 80 см, ширина 45 см, а высота 55 см. Сколько литров воды надо влить в этот аквариум, чтобы уровень воды был ниже верхнего края аквариума на 10 см?

Применение формул объема и площади поверхности прямоугольного параллелепипеда для решения практических задач и математического моделирования

Цель урока: На практике научиться применять формулы объёма и площади поверхности прямоугольного параллелепипеда.

Инструменты: мультимедийная установка, мел, доска, макеты параллелепипедов.

Ход урока

I. Проверка домашнего задания.

II. Устный опрос.

1. Сколько ребер у прямоугольного параллелепипеда? Какой фигурой они являются?
2. Сколько граней у прямоугольного параллелепипеда? Какой фигурой они являются?
3. Сколько вершин у прямоугольного параллелепипеда? Какой фигурой они являются?

III.

Работа по готовым чертежам.

1. Что такое a, b и c?
2. Как найти площадь боковой грани? Есть ли еще грани с такой же площадью?
3. Как найти площадь верхней грани?
4. Как найти площадь передней грани?
5. Записать на доске формулу для нахождения площади поверхности параллелепипеда.
6. Записать формулу для нахождения объёма параллелепипеда.
7. В каких единицах измеряется площадь поверхности параллелепипеда, а в каких объём.

IV. Решить задачу по чертежу, изображенному на рисунке.

Найти площадь поверхности и объём прямоугольного параллелепипеда.

Решение.

1. 3*4 = 12 (кв. см) – площадь передней поверхности.
2. 3*5 = 15 (кв. см) – площадь боковой поверхности.
3. 4*5 = 20 (кв. см) – площадь верхней поверхности.
4. 2*(12+15+20) = 94 (кв. см) – площадь боковой поверхности параллелепипеда.

Ответ: 94 кв.см.

V. Практическая часть. Раздать параллелепипеды

1. Измерить ребра параллелепипеда (длину, высоту и ширину). Записать результаты в тетрадь.
2. Найти площадь боковой поверхности параллелепипеда.
3. Найти объем параллелепипеда.
4. Подписать грань параллелепипеда площадь, которой равна

• Вариант 1 – 14 кв. см
• Вариант 2 – 18 кв. см
• Вариант 3 – 48 кв. см

VI. Письменная работа на доске с фронтальным обсуждением.

Задача.

Найти площадь поверхности и объём прямоугольного параллелепипеда с вырезом.

Решение.

1. 2*(4*5+5*5+5*4) = 130 кв. см – площадь поверхности.
2. 5*5*4 = 100 куб. см – объём параллелепипеда.

Ответ: 130 кв. см и 100 куб. см.

VII. Задача с практическим содержанием.

Сколько ведер воды по 8 литров каждое, налито в аквариум, изображенный на рисунке.

Мы знаем, что 1 литр = 10 куб.дм.

1. 25-5 = 20 (см) – высота налитой воды.
2. 20*40*60 = 48000 (куб. см) – объём воды в аквариуме.
   48000 куб. см = 48 куб. дм = 48 литров
3. 48:8 = 6 (вед.) – воды потребуется.

Ответ: 6 ведер.

VIII. Выставление оценок.

IX. Домашнее задание.

как найти полную и боковую, формула для определения

Что такое площадь поверхности параллелепипеда

Определение

Параллелепипед — четырехугольная призма, основаниями которой являются параллелограммы. Частный случай этой геометрической фигуры — прямой параллелепипед, у которого все грани являются прямоугольниками.

В общем случае площадь — это численное значение, характеризующее размер двумерной геометрической фигуры.

Параллелепипед может существовать только в трех измерениях, поэтому для него вводится понятие площади поверхности. В геометрическом смысле площадь поверхности объемной фигуры является совокупностью площадей ее граней.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Формула нахождения полной площади

В задачах чаще всего имеется дело с прямоугольным параллелепипедом. Для него полная площадь поверхности вычисляется следующим образом:

\(S=2\cdot(a\cdot b+a\cdot c+b\cdot c)\)

где a, b и c — длины ребер, исходящих из любой вершины параллелепипеда.

Рассмотрим то, как данная формула выводится. Как уже упоминалось выше, площадь поверхности объемной фигуры является совокупностью площадей ее граней. Для наглядности возьмем параллелепипед ABCDA₁B₁C₁D₁.

Рисунок 1

Полная площадь его поверхности равняется сумме площадей всех граней: \(S_{пар}=S_{AA_1D_1D}+S_{DD_1C_1C}+S_{CC_1B_1B}+S_{BB_1A_1A}+S_{ABCD}+S_{A_1B_1C_1D_1}\)

Согласно свойствам параллелепипеда, его противоположные грани равны между собой. Следовательно, нет необходимости вычислять площадь всех шести граней, можно ограничиться тремя, а затем их сумму умножить на 2:

\(S_{пар}=2\cdot\left(S_{AA_1D_1D}+S_{BB_1A_1A}+S_{ABCD}\right)\)

Грани прямого параллелепипеда являются прямоугольниками. Площадь данной фигуры равняется произведению ее сторон:

\(S_▭=a\cdot b\)

У выбранных нами для расчета площади граней есть три общие стороны: AB, AD и AA₁. Для удобства обозначим их как a, b и c соответственно.

Рисунок 2

Таким образом:

 \(S_{ABCD}=a\cdot b\)

\(S_{AA_1D_1D}=a\cdot c\)

\(S_{BB_1A_1A}=b\cdot c\)

Подставим данные значения в обозначенную выше формулу площади параллелепипеда:

\(S_{пар}=2\cdot\left(a\cdot b+a\cdot c+b\cdot c\right)\)

Вычисление площади боковой поверхности прямоугольного параллелепипеда

Кроме полной площади поверхности, в расчетах иногда необходимо вычислить площадь боковой поверхности, то есть совокупность площадей боковых граней, без учета оснований.

Для этого есть три взаимосвязанные формулы:

1. \(S_{бок}=P_{осн}\cdot h,\) где \(P_{осн}\) — периметр основания параллелепипеда; h — высота. На рисунке выше она равняется стороне, обозначенной как c.
2. \(S_{бок}=2\cdot a\cdot c+2\cdot b\cdot c\), где a, b и c — длины ребер, исходящих из любой вершины параллелепипеда.
3. \(S_{бок}=2\cdot c\cdot(a+b).\)

Примеры решения задач

Задача

Вычислить полную площадь поверхности прямоугольного параллелепипеда ABCDA₁B₁C₁D₁.

Рисунок 3

Дано: AB = 3, A₁B = 6, AD = 5.

Решение

Для расчета полной площади необходимо знать длины трех сторон. В данном случае нам понадобится вычислить длину стороны AA₁. Так как длина диагонали A

1B известна, сделать это нетрудно.

Воспользуемся теоремой Пифагора:

\(A_1B=\sqrt{{AA_1}^2+{AB}^2}\)

Соответственно, \({AA_1}=\sqrt{{A_1B}^2-{AB}^2}=\sqrt{6^2-3^2}=\sqrt{36-9}=\sqrt{25}=5\)

Подставим известные значения в формулу расчета площади поверхности:

\(S=2\cdot(a\cdot b+a\cdot c+b\cdot c)\)

\(S=2\cdot(AB\cdot AD+AB\cdot AA_1+AD\cdot AA_1)=2\cdot(3\cdot5+3\cdot5+5\cdot5)=2\cdot(15+15+25)=2\cdot55=110\)

Ответ: S=110.

Задача 2

Вычислить длину стороны прямого параллелепипеда ABCDA₁B₁C₁D₁.

Рисунок 4

Дано: S_пов=96, S_бок=60, b=6.

Решение

Так как нам известна одна из сторон основания — b а в основании параллелепипеда лежит прямоугольник, найти вторую сторону проще всего будет через площадь этого основания:

\(S=a\cdot b\)

Отличие площади боковой поверхности от полной в том, что в ней не учитываются нижняя и верхняя грани фигуры. Следовательно, их разность будет равняться двум площадям основания. Вычислим это значение:

\(S_{пов}-S_{бок}=2\cdot a\cdot b+2\cdot a\cdot c+2\cdot b\cdot c-2\cdot a\cdot c-2\cdot b\cdot c=2\cdot a\cdot b\)

Преобразуем выражение так, чтобы вычислить длину неизвестной стороны:

\(2\cdot a\cdot b=S_{пов}-S_{бок}\)

\(a=\frac{S_{пов}-S_{бок}}{2\cdot b}=\frac{96-60}{2\cdot6}=\frac{36}{12}=3\)

Ответ: a=3.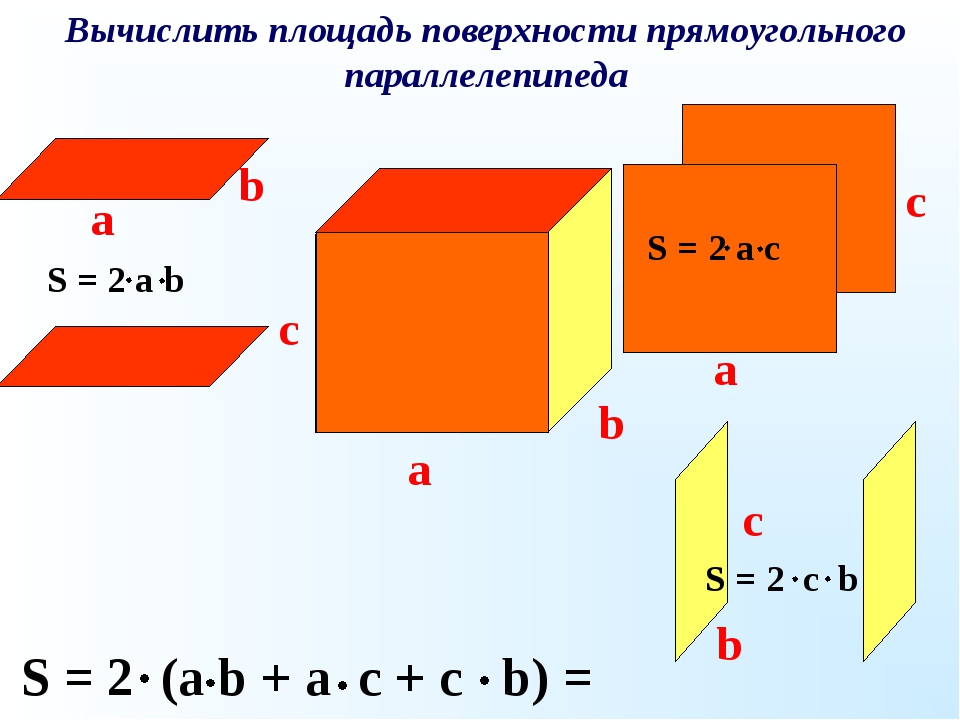

Рассчитать площадь параллелепипеда. Вычисляем площадь параллелепипеда

Параллелепипед – это четырехугольная призма, в основании имеющая параллелограмм. Существуют готовые формулы для расчета боковой и полной площади поверхности фигуры, для которых необходимы лишь длины трех измерений параллелепипеда.

Как найти площадь боковой поверхности прямоугольного параллелепипеда

Необходимо различать прямоугольный и прямой параллелепипед. Основание прямой фигуры может представлять собой любой параллелограмм. Площадь такой фигуры необходимо вычислять по другим формулам.

Сумма S боковых граней прямоугольного параллелепипеда вычисляется по простой формуле P*h, где P – периметр и h – высота. На рисунке видно, что у прямоугольного параллелепипеда противоположные грани равны, а высота h совпадает с длиной ребер, перпендикулярных основанию.

Площадь поверхности прямоугольного параллелепипеда

Полная площадь фигуры состоит из боковой и площади 2-х оснований. Как найти площади прямоугольного параллелепипеда:

Где a, b и c – это измерения геометрического тела.
Описанные формулы просты для понимания и полезны при решении множества задач геометрии. Пример типового задания представлен на следующем изображении.

При решении подобного рода задач следует помнить, что основание четырехугольной призмы выбирается произвольно. Если за основание принять грань с измерениями x и 3, то значения Sбок будет иным, а Sполн останется 94 см2.

Площадь поверхности куба

Куб – это прямоугольный параллелепипед, у которого все 3 измерения равны между собой. В связи с этим формулы полной и боковой площади куба отличаются от стандартных.

Периметр куба равен 4a, следовательно, Sбок= 4*a*a = 4*a2. Данные выражения не обязательны для заучивания, но значительно ускоряют решение заданий.

Пример решения задачи

Приведенные формулы могут использоваться в ходе поиска диагоналей параллелепипеда.

Для нахождение B1D достаточно применить теорему Пифагора: сумма квадратов катетов равна квадрату гипотенузы.

Параллелепипед — это многогранник, который представляет собой частный вид прямоугольной шестигранной призмы. В основании параллелепипеда лежит прямоугольник или равносильный ему четырехугольник, а в качестве боковых поверхностей выступают параллелограммы. Как и любая призматическая фигура, параллелепипед широко распространен в реальной жизни, но в большинстве случаев реальный многогранник принимает форму прямоугольного параллелепипеда.

Геометрия параллелепипеда

Прямоугольный параллелепипед представляет собой два одинаковых прямоугольника, лежащие в параллельных плоскостях и четыре соединяющих их прямоугольника, которые образуют боковую поверхность фигуры. В общем случае параллелепипед представляет собой частный случай прямой четырехугольной призмы. Параллелепипед — наиболее распространенная в реальной жизни фигура. Именно форму данного многогранника имеют такие объекты как дома, комнаты, кирпичи, картонные коробки, блоки компьютеров, упаковки молока, спичечные коробки и многое другое.

Реальный мир состоит их различных геометрических фигур, поэтому вам может понадобиться калькулятор, который мгновенно посчитает площадь поверхности объекта, имеющего форму прямоугольного параллелепипеда, будь то корпусная мебель, кладовка или системный блок стационарного компьютера.

Площадь поверхности параллелепипеда

Площадь полной поверхности такой призмы определяется как сумма площадей всех граней. Параллелепипед представляет собой шестигранник, каждая пара граней которого равны между собой. Это означает, что каждая грань параллелепипеда имеет свою конгруэнтную пару. Таким образом, площадь поверхности данной призматической фигуры выражается как двойная сумма площадей каждой грани.

S = 2 (Sa + Sb + Sc)

Так как каждая грань параллелепипеда представляет собой обычный прямоугольник, то площадь одной грани определяется как произведение сторон многоугольника. Если призматическая фигура имеет стороны a, b и c, то площадь ее полной поверхности будет равна:

S = 2 (ab + bc + ac)

Для более простого понимания можем представить формулу через длину, ширину и высоту параллелепипеда. В этом случае в формуле будет лишь небольшое изменение:

S = 2 (ab + bh + ah)

Таким образом, для определения площади полной поверхности призматической фигуры вам понадобится узнать три ее параметра. Введите эти данные в форму онлайн-калькулятора и вы получите мгновенный результат. Кроме того, калькулятор сразу подсчитает длину диагонали многогранника. Расчет площади поверхности призматической фигуры может понадобиться вам во многих ситуациях.

Примеры из жизни

Покраска стен

Допустим, вы хотите покрасить стены, пол и потолок кухни белой краской. Вам необходимо купить достаточное количество краски для обработки выбранного помещения. Зная, что расход масляной краски на 1 квадратный метр поверхности составляет приблизительно 200 грамм, вы можете определить, сколько материала вам понадобится для работы. Пусть высота кухонного помещения составляет 3 м, ширина 2 м, а длина — 5 м. Введите эти данные в онлайн-калькулятор и вы получите результат в виде:

Таким образом, вам понадобится покрасить 62 квадратных метров поверхности. Для этого вам потребуется купить 12,4 кг масляной краски или 5 банок краски по 2,8 кг.

Производство

Допустим, вы работаете на производстве и покрываете стальной квадратный профиль защитным покрытием, окуная детали в ванную с раствором. Для правильного расчета параметров покраски вам необходимо знать площадь поверхности одного стального профиля, который имеет форму параллелепипеда. Стандартный квадратный профиль имеет размеры: длина 6 м, сторона а = 80 мм, сторона b = 80 мм. Для правильного расчета вам необходимо подставить все размеры в одних единицах измерения, к примеру, в сантиметрах. В этом случае вбейте в онлайн-калькулятор три стороны параллелепипеда, которые равны 600, 8 и 8. Вы получите результат в виде:

Таким образом, полная площадь поверхности стального профиля составляет 19 328 квадратных сантиметров или 1,9828 квадратных метра. Зная площадь поверхности одного профиля, вы легко сможете определить параметры покраски деталей защитным покрытием.

Заключение

Большое количество реальных объектов имеет форму параллелепипеда: это и кирпичи, и комнаты, и здания, и детали машин, и многое другое. Расчет площади данного многогранника может понадобиться в самых неожиданных ситуациях, как-то житейские проблемы или профессиональные расчеты. Наш онлайн-калькулятор поможет вам быстро определить объемы и площади поверхностей любых правильных геометрических фигур.

Одной из самых простых можно назвать параллелепипед. Он имеет форму призмы, в основании которой расположен параллелограмм. Не составляет труда подсчитать площадь параллелепипеда, поскольку формула очень проста.

Призму составляют грани, вершины и рёбра. Распределение этих составляющих элементов выполнено в том минимальном количестве, которое необходимо для образования этой геометрической формы. Параллелепипед заключает в себе 6 граней, которые соединяются посредством 8-ми вершин и 12-ти рёбер. Причём противоположные стороны параллелепипеда всегда будут равны между собой. Поэтому, чтобы узнать площадь параллелепипеда, достаточно определить размеры трёх его граней.

Параллелепипед (в переводе с греческого языка термин означает «параллельные грани») обладает некоторыми свойствами, которые следует упомянуть. Во-первых, симметричность фигуры подтверждается только в середине каждой своей диагонали. Во-вторых, проведя между любыми из противоположных вершин диагональ, можно обнаружить, что все вершины имеют единую точку пересечения. Также стоит отметить то свойство, что противоположные грани всегда равны и будут обязательно параллельны между собой.

В природе различают такие разновидности параллелепипедов:

прямоугольный — состоит из граней прямоугольной формы;

прямой — имеет только боковые грани прямоугольные;

наклонный параллелепипед имеет в составе боковые грани, которые поставлены неперпендикулярно основаниям;

куб — состоит из граней квадратной формы.

Попробуем найти площадь параллелепипеда на примере прямоугольного типа этой фигуры. Как нам уже известно, все его грани прямоугольные. И поскольку количество этих элементов сводится к шести, то, узнав площадь каждой грани, нужно суммировать получившиеся результаты в одно число. А найти площадь каждой из них не составит труда. Для этого необходимо умножить две стороны прямоугольника.

Используется математическая формула, чтобы определить площадь прямоугольного параллелепипеда. Она состоит из знаковых символов, обозначающих грани, площадь, и выглядит так: S=2(ab+bc+ac), где S — площадь фигуры, a, b — стороны основания, c — боковое ребро.

Приведём примерное вычисление. Допустим, a = 20 см, b = 16 см, c = 10 см. Теперь нужно перемножить числа в соответствии с требованиями формулы: 20*16+16*10+20*10 и получаем число 680 см2. Но это будет лишь половина фигуры, так как мы узнали и суммировали площади трёх граней. Поскольку каждая грань имеет своего «двойника», нужно удвоить результирующее значение, и получаем площадь параллелепипеда, равную 1360 см2.

Чтобы вычислить площадь боковой поверхности, применяют формулу S=2c(a+b). Площадь основания параллелепипеда можно узнать, умножая длины сторон основания друг на друга.

В повседневном быту параллелепипеды можно встретить часто. О их существовании нам напоминает форма кирпича, деревянного ящика обычного спичечного коробка. Примеров каждый сможет найти в изобилии вокруг нас. В школьных программах по геометрии на изучение параллелепипеда отведено несколько уроков. Первые из них демонстрируют модели прямоугольного параллелепипеда. Затем ученикам показывают, как вписывать в него шар или пирамиду, другие фигуры, находить площадь параллелепипеда. Одним словом, это простейшая трёхмерная фигура.

В 5 классе в курсе математики изучается тема прямоугольного параллелепипеда. Сегодня мы поговорим о формулах для нахождения площади прямоугольного параллелепипеда боковой поверхности и площади полной поверхности этой фигуры, которые наиболее часто вызывают затруднение у учеников при изучении этой темы.

Определения

Параллелепипед – это фигура, который состоит из шести четырехугольников. Если в основании этой фигуры находится прямоугольник, то многогранник называется прямоугольным параллелепипедом.

Прямоугольный параллелепипед имеет четыре боковые грани. Две из них называются основанием многогранника. Для обозначения вершин фигуры используют большие латинские буквы.

Если две грани не имеют общего ребра, то они называются противоположными. Так как каждая грань является прямоугольником, где противоположные стороны равны, то и противоположные грани прямоугольного параллелепипеда равны.

Стороны граней – это ребра, фигура имеет 12 ребер. Длина ребер определяет основные характеристики прямоугольного параллелепипеда: площадь, периметр, объем.

Рис. 1. Прямоугольный параллелепипед

Примеры таких фигур мы часто встречаем в нашей жизни: кирпич, коробка, системный блок компьютера.

Математическая фигура – прямоугольный параллелепипед активно используется в искусстве, архитектуре и прочих областях.

Различают несколько видов параллелепипедов, с основанием в виде квадрата, параллелограмма или прямоугольника.

Формула для нахождения площади

Для того, чтобы найти площадь боковой поверхности прямоугольного параллелепипеда, необходимо вычислить по отдельности площадь каждой боковой грани, а затем просуммировать получившиеся значения.

$S = ac, a, b, c$ – стороны фигуры.

Рис. 2. Прямоугольный параллелепипед

А так как противоположные грани равны, то есть $AMPD = BNKC$, $AMNB = DPKC$, их сумма и будет площадью боковой поверхности многоугольника.

Соответственно, чтобы вычислить площадь полной поверхности прямоугольного параллелепипеда необходимо сложить площадь боковой поверхности и две площади основания. В итоге получится формула площади прямоугольного параллелепипеда.

$S = 2(ab + ac) + 2 bc = 2(ab + ac + bc)$

Иногда для уточнения возле знака площади пишут краткое обозначение например, S п.п – площадь полной поверхности, либо S б.п – площадь боковой поверхности. Это помогает вовремя выполнения задание не перепутать нужные данные.

Пример задания

Найти площадь полной поверхности прямоугольного параллелепипеда, если длина и ширина основания 4 см и 3 см соответственно, а высота равна 2 см.

Параллелепипед — самая распространенная фигура из тех, что окружают людей. Большинство помещений представляют собой именно его. Особенно важно знать площадь параллелепипеда, хотя бы его боковых граней, во время ремонта. Ведь нужно точно знать, сколько материала приобрести.

Что он собой представляет?

Это призма с четырехугольным основанием. Поэтому у нее четыре боковых грани, которые являются параллелограммами. То есть такое тело имеет всего 6 граней.

Для определения параллелепипеда в пространстве у него определяют площадь и объем. Первая может быть как отдельно для каждой грани, так и для всей поверхности. К тому же выделяют еще и площадь только боковых граней.

Какие существуют виды параллелепипедов?

Наклонный. Такой, у которого боковые грани образуют с основанием угол, отличный от 90 градусов. У него верхний и нижний четырехугольники не лежат друг напротив друга, а сдвинуты.

Прямой. Параллелепипед, боковые грани которого являются прямоугольниками, а в основании лежит фигура с произвольными величинами углов.

Прямоугольный. Частный случай предыдущего вида: в его основании находится прямоугольник.

Куб. Особый тип прямого параллелепипеда, в котором все грани представлены квадратами.

Некоторые математические особенности параллелепипеда

Может возникнуть ситуация, когда они окажутся полезными в том, чтобы найти площадь параллелепипеда.

• Грани, которые лежат напротив друг друга, не только параллельны, но и равны.
• Диагонали параллелепипеда точкой пересечения делятся на равные части.
• Более общий случай, если отрезок соединяет две точки на поверхности тела и проходит через точку пересечения диагоналей, то он делится этой точкой пополам.
• Для прямоугольного параллелепипеда справедливо равенство, в котором в одной его части стоит квадрат диагонали, а в другой — сумма квадратов его высоты, ширины и длины.

Площади прямого параллелепипеда

Если обозначить высоту тела как «н», а периметр основания буквой Р ос, то вся боковая поверхность может быть вычислена по формуле:

S бок = Р ос * н

Используя эту формулу и определив площадь основания, можно сосчитать полную площадь:

S = S бок + 2 * S ос

В последней записи S ос.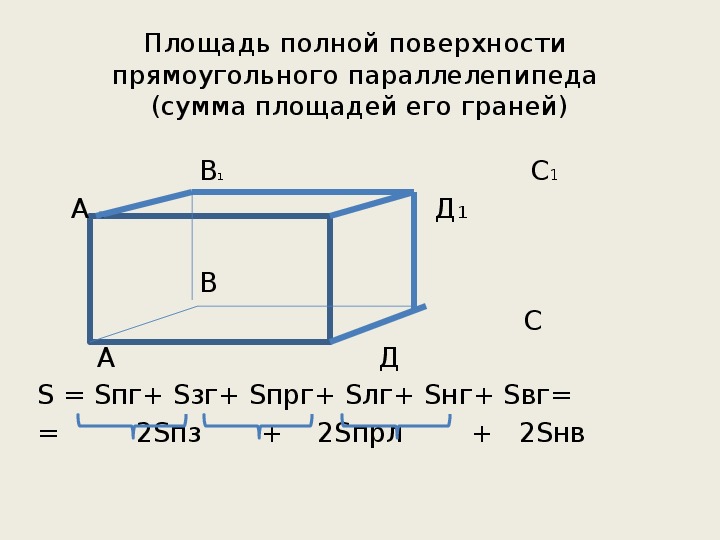 , то есть площадь основания параллелепипеда, может быть вычислена по формуле для параллелограмма. Другими словами, потребуется выражение, в котором нужно перемножить сторону и высоту, опущенную на нее.

Площади прямоугольного параллелепипеда

Принято стандартное обозначение длины, ширины и высоты такого тела буквами «а», «в» и «с» соответственно. Площадь боковой поверхности будет выражаться формулой:

S бок = 2 * с * (а + в)

Чтобы вычислить полную площадь прямоугольного параллелепипеда, потребуется такое выражение:

S = 2 * (ав + вс + ас)

Если окажется необходимым узнать площадь его основания, то достаточно вспомнить, что это прямоугольник, а значит, достаточно перемножить «а» и «в».

Площади куба

Его боковая поверхность образована четырьмя квадратами. Значит, чтобы ее найти, потребуется воспользоваться известной для квадрата формулой и умножить ее на четыре.

S бок = 4 * а 2

А из-за того, что его основания — такие же квадраты, полная площадь определится по формуле:

S = 6 * а 2

Площади наклонного параллелепипеда

Поскольку его грани — это параллелограммы, то нужно узнать площадь каждого из них и потом сложить. К счастью, противолежащие равны. Поэтому вычислять площади нужно только три раза, а потом умножить их на два. Если записать это в виде формулы, то получится следующее:

S бок = (S 1 + S 2) * 2,

S = (S 1 + S 2 + S 3) * 2

Здесь S 1 и S 2 являются площадями двух боковых граней, а S 3 — основания.

Задачи по теме

Задание первое. Условие. Необходимо узнать длину диагонали куба, если площадь всей его поверхности равна 200 мм 2 .

Решение. Начать нужно с получения выражения для искомой величины. Ее квадрат равен трем квадратам стороны куба. Это значит, что диагональ равна «а», умноженной на корень из 3.

Но сторона куба неизвестна. Здесь потребуется воспользоваться тем, что известна площадь всей поверхности. Из формулы получается, что «а» равно квадратному корню из частного S и 6.

Ответ. Диагональ куба равна 10 мм.

Задание второе. Условие. Необходимо вычислить площадь поверхности куба, если известно, что его объем равен 343 см 2 .

Решение. Потребуется воспользоваться той же формулой для площади куба. В ней опять неизвестно ребро тела. Но зато дан объем. Из формулы для куба очень просто узнать «а». Оно будет равно кубическому корню из 343. Простой подсчет дает такое значение для ребра: а = 7 см.

Ответ. S = 294 см 2 .

Задание третье. Условие . Дана правильная четырехугольная призма со стороной основания 20 дм. Необходимо найти ее боковое ребро. Известно, что площадь параллелепипеда равна 1760 дм 2 .

Решение. Начинать рассуждения нужно с формулы для площади всей поверхности тела. Только в ней нужно учесть, что ребра «а» и «в» равны. Это следует из утверждения о том, что призма правильная. Значит, в его основании лежит четырехугольник с равными сторонами. Отсюда а = в = 20 дм.

Учитывая это обстоятельство, формула площади упростится до такой:

S = 2 * (а 2 + 2ас).

В ней известно все, кроме искомой величины «с», которая как раз и является боковым ребром параллелепипеда. Чтобы его найти, нужно выполнить преобразования:

• разделить все неравенство на 2;
• потом перенести слагаемые так, чтобы слева оказалось слагаемое 2ас, а справа — деленная на 2 площадь и квадрат «а», причем последнее будет со знаком «-»;
• затем поделить равенство на 2а.

В итоге получится выражение:

с = (S/2 — а 2) / (2а)

После подстановки всех известных величин и выполнения действий получается, что боковое ребро равно 12 дм.

Ответ . Боковое ребро «с» равняется 12 дм.

Задание четвертое. Условие. Дан прямоугольный параллелепипед. Одна из его граней имеет площадь, равную 12 см 2 . Необходимо вычислить длину ребра, которое перпендикулярно этой грани. Дополнительное условие: объем тела равен 60 см 3 .

Решение. Пусть известна площадь той грани, которая расположена лицом к наблюдателю. Если принять за обозначение стандартные буквы для измерений параллелепипеда, то в основании ребра будут «а» и «в», вертикальное — «с». Исходя из этого, площадь известной грани определится как произведение «а» на «с».

Теперь нужно воспользоваться известным объемом. Его формула для прямоугольного параллелепипеда дает произведение всех трех величин: «а», «в» и «с». То есть известная площадь, умноженная на «в», дает объем. Отсюда получается, что искомое ребро можно вычислить из уравнения:

Элементарный расчет дает результат 5.

Ответ. Искомое ребро равно 5 см.

Задание пятое. Условие. Дан прямой параллелепипед. В его основании лежит параллелограмм со сторонами 6 и 8 см, острый угол между которыми равен 30º. Боковое ребро имеет длину 5 см. Требуется вычислить полную площадь параллелепипеда.

Решение. Это тот случай, когда нужно узнать площади всех граней по отдельности. Или, точнее, трех пар: основание и две боковые.

Поскольку в основании расположен параллелограмм, то его площадь вычисляется как произведение стороны на высоту к ней. Сторона известна, а высота — нет. Ее нужно сосчитать. Для этого потребуется значение острого угла. Высота образует в параллелограмме прямоугольный треугольник. В нем катет равен произведению синуса острого угла, который ему противолежит, на гипотенузу.

Пусть известная сторона параллелограмма — это «а». Тогда высота будет записана как в * sin 30º. Таким образом, площадь основания равна а * в * sin 30º.

С боковыми гранями все проще. Они — прямоугольники. Поэтому их площади — это произведение одной стороны на другую. Первая — а * с, вторая — в * с.

Осталось объединить все в одну формулу и сосчитать:

S = 2 * (а * в * sin 30º + а * с + в * с)

После подстановки всех величин получается, что искомая площадь равна 188 см 2 .

Ответ. S = 188 см 2 .

Площадь поверхности и объем параллелепипеда

Примечание. Это часть урока с задачами по геометрии (раздел теорема стереометрия — параллелепипед). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√»

Задача Основание прямоугольного параллелепипеда — ромб. Найдите площадь боковой поверхности параллелепипеда, если площади его диагональных сечений равны P и Q

Решение.
Площадь первого сечения выразим как
P = hd₁ , где
h — высота параллелепипеда
d₁ — длина диагонали

Площадь второго сечения выразим как
Q= hd₂ , где
h — высота параллелепипеда
d₂ — длина диагонали

Соответственно,
d₁ = P / h
d₂ = Q / h

Площадь боковой поверхности равна
S = 4ah, где
a — длина стороны ромба
h — высота параллелепипеда

По теореме Пифагора
a = sqrt( ( d₁ / 2 )² + ( d₂ / 2 )² )
a = sqrt( d₁² / 4  + d₂² / 4 )
a = sqrt( d₁² + d₂² ) / 2

Тогда
S = 4ah
S = 4h sqrt( d₁² + d₂² ) / 2
S = 2h sqrt( d₁² + d₂² )

поскольку
d₁ = P / h
d₂ = Q / h

то
S = 2h √( ( P / h )_{² + ( Q / h )² )
S = 2h √( P ² + Q² ) / h
S = 2 √( P ² + Q² )}

Ответ: S = 2 √( P ² + Q² )

Задача

Вычислить объем прямоугольного параллелепипеда, диагональ которого а образует с плоскостью основания угол а, а с боковой гранью – угол β.

Обчислити об’єм прямокутного паралелепіпеда, діагональ якого а утворює з площиною основи кут а, а з бічною гранню кут β.

Решение. Рiшення.

По условию AC’ = a ∠C’AC = α ∠AC’B = β Тогда V = AB х BC х CC´; AB = a sin β; AC = a cos α; CC´ = a sin α; BC2 = AC2 — AB2 a2cos2α — a2sin2β = a2( cos2α — sin2β ) (cos2α — sin2β > 0 т. к. АС – гипотенуза, а АВ – катет).

За умовою AC’ = a ∠C’AC = α ∠AC’B = β Тоді V = AB х BC х CC´; AB = a sin β; AC = a cos α; CC´ = a sin α; BC2 = AC2 — AB2 a2cos2α — a2sin2β = a2( cos2α — sin2β ) (cos2α — sin2β > 0 т.к. АС – гіпотенуза, а АВ – катет).

Задача

В параллелепипеде длины трех ребер, выходящих из одной вершины, равны а, b, с. Ребра а и b взаимно перпендикулярны, а ребро с образует с каждым из них угол α. Найти объем параллелепипеда.

У паралелепіпеді довжини трьох ребер, що виходять з однієї вершини, дорівнюють а, b, с. Ребра а і b взаємно перпендикулярні, а ребро с утворює з кожним з них кут α. Знайти об’єм паралелепіпеда.

Решение. Рiшення.

Так как углы, образуемые ребром с с ребрами а и b, равны, то треугольник АОВ равнобедренный и прямоугольный, катеты которого АВ=ОВ=с*cosα, а гипотенуза ОА= *c*cosα

Так як кути, утворені ребром с з ребрами а і b рівні, то трикутник АОВ і прямокутний рівнобедрений, катети якого АВ=ОВ=с*cosα,  а гіпотенуза ОА= *c*cosα

 Параллепипед | Описание курса | Призма с треугольником в основании 

   

Многогранники площади поверхностей и объемы многогранников призма

Приложение №2.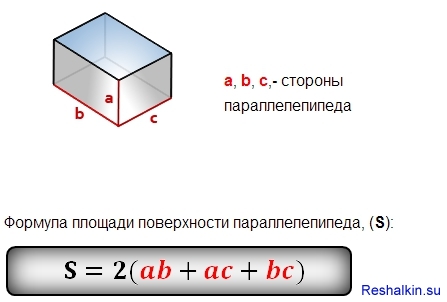

Многогранники.

Площади поверхностей и объемы многогранников.

Призма.

Призма называется прямой, если ее боковые ребра перпендикулярны основаниям.

Призма назывется правильной если она прямая и ее основания – правильные многогранники.

ABCD – квадрат

Площадь боковой поверхности – это сумма площадей боковых граней.

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы (длину бокового ребра)

сумма длин всех сторон основания

Объем призмы равен произведению площади ее основания на высоту

Параллелепипед

Параллелепипед – призма, основанием которой служит параллелограмм.

В любом параллелепипеде:

-противоположные грани равны и параллельны

-диагонали пересекаются в одной точке и делятся в ней пополам

Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.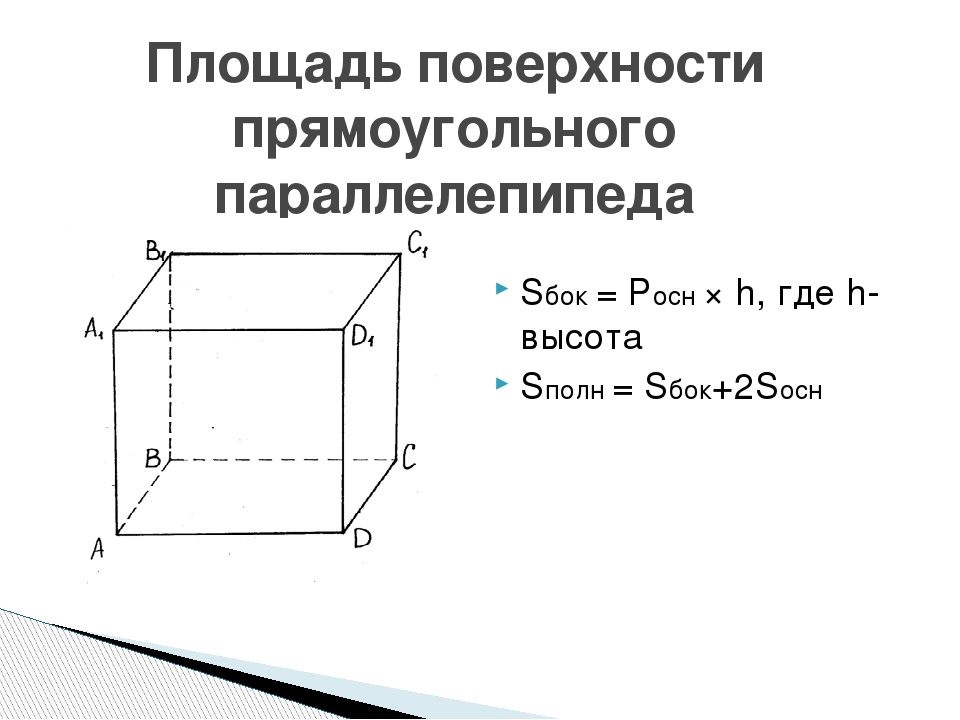

Все диагонали прямоугольного параллелепипеда равны

Задача.

В прямом параллелепипеде стороны основания равны 6 м и 8 м образуют угол , боковое ребро равно 5 м. Найдите полную поверхность этого параллелепипеда и его объем.

Дано: прямой параллелепипед, ABCD – параллелограмм, AD = 6 м, АВ = 8 м, , .

Найти: S и V параллелепипеда.

Решение:

1. Полная поверхность параллелепипеда вычисляется по формуле:

2. Полная поверхность основания параллелепипеда вычисляется по формуле:

, так как параллелограмм – ABCD

3. Полная поверхность бока параллелепипеда вычисляется по формуле:

Периметр основания вычисляется по формуле:

(м)

4. Полная поверхность параллелепипеда равна:

5. Объем параллелепипеда вычисляется по формуле:

Ответ: ,

Задача

В

прямом параллелепипеде стороны основания 3 см и 6 см, а одна из диагоналей основания 4 см. Найдите большую диагональ параллелепипеда, зная, что диагональ образует с плоскостью основания угол .

Решение:

1. Так как основанием прямого параллелепипеда служит параллелограмм, а у параллелограмма сумма квадратов диагоналей равна сумме квадратов его сторон, то неизвестная диагональ равна

2. Из прямоугольного треугольника найдем ребро

3. Большая диагональ параллелепипеда является гипотенузой прямоугольного треугольника , тогда см.

Пирамида

Пирамида называется правильной, если ее основание – правильный многоугольник, а высота ее проходит через центр основания.

Высота боковой грани правильной пирамиды называется апофемой пирамиды.

Правильная треугольная пирамида называется тетраэдром.

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему (1)

Задача

Основанием пирамиды является прямоугольник со сторонами 3 м и 4 м. Каждое боковое ребро пирамиды равно 13 м. Найдите высоту пирамиды и площадь боковой поверхности.

Решение.

1. Так как по условию все боковые ребра равны. то вершина проектируется в центр описанной около основания окружности, то есть в точку О пересечения диагоналей.

2. Следовательно, высота пирамиды равна катету прямоугольного треугольника OSD, у которого катет равен половине диагонали прямоугольника, а гипотенузой является боковое ребро.

3. Найдем диагональ прямоугольника

4. Высота пирамиды

5. Для нахождения площади боковой поверхности нужно знать длины апофем SK и SM:

из прямоугольного треугольника SKD найдем

из прямоугольного треугольника SMD найдем

Найдем площадь боковой поверхности:

,

Задача

Одно ребро тетраэдра равно 4, каждое из остальных равно 4. Найдите объем тетраэдра.

Решение.

1. Пусть ВС=4, АВ=АС=ЕА=ЕВ=ЕС=3

2. , где Н=ЕО

3. , где и ВС = 4. Из прямоугольного треугольника ADC найдем . Таким образом,

4. АЕ=ЕВ=ЕС, следовательно, точка О – центр описанной окружности около основания АВС и ОА=R.

5. Из прямоугольного треугольника АЕО находим , где АЕ=3. Так как АО=R, то , тогда

Усеченная пирамида

Если пирамиду пересечь плоскостью, параллельной основанию, то получится новый многогранник, который называется усеченной пирамидой.

Н-высота

и — площади оснований.

Формулы площадей многоугольников.

1. Треугольник

,

, где

2. Параллелограмм

,

3. Ромб

4. Трапеция

5. Круг

6. Теорема косинусов

Для

7. Свойства диагоналей параллелограмма.

Для параллелограмма ABCD

Задачи

1. Стороны основания прямоугольного параллелепипеда имеют длины 6 см и 8 см, длина диагонали параллелепипеда 26 см. Найдите высоту параллелепипеда и площадь диагонального сечения.

2. В правильной четырехугольной призме диагонали боковой грани 23 см, а диагональ основания 20 см. Найдите диагональ призмы.

3. Найдите диагональ прямоугольного параллелепипеда, если диагонали его граней имеют длины 11 см, 19 см и 20 см.

4. Стороны основания прямого параллелепипеда 6 см и 7 см, а диагональ основания 11 см. Высота параллелепипеда 10 см. Найдите площадь диагональных сечений.

5. В основании прямого параллелепипеда ромб со стороной 6 см и острым углом . Найдите диагонали параллелепипеда, если меньшая диагональ составляет с плоскостью основания угол в .

6. Стороны основания прямого параллелепипеда 6 см и 8 см, а диагонали параллелепипеда наклонены к основанию под углами и . Найдите длины этих диагоналей.

7. Стороны основания прямого параллелепипеда имеют длины 2 см и 7 см, а один из углов основания . Меньшая диагональ параллелепипеда имеет длину 8 см. Найдите площадь боковой поверхности параллелепипеда.

8. Стороны основания прямого параллелепипеда имеют длины 35 дм и 13 дм, а один из углов основания . Большая диагональ параллелепипеда составляет с плоскостью основания угол . Найдите площадь полной поверхности параллелепипеда.

9. Стороны основания прямого параллелепипеда имеют длины 9 см и 3 см. Диагонали параллелепипеда составляют с плоскостью основания углы и . Найдите площадь боковой поверхности параллелепипеда и длины его диагоналей.

10. Сторона основания правильной четырехугольной пирамиды 12 см, а боковое ребро 10 см. Найдите площадь полной поверхности пирамиды.

11. Стороны основания правильной четырехугольной пирамиды равно 10 см, а двугранный угол при основании равен . Найдите площадь полной поверхности пирамиды.

12. Высота правильной четырехугольной пирамиды равна 4 см. Найдите площадь полной поверхности пирамиды, если двугранный угол при основании ее равен .

13. Сторона основания правильной четырехугольной пирамиды равна 30 см, а высота 5 см. Найдите площадь полной поверхности пирамиды.

14. Высота правильной треугольной пирамиды равна 5 см, а боковое ребро 13 см. Найдите площадь полной поверхности пирамиды.

15. Высота правильной треугольной пирамиды равна 5 см. Найдите площадь полной поверхности пирамиды, если боковое ребро ее наклонено к плоскости основания под углом .

16. Диагональ прямоугольного параллелепипеда имеет длину 81 см. Найдите объем этого параллелепипеда. Сели его измерения относятся как 2:7:26

17. Найдите объем прямоугольного параллелепипеда, если длины диагоналей его граней равны 7 см, 8 см и 9 см.

18. Диагональ прямоугольного параллелепипеда составляет с одной его гранью угол , а с другой . Найдите объем параллелепипеда, если длина его диагонали 12 см.

19. Каждое ребро параллелепипеда имеет длину 5 см, один из углов основания , а с другой . Найдите объем параллелепипеда, если длина его диагонали 12 см.

20. Каждое ребро прямого параллелепипеда имеет длину 5 см, один из углов основания . Найдите объем и площадь полной параллелепипеда.

21. Стороны основания прямого параллелепипеда имеют длины 3 и 8 дм, а один из углов основания . Найдите объем параллелепипеда и площади его диагональных сечений, если площадь боковой поверхности его равна 220 .

22. Найдите объем правильной четырехугольной призмы, в которой длина диагонали 7 см, а длина диагонали боковой грани 5 см.

23. — правильная треугольная призма. Найдите площадь сечения этой призмы плоскостью, проходящей через ребро ВС и середину ребра , если ВС = 10 см, = 30 см.

24. В прямом параллелепипеде длины сторон основания равны 7 b 11 см, а длина одной из диагоналей основания равна 12 см. Найдите площади диагональных сечений параллелепипеда и длину меньшей из его диагоналей, если длина бокового ребра равна 16 см.

25. — правильная треугольная призма. Найдите площадь сечения этой призмы плоскостью, проходящей через ребро АС и вершину , если АС- 14 см, =7 см.

26. Дана прямая треугольная призма , в которой АВ = 16 см, АС = 10 см, ВАС = . Найдите площадь полной поверхности призмы, если длина диагонали боковой грани равна 20 см.

27. Высота правильной четырехугольной пирамиды равна 12 см, а величина двугранного угла при основании пирамиды равна . Найдите площадь полной поверхности пирамиды.

28. Основанием прямого параллелепипеда служит ромб, длина стороны которого равна 5 см, а величина острого угла . Найдите площадь полной поверхности параллелепипеда, если длина его большей диагонали равна 10 см.

29. Дана треугольная пирамида SАВС в которой . Найдите площадь полной поверхности этой пирамиды, если АВ = АС = 13 см, ВС = 10 см, а грань SВС составляет с плоскостью основания угол .

30. Длины сторон основания прямого параллелепипеда равны 10 и см, а величина угла между ними равна

31. Длины сторон основания прямой треугольной призмы равны 5, 6 и 9 см. Найдите объем призмы, если длина диагонали боковой грани, проходящей через сторону основании, имеющую наибольшую длину, равна 15 см.

32. Найдите объем правильной четырехугольной пирамиды, если высота ее равна 8 см, а боковое ребро составляет с плоскостью основания угол .

Формулы площади поверхности геометрических фигур.

Площадь геометрической фигуры — численная характеристика геометрической фигуры, показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Площадь куба

Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.

Формула площади куба

где

S

— площадь куба,

a

— длина грани куба.

Площадь прямоугольного параллелепипеда

Формула площади поверхности прямоугольного параллелепипеда

S = 2(

a · b

+

a · h

+

b · h

)
где

S

— площадь прямоугольного параллелепипеда,

a

— длина,

b

— ширина,

h

— высота.

Площадь цилиндра

Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.

Формула для вычисления площади боковой поверхности цилиндра

Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.

Формула для вычисления площади полной поверхности цилиндра

S = 2

π R h

+ 2

π R

² = 2

π R

(

R

+

h

)
где

S

— площадь,

R

— радиус цилиндра,

h

— высота цилиндра,

π = 3. 141592

.

Площадь конуса

Площадь боковой поверхности конуса равна произведению его радиуса и образующей умноженному на число

π

.

Формула площади боковой поверхности конуса:

Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности.

Формула площади полной поверхности конуса:

S =

π R

² +

π R l

=

π R

(

R

+

l

)
где

S

— площадь,

R

— радиус основания конуса,

l

— образующая конуса,

π = 3.141592

.

Площадь шара

Формулы площади шара

• Площадь поверхности шара равна четырем его радиусам в квадрате умноженным на число

  π

  .

• Площадь поверхности шара равна квадрату его диаметра умноженного на число

  π

  .

где

S

— площадь шара,

R

— радиус шара,

D

— диаметр шара,

π = 3. 141592

.

Добавить комментарий

Параллелепипед

Свойства параллелепипеда

1) Параллелепипед имеет трехмерную форму.

2) Имеет 6 граней.

3) У него 12 ребер и 8 вершин.

4) Грани параллелепипеда — параллелограмм.

5) Это призма с параллелограммом в основании.

6) Каждое лицо кажется зеркальным отражением противоположного лица.

7) Диагональ каждой грани называется диагональю грани.

8) Диагональ трехмерного тела параллелепипеда называется диагональю тела.

Объем параллелепипеда

Для данного параллелепипеда пусть «A» будет площадью нижней грани, а «h» — высотой, тогда формула объема будет иметь следующий вид:

Объем параллелепипеда = A × h

Поскольку нижняя грань представляет собой параллелограмм, ее площадь «A» можно рассчитать по формуле:

A = Площадь параллелограмма = основание × высота.

В векторной форме:

Объем параллелепипеда, охватываемого точками a, b и c, определяется по формуле:

Объем = Площадь основания × высота

= | a × b | | c | cos ø

= | (а × б).c |

Площадь поверхности параллелепипеда

1) Площадь боковой поверхности (L.S.A.)

Это произведение периметра основания и высоты параллелепипеда.

L.S.A. = Периметр основания × высота

2) Общая площадь поверхности (T.S.A.)

Это сумма LSA и площади двух оснований.

Т.С.А. = Л.С.А. + 2 (базовая площадь)

В основном есть два типа параллелепипедов:

1.Куб

2. Кубоид

Куб

Куб представляет собой параллелепипед, все шесть граней которого имеют квадратную форму.

Пример: игральные кости, кубик льда, кубик Рубика и т. 2})} = \ sqrt {(2)} \ times (a) \] единиц

5.2}} = \ sqrt 3 \ times \ left (a \ right) \] units

Кубоид

Кубоид — это параллелепипед, все шесть граней которого имеют прямоугольную форму.

Представляет собой объемную коробчатую конструкцию.

Пример: коробка для спичек, пыльник, кирпичи, ящик для инструментов и т. Д.

Пусть длина, ширина и высота кубоида обозначены l, b и h соответственно. Тогда

1) Объем кубоида = Площадь нижней грани (прямоугольная) × Высота

= (l × b) × (h)

= l × b × h

2) L.S.A. = периметр основания (прямоугольник) × высота

= 2 (l + b) × (h)

= 2 (l + b) h

L.S.A. кубоида также можно принять за площадь четырех стен кубовидной комнаты.

3) Т.С.А. = Л.С.А. + 2 (Базовая площадь)

= 2 (l + b) h + 2 (lb)

= 2 (lb + bh + lh)

4) Диагональ лица

Здесь диагональ лица такая же, как и диагональ Прямоугольник. Диагональ грани — это линия, соединяющая две вершины, находящиеся на одной грани, но не на одном ребре.2}} \]

Решенные примеры:

Q.1. Найдите сторону куба площадью 600 см2.

Отв. Площадь поверхности куба = 6 (сторона) 2

Дано, площадь поверхности куба = 600 см2

⇒ 6 (сторона) 2 = 600 см2

⇒ (сторона) 2 = 100 см2

⇒ сторона куба = 10 см.

Q.2. Найдите том, L.S.A., T..S.A. и диагональ тела Кубоида длиной 3 см, шириной 4 см и высотой 5 см.

Отв. a.) Объем кубоида = l × b × h

= 3 см × 4 см × 5 см

= 60 см3

b.) L.S.A. = 2 (l + b) h

= 2 × (3 см + 4 см) × 5 см

= 70 см2

c.) Т.С.А. = 2 (фунт + bh + hl)

= 2 × {(3 см × 4 см) + (4 см × 5 см) + (5 см × 3 см)}

= 2 × (12 см2 + 20 см2 + 15 см2)

= 2 × 47 см2

= 94 см2

d. 2}} \]

= \ [\ sqrt {9 + 16 + 25} \] см

= \ [\ sqrt {50} \] см

= 5 \ [\ sqrt {2} \] см

Q.3. Внутренние размеры кубовидной комнаты — 12 м × 8 м × 4 м. Найдите общую стоимость белой стирки всех четырех стен комнаты, если стоимость побелки составляет рупий. 5 за кв. Метр.

Отв. Пусть длина помещения = l = 12 м

ширина помещения = b = 8 м

высота помещения = h = 4 м

Площадь четырех стен помещения = L.Площадь прямоугольного помещения = 2 (l + b) × h

= 2 (12 + 8) × 4

= 2 × 20 × 4

= 160 м2

Учитывая, стоимость стирки белого на м2 = Rs. 5

Следовательно, общая стоимость белой стирки четырех стен комнаты = Rs.(160 × 5) = рупий. 800.

Площадь параллелограмма — объяснение и примеры

Как следует из названия, параллелограмм — это четырехугольник, образованный двумя парами параллельных прямых . Он отличается от прямоугольника величиной углов при углах. В параллелограмме противоположные стороны равны по длине, а противоположные углы равны по размеру, а в прямоугольнике все углы равны 90 градусам.

Из этой статьи вы узнаете, как рассчитать площадь параллелограмма по формуле площади параллелограмма.

Чтобы узнать, чем его площадь отличается от других четырехугольников и многоугольников, посетите предыдущие статьи.

Как найти площадь параллелограмма?

Площадь параллелограмма — это пространство, ограниченное двумя парами параллельных линий. Прямоугольник и параллелограмм имеют схожие свойства, поэтому площадь параллелограмма равна площади прямоугольника.

Площадь параллелограмма Формула

Рассмотрим параллелограмм ABCD , показанный ниже.Площадь параллелограмма — это пространство, ограниченное сторонами AD, DC, CB, и AB.

Площадь состояний формулы параллелограмма;

Площадь параллелограмма = основание x высота

A = (b * h) кв.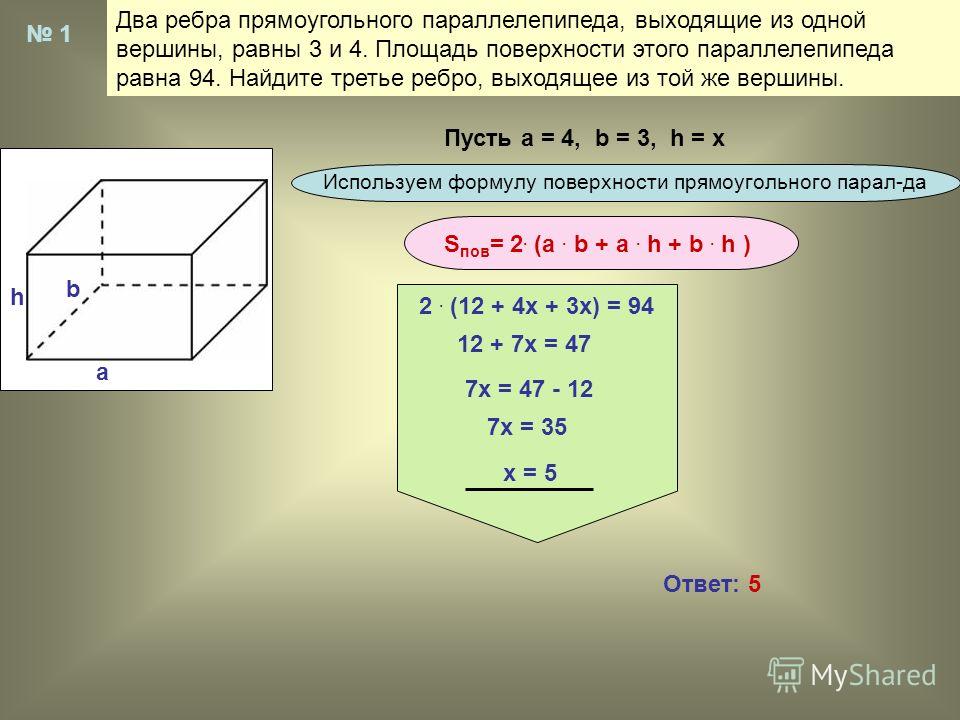 единиц

Где b = основание параллелограмма и,

h = высота или высота параллелограмма.

Высота или высота — это перпендикулярная линия (обычно пунктирная) от вершины параллелограмма к любому из оснований.

Пример 1

Вычислите площадь параллелограмма, основание которого 10 сантиметров, а высота 8 сантиметров.

Раствор

A = (b * h) кв. единицы.

A = (10 * 8)

A = 80 см ²

Пример 2

Вычислите площадь параллелограмма с основанием 24 дюйма и высотой 13 дюймов

Решение

А = (ш * в) кв.единицы.

= (24 * 13) квадратный дюйм.

= 312 квадратных дюймов.

Пример 3

Если основание параллелограмма в 4 раза больше высоты, а площадь равна 676 см², найдите основание и высоту параллелограмма.

Решение

Пусть высота параллелограмма = x

и основание = 4x

Но площадь параллелограмма = b * h

676 см² = (4x * x) кв. единиц

676 = 4x ²

Разделим обе стороны на 4, чтобы получить,

169 = x ²

Найдя квадратный корень из обеих сторон, мы получим

x = 13.

Заменитель.

Основание = 4 * 13 = 52 см

Высота = 13 см.

Следовательно, основание и высота параллелограмма 52 см и 13 см соответственно.

Помимо формулы площади параллелограмма, существуют другие формулы для вычисления площади параллелограмма.

Давайте посмотрим.

Как найти площадь параллелограмма без высоты?

Если высота параллелограмма нам неизвестна, мы можем использовать концепцию тригонометрии, чтобы найти его площадь.

Площадь = ab sine (α) = ab sine (β)

Где a и b — длина параллельных сторон, а β или α — угол между сторонами параллелограмма.

Пример 4

Найдите площадь параллелограмма, если его две параллельные стороны составляют 80 см и 40 см, а угол между ними составляет 56 градусов.

Решение

Пусть a = 80 см и b = 40 см.

Угол между a и b = 56 градусов.

Площадь = ab sine (α)

Заменитель.

A = 80 × 40 синус (56)

A = 3200 синус 56

A = 2652,9 кв. См.

Пример 5

Вычислите углы между двумя сторонами параллелограмма, если длина его сторон составляет 5 м и 9 м, а площадь параллелограмма равна 42,8 м ² .

Решение

Площадь параллелограмма = ab синус (α)

42,8 м ² = 9 * 5 синус (α)

42.8 = 45 синус (α)

Разделим обе части на 45.

0,95111 = sin (α)

α = синус ^-1 0,95111

α = 72 °

Но β + α = 180 °

β = 180 ° — 72 °

= 108 °

Следовательно, углы между двумя параллельными сторонами параллелограмма равны; 108 ° и 72 °.

Пример 6

Вычислите высоту параллелограмма, параллелограммы которого равны 30 см и 40 см, а угол между этими двумя сторонами равен 36 градусам. Примем основание параллелограмма равным 40 см.

Решение

Площадь = ab sine (α) = bh

30 * 40 синус (36) = 40 * h

1,200 синус (36) = 40 * h.

Разделите обе стороны на 40.

h = (1200/40) синус 36

= 30 синус 36

h = 17,63 см

Итак, высота параллелограмма составляет 17,63 см.

Как найти площадь параллелограмма по диагоналям?

Предположим, что d ₁ и d ₂ — диагонали параллелограмма ABCD, , тогда площадь параллелограмма задается как,

A = ½ × d ₁ × d ₂ синус ( β) = ½ × d ₁ × d ₂ синус (α)

Где β или α — угол пересечения диагоналей d ₁ и d ₂ .

Пример 7

Вычислите площадь параллелограмма, диагонали которого составляют 18 см и 15 см, а угол пересечения диагоналей равен 43 °.

Решение

Пусть d ₁ = 18 см и d ₂ = 15 см.

β = 43 °.

A = ½ × d ₁ × d ₂ синус (β)

= ½ × 18 × 15 синус (43 °)

= 135 синус 43 °

= 92,07 см ²

Следовательно, площадь параллелограмма 92.07 см ² .

Практические вопросы

1. Флаг имеет основание 2,5 фута и высоту 4,5 фута. Если флаг имеет форму параллелограмма, найдите площадь флага.
2. Рассмотрим параллелограмм, площадь которого в два раза больше площади треугольника. Если обе эти формы имеют общее основание, какова связь между их высотой?

Ответы

1. 25 футов ²
2. Высоты параллелограмма и треугольника будут равны.

Предыдущий урок | Главная страница | Следующий урок

Определители и объемы

Пусть A — матрица размера n × n со столбцами v1, v2, . .., vn, и пусть T: Rn → Rn — соответствующее преобразование матрицы T (x) = Ax. Тогда T (e1) = v1 и T (e2) = v2, поэтому T переводит единичный куб C в параллелепипед P, определяемый v1, v2, …, vn:

Поскольку единичный куб имеет объем 1 и его изображение имеет объем | det (A) |, преобразование T масштабировало объем куба в | det (A) |.Перефразируя:

Обозначение T (S) означает изображение области S при преобразовании T. В обозначении построителя множеств это подмножество

T (S) = CT (x) | xinSD.

Фактически, T масштабирует объем любой области в Rn с тем же коэффициентом, даже для округлых областей.

Проба

Пусть C — единичный куб, пусть v1, v2, …, vn — столбцы A, и пусть P — паралелепипед, определяемый этими векторами, так что T (C) = P и vol (P) = | det (А) |. Для A> 0 обозначим AC кубом со сторонами A, i.е., паралелепипед, определяемый векторами Ae1, Ae2, …, Aen, и AP мы определяем аналогично. По второму определяющему свойству T переводит AC в AP.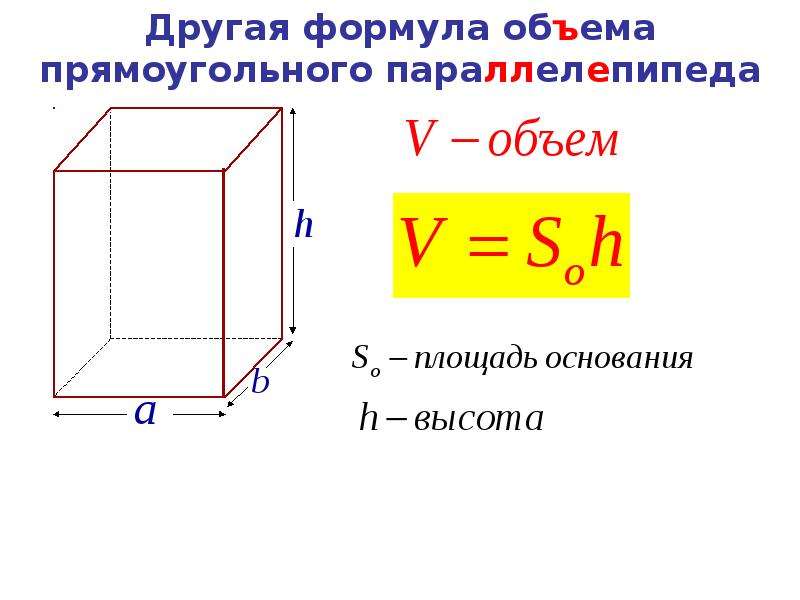 Объем AC равен An (мы масштабировали каждый из n стандартных векторов в A раз), а объем AP равен An | det (A) | (по той же причине), поэтому мы показали, что T масштабирует объем AC на | det (A) |.

Ae2Ae1ACvol (AC) = AnTF || v1v2 || GAv2Av1APvol (AP) = An | det (A) |

По первому определяющему свойству изображение переводчика AC является переводом AP:

Т (х + АС) = Т (х) + АТ (С) = Т (х) + AP.

Поскольку перевод не изменяет объемы, это доказывает, что T масштабирует объем перевода AC на | det (A) |.

На этом этапе нам нужно использовать технику многомерного исчисления, поэтому мы дадим только представление об остальной части доказательства. Любую область S можно аппроксимировать набором очень маленьких кубиков вида x + AC. Затем изображение T (S) аппроксимируется изображением этого набора кубиков, который представляет собой набор очень маленьких паралелепипедов вида T (x) + AP.

Объем S приблизительно равен сумме объемов кубов; фактически, когда A стремится к нулю, предел этой суммы в точности равен vol (S). Точно так же объем T (S) равен сумме объемов паралелэпипедов, считая в пределе A → 0. Ключевым моментом является то, что объем каждого куба масштабируется на | det (A) |. Следовательно, сумма объемов паралеллепипедов равна | det (A) | умножить на сумму объемов кубиков. Это доказывает, что vol (T (S)) = | det (A) | vol (S).

Параллелепипед — Калькулятор геометрии

1D линия, круговая дуга, парабола, спираль, кривая Коха 2D Правильные многоугольники: Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, девятиугольник, десятиугольник, шестиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольника Другие многоугольники: треугольник, прямоугольный треугольник, равнобедренный треугольник, ИК-треугольник, четырехугольник, прямоугольник, золотой прямоугольник, ромб, параллелограмм, полуквадратный воздушный змей, воздушный змей, воздушный змей, правая трапеция, равнобедренная трапеция, трех равносторонняя трапеция, трапеция, циклический четырехугольник, тангенциальный четырехугольник, стрелка, вогнутый четырехугольник, крест Антипараллелограмм, Форма дома, Симметричный пятиугольник, Вырезанный прямоугольник, Вогнутый пятиугольник, Вогнутый правильный пятиугольник, Параллелогон, Вытянутый шестиугольник, Вогнутый шестиугольник, Стрелка-шестиугольник, Прямоугольный шестиугольник, L-образная форма, Острый перегиб, T-образная форма, Усеченный квадрат, Рамка, Открытая рамка, сетка, крест, форма X, форма H, тройная звезда, четыре звезды, пентаграмма, гексаграмма, уникурсальная гексаграмма, октаграмма, звезда Лакшми, многоугольник с двойной звездой, многоугольник, многоугольник 90 581 Круглые формы: Круг, Полукруг, Круговой сектор, Круговой сегмент, Круговой слой, Круговой центральный сегмент, Круглый угол, Круглый угол, Круговая касательная стрелка, Форма капли, Полумесяц, Остроконечный овал, Ланцетная арка, Бугорок, Кольцо, Кольцевой сектор , Изогнутый прямоугольник, закругленный многоугольник, закругленный прямоугольник, эллипс, полуэллипс, эллиптический сегмент, эллиптический сектор, эллиптическое кольцо, стадион, спираль, бревно. Спираль, Треугольник Рело, Циклоида, Двойная Циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой дуговый многоугольник, Коготь, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник 3D Платоновых тел: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр архимедова Solids: усеченный тетраэдр, кубооктаэдр, усеченный куб, усеченный октаэдр, ромбокубооктаэдр, усеченный кубооктаэдр, икосододекаэдр, усеченный додекаэдр, усеченный икосаэдр, Snub куб, ромбоикосододекаэдр , Усеченный икосододекаэдр, Snub Додекаэдр Каталонских Сухой остаток: триакистетраэдр, ромбический додекаэдр, триакисоктаэдр, тетракисгексаэдр, дельтоидальный икоситетраэдр, гексакис октаэдр, ромбический триаконтаэдр, триакисикосаэдр, пентакисдодекаэдр, Пятиугольные Icositetrahedron, дельтоидальный гексеконтаэдр, гексакис Икосаэдр, Пятиугольный гексеконтаэдр Твердые тела Джонсона: Пирамиды, купола, ротонда, удлиненные пирамиды, гиро-продолговатые пирамиды, бипирамиды, удлиненные бипирамиды, гиро-продолговатая квадратная дипирамида, гиробифастигедрон, дисфагениум Sphenocorona, Disphenocingulum Другие многогранники: Кубоид, квадратный столб, треугольная пирамида, квадратная пирамида, правильная пирамида, пирамида, квадратная пирамида, правильная пирамида, створка, правильная бипирамида, бипирамида, двуугольник, двуугольник , Клин, полутетраэдр, ромбоэдр, параллелепипед, правильная призма, призма, наклонная призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клин-кубоид, полукубоид, скошенный кубоид, слиток, скошенный призматический трехгранник , Разрезанный кубоид, усеченный кубоид, кубоид с тупыми краями, удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый кубоид, полый кубоид, полая пирамида, полый ствол, звездная пирамида, звездчатый октаэдр, малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр Круглые формы: Сфера, полусфера, сферический угол, цилиндр, отрезной цилиндр, наклонный цилиндр, изогнутый цилиндр, эллиптический цилиндр der, обобщенный цилиндр, конус, усеченный конус, косой круговой конус, эллиптический конус, общий конус, общий усеченный конус, биконус, усеченный биконус, заостренный столб, закругленный конус, капля, сфероид, эллипсоид, полуэллипсоид, сферический сектор, сферическая крышка , Сферический сегмент, сферический центральный сегмент, двойной калот, сферический клин, полуцилиндр, диагонально разрезанный пополам цилиндр, цилиндрический клин, цилиндрический сектор, цилиндрический сегмент, цилиндр с плоским концом, полуконус, конический сектор, конический клин, сферическая оболочка, полусферическая оболочка, Цилиндрическая оболочка, вырезанная цилиндрическая оболочка, косая цилиндрическая оболочка, полый конус, усеченный полый конус, сферическое кольцо, тор, тор шпинделя, тороид, сектор тора, сектор тороида, арка, тетраэдр Рело, капсула, сегмент капсулы, двойная точка, антиконус, Усеченный антиконус, сферический цилиндр, линза, вогнутая линза, ствол, форма яйца, параболоид, гиперболоид, олоид, твердые тела Штейнмеца, твердое тело вращения 4D Тессеракт, Гиперсфера

Anzeige Расчеты на параллелепипеде. У параллелепипеда противоположные грани и ребра равны. Введите три длины ребра и три угла в одной из вершин и выберите количество десятичных знаков. Затем нажмите Рассчитать. Пожалуйста, введите углы в градусах, здесь вы можете конвертировать угловые единицы. α — угол при bc, β — угол при ac и γ — угол при ab. Формулы: A = 2 * (a * b * sin (γ) + a * c * sin (β) + b * c * sin (α)) V = abc * √ 1 + 2 * cos ( α) * cos (β) * cos (γ) — cos² (α) — cos² (β) — cos² (γ) Длины кромок имеют одинаковую единицу измерения (например,г. метр), площадь имеет эту единицу в квадрате (например, квадратный метр), объем имеет эту единицу в степени трех (например, кубический метр). Аудио / видео имеет этот блок -1 . Поделиться: © Jumk.de Веб-проекты Anzeige

Расчет формулы объема и площади в Excel

Программа Excel — лучший калькулятор. Мы привыкли использовать для расчетов традиционные бухгалтерские калькуляторы, хотя все их возможности поддерживаются программой Excel. Более того, у него есть неоспоримые преимущества.

В некоторых формулах вы можете выполнить только один математический расчет для расчета калькуляции. В таких случаях при изменении данных нужно все изменить. Но если все данные распределены по ячейкам и формула будет относиться только к единицам, то при любых изменениях менять не нужно. Одна формула может использоваться много раз. Чтобы понять, как это работает, лучше привести несколько практических примеров.

Как рассчитать объем и площадь в Excel

В ячейку A1 записываем формулу расчета объема параллелепипеда: a = 6 см; б = 8 см; c = 12 см.

В ячейку А2 записываем формулу расчета площади круга: r = 25 см.

В ячейке A3 формула содержит функцию без аргументов PI (), которая сама по себе содержит общее количество PI (а не 3,14). Поэтому значения ячеек A2 и A3 немного отличаются.

Расчет арифметических формул в Excel

Допустим, нам нужно вычислить формулу в Excel:

Чтобы получить результат расчета, просто записываем в одну строку:

5 арифметических операций: суммирование, вычитание, умножение, деление и представление в степень (^). Если писать все в одну строчку, то надо соблюдать правила арифметической последовательности. Для этого нужно использовать круглые скобки.

Формула для расчета объема шара в Excel

Например, нам нужно регулярно рассчитывать объемы сфер разного радиуса.

Формула для вычисления объема шара выглядит так:

Предыдущие примеры плохо подходят для решения этой проблемы, так как они не используют значения переменных в формулах, а только константы.3 (A2 — ссылка на ячейку).

В ячейку A2 мы введем разные радиусы, и после каждого ввода в ячейку B2 мы получим результат вычисления объема сфер, соответствующего его радиусу.

Примечание. Если вы используете несколько вычислений в Excel или формулы, которые содержат ссылки на ячейки в качестве значений переменных, вам всегда нужно подписывать каждую ячейку входящими данными и формулами. Это позволит избежать ошибок и легко прочитать значения или результаты расчета формул.

Площадь параллелограмма с учетом сторон и угла.

Калькулятор

[1] 2020/03/23 18:52 Младше 20 лет / Высшая школа / Университет / аспирант / Немного /

Цель использования

Тест по геометрии .

Комментарий / запрос

Не могли бы вы рассказать, как вы получили решение?

[2] 2019/07/14 14:58 Уровень 40 лет / Самостоятельно занятые люди / Полезные /

Цель использования

Рассчитайте площадь параллелограмма, необходимую для построения узора для деревянного художественного проекта.

[3] 2019/04/18 02:24 До 20 лет / Средняя школа / Университет / аспирант / Немного /

Цель использования

Домашнее задание Precalc

Комментарий / запрос

Шаг -пошаговый процесс, показывающий пользователям, как перейти от цифр к ответам.

[4] 2018/12/05 16:45 Моложе 20 лет / Другое / Немного /

Цель использования

решение математической задачи, дал мне ответ, но никаких шагов для его решения нет

[5] 2018/11/22 03:22 Моложе 20 лет / Начальная школа / Младший школьник / Очень /

Цель использования

Для выполнения домашнего задания по математике

Комментарий / Запрос

все сработало хорошо

[6] 2018/04/12 04:28 Моложе 20 лет / Средняя школа / Университет / аспирант / Очень /

Цель использования

Программа

[7] 2018/01 / 18 12:09 Моложе 20 лет / Старшая школа / Университет / аспирант / Не совсем /

Цель использования

для слов моих неизвестных вопросов

Комментарий / запрос

Я не вижу процесса, в котором это происходит
Вы добавляете кнопку ниже, по крайней мере, для студентов, которые хотят изучать

[8] 2017/06/13 01:13 Уровень 60 и старше / Самостоятельно занятые люди / Очень /

Цель использования

На карте участка, которая представляла собой идеальный параллелограмм, проверьте квадратные футы (и площадь).

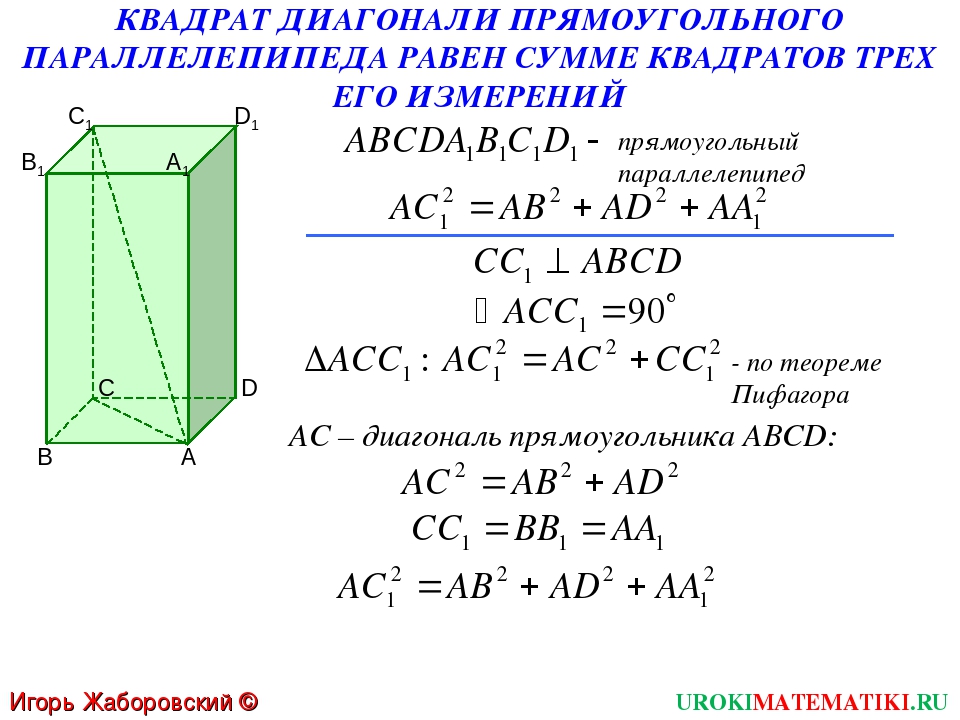
Комментарий / запрос

Для нематематических основных единиц измерения и синтаксиса символов всегда неприятно. Было бы здорово ввести угол в десятичном формате или в градусах-минутах-секундах (преобразование несложно, но требует дополнительных шагов). Также неплохо было бы иметь формулу Excel. В Excel функция Sin требует ввода в радианах, поэтому side1 * side2 * sin (pi () / 180)

[9] 26.03.2017 10:00 Моложе 20 лет / Средняя школа / Университет / Аспирант / Полезное /

Цель использования

Математическая версия

Комментарий / запрос

как вы получили площадь с заданными сторонами и углом? Какой был метод?

from Keisan

Площадь параллелограмма = основание * высота = a * (b * sinθ)

[10] 2015/10/10 02:45 Уровень 30 лет / Учитель / Исследователь / Очень /

Цель использования

Знать площадь параллелограмма с учетом сторон и угла

Комментарий / запрос

Это очень просто и быстро.

Кубоид | Определение, форма, площадь и свойства

Кубоид — это не куб. Куб может быть кубоидом , но также может быть прямоугольная призма. Кубоид — это частный случай параллелепипеда, трехмерного тела с шестью гранями в форме параллелограмма. Обувная коробка — это кубоид. Пара кубиков, кубики и учебники в твердом переплете — кубоиды. Книги, картонные коробки и плитки мороженого Klondike® имеют форму куба. Если трехмерный объект имеет шесть параллелограммов, которые встречаются под прямым углом, это кубоид.

Содержание

1. Параллелограмм
2. Параллелепипед
3. Кубоид
4. Свойства кубоидов
5. Расчет объема кубоидов
6. Попробуй!
7. Площадь поверхности кубоидов
8. Пример проблемы!

Параллелограмм

Параллелограмм — многоугольник с двумя парами параллельных сторон. Итак, прямоугольники и квадраты — параллелограммы:

[вставить рисунок квадрата, явно наклонного параллелограмма и прямоугольника]

Параллелепипед

Если собрать из шести параллелограммов трехмерное тело, получится многогранник, называемый параллелепипедом :

[вставить рисунок параллелепипеда с явно наклоненными сторонами]

Другое название этой трехмерной формы — прямоугольная призма или правая призма.

Кубоид

Если у вас есть параллелепипед с вершинами, составляющими 90 °, у вас есть кубоид :

[вставить чертеж прямоугольной формы; ИЛИ вместо этих трех рисунков рассмотрите видео, в котором параллелограмм преобразуется в трехмерную форму наклонной коробки, а затем выпрямляется, чтобы создать форму коробки для обуви с прямыми углами]

Свойства кубоидов

Все кубоиды имеют следующие свойства:

1. Три измерения ширины, длины и глубины (или высоты)
2. Шесть прямоугольных граней
3. Все вершины равны 90 °

Эти три свойства означают, что противоположные стороны кубоида параллельны и конгруэнтны друг другу.

Эти условия приводят к форме коробки, такой как коробка из-под обуви, коробка хлопьев или учебник.

Расчет объема кубоидов

Чтобы найти объем любого кубоида, формула:

• V = длина x ширина x высота (или глубина)
• V = л / ч

Поскольку объект трехмерен, объем выражается в кубе — третьей степени — любых используемых вами линейных единиц: кубических метров, кубических футов, кубических ярдов и т. Д.

Попробуй!

Вот транспортный контейнер, который вы видите сложенным, как детские кубики, на грузовых кораблях:

[вставить фотографию 40-футового транспортного контейнера без авторских прав]

Наружные размеры 8 футов в ширину, 8.5 футов в высоту и 40 футов в длину. Какой объем контейнера?

• V = л / ч
• V = 8 футов x 8,5 футов x 40 футов
• V = 2720 кубических футов

Площадь поверхности кубоидов

Чтобы вычислить площадь поверхности любого кубоида, вам необходимо знать площадь поверхности каждой грани. Затем вы складываете все шесть областей вместе.

Поскольку противоположные грани совпадают, вам нужно всего три грани, которые вы можете умножить на два, а затем сложить. Вы используете каждое измерение (ширину, длину и высоту или глубину) два раза и только два раза в формуле.

Формула:

Площадь поверхности всегда измеряется в квадратных единицах линейного измерения, второй степени. 2

Пример проблемы!

Декоративный ящик для хранения, который вы используете для хранения трофеев и лент на соревнованиях по математике, имеет размеры 12 дюймов в длину x 8.3

Кубоид — это прямоугольная призма, параллелепипед с вершинами (углами) 90 °. Кубоиды повсюду: кирпичи, здания, бутерброды с мороженым, учебники, коробки из-под обуви, игровые кости, транспортные контейнеры, коробки с хлопьями и во многих других уголках вашего мира. Вы можете легко вычислить как площадь поверхности, так и объем любого кубоида, если вы знаете его ширину, длину и высоту (или глубину).

Следующий урок:

Dodecagon

.