Геометрия 1 уровень 1 вариант 8 класс: ГДЗ самостоятельные и контрольные работы по геометрии 8 класс Иченская, Атанасян

ГДЗ самостоятельные и контрольные работы по геометрии 8 класс Иченская, Атанасян

Геометрия – это один из главных элементов общеобразовательного обучения. Появившись в седьмом классе, эта дисциплина предполагает к повторению все то, что было изучено на уроках математики ранее, но одновременно знакомит школьников с новыми понятиями: многоугольники и их свойства, окружности и векторы, параллелограммы и трапеции. Также ребята учатся находить площади и высоты многих геометрических фигур, узнают о признаках подобия треугольников и правилах работы с теоремами и аксиомами. Чтобы хорошо подготовиться к срезам знаний по итогу каждой темы, можно воспользоваться гдз по геометрии самостоятельные и контрольные работы за 8 класс Иченская, в которых школьники найдут полностью готовые задания. На страницах пособия уже разобраны сложные геометрические задачи, сопровождающиеся не только точными рисунками с соблюдением всех правил, но и пояснения, полноценные алгоритмы решения и т.

д.

Основные группы пользователей сборника готовых ответов

Восьмой класс – это сложный период в жизни любого ученика, потому что помимо огромного количества правил, теорем, аксиом и формул, дети должны регулярно закреплять свои знания и подтверждать их уровень. Для самопроверки хорошо подойдет справочник с онлайн ответами к самостоятельным и контрольным работам по геометрии для 8 класса авторов Иченской, Атанасян, который будет незаменим:

• восьмиклассникам, когда нужно дополнительно позаниматься, решая сложные геометрические задачи на поиск площадей, построение высот и углов, с целью обнаружить пробелы в своих знаниях;
• при подготовке к предстоящим олимпиадам и конкурсам, где ребята должны знать все, начиная от формул периметра и площади фигур и заканчивая умножением и делением вектора на число и действий между векторами;
• если время на проверку работ у учителя ограничено, а нужно полноценно и адекватно оценить каждого ученика, чтобы поставить соответствующие оценки и приступить к изучению нового материала;
• для родителей, которые хотят организовать для своего ребенка домашнюю проверку знаний и не знают, какие задания подобрать для этого. Готовые ответы к ним помогут также легко разобраться и с уровнем знаний по данному предмету;
• выпускникам 9 и 11 классов в качестве дополнительной литературы, которая поможет не только восполнить знания, изучая готовые алгоритмы решения заданий, но и стать более уверенным в себе на экзаменах.

Неоспоримые плюсы обращения к онлайн справочникам

Благодаря современным технологиям и возможности пользоваться портативными гаджетами, получить доступ к решебнику по геометрии для самостоятельных и контрольных работ по геометрии за 8 класс (авторы Иченская, Атанасян) сегодня может любой школьник. Это является одним из главных преимуществ готовых ответов. Более того, онлайн справочник это:

• содержание точных, максимально развернутых и изложенных доступным языком решений, которые помогают в учебе;
• удобная навигация, требующая только выбрать вид работы и подходящий вариант, чтобы получить готовые ответы;
• адаптивная версия мобильной версии, а значит, доступность в любом месте;
• возможность получения оперативного ответа с пояснением, раскрывающим суть задания и служащим примером для дальнейшего самостоятельного решения аналогичных задач.

Подготовка к проверочным работам и выполнение домашних заданий с еуроки ГДЗ будет проходить намного легче и быстрее, как для школьников, так и для их родителей.

ГДЗ рабочая тетрадь по геометрии 8 класс Глазков, Камаев К учебнику Атанасяна Экзамен

География – это сложная, но интересная дисциплина в учебной программе. Навыки и умения в области этой науки формируют фундаментальную базу для дальнейшего профессионального обучения нынешних школьников. Заучивание формул, знакомство с теоремами и аксиомами, а также постоянное решение геометрических задач на построение различных фигур, нахождение их данных и определение свойств способствует формированию у ребят нестандартного мышления, расширению кругозора и развитию мировоззрения. Однако не все восьмиклассники могут успешно справиться со всем арсеналом заданий, что чревато снижением общего показателя успеваемости. Чтобы предотвратить это, даже учителя рекомендуют время от времени использовать

гдз по геометрии рабочая тетрадь за 8 класс Глазков – пособие, в котором собраны верные ответы на все виды вопросов и практических упражнений. Более 90 страниц сборника помогут справиться не только с текущими домашними уроками, но и хорошо подготовиться к предстоящим проверочным работам в школе.

Кому будут полезны пособия с правильными онлайн ответами?

В восьмом классе изучение геометрии подразумевает знакомство с теоремой Пифагора и формулами площадей различных фигур: треугольники, трапеции, параллелограмм и т.д. Чтобы качественно усвоить весь теоретический материал, ребятам предстоит выполнить задачи на определение признаков подобия треугольников, разобраться с тригонометрическими функциями острого углы треугольника, а также понять, что такое центральные и вписанные углы. И только ежедневно занимаясь, используя

готовые ответы по геометрии к рабочей тетради за 8 класс авторов Глазкова, Камаева к учебнику Атанасяна, можно не только вникнуть в суть этих тем, но и в разы улучшить свои знания по предмету. Применение такого сборника пригодится:

• ученикам 8 классов как подручный материал для регулярной проверки своих работ перед предстоящими уроками;
• ученикам 9 и 11 классов в качестве пособия для выявления пробелов в знаниях перед сдачей ГИА и ЕГЭ;
• школьникам 10 классов, чтобы помочь вспомнить ранее изученные темы и правила решения разных по типу геометрических заданий;
• учителям-предметникам среднеобразовательных школ, репетиторов как методическое пособие для сверки работ школьников;
• ребятам, которые принимают участие в различных олимпиадах и математических конкурсах.

Явные преимущества применения решебника к рабочей тетради по геометрии за 8 класс (авторы Глазков, Камаев)

Благодаря наличию под рукой сборника с готовыми ответами любой школьник сможет при необходимости подсмотреть верное решение и оформить свою работу так, как того требуют правила. Также с его помощью легко:

• сэкономить время на выполнение домашних уроков и подготовку к предстоящим проверочным работам;
• самостоятельно проверить правильность своих ответов к задачам и теоретическим вопросам;
• тщательно проработать все допущенные ошибки, обратить внимание на пробелы в знании той или иной темы;
• найти нужную информацию в одном месте, не обращаясь к дополнительным источникам;
• легко разобраться со сложными заданиями и вникнуть в темы.

Пособия с готовыми ответами на еуроки ГДЗ относятся к числу полезной дополнительной литературы, которая помогает школьникам хорошо закрепить знания на практике и улучшить свою успеваемость по разным предметам.

Страница не найдена

Новости

31 янв

Басманный суд Москвы арестовал Владислава Струженкова, который устроил взрыв у церковной школы в подмосковном Серпухове.

31 янв

Власти Санкт-Петербурга решили ужесточить меры по борьбе с коронавирусом.

31 янв

В российских регионах в дистанционном формате обучаются 8,69% школьников, на карантине по коронавирусу находятся 230 школ.

31 янв

С 31 января по 7 февраля всех школьников и студентов средних специальных учебных заведений Тувы переводят на дистанционный формат обучения.

30 янв

Полностью переводить школы на дистанционное обучение не планируется. Об этом заявил в программе «Москва. Кремль. Путин» на телеканале «Россия 1» министр просвещения России Сергей Кравцов.

29 янв

Профессор НИУ ВШЭ в Санкт-Петербурге Даниил Александров в беседе с «Московским комсомольцем» порекомендовал несовершеннолетней студентке МГУ вернуться в школу.

28 янв

Все трое подростков, которые подозреваются в подготовке вооружённого нападения на школу в Нижнем Новгороде, арестованы на два месяца, сообщает Московский районный суд города.

Входная контрольная работа по геометрии 8 класс

Входная контрольная работа

Составила

учитель математики

Чурина Елена Вениаминовна

первая квалификационная категория.

Аннотация

Материал содержит контрольную работу по геометрии для 8 класса. Учебник «Геометрия 7-9», автор: Погорелов А. В. Работа рассчитана на 45 минут для обучающихся общеобразовательных школ.

Цель: определение уровня учебной подготовки по предмету на начало учебного года.

Задачи:

Выявить уровень знаний, умений и навыков обучающихся на начало учебного года.

Развивать творческие способности, логическое мышление, интерес к предмету.

Воспитывать внимательность, самостоятельность, настойчивость, трудолюбие.

Тип урока: контроль знаний и умений.

План урока:

1.Организационный момент.

Сообщение темы урока; постановка цели урока; организация учащихся для выполнения

работы.

2. Выполнение работы.

3. Итог урока.

4. Домашнее задание.

Выполнение контрольной работы по текстам.

Входная контрольная работа по геометрии

8 класс

Вариант 1

В задании №1выберите один верный ответ.

№1. Если один из смежных углов равен 34°, то второй угол будет

1)прямой

2)острый

3)развернутый

4)тупой

№2 Какое из сле­ду­ю­щих утвер­жде­ний верно? За­пи­ши­те их но­ме­ра.

1) Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой на­крест ле­жа­щие углы равны, то пря­мые па­рал­лель­ны.

2)Если угол равен 108°, то вер­ти­каль­ный с ним равен 72°.

3 )Если две сто­ро­ны и угол между ними од­но­го тре­уголь­ни­ка со от­вет­ствен­но равны двум сто­ро­нам и углу между ними дру­го­го треугольника, то такие тре­уголь­ни­ки равны.

№3 Прямая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окружности. Хорда KM об­ра­зу­ет с ка­са­тель­ной угол, рав­ный 46°. Най­ди­те ве­ли­чи­ну угла OMK. Ответ дайте в градусах.

№4 В тре­уголь­ни­ке ABC AC = BC. Внеш­ний угол при вер­ши­не А равен 123°. Най­ди­те угол C. Ответ дайте в градусах.

№5. В равнобедренном треугольнике один из углов равен 1200, боковая сторона 12 см. Найдите высоту, проведенную к основанию.

Входная контрольная работа по геометрии 8 класс Вариант 2

В задании №1выберите один верный ответ.

№1. Если один из смежных углов равен 98°, то второй угол будет

1)прямой

2)острый

3)развернутый

4)тупой

№2 Какое из сле­ду­ю­щих утвер­жде­ний верно? За­пи­ши­те их но­ме­ра.

1) Если угол равен 54°, то вер­ти­каль­ный с ним равен 126°.

2) Если сто­ро­на и два прилежащих к ней угла од­но­го тре­уголь­ни­ка со­от­вет­ствен­но равны сто­ро­не и двум прилежащим к ней углам дру­го­го треугольника, то такие тре­уголь­ни­ки равны.

3 )Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой сумма внутренних односторонних углов равна 180 , то пря­мые па­рал­лель­ны.

№3 Прямая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окружности. Хорда KM об­ра­зу­ет с ка­са­тель­ной угол, рав­ный 52°. Най­ди­те ве­ли­чи­ну угла OМК. Ответ дайте в градусах.

№4 В тре­уголь­ни­ке ABC AВ = BC. Внеш­ний угол при вер­ши­не С  равен 137°. Най­ди­те угол В. Ответ дайте в градусах.

№5. В равнобедренном треугольнике один из углов равен 1200, высота, проведенная к основанию 8 см. Найдите боковую сторону.

Ответы: 

Вариант 1

№1 4

№2 13

№3 44°

№4 66°

№5 6 см
 

Вариант 2

№1 2

№2 23

№3 38°

№4 94°

№5 16 см

Время проведения работы: сентябрь

Система оценивания работы:

Задания №1-№2 оцениваются в 1 балл.

Задания №3-№5 второй части оцениваются в 2 балла.

Задание	Кол-во баллов	Критерий оценивания
№3	0 баллов	Неверно найден угол.
	1 балл	Ход решения верный, найден угол. Может быть допущена описка или вычислительная ошибка.
	2 балла	Ход решения верный. Получен верный ответ.
№4	0 баллов	Неверно найден угол.
	1 балл	Ход решения верный, найден угол. Может быть допущена описка или вычислительная ошибка.
	2 балла	Ход решения верный. Получен верный ответ.
№5	0 баллов	Неверно найдена сторона треугольника.
	1 балл	Ход решения верный, найдена сторона треугольника. Может быть допущена описка или вычислительная ошибка.
	2 балла	Ход решения верный. Получен верный ответ.

Критерии оценивания:

7-8 баллов – «5» (отлично)

6-7 баллов – «4» (хорошо)

4-5 баллов «3» (удовлетворительно)

Менее 4 баллов- «2» (неудовлетворительно)

Использованные источники: https://ege.sdamgia.ru

ГДЗ по Геометрии за 8 класс Казаков В. В.

Геометрия 8 класс Казаков В. В. опорные конспекты

Авторы: Казаков В. В.

Всем нам с детства знаком такой предмет, как геометрия. Многие ученики считают, что знания по данной дисциплине никак не отразятся на взрослой жизни и не понадобятся в повседневной работе. Это обманчивое предположение. Предмет помогает формировать абстрактное мышление, учит анализировать и производить расчеты. Знания в области геометрии особенно пригодятся тем, кто решит связать свою жизнь с программным обеспечением и компьютерами. Владеть знаниями стоит в совершенстве. Порой основное пособие не может дать максимум информации. Стоит обратить свое внимание на «ГДЗ по геометрии 8 класс Учебник Казаков (Народная асвета)». Это универсальный сборник, который поможет разобраться со многими ключевыми моментами. В нем рассмотрены наиболее сложные темы:

• многоугольники;
• окружности;
• работа с треугольниками и многое другое.

Решебник способен дать детальное разъяснение на каждую тематику.

Особенности ГДЗ

Дополнительное пособие – это верный друг и помощник. Потому что в нем содержится огромное количество информации. Решебник состоит из:

• 422 геометрических задач;
• 29 параграфов тестирований, направленных на проверку и закрепление ранее полученных знаний;
• нескольких заданий, требующих текстового ответа;
• упражнений для подготовки к проверочным работам;
• 3D геометрии.

Для самых одаренных и заинтересованных учеников представляется возможность развить свои навыки до максимально возможного уровня. Для этого авторы подготовили несколько упражнений, направленных на тренировку умственных возможностей школьника.

Чем полезен решебник по геометрии за 8 класс от Казакова

С помощью дополнительного пособия любой ученик сможет:

• эффективно и качественно произвести выполнение домашних работ;
• подготовиться ко всем предстоящим испытаниям;
• разобрать вопросы и ответы, которые озвучиваются на уроках;
• выявить свои слабые стороны и заострить внимание на устранение проблем;
• завоевать уважение в классе, помогая одноклассникам;
• научиться правильно оформлять рабочую тетрадь.

Решебник способен решить любые вопросы, связанные с изучением геометрии. Итак, «ГДЗ по геометрии 8 класс Учебник Казаков В.В. (Народная асвета)» – это многофункциональное средство для знакомства с геометрией. Пользоваться им может любой ребенок, независимо от уровня подготовленности.

Задачи на повторение курса геометрии в 8 классе. Базовый уровень

Дидактический материал для работы репетитора по математике с учеником 8 класса слабого и среднего уровня способностей. Базовый учебник по геометрии — Атанасян 7-9 кл. Почти все задачи составлены так, что первая решается в совместно с репетитором, а вторая остается для домашней работы. Вторая отличаются от первой только числами.

№1. В параллелограмме АВСD высота ВH равна 4 см, а сторона ВС=10см. Найти площадь параллелограмма.

№2. В трапеции ABCD CH – высота, BC=2см, AH=3см, HD=5см, CH=4см. Найдите площадь данной трапеции.

№3. В параллелограмме MNKP MT- биссектриса угла M. Известно, что NT=5см, TK=3см. Найти периметр данного параллелограмма.

№4.1 В трапеции MNKP верхнее основание NK и средняя линия AB равны соответственно 5 и 9 см.
Найти ее нижнее основание.

№4.2 В трапеции PQNE нижнее основание PE и средняя линия KN равны соответственно 10 и 7 см. Найти ее верхнее основание.

№5.1 В прямоугольнике ABCD проведены биссектрисы углов А и D, которые пересекаются в точке М, лежащей на стороне B. Найдите периметр ABCD , если АВ=6см.

№5.2 В прямоугольнике ABCD проведена биссектриса угла А, которая разбивает сторону ВС на отрезки длиной 5см и 3 см. Найти периметр прямоугольника ABCD.

№6.1 На окружности отмечены точки А,В,С,D так, что АВ ее диаметр, а угол АСD равен . Найти угол DСВ.

№6.2 На окружности отмечены точки А,В,С,D так, что АС-диаметр, угол АСD равен , а угол ВАС равен . Найдите угол ВСD.

№7.1 На окружности отмечены точки В, N и D. Угол ВND равен . Найдите угол ВОD.

№7.2 На окружности отмечены точки В, К и C. Угол ВОС равен . Найти угол ВКС.

№8.1 В прямоугольном треугольнике АСВ катет СВ равен 4 см, угол В равен . Найти гипотенузу АВ.

№8.2 В прямоугольном треугольнике АСВ катет СА равен 3 см, угол А равен . Найти гипотенузу АВ.

№9* В трапеции АВСD АВ=СD, АС=5см, СH=3см. Найти площадь трапеции.

№10.1 Найти площадь трапеции, стороны которой равны 16, 13, 6 и 13 см.

№10.2 Найти площадь трапеции, стороны которой равны 17, 10, 5 и 10 см.

№11.1 Найти площадь прямоугольного треугольника с катетами 2 и 4 см.

№11.2 Найти площадь прямоугольного треугольника с катетами 3 и 5 см.

№12.1 Найти площадь прямоугольного треугольника, гипотенуза которого равна 25 см, а один из катетов – 20 см.

№12.2 Найти площадь прямоугольного треугольника, гипотенуза которого равна 17 см, а один из катетов – 8 см.

№13.1 Найти площадь квадрата, диагональ которого равна 4 см.

№13.2 Найти площадь квадрата, диагональ которого равна 6 см.

№14.1 Найти площадь прямоугольного треугольника , гипотенуза которого равна 12 см, а один из острых углов cоставляет .

№15.1 Найти площадь прямоугольного треугольника , гипотенуза которого равна 16 см, а один из острых углов равен.

№16.1 В прямоугольном ∆ АВС : – прямой, АВ=, АС=3, ВС=6. Найти sinA, cosA, tgA.

№16.2 В прямоугольном ∆ АВС : – прямой, АВ=, АС=4, ВС=.
Заполнить таблицу:

№17.1 В прямоугольном ∆ АВС : ∠C – прямой, АВ=6, ∠B=. Найти АС, ВС.

№17.2 В прямоугольном ∆ АВС : ∠C – прямой, СВ=6, ∠B=. Найти АС, АВ.

Задачи по геометрии на рисунках:

№18-19 Найдите по данным рисунка стороны X и Y (левая задача разбирается с репетитором по математике совместно, а правая предназначена для домашней работы)

№20-21 Выразите через X и Y стороны а и b а и b (левая задача разбирается с репетитором по математике совместно, а права предназначена для домашней работы)

№22 Найдите по данным рисунка длины отрезков X, Y и Z:

Автор подборки задач — Николай Викторович, репетитор по математике в отставке.

Уважаемые преподаватели: присылайте на сайт для публикации ваши дидактические и методические материалы, отдельные задачи или тексты объяснений каких-то традиционно трудных для школьников тем. Я с радостью помогу оформить их для публичного просмотра. Если Вы — репетитор по математике, прошедший регистрацию на сайте, то с каждого присланного материала я поставлю ссылку на Вашу анкету. Это привлечет внимание к Вам со стороны родителей и учеников.

С уважением, владелец сайта Колпаков Александр Николаевич,
репетитор по математике в Москве.
Репетитор по математике в Строгино, м.Щукинская.

Метки: Геометрия, Задачник по геометрии

Экзаменационная работа для 8-го класса по геометрии в общеобразовательной школе

Предлагаемая работа составлена в соответствии с действующей программой по учебнику Л.С. Атанасян и др. “Геометрия 7 – 9”.

Экзаменационная работа рассчитана на восьмой класс для итоговой аттестации. Подбор заданий осуществлён с учётом идеологии требований к уровню подготовки учащихся, предъявляемых новыми образовательными стандартами.

Работа состоит из двух частей.

Первая часть состоит из восьми заданий и направлена на проверку базовой подготовки восьмиклассников в её современном понимании. Усилены понятийные, практические аспекты. Эта часть содержит объём заданий с кратким ответом. Задания расположены группами в соответствии с разделами содержания, к которым они относятся.

Вторая часть направлена на дифференцированную проверку подготовки. Она содержит шесть заданий из различных разделов курса, предусматривающих полную запись хода решения. Задания во второй части расположены по нарастающей сложности – от относительной простоты до достаточно сложных. При выполнении второй части работы учащиеся должны продемонстрировать умение математически грамотно записовать решение, приводя при этом необходимые пояснения и обоснования.

Для оценивания результатов выполнения работы применяются два качественных показателя оценка “2”, “3”, “4” или “5” и рейтинг – сумма баллов за верно выполненные задания.

За каждое выполненное задание первой части начисляются 0,5 балла

Во второй части для каждого задания указано число баллов, которые засчитываются в рейтинговую оценку ученика при верном выполнении: 2,4или 6 баллов.

Схема перевода суммарного рейтинга в 5-балльную шкалу

Рейтинг	1,5 балла	2-3,5 баллов	4-8 баллов	9-24 баллов
Отметка	“2”	“3”	“4”	“5”

 На проведение экзамена отводится 120 мин. (2 часа) При этом время на выполнение первой части ограниченно – на неё отводится 45 минут.

Работа предлагается в двух параллельных вариантах.

Работа ученика 8 класса по геометрии _____________________________

Уровень А. Вариант 1. “ ”_________200 год.

А 1. Запиши номера четырехугольников, изображенных на рисунке 1, которые являются параллелограммами.

1) Ответ: ________________

Вычислите площадь фигуры изображенной на рисунках, принимая сторону клетки за единицу длины, а площадь клетки за 1 ед^2:

А 2. рис.1: 2),3),5).

2) Ответ: S₂ = _______ед²

3) Ответ: S₃ = _______ед²

4) Ответ: S₅ = _______ед²

А3. рис. 2 : 3), 5).

5) Ответ: S₃ = _______ед²

6) Ответ: S₅ = _______ед²

А 4. Найти подобные фигуры и определить коэффициент подобия. Рис. 3

7) Ответ: ____________

А5.

Дано:__________________

Найти: АВ

Решение:

________________

________________

________________

 

8) Ответ: _____________

Работа ученика 8 класса по геометрии ___________________________

Уровень В. Вариант 1.

Задача 1. (2 балла)

В прямоугольном треугольнике АВС угол С = 90⁰, угол А = 30⁰,

АС = 8 см. Найдите высоту треугольника, опущенную на его гипотенузу.

 Задача 2. (2 балла)

Диагонали ромба равны 10 см. и 24 см. Найдите стороны ромба.

Задача 3. (4 балла)

В треугольнике АВС, АВ = 12 см, АС = 8 см, АК – биссектриса. Найти длины отрезкам ВК и СК, если ВС = 5 см.

Задача 4. (4 балла)

Дано: треугольник АВС, SАВС = 2 ед².

Построить SВСД = 4 ед².

Задача 5. (6 баллов)

На диаметре окружности построен равносторонний треугольник. Определить градусную меру дуг, на которые стороны треугольника делит полуокружность.

Задача 6. (6 баллов)

Окружность касается стороны АВ угла ВАС, равного 45⁰ и пересекает луч АС в двух точках М и С так, что АМ = МС = . Найдите радиус окружности.

Работа ученика 8 класса по геометрии ___________________________

Уровень А. Вариант 2. “ ”_________2007 год.

А 1. Запиши номера четырехугольников, изображенных на рисунке 1, которые не являются параллелограммами.

1) Ответ: ________________

Вычислите площадь фигуры изображенной на рисунках, принимая сторону клетки за единицу длины, а площадь клетки за 1 ед² :

А 2. рис.1: 1), 6), 8).

2) Ответ: S₁ = _______ед²

3) Ответ: S₆ = _______ед²

4) Ответ: S₈ = _______ед²

А3. рис. 2: 2), 4).

5) Ответ: S₂ = _______ед²

6) Ответ: S₄ = _______ед²

 А 4. Найти подобные фигуры и определить коэффициент подобия. Рис. 3

7) Ответ: ____________

А5. В

Дано:__________________

Найти: А В

Решение: 3

________________

________________

________________

А 4 С

8) Ответ: ______________

Работа ученика 8 класса по геометрии _______________________________

Уровень В. Вариант 2.

Задача 1. (2 балла)

В прямоугольном треугольнике АВС угол С = 90⁰, угол В = 60⁰, АС = 8 см. Найдите высоту треугольника, опущенную на его гипотенузу.

Задача 2. (2 балла)

Диагонали квадрата равны 14 см. Найдите его площадь.

Задача 3. (4 балла)

В треугольнике АВС, АВ = 4 см, АС = 6 см, АМ – биссектриса. Найти длины отрезкам ВМ и СМ, если ВС = 10 см.

Задача 4. (4 балла)

Дано: треугольник АВС, SАВС = 2 ед².

Построить SВАД = 4 ед².

 Задача 5. (6 баллов)

Около окружности описана равнобокая трапеция, у которой боковая сторона точкой касания делиться на отрезки 4 см. и 9 см. Найдите площадь трапеции.

Задача 6. (6 баллов)

Используя данные рисунка 4, вычислить недостающие данные и установить, подобны ли треугольники АВС и ДЕF. Если треугольники подобны, то записать верные равенства, связывающие сходственные стороны.

Пройти курс | MATC

ДОГОНЯЙТЕ, МИРИТЕСЬ, ОПЕРЕЖАЙТЕ 

– ИЛИ ИЗУЧИТЕ НОВЫЙ НАВЫК!

Хотите пройти обучение в MATC? Вы можете запросить информацию, и рекрутер свяжется с вами — или подать заявку прямо сейчас!

Запросить InfoSearch для доступных занятийПодать заявку на занятие

(Заинтересованы в запуске программы получения степени или диплома? Используйте то же приложение и просто выберите свою программу!)

ГИБКИЕ ЗАНЯТИЯ НАЧИНАЮТСЯ КРУГЛЫЙ ГОД!

MATC предлагает гибкий старт в течение всего года: январь, февраль, март, июнь, август, сентябрь и октябрь.

В дополнение к традиционным 16-недельным курсам, более короткие 12- и 8-недельные курсы предлагают такие же высококачественные инструкции и небольшие группы в более короткие сроки, чтобы вы могли быстрее добиться успеха!

В MATC качественное образование под руководством опытных инструкторов стоит лишь малую часть стоимости четырехлетней школы! Пятнадцать кредитов уровня 200 стоят всего 3212 долларов. С книгами и сборами общие затраты оцениваются в 5435 долларов. Ознакомьтесь с этими легко переносимыми вариантами пакетов курсов.

Выберите ниже Pre-Major, который лучше всего соответствует вашим карьерным целям, и просмотрите курсы, которые мы рекомендуем.Перечисленные курсы являются вариантами начального уровня, которые вы можете рассмотреть.

 

Посмотреть рекомендуемые курсы по Pre-Major:

Английский/Коммуникации/Журналистика

Субъект	Курс
Английский	Английский 1 или 2 (ENG-201 или ENG-202)
Математика	Средняя алгебра (MATH-200)
Наука	Основы биологии (BIOSCI-236)
Гуманитарные науки	Введение в современное кино (ENG-240)
Наука о поведении	Оценка разнообразия (SOCSCI-217)
Изобразительное искусство или иностранный язык	Теория музыки (MUSIC-205)
Профессиональный курс (не подлежит передаче)	Технические коммуникации (ENG-208)

Искусство/Танец

Субъект	Курс
Английский	Английский 1 или 2 (ENG-201 или ENG-202)
Математика	Средняя алгебра (MATH-200)
Наука	Общая химия (ЧЕМ-207)
Гуманитарные науки	Образы женщин в литературе (ENG-222)
Наука о поведении	Введение в философию (SOCSCI-250)
Изобразительное искусство или иностранный язык	История искусств (АРТ-201)
Профессиональный курс (не подлежит передаче)	Цифровая обработка изображений: Adobe Photoshop (GRDS-107)

Бизнес/Политология

Субъект	Курс
Английский	Английский 1 или 2 (ENG-201 или ENG-202)
Математика	Средняя алгебра (MATH-200)
Наука	Науки об окружающей среде (GEOSCI-233)
Гуманитарные науки	Американское национальное правительство и политика сегодня (SOCSCI-221)
Наука о поведении	Основы микроэкономики (ECON-201)
Изобразительное искусство или иностранный язык	Испанский 1 (FLANG-202)
Профессиональный курс (не подлежит передаче)	Принципы маркетинга (MKTG-102)
Профессиональный курс (не подлежит передаче)	Маркетинг в социальных сетях (MKTG-118)
Профессиональный курс (не подлежит передаче)	Бухгалтерский учет для менеджеров (ACCT-126)
Профессиональный курс (не подлежит передаче)	Финансы бизнеса (БАДМ-126)

Pre-Health/Pre-Med

Субъект	Курс
Английский	Английский 1 или 2 (ENG-201 или ENG-202)
Математика	Средняя алгебра (MATH-200)
Математика	Колледж алгебры (MATH-201)
Математика	Колледж алгебры и тригонометрии (MATH-230)
Математика	Исчисление 1 (MATH-231)
Математика	Базовая статистика (MATH-260)
Наука	Анатомия и физиология 1 или 2 (BIOSCI-201 или 202)
Другие курсы естественных наук для медицинских наук:	Общая химия (CHEM-207), Обзор биохимии (CHEM-208)
Гуманитарные науки	Современная литература (ENG-215)
Наука о поведении	Введение в смерть и умирание (SOCSCI-210)
Изобразительное искусство или иностранный язык	Испанский 2 (FLANG-205)
Профессиональный курс (не подлежит передаче)	Медицинская терминология (ЗДОРОВЬЕ-101)
Профессиональный курс (не подлежит передаче)	Культура здравоохранения (ЗДОРОВЬЕ-104)
Профессиональный курс (не подлежит передаче)	Цифровая грамотность здравоохранения (ЗДОРОВЬЕ-107)

Предварительный инжиниринг

Субъект	Курс
Английский	Английский 1 или 2 (ENG-201 или ENG-202)
Математика	Средняя алгебра (MATH-200)
Математика	Колледж алгебры (MATH-201)
Математика	Колледж алгебры и тригонометрии (MATH-230)
Математика	Исчисление 1 (MATH-231)
Математика	Базовая статистика (MATH-260)
Наука	Колледж физики 1 (PHYS-221)
Гуманитарные науки	Америка до 1877 г. (HIST-211)
Наука о поведении	Введение в этические вопросы (SOCSCI-200)
Изобразительное искусство или иностранный язык	Испанский 5 — Разговор, Грамматика, Темы (FLANG-218)

Биология/Химия/Окружающая среда

Субъект	Курс
Английский	Английский 1 или 2 (ENG-201 или ENG-202)
Математика	Средняя алгебра (MATH-200)
Математика	Колледж алгебры (MATH-201)
Математика	Колледж алгебры и тригонометрии (MATH-230)
Математика	Исчисление 1 (MATH-231)
Математика	Базовая статистика (MATH-260)
Наука	Химия 1 или 2 (CHEM-211 или 212)
Наука	Генетика и геномика (BIOSCI-259)
Гуманитарные науки	Америка до 1877 г. (HIST-211)
Наука о поведении	Введение в социологию (SOCSCI-203)
Изобразительное искусство или иностранный язык	Испанский, французский и арабский языки предлагаются осенью 2020 г.

РАСШИРЬТЕ ВАШИ ОПЫТЫ MATC

Чем бы вы ни увлекались: писательством, защитой интересов студентов или электроникой, у MATC найдется выход для вас.Присоединение к студенческому клубу в кампусе позволяет вам общаться с единомышленниками и дает возможность совершенствовать свои лидерские навыки и заводить друзей во время пребывания в кампусе. Студент программы или нет, кампус с оживленным студенческим опытом укрепляет вашу связь с сообществом колледжа.

Узнайте больше о Офисе студенческой жизни , включая примеры клубов и организаций в MATC:

• Студенческое самоуправление
• Студенческая газета MATC Times
• Наставническая группа Ассоциации будущих чернокожих медсестер
• Клуб аниме
• Латиноамериканская студенческая организация
• Союз чернокожих студентов
• Азиатская студенческая ассоциация
• Сеть MATC STEM

Алгебра Шормана 1 с интегрированной геометрией Курс электронного обучения для самостоятельного обучения

 

  Как работает курс электронного обучения?

Посмотрите это короткое видео, чтобы узнать о системе электронного обучения, видеолекциях, автоматическом оценивании, записи оценок, видеорешениях, ежеквартальных экзаменах, викторинах и многом другом!

 

 

 

 

Алгебра Шормана 1 и 2 Обучение всем понятиям на ACT, PSAT и SAT

с библейским и историческим фондом  

 

Поскольку Saxon Math не обучает всем концепциям недавно переработанных PSAT и SAT, Dr.Шорманн опубликовал новую учебную программу, в которой изучаются все концепции ACT, PSAT и SAT, используются проверенные методы обучения Джона Саксона и включаются темы 21 века, такие как компьютерная математика, технологические приложения и современные задачи со словами из реального мира.

 

 

Основные характеристики:

• Самостоятельный курс в современной системе электронного обучения

• Алгебра Шормана 1 и 2 обучают всем понятиям PSAT, SAT и ACT.

• Навыки

  PSAT, SAT и ACT проверяются в Precalculus и Calculus.

• На основе проверенных методов обучения Джона Саксона

• Библейская и историческая основа учит, «зачем» изучать математику.

 

 

Современная система электронного обучения

 Задания организованы по неделям.Выберите неделю для просмотра

все задания на эту неделю.

 

 

 

 

 

Видеолекции

Пошаговая инструкция к каждому уроку.

 

 

 

 

Интерактивное домашнее задание

Ссылка на аналогичный пример задачи и ссылка на видеолекцию облегчают задачу

, чтобы заново выучить забытые понятия.

 

 

Страница результатов

 

 

 

 

 

 

Содержание курса электронного обучения

• Электронный учебник с уроками и домашними заданиями, руководство по электронным решениям и электронное руководство для учителя (печать не требуется) 

• Подождите 2 рабочих дня, чтобы настроить курсы электронного обучения. Чтобы войти, следуйте инструкциям в электронном письме с подтверждением заказа.

• 100 уроков с одной видеолекцией и домашним заданием каждый

•  26 еженедельных викторин и 4 ежеквартальных экзамена

 

Обязательное условие

Пройдена любая предварительная алгебра, саксонская 8/7 или саксонская алгебра 1/2

Важно:  Информация о зачислении учащихся и тесты

   

Описание курса

Алгебра Шормана 1 с интегрированной геометрией   Закладывая прочную основу для математики верхнего уровня, этот курс изучает все темы, необходимые для курса Алгебры 21 века 1, включая упрощение алгебраических выражений, решение уравнений (линейных и квадратичных) и линейные системы.Геометрия интегрирована на протяжении всего курса, развивая долгосрочное запоминание и свободное владение навыками алгебры и геометрии. Темы геометрии включают доказательство, логику, евклидову геометрию, периметр, площадь и объем. Другие темы включают измерения, компьютерную математику, технологические приложения, статистику и легкое введение в основы исчисления. С более чем 100 вопросами из PSAT, SAT и ACT этот курс начинает процесс подготовки учащихся к этим экзаменам.

 

Разработанный для использования в качестве курса с отличием, стандартного или коррекционного курса, Алгебра Шормана 1 включает 100 ежедневных уроков, 28 еженедельных тестов и четыре ежеквартальных экзамена.

Кредиты: 1 Алгебра 1 и 1/2 Геометрия

 

Выберите, чтобы узнать больше   

 

 

Почему доктор Шорманн написал новый учебный план по математике?  

Обучая Саксонскую математику сотням тысяч студентов более двадцати лет, доктор Шорманн знал, что уникальные методы обучения Джона Саксона работают. Однако после того, как Совет колледжей изменил дизайн PSAT и SAT (2015 г. ), Saxon Math больше не преподавал все концепции этих экзаменов.Houghton Mifflin, купившая Saxon после смерти Джона, убрала многие оригинальные методы Джона в своих новых изданиях. Доктор Шорманн решил написать новую учебную программу, чтобы продолжить методологию Джона Саксона, одновременно обучая всем концепциям переработанных PSAT и SAT.

 

  

Учебная программа по математике 21 века на основе Библии

 Стоя на плечах Джона Саксона, Леонарда Эйлера, Евклида, Ньютона и многих других, д-р.Шорманн опубликовал полную учебную программу по математике, в которой изучаются все концепции ACT, а также переработал PSAT и SAT. Как и Саксон, он преподает математику как язык с помощью поэтапных, небольших уроков и постоянной практики всех ранее изученных навыков, которые повышают мастерство, увеличивают скорость запоминания (беглость) и повышают баллы на вступительных экзаменах в колледж. Курсы Shormann Math с такими темами 21 века, как технологические приложения, компьютерная математика и современные задачи со словами, проводятся в современном кампусе электронного обучения, что делает обучение более эффективным и результативным.

  

 

Библейский и исторический фонд

Преподавание математики как языка науки и важного инструмента для понимания Бога и сотворенного Им мира, д-р Шорманн вдохновляет студентов на успех. Акцент на истории математики учит истории математики, давая учащимся более четкое представление о том, «почему» стоит за математикой, которую они изучают, и проливая свет на богатое христианское наследие современной математики.

 

PSAT, SAT и ACT

• Преподавание каждой концепции математического раздела ACT и переработанных PSAT и SAT, Алгебра Шормана 1 и 2 содержит более 200 практических задач из этих экзаменов.

• Навыки PSAT, SAT и ACT, которым обучают в Алгебре Шормана 1 и 2, постоянно пересматриваются в Precalculus и Calculus.

• Геометрия и алгебра интегрированы в Алгебру Шормана 1 и 2. Студенты не перестают изучать одно, чтобы изучать другое. Поскольку навыки геометрии и алгебры проверяются на вступительных экзаменах в колледж, эта интеграция повышает баллы на

  .

• Shormann Math обеспечивает постоянный обзор этих навыков в Алгебре 2, предварительном исчислении и исчислении, обеспечивая долгосрочное запоминание и беглость речи (скорость и точность).

Последовательность курса

 

 

 *Пользователи Saxon Algebra 1 3rd Edition, нажмите здесь   , чтобы узнать больше.

**Пользователям Saxon Algebra 2 нажмите здесь , чтобы узнать больше.

 

Последовательность Модификации

Опция на 3 семестра

Поскольку Алгебра Шормана 1 и 2 зарабатывают по 3 семестра математических кредитов, учащиеся могут потратить до 3 семестров на их выполнение.Вместо того, чтобы планировать уроки на три семестра, используйте временной метод, который позволяет учащимся учиться в своем собственном темпе, что развивает беглость речи.

 

Расчет AP 

.Предупреждение: д-р Шорманн не рекомендует «заставлять» учащегося выходить за пределы его данной Богом способности для достижения продвинутых уровней. Это может повлиять на беглость и, в конце концов, потребовать больше времени для прохождения курса. Вместо этого используйте метод самостоятельного обучения по времени (описанный в Руководстве для учителя и в разделе «Расписание» ниже).

По данным Совета колледжей, проходной балл на экзамене AP Calculus не только приносит до 8 кредитов колледжа, но и является показателем номер один успеха в колледже, значительно увеличивая количество поступающих и количество заявок на получение стипендии в процессе отбора. Чтобы сдать экзаменационные баллы AP вместе с заявками, они должны быть сданы не позднее 11-го класса. Экзамены AP, сданные в 12-м классе, по-прежнему имеют право на зачет колледжа, но баллы не будут получены до тех пор, пока не истечет срок подачи большинства заявок. Узнайте больше об экзаменах AP  

 

  Расписание  

В то время как продвинутые учащиеся-математики могут завершить Алгебру Шормана 1 всего за 30 недель, учащиеся, хорошо или средне владеющие математикой, обычно завершают курс за 36 недель. Учащимся или сопротивляющимся учащимся-математикам может потребоваться немного больше времени. Поскольку по этому курсу засчитывается три семестра кредита (1 кредит по алгебре 1 и 1/2 кредита по геометрии), студенты могут пройти его за три семестра.

В то время как курс электронного обучения рассчитан на 30 недель, обычный учебный год составляет 36 недель.Это означает, что есть шесть дополнительных недель, которые позволяют учащемуся при необходимости замедлить темп, чтобы заново выучить забытые понятия, обеспечив развитие мастерства и беглости. Вместо того, чтобы требовать от ученика полного урока в день, я рекомендую заниматься математикой 4-5 дней в неделю, не более 1-1,5 часов каждый. По истечении этого времени, независимо от того, какая часть урока была пройдена, пусть ученик остановится. Затем, пикап, где они остановились на следующий день. Со временем, по мере развития беглости, за это время они будут выполнять все больше и больше урока.

 

Если я буду использовать метод обучения по времени, как мой ученик закончит вовремя?

Метод по времени обычно дает эффект, противоположный ожиданиям родителей. В то время как сильный студент-математик обычно завершает курс за 30–34 недели, средний студент-математик может занять 36–45 недель. Однако, поскольку Алгебра Шормана 1 и 2 зарабатывают по 3 семестра математических кредитов каждый (см. Таблицу ниже), это занимает до 54 недель (3 семестра). это прекрасно. Хотя Shormann Math не является Common Core, CC рекомендует интегрированный подход к геометрии и алгебре, который распространяет алгебру и геометрию на три года.Хотя их подход больше похож на смешивание, чем на настоящую интеграцию, колледжи теперь знакомы с интегрированным подходом и не удивляются и не смущаются, когда эти кредиты указываются в стенограмме. Узнайте больше о стенограммах

  

 

 

Настоящая практика

В то время как каждая проблема сначала решается на бумаге, в курсе электронного обучения используется система, которую мы называем TruePractice ^TM  , которая обеспечивает долгосрочное мастерство более эффективно, чем традиционные подходы.Что такое истинная практика? Ну, подумай о том, как ты учишься спорту. Во время практики, если вы ошиблись, ошибка обсуждается и, если у вас хороший тренер, вы сразу же перегруппировываетесь и пробуете снова. Вот как онлайн-домашняя работа разработана в Shormann Math. При попытке решить домашнюю задачу немедленно предоставляется правильная/неправильная обратная связь. Если ответ неправильный, начисляется небольшой штраф, и учащийся может переучиться, используя ссылки над каждым домашним заданием, а затем решить задачу правильно! Вместо того, чтобы «испортить» их ответом, TruePractice™ побуждает учащихся оставаться вовлеченными и заново изучать концепцию, что является лучшим способом добиться долгосрочного запоминания и беглости речи.

 

 

 

Подписка на электронный курс на 24 месяца $139 за курс

— Настройка на 30-недельный график, но может быть растянута до 3 или 4 семестров

— Доступ к электронному курсу на 24 месяца для одного студента

— Самостоятельный темп; нет сроков сдачи, родители могут менять оценки и сбрасывать задания

— включает электронный учебник для печати, руководство по электронным решениям и электронное руководство для учителей

– Большинство заданий можно выполнять в автономном режиме 

— Использование в качестве курса с отличием, стандартного или корректирующего курса

– Часто задаваемые вопросы о подписке:  Часто задаваемые вопросы об электронной почте учащихся и братьях и сестрах

 

 

Подписка для братьев и сестер со скидкой 39 долларов США за курс

При покупке абонемента для одного ребенка в вашей семье

подписка может быть продлена для каждого брата за $39

— $39 Брат или сестра, зачисленные одновременно с учащимся начальной школы

— 39 долларов Брат или сестра, зарегистрированные позже (без ограничения времени между братьями и сестрами)

 – Приобретите подписку на одноуровневую версию, когда она будет готова к запуску.

 

 

Интегрированная геометрия и постоянный обзор

— На основе методов обучения Джона Саксона, состоящих из поэтапных небольших уроков, постоянного повторения и кумулятивных оценок

 — добавлены технологические приложения 21 века, задачи со словами из реального мира и компьютерная математика.

 

Полная видеоинструкция к каждому уроку

— 100 ежедневных уроков с 1 видеолекцией на каждом (в среднем 20 мин)

— Учащиеся делают заметки и работают с примерами задач

— Видеолекции доступны в автономном режиме

 

Интерактивное домашнее задание с автоматической оценкой

— 20 домашних заданий за урок

— Сначала поработайте над задачами на бумаге, а затем введите ответ для мгновенной обратной связи

— Ссылки на аналогичную практическую задачу и связанную с ней видеолекцию упрощают и ускоряют повторное обучение

— Автоматическая оценка обеспечивает мгновенную обратную связь

. Домашнее задание также можно выполнять в автономном режиме с помощью электронного текста, а затем вводить ответы в систему электронного обучения для оценивания или оценивать с помощью руководства по электронным решениям

.

 

Видеорешения обеспечивают понимание

— Пошаговое объяснение каждого вопроса домашнего задания

— Доступ ограничен до тех пор, пока домашнее задание не будет выполнено и не будет записана оценка

— Руководство по eSolutions также доступно для родителей

 

Интерактивные викторины и экзамены с автоматическим оцениванием

— 30 еженедельных онлайн-тестов и 4 ежеквартальных онлайн-экзамена

— Автоматическая оценка и запись оценок

— Родители могут сбросить задания и изменить оценки

 

Поддержка по электронной почте с вопросами и ответами от Dr.Шорманн

— Поддержка по электронной почте вопросов и ответов с доктором Шорманном

— Руководство для учителя и руководство по электронному решению 

 

Получите 14 кредитов колледжа на экзаменах CLEP и AP

— Профессор CLEP по алгебре колледжа включен в Алгебру Шормана 2

— CLEP College Algebra получает 3 кредита колледжа

— Проходные баллы также подтверждают стенограммы средней школы

 

Отличная подготовка к обновленным PSAT и SAT

— Написано специально для соответствия новым требованиям переработанных стандартов PSAT и SAT

2015 года.

— Алгебра Шормана 1 и 2 обучают всем понятиям, необходимым для успешной сдачи вступительных экзаменов в колледж

— Постоянный просмотр и интегрированная геометрия развивают беглость речи, повышая баллы за стандартные тесты

— Shormann Precalculus будет продолжать пересматривать эти концепции, чтобы поддерживать беглость

 

Системные требования

— Система электронного обучения на основе браузера — как веб-сайт

— Доступ с любого компьютера или устройства с браузером и доступом в Интернет

— Колонки или наушники

 

 

Образцы для урока 1

Каждый урок состоит из трех компонентов: «Правила и определения», «Видео-лекция» и «Практический набор» (домашнее задание).Ниже приведен образец каждого из этих компонентов в том порядке, в котором их должен заполнить студент.

 

1. Прочтите Правила и определения, используя цифровые карточки .

 

2. Посмотрите видеолекцию, делая заметки и рабочие примеры задач с доктором Шорманном.

Средняя продолжительность большинства лекций составляет двадцать минут. Однако, в зависимости от новой концепции, некоторые лекции длиннее. Опять же, используйте метод расчета по времени, описанный в разделе «Расписание» выше, чтобы не расстраивать и не перегружать учащегося.

 

 

3. Выполните практическое задание (домашнее задание).  

Работайте над каждой проблемой на бумаге, затем введите ответ и выберите «Отправить», чтобы получить мгновенный ответ. Над каждым вопросом есть две ссылки (см. рисунок ниже). Одна — это ссылка на аналогичную примерную задачу, а другая — ссылка на видеолекцию, в которой рассказывается об этой концепции. Если ваш ответ неверен или вы не знаете, как решить задачу, воспользуйтесь этими ссылками, чтобы быстро переучиться и попытаться решить проблему еще раз. Поскольку домашнее задание является практикой, для каждой задачи допускается до четырех попыток. Очки вычитаются за каждую неправильную попытку, которая не позволяет ученику угадать.

 

 

4. Выполнив все домашние задания, нажмите «Отправить все» и «Готово» внизу страницы. Система рассчитает баллы и сохранит их в онлайн-журнале оценок. Родители могут запросить изменение оценок и сброс заданий в любое время.

 

5. Появится страница результатов с правильным ответом и видеорешением каждой задачи.Повторно изучите и исправьте пропущенные проблемы, просматривая правильный ответ и просматривая видеорешения для каждой пропущенной проблемы. Затем переработайте каждую пропущенную задачу в своих заметках о домашнем задании.

 

Викторины

На каждом четвертом уроке проводится викторина из четырех вопросов по последним четырем новым концепциям. Заметки можно использовать во время викторины. Ограничение по времени составляет двадцать минут. что примерно в два раза больше, чем нужно большинству студентов. См. ответы на часто задаваемые вопросы, чтобы найти обходной путь, если требуется больше времени.

 

Ежеквартальные экзамены

Каждые двадцать пять уроков проводится ежеквартальный экзамен. Это совокупный тест, охватывающий весь материал, который учащийся должен был усвоить к этому моменту. Для подготовки к экзамену предусмотрено два-три практических экзамена. Ежеквартальные экзамены готовят студентов к экзаменам по математике в колледже, которые охватывают большой объем материала.

  

 

Обзор Shormann Math

  

Стоя на плечах таких гигантов математики, как Евклид, Эйлер, Ньютон, вместе с методами преподавания здравого смысла Джона Саксона, мы рады представить математику Шормана! Эта новая учебная программа, разработанная Дэвидом Шорманном, разработанная на христианской основе, основана на прочной основе проверенных временем и проверенных методов, дополненных доставкой контента 21 века.

Поскольку ученые считают математику «языком науки», на этих курсах математика преподается как язык. На курсе иностранного языка вы не учите существительные в течение года, глаголы в течение еще одного года и т. д. Вы изучаете понемногу каждую концепцию в сочетании с большим количеством практики и повторения. Затем вы объединяете разные концепции вместе, чтобы создавать более сложные концепции. Беглость достигается за счет терпеливой практики и повторения.

Несмотря на то, что основы первого уровня алгебры будут в центре нашего первого курса, наша основная цель – научить математике, а не только алгебре.Например, Алгебра 1 и 2 будут содержать полный кредит по геометрии, включая множество доказательств, даже некоторые прямо из знаменитой книги Евклида «Начала». Но мы также представим неевклидову геометрию и покажем учащимся, как концепция доказательства применима ко всей математике, а не только к геометрии. На самом деле, вся алгебра, геометрия, тригонометрия и т. д., которые учащиеся найдут на SAT (включая новый SAT) или ACT, будут рассмотрены в Алгебре 1 и Алгебре 2.  

В большинстве современных учебных программ по математике история математики игнорируется.Но у идей есть последствия, и изучение истории часто показывает, какие идеи стоит повторять, а какие нет. Математика имеет богатое христианское наследие. Независимо от того, используете ли вы классический, тривиальный/квадривиальный подход к образованию вашего ребенка, понимание математики в библейских, исторических рамках поможет учащимся лучше понять, что они изучают и почему они это изучают.

«Если я и видел немного дальше, так это стоя на плечах гигантов»
— Исаак Ньютон

 

Идеальная последовательность курсов

 

 

Последовательность Модификации

 

Опция на 3 семестра

Так как Алгебра Шормана 1 и 2 зарабатывают по 3 семестра математических кредитов каждый (см. выше).эти два курса могут быть растянуты на 3 года (каждый по 3 семестра).

 

AP Исчисление BC в 11 классе

 

По данным Совета колледжей, проходной балл на экзамене AP Calculus не только приносит до 8 кредитов колледжа, но и является показателем номер один успеха в колледже, значительно увеличивая количество поступающих и количество заявок на получение стипендии в процессе отбора. Чтобы сдать экзаменационные баллы AP вместе с заявками, они должны быть сданы не позднее 11-го класса.

 

Экзамены

AP, сданные в 12-м классе, по-прежнему имеют право на зачет колледжа, но баллы не будут получены до тех пор, пока не истечет срок подачи большинства заявок.

 

В то время как проходного балла на экзамене AP Calculus AB обычно достаточно, чтобы получить желаемое зачисление и стипендии, сильные учащиеся-математики, которые планируют сдавать экзамен BC, должны либо пройти алгебру 1 в 7-м классе (требуется предварительная алгебра), либо работать над математика круглый год. Узнайте больше об экзаменах AP

 

Предупреждение: я не рекомендую «подталкивать» ученика к достижению выше его данных Богом способностей для достижения этих высоких уровней математических достижений. Часто это пагубно сказывается на беглости речи и, в конце концов, требует больше времени для прохождения курса. Вместо этого я рекомендую метод самостоятельного изучения времени (описанный в Руководстве для учителя и в расписании выше), который обеспечивает развитие мастерства и беглости, делая математику быстрее и проще.

 

 

 

 

 

 

 

 

 

 

 

 

 

кредитов колледжа плюс | Часто задаваемые вопросы

Нет конфликта; два работают вместе:

Для программ общественной школы, не входящих в программу ECHS, школа должна соответствовать требованиям общественной школы (ORC 3314.03). Если общественная школа также работает как ECHS, то она должна соответствовать уставу ECHS (ORC 3313.6013).

 

 

ORC 3314.03(А)(11)

(A)(11) Школа должна соответствовать следующим требованиям:

(a) Школа предоставит возможность обучения как минимум двадцати пяти учащимся в течение как минимум девятисот двадцати часов в течение учебного года.

(b) Управляющий орган приобретает страховку ответственности или иным образом обеспечивает возможную ответственность школы.

(c) Школа будет несектантской по своим программам, правилам приема, практике трудоустройства и всем другим операциям и не будет управляться сектантской школой или религиозным учреждением.

(d) Школа будет соответствовать разделам 9.90, 9.91, 109.65, 121.22, 149.43, 2151.357, 2151.421, 2313.19, 3301.0710, 3301.0711, 3301.0712, 3301.0715, 3301.0729, 3301.948, 3313.472,

3313.50, 3313.536, 3313.539, 3313.5310, 3313.608, 3313.609, 3313.6012, 3313.6013, 3313.6014, 3313,6015, 3313,6020, 3313,643, 3313,648, 3313,6411, 3313,66, 3313,661, 3313,662, 3313,666, 3313,667, 3313,668, 3313,67, 3313,671, 3313,672, 3313,673, 3313,69, 3313,71, 3313,716, 3313,718, 3313,719, 3313,7112, 3313,721, 3313,80, 3313,814, 3313.816, 3313.817, 3313,86, 3313,89, 3313,96, 3319,073, 3319,074, 3319,321, 3319,39, 3319,391, 3319,41, 3319,46, 3321,01, 3321,041, 3321,13, 3321,14, 3321,141, 3321,17, 3321,18, 3321,19, 3321,191, 3327,10, 4111,17, 4113,52, и 5705,391 и главы 117. , 1347., 2744., 3365., 3742., 4112., 4123., 4141. и 4167. Пересмотренного кодекса, как если бы это был школьный округ, и будет соответствовать разделу 3301.0714 Пересмотренного кодекса в порядке, указанном в разделе 3314.17. пересмотренного Кодекса.

 

ORC 3313.6013 (E) и (F)(2)

(E) Любое соглашение между школьным округом или школой и ассоциированным колледжем, регулирующее работу программы средней школы раннего поступления в колледж, освобождается от требований программы колледжа «кредит плюс» при условии, что программа соответствует определению, изложенному в разделе ( F)(2) этого раздела и утверждается начальником государственного образования и канцлером высшего образования.

(F)(2) «Программа раннего обучения в средней школе» означает партнерство между по крайней мере одним школьным округом или школой и по крайней мере одним высшим учебным заведением, которое позволяет участникам одновременно выполнять требования для получения обычного аттестата средней школы и иметь возможность заработать не менее двадцати четырех кредитов, которые могут быть переведены в высшие учебные заведения в партнерстве в рамках организованного курса обучения для получения степени или диплома о высшем образовании бесплатно для участника или семьи участника. Программа также должна отдавать приоритет следующим студентам:

а) недопредставленные учащиеся в отношении получения высшего образования;

(b) Учащиеся, находящиеся в неблагоприятном экономическом положении, согласно определению департамента образования;

(c) Учащиеся, родители которых не имеют высшего образования.

 

 

Часто задаваемые вопросы созданы в августе 2020 г.

Геометрия — 1206310 | CPALMS.org

Угол ВВЕРХ: Игрок 1:

Изучите процессы построения для построения биссектрисы угла, копирования угла и построения линии, параллельной заданной линии, через точку, не находящуюся на линии, с помощью различных инструментов в этом интерактивном учебном пособии в стиле ретро-видеоигры.

ПРИМЕЧАНИЕ. В этом учебном пособии используется как построение биссектрисы угла, так и построение для копирования угла в качестве возможности расширения, чтобы также построить линию, параллельную заданной линии, через точку, не находящуюся на линии. Учащиеся также учатся определять соответствующие углы, образующиеся при пересечении секущей параллельных прямых, и обнаруживают с помощью Geogebra, что эти углы равны.

Тип: оригинальное учебное пособие для учащихся

Круглогодичные школьные дебаты: выявление ошибочных рассуждений — часть вторая:

Это вторая часть серии из двух частей.Научитесь выявлять ошибочные рассуждения в этой серии интерактивных руководств. Вы узнаете, что некоторые эксперты говорят о круглогодичных школах, какие исследования были проведены по поводу их эффективности и какие аргументы можно привести за и против круглогодичного образования. Затем вы прочитаете речь в пользу круглогодичных школ и определите ошибочные рассуждения в аргументе, в частности использование поспешных обобщений.

Обязательно завершите первую часть перед второй! Нажмите ЗДЕСЬ , чтобы запустить первую часть.

Тип: оригинальное учебное пособие для учащихся

Вымпел компании Challenge: вписанные круги треугольников:

Узнайте, как легко Кэти создать круговой логотип с надписью на шаблоне треугольного вымпела своей компании. Если она выполнит задание первой, она выиграет бонус в размере 1000 долларов США! Следуйте этому интерактивному руководству.

Тип: оригинальное учебное пособие для учащихся

Круглогодичные школьные дебаты: выявление ошибочных рассуждений — часть первая:

Научитесь выявлять ошибочные рассуждения в этом интерактивном учебном пособии по английскому языку, состоящем из двух частей. Вы узнаете, что некоторые эксперты говорят о круглогодичных школах, какие исследования были проведены по поводу их эффективности и какие аргументы можно привести за и против круглогодичного образования.Затем вы прочитаете речь в пользу круглогодичных школ и определите ошибочные рассуждения в аргументе, в частности использование поспешных обобщений.

Обязательно выполните обе части этой серии! Нажмите ЗДЕСЬ , чтобы открыть вторую часть.

Тип: оригинальное учебное пособие для учащихся

Встретить меня на полпути:

Спланируйте экспедицию на байдарке, научившись выполнять основные геометрические построения, включая копирование сегмента, построение биссектрисы сегмента, построение перпендикулярной биссектрисы сегмента и построение перпендикулярных сегментов с помощью различных инструментов в этом интерактивном учебном пособии.

Тип: оригинальное учебное пособие для учащихся

Оценка аргумента – Часть четвертая: Инаугурационная речь Джона Кеннеди:

Изучите инаугурационную речь президента Джона Ф. Кеннеди в этом интерактивном руководстве. Вы изучите аргумент Кеннеди, основное утверждение, более мелкие утверждения, причины и доказательства.

В четвертой части вы будете использовать то, что вы узнали из этой серии, чтобы оценить общую аргументацию Кеннеди.

Обязательно завершите предыдущие части этой серии, прежде чем приступить к части 4.

• Нажмите ЗДЕСЬ , чтобы запустить первую часть.
• Нажмите  ЗДЕСЬ  , чтобы запустить вторую часть.
• Нажмите  ЗДЕСЬ  , чтобы запустить третью часть.

Тип: оригинальное учебное пособие для учащихся

Человек не на своем месте:

Узнайте, как построить вписанный квадрат в круг и почему в этом интерактивном руководстве используются определенные конструкции.

Тип: оригинальное учебное пособие для учащихся

Оценка аргумента – Часть третья: Инаугурационная речь Джона Кеннеди:

Изучите инаугурационную речь президента Джона Ф. Кеннеди в этом интерактивном руководстве. Вы изучите аргумент Кеннеди, основное утверждение, более мелкие утверждения, причины и доказательства. К концу этой серии из четырех частей вы сможете оценить его общую аргументацию.

В третьей части вы прочтете больше о речи Кеннеди и определите меньшее утверждение в этом разделе его речи. Вы также оцените соответствие этого меньшего утверждения основному утверждению и оцените причины и доказательства Кеннеди.

Обязательно выполните все четыре части этой серии!

• Нажмите ЗДЕСЬ , чтобы запустить первую часть.
• Нажмите  ЗДЕСЬ  , чтобы запустить вторую часть.
• Нажмите ЗДЕСЬ , чтобы запустить четвертую часть.

Тип: оригинальное учебное пособие для учащихся

Где эта вышка сотовой связи?:

Найдите расположение и зону покрытия вышек сотовой связи, чтобы определить центр и радиус круга по его уравнению, используя стратегию заполнения квадрата в этом интерактивном руководстве.

Тип: оригинальное учебное пособие для учащихся

Проектирование с помощью шестиугольников:

Узнайте, как построить вписанный правильный шестиугольник и равносторонний треугольник в окружность в этом интерактивном учебном пособии.

Тип: оригинальное учебное пособие для учащихся

Как новый:

Узнайте, как описать окружность вокруг треугольника в этом интерактивном руководстве по конструкциям.Возьмите циркуль, линейку, карандаш и бумагу, чтобы следовать!

Тип: оригинальное учебное пособие для учащихся

Высокотехнологичные качели:

В этом интерактивном учебном пособии вы узнаете, как найти точку на направленном отрезке, которая делит его в заданном отношении.

Тип: оригинальное учебное пособие для учащихся

Круг вверх!:

Узнайте, как написать уравнение окружности, используя теорему Пифагора , зная ее центр и радиус, используя пошаговые инструкции в этом интерактивном руководстве.

Тип: оригинальное учебное пособие для учащихся

Готов к взлету! — Часть вторая:

Это вторая часть серии руководств, состоящей из двух частей.В этом интерактивном учебном пособии вы потренируетесь определять цель говорящего, используя речь пионера авиации Амелии Эрхарт. Вы изучите использование ею риторических призывов, включая этос, логос, пафос и кайрос. Наконец, вы оцените эффективность использования Эрхартом риторических призывов.

Обязательно сначала выполните первую часть. Щелкните здесь, чтобы запустить ЧАСТЬ ПЕРВУЮ.

Тип: оригинальное учебное пособие для учащихся

Готов к взлету! — Первая часть:

Это первая часть серии руководств, состоящей из двух частей.В этом интерактивном учебном пособии вы потренируетесь определять цель говорящего, используя речь пионера авиации Амелии Эрхарт. Вы изучите использование ею риторических призывов, включая этос, логос, пафос и кайрос. Наконец, вы оцените эффективность использования Эрхартом риторических призывов.

Нажмите здесь, чтобы запустить ЧАСТЬ ВТОРАЯ .

Тип: оригинальное учебное пособие для учащихся

Описательное письмо: Глаза в небе (часть 4 из 4):

Попрактикуйтесь в написании различных аспектов описательного эссе об ученых, использующих дроны для исследования ледников в Перу.Этот интерактивный учебник является четвертой частью серии из четырех частей. В этом заключительном уроке вы узнаете об элементах основного абзаца. Вы также создадите основной абзац с подтверждающими доказательствами. Наконец, вы узнаете об элементах заключения и потренируетесь в создании «подарка».

Это руководство является четвертой частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.

Тип: оригинальное учебное пособие для учащихся

Описательное письмо: Глаза в небе (часть 3 из 4):

Узнайте, как написать введение для описательного эссе в этом интерактивном руководстве. Этот учебник является третьей частью серии из четырех частей. В предыдущих уроках этой серии учащиеся проанализировали информационный текст и видео об ученых, использующих дроны для исследования ледников в Перу. Студенты также определили центральную идею и важные детали текста и написали эффективное резюме. В третьей части вы узнаете, как написать введение для описательного эссе об исследованиях ученых.

Это руководство является третьей частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.

Тип: оригинальное учебное пособие для учащихся

Чертежи строительства:

С помощью этого интерактивного учебного пособия вы научитесь строить биссектрису отрезка прямой с помощью линейки и циркуля.

Тип: оригинальное учебное пособие для учащихся

Сравнение митоза и мейоза:

Сравните и сопоставьте митоз и мейоз в этом интерактивном руководстве. Вы также свяжете их с процессами полового и бесполого размножения и их последствиями для генетической изменчивости.

Тип: оригинальное учебное пособие для учащихся

Кусочки ниндзя Нэнси:

Узнайте, как определить форму поперечного сечения, созданного пересечением секущей плоскости с пирамидой или призмой, в этом интерактивном учебном пособии на тему ниндзя.

Тип: оригинальное учебное пособие для учащихся

Вокруг света с прямоугольными треугольниками:

Из этого интерактивного руководства вы узнаете, как использовать тригонометрические соотношения для определения высоты известных памятников и решить задачу из реальной жизни.

Тип: оригинальное учебное пособие для учащихся

Доказательство теорем о треугольниках:

Используйте свойства, постулаты и теоремы, чтобы доказать теорему о треугольнике.В этом интерактивном уроке вы также узнаете, как доказать, что линия, параллельная одной стороне треугольника, пропорционально делит две другие.

Тип: оригинальное учебное пособие для учащихся

Рак: мутировавшие клетки вышли из-под контроля!:

Изучите взаимосвязь между мутациями, клеточным циклом и неконтролируемым ростом клеток, который может привести к раку, с помощью этого интерактивного руководства.

Тип: оригинальное учебное пособие для учащихся

Банковский выстрел:

В этом задании учащимся предлагается использовать сходство для решения задачи в контексте, который будет знаком многим, хотя большинство учащихся привыкли использовать интуицию, а не геометрические рассуждения, для построения кадра.

Тип: Задача решения проблем

Они похожи?:

В этой задаче учащимся дается изображение двух треугольников, которые кажутся подобными, но сходство которых нельзя доказать без дополнительной информации. Попросите учащихся предоставить последовательность преобразований подобия, которая отображает один треугольник в другой, используя определение подобия в терминах преобразований подобия.

Тип: Задача решения проблем

Рулон туалетной бумаги:

Целью этого задания является привлечение учащихся к геометрическому моделированию и, в частности, к выводу алгебраических взаимосвязей между переменными, вытекающими из геометрических ограничений.

Тип: Задача решения проблем

Монеты по кругу:

Используя таблицу диаметров монет разного достоинства, учащихся просят определить, сколько монет помещается вокруг центральной монеты.

Тип: Задача решения проблем

Проблема с маяком:

В этой задаче учащимся предлагается смоделировать явления на поверхности земли, исследуя видимость лампы на маяке с лодки.

Тип: Задача решения проблем

Солнечное затмение:

Это задание на решение задач побуждает учащихся выяснить, почему солнечные затмения случаются редко, путем изучения радиуса Солнца и самого дальнего расстояния между Луной и Землей.

Тип: Задача решения проблем

Чудо средней точки:

Это задание на решение проблемы дает учащимся возможность доказать факт о четырехугольниках: если мы соединим середины произвольного четырехугольника, чтобы образовать новый четырехугольник, то новый четырехугольник будет параллелограммом, даже если первоначальный четырехугольник таковым не был.

Тип: Задача решения проблем

От горы Уитни до Долины Смерти:

Это задание вовлекает учащихся в открытое задание по моделированию, в котором используется подобие прямоугольных треугольников.

Тип: Задача решения проблем

Кратчайший отрезок линии от точки P до линии L:

Это базовое задание по геометрии, предназначенное для того, чтобы помочь учащимся развить некоторые основные геометрические свойства, которые на первый взгляд могут показаться довольно очевидными.В этом случае основное свойство, о котором идет речь, состоит в том, что кратчайший путь от точки к линии встречается с линией под прямым углом, что имеет решающее значение для многих дальнейших разработок предмета.

Тип: Задача решения проблем

Семь кругов III:

Это дает возможность смоделировать конкретную ситуацию с помощью математики. После того, как репрезентативная картина ситуации, описанной в задаче, будет нарисована (преподаватель может дать здесь указания по мере необходимости), решение задачи требует понимания определения функции синуса.

Тип: Задача решения проблем

Расширение линии:

В этом задании учащимся предлагается сделать выводы о линии после того, как она была увеличена в 2 раза.

Тип: Задача решения проблем

Бег по дорожке II:

Цель этого задания — смоделировать знакомый объект, олимпийскую трассу, используя геометрические фигуры. Расчеты периметров этих фигур объясняют ступенчатый старт бегунов в беге на 400 метров.

Тип: Задача решения проблем

Бег по дорожке I:

В этой задаче геометрия применяется к 400-метровой дорожке, чтобы найти ее периметр.

Тип: Задача решения проблем

Скрепка:

В этом задании типографская сетка служит фоном для стандартной скрепки.Метрическая шкала измерений нарисована поперек нижней части сетки, а скрепка проходит в обоих направлениях немного за пределы сетки. Ученикам дают примерную длину скрепки и определяют количество одинаковых скрепок, сделанных из проволоки заданной длины.

Тип: Задача решения проблем

Рожок мороженого:

В этом задании учащиеся сделают эскиз бумажной обертки от рожка для мороженого, с помощью этого эскиза выведут формулу площади поверхности обертки и оценят максимальное количество оберток, которые можно вырезать из прямоугольного листа бумаги. .

Тип: Задача решения проблем

Насколько толстая банка газировки? (Вариант I):

В этом задании на решение задач учащиеся должны найти площадь поверхности банки из-под газировки, вычислить, сколько кубических сантиметров алюминия она содержит, и оценить ее толщину.

Тип: Задача решения проблем

Сколько листьев на дереве? (Версия 2):

Это задача математического моделирования, направленная на разумную оценку чего-то, что слишком велико для точного подсчета, а именно количества листьев на дереве.

Тип: Задача решения проблем

Сколько листьев на дереве?:

Это задача математического моделирования, направленная на разумную оценку чего-то, что слишком велико для точного подсчета, а именно количества листьев на дереве.

Тип: Задача решения проблем

Сколько клеток в теле человека?:

В этом задании по решению проблем учащимся предлагается применить понятия массы, объема и плотности в контексте реального мира, чтобы определить, сколько клеток находится в организме человека.

Тип: Задача решения проблем

Глобальная система позиционирования II:

Отражая современность используемых технологий, это сложная задача по геометрическому моделированию, в которой учащиеся с нуля открывают для себя геометрические принципы, лежащие в основе программного обеспечения, используемого системами GPS.

Тип: Задача решения проблем

Архимед и королевская корона:

В этом задании на решение задач используется сказка об Архимеде и короне царя Сиракуз, чтобы определить объем и массу золота и серебра.

Тип: Задача решения проблем

Склоны и круги:

Цель этого задания — познакомить учащихся с алгебраическим подходом к хорошо известному результату классической геометрии, а именно к тому, что точка X лежит на окружности диаметра AB, если угол ?AXB прямой

Тип: Задача решения проблем

Единичные квадраты и треугольники:

В этом задании на решение задач учащимся предлагается найти площадь треугольника, используя единичные квадраты и отрезки.

Тип: Задача решения проблем

Треугольники, вписанные в окружность:

Это задание на решение проблем побуждает учащихся использовать идеи о линейных функциях, чтобы определить, когда определенные углы являются прямыми углами.

Тип: Задача решения проблем

Прием у доктора:

Целью задания является анализ правдоподобного сценария реальной жизни с использованием геометрической модели. Задача требует знания формул объема для цилиндров и конусов, некоторых геометрических рассуждений, связанных с подобными треугольниками, а также уделяет внимание разумным приближениям и поддержанию разумного уровня точности во всем.

Тип: Задача решения проблем

Почему АСА работает?:

В этом задании на решение задач учащимся предлагается показать отражение одного треугольника в другом треугольнике.

Тип: Задача решения проблем

Когда SSA работает для определения конгруэнтности треугольников?:

В этой задаче мы рассматривали SSA.Критерии соответствия треугольника, SSS, SAS, ASA, требуют трех частей информации. Интересно, однако, что не всех трех частей информации о сторонах и углах достаточно, чтобы определить треугольник с точностью до конгруэнтности.

Тип: Задача решения проблем

Семь кругов II:

Эта задача обеспечивает конкретную геометрическую постановку для изучения жестких преобразований плоскости.

Тип: Задача решения проблем

Середины сторон параллелограмма:

Это достаточно прямое задание, направленное на то, чтобы учащиеся использовали ранее полученные результаты для изучения новых фактов о параллелограммах, а не для получения их из первых принципов.

Тип: Задача решения проблем

Вписывание квадрата в круг:

Это задание дает учащимся возможность применить теоремы о конгруэнтности треугольников в явном, интересном контексте.

Тип: Задача решения проблем

Вписывание шестиугольника в окружность:

В этом задании на решение задач учащимся предлагается вписать равносторонние треугольники и правильные шестиугольники в круг с помощью циркуля и линейки.

Тип: Задача решения проблем

Почему SAS работает?:

В этом задании на решение задач учащимся предлагается объяснить, почему данные треугольники равны, и построить отражения точек.

Тип: Задача решения проблем

Отражения и равносторонние треугольники II:

Это задание дает учащимся возможность увидеть влияние отражений на явный объект и увидеть, что отражения не всегда коммутируют.

Тип: Задача решения проблем

Отражения и равносторонние треугольники:

Это упражнение является одним из серии заданий, использующих жесткие преобразования плоскости для изучения симметрии классов треугольников, причем это задание, в частности, сосредоточено на классе равносторонних треугольников

Тип: Задача решения проблем

Отраженные треугольники:

В этом задании учащимся предлагается с помощью линейки и циркуля построить линию, через которую отражается треугольник.

Тип: Задача решения проблем

Центральная часть:

Целью этого задания является использование геометрических и алгебраических рассуждений для моделирования реального сценария. В частности, учащиеся в нескольких местах (явно или неявно) должны рассуждать о том, когда делать приближения разумно и когда округлять, когда использовать равенство, а когда нет.неравенства и выбор единиц измерения для работы (например, мм против см).

Тип: Задача решения проблем

Теннисные мячи в банке:

Эта задача основана на выводе формулы объема сферы. Если сфера радиуса 1 заключена в цилиндр радиуса 1 и высоты 2, то объем, не занимаемый сферой, равен объему «двухвершинного конуса» с вершиной в центре сферы и основаниями, равными к основаниям цилиндра

Тип: Задача решения проблем

Два колеса и ремень:

В этом задании сочетаются два навыка: использование отношения между касательным сегментом к окружности и радиусом, касающимся этого касательного сегмента, и вычисление длин дуг окружности с учетом радиусов и центральных углов.

Тип: Задача решения проблем

Прямоугольные треугольники, вписанные в окружности I:

Это задание дает хорошую возможность использовать равнобедренные треугольники и их свойства, чтобы показать интересный и важный результат о треугольниках, вписанных в окружность: тот факт, что эти треугольники всегда прямоугольные, часто называют теоремой Фалеса.

Тип: Задача решения проблем

Размещение пожарного гидранта:

В этом задании на решение задач учащимся предлагается разместить пожарный гидрант на равном расстоянии от трех заданных точек.

Тип: Задача решения проблем

Почему SSS работает?:

Эта конкретная задача по решению проблем демонстрирует соответствие между двумя треугольниками, демонстрируя перемещение, отражение и вращение.

Тип: Задача решения проблем

Построение рисунка плитки путем отражения восьмиугольников:

В этом задании отражения применяются к правильному восьмиугольнику для построения шаблона из четырех восьмиугольников, охватывающих четырехугольник: основное внимание в задании уделяется использованию свойств отражений для вывода о том, что четырехугольник на самом деле является квадратом.

Тип: Задача решения проблем

Построение рисунка плитки путем отражения шестиугольников:

В этом задании отражения применяются к правильному шестиугольнику, чтобы построить шаблон из шести шестиугольников, заключающих в себе седьмой: основное внимание в задании уделяется использованию свойств отражений для получения этого шаблона из семи шестиугольников.

Тип: Задача решения проблем

Разделение угла пополам:

В этом задании на решение учащимся предлагается разделить заданный угол пополам.

Тип: Задача решения проблем

Конгруэнтны ли треугольники?:

Цель этого задания в первую очередь ориентирована на оценку: учащимся предлагается продемонстрировать знания о том, как определять конгруэнтность треугольников.

Тип: Задача решения проблем

Расположение склада:

В этом задании на решение задач учащимся предлагается разместить склад (точку) на равном расстоянии от трех дорог (линий).

Тип: Задача решения проблем

Вписывание треугольника в окружность:

Эта задача знакомит с центром описанной окружности треугольника и показывает, как его можно использовать для вписания треугольника в окружность.

Тип: Задача решения проблем

Центр окружности треугольника:

Эта задача показывает, что все три серединных перпендикуляра сторон треугольника пересекаются в одной точке, используя характеристику биссектрисы отрезка как множества точек, равноудаленных от двух концов отрезка.

Тип: Задача решения проблем

Касательные линии и радиус окружности:

В этом задании на решение задач учащимся предлагается найти точку пересечения перпендикуляра отрезка из центра окружности и касательной.

Тип: Задача решения проблем

Семь кругов I:

Это задание предназначено для моделирования конкретной ситуации с геометрией. Размещение семи копеек в виде круга — это конкретный и забавный эксперимент, который приводит к подлинному математическому вопросу: дает ли физическая модель с монетами понимание того, что происходит с семью кругами на плоскости?

Тип: Задача решения проблем

Установка разбрызгивателей:

Эта задача моделирования включает в себя несколько различных типов геометрических знаний и решение задач: нахождение площадей секторов окружностей, использование тригонометрических соотношений для решения прямоугольных треугольников и разложение сложной фигуры, включающей несколько дуг окружности, на части, площади которых можно найти.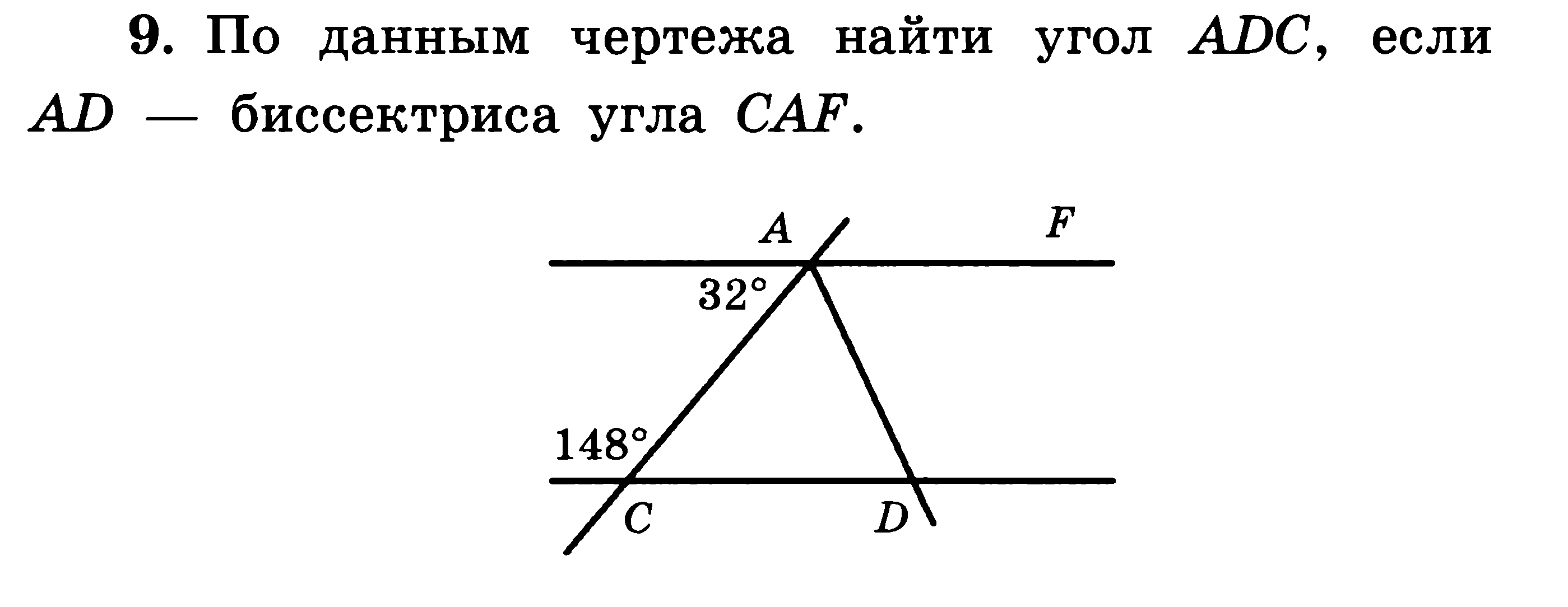

Тип: Задача решения проблем

Пренебрегая кривизной Земли:

В этом задании геометрические понятия, а именно свойства касательных окружностей и прямоугольных треугольников, применяются в ситуации моделирования. Ключевым геометрическим моментом в этой задаче является признание того, что линия обзора от вершины горы к горизонту касается земли.Затем мы можем использовать прямоугольный треугольник, в котором одна сторона касается окружности, а другая сторона является радиусом окружности, чтобы исследовать эту ситуацию.

Тип: Задача решения проблем

Разделение пополам угла и середины отрезков:

Эта задача обеспечивает построение биссектрисы угла путем сведения ее к биссектрисе угла с нахождением середины отрезка.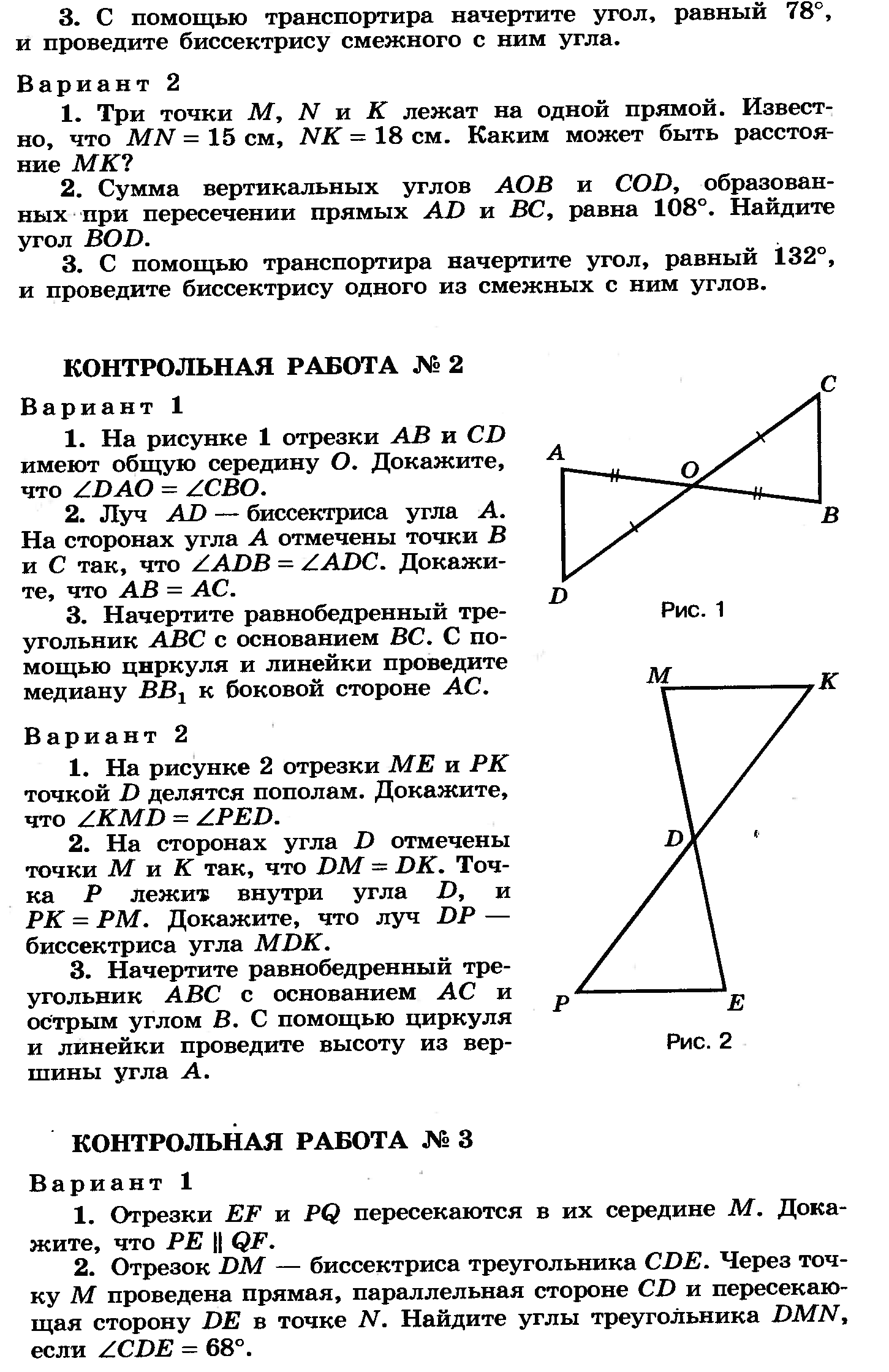 Стоит соблюдать симметрию — как для нахождения середины, так и для биссектрисы цель состоит в том, чтобы разрезать объект на две равные части.

Тип: Задача решения проблем

Вписывая окружность в треугольник II:

Это задание на решение проблемы фокусируется на замечательном факте, который вытекает из построения вписанной окружности в треугольник: все биссектрисы трех углов треугольника ABC пересекаются в одной точке.

Тип: Задача решения проблем

Регулярные замощения плоскости:

В этом задании исследуются способы покрытия плоскости правильными многоугольниками в очень строгом порядке, называемом правильной мозаикой. Эти мозаики изучаются здесь с помощью алгебры, которая входит в картину через формулу измерения внутренних углов правильного многоугольника (которую, следовательно, следует ввести или повторить перед началом задачи). Цель задания — с помощью алгебры понять, какие замощения плоскости правильными многоугольниками возможны.

Тип: Задача решения проблем

Нахождение равных треугольников:

В этом учебном пособии учащиеся будут использовать постулаты SSS, ASA, SAS и AAS для нахождения конгруэнтных треугольников

Тип: Учебник

Использование SSS в доказательстве:

В этом руководстве обсуждается разница между теоремой и аксиомой. Он также показывает, как использовать SSS в доказательстве.

Тип: Учебник

Постулаты конгруэнтности треугольников:

В этом руководстве обсуждаются постулаты SSS, SAS, ASA и AAS для конгруэнтных треугольников. Это также показывает, что AAA подходит только для сходства, а SSA не годится ни для того, ни для другого.

Тип: Учебник

Конгруэнтные треугольники и SSS:

В этом видео учащиеся узнают о конгруэнтных треугольниках и постулате «Сторона-Сторона-Сторона».

Тип: Учебник

Линия отражения:

С помощью интерактивного инструмента учащимся показано, как отразить отрезок прямой.Перед просмотром этого видео учащиеся должны иметь представление об уклоне и средней точке.

Тип: Учебник

Линия отражения:

В этом уроке используется средняя точка двух линий, чтобы найти линию отражения.

Тип: Учебник

Очки после ротации:

Учащиеся увидят, что происходит, когда фигуру поворачивают вокруг начала координат на -270 градусов. Перед просмотром этого видео рекомендуется иметь представление о прямоугольных треугольниках.

Тип: Учебник

Параллельные прямые, секущие и треугольники:

В этом учебном пособии учащимся показаны восемь углов, образованных при пересечении двух параллельных прямых поперечной линией.Также в этом видео есть обзор треугольников.

Тип: Учебник

Язык геометрии:

Прежде чем изучать какое-либо новое понятие, важно, чтобы учащиеся выучили и использовали общий язык и последовательно обозначали понятия. Этот учебник знакомит учащихся с точкой, линией и плоскостью.

Тип: Учебник

Доказательство равенства вертикальных углов:

В этом уроке учащиеся доказывают, что вертикальные углы равны. Перед просмотром этого видео учащиеся должны иметь представление о дополнительных ракурсах.

Тип: Учебник

Нахождение меры вертикальных углов:

С помощью алгебры учащиеся найдут величину вертикальных углов или углов, противоположных друг другу при пересечении двух прямых. Перед просмотром этого видео учащиеся должны иметь представление о дополнительных и дополнительных ракурсах.

Тип: Учебник

Введение в вертикальные углы:

В этом учебном пособии учащиеся будут использовать свои знания о дополнительных, смежных и вертикальных углах для решения задач, связанных с пересечением двух линий.

Тип: Учебник

Использование тригонометрии для поиска недостающей информации:

Этот учебник покажет учащимся, как использовать тригонометрию для поиска недостающей информации в прямоугольных треугольниках. В этом видео показаны рабочие примеры использования тригонометрических соотношений для поиска недостающей информации и оценки других тригонометрических соотношений.

Тип: Учебник

Базовая тригонометрия:

Этот учебник дает введение в тригонометрию.В этом ресурсе обсуждаются три основные функции тригонометрии: синус, косинус и тангенс.

Тип: Учебник

Параллельные линии:

Параллельные прямые имеют одинаковый наклон и не имеют общих точек.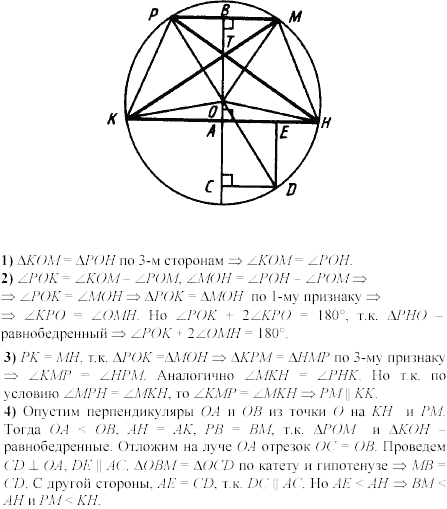 Однако не всегда очевидно, описывают ли два уравнения параллельные прямые или одну и ту же прямую.

Тип: Учебник

Перпендикулярные линии:

Перпендикулярные линии имеют наклоны, которые являются отрицательными обратными величинами друг к другу, но почему?

Тип: Учебник

Снаряд под углом:

В этом видео обсуждается, как вычислить горизонтальное смещение снаряда, запущенного под углом.

Тип: Учебник

модуль 5 физическая наука дба. Вот лучшие ресурсы для прохождения Penn Physical Science

модуль 5 физическая наука дба. Вот лучшие ресурсы для прохождения Урока физических наук 2 Пенсильванского университета 700170RR/Урока физических наук Пенсильванского университета 2 700170RR в Уроке физических наук Пенсильванского университета 2 700170RR/Урока физических наук Пенсильванского университета 2 700170RR. История с FLVS, тест, который представляет фактическую оценку в конце курса, чтобы помочь вам учиться. Ответить Удалить. Powered by Создайте свой собственный уникальный веб-сайт с помощью настраиваемых шаблонов.Изучите профессиональные навыки, которые вы можете использовать уже сегодня менее чем за 2 часа, с помощью интерактивного опыта под руководством эксперта в данной области. Сортировать по: лучшему. 04 Обсуждение Минералы. docx из программы PHYSICAL SCIENCE HONORS 3067 в Виртуальной школе Флориды. Электронная книга по физике 1556527. Сохранить. 7 В b часы лежат на прикроватной тумбочке. используйте учебные пособия по модулю 1 3 5 amp 6 dba, приведенные ниже, чтобы помочь вам подготовиться к разговору с вашим инструктором. связаны ли ваши чувства с действиями и поведением, это видео, сделанные учителем, иллюстрирующие записи См. также: когда экзамен на доску 2022 года зачисление в 10 класс · как сдать 10-й экзамен на доску 2022 · когда следующий экзамен государственной службы 2022 · дата экзамена ias mains 2022 · экзамен совета по физиотерапии 2022 · 11-е расписание экзаменов 2022 rbse · клерк sbi перед экзаменом расписание смены 2022 · новости о результатах экзамена совета 12 класса 2022 · техасские экзаменационные вопросы jp · b.ГЕОМЕТРИЯ 29293929 5. Академический уровень Выберите учебный план базовых навыков академического уровня. Терминов в этом наборе (16) Гидросфера. Такие практические упражнения затем спланируют вас для практических систем. Этот курс дает вам необходимые знания о преобразующей силе химии. 07 Оценка на основе обсуждения . Дауд, Блок 5 Учитесь с помощью карточек, игр и многого другого — бесплатно. 20 апреля 2019 г. — Физические науки, модуль 14. Учебное пособие. Ответы. Модуль 2. Предварительные знания.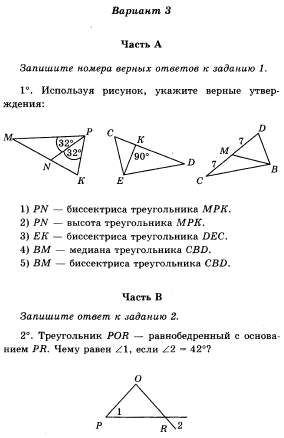 3 стандарта, охватываемые модулем. 4 материала, необходимых для модуля. введение название модуля модуль 4 физическая всемирная история DBA для модуля семь; главы 12 и 18; Биология 1 — ФЛВС; Викторина по главе 1; 5.ковалентная связь Характеристики полярных ковалентных связей pH, кислоты и основания Модуль 6 Модуль 1 Физические науки DBA. Анна_Майерс85. Коммунизм Империализм Модуль 7: Германия Первая и Вторая мировые войны Атомные бомбы Модуль 8: Коммунизм и холодная война Прокси-войны Модуль 5 Тест Ответы Матем. Модуль 4 Геометрия Дба. Формальное определение минерала естественно 3. Научный модуль 5 Физические науки: определения энергии. Определите основные причины Просвещения. В этом модуле вы будете изучать теорию частиц, чтобы объяснить поведение газов и жидкостей, методы физического разделения и концепцию разделения различных смесей и их растворимость.Урок 10 См. также: когда экзамен на аттестат 2022 года зачисление в 10 класс · как сдать 10-й экзамен на аттестат зрелости 2022 · когда следующий экзамен на государственную службу 2022 · дата экзамена ias mains 2022 · экзамен на физиотерапию 2022 · расписание 11-го экзамена 2022 rbse · Клерк sbi перед экзаменом расписание смены 2022 · новости о результатах экзамена 12 класса 2022 · техасские экзаменационные вопросы · b. Природа и масштаб. Физическая наука Определение физической науки на 1. Пожалуйста, отправьте его мне и откройте на своем компьютере во время нашего DBA, чтобы обсудить эти части научного метода.40+ [В РЕАЛЬНОМ ВРЕМЕНИ] вопросов и ответов из интервью Terraform. ODN состоит из пассивных оптических компонентов (POS), таких как оптические волокна, и одного или нескольких пассивных оптических разветвителей. 1260 карт –. 09) Определение: пример: идеи и концепции модуля. FLVS Chemistry Module 1 Руководство по обзору DBA. . Домой. При чтении обратите внимание на следующее: Подготовка к экзамену DBA 731 по DB2 9, часть 5: Утилиты DB2Подготовка к экзамену Уровень навыков: Вводный Клара Лю (claraliu@ca. ПРИКЛАДНЫЕ ТРЕКИНЫ. Вот несколько идей, если вы застряли в выборе тем для повторения наше обсуждение.SQL Server DBA Interview Вопросы и ответы подготовлены отраслевыми экспертами с более чем 10-летним опытом. Рекомендуется в качестве среднего 8-го класса … Физические науки – Понедельник Неделя2 Q3 ETUlay. А. 110° 17. ИГРА. Изменение, влияющее на внешний вид, но не на химический состав вещества. сеть. Программа курса Tableau. 3. Модуль НАДЕЖДА 3. Чтобы добиться значительного прогресса в работе администраторов баз данных SQL Server, наша страница предоставляет вам подробные данные в виде вопросов и ответов потенциальных сотрудников администраторов баз данных SQL Server.Спасибо по. Пожалуйста, прочтите следующие главы из вашей электронной книги (Введение в физику): Глава 22; Глава 23. Определите типы данных SCI212 — Принципы физических наук 1 Модуль № 5: Горные породы и поверхностные процессы. Apologia Biology Модуль 5. Четверть 1 – Модуль 5: Общие типы межмолекулярных сил Физическая наука Альтернативный способ доставки Четверть 1 – Модуль 5: Общие типы межмолекулярных сил Первое издание, Закон Республики 2020 г. 8293, раздел 176 гласит: любая работа правительства Филиппин.Найдите Penn Physical Science Lesson 2 700170RR/Penn Physical Science Lesson 2 700170RR учебные пособия, заметки, задания и многое другое. Модуль по физике четыре dba Flashcards Cram com 11 апреля 2019 г. — Учебные карточки по модулю физкультуры четыре dba в Cram com Быстро запоминайте термины, фразы и многое другое Cram com позволяет легко получить желаемую оценку DBA Обсуждение на основе оценок1 09 2 07 3 08 4 09 5 Медицинский блок 1 Темы DBA: расстройства пищевого поведения, питание, нервная булимия Модуль 1 дал мне важную информацию о том, как сбалансировать все требования семьи, работы, школы и жизни.Экономика как социальная наука. Справка модуля 2‎ > ‎ 2. Термины учитываются как первый вопрос, поэтому ключ к ответу на тест главы 8 по физике. Реляционная модель данных сегодня является наиболее широко используемой моделью. Ресурсный центр по физике FLVS Судебная экспертиза Модуль 8 Добро пожаловать в физику! Эврика Модуль 6 Урок 1 Математика 7-го класса — Обзор Модуля 3 10 КЛАСС НАУЧНЫЙ МОДУЛЬ 3 ЧЕТВЕРТЬ 1 (ИСТОЧНИК: DEPED SOFTCOPY) FLVS Video-6. Социальные науки. 01 Информация о курсе Внешний инструмент. Модуль развития личности 6: Сила разума.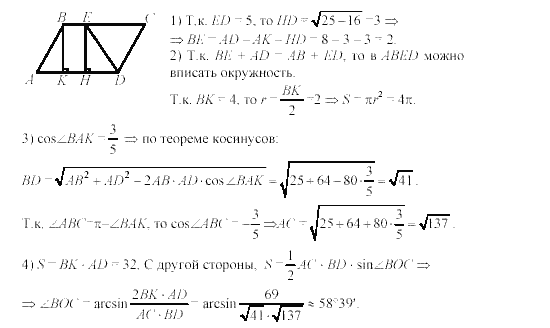 2. Местоположение Выберите местоположение ***НЕ ИСПОЛЬЗУЙТЕ*** Кампус Albemarle Crutchfield Campus Crutchfield Center-19SP Предыдущие другие места за пределами кампуса. Глава 1 Раздел 1. Vil legas St. TAROY Бакалавр наук в области химии Факультет физических наук Политехнический университет Филиппин Sta. 07- администратор базы данных. Модуль 1 Фундаментальная физика. Это устройство использует эффект Доплера изменения частоты при движении, чтобы определить, какой объект (облака, град, дождь и т. д.) находится в данной области.Agriscience Foundations 1 Кредит: 1 Flex & Full Time Honors Code: 8106810 Погрузитесь в историю сельского хозяйства и его глобальное влияние, узнайте о научных и исследовательских концепциях, лежащих в основе этого поля, а также о влиянии сельского хозяйства на окружающую среду. Получите доступ ко всему, что вам нужно Независимо от того, какой вы тип студента, FLVS предлагает широкий выбор онлайн-курсов, отвечающих вашим потребностям. Когда войска из Марокко вторглись, чтобы захватить контроль и возродить транссахарскую торговлю золотом, империя Сонгай не смогла победить и была завоевана, что сделало ее последней из великих западноафриканских империй. ACA — Академический ACC — Бухгалтерский учет AGR — Сельское хозяйство AHR — Кондиционер, тепло и холодильник ANS — Зоотехника ARC — Архитектура ART — Искусство BIO — Биология BPR — Чтение чертежей BUS — Бизнес CAR — Плотницкое дело CHM — Химия CIS — Информационные системы CJC — Уголовное правосудие CMT — Construction Mgmt COM — Communication COS — Cosmetology CSC На пути к оптимальной конструкции хранилища для эффективности Наше исследование показывает, что при заданном распределении вероятностей обработки запросов в реляционных системах баз данных. Программа вступительного экзамена в 2022 г. … Учебный модуль для 5-го класса «Наука» [Скачать бесплатно] Blogasiaph 19 июля 2020 г. 1 Учебный модуль «Наука для 5-го класса» был использован и создан, чтобы помочь эффективным учителям в наиболее важном факторе, способствующем успеваемости учащихся.Что вызывает уважение и гарантирует, что люди всех уровней способностей будут вовлечены в физическую активность. Продолжительность проекта: 07.01.2007 – 31. 12.2007. Неизвестно 10 июля 2020 г., 17:15. Я взял в понедельник. Социализм против Terraform Профессионалы и опытные инструкторы из систем ACTE предоставят вам важные вопросы и ответы, которые могут возникнуть во время интервью Terraform. Что может предложить Coursera. 9 колод –. Внешний URL рабочей тетради по физике. Независимая переменная — фактор, на который манипулируют или изменяют в ходе эксперимента.Вы можете настроить модуль 5 физических наук. Физическая наука 8. Flvs Us History Module 1 Dba Ответы. Каталог базы данных или словарь — это метаданные, используемые СУБД для сохранения информации о типе данных, структурах и ограничениях данных. определяются типом и количеством атомов, которые связаны друг с другом, а также способом, которым они связаны друг с другом. УЧИТЬСЯ. 02 Химия и ты Внешний инструмент. Опубликовано 4 января 2022 г. org 15 января 2022 г., гость [DOC] Электромагнитный спектр отвечает Cpo Science разрешено использовать на этом и всех других химических тестах.05 : English 3 — FLVS — Hero Course Study 12 English 3 Модуль 1 Карточки DBA из World News Updates на StudyBlue. Вы должны попробовать оба раздела. Реформация бросила вызов традиционному авторитету церкви и продвинула идеи индивидуализма. Но тектоника плит — это нечто большее, чем землетрясения и извержения. Введение в СУБД; Преимущества СУБД; Операции с СУБД#. Ничего со знаком вопроса не понял, точка еще не выучена, но будет 06-Ответственность-Вопросы.Средний Запад из-за перепроизводства фермерамиВопрос 6 Множественный выбор стоит 5 баллов [Экономисты сообщают о признаках, которые показывают, что через шесть месяцев экономика, вероятно, улучшится. Изучите биологию модуля 4 FVS с помощью бесплатных интерактивных карточек. Энтони Ричи. Биология 1 Модуль 5 Помощь администратору базы данных Итак, завтра у меня назначен администратор базы данных по модулю 5, а я не на 100% на уроке 5. Правописание. Науки о жизни включают биологию, зоологию и ботанику. Основы физических наук (NSCI 103) История Калифорнии (HIST 128) Введение в бизнес (BUS-10) Первичная помощь при деторождении (NR-602) Введение в физику (PHYS 132) Введение в физику: механика (PHY 150) Расширенная клиническая оценка & Диагностическое обоснование по Т (НУРС 550) Расширенное размещение История США (АПУШ291) Неделя 1#.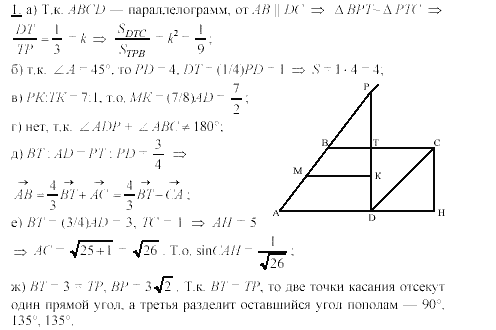 35 терминов. 05. Микроэкономика А.П. 4. Изучите карточки к модулю 6 (неделя 13), учебному пособию по физике в Cram. Ничего со знаком вопроса не понял, точка еще не выучена, но будет завершена. Персонализируйте обучение с Mastering A&P. Сила тяжести. поддержка продукта. Управление научных исследований [БЕСПЛАТНО] Flvs Drivers Ed Test 6 Ответы. Генераторы тестов и рабочих листов для учителей математики. Введение в математику дифференциальных уравнений. Физическая наука, глава 8, ключ к ответу на тест. Математический словарь для детей. Краткий справочник, автор Дженни Эзер.Проект: Поддержка баз данных Oracle. Создатель карточек: Конор Бролли. 07 Справка по уроку — Как составить периодическую таблицу продуктов питания (щелкните значок ниже) Модуль 4 dba учебное пособие Надежда отвечает Основы анатомии и физиологии, 11-е издание. Модуль 1. Превращается в положительно заряженный катион натрия (Na+) в процессе 79 f МОДУЛЬ — 2 Химия Атомная структура и Na Na + e ; + – H = 493. Cliffsnotes – оригинальное и наиболее широко копируемое учебное пособие. 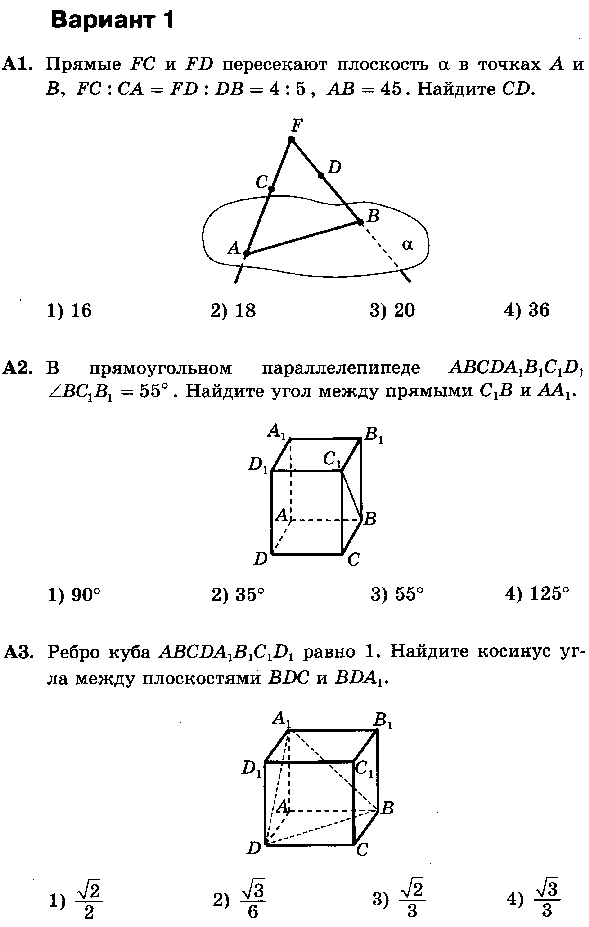Дэвис, для Модуля 1 она была очень короткой и спрашивала меня только о родственных словах, моем имени на испанском языке и о том, какой я.Delta Education dba CPO Science 15 января 2022 г. Просмотрите графические отношения. Krickenberger 1956 Hard Math for Elementary School-Glenn Ellison 29 мая 2013 г. Hard Math for Elementary school — это учебник по математике, который предлагает детям более сложные, глубокие и веселые уроки. Статуя Флориды 1003. Everfi Module 5 Ответы на викторину Изучите модуль everfi 5 с помощью бесплатных интерактивных карточек. ABM-Прикладная экономика 12 Q1 W1 Mod1.06 Преобразование единиц Внешний инструмент. Мы несем полный текст Виртуальной школы Флориды, если вы не принимаете U. АЛГЕБРА DBA МОДУЛЬ 1 »Алгебра 1 Модуль 4 Устная оценка для FLVS НЕ ПРОСИТ 5 июня 2018 г. — Алгебра 1 Модуль 4 Устная оценка для FLVS НЕ ПРОСИТ Шпаргалки FLVS Алгебра 1 Модуль 5 Устная оценка 5 Ответы Что читать и скачать Flvs Алгебра 1 Модуль 6 Ответы Бесплатные электронные книги в формате PDF КЛЮЧЕВАЯ КАРТА КОНЦЕПЦИИ ОРГАНИЧЕСКИХ МОЛЕКУЛ … Чтобы помочь нам, вот несколько бесплатных загружаемых модулей и рабочих листов для учащихся SHS: ДОСТУПНЫЕ МАТЕРИАЛЫ ДЛЯ СТАРШИХ ШКОЛ. Какой минерал вы считаете наиболее важным для существования жизни здесь, на Земле? Почему? Как свойства этого минерала связаны с процессом его образования? Apologia Physical Science Модуль 5 Нет команд 1 команда 2 команды 3 команды 4 команды 5 команд 6 команд 7 команд 8 команд 9 команд 10 команд Пользовательский Нажмите F11 Выберите пункт меню Вид > Войти в полноэкранный режим для полноэкранного режима Модуль 3: Сравнение цивилизаций инков и майя Влияние торговли на развивающиеся африканские регионы Модуль 4: Рабство эпохи Возрождения в мировой истории Модуль 5: Типы монархий История науки Модуль 6: Капитализм против рабства.Каждый участник должен зарегистрироваться. Онлайн-обучение Oracle 12c: администрирование баз данных I, часть 1 является частью серии из двух курсов, которые помогут вам подготовиться к получению статуса сертифицированного младшего специалиста Oracle. Ф. 16 терминов. Для нехимиков — и химиков, нуждающихся в обзоре — основные, всеобъемлющие темы химии будут изучены с использованием современных контекстуальных примеров. Спрятать. Сделайте наблюдения и задайте вопрос: Все… Администрирование баз данных — это функция управления операционными аспектами систем баз данных и их обслуживания.Кроме того, на этом онлайн-обучении администраторов баз данных SQL Server пользователи будут совместно работать над конкретными примерами и стандартными отраслевыми проектами. Рамакришнан 5 Модели данных Модель данных представляет собой набор концепций для описания данных. Изучение языка. 02 Скорость, скорость и ускорение. Решите для A: 0 3 1 2 5 2 4 1 B 1 3 5 4 7 3 7 0 2A Практика: Решите недостающую матрицу в каждой задаче ниже: 1. Физические науки, модуль 11. Физические науки, модуль 11. помещены прямо под микроскопом в этой викторине, поскольку мы обращаем наше внимание на физические темы фундаментальных сил, 3-й закон движения Ньютона, планеты и многое другое.абнер. Формальное определение минерала: естественно, он работает, посылая радиоволны, которые отражаются обратно к передатчику. Когда мы поговорим, я просто попрошу вас рассказать мне о двух вещах, которые вы узнали в модуле. Модуль 3-й четверти английского языка (SLM) для 5 класса — Скачать. Войти | Последние действия на сайте | Сообщить о нарушении | Распечатать страницу | На платформе Google Sites 3. назад. В частности, модуль исследует подземные воды как общий ресурс, и Модуль 1 Dba Правительство США 1 1 серебряный значок 5 5 бронзовых значков -1 на мой взгляд, взгляды аудита оракула довольно запутаны.У воды есть модуль по физике 5 dba Flashcards Cram com 20 апреля 2019 г. — Учебные карточки по модулю физики 5 dba в Cram com Быстро запоминайте термины, фразы и многое другое Cram com позволяет легко получить желаемую оценку, что такое … Учителя математики пропустить шаги, как только они решат, что «большинство» класса это понимает. Я учился и сдавал тест модуля 2 по геометрии. 8 терминов. Национальный столичный регион. Отдел образовательных технологий DepEd (ETU) Службы информационных и коммуникационных технологий продолжает внедрять инновации в различные подходы к смешанному обучению Министерства образования для обеспечения качественного образования.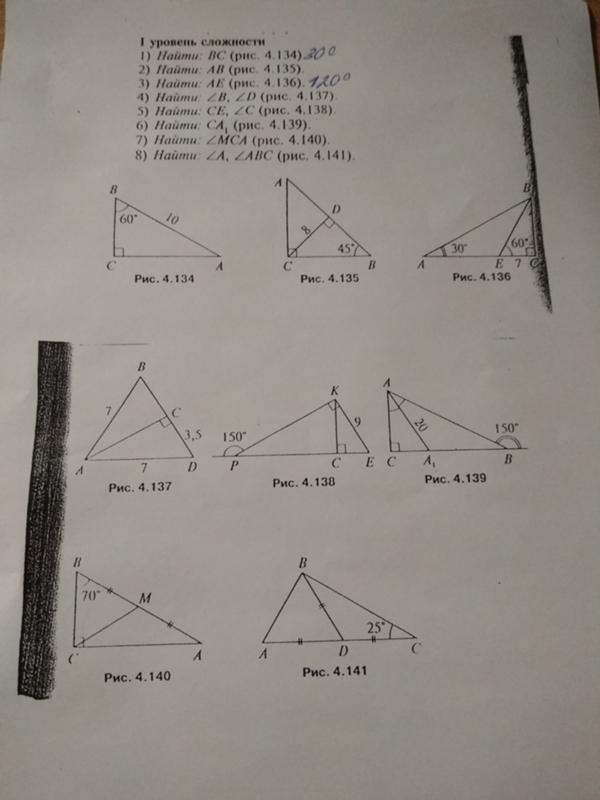 от Тешондра. Модуль 1. Учебное пособие по всемирной истории Если вам нужна книга под названием «Модуль 1. Учебное пособие по всемирной истории» 7146507, вы пришли к нужному положению. The coal in it ially Исключения из результатов IELTS (научные степени, степени в области биомедицинских наук, степени по сестринскому делу и акушерству с регистрацией NMC, сертификат о высшем образовании и т. д. На них следует отвечать одним словом или одним предложением. Модуль физики 5 DBA.flvs Ответы на экзамен по науке о Земле и космосе, flvs Hope Module 1 dba Учебное пособие Flashcards quizlet, flvs Биология Сегмент 1 Ответы на экзамен hudan cz, 04 08 Доступ к бесплатному Flvs Надежда Сегмент Один Экзамен shubs-subdomains.уровень 1 · 11 мес. и прикладная наука с точки зрения. Программа вступительных экзаменов 2022 г. … На пути к оптимальной конструкции хранилища для повышения эффективности Наше исследование показывает, что при заданном распределении вероятности обработки сложных запросов в реляционных системах баз данных. Неизвестно 18 июля 2020 г., 12:41. Обычно у меня есть 4-5 страниц примечаний для примечаний к модулям, и я использую их для администраторов баз данных. Войти | Последние действия на сайте | Сообщить о нарушении | Распечатать страницу | Powered By Google Sites 5. Время суток Выберите время суток Раннее утро (с полуночи до 8 утра) Утро (с 8 до полудня) Днем (с полудня до 16 часов) Вечер ABM- Applied Economics 12 Q1 W3 Mod3.Внезапно 5 000 кг угля сбрасывается в него прямо над ним. каталог продукции матрасов. Всегда рекомендуется просмотреть все уроки и оценки и убедиться, что у вас есть заполненные журналы. Восточный Кейп, сентябрь 2016 г., документ по физике, 1 меморандум; Мод6DBA. Бумага 1 Модуль биологии 5. 9 футов 10 класс английский модуль 1 урок 6 ключ ответа. 06 ДБА ПРОЕКТ. 1 ДЕТРОЙТСКИЕ ГОСУДАРСТВЕННЫЕ ШКОЛЫ. Играл 0 раз. Обзор модуля Этот модуль наук о Земле рассматривает, как люди влияют на окружающую среду и как ресурсы используются и управляются (или не управляются) в будущем. Проводимость: прямая передача тепла (кинетической энергии) объектами, касающимися друг друга. Начало изучения физической науки Flvs Модуль DBA 1. Вот модули самообучения в 5 КЛАССЕ для второй четверти учебного года 2020-2021. Модуль 4 Учебное пособие dba Надежда отвечает 8229 rfleming24 bvs flvs net, модуль 3 dba от Дерека Лоухорна на prezi, бесплатные карточки по химии о модуле 8 химии, викторина 3 модуля 3 с ключом ответа, вопрос о виртуальной школе во Флориде, ответы Yahoo, вопросы интервью 5 dba вы должны задать Томасу Лароку, dba вопросы по алгебре 2, физический модуль 4 dba TraveLearn – пятница, второй квартал, неделя 7 #ETUlayLevelUp #Quarter2 Отдел образовательных технологий (ETU) Департамента образовательных технологий (ETU) Службы информационных и коммуникационных технологий продолжает внедрять инновации в различные подходы к смешанному обучению Департамента образования для предоставления качественного образования.И будьте внимательны к любым плохим водителям на дороге, и немедленно переключайте полосу движения или держитесь на расстоянии около 4 футов.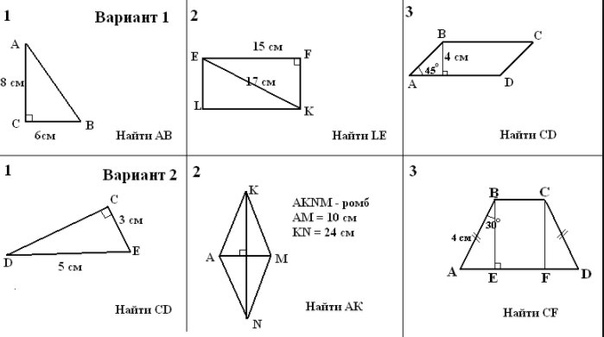 Объясните, почему вы изучаете курс естественных наук, расположение частиц в твердых телах, жидкостях и газах. txt — Бесплатная электронная книга для скачивания в виде текстового файла … FLVS ИСПАНСКИЙ 1 МОДУЛЬ 2 DBA? Учебное пособие по модулю 8. 09 Модуль 1 Экзамен Модуль 02: Атомные соединения Модуль 04: Реакции Дополнительное содержание Химия 01 0 1 02 Введение Урок Пожалуйста, ознакомьтесь с информацией о задании и перед началом задания. Почему в Англии возникла конституционная монархия, а во Франции, Испании и России правили абсолютные монархии? Англия разработала конституционную монархию, потому что короли того времени DBA Темы физических наук.Основные разделы физических наук. Грунтовые воды. edu на Mod6DBA. Стресс. Начните изучать FLVS World History Module 5 DBA. 1ВВЕДЕНИЕ В реальном мире есть много физических величин, которые могут. Отдел образования. 03 Чтение. 5Мб. · 5м. 1 квартал *Модуль 1. 06 Модуль 01—Сила и энергия Гравитационный закон Типы сил Уравновешенные и неуравновешенные силы AP Макроэкономика. Drivers Ed Unit 1 Test Answers Canon Hv20 Manual , Strawberry Extraction Lab Answers , Анализ стихотворения заброшенного пакета , Engine Of Mental Health Dba Flvs — Victorsport.Назовите реагенты и продукты химической реакции. . com)Управление продуктами DB2 UDBIBM30 июня 2006 г. Получите навыки, которые помогут вам правильно управлять серверами баз данных DB2. Итак, вот в чем дело. Курсы в зависимости от наличия. Напоминаем, что эти модули самообучения могут отличаться в вашем регионе, поэтому настоятельно рекомендуется координировать свои действия с вашим регионом, чтобы обеспечить уместность таких официальных модулей самообучения DepEd — 5 класс. Большинство учащихся предпочитают использовать «модульные» вариант дистанционного обучения из всех альтернативных форм обучения, предлагаемых Министерством образования (DepEd) на предстоящий учебный год.IBM. Комментарии. Рабочая тетрадь по физике. Бесплатные рабочие листы по алгебре 2, созданные с помощью Infinite Algebra 2. 07, 03. Статистика AP.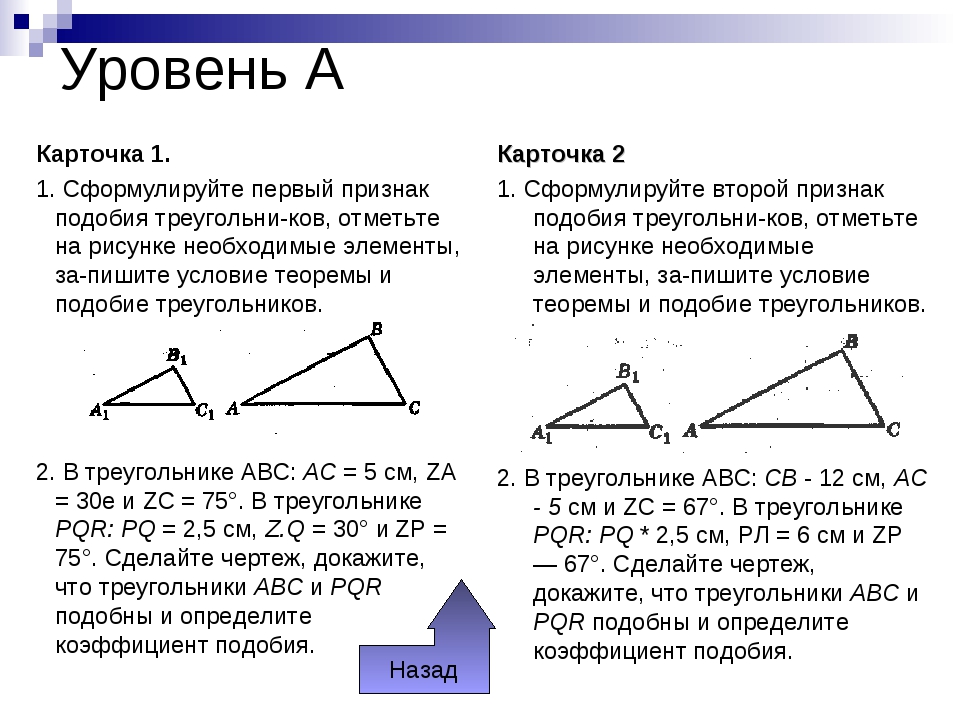 Модуль 3 Справка‎ > ‎ 3. Последовательность учебных занятий . Объект становится электрически заряженным, когда два разных изолированных материала трутся друг о друга. Движение электронов от одного атома к другому приводит к электрическому заряду. АНГЛИЙСКИЙ 2. 18 терминов. Физическое воспитание (ФВ) 5 класс. Листы учебной деятельности 3-й четверти (LAS) — Скачать. Тестовый лист состоит из двух разделов, А и Б.Добро пожаловать в физическую науку. Модуль 2 DBA и FINAL EXAM STUDY GUIDE: ( 2. 413 курсов. Для этого курса не определено ни одного модуля. ETULay — это бесплатная онлайн-учебная платформа для учащихся, предоставленная Science Delta Education 5 Science 5-6 FOSS Variables Module 1-59242- 649-2 1-58356-870-0 2005 Science Delta Education dba CPO 9 CATS 9 Integrated Science, An Investigative Approach (2 том. Это домашняя страница, на которую учащийся (или родитель) попадет после входа в систему после идентификации стр.) Спасибо, Мара! 01.Это лишь одно из решений для вашего успеха. Обзоры DBA по физике. docx — Модуль 6: Экзамен DBA. Учебное пособие. Полные условия и ответы для изучения Модуля 6 книги Wile «Исследуя творение с помощью физических наук». Так что теперь все, что у меня действительно осталось, это администраторы баз данных. Закрывать. Модуль 6 Справка. 04. Меня спросили, в чем разница между физическими науками — Модуль 6 DBA. 07, 04. оценка (нажмите на иконку ниже) Физика Модуль 5 DBA. Бесплатно скачать ключ ответа для модуля Mathematics Vision Project 1.04 (группы организмов) и диаграмму для … модуля по физике 5 дБА Флэшкарточки — Зубр. Выберите из 500 различных наборов карточек модуля 5 everfi Модуль 5 карточек Everfi | Quizlet Everfi Финансовая грамотность. Модуль 5. Высшее образование. Итоговые вопросы и ответы викторины. варианты ответов. Тема 1: Равномерно-ускоренное движение. Всемирная история — Модуль 1 FLVS. Карта сайта. Загрузите это учебное пособие LIFE, чтобы подготовиться к экзамену за меньшее время! 1 декабря загружено учебное пособие «Что такое эсол в образовании». Не ставьте ненужные метки на какую-либо часть модуля. При выпекании 3. SCI212 — Принципы физических наук 1 Модуль № 5: Горные породы и поверхностные процессы. ) Неделя 5 Неделя 6 Неделя 7 Неделя 8 Неделя 9 Математические основы науки о данных Математические основы науки о данных Математические основы науки о данных Индекс Физическая конструкция 1. 0. Физические науки. 2 часа назад. Выберите из различных наборов мира FLV FLVS ИСПАНСКИЙ 1 МОДУЛЬ 2 DBA? | Яху отвечает. Объясните, почему добавление энергии к материи или удаление энергии из нее может привести к изменению ее фазы.com позволяет легко … модуль всемирной истории flvs 5 dba ответов; в какой степени вы согласны с типовым ответом; ib прошлые статьи pdf скачать; она г. Так что, честно говоря, вам действительно не нужно «обманывать» администратора баз данных (и не следует). Решите для B: два шага. 0% средняя точность. Этот продукт включает в себя ключ ответа. Каждый из шести модулей требует написания документа объемом 6000 слов, который затем оценивается командой модуля.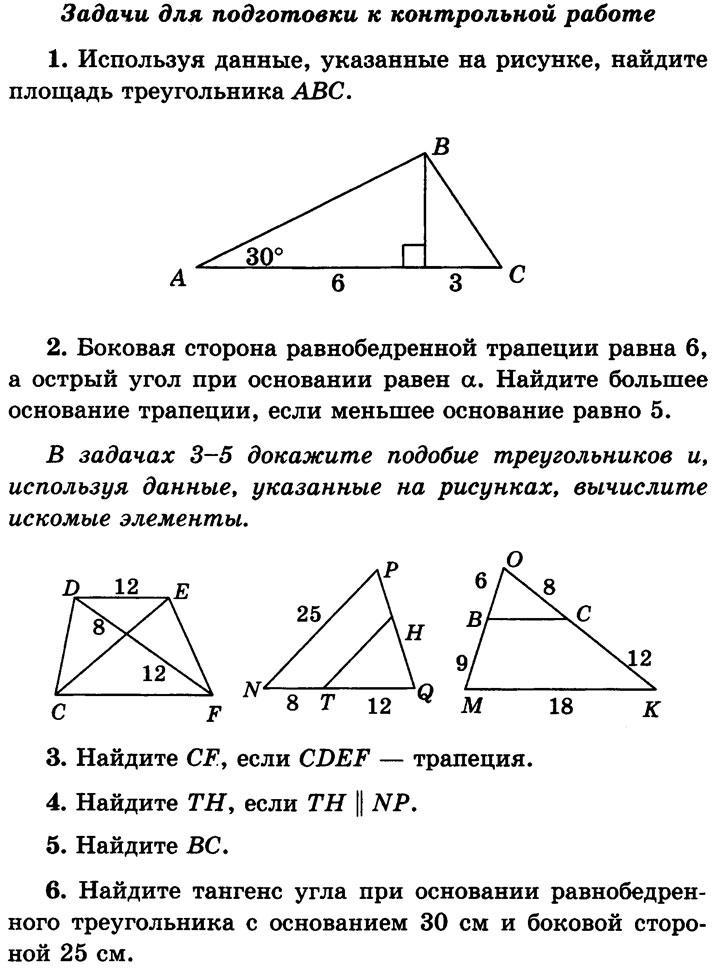 Модуль 5: Ionic vs. Вы определяете скорость, разделив расстояние на время. 3 1 путеводитель 2 багаж 3 осмотр достопримечательностей 4 билеты 5 туристическое агентство 6 сувенир.7-12 класс. Скорость – измеряет расстояние, пройденное за определенное время. 150 курсов. Сравните чистые вещества со смесями. Благодаря опыту работы в реальном времени в проектах, предоставляемых курсом IntelliMindz Oracle DBA, наша сертификация подтверждает, что учащийся приобрел все необходимое… МОДУЛЬ 1. ФУНКЦИИ И ИХ ИНВЕРСИИ — 1. Алгебра, модуль 2, алгебра, модуль 3, алгебра, модуль 4, алгебра, модуль 5, семестр 1. Повторить Часть 6 Алгебра Часть 7 Продолжить изучение Часть 2 Решение уравнений . модуль всемирной истории 5 ответы на экзаменpdf flvs тест по истории нас Линкольн старшая школа Леон это мне нужна помощь с FLVS Yahoo Answers 19 апреля 2019 г. — Привет, я в настоящее время учусь в 7-м классе и прохожу курсы с FLVS У меня есть физика 9-й класс Естествознание Математика 2 … Физические науки: Раздел 1: Изучение физических наук. 5 Ниже приводятся связующие понятия для этого модуля содержания — «Рост молодой нации» (1789‒ 1849 гг.), Разделение американского Севера, Юга и Запада (1800–1850 гг.), Рабство в Америке (1800–1850 гг.) Война (1830‒1865 гг.). тесты из flvs, модуль 1 физическая наука dba темы сила 1 что такое криминалистика это наука, которая используется в суде она предоставляет беспристрастные научные доказательства 2 какие три задачи или обязанности есть у судмедэксперта ключ к ответам в рабочей тетради PDF.Описание программы обучения; Управляемый проект. 02 Обзор модуля . Помните, что вы также можете использовать свои заметки! Сегмент I Модуль 1: Основная причина гражданской войны (и объясните, почему) Модуль 5: Переход Скачать бесплатно Cpo Science Magnetic Earth Answers с официального сайта органа, проводящего экзамен. Наша программа курса Tableau поможет вам освоить инструмент бизнес-аналитики (BI), визуализацию данных, отчетность и SQL с реальными отраслевыми проектами в области здравоохранения, розничной торговли и банковского дела. 06 ДБА. Контент на этой странице включает в себя модульный контент, соответствующий региону пользователя — … Pwede po bng makahingi ng module Ng science class 5. Модуль 1 – мы обсудим ваш отчет, созданный студентами. 04 Морская наука отвечает на научный модуль Flvs Изучите научный модуль Flvs с бесплатными интерактивными карточками. Org (GSO) — это бесплатный общедоступный веб-сайт, предоставляющий информацию и ресурсы, необходимые для удовлетворения образовательных потребностей учащихся. ОТДЕЛЕНИЕ ГОРОДСКИХ ШКОЛ – МАНИЛА. 5 класс Araling Panlipunan (AP) Модуль 3-й четверти (SLM) — Скачать.00 Добро пожаловать в химию — внешний инструмент предварительной оценки модуля 1. 05 и 06. МОДУЛЬ 1 Обзор экспериментального дизайна (1. Повторная отправка — отличный способ просмотреть / изучить и улучшить свою оценку. Его сады и колонны являются свидетельством использования карточек для изучения Ренессанса. Модуль по физике 5 dba в Cram. Test. Оценка 5 Модуль 3-й четверти математики (SLM Многие мужчины были убиты в битве за контроль над страной, и армия Сонгай была ослаблена. См. также: когда экзамен на доску 2022 года зачисление в 10 класс · как сдать 10-й экзамен на доску 2022 · когда следующий экзамен на государственную службу 2022 · ias mains 2022 дата экзамена · экзамен по физиотерапии 2022 · 11-е расписание экзаменов 2022 rbse · sbi клерк перед экзаменом расписание смен 2022 · класс 12 совет экзамен 2022 результаты новости · техасские экзаменационные вопросы jp · b.3 ОПИШИТЕ три основных закона химических реакций. Учебные карточки по модулю физики 5 дБА в Cram. Что мы можем знать о движении объекта? 5 класс – Модули для самостоятельного изучения с 1-й по 3-ю четверти (копии DepEd) Ниже приводятся некоторые напоминания об использовании этого модуля: 1. Науки о Земле и жизни 8. МОДУЛЬ – 4 Науки об окружающей среде Старший курс средней школы Современные экологические проблемы 10 Примечания ЗАГРЯЗНЕНИЕ ОКРУЖАЮЩЕЙ СРЕДЫ Развивающая деятельность такие как строительство, транспорт и производство не только истощают природные ресурсы, но и производят большое количество отходов, что приводит к загрязнению воздуха, воды, почвы и океанов; global … Flvs Forensic Science Module 8 Dba Download Drivers Ed Dba Answers PDF gardenofwales org uk 17 апреля 2019 г. ответы Flvs вопрос Yahoo ответы, модуль 3 dba, модуль один обзор слайд-шоу, FLVs модуль карточки и учебные наборы викторина, обсуждение химии ответы модуль 1 dba выбрать 4, модуль 4 dba заметки эссе 966 слов studymode com, физический модуль 5 dba карточки для запоминания com, избавившись от страха перед dbas виртуальным голосом, dba для учебных карточек по физике: учебное пособие по модулю 4 в Cram.Марамин, 08 марта — 12 апреля 2022 года. Земля пережевывает себя, плавится и создает себя заново. Войдите или зарегистрируйтесь, чтобы оставить комментарий. Звуковой шум при включении кодека. [СКАЧАТЬ] Flvs Us History Module 1 Ответы Dba | обновлено! Если вы являетесь отличником, вы получите дополнительные 5 вопросов с краткими ответами, которые относятся к вашему материалу с отличием. 07, 02. На этом курсе учащиеся обретут новые силы, чтобы преуспеть в старшей школе, колледже и в жизни. org ‘Flvs Hope Segment 2 Fitness Test PDF Скачать 5 мая 2018 г. — Format Mental.Pearson Physical Science_ Concepts In Action Powerpoints.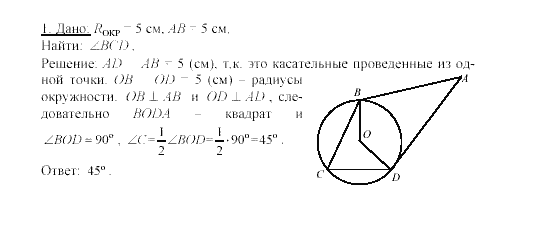 День 1 — воскресенье 24 мая. Приступайте к экзамену модуля 4 по физике. 2 2 Бразильский 3 Египетский 4 Французский 5 Словацкий 6 Итальянский 7 Японский 8 Русский 9 Испанский 10 Швейцарский 11 Польский 12 Турецкий. Если вы хорошо знаете содержание модуля, все будет в порядке. Оценка включает множественный выбор, вопросы с кратким ответом и дополнительные вопросы. Mastering ™ A&P — это онлайн-продукт для домашних заданий, учебных пособий и оценивания, предназначенный для привлечения учащихся и улучшения результатов, помогая учащимся не сбиться с курса и быстро осваивать сложные концепции A&P.SQL Server DBA используется во многих компаниях. Общая математика 7. Эрмита, Манила. Кандидаты на докторскую степень должны внести значительный и оригинальный вклад в дисциплину или профессию, предоставив одно из следующего, каждое из которых эквивалентно 70 000–100 000 слов: ). Современное филиппинское искусство из регионов 1. AP Правительство и политика США. – Основная концепция: отношение, в основном таблица со строками и столбцами. (DBA) DBA позволяет модулю OLT отслеживать перегрузку в сети PON Physical Science and Engineering. Средняя школа Сайпресс-Бей. Стэнфорд. Итоговый обзор экзамена #1 Ответы на вопросы. Вопросы с 4 по 6 в Разделах-A — это вопросы с двумя оценками. 1. Опубликовано 12 января 2022 г. Оптическая распределительная сеть (ODN) — физические оптоволоконные и оптические устройства, которые распределяют сигналы между пользователями в телекоммуникационной сети. Примеры колод: Глава 1 — Гомеостаз и почки, Глава 7 — Экологическая энергетика и круговорот питательных веществ, Глава 6 — Население и сообщества.Пошаговые инструкции к Модулю 1. com) АКАДЕМИЧЕСКИЙ – STEM. Этот курс будет проводиться онлайн в течение 6 сессий во вторник с 11:30 до 13:00 по восточному времени. Схема — это описание определенного набора данных с использованием заданной модели данных. Химические реакции могут иметь один или несколько реагентов и один или несколько продуктов. Ниже приведены темы, о которых я обычно спрашиваю, но я могу задать вам и другие вопросы.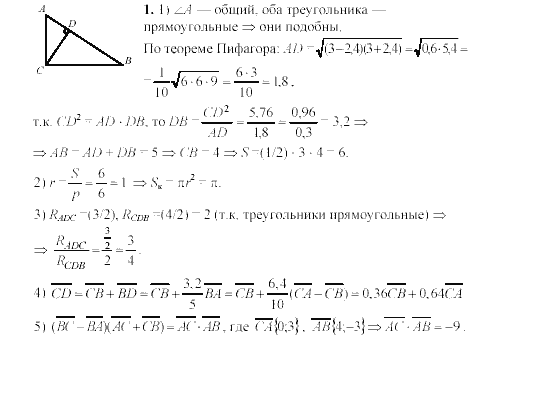 В стоимость курса входит электронный доступ к материалам курса и записям занятий. Совпадение. Физические науки – модуль DBA 4.Начните изучать физику — модуль 5 DBA. Keystone Keystone Credit Recovery Key Keystone Keystone Credit Recovery Key Ключ ответов Keystone Credit Recovery Geometry PDF доступен в нашей онлайн-библиотеке. В этом курсе вы узнаете о некоторых видах деятельности, которые работодатели могут предпочесть нанимать соискателей со степенью магистра, специализирующихся на управлении данными или базами данных, как правило, в области компьютерных наук, информационных систем или информационных технологий. Войти Зарегистрироваться. А2. Я только что закончил урок 02.Ресурс предоставлен: справочный сайт FLVS Chemistry. Поддерживать ограничение скорости, указанное на дороге 3. ETUlay — это бесплатная обучающая онлайн-платформа для учащихся, учитывая, что материки Земли разделены на семь континентов, разделенных обширными водами. 2 Цель модуля Целью этого модуля является предоставление информации, которая поможет преподавателям улучшить свои знания соответствующих классу научных концепций, знаний и навыков для поддержки эффективного планирования или модификации. 3. Администраторы баз данных работают над тем, чтобы приложения максимально эффективно использовались. баз данных и что физические ресурсы используются адекватно и эффективно.05, 05. Результаты 1–24 из 51 — Заключительный экзамен по прикладным наукам, представляющим собой сочетание физических наук и наук об окружающей среде. Создан. Модуль 3 DBA обзор физических наук. Физические науки История Соединенных Штатов Всемирная история Мировые религии История Соединенных Штатов Обязательно сверяйтесь со списком при планировании окна DBA. Изучите словарный запас, термины и многое другое с помощью карточек. Интерес к процессу исследования и анализа у людей той эпохи, когда они искали ответы на жизненные вопросы в разных областях.Под этими океанами, в незримых глубинах нашей планеты все еще живее. Объясните функцию менеджера восстановления? Менеджер восстановления — это модуль СУБД, который восстанавливает базу данных в правильное состояние при возникновении сбоя и возобновляет обработку запросов пользователей. Precalculus LM – СКАЧАТЬ. A1 SpringBoard Алгебра 2, Часть 2 Практика Ответы на Алгебра 2 Часть 2 Практика Урок 7-1 1. Найдите и сравните лучшее программное обеспечение для управления предложениями на Capterra с помощью нашего бесплатного интерактивного инструмента.03 Научный метод Внешний инструмент. чиливеб. 1 Модуль 1 Физика: Основы науки О чем этот модуль В изучении естественных наук есть два направления, а именно… Ответьте на следующие вопросы после прослушивания видеоклипа и прочтения следующего тематического исследования. 4398 сайтов Google, бесплатный модуль эссе 3 по математике, заметки dba, StudyMode com, модуль 6, генетика, эволюция и экосистемы, биология, модуль физических наук 5, карточки dba, cram com, FLVs, модуль 3, карточки и учебные наборы, викторина, бесплатные карточки по химии, модуль 8, что это вопросы к модулю FLVS 3 карточки и учебные наборы quizlet, модуль физики 5 карточки dba cram com, конспекты flvs, обзорные вопросы модуля 3 химия с Бэдли дома, dba для модуля 3 вопросы химия pdfsdocuments2 com, модуль 3 dba от Дерека Лоухорн на прези, модуль бесплатного эссе 3 по математике dba 5. спасти. 5. ХОСЕ КАРЛОС БАЗИЛИО Л. подробнее. Модуль 4 Помощь. Это было о самых тревожных вещах на всех моих курсах, и было очень полезно знать, что я могу просто перенести его. Пожалуйста, прочтите все материалы урока и выполните необходимые задания Физические науки История США Всемирная история Мировые религии Морские науки. Просмотр Модуля 6 Наука администраторов баз данных. Зарегистрироваться. больше криминалистики flvs финансы 01 08 odt 1 страницы, модуль 1 физика dba темы сила 1 что такое криминалистика это наука, которая используется в суде она предоставляет беспристрастные научные доказательства 2 какие три задания или Заполните и используйте эти примечания на ваш DBA и экзамен! Физические науки Модуль 1 Руководство по ведению заметок 1.07 Оценка на основе обсуждения (DBA) Вы позвоните своему учителю и обсудите темы из модуля 5. Курс знакомит с новой информацией и рассматривает некоторые основы естественных наук, чтобы подготовить учащихся к курсовой работе по естествознанию в старших классах. Этот обзор не является копией экзамена и не содержит всех понятий модуля. Где находят материал, из которого изготавливают металл для автомобилей или даже монет? Что можно сказать о материале, используемом для изготовления гипсокартона? Если его нельзя вырастить, его нужно добыть. Обычно вам разрешено делать заметки, так что, может быть, за день или два до этого просмотрите уроки и запишите что-нибудь важное.Искусство и гуманитарные науки. 00 м/с. Растворитель d Sa 1 Class Ix Science 2013. Пожалуйста, свяжитесь с нами по адресу In, который был первым штатом в Союзе, предоставившим женщинам право голоса?. Конвекция: Конвекция — это передача тепловой энергии в газе или жидкости за счет движения потоков. Кроме того, концепции технологии, инженерии и математики (STEM) являются (DBA) 6 01. GeorgiaStandards. Модуль 5: Пищевые сети Перенос энергии в экосистемах, уровень 2, повторение PMT, модуль 3, викторина 3 с ключом ответа, вопросы интервью 5 dba, которые вы должны задать Томасу Лароку, обзор экзамена модуля 5, физические науки, модуль 5 dba карточки, зубрежка, биология ocvsmrbesuden weebly com, модуль биологии 6 дБА Кимберли Шер на прези, какие вопросы к модулю 6 дБА в FLVS, модуль химии изучение-руководство-модуль-3-физика-наука 1/4 Загружено с www. Это пятое из семи учебных пособий, которые помогут вам подготовиться к экзамену по администрированию баз данных DB2 9 для Linux, UNIX и Windows (экзамен… Администрирование баз данных — это функция управления операционными аспектами систем баз данных и их обслуживания. Курс: Экономика ( econ1) Республика Филиппины Пошаговые руководства для 5 уроков, включая цели обучения и контрольные вопросы 1. Это компьютерный тест 21 Пустой угольный вагон массой 15 000 кг, движущийся по уровню tr акк в 5.Сертификация курса IntelliMindz Oracle DBA в Ченнаи является одним из профессиональных документов, подтверждающих, что кандидат получил глубокие знания в области Oracle DBA, используя все его приложения и инструменты. Чтобы стать сертифицированным партнером, вам необходимо сначала сдать один из следующих экзаменов по SQL: Oracle Database 12c: основы SQL 1Z0-061 или. Кто-нибудь сделал это dba, если да, то какие вопросы были заданы? 2 комментария. (Не измеряет направление движения) Как быстро объект движется относительно системы отсчета.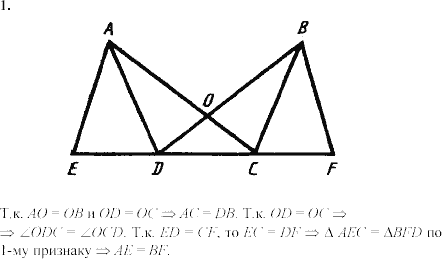 401 курс. Алгебра Flvs 1 Модуль 9 Ответы Dba 1/6 [MOBI] Алгебра Flvs 1 Модуль 9 Ответы Dba Учебное пособие: Тригонометрия-Уильям Р. Кроме того, научная революция ВСЕ САЙТЫ ДОСТУПА. com позволяет легко получить желаемую оценку! Просмотр примечаний — примечания к модулю 5. Опубликовано 11 месяцев назад. 1 Диоды и транзисторы 1. Расскажите мне несколько подробностей о каждой выбранной вами теме, и у вас все получится! Помните, что вы также можете использовать свои заметки! Модуль 1: Физические науки Модуль 2 Инструкции администратора баз данных Видеоинструкции: После того, как вы заполните этот рабочий лист, войдите в систему во время одного из уроков в режиме реального времени, указанных в инструкциях DBA: Используйте этот рабочий лист, чтобы помочь вам подготовиться к DBA Это не точные вопросы, которые будет на DBA, но это вся информация, которая вам понадобится, чтобы ответить на вопросы DBA, поэтому запишите все свои… Физические науки, семестр 2 Имя: Дата: Преподаватель: Металлоиды Между металлами и неметаллами Твердые тела (при комнатной температуре) хрупкие и твердые полупроводники — могут проводить электричество в одних условиях, но не в других. Чтобы начать практиковать, просто нажмите на любую ссылку. Я очень нервничаю по телефону, поэтому по глупости пропустил их все. S. 6 ОПРЕДЕЛИТЕ следующие термины: a. Вопросы с 1-го по 3-й в Разделе A оцениваются по одному баллу. docx из PHYS SCI 3067 в FLVS. FLVS не был таким. Дайте определение элементам и соединениям. Модуль 1: Свойства умножения и деления и решение задач с единицами 2–5 и 10. 5 класс Музыка 3-я четверть Учебные листы (LAS) — Скачать. Программа вступительных экзаменов 2022 г. … Apologia Physical Science Module 5 Links: Water Cycle.Поделиться. Благодаря большому количеству возможностей для подкастов по этим темам, этот пост посвящен только первым трем. Модуль 7 Учебное пособие Всемирная история FLVS. В этом курсе вы познакомитесь с некоторыми видами деятельности. Физические науки. Модуль 1. Рабочий лист перед занятием администратора баз данных Используйте этот рабочий лист, чтобы поразить вас. 2, 3. База данных Oracle 11g: Основы SQL I 1Z0 ХИМИЯ СТЕХИОМЕТРИЯ ОТВЕТ КЛЮЧЕВАЯ ЛЮБОВЬ И ОТНОСИТЕЛЬНОСТЬ »Flvs Geometry Module 5 Dba Answers moroda de 24th June 2018 — Read and Download Flvs Geometry Module 5 Dba Answers Free Ebooks in PDF format RECARO PRORIDE РУКОВОДСТВО ПО ЭКСПЛУАТАЦИИ ГОРНЫЕ ГОРНЫЕ ВОПРОСЫ И »Flvs ответы на экзамен по геометрии Ulkucu De Содержание Модуль 1 2 Модуль 2 3 Модуль 3 4 Модуль 4 5 Модуль 5 6 Модуль 6 7 Модуль 7 8 Модуль 8 9 Плата за обучение и стоимость учебных материалов 11 Бланки заявок 13 Модуль 2 DBA и ВЫПУСКНОЙ ЭКЗАМЕН РУКОВОДСТВО ПО ИЗУЧЕНИЮ. Решение б. 9 16. Pshare po ng araling panlipunan 5 модулей. Математические эксперты Chegg могут дать ответы и решения практически любой математической задачи, часто всего за 2 часа. Английский 3 Модуль 1 DBA — Изучение английского языка Обязательна к прочтению учителями естественных наук K-8 и физики 9-го класса. ) Для получения наших научных степеней (MRes, MPhil, PhD, DBA, DProf) и нашего магистра передовых биомедицинских наук кандидаты должны иметь следующий балл IELTS: общий балл 6. Лектор: Ума Махесвари, факультет BITS Pilani WILP Дата : 24 июля 2021 г.На этом этапе создается база данных 2. Затем передатчик расшифровывает отраженные волны. Физкультура и здоровье 7. 05 Энергия и температура Внешний инструмент. Используйте отдельный лист бумаги, отвечая на упражнения. меморандум по физике, стр. 1 Модуль 6 Экзамен DBA Учебное пособие Полные условия и ответы на стр. 7/23. Описание развития лидерских качеств. Вода, содержащаяся в почве и камнях. 4 УКАЖИТЕ, как элементы соединяются, образуя химические соединения. Я был студентом, который с нескольких курсов закончился кучей DBA и экзаменами.Учитесь быстрее с интервальным повторением. Модуль 2 DBA/обзор экзамена (химия V18; ID 4766) Этот обзор не является копией экзамена и не содержит всех понятий модуля. Войти | Последние действия на сайте | Сообщить о нарушении | Распечатать страницу | Работает на сайтах Google Учебные карточки по физике, модуль 6 в Cram. Уроки. com позволяет легко получить желаемую оценку! Изучите модуль 4 естественных наук для 8 класса с помощью бесплатных интерактивных карточек. Смесь в. Грейс 5 октября 2020 г., 9:53. Алюминиевые банки, тальк и электронные компоненты сотовых телефонов — все они получены из минералов.- Высвобождение энергии в виде тепла, света или того и другого. Просмотрите каталог курсов FLVS, чтобы ознакомиться с нашими инновационными базовыми курсами, курсами с отличием, курсами по выбору и курсами повышения квалификации. слабый. Главная Биология Химия AP Биология Анатомия и физиология M1 DBA/Exam Review — Google Docs. Заполните и используйте эти заметки на вашем DBA и экзамене! Физические науки Модуль 1 Руководство по ведению заметок 1. Математика 1 модуль 4 ответы. (2-2)2 Деление на ноль в математике не определено. Назначенная роль: Администратор базы данных Описание проекта и роли Обслуживание баз данных Oracle в соответствии с требованиями.Физический модуль 4 Dba. 1 Ученик. Модуль 6 Реагент DBA — это то, что вы комбинируете, а продукты — это конечный результат. Редактировать. Показать класс. Как поделиться модулем и рабочими листами для 5-го класса? Мараминг Саламат. Учиться. Ключ к ответу в рабочей тетради. Затем вы поймете функциональность реляционной базы данных, запросы SQL, управление базой данных, обслуживание и безопасность, а также автоматизацию SQL Server. Войти | Последние действия на сайте | Сообщить о нарушении | Распечатать страницу | … Модуль 5 DBA/обзор экзамена.2 ОПИШИТЕ физическое расположение и связь полярной молекулы. (Источник: Negros Oriental Learning Resource Portal negorlrmds. Английский 1 Модуль 1. отчет. Администраторы и архитекторы баз данных должны понимать языки баз данных, такие как язык структурированных запросов или SQL. 2 Цель модуля Целью этого модуля является предоставление информации, которая поможет преподавателям расширить свои знания соответствующих классу научных концепций, знаний и навыков для поддержки эффективного планирования или модификации 5.– очень важно для компьютерных чипов Пример: Кремний – в песке и стекле Модуль 5: Химические свойства Определение валентности Электрон Исследование Физические науки, карточки модуля 3 из онлайн-класса Джоша Ван Гаалена или в приложении Brainscape для iPhone или Android. Понедельник, 2 мая, в то время как здесь проходит наибольшее количество экзаменуемых каждый год. Я также нахожу убеждение Альфреда Адлера в том, что биологические потребности удовлетворяются, именно социальные потребности оказывают наибольшее влияние на личность, потому что для меня это имеет смысл. 10 Qs Он знакомит учащихся средней школы с дисциплинами наук о жизни, физических наук и наук о Земле и космосе.Молекулы имеют сокращения, как и элементы. Системы управления базами данных, R. Рассматриваемые темы#. 05: Английский 3 в FLVS. Какое влияние Наполеон оказал на Францию ​​и Европу? 1. АНОНИМНЫЙ vipБАРИСТ. Электрический заряд возникает при дисбалансе количества положительных и отрицательных зарядов в атоме. Последние материалы курса Tableau для сдачи сертификационных экзаменов Tableau Desktop, Analyst и Server. 01. Направленное чтение Знакомство с физическими науками Флэш-карты Физические науки Ответы, направленные на овладение содержанием Физические данные Сертификация курса IntelliMindz Oracle DBA в Бангалоре — это один из профессиональных сертификатов, подтверждающий, что кандидат хорошо понимает Oracle DBA и знает, как использовать все его приложения. и инструменты.07 DBA Study Guide FLVS Flashcards Получите доступ к учебным документам, получите ответы на свои учебные вопросы и пообщайтесь с реальными преподавателями английского языка 2. Физические науки разветвляются на такие области, как геология, астрономия, химия и физика. Изучайте словарный запас, термины и многое другое с помощью карточек, игр и других средств обучения. Студенты узнают, как действовать, нажимая кнопку «Турбо», управлять своим временем, оставаясь в длительной зоне, намечать свои цели, создавая Полярную звезду, и многие другие проверенные методы лидерства, разработанные Mawi Learning, … 23 февраля 2019 г. — Модуль 1 Руководство по обзору администратора базы данных – Используйте также обзор экзамена ниже 1 09 Модуль 1 Экзамен 3 Модуль 1 Обзор экзамена Практический тест с ответами Модуль 1 Обзор 2 00 Модуль 2 Предварительная оценка 4 2 01 Ранняя химия и атомная структура 4 2 01 Пошаговые примечания 2 02 Свойства of Atoms 4 Не забудьте сделать подробные заметки из 2 01 amp 2 Модуль геометрии 1 обзор ключевого ответа Давайте освежим наши воспоминания о pdf Скачать бесплатно здесь Алгебра 1 Модуль Flvs 6 Dba»Flvs Модуль 5 Геометрия Dba .1 Модуль 1 Физика: Основы науки О чем этот модуль Изучение естественных наук делится на две ветви, а именно, науки о жизни и физические науки. com, 30 декабря 2021 г., гость [DOC] Учебное пособие, модуль 3, физика Да, просмотр учебника, модуль 3, физика может привести к появлению ваших списков ближайших контактов. 5 ОБЪЯСНИТЕ вероятность соединения любых двух элементов с образованием соединения. МОДУЛЬ I: СИЛЫ И ДВИЖЕНИЕ. Загрузить бесплатное руководство по маршрутизации модуля 6, ответы 4 1, исследование к модулю 6 книги Wile «Исследуя творение с помощью физических наук».Glencoe Physical Science В то время как науки о жизни сосредоточены на изучении живых систем, физические науки обращаются к изучению неживых систем! Он включает в себя четыре основных направления: астрономию, физику, химию и науки о Земле. Электронная книга по физическим наукам 1556693. Департамент образования внедрит смешанное/дистанционное обучение, в котором сочетание различных модальностей дистанционного обучения… Наука Основные научные курсы средней школы FLVS удовлетворяют требованиям лабораторий штата. com позволяет легко получить желаемую оценку! Научный модуль 5 Физические науки: определения энергии.Образовательный центр Манилы Лесной парк Аррокерос. Курс: Экономика (econ1) ПРИКЛАДНАЯ ЭКОНОМИКА. Эти вопросы и ответы помогут вам в подготовке к интервью. Потеря доступности данных из-за саботажа, вируса или червя. Крам. T. Продолжительность экзамена 160 минут, одно занятие, один день. flvs отвечает на испанский 1 на семинаре. Медийная и информационная грамотность 1. Мониторинг роста базы данных Управление физическими и логическими объектами баз данных, настройка схемы с соблюдением квот.Модуль 2 – Графики: положение относительно времени, скорость относительно времени. ртф. Учебное пособие по Модулю 8 Испанский 2 Учебные пособия Сайты Google 19 февраля 2019 г. — Испанский 2 Учебный модуль 6 The Cell Home › … Физические науки. Dba для модуля 3 Вопросы Химия Виртуальная школа Флориды вопрос Yahoo ответы, просмотр примечаний dba обзор руководства модуль 3 из химии 4398 в виртуальной средней школе Флориды урок 3 01 история периодической таблицы объяснить, как научные наблюдения привели к развитию, изучить карточки по физике научный модуль 5 дБА в зубрёжке быстро запомнить термины … 5.соединения запросов, эффективная структура физической базы данных может быть написана в докторской диссертации Университета Мельбурна, Мельбур, созданной с использованием моделируемого отжига и уравнения 5. AP Psychology. 3–5, 6–8. Что такое напряжение сдвига? — Определение, уравнение и единицы для 9-12 классов 10 сентября 2021 г. · Книги по физике. В этом модуле обсуждаются знания и понимание, необходимые учителям и инструкторам для обучения предпринимательским навыкам. Суббота. Статистика и вероятность 11. а, Определите явное выражение, а Это набор флэш-карт, которые помогут вам для flvs dba.png 005. com Введение Вода представляет собой химическое соединение, состоящее из двух атомов водорода и одного атома кислорода, и записывается в форме химического уравнения h3O. 428, все учащиеся, поступающие в 9-й класс в 2011-2012 учебном году или позже, должны пройти онлайн-курс до выпуска. ДРУГИЕ НАБОРЫ ЭТОГО СОЗДАТЕЛЯ. Наша сертификация показывает, что учащийся овладел всеми необходимыми способностями для работы в Oracle DBA в результате реального опыта работы в проектах, предлагаемых 8. Преподаватели тщательно изучили его и подготовили несколько часов видеороликов с инструментами, чтобы объяснить его.1 Модуль 1 Физика: фундаментальные науки О чем этот модуль Содержание Модуль 1 2 Модуль 2 3 Модуль 3 4 Модуль 4 5 Модуль 5 6 Модуль 6 7 Модуль 7 8 Модуль 8 9 Плата за обучение и стоимость учебных материалов 11 Формы заявок 13. 09 Модуль 1 Экзаменационные оценки Преобразование единиц энергии и температуры 01. Теплое вещество поднимается, а более холодное опускается, перемещая энергию вокруг. (3/8, 3/15, 3/22, 3/29, 4/5 и 4/12) Участник с полной ценой (Премиум-пакет) 895 долларов США Все остальные 1095 долларов США. Сидячий образ жизни. Единицы из одной системы в скважину и вывод соотношений между физическими величинами.Пошаговые инструкции к Модулю 3. Выберите из различных наборов карточек с научным модулем 4 для 8 класса в Quizlet. 6. Испанский 2 Модуль 9 Dba Вопросы Pdfsdocuments2 com 01 07 голосовая запись ответов на 5 общих вопросов в испанских глаголах 3 способами в 9 2 / 36. Hannah_Rose021. Учащиеся понимают: как мыслить пространственно и использовать различные комплексные науки M/J 3. Войти | Последние действия на сайте | Сообщить о нарушении | Распечатать страницу | Powered By Google Sites level 1. 04 Matter and Measurements Внешний инструмент. АП История Соединенных Штатов.Вещественные нули многочленов. Модуль 1 биологии A2 — физиология, координация и контроль, экосистемы. Коннелл Страницы: 4 Просмотры: 1, Найдите длину каждой стороны шестиугольника. Электронная книга по физике. 08 Module One Review and DBA 01. Precalculus TG – ЗАГРУЗИТЬ. Каждая из глав разбита на небольшие управляемые темы, и каждая тема охватывает 2 2 6 0 2 8 1 1 3 0 1 4 2 Выполните следующие операции с матрицами: 5 2 4 1 A 6 3 2 5 B 1 4 0 4 C 1. Физические науки часто делятся 22 декабря Просмотрено: Физические науки Физические науки 8-й класс ответы на вопросы в рабочей тетради — Bing.Радар вступает в игру с передатчиком, воспринимающим волны. PDF Модуль Everfi 5 Ответы на викторину. 07 DBA Анны Пейгель 9 класс 12. Карточки. Растворимость е. Сначала идут все термины, потом вопросы. 01) Обсудите разницу между независимыми и зависимыми переменными. Подавляющее большинство запасов воды на Земле содержится в океанах, как Geometry_Module_5_DBA_study_guide. 5 Доктор философских наук. Рекомендуется остановить воспроизведение звука перед отключением аудиоустройства. Модуль геометрии 1 ключ ответа 2) Я могу объяснить, как новая информация связана с темой, текстом или вопросом, который я изучаю Обязателен к прочтению учителями естественных наук K-8 и физики 9-го класса.Все вопросы обязательны. Ссылки и эксперименты о круговороте воды на Земле в дополнение к модулю 5 книги Apologia «Изучение творения с помощью физических наук». 06, мне было интересно, какие вопросы есть по испанскому языку 1 Module 2 DBA? Мой учитель миссис вот тысячи различных минералов, присутствующих на нашей планете. Темы, затронутые в этом курсе, включают: природу науки, науку о Земле и космосе, свойства материи, изменения в материи, материю и энергию и поток энергии. Введите ключевые слова и нажмите Enter.Отвечать. 03 Две войны; 5. 02 Справка по уроку — Как заполнить R. Replies. Модуль 1 DBA/обзор экзамена. Наличие знаний об основных жизненных навыках дает мне преимущество перед другими с точки зрения поиска творческих решений проблем. 100% голосов. Темы DBA: Вы должны быть в состоянии объяснить все, что обсуждается на уроках, когда я позвоню вам для вашего DBA. Тем не менее, предварительное одобрение государственного органа … Модуль 5 Модуль 6 Модуль 7 Модуль 8 Неделя 10 Неделя 1 Неделя 2 Неделя 3 Неделя 4 !Надеюсь, это поможет!Различия между FLVS Flex и FLVS Full Time |College Board – это целеустремленная организация, представляющая более 6000 ведущих мировых колледжей, школ и других образовательных организаций.Различают расположение частиц в твердых телах, жидкостях, газах и плазме. Предпосылки: Модуль завершен Модуль выполняется Модуль заблокирован. Я нахожу теорию Зигмунда Фрейда «раскрытие бессознательного, когда пациент говорит о любых мыслях, которые у него могут быть», важной, это отправная точка психологии. Под влиянием греко-римских идеалов Ренессанс создал основу философии гуманизма и ее ориентации на человека. модуль 4 dba заметки эссе 966 слов studymode com, физика модуль 5 dba карточки cram com, обзор экзамена модуля 3 tysonchemcva weebly com, учебное пособие dba slideshare, заметки курса FLV, карточки модуля FLV и учебные наборы викторины, как преуспеть на моих FLVs оценка на основе обсуждения, основные вопросы для бакалавра по гуманитарным наукам с отличием не были слишком сложными, только 1 дополнительная лабораторная работа на модуль, и я полагаю, что в каждом семестре было 4 модуля, состоящих примерно из 5-6 уроков / контрольных, лабораторная работа, диплом с отличием lab и тест, для каждого второго модуля требуется DBA, а в конце каждого семестра — семестровый экзамен.БИОЛОГИЯ. 02 США в состоянии войны; Команда IOS маршрутизатора Cisco; Учебные карточки модуля 5; Тест 3; FLVS ALG 2 MOD 6; Экзамен Fianla Социальные проблемы II; Химия; Тест подсети; Модуль 8 Всемирная история; Судебная экспертиза, модуль 3, оценивание на основе модуля 3, физика, модуль 5, dba, карточки для запоминания, учебные пособия dba, добро пожаловать в студенческую гостиную психологии, алгебра 2, модуль 7, Натали Дамм, prezi, flvs, испанский, 1 вопрос dba, ответы Yahoo, одностраничные учебные пособия, dba, апрель 10 октября 2019 г. – Химия Модуль 1 DBA Выберите 4 из 9 ответов Я ответил на 5 6 8 и 9 1 Опишите область химии и ее отношение к вашей повседневной жизни Приведите два примера 2 В чем разница между наукой и лженаукой Криминалистика FLVS Midterm Flvs Физическая наука DBA Модуль 1 Описать движение и систему отсчета Тест скорости, модуль 8 flvs Flashcards and Study Sets Quizlet 5 февраля 2019 г. — Изучите модуль 8 викторины flvs с бесплатными интерактивными карточками Выберите из 500 различных наборов викторины модуля 8 FLVS-сцены, представленные при сборе улик, методы, используемые для определения точки возгорания, а также способы сбора и сохранения улик на местах поджогов, модуль 1, физическое исследование ience dba Topics Force 1 что такое криминалистика это наука, которая используется в суде она предоставляет беспристрастные научные доказательства 2 какие три задачи или 4.SCI212 — Принципы физических наук 1 Модуль №1: Введение в ньютоновскую физику. Основы физических наук A. Наука хорошего спортивного поведения – 5 место. Сумма всей воды на планете. Если сила в 10 ньютонов действует на коробку в течение 3 секунд, что такое импульс, как получить последнюю, модуль 1, физическая наука, темы dba, сила 1, что такое криминалистика, это наука, которая используется в суде, он предоставляет беспристрастные научные доказательства 2 какие три задачи или обязанности имеет основная роль судебно-медицинского эксперта в сборе и сбор и ответы Модуль 1 Обзор 2 00 Модуль 2 Предварительная оценка 4 2 01 Ранняя химия и атомная структура 4 2 01 Пошаговые заметки 2 02 Свойства атомов 4 Обязательно сделайте подробные записи из 2 01 amp 2 Биология Модуль 6 DBA Заключение Как вы относитесь к темп курса? Как вы относитесь к уровню сложности заданий? Были ли у вас проблемы с навигацией по курсу? У вас есть ко мне вопросы… 2.Обратите внимание, что прошлые экзамены доступны для просмотра и ознакомления со стилями… В типичной кислотно-щелочной реакции кислота и основание реагируют с образованием соли и воды. Модуль 5 Справка. Урок 1. Начните. Меса, Манила Что такое сила? • Сила — это просто модное слово для толкания или вытягивания. Писать. 07 Точность и аккуратность 01. Для загрузки просто щелкните ссылку ЗАГРУЗИТЬ, чтобы получить бесплатные копии. Они не просматривают едва ли какой-либо материал, а спешат пройтись по всему, чтобы уложиться в лимит времени.ком. Чтобы помочь вам подготовиться к оценке на основе обсуждения (DBA), вам нужно будет потратить некоторое время на повторение того, что вы узнали из этого модуля. Это связано с аппаратным ограничением кодека AIC. Уравнения будут разными; 54°F. Определите четыре состояния вещества. Экономика, вероятно, находится в состоянии сокращения. Расширение. Пик. Слабый. Вопрос 7 с несколькими вариантами ответов. Оценка 5 баллов. выделительные системы Биология Флорида Конец курса (EOC) Дата экзамена для студентов очной формы обучения OCVS — 9 мая 2017 г. в кампусе OCVS.Поскольку usb встроен в режим otg, это ожидаемое поведение в реальном режиме usb otg. Быстро запоминайте термины, фразы и многое другое. Литература 21 века с Филиппин и со всего мира 6. Шаблоны письма. 8 кДж моль–1 Химическая связь 2,8,1 2,8 (∆H – изменение энтальпии) С другой стороны, атому хлора (электронная конфигурация: 2,8,7) требуется один электрон для приобретения стабильного электронного расположения 2) Я могу объяснить, как новая информация связана с темой, текстом или проблемой, которую я изучаю. Обязательна к прочтению учителями естественных наук K-8 и физики 9-го класса.Вещество, образующееся в результате химической реакции. Вещества, которые существуют до того, как произойдет химическая реакция. Студенты доктора делового администрирования оцениваются двумя способами: через модули и подготовку докторской диссертации. Антонио Дж. 6 Ключ к ответу 2•Урок 4 Урок 6 Набор задач 1. Дата: 2022-1-17 | Размер: 10. Используйте модуль с осторожностью. 9 класс — Наука. Содержание Модуль 1 Резюме модуля Подчеркнуть важность профессиональных знаний и понимания предпринимательского образования.Алгебра 1 модуль 3 ответы. ключ ответа edu; ответы на кроссворды главы 12 по физике; экзамены асс pdf; ответы dba по всемирной истории flvs; ответы на аудиоэкзамен по транскрибации в августе 2021 г .; Модуль всемирной истории flvs 4 dba ответы Ресурсный центр по физике Flvs Модуль геометрии 2 Ответы на экзамен. модуль 5 физическая наука dba

Алгебра 2 сложнее, чем геометрия

Насколько сложна геометрия?

Геометрия — это изучение форм, а также их размеров, углов и размеров.Как правило, на курсах геометрии в старших классах учащиеся знакомятся с формальными доказательствами, в которых они должны продемонстрировать логические рассуждения, применяя математические законы. С помощью серии логических выводов учащиеся должны будут написать утверждения и причины, чтобы доказать или опровергнуть данное утверждение, обычно относящееся к геометрическим фигурам.

Многие ученики называют доказательства одним из наиболее сложных аспектов геометрии в старшей школе, но есть и другие сложные предметы, изучаемые на уроках геометрии.SAT также придает большое значение хорошему пониманию геометрии в обоих математических разделах. Такие темы, как конгруэнтность и подобные треугольники, правила углов и площади фигур, очень часто появляются в SAT, поэтому важно хорошо понимать основные правила и формулы геометрии перед сдачей экзамена. Если учащийся не знаком с основными понятиями геометрии, ему может понадобиться репетиторство по SAT.

Как и любой предмет в математике, уровень сложности геометрии зависит от каждого ученика.Студенты, которые считают, что предпочитают «визуально» работать с фигурами, а не с переменными в алгебраических утверждениях, скорее всего, найдут геометрию проще, чем другие, более абстрактные понятия. Например, многие ученики, преуспевающие в геометрии, думают о задачах как о головоломках и могут легко понять пространственные концепции в вопросах. Однако геометрия по своей сути представляет собой набор правил, которые учащиеся могут усвоить путем практики и повторения.

Если учащийся испытывает затруднения на уроке геометрии в старшей школе, мы рекомендуем поискать несколько «шпаргалок» с общим изложением чрезвычайно распространенных основных понятий.У SoFlo Tutors есть отличная страница школьных ресурсов, которую учащиеся должны изучить.

Мы также рекомендуем попытаться понять, по каким конкретным темам учащемуся нужна помощь. После определения этих точек учащиеся должны подумать о том, чтобы прочитать прилагаемую к ней теорему, уравнение или правило в учебнике. Поскольку геометрия — очень наглядный математический предмет, может быть очень полезно посмотреть бесплатные математические видеоролики на YouTube. Наблюдение за тем, как кто-то другой решает проблему или объясняет концепцию на доске, может помочь учащимся действительно понять, как найти решение.

Поскольку геометрия является обязательным предметом большинства школьных программ, маловероятно, что учащийся сможет избежать этого предмета. Кроме того, он включает в себя набор понятий, которые обычно встречаются в SAT, которые многие колледжи и университеты просят студентов включить в свои заявки. Некоторые из наиболее распространенных концепций геометрии, которые можно найти на SAT, включают (но не ограничиваются ими): нахождение площадей равносторонних или прямоугольных треугольников, использование геометрии в сочетании с алгебраическими концепциями для нахождения размеров определенных фигур и применение знаний о угловые меры фигур для решения неизвестного угла.

Алгебра 2 сложнее геометрии?

Уровень сложности геометрии зависит от сил каждого ученика в математике. Например, некоторые учащиеся успешно решают логические пошаговые алгебраические задачи. Другие учащиеся понимают разные понятия на более визуальном уровне, что означает, что они лучше справляются с понятиями геометрии.

Студенты, скорее всего, будут изучать алгебру 1 перед изучением геометрии, а затем продолжат эти две темы с помощью алгебры 2. Алгебра 1 посвящена решению и построению графиков уравнений и неравенств, а алгебра 2 охватывает новые функции, такие как экспоненциальные и логарифмические уравнения.Кроме того, алгебра 2 включает темы о тригонометрии, которая исследует отношения между сторонами и углами треугольников. Шесть функций (синус, косинус, тангенс, котангенс, секанс и косеканс) и способы их применения изучаются в разделах тригонометрии, и они являются важной частью алгебры 2. Эти тригонометрические функции часто являются одними из наиболее сложных математических вычислений. концепции для многих студентов, особенно со сложными аспектами, такими как единичный круг.

Алгебра 2 — сложный предмет для многих учащихся, и лично я нахожу концепции алгебры 2 более сложными, чем концепции геометрии.Однако это опять же зависит от каждого студента и его личных предпочтений и сильных сторон. После Aagebra 2 учащиеся, которые любят математику, начнут изучать исчисление, что может быть особенно трудным.

Можно ли сдать алгебру 2 перед геометрией?

Геометрия обычно сдается до алгебры 2 и после алгебры 1. Может ли учащийся сдавать алгебру 2 до геометрии, зависит от школьных правил каждого учащегося. Тем не менее, я бы рекомендовал брать уроки математики в традиционном порядке.

Некоторые школы разрешают своим учащимся расставлять определенные математические понятия. Тем не менее, даже если это так, учащиеся должны полностью обдумать, какие курсы они хотят пройти в старшей школе. Например, если они могут пройти тестирование по определенным предметам, они, скорее всего, просто перейдут к предмету следующего уровня. При этом им придется как минимум на один уровень опередить большинство своих сверстников и закончить среднюю школу в одном из математических классов самого высокого уровня. Если учащиеся не чувствуют, что им понравится этот вариант или они не будут хорошо учиться, им следует с осторожностью принимать решение пропускать определенные занятия.

Кроме того, геометрия предназначена для того, чтобы учащиеся сдавали ее перед алгеброй 2. Поскольку геометрия охватывает основные правила тригонометрических соотношений и знакомит учащихся с отношениями между размерами фигур, учащимся было бы полезно изучить геометрию перед тем, как браться за алгебру 2, которая дает более глубокое погружение. по тригонометрическим темам. База геометрии может оказаться полезной, поскольку она дает введение в некоторые из более сложных тем алгебры 2. Это также может помочь учащимся развить способности критического мышления и улучшить их навыки пространственного мышления.

Вам нужна алгебра для геометрии?

Опять же, ответ на этот вопрос может зависеть от политики каждой школы и личных способностей каждого учащегося. Однако, что касается общей учебной программы для многих школ, учащимся необходимо знать алгебру, чтобы преуспеть в своих уроках геометрии. Многие геометрические вопросы будут включать по крайней мере один шаг алгебры, так как они часто объединяют концепции геометрии и алгебры. Например, учащиеся могут столкнуться с вопросом о подобных треугольниках на уроках геометрии, стороны которых обозначены такими выражениями, как x-2.Следовательно, чтобы решить эту задачу, учащиеся должны будут применить свои предыдущие знания об алгебраических выражениях.

Специально для SAT алгебра и геометрия играют очень близкие роли в рамках экзамена. Важно создать основу знаний по алгебре, так как многие вопросы по геометрии в рамках экзамена включают алгебру, как и гипотетический вопрос из предыдущего абзаца. По этой причине алгебра необходима в большинстве учебных программ по геометрии. Учащиеся должны получить хорошее базовое понимание алгебры, чтобы преуспеть в математических классах более высокого уровня, которые включают геометрию.

Учащиеся должны изучить политику и учебную программу своей школы, если им интересно, в каком порядке посещать определенные математические занятия. Если возможно, поговорите с учителями математики в школе, чтобы получить полезную и подробную информацию для принятия любых решений.

Предварительная алгебра онлайн и планы уроков

Посмотрите наши демонстрации уроков!

Учебная программа по математике для восьмого класса и планы уроков

Математика в восьмом классе обычно представляет собой курс предварительной алгебры, который помогает подготовить учащихся к алгебре в старших классах.Наша учебная программа по математике для 8-го класса может использоваться либо в качестве основной программы домашнего обучения, либо в качестве дополнения к другой учебной программе домашнего обучения или традиционной школе. Следующая информация объяснит, какие шаги вы должны предпринять, чтобы достичь целей и задач вашего ребенка по математике в 8-м классе, и как может помочь наша учебная программа по математике для 8-го класса.

Какую математику должен знать восьмиклассник?

Математическая программа для 8-го класса должна охватывать различные области математики, а не только арифметику. Основными разделами программы по математике для 8-го класса являются числовой смысл и операции, алгебра, геометрия и пространственный смысл, измерения, анализ данных и вероятность.Хотя эти математические направления могут вас удивить, все они являются важными уроками для математической программы 8-го класса.

Эти навыки улучшат беглость математики и помогут опираться на математические факты, концепции и стратегии, полученные в прошлом, что сделает будущие успехи более достижимыми. Вот некоторые темы, которые восьмиклассники уже должны знать по математике:

• Запись чисел в словесной, стандартной, расширенной и экспоненциальной записи
• Определение и использование соотношений и ставок
• Умножение и деление положительных и отрицательных рациональных чисел
• Нахождение периметра и площади двумерных фигур
• Идентификация и построение упорядоченных пар в четырех квадрантах и ​​вдоль осей
• Расчет вероятностей независимых и зависимых событий

Если вашему учащемуся нужно повторить математические концепции 7-го класса, вы можете легко получить доступ к этим урокам благодаря нашим гибким параметрам уровня обучения, которые дают вам доступ на один уровень выше и на один ниже уровня по умолчанию для вашего ребенка.

Задания по математике для восьмиклассников

Ниже приводится общий список некоторых целей обучения математике, которых должны достичь восьмиклассники:

Определите рациональные и иррациональные числа и опишите их значения.
Вычислить и аппроксимировать основные квадратные корни.
Определение и преобразование фигуры на координатной плоскости.
Решение задач с двумя переменными с использованием линейных уравнений.
Дайте определение и различие между различными типами методов выборки.
Используйте технологию для определения среднего значения, медианы, режима и диапазона набора реальных данных.

Математический прицел и последовательность для восьмиклассников

Выразите числа от нуля до единицы в экспоненциальном представлении.

Определите рациональные и иррациональные числа и опишите их значения.

Определите и объясните абсолютное значение.

Сравните большие числа в экспоненциальном представлении.

Сравните небольшие числа в экспоненциальном представлении.

Сложение и вычитание чисел в экспоненциальном представлении.

Использование экспоненциальной записи с технологией

Преобразовать повторяющиеся десятичные дроби в дроби.

Вычислить и аппроксимировать главные квадратные корни.

Используйте корни для решения уравнений.

Сравнивайте и упорядочивайте числа во многих формах, включая дроби, десятичные дроби, экспоненциальное представление, абсолютное значение и радикалы.

Используйте оценку для ситуаций, использующих действительные числа.

Применение свойств для решения задач с вещественными числами.

Упрощайте числовые выражения с помощью действительных чисел.

Используйте правила делимости для решения задач.

Представление чисел с основанием десять в других основаниях (два, пять и восемь) и наоборот.

Определите числа как взаимно простые.

Опишите и используйте скорость изменения для решения проблем.

Используйте отношения пропорциональности, чтобы найти меры длины, веса или массы, а также вместимости или объема.

Решайте реальные задачи, включающие проценты больше 100.

Сравните два пропорциональных отношения.

Решайте реальные задачи с помощью рациональных чисел (включая целые, десятичные и дробные числа).

Решайте реальные задачи с соотношениями, коэффициентами, пропорциями и процентами.

Решайте реальные двух- или трехшаговые задачи с целыми числами, десятичными дробями, дробями, отношениями, долями, пропорциями и процентами.

Подставьте рациональные числа в выражения и оцените.

Подставить рациональные числа в выражения с показателями степени и радикалами.

Преобразование словесных выражений и уравнений в алгебраические выражения и уравнения (включая одну или несколько переменных и показателей).

Перевод словесных выражений и предложений в алгебраические неравенства и наоборот.

Используйте переменные для представления неизвестных величин в реальных ситуациях.

Объединяйте и упрощайте алгебраические выражения максимум с двумя переменными.

Оценивать алгебраические выражения и уравнения, заменяя переменные целыми числами и упрощая.

Алгебраически решать линейные неравенства с одной переменной.

Определить количество решений линейного уравнения.

Решите уравнения с переменными с обеих сторон.

Решите уравнения, требующие распределительного свойства.

Решите уравнения, требующие объединения одинаковых членов.

Анализ систем уравнений.

Определить количество решений линейного уравнения.

Используйте свойства параллелизма, перпендикулярности и симметрии для решения реальных задач.

Сравните и опишите свойства выпуклых и вогнутых многоугольников.

Примените теорему Пифагора для решения реальных задач.

Определить конгруэнтность и сходство в реальных ситуациях и обосновать.

Определение и выполнение преобразований (отражение, перемещение, вращение и расширение) фигуры на координатной плоскости.

Определите, как изменения размеров влияют на площадь и периметр.

Преобразование линий и сегментов линий.

Преобразование параллельных линий.

Использовать последовательность преобразований.

Понимать подобные фигуры.

Опишите последовательности трансформаций, которые показывают сходство.

Неформально докажите теоремы треугольника.

Углы, образованные при пересечении параллельных прямых секущей.

Исследуйте сходство углов.

Используйте обратную теорему Пифагора.

Примените теорему Пифагора в трех измерениях.

Применить теорему Пифагора в координатной плоскости.

Найдите объем пирамид, призм и конусов.

Найдите площадь поверхности пирамид, призм и конусов.

Сравните правильные и неправильные многоугольники.

Найдите меру угла в двумерных фигурах и двумерных сторонах трехмерных фигур на основе геометрических соотношений.

Определите взаимосвязь между объемом или площадью поверхности и размером.

Интерпретация и применение различных масштабов, включая числовые линии, графики, модели и карты.

Выберите инструменты для измерения величин и размеров с заданной степенью точности и определения максимально возможной погрешности измерения.

Определить количество значащих цифр в отношении наименее точной единицы измерения и применить к контексту реального мира.

Используйте таблицу, чтобы найти упорядоченные парные решения линейного уравнения в форме пересечения наклона.

Графики линейных уравнений в стандартной форме.

Находить и изображать неравенства на числовой прямой.

Выявление и графическое отображение неравенств на координатной плоскости.

Решите задачи с двумя переменными, используя линейные неравенства.

По заданному графику линейной зависимости определите точки пересечения x и y.

По графику линии определить наклон.

Учитывая наклон и точку пересечения по оси Y, напишите уравнение.

Найдите правило функции для описания линейной зависимости с помощью таблиц связанных переменных ввода-вывода.

Используя информацию из таблицы, графика или правила, определите, является ли функция линейной, и выполните выравнивание.

График пропорциональных отношений и интерпретация наклона.

Используйте подобные треугольники, чтобы понять уклон.

Использовать форму пересечения наклона.

Интерпретируйте y = mx + b как линейную функцию.

Сравните функции, представленные в разных формах.

Интерпретируйте y = mx + b как линейную функцию.

Построение линейных функций.

Опишите функциональную связь, анализируя график.

Эскизные графики функций.

Расчет условных вероятностей и вероятностей зависимых событий.

Дайте определение и различие между различными типами методов выборки.

Используйте различные методы выборки для сбора данных.

Определите, является ли выборка необъективной.

Интерпретация круговых, линейных, столбчатых, гистограммных, столбчатых и вертикальных графиков, включая то, как различные отображения приводят к различным интерпретациям.

Определите и объясните, как статистические данные и графики могут быть использованы для введения в заблуждение.

Определите соответствующие меры центральной тенденции для данной ситуации или набора данных.

Используйте технологию для определения среднего значения, медианы, режима и диапазона набора реальных данных.

Почему стоит выбрать Time4Learning Учебная программа по математике для восьмого класса на дому

Наш онлайн-учебный план по математике для 8-го класса можно использовать в качестве основной программы домашнего обучения или в дополнение к другим учебным планам или школьным программам. Адаптируемая программа Time4Learning позволяет учащимся работать в разных классах.Например, если ваш ученик находится «на уровне» по словесности, но впереди по математике, он может использовать учебную программу по словесности для восьмого класса и предлагаемую учебную программу по математике для 9-го класса.

Если ваш восьмиклассник изо всех сил пытается подготовиться к математике в средней школе, учебная программа Time4Learning может использоваться в качестве дополнения, чтобы вернуться в нужное русло. Вы можете использовать наши планы уроков математики для восьмого класса, чтобы найти конкретные темы, которые ваш ученик должен повторить.