Конспект урока определение координаты движущегося тела 9 класс: Конспект урока по физике «Определение координаты движущегося тела» 9 класс

Конспект урока по физике «Определение координаты движущегося тела» 9 класс

Тема урока: «Определение координаты движущегося тела»

Цель урока: Ввести понятия векторная и скалярная величина, координата, проекция вектора, модуль вектора. Сформулировать правила определения знака проекции.

Тип уроки: Комбинированный урок.

Проверка знаний:

1. Что называется механическим движением?

2. Что входит в понятие «система отсчета»?

3. Почему невозможно описать движение без выбора системы отсчета?

4. Какие точки катящегося вагона движутся и какие находятся в покое относительно дороги?

5. Что такое материальная точка?

6. Какое движение называется поступательным?

7. Что такое траектория?

8. Что такое пройденный путь?

9. Что такое перемещение?

10. ответить на вопросы к §2.

11. ответить на вопросы упр. 2 № 1,2.

12. Траектории движения двух материальных точек пересекаются.

    Означает ли это, что тела сталкиваются? Приведите пример, подтверждающий ваш ответ.

13. Тело, брошенное вертикально вверх, поднялось на высоту 20 м и упало в ту же точку. Чему равен путь, пройденный телом за то время, пока оно двигалось вверх? За время, пока оно двигалось вниз? За все время движения?

14. При каком условии путь равен модулю перемещения тела? Может ли модуль перемещения быть больше пройденного пути? Приведите примеры таких движений.

15. Автомобиль проехал 100 км. а) Какие точки колеса совершили максимальное перемещение? Минимальное? б) Какие точки колеса прошли максимальный путь? Минимальный?

16. Два тела, двигаясь прямолинейно, совершили одинаковые перемещения. Обязательно ли одинаковы пройденные ими пути? Ответ поясните примером.

План изложения нового материала:

1. Определение координаты движущегося тела.

2. Векторные и скалярные величины.

3. Проекция вектора.

4. Правило определения знака проекции.

5. Уравнение, с помощью которого можно определить координату тела.

6. Модуль вектора.

1. Изложение нового материала.

Определение координаты движущегося тела. При решении задач обычно составляют уравнения, связывающие физические величины, а затем решают эти уравнения. Если величины векторные, приходится «следить» не только за модулем каждой такой величины, но и за ее направлением. Решение задач значительно упрощается благодаря тому, что одну векторную величину можно задать с помощью нескольких скалярных величин следующим образом.

Любую векторную величину можно представить в виде суммы трех векторных величин,

направленных вдоль осей координат. Эти векторные величины называют ее составляющими. Каждую составляющую векторной величины можно охарактеризовать просто числом: модуль этого числа равен модулю составляющей, а знак числа определяется направлением составляющей. Если она направлена в положительном направлении оси координат, — это число положительное, а если в отрицательном, — отрицательное. Это число называется проекцией данной векторной величины на соответствующую координатную ось.

Проекции векторной величины а на оси координат х, у, z обозначаются а_х, а_у и а_г. Они измеряются в тех же единицах, что и модуль этой величины. Например, проекция перемещения измеряется в метрах, а проекция скорости — в метрах в секунду.

Свяжем проекции перемещения тела с его координатами. Для наглядности ограничимся движением на плоскости.

Пусть тело из точки с координатами х_0, у₀ переместилось в точку с координатами х, у. Тогда перемещение s — это вектор, проведенный из точки с координатами х_0,, у₀ в точку с координатами х, у. Следовательно,

s_x = х — х₀, s_y=y-y_0. • Таким образом,

x = x₀ + s_x, y = y_Q+s_y.

Обращаем внимание: в этих формулах стоит знак

«плюс», независимо от того, в каком направлении двигалось тело — в положительном направлении оси или в отрицательном.

2. Отработка знаний и умений.

Решение задачи упр.3 №1

Задание на дом: §3 упр.3 №2.

«Определение координат движущегося тела» 9 класс

Физика 9 класс

Урок 2. Траектория, путь и перемещение. Определение координаты движущегося тела.

Цели урока: введение понятий “перемещение”, “путь”, “траектория”.

Задачи урока:

образовательная: научить определять координаты движущегося тела.

развивающая: развивать логическое мышление, правильную физическую речь, использовать соответствующую терминологию.

воспитательная: достигать высокой активности класса, внимания, сосредоточенности учащихся.

Ход урока.

1. Организационный момент (1 мин).

Здравствуйте, ребята. Сегодня мы с вами продолжим изучать тему “Законы взаимодействия и движения тел” и на уроке познакомимся с тремя новыми понятиями из этой темы.

2. Актуализация знаний. Проверка домашнего задания (10 мин).

А пока проверим выполнение вами домашнего задания к данному уроку.

У доски работает 3 человека устно по вопросам к § 1 и упражнение 1.

Четверо учеников работают по карточкам с индивидуальными заданиями, которые выполняются во время устного ответа. (Приложение 1)

3. Изучение нового теоретического материала (15 мин).

Тема урока «Траектория, путь и перемещение. Определение координаты движущегося тела».

Слайд 1

С изменениями координат тела связана величина, вводимая для описания движения, – перемещение.

Перемещением тела (материальной точки) называется вектор, проведенный из начального положения тела в его конечное положение.

Перемещение принято обозначать буквой  . В СИ перемещение измеряется в метрах (м).

Перемещение – величина векторная, т.е. кроме числового значения имеет еще и направление. Векторную величину изображают в виде отрезка, который начинается в некоторой точке и заканчивается острием, указывающим направление. Такой отрезок-стрелка называется вектором.

Слайд 2

В процессе движения материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом движущаяся точка “описывает” в пространстве какую-то линию. Иногда эта линия видна, – например, высоко летящий самолет может оставлять за собой след в небе. Более знакомый пример – след куска мела на доске.

Воображаемая линия в пространстве, по которой движется тело называется траекторией движения тела.

Траектория движения тела – это непрерывная линия, которую описывает движущееся тело (рассматриваемое как материальная точка) по отношению к выбранной системе отсчета.

Длина траектории – это путь. Путь увеличивается, если тело движется. И остается неизменным, если тело покоится. Таким образом, путь не может уменьшаться с течением времени.

Слайд 3

Движение, при котором все точки тела движутся по одинаковым траекториям, называется поступательным.

В зависимости от траектории движения могут быть прямолинейными (падение тел в опыте Галилея) и криволинейными (движение брошенного под углом к горизонту мяча).

Траектория одного и того же движения различна в разных системах отсчета.

Например, для пассажира равномерно двигающегося поезда падающий в вагоне мячик двигается вертикально вниз, а для человека, стоящего на перроне, тот же мячик двигается по параболической траектории.

Слайд 4

Чем же отличается путь от перемещения? Эти два понятия часто смешивают, хотя на самом деле они очень сильно отличаются друг от друга. Рассмотрим эти отличия:

• Путь – скаляр, а перемещение вектор.

• Путь зависит от траектории, а перемещение нет.

• Перемещение может быть положительным и отрицательным, а путь всегда строго положителен.

• При движении тела путь может только увеличиваться, а модуль перемещения может как увеличиваться, так и уменьшаться.

• Если тело вернулось в начальную точку, его перемещение равно нулю, а путь нулю не равен.

Слайд 5

Проекция вектора на ось. Важным понятием является понятие проекции вектора.

Проекцию считают положительной (а_х > 0), если от проекции начала вектора к проекции его конца нужно идти по направлению оси.

Другими словами, проекция вектора положительна, если угол между направлением вектора и осью ОХ острый.

В противном случае проекция вектора отрицательна (а_x < 0).

Если вектор перпендикулярен оси, то при любом направлении вектора его проекция на ось равна нулю (а_х = 0).

Слайд 6-7

5. Упражнения и вопросы для повторения (10 мин).

Вопросы:

1. Путь или перемещение мы оплачиваем при поездке в такси? (Путь.)

2. Мяч упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. Найти путь и перемещение мяча. (Путь 4 м, перемещение 2 м.)

3. Велосипедист движется по окружности с радиусом 30 м. Чему равны путь и перемещение велосипедиста за половину оборота? За полный оборот? {Пройденный за пол оборота путь равен l = пR = 94,2 м, перемещение S = 2R= 60 м. За один оборот путь l = 2πR = 188,4 м, перемещение S₂ = 0.)

Задача: Автомобиль переместился из точки с координатой Х₀=200м в точку с координатой Х=-200м. Определите проекцию перемещения автомобиля.

Слайд 8

Сборник задач В.И. Лукашик № 98, 102, 104, 106, 108

6. Итог урока (2 мин).

Повторение понятий урока: перемещение, траектория, путь.

7. Домашнее задание (2 мин).

§ 2,3 вопросы после параграфа, упражнение 2 (стр.12), 3 (стр 15.)

Заполнить таблицу:

4. Домашняя лабораторная работа.  

1. Заполните водой до горловины пластмассовую бутылку со шкалой.

2. Флакончик со шкалой заполните водой на 1/5 его объема.

3. Наклоните бутылку так, чтобы вода подошла к горловине, но не вытекала из бутылки.

4. Быстро опустите флакончик с водой в бутылку (не закрывая его пробкой) так, чтобы горловина флакончика вошла в воду бутылки. Флакончик плавает на поверхности воды в бутылке. Часть воды при этом из бутылки выльется

5. Завинтите крышку бутылки.

6. Сжимая боковые стенки бутылки, опустите поплавок на дно бутылки.

7. Ослабляя давление на стенки бутылки, добейтесь всплытия поплавка. Определите путь и перемещение поплавка:__________________________________________

8. Опустите поплавок на дно бутылки. Определите путь и перемещение поплавка:_______________________________________________________________________

9. Заставьте поплавок всплыть и утонуть. Каков путь и перемещение поплавка в этом случае?_________________________________________________________________________

Список литературы

1. Перышкин А.В., Гутник Е.М. Физика. 9 кл.: учеб.для общеобразоват.учреждений – 9-е изд., стереотип. – М.: Дрофа, 2005.

2. Волков В.А. Универсальные поурочные разработки по физике: 9 класс.-М.:ВАКО, 2012

3. Иванова В.В., Минькова Р.Д. Рабочая тетрадь по физике. 9 класс-М.: Издательство «Экзамен», 2012

4. Харченко Н.И. «Перемещение. Траектория. Путь»

http://festival.1september.ru/articles/563378/

Определение координаты движущегося тела

На прошлом уроке мы с вами говорили о пути и перемещении тела. Давайте вспомним, что путь — это скалярная величина, равная длине траектории, которую описывает тело за некоторый промежуток времени.

А перемещением называется направленный отрезок прямой, соединяющий начальное и конечное положения тела.

Так как перемещение — это векторная величина, то есть имеет модуль и направление, то складывать и вычитать перемещения необходимо по правилам сложения и вычитания векторов. Однако при решении большинства задач, используется понятие не вектора, а проекции вектора на ось координат.

— А что такое проекция вектора и каковы её свойства?

На это вопрос мы с вами и попытаемся сегодня ответить. Начнём с простого — с понятия проекция точки на ось. Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.

На представленном рисунке точка А₁ — это проекция точки А на ось Ox, а точка B₁ — проекция точки B на ось Oy.

Теперь разберёмся с проекцией вектора на ось. Согласно определению, проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора на эту ось, взятая со знаком «плюс» или «минус».

Знак «плюс» берут, если угол между вектором и осью острый, а «минус» — если угол тупой.

Обозначать проекцию вектора будем той же буквой, что и вектор, но с индексом внизу (например, a_x — это проекция вектора a на ось Ox).

— А если вектор перпендикулярен оси?

Тогда проекция этого вектора равна нулю.

Проекцию вектора можно выразить через его модуль и угол между вектором и осью. Итак, пусть у нас есть вектор a направленный под некоторым острым углом к координатной оси Ox. Укажем проекцию этого вектора на ось.

У нас с вами получился прямоугольный треугольник, гипотенуза которого равна длине вектора a, а катет AB₁ — это проекция вектора a на ось Ox.

Тогда, на основании определения косинуса острого угла, мы можем записать, что проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью:

Это правило справедливо при любых значениях угла φ. Например, для углов, больше 90^о, косинус угла φ отрицательный. Тогда по формуле получается, что проекция вектора на ось также отрицательна, как и должно быть по определению проекции.

— А можно ли найти модуль и направление вектора по его проекциям на координатные оси?

Чтобы ответить на этот вопрос рассмотрим вектор, лежащий в плоскости xOy. Вектор, лежащий в заданной плоскости, определяется двумя проекциями на оси координат.

Обратим внимание на важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.

Но вернёмся к нашему прошлому уроку. На нём мы с вами говорили о том, что положение тела, которое совершило некоторое перемещение, можно найти графически. Для этого достаточно отложить вектор перемещения от начального положения этого тела. Однако в большинстве случаев необходимо уметь вычислять положение тела, то есть уметь определять его координаты. Давайте на примере решения задачи посмотрим, как можно определить координату движущегося тела, зная координату его начального положения и вектор перемещения.

Итак, два поезда идут по параллельным путям в противоположных направлениях и встречаются в шестидесяти километрах к востоку от железнодорожного вокзала. Продолжив движение через некоторое время t первый поезд удалился от места встречи на 50 километров в восточном направлении, а второй — на 80 километров в западном. Определите координаты каждого поезда относительно вокзала и расстояние между ними через промежуток времени t.

Физика 9кл. Определение координаты движущегося тела

Физика 9кл. Определение координаты движущегося тела

Подробности

Просмотров: 246

 

В большинстве задач необходимо вычислить положение тела, т. е. определить его координаты.

1. С какими величинами производят вычисления — с векторными или скалярными?

Вычисления производят не с векторами, а со скалярными величинами, т.е. с проекциями векторов на координатные оси и с модулями векторов или их проекций.

2. При каком условии проекция вектора на ось будет положительной, а при каком — отрицательной?

Проекция вектора на ось считается положительной, если вектор сонаправлен с этой осью.
Проекция вектора на ось считается отрицательной, если вектор направлен противоположно оси.

3. Как рассчитать изменение координаты тела за время t?

l = |х — х₀| = s_x
Проекция вектора перемещения s на ось координат равна изменению координаты тела..

4. По какому уравнению можно определить координату тела, зная координату его начального положения и вектор перемещения?

где
х — конечная координата тела,
х_о — начальная координата тела,
s_x — проекция вектора перемещения на координатную ось OX.

5. Как рассчитать координату движущегося тела, зная координату его начального положения и вектор перемещения?

Задача.

Два автобуса едут по шоссе навстречу друг другу и встречаются в 1000 м справа от остановки О (смотри чертеж).
Продолжая движение, за некоторое время t первый автобус переместился от места встречи на 600 м (вправо),
а второй — на 500 м (влево).
Определите координаты каждого автобуса относительно остановки и расстояние между ними через время t после их встречи.

Проведём координатную ось ОХ параллельно прямой, вдоль которой движутся автобусы, и направим её вправо.
Начало этой оси (х = 0) — точку О — совместим с остановкой, приняв её за тело отсчёта, т.к. в задаче требуется определить положение автобусов по отношению к остановке.

Спроецировав начала и концы векторов перемещения s₁ и s₂ на ось ОХ, получим отрезки s_1x и s_2x, которые являются проекциями указанных векторов.
Проекция вектора на ось считается положительной, если вектор сонаправлен с этой осью, и отрицательной, если вектор направлен противоположно оси.

Значит, в данном случае:
s_1x > 0,
s_2x < 0.

Из чертежа видно, что координаты х₁ и х₂ можно найти следующим образом:
x₁ = x₀ + s_1x
х₂ = х₀ + s_2x

Расстояние l между двумя телами равно модулю разности их координат:
l = |х₁ — х₂|

По уравнениям можно рассчитать искомые координаты х₁ и х₂.
Но какие числа следует подставить в уравнения вместо символов х₀, s_1x и s_2x?

Согласно условию задачи автобусы встретились на расстоянии 1000 м от остановки, значит, длина отрезка Ох₀ равна 1000 м.
Координата x₀ находится на положительной полуоси ОХ, т. е. х₀ > 0.
Значит, х₀ = 1000 м.

Поскольку ось ОХ параллельна векторам перемещений автобусов, длины проекций s_1x и s_2x равны соответственно длинам векторов s₁ и s₂ (как противоположные стороны построенных на них прямоугольников).
А это означает, что модуль каждой проекции равен модулю соответствующего ей вектора.

Указанные в задаче расстояния (600 м и 500 м), на которые сместились автобусы за время t, представляют собой модули векторов их перемещений.
Значит, модуль проекции s_1x равен 600 м, а модуль проекции s_2x равен 500 м.

Поскольку проекция s_1x положительна, то можно записать:
s_1x = 600 м.
Но проекция s_2x отрицательна, поэтому:
s_2x = -500 м.

Далее можно легко рассчитать по уравнениям координаты автобусов х₁ и х₂.

Следующая страница — смотреть

Назад в «Оглавление» — смотреть

Определение координаты движущегося тела интернет урок. Движение тела по окружности

Как определить координаты движущегося тела? Для этого необходимо знать такие понятия, как механическое движение, пройденный путь, скорость, перемещение.

Механическое движение

При механическом движении происходит изменение положения тела в пространстве относительно других тел за промежуток времени. Оно бывает равномерным и неравномерным.

Равномерное движение

При равномерном движении тело за равные промежутки времени проходит одинаковые расстояния (т. е. движется с постоянной скоростью).

Путь, пройденный при равномерном движении равен: Sx=Vxt=x-xо

Следовательно, при равномерном движении координата тела изменяется по следующей зависимости:

Рис. 1. Формула координаты тела при прямолинейном равномерном движении

• Xо – начальная координата тела;
• X – координата в момент времени t;
• Vx – проекция скорости на ось X.

Неравномерное движение

Неравномерное движение – движение, при котором тело за равные промежутки времени проходит неодинаковые расстояния (движется с непостоянной скоростью), то есть движется с ускорением.

Если тело движется неравномерно, то скорость тела в разные моменты отличается не только по величине, но и (или) по направлению. Средняя скорость тела при неравномерном движении определяется по формуле: V (ср)= S (весь)/t (весь)

Ускорение – величина, показывающая, как изменяется скорость за 1 секунду.

Рис. 2. Формула ускорения

Следовательно, скорость в любой момент времени можно найти следующим образом:

V=Vо+at

Если скорость с течением времени увеличивается, то a больше 0, если скорость с течением времени уменьшается, то a меньше 0.

Как найти путь при равноускоренном движении?

Рис. 3. Прямолинейное равноускоренное движение

Пройденный путь численно равен площади под графиком. То есть Sx=(Vox+Vx)t/2

Скорость в любой момент времени равна Vx=Vox+axt, следовательно Sx=Voxt+axt2/2

Так как перемещение тела равно разности конечной и начальной координат (Sx=X-Xo), то координата в любой момент времени вычисляется по формуле X=Xo+Sx, или

X=Xo+Voxt+axt2/2

Движение тела по вертикали

Если тело движется по вертикали, а не по горизонтали, то такое движение всегда является равноускоренным. Когда тело падает вниз, то падает оно всегда с одинаковым ускорением – ускорением свободного падения. Оно всегда одинаковое: g=9,8 м/кв.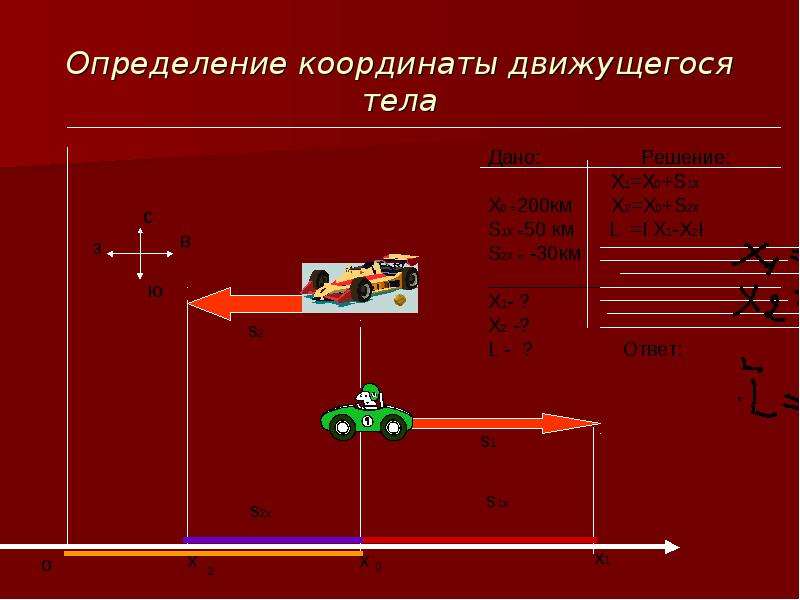 с.

При движении по вертикали формула скорости приобретает вид: Vy=Voy+gt ,
где Vy и Voy – проекции начальной и конечной скоростей на ось OY.

Движение тела по окружности

При движении по окружности численное значение скорости может и не изменяться, но поскольку обязательно изменяется направление, то движение по окружности – это всегда равноускоренное движение.

Что мы узнали?

Тема «Определение координаты движущего тела», которую изучают в 9 классе, поможет ученикам систематизировать информацию о том, что движение может быть равномерным и неравномерным. Так же для того чтобы знать пройденный путь, нужно выбрать тело отсчета и использовать прибор для отсчета времени.

Оценка доклада

Средняя оценка: 4 . Всего получено оценок: 6.

Тема урока: «Определение координаты движущегося тела»

Цель урока: Ввести понятия векторная и скалярная величина, координата, проекция вектора, модуль вектора.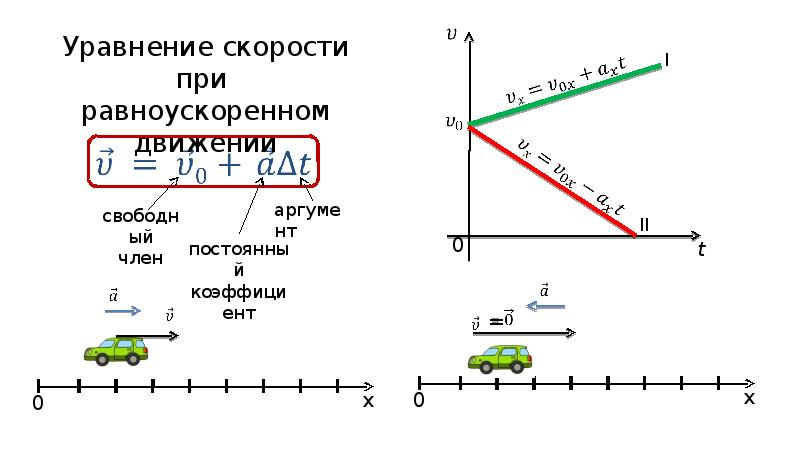 Сформулировать правила определения знака проекции.

Тип уроки: Комбинированный урок.

Проверка знаний:

1. Что называется механическим движением?

2. Что входит в понятие «система отсчета»?

3. Почему невозможно описать движение без выбора системы отсчета?

4. Какие точки катящегося вагона движутся и какие находятся в покое относительно дороги?

5. Что такое материальная точка?

6. Какое движение называется поступательным?

7. Что такое траектория?

8. Что такое пройденный путь?

9. Что такое перемещение?

10. ответить на вопросы к §2.

11. ответить на вопросы упр. 2 № 1,2.

Траектории движения двух материальных точек пересекаются. Означает ли это, что тела сталкиваются? Приведите пример, подтверждающий ваш ответ.

Тело, брошенное вертикально вверх, поднялось на высоту 20 м и упало в ту же точку. Чему равен путь, пройденный телом за то время, пока оно двигалось вверх? За время, пока оно двигалось вниз? За все время движения?

При каком условии путь равен модулю перемещения тела? Может ли модуль перемещения быть больше пройденного пути? Приведите примеры таких движений.

Автомобиль проехал 100 км. а) Какие точки колеса совершили максимальное перемещение? Минимальное? б) Какие точки колеса прошли максимальный путь? Минимальный?

Два тела, двигаясь прямолинейно, совершили одинаковые перемещения. Обязательно ли одинаковы пройденные ими пути? Ответ поясните примером.

План изложения нового материала:

Определение координаты движущегося тела.

Векторные и скалярные величины.

Проекция вектора.

Правило определения знака проекции.

Уравнение, с помощью которого можно определить координату тела.

Модуль вектора.

1. Изложение нового материала.

Определение координаты движущегося тела . При решении задач обычно составляют уравнения, связывающие физические величины, а затем решают эти уравнения. Если величины векторные, приходится «следить» не только за модулем каждой такой величины, но и за ее направлением. Решение задач значительно упрощается благодаря тому, что одну векторную величину можно задать с помощью нескольких скалярных величин следующим образом.

Любую векторную величину можно представить в виде суммы трех векторных величин, направленных вдоль осей координат. Эти векторные величины называют ее составляющими. Каждую составляющую векторной величины можно охарактеризовать просто числом: модуль этого числа равен модулю составляющей, а знак числа определяется направлением составляющей. Если она направлена в положительном направлении оси координат, — это число положительное, а если в отрицательном, — отрицательное. Это число называется проекцией данной векторной величины на соответствующую координатную ось.

Проекции векторной величины а на оси координат х, у, z обозначаются а х , а у и а г . Они измеряются в тех же единицах, что и модуль этой величины. Например, проекция перемещения измеряется в метрах, а проекция скорости — в метрах в секунду.

Свяжем проекции перемещения тела с его координатами. Для наглядности ограничимся движением на плоскости.

Пусть тело из точки с координатами х 0, у 0 переместилось в точку с координатами х, у. Тогда перемещение s — это вектор, проведенный из точки с координатами х 0, , у 0 в точку с координатами х, у. Следовательно,

s x = х — х 0 , s y =y -y 0. Таким образом,

x = x 0 + s x , y = y Q +s y .

Обращаем внимание: в этих формулах стоит знак «плюс», независимо от того, в каком направлении двигалось тело — в положительном направлении оси или в отрицательном.

2. Отработка знаний и умений.

Решение задачи упр.3 №1

Задание на дом: §3 упр.3 №2.

Есть одна фундаментальная вещь! У меня есть пример, когда студенты до второго курса технического ВУЗа допускали глупые ошибки, потому что недостаточно понимали это.

Положение тела можно задать набором координат. Например, (50, -70, 10), что означает «тело сдвинуто от начала координат на 50 единиц по оси X, на 70 единиц против оси Y, на 10 единиц по Z».

В математике три (или два) числа с указанием координат называются вектором или радиус-вектором . Чтобы представить радиус-вектор в терминах «направленного отрезка-стрелочки», надо вообразить эту стрелку, исходящую из начала координат, и указывающую в интересующую нас точку.

Радиус-вектор точки A.

Зачем вообще нужны эти векторы, ведь, казалось бы, можно обойтись точками?

Но дело в том, что многие уравнения в физике записаны именно векторами (т.к. многие тела движутся в пространстве в каком-либо направлении), и если мы будем воспринимать точки как вектора, то нам будет легче проводить все расчёты.

К тому же есть множество калькуляторов, которые отлично работают с векторами – это позволяет вместо ряда уравнений для скаляров написать всего одно уравнение для векторов.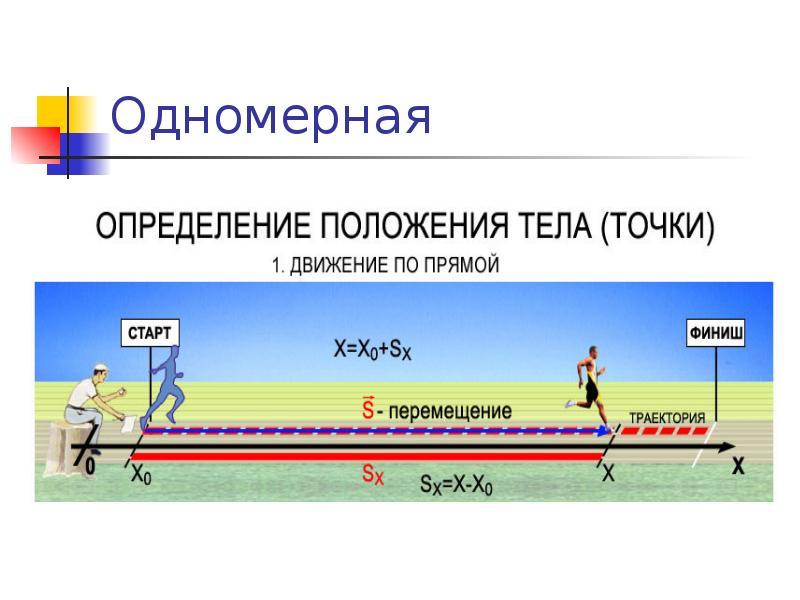 Так что стоит помнить, что вектор – это не только «стрелочка», но и упорядоченный набор чисел.

Кроме того, векторная запись – это отличный способ не запутаться в знаках. Опыт показывает, что ученики и студенты допускают ощутимо больше ошибок со знаками, когда не пользуются векторной записью.

Смотрите, как можно расписать векторные уравнения очень простым способом.

Векторное уравнение:

В скалярной форме выглядит как система уравнений:

Т.е. чтобы превратить векторное уравнение в скалярное, достаточно расписать проекции этого уравнения на все оси, что значит заменить вектор «» на скаляры «x» и «y», а вектор «» на проекции «v x » и «v y ».

Как определять координаты движущегося тела

Допустим, тётя Люда на Камазе выехала из Москвы и проехала по трассе на север 90 километров. А затем развернулась обратно и проехала 150 километров (утюг, например, забыла выключить в Подмосковье). А дядя Витя на коне за это же время стартовал на 200 км южнее Москвы, и проскакал 120 км на север.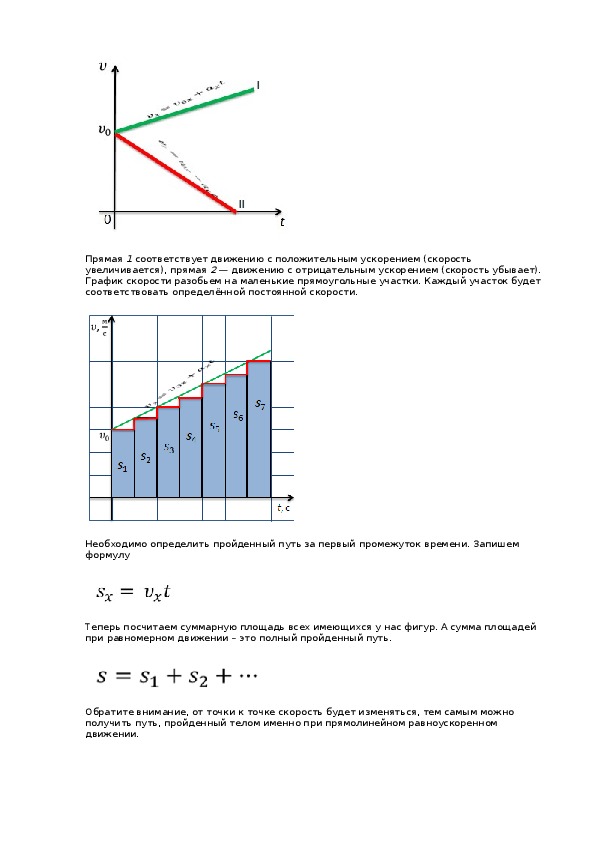

Вопрос: на каком расстоянии друг от друга тётя Люда и дядя Витя?

Примем Москву за начало координат. Введём также одну координатную ось, и направим её на север. Назовём ось X.

Стартовая позиция тёти Люды:

Первое перемещение тёти Люды обозначим как и его проекция на X равна = 90 км (вспоминаем, что она сначала ехала на север).

Второе перемещение тёти Люды и его проекция на X равна = -150 км (минус – потому что вектор направлен против оси X (вниз)).

Тогда последнее местоположение тёти Люды равно

Т.е. начальное положение + 1-е передвижение + 2-е передвижение.

Если переписать в скалярном виде, получается:

x L2 = r L0x + S L1x + S L2x = 0 + 90 — 150 = -60 км

Стартовая позиция дяди Вити на 200 км южнее Москвы, то есть проекция = -200 км. А проекция перемещения дяди Вити равна =120 км.

А радиус-вектор последнего местоположения дяди Вити равен: Т.е. также: стартовая позиция + 1-е перемещение.

Если спроецировать на оси, получится:

x V1 = r V0x + S V1x = -200 + 120 = -80 км.

Расстояние между дядей Витей и тётей Людой равно модулю от разности их радиус-векторов

D LV = |-60 — (-80)| = 20 км

Обратите внимание, что здесь всегда используется модуль, поскольку расстояние между объектами никогда не может быть отрицательным.

Если бы у нас была задача с двумя координатами, мы бы её решали примерно так же, за исключением двух моментов:

1. Векторные уравнения мы расписывали бы как системы из двух уравнений с проекциями.
2. Модуль вектора мы рассчитывали бы по теореме .

Редактировать этот урок и/или добавить задание и получать деньги постоянно* Добавить свой урок и/или задания и получать деньги постоянно

На данном уроке, тема которого: «Определение координаты движущегося тела» мы поговорим о том, как можно определять место нахождения тела, его координату. Поговорим о системах отсчета, рассмотрим для примера задачу, а также вспомним, что такое перемещение

Представьте: вы изо всей силы бросили мяч. Как определить, где он будет находиться через две секунды? Можно подождать две секунды и просто посмотреть, где он. Но, даже не глядя, вы приблизительно можете предсказать, где будет мяч: бросок был сильнее обычного, направлен под большим углом к горизонту, значит, полетит высоко, но недалеко… Используя законы физики, можно будет точно определить положение нашего мяча.

Определить положение движущегося тела в любой момент времени — это и есть основная задача кинематики.

Начнем с того, что у нас есть тело: как определить его положение, как объяснить кому-то, где оно находится? Об автомобиле мы скажем: он на дороге за 150 метров перед светофором или на 100 метров за перекрестком (см. рис. 1).

Рис. 1. Определение местоположения машины

Или на трассе за 30 км к югу от Москвы. О телефоне на столе скажем: он сантиметров на 30 правее клавиатуры или рядом с дальним углом стола (см. рис. 2).

Рис. 2. Положение телефона на столе

Заметьте: мы не сможем определить положение автомобиля, не упомянув другие объекты, не привязавшись к ним: светофор, город, клавиатуру. Мы определяем положение, или координаты, всегда относительно чего-то.

Координаты — это набор данных, по которому определяется положение того или иного объекта, его адрес.

Примеры упорядоченных и неупорядоченных имен

Координата тела — это его адрес, по которому мы его можем найти. Он упорядоченный. Например, зная ряд и место, мы точно определяем, где находится наше место в зале кинотеатра (см. рис. 3).

Рис. 3. Зал кинотеатра

Буквой и цифрой, например e2, точно задается положение фигуры на шахматной доске (см. рис. 4).

Рис. 4. Положение фигуры на доске

Зная адрес дома, например улица Солнечная 14, мы будем искать его на этой улице, на четной стороне, между домами 12 и 16 (см. рис. 5).

Рис. 5. Поиск дома

Названия улиц не упорядочены, мы не будем искать Солнечную улицу по алфавиту между улицами Розовой и Тургенева. Также не упорядочены номера телефонов, номерные знаки автомобилей (см. рис. 6).

Рис. 6. Неупорядоченные имена

Эти номера, идущие подряд, — это лишь совпадение, не означающее соседства.

Мы можем задать положение тела в разных системах координат, как нам удобно. Для того же автомобиля, можно задать точные географические координаты (широту и долготу) (см. рис. 7).

Рис. 7. Долгота и широта местности

Рис. 8. Местоположение относительно точки

Причем если мы выберем разные такие точки, то получим разные координаты, хотя они будут задавать положение одного и того же автомобиля.

Итак, положение тела относительно разных тел в разных системах координат будет разным. А что такое движение? Движение — это изменение положения тела со временем. Поэтому описывать движение мы будем в разных системах отсчета по-разному, и нет смысла рассматривать движение тела без системы отсчета.

Например, как движется стакан с чаем на столе в поезде, если сам поезд едет? Смотря относительно чего. Относительно стола или пассажира, сидящего рядом на сидении, стакан покоится (см. рис. 9).

Рис. 9. Движение стакана относительно пассажира

Относительно дерева около железной дороги стакан движется вместе с поездом (см. рис. 10).

Рис. 10. Движение стакана вместе с поездом относительно дерева

Относительно земной оси стакан и поезд вместе со всеми точками земной поверхности будут еще и двигаться по окружности (см. рис. 11).

Рис. 11. Движение стакана с вращением Земли относительно земной оси

Поэтому нет смысла говорить о движении вообще, движение рассматривается в привязке к системе отсчета.

Всё, что мы знаем о движении тела, можно разделить на наблюдаемое и вычисляемое. Вспомним пример с мячом, который мы бросили. Наблюдаемое — это его положение в выбранной системе координат, когда мы его только бросаем (см. рис. 12).

Рис. 12. Наблюдение

Это момент времени, когда мы его бросили; время, которое прошло после броска. Пусть на мяче нет спидометра, который показал бы скорость мяча, но ее модуль, как и направление, тоже можно узнать, используя, например, замедленную съемку.

С помощью наблюдаемых данных мы можем предсказать, например, что мяч через 5 секунд упадет за 20 м от места броска или через 3 секунды попадет в верхушку дерева. Положение мяча в любой момент времени — это в нашем случае вычисляемые данные.

Что определяет каждое новое положение движущегося тела? Его определяет перемещение, потому что перемещение — это вектор, характеризующий изменение положения. Если начало вектора совместить с начальным положением тела, то конец вектора укажет на новое положение переместившегося тела (см. рис. 13).

Рис. 13. Вектор перемещения

Рассмотрим несколько примеров на определение координаты движущегося тела по его перемещению.

Пусть тело двигалось прямолинейно из точки 1 в точку 2. Построим вектор перемещения и обозначим его (см. рис. 14).

Рис. 14. Перемещение тела

Тело двигалось вдоль одной прямой, значит, нам будет достаточно одной оси координат, направленной вдоль перемещения тела. Допустим, мы наблюдаем за движением со стороны, совместим начало отсчета с наблюдателем.

Перемещение — вектор, удобнее работать с проекциями векторов на оси координат (у нас она одна). — проекция вектора (см. рис. 15).

Рис. 15. Проекция вектора

Как определить координату начальной точки, точки 1? Опускаем перпендикуляр из точки 1 на ось координат. Этот перпендикуляр пересечет ось и отметит на оси координату точки 1. Так же определяем координату точки 2 (см. рис. 16).

Рис. 16. Опускаем перпендикуляры на ось ОХ

Проекция перемещения равна:

При таком направлении оси и перемещения будет по модулю равна самому перемещению .

Зная начальную координату и перемещение, найти конечную координату тела — дело математики:

Уравнение

Уравнение — это равенство, содержащее неизвестный член. В чем его смысл?

Любая задача заключается в том, что что-то нам известно, а что-то — нет, и неизвестное нужно найти. Например, тело из некоторой точки переместилось на 6 м в направлении оси координат и оказалось в точке с координатой 9 (см. рис. 17).

Рис. 17. Начальное положение точки

Как найти, из какой точки тело начало движение?

У нас есть закономерность: проекция перемещения — это разность конечной и начальной координат:

Смысл уравнения будет в том, что перемещение и конечную координату мы знаем () и можем подставить эти значения, а начальную координату не знаем, она будет неизвестным в этом уравнении:

И уже решая уравнение, мы получим ответ: начальная координата .

Рассмотрим другой случай: перемещение направлено в сторону, противоположную направлению оси координат.

Координаты начальной и конечной точек определяются так же, как и раньше, — опускаются перпендикуляры на ось (см. рис. 18).

Рис. 18. Ось направлена в другую сторону

Проекция перемещения (ничего не меняется) равна:

Обратите внимание, что больше, чем , и проекция перемещения , когда она направлена против оси координат, будет отрицательной.

Конечная координата тела из уравнения для проекции перемещения равна:

Как видим, ничего не меняется: в проекции на ось координат конечное положение равно начальному положению плюс проекция перемещения. В зависимости от того, в какую сторону тело переместилось, проекция перемещения будет положительной или отрицательной в данной системе координат.

Рассмотрим случай, когда перемещение и ось координат направлены под углом друг к другу. Теперь одной оси координат нам недостаточно, нужна вторая ось (см. рис. 19).

Рис. 19. Ось направлена в другую сторону

Теперь перемещение будет иметь ненулевую проекцию на каждую ось координат. Эти проекции перемещения будут определяться, как и раньше:

Заметьте, модуль каждой из проекций в этом случае меньше модуля перемещения. Модуль перемещения можем легко найти, используя теорему Пифагора. Видно, что если построить прямоугольный треугольник (см. рис. 20), то его катеты будут равны и , а гипотенуза равна модулю перемещения или, как часто записывают, просто .

Рис. 20. Треугольник Пифагора

Тогда по теореме Пифагора запишем:

Автомобиль находится в 4 км к востоку от гаража. Воспользуйтесь одной осью координат, направленной на восток, с началом отсчета в гараже. Укажите координату автомобиля в заданной системе через 3 минуты, если автомобиль этим временем ехал со скоростью 0,5 км/мин на запад.

В задаче ничего не сказано о том, что автомобиль поворачивал или изменял скорость, поэтому считаем движение равномерным прямолинейным.

Изобразим систему координат: начало координат у гаража, ось х направлена на восток (см. рис. 21).

Автомобиль изначально был в точке и двигался по условию задачи на запад (см. рис. 22).

Рис. 22. Движение автомобиля на запад

Проекция перемещения, как мы неоднократно писали, равна:

Мы знаем, что автомобиль проезжал по 0,5 км каждую минуту, значит, чтобы найти суммарное перемещение, нужно скорость умножить на количество минут :

На этом физика закончилась, осталось математически выразить искомую координату. Выразим ее из первого уравнения:

Подставим перемещение:

Осталось подставить числа и получить ответ. Не забывайте, что автомобиль двигался на запад против направления оси х, это значит, что проекция скорости отрицательна: .

Задача решена.

Главное, чем мы сегодня пользовались для определения координаты, — выражение для проекции перемещения:

И из него мы уже выражали координату:

При этом сама проекция перемещения может быть задана, может вычисляться как , как в было в задаче о равномерном прямолинейном движении, может вычисляться сложнее, что нам еще предстоит изучить, но в любом случае координату движущегося тела (где тело оказалось) можно определить по начальной координате (где тело было) и по проекции перемещения (куда переместилось).

На этом наш урок окончен, до свидания!

Список литературы

1. Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. — 2-е издание, передел. — X.: Веста: Издательство «Ранок», 2005. — 464 с.
2. Перышкин А.В., Гутник Е.М. Физика: 9 класс. Учебник для общеобразовательных учреждений. — 14-е изд. — М.: Дрофа, 2009.

1. Class-fizika.narod.ru ().
2. Av-physics.narod.ru ().
3. Class-fizika.narod.ru ().

Домашнее задание

1. Что такое перемещение, путь, траектория?
2. Как можно определить координаты тела?
3. Запишите формулу для определения проекции перемещения.
4. Как будет определяться модуль перемещения, если перемещение имеет проекции на две оси координат?

План-конспект урока по физике по теме: Повторно – обобщающий урок по теме: «Кинематика» ❤️

Home ⇒ 📌Механика ⇒ План-конспект урока по физике по теме: Повторно – обобщающий урок по теме: «Кинематика»

Цель урока: повторить материал темы: «Кинематика»; развивать навыки самостоятельного решения качественных, графических и вычислительных задач,умения работать в коллективе, анализировать, сравнивать, систематизировать знания.

Ход урока

Организационный момент.

Класс делится на группы по 4 человека. Каждая группа получает индивидуальное задание на карточках. В течение 20 – 25 минут учащиеся коллективно решают предложенные задачи, отвечают на вопросы. Необходимо, чтобы группы были приблизительно одинаковы

по уровню подготовки и в каждой был ученик, обладающий хорошими организаторскими способностями, играющий роль консультанта.

Карточка №1

1 Какое движение материальной точки называется прямолинейным и равномерным?

2 Запишите формулу для координаты х материальной точки при её прямолинейном равномерном движении и поясните смысл входящих в неё величин.

3 На рисунке изображен график зависимости от времени координаты Х точи, движущейся вдоль оси Ох. Найдите скорость на каждом участке графика и путь l, пройденный точкой за все время движения.

/> Х

Ответ: Vx1= — 2 м/с

Vx2= 0

t Vx3= 2 м/с

L = 10 м

4 Автомобиль одну четверть времени своей поездки двигался со скоростью V1=36 км/ч, а три четверти времени со скоростью V2= 54 км/ч. Чему равна средняя скорость Vср автомобиля на всем пути.

5 Конец минутной стрелки на Спасской башне Кремля за время t= 60 с прошел путь l=37cм.

Какова длина стрелки R?

Карточка № 2

1 Что называется перемещением Δr материальной точки? Изобразите на рисунке траекторию криволинейного движения материальной точки и её перемещение за время Δt.

2 Запишите формулу, связывающую радиус — вектор r материальной точки с вектором скорости V при прямолинейном равномерном движении, предположив начальный радиус-вектор точки равным r0. Запишите это уравнение в проекции на ось Х.

3 Материальная точка движется прямолинейно вдоль оси Ох. Проекция Vx её cкорости изменяется со временем, как показано на рисунке. Опишите как движется точка в интервале

V времени 0 -2с. Найдите отношение axl/axll проекций ускорений на ось

Ох, с которыми точка двигалась в течение интервалов времени

(0 – 1с) и (1 – 2с)

0 t

4 Материальная точка, двигаясь равноускоренно с нулевой начальной скоростью, за пятую секунду прошла путь l. равный 9 м. Чему равно ускорение а, с которым двигалась точка?

5. Снаряд, вылетевший из орудия под углом к горизонту, находился в полете 12с. Какой наибольшей высоты достиг снаряд?

Отчеты групп о выполнении работы. 2 ученика одновременно решают задачи у доски,

один из учеников отвечает на устные вопросы. Обсуждается одна из наиболее интересных задач.

Подводим итоги урока.

Домашняя работа: краткие итоги главы 1, стр. 45 – 46, № 69, 226

Поурочные планы. Физика, 9 кл. 3 ч/нед. Перышкин А.В., Гутник Е.М. — Медиатека

Поурочные планы. Физика, 9 кл. 3 ч/нед. Перышкин А.В., Гутник Е.М.   Урок 1. Материальная точка. Система отсчета [doc, 43,0 Kb]   Урок 2. Перемещение [doc, 220,0 Kb]   Урок 3. Определение координат движущегося тела [doc, 69,5 Kb]   Урок 4. Перемещение при прямолинейном равномерном движении [doc, 64,0 Kb]   Урок 5. Решение задач [doc, 40,5 Kb]   Урок 6. Прямолинейное равноускоренное движение [doc, 39,5 Kb]   Урок 7. Решение задач [doc, 39,0 Kb]   Урок 8. Скорость прямолинейного равноускоренного движения. График скорости [doc, 137,5 Kb]   Урок 9. Перемещение при прямолинейном равноускоренном движении [doc, 100, 0 Kb]   Урок 15. Относительность движения [doc, 48,5 Kb]   Урок 17. Контрольная работа № 1 по теме «Основы кинематики» [doc, 46,0 Kb]   Урок 19. Инерциальные системы отсчета. 1-й закон Ньютона [doc, 43,5 Kb]   Урок 20. 2-й закон Ньютона [doc, 43,5 Kb]   Урок 29. Ускорение свободного падения на Земле и других небесных телах [doc, 44,5 Kb]   Урок 30. Прямолинейное и криволинейное движение [doc, 42,0 Kb] Список категорий

Кинематические уравнения и кинематические графики

Урок 4 этого раздела в классе физики был посвящен использованию графиков скорость-время для описания движения объектов. В этом Уроке подчеркивалось, что наклон линии на графике скорость-время равен ускорению объекта, а площадь между линией и осью времени равна смещению объекта. Таким образом, графики зависимости скорости от времени можно использовать для определения числовых значений и отношений между величинами перемещения (d), скорости (v), ускорения (a) и времени (t).В Уроке 6 основное внимание уделялось использованию четырех кинематических уравнений для описания движения объектов и предсказания численных значений одного из четырех параметров движения — смещения (d), скорости (v), ускорения (a) и время (т). Таким образом, теперь есть два метода решения задач, связанных с числовыми соотношениями между перемещением, скоростью, ускорением и временем. В этой части Урока 6 мы исследуем отношения между этими двумя методами.

Пример задачи — графическое решение

Рассмотрим объект, который движется с постоянной скоростью +5 м/с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м/с в течение следующих 5 секунд. Такое словесное описание движения может быть представлено графиком скорость-время. График показан ниже.

Горизонтальная часть графика изображает движение с постоянной скоростью, что соответствует словесному описанию. Участок графика с положительным наклоном (т. е. с наклоном вверх) изображает положительное ускорение, соответствующее словесному описанию объекта, движущегося в положительном направлении и ускоряющегося с 5 м/с до 15 м/с. Наклон линии можно вычислить, используя коэффициент подъема относительно пробега.Между 5 и 10 секундами скорость линии увеличивается с 5 м/с до 15 м/с и продолжается от 5 до 10 с. Это общий подъем +10 м/с и общий пробег 5 с. Таким образом, уклон (соотношение подъем/спуск) равен (10 м/с)/(5 с) = 2 м/с ² . По графику скорость-время определено ускорение объекта, равное 2 м/с ² в течение последних пяти секунд движения объекта. Смещение объекта также можно определить с помощью графика зависимости скорости от времени. Площадь между линией на графике и осью времени представляет смещение; эта область принимает форму трапеции.Как обсуждалось в Уроке 4, площадь трапеции можно приравнять к площади треугольника, лежащего на вершине площади прямоугольника. Это показано на диаграмме ниже.

Общая площадь равна площади прямоугольника плюс площадь треугольника. Расчет этих площадей показан ниже.

Прямоугольник	Треугольник
Площадь = основание * высота Площадь = (10 с) * (5 м/с) Площадь = 50 м	Площадь = 0.5 * база * высота Площадь = 0,5 * (5 с) * (10 м/с) Площадь = 25 м

Общая площадь (прямоугольник плюс треугольник) равна 75 м.кв. Таким образом, перемещение объекта за 10 секунд движения составляет 75 метров.

Приведенное выше обсуждение иллюстрирует, как графическое представление движения объекта может использоваться для извлечения числовой информации об ускорении и смещении объекта. После построения график зависимости скорости от времени можно использовать для определения скорости объекта в любой момент времени в течение 10 секунд движения.Например, скорость объекта в 7 секунд может быть определена путем считывания значения координаты y в координате x 7 секунд. Таким образом, графики скорости-времени можно использовать для выявления (или определения) числовых значений и взаимосвязей между величинами смещения (d), скорости (v), ускорения (a) и времени (t) для любого заданного движения.

 

Пример задачи — решение с использованием кинематического уравнения

Теперь рассмотрим то же словесное описание и соответствующий анализ с помощью кинематических уравнений.Словесное описание движения было:

Объект, который движется с постоянной скоростью +5 м/с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м/с в течение следующих 5 секунд

Кинематические уравнения могут быть применены к любому движению, для которого ускорение является постоянным. Поскольку это движение имеет две отдельные стадии ускорения, любой кинематический анализ требует, чтобы параметры движения для первых 5 секунд не смешивались с параметрами движения для последних 5 секунд.В таблице ниже перечислены заданные параметры движения.

t = 0 с — 5 с	т = 5 с — 10 с
v i = 5 м/с v f = 5 м/с t = 5 с a = 0 м/с 2	v i = 5 м/с v f = 15 м/с t = 5 с

Обратите внимание, что ускорение в течение первых 5 секунд указано как 0 м/с ² , несмотря на то, что это явно не указано.Фраза постоянная скорость указывает на движение с нулевым ускорением. Ускорение объекта за последние 5 секунд можно рассчитать с помощью следующего кинематического уравнения.

v _f = v _i + a*t

Здесь показаны подстановка и алгебра.

15 м/с = 5 м/с + а*(5 с)
15 м/с — 5 м/с = a*(5 с)

10 м/с = a*(5 с)

(10 м/с)/(5 с) = a

a = 2 м/ с ²

Это значение ускорения объекта в течение времени от 5 с до 10 с согласуется со значением, определенным по наклону линии на графике скорость-время.

Смещение объекта за все 10 секунд также можно рассчитать с помощью кинематических уравнений. Поскольку эти 10 секунд включают в себя два совершенно разных интервала ускорения, расчеты для каждого интервала необходимо выполнять отдельно. Это показано ниже.

t = 0 с — 5 с	т = 5 с — 10 с
d = v i *t + 0,5*a*t 2 d = (5 м/с)*(5 с) +0.5*(0 м/с 2 )*(5 с) 2 d = 25 м + 0 м д = 25 м	d = ((v i + v f )/2)*t d = ((5 м/с + 15 м/с)/2)*(5 с) d = (10 м/с)*(5 с) д = 50 м

Общее перемещение за первые 10 секунд движения составляет 75 метров, что соответствует значению, определенному по площади под линией на графике скорость-время.

Анализ этого простого движения иллюстрирует значение этих двух представлений движения — графика скорость-время и кинематических уравнений.Каждое представление можно использовать для извлечения числовой информации о неизвестных величинах движения для любого заданного движения. Приведенные ниже примеры предоставляют полезную возможность для тех, кому требуется дополнительная практика.

Проверьте свое понимание

1. Rennata Gas движется по городу со скоростью 25,0 м/с и начинает ускоряться с постоянной скоростью -1,0 м/с ² . В конце концов Ренната полностью останавливается.

а. Представьте ускоренное движение Реннаты, нарисовав график зависимости скорости от времени.Используйте график зависимости скорости от времени, чтобы определить это расстояние.
б. Используйте кинематические уравнения для расчета расстояния, которое проходит Ренната при замедлении.

2. Отто Эмиссион едет на своей машине со скоростью 25,0 м/с. Отто ускоряется со скоростью 2,0 м/с ² в течение 5 секунд. Затем Отто поддерживает постоянную скорость еще 10,0 секунд.

а. Представьте 15 секунд движения Отто Эмиссион, нарисовав график зависимости скорости от времени.Используйте график, чтобы определить расстояние, пройденное Отто за все 15 секунд.
б. Наконец, разбейте движение на два сегмента и используйте кинематические уравнения для расчета общего расстояния, пройденного за все 15 секунд.

3. Люк Аутбело, человек, мастер по стрельбе из пушечного ядра, был сброшен с края обрыва с начальной восходящей скоростью +40,0 м/с. Люк ускоряется с постоянным нисходящим ускорением -10,0 м/с ² (приблизительное значение ускорения свободного падения).

а. Нарисуйте график зависимости скорости от времени для первых 8 секунд движения Люка.
б. Используйте кинематические уравнения, чтобы определить время, необходимое Люку Отбело, чтобы вернуться на исходную высоту скалы. Укажите это время на графике.

 

4. Чак Вагон движется с постоянной скоростью 0,5 мили в минуту в течение 10 минут. Затем Чак замедляется со скоростью -0,25 мили/мин ² в течение 2 минут.

а. Нарисуйте график скорости во времени для движения Чака Вагона. Используйте график зависимости скорости от времени, чтобы определить общее расстояние, пройденное Чаком Вагоном за 12 минут движения.
б. Наконец, разбейте движение на два сегмента и используйте кинематические уравнения, чтобы определить общее расстояние, пройденное Чаком Вагоном.

 

5. Вера Сайд мчится по межштатной автомагистрали со скоростью 45,0 м/с. Вера смотрит вперед и наблюдает за аварией, в результате которой посреди дороги образовалась авария.К моменту, когда Вера бьет по тормозам, она находится в 50,0 м от пайлапа. Она замедляется со скоростью -10,0 м/с ² .

а. Постройте график зависимости скорости от времени для движения Веры Сайд. Используйте график, чтобы определить расстояние, которое Вера преодолела бы до полной остановки (если бы она не столкнулась с нагромождением).
б. Используйте кинематические уравнения, чтобы определить расстояние, которое Вера Сайд преодолела бы до полной остановки (если бы она не столкнулась с нагромождением). Столкнется ли Вера с машинами в толпе? То есть проедет ли Вера больше 50.0 метров?

 

6. Эрл Э. Берд движется со скоростью 30,0 м/с за 10,0 секунд. Затем он ускоряется со скоростью 3,00 м/с ² в течение 5,00 секунд.

а. Постройте график зависимости скорости от времени для движения Эрла Э. Берда. Используйте график, чтобы определить общее пройденное расстояние.
б. Разделите движение Earl E. Bird на два временных сегмента и используйте кинематические уравнения для расчета полного перемещения.

Ответы на вышеуказанные вопросы

Ответ на вопрос 1

а.График скорость-время для движения:

Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.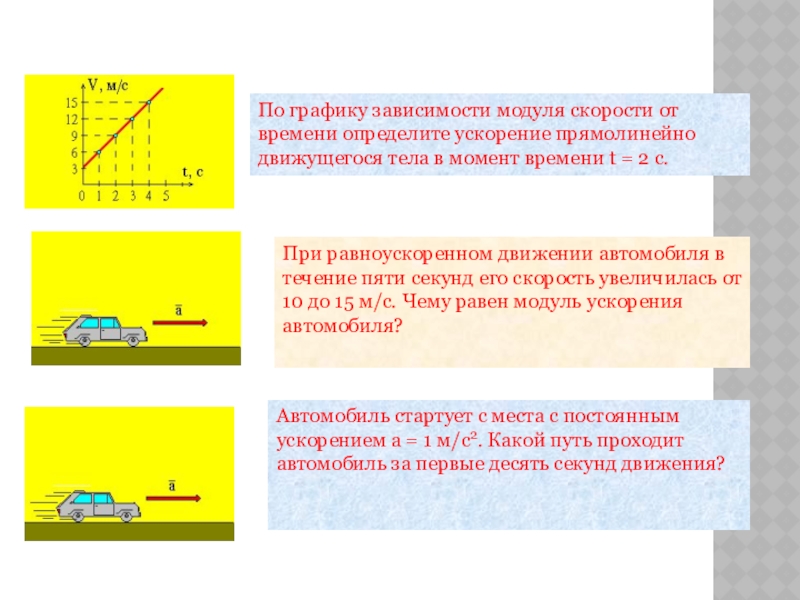

Площадь = 0,5*b*h = 0,5*(25,0 с)*(25,0 м/с)

Площадь = 313 м

б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.

Дано: v i = 25.0 м/с v f = 0,0 м/с а = -1,0 м/с 2

Найти: д = ??

(0 м/с) ² = (25,0 м/с) ² + 2 * (-1,0 м/с ² )*d

0.0 м ² /с ² = 625,0 м ² /с ² + (-2,0 м/с ² )*d

0,0 м ² /с ² — 625,0 м ² /с ² = (-2,0 м/с ² )*d

(-625,0 м ² /с ² )/(-2,0 м/с ² ) = d

313 м = д

 

 

Ответ на вопрос 2

а. График зависимости скорости от времени для движения:

 

Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.

Площадь = 0.5*b _tri *h _tri + b _rect1 *h _rect1 + b _rect2 *h _rect2

Площадь = 0.5*(5,0 с)*(10,0 м/с) + (5,0 с)*(25,0 м/с) + (10,0 с)*(35,0 м/с)

Площадь = 25 м + 125 м + 350 м

Площадь = 500 м

б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.

Сначала найдите d за первые 5 секунд:

Дано: v i = 25.0 м/с т = 5,0 с а = 2,0 м/с 2

Найти: д = ??

d = v _i *t + 0,5*a*t ²

d = (25,0 м/с)*(5,0 с) + 0. 5*(2,0 м/с ² )*(5,0 с) ²

d = 125 м + 25,0 м

д = 150 м

Теперь найдите d за последние 10 секунд:

Дано: v i = 35,0 м/с т = 10,0 с а = 0.0 м/с 2

Найти: д = ??

(Примечание: скорость на отметке 5 секунд можно найти, зная, что автомобиль ускоряется с 25,0 м/с до +2,0 м/с ² в течение 5 секунд. Это приводит к изменению скорости a*t = 10 м/с и, следовательно, скорость 35,0 м/с.)

d = v _i *t + 0.5*а*т ²

d = (35,0 м/с)*(10,0 с) + 0,5*(0,0 м/с ² )*(10,0 с) ²

d = 350 м + 0 м

d =350 м

Общее расстояние за 15 секунд движения равно сумме этих двух расчетов расстояния (150 м + 350 м):

расстояние = 500 м

 

 

Ответ на вопрос 3

а. График скорость-время для движения:

б. Время подъема и падения на исходную высоту в два раза превышает время подъема на пик. Таким образом, решение заключается в том, чтобы найти время, чтобы подняться до пика, а затем удвоить его.

Дано: v i = 40,0 м/с v f = 0.0 м/с а = -10,0 м/с 2

Найти: т вверх = ?? 2*t вверх = ??

v _f = v _i + a*t _вверх

0 м/с = 40 м/с + (-10 м/с2)*t _до

(10 м/с ² )*t _до = 40 м/с

t _up = (40 м/с)/(10 м/с ² )

т _до = 4. 0 с

2*t _до = 8,0 с

 

 

 

Ответ на вопрос 4

а. График скорость-время для движения:

Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади прямоугольника плюс площадь треугольника.

Площадь = b _{прямоугольная} *h _{прямоугольная} + 0,5*b _{тройная} *h _{тройная}

Площадь = (10,0 мин)*(0,50 мили/мин) + 0,5*(2,0 мин)*(0,50 мили/мин)

Площадь = 5 миль + 0,5 мили

Площадь = 5,5 мили

б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.

Сначала найдите d за первые 10 минут:

Дано: v i = 0. 50 миль/мин т = 10,0 мин а = 0,0 миль/мин 2

Найти: д = ??

d = v _i *t + 0,5*a*t ²

d = (0,50 миль/мин)*(10.0 мин) + 0,5*(0,0 миль/мин ² )*(10,0 мин) ²

d = 5,0 миль + 0 миль

d = 5,0 миль

Теперь найдите d за последние 2 минуты:

Дано: v i = 0,50 миль/мин т = 2,0 мин а = -0.25 миль/мин 2

Найти: д = ??

d = v _i *t + 0,5*a*t ²

d = (0,50 миль/мин)*(2,0 мин) + 0,5*(-0,25 м/с ² )*(2,0 мин) ²

d = 1,0 мили + (-0,5 мили)

d = 0,5 мили

Общее расстояние за 12 минут движения равно сумме этих двух расчетов расстояния (5. 0 миль + 0,5 мили):

расстояние = 5,5 мили

 

 

Ответ на вопрос 5

а. График скорость-время для движения:

Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.

Площадь = 0.5*b*h = 0,5*(4,5 с)*(45,0 м/с)

Площадь = 101 м

 

б.

Дано: v i = 45,0 м/с v f = 0,0 м/с а = -10,0 м/с 2

Найти: д = ??

v _f ² = v _i ² + 2*a*d

(0 м/с) ² = (45. 0 м/с) ² + 2 * (-10,0 м/с ² )*d

0,0 м ² /с ² = 2025,0 м ² /с ² + (-20,0 м/с ² )*d

0,0 м ² /с ² — 2025,0 м ² /с ² = (-20,0 м/с ² )*d

(-2025,0 м ² /с ² )/(-20,0 м/с ² ) =d

101 м =d

Так как место аварии находится менее чем в 101 м от Веры, она действительно врежется в нагромождение перед полной остановкой (если не отклонится в сторону).

 

 

 

Ответ на вопрос 6

а. График скорость-время для движения:

Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.

Площадь = 0,5*b _tri *h _tri + b ₁ *h ₁ + b ₂ *h ₂

Площадь = 0,5*(5,0 с)*(15,0 м/с) + (10,0 с)*(30,0 м/с) + (5,0 с)*(30,0 м/с)

Площадь = 37,5 м + 300 м + 150 м

Площадь = 488 м

 

б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.

Сначала найдите d за первые 10 секунд:

Дано: v i = 30,0 м/с т = 10,0 с а = 0,0 м/с 2

Найти: д = ??

d = v _i *t + 0.5*а*т ²

d = (30,0 м/с)*(10,0 с) + 0,5*(0,0 м/с ² )*(10,0 с) ²

d = 300 м + 0 м

d =300 м

Теперь найдите d за последние 5 секунд:

Дано: v i = 30,0 м/с т = 5. 0 с а = 3,0 м/с 2

Найти: д = ??

d = v _i *t + 0,5*a*t ²

d = (30,0 м/с)*(5,0 с) + 0,5*(3,0 м/с ² )*(5,0 с) ²

d = 150 м + 37,5 м

д = 187.5 м

Общее расстояние за 15 секунд движения равно сумме этих двух расчетов расстояния (300 м + 187,5 м):

расстояние = 488 м

Что такое положение в физике? — Определение и примеры — Видео и стенограмма урока

Векторы и скаляры

Когда дело доходит до положения, важно направление.Говоря, что вы находитесь на положительных 6 метрах в направлении x, вы говорите, что находитесь на 3 метра правее оси y. Это направление.

Число, для которого важно направление, называется вектором .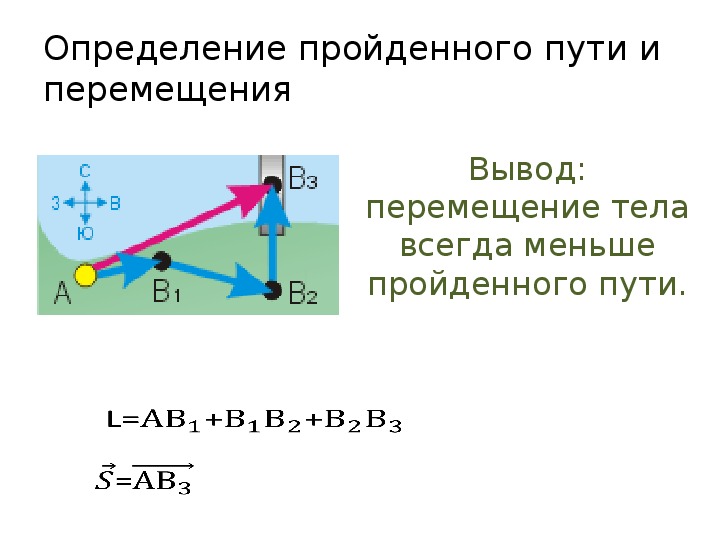 Число, направление которого не имеет значения, называется скаляром . Например, температура является скаляром. Потому что у него никогда нет направления. Температура может быть 70 градусов по Фаренгейту, но она не поднимается до 70 градусов по Фаренгейту. Это может быть 40 градусов по Цельсию, но никогда 40 градусов по Цельсию не направляются на запад.Это не то, как работает температура. Температура является скаляром.

Позиция является вектором, потому что направление имеет значение. Но расстояние является скаляром. Расстояние — это расстояние, которое вы проехали. Например, если вы бегаете по комнате с осью на полу, вы можете пробежать очень длинный путь, пока не пройдете в общей сложности 50 метров. Но ваша позиция не 50 метров. Например, ваша позиция может быть отрицательной на 3 метра по оси X и положительной на 4 метра по оси Y. Направление, в котором вы бежали, не имело значения для вашего расстояния — вы все равно преодолели 50 метров.Так что с расстоянием направление не имеет значения. Расстояние является скаляром.

Графики положение-время

Когда ваше положение меняется с течением времени, вы можете показать это с помощью графика положение-время. График положение-время выглядит следующим образом, с положением по оси Y и временем по оси X:

График положение-время

Если вы не двигаетесь, вы получите плоскую линию, например:

Нет движения

Если вы не двигаетесь в начале координат, это будет выглядеть так:

Нет движения в начале

Но если вы не двигаетесь в позиции, которая не является исходной, это будет выглядеть так:

Нет движения в позиции, отличной от исходной

Если вы движетесь с постоянной скоростью, вы получите диагональную линию. Если вы движетесь к исходной точке, это будет выглядеть так:

Движение к происхождению

Если вы удаляетесь от начала координат, это будет выглядеть так:

Движение от источника

Пример

Вам необходимо построить график положение-время по некоторым данным. Например, вы можете получить такие данные:

. Данные для велосипедиста

Эти данные показывают, как велосипедист менял положение в течение дня, отправляясь на работу, а затем снова возвращаясь домой.Приостановите видео и попробуйте построить график этих данных. Я покажу вам решение через минуту.

Если вы еще этого не сделали, приостановите воспроизведение видео сейчас.

Итак, если вы все еще слушаете видео, значит, вы попробовали построить график. Сейчас я покажу вам, как это должно было выглядеть. Ваш график должен выглядеть так:

Пример графика положение-время для велосипедиста

Велосипедист поехал на работу с постоянной скоростью, некоторое время оставался в том же положении, потому что был на работе, а затем поехал домой.Вы могли бы даже заметить, что он ехал на работу быстрее, чем домой. Может быть, он опоздал!

Резюме урока

Позиция — это место, где кто-то или что-то находится или находится. В физике положение обычно представляет собой число на оси. У вас может быть ось X, которая выглядит как в разделе выше, или ось Y, также в разделе выше. Вы можете находиться на положительных 6 метрах по оси x и на отрицательных 3 метрах по оси y. Это ваша позиция.

Когда дело доходит до позиции, важно направление. Говоря, что вы находитесь на положительных 6 метрах по оси x, вы говорите, что находитесь на 6 метров справа от оси y. Это направление. Число, для которого имеет значение направление, называется вектором . Число, направление которого не имеет значения, называется скаляром . Позиция — это вектор, потому что направление имеет значение. Но расстояние является скаляром. Расстояние — это расстояние, которое вы проехали. Например, если вы бегаете по комнате с топорами на полу, вы можете пробежать очень длинный путь, пока не пробежите в общей сложности 50 метров.Но ваша позиция не 50 метров. Направление, в котором вы бежали, не имело значения для вашего расстояния — вы все равно преодолели 50 метров. Итак, с расстоянием направление не имеет значения. Расстояние является скаляром.

Когда ваше положение меняется с течением времени, вы можете показать это с помощью графика положение-время. График положение-время выглядит так же, как в разделе выше, с положением на оси Y и временем на оси X. Если вы не двигаетесь, вы получите плоскую линию, как показано выше. Если вы движетесь с постоянной скоростью, вы получите диагональную линию.

Результаты обучения

После этого урока вы сможете:

• Определять положение и расстояние
• Отличие вектора от скаляра
• Определение назначения и интерпретация графиков положение-время

Скорость в зависимости от времени: определение смещения объекта — видео и расшифровка урока

Перемещение с графиком зависимости скорости от времени

Но мы также можем выполнять другие расчеты с единицами измерения зависимости скорости от времени.график времени. Что, если вместо деления мы умножим? Скорость, умноженная на время, равна… ну, метры в секунду, умноженные на секунды, равны метрам. Отсюда следует, что если мы умножим скорость на время, мы сможем вычислить метры, пройденные объектом. В физике это называется смещением и представляет собой изменение положения от начальной до конечной точки. Этот процесс не так прост; это больше, чем просто умножение пары очков. По скорости против.график времени, площадь между линией графика и осью времени равна смещению объекта за этот период времени. Это официальное определение, но оно станет намного яснее, если мы посмотрим на пример.

График смещения Пример задачи

Посмотрите на этот график зависимости скорости бегуна от времени на прямой дорожке.

Из графика видно, что бегун разгоняется от полной остановки до максимальной скорости 12 метров в секунду, затем замедляется до полной остановки.Вся гонка занимает 12 секунд. Мы можем определить смещение бегуна за 12-секундный забег, рассчитав площадь между линией графика и осью времени. Надеюсь, вы помните, что вам нужна следующая формула для вычисления площади треугольника:

Площадь = (1/2) x основание x высота

Для этой задачи вы можете видеть на графике, что основание составляет 12 секунд. Высота 12 метров в секунду. Подставим их в уравнение: Площадь = (1/2) x (12с) x (12 м/с) , что равно 72 метра .Наш бегун пробежал 72 метра за 12 секунд. Его водоизмещение составляет 72 метра.

Помните: перемещение является векторной величиной, требующей как величины, так и направления. На графике с прямолинейным движением направление либо положительное — движение вперед, либо отрицательное — движение назад. В этой задаче смещение положительное, что говорит нам о том, что бегун двигался вперед от своего исходного положения. Этот метод также работает, если объект движется назад и если линия графика находится ниже оси времени.Просто помните, что если скорость отрицательна, вам нужно сохранить этот отрицательный знак. Вы также можете определить смещение, если объект движется с постоянной скоростью. Вместо того, чтобы вычислять площадь треугольника, это был бы прямоугольник, подобный этому.

График объекта, движущегося с постоянной скоростью, представляет собой прямоугольник.

Площадь = основание x высота

Итоги урока

Пришло время сделать краткий обзор.Вы можете использовать график зависимости скорости от времени для расчета смещения объекта при прямолинейном движении. Площадь между линией графика и осью времени равна смещению объекта за этот период времени. Смещение может быть положительным, если линия находится выше оси времени, или отрицательным, если линия ниже оси времени. Всегда не забывайте указывать знак смещения, потому что смещение является векторной величиной.

Результат обучения

Просмотрите этот урок, чтобы узнать, как использовать скорость и скорость.временной график для определения смещения объекта.

Перемещение, Скорость, Ускорение

Мы живем в мире, который определяется тремя пространственными измерениями и одним измерение времени. Объекты перемещаются внутри этой области двумя способами. Объект транслирует , или изменяет адрес с одного указать на другое. И объект вращается, или изменяет свою ориентацию .В общем, движение объекта предполагает как перевод во всех три направления, и вращение вокруг три главные оси.

На этой странице мы будем рассматривать только перевод объекта. Мы можем указать местоположение объекта в в любое время t , указав три координаты x, y, и z в ортогональной системе координат. Ан ортогональная система координат имеет каждый его координатных направлений перпендикулярны всем другим координатным направлениям.Изначально наш объект находится в точке «0», с координатами x0, y0, и z0 в момент времени t0 . В общем случае объект перемещается по домену до тех пор, пока в более позднее время t1 объект находится в точке «1» с координатами x1, y1, и z1 . Мы можем указать смещение — d в каждом направлении координат по разнице координат от точки «0» до точки «1». X-смещение равно (x1 — x0), смещение по оси y равно (y1 — y0), а смещение по оси z равно (z1 — z0). На этой веб-странице, для простоты, мы будем рассматривать только координату x. Тогда смещение определяется как:

д = х1 — х0

Смещение – это векторная величина, а значит, перемещение имеет размер и направление, связанное с ним. Направление — от точки «0» до пункт «1». Индивидуальные смещения x-, y-, и z- являются компоненты вектора смещения в координатных направлениях. Все величины, полученные из смещения, также являются векторными величинами.

скорость -V объекта через домен это изменение местоположения во времени. В направлении X средняя скорость равна смещению, деленному на по интервалу времени:

V = (x1 — x0) / (t1 — t0)

Это всего лишь средняя скорость, и объект может ускоряться и замедляться между точками «0» и «1».В любой момент объект может иметь скорость, отличную от средней. Если мы сократим разницы во времени до очень малого (дифференциального) размера, мы можем определить мгновенная скорость дифференциальное изменение положения, деленное на дифференциальное изменение во времени;

V = дх/дт

где символ д/дт — дифференциал от исчисления. (Для младших школьников, у вас только что был первый урок по математике! .. это было не так уж плохо, не так ли? Если это не имеет смысла, не беспокойтесь и просто продолжайте читал..через несколько лет будет смысл.)

Когда мы изначально указываем местоположение нашего объекта с помощью x0, y0, z0, и t0 координаты, мы также должны указать начальную мгновенную скорость V0 . Аналогично в конечная позиция x1, y1, z1, и t1 , скорость меняется на скорость V1 .Опять же, для простоты мы рассматриваем только x-компоненту скорости. В действительности скорость изменяется во всех трех направлениях. Скорость это векторная величина и имеет как величину, так и направление. Направление совпадает с направлением смещения, от которого мы определили скорость.

Ускорение (а) объекта через домен равно изменение скорости во времени. В направлении X среднее ускорение есть изменение скорости разделить на интервал времени:

а = (V1 — V0) / (t1 — t0)

Как и в случае со скоростью, это только среднее значение. ускорение.В любой момент объект может иметь ускорение, отличное от среднего. Если мы сократим разницы во времени до очень малого (дифференциального) размера, мы можем определить мгновенное ускорение – дифференциальное изменение скорости, деленное на в дифференциальное изменение во времени:

а = дв/дт

От Ньютона второй закон движения, мы знаем, что силы, действующие на объект, вызывают ускорения.Если мы можем определить силы, действующие на объект, и то, как силы изменяются со временем, мы можем использовать уравнения, представленные на этом слайде, для определения ускорения, скорости, перемещения и, следовательно, местоположение объекта как функция времени. Авиационные инженеры используют эту информацию для прогнозирования движение самолета, или полет ракеты.

---

Деятельность:

---

Экскурсии с гидом

---

Навигация ..

Домашняя страница руководства для начинающих

15.

1 Виды сил | Силы

Поле — это область в пространстве, где на объект (с определенными свойствами) действует сила. Полевые силы являются бесконтактными силами. Бесконтактные силы – это силы, действующие на расстоянии. Они не должны соприкасаться. Наиболее распространенные примеры полей:

Когда мы обсуждали контактные силы, мы говорили о толчках и притяжениях.Однако с полевыми силами лучше говорить о отталкивании и притяжении .

Гравитационные силы

Вы когда-нибудь задумывались, почему вещи падают вниз, а не вверх?

Вы можете продемонстрировать гравитационный эффект, сбрасывая предметы разной массы с одинаковой высоты. Используйте теннисный мяч и скрученный лист бумаги (чтобы они были примерно одинакового размера и формы).Бросьте их с одной высоты и посмотрите, заметят ли ученики разницу в том, как они падают. Спросите учащихся, почему, по их мнению, предметы упали. Что-то давит на них? Или тянуть их вниз? Попросите их обсудить свои идеи друг с другом.

Модели, представленные в этой главе, очень полезны, если у вас есть доступ в Интернет. В противном случае поощряйте учащихся взаимодействовать с ними в свободное время дома или по мобильному телефону.

Мы уже сталкивались с гравитацией на планете Земля и за ее пределами в предыдущих классах.

Сила, которая заставляет предметы падать на Землю и не дает нам упасть с планеты, называется гравитационной силой . Силы гравитации существуют между любыми двумя объектами с массой, и они являются силами притяжения (тяги).

Ньютон разработал свой Закон всемирного тяготения, описывающий силу притяжения между телами с массой в 1687 году. Работа Ньютона по описанию теории гравитации могла быть вдохновлена ​​наблюдением за падением яблока с дерева.

Строго говоря, говоря о «гравитации», мы имеем в виду именно гравитационную силу притяжения, возникающую между Землей (или другим небесным телом, например планетой) и другими объектами, в отличие от гравитационной силы вообще, действующей между любыми два объекта с массой. Например, мы бы назвали гравитационную силу, притягивающую объекты к Луне, гравитационной силой Луны.

Что такое гравитация?

Гравитационная сила — это сила, которая притягивает объекты с массой друг к другу. Любой объект с массой оказывает гравитационное воздействие на любой другой объект с массой . Земля притягивает вас, парты в вашем классе и стулья в вашем классе, удерживая вас на поверхности и не давая улететь в космос.

Гравитация — это сила, поэтому она измеряется в ньютонах.

Сила притяжения Земли притягивает все к центру Земли, поэтому, когда вы роняете предмет, например книгу или яблоко, он падает на землю. Однако знаете ли вы, что вы, ваш стол, ваш стул, падающее яблоко и книга оказывают одинаковое, но противоположное притяжение на Землю? Как вы думаете, почему эти силы на Земле не вызывают заметного движения Земли?

---

---

Земля имеет гораздо большую массу, чем человек или стол, и поэтому она ускоряется на гораздо меньшую величину, хотя сила, действующая на Землю со стороны стола, равна силе, действующей на стол со стороны Земли ( только в разные стороны).Вот почему Земля не движется заметно.

Стрелки показывают направление гравитационного поля Земли. Все стрелки указывают на центр Земли, потому что гравитационная сила всегда притягивает.

Моделирование PhET в боксе для посещений может быть использовано для очень простой демонстрации того, как гравитационная сила между двумя объектами увеличивается с массой и уменьшается с увеличением расстояния между объектами. Вы можете отключить значения и использовать положение фигурок, дергающих за веревки, чтобы качественно продемонстрировать отношения.

Земля притягивает нас, потому что у нее такая большая масса, и поэтому мы все время притягиваемся вниз к центру Земли.

Эти армейские парашютисты только что выпрыгнули из задней части самолета и упали на Землю из-за гравитации.

Чем больше масса объектов, тем больше сила между ними.Это означает, что два небольших объекта будут иметь очень слабое гравитационное притяжение, поэтому оно не оказывает заметного эффекта. Однако более крупные объекты, такие как Луна и Земля, обладают гораздо большей гравитационной силой.

Как мы знаем из Планеты Земля и за ее пределами, все планеты в нашей Солнечной системе удерживаются на орбитах вокруг Солнца силой гравитационного притяжения между Солнцем и планетами.

Планеты движутся вокруг Солнца в нашей Солнечной системе. Существует гравитационная сила притяжения между Солнцем и планетами, а также между планетами и их лунами.

Вторым фактором, влияющим на гравитационную силу притяжения между объектами, является расстояние между ними. Чем дальше объекты друг от друга, тем меньше гравитационная сила.

Между нами и Солнцем существует гравитационная сила притяжения, но мы этого не замечаем, так как находимся так далеко друг от друга и очень малы.

Все компоненты нашей Вселенной удерживаются вместе гравитационной силой. Подводя итог, мы можем сказать:

• Чем больше масса объектов, тем сильнее гравитационная сила притяжения между ними.

• Чем ближе объектов друг к другу, тем сильнее гравитационная сила между ними.

Заметка о падающих предметах

Полезный способ продемонстрировать гравитацию Земли — посмотреть на падающие предметы. Ниже приведено дополнительное дополнительное задание, в котором учащиеся бросают различные предметы. Вы можете проголосовать в классе, чтобы узнать, думают ли учащиеся, что яблоко или пакетик сахара упадут на землю первыми.(Ответ: они упадут на землю одновременно, если сопротивлением воздуха можно пренебречь.) Очень вероятно, что у учащихся сложится предубеждение, что более тяжелые предметы падают быстрее. В данный момент не важно, чтобы ответы учащихся были правильными, и не пытайтесь подвести их к правильному ответу. Они, надеюсь, откроют это для себя в следующем эксперименте.

В этом исследовании учащиеся должны работать в парах. Сначала они одновременно роняют целое яблоко и половинку яблока с одинаковой высоты.Затем они будут экспериментировать с мячами разной массы (но одинакового размера) и мячами одинаковой массы (но разного объема). Очень сложно ронять предметы в одно и то же время так, чтобы они упали на пол одновременно, поэтому позвольте учащимся повторить эксперимент несколько раз, пока они не будут уверены, что роняют предметы одновременно. Если им трудно увидеть, какой предмет падает на землю первым, предложите учащимся прислушаться к тому количеству звуков, которые они слышат — один или два — при ударе предметов.Учащимся, возможно, придется повторить это исследование много раз, поскольку оно, скорее всего, противоречит их предубеждениям. Совет по безопасности: лучше заранее разрезать яблоки пополам.

После того, как учащиеся закончат свой эксперимент, вы можете продемонстрировать эффекты сопротивления воздуха, бросив молоток и перо. Предложите учащимся проголосовать за то, что произойдет, если вы бросите молоток и перо. Будьте готовы объяснить учащимся, что сопротивление воздуха замедляет падение пера и что, если бы не было сопротивления воздуха, оба пера падали бы с одинаковой скоростью и одновременно ударялись об пол.

ИССЛЕДОВАТЕЛЬСКИЙ ВОПРОС: Падают ли разные предметы с одинаковой скоростью?

ГИПОТЕЗА:

Как вы думаете, что произойдет?

---

Ответ зависит от учащегося.

МАТЕРИАЛЫ И АППАРАТЫ:

• молоток
• перо
• два мяча одинаковой массы, разного объема (один комплект на пару)
• два мяча одинакового объема, разной массы (один комплект на пару)

Видео перьев и монет, падающих в вакууме

МЕТОД:

1. Работайте в парах, по очереди будьте тем, кто роняет предмет (экспериментатор), и тем, кто наблюдает за падением предметов (наблюдателем).
2. Заполните столбец «прогноз» в таблице ниже.
3. Экспериментатор: встаньте на стул или стол и возьмите два шара одинаковой массы, один в одну руку, а другой в другую.
4. Экспериментатор: поднимите два мяча на одной высоте перед собой и бросьте их точно в одно и то же время.
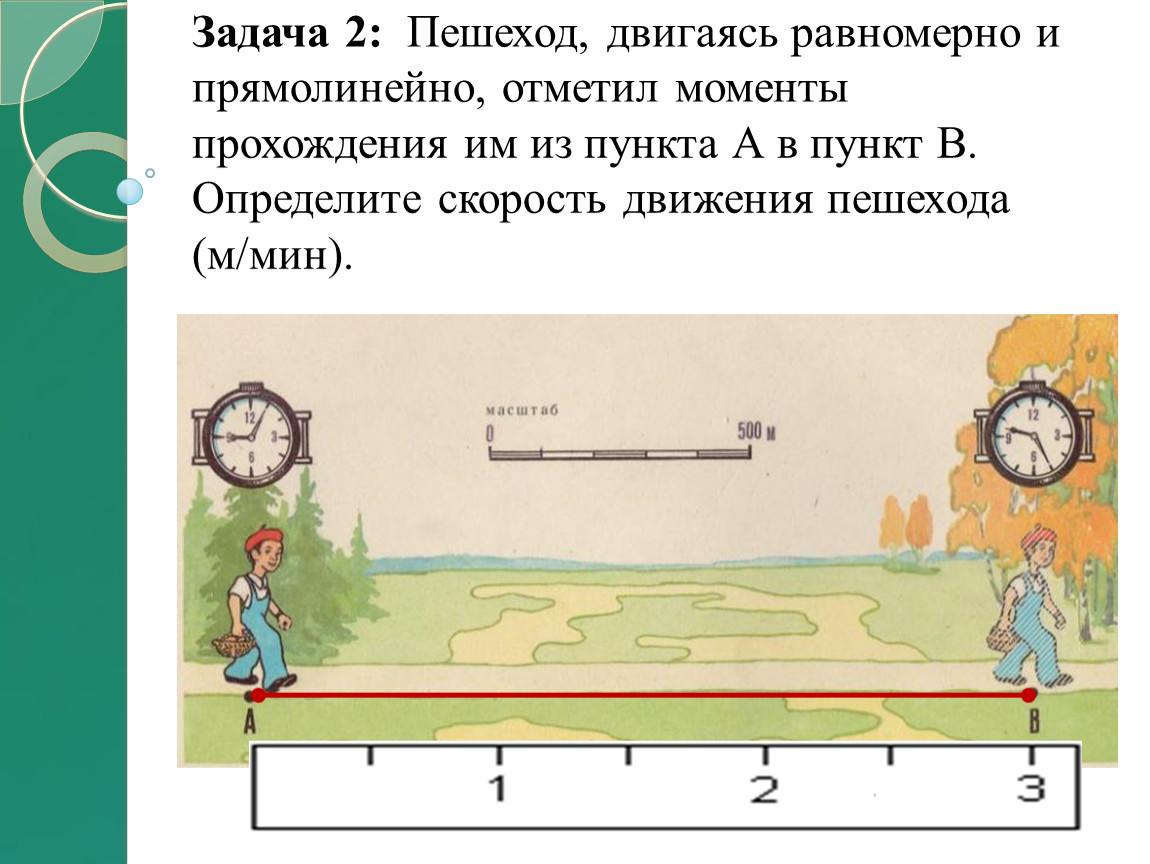
5. Наблюдатель: обратите внимание на то, что происходит, в частности, что приземлится первым.
6. Поменяйтесь местами и повторите эксперимент, используя два шара одинакового объема, но разной массы.
7. Теперь ваш учитель продемонстрирует вам и бросит молоток и перо. Перед тем, как учитель бросит молоток и перо, запишите в колонку прогнозов падение молотка и пера.
8. Запишите, что произошло с молотком и пером, и ответьте на приведенные ниже вопросы.

РЕЗУЛЬТАТЫ И НАБЛЮДЕНИЯ:

Что вы оставили неизменным в этом эксперименте?

---

Высота, на которую падают предметы.

Что вы изменили в этом эксперименте?

---

Тип сбрасываемых объектов, в частности масса и объем объектов.

В приведенной ниже таблице запишите, что, по вашему мнению, произойдет в столбце «прогноз», прежде чем проводить эксперимент.Как вы думаете, что произойдет, если вы бросите каждую пару предметов с одной и той же высоты в одно и то же время? Как вы думаете, что приземлится первым?

Объекты	Прогноз	Наблюдение
Мячи: одинаковой массы, разного объема
Мячи: разная масса, одинаковый объем
Молоток и перо

ОЦЕНКА:

Насколько надежным был ваш эксперимент? Как бы вы могли улучшить свой метод?

---

---

---

Ответ зависит от учащегося. Примеры ответов могут включать: Трудно бросать предметы одновременно. Лучше сбрасывать предметы с большей высоты. На результаты могло повлиять сопротивление воздуха, и было бы лучше сбрасывать предметы в вакууме.

ВЫВОДЫ:

Напишите заключение по этому расследованию.

---

---

---

Учащиеся должны были обнаружить, что половина яблока и целое яблоко упали на пол одновременно.Они также должны были обнаружить, что шары одинаковой массы падают на пол в одно и то же время, а также шары одного объема падают на пол в одно и то же время. Из этого они должны сделать вывод, что все падающие предметы падают с одинаковой скоростью, независимо от их формы или размера, если сопротивлением воздуха можно пренебречь. (Дополнительно: они ускоряют с той же скоростью). В случае падения молотка и пера учащиеся должны были обнаружить, что молоток приземлился первым. Это происходит из-за эффекта сопротивления воздуха, замедляющего падение пера.

Заблуждения о падающих предметах (видео)

ВОПРОСЫ:

Что приземлилось первым, яблоко или половинка яблока?

---

Они оба должны были приземлиться в одно и то же (или почти в одно и то же) время.

Считая шары одинаковой массы, какой из них приземлился первым, больший или меньший?

---

Они оба должны были приземлиться одновременно.

Учитывая шары одинакового объема, какой из них приземлился первым, более тяжелый или более легкий?

---

Они оба должны были приземлиться одновременно.

Как вы думаете, почему два упавших мяча всегда приземлялись одновременно?

---

---

В идеальной ситуации все предметы, сброшенные с одной высоты, приземлятся одновременно.Это связано с тем, что гравитационная сила Земли заставляет каждый объект ускоряться на одну и ту же величину каждую секунду, независимо от того, насколько он тяжелый или каков его объем.

Примечание для продвинутого учителя:

Согласно универсальному закону гравитации, гравитационная сила Земли притягивает объект с силой, пропорциональной массе объекта и массе Земли. Во всех случаях масса Земли одинакова, поэтому любые различия в силе гравитации на объекты на Земле зависят только от разницы в массе сбрасываемых объектов.

Согласно второму закону Ньютона, результирующая сила, действующая на объект F, определяется формулой F=ma, где m — масса объекта, а a — ускорение, создаваемое результирующей силой F.

Как вы думаете, почему молот приземлился раньше пера?

---

---

---

---

В реальной ситуации воздух вокруг нас влияет на то, как предметы падают. Когда объект движется по воздуху, он испытывает сопротивление воздуха. Перо намного легче молотка, поэтому влияние сопротивления воздуха на перо гораздо больше. Суммарная сила, действующая вниз на падающий объект, представляет собой силу гравитации за вычетом силы сопротивления воздуха. Поскольку перо намного легче молотка, результирующая сила, действующая на него, будет меньше, поэтому оно будет испытывать меньшее ускорение по направлению к земле и падать медленнее.

Примечание для продвинутого учителя:

Сопротивление воздуха — это сила сопротивления, действующая для замедления объекта.Величина силы зависит от квадрата скорости падающего объекта, площади поверхности падающего объекта и плотности жидкости, в которую он падает (в данном случае воздуха). Очень легкие объекты замедляются за счет сопротивления воздуха, например, перья или тонкие листы бумаги. Это потому, что их гравитационная сила очень мала по сравнению с сопротивлением воздуха. Очень большие объекты также замедляются из-за сопротивления воздуха. Это объясняет, почему парашют замедляет ваше падение. Перед раскрытием парашюта сопротивление воздуха невелико.После раскрытия широкий парашют испытывает большее сопротивление воздуха, которое затем замедляет вас.

Очень важно, чтобы учащиеся понимали разницу между массой и весом. В науке вес — это сила, но учащиеся привыкли использовать слово «вес» при описании своей массы. Вес – это сила, с которой объект сталкивается под действием силы тяжести. На Земле все объекты притягиваются вниз к центру Земли, и наш вес указывает на величину этого притяжения.Вес будет варьироваться в зависимости от нашего положения в пространстве, но наша масса должна оставаться постоянной независимо от нашего положения.

Вы, вероятно, уже много раз слышали термин «вес» либо на уроках естественных наук, либо в разговорах с другими. Многие люди неправильно используют термин «вес» в повседневном языке. Например, родственник может сказать вам: «Мой вес увеличился на 2 кг за праздники, так как я съел слишком много еды.» Что не так с этим утверждением? Обсудите это со своим классом и учителем.

---

---

Это утверждение неверно, так как родственница приравнивает свой вес к килограммам. Килограммы — это мера массы, а не веса. Ее масса могла увеличиться на 2 килограмма.

• вес
• масса
• свободное падение
• гравитационное ускорение

Слово масса происходит от греческого слова маза , что означает кусок теста или пирог.

масса объекта — это количество материи в объекте.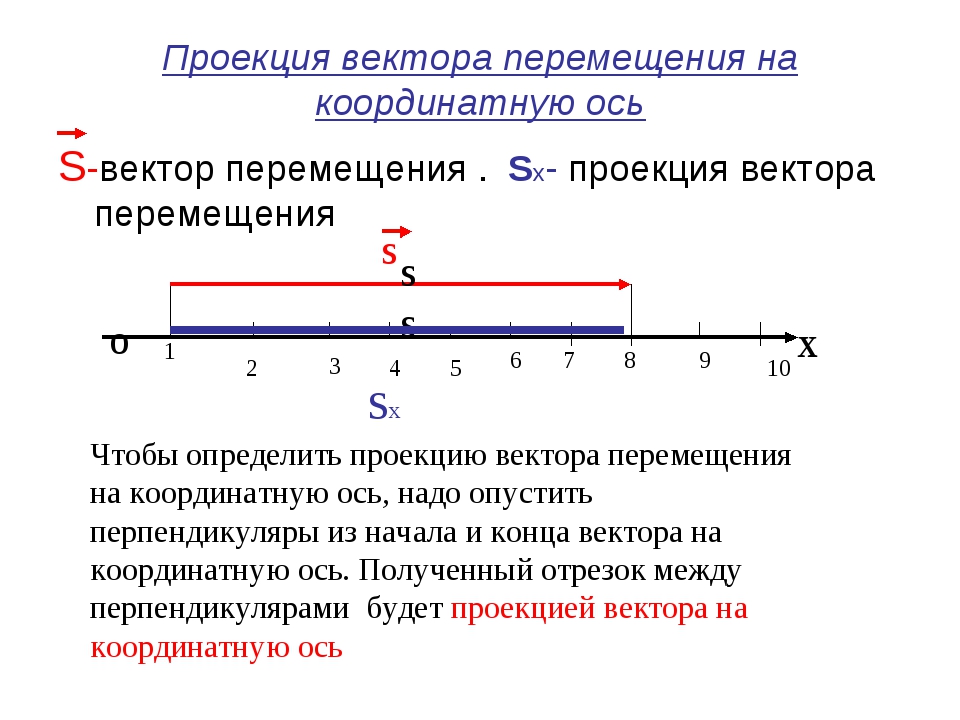 Он говорит вам, сколько частиц у вас есть. Вы помните, что узнали об атомах в «Материи и материалах»? Так, например, масса деревянного бруска говорит нам, сколько в нем атомов. Масса измеряется в килограммах (кг) и не зависит от того, где вы ее измеряете. Деревянный брусок массой 10 кг на Земле также имеет массу 10 кг на Луне.

Однако вес объекта может меняться, так как он зависит от массы объекта, а также силы гравитационной силы, действующей на него.Вес измеряется в ньютонах (Н), так как это гравитационная сила притяжения, действующая на объект со стороны Земли (или Луны, или любой другой планеты). Следовательно, вес объекта будет меняться при взвешивании в разных местах. Вес 10-килограммового блока на Земле будет отличаться от веса на Луне. Как вы думаете, почему это так? Будет ли вес больше или меньше, чем на Луне?

---

---

---

Земля намного больше Луны, поэтому сила притяжения между Землей и блоком будет больше, чем сила между Луной и блоком.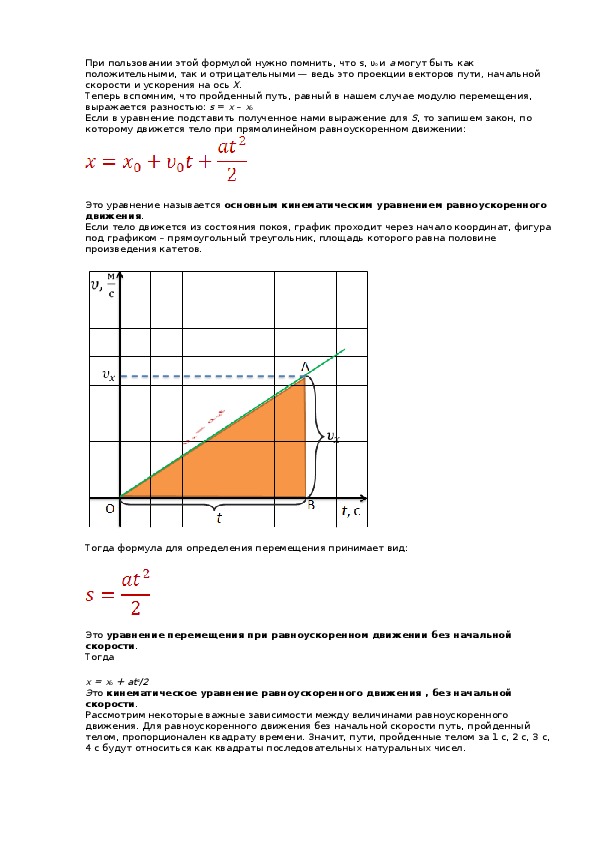

Масса, вес и гравитация (видео).

СЛЕДИТЕЛЬНЫЙ ВОПРОС: Какая связь между массой предмета и его весом?

ГИПОТЕЗА: Напишите гипотезу для этого исследования.

---

---

Ответ зависит от учащегося.

МАТЕРИАЛЫ И АППАРАТЫ

• четыре штуки с шагом 500 г (одна по 500 г, одна по 1 кг, одна по 1,5 кг и одна по 2 кг)
• пружинный баланс
• весы с тремя балками

Для измерения массы объектов можно использовать любой измеритель массы.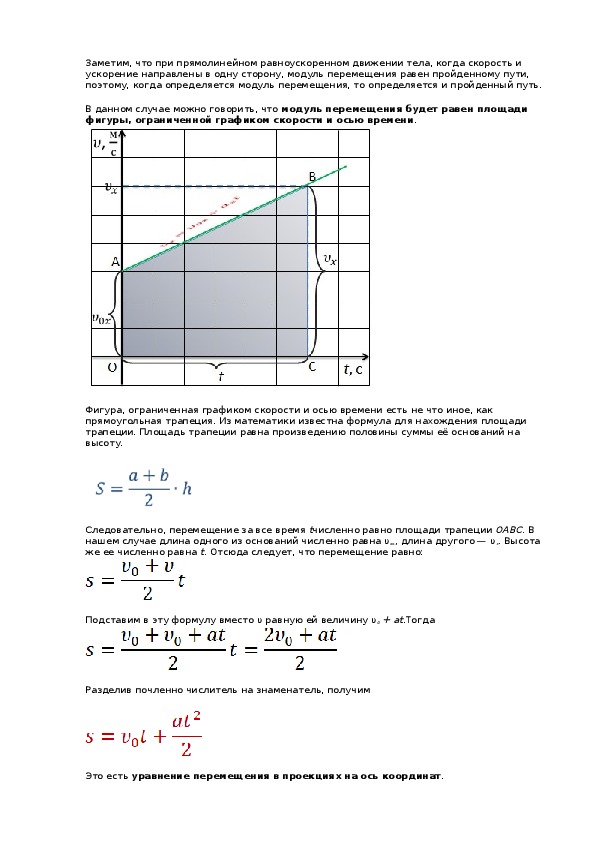 Также можно использовать кухонные весы или электронные весы.

МЕТОД:

1. Измерьте массу штук на трехрычажных весах.
2. Измерьте вес каждой части груза с помощью пружинных весов.
3. Запишите массу и соответствующую массу в таблицу результатов.
4. Нарисуйте график своих результатов.
5. Вычислить градиент графика.

РЕЗУЛЬТАТЫ:

Запишите свои результаты в следующую таблицу.

Пример результатов при использовании предложенной массы штук:

Масса (кг)	Вес (Н)
0,5	4. 8
1	9,8
1,5	14,7
2	19.6

Что такое зависимая переменная?

---

Что такое независимая переменная?

---

Масса

Таким образом, вес отложен по оси Y по сравнению с массой по оси X

Начертите график в отведенном ниже месте.

Ваш график должен быть прямой линией. Используйте пространство ниже, чтобы вычислить градиент вашего графика.

Градиент должен быть 9,8.

Возможно, вам придется напомнить учащимся о вычислении уклона прямой линии.Они должны были рассмотреть эту тему в математике, но было бы полезно напомнить им. Им нужно выбрать две координаты на своей прямой. Они могут выбрать любые две координаты, которые следует обозначить как (x1; y1) и (x2; y2). Формула градиента прямой линии: градиент = подъем/разгон = (y2 — y1)/(x2 — x1)

Пример расчета: градиент = (9,8 — 4,8)/(1 — 0,5) = 9,8

Учащиеся могут не получить правильный ответ для градиента, если они неправильно построили график или если пружинные балансы не откалиброваны должным образом. Они могут получить ответ ближе к 10. Градиент графика дает гравитационное ускорение на Земле. Это будет объяснено в тексте после расследования.

ВЫВОД:

Напишите заключение по этому расследованию.

---

Вес объекта прямо пропорционален его массе.

Вес — это сила тяжести, притягивающая вас к центру Земли. Измеряется в ньютонах. На Земле гравитационная сила заставляет нас всех ускоряться по направлению к центру Земли. Ускорение называется гравитационным ускорением . На Земле это 9,8 м/с ² . Градиент, который мы рассчитали в последнем исследовании, должен был дать вам число, близкое к 9,8 м/с ² , что является гравитационным ускорением.

Объекты находятся в состоянии свободного падения , когда единственная сила, действующая на них, — это сила гравитации.

Вес (Вт) рассчитывается путем умножения массы объекта (м) на ускорение свободного падения (г):

Вт = м × г

Мы использовали эту формулу в последнем разделе о трении для расчета веса и, следовательно, нормальной силы, действующей на объект.

А что, если бы вы отправились на Луну?

Луна в 6 раз меньше Земли.

Масса Земли 5,972×10 ²⁴ кг.

Луна также имеет собственную гравитацию. Сила гравитации на поверхности Луны составляет одну шестую силы тяжести на поверхности Земли, поэтому вы будете весить одну шестую того, что вы делаете на Земле на Луне. На Юпитере вы будете весить в 2,5 раза больше, чем на Земле, поскольку гравитация Юпитера в 2,5 раза больше земной. Несмотря на то, что вы будете весить по-разному (и чувствовать себя легче на Луне и тяжелее на Юпитере), ваша фактическая масса останется неизменной в обоих случаях.

Масса космонавта остается неизменной, где бы ее ни измеряли. Однако вес астронавта зависит от того, где вы его измеряете, так как вы можете видеть, что астронавт весит 1200 Н на Земле и только 200 Н на Луне.

Так сколько бы ты весил на Луне? Представьте, что у вас есть масса 60 кг. Ваш вес на Земле будет 60 х 9,8 = 588 Н. Гравитационное ускорение на Луне 1,6 м/с ² , поэтому ваш вес на Луне будет 60 х 1,6 = 96 Н.

Весы для ванной измеряют вес и преобразуют его в массу.

Расчет веса и массы

Это короткое упражнение для тренировки вычислений. Учащиеся могут выполнить это задание в качестве домашнего задания.

ВОПРОСЫ:

Феррари имеет массу 1485 кг. Каков его вес на Земле?

Феррари.

вес = 1485 х 9,8 = 14553Н

Линдиве на Земле имеет массу 50 кг. Какова ее масса на Луне?

---

50 кг, так как масса объекта не зависит от положения.

Ян имеет массу 78 кг. Его друг Сэм говорит, что на Луне он будет весить 24 Н. Сэм прав? Объясните с помощью расчета.

вес на Луне = 78 х 1,6 = 124,8 Н

Сэм неверен.

У вас есть яблоко массой 220 г, каков его вес на Земле и на Луне?

масса = 220 г = 0. 22 кг.

вес на Земле = 0,22 х 9,8 = 2,156 Н

вес на Луне = 0,22 х 1,6 = 0,352 Н

Если на Луне корова весила 1340 Н, какова ее масса?

Трикотажная корова.

масса = 1340/1,6=837.5 кг

Моделирование PhET, указанное в ссылке для посещения, можно использовать, чтобы легко показать, как изменяется вес объектов. Эту симуляцию можно использовать на многих различных уровнях, в зависимости от сложности концепций, которые вы хотите проиллюстрировать. Ссылка на pdf-файл с советами по обучению от команды PhET доступна здесь: http://phet. colorado.edu/files/teachers-guide/mass-spring-lab-guide.pdf

Вы когда-нибудь задумывались, каково это — ходить по другим планетам? Узнайте, сколько бы вы весили на других планетах, в следующем упражнении.

Это необязательное действие . В этом упражнении учащиеся рассчитывают свой вес на семи других планетах нашей Солнечной системы.Хотя их масса останется прежней, они будут «чувствовать» себя легче или тяжелее из-за различий в силе гравитационного поля на поверхностях других планет. Следует подчеркнуть, что их масса всегда остается неизменной, а меняется только их вес. Если у вас нет доступа к весам, вы можете либо попросить учащихся оценить свою массу, либо предоставить им примерный номер.

МАТЕРИАЛЫ:

• весы
• калькулятор

ИНСТРУКЦИИ:

Измерьте свою массу в килограммах. Запишите значение в таблицу ниже.

Используйте значения ускорения силы тяжести на разных планетах, чтобы рассчитать, сколько вы будете весить на этой планете.

Планета	Ваша масса (кг)	Значение g (м/с 2 )	Ваш вес (Н)
Земля		9,8
Меркурий		3,6
Венера		8,8
Марс		3,8
Юпитер		26
Сатурн		11,2
Уран		10,5
Нептун		13,3

Пример ответов для учащегося весом 50 кг

Планета	Ваша масса (кг)	Значение g (м/с 2 )	Ваш вес (Н)
Земля	50	9,8	490
Меркурий	50	3,6	180
Венера	50	8,8	440
Марс	50	3,8	190
Юпитер	50	26	1300
Сатурн	50	11,2	560
Уран	50	10,5	525
Нептун	50	13,3	665

ВОПРОСЫ:

На каких планетах вы бы чувствовали себя тяжелее, чем на Земле?

---

Вам было бы тяжелее на Юпитере и Нептуне.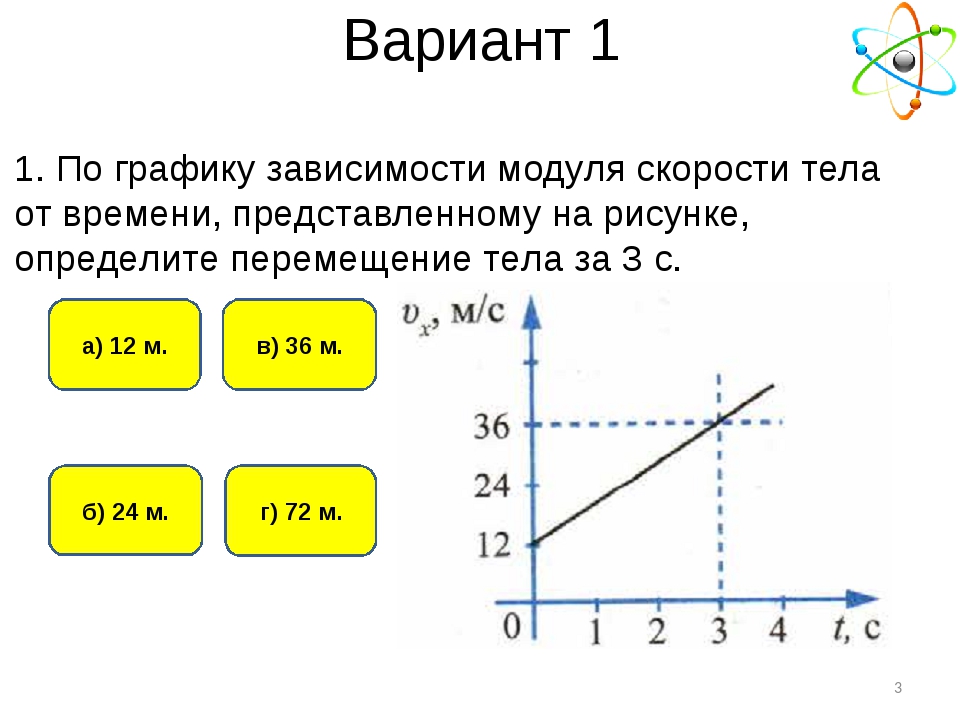

На каких планетах вы бы чувствовали себя легче, чем на Земле?

---

Вам будет легче на Меркурии, Венере, Марсе, Сатурне и Уране.

Вес человека – это сила гравитационного притяжения к Земле, которую испытывает человек.Кто-то в свободном падении чувствует себя невесомым, но не потерял в весе. Они все еще испытывают гравитационное притяжение Земли.

Единственная причина, по которой астронавты плавают, заключается в том, что они находятся в свободном падении, и их движущийся космический корабль также находится в свободном падении вместе с ними, падая с той же скоростью. Следовательно, астронавты кажутся парящими по сравнению с космическим кораблем, потому что оба они падают с одинаковой скоростью.

Космонавты испытывают невесомость.

Наблюдайте за сверхзвуковым свободным падением Феликса Баумгартнера обратно на Землю. Он испытал свободное падение или невесомость.

Заметка о невесомости

Термин «невесомость» вызывает много путаницы у учащихся. Смешение фактического веса человека с его ощущением веса является источником многих заблуждений. Невесомость относится только к чьему-то ощущению своего веса или его отсутствия.Невесомость — это чувство, которое испытывает человек, когда нет никаких внешних объектов, соприкасающихся с человеком, оказывающим на них толчок или притяжение (мы называем эти контактные силы, потому что они возникают из-за того, что предметы соприкасаются или соприкасаются друг с другом).

Вес человека – это сила гравитационного притяжения к Земле, которую испытывает человек. Кто-то в свободном падении чувствует себя невесомым, но не потерял своего веса. Они все еще испытывают гравитационное притяжение Земли.

Учащиеся также часто не понимают, почему астронавты на орбите вокруг Земли парят в своих космических кораблях. Одно распространенное заблуждение состоит в том, что в космосе нет гравитации, поэтому астронавты могут летать. На самом деле, на низкой околоземной орбите гравитация Земли составляет около 90% ее силы на поверхности Земли. Единственная причина, по которой астронавты плавают, заключается в том, что они находятся в свободном падении, и их космический корабль также находится в свободном падении вместе с ними, падая с той же скоростью. Следовательно, астронавты кажутся парящими по сравнению с космическим кораблем, потому что оба они падают с одинаковой скоростью.Другим примером является то, что орбитальные космические корабли по существу находятся в свободном падении, поскольку «ничто» не замедляет их движение к центру Земли, но из-за их орбитальной скорости они никогда не приближаются к Земле.

В поле «Посетить» есть отличная ссылка на видео о том, как кто-то испытывает свободное падение.

Магнитные силы

• магнит
• магнитный материал
• сплав

Некоторые материалы имеют сильные магнитные поля вокруг себя.Их называют магнитами. Все магниты имеют два полюса, северный и южный.

Пример стержневого магнита с северным и южным полюсами.

Другие материалы сильно притягиваются к магнитам. Эти материалы называются магнитными. Магниты воздействуют на другие магниты и магнитные материалы. Какие материалы являются магнитными? Давайте исследовать.

ИССЛЕДОВАТЕЛЬСКИЙ ВОПРОС: Какие материалы являются магнитными, а какие нет?

ГИПОТЕЗА:

Напишите гипотезу для этого исследования.

---

Ответ зависит от учащегося. Есть много различных возможных гипотез для этого исследования. Примером может быть: Только некоторые материалы являются магнитными.

МАТЕРИАЛЫ И АППАРАТЫ:

• стержневые магниты
• бумага
• дерево
• пластик
• железо
• алюминий
• сталь

МЕТОД:

1. Держите различные предметы рядом с стержневым магнитом (не касаясь), чтобы увидеть, притягиваются ли они к магниту.
2. Заполните таблицу, указав, притягиваются ли предметы к магниту.

Учащиеся должны заметить, что неметаллы не притягиваются к магнитам и что медь, даже если это металл, не притягивается.

Как уничтожить магнит.

РЕЗУЛЬТАТЫ:

Заполните следующую таблицу.

Материал	Магнитный (ДА/НЕТ)
бумага
дерево
пластик
железо
алюминий
сталь
медь

Материал	Магнитный (ДА/НЕТ)
Бумага	НЕТ
дерево	НЕТ
пластик	НЕТ
железо	ДА
алюминий	НЕТ
сталь	ДА
медь	НЕТ

ВЫВОД:

Какой вывод вы можете сделать из своих результатов?

Не все материалы являются магнитными. Лишь некоторые металлы обладают магнитными свойствами, например железо.

Не все металлы притягиваются к магнитам. Те, которые притягиваются к магнитам, известны как магнитных материалов. Магнитных материалов очень мало. Это железо, никель и кобальт. Сплавы, в состав которых входят любые магнитные материалы, также могут притягиваться к магнитам. Сталь — это сплав, содержащий железо, поэтому сталь может притягиваться к магниту.

Сплав представляет собой смесь металлов.

Итак, теперь мы знаем, что магнитные силы могут действовать на расстоянии, но могут ли они по-прежнему действовать, если что-то мешает? Давайте разберемся.

Магнитные силы являются бесконтактными силами и могут действовать на расстоянии. Однако обычные магниты не имеют очень сильных магнитных полей. Чем дальше объект от магнита, тем слабее сила, которую он испытывает. Магнит должен действовать через большинство веществ.Если объект, помещенный между магнитом и металлом, слишком толстый, то металл может быть слишком далеко от магнита, чтобы испытывать достаточно сильную силу. Таким образом, это отсутствие притяжения связано с силой магнитного поля, а не с «блокирующей» способностью материала. В этом исследовании вы можете исследовать это, используя тонкий кусок дерева и толстый кусок дерева. Магнитное поле может действовать через тонкую древесину, что означает, что древесина не является «блокатором» магнитной силы. Таким образом, если толстая древесина препятствует притяжению скрепок, видно, что имеет значение расстояние между скрепками и магнитом, а не материал (дерево).

МАТЕРИАЛЫ:

• стержневые магниты
• бумага
• тонкий кусок дерева
• толстый кусок дерева
• фольга
• скрепки

ИНСТРУКЦИИ:

Держите два северных полюса близко друг к другу. Что ты заметил?

---

Два полюса отталкивают друг друга. Есть «толкающая» сила.

Держите два южных полюса близко друг к другу. Что ты заметил?

---

Два полюса отталкивают друг друга.Есть «толкающая» сила.

Держите северный полюс и южный полюс близко друг к другу. Что ты заметил?

---

Два полюса притягиваются друг к другу. Между полюсами действует сила притяжения.

Положите скрепки на стол.

Попробуйте подобрать скрепки с помощью магнита, но поместите один из других материалов между магнитом и скрепками. Скрепки все еще притягиваются к магниту?

Магнит должен проходить сквозь любые материалы, если они достаточно тонкие.Именно расстояние между магнитом и скрепками будет влиять на притяжение. Таким образом, тонкий кусок дерева не должен препятствовать притяжению, но более толстая древесина будет удерживать скрепки достаточно далеко от магнита, чтобы сделать притяжение слишком слабым, чтобы поднять скрепки.

Попробуйте разные материалы между магнитом и скрепкой.

ВОПРОСЫ:

Имелись ли какие-либо материалы, препятствовавшие захвату скрепок магнитом.

---

Единственным материалом, который мог помешать магниту захватить скрепки, был толстый кусок дерева.

Что эта активность говорит нам о природе магнитной силы?

---

---

Действует на расстоянии. Он сильнее всего ближе к магниту и слабее по мере удаления от магнита.

В последнем упражнении мы видели, что одноименные полюса отталкиваются, а противоположные полюса притягиваются. Мы также видели, что магнитная сила действует на расстоянии. Магниту не нужно касаться чего-либо, чтобы воздействовать на него силой. Таким образом, магнитная сила является бесконтактной или полевой силой.

Что такое силовое поле? Можем ли мы это увидеть? Давайте исследуем, возможно ли увидеть магнитное поле.

Что такое магнитное поле?

Железные опилки выравниваются с магнитным полем. Объясните учащимся, что железные опилки показывают поле в двух измерениях, но на самом деле поле окружает магнит в трех измерениях.

МАТЕРИАЛЫ:

• железные опилки
• два стержневых магнита
• бумага

ИНСТРУКЦИИ:

1. Положите стержневой магнит на стол.
2. Положите бумагу на магнит.
3. Высыпьте железные опилки на бумагу.
4. Пальцем медленно протолкните опилки вокруг магнита.
5. Запишите образец и нарисуйте его ниже.

Здесь показан рисунок вокруг стержневого магнита.

1. Снимите бумагу с магнита.
2. Поместите второй магнит рядом с первым так, чтобы разные полюса были обращены друг к другу.
3. Положите бумагу обратно на магниты.
4. Переместите железные опилки вокруг двух магнитов, особенно между магнитами.
5. Нарисуйте узор в пространстве ниже.

Схема притяжения двух противоположных полюсов.

1. Снимите бумагу с магнита.
2. Переместите второй магнит так, чтобы его полюса были обращены друг к другу.
3. Положите бумагу обратно на магниты.
4. Переместите железные опилки вокруг двух магнитов, особенно между магнитами.
5. Нарисуйте узор в пространстве ниже.

Схема между двумя отталкивающимися полюсами.

Как мы видели, можно визуализировать магнитное силовое поле вокруг магнита. Мы знаем из нашей предыдущей деятельности, что магнитная сила действует на расстоянии. Поле — это пространство вокруг магнита, в котором он может притягивать или отталкивать другой магнит.

В последнем упражнении железные опилки показали двухмерное изображение поля, но на самом деле поле окружает магнит в трех измерениях.

Магнитное поле вокруг подковообразного магнита.

Как нарисовать силовое поле? Образец, который вы видели с помощью ваших магнитов, может быть представлен линиями поля .Линии поля используются, чтобы показать то, что мы на самом деле не можем видеть. Чем ближе сближены силовые линии, тем сильнее описываемое поле. Чем больше линий поля нарисовано, тем сильнее поле. Силовые линии идут от северного полюса к южному полюсу. На следующей диаграмме показаны линии поля вокруг стержневого магнита.

На следующих диаграммах показаны силовые линии между стержневыми магнитами, которые притягиваются и отталкиваются.

Противоположные полюса притягиваются.

Как полюса отталкиваются.

Поле сильнее всего рядом с магнитом и ослабевает по мере удаления от магнита.

Знаете ли вы, что Земля похожа на стержневой магнит с северным и южным полюсами? Земля имеет магнитное поле. Вы можете представить себе магнитное поле Земли так, как будто через ядро ​​проходит стержневой магнит, южный полюс которого находится под северным полюсом Земли. Никто не знает наверняка, но теория состоит в том, что сверхгорячее жидкое железо в ядре Земли движется вращательно, и эти вращательные силы приводят к слабым магнитным силам вокруг оси вращения Земли.

У Земли есть магнитное поле, как будто через ядро ​​проходит большой стержневой магнит, южный полюс которого находится под северным магнитным полюсом Земли.

Где находится настоящий Северный полюс. youtube.com/embed/Roq20IV4yP0″/>

Вот почему мы можем использовать компас, чтобы определить направление. У компаса есть стрелка с небольшим магнитом. Стрелка указывает на магнитный север, потому что маленький магнит притягивается к противоположному магнитному полю и может использоваться для определения направления.

Компас со стрелкой, указывающей на север.

Южное сияние также называют Aurora Australis, а северное сияние называют Aurora Borealis.

Вы когда-нибудь слышали о южном или северном сиянии? Вы знаете, как происходит это явление?

Южное сияние, вид с Международной космической станции.

Заряженные частицы покидают поверхность Солнца и движутся наружу во всех направлениях.Когда заряженные частицы достигают Земли, некоторые из них захватываются магнитным полем Земли в областях в космосе вокруг земной атмосферы, называемых поясами. Иногда заряженные частицы покидают пояса и движутся по спирали вдоль силовых линий магнитного поля к магнитным полюсам, где они входят в атмосферу Земли. Затем они взаимодействуют с частицами атмосферного газа, вызывая красивые световые шоу.

Что вызывает северное сияние?

Некоторые жидкости также могут намагничиваться в присутствии сильного магнитного поля.Их называют феррожидкостями.

Пример феррожидкости, жидкости, которая может намагничиваться в магнитном поле.

Магнитная жидкость (видео).

Электростатические силы

Помните ли вы, что изучали статическое электричество в Гр. 8? Давайте быстро повторим некоторые из уже известных нам понятий.

Несмотря на то, что эти эксперименты проводились в Gr.8, важно, чтобы учащиеся выполняли их снова в качестве деятельности.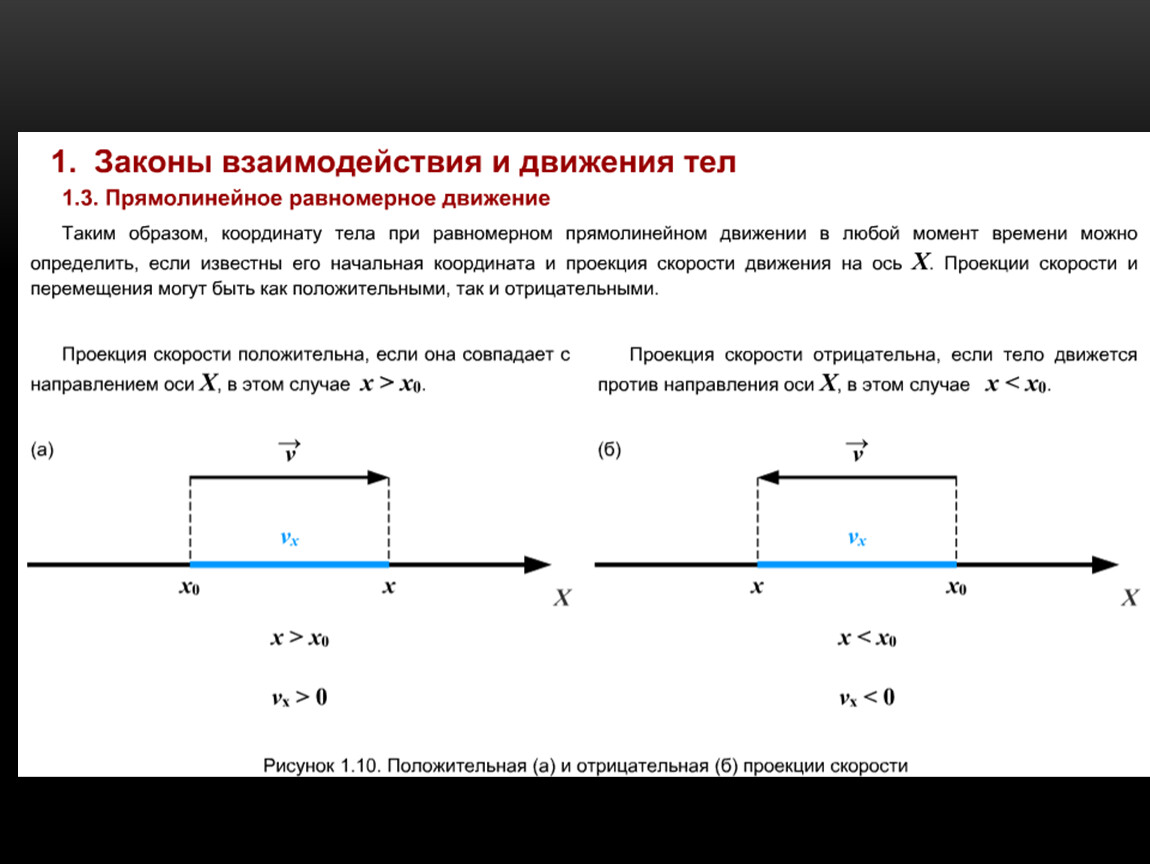 Это поможет им понять, как работают электроскоп и генераторы Ван де Граафа.

Вы также можете выполнять это упражнение, используя пластиковую расческу, а не воздушные шарики. В противном случае вы можете использовать кусочки бумаги вместо волос ученика, так как не все волосы будут вести себя следующим образом.

МАТЕРИАЛЫ:

• воздушные шары (или пластиковая расческа)
• стеклянная палочка
• кусок трикотажа (шерсть)
• Стержень из ПВХ
• пластиковая линейка
• маленькие кусочки бумаги
• водопроводный кран

ИНСТРУКЦИИ:

Надуйте воздушный шар и завяжите его, чтобы воздух не выходил.

Держите шарик на небольшом расстоянии от волос. Что ты заметил?

---

Потри волосы шариком.

Теперь держите шарик на небольшом расстоянии от волос.Что ты видишь?

---

Волосы должны «подняться» и прилипнуть к шарику.

Затем держите стеклянную палочку над маленькими кусочками бумаги. Что ты заметил?

---

Натрите стеклянную палочку трикотажем.

Держите стеклянную палочку над кусочками бумаги. Что ты заметил?

---

Кусочки бумаги прилипают к стеклянной палочке.

Еще раз потрите стеклянную палочку о трикотаж.

Откройте кран, чтобы потекла тонкая струйка воды.

Поднесите стеклянную палочку к струе воды. Что ты заметил?

---

Струя воды наклоняется к стеклянной палочке.

ВОПРОСЫ:

Что ты сделал, чтобы твои волосы прилипали к шарику?

---

Энергично потер баллоном.

Что будет, если потереть стеклянную палочку о трикотаж?

---

---

Электроны переносятся со стеклянной палочки на трикотаж за счет трения.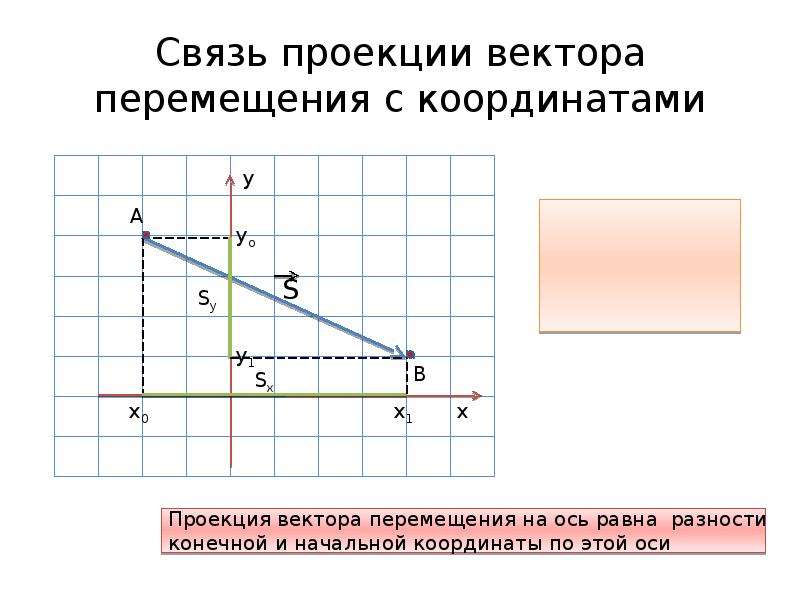 Стеклянная палочка становится положительно заряженной, а вата – отрицательно.

Почему стеклянная палочка притянула струю воды?

---

---

Вода имеет положительные и отрицательные заряды.Отрицательные заряды притягивались к положительно заряженному стержню.

Давайте рассмотрим пример расчесывания волос подробнее, чтобы понять, что происходит. Вы провели пластиковой расческой по поверхности волос. Когда две поверхности трутся друг о друга, между ними возникает трение . Трение между двумя поверхностями может вызвать перенос электронов с одной поверхности на другую.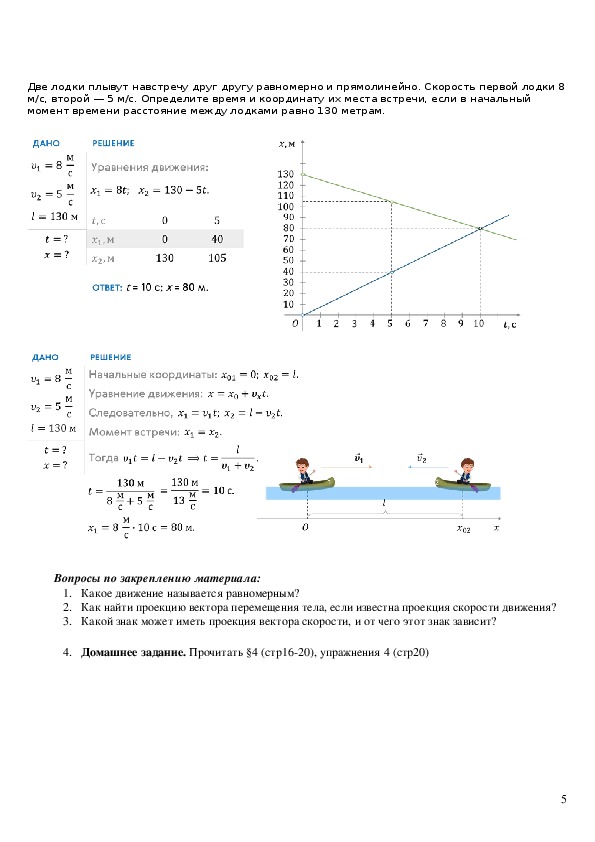

Чтобы понять, как могут переноситься электроны, нам нужно вспомнить, что мы узнали о структуре атома.

Где расположены электроны в атоме?

---

Электроны расположены в пространстве вокруг ядра.

Какой заряд имеет протон?

---

Какой тип заряда у электрона?

---

Каков заряд нейтрона?

---

Нейтроны не заряжены.Они нейтральны.

Атом удерживается вместе электростатическим притяжением между положительно заряженным ядром и отрицательно заряженными электронами. Внутри атома электроны, находящиеся ближе всего к ядру, удерживаются сильнее всего, в то время как те, что находятся дальше, испытывают более слабое притяжение.

В норме атомы содержат одинаковое количество протонов и электронов. Это означает, что атомы обычно нейтральны , потому что они имеют одинаковое количество положительных и отрицательных зарядов, поэтому заряды уравновешивают друг друга.Все объекты состоят из атомов, и поскольку атомы обычно нейтральны, объекты также обычно нейтральны.

Однако, когда мы трёмся друг о друга двумя поверхностями, например, когда вы расчёсываете волосы или трёте о волосы воздушный шар, трение может привести к переносу электронов с одного объекта на другой. Помните, что протоны зафиксированы в ядре и поэтому не могут перемещаться между атомами. Между атомами могут передаваться только электроны. Некоторые объекты отдают электроны легче, чем другие объекты.Посмотрите на следующую диаграмму, которая объясняет, как это происходит.

Какой объект на диаграмме отдал часть своих электронов?

---

У этого объекта теперь больше положительных или больше отрицательных зарядов?

---

Имеет больше положительных зарядов.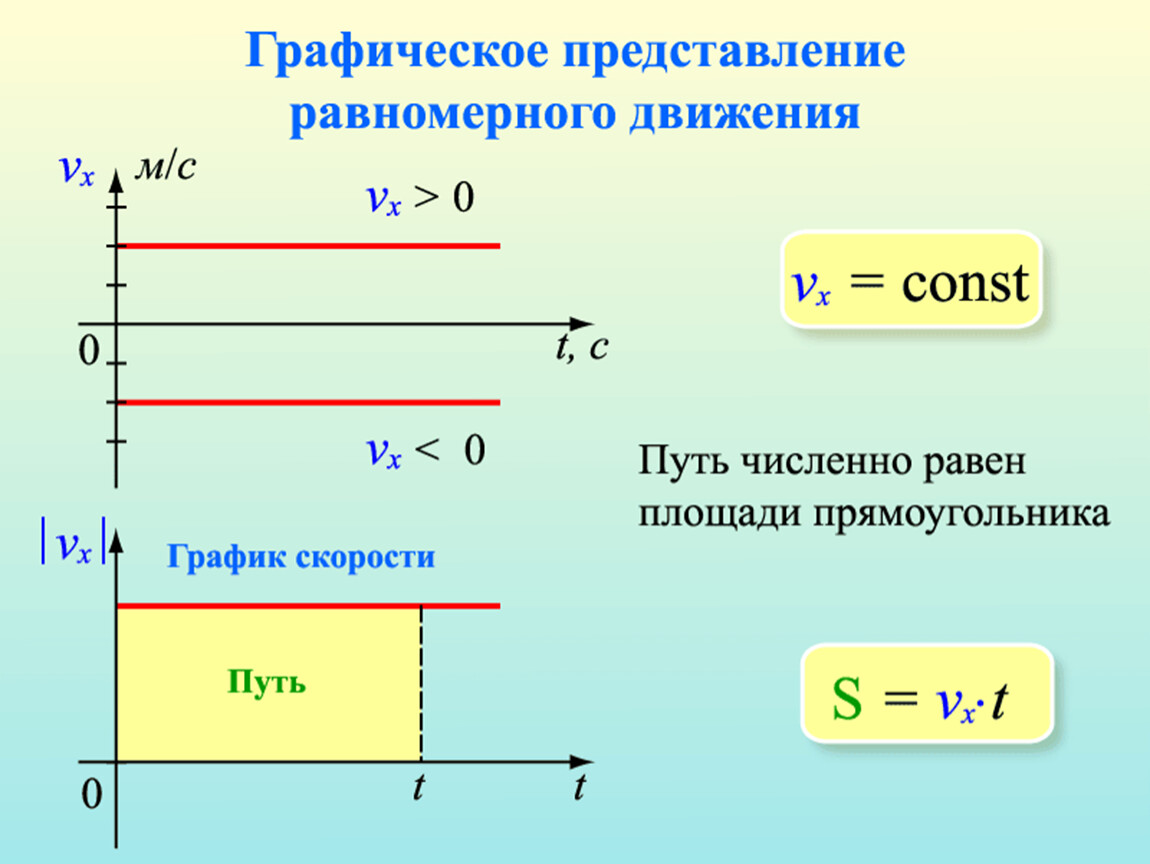

Какой объект на диаграмме получил электроны?

---

У этого объекта теперь больше положительных или больше отрицательных зарядов?

---

Имеет больше отрицательных зарядов.

Когда в объекте больше электронов, чем протонов, мы говорим, что объект отрицательно заряжен .

Когда в объекте меньше электронов, чем протонов, мы говорим, что объект положительно заряжен .

Помните, что движутся только внешние электроны, а не протоны, находящиеся в ядре атома.

Взгляните на следующие диаграммы, иллюстрирующие это.

Теперь мы понимаем перенос электронов, происходящий в результате трения между телами. Но как это привело к тому, что ваши волосы встали дыбом, когда вы поднесли заряженный шарик к волосам в последнем упражнении? Давайте посмотрим, что происходит, когда противоположно заряженные объекты сближаются.

Это забавная демонстрация того, как одноименные заряды отталкиваются, а разноименные притягиваются.Если у вас достаточно материалов, позвольте учащимся попробовать это сделать самостоятельно. Если у вас недостаточно материалов, сделайте это в качестве демонстрации, но дайте учащимся возможность немного поиграть.

Сначала потренируйтесь в этом упражнении несколько раз, чтобы убедиться, что вы правильно поняли метод. Помните, что очень легко случайно заземлить стержни, поэтому работайте с осторожностью. Лучше всего это будет работать в сухой день. Это будет зависеть от района, в котором вы живете.

На семинаре-мозговом штурме с учителями-добровольцами и учеными в начале 2013 года мы сняли быструю демонстрацию этой задачи, когда группа ее обсуждала. Вы можете посмотреть этот короткий клип здесь: bit.ly/1fFbbbJ

МАТЕРИАЛЫ:

• 2 изогнутых часовых стекла
• 2 стержня из плексигласа
• ткань: шерсть или нейлон
• пластиковый стержень
• маленькие кусочки рваной бумаги

ИНСТРУКЦИИ:

1. Положите на стол перевернутое часовое стекло.
2. Сбалансируйте второе часовое стекло вертикально на первом часовом стекле.
3. Энергично потрите тканью один из стержней из плексигласа.
4. Сбалансируйте стержень из плексигласа на верхней части часового стекла.
5. Энергично протрите второй стержень из плексигласа той же тканью.
6. Поднесите второй стержень из плексигласа к стороне первого заряженного стержня из плексигласа. Что, по вашему мнению, происходит?

Второй стержень из плексигласа должен отталкивать первый, поскольку у них одинаковые заряды, поэтому учащиеся должны видеть, как второй стержень «толкает» первый по кругу.

Возможно, вам придется снова потереть первый плексигласовый стержень между попытками, так как заряд рассеивается.

1. Повторите упражнение, но вместо второго плексигласового стержня используйте пластиковый стержень. Что, по вашему мнению, происходит?

Теперь стержни имеют противоположные заряды, поэтому второй стержень должен «тянуть» другой стержень по кругу.

1. Затем поднесите палочку, которую вы натерли, ближе к маленьким кусочкам рваной бумаги на столе. Что вы наблюдаете?

Учащиеся должны уметь поднимать листы бумаги заряженным стержнем.

ВОПРОСЫ:

Что произошло, когда вы поднесли второй стержень из плексигласа близко к первому стержню из плексигласа?

---

---

Когда стержни одинаковые (т.е. оба плексигласа) то первый стержень должен отойти от второго и верхнее часовое стекло повернется по кругу.

Что произошло, когда вы приблизили пластиковый стержень к первому стержню из плексигласа?

---

---

При использовании двух разных материалов первый стержень должен двигаться к пластиковому стержню, а часовое стекло поворачивается по кругу к пластиковому стержню.

Что произошло, когда вы приблизили пластиковый стержень к кусочкам бумаги?

---

Кусочки бумаги притянулись к стержню.

Когда мы терли плексигласовые стержни тканью, электроны переносились с плексигласа на ткань.Какой заряд теперь имеют стержни из плексигласа?

---

Оба плексигласовых стержня теперь имеют одинаковый заряд . Вы замечали, что объекты с одинаковым зарядом стремятся оттолкнуть друг друга? Мы говорим, что они отталкивают друг друга.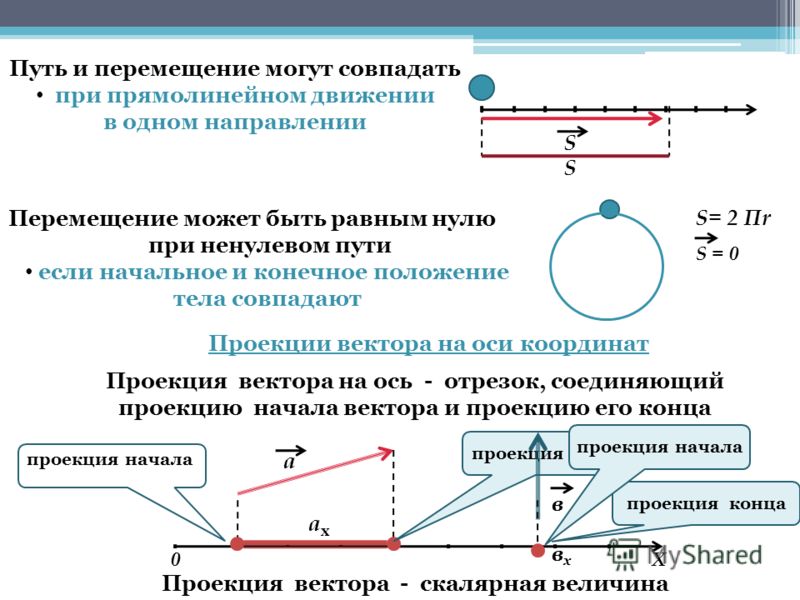 Это электростатическая сила отталкивания.

Когда мы натирали пластиковый стержень тканью, электроны переносились с ткани на пластиковый стержень. Какой заряд теперь имеет пластиковый стержень?

---

Стержень из плексигласа и пластиковый стержень теперь имеют противоположных зарядов.Вы замечали, что объекты с разным зарядом притягиваются друг к другу? Мы говорим, что они притягивают друг друга. Это электростатическая сила притяжения.

Как и в случае с гравитационной и магнитной силой, расстояние между заряженными объектами влияет на силу электростатической силы. Чем ближе заряженные объекты, тем сильнее сила. Чем больше заряжены объекты, тем сильнее электростатическая сила между ними.

Теперь мы наблюдали фундаментальное поведение зарядов.Подводя итог, мы можем сказать:

• Если сблизить два отрицательно заряженных объекта, они будут отталкиваться друг от друга.
• Если сблизить два положительно заряженных объекта, они будут отталкиваться друг от друга.
• Если положительно заряженный объект приблизить к отрицательно заряженному объекту, они будут притягиваться друг к другу.

Помните, одинаковых зарядов отталкиваются, и противоположных зарядов притягиваются.

Противоположности притягиваются и как бы отталкиваются (видео)

Вы когда-нибудь задумывались, откуда берется молния? Продемонстрируем электростатическую искру.

Это необязательное действие , расширение . Генератор Ван де Граафа можно использовать для самых разных развлечений. Вы можете использовать его для объяснения различных концепций статического электричества. Есть несколько веб-сайтов с идеями и предложениями для забавных мероприятий и видеороликов с демонстрациями, например, этот: http://www.nationalstemcentre.org.uk/elibrary/resource/2088/van-de-graaff-generator

.

[ссылка]

Цель этого упражнения — показать, как образуются искры, чтобы вы могли объяснить, как работает молния. Если у вас нет генератора Ван-де-Граафа, используйте видеоклип (например, этот, представленный в поле для посещений) из Интернета.

Большие искры, маленькие искры.

МАТЕРИАЛЫ:

ИНСТРУКЦИИ

Поднесите небольшой металлический шар к генератору. Что ты видишь?

---

Учащиеся должны увидеть искру между генератором и шаром.

Генератор Ван де Граафа.

Вы видели искры? Генератор Ван де Граафа можно использовать для демонстрации эффектов электростатического заряда. Большой металлический купол наверху заряжается положительно при включении генератора. Когда купол заряжен, его можно разрядить, поднеся к куполу другую изолированную металлическую сферу.Электроны прыгнут на купол из металлической сферы и вызовут искру.

Фундаментальная идея использования трения в машине для создания заряда восходит к 17 веку, но генератор был изобретен Робертом Ван де Граафом только в 1929 году в Принстонском университете.

Какое отношение эта маленькая искра имеет к мощному удару молнии?

Молния — это огромный электростатический разряд.

Как выжить при ударе молнии.

Во время грозы облака заряжаются. Трение между облаками и влага в облаках заставляют облака заряжаться. Нижняя часть облаков (ближайшая к земле) становится отрицательно заряженной, а верхняя часть облака становится положительно заряженной. Когда накопление заряда становится слишком большим, электроны перемещаются из нижней части облака на землю, где они «заземляются». Передача энергии массивна и приводит к чрезвычайно яркому свету, теплу и звуку.Вспышка молнии — это массивный разряд между заряженными областями внутри облаков или между облаками и Землей. Удар грома, который мы слышим, — это движение воздуха в результате движения электронов.

Молния чрезвычайно опасна. Если электроны движутся через человека по пути к земле, то большое количество энергии наносит значительный ущерб. Такой человек может получить серьезную травму, вплоть до смерти.

В ЮАР один из самых высоких показателей ударов молнии в мире.

Какие меры предосторожности следует принимать во время грозы? Молния может ударить далеко от дождевой тени грозы. Это означает, что даже если буря кажется далекой, все равно лучше принять меры предосторожности. Самое безопасное место во время грозы – это помещение. Держитесь подальше от окон и металлических предметов. Если вы не можете попасть внутрь, не стойте рядом с высокими объектами или металлическими предметами, потому что, если ударит молния, она обычно поразит самый высокий объект в этом районе.Если вы едете в машине во время грозы, оставайтесь в машине, пока не утихнет гроза.

Лаборатория 5 — Равномерное круговое движение

Введение

Если вы когда-либо были на аттракционе в парке развлечений, который движется по криволинейной или круговой траектории, то вы испытали на себе силу, называемую центростремительной силой, толкающую вас в аттракцион. Будь то задняя стенка «Раундапа» или «Ротора», поездка, в которой пол уходит из-под ваших ног, или ремень безопасности «американских горок», который обеспечивает силу, вы постоянно ускоряетесь к центру поездки. кривизны.Если бы — чего вы больше всего боитесь в такой поездке — эта сила внезапно исчезла, вы бы двинулись в направлении, касательном к круговой траектории. Вот что происходит, когда вы едете по холму на американских горках как раз перед тем, как ремень безопасности сработает. На рис. 1 сравнивается движение при наличии центростремительной силы с результирующим движением тела, если бы центростремительная сила внезапно прекратилась.

Рисунок 1 : Объект в круговом движении

В качестве другого примера рассмотрим шар, привязанный к веревке и вращающийся по кругу, как показано на рис.2а. Натяжение нити прикладывает к мячу центростремительную силу , заставляя его двигаться по круговой траектории. Нить тянет мяч к центру круга, в то время как мяч тянется наружу по струне и, следовательно, по вашей руке в соответствии с третьим законом Ньютона о действии и противодействии. Таким образом, эта направленная наружу сила не действует на шар, хотя ее обычно неправильно называют центробежной силой, действующей на шар. При прекращении действия центростремительной силы, как, например, на рис.2б, когда струна рвется, объект движется в направлении скорости в этот момент. Это направление касается окружности в этой точке.

Рисунок 2 : Вид сверху на мяч на нити до и после разрыва нити

Центростремительную силу, которая удерживает вас в поездке, можно определить с помощью нескольких измерений и расчетов. В этом эксперименте вы определите, какие переменные должны быть известны, чтобы определить центростремительную силу, необходимую для удержания массы, движущейся по круговой траектории с постоянной скоростью.

Обсуждение принципов

Второй закон Ньютона гласит, что результирующая сила

F _net

, действующая на движущееся тело, равна произведению массы тела

m

на его ускорение

a.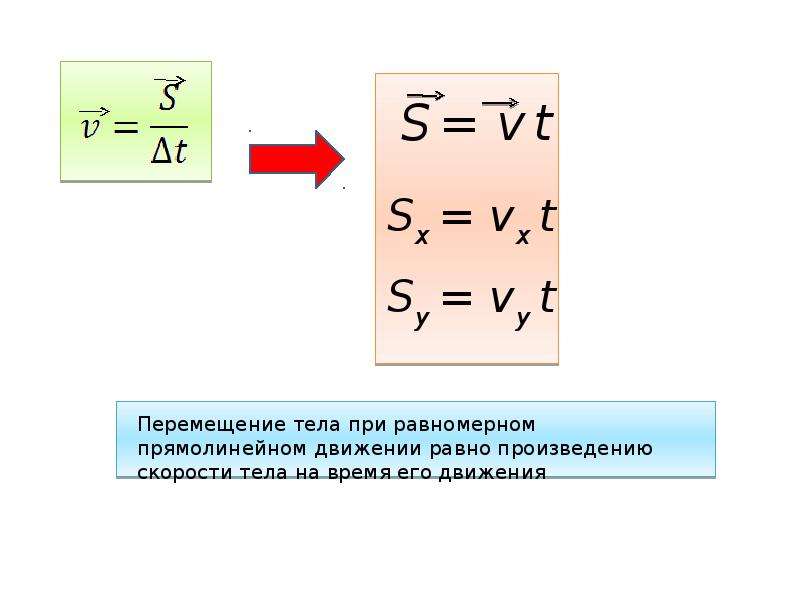

( 1 )

F _нетто = ма Применяя второй закон Ньютона к круговому движению, удобно использовать координаты, параллельные и перпендикулярные движению объекта. Для тела, движущегося прямолинейно, ускорение обусловлено изменением модуля скорости.Для тела, движущегося по круговой траектории с постоянной скоростью, величина | в | скорости не меняется, но направление вектора скорости v постоянно меняется. В этом случае объект не имеет ускорения в направлении, параллельном его движению и

F _||

в уравнении. (2)

F _|| = ма _||

равно нулю. Это движение называется равномерным круговым движением — движением по круговой траектории с постоянной скоростью. Поскольку вектор скорости изменяется во времени, объект, совершающий равномерное круговое движение, ускоряется.Концептуально использование параллельных и перпендикулярных координат удобно, потому что параллельная сила отвечает за изменение скорости, а перпендикулярная сила (или центростремительная сила) отвечает за изменение направления.

Центростремительное ускорение

Какое ускорение необходимо, чтобы тело двигалось по окружности с постоянной скоростью? См. рис. 3а ниже. В некоторый момент частица находится на вершине радиус-вектора r. В другой момент

Δt через

частица находится на вершине радиус-вектора r’.За небольшой промежуток времени

Δt

тело движется по дуге длиной

vΔt

. Если

Δt

достаточно мало, длина дуги примерно равна расстоянию между положением тела в начале интервала

Δt

и положением в конце интервала. Этот прямолинейный отрезок вместе с двумя радиусами образует равнобедренный треугольник, показанный на рис. 3а.

Рисунок 3 : Геометрические соображения

На рис. 3b показаны векторы скорости в двух положениях.Обратите внимание, что величина вектора скорости не меняется. На рис. 3c перерисованы два вектора скорости без изменения их длины или ориентации. Стрелка, соединяющая вершины векторов скорости, представляет изменение

Δv

скорости частицы из-за изменения направления в течение временного интервала

Δt

. Обратите внимание, что по мере того, как

Δt

становится меньше, угол между направлением

Δv

и

v

и

v’

приближается к прямому углу 90°.Поскольку касательная к окружности перпендикулярна ее радиусу, отсюда следует, что угол

θ

между

v

и

v’

, как показано на рис. 3с, такой же, как угол между двумя радиусами на рис. 3а. Из тригонометрии мы знаем, что эти два треугольника конгруэнтны, а значит, отношения их сторон должны быть равны. Таким образом, мы можем написать следующее выражение Разделив обе стороны на

Δt / v

, получим Конечно

Δv/Δt

это ускорение тела, и оно в направлении

Δv

.Из рис. 3в видно, что ускорение направлено к центру окружности. Величина центростремительного ускорения

a _c

определяется выражением а центростремительная сила Поскольку измерить скорость тела напрямую сложно, вместо этого вы будете вычислять скорость по величинам, которые легче измерить. Величину вектора скорости можно определить, измерив расстояние, которое объект проходит за единицу времени.Если

T

— это период (время, необходимое для того, чтобы объект совершил один полный оборот), то скорость равна расстоянию, пройденному за этот один оборот, деленному на период. Подставляя это в уравнение. (6) для центростремительного ускорения дает

( 9 )

a _c = = 4 π ² f ² r = 4 π ² T ⁻² r где

f = 1/T

— число оборотов в секунду, измеренное в герцах.Теперь уравнение (7) можно записать через измеряемые величины

m

,

T

и

r

как

Объектив

В этом эксперименте вы измерите период вращения объекта и рассчитаете центростремительную силу, действующую на него. Вы сравните эту центростремительную силу с эквивалентной силой, необходимой для удержания объекта на том же радиусе.

Оборудование

• Аппарат кругового движения
• Ассорти весов
• Пузырьковый уровень
• Остаток средств
• Секундомер
• метр палка
• Весна

Процедура

Хотя было бы интереснее провести это исследование на полпути, простой лабораторный прибор, показанный на рис. 4 ниже будет использоваться для изучения природы центростремительной силы. Используя прибор центростремительной силы, вы можете измерить частоту вращения объекта, движущегося по круговой траектории известного радиуса. уравнение (10)

F _c = 4 π ² mf ² r

можно использовать для вычисления центростремительной силы, действующей на объект.

Описание аппарата

На рис. 4 показано устройство и его различные компоненты. Нижняя часть основания снабжена регулируемыми винтами, которые можно использовать для выравнивания всего устройства.Перекладина с противовесом на конце может перемещаться для изменения положения вращающейся массы. Стрелку можно перемещать вдоль прорези и располагать прямо под кончиком вращающейся массы. Это помогает измерить радиус кругового пути вращающейся массы.

Рисунок 4 : Эскиз, показывающий компоненты аппарата

В этом аппарате центростремительная сила обеспечивается пружиной. Когда пружина прикреплена к вращающейся массе

M _R

, она втягивается, как показано на рис.5а и рис. 6б. Чтобы вернуть вращающуюся массу выше указателя или индикатора радиуса, струну пропускают через шкив, и к концу струны добавляется достаточно массы, чтобы вернуть вращающуюся массу выше индикатора радиуса.

Рисунок 5 : Эскиз начальной установки

Рисунок 6 : Фото первоначальной настройки

На рис. 5b и рис. 6с вес

m _h г

подвешенной массы

m _h

как раз уравновешивает силу упругости пружины, когда вращающийся объект

M _R

находится над стрелкой или столб указателя радиуса.На рис. 7 пружина растягивается на столько же, сколько масса

M _R

вращается по траектории с тем же радиусом, что и на рис. 5b. Величины двух сил

F _c

и

m _h g

должны точно совпадать, поскольку обе силы вызывают одинаковое удлинение пружины.

Рисунок 7 : Эскиз, показывающий круговой путь объекта

Процедура A: Измерение периода вращения

1

Выровняйте аппарат тремя регулировочными винтами в основании.Предмет находится в горизонтальном положении, когда перекладина остается зафиксированной в любом положении. При необходимости используйте пузырьковый уровень, чтобы помочь вам в этом процессе.

2

Взвесьте вращающуюся массу

M _R

и занесите это значение в рабочий лист.

3

Установите индикатор радиуса на наименьший радиус и измерьте

r

. Радиус измеряется от центра стойки (оси вращения) до центра указателя радиуса. Запишите

r

в таблицу данных на рабочем листе.

4

Переместите перекладину, пока кончик вращающейся массы не окажется над индикатором радиуса.

5

Присоедините пружину к вращающейся массе. Прикрепите струну к вращающейся массе, пропустите струну через шкив и прикрепите ее к подвеске массы на другом конце. Добавляйте грузы к подвеске до тех пор, пока кончик вращающегося груза не окажется над индикатором радиуса. Запишите значение общей подвешенной массы

м _ч

в таблицу данных 1 на рабочем листе.

6

Снимите грузы и подвеску и поверните перекладину.Следите за тем, чтобы кончик вращающейся массы касался индикатора радиуса при каждом обороте. Возможно, вам придется немного потренироваться, прежде чем вы начнете собирать данные. Важно равномерно вращать вал. ВНИМАНИЕ: Не допускайте попадания волос и одежды на устройство во время его движения! С помощью таймера запишите время, необходимое для 50 оборотов. Запишите это время в таблицу данных 1 на рабочем листе.

7

Отсоедините пружину и сдвиньте индикатор радиуса примерно на 1 см. Измерьте и запишите это новое значение радиуса в Таблицу данных 1.

8

Повторите шаги с 4 по 6 и введите значения в Таблицу данных 1.

9

Повторите шаг 7 еще для трех позиций индикатора радиуса, всего 5 радиусов.

КПП 1:
Попросите вашего ТА проверить значения таблицы данных 1, прежде чем продолжить.

10

Рассчитайте и запишите период вращения

T

в Таблицу данных 2.

11

Рассчитайте и запишите частоту вращения

f

в Таблицу данных 2.

12

Рассчитайте и запишите центростремительное ускорение в Таблицу данных 2.

13

Вычислите центростремительную силу.

14

Рассчитайте процентную разницу между экспериментальным значением центростремительной силы и силой подвешенной массы,

м _ч г

и запишите значения в Таблицу данных 2. См. Приложение B. Примечание : Если разница в процентах превышает 15 % для одного испытания, вы должны повторить это испытание.

КПП 2:
Попросите вашего ТА проверить ваши значения и расчеты в Таблице данных 2.

Процедура B: Участок

м _ч г

против

a _c

15

Используя Excel, постройте график

м _ч г

против

a _c

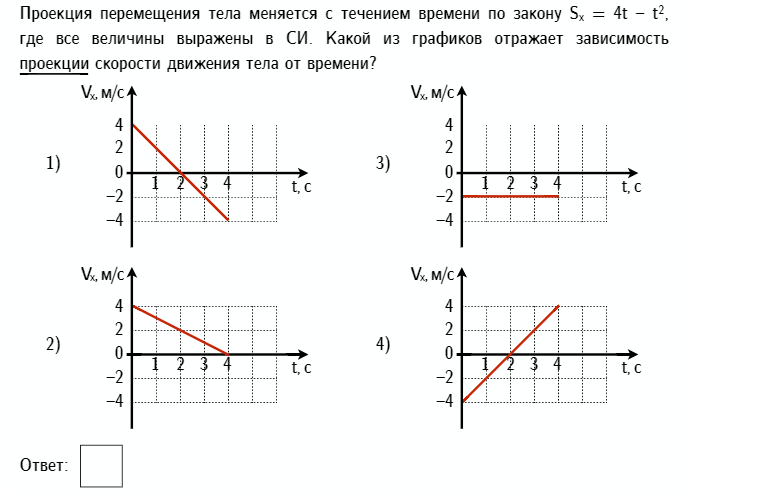. См. Приложение G.

16

Используйте параметр линии тренда в Excel, чтобы найти наклон.См. Приложение Н.

17

По наклону определяют величину вращающейся массы.

18

Сравните значение вращающейся массы, полученное из наклона, с измеренным значением, вычислив разницу в процентах.

КПП 3:
Попросите вашего ТА проверить ваш график и расчеты.

Copyright © 2010 Advanced Instructional Systems, Inc.и Университет штата Северная Каролина. | Кредиты

%PDF-1.4 % 1483 0 объект > эндообъект внешняя ссылка 1483 1240 0000000016 00000 н 0000025157 00000 н 0000025256 00000 н 0000028993 00000 н 0000029246 00000 н 0000038887 00000 н 0000038930 00000 н 0000038954 00000 н 0000047369 00000 н 0000047393 00000 н 0000056772 00000 н 0000056796 00000 н 0000066187 00000 н 0000066211 00000 н 0000075996 00000 н 0000076020 00000 н 0000085774 00000 н 0000085798 00000 н 0000085995 00000 н 0000086192 00000 н 0000086434 00000 н 0000086681 00000 н 0000087711 00000 н 0000087902 00000 н 0000088971 00000 н 0000089221 00000 н 0000089464 00000 н 00000

00000 н 00000

00000 н 00000 ^{00000 н 00000 00000 н 00000 00000 н 0000093280 00000 н 0000102671 00000 н 0000102696 00000 н 0000113193 00000 н 0000113217 00000 н 0000113240 00000 н 0000121260 00000 н 0000121284 00000 н 0000121307 00000 н 0000121331 00000 н 0000121355 00000 н 0000121378 00000 н 0000121401 00000 н 0000129819 00000 н 0000129843 00000 н 0000137304 00000 н 0000137329 00000 н 0000147543 00000 н 0000147568 00000 н 0000148391 00000 н 0000148414 00000 н 0000161032 00000 н 0000161055 00000 н 0000161078 00000 н 0000161102 00000 н 0000161125 00000 н 0000161149 00000 н 0000161173 00000 н 0000161197 00000 н 0000161222 00000 н 0000170318 00000 н 0000170341 00000 н 0000170993 00000 н 0000171016 00000 н 0000171675 00000 н 0000171697 00000 н 0000171907 00000 н 0000171929 00000 н 0000172162 00000 н 0000172184 00000 н 0000172417 00000 н 0000172440 00000 н 0000173215 00000 н 0000173239 00000 н 0000174503 00000 н 0000174525 00000 н 0000174758 00000 н 0000174780 00000 н 0000175013 00000 н 0000175035 00000 н 0000175268 00000 н 0000175290 00000 н 0000175523 00000 н 0000175546 00000 н 0000176255 00000 н 0000176277 00000 н 0000176510 00000 н 0000176532 00000 н 0000176765 00000 н 0000176788 00000 н 0000177138 00000 н 0000177160 00000 н 0000177393 00000 н 0000177416 00000 н 0000178485 00000 н 0000178507 00000 н 0000178740 00000 н 0000178762 00000 н 0000178995 00000 н 0000179017 00000 н 0000179250 00000 н 0000179272 00000 н 0000179524 00000 н 0000179548 00000 н 0000180749 00000 н 0000180772 00000 н 0000181329 00000 н 0000181353 00000 н 0000183007 00000 н 0000183029 00000 н 0000183262 00000 н 0000183284 00000 н 0000183517 00000 н 0000183539 00000 н 0000183772 00000 н 0000183795 00000 н 0000184427 00000 н 0000184449 00000 н 0000184656 00000 н 0000184680 00000 н 0000185876 00000 н 0000185898 00000 н 0000186125 00000 н 0000186149 00000 н 0000187481 00000 н 0000187503 00000 н 0000187736 00000 н 0000187758 00000 н 0000187962 00000 н 0000187985 00000 н 0000189058 00000 н 0000189080 00000 н 0000189344 00000 н 0000189366 00000 н 0000189573 00000 н 0000189597 00000 н 00001}

00000 н 00001 00000 н 00001 00000 н 00001 youtube.com/embed/knwiWm4DpvQ»/> 00000 н 0000193842 00000 н 0000193866 00000 н 0000195100 00000 н 0000195123 00000 н 0000195528 00000 н 0000195551 00000 н 0000196117 00000 н 0000196139 00000 н 0000196372 00000 н 0000196394 00000 н 0000196627 00000 н 0000196649 00000 н 0000196842 00000 н 0000196864 00000 н 0000197097 00000 н 0000197119 00000 н 0000197352 00000 н 0000197374 00000 н 0000197563 00000 н 0000197585 00000 н 0000197774 00000 н 0000197797 00000 н 0000198453 00000 н 0000198477 00000 н 0000199940 00000 н 0000199964 00000 н 0000201420 00000 н 0000201443 00000 н 0000201725 00000 н 0000201749 00000 н 0000202973 00000 н 0000202995 00000 н 0000203184 00000 н 0000203206 00000 н 0000203439 00000 н 0000203461 00000 н 0000203709 00000 н 0000203732 00000 н 0000204340 00000 н 0000204362 00000 н 0000204595 00000 н 0000204617 00000 н 0000204850 00000 н 0000204872 00000 н 0000205122 00000 н 0000205146 00000 н 0000206571 00000 н 0000206593 00000 н 0000206826 00000 н 0000206849 00000 н 0000207610 00000 н 0000207632 00000 н 0000207865 00000 н 0000207889 00000 н 0000209130 00000 н 0000209153 00000 н 0000210319 00000 н 0000210341 00000 н 0000210574 00000 н 0000210597 00000 н 0000211622 00000 н 0000211646 00000 н 0000212838 00000 н 0000212860 00000 н 0000213093 00000 н 0000213116 00000 н 0000214053 00000 н 0000214075 00000 н 0000214308 00000 н 0000214330 00000 н 0000214563 00000 н 0000214585 00000 н 0000214786 00000 н 0000214808 00000 н 0000215041 00000 н 0000215064 00000 н 0000215360 00000 н 0000215382 00000 н 0000215615 00000 н 0000215639 00000 н 0000217164 00000 н 0000217188 00000 н 0000218807 00000 н 0000218831 00000 н 0000220411 00000 н 0000220435 00000 н 0000221742 00000 н 0000221765 00000 н 0000222497 00000 н 0000222521 00000 н 0000224182 00000 н 0000224204 00000 н 0000224397 00000 н 0000224421 00000 н 0000225618 00000 н 0000225641 00000 н 0000226058 00000 н 0000226080 00000 н 0000226313 00000 н 0000226335 00000 н 0000226568 00000 н 0000226592 00000 н 0000227776 00000 н 0000227799 00000 н 0000228968 00000 н 0000228991 00000 н 0000230011 00000 н 0000230035 00000 н 0000231234 00000 н 0000231257 00000 н 0000232100 00000 н 0000232122 00000 н 0000232355 00000 н 0000232378 00000 н 0000233371 00000 н 0000233393 00000 н 0000233626 00000 н 0000233649 00000 н 0000234522 00000 н 0000234546 00000 н 0000235869 00000 н 0000235891 00000 н 0000236124 00000 н 0000236148 00000 н 0000237344 00000 н 0000237366 00000 н 0000237632 00000 н 0000237654 00000 н 0000237887 00000 н 0000237909 00000 н 0000238142 00000 н 0000238166 00000 н 0000239498 00000 н 0000239521 00000 н 0000240670 00000 н 0000240692 00000 н 0000240925 00000 н 0000240947 00000 н 0000241180 00000 н 0000241202 00000 н 0000241445 00000 н 0000241468 00000 н 0000242623 00000 н 0000242647 00000 н 0000243958 00000 н 0000243980 00000 н 0000244213 00000 н 0000244236 00000 н 0000244938 00000 н 0000244961 00000 н 0000245366 00000 н 0000245388 00000 н 0000245621 00000 н 0000245643 00000 н 0000245876 00000 н 0000245899 00000 н 0000246838 00000 н 0000246860 00000 н 0000247093 00000 н 0000247115 00000 н 0000247304 00000 н 0000247328 00000 н 0000249051 00000 н 0000249074 00000 н 0000249512 00000 н 0000249534 00000 н 0000249761 00000 н 0000249785 00000 н 0000251493 00000 н 0000251516 00000 н 0000252153 00000 н 0000252175 00000 н 0000252408 00000 н 0000252431 00000 н 0000253322 00000 н 0000253346 00000 н 0000255070 00000 н 0000255092 00000 н 0000255279 00000 н 0000255302 00000 н 0000255719 00000 н 0000255742 00000 н 0000256088 00000 н 0000256110 00000 н 0000256337 00000 н 0000256361 00000 н 0000257783 00000 н 0000257806 00000 н 0000258804 00000 н 0000258828 00000 н 0000260502 00000 н 0000260524 00000 н 0000260757 00000 н 0000260781 00000 н 0000262268 00000 н 0000262290 00000 н 0000262523 00000 н 0000262546 00000 н 0000263711 00000 н 0000263735 00000 н 0000264976 00000 н 0000264998 00000 н 0000265231 00000 н 0000265254 00000 н 0000266139 00000 н 0000266162 00000 н 0000267074 00000 н 0000267096 00000 н 0000267329 00000 н 0000267351 00000 н 0000267565 00000 н 0000267587 00000 н 0000267820 00000 н 0000267842 00000 н 0000268046 00000 н 0000268068 00000 н 0000268275 00000 н 0000268297 00000 н 0000268556 00000 н 0000268579 00000 н 0000269226 00000 н 0000269248 00000 н 0000269460 00000 н 0000269482 00000 н 0000269715 00000 н 0000269737 00000 н 0000269945 00000 н 0000269969 00000 н 0000271326 00000 н 0000271349 00000 н 0000272021 00000 н 0000272044 00000 н 0000272709 00000 н 0000272732 00000 н 0000273897 00000 н 0000273921 00000 н 0000275505 00000 н 0000275528 00000 н 0000276562 00000 н 0000276585 00000 н 0000277545 00000 н 0000277569 00000 н 0000279241 00000 н 0000279265 00000 н 0000280474 00000 н 0000280497 00000 н 0000281160 00000 н 0000281182 00000 н 0000281371 00000 н 0000281394 00000 н 0000282145 00000 н 0000282167 00000 н 0000282400 00000 н 0000282423 00000 н 0000282700 00000 н 0000282722 00000 н 0000282955 00000 н 0000282979 00000 н 0000284274 00000 н 0000284296 00000 н 0000284529 00000 н 0000284551 00000 н 0000284784 00000 н 0000284807 00000 н 0000285854 00000 н 0000285876 00000 н 0000286109 00000 н 0000286131 00000 н 0000286364 00000 н 0000286386 00000 н 0000286642 00000 н 0000286664 00000 н 0000286897 00000 н 0000286919 00000 н 0000287152 00000 н 0000287175 00000 н 0000287914 00000 н 0000287938 00000 н 0000289749 00000 н 0000289773 00000 н 00002 00000 н 00002 00000 н 00002 00000 н 00002

00000 н 00002 00000 н 0000293659 00000 н 0000293682 00000 н 0000294784 00000 н 0000294806 00000 н 0000295039 00000 н 0000295062 00000 н 0000295630 00000 н 0000295652 00000 н 0000295885 00000 н 0000295908 00000 н 0000296662 00000 н 0000296685 00000 н 0000297659 00000 н 0000297683 00000 н 0000299049 00000 н 0000299073 00000 н 0000300440 00000 н 0000300463 00000 н 0000300958 00000 н 0000300982 00000 н 0000302522 00000 н 0000302545 00000 н 0000303316 00000 н 0000303339 00000 н 0000304447 00000 н 0000304471 00000 н 0000305750 00000 н 0000305772 00000 н 0000306005 00000 н 0000306027 00000 н 0000306260 00000 н 0000306283 00000 н 0000307386 00000 н 0000307410 00000 н 0000309039 00000 н 0000309063 00000 н 0000310302 00000 н 0000310324 00000 н 0000310557 00000 н 0000310579 00000 н 0000310812 00000 н 0000310834 00000 н 0000311023 00000 н 0000311045 00000 н 0000311278 00000 н 0000311300 00000 н 0000311533 00000 н 0000311555 00000 н 0000311788 00000 н 0000311810 00000 н 0000312025 00000 н 0000312048 00000 н 0000312531 00000 н 0000312553 00000 н 0000312786 00000 н 0000312809 00000 н 0000313929 00000 н 0000313952 00000 н 0000314266 00000 н 0000314288 00000 н 0000314521 00000 н 0000314544 00000 н 0000315560 00000 н 0000315582 00000 н 0000315815 00000 н 0000315837 00000 н 0000316070 00000 н 0000316094 00000 н 0000317645 00000 н 0000317667 00000 н 0000317900 00000 н 0000317922 00000 н 0000318115 00000 н 0000318137 00000 н 0000318326 00000 н 0000318348 00000 н 0000318581 00000 н 0000318605 00000 н 0000320145 00000 н 0000320167 00000 н 0000320400 00000 н 0000320422 00000 н 0000320655 00000 н 0000320678 00000 н 0000321730 00000 н 0000321754 00000 н 0000322963 00000 н 0000322986 00000 н 0000324027 00000 н 0000324049 00000 н 0000324242 00000 н 0000324266 00000 н 0000325531 00000 н 0000325553 00000 н 0000325746 00000 н 0000325768 00000 н 0000326001 00000 н 0000326025 00000 н 0000327542 00000 н 0000327565 00000 н 0000328333 00000 н 0000328355 00000 н 0000328544 00000 н 0000328566 00000 н 0000328799 00000 н 0000328821 00000 н 0000329028 00000 н 0000329051 00000 н 0000330111 00000 н 0000330134 00000 н 0000331025 00000 н 0000331048 00000 н 0000331346 00000 н 0000331368 00000 н 0000331601 00000 н 0000331623 00000 н 0000331856 00000 н 0000331880 00000 н 0000333518 00000 н 0000333541 00000 н 0000334409 00000 н 0000334431 00000 н 0000334620 00000 н 0000334643 00000 н 0000334956 00000 н 0000334979 00000 н 0000335581 00000 н 0000335603 00000 н 0000335792 00000 н 0000335816 00000 н 0000337143 00000 н 0000337167 00000 н 0000338481 00000 н 0000338503 00000 н 0000338736 00000 н 0000338759 00000 н 0000339041 00000 н 0000339064 00000 н 0000339906 00000 н 0000339928 00000 н 0000340161 00000 н 0000340185 00000 н 0000341739 00000 н 0000341761 00000 н 0000341950 00000 н 0000341973 00000 н 0000342428 00000 н 0000342450 00000 н 0000342683 00000 н 0000342707 00000 н 0000344011 00000 н 0000344035 00000 н 0000345472 00000 н 0000345496 00000 н 0000347223 00000 н 0000347245 00000 н 0000347478 00000 н 0000347500 00000 н 0000347733 00000 н 0000347756 00000 н 0000348880 00000 н 0000348903 00000 н 0000349891 00000 н 0000349914 00000 н 0000350546 00000 н 0000350568 00000 н 0000350801 00000 н 0000350824 00000 н 0000351185 00000 н 0000351209 00000 н 0000352494 00000 н 0000352517 00000 н 0000353535 00000 н 0000353559 00000 н 0000354785 00000 н 0000354807 00000 н 0000355045 00000 н 0000355067 00000 н 0000355300 00000 н 0000355322 00000 н 0000355555 00000 н 0000355577 00000 н 0000355810 00000 н 0000355832 00000 н 0000356065 00000 н 0000356087 00000 н 0000356320 00000 н 0000356343 00000 н 0000356703 00000 н 0000356726 00000 н 0000357729 00000 н 0000357751 00000 н 0000357958 00000 н 0000357982 00000 н 0000359320 00000 н 0000359344 00000 н 0000360556 00000 н 0000360579 00000 н 0000361464 00000 н 0000361486 00000 н 0000361719 00000 н 0000361741 00000 н 0000361974 00000 н 0000361997 00000 н 0000362290 00000 н 0000362314 00000 н 0000363865 00000 н 0000363889 00000 н 0000365446 00000 н 0000365470 00000 н 0000366787 00000 н 0000366810 00000 н 0000367686 00000 н 0000367709 00000 н 0000368005 00000 н 0000368028 00000 н 0000368748 00000 н 0000368772 00000 н 0000370052 00000 н 0000370075 00000 н 0000371004 00000 н 0000371027 00000 н 0000372028 00000 н 0000372050 00000 н 0000372243 00000 н 0000372265 00000 н 0000372498 00000 н 0000372521 00000 н 0000372864 00000 н 0000372886 00000 н 0000373119 00000 н 0000373141 00000 н 0000373346 00000 н 0000373368 00000 н 0000373601 00000 н 0000373625 00000 н 0000374947 00000 н 0000374971 00000 н 0000376239 00000 н 0000376261 00000 н 0000376465 ​​00000 н 0000376488 00000 н 0000377507 00000 н 0000377529 00000 н 0000377762 00000 н 0000377786 00000 н 0000379228 00000 н 0000379250 00000 н 0000379483 00000 н 0000379506 00000 н 0000380267 00000 н 0000380289 00000 н 0000380522 00000 н 0000380546 00000 н 0000381775 00000 н 0000381798 00000 н 0000382282 00000 н 0000382306 00000 н 0000383669 00000 н 0000383691 00000 н 0000383918 00000 н 0000383942 00000 н 0000385143 00000 н 0000385165 00000 н 0000385398 00000 н 0000385420 00000 н 0000385653 00000 н 0000385677 00000 н 0000387057 00000 н 0000387079 00000 н 0000387312 00000 н 0000387335 00000 н 0000387679 00000 н 0000387703 00000 н 0000389155 00000 н 0000389179 00000 н 00003

00000 н 00002

00000 н 00003 00000 н 00003 00000 н 00003

00000 н 00003

00000 н 00003

00000 н 00003 00000 н 0000393243 00000 н 0000393476 00000 н 0000393498 00000 н 0000393731 00000 н 0000393753 00000 н 0000393986 00000 н 0000394010 00000 н 0000395607 00000 н 0000395629 00000 н 0000395862 00000 н 0000395885 00000 н 0000396977 00000 н 0000397000 00000 н 0000398042 00000 н 0000398064 00000 н 0000398297 00000 н 0000398320 00000 н 0000399475 00000 н 0000399497 00000 н 0000399724 00000 н 0000399746 00000 н 0000399979 00000 н 0000400003 00000 н 0000401239 00000 н 0000401262 00000 н 0000402300 00000 н 0000402323 00000 н 0000403433 00000 н 0000403457 00000 н 0000404641 00000 н 0000404665 00000 н 0000406231 00000 н 0000406255 00000 н 0000407888 00000 н 0000407910 00000 н 0000408143 00000 н 0000408165 00000 н 0000408398 00000 н 0000408422 00000 н 0000409860 00000 н 0000409882 00000 н 0000410122 00000 н 0000410144 00000 н 0000410377 00000 н 0000410400 00000 н 0000411409 00000 н 0000411431 00000 н 0000411664 00000 н 0000411686 00000 н 0000411919 00000 н 0000411942 00000 н 0000412401 00000 н 0000412425 00000 н 0000413790 00000 н 0000413814 00000 н 0000415085 00000 н 0000415109 00000 н 0000416617 00000 н 0000416640 00000 н 0000417414 00000 н 0000417436 00000 н 0000417691 00000 н 0000417713 00000 н 0000417946 00000 н 0000417969 00000 н 0000418665 00000 н 0000418687 00000 н 0000418920 00000 н 0000418942 00000 н 0000419187 00000 н 0000419210 00000 н 0000419709 00000 н 0000419731 00000 н 0000419964 00000 н 0000419986 00000 н 0000420219 00000 н 0000420241 00000 н 0000420474 00000 н 0000420496 00000 н 0000420703 00000 н 0000420725 00000 н 0000420958 00000 н 0000420980 00000 н 0000421213 00000 н 0000421236 00000 н 0000421859 00000 н 0000421883 00000 н 0000423153 00000 н 0000423175 00000 н 0000423431 00000 н 0000423454 00000 н 0000424591 00000 н 0000424613 00000 н 0000424846 00000 н 0000424870 00000 н 0000426165 00000 н 0000426188 00000 н 0000427166 00000 н 0000427189 00000 н 0000427836 00000 н 0000427858 00000 н 0000428047 00000 н 0000428069 00000 н 0000428296 00000 н 0000428318 00000 н 0000428551 00000 н 0000428574 00000 н 0000429695 00000 н 0000429717 00000 н 0000429950 00000 н 0000429972 00000 н 0000430205 00000 н 0000430229 00000 н 0000431605 00000 н 0000431628 00000 н 0000432782 00000 н 0000432804 00000 н 0000433037 00000 н 0000433061 00000 н 0000434256 00000 н 0000434278 00000 н 0000434547 00000 н 0000434571 00000 н 0000436149 00000 н 0000436171 00000 н 0000436404 00000 н 0000436428 00000 н 0000437620 00000 н 0000437642 00000 н 0000437896 00000 н 0000437918 00000 н 0000438151 00000 н 0000438175 00000 н 0000439389 00000 н 0000439413 00000 н 0000440661 00000 н 0000440683 00000 н 0000440876 00000 н 0000440898 00000 н 0000441131 00000 н 0000441155 00000 н 0000442752 00000 н 0000442775 00000 н 0000443146 00000 н 0000443168 00000 н 0000443401 00000 н 0000443424 00000 н 0000444160 00000 н 0000444183 00000 н 0000444789 00000 н 0000444811 00000 н 0000445044 00000 н 0000445066 00000 н 0000445299 00000 н 0000445322 00000 н 0000446345 00000 н 0000446368 00000 н 0000447333 00000 н 0000447355 00000 н 0000447588 00000 н 0000447610 00000 н 0000447839 00000 н 0000447863 00000 н 0000449115 00000 н 0000449137 00000 н 0000449370 00000 н 0000449394 00000 н 0000450889 00000 н 0000450913 00000 н 0000452471 00000 н 0000452495 00000 н 0000453969 00000 н 0000453992 00000 н 0000455143 00000 н 0000455165 00000 н 0000455372 00000 н 0000455394 00000 н 0000455627 00000 н 0000455650 00000 н 0000456555 00000 н 0000456579 00000 н 0000457846 00000 н 0000457869 00000 н 0000458212 00000 н 0000458234 00000 н 0000458467 00000 н 0000458489 00000 н 0000458722 00000 н 0000458744 00000 н 0000458977 00000 н 0000458999 00000 н 0000459232 00000 н 0000459256 00000 н 0000460560 00000 н 0000460582 00000 н 0000460815 00000 н 0000460837 00000 н 0000461044 00000 н 0000461066 00000 н 0000461299 00000 н 0000461322 00000 н 0000462015 00000 н 0000462039 00000 н 0000463572 00000 н 0000463594 00000 н 0000463827 00000 н 0000463851 00000 н 0000465311 00000 н 0000465333 00000 н 0000465587 00000 н 0000465609 00000 н 0000465842 00000 н 0000465866 00000 н 0000467221 00000 н 0000467243 00000 н 0000467511 00000 н 0000467535 00000 н 0000468872 00000 н 0000468894 00000 н 0000469127 00000 н 0000469150 00000 н 0000469784 00000 н 0000469807 00000 н 0000470562 00000 н 0000470585 00000 н 0000471748 00000 н 0000471771 00000 н 0000472920 00000 н 0000472942 00000 н 0000473149 00000 н 0000473171 00000 н 0000473404 00000 н 0000473428 00000 н 0000474935 00000 н 0000474959 00000 н 0000476423 00000 н 0000476447 00000 н 0000477695 00000 н 0000477717 00000 н 0000477944 00000 н 0000477968 00000 н 0000479199 00000 н 0000479221 00000 н 0000479454 00000 н 0000479476 00000 н 0000479709 00000 н 0000479731 00000 н 0000479964 00000 н 0000479987 00000 н 0000480622 00000 н 0000480645 00000 н 0000481186 00000 н 0000481208 00000 н 0000481441 00000 н 0000481464 00000 н 0000481855 00000 н 0000481879 00000 н 0000483064 00000 н 0000483086 00000 н 0000483279 00000 н 0000483302 00000 н 0000484136 00000 н 0000484158 00000 н 0000484391 00000 н 0000484413 00000 н 0000484646 00000 н 0000484669 00000 н 0000485843 00000 н 0000485865 00000 н 0000486098 00000 н 0000486120 00000 н 0000486353 00000 н 0000486377 00000 н 0000487836 00000 н 0000487858 00000 н 0000488091 00000 н 0000488113 00000 н 0000488346 00000 н 0000488369 00000 н 0000489330 00000 н 0000489352 00000 н 0000489559 00000 н 0000489582 00000 н 00004 _{00000 н 00004} 00000 н 00004 00000 н 00004

00000 н 00004

00000 н 00004 00000 н 00004

00000 н 00004

00000 н 0000494498 00000 н 0000494520 00000 н 0000494753 00000 н 0000494775 00000 н 0000495008 00000 н 0000495030 00000 н 0000495263 00000 н 0000495285 00000 н 0000495518 00000 н 0000495541 00000 н 0000496093 00000 н 0000496117 00000 н 0000497622 00000 н 0000497644 00000 н 0000497877 00000 н 0000497901 00000 н 0000499452 00000 н 0000499475 00000 н 0000500104 00000 н 0000500126 00000 н 0000500398 00000 н 0000500421 00000 н 0000500958 00000 н 0000500981 00000 н 0000501968 00000 н 0000501990 00000 н 0000502175 00000 н 0000502199 00000 н 0000503614 00000 н 0000503637 00000 н 0000504519 00000 н 0000504542 00000 н 0000505139 00000 н 0000505162 00000 н 0000506199 00000 н 0000506221 00000 н 0000506414 00000 н 0000506438 00000 н 0000507840 00000 н 0000507862 00000 н 0000508095 00000 н 0000508119 00000 н 0000509724 00000 н 0000509748 00000 н 0000510942 00000 н 0000510964 00000 н 0000511197 00000 н 0000511220 00000 н 0000512061 00000 н 0000512084 00000 н 0000512759 00000 н 0000512782 00000 н 0000513287 00000 н 0000513311 00000 н 0000514857 00000 н 0000514880 00000 н 0000515677 00000 н 0000515700 00000 н 0000516763 00000 н 0000516787 00000 н 0000518310 00000 н 0000518333 00000 н 0000518921 00000 н 0000518944 00000 н 0000520061 00000 н 0000520084 00000 н 0000520422 00000 н 0000520445 00000 н 0000520918 00000 н 0000520940 00000 н 0000521173 00000 н 0000521196 00000 н 0000521475 00000 н 0000521497 00000 н 0000521730 00000 н 0000521752 00000 н 0000521941 00000 н 0000521963 00000 н 0000522196 00000 н 0000522220 00000 н 0000523694 00000 н 0000523716 00000 н 0000523949 00000 н 0000523971 00000 н 0000524178 00000 н 0000524201 00000 н 0000525125 00000 н 0000525148 00000 н 0000526078 00000 н 0000526101 00000 н 0000527041 00000 н 0000527064 00000 н 0000527941 00000 н 0000527964 00000 н 0000528906 00000 н 0000528928 00000 н 0000529163 00000 н 0000529186 00000 н 0000529598 00000 н 0000529621 00000 н 0000529898 00000 н 0000529920 00000 н 0000530153 00000 н 0000530177 00000 н 0000531423 00000 н 0000531446 00000 н 0000531729 00000 н 0000531752 00000 н 0000532648 00000 н 0000532671 00000 н 0000533547 00000 н 0000533569 00000 н 0000533796 00000 н 0000533818 00000 н 0000534051 00000 н 0000534073 00000 н 0000534300 00000 н 0000534324 00000 н 0000535528 00000 н 0000535552 00000 н 0000537249 00000 н 0000537272 00000 н 0000538283 00000 н 0000538307 00000 н 0000539927 00000 н 0000539949 00000 н 0000540182 00000 н 0000540204 00000 н 0000540437 00000 н 0000540459 00000 н 0000540731 00000 н 0000540753 00000 н 0000540942 00000 н 0000540965 00000 н 0000541956 00000 н 0000541979 00000 н 0000542785 00000 н 0000542807 00000 н 0000543062 00000 н 0000543085 00000 н 0000543718 00000 н 0000543742 00000 н 0000545067 00000 н 0000545089 00000 н 0000545322 00000 н 0000545345 00000 н 0000545625 00000 н 0000545648 00000 н 0000545945 00000 н 0000545968 00000 н 0000546909 00000 н 0000546931 00000 н 0000547164 00000 н 0000547186 00000 н 0000547400 00000 н 0000547423 00000 н 0000547918 00000 н 0000547942 00000 н 0000549244 00000 н 0000549266 00000 н 0000549499 00000 н 0000549521 00000 н 0000549754 00000 н 0000549778 00000 н 0000551237 00000 н 0000551259 00000 н 0000551492 00000 н 0000551514 00000 н 0000551747 00000 н 0000551769 00000 н 0000552002 00000 н 0000552024 00000 н 0000552260 00000 н 0000552282 00000 н 0000552531 00000 н 0000552555 00000 н 0000553982 00000 н 0000554004 00000 н 0000554237 00000 н 0000554261 00000 н 0000555438 00000 н 0000555462 00000 н 0000556649 00000 н 0000556673 00000 н 0000558075 00000 н 0000558097 00000 н 0000558330 00000 н 0000558354 00000 н 0000559899 00000 н 0000559923 00000 н 0000561394 00000 н 0000561416 00000 н 0000561649 00000 н 0000561671 00000 н 0000561904 00000 н 0000561928 00000 н 0000563313 00000 н 0000563336 00000 н 0000564327 00000 н 0000564350 00000 н 0000565072 00000 н 0000565094 00000 н 0000565327 00000 н 0000565349 00000 н 0000565582 00000 н 0000565606 00000 н 0000566913 00000 н 0000566936 00000 н 0000567719 00000 н 0000567741 00000 н 0000567974 00000 н 0000567996 00000 н 0000568245 00000 н 0000568268 00000 н 0000569398 00000 н 0000569421 00000 н 0000570066 00000 н 0000570088 00000 н 0000570321 00000 н 0000570344 00000 н 0000571241 00000 н 0000571264 00000 н 0000572102 00000 н 0000572124 00000 н 0000572357 00000 н 0000572381 00000 н 0000574062 00000 н 0000574085 00000 н 0000575218 00000 н 0000575240 00000 н 0000025411 00000 н 0000028969 00000 н трейлер ] >> startxref 0 %%EOF 1484 0 объект > эндообъект 1485 0 объект >/Кодировка >>> /DA (/Helv 0 Tf 0 г ) >> эндообъект 2721 0 объект > ручей HV}PSIHB@.

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт

00000 н 00003 00000 н 00003 00000 н 00003 00000 н 00003

00000 н 00003 00000 н 00003