Площадь корень: Страница не найдена

Арифметический квадратный корень 8 класс онлайн-подготовка на Ростелеком Лицей

Арифметический квадратный корень

Пусть известно, что площадь квадрата равна 64 см². Чему равна длина стороны этого квадрата?

Обозначим длину стороны за х см.

Тогда выражение для площади S = х·х = х² (см²).

Получим уравнение х² = 64.

У этого уравнения два корня – х₁ = 8 и х₂ = -8.

Но длина стороны квадрата не может быть отрицательным числом, поэтому условию задачи удовлетворяет только х₁.

Квадратным корнем из числа а называют число, квадрат которого равен а.

То есть квадратными корнями из 64 являются числа 8 и -8.

Число 8 – неотрицательный корень из 64, другими словами – арифметический.

Арифметическим квадратным корнем из числа а называется такое неотрицательное число, квадрат которого равен а.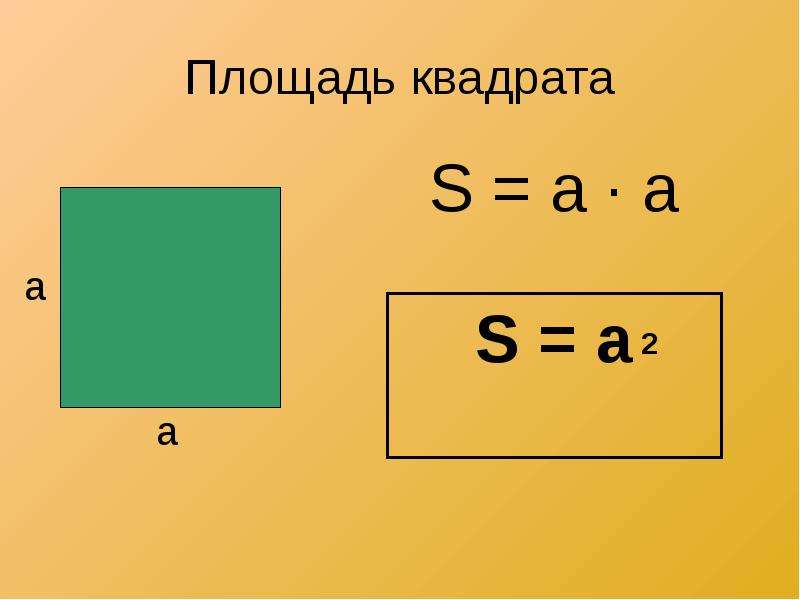

Арифметический квадратный корень из числа а обозначают a. Знак √ называют знаком арифметического квадратного корня или знаком радикала. Выражение, стоящее под знаком корня, называют подкоренным выражением. Запись a читают как «квадратный корень из а», слово «арифметический» при этом опускают.

Приведем примеры нахождения (еще говорят извлечения) арифметических квадратных корней.

4=2, так как 2 – неотрицательное и 2^{2= 4.}

1,21=1,1, так как 1,1 – число неотрицательное и 1,1² = 1,21.

0=0, так как 0 число неотрицательное и 0^{2= 0.}

В общем случае a=b, если выполняются два условия: b≥0 и b2=a.

При а<0 выражение a не имеет смысла.

Арифметический квадратный корень из отрицательных чисел не существует.

Например, -16 не имеет смысла, т. к. нет такого действительного числа a, которое в квадрате равно отрицательному числу: a2=-16.

При любом а, при котором выражение a имеет смысл, верно равенство (a)2=a.

Чтобы найти квадратный корень из числа, необходимо хорошо знать квадраты чисел.

Часто используемые квадраты целых чисел:

1² = 1

1	2	3	4	5	6	7	8	9	10
1	4	9	16	25	36	49	64	81	100

11	12	13	14	15	16	17	18	19	20	25
121	144	169	196	225	256	289	324	361	400	625

Значит, 81=9; 121=11 и т. 2=400\\ \hline \end{array}\]

Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\] Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\), то первоначально вы должны найти значения \(\sqrt{25}\) и \(\sqrt{49}\), а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\]

Если значения \(\sqrt a\) или \(\sqrt b\) при сложении \(\sqrt a+\sqrt b\) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt 2+ \sqrt {49}\) мы можем найти \(\sqrt{49}\) – это \(7\), а вот \(\sqrt 2\) никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt 2+7\). Дальше это выражение, к сожалению, упростить никак нельзя   \(\bullet\) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad \sqrt a:\sqrt b=\sqrt{a:b}\] (при условии, что обе части равенств имеют смысл)
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot 2}=\sqrt{64}=8\);   \(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\);   \(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}= 5\cdot 8=40\).   \(\bullet\) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\). Так как \(44100:100=441\), то \(44100=100\cdot 441\). По признаку делимости число \(441\) делится на \(9\) (так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\), то есть \(441=9\cdot 49\).
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}= \sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\] Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}= \sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{ \dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot \sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
\(\bullet\) Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\) (сокращенная запись от выражения \(5\cdot \sqrt2\)). Так как \(5=\sqrt{25}\), то \[5\sqrt2=\sqrt{25}\cdot \sqrt2=\sqrt{25\cdot 2}=\sqrt{50}\] Заметим также, что, например,

1) \(\sqrt2+3\sqrt2=4\sqrt2\),
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\). 2\), поэтому \(\sqrt{16}=4\). А вот извлечь корень из числа \(3\), то есть найти \(\sqrt3\), нельзя, потому что нет такого числа, которое в квадрате даст \(3\).
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\) и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\) (число “пи”, приблизительно равное \(3,14\)), \(e\) (это число называют числом Эйлера, приблизительно оно равно \(2,7\)) и т.д.
\(\bullet\) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся

множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\).
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.  

Факт 5.
\(\bullet\) Модуль вещественного числа \(a\) – это неотрицательное число \(|a|\), равное расстоянию от точки \(a\) до \(0\) на вещественной прямой. 2\\ &2>2,25 \end{aligned}\] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1<0,5\).
Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3<\sqrt2\) нельзя (убедитесь в этом сами)!

  \(\bullet\) Следует запомнить, что \[\begin{aligned} &\sqrt 2\approx 1,4\\[1ex] &\sqrt 3\approx 1,7 \end{aligned}\] Знание приблизительного значения данных чисел поможет вам при сравнении чисел!   \(\bullet\) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. 2=168\cdot 168=28224\).
Следовательно, \(\sqrt{28224}=168\). Вуаля!

Как растут корни винограда

Тим Мартинсон (Tim Martinson), старший специалист, Корнельский университет (Cornell University)

Фото Красохиной С.И.

По сравнению с надземными частями куста винограда корневая структура и ее функции являются большей загадкой для большинства виноградарей. Корни извлекают питательные вещества и воду из почвы, а также являются доминирующим органом для хранения углеводов и питательных веществ (запасов винограда) в период покоя (см. Показатели запасов питательных веществ).

Они также оказывают физическую поддержку лозе, удерживая растение в почве, и производят гормоны, которые регулируют рост побегов и реакцию куста на условия окружающей среды (см. Как нормирование побегами, листьями и гроздями влияет на качество урожая и зимостойкость почек).

Но корни скрыты под землей — поэтому сезонный характер их роста и функции не могут быть непосредственно обнаружены. Рост и развитие виноградной лозы над землей проходит через биологические фазы — распускание почек, цветение, начало созревания ягод, сбор урожая и листопад. Но сезонный цикл роста корней, который проходит под землей, менее очевиден (см. Жизнь корней винограда).

На фото: надземная и подземная часть куста винограда после раскопки корнеобитаемого слоя, сорт Конкорд.

Прямая корреляция

Исследователи считают, что кусты выделяют от 30 до 60% фотосинтатов для роста корней. У взрослого куста лозе площадь поверхности корней оценивается примерно в 100 квадратных метров по сравнению с 10 квадратными метрами площади листьев. В то время как большинство «тонких корней», которые поглощают воду и питательные вещества, сосредоточены в верхнем метре почвы, часть корней может вырасти на большие глубины (до 30 м) и простираться на несколько метров от основания лозы (см. Раскопки корней на винограднике).

Виноградное растение всегда пытается поддерживать соотношение корень: побег в разумных пределах, а размер куста напрямую коррелирует с размером корневой системы.

Структура корней

Виноградник обычно закладывают саженцами, то есть с помощью вегетативного размножения, и первоначально корни формируются как наросты камбиального слоя черенка в условиях высокой влажности. На черенках корни обычно образуются вблизи междоузлия. Эти образовавшиеся корни становятся основными структурными корнями, которые впоследствии, по мере роста и развития куста, разветвляются на боковые (вторичные и третичные) корни.

Боковые разветвления могут образовываться в любом месте вдоль корневой системы, и их формирование зависит от способности куста винограда реагировать на условия окружающей среды (наличие воды, наличие питательных веществ) и распространяться на эти области. В отличие от побегов и листьев, которые имеют заранее запрограммированное и предсказуемое расположение, модели роста и ветвления корней очень гибки и очень чувствительны к местным условиям почвы.

Рост корня происходит в меристеме кончика корня, где идет деление клеток (зона деления корня). Кончик корня покрыт слизистой корневым чехликом, который защищает от истирания частицами почвы. За этой зоной находится ячейка роста корня, называемая «зона удлинения», где клетки начинают образовывать два слоя. Внешний слой — это кора, где происходит поглощение и хранение питательных веществ. Внутренний слой дифференцируется в ксилему и флоэму, отвечающую за транспортировку воды и питательных веществ вверх и вниз по растению. 

Максимальное поглощение происходит за несколько миллиметров от кончика корня, где образуются многочисленные корневые волоски, которые значительно увеличивают площадь поверхности для поглощения. Вдали от кончика корня эти наружные слои и корневые волоски стираются, оставляя центральный цилиндр и его сосудистую систему для транспортировки к штамбу, побегам и другим частям куста винограда. Слой клеток вне ксилемы развивается в камбий, который увеличивает диаметр корней и может инициировать образование и развитие новых боковых корневых меристем. Внешний «пробковый камбий» образует и развивает внешние закаленные клеточные слои, которые содержат субарин — воскообразное водостойкое вещество, образующее своего рода барьер между почвой и проводящими тканями корня.

Тонкие корни вызывают ассоциации с микоризными грибами — симбиотическими отношениями, в которых гриб усиливает поглощение питательных веществ из почвы — и, в свою очередь, снабжаются углеводами для поддержки роста и развития из фотосинтезирующих листьев винограда.

На  фото: распределение  корней у подвоя  Рипариа глуар, который склонен к боковому росту корней, образовывая при этом поверхностную корневую систему. Другие подвои, такие как Кудерк 3309 , имеют склонность к вертикальному росту корней.

Развитие корней в течение сезона.

В состоянии покоя клетки, окружающие сосуды ксилемы в корнях, наполняются крахмалом и азотом, который откладывается, начиная с начала созревания ягод, но также мобилизуется из листьев по мере их старения осенью.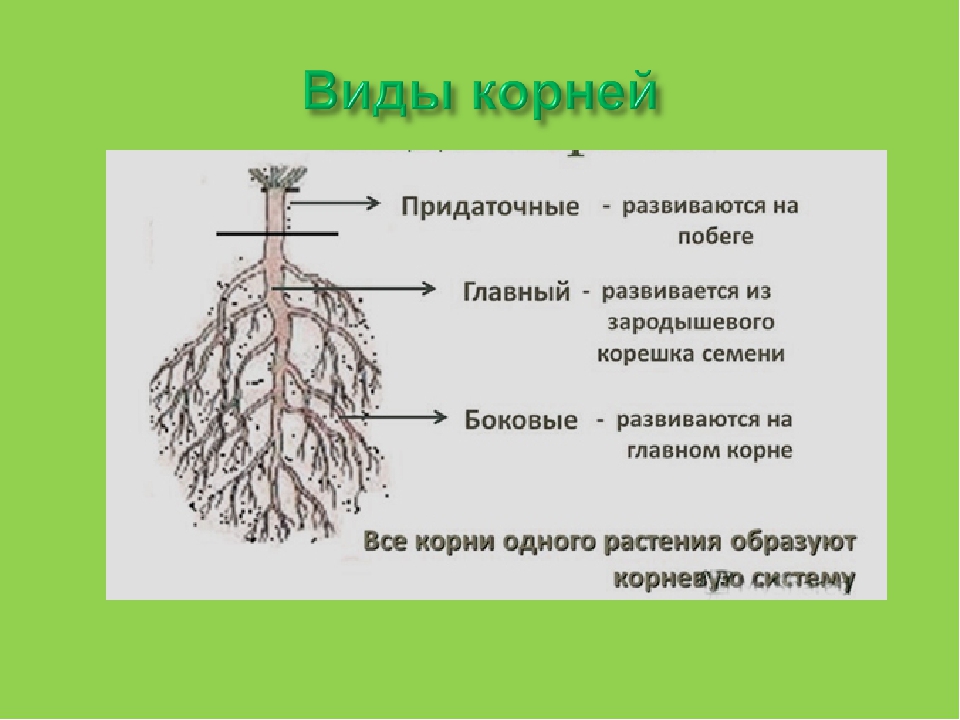 Эти запасы являются тем, что весной способствует распусканию почек и функционированию молодых побегов.

Первым видимым признаком перехода куста винограда от периода покоя к активному росту часто является поток сока ксилемы из обрезанных ран, называемого плач.

Движущей силой этого плача куста винограда является метаболическая активность в тканях корня, так как почва весной начинает прогреваться и запускаются процессы жизнедеятельности растения. Поскольку хранимый крахмал и белки превращаются в сахара и аминокислоты, они высвобождаются в ксилему.

Результирующее осмотическое давление (из-за высокой концентрации сахаров в соке ксилемы) втягивает воду в корни, и этого достаточно для поднятия воды (и питательных веществ) к кончикам побегов — там, где она увлажняет почки, начиная процесс распускания почек.

Когда почки начинают набухать, кончики побегов производят ауксины, которые в конечном итоге транспортируются (через флоэму) вниз к корням, чтобы стимулировать рост корней. Они взаимодействуют с гиббереллинами, образующимися на кончиках корней (способствуя удлинению клеток). Этот процесс требует времени, потому что спящие почки изолированы от сосудистой системы виноградной лозы и нуждаются в повторном соединении с ней — процессе, который, как считается, завершается в период цветения (см. Как виноград начинает сезон вегетации после зимы).

Таким образом, весной рост корней отстает от роста побегов — и сухой вес корней между периодами начала распускания почек и цветением фактически уменьшается, так как ресурсы запасов растения мобилизуются для поддержки роста побегов в начале сезона. По мере появления зеленой массы рост корней ускоряется, достигая пика между цветением и образованием ягод, а затем постепенно снижается во время созревания ягод.

Хотя корневая биомасса увеличивается от с периода конца цветения до листопада, большая часть биомассы сосредоточена в более крупных, постоянных структурных корнях.

Тонкие корни — это место, где происходит поглощение питательных веществ и воды. Они недолговечны (срок жизни их составляет меньше 5 недель) и часто заменяются — вполне вероятно, потому что они истощают в месте своего нахождения питательные вещества и водоснабжение. На цикле жизни тонких корней основано эффективное внесение удобрений (Когда лучше делать корневую подкормку).

По мере того как зеленый полог куста винограда становится устойчивым после цветения, часть фотосинтатов возвращается к корням и пополняет запасы лозы — процесс, который ускоряется по мере созревания ягод, формирования перидермы и прекращения роста зеленых побегов.

Реакция корней на экологические стрессы и технологические приемы

Зеленые операции . Рост корня зависит от потока ауксина из почек и новых побегов. Незначительная обрезка, оставление большого количества однолетних побегов приведет к большему количеству листьев, и рано появившаяся большая площадь листьев будет стимулировать рост корней. Жёсткая обрезка или травмы, полученные в ходе перезимовки от морозов, что ограничивает рост побегов в начале сезона, также ограничивают и рост корней. Прищипка зеленого побега временно приведет к паузе в росте корня.

Водный стресс (засуха). В течение вегетационного периода транспирация водяных паров через устьица листьев приводит к наибольшему поглощению воды из почвы (см. Как виноград реагирует на засуху). Поскольку запасы почвенной воды истощаются, потребность листьев в транспирации превышает поглощение корнями. По мере высыхания почвы ткани корня увеличивают выработку абсциссовой кислоты (АБК), которая транспортируется к листьям и сигнализирует о закрытии устьиц, уменьшая потерю воды, но также уменьшая выброс углекислого газа – обмен, необходимый для процесса для фотосинтеза. Рост побегов замедляется, но АБК может вызывать противоположный эффект у корней. По-видимому, он блокирует транспорт K + (ионов калия) в ксилему, вызывая импорт воды в растущие ткани корня. Поэтому при небольшой нехватке воды корни могут поддерживать рост и эксплуатировать новую (менее истощенную) почву.

Избыток влаги: всем известно, что лозы «не любят мокрые ноги» — и лучше справляются с грубой, чем с тонкой текстурой. Корневое дыхание требует поглощения растворенного в почве кислорода, который быстро истощается в заболоченных почвах. В течение длительного периода заболачивания недостаток дыхания ограничивает функцию клеток, а также поглощение корнями питательных веществ и воды.

Избыток питательных веществ : Потребность куста в росте и развитии надземной части, как правило, стимулирует усвоение питательных веществ, а механизмы обратной связи могут «отключить» усвоение питательных веществ. Но поглощение может превышать требования роста лозы, и избыточное предложение может накапливаться — часто в вакуолях в клетках, где запасы обеспечивают страховку от истощения питательных веществ.

Нехватка питательных веществ: при недостатке питательных веществ рост побегов замедляется из-за ограничивающих рост запасов в клетках. Корни поглощают и истощают питательные вещества в окружающей корневой зоне. Местное истощение может перенаправить поглощение на другие корни, исследуя более богатые питательными веществами районы.

Если общий запас питательный веществ у винограда в макроэлементах (N, P, K) недостаточен, то корневые клетки снижают выработку цитокининов, которые при транспортировке к макушке побегов стимулируют рост и деление клеток.

Однако более низкий уровень цитокининов в корнях в ответ на дефицит азота может увеличить скорость роста корней — предположительно, чтобы корни могли улучшить усвоение питательных веществ, используя новую почву, в которой еще не было истощения.

Выводы.

Корневая система куста винограда скрыта под землей, но ее рост и общая «доля» фотосинтатов, усвоенных лозой, критически важны для здоровья и развития надземных структурных элементов куста, побегов, листьев и ягод (Корневая система винограда).

Корни поглощают питательные вещества, снабжают водой, обеспечивают поддержку и вырабатывают гормоны, которые регулируют общий рост куста винограда.

Они образуют симбиотические отношения с микоризными грибами, усиливающими поглощение питательных веществ и воды сверх того, что могли бы обеспечить сами корни.

У них есть гибкая зона роста, которая реагирует на переменные условия почвы.

Корни являются наиболее важными органами хранения запасов, обеспечивающих потребность в сахарах и азоте в начале вегетационного периода.

Хотя мы не можем непосредственно наблюдать за ростом и развитием корней под землей, мы знаем, что функции корней столь же важны, как и зеленый полог и ягоды винограда, которыми виноградари активно управляют при возделывании своего виноградника.

Источник, перевод. Красохиной С.И.

Понятие об извлечении корня

S = 8² = 64 (м²).

Задача 2. Площадь квадратного участка равна 81 м². Вычислить его сторону.

Эта задача является обратной по отношению к первой. В первой задаче была известна длина стороны квадрата и требовалось найти его площадь; здесь, наоборот, известна площадь квадрата, требуется найти длину его стороны.

Обозначим неизвестную длину стороны квадрата через x метров. Тогда площадь квадрата будет равна x² м2. Но по условию эта площадь равна 81 м². Получаем уравнение:

x² = 81.

Значит, чтобы решить задачу 2, надо найти число, квадрат которого был бы равен 81. Из таблицы квадратов найдем, что таким числом является 9. Действительно,

9² = 9 * 9 = 81.

Число 9 называется корнем второй степени или, короче, квадратным корнем из 81. Точно так же 7 является квадратным корнем из 49, так как 7² = 49; число — квадратный корень из, так как.

Определения. 1. Квадратным корнем из числа a называется число, квадрат которого равен a.

2. Действие, посредством которого отыскивается квадратный корень, называется извлечением квадратного корня.

Извлечение корня (квадратного) является действием, обратным возведению в квадрат: при возведении в квадрат известно число, требуется найти его квадрат; при извлечении квадратного корня известен квадрат числа, требуется найти само число.

Поэтому правильность извлечения квадратного корня можно проверить, возведя найденный корень в квадрат; если получится данное число, значит, корень найден верно.

Рассмотрим уравнение

x² = a (1)

при различных значениях a.

1) Пусть a < 0.

В этом случае уравнение (1) не имеет решений. Действительно, какое бы значение x мы ни взяли, квадрат его будет всегда неотрицательным числом (т. е. положительным числом или нулем) и, следовательно, не может равняться отрицательному числу a.

2) Пусть a = 0.

Очевидно, что в этом случае уравнение (1) имеет единственное решение x = 0.

Действительно, 0² = 0 * 0 = 0, если же x ≠ 0, то и x² ≠ 0.

3) Пусть a > 0.

В этом случае, как мы уже видели на примере уравнения x² = 81, уравнение может иметь решение.

Из всего сказанного можно сделать вывод:

Для того чтобы из числа можно было извлечь квадратный корень, необходимо, чтобы оно было неотрицательным числом, то есть положительным числом или нулем.

Иррациональные числа: Корень из двух

Несложно заметить: число √2 встречается там, где речь идёт о квадратах или удвоении площади. И где же это происходит? Начнём, пожалуй, с вещей, которые ежедневно попадают нам в руки. Таких, как бумага в принтере.

Формат бумаги — стандартизованный размер бумажного листа. Все страны мира, кроме Канады и США, пользуются международным стандартом ISO 216. Все форматы бумаги ISO имеют одно и то же соотношение сторон, равное 1 ÷ √2, так называемому отношению Лихтенберга (немецкий учёный Георг Лихтенберг в 1768 году первый заметил преимущества использования бумажного листа с таким отношением сторон).

Интересно следующее: поскольку отношение большей стороны к меньшей постоянно, при последовательном разрезании листа А0 на меньшие форматы левый нижний край, правый верхний и точки, в которых сходятся три разреза, согласно теореме Фалеса, будут лежать на одной прямой.

Этот формат был создан в 1975 году на основе немецкого стандарта DIN 476 и отличается от него только бо́льшими допустимыми погрешностями. Базовый лист бумаги (А0) имеет площадь в 1 м² и соотношение сторон 1 ÷ √2. Все остальные размеры получаются разрезанием длинной стороны на две равные части, то есть площадь следующего листа равна половине площади предыдущего. Такое соотношение сторон сохраняется для всех последующих меньших форматов.

Арифметически это связано с равенством  . А именно: пусть стороны листа были x и √2x. Уменьшая вторую сторону в два раза и оставляя первую неизменной, мы уменьшаем площадь прямоугольника в два раза. Стороны стали x и . Найдём теперь отношение меньшей стороны к большей:

У фотографов тоже есть причина использовать число √2. Рассмотрим круг радиусом R. Его площадь равна πR². Если мы хотим построить круг вдвое большей площади, как вы думаете, на какое число необходимо умножить радиус? А если вдвое меньшей — на какое разделить? Опять нас ждёт встреча с числом √2.

Как это связано с фотографией? Когда мы снимаем в ручном режиме, то настраиваем фокус и экспозицию. Последняя определяется выдержкой и диафрагмой объектива — отверстием переменного радиуса, которое позволяет регулировать поток света, попадающего через объектив на плёнку или матрицу фотоаппарата. Если свет яркий, отверстие диафрагмы уменьшают, чтобы не засветить кадр. Если же света мало — пасмурный день или вообще ночное время, — отверстие диафрагмы увеличивают, иначе кадр получится слишком тёмным. Размеры диафрагмы имеют фиксированное значение: при закрытии на одно деление площадь отверстия уменьшается вдвое, ну а радиус, соответственно, в √2 раз. Делениям на шкале диафрагмы соответствуют так называемые диафрагменные числа: 2; 2,8; 4; 5,6; 8; 11; 16; 22 и так далее. Закономерность неочевидна, но на самом деле это не что иное, как приближённые значения степеней числа √2 (округлённые почему-то не по математическим законам):

Это связано с тем, что если мы хотим получить ряд кругов площадью каждый вдвое меньше предыдущего, то радиус исходного круга мы должны будем последовательно делить на √2. Таким образом, отношение радиусов двух произвольных кругов из этого ряда всегда будет равно степени числа √2.

Поиск гармонии

Пифагорейцы изучали связь между гармонией природы и математикой, поэтому они искали числовые пропорции во всех окружающих явлениях. И, надо сказать, преуспели в этом. Например, выяснилось, что гармонические соотношения между нотами соответствуют определённым отношениям целых чисел (стоит ли говорить, что частоту звука можно напрямую связать с длиной струны — геометрической величиной).

Число √2 как пропорциональное отношение часто встречается в архитектуре: оно есть во всех квадратах, которые только можно начертить. Поэтому корень из двух занимает почётное место в искусстве, прежде всего в архитектуре и дизайне.

В барселонском парке Гуэль, спроектированном великим Антонио Гауди, вместо чётких прямых линий мы наблюдаем очертания различной кривизны; центральным элементом паркового ансамбля является терраса, поддерживаемая греческими колоннами. Изогнутый потолок, причудливые формы постройки могут вызвать ложное ощущение, что архитектор не придерживался какой-либо рациональной системы. Однако если посмотреть план сооружения, сразу видно, что его стабильность обеспечена геометрией квадратов, в вершины которых Гауди поместил вершины колонн. Ещё на чертеже можно заметить правильные восьмиугольники (октагоны), в которых тоже скрыто наше любимое число √2, ведь в каждом октагоне есть как минимум три квадрата.

Слабость к правильному вось­миугольнику питали архитекторы разных эпох. Купол кафедрального флорентийского собора Санта-Мария-дель-­Фьоре, Башня Ветров в Афинах, замок ­Кастель-дель-Монте на юге Италии, Капелла Карла Великого в немецком Ахене и многие другие постройки, всех не перечислить, имеют форму октагона.

Возможно, корень из двух не самое примечательное иррациональное число. Есть множество иррациональных чисел (π, экспонента е) и соотношений (например, золотое сечение), о которых можно рассказать больше интересного. Но важно понимать, что изучение таких чисел началось именно с √2. Его открытие перевернуло представления человечества о числе, положило начало изучению чисел как непрерывного множества и расширило возможности познания мира. В результате идея, что числа лежат в основе всех проявлений науки и техники, сегодня уже не вызывает сомнений. 

проверочное слово к буквам «д», «о»

Безударный глас­ный в сло­ве «пло­щад­ка» про­ве­рит одно­ко­рен­ное суще­стви­тель­ное «пло́щадь». Написание бук­вы «д» дока­жут их падеж­ные фор­мы — нет пло­ща­ди, пло­ща­док и род­ствен­ное сло­во «пло­ща­доч­ка»

В корне сло­ве «площад­ка» удар­ным явля­ет­ся глас­ный вто­ро­го сло­га, из-за чего неяс­но слы­шит­ся в без­удар­ной пози­ции пер­вый гласный:

площа́дка — корень/суффикс/окончание

Возникает сомне­ние, какую бук­ву, «о» или «а», сле­ду­ет писать в этом слове.

Правописание слова «площадка»

Обычно без­удар­ные глас­ные в сло­вах про­ве­ря­ют уда­ре­ни­ем, так как в без­удар­ном поло­же­нии пишет­ся та же глас­ная бук­ва, кото­рая высту­па­ет в том же сло­ге, когда она нахо­дит­ся под уда­ре­ни­ем в любой грам­ма­ти­че­ской фор­ме сло­ва или в подо­бран­ных одно­ко­рен­ных лексемах.

Понаблюдаем, как мож­но про­ве­рить без­удар­ные глас­ные в корне сле­ду­ю­щих слов:

• окно́ — о́кна;
• каче́ли — ка́чка;
• весёлый — ве́село;
• появи́лись — я́вка.

Чтобы выбрать бук­ву «о» или «а» в корне суще­стви­тель­но­го «пло­щад­ка», поищем про­ве­роч­ное сло­во. В пра­виль­ном напи­са­нии без­удар­но­го глас­но­го помо­жет одно­ко­рен­ное суще­стви­тель­ное «пло́щадь».

Вывод

В корне сло­ва «пло­щад­ка» пра­виль­но пишет­ся бук­ва «о», что дока­жет про­ве­роч­ное сло­во «пло­щадь».

Второе ошиб­ко­опас­ное место в рас­смат­ри­ва­е­мом сло­ве — это соче­та­ние «ща», кото­рое по пра­ви­лу орфо­гра­фии пишем толь­ко с бук­вой «а».

Проверяем букву «д» в слове «площадка»

Перед суф­фик­сом -к- оглу­ша­ет­ся конеч­ный соглас­ный кор­ня сло­ва, и вме­сто него слы­шит­ся пар­ный глу­хой соглас­ный [т]:

[п л а щ’ а т к а]

Чтобы и здесь не сде­лать орфо­гра­фи­че­скую ошиб­ку, изме­ним рас­смат­ри­ва­е­мое сло­во и род­ствен­ное суще­стви­тель­ное «пло­щадь» по паде­жам, в резуль­та­те чего глас­ный, появив­ший­ся после соглас­но­го, тре­бу­ю­ще­го про­вер­ки, высве­тит нуж­ный соглас­ный в корне:

• пло­щадь — нет площади;
• площа́дка — мно­го площадок.

Второй спо­соб про­вер­ки напи­са­ния бук­вы «д» в корне ана­ли­зи­ру­е­мо­го суще­стви­тель­но­го — поиск род­ствен­но­го сло­ва. Однокоренное суще­стви­тель­ное «пло­ща­доч­ка» про­из­но­сит­ся с чет­ко зву­ча­щим соглас­ным «д».

Вывод

Проверочные сло­ва к сло­ву «пло­щад­ка» — «пло­щадь», «пло­ща­доч­ка»; фор­мы суще­стви­тель­ных — «пло­ща­ди», «пло­ща­док».

Примеры

А ты зна­ешь, где нахо­дит­ся дет­ская площа́дка в парке?

Наша дет­ская площа́дка хоро­шо обо­ру­до­ва­на для подвиж­ных игр малышей.

Лестничная площа́дка выло­же­на кра­си­вой цвет­ной плиткой.

Скачать ста­тью: PDF

7 способов найти площадь прямоугольника

1. Если известны две соседние стороны

Просто перемножьте две стороны прямоугольника.

• S — искомая площадь прямоугольника;
• a и b — соседние стороны.

2. Если известны любая сторона и диагональ

Найдите квадраты диагонали и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте длину известной стороны на полученное число.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).

3.

Если известны любая сторона и диаметр описанной окружности

Найдите квадраты диаметра и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте известную сторону на полученное число.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• D — диаметр описанной окружности.

4. Если известны любая сторона и радиус описанной окружности

Найдите квадрат радиуса и умножьте результат на 4.

Отнимите от полученного числа квадрат известной стороны.

Найдите корень из результата и умножьте на него длину известной стороны.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• R — радиус описанной окружности.

5. Если известны любая сторона и периметр

Умножьте периметр на длину известной стороны.

Найдите квадрат известной стороны и умножьте полученное число на 2.

От первого произведения отнимите второе и разделите результат на 2.

6. Если известны диагональ и угол между диагоналями

Найдите квадрат диагонали.

Разделите полученное число на 2.

Умножьте результат на синус угла между диагоналями.

• S — искомая площадь прямоугольника;
• d — любая диагональ прямоугольника;
• α — любой угол между диагоналями прямоугольника.

7. Если известны радиус описанной окружности и угол между диагоналями

Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.

Умножьте полученное число на 2, а потом на синус угла между диагоналями.

• S — искомая площадь прямоугольника;
• R — радиус описанной окружности;
• α — любой угол между диагоналями прямоугольника.

Читайте также 🎓❓📐

{2} = \ left (-3 \ right) \ cdot \ left (-3 \ right) = 9 $$

3 и -3 считаются квадратными корнями из 9.

Все положительные действительные числа имеют два квадратных корня, один положительный квадратный корень и один отрицательный квадратный корень. {2} = a \ cdot a = \ left (-a \ right) \ cdot \ left (-a \ right) $$

Квадратный корень записывается с помощью символа корня √, а число или выражение внутри символа корня, обозначенное ниже a, называется подкоренным выражением.

$$ \ sqrt {a} $$

Чтобы указать, что нам нужен как положительный, так и отрицательный квадратный корень из подкоренной части, мы помещаем символ ± (читается как плюс минус) перед корнем.

$$ \ pm \ sqrt {9} = \ pm 3 $$

У нуля один квадратный корень, равный 0.

$$ \ sqrt {0} = 0 $$

Отрицательные числа не имеют действительных квадратных корней, поскольку квадрат либо положительный, либо 0.

Если квадратный корень целого числа является другим целым числом, квадрат называется полным квадратом.Например, 25 — это идеальный квадрат, так как

$$ \ pm \ sqrt {25} = \ pm 5 $$

Если подкоренное выражение не является точным квадратом, то есть квадратный корень не является целым числом, вам нужно приблизительно вычислить квадратный корень

$$ \ pm \ sqrt {3} = \ pm 1.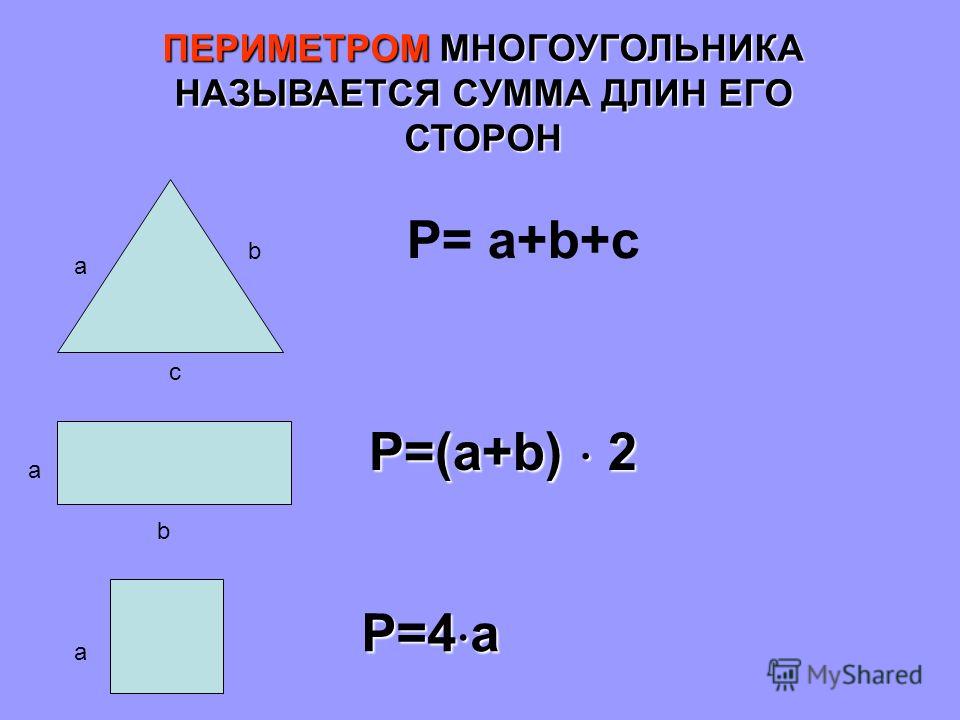 73205 … \ приблизительно \ pm 1,7 $$

Квадратные корни из чисел, не являющихся полным квадратом, являются членами иррациональных чисел. Это означает, что они не могут быть записаны как частное двух целых чисел. Десятичная форма иррационального числа не прерывается и не повторяется.Иррациональные числа вместе с рациональными числами составляют действительные числа.

---

Видеоурок

Приблизительно квадратный корень из 250

Калькулятор квадратного корня

. Найдите квадратный корень за один простой шаг.

Наш калькулятор квадратного корня вычисляет квадратный корень любого положительного числа, которое вы хотите. Просто введите выбранный номер и ознакомьтесь с результатами. Все рассчитывается быстро и автоматически ! С помощью этого инструмента вы также можете оценить квадрат желаемого числа (просто введите значение во второе поле), что может оказаться большим подспорьем в поиске точных квадратов из формулы квадратного корня. Вы боретесь с основными арифметическими операциями: сложение квадратных корней, вычитание квадратных корней, умножение квадратных корней или деление квадратных корней? Уже нет! В следующем тексте вы найдете подробное объяснение о различных свойствах квадратного корня, например, как упростить квадратный корень, с множеством различных примеров . Из этой статьи вы раз и навсегда узнаете, как находить квадратные корни!

Вы когда-нибудь задумывались, каково происхождение символа квадратного корня √? Уверяем вас, что эта история не так проста, как вы могли подумать вначале.Происхождение символа корня восходит к древним временам, как происхождение знака процента.

Если вам нужен график квадратного корня или свойства функции квадратного корня, перейдите непосредственно в соответствующий раздел (просто нажмите на ссылки выше!). Здесь мы объясняем, что такое производная квадратного корня, используя определение фундаментального квадратного корня; мы также подробно рассмотрим, как вычислять квадратные корни из экспонент или квадратные корни из дробей. Наконец, если вы будете достаточно настойчивы, вы обнаружите, что квадратный корень из отрицательного числа на самом деле возможен.Таким образом, мы вводим комплексных чисел , которые находят широкое применение в физике и математике.

Символ квадратного корня √

Операция извлечения квадратного корня из числа была известна еще в древности. Самая ранняя глиняная табличка с правильным значением √2 = 1,41421 до 5 знаков после запятой происходит из Вавилонии (1800 г. до н.э. — 1600 г. до н.э.) г. Многие другие документы показывают, что квадратные корни также использовали древние египтяне, индийцы, греки и китайцы. Однако происхождение корневого символа √ все еще остается в значительной степени спекулятивным.

• Многие ученые считают, что квадратные корни происходят от буквы «r» — первой буквы латинского слова Radix, означающего корень,
• другая теория утверждает, что символ квадратного корня был взят из арабской буквы ج , которая была помещена в исходной форме ﺟ в слове جذر — корень (арабский язык пишется справа налево).

Первое использование символа квадратного корня √ не включало горизонтальную «черту» над числами внутри символа квадратного корня (или радикала), √‾.«Бар» на латыни известен как vinculum, что означает облигация . Хотя радикальный символ с винкулумом сейчас используется в повседневной жизни, мы обычно опускаем эту черту во многих текстах, например, в статьях в Интернете. Обозначение высших степеней корня было предложено Альбертом Жираром, который поместил указатель степени в начало знака корня, например, ³√ или ⁴√.

Последний вопрос: почему операция извлечения квадратного корня называется корнем независимо от ее истинного происхождения? Объяснение станет более очевидным, если мы запишем уравнение x = ⁿ√a в другой форме: xⁿ = a.x называется корнем или радикалом, потому что это скрытое основание a. Таким образом, слово радикальный не означает далеко идущий или крайний , а вместо этого основополагающий, достигающий первопричины .

Определение квадратного корня

В математике традиционными операциями с числами являются сложение, вычитание, умножение и деление. Тем не менее, мы иногда добавляем в этот список некоторые более сложные операции и манипуляции: квадратные корни , возведение в степень, логарифмические функции и даже тригонометрические функции (например,г., синус и косинус). В этой статье мы сосредоточимся только на определении квадратного корня.

Квадратный корень из заданного числа x — это каждое число y , квадрат которого y² = y * y дает исходное число x . Следовательно, формула квадратного корня может быть выражена как:

√x = y ⟺ x = y² ,

, где ⟺ — математический символ, который означает тогда и только тогда, когда . Каждое положительное действительное число всегда имеет два квадратных корня — первый положительный, а второй отрицательный. (0,5)

В геометрической интерпретации квадратный корень из данной площади квадрата дает длину его стороны. Вот почему в названии √ есть слово , квадрат . Аналогичная ситуация и с кубическим корнем ∛ . Если вы берете кубический корень из объема куба, вы получаете длину его ребер. В то время как квадратные корни используются при рассмотрении площади поверхности, кубические корни полезны для определения величин, относящихся к объему, например плотности.

Как найти квадратный корень?

Может быть, мы не очень скромны, но мы думаем, что лучший ответ на вопрос, как найти квадратный корень, прост: используйте калькулятор квадратного корня! Вы можете использовать его как на компьютере, так и на смартфоне, чтобы быстро вычислить квадратный корень из заданного числа.К сожалению, бывают ситуации, когда можно рассчитывать только на себя, что тогда? Чтобы подготовиться к этому, вы должны запомнить несколько основных идеальных квадратных корней:

• квадратный корень из 1: √1 = 1 , так как 1 * 1 = 1 ;
• квадратный корень из 4: √4 = 2 , так как 2 * 2 = 4 ;
• квадратный корень из 9: √9 = 3 , так как 3 * 3 = 9 ;
• квадратный корень из 16: √16 = 4 , так как 4 * 4 = 16 ;
• квадратный корень из 25: √25 = 5 , так как 5 * 5 = 25 ;
• квадратный корень из 36: √36 = 6 , так как 6 * 6 = 36 ;
• квадратный корень из 49: √49 = 7 , так как 7 * 7 = 49 ;
• квадратный корень из 64: √64 = 8 , так как 8 * 8 = 64 ;
• квадратный корень из 81: √81 = 9 , так как 9 * 9 = 81 ;
• квадратный корень из 100: √100 = 10 , так как 10 * 10 = 100 ;
• квадратный корень из 121: √121 = 11 , так как 11 * 11 = 121 ;
• квадратный корень из 144: √144 = 12 , так как 12 * 12 = 144 ;

Приведенные выше числа являются простейшими квадратными корнями, потому что каждый раз вы получаете целое число. Попробуй их запомнить! Но что делать, если есть число, у которого нет такого красивого квадратного корня? Есть несколько решений. Прежде всего, можно попробовать предсказать результат методом проб и ошибок . Допустим, вы хотите вычислить квадратный корень из 52 :

1. Вы знаете, что √49 = 7 и √64 = 8 , поэтому значение √52 должно быть между 7 и 8 .
2. Число 52 ближе к 49 (фактически ближе к 7 ), поэтому вы можете попробовать угадать, что √52 — это 7.3 .
3. Затем возводите в квадрат 7,3 , получая 7,3² = 53,29 (как говорит формула квадратного корня), что больше, чем 52 . Вы должны попробовать с меньшим числом, скажем 7.2 .
4. Квадрат 7,2 равен 51,84 . Теперь у вас меньше номер, но он намного ближе к 52 . Если такая точность вас устраивает, можете закончить оценку здесь. В противном случае вы можете повторить процедуру с выбранным числом от 7.2 и 7.3 , например, 7.22 и так далее и так далее.

Другой подход состоит в том, чтобы сначала упростить квадратный корень, а затем использовать приближения квадратных корней из простых чисел (обычно с округлением до двух знаков после запятой):

• квадратный корень из 2: √2 ≈ 1,41 ,
• квадратный корень из 3: √3 ≈ 1,73 ,
• квадратный корень из 5: √5 ≈ 2,24 ,
• квадратный корень из 7: √7 ≈ 2.65 ,
• квадратный корень из 11: √11 ≈ 3,32 ,
• квадратный корень из 13: √13 ≈ 3,61 ,
• квадратный корень из 17: √17 ≈ 4,12 ,
• квадратный корень из 19: √19 ≈ 4,34 и т. Д.

Давайте попробуем снова найти квадратный корень из 52 . Вы можете упростить его до √52 = 2√13 (вы узнаете, как упростить квадратный корень в следующем разделе), а затем замените √13 ≈ 3,61 . Наконец, произведем умножение √52 ≈ 2 * 3.61 = 7,22 . Результат такой же, как и раньше!

Вы можете проверить, является ли число простым или нет, с помощью нашего калькулятора простых чисел. Простое число — это натуральное число (больше единицы), которое не может быть получено как произведение двух меньших натуральных чисел. Например, 7 — простое число, потому что вы можете получить его, только умножив 1 * 7 или 7 * 1 . С другой стороны, число 8 не является простым, потому что вы можете сформировать его, умножив 2 * 4 или 4 * 2 (помимо произведения 1 и самого 8).

Калькулятор квадратного корня

В некоторых ситуациях вам не нужно знать точный результат вычисления квадратного корня. В этом случае наш калькулятор квадратного корня — лучший вариант для оценки значения каждого квадратного корня , который вы хотите. Например, предположим, вы хотите узнать, больше ли 4√5 , чем 9 . Из калькулятора вы знаете, что √5 ≈ 2,23607 , поэтому 4√5 ≈ 4 * 2,23607 = 8,94428 . Он очень близок к 9 , но не больше его! Калькулятор квадратного корня дает окончательное значение с относительно высокой точностью (до пяти цифр в приведенном выше примере).С помощью калькулятора значащих цифр вы можете вычислить этот результат до любого количества значащих цифр.

Помните, что наш калькулятор автоматически пересчитывает числа, введенные в любое из полей. Вы можете найти квадратный корень из определенного числа, заполнив первое окно, или получить квадрат числа, введенного вами во втором окне. Второй вариант удобен в для нахождения идеальных квадратов , которые необходимы во многих аспектах математики и естествознания.Например, если вы введете 17 во второе поле, вы обнаружите, что 289 — это полный квадрат.

В некоторых приложениях квадратного корня, особенно относящихся к таким наукам, как химия и физика, предпочтение отдается результатам в научной нотации. Короче говоря, ответ в научном представлении должен иметь десятичную точку между первыми двумя ненулевыми числами и будет представлен как десятичная дробь, умноженная на 10, возведенная в степень. Например, номер 0.00345 записывается как 3,45 * 10⁻³ в экспоненциальном представлении, тогда как 145,67 записывается как 1,4567 * 10² в экспоненциальном представлении. Результаты, полученные с помощью калькулятора квадратного корня, можно преобразовать в экспоненциальную нотацию с помощью калькулятора.

Как упростить извлечение квадратного корня?

Во-первых, давайте спросим себя, какие квадратные корни можно упростить. Чтобы ответить на него, вам нужно взять число, стоящее после символа квадратного корня, и найти его множители.Если какой-либо из его множителей является квадратным числом (4, 9, 16, 25, 36, 49, 64 и т. Д.), То вы можете упростить квадратный корень. Почему эти числа квадратные? Они могут быть соответственно выражены как 2², 3², 4², 5², 6², 7² и так далее. Согласно определению квадратного корня, вы можете назвать их полными квадратами . У нас есть специальный инструмент, называемый калькулятором коэффициентов, который может быть здесь очень кстати. Давайте посмотрим на несколько примеров:

• Можно ли упростить √27? С помощью упомянутого выше калькулятора вы получаете множители 27: 1, 3, 9, 27.(1/2) ⟺ √ (x * y) = √x * √y ,

  Как вы можете использовать эти знания? Аргумент квадратного корня обычно не является точным квадратом, который можно легко вычислить, но он может содержать идеальный квадрат среди своих множителей. Другими словами, вы можете записать это как умножение двух чисел, где одно из чисел представляет собой полный квадрат, например, 45 = 9 * 5 (9 — это полный квадрат). Требование иметь по крайней мере один множитель , который является полным квадратом, необходимо для упрощения квадратного корня. (1/2) = √9 * √5 = 3√5 .

  Вы успешно упростили свой первый квадратный корень! Конечно, вам не обязательно записывать все эти расчеты. Если вы помните, что квадратный корень эквивалентен степени половины , вы можете сократить их. Попрактикуемся в упрощении квадратных корней на некоторых других примерах:

  • Как упростить квадратный корень из 27? √27 = √ (9 * 3) = √9 * √3 = 3√3 ;
  • Как упростить квадратный корень из 8? √8 = √ (4 * 2) = √4 * √2 = 2√2 ;
  • Как упростить квадратный корень из 144? √144 = √ (4 * 36) = √4 * √36 = 2 * 6 = 12 .

  В последнем примере вам вообще не нужно было упрощать квадратный корень, потому что 144 — это полный квадрат. Вы можете просто вспомнить, что 12 * 12 = 144. Однако мы хотели показать вам, что с помощью процесса упрощения вы также можете легко вычислить квадратные корни из полных квадратов. Это полезно, когда имеет дело с большими числами .

  Наконец, вы можете спросить, как упростить корни более высокого порядка, например, кубические корни. Фактически, этот процесс очень похож на квадратные корни, но в случае кубических корней вы должны найти хотя бы один множитель, который представляет собой идеальный куб , а не идеальный квадрат, т.е.е., 8 = 2³, 27 = 3³, 64 = 4³, 125 = 5³ и так далее. Затем вы делите свое число на две части и кладете под кубический корень. Возьмем следующий пример упрощения ³√192:

  ∛192 = ∛ (64 * 3) = ∛64 * ∛3 = 4∛3

  На первый взгляд это может показаться немного сложным, но после некоторой практики вы сможете упростить корни в своей голове . Доверься нам!

  Сложение, вычитание, умножение и деление квадратных корней

  Сложение квадратных корней и вычитание квадратных корней

  К сожалению, сложение или вычитание квадратных корней не так просто, как сложение / вычитание обычных чисел. Например, если 2 + 3 = 5, это не означает, что √2 + √3 равно √5. Это неправильно! Чтобы понять, почему это так, представьте, что у вас есть два разных типа фигур: треугольники 🔺 и круги 🔵. Что произойдет, если вы добавите один треугольник к одному кругу 🔺 + 🔵? Ничего такого! У вас остались один треугольник и один круг 🔺 + 🔵. С другой стороны, что произойдет, если вы попытаетесь добавить три треугольника к пяти треугольникам: 3 🔺 + 5 🔺? У нас получится восемь треугольников 8 🔺.

  Сложение квадратного корня очень похоже на это.Результат сложения √2 + √3 по-прежнему равен √2 + √3. Вы не можете упростить это дальше. Однако это другая ситуация, когда оба квадратных корня имеют одинаковое число под символом корня . Затем мы можем складывать их как обычные числа (или треугольники). Например, 3√2 + 5√2 равно 8√2. То же самое и с вычитанием квадратных корней. Давайте посмотрим на другие примеры, иллюстрирующие это свойство квадратного корня:

  • Что такое 6√17 + 5√17 ? Ответ: 6√17 + 5√17 = 11√17 ;
  • Что такое 4√7 - 7√7 ? Ответ: 4√7 - 7√7 = -3√7 ;
  • Что такое 2√2 + 3√8 ? Ответ: 2√2 + 3√8 = 2√2 + 6√2 = 8√2 , потому что мы упростили √8 = √ (4 * 2) = √4 * √2 = 2√2;
  • Что такое √45 - √20 ? Ответ: √45 - √20 = 3√5 - 2√5 = √5 , потому что мы упростили √45 = √ (9 * 5) = √9 * √5 = 3√5 и √20 = √ (4 * 5) = √4 * √5 = 2√5;
  • Что такое 7√13 + 2√22 ? Ответ: 7√13 + 2√22 , мы не можем упростить это дальше;
  • Что такое √3 - √18 ? Ответ: √3 - √18 = √3 - 3√2 , мы не можем упростить это дальше, чем это, но мы, по крайней мере, упростили √18 = √ (9 * 2) = √9 * √2 = 3√ 2. (1/2) ⟺ √x * √y = √ (x * y) .

    В отличие от сложения, вы можете умножить каждые на два квадратных корня. Помните, что умножение имеет коммутативные свойства , это означает, что порядок, в котором умножаются два числа, не имеет значения. Несколько примеров должны прояснить этот вопрос:

    • Что такое √3 * √2 ? Ответ: √3 * √2 = √6 ;
    • Что такое 2√5 * 5√3 ? Ответ: 2√5 * 5√3 = 2 * 5 * √5 * √3 = 10√15 , потому что умножение коммутативно;
    • Что такое 2√6 * 3√3 ? Ответ: 2√6 * 3√3 = 2 * 3 * √6 * √3 = 6√18 = 18√3 , мы упростили √18 = √ (9 * 2) = √9 * √2 = 3√ 2.(1/2) ⟺ √x / √y = √ (x / y) .

      Все, что вам нужно сделать, это заменить знак умножения на деление. Однако дивизия — это не коммутативный оператор ! Вы должны отдельно вычислять числа перед квадратными корнями и числа под квадратными корнями. (1/2) .(1/2) ⟺ √x / √y = √ (x / y) ,

      , где x / y — дробь. Ниже вы можете найти несколько примеров квадратных корней из дроби:

      • квадратный корень из 4/9: √ (4/9) = √4 / √9 = 2/3 ,
      • квадратный корень из 1/100: √ (1/100) = √1 / √100 = 1/10 ,
      • квадратный корень из 1/5: √ (1/5) = √1 / √5 = 1 / √5 = √5 / 5 .

      Оставлять корни в знаменателе — не очень хорошая привычка. Вот почему мы избавились от него в последнем примере.Мы просто умножили числитель и знаменатель на одно и то же число (мы всегда можем это сделать, так как число, которое мы умножаем на 1), в данном случае на √5 .

      Функция квадратного корня и график

      Функции играют жизненно важную роль не только в математике, но и во многих других областях, таких как физика, статистика или финансы. Функция f (x) — это не что иное, как формула, которая говорит, как значение f (x) изменяется с аргументом x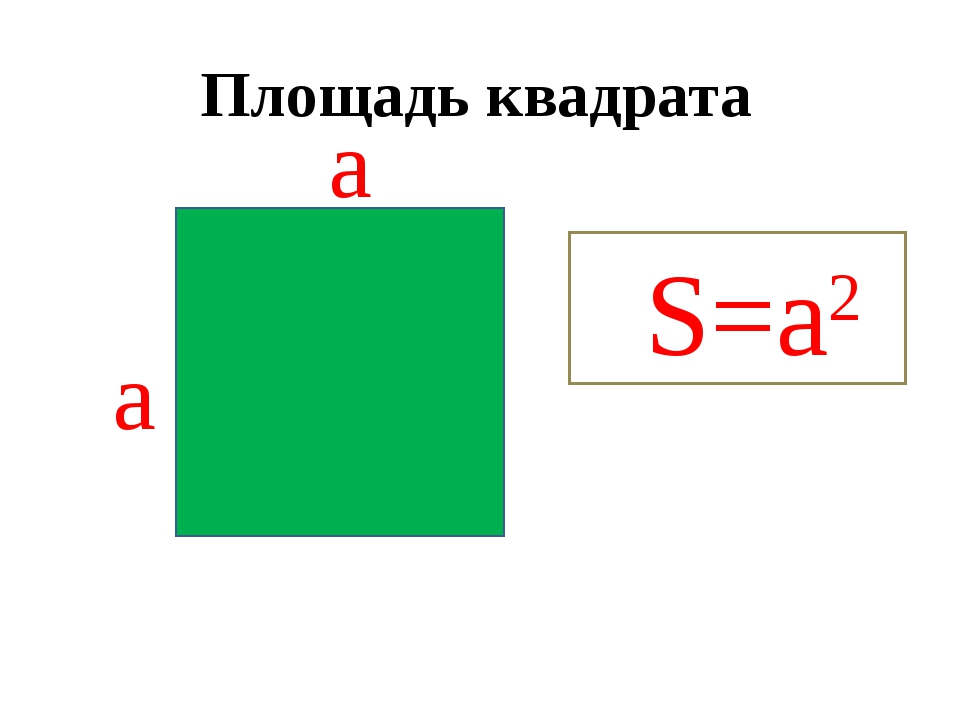 . Чтобы увидеть некоторые примеры, ознакомьтесь с нашими финансовыми инструментами, созданными финансовыми специалистами, например, калькулятор сложных процентов или калькулятор будущей стоимости.Там вы найдете несколько функций, которые можно применить в реальной жизни. Они очень полезны, если вы хотите знать, как рассчитать сложные проценты или оценить будущую стоимость аннуитета.

      Ниже вы можете найти график квадратного корня, состоящий из половин параболы . Проверьте его и попробуйте проверить, например, является ли функция квадратного корня x = 9 3 и x = 16 равным 4 (как и должно быть).

      Давайте вернемся к функции квадратного корня f (x) = √x и исследуем ее основные свойства .Мы рассматриваем только положительную часть f (x) (как вы можете видеть на графике квадратного корня выше). Итак, функция квадратного корня:

      • — это непрерывный и растущий для всех неотрицательных x ,
      • — это , дифференцируемое для всех положительных значений x (дополнительные сведения см. В разделе о производной квадратного корня),
      • приближается к пределу бесконечности , когда x приближается к бесконечности ( lim √x → ∞ , когда x → ∞ ),
      • — это действительное число для всех неотрицательных x и комплексное число для всех отрицательных x (подробнее об этом мы пишем в разделе квадратного корня из отрицательного числа).

      Вы, наверное, уже заметили, что квадратный корень из площади квадрата дает длину его стороны. Эта функция используется в одном из наших строительных калькуляторов — калькуляторе квадратных метров. Если вы планируете что-либо отремонтировать в будущем, эти инструменты могут вам очень помочь. Не забывайте их использовать!

      Производная квадратного корня

      Производная функции сообщает нам, насколько быстро эта функция изменяется вместе со своим аргументом. Один из простейших примеров в физике — это положение объекта и его скорость (скорость изменения положения). Допустим, функция x (t) описывает, как расстояние движущегося автомобиля от определенной точки изменяется со временем t . Вы знаете, что определяет, насколько быстро меняется пройденное вами расстояние? Ответ — скорость машины! Таким образом, производная положения x (t) равна скорости v (t) (скорость также может зависеть от времени). Для обозначения производной мы обычно используем апостроф v (t) = x '(t) или символ производной v (t) = dx (t) / dt .(-1/2) = 1 / (2√x) .

      Так как число в отрицательной степени на единицу больше этого числа, оценка вывода будет включать дроби. У нас есть инструмент, который может оказаться незаменимым при сложении или вычитании дробей с разными знаменателями. Он называется калькулятором НОК и объясняет, как найти наименьшее общее кратное.

      Производная квадратного корня необходима для получения коэффициентов в так называемом разложении Тейлора . Мы не хотим слишком углубляться в детали, поэтому, вкратце, серия Тейлора позволяет вам аппроксимировать различные функции с помощью многочленов, которые намного проще вычислить.Например, разложение Тейлора √ (1 + x) около точки x = 0 дается следующим образом:

      √ (1 + x) = 1 + 1/2 * x - 1/8 * x² + 1/16 * x³ - 5/128 * x⁴ + ... ,

      , что действительно для -1 ≤ x ≤ 1 . Хотя в приведенном выше выражении содержится бесконечное количество членов, чтобы получить приблизительное значение, вы можете использовать всего несколько первых членов. Давай попробуем! С x = 0,5 и первыми пятью членами вы получите:

      √ (1,5) = 1 + 1/2 * 0.5 - 1/8 * 0,25 + 1/16 * 0,125 - 5/128 * 0,0625 ,

      √ (1,5) ≈ 1,2241 ,

      , а действительное значение, предоставленное нашим калькулятором, составляет √ (1,5) ≈ 1,2247 . Достаточно близко!

      Пока что это было много математики и уравнений. Для тех из вас, кто достаточно настойчив, мы подготовили следующий раздел, в котором объясняется, как вычислить квадратный корень из отрицательного числа.

      Корень квадратный из отрицательного числа

      В школе вас, вероятно, учили, что квадратного корня из отрицательного числа не существует.Это верно, если рассматривать только действительные числа. Давным-давно для выполнения сложных вычислений математикам пришлось ввести более общий набор чисел — комплексные числа . Их можно выразить в следующей форме:

      х = а + Ь * я ,

      , где x — комплексное число с действительной частью a и мнимой частью b . Что отличает комплексное число от действительного, так это мнимое число i .Вот несколько примеров комплексных чисел: 2 + 3i , 5i , 1,5 + 4i , 2 . Вы можете быть удивлены, увидев там 2 , которое является настоящим числом. Да, но это также комплексное число с b = 0 . Комплексные числа являются обобщением действительных чисел.

      Пока что воображаемое число i , наверное, до сих пор для вас загадка. Что это вообще такое? Что ж, хотя это может показаться странным, это определяется следующим уравнением:

      я = √ (-1) ,

      , и это все, что вам нужно для вычисления квадратного корня из каждого числа, независимо от того, положительное оно или нет.Давайте посмотрим на несколько примеров:

      • квадратный корень из -9: √ (-9) = √ (-1 * 9) = √ (-1) √9 = 3i ,
      • квадратный корень из -13: √ (-13) = √ (-1 * 13) = √ (-1) √13 = i√13 ,
      • квадратный корень из -49: √ (-49) = √ (-1 * 49) = √ (-1) √49 = 7i .

      Разве это не просто? Эта проблема не возникает с кубическим корнем, поскольку отрицательное число можно получить, умножив три одинаковых отрицательных числа (чего нельзя сделать с двумя отрицательными числами). 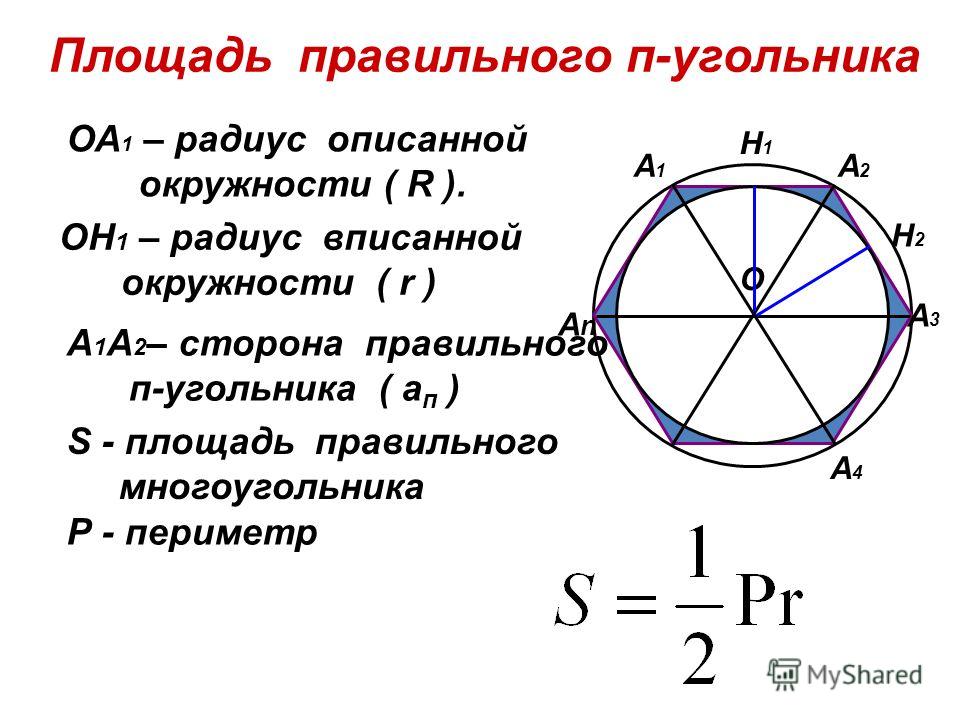Например:

      ³√ (-64) = ³√ [(- 4) * (- 4) * (- 4)] = -4 .

      Это, вероятно, все, что вам следует знать о квадратных корнях. Мы ценим, что вы остались с нами до этого момента! В качестве награды испеките себе что-нибудь сладкое 🙂 Воспользуйтесь нашим калькулятором идеальных блинов, чтобы узнать, как приготовить идеальный блин, каким бы он вам ни нравился. Вам может понадобиться наш калькулятор граммов в чашки, чтобы помочь вам в этом. Он работает в обоих направлениях, то есть для преобразования граммов в чашки и преобразования чашек в граммы.А если вы спросите себя: «Сколько калорий мне нужно съедать в день?», Воспользуйтесь нашим удобным калькулятором калорий!

      FAQ

      Может ли число иметь более одного квадратного корня?

      Да, на самом деле все положительные числа имеют 2 квадратных корня , один положительный, а другой равный первому, но отрицательный. Это связано с тем, что если вы умножите два негатива вместе, негативы аннулируются и результат будет положительным.

      Как найти квадратный корень без калькулятора?

      1. Вычислите квадратного корня.Ближайшее квадратное число приемлемо, если вы в затруднении.
      2. Разделите число, из которого вы хотите найти квадратный корень, на оценку.
      3. Добавьте оценку к результату шага 2.
      4. Разделите результат шага 3 на 2. Это ваша новая оценка .
      5. Повторите шаги 2–4 с новой оценкой. Чем больше раз это повторяется, тем точнее будет результат.

      Как вычислить квадратные корни?

      1. Найдите ближайшее квадратное число выше и ниже числа, о котором вы думаете.
      2. Квадратный корень будет между квадратными корнями этих чисел.
      3. Близость числа к квадратному корню указывает, насколько близок корень. Например, 26 очень близко к 25, поэтому корень будет очень близок к 5.
      4. Попробуйте несколько раз разобраться в этом .

      Является ли квадратный корень из 2 рациональным числом?

      Нет, корень квадратный из 2 не рационально . 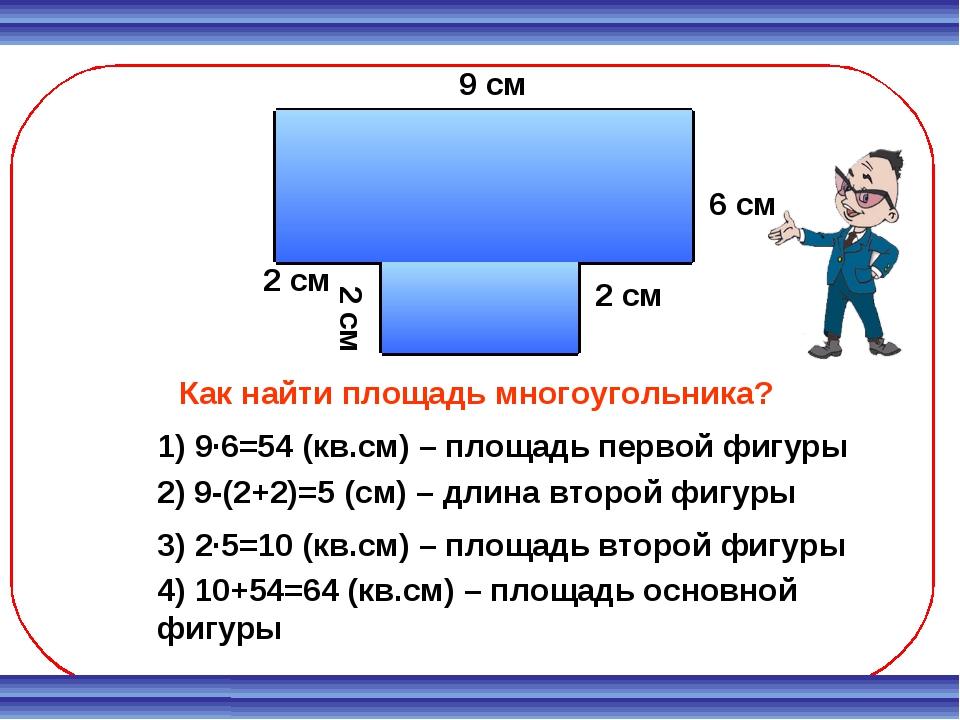Это связано с тем, что, когда 2 записывается как дробь, ² / ₁ , она никогда не может иметь только четные показатели, и поэтому рациональное число не может быть возведено в квадрат для его создания.

      Как избавиться от квадратного корня?

      В алгебре возведение в квадрат обеих частей уравнения избавит от любых квадратных корней . Результатом этой операции является то, что квадратные корни будут заменены любым числом, из которого они находили квадратный корень.

      Являются ли квадратные корни рациональными?

      Некоторые квадратные корни являются рациональными , а другие — нет. Вы можете определить, является ли квадратный корень рациональным или нет, выяснив, может ли число, которое вы извлекаете квадратным корнем, быть выражено только в терминах четных показателей (например,грамм. 4 = 2 ² /1 ² ). Если может, то его корень рациональный .

      Является ли квадратный корень из 5 рациональным числом?

      Квадратный корень из 5 — это , а не рациональное число . 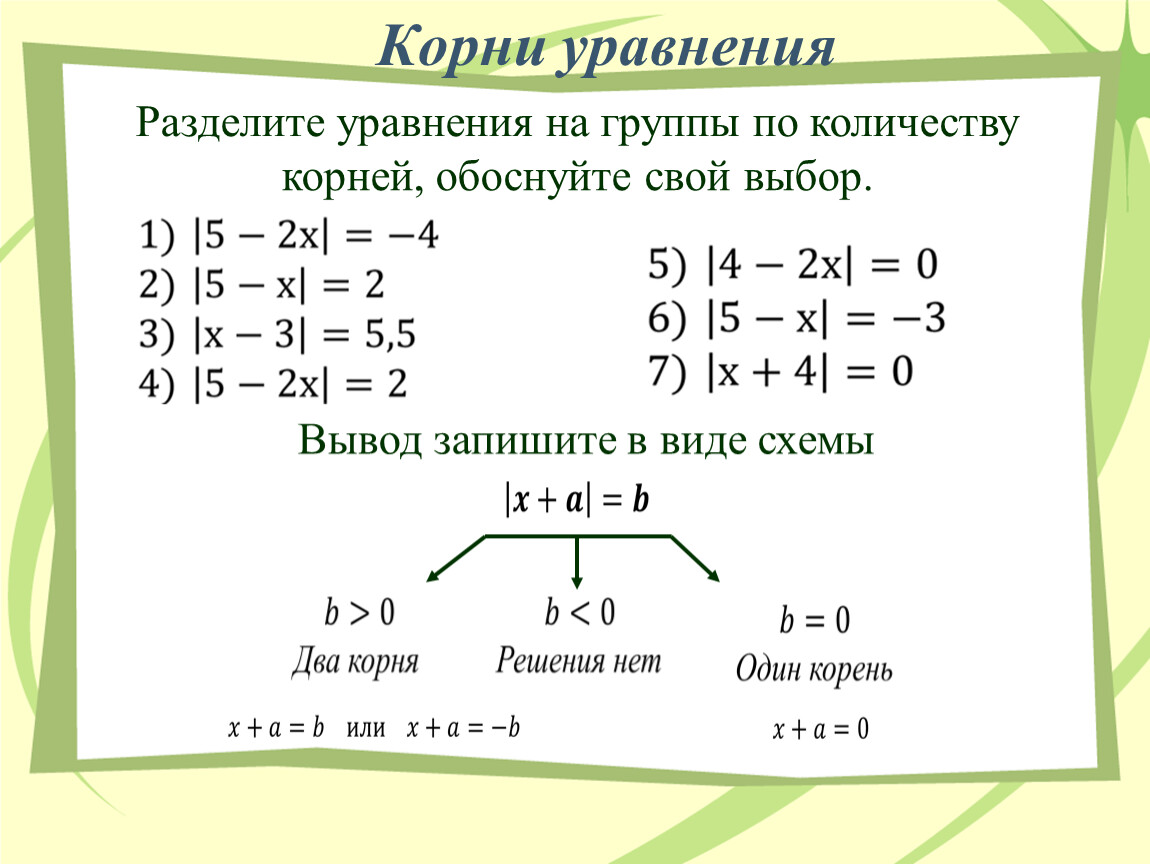Это связано с тем, что 5 не может быть выражено дробью, если числитель и знаменатель имеют четные показатели. Это означает, что рациональное число нельзя возвести в квадрат, чтобы получить 5.

      Является ли квадратный корень из 7 рациональным числом?

      Результатом квадратного корня 7 является иррациональное число .7 не может быть записано в виде дроби только с четными показателями, что означает, что число, возведенное в квадрат для достижения 7, не может быть выражено как дробь целых чисел, и поэтому не является рациональным.

      Какова производная квадратного корня из x?

      Производная квадратного корня x равна ^{x — 1 / ₂} / ₂ или ¹ / _{2SQRT (x)} . Это связано с тем, что квадратный корень из x может быть выражен как x ^{1 / ₂} , от которого обычно происходит дифференцирование.

      Как найти квадратный корень из десятичной дроби?

      1. Преобразует десятичную дробь в дробь .
      2. Найдите любой квадратный корень из дроби или оцените его. Сделайте дробью, равной квадратному корню, который вы нашли в квадрате.
      3. Отмените квадратный корень и квадрат, оставив дробь.
      4. Запишите дробь как десятичную в качестве окончательного ответа.

      Квадратные корни — объяснение и примеры

      В математике квадратный корень из числа x таков, что число y является квадратом x, упрощение записывается как y ² = x.

      Например, 5 и — 5 являются квадратными корнями из 25, потому что:

      5 x 5 = 25 и -5 x -5 = 25.

      Квадратный корень числа x обозначается знаком корня √x или x ^1/2 . Например, квадратный корень из 16 представлен как: √16 = 4. Число, квадратный корень которого вычисляется, называется подкоренным выражением. В этом выражении √16 = 4, число 16 — подкоренное выражение.

      Что такое квадратный корень?

      Квадратный корень — это операция, обратная возведению числа в квадрат. Другими словами, извлечение квадратного корня — это операция, которая отменяет показатель степени 2.

      Свойства

      • Полное квадратное число имеет точный квадратный корень.
      • Четное совершенное число имеет четный квадратный корень.
      • Нечетное совершенное число имеет нечетный квадратный корень.
      • Квадратный корень отрицательного числа не определен.
      • Только числа, оканчивающиеся четным числом нулей, имеют квадратные корни.

      Как найти квадратный корень из чисел?

      Есть несколько способов найти квадрат чисел.Мы увидим некоторые из них здесь.

      Повторное вычитание

      Этот метод включает в себя успешное и многократное вычитание нечетных чисел, таких как 1, 3, 5 и 7, из числа до тех пор, пока не будет достигнут ноль. Квадрат числа равен числу или частоте вычитания числа

      Предположим, нам нужно вычислить квадрат совершенного числа, такого как 25, операция выполняется как:

      25 — 1	= 24
      24-3	= 21
      21-5	= 16
      16-7	= 9

      Вы можете заметить, что частота вычитания равна 5, поэтому квадратный корень из 25 равен 5.

      Факторизация на простые множители

      В этом методе точное квадратное число факторизуется путем последовательного деления. Простые множители группируются в пары, и вычисляется произведение каждого числа. Следовательно, произведение представляет собой квадратный корень из числа. Чтобы найти квадрат совершенного числа, такого как: 144, выполняется как:

      • 144 = 2 × 2 × 2 × 2 × 3 × 3.
      • Соедините простые множители.
      • Выбор одного числа из каждой пары.
      • 2 × 2 × 3 = 12.
      • Таким образом, √144 = 12.

      Метод деления

      Метод деления — это подходящий метод вычисления квадрата большого числа. Это следующие шаги:

      • Полоса помещается над каждой парой цифр, начиная с правой стороны.
      • Разделите левое конечное число на число, квадрат которого меньше или эквивалентен числам под левым концом.
      • Возьмите это число в качестве делителя и частного. Точно так же возьмите крайнее левое число в качестве делимого.
      • Разделите, чтобы получить результат
      • Потяните вниз следующее число с полосой справа от остатка
      • Умножьте делитель на 2.
      • Справа от этого нового делителя найдите подходящий дивиденд. Этот процесс повторяется до тех пор, пока мы не получим в качестве остатка ноль. Следовательно, квадрат числа равен частному.

      Квадратный корень из 225 вычисляется как

      • Начинайте деление с крайней левой стороны.
      • В этом случае 1 — это наше число, квадрат которого меньше 2.
      • Если присвоить 1 как делитель и частное и умножить его на 2, получим:
      • Выполните шаги, чтобы получить 15 как частное.

      Практические вопросы

      1. Оценить √144 + √196
      2. Упростить √25 x √25
      3. Найдите квадратный корень из 1000000.
      4. В школьной аудитории 3136 мест, если количество мест в ряду равно количеству мест в столбцах. Подсчитайте количество мест в ряду.
      5. Вычислить √5625.
      6. Квадратный сад имеет площадь 16 квадратных метров. Рассчитайте периметр сада.
      7. Какое наименьшее число нужно добавить к 570, чтобы получился идеальный квадрат.
      8. Оценить √0,9 + √2,5.
      9. Найдите квадратный корень из первого совершенного четырехзначного числа.
      10. Что такое √0,0025?

      Ответы на практические вопросы

      1. √144 + √196

      = 12 + 13

      = 25

      2. √25 x √25

      = 5 x 5

      = 25

      3. √1000000

      1000000 имеет четное число нулей, поэтому выбирайте каждый ноль из пары.

      = 1000

      4. Равное количество строк и столбцов

      Количество мест в ряду и столбце = √ 3136

      56 мест

      5. √5625

      = 75

      6. √16 = 4

      Периметр = 4 x 4

      = 16 метров

      7. 570 + 6 = 576

      √576 = 24

      8. √0.9 + √2.5

      = 0.3 + 0. 5

      = 0.8

      9 Первое совершенное четырехзначное число — 1024

      10. 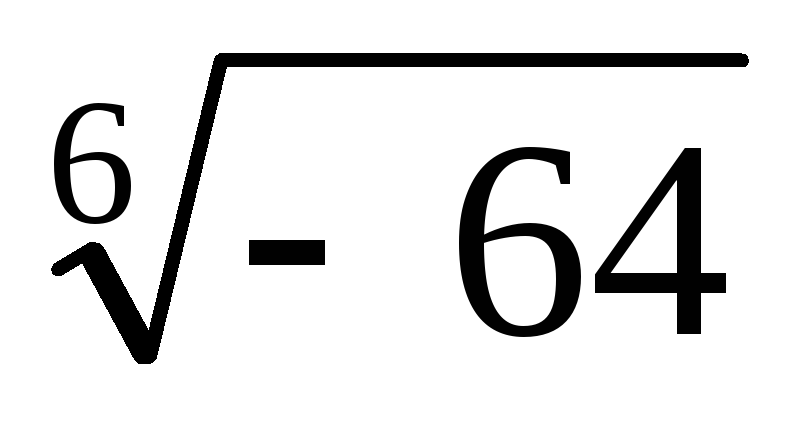√0.0025

      = 0. 05

      Предыдущий урок | Главная страница | Следующий урок

      Квадратные корни

      Как мы их делаем?

      Квадратный корень из числа б является решением уравнения Икс 2 знак равно б .Все числа, кроме 0 имеет два квадратных корня, положительный и отрицательный. Положительный квадратный корень — это главный квадратный корень и написано б . Чтобы обозначить отрицательный корень, напишите — б и чтобы указать оба корня, напишите ± б .

      Итак, мы звоним 5 «квадратный корень» из 25 и писать 25 знак равно 5 так как 5 2 знак равно 25 .(Подробнее об этом см. Экспоненты.) Поскольку ( — 5 ) 2 также равно 25 это также «квадратный корень» из 25 , но мы пишем — 25 знак равно — 5 потому что это не главный квадратный корень.

      Не все целые числа имеют квадратный корень из целого числа. Например 2 знак равно 1,414213562 … (Десятичная дробь продолжается вечно и никогда не повторяет шаблон.Это называется иррациональное число .)

      Как вы можете оценить значение квадратного корня, например 70 ? Что ж, вы могли сначала заметить, что 64 знак равно 8 а также 81 год знак равно 9 , поскольку 64 а также 81 год оба являются полными квадратами. 70 находится посередине 64 а также 81 год , так 8 < 70 < 9 . С 70 ближе к 64 чем 81 год , 70 ближе к 8 .

      Чтобы найти лучшее приближение, вы можете использовать калькулятор:

      70 ≈ 8,3666

      Совершенные квадраты и квадратные корни [видео]

      Квадратный корень и идеальный квадрат

      Квадратный корень и полный квадрат. Квадратный корень из числа — это результат, обратный возведению числа в квадрат или возведению числа во вторую степень. Квадратный корень — это число, которое при умножении само на себя дает это значение. Например, квадратный корень из 4 равен 2, потому что 2 умножения на себя равно 4.

      4 — правильный квадрат. Полный квадрат — это значение, состоящее из квадратного корня из целого числа. Квадратный корень из 4 равен 2, поэтому квадратный корень представляет собой целое число, что означает, что четверка является полным квадратом. Другой пример полного квадрата — 9.

      Квадратный корень из 9 равен 3. Квадратный корень — это целое число, что означает, что 9 — это полный квадрат. Квадратный корень равен 3. 3 не является полным квадратом, потому что квадратный корень из 3 не является целым числом. Квадратный корень 3 на самом деле является иррациональным числом.

      Вы можете найти значение на своем калькуляторе, но оно продолжается вечно. Корни могут быть выражены в экспоненциальной форме в виде дробей. Квадратный корень из 3, который мы могли бы записать, равен 3 в степени 1/2. Они эквивалентны.

      Вы можете записать кубический корень из 8 также как дробь, как показатель степени с дробью, так что это будет от 8 до 1/3 степени. Кубический корень из восьми.Это очень похоже на нахождение квадратного корня из числа, но когда вы находите кубический корень, вы находите, какое число, умноженное на три раза, дает вам восемь.

      Куб восьмерки равен 2, потому что 2 умножить на 2 умножить на 8. Некоторые корни имеют коэффициенты, например 4 квадратных корня из 7. Коэффициент — это число перед корнем, и если коэффициент не показан, как в случае с этими числами квадратный корень из 4, квадратный корень из 9, квадратный корень из 3 или кубический корень из 8, тогда это понимается как 1, так как любое число, умноженное на одно, равно самому себе.

      Но этот коэффициент — это просто число, умноженное на радикал, например, 4 умноженное на квадратный корень из 7, и написано без всякого знака умножения, что означает, что это 4 умноженный на квадратный корень из семи.

      Как найти квадратный корень вручную

      Как вручную найти квадратный корень

      Как найти квадратный корень вручную

      Вот почти забытое искусство: с появлением электронных калькуляторы, скорее всего, доживут до XXI века только на бумаге и в воспоминаниях стариков.

      Из какого числа вы хотите найти квадратный корень? Вот один из них, который мы будем использовать:

      46656
       

      Сначала разделите число, которое нужно извлекать из квадратного корня, на пары цифр, начиная с десятичной точки.То есть никакая пара цифр не должна пересекаться десятичная точка. (Например, разделите 1225 на «12 25», а не на «1 22 5»; 6.5536 на «6,55 36», а не на «6,5 53 6».)

      Затем вы можете поместить несколько линий на каждую пару цифр и полосу на слева, что-то вроде длинного деления.

           + --- ---- ----
           | 4 66 56
       

      Найдите наибольшее число, квадрат которого меньше или равен ведущему пара цифр. В этом случае первая пара цифр — 4; самое большое число квадрат которого меньше или равен 4 равен 2.

      Поместите это число слева, и над первой парой цифр.

             2
           + --- ---- ----
        2 | 4 66 56
       

      Теперь возведите это число в квадрат и вычтите из первой пары цифр.

             2
           + --- ---- ----
        2 | 4 66 56
           | -4
           + ----
             0
       

      Выдвинуть левую скобу; умножьте последнюю (и единственную) цифру левой число на 2, поместите его слева от разницы, которую вы только что вычислили, и оставьте рядом с ним пустой десятичный знак.

             2
           + --- ---- ----
        2 | 4 66 56
           | -4
           + ----
       4_ | 0
       

      Затем опустите следующую пару цифр и поместите ее вправо разницы.

             2
           + --- ---- ----
        2 | 4 66 56
           | -4
           + ----
       4_ | 0 66
       

      Найдите наибольшее число для этого пустого десятичного разряда, чтобы число, умноженное на уже существующее число плюс десятичный разряд, будет меньше чем текущая разница. Например, если 1 * 41 равно ≤ 66, то 2 * 42 ≤ 66 и т. Д. В данном случае это 1. Поместите это число в оставленное вами поле, и в следующем десятичном разряде в строке результатов вверху.

             2 1
           + --- ---- ----
        2 | 4 66 56
           | -4
           + ----
       41 | 0 66
       

      Теперь вычтите продукт, который вы только что нашли.

             2 1
           + --- ---- ----
        2 | 4 66 56
           | -4
           + ----
       41 | 0 66
           | - 41
           + --------
                 25
       

      Теперь повторите, как и раньше: возьмите число в левом столбце (здесь 41) и удвойте его последнюю цифру (что даст вам 42).Скопируйте это ниже в левый столбец и оставьте рядом с ним пустое место. (Двойная последняя цифра с переносом: для Например, если у вас было не 41, а 49, что составляет 40 + 9, вы должны скопировать 40 + 18 что равно 58.) Также опустите следующую пару цифр справа.

             2 1
           + --- ---- ----
        2 | 4 66 56
           | -4
           + ----
       41 | 0 66
           | - 41
           + --------
      42_ 25 56
       

      Теперь найдите самую большую цифру (назовите ее #) такую, что 42 # * # ≤ 2556. Здесь, получается, что 426 * 6 = 2556 точно.

             2 1 6
           + --- ---- ----
        2 | 4 66 56
           | -4
           + ----
       41 | 0 66
           | - 41
           + --------
      426 | 25 56
           | - 25 56
           + -------------
                       0
       

      Когда разница равна нулю, у вас есть точный квадратный корень, и вы Выполнено. В противном случае вы можете продолжать находить больше десятичных знаков до тех пор, пока как ты хочешь.

      ---

      Вот еще один пример с меньшим количеством аннотаций.

      
                7. 2 8 0 1 ...
             + ----------------------
      7 | 53. 00 00 00 00 00
             | 49
             + ----------------------
      142 | 4 00
             | 2 84
             + ----------------------
      1448 | 1 16 00
             | 1 15 84
             + ----------------------
      14560 | 16 00
             | 0
             + ----------------------
      145601 | 16 00 00
             | 14 56 01
             + ----------------------
             | 1 43 ​​99 00
                               ...
      
       

      ---

      Джон Керл
      john dot r dot kerl at lmco точка com
      Июль 1998 г.

      Текущий адрес (по состоянию на 2005 г.):
      [email protected]
      ← Прочие документы

      Квадратный корень из 13 — Как найти квадратный корень из 13?

      Символ квадратного корня записывается как (√) и является неотъемлемой частью математики. Как только вы поймете основы нахождения квадратного корня из числа, вы сможете решить любую проблему, связанную с квадратным корнем.
      Сегодня давайте найдем квадратный корень из 13 и исследуем ответ на такие вопросы, как: квадратный корень из 13 — рациональное число и квадратный корень из 13 — в радикальной форме.

      • Квадратный корень из 13 : √13 = 3,60555128
      • Квадрат 13:13 ² = 169

      Что такое квадратный корень из 13?

      Квадратный корень из 13 выражается как √ 13 в радикальной форме и как 13 ^½ в экспоненциальной форме.
      Квадратный корень из 13 с округлением до 5 знаков после запятой составляет ± 3,60555.

      ---

      Является квадратный корень из 13 рациональным или иррациональным?

      Число, которое не может быть выражено как отношение двух целых чисел, является иррациональным числом. Десятичная форма иррационального числа является неограничивающей (т. Е. Никогда не заканчивается) и неповторяющейся (т. Е. Десятичная часть числа никогда не повторяет шаблон). Теперь давайте посмотрим на квадратный корень из 13.

      Является квадратный корень из 13 рациональным или иррациональным?

      Как вы думаете, десятичная часть останавливается после 3.60555128? Нет, он бесконечен, и вы не можете увидеть узор в десятичной части.

      • Квадратный корень из √13 — иррациональное число.

      ---

      Как найти квадратный корень из 13?

      квадратного корня можно вычислить с помощью различных методов:

      • Путем упрощения радикала чисел, которые представляют собой точные квадраты.
      • По методу деления на полные и несовершенные квадраты

      13 — простое число и, следовательно, не является полным квадратом.Следовательно, квадратный корень из 13 можно вычислить только методом деления в длину.

      Упрощенная радикальная форма квадратного корня из 13

      Чтобы упростить извлечение квадратного корня из 13, сначала представим 13 как произведение его простых множителей.

      • Факторизация на простые числа 13 = 1 × 13.
      • √13 находится в самом низком виде и не может быть далее упрощен.
      • Мы выразили квадратный корень из 13 в радикальной форме.

      Квадратный корень из 13 по длинному делению

      Давайте проследим шаги, чтобы найти квадратный корень из 13 делением в столбик.

      • Шаг 1: Сгруппируйте цифры в пары справа налево, поместив над ними полосу.
      • Шаг 2: Найдите наибольшее число, такое, что при умножении его на себя, произведение меньше или равно 13. Мы знаем, что 3 × 3 равно 9 и меньше 13. Теперь давайте разделим 13 ÷ 3.
      • Шаг 3: Давайте поместим десятичную точку и пары нулей после нее, чтобы продолжить наше деление.
      • Теперь умножьте частное на 2, и произведение станет начальной цифрой нашего следующего делителя.
      • Шаг 4: Выберите число в месте единиц для нового делителя так, чтобы его произведение с числом было меньше или равно 400. Мы знаем, что 6 находится в разряде десятков, а наше произведение должно быть 400 и ближайшим умножением равно 66 × 6 = 396
      • Шаг 5: Введите следующую пару нулей и умножьте частное 36 (без учета десятичной дроби) на 2, то есть 72, и начальную цифру нового делителя.
      • Шаг 6: Выберите наибольшую цифру в разряде единиц для нового делителя так, чтобы произведение нового делителя на цифру в разряде единиц было меньше или равно 400.Мы видим, что 721 при умножении на 1 дает 721, что больше 400. Следовательно, мы возьмем 720 × 0 = 0, что меньше 400.
      • Шаг 7: Добавьте еще пары нулей и повторите процесс поиска нового делителя и произведения, как это было сделано на шаге 2.
      • Шаг 8: Выберите самую большую цифру в месте единиц для нового делителя так, чтобы произведение нового делителя на цифру в разряде единиц было меньше или равно 40000. Мы видим, что 7205 при умножении на 5 дает 36025, что меньше 40000.
      • Таким образом, квадратный корень из 13, полученный путем деления в столбик, равен 3,60555128.

      Можете ли вы попробовать аналогичным образом выразить квадратный корень из 17? Ответ √17 должен быть 4,123

      .
      • Можете ли вы представить себе квадратное уравнение с корнем √13?
      • Поскольку (-√13) ² = 13, можем ли мы сказать, что -√13 также является квадратным корнем из 13?
      • Корень квадратный из 13 в радикальной форме выражается как √13.
      • Квадратный корень из 13 выражается как 13 ^½ в экспоненциальной форме.
      • Реальные корни √13 равны ± 3,605

      Часто задаваемые вопросы о квадратном корне из 13

      Что такое квадратный корень из 13?

      Квадратный корень из 13 равен √13 = 3,60555128.

      Что такое квадрат 13?

      Площадь 13 — 169.

      Как вычислить квадратный корень из 13?

      Мы можем найти квадратный корень из 13 различными методами.

      1. Повторное вычитание
      2. Основная факторизация
      3. Оценка и приближение
      4. Длинный дивизион

      Если вы хотите узнать больше о каждом из этих методов, щелкните здесь.

      Что такое квадратный корень из 13 в простейшей радикальной форме?

      √13 — простейшая радикальная форма.

      Является ли квадратный корень из 13 иррациональным числом?

      √13 = 3,60555128. √13 — иррациональное число.

      .