6.1.2. Задачи на пропорцию математика-повторение
Задача 1. Толщина 300 листов бумаги для принтера составляет 3, 3 см. Какую толщину будет иметь пачка из 500 листов такой же бумаги?
Решение. Пусть х см — толщина пачки бумаги из 500 листов. Двумя способами найдем толщину одного листа бумаги:
3,3:300 или х:500.
Так как листы бумаги одинаковые, то эти два отношения равны между собой. Получаем пропорцию (напоминание: пропорция — это равенство двух отношений):
3,3:300=х:500. Неизвестный средний член пропорции равен произведению крайних членов пропорции, деленному на известный средний член. (Подробно о пропорции и нахождению ее крайнего, среднего членов читайте в статье: «6.1.1. Пропорция. Основное свойство пропорции.»)
х=(3,3·
х=5,5. Ответ: пачка 500 листов бумаги имеет толщину 5,5 см.
Это классическое рассуждение и оформление решения задачи. Такие задачи часто включают в тестовые задания для выпускников, которые обычно записывают решение в таком виде:
или решают устно, рассуждая так: если 300 листов имеют толщину 3,3 см, то 100 листов имеют толщину в 3 раза меньшую. Делим 3,3 на 3, получаем 1,1 см. Это толщина 100 листовой пачки бумаги. Следовательно, 500 листов будут иметь толщину в 5 раз большую, поэтому, 1,1 см умножаем на 5 и получаем ответ: 5,5 см.
Разумеется, это оправдано, так как время тестирования выпускников и абитуриентов ограничено. Однако, на этом занятии мы будем рассуждать и записывать решение так, как положено это делать в 6 классе.
Задача 2. Сколько воды содержится в 5 кг арбуза, если известно, что арбуз состоит на 98% из воды?
Решение.
Вся масса арбуза (5 кг) составляет 100%. Вода составит х кг или 98%. Двумя способами можно найти, сколько кг приходится на 1% массы.
5:100 или х:98. Получаем пропорцию:
5:100 = х:98.
х=(5·98):100;
х=4,9 Ответ: в 5кг арбуза содержится 4,9 кг воды.
Задача 3. Масса 21 литра нефти составляет 16,8 кг. Какова масса 35 литров нефти?
Решение.
Пусть масса 35 литров нефти составляет х кг. Тогда двумя способами можно найти массу 1 литра нефти:
16,8:21 или х:35. Получаем пропорцию:
16,8:21=х:35.
Находим средний член пропорции. Для этого перемножаем крайние члены пропорции (16,8 и 35) и делим на известный средний член (
Умножаем числитель и знаменатель дроби на 10, чтобы в числителе и знаменателе были только натуральные числа. Сокращаем дробь на 5 (5 и 10) и на 3 (168 и 3).
Ответ: 35 литров нефти имеют массу 28 кг.
Задача 4. После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля?
Решение.
Пусть площадь всего поля х га, что составляет 100%. Осталось вспахать 9 га, что составляет 100% — 82% = 18% всего поля. Двумя способами выразим 1% площади поля. Это:
х:100 или 9:18. Составляем пропорцию:
х:100 = 9:18.
Находим неизвестный крайний член пропорции. Для этого перемножаем средние члены пропорции (100 и 9) и делим на известный крайний член ( 18). Сокращаем дробь.
Ответ: площадь всего поля 50 га.
www.mathematics-repetition.com
Определение пропорции, задачи на пропорцию
Пропо́рция – равенство двух отношений, т. е. равенство вида a : b = c : d, или, в других обозначениях, равенство
Если a : b = c : d, то a и d называют крайними, а b и c — средними членами пропорции.
От « пропорции» никуда не деться, без нее не обойтись во многих задачах. Выход только один – разобраться с этим отношением и пользоваться пропорцией как палочкой-выручалочкой.
Прежде чем приступать к рассмотрению задач на пропорцию, важно вспомнить основное правило пропорции:
В пропорции
произведение крайних членов равно произведению средних
Если какая-то величина в пропорции неизвестна, ее легко будет найти, опираясь на это правило.
Например,
или
То есть неизвестная величина пропорции – значении дроби, в знаменателе которой – то число, которое стоит напротив неизвестной величины, в числителе – произведение оставшихся членов пропорции (независимо от того, где эта неизвестная величина стоит).
Задача 1.
Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?
Решение:+ показать Мы понимаем, что уменьшение веса семени во сколько-то раз, влечет за собой уменьшение веса получаемого масла во столько же раз. То есть величины связаны прямой зависимостью. Заполним таблицу: Неизвестная величина – значение дроби , в знаменателе которой – 21 – величина, стоящая напротив неизвестного в таблице, в числителе – произведение оставшихся членов таблицы-пропорции. Поэтому получаем, что из 7 кг семени выйдет 1,7 кг масла. Ответ: 1,7 Чтобы правильно заполнять таблицу, важно помнить правило: Одинаковые наименования нужно записывать друг под другом. Проценты записываем под процентами, килограммы под килограммами и т.д
Задача 2.
Перевести в радианы.
Решение:+ показать Мы знаем, что . Заполним таблицу: Откуда Ответ:
Задача 3.
На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 27?
Решение: + показать
Решение: + показать Все поле составляет 100%, и поскольку вспахано 82%, то осталось вспахать 100%-82%=18% поля. Заполняем таблицу: Откуда получаем, что все поле составляет (га). Ответ: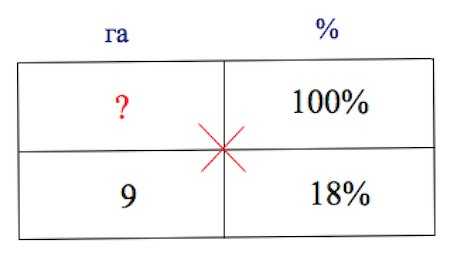 
А следующая задача – с засадой.
Задача 5.
Расстояние между двумя городами пассажирский поезд прошел со скоростью 80км/ч за 3 часа. За сколько часов товарный поезд пройдет то же расстояние со скоростью 60 км/ч?
Решение: + показать время, которое потребуется товарному поезду, чтобы пройти то же расстояние, что и пассажирским, есть часа. То есть, получается, что идя с меньшей скоростью, он преодолевает (за одно и тоже время) расстояние быстрее, нежели поезд с большей скоростью. В чем ошибка рассуждений? До сих пор мы рассматривали задачи, где величины были прямопропорциональны друг другу, то есть рост одной величины во сколько-то раз, дает рост связанной с ней второй величины во столько же раз (аналогично с уменьшением, конечно). А здесь у нас другая ситуация: скорость пассажирского поезда больше скорости товарного во сколько-то раз, а вот время, требуемое на преодоление одного и того же расстояния, требуется пассажирскому поезду меньшее во столько же раз, нежели товарному поезду. То есть величины друг другу обратно пропорциональны. Схему, которой мы пользовались до сих пор, надо чуть изменить в данном случае. Решение: Рассуждаем так: Пассажирский поезд со скоростью 80 км/ч ехал 3 ч, следовательно, он проехал км. А значит товарный поезд это же расстояние преодолеет за ч. То есть, если бы мы составляли пропорцию, нам следовало бы поменять местами ячейки правой колонки предварительно. Получили бы: ч. Ответ: .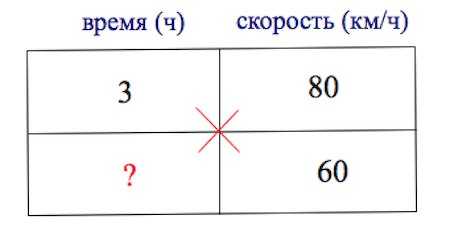
Если вы будете решать эту задачу аналогично предыдущей, то получите следующее:
Поэтому, пожалуйста, будьте внимательны при составлении пропорции. Разберитесь сначала, с какой зависимостью имеете дело – с прямой или обратной.
egemaximum.ru
План-конспект урока по алгебре (6 класс) на тему: Пропорция.Решение задач с помощью пропорций.
«ПРОПОРЦИЯ. РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ПРОПОРЦИИ»
(6 класс)
Образовательная цель урока: проверка умений и навыков учащихся по теме «Пропорция», формирование навыков решения задач с помощью пропорции.
Воспитательная цель урока: развитие интереса к математике, воспитание любви к Родине, формирование основ выбора профессии.
Оборудование: компьютер, видеопроектор, экран
Задачи урока:
• обучить учащихся умению самостоятельно решать и составлять задачи на пропорцию;
• развивать навык самоанализа и самоконтроля учебной деятельности;
• развивать интерес к предмету и активность каждого ученика на уроке.
План урока
1. Организационный момент
2. Разминка
3. Основная часть урока. Решение задач
4. Контроль умений и знаний
5. Подведение итогов.
Ход урока
1. Здравствуйте ребята!
Ребята, сегодня у нас урок по теме «Пропорция. Решение задач с помощью пропорции». Нам предстоит повторить теоретический материал по данной теме и практически его применить. В конце урока будет проведен контроль знаний по данной теме. А сначала мы проведем небольшую разминку.
2.Разминка.
Веселые задачи.
Задача 1.
Вышел как-то бегемот из болота.
Был задумчив бегемот отчего-то.
Был рассеян бегемот и невесел —
Сосчитать не мог, сколько весил.
Знал, что втрое тяжелее крокодила,
Тот же втрое тяжелее, чем горилла,
А горилла, растолстев от бананов,
Весит 250 килограммов.
Не сочтя за лишний труд и заботу,
Не могли бы вы помочь бегемоту?
(2250 кг)
Задача 2.
На лугу один барашек
Съел семь штук душистых кашек.
И ушло на этот труд
У барашка пять минут.
Разобраться помогите:
При подобном аппетите
Сколько штук душистых кашек съест за час один барашек?
(84)
Задача 3
Два носорога
И три бегемота
Выпили вместе
Сто литров компота.
Если досталось
Всем поровну строго,
Много ли выпили
Два носорога?
(40)
Вопрос. Какая из этих трех задач решается с помощью пропорции?
3.Основная часть урока.
Перед вами станет вопрос: какую профессию выбрать? Профессий много, как же тут разобраться? Чтобы узнать как можно больше о них, на наших уроках мы иногда можем путешествовать, встречаясь с людьми разных профессий с различных предприятий, знакомиться с их продукцией. А как мы будем это делать, вы сегодня увидите. Собираясь в путешествие, люди собирают багаж. И мы возьмем с собой багаж — багаж знаний по теме «Пропорция».
Вопросы учителя.
1. Что называют отношением двух чисел?
(Частное двух чисел называют отношением этих чисел )
2. Что показывает отношение двух чисел? (Отношение двух чисел показывает, во сколько раз первое число больше второго или какую часть первое число составляет от второго.)
3. Что такое пропорция? (Пропорцией называется равенство двух отношений.)
4. Прочитайте пропорцию разными способами: а : Ь = с : d
5. Как называются числа х и у в пропорции х : а = Ь : у? (Крайние члены.)
6. Как называются числа m и n в пропорции а : m = n : b? (Средние члены.)
7. Сформулируйте основное свойство пропорции. (В верной пропорции произведение крайних членов равно произведению средних.)
8. Как найти неизвестный крайний член пропорции? (Чтобы найти неизвестный крайний член пропорции, нужно произведение средних членов разделить на известный крайний член)
9. Как найти неизвестный средний член пропорции? (Чтобы найти неизвестный средний член пропорции, нужно произведение крайних членов разделить на известный средний член.)
Учитель. Молодцы, ребята! Вы собрали хороший багаж знаний по теме! Я надеюсь, он нам пригодится в пути.
— Пора отправляться в дорогу. Путешествуя, выясним, как вы сможете на практике применять знания по теме «Пропорции». Ведь данная тема служит основой для решения многих задач практического характера. С задачами, решение которых сводится к составлению пропорций, встречаются люди любой профессии.
— Итак, в путь!
. Мы посетим одно из самых крупных предприятий Мордовии ОАО «Мордовцемент».
— Перед рабочими возникла проблема. Нужно решить следующую задачу.
Задача 1.
Для перевозки сырья требуется 16 вагонов грузоподъемностью 60 тонн. Сколько потребуется вагонов грузоподъемностью 80 тонн для перевозки этого же груза?
(Разбор решения задачи происходит совместно с учителем.)
Решение. Пусть для перевозки сырья потребуется х вагонов грузоподъемностью 80 тонн,
- 16 в-60 т
- х в — 80 т
16 : х = 80 : 60;
х= 16*60 : 80;
х = 12
Ответ: 12 вагонов.
Продолжаем наше путешествие. Теперь в Ромоданове. Заглянем на сахарный завод. Поможем рабочим этого предприятия решить следующую задачу :
Задача 2.
В сахарной свекле содержится 18,5 % сахара. Сколько сахара содержится в 50 т сахарной свеклы?
(Один ученик решает задачу у доски, остальные в тетради с последующей проверкой решения.)
Решение:
Пусть х тонн сахара содержится в 50 тонн сахарной свеклы,
- 50 т — 100%
- Х т — 18,5%
50 : х = 100 : 18,5;
х = 50*18,5 : 100;
х = 9,25 Ответ: 9,25 тонн.
Сообщение ученика по теме: «Пропорции в Древней Греции».
Слово «пропорция» происходит от латинского слова proportio, означающего вообще соразмерность, определенное соотношение частей между собой. В древности учение о пропорциях было в большом почете у пифагорейцев. С пропорциями они связывали мысли о порядке и красоте в природе, о созвучных аккордах в музыке и гармонии во вселенной. Поэтому некоторые виды пропорций они называли «музыкальными» и «гармоническими».
В VII книге «Начал» Евклида изложена теория отношений и пропорций для целых чисел.
Из пропорции а : Ь = с : d Евклид выводит следующие производные пропорции:
b : а = d : с (а+b) : b = (с+d): d
а : с = b : d (а-b) : b = (с-d) : d
с : (а-b) = с : (с-d)
Основное свойство пропорции.
Евклид доказал основное свойство пропорции: произведение крайних членов равно произведению средних членов.
Пропорциями пользовались для решения разных задач и в древности и в средние века. Определенные типы задач легко и быстро решаются и теперь при помощи пропорций.
Пропорции и пропорциональность применяются и применялись не только в математике, но и в архитектуре, искусстве.
С пропорциями имели дело строители уже в Древнем мире. Правильное соотношение размеров возводимых ими дворцов и храмов придавало этим зданиям ту необыкновенную красоту, которая и сегодня восхищает нас.
Продолжаем наше путешествие.
Заглянем на предприятие Большеберезниковского района маслодельный завод
— Перед рабочими завода встала проблема. Нужно решить задачу.
Задача 3.
Из 110 литров молока получается 5 кг сливочного масла. Сколько нужно литров молока для получения 20 кг сливочного масла?
(Один ученик решает задачу на доске, остальные в тетради с последующей проверкой решения.)
Решение:
Пусть х литров молока потребуется для получения 20 кг сливочного масла,
- 110 л — 5 кг
- X л — 20 кг
110 : х = 5 : 20;
Х = 110*20 : 5;
х = 440
Ответ: 440 литров.
4.Контроль умений и знаний.
Учитель. Ребята, сейчас мы сыграем в игру «Кто хочет стать отличником».
У вас на столах лежат карточки с цифрами 1,2, 3 и значки Умника. Отвечая на вопросы теста, вы должны поднять нужную карточку. При правильном ответа вы берете себе один значок. По количеству набранных значков в конце урока вам будет выставлена оценка
Тест
1. Пропорцией называется:
1) равенство двух сумм;
2) равенство двух отношений; +
3) равенство двух произведений.
2. Выберите верное утверждение:
1) в верной пропорции произведение средних членов равно произведению крайних; +
2) в верной пропорции сумма средних членов равна сумме крайних;
3) в верной пропорции разность средних членов равна разности крайних.
3. Какое из данных равенств является пропорцей?
1) 2,5 : 5 = 4 + 1;
2) 30 : 5 = 60 : 10; +
3) 48 — 40 = 48 : 6.
4. В пропорции 3,6 : 1,2 = 6,3: 2,1 средние члены равны:
1) 3,6 и 6,3;
2) 1,2 и 6,3; +
3) 1,2 и 2,1.
5. В пропорции 14,7 : 0,7 = 18,9 : 0,9 крайние члены равны:
1) 14,7 и 0,7,
2) 18,9 и 0,9;
3) 14,7 и 0,9. +
6. Две величины называются прямо пропорциональными, если:
1) при увеличении одной из них в несколько раз другая увеличивается во столько же раз; +
2) при уменьшении одной из них в несколько раз другая увеличивается во столько же раз.
7. Две величины называются обратно пропорциональными, если:
1) при уменьшении одной величины в несколько раз другая увеличивается во столько же раз; +
2) при увеличении одной величины в несколько раз другая увеличивается во столько же раз.
8. Зависимость между какими величинами является прямо пропорциональной?
1) путь, пройденный автомашиной с постоянной скоростью, и время ее движения; +
2) скоростью движения автомашины на участке определенной длины и временем ее движения.
9. Зависимость между какими величинами является обратно пропорциональной?
1) ценой товара и его количеством, купленным на определенную сумму; +
2) ценой и стоимостью товара определенного количества.
Подведение итогов. Выставление оценок
9 значков — «5»;
7 значков — «4»;
5 значков — «3».
Дополнительное задание. (При наличии времени.)
По краткой записи составьте и решите задачу.
количество стоимость
I покупка 11,2 кг 516 руб
II покупка 33,6 кг х руб
скорость время
I автомашина 75 км/ч 3 ч
II автомашина 112,5 км/ч х ч
5. Домашнее задание.
Составьте и решите задачу по теме «Пропорция».
Заключительное слово учителя. Дорогие ребята! Наш урок подошел к концу, но жизнь откроет перед вами еще много неизвестного и интересного в области математики. И закончить я бы хотела словами Софьи Васильевны Ковалевской
«С того человека и взыщется много,
Кому было много талантов дано».
Пусть ты не станешь Пифагором,
Каким хотел бы, может быть.
Но будешь — ты рабочим иль ученым
И будешь родину любить.
Как воздух математика нужна
Создателям машин, воздушных кораблей.
Как трудно нам пришлось бы без Ньютонов,
Каких дала история до наших дней.
В наше время, чтобы строить
И машиной управлял,,
Нужно прежде только в школе
Математику познать.
— До свидания! Спасибо всем!
Список используемой литературы:
1. Программы для общеобразовательных школ, гимназий, лицеев. — М: Дрофа, 2001.
2. Математика, 6 класс: Учебник /Под ред. Н.Я. Виленкина и др.
3. Дидактические материалы по математике, 6 класс/ А.С. Чесноков, К.И. Пешков.
Интернет-ресурсы:
1. http://edurm.ru
1. http://festival.1september.ru/
2. http://www/mordovcement.ru
3. http://vestnik.fa.ru/
nsportal.ru
Методическая разработка по алгебре (6 класс) на тему: Пропорции.Решение задач с помощью пропорций.
КАРТАЛИНСКИЙ РАЙОННЫЙ ОТДЕЛ ОБРАЗОВАНИЯ
МОУ ЕЛЕНИНСКАЯ СОШ
для учащихся 6 класса
Подготовила:
учитель математики
ЯРКЕЕВА Л.М.
ЕЛЕНИНКА 2015 год
Тема: Пропорция. Решение задач с помощью пропорции.
Тип урока: урок-путешествие
Цель урока: проверить умение находить неизвестный член пропорции; решать задачи с помощью пропорции.
Ход урока.
Учитель: Пройдет еще немного времени и перед вами встанет вопрос: какую профессию выбрать? Профессий много, как же тут разобраться? Вы уже знакомы с профессиями своих родственников, с профессией учителя. Но ведь существует еще много интересных. Чтобы узнать как можно больше о них, на наших уроках мы иногда можем путешествовать, встречаясь с людьми разных профессий с различных предприятий, знакомиться с продукцией этих предприятий. А как мы это будем делать — вы сегодня увидите. Это не совсем обычный урок. Мы с вами отправляемся в поездку по некоторым местам нашего города. Путешествуя, выясним, как вы усвоили тему: «Пропорция». Ведь данная тема служит основой для решения многих задач практического характера. С задачами, решение которых сводится к составлению пропорции, встречаются люди разных профессий. Итак, в путь!
КАРТА ПУТЕШЕСТВИЯ
УНИВЕРСИТЕТ
ШКОЛА ХЛЕБОЗАВОД
САХАРНЫЙ ЗАВОД ДОМСТРОЙ
1.Станция «УНИВЕРСИТЕТ».
Учитель: Внимание. На нашем пути студенческий городок. Заглянем в одну из аудиторий университета. Здесь идет конференция по истории математики.
1.1 Историческая справка (сообщение делает ученик). Ученые в Древней Греции не признавали дробных чисел и из-за этого у них возникали затруднения с измерением величин. Пришлось греческим ученым придумать способ, как обходиться в науке без того, чтобы выражать длины, площади и объемы числами. Так было создано учение об отношениях величин, о равенстве таких отношений. Равенство двух отношений стало потом называться латинским словом «пропорция». С пропорциями имели дело строители уже в Древнем мире.
Правильное соотношение размеров возводимых ими дворцов и храмов придавало этим зданиям ту необыкновенную красоту, которая и сегодня восхищает нас.
Учитель: А в другой аудитории идет практическое занятие. Давайте примем в нем участие.
1.2.Устная работа:
— Какие из данных равенств являются пропорциями? Почему?
а) 2,5 : 0,5 = 4 + 1,
2 1
б) 30 : 5 = 7 : 21.
-Допишите недостающие члены пропорции:
а) 104 : … = 160 : 20,
б) 10 : 5 = … : …
Сколько решений имеет пропорция?
Проверьте составленную пропорцию двумя способами. Назовите крайние и средние члены пропорции.
— Проверьте, правильно ли найден неизвестный член пропорции:
75 : 9 = 9 : у
75 * у = 9 * 9
75 * 9
у = 9
у = 75
-Из чисел 4, 2, 5, 10 составьте пропорцию. Как из данной пропорции получить верную пропорцию?
Учитель: Так как следующие станции связаны с решением задач практического характера, давайте ответим на следующие вопросы:
— Какие величины называются прямо пропорциональными?
— Какие величины называются обратно пропорциональными?
— Приведите примеры прямо пропорциональных величин.
— Приведите примеры обратно пропорциональных величин.
2.Станция «ХЛЕБОЗАВОД»
Один ученик решает у доски с объяснением.
Задача: При выпечке хлеба из килограмма ржаной муки пекарь получит 1,4 кг хлеба. Сколько килограммов муки расходуется на выпечку 21 ц хлеба?
1 кг — 1,4 кг
х кг — 2100 кг
Прямая пропорциональность.
1 1, 4
х = 2100
х = 1500 кг
Ответ: 15 центнеров.
Учитель: Итак, где мы сейчас побывали? О какой профессии узнали из этой задачи?
3. Станция «ДОМСТРОЙ».
Один ученик решает около доски с объяснением.
Задача: Пять каменщиков могут закончить работу за 9 дней. Инженер попросил ускорить работу и для этого добавил еще 10 каменщиков. За какое время они закончат работу, считая, что все каменщики будут работать с одинаковой производительностью?
Решение: Пусть за х дней каменщики закончат работу.
5 каменщ. — 9 дней
15 каменщ. — х дней
Обратная пропорциональность.
5 х
15 = 9
х = 3
Ответ: 3 дня.
Вопрос классу: Каким свойством пользовались при решении задачи? Сформулируйте.
Учитель: В какой организации мы побывали? Чем занимается эта организация? С какими профессиями мы познакомились?
4. Станция «САХАРНЫЙ ЗАВОД»
Один ученик решает у доски с объяснением.
Задача: В сахарной свекле содержится 18,5% сахара. Сколько сахара содержится в 50 т сахарной свеклы?
Решение: Пусть х т сахара содержится в 50 т сахарной свеклы.
50т — 100%
х т — 18,5%
Обратная пропорциональность.
50 100
х = 18,5
х = 9,25
Ответ: 9,25 т
Работа с плакатом.
50 т — 100% х т — 100%
х т — 18,5% 9, 25 т — 18,5%
Вопросы к классу:
1. Что вы видите на доске?
(Краткая запись задачи и краткая запись обратной задачи).
2. По краткой записи обратной задачи сформулируйте условие.
(Условие: В сахарной свекле содержится 18,5% сахара. Сколько надо взять сахарной свеклы, чтобы в ней содержалось 9, 25 т сахара?)
Учитель: Где мы с вами побывали? Какой продукт там изготавливали? Из чего получается сахар?
5. Физкультминутка
Дружно встал 6 «а» класс — это «раз».
Повернулась голова — это «два».
Влево, вправо посмотри — это «три».
Свои плечи развернули на «четыре».
Пальцы надо нам размять — это «пять».
Всем ребятам надо сесть — это «шесть».
6. Станция «ШКОЛА».
Самостоятельная работа.
1 вариант:
1. Найдите неизвестный член пропорции 2,8 : 3,2 = 2,1 : х.
Ответ: х = 2,4.
2. Решите задачу:
На 20 км пути автомашина расходует 3,2 л горючего. Сколько горючего автомашина израсходует на 50 км пути?
Ответ: 8л.
2 вариант:
1. Найдите неизвестный член пропорции у : 2,1 = 4,5 : 3,5.
Ответ: у = 2,7.
2. Решите задачу:
Участок клубники 24 человека пропололи за 6 дней. За сколько дней выполнят ту же работу 36 человек, если будут работать с такой же производительностью?
Ответ: 4 дня.
7. Подведение итогов урока, рефлексия.
8. Домашнее задание: Придумайте две новые станции, две задачи и решите их.
nsportal.ru
Урок на тему: «Виды задач на пропорции» 6 класс
Тема: «Виды задач на пропорции»
Цели:
- Продолжить формирование навыков решения задач на пропорции
- Развитие логического мышления
- Воспитание самостоятельности
Оборудование: раздаточный материал (карточки с набором задач)
Ход урока:
- Организационный момент и проверка домашнего задания.
- Актуализация теоретических знаний:
(выполняется на листке, один правильный ответ – 1 балл, проверяется учителем в течение урока)
- Две величины прямо пропорциональны, если… при возрастании (убывании) одной величины возрастает (убывает) вторая.
- Две величины обратно пропорциональны, если… при возрастании (убывании) одной величины убывает (возрастает) вторая.
- Все ли величины прямо или обратно пропорциональны? Нет, есть величины не пропорциональные вообще.
- Сформулировать основное свойство пропорции.Произведение крайних членов пропорции = произведению средних.
- Привести пример прямо пропорциональной зависимости.
- Фронтальное решение задач.
№ 749
№ 799
№ 803
- Самостоятельная работа: решение задач на карточках (прилагаются)
- Подведение итогов урока.
- Домашнее задание: п. 21-22 повторить, № 811, № 819 решить.
Просмотр содержимого документа
«урок на тему: «Виды задач на пропорции» 6 класс »
Тема: «Виды задач на пропорции»
Цели:
Продолжить формирование навыков решения задач на пропорции
Развитие логического мышления
Воспитание самостоятельности
Оборудование: раздаточный материал (карточки с набором задач)
Ход урока:
Организационный момент и проверка домашнего задания.
Актуализация теоретических знаний:
(выполняется на листке, один правильный ответ – 1 балл, проверяется учителем в течение урока)
Две величины прямо пропорциональны, если… при возрастании (убывании) одной величины возрастает (убывает) вторая.
Две величины обратно пропорциональны, если… при возрастании (убывании) одной величины убывает (возрастает) вторая.
Все ли величины прямо или обратно пропорциональны? Нет, есть величины не пропорциональные вообще.
Сформулировать основное свойство пропорции. Произведение крайних членов пропорции = произведению средних.
Привести пример прямо пропорциональной зависимости.
Фронтальное решение задач.
№ 749
№ 799
№ 803
Самостоятельная работа: решение задач на карточках (прилагаются)
Подведение итогов урока.
Домашнее задание: п. 21-22 повторить, № 811, № 819 решить.
Приложение
Задачи на пропорцию
1.При изготовлении 9 одинаковых приборов потребовалось 300г серебра. Сколько серебра потребуется для изготовления 6 таких приборов?
2.Для изготовления 18 одинаковых приборов потребовалось 27г платины. Сколько платины потребуется для изготовления 28 таких приборов?
3.Трое маляров могут закончить работу за 5дней. Для ускорения работы добавили еще двух маляров. За какое время они закончат работу, если все маляры работают с одинаковой производительностью?
4.Для строительства стадиона 5 бульдозеров расчистили площадку за 210 мин. За какое время 7 бульдозеров расчистили бы эту площадку?
5.Для приготовления борща на каждые 100г мяса надо взять 60г свёклы. Сколько свёклы надо взять на 650 г мяса?
6.Для перевозки груза потребовалось 24 машины грузоподъемностью 7,5т. Сколько нужно машин грузоподъемностью 4,5т, чтобы перевезти тот же груз?
7. В 80 кг картофеля содержится 14кг крахмала. Найдите процентное содержание крахмала в таком картофеле.
8.Из 20кг яблок получается 16 кг яблочного пюре. Сколько яблочного пюре получится из 45 кг яблок?
9.На изготовления 12 костюмов требуется 49,8 м ткани. Сколько таких же костюмов можно сшить из 74,7м той же ткани?
10.Для погрузки нефти нужно 35 цистерн емкостью 60м3 каждая. Однако на железной дороге оказалось только цистерны емкостью 70м3. Сколько таких цистерн потребуется для погрузки того же количества нефти?
11.На изготовления 3,5 кг ржаного хлеба требуется 2,5 кг муки. Сколько хлеба можно испечь из 17,5 т ржаного хлеба?
12. Из 79 л молока получается 3,2кг сливочного масла. Сколько нужно взять молока, чтобы получить 16 кг масла?
13.12 тракторов одинаковой мощности могут вспахать поле за 88ч. Сколько нужно таких же тракторов, чтобы вспахать это поле за 33ч?
14.Из 0,3 т свежих яблок получилось 57 кг сушеных. Сколько получится сушеных яблок из 2,1т свежих?
15. 16 солдат могут отрыть окоп полного профиля за 21ч. Сколько солдат нужно поставить на эту работу, чтобы окоп был готов через 14ч?
kopilkaurokov.ru
| 1. | Прямо пропорциональные величины | 2 вид — интерпретация | лёгкое | 1 Б. | Выбор задачи, в которой величины прямо пропорциональны. |
| 2. | Обратно пропорциональные величины | 2 вид — интерпретация | лёгкое | 1 Б. | Выбор задачи, в которой величины обратно пропорциональны. |
| 3. | Прямая или обратная пропорциональность | 2 вид — интерпретация | среднее | 1 Б. | Следует определить, является ли зависимость между величинами прямо или обратно пропорциональной. |
| 4. | Расстояние и объём бензина | 2 вид — интерпретация | среднее | 2 Б. | Следует составить пропорцию для решения задачи, прямая пропорциональность. |
| 5. | Длина и ширина прямоугольника | 2 вид — интерпретация | среднее | 2 Б. | Следует составить пропорцию для решения задачи, обратная пропорциональность. |
| 6. | Стоимость картофеля | 2 вид — интерпретация | среднее | 2 Б. | Необходимо составить пропорцию для решения задачи, прямая пропорциональность. |
| 7. | Хлопковое семя и масло | 2 вид — интерпретация | сложное | 5 Б. | Решение текстовой задачи. |
| 8. | Количество машин и грузоподъёмность | 2 вид — интерпретация | сложное | 5 Б. | Решение текстовой задачи. |
| 9. | Количество посаженных деревьев | 2 вид — интерпретация | сложное | 4 Б. | Решение текстовой задачи. |
| 10. | Новая цена сыра | 2 вид — интерпретация | сложное | 4 Б. | Решение задачи на проценты. |
www.yaklass.ru
Конспект урока математики 6 класс «Решение задач с помощью пропорций»
Урок математики в 6 классе по теме
«Решение задач с помощью пропорций»
Цели урока:
Обучающие:
закрепление умения выполнять практические задания по измерению длин;
совершенствование умения составлять пропорции и отношения, проводить необходимые вычисления;
усиление прикладной и практической направленности изученной темы;
формировать умения и навыки в решении уравнений и задач по теме, повторяя при этом название членов пропорции, основное свойство пропорции;
прививать любовь к математике, желание познавать новое, навык самостоятельности в работе;
установление внутрипредметных и межпредметных связей с другими темами курса математики.
Развивающие:
развить мышление, внимание, память, умение анализировать, сопоставлять, сравнивать;
расширение кругозора учащихся;
Воспитательные:
воспитание интереса к предмету и смежным дисциплинам,
воспитывать честность в оценке своих знаний; учить трудолюбию, аккуратности.
воспитывать чувство прекрасного, чувство патриотизма.
Тип урока: урок комплексного применения знаний, умений и навыков.
Оформление:
Презентация по уроку, флипчарты.
Листы настроения для каждого ученика.
Цветные карандаши.
Опорные схемы по теме для каждого учащегося.
Листы самооценивания.
Раздаточный материал( карточки для индивидуальной работы, карточки с высказываниями для групповой работы, карточки для самостоятельной работы, материал для исследовательской работы).
Цветик-семицветик с вопросами по пропорции.
Плакат «Рефлексия», стикеры.
Ход урока
I. Организационный момент
Учитель:
– Здравствуйте, ребята!!
( Рифмованное начало урока )
Начиная наш урок,
Ну-ка ты проверь, дружок:
Все ль на месте,
Все ль в порядке,
Ручка, книжка и тетрадка?
– Тихо сели девочки! (пауза)
– Тихо сели мальчики! (пауза)
–Долгожданный дан звонок.
Начинается урок.
Девизом сегодняшнего урока будут слова «Незнающие пусть научатся, а знающие- вспомнят еще раз».
Кто-то сегодня будет доволен, что сумел решить сам или с помощью одноклассников трудную задачу; кто-то тем, что он узнал что-то новое; а кто-то тем, что ему повезло, и не пришлось думать над задачей.
Перед вами листок настроения
Вы моё настроение видите, оно зависит от вас, от ваших знаний. А какое ваше настроение? Покажите его, закрасив желтым карандашом то личико, которое соответствует вашему настроению к началу урока. (учащиеся цветными карандашами закрашивают личико, соответствующее настроению)
Учитель: Тема нашего урока зашифрована в ребусе . Постарайтесь, работая в парах, распознать тему урока. (Ребята, работая в парах сидящие за одной партой, расшифровывают ребус. В итоге у них должно получиться слово «Пропорция»).Слайд № 3
Учитель: Итак, мы сегодня мы будем говорить о пропорции. Тема для вас уже знакома. Давайте попробуем вместе сформулировать цели и задачи нашего урока.
Ученики пытаются вывести, что им нужно знать, уметь на уроке. Все их предложения обобщаются и вывешиваются в виде тезисов: (слайд №4)
Знать : понятие пропорции, ее члены; основное свойство пропорции.
Уметь: решать уравнения и задачи с применением основного свойства пропорции.
Учитель:
— Запишите число. «Классная работа». Итак, в добрый путь.
(ученики работают в своих тетрадях).
Учитель: «Говорят «Математика- гимнастика ума», а что такое – гимнастика? Это система упражнений для физического развития человека. Гимнаст- человек ловкий, сильный, стройный. Математика развивает ум, тренирует память, закаляет характер. Наш урок мы традиционно начнем с разминки.
2. Устная работа, направленная на повторение пройденного материала.
У меня необычный цветок. На каждом его лепестке написан вопрос по теме:
«Пропорция». С помощью этого цветка мы вместе вспомним теоретические знания. Вы будете по одному отрывать лепестки и отвечать на вопросы. ( Учитель в руках держит цветик- семицветик, на лепестках которого написаны вопросы по пропорции. Ученик отрывает листок, читает вопрос, отвечает.).
1. Что называют отношением двух чисел?
{Частное двух чисел называют отношением этих чисел}
2. Что такое пропорция?
{Равенство двух отношений называют пропорцией}.
3. Как называют числа составляющие пропорцию?
{Числа, составляющие пропорцию, называют членами этой пропорции}
4. Сформулируйте основное свойство пропорции.
{Произведение крайних членов равно произведению средних членов}.
5 . Какие виды пропорциональностей вам известны?
6. Какие величины называют прямо пропорциональными?
{Две величины называют прямо пропорциональными, если с увеличением одной из них в несколько раз другая увеличивается во столько же раз}.
7. Какие величины называют обратно пропорциональными?
{Две величины называют обратно пропорциональными, если с увеличением одной из них в несколько раз другая уменьшается во столько же раз}.
(слайд №5)
Учитель обращается к ученикам с вопросом :» Какую связь можно установить в нашей проделанной работе? Как вы можете ее выразить через высказывание? «
Предпологаемые выводы учеников:
-Чем больше лепестков сорвано со цветка, тем больше материала мы повторили.
-Чем меньше лепестков остается на цветке, тем больше материала мы повторили.
Подводят игог по видам пропорции.
3. Актуализация знаний учащихся ( на данном этапе проходит несколько различных видов работы: индивидуальная, работа в парах, фронтальная, групповая).
А). индивидуальная работа на доске .
Задание для первого ученика. Реши задачу: «Для варки варенья из вишни на 6 кг ягод берут 4 кг сахарного песка. Сколько сахарного песка надо взять на 4 кг ягод?» Письменное решение.
Задание для второго ученика, сидящего на своем рабочем месте. Ответить на вопрос следующей задачи: «Имеются деньги на покупку 30 карандашей. а) Сколько тетрадей можно купить на те же деньги, если тетрадь дешевле карандаша в 2 раза? б) Сколько ручек можно купить на те же деньги, если ручка дороже карандаша в 10 раз? «
Б). индивидуальная работа на интерактивной доске : собрать из предложенных отношений верные равенства. (Работа с флипчартами: с помощью перетаскивания частей, собрать пропорции).
В). математический бой : «Ты-мне, я-тебе». Работа двух ребят на доске. Суть игры состоит в следующем: каждый из ребят обменивается вопросом, получив свое задание, выполняет его.
Г). Работа остальных учащихся класса : цифровой диктант
Ваша задача правильно разгадать код. Если вы согласны с утверждением, то ставите цифру 1, а если не согласны, то 0.
( учитель зачитывает предложение, ученики ставят соответствующую цифру)
1. Цифровой диктант.
А) Пропорция – это равенство двух отношений. (1)
Б) Произведение крайних членов верной пропорции равно произведению её средних членов. (1)
В) В пропорции 2: 5 = 10 : 25 числа 2 и 25 называются средними членами пропорции.(0)
Г) Количество товара и его стоимость при постоянной цене являются пропорциональными величинами. ( 1)
1101 – это код. ( Вывешивается на доску)
Вы получили доступ к выполнению заданий на уроке. Сядьте удобно и чтобы не скучать на уроке поработаем с выражениями на прямую и обратную пропорциональность.
2. Верно-неверно.
(Учащиеся, работая группами, отмечают знаком «+» верные высказывания, знаком «-» неверные высказывания. Каждая группа получает листок с высказываниями. Проверка задания проводится с помощью интерактивной доски. К этому моменту доска должна уже освободиться. (Индивидуальную работу ученика, работающего у доски, проверяет учитель, если в классе достаточное количество ребят, может проверить один из учащихся.) Ответы закрыты, используя эффект «шторки»).
Предполагаемые высказывания:
1. Периметр квадрата и длина стороны квадрата – прямо пропорциональные величины.
2. Длина стороны квадрата и площадь квадрата – прямо пропорциональные величины.
3. Если скорость движения постоянна, то пройденный путь и время движения – прямо пропорциональные величины.
4. Выручка кассы кинотеатра обратно пропорциональна количеству проданных билетов.
5. При постоянной цене стоимость товара и его количество – обратно пропорциональные величины.
6. Если площадь прямоугольника постоянная величина, то его длина и ширина – обратно пропорциональные величины.
(Результаты работы на уроке учащиеся выставляют в листах самооценивания. С нормами оценивания они знакомы, поскольку выполняют такую работу регулярно. На доску вывешивается шкала оценивания).
Учитель. На простейшие вопросы вы ответили на «5».
Покажите на примерах, как умеете считать.
III. Работа в тетрадях (12 мин) (слайды №6, 7)
Решение задач с содержанием регионального компонента.
В 28 кг картофеля, выращенным компанией «Иволга», содержится 4,2 кг крахмала. Сколько кг крахмала содержится в 35 кг картофеля?
Бригада по строительству нового комплекса для международной выставки «ЭКСПО-2017» из 8 рабочих выполняет задание за 12 дней. Сколько рабочих сможет выполнить это задание за 8 дней, работая с той же производительностью?
IV. Валеологическая пауза (музыкальная физ минутка)
Физминутка для глаз.
Напишите глазами свою фамилию, имя и рядом ту оценку, которую вы хотели бы получить сегодня на уроке.
Исторический ракурс по пропорции. ( дополнительный материал по пропорции подготовили двое учащихся к данному уроку, получив задание в качестве домашнего после предыдущего урока. На кануне урока задание проверяется учителем и редактируется по необходимости, т.к. ученики могут подготовить большой объем информации, используя материалы Интернета)
1ученик: Само слово «пропорция» (от латинского proportio) означает «соразмерность», определенное соотношение частей между собой.
Учение о пропорциях особенно успешно развивалось в IV в до н.э. в Древней Греции, славившейся произведениями искусства, архитектуры, развитыми ремеслами. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке. Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.
2 ученик: Первым ввел термин «золотое сечение» Леонардо да Винчи. Его личность одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды». Он снискал славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения. (слайды №9, 10)
«Золотым сечением» и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей и это отношение равно 8:5. «Золотое сечение» чаще всего применяется в произведениях искусства, архитектуры, также взято из законов природы.
Даже растения имеют «золотое сечение».Если мы рассмотрим расположение листьев на стебле то можно заметить, что между двумя парами листьев расположена третья на месте « золотого» сечения. Этот звездчатый пятиугольник называется “пентаграммой”. Она считалась символом здоровья и служила опознавательным знаком. Звезда построена по принципу “золотого сечения”. “Золотым сечением” математики древности называли деление отрезка, при котором длина всего отрезка относится к длине его большей части так же, как длина большей части к меньшей, т. е. 
.
VII. Исследовательская работа на проверку свойства «Золотого сечения».
(Работа в группах)
— У вас на столе лежат звездочки разных размеров. Измерьте нужные отрезки. Составьте пропорцию и проверьте равенство.
— Какое число у вас получилось? ( 1,6)
— Почему у всех примерно одинаковый ответ, ведь звездочки разной величины?
Вывод. Отношения равны. В этом и заключается свойство “Золотого сечения”.
6. Самостоятельная работа на проверку понимания изученного материала по теме «Пропорция»
(Самостоятельная работа проводится по уровням знаний учащихся.Самостоятельная работа содержит цветные задачи в соответствии уровнем слайд № 11)
1 вариант.
1. На пошив 9 рубашек ушло 18 м ткани. Сколько метров уйдет на пошив 12 таких рубашек?
2. 6 одинаковых труб заполняют бассейн за 24 минуты. За сколько минут заполнят бассейн 9 таких труб?
3. Решите уравнение: х:3,5=2,4:0,8.
2 вариант.
1. Из 9,6 кг помидоров получают 4 л томатного сока. Сколько литров сока можно получить из 96 кг помидоров?
2. Для строительства здания необходимо расчистить площадку. За какое время расчистят эту площадку 6 бульдозеров, если такую же площадку 4 бульдозера с такой же производительностью расчистят за 9 часов?
3. Решите уравнение: х:0,75=1,4:0,25
Учащиеся работают в тетрадях для дополнительных работ и сдают их для проверки. Правильное решение и ответы показываются на слайде № 12 .
7.Итог урока. 2 мин.
— Ребята! Давайте вернемся к целям и задачам нашего урока. Как вы думаете, все ли мы сделали для того чтобы достигнуть цели нашего урока и выполнить его задачи?
-Оцените вашу работу на уроке?
-А вашего товарища?
— Кто еще хочет оценить себя или своего друга?
-Соответствует ли ваше желание с той оценкой, которую вы получили на уроке?
-Что вам больше всего сегодня понравилось на уроке?
— А что не понравилось?
-Выскажите ваше мнение об уроке.
Выберите личико на слайде настроения, которое соответствует вашему настроению к концу урока.
На стикерах напишите ваше мнение об уроке начиная со слов (слайд № 13)
Сегодня я узнал…
Я смог…
Урок дал мне для жизни…
Я научился…
Я понял, что…
Мне захотелось…
Я приобрел…
Было интересно…
Было трудно…
У меня получилось…
Я выполнил задание…
Теперь я могу…
Я почувствовал, что…
Я попробую…
Меня удивило…
( На стене висит плакат рефлексии с содержащими на них карманчиками. Мнение об уроке ученики вкладывают в соответствующий карманчик, начинающий одной из фраз….).
Домашнее задание (слайд №14)
1. Практическое задание «Найти отношение собственного роста к расстоянию от подошвы до поясницы. Проделайте такой опыт с несколькими членами вашей семьи». Сделай вывод.
2. Повторить материал учебника п.2-п.4, №169, 175.
VIII. Прощание с детьми (Слайд 15)
Пусть каждый день и каждый час
Вам новое добудет.
Пусть добрым будет ум у вас,
А сердце умным будет.
С. Маршак
Список литературы:
1. Ребусы по математике. Материал из Интернета.
2. «Золотое сечение». Материал из Интернета.
3. Учебное пособие для 6 класса»Математика»автора
infourok.ru