Экспериментальное задание «Жесткость пружины»
Экспериментальное задание по теме
« Измерение коэффициента жесткости пружины и экспериментальная проверка закона Гука.»
Выполнил:
Буторов Евгений Борисович
учитель физики
МБОО Дмитриево Помряскинская СШ
Старомайнского района
Ульяновской области
Тема: Измерение коэффициента жесткости пружины и экспериментальная проверка закона Гука.
Цели:
Образовательная: Экспериментально подтвердить прямо пропорциональную зависимость силы упругости от удлинения, рассчитать коэффициент жесткости пружины, используя результаты эксперимента (ОК3 Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность)
Развивающая: развивать способность анализировать (ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их выполнение и качество).
Воспитательная: воспитывать устойчивый интерес к специальности (ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес)
Оборудование: штатив с муфтой и лапкой, пружина, динамометр с пределом измерения 5Н, измерительная лента с миллиметровыми делениями, грузы.
Теория
Соотношение между силой упругости и деформацией упругого тела, описываемое формулой Fупр = k∆l, открыл английский ученый Роберт Гук в 1660 году, поэтому это соотношение носит его имя и называется законом Гука.
Удлинение пружины в результате ее растяжения обозначается ∆l =l — l0, где l0 — начальная длина, l — длина растянутой пружины.
Коэффициент k называют жесткостью пружины. Чем жестче пружина, тем труднее ее растянуть, и тем большее значение будет иметь k.
Сила упругости растянутой пружины уравновешивает силу тяжести, действующую на груз, т.е.
Fупр = FТ = mg = Р.
Порядок выполнения работы
В тетради запиши теорию по данной теме, используя план:
сделать рисунок;
ввести условные обозначения:
l0— ……………………………………….
∆l
l – ……………………………………….
Δl = l-l0 ………………………………….
Fупр-…………………………………….
mg — ……………………………………
k — ……………………………………….
Соберите установку эксперимента, закрепив пружину в лапке с муфтой.
Измерьте длину не деформированной пружины l0.
Подвесьте 1 груз, измерьте длину пружины с подвешенным грузом; рассчитайте удлинение; при помощи динамометра определите вес 1 груза.

Повторите действие п.4 для 2-х, 3-х, 4-х грузов.
Рассчитайте коэффициент жесткости пружины для каждого случая, найдите среднее значение коэффициента жесткости пружины kср.
Найдите абсолютную и относительную погрешности для коэффициента жесткости пружины:
Δkср
Заполнить таблицу:
м
l,
м
Δl,
м
P,Н
k,
Н/м
kср,
Н/м
Δkср,Н/м
,
%
1 груз
2 груза
3 груза
4 груза
Постройте график зависимости Fупр(Δl), выбрав удобный масштаб, по графику определить вид приблизительной математической зависимости.

Записать вывод, основываясь на поставленную цель; записать рассчитанный коэффициент жесткости пружины с погрешностью в виде k=kср± Δkср.
Контрольные вопросы.
Когда возникает сила упругости?
Как найти удлинение пружины?
Как рассчитать жёсткость пружины?
Груз неподвижно висит на пружине. Что можно сказать в этом случае о силе тяжести груза и силе упругости пружины?
Чем является график зависимости силы упругости от удлинения пружины?
Каково направление силы упругости?
От чего зависит коэффициент жесткости? В каких единицах измеряется?
Коэффициент жесткости пружины
Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины.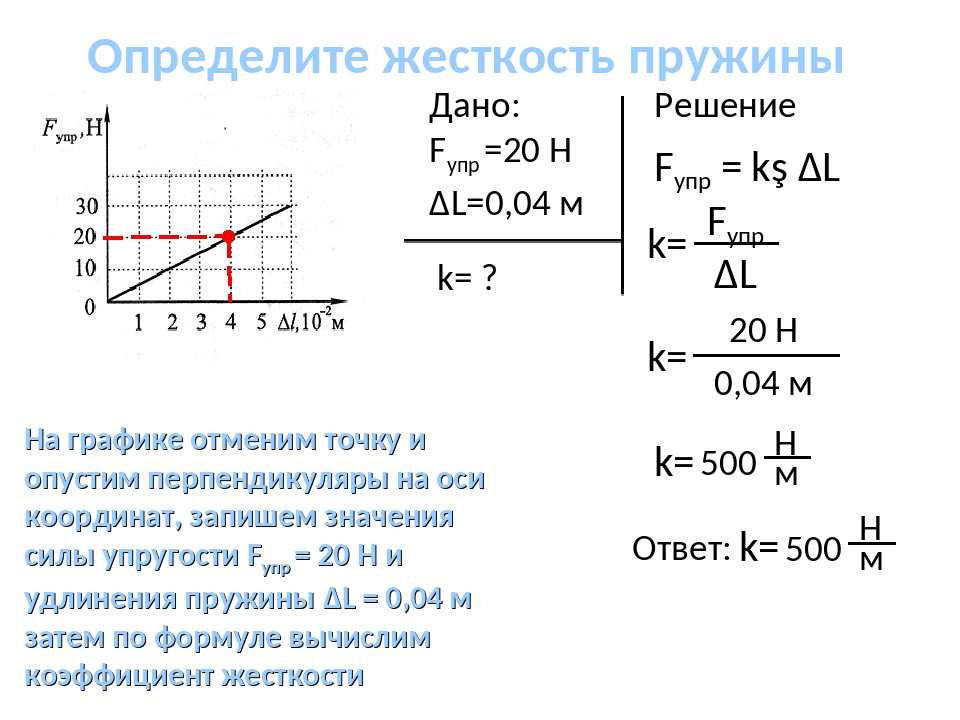 Что же это за величина, и как она связана с деформацией тел и законом Гука?
Что же это за величина, и как она связана с деформацией тел и законом Гука?
Блок: 1/7 | Кол-во символов: 250
Источник: https://LivePosts.ru/articles/education-articles/fizika/kak-najti-koeffitsient-zhyostkosti-pruzhiny-formula-opredelenie
Определение и свойства
Коэффициент упругости по определению равен силе упругости, делённой на изменение длины пружины: Коэффициент упругости зависит как от свойств материала, так и от размеров упругого тела. Так, для упругого стержня можно выделить зависимость от размеров стержня (площади поперечного сечения и длины ), записав коэффициент упругости как Величина называется модулем Юнга и, в отличие от коэффициента упругости, зависит только от свойств материала стержня.
Блок: 2/6 | Кол-во символов: 478
Источник: https://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D1%83%D0%BF%D1%80%D1%83%D0%B3%D0%BE%D1%81%D1%82%D0%B8
Типы пружин
Пружины можно классифицировать по направлению прилагаемой нагрузки:
- пружины растяжения; предназначены для работы в режиме растягивания, при деформации их длина увеличивается; как правило, такие устройства имеют нулевой шаг, т.

- пружины сжатия под нагрузкой, напротив, укорачиваются; в исходном состоянии между их витками есть некоторое расстояние, как, например, в амортизаторах автомобильных подвесок.
В данной статье рассматриваются пружины, представляющие собой цилиндрические спирали. В технике применяется много других разновидностей упругих устройств: пружины в виде плоских спиралей (используются в механических часах), в виде полос (рессоры), пружины кручения (в точных весах), тарельчатые (сжимающиеся конические поверхности) и т.п. Своего рода пружинами являются амортизирующие изделия из полимерных эластичных материалов, прежде всего резины. Во всех этих устройствах используется один и тот же принцип — запасать энергию упругой деформации и возвращать ее.
Блок: 2/5 | Кол-во символов: 1113
Источник: https://spravochnick.ru/fizika/zhestkost_pruzhiny_formula/
Определение и формула жесткости пружины
При рассмотрении того, что такое коэффициент жесткости пружины следует уделить внимание понятию упругости. Для ее обозначения применяется символ F. При этом сила упругости пружины характеризуется следующими особенностями:
Для ее обозначения применяется символ F. При этом сила упругости пружины характеризуется следующими особенностями:
- Проявляется исключительно при деформации тела и исчезает в случае, если деформация пропадает.
- При рассмотрении, что такое жесткость пружины следует учитывать, после снятия внешней нагрузки тело может восстанавливать свои размеры и форму, частично или полностью. В подобном случае деформация считается упругой.
Не стоит забывать о том, что жесткость – характеристика, свойственная упругим телам, способным деформироваться. Довольно распространенным вопросом можно назвать то, как обозначается жесткость пружины на чертежах или в технической документации. Чаще всего для этого применяется буква k.
Слишком сильная деформация тела становится причиной появления различных дефектов. Ключевыми особенностями можно назвать следующее:
- Деталь может сохранять свои геометрические параметры при длительной эксплуатации.
- При увеличении показателя существенно снижается сжатие пружины под воздействие одинаковой силы.

- Наиболее важным параметром можно назвать коэффициент жесткости. Он зависит от геометрических показателей изделия, типа применяемого материала при изготовлении.
Довольно большое распространение получили красные пружины и другого типа. Цветовое обозначение применяется в случае производства автомобильных изделий. Для расчета применяется следующая формула: k=Gd 4 /8D 3 n. В этой формуле указываются нижеприведенные обозначения:
- G – применяется для определения модуля сдвига. Стоит учитывать, что это свойство во многом зависит от применяемого материала при изготовлении витков.
- d – диаметральный показатель проволоки. Она производится путем проката. Этот параметр указывается также в технической документации.
- D – диаметр создаваемых витков при накручивании проволоки вокруг оси. Он подбирается в зависимости от поставленных задач. Во многом диаметр определяет то, какая нагрузка оказывается для сжатия устройства.
- n – число витков.
 Этот показатель может варьировать в достаточно большом диапазоне, также влияет на основные эксплуатационные характеристики изделия.
Этот показатель может варьировать в достаточно большом диапазоне, также влияет на основные эксплуатационные характеристики изделия.
Рассматриваемая формула применяется в случае расчета коэффициента жесткости для цилиндрических пружин, которые устанавливаются в самых различных механизмах. Подобная единица измеряется в Ньютонах. Коэффициент жесткости для стандартизированных изделий можно встретить в технической литературе.
Блок: 2/7 | Кол-во символов: 2525
Источник: https://MyTooling.ru/instrumenty/vyvod-opredelenie-zhestkosti-pruzhiny
Физические характеристики пружин
Цилиндрические пружины характеризуются рядом параметров, сочетание которых обуславливает их жесткость — способность сопротивляться деформации:
- материал; пружины чаще всего изготавливают из стальной проволоки, причем сталь в них применялася особая, ее характеризует среднее или высокое содержание углерода, низкое содержание других примесей (низколегированный сплав) и особая термообработка (закалка), придающая материалу дополнительную упругость;
- диаметр проволоки; чем он меньше, тем эластичнее пружина, но тем меньше ее способность запасать энергию; пружины сжатия изготавливают, как правило, из более толстой проволоки, чем пружины растяжения;
- форма сечения проволоки; не всегда проволока, из которой намотана пружина, имеет круглое сечение; уплощенное сечение имеют пружины сжатия, чтобы при максимальном сокращении длины (виток «садится» на соседний виток) конструкция была более устойчивой;
- длина и диаметр пружины; длину пружины следует отличать от длины проволоки, из которой она намотана; эти два параметра согласуются через количество витков и диаметр пружины, который, в свою очередь, не следует путать с диаметром проволоки.

Существуют и другие физические характеристики, влияющие на работоспособность пружин. Например, при повышении температуры металл становится менее упругим, а при существенном ее понижении может стать хрупким. При интенсивной эксплуатации пружина со временем теряет часть упругости по причине постепенного разрушения связей между атомами кристаллической решетки.
Блок: 3/5 | Кол-во символов: 1530
Источник: https://spravochnick.ru/fizika/zhestkost_pruzhiny_formula/
Расчет пружины сжатия из проволоки прямоугольного сечения
Жесткость пружины из проволоки или прутка прямоугольного сечения при тех же габаритах, что и из круглой проволоки может быть гораздо больше. Соответственно и сила сжатия пружины может быть больше.
Основным отличием в расчете, как вы уже догадались, является определение жесткости витка (C 1 ) , задающей жесткость пружины (C ) в целом.
Далее представлены скриншот программы и формулы для цилиндрической стальной пружины из прямоугольной проволоки, у которой поджаты по ¾ витка с каждого конца и опорные поверхности отшлифованы на ¾ длины окружности.
Внимание!!!
После выполнения расчета по программе выполняйте проверку касательных напряжений!!!
4. I =(D 1 / B ) -1
5. При 1/3: Y =5,3942*(H / B ) 2 -0,3572*(H /B )+0,5272
При 1: Y =5,4962*(H / B ) (-1.715)
При 2H / B : Y =3 ,9286 *(H / B ) (-1. 2339 )
6. При H B : C 1 =(78500* H 4 )/(Y * (D 1 — B ) 3)
При H > B : C 1 =(78500* B 4 )/(Y * (D 1 — B ) 3)
8. T nom =1,25*(F 2 / C 1 )+H
9. T max =π*(D 1 — B )*tg (10 ° )
T max =π*(D 1 — B )*tg (10 ° )
11. S 3 = T — H
12. F 3 = C 1 * S 3
14. N расч =(L 2 — H )/(H +F 3 / C 1 — F 2 / C 1 )
16. C = C 1 / N
17. L 0 = N * T + H
18. L 3 = N * H + H
19. F 2 = C * L 0 — C * L 2
21. F 1 = C * L 0 — C * L 1
22. N 1 = N +1,5
23. A =arctg (T /(π *(D 1 — H )))
24. L разв =π* N 1 *(D 1 — H )/cos (A )
L разв =π* N 1 *(D 1 — H )/cos (A )
25. Q =H *B * L разв *7,85/10 6
Блок: 3/6 | Кол-во символов: 1488
Источник: https://svetvam.ru/diy/formula-udlineniya-pruzhiny-kak-naiti-koefficient-zh-stkosti.html
Жёсткость деформируемых тел при их соединении
Параллельное соединение пружин.
Последовательное соединение пружин.
При соединении нескольких упруго деформируемых тел (далее для краткости — пружин) общая жёсткость системы будет меняться. При параллельном соединении жёсткость увеличивается, при последовательном — уменьшается.
Параллельное соединение
При параллельном соединении пружин с жёсткостями, равными жёсткость системы равна сумме жёсткостей, то есть
Последовательное соединение
При последовательном соединении пружин с жёсткостями, равными общая жёсткость определяется из уравнения:
Блок: 3/6 | Кол-во символов: 601
Источник: https://ru. wikipedia.org/wiki/%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D1%83%D0%BF%D1%80%D1%83%D0%B3%D0%BE%D1%81%D1%82%D0%B8
wikipedia.org/wiki/%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D1%83%D0%BF%D1%80%D1%83%D0%B3%D0%BE%D1%81%D1%82%D0%B8
Расчет в Excel жесткости витка пружины
Жесткость витка пружины – это «краеугольный камень в фундаменте» расчетов, зависящий лишь от модуля сдвига материала, из которого пружина навита и её геометрических размеров.
C 1 = G * X 4 /(Y *(D 1 — B ) 3 )
В этой формуле:
G – модуль сдвига материала проволоки
Для пружинной стали:
G ≈78500 МПа ±10%
Для пружинной бронзы:
G ≈45000 МПа ±10%
X – минимальный размер сечения проволоки
Для круглой проволоки – это её диаметр:
X = D
Для прямоугольной проволоки:
X = H при H B
X = B при B H
H – высота сечения проволоки в направлении параллельном оси навивки пружины
B – ширина сечения проволоки в направлении перпендикулярном оси навивки пружины
Для круглой проволоки:
H = B = D
D 1 — наружный диаметр пружины
(D 1 — B ) – средний диаметр пружины
Y – параметр жесткости сечения проволоки
Для круглой проволоки:
Y = 8
Для прямоугольной проволоки:
Y = f (H / B )
Что это за функция — f (H / B ) ? В литературе она всегда задана в виде таблицы, что не всегда удобно, особенно для промежуточных значений H / B , которых попросту нет.
Выполним в MS Excel табличных данных в первых двух столбцах аналитическими функциями, разбив для повышения точности табличные значения на три группы.
На графиках, представленных ниже, Excel нашел три уравнения для определения параметра Y при различных значениях аргумента — отношения высоты проволоки к ширине — H / B . Красные точки – это заданные значения из таблицы (столбец №2), черные линии – это графики найденных аппроксимирующих функций. Уравнения этих функций Excel вывел непосредственно на поля графиков.
В таблице в столбце №3 размещены посчитанные по полученным формулам значения параметра жесткости сечения проволоки Y , а в столбцах №4 и №5 — абсолютные Δ абс и относительные Δ отн погрешности аппроксимации.
Как видно из таблицы и графиков полученные уравнения весьма точно замещают табличные данные! Величина достоверности аппроксимации R 2 очень близка к 1 и относительная погрешность не превышает 2,7%!
Применим на практике полученные результаты.
Блок: 2/6 | Кол-во символов: 2101
Источник: https://svetvam.ru/diy/formula-udlineniya-pruzhiny-kak-naiti-koefficient-zh-stkosti.html
Коэффициент жесткости соединений пружин
Приведенный выше показатель коэффициента жесткости детали при параллельном или последовательном соединении определяет многие характеристики соединения. Довольно часто проводится определение тому, чему равно удлинение пружины. Среди особенностей параллельного или последовательного соединения можно отметить нижеприведенные моменты:
- При параллельном подключении удлинение обоих изделий будет равным. Не стоит забывать о том, что оба варианта должны характеризоваться одинаковой длиной в свободном положении. При последовательном показатель увеличивается в два раза.
- Свободное положение – ситуация, в которой деталь находится без прикладывания нагрузки. Именно оно в большинстве случаев учитывается при проведении расчетов.
- Коэффициент жесткости изменяется в зависимости от применяемого способа подсоединения.
 В случае параллельного соединения показатель увеличивается в два раза, при последовательном уменьшается.
В случае параллельного соединения показатель увеличивается в два раза, при последовательном уменьшается.
Для проведения расчетов нужно построить схему подключения всех элементов. Основание представлено линией со штриховкой, изделие обозначается схематически, а тело в упрощенном виде. Кроме этого, от упругой деформации во многом зависит кинетическая и другая энергия.
Блок: 4/7 | Кол-во символов: 1218
Источник: https://MyTooling.ru/instrumenty/vyvod-opredelenie-zhestkosti-pruzhiny
Коэффициент жесткости цилиндрической пружины
На практике и в физике довольно большое распространение получили именно цилиндрические пружины. Их ключевыми особенностями можно назвать следующие моменты:
- При создании указывается центральная ось, вдоль которой и действует большинство различных сил.
- При производстве рассматриваемого изделия применяется проволока определенного диаметра. Она изготавливается из специального сплава или обычных металлов.
 Не стоит забывать о том, что материал должен обладать повышенной упругостью.
Не стоит забывать о том, что материал должен обладать повышенной упругостью. - Проволока накручивается витками вдоль оси. При этом стоит учитывать, что они могут быть одного или разного диаметра. Довольно большое распространение получил вариант исполнения цилиндрического типа, но большей устойчивостью характеризуется цилиндрический вариант исполнения, в сжатом состоянии деталь обладает небольшой толщиной.
- Основными параметрами можно назвать больший, средний и малый диаметр витков, диаметр проволоки, шаг расположения отдельных колец.
Не стоит забывать о том, что выделяют два типа деталей: сжатия и растяжения. Их коэффициент жесткости определяется по одной и той же формуле. Разница заключается в следующем:
- Вариант исполнения, рассчитанный на сжатие, характеризуется дальним расположением витков. За счет расстояние между ними есть возможность сжатия.
- Модель, рассчитанная на растяжение, имеет кольца, расположенные практически вплотную.
 Подобная форма определяет то, что при максимальная сила упругости достигается при минимальном растяжении.
Подобная форма определяет то, что при максимальная сила упругости достигается при минимальном растяжении. - Также есть вариант исполнения, который рассчитан на кручение и изгиб. Подобная деталь рассчитывается по определенным формулам.
Расчет коэффициента цилиндрической пружины может проводится при использовании ранее указанной формулы. Она определяет то, что показатель зависит от следующих параметров:
- Наружного радиуса колец. Как ранее было отмечено, при изготовлении детали применяется ось, вокруг которой проводится накручивание колец. При этом не стоит забывать о том, что выделяют также средний и внутренний диаметр. Подобный показатель указывается в технической документации и на чертежах.
- Количества создаваемых витков. Этот параметр во многом определяет длину изделия в свободном состоянии. Кроме этого, количество колец определяет коэффициент жесткость и многие другие параметры.
- Радиуса применяемой проволоки. В качестве исходного материала применяется именно проволока, которая изготавливается из различных сплавов.
 Во многом ее свойства оказывают влияние на качества рассматриваемого изделия.
Во многом ее свойства оказывают влияние на качества рассматриваемого изделия. - Модуля сдвига, который зависит от типа применяемого материала.
Коэффициент жесткости считается одним из наиболее важных параметров, который учитывается при проведении самых различных расчетов.
Блок: 5/7 | Кол-во символов: 2693
Источник: https://MyTooling.ru/instrumenty/vyvod-opredelenie-zhestkosti-pruzhiny
Это соотношение выражает суть закона Гука. А значит, чтобы найти коэффициент жесткостипружины, следует силу растяжения тела разделить на удлинение данной пружины
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества.
Закон Гука может быть обобщен и на случай более сложных деформаций. В технике часто применяются спиралеобразные пружины (рис. 1.12.3). Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Закрепите вертикально один конец пружины, второй же ее конец оставьте свободным. Жесткость – это способность детали или конструкции противодействовать приложенной к нему внешней силе, по возможности сохраняя свои геометрические параметры.
Различные пружины предназначены для работы на сжатие, растяжение, кручение или изгиб. В школе на уроках физики детей учат определять коэффициентжесткости пружины, работающей на растяжение. Для этого на штативе вертикально подвешивается пружина в свободном состоянии.
Вычисление силы Архимеда. Количество теплоты и калориметр. Теплота плавления/кристаллизации и парообразования/конденсации. Теплота сгорания топлива и КПД тепловых двигателей. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис.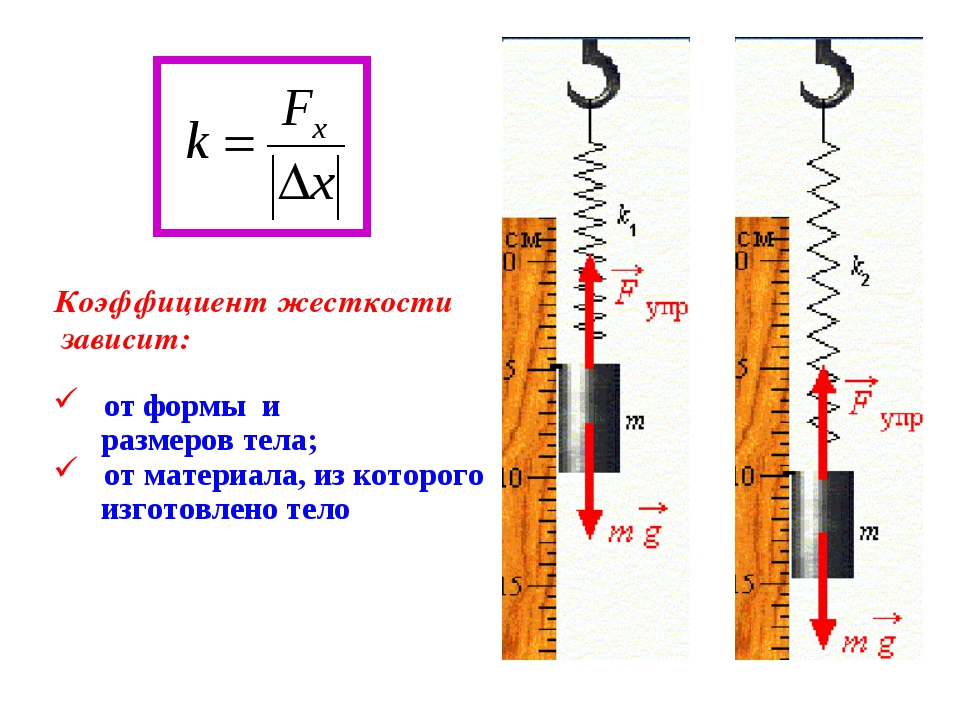 1.12.2).
1.12.2).
Поэтому ее часто называют силой нормального давления. Деформация растяжения пружины. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала. С точки зрения классической физики пружину можно назвать устройством, которое накапливает потенциальную энергию путем изменения расстояния между атомами материала, из которого эта пружина сделана.
Блок: 5/6 | Кол-во символов: 2054
Источник: https://svetvam.ru/diy/formula-udlineniya-pruzhiny-kak-naiti-koefficient-zh-stkosti.html
Примеры задач на нахождение жесткости
Задача 1
На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.
- Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
- По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.
Ответ: жесткость пружины составит 2500 Н/м.
Задача 2
Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.
- Найдем силу тяжести, деформирующей пружину: F = mg = 10 · 9.8 = 98 Н.
- Определим коэффициент упругости: k = F/x = 98 / 0.04 = 2450 Н/м.
- Рассчитаем, с какой силой действует второй груз: F = mg = 25 · 9.8 = 245 Н.
- По закону Гука запишем формулу для абсолютного удлинения: x = F/k.
- Для второго случая подсчитаем длину растяжения: x = 245 / 2450 = 0,1 м.
Ответ: во втором случае пружина растянется на 10 см.
Блок: 6/7 | Кол-во символов: 919
Источник: https://LivePosts.ru/articles/education-articles/fizika/kak-najti-koeffitsient-zhyostkosti-pruzhiny-formula-opredelenie
Единицы измерения
Основной единицей измерения коэффициента жесткости в системе СИ является:
В СГС:
= дин/см
Блок: 5/6 | Кол-во символов: 128
Источник: http://ru. solverbook.com/spravochnik/koefficienty/koefficient-zhestkosti-pruzhiny/
solverbook.com/spravochnik/koefficienty/koefficient-zhestkosti-pruzhiny/
Видео
Из этого видео вы узнаете, как определить жесткость пружины.
Блок: 7/7 | Кол-во символов: 69
Источник: https://LivePosts.ru/articles/education-articles/fizika/kak-najti-koeffitsient-zhyostkosti-pruzhiny-formula-opredelenie
Особенности расчета жесткости соединений пружин
Приведенная выше информация указывает на то, что коэффициент жесткости является довольно важным параметром, который должен рассчитываться при выборе наиболее подходящего изделия и во многих других случаях. Именно поэтому довольно распространенным вопросом можно назвать то, как найти жесткость пружины. Среди особенностей соединения отметим следующее:
- Провести определение растяжения пружины можно при вычислении, а также на момент теста. Этот показатель может зависеть в зависимости от проволоки и других параметров.
- Для расчетов могут применяться самые различные формулы, при этом получаемый результат будет практически без погрешностей.
- Есть возможность провести тесты, в ходе которых и выявляются основные параметры. Определить это можно исключительно при применении специального оборудования.
Как ранее было отмечено, выделяют последовательный и параллельный метод соединения. Оба характеризуются своими определенными особенностями, которые должны учитываться.
В заключение отметим, что рассматриваемая деталь является важной частью конструкции различных механизмов. Неправильный вариант исполнения не сможет прослужить в течение длительного периода. При этом не стоит забывать о том, что слишком сильная деформация становится причиной ухудшения эксплуатационных характеристик.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Блок: 7/7 | Кол-во символов: 1412
Источник: https://MyTooling. ru/instrumenty/vyvod-opredelenie-zhestkosti-pruzhiny
ru/instrumenty/vyvod-opredelenie-zhestkosti-pruzhiny
Количество использованных доноров: 6
Информация по каждому донору:
- https://MyTooling.ru/instrumenty/vyvod-opredelenie-zhestkosti-pruzhiny: использовано 4 блоков из 7, кол-во символов 7848 (42%)
- http://ru.solverbook.com/spravochnik/koefficienty/koefficient-zhestkosti-pruzhiny/: использовано 1 блоков из 6, кол-во символов 128 (1%)
- https://LivePosts.ru/articles/education-articles/fizika/kak-najti-koeffitsient-zhyostkosti-pruzhiny-formula-opredelenie: использовано 3 блоков из 7, кол-во символов 1238 (7%)
- https://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D1%83%D0%BF%D1%80%D1%83%D0%B3%D0%BE%D1%81%D1%82%D0%B8: использовано 2 блоков из 6, кол-во символов 1079 (6%)
- https://spravochnick.ru/fizika/zhestkost_pruzhiny_formula/: использовано 2 блоков из 5, кол-во символов 2643 (14%)
- https://svetvam.
 ru/diy/formula-udlineniya-pruzhiny-kak-naiti-koefficient-zh-stkosti.html: использовано 3 блоков из 6, кол-во символов 5643 (30%)
ru/diy/formula-udlineniya-pruzhiny-kak-naiti-koefficient-zh-stkosti.html: использовано 3 блоков из 6, кол-во символов 5643 (30%)
Физика нуклеиновых кислот | Научно-образовательный центр по нанотехнологиям МГУ
IV курс, VII семестр, специализация «Наноструктуры биологической мембраны» (подгруппа НБ2).
Лившиц Михаил Аронович (дфмн, зав. лаб Физики битополимеров Института молекулярной биологии РАН).
24 часа.
Компетенция: иметь чёткое представление о физико-химических свойствах молекулы ДНК, ее геометрии, ее полимерных свойствах, условиях стабилизации.
Программа
Гибкость полимерных молекул. Идеальная свободно-сочлененная цепь. Размеры полимерного клубка. Энтропийная упругость, высокоэластичность.
Объемные взаимодействия. Хороший/плохой растворитель, θ -точка. Набухание клубка в хорошем растворителе. Коэффициент набухания по П.Флори. Конденсация полимерных клубков и гелей в плохом растворителе.
Экспериментальное определение размеров полимерных клубков. Малоугловое упругое светорассеяние. Радиус инерции клубка. Вискозиметрия, скорость седиментации . Гидродинамический радиус. Броуновское движение клубка.
Малоугловое упругое светорассеяние. Радиус инерции клубка. Вискозиметрия, скорость седиментации . Гидродинамический радиус. Броуновское движение клубка.
Изгибная упругость молекулы ДНК. “Червеобразная” модель. Персистентная длина ДНК. Влияние ионной силы. Исключенный объем ДНК. Крутильная жесткость ДНК, флуктуации спирального вращения.
Природа аномально высокой торсионной жесткости ДНК. Составная модель, описывающая упругие свойства молекулы ДНК – сплошной стержень, охваченный жесткой на растяжение-сжатие спиралью.
Статическая и динамическая гибкость. “Кривые” ДНК. Аномальная задержка в геле.
Термодинамическая устойчивость двойной спирали ДНК. Энтальпийно-энтропийная компенсация. Способы наблюдения плавления ДНК. Статистическая термодинамика перехода спираль-клубок в гомополимере: минимизация свободной энергии. Энергия границ, параметр кооперативности. Степень спиральности, средняя длина спирального участка. Длина кооперативности.
Модель Изинга. Отличие перехода спираль-клубок в линейном полимере от истинных фазовых переходов. Теорема Ландау об одномерных системах.
Теорема Ландау об одномерных системах.
Плавление гетерополимера. Дифференциальные кривые плавления и денатурационные карты для ДНК Умеренных размеров (103-104 п.о.). Ширина кривой плавления высокомолекулярной ДНК.
Полиэлектролитные свойства ДНК. Конденсация противоионов.
Эксперименты по «сверхрастяжению» отдельной молекулы ДНК. Растяжение двуспиральной (ds) и однонитевой (ss) ДНК. Теоретические и экспериментальные подтверждения того, что переход в растянутое состояние (B – S) является плавлением, т.е. (ds-ss), а не (ds-ds) переходом.
Кольцевые замкнутые ДНК. Сверхспирализация. Топоизомеразы I и II. Число и плотность сверхвитков. Экспериментальное определение числа сверхвитков: титрование интеркалятором и двумерный электрофорез. Определение свободной энергии сверспирализации с помощью интеркалятора и из равновесных распределений топоизомеров.
Геометрия и топология КЗ ДНК: порядок зацепления, осевая закрутка, райзинг. Определение торсионной жесткости ДНК с использованием наблюдаемой дисперсии порядка зацепления и расчетной дисперсии райзинга.
Плавление КЗ ДНК. Снижение кооперативности диктуется свободной энергией райзинга.
Неканонические структуры ДНК. Кресты в палиндромах. Z –форма в (GC)n –повторах. Н-форма в гомопурин-гомопиримидиновых повторах при кислых pH. А-форма. Параллельные двойные спирали ДНК. Триплексы. Квадруплексы. G-квартеты.
Список литературы
1. А.Ю.Гросберг, А.Р.Хохлов. Статистическая физика макромолекул. «Наука», 1989
2. Ч.Кантор, П.Шиммел. Биофизическая химия, т.1, 2, 3. 1984, 1985
3. М.В.Волькенштейн. Биофизика. «Наука», 1988
4. А.В.Вологодский. Топология и физические свойства кольцевых ДНК. «Наука», 1988
5. М.Д.Франк-Каменецкий. Век ДНК, Изд-во «КДУ», 2004
6. I.Rouzina, V.Bloomfield. Biophys. J. 80, 882-893, 2001
7. C.Bustamante et.al. Nature, 442, 836-839, 2006
Программу составил зав. лаб. физики биополимеров ИМБ РАН д. ф-м. н. М.А.Лившиц
Аннотированный список лекций
Лекция 1. Гибкость полимерных молекул. Идеальная свободно-сочлененная цепь. Размеры полимерного клубка. Энтропийная упругость, высокоэластичность.
Размеры полимерного клубка. Энтропийная упругость, высокоэластичность.
Лекция 2. Объемные взаимодействия. Хороший/плохой растворитель, θ -точка. Набухание клубка в хорошем растворителе. Коэффициент набухания по П.Флори. Конденсация полимерных клубков и гелей в плохом растворителе.
Лекция 3. Экспериментальное определение размеров полимерных клубков. Малоугловое упругое светорассеяние. Радиус инерции клубка. Вискозиметрия, скорость седиментации . Гидродинамический радиус. Броуновское движение клубка.
Лекция 4. Изгибная упругость молекулы ДНК. “Червеобразная” модель. Персистентная длина ДНК. Влияние ионной силы. Исключенный объем ДНК. Крутильная жесткость ДНК, флуктуации спирального вращения.
Лекция 5. Природа аномально высокой торсионной жесткости ДНК. Составная модель, описывающая упругие свойства молекулы ДНК – сплошной стержень, охваченный жесткой на растяжение-сжатие спиралью.
Статическая и динамическая гибкость. “Кривые” ДНК. Аномальная задержка в геле.
Лекция 6. Термодинамическая устойчивость двойной спирали ДНК. Энтальпийно-энтропийная компенсация. Способы наблюдения плавления ДНК. Статистическая термодинамика перехода спираль-клубок в гомополимере: минимизация свободной энергии. Энергия границ, параметр кооперативности. Степень спиральности, средняя длина спирального участка. Длина кооперативности.
Термодинамическая устойчивость двойной спирали ДНК. Энтальпийно-энтропийная компенсация. Способы наблюдения плавления ДНК. Статистическая термодинамика перехода спираль-клубок в гомополимере: минимизация свободной энергии. Энергия границ, параметр кооперативности. Степень спиральности, средняя длина спирального участка. Длина кооперативности.
Лекция 7. Модель Изинга. Отличие перехода спираль-клубок в линейном полимере от истинных фазовых переходов. Теорема Ландау об одномерных системах.
Плавление гетерополимера. Дифференциальные кривые плавления и денатурационные карты для ДНК Умеренных размеров (103-104 п.о.). Ширина кривой плавления высокомолекулярной ДНК.
Полиэлектролитные свойства ДНК. Конденсация противоионов.
Лекция 8. Эксперименты по «сверхрастяжению» отдельной молекулы ДНК. Растяжение двуспиральной (ds) и однонитевой (ss) ДНК. Теоретические и экспериментальные подтверждения того, что переход в растянутое состояние (B – S) является плавлением, т.е. (ds-ss), а не (ds-ds) переходом.
Лекция 9. Кольцевые замкнутые ДНК. Сверхспирализация. Топоизомеразы I и II. Число и плотность сверхвитков. Экспериментальное определение числа сверхвитков: титрование интеркалятором и двумерный электрофорез. Определение свободной энергии сверспирализации с помощью интеркалятора и из равновесных распределений топоизомеров.
Лекция 10. Геометрия и топология КЗ ДНК: порядок зацепления, осевая закрутка, райзинг. Определение торсионной жесткости ДНК с использованием наблюдаемой дисперсии порядка зацепления и расчетной дисперсии райзинга.
Плавление КЗ ДНК. Снижение кооперативности диктуется свободной энергией райзинга.
Лекция 11. Неканонические структуры ДНК. Кресты в палиндромах. Z –форма в (GC)n –повторах. Н-форма в гомопурин-гомопиримидиновых повторах при кислых pH. А-форма. Параллельные двойные спирали ДНК. Триплексы. Квадруплексы. G-квартеты.
Промежуточная аттестация и Список вопросов в билетах
— по пунктам программы.
Примеры решения задач по теме «Силы упругости.
 Закон Гука»
Закон Гука»Примеры решения задач по теме «Силы упругости. Закон Гука»
- Подробности
- Просмотров: 1159
«Физика — 10 класс»
При решении задач по этой теме надо иметь в виду, что закон Гука справедлив только при упругих деформациях тел. Сила упругости не зависит от того, какая происходит деформация: сжатия или растяжения, она одинакова при одинаковых Δl. Кроме этого, считается, что сила упругости вдоль всей пружины одинакова, так как масса пружины обычно не учитывается.
Задача 1.
При помощи пружинного динамометра поднимают с ускорением а = 2,5 м/с2, направленным вверх, груз массой m = 2 кг. Определите модуль удлинения пружины динамометра, если её жёсткость k = 1000 Н/м.
Р е ш е н и е.
Согласно закону Гука, выражающему связь между модулем внешней силы , вызывающей растяжение пружины, и её удлинением, имеем F = kΔl. Отсюда
Для нахождения силы воспользуемся вторым законом Ньютона. На груз, кроме силы тяжести m, действует сила упругости пружины, равная по модулю F и направленная вертикально вверх. Согласно второму закону Ньютона m = F + m.
На груз, кроме силы тяжести m, действует сила упругости пружины, равная по модулю F и направленная вертикально вверх. Согласно второму закону Ньютона m = F + m.
Направим ось OY вертикально вверх так, чтобы пружина была расположена вдоль этой оси (рис. 3.16). В проекции на ось OY второй закон Ньютона можно записать в виде mау = Fy + mgy
Так как ау = a, gy = -g и Fy = F, то F = mа + mg = m(а + g).
Следовательно,
Задача 2.
Определите, как изменяется сила натяжения пружины, прикреплённой к бруску массой m = 5 кг, находящемуся неподвижно на наклонной поверхности, при изменении угла наклона от 30° до 60°. Трение не учитывайте.
Р е ш е н и е.
На брусок действуют сила тяжести, сила натяжения пружины и сила реакции опоры (рис. 3.17).
Условие равновесия бруска: m + + yпp = 0.
Запишем это условие в проекциях на оси ОХ и OY:
Из первого уравнения системы получим Fyпp = mg sinα.
При изменении угла наклона изменение силы упругости найдём из выражения ΔFyпp = mg(sinα2 — sinα1) = 5 • 10 • (0,866 — 0,5) (Н) = 18,3 Н.
Задача 3.
К потолку подвешены последовательно две невесомые пружины жёсткостями 60 Н/м и 40 Н/м. К нижнему концу второй пружины прикреплён груз массой 0,1 кг. Определите жёсткость воображаемой пружины, удлинение которой было бы таким же, как и двух пружин при подвешивании к ней такого же груза (эффективную жёсткость).
Р е ш е н и е.
Так как весом пружин можно пренебречь, то очевидно, что силы натяжения пружин равны (рис. 3.18). Тогда согласно закону Гука
Fynp1 = Fупр2; k1x1 = k2х2. (1)
На подвешенный груз действуют две силы — сила тяжести и сила натяжения второй пружины.
Условие равновесия груза запишем в виде mg = k2х2.
Из этого уравнения найдём удлинение
Подставив выражение для х2 в уравнение (1), получим для удлинения
Определим теперь эффективную жёсткость. Запишем закон Гука для воображаемой пружины:
Запишем закон Гука для воображаемой пружины:
Подставив в формулу (2) выражения для удлинений x1 и х2 пружин, получим
Для эффективной жёсткости получим выражение
Задача 4.
Через блок, закреплённый у края стола, перекинута нерастяжимая нить, к концам которой привязаны брусок массой m1 = 1 кг, находящийся на горизонтальной поверхности стола, и пружина жёсткостью k = 50 Н/м, расположенная вертикально. Ко второму концу пружины привязана гиря массой m2 = 200 г (рис. 3.19). Определите удлинение пружины при движении тел. Силу трения, массы пружины, блока и нити не учитывайте.
Р е ш е н и е.
На брусок действуют сила тяжести, сила реакции опоры и сила натяжения нити.
На гирю действуют сила тяжести и сила натяжения пружины.
Согласно второму закону Ньютона для бруска и гири запишем:
m11 = m1 + + ;
m22 = m + упр.
В проекциях на выбранные оси координат запишем: на ось ОХ: m1а1 = Т;
на ось OY:
Так как нить нерастяжима, то модули ускорений равны: а1 = а2 = а.
В силу условия малых масс пружины, нити и блока можно записать: T2 = Fупр и Т1 = Т2 = Т.
Учтя последние равенства, систему уравнений (1) запишем в виде
Выразив ускорение из первого уравнения системы и подставив его во второе, получим
Из этого уравнения найдём силу натяжения нити:
Так как согласно закону Гука Fупр = kx, то
Тогда удлинение пружины
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Динамика — Физика, учебник для 10 класса — Класс!ная физика
Основное утверждение механики —
Сила —
Инертность тела. Масса. Единица массы —
Первый закон Ньютона —
Второй закон Ньютона —
Принцип суперпозиции сил —
Примеры решения задач по теме «Второй закон Ньютона» —
Третий закон Ньютона —
Геоцентрическая система отсчёта —
Принцип относительности Галилея. Инвариантные и относительные величины —
Силы в природе —
Сила тяжести и сила всемирного тяготения —
Сила тяжести на других планетах —
Примеры решения задач по теме «Закон всемирного тяготения» —
Первая космическая скорость —
Примеры решения задач по теме «Первая космическая скорость» —
Вес. Невесомость —
Деформация и силы упругости. Закон Гука —
Примеры решения задач по теме «Силы упругости. Закон Гука» —
Силы трения —
Примеры решения задач по теме «Силы трения» —
Примеры решения задач по теме «Силы трения» (продолжение) —
Инвариантные и относительные величины —
Силы в природе —
Сила тяжести и сила всемирного тяготения —
Сила тяжести на других планетах —
Примеры решения задач по теме «Закон всемирного тяготения» —
Первая космическая скорость —
Примеры решения задач по теме «Первая космическая скорость» —
Вес. Невесомость —
Деформация и силы упругости. Закон Гука —
Примеры решения задач по теме «Силы упругости. Закон Гука» —
Силы трения —
Примеры решения задач по теме «Силы трения» —
Примеры решения задач по теме «Силы трения» (продолжение) —
Уточнение закона физики – Наука – Коммерсантъ
Упругие свойства материалов интересовали человечество с древнейших времен. Существенный прогресс в понимании упругости был достигнут в работах Роберта Гука, английского исследователя, работавшего во второй половине XVII века. Считается, что наряду с Исааком Ньютоном Гук «ответственен» за закон всемирного тяготения.
В теории упругости он известен открытием закона Гука, который гласит, что сила, которая требуется, чтобы растянуть материал (см. рисунок), оказывается пропорциональна величине растяжения. Коэффициент пропорциональности характеризует конкретный материал и называется объемным модулем Юнга. Для тонких пластин удобно работать с модулем Юнга Y, который получается умножением объемного модуля Юнга на толщину пластины. (Модуль Юнга в системе единиц СИ измеряется в ньютонах на метр (н/м).) Кроме растяжения или сжатия в плоскости у тонких пластин возникает возможность изгиба. Энергия, связанная с изгибом, определяется величиной изгибной жесткости. (В системе СИ изгибная жесткость измеряется в джоулях.)
Возникающий при уменьшении толщины пластины до одного атомарного слоя объект принято называть кристаллической мембраной. Самый известный пример — это графен, который представляет собой один слой атомов углерода, расположенных в узлах шестигранных (сотовых) ячеек. Графен был получен в лаборатории Андреем Геймом и Константином Новоселовым в 2004 году. –19 джоулей.
–19 джоулей.
Как известно из школьного курса физики, атомы в кристаллах совершают тепловые колебания около своих положений равновесия. Эти же тепловые колебания могут вызывать изгибные деформации мембраны. Можно оценить, как величина изгибных деформаций, вызванных тепловыми флуктуациями, растет с увеличением продольного размера мембраны, и найти, при каком размере она сравнивается с толщиной мембраны. Последняя для одноатомного слоя имеет порядок долей нанометра (нм). Соответствующая длина, называемая длиной Гинзбурга, оказывается для графена исключительно маленькой. Она равна 1 нм при комнатной температуре. Поэтому для всех исследуемых в лабораториях образцах графена тепловые изгибные флуктуации оказываются принципиально важны. Для сравнения можно оценить длину Гинзбурга для листа бумаги толщиной 1 мм. Она оказывается равной 1000 км при комнатной температуре! Именно поэтому в обычной жизни мы, как правило, не встречаемся с проявлением тепловых изгибных флуктуаций.
Несмотря на то что роль длины Гинзбурга в физике кристаллических мембран была осознана только в середине 1980-х годов, важность тепловых изгибных флуктуаций была понятна еще с 1930-х годов. В это время Лев Ландау и Рудольф Пайерлс, английский физик-теоретик, один из пионеров концепции дырочной проводимости в полупроводниках и теории экситонов, независимо друг от друга показали, что бесконечные кристаллические мембраны из-за тепловых изгибных флуктуаций должны разрушаться, превращаясь в бесформенный комок атомов. Другими словами, получается, что их результат, который до сих пор входит в стандартные учебники по теоретической физике, например, в курс Ландау и Лифшица, запрещает существование графена!
В это время Лев Ландау и Рудольф Пайерлс, английский физик-теоретик, один из пионеров концепции дырочной проводимости в полупроводниках и теории экситонов, независимо друг от друга показали, что бесконечные кристаллические мембраны из-за тепловых изгибных флуктуаций должны разрушаться, превращаясь в бесформенный комок атомов. Другими словами, получается, что их результат, который до сих пор входит в стандартные учебники по теоретической физике, например, в курс Ландау и Лифшица, запрещает существование графена!
Как же примерить ставшее классическим утверждение Ландау—Пайерлса и чешуйки графена, имеющиеся в настоящее время во многих лабораториях мира. Как это обычно бывает для многих вопросов, разгадка скрыта в деталях. Обратим внимание на то, что, согласно результату Ландау—Пайерлса, не существует кристаллических мембран бесконечных размеров. При любой заданной температуре существует предельный продольный размер мембраны, когда изгибных тепловых флуктуаций недостаточно для разрушения мембраны. Подчеркнем, что этот размер не нужно путать с длиной Гинзбурга! Если оценить такой предельный размер для графена при комнатной температуре, то получится гигантская длина. Так как в лабораториях чешуйки графена обычно имеют размер всего несколько микрометров, то, казалось бы, разгадка найдена!
Подчеркнем, что этот размер не нужно путать с длиной Гинзбурга! Если оценить такой предельный размер для графена при комнатной температуре, то получится гигантская длина. Так как в лабораториях чешуйки графена обычно имеют размер всего несколько микрометров, то, казалось бы, разгадка найдена!
Как это часто бывает в физике, самое простое объяснение явления не всегда оказывается правильным. Утверждение Ландау—Пайерлса основано на предположении, что изгибные тепловые флуктуации не взаимодействуют друг с другом, как говорят, являются гармоническими. Оказывается, что для графена такая идеализация справедлива только для очень маленьких размеров, меньше длины Гинзбурга. Для графена микронного размера игнорировать взаимодействие изгибных флуктуаций между собой оказывается принципиально неправильным. Их взаимодействие приводит к тому, что изгибная жесткость мембраны начинает расти степенным образом с увеличением продольного размера, то есть чем больше размер мембраны, тем все труднее становится ее изогнуть. Этот эффект был теоретически предсказан в середине 80-х годов прошлого века. Он приводит к тому, что бесконечная кристаллическая мембрана оказывается устойчивой при температурах ниже некоторой критической. Для графена критическая температура оказывается выше 10 тыс. градусов Кельвина. Такая высокая критическая температура означает, что тепловые изгибные флуктуации никогда не разрушают графен, так как при таких высоких температурах уже расплавится кристаллическая решетка.
Этот эффект был теоретически предсказан в середине 80-х годов прошлого века. Он приводит к тому, что бесконечная кристаллическая мембрана оказывается устойчивой при температурах ниже некоторой критической. Для графена критическая температура оказывается выше 10 тыс. градусов Кельвина. Такая высокая критическая температура означает, что тепловые изгибные флуктуации никогда не разрушают графен, так как при таких высоких температурах уже расплавится кристаллическая решетка.
Взаимодействие изгибных флуктуаций приводит к ряду интересных явлений в кристаллических мембранах, которые называют термином аномальная упругость. В области малых продольных деформаций нарушается закон Гука: деформация мембраны как целого становится степенной функцией приложенной силы со значением показателя степени меньше единицы, который к тому же не зависит от типа атомов мембраны, то есть является универсальным. Линейный закон Гука восстанавливается только при достаточно больших значениях деформации. Недавно такой нелинейный закон Гука для графена был измерен экспериментально. Также у графена в широкой области параметров оказывается отрицательным коэффициент Пуассона. Напомним, что положительный коэффициент Пуассона характеризует, как при растяжении в одном направлении материал сжимается в поперечном направлении. У графена вместо сжатия в поперечном направлении происходит растяжение! Наконец, вплоть до ультранизких температур коэффициент теплового расширения графена оказывается отрицательным, то есть графен при нагреве сжимается, вместо того чтобы расширяться, как это делает большинство веществ.
Также у графена в широкой области параметров оказывается отрицательным коэффициент Пуассона. Напомним, что положительный коэффициент Пуассона характеризует, как при растяжении в одном направлении материал сжимается в поперечном направлении. У графена вместо сжатия в поперечном направлении происходит растяжение! Наконец, вплоть до ультранизких температур коэффициент теплового расширения графена оказывается отрицательным, то есть графен при нагреве сжимается, вместо того чтобы расширяться, как это делает большинство веществ.
В заключение можно сказать, что физика кристаллических мембран, в частности графена, в очередной раз подтверждает, что в настоящей науке не бывает абсолютных истин: все законы выводятся в рамках некоторых предположений, о которых не стоит забывать. В теории кристаллических мембран все еще осталось значительное количество вопросов, связанных с аномальной упругостью, требующих теоретического и экспериментального изучения. В частности, этим занимаются ученые из Физико-технического института им. А. Ф. Иоффе РАН, Института теоретической физики им. Л. Д. Ландау РАН и Сколковского института науки и технологий в рамках гранта РФФИ 20-52-12019.
А. Ф. Иоффе РАН, Института теоретической физики им. Л. Д. Ландау РАН и Сколковского института науки и технологий в рамках гранта РФФИ 20-52-12019.
Игорь Бурмистров, доктор физико-математических наук, заместитель директора Института теоретической физики им. Л. Д. Ландау РАН
Химические показатели воды – жесткость
Жесткость воды определяется содержанием в воде солей жесткости (кальция и магния). Она выражается в миллиграмм-эквивалентах на литр (мг-экв/л). Различают карбонатную (временную) жесткость, некарбонатную (постоянную) жесткость и общую жесткость воды.
Карбонатная жесткость (устранимая), определяется наличием в воле двууглекислых солей кальция и магния — характеризуется содержанием в воде гидрокарбоната кальция, который при нагревании или кипячении воды разлагается на практически нерастворимый карбонат и углекислый газ. Поэтому её еще называют временной жесткостью.
Некарбонатная или постоянная жесткость — содержание некарбонатных солей кальция и магния — сульфаты, хлориды, нитраты. При нагревании или кипячении воды они остаются в растворе.
При нагревании или кипячении воды они остаются в растворе.
Общая жесткость — определяется как суммарное содержание в воде солей кальция и магния, выражается как сумма карбонатной и некарбонатной жесткости. При оценке жесткости воды обычно воду характеризуют следующим образом:
Очень мягкая вода — до 1,5 мг-экв/л
Мягкая вода — от 1,5 до 4,0 мг-экв/л
Вода средней жесткости — от 4,0 до 8,0 мг-экв/л
Жесткая вода — от 8,0 до 12,0 мг-экв/л
Очень жесткая вода — более 12 мг-экв/л
Вода поверхностных источников, как правило, относительно мягкая (3…6 мг-экв/л) и зависит от географического положения — чем южнее, тем жесткость воды выше. Жесткость подземных вод зависит от глубины и расположения горизонта водоносного слоя и годового объема осадков.
Жесткость воды из слоёв известняка составляет обычно 6 мг-экв/л и выше.
По нормам СанПиН 2.1.4.1074-01 жесткость питьевой воды должна быть не выше 7,0 мг-экв/л.
Жесткая вода просто неприятна на вкус, в ней излишне много кальция. Постоянное употребление внутрь воды с повышенной жесткостью приводит к снижению моторики желудка, к накоплению солей в организме, и, в конечном итоге, к заболеванию суставов (артриты, полиартриты) и образованию камней в почках и желчных путях. Хотя очень мягкая вода не менее опасная, чем излишне жесткая. Самая активная — это мягкая вода. Мягкая вода способна вымывать из костей кальций. У человека может развиться рахит, если пить такую воду с детства, у взрослого человека становятся ломкие кости. Есть еще одно отрицательное свойство мягкой воды. Она, проходя через пищеварительный тракт, не только вымывает минеральные вещества, но и полезные органические вещества, в том числе и полезные бактерии. Вода должна быть жесткостью 1,5-2 мг-экв/л. Использование воды с большой жесткостью для хозяйственных целей также нежелательно. Жесткая вода образует налет на сантехнических приборах и арматуре, образует накипные отложения в водонагревательных системах и приборах. В первом приближении это заметно на стенках, например, чайника.
Постоянное употребление внутрь воды с повышенной жесткостью приводит к снижению моторики желудка, к накоплению солей в организме, и, в конечном итоге, к заболеванию суставов (артриты, полиартриты) и образованию камней в почках и желчных путях. Хотя очень мягкая вода не менее опасная, чем излишне жесткая. Самая активная — это мягкая вода. Мягкая вода способна вымывать из костей кальций. У человека может развиться рахит, если пить такую воду с детства, у взрослого человека становятся ломкие кости. Есть еще одно отрицательное свойство мягкой воды. Она, проходя через пищеварительный тракт, не только вымывает минеральные вещества, но и полезные органические вещества, в том числе и полезные бактерии. Вода должна быть жесткостью 1,5-2 мг-экв/л. Использование воды с большой жесткостью для хозяйственных целей также нежелательно. Жесткая вода образует налет на сантехнических приборах и арматуре, образует накипные отложения в водонагревательных системах и приборах. В первом приближении это заметно на стенках, например, чайника.
При хозяйственно-бытовом использовании жесткой воды значительно увеличивается расход моющих средств и мыла вследствие образования осадка кальциевых и магниевых солей жирных кислот, замедляется процесс приготовления пищи (мяса, овощей и др.), что нежелательно в пищевой промышленности. Во многих случаях использование жесткой воды для производственных целей (для питания паровых котлов, в текстильной бумажной промышленности, на предприятиях искусственного волокна и др.) не допускается, так как это связано с рядом нежелательных последствий.
В системах водоснабжения — жесткая вода приводит к быстрому износу водонагревательной технике (бойлеров, батарей центрального водоснабжения и др.). Соли жесткости (гидрокарбонаты Ca и Mg), отлагаясь на внутренних стенках труб, и образуя накипные отложения в водонагревательных и охлаждающих системах, приводят к занижению проходного сечения, уменьшают теплоотдачу. Не допускается использовать воду с высокой карбонатной жесткостью в системах оборотного водоснабжения.
Физика — Жесткость: меньше значит больше
• Физ. Rev. Focus 7, 13
Пузырьки материала с отрицательной жесткостью, внедренные в более обычный материал, могут привести к получению композитов с очень высокой жесткостью.
© 2001 Photodisc, Inc.
Не слишком гибкий. Пузырьки материала с отрицательной жесткостью, внедренные в более обычный материал, могут привести к получению композитов с очень высокой жесткостью, возможно, достаточно хорошей для улучшения крыльев самолетов.© 2001 Photodisc, Inc.
Не слишком гибкий. Пузырьки материала с отрицательной жесткостью, внедренные в более обычный материал, могут привести к получению композитов с очень высокой жесткостью — возможно, достаточно хорошей для улучшения крыльев самолета. × Когда вы пытаетесь сжать пружину, она отталкивается. Материаловеды называют это свойство положительной жесткостью. Хотя можно создавать материалы с отрицательной жесткостью, они нестабильны. Один толчок, и они либо разлетятся, либо рухнут во что-то с положительной жесткостью.Теперь исследователь сообщает в PRL от 26 марта, что теоретически можно значительно увеличить общую положительную жесткость материала, добавив в него маленькие пузырьки отрицательной жесткости. В другой экспериментальной работе он доказал эту концепцию. Неожиданный прогресс может быть однажды использован для создания более жестких крыльев самолетов, более тихих автомобилей и, возможно, даже временных заменителей сухожилий.
Хотя можно создавать материалы с отрицательной жесткостью, они нестабильны. Один толчок, и они либо разлетятся, либо рухнут во что-то с положительной жесткостью.Теперь исследователь сообщает в PRL от 26 марта, что теоретически можно значительно увеличить общую положительную жесткость материала, добавив в него маленькие пузырьки отрицательной жесткости. В другой экспериментальной работе он доказал эту концепцию. Неожиданный прогресс может быть однажды использован для создания более жестких крыльев самолетов, более тихих автомобилей и, возможно, даже временных заменителей сухожилий.
Механические конструкции ограничены жесткостью. Никто не хочет летать на самолете с крыльями, которые хлопают, как мокрая лапша в турбулентном воздухе.Один из способов, которым инженеры увеличивают жесткость материала, — это смешивание его со вторым материалом для образования композита. Но как только геометрия и состав зафиксированы, серия математических теорем тридцатилетней давности устанавливает окончательный верхний предел жесткости. Увеличение верхнего предела требует более тяжелых или дорогих материалов; но есть загвоздка. «Все эти теоремы молчаливо предполагают, что жесткость положительна», — говорит материаловед из Висконсинского университета Родерик Лейкс.
Увеличение верхнего предела требует более тяжелых или дорогих материалов; но есть загвоздка. «Все эти теоремы молчаливо предполагают, что жесткость положительна», — говорит материаловед из Висконсинского университета Родерик Лейкс.
Добавление отрицательной жесткости переворачивает все эти предположения с ног на голову. Вместо того, чтобы оказывать обычную восстанавливающую силу, которая пытается сопротивляться деформации, материалы с отрицательной жесткостью используют энергию, запасенную в их нестабильном равновесном состоянии, чтобы помочь деформации протекать быстрее. Поскольку они нестабильны, материалы с отрицательной жесткостью обычно быстро разрушаются. Но небольшие пузырьки отрицательной жесткости могут сохраняться на фоне материала положительной жесткости. В некоторых случаях композит будет иметь более низкую общую жесткость, но в своей статье PRL Лейкс математически показывает, что может произойти и обратное.
«Две фазы взаимодействуют друг с другом в некоторых геометриях, и в итоге вы получаете нулевой эффект», — говорит Лейкс. «Но это не линейное сложение, и иногда жесткости складываются обратно пропорционально, давая более положительную жесткость». Хотя в его статье представлено математическое обоснование эффекта, это не просто теоретическая фантазия. В отдельной статье [1] Лейкс показывает, что когда трубки из силиконового каучука сгибаются, как частично сплющенные банки из-под газировки, они имеют отрицательную жесткость. Когда трубы с изгибом смешиваются с трубками без изгиба, жесткость композита возрастает на порядки, как и предсказывает его теория.По словам Лейкса, композит высокой жесткости также имеет тенденцию быстро гасить вибрации, что делает материалы потенциально идеальными для крыльев самолетов и автомобилей.
«Но это не линейное сложение, и иногда жесткости складываются обратно пропорционально, давая более положительную жесткость». Хотя в его статье представлено математическое обоснование эффекта, это не просто теоретическая фантазия. В отдельной статье [1] Лейкс показывает, что когда трубки из силиконового каучука сгибаются, как частично сплющенные банки из-под газировки, они имеют отрицательную жесткость. Когда трубы с изгибом смешиваются с трубками без изгиба, жесткость композита возрастает на порядки, как и предсказывает его теория.По словам Лейкса, композит высокой жесткости также имеет тенденцию быстро гасить вибрации, что делает материалы потенциально идеальными для крыльев самолетов и автомобилей.
«Это весьма инновационно и увлекательно», — говорит Лоуренс Кац, инженер-биомедик из Университета Кейс Вестерн Резерв в Кливленде, штат Огайо. Кац предполагает, что материалы с отрицательной жесткостью также можно использовать в медицинских целях. «Если бы материал с отрицательной жесткостью можно было поместить в сухожилие, находящееся под напряжением, он превратился бы в каркас, оставляющий место для роста естественных тканей», — говорит Кац.
–Марк Силл
Марк Силл – независимый научный писатель из Хьюстона, штат Техас.
Ссылки
- R. S. Lakes, Philos. Маг. лат. 81, 95-100 (2001)
Тематические области
Статьи по теме
Еще статьиFrontiers | Динамика прерывистого скольжения в моделях пучков волокон с переменной жесткостью и числом скольжения
1 Введение
Модели пучков волокон (FBM) являются одним из наиболее важных теоретических подходов к повреждению и разрушению неупорядоченных материалов [1].В рамках FBM образец дискретизируется как пучок параллельных волокон, на которые действует внешняя нагрузка вдоль направления волокон [2, 3]. Модуль Юнга волокон обычно считается постоянным, так что неоднородность материалов полностью представлена случайностью прочности волокон. Даже в простейшем виде ФБМ давали глубокое представление о процессе разрушения разнородных материалов [2, 4, 5], позволяя также встроить процессы разрушения в общие рамки статистической физики [1, 6, 7] и прояснить его аналогия с фазовыми переходами и критическими явлениями [8–13].
Вскоре после того, как Пейрес в 1927 г. [14] представил базовую концепцию FBM, модель была расширена для учета зависимости от времени и эффектов усталости [15]. Последующие разработки модели в течение последних десятилетий показали, что варьируя механический отклик [16] (хрупкое, пластическое) и реологическое (вязкоупругое) поведение [17–20] отдельных волокон, кроме того, степень неупорядоченности прочности [21 –23], диапазон распределения нагрузки (локальный, глобальный) [11, 24, 25] после разрушения и способ нагружения [19, 20, 26] (квазистатическое, ползучести, усталостное) модель способна захватывать широкий спектр поведения материалов.Благодаря этой гибкости модель нашла широкое применение: от разрушения композитов, армированных волокном [25, 27], до гранулированных материалов, где силовые цепи рассматривались как несущие нагрузку волокна [28, 29], до разрыва биологические материалы [30].
Недавно мы предложили расширение FBM [31, 32] для описания механического отклика систем со сложной микроструктурой, которые реагируют на внешнюю нагрузку локальными перестройками, например, частиц, как в гранулированных материалах [28, 32]. 33] и в агломератах диполярных частиц [34], или путем активации внутренней запасенной длины, такой как шелк паука [35].Особой областью, где динамика прерывистого скольжения может быть использована для технологических приложений, является разработка нанокомпозитов, в частности композитов углеродных нанотрубок (УНТ), где УНТ встроены в полимерную матрицу. Одним из интересных свойств нанокомпозитов УНТ является способность поглощать энергию колебаний, что в сочетании с высокой прочностью и устойчивостью к усталости делает их идеальными кандидатами для новых многофункциональных композитных структур [36]. Недавние экспериментальные исследования показали, что усиление демпфирования может быть связано с прерывистым скольжением УНТ-матрицы, вызванным сильным упругим несоответствием, которое приводит к локализации напряжения сдвига на границах раздела [37].Чтобы представить микромасштабную сложность, лежащую в основе динамики прерывистого скольжения, предполагалось, что волокна в нашей модели подвергаются последовательности событий прерывистого скольжения: когда локальная нагрузка достигает порога отказа, волокно не разрывается, вместо этого его нагрузка падает до нуля, но волокно снова способно выдерживать нагрузку.
33] и в агломератах диполярных частиц [34], или путем активации внутренней запасенной длины, такой как шелк паука [35].Особой областью, где динамика прерывистого скольжения может быть использована для технологических приложений, является разработка нанокомпозитов, в частности композитов углеродных нанотрубок (УНТ), где УНТ встроены в полимерную матрицу. Одним из интересных свойств нанокомпозитов УНТ является способность поглощать энергию колебаний, что в сочетании с высокой прочностью и устойчивостью к усталости делает их идеальными кандидатами для новых многофункциональных композитных структур [36]. Недавние экспериментальные исследования показали, что усиление демпфирования может быть связано с прерывистым скольжением УНТ-матрицы, вызванным сильным упругим несоответствием, которое приводит к локализации напряжения сдвига на границах раздела [37].Чтобы представить микромасштабную сложность, лежащую в основе динамики прерывистого скольжения, предполагалось, что волокна в нашей модели подвергаются последовательности событий прерывистого скольжения: когда локальная нагрузка достигает порога отказа, волокно не разрывается, вместо этого его нагрузка падает до нуля, но волокно снова способно выдерживать нагрузку. Модель успешно применялась для анализа механического отклика сыпучих материалов на сдвиг [33] и влияния укрепления корней на устойчивость грунтов [29]. Дополняя прерывисто-скользящую ФБМ восстановительным механизмом, она оказалась способной описать процесс разрушения снега [38, 39].
Модель успешно применялась для анализа механического отклика сыпучих материалов на сдвиг [33] и влияния укрепления корней на устойчивость грунтов [29]. Дополняя прерывисто-скользящую ФБМ восстановительным механизмом, она оказалась способной описать процесс разрушения снега [38, 39].
В базовой настройке модели предполагается, что волокна сохраняют свою первоначальную жесткость в течение всей истории их повреждения [31, 32], что является грубым упрощением. Разумно предположить, что события перестройки приводят к ухудшению локальной жесткости или к упрочнению, например, из-за повреждения или активизации накопленной длины внутри материала соответственно. Кроме того, волокна пучка могут подвергаться одинаковому количеству событий скольжения, хотя в расширенной выборке количество возможных реструктуризаций может иметь пространственные вариации.Чтобы сделать прерывистое скольжение FBM более реалистичным, в настоящей статье мы устраняем эти ограничения, допуская изменение жесткости волокон в результате проскальзывания, и фиксируем флуктуации количества циклов прерывистого скольжения, разрешенных для волокна. В предположении о глобальном распределении нагрузки мы получаем аналитические выражения для макроскопического определяющего отклика пучка как для закаленного, так и для отожженного беспорядка порогов разрушения, где активируется проскальзывание. Изменение жесткости обрабатывается мультипликативно, что позволяет использовать единую структуру снижения жесткости и повышения жесткости.Мы демонстрируем, что прерывистая динамика приводит к пластическому поведению на макроуровне, и исследуем последствия новых степеней свободы модели.
В предположении о глобальном распределении нагрузки мы получаем аналитические выражения для макроскопического определяющего отклика пучка как для закаленного, так и для отожженного беспорядка порогов разрушения, где активируется проскальзывание. Изменение жесткости обрабатывается мультипликативно, что позволяет использовать единую структуру снижения жесткости и повышения жесткости.Мы демонстрируем, что прерывистая динамика приводит к пластическому поведению на макроуровне, и исследуем последствия новых степеней свободы модели.
2 Динамика прерывистого скольжения с переменной жесткостью
Модель состоит из N параллельных волокон, которые характеризуются одинаковым начальным значением жесткости E=1. При увеличении внешней нагрузки σ волокна имеют линейно-упругое поведение вплоть до пороговой нагрузки σth. Когда нагрузка на волокно превышает порог разрушения, мы предполагаем, что волокно не рвется, а проскальзывает и растягивается за счет увеличения своей равновесной длины до тех пор, пока нагрузка не упадет до нуля. Неоднородность материала представлена случайностью порогов проскальзывания, которые выбираются из распределения вероятностей p(σth). Событие проскальзывания является мгновенным в том смысле, что оно не требует времени, однако после завершения проскальзывания волокно снова может выдерживать нагрузку. В качестве важного шага обобщения модели мы допускаем изменение жесткости волокон после проскальзывания мультипликативным образом, т. е. жесткость обновляется как
Неоднородность материала представлена случайностью порогов проскальзывания, которые выбираются из распределения вероятностей p(σth). Событие проскальзывания является мгновенным в том смысле, что оно не требует времени, однако после завершения проскальзывания волокно снова может выдерживать нагрузку. В качестве важного шага обобщения модели мы допускаем изменение жесткости волокон после проскальзывания мультипликативным образом, т. е. жесткость обновляется как
, где a≥0 — параметр жесткости модели.Обратите внимание, что частный случай a=0 фиксирует немедленный необратимый отказ волокна сразу при первом проскальзывании, что по существу приводит к той же динамике, что и классическая модель пучка волокон [2, 4, 40]. Выбор параметра a=1 восстанавливает исходную модель прерывистого скольжения, в которой жесткость не меняется в течение истории нагружения волокон [31, 32]. В нашем настоящем исследовании мы фокусируемся на диапазонах параметров 0 Для практических применений модели снижение жесткости (a<1) обычно вызывается внутренними повреждениями единиц материала, представленных волокнами. Увеличение жесткости (а<1) происходит, например, в зернистых материалах при сжатии, где реструктуризация силовых цепей может сопровождаться ужесточением [28], и в биологических материалах, таких как шелк паука, которые реагируют на возрастающую нагрузку активацией запасенных длина [41].
Для практических применений модели снижение жесткости (a<1) обычно вызывается внутренними повреждениями единиц материала, представленных волокнами. Увеличение жесткости (а<1) происходит, например, в зернистых материалах при сжатии, где реструктуризация силовых цепей может сопровождаться ужесточением [28], и в биологических материалах, таких как шелк паука, которые реагируют на возрастающую нагрузку активацией запасенных длина [41].
После завершения проскальзывания волокно слипается, так что оно снова может выдерживать нагрузку, описываемую определяющим законом
, где ε обозначает деформацию волокна.уравнение 2 учитывает, что релаксированная длина волокна увеличивается с порогом деформации εth=σth/E проскальзывания. Следствием этой динамики является то, что волокна могут снова удовлетворять условию проскальзывания и в конечном итоге могут подвергаться последовательности прерывистого скольжения, представляющей собой постепенную реструктуризацию материала. Для описания таких последовательностей задается число разрешенных событий скольжения K≥1, которое сначала предполагается фиксированным для всех волокон пучка. Это следует из уравнения 1 видно, что после k циклов прерывистого скольжения жесткость E’ волокна имеет значение
Это следует из уравнения 1 видно, что после k циклов прерывистого скольжения жесткость E’ волокна имеет значение
, которое может быть больше или меньше начального значения E для a>1 и a<1 соответственно.Ключевым вопросом является то, при каких пороговых нагрузках происходят последующие события проскальзывания. В простейшем случае можно считать, что пороговое значение σth фиксировано для всей истории волокна, что дает представление о закаленном беспорядке микроструктуры материалов. Также может случиться так, что после событий реструктуризации локальные физические свойства системы изменяются, что можно зафиксировать, назначая волокну новое пороговое значение из одного и того же распределения вероятностей p(σth) каждый раз, когда происходит проскальзывание (отожженный беспорядок).
Для взаимодействия волокон предполагается глобальное распределение нагрузки таким образом, что волокна натягиваются между двумя жесткими нагрузочными пластинами, что обеспечивает глобальную реакцию всей системы на локальные события проскальзывания. Однако глобальное распределение нагрузки не означает равной нагрузки на волокна в нашей системе прерывистого скольжения, поскольку волокна, испытавшие разное количество проскальзываний, имеют разную жесткость и длину в расслабленном состоянии, следовательно, они сохраняют разные нагрузки. После фиксации типа беспорядка можно определить пороговые деформации скольжения по соответствующим порогам напряжений.Волокно, проскальзывающее k раз при последовательных порогах деформации εth(1),εth(2),…,εth(k) до приложенной извне деформации ε, удерживает нагрузку
Однако глобальное распределение нагрузки не означает равной нагрузки на волокна в нашей системе прерывистого скольжения, поскольку волокна, испытавшие разное количество проскальзываний, имеют разную жесткость и длину в расслабленном состоянии, следовательно, они сохраняют разные нагрузки. После фиксации типа беспорядка можно определить пороговые деформации скольжения по соответствующим порогам напряжений.Волокно, проскальзывающее k раз при последовательных порогах деформации εth(1),εth(2),…,εth(k) до приложенной извне деформации ε, удерживает нагрузку
где сумма порогов отказов ε0k=∑j=1kεth(j) определяет релаксированную длину ε0k волокна. Далее мы выводим макроскопическое определяющее соотношение расслоения для случаев закаленного и отожженного беспорядка порогов скольжения с глобальным распределением нагрузки. Наша главная цель состоит в том, чтобы исследовать последствия изменения жесткости и флуктуаций количества событий скольжения, которые могут испытать волокна.
2.1 Закаленный разлад Пороги разрушения
Закаленный разлад означает, что проскальзывания волокна всегда происходят при одном и том же пороге напряжения σth, заданном ему в начальном состоянии системы. Однако соответствующие пороговые деформации не являются постоянными, что показано на рисунке 1, где история повреждения одиночного волокна представлена с параметром жесткости a<1. Можно заметить, что, несмотря на постоянную пороговую нагрузку σth, значения деформации εth(1),εth(2),εth(3),… при проскальзывании постепенно увеличиваются из-за ухудшения жесткости.Это следует из уравнения 4 видно, что пороговые деформации εth(k)(k=1,…,K) последовательных проскальзываний волокна определяются его начальным порогом деформации εth(1) и параметром жесткости a модели как
εth( k)=εth(1)ak−1.(5) РИСУНОК 1 . Механический отклик одиночного волокна в случае гашеного беспорядка, когда порог скольжения σth фиксирован для всей истории повреждения волокна. Значение a установлено равным а=0,8, так что происходит постепенное ухудшение жесткости в течение последующих периодов прерывистого скольжения.Поскольку жесткость изменяется, пороговые деформации скольжения возрастают εth(1)<εth(2)<εth(3), несмотря на фиксированный порог напряжений σth волокна.
Значение a установлено равным а=0,8, так что происходит постепенное ухудшение жесткости в течение последующих периодов прерывистого скольжения.Поскольку жесткость изменяется, пороговые деформации скольжения возрастают εth(1)<εth(2)<εth(3), несмотря на фиксированный порог напряжений σth волокна.
Релаксированная длина ε0(k) волокна после k -го проскальзывания является суммой всех предыдущих пороговых деформаций, что дает
ε0(k)=εth(1)(1+1a+1a2+⋯+1ak−1 ).(6) Для суммы геометрического ряда внутри скобок введем сокращенное обозначение S(a,k), так что уравнение 6 упрощается до ε0(k)=εth(1)S(a,k).Здесь значение S(a,k) можно привести к закрытой форме S(a,k)=(a−k−1)/(a−1−1) для a≠1. Приведенные выше выражения справедливы как для постепенной деградации a<1, так и для повышения жесткости a>1, что приводит к увеличению и уменьшению последовательности порогов деформации событий скольжения, соответственно. Отметим, что в частном случае исходной прерывистой модели с a=1 сумма S(a,k) принимает значение S(a,k)=k.
2.1.1 Вывод определяющего уравнения с переменной жесткостью
Чтобы получить замкнутую аналитическую форму для определяющего уравнения, мы предположим контролируемую деформацией нагрузку пучка между двумя жесткими пластинами.При заданной деформации ε в процессе нагружения пучок представляет собой смесь подмножеств волокон, которые либо не повреждены (без проскальзывания), либо претерпели различное количество проскальзываний k , где выполняется 1≤k≤K. На основе уравнений 4–6 индекс разрушения k волокон может быть выражен через их начальные пороги разрушения εth(1) и приложенную извне деформацию ε как
εS(a,k)<εth(1)<εS( a,k+1), 1≤kМакроскопический определяющий отклик системы может быть получен суммированием нагрузки σk(ε), выдерживаемой подмножествами волокон, которые претерпели ровно k случаев проскальзывания
σ(ε)=∑k=0Kσk(ε).(8) Частичные нагрузки σk(ε) могут быть выражены через распределение беспорядка как ∫ε/S(a,k+1)ε/S(a,k)[ε−ε1S(a,k)]p(ε1)dε1 для 1≤k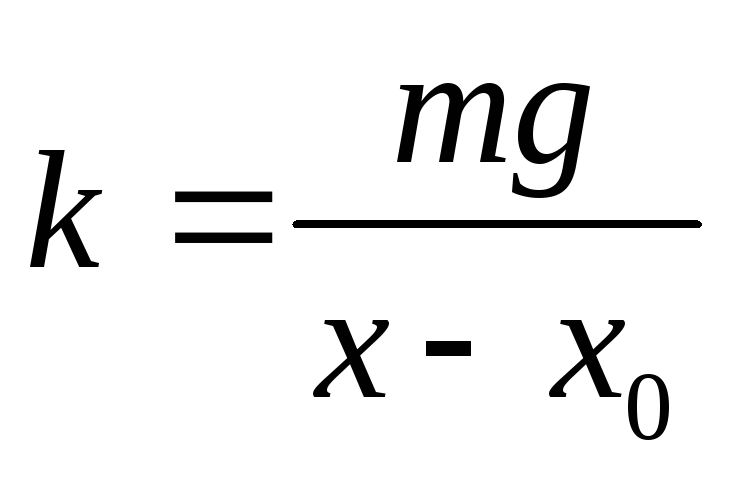 Обратите внимание, что пределы интегрирования охватывают разделение подмножеств волокон, заданное уравнением.7. В предельном случае малой деформации ε→0 только первый член уравнения 9 имеет конечный вклад, восстанавливающий ожидаемое линейное поведение σ(ε)≈Eε с исходной жесткостью. В противоположном пределе ε→+∞ только последний член уравнения 11, который показывает, что после числа K допустимых событий скольжения волокна все еще сохраняют нагрузку, и появляется линейное поведение
Обратите внимание, что пределы интегрирования охватывают разделение подмножеств волокон, заданное уравнением.7. В предельном случае малой деформации ε→0 только первый член уравнения 9 имеет конечный вклад, восстанавливающий ожидаемое линейное поведение σ(ε)≈Eε с исходной жесткостью. В противоположном пределе ε→+∞ только последний член уравнения 11, который показывает, что после числа K допустимых событий скольжения волокна все еще сохраняют нагрузку, и появляется линейное поведение
С асимптотической жесткостью Ea=aKE. В правой части 〈εth(1)〉 обозначает средний порог проскальзывания в начальном состоянии расслоения.Между двумя пределами при промежуточных деформациях второй член уравнения. 10 контролирует макроскопический отклик, так как волокна постепенно подвергаются все большему количеству случаев скольжения.
Конститутивное поведение пучка прерывистого скольжения показано на рис. 2 для нескольких значений максимального числа K событий скольжения при фиксированном значении параметра жесткости a=0,8. Для явных расчетов мы рассмотрели экспоненциально распределенные пороги скольжения с функцией плотности вероятности
Для явных расчетов мы рассмотрели экспоненциально распределенные пороги скольжения с функцией плотности вероятности
, где параметр λ установлен равным λ=1.Это распределение беспорядка имеет то преимущество, что все выражения уравнений 9–11 могут быть получены аналитически. При представлении результатов мы перемасштабировали напряжение σ и деформацию ε с пределом прочности σc0 и εc0 простого FBM с равным распределением нагрузки с тем же пороговым распределением, при котором волокна ломаются, когда нагрузка превышает их прочность. Заметим, что определяющее уравнение этого классического ФБМ совпадает с σ0(ε) уравнения 9. Видно, что при промежуточных деформациях проявляется пластическое поведение, которое становится более выраженным при более высоких значениях К , т.е.е. кривые упрочнения стремятся к асимптотическим прямым линиям по формуле 12, которым предшествуют все более и более продолжительные режимы плато, несмотря на снижение жесткости. Модель также может учитывать окончательный разрыв волокон после завершения разрешенного числа K циклов прерывистого скольжения, опуская член σK (ε) в уравнении. 8. Разрыв волокна подразумевает, что в пределе ε→∞ несущая способность пучка постепенно уменьшается, так что следует σ(ε)→0, однако при увеличении числа актов проскальзывания K возникает более широкое пластическое плато, аналогичное упрочняющие связки (см. рис. 2).
РИСУНОК 2 . Конститутивное поведение расслоения прерывистого скольжения с закаленным беспорядком порогов скольжения согласно уравнению. 8, включая как случаи остаточной жесткости (сплошные линии), так и окончательное разрушение волокон (пунктирные линии) после завершения K случаев проскальзывания. Стрелками отмечены кривые разгрузки, которые начинаются при различных деформациях εm определяющей кривой пучка разупрочнения К=5. Значение параметра жесткости равно а=0,8.
2.1.2 Влияние различной жесткости волокна на макроскопический отклик прерывисто-скользящих пучков
Значение параметра жесткости и оказывает важное влияние на общее поведение системы. Из уравнений 5, 6 можно сделать вывод, что для случая усиления a>1 последовательные события проскальзывания быстро следуют друг за другом, так что асимптотический режим уравнения 12 достигается при относительно низкой деформации. При уменьшении до при постоянном значении К пластический режим, предшествующий закалке, становится все более и более продолжительным (см. иллюстрацию на рис. 3).При наименьших значениях параметра жесткости и режим упрочнения достигается только при очень высоких деформациях, что затрудняет точную структуру кривых σ(ε) на рис. 3. Поэтому далее проанализируем появление режима плато при низких и значений на рисунке 4 с использованием логарифмической шкалы по горизонтальной оси, представляющей также частичные нагрузки σk(ε) подмножеств волокон с различными индексами разрушения. Видно, что при снижении параметра жесткости пластическое плато развивается как стационарный режим, украшенный некоторыми колебаниями.Видно, что при более высоких значениях a , когда жесткость медленно ухудшается, кривые σk(ε) сильно перекрывают друг друга и их пиковая нагрузка быстро уменьшается с k . При уменьшении a возникает стационарное состояние, так как кривые σk(ε) все больше расходятся, а их пиковая нагрузка увеличивается, приближаясь к σc классического FBM, что совпадает с σk=1(ε).
При уменьшении до при постоянном значении К пластический режим, предшествующий закалке, становится все более и более продолжительным (см. иллюстрацию на рис. 3).При наименьших значениях параметра жесткости и режим упрочнения достигается только при очень высоких деформациях, что затрудняет точную структуру кривых σ(ε) на рис. 3. Поэтому далее проанализируем появление режима плато при низких и значений на рисунке 4 с использованием логарифмической шкалы по горизонтальной оси, представляющей также частичные нагрузки σk(ε) подмножеств волокон с различными индексами разрушения. Видно, что при снижении параметра жесткости пластическое плато развивается как стационарный режим, украшенный некоторыми колебаниями.Видно, что при более высоких значениях a , когда жесткость медленно ухудшается, кривые σk(ε) сильно перекрывают друг друга и их пиковая нагрузка быстро уменьшается с k . При уменьшении a возникает стационарное состояние, так как кривые σk(ε) все больше расходятся, а их пиковая нагрузка увеличивается, приближаясь к σc классического FBM, что совпадает с σk=1(ε). В пределе a→0 стационарный режим напряжения исчезает, поскольку функции σk(ε) становятся почти полностью разделенными (см. рис. 4D).
В пределе a→0 стационарный режим напряжения исчезает, поскольку функции σk(ε) становятся почти полностью разделенными (см. рис. 4D).
РИСУНОК 3 . Влияние значения параметра жесткости и на макроскопическое поведение пучка, в котором всем волокнам разрешено выполнять K=10 циклов прерывистого скольжения. Также включены определяющие кривые упрочнения (сплошные линии) и размягчения (штриховые линии) пучков. Пороги скольжения имеют экспоненциальное распределение. Волокна сохраняют свою конечную жесткость, так что все пучки твердеют, даже если асимптотические режимы не видны для самых низких a .
РИСУНОК 4 . Возникновение режима плато при уменьшении параметра жесткости a при фиксированном значении максимально допустимого для волокон числа К=5 прерывистых циклов. Частичные нагрузки σk(ε) из уравнений 9–11, выдерживаемые подмножествами волокон, которые претерпели ровно k случаев проскальзывания, также показаны для k=0,1,2,3,4,5 для четырех различных значений жесткости. параметр a : (A) 0,8, (B) 0,5, (C) 0,2 и (D) 0.05. Также представлена определяющая кривая всего пучка σ(ε) как для упрочнения (сплошная красная линия), так и для размягчения (штриховая красная линия). На горизонтальной оси используется логарифмическая шкала из-за больших деформаций, возникающих при низких значениях и .
параметр a : (A) 0,8, (B) 0,5, (C) 0,2 и (D) 0.05. Также представлена определяющая кривая всего пучка σ(ε) как для упрочнения (сплошная красная линия), так и для размягчения (штриховая красная линия). На горизонтальной оси используется логарифмическая шкала из-за больших деформаций, возникающих при низких значениях и .
Разделение кривых σk(ε) в нижнем пределе и также показывает, что их функциональная форма практически одинакова и определяется определяющим уравнением классической модели расслоения σk=0(ε). Общая форма определяющей кривой FBM имеет высокую степень устойчивости для широкого класса распределений беспорядка [2], что подразумевает устойчивость макроскопического поведения FBM прерывистого скольжения, представленного выше, к распределению порогов скольжения p (ε-й (1)).
Очень важным следствием динамики прерывистого скольжения является то, что при разгрузке σ→0 пучка остается остаточная деформация εr, которая зависит от максимальной деформации εm, достигнутой до начала разгрузки. Если волокна сохраняют свое последнее значение жесткости после K циклов прерывистого скольжения, остаточная деформация монотонно возрастает и имеет верхний предел εrmax, который может быть реализован, если разгрузка начинается по асимптотическому линейному режиму упрочняющегося пучка. Значение εrmax можно получить из уравнения12 с использованием условия σ(εrmax)=0, что дает
Если волокна сохраняют свое последнее значение жесткости после K циклов прерывистого скольжения, остаточная деформация монотонно возрастает и имеет верхний предел εrmax, который может быть реализован, если разгрузка начинается по асимптотическому линейному режиму упрочняющегося пучка. Значение εrmax можно получить из уравнения12 с использованием условия σ(εrmax)=0, что дает
Для промежуточных начальных точек εm остаточная деформация εr может быть определена из условия σ(εr)=0 в определяющем уравнении 8 с учетом также того, что на кривой разгрузки проскальзывания не происходит. Это приводит к окончательному виду
)∫εthminεm/S(a,K)ε1p(ε1)dε11−P(εm)+∑k=1K−1ak∫εm/S(a,k+1)εm/S(a,k)p(ε1dε1) +aK∫εthminεm/S(a,K)p(ε1)dε1,(15), которая сходится к εrmax в пределе εm→∞.Отметим, что начальная точка разгрузки εm фигурирует в верхней границе интегралов. Остаточная деформация εr упрочняющих связок представлена на рис. 5 для нескольких значений максимального числа скольжения K . Из уравнений (14, 15) следует, что при увеличении числа актов проскальзывания K и уменьшении параметра жесткости a упрочняющие связки сохраняют более высокую пластическую деформацию, что также подтверждается численными результатами рисунка.
Из уравнений (14, 15) следует, что при увеличении числа актов проскальзывания K и уменьшении параметра жесткости a упрочняющие связки сохраняют более высокую пластическую деформацию, что также подтверждается численными результатами рисунка.
РИСУНОК 5 .Остаточная деформация εr упрочняющих (сплошные линии) и разупрочняющихся (штриховые линии) прерывистых связок в зависимости от максимальной деформации εm, достигаемой перед началом разгрузки при различных значениях числа скольжения K при параметре жесткости a=0,8. Оставшаяся деформация εr масштабируется с соответствующим максимальным значением εrmax случая упрочнения, заданным уравнением. 14. Для смягчения пучков получается немонотонное поведение. Кроме того, даже максимальные значения кривых εr(εm) оказываются ниже соответствующих кривых упрочняющих связок.
Примеры кривых разгрузки представлены на рис. 2 для случая размягчения пучков, когда волокна обрываются после К шликеров. Поскольку при убывающей нагрузке проскальзывания не может быть, то кривые разгрузки всегда прямолинейны и имеют наклон, т. е. модуль разгрузки уменьшается с увеличением εm. Аналитическое выражение модуля разгрузки Eu совпадает со знаменателем уравнения 15 умножить на начальную жесткость E волокон
Поскольку при убывающей нагрузке проскальзывания не может быть, то кривые разгрузки всегда прямолинейны и имеют наклон, т. е. модуль разгрузки уменьшается с увеличением εm. Аналитическое выражение модуля разгрузки Eu совпадает со знаменателем уравнения 15 умножить на начальную жесткость E волокон
Из выражения видно, что модуль разгрузки Eu при заданном εm представляет собой средневзвешенное значение модулей Eak подмножеств волокон с числами скольжения k=0,1,…,K, где веса определяются распределением p(ε1) порогов скольжения. В пределе εm→∞ модуль разгрузки Eu сходится к асимптотическому значению Eu→Ea=EaK.
Для модуля разгрузки пучков размягчения последний член в скобках следует опустить, чтобы учесть окончательное разрушение волокон.Из рис. 2 также можно сделать вывод, что остаточная деформация разупрочняющих связок не является монотонной, т. е. функция εr(εm) имеет максимум и убывает при разгрузке по хвосту режима разупрочнения определяющей кривой σ(ε). Такое поведение может быть реализовано на рис. 2 за счет изменения порядка конечных точек кривых разгрузки. Из рис. 5 видно, что даже максимальное значение остаточной деформации разупрочняющихся связок значительно меньше соответствующей максимальной остаточной деформации εrmax упрочняющих.
Такое поведение может быть реализовано на рис. 2 за счет изменения порядка конечных точек кривых разгрузки. Из рис. 5 видно, что даже максимальное значение остаточной деформации разупрочняющихся связок значительно меньше соответствующей максимальной остаточной деформации εrmax упрочняющих.
Из рис. 4 следует, что если пластическую площадку удается идентифицировать, то ее протяженность практически одинакова для упрочняющихся (без разрыва) и разупрочняющихся (разрушающихся после K шликеров) связок. При заданном наборе параметров a,K расширение плато может быть охарактеризовано асимптотическим значением εrmax остаточной деформации (уравнение). 14 закалочных пучков. Интересно отметить, что в случае a>1 значение S(a,K) в уравнении 14 сходится к S≈1/(1−a−1) при K→∞, откуда следует конечный предел остаточной деформации
εrmax→11−a−1〈εth(1)〉, (17) и, следовательно, расширения плато, когда волокна становятся более жесткими после событий скольжения.Однако в случае ухудшения жесткости a<1 сумма S(a,K) не имеет конечного предела для больших значений K , что приводит к монотонно расширяющемуся плато по мере увеличения максимального числа скольжения K .
3 Колебания максимального числа событий проскальзывания
Модели пучков волокон с динамикой прерывистого проскальзывания могут применяться для понимания накопления повреждений и разрушения в большом количестве систем, где микромасштабная реструктуризация играет доминирующую роль. Однако в данной форме модели максимальное количество допустимых циклов прерывистого скольжения фиксировано для всех волокон, что является очень сильным ограничением и ограничивает применимость модели в реальных условиях.В этом разделе мы расширим модель, чтобы отразить эффект колеблющегося числа скольжения K .
Мы предполагаем, что K является случайной величиной, выбранной из функции плотности вероятности g(K), определенной в диапазоне 0≤K<∞, с условием нормализации
Обратите внимание, что вероятность волокон с K=0 равна включены, что означает, что некоторые волокна всегда остаются неповрежденными в процессе загрузки.
Определяющее уравнение σ(ε) прерывистого пучка волокон с флуктуирующим максимальным числом актов скольжения K может быть получено усреднением вкладов подмножеств волокон постоянного K Уравнения 9–11 с распределением g (K)
σ(ε)=(g(0)+[1−g(0)][1−P(ε)])Eε+∑K=1∞g(K)∑k=1K−1Eak∫ ε/S(a,k+1)ε/S(a,k)[ε−S(a,k)ε1]p(ε1)dε1+∑K=1∞g(K)EaK∫εthminε/S(a ,k)[ε−S(a,k)ε1]p(ε1)dε1. (19)
(19) Первый член правой части уравнения. 3 представлена нагрузка, выдерживаемая неповрежденными волокнами, с учетом того, что волокно может быть целым либо потому, что никогда не может проскальзывать K=0, либо потому, что оно повреждаемое K>0, но при текущем напряжении не испытало проскальзывания k=0. Второй член обозначает те волокна, которые совершили проскальзывание ровно k раз и еще могут пройти дальнейшие циклы прерывистого скольжения k , которое мы используем для явных вычислений, чтобы продемонстрировать результаты общих выводов. Здесь параметр 〈K〉 обозначает среднее число промахов K внутри пучка. Предполагая, что дефекты, ответственные за события скольжения, возникают вдоль волокон некоррелированным образом, пуассоновское распределение, контролируемое средним значением 〈K〉, дает адекватное описание статистики максимального числа скольжения K [42]. , что дает и для асимптотического модуля Юнга Ea и для максимального значения постоянного деформации εrmax соответственно. РИСУНОК 6 . Сравнение определяющих кривых пучков прерывистого скольжения с постоянным ( штриховые линии ) и флуктуирующим ( сплошные линии ) максимальным числом актов скольжения для случая упрочнения при параметре жесткости а=0,8. Постоянные значения K устанавливаются равными среднему 〈K〉 распределения Пуассона.Естественным выбором для g(K) является распределение Пуассона. Основополагающая реакция размягчающихся связок с колеблющимся максимальным числом скольжения также может быть получена из уравнения. 3, пропуская последний член, который представляет вклад волокон с индексом отказов k=K. На рис. 7 сравнивается поведение размягчающихся прерывистых проскальзывающих связок с постоянными и флуктуирующими числами максимального скольжения, где среднее 〈K〉 устанавливалось равным фиксированным значениям K соответствующих связок. РИСУНОК 7 . В материалах со сложной микроструктурой события проскальзывания могут сопровождаться изменением локальных свойств материала. В нашей модели пучка волокон это поведение можно до некоторой степени зафиксировать, назначая волокну новое пороговое значение после каждого события проскальзывания из того же распределения вероятностей p(σth). Этот тип отожженного беспорядка приводит к конститутивному поведению, качественно аналогичному случаю закаленного беспорядка, но с более сложной динамикой.После тыс. случаев проскальзывания нагрузка σ, удерживаемая волокном, определяется уравнением 4 общей конструкции модели, однако теперь порог напряжения σth не является фиксированным для волокна, вместо этого после каждого последующего события проскальзывания генерируется новый порог σth(i) из того же распределения p(σth). , где εk= σth(k)/E — значения деформации, которые имеют одно и то же распределение p(εth) для всей истории волокна.уравнение 24 показано, что, хотя пороги напряжения σth(k) генерируются с тем же распределением, соответствующие значения деформации εk все же должны быть преобразованы для получения порогов деформации, при которых происходит проскальзывание волокон. Конструктивное поведение одиночного волокна и отношение переменных εth(k) и σth(k) показаны на рисунке 8. РИСУНОК 8 . Конститутивное поведение одиночного волокна с отожженным беспорядком порогов скольжения. Значение параметра жесткости равно а=0.8, так что жесткость волокна постепенно уменьшается (сравните с рис. 1). Последовательные пороги σth(k) получаются из одного и того же распределения вероятностей p(σth), затем соответствующие пороги деформации εth(k) получаются из уравнения 24. На основании приведенных выше выражений определяющее уравнение σ(ε) всего пучка с фиксированным числом разрешенных проскальзываний K можно представить в виде , где снова суммируются несущие вклады подмножеств волокон с разными числами скольжения k=0, 1,…,K: первый член представляет собой нагрузку, удерживаемую волокнами, которые не повреждены k=0 при деформации е; второй представляет собой сумму вкладов волокон, которые претерпели ровно 1≤k На рис. 9 сравниваются определяющие реакции прерывистых связок с закаленным и отожженным беспорядком для случая упрочнения с фиксированными значениями числа событий скольжения K . Можно заметить, что два набора кривых имеют качественно сходное поведение. При К=1 между двумя типами беспорядка нет разницы, поэтому соответствующие кривые должны совпадать, однако более значительные количественные различия закалочного и отожженного откликов наблюдаются при более высоких значениях К .Последовательность независимых одинаково распределенных порогов разрушения отожженного беспорядка приводит к более широким режимам плато с более высоким значением среднего напряжения вдоль плато. При больших деформациях оба набора кривых сходятся к асимптотическим прямым, наклон которых Ea=aKE не зависит от типа беспорядка. Из-за качественного сходства макроскопических откликов закаленных и отожженных пучков прерывистого беспорядка мы опускаем детали дальнейших сравнений. РИСУНОК 9 . Мы представили расширение моделей пучков волокон для динамики прерывистого скольжения, включающее эффект изменения жесткости волокон после событий скольжения и флуктуации числа циклов прерывистого скольжения, которые волокна могут испытать при возрастающем внешнем воздействии. нагрузка.Динамика прерывистого скольжения подразумевает, что, когда нагрузка на волокно превышает его локальную прочность, волокно не разрывается, а соскальзывает, что увеличивает его длину в расслабленном состоянии. В результате нагрузка на волокно падает до нуля, однако волокно сохраняет свою несущую способность. FBM имеет высокую степень сложности, что делает его гибким для описания поведения различных материалов. Мы проанализировали модель в пределе среднего поля, т.е. предполагалось глобальное распределение нагрузки (GLS). Однако в прерывисто-скользящих ФБМ GLS не предполагает одинаковой нагрузки на волокна, так как при заданной деформации волокна пучка могут иметь разную длину в расслабленном состоянии и значения жесткости.Получены замкнутые аналитические формы для макроскопического определяющего отклика пучка как при закаленном, так и при отожженном беспорядке порогов скольжения. Эти результаты показали, что в макромасштабе пучок проявляет пластическое поведение, т. е. кривые σ(ε) имеют платообразный режим, который становится шире с увеличением числа сдвигов. Детально проанализирована роль изменения жесткости волокон в возникновении пластического плато. При снятии нагрузки с пучка остаются остаточные деформации, которые монотонно возрастают с максимальной деформацией, достигнутой перед началом разгрузки для упрочняющих пучков, в то время как в случае разупрочнения получается немонотонное поведение.Остаточная деформация размягчающихся связок оказалась меньше, чем у их упрочняющих аналогов. Асимптотическое значение остаточной деформации упрочняющих связок может быть использовано для характеристики расширения режима плато при различных параметрах жесткости и . Наши расчеты показали, что при увеличении числа разрешенных проскальзываний K протяженность плато имеет конечный предел для пучков жесткости a>1, а при деградации жесткости a<1 она расходится. Мы показали, что флуктуации количества циклов прерывистого скольжения, разрешенных для волокон, влияют на поведение как упрочняющих, так и размягчающихся пучков. Сравнение упрочняющих связок с постоянными и переменными числами скольжения с одинаковым средним значением показало, что большие колебания приводят к более узкому пластическому режиму, влияющему также на асимптотическую жесткость и остаточную деформацию пучка. Для размягчающихся связок колебания числа скольжения приводят к более низкой и более высокой несущей способности при малых и больших деформациях, соответственно, по сравнению с их аналогами с постоянным числом скольжения. Отожженный беспорядок порогов скольжения приводит к качественно аналогичному макроскопическому отклику на закаленный беспорядок, однако его описание связано с более высокой математической сложностью. Здесь мы сосредоточились на влиянии изменяющейся жесткости и флуктуирующего числа волокон на макроскопическое поведение прерывистого скольжения FBM и продемонстрировали, что, изменяя его параметры, модель способна отражать несколько аспектов макромасштабных последствий прерывистая динамика. Несмотря на то, что модель сложна, ее можно расширить, чтобы она соответствовала конкретным приложениям. Например, когда последовательные события скольжения приводят к накоплению внутренних повреждений волокон, ухудшение жесткости волокон может сопровождаться снижением их прочности. Эта корреляция локальной прочности и жесткости может быть зафиксирована моделью таким образом, что в случае проскальзывания волокна получают новый порог разрушения (отожженный беспорядок) из распределения, которое имеет ту же функциональную форму, что и исходное, однако его среднее значение равно постепенно уменьшаются. Необработанные данные, подтверждающие выводы этой статьи, будут предоставлены авторами без неоправданных оговорок. ZH, IK и FK провели аналитические расчеты, ZH провела компьютерное моделирование. ZH и FK провели анализ данных, задумали и разработали исследование и составили рукопись. Проект финансируется совместно Европейским Союзом и Европейским социальным фондом.Это исследование было поддержано Национальным фондом исследований, развития и инноваций Венгрии, финансируемым в рамках схемы финансирования K-16 Проект №. K 119967. Исследование финансировалось Тематической программой повышения квалификации Министерства инноваций и технологий Венгрии (ED_18-1-2019-0028) в рамках тематической программы «Автомобильная промышленность» Университета Дебрецена. Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов. Авторы благодарны Герго Палу за обсуждения. 1. Herrmann HJ, and Roux S eds. Статистические модели разрушения неупорядоченных сред В кн.: Случайные материалы и процессы . Google Scholar 2. Хансен А., Хеммер П., Прадхан С. Модель пучка волокон: моделирование разрушения материалов. В кн.: Статистическая физика разрушения и разрушения .Хобокен, Нью-Джерси: Wiley (2015). Google Scholar 3. Kun F, Raischel F, Hidalgo RC, Herrmann HJ. Расширения моделей пучков волокон. В: Бхаттачарья П. и Чакрабарти Б.К., редакторы. Моделирование критических и катастрофических явлений в науках о Земле: подход статистической физики. Конспект лекций по физике . Берлин, Германия: Springer-Verlag Berlin Heidelberg New York (2006). п. 57–92. Полнотекстовая перекрестная ссылка | Google Scholar 4. Идальго Р.С., Кун Ф., Ковач К., Пагонабаррага И.Лавинная динамика моделей пучков волокон. Phys Rev E — Stat Nonlinear Soft Matter Phys (2009) 80:051108. doi:10.1103/PhysRevE.80.051108 Полный текст CrossRef | Google Scholar 6. Sinha S, Kjellstadli JT, Hansen A. Полный текст CrossRef | Google Scholar 7. Данку З., Одор Г., Кун Ф.Лавинная динамика в многомерных моделях пучков волокон. Phys Rev E (2018) 98:042126. doi:10.1103/physreve.98.042126 Полный текст CrossRef | Google Scholar 8. Андерсен Дж. В., Сорнетт Д., Леунг К. Трикритическое поведение при разрыве, вызванном беспорядком. Phys Rev Lett (1997) 78:2140–3. doi:10.1103/physrevlett.78.2140 Полный текст CrossRef | Google Scholar 9. Йошиока Н., Кун Ф., Ито Н. Кертес Линия явлений термически активируемого пробоя. Phys Rev E — Stat Nonlinear Soft Matter Phys (2010) 82:055102. doi:10.1103/PhysRevE.82.055102 Полный текст CrossRef | Google Scholar 10. Карпас Э., Кун Ф. Индуцированный беспорядком переход от хрупкости к квазихрупкости в пучках волокон. Полный текст CrossRef | Google Scholar 12. Рой С., Рэй П. Критическое поведение в модели пучка волокон: исследование перехода от хрупкого к квазихрупкому. Epl (2015) 112:26004.doi:10.1209/0295-5075/112/26004 Полный текст CrossRef | Google Scholar 14. Peires FT. Испытания на растяжение хлопчатобумажной пряжи. V.- «Самое слабое звено», теоремы о прочности длинных составных образцов. J Textil Inst (1926) 17:T355–368. Google Scholar 15. Коулман Б.Д. Зависимость механического разрушения пучков волокон от времени. III. Правило нарушения степенного закона. Trans Soc Rheol (1958) 2:195–218. doi:10.1122/1.548830 Полный текст CrossRef | Google Scholar 16.Райшель Ф., Кун Ф., Херрманн Х.Дж. Процесс разрушения пучка пластиковых волокон. Phys Rev E — Stat Nonlinear Soft Matter Phys (2006) 73:066101. doi:10.1103/PhysRevE.73. Полный текст CrossRef | Google Scholar 17. Нехад Х., Хелмштеттер А., Герджума Р.Э., Сорнетт Д. Андраде и критические законы наработки на отказ в композитах с волокнистой матрицей: эксперименты и модель. J Mech Phys Solid (2005a) 53:1099. doi:10.1016/j.jmps.2004.12.001 Полный текст CrossRef | Академия Google 19.Кун Ф., Морено Ю., Идальго Р.С., Херрманн Х.Дж. Ползучесть имеет два класса универсальности. Europhys Lett (2003) 63:347–53. doi:10.1209/epl/i2003-00469-9 Полный текст CrossRef | Google Scholar 20. Идальго Р.С., Кун Ф., Херрманн Х.Дж. Ползучий разрыв пучков вязкоупругих волокон. Phys Rev E — Stat Nonlinear Soft Matter Phys (2002a) 65:032502. doi:10.1103/PhysRevE.65.032502 Полный текст CrossRef | Google Scholar 21. Идальго Р.С., Ковач К., Пагонабаррага И., Кун Ф.Класс универсальности расслоений с сильными неоднородностями. Europhys Lett (2008) 81:54005. doi:10. Полный текст CrossRef | Google Scholar 22. Рой С., Кунду С., Манна С.С. Модель пучка волокон с сильно неупорядоченными порогами нарушения. Phys Rev E — Stat Nonlinear Soft Matter Phys (2015) 91:032103. doi:10.1103/PhysRevE.91.032103 Полный текст CrossRef | Google Scholar 23. Данку З., Кун Ф. Процесс разрушения пучка волокон с сильным расстройством. J Stat Mech (2016) 2016:073211. doi:10.1088/1742-5468/2016/07/073211 CrossRef Полный текст | Google Scholar 24. Идальго Р.С., Морено Ю., Кун Ф., Херрманн Х.Дж. Модель разрушения с переменным диапазоном взаимодействия. Phys Rev E — Stat Nonlinear Soft Matter Phys (2002b) 65:046148. doi:10.1103/PhysRevE.65.046148 Полный текст CrossRef | Google Scholar 25. Phoenix SL, Newman WI. Оптические пучки, зависящие от времени, с локальным распределением нагрузки. II. общие волокна Вейбулла. Phys Rev E — Stat Nonlinear Soft Matter Phys (2009) 80:066115. Полный текст CrossRef | Google Scholar 26. Бхаттачарья П., Прадхан С., Чакрабарти Б.К. Фазовый переход в моделях расслоения с рекурсивной динамикой. Phys Rev E — Stat Nonlinear Soft Matter Phys (2003) 67:046122. doi:10.1103/PhysRevE.67.046122 Полный текст CrossRef | Google Scholar 27. Кертин В.А. Размерное масштабирование прочности гетерогенных материалов. Phys Rev Lett (1998) 80:1445. doi:10.1103/physrevlett.80.1445 Полный текст CrossRef | Google Scholar 28. Hidalgo RC, Grosse CU, Kun F, Reinhardt HW, Herrmann HJ. Эволюция перколяционных силовых цепочек в сжатых гранулированных средах. Phys Rev Lett (2002c) 89:205501. doi:10.1103/PhysRevLett.89.205501 PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar 29. Михлмайр Г., Ор Д., Коэн Д. Модели пучков волокон для снятия напряжения и выброса энергии при сдвиге гранул. Phys Rev E — Stat Nonlinear Soft Matter Phys (2012) 86:061307. Полный текст CrossRef | Google Scholar 30. Лейтон Б.Е., Састри А.М. Микромеханические модели с равным и локальным распределением нагрузки для коллагенов: количественные сравнения реакции тканей крыс без диабета и диабета. Acta Biomater (2006) 2:595. doi:10.1016/j.actbio.2006.05.013 PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar 31. Халас З., Кун Ф.Модель пучка волокон с прерывистой динамикой. Phys Rev E — Stat Nonlinear Soft Matter Phys (2009) 80:027102. doi:10.1103/PhysRevE.80.027102 Полный текст CrossRef | Google Scholar 33. Михлмайр Г., Чалари А., Кларк А., Ор Д. Волоконно-оптический акустический эмиссионный (АЭ) высокого разрешения мониторинг обрушения склона. Оползни (2017) 14:1139–46. doi:10.1007/s10346-016-0776-5 Полный текст CrossRef | Google Scholar 34. Фурст Э.М., Гаст А.П. Микромеханика диполярных цепочек с помощью оптического пинцета. Полный текст CrossRef | Google Scholar 36. Зур Дж., Кораткар Н.А. Рассеяние энергии в композитах из углеродных нанотрубок: обзор. J Mater Sci (2008) 43:4370–82. doi:10.1007/s10853-007-2440-x Полный текст CrossRef | Google Scholar 37. Zhou X, Shin E, Wang K, Bakis C. Характеристики межфазного демпфирования композитов на основе углеродных нанотрубок. Compos Sci Technol (2004) 64:2425–37.doi:10.1016/j.compscitech.2004.06.001 Полный текст CrossRef | Google Scholar 38. Capelli A, Reiweger I, Lehmann P, Schweizer J. Модель пучка волокон с механизмами восстановления, зависящими от времени, для имитации постепенного разрушения снега. Phys Rev E (2018) 98:023002. doi:10.1103/PhysRevE.98.023002 PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar 39. Капелли А., Райвегер И., Швейцер Дж. Изучение разрушения снега с помощью моделей пучков волокон. Полный текст CrossRef | Google Scholar 40. Прадхан С., Хансен А., Чакрабарти Б.К. Процессы разрушения в пучках эластических волокон. Rev Mod Phys (2010) 82:499. doi:10.1103/revmodphys.82.499 Полный текст CrossRef | Google Scholar 42. Йейтс Р., Гудман Д. Вероятностные и случайные процессы: удобное введение для инженеров-электриков и программистов . Хобокен, Нью-Джерси: John Wiley & Sons (2005). Google Scholar 43.Huang Y, Tangpong X. Модель распределенного трения для рассеяния энергии в композитах на основе углеродных нанотрубок. Commun Nonlinear Sci Numer Simulat (2010) 15: 4171–80. doi:10.1016/j.cnsns.2010.01.017 Полный текст CrossRef | Google Scholar 44. Ван Т.Ю., Лю С.К., Цай Дж.Л. Микромеханическая модель прерывистого скольжения для характеристики демпфирующих характеристик нанокомпозитов с однослойными углеродными нанотрубками. Полный текст CrossRef | Академия Google 45.Формика Г., Лакарбонара В. Трехмерное моделирование межфазного прерывистого скольжения в нанокомпозитах из углеродных нанотрубок. Int J Plast (2017) 88: 204–17. doi:10.1016/j.ijplas.2016.10.012 CrossRef Полный текст | Google Scholar Мы провели измерения магнитооптического эффекта Керра с временным разрешением (TR-MOKE) для [Co (6. a Сигнал магнитооптического эффекта Керра с временным разрешением (открытые символы) с одиночными экспоненциальными аппроксимирующими кривыми (штриховые линии) для длины волны импульса накачки λ накачки = 800 нм. Значения плотности потока накачки F P указаны рядом с экспериментальными данными. Данные смещены вверх для облегчения распознавания. Столбики погрешностей представляют собой стандартную ошибку усредненных необработанных данных. b Время перемагничивания τ R относительно плотности потока энергии для λ насоса = 800 нм (квадрат) и λ насоса = nm 800. (1) где T e , T l , и T s 6 — спиновая температура решетки, соответственно, и 5 s 6. C e , C l , и C s — удельные теплоемкости решетки электрона и спина соответственно. G el , G es , и G ls , и G ls , электрон-спиновое взаимодействие, электрон-спиновое взаимодействие, электрон-спин-лед каналы, соответственно, электрон-спин (4) , где A — это постоянная решетка, A Ex0 6 Коэффициент биржи-жесткости на 0 к, V Громкость клеток, T F Ферми, S = 3/2 спиновое квантовое число, M намагниченность и G 2 функция, основанная на функции Дебая второго порядка 23 (уравнение(3)). T F — температура Ферми, выбранная для того, чтобы FCC CO ( т F = 16,87 RY / K B 6) 31 . D = SM [ T S ] Q ] M M M A A 2 , где Q M — Магниновая волна № Q M 65 M = K F = (6π 2 ) 1/3 A -1 и K F — это номер волны Ферми. G-3TM состоит из нескольких свободных параметров, поэтому к фитингу следует подходить с осторожностью.Во-первых, разрешенные сроки разрабатываемость R ( т ) Данные были использованы для оценки значений для C E , C C L , и G EL , учитывая только электрон и решетка, на основе двухтемпературной модели 32,33 . При полном анализе с использованием G-3TM были подобраны данные отражательной способности и MOKE. В качестве ограничения при анализе использовались измеренные значения степени размагничивания ( D размагничивания ) (рис. Для случая длины волны импульса накачки λ накачка = 800 нм, a Данные магнитооптического эффекта Керра с временным разрешением (TR-MOKE), измеренные для 1. Прибор Г-3ТМ определяет временную эволюцию спиновой, электронной и температуры решетки на длине волны импульса накачки λ накачки = 800 нм (рис.2б, в) и λ накачки = 400 нм (рис. 2д, е). Случаи для очень высоких F P , соответствующих T s , очень близких к температуре Кюри (1131 K), не рассматриваются, где G-3TM может быть недействительным. Встроенное значение C E было 1.8 ~ 2.1 × 10 3 J (M 3 K 2 ) -1 и, C L было 1,8 ~ 5,0 × 10 6 Дж (м 3 К) −1 34,35 .(все параметры подгонки приведены в дополнительном примечании 2). C s должны зависеть от температуры отжима T s . В оригинальной статье Мэнчона 23 , на которой находится G-3TM, C s определяется из численной производной спиновой энергии. На рис. 6 представлено сравнение определяющих кривых расслоения прерывистого скольжения с постоянным и распределенным по Пуассону максимальным числом событий скольжения таким образом, что константа K с принимается равной среднему 〈K〉 пуассоновской функции .Можно видеть, что функциональная форма двух наборов определяющих кривых практически одинакова. При малых значениях K=〈K〉 соответствующие кривые ложатся относительно близко друг к другу, однако отклонения возрастают с увеличением 〈K〉. Причина в том, что стандартное отклонение распределения Пуассона растет как квадратный корень из среднего 〈K〉, так что при более высоких значениях 〈K〉 распределение 20 становится шире и колебания K становятся более актуальными. Колебания K влияют также на асимптотику σ(ε) упрочняющих связок
На рис. 6 представлено сравнение определяющих кривых расслоения прерывистого скольжения с постоянным и распределенным по Пуассону максимальным числом событий скольжения таким образом, что константа K с принимается равной среднему 〈K〉 пуассоновской функции .Можно видеть, что функциональная форма двух наборов определяющих кривых практически одинакова. При малых значениях K=〈K〉 соответствующие кривые ложатся относительно близко друг к другу, однако отклонения возрастают с увеличением 〈K〉. Причина в том, что стандартное отклонение распределения Пуассона растет как квадратный корень из среднего 〈K〉, так что при более высоких значениях 〈K〉 распределение 20 становится шире и колебания K становятся более актуальными. Колебания K влияют также на асимптотику σ(ε) упрочняющих связок Отметим, что среднее значение 〈aK〉 рассчитывается с распределением g(K) максимального числа скольжения K , а средний порог 〈εth(1)〉 определяется неупорядоченной прочностью волокон p(εth).
Отметим, что среднее значение 〈aK〉 рассчитывается с распределением g(K) максимального числа скольжения K , а средний порог 〈εth(1)〉 определяется неупорядоченной прочностью волокон p(εth). Интересно отметить, что в отличие от случая упрочнения отклонения соответствующих определяющих кривых более выражены при малых деформациях. Положение максимумов соответствующих кривых σ(ε) практически совпадает, однако пучки флуктуирующего K держат меньшую нагрузку, чем их постоянный аналог K . При увеличении деформации ε кривые пересекаются, что указывает на более высокую несущую способность пучков с колеблющимся K . При больших деформациях ε→∞ напряжение должно стремиться к нулю при постоянном максимальном числе скольжения, однако конечная жесткость связок с колеблющимся К не равна нулю.Это эффект тех волокон, которые не могут скользить K=0, что приводит к конечной асимптотической жесткости Ea=g(0)E=e−〈K〉E. При увеличении среднего числа скольжения 〈K〉 доля неразрывных волокон экспоненциально стремится к нулю, увеличивая разницу постоянных и флуктуирующих пучков K при низких значениях K (см. рис. 7).
Интересно отметить, что в отличие от случая упрочнения отклонения соответствующих определяющих кривых более выражены при малых деформациях. Положение максимумов соответствующих кривых σ(ε) практически совпадает, однако пучки флуктуирующего K держат меньшую нагрузку, чем их постоянный аналог K . При увеличении деформации ε кривые пересекаются, что указывает на более высокую несущую способность пучков с колеблющимся K . При больших деформациях ε→∞ напряжение должно стремиться к нулю при постоянном максимальном числе скольжения, однако конечная жесткость связок с колеблющимся К не равна нулю.Это эффект тех волокон, которые не могут скользить K=0, что приводит к конечной асимптотической жесткости Ea=g(0)E=e−〈K〉E. При увеличении среднего числа скольжения 〈K〉 доля неразрывных волокон экспоненциально стремится к нулю, увеличивая разницу постоянных и флуктуирующих пучков K при низких значениях K (см. рис. 7). Сравнение определяющих кривых пучков прерывистого скольжения с постоянным ( штриховые линии ) и флуктуирующим ( сплошные линии ) максимальным числом актов скольжения для случая разупрочнения при параметре жесткости а=0.8. Постоянные значения K устанавливаются равными среднему 〈K〉 распределения Пуассона.
Сравнение определяющих кривых пучков прерывистого скольжения с постоянным ( штриховые линии ) и флуктуирующим ( сплошные линии ) максимальным числом актов скольжения для случая разупрочнения при параметре жесткости а=0.8. Постоянные значения K устанавливаются равными среднему 〈K〉 распределения Пуассона. 4 Пороги разрушения после отжига
 Отсюда следует, что пороговые деформации εth(1),εth(2),…,εthk последовательных событий поскальзывания могут быть получены как
Отсюда следует, что пороговые деформации εth(1),εth(2),…,εthk последовательных событий поскальзывания могут быть получены как

 Сравнение определяющих кривых упрочнения прерывистых связок с закаленным ( штриховые линии ) и отожженным ( сплошные линии ) порогами разрушения для нескольких значений фиксированного числа разрешенных событий проскальзывания K при параметре жесткости а=0,8 .
Сравнение определяющих кривых упрочнения прерывистых связок с закаленным ( штриховые линии ) и отожженным ( сплошные линии ) порогами разрушения для нескольких значений фиксированного числа разрешенных событий проскальзывания K при параметре жесткости а=0,8 . 5 Обсуждение
 Чтобы повысить применимость модели, мы ввели параметр, который контролирует изменение жесткости волокон после проскальзывания мультипликативным образом, допуская как постепенную деградацию, так и повышение жесткости.Во время своей истории нагружения волокна могут пройти последовательность циклов прерывистого скольжения. В построении нашей модели пороги разрушения, при которых активируется проскальзывание, могут быть либо зафиксированы для всего процесса разрушения волокна (закаленный беспорядок), либо могут быть выбраны из распределения вероятностей (отожженный беспорядок), представляющего фиксированный структурный беспорядок материалов и эффект локального изменения поведения материала после проскальзывания соответственно. В качестве еще одного нового элемента нашего исследования максимальное количество событий поскальзывания рассматривается как случайная величина внутри набора, отобранного из распределения вероятностей.Общее количество разрешенных событий проскальзывания и пороговые нагрузки, при которых активируется проскальзывание, являются независимыми случайными величинами.
Чтобы повысить применимость модели, мы ввели параметр, который контролирует изменение жесткости волокон после проскальзывания мультипликативным образом, допуская как постепенную деградацию, так и повышение жесткости.Во время своей истории нагружения волокна могут пройти последовательность циклов прерывистого скольжения. В построении нашей модели пороги разрушения, при которых активируется проскальзывание, могут быть либо зафиксированы для всего процесса разрушения волокна (закаленный беспорядок), либо могут быть выбраны из распределения вероятностей (отожженный беспорядок), представляющего фиксированный структурный беспорядок материалов и эффект локального изменения поведения материала после проскальзывания соответственно. В качестве еще одного нового элемента нашего исследования максимальное количество событий поскальзывания рассматривается как случайная величина внутри набора, отобранного из распределения вероятностей.Общее количество разрешенных событий проскальзывания и пороговые нагрузки, при которых активируется проскальзывание, являются независимыми случайными величинами. После завершения всех циклов прерывистого скольжения волокно может либо сохранить свою окончательную жесткость, либо подвергнуться предельному разрыву, что приводит к глобальному упрочнению и размягчению пучка в пределе больших деформаций соответственно.
После завершения всех циклов прерывистого скольжения волокно может либо сохранить свою окончательную жесткость, либо подвергнуться предельному разрыву, что приводит к глобальному упрочнению и размягчению пучка в пределе больших деформаций соответственно. Наши расчеты показали, что параметр жесткости контролирует степень перекрытия вкладов подмножеств волокон с различным индексом разрушения.В пределе низкого параметра жесткости а≪1 пластическое плато украшено хорошо разделенными максимумами, а при медленно убывающей жесткости а≲1 и высоких значениях числа скольжения К получается гладкое горизонтальное плато.
Наши расчеты показали, что параметр жесткости контролирует степень перекрытия вкладов подмножеств волокон с различным индексом разрушения.В пределе низкого параметра жесткости а≪1 пластическое плато украшено хорошо разделенными максимумами, а при медленно убывающей жесткости а≲1 и высоких значениях числа скольжения К получается гладкое горизонтальное плато.
 Определяющие кривые с режимами разупрочнения и колебаниями вдоль плато могут быть реализованы только в экспериментах с контролируемой деформацией. При нагрузке, контролируемой напряжением, за событиями проскальзывания следует перераспределение нагрузки внутри пучка, которое может вызвать дальнейшие проскальзывания и, в конечном итоге, вызвать целую лавину проскальзывающих волокон, пока пучок не стабилизируется. Что касается следующего, мы собираемся исследовать влияние различной жесткости и флуктуирующего числа скольжения на динамику и статистику лавин скольжения, что может иметь отношение к пониманию реструктурирующих лавин сыпучих материалов и землетрясений.
Определяющие кривые с режимами разупрочнения и колебаниями вдоль плато могут быть реализованы только в экспериментах с контролируемой деформацией. При нагрузке, контролируемой напряжением, за событиями проскальзывания следует перераспределение нагрузки внутри пучка, которое может вызвать дальнейшие проскальзывания и, в конечном итоге, вызвать целую лавину проскальзывающих волокон, пока пучок не стабилизируется. Что касается следующего, мы собираемся исследовать влияние различной жесткости и флуктуирующего числа скольжения на динамику и статистику лавин скольжения, что может иметь отношение к пониманию реструктурирующих лавин сыпучих материалов и землетрясений. Благодаря своей гибкости модель может служить отправной точкой для разработки более реалистичных микромеханических моделей полимерных композитов, армированных углеродными нанотрубками, где высокая демпфирующая способность материала возникает из-за прерывистого скольжения, возникающего на границе УНТ-матрица. Наш подход может дополнить недавно разработанные микромеханические модели нанокомпозитов УНТ [43–45], обеспечивая эффективную основу для представления двух источников беспорядка (локальная прочность и число скольжения), деградации и повышения жесткости после событий скольжения и размягчения или отверждения после достигнуто максимальное число промахов.Работа в этом направлении ведется.
Благодаря своей гибкости модель может служить отправной точкой для разработки более реалистичных микромеханических моделей полимерных композитов, армированных углеродными нанотрубками, где высокая демпфирующая способность материала возникает из-за прерывистого скольжения, возникающего на границе УНТ-матрица. Наш подход может дополнить недавно разработанные микромеханические модели нанокомпозитов УНТ [43–45], обеспечивая эффективную основу для представления двух источников беспорядка (локальная прочность и число скольжения), деградации и повышения жесткости после событий скольжения и размягчения или отверждения после достигнуто максимальное число промахов.Работа в этом направлении ведется. Заявление о доступности данных
Вклады авторов
 Все авторы прочитали и одобрили рукопись.
Все авторы прочитали и одобрили рукопись. Финансирование
Конфликт интересов
Благодарности
Ссылки
 Амстердам, Нидерланды: Эльзевир (1990).
Амстердам, Нидерланды: Эльзевир (1990). Локальная модель пучка волокон с распределением нагрузки в более высоких измерениях. Phys Rev E — Stat Nonlinear Soft Matter Phys (2015) 92:020401. doi:10.1103/PhysRevE.92.020401
Локальная модель пучка волокон с распределением нагрузки в более высоких измерениях. Phys Rev E — Stat Nonlinear Soft Matter Phys (2015) 92:020401. doi:10.1103/PhysRevE.92.020401 Epl (2011) 95:16004. doi:10.1209/0295-5075/95/16004
Epl (2011) 95:16004. doi:10.1209/0295-5075/95/16004 066101
066101 1209/0295-5075/81/54005
1209/0295-5075/81/54005 doi:10.1103/PhysRevE.80.066115
doi:10.1103/PhysRevE.80.066115 doi:10.1103/PhysRevE.86.061307
doi:10.1103/PhysRevE.86.061307 Phys Rev Lett (1999) 82:4130. doi:10.1103/physrevlett.82.4130
Phys Rev Lett (1999) 82:4130. doi:10.1103/physrevlett.82.4130 Front Phys (2020) 8:236.doi:10.3389/fphy.2020.00236
Front Phys (2020) 8:236.doi:10.3389/fphy.2020.00236 J Compos Mater (2016) 50: 57–73. doi:10.1177/0021998315570371
J Compos Mater (2016) 50: 57–73. doi:10.1177/0021998315570371 Обзор биологии атеросклероза, жесткости стенок, физики эластичности и ее измерения на основе ультразвука – отпечаток пальца – Калифорнийский университет в Дэвисе
Обзор биологии атеросклероза, жесткости стенки, физики эластичности и ее измерения на основе ультразвука — отпечаток пальца
— Калифорнийский университет в Дэвисе Медицина и науки о жизни
Сверхбыстрая динамика обменной жесткости в многослойном Co/Pt
Время перемагничивания, зависящее от флюенса
 2 Å)/Pt (7,7 Å)] 5 многослойная пленка, магнитные свойства которой, такие как перпендикулярная магнитная анизотропия и намагниченность насыщения, хорошо известны 7,24,25,26,27 . Подробная экспериментальная конфигурация была опубликована в другом месте 28 . Сигналы TR-MOKE измерялись для 1,7 ≤ F P ≤ 28,5 мДж см -2 для временных задержек до 30 пс. Чтобы исключить эффект дихроичного обесцвечивания, эксперименты проводятся с пучком накачки на длинах волн как 400, так и 800 нм (λ накачка ).График TR-MOKE в зависимости от времени при различных плотностях потока показан на рис. 1а для случая насоса λ = 800 нм, в то время как существенной разницы в общей тенденции для случая насоса λ = 400 нм не наблюдается. Сигналы были нормированы по их максимальным изменениям для сравнения динамического поведения при перемагничивании для различных условий. Внешнее магнитное поле напряженностью 1.
2 Å)/Pt (7,7 Å)] 5 многослойная пленка, магнитные свойства которой, такие как перпендикулярная магнитная анизотропия и намагниченность насыщения, хорошо известны 7,24,25,26,27 . Подробная экспериментальная конфигурация была опубликована в другом месте 28 . Сигналы TR-MOKE измерялись для 1,7 ≤ F P ≤ 28,5 мДж см -2 для временных задержек до 30 пс. Чтобы исключить эффект дихроичного обесцвечивания, эксперименты проводятся с пучком накачки на длинах волн как 400, так и 800 нм (λ накачка ).График TR-MOKE в зависимости от времени при различных плотностях потока показан на рис. 1а для случая насоса λ = 800 нм, в то время как существенной разницы в общей тенденции для случая насоса λ = 400 нм не наблюдается. Сигналы были нормированы по их максимальным изменениям для сравнения динамического поведения при перемагничивании для различных условий. Внешнее магнитное поле напряженностью 1.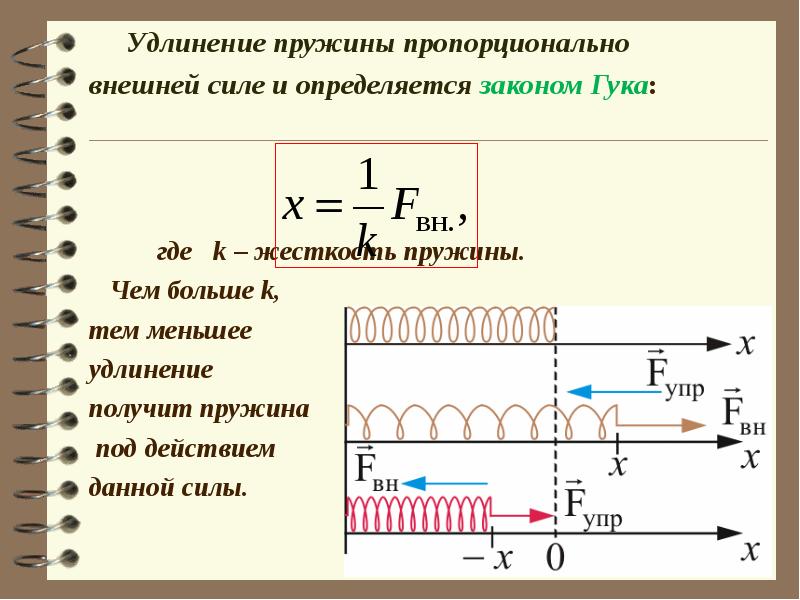 7 кЭ прикладывалось нормально к поверхности пленки. На всех измеренных кривых отчетливо видна динамика фотоиндуцированного размагничивания и последующего перемагничивания.Максимальное изменение размагничивания наблюдается около t = 0,3 пс для всех случаев флюенса. В случае насоса λ = 800 нм, как F P было увеличено с 1,7 до 28,5 млн. К.М. -2 , Ремагнитация была замедлена на F P > 9,9 MJ CM -2 . Характер перемагничивания при 1,7 ≤ F P ≤ 16,5 мДж см −2 хорошо описывается одной экспоненциальной кривой (рис. 1а, пунктирные линии), что дает характерное время τ
7 кЭ прикладывалось нормально к поверхности пленки. На всех измеренных кривых отчетливо видна динамика фотоиндуцированного размагничивания и последующего перемагничивания.Максимальное изменение размагничивания наблюдается около t = 0,3 пс для всех случаев флюенса. В случае насоса λ = 800 нм, как F P было увеличено с 1,7 до 28,5 млн. К.М. -2 , Ремагнитация была замедлена на F P > 9,9 MJ CM -2 . Характер перемагничивания при 1,7 ≤ F P ≤ 16,5 мДж см −2 хорошо описывается одной экспоненциальной кривой (рис. 1а, пунктирные линии), что дает характерное время τ 6 R
6 перемагничивания (светлый квадрат на рис.1б). Заметим, что τ R резко возросло, так как F P увеличилось лишь в несколько раз. Аппроксимация одной экспоненциальной кривой недействительна для F P > 16,5 мДж см -2 .
 Аналогичная тенденция наблюдается для случая насоса λ = 400 нм, где τ R также аппроксимируется одной экспоненциальной кривой.
Аналогичная тенденция наблюдается для случая насоса λ = 400 нм, где τ R также аппроксимируется одной экспоненциальной кривой. 3\\ C_s(T_s)\frac{{dT_s}}{{dt}} = — G_{es}\left[ {T_e,T_s} \right] \times (T_s — T_e) — G_{ls} \times (T_s — T_l)$$
3\\ C_s(T_s)\frac{{dT_s}}{{dt}} = — G_{es}\left[ {T_e,T_s} \right] \times (T_s — T_e) — G_{ls} \times (T_s — T_l)$$ 2,$$
2,$$ Особенности г E [ E 9000 E , T 69 , T S ] подробно описаны в дополнительной примесе 1. G ES0 (EQ. ( 4)) является независимым от температуры каналом электрон-спинового взаимодействия. В статическом случае хорошо известно, что A EX \ (\ propto \) ( J EX A -1 ) < S 2 > , где J ex — константа обменного взаимодействия, a — постоянная решетки.Пропорциональность зависит от параметров материала, таких как периодическая конфигурация решетки. Поскольку A ex можно легко измерить, а не J ex , мы сосредоточимся на подсчете A ex на сверхбыстрой временной шкале. Когда соотношение между A EX и J EX и EX продлен, мы поставили A EX ( T ) \ (\ Propto \) A EX0 < M ( T ) 2 > \ (\ propto \) ( j EX A 8 -1 ) < S ( т ) 2 7 2 >, где температура T зависимость включена в < M ( T ) 2 > без затрагивания J EX .
Особенности г E [ E 9000 E , T 69 , T S ] подробно описаны в дополнительной примесе 1. G ES0 (EQ. ( 4)) является независимым от температуры каналом электрон-спинового взаимодействия. В статическом случае хорошо известно, что A EX \ (\ propto \) ( J EX A -1 ) < S 2 > , где J ex — константа обменного взаимодействия, a — постоянная решетки.Пропорциональность зависит от параметров материала, таких как периодическая конфигурация решетки. Поскольку A ex можно легко измерить, а не J ex , мы сосредоточимся на подсчете A ex на сверхбыстрой временной шкале. Когда соотношение между A EX и J EX и EX продлен, мы поставили A EX ( T ) \ (\ Propto \) A EX0 < M ( T ) 2 > \ (\ propto \) ( j EX A 8 -1 ) < S ( т ) 2 7 2 >, где температура T зависимость включена в < M ( T ) 2 > без затрагивания J EX . Для простоты мы использовали приближение Дж ex ~ 2 aA ex0 16 . В G-3TM G el по-прежнему считается постоянным, поскольку ожидается, что скорость релаксации между электроном и решеткой будет просто пропорциональна разности температур. G ls также было задано постоянным на протяжении всего моделирования.
Для простоты мы использовали приближение Дж ex ~ 2 aA ex0 16 . В G-3TM G el по-прежнему считается постоянным, поскольку ожидается, что скорость релаксации между электроном и решеткой будет просто пропорциональна разности температур. G ls также было задано постоянным на протяжении всего моделирования. 2а, г). Измерение петли гистерезиса — лучший способ оценить демаг D . Петли гистерезиса были измерены при t = −2 пс и 0,3 пс (максимальное размагничивание) с использованием одной и той же установки TR-MOKE с модуляцией зондирующего пучка для всех F P (раздел «Методы»). Пример измерений для F P = 13,2 мДж см −2 (рис. 2а, вставка) показывает, что D демаг составляет 70%.Превосходное соответствие было установлено во всех случаях (см. Дополнительное примечание 2, где описано использование измерения R ( t ) и D demag для подгонки).
2а, г). Измерение петли гистерезиса — лучший способ оценить демаг D . Петли гистерезиса были измерены при t = −2 пс и 0,3 пс (максимальное размагничивание) с использованием одной и той же установки TR-MOKE с модуляцией зондирующего пучка для всех F P (раздел «Методы»). Пример измерений для F P = 13,2 мДж см −2 (рис. 2а, вставка) показывает, что D демаг составляет 70%.Превосходное соответствие было установлено во всех случаях (см. Дополнительное примечание 2, где описано использование измерения R ( t ) и D demag для подгонки).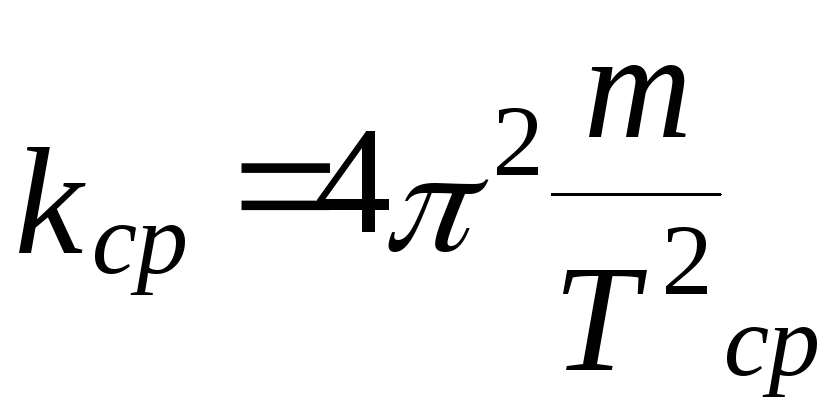 7 ≤ F P (флюенс накачки) ≤ 16,5 мДж·см −2 ; вставка: петли гистерезиса с модуляцией зондирующего пучка, измеренные при времени задержки t = -2 пс (пунктирная линия) и 0,3 пс (сплошная линия) при F P = 13,2 мДж см −2 . Температура спина T S 9065 S (красный), электронная температура T E 6 (черный) и решетка T L (синий) во время начальных 30 PS на P = b 3 и c 9.9 мДж см -2 . Для случая насоса λ = 400 нм, d Данные TR-MOKE, измеренные для 4,1 ≤ F P ≤ 16,3 мДж см -2 . T S 9065 S (красный), T E (черный), и T L (синий) во время начальных 30 PS для F 6 = e 4.1, f 16,3 мДж см -2 .
7 ≤ F P (флюенс накачки) ≤ 16,5 мДж·см −2 ; вставка: петли гистерезиса с модуляцией зондирующего пучка, измеренные при времени задержки t = -2 пс (пунктирная линия) и 0,3 пс (сплошная линия) при F P = 13,2 мДж см −2 . Температура спина T S 9065 S (красный), электронная температура T E 6 (черный) и решетка T L (синий) во время начальных 30 PS на P = b 3 и c 9.9 мДж см -2 . Для случая насоса λ = 400 нм, d Данные TR-MOKE, измеренные для 4,1 ≤ F P ≤ 16,3 мДж см -2 . T S 9065 S (красный), T E (черный), и T L (синий) во время начальных 30 PS для F 6 = e 4.1, f 16,3 мДж см -2 .
 При подгонке наших данных мы обнаружили, что подгонка становится достаточно хорошей, если C s меньше ~10 4 Дж (m 3 K) −1 во всех случаях.Таким образом, мы использовали малое значение C с = 100 Дж (m 3 K) −1 для всех случаев. Верхний предел подобранного значения C s (~10 4 J (m 3 K) −1 ) в настоящей работе кажется немного меньшим, чем приведенные значения, определенные из 3ТМ. Например, в Ref. 35 , C s Ni и FeCuPt составляют 0,2 × 10 6 J (м 3 К) –1
При подгонке наших данных мы обнаружили, что подгонка становится достаточно хорошей, если C s меньше ~10 4 Дж (m 3 K) −1 во всех случаях.Таким образом, мы использовали малое значение C с = 100 Дж (m 3 K) −1 для всех случаев. Верхний предел подобранного значения C s (~10 4 J (m 3 K) −1 ) в настоящей работе кажется немного меньшим, чем приведенные значения, определенные из 3ТМ. Например, в Ref. 35 , C s Ni и FeCuPt составляют 0,2 × 10 6 J (м 3 К) –1
Максимальные значения электронов температуры T E 9065 E MAX 9067 и температура спина T S S MAX 9067 MAX AT T = 0,3 PS увеличиваются как F P увеличен; например, T s max at t = 0,3 ps изменяется от 564 до 1040 K как05 F
увеличивается. от 7 до 9,9 мДж см -2 (насос λ = 800 нм). Высокий F P увеличивает количество энергии, передаваемую в подсистемы, так что увеличение т E MAX и T и S S Max . Температура равновесия, при которой T — E 6661 T 6 = — = 6660666 = 66 = 66 6 = 666666 = 666666 = 666666666 = 66 606666 = 6666661 6666 = 66 = 6 60666 = 6 также увеличились как F 6 P , но очень интересно отметить, что разница между T E E MAX и S S S 6 S Макс Макс по существу приобрели F P (рис.2б, в, рис. 2д, е). В контексте Г-3ТМ это наблюдение указывает на то, что канал взаимодействия G es между электронной и спиновой подсистемами сокращается, что приводит к увеличению теплового разделения спиновой системы от электронной подсистемы как а также, таким образом, увеличение времени, необходимого для достижения теплового равновесия.
от 7 до 9,9 мДж см -2 (насос λ = 800 нм). Высокий F P увеличивает количество энергии, передаваемую в подсистемы, так что увеличение т E MAX и T и S S Max . Температура равновесия, при которой T — E 6661 T 6 = — = 6660666 = 66 = 66 6 = 666666 = 666666 = 666666666 = 66 606666 = 6666661 6666 = 66 = 6 60666 = 6 также увеличились как F 6 P , но очень интересно отметить, что разница между T E E MAX и S S S 6 S Макс Макс по существу приобрели F P (рис.2б, в, рис. 2д, е). В контексте Г-3ТМ это наблюдение указывает на то, что канал взаимодействия G es между электронной и спиновой подсистемами сокращается, что приводит к увеличению теплового разделения спиновой системы от электронной подсистемы как а также, таким образом, увеличение времени, необходимого для достижения теплового равновесия. Это явление может быть причиной увеличения τ R по мере увеличения F P , как показано на рис.1б.
Это явление может быть причиной увеличения τ R по мере увеличения F P , как показано на рис.1б.
Рисунок 3А — график г ES (уравнение 6666 (EQ. (4)) как функция T E и S S 6. По мере увеличения T s G es увеличивается, а затем уменьшается для данной электронной температуры. Значения T E , T S , и G E ES 6 Определенные из фитинга до наших экспериментальных данных на насосе λ = 800 нм показаны в серых изогнутых линия на рис.3а и снова на рис. 3б для различных F P . Случай T s = T e также представлен в виде пунктирной кривой для справки на рис. 3b. Немонотонность G es по отношению к T s является прямым следствием уравнения. (3). G es монотонно возрастает с ростом T s при низких F P = 1.7 и 3,3 мДж см 90 667 -2 90 668 , но при высоких значениях 90 005 F 90 665 P 90 666 > 6,6 мДж см 90 667 -2 90 668 наблюдается рост, а затем уменьшение. Мы подозреваем, что различные экспериментальные результаты динамики сверхбыстрого размагничивания могут быть вызваны этой другой тенденцией G es при высоких F P 36,37,38 .
(3). G es монотонно возрастает с ростом T s при низких F P = 1.7 и 3,3 мДж см 90 667 -2 90 668 , но при высоких значениях 90 005 F 90 665 P 90 666 > 6,6 мДж см 90 667 -2 90 668 наблюдается рост, а затем уменьшение. Мы подозреваем, что различные экспериментальные результаты динамики сверхбыстрого размагничивания могут быть вызваны этой другой тенденцией G es при высоких F P 36,37,38 .
3D-карта г E 60005 E 60005 S (температура спина) и т E 6 (электронная температура). Темно-серая линия: траектория G es при 9,9 мДж см -2 для от -1 до 0,3 пс. b G es по сравнению с T s для от -1 до 0,3 ps при 1,7 ≤ F 6 9 флюенс 9,6 909 мДж см -2 (длина волны импульса накачки λ накачки = 800 нм). Черная пунктирная линия: T e = T s . C G G E -S Время задержки ( T ) от -1 до 3 PS при 1,7 ≤ F P ≤ 9,9 MJ CM -2 (насос λ = 800 нм). Вертикальная пунктирная линия: t = 0,3 пс. D Каналы взаимодействия ( G ES , G , EL EL , и G LS 6) VS F P AT T = 0.3 пс для случая 800- и 400-нм λ накачки . Столбики погрешностей представляют собой самую низкую область стандартной ошибки (<5%) для каждого параметра подбора с помощью G-3TM.
Темно-серая линия: траектория G es при 9,9 мДж см -2 для от -1 до 0,3 пс. b G es по сравнению с T s для от -1 до 0,3 ps при 1,7 ≤ F 6 9 флюенс 9,6 909 мДж см -2 (длина волны импульса накачки λ накачки = 800 нм). Черная пунктирная линия: T e = T s . C G G E -S Время задержки ( T ) от -1 до 3 PS при 1,7 ≤ F P ≤ 9,9 MJ CM -2 (насос λ = 800 нм). Вертикальная пунктирная линия: t = 0,3 пс. D Каналы взаимодействия ( G ES , G , EL EL , и G LS 6) VS F P AT T = 0.3 пс для случая 800- и 400-нм λ накачки . Столбики погрешностей представляют собой самую низкую область стандартной ошибки (<5%) для каждого параметра подбора с помощью G-3TM. G es не подходит для параметра G-3TM. E G G E / G / G 6/ G 6- F 6 P AT T = 0,3 PS Для случая насоса 800 и 400 Нм λ . Столбики погрешностей представляют собой самую низкую область стандартной ошибки (<5%) для каждого параметра подбора с помощью G-3TM.
G es не подходит для параметра G-3TM. E G G E / G / G 6/ G 6- F 6 P AT T = 0,3 PS Для случая насоса 800 и 400 Нм λ . Столбики погрешностей представляют собой самую низкую область стандартной ошибки (<5%) для каждого параметра подбора с помощью G-3TM.
Динамическое изменение G es в фемтосекундной шкале времени показано для различных F P на рис. 3c. При низких F P наблюдается простое возрастание и уменьшение G es с максимумом при t = 0,3 пс. Время максимума G es совпадает со временем, когда D демаг наибольшая.На высоких F P , G es быстро достигает первого пика сразу после прихода импульса накачки, снижается до минимума примерно во время максимума D demag5
t = 0,3 пс), а затем снова увеличилось. Сравнение между поведением г ES , г , а г EL 6 при т = 0.3 PS под различными F P (рис. 3D) показывает, что G EL 6 — самый сильный канал, г ES 6 увеличился на низком уровне F P , но уменьшается при высокой F P ; эта тенденция может быть результатом особенности G es (рис. 3a, b). С другой стороны, G ls является самым слабым каналом (которым часто пренебрегают), но становится сопоставимым с G es по мере увеличения F P . G LS 65 LS участвует в сочетании спин-орбиты 23 , что может быть сильнее как T или D или D или 39 39 .
Сравнение между поведением г ES , г , а г EL 6 при т = 0.3 PS под различными F P (рис. 3D) показывает, что G EL 6 — самый сильный канал, г ES 6 увеличился на низком уровне F P , но уменьшается при высокой F P ; эта тенденция может быть результатом особенности G es (рис. 3a, b). С другой стороны, G ls является самым слабым каналом (которым часто пренебрегают), но становится сопоставимым с G es по мере увеличения F P . G LS 65 LS участвует в сочетании спин-орбиты 23 , что может быть сильнее как T или D или D или 39 39 .
Приведенное выше обсуждение показывает, что динамика фотоиндуцированного размагничивания и перемагничивания в спиновой системе Co/Pt в основном определяетсяНа рисунке 3e показано отношение G es к G ls при t = 0,3 ps для различных плотностей потока.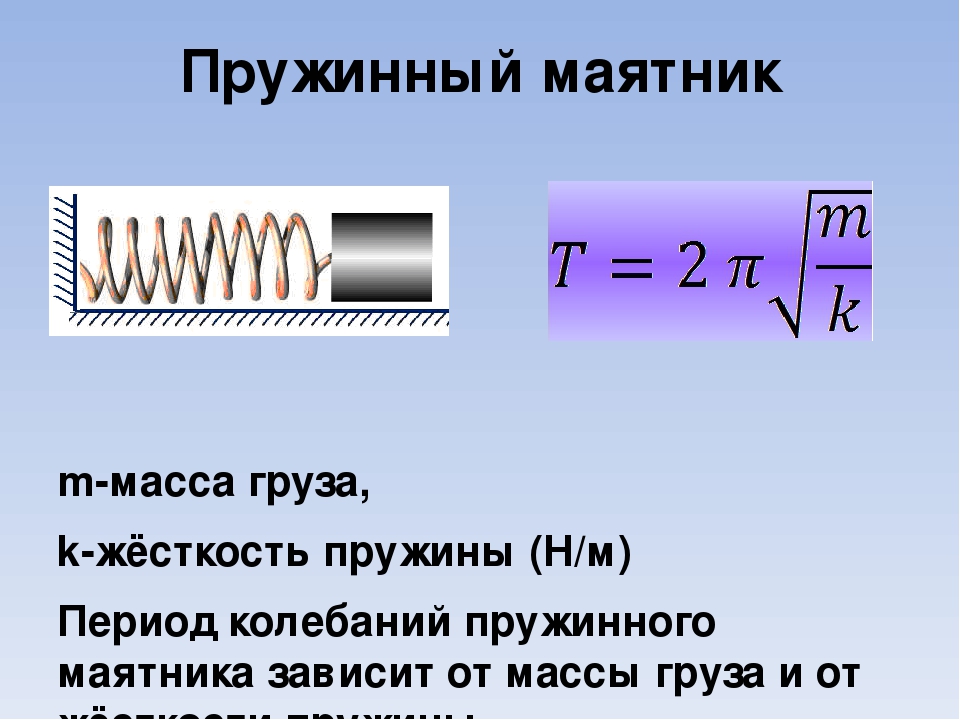 г ES / G LS / G LS превышает 10 для F P <6.6 MJ CM -2 для насоса λ = 800 и 400 нм. Этот дисбаланс означает, что в этом режиме доминирует спин-электронное взаимодействие.Для F P ≥ 6,6 MJ CM -2 , G E / G — G G LS 6 подходит к асимптотически, что указывает на то, что взаимодействие спин-решетки становится все более важным. Фитинг G-3TM дает значения для G es . Уравнения (2) и (4) позволяют рассчитать A ex0 , не зависящий от температуры коэффициент обменной жесткости. Расчетное значение A ex0 оказывается равным 10.01 пДж м -1 вообще F P ; это значение хорошо согласуется с заявленным значением для многослойного соединения Co/Pt 40,41 .
г ES / G LS / G LS превышает 10 для F P <6.6 MJ CM -2 для насоса λ = 800 и 400 нм. Этот дисбаланс означает, что в этом режиме доминирует спин-электронное взаимодействие.Для F P ≥ 6,6 MJ CM -2 , G E / G — G G LS 6 подходит к асимптотически, что указывает на то, что взаимодействие спин-решетки становится все более важным. Фитинг G-3TM дает значения для G es . Уравнения (2) и (4) позволяют рассчитать A ex0 , не зависящий от температуры коэффициент обменной жесткости. Расчетное значение A ex0 оказывается равным 10.01 пДж м -1 вообще F P ; это значение хорошо согласуется с заявленным значением для многослойного соединения Co/Pt 40,41 .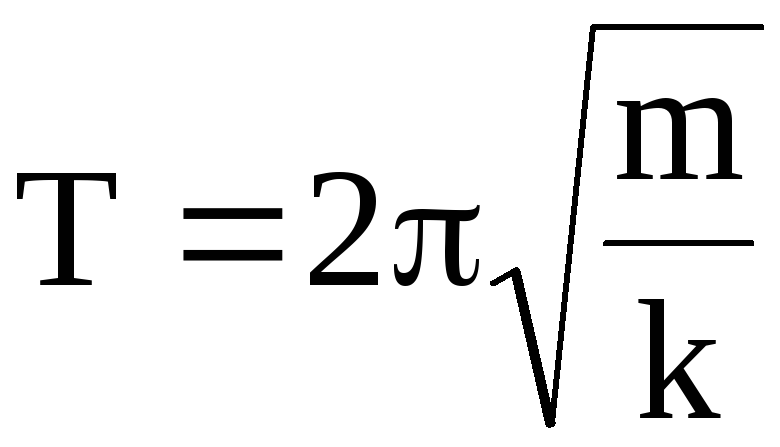 Другие методы анализа 42,43 также могут воспроизвести медленную скорость намагничивания при высокой плотности потока энергии. Следует отметить, что Г-3ТМ на основе гамильтониана лазерно-индуцированного размагничивания 23 позволяет отдельно контролировать нестационарные G es и G ls , а также их соотношение G es / G ls .В этой работе мы отмечаем, что отношение, по-видимому, играет важную роль в определении динамики спина с избыточной энергией на временной шкале менее пс.
Другие методы анализа 42,43 также могут воспроизвести медленную скорость намагничивания при высокой плотности потока энергии. Следует отметить, что Г-3ТМ на основе гамильтониана лазерно-индуцированного размагничивания 23 позволяет отдельно контролировать нестационарные G es и G ls , а также их соотношение G es / G ls .В этой работе мы отмечаем, что отношение, по-видимому, играет важную роль в определении динамики спина с избыточной энергией на временной шкале менее пс.
Физика — модуль Юнга — Бирмингемский университет
Один из самых важных тестов в инженерии — это знание того, когда объект или материал согнется или сломается, и свойство, которое говорит нам об этом, — модуль Юнга. Это мера того, насколько легко материал растягивается и деформируется.
Согнется или сломается?
Провода подчиняются закону Гука, как и пружины. Когда приложена сила F , она распространится на некоторое расстояние x , что может быть просто описано уравнением F = kx
Когда приложена сила F , она распространится на некоторое расстояние x , что может быть просто описано уравнением F = kx
В то время как k для пружины — это жесткость пружины, величина растяжения проволоки зависит от ее площади поперечного сечения, длины и материала, из которого она изготовлена. Модуль Юнга ( E ) — это свойство материала, которое говорит нам, насколько легко он может растягиваться и деформироваться, и определяется как отношение растягивающего напряжения ( σ ) к деформации растяжения ( ε ).Где напряжение — это количество силы, приложенной к единице площади ( σ = F/A ), а деформация — удлинение на единицу длины ( ε = дл/л ).
Поскольку сила F = мг , мы можем получить модуль Юнга проволоки, измерив изменение длины ( dl ) при приложении гирь массой м (при условии, что г = 9,81 метра на секунда в квадрате).
Относится ли модуль Юнга к исследованиям?
Имеет ли модуль Юнга отношение к исследованиям?
Что важно знать?
Для разных типов материалов графики напряжения-деформации могут выглядеть очень по-разному.Хрупкие материалы, как правило, очень прочные, потому что они могут выдерживать большие нагрузки, они не сильно растягиваются и могут внезапно сломаться. Пластичные материалы имеют большую область упругости, где зависимость между напряжением и деформацией является линейной, но при первом обороте (предел упругости) линейность нарушается, и материал больше не может вернуться к своей первоначальной форме. Второй пик — это предел прочности при растяжении, и он говорит нам о максимальном напряжении, которое материал может выдержать до разрыва. Пластмассовые материалы не очень прочные, но выдерживают большую нагрузку.Модуль Юнга задается градиентом линии на графике напряжения-деформации.
В эксперименте, показанном на видео выше, мы измерили модуль Юнга медной проволоки, которая не сильно растягивается. Таким образом, можно использовать реперный маркер, например, ленту, чтобы определить исходную и увеличенную длину. Выполнение многократных измерений с различными массами увеличит количество точек на графике напряжения-деформации и сделает расчет модуля Юнга более надежным. Еще одна вещь, о которой нужно позаботиться, — это измерение площади поперечного сечения провода.Дефекты проволоки могут означать, что диаметр не является абсолютно постоянным по всей ее длине, поэтому может помочь среднее значение нескольких показаний микрометра.
Таким образом, можно использовать реперный маркер, например, ленту, чтобы определить исходную и увеличенную длину. Выполнение многократных измерений с различными массами увеличит количество точек на графике напряжения-деформации и сделает расчет модуля Юнга более надежным. Еще одна вещь, о которой нужно позаботиться, — это измерение площади поперечного сечения провода.Дефекты проволоки могут означать, что диаметр не является абсолютно постоянным по всей ее длине, поэтому может помочь среднее значение нескольких показаний микрометра.
Как это применимо ко мне?
Изучение механических свойств материалов важно, потому что оно помогает нам понять, как ведут себя материалы, и позволяет нам разрабатывать новые продукты и улучшать существующие. В качестве примера темы исследования в Бирмингеме рассматривалась разработка шестов для прыжков, используемых спортсменами, занимающимися прыжками в высоту, для достижения максимальной производительности.Эти шесты должны быть легкими, чтобы обеспечить быстрый разбег, но также должны сохранять энергию упругой деформации при изгибе шеста. Шест должен преобразовывать энергию упругости в кинетическую энергию по мере того, как он выпрямляется, и быть в состоянии выдерживать нагрузки, вызванные весом прыгуна, а также выдерживать многократные использования спортсменом.
Шест должен преобразовывать энергию упругости в кинетическую энергию по мере того, как он выпрямляется, и быть в состоянии выдерживать нагрузки, вызванные весом прыгуна, а также выдерживать многократные использования спортсменом.
В небольших масштабах существует множество продуктов, содержащих биологические (например, фармацевтические препараты, препараты для лечения бесплодия, тканевая инженерия) и небиологические микрочастицы (например,г. химикаты, сельское хозяйство, уход за домом). Благодаря пониманию их механических свойств мы можем прогнозировать их поведение при производстве и обработке, максимизировать их эксплуатационные возможности.
Модуль Юнга материала полезно знать, чтобы предсказать поведение материала под действием силы. Это важно практически для всего, что нас окружает, от зданий до мостов, транспортных средств и многого другого.
Следующие шаги
Эти ссылки предоставляются для удобства и только в информационных целях; они не являются подтверждением или одобрением Бирмингемским университетом какой-либо информации, содержащейся на внешнем веб-сайте. Университет Бирмингема не несет ответственности за точность, законность или содержание внешнего сайта или последующих ссылок. Пожалуйста, свяжитесь с внешним сайтом для получения ответов на вопросы, касающиеся его содержания.
Университет Бирмингема не несет ответственности за точность, законность или содержание внешнего сайта или последующих ссылок. Пожалуйста, свяжитесь с внешним сайтом для получения ответов на вопросы, касающиеся его содержания.
Что такое единица жесткости? – М.В.Организинг
Что такое единица жесткости?
В Международной системе единиц жесткость обычно измеряется в ньютонах на метр ( ). В имперских единицах жесткость обычно измеряется в фунтах на дюйм.
Как повысить жесткость материала?
В более общем случае жесткость рассчитывается как F/Δ. К ↑ k, ↑ A и E (для кручения, G и J) или ↓ L. Если геометрия остается неизменной, простое увеличение модуля упругости при выборе другого материала повысит жесткость.
Какая формула жесткости?
Его жесткость равна S = F/δ, где F — общая нагрузка, а δ — прогиб при изгибе. Рисунок 5.7 (c) Балка квадратного сечения, нагруженная на изгиб.Его жесткость S = F/δ, где F — нагрузка, а δ — прогиб при изгибе.
Что такое модуль жесткости?
Жесткость относится к тому, как компонент изгибается под нагрузкой, возвращаясь к своей первоначальной форме после снятия нагрузки. Со стороны материала жесткость зависит от модуля упругости, также известного как модуль Юнга и сокращенно E. Модуль Юнга — это отношение напряжения к деформации при очень малых деформациях.
Что вызывает нормальную деформацию?
Нормальная деформация вызывается силами, перпендикулярными плоскостям или площадям поперечного сечения материала, например, в объеме, который находится под давлением со всех сторон, или в стержне, который вытягивается или сжимается в длину.
Зависит ли стресс от напряжения?
Да, напряжение зависит от напряжения. Эту связь легко объяснить с помощью закона Гука. Этот закон гласит, что «деформация в твердом теле пропорциональна приложенному напряжению в пределах предела упругости этого твердого тела». После предела упругости тело начинает деформироваться.
Кто приходит первым стресс или напряжение?
Кривая напряжения-деформации представляет собой поведение материала, когда он подвергается нагрузке, и по кривой SN мы можем сказать, что напряжение возникает только тогда, когда есть деформация (или она вот-вот деформируется), вызванная некоторыми механическими или физическими силами.Поэтому напряжение всегда приходит первым, а потом только стресс порождает.
Стресс вызывает напряжение или напряжение вызывает стресс?
Существует три вида напряжения: сжатие, растяжение и сдвиг. Стресс может вызвать деформацию, если она достаточна для преодоления силы объекта, находящегося под нагрузкой. Деформация – это изменение формы или размера в результате приложенных сил (деформация). Камни деформируются только при нагрузке.
Коллективное движение приводимых в движение полугибких нитей, настроенное на мягкое отталкивание и жесткость | Группа биофизики
Джеффри М.Мур, Тайлер Н. Томпсон, Мэтью А. Глейзер и Мередит Д. Беттертон (2020 г.). Мягкая материя 16, 9436-9442. DOI: 10.1039/D0SM01036G. архив DOI: 1909.11805. Скачать
Глейзер и Мередит Д. Беттертон (2020 г.). Мягкая материя 16, 9436-9442. DOI: 10.1039/D0SM01036G. архив DOI: 1909.11805. Скачать
В системах с активной материей самодвижущиеся частицы могут самоорганизоваться, чтобы совершать коллективное движение, что приводит к постоянному динамическому поведению вне равновесия. В клетках цитоскелетные нити и моторные белки проявляют активность и самоорганизацию в сложные структуры, важные для клеточной механики, подвижности и деления.Коллективная динамика систем цитоскелета может быть воссоздана с помощью экспериментов по скольжению филаментов, в которых филаменты цитоскелета приводятся в движение поверхностно-связанными моторными белками. В ходе этих экспериментов наблюдалось разнообразное поведение, включая стаи, полярные потоки, закрученные вихри и спирали из одиночных нитей. Недавние эксперименты с микротрубочками и кинезиновыми моторными белками показали, что эффективное отталкивающее взаимодействие между филаментами может регулироваться краудинговыми агентами в растворе, изменяя коллективное поведение. Добавление краудера уменьшало пересечение филаментов, способствовало выравниванию и приводило к переходу от активных, изотропно ориентированных филаментов к локально выровненным полярным потокам. Эти результаты предполагают, что настраиваемое мягкое отталкивание может управлять активным фазовым поведением, но как изменение стерических взаимодействий и жесткости филаментов влияет на коллективное движение, до конца не изучено. Здесь мы используем моделирование движущихся филаментов с регулируемым мягким отталкиванием и жесткостью, чтобы лучше понять, как взаимодействие между гибкостью филаментов и стерическими эффектами может привести к различным активным стационарным состояниям.Мы идентифицируем закрученные стаи, полярные потоки, полосы изгиба и спирали и описываем физику, управляющую переходами между этими состояниями. Помимо отталкивания, настройка жесткости филаментов может способствовать коллективному поведению и контролировать переход между активными изотропными филаментами, локально выровненными стаями и полярными потоками.
Добавление краудера уменьшало пересечение филаментов, способствовало выравниванию и приводило к переходу от активных, изотропно ориентированных филаментов к локально выровненным полярным потокам. Эти результаты предполагают, что настраиваемое мягкое отталкивание может управлять активным фазовым поведением, но как изменение стерических взаимодействий и жесткости филаментов влияет на коллективное движение, до конца не изучено. Здесь мы используем моделирование движущихся филаментов с регулируемым мягким отталкиванием и жесткостью, чтобы лучше понять, как взаимодействие между гибкостью филаментов и стерическими эффектами может привести к различным активным стационарным состояниям.Мы идентифицируем закрученные стаи, полярные потоки, полосы изгиба и спирали и описываем физику, управляющую переходами между этими состояниями. Помимо отталкивания, настройка жесткости филаментов может способствовать коллективному поведению и контролировать переход между активными изотропными филаментами, локально выровненными стаями и полярными потоками.
